Z 8836:2017 (ISO 13099-2:2012)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語,定義及び記号 ·········································································································· 1
3.1 用語及び定義 ················································································································ 1
3.2 記号 ···························································································································· 3
4 原理······························································································································· 3
5 顕微鏡法························································································································· 4
6 電気泳動光散乱(ELS)法 ································································································· 5
6.1 概要 ···························································································································· 5
6.2 セル ···························································································································· 5
6.3 参照光光学配置 ············································································································· 6
6.4 クロスビーム光学系 ······································································································· 7
6.5 信号処理 ······················································································································ 7
6.6 電気泳動移動度の決定 ···································································································· 9
7 ゼータ電位の計算 ············································································································ 10
8 操作手順························································································································ 11
8.1 必要条件 ····················································································································· 11
8.2 検証 ··························································································································· 12
8.3 測定誤差の要因 ············································································································ 14
8.4 測定の報告 ·················································································································· 15
附属書A(参考)細管セル内での電気浸透流 ············································································ 17
附属書JA(参考)ゼータ電位の理論モデルの概要 ····································································· 20
参考文献 ···························································································································· 24
Z 8836:2017 (ISO 13099-2:2012)
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本粉体工業技術協会(APPIE)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本工業規格 JIS
Z 8836:2017
(ISO 13099-2:2012)
コロイド分散系−ゼータ電位の光学的測定法
Colloidal systems-Methods for zeta-potential determination-
Optical methods
序文
この規格は,2012年に第1版として発行されたISO 13099-2を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項及び附属書JAは,対応国際規格にはない事項であ
る。
1
適用範囲
この規格は,顕微鏡法及び電気泳動光散乱法を用いて,液中に分散した粒子の電気泳動移動度を測定す
る方法について規定する。測定した電気泳動移動度及び適切な理論モデルによって,表面電荷の推定及び
ゼータ電位の決定が可能になる。
注記1 ISO 13099-1に対応する日本工業規格はないため,これを翻訳し,その概念を附属書JAに示
す。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を次に示す。
ISO 13099-2:2012,Colloidal systems−Methods for zeta-potential determination−Part 2: Optical
methods(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Q 0030 標準物質に関連して用いられる用語及び定義
注記 対応国際規格:ISO Guide 30,Terms and definitions used in connection with reference materials
ISO 13099-1,Colloidal systems−Methods for zeta-potential determination−Part 1: Electroacoustic and
electrokinetic phenomena
3
用語,定義及び記号
この規格で用いる主な用語,定義及び記号は,次による。
3.1
用語及び定義
2
Z 8836:2017 (ISO 13099-2:2012)
3.1.1
ブラウン運動(Brownian motion)
媒体分子の熱運動によって引き起こされる液体中の懸濁粒子のランダムな運動。
3.1.2
ドップラーシフト(Doppler shift)
波の発生源に対して相対運動する観測者が観測する波の周波数及び波長の変化。
3.1.3
表面電位(electric surface potential)
表面から十分離れた液体部分を基準にした表面との電位差。
注記 単位はボルト(V)。
3.1.4
ゼータ電位,ζ(zeta-potential)
ζ電位(ζ-potential)
界面動電位(electrokinetic potential)
すべり面上と表面から十分離れた液体部分との電位差。
注記 単位はボルト(V)。
3.1.5
電気浸透(electroosmosis)
液体中の対イオンが,印加電場下で液体とともに荷電固体表面に対して移動する現象。この現象によっ
て液体は,粒子充塡層,多孔体,毛細管又は膜を通過する。
3.1.6
電気浸透速度,veo(electroosmotic velocity)
電気浸透において荷電固体表面から十分離れた点での均一な液体の速度。
注記 単位はメートル毎秒(m/s)。
3.1.7
電気泳動移動度,μ(electrophoretic mobility)
単位電場当たりの電気泳動速度。
注記1 電気泳動移動度は,粒子が低電位(負電極)の方向に移動するなら正であり,逆の場合は負
である。
注記2 単位は平方メートル毎ボルト毎秒[m2/(V・s)]。
3.1.8
電気泳動速度,ve(electrophoretic velocity)
電気泳動による粒子の速度。
注記 単位はメートル毎秒(m/s)。
3.1.9
すべり面(slipping plane)
せん断面(shear plane)
せん断応力の影響によって,液体が固体表面に対して滑ることによって生じる概念的な面。
3
Z 8836:2017 (ISO 13099-2:2012)
3.2
記号
a
粒子半径
D
拡散係数
E
電場強度
kB
ボルツマン定数
I
光強度
NA
アボガドロ数
n
媒体の屈折率
Rcap
細管の半径
S(ω)
散乱光の周波数パワースペクトル
Г
ローレンツ半値幅
ε
媒体の誘電率
ζ
ゼータ電位(界面動電位)
η0
媒体の粘性率
θ
入射光と散乱光とのなす角度
θ'
交差する2本の光線のなす角度
κ
デバイ長の逆数
λ
波長
μ
電気泳動移動度
μeo
液体の電気浸透移動度
ν
周波数
ξ
散乱光と電場方向とのなす角度
τ
自己相関関数における相関時間
φ
体積分率
ω
角周波数(=2πν)
4
原理
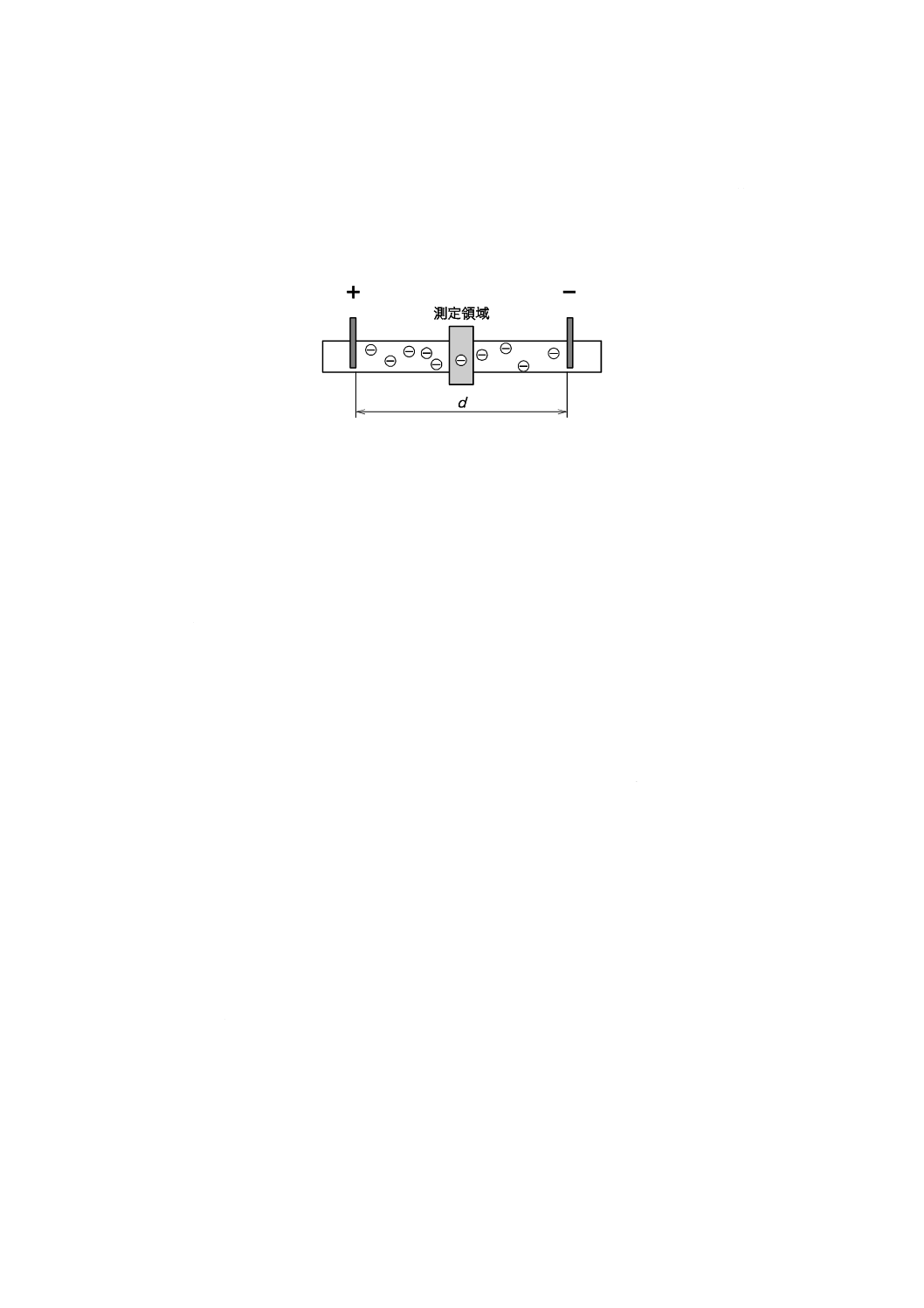
荷電粒子の懸濁溶液が,一定間隔の一対の電極をもつセル中に存在するとする(図1参照)。このセルは,
内壁に電極をもつ容器,又は両端に電極をもち,断面が円筒形又は角形の細管である。この電極間に電場
を印加すると,荷電粒子は,反対符号の電極に,電気泳動によって,引き寄せられる。細管壁が荷電して
いる場合,電気浸透効果によって,管壁に沿った媒体流れが生じるが,この流れの方向及び速度は,壁面
電荷の正負及び電荷量に依存する。したがって,セルに対する粒子の相対速度は,電気泳動速度及び電気
浸透速度を合算したものとなる。ここで注意を要することは,電場印加後,粒子が終末電気泳動速度に到
達する時間は,セル中の全溶液の電気浸透速度が十分に発達する時間と比べると,極めて短いことである。
この時間の違いを理解しないと,正しく測定できない場合がある。ある位置で測定される粒子速度は,ビ
デオ顕微鏡法又は電気泳動光散乱を利用するレーザドップラー法によって決定される。すなわち,泳動粒
子のセルに対する相対的な速度及び方向が決定される。電極間距離及び印加電圧が既知である場合には,
粒子の電気泳動移動度が決定され,その値から,理論計算によってゼータ電位が算出される。
電場中の粒子運動の観察には,二つの手法がある。歴史上,最初の手法は,顕微鏡下で粒子像を観察す
るもので,“顕微鏡法”又は“ミクロ電気泳動法”と呼ばれる。第二の手法は,粒子の散乱光を測定し,そ
4
Z 8836:2017 (ISO 13099-2:2012)
のドップラー周波数シフト量から電気泳動移動度を算出するものである。この方法は,“電気泳動光散乱
法”と呼ばれている。
これらの手法においては,セル定数は,既知の導電性をもつ溶液を用いた測定又は理論計算によって,
決めなければならない。また,ゼータ電位が既知の粒子を用いた検定によって,そのセルのセル定数を決
定することもできる。
d
電極間距離
図1−電気泳動測定の概念図
5
顕微鏡法
顕微鏡法の主原理は,二世紀以上前から,ミクロ電気泳動法として発展してきた(文献[1])。直流又は
交流の電場下で移動する粒子に,光を照射すると,散乱光によって粒子挙動が観察できる。この光照射は,
明視野,暗視野又はその両方の下で行うことが可能である(文献[2])。明視野光照射で得られるコントラ
ストでは,粒径0.2 μm以下の粒子を検出することはできない。一方,暗視野光照射は,ナノメートル領域
の泳動粒子像を捕らえるのに適している。
マイクロメートルのサイズの泳動粒子像の測定に関しては,幾つかの方法があり,その手法は,手動,
半自動及び全自動に分類される。手動法では,1個又は複数個の粒子の動きを,目とストップウォッチと
で追跡する。したがって,測定には,長時間かかり,使いづらく,不正確な手法である。
半自動法では,照射光走査装置又はく(矩)形プリズム回転装置を用いて光照射粒子を手動で顕微鏡追
跡する。光走査速度又はプリズム回転速度を半自動的に制御し,粒子の顕微鏡観察像が静止状態に見える
条件から電気泳動速度を算出する(文献[3][4])。これらの方法は,均一な電気泳動移動度をもつ試料だけ
に適用可能である。
電気泳動移動度に分布のある試料に対しては,手動の顕微鏡観察法を自動電気泳動光散乱シグナル分析
と組み合わせる方法が利用できる(文献[5][6])。
最近の電荷結合素子(CCD)及びコンピュータの出現によって,粒子像を断続的にコンピュータに送り,
高度な画像解析法を用い,時間が刻印されたビデオの各コマから,電場下での粒子の移動軌跡を再現する
ことが可能となった。ただし,この手法は,ビデオに映る鮮明度のある粒子に限り有効である。1コマの
時間間隔及び粒子の移動距離から,各粒子の速度が正確に算出され,印加電場強度と組み合わせると,電
気泳動移動度が計算される。暗視野照射を用いると,この手法はナノ粒子に対しても利用できる。この手
法では,電場の超短時間印加が可能なため,熱泳動又は電気化学的汚染の影響が避けられる。粒子濃度は,
個々の粒子を追跡するため,極めて低濃度でなければならない。
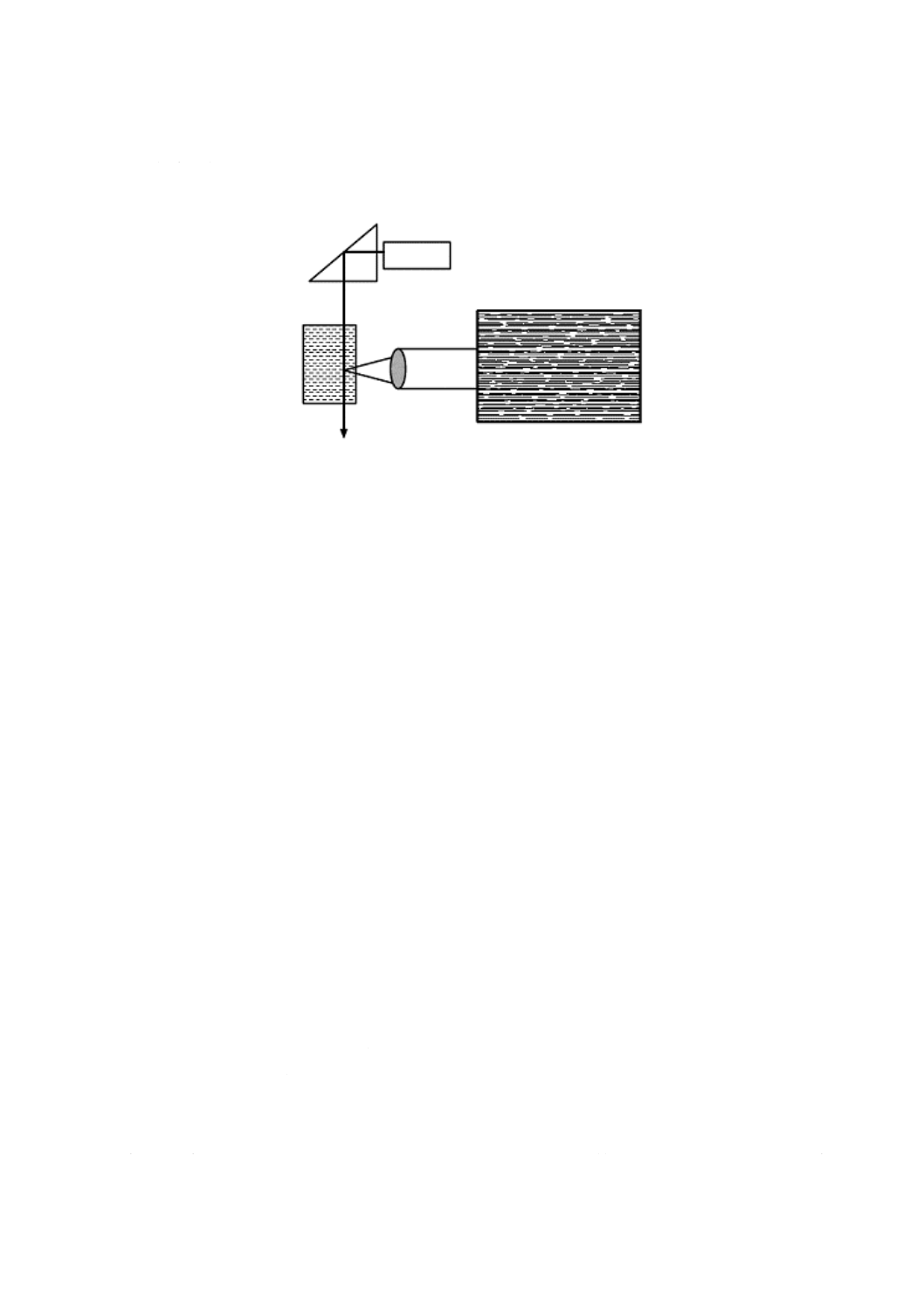
最近の装置では,散乱角90°の光学配置が一般的である。レーザ光は,顕微鏡焦点面を照らし,レーザ
光束及び顕微鏡の光軸は,いずれも電場と垂直である。図2では,電場の方向は紙面に対して垂直である。
電気浸透の影響を避けるために,レーザ光及び顕微鏡焦点は,静止面上にあることが必要である。これは
5
Z 8836:2017 (ISO 13099-2:2012)
附属書Aで説明する。粒子の電気泳動運動を正確に測定するためには,この位置を精度よく設定する必要
がある(文献[7])。
1 レーザ
3 顕微鏡対物レンズ
5 プリズム
2 セル管路の断面
4 ビデオカメラ
図2−代表的な電気泳動ビデオ顕微鏡
6
電気泳動光散乱(ELS)法
6.1
概要
電気泳動光散乱(ELS)法は,散乱光のドップラー効果を用いて,多数の粒子の電気泳動移動度を間接
的に測定する方法である。ELS法は,電場下の液中に分散した粒子に位相のそろった光を入射する。荷電
粒子は,その電荷の符号に応じて,陽極又は陰極のいずれかの方向に移動する。この移動によって粒子か
らの散乱光周波数は,ドップラー効果によってシフトする。このシフトした周波数分布から,粒子の電気
泳動移動度の分布が決定できる。ELS法は,校正用標準粒子を必要とせず,水系又は非水系のいずれかの
媒体中に懸濁した複合粒子試料の電気泳動を迅速,正確,自動的かつ再現よく測定することができる(文
献[8])。
6.2
セル
多くの種類の測定セルが用いられている。セルは,測定粒子を含む試料を保持する機能,試料に電界を
供給する機能,並びに入射光及び散乱光の光路を確保する3種類の機能をもっている。セルによっては,
液が流動できるように設計されており,試料のpHなどを調製する自動滴定装置の追加も可能である。ま
た,極端に濃厚でない試料の電気泳動移動度の測定が容易にできるように,入射光及び散乱光に対して透
明電極及び多重屈折が利用できるように設計されたセルもある(文献[9])。測定点の電界は,安定,均一
かつ平行でなければならない。この状態を作るために,く(矩)形セルの場合は,二つの電極間は互いに
非常に近接して配置しなければならない。細管セルの場合には,電界経路は閉じていなければならない。
電圧を電極に印加すると,イオンが存在する液中では電流が流れる。この電流値が高いと,ジュール熱を
引き起こし,電極で電気分解が生じる場合もある。したがって,セル及び電極材料の適切な選定,応答が
十分に速い温度制御,適切な電場印加時間及び電界強度が,正確かつ再現性のある結果を得るための重要
な要素である。
電極上の分極を抑え,試料粒子の均一な分布を保持し,加熱の影響を最小に抑えるために,電圧印加停
1
3
4
2
5
6
Z 8836:2017 (ISO 13099-2:2012)
止時間を挟みながら電場の極性を定期的に反転させる。閉じたガラス細管セルでは,ガラス表面の荷電の
ため,液の電気浸透が生じ,細管断面上で放物線状の流れとなる。したがって,液が動かない静止面と呼
ばれる面が存在する。粒子の電気泳動速度は,この静止面上で測定する,又は粒子の電気泳動による動き
から液の動きを分離するために,細管断面上の幾つかの位置で測定する方法もある。また,使い捨てセル
を用いる装置もある。
6.3
参照光光学配置
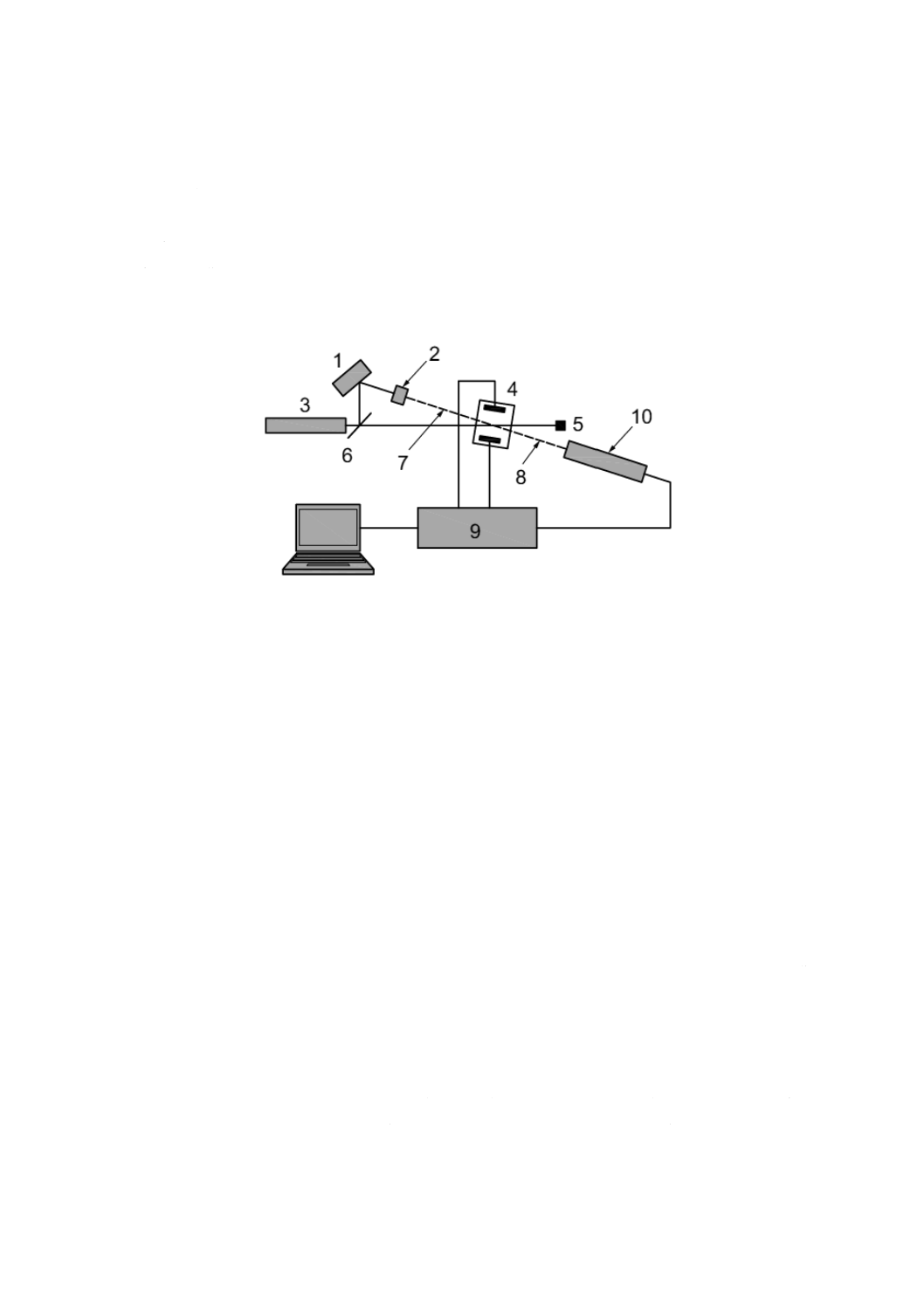
典型的な小角光散乱測定装置の例を,図3に示す。
1 光変調器
6 ビームスプリッタ
2 光減衰器
7 参照光
3 レーザ
8 散乱又は参照光
4 電極を備えた試料セル
9 プロセッサ
5 ビームストップ
10 光検出器
図3−参照光光学系の構成例
ヘテロダイン検出法を用いた小角散乱光学系がよく使用されている。散乱角は,15°〜30°が多く用い
られる。小角を使うことによってブラウン運動に起因するスペクトル広がりを低減することができる。非
球形粒子は,回転拡散の影響で球形粒子によってスペクトルが広がる。試料はあらかじめ分散させて測定
セルに入れる。液体の粘度,誘電率及び屈折率は温度に依存するので,セルを温度制御するか,又は温度
を正確に求めておく必要がある。所定の電位勾配を得るために,電極間隔が既知のセルの電極間に印加す
る。また,測定用電極を用いて一定間隔の電位勾配を直接測定する方法もある。波長が既知のレーザ光は,
入射光及び参照光と呼ばれる2本の光線に分割される。入射光はセル窓を屈折して試料を照射し,試料中
の粒子から散乱光が生じる。セルを通過又は通過しない参照光と,ミラー,レンズ又は光ファイバで集光
した粒子からの散乱光とを重ね合わせた信号を光電子増倍管又はアバランシェフォトダイオードの光検出
器によって検出する。光変調器を用いて2本に分割された光線の一方又は両方を元のレーザ光周波数から
数百Hzシフトさせることによって,所定の周波数差を作る。こうすることでブラウン運動によるドップ
ラーシフト周波数の原点をシフトさせ,粒子の移動方向を認識し,低周波領域の干渉の影響を最小限に抑
えることができる。コヒーレント検出及び散乱体積を制御するために,検出器前のアパーチャは可変にな
っていることがある。検出した信号は,デジタル相関器,スペクトラムアナライザ,振幅重み付位相構造
関数システムなどの信号処理装置に送られる。セルに印加する電圧は,データ測定と同期して反転できる
7
Z 8836:2017 (ISO 13099-2:2012)
ようになっている。装置の制御は,ゼータ電位を計算するコンピュータを用いる場合が多い。
6.4
クロスビーム光学系
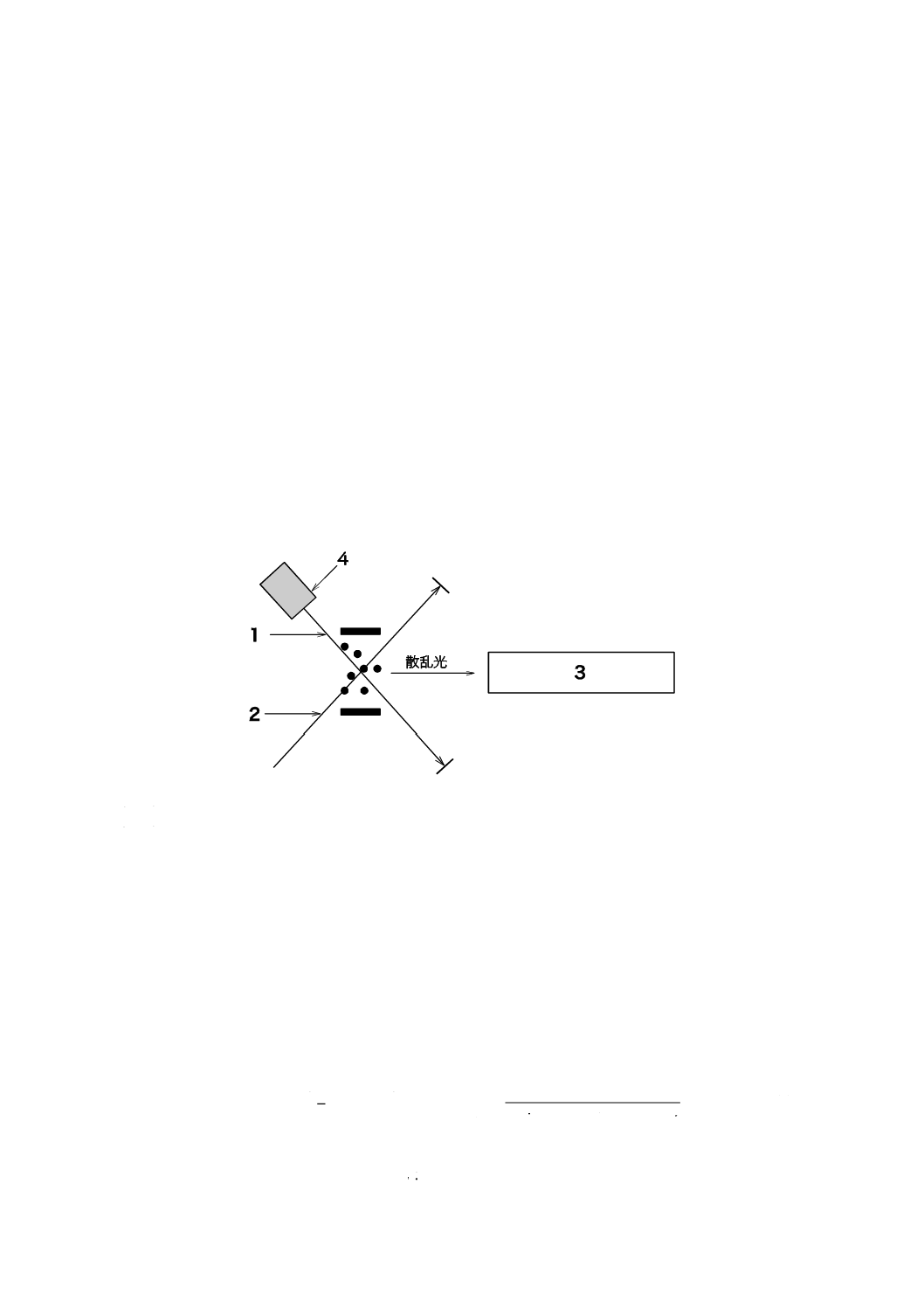
今日ではあまり一般的な光学系ではないが,他の測定法としてクロスビーム法がある(図4参照)。クロ
スビーム法は主光線を2本の等しい強度の光線に分割し,一方又は両方の光線の周波数を変調する。2本
の光線は,セルの一方向から対称的に交差するよう入射する。検出器は,セルに対して光源と逆方向に配
置する。各粒子に照射される2本の光線からそれぞれ異なった散乱角で散乱された光を合成し観測する。
散乱光のドップラー周波数シフト量は,いずれの散乱角にも無関係で,2本の光線のなす角で決定される。
この光学系は,次のような別の簡単な説明(フリンジモデル)も可能である。すなわち,可干渉な2本の
光線はセル内で干渉しま(縞)を形成する。干渉しまの間隔は,波長及び2本の光線のなす角で決まる。
粒子が干渉しま中を移動するときの散乱光強度の時間変化(測定周波数)から,電気泳動速度を検出する。
粒子の速度及び方向(荷電の正負)の両方を決定するために光変調器を用いて,干渉しまの移動速度を
一方向に制御する。測定周波数が変調器で作られた周波数差よりも高い場合,移動する干渉しまの中を運
動する粒子は,その動きが干渉しまの移動方向と反対方向であることを意味する。測定周波数が干渉しま
の周波数よりも低い場合は,粒子は干渉しまの動きと同じ方向に移動していることを示している。
なお,干渉しまの移動速度は常に予想される最大粒子速度よりも大きくなるように設定する。
1 ビーム1
3 光検出器
2 ビーム2
4 光変調器
図4−クロスビーム光学系の構成
6.5
信号処理
6.5.1
スペクトル分析
大きさ及び電気泳動移動度に分布をもつ粒子の場合,それらの粒子は,ある強度の直流電場下で電気泳
動運動とともにブラウン運動を行っている。
参照光光学装置による周波数パワースペクトルS(ω)(又は,電気泳動図と呼ばれる。)は,式(1)から求
める(文献[8])。
()
()
(
)
[
]
∑∑
=
∆
∆
=
+
∆
+
+
=
max
min
max
,s
min
,s
2
2
,s
M
,s
L
2
L
π
2
2
π
2
d
d
i
v
v
j
i
ij
i
ij
Γ
v
Γ
I
I
I
S
ω
ω
ω
δ
ω
μ
················· (1)
ここに,
IL: 参照光強度
Is, ij: iの大きさ(球形粒子においては直径)でjの移動度をも
8
Z 8836:2017 (ISO 13099-2:2012)
つ粒子からの散乱強度
Γ: iの大きさの粒子のローレンツ分布の半値幅
ω: 角周波数
ωM: 光変調器周波数
Δνs, ij: iの大きさでjの移動度をもつ粒子の電気泳動運動から
生じる周波数シフト
δ(ω): ω=0におけるデルタ関数
分母にある記号∓は,二つのピークがパワースペクトルにあることを意味する。一つは観察できないマ
イナスの周波数域に,他は観測可能なプラスの周波数域に位置する。光変調器周波数ωMを大きくするこ
とによって,次の項(ωM+2πΔνs, ij)は常に正になるので,マイナス符号を使うことが可能となる。
式(1)によると,全ての粒子の電気泳動スペクトルは,全電気泳動移動速度のパワースペクトルに加えて
粒子のブラウン運動によって生じる固有の広がりをもっている。ブラウン運動による広がりは,粒子径が
小さくなる,又は散乱角度が大きくなる場合は,より顕著になる。ブラウン運動によるパワースペクトル
の広がり程度を測定するには,電場をかけないで測定を行うことが必要である。
全体のパワースペクトルからのブラウン運動だけのパワースペクトルを差し引くことによって,電気泳
動移動度分布が求まる(文献[10])。
6.5.2
自己相関関数
自己相関関数は,周波数パワースペクトルのフーリエ変換形である。式(2)は参照光光学系における相関
時間τの関数としての自己相関関数[G(2)( τ)]を示す。
()
(
)(
)
[
]
τ
ω
τ
τ
ij
i
ij
d
d
i
v
v
j
v
Γ
I
I
I
G
,s
M
,s
L
2
L
)2(
π
2
cos
exp
2
max
min
max
,s
min
,s
∆
+
−
+
=
∑∑
=
∆
∆
=
·············· (2)
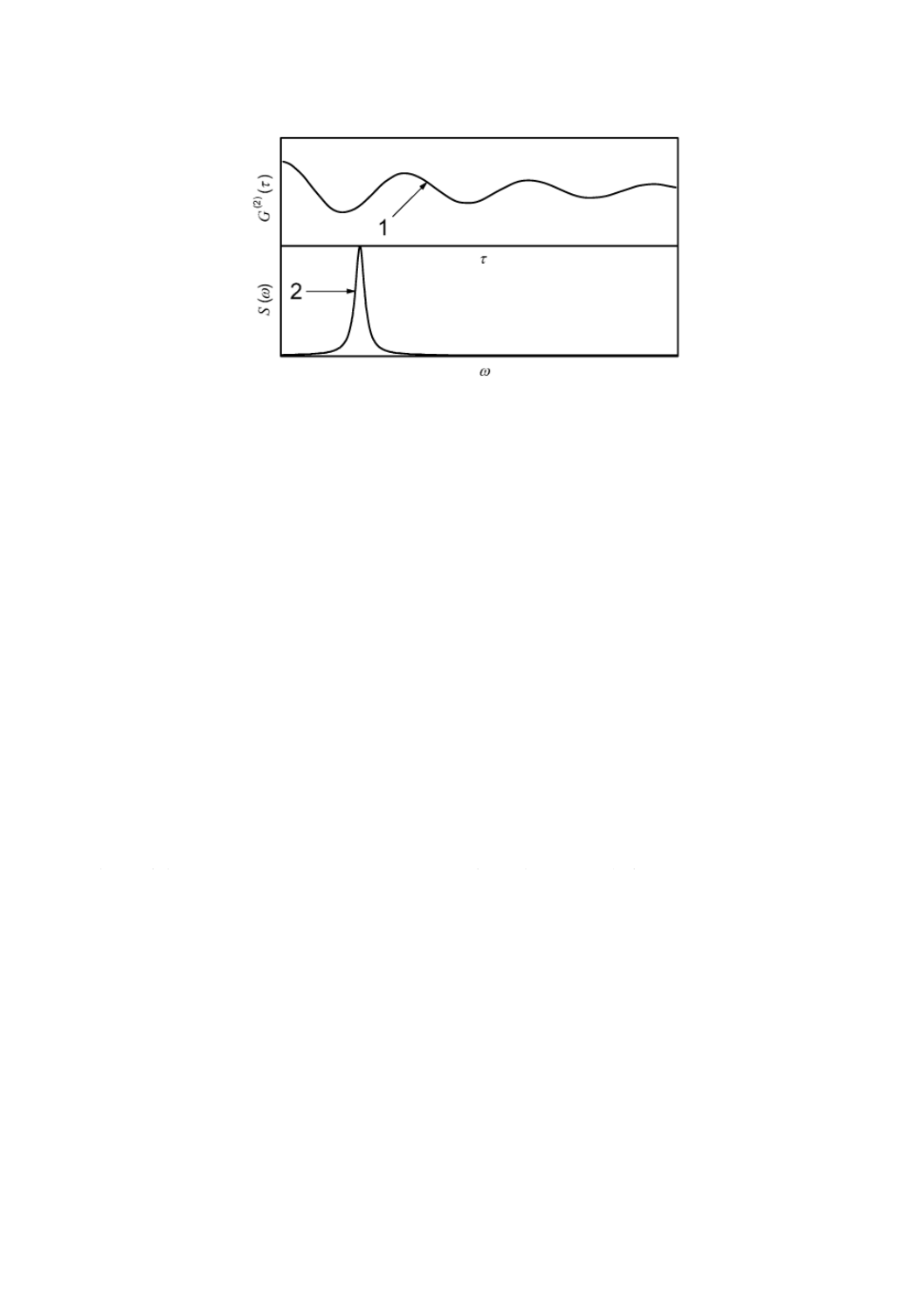
図5には,電気泳動速度スペクトルとともに典型的な自己相関関数を示す。式(2)の自己相関関数では,
指数関数部分はランダムなブラウン運動に,余弦関数部分は電気泳動運動に由来する。パワースペクトル
のピーク位置は,光変調器の周波数及び粒子の電気泳動運動速度に関連する。ピーク形状は,粒子のブラ
ウン運動,移動度スペクトル及びレーザビーム幅に由来する。
9
Z 8836:2017 (ISO 13099-2:2012)
1 自己相関関数曲線
G(2) (τ) 自己相関関数
τ 相関時間
2 周波数パワースペクトル曲線
S(ω) 周波数パワースペクトル
ω 角周波数
図5−電気泳動光散乱法の典型的な自己相関関数及びスペクトル
6.5.3
位相解析光散乱法(PALS)
非極性溶媒中の粒子の電気泳動移動度は非常に小さいので,光変調器周波数と実測された電気泳動運動
によるドップラー周波数シフト量との差は小さくなる。その周波数差は,1 Hz未満である。また高イオン
濃度溶液中の懸濁粒子においては,ジュール熱の影響が無視できる極めて低電場条件下でだけ,測定が可
能である。したがって,この場合も微小なドップラー周波数シフトを検出することが必要になる。
このように周波数シフトが微小な場合,スペクトル分析又は自己相関関数解析は,もはや十分な解決策
ではなく,位相解析光散乱法(PALS)がよりよい選択肢となる(文献[11])。PALSは,粒子の電気泳動移
動度によって生じる小さな振動要素に由来する非常に小さな周波数シフトを検知する方法である。PALS
処理(振幅重み付きの構造関数処理とも呼ばれる。)では,演算機内で合成された光変調器周波数が,正弦
波又は余弦波を与える。検出された信号は,正弦波又は余弦波によって増幅され,二つの導関数(同相の
構成要素及び求積構成要素)を作成する。これらの二つの要素から解かれた逆正接・ベクトルは一定の振
幅値を導出し,その変化速度が単位時間当たりの位相差を与えることとなる。
この手法は,原理的に0.001 Hz程度の分解能をもつが,実際にはノイズ又は他の原因のために,その分
解能を達成できない。それでもPALSは,0.002 Hz程度の周波数シフトが観察できている。得られる電気
泳動移動度は,その平均値だけである。
実例では,印加電圧の高速及び低速反転を組み合わせたスペクトル分析方法及びPALSを併用すること
によって,セル電極の分極化を防ぎ,電気泳動及び電気浸透の影響を切り離すことが可能になる。この手
法によって,電気泳動移動度の平均値及び移動度分布が得られる(文献[12])。
6.5.4
変調ブラウン運動パワースペクトル法
この方法では,交流電場下で粒子の電気泳動運動の平均振幅を測定し,パワースペクトル分析を適用す
る。移動度の符号は別途,直流電場下で測定することによって決定する。ただし,トレーサビリティのあ
る移動度をもつ標準物質による一点校正が必要である。
6.6
電気泳動移動度の決定
ドップラー周波数シフト量と粒子の電気泳動移動度μとの関係は,装置の光学配置に依存する。式(3)及
び式(4)は,それぞれ,参照光光学系及びクロスビーム光学系に使用される(文献[8])。
10
Z 8836:2017 (ISO 13099-2:2012)
(
)
(
)
[
]
ξ
θ
θ
λ
ω
μ
+
∆
=
2
/
sin
2
/
sin
π
4
0
E
n
···················································· (3)
( )2/
sin
π
4
0
θ
λ
ω
μ
′
∆
=
E
n
··································································· (4)
ここに,
Δω: ドップラー周波数シフト量
λ0: 真空中のレーザ波長
n: 媒体の屈折率
E: 電場強度
θ: 入射光と散乱光とのなす角度
ξ: 散乱光と電場方向とのなす角度
θ′: 交差する2本の光線のなす角度
7
ゼータ電位の計算
ゼータ電位計算のために用いられる種々の理論の詳細な説明については,ISO 13099-1を参照する。
非伝導性の球に対するゼータ電位ζと電気泳動移動度μとの関係式である式(5)は,ヘンリーの式として
広く一般に知られている(文献[13])。
()
a
fκ
η
ζε
μ
0
3
2
=
··········································································· (5)
ここに,
η0: 媒体の粘性率
κ: デバイ長の逆数
ε: 媒体の誘電率
a: 粒子半径
f(κa): f(κa)κa→0=1からf(κa)κa→∞=3/2に変化する単調関数
式(5)は,次のことを仮定することで導出される。
a) 粒子が受ける総電場は,印加電場及び粒子電荷に由来する電場の和で与えられる。
b) 粒子の運動によって生じた電場のひずみ(すなわち,緩和効果)は無視する。
c) 流体力学方程式中の慣性項は無視する。
d) 表面電位は,kBT/eよりもかなり小さい。
注記 Tは絶対温度,eは電気素量である。
κa≫1の場合,式(5)中のf(κa)は3/2の値を取り,スモルコフスキーの式となる。典型的には,水系懸濁
液中の大きな粒子に対して適用される。
κa≪1の場合,式(5)中のf(κa)は1の値を取り,ヒュッケルの式となる。典型的には,非水系懸濁液中の
小さな粒子に対して適用される。
これら理論の概要を,附属書JAに示す。
ζ及びμの関係については,a)からd)の仮定をせず,より正確な又は厳密なモデルが多く存在する。し
かし,これらのモデルの手法による計算には煩雑な処理及び試料に関する他のパラメータが必要である。
さらに多くの場合,これらのパラメータは求めるのが難しい。
希薄懸濁液中の導電性粒子及び非球形粒子に対する電気泳動移動度とゼータ電位との関係は報告されて
11
Z 8836:2017 (ISO 13099-2:2012)
いるが,その実用系への適用は限定的である。
また,ほとんどの試料の粒子は多分散のため,異なったκaの値をもつ。このような系に対し正確なゼー
タ電位分布を得るには,分布の各成分に対して複雑で異なった計算が必要なため,実用的ではない。
8
操作手順
8.1
必要条件
8.1.1
装置の設置
装置は,過度の電気的ノイズ,機械的振動及び温度変化のない清浄な環境に設置した方がよい。また,
日光及び空気の流れも避けた方がよい。操作場所は,設置した場所での健康及び安全に関する法規に従わ
なければならない。装置は,除振機能の付いた堅ろう(牢)な光学系をもち,堅固な作業台又は頻繁に使
用する場合には光学系の再調整が不要な作業台を準備した方がよい。
警告 装置は,致命的な眼の損傷を起こす可能性のあるレーザを装備している。レーザ光の光路及び
反射光を直接のぞ(覗)き込まない。高い反射率をもつ表面でレーザ光を遮らない。また,レ
ーザ光反射に関する安全基準を遵守する。
8.1.2
分散液
試料セルが,用いる溶媒に適しているかどうかを確認する。粒子の電気泳動移動度は懸濁液体の化学的
特性に強く依存する。測定のために濃厚懸濁液を希釈する場合,分散液のpH及びイオン濃度は共に極め
て重要な特性であるので,これらの条件を一定に保たなければならない。
8.1.3
測定セル
使用する装置に依存するが,セルを選ぶこともできる。使い捨てのセルも存在する。汚染の可能性を防
ぐために,試験の前にセルを注意深く洗浄する必要がある。イオン濃度が低い溶液に対して行う測定では,
それ以前の測定が高イオン濃度で行われていた場合,結果が変わる可能性がある。前回の試験から残って
いるイオンを十分に洗い流し,確認する必要がある。電極表面の状態は以前の測定によって汚れていると,
電位勾配の評価に誤差を生じさせる。セル壁が汚れたままであると,細管セル中の電気浸透流が予測どお
りでなくなる場合がある。
液体の粘度は温度の関数であるため,セルの温度を注意深く制御することが重要である。例えば,水系
試料の場合,その粘度は約2 %/℃変化する。移動度は粘度に依存するため,この影響が大きいことに注意
する。
直流電圧が,その極性を反転するまでの一定時間,電極間に印加される。伝導率が高い溶液の場合,短
時間だけ印加される。この操作方法はジュール熱による影響を抑えるのに役立つ。短時間の電圧印加はパ
ワースペクトル中に偽のピークが現れることがある。このような場合,PALSを用いた測定が有効である
(文献[11])。
8.1.4
試料の検査,調製,希釈及び濃度
8.1.4.1
試料の検査
測定された電気泳動移動度は,試験試料が系全体を代表し,かつ,適切にサンプリングされているとき
にだけ,試料の値として取り扱うことができる。
対象物質を目視又は顕微鏡を用いて観察し,粒子が適切に分散しているかどうか,又は沈殿が生じてい
かないかを確認する。測定にかかる時間よりも粒子が早く沈降する場合は,レーザの光路内に粒子が残っ
ておらず,測定を行うことができない。多分散試料では,大きな粒子は沈降し,小さな粒子だけが測定さ
れる。
12
Z 8836:2017 (ISO 13099-2:2012)
8.1.4.2
試料の調製
測定のための試料調製の間,試験に用いる試料の電気泳動移動度が変化しないように十分な注意を払う
ことが望ましい。ガラスビーカー及び注入器のような取扱器具は,表面に試料中のイオンが吸着したり,
事前の洗浄過程で残留した汚染物質が混入したりすることがある。さらに,取扱器具から試料へと汚染物
質が染み出ることがある。試料と化学反応を起こさないのであれば,使い捨てのプラスチック製調製用ビ
ーカー及びピペットの使用が望ましい。
8.1.4.3
試料の希釈
幾つかの実例にあるように,特殊なセルを採用すると,小さな散乱角であっても比較的高い濃度域で電
気泳動移動度の測定が可能である(文献[9])。小さな散乱角の光学設定をもつ装置では多くの場合,散乱
光が測定セルを通過するためには試料を希釈する必要がある。
ゼータ電位は,粒子の特性であるばかりでなく,粒子表面及びその周りの液体の間の化学平衡にも依存
している。液体の化学的性質及びイオン組成の小さな変化も,この化学平衡に影響し,その結果ゼータ電
位に影響を与える。
このことは,試料を測定可能な程度まで希釈する必要がある場合に問題となる。特殊な測定が行われな
いとしても,希釈によって液体の化学組成が変化する可能性がある。試料調製は,ゼータ電位が当初の系
から希釈された試料において変化しないような手順で行わなければならない。
この手順では,希釈に際して,当初の系及び希釈された系で,粒子及び粒子表面特性の同一性が保たれ
ているばかりではなく,溶液条件が同じに保たれていなければならない。試料の希釈及び界面活性剤の安
定性の双方を考慮しなければならない場合,この条件を満たすことは容易ではない。このように試料調製
の手順は,液体の組成に甚大な影響を与える可能性がある。
試料調製は,いわゆる平衡希釈の手順を用いなければならず,希釈液は当初の系と同じ液体でなければ
ならない。希釈の後で,唯一変化するパラメータは粒子濃度だけである。平衡希釈に基づく試料調製だけ
が,当初の系と希釈後の試料との間で同一なゼータ電位の値を与える。
希釈に使用する液体を得るには二つの手段がある。一つは,沈降又は遠心を使用した上澄み液の抽出で
ある。この上澄み液は,個々の測定手法に最適な濃度まで最初の試料を希釈するのに使用することができ
る。この方法は,液体との十分な密度差をもつ大きな粒子に適しており,ナノ粒子及び柔らかな生体系の
粒子ではあまり有用ではない。
もう一つの手段は透析の使用であり,ナノ粒子及び柔らかな生体系の粒子に適している。透析膜では,
イオン及び分子は透過するが粒子は透過しないことが必要である。
試料の扱い及び希釈液の作製についての正確な詳細報告を,結果に付随して示さなければならない。採
用した方法が少なくとも安定で矛盾のないのものであったことを提示するために,試料に対して正確な希
釈及び測定を複数回行うことが望ましい。
8.2
検証
8.2.1
標準物質
標準物質の使用に関する手引は,JIS Q 0030による。
標準物質は,電気泳動移動度の時間及び温度変化が試験されており,十分に均質かつ安定であることが
望ましい。表示される電気泳動移動度の値は,数人の測定者によって測定され,かつ,厳格に証明された
ものでなければならない。標準物質は,サンプリング手順及び希釈方法,並びに必要に応じて測定手順に
関し,明確に文書化されていることが望ましい。
認証標準物質は,装置の校正,測定方法の妥当性確認,又は物質に対して数値を特定する目的で使用す
13
Z 8836:2017 (ISO 13099-2:2012)
る。認証標準物質には,電気泳動移動度の単位を精確に実現するためのトレーサビリティを立証する手順
を経て認証された電気泳動移動度,及び信頼水準を表明した不確かさが記載された認証書が添付されてい
ることが望ましい。現時点では,使用可能な認証標準物質はなく,多くの使用可能な標準試料は電気泳動
移動度の単位に対する独立したトレーサビリティをもっていない。
注記1 標準物質の使用についての手引には,JIS Q 0031,JIS Q 0032,JIS Q 0033,JIS Q 0034及び
JIS Q 0035もある。
注記2 電気泳動移動度の標準物質は頒布されているが,電気泳動移動度からゼータ電位を導くには
附属書JAに示すような理論モデルの仮定が必要であるため,ゼータ電位の標準物質として
は認証されていない。
8.2.2
繰返し性
電気泳動移動度(測定)の要求される繰返し性を達成するために,次のような段階を踏む。
a) 装置を適切に設置し,操作条件を適切に設定し,十分な暖機運転をする。
b) 標準物質に示された測定手順に従う。
c) 小分けした同一の試験試料,又は適切な濃度に希釈した同一の試料に対して,連続測定を3回行う。
電気泳動移動度の絶対値が2×10−8 m2/ (V・s)より高く規定されている標準物質を使用し,その標準物質
の測定から得られた電気泳動移動度の平均値に対する変動係数が10 %以下である場合,装置は,繰返し性
の要求事項に合致すると考えられる。
8.2.3
中間精度
中間精度に関する試験は,同一の試験試料ではなく小分けした異なる複数の試験試料,又は適切な濃度
に希釈した異なる複数の試料を使用しなければならない。それ以外は,8.2.2に規定した手順に従わなけれ
ばならない。
電気泳動移動度の絶対値が2×10−8 m2/(V・s)より高く規定されている標準物質を使用し,その標準物質
の測定から得られた電気泳動移動度の平均値に対する変動係数が15 %以下である場合,装置は,中間精度
の要求事項に合致すると考えられる。
注記 中間精度(intermediate precision)とは,一般に,同一の試験試料を同一の測定者が同一の測定
手順を用いて短期間に測定した繰返し性(repeatability)と,同一の測定対象を異なる測定者が
異なる測定系で測定した場合の再現性(reproducibility)との間の,中間の再現精度のことを指
す。この規格の中では,再現性(reproducibility)は真度(trueness)によって置き換えられてい
る。
8.2.4
真度
装置操作の真度は,国家標準機関,測定能力が承認された国家標準,若しくは国際標準に合致すること
が認証されたその他の研究拠点によって扱われている認証標準物質,又はJIS Q 0030で記載されているよ
うに,特定条件下の光学的手法によって決定された規定の電気泳動移動度をもち,信頼できる原料から成
る剛体球で均質かつ安定な標準物質を使用することによって決定されなければならない。中間精度の試験
は,8.2.3に規定した手順に従わなければならない。
絶対値が2×10−8 m2/(V・s)より高く規定されている標準物質の電気泳動移動度認証値の10 %以内に,電
気泳動移動度の3回の測定の平均値が収まっている場合,装置は,真度の要求事項に合致すると考えられ
る。より大きな誤差が観測された場合は,助言を受けたり,装置の操作法を調べたりした方がよい。
注記 標準物質の手引には,JIS Q 0031,JIS Q 0032,JIS Q 0033,JIS Q 0034及びJIS Q 0035もある。
14
Z 8836:2017 (ISO 13099-2:2012)
8.3
測定誤差の要因
8.3.1
測定試料の残留による汚染
測定誤差の要因には,セルの洗浄が不十分で,試料が残留する場合などがある。測定を終えた試料のイ
オン濃度が,次に測定する試料より高かった場合,洗い流しによる洗浄操作自体が不適切と考えられる。
イオン濃度が高い試料を測定する場合は,その試料専用のセルを個別にもつことが望ましい。
8.3.2
試料の調製手順
粒子のゼータ電位は,粒子を分散させている分散媒の影響を強く受ける。試料を高濃度の懸濁液からサ
ンプリングする場合,ゼータ電位が変化しないよう,液相中のイオンの状態を保たなければならない。イ
オンの状態を保つため,沈降又はフィルタを使用して作製した上澄み液の使用を推奨する。代わりの方法
として,濃度状態を模擬した緩衝液を作製し使用してもよい。上澄み液又は緩衝液を保管するガラス器具
又は容器は,必ず洗浄し,イオンによる汚染がない状態にしなければならない。
8.3.3
試料
移動度を測定するためには,測定の間,粒子は試料セル中に分散され,かつ,光路にとどまっていなけ
ればならない。このため,所定の時間内における測定可能な粒子の大きさは,粒子の密度によって決まる。
細管セルにおいて,粒子は非常に短い距離でセル底に沈降する。沈降粒子の場合,細管セル使用時におけ
る測定可能な時間は,平行板セルを使用する場合と比べて短い。また粒子は,検出可能な十分強い散乱光
を発しなければならない。このため,所定の濃度における測定可能な最小粒子径は,検出可能な散乱光の
強さで決まる。
PALS法では,非常に小さい粒子に対する低い移動度を決定することが可能である。その理由は,PALS
法における演算処理では,非常に多くの測定を繰り返すことによって,拡散項の影響の大半を取り除いた
移動度の一次モーメントが得られ,ブラウン運動の影響を極端に小さくできるからである。
8.3.4
溶媒
使用するレーザ波長に対して,溶媒は透明で非吸収なものが望ましい。粘度は,10 mPa・s以下の,あま
り高くないことが望ましい。測定温度で揮発しないものが望ましい。
8.3.5
測定温度
水の粘度は,室温付近では2 %/℃で変化する。電場の強さによる粒子の終末速度は,粘性抵抗に依存す
る。このため,ゼータ電位を正確に比較するには,既知の温度条件下で行わなければならない。測定試料
を装置と異なった温度条件下で調製した場合,試料及び装置の温度が一致するまで待たなければならない。
8.3.6
光路における結露
室温より低い温度での測定では,光路における結露を避けるため,予防措置をとる。乾燥空気又は窒素
で清浄化しておくことが望ましい。
8.3.7
光学面上の粒子,指紋又は引っかききず
セルの光学面上の引っかききず及び汚れからくるフレアの影響は,参照光光学系の装置では小さいが,
クロスビーム光学系の装置では潜在的な問題であり,最悪の場合は測定が不可能になる。
8.3.8
印加電圧
生理食塩水中の赤血球(細胞)のようにイオン強度が大きい懸濁液を測定する場合,ジュール熱による
熱対流が生じ問題となる。この場合,懸濁液の温度は,装置の設定温度とかなり異なってくる。この結果,
実際の粘度と設定温度における粘度とに違いが生じる。最悪の場合,熱せられた電極表面で細胞が焦げた
り,電気分解によって電極表面に発生した気泡が粒子の動きを阻害したりすることもある。この影響を最
小限に抑えるには,印加電圧を下げ,電圧の正負を短い時間で反転し,電圧の反転と同期した測定をする
15
Z 8836:2017 (ISO 13099-2:2012)
ことが望ましい。
8.3.9
パラメータ
誘電率,粘度,屈折率,温度,電気伝導率,電場などのパラメータが不適切に入力された場合,誤差の
要因になる。
8.3.10 気泡
気泡は,試料の注入操作若しくは溶存空気から,又は電極表面における電気分解のような電気化学的反
応によって発生する。細管セルの壁面に付着した気泡によって,電場がひずみ,静止面の位置が不確かに
なる。電極表面に付着した気泡の存在で,電気伝導率の測定は不正確になる。
8.3.11 セル被覆の損傷
被覆した細管セルを使用する場合がある。細管セル内壁表面の電荷を中和するような被覆をすると,セ
ルの任意の点における測定も可能になる。ただし,このような被覆はもろく,被覆に対し化学的に不適切
な懸濁液を使用することによって容易に破壊される。
8.3.12 電気泳動移動度からゼータ電位を計算する際の理論の選択
ゼータ電位は移動度から計算する。計算に使用する適切な理論及び計算式は,懸濁液の状態に依存する。
詳細は,附属書JAに示す。
8.3.13 試料の安定性
試料が安定していることを実証するためには,連続した時間内で,一連の測定を実施することが望まし
いが,特定の実験の不安定性を検討してもよい。例えば,懸濁液中の粒子からイオン種が解離すると,時
間とともにpH又は電気伝導率が変化し,その結果,移動度も変化する。測定の前後で懸濁液のpH又は電
気伝導率を測定することが望ましい。これによって,試料の安定・不安定性が判定できる。試料が急速な
不安定性を示す場合は,試料をいかに調製し,測定できるかを工夫するのがよい。試料の調製及び装置の
測定手順が時間ごとに変化する場合は,最終結果に違いが生じる。このような場合は,絶対値ではなく変
化速度を記録することが望ましい。
8.4
測定の報告
測定に使用した装置が,ゼータ電位及び電気泳動移動度の各平均値,また各々の分布をそれぞれ出力す
る場合,測定の報告にはこれらの情報を記載することが望ましい。測定の報告には,次の詳細情報を記載
する。
a) 表題及び各ページを識別できる情報
b) 試料を識別する情報及び試料入手年月日
c) 装置の型番及び製造番号
d) 試料
− 粒子特性
− 分散媒
− 粒子状物質の濃度
− 添加剤
− イオン種及びその濃度
− pH及び電気伝導率
e) 試料の調製方法
− 希釈方法
− 超音波処理条件:周波数及び出力
16
Z 8836:2017 (ISO 13099-2:2012)
− 試料調製に関する追加情報
f)
測定条件:
− 測定時の粒子濃度
− 測定温度
− 分散媒の粘度,誘電率及び屈折率
− 印加電圧及び電場強度
g) 測定者情報:
− 施設名及び場所
− 測定者名
− 測定日
h) 報告の終わりを識別する情報
17
Z 8836:2017 (ISO 13099-2:2012)
附属書A
(参考)
細管セル内での電気浸透流
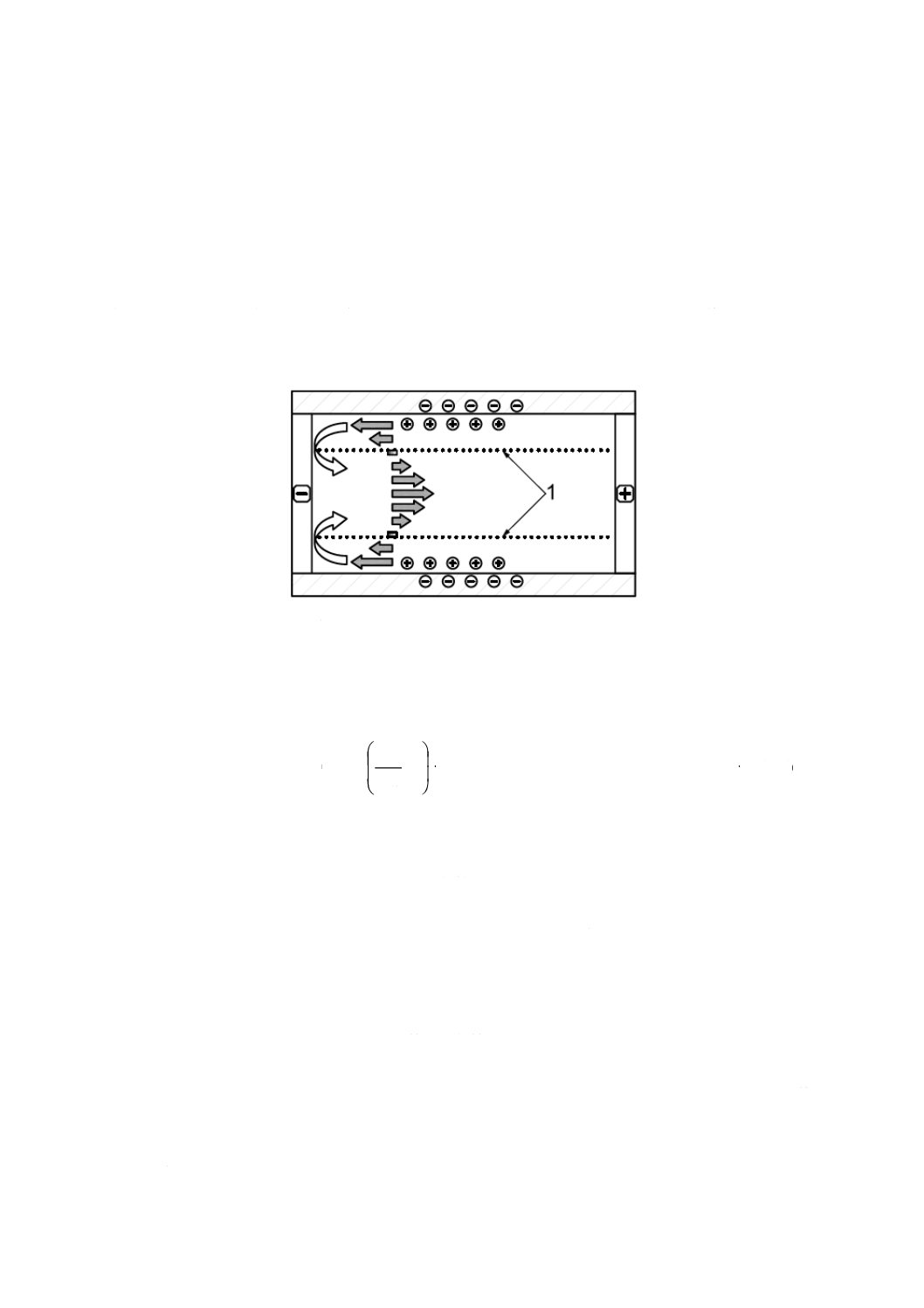
電気浸透流とは,荷電壁面に対する液の流動である。細管型の電気泳動セルに電場を印加すると,細管
セル表面近傍の液は電場に沿って移動する。細管の両端が閉じている場合,壁面に沿って移動する液は,
細管端で反転し,毛細管の中央部に押し出され,図A.1に示すように,反対方向に放物線状に流れる。全
壁面が同じ荷電状態にある単純な形状の細管に対しては,液の流速分布は理論的に予測可能である。
1:静止面
図A.1−細管中の液の流速分布
円筒型細管内の電気浸透による液の移動度(μ0,eo)は,式(A.1)によって求める。
()
−
=
1
2
2
cap
2
eo
,0
eo
R
r
r
μ
μ
······························································ (A.1)
ここに,
μ0,eo: 電気浸透による壁面での液の移動度
r: 中心軸からの距離
Rcap: 細管の半径
同様の式は,角型細管についても導出されている(文献[14])。放物線状の流れ分布の形状は,表面状態
に依存するμ0,eoの値によって変化する。電気泳動光散乱法では,観察されるドップラー周波数シフト量は,
電気浸透による液流動の影響も受けるので,単に粒子移動だけではなく,粒子の電気泳動,ブラウン運動
及び液の電気浸透流に依存している。粒子の運動を正確に知るためには,測定は液が静止するμeo=0で行
う必要がある。この位置を静止面と呼ぶ。円筒状の細管では,この位置はr=0.707 Rcapの円となる。角型
の細管では,静止面は長方形となり,その壁面からの距離は細管の幅と高さとの比によって決定する。こ
の幅の高さに対する比が3の場合,上下の静止面は,細管の高さに対してそれぞれ84 %及び16 %の位置
になる。
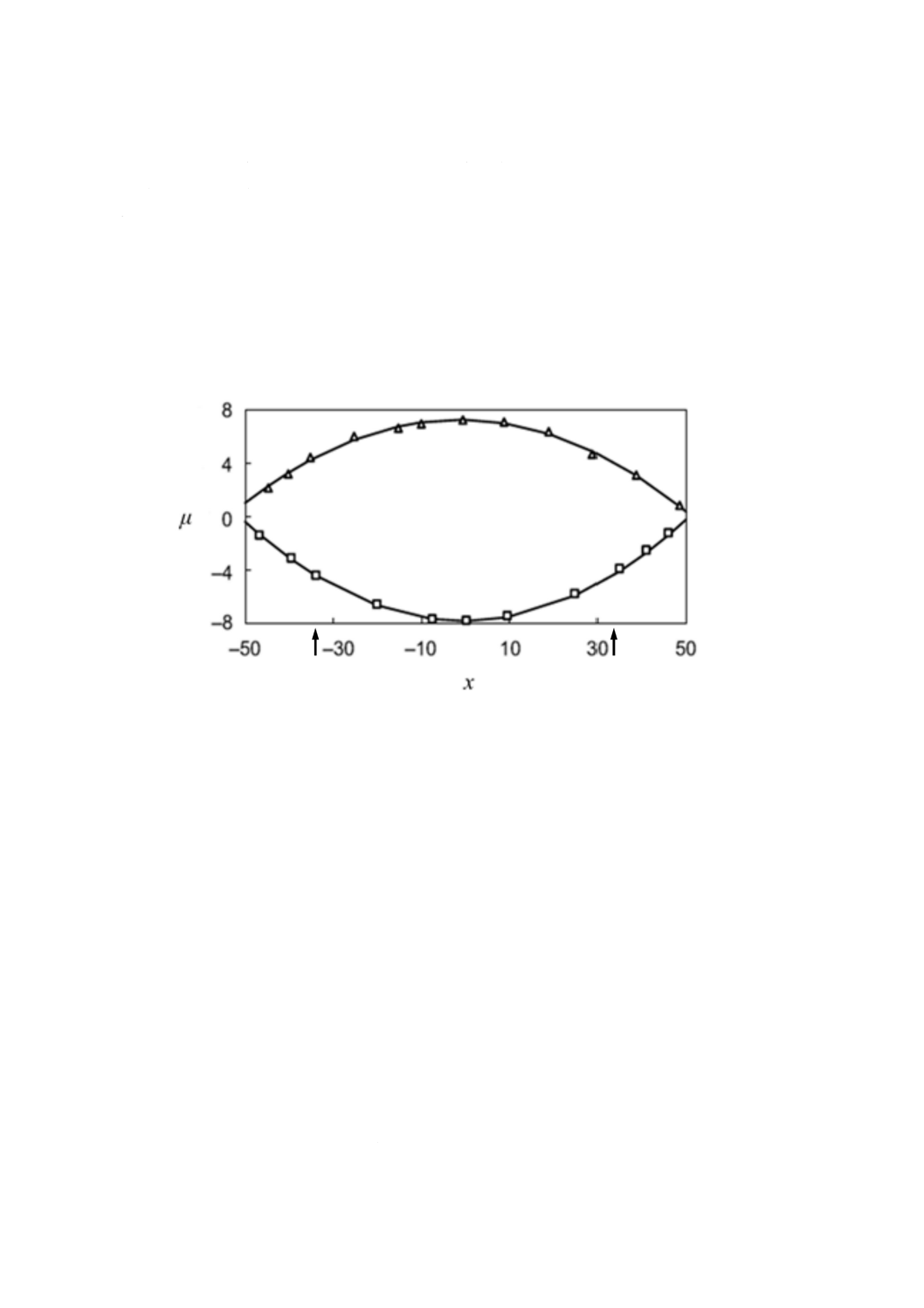
図A.2は,角型細管セル中の異なる位置で観察される見かけの電気泳動移動度の値を示す。四角(□)
は,移動度が−4.2×10−8 m2/(V・s)のポリスチレンラテックス試料(a=155 nm)の見かけの電気泳動移動
18
Z 8836:2017 (ISO 13099-2:2012)
度を示す。三角形(△)は,臭化ナトリウムの1 mol/m3水溶液中における正電荷ドデシルトリメチルアン
モニウムイオンの吸着したポリスチレンラテックス試料(a=45 nm)の見かけの電気泳動移動度を示す。
二つの矢印は電気浸透流速がゼロとなり,正確な電気泳動移動度が得られる二つの静止面の位置を示して
いる。
実際,入射光が静止面に照射された場合,電気浸透流の影響はほとんど消失する。入射光には一定の厚
さがあるので,当然,静止面付近の一定の厚さ内の粒子が測定される。角型細管の場合,静止面上下に微
小な電気浸透流が存在するが,互いに逆方向のため平均化されて,その電気浸透流への影響はなくなる。
円筒細管の場合,静止面が平面ではないため,入射光の中心が静止面に正確に入射していても,液流速ゼ
ロからのずれの影響が生じる。
μ:電気泳動移動度[10−8 m2/(V・s)]
x:位置(%)
図A.2−異なる位置で観察される見かけの電気泳動移動度の値(文献[8])
試料及び空気又はその他のガス気泡に由来するイオンほかの物質が吸着した場合,細管の各表面のポテ
ンシャルは,不均一になり得る。その場合,非対称の液流速分布となる。角型の細管の場合,この流速分
布は上下表面の表面電位を決定するために利用できる(文献[15])。
その他の電気浸透流の問題点は,移動度分布測定値の広がりである。いずれの光源でもある程度の厚さ
があるので,入射光の中心が静止面上にあっても,入射光の一部はある方向への流れを照射し,他の一部
は逆方向への流れを照射する。粒子が全く同じ移動度をもつときでさえ,移動度の測定値は単一の値では
なく分布をもつ。ただし,その平均値は正しい値である。細管中心では,流速分布の勾配が平たん(坦)
となり,液と粒子とは似た流れになる。したがって,分布の広がりは最小となる。そのため,電気浸透流
の影響を最小にする一つの方法は,細管の中心及び静止面の2か所で測定を行うことである。すなわち,
中心で測定した正確な移動度分布と,静止面での正確な平均値とを組み合わせ,測定値とする。
電気浸透流を低減する一つの方法は,壁面のゼータ電位を低くする物質で細管の内部表面を被覆するこ
とである。特に,ポリエチレングリコール‐ポリエチレンイミン(PEG-PEI)を被覆又は結合させると,
広いpH,イオン強度にわたり,電気浸透流が顕著に低減する。しかし,被覆の安定性及び簡便さは,広く
19
Z 8836:2017 (ISO 13099-2:2012)
用いる手法としては,改善の余地が大きい。
液の電気浸透流を回避するもう一つの方法は,高い周波数(10 Hz以上)で切り替える交流電場を使用
することである。この着想の重要な点は,液が終末速度に達する時間が,粒子のそれよりもはるかに長い
ところにある。静止粒子が電気泳動速度に達するのに必要な加速時間はナノからマイクロ秒の範囲である
が,液の場合は,0.1秒の領域にある。電極が高速で反転した場合,液は静止状態で,電気浸透流は発生し
ない(文献[16][17])。したがって,細管のいずれの場所でも測定を実施することができる。しかし,高周
波場を用いることによって,分布の分解能は必然的に低下し,電場の変調によって副次的なバンドが生成
する。これは,特に分布の広い移動度をもつ物質に対するスペクトルを複雑化する。この複雑化を避ける,
一つの方法は,通常の直流での測定及び高周波反転測定の利点を利用することである。まず高周波反転測
定から試料の平均移動度を測定する。次に,液の電気浸透のため正確ではないが,副次的なバンドのない
直流での電気泳動測定を行い,高周波測定から得られた正確な平均値で補正して,電気泳動分布を得るも
のである(文献[12])。
20
Z 8836:2017 (ISO 13099-2:2012)
附属書JA
(参考)
ゼータ電位の理論モデルの概要
JA.1 ゼータ電位及びすべり面
液中の荷電粒子の表面近傍全体では,電気的中性の原理が成立し,表面電荷と当量で反対符号の電荷が
粒子表面の周りにイオンの形で集まる。これらのイオンは静電引力及び熱運動による拡散力によって,あ
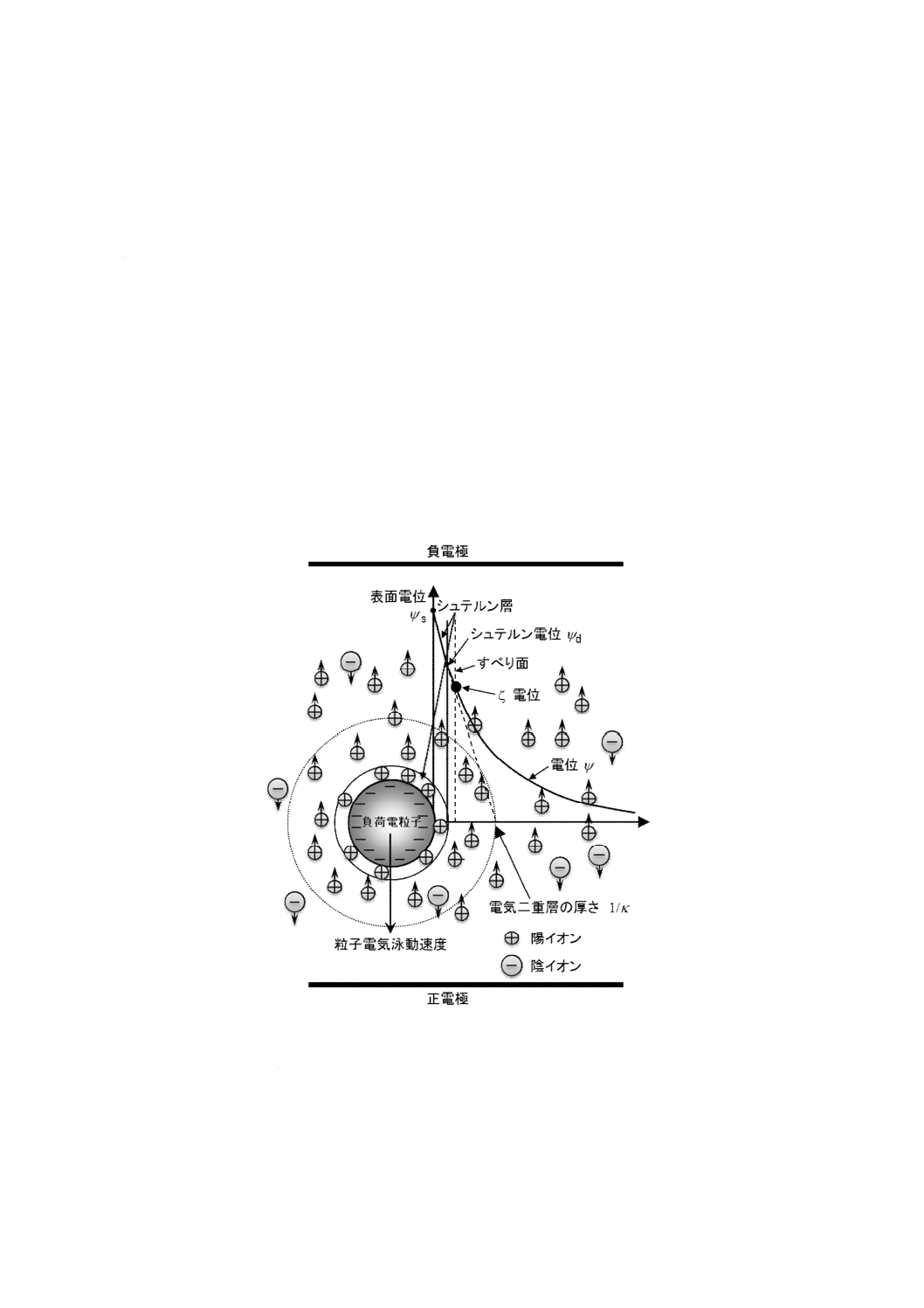
る平衡分布を取り,図JA.1に示すように,粒子の周りに雲状に存在する。このイオンの雲状分布を拡散電
気二重層と呼ぶ。このような溶液に外部電場を印加すると,粒子と拡散電気二重層とはそれぞれ反対符号
の電極に静電的に引っ張られる。このとき,粒子表面に強い親和性をもつ表面近傍の液体分子及びイオン
は,粒子に追随して運動し,その外側の溶液は逆方向に運動する。したがって,両者の界面には相対運動
が生じる。この界面は“すべり面”と呼ばれ,すべり面の電位がゼータ電位である。このような定義から,
ゼータ電位の絶対値の物理的意味は不明瞭であるが,粒子荷電を相対的に論じる場合には,一つの尺度と
して重要である。
ψ
:粒子周りの電位
ψs :粒子表面電位
1/κ :デバイ長
図JA.1−電場下における荷電粒子のすべり面及びゼータ電位の模式図
21
Z 8836:2017 (ISO 13099-2:2012)
JA.2 球形粒子周りの電位分布及びデバイ長
電解質水溶液中の荷電球形粒子に対し,電力束のガウス定理より導かれる粒子周りの電位ψ及び電荷密
度ρに関するポアソンの式,並びにイオンに働く拡散力と静電力とのバランスから導出されるボルツマン
の式を適用すると,式(JA.1)のポアソン-ボルツマン式が導出される。
∑
∑
=
=
−
=
∇
T
k
e
z
e
z
n
e
z
n
i
i
i
i
i
B
0
2
exp
ψ
ε
ε
ε
ρ
ψ
·························· (JA.1)
ここに,
ε: 媒体の誘電率
ni,n0i: 任意点及び粒子表面から十分離れた点でのイオン濃度(添
え字iはイオン種)
zi: イオン価数(添え字iはイオン種)
e: 電気素量
kB: ボルツマン定数
T: 絶対温度
簡単のため電解質が塩化ナトリウムなどのようにz-z型の対称型電解質で,z+=z−=z, n0+=n0−=n0が成
立し,電位が低くzeψ<kBT(常温でz=1のとき,ψ<25 mV)が成立する場合には,粒子中心からの位置
rでの電位ψは,解析的に導出され,式(JA.2)及び式(JA.3)で与えられる。
(
)
[
]
a
r
r
a
−
−
=
κ
ψ
ψ
exp
s
···························································· (JA.2)
T
k
e
z
n
B
2
2
0
2
ε
κ=
······································································· (JA.3)
ここに,
a: 粒子半径
ψs: 粒子表面電位
κは式(JA.3)から分かるように,溶液のイオン濃度n0の尺度である。粒子径が十分に大きいとすると,式
(JA.2)は平板に対する式,ψ=ψsexp(−κh)に帰着する。ただし,hは平板表面からの距離である。ここで,
粒子表面h=0で,ψの接線を引くと,そのψ=0との交点がh=1/κとなる。1/κは“デバイ長”又は“電
気二重層の厚さ”と呼ばれ,図JA.1で概念的に示されるように,拡散電気二重層の広がり(厚さ)を表す
尺度となる。25 ℃の水溶液の場合,デバイ長は式(JA.4)で与えられる。
C
z
10
10
0.3
1
−
×
=
κ
······································································· (JA.4)
ここに,
1/κ: デバイ長又は電気二重層の厚さ(m)
C: 電解質モル濃度(mol/dm3)
これから分かるように,C又はzの値が増すと,1/κは小さくなり電気二重層は圧縮される。z=1, C=10−3
mol/dm3の場合,1/κ〜10−8 m (=10 nm)となる。1粒子のもつ全電荷Q及び表面電荷密度σは,周りのイオ
ンのもつ電荷との釣合から式(JA.5)で与えられる。
(
)
s
2
1
4
4
ψ
κ
ε
π
σ
π
a
a
a
Q
+
=
=
··················································· (JA.5)
22
Z 8836:2017 (ISO 13099-2:2012)
溶液中の粒子電荷は,ψsとκとで決まることが分かる。κの値は式(JA.3)で計算されるが,ψsの値を求め
ることは難しい。ゼータ電位はこのψsの近似値として用いられる。
JA.3 電気泳動速度からのゼータ電位の導出
JA.1で示すように,電場下の荷電粒子と拡散電気二重層とはそれぞれ反対方向に泳動するので,その相
対速度u∞の測定からゼータ電位が求められる。κaの値が極端な場合には,比較的簡単に電場強度E当た
りの粒子の泳動速度,すなわち,電気泳動移動度μ(=u∞/E)を導出することができる。
a) κa≪1の場合 この場合,κの値は極めて小さい。これは,溶媒中のイオン濃度が極めて低く,粒子
の泳動に比べて,溶媒中のイオン泳動の影響は無視してよいことを意味する。したがって,強度Eの
電場中の荷電粒子に働く力QEは,ストークスの流体抗力と釣り合うため,式(JA.6)が成立する。
∞
=
u
a
E
Q
0
6
η
π
····································································· (JA.6)
ここに,
η0: 媒体の粘性率
式(JA.5)において,κa≪1, ψs≈ζとすると,式(JA.6)によって,電気泳動移動度とゼータ電位との関係は式
(JA.7)で与えられる。
0
3
2
η
ζ
ε
μ=
············································································· (JA.7)
この式は,ヒュッケルの式として知られている。
b) κa≫1の場合 この場合,溶媒中のイオン濃度が極めて高い。これは,電気二重層の厚さが極めて薄
いこと,すなわち,粒子表面を平板と考えてよいことを意味している。図JA.2に示すような粒子表面
平板に固定した座標系において,−x方向に電場Eを印加すると,負に荷電している粒子表面(表面
積A)はx方向に一定速度u∞で泳動し,y方向の速度分布及びポテンシャル分布は図中のようになる。
いま,溶液の微小要素AΔyに働く力を考えると,定常状態では静電力と流体の粘性力がバランスし,
式(JA.8)が成立する。
y
A
y
d
y
u
d
y
A
E
∆
=
∆
−
2
2
0
)
(
η
ρ
····················································· (JA.8)
ここに,
y: 表面に垂直な座標軸
x: 表面に平行な表面上の座標軸
Δy: y軸方向の微小距離差
u(y): 座標yにおける流体速度
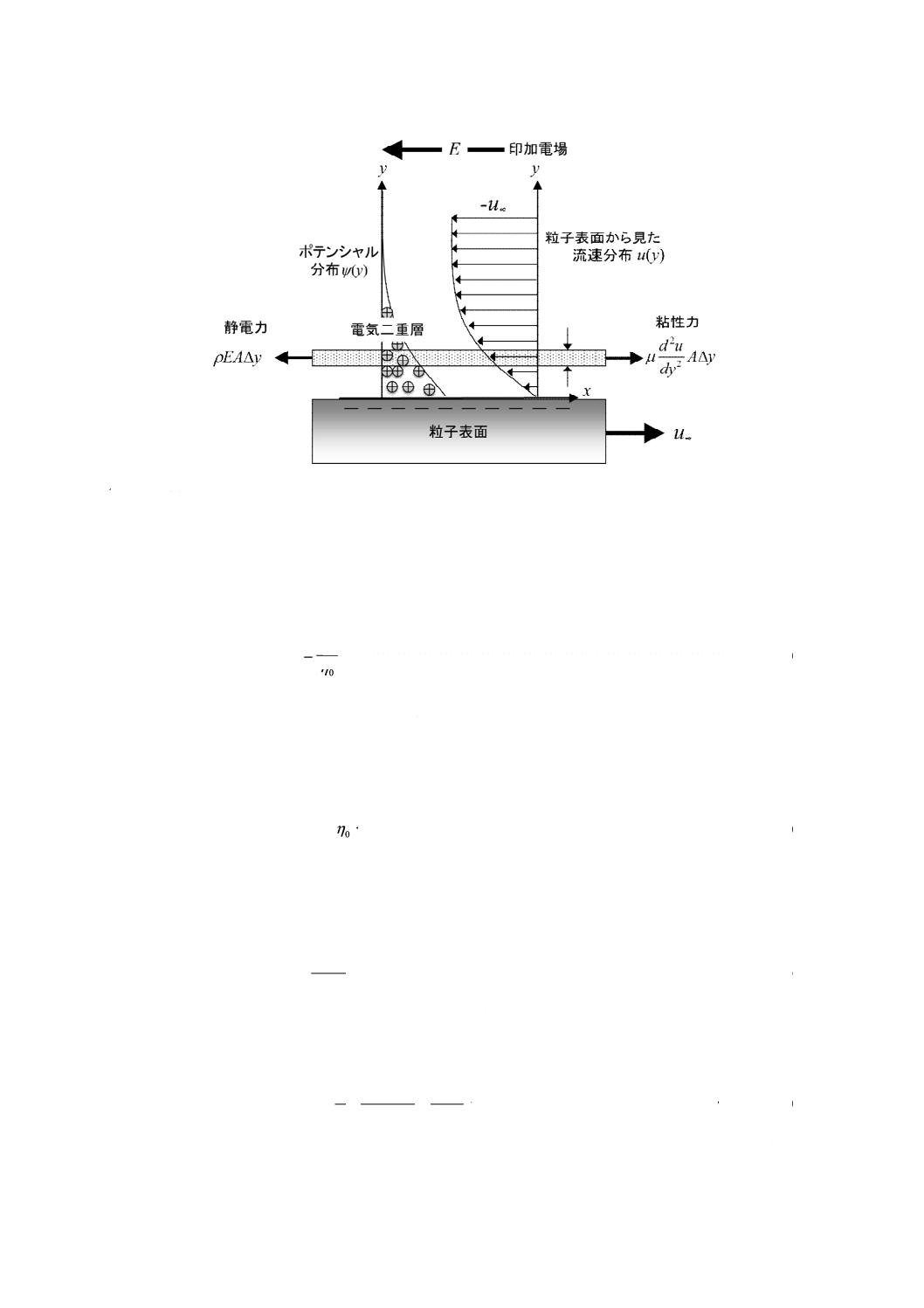
23
Z 8836:2017 (ISO 13099-2:2012)
A :表面積
y :表面に垂直な座標軸
x :表面に平行な表面上の座標軸
Δy:y軸方向の微小距離差
u(y):座標yにおける流体速度
E:印加電場
u∞:粒子表面速度
ψ(y):y方向のポテンシャル分布
図JA.2−κa≫1の場合における粒子から見た粒子表面平板上の媒体流れ及び電場
式(JA.8)の電荷密度ρに式(JA.1)を代入し,境界条件(y→∞において,ψ→0, u→−u∞,dψ/dx→0, du/dy→
0, かつ,y=0にてψ=ζ, u=0)を用いると,式(JA.9)が導出される。
E
u
0η
ζ
ε
=
∞
··········································································· (JA.9)
この式は,表面近傍の流体速度場と印加電場とが表面に平行であれば成立することは明らかである。電
場と速度場の表面近傍での平行性は,表面が絶縁体であれば成立することは証明されており,粒子の表面
がx方向と角度θ傾いた微小平板で近似できるとすると,印加電場はEcosθ,相対速度はu∞cosθとなるだ
けで,式(JA.9)は成立する。したがって,粒子の電気泳動移動度μは,粒子形状によらず成立するスモル
コフスキー式と呼ばれる式(JA.10)で与えられる。
0η
ζ
ε
μ=
·········································································· (JA.10)
c) ヘンリーの式 上記のようにκaの値が極端な場合,粒子の電気泳動移動度は比較的簡単に導出可能で
ある。しかし,その中間領域での電気泳動移動度は,印加電場の粒子の存在による電場のひずみ並び
に表面近傍の電気二重層への影響を考慮した運動方程式及び連続の式を解く必要がある。ヘンリーに
よると,表面電位が余り高くない場合,電気泳動移動度μは式(JA.11)で与えられる(文献[18])。
()
a
fκ
η
ζ
ε
μ
0
3
2
=
···································································· (JA.11)
f(κa)は,ヘンリー関数で,κa→0でf(κa) →1,κa→∞でf(κa) →3/2となり,両極端がそれぞれ,ヒュッケ
ルの式,スモルコフスキーの式に一致する。f(κa) は,積分を含む複雑な関数となるので,式(JA.12)の近似
式が提案されている(文献[18])。
()
()
13
.1
144
.0
2
1
2
3
a
a
f
κ
κ
+
−
=
···················································· (JA.12)
0.1<κa<100の領域ではヘンリーの式を用いる必要のあることが知られている。ただし,その導出過程
で,式(JA.2)を用いているため,ゼータ電位が余り高くない場合にだけ利用可能である。
Δy
24
Z 8836:2017 (ISO 13099-2:2012)
参考文献
[1] Reuss, A. Mem. Soc. Imp. D. Moscow 1807, 11, p. 327
[2] Zsigmondy, R. Colloids and the ultramicroscope. New York, NY: Wiley, 1914
[3] Gittens, G.J., James, A.M. An improved microelectrophoresis apparatus and technique for studying biological
cells surfaces. Anal. Biochem. 1960, 1, pp. 478‒485
[4] Goetz, P.J., Penniman, J.G. A new technique for microelectrophoretic measurements. Am. Lab. 1976, 8, pp.
21-30
[5] Goetz, P.J. System 3000 automated electrokinetic analyzer for biomedical applications. In: Schutt, W.,
Klinkmann, H., editors. Cell electrophoresis. New York, NY: de Gruyter, 1985, pp. 41-55
[6] OʼBrien, R .W., C annon, D .W., Rowlands, W.N. Electroacoustic determination of particle size and
zeta-potential. J. Colloid Interface Sci. 1995, 173, pp. 406-418
[7] Sutherland, W.H., Pritchard, J.A.V. An improved apparatus for micro-electrophoresis. In: Preece, A.W.,
Sabolovic, D., editors. Cell electrophoresis: Clinical application and methodology. Elsevier, 1979, pp.
421-31
[8] Xu, R. Particle characterization: Light scattering methods. Chapter 6. Dordrecht: Kluwer, 2000, pp. 299-343
[9] Xu, R. Progress in nanoparticles characterization: Sizing and zeta-potential measurement. Particuology 2008, 6,
pp. 112-115
[10] Xu, R. Methods to resolve mobility from electrophoretic laser light scattering measurement. Langmuir 1993, 9,
pp. 2955-2962
[11] Miller, J.F. The determination of very small electrophoretic mobilities in polar and non polar colloidal
dispersions using phase analysis light scattering. J. Colloid Interface Sci. 1991, 143, pp. 532-553
[12] Connah, M.L., Kaszuba, M., Morfesis, A. High resolution zeta-potential measurements: Analysis of
multi-component mixtures. J. Disper. Sci. Technol. 2002, 23, pp. 663-669
[13] Henry, D.C. The cataphoresis of suspended particles−Part I: The equation of cataphoresis. Proc. R. Soc.
London Ser. A 1931, 133, pp. 106-129
[14] Burns, N.L. Surface characterization through measurement of electroosmosis at flat plates. J. Colloid Interface
Sci. 1996, 183, pp. 249-259
[15] Mori, S., Okamoto, H. A unified theory of determining the electrophoretic velocity of mineral particles in the
rectangular micro-electrophoresis cell. Fusen 1980, 27, pp. 117-126
[16] Schätzel, K., Weise, W., Sobotta, A., Drewel, M. Electroosmosis in an oscillating field: Avoiding distortions in
measured electrophoretic mobilities. J. Colloid Interface Sci. 1991, 143, pp. 287-293
[17] Minor, M., van der Linde, A.J., van Leeuwen, H.P., Lyklema, J. Dynamic aspects of electrophoresis and
electroosmosis: A new fast method for measuring particle mobility. J. Colloid Interface Sci. 1997, 189, pp.
370-375
[18] Masliyah, J.H., Bhattacharjee, S., “Electrokinetic and Colloid Transport Phenomena”, New Jersey, John Wiley
& Sons, Inc., 2006, p.318
[19] JIS Q 0031 標準物質−認証書及びラベルの内容
[20] JIS Q 0032 化学分析における校正及び認証標準物質の使い方
25
Z 8836:2017 (ISO 13099-2:2012)
[21] JIS Q 0033 認証標準物質の使い方
[22] JIS Q 0034 標準物質生産者の能力に関する一般要求事項
[23] JIS Q 0035 標準物質−認証のための一般的及び統計的な原則








