Z 8831-3:2010 (ISO 15901-3:2007)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 記号······························································································································· 3
5 原理······························································································································· 5
5.1 概要 ···························································································································· 5
5.2 測定方法 ······················································································································ 6
6 測定手順························································································································· 6
6.1 試料のサンプリング ······································································································· 6
6.2 試料前処理 ··················································································································· 7
6.3 吸着量測定 ··················································································································· 7
7 装置性能の検証 ················································································································ 7
8 装置校正························································································································· 7
9 ミクロ細孔容積の評価 ······································································································· 7
9.1 ミクロ細孔容積評価法の一般原理······················································································ 7
9.2 デュビニン・ラドシュケビッチ(Dubinin/Radushkevich)法によるミクロ細孔容積の測定 ··········· 9
9.3 吸着等温線の比較によるミクロ細孔の解析 ········································································· 10
9.4 ホルバス・カワゾエ(HK)法及びサイトウ・フォリー(SF)法によるミクロ細孔径分布の解析 ·· 14
9.5 非局所密度はん(汎)関数理論(NLDFT)によるミクロ孔細孔分布の解析 ······························ 15
10 試験結果報告 ················································································································ 18
附属書A(参考)HK法及びSF法 ·························································································· 20
附属書B(参考)NLDFT法··································································································· 23
参考文献 ···························································································································· 26
Z 8831-3:2010 (ISO 15901-3:2007)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本粉体工業技術協会(APPIE)及
び財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,
日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権及び出願公開後の実用新案登録出願にかかわる確認について,責
任はもたない。
JIS Z 8831の規格群には,次に示す部編成がある。
JIS Z 8831-2 第2部:ガス吸着によるメソ細孔及びマクロ細孔の測定方法
JIS Z 8831-3 第3部:ガス吸着によるミクロ細孔の測定方法
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8831-3:2010
(ISO 15901-3:2007)
粉体(固体)の細孔径分布及び細孔特性−
第3部:ガス吸着によるミクロ細孔の測定方法
Pore size distribution and porosity of solid materials-
Part 3: Analysis of micropores by gas adsorption
序文
この規格は,2007年に第1版として発行されたISO 15901-3を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,低温ガス吸着によるミクロ細孔性物質のミクロ細孔(細孔内径2 nm以下)の容積及び比
表面積の測定方法について規定する(参考文献[1]〜[7]参照)。これらは,相対的かつ非破壊的試験である。
この方法は,測定時にミクロ細孔内に拡散できる物理吸着ガスを用いる。また,この方法は,IUPAC分類
(JIS Z 8831-2の図1及びJIS Z 8830を参照)のI型,II型,IV型又はVI型の吸着等温線に対して有効で
ある。ただし,化学吸着又は吸収が起こる場合には,この方法は適用できない。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 15901-3:2007,Pore size distribution and porosity of solid materials by mercury porosimetry and
gas adsorption−Part 3: Analysis of micropores by gas adsorption(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8830 気体吸着による粉体(固体)の比表面積測定方法
注記 対応国際規格:ISO 9277,Determination of the specific surface area of solids by gas adsorption
using the BET method(MOD)
JIS Z 8831-2 粉体(固体)の細孔径分布及び細孔特性−第2部:ガス吸着によるメソ細孔及びマクロ
細孔の測定方法
注記 対応国際規格:ISO 15901-2,Pore size distribution and porosity of solid materials by mercury
porosimetry and gas adsorption−Part 2: Analysis of mesopores and macropores by gas adsorption
(MOD)
ISO 3165,Sampling of chemical products for industrial use−Safety in sampling
2
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ISO 8213,Chemical products for industrial use−Sampling techniques−Solid chemical products in the form of
particles varying from powders to coarse lumps
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1
吸着質(adsorbate,adsorptive)
吸着した状態の物質(adsorbate),及び吸着されるガス又は蒸気(adsorptive)。
注記 英語ではadsorbateとadsorptiveとが区別されているが,日本語では両者を吸着質としている。
3.2
吸着(adsorption)
固体の外部表面及び吸着可能な内部表面上での吸着質の濃縮現象。
3.3
吸着材(adsorbent)
その上で吸着が起こる固体物質。
注記 吸着剤ともいう。
3.4
吸着等温線(adsorption isotherm)
一定温度における吸着量と吸着質ガス(adsorptive)の平衡圧力との関係。
3.5
吸着量(adsorbed amount)
ある圧力p及び温度Tにおいて吸着したガスのモル数(物質量)。
3.6
平衡吸着圧力(equilibrium adsorption pressure)
吸着した状態の吸着質(adsorbate)と平衡にある気相中の吸着質(adsorptive)の圧力。
3.7
単分子層吸着量(monolayer amount)
吸着材表面上に単分子の層を形成するときの,吸着質のモル数。
3.8
単分子層吸着容量(monolayer capacity)
標準状態の温度及び圧力(standard temperature and pressure,STP)でのガスとして表現される,単分子層
吸着量の体積相当量。
3.9
マクロ細孔(macropore)
50 nmよりも大きな径をもつ細孔。
注記 マクロ孔又はマクロポアともいう。
3.10
メソ細孔(mesopore)
2〜50 nmの間の径をもつ細孔。
注記 メソ孔又はメソポアともいう。
3
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.11
ミクロ細孔(micropore)
2 nm以下の径をもつ細孔。
注記 ミクロ孔,ミクロポア,マイクロ孔,マイクロ細孔又はマイクロポアともいう。
3.12
物理吸着(physisorption)
圧力又は温度の小さな変化に対して可逆的である,弱い結合による吸着。
3.13
細孔径(pore size)
細孔の径,すなわち,シリンダ型細孔の直径又はスリット型細孔の面間距離。
3.14
相対圧(relative pressure)
飽和蒸気圧力p0に対する平衡吸着圧力pの比。
3.15
飽和蒸気圧(saturation vapour pressure)
吸着温度で液化する吸着質の蒸気圧。
3.16
体積吸着量(volume adsorbed)
標準状態の温度及び圧力(STP)での,ガスとして表現される吸着量の体積相当量又は吸着質(adsorbate)
の液体体積として表現される吸着量の体積相当量。
4
記号
この規格で用いる記号,意味及び単位は,次による。単位質量当たりで示される値は,すべてグラム当
たりである。
記号
意味
単位
KAa
吸着質ガスのカークウッド・ミューラー(Kirkwood-Mueller)定数
J·cm6
KAs
吸着状態にある吸着質のカークウッド・ミューラー定数
J·cm6
as
比表面積
m2·g−1
as,ref
参照試料の比表面積
m2·g−1
am
分子断面積(分子占有面積ともいう。)
nm2
αa
吸着質ガスの分極率
cm3
αs
規格化された吸着量a)
1
α(s*)
吸着材の分極率
cm3
β
親和係数(affinity coefficient)a)
1
c
光速
m·s−1
da
吸着質ガス分子の直径
nm
dHS
剛体球の直径
nm
dp
細孔直径又は細孔径
nm
ds
吸着材表面原子の直径
nm

4
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
記号
意味
単位
d0
d0=(ds+da)/2,吸着質ガス分子と吸着材表面原子との間の距離
nm
E
吸着ポテンシャル
J·mol−1
E0
特性吸着エネルギー(characteristic adsorption energy)
J·mol−1
εff
ガス−ガス間のレナード・ジョーンズ(Lennard-Jones)ポテンシャルパラメータ K
εsf
ガス−固体間のレナード・ジョーンズポテンシャルパラメータ
K
kB
ボルツマン定数(1.380 650 5×10−23)
J·K−1
L
原子核間細孔径
nm
ma
吸着したガス(吸着物)の質量
g
me
電子の質量
kg
ms
試料質量
g
NA
アボガドロ数(6.022 141 5×1023)
mol−1
Na
単分子層の単位面積(m2)当たりの原子数
m−2
Ns
吸着材の単位面積(m2)当たりの原子数
m−2
na
吸着材単位質量当たりの吸着量
mol·g−1
nm
吸着材単位質量当たりの単分子層吸着量
mol·g−1
p
吸着した状態の吸着質と平衡にある吸着質ガスの圧力
Pa
P0
吸着質ガスの飽和蒸気圧
Pa
p/p0
吸着質ガスの相対圧a)
1
R
気体定数(ガス定数)(8.314 472)
J·mol−1·K−1
ρg
ガス密度
g·cm−3
ρg,STP
標準状態(273.15 K,101 325.02 Pa)のガス密度
g·cm−3
ρl
液体密度
g·cm−3
σ
相互作用エネルギーがゼロとなる2分子間の距離
nm
σff
ガス−ガス間レナード・ジョーンズポテンシャルの距離パラメータ
nm
σsf
ガス−固体間レナード・ジョーンズポテンシャルの距離パラメータ
nm
T
温度
K
Tcr
臨界温度
K
t
吸着層の統計的厚さb)
nm
Va
吸着材単位質量当たりの吸着質の液体相当体積
cm3·g−1
Vg
吸着材単位質量当たりの吸着質の標準状態(273.15 K,101 325.02 Pa)換算体積 cm3·g−1
Vmicro
ミクロ細孔容積
cm3·g−1
W
細孔径(スリット型細孔)
nm
χa
吸着質ガスの反磁性磁化率
cm3
χs
吸着材の反磁性磁化率
cm3
注記 物性定数については,適宜丸めた値を用いても差し支えない。
注a) 現在,一般に無次元と決められている次元1のすべての量に対して,SI単位は1である[JIS Z
8202-0(参考文献[43]参照)]。
b) 記号tは一般的に時間を表すために使用されているのに対し,ガス吸着による細孔径分布解析で
の一般的慣習として,tは液体状の吸着層の統計的厚さを表現するために使用されている。した
がって,この規格における記号tのすべては,時間ではなく統計的厚さに対応する。
5
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
原理
5.1
概要
この測定方法は,一定の低温下でのガスの吸着及び脱着(脱離ともいう。)の測定,並びにそれによって
得られる吸着等温線の初期低圧部分におけるデータの評価に基づくものである。用いる気体は,固体表面
に物理吸着するものであり,特に77.4 Kにおける窒素,77.4 K及び87.3 Kにおけるアルゴン,並びに195
K及び273.15 Kにおける二酸化炭素がよく用いられる。ガス分子の大きさの違いによる細孔への拡散性が
異なること及び測定温度が違うことで,異なる測定結果が得られる可能性がある。ミクロ細孔では,分子
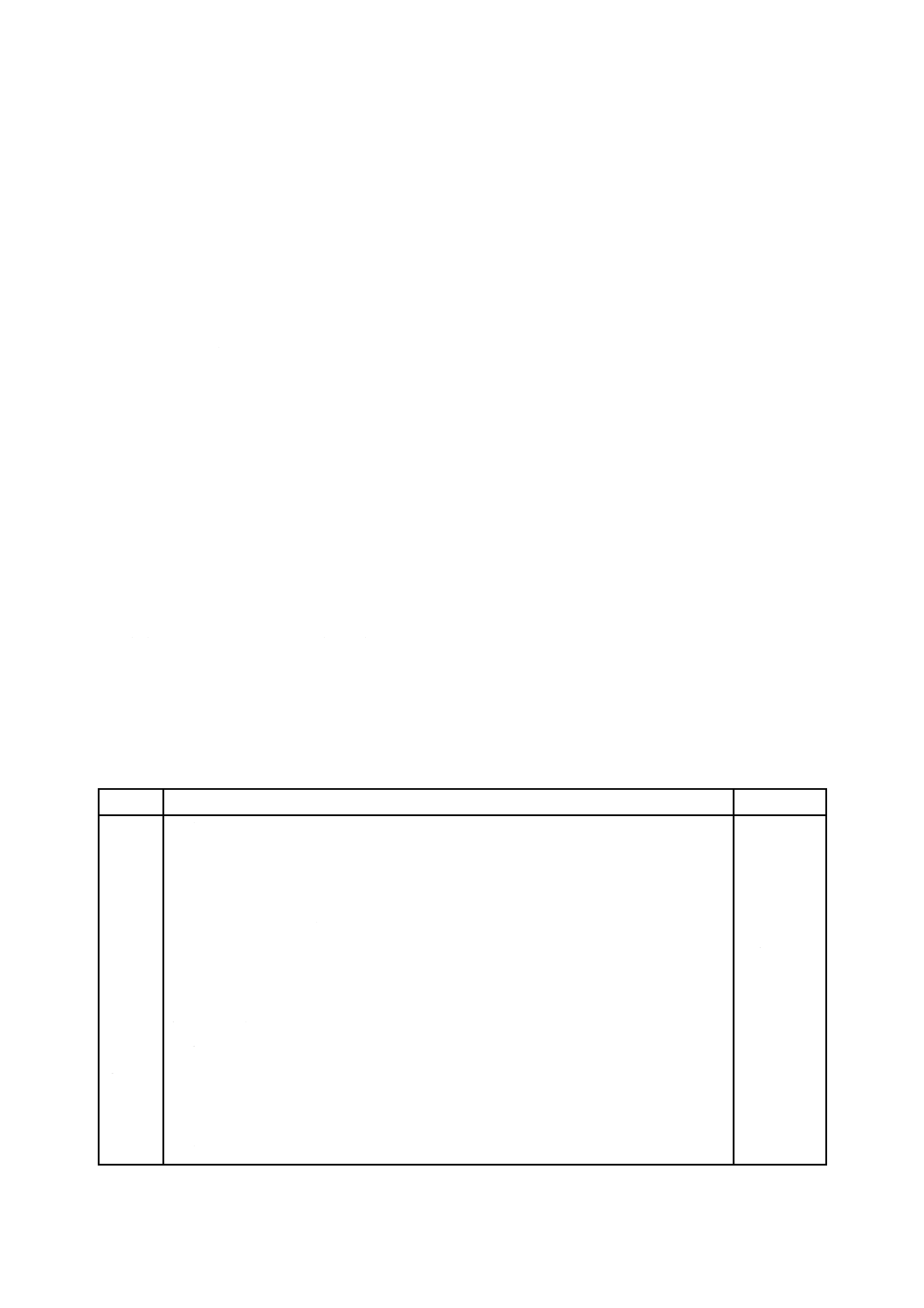
と細孔壁との相互作用ポテンシャルが,相対する壁との相互作用ポテンシャルと重なり合う(図1参照)
ので,物理吸着力は広い細孔及び外表面のそれよりも強い。その結果,ミクロ細孔は,非常に低い相対圧
(p/p0<0.01)において吸着質で充てんされる(この現象は,特に“ミクロ細孔フィリング”又は“ミクロ
ポアフィリング”と呼ばれる。)。ミクロ細孔の典型的な部分は,吸着等温線の原点付近での大きくて急激
な立ち上がり,及びその後の平たん部(プラトー)に続く折れ曲がりである。ミクロ細孔は,ミクロ細孔
容積及びミクロ細孔径分布で評価される。細孔径が分子直径に近いので,細孔径を評価する上でガスの選
択は重要である。
注記 対応国際規格では,吸着温度に77 K,77.35 K及び77.4 Kというように種々の値を用いている。
この規格では,変更しないでそのまま記載した。
X軸:細孔壁間の距離
Y軸:ポテンシャル・エネルギー
図1−無限に長いスリット状細孔における流体と表面との間の強調化された
相互作用ポテンシャルの細孔径依存性(参考文献[8]参照)
ゼオライト,分子ふるい炭素などのようなミクロ細孔性物質の細孔径及び細孔容量の解析は,困難であ
る。なぜならば,0.5〜1 nmの細孔への充てんは相対圧10−7〜10−5で起こり,この場合,拡散速度及び吸
着平衡が非常に遅いからである。87.3 Kでのアルゴンは,77.4 Kにおける窒素に比較してかなり高い相対
圧になってから0.5〜1 nmのミクロ細孔を充てんする。このように,窒素吸着に比較して高い細孔充てん
6
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
圧及び高い温度は,拡散及び平衡過程を促進させる。したがって,ミクロ細孔性物質の細孔解析には液体
アルゴン温度(87.3 K)でのアルゴンを吸着質として用いると有利である。しかしながら,77.4 Kにおけ
る窒素吸着の場合と同様に,ほとんどの狭いミクロ細孔を充てんするには,アルゴンの場合でもそれに必
要な絶対圧力は非常に低い。このような低い圧力では,拡散障害というよく知られた問題が生じる。すな
わち,このような条件では窒素分子又はアルゴン分子でも,活性炭素繊維,分子ふるい炭素などに存在す
る最も狭い細孔に入りにくくなる。このため,誤った吸着等温線が得られる可能性があり,細孔容積など
を過小評価することになる。これらの問題を解決する一つの可能性は(少なくともミクロ細孔性炭素材料
に対しては),273.15 Kにおける二酸化炭素の使用にある。この温度での二酸化炭素の飽和蒸気圧は,約
3.48 MPaである。すなわち,ミクロ細孔フィリングを検知するために必要な低い相対圧を達成するための,
ターボ分子ポンプレベルの高真空状態を必要としない。101 325 Pa(1 atm)までの二酸化炭素吸着で,約
1.5 nmまでの最も小さなミクロ細孔を検出できる。このような比較的高い温度及び圧力では,大きな拡散
障害はなく,低温での窒素及びアルゴンによる実験に比べ,平衡に速く到達する。
5.2
測定方法
吸脱着等温線を求めるために必要とされる実験データは,圧力をステップ状に順次変化させる逐次方式
又は圧力を連続的に変化させる方式によって,平衡圧を観測する容量法又は平衡状態における質量を測定
する質量法によって得ることができる。吸脱着平衡は長い時間を要するので,平衡値測定を確実にする逐
次方式が推奨される。
容量法は,校正された体積及び圧力の測定に基づく(JIS Z 8830の図5を参照)。一般的な気体の状態方
程式を適用して,導入されたガスの量及び接続部分を含む試料容器中のフリースペースを充てんするガス
の量の差として,吸着量を計算する。平衡に到達したかどうかは,フリースペース中の圧力をモニターす
ることによって判断できる。ミクロ細孔への物理吸着は,メソ細孔への吸着現象より実質的に低い相対圧
で起きるので(5.1参照),測定が広い圧力範囲にわたる。よって,圧力測定には特に十分な注意が必要で
ある。その結果,平衡圧を十分な精度で測定するために,二つ以上の圧力変換器を備える必要がある。十
分な精度で10−7≦p/p0≦1の相対圧範囲で窒素及びアルゴンのようなガスを用いて,それらの沸点で吸着
を研究するためには,0.133 kPa(1 Torr),1.33 kPa(10 Torr)及び133 kPa(1 000 Torr)という異なる最大
圧力測定可能な圧力変換器を組み合わせて用いることが望まれる。さらに,試料セル及びマニフォールド
を可能な限り高真空で排気するために,適切な高真空用排気システムを必要とする。必要な高真空状態は,
ターボ分子ポンプを使って達成できる。約13 Pa以下のガス圧(77 Kでの窒素ガス及び87 Kでのアルゴン
でp/p0<10−5)に対しては,クヌーセン効果による試料バルブの細管に沿った圧力差を考慮に入れなけれ
ばならない(熱遷移補正)。
注記 単位“Torr”の使用については,用途が限定されている。
質量法測定では,吸着した質量は直接測定する(JIS Z 8830の図6を参照)が,圧力に依存する浮力の
補正が必要である。平衡に到達しているか否かは,質量指示計をモニターすることで判断できる。0.1〜100
Paの圧力範囲では,気体流は測定に対して深刻な影響を及ぼす。試料は温度測定端子と直接接触していな
いので,試料の正しい温度を実験的に確認することが必要である。
6
測定手順
6.1
試料のサンプリング
試料のサンプリングは,ISO 3165及びISO 8213に従って実施する。試験のための試料はロットを代表
するものとし,適切な量の採取が望ましい。サンプリングにおける2番目の試料を用いた繰返し測定が望
7
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ましい。
6.2
試料前処理
物理吸着物質を取り除くために,昇温下1 Pa以下の真空下で脱ガスすることが望ましい。この工程中,
不可逆的な表面構造変化を避けることが望ましい。脱ガス処理での最高温度は,熱質量分析(JIS Z 8830
の図3を参照)によって決定できる。それ以外の方法としては,脱ガスの時間及び温度を変化させて吸着
測定を繰り返すことが望ましい(JIS Z 8830の図4を参照)。また,試料から物質が排出される温度は示差
走査熱量法によって決定でき,排出ガスも分析可能である。
替わりの方法としては,高純度の不活性ガス(例えば,ヘリウム又は窒素)流通下で加熱脱ガスする方
法がある。脱ガスの完了は,15〜30分間の試料の質量変化又は試料セル内の圧力変化がないことで示され
る。以上の処理で得られる乾燥試料の質量を測定する。
6.3
吸着量測定
吸着量は,JIS Z 8830又はJIS Z 8831-2に従って測定する。
7
装置性能の検証
装置の校正及び性能を確認するため,認証標準物質又は測定者が選んだ特定の標準物質(機関内標準物
質)を用いて定期的に試験測定をすることが望ましい。機関内標準物質は,認証標準物質にトレーサブル
でなければならない。
注記 認証標準物質は,国家標準機関によって提供され,現在,ドイツBAM及び米国NISTから入手
可能である。
Bundesanstalt für Materialforschung und-prüfung (BAM)
Division I. 1 Inorganic Chemical Analysis; Reference Materials
Branch Adlershof,Richard-Willstätter-Straße 11,D-12489 Berlin,Germany
Standard Reference Materials Program
National Institute of Standards and Technology (NIST)
100 Bureau Drive,Stop 2322
Gaithersburg,MD 20899-2322,USA
上記の情報は,この規格の利用者に便宜を与えるためのものであり,それらの製品をJIS(ISO)
が保証するものではない。もし,同じ結果を与えるならば同等の製品を使うことができる。
8
装置校正
個々の構成要素の校正は,製造業者の推奨に従って行うことが望ましい。一般に,圧力変換器及び温度
センサの校正は,校正証明書を添付した圧力計及び温度計と対照することによって行う。マニフォールド
容積の校正は,一定温度で既知の体積をもつトレース可能な空間又は固体を用い,適切な圧力と温度との
関係を測定することによって行う。サンプル容器の校正は,一般に,JIS Z 8831-2の9.3.4に規定するフリ
ースペースの測定によって行う。
9
ミクロ細孔容積の評価
9.1
ミクロ細孔容積評価法の一般原理
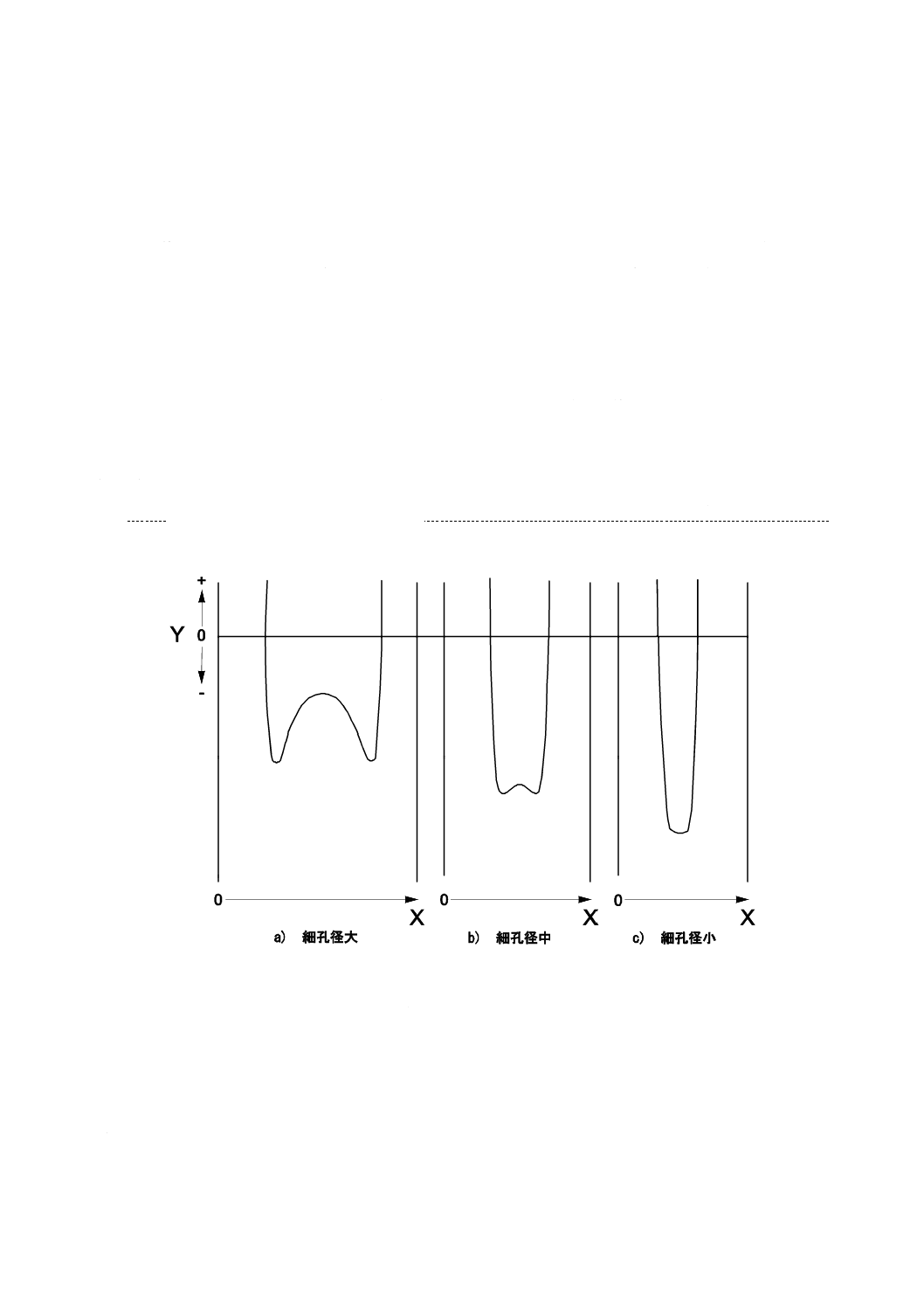
Vg=f(p/p0)又はma=f(p/p0)Tで示される吸着等温線は,均等目盛(図2参照),望ましくは対数目盛(図3
8
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
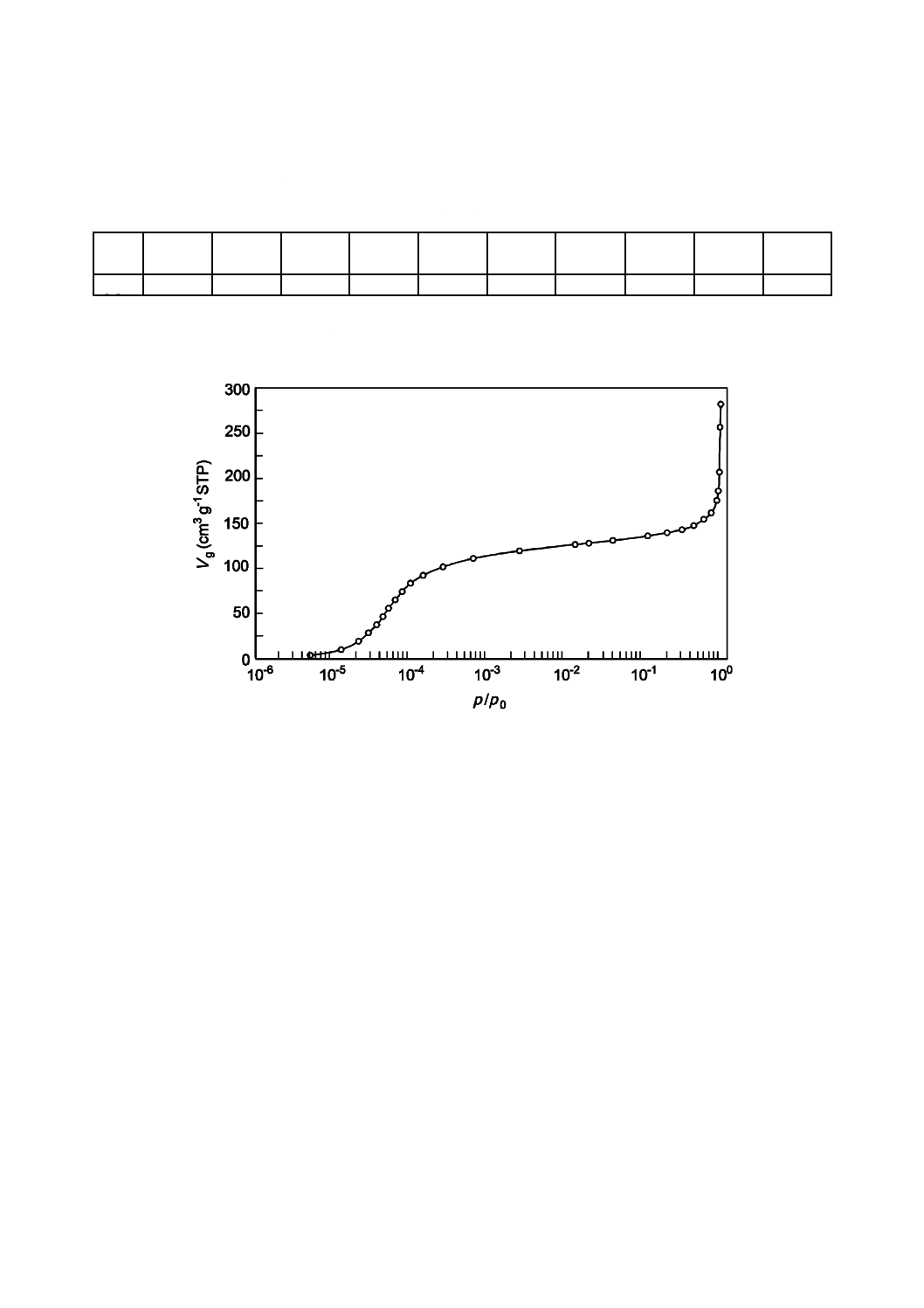
参照)の相対圧に対してプロットすることで得られる。
図2−ゼオライトへの87.3 Kアルゴン吸着等温線のリニアプロット
図3−ゼオライトへの87.3 Kアルゴン吸着等温線の片対数プロット
外部表面積又はメソ細孔の容積が無視できる場合,ミクロ細孔が発達した試料の吸着等温線は,ラング
ミュア型(IUPACのI型,JIS Z 8830の図1を参照)を示す。平たん部の吸着量は,ミクロ細孔容積に相
当する。マクロ細孔がある場合には,相対圧1付近で吸着量の急激な増加が見られる。
平たん部での吸着量は,吸着容量の尺度である。細孔容積を得るには,吸着質の密度がその吸着温度で
液体の密度と等しいと仮定する。その場合の細孔容積は,式(1)で計算する。
(
)
s
1
a
a
m
m
V =
ρ
········································································· (1)
9
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9.2
デュビニン・ラドシュケビッチ(Dubinin/Radushkevich)法によるミクロ細孔容積の測定
もともとこの方法は,活性炭のミクロ細孔を調べるために開発され(参考文献[9]参照),色々なミクロ
細孔をもつ試料に使用されている(参考文献[10]〜[13]参照)。ミクロ細孔をもつ試料への純ガスの吸着等
温線は,ポラニの吸着ポテンシャル理論(参考文献[14]参照)で説明できる。各々の吸着質/吸着材の系
は,吸着ポテンシャルEで説明される。Eは,吸着材の化学的性質によって影響を受ける。規定の相対圧
p/p0で満たされた細孔の容積Vaは,全ミクロ細孔容積Vmicroの一部であり,吸着ポテンシャルEの関数と
なり,式(2)で示す。
()
E
f
V=
a
················································································· (2)
デュビニンによれば,吸着ポテンシャルは,吸着分子が気相になるときに必要な仕事量である。T<Tcr
の場合にポラニのポテンシャルは,式(3)によって計算する。
p
p
T
R
E
0
ln
=
············································································· (3)
ある吸着材に対する温度不変の(温度に依存しない)“特性曲線”(つまり,Eに対してVaをプロットし
たもの)といったポラニの概念に基づいて,デュビニン・ラドシュケビッチは,実験式(4)を導いた。
−
=
2
0
0
micro
a
ln
exp
p
p
E
T
R
V
V
β
···················································· (4)
特性吸着エネルギーE0は,細孔径分布と関連付けられる。親和係数βは,ある特定の吸着質の特性曲線
に対する,(与えられた吸着材での)異なった吸着質の特性曲線の尺度となり得る。よって,デュビニンの
等温線は,直線となる対数式(5)で記述できる。
2
0
micro
a
lg
lg
lg
−
=
p
p
D
V
V
······························································ (5)
ここに,
2
0
303
.2
=
E
T
R
D
β
······································································· (6)
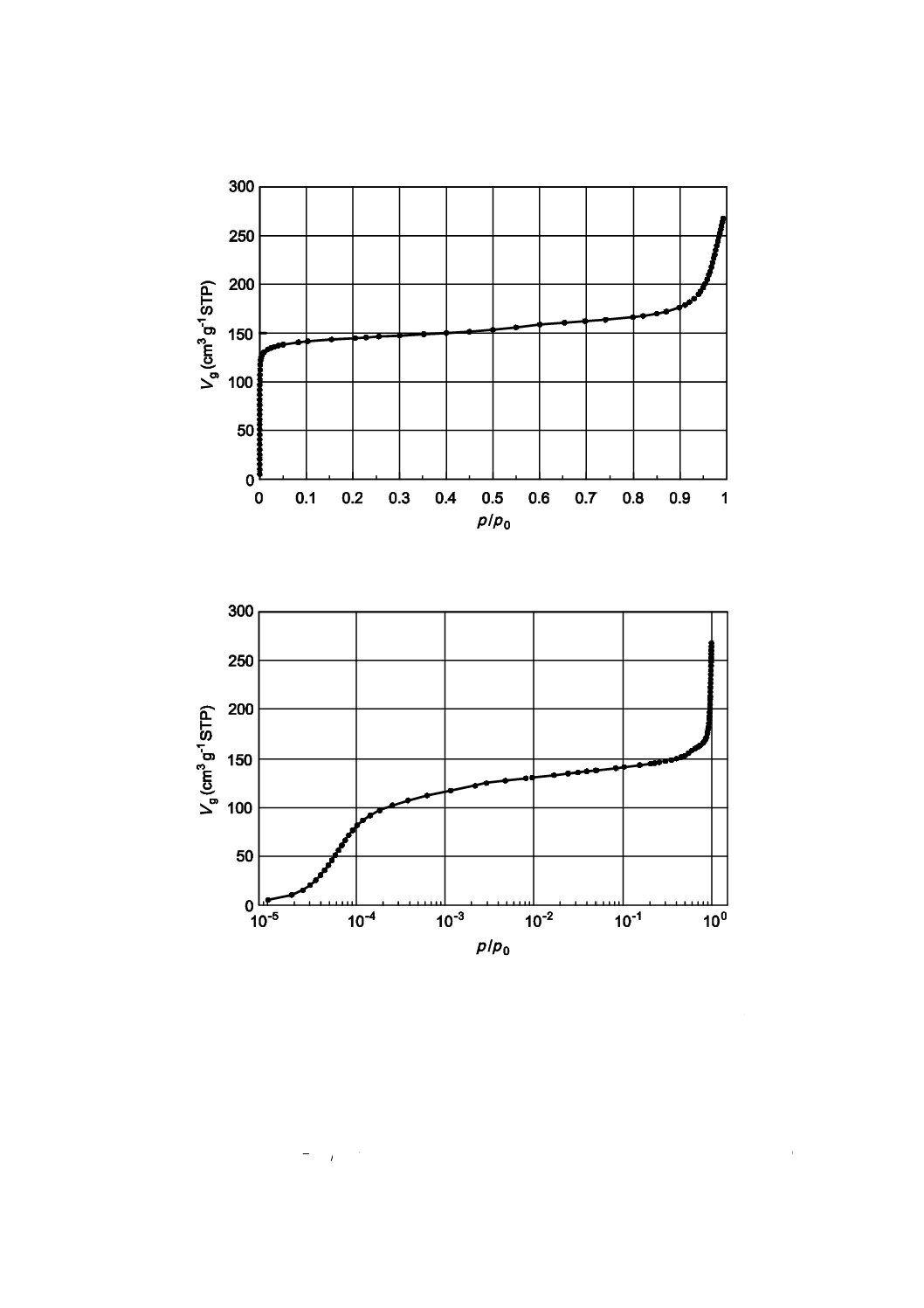
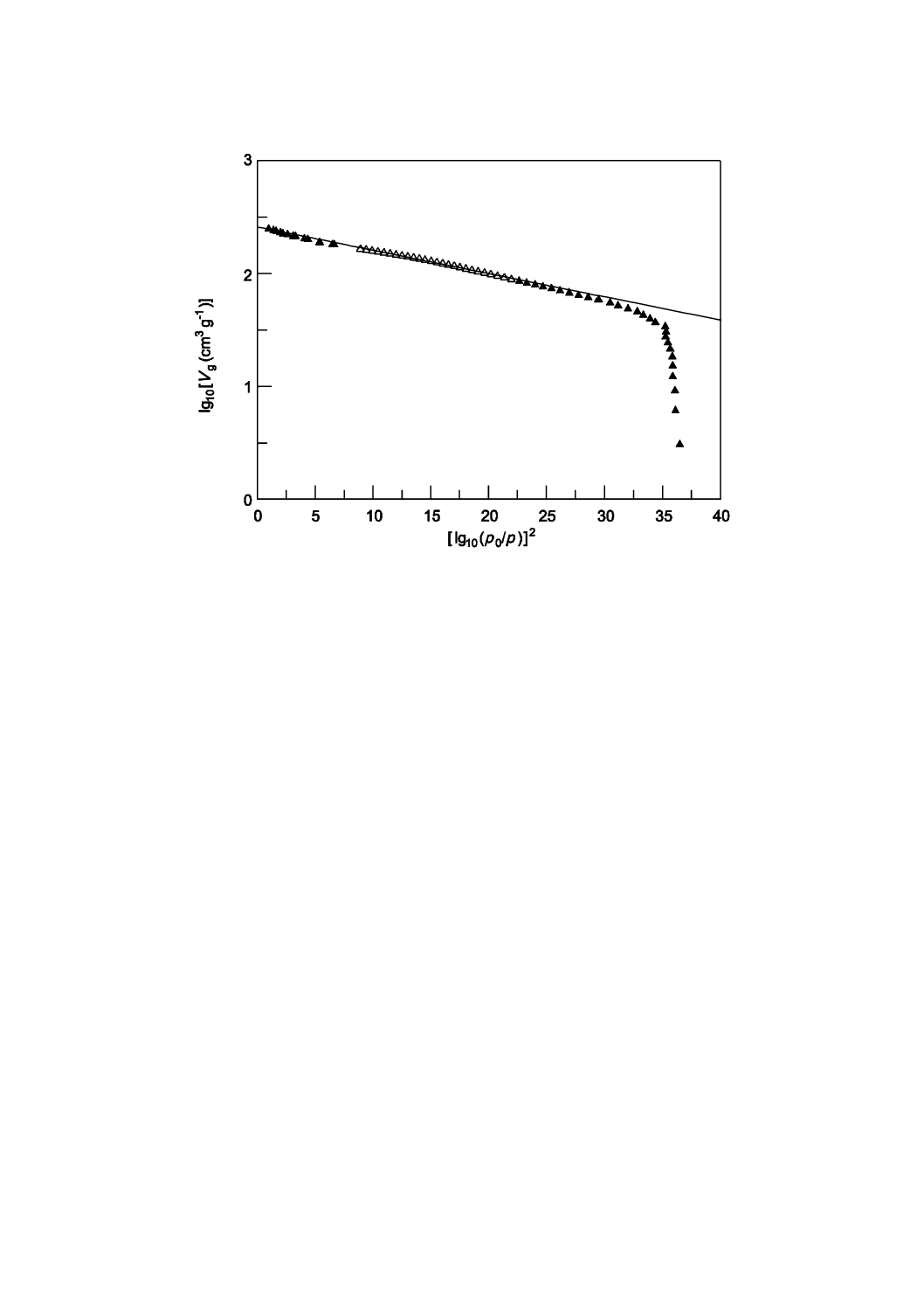
評価のためのデータは,10−4<p/p0<10−1の相対圧範囲で求めることが望ましい。次に,データを
2
0
lg
p
p
に対するlgVaの図にプロットする(図4参照)。回帰直線のこう配は,パラメータDを示す。縦軸の切片
から全ミクロ細孔容積Vmicroが計算できる。
10
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
▲ 実験データ点
△ デュビニン・ラドシュケビッチ(DR)フィットに使われる実験データポイント
図4−活性炭への77.4 Kでの窒素吸着等温線のデュビニン・ラドシュケビッチプロット
9.3
吸着等温線の比較によるミクロ細孔の解析
9.3.1
ミクロ細孔解析の一般原理
この方法では,ある試料の吸着等温線を,類似した化学的な表面組成をもつ無孔性の参照試料と比較す
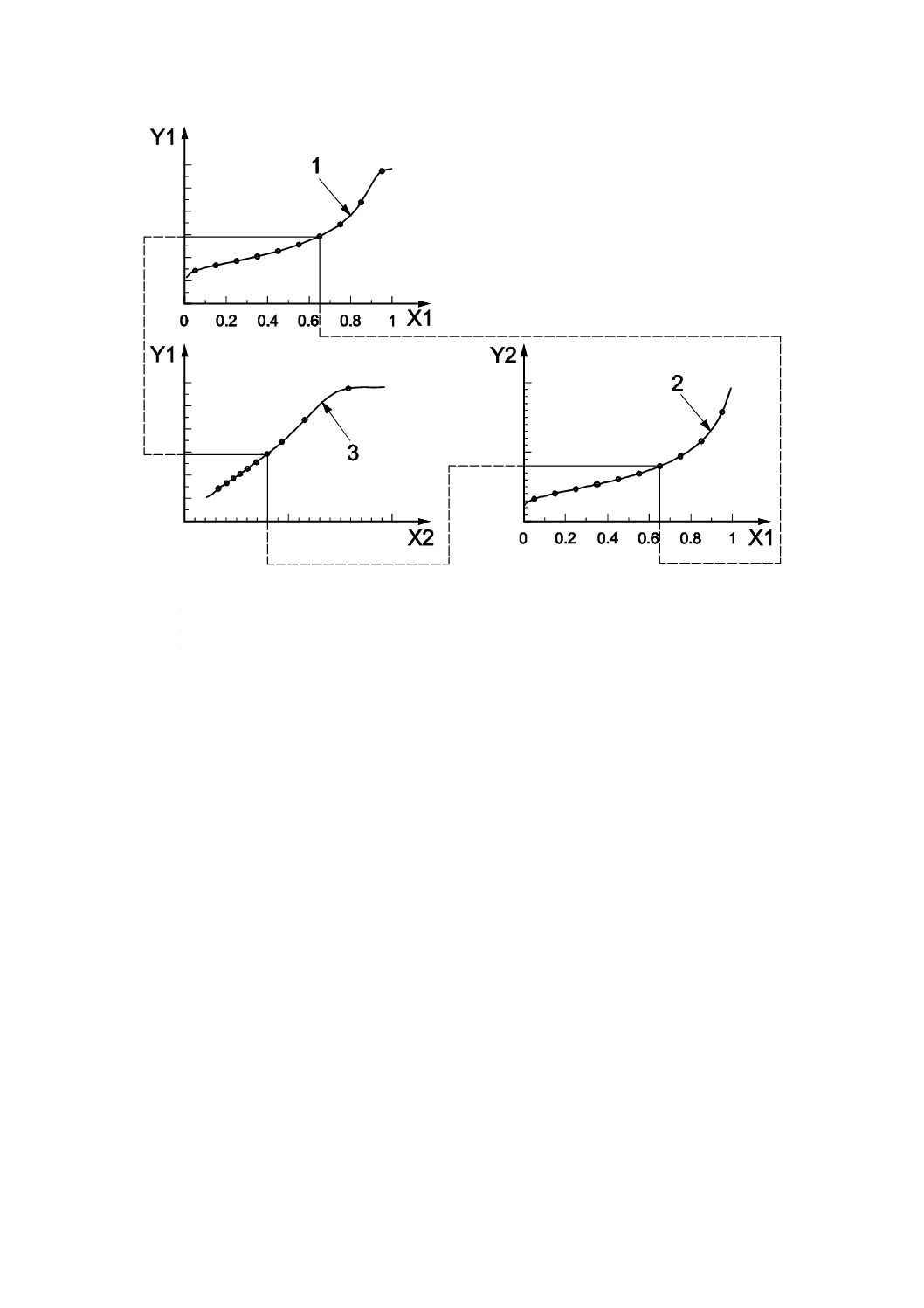
る。手順を,図5に示す。
注記1 図5の手順は,9.3.2及び9.3.3を参照。
11
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X1軸:p/p0
X2軸:t又はαs
Y1軸:Va又はna
Y2軸:t又はαs
1:試料吸着等温線
2:参照吸着等温線
3:結果として得られる比較図形
図5−t-プロット又はαs-プロットにおける図示方法
比較プロット図では,測定された吸着等温線は,t-プロット又はαs-プロットという形に書き直される。
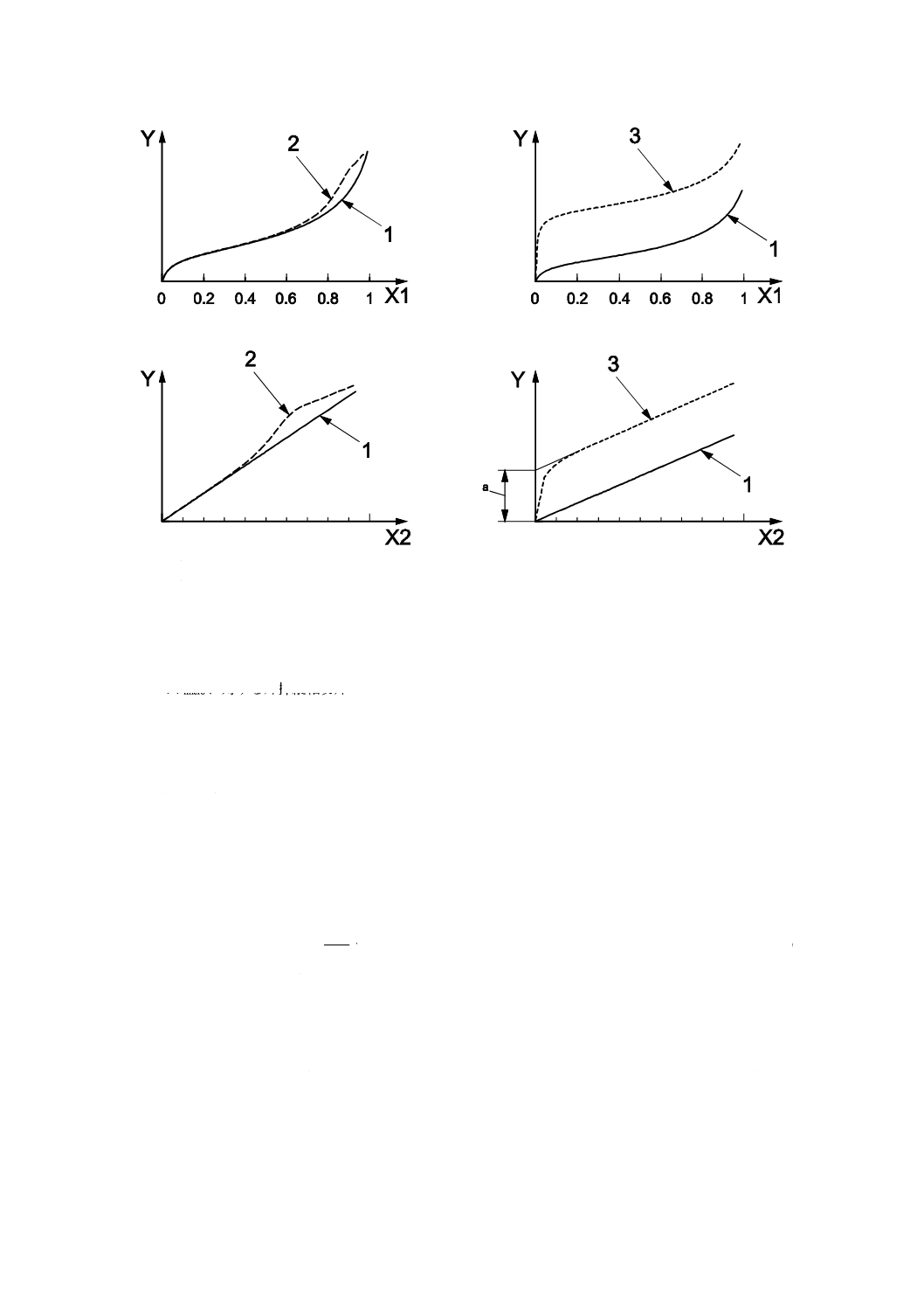
つまり,相対圧p/p0の代わりにt又はαsに対して吸着量の変化がプロットされる。特徴的な比較プロット
を,図6に示す。
注記2 図6の詳細は,9.3.2及び9.3.3を参照。
12
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X1軸:p/p0
X2軸:t又はαs
Y軸 :Va又はna
1:無孔性物質
2:メソ細孔性物質
3:ミクロ細孔性物質
a:Vmicroに対する外挿縦軸切片
図6−3種類の物質における吸着等温線(上)及びt-プロット又はαs-プロット図(下)
比較図(図6参照)の解釈を行うための前提条件を,次に示す。
a) メソ細孔領域で表面が平滑である。
b) ミクロ細孔フィリング及び毛管凝縮が,明確に異なった圧力範囲で起こる。
c) 多分子層吸着は,比較図で直線を与える。結果として比較プロットでは直線になる。しかし,細孔の
存在は,直線から上への偏移を引き起こす。これは,ある範囲の細孔径に割り当てられる細孔容積の
計算を可能にする。直線部分では,未充てんの細孔の比表面積asは,傾斜bから式(7)によって求める。
ref
ref
s,
s
b
a
b
a=
················································································ (7)
ここに,
as,ref: 参照物質の比表面積
bref: 参照物質の傾斜
縦軸切片は,この相対圧で満たされている細孔容積と一致する。それは,式(1)で計算する。
ミクロ細孔の割合が大きい場合,直線部分の前にある初期の部分で急激な増加を示す。ミクロ細孔だけ
が発達した材料では,その直線部分のこう配は外部表面積を示す。メソ細孔/マクロ細孔が存在する場合
は,外部表面積にそれらの細孔壁の表面積を加えたものになる。直線部分を外挿したときの縦軸切片は,
ミクロ細孔容積Vmicroを示す。計算は,式(1)による。もしミクロ細孔がなければ,初期の部分が直線にな
り,比表面積はBET法で計算された値と一致する(JIS Z 8830参照)。
13
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9.3.2
t-プロット法
t-プロット法は,リッペンス及びデボア(Lippens and deBoer)の報告による(参考文献[15]〜[18]参照)。
吸着量は,無孔性試料の標準等温線から計算される吸着層の統計的厚さtの関数として,式(8)で示される。
t
m
a
s
a
3
10
σ
n
n
a
V
t
=
=
········································································ (8)
注記1 対応国際規格では,式(8)を次のように記載しているが,それぞれの記号がもつ次元を考慮し
て修正した。
t
m
a
s
a
σ
n
n
a
V
t
=
=
ここに,σtは単分子層の厚さを示し,窒素では通常0.354 nmである。参照する試料の比表面積as又は単
分子層吸着量nmは,JIS Z 8830によって決定できる。式(8)は,あらゆる吸着材と吸着質との間で適用可能
である。参照試料は,類似の化学的組成をもつものでもよい。77 Kの窒素の場合,分子断面積にam=0.162
nm2を使用し,密度0.807 9 g・cm−3の液体状吸着質の六方最密充てんを仮定すれば,式(8)は,式(9)になる。
m
a
m
a
354
.0
354
.0
n
n
V
V
t
=
=
································································· (9)
ここに, Vm:吸着材単位質量当たりの単分子層吸着量に相当する吸着質の液体
相当体積(cm3·g−1)
この場合,吸着層の統計的厚さt(平均的厚さ)は,文献に示され,JIS Z 8831-2で使用されている普遍
的t-カーブから求めることができる。
t-プロットの図で得られる直線部分のこう配から,式(9)を用いて比表面積が計算できる。吸着量が標準
状態(STP)でのcm3・g−1で,吸着層の統計的厚さtがnmで,こう配dVg/dtの次元がcm3・g−1・nm−1であ
る場合には,比表面積m2・g−1は,式(10)で計算する。
t
V
a
d
d
8
546
.1
g
s=
······································································· (10)
ミクロ細孔容積Vmicroは,縦軸の切片から式(11)で求める。
g
micro
8
546
001
.0
V
V
=
··································································(11)
注記2 上記の説明で,ミクロ細孔中にある窒素の密度は,液体窒素の密度に等しいと仮定している。
0.001 546 8という係数は,標準状態(STP)での窒素ガスの体積を液体体積に換算するとき
の係数である。Vmicroは,“有効”ミクロ細孔容積と考えることができ,過度に単純化された
ものであると認識される。なぜなら,ミクロ細孔中の窒素の密度は,液体密度とは等しくな
いかもしれないからである。
9.3.3
αs法
この方法は,層の厚さ計算を使用しない。その代わりに,参照試料の吸着量が,選択された相対圧に関
連付けられる。一般に,p/p0=0.4が用いられる。これは77 Kの窒素の場合に,多くの材料で,この相対
圧では,単分子層吸着は完了しているが,毛管凝縮は始まっていないことが理由である(ただし,2〜5 nm
の細孔直径をもつメソ細孔が存在する吸着材は例外である)。参照値となる規格化された吸着量αsは,参
照等温線を用いて,式(12)で計算する。
)4.0(
)4.0(
a
a
a
a
s
n
n
V
V
=
=
α
································································· (12)
αs-プロット図では,測定された吸着量はαsの関数として示される。αs-プロット図は,t-プロットの場合
14
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
と類似の形になり,同じ手順で比表面積及びミクロ細孔容積が計算できる。
9.4
ホルバス・カワゾエ(HK)法及びサイトウ・フォリー(SF)法によるミクロ細孔径分布の解析
ホルバス及びカワゾエ(参考文献[19],[20]参照)は,ミクロ細孔性材料に対する窒素吸着等温線から有
効細孔径分布を計算するための半経験的な解析法を提案している。もともとのHK法は,エベレット及び
ポール(Everett and Powl)の研究(参考文献[8]参照)に基づいており,分子ふるい炭素及び活性炭に見ら
れるスリット細孔に閉じ込められた流体(窒素)を考慮に入れている。エベレット及びポールは,グラフ
ァイト化された炭素の2層間のスリットに吸着した希ガス原子に対するポテンシャル・エネルギーを計算
した。2層の原子間距離をlとする。吸着した流体は,平均ポテンシャル場によって影響されるバルクの
液体であると考えられ,平均ポテンシャル場は吸着材と吸着質との間の相互作用を示す。用語“平均場”
は,強い空間依存を示す吸着質分子と吸着材との間のポテンシャル相互作用が平均的で均一なポテンシャ
ル場によって置き換えられることを示す。ホルバス及びカワゾエは,熱力学の論拠を用い,有効細孔径を
dp=l−ds(ここでdsは,吸着材分子の直径)とすることで,平均ポテンシャルが,充てん圧力p/p0と有効
細孔径との関係[式(13)で示される]をもたらす吸着の自由エネルギー変化と関係付けられることを見い
だした。
(
)
(
)
(
)
0
HK
0
4
Aa
a
As
s
A
0
,,
2
ln
d
l
f
d
l
K
N
K
N
T
R
N
p
p
σ
σ
−
+
=
········································ (13)
ここに,
(
)
(
)
(
)
()
()9
0
10
3
0
4
9
0
10
3
0
4
0
HK
9
3
9
3
,,
d
d
d
l
d
l
d
l
f
σ
σ
σ
σ
σ
+
−
−
−
−
=
····························· (14)
パラメータd0,σ,KAs及びKAaは,式(15)〜式(18)によって計算する。
2
s
a
0
d
d
d
+
=
············································································ (15)
0
6
1
5
2
d
=
σ
············································································ (16)
()
()
a
a
s
s
a
s
2
e
As
*
*
6
χ
α
χ
α
α
α
+
=
c
m
K
··································································· (17)
a
a
2
e
Aa
2
3
χ
α
c
m
K=
···································································· (18)
式(13)は,細孔径及び形状に対するミクロ細孔フィリングが特有の相対圧で起こることを示している。
この特有の相対圧は,吸着材と吸着質との相互作用エネルギーと直接に関係する。
サイトウ及びフォリーは,ゼオライトの87 Kでのアルゴン吸着等温線に対する有効細孔径分布の解析に
HK法を拡張した(参考文献[21],[22]参照)。SF法もエベレット及びポールのポテンシャル式(参考文献
[8]参照)を基礎とするが,シリンダ型細孔形状に対するものである。HK法を誘導した論法に従い,サイ
トウ及びフォリーは,ミクロ細孔フィリングが起こる相対圧p/p0と有効細孔直径dpとを関連付けるHK式
に類似した式(19)を導き出した。
(
)
()
(
)
0
SF
4
0
Aa
a
As
s
A
0
,,
,
π
4
3
ln
d
l
f
d
K
N
K
N
T
R
N
p
p
β
α
+
=
································· (19)
ここに,
15
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)∑
∞
=
−
−
+
=
0
4
0
10
0
2
0
0
SF
2
2
32
21
2
1
1
1
,,
,
k
k
k
k
l
d
l
d
l
d
k
d
l
f
β
α
β
α
··········· (20)
パラメータKAs及びKAaは,式(17)及び式(18)によって計算する。パラメータαk及びβkは,式(21)及び式
(22)で定義する。
1
2
5.4
−
−
−
=
k
k
k
kα
α
································································· (21)
1
2
5.1
−
−
−
=
k
k
k
kβ
β
·································································· (22)
ここに,α0=β0=1である。
HK法及びSF法の計算を行うために,吸着質パラメータαa,χa,da及びNaと同様に,吸着材パラメータ
αs,χs,ds,Nsの値が必要である。計算結果は,これらの定数の選択に対して非常に敏感である。窒素/
カーボン(窒素を吸着質,カーボンを吸着材とした系)及びアルゴン/ゼオライトの組合せに対する材料
パラメータは,附属書Aによる[DIN 66135-4(参考文献[23]参照)による]。
9.5
非局所密度はん(汎)関数理論(NLDFT)によるミクロ孔細孔分布の解析
9.5.1
背景
非局所密度はん(汎)関数理論(NLDFT),分子動力学及びモンテカルロシミュレーションのようなコ
ンピュータシミュレーション方法は,吸着及び多孔質内に閉じ込められた不均質な流体の挙動を記述する
ための強力な手段として開発された(参考文献[24]〜[32]参照)。これらの方法は,固体壁の近傍で振動す
る密度関数(プロファイル),又はスリット,シリンダ若しくは球状のような単純な幾何学構造内に閉じ込
められた流体の挙動を正確に記述する。それらは,表面及び細孔に吸着した流体の平衡密度プロファイル
の計算を可能とし,それによって吸脱着等温線,吸着熱及び他の熱力学量が導かれる。吸着及び細孔内の
流体の相挙動を研究するための,コンピュータシミュレーションによる密度はん(汎)関数理論(DFT)
及び分子モデリングの応用に関する先駆的な研究は,エバンス及びタラゾナ(Evans and Tarazona)(参考
文献[24]参照)によって行われた。シートン(Seaton)ら(参考文献[25]参照)は,メソ細孔及びミクロ細
孔の両領域で細孔径分布の計算のためにDFTを最初に適用した。細孔径分析にDFTを応用するこの最初
の試みでは,いわゆる局所バージョンのDFTが使われた。それは,細孔フィリングの巨視的,熱力学的記
述に関して顕著な改良をもたらしているが,狭いミクロ細孔に対しては不正確である。正確さにおける顕
著な改良がNLDFTを用いて得られた。その最初の報告は,ミクロ細孔性炭素の細孔径解析に関するもの
であり,1993年にラストスキ(Lastoskie)ら(参考文献[26]参照)によってなされた。そのときから,NLDFT
がミクロ及びメソ多孔体の細孔径解析のためにしばしば応用されてきた(参考文献[27],[28]参照)。NLDFT
法は,現在では多くの吸着材/吸着質系に対して市販品として提供されている。古典的で巨視的な熱力学
モデルと比較して,NLDFT法は分子レベルで細孔内に閉じ込められた流体の挙動を記述する。このアプリ
ケーションは,ガスの分子特性と異なった細孔径内での吸着特性とを関連付ける。そして,NLDFT法に基
づいた細孔径評価法は,ミクロ細孔及びメソ細孔の全領域に適用可能となる(参考文献[26],[28]参照)。
9.5.2
非局所密度はん(汎)関数理論(NLDFT)の概要
実験中では,細孔内の吸着流体はバルクガス相と平衡であり,したがって,一般的なNLDFTはグラン
ドカノニカルアンサンブルの系で表現することができる。グランドカノニカルポテンシャル関数Ω[ρ(r)]は,
式(23)で表される。
16
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
[
]
()
[
]
()
()
[
]
∫
−
−
=
Ω
r
r
r
r
F
r
ext
d
ν
μ
ρ
ρ
ρ
············································· (23)
ここに,
ρ(r): 一般的な三次元配位子rでの平衡流体密度
F: 固有ヘルムホルツ自由エネルギーであり,外
場のない場合,それは平衡状態でのガスの分
子密度ρ(r)の関数F[ρ(r)]で表される。
νext(r): 壁によって与えられた外部ポテンシャル
μ: 化学ポテンシャル
外部ポテンシャルνext(r)は,仮定される細孔モデルに依存する。
例えば,炭素材料(カーボン)の細孔を表現するためにしばしば用いられるスリット型細孔モデルに対
して,このポテンシャルは外部ポテンシャルνext(z)を計算するために,式(24)の形となる。
()
()
(
)z
W
z
z
−
+
=
sf
sf
ext
φ
φ
ν
····························································· (24)
ここに,
φsf(z): 分子と細孔壁間の固体−流体相互作用ポテ
ンシャル
W: 細孔径
z: 壁からの距離
多孔性の炭素材料(ポーラスカーボン)に対して一般的に受け入れられている固体−流体間ポテンシャ
ルは,スティール(Steele)のポテンシャル(参考文献[26]参照)であり,それは1枚のグラファイト層と
ガス分子との相互作用であり,式(25)で示される。
()
()
(
)
∆
+
∆
−
−
∆
=
3
4
sf
4
sf
10
sf
sf
s
sf
sf
61
.0
3
52
π
2
z
z
z
z
σ
σ
σ
σ
ρ
ε
φ
······················ (25)
ここに,
εsf: ガス−壁面間のレナード・ジョーンズポテン
シャルパラメータ
σsf: ガス−壁面間相互作用の距離パラメータ
ρs: グラファイトの密度
Δ: グラファイト層間距離
シリンダ(参考文献[33]参照)及び球状(参考文献[34]参照)を含む他の細孔形状並びにそれらの適切な
ポテンシャルも検討されている。それらは,幾つかのメソ細孔性分子ふるいシリカ(例えば,MCM-41,
SBA-16)にも適用可能である。
固有ヘルムホルツ自由エネルギーFは,三つの成分からなる。
a) 理想気体の自由エネルギーFid:厳密な表現で与えられる(参考文献[24]参照)。
b) 過剰自由エネルギーFex:これは二つのタイプの分子間相互作用を考慮している。
− Fatt:引力からくる自由エネルギー
− FHS:剛体球の標準系として記述される分子間の反発力
自由エネルギーFの三つの成分は,流体密度分布の関数であり,式(26)で示される。
()
()
[
]
()
[
]
()
[
]
()
[
]
r
F
r
F
r
F
r
F
r
ρ
ρ
ρ
ρ
ρ
HS
att
id
:
+
+
=
······································ (26)
引力相互作用項Fattは,式(27)によって計算する。
()()(
)
∫∫
′
−
′
′
=
r
r
r
r
r
r
F
att
att
d
d
2
1
φ
ρ
ρ
················································ (27)
ここで,φattは引力ポテンシャルであり,ウィークス・チャンドラー・アンダーソン(Weeks-Chandler-
Anderson,WCA)の方法(参考文献[25]参照)でモデル化され,rsc<rmに対して式(28)で,及びrm<rscに
対して式(29)で,それぞれ求める。
17
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
ff
sc
att
ε
φ
−
=
r
··········································································· (28)
()
−
=
6
sc
ff
12
sc
ff
ff
sc
att
4
r
r
r
σ
σ
ε
φ
····················································· (29)
ここに,
rsc: 分子間の距離(スカラー量)
rm: 最小ポテンシャル
εff: レナード・ジョーンズ流体−流体間相互作
用ポテンシャル
σff: レナード・ジョーンズ流体−流体間相互作
用ポテンシャルの距離パラメータ
WCAの方法は,モンテカルロシミュレーション(参考文献[28]参照)と比較して,良い結果を与えるこ
とが証明されている。
反発力を計算に入れるため,不均一剛体球流体に対する幾つかの関数が開発された。この中には,加重
密度近似(参考文献[29]参照),基本的な測定理論(参考文献[30],[31]参照),及び平滑化した密度近似(参
考文献[23]参照)がある。タラゾナら(参考文献[24]参照)によって提案された平滑化した密度近似は,現
在,細孔解析に用いられているほとんどのNLDFT解析に使用されている。この手法では,剛体球システ
ムの自由エネルギーFHS[ρ(r)]が平滑化した密度
)
(r
ρ
に対して計算され,式(30)で与えられる。
()
[
]
()
()
[
]
∫
=
HS
HS
HS
;
d
d
r
f
r
r
r
F
ρ
ρ
ρ
·················································· (30)
ここに,
dHS: 剛体球直径
()
[
]
∫
HS
HS
;d
r
fρ
: 1分子当たりの過剰自由エネルギー(剛体
球流体に対するカーナハン・スターリング
(Carnahan-Starling)の状態方程式(参考
文献[24],[28]参照)で計算できる。
平滑化した密度
)
(r
ρ
は,タラゾナ(参考文献[24]参照)によって提案された重み関数を用いることによ
って得られる。
分子密度分布ρ(r)は,与えられた細孔モデルでの平衡流体分布の重要な説明となる。平衡状態を基礎と
した密度関数ρ(r)は,相当するグランドポテンシャルΩ [ρ(r)]を最小化することによって決定される。Ωの
最小値は,オイラー・ラグランジェ(Euler-Lagrange)式(参考文献[24]参照)又は不確定ラグランジェ
(Lagrange)乗数法(参考文献[32]参照)を使用することによって計算される。ρ(r)の実際の数値は,反復
計算によって求める。一度ρ(r)が決定されると,ほかの熱力学的特性である吸着等温線,吸着熱,自由エ
ネルギー,相変化などが計算できる。
9.5.3
細孔径解析への応用−NLDFTのカーネル及び積分吸着式
実験で得た吸着等温線から細孔径分布を計算するときにこの理論を適用するためには,理論モデル等温
線を統計力学的手法によって計算しなければならない。実際には,これらの等温線は,モデル細孔内流体
の平衡密度プロファイルρ(r)の積分によって計算する。ある吸着質において,与えられた範囲内の分割さ
れた細孔径に対して個々に計算された等温線は,モデルデータベースとなる。カーネルと呼ぶこのような
等温線のセットは,与えられた吸着系に対する理論的な参照等温線とみなすことができ,対応する系に対
し測定した吸着等温線からの細孔径分布の計算に使用することができる。
仮定した幾何学的細孔モデル,ガス−ガス間とガス−固体間との相互作用パラメータの値,及びモデル
で用いた仮定などの幾つかの因子が,カーネルの数値に影響することを理解することが重要である。その
18
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
モデルが流体のバルク性質(例えば,バルク液体−ガス平衡密度及び平衡圧力,液体−ガス界面張力)を
正しく再現するように相互作用パラメータ(液体−液体間及び液体−固体間)を調整することが一般的に
行われる。表面張力の正確な予測は,細孔内の毛管凝縮及び脱着(脱離)の定量的記述に使用するいかな
るモデルに対しても必要な条件である。固体−液体間ポテンシャルのパラメータは,特性が明確であり,
かつ,非多孔性(無孔性)の吸着材の標準吸着等温線にフィットするように決定する。
幾つかの吸着モデルが研究され,種々の材料のガス吸着に対してパラメータが計算され,文献として発
表されている。例えば,窒素/炭素材料,二酸化炭素/炭素材料及びアルゴン/炭素材料の系のガス−ガ
ス間及びガス−固体間相互作用パラメータは,参考文献[26],[28],[35],[36]に記載されている。窒素/
シリカ及びアルゴン/シリカの系に対する適切なパラメータは,参考文献[28],[37]に記載されている。幾
つかの吸着系のDFT解析に使用するパラメータの参考文献は,表B.1及び表B.2に記載する。
細孔径分布の計算は,積分吸着式(integral adsorption equation,IAE)の解を求めることであり,それは
理論吸脱着等温線のカーネルを実験吸着等温線と関係付けることである(参考文献[4]参照)。実験吸着等
温線からの吸着量データN(p/p0)は,式(31)で示されるIAE式から求める。
W
W
f
W
p
p
N
p
p
N
W
W∫
=
max
min
d)
(
)
,
/
(
)
/
(
0
0
··············································· (31)
ここに,
W:細孔径(スリット型細孔の壁間距離,又は
シリンダ型及び球状型細孔の直径)
N(p/p0, W):異なる細孔径に対する理論等温線カーネル
f(W):細孔径分布関数
独立した個々の細孔径に相当する等温線に,その細孔径の相対分布f(W)を乗じたものを,該当する細孔
径範囲にわたって加え合わせることで,全等温線が構成されるという仮定をIAE式は反映している。与え
られた系(吸着質/吸着材)におけるN(p/p0,W)等温線(つまり,カーネル)のセットは,密度はん(汎)
関数法又はモンテカルロシミュレーションによって与えられ,細孔径分布はIAE式を数値的に解くことに
よって求められる。一般的にIAEは,一意的に解が得られないという“不良設定問題”(ill-posed problem)
を抱え,ある程度の正則化(規則化)が必要である。正則化アルゴリズム(参考文献[38]〜[40]参照)によ
って,意味のある安定した解が得られる。計算の妥当性を確認するために,計算されたNLDFT等温線(フ
ィッティング等温線)を実験吸着等温線と比較する。
10 試験結果報告
次に示すように,測定条件及び計算に用いた定数のまとめを個々の結果に対して提供することが望まし
い。
a) 測定機関,測定者及び日付
b) 試料性状(例えば,化学組成,純度,粒子径分布,サンプリング方法,試料縮分など)
c) 試料の入手先
d) 脱ガス後の試料質量(g)
e) 測定方法及び使用装置
f)
試料の前処理
g) 脱ガス条件:温度及び真空排気圧力
h) 装置及び構成要素の校正で得た定数
i)
細孔径及び表面積解析に用いたモデル/方法
19
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
j)
SF法及びHK法を利用した際の吸着質ガス及び吸着材に対する物質パラメータ
k) NLDFT法を用いた際のカーネルの記載(例えば,吸着質ガス/吸着材の組合せ,仮定した細孔径形状,
吸着/脱着等温線など)
l)
ミクロ細孔容積(cm3·g−1)
m) 全細孔容積(cm3·g−1)
n) 比表面積(m2·g−1)
o) 累積細孔容積のプロット及び表,並びに細孔容積分布(HK法,SF法及びNLDFT法に対して)

20
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
HK法及びSF法
A.1 物性定数,吸着材及び吸着質ガスのパラメータの例
ホルバス・カワゾエ(HK)法及びサイトウ・フォリー(SF)法で適用した吸着質ガス及び吸着材のモ
デルパラメータの例を,表A.1及び表A.2に示す。それらの定数は,ホルバス・カワゾエ(参考文献 [19],
[20] 参照)とサイトウ・フォリー(参考文献 [21],[22] 参照)の原著から転載した。表に記載されたパラ
メータの値は,それらの文献で見いだすことができる。したがって,意味のある結果を示すために,SF法
及びHK法の計算で採用された吸着質ガス及び吸着材のパラメータを解析レポートに記述することが重要
である。
注記 DIN 66135-4を参照。
表A.1−吸着材のパラメータ
物理量
単位
記号
炭素a)
ゼオライトb)
分極率
10−24 cm3
α(s*)
1.02
2.50
磁化率
10−29 cm3
χs
13.5
1.30
表面密度
(細孔壁1 m2当たりの
原子数)
1019 m−2
Ns
3.84
1.31
直径
nm
ds
0.34
0.28
注a) 参考文献[19],[20]参照
b) 参考文献[21],[22]参照
表A.2−吸着質ガスのパラメータ
物理量
単位
記号
窒素a)
アルゴンb)
分極率
10−24 cm3
αa
1.46
1.63
磁化率
10−29 cm3
χa
2.00
3.25
表面密度
(単分子層1 m2当たりの
原子数)
1018 m−2
Na
6.70
8.52
直径
nm
da
0.30
0.34
注a) 参考文献[19],[20]参照
b) 参考文献[21],[22]参照
表A.3に規定する数値は,表A.1及び表A.2に規定する吸着質ガス及び吸着材の物性定数を用いて計算
する。
表A.3−HK法に基づく炭素のスリット型細孔における窒素のミクロ細孔フィリングが
77.35 Kで起こるときの相対圧力と細孔径との関係
dp
nm
0.4
0.5
0.6
0.7
0.8
1.0
1.2
1.4
1.7
2.0
p/p0 1.8×10−7 1.2×10−5 1.7×10−4 9.6×10−4 3.2×10−3 1.4×10−2 3.5×10−2 6.3×10−2 1.1×10−1 1.6×10−1
21
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.4に規定する数値は,表A.1及び表A.2に規定する物性定数を用いて計算する。
表A.4−SF法に基づくシリンダ型ゼオライト細孔におけるアルゴンのミクロ細孔フィリングが
87.27 Kで起こるときの相対圧力と細孔径との関係
dp
nm
0.4
0.5
0.6
0.7
0.8
1.0
1.2
1.4
1.7
2.0
p/p0
5.7×10−7 9.8×10−6 1.4×10−4 8.7×10−4 3.1×10−3 1.5×10−2 3.9×10−2 7.2×10−2 1.3×10−1 1.9×10−1
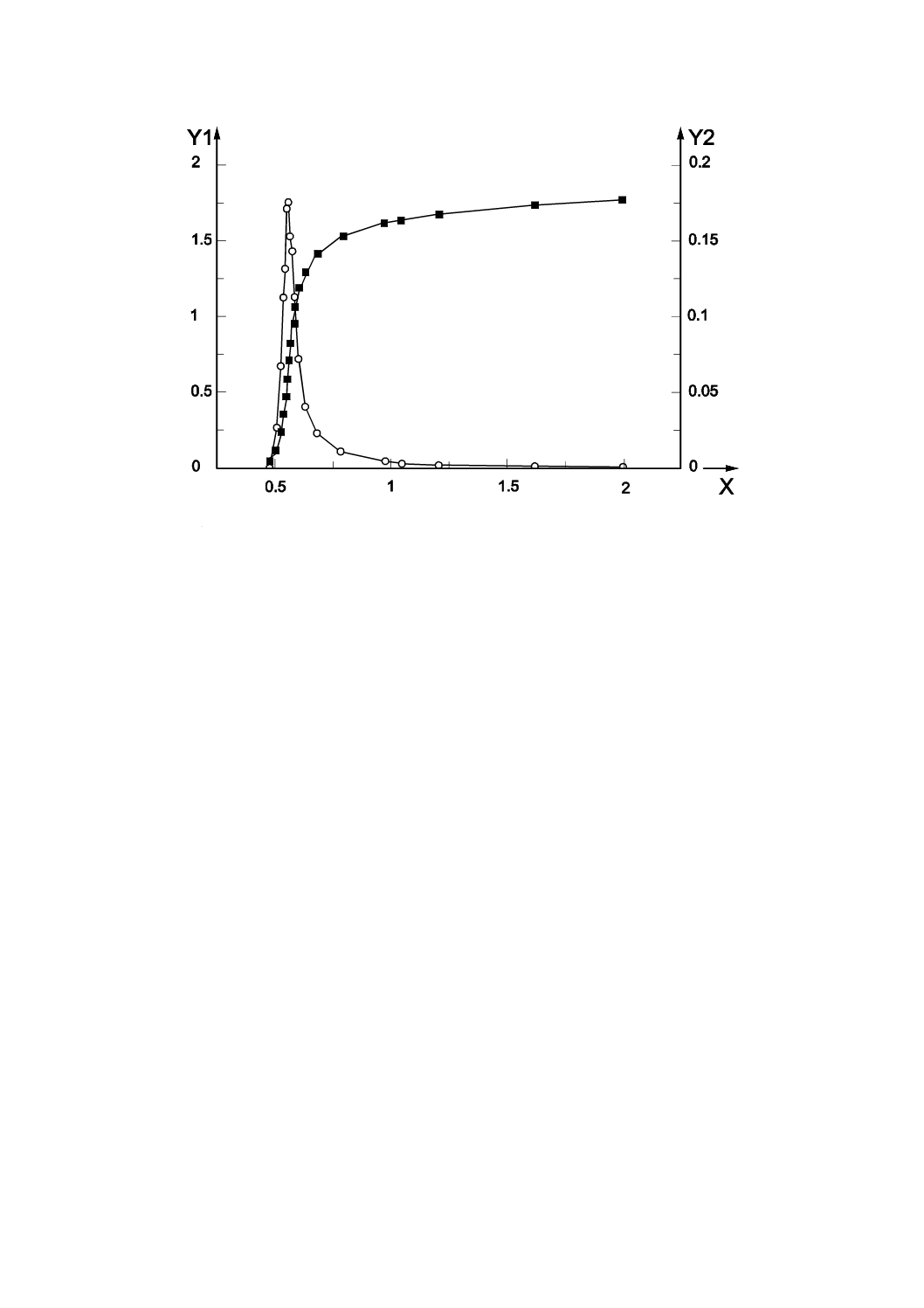
A.2 サイトウ・フォリーミクロ細孔解析の応用例
図A.1−A型ゼオライトの87.3 Kにおけるアルゴン吸着等温線の実験結果
22
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X
細孔径(nm)
Y1
微分細孔容積(cm3・g−1・nm−1)
Y2
累積細孔容積(cm3・g−1)
■
累積細孔容積
○
微分細孔容積
図A.2−A型ゼオライトのサイトウ・フォリー細孔径分布
図A.2でプロットされた値は,図A.1で示されたアルゴン吸着等温線から得られる。計算に用いた吸着
質ガス及び吸着材のパラメータは,表A.1及び表A.2に示した値に対応する。

23
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
NLDFT法
B.1
計算で用いる吸着質ガス−吸着質ガス及び吸着質ガス−吸着材の分子間相互作用パラメータの例
吸着質ガス−吸着質ガス及び吸着質ガス−吸着材の分子間相互作用パラメータの例を,表B.1及び表B.2
に示す。
表B.1−NLDFT計算に対する吸着質ガス−吸着質ガスの分子間ポテンシャルのパラメータ
ガス
εff/kB
K
σff
nm
dHS
nm
窒素a)
94.45
0.357 5
0.357 5
アルゴンb)
118.05
0.330 5
0.338 0
二酸化炭素a)
253.9
0.345 4
0.349 5
注a) 参考文献[28],[36]参照
b) 参考文献[37]参照
表B.2−NLDFT計算に対する吸着質ガス−吸着材の分子間ポテンシャルのパラメータ
ガス−固体
εsf/kB
K
σsf
nm
NS
窒素−炭素b)
53.22
0.349 4
炭素a):Ns=0.038 19 nm−2
二酸化炭素−炭素b)
81.5
0.343 0
−
窒素−シリカc)
147.3
0.317 0
シリカa):Ns=0.015 3 nm−2
アルゴン−シリカd)
171.24
0.300 0
−
注a) 参考文献[28]参照
b) 参考文献[28],[36]参照
c) 参考文献[28],[37]参照
d) 参考文献[37]参照
B.2
NLDFTミクロ細孔解析の応用例
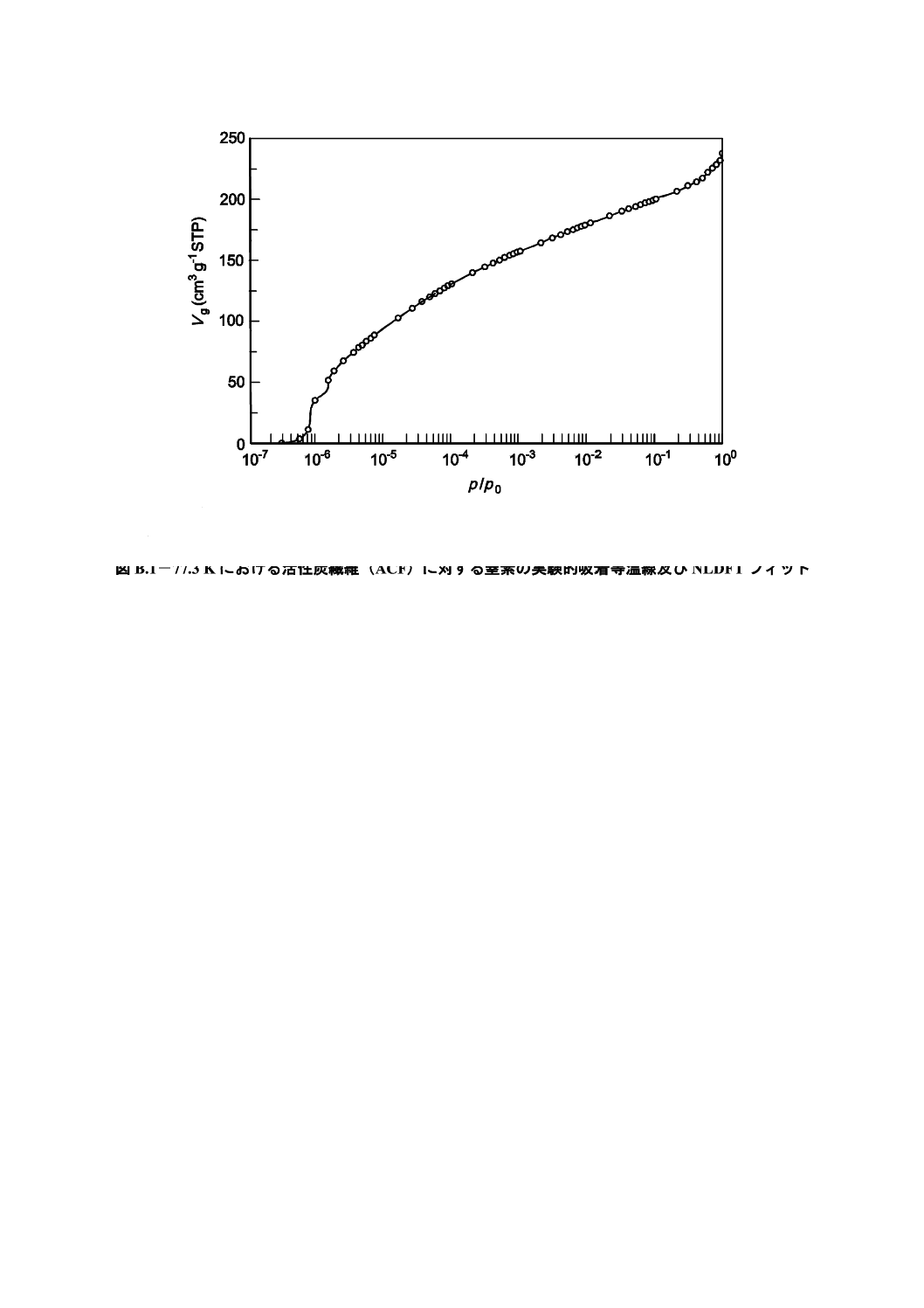
図B.1のプロットは,スリット型細孔を仮定し,表B.1及び表B.2に示した吸着質ガス/吸着材のパラ
メータを用いて得られた。
24
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
○
活性炭素繊維上の窒素(77.3 K)
-
NLDFTフィット
図B.1−77.3 Kにおける活性炭繊維(ACF)に対する窒素の実験的吸着等温線及びNLDFTフィット
25
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
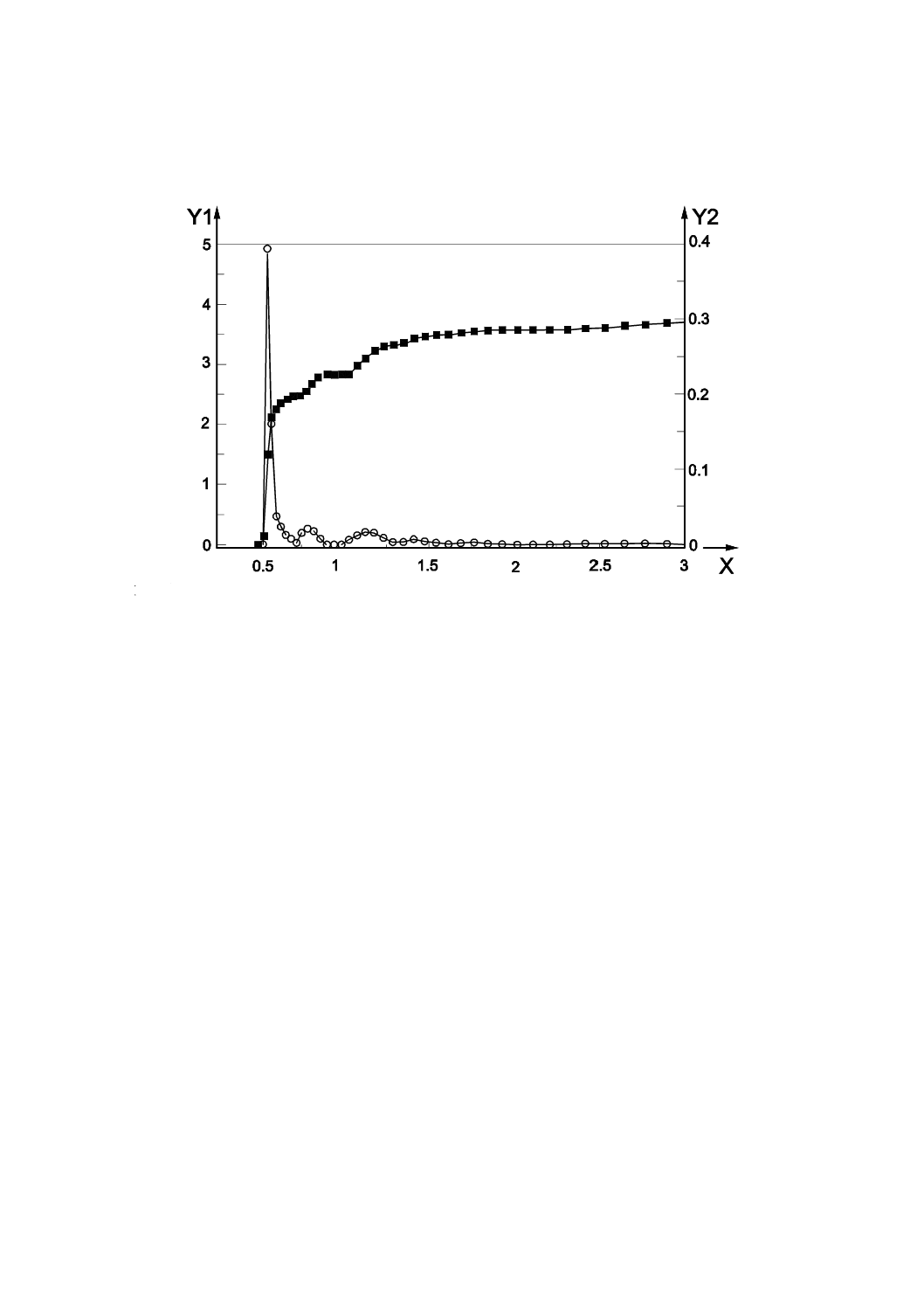
図B.2は,スリット型細孔に基づいて,表B.1及び表B.2に示した吸着質ガス及び吸着材の分子間相互
作用パラメータを用いて計算された。
X
細孔径(nm)
Y1
微分細孔容積(cm3・g−1・nm−1)
Y2
累積細孔容積(cm3・g−1)
■
累積細孔容積
○
微分細孔容積
図B.2−図B.1に示される窒素の吸着等温線から得られる活性炭繊維のNLDFT細孔径分布
26
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] Gregg, S.J., Sing, K.S.W. Adsorption, Surface Area and Porosity. 2nd ed., Academic Press, London 1982
[2] Mikhail, R.Sh. and Robens, E. Microstructure and Thermal Analysis of Solid Surfaces. Wiley, Chichester 1983
[3] Kaneko, K. Journal of Membrane Science, 96 (1994), 59
[4] Ross, S., Olivier, J.P. On Physical Adsorption. Wiley and Sons, New York (1964)
[5] Conner, W.C. In Fraissard, J. (Ed.) Physical Adsorption Experiment, Theory and Applications. Kluwer,
Dordrecht 1997, S. 33-63
[6] Lowell, S., Shields, J.E., Thomas, M.A. and Thommes M. Characterization of Porous Solids and Powders
Surface Area, Pore Size and Density. Kluwer, Dordrecht. 2004
[7] Rouquerol, F., Rouquerol, J., Sing, K.S.W. Adsorption by Powders and Porous Solids. Academic Press, San
Diego 1999
[8] Everett, D.H. and Powl, J.C.. J. Chem. Soc. Faraday Trans. I, 72 (1976) 619
[9] Dubinin, M.M. Quart. Rev. Chem. Soc., 9 (1955), 101
[10] Dubinin, M.M. In Progress in Surface and Membrane Science, 9 (D.A. Cadenhead ed.), Academic Press 1975
[11] Dubinin, M.M. Chem. Rev., 60 (1969) 235
[12] Stoeckli, H.F. J. Colloid Interface Sci., 59 (1977), 1, 185
[13] Dubinin, M.M. Stoeckli, H.F. J. Colloid Interface Sci., 75 (1980), 1, 34
[14] Polanyi, M. Verh. dtsch. physik. Ges., 16 (1914), 1012
[15] Lippens, B.C., Linsen, B.G., deBoer, J. H. J. Catalysis, 3 (1964), 32
[16] Lippens, B.C., deBoer. J.H. J. Catalysis 4 (1965) 319
[17] deBoer, J.H., Linsen, B.G., Osinga, Th. J. J. Catalysis, 4 (1965), 643
[18] Sing, K.S.W in Everett, D.H., Ottewill, R.H. (eds.), Surface Area Determination. Butterworths, London 1970,
25
[19] Horvath, G. and Kawazoe, K. J. Chem Eng. Japan, 16 (1983), 470
[20] Horvath, G. Energetic interactions in phase and molecular level pore characterization in nano-range, Colloids
& Surfaces A Physicochemical and Engineering Aspects, 141 (1998), 295−304
[21] Saito, A., Foley, C. AIChE Journal, 37 (1991), 429
[22] Saito, A., Foley, C. Microporous Materials, 3 (1995), 531
[23] DIN 66135-4,Partikelmesstechnik−Mikroporenanalyse mittels Gasadsorption−Teil 4: Bestimmung der
Porenverteilung nach Horvath-Kawazoe und Saito-Foley
[24] Tarazona, P. Physical Review, 31, 2672 (1985); Evans, R., Tarazona, P. Phys. Rev. A, 31 (1985), 2672;
Tarazona, P., Evans, R. Mol Phys., 52 (1984), 847
[25] Seaton, N.A., Walton, J.R.B.,Quirke, N. Carbon, 27 (1989), 853
[26] Lastoskie, C.M., Gubbins, K., Quirke, N. J. Phys. Chem., 97 (1993), 4786
[27] Olivier, J.P. J. Porous Mat., 2 (1995), 9
[28] Ravikovitch, P., Vishnyakov, A., Neimark, A.V. Phys. Rev.E. 64 (2001), 011602
[29] Curtin, W.A., Ashcroft, N.W. Phys. Rev.A. 32 (1985), 2909
[30] Kierlik, E., Rosinberg, M.L. Phys. Rev.A. 42 (1990), 3382
27
Z 8831-3:2010 (ISO 15901-3:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[31] Rosenfeld Y. Phys. Rev. Lett., 63 (1989), 980
[32] Neimark, A.V. Langmuir, 11 (1995), 4183
[33] Ravikovitch, P.I., Domhnaill, S.C., Neimark, A.V., Schueth, F., Unger, K.K. Langmuir, 11 (1995), 4765
[34] Ravikovitch, P.I. and Neimark, A.V. Langmuir, 2002, 18, 1550
[35] Sweatman, M.B. and Quirke, N. Langmuir, 17 (2001), 5011
[36] Ravikovitch, P.I., Vishnyakov, A., Russo, R. and Neimark, A.V. Langmuir, 16 (2000), 2311
[37] Neimark, A.V., Ravikovitch, P.I. Microporous and Mesoporous Material, 44−45 (2001), 697
[38] Lawson, C.L., Hanson, R.J. Solving Least squares problems SIAM, Philadelphia, 1995
[39] Provencher, S.W. Computer Phys. Commun., 27 (1982), 213
[40] Wahba, G., SIAM J. Numer. Anal., 14 (1977), 651
[41] IUPAC Recommendations 1984, Sing, K.S.W., Everett, D.H., Haul, R.A.W., Moscou, L., Pierotti, R.A.,
Rouquérol, J., Siemieniewska, T. Reporting Physisorption Data for Gas/Solid Systems with Special Reference
to the Determination of Surface Area and Porosity, Pure & Appl, Chem., 57 (1985), 4, 603−619
[42] IUPAC Recommendations 1994, Rouquérol, J., Avnir, D., Fairbridge, C.W., Everett, D.H., Haynes, J.H.,
Pernicone, N., Ramsay, J.D.F., Sing, K.S.W., Unger, K.K. Recommendations for the Characterization of
Porous Solids, Pure & Appl. Chem., 66 (1994), 8, 1739−1785
[43] JIS Z 8202-0 量及び単位−第0部:一般原則
注記 対応国際規格:ISO 31-0,Quantities and units−Part 0: General principles(IDT)












