Z 8827-1:2018 (ISO 13322-1:2014)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語,定義及び記号 ·········································································································· 2
3.1 用語及び定義 ················································································································ 2
3.2 記号 ···························································································································· 4
4 撮像準備························································································································· 4
4.1 はじめに ······················································································································ 4
4.2 手順 ···························································································································· 5
5 試料調製のための要件 ······································································································· 5
5.1 測定試料の分割及び縮分 ································································································· 5
5.2 接触粒子 ······················································································································ 6
5.3 試料台上での試料粒子の分布 ··························································································· 6
5.4 必要計測粒子数 ············································································································· 6
5.5 粒子を分散する流体 ······································································································· 6
6 画像の品質 ······················································································································ 6
6.1 一般的事項 ··················································································································· 6
6.2 粒子画像の画素 ············································································································· 7
7 画像解析························································································································· 7
7.1 一般的事項 ··················································································································· 7
7.2 粒子径区分及び倍率 ······································································································· 8
8 計数法···························································································································· 8
8.1 一般的事項 ··················································································································· 8
8.2 粒子画像の境界 ············································································································· 8
8.3 測定領域の境界上に存在する粒子······················································································ 9
8.4 接触している粒子 ········································································································· 11
8.5 測定 ··························································································································· 11
9 測定粒子径結果の計算 ······································································································ 12
10 校正及びトレーサビリティ ······························································································ 12
10.1 一般的事項 ················································································································· 12
10.2 推奨事項及び必要事項 ·································································································· 12
11 精度 ···························································································································· 13
11.1 一般的事項 ················································································································· 13
11.2 標準物質 ···················································································································· 13
11.3 機器の準備 ················································································································· 14
Z 8827-1:2018 (ISO 13322-1:2014) 目次
(2)
ページ
11.4 適格性試験 ················································································································· 14
11.5 適格性確認 ················································································································· 14
12 報告書 ························································································································· 15
附属書A(参考)要求精度を満たすために必要な計数粒子数の推定について ··································· 16
附属書B(参考)粒子検出のための標準的な二値化の方法 ··························································· 20
附属書C(参考)画像解析法フローチャート ············································································ 21
附属書D(参考)参考文献 ···································································································· 22
Z 8827-1:2018 (ISO 13322-1:2014)
(3)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
粉体工業技術協会(APPIE)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業
規格を改正すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業
規格である。これによって,JIS Z 8827-1:2008は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 8827の規格群には,次に示す部編成がある。
JIS Z 8827-1 第1部:静的画像解析法
JIS Z 8827-2 第2部:動的画像解析法
日本工業規格 JIS
Z 8827-1:2018
(ISO 13322-1:2014)
粒子径解析−画像解析法−第1部:静的画像解析法
Particle size analysis-Image analysis methods-
Part 1: Static image analysis methods
序文
この規格は,2014年に第2版として発行されたISO 13322-1を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,粒子径分布の測定を目的とする静的画像解析の方法について規定する。このとき,撮像装
置の光学系に対する粒子の相対速度はゼロであり,粒子は,撮像装置の対物面内で,適切に分散し,固定
されているものとする。得られる画像に対して試料の移動が影響しないことを条件に,試料台又はカメラ
を移動させることによって,視野を対物面内で移動させて撮像することは,許容される。撮像装置によっ
て取得された画像に対して,粒子径解析を行う。
この規格は,光学的方法又は電子顕微鏡で得られるデジタル画像の解析を対象とする。撮像装置の粒子
検出条件の設定及びその校正は粒子径測定の精度を確保するために重要であるが,この規格では画像取得
法については規定せず,粒子画素計数に基づく粒子投影像評価法を規定する。
個数基準又は体積基準のいずれにおいても,粒子径分布の範囲によって,所定の信頼限界内で要求精度
を保証するために計測すべき粒子個数は大きく異なる。その例を,附属書Aに記載する。
解析の自動化は,必要とされる精度に応じて十分な数の粒子を計測するために利用可能である。
この規格は,試料調製法については規定しない。しかし,最終的な解析結果の正確度及び精密度を保証
するために,測定試料の抽出,分散及び試料台への固定は,画像処理法の一連の流れの中で本質的なもの
である。
注記1 試料抽出及び試料調整法の詳細については,JIS Z 8824及びJIS Z 8833を参照。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 13322-1:2014,Particle size analysis−Image analysis methods−Part 1: Static image analysis
methods(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の一部を構成する。これらの引用規
格は,その最新版(追補を含む。)を適用する。
2
Z 8827-1:2018 (ISO 13322-1:2014)
JIS Z 8819-1 粒子径測定結果の表現−第1部:図示方法
注記 対応国際規格:ISO 9276-1,Representation of results of particle size analysis−Part 1: Graphical
representation(IDT)
JIS Z 8819-2 粒子径測定結果の表現−第2部:粒子径分布からの平均粒子径又は平均粒子直径及びモ
ーメントの計算
注記 対応国際規格:ISO 9276-2,Representation of results of particle size analysis−Part 2: Calculation
of average particle sizes/diameters and moments from particle size distributions(IDT)
JIS Z 8833 粒子特性を評価するための粉体材料の縮分
注記 対応国際規格:ISO 14488,Particulate materials−Sampling and sample splitting for the
determination of particulate properties(MOD)
3
用語,定義及び記号
3.1
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1.1
面積相当径(area equivalent diameter)
粒子の投影面積と等しい円の直径。
注記 ヘイウッド径(Heywood径)又は円相当径とも呼ばれる。
3.1.2
二値化画像(binary image)
各画素の濃度の値が0か1のどちらかの値を取る画素の配列からなるデジタル画像。通常,これは表示
装置に“明”,“暗”の領域として,又は2色を付けて表示される。
3.1.3
(画像の)コントラスト[contrast (of an image)]
(粒子径解析における)粒子像とその周辺のバックグラウンドとの濃淡値の差。
3.1.4
境界検出(edge detection)
粒子と背景との境界を検出すること。
注記 3.1.13参照。
3.1.5
フェレー径(Feret diameter)
粒子の像を2本の平行線で挟んだときの平行線の間隔。
3.1.6
視野(field of view)
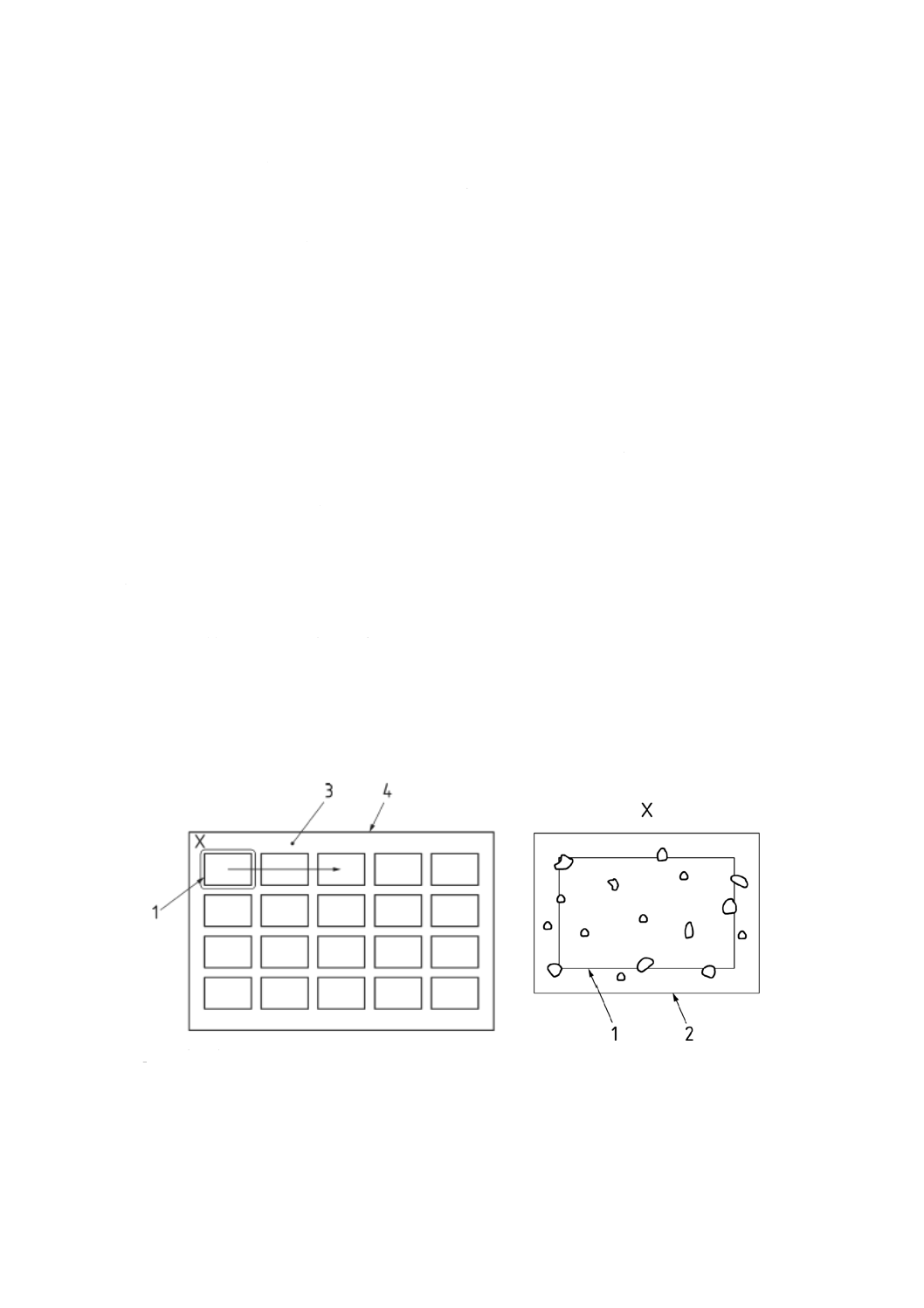
観測装置で見える領域(図1参照)。
注記 デジタル撮像装置の全画像領域はこの視野に等しい。
3.1.7
濃淡画像(grey image)
各画素の明暗濃度として,0,1,及びその中間の階調が許容される画像。グレーイメージともいう。
3
Z 8827-1:2018 (ISO 13322-1:2014)
3.1.8
画像解析(image analysis)
画像から定量的又は論理的な結果を得る過程及びデータ解析操作。
3.1.9
全測定領域(measurement field)
一連の測定領域全てによって構成される領域(図1参照)。
3.1.10
測定領域(measurement frame)
画像解析によって粒子計測を行う視野の中の領域(図1参照)。
注記 測定領域の集合が全測定領域を構成する。
3.1.11
画素(pixel, picture element)
水平方向及び垂直方向の両方向に一定間隔でサンプリングして得られるデジタル画像の最小単位の領域。
3.1.12
ラスターパターン(raster pattern)
全測定領域を測定領域で走査するときの順序(図1参照)。
3.1.13
セグメンテーション法,粒子抽出法(segmentation method)
着目粒子を周辺から切り出すのに用いる方法。
注記1 背景から粒子を分離する方法。
注記2 3.1.4参照。
3.1.14
しきい値(threshold)
濃淡画像において粒子と背景とを区別する値。
1
測定領域
2
視野
3
(測定領域の)ラスターパターン
4
全測定領域
X 一つの視野の拡大図
図1−“視野”,“測定領域”,“ラスターパターン”及び“全測定領域”の説明
4
Z 8827-1:2018 (ISO 13322-1:2014)
3.2
記号
この規格で用いる主な記号を,次に示す。
Ai
:粒子iの投影面積
α1
:水平方向校正係数
α2
:垂直方向校正係数
d
:最小代表長さ
dc
:円の直径
N
:測定する粒子の総個数
nc
:円内の測定画素数
nj
:粒子径範囲Δxj内の粒子個数
Pi
:粒子iが測定領域内に存在する確率[マイルズ・ランテュージュル(Miles-Lantuejoul)因子とも
いう。]
φi
:アスペクト比
σ
:標準偏差
Vi
:粒子iの体積
xA,i
:粒子iの面積相当径
xF1
:対象物の水平方向フェレー径
xF2
:対象物の垂直方向フェレー径
xi
:粒子iの寸法
xFmax,i :粒子iの最長寸法。最大フェレー径ともいう。
xFmin,i :粒子iの最短寸法。最小フェレー径ともいう。
x1
:対象物の水平方向の寸法
x1, m
:対象物のSI単位での水平方向寸法
x1, p
:画素数で表した対象物の水平方向寸法
x2
:対象物の垂直方向の寸法
x2, m
:対象物のSI単位での垂直方向寸法
x2, p
:画素数で表した対象物の垂直方向の寸法
x10, 3 :体積基準でふるい下積算分率10 %になる粒子径
x90, 3 :体積基準でふるい下積算分率90 %になる粒子径
Z1
:長方形測定領域の水平方向の辺の寸法
Z2
:長方形測定領域の垂直方向の辺の寸法
4
撮像準備
4.1
はじめに
この手法による正確な粒子径測定のためには,測定を実施する目的,撮像装置の設定及び校正について
の十分な理解が不可欠である。
撮像装置の最終的な設定及び校正には,試行錯誤による微調整が必要になる。未知の試料の粒子径範囲
は,撮像装置の設定に影響するが,最初の画像が得られるまではこれは未知である。望まれる粒子径測定
の精度を得るためには,撮像装置の調整及びその撮像結果の確認が必要となる。これは,熟練者によって
なされなければならない。
5
Z 8827-1:2018 (ISO 13322-1:2014)
撮像装置の設定及び操作は,撮像条件に対応した製造業者の推奨に従ってなされることが望ましい。
高精度の粒子径計測を実施するために,照明は視野において一様で,高いコントラストの画像を得られ
ることが望ましい。また,撮影倍率は,焦点が合い,最小粒子に対して要求精度に見合う適切な画素数が
割り当てられることが望ましい。最小寸法に対する画素数は,直線寸法又はそれらから求められる寸法を
測定する場合に影響する。
画像のゆがみは,様々な原因によって生じるが,ゆがみの存在及びその画像への影響は,既知の大きさ
の粒子又は粒子と類似した光学特性をもつ参照物質を視野の複数の位置,又は配向で観察することによっ
て確認することができる。画像法では,2次元,すなわちX,Yの情報しか得られないことに注意が必要
である。
4.2
手順
測定者は,画像解析の目的をあらかじめ理解しておくことが望ましい。例えば,各粒子径区分の個数に
よる粒子径分布が必要なのか,粒子径区分内の粒子の体積が必要なのか,最終結果に求められる正確度及
び精密度はどの程度か,というようなことである。これらの事項は,測定を実施する際の設定値の選択及
び方法に大きな影響を与える。
試料及び使用する機器ごとに,測定者は次の手順に従って確認を行わなければならない。
a) 使用する撮像装置の測定領域のX軸,Y軸の両方に対して,認証校正格子又は同等の参照物質を用い
て,適切な校正が行われている。
b) 使用する光学倍率が適切か,すなわち,最小粒子の画像において,要求精度を得るために必要な十分
な画素数が確保されている。
c) 照明法及び焦点の設定によって,収集された画像において高いコントラスト及び一様な照明が得られ
るものになっている。
d) 測定領域内の粒子が,できるだけ接触していないような分散状態になっている。
e) 複数に分割された試料から得られた十分な数の画像から最終的に合計で,個数基準又は体積基準に応
じて,及び粒子径分布の幅(JIS Z 8833参照)に応じて,適切な数の粒子個数を得られている。また,
測定対象の中の最大粒子が統計的に十分な数が含まれている(附属書A参照)。
f)
画像解析を行う場合,広領域を走査できるX,Y自動ステージ,又は手動の移動ステージを用いるこ
とがある。広領域に試料粒子を固定したスライドを用いることによって,多くの測定領域を取ること
が可能である。このとき,測定領域の間にスペースを設け,測定領域の重なりを全くなくすことが要
求される。測定領域の重なりを許すような画像解析法,又は測定領域の辺にかかる粒子を計数するよ
うな方法を採用する場合,各粒子が一度だけ含まれることを保証する手順を用いなければならない。
詳細については,8.3を参照。
g) 照明,焦点,倍率などによって画像の質が適正に調整されたならば,測定の最後まで一定であること
が望ましい。この要求は,使用する装置の性能に依存する。
h) 画像法を認証標準物質の測定に用いる場合には,画像取得操作の後に,a)で規定した校正を再度行っ
て,測定された偏差を全て記録することが望ましい。
i)
測定対象の試料に対して設定した条件は,全て記録しなければならない。
5
試料調製のための要件
5.1
測定試料の分割及び縮分
実際の測定に必要となるのはごく少量の試料なので,測定試料が全体を代表するようにJIS Z 8833に従
6
Z 8827-1:2018 (ISO 13322-1:2014)
ってサンプリングしなければならない。
5.2
接触粒子
粒子が接触しているかどうかを判定できるように,撮像装置の光学解像度を,適切に選ばなければなら
ない。光学解像度は,4.2 b)の要件も満たすことが望ましい。
互いに接触した粒子の数を最少にすることが望ましい。この規格で規定する測定方法は,孤立した粒子
に対して適用する。適切な分離を行わずに接触粒子を1個の粒子として測定すると,粒子径分布測定に誤
差が生じる。
画像解析だけでは接触粒子を見つけることは困難である。しかし,測定結果に対する接触粒子の影響は,
1画像当たりの粒子の数を増減することによって,実験的に調査することができる。粒子の数を変えるこ
とができない場合は,同様の大きさ及び形状の標準物質を使って,その影響を調査することができる。
5.3
試料台上での試料粒子の分布
試料粒子は,視野で十分に分散していることが望ましい。多くの粒子計数が必要とされるならば,複数
の視野を測定する。この場合,全測定領域での顕著な粒子径偏析がないことを確認することが望ましい。
また,4.2 f)に示した要求にも従うことが望ましい。
5.4
必要計測粒子数
必要な測定最少粒子数は,最終結果として求める粒度分布が個数基準によるか,又は体積基準であるか
どうかに依存する。計測が母集団の値を代表するように十分気を付ける(JIS Z 8833参照)。これは,元の
サンプルを分割して少なくとも三つの測定試料を調整することによって確かめることができる。ただし,
それぞれの測定試料は,測定に必要な十分な数の粒子を含んでいる必要がある。得られた結果を統計解析
することで,サンプル抽出及び分散を含む測定法の再現性を確認できる。
注記 必要となる計測粒子数についての詳細は,附属書Aを参照。
5.5
粒子を分散する流体
静止画像法では,気相中の粒子を測定することが多いが,この場合には適切なコントラストが保たれて
いることが望ましい。また,液体中に分散した粒子の場合,分散媒は清浄かつ粒子を含まず透明で,分散
媒の屈折率はコントラストを高めるために測定粒子の屈折率とできるだけ異なることが求められる。生物
標本のように混合光学背景中に粒子が存在する場合,粒子ごとの動的しきい値選択などの方法が必要にな
る場合があるかもしれない。
警告 混合光学背景で自動パラメータ選択によって粒子抽出する場合には,得られた値が真の粒子径
かどうか確認する方法がなく,粒子径に偏りが発生し精度が悪化する。
注意 光学特性の異なる粒子の混合系では,しきい値設定の誤差が粒子径に偏りをもたらすので,得
られる粒子径は不正確なものとなる。
6
画像の品質
6.1
一般的事項
粒子径解析には,撮像された画像中で粒子が十分に分散していることが重要である。測定領域中での粒
子濃度を減少させることによって,接触したり重なり合ったりしている粒子数を減少させることができる
(5.2参照)。しかし,これは高精度計測に必要となる十分な粒子数の計数とは相反するため,一定の妥協
は許容される。
得られた画像のコントラストは,要求測定精度と対応していることが望ましい。粒子と背景との輝度差
として,濃淡画像の輝度の分解能の数倍を確保しなければならない。
7
Z 8827-1:2018 (ISO 13322-1:2014)
個々の粒子画像に含まれる画素数が,測定結果の精度に大きく影響を及ぼす。粒子投影面積を幾つかの
粒子の平均値として計測する場合に限れば,最小粒子が数画素しか含まないような計測からも許容できる
結果を得られる場合がある。個々の粒子について詳細な情報を得るためには,更に多くの画素数が必要と
なる。
6.2
粒子画像の画素
粒子画像を構成する画素数及び固定された画素配列に対する粒子画像の相対的な位置は,粒子画像から
得られる粒子径に大きな影響を及ぼす。
画像解析法は,標準物質の認証のための計測法として利用可能であるし,一般の計測にも利用される。
それぞれの場合に対して,定義された正確度及び精密度を達成するために必要な測定条件は大きく異なり,
したがって,異なる方法論が必要になる。
6.2.1
標準物質の計測
標準物質としては多くの場合,球形で単分散又は非常に狭い粒子径分布の粒子が採用される。このよう
な粒子を高精度で計測するためには,個々の粒子画像が十分な数の画素を含むことが必要である。二値化
された粒子画像に基づく粒子径計測誤差は,次の二つの原因で生じる。
a) 粒子画像に含まれる画素数,及び固定された画素配列に対する粒子中心の偏位による場合。画素サイ
ズは有限であり,個々の粒子に含まれる画素数は粒子投影面積に対して(区分求積の意味で)無限に
多いわけではない。このため,セグメンテーション処理によって粒子に含まれる画素数に揺らぎが生
じると,得られる粒子径も変化する。この画素数は,同じサイズの粒子であっても,格子状画素配列
と粒子中心との相対的位置関係によって変化する。このために,完全に単分散な粒子を計測しても,
得られる粒子径には一定の広がりが生じる。
b) 二値化におけるしきい値の設定及び制御による場合。画素が粒子に含まれるか外れるかを決めるしき
い値設定における誤差は得られる粒子径に偏りを生じる。参考文献[12]で示されているように,しき
い値調整の影響を詳細に検討しておく必要がある。誤差又は偏りが生じないことを明示できないよう
な自動しきい値設定機能は,標準物質の測定に用いてはならない。
画素数基準で表される粒子径(dc)及び画素数(nc)の円について,ncの統計的分布についての標準偏
差は式(1)で近似的に表される(参考文献[4])。
2
1
c
c
2
68
.0
)
(
=
d
n
σ
······································································ (1)
逆に式(1)によって,任意の標準偏差σに対し,dcの画像を形成するncを推定することができる。
注記 粒子当たりの画素数を大きくしようとすると,測定領域中の測定粒子個数を減少させてしまう。
6.2.2
一般の粒子径計測
一般的な粒子径計測では(単分散標準物質の場合に比べて)粒子径範囲は広くなる。この場合には,最
大粒子が測定領域に正しく含まれ,最小粒子に計測目的に必要となる精度に対応して適正な画素数が含ま
れるように,全体のバランスを取る必要がある。しきい値は8.2に記載のように設定してよい。
7
画像解析
7.1
一般的事項
最新の画像解析装置には,通常,解析前画像の画質向上,及び接触粒子自動分離を行うアルゴリズムが
8
Z 8827-1:2018 (ISO 13322-1:2014)
搭載されている。このような画質向上機能は,現画像の粒子との対応関係が明確であり,かつ,画質向上
操作が粒子径計測結果に新たな誤差と偏りをもたらさないことが確認できる場合にだけ,利用してもよい。
不規則形状の粒子又は鋭角先端をもつ粒子の場合には,粒子画像が変形するので,粒子分割アルゴリズム
は用いないほうがよい。接触した不規則形状粒子は計測から除外するのが望ましい。この場合には,測定
領域から除外した粒子の割合を記録することが望ましい(8.4参照)。球形粒子の場合には,接触粒子の分
離による面積変化は小さいので,分離機能を用いることができる。画像解析法による粒子径計測の標準的
な手順を図C.1に示す。
7.2
粒子径区分及び倍率
画像解析における粒子のサイズ解像度の理論的限界は1画素である。ただし,画素数が少なければ得ら
れる粒子径の不確かさは増加する。得られた粒子ごとの二値化画像は,分解能を1画素として保存するこ
とが望ましい。画像圧縮は必ず精度及び解像度を悪化させることに留意する。一方,粒子径分布の測定結
果を報告するためには粒子径区分を定義する必要がある。それぞれの粒子径区分に含まれる粒子径幅は,
計数総粒子数・粒子径分布幅・想定される最小粒子が含む画素数によって決まる測定精度に適合すること
が求められる。このため,定量的な粒子径分布測定結果の報告に先立って画素数をSIによる長さ単位に変
換することを推奨する。
撮像倍率は,計数対象となる最小粒子の投影面積が測定の要求精度に適合する画素数を含むように設定
することが望ましい。画像中の全ての粒子の粒子径を測定し,1画素解像度で画像保存することが望まし
い。粒子径分布の最終結果は粒子径区分ごとに集計し,報告する。この粒子径区分は,通常,分布の狭い
試料の場合には等分割に,分布の広い試料の場合には対数で等分割による。分割幅は,全計数粒子の最大
粒子径範囲に基づいて決定することが望ましい。各粒子は,粒子径が各粒子径区分の最小値以上,最大値
未満のときに当該区分に算入する。
8
計数法
8.1
一般的事項
粒子径分布は,各測定領域においてソフトウェアの選択基準に適合した粒子画像を計数し,全ての測定
領域の結果を合計して定める。
8.2
粒子画像の境界
セグメンテーション法(粒子抽出法)は複数存在する。例えば,次のとおり。
a) しきい値法
b) 境界検出法
注記1 詳細情報は,附属書Bを参照。
これらの方法を選択するときには,あらかじめ標準物質を用いた測定によって,どのような方法及びパ
ラメータ設定が最もよい結果を与えるか,また,実際の測定対象である物質の特性に適合する方法・設定
であるかを試験することが望ましい。
注記2 光学顕微鏡を用いる場合,実際の粒子の光学的外観は,粒子屈折率,媒体の屈折率,粒子表
面構造,照射光の種類に依存する。さらに,撮像センサ上の光学的な粒子像は僅かに焦点か
らずれている場合もあり,また,これは離散的な画素配列にデジタル的にサンプリングされ
ている。これらの全ての効果が粒子画像の境界像に影響を与えている。
必要ならば,しきい値法は手動で設定することができる。
例 50 %しきい値法が適用可能である場合には,次の手順となる。まず,代表的な粒子の境界から数
9
Z 8827-1:2018 (ISO 13322-1:2014)
画素は離れた背景部分の小さな領域を選んで背景値を得る。次に,完全に粒子に属する画素であ
ると認められる数画素の信号強度を前景値(粒子信号)として採用する。背景値と前景値との平
均をしきい値とする(参考文献[2]参照)。
注記3 手動によるしきい値レベルの設定は,元画像と二値化画像とを直接比較することで主観的に
確認できる。このような主観的方法は妥当性確認に適合しないが,条件設定の誤りを容易に
検出できる。
第二の選択肢は,“自動しきい値設定”の機能を用いることである。ただし,このように自動しきい値法
を採用する場合には事前に,実際の測定対象である粒子と類似の光学特性をもつ認証標準物質を用いた妥
当性確認を行う必要がある。これには認証標準物質又は認証校正用格子を用いることができる。適用した
しきい値が粒子径に対して独立になっていることを確認する。
注意 特に,液体懸濁粒子の測定においては,測定対象粒子と異なる光学特性をもつ校正用格子又は
標準物質を用いて設定したしきい値レベルは,結果として得られる粒子径に相当の偏りをもた
らす。
注意 不適切なしきい値レベル設定は,得られる粒子径に大きな偏りをもたらす。この偏りは粒子径
に依存する。全ての粒子が影響を受けるが,一定の解像度の下で粒子径が小さくなるほど相対
的影響が大きくなる。
8.3
測定領域の境界上に存在する粒子
8.3.1
測定領域にある全ての粒子の計数方法
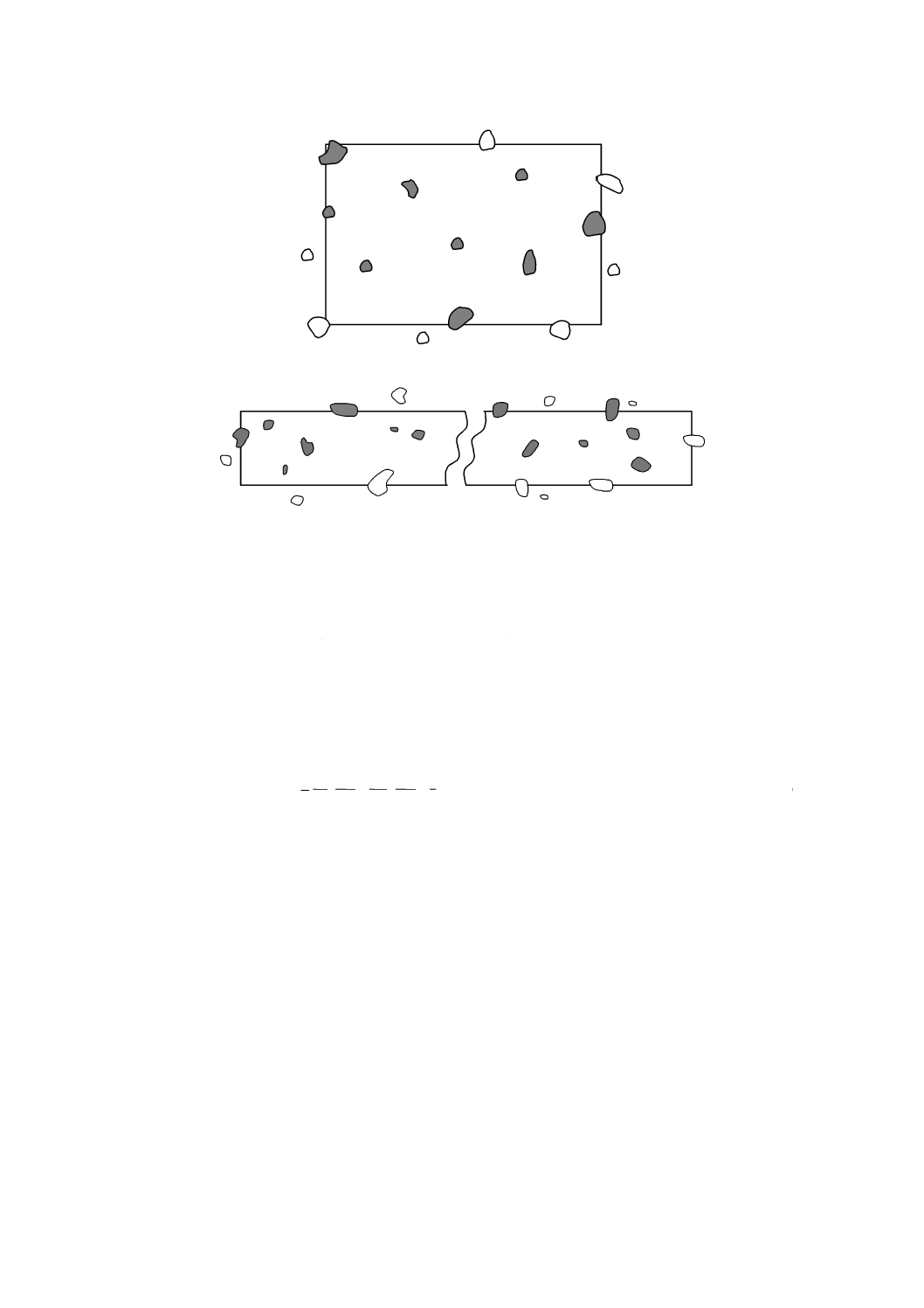
視野に存在する全ての粒子を測定すると,幾つかの粒子は視野の縁辺によって切られるので,最終的に
得られる粒子径分布の精度は低下する。これを避けるために,視野の中に測定領域を設定する。測定領域
は,次のように利用する。
a) 全ての粒子に対して代表計数点(例えば,重心)として1画素を割り振る。この代表計数点が測定領
域内に含まれる粒子だけを計数する[図2 a)参照]。測定領域としては,測定対象粒子が視野の縁辺に
よって切られることがない程度に,測定領域の縁辺と視野の縁辺との間に十分なスペースを設けるこ
とができれば,どのような形状でも採用することができる。
b) 下辺及び右辺を除外縁辺と定義した長方形の測定領域を使用する。測定領域内に一部又は全てが入っ
ていて,除外縁辺に接触していない粒子を測定対象粒子とする[図2 b)参照]。測定対象粒子が視野の
縁辺で切られないように,測定領域上辺と左辺とから視野の縁辺までとの間に十分なスペースが必要
である。この計数方法では,ほぼ全ての粒子を数え落としなく計数できる。測定領域の対辺にまたが
るような粒子は除外されることになるが,このような粒子は,その倍率で測定するには大きすぎるか,
又は面積だけで粒子径分布を表現することには適さないような針状粒子である。測定領域の境界上に
存在する粒子を全て除外する画像解析システムでは,粒子径の範囲及び粒子形状に対して異なる寸法
の有効測定領域を採用している。
10
Z 8827-1:2018 (ISO 13322-1:2014)
a) 重心が測定領域内にある粒子の計数
b) 下辺及び右辺を除外縁辺とした場合の粒子の計数
注記 黒塗りの粒子は計測され,白抜きの粒子は計測されない。
図2−測定領域の境界に存在する粒子の取扱い
8.3.2
測定領域で切られて無視された粒子の取扱い
粒子全体が完全に測定領域に含まれている粒子を測定対象とする。測定領域外又は測定領域の境界上に
存在する粒子は,全て無視する。この場合,測定領域に粒子が含まれる確率は,粒子径に反比例する。そ
のため,粒子径が大きくなるほど測定誤差が大きくなる。水平フェレー径(xF1)及び垂直フェレー径(xF2)
をもつ粒子(i)が,横(Z1)及び縦(Z2)の大きさの長方形の測定領域に含まれる確率(Pi)は,式(2)で
表される(参考文献[3][5])。
2
1
F2
2
F1
1
)
)(
(
Z
Z
x
Z
x
Z
Pi
−
−
=
······························································· (2)
したがって,測定領域に含まれる粒子数は,計測数を確率(Pi)で除して求めることが望ましい。
注記 特に,測定領域に比べて粒子が十分小さいとはいえない場合,境界効果による誤差を最小化す
るためには,非常に多くの測定フレームが要求される。
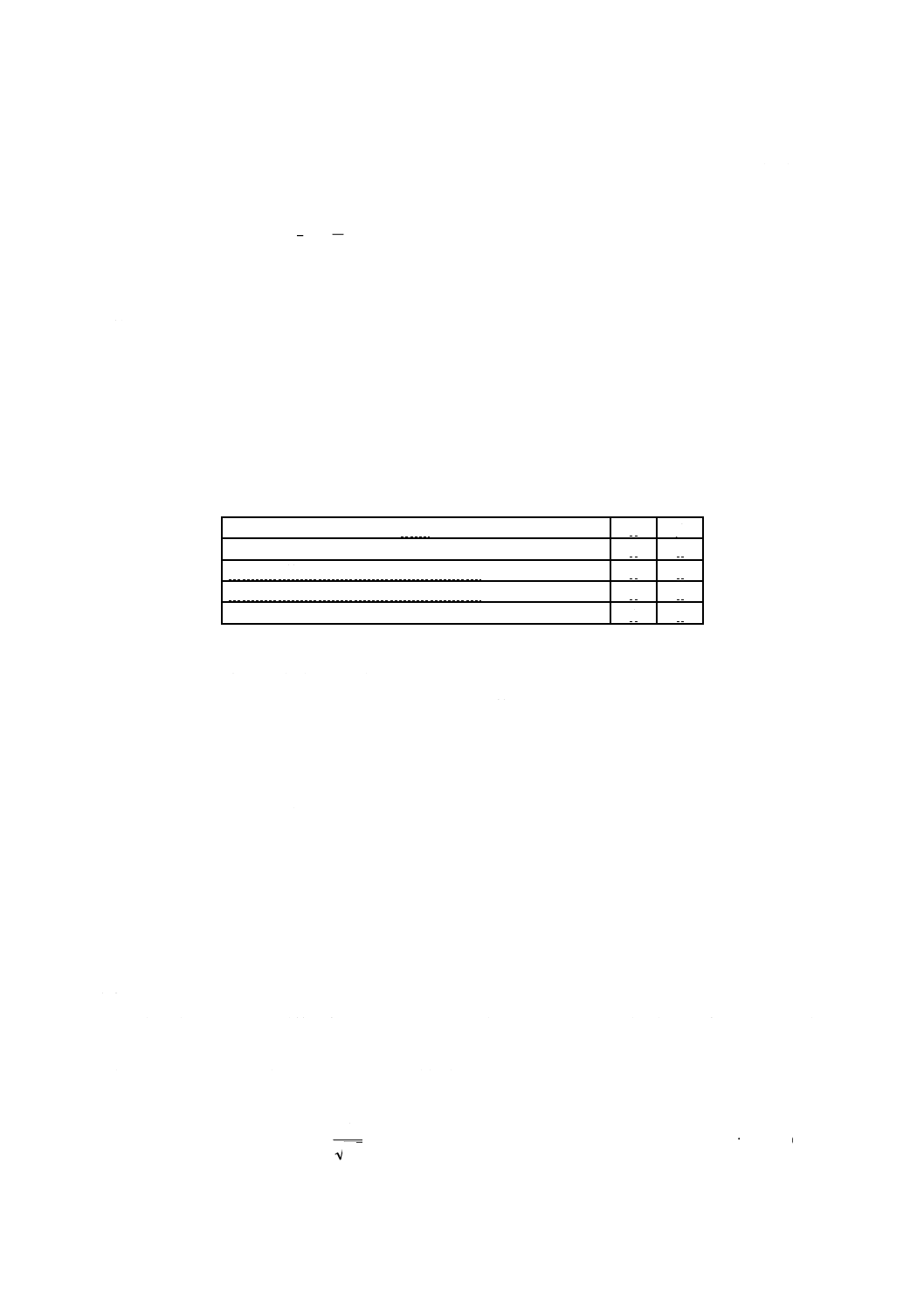
例 2単位〜10単位の粒子径範囲にある粒子数を計測するのに,1辺100単位×100単位の正方形測定
領域を使用した場合。粒子全体が測定領域に含まれる粒子の数及びそのときの補正係数を,表1
に示す。

11
Z 8827-1:2018 (ISO 13322-1:2014)
表1−補正された計数の例
直径
xi
任意単位
実測個数
ni
確率
Pi
補正個数
ni/Pi
2
81
0.96
84
4
64
0.92
70
6
49
0.88
56
8
36
0.85
42
10
25
0.81
31
8.3.3
接続測定領域による解析法
上記境界効果による影響を最小限にし,有効粒子径計数に含まれる粒子数を最大化する方法の選択肢と
して,(く形)測定領域の辺を重ね合わせるようにして接続する方法がある。この方法を採用するときには,
次の測定領域を撮像するためのステージ移動が高精度・精密である必要がある。ステージ移動によって各
粒子がいずれの測定領域に算入されるかが確定するので,ステージ移動が高精度・精密であることは,粒
子の重複計数を避けるために不可欠な条件になる。
各測定領域の画像処理では,境界にかかる粒子を識別し,粒子位置情報は次の隣接測定領域の処理に送
られる。境界にかからず完全に測定領域に含まれる全ての粒子は当該領域内で計数し記録する。隣接測定
領域の重なりの程度は,あらかじめ分かっている粒子径分布と倍率とから決定する。測定領域の重なりは,
全ての粒子がいずれか一つの測定領域内で計数されるように設定されることが望ましい。
この方法では,全測定領域の外縁境界にかからない全ての粒子を数え落としなく計数できる。
8.4
接触している粒子
プレパラートの調製では,接触粒子数を最小化する方法を選ぶことが望ましい。しかし,それでもなお,
測定領域内に接触粒子が全く存在しないようにすることは難しいので,何らかの処理が必要となる。
接触粒子を自動的に認識することは難しいが,次の方法で対応する。
a) 何らかの数値的な接触粒子分割アルゴリズムを利用して“生成された”粒子を計数する方法
b) 形状係数のような判定基準を用いる方法
c) 手動処理による方法:評価用スライドに対する統計分析で,一定の判定基準が得られる。
画像中の粒子径を変化させてしまう可能性があるので,凝集粒子を独立粒子に分離する方法としては数
値的処理は用いないほうがよい。このような方法で得られた粒子径分布は,トレーサビリティを満たさな
い。元画像から得られた結果と比較することで,凝集粒子を検出するこのような方法の妥当性を詳しく調
べることができる。球形粒子が接触している程度なら,粒子投影面積に対する影響が小さいので分離可能
である。
形状係数による接触粒子の判別は容易ではない。特に,密に重なった凝集粒子では,実際に形状の異な
る粒子か,又は特に大きい粒子かを区別できない。接触粒子を排除できない場合には,様々な技術,例え
ば,フラクタル解析による凝集体の評価,モデルに基づく粒子分離などを,注意深く利用することで粒子
分離を行ってもよい。認証標準物質の測定においては,このような手順を採用しないほうがよい。
8.5
測定
粒子周囲長の測定は,使用する画像解析システムに強く依存する。測定するのは画素数で表された粒子
の投影面積であり,次に最大・最小フェレー径である。これらを用いて識別度の高い粒子形状記述子(形
状係数)を定義することができる。したがって,画像解析法では次の主要パラメータを用いるのがよい。
12
Z 8827-1:2018 (ISO 13322-1:2014)
a) 粒子投影面積(Ai)
b) 粒子の最大径,又は最大フェレー径(xFmax,i)
c) 各粒子の最小径,又は最小フェレー径(xFmin,i)
これらの値は,式(3)に従って面積相当径(xA,i)を,また,式(4)に従ってアスペクト比(φi)を算出する
ために使用される。
π
4
,
A
i
i
A
x
=
·············································································· (3)
i
i
i
x
x
φ
max,
F
min,
F
=
··············································································· (4)
装置が正方形の画素を使用していない場合には,適切な補正が必要である。画像解析法を用いて得られ
た粒子径測定結果と体積又は質量基準の測定結果とを比較する場合,粒子iの体積Viは,各粒子の投影面
積相当径(xA,i)から式(5)に従って計算できる。
6
)
π(
3
A,i
i
x
V=
············································································· (5)
9
測定粒子径結果の計算
画像解析法による粒子径分布計測では,個数基準の分布が得られる。ただし,分布の各粒子径区分に含
まれる粒子数は,箇条8で規定した方法で補正されている。
平均粒子径の計算は,JIS Z 8819-2による。
10 校正及びトレーサビリティ
10.1 一般的事項
画素をSI長さ単位(ナノメートル,マイクロメートル,ミリメートルなど)に変換するために,最初に
装置を校正する。校正手順には,視野の均一性の確認を含める。校正手順においては,全ての測定が計測
標準にトレーサビリティをもつことが不可欠である。これは,認証された標準対物マイクロメータ(マイ
クロスケール)を用いて画像解析装置を校正することで実現できる。校正は,通常の解析と同等の照明及
びコントラストの条件で行わなければならない。
例 ガラスにクロムマークした認証校正対物格子はイギリス国立物理学研究所(National Physical
Laboratory)から入手可能。認証球形粒子(SRM475,SRM484)はアメリカ国立標準技術研究所
(National Institute of Standards Technology)(NIST)から入手可能。ほかにも,対SIトレーサビリ
ティをもつ商用認証標準物質は市場に存在する。この情報はこの規格の利用者の便宜を図って記
載するもので,これらを推奨するものではない。同じ結果が得られる場合は,これらと同等の他
のものを利用してもよい。国内では,JCSS(Japan Calibration Service System)による校正事業者
登録制度によって,長さの登録区分に登録された事業者から校正用スケールの校正証書を得るこ
とができる。
10.2 推奨事項及び必要事項
10.2.1 接触粒子
領域内の全ての粒子を計数して,面積,最大フェレー径及び最小フェレー径の結果を報告するのが望ま
しい。
13
Z 8827-1:2018 (ISO 13322-1:2014)
過剰な接触粒子数が観察された場合には,試料を希釈することによって,画像当たりの粒子数を減らし,
より多くの測定領域を用いて測定を繰り返す(8.4及び5.2を参照)。
10.2.2 画像のひずみ
画像のひずみは,次のようにして判別する。
a) 校正用対物格子の計数線から幾つかのグリッドを用いて,1個の正方形を選択する。それを中央に置
き,幅x1及び高さx2を測定する。x1,x2,及びこの正方形に含まれる画素数は,要求校正精度を達成
するのに十分な数でなければならない。
b) 選択した正方形を視野の4隅にそれぞれ置き,幅x1及び高さx2を測定する。
c) 最終結果にx1及びx2の5個の値を報告する。
10.2.3 校正
画像機器の各設定は,次のように校正する。
a) 画素数で表される画像サイズと実際のSI単位による長さとの対応を,校正用格子上の複数の正方格子
を用いて決定する。
b) 式(6)に従って計算したα1及び式(7)に従って計算したα2を報告する。
p,1
m
,1
1
x
x
α=
·················································································· (6)
ここに, x1,m: 実寸法で表した水平長
x1,p: 画素数で表した水平長
p,2
m
,2
2
x
x
α=
················································································· (7)
ここに, x2,m: 実寸法で表した垂直長
x2,p: 画素数で表した垂直長
注記 ラインスキャナを用いる場合と同様にマトリックスカメラを使用する場合にも,x1又はx2のど
ちらか,及びα1又はα2のどちらかを報告することにしてもよい。
11 精度
11.1 一般的事項
機器の正しい操作について適正な手順で確認を行うことが望ましい(4.2参照)。
11.2 標準物質
精度確保のため,トレーサビリティをもつ球形の認証標準物質(以下,CRMという。)を使用する。例
えば,国家計量標準機関に対してトレーサブルである認証値をもつ粒子である。これは例えば,それらの
機関が直接校正した粒子,又はそれら機関が製造したCRMを用いて校正された粒子である。これによっ
て,測定装置として装置が正しく機能していることを保証する。装置の改造又は大規模メンテナンスが必
要となった場合には,再度トレーサビリティをもつCRMを用いて機器の精度を確保する。
精度確保のためには,トレーサビリティをもつ球形CRMが必要である。これらは,画像解析に適した
粒子であるとされていること,分布がx90, 3/x10, 3の比率で最低でも1.5の球状粒子であること,並びに一様
な密度及び光学特性をもつ粒子であること,が求められる。これらはJIS Q 0034(参考文献[6])に従って
製造されていることが望ましい。また,質量基準又は体積基準の各粒子径区分における割合が,対SIトレ
ーサブルであってこれらが計量標準に従って値付けされていることが望ましい。
試料抽出及び試料調製についての再現性のある手続が確保でき,これが詳細に記録されていることは極
14
Z 8827-1:2018 (ISO 13322-1:2014)
めて重要である。そのような手順に厳密に従って,操作を行わなければならない。また,この記録のタイ
トル及びバージョンを報告しなければならない。トレーサビリティをもつCRMを用いた測定結果が所定
の範囲に収まれば,測定機器はその本来の精度性能を発揮するであろう。
日常的な測定機器の適格性確認には,画像解析法に適した非球形(非認証)の標準物質を利用しても差
し支えない。x90, 3/x10, 3の比率が,最低でも1.5であるような既知の粒子径分布をもつ試料を用いることが
望ましい。
非球形粒子を用いる場合には,アスペクト比は1:3までとする。常に安定して適正な結果が得られるこ
とが確認されている詳細な測定手続に従って,一つ以上の画像解析装置で得られた粒子径分布が文書で記
録されていることが必要である。画像解析法ではない方法で得られた参照値を用いると,結果に大きな偏
りをもたらす可能性がある。試料抽出が必要な場合には,適切な結果が得られることが証明されている方
法に従う(JIS Z 8833参照)。サンプリング,分散及び測定法についての既存の手順が利用不可能な場合に
は,最終結果とともに用いた手順を報告しなければならない。
11.3 機器の準備
機器マニュアルに記載されている指示及びアドバイスに従う。装置の動作は,製造業者による操作適格
性試験(OQテスト)又はそれに相当する試験に合格していなければならない。また,試験の日付及び結
果を記録する。解析モードが選択可能な場合には,計測の目的にかなったモードを選択する(4.2参照)。
十分に訓練を受けた操作者が,機器の準備及び適格性試験を行わなければならない。測定結果の表示機能
は,JIS Z 8819-1に適合するふるい下積算分布を出力するように設定する。
11.4 適格性試験
測定はCRM試験の手順に従わなければならない。適正な測定領域数を用いて少なくとも三つの測定試
料を用いた測定を行うことが望ましく,これによる平均値を測定結果として用いるのがよい。測定中に元
画像と二値化画像とを同時表示できる機能を用いることが望ましい。
11.5 適格性確認
適格性確認は,個数基準又は体積基準で与えられているCRMを用いて行う。95 %許容差がCRMの各
パラメータの値付けに記載されている。これによって各パラメータに対する最大値・最小値が決まる。計
測された粒子径分布が次の基準を満たすとき,この規格の要求する適格性が確認される。
a) 計数した粒子数が,要求精度に対して必要となる計測数を,規定の信頼区間の範囲で超過している。
b) 接触粒子数が規定の制限を下回っている。球形CRMを用いる場合には,形状記述子を用いたフィル
タリングによってこの影響を低減できる。
c) 質量基準又は体積基準で,ふるい下積算分布の10〜30パーセンタイルの区間で測定される粒子径が,
同区間で記載されている標準物質の最大・最小値を相対値で3 %以上外れない。
d) 質量基準又は体積基準で,ふるい下積算分布の30〜70パーセンタイルの区間で測定される粒子径が,
同区間で記載されている標準物質の最大・最小値を相対値で2.5 %以上外れない。
e) 質量基準又は体積基準で,ふるい下積算分布の70〜90パーセンタイルの区間で測定される粒子径が,
同区間で記載されている標準物質の最大・最小値を相対値で4 %以上外れない。
大きな偏差が得られた場合には,可能性のあるエラーを全て確認すること及び/又は専門家の助言を求
める。特に,高精度が要求される場合には,より信頼区間の狭いCRMを選ぶことが望ましい。サンプリ
ング,分散及び測定を含む全手順には偏差が最小であるものを使用することが望ましい。
15
Z 8827-1:2018 (ISO 13322-1:2014)
12 報告書
試験報告書には,次の情報を含むことが望ましい。
a) 測定試料の識別名
b) 日本工業規格の番号(JIS Z 8827-1)
c) 粒子の公称質量,体積,及び組成の全ての定量的な記述とともに,試料抽出のために使用した方法全
体の記載及び試料抽出手順の各ステージで使用した製品
d) 使用したシステム(ハードウェア及びソフトウェア)
e) 画像サイズ
f)
画像解像度
g) 使用した測定領域の数
h) 合計の計数粒子数
測定結果は,JIS Z 8819-1及びJIS Z 8819-2に従って表及びグラフで報告することが望ましい。
試料ごと,また,撮像装置の設定ごとに,代表的な視野で得られた画像を提出することが望ましい。

16
Z 8827-1:2018 (ISO 13322-1:2014)
附属書A
(参考)
要求精度を満たすために必要な計数粒子数の推定について
A.1 一般
個数基準での粒子径分布計測において,得られる平均粒子径などの統計指標値が所定の信頼区間によっ
て規定される精度を満足するために必要となる,計数(計測)されるべき最小粒子数の推定は,増田・後
藤(参考文献[1]),Wedd(参考文献[7]),吉田(参考文献[13])によって議論されている。この結果は,最
終的に粒子径分布を個数基準で表示するのか体積基準で表示するのかにも依存する。体積基準での粒子径
分布を一定の精度で得るためには,個数基準の場合よりも分布の各粒子径分画に更に多くの粒子数を計数
することが必要になる。これは,体積基準の場合には粒子径の3乗の重みが付くからで,例えば100 µm
の粒子1個と同体積になるためには10 µmの粒子数は1 000個必要であることを考えれば,このことは容
易に理解できるであろう。
A.2 平均粒子径の推定のために必要な粒子数の計算
A.2.1 計算法の概略
必要精度を得るために必要になる計数粒子数の推定値をn*とする。もう少し詳しく書くと,n*は,サン
プルの平均粒子径が,母集団の平均粒子径に対して相対誤差δの範囲に入る確率がPになるようなサンプ
ル粒子数であると定義できる。参考文献[1]では,母集団の粒子径分布が個数基準で対数正規分布であると
きに,与えられた相対誤差δと確率Pとに対するn*の計算法が示されており,それは次の手順で計算でき
る。
与えられた確率Pによって決まる中間変数uを,式(A.1)で定義する。
2
1
)
(
P
u
−
=
−
φ
········································································ (A.1)
ここで,φは積算正規分布関数である。幾つかの代表的な確率Pの値に対応するuの計算値を表A.1に
示す。
表A.1−確率Pが50 %以上のときの確率Pに対応するu(P)の値
(確率50 %以下では信頼水準として低すぎる点に留意)
P(%)
50
68.3
75
80
90
95
97.5
99
99.5
99.8
99.9
u
0.67
1.00
1.15
1.28
1.64
1.96
2.24
2.58
2.81
3.09
3.29
次に,母集団の粒子径分布のsを式(A.2)で定義する。これは,個数基準対数正規分布の場合には84パ
ーセンタイル値x84, 0及び50パーセンタイル値x50, 0を用いて計算できる。
s=ln(sg)=ln(x84, 0)−ln(x50, 0) ······················································· (A.2)
ここで,sgは幾何標準偏差で,対数正規分布の場合に分布の広がりを規定する値であり,対数正規分布
の場合には分布の基準(重み)によらない。lnは自然対数を表す。
注記 なお,参考文献[1]では標準偏差及び幾何標準偏差を表すのにσ及びσgの記号を用いているが,
ISO 9276-5に従ってここではs及びsgの記号を用いた。
次に式(A.2)で求めた標準偏差s及び式(A.1)(又は表A.1)のuの値(例えば,P=95 %のときにu=1.96)
17
Z 8827-1:2018 (ISO 13322-1:2014)
を用いて,新たな中間変数ωを式(A.3)のように計算する。
ω=u2α2s2(2c2s2+1) ·································································· (A.3)
ここに
2
α
β
c
+
=
である。αは粒子径の何乗の値の平均を計算するのかを表す指数で,粒子径の(長さの)平均を計算する
ならα=1,粒子体積の平均を計算してから立方根をとる(平均体積径)ならα=3とする。βは平均径を
計算するときの基準(個数基準か体積基準か)によって決まる定数(または,これを“重み”という。)で,
個数基準ならβ=0,質量基準ならβ=3とする。
以上で得られたωの値と要求する相対誤差δ(例えば,相対誤差1 %ならδ=0.001,相対誤差3.16 %な
らδ=0.031 6とする)から,必要粒子数n*は式(A.4)で与えられる。
n*=ωδ−2 ·············································································· (A.4)
表A.2に定数α及びβの値を示す。
表A.2−平均径の種類に対応する定数α及びβの値
種類
α
β
個数基準算術平均長さ径(個数平均径)
1
0
個数基準算術平均体積径(平均体積径)
3
0
重み付き体積平均粒子径(体積平均径)
1
3
重み付き表面積平均粒子径(ザウター径,体面積平均径)
1
2
A.2.2 計算例
ここでは,5 %の相対誤差(d=0.005),確率95 %(P=0.95で表A.1によって対応するuはu=1.96)で
質量(体積)中位径を求めるために必要となる粒子数の計算例を示す。この場合,表A.2によって,α=6,
β=0であるから,これらを式(A.3)に代入して,
n*=[36u2s2(18s2+1)]δ−2
となる。したがって,この例では与えられたu及びδの値に対して,必要粒子数は次のように計算される。
n*=55 319s2(18s2+1)
ここに,s=ln(sg)
母集団の幾何標準偏差sgが分かっているか,式(A.2)で与えられたパーセンタイル値から計算して,上式
に代入する。例えば,sg=1.1をsg=1と近似して(整数値に丸めて)代入すると,n*=585を得る(参考
文献[1]の表2参照)。これは,相当に狭い分布,ほとんど単一サイズと呼べるような分布の場合の値にな
る。
A.3 体積基準対数正規分布を用いる場合の例
粒子径分布のQ3=90 %(質量基準90パーセンタイル値x90, 0,JIS Z 8833参照)を一定の不確かさ(標
準偏差で表示される。)で求めるために,必要粒子数n*の計算例を示す。
体積基準粒子径分布が無次元化パラメータ(z)(ISO 9275-5参照)を用いて式(A.5)の正規分布(確率密
度関数)で表されるとする。
2
5.0
*
3
π
2
1
)
(
z
e
z
q
−
=
··································································· (A.5)
18
Z 8827-1:2018 (ISO 13322-1:2014)
体積基準対数正規分布は,式(A.5)でパラメータ(z)を,粒子径(x)から中位径(x50, 3)及びs=ln(sg)
を用いて式(A.6)のように計算する場合に与えられる。
3,
50
g
3,
50
g
3,
50
log
log
1
ln
ln
1
ln
1
x
x
s
x
x
s
x
x
s
z
=
=
=
··································· (A.6)
ここで,幾何標準偏差sgは分布の広がりを特徴付ける量でsg=x84, 3/x50, 3と等しくなる。log(sg)の値は0.05
〜0.5程度の値を取る(表A.3参照)。
なお,log(x)は常用対数(底を10とする)を表す。
表A.3−分布の広がりを表す各値の対応関係
log(sg)
3,
50
3
,
84
g
x
x
s=
3
,
10
3
,
90
x
x
0.01
1.02
1.06
0.05
1.12
1.34
0.1
1.26
1.80
0.2
1.58
3.26
0.3
2.00
5.87
0.5
3.16
19.12
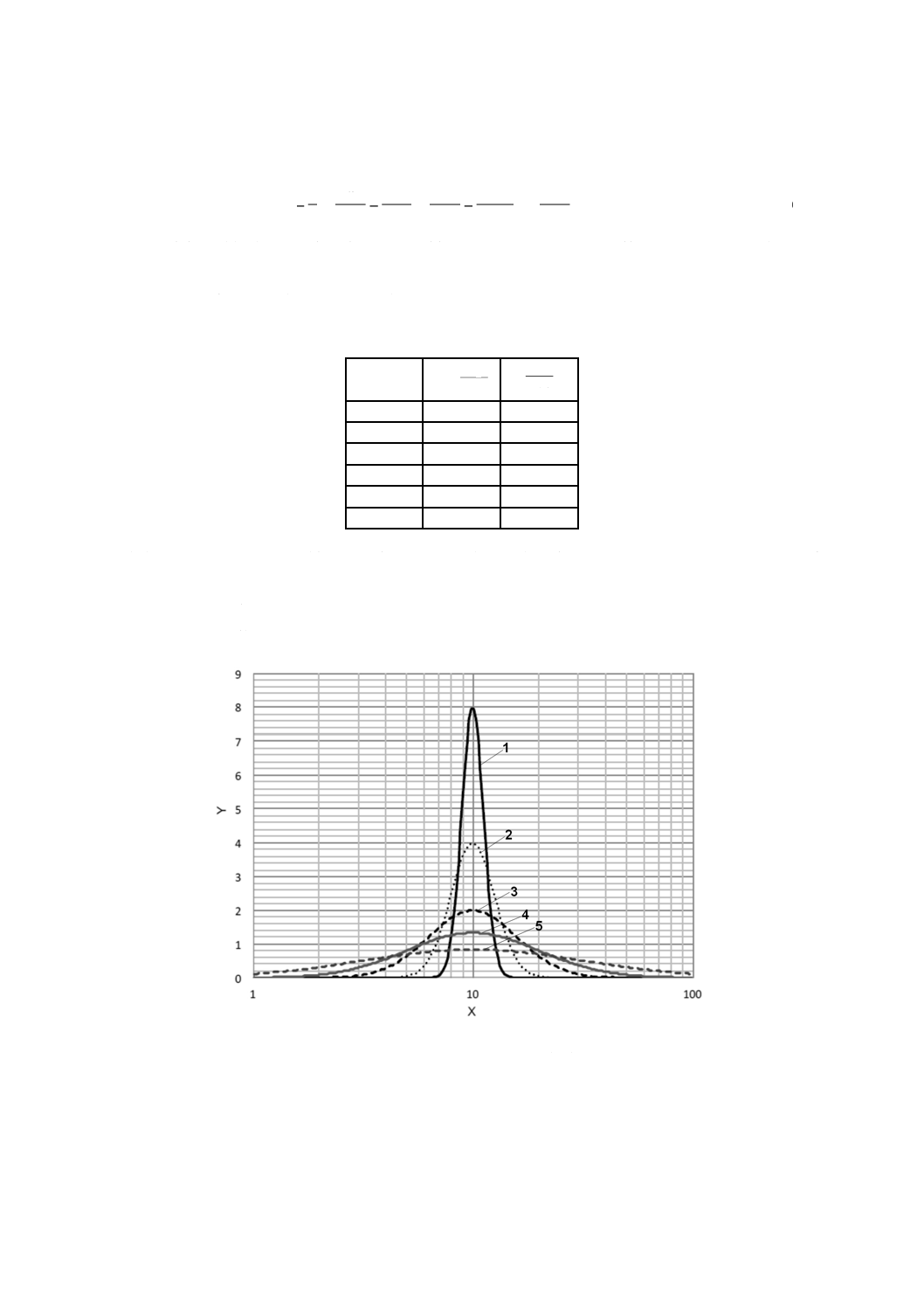
中位径x50,3=10 µmとした(幾つかの広がりをもつ。)粒子径分布について,1 µm〜100 µmの間を対数
軸上で等間隔になるように粒子径分画を取って,普通の表計算ソフトを用いて計算した計算例を示す。対
数正規分布は0から無限大の間の分布ではあるが,それを下限1 µm・上限100 µmでカットして計算して
いることになる。計算結果を,図A.1に示す。
log(sg)
1
0.05
2
0.1
3
0.2
4
0.3
5
0.5
X 粒子径(μm)
Y 頻度
図A.1−対数正規分布の例
19
Z 8827-1:2018 (ISO 13322-1:2014)
式(A.5)及び式(A.6)で与えられる体積基準の頻度分布(確率密度関数)から個数基準積算分布Q0(x)及び
体積基準積算分布Q3(x)を,JIS Z 8819-1に規定されている計算法に従って普通の表計算ソフトで求めた。
この分布に基づいて,体積分布の90 %径と99.9 %径との間に入る粒子の数を式(A.7)で求めた。
n0=n(Q0(x|Q3(x)≈99.9 %)−Q0(x| Q3(x)≈90 %)) ·········································· (A.7)
ここで,nはサンプル中の総粒子数である。99.9 %は分布の最大値を代表する値として選んだ。ただし,
横軸の99.9 %径x|Q3(x)≈99.9 %及び99.9 %径x|Q3(x)≈90 %の近似値,並びにそれに対応する個数基準の値Q0の近
似値は,表計算ソフトの計算値から読み取った。
ここで求めたn0の値がnに比べて十分に小さい場合,この範囲の粒子についてだけ求めた標準偏差はポ
ワソン分布を用いて式(A.8)のように推定できる(JIS Z 8833参照)。
0
0)
(
n
n
σ
=
··········································································· (A.8)
この分画の相対不確かさ
0
0n
n
を一定のレベル(例えば,1 %,3.16 %,5 %など)に設定するとき,
この分画に必要となる粒子数n0が計算できる(例えば,1 %の不確かさのためには10 000の粒子数がこの
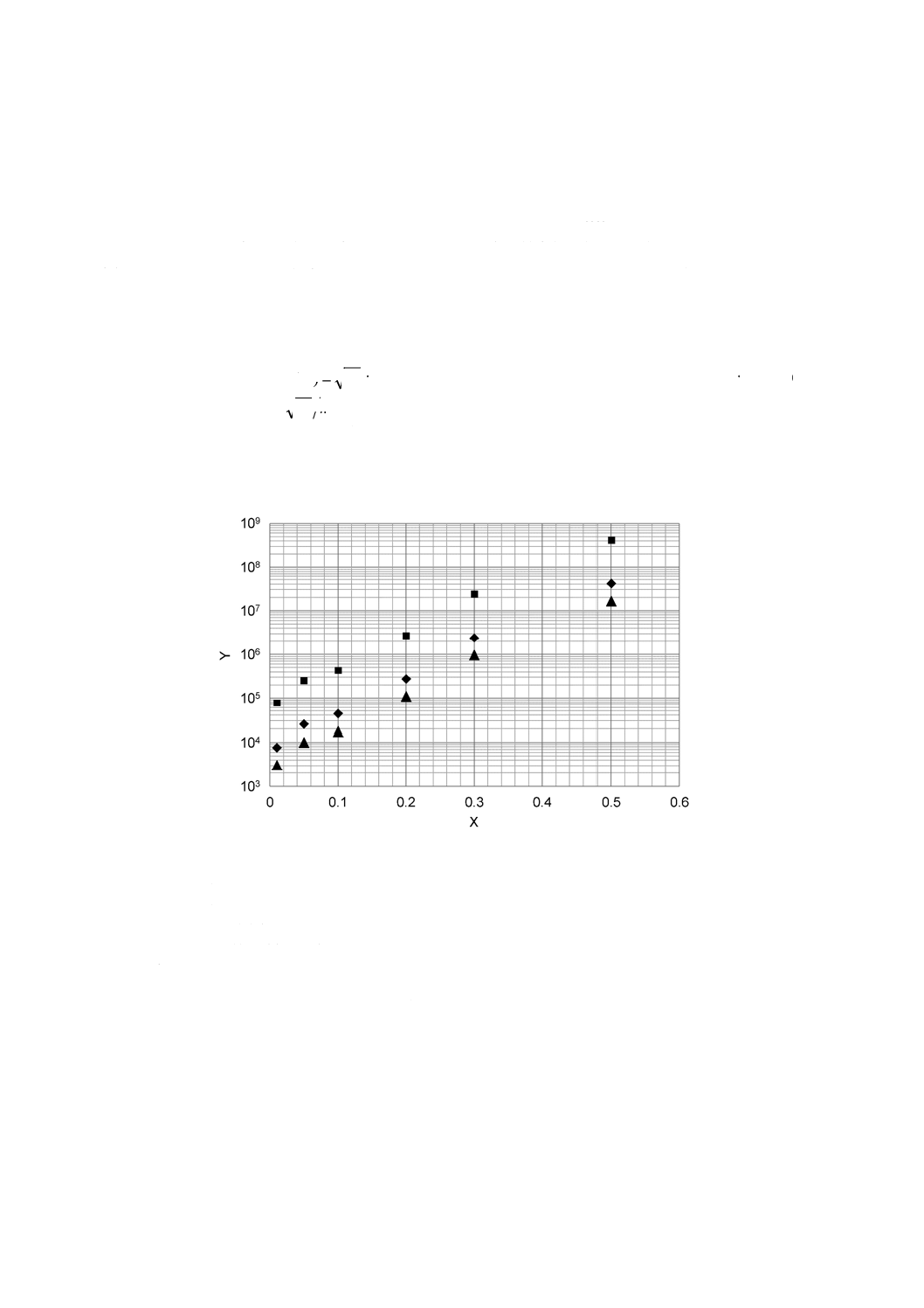
分画の中になければならない。)。このためにn*は,式(A.7)をnについて解けば得られる。図A.2に,以上
の計算で求められる,幾つかの分布幅及び不確かさのレベルに対応して必要粒子数を示した。
不確かさ
■ 1 %
◆ 3.16 %
▲ 5 %
X 分布幅log(sg)
Y 最小計数粒子数n*
注記 分布幅を表す場合のlog(sg)とx84, 3/x50, 3,x90, 3/x10, 3との関係については,表A.3参照。
図A.2−体積基準90 %径(Q3=90 %)を標準偏差で表された
所定の不確かさで求めるために必要粒子数n*
20
Z 8827-1:2018 (ISO 13322-1:2014)
附属書B
(参考)
粒子検出のための標準的な二値化の方法
B.1
総論
二値化の目的は,次のとおりである。
a) 各画素が粒子に属するかどうかを決める。
b) 粒子の輪郭線を決める。
b)の輪郭線決定法では,画素分解能より細かい補完法を用いるものが多い。この規格では当面,画素計
数によって粒子投影面積を決定する方法だけを用いることにした。
濃淡画像の二値化法の選択においては,撮像法の物理的特性を考慮する必要がある点に留意する必要が
ある(参考文献[12])。
また,粒子径及び粒子形状を決めるアルゴリズムの選択にあっては,選択した二値化法に対応している
ことに留意する必要があり,これによって,同じ粒子画像から同じ測定結果が得られるようにする必要が
ある。
B.2
二値化法
B.2.1 しきい値法
しきい値法では,濃淡画像において一定レベル以上の画素が粒子に含まれるとする。逆に一定レベル以
下の画素は背景に所属する。(粒子・背景の)濃淡が逆でも意味は同じである。二値化後は,通常,粒子と
背景とを区別するために白黒画像として表示される。
自動しきい値決定アルゴリズムでは,画像全体の濃淡分布,又は画像そのものの情報を用いてしきい値
レベルを決定する(参考文献[10] [11])。しきい値は,全測定領域全体で一定値を取るように定める方法も
あり,画像の一部ごとに別のしきい値を与える方法もあり得る。最適なしきい値決定は,撮像システム及
び粒子の光学的特性によって異なる。
高コントラストの粒子光学像に用いることができる,理想的なステップ関数に対応する理論的濃淡輝度
はGoodmanによって議論されている(参考文献[8])。それによると,非コヒーレント光源を用いる撮像シ
ステムによる画像では粒子と背景の間の50 %のしきい値を取る。しかしながら,実際の粒子の場合,その
他の撮像システムを用いる場合には,この50 %しきい値の設定が最適であるとは限らない。
B.2.2 境界検出法
境界検出アルゴリズムは,粒子輪郭線を決定するために利用される。一般的な境界検出アルゴリズムで
は,必ずしも閉曲線が得られない場合がある点には留意が必要である。
21
Z 8827-1:2018 (ISO 13322-1:2014)
附属書C
(参考)
画像解析法フローチャート
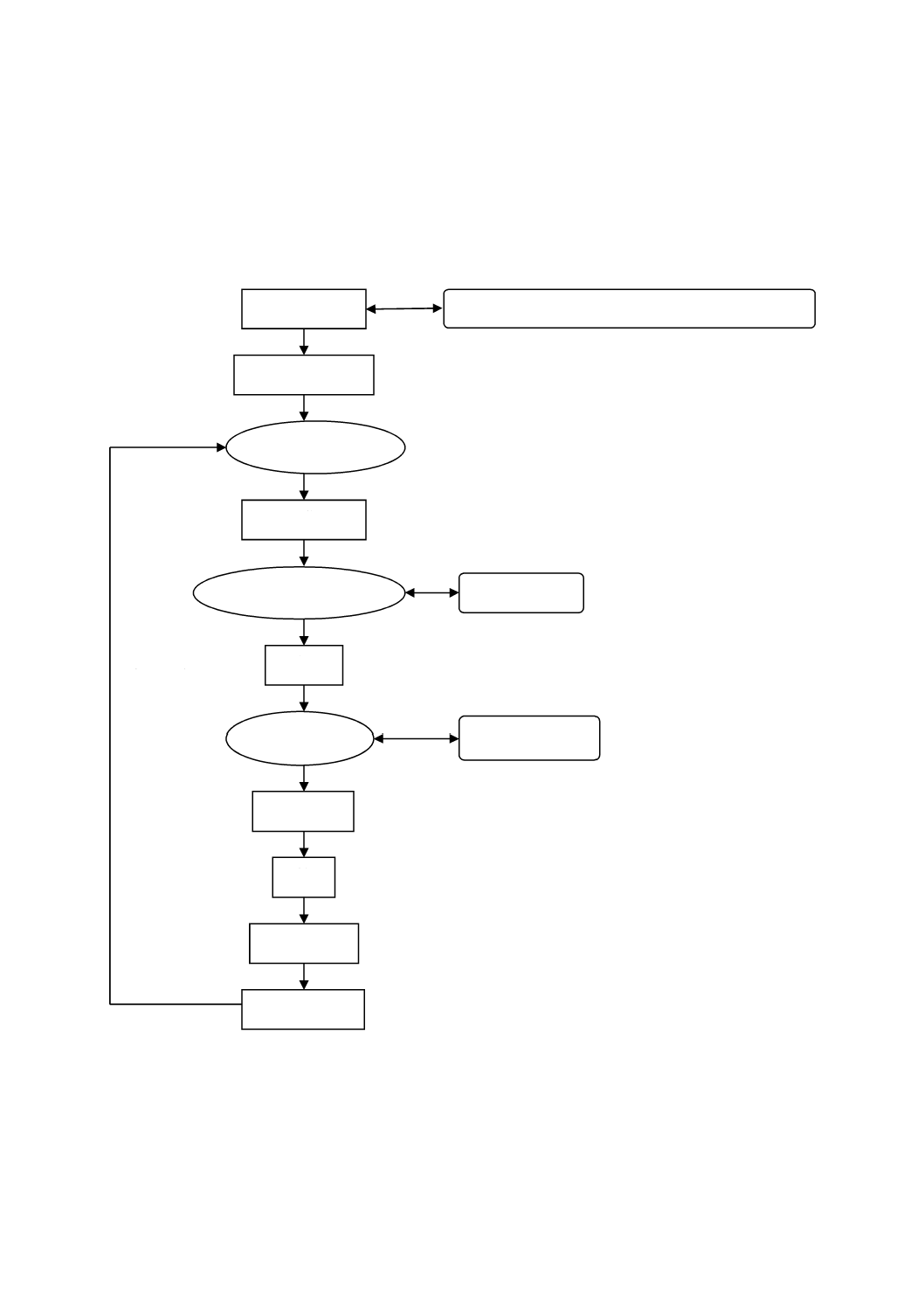
図C.1は,画像解析法フローチャートの一例である。
図C.1−典型的な画像解析法フローチャート
観察画像表示
フォーカス・照明・コントラスト及び倍率調整
測定条件の設定
観察画像確認
計測画像入力
計測対象濃淡画像
二値化
二値化画像
二値化画像処理
粒子検出
計測
データ記憶
結果表示印刷
濃淡画像処理
繰返し計測
22
Z 8827-1:2018 (ISO 13322-1:2014)
附属書D
(参考)
参考文献
[1] Masuda H., and Gotoh K., Study on the sample size required for the estimation of mean particle diameter.
Advanced Powder Technol., 1999, 10(2) p. 159-173
[2] Bell J.M., BCR Draft Method For Particle Size Distributions By Scanning Electron Microscopy and Image
Analysis. ICI Chemicals and Polymers Limited, Runcorn, England:1993.
[3] Kendall D.G., and Harding E.F. ed., Stochastic Geometry. p.228, Wiley & Sons, NY:1974
[4] Kendall D.G., and Moran P.A.P., Geometrical Probability. Charles Griffin, London, 1963
[5] Lantuejoul C., Microscopica Acta, 1980, S4 p.266
[6] JIS Q 0034 標準物質生産者の能力に関する一般要求事項
注記 対応国際規格:ISO Guide 34:2009,General requirements for the competence of reference material
producers(IDT)
[7] Wedd M.W., Procedure for Predicting a Minimum Volume or Mass of Sample to Provide a Given Size
Parameter Precisiotn. Part.Part.Syst.Charact. 2001, 18 pp.109-113
[8] Goodman J.W., Introduction to Fourier Optcs. Roberts&Company Publishers, third edition, December 2003
[9] Wedd M.W., The Influence of Pixel Numbers and Image Centering upon Particle Size Analysis Accuracy.
Part.Part.Syst.Charact. 2010, 27 pp.71-75
[10] Sahoo P., Soltani S., Wong A., A Survey of Thresholding Techniques. Comput. Vis. Graph. Image Process. 1988
February, 41 pp.233-260
[11] Sezgin M., and Sankur B., Survey over Image Thresholding Techniques and Quantitative Performance
Evaluation. J.Electron.Imaging. 2004, 13 p.146
[12] Klein T., Buhr E., Jhonsen K.P., Frase C.G., Traceable Measurement of Nanoparticle Size using a Scanning
Electron Microscope in Transmission Mode (TSEM). Meas.Sci.Technol. 2011, 22 p.094002
[13] Yoshida H., Mori Y., Masuda H., Yamamoto T., Particle Size Measurement of Standard Reference Particle
Candidates and Theoretical Estimation of Uncertainty Region. Advanced Powder Technology. 2009 March 20
pp.145-149
[14] JIS Z 8824 粒子径測定のための試料調製−粉体の液中分散方法
注記 対応国際規格:ISO 14887,Sample preparation−Dispersing procedures for powders in liquids
(MOD)







