Z 8462-7:2018 (ISO 11843-7:2012)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 3
4 定量分析及びバックグラウンドノイズ ·················································································· 4
4.1 分析における誤差の原因 ································································································· 4
4.2 バックグラウンドノイズの確率過程··················································································· 4
5 精度の理論 ······················································································································ 5
5.1 自己共分散関数に基づく理論 ··························································································· 5
5.2 パワースペクトルに基づく理論 ························································································ 6
6 FUMI理論の実践的な利用法 ····························································································· 10
6.1 ノイズパラメータの推定 ································································································ 10
6.2 SD推定の手順 ·············································································································· 11
附属書A(参考)この規格で用いる記号及び略号 ······································································ 14
附属書B(参考)式(7)の導出 ································································································· 15
附属書C(参考)式(14)〜式(16)の導出 ···················································································· 16
参考文献 ···························································································································· 18
Z 8462-7:2018 (ISO 11843-7:2012)
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人日本規格協会(JSA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 8462の規格群には,次に示す部編成がある。
JIS Z 8462-1 第1部:用語及び定義
JIS Z 8462-2 第2部:検量線が直線である場合の方法
JIS Z 8462-3 第3部:検量線がない場合に応答変数の限界値を求める方法
JIS Z 8462-4 第4部:与えられた値が検出可能か否かの判定方法
JIS Z 8462-5 第5部:検量線が線形及び非線形である場合の方法
JIS Z 8462-6 第6部:測定値がポアソン分布に従う場合の限界値及び検出可能な最小値を正規分布近
似によって求める方法
JIS Z 8462-7 第7部:分析機器ノイズの確率論的性質に基づく方法
日本工業規格 JIS
Z 8462-7:2018
(ISO 11843-7:2012)
測定方法の検出能力−第7部:分析機器ノイズの
確率論的性質に基づく方法
Capability of detection-
Part 7: Methodology based on stochastic properties of instrumental noise
序文
この規格は,2012年に第1版として発行されたISO 11843-7を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
JIS Z 8462の規格群は,検量線が線形及び非線形である場合の正味状態変数(測定対象量)の確率分布
を基礎とする。この規格では,計測した応答から得られる推定値に伴う不確かさが,主に機器分析のベー
スラインノイズに起因することに焦点を絞る。ほとんど全てではないとしても,多くの分析機器では,サ
ンプル量が検出可能な最小値程度に少ない場合は,ベースラインノイズが不確かさの主要な要因と考えら
れる。この規格で示す方法は,適用可能な範囲内においては,実サンプルの繰返し実験を省略できるため,
これに必要な時間及びエネルギーを節約することができる。
この規格の基本的な概念は,数学的に厳密に定義されている確率過程によって,応答変数の確率分布を
数学的に記述することにある。この記述は,検出可能な最小値を直接導出する。応答変数と正味状態変数
との関係は,線形及び非線形の検量線に適用できる。この規格の方法に従えば,JIS Z 8462-2及びJIS Z
8462-5との適合性が確保できる。
検出可能な最小値の定義及び応用性は,JIS Z 8462-1及びJIS Z 8462-2に規定されており,精度プロフ
ァイルの定義及び応用性は,JIS Z 8462-5に規定されている。精度プロファイルは,精度が正味状態変数
の値に依存して変化する様子を表す。この規格は,バックグラウンドノイズが支配的である機器分析にお
いて,JIS Z 8462の規格群の基本的概念を実践的に使用する方法を規定している。
検出可能な最小値xdは,正味状態変数の単位で一般的に記述する。検量線が線形である場合は,この規
格の方法で推定された応答変数の標準偏差(SD)又は変動係数(CV)は,正味状態変数のSD又はCVに
線形的に変換し,検出可能な最小値xdの推定に利用できる。
検量線が非線形である場合は,この規格における応答変数の精度プロファイルは,JIS Z 8462-5に規定
するように,正味状態変数の精度プロファイルを変換する必要がある。JIS Z 8462-5は,内容を変更する
ことなく,この変換のために利用できる。
1
適用範囲
この規格は,測定の不確かさの主要な要因がバックグラウンドノイズである場合に,検出可能な最小値
を求める数学的方法について規定する。検出可能な最小値は,バックグラウンドノイズの確率的な特性か
2
Z 8462-7:2018 (ISO 11843-7:2012)
ら直接的及び数学的に導く。
なお,バックグラウンドノイズは,サンプルを分析機器で測定しているか否かにかかわらず,分析機器
には普遍的に存在する。
この規格は,次の基本的方法を規定する。
− バックグラウンドノイズの確率的特性の抽出方法
− SD又はCVを推定するための,この特性の利用方法
− 上記の方法で得られたSD又はCVに基づく,検出可能な最小値の計算方法
機器出力のバックグラウンドノイズが他の測定の不確かさの要因よりも影響が大きい場合,この規格の
方法は,測定機器の種類に関係なく,有効である。この方法は,可視紫外吸光光度分析法,原子吸光分析
法,原子蛍光分光法,発光分光分析法,液体クロマトグラフィ,ガスクロマトグラフィなどに適している。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 11843-7:2012,Capability of detection−Part 7: Methodology based on stochastic properties of
instrumental noise(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8101-1 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: General statistical terms
and terms used in probability(IDT)
JIS Z 8101-2 統計−用語及び記号−第2部:統計の応用
注記 対応国際規格:ISO 3534-2,Statistics−Vocabulary and symbols−Part 2: Applied statistics(IDT)
JIS Z 8101-3 統計−用語と記号−第3部:実験計画法
注記 対応国際規格:ISO 3534-3,Statistics−Vocabulary and symbols−Part 3: Design of experiments
(IDT)
JIS Z 8402-1 測定方法及び測定結果の精確さ(真度及び精度)−第1部:一般的な原理及び定義
注記 対応国際規格:ISO 5725-1,Accuracy (trueness and precision) of measurement methods and results
−Part 1: General principles and definitions(IDT)
JIS Z 8462-1:2001 測定方法の検出能力−第1部:用語及び定義
注記 対応国際規格:ISO 11843-1:1997,Capability of detection−Part 1: Terms and definitions(IDT)
JIS Z 8462-2:2003 測定方法の検出能力−第2部:検量線が直線である場合の方法
注記 対応国際規格:ISO 11843-2:2000,Capability of detection−Part 2: Methodology in the linear
calibration case(IDT)
JIS Z 8462-5:2011 測定方法の検出能力−第5部:検量線が線形及び非線形である場合の方法
注記 対応国際規格:ISO 11843-5:2008,Capability of detection−Part 5: Methodology in the linear and
non-linear calibration cases(IDT)
3
Z 8462-7:2018 (ISO 11843-7:2012)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS Z 8462-1:2001,JIS Z 8462-2:2003,JIS Z 8462-5:2011,JIS Z
8101-1〜JIS Z 8101-3及びJIS Z 8402-1によるほか,次による。この規格で用いる記号及び略号は,附属書
Aを参照する。
3.1
精度プロファイル(precision profile)
<測定方法の検出能力> 応答変数又は正味状態変数のSDであり,正味状態変数の関数で表した数学
的記述(JIS Z 8462-5:2011の3.4参照)。
注記1 応答変数又は正味状態変数のCVであり,正味状態変数の関数で表した記述も同様に精度プ
ロファイルという。
注記2 精度は,観測された応答変数のSD若しくはCVで表すか,又は検量線から推定された正味
状態変数のSD若しくはCVで表す(JIS Z 8462-5:2011参照)。
注記3 <>は,この用語の定義が,この記号で示される特定分野にだけ適用することを示す。
3.2
検出可能な最小正味状態変数値,xd(minimum detectable value of the net state variable)
確率(1−β)で測定対象系が基底状態(ブランク状態)にないと判断される,実際の状態における正味
状態変数Xの値(JIS Z 8462-5:2011の3.2参照)。
注記1 正味状態変数のSD及びσX(X)が一定であると仮定する場合,検出可能な最小値xdは,式(1)
によって定義する。
xd=(kc+kd)σX ············································································ (1)
ここに,
kc: 第1種の過誤の確率に対応する係数
kd: 第2種の過誤の確率に対応する係数
応答変数のSD,つまりσYが一定[すなわちσY(X)=σY]であるという仮定の場合,検出可能な最小値は,
次の式(2)によって計算できる。
xd=(kc+kd)( σY/|dY/dX|) ································································ (2)
ここに, |dY/dX|: 検量線の傾きの絶対値。線形を対象としているので,一定
である。
注記2 正味状態変数が正規分布に従っている場合,第1種の過誤の確率及び第2種の過誤の確率α
=β=5 %に対応する係数は,kc=kd=1.65であり,式(1)は,xd=3.30σXと簡単になる。
注記3 kc=kd=1.65の場合,式(1)はσX/xd=1/3.30=30 %となる。そのため,精度プロファイルから,
xdは,CVが30 %となるXとして求まる。ここで,1/3.30=30 %としたのは,一般的に精度
プロファイルの精度がそれほど高くなく,2桁の有効数字で十分だからである。
注記4 異なるタイプの精度プロファイルを定義できるが,これらは互いに変換可能である。
例えば,応答変数のSD,つまりσY(X)は,検量線[Y=f(X)]の微分の絶対値|dY/dX|によって,
正味状態変数のSD,つまりσX(X)に変換可能である。すなわち,[σX(X)=σY(X)/|dY/dX|]である
(JIS Z 8462-5:2011参照)。
注記5 JIS Z 8462-5:2011参照。
4
Z 8462-7:2018 (ISO 11843-7:2012)
4
定量分析及びバックグラウンドノイズ
4.1
分析における誤差の原因
一般に,サンプルから測定値を求める定量分析は,調製,機器分析,データ解析及び検量で構成する。
分析における,これらの分析手順は,物理的に互いに独立であると同時に,確率論的にも互いに独立であ
る。
この規格は,機器分析だけに適用できる。ただし,上記以外の分析手順に起因する誤差も,同様に,最
終的な値である正味状態変数の誤差に影響する。すなわち,測定値の推定に関わる合成不確かさは,関与
する手順に関連する全ての不確かさの伝ぱ(播)に依存する。そのため,次の条件が,この規格を利用す
る際に必要である。
クロマトグラフィにおける検出可能な最小値に近い濃度では,測定機器へのサンプル注入に起因する誤
差(例えば,最近の機器ではCV=0.3 %)は,バックグラウンドノイズ(3.2によって,CV=30 %)ほど,
重要ではない。ノイズ以外の要素が,ノイズに匹敵する影響をもつ場合には,この規格の方法は適用でき
ない。
データ解析は,通常,ピーク高さ,面積などのような,雑音を含む機器出力からシグナル成分を抽出す
る処理である。ここで,ピーク高さとは山形のシグナルでの頂上の相対的な高さを,面積とはシグナル領
域における強度の積分を,それぞれ意味する。この処理の統計的影響をこの規格では扱う。シグナルをデ
ジタルフィルタ又はアナログフィルタ処理した後の分析にも適用できる。
4.2
バックグラウンドノイズの確率過程
応答変数の典型的な例は,クロマトグラフィにおいて測定する面積及び高さである。この規格では,出
力強度の差[式(6)]及び面積[式(10)及び式(11)]は,機器出力の強度Yiの差及び積算値としている。応
答変数は,同一機器での連続測定から得たものであっても,通常は互いに独立である。一方,一連の強度
Yiは,自己相関のある確率過程として定式化し,多くの場合,1/f(ノイズ)であると解釈している[1]。
1/f(ノイズ)のパワースペクトルP(f)は,式(3)のとおり周波数fに反比例する傾きをもつ。
()
f
f
P
1
∝
················································································ (3)
ここに,
f: 周波数,ゼロに近い値
数学の理論では,最も簡単な確率過程のモデルは,ホワイトノイズである。wiをホワイトノイズのポイ
ントiにおける確率変数とする。定義によって,どのポイントiにおいても,ホワイトノイズの平均はゼ
ロ,そのSD,すなわちw~は一定である。i≠jの場合,ノイズ強度wi及びwjが互いに独立であることは,
ホワイトノイズの重要な特徴である。
マルコフ過程は,強度Mi及びMjが互いに独立ではない(i≠j)という数学的モデルである。機器出力の
変化に自己相関がある場合,マルコフ過程を,その変化の主要な成分とみなす[式(9)参照]。ポイントi
のマルコフ過程は,次の式(4)で定義できる。
Mi=ρMi−1+mi ··········································································· (4)
ここに,
mi: ポイントiにおけるホワイトノイズの確率変数
ρ: 前の状態Mi−1を現状態Miがどの程度保持しているかを示す度
合い(−1<ρ<1)
5
Z 8462-7:2018 (ISO 11843-7:2012)
5
精度の理論
5.1
自己共分散関数に基づく理論
ワインフォードナー(Winefordner)及び彼の共同研究者が提案した理論[2][3][4]は,式(5)のとおり自己共
分散関数に基づいている。
]
[
0
s
0+
s
t
τ
t
Y
Y
E
)
ψ(τ ≡
······································································· (5)
ここに, E[·]: 角括弧内にある確率変数のt0における期待値
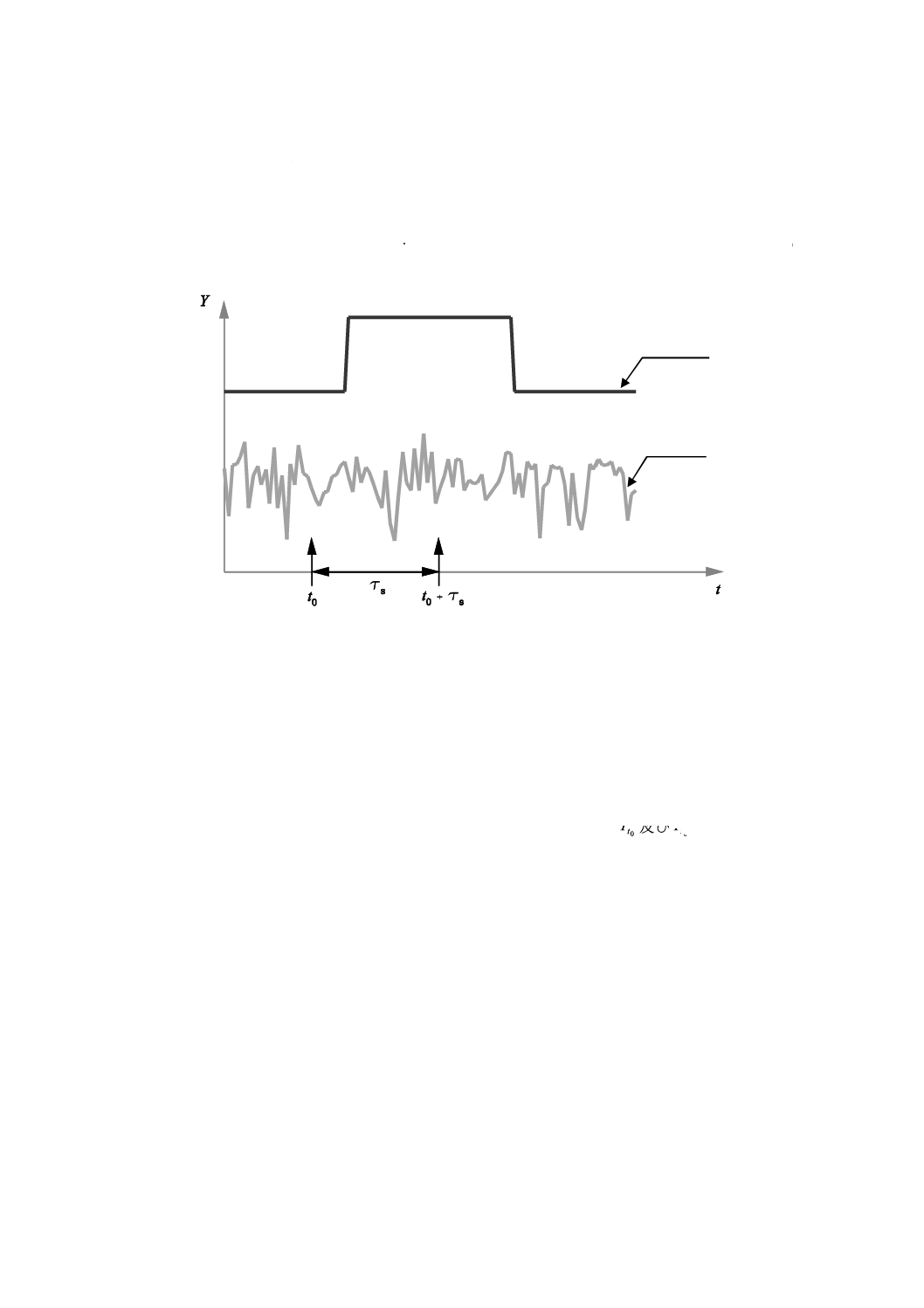
図1−シグナル,ノイズ及び強度の差(t0及びt0+τsにおける)
図1の上半分は,シグナルをく(矩)形波(近似的な描写)として示す。シグナルに加わるノイズ(バ
ックグラウンドに相当する)は,図の下半分に描かれている振動する曲線で示される。t0は,シグナルの
バックグラウンド部分の時刻を表し,t0+τsはシグナル自身の時刻を表す。測定(シグナル検出)とは,時
刻t0及びt0+τsでの強度の差を求めることである。バックグラウンドノイズが存在しなければ,シグナル
の値は,t0において0となる。サンプルを測定した場合は,シグナルの値は,t0+τsにおいて有限の値をも
つ。この規格の測定モデルでは,シグナルとノイズとは重なり合い,このランダムな混合過程によって,
時刻tiにおける強度はYiとする。時刻t0及びt0+τsにおける強度をそれぞれ
0tY及び
s
0τ
+
tY
と表し,その強度
の差を式(6)で表す。
ノイズ
シグナル
6
Z 8462-7:2018 (ISO 11843-7:2012)
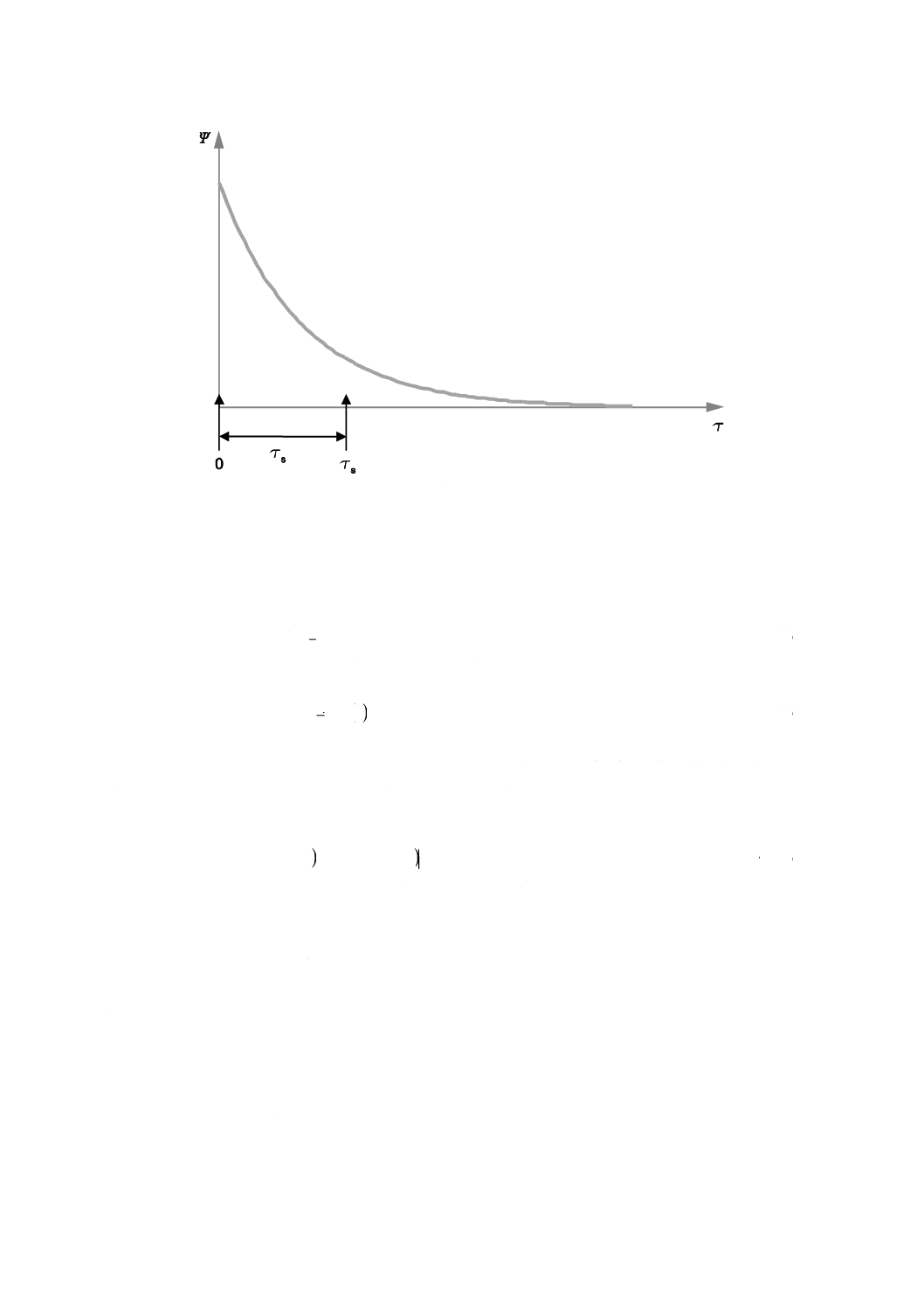
図2−ノイズの自己共分散関数
時刻0及びτsにおける自己共分散関数Ψ(τ)の値の差は,式(7)の右辺に対応する。
分析化学的な分光測定では,強度の差は,バックグラウンドゆらぎに支配される検出可能な最小値の近
傍で,しばしば利用する。強度の差,例えば,バックグラウンド補正を行ったシグナル強度は,次の式(6)
で表す[2][3][4]。
0
s
0
Δ
t
τ
t
Y
Y
Y
−
=
+
·········································································· (6)
ここに,
ΔY: 応答変数Y
強度の差の分散を,式(7)[2][3][4]によって示す[式(7)の導出に関しては,附属書B参照]。
()
()
[
]
s
2
Δ
0
2
τ
ψ
ψ
σY
−
=
··································································· (7)
図2に示すように,実際の自己共分散関数,Ψ(0)及びΨ(τs)をバックグラウンドノイズの観測から求めれ
ば,式(7)は実際の測定で利用できる。式(7)を式(2) (σY=σΔY)に代入すれば,検出可能な最小値が得られる。
自己共分散関数とパワースペクトル密度とをフーリエ変換によって関係付けるウィーナー・ヒンチンの
定理[5]が利用できる。
()
()()
(
)
∫∞
=
0
s
2
b
s
d
π
2
cos
f
fτ
f
G
f
S
τ
ψ
················································· (8)
ここに, Sb(f): 観測したバックグラウンドノイズのパワースペクトル
G(f): 測定機器の周波数応答
式(8)は,測定値のSD,つまり式(7)のパワースペクトルによる推定を表す。
5.2
パワースペクトルに基づく理論
ベースラインのパワースペクトルから,機器分析で測定した面積及び高さのSDを導く理論を,FUMI
(function of mutual information)理論[6][7][8]という。これらの測定値は,図3に示すように,機器出力を,
積分範囲で積分した値である。シグナル(形状及び大きさ)が一定で,面積又は高さの測定値の誤差の要
因がノイズだけなら,積分範囲内のノイズの面積又は高さと誤差は等しい。簡単にいうと,面積又は高さ
の測定誤差は,ノイズの面積又は高さに等しい。ノイズによって生成された面積のSDは,高さ測定値又
は面積測定値のSDと一致する。
7
Z 8462-7:2018 (ISO 11843-7:2012)
1
c+
kt
fkt
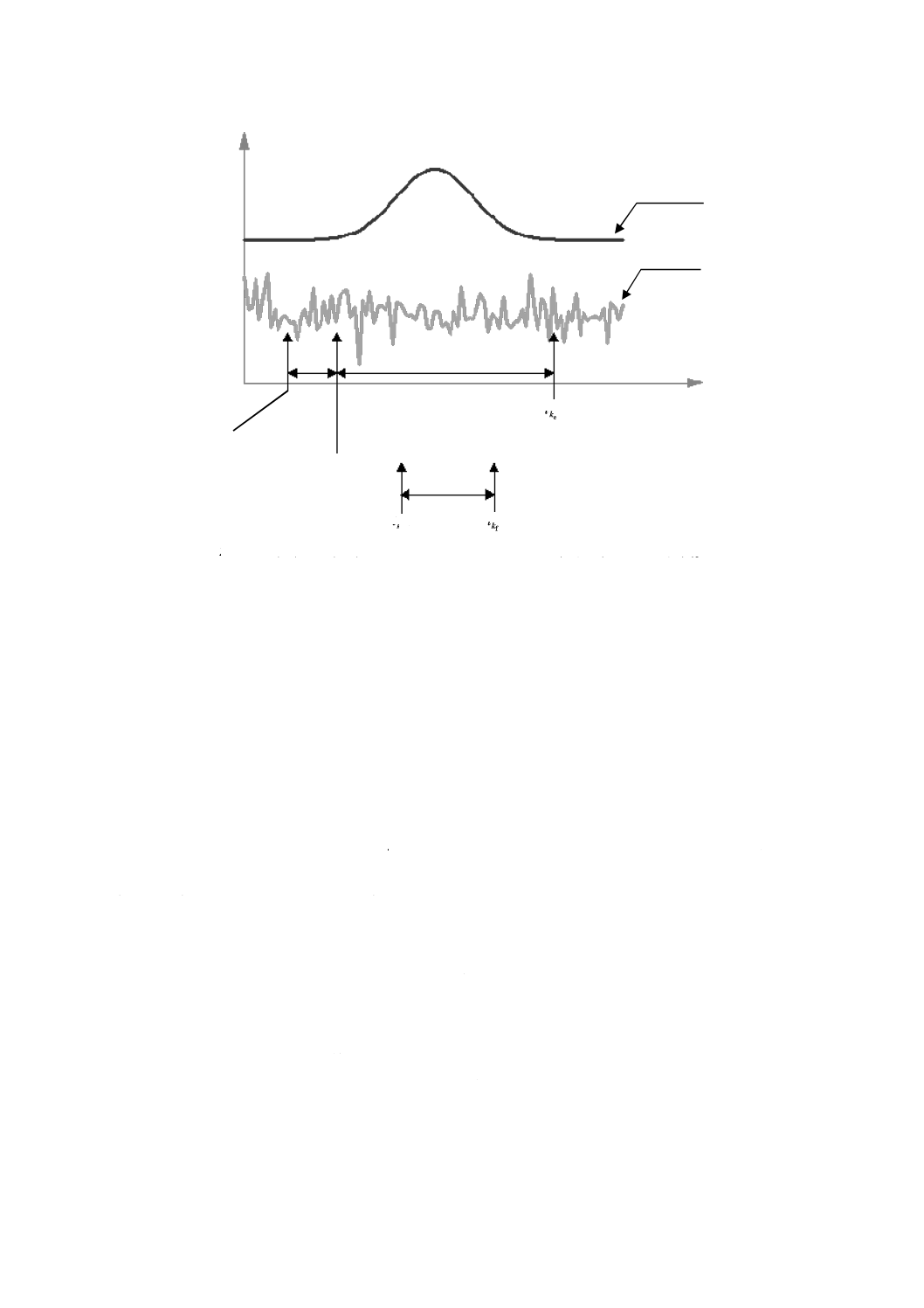
Z: ゼロウィンドウ(ベースラインのノイズデータの平均を取るための区間。
この区間のデータポイント数をbとする。)
S: シグナル領域(シグナルが立ち上がってから立ち下がるまでの領域)
I: 積分範囲
kc: 積分範囲の開始のデータポイントから一つ前のデータポイント
ke: シグナル領域の最終データポイント
kf: 積分範囲の最終データポイント
(他の記号は附属書Aに示す。)
図3−シグナル,ノイズ,ゼロウィンドウ及び積分領域
積分範囲のデータポイント数は,kf−kcである。
FUMI理論では,ポイントiにおけるノイズ強度Yiは,式(9)のとおりホワイトノイズとマルコフ過程(Mi)
とをランダムに足し合わせた値としている。
Yi=wi+Mi ················································································ (9)
FUMI理論の目的は,積分範囲内のノイズの面積AFのSDを求めることである(図3参照)。
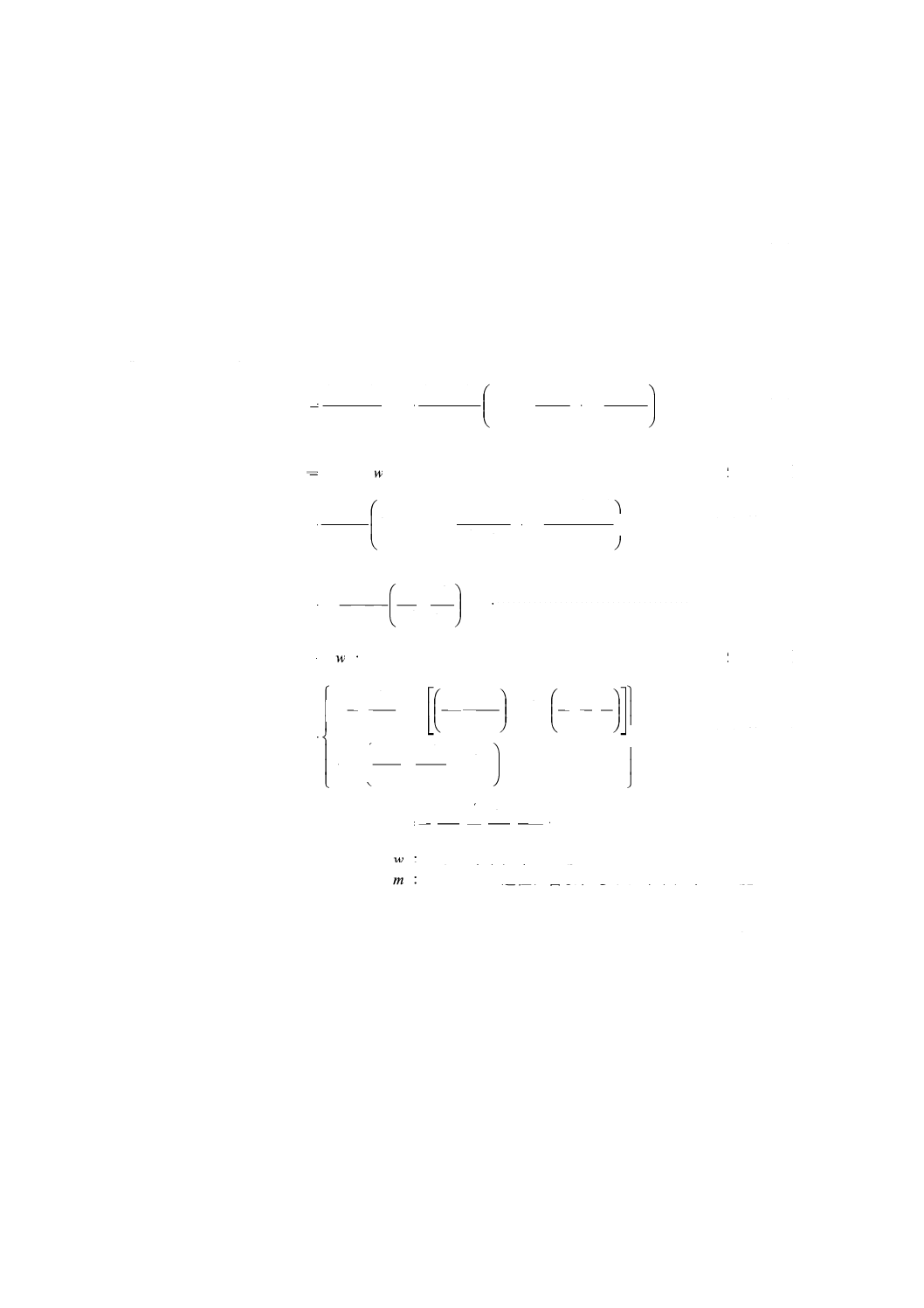
実際の測定において,特にクロマトグラフィにおいて,図4に示すように,様々な積分手法が用いられ
る。その方法には,シグナルが立ち上がったデータポイントからシグナルが立ち下がったデータポイント
まで水平のベースラインを引き,その領域を積分する方法と,シグナルが立ち上がったデータポイントと
シグナルが立ち下がったデータポイントとを直接斜線で結び,その領域を積分する方法とがある。測定値
は,領域[kc+1, kf]内における,水平又は斜めのベースラインを基準とした強度の積分である。水平なベー
スラインは,ゼロポイント(t0)の(補正された)強度から水平に引き,斜めのベースラインは,シグナ
ル領域の両端(0, ke)の強度を直線で結ぶ。後者は,緩やかに変化するバックグラウンド(クロマトグラ
フィでは,“ドリフト”という。)に対して,しばしば有効である。
I
t
S
Z
Y
t0
t−b+1
ekt
ノイズ
シグナル
8
Z 8462-7:2018 (ISO 11843-7:2012)
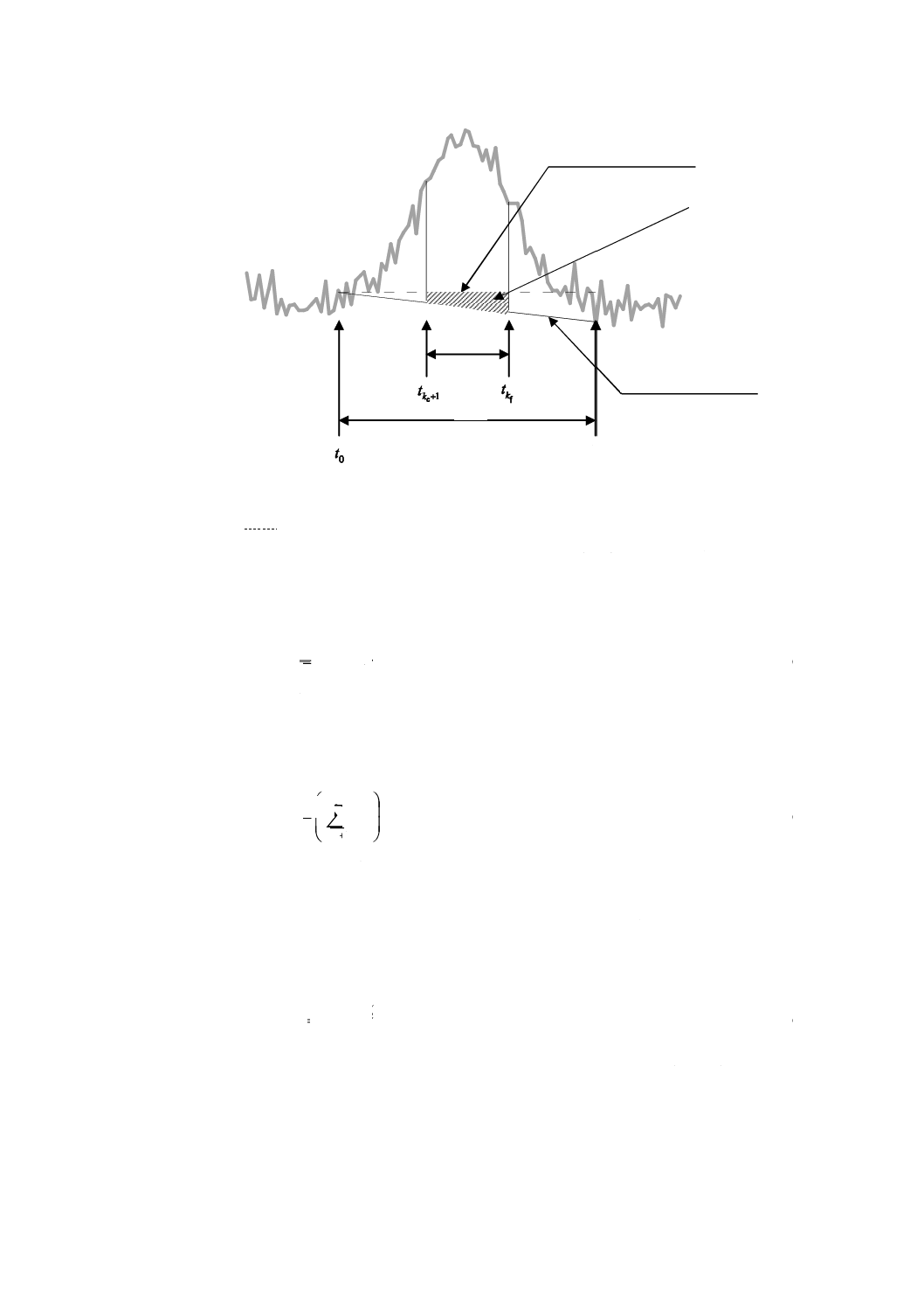
S: シグナル領域
I: 積分範囲
注a) 式(11)で用いる台形の面積とは,この部分をいう。
図4−水平線(破線)及び斜線(実線)を用いた領域[
f
c1,k
k
t
t+
]での積分様式
ベースラインが水平の場合,ノイズによって生成された面積は,シグナルがない場合の積分範囲でノイ
ズによるランダムな軌道と水平線とに挟まれた面積であり,式(10)で表す。
∑+
=
=
f
c1
F
Δ
k
k
i
it
Y
A
··········································································· (10)
ここに,
Yi: ノイズ強度
Δt: 連続するデータの時間間隔
AF: Yの応答変数
ベースラインが傾いている場合,ノイズによって生成された面積は,式(11)で表す。
T
1
F
f
c
Δ
A
t
Y
A
k
k
i
i
−
=∑+
=
···································································(11)
ここに,
AT: 積分範囲の両端(kc+1及びkf)を通るそれぞれの垂直線と,
斜線及び水平線とで囲まれた台形の面積(図4参照)。積分範
囲で斜線が水平線より上にあれば正,下にあれば負である。
図4に示す台形の面積の符号は,負である。
ノイズによって水平線の周囲に生成された面積AFのSDであるσFの一般的表現は,次の式(12)によって
表す。
[]
(
)2
1
2
F
F
A
E
σ=
········································································· (12)
ここに, E[·]: 角括弧内にある確率変数の期待値。
ノイズによって生成された面積の水平線(破線)上での集合
平均[式(11)の右辺第1項]はゼロであり,かつ,台形ATの
集合平均もゼロであるから(附属書C参照),E[AF]=0となる。
上記の導出は,ゼロレベル,すなわちY0=0には不確かさが存在しないという仮定に基づいている。し
かし,このタイプの不確かさは,実際には存在するため,考慮しなければならない。クロマトグラフィで
水平のベースライン
斜線のベースライン
I
S
a)
e
k
t
9
Z 8462-7:2018 (ISO 11843-7:2012)
は,実際の強度と,ゼロレベルつまりゼロウィンドウ区間でのバックグラウンド強度の平均値との差を測
定するのが,一般的である(図3参照)。
ゼロウィンドウを用いて測定した面積(ノイズに生成された面積)のSDの二乗は,次の式(13)によって
表す[6][7][8]。
σY2=σZ2+σF2 ··········································································· (13)
ここに,
σZ2: ゼロウィンドウに起因する分散
σF2: 面積測定値に起因する分散[σFについては式(12)参照]
式(14)及び式(15)の導出を,附属書Cに要約する。式(13)を式(2)に代入すれば,検出可能な最小値を計算
できる。
分散σZ2は,次の式(14)によって表す[6][7][8]。
(
)
(
)
(
)
2
2
2
2
2
2
2
c
f
2
2
c
f
2
Z
~
1
1
1
1
2
1
~
m
ρ
ρ
ρ
ρ
ρ
ρ
b
ρ
b
k
k
w
b
k
k
σ
b
b
−
−
+
−
−
−
−
−
+
−
=
················ (14)
シグナル領域における積分の影響は,次の式(15)によって表す[6][7][8]。
(
)
2
c
f
2
F
~w
k
k
σ
−
=
···························································· (15) 第1項
(
)
(
)
2
2
2
2
c
f
2
~
1
1
1
1
2
1
1
c
f
c
f
m
ρ
ρ
ρ
ρ
ρ
ρ
k
k
ρ
k
k
k
k
−
−
+
−
−
−
−
−
+
−
−
············· (15) 第2項
2
2
2
2
2
~
1
1
1
1
c
f
c
m
ρ
ρ
ρ
ρ
ρ
k
k
k
−
−
−
−
+
−
·········································· (15) 第3項
2
2~w
α
+
···································································· (15) 第4項
2
1
1
1
2
2
1
2
2
2
~
1
1
1
1
1
1
2
1
1
c
f
c
e
c
f
c
c
e
c
f
e
m
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
α
ρ
ρ
α
k
k
i
k
k
i
k
k
k
k
k
k
k
k
−
−
+
−
−
−
−
−
−
−
+
∑
−
=
−
−
−
+
−
−
−
−
+
−
·········· (15) 第5項
ここに,
(
)(
)
e
c
f
c
f
2
1
k
k
k
k
k
α
+
+
−
=
······························· (16)
w~: ホワイトノイズのSD
m~: マルコフ過程に含まれるホワイトノイズのSD
ρ: マルコフ過程のパラメータ(定数)
kc,kf,ke: 図3及び図4によって定義
b: ゼロウィンドウ内[−b+1, 0]での連続するデータポイン
ト数
式(15)の五つの項は,測定の不確かさに対して次のような確率論的な寄与がある。
− 第1項: 積分範囲(データポイント数:kf−kc)におけるホワイトノイズに起因する誤差
− 第2項: 積分範囲(データポイント数:kf−kc)におけるマルコフ過程に起因する誤差
− 第3項: ゼロポイント(t0)と積分の開始ポイントとの間にあるkc個のデータポイントの影響
− 第4項: 斜めのベースラインにおけるホワイトノイズの影響
− 第5項: 斜めのベースラインにおけるマルコフ過程の影響
10
Z 8462-7:2018 (ISO 11843-7:2012)
6
FUMI理論の実践的な利用法
6.1
ノイズパラメータの推定
式(13)〜式(16)で示すFUMI理論を適用する場合に必要な全てのパラメータは,実験データから決定する。
図3に示すとおり,シグナルパラメータ(b,kc,kf,ke)は,選択したピークの形から設定できる。一方,
ノイズパラメータ(w~,m~及びρ)は,次に示すように,ノイズパワースペクトル密度から自動的に決定
される。
ノイズパワースペクトル密度は,ノイズデータYiのフーリエ変換から求める。フーリエ変換及び逆フー
リエ変換は,次の式(17)及び式(18)によって表す。
∑
−
=
∧=
1
0
N
i
ki
i
k
W
Y
Y
·········································································· (17)
∑
−
=
−
∧
=
1
0
1N
k
ki
k
i
W
Y
N
Y
····································································· (18)
ここに,
N: フーリエ変換領域に含まれるデータポイント数
W: exp[−j(2π/N)]
j: 虚数単位
確率過程Yiのパワースペクトル密度P(k)は,次の式(19)によって表す。
()
N
Y
Y
k
P
k
kˆ
ˆ
=
············································································ (19)
ここに,
k
Yˆ:
k
Yˆの共役複素数
式(9)で示すモデルノイズを採用する場合は,式(19)のパワースペクトル密度は,次の式(20)によって表す
[6][7][8]。
()
2
2
2
2
2
~
]
)
(
π
4
)
1
[(
)
1(
~
w
k/N
ρ
ρ
m
k
P
+
+
−
−
=
·········································· (20)
FUMI理論に必要なノイズパラメータ(w~,m~,ρ)は,式(20)を実際のバックグラウンドノイズのパワ
ースペクトル密度に非線形最小二乗法を当てはめることによって求める。
式(19)及び式(20)に含まれているフーリエ変換の第1項
0ˆYは直流成分であり,対応するパワースペクト
ル密度P(0)を無視する。式(20)の周波数kは整数であり,1からナイキスト周波数であるN/2までの範囲に
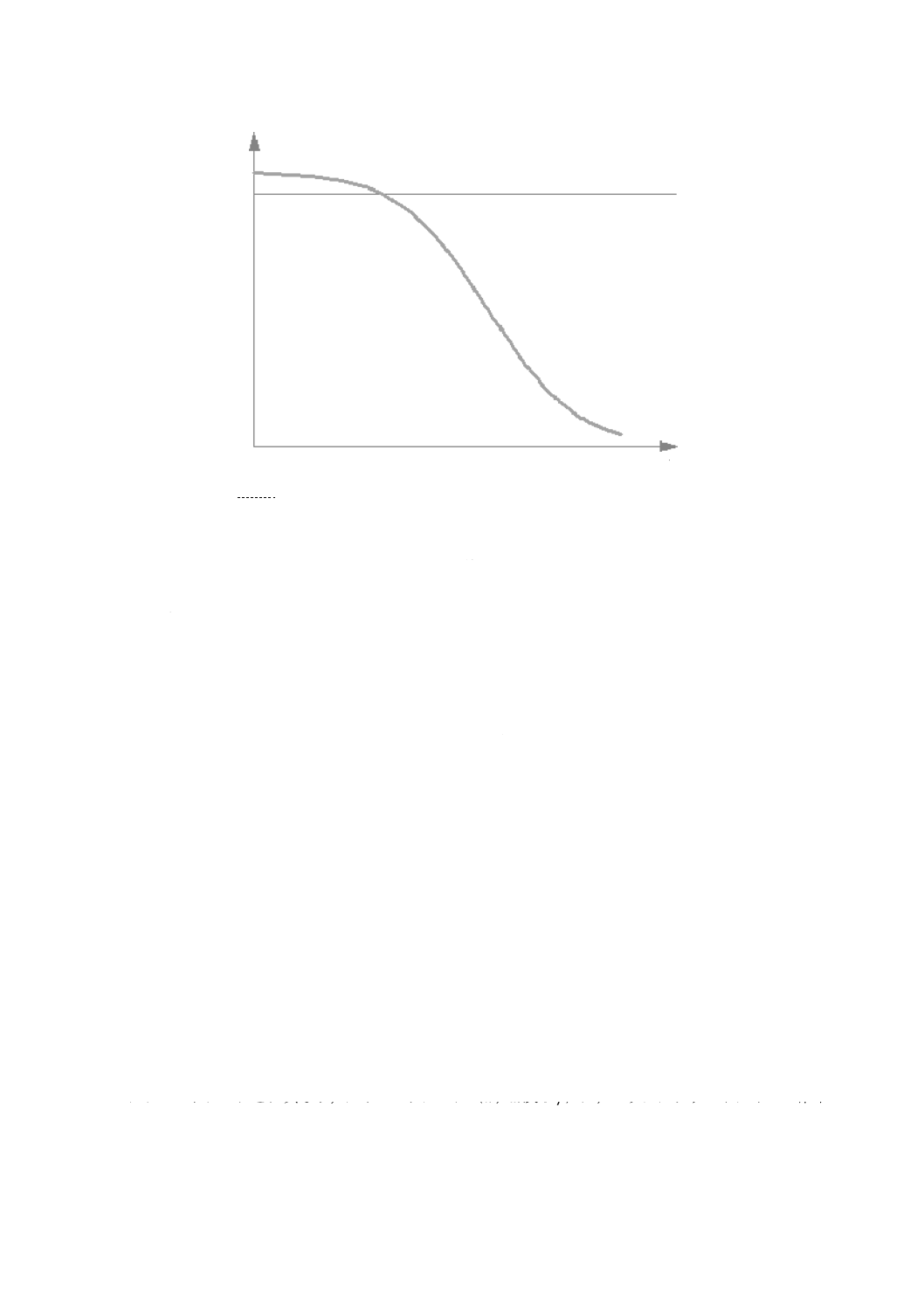
わたる。式(20)の典型例を,図5に示す。
実際の測定では,周波数kをHz(ヘルツ)で表すことが多い。Δtを,連続するデータの時間間隔(デ
ータYiの収集に使用したアナログ−デジタル変換器のサンプリング間隔)とする。k(=1, 2, …, N/2)に
対応する周波数は,k/(Δt N)である。
11
Z 8462-7:2018 (ISO 11843-7:2012)
f
注記 この図は,連続ノイズをモデルにしている。
図5−モデルノイズのパワースペクトル密度
実際には,パワースペクトル密度は,図5の理論曲線が示すほど,滑らかではない。観測されたものは,
滑らかな理論曲線の回りを振動するように見える場合がある。
6.2
SD推定の手順
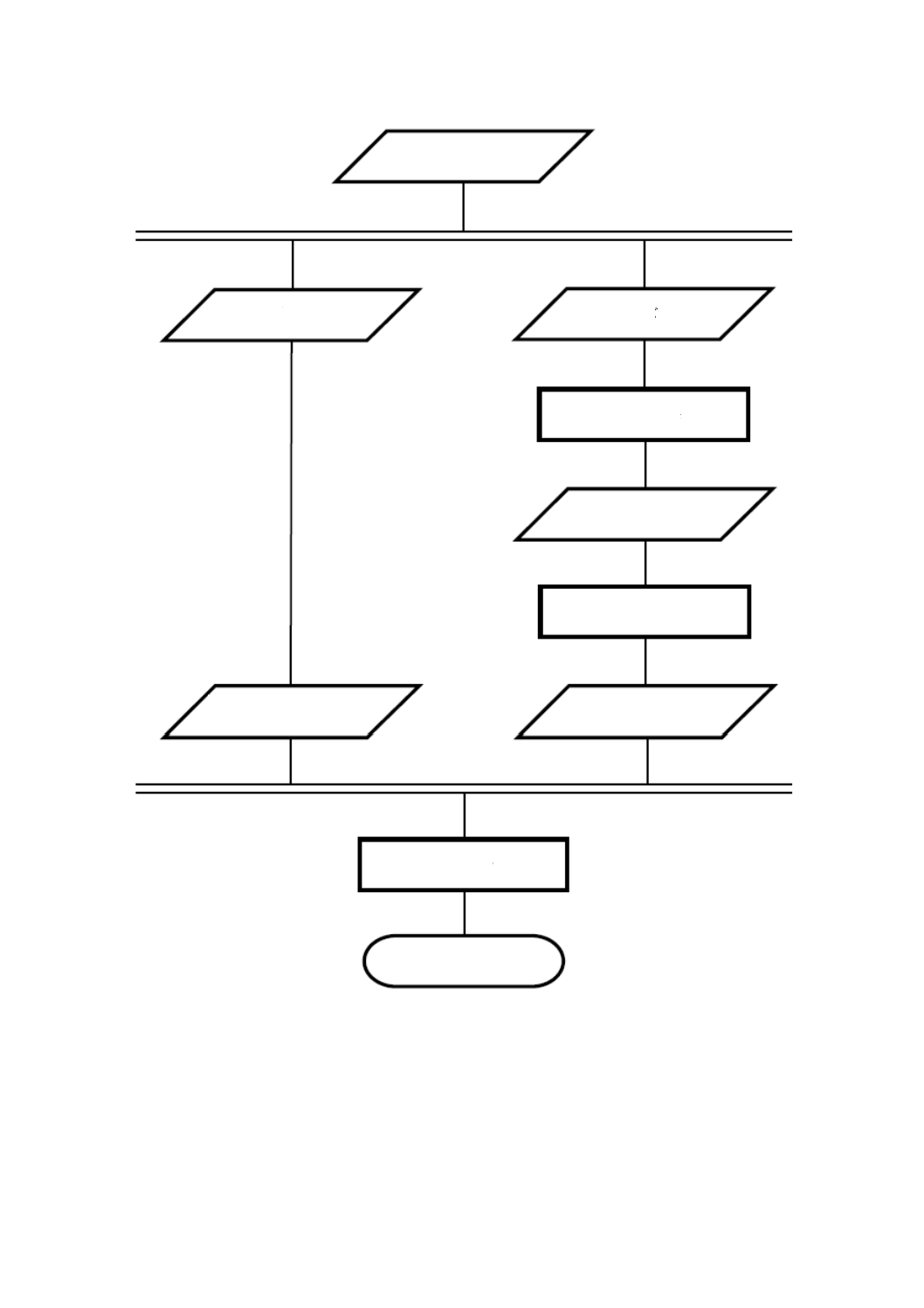
FUMI理論は,測定した面積のSDを推定するために,機器出力を使い,検出可能な最小値を導出する。
その手順を,図6に示す。
デジタル機器出力,例えば,クロマトグラム及びスペクトルは,シグナルパラメータ及びノイズパラメ
ータを抽出するために必要である。シグナルパラメータは,シグナルの立ち上がりをデータポイント0と
し,そのデータポイント0からデータポイントkeの範囲にわたるシグナル領域,データポイントkc+1か
らデータポイントkfの範囲にわたる積分領域,及びデータポイント0からデータポイント(−b+1)の範
囲にわたるゼロウィンドウを含む(図3参照)。シグナル領域のデータポイント数は(ke+1),積分領域の
データポイント数は(ke−kc),ゼロウィンドウのデータポイント数はbデータポイントで,それぞれを構
成する。
シグナルパラメータは,任意であるが実践では次の指標が有用である。図3に示すようなガウス型ピー
クでは,σを標準偏差(幅)及びシグナルの中心をガウス型ピークの平均とすると,シグナル領域の範囲
は,ピークの中心から±3σ,±4σなどの範囲がよく用いられる(ke=6σ又は8σ)。多くの場合,ピーク高
さ又は全面積が典型的な測定値である。ピーク高さ測定においては,(kf=kc+1)である。全面積測定では,
(kf=ke−1)及び(kc=0)である。いずれの場合においても,積分領域のデータポイント数は,(kf−kc)
である。精度の観点からは,図3に示すように,シグナル領域の一部だけを積算することも有効である。
図3に示すように,経験的に,ゼロウィンドウは,シグナル領域よりかなり狭い領域として,設定できる。
注記 図3のほか,図4も参照するのがよい。
シグナルパラメータとは異なり,ノイズパラメータ(w~,m~及びρ)は,バックグラウンドノイズの確率
論的性質に従って,一意に決定する。液体クロマトグラフィの例を,表1に示す。第1段階は,シグナル
が存在しないバックグラウンド領域を識別することである。
P(f)

12
Z 8462-7:2018 (ISO 11843-7:2012)
表1−液体クロマトグラフィ[6]におけるノイズパラメータ推定の例
w~
m~
ρ
実験A
14
3.7
0.99
実験B
12
9.0
0.94
実験C
14
5.6
0.99
第2段階は,この領域のバックグラウンドノイズをフーリエ変換し,式(19)に従って,パワースペクト
ル密度を得ることである。ドリフトなどの低周波ノイズを評価するには,データ数はシグナル領域のデー
タ数の10倍あった方がよい。また,高速フーリエ変換[FFT(fast Fourier transform)]のデータポイント
数は通常2の累乗(又は2のn乗)である。シグナル領域のデータ数が50又は100で,FFTを用いてバッ
クグラウンドノイズのパワースペクトル密度を計算する場合,式(19)のデータポイント数Nは,512又は
1024が適切である。
第3段階は,上記の計算によって得られたバックグラウンドノイズのパワースペクトル密度に,理論曲
線[式(20)]を最小二乗法に当てはめることである。FFT領域のデータポイント数が少ない(例えば,32)
と,ノイズパラメータの推定に支障が生じることがある。
上記のように決定したシグナルパラメータ及びノイズパラメータを式(13)〜式(16)に代入し,FUMI理論
の最終的な値(精度)を得る。
FUMI理論の適用範囲はかなり広いが,次の二つの典型的な状況には適用できない。
− バックグラウンドノイズが主要な誤差原因ではない場合である。例えば,質量分析において,イオン
化がノイズよりも大きな誤差を生じる場合,FUMI理論は面積測定値のSDを過小評価する。
− 実際の機器ノイズがホワイトノイズとマルコフ過程との混合過程では,適切に近似できないノイズを
含んでいる場合である。一例は,強いスパイクノイズである。
検出可能な最小値は,正味状態変数のCVが30 %を示す正味状態変数の値として,精度プロファイルか
ら作図によって求める。検量線が線形の場合は,正味状態変数の精度プロファイルと応答変数の精度プロ
ファイルとは同一である[9][10]ため,応答変数のCVにも,この方法を同様に適用可能である。しかし,非
線形の検量線の場合は,応答変数の精度プロファイルと正味状態変数の精度プロファイルとは異なる。こ
の場合は,JIS Z 8462-5の方法を用いて精度プロファイルを変換することによって,検出可能な最小値を,
同様に推定できる。
13
Z 8462-7:2018 (ISO 11843-7:2012)
図6−FUMI理論の手順
機器出力
シグナル
ノイズ
フーリエ変換
パワースペクトル
式(20)への当てはめ
ノイズパラメータ
シグナルパラメータ
式(13)
精度
14
Z 8462-7:2018 (ISO 11843-7:2012)
附属書A
(参考)
この規格で用いる記号及び略号
SD:
標準偏差
CV:
変動係数(標準偏差を平均値で除したもの)
X:
正味状態変数
Y:
応答変数(測定された面積又は高さ)
ti:
均一な間隔で配置された時間 t1, t2, …
Δt:
ti+1−ti,データ収集に用いたアナログ−デジタル変換の変換時間の間隔
Yi:
時刻tiにおける機器出力の強度(Yiの積算値はYである。)
Yt:
時刻tにおける機器出力の強度(Ytの積算値はYである。)
xd:
検出可能な最小正味状態変数値
kc:
第1種の過誤の確率に対応する係数
kd:
第2種の過誤の確率に対応する係数
σY(X):
Xの関数としての応答変数のSD
σX(X):
Xの関数としての正味状態変数のSD
|dY/dX|: 検量線の傾きの絶対値
E[·]:
角括弧内にある確率変数の期待値
ψ(τ):
式(5)によって定義するラグτで規定する自己共分散関数
wi:
平均が0及びSDがw~であるホワイトノイズのポイントiにおける確率変数
w~:
ホワイトノイズwiのSD
Mi:
ポイントiにおけるマルコフ過程の確率変数
Mi−1:
ポイントi−1におけるマルコフ過程の確率変数
mi:
式(4)によって定義し,ポイントiにおけるマルコフ過程に含まれるホワイトノイズ
m~:
マルコフ過程に含まれるホワイトノイズmiのSD
ρ:
式(4)によって定義し,前の状態Mi−1の保持の程度を示す比
AF:
ノイズによって生成された面積
FUMI:
相互情報量の関数(function of mutual information)
15
Z 8462-7:2018 (ISO 11843-7:2012)
附属書B
(参考)
式(7)の導出
ポイントt0及びt0+τsにおける強度の差の分散は,次の式(B.1)によって表す。
(
)
[
][
][]
[
]
0
s
0
0
s
0
0
s
0
2
2
2
2
2
Δ
t
τ
t
t
τ
t
t
τ
t
Y
Y
Y
E
Y
E
Y
E
Y
Y
E
σ
+
+
+
−
+
=
−
=
······················· (B.1)
自己共分散関数の定義[式(5)]によって,式(B.1)の右辺第2項は,次の式(B.2)によって表す。
()[]
2
0
0
tY
E
ψ
≡
·········································································· (B.2)
バックグラウンドゆらぎを定常と仮定したことによって,式(B.1)の右辺第1項と第2項とは等しい[式
(B.3)]。
[
][]
2
0
s
0
t
τ
t
Y
E
Y
E
=
+
······································································ (B.3)
このため,式(B.1)は,次の式(B.4)のように表す。
()
[
]
0
s
0
2
0
2
2
Δ
t
τ
t
Y
Y
Y
E
ψ
σ
+
−
=
·························································· (B.4)
自己共分散関数の定義[式(5)]に着目し,式(7)を得る。
16
Z 8462-7:2018 (ISO 11843-7:2012)
附属書C
(参考)
式(14)〜式(16)の導出
ホワイトノイズの確率変数が互いに独立であることが,式(14)〜式(16)の導出の基本的な仮定である。
0
]
[
=
j
iw
w
E
(i ≠ jの場合) ···················································· (C.1)
2
~
]
[
w
w
w
E
j
i
=
(i = jの場合) ···················································· (C.2)
0
]
[
=
j
im
m
E
(i ≠ jの場合) ···················································· (C.3)
2
~
]
[
m
m
m
E
j
i
=
(i = jの場合) ···················································· (C.4)
0
]
[
=
j
im
w
E
··········································································· (C.5)
ここで,式(C.5)はいかなる条件下でも成り立つ。導出された式は,ベースラインが水平な場合を含むの
で,この附属書では,ベースラインは斜めの場合の式を導く。
ゼロポイント(Y0=0)とデータポイントkeにおける観測値
e
k
Yを通る斜めのベースラインの傾きは,
e
e
k
Ykで
ある。すると,積分区間の両端の高さは,次の式(C.6)及び式(C.7)となる。
(
)1
c
e
e
+
k
k
Yk
(データポイントkc+1の場合) ···························· (C.6)
f
e
ek
k
Yk
(データポイントkfの場合) ································· (C.7)
ここで,Yiは式(9)で与えられる。斜線,水平線及び二つの垂直線で囲まれた台形[図4の注a)参照]は,
次の面積をもつ。
e
T
k
αY
A=
·············································································· (C.8)
ここで,αは,式(16)で与えられる。ノイズによって生成された面積を表す式(11)は,次の式(C.9)で表す。
e
f
c1
F
k
k
k
i
i
αY
Y
A
−
=∑+
=
·································································· (C.9)
ここで,式(11)のΔtは,単位時間と仮定している。式(C.9)の分散が,目的の式[式(15)]である。
式の導出の前に,マルコフ過程の和を,面積測定値の簡単な例として,取り上げる。M0=0の場合,式
(4)で定義するマルコフ過程は,次の式(C.10)〜式(C.12)で表す。
M1=m1 ················································································ (C.10)
M2=ρm1+m2 ········································································ (C.11)
…
Mk=ρk−1m1+ρk−2m2+...+ρmk−1+m ··········································· (C.12)
マルコフ過程の和は,次の式(C.13)で表す。
(
)
(
)
(
)
k
k
k
k
k
i
i
m
m
ρ
m
ρ
ρ
ρ
m
ρ
ρ
ρ
M
+
+
+
+
+
+
+
+
+
+
+
+
+
=
−
−
−
=∑
1
2
2
2
1
1
2
1
1
1
1
Κ
Κ
Κ
········ (C.13)
定義のE[mi]=0によって,式(C.13)の平均はゼロであるが,その分散は有限な値をとる[式(C.14)]。

17
Z 8462-7:2018 (ISO 11843-7:2012)
(
)
(
)
(
)
2
2
2
2
2
2
2
1
2
2
1
~
~
1
~
1
~
1
m
m
ρ
m
ρ
ρ
ρ
m
ρ
ρ
ρ
M
E
k
k
k
i
i
+
+
+
+
+
+
+
+
+
+
+
+
+
=
−
−
=∑
Κ
Κ
Κ
(C.14)
この式(C.14)は,次の簡単な式(C.15)となる。
(
)
−
−
+
−
−
−
−
=
∑
=
2
2
2
2
2
2
1
1
1
1
1
2
1
~
ρ
ρ
ρ
ρ
ρ
ρ
k
ρ
m
M
E
k
k
k
i
i
·························· (C.15)
kf−kcを式(C.15)のkに代入し,式(15)の第2項を得る。式(15)の第1項は,データポイントkfからデータ
ポイントkcまでの間のホワイトノイズの和である。式(15)のその他の項は,式(C.1)〜式(C.5)及び式(C.9)〜
式(C.15)を考慮して得る[7]。付け加えると,E[wi]=0及びE[mi]=0の仮定の下では,E[AF]=0である。
ゼロウィンドウの設定に伴う不確かさも,同様な方法で導く[8]。ゼロレベルL0は,連続したbデータの
平均値として定義する[式(C.16)]。
=∑
=
b
i
iY
b
L
1
0
1
······································································· (C.16)
ここで,Yiは式(9)から得る。ゼロレベルの設定は,次の式(C.17)で示す面積を積分領域内に作ることに
よって,積分領域内でのバックグラウンドを補正することを意味する。
(kf−kc)L0 ·············································································· (C.17)
よって,ゼロウィンドウの設定に伴う不確かさは,次の式(C.18)によって表す。
σZ2=(kf−kc)2E[L02]·································································· (C.18)
ここで,定義によって,E[L0]=0である。式(C.16)の∑
=
b
i
iY
1
の代わりに,式(C.13)を用いて,式(14)の第2
項に一致する式を得る[8]。式(14)の第1項は,ホワイトノイズだけの影響を表す。
18
Z 8462-7:2018 (ISO 11843-7:2012)
参考文献
[1] Ingle, J.D. Jr. and S.R. Crouch. Spectrochemical Analysis. Prentice-Hall, Inc., New Jersey, 1988
[2] Alkemade, C.Th.J., W. Snelleman, G.D. Boutilier, B.D. Pollard, J.D. Winefordner, T.L. Chester and N.Omenetto.
A review and tutorial discussion of noise and signal-to-noise ratios in analytical spectrometry-I. Fundamental
principles of signal-to-noise ratios. Spectrochim. Acta, 33B, pp. 383-399, 1978
[3] Boutilier, G.D., B.D. Pollard, J.D. Winefordner, T.L. Chester and N. Omenetto. A review and tutorial discussion
of noise and signal-to-noise ratios in analytical spectrometry-II. Fundamental principles of signal-to-noise ratios.
Spectrochim. Acta, 33B, pp. 401-415, 1978
[4] Alkemade, C.Th. J., W. Snelleman, G.D. Boutilier and J.D. Winefordner. A review and tutorial discussion of
noise and signal-to-noise ratios in analytical spectrometry-III. Multiplicative noises. Spectrochim. Acta, 35B, pp.
261-270, 1980
[5] 日野幹雄:スペクトル解析,朝倉書店,(1977)
注記:Hino, M. Spectral Analysis (Supekutoru Kaiseki). Asakura Shoten, Tokyo, 1982
[6] Hayashi, Y. and R. Matsuda. Deductive prediction of measurement precision from signal and noise in liquid
chromatography. Anal. Chem., 66(18), pp. 2874-2881, 1994
[7] Hayashi, Y. and R. Matsuda. Prediction of precision from signal and noise measurement in liquid
chromatography: Mathematical relationship between integration domain and precision, Chromatographia, 41,
pp. 75-83, 1995
[8] Poe, R.B., Y. Hayashi and R. Matsuda. Precision-optimization of wavelengths in diode-array detection in
separation science. Anal. Sci., 13, pp. 951-962, 1997
[9] Kotani, A., Y. Yuan, B. Yang, Y. Hayashi, R. Matsuda and F. Kusu. Selection of the optimal solvent grade for the
mobile phase in HPLC with electrochemical detection based on FUMI theory. Anal. Sci., 25, pp. 925-929, 2009
[10] Kotani, A., S. Kojima, Y. Hayashi, R. Matsuda and F. Kusu, Optimization of capillary liquid chromatography
with electrochemical detection for determining femtogram levels of baicalin and baicalein on the basis of the
FUMI theory. J. Pharm. Biomed. Anal., 48, pp. 780-787, 2008








