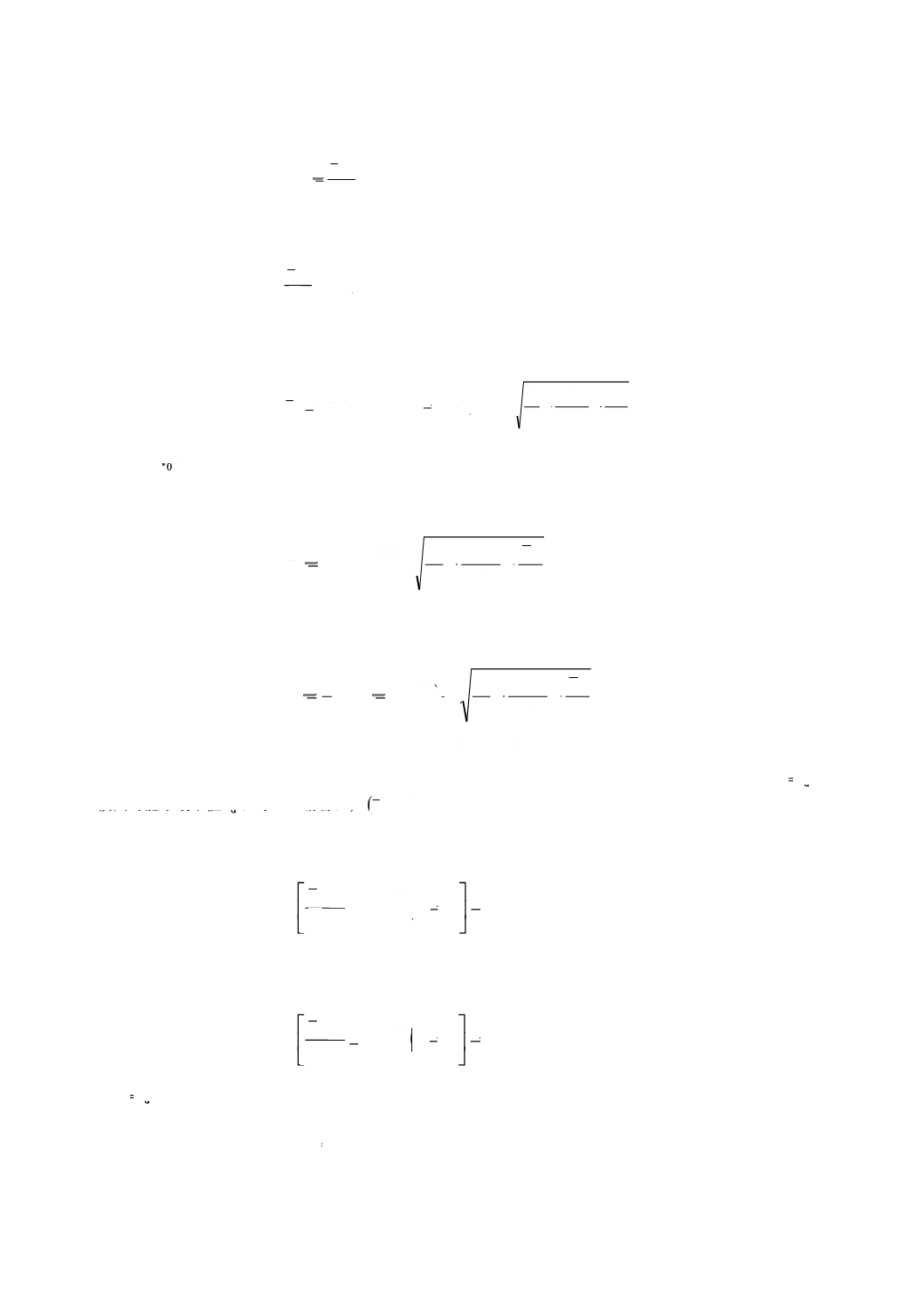Z 8462-2:2003
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人日本規格協会(JSA)から,工業標準
原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大
臣が制定した日本工業規格である。
制定に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO 11843-2:2000,Capability of detection
- Part 2: Methodology in the linear calibration caseを基礎として用いた。
JIS Z 8462-2:2003には,次に示す附属書がある。
附属書A(規定)記号及び略語
附属書B(参考)式の誘導
附属書C(参考)例
JIS Z 8462-2:2003には,次に示す部編成がある。
JIS Z 8462-1 測定方法の検出能力 ― 第1部:用語及び定義
Z 8462-2:2003
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 2
3. 用語及び定義 ·················································································································· 3
4. 実験計画 ························································································································ 3
4.1 一般的事項 ··················································································································· 3
4.2 参照状態の選択 ············································································································· 3
4.3 参照状態の数I,測定操作の反復回数J,K,Lの選択 ··························································· 3
5. 一連の測定における限界値yc,xc及び検出可能な最小値xd······················································· 4
5.1 基本的仮定 ··················································································································· 4
5.2 ケース1―標準偏差が一定の場合 ······················································································ 4
5.3 ケース2―標準偏差が正味状態変数と直線関係にある場合······················································ 6
6. 測定方法の検出可能な最小値 ····························································································· 9
7. 報告と結果の適用 ··········································································································· 10
7.1 限界値 ························································································································ 10
7.2 検出可能な最小値 ········································································································· 10
附属書A(規定)記号及び略語 ······························································································ 11
附属書B(参考)式の誘導 ···································································································· 13
B.1 ケース1―標準偏差が一定の場合 ····················································································· 13
B.2 ケース2―正味状態変数と直線関係となる標準偏差 ····························································· 16
附属書C(参考)例 ············································································································· 18
C.1 例1 ··························································································································· 18
C.2 例2 ··························································································································· 19
参考文献 ···························································································································· 22
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8462-2:2003
測定方法の検出能力−
第2部:検量線が直線である場合の方法
Capability of detection - Part 2: Methodology in the linear calibration case
序文 この規格は,2000年に第1版として発行されたISO 11843-2:2000,Capability of detection - Part 2:
Methodology in the linear calibration caseを翻訳し,技術的内容及び規格票の様式を変更することなく作成し
た日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
ある状態変数に関する測定方法の検出能力についての理想的な条件は,観測された各測定対象系の実際
の状態が,基底状態と等しいか又は異なるかということを確実に識別できることである。しかし,実際に
は,系統的及び偶然の誤差のために,次のような理由で,この理想的な条件を満足することはできない:
― 基底状態を含むすべての参照状態は,その状態変数については未知であるというのが実情である。し
たがって,すべての状態は基底状態との差,すなわち正味状態変数としてだけ正しく特性付けられる。
実際は,参照状態の状態変数は既知であると仮定される場合が多い。言い換えると,基底状態に対
する状態変数の値はゼロと設定する;例えば分析化学において,ブランク物質に含まれる未知の分析
対象成分の濃度又は量は通常ゼロであるとみなし,測定対象成分の正味濃度又は正味量の値を報告す
る。特に微量成分分析においては,測定対象成分の濃度又は量は利用可能なブランク物質との差とし
てしか推定することはできない。誤った判断をしないために,基底状態との差,すなわち正味状態変
数としてだけデータを報告することが一般的に推奨される。
備考 JIS Q 0030及びJIS Z 8461においては,状態変数と正味状態変数が区別されていない。その結
果,これらの文書においては,特にことわらずに参照状態の状態変数が既知であるとみなして
いる。
参考 JIS Q 0030では標準物質に関する定義が述べられており,検量線に関する統計的取扱いに関す
る事項はむしろJIS Q 0033の方で言及されている。
― 校正の段階とサンプリング及び試料調製過程において,測定結果にランダムな変動が加わる。
この規格では,次の二つの確率についての要件を規定した:
― 測定対象系が基底状態にあるとき,これが基底状態にないものと(誤って)判定する確率をαとする;
― 正味状態変数の値が検出可能な最小値(dx)に等しい測定対象系について,これが基底状態にないと(誤
って)判定する確率をβとする。
1. 適用範囲 この規格は次の目的のための基本的方法を規定する:
― 正味状態変数の限界値,応答変数の限界値及び検出可能な最小正味状態変数値を推定するための実験
を計画する,
― 校正関数(検量線)が直線であり,応答変数の標準偏差が一定の場合又は正味状態変数と直線関係に
2
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ある場合に,実験データから正味状態変数の限界値,応答変数の限界値,及び検出可能な最小正味状
態変数値を推定する。
この規格に規定する方法は,物質中に含まれる特定成分の存在の有無,サンプル又はプラントからのエ
ネルギーの放射,外力による静力学的形状変化のチェックなど,種々の場合に適用することができる。
二つの限界値は,一連の測定対象系の未知の状態を評価するための実際の一連の測定から導くことがで
き,一方,測定方法の特性としての検出可能な最小正味状態変数値は,適切な測定プロセスを選択すると
きに役立つ。測定プロセス,試験室,又は測定方法を特性化するために,関連する各水準,すなわち一連
の測定,測定プロセス,試験室,又は測定方法に関して適正なデータが得られれば,検出可能な最小値を
示すことができる。検出可能な最小値は,一連の測定,測定プロセス,試験室,又は測定方法ごとに異な
る場合もある。
参考 測定方法,測定プロセス,測定方法のタイプについては,JIS Z 8462-1に付された解説を参考
にされたい。
JIS Z 8462シリーズは,基本的に連続な量に適用することができる。また応答変数の期待値と状態変数
値との関数関係が校正関数(検量線)によって表される測定プロセス及び測定装置に適用することができ
る。応答変数又は状態変数がベクトル量の場合,JIS Z 8462シリーズの方法は,ベクトルの成分又は成分
の関数に対して別々に適用することができる。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide21に基づき,IDT(一致している),MOD(修
正している),NEQ(同等でない)とする。
ISO 11843-2:2000,Capability of detection - Part 2: Methodology in the linear calibration case (IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発効年(又は発行年)を付記してあるものは,記載の年の版だけがこの
規格の規定を構成するものであって,その後の改正版・追補には適用しない。発効年(又は発行年)を付
記していない引用規格は,その最新版(追補を含む)を適用する。
JIS Z 8101-1:1999 統計―用語と記号―第1部:確率及び一般統計用語
備考 ISO 3534-1:1993 Statistics - Vocabulary and symbols - Part 1: Probability and general statistical
termsからの引用事項は,この規格の該当事項と同等である。
JIS Z 8101-2:1999 統計―用語と記号―第2部:統計的品質管理用語
備考 ISO 3534-2:1993 Statistics - Vocabulary and symbols - Part 2: Statistical quality controlからの引
用事項は,この規格の該当事項と同等である。
JIS Z 8101-3:1999 統計―用語と記号―第3部:実験計画法
備考 ISO /FDIS 3534-3:1999 Statistics - Vocabulary and symbols - Part 3: Design of experimentsが,こ
の規格と一致している。
JIS Z 8461:2001 標準物質を用いた校正(検量線が直線の場合)
備考 ISO 11095:1996 Linear calibration using reference materialsが,この規格と一致している。
JIS Z 8462-1:2001 測定方法の検出能力―第1部:用語及び定義
備考 ISO 11843-1:1997 Capability of detection - Part 1: Terms and definitionsが,この規格と一致して
いる。
JIS Q 0030:1997 標準物質に関連して用いられる用語及び定義
3
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 ISO Guide 30:1992 Terms and definitions used in connection with reference materialsが,この規
格と一致している。
3. 用語及び定義 この規格で用いる主な用語の定義は,JIS Z 8101(すべての部),JIS Q 0030,JIS Z 8461,
及びJIS Z 8462-1による。
4. 実験計画
4.1
一般的事項 実際の状態を定量する手順には,サンプリング,試料調製,及び(機器などによる)
測定そのものが含まれる。この手順の各ステップで誤差が発生する可能性があるため,特性付け,すなわ
ち,試料調製及び実際の状態を定量するときの操作,並びに,校正(検量線作成)に使用するすべての参
照状態及び基底状態に対して,同一の手順を適用しなければならない。
値が未知である実際の状態と基底状態との差を定量するためには,両者を比較するのに適した実験計画
を採用する必要がある。このような実験に必要な実験のセットは,測定対象の実際の状態と校正(検量線
作成)に使用するすべての参照状態から成り立つ。理想的には,定量結果に影響を及ぼすことが知られて
いる要因をすべて一定に保ち,試料調製の順序及び測定の順序をランダム化することによって,未知の要
因を管理することが望ましい。
実際には,関連する状態の試料調製と定量がある時間連続して行われるため,このように試料調製の順
序と測定の順序をランダム化して要因を一定に保つことは困難なことがある。しかし,時間とともに変動
する主要なかたよりを防ぐため,校正(検量線作成)の半分ずつを値が未知である状態の測定の前後に行
うことが強く望まれる。ところが,これは一連の測定の量(サンプル数)があらかじめ分かっていて,し
かもそのために十分時間があるときにだけ可能である。影響要因の中に管理できない要因がある場合は,
検証されない仮定をすべて記述して,その測定結果は条件付きであることを付記しなければならない。
測定方法には,あらかじめサンプルの化学的又は物理的処理を必要とするものが多い。これらの測定手
順の各ステップがいずれも測定結果を変動させる。測定を繰り返す必要がある場合は,試料調製と測定を
すべて繰り返さなければならない。しかし,測定手順全体が繰り返されない場合も多い。特に測定ごとに
試料調製のステップがすべて繰り返されるとは限らない;5.2.1の備考を参照。
4.2
参照状態の選択 参照状態が対象とする正味状態変数の値の範囲には,次の値を含めることが望ま
しい。
― 正味状態変数のゼロ値,すなわち,分析化学におけるブランク物質のサンプル,及び
― 検出可能な最小値に関する事前の情報が示唆する値に近い値を1個以上;もしこの要件が満たされな
い場合は,適切な正味状態変数の他の値を用いて校正実験を繰り返すことが望ましい。
参照状態は,(対数値を含む)正味状態変数の値が,最小値と最大値の間においてほぼ等間隔となるよう
選択するのがよい。
参照状態を表すために標準物質を調製して使用する場合,その組成は可能な限り測定対象物質の組成に
近くなければならない。
4.3
参照状態の数I,測定操作の反復回数J(各参照状態に対する試料調製数),K(実際の状態に対する
試料調製数),L(各試料調製に対する繰返し測定回数)の選択 参照状態,試料調製数,及び,繰返し測
定回数は次のとおりとする。
― 校正実験に使用する参照状態の数Iは,3以上でなければならない;推奨値はI = 5である;
― (基底状態を含む)各参照状態に対する試料調製数Jは,同一であることが望ましい;推奨値はJ = 2
4
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
以上である;
― 実際の状態に対する試料調製数Kは,各参照状態の試料調製数Jと同一とすることが望ましい;
― 各試料調製当たりの繰返し測定回数Lは,同一とする;推奨値は,L = 2以上である。
備考 5.に規定する限界値及び検出可能な最小値の式は,試料調製当たりの繰返し測定回数が,参照
状態及び実際の状態の測定すべてについて同一でなければ成立しない。
試料調製のばらつき及びコストは,一般に,測定におけるばらつき及びコストよりはるかに大きいため,
ばらつきとコストとの関係を最適化することによって,J,K,及びLの最適値が導かれる。
5. 一連の測定における限界値yc,xc及び検出可能な最小値xd
参考 ここで用いる記号yc,xc,及びxdは、JIS Z 8462-1で用いていた記号yC,xC,及びxDと同一である。
参考 以下で用いられる用語“検出可能な最小値”は、“検出可能な最小正味状態変数値”を意味する。
5.1
基本的仮定 次に示す限界値と検出可能な最小値の計算手順はJIS Z 8461に示された仮定に基づい
ている。ただし,JIS Z 8461の方法が少し一般化されて使用されている;5.3を参照。
JIS Z 8461の基本的仮定は,
― 校正関数(検量線)は直線である,
― すべての試料及び参照状態の応答変数の測定値は独立で正規分布し,その標準偏差を残差標準偏差と
呼ぶ。
― この残差標準偏差は一定,すなわち,正味状態変数値に依存しないか(ケース1),又は正味状態変数
値の一次関数である(ケース2)
である。
実際のデータに,この規格が適用可能であるか否か,及び上記の二つのケースのいずれを選択するかに
ついては,事前の知識及びグラフ化されたデータの視覚的な判断に基づいて決定する。
5.2
ケース1―標準偏差が一定の場合
5.2.1
モデル 次の式で表されるモデルは,校正関数(検量線)が直線であり,標準偏差が一定であると
いう仮定に基づく。
ij
i
ij
bx
a
Y
ε
+
+
=
··········································································· (1)
ここに,
ix: 参照状態iにおける正味状態変数;
ij
ε: サンプリング,試料調製及び測定誤差のラ
ンダム成分を表す確率変数。
ij
εは独立な正規分布に従う変数であり,その期待値はゼロ,残差標準偏差はσとすると,ij
ε〜N (0;
2
σ)
と表せる。したがって,応答変数の値ij
Yは期待値E (ij
Y) =a+
i
bx,ixには依存しない分散V (ij
Y) =
2
σをも
つ確率変数である。
備考 参照状態iについて,J個のサンプルを調製し,それぞれについてL回,合計J×L回測定を行
う場合,ij
Yは調製した試料について得られるL回の測定の平均値である。
参考
ij
ε〜N (0;
2
σ)はij
εが平均値0,標準偏差σの正規分布に従う事を示す。
5.2.2
校正関数(検量線)と残差標準偏差の推定 JIS Z 8461によって,a,b及び
2
σの推定値(備考を
参照)は次の式から得られる。
5
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)(
)
xx
I
i
J
j
ij
i
s
y
y
x
x
b
∑∑
=
=
−
−
=
1
1
ˆ
······························································ (2)
x
bˆ
y
aˆ
−
=
················································································· (3)
(
)
∑∑
=
=
−
−
−
×
=
I
i
J
j
i
ij
x
b
a
y
J
I
1
1
2
2
ˆ
ˆ
2
1
ˆσ
·········································· (4)
上式で使用する記号と,この規格の他の箇所で使用する記号の定義は,附属書Aを参照。
備考 推定値は記号∧で表し,未知であるパラメータ自体と区別する。
参考 原国際規格では式(2)において,二つめのΣの下のj=1をj-1と誤記されている。
5.2.3
限界値の計算 応答変数の限界値は,次の式から得られる。
()
xx
s
x
J
I
K
t
a
y
2
95
.0
1
1
ˆ
ˆ
+
×
+
+
=
σ
ν
c
··········································· (5)
正味状態変数の限界値は,次の式から得られる。
()
xx
s
x
J
I
K
b
t
x
2
95
.0
1
1
ˆ
ˆ
+
×
+
=
σ
ν
c
··············································· (6)
ここで,
()
ν
95
.0t
は,自由度ν = I×J−2のt分布の95%点である。
これらの式の導出は,附属書Bを参照。
5.2.4
検出可能な最小値の計算 検出可能な最小値は,次の式から得られる。
xx
s
x
J
I
K
b
x
2
1
1
ˆ
ˆ
+
×
+
=σ
δ
d
······················································ (7)
ここで,非心度の値δ=(
)
β
α
ν;
;
は,自由度ν = I×J−2,非心度δの非心t分布に従う確率変数(
)
δ
ν;
T
が次の式
を満たすように求める。
(
)
()
[
]β
ν
δ
ν
α
=
≤
−
1t
T
P
;
ここで,t1−α (ν)は,自由度νのt分布の(1−α)分位点である。
6
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この式の導出は,附属書Bを参照。
α = β及びν>3の場合,次の式でδの良好な近似値が与えられる。
(
)
()
ν
β
α
ν
δ
α
−
≈
1
2t
;
;
································································ (8)
ν = 4及びα = β = 0.05の場合,この近似値の相対誤差は5%である。またt1−α(ν)は,自由度ν = I×J−2の
t分布の(1−α)分位点である。
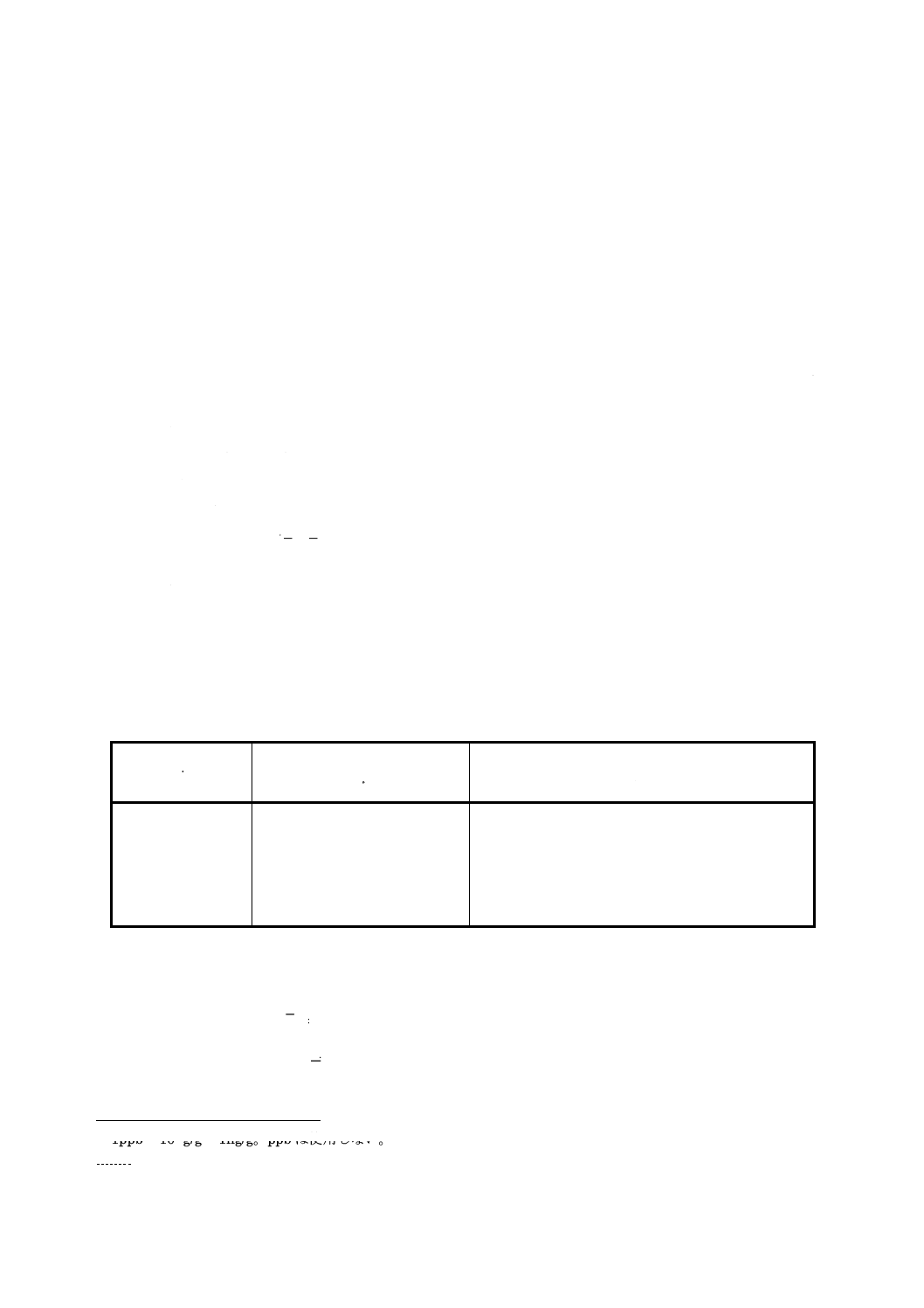
表1に,α = β = 0.05の場合について,νを変えたときのδ = (
)
β
α
ν;
;
の値を示す。
α = β及びν>3の場合,dxは次の式で近似される。
()
cx
s
x
J
I
K
b
t
x
xx
2
1
1
ˆ
ˆ
2
2
95
.0
d
=
+
×
+
≈
σ
ν
································· (9)
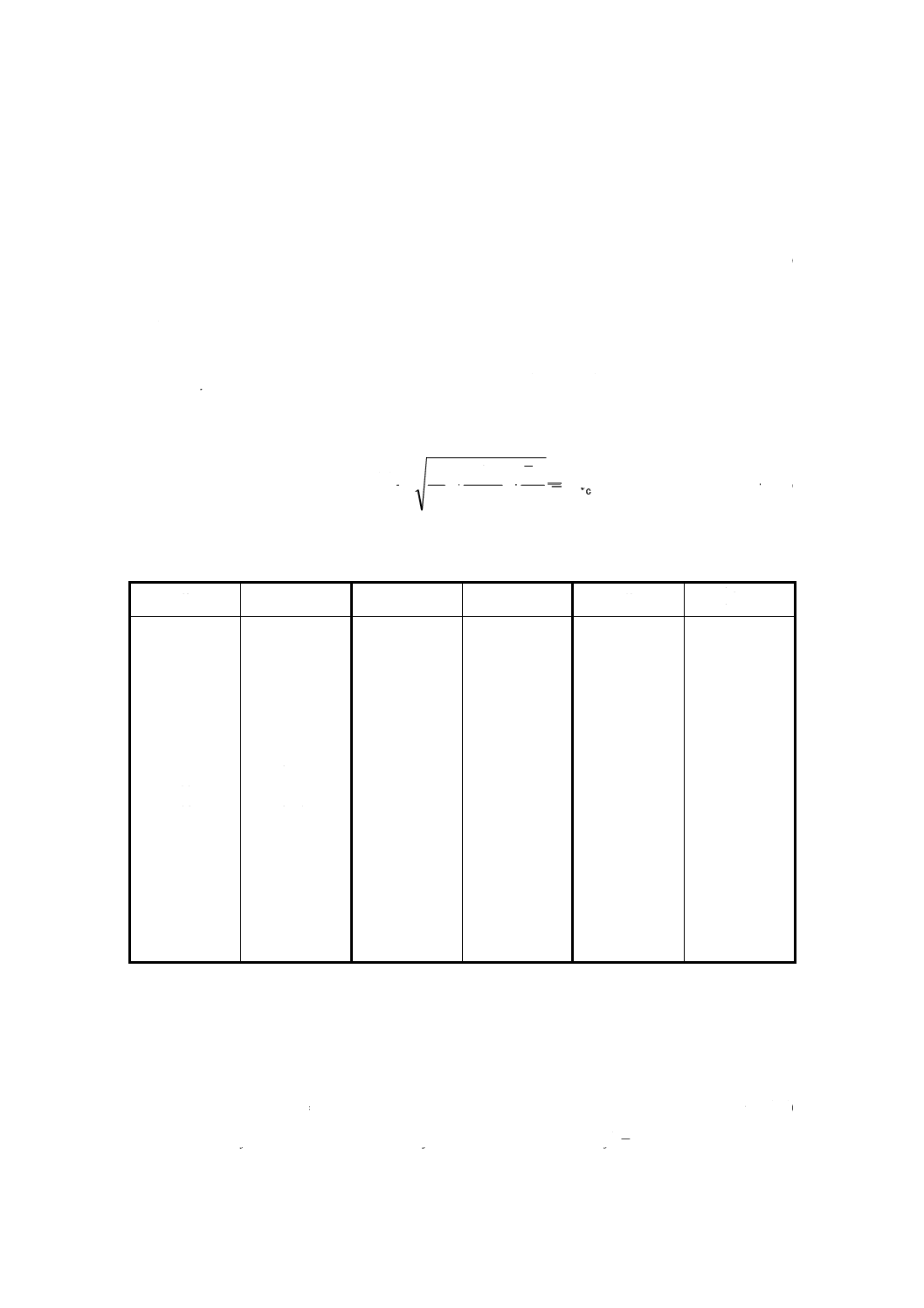
表1 α = β = 0.05,自由度νの場合の非心度の値
ν
(
)
β
α
ν
δ
;
;
ν
(
)
β
α
ν
δ
;
;
ν
(
)
β
α
ν
δ
;
;
2
5.516
19
3.415
36
3.354
3
4.456
20
3.408
37
3.352
4
4.067
21
3.402
38
3.350
5
3.870
22
3.397
39
3.349
6
3.752
23
3.392
40
3.347
7
3.673
24
3.387
41
3.346
8
3.617
25
3.383
42
3.344
9
3.575
26
3.380
43
3.343
10
3.543
27
3.376
44
3.342
11
3.517
28
3.373
45
3.341
12
3.496
29
3.370
46
3.339
13
3.479
30
3.367
47
3.338
14
3.464
31
3.365
48
3.337
15
3.451
32
3.362
49
3.336
16
3.440
33
3.360
50
3.335
17
3.431
34
3.358
18
3.422
35
3.356
5.3
ケース2―標準偏差が正味状態変数と直線関係にある場合
5.3.1
モデル 次の式で表されるモデルは,検量線が直線であり,標準偏差が正味状態変数と直線関係に
あるという仮定に基づく。
ij
i
ij
bx
a
Y
ε
+
+
=
········································································· (10)
ここで,xi,a,b,ij
Yの定義は5.2.1による。ij
εは独立で,期待値がE (ij
ε) = 0,分散が次の式で表される
正規分布に従う。
7
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
()(
)2
2
i
i
ij
dx
c
x
V
+
=
=σ
ε
······························································ (11)
すなわち,残差標準偏差はxと直線関係にある。
()
i
i
dx
c
x
+
=
σ
··········································································· (12)
モデルのパラメータa,b,c,及びdは,5.3.2及び5.3.3に規定する二段階からなる方法によって推定す
る。
5.3.2
残差標準偏差と正味状態変数間の直線関係の推定 パラメータc,dは,正味状態変数xを説明変
数,Sを目的変数として,標準偏差が
(
)
∑
−
−
=
=
J
j
i
ij
i
y
y
J
s
1
2
1
1
································································ (13)
である線形回帰分析によって推定する。分散V(S)の値は
2
σに比例するため,重み付き回帰分析(参考文献
[1]及び[2]を参照)を実施する必要があり,重みは
()(
)2
2
1
1
i
i
i
dx
c
x
w
+
=
=σ
································································ (14)
である。
しかし,分散
()ix
2
σ
は推定されていない未知のパラメータc及びdに依存する。そのため,重みを
()2
1
qi
qi
ˆ
wˆ
σ
=
············································································· (15)
とする次の反復計算を推奨する。第1回目の反復(q = 0)には
i
i
s
ˆ
=
0
σ
,ここでsiの値は経験標準偏差(標本
標準偏差)である。その後の反復q = 1,2,・・・では
i
q
q
qi
x
dˆ
cˆ
ˆ
+
=
σ
·········································································· (16)
とするが,これは次の補助値を計算することによって
8
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
∑
∑
∑
∑
=
+
=
+
=
+
=
+
=
+
=
=
=
=
=
I
i
i
i
qi
,
q
I
i
i
qi
,
q
I
i
i
qi
,
q
I
i
i
qi
,
q
I
i
qi
,
q
s
x
wˆ
T
s
wˆ
T
x
wˆ
T
x
wˆ
T
wˆ
T
1
5
1
1
4
1
1
2
3
1
1
2
1
1
1
1
;
;
;
;
······································································· (17)
2
2
1
3
1
1
1
5
1
2
1
4
1
3
1
1
,
q
,
q
,
q
,
q
,
q
,
q
,
q
q
T
T
T
T
T
T
T
cˆ
+
+
+
+
+
+
+
+
−
−
=
························································ (18)
2
2,1
3,1
1,1
4,1
2,1
5,1
1,1
1
ˆ
+
+
+
+
+
+
+
+
−
−
=
q
q
q
q
q
q
q
q
T
T
T
T
T
T
T
d
················································· (19)
を得る。この反復は急速に収束するため,q = 3の結果の値
;
σ
x
dˆ
cˆ
ˆ
3
3
3
+
=
を最終結果,すなわち
()x
ˆ
ˆ
σ
σ=
3
,
0
3
σˆ
cˆ=
及び
dˆ
dˆ=
3
としてよい。
()
x
d
x
ˆ
ˆ
ˆ
0+
=σ
σ
····································································· (20)
参考 原国際規格では式(20)において,
)
(ˆx
d
と誤記されている。
5.3.3
校正関数(検量線)の推定 パラメータa,bは,
ij
yを目的変数,xiを説明変数,重みを
();
i
i
x
ˆ
w
2
1
σ
=
とした重み付き線形回帰分析(参考文献[1]及び[2]を参照)によって推定される。
ここに
()ix
ˆ2
σ
は式(20)によるxiの分散の予測値である。
9
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑∑
∑∑
∑
∑
∑
=
=
=
=
=
=
=
=
=
=
=
=
I
i
J
j
ij
i
i
I
i
J
j
ij
i
I
i
i
i
I
i
i
i
I
i
i
y
x
w
T
y
w
T
x
w
J
T
x
w
J
T
w
J
T
1
1
5
1
1
4
1
2
3
1
2
1
1
;
;
;
;
································································· (21)
によってa,bの推定値は
22
3
1
5
2
4
3
T
T
T
T
T
T
T
aˆ
−
−
=
·········································································· (22)
22
3
1
4
2
5
1
T
T
T
T
T
T
T
bˆ
−
−
=
·········································································· (23)
と求められる。
参考 原国際規格では式(21)において,T4及びT5の式で二つめのΣの下のj=1をj=lと誤記されている。
また,原国際規格ではΣの前に係数Jが掛かっているのは,誤記である。
5.3.4
限界値の計算 応答変数の限界値は
()
2
2
1
2
0
95
.0
ˆ
1
ˆ
ˆ
σ
σ
ν
+
+
+
=
xxw
w
s
x
T
K
t
a
yc
············································ (24)
によって与えられ,正味状態変数の限界値は
()
2
2
1
2
0
95
.0
ˆ
1
ˆ
ˆ
σ
σ
ν
+
+
=
xxw
w
s
x
T
K
b
t
xc
················································ (25)
となる。ここに,
1
2T
/
T
xw=
·············································································· (26)
1
22
3
T
/
T
T
sxxw
−
=
······································································· (27)
10
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)2
1
1
2
ˆ
ˆ
2
1
ˆ
∑∑
=
=
−
−
−
×
=
I
i
J
j
i
ij
i
x
b
a
y
w
J
I
σ
····································· (28)
また,
()
ν
95
.0t
は,自由度ν = I×J−2のt分布の95%分位点であり,sxxwは附属書Aに定義される。
5.3.5
検出可能な最小値の計算 検出可能な最小値は
()
2
2
1
2
1
σ
σ
δ
ˆ
s
x
T
K
x
ˆ
bˆ
x
xxw
w
+
+
=
d
d
······················································ (29)
によって与えられる。ここで,δ = δ (ν; α; β)は5.2.4で定義された非心度の値である。
()
d
2x
ˆσ
はxdの値に依存しているが,その値は計算されていないため,反復計算によってこれを求める。
反復計算は()
0
0
d
σ
σ
ˆ
x
ˆ
=
からスタートしてxd0を得る。次に()
()
d0
1
d
x
ˆ
x
ˆ
σ
σ
=
を計算し,これをxdの式に代入
してxd1を得る。このステップを繰り返す。1回目の反復計算においてすらxdの値はほとんど変わらないこ
とが多い。したがって,反復計算を3回行えば十分妥当なxdの値が得られる。
6. 測定方法の検出可能な最小値 ある特定の校正(検量線)によって得た検出可能な最小値は,一連の
測定が観測された実際の状態の正味状態変数の値がゼロではないと判定するための,その校正による測定
プロセスの能力を示す,すなわち,1−βの確率でゼロではないと判定されうる正味状態変数の最小値であ
る。この検出可能な最小値は,校正ごとに異なる。検出可能な最小値は,
― 同一タイプの測定プロセスに基づく特定の測定プロセス
― 同一測定方法に基づくあるタイプの測定プロセス,又は
― 測定方法
といった様々な測定系列について,それぞれ当該測定プロセスの特性,当該測定プロセスのタイプ,又は
当該測定方法に付随するパラメータをもつ確率分布に従う確率変数の実現値とみなすことができる。
検出可能な最小正味状態変数値xdを求めるために,連続m回の校正を行ったとすれば,m個の検出可能
な最小値,xd1, … xdm,は,次の条件下でその測定プロセスの検出可能な最小値を求めるのに用いるこ
とができる。
a) 測定プロセスが変更されていない。
b) 検出可能な最小正味状態変数値xdの分布が単峰性であり,はずれ値が存在しない。
c) 各校正において実験計画(参照状態の数I,測定方法の反復回数J,K及びLを含む)が同一で
ある。
これらの条件下では,xdi (i = 1,・・・,m)の値の中央値をその測定プロセスの検出可能な最小値として
推奨するが,中央値の代わりに別の要約統計量xdiを使用した場合は,使用した統計量は報告されねばなら
ない。
これらの条件のいずれかが満たされない場合は,その測定プロセスの検出可能な最小値が十分明らかに
されたとは言えず,共通の値を求めようとしてはならない。
p個の試験室において同一の測定方法を適用し,それぞれの試験室で試験室内の測定プロセスの検出可
能な最小値を求める場合,測定プロセスの検出可能な最小値を求める場合と同じように上記のa)〜c)に相
当する条件が成り立つならば,p個の試験室の検出可能な最小値の中央値を,その測定方法の検出可能な
最小値として推奨する;もし,中央値の代わりに試験室の検出可能な最小値の別の要約統計量を使用した
11
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
場合は,使用した統計量は報告されねばならない。
7. 報告と結果の適用
備考 限界値と検出可能な最小値を求める例については,附属書Cを参照。
7.1
限界値 実際の状態を調査し判定する際には,正味状態変数と応答変数の限界値だけが適用される
べきである。(1回の)校正によって導いた測定プロセスのこれらの限界値は,その一連の測定における測
定対象系についてだけ使用できる,未知の状態を評価するための判定限界(decision limit)である。同一測定
プロセスの連続した校正を見ると,限界値は校正ごとに変化することがある。しかし,それぞれの限界値
は特定の一連の測定に属する判定限界であるため,各校正を通じての全体的な限界値を計算しても無意味
であり,これらを限界値として使用することは論理的に妥当ではない。
正味状態変数又は応答変数の値が限界値以下の場合は,観測した実際の状態と基底状態との間には差は
見られないと言ってよい。しかし,第2種の誤りを犯す可能性があるため,この値は観測された状態が確
実に基底状態にあることを示すものと解釈してはならない。したがって,このような結果を“ゼロ”又は
“検出可能な最小値より小”と報告することは許容できない。得られた値とその不確かさは必ず報告しな
ければならないし,その値が限界値より大きくない場合は,“検出されず”と注記すべきである。
7.2
検出可能な最小値
特定の校正から導かれた検出可能な最小値は,実際の測定プロセスの検出能力が意図された目的のため
に十分であるか否かを示す。十分でない場合は,J,K,Lの数を修正する必要があるかもしれない。
6.に述べた条件において行った2回以上の校正から導かれた検出可能な最小値は,異なる試験室及び方
法それぞれについての比較,選択,又は審査を行うのに役立つかもしれない。
12
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定)記号及び略語
a
一次関数
ε
+
+
=
bx
a
y
の切片
aˆ
切片aの推定値
b
一次関数
ε
+
+
=
bx
a
y
の傾き
bˆ
傾きbの推定値
c
残差標準偏差を表す一次関数()
dx
c
x
+
=
σ
の切片
cˆ
切片cの推定値
d
残差標準偏差を表す一次関数()
dx
c
x
+
=
σ
の傾き
dˆ
傾きdの推定値
()
E
(括弧内の確率変数の)期待値
I
校正実験に使用する参照状態の数
I
i
,
,Κ
1
=
参照状態の識別変数
J
各参照状態に対する試料調製数
J
j
,
,Κ
1
=
参照状態及び基底状態に対する試料調製の識別変数
K
実際の状態に対する試料調製数
K
k
,
,Κ
1
=
実際の状態に対する試料調製数の識別変数
L
各試料調製に対する繰返し測定回数
L
l
,
,Κ
1
=
試料調製当たりの繰返し測定回数の識別変数
M
乗数
m
連続校正回数
N
校正実験における試料調製数,各参照状態に対する試料調製数が同一の場合は
N =I×J,校正実験における全測定回数はN×L
Κ
,
,
,2
1
0
=
q
反復計算ステップの数
s
経験的標準偏差
(
)
∑
=
−
=
I
i
i
xx
x
x
J
s
1
2
参照状態(基底状態を含む)に対して選択した正味状態変数の値の平均値からの残
差平方和
(
)
∑
=
−
=
I
i
w
i
i
xxw
x
x
w
J
s
1
2
参照状態(基底状態を含む)に対して選択した正味状態変数の値の重み付き平均値
からの重み付き偏差平方和
T
重み付き線形回帰分析に関する補助値
()
V
(括弧内の確率変数の)分散
i
w
ixの重み付き値
qi
wˆ
q回目の反復計算におけるixの重み付き値
X
正味状態変数,
0z
Z
X
−
=
x
正味状態変数の(個々の)値
Ix
x
,
,Κ
1
基底状態を含む参照状態に対して選択した正味状態変数Xの値
cx
正味状態変数の限界値
dx
検出可能な最小正味状態変数値
∑=
=
I
i
ix
I
x
1
1
参照状態(基底状態を含む)に対して選択した正味状態変数の値の平均値
bˆ
aˆ
y
xˆ
a−
=
個々の実際の状態に対する正味状態変数の推定値
∑
∑
=
=
=
I
i
i
I
i
i
i
w
w
x
w
x
1
1
参照状態(基底状態を含む)に対して選択した正味状態変数の重み付き平均値
Y
応答変数
cy
応答変数の限界値
ijl
y
i番目の参照状態におけるj番目の試料のl番目の測定値
13
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
kl
k
y
y
,
,Κ
1
一連の測定において,個々の実際の状態におけるk番目の試料に対して得られた応
答変数の値
∑∑
=
=
×
=
K
k
L
l
kl
a
y
K
y
1
1
L
1
個々の実際の状態における観測値の平均値
∑∑∑
=
=
=
×
×
=
I
i
J
j
L
l
ijl
y
L
J
I
y
1
1
1
1
測定値ijl
yの平均値
∑=
=
L
l
ijl
ij
y
L
y
1
1
i番目の参照状態におけるj番目の試料の測定値の平均値
∑∑
=
=
×
=
J
j
L
l
ijl
i
y
L
J
y
1
1
1
i番目の参照状態における測定値の平均値
0y
x = 0におけるK×L個の測定値の平均値
Z
状態変数
0z
基底状態における状態変数の値
α
帰無仮説“対象の状態は,状態変数に関して基底状態とは異なっていない”が真で
ある一連の測定において,観測された個々の実際の状態に対し,この帰無仮説を誤
って棄却する確率(第1種の誤りの確率),推奨値が存在しない場合,αの値はα =
0.05に固定する。
β
正味状態変数が求めるべき検出可能な最小値に等しい一連の測定において,観測さ
れた個々の実際の状態に対し,帰無仮説“対象の状態は,状態変数に関して基底状
態とは異なっていない”を誤って採択する確率(第2種の誤りの確率),推奨値が
存在しない場合,βの値はβ = 0.05に固定する。
δ
非心t分布の非心度
ε
サンプリング,試料調製及び測定誤差のランダム成分を表す応答変数測定の成分
ν
自由度
σdiff
平均値yと切片の推定値aˆの差の標準偏差
σˆ
残差標準偏差の推定値
qi
ˆσ
q回目の反復計算におけるixの標準偏差
0
σˆ
x=0における残差標準偏差の推定値
14
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考)式の誘導
この附属書は,本体及び附属書(規定)に関連する事柄を補足するもので,規定の一部ではない。
B.1
ケース1―標準偏差が一定の場合 本体5.1の仮定を設け,標準偏差が一定であると仮定する場合,
回帰係数の推定値aˆ及びbˆは,次の期待値の正規分布に従う。
()
()b
bˆ
E
;
a
aˆ
E
=
=
また,分散は次の式で表される。
()
()
xx
xx
s
b
V
s
x
J
I
a
V
2
2
2
ˆ
1
ˆ
σ
σ
=
+
×
=
;
ここで,2
σは各調製試料に対するL回の繰返し測定の平均値からの残差の分散である。基底状態(z=0z,
x= 0)において,応答変数をK×L回測定すると,K×L個の値の平均値
0yと切片aˆの推定値の差は,次の期
待値の正規分布に従う。
(
)
()
()
0
0
0
=
−
=
−
=
−
a
a
aˆ
E
y
E
aˆ
y
E
また,分散は次の式で表される。
(
)
()
()
2
2
2
2
2
0
0
1
1
1
ˆ
ˆ
σ
σ
σ
+
×
+
=
+
×
+
=
+
=
−
xx
xx
s
x
J
I
K
s
x
J
I
K
a
V
y
V
a
y
V
(
0y−aˆ)は正規分布に従うため,次の確率変数は標準正規分布に従う。
diff
σ
a
y
U
ˆ
0−
=
また,次の不等式が成り立つ確率は0.95となる。
95
.0
0
ˆ
u
a
y
≤
−
diff
σ
2diff
σ
は未知なので,その値は次のように推定される。
2
2
2
ˆ
1
1
ˆ
σ
σ
+
×
+
=
xx
s
x
J
I
K
diff
ここで,
2
σˆは代わりに使用する回帰分析の残差分散の推定値である。
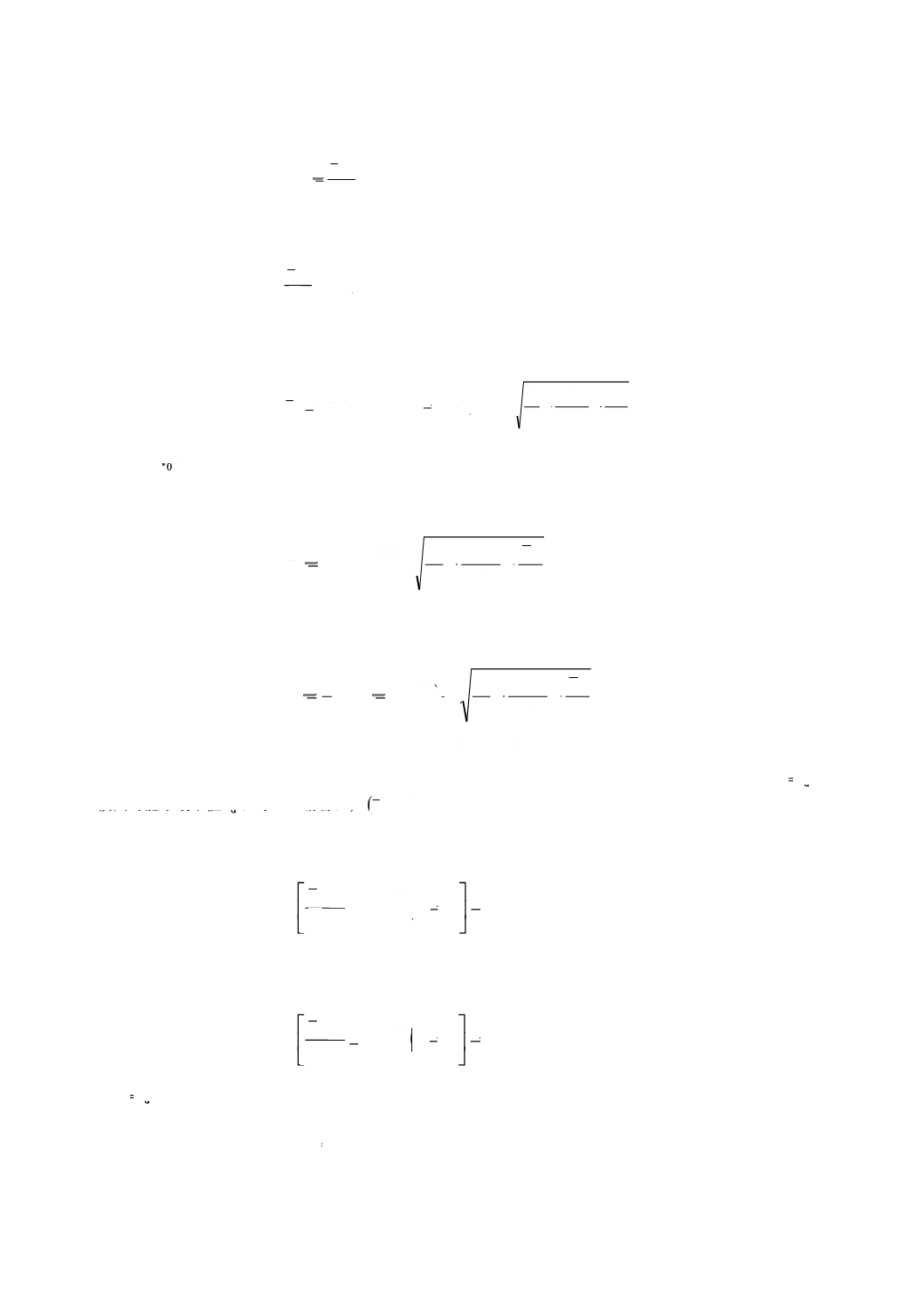
15
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
diff
σ
ν
ˆ
ˆ
0
a
y
T
−
=
次の確率変数は自由度ν = I×J−2のt分布に従う。また,次の不等式が成り立つ確率は0.95となる。
()
ν
σ
95
.0
0
ˆ
ˆ
t
a
y
≤
−
diff
すなわち
()
()
xx
s
x
J
I
K
t
a
t
a
y
2
95
.0
95
.0
0
1
1
ˆ
ˆ
ˆ
ˆ
+
×
+
+
=
+
≤
σ
ν
σ
ν
diff
ここで,
()
ν
95
.0t
は自由度νのt分布の95%点である。
この不等式の右辺が次の式で表される応答変数の限界値を与える。
()
xx
s
x
J
I
K
t
a
y
2
95
.0
1
1
ˆ
ˆ
+
×
+
+
=
σ
ν
c
また,正味状態変数の限界値は次の式で表される。
()
xx
s
x
J
I
K
b
t
b
a
y
x
2
95
.0
1
1
ˆ
ˆ
ˆ
ˆ
+
×
+
=
−
=
σ
ν
c
c
これらの値は,t分布の他の分位点を用いるのが適切な場合にも,同様な式で表すことができる。
検出可能な最小正味状態変数値dxを求めるためには,正味状態変数の真の値xが正味状態変数
dx
x=
の
検出可能な最小値dxに等しい場合に,(
)
diff
σˆ
aˆ
y−
の分布を調べる必要がある。この状態は確率1−βで検
出しなければならない。すなわち,次の式が成立しなければならない。
()
β
ν
σ
−
=
=
>
−
1
ˆ
ˆ
95
.0
d
diff
x
x
t
a
y
P
言いかえれば
()
β
ν
σ
=
=
≤
−
d
diff
x
x
t
a
y
P
95
.0
ˆ
ˆ
dx
x=
の場合,yの期待値は次の式から得られる。
()
d
bx
a
y
E
+
=
したがって

16
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
d
bx
aˆ
y
E
=
−
となる。また,(
)
2
diff
σ
=
−a
y
V
ˆ
となるが,これは,= 0の場合にも成立する。以上から,次の式が成立
する。
()
(
)
()
()
()
()
(
)
()
[
];
;
diff
diff
diff
d
diff
d
d
diff
d
d
d
diff
ν
δ
ν
ν
ν
ν
χ
δ
ν
σ
σ
σ
σ
ν
σ
ν
σ
95
.0
95
.0
2
95
.0
95
.0
95
.0
/
/
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
t
T
P
t
U
P
t
bx
bx
a
y
P
x
x
t
bx
bx
a
y
P
x
x
t
a
y
P
≤
=
≤
+
=
≤
+
−
−
=
=
≤
+
−
−
=
=
≤
−
(
)
diff
dσ
bx
aˆ
y
U
−
−
=
は標準正規分布に従い,
diff
diffσ
σˆ
はUとは独立に
()ν
ν/
2x
の分布に従うため,
確率変数(
)
δ
ν;
T
は自由度ν,非心度δの非心t分布に従う。必要な場合は,α= 0.05又は適切なその他のα
の値に対して,次の式を満足させる自由度νの非心t分布の非心度の値として
(
)
β
α
ν
δ
δ
;
;
=
を求めること
ができる。
(
)
()
[
]β
ν
δ
ν
α
=
≤
−
1t
T
P
;
また,
diff
d
σ
δ
bx
=
から,検出可能な最小正味状態変数値に対する次の表現が導かれる。
xx
s
x
J
I
K
b
b
x
2
1
1
+
×
+
=
=
σ
δ
σ
δ
diff
d
検出可能な最小値の推定値を得るためには,この式にb及びσの推定値を代入する。すなわち,
xx
s
x
J
I
K
b
x
2
1
1
ˆ
ˆ
ˆ
+
×
+
=σ
δ
d
応答変数cyの限界値はaˆとσˆの定数倍の和であり,正味状態変数の限界値はσˆ/bˆの定数倍である。推奨
に従って,参照状態の正味状態変数値が最小値をゼロとして等間隔に配置され,かつ,α= 0.05とし,K
が次の値のいずれかである場合,
― K = 1(実際の状態の測定に対する試料調製1個),又は
17
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
― K = J(参照状態に対する試料調整と同じ回数の試料調整を実際の状態の測定に対して行う)
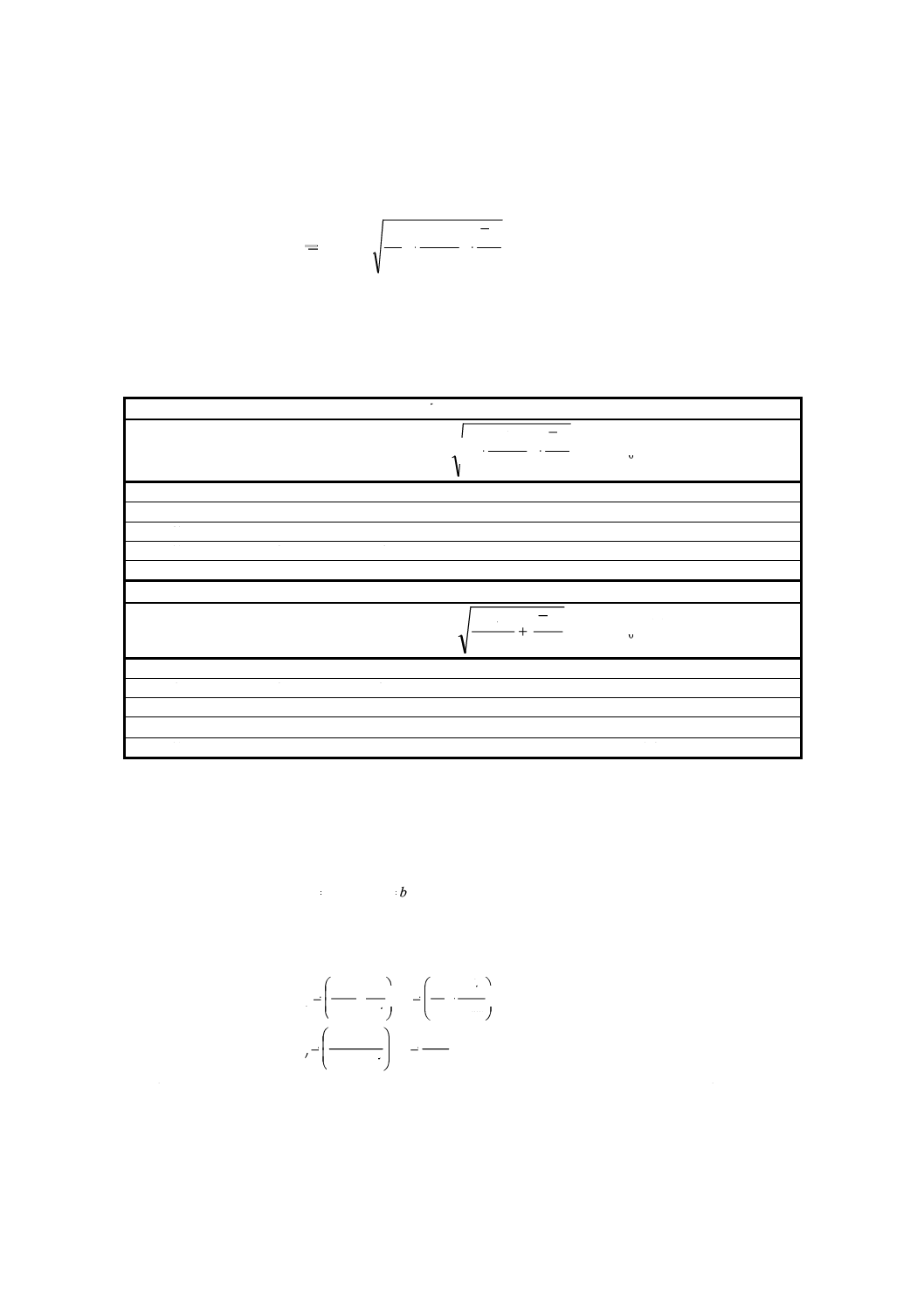
限界値の式中の次の乗数は,参照状態の数Iと,各参照状態に対する試料調製数Jだけの関数となる。
()
xx
s
x
J
I
K
t
M
2
95
.0
1
1
+
×
+
=
ν
各変数の値を変えた場合のMの値を附属書B表1に掲げる。
附属書B表1 乗数Mの値
K = 1の場合
I
J
J
I×
xx
s
x
J
I
2
1
1
+
×
+
()
ν
95
.0t
M
3
1
3
1.35
6.31
8.52
3
2
6
1.19
2.13
2.54
5
1
5
1.26
2.35
2.97
5
2
10
1.14
1.86
2.12
5
4
20
1.07
1.73
1.86
K = Jの場合
I
J
J
I×
xx
s
x
J
I
I
2
1+
×
+
()
ν
95
.0t
M
3
1
3
1.35
6.31
8.54
3
2
6
0.96
2.13
2.04
5
1
5
1.26
2.35
2.97
5
2
10
0.89
1.86
1.66
5
4
20
0.63
1.73
1.09
B.2
ケース2―正味状態変数と直線関係となる標準偏差 本体5.1の仮定の下で,標準偏差が正味状態変
数と直線関係にある場合には,回帰係数推定値aˆ及びbˆは,次の期待値の正規分布に従う。
()
()b
bˆ
E
a
aˆ
E
=
=
;
また,分散は次の式で表される。
()
()
xxw
xxw
w
s
T
T
T
T
bˆ
V
s
x
T
T
T
T
T
aˆ
V
2
2
22
3
1
1
2
2
1
2
22
3
1
3
1
σ
σ
σ
σ
=
−
=
+
=
−
=
ここで
2
σは,各試料調整iに対するL回の繰返し測定の平均値からの残差の分散がi
w
2
σとなるよう定義
する。
基底状態(Z=0z,X= 0)において,応答変数をK×L回測定すると,K×L個の値の平均値yと切片aˆの推
定値の差は,次の期待値の正規分布に従う。

18
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
()
()
0
=
−
=
−
=
−
a
a
aˆ
E
y
E
aˆ
y
E
また,分散は次の式で表される。
(
)
()
()
diff
2
2
2
1
20
1
σ
σ
σ
=
+
+
=
+
=
−
xxw
w
s
x
T
K
aˆ
V
y
V
aˆ
y
V
2diff
σ
は未知だが,その値は次のように推定される。
()
2
2
1
20
20
2
1
σ
σ
σ
σ
ˆ
s
x
T
K
ˆ
aˆ
Vˆ
K
ˆ
ˆ
xxw
w
+
+
=
+
=
diff
ここで,
20
σˆの値は等式(20)から得られ,
2
σˆは重み付き回帰分析の残差分散の推定値である。ここではこ
れらの値を使用する。
ケース1の場合と同じく,応答変数の限界値は次の式から得られる。
()
()
2
2
1
20
95
.0
95
.0
ˆ
1
ˆ
ˆ
ˆ
ˆ
σ
σ
ν
σ
ν
+
+
+
=
+
=
xxw
w
s
x
T
K
t
a
t
a
y
diff
c
そして,正味状態変数の限界値は次の式から得られる。
()
()
2
2
1
20
95
.0
95
.0
ˆ
1
ˆ
ˆ
ˆ
ˆ
σ
σ
ν
σ
ν
+
+
=
=
xxw
w
s
x
T
K
b
t
b
t
x
diff
c
これらの値は,t分布の他の分位点を用いるのが適切な場合にも,同様な式で表すことができる。
これらの式はi= 1,...Iに対して重み値をすべて1,すなわちi
w= 1とし,
J
I
T
×
=
1
,
x
xw=,
xx
xxws
s
=
及び
20
σˆ=
2
σˆとすれば,標準偏差が一定の場合の式となる。
検出可能な最小正味状態変数値は次の式から得られる。
b
x
diff
d
σ
δ
=
ここで,x=dxについては,次の式が成り立つ。
(
)
(
)
()aˆ
V
x
x
y
V
x
x
aˆ
y
V
x,
+
=
=
=
−
=
d
d
diff
d
2
σ
bと
2
,d
diffx
σ
の推定値,すなわちbˆと次の値
(
)
()
()
2
2
1
2
2
,
ˆ
1
ˆ
ˆ
ˆ
ˆ
ˆ
σ
σ
σ
+
+
=
+
=
=
xxw
w
x
s
x
T
K
x
a
V
x
x
y
V
d
d
diff
d
をこの式に代入すれば,次のとおり検出可能な最小正味状態変数値が得られる。
19
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
2
2
1
2
1
σ
σ
δ
ˆ
s
x
T
K
x
ˆ
bˆ
x
xxw
w
+
+
=
d
d
()
dx
ˆ2
σ
は計算されていないdxの値によって決まるため,本体5.3.5の反復計算を実施する必要がある。
20
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考)例
この附属書は,本体及び附属書(規定)に関連する事柄を補足するもので,規定の一部ではない。
C.1 例1 食品又は医薬品中の水銀含有量(ng/g)1)を原子吸光分析法によって測定する。各サンプルを
マイクロ波(MLS-1200)法によって分解し,硝酸/二クロム酸カリウム溶液に溶かす。これらの溶液をバ
リアンVGA-76還元気化システムから金メッキ箔濃縮システム(MCA-90)に導き,繰返し原子吸光測定
に供する。校正関数(検量線)を推定し,検出能力を求めるため,ブランク濃度(x= 0)と正味濃度x= 0.2ng/g,
0.5ng/g,1.0ng/g,2.0ng/g,3.0ng/gの標準サンプル6個を3回調製し,各調製された試料を1回ずつ測定す
る。したがって,I = 6,J = 3,L = 1である。
校正関数(検量線)は直線であり,標準偏差一定及び応答変数の正規分布の仮定が成立するものとする;
α及びβはあらかじめα = β = 0.05に固定する。分析対象物質中の水銀濃度を定量するために,二つの異なっ
たアプローチを検討することにする。
a) 1回測定を行う(K = L = 1)。
b) 測定用のサンプルを3個調製し,それぞれについて1回測定を行い(K = 3,L = 1),観測値の平均
値a
yを測定結果として使用する。
校正実験(検量線作成実験)の結果を附属書C表1に示す。
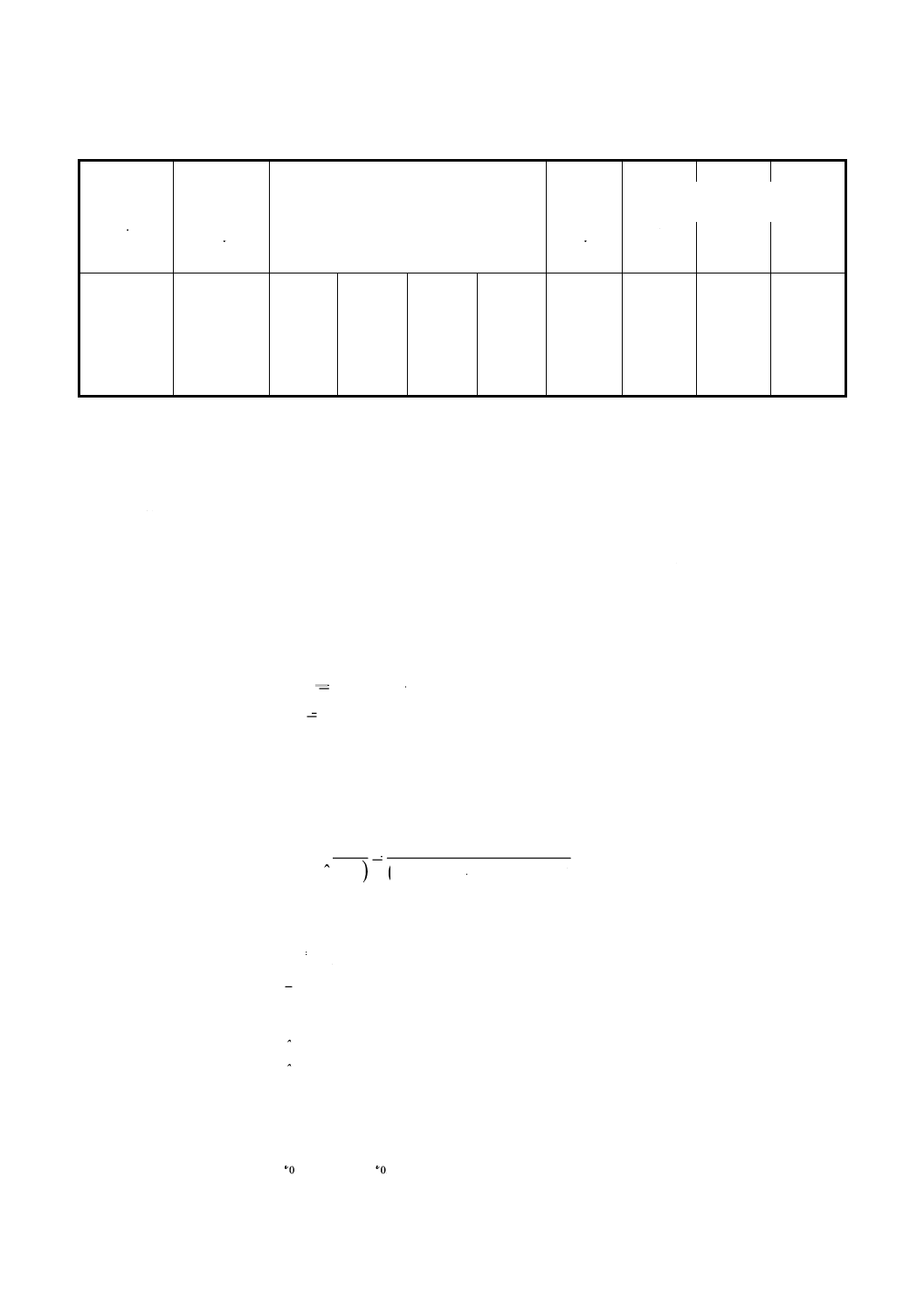
附属書C表1
食品又は医薬品中の水銀含有量の定量を行うための校正(検量線作成用)実験校正実験の結果
標準サンプル
i
正味水銀濃度
ix
吸光度
ij
y
1
0
0.003
−0.001
0.002
2
0.2
0.004
0.005
0.005
3
0.5
0.011
0.011
0.012
4
1.0
0.023
0.023
0.023
5
2.0
0.048
0.047
0.048
6
3.0
0.071
0.072
0.072
統計的解析によって次の値が得られる。
1167
.1
=
x
ng/g
425
.
20
=
xx
s
1) 1ppb = 10-9g/g = 1ng/g。ppbは使用しない。
参考 計量法ではppbの使用は認められている。

21
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
10
9959
.9
ˆ
−
×
=
a
02374
.0
ˆ=
b
3
10
1099
.1
ˆ
−
×
=
σ
ν = N−2 = 16であるため
()
()
746
.1
16
95
.0
95
.0
=
=t
t
ν
(
)
(
)
440
.3
05
.0;
05
.0;
16
=
=δ
β
α
ν
δ
;
;
()
(
)
492
.3
2
95
.0
=
ν
t
アプローチ a)の結果は次のとおりである。
応答変数の限界値(式(5)参照)
cy=0.00215
正味濃度の限界値(式(6)参照)
cx=0.086ng/g
検出可能な最小正味濃度(式(9)参照)
dx=0.173ng/g
― 正味水銀濃度がブランク濃度より高いサンプルであると解釈される吸光度の最小値は,cy= 0.00305
(応答変数限界値)である。
― (確率1−β = 0.95で)ブランク濃度から識別可能なサンプル中の正味水銀濃度の最小値は,dx=
0.173ng/g(検出可能な最小正味濃度)である。
アプローチ b)の結果は次のとおりである。
応答変数の限界値(式(5)参照)
cy=0.00140
正味濃度の限界値(式(6)参照)
cx=0.055ng/g
検出可能な最小正味濃度(式(9)参照)
dx=0.110ng/g
参考1. ycの計算結果を,原国際規格ではそれぞれ,0.00305及び0.00230としているが,共に
4
10
9959
.9
ˆ
−
×
=
a
を用いて計算された結果である。正しくは前に示すように,
5
10
9959
.9
ˆ
−
×
=
a
を用いて計算しなければならない。
2. 検出可能な最小正味濃度について,原国際規格では式(7)を参照すると誤記している。
C.2 例2 2) 抽出液100μl中のトルエンの量をガスクロマトグラフィー/質量分析法(GC/MS)によって
測定する。サンプル100μlをGC/MSシステムに注入する。6種類の標準サンプルを使用する。トルエンの
含有量は4.6pg/100μlから15000pg/100μlの範囲にあることが分かっている。各サンプルを4個用意し,1
回ずつ注入,測定を行う(I = 6,J = 4,L = 1,N = 24)。測定結果を附属書C表2に示す。
測定結果をグラフに表すと,トルエンの量と応答変数(ピーク面積)は十分直線関係にあり,ピーク面
積の標準偏差とトルエンの量も直線関係にある。さらに,応答変数が正規分布に従うものと仮定すれば,
本体5.3の方法によって検出能力を求めることができる。
2) D.M. Rocke and S. Lorenzato,A Two-Component Model for Measurement Error in Analytical Chemistry,
Technometrics,1955,37,pp. 181-182
22
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C表2
抽出液100μl中のトルエン量に関する校正実験の結果
(1)
(2)
(3)
(4)
(5)
(6)
(7)
標準サンプル
正味トルエン量
ピーク面積
経験的
標準偏差
反復計算における標準偏差の予測値
i
ix
pg/100 μl
ij
y
is
1
i
ˆ1
σ
2
i
ˆ2
σ
3
i
ˆ3
σ
1
4.6
29.80
16.85
16.68
19.52
6.20
4.56
5.17
5.15
2
23
44.60
48.13
42.27
34.78
5.65
7.07
7.93
7.92
3
116
207.70
222.40
172.88
207.51
21.02
19.73
21.87
21.88
4
580
894.67
821.30
773.40
936.93
73.19
82.91
91.43
91.57
5
3000
5350.65
4942.63
4315.79
3879.28
652.98
412.46
454.22
455.02
6
15000
20718.14 24781.61 22405.76 24863.91
2005.02
2046.54
2253.14
2257.23
c及びdを推定するため,本体5.3.2の反復再重み付き線形回帰分析を行うと,次の推定線形回帰式が得
られる。
反復計算1:
i
ˆ1
σ=3.93323+0.136174ix
反復計算2:
i
ˆ2
σ=4.48284+0.149911ix
反復計算3:
i
ˆ3
σ=4.46228+0.150185ix
附属書C表2の(5)から(7)欄に,対応する標準偏差の予測値を掲げる。3回反復計算を行えば結果が安定
するため,第3回目の反復計算の結果の式を推定手順の前半の最終結果として使用することができる。す
なわち,
()
46228
.4
ˆ
150185
.0
46228
.4
ˆ
0=
+
=
σ
σ
x
x
検量線のパラメータa及びbは,(3)欄のij
yを従属変数値,(2)欄のixを独立変数値とし,次の重み付け値
を用いて,本体5.3.3の重み付き線形回帰分析を行って推定する。
()(
)2
2
150185
.0
46228
.4
1
ˆ
1
i
i
i
x
x
w
+
=
=σ
回帰分析の結果次の値が得られる。
∑=
=
I
i
i
w
J
T
1
1
=0.223306
w
x =15.5669
xxw
s
=606.224
aˆ =12.2185
bˆ =1.52727
2
σˆ =1.05954
ν =N−2=22
()
ν
95
.0t
=
95
.0t
(22)=1.717
23
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
したがって,K = 1の場合次の値が得られる。
参考 丸めの誤差によって,下1けたの数値が上記の計算結果と異なる場合がある。
応答変数の限界値(式(24)参照)
cy= 20.82
抽出液100μl中の正味トルエン量の限界値(式(25)参照)
cx= 5.63pg
検出可能な最小値は反復計算を行って求める。
α = β = 0.05,(
)
β
α
ν
δ
;
;
= δ (22; 0.05; 0.05) = 3.397(本体表1参照)及び()
0
0
σ
σ
ˆ
x
ˆ
=
d
の場合,1回目のdxの
値(等式(29)参照)は
0
dx = 11.139である。したがって,()1
dx
ˆσ
=6.1352,
1dx= 14.553となる。
()2
dx
ˆσ
=6.6479であるから,2回目の計算によって
2
dx = 15.627pg/100μl,及び
()3
dx
ˆσ
=6.8092であり,最終的にdx=
3
dx= 15.967pg/100μlを得る。
正味トルエン濃度がブランク濃度より高いサンプルであると解釈される最小ピーク面積は,cy= 20.82
(応答変数の限界値)である。
(確率1−β =0.95で)ブランク濃度から識別可能な抽出液100μlサンプル中の最小正味トルエン量は,
dx= 15.97pg/100μl(検出可能な最小正味トルエン濃度)である。
24
Z 8462-2:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1]
Draper N.R. and Smith H. Applied Regression Analysis. Wiley, New York, 1981.
参考 日本で翻訳書が出されている。中村慶一訳,応用回帰分析,森北出版株式会社,東京,1968
[2]
Montgomery D.C. and Peck E.A. Introduction to Linear Regression Analysis. Wiley, New York, 1992.
[3]
Currie L.A. Nomenclature in Evaluation of Analytical Methods Including Detection and Qualification Capabilities.
IUPAC Recommendations 1995. Pure and Applied Chemistry,67,1995,pp. 1699-1723.