Z 8461 : 2001 (ISO 11095 : 1996)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人 日本規格協会 (JSA) から工業標
準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業
大臣が制定した日本工業規格である。
JIS Z 8461には,次に示す附属書がある。
附属書A(規定) 記号及び略語
附属書B(規定) 繰返し数が異なる場合の基本的方法
附属書C(参考) 参考文献
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8461 : 2001
(ISO 11095 : 1996)
標準物質を用いた校正
(検量線が直線の場合)
Linear calibration using reference materials
序文 この規格は,1996年に第1版として発行されたISO11095,Linear calibration using reference materials
を翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
校正(検量線作成)は,ほとんどすべての測定手順において重要な作業である。校正(検量線作成)は,
特定の条件下で,測定システムが示す値と,対応する幾つかの“標準”の採択値との関係を確立する一連
の作業である。この規格における標準とは,標準物質をいう。
標準物質 (RM) とは,測定システムを検証するため,一つ以上の特性が十分良好に確立された(天然)物
質又は人工物をいう。RMには幾つかの種類が存在する。
a) 自家製標準物質とは,ユーザーが自己の使用に供するために作成したRMをいう。
b) 市販の標準物質とは,ユーザー以外が提供するRMをいう。
c) 認証標準物質とは,その資格を承認された機関が提出し,かつ,認証するRMをいう。
1. 適用範囲 この規格は,
a) 測定システムを校正(検量線作成)し,“校正(検量線作成)”した測定システムを統計的に管理され
た状態に維持するために必要な一般的原理について概説し,
b) 次のことを行うための基本的方法を規定する。
− 測定値の可変性に関連する二つの仮定のいずれか一つに基づく直線で表される校正関数(検量線)の
推定
− 校正関数(検量線)の直線性の仮定と,測定値の可変性に関する仮定のチェック
− ある新規,かつ,未知の量に関して校正関数(検量線)によって得られた測定値を変換することによ
る,その量の値の推定
c) 次のことに関して校正関数(検量線)を拡張適用する場合の管理方法を規定する。
− 校正関数(検量線)を更新すべき時期の決定
− 校正関数(検量線)により変換した後の,測定値の不確かさの推定
d) 基本的方法に対して,特殊な条件下での二つの代替法を規定する。
e) 例を用いて基本的方法と管理方法の説明を行う。
この規格は,標準物質が入手できる測定システムに適用することができる。
この規格は,直線で表される校正関数(検量線)が仮定された測定システムに適用することができ
る。この規格は,直線性の仮定を検証する方法を規定する。校正関数(検量線)が非直線であること
2
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
が既知の場合は,この規格を適用することはできない。ただし,8.3に述べる“ブラケティング法”を
適用する場合を除く。
この規格は,各種のRMを区別せず,測定システム校正(検量線作成)のために選択されたRM採
択値には誤差がないものとする。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
している),NEQ(同等でない)とする。
ISO 11095:1996, Linear calibration using reference materials (IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格)のうちで,発行年を付記してあるものは,記載の年の版だけがこの規格の規定を
構成するものであって,その後の改正版・追補には適用しない。
JIS Z 8101-1 : 1999 統計−用語と記号−第1部:確率及び一般統計用語
備考 ISO 3534-1 : 1993, Statistics−Vocabulary and symbols−Part 1 : Probability and generalstatistical
termsからの引用事項は,この規格の該当事項と同等である。
JIS Z 8101-2 : 1999 統計−用語と記号−第2部:統計的品質管理用語
備考 ISO 3534-2 : 1993, Statistics−Vocabulary and symbols−Part 2 : Statistical quality controlからの引
用事項は,この規格の該当事項と同等である。
JIS Q 0030 : 1997標準物質に関連して用いられる用語及び定義
備考 ISO Guide 30 : 1992, Terms and definitions used in connection with reference materialsが,この規
格と一致している。
3. 定義 この規格で用いる主な用語の定義は,JIS Z 8101-1及びJIS Z 8101-2によるほか,次による。
3.1
標準物質 (reference material) 測定システムを検証するため,一つ以上の特性が十分良好に確立され
た物質又は人工物
4. 一般原理 校正(検量線作成)とは,測定システムと,標準物質及びその採択値によって表される“参
照”システムとの間に存在する可能性がある系統的な差違を決定する手順をいう。この規格においては,
システムという用語(測定システム及び参照システム)は,測定器具だけでなく,手順,オペレーター及
び当該測定器具に関連する環境条件の集合を表す。
校正(検量線作成)手順の出力は,将来の測定結果を変換するための校正関数(検量線)である。この
規格においては,“変換”という用語は,次のいずれか一つを表す。
− 標準物質 (RM) の採択値と観測値が同じ単位の場合,将来の測定値の補正
− 観測された測定値の単位からRMの単位への変換
校正関数(検量線)の有効性は,次の二つの条件によって決まる。
a) 校正関数(検量線)の計算に使用された測定値が測定システムを使用する通常の条件を代表する。
b) 測定システムが管理状態にある。
校正(検量線作成)実験は,項目a)を満足するよう計画しなければならない。管理方法は,システムが
管理状態から逸脱したと考えるしかないとき,可能な限り速やかにこれを検知する。
この規格の手順は,参照システムと直線関係にある測定システムに適用できるだけである。直線性の仮
3
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定が妥当か否かをチェックするためには,校正(検量線作成)実験にRMを3個以上使用する必要がある。
このことは,基本的方法において説明する。基本的方法は,RMを数個使用し,校正(検量線作成)実験
において収集されたデータを解析する計画と手法を提供する。直線性が明確に成立する場合は,基本的方
法より簡単な代替法を用いて1点に基づく直線で表される校正関数(検量線)を推定することができる。
この“1点校正(検量線作成)”法(ゼロ水準変換に従う)は,仮定に関するいかなる検定も考慮していな
いが,これまでの実験において,より徹底的に検討されたシステムを敏速,かつ,容易に“再校正(検量
線作成)”する方法である。直線性が疑わしい場合は,“ブラケティング法”と呼ぶもう一つの方法を適用
する。
基本的方法と1点校正(検量線作成)法は,校正(検量線作成)に注がれた労力がプロセスの安定期間
全体を通じて有効であるという仮定に基づく。校正(検量線作成)の有効期間を調べるためには,管理方
法が適切でなければならない。管理方法は,システムに究明又は再校正(検量線作成),若しくはその両方
を必要とする変化が発生したか否かを検出するよう計画される。管理方法は,また,与えられた校正関数
(検量線)によって変換された値の精度を決定する簡単な方法を提供する。
ブラケティング法は,大きな労力を要するが,より精確に未知量の値を決定する方法である。この方法
では,二つのRMによって各未知量を可能な限り短い間隔で取り囲み(ブラケティングし),未知量の測
定値と二つのRMの測定値から未知量に関する変換値を抽出する。この方法で測定プロセスの安定性を仮
定するのは,短い期間(未知量とRM2個の測定期間)についてだけである。直線性は二つのRMの値の
間においてだけ仮定される。
5. 基本的方法
5.1
一般 この箇条では,RMが数個(3個以上)利用できる場合に,直線で表される校正関数(検量線)
を推定し,それを用いる方法について述べる。RMが複数個存在すれば,校正関数(検量線)の直線性を
検証することができる。
5.2
仮定
5.2.1 RMの採択値には,誤差が存在しないものと仮定する(この規格では,この仮定をチェックしない。)。
しかし,実際にはRMの採択値には不確かさが付記されて引用される。その不確かさがこれらのRMの測
定値の誤差の大きさに比べて小さい場合には,RMの採択値に誤差がないという仮定は成立するものと考
えられる(参考文献[1]参照)。
備考1. 測定器の示す値を読み取る前に,RMが化学的に処理されるか,又はある場合には物理的に
処理される状況では,この規格は,新たな測定結果の変換に伴う不確かさを過小評価するこ
とがある。
5.2.2
校正関数(検量線)は直線であると仮定する(この仮定は検証される。)。
5.2.3
所与のRMの繰り返された測定値は独立に正規分布に従うものと仮定し,その分散は“残差分散”
と呼ぶ(この規格では,独立性と正規性の仮定はチェックしない。)。残差分散の平方根を残差標準偏差と
呼ぶ。
5.2.4
残差標準偏差は,RMの採択値に対して一定であるか,又は比例するものと仮定する(この仮定は,
検証される。)。
5.3
校正(検量線作成)実験
4
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.3.1
実験条件 実験条件は,測定システムの通常の操作条件と同じでなければならない。すなわち,例
えば,オペレータが二人以上で一つの測定装置を使用する場合,校正(検量線作成)実験にもオペレータ
ーが二人以上参画するものとするのがよい。
5.3.2
RMの選択 選択したRMの値の範囲が,(可能な限り)測定システムの通常の操作条件で測定さ
れ得る値の範囲を含むことが望ましい。
選択したRMの組成は,可能な限り測定対象物質の組成を近似していることが望ましい。
RMの値は,測定システムの通常の操作条件で測定され得る値の範囲の全体にほぼ等間隔で配置するの
がよい。
5.3.3
RMの個数,N 校正関数(検量線)の評価には,少なくとも3個のRMを使用することが望まし
い。
校正関数(検量線)の初めての評価には,RMを4個以上[校正関数(検量線)の直線性に疑いがもた
れる区間については,いずれの区間でも少なくとも3個]使用することが望ましい。
5.3.4
繰返し回数,K 各RMは,少なくとも2回測定するのがよい(実際には,可能な限り多数回繰り
返すことを薦める。)。
すべてのRMについて,同一回数の繰返し測定を行うのがよい。
繰返し測定の時期と条件は,操作条件のすべてを代表することを保証するために必要な程度広い範囲に
わたることが望ましい。
5.4
データ解析の方策
5.4.1
データをプロットして,次のことを調査する。
a) 校正(検量線作成)実験時の測定システムの管理状態
b) 直線性の仮定
c) RMの採択値の関数としての測定値のばらつき
5.4.2
残差標準偏差一定の仮定の下で直線で表される校正関数(検量線)を推定する。
5.4.3
校正関数(検量線)と残差をプロットする。残差プロットは,直線性又は, 残差標準偏差一定の
仮定からの逸脱を示す強力な指標である。 残差標準偏差一定の仮定が明らかに成立する場合は,ステップ
5.4.4を省略してステップ5.4.5へ進み,その仮定が成立しない場合はステップ5.4.4を実行する。
5.4.4
比例する残差標準偏差の仮定の下で直線で表される校正関数(検量線)を推定し,校正関数(検量
線)と残差をプロットする。
参考 “比例する残差標準偏差の仮定” (the assumption of proportional residual standard deviation) は,
“残差標準偏差がRMの採択値に比例する”という仮定を意味する。(5.2.4参照)
5.4.5
校正関数(検量線)の不適合性(当てはまりの悪さ)を評価する。繰返し測定値のばらつきに比べ
て,不適合性(当てはまりの悪さ)を表すばらつきが大きい場合は,校正(検量線作成)実験で実施した
手順を調査し,校正関数(検量線)の直線性の仮定を再検討する。直線性の仮定が成立しない場合は,8.3
に述べるブラケティング法を適用するのも一つの方法である。
備考2. この規格の目的を超えるが,データに2次以上の高次曲線を当てはめる手法もある(参考文献
[2]及び[3]参照)。
5.4.6
校正関数(検量線)によって,将来の測定値を変換する。
次の箇条は,この方策の六つのステップについて述べる。9.では,例を用いて基本的方法を説明する。
6. 基本的方法の各ステップ
5
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.1
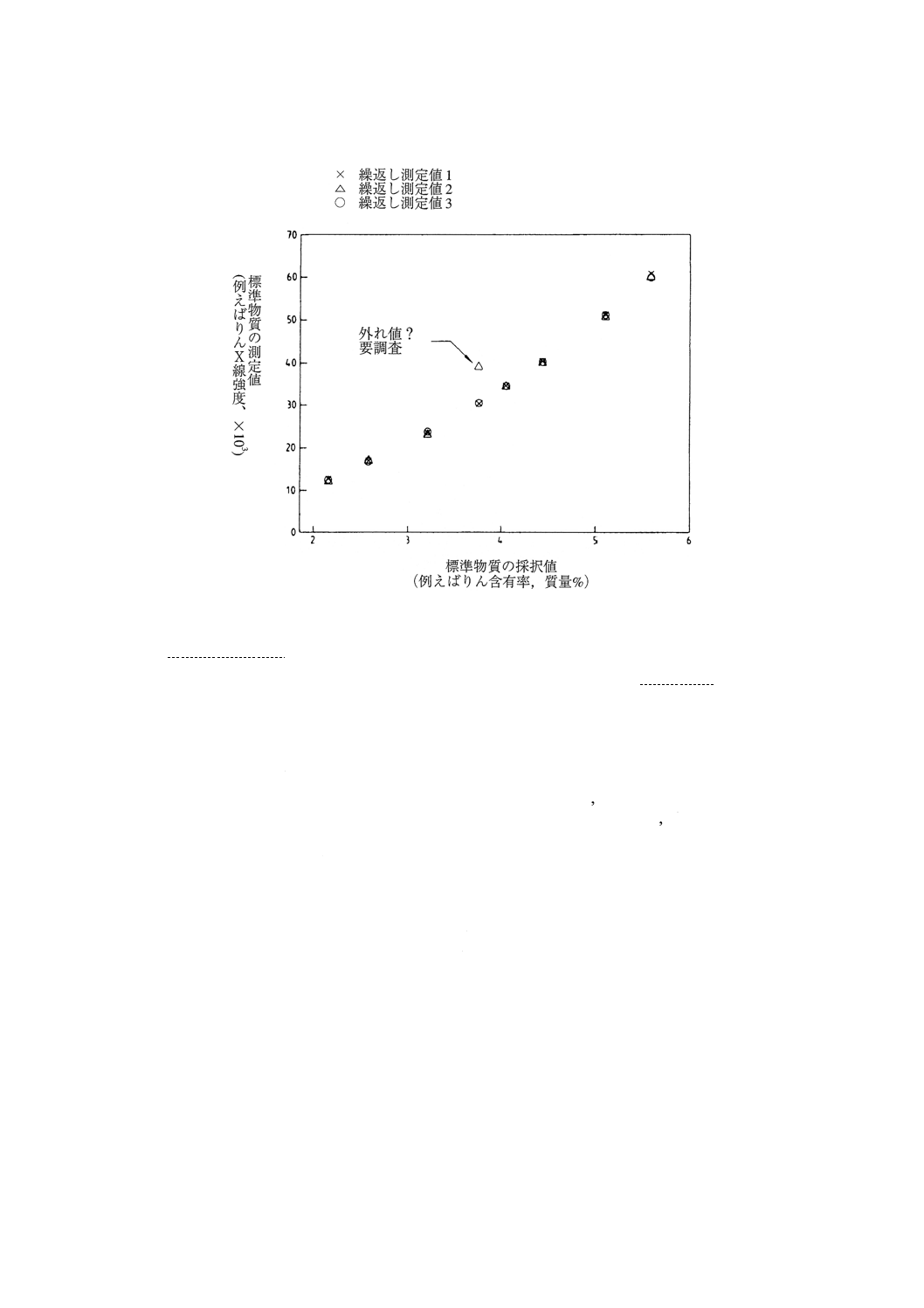
校正(検量線作成)実験において収集したデータのプロット 図1は,測定値を標準物質の採択値
に対してプロットした図である。図1から図5までは,シミュレーション・データを基にして描いた。プ
ロットからどのような情報が得られるかを示すために,これら五つの図を示した。8.では,データ,プロ
ット及び解析を総合した例を示す。
図1のようなプロットの主な目的は,校正(検量線作成)実験における測定システムの通常とは異なる
挙動を視覚的に検出し,外れ値の可能性がある値を特定することにある。可能であれば,データを測定順
にラベルし,明白な時間的トレンドを探すとよい。幾つかのデータが疑わしいか,又は時間的トレンドが
明白であるなら,異常の原因を究明するために調査をしなければならない。異常の原因を取り除いたら,
直ちに校正(検量線作成)実験を繰り返し,新しいデータを収集して校正関数(検量線)を確立すべきで
ある。
もし1個又は限られた個数の外れ値の原因が明らかで,かつ,その原因が他の測定値に影響を及ぼさな
い場合には,その外れ値を排除してもよい。その結果,校正(検量線作成)実験のバランスは崩れる。す
なわち,測定値数Knは,定数Kとはならず標準物質ごとに変わってくる。それでも校正関数(検量線)
の推定は,附属書Bに掲げる公式に置き換えることによって,6.2,6.4及び6.5に述べる公式に従って進
めることができる。
図1によって,校正関数(検量線)に直線性を仮定することが可能かどうかの初期判断を行うことがで
き,また, 残差標準偏差一定の仮定について直感的に判断することができる。図1に,プロットしたデ
ータを通る直線を引けば,校正関数(検量線)の直線性を視覚的にチェックすることができる(図1のデ
ータを結ぶ線は,少し曲がっていると思われる。)。 残差標準偏差一定の仮定は,与えられた標準物質に関
する図1の各点の広がりを見れば分かる。標準物質の採択値が大きくなるにつれて広がりが大きくなれば,
残差標準偏差一定の仮定はおそらく正しくないであろう(図1は,これには該当しないと思われる。)。6.3
では,直線性と 残差標準偏差一定の仮定をチェックするための更に精密なプロットを示す。
6
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1 校正(検量線作成)実験において収集されたデータ
参考 JIS Z 8101-1 : 1999では“replication”を“反復”としているが,この規格の図1〜3では,用い
られている意味を考慮し“replicate1, 2, 3”を“繰返し測定値1, 2, 3”とした。
6.2
残差標準偏差一定を仮定した直線で表される校正関数(検量線)の推定
6.2.1
モデル 校正関数(検量線)の直線性と残差標準偏差一定の仮定は,次のモデルによって表される。
ynk=β0+β1xn+εnk
ここに
xn: n番目の標準物質の採択値 (n=1, …, N)
ynk: n番目の標準物質のk番目の測定値 (k=1, …, K)
β0+β1xn: n番目の標準物質測定値の期待値
εnk: ynkの,n番目の標準物質測定値の期待値からの偏差(これらの偏差は
独立で,平均値0,分散σ2の正規分布に従うものと仮定する。)
β0,β1及びσ2: 校正(検量線作成)実験において収集したデータから推定す
る三つのパラメータ
β0:: 校正関数(検量線)の切片
β1: 校正関数(検量線)の傾き
σ2: 測定システムの精度の尺度
6.2.2
パラメータの推定値 パラメータβ0,β1及びσ2の推定値は,次に示す式を用いるか,又はy及びx
について同じ個数のデータを入力できる直線回帰ソフトウェアを用いて求めることができる。
備考3. パラメータ自体は未知であるため,この規格においては,その推定値には記号^をつけて識
別する。
7
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)(
)
(
)
∑
∑
=
=
−
−
−
=
N
n
n
N
n
n
n
x
x
y
y
x
x
1
2
1
2
1ˆβ
x
y
1
0
ˆ
ˆ
β
β
−
=
(
)2
SSE
ˆ2
−
=NK
σ
ここに
∑
=
=
N
n
n
x
N
x
1
1
∑
=
=
K
k
nk
n
y
K
y
1
1
∑
=
=
N
n
n
y
N
y
1
1
NK=N×K
n
n
x
y
1
0
ˆ
ˆ
ˆ
β
β+
=
n
nk
nk
y
y
e
ˆ
−
=
(
)
∑∑
=
=
=
N
n
K
k
nk
e
1
1
2
SSE
6.3
校正関数(検量線)及び残差のプロット 図2及び図3を用いて,6.2のモデルに関する仮定が成立
するか否かを調べることを薦める。
6.3.1
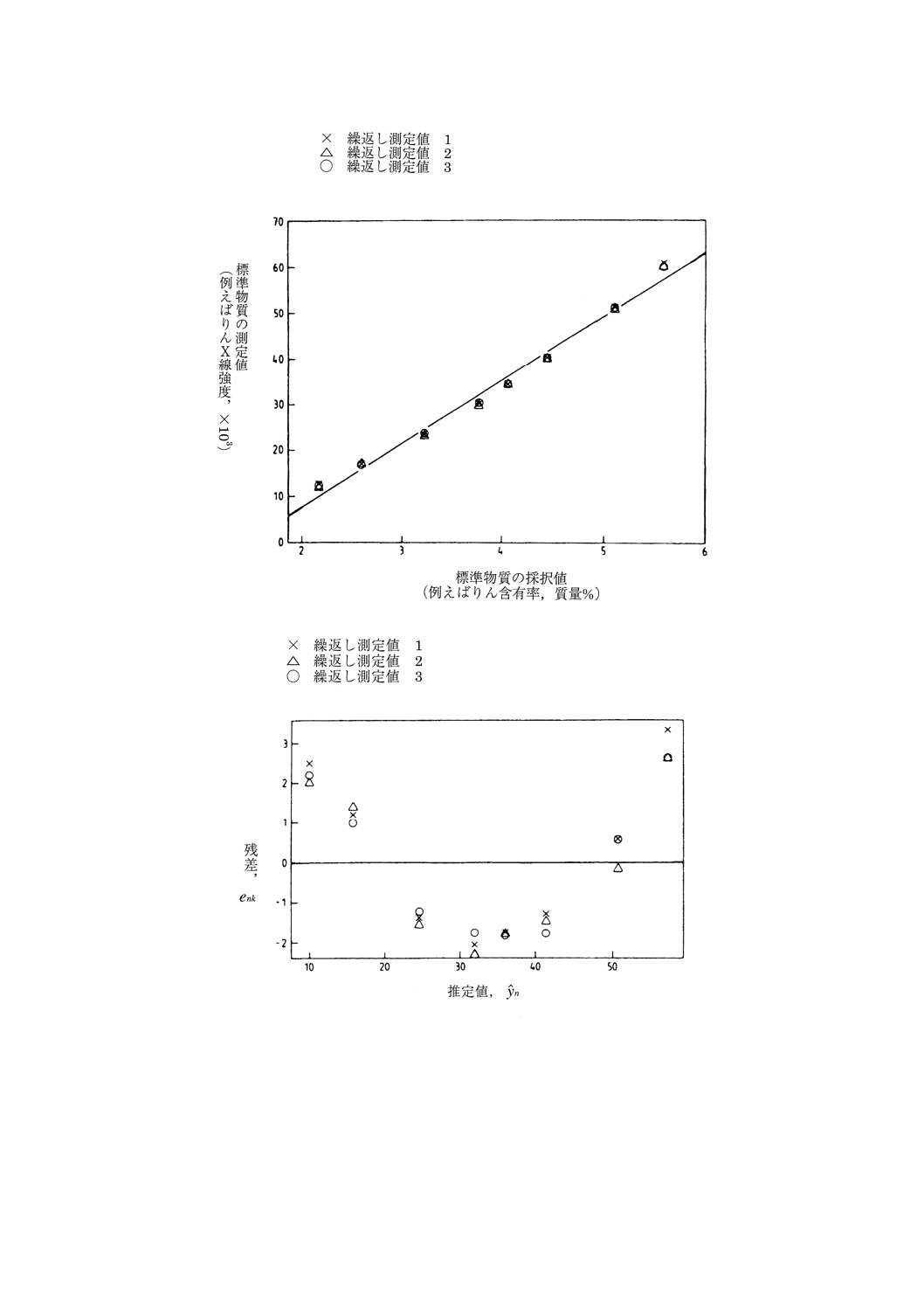
校正関数(検量線)のプロット 図2は,図1に,推定された校正関数(検量線)を追加したもの
である。
図2のプロットでは,主として6.2.2に述べた計算をチェックする。また,校正関数(検量線)の直線性
の仮定を視覚的にチェックすることができる。
8
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2 校正曲線
図3 残差対適合値のプロツト
9
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.2
残差対適合値のプロット 残差enk対適合値
n
yˆのプロット(図3)は,直線性と残差標準偏差一定
の仮定が成立しないことを検出するための強力な手段である。これら二つの仮定が成立する場合,図3で
は,プロットがゼロを中心にしてランダムに分布することになる。直線性の仮定が成立しない場合は,残
差と適合値の間に系統的なパターンが現れる(図3がこれに該当する。)。 残差標準偏差一定の仮定が成
立しない場合は,データのばらつきは,適合値が増加するに従って,大きくなるか又は小さくなる。図3
の場合は,残差のばらつきは,どの適合値についてもほぼ一定である。したがって,図3の場合,残差標
準偏差一定の仮定が成立するとみなすことができる。
備考4. 図8に,残差標準偏差一定の仮定が成立しない場合を示す。
残差標準偏差一定の仮定が成立しない場合は,校正(検量線作成)実験において収集したデータを再度
解析しなければならない。RMの繰返し測定値の標準偏差対RMの採択値のプロットは,比例する残差標
準偏差の仮定が成立するか否かを示す。図9は,その場合のプロットである。
a) 比例する残差標準偏差の仮定が成立すると思われる場合は,ステップ6.4に従ってデータを再度解析
することができる。
b) 比例する残差標準偏差の仮定は成立しないが,残差標準偏差をRMの採択値と関連付ける(例えば,
反比例関係を示す。)モデルが存在する場合は,ステップ6.4に示すアプローチと類似したアプローチ
をとることができる。
直線性の仮定が成立しない場合は,8.3において述べるブラケティング法を適用する。
備考5. この規格の範囲を超えるが,データに2次又は高次曲線を当てはめる手法もある(参考文献
[2]及び[3]参照)。
εnk値の独立性と正規性の仮定を検定することは,この規格の範囲外である。ステップ6.5が有効である
ためには,これら二つの仮定が必ず成立しなければならないが,これらの仮定は,残差を検討することに
よってもチェックすることができる。例えば,残差の正規確率プロットでは,正規性の仮定をチェックす
ることができ,残差対時間のプロットでは,測定値の独立性の仮定をチェックすることができる。詳細に
ついては参考文献[3]を参照されたい。
6.4
比例する残差標準偏差を仮定した校正関数(検量線)の推定と,校正関数(検量線)及び残差のプ
ロット
6.4.1
モデル ステップ6.2.1に示したモデルに代わるもう一つのモデルは,校正関数(検量線)は直線
であるが,RM採択値の増加につれて残差標準偏差も増加するモデルである。これは,次の式で表される。
ynk=γ0+γ1xn+ηnk
ここに
xn:
n番目のRMの採択値 (n=1, …, N)
ynk:
n番目のRMのk番目の測定値 (k=1, …, K)
γ0+γ1xn: n番目のRMの測定値の期待値
ηnk:
ynkの,n番目のRMの測定値の期待値からの偏差(これらの偏差
は独立で,平均0,分散が
2n
xに比例する正規分布に従うものと仮
定する。),すわなち,
var(ηnk)=var (ynk) =
2
2r
n
x
γ0,γ1及びr2: 校正(検量線作成)実験で得られたデータから推定する三
つのパラメータ
γ0及びγ1:
校正関数(検量線)の切片と傾き
r2:
測定システムの相対精度の尺度
このモデルは,6.2.1のモデルと同等なモデル,すなわち,誤差分散が一定であるモデルへ変換すること
10
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ができる。
この変換を行うため,次の式の両辺をxnで割る。
ynk=γ0+γ1xn+ηnk
したがって,次の式が得られる。
n
nk
n
n
nk
x
x
x
y
η
γ
γ
+
+
=
1
0
これは,次の式と同等である。
znk=γ1+γ0ωn+εnk
ここに
znk=ynk/xn
ωn=1/xn
εnk=ηnk/xn
6.2に示した式の各項に正しく代入すれば,この新しいモデルを同じ方法で解析することができる。
6.4.2
パラメータの推定 パラメータγ0,γ1及びr2の値は,次の式か,又は,y,x及び重み (1/x2) のそ
れぞれについて,同じ個数のデータを入力できる重み付き線形回帰分析のソフトウェアを用いて推定する
ことができる。また,重み付きでない線形回帰分析のソフトウェアを用いても,二つの入力変数をz及び
ωとすれば,これと同じ結果が得られる。
(
)(
)
(
)
∑
∑
=
=
−
−
−
=
N
n
n
N
n
n
n
w
w
z
z
w
w
1
2
1
0ˆγ
w
z
0
1
ˆ
ˆ
γ
γ
−
=
(
)2
WSSE
ˆ2
−
=NK
r
ここに
NK=N×K
n
nk
nk
x
y
z =
n
n
x
w
1
=
∑
=
=
N
n
n
w
N
w
1
1
∑
=
=
K
k
nk
n
z
K
z
1
1
∑
=
=
N
n
nz
N
z
1
1
n
n
w
y
y
z
0
1ˆ
ˆ
ˆ
+
=
n
nk
nk
z
z
u
ˆ
−
=
(
)
∑∑
=
=
=
N
n
K
k
nk
u
1
1
2
WSSE

11
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.3
校正関数(検量線)と残差のプロツト6.3の場合と同じく,次の2種類のプロットを用いることが
望ましい。
a) 推定された校正関数(検量線)
x
y
1
0
ˆ
ˆ
ˆ
γ
γ+
=
及び図1のデータのプロット
b) 重み付きで当てはめた値
nzˆに対する重み付き残差unkのプロット
これらのプロットの解釈方法は,図2及び図3の場合と同じである。
6.5
校正関数(検量線)の当てはまりの評価
6.5.1
一般 分散分析 (ANOVA) 表を作成した後,次の二つを比較する。
− 6.2又は6.4において選択したモデルの不適合性(当てはまりの悪さ)を表すばらつき
− 測定を正確に繰り返すためのシステムの能力不足を表す純誤差のばらつき
各RMの測定が繰り返されているので,この比較を行うことができる。
有意水準αの値の選択は,個々の目的に応じて決まり,この規格の使用者が決定するものとする。
参考 純誤差とは,測定の繰返しによってだけ生ずる純粋な繰返し誤差をいう。JIS Z 8101-3 : 1999
参照。
6.5.2
残差標準偏差一定のモデル(6.2において定義)
6.5.2.1
表1に示す分散分析表は,次の式,又はほとんどの線形回帰分析のソフトウェアの出力を用いて,
得ることができる。
表1 残差標準偏差一定を仮定した場合の不適合性(当てはまりの悪さ)と純誤差を比較する分散分析表
要因
自由度,DF
平方和,SS
SS/DF
F
校正関数(検量線) 1
SSR=SST−SSE
残差
NK-2
SSE
2
SSE
ˆ
−
=NK
σ
不適合性(当ては
まりの悪さ)
N-2
SSE−SSP
2
SSP
SSE
ˆ21
−
−
=
N
σ
2P
21
ˆ
ˆ
σ
σ
純誤差
NK-N
SSP
N
NK−
=
SSP
ˆ2P
σ
合計
NK-1
SST
(
)
∑∑
=
=
−
=
N
n
K
k
nky
y
1
1
2
SST
(
)
∑∑
=
=
−
=
N
n
K
k
n
nky
y
1
1
2
SSP
SSEは6.2.2の定義による。
6.5.2.2
純誤差によるばらつきは,
2Pˆσで推定される。このばらつきは,データに当てはめたモデル(y=β0
+β1x)と独立である。不適合性(当てはまりの悪さ)を表すばらつきは
21ˆσで推定する。6.2.1で定義し左
モデルの妥当性は,
2P
21
ˆ
ˆ
σ
σ
とF (1-α) (N-2 ; NK-N) の比較によって検定される。ここでF(1-α) (N-2; NK-N) は,
自由度がN-2及びNK-NのF分布の(1-α)分位点である。
a)
2P
21
ˆ
ˆ
σ
σ
がF (1-α) (N-2; NK-N) より大きくない場合は,線形モデルを棄却する根拠はない。
b)
2P
21
ˆ
ˆ
σ
σ
がF (1-α) (N-2; NK-N) より大きい場合,純誤差によるばらつきに比べて,不適合性(当てはま
りの悪さ)を表すばらつきが大きくなる潜在的な原因を調査しなければならない。一般に共通する原
因は,校正関数(検量線)の直線性の仮定が十分には成り立っていないことである(図2及び図3参
照)。もう一つ考えられる原因は,校正(検量線作成)実験を実施した条件(例えば,繰返し測定が正
しく行われずに,測定値の読みとりを繰り返すなど)であることもある。

12
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.5.3
比例する残差標準偏差のモデル(6.4において定義) 比例する残差標準偏差のモデルを用いた場
合には,分散分析表は表2に示したようになる。
2P
21
ˆ
ˆr
r
については,6.5.2.2に述べた
2P
21
ˆ
ˆ
σ
σ
に対する検定,解釈,結論及び注意がそのまま適用される。
表2 比例する残差標準偏差を仮定した場合の不適合性(当てはまりの悪さ)と純誤差を比較する分散分
析表
要因
自由度,DF
平方和,SS
SS/DF
F
校正関数(検量線) 1
WSSR=WSST
−
WSSE
残差
NK-2
WSSE
2
WSSE
ˆ2
−
=NK
r
不適合性(当ては
まりの悪さ)
N-2
WSSE−WSSP
2
WSSP
WSSE
ˆ21
−
−
=
N
r
2p
21
ˆ
ˆ
r
r
純誤差
NK-N
WSSP
N
NK
r
−
=WSSP
ˆ2P
合計
NK-1
WSST
(
)
∑∑
=
=
−
=
N
n
K
k
nkz
z
1
1
2
WSST
(
)
∑∑
=
=
−
=
N
n
K
k
n
nkz
z
1
1
2
WSSP
WSSEは6.4.2の定義による。
6.6
校正関数(検量線)による測定値の変換 いったん校正(検量線作成)実験が行われると,校正関
数(検量線)により,(既知の値又は採択値をもつ標準物質とは逆の手順で)未知の量の測定値を変換する
ことができる。これらの測定値を変換することにより,未知の量の真の値を推定する一つの値x0*が得ら
れる。この変換は,残差分散に関する仮定に応じて次のように行われる。
新たな未知の量をp回測定し,測定値y01,y02,…,y0pを得る。これらのp個の測定値の平均値
0yは,
次の式で与えられる。
∑
=
=
p
k
k
y
p
y
1
0
0
1
p=1の場合は
01
0
y
y=
である。
a) 残差標準偏差一定のモデルを選択した場合は,
1
0
0
0
ˆ
β
β
−
=
y
x
b) 比例する残差標準偏差のモデルを選択した場合は,
1
0
0
0
ˆ
ˆ
γ
γ
−
=
y
x
この規格では;校正(検量線作成)実験に基づく校正関数(検量線)に含まれる未知パラメータの
推定について,パラメータごとに設定する信頼区間(参考文献[2]参照)も,複数のパラメータを多変
量として設定する信頼区間(参考文献[4]及び[5]参照)も規定しない。この規格は,それに代えて,種々
な利点の中でも特に一定の期間RMを少数個モニターしたときに得られるばらつきに基づく信頼区間
を導出することができるという利点をもっ管理方法を規定する。
13
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7. 管理方法
7.1
一般 校正関数(検量線)を,長期間使用する場合は,校正曲線の有効性をチェックするための,
また,好ましくないばらつきの原因を特定しこれを排除できるようにするための管理方法を取り入れるこ
とが望ましい。管理方法は,システムが不安定になったり偏りを生じたりして,校正関数(検量線)が有
害ではないにしても無益になった可能性がある場合,これを速やかに検知する目的で,定期的に測定シス
テムを監視するためのものである。
この検知は,管理図の手法を用いて,RMm個のセットに対する[校正関数(検量線)による変換後の]
測定値を監視することにより行う。
備考6. このアプローチは,ISO 7870 [6] とISO 8258 [7] に記述されている従来の管理図の応用である。
校正(検量線作成)実験の間に収集したデータから,まず管理図を作成する。次にこの管
理図を用いて,校正関数(検量線)を再度推定する必要があるか否かを決定する。同じ管理
図はまた,校正関数(検量線)によって変換された後の測定値の不確かさを推定するために
も用いられる。
7.2
上方及び下方管理限界の計算
7.2.1
残差標準偏差一定のモデル
a) 上方管理限界Udと下方管理限界Ldを,次の式によって計算する。
(
)(
)2
ˆ
ˆ
2
1
1
d
−
=
−
NK
t
U
ς
β
σ
(
)(
)2
ˆ
ˆ
2
1
1
d
−
−
=
−
NK
t
L
ς
β
σ
ここで
∂: 校正(検量線作成)実験から得られた推定値σ2の平方根(6.2.2参照)
NK-2:
σ2の推定に伴う自由度(6.5参照)
1ˆβ: 校正(検量線作成)実験から得られたβ1の推定値(6.2.2参照)
α:
この管理図で用いる有意水準
t(1-ζ/2) (NK-2): 自由度NK-2のt分布の(1-ζ/2)分位点,すなわち,
P[t>t(1−ζ/2) (NK-2) ]=ζ/2
ζ: 個々のRMに対する有意水準であり,m個全部のRMに対する一括し
た有意水準がαになるような限界UdとLdを与えるもの。ζは(αが小
さい場合には)次の式で与えられる。
(
)
−
−
=
m
α
ς
1
ln
exp
1
m
α
≈
b) 管理図に上方管理限界Udと下方管理限界Ldをプロットする。
7.2.2
比例する残差標準偏差のモデル
a) 上方管理限界Ucと下方管理限界Lcを次の式によって計算する。
(
)(
)2
ˆ
ˆ
2
1
1
c
−
=
−
NK
t
r
U
ς
γ
14
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)(
)2
ˆ
ˆ
2
1
1
c
−
−
=
−
NK
t
r
L
ς
γ
ここで
rˆ:
校正(検量線作成)実験から得られた推定値
2ˆrの平方根(6.4.2参照)
NK-2:
2ˆrの推定に伴う自由度(6.5参照)
1ˆγ:
校正(検量線作成)実験から得られたγ1の推定値(6.4.2参照)
備考7
. α,t(1−ζ/2) (NK−2) 及びζは,7.2.1a)の定義による。
b) 管理図に上方管理限界Ucと下方管理限界Lcをプロットする。
7.3
データの収集とプロット
7.3.1
m個のRMを,それらの採択値が測定システムの通常の測定条件において生じる値の範囲を含むよ
うに選択する。RMは最低限2個必要であるが,3個使用することを推奨する。校正(検量線作成)実験
において使用したRMとは異なるRMを使用することが望ましいが,これは必す(須)ではない。
7.3.2
定期的に(例えば,1日1回又は1直当たり1回など)これらのm個のRMのそれぞれを1回ずつ
測定する。
7.3.3
m個のRMのそれぞれについて変換した値を求める(6.6参照)。これらの変換値を
ix (i=1, …, m)
で表す。
7.3.4
変換値
ixとRMの採択値xiの差diを次の式で計算する。
i
i
i
x
x
d
−
=
7.3.5
校正(検量線作成)モデルとして 残差標準偏差一定を仮定する場合,差diを管理値とする。
校正(検量線作成)モデルとして比例する残差標準偏差を仮定する場合,diをxiで割って正規化し,そ
の値ciを管理値とする。すなわち,
i
i
i
i
x
x
x
c
−
=
7.3.6
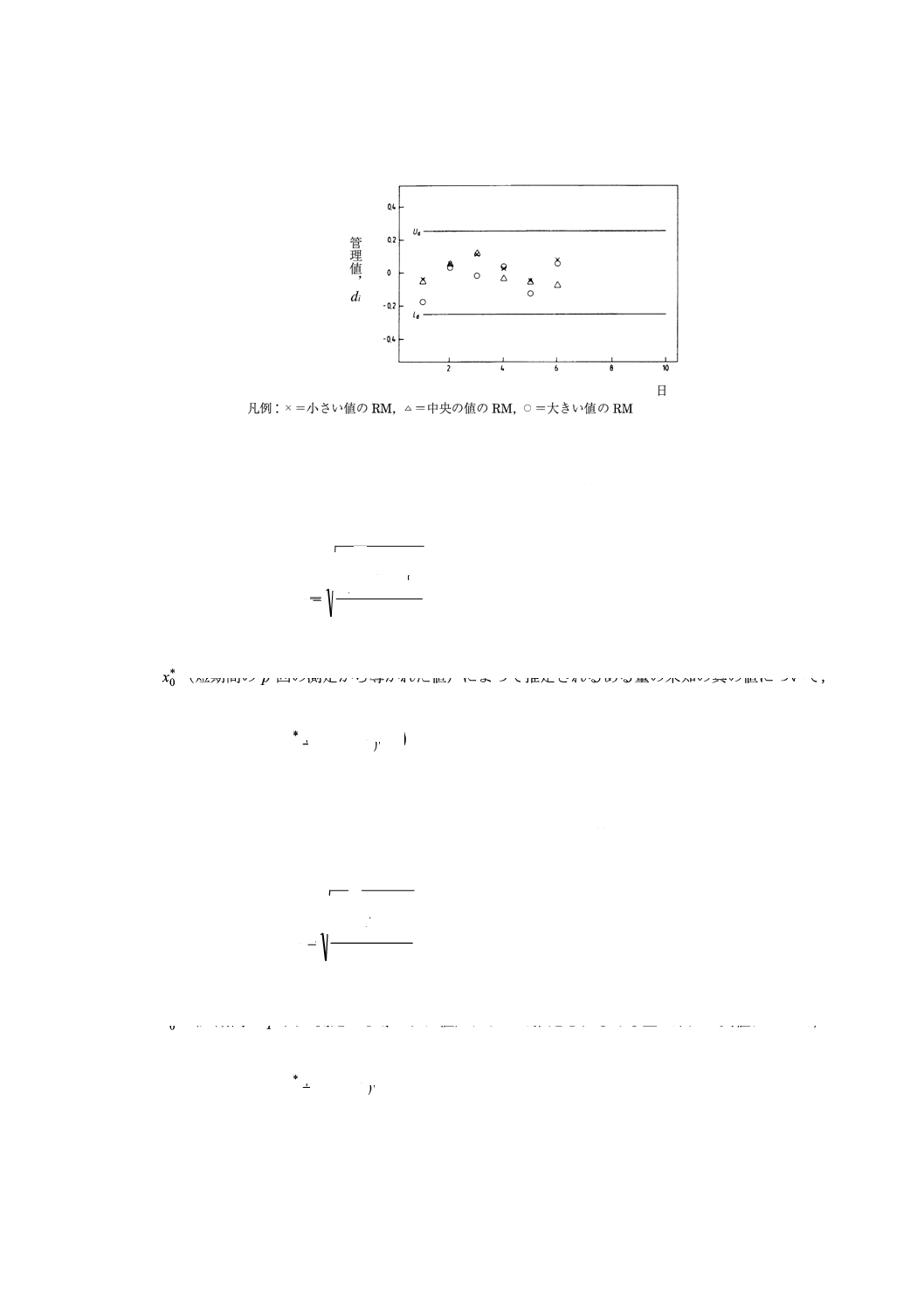
管理図上に,該当する管理値(di又はci)をm個のRMを測定した時間に対してプロットする。図
4は,残差標準偏差一定のモデルに対する管理図を示す。比例する残差標準偏差のモデルについても同様
の管理図を描くことができる(図12参照)。
7.4
システムの状態の決定 残差標準偏差一定のモデルにおいて,1個又はそれ以上のdiの値が管理限
界Ud及びLdの外に出た場合,システムは,その時点で管理はずれの状態にあると判断する。このとき,m
個のRMを再測定しなければならない。再測定したm個のRMの測定値の少なくとも1個がなお管理限界
の外にある場合,その時点で間題の原因をつきとめるため調査を行う。問題の性質によっては,新たな校
正(検量線作成)実験を行って,校正関数(検量線)を再推定しなければならないかもしれない。
比例する残差標準偏差のモデルにおいても,ciの値と管理限界Uc及びLcを比較することによって,同様
の手順となる。
7.5
変換値の不確かさの推定
7.5.1
得られた校正関数(検量線)が有効な期間中の推定 上の管理方法を校正関数(検量線)に適用し
ている場合,変換値の不確かさは,(管理方法のために選択したm個の中の)2個のRM,すなわち,最大
及び最小のRMに対するプールされた分散で近似される。これは,変換値の分散は,校正(検量線作成)
実験の際に生じた値の範囲の両端で大きく中間で小さいと予想されるからである。したがって,両極端の
RMの変動から導かれる変換値の信頼区間は,実際に生じる値の範囲の端部の値についてはほぼ正しく,
範囲の中央の値については大きめになる。
15
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
このような信頼区間を求めるため,該当するモデル(残差標準偏差一定又は比例する残差標準偏差)に
ついて,7.5.1.1に述べる計算を行う。
図4 残差標準偏差一定を仮定した場合の校正曲線を検証する管理図
7.5.1.1
残差標準偏差一定のモデル 最小及び最大のRMに対する管理値をそれぞれdlj,dmjと表す。こ
こで,jは測定が行われた時間を示す。すると,測定システムが統計的管理状態にある間のj回の測定の期
間全体について,変換値の標準偏差は,
(
)
J
d
d
J
j
j
j
2
ˆ
1
2m
2l
cal
∑
=
+
=
σ
で近似的に求められ,その目由度は2Jである。
変換値
0x(短期間のp回の測定から導かれた値)によって推定されるある量の未知の真の値について,
信頼水準(1-α)の信頼区間は近似的に
(
)()
J
t
x
2
ˆ
2
1
cal
0
α
σ
−
±
で得られる。ここでt(1-α/2) (2J)は,自由度2Jのt分布の(1-α/2)分位点である。
7.5.1.2
比例する残差標準偏差のモデル 最小及び最大のRMに対する管理値をそれぞれclj,cmjと表す。
ここでjは測定が行われた時間を示す。すると,測定システムが統計的管理状態にある間のJ回の測定の
期間全体について,変換値の変動係数は,
(
)
J
c
c
r
J
j
j
j
2
ˆ
1
2m
2l
cal
∑
=
+
=
で近似的に求められ,その自由度は2Jである。
変換値
0x(短期間のp回の測定から導かれた値)によって推定されるある量の未知の真値について,
信頼水準(1-α)の信頼区間は近似的に
(
)()
−
±
0
2
1
cal
0
2
ˆ
x
J
t
r
x
α
で得られる。ここで,t(1−α/2) (2J)は,自由度2Jのt分布の (1−α/2) 分位点である。
16
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.5.2
再校正(検量線作成)を含む期間にわたっての推定 校正(検量線作成)作業による変動が不確か
さの表記に含まれることを保証するため,各校正(検量線作成)間隔から1セットの管理値 (dlj, dmj) 又は
(clj, cmj) を取り出し,
cal
ˆσ又
cal
ˆcと同じ公式を適用する。ただし,jは今の場合,再校正(検量線作成)の
番号を示す。
8. 基本的方法の代替となる二つの方法
8.1
一般 特別の条件においては,二つの代替方法を用いて測定プロセスを校正(検量線作成)するこ
とができる。これら二つの方法は,実際は,基本的方法においてRMを1個又は2個しか使用しない特別
の場合である。1点校正(検量線作成)法は,校正関数(検量線)の直線性に疑問がないとき,測定シス
テムを敏速に“再校正(検量線作成)”する手法である。ブラケティング法は大きな労力を要するが,最小
限の仮定で未知の量の値を高精度で測定する手法である。
8.2.1
点校正(検量線作成)法
8.2.1
一般 この方法は,与えられた範囲 [0, …, M] において,関数の直線性に疑問がないとき,敏速
に再校正(検量線作成)を行う場合に便利である。あるダイアル(使用する測定器のダイアル)を調整す
ることによって,真の値が0である未知の量が0として測定されるような“ゼロ点”を設定する。この方
法では,ブランク(真の値が0の量)と,RMが1個使用される。
この方法は,歴史的には1点校正(検量線作成)と呼ばれてきたが,実際はブランクを1個とRMを1
個使用する2点校正(検量線作成)である。このいわゆる“1点校正(検量線作成)”は,ブランクに疑問
があるため,不十分,かつ,不確実な方法である。したがって,これを校正(検量線作成)に使用するこ
とは好ましくなく,使用するとしても,主として既存の直線で表される校正関数(検量線)のチェックに
止めるべきである。
8.2.2
仮定 次のことを仮定する。
a) この方法に使用するRM1個とブランクの採択値には誤差がない(検証しない仮定)。
b) 校正関数(検量線)は範囲 [0, …, M] 全体を通じて直線で表される(検証しない仮定)。
c) 残差標準偏差は一定である(検証しない仮定)。
8.2.3
1点校正(検量線作成)実験
a) 実験条件:実験条件は,測定システムの通常の操作条件と同じにする。
b) RMの選択:この実験のために選択する唯一のRMは,(可能な限り)測定システムの通常の条件で測
定される値より大きい採択値をもつものとする。
c) 繰返し数:RMは少なくとも2回測定する。
8.2.4
校正関数(検量線)の推定
8.2.4.1
モデル このモデルは,6.2.1において定義した残差分散の一定な基本的方法のモデルに類似して
いるが,切片をもたない。このモデルは,次の式で表される。
yk=βx+εk
ここで
x:
使用するRM1個の採択値
yk: 使用するRM1個のk番目の測定値 (k=1, …, K)
εk: ykの,RM測定値の期待値からの偏差(これらの偏差は独立であり,
平均値0,分散σ2の正規分布に従うものと仮定)
β及びσ2:
校正(検量線作成)実験において収集したデータから推定す
る二つのパラメータ
17
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2.4.2
β及びσ2の推定値 β及びσ2の推定値は,次の式から得られる。
x
y
=
βˆ
(
)
∑
=
−
−
=
K
k
k
y
y
K
1
2
2
1
1
ˆσ
ここで
∑
=
=
K
k
k
y
K
y
1
1
8.2.4.3
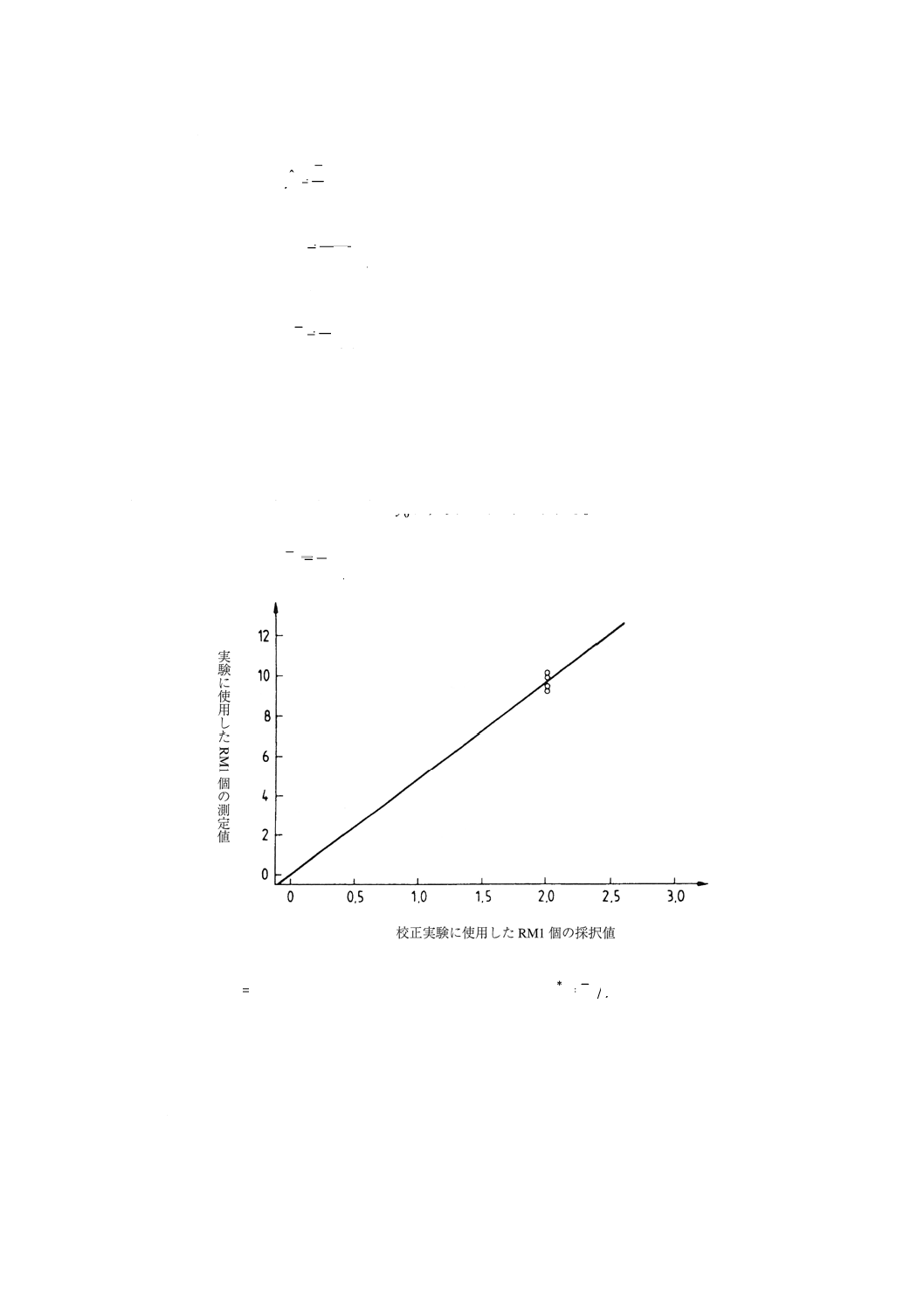
デタのプロット 実験において収集したデータを,図5に示すとおりプロットする。
図5のプロットによって,究明すべき潜在的な異常値を視覚的に特定することができる。図5は,また,
必ず原通る直線で表される校正関数(検量線)を表す。
8.2.5
校正関数(検量線)による測定値の変換 ある未知の量をp回測定して,測定値y01,y02,…,y0p
をp個得る。これらの測定値p個の平均値
0yは,次の式で与えられる。
∑
=
=
p
k
k
y
p
y
1
0
0
1
図5 1点校正実験におけるデータ
p=1の場合は,
01
0
y
y=
である。これらの測定値を変換して,
βˆ
0
0
y
x =
として結果が得られる。
備考8. 原則として,ブランクは必ずしも真の値0をもつものではなく,測定値がybとして知られて
いる採択値xbをもつ。xbが無視できない場合は,8.2.3に述べた1点校正(検量線作成)方法
は,次のように修正してこれを使用することができる。
a) ブランクを測定して,測定器のダイアルがybを指すように調整する。
b) 値が0のブランクの場合と同じように,使用するRMを1個測定する。
c) モデルは,次の式で表されることとなる。
yk-yb=β (x−xb)+εk
18
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) βの推定値は,次の式で表される。
(
)(
)
b
b
ˆ
x
x
y
y
−
−
=
β
e) σ2の推定値は,同じ式が使える。
f) P回測定された未知の量の真の値 (y01,y02,…,y0p) の推定値は,次のとおりである。
(
)βˆ
b
0
b
0
y
y
x
x
−
+
=
8.3
ブラケティング手法
8.3.1
一般 この方法は,測定システムの通常の操作において測定される値の範囲全体について校正関数
(検量線)の直線性に若干疑問があるときに有効である。また,この方法は,測定プロセスの安定性を問
題にする場合にも有効である。この方法の原理は,校正関数(検量線)の直線性を仮定する区間を可能な
限り限定することにある。このため,標準物質 (RM) の二つの値で未知の量を可能な限り短い間隔で取り
囲む(ブラケティングする。)。二つのRM値によって未知の各量を狭い間隔で取り囲むことと,手順に要
する時間(未知の量と二つのRMの測定時間)が短いことによって,このブラケティング法は,一般に未
知の量の変換値を高い精確さで求めることができる。
未知の量とRM2個は,同時に測定する。未知の量の値は,二つのRM値の間の直線補間によって直接
推定する。
8.3.2
仮定 ブラケティング法ではRM値を2個しか使用しないため,次のいずれの仮定もチェックする
ことはできない。
a) RM2個の採択値には誤差がない。
b) RM2個の間の校正関数(検量線)は直線である。
c) 残差標準偏差は一定である。
8.3.3
ブラケティング実験
a) 実験条件:実験条件は,同一RMの測定の変動が可能な限り小さくなるよう設定する。
b) RMの選択:2個のRM値の間隔は可能な限り小さくし,かつ,測定対象の未知の量の値をその間に
挟まなければならない。
c) RMの数:未知の量1個につきRMを2個使用する。
d) 繰返し数:2個のRMと未知の量はいずれも少なくとも2回測定する。
8.3.4
未知の量の推定
8.3.4.1
モデル このモデルは, 残差標準偏差一定の基本的方法のモデルと同じである(6.2参照)。す
なわち,このモデルは,次の式で表される。
yik=β0+β1xi+εik
ここで
i:
RM2個 (i=1, 2) と未知量 (i=0) を示す添字
x1及びx2:
RMの採択値
x0:
未知量の未知の真の値
y1kとy2k及びy0k: それぞれ2個のRMと未知量の測定値 (k=1, …, K)
εik:
yikの,(iの値に応じて)RM又は未知量の測定値の期待値からの偏
差(これらの偏差は,平均値0,分散σ2のランダムな分布と仮定)。
β0,β1, x0及びσ2: ブラケティング実験において収集されたデータから推
定する4パラメータ(β0及びβ1は,パラメータx0に影響
するために推定するものであり,それ以外の意味はな
19
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い。)。
8.3.4.2
x0及び残差分散σ2の推定値 x0及び残差分散σ2の推定値は,次の式で求められる。
(
)
(
)
1
2
2
0
1
1
0
2
0ˆ
y
y
y
y
x
y
y
x
x
−
−
−
−
=
(
)
(
)
(
)
(
)1
3
ˆ
1
2
0
0
1
2
2
2
1
2
1
1
2
−
−
+
−
+
−
=
∑
∑
∑
=
=
=
K
y
y
y
y
y
y
K
k
k
K
k
k
K
k
k
σ
ここに
i=0,1,2のとき,
∑
=
=
K
k
ik
i
y
K
y
1
1
9. 例
9.1
一般 ここでは,測定システムに関する直線で表される校正関数(検量線)を推定する基本的方法
と,当該測定システムを監視する管理方法の例を示す。この例は,参考文献 [8] に基づくものである。
9.2
基本的方法
9.2.1
背景とデータ 0.5μmから12μmの範囲にある集積回路フォトマスクの線間隔は,光学的撮像シス
テム(測定用アタッチメントをもつ光学顕微鏡)によって測定する。このようなシステムは,国立標準技
術研究所 (NIST: NationalInstituteofStandardsandTechnology) が提供する標準物質SRM-474を用いて校正(検
量線作成)することができる。SRM-474は各種機能のほかに,間隔が0.5μmから12μmの範囲で,ランダ
ムに配列された直線を10個もっている。ここでは,光学的撮像システムに対して行われた校正(検量線作
成)実験について述べる。標準の線間隔10個は,それぞれ4回測定された。測定値の間の独立性を保証す
るため,2週間間隔をあけて反復測定が行われた。表3のデータは,NISTが採択値を規定する線間隔10
個 (N=10) のそれぞれについて反復測定された値4個 (K=4) を示す。
9.2.2
データのプロット 図6に示す実験において収集されたデータのプロットでは,校正(検量線作成)
実験において明白な異常値が現れたことも,システムが異常な挙動を行ったことも特定されない。これは,
校正関数(検量線)の直線性を裏付けるが,各NIST値が増加すると,そのNIST値に対するデータの広が
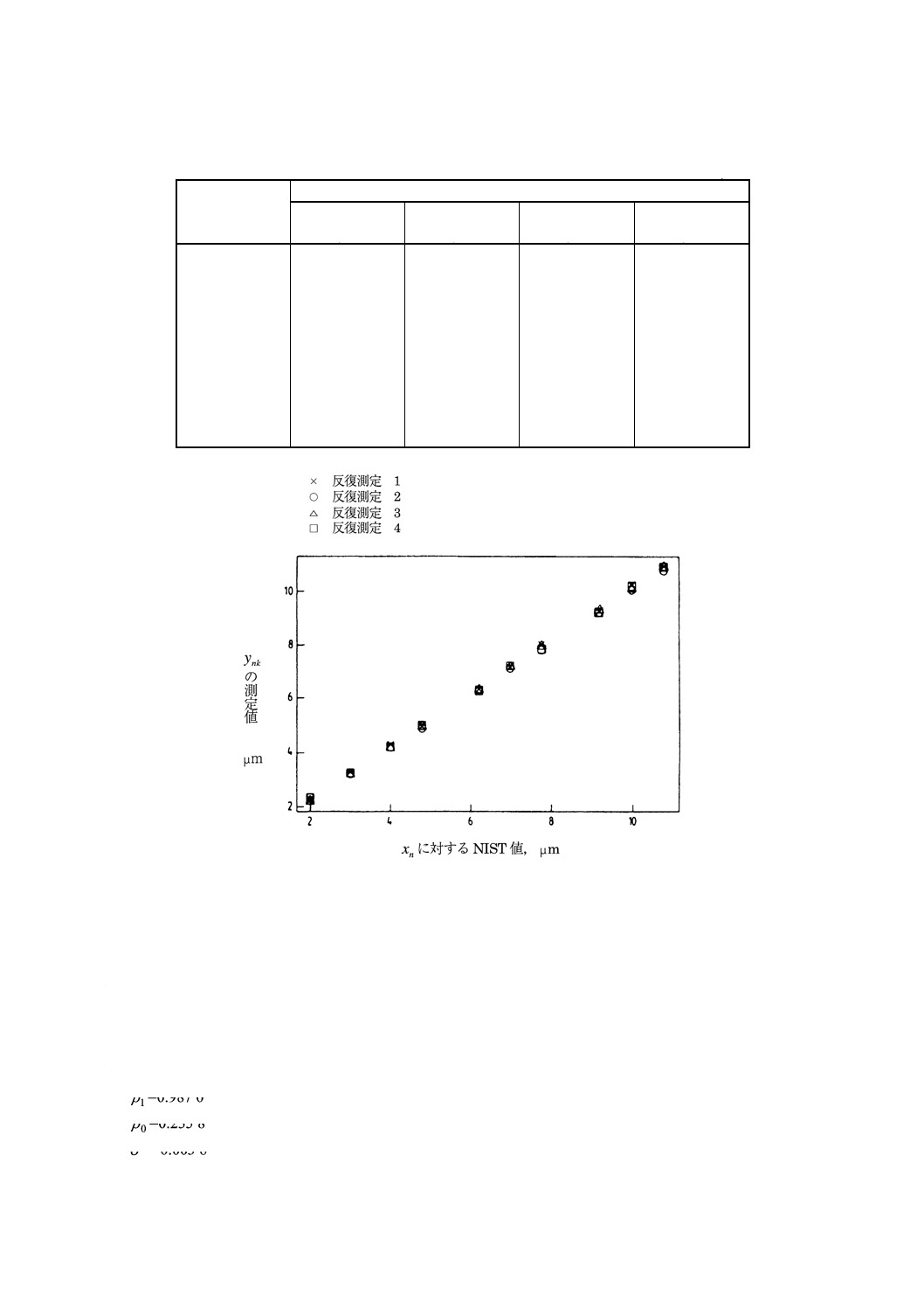
りが拡大するところから, 残差標準偏差一定の仮定に関して疑いが生ずる。
20
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3 線間隔の校正(検量線作成)実験
単位μm
NIST値
xn
測定値
反復測定値1
yn1
反復測定値2
yn2
反復測定値3
yn3
反復測定値4
yn4
6.19
6.31
6.27
6.31
6.28
9.17
9.27
9.21
9.34
9.23
1.99
2.21
2.19
2.22
2.20
7.77
8.00
7.81
7.95
7.84
4.00
4.27
4.15
4.15
4.15
10.77
10.93
10.73
10.92
10.89
4.78
4.95
4.87
5.00
5.00
2.99
3.24
3.17
3.21
3.21
6.98
7.14
7.07
7.18
7.20
9.98
10.23
10.02
10.07
10.17
図6 線間隔校正実験において収集されたデータ
9.2.3
残差標準偏差一定を仮定した直線で表される校正関数(検量線)の推定 6.2.2の式によって次の
値が得られるぐ
a) N=10, K=4
b)
x=6.462
c) yiは,表4による。
d)
y=6.614
e) SSE=0.146 2
f)
1ˆβ=0.987 0
g)
0ˆβ=0.235 8
h)
2ˆσ=0.003 8
21
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
校正関数(検量線)は,次のとおりである。
yˆ=0.235 8+0.987x
適合値
n
yˆは,この式のxを表3のNIST値xnで置き換えることによって得られる。
残差は,次の式で与えられる。
n
nk
nk
y
y
e
ˆ
−
=
表5に残差を示す。
表4 yiの値
i
1
2
3
4
5
6
7
8
9
10
yi
6.292 9.263 2.205 7.900 4.180 10.868 4.955 3.208 7.148 10.12
表 5 残差標準偏差一定を仮定した線形校正
単位μm
NIST値
適合値
残差
xn
n
yˆ
en1
en2
en3
en4
6.19
6.345 5
−0.035 5
−0.075 5
−0.035 5
−0.065 5
9.17
9.286 9
−0.016 9
−0.076 9
0.053 1
−0.056 9
1.99
2.200 0
0.010 0
−0.010 0
0.020 0
0.000 0
7.77
7.905 0
0.095 0
−0.095 0
0.045 0
−0.065 0
4.00
4.183 9
0.086 1
−0.033 9
−0.033 9
−0.033 9
10.77
10.866 2
0.063 8
−0.136 2
0.053 8
0.023 8
4.78
4.953 8
−0.003 8
−0.083 8
0.046 2
0.046 2
2.99
3.187 0
0.053 0
−0.017 0
0.023 0
0.023 0
6.98
7.125 3
0.014 7
−0.055 3
0.054 7
0.074 7
9.98
10.086 4
0.143 6
−0.066 4
−0.016 4
0.083 6
図7 残差標準偏差一定を仮定した線間隔の校正曲線
9.2.4
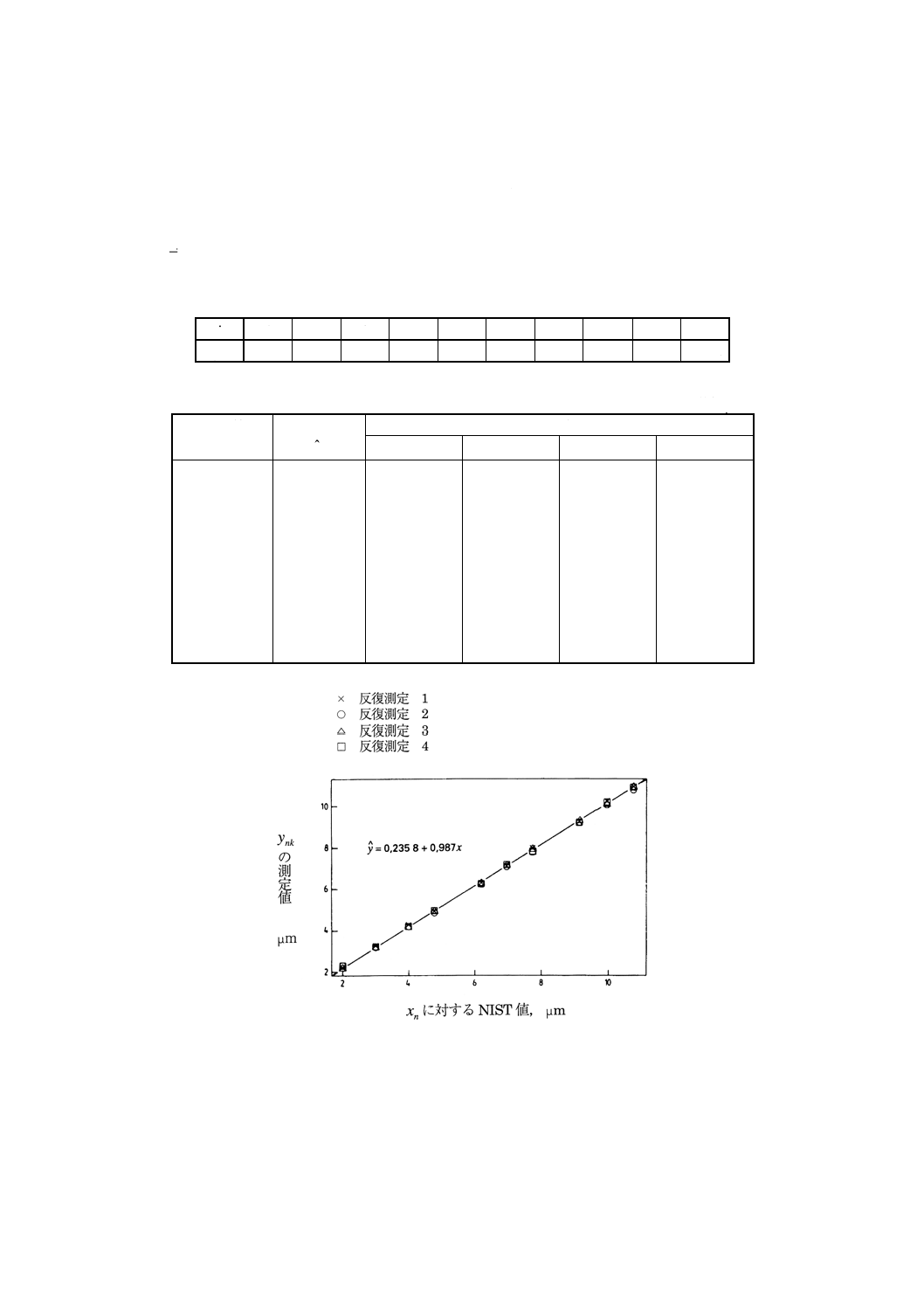
校正関数(検量線)と残差のプロツト 校正関数(検量線)のプロット(図7)によって,校正関
数(検量線)の直線性の仮定が妥当であることが確認される。
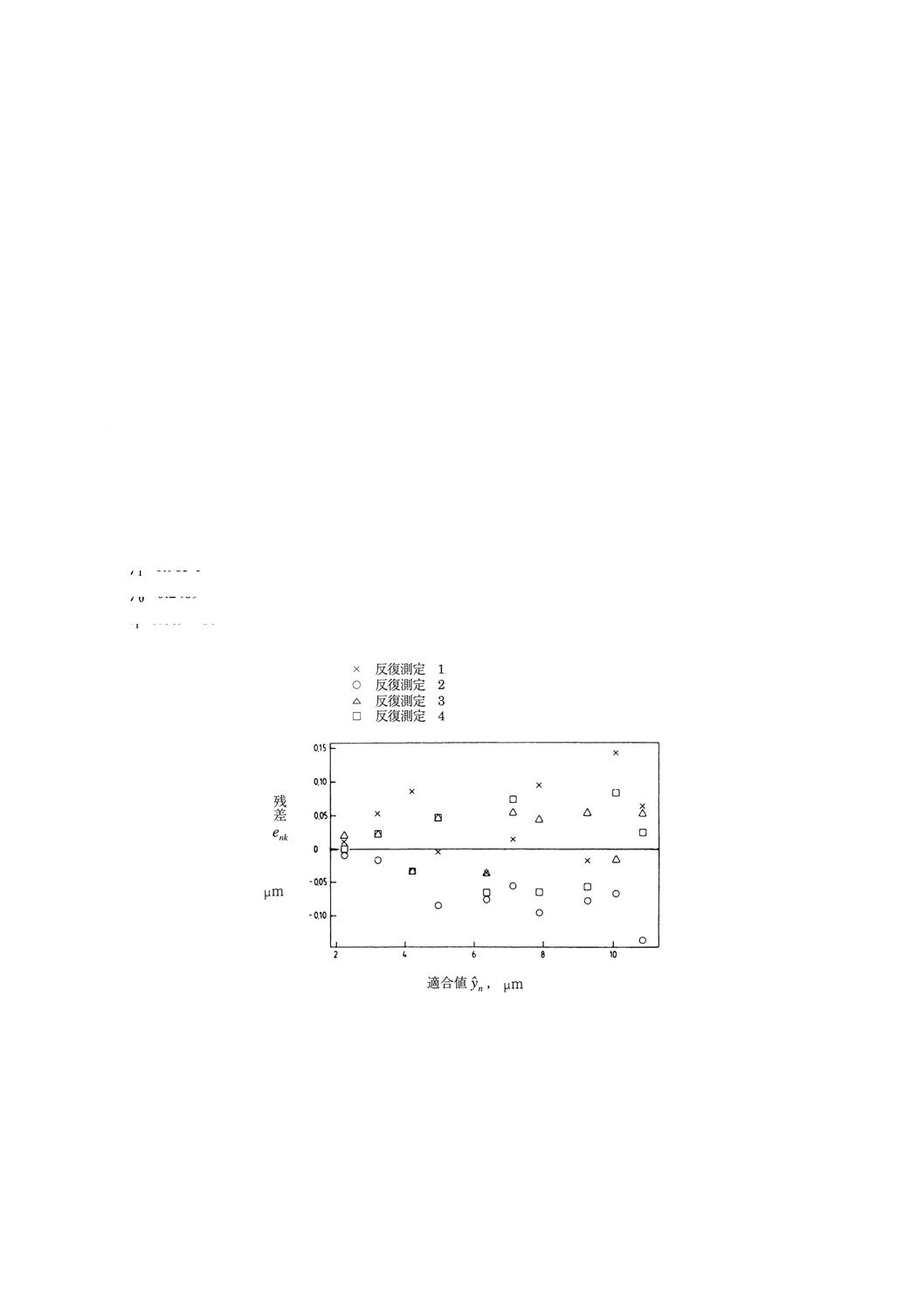
残差のプロット(図8)は,反復測定2の残差が一貫して他の反復測定残差より小さいことを示す。こ
の事実は,表3の当初のデータにおいても,反復測定2の測定値が一貫して他の反復測定値より低いこと
22
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
にさかのぼることができる。この現象を確定的に説明し得る事実はなく,反復測定2のデータは,通常の
測定条件において測定システムに起こり得るものとして保持された。
6.2.1及び6.4.1において提案したモデルニつより更に精密なモデルを用いてこれらのデータを解析すれ
ば,反復測定値の間の系統的な差違を反映した考察ができるであろう。議論を簡単にするため,かっ,基
本的方法と管理方法を示すことが目的であるから,ここではこの効果を無視して,今まで述べた方策とこ
れに関連するモデルを追及することとする。
図8はまた, 残差標準偏差一定の仮定が成立しないことを示唆する。これは,RMの反復測定値の標準
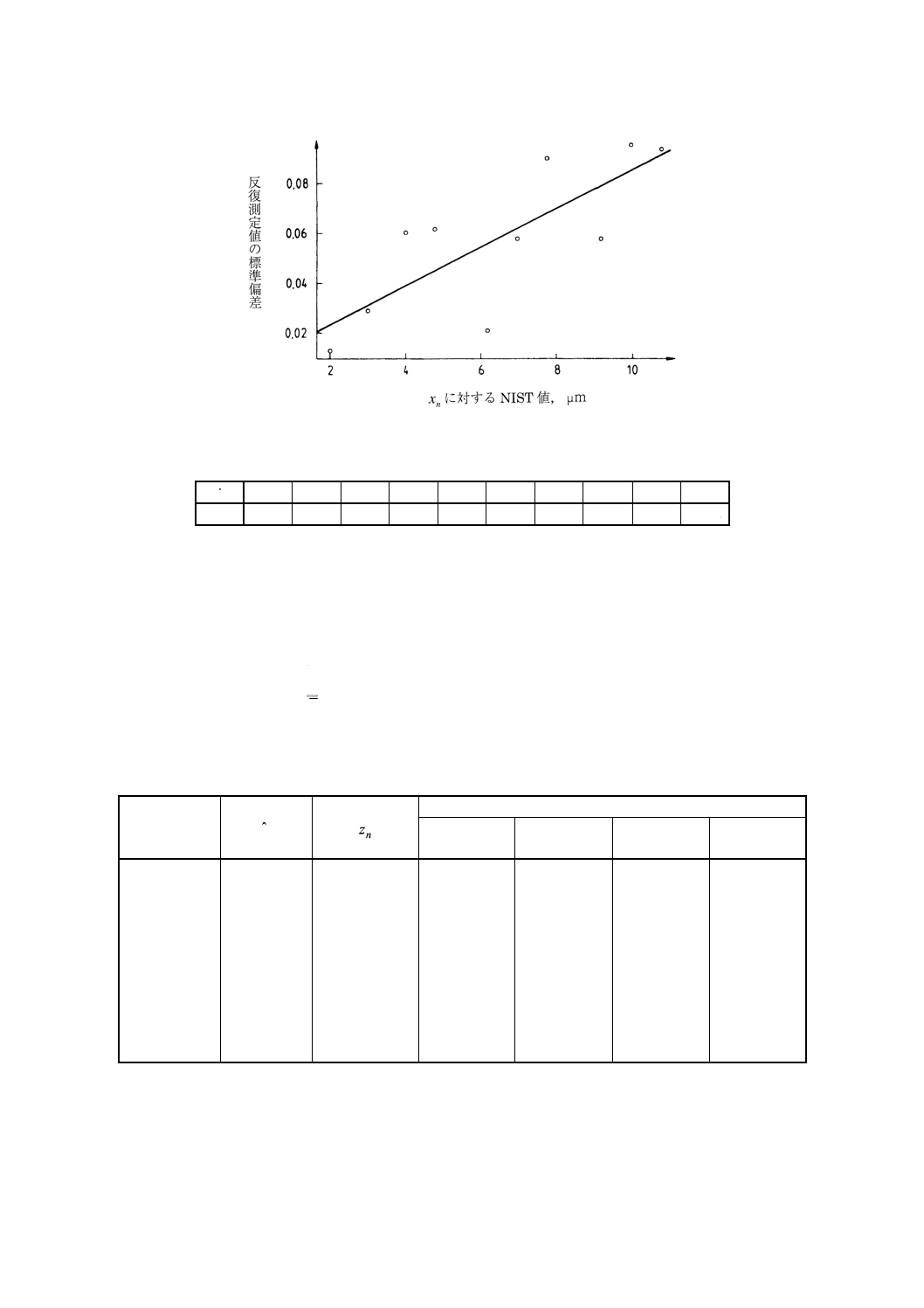
偏差と採択値を対比してプロットした図9によって確認される。
9.2.5
比例する残差標準偏差を仮定した校正関数(検量線)の推定 比例する残差標準偏差を仮定して校
正関数(検量線)を推定し,その校正関数(検量線)と残差をプロットする。
6.4.2の式によって,次の値が得られる。
a) N=10, K=4
b)
w=0.203
c) zi.は,表6による。
d)
z=1.035
e) WSSE=0.003 4
f)
1ˆγ=0.985 1
g)
0ˆγ=0.2469
h)
1ˆr=0.889×10−4
図8 残差標準偏差一定を仮定した線間隔の残差対適合値
23
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図9 線間隔反復測定値の標準偏差NIST値
表6 zi.の値
i
1
2
3
4
5
6
7
8
9
10
zi
1.017 1.010 1.108
L017
1.045 1.009 1.037 1.073 1.024 1.014
校正関数(検量線)は,次の式で表される。
yˆ=0.2469+0.9851x
適合値n
yˆは,この式のxをNIST値xnで置き換えることによって得られる。表7に適合値を示す。
重み付き適合値は,次の式のxをNIST値xnで置き換えることによって得られる。
zˆ=0.985 1+0.2469/x
重み付き残差は,次の式で与えられる。
n
nk
nk
z
z
u
ˆ
−
=
表7に重み付き残差を示す。
図10は,当初のデータと比例する残差標準偏差を仮定した校正関数(検量線)を示す。
表7 比例する残差標準偏差を仮定した線形校正
NIST値
適合値
重み付き適合値
重み付き残差
xn
n
yˆ
nzˆ
μm
μm
un1
un2
un3
un4
6.19
6.344 9
1.025 0
−0.005 6
−0.012 1
−0.005 6
−0.010 5
9.17
9.280 7
1.012 1
−0.001 2
−0.007 7
0.006 5
−0.005 5
1.99
2.207 4
1.109 2
0.001 3
−0.008 7
0.006 4
−0.003 7
7.77
7.901 5
1.016 9
0.012 7
−0.011 8
0.006 2
−0.007 9
4.00
4.187 5
1.046 9
0.020 6
−0.009 4
−0.009 4
−0.009 4
10.77
10.856 9
1.008 1
0.006 8
−0.011 8
0.005 9
0.003 1
4.78
4.955 9
1.036 8
−0.001 2
−0.018 0
0.009 2
0.009 2
2.99
3.192 5
1.067 7
0.015 9
−0.007 5
0.005 9
0.005 9
6.98
7.123 2
1.020 5
0.002 4
−0.007 6
0.008 1
0.011 0
9.98
10.078 6
1.009 9
0.015 2
−0.005 9
−0.000 9
0.009 2
24
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図10 比例する残差標準偏差を仮定した線間隔の校正曲線
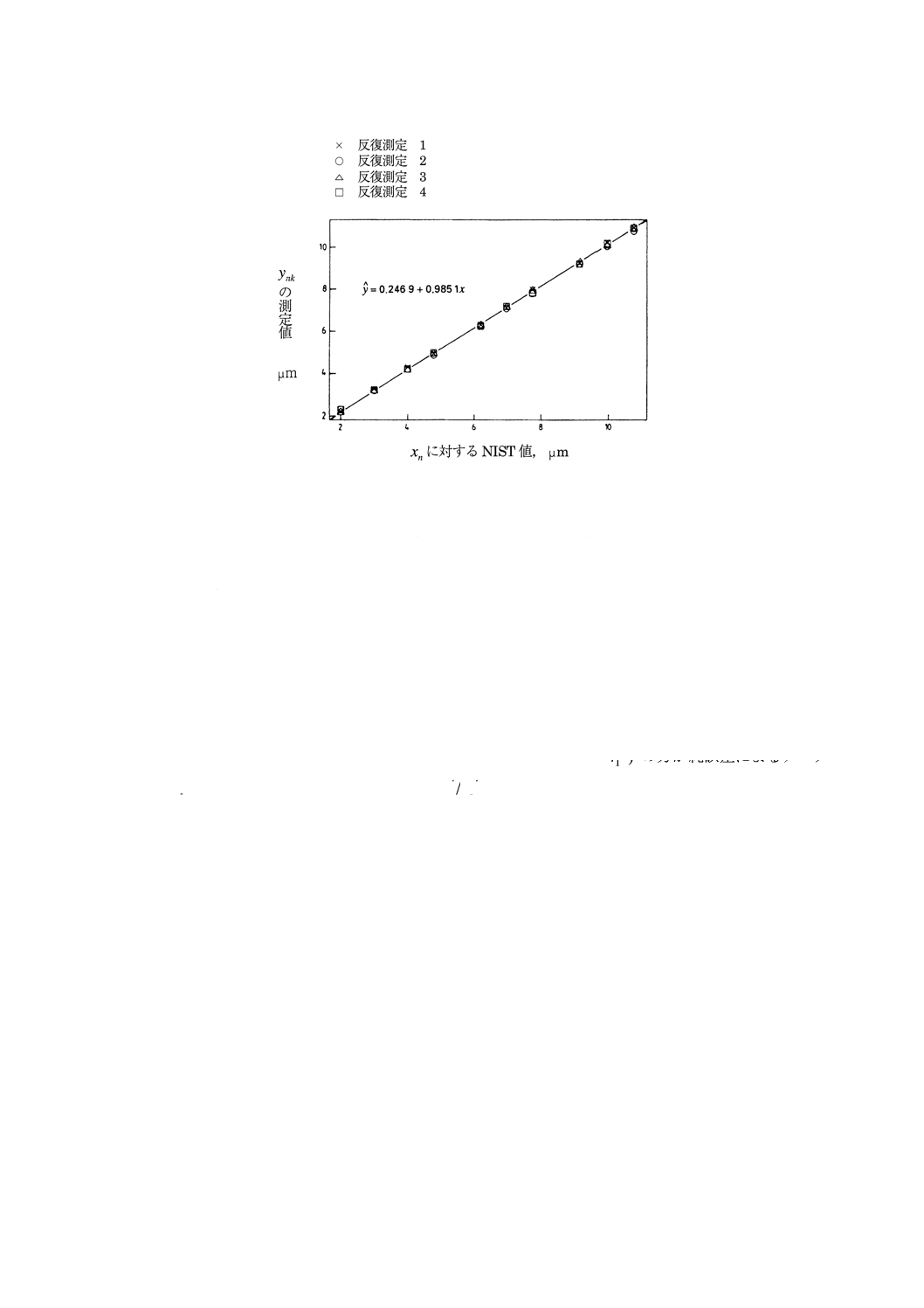
図10は,図7と同じように直線性の仮定を裏付ける。直線で表される校正関数(検量線)の係数は,図
7の場合から若干変わった。この変化は,小線間隔の測定値よりも大線間隔の測定値に小さな重み付けを
行つた結果である(比例する残差標準偏差を仮定)。
図11は,重み付き残差のプロットを示す。
図11の重み付き残差は,ランダムに分布しているように思われる。図8において見られた広がり増大の
傾向が消滅し,比例する残差標準偏差の仮定に更に強固な根拠を与えている。図11は,図8の場合と同じ
く,反復測定2の重み付き残差が小さいことを示している。
9.2.6
校正関数(検量線)の不適合性(当てはまりの悪さ)の推定 表8は,6.5.3において示した比例
する残差標準偏差を仮定したモデルの分散分析表を示す。
分散分析表から,不適合性(当てはまりの悪さ)による残差の変動性 (
2
1ˆr) の方が純誤差によるデータ
の変動性 (
2ˆp
r) よりも小さいことが分かる。比率
2
2
1
ˆ
ˆ
p
r
r
,F0.95 (8.30) 値,すなわち2.27よりも小さい。こ
れによって,この例について述べた校正(検量線作成)実験に関する直線性の仮定が妥当であることが確
認される。

25
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図11 比例する残差標準偏差を仮定した線間隔の重み付き残差対重み付き適合値
表8 比例する残差標準偏差を仮定した線間隔の不適合性(当てはまりの悪さ)と純誤差を比較する分散
分析表
要因
自由度,DF
平方和,SS
SS/DF
F
校正関数(検量線)
1
WSSR=0.036 9
MSR=0.036 9
残差
38
WSSE=0.003 4
2ˆr=0.89×10-4
不適合性(当てはまりの悪さ) 8
WSSE−WSSP=0.0005 5
2
1ˆr=0.69×10-4
2p
2
1
ˆ
ˆ
r
r
=0.73
純誤差
30
WSSP=0.002 8
2pˆr=0.94×10-4
合計
39
WSST=0.040 3
9.2.7
将来の測定値の変換 6.4で得た校正関数(検量線)に基づき,新規,かつ,未知の線間隔の測定
値を,次のとおり変換する。
a) 未知の線間隔の単一測定値y0から,次の線間隔決定値が得られる。
1
985
.0
9
246
.0
0
0
−
=
y
x
b) 同一の未知線間隔y01,y02,…,y0pの測定値p個から,次の単一線間隔決定値が得られる。
1
985
.0
9
246
.0
0
0
−
=
y
x
9.3
管理方法
9.3.1
背景とデータ
管理方法のために線間隔が2個選択された (m=2) 。これらの線間隔2個は,通常の測定条件において発
生する値の範囲を可能な限り広く含むよう選択されたものである。線間隔は,それぞれ毎日測定された。
表9に,最初の7日間の測定値と,NIST値xiを示す。
9.3.2
上方及び下方管理限界の計算 αの値を0.05とすると,6.4.2から次の値が得られる。
4
2
10
889
.0
ˆ
−
×
=
r
1
985
.0
ˆ1=
γ
26
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
NK−2=38
ζ=0.025
これらの値から,次の値が得られる。
Uc=0.009 4×2.3342/0.985 1=0.022 3
Lc=−0.022 3
図12に限界値をプロットする。
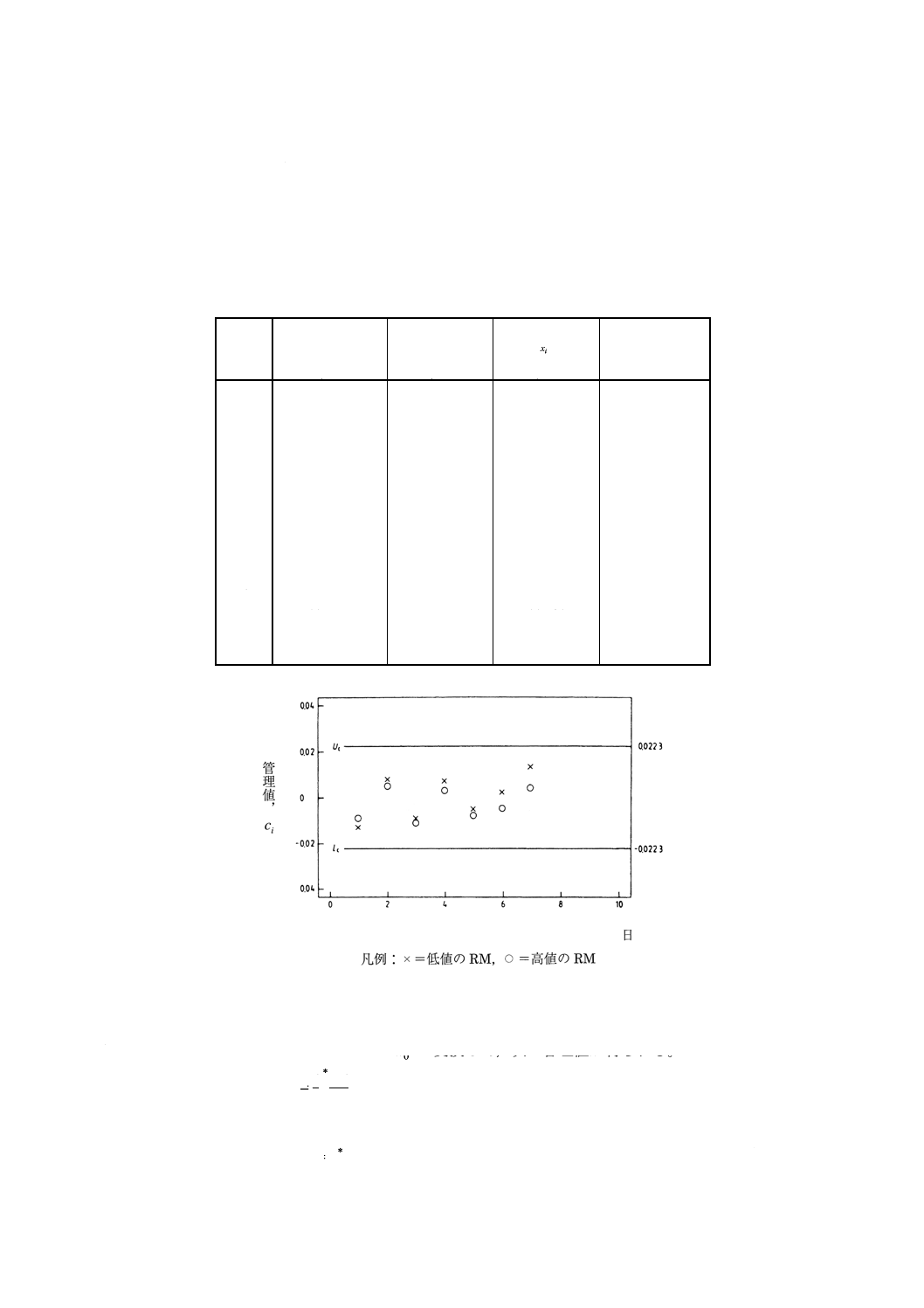
表9 管理方法のために収集されたデタ
日
NIST値
測定値
変換値
管理値
xi
μm
yi
μm
ix
μm
ci
1
2.99
3.154:
2.915
−0.013
10.77
10.760
10.673
−0.009
2
2.99
3.215
3.013
0.008
10.77
10.909
10.823
0.005
3
2.99
3.165
2.962
−0.009
10.77
10.740
10.652
−0.011
4
2.99
3.213
3.011
0.007
10.77
10.892
10.806
0.003
5
2.99
3.179
2.976
−0.005
10.77
10.772
10.685
−0.008
6
2.99
3.198
2.996
0.002
10.77
10.807
10.720
−0.005
7
2.99
3.230
3.028
0.013
10.77
10.897
10.811
0.004
図12 比例する残差標準偏差を仮定した線間隔校正曲線を検証するための管理図
9.3.3
データの変換及びプロット
a) 校正関数(検量線)を用いてyiの値を
0xへ変換して,次の管理値が得られる。
i
i
i
i
x
x
x
c
−
=
校正関数(検量線)は,比例する残差標準偏差のモデルを用いて誘導された。管理方法は,管理値
として,通常の差の値 (
i
i
i
x
x
d
−
=
) に代えて,正規化された差の値を使用した。表9に管理値を示
27
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
す。
b) 管理値を管理図にプロットする(図12)。
9.3.4
システム状態の決定 システムは管理状態にあると思われ,7日目に更新する必要はない。
9.3.5
校正関数(検量線)有効期間中における変換値の不確かさの推定 管理図にはRMが2個しか使用
されていないため,管理値ci全体を用いて,変換値の変動係数の推定値を計算する。その推定値は,次の
とおりである。
(
)
9
007
.0
2
ˆ
1
2m
2l
cal
=
+
=
∑
=
J
c
c
r
J
j
j
j
ここに,
2J=自由度14
ある量について,信頼水準0.95において,変換値
0xから推定されるその量の未知の真の値に対する近
似信頼区間は,次のとおりである。
(
)()
−
×
±
=
±
0
0
0
2
1
cal
0
145
.2
9
007
.0
2
ˆ
x
x
x
J
t
r
x
α
x
28
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) 記号及び略語
N:標準物質の個数
K又はKn:標準物質1個当たりの繰返し測定値数
NK:全標準物質の測定値数の合計数
x:標準物質の採択値
xb:ブランクの採択値
x:全採択値の平均値
w:標準物質採択値の逆数 (1/x)
w:採択値の逆数の全平均値
y:標準物質の測定値
yb:ブランクの測定値
y:全測定値の平均値
y:標準物質の測定値の平均値
z:あるRMの測定値の採択値に対する比 (y/x)
β0: 残差標準偏差一定を仮定した校正関数(検量線)の切片
β1: 残差標準偏差一定を仮定した校正関数(検量線)の傾き
γ0:比例する残差標準偏差を仮定した校正関数(検量線)の切片
γ1:比例する残差標準偏差を仮定した校正関数(検量線)の傾き
ε:直線性及び 残差標準偏差一定を仮定した場合の測定値の期待値からの偏差
η:直線性及び比例する残差標準偏差を仮定した場合の測定値の期待値からの偏差
e:直線性及び 残差標準偏差一定を仮定した場合の残差
u:直線性及び比例する残差標準偏差を仮定した場合の重み付き残差
σ2:一定のときの残差分散(εの分散)
2p
σ: 残差標準偏差一定を仮定した場合の純誤差の分散
21
σ: 残差標準偏差一定を仮定した場合の不適合性(当てはまりの悪さ)を表す分散
r2:比例する残差分散(η/xの分散)
2pr:比例する残差標準偏差を仮定した場合の純誤差に関連する分散
21r:比例する残差標準偏差を仮定した場合の不適合性(当てはまりの悪さ)に関連する分散
SSE:残差eの平方和
WSSE:重み付き残差uの平方和
SST, WSST:残差標準偏差一定又は比例する残差標準偏差を仮定した場合の全平方和
SSP, WSSP:残差標準偏差一定又は比例する残差標準偏差を仮定した場合の純誤差の平方和
SSR, WSSR:残差標準偏差一定又は比例する残差標準偏差を仮定した場合,校正関数(検量線)で説明
される平方和
α:有意水準
1−α:信頼水準
F(1-α) (n1: n2):自由度n1及びn2のF分布の(1−α)分位点
t(1-ζ) (n1):自由度n1のt分布の(1−ζ)分位点
29
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Ud:残差標準偏差一定を仮定した場合の上方管理限界
Ld:残差標準偏差一定を仮定した場合の下方管理限界
Uc:比例する残差標準偏差を仮定した場合の上方管理限界
Lc:比例する残差標準偏差を仮定した場合の下方管理限界
d:残差標準偏差一定を仮定した場合の管理値
c:比例する残差標準偏差を仮定した場合の管理値
30
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(規定) 繰返し数が異なる場合の基本的方法
各RMについての繰返し数Knが変わる場合,校正関数(検量線)は,本体の6.2.2,6.4.2及び6.5の式
を修正して推定することができる。
B.1 β0,β1,及びσ2の推定値は,次の式を用いて計算する。
(
)
(
)
(
)
∑
∑
∑
=
=
=
−
−
−
=
N
n
n
n
N
n
K
k
nk
n
x
x
K
y
y
x
x
n
1
2
1
1
1ˆβ
x
y
1
0
ˆ
ˆ
β
β
−
=
(
)2
SSE
ˆ2
−
=NK
σ
ここに
∑
=
=
N
n
n
K
NK
1
∑
=
=
N
n
n
nx
K
NK
x
1
1
∑∑
=
=
=
N
n
K
k
nk
n
y
NK
y
1
1
1
n
n
x
y
1
0
ˆ
ˆ
ˆ
β
β+
=
n
nk
nk
y
y
e
ˆ
−
=
(
)
∑∑
=
=
=
N
n
K
k
nk
n
e
1
1
2
SSE
B.2 γ0,γ1及びr2の推定値は,次の式を用いて計算する。
(
)
(
)
(
)
∑
∑
∑
=
=
=
−
−
−
=
N
n
n
n
N
n
K
k
nk
n
w
w
K
z
z
w
w
n
1
2
1
1
0ˆγ
w
z
0
1
ˆ
ˆ
γ
γ
−
=
(
)2
WSSE
ˆ2
−
=NK
r
ここに
∑
=
=
N
n
n
K
NK
1
n
nk
nk
x
y
z =
31
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
n
n
x
w
1
=
∑
=
=
N
n
n
nw
K
NK
w
1
1
∑∑
=
=
=
N
n
K
k
nk
n
z
NK
z
1
1
1
n
w
z
0
1
ˆ
ˆ
ˆ
γ
γ+
=
n
nk
nk
z
z
u
ˆ
−
=
(
)
∑∑
=
=
=
N
n
K
k
nk
n
u
1
1
2
WSSE
B.3 不適合性(当てはまりの悪さ)は,次のようにして評価する。本体の表1及び表2の中の式を次の式
と置き換えて,これらの表を適用する。
∑
=
=
n
K
k
nk
n
n
y
K
y
1
1
(
)
∑∑
=
=
−
=
N
n
K
k
nk
n
y
y
1
1
2
SST
(
)
∑∑
=
=
−
=
N
n
K
k
n
nk
n
y
y
1
1
2
SSP
SSEはB.1の定義による。
∑
=
=
n
K
k
nk
n
n
z
K
z
1
1
(
)
∑∑
=
=
−
=
N
n
K
k
nk
n
z
z
1
1
2
WSST
(
)
∑∑
=
=
−
=
N
n
K
k
n
nk
n
z
z
1
1
2
WSSP
WSSEはB.2の定義による。
32
Z 8461 : 2001 (ISO 11095 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 参考文献
[1] Mandel, J. Fitting straight lines when both variables are in error. Journal of Quality Technology, 16 (No.1) ,
1984, pp.1-14
[2] Graybill, F. Theory arid Applications of the Linear Model. Duxbury Press, North Scituate, MA, 1976
[3] Draper, N. and Smith, H. Applied Regression Analysis.2nd edn. , Wiley, New York, 1981
[4] Carroll, R. , Spiegelman, C. and Sacks, J. A quick and easy multiple-use calibration curve procedure,
Technometr'ics.30, 1988, pp.137-141
[5] Mee, R. , Eberhardt, K. and Reeve, C. Calibration and simultaneous tolerance intervals for regression.
Techrtometrics, 33, 1991, pp.211-219
[6] ISO 7870 : 1993, Control charts−General guide and introduction
参考 ISO 7870 : 1993は,JIS Z 9020 : 1999管理図−一般指針と一致している。
[7] ISO 8258 : 1991, Shewhart control charts
参考 ISO 8258 : 1991からの引用事項は,JIS Z 9021 : 1998 シューハート管理図の該当事項と
同等である。
[8] Croarkin, C. and Varner, R. Measurement assurance for dimensional measurements on integrated-circuits
photomasks. NBS Technical Note 1164, 1982
JIS Z 8461 [標準物質を用いた校正(検量線が直線の場合)]原案作成委員会 構成表
氏名
所属
(委員長)
宮 津 隆
帝京科学大学 理工学部
尾 島 善 一
東京理科大学 理工学部
鹿 庭 なほ子
国立医薬品食品衛生研究所 薬品部
城 道 修
メルシャン株式会社 中央研究所
小 林 経 明
社団法人 日本鉄鋼連盟 標準化センター
久 本 泰 秀
社団法人 日本分析機器工業会(株式会社日立製作所)
榎 原 研 正
計量研究所 計測システム部
高 津 章 子
物質工学工業技術研究所 計測科学部
新行内 康 慈
帝京科学大学 理工学部
(事務局)
橋 本 進
財団法人 日本規格協会
安 田 順 子
財団法人 日本規格協会












