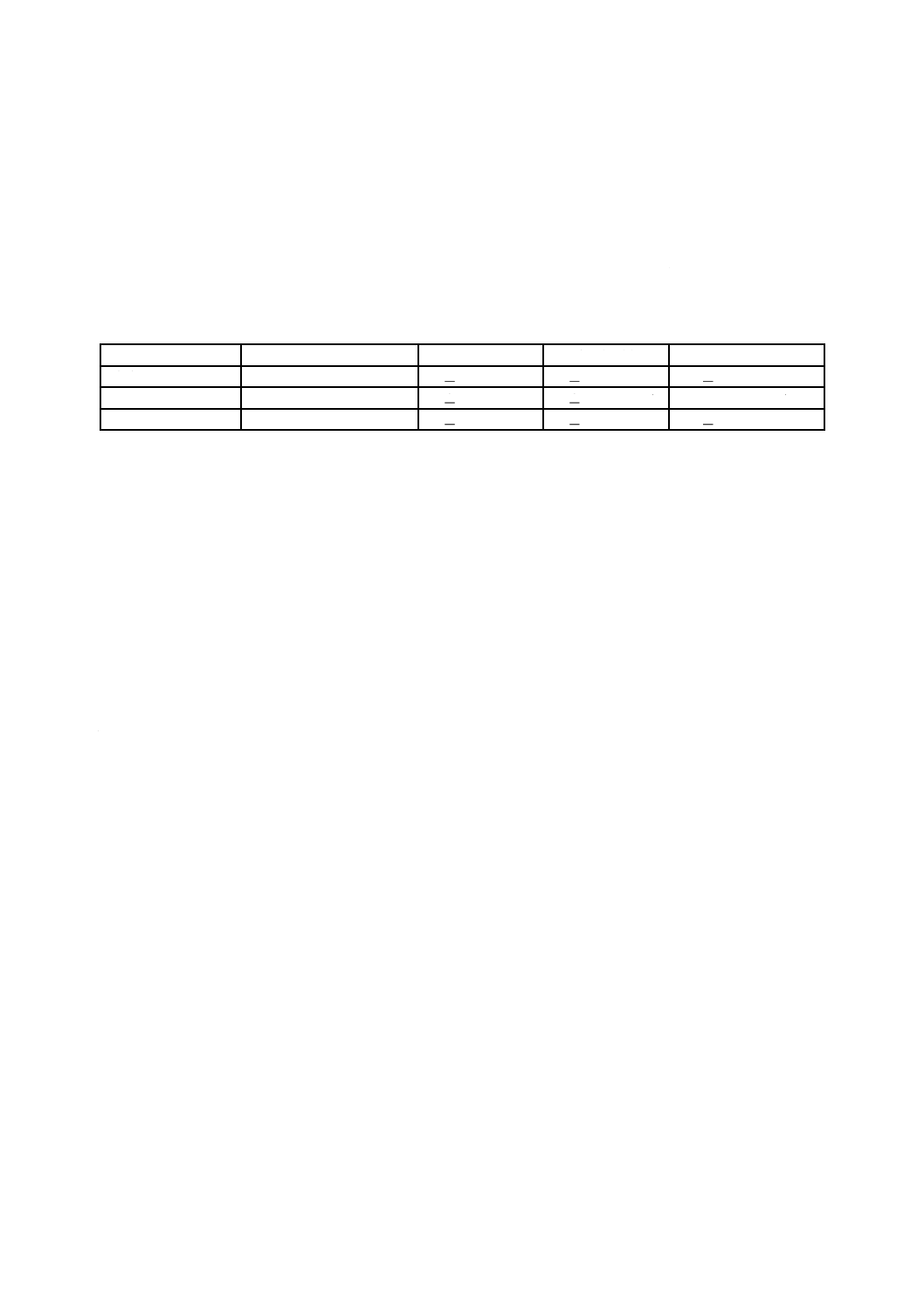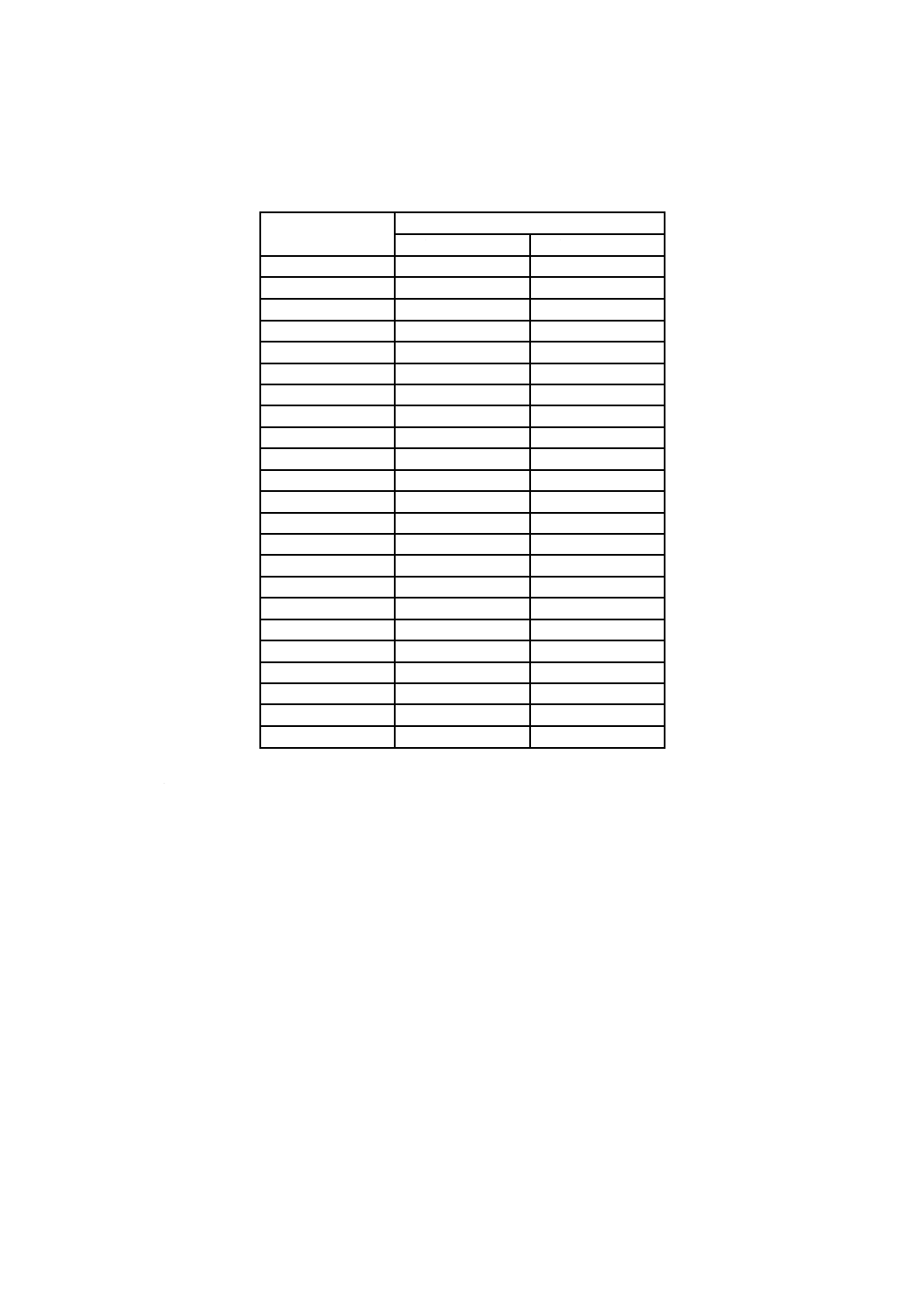Z 8405:2008 (ISO 13528:2005)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
0 序文······························································································································· 1
0.1 技能試験の目的 ············································································································· 1
0.2 JIS Q 0043 ···················································································································· 1
1 適用範囲 ························································································································· 4
2 引用規格 ························································································································· 4
3 用語及び定義 ··················································································································· 5
4 技能試験の計画及び解釈のための統計ガイドライン ································································ 5
4.1 処置信号及び警戒信号 ···································································································· 5
4.2 付与された値の不確かさの上限に関するガイドライン ··························································· 6
4.3 測定の繰返し回数の選択のためのガイドライン ···································································· 7
4.4 試料の均質性及び安定性 ································································································· 7
4.5 操作上規定される測定方法······························································································· 7
4.6 データの報告 ················································································································ 8
4.7 技能試験結果の有効期間 ································································································· 8
5 付与された値及びその標準不確かさの決定 ············································································ 8
5.1 付与された値の決定方法の選択························································································· 8
5.2 定式化 ························································································································· 9
5.3 認証参照値 ··················································································································· 9
5.4 参照値 ························································································································· 9
5.5 熟練試験所による合意値 ································································································ 11
5.6 参加試験所による合意値 ································································································ 12
5.7 付与された値の比較 ······································································································ 17
5.8 欠測値 ························································································································ 17
6 技能評価のための標準偏差の求め方 ···················································································· 18
6.1 技能評価のための標準偏差の求め方の選択 ········································································· 18
6.2 規定値を用いる場合 ······································································································ 18
6.3 達成期待レベルを用いる場合··························································································· 18
6.4 一般的なモデルを用いる場合··························································································· 19
6.5 精度評価実験結果を用いる場合························································································ 20
6.6 単一技能試験スキームによって得たデータを用いる場合 ······················································· 20
6.7 技能試験から得た精度の値と設定値との比較 ······································································ 21
7 成績を表す統計量[performance statistics(成績を表す統計指標)]の計算 ································· 21
7.1 試験所のかたよりの推定値······························································································ 21
7.2 パーセンテージ差分 ······································································································ 24
7.3 順位及びパーセンテージ順位··························································································· 26
Z 8405:2008 (ISO 13528:2005) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
7.4 z-スコア ······················································································································ 27
7.5 En数 ··························································································································· 30
7.6 z′-スコア······················································································································ 30
7.7 ζ-スコア ···················································································································· 31
7.8 Ezスコア ····················································································································· 32
7.9 不確かさが報告されたときのデータ解析例 ········································································· 32
7.10 成績スコアの複合表示方法 ···························································································· 37
8 単一技能試験ラウンドから得た複数の測定対象に対する成績スコアを組み合わせる図式表現の方法 37
8.1 用途 ··························································································································· 37
8.2 成績スコアのヒストグラム······························································································ 37
8.3 標準化された試験所のかたよりの棒グラフ ········································································· 39
8.4 標準化された併行性の棒グラフ························································································ 40
8.5 Youdenプロット ··········································································································· 40
8.6 併行精度の標準偏差のプロット························································································ 46
8.7 分割試料 ····················································································································· 49
9 複数回の技能試験スキームの成績スコアを組み合わせるための図式表現の方法 ··························· 54
9.1 用途 ··························································································································· 54
9.2 z-スコアのシューハート管理図 ························································································ 54
9.3 z-スコアの累積和管理図 ································································································· 57
9.4 試験所平均に対する標準化した試験所のかたよりのプロット ················································· 58
9.5 ドットプロット ············································································································ 59
附属書A(規定)記号 ·········································································································· 61
附属書B(規定)試料の均質性試験及び安定性試験 ···································································· 62
附属書C(規定)ロバストな解析 ··························································································· 66
Z 8405:2008 (ISO 13528:2005)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人日本規格協会(JSA)から,工業標準
原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大
臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8405:2008
(ISO 13528:2005)
試験所間比較による技能試験のための統計的方法
Statistical methods for use in proficiency testing by
interlaboratory comparisons
0
序文
この規格は,2005年に第1版として発行されたISO 13528を基に,技術的内容及び対応国際規格の構成
を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
0.1
技能試験の目的
試験所間比較による技能試験は,固有の試験又は測定に対する個々の試験所の技能の評価,及び試験所
の技能を継続的にモニターするために使用する。技能試験の目的の全体的な解説に関しては,JIS Q 0043-1
の序文を参照されたい。統計的な表現をすれば,試験所の技能は三つの統計的特性によって示すことがで
きる。すなわち,試験所のかたより,安定性及び併行精度である。試験所のかたより及び併行精度(繰返
し性)は,JIS Z 8101-1,JIS Z 8101-2,JIS Z 8402-1に規定する。試験所の測定結果の安定性は,JIS Z 8402-3
に規定する中間精度によって評価する。
試験所のかたよりは,標準物質を用いた試験が可能な場合,JIS Z 8402-4に規定する手順に基づいて評
価できる。それ以外の場合では,試験所のかたよりの情報を,試験所間比較による技能試験を行うことに
よって求めることが広く行われている。そして,この技能試験からのデータを用いて試験所のかたよりの
推定値を得ることは,当該データ解析の重要な側面である。ただし,安定性及び併行精度は技能試験中に
得るデータに影響を与えるため,ある試験所の単一ラウンドの技能試験において,安定性又は併行精度の
不足の影響によってかたよりのあるデータを得ることがある。したがって,試験所の技能のこの側面を定
期的に評価することが重要である。
安定性は,保持試料の再試験,又は標準物質若しくは社内標準物質(私的な標準物質として使用するた
めに試験所が保有する物質)の測定を定期的に実施することによって評価する。この手法はJIS Z 8402-6
に規定する。また,安定性は技能試験から求めた試験所のかたよりの推定値を管理図にプロットすること
からも評価できる。これによって,個々の技能試験スキームの個別のラウンドの結果を調べても明らかに
ならない情報を与えられるが,これはこの種のデータ解析の別の重要な側面である。
併行精度の評価に適したデータは,試験所の通常業務中に実施した試験から,又は併行精度を評価する
ため,特に試験所内で実施した追加試験によって得る。したがって,併行精度の評価は必ずしも技能試験
の重要な側面ではないが,試験所はなんらかの方法によって併行精度を監視することが重要である。併行
精度を評価するには,JIS Z 8402-6で規定しているとおり,二重測定の範囲を管理図にプロットすること
によって評価する。
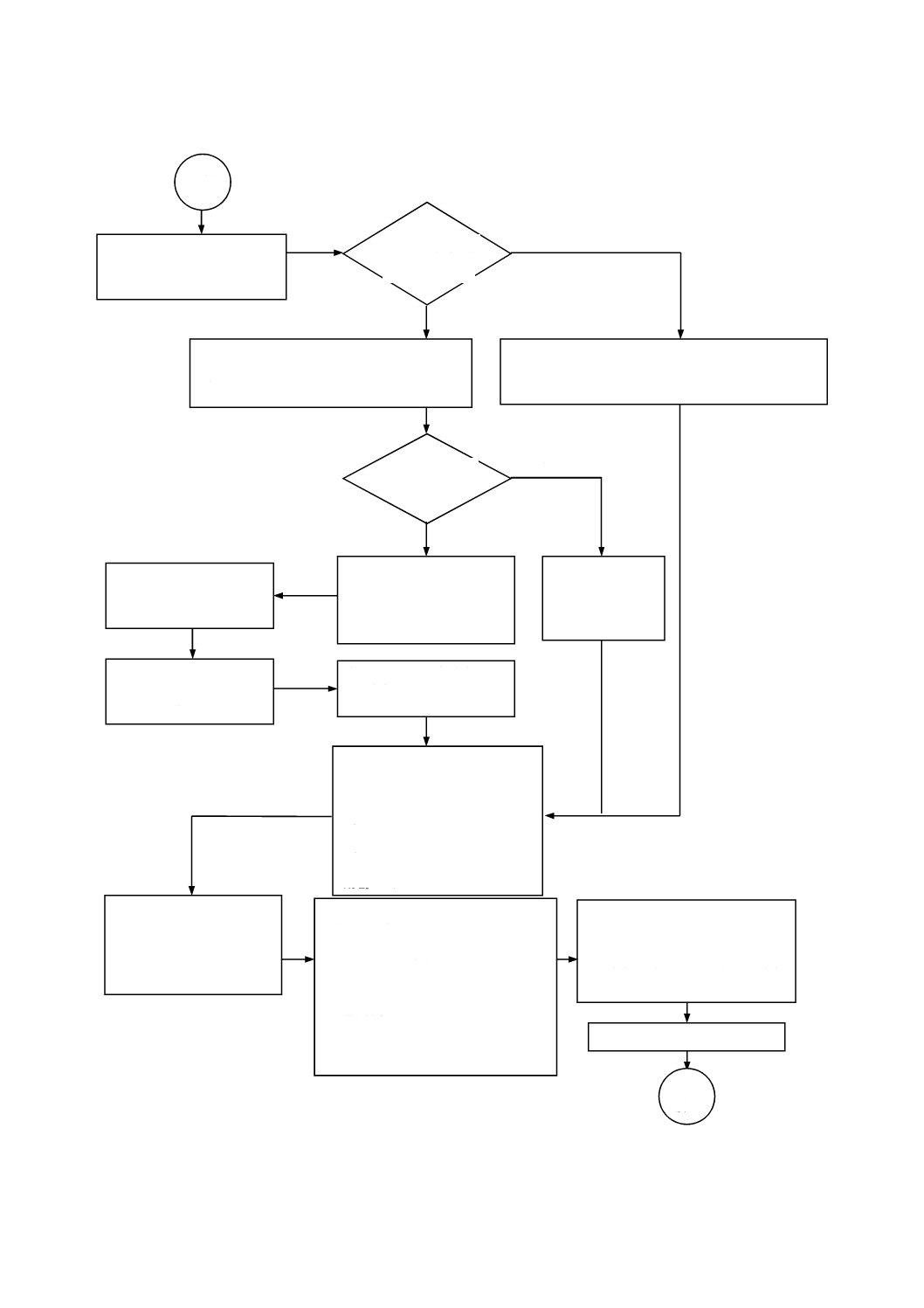
フローチャート(図1)は,この規格に規定する手法の適用方法を示す。
0.2
JIS Q 0043
2
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Q 0043-1は各種の技能試験スキームを示し,更に技能試験スキームの構成及び計画に関する指針を
規定する。JIS Q 0043-2は,試験所認定機関による技能試験スキームの選択及び使用に関する指針を規定
する。当該分野の詳細な情報に関しては,それらの文書を参照する(ここでは情報は再掲しない。)。JIS Q
0043-1の附属書では,技能試験スキームに使用する統計的手法を簡略ではあるが説明している。
この規格はJIS Q 0043に対する補足であり,技能試験中の統計的手法の使用に関して,同規格に欠けて
いる詳細な指針を与える。この規格の大部分は,分析試験所の技能試験に関するハーモナイズドプロトコ
ルに基づいているが[1],すべての測定方法に使用することを目的とする。
3
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1−技能試験スキームを実施時,統計的手法の使用が必要な各種活動を示すフローチャート
いいえ
附属書Bによって試料調製方法を
チェック
開始
付与された値とその
不確かさを技能試験前に
決定しているか?
次から一つを適用する。
5.2 定式化 5.3 認証参照値 5.4 参照値
次から一つを適用する。
5.5 熟練試験所による合意値 5.6 参加試験所による合意値
次を使用する付与された値の
決定方法を確認する。
4.2 付与された値の不確かさ
の上限に関するガイドライン
次から一つを適用する。
6.2 規定値
6.3 達成期待レベル
6.4 一般的なモデル
6.5 精度評価実験結果
次を適用する。
6.6 単一技能試験
スキームによっ
て得たデータ
次によって,使用した反復測定
数を確認する。
4.3 測定の繰返し回数の選択の
ためのガイドライン
単一ラウンドの技能試験スキー
ムを実施する
該当する場合,次を適用する。
5.7 付与された値の比較
6.7 技能試験から得た精度の値
と設定値との比較
次のうち一つ又は複数を使用し,ラウンドの
性能統計をグラフィカルに表示する。
8.2 成績スコアのヒストグラム
8.3 標準化された試験所のかたよりの
棒グラフ
8.4 標準化された併行性の棒グラフ
8.5 Youdenプロット
8.6 併行精度の標準偏差のプロット
8.7 分割試料
次のうち一つを使用し,複数ラウンドに
わたる性能統計を組み合わせる。
9.2 z-スコアのシューハート管理図
9.3 z-スコアの累積和管理図
9.4 試験所平均に対する標準化した試験
所のかたよりのプロット
結果を参加者に報告する
開始に
戻る
はい
技能試験の前に,
技能評価の標準偏差
を決定する
はい
いいえ
次の中から一つを使用し,ラウンドの
性能統計を計算する。
7.1 試験所のかたよりの推定値
7.2 パーセンテージ差分
7.3 順位及びパーセンテージ順位
7.4 z-スコア
7.5 En 数
7.6 z′-スコア
7.7ζ(ゼータ)-スコア
7.8 Ezスコア
4
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1
適用範囲
この規格は,JIS Q 0043(すべてのパート)を補足するものであり,技能試験スキームから得たデータ
を解析するためにオーガナイザが使用する適切な統計的手法の詳細を説明し,当該スキーム中の参加者及
び認定団体による実際の使用に関する勧告を与える。
この規格は,試験所が得た測定結果が,許容できないレベルのかたよりの証拠を表しているものではな
いことを証明するために適用する。(同等性の証明に適用できるが,同等性をもたないことの証明には用い
ることができない。)
これは,定量的データに適用できるが,定性的データには適用できない。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 13528:2005,Statistical methods for use in proficiency testing by interlaboratory comparisons (IDT)
なお,対応の程度を表す記号(IDT)は,ISO/IEC Guide 21に基づき,一致していることを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS Q 0043-1:1998,試験所間比較による技能試験 第1部:技能試験スキームの開発及び運営
注記 対応国際規格:ISO/IEC Guide 43-1:1997,Proficiency testing by interlaboratory comparisons−Part
1:Development and operation of proficiency testing schemes (IDT)
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
注記 対応国際規格:ISO 3534-1:1993,Statistics−Vocabulary and symbols−Part 1:Probability and
general statistical terms (MOD)
JIS Z 8101-2 統計−用語と記号−第2部:統計的品質管理用語
注記 対応国際規格:ISO 3534-2:1993,Statistics−Vocabulary and symbols−Part 2:Statistical quality
control (MOD)
JIS Z 8402-1 測定方法及び測定結果の精確さ(真度及び精度)−第1部:一般的な原則及び定義
注記 対応国際規格:ISO 5725-1,Accuracy (trueness and precision) of measurement methods and results
−Part 1:General principles and definitions (IDT)
JIS Z 8402-2 測定方法及び測定結果の精確さ(真度及び精度)−第2部:標準測定方法の併行精度及
び再現精度を求めるための基本的方法
注記1 対応国際規格:ISO 5725-2,Accuracy (trueness and precision) of measurement methods and
results−Part 2:Basic method for the determination of repeatability and reproducibility of a
standard measurement method (IDT)
注記2 ISO 5725-2は,対応国際規格では参考文献となっているが,規定事項として引用している
ため,引用規格に追加する。
JIS Z 8402-5:2002 測定方法及び測定結果の精確さ(真度及び精度)−第5部:標準測定方法の精度
を求めるための代替法
注記1 対応国際規格:ISO 5725-5,Accuracy (trueness and precision) of measurement methods and
results−Part 5:Alternative methods for the determination of the precision of a standard
measurement method (IDT)
5
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記2 この規格は対応国際規格では参考文献となっているが,規定事項として引用しているため,
引用規格に追加する。
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS Z 8101-1,JIS Z 8101-2及びJIS Z 8402-1によるほか,次に
よる。
なお,この規格で用いる記号の一覧を附属書Aに規定する。
3.1
試験所間比較 (interlaboratory comparison)
あらかじめ決定された条件に従う,二つ以上の試験所による同一又は類似の試験品目についての試験の
企画・調整,実施及び評価。
注記 この定義は,JIS Q 0043-1を採用したものである。
3.2
技能試験 (proficiency testing)
試験所間比較の手段による試験所試験成績の決定。
3.3
付与された値 (assigned value)
特定量に属する値であり,場合によって慣例に基づいて,特定の目的に適合する不確かさをもつことが
認められたもの。
3.4
技能評価のための標準偏差 (standard deviation for proficiency assessment)
使用可能な情報に基づく,技能評価に使用するばらつきの尺度。
3.5
z-スコア (z-score)
試験所のかたよりの標準化された尺度。付与された値と技能評価のための標準偏差を用いて計算する。
3.6
コーディネータ (coordinator)
技能試験スキームの作業に必要な全活動を調整する責任をもつ組織(又は者)
4
技能試験の計画及び解釈のための統計ガイドライン(JIS Q 0043-1,5.4.2参照)
4.1
処置信号及び警戒信号
4.1.1
この規格は,技能試験中に得られるデータに対して,処置信号又は警戒信号を発信するかどうかを
判断するための基準となる値又はグラフィックな基準を示す。優秀なスタッフがおり,運営が良好である
試験所においても,異常な結果が発生することがある。さらに,標準化された測定方法が,精度評価実験
によって実証された場合であっても,数回の技能試験スキームの後に不具合が明らかになることがある。
技能スキーム自体に不具合がある場合もある。これらの理由によって,ここに規定する基準を用いて,検
討対象の測定方法を実施するのに不適格であるとして,試験所を不良と判定してはならない。技能試験を
試験所判定に使用する場合には,その目的に合った適切な基準を設定しなければならない。
4.1.2
ここに規定する基準は,技能評価のための標準偏差が実際に観測された結果に基づいている場合
(6.4〜6.6による方法の一つを使用した場合)に,この基準によって示される処置信号が,その測定結果
6
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
についての調査及び是正処置を必要とすることを意味するように,設計している。
4.1.3
コーディネータは,対象となる測定の技能試験データに予想されるばらつきについて,主な変動原
因を理解していることが望ましい。データ解析の第1手順では,測定結果の分布を調べ,予想していなか
った変動原因が存在するかどうかを検討する。例えば,測定結果の分布が二山になっている場合は,異な
った方法による測定,汚染された試料の測定,又は記載不備の指示書に基づく測定の結果によって得る分
布が混在している可能性がある。この状況では,懸案となる事項をデータ解析や評価の前に解決しておく
必要がある。認定機関は,技能試験が不合格の場合の対処方針を用意しておかなければならない。フォロ
ーアップ処置は,認定機関の方針又は試験所の品質マネジメントの手順によって決定する。ただし,試験
所が技能試験の結果,不合格となった場合には,一般的に推奨される処置が存在する。技能試験における
不満足な結果に対する試験所による処置のガイダンスは4.1.4による。
4.1.4
技能評価に用いる標準偏差が実際に観測された結果に基づくスキームで,結果が処置信号を示した
場合,試験所は,必要に応じてコーディネータ又は認定機関と協議の上,適切な調査及び是正処置を決定
しなければならない。上記の実施を回避する正当な理由がない場合,試験所はその手順を確認し,試験所
のスタッフによるそのような結果の再発を防止するために,一つ又は複数の是正処置を特定しなければな
らない。試験所はコーディネータに問題の原因に関して助言を求めたり,又は,他の専門家に相談するよ
うにコーディネータに依頼してもよい。試験所は,それ以後も,是正処置の有効性を評価するために技能
試験スキームに参加しなければならない。適切な是正処置の候補を次に示す。
a) スタッフが測定手順を理解し,これに従っていることを確認する。
b) 測定手順の詳細がすべて正しいことを確認する。
c) 装置の校正,及び試薬の組成を確認する。
d) 疑わしい装置又は試薬を交換する。
e) スタッフ,装置及び試薬又はこれらの組合せを別の試験所と比較試験する。
技能試験結果の試験所認定機関による使用はJIS Q 0043-2,6.を参照。
4.2
付与された値の不確かさの上限に関するガイドライン
付与された値Xは標準不確かさΧ
uをもつが,その標準不確かさは,これを導出した方法によって,ま
た,複数の試験所における測定結果から導出した場合には試験所の数,又は他の要因にも依存し決定する。
付与された値の標準不確かさの計算の方法は箇条5による。
技能試験の標準偏差σˆは,技能試験で検出される試験所のかたよりの推定値の大きさを評価するために
用いる。技能試験の標準偏差を求める方法は箇条6に,これと試験所のかたよりの推定値とを比較する基
準は箇条7による。
付与された値の標準不確かさ
Χ
uが技能試験の標準偏差σˆと比較して非常に大きい場合,試験所内の原
因ではなく付与された値の決定が不正確であることに起因して,処置信号及び警戒信号を受ける試験所が
存在するという危険がある。この理由で,付与された値の標準不確かさを正しく定め,技能試験スキーム
に参加する試験所に報告しなければならない(JIS Q 0043-1のA.1.4及びA.1.6を参照)。
次の式が成立する場合,付与された値の不確かさは無視することができ,技能試験結果の解釈に含める
必要はない。
σˆ
3.0
≦
X
u
············································································· (1)
これらのガイドラインが満たされない場合,コーディネータは次のことを検討しなければならない。
a) その不確かさが上記のガイドラインを満たすような,付与された値の決定方法を探す。
b) 付与された値の不確かさを技能試験結果の解釈に使用する(En数については7.5,z'-スコアについて
7
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は7.6を参照)。
c) 技能試験の参加者に,付与された値の不確かさが無視できないことを通知する。
例 11試験所の試験結果の平均xを付与された値Xとし,同一の11試験所の試験結果の標準偏差
を技能試験の標準偏差とした場合,σˆ=sとなる。この場合の付与された値の標準不確かさの近
似値はX
u
= s /11=0.3sによって推定できるため,要件は満足しているようにみえる。ただし,
11試験所未満の場合にはこの要件は満足しないことになる。さらに,この試料が不均質若しく
は不安定である場合,又は試験所の結果に共通のかたよりを発生する要因がある場合(例えば,
すべてが同一の参照標準を用いている場合),付与された値の不確かさはs /11より大きくな
る。
4.3
測定の繰返し回数の選択のためのガイドライン
併行測定のばらつきは,技能試験における試験所のかたより間のばらつきに影響する。併行測定のばら
つきが技能試験の標準偏差と比較して非常に大きい場合,併行測定のばらつきが技能試験に誤った結果を
もたらすという危険がある。この状況では,ある試験所はある一回のラウンドでは大きなかたよりを示す
が,次のラウンドでは示さないことがあり,このため,原因の特定が困難になる。
この理由によって,併行測定のばらつきの影響を抑えることが必要と考えられる場合,各試験所での技
能試験で実施する測定の繰返し回数nを次の式のように選択しなければならない。
σ
σ
ˆ
.
n
/
r
3
0
≦
·········································································· (2)
ここに,
r
σ: 過去の共同実験によって求められた併行標準偏差
係数0.3の根拠は,この基準を満たしていれば,併行標準偏差の影響が技能試験の標準偏差の約10 %を
超えないことに基づく。
さらに,試験所はすべて同じ回数の繰返し測定を実施するものとする(この規格で以後に規定する解析
方法は,この要件が満たされることを前提としている)。式(2)が満たされない場合には,繰返し測定の回
数を増やさなければならない,又は技能試験結果を慎重に解釈しなければならない。
ここでは,すべての試験所が一般にほぼ同一の併行精度であることを想定している。この想定がなりた
たない場合もあり得る。このような場合,この規格に規定された方法を適用する際に,次の方策によって
もよい。コーディネータは,併行標準偏差の代表的な値を用いて,反復測定回数nを設定する。次に,各
試験所はそれぞれの併行標準偏差によって,式(2)を満たすことを確認する。満たさない場合には,測定手
順に定められた測定の繰返し回数を,式(2)を満たす繰返し回数に変更し,変更後の回数の測定値の平均値
を測定結果とする。
4.4
試料の均質性及び安定性(JIS Q 0043-1の5.6.2及び5.6.3参照)
技能試験に使用する試料が均質及び安定であることを適切に確認するための方法は,附属書Bによる。
附属書Bの均質性基準が満たされないような試料調製方法が使用される場合,参加者は複数の試料を試
験しなければならない,又は技能試験の標準偏差に,附属書Bに規定するように,試料の不均質性による
分を含めなければならない。
4.5
操作上規定される測定方法
操作が定義された測定方法を用いる場合,その測定結果は測定手順に依存する。例えば,粒子状物質の
粒度分布は,角穴又は丸穴のいずれのふるいを用いるかによって決まることもある。どのふるいを用いる
ことが望ましいかについての適切な理由はないが,ふるいの種類を指定していなければ,異なった種類の
ふるいを使用する試験所間で結果が異なる場合がある。付与された値を定めるために参加者が使用した方
8
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
法と異なる方法を使用すると,実施の際は不具合がなくても,その結果にかたよりを示すことがある。
参加者が,操作が定義された方法を自由に選択するとき,その中から有効なコンセンサスが得られない
場合がある。この問題を解決するために二つの対策がある。
a) 標準化された方法を複数の参加者がルーチン的に用いている場合,これに対して付与された値を定め,
参加者に,その値を技能試験に使用するように指示する。
b) それぞれの方法に対し,別々の付与された値を用いる。
測定手順ではないが,測定対象を指定する場合にも類似な状況が発生し,同一の選択を行う必要がある。
4.6
データの報告(JIS Q 0043-1の6.2.3参照)
技能試験に必要な計算のため,個々の測定結果を
2
/
r
σ
の値を超えて丸めないことが望ましい。
参加者は,測定結果の実際の値をそのまま報告するよう求められる。測定結果を切り捨ててはならない
(すなわち,結果を“<0.1”又は“検出限界未満”の形式で報告してはならない)。同様に,負の結果が観
測された場合には,実際の負の値を報告する(すなわち,測定結果が論理的に負にならない場合であって
も,結果をゼロとして報告しない)。試料について切り捨てた値で結果を報告した場合,又は結果が負の場
合にゼロと報告した場合,参加者に対して当該試料に対応するすべてのデータを解析から除外することを
通知しなければならない。必要ならば,結果が検出限界未満であることを参加者が表示するボックスを,
結果の報告に使用するフォームに設けてもよい。
4.7
技能試験結果の有効期間
技能試験スキームの単一ラウンド中に試験所によって得られた結果の有効期間は,試験所が当該試験を
実施した時期に限定される。したがって,試験所が満足な結果を単一ラウンド中で得たとしても,その試
験所は,この結果を別の時期のデータも信頼できるデータであることを主張するために用いてはならない。
品質システムを実施し,十分な結果の履歴を多数のラウンドの技能試験スキームに参加して得た試験所
は,一貫して信頼できるデータを得ることができる証拠としてこの結果を使用できる。
5
付与された値及びその標準不確かさの決定
5.1
付与された値の決定方法の選択
付与された値Xの決定方法を5.2〜5.6に5通り規定する。JIS Q 0043-1に規定するように,コーディネ
ータは,技術専門家からの助言に基づき,その責任において,付与された値の決定方法を選択する。5.5
及び5.6による方法は,スキームに参加する試験所の数が少ない場合に適用することは困難である。通常,
この規格では,箇条5による付与された値の標準不確かさX
uの算出法は適切である。健全な統計的基礎を
備え,スキームの計画を文書によって示している方法がある場合は,その方法を用いてもよい。
付与された値を決定するのは,コーディネータの責任である。コーディネータは,各参加機関の結果が
コーディネータにすべて通知されるまで,付与された値を参加機関に知らせてはならない。コーディネー
タは,付与された値の決定方法,この付与された値の決定に関与した試験所について,付与された値のト
レーサビリティ及び計測の不確かさに関する記述をそれぞれ示した詳細な報告を用意する。
“計測における不確かさの表現のガイド(以下,GUMという。)”は,計測の不確かさの評価に関する
指針である。
この規格では,ロバストな統計的手法が最適であると考えられる場合には,それを用いることが望まし
い。(例えば,5.5及び5.6)。このほか,健全な統計的基礎を備え,算出法を文書によって規定している場
合,外れ値の検出及び除去に必要な手順を用いることができる。外れ値の検定に関する指針は,JIS Z 8402-2
による。
9
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2
定式化[JIS Q 0043-1のA.1.1 a) 参照]
5.2.1
一般
この手法では,ある成分を一定割合にて混合するか,又は一定割合のある成分を基材に追加することに
よって試験試料を調製する。この場合,成分の使用質量から付与された値Xを求める。
この手法が特に有用なのは,試験試料をこの方法を用いて個々に調製し,その試料に含まれる各成分の
割合,又は追加された成分の割合を決定するという場合,すなわち,試験試料を1回で大量に調製しなく
ても,均質性が確保される場合である。ただし,添加した試料が試験物質中で緩やかに結合する場合,又
は他の物質に変化するような場合には,別の手法を用いてもよい。
5.2.2
付与された値の標準不確かさuX
試験試料の付与された値を定式化手法によって計算する場合,標準不確かさは,GUMに規定される手
法を用いて,各不確かさを合成することによって求める。例えば,化学分析における不確かさ要因は,主
に,重量法及び容量法に関連するものである。
(化学分析において)この方法の使用に当たっては,次の点を十分に確認しなければならない。
a) 基材に添加する成分が元々含まれていない,又は基材中に含まれている添加する成分の割合が正確に
分かっている。
b) 各成分が互いに均質に混合している(必要な場合)。
c) 誤差要因をすべて特定している(例えば,水銀化合物水溶液濃度では,ガラスによる水銀化合物の吸
収量の程度が分からないため,用いる容器によって濃度が変動する。)。
d) 各成分とマトリックスの間との交互作用がない。
5.2.3
例 硬化コンクリートのセメント含有量の定量
この場合,コンクリート試料片は,各成分(セメント,骨材,水)の量を測定し,各コンクリート試料
を固めるために互いに混ぜ合わせて作成する。この手法の利点は,試料片を作成する精度がセメント含有
量の定量に用いる分析方法の精度より高いことによる。
5.3
認証参照値[JIS Q 0043-1のA.1.1 b) 参照]
5.3.1
一般
この手法では,技能試験に使用する物質が認証標準物質(CRM)である場合,その認証参照値を付与され
た値Xとして使用する。
5.3.2
付与された値の標準不確かさuX
認証標準物質を試験物質として使用する場合,付与された値の標準不確かさは,校正証明書に記載され
た不確かさに関する情報から得る。
この手法は,技能試験の各参加機関に認証標準物質の試料を提供すると,多額の費用がかかる場合があ
る。
5.3.3
例 骨材のロサンゼルス値
“ロサンゼルス値”とは,道路建設に使用する骨材の機械的強度の尺度で,単位は“LA”である。標準
物質を認証する作業において,多数の特別な骨材試料を用意し,この試料の一部を28の試験所で実施する
共同試験に使用した結果,付与された値XCRM =21.62 LA,標準不確かさ
CRM
;
X
u
=0.26 LAを得た。この骨
材の残りの試料は,技能試験に使用することができた。
5.4
参照値[JIS Q 0043-1のA.1.1 c) 参照]
5.4.1
一般
この手法では,参加機関への配布に備えて,標準物質(RM)として使用する予定の試験物質の試料をまず
10
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
用意する。次に,その用意した試験試料から多数の試料をランダムに選択し,ある一つの試験所が,認証
標準物質を用いて,適切な測定方法を用い,併行精度条件に従って試験する(JIS Z 8101-2の規定に従う)。
最後に,試験物質をCRMの認証参照値を用いて校正することによって,付与された値XRMを求める。
5.4.2
付与された値の標準不確かさuX
試験物質及びCRMの一連の試験結果から試験物質の付与された値を求める場合,付与された値の標準
不確かさは,試験結果及びCRMの認証参照値の不確かさから求める。試験物質とCRMが同一でない場合
(基質,組成,結果のレベル),これが原因となる不確かさも含める。
この方法で付与された値は,その標準不確かさが求められていれば,CRMの認定値にトレーサブルであ
る。さらに,この方法は費用が高いCRMを全参加機関に配布する必要がない。これらが他の方法より優
れる理由である。ただし,この方法は試験物質と試験条件の間に相互作用がないことを前提としている。
5.4.3の例は,単一CRMとの直接比較によって,試験物質の付与された値を求める,という単純なケー
スにおける不確かさの算出法を示している。
5.4.3
例 骨材のロサンゼルス値
5.3の例中のCRMを用いて別の類似の骨材RMに値付けできる。値付けするには,一つの試験所で二つ
の骨材試料に対して同一の測定方法を使用し,併行条件によって一連の試験を実施する必要がある。
このとき,次の式が成立する。
D
X
X
+
=
CRM
RM
·········································································· (3)
ここに,
XCRM: CRMの付与された値
XRM: RMの付与された値
Di: i番目の試料に対するRMとCRMの平均測定結果の間の
差分(RM−CRM)
D: 差分Diの平均
RMの付与された値の標準不確かさは,次のように計算できる。
2
2
CRM
;
RM
;
D
X
X
u
u
u
+
=
··························································· (4)
表1は一連の試験から得られるデータの例,及び差分の標準の不確かさuDを計算する方法を示す。
この結果によって式(5)及び式(6)を得る。
35
.
23
73
.1
62
.
21
RM
=
+
=
X
LA units ········································ (5)
35
.0
24
.0
26
.0
2
2
RM
;
=
+
=
X
u
LA units ···································· (6)
ここに,0.26:CRMの付与された値の標準不確かさ(5.3の例)
0.24:Dの標準不確かさ

11
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−CRMとRM間の平均差分及びこの差分の標準の不確かさの計算
試料
RM
CRM
平均値の差分
RM−CRM
単位LA
試験1
単位LA
試験2
単位LA
試験1
単位LA
試験2
単位LA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
20.5
21.1
21.5
22.3
22.7
23.6
20.9
21.4
23.5
22.3
23.5
22.5
22.5
23.4
24.0
24.5
24.8
24.7
24.9
27.2
20.5
20.7
21.5
21.7
22.3
22.4
21.2
21.5
23.5
22.9
24.1
23.5
23.5
22.7
24.2
24.4
24.7
25.1
24.4
27.0
19.0
19.8
21.0
21.0
20.5
20.3
21.5
21.9
21.0
22.0
20.8
21.0
21.0
22.0
22.1
22.3
22.0
21.9
22.4
24.5
18.0
19.9
21.0
20.8
21.0
20.3
21.8
21.7
21.0
21.3
20.6
22.0
21.0
22.0
21.5
22.5
21.9
21.9
22.6
23.7
2.00
1.05
0.50
1.10
1.75
2.70
−0.60
−0.35
2.50
0.95
3.10
1.50
2.00
1.05
2.30
2.05
2.80
3.00
2.15
3.00
平均差分 D
標準偏差
Dの標準不確かさ(標準偏差/20)
1.73
1.07
0.24
注記 このデータは,ロサンゼルス(LA)試験から得られた骨材の機械的強度の測定値である。
5.5
熟練試験所による合意値[JIS Q 0043-1のA.1.1 d) 参照]
5.5.1
一般
この手法では,参照値(5.4)の手法の場合と同様に,参加機関への配布の備えて試験物質の試料をまず用
意する。次に,この試料からランダムにサンプルを取り出し,幾つかの熟練試験所が分析する。付与され
た値及びその不確かさをラウンド完了後に求める場合には,この熟練試験所グループはこのラウンドの技
能試験スキームの参加機関であってもよい。熟練試験所グループが報告した結果のロバストな平均値を,
付与された値Xとする。ロバストな平均値は附属書CのアルゴリズムAを用いて算出する。
使用した計算方法が健全な統計的基礎を備えたものであり,その方法が文書によって報告される場合は,
アルゴリズムAの代わりに他の計算方法を用いてもよい。
5.5.2
付与された値の標準不確かさuX
p個の熟練試験所がそれぞれ試験物質の測定値xiを,計測の標準不確かさの推定値uiとともに報告し,
更に付与された値Xを,アルゴリズムAを用いて算出したロバストな平均値とした場合,付与された値X
の標準不確かさは次の式によって推定できる。
∑
=
×
=
p
i
i
X
u
p
u
1
2
25
.1
························································· (7)
熟練試験所が標準不確かさを報告しない場合,又は不確かさを独立して(例えば,試験所認定機関によ
12
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
って)検証していない場合,付与された値の標準不確かさを5.6に従って求めなければならない。
注記 係数1.25とは,正規分布からサンプリングされた大きな試料(p>10)から求められた,中央値の
標準偏差と算術平均値の標準偏差との比のことである。正規分布からサンプリングされたデー
タを,附属書Cのアルゴリズムによってロバストな平均値を算出したときの,平均値の標準偏
差の詳しい値は不明であるが,算術平均値の標準偏差と中央値の標準偏差との間のいずれかの
値をとるため,式(7)を用いれば標準不確かさuXの保守的な(現実より大きな)推定値が得られ
る。p<10の場合,適切な係数は1.25より小さいため式(7)は二重に保守的な値を算出する。
この手法では,熟練試験所の結果に未知のかたよりがある可能性,更に各熟練試験所から提出された不
確かさの信頼性が高くない可能性がある。
5.5.3
例 骨材の岩石の分類学的分析
骨材試料を配布し,参加者が試料の岩石の分類学的組成を決定する場合にこの手法を使用できる。骨材
の分類には技能及び経験が必要であり,利用可能な標準物質がないため,小グループの専門家の合意がこ
の場合の値付けに最良の方法となるであろう。
5.6
参加試験所による合意値[JIS Q 0043-1のA.1.1 e) 参照]
5.6.1
一般
この手法では,1ラウンドの技能試験スキームの全参加機関が報告した結果から,附属書Cのアルゴリ
ズムAを用いて求めたロバストな平均値を,付与された値Xとする。
健全な統計的基礎があり,計算方法を文書によって規定している場合は,アルゴリズムAの代わりにそ
の計算方法を用いてもよい。例えば,中央値が得られ,中央値の絶対偏差を式(C.2)の代わりに使用できる
場合に,C.1の計算は式(C.1)まで行えばよい。
この手法は,測定方法を標準化し,規定している場合に,特に有用である。
5.6.2
付与された値の標準不確かさuX
アルゴリズムAを用いて計算したロバストな平均を付与された値とするとき,付与された値Xの標準不
確かさは次の式のように推定できる。
p
s
uX
/
*
25
.1
×
=
······························································ (8)
ここで,s*は,附属書CのアルゴリズムAを用いて計算した,ロバストな標準偏差である(このとき,
ある参加機関の“結果”は,全参加機関による試験物質の測定値の平均値となる)。
この手法には,次のような制約がある。
a) 各参加機関から提出された値によって示した範囲の中に真の値が存在しない場合がある。
b) 誤った方法を適用することによって合意値がかたよる可能性がある。さらに,このかたよりは上記の
計算によって求めた付与された値の標準不確かさに反映されない。
微量成分の定量において,上記条件のいずれもが発生する可能性がある。
5.6.3
例 抗体の濃度
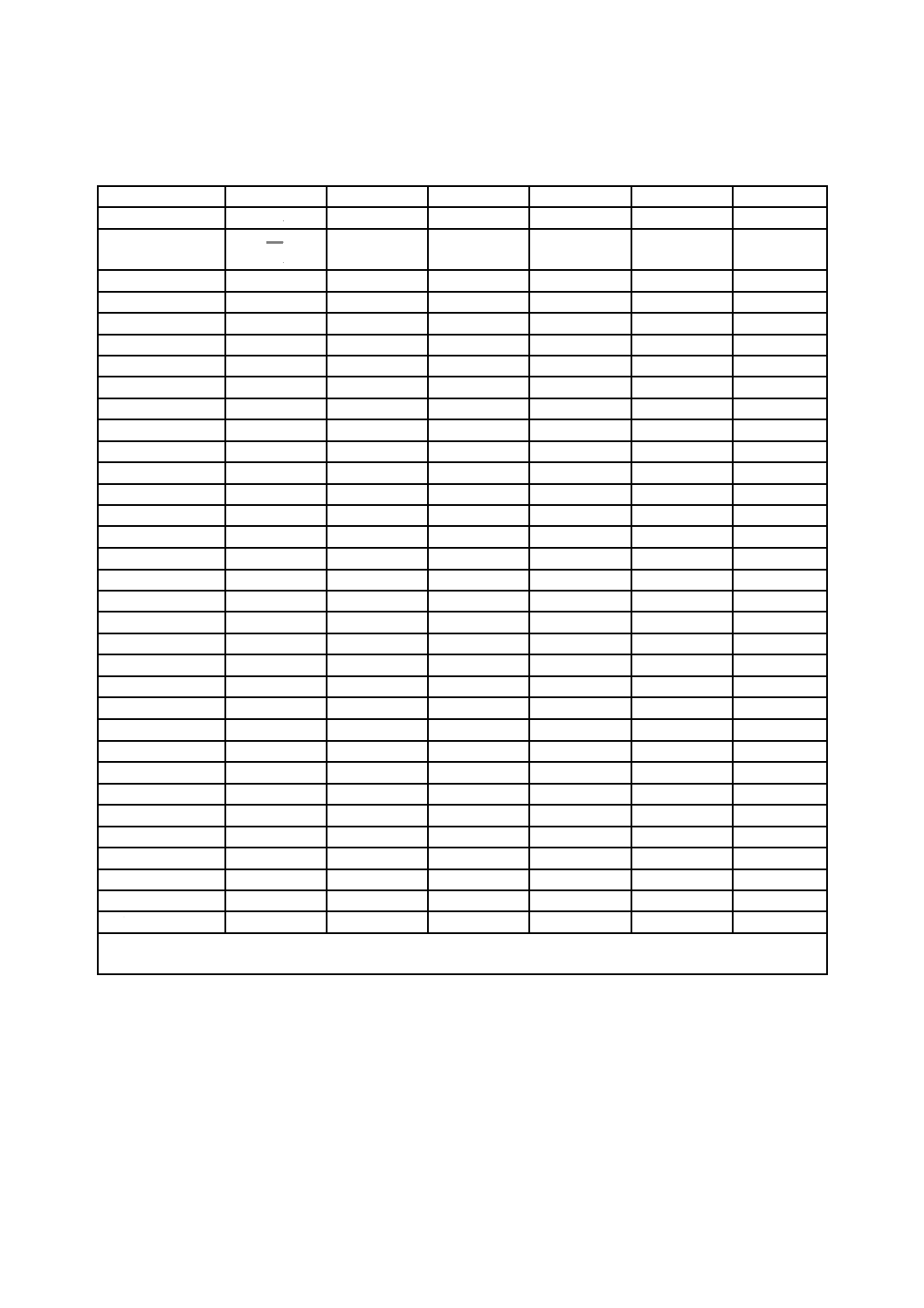
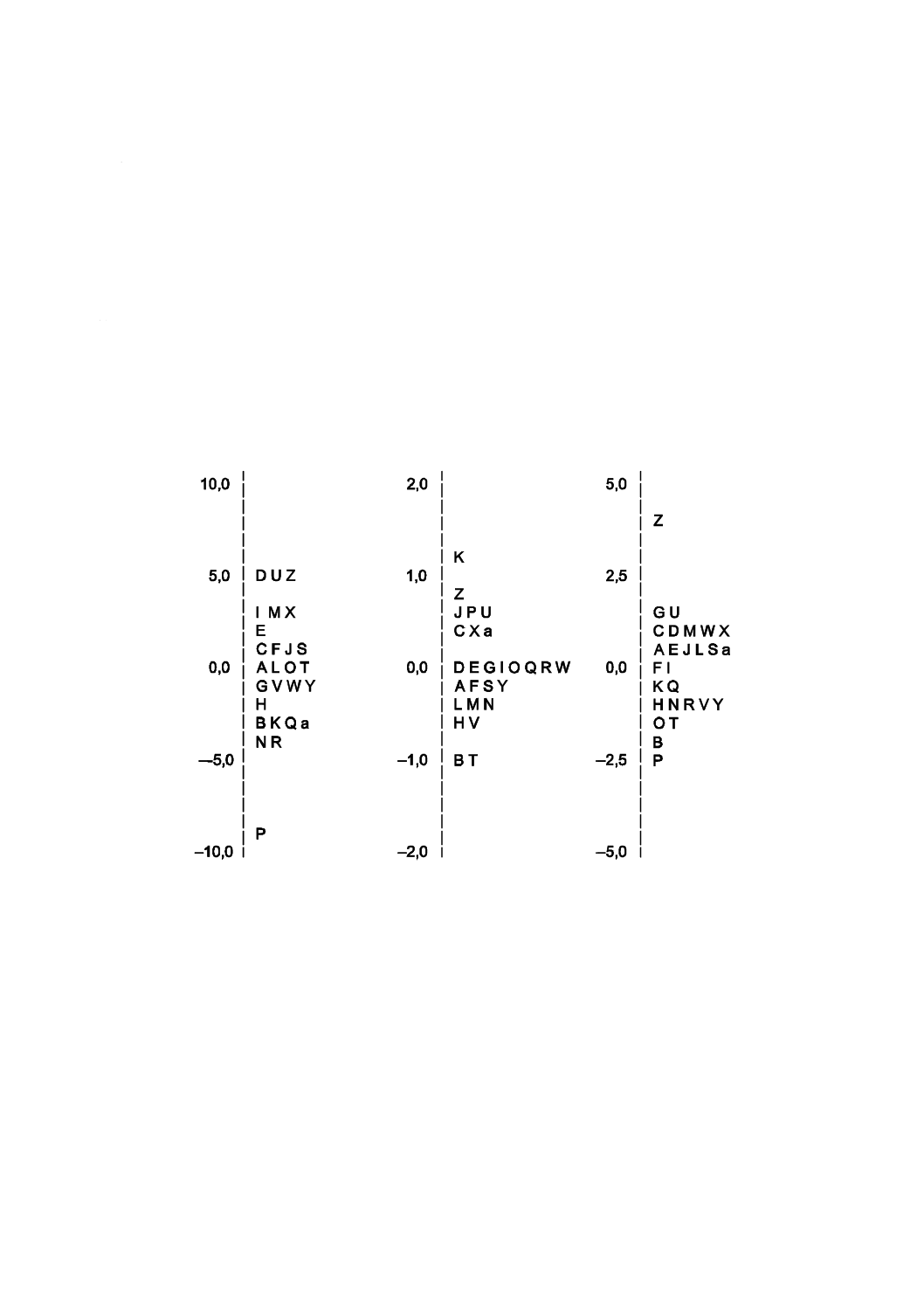
表2は,3種のアレルゲン(アレルギー誘引物質)特異のIgE(免疫グロブリンE)抗体の濃度を定量す
る1ラウンドの技能試験のデータを示している。図2は,同一のデータをヒストグラムで表示したもので
ある。
アルゴリズムAを適用して,データは昇順に並べられ,ロバスト法によって平均値及び標準偏差の初期
推定値が計算され,その後,このアルゴリズムの反復法が適用される。表3は,表2から計算したアレル
ゲン特異IgE抗体d1の結果を示す。
13
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
次に示すスプレッドシート法によって,アルゴリズムAに必要な計算を行う。
a) ステップ1:表3の反復0のところに示すとおり,昇順にカラムに記入する。それらの平均値及び標
準偏差(表3中の10.91及び3.13)を計算する。ロバスト法による平均値及びロバスト法による標準
偏差(表3中の10.85及び3.53)をC.1に示す式を用いて計算する。
b) ステップ2:表3中の反復1に示すデータを,次のカラムにコピーする。C.1中に示す式を用いてカッ
トオフ値(表3中の5.56及び16.15)を計算するためにロバスト平均値とロバスト標準偏差の初期値
を使用する。カットオフ値の外側のデータをカットオフ値と入れ替える(2.18を5.56に,16.30を16.15
に置き換える)。変更されたデータの新たな平均値と標準偏差(表3中の11.03及び2.81)を計算する。
附属書Cの式によって,ロバスト平均値はこの平均値と同一(11.03)になり,ロバスト標準偏差(3.19)
は,標準偏差に1.134を乗じて求める。
c) ステップ3:スプレッドシートを使用すると,データのカラムをこれ以上作成する必要はない。代わ
りに,第2データカラム最上部にあるカットオフ値の計算を変更し,同一カラムの最下部にあるロバ
スト平均値及びロバスト標準偏差を使用できるようにする。これによって,表3の繰返し2に示すカ
ットオフ値(6.24及び15.82)を得る。カットオフ値の外側のデータをカットオフ値に変更する操作を,
繰返しが収束するまで繰り返すことによって,この計算は終了する。データを入れ替えると,スプレ
ッドシートは自動的に平均値,標準偏差及びカットオフ値を更新するが,値の変化分は,無視できる
くらい次第に小さくなる。
他の二つのアレルゲン特異IgE抗体のロバスト平均値及び標準偏差も同様に計算する。
試験所Pのd1に対する結果は,Grubbsの検定によって,外れ値としては分類されないことに注意する
必要がある。したがって,JIS Z 8402-2に規定するこの例の外れ値検定を使用すると,平均値及び標準偏
差が全データから計算でき,表3の繰返し0に示す値を得る。ロバスト法によって,試験所Pの低い結果
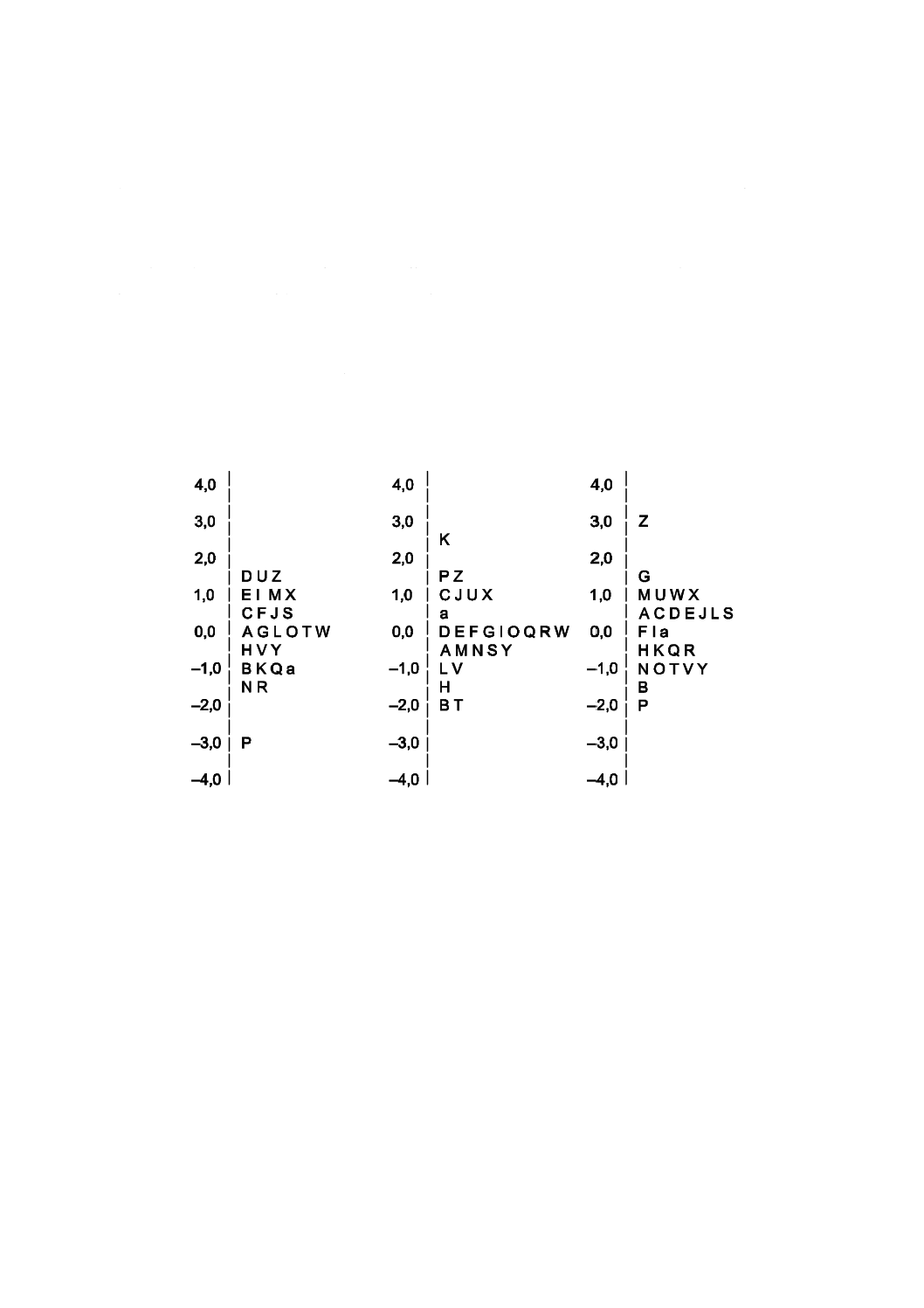
及び試験所D,U,Zの高い結果はロバスト推定値に影響しない。図9によって,試験所の結果が調査に
値するかどうかを判定できる。例えば,図9では,試験所Zが3レベルのすべてにおいて,大きな正のz-
スコアを示していることが分かる。

14
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−3個のアレルゲン特異IgE抗体(d1,f1,e3)の濃度
p=27の試験所が報告したデータ
試験所
濃度
d1
kU/L
f1
kU/L
e3
kU/L
A
11.30
1.69
5.02
B
8.29
0.74
2.52
C
11.90
2.23
5.15
D
15.60
1.76
5.15
E
13.40
1.91
4.84
F
12.50
1.71
4.54
G
10.40
1.88
5.94
H
9.38
1.14
3.50
I
14.20
1.74
4.48
J
12.10
2.39
4.75
K
8.10
3.10
3.70
L
10.80
1.39
4.70
M
13.80
1.52
5.59
N
7.00
1.50
3.40
O
10.85
1.80
2.80
P
2.18
2.52
1.88
Q
8.39
1.83
3.80
R
6.95
1.92
3.52
S
11.80
1.58
4.86
T
10.90
0.80
2.80
U
16.30
2.39
5.60
V
9.71
1.21
3.33
W
10.50
1.93
5.35
X
13.60
2.23
5.53
Y
10.10
1.63
3.18
Z
16.07
2.69
8.22
a
8.47
2.16
4.64
p
27
27
27
ロバスト平均x*
11.03
1.83
4.35
ロバスト標準偏差s*
3.04
0.50
1.25
注記 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1
リットル(L)当たりの値として示す。

15
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記1 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リットル(L)当たり
の値として示す。
注記2 表2に示す数値は,小数点以下2けたの計算を手作業で行い,得たものである。
注記3 この規格の図では対応国際規格に合わせて,小数点は“,”を用いた。
図2−3種のアレルゲン特異IgE抗体の濃度−
報告したデータのヒストグラム(表2のデータから)
アレルゲンd1
アレルゲンf1
アレルゲンe3
16
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3−3種のアレルゲン特異IgE抗体の濃度
抗体d1のロバスト平均値及び標準偏差の計算
繰返し
0
1
2
3
4
5
δ=1.5 s*
-
5.30
4.79
4.62
4.58
4.56
x*−δ
x* + δ
-
-
5.56
16.15
6.24
15.82
6.41
15.65
6.45
15.61
6.47
15.59
P
2.18
5.56
6.24
6.41
6.45
6.47
R
6.95
6.95
6.95
6.95
6.95
6.95
N
7.00
7.00
7.00
7.00
7.00
7.00
K
8.10
8.10
8.10
8.10
8.10
8.10
B
8.29
8.29
8.29
8.29
8.29
8.29
Q
8.39
8.39
8.39
8.39
8.39
8.39
a
8.47
8.47
8.47
8.47
8.47
8.47
H
9.38
9.38
9.38
9.38
9.38
9.38
V
9.71
9.71
9.71
9.71
9.71
9.71
Y
10.10
10.10
10.10
10.10
10.10
10.10
G
10.40
10.40
10.40
10.40
10.40
10.40
W
10.50
10.50
10.50
10.50
10.50
10.50
L
10.80
10.80
10.80
10.80
10.80
10.80
O
10.85
10.85
10.85
10.85
10.85
10.85
T
10.90
10.90
10.90
10.90
10.90
10.90
A
11.30
11.30
11.30
11.30
11.30
11.30
S
11.80
11.80
11.80
11.80
11.80
11.80
C
11.90
11.90
11.90
11.90
11.90
11.90
J
12.10
12.10
12.10
12.10
12.10
12.10
F
12.50
12.50
12.50
12.50
12.50
12.50
E
13.40
13.40
13.40
13.40
13.40
13.40
X
13.60
13.60
13.60
13.60
13.60
13.60
M
13.80
13.80
13.80
13.80
13.80
13.80
I
14.20
14.20
14.20
14.20
14.20
14.20
D
15.60
15.60
15.60
15.60
15.60
15.59
Z
16.07
16.07
15.82
15.65
15.61
15.59
U
16.30
16.15
15.82
15.65
15.61
15.59
平均値
10.91
11.03
11.03
11.03
11.03
11.03
標準偏差
3.13
2.81
2.72
2.69
2.68
2.68
新 x*
10.85
11.03
11.03
11.03
11.03
11.03
新s*
3.53
3.19
3.08
3.05
3.04
3.04
注記 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リットル(L)当たり
の値として示す。
17
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.7
付与された値の比較
5.2〜5.4による方法を用いて付与された値Xを定める場合,各ラウンドの技能試験スキームが一巡した
後,各参加機関のこのラウンドの結果から求めたロバストな平均値x*を付与された値と比較しなければな
らない。5.5及び5.6による方法を用いて付与された値を定める場合,可能であれば,この値と優れた試験
所が求めた参照値とを比較しなければならない。差分x*−Xの標準不確かさを,次の式によって推定する。
2
2
+
*)
25
.1(
X
u
p
s
ここに,
s*: ロバストな標準偏差
p: 試験所の数
差分が不確かさの2倍より大きい場合,理由を調査する。想定される理由は次のとおりである。
− 測定方法が原因のかたより
− 試験所の結果に含まれる,共通のかたより
− 5.2による定式化手法を用いた場合,5.2.2の手法を用いる際の条件の未評価
− “熟練試験所による合意値”手法を用いた場合であれば,熟練試験所が共通してもつ結果中のかたよ
り
− ロバストな平均値を,合意の上付与された値として用いた場合,参加機関が用いた手法がかたよりを
もつ,又はかたよりをもつ幾つかの参加機関が含まれる場合
5.8
欠測値
技能試験の反復測定回数nが2以上の場合,結果の解析の第1ステップは,各試験所が提出した結果の
各平均値及び各標準偏差を計算することである。次に,平均値を用いて,例えば,箇条7によって成績を
表す統計量を計算して,8.2及び8.3によってヒストグラム又は棒グラフを作成する。標準偏差を用いて,
例えば,8.4及び8.6によって併行精度尺度のプロットを作成する。
すべての参加機関は測定の反復を同一の回数行うべきであるが,例えば,無効な試験又は繰返しのでき
ない試験があった場合,全参加機関が同一測定回数の結果を報告できるとは限らない。このような場合,
次の手順を行うことが望ましい。
ある試験所が少なくとも0.59n回の反復測定結果を報告できる場合,その試験所の測定結果の平均値及
び標準偏差を技能試験結果の計算に含めなければならず,n回の測定結果を報告した他の試験所と同等に
取り扱わなければならない。この報告には,全試験所の測定の回数をすべて示さなければならない。
試験所が報告する反復測定の回数が0.59 n回未満である場合,その結果を,他の試験所に影響する統計
計算に含めてはならない。例えば,この結果を5.6による付与された値の計算,又は6.6による技能評価
のための標準偏差の計算に含めてはならない。しかし,この結果を,箇条7による自身の成績を表す統計
量の計算に用いてもよい。また,箇条8によるグラフに含めてもよい。ただし,この報告には,報告され
た測定の回数,及びその測定回数がこの技能試験スキームが求める数より小さいことを示さなければなら
ない。
注記 乗数0.59の理由は,次のとおりである。n回の反復測定の平均値の標準偏差は
n
/
r
σ
である。
この反復測定回数が減少すると,標準偏差は増加する。したがって,実際の反復測定回数がn
から0.59 nに減少した場合,標準偏差は1.3倍となる。
この値は技能試験で適合と判定される標準偏差の増加の限界値である。したがって,限界値0.59nを使
用すると,標準偏差がこれより大きくなるのを防止できる。この規則はし(恣)意的な基準によって決め
18
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
られたことが明らかであるため,コーディネータは必要な場合,技能試験スキーム参加機関の助言を得て
これを変更してもよい。
6
技能評価のための標準偏差の求め方(JIS Q 0043-1のA.2.1.3参照)
6.1
技能評価のための標準偏差の求め方の選択
技能評価のための標準偏差σˆの決定方法を6.2〜6.6に5通り規定する。コーディネータは,スキームの
メンバー及び適切な認定団体と協議し,適切な規制を考慮して,コーディネータの責任において,技能評
価のための標準偏差の決定方法を選択しなければならない。6.6による方法は,スキームに参加する試験所
の数が少ない場合に適用することは望ましくない。標準偏差σˆは,コーディネータの責任によって決定す
る。コーディネータは標準偏差の求め方の詳細な報告を用意しなければならない。
注記 JIS Q 0043-1では,技能評価のための標準偏差として記号sを用いる。これは技能試験のため
の標準偏差として標本標準偏差(不偏分散の平方根)を用いるというこの規格の通常の手法の
場合であれば問題はない。しかしこの規格では,技能評価のための標準偏差を標本標準偏差の
算出法以外の方法によって求めることがあるため,記号sではない他の記号で表すことが望ま
しい。したがって,この規格では,σˆを技能評価のための標準偏差として用いる。
6.2
規定値を用いる場合
6.2.1
一般
これは,ある種特定のデータ解釈作業,又は法令によって規定している要件から,技能評価のための標
準偏差を設定する手法である。
この手法の利点は,技能評価のための標準偏差が,“目的適合性”をその測定方法が満たすかどうか,と
いうことと直接結びついていることである。
6.2.2
例 ナッツ,ナッツ製品,干しいちじく,干しいちじく製品中のアフラトキシン
法定限度が10 µg/kgである場合,アフラトキシンの試験に使用する方法の再現精度の変動係数は50 %
を超えないことを規定した法令がある。したがって,試験物質を技能試験スキームに使用し,アフラトキ
シン含有量が10 µg/kgである場合,この法令は,この物質の再現標準偏差が5 µg/kgを超えないことを求
めている。この場合,技能評価の標準偏差としても5 µg/kgを設定するのがよい。
6.3
達成期待レベルを用いる場合
6.3.1
一般
この手法では,技能評価のための標準偏差を,コーディネータ及びスキームのメンバーが達成を期待す
る実施レベルに対応する値に設定する。
この手法では,技能評価のための標準偏差が,“目的適合性”をその測定方法が満たすかどうか,という
ことと同等になる。
技能評価のための標準偏差σˆを規定又は達成期待ラインの設定によって選択した場合,選択した値が測
定方法の再現精度に関して現実的でない可能性がある。この方法の併行精度及び再現精度に関する情報が
入手可能な場合,次の方法を用いて,選択したσˆの値が現実的であることを確認する。
次の値を得た場合,
R
σ
再現標準偏差
r
σ
併行標準偏差
試験所間標準偏差を,次の式によって計算する。
19
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
σL =
2
2
r
R
σ
σ
−
······································································ (9)
L
σ及び
r
σの値と選択した値∃σとを式(10)に代入することによって,係数φの値を計算する。
σˆ=(
)
(
)n
/
r2
2
L
σ
σ
φ
+
×
························································ (10)
ここに, n: 各試験所が実施する反復測定の回数
求めた値φが小さい場合(例えばφ<0.5),選択した値σˆは,試験所が現実に達成できない反復精度のレ
ベルに対応することを意味する。
6.3.2
例1 ヒト血清中のグルコース測定
濃度が非常に低い場合(60 mg/dL未満)でも,許容範囲±6 mg/dLが認められれば,臨床検査室は,血
液グルコースレベルを付与された値の±10 %の範囲で定量できることを意味する。この情報を利用して次
のように技能評価の標準偏差を計算する。
a) 付与された値Xが60 mg/dL未満の場合
σˆ=6.0/3.0 =2.0 mg/dL
b) 付与された値Xが60 mg/dLを超える場合
σˆ=0.1 X/3.0 = 0.033 X mg/dL
ここで導入した係数3.0は,z-スコアの解釈に使用する棄却限界値3.0に対応する(7.4参照)。
6.3.3
例2 硬化コンクリートのセメント含有量の定量
コンクリートのセメント含有量は通常,立方メートル当たりのコンクリートに対するセメントのキログ
ラム表示の質量(すなわちkg/m3)で示す。実際には,コンクリートをセメント含有量25 kg/m3の幅の品
質グレードによって製造しており,試験所がこのグレードを正確に確認することが望ましい。このため,
選択した値σˆの値は25 kg/m3の半分を超えないことが望ましい。コンクリートの平均セメント含有量が
260 kg/m3の試料を用いる再現性実験によって次の結果を得た。
R
σ= 23.2 kg/m3及び
r
σ= 14.3 kg/m3。
したがって,式(11)が成り立つ。
σL =
2
2
3
14
2
23
.
.
−
= 18.3 kg/m3 ············································ (11)
nを2とし,σL=18.3 kg/m3,
r
σ=14.3 kg/m3,σˆ=12.5 kg/m3を式(10)に代入して,次の結果を得る。
12.5 = (
)
(
)2
/
3.
14
3.
18
2
2
+
φ
·················································· (12)
これを計算すると,φ=0.40となる。したがって,σˆ=12.5 kg/m3を選択すると,試験所が達成できる試
験所間標準偏差は,係数0.4だけ再現性実験で得た値より小さくなる。これは明らかに非現実的な値であ
る。
6.4
一般的なモデルを用いる場合
6.4.1
一般
この手法では,技能評価のための標準偏差の値を,測定方法の再現精度の一般的なモデルから求める。
この手法の欠点は,特定の測定方法の真の再現精度が,モデルから得る値と大幅に異なる場合があるこ
とである。これは,(例えば6.4.2のような)一般的なモデルを使用すると,再現精度の値は測定量のレベ
ルだけに依存することになり,測定対象量,測定方法,又は試料の大きさや量が無視されるためである。
6.4.2
例 Horwitz曲線
Horwitz[3]が示した分析方法の再現精度の一般的なモデルを使用すると,再現標準偏差を求める次の式を
20
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
得る。
8495
.0
02
.0
=
c
R
σ
······························································ (13)
ここでcは化学種の濃度であり,単位は無次元(質量分率)である。
6.5
精度評価実験結果を用いる場合
6.5.1
一般
この手法では,技能試験スキームに使用する測定方法を標準化している場合,更に,その方法の併行精
度と再現精度に関する情報を得ることができる場合に,技能評価のための標準偏差σˆを次の情報を用いて
計算すると,試験所間標準偏差は次の式で表される。
L
σ=
2
2
r
R
σ
σ
−
··································································· (14)
ここに,
R
σ:
r
σ:
再現標準偏差
併行標準偏差
さらに,技能評価のための標準偏差を次の式によって求める。
∃σ=
(
)n
r/
2
2
L
σ
σ
+
················································································ (15)
ここに,
n: 各試験所が1ラウンドのスキームに実施する反復測定の回数
試験結果の平均値を元に,併行標準偏差及び再現標準偏差を求めている場合,関数関係はJIS Z 8402-2
に規定する方法から得る。次に,この関係を用いて,技能試験に使用する付与された値に適切な,併行標
準偏差及び再現標準偏差の値を計算する。
6.5.2
例 硬化コンクリートのセメント含有量の定量
6.3の例に使用したものと同一データによって,式(15)から,次の技能試験のための標準偏差を得る。
∃σ=
(
)2/
3.
14
3.
18
2
2
+
= 20.9 kg/m3 ········································· (16)
ここでは,n= 2の反復測定を実施することを前提としている。
6.6
単一技能試験スキームによって得たデータを用いる場合
6.6.1
一般
この手法では,1ラウンドのスキームの参加者の技能評価のための標準偏差σˆを,同一ラウンド中の参
加者が報告する結果から求める。標準偏差は全参加者が報告する結果のロバストな標準偏差で表され,こ
れは,附属書CのアルゴリズムAを用いて計算する。この手法では,ある参加者が報告する結果は,該当
ラウンドの参加者が得るn回の反復測定の平均でなければならない。
使用した計算方法が健全な統計的基礎を備えたものであり,その方法を文書によって報告する場合は,
アルゴリズムAの代わりに他の計算方法を用いてもよい。
他の計算方法をアルゴリズムAの代わりに用いてもよい。ただし,その計算方法が妥当な統計的基礎を
備えた手法であり,その手法の詳細な報告を用意する。
この手法の欠点は,σˆの値がラウンドごとに大きく変化し,試験所が複数ラウンドにまたがる傾向を調
べるためにz-スコアの値を使用するのが難しくなることである。この欠点は,多数のラウンドから,附属
書CのアルゴリズムSを用いて計算した標準偏差のロバストなプール値を使用することによって,確立し
21
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
たスキーム中で克服できる。
6.6.2
例 抗体濃度
表2及び表3にこの手法の例を示す。
6.7
技能試験から得た精度の値と設定値との比較
参加者の成績の確認として,更に,参加者に対するスキームの効用を評価するため,コーディネータは
次の手順を適用するのがよい。技能試験スキームの各ラウンドから得た結果を用いて,更に,JIS Z 8402-5
に規定するロバストな方法を用いて,測定方法の併行標準偏差及び再現標準偏差の推定値を計算する。こ
の推定値を時系列として,精度試験から得た併行標準偏差及び再現標準偏差の値(可能な場合)とともに,
グラフにプロットする。
次に,コーディネータはこのグラフを検討する。技能試験から得た精度値が係数2以上で精度実験から
得た値と異なっていることをこのグラフが示す場合,コーディネータは原因を調査する。測定方法の精度
が時間経過とともに向上していないことをグラフが示す場合,次のことが想定される。
− 参加試験所が処置信号及び警戒信号の原因を調査していない,又は是正処置を適切に実施していな
い。
− 参加試験所が,処置信号及び警戒信号の原因を特定できない。
− 方法が統計的管理の状態にあり,信頼性の高い結論が方法から得たデータに基づいている。
7
成績を表す統計量[performance statistics(成績を表す統計指標)]の計算
7.1
試験所のかたよりの推定値[JIS Q 0043-1のA.2.1.4 a) 参照]
7.1.1
一般
xを,ある技能試験スキームの試料の一特性について,参加試験所によって報告された結果(又は結果
の平均)を表すものとする。
次に,Xを付与された値とすると,試験所のかたよりDの推定値は次の式によって計算できる。
D = x−X ················································································ (17)
ここで,試験所のかたよりの絶対値をとって|D|としたり,D2を使った統計量(指標)は,かたより
の符号が隠れるため,使用しないほうがよい。
7.1.2
試験所のかたよりについての解釈
参加試験所の(複数の)報告値によって計算した結果,その試験所のかたよりが,ひとつでも,±3.0σˆ
の範囲から外れた場合,この結果は“処置信号”が発生したと考えなければならない。同様に,試験所の
かたよりが±2.0σˆの範囲から外れた場合,“警戒信号”が発生したと考えるべきである。あるラウンドで
一つの“処置信号”が発生したり,又は二つのラウンドで継続して“警戒信号”が発生した場合は,調査
を要する異常が発生した証拠と考えなければならない。この判断基準は,7.4によるz-スコアのものと同等
であり,処置信号及び警戒信号の基準は全く同じである。
乗数2.0及び3.0を,ここで(更に,後述する他の同様な基準において)使用する理由は,次のとおりで
ある。X及びσˆがx値を導く元となる母集団の平均及び標準偏差の良好な推定値であり,基礎となる分布
が正規分布である場合,D値は平均値ゼロ,標準偏差σˆの正規分布をとる。このような状況では,試験所
の推定したかたよりの約0.3 %だけが−3.0 σˆ< D < 3.0σˆの範囲の外側に,同様に約5 %が−2.0 σˆ < D <
2.0 σˆの外側にくる。これらの確率は非常に低いため,実際に問題が存在しない場合は,処置信号は発生
しにくい。したがって,処置信号が発生したということは,異常を特定できる十分な理由があるといえる。
技能評価のための標準偏差を6.2,6.3又は6.4によるいずれかの方法によって固定した場合は,その値
22
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は(技能試験時の)再現標準偏差とは大きく異なる可能性があり,上記の確率0.3 %及び5.0 %の考え方
は適用できない。
技能を評価するための標準偏差を6.2又は6.3による方法のいずれかによって固定した場合は,それが(規
格,法令などに)規定したり,一般的に合意された性能基準と直接比較が実施できるように使われていれ
ば,参加試験所にとって適切な成績を表す統計量を得るために役立つ場合もある。例えば,6.3の例の場合,
グルコース試料の誤差の目標値が付与された値の±10 %であれば,この例に従って,技能評価の標準偏差
3.33 %を求め,z-スコアを計算し,7.4に従う。同様に,試験所のかたよりをパーセンテージ差分として計
算し(7.2に規定),これを目標値10 %と直接比較すればよい。
7.1.3
例 抗体濃度
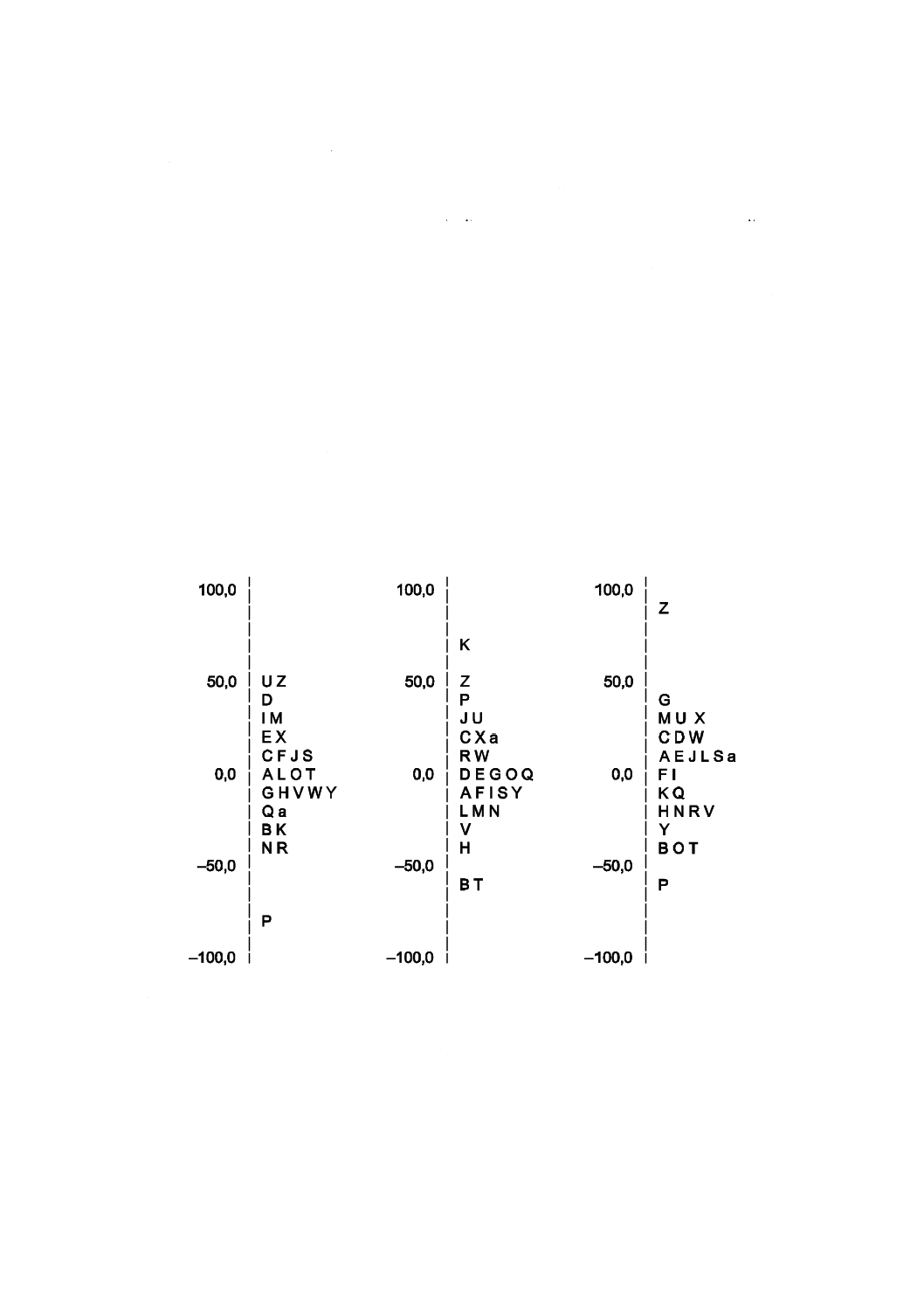
表4は,この方法を表2のデータに適用した結果を示し,図3のヒストグラムは試験所のかたよりの推
定値を示す。図2と図3との比較から,試験所のかたよりは元のデータと同一分布を示すことが分かる(丸
めによる若干の影響を除く。)。ただし,ゼロを中心の値としている。
注記 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リットル(L)当たりの
値として示す。
図3−3種のアレルゲン特異IgE抗体の濃度−
試験所のかたよりの推定値のヒストグラム(データは表4から)
アレルゲンd1
アレルゲンf1
アレルゲンe3

23
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−3種のアレルゲン特異IgE抗体の濃度(d1,f1,e3)
試験所のかたよりの推定値
試験所
濃度
d1
kU/L
f1
kU/L
e3
kU/L
A
0.27
−0.14
0.67
B
−2.74
−1.09 W
−1.83
C
0.87
0.40
0.80
D
4.57
−0.07
0.80
E
2.37
0.08
0.49
F
1.47
−0.12
0.19
G
−0.63
0.05
1.59
H
−1.65
−0.69
−0.85
I
3.17
−0.09
0.13
J
1.07
0.56
0.40
K
−2.93
1.27 W
−0.65
L
−0.23
−0.44
0.35
M
2.77
−0.31
1.24
N
−4.03
−0.33
−0.95
O
−0.18
−0.03
−1.55
P
−8.85 W
0.69
−2.47
Q
−2.64
0.00
−0.55
R
−4.08
0.09
−0.83
S
0.77
−0.25
0.51
T
−0.13
−1.03 W
−1.55
U
5.27
0.56
1.25
V
−1.32
−0.62
−1.02
W
−0.53
0.10
1.00
X
2.57
0.40
1.18
Y
−0.93
−0.20
−1.17
Z
5.04
0.86
3.87 A
a
−2.56
0.33
0.29
3.0 σˆ
9.12
1.50
3.75
2.0 σˆ
6.08
1.00
2.50
−2.0 σˆ
−6.08
−1.00
−2.50
−3.0 σˆ
−9.12
−1.50
−3.75
注記1 濃度データの後の記号 A=処置信号,W=警戒信号
注記2 本表の試験所のかたよりは,表2中のロバスト平均値を3レベルの付与された値として使用し,
表2中のデータから求めたものである。表の最下部に示す処置限界と警戒限界は,表2のロバ
スト標準偏差を技能評価用標準偏差として使用し計算した。
注記3 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リッ
トル(L)当たりの値として示す。
24
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.2
パーセンテージ差分[JIS Q 0043-1のA.2.1.4 b) 参照]
7.2.1
一般
7.1の表記法によって,パーセンテージ差分を次の式によって計算する。
D% = 100 (x−X ) / X ································································ (18)
7.2.2
パーセンテージ差分の解釈
パーセンテージ差分については,7.1の試験所のかたよりで示したものと同じ考え方で解釈する。すなわ
ち,参加者が報告する結果が発生するパーセンテージ差分が±300 σˆ/X %の範囲から外れた場合,この
結果は“処置信号”が発生したものと考えなければならない。同様に,パーセンテージ差分が±200 σˆ/X %
の範囲から外れた場合,“警戒信号”が発生したものと考えなければならない。一回の“処置信号”又は二
つのラウンドで継続した“警戒信号”は,調査が必要な異常が発生した証拠であると考えなければならな
い。
7.2.3
例 抗体濃度
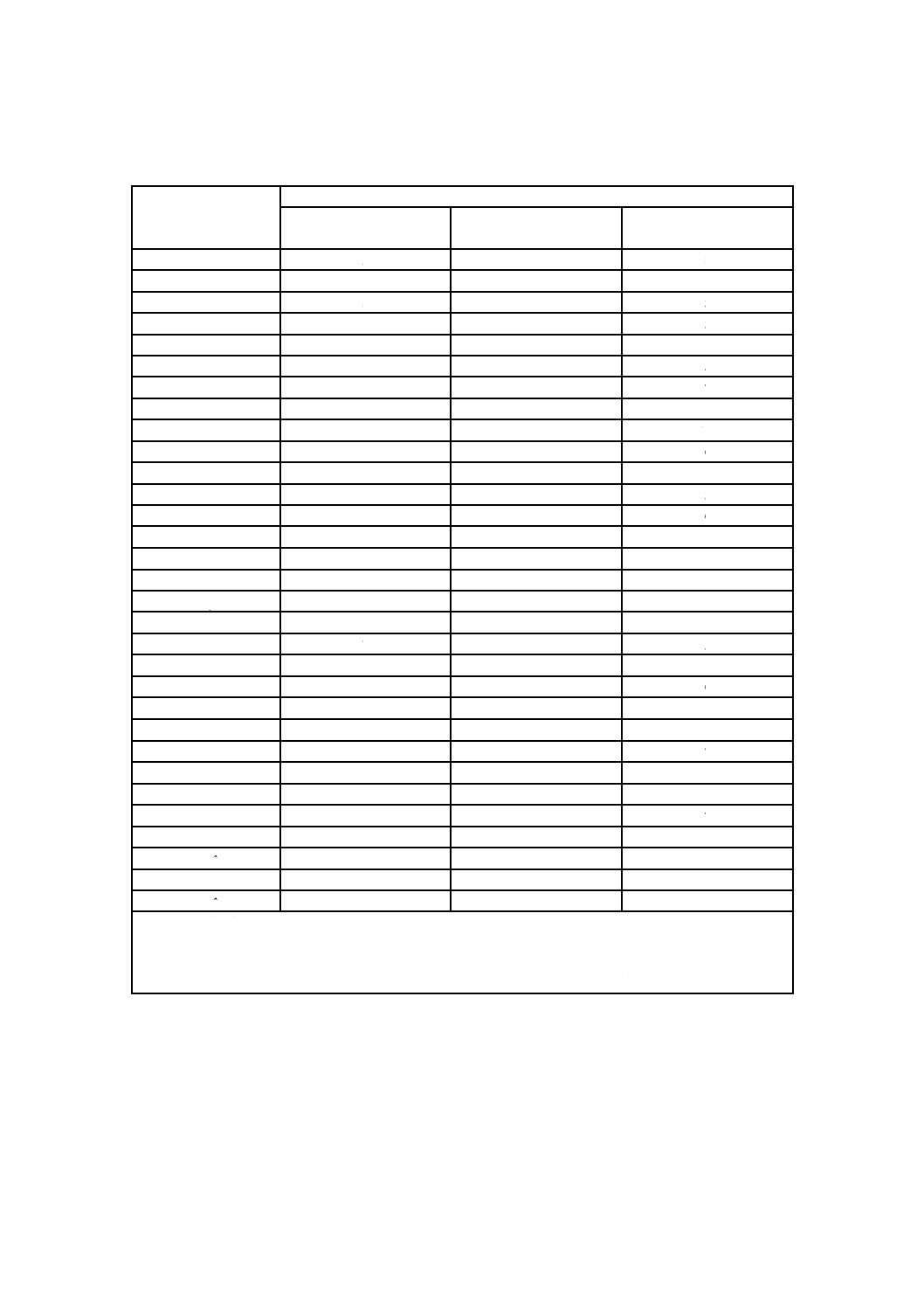
表5は,この方法を表2中のデータに適用した結果を示す。図4のヒストグラムは,パーセンテージ差
分を示す。図2と図4とを比較すると,パーセンテージ差分が元のデータと同一の分布を示していること
が分かる(丸めによるわずかな影響は考えない。)。ただし,中心の値はゼロであり,これは試験所のかた
よりの推定値と同様である。
注記 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リットル(L)当たりの
値として示す。
図4−3種のアレルゲン特異のIgE抗体の濃度−
パーセンテージ差分のヒストグラム(データは表5から)
アレルゲンd1
アレルゲンf1
アレルゲンe3
25
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5−3種のアレルゲン特異IgE抗体の濃度(d1,f1,e3)
パーセンテージ差分
試験所
パーセンテージ差分
d1
%
f1
%
e3
%
A
2
−8
15
B
−25
−60 W
−42
C
8
22
18
D
41
−4
18
E
21
4
11
F
13
−7
4
G
−6
3
37
H
−15
−38
−20
I
29
−5
3
J
10
31
9
K
−27
69 W
−15
L
−2
−24
8
M
25
−17
29
N
−37
−18
−22
O
−2
−2
−36
P
−80 W
38
−57
Q
−24
0
−13
R
−37
5
−19
S
7
−14
12
T
−1
−56
−36
U
48
31
29
V
−12
−34
−23
W
−5
5
23
X
23
22
27
Y
−8
−11
−27
Z
46
47
89 A
a
−23
18
7
300
X
/
ˆσ
82.7
82.0
86.2
200
X
/
ˆσ
55.1
54.6
57.5
−200
X
/
ˆσ
−55.1
−54.6
−57.5
−300
X
/
ˆσ
−82.7
−82.0
−86.2
注記1 濃度データの後の記号 A=処置信号,W= 警戒信号
注記2 本表中のパーセンテージ差分は,表2のロバスト平均値を3レベルの付与された値として使用
し,表2中のデータから求めた。表の最下部に示す処置限界及び警戒限界は,表2中のロバス
ト標準偏差を,技能評価の標準偏差として使用することによって計算した。
26
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3
順位及びパーセンテージ順位[JIS Q 0043-1のA.2.1.4 c) 参照]
7.3.1
一般
1ラウンドの技能試験中のp試験所から得た結果によって,順位1を最も低い結果を報告する試験所に,
順位2を次に低い結果を報告する試験所に割り当て,以下同様の割当て方法によって順位を求める。最も
高い結果を報告する試験所に順位pを割り当てる。二つ以上の結果が等しい場合,同一の平均順位を割り
当てる。例えば,表2の場合,試験所Cと試験所Xが共に,f1の濃度2.23を報告している。二つの試験
所には順位21と22が割り当てられるため,表6中,双方にランク21.5が割り当てられている。一試験所
当たり複数の測定が行われた場合,各測定量に個別に順位を割り当てる。
順位をi =1,2,...,pによって表す場合,パーセンテージ順位は100(i −0.5 )/ p %として計算する。パー
センテージ順位の計算例を表6に示す。
7.3.2
順位及びパーセンテージ順位についての解釈
順位又はパーセンテージ順位の解釈に当たり,データが特定の確率分布に従っているという仮定は不要
であり,また,これを算出するのに付与された値や技能評価のための標準偏差は使用しない。したがって,
順位及びパーセンテージ順位は,最も極端な結果を報告した試験所を特定するための簡単な方法として使
える。これは特定の早期ラウンドの技能試験スキームに特有な方法であり,これを用いて技能が最も改善
できそうな試験所を特定するのに使うことができる。ただし,JIS Q 0043-1:1998,6.6.5に規定した警告に
注意しなければならない。すなわち,“成績に応じた試験所の順位付け一覧表による成績の報告は,技能試
験においては望ましくない。順位付けは,誤解されたり誤用されやすいため,特段の注意の下でだけ用い
ることが望ましい。”
27
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表6−3種のアレルゲン特異IgE抗体の濃度(d1,f1,e3)
順位及びパーセンテージ順位
試験所
順位
パーセンテージ順位
d1
f1
e3
d1
%
f1
%
e3
%
A
16
10
19
57
35
69
B
5
1
2
17
2
6
C
18
21.5
20.5
65
78
74
D
25
13
20.5
91
46
74
E
21
17
17
76
61
61
F
20
11
13
72
39
46
G
11
16
26
39
57
94
H
8
3
8
28
9
28
I
24
12
12
87
43
43
J
19
23.5
16
69
85
57
K
4
27
10
13
98
35
L
13
5
15
46
17
54
M
23
7
24
83
24
87
N
3
6
7
9
20
24
O
14
14
3.5
50
50
11
P
1
25
1
2
91
2
Q
6
15
11
20
54
39
R
2
18
9
6
65
31
S
17
8
18
61
28
65
T
15
2
3.5
54
6
11
U
27
23.5
25
98
85
91
V
9
4
6
31
13
20
W
12
19
22
43
69
80
X
22
21.5
23
80
78
83
Y
10
9
5
35
31
17
Z
26
26
27
94
94
98
a
7
20
14
24
72
50
7.4
z-スコア[JIS Q 0043-1のA.2.1.4 d) 参照]
7.4.1
一般
7.2の記法によって,z -スコアを次の式のとおり計算する。
z =(x −X )/ σˆ ······································································· (19)
ここに,
σˆ: 技能評価の標準偏差
注記 JIS Q 0043では,z-スコア定義中の標準偏差に対し記号sを使用する。これは,この量を多数
の結果の標本標準偏差として求める場合には適切であるが,例えば,精度実験結果から又は6.4
の一般的なモデルを参照して,標準偏差を計算するような場合には不適切である
7.4.2
z-スコアの解釈
参加試験所の(複数の)報告値によって計算した結果,その試験所のかたよりが,一つでも,±3.0の範
囲から外れた場合,この結果によって“処置信号”が発生されたものと考えなければならない。同様に,
試験所のかたよりが±2.0の範囲から外れた場合,“警戒信号”が発生されたものと考えなければならない。
28
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
あるラウンドで一つの“処置信号”が現れたり,又は二つのラウンドで継続して“警戒信号”が発生した
場合は,調査を要する異常が発生した証拠と考えなければならない。
多数の試験所が参加した技能試験スキームでは(例えば,100以上の試験所),z-スコアの補足説明をす
るために,7.9及び/又は図6に示す正規確率プロットを用いてもよい。この対極として,少数の試験所
(例えば,10未満の試験所)しかない場合には,“処置信号”又は“警戒信号”を使用しなくてもよい。
この場合は,個々のラウンドの結果よりも,複数ラウンドにわたるz-スコアを組み合わせたグラフィカル
な方法によって試験所の成績を表示したほうが有用である。
7.4.3
例 抗体濃度
表2に従って計算したロバスト平均及び標準偏差を用いて得たz -スコアを表7に示す。そのヒストグラ
ムを図5に示す。図2と図5との比較によって,z -スコアが元のデータと同一分布になることが分かる(丸
めによる若干の影響は別とする。)。ただし,中央値はゼロであり,これは試験所のかたよりの推定値と同
様である。
図5−3種のアレルゲン特異IgE抗体の濃度−
z-スコアのヒストグラム(データは表7から)
アレルゲンd1
アレルゲンf1
アレルゲンe3

29
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表7−3種のアレルゲン特異IgE抗体の濃度(d1,f1,e3)−z-スコア
試験所
z-スコア
d1
f1
e3
A
0.09
−0.28
0.54
B
−0.90
−2.18 W
−1.46
C
0.29
0.80
0.64
D
1.50
−0.14
0.64
E
0.78
0.16
0.39
F
0.48
−0.24
0.15
G
−0.21
0.10
1.27
H
−0.54
−1.38
−0.68
I
1.04
−0.18
0.10
J
0.35
1.12
0.32
K
−0.96
2.54 W
−0.52
L
−0.08
−0.88
0.28
M
0.91
−0.62
0.99
N
−1.33
−0.66
−0.76
O
−0.06
−0.06
−1.24
P
−2.91 W
1.38
−1.98
Q
−0.87
0.00
−0.44
R
−1.34
0.18
−0.66
S
0.25
−0.50
0.41
T
−0.04
−2.06 W
−1.24
U
1.73
1.12
1.00
V
−0.43
−1.24
−0.82
W
−0.17
0.20
0.80
X
0.85
0.80
0.94
Y
−0.31
−0.40
−0.94
Z
1.66
1.72
3.10 A
a
−0.84
0.66
0.23
注記1 濃度データの後の記号 A=処置信号,W= 警戒信号
注記2 本表のz -スコアは,表2中のロバスト平均値を3レベルの付与された値として使用する
ことによって,更に,表2のロバスト標準偏差を技能評価の標準偏差として使用するこ
とによって,表2中のデータから求めている。この例中のz -スコアを求める式は次のと
おりである。
(
)
(
)
*
*
ˆ
s
x
x
X
x
z
−
=
−
=
σ
30
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.5
En数[JIS Q 0043-1のA.2.1.4 e) 参照]
この成績を表す統計量は次の式によって求める。
2
ref
2
lab
U
U
X
x
En
+
−
=
···························································· (20)
ここに,
X: 参照試験所で決定し付与された値
Uref: Xの拡張不確かさ
Ulab: 参加者の結果xの拡張不確かさ
z-スコアに使用する棄却限界値2.0及び3.0とは異なり,En数における棄却限界値は通常1.0を使用する。
これは,標準偏差の代わりに拡張不確かさを分母に用いてEn数を計算するためである。
注記1 参加者が不確かさを十分理解していない場合,参加者の算出方法が均一でない場合には,En
数の使用には注意すべきである。しかし,不確かさに関する情報を,技能試験の結果の解釈
に含めて使用すると,このような難しい問題をより良く理解するために大いに役立つ。
包含係数2.0を用いて拡張不確かさを計算する場合,En数における棄却限界値1.0は,z-スコアにおける
棄却限界値2.0と等価である。
注記2 GUMに従って不確かさを推定する場合,En数は各結果に関連する拡張不確かさ推定の有効
性を表す。|En|<1であれば,不確かさの推定値がGUMによる拡張不確かさの定義に合致して
いることを客観的に示している。
7.6
z′-スコア
7.6.1
一般
7.4の記法によって,z′-スコアは次の式のとおり計算する。
(
)
2
2ˆ
/
X
u
X
x
z'
+
−
=
σ
·························································· (21)
ここに,
uX: 標準の付与された値Xの不確かさ
式(21)は,付与された値が技能試験参加者の報告結果を使用せずに計算された場合に使用できる。すな
わち,付与された値を5.2,5.3及び5.4による方法によって得た場合並びに5.5による方法を使用した場
合,及び熟練試験所が技能試験に参加していない場合にも用いてよい。5.6による方法を使用した場合は,
付与された値は参加者が報告した結果を含んでいるため,式(21)に定義するz′-スコアの使用は有効でない。
7.6.2
z′-スコアの解釈
z′-スコアは,z-スコア(7.4参照)と同一の方法によって,更に,同一の棄却限界値2.0及び3.0を用い
て解釈する。
注記 試験所のかたより及びパーセンテージ差分の解釈に関する7.1及び7.2による基準は同様に,σˆ
を
2
2ˆ
X
u
+
σ
に置き換えることによって適用できる。
7.6.3
z′-スコアの使用
7.4によるz-スコアと7.6によるz′-スコアの式とを比較すると,あるラウンドの技能試験スキームのz′-
スコアがすべて,対応するz -スコアより次に示す一定の係数だけ小さい。
2
2ˆ
/ˆ
X
u
+
σ
σ
4.2による付与された値の不確かさの限界に関するガイドラインが満たされる限りにおいては,この係数
31
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は次の式の範囲に収まる。
0.96
≦
≦
2
2ˆ
/ˆ
X
u
+
σ
σ
1.00 ··············································· (22)
したがって,このような場合は,z′-スコアはほぼz-スコアと等しく,付与された値の不確かさは無視し
てもよい。
4.2のガイドラインが満たされない場合は,z′-スコアとz-スコアとの差が広がることによって,一部の
z-スコアが棄却限界値2.0又は3.0を超え,したがって,“処置信号”又は“警戒信号”を発生する程度と
なっても,対応するz′-スコアは上記の棄却限界値を超えず,信号を発生しないこともある。
z-スコア又はz′-スコアのいずれを使用するかを決めるためには,技能試験の実施者は次の点を考慮しな
ければならない。
a) 付与された値の不確かさが4.2のガイドラインを満たすかどうか。満たす場合は,z′-スコアを用いて
も効用はないであろう。
b) このガイドラインが満たされない場合は,技能試験の参加者にこれを説明するという複雑さと難しさ
とが伴うが,z′-スコアを使用することが望ましい。
c) 技能試験の結果によって“警戒信号”又は“処置信号”を発生した場合,試験所が受ける影響の重大
性はどれほどか。その技能試験の結果によって,一部のユーザグループの試験所がその測定方法を使
う資格を奪われることにならないか。
7.7
ζ-スコア
7.7.1
一般
7.4に示したように,ζ-スコアを次の式によって求める。
2
2
/)
(
X
xu
u
X
x
+
−
=
ζ
······························································ (23)
ここに,
ux: 試験所による結果xの標準不確かさの推定値
uX: 付与された値Xの標準不確かさ
式(23)は,付与された値を参加者の報告した結果を用いて計算していない場合に使用することができる。
すなわち,付与された値が5.2,5.3及び5.4による方法によって得られた場合並びに5.5による方法を使
用した場合,及び5.5による熟練試験所が技能試験に参加していない場合に使用することができる。5.6に
よる方法を使用した場合は,付与された値は参加者が報告した結果を含んでいるため,式(23)に定義するζ-
スコアの使用は有効でない。
注記1 ζ-スコアは,拡張不確かさU(x)ではなく標準不確かさu(x)を使用するところが,En数とは異な
る。
注記2 現状(2005年)ではまだ,技能試験スキームに参加試験所の測定の不確かさに関する情報を
各種スコアに組み込むのは一般的でない。しかし,不確かさの情報はより広く報告されるよ
うになるであろう。7.7では情報が提供されるようになったとき,その情報を技能試験結果に
どう組み込むかのガイダンスを技能試験実施者に提供する。測定の不確かさに関する情報は
現在JIS Q 17025が要求しているため,国際標準への適合を要求する試験所に関連する技能
試験スキームの場合,技能試験実施者は不確かさ情報の取扱方法に関するガイダンスを必要
としている。
7.7.2
ζ-スコアの解釈
試験所の結果の標準不確かさの推定値を確認するためのシステムが有効に機能している場合は,ζ-スコ
32
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
アをz-スコアの代わりに使用することができる。その場合,同一の棄却限界値2.0及び3.0を用いてz-スコ
アと同一の方法によって解釈しなければならない(7.4を参照)。
このようなシステムが機能していない場合は,ζ-スコアはz -スコアとともに使用するに留め,次に規定
するように,試験所の成績を改善する補助的な手段としてだけ使用しなければならない。すなわち,試験
所のz-スコアが繰返し棄却限界値3.0を超える場合,試験手順を逐一確認し,その測定手順の不確かさの
バジェット表を求めるための値として使用するのが有効である。不確かさのバジェット表を作成すること
によって,その手順のなかで最も大きな不確かさが発生している手順中のステップを特定することができ,
試験所は改善のためにどこに作業を集中すべきかを判定できる。 ζ-スコアもまた繰返し棄却限界値3.0を
超えている場合には,その試験所が作成した不確かさのバジェット表が不確かさの重要な原因をすべて網
羅していないことを意味する(すなわち,試験所が重要な要因を見逃している。)。
試験所が大きなかたよりをもち,その不確かさの間隔X ± Uxの間に付与された値が入らない場合にも,
ζ-スコア又はEn数が大きくなる。
7.8
Ezスコア
Ezスコアは,次の式によって定義できる。
(
)
x
X
z
U
U
X
x
E
−
−
=
−
及び
(
)
x
X
z
U
U
X
x
E
+
−
=
+
ここで,Xは,7.4又は7.6によって求める付与された値である。参照値は7.5を用いて求める。UXはX
の拡張不確かさである。
xは試験所の値であり,Uxはxの拡張不確かさである。Uxは7.4及び7.6の2σˆ又は3σˆ,並びに7.5の
Ulabのいずれかをとることができる。
通常,Ezの値を棄却限界値1.0と比較する。
a) Ez−とEz+の双方が‒1.0〜1.0の範囲に入る場合,試験所の成績は満足である。
b) Ez−とEz+の一方が‒1.0〜1.0の範囲外にある場合には,試験所の成績はどちらともいえない。
c) Ez−とEz+の双方が‒1.0より小さい場合,又は双方が1.0より大きい場合,試験所の成績は不満足であ
る。
7.9
不確かさが報告されたときのデータ解析例
7.9.1
一般
図6及び図7に示すグラフは,試験所の結果及びその不確かさを要約したものである。最大のかたより
を示す試験所は,同時に最大のz-スコアの絶対値を示している(このような試験所は,グラフのいずれか
の端に現れる。)。
表8に示すのは,181の試験所が水中の鉛分析に関する不確かさを報告した試験から得られた実際のデ
ータである。このデータの単位はmol/Lであるが,値には1010を乗じて扱いやすくしている。表8は,測
定結果が同じ不確かさ又は同じかたよりをもっていないことを示す。それぞれの結果は,方法のかたより
と試験所のかたよりとの和からなるかたよりDiをもつ。また,そこで使われた各方法が,再現標準偏差
R
σ
をもっていることは自明である。試験所は各種の方法を用いて定量を行い,不確かさを計算した。ここで
の不確かさは拡張不確かさとして扱われている。表8のデータを,昇順に並べ替え,その順に番号付けし
てはいるが,報告されたままのものである。U =0は不確かさが報告されなかったことを示している。表中
33
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の幾つかの値は有効性に疑問があり,更に調査の必要があるもの,グラフには示すことができない極端な
結果もある。特に,負の値はグラフに示していないが,統計指標の計算には使われている。負の鉛含有量
など論理的にはありえないが,このようなデータは4.6によるように結果を報告することが要求される例
である。
7.9.2
付与された値とその不確かさ
付与された値は,附属書CのアルゴリズムAを用いて,5.6に示したロバストな平均値として計算した。
付与された値は,次の式で求められる。
X = x* = 605 × 10−10 mol/L ··························································· (24)
ロバストな標準偏差を,次の式で求める。
s* = 142 × 10−10 mol/L ································································ (25)
付与された値の標準不確かさは,5.6によって,次のようになる。
uX = 1.23 × s * /181= 13 × 10−10 mol/L ··········································· (26)
7.9.3
技能評価のための標準偏差
技能評価のための標準偏差は,6.6のように,ロバストな標準偏差として求められる。
σˆ= s* = 142 × 10−10 mol/L ·························································· (27)
7.9.4
付与された値の不確かさを解釈するためのガイドライン
付与された値の不確かさは,4.2のガイドラインによると,次の場合には無視できる。
uX ≦ 0.3σˆ ············································································· (28)
この例中のuX = 1.25×s */p 及びσˆ= s*を使うと,p > 16の場合の計算結果は式(28)が満たされる。p =
181の参加試験所数の場合は,この基準は容易に満足される。したがって,これらのデータについては7.6
によるz′-スコアを考慮する必要性は存在しない。
7.9.5
正規確率プロットを使用した多数の試験所のデータ解析
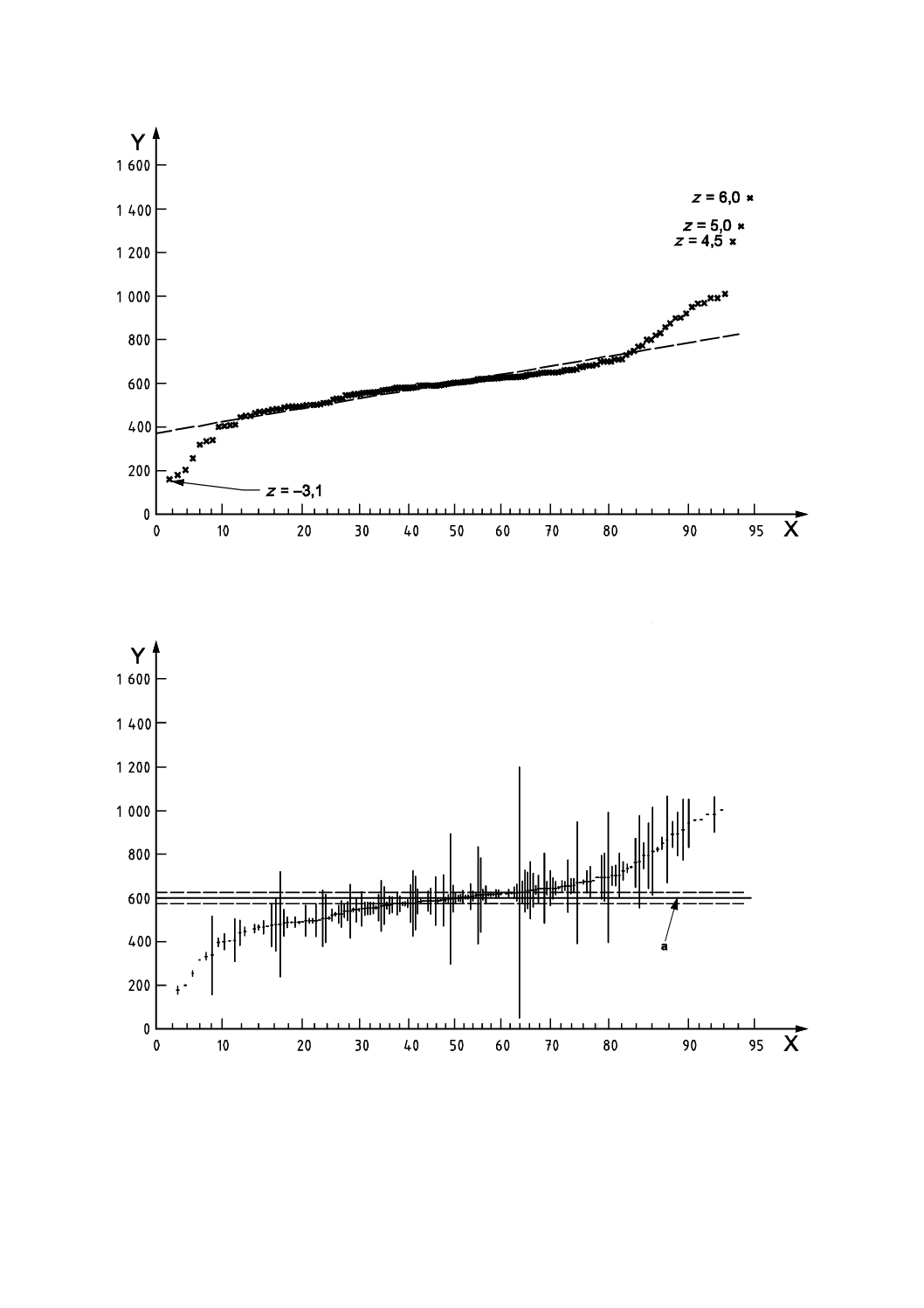
図6に示す結果は181の試験所をパーセンテージ順位によってプロットしたものであり(7.3の計算),
パーセンテージ順位に関して正規確率スケールを付している。0 mol/Lより小さいもの,1 600×10−10 mol/L
を超える結果は図6に示していない。
z-スコアは,z = (x−605)/142として計算できる。試験所のz-スコアが3.0より大きい場合,又は−3.0より
小さい場合は,z-スコアの値を図6の対応する値の脇に示した。
平均値605×10−10 mol/L,標準偏差142×10−10 mol/Lの正規分布の累積分布関数を破線の直線で図6に示
す。
ロバストなアルゴリズムに使用される最終しきい値は,式(29)及び式(30)のとおりである。
x* − 1.5 s* = 605 − 1.5 × 142 = 392 × 10−10 mol/L ······························· (29)
x* + 1.5 s* = 605 + 1.5 × 142 = 818 × 10−10 mol/L ······························· (30)
図6では,幾つかの点は破線から向きを変えて離れ上記の範囲外に位置する。この意味するところは,
34
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
すべての測定結果が同一の正規母集団から抽出されたのではない,ということである。破線から離れてい
る点は,破線に近い点より大きな分散をもつ母集団から抽出している。
z-スコアが3.0より大きく,−3.0より小さい結果も破線から離れていることも図6から分かる。これは,
これらのz-スコアが“処置をとるべき”信号を発生させているということの証拠である(z -スコアが3.0
より大きく,−3.0より小さい測定結果が多数得られるが,ただし,図6のようにプロットした場合,すべ
ての点の分布が破線に近くなる,という可能性もある。この場合,この図はz-スコアが処置信号を発生す
るものとして扱うべきという結論の証拠とすることにはならない。)。
図7に示すのは,z -スコアが±3.0の範囲に入る試験所だけの結果であり,縦線は報告された不確かさ
を示す(不確かさが非常に大きい二つの試験所,24及び112の結果は図7に示されない。)。図7中の横線
(実線)は付与された値を表し,その上下にある破線は付与された値の拡張不確かさを示す。
試験所が実施したこの結果の拡張不確かさの計算が正しい場合は,図7の中でほぼすべての縦線が付与
された値±その(片側の)拡張不確かさによって定義した領域にかかるはずである。ただし,図7には多
数の試験所が付与された値の両側に位置し,その縦線はこの領域に達していないケースもある。このこと
は,多数の試験所が正しい不確かさの計算を実施していないことを意味する。すなわち,不確かさの重要
な原因のすべてを計算に取り込んでいない可能性が非常に高い。

35
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表8−181試験所による水中鉛含有量の定量値(mol/L×1010)及び試験所が報告した結果の拡張不確かさ(U)
試験所
結果
U
試験所
結果
U
試験所
結果
U
試験所
結果
U
1
−960 000
0
47
530
9
93
603
13
139
680
8
2
−12 100
0
48
530
40
94
604
18
140
680
50
3
−4 800
0
49
530
60
95
608
30
141
680
70
4
−3 860
0
50
545
30
96
608
8
142
685
0
5
−1 500
0
51
545
43
97
609
9
143
700
0
6
−1 010
0
52
545
123
98
610
61
144
700
100
7
−1 000
0
53
550
8
99
613
22
145
700
110
8
−1 000
0
54
550
55
100
618
7
146
700
300
9
−965
0
55
550
5
101
618
224
147
708
44
10
−483
0
56
555
79
102
618
170
148
709
48
11
160
20
57
556
30
103
620
25
149
710
100
12
180
20
58
557
28
104
620
40
150
729
41
13
203
0
59
557
28
105
621
6
151
740
20
14
256
13
60
559
26
106
622
9
152
748
3
15
319
0
61
560
7
107
622
6
153
767
113
16
335
18
62
560
60
108
623
18
154
772
213
17
340
180
63
569
116
109
625
15
155
800
60
18
400
20
64
570
86
110
626
5
156
800
150
19
404
36
65
571
16
111
627
0
157
821
203
20
407
0
66
572
40
112
627
1 010
158
830
10
21
410
97
67
574
35
113
627
15
159
857
27
22
444
58
68
578
0
114
628
3
160
874
200
23
450
20
69
579
52
115
629
26
161
898
59
24
450
3 400 000
70
579
35
116
630
40
162
900
100
25
463
19
71
579
8
117
630
580
163
920
140
26
470
10
72
579
10
118
632
50
164
950
110
27
470
30
73
579
17
119
637
96
165
965
0
28
474
0
74
579
87
120
639
83
166
968
0
29
480
100
75
580
150
121
640
130
167
990
0
30
482
122
76
582
122
122
640
77
168
990
80
31
483
241
77
589
57
123
642
20
169
1 010
0
32
490
60
78
589
10
124
647
63
170
1 250
140
33
492
25
79
590
0
125
647
0
171
1 320
410
34
492
1
80
590
0
126
650
160
172
1 450
460
35
493
24
81
590
45
127
650
30
173
1 640
241
36
493
5
82
590
60
128
650
80
174
1 900
46
37
495
0
83
590
0
129
650
48
175
2 413
20
38
500
70
84
591
112
130
650
30
176
2 460
0
39
500
10
85
591
9
131
653
5
177
2 900
900
40
500
10
86
594
4
132
658
27
178
10 000
0
41
501
75
87
594
119
133
660
20
179
386 000
31 000
42
504
0
88
597
9
134
660
120
180
670 000
60 000
43
510
130
89
600
20
135
660
34
181
630×106 60×106
44
510
110
90
600
300
136
663
32
45
512
6
91
603
60
137
675
280
46
526
26
92
603
24
138
675
0
36
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X軸: 試験所パーセンテージ順位,%
Y軸: 鉛含有量,mol/L×1010
注記 19試験所の結果は含まれない。
図6−162試験所による水中鉛含有量の定量結果の正規確率プロット
X軸:試験所-パーセンテージ順位,%
Y軸:鉛含有量,mol/L×1010
a :付与された値±その拡張不確かさ
注記 25試験所の結果は,含まれていない。
図7−156試験所による水中鉛含有量の確定に対する拡張不確かさの正規確率プロット
37
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.10 成績スコアの複合表示方法
技能試験スキームの単一ラウンド内では,複数の試験項目又は複数の測定対象に対して結果が得られる
というのが一般的である。この場合は,各試験項目及び各測定対象に対する結果は,7.2〜7.9に従って解
釈する。すなわち各試験項目と各測定対象に対する結果とは別々に解析される。技能試験の中には,二つ
以上の物質を特に設計された複数の水準で試験を行うスキームがあり,その中で併行精度,線形性などの
技能をみる場合もある。このような場合,技能試験の実施者はそこで使われる統計手法の計画及び手順を
参加者に十分説明しなければならない。二つの類似な物質をスキームに組み込み,Youden図として表示す
ることを目的とする場合は,特に8.5による方法を適用する。
さらに,複数の試験項目又は複数の測定対象の結果が得られる場合は,箇条8によるグラフ表示の方法
を併用することが望ましい。そこでは,スコアを組み合わせることによって,高い値をもつ個々のスコア
が隠ぺい(蔽)されないように,更に,個々のスコアの表には現れない測定対象が異なる結果間の相関な
ど,試験所の成績に関する追加情報を明示してもよい。
多数の測定対象が試験されるスキームの場合は,処置信号及び警戒信号の数によって,これらの信号を
一つ又は複数もった試験所が特定できるようにしてもよい。それらの試験所には,7.2〜7.9による方法を
使った詳細な結果の報告を示すのもよい。 いずれの信号も表示されない試験所には簡単な報告だけでよい。
注記 同一の測定対象に複数の試験項目がある場合に複合スコアを使用すること(z-スコアの平均値,
合計,値又は差分の絶対値,二乗差分の平均値若しくは合計値),又は複数の測定対象に対する
結果がある場合に複合スコアを使用すること(z-スコアの絶対値の平均値,又は評価限界値に
対する差分の絶対値の平均値)は望ましくない。なぜなら,平均(又は合計)z -スコアには,
他のスコアが低い場合,又は他のスコアも高いが符号が逆の場合に,1試験項目の高いスコア
が隠されることがあるという重大な欠陥があるからである。差分の絶対値の平均値(又は合計
値)及び二乗差分の和は,他のスコアが低いとき,1試験項目の高いスコアが隠される場合が
あるという重大な欠陥がある。z-スコアの絶対値の平均値及び,評価限界値に対する差分の絶
対値の平均値も,同様の欠陥をもつ。
8
単一技能試験ラウンドから得た複数の測定対象に対する成績スコアを組み合わせる図式表現の方法
(JIS Q 0043-1のA.2.2.1参照)
8.1
用途
コーディネータは,技能試験スキームの各ラウンドから得た成績スコアを用いて,8.2及び8.3によるグ
ラフを作成する。z-スコアを使用するとグラフの軸を標準化できるので,表現及び解釈を容易にできると
いう利点がある。グラフは参加者が利用でき,各参加者に自身の結果が他の参加者の得た結果とどのよう
な関係にあるのかが分かるようにする。そのために,文字符号又は数字符号を用いて参加者を表示し,各
参加者は自身の結果を識別することができるが,他の結果をどの参加者が得たのかは分からないようにす
べきである。さらに,グラフはコーディネータからも使用でき,スキームの総合的な有効性を判定できる
ようにするとともに,技能の審査に用いられる基準を見直す必要があるときにも,見ることができるよう
にする。
8.2
成績スコアのヒストグラム
8.2.1
一般
z-スコアのヒストグラムを作成するため,ある特性の測定に関するz-スコアを,1ラウンドの技能試験ス
キームから収集し,図8に示すヒストグラムに表す。ヒストグラムの間隔を0.3〜0.5くらいにすると,ヒ
38
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ストグラムが見やすい。±2.0及び±3.0の位置に線を引き,技能の評価基準を示す。ヒストグラムの範囲
は約±6.0とする。結果がこの範囲に収まらない場合,又は中央付近に測定点が密に集まっている場合には,
(分析者は)別の範囲を用いてもよい。
試験所のかたより,又は差の百分率のヒストグラムが好ましい場合,同等なヒストグラム間隔,警戒限
界,及び処置限界を次に示す。この場合,技能を評価する際の処置限界は,標準偏差から計算する代わり
に,定められた要求値,又は一般に認められている要求値から直接求めた方が簡単である。
表9−成績スコアの警戒限界と処置限界
性能統計
ヒストグラム間隔
警戒限界
処置限界
ヒストグラムの範囲
試験所のかたより
0.3σˆ 〜 0.5σˆ
± 2.0σˆ
± 3.0σˆ
± 6.0σˆ
差の百分率
30σˆ / X 〜 50σˆ / X
± 200σˆ / X
± 300σˆ / X
± 600σˆ / X
zスコア
0.3 〜 0.5
± 2.0
± 3.0
± 6.0
ヒストグラムは,測定される特性量の数が少ない場合,又は多数の異なる特性量を測定する場合に適し
たグラフ表示の方法である。個々の参加者は,(ヒストグラム上での)自身の採点の位置を確認することが
できるので,自身の成績を評価することによって,自身の方法を検討する必要性があるかどうかを知るこ
とができる。高いz-スコアを示した参加者はヒストグラムを使用し,他の参加者が得たスコアと比較して
自身のスコアがどの程度正常値から外れているのかを知ることができる。
コーディネータはヒストグラムから参加者が技能の評価基準を達成できない頻度を知ることができる。
ヒストグラムの端が±3.0の限界の外側に伸びた場合,その誤りの原因は個々の参加者にあるのではなく,
むしろ使われた測定方法にあると考えられる。(その場合)この測定方法を改善するか,又はその技能の評
価基準を緩和することが望ましい(σˆを増加させる)。(逆に)ヒストグラムがおおむね±2.0の限界内に
収まり,この限界の外にあるz-スコアが一つ又は二つの場合には,技能の評価基準をより厳しくしてもよ
い (σˆを減少させる)。
8.2.2
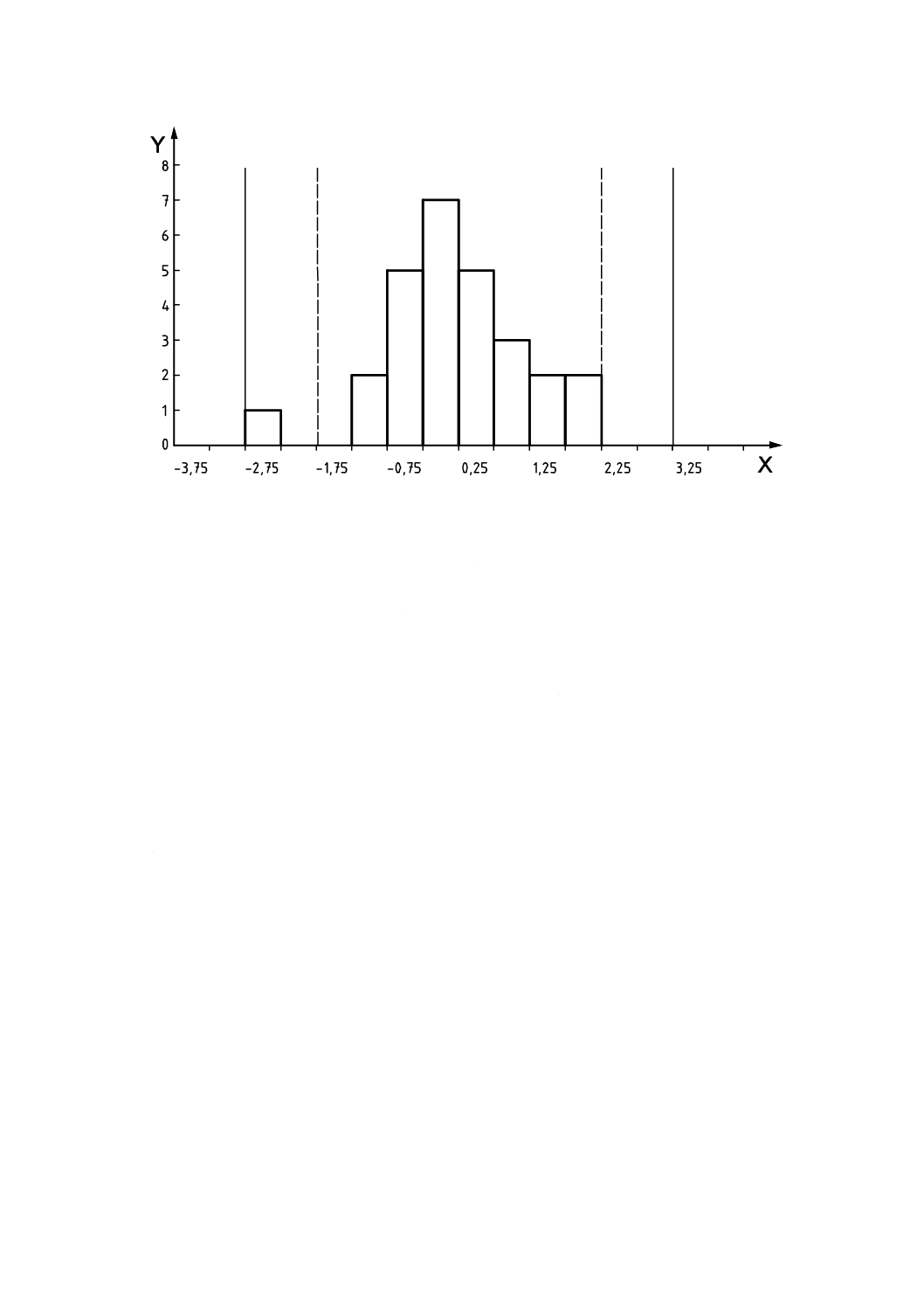
例 抗体濃度
d1のz-スコアを図8にヒストグラム形式によって示す。
39
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X: アレルゲンd1のz-スコア
Y: 試験所数
図8−1ラウンドの技能試験に基づくz-スコアのヒストグラム
(アレルゲンd1のデータは表7から)
8.3
標準化された試験所のかたよりの棒グラフ
8.3.1
一般
棒グラフを作成するには,収集したz-スコアを図9に示す棒グラフの様式にプロットする。この図では,
各参加者のz-スコアを一つにグループ化している(z-スコアは,JIS Z 8402-2においてh統計量と呼ばれて
いるものと同じ統計量であり,ここに示す棒グラフは,JIS Z 8402-2に規定するh統計量のプロットと同
一のグラフである。)。
棒グラフは,多数の類似した特性量のz-スコアを一つのグラフに表示するのに適した方法である。これ
によって,ある参加者のz-スコアに何らかの共通した特性があるかどうか,例えば,ある参加者が高いz-
スコア(一般的には成績が悪いことを示す)を幾つか示しているというようなことを明らかにできる。
8.3.2
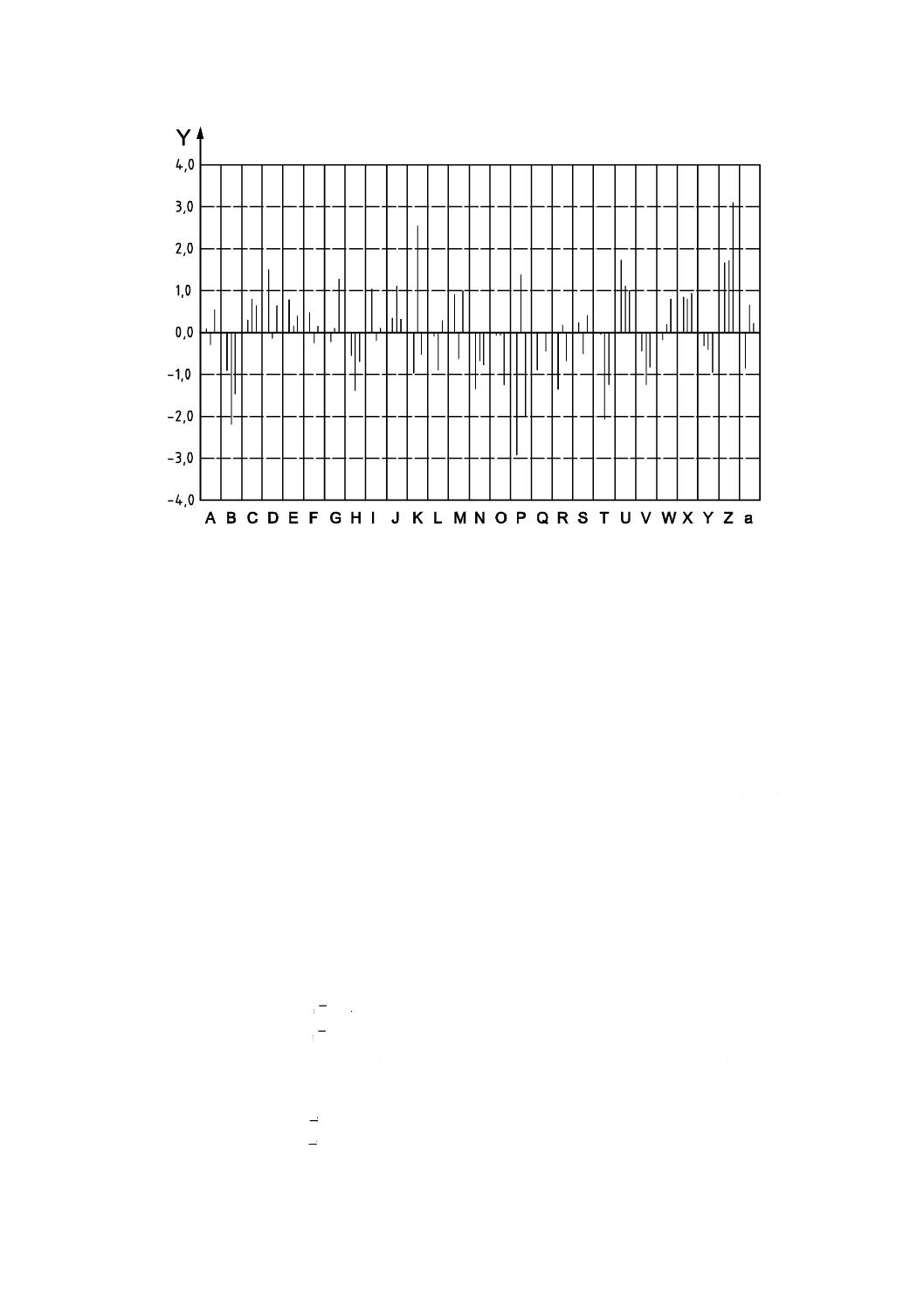
例 抗体濃度
表7のz-スコアを,図9の棒グラフとしてプロットする。このグラフから,試験所B及びZは,三つの
レベルにほぼ同一量の影響を与えるかたよりの原因を調査すべきであることが分かる。一方,試験所K及
びPは,z-スコアの符号が抗体種別に依存していることが分かる。
40
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Y軸: z-スコア
注記 A〜aは試験所番号を示す。
図9−参加者が3種のアレルゲン特異IgE抗体の濃度を定量する1ラウンドの技能試験の
z-スコア (4.0〜−4.0) の棒グラフ−(データは表7から)
8.4
標準化された併行性の棒グラフ
1ラウンドの技能試験において反復測定が行われた場合,その結果を用いて,JIS Z 8402-2に規定してい
るk統計量のグラフを計算できる。
8.5
Youdenプロット
8.5.1
一般
1ラウンドの技能(試験)スキーム中で,類似した物質からなる二つの試料を試験する場合,結果を検
討するための多くの情報をもたらす図式表現の手法として,Youdenプロットを用いてもよい。このグラフ
は,一つの物質から得られたz-スコアを,他の物質から得られたz-スコアに対してプロットすることによ
って作成される。このプロットの解釈を補助するためには,8.5.2に従って計算した信頼域だ円を使用する。
元の測定値,試験所のかたより,又はかたよりの百分率のYoudenプロットは,z-スコアを用いて次の手順
によって得ることができる。
信頼域だ円を,測定値本来の単位で表示されたグラフ上にプロットする場合には,次の式を用いて上記
の一連の点を元の単位に変換する。
B
B
,.
B
B
A
A
,.
A
A
z
s
x
x
z
s
x
x
×
+
=
×
+
=
試験所のかたよりDA及びDBを示す軸をもつグラフ上に信頼域だ円をプロットする場合には,次の式
を用いて一連の点を変換する。
B
B
B
A
A
A
z
s
D
z
s
D
×
=
×
=
かたよりの百分率DA%及びDB%を示す軸をもつグラフ上に信頼域だ円をプロットする場合には,次の式
41
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を用いて一連の点を変換する。
B
B
B
B%
A
A
A
A%
/
100
/
100
x
z
s
D
x
z
s
D
×
=
×
=
結合z-スコアは,Youdenプロットをよりよく解釈するために用いることができる。結合z-スコアの最大
値は信頼域だ円の計算における有意水準の最大値100α %に対応するため,この結合z-スコアを用いて,
Youdenプロット上の最も外側にある点を特定することができる。場合によっては,ひとつ又はそれ以上の
外れ値の点を除外して信頼域だ円を計算し直さなければならない。このとき,結合z-スコアを,除外する
点を特定するための目安として用いることができる。
作成したYoudenプロットから,次のような解釈をする。
a) 他のデータからかけ離れた位置にプロットされた点に注目する。ある試験所が正しい方法で試験を行
わなかったため,その結果にかたよりが生じている場合には,その点はだ円長軸に沿って大きく外れ
ることになる。このような点は,ある試験所が,測定結果のレベルにおいて時間経過とともに大きな
変動をもった場合にも見られる。長軸から離れた点は,ある参加者の併行精度が悪いことを表す。
b) プロットを検査し,二つの試料の測定結果の間に関係があることを示す証拠があるか調べる。それが
認められた場合,多くの試験所に共通する試験所間変動の原因があることを示しており,測定方法を
適切に指定していなかった証拠となる。次に,試験方法を検討することによって,一般的には,この
方法の再現性は改善される。8.5.3による順位相関検定を用いて,二つの試料間の関係が統計的に有意
かどうか検査することができる。相関係数はデータ中の異常値に対して敏感であるため,ここでは順
位相関係数を用いることがより望ましい。
8.5.2
信頼域だ円(ジャクソンの方法[2]に基づく)
8.5.2.1
一般
二つの試料A及びBについて考える。Aから得られた結果を
xA,1, xA,2, ..., xA,p
Bから得られた結果を
xB,1,xB,2, ..., xB,p
と表す。ここでpは試験所の数である。
2組のデータの平均値と標準偏差
B
A
B,.
A,.
s
s
x
x
及び相関係数ρˆを計算する。二つの試料のz-スコアを次のように計算する。
A
,.
A
,
A
,
A
/)
(
s
x
x
z
i
i
−
=
································································ (31)
ここに, i = 1, 2, ...,p
B
,.
B
,
B
,
B
/)
(
s
x
x
z
i
i
−
=
································································· (32)
ここに, i = 1, 2, ..., p
さらに,二つの試料の結合スコアを計算する。
2
,B
,B
,
A
2
,
A
B,
A,
ˆ
2
i
i
i
i
i
z
z
z
z
z
+
−
=
ρ
····················································· (33)
標準化された変数を次のように定義する。
42
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A
,.
A
A
A
/)
(
s
x
x
z
−
=
··································································· (34)
B
,.
B
B
B
/)
(
s
x
x
z
−
=
··································································· (35)
標準化された変数について,信頼域だ円はホテリングのT 2を用いて次の式のように表す。
2
2
2B
B
A
2A
)
ˆ
1(
ˆ
2
T
z
z
z
z
ρ
ρ
−
=
+
−
····················································· (36)
ここに
{
}
)1
,2(
)2
/(
)1
(
2
)
1(
2
−
−
−
=
−
p
F
p
p
T
α
··············································· (37)
ここに,F(1−α)(2,p−1)は,自由度が2及び(p−1)であるF-分布表の(1−α)分位点である。−T≦zA≦T とな
る一連の点を式(38)に対してプロットすることによって,z-スコアzA及びzBを座標軸とするグラフ上に信
頼域だ円を描くことができる。
)
)(
ˆ
1(
ˆ
2A
2
2
A
B
z
T
z
z
−
−
±
=
ρ
ρ
····················································· (38)
注記
信頼域だ円を計算するロバストな方法を定める必要があるが,その方法は詳細には今のとこ
ろ確立していないため,未解決である。(zA,B,i)2/(1−ρˆ2)が自由度2のカイ二乗分布に近似的
に従うことを用いると,外れ値の除外に注意してカットオフ値条件を計算することができる
が,修正補正係数をシミュレーションによって求めなければならない場合がある。
8.5.2.2
例 抗体濃度
表10は,抗体濃度が類似した二つの試料を試験することによって得られたデータ及び信頼域だ円を求め
るために必要な計算を示す。p=29試験所及び有意水準100α % = 5 %を使用すると,F(1−α)(2,p−1) = 3.34
が得る。したがって,T=2.632となり,標準化変数に関しては,95 %信頼域だ円は次の式のように表す
ことができる。
2
Az−1.412zAzB+
2
Bz=3.48 ····························································· (39)
図10に,z-スコアを表すポイント及び確率水準100α % =5 %,1 %及び0.1 %のだ円を示す。結合ス
コアを表10に示す。
図10では,二つの試験所(番号5及び23)が右上の象限に存在することが分かる。この二つの結合z-
スコアは1.641及び2.099である。試験所26は物質Bに高いz-スコアをとり,結合z-スコアは2.059であ
る。試験所5,23及び26に続いて,次に高い結合z-スコアをもつ試験所は8である(結合スコアは1.501)。
試験所23及び26の点は,確率水準5 %と1 %のだ円の間にあるため,その結果を,警戒信号が発生す
るものとして扱い,次のラウンドのスキームでの結果がどこに位置するか確認するのがよい。

43
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表10−二つの類似アレルゲンの抗体濃度に関するデータと計算
試験所
データ
z-スコア
結合スコア
アレルゲン
アレルゲン
アレルゲン
アレルゲン
A
B
A
B
i
xA, i
xB,i
zA,i
zB,i
zA,B,i
1
12.95
9.15
0.427
0.515
0.370
2
6.47
6.42
−1.540
−0.428
1.275
3
11.40
6.60
−0.043
−0.366
0.336
4
8.32
4.93
−0.978
−0.942
0.737
5
18.88
13.52
2.228
2.023
1.641
6
15.14
8.22
1.092
0.194
0.965
7
10.12
7.26
−0.432
−0.138
0.349
8
17.94
9.89
1.942
0.770
1.501
9
11.68
4.17
0.042
−1.204
1.234
10
12.44
7.39
0.272
−0.093
0.344
11
6.93
7.78
−1.400
0.042
1.430
12
9.57
5.80
−0.599
−0.642
0.477
13
11.73
5.77
0.057
−0.652
0.693
14
12.29
6.97
0.227
−0.238
0.429
15
10.95
6.23
−0.180
−0.493
0.388
16
10.95
5.90
−0.180
−0.607
0.497
17
11.17
7.74
−0.113
0.028
0.134
18
11.20
8.63
−0.104
0.335
0.415
19
7.64
3.74
−1.185
−1.353
0.986
20
12.17
7.33
0.190
−0.114
0.282
21
10.71
5.70
−0.253
−0.676
0.529
22
7.84
6.07
−1.124
−0.549
0.833
23
20.47
15.66
2.710
2.762
2.099
24
12.60
11.76
0.321
1.415
1.210
25
11.37
4.91
−0.052
−0.949
0.913
26
11.36
13.51
−0.055
2.019
2.059
27
10.75
5.48
−0.241
−0.752
0.607
28
12.21
9.77
0.203
0.729
0.603
29
7.49
5.82
−1.230
−0.635
0.902
平均値
標準偏差
相関係数
11.54
7.66
0.00
0.00
3.29
2.90
1.00
1.00
0.706
0.706
注記1 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リットル(L)
当たりの値として示す。
注記2 本表中のz-スコアは,表の最下部に示すまるめ値を使用するのではなく,平均値と標準偏差のまるめな
いままの値を用いて計算したものである。
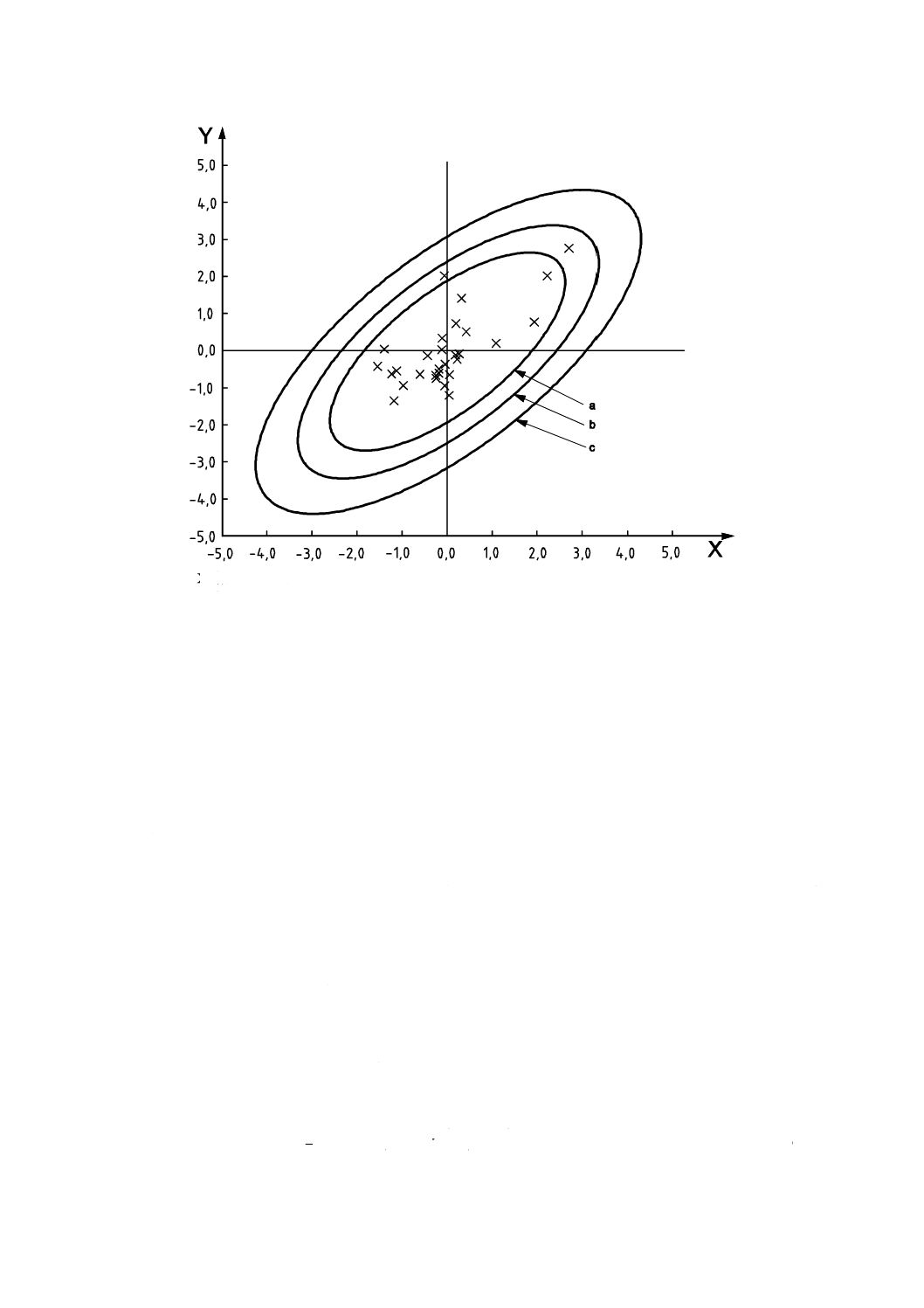
44
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X 軸:アレルゲンAのz-スコア
Y 軸:アレルゲンBのz-スコア
a :5 %水準
b :1 %水準
c :0.1 %水準
図10−表10中のz-スコアのYoudenプロット
8.5.3
順位相関検定
8.5.3.1
一般
順位相関検定は次に規定するようにスピアマンの相関係数を用いて行う。試料Aの観測結果をその順位
に置き換える(すなわち,最小値を1に,次に小さい値を2に,以下同様に置き換え,最大値をpに置き
換える)。試料Bの観測結果についても同様の操作を行う。観測結果の中に同じ値がある場合には,これ
らの観測値群を,観測値群の順位の平均値に置き換える。順位に関する二つの数列の間の相関係数を計算
し,この結果を表11の値と比較する。計算値が表の値より大きい場合,二つの変数の関係を有意とみなす。
順位相関係数は次の簡略化した手法によって計算してもよい。ここで,
p
k
k
k
,
A
2,
A
1,
A
,
,
,
Κ
が,試料Aに関する試験所の順位を表すとする。同様に試料Bに関する順位を
p
k
k
k
,B
2,B
1,B
,
,
,
Κ
とすると,順位相関係数は次の式で計算してもよい。
{
})1
(
/
)
(
6
1
2
2
,B
,
A
−
−
−
=
∑
p
p
k
k
i
i
k
ρ
··············································· (40)
45
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここで,総和記号はpか所の試験所に関する総和を意味する。
表11−順位相関係数の棄却限界値
データ点数
棄却限界値
有意水準5 %
有意水準1 %
8
0.738
0.881
9
0.683
0.833
10
0.648
0.794
11
0.623
0.818
12
0.591
0.780
13
0.566
0.745
14
0.545
0.716
15
0.525
0.689
16
0.507
0.666
17
0.490
0.645
18
0.476
0.625
19
0.462
0.608
20
0.450
0.591
21
0.438
0.576
22
0.428
0.562
23
0.418
0.549
24
0.409
0.537
25
0.400
0.526
26
0.392
0.515
27
0.385
0.505
28
0.377
0.496
29
0.370
0.487
30
0.364
0.478
8.5.3.2
例 抗体濃度
ランク相関係数の計算例を表12に示す。計算したランク相関係数は0.605であり,この値は表11中の
表形式の値である,29個のデータポイントの1 %水準である0.487より大きい。したがって,図10に示
される関係は統計的に有意であると結論できる。
46
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表12−表10のデータに対するランク相関係数の計算
試験所
i
データ
ランク
差分
i,
i,
k
k
B
A−
アレルゲン
A
zA,i
アレルゲン
B
zB,i
アレルゲン
A
kA,i
アレルゲン
B
kB,i
1
12.95
9.15
25
23
2
2
6.47
6.42
1
13
12
3
11.40
6.60
17
14
3
4
8.32
4.93
6
4
2
5
18.88
13.52
28
28
0
6
15.14
8.22
26
21
5
7
10.12
7.26
8
16
8
8
17.94
9.89
27
25
2
9
11.68
4.17
18
2
16
10
12.44
7.39
23
18
5
11
6.93
7.78
2
20
18
12
9.57
5.80
7
8
1
13
11.73
5.77
19
7
12
14
12.29
6.97
22
15
7
15
10.95
6.23
11.5
12
0.5
16
10.95
5.90
11.5
10
1.5
17
11.17
7.74
13
19
6
18
11.20
8.63
14
22
8
19
7.64
3.74
4
1
3
20
12.17
7.33
20
17
3
21
10.71
5.70
9
6
3
22
7.84
6.07
5
11
6
23
20.47
15.66
29
29
0
24
12.60
11.76
24
26
2
25
11.37
4.91
16
3
13
26
11.36
13.51
15
27
12
27
10.75
5.48
10
5
5
28
12.21
9.77
21
24
3
29
7.49
5.82
3
9
6
二乗差分の和
p(p2−1)
計算したランク相関係数
1 % 有意水準に対する表形式の棄却限界値
1 605.50
24 360
0.605
0.487
注記 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,試料1リットル(L)当
たりの値として示す。
8.6
併行精度の標準偏差のプロット
8.6.1
一般
あるラウンドの技能試験スキームにおいて参加者がn個の反復測定を実施した場合,その結果から異常
な平均と標準偏差が発生した試験所を特定するためのプロットを作成することができる。このグラフは,
各試験所の試験所内標準偏差siを,試験所の対応する平均xiに対してプロットすることによって作成され
る。

47
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
X =x* :アルゴリズムAによって計算されるx1,x2,...,xpのロバストな平均
S =s* :アルゴリズムSによって計算されるs1,s2,...,spのロバストなプール値
とし,これらのデータは正規分布に従うと仮定する。試験所の平均値又は試験所内標準偏差のいずれかの
母集団の値について試験所間の差異はないという帰無仮説を立てると,統計値
2
2
ln
)1
(2 −
+
−
S
s
n
S
X
x
n
i
i
は,近似的に自由度2のχ2分布に従う。したがって,有意水準1 %の棄却域は式(41)を縦軸(標準偏差)
にとり,横軸に式(42)の平均値を示したグラフをプロットすることによって図示することができる。
−
−
−
±
=
2
299
.0;2
)1
(2
1
exp
S
X
x
n
n
S
s
χ
································· (41)
まで
から
n
S
X
n
S
X
x
299
.0;2
299
.0;2
χ
χ
+
−
=
····························· (42)
注記 このCircle Techniqueはvan Nuland [6]によって導入された。この方法は標準偏差の分布として単
純な正規近似を用いているため,棄却域が負の標準偏差の領域まで広がる可能性がある。ここ
で示した方法は,この問題を避けるような標準偏差の近似的な分布を用いているが,棄却域は
原典にあるような円形ではなくなっている。また,原典の方法で中心点として用いられていた
単純平均の代わりに,ここではロバストな値を用いている。
8.6.2
例 抗体濃度
表13は,血清試料中のある種の抗体の濃度を定量した結果を示す。各試験所は4種の反復定量を併行精
度の条件のもとで実施した。上記の式を用いて,図11に示すプロットを得た。このプロットは複数の試験
所が処置信号又は警戒信号を受けることを示す。
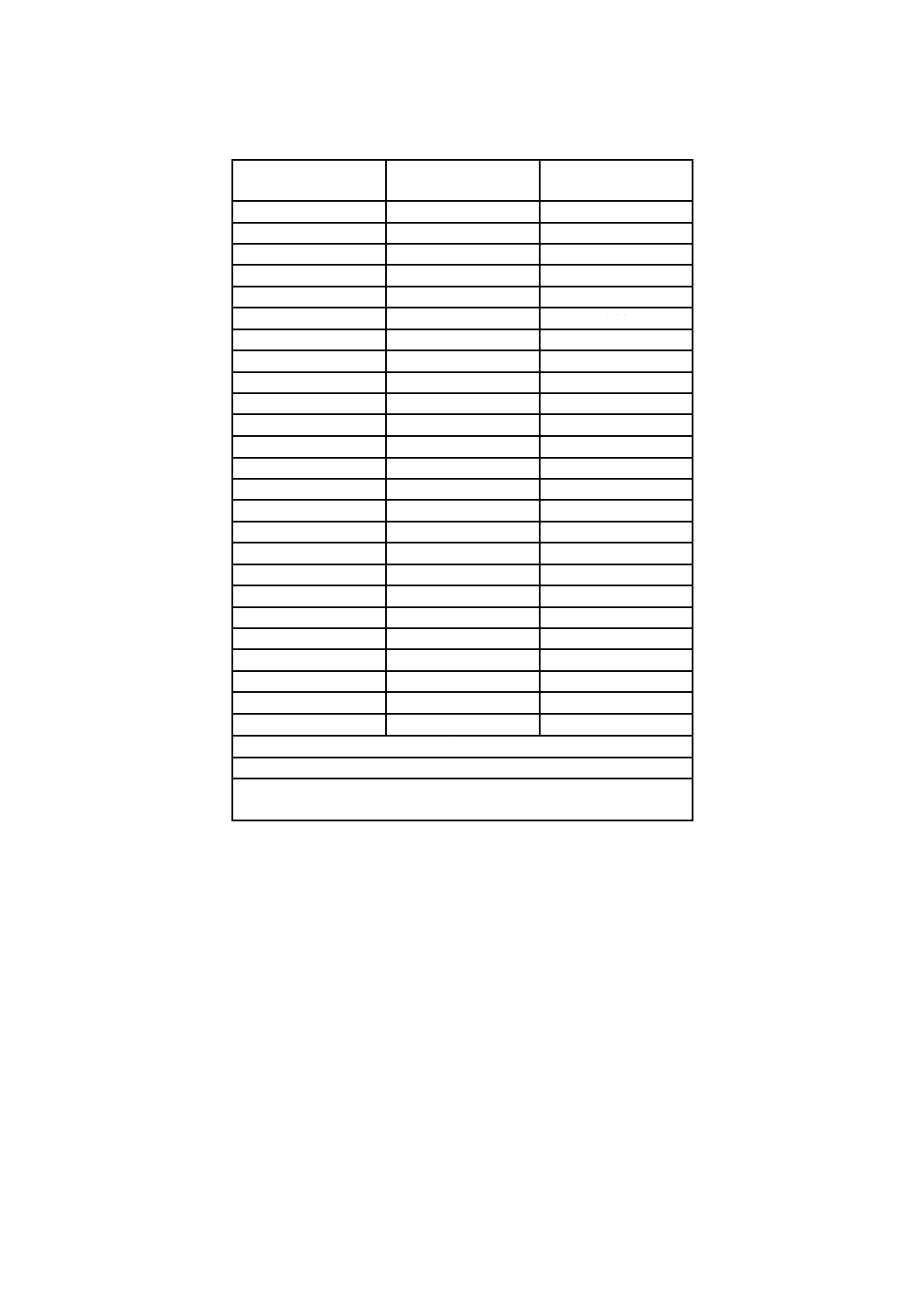
48
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表13−血清試料中のある抗体の濃度(各試験所の1試料に4種の反復定量)
試験所
平均
kU/L
標準偏差
kU/L
1
2.15
0.13
2
1.85
0.21
3
1.80
0.08
4
1.80
0.24
5
1.90
0.36
6
1.90
0.32
7
1.90
0.14
8
2.05
0.26
9
2.35
0.39
10
2.03
0.53
11
2.08
0.25
12
1.25
0.24
13
1.13
0.72
14
1.00
0.26
15
1.08
0.17
16
1.20
0.32
17
1.35
0.4
18
1.23
0.36
19
1.23
0.33
20
0.90
0.43
21
1.48
0.40
22
1.20
0.55
23
1.73
0.39
24
1.43
0.30
25
1.28
0.22
ロバスト平均値
1.57
ロバスト標準偏差
0.34
注記 データは,国際標準物質の濃度によって定義される単位(U)を
1 000倍の(kU)とし,試料1リットル(L)当たりの値として示す。
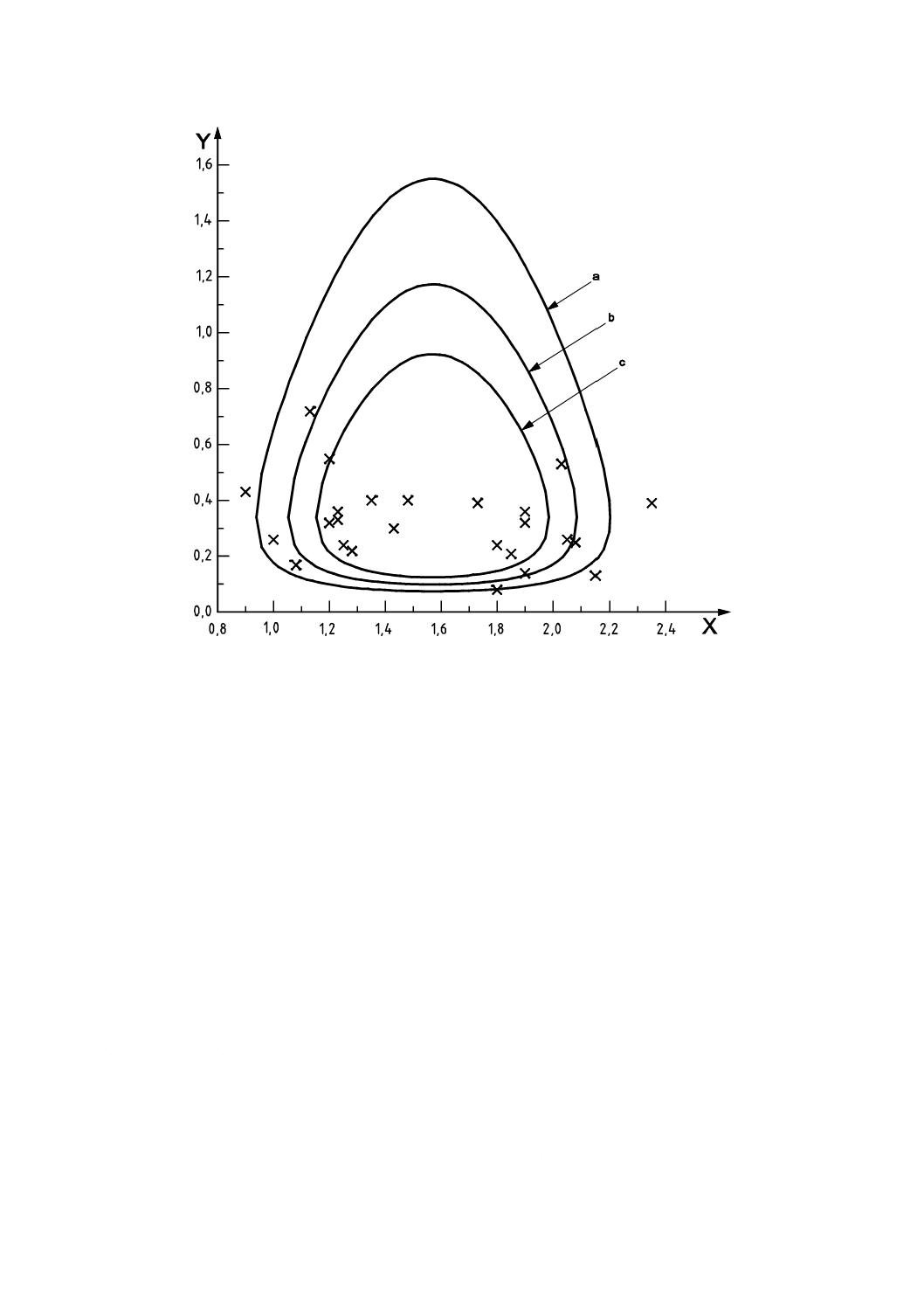
49
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X軸: 平均値
Y軸: 標準偏差
注記 データは,国際標準物質の濃度によって定義される単位(U)を1 000倍の(kU)とし,
試料1リットル(L)当たりの値として示す。
a
: 0.1 %水準
b
: 1 %水準
c
: 5 %水準
図11−25の試験所の平均値に対する標準偏差のプロット
(データは表13から)
8.7
分割試料(JIS Q 0043-1,A.3.1.2を参照)
8.7.1
一般
分割試料は,二つの試験所の詳細な比較を行う必要がある場合に用いる手法である。例えば,ある納入
業者が試験所を運営する一方,ある顧客が別の試験所を運営しているようなときに,この二つの組織がこ
の二つの試験所の測定が一致することを望んでいる場合である。複数の試料が得られ,それらが様々な興
味深い特性を示すとき,各試料をそれぞれ二つの部分に分け,各試験所に反復定量を行うのに必要な数量
(少なくとも二つ)を分与する。
二つ以上の試験所が関与することもあるが,その場合には,一つの試験所を参照試験所として扱い,そ
れ以外は次に規定する手法を用いてこの参照試験所と比較する。
分割試料実験から得られたデータを用いて,二つの試験所の反復測定間の偏差,及び各試料に関する各試
験所の測定結果の平均値の差を示すグラフを作成する。それ以降の解析は,これらのグラフからどのよう
50
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
な推論を行うかによる。
8.7.2
例 抗体濃度
21個の血清試料中のある抗体の濃度は,二つの試験所X及びYでラジオイムノアッセイ(放射免疫測
定法)によって測定された。各試験所では,全測定を同一分析ラン内で二重測定によって実施した。得ら
れた濃度(単位:U/L)を表14に示す。測定範囲が広く,相対差分が適切であるため,計算を行う前に,
自然対数をとることによってデータを変換する。変換したデータを表15に示す。表15の統計を示すグラ
フを図12,図13及び図14に示す。
反復定量の範囲のグラフから,試験所Xの反復の値間の偏差は試験所Yの値より大きいようにみえる。
各統計のプール値は表15に示し,必要な場合,F-検定を用いて比較してもよい。第3のグラフを見ると,
各ポイントに顕著なパターン又は傾向は見あたらない。ただし,図12及び図13中の反復定量の範囲はほ
とんどすべて0.2より小さく,図14の試験所間の差異の多数はこれより大きい。これは,試験所間の差異
が試料に依存することを意味するから,この特徴を調査しなければならない。試験所間の平均差分の計算
を表15に示す。この平均差分を用いて,試験所間差分の重要性を表示できるが,以後の試料分析時に得る
可能性のある試験所間の差分の予測には使用しない。したがって,変換したデータによって,平均して
ln(Y)−ln(X) = 0.443となり,Y/X=1.6を得る。ここで,試験所Yが得る結果は,平均して試験所Xより係
数1.6だけ高くなっている。ただし,一部の試料では,差分が更に大きくなり,他の試料では,試験所X
のほうが高い結果を得ている。
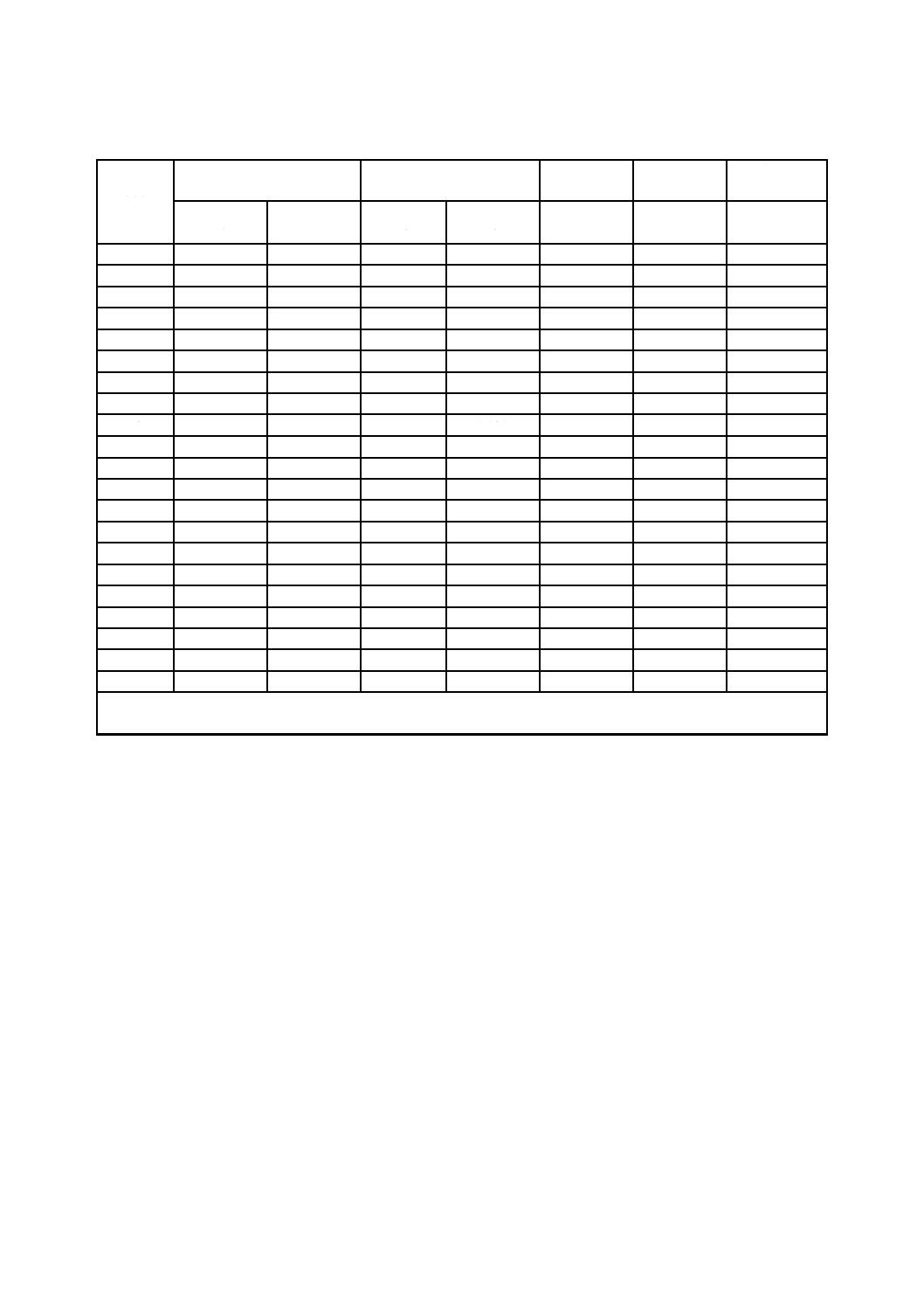
51
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表14−21の血清試料中のある抗体の濃度
試料i
試験所X
試験所Y
試験所X
試験所Y
試験所
X及びY
反復1
U/L
反復2
U/L
反復1
U/L
反復2
U/L
平均
U/L
平均
U/L
平均
U/L
1
19.106
18.174
11.473
11.705
18.640
11.589
15.115
2
6.424
7.171
5.812
5.812
6.798
5.812
6.305
3
6.619
5.989
11.705
11.473
6.304
11.589
8.947
4
0.543
0.664
0.861
0.905
0.604
0.883
0.743
5
43.816
46.063
49.899
55.147
44.940
52.523
48.731
6
2.096
2.535
24.047
26.843
2.316
25.445
13.880
7
10.591
9.875
9.116
8.671
10.233
8.894
9.563
8
13.874
13.599
12.554
12.807
13.737
12.681
13.209
9
1.974
2.363
1.094
1.020
2.169
1.057
1.613
10
9.393
10.591
13.736
14.585
9.992
14.161
12.076
11
1.840
1.616
2.484
2.460
1.728
2.472
2.100
12
31.817
34.124
48.424
55.147
32.971
51.786
42.378
13
1.150
1.051
2.014
2.270
1.101
2.142
1.621
14
0.625
0.684
1.051
1.174
0.655
1.113
0.884
15
73.700
79.838
119.104
127.740
76.769
123.422
100.096
16
2.181
2.340
2.560
3.065
2.261
2.813
2.537
17
8.415
8.166
5.755
5.585
8.291
5.670
6.980
18
1.419
1.632
8.846
8.846
1.526
8.846
5.186
19
0.861
0.887
2.612
3.065
0.874
2.839
1.856
20
10.697
10.486
15.029
14.880
10.592
14.955
12.773
21
0.230
0.177
0.795
0.795
0.204
0.795
0.499
注記 データは,国際標準物質の濃度によって定義される単位(U)を用い,試料1リットル(L)当たりの値として示
す。
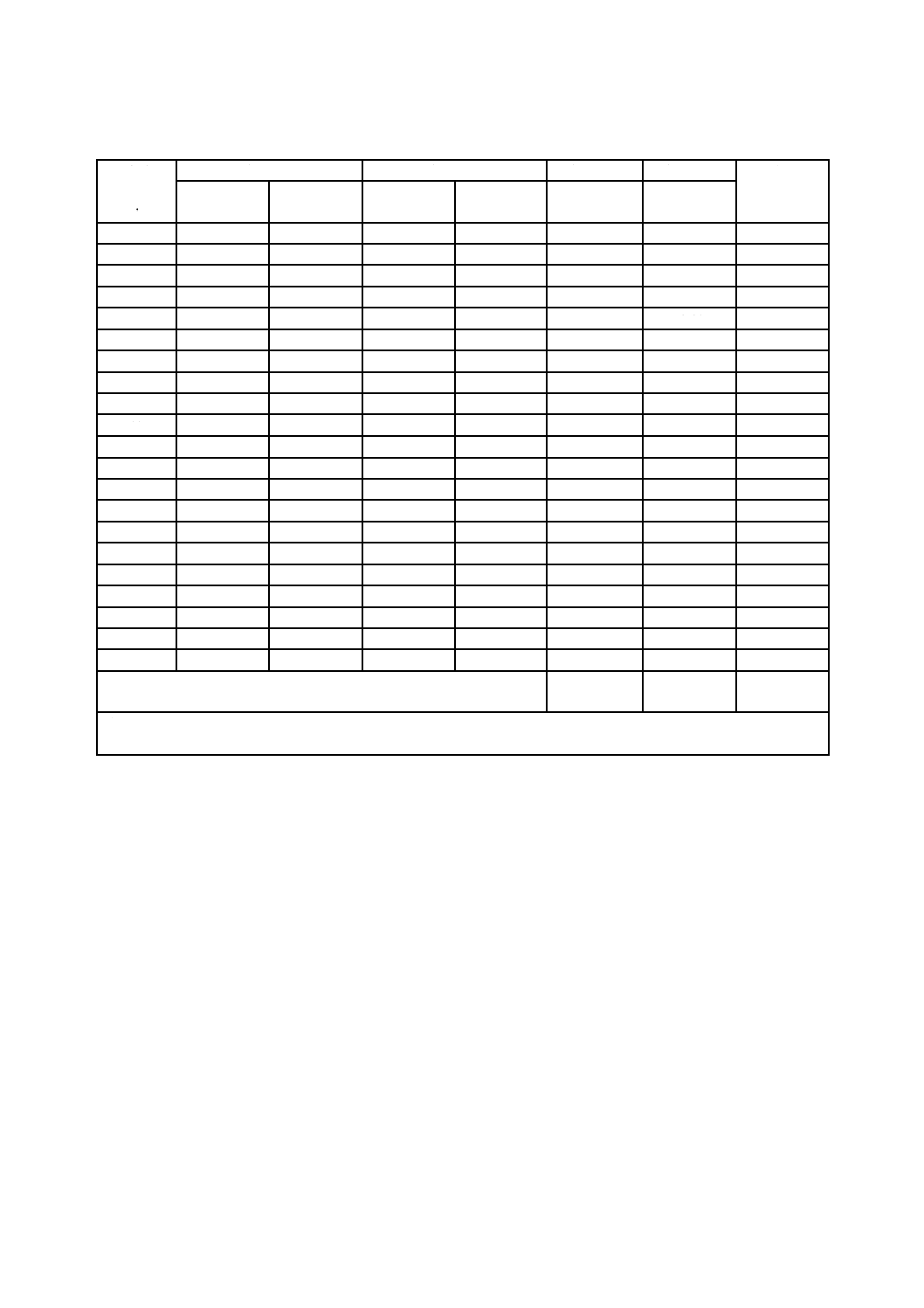
52
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表15−表14のデータのln(濃度)と統計
試料
i
試験所 X
試験所 Y
試験所 X
試験所 Y
差分
Y−X
ln U/L
反復1
ln U/L
反復2
ln U/L
反復1
ln U/L
反復2
ln U/L
範囲
ln U/L
範囲
ln U/L
1
2.95
2.90
2.44
2.46
0.05
0.02
−0.475
2
1.86
1.97
1.76
1.76
0.11
0.00
−0.155
3
1.89
1.79
2.46
2.44
0.10
0.02
0.610
4
−0.61
−0.41
−0.15
−0.10
0.20
0.05
0.385
5
3.78
3.83
3.91
4.01
0.05
0.10
0.155
6
0.74
0.93
3.18
3.29
0.19
0.11
2.400
7
2.36
2.29
2.21
2.16
0.07
0.05
−0.140
8
2.63
2.61
2.53
2.55
0.02
0.02
−0.080
9
0.68
0.86
0.09
0.02
0.18
0.07
−0.715
10
2.24
2.36
2.62
2.68
0.12
0.06
0.350
11
0.61
0.48
0.91
0.90
0.13
0.01
0.360
12
3.46
3.53
3.88
4.01
0.07
0.13
0.450
13
0.14
0.05
0.70
0.82
0.09
0.12
0.665
14
−0.47
−0.38
0.05
0.16
0.09
0.11
0.530
15
4.30
4.38
4.78
4.85
0.08
0.07
0.475
16
0.78
0.85
0.94
1.12
0.07
0.18
0.215
17
2.13
2.10
1.75
1.72
0.03
0.03
−0.380
18
0.35
0.49
2.18
2.18
0.14
0.00
1.760
19
−0.15
−0.12
0.96
1.12
0.03
0.16
1.175
20
2.37
2.35
2.71
2.70
0.02
0.01
0.345
21
−1.47
−1.73
−0.23
−0.23
0.26
0.00
1.371
プールした範囲
試験所間の平均差分
0.119
0.083
0.443
注記 データは,国際標準物質の濃度によって定義される単位(U)を用い,試料1リットル(L)当たりの値として示す。
プールした範囲は,附属書Cのアルゴリズムに従って計算する。
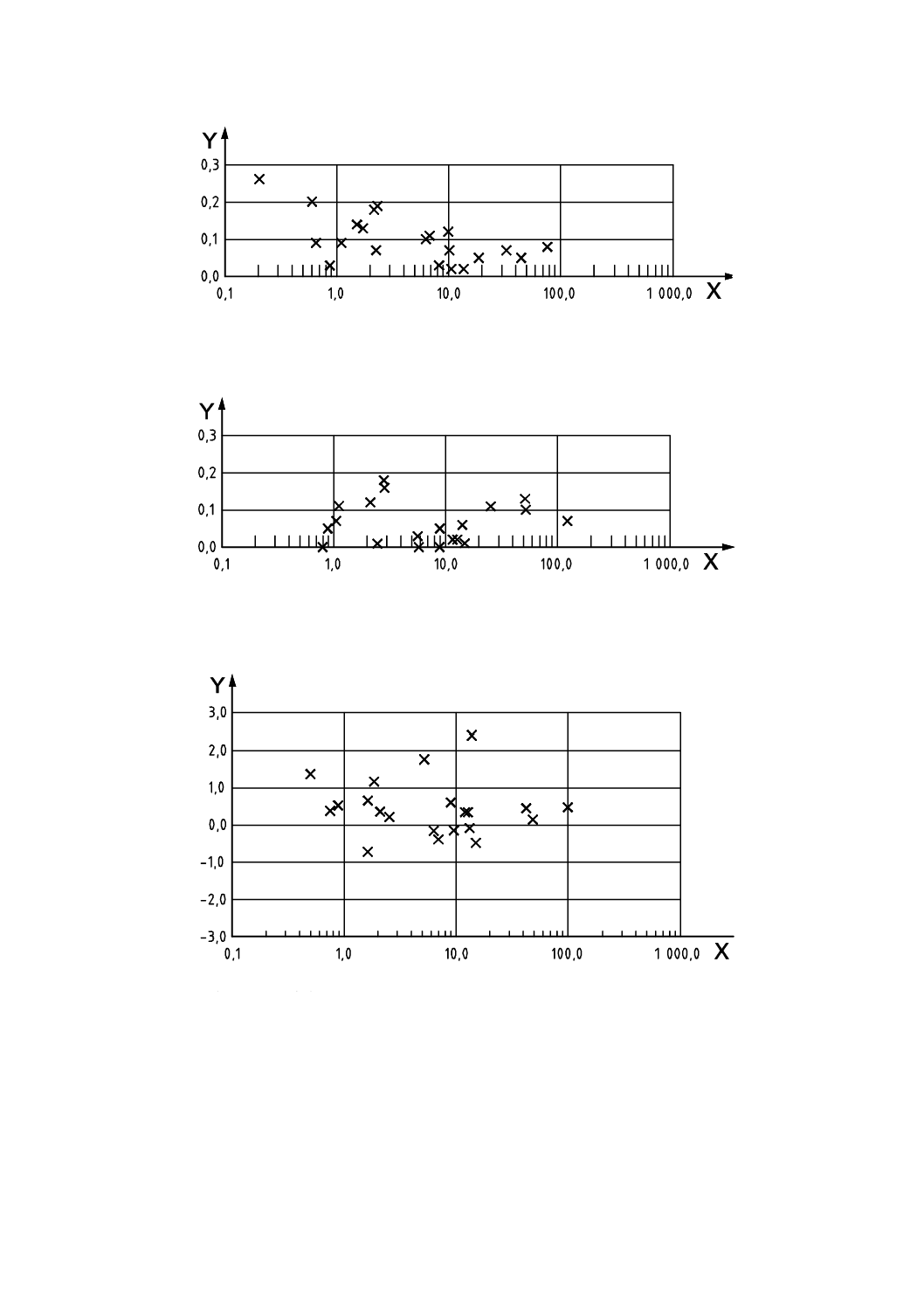
53
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X軸:試験所Xの平均濃度,%
Y軸:試験所Xの差分ln(濃度)
図12−試験所Xの反復定量の範囲(ln濃度から計算した範囲による)
X軸:試験所Yの平均濃度,%
Y軸:試験所Yの差分ln(濃度)
図13−試験所Yの反復定量の範囲(ln濃度から計算した範囲による)
X軸:試験所X,Yの平均濃度,%
Y軸:差分ln(濃度),試験所Y−試験所X
図14−試験所平均Y−Xの差分(ln濃度から計算した差分)
54
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9
複数回の技能試験スキームの成績スコアを組み合わせるための図式表現の方法(JIS Q 0043-1,A.3.2
参照)
9.1
用途
標準化スコアを複数ラウンドにわたって組み合わせる場合,9.2又は9.3に従って,グラフを作成するこ
とをコーディネータは考慮する。複数ラウンドのスコアを組み合わせたグラフを使用することによって,
各ラウンドのスコアを個別に検査した場合に現れない,結果の傾向や他の特徴を特定できる。
注記 試験所が得たスコアを複数ラウンドにわたって組み合わせるがグラフィック表示をしない“ラ
ンニングスコア”の使用は望ましくない。あるラウンドに使用する試験物質には現れるが,他
のラウンドには現れない不良が試験所に発生する場合がある。ランニングスコアはこの不良を
隠す場合がある。処置信号と警戒信号の数のカウントという形式のランニングスコアを使用し
た場合は7.9による。
9.2
z-スコアのシューハート管理図
9.2.1
一般
この図を作成するには,試験所のz-スコアを個々のポイントとしてプロットし,表16及び図15に示す
スタイル上で処置限界及び警戒限界を±2.0及び±3.0に設定する。複数特性を各ラウンド中に測定する場
合,差分特性のz-スコアを同一グラフ上にプロットしてよいが,差分特性のポイントは別のプロット記号
及び/又は異なった色を用いてプロットしたほうがよい。シューハート管理図のプロットに関しては,JIS
Z 9021[4]を参照。
シューハート管理図は,z-スコアに大きな値のエラーを発生させるような問題の特定に効果的な方法で
ある。
シューハート管理図を解釈する規則とは,次の場合に管理外れ信号を発出することである。
a) 単一ポイントが処置限界(± 3.0)の外側に現れる
b) 三つの連続する点のうち二つが,同一の警戒限界(±2.0)の外側に現れる
このようなシューハート管理図が管理外れ信号を発行する場合,4.1による処置を行う。技能評価の標準
偏差σˆは必ずしも試験所のかたよりx−Xの標準偏差ではないため,シューハート管理図の処置限界と警戒
限界に通常関連する確率水準は適用しないことに注意する。
9.2.2
例 アレルゲン濃度
表16のデータを図15にプロットする。
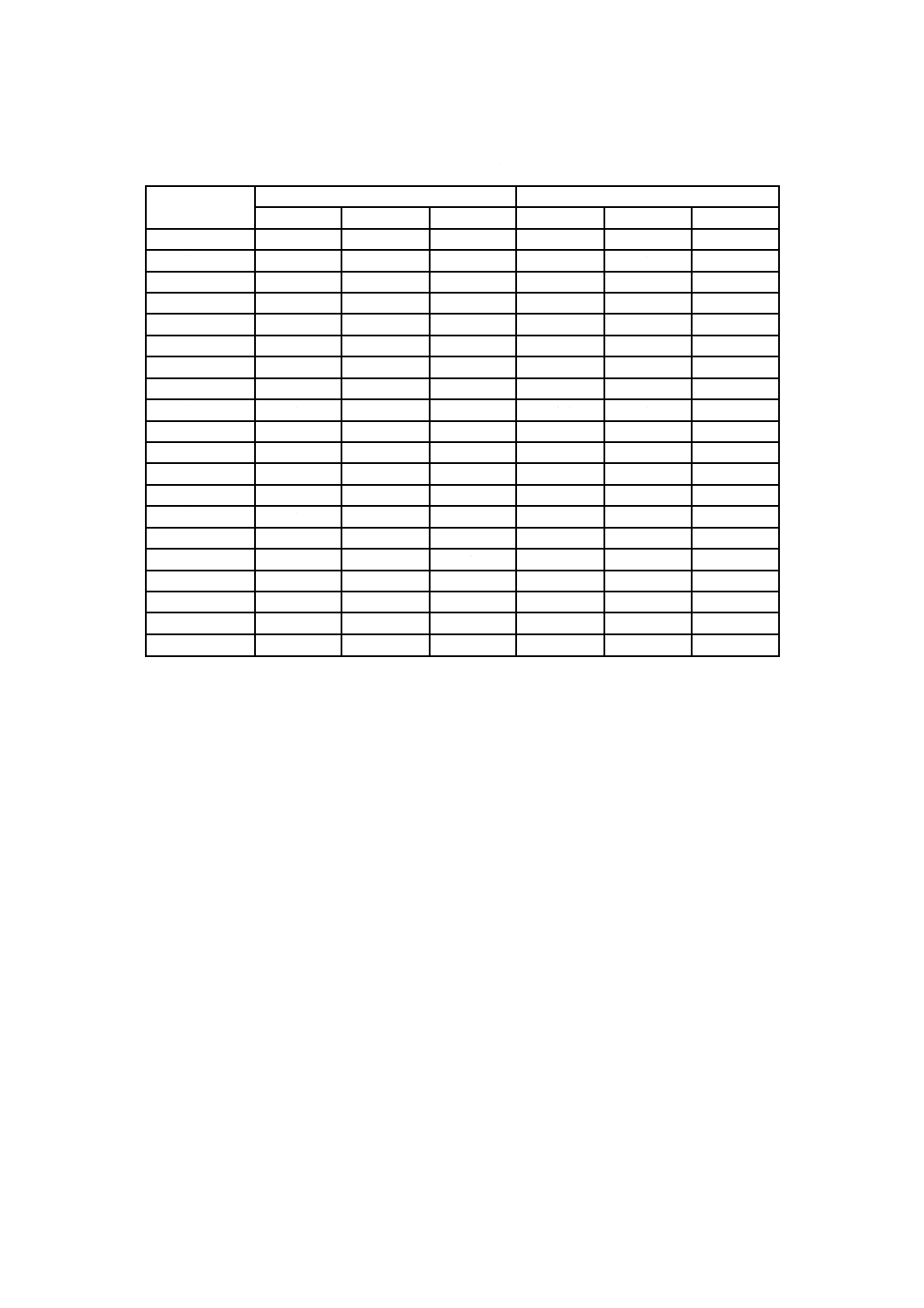
55
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表16−3種のアレルゲン濃度の定量に必要な技能試験スキームの
20ラウンドのデータ (d1,f1,e3)
ラウンド日付
アレルゲンのz-スコア
z-スコアの累積和
d1
f1
e3
d1
f1
e3
1991年9月
−1.4
−0.2
−0.5
−1.4
−0.2
−0.5
1991年12月
−0.9
−1.3
−1.0
−2.3
−1.5
−1.5
1992年3月
0.2
1.6
1.0
−2.1
0.1
−0.5
1992年6月
1.0
−0.5
−1.1
−0.4
1992年9月
−0.4
−1.2
−1.5
−1.5
−1.6
−2.0
1992年12月
0.0
0.3
−0.8
−1.5
−1.3
−2.8
1993年3月
0.9
−0.1
−1.1
−0.6
−1.4
−3.9
1993年6月
2.0
0.3
1.0
1.4
−1.1
−2.9
1993年9月
1.7
2.6
3.1
1.5
1993年12月
−0.8
−1.3
−0.6
2.3
0.2
−3.5
1994年3月
−1.0
1.6
0.4
1.3
1.8
−3.1
1994年6月
−2.0
0.8
0.4
−0.7
2.6
−2.7
1994年9月
−1.6
4.0
−0.8
−2.3
6.6
−3.5
1994年12月
1.5
1.1
−0.8
7.7
1995年3月
0.1
0.3
−1.5
−0.7
8.0
−5.0
1995年6月
−1.9
0.1
−0.5
−2.6
8.1
−5.5
1995年9月
−0.7
1.2
0.4
−3.3
9.3
−5.1
1995年12月
0.3
−1.9
−0.8
−3.0
7.4
−5.9
1996年3月
−1.3
−1.1
−4.3
6.3
1996年6月
−0.4
1.9
0.0
−4.7
8.2
−5.9
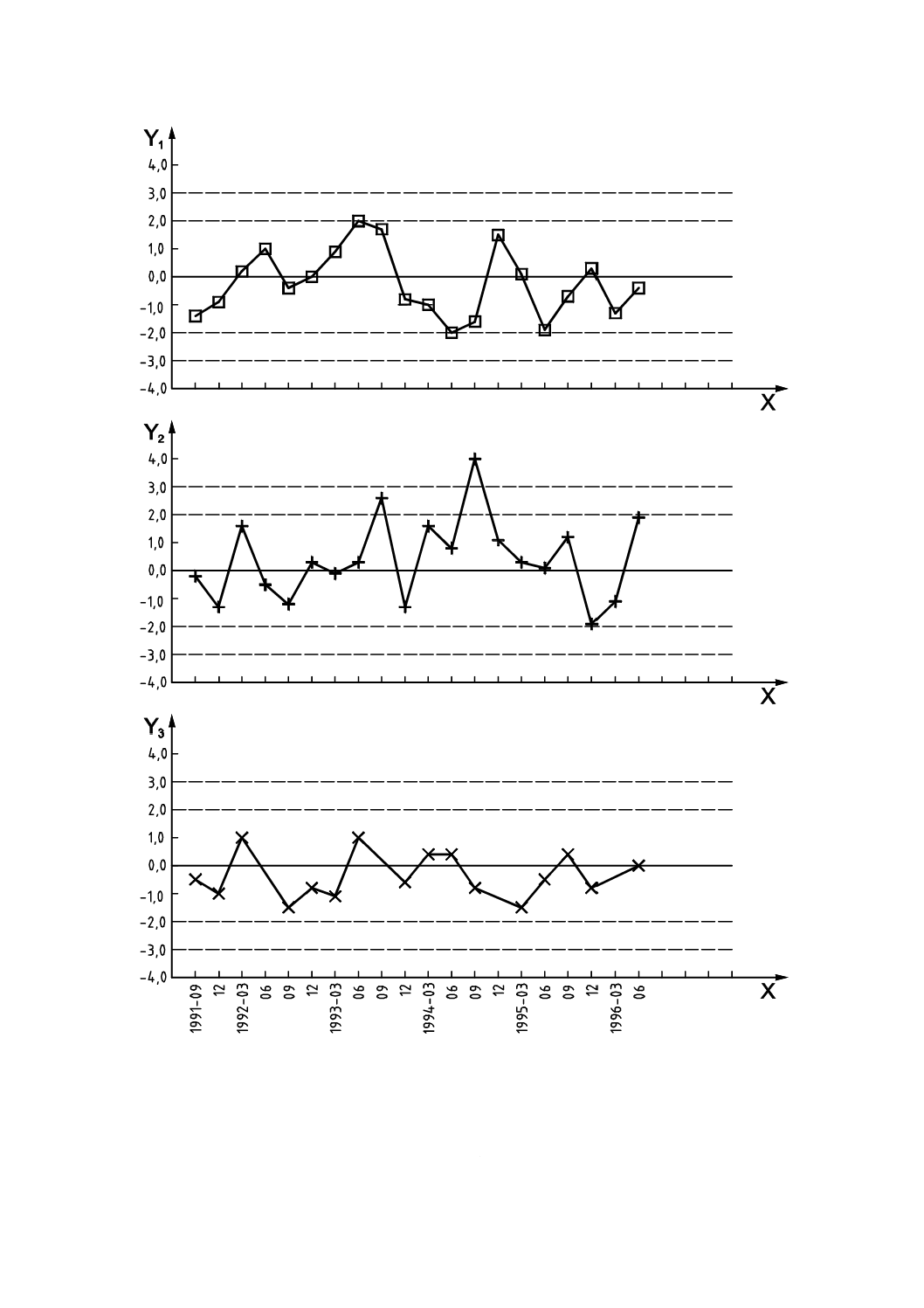
56
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X軸:ラウンドの日付
Y1軸:アレルゲンd1のz-スコア
Y2軸:アレルゲンf1のz-スコア
Y3軸:アレルゲンe3のz-スコア
図15−20ラウンドの技能試験スキームにおけるある試験所データの
シューハート管理図(データは表16から)
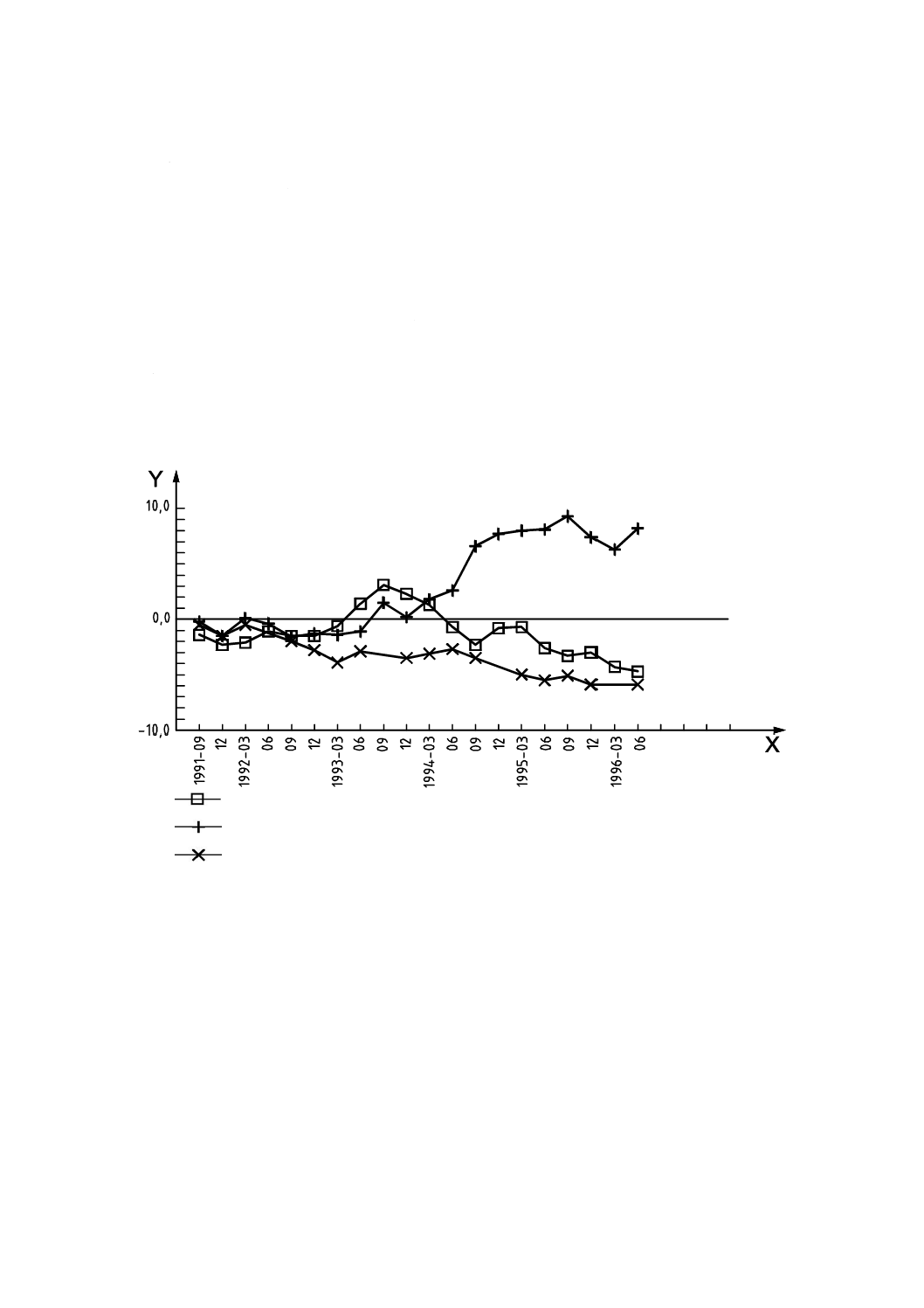
57
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9.3
z-スコアの累積和管理図
9.3.1
一般
この図を作成するには,複数ラウンドの技能試験にわたって試験所が得るz-スコアの累積和(cusum)を計
算し,図16に示すようにプロットする。累積和図の目的はz-スコアがゼロから離れる場合を検出すること
であるため,累積和の目標値はゼロであり,累積和はz-スコアの累積和として簡単に計算できる。累積和
図のプロットに関しては,ISO/TR 7871[5]を参照。
各ラウンドで複数の特性を測定する場合,別々の累積和を各特性に対して計算する。
累積和管理図は,複数ラウンドにわたり存在する特性決定中のかたよりを発生する問題を特定するのに
有効な方法である。このような累積和管理図が管理外れ信号を発生する場合,4.1による処置を行う。
9.3.2
例 アレルゲン濃度
表16は3種のアレルゲンの定量値に対してそれらから得たz-スコア及び累積和を示す。累積和を図16
に示す。このグラフは,1994年3月以降の試験所の結果に変化が生じたことを示す。
アレルゲン d1
アレルゲン f1
アレルゲン e3
X軸:ラウンドの日付
Y軸:z-スコアの累積和
図16−20ラウンドの技能試験スキームにおけるある試験所データの累積和管理図
(データは表16から)
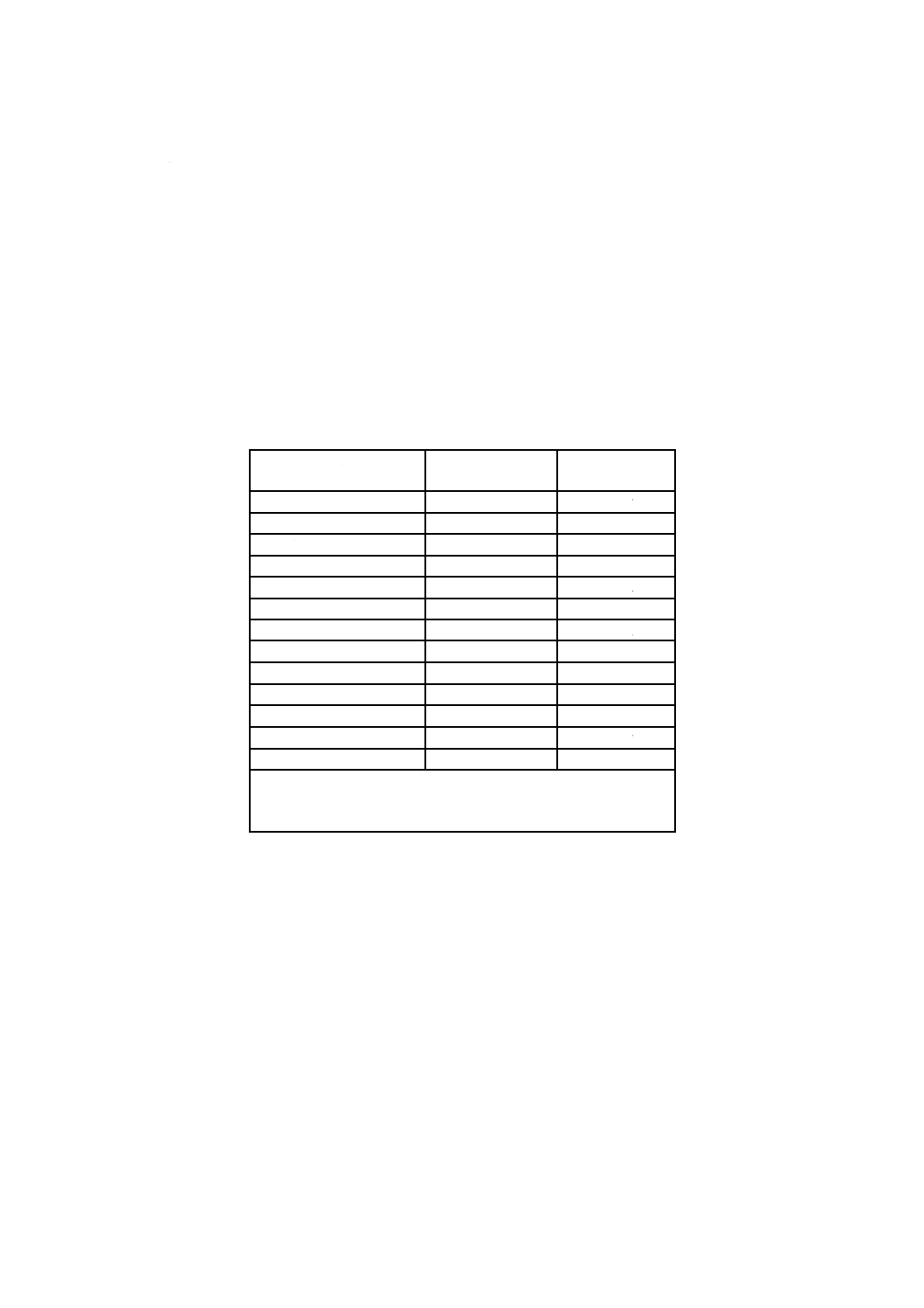
58
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9.4
試験所平均に対する標準化した試験所のかたよりのプロット
9.4.1
一般
あるラウンドの技能試験から別ラウンドの試験への広範囲にわたり特性のレベルが変化する場合,レベ
ルに対するz-スコア又は他の標準化スコアのプロットは,試験所のかたよりがレベルによって変化するか
どうかを示す。
9.4.2
例 アレルゲン濃度
表17はある試験所が13ラウンドの技能試験にわたって報告したアレルゲン濃度の定量結果を示す。図
17は,濃度レベルに対してプロットしたz-スコアを示す。このグラフは,濃度レベルが高くなると試験所
は正のz-スコアを得る傾向にあることを示す。このデータによって,回帰分析を用いてこの傾向が統計的
に有意であることを実証できる。
表17−ある試験所におけるアレルゲン濃度d1の定量
日付
平均濃度
kU/L
z-スコア
1992年6月
12.00
0.7
1992年9月
4.82
−1.3
1992年12月
17.20
2.3
1993年3月
8.53
1.3
1993年6月
8.47
1.4
1993年9月
2.57
0.3
1993年12月
1.94
0.2
1994年3月
3.78
−0.1
1994年6月
2.07
−0.5
1994年9月
19.50
2.1
1994年12月
3.13
1.3
1995年3月
16.70
1.7
1995年6月
5.12
0.5
注記 データは,国際標準物質の濃度によって定義される単位(U)
を1 000倍の(kU)とし,試料1リットル(L)当たりの値とし
て示す。
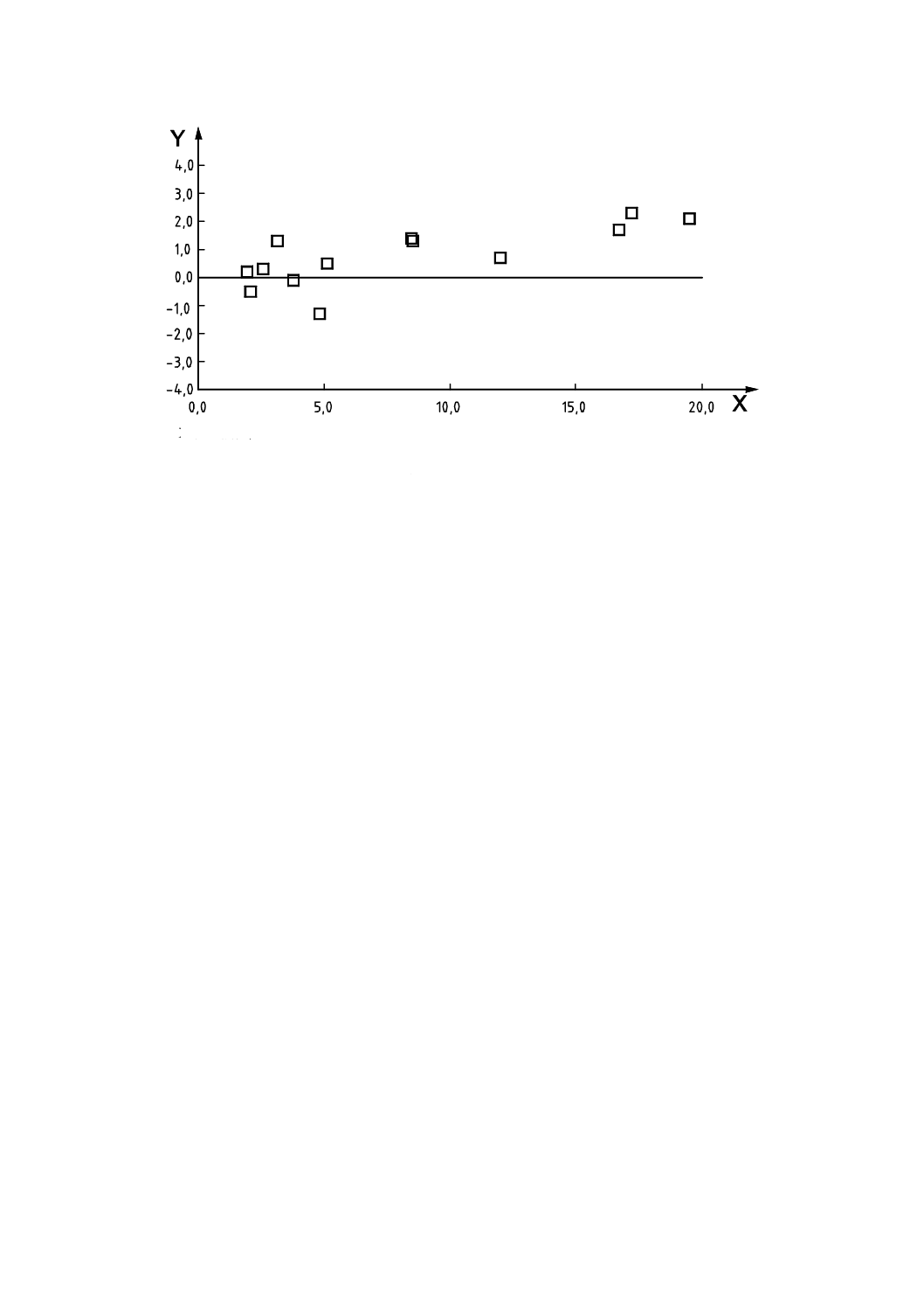
59
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X軸:濃度,kU/L
Y軸:アレルゲンd1のz-スコア
図17−ある試験所におけるアレルゲンd1の定量における濃度レベルとz-スコアの関係
9.5
ドットプロット
複数の試験項目を1ラウンドの技能試験にて同一の測定対象に関して試験する場合にもシューハート管
理図などのプロットは有用である。ドットプロットはシューハートプロットに似ているが,各時間間隔で
複数のポイントを対象としており,ラインが各時間間隔における成績測定の平均とつながっている。
次に示す例はグルコースを3か月ごとに五つの異なった試料によって試験している状況である。解釈の
受入基準は,付与された値60 mg/dL以上に対して±10 %,付与された値60 mg/dL未満に対して6.0 mg/dL
である。この状況及び広範囲の値は,付与された値ごとに技能試験の固定標準偏差3.33 %又は2.0 mg/dL
を用いて実施するz-スコアによる評価に適している。
図18のグラフは,第1ラウンド及び第3ラウンドにおいて,±3限界値の外側に出ているものがあり,
また,少数の疑わしい値がこのシリーズ中にあることを示す。このデータセット中,この試験所の第1ラ
ウンドの併行精度は低く,かたよりは若干高い。第2ラウンドでは,精度問題を修復しているが,かたよ
りは調整していない。第3ラウンドでは,かたよりは修正しているが,最初の精度問題が再発している。
第4ラウンドには類似のかたよりがあるが,精度は良好である。
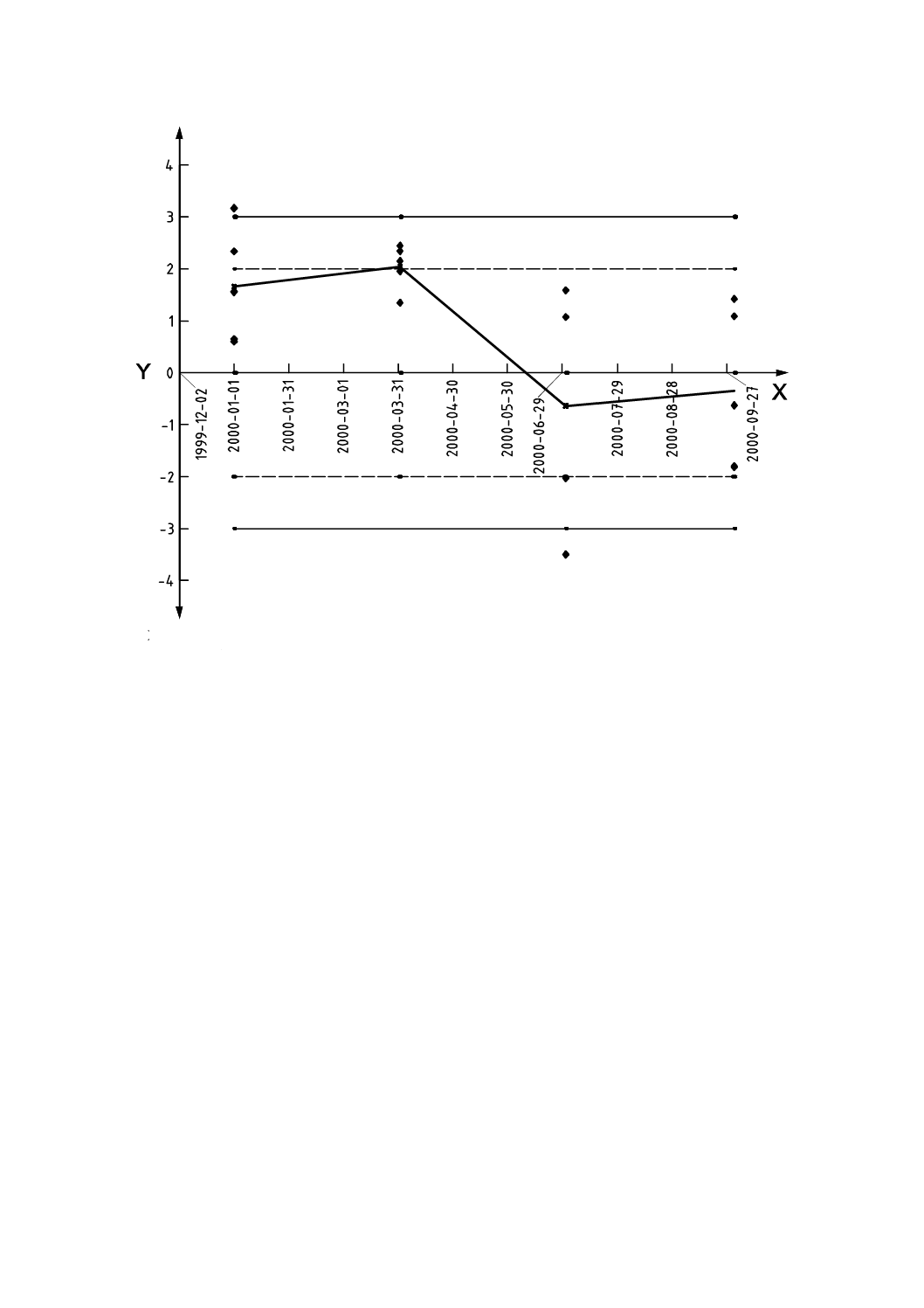
60
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X:試験日付
Y:z-スコア
図18−4回の技能試験におけるグルコースのz-スコア
61
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
記号
g
均質性試験における試験対象試料数
n
試料当たりの併行測定数
p
1ラウンドの技能試験に参加した試験所数
ss
試料間標準偏差
sx
標本平均の標準偏差
s*
ロバストな標準偏差(ロバストなアルゴリズムによって計算した標準偏差)
X
u
付与された値の標準不確かさ
wt
試験部分間の範囲
x
測定結果
x*
ロバストな平均(ロバストなアルゴリズムによって計算した平均)
z
技能評価に使用するスコア
D
試験所のかたより
X
技能評価のための付与された値
L
σ
試験所間標準偏差
σˆ
技能評価のための標準偏差
r
σ
併行標準偏差
R
σ
再現標準偏差
φ
認知に得た値σˆの検査に使用する係数
62
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(規定)
試料の均質性試験及び安定性試験
序文
この附属書は,技能試験に使用する試料が均質及び安定であることを適切に確認するための方法につい
て規定する。
B.1
均質性試験の手順
次の手順に従う。
a) 均質性試験を実施する試験所を選択する。均質性試験に使用する測定方法や測定する対象試験物質の
特性について,試料間の不均質性について感度の高いものを選択すれば,すべての測定対象に対して
均質性試験を実施しなくてもよい。この場合,粉体においては,十分に選別された特性のもの(すな
わち,一定の目開きのふるいを通過した粒度のもの)を選ぶ必要がある。試料のある小部分を測定す
る場合,小部分の特性の均質化はより困難であり,したがって均質性試験において色々面倒な問題が
起こりやすい(十分に選別された特性のものとは,個々の粒子が唯一の値を示すような特性のもので
ある。個々の粒がさまざまな度合いの特性を示す場合には,そのような粉体は十分に選別された特性
のものとはいえない。)。
b) 1ラウンドの技能試験スキーム用に試料を準備し,こん包する。この場合,スキームへの参加者及び
均質性試験を実施するために必要な十分な数の試料を確保する必要がある。
c) 最終的にこん包した試料からランダムにある試料数gを選択する。ここでg≧10とする。同一の手順
によって作成した類似の試料で実施した以前の均質性試験から適切なデータが得られる場合は,均質
性試験に使用する試料数を少なくしてもよい。
d) 試験部分間差分を最小にする適切な手法を用いて,各試料から二つの試験部分を作成する。
e) 2 gの試験部分をランダムな順序で取り出し,一連の測定を併行条件下にてすべて実施して測定結果を
取得する。
f)
B.3によって,一般平均x.,.,試料内標準偏差sW,試料間標準偏差sSを計算する。
B.2
均質性試験の評価基準
試料間標準偏差sSを技能評価のための標準偏差σˆと比較する。次の場合にはこの試料が十分均質である
とみなす。
sS≦ 0.3σˆ ············································································· (B.1)
この式の係数0.3の根拠は,この基準が満たされる場合,試料間標準偏差によって生じる技能試験の標
準偏差が約10 %を超えないということである。この基準が満たされない場合,コーディネータは次の可
能性を考慮する必要がある。
a) 試料作成手順を検査し,改善の可能性を調べる。
b) 多数の試料を技能スキーム中の各参加者に配布し,各試料について測定結果を取得するように要求す
る。試料の不均質性によって,試料内標準偏差が次の式のように増加する。
63
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
σr1=
2
S
2s
r+
σ
······································································· (B.2)
σr1を測定の繰返し回数の選択のためのガイドライン,式(2)中の
r
σの代わりに使用する。
c) 次の式によってσˆを計算して,試料間標準偏差を技能試験のための標準偏差に使用する。
σˆ=
2
S
2
1ˆ
s
+
σ
········································································· (B.3)
ここに,
σˆ1: 試料の不均質性に許容度を含まない技能試験の標準偏差で
ある。
B.3
均質性試験に使用する式
均質性試験からのデータを次のように表す。
xt,k
ここに,
t: 試料を表す(t = 1 , 2 ..., g)
k: 試験部分を表す(k = 1, 2)
試料平均を次の式によって定義する。
xt,.=(xt,1+xt,2)/2 ···································································· (B.4)
さらに試験部分間範囲を,次の式によって定義する。
1,
=
t
t
x
w
−
2,tx
····································································· (B.5)
一般平均を計算する。
g
x
x
t/
.,.
,.
∑
=
········································································ (B.6)
試料平均の標準偏差を次の式によって計算する。
)1
(
)
(
2
.,.
,.
g
x
x
s
t
x
∑
=
····················································· (B.7)
さらに,試料内標準偏差を次の式によって計算する。
)
2(
2
w
g
w
s
t
∑
=
································································· (B.8)
ここで,総和は試料全体を対象とする(t = 1,2,...,g)。
最後に,試料間標準偏差を次の式によって計算する。
(
)2
2
w
2
S
s
s
s
x
=
·································································· (B.9)
注記 範囲を使用する代わりに,試験部分間標準偏差として次の標準偏差を用いてもよい。
st=wt/2
B.4
安定性試験の手順
a) 均質性試験と同一の試験所を使って安定性試験を行う。同一の測定方法を使用し,同一の試験物質特
性を測定する。
b) 均質性試験と安定性試験との間に,技能試験の参加者が試験した試料が受ける時間の遅延と同様の時
64
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
間の遅延を許容する。
c) 試料の数量gをランダムに選択する。ここでg≧ 3である。
d) 均質性試験と同一の手法を使用し,二つの試験部分を各試料から用意する。
e) 2 gの試験部分をランダムな順序によって取り出し,それぞれから測定結果yt,kを採取し,併行精度条
件下での全測定を実施する。
f)
安定性試験から得た測定値の一般平均
.,.
yを計算する。
B.5
安定性試験の評価基準
均質性試験から得た測定値の一般平均を,安定性試験から得た結果の一般平均と比較する。この試料が
十分安定と考えられるのは,次の式が成立する場合である。
.,.
x−
.,.
y
σˆ
3.0
≦
··································································· (B.10)
この基準が満たされない場合,試料作成及び保管手順を検査し,改善の可能性を確認する。
B.6
例 きなこ中の銅 (µg/g)
きなこ(大豆粉)を試験物質として使用する技能試験スキームでは,精度実験結果を用いて技能評価の
標準偏差をσˆ= 1.1 µg/gに設定した。式(B.1)に基づくと,試料間標準偏差は次の値より小さくなければな
らない。
0.3 × 1.1 = 0.330 µg/g
均質性試験の場合,技能試験スキームに用意したきなこ試料から12をランダムに選択し,各試料から,二
つの試験部分の銅含有量を定量した。このデータを表B.1に示す。試料平均と試験部分間の範囲も併せて
示す。
B.3中の式を用いて,次の値を計算する。
一般平均
x.,. = 10.02 µg/g
試料平均の標準偏差
sx = 0.340 µg/g
試料内標準偏差
sW = 0.246 µg/g
試料間標準偏差
sS = 0.292 µg/g
この値は0.330 µg/gより小さいため,試料は技能試験スキームに使用可能な均質性を備えていると結論
できる。
安定性試験のため,3試料を同一の試験所が1か月後に試験し,結果として平均値
.,.
y= 10.78 µg/gを得
た。差分
.,.
y−
.,.
x=0.76 µg/g は,0.3σˆ= 0.33 µg/gより大きいため,試料の安定性は十分でない。

65
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.1−きなこの銅に対する均質性試験の測定結果 (µg/g)
試料番号
t
試験部分
1
試験部分
2
試料平均
xt,.
試験部分間の範囲
wt
1
10.5
10.4
10.45
0.1
2
9.6
9.5
9.55
0.1
3
10.4
9.9
10.15
0.5
4
9.5
9.9
9.70
0.4
5
10.0
9.7
9.85
0.3
6
9.6
10.1
9.85
0.5
7
9.8
10.4
10.10
0.6
8
9.8
10.2
10.00
0.4
9
10.8
10.7
10.75
0.1
10
10.2
10.0
10.10
0.2
11
9.8
9.5
9.65
0.3
12
10.2
10.0
10.10
0.2
66
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(規定)
ロバストな解析
序文
この附属書は,ロバストな方法について規定する。
C.1 ロバストな解析:アルゴリズムA
このアルゴリズムによって,アルゴリズムを適用する対象データの平均及び標準偏差のロバストな推定
値を得る。
注記1 この附属書中のアルゴリズムA及びアルゴリズムSは,JIS Z 8402-5から引用している。
注記2 ロバスト性は推測アルゴリズムの特性であり,アルゴリズムの結果としての推定値の特性で
はない。したがって,このようなアルゴリズムによって計算される平均及び標準偏差を“ロ
バスト”と称するのは厳密には正しくない。ただし,用語が過度に複雑になるのを避けるた
め,この規格では,“ロバストな平均”及び“ロバストな標準偏差”を用いるものとし,それ
ぞれ,ロバストなアルゴリズムを用いて計算される母集団平均の推定値又は母集団標準偏差
の推定値を意味する。
p個のデータを,昇順に並べ替え,次のように表す。
x1, x2,...,xi,...,xp
このデータのロバスト平均及びロバスト標準偏差をx*及びs*によって示す。
x*及びs*の初期値を次のように計算する。
x* = xiの中央値 (i= 1, 2, …, p) ·················································· (C.1)
s* = 1.483 x |xi‒ x*|の中央値 (i= 1, 2, …, p) ································ (C.2)
x*及びs*の値を次のように更新する。
δ= 1.5s* ················································································ (C.3)
それぞれのxi(i = 1, 2, ..., p)について,次の計算を行う。
+
>
+
−
<
−
=
それ以外
,
の場合
,
の場合
,
i
i
i
i
x
x
x
x
x
x
x
x
δ
δ
δ
δ
··············································· (C.4)
x* 及び s*の新しい値を次の式から計算する。
p
x
x
i
∑
=
*
*
······································································ (C.5)
∑
=
)1
(
)
(
134
.1
2
*
*
*
p
x
x
s
i
·············································· (C.6)
ここで,総和はすべてのiについて行う。
ロバストな推定値x*及びs*は繰返し計算によって求める。すなわち,x*及びs*の値を変更しながらこの
プロセスが収束するまで何回か更新する。ロバストな標準偏差及びロバストな平均中の等価な数字の第三
有効数字が,ある繰返しと次の繰返しとの間で変化しない場合に収束したものとみなす。この方法は,コ
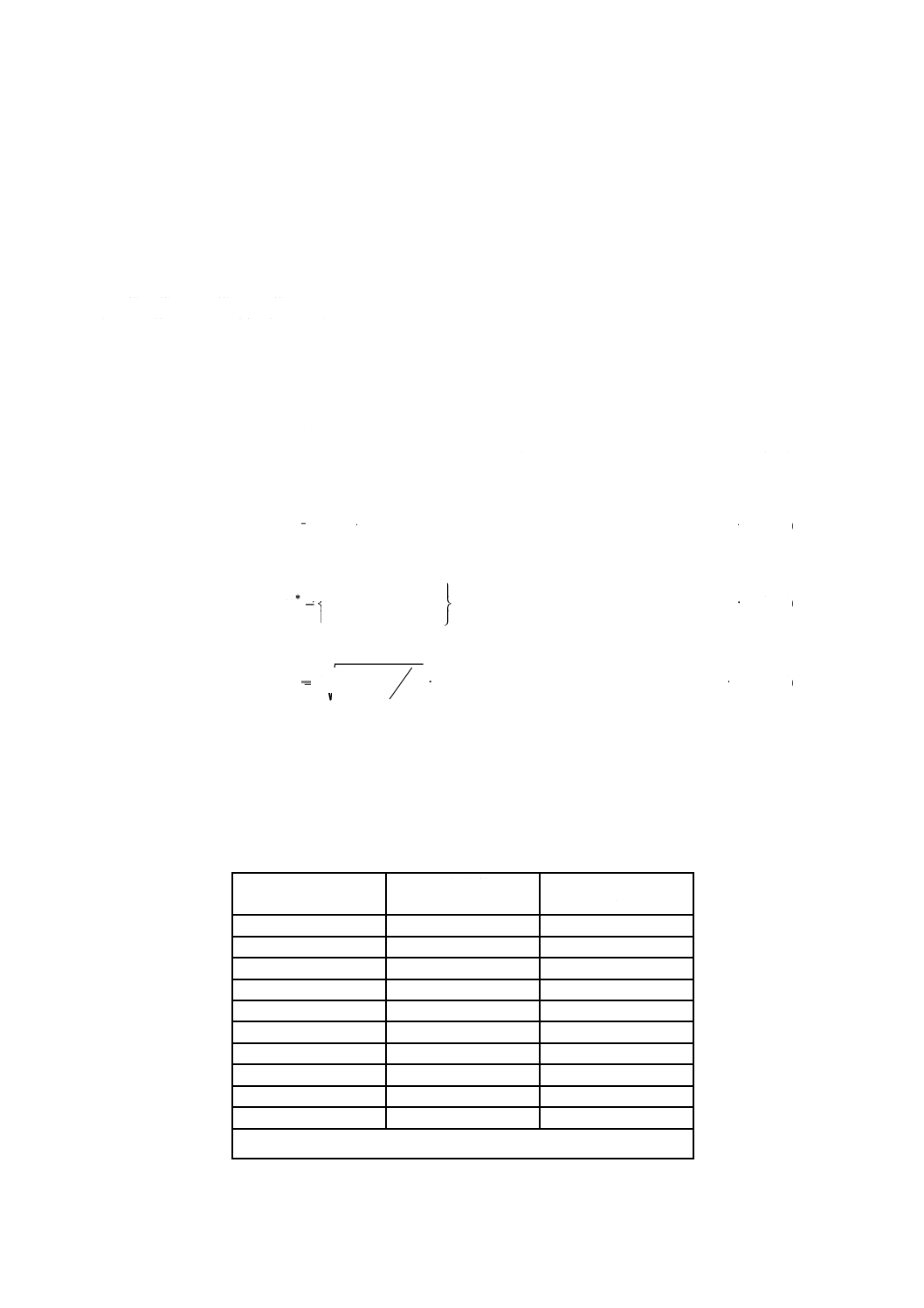
67
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ンピュータ上でプログラムするための簡単な方法である。
C.2 アルゴリズムS
このアルゴリズムは標準偏差 (又は範囲)に適用し,標準偏差又は適用対象の範囲のロバストなプール値
を発生する。
p個のデータを昇順に並べ替え,次のように表す。
w1,w2,...,wi,...,wp
(これは範囲又は標準偏差である)
ロバストなプール値をw*,各wiに対応する自由度をνによって表す(wiが範囲である場合,ν=1である。
wiが試験結果の標準偏差である場合,ν=n−1となる)。アルゴリズムに必要な値ξ及びηを表C.1から取
り出す。
w*の初期値を次のように計算する。
w*= wiの中央値 (i= 1,2, …, p) ············································ (C.7)
w*の値を次のように更新する。次の式を計算する。
*
×
=
w
η
ψ
············································································· (C.8)
それぞれのwi(i = 1,2,...,p)に対し,次の計算を行う。
>
=
それ以外
,
の場合
,
i
i
i
w
w
w
ψ
ψ
························································· (C.9)
w*の新しい値を次の式によって計算する。
p
w
w
i
∑
=
2
*
*
)
(
ξ
······························································ (C.10)
ロバストな推定値w*は繰返し計算によって求める。すなわち,値w*を何回か更新し,このプロセスが
収束するまで更新し続ける。ある繰返しから次の繰返しを行ったとき,ロバストな範囲の第3有効数字に
変化がない場合に収束したものとみなす。この方法はコンピュータ上でプログラムするための簡単な方法
である。
表C.1−ロバストな解析に必要な係数: アルゴリズムS
自由度
ν
限界係数
η
調整係数
ξ
1
1.645
1.097
2
1.517
1.054
3
1.444
1.039
4
1.395
1.032
5
1.359
1.027
6
1.332
1.024
7
1.310
1.021
8
1.292
1.019
9
1.277
1.018
10
1.264
1.017
注記 ξ及びηの値はJIS Z 8402-5:2002の附属書Bから得る。
68
Z 8405:2008 (ISO 13528:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1]
THOMPSON,M and WOOD,R: The international harmonized protocol for the proficiency testing of
(chemical) analytical laboratories(分析試験所の技能試験のためのハーモナイズドプロトコル),
AOAC,1993年9月
[2]
JACKSON,J.E.: Quality control methods for two related variables.(二つの関連変数の品質管理方
法),Indusrial Quality Control,7,1956,pp. 2-6
[3]
HORWITZ, W.: Evaluation of analytical methods used for regulations of food and drugs(食品と
薬物の規制に使用する分析方法の評価),Anal. Chem.,54,1982,pp.67A-76A
[4]
JIS Z 9021 シューハート管理図
[5]
ISO/TR 7871 累積和図−累積和手法を使用する品質管理とデータ分析のガイダンス
[6]
VAN NULAND,Y. ISO 9002 and circle technique,(ISO 9002 とサークル技法),Qual. Eng.,5,
1992,pp. 269-291
[7]
Guide to the expression of uncertainty in measurement (GUM):1993,計測における不確かさの表現
のガイド (BIPM; IEC,IFCC; ISO; IUPAC; IUPAP,OIML(1995年に修正再販)
[8]
JIS Z 8402-3 測定方法及び測定結果の精確さ(真度及び精度)−第3部:標準測定方法の中
間精度
[9]
JIS Z 8402-4 測定方法及び測定結果の精確さ(真度及び精度)−第4部:標準測定方法の真
度を求めるための基本的方法
[10]
JIS Z 8402-6 測定方法及び測定結果の精確さ(真度及び精度)−第6部:精確さに関する値
の実用的な使い方
[11]
JIS Q 17025 試験所及び校正機関の能力に関する一般要求事項
[12]
JIS Q 0043-2 試験所間比較による技能試験 第2部:試験所認定機関による技能試験スキー
ムの選定及び利用