JISZ8404-2:2008 測定の不確かさ－第２部：測定の不確かさの評価における繰返し測定及び枝分かれ実験の利用の指針

Z 8404-2：2008 (ISO/TS 21749：2005)

（1）

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

ページ

序文 ··································································································································· 1

1 適用範囲 ························································································································· 2

2 引用規格 ························································································································· 2

3 用語及び定義 ··················································································································· 3

4 不確かさの評価の統計的方法 ······························································································ 5

4.1 GUMのアプローチ ········································································································ 5

4.2 チェック用標準 ············································································································· 6

4.3 不確かさの評価のステップ······························································································· 7

4.4 この規格における例 ······································································································· 7

5 不確かさのタイプAの評価 ································································································ 8

5.1 一般 ···························································································································· 8

5.2 不確かさのタイプAの評価における時間の役割 ··································································· 9

5.3 測定方法 ····················································································································· 14

5.4 材料の不均質性 ············································································································ 16

5.5 測定の方法によるかたより······························································································ 18

6 不確かさのタイプBの評価 ······························································································· 25

7 不確かさの伝ぱ（播） ······································································································ 26

7.1 一般 ··························································································································· 26

7.2 一変数関数に関する公式 ································································································ 27

7.3 二変数関数に関する公式 ································································································ 27

8 事例−ゲージ調査からの不確かさのタイプAの評価 ······························································ 28

8.1 目的及び背景 ··············································································································· 28

8.2 データの収集及びチェック用標準····················································································· 29

8.3 併行精度，日間及び長時間効果の解析 ··············································································· 29

8.4 プローブのかたより ······································································································ 30

8.5 配線のかたより ············································································································ 32

8.6 不確かさの計算 ············································································································ 34

附属書A（規定）記号 ·········································································································· 36

参考文献 ···························································································································· 37

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

日本工業規格 JIS

Z 8404-2：2008

(ISO/TS 21749：2005)

測定の不確かさ−第2部：測定の不確かさの

評価における繰返し測定及び

枝分かれ実験の利用の指針

Measurement uncertainty−Part 2: Measurement uncertainty for metrological

applications−Repeated measurements and nested experiments

序文

この規格は，2005年に第1版として発行されたISO /TS 21749を基に，技術的内容及び対応国際規格の

構成を変更することなく作成した日本工業規格である。

なお，この規格で点線の下線を施してある参考事項は，対応国際規格にはない事項である。

試験，校正及びその他のための試験所は，測定結果及びそれに伴う不確かさを報告することが頻繁に求

められる。不確かさの評価は，時間及び資源が必要な継続的なプロセスである。特に，試験所が実施して

いる多くの試験及びその他の操作には複数の不確かさの要因が絡み合っている。“Guide to the expression of

uncertainty in measurement”（以下，GUMという。）に示す，不確かさの成分を合成するというアプローチ

に沿って，この規格では，個々の成分，とりわけタイプAの（統計的）評価に基づいた個々の成分を評価

するために，分散分析を利用することに焦点をあてている。

試験所は，解析において不確かさの成分への分解ができるように，適切な回数の測定を実施するという

実験の計画をまとめる。計画及び実施，また，その後の解析及び不確かさの評価という点から見ると，実

験には，特に統計的解析のようなデータ解析手法に習熟していることが求められる。したがって，試験所

の要員は，必要となる資源について知しつ（悉）し，必要なデータ収集及び解析を計画することが重要で

ある。

この規格では，タイプAの評価に基づく不確かさの成分を，測定機器，試験品目又はチェック用標準に

よる複数の測定結果の統計解析から評価できる。

この規格の一つの目的は，例えば，現在進行中の製造検査として実施する，試験品目の測定の不確かさ

の評価について指針を示すことである。このような不確かさには，測定プロセスそれ自体からの寄与分，

及び製造プロセスの変動からの寄与分が含まれる。両タイプの寄与分には，オペレータ，環境条件及びそ

の他の効果によるものが含まれる。測定プロセスの効果と製造変動の効果とを分離するために，チェック

用標準の測定によって測定プロセスそれ自体についてのデータを得ることができる。このような測定は，

試験品目について行った測定と名目上は同じである。特に，チェック用標準の測定は，時間に依存した効

果を明確にするために用いているので，このような効果を評価して，チェック用標準の測定のデータベー

スと対比させることができる。これらの量のベースラインを履歴データから確定してしまえば，これらの

標準は，プロセスのかたより及び長期的ドリフトを管理する上でも有用になる。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

箇条4では，GUMで推奨されているアプローチに含まれる不確かさ評価の統計的方法，チェック用標

準の使用，不確かさの評価のステップ，及びこの規格の事例について簡単に説明する。箇条5はこの規格

の主要部分であり，タイプAの評価を検討する。時間に依存した不確かさの要因の取扱いでは，分散分析

の枝分かれ計画を使用する。測定方法，材料の不均質性，測定の方法によるかたよりなどの不確かさの要

因と関連する不確かさ解析を検討する。箇条6では，完全性を確保するために，タイプB（非統計的）の

不確かさの評価について検討する。GUMにある不確かさの伝ぱ（播）則は広く使われている。箇条7で

は，この伝ぱ（播）則を一変数，二変数の幾つかの関数に適用した公式を提示する。箇条8では，一事例

として，ゲージ調査に対する不確かさのタイプAの評価について検討する。そこでは，様々な要因による

様々な不確かさの成分が得られる。附属書Aでは，この規格で使用する統計的記号の表を規定する。

適用範囲

この規格は，GUMに採用されているアプローチに従って，不確かさの成分を求め，合成する基本的な

手順を確立する。この基本手順には，個々の成分，特に不確かさのタイプAの評価として分類される，統

計的方法に基づく不確かさ成分を評価するために分散分析を使用する統計的枠組みが追加されている。完

全なものとするために，不確かさのタイプBの評価（非統計的方法）の短い記述も含めた。

この規格は，不確かさの成分が，繰返し測定，測定機器，試験項目又は検査用標準の統計解析から見積

もることができるような実験的状況について規定する。

この規格は，1段，2段又は3段の枝分かれ実験から不確かさを見積もる場合だけを規定する。より複雑

な実験的状況，例えば，測定者の影響と測定機器の影響との交互作用又は交差的な影響が存在するような

状況は取り扱わない。

この規格は，破壊測定，又は動的に変化するシステム（例えば，流体，電流又は電気通信システム）に

対する測定のように，繰返しができない測定には適用できない。また，標準物質（特に化学物質）の認証

及び“ひょう（秤）量法”として知られている方法で測定対象物（artefact）が比較されるような校正を，

特別の対象としているわけではない。標準物質の認証については，JIS Q 0035を参照。

共同実験の結果を利用できる場合の手法は，この規格の第1部に規定する。この規格の第1部とこの規

格との主な違いは，第1部が再現性データ（併行精度の影響が避けられない）に関するものであるのに対

して，この規格は併行精度データ及びデータ処理のための分散分析に焦点を絞っているところである。

この規格は，様々な測定，例えば，長さ，角度，電圧，抵抗，質量，密度などの測定に適用する。

注記この規格の対応国際規格及びその対応の程度を表す記号を，次に示す。

ISO /TS 21749:2005，Measurement uncertainty for metrological applications−Repeated measurements

and nested experiments (IDT)

なお，対応の程度を表す記号(IDT)は，ISO/IEC Guide 21に基づき，一致していることを示す。

引用規格

次に掲げる規格は，この規格に引用されることによって，この規格の規定の一部を構成する。これらの

引用規格は，その最新版（追補を含む。）を適用する。

JIS Q 0035 標準物質の認証−一般的及び統計学的原則

注記1 対応国際規格：ISO Guide 35，Certification of reference materials−General and statistical

principles（IDT）

注記2 ISO Guide 35は，対応国際規格では参考文献となっているが，規定事項として引用されて

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

いるため，引用規格に追加する。

JIS Z 8101-1 統計−用語と記号−第1部：確率及び一般統計用語

注記対応国際規格：ISO 3534-1:1993，Statistics−Vocabulary and symbols−Part 1: Probability and

general statistical terms（MOD）

JIS Z 8101-2 統計−用語と記号−第2部：統計的品質管理用語

注記対応国際規格：ISO 3534-2:1993，Statistics−Vocabulary and symbols−Part 2: Statistical quality

control（MOD）

JIS Z 8101-3 統計−用語と記号−第3部：実験計画法

注記対応国際規格：ISO 3534-3，Statistics−Vocabulary and symbols−Part 3: Design of experiments

（IDT）

JIS Z 8402-1 測定方法及び測定結果の精確さ（真度及び精度）−第1部：一般的な原理及び定義

注記対応国際規格：ISO 5725-1，Accuracy (trueness and precision) of measurement methods and results

−Part 1: General principles and definitions（IDT）

JIS Z 8402-2 測定方法及び測定結果の精確さ（真度及び精度）−第2部：標準測定方法の併行精度及

び再現精度を求めるための基本的方法

注記対応国際規格：ISO 5725-2，Accuracy (trueness and precision) of measurement methods and results

−Part 2: Basic method for the determination of repeatability and reproducibility of a standard

measurement method（IDT）

JIS Z 8402-3 測定方法及び測定結果の精確さ（真度及び精度）−第3部：標準測定方法の中間精度

注記対応国際規格：ISO 5725-3，Accuracy (trueness and precision) of measurement methods and results

−Part 3: Intermediate measures of the precision of a standard measurement method（IDT）

JIS Z 8402-4 測定方法及び測定結果の精確さ（真度及び精度）−第4部：標準測定方法の真度を求め

るための基本的方法

注記対応国際規格：ISO 5725-4，Accuracy (trueness and precision) of measurement methods and results

−Part 4: Basic methods for the determination of the trueness of a standard measurement method

（IDT）

JIS Z 8402-5 測定方法及び測定結果の精確さ（真度及び精度）−第5部：標準測定方法の精度を求め

るための代替法

注記対応国際規格：ISO 5725-5，Accuracy (trueness and precision) of measurement methods and results

−Part 5: Alternative methods for the determination of the precision of a standard measurement

method（IDT）

JIS Z 8402-6 測定方法及び測定結果の精確さ（真度及び精度）−第6部：精確さに関する値の実用的

な使い方

注記対応国際規格：ISO 5725-6，Accuracy (trueness and precision) of measurement methods and results

−Part 6: Use in practice of accuracy values（IDT）

Guide to the expression of uncertainty in measurement (GUM)，BIPM/IEC/IFCC/ISO/IUPAC/IUPAP/

OIML（計測における不確かさの表現のガイド）

用語及び定義

この規格で用いる主な用語及び定義は，JIS Z 8101-1，JIS Z 8101-2，JIS Z 8101-3及びJIS Z 8402（すべ

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

ての部）によるほか，次による。

3.1

測定量（measurand）

測定されるべき明確に定義された物理量で，基本的に固有の値によって特性付けられる量。

3.2

測定の不確かさ（uncertainty of measurement）

測定の結果に伴う，合理的に測定される量に結び付けられ得る値のばらつきを特徴付けるパラメータ又

はパラメータの推定値。

3.3

タイプAの評価（Type A evaluation）

統計的方法を用いた不確かさの評価方法。

3.4

タイプBの評価（Type B evaluation）

統計的方法以外の手段による不確かさの評価方法。

3.5

標準不確かさ（standard uncertainty）

単一の不確かさ成分について標準偏差で表される測定の結果の不確かさ。

注記この規格の第1部及びGUMでは，次のように定義している。

“標準偏差で表される，測定の結果の不確かさ”

3.6

合成標準不確かさ（combined standard uncertainty）

特定の測定又は一連の測定の結果の標準偏差であって，一つ以上の不確かさの成分を計算に入れたもの。

注記この規格の第1部及びGUMでは，次のように定義している。

“測定の結果が幾つかの測定量以外の量の値から求められるときの，測定の結果の標準不確

かさであり，これらの各量の変化に応じて測定結果がどれだけ変わるかによって重み付けした，

測定量以外の量の分散又は共分散の和の正の平方根に等しい。”

3.7

拡張不確かさ（expanded uncertainty）

合成標準不確かさに包含係数を乗じたもの。ただし，包含係数は，通常，合成標準不確かさの自由度及

び希望する包含率に応じて，t分布から選ばれた限界値である。

注記この規格の第1部及びGUMでは，次のように定義している。

“測定の結果について，合理的に測定量に結び付けられ得る値の分布の大部分を含むと期待

される区間を定める量。”

3.8

有効自由度（effective degrees of freedom）

二つ以上の変数成分で構成された標準偏差に対応する自由度。

注記有効自由度は，ウェルチ=サタスウェイト（Welch-Satterthwaite）の近似を用いて計算できる

（GUM，G.4参照）。

3.9

枝分かれ実験計画（nested design）

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

ある因子のすべての水準が，他のすべての因子の一つの水準だけに現れる実験の計画。

注記1 この定義は，JIS Z 8101-3から採用した。

注記2 “水準”の定義については，JIS Z 8101-3を参照。

3.10

固定効果（fixed effects）

因子がとり得る値の中から，実験に際し事前に設定した水準から生じる効果。

注記例えば，5名のオペレータの違いを評価する場合には，オペレータを因子とし5名のそれぞれ

を水準とする。各オペレータのかたより（各オペレータの効果）をα1，…，α5で表すと，この

かたよりは，各オペレータに固有であって，同じ実験を更に繰り返しても再現すると考えられ

る。このように効果が一定値で再現するものを固定効果（母数効果）という。オペレータの効

果を評価し，その原因を突き止め，標準化することによって，技能の向上を目的とする場合に

適している。

3.11

偶然効果（random effects）

各因子の水準において，因子がとり得る値の母集団からサンプリングした結果生じる効果。

注記例えば，5日にわたる実験で，実験日の影響を評価する場合には，実験日を因子とし5日のそ

れぞれを水準とする。各実験日の影響（効果）をβ1，…，β5で表すとする。これをかたよりと

して評価し，同じ実験を更に繰り返しても，実験日が異なり再現するとは考えられない。この

ように影響（効果）が再現せず，確率的変動として扱うことがふさわしいものを偶然効果（変

量効果）という。オペレータの効果についても，オペレータの集団の中からランダムに割り当

てられたオペレータを水準として，オペレータが異なることによって，ばらつきがどの程度増

大するのかを一般的に評価することを目的とする場合には，オペレータも偶然効果として扱う

ことができる。

3.12

バランス型枝分かれ計画（balanced nested design）

上位の因子内で水準数が一定の枝分かれ計画。

注記この定義はJIS Z 8101-3から採用した。

3.13

偶然誤差の平均平方（mean square for random errors）

誤差の二乗の和を対応する自由度で除したもの。

注記 “自由度”の定義については，JIS Z 8101-1を参照。

不確かさの評価の統計的方法

4.1

GUMのアプローチ

GUMは，測定結果がすべての認識された有意な系統的効果に対して補正されること，その結果が測定

量の最良の（又は少なくともかたよりのない）推定となること，及び測定システムの完全なモデルが存在

することを推奨している。このモデルは，一連の入力量（測定量はこれに依存する。）と測定量（出力量）

との関数関係を示すものである。不確かさの評価の目的は，測定量に合理的に結びつけられ得る値の分布

の大部分を包含すると期待できる間隔を決定することである。かたよりは正確に定量化できないので，測

定結果をかたよりに関して補正すると，更に補正をしたことによる不確かさをもつことになる。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

モデル化プロセスから始まる一般的アプローチは，次による。

注記このアプローチは，相互に独立している入力量に関係しており，また，相互に依存する入力量

に更に一般化できる（GUM，5.2参照）。

a) モデル入力量（影響量を含む。）をモデル出力量（測定量）に関連付けるための，測定プロセス又は測

定システムの数学的モデル（関数関係）を作成する。多くの場合，このモデルは，測定結果を計算す

るために使用する公式（一つ又は複数）であり，必要に応じて，不確定な効果，環境による効果及び

測定結果に影響を与えることのあるかたより補正のような，その他の効果で拡大される。

b) モデル中の入力量に，最良推定値及びこの標準不確かさ（標準偏差として表現した不確かさ）を割り

当てる。

c) 各入力量に起因する，測定結果の標準不確かさへの寄与分を評価する。これらの寄与分は，入力量に

かかわる偶然効果及び系統効果の両者の不確かさを考慮しなければならず，また，それ自体は，より

詳細な不確かさの評価を含んでいることがある。

d) 測定結果の（合成）標準不確かさを得るために，これらの標準不確かさを合成する。この不確かさの

評価は，GUMに従って，不確かさの伝ぱ（播）則を用いて行うか，又は不確かさの伝ぱ（播）則が

適用できない場合，若しくは適用できるかどうか分からない場合には，より一般的な解析的方法又は

数値的方法によって行う。

e) 適切な場合は，拡張不確かさと，それによって規定の信頼度における測定量に対する包含間隔を得る

ために，測定結果の標準不確かさとに包含係数を乗じる。GUMは，包含係数を計算するために使用

できるアプローチを示す。すべての入力量の標準不確かさに対する自由度が無限である場合，包含係

数は正規分布から求める。それ以外では，合成標準不確かさに対する（有効）自由度は，入力量の最

適推定の標準不確かさに対する自由度から，ウェルチ=サタスウェイト（Welch-Satterthwaite）の公式

を用いて推定する。

GUMは，標準不確かさの評価に，適切などのような方法を用いることも認めている。GUMは，不確か

さの評価方法を，併行観察結果の統計的処理によるタイプAの評価と，その他の手段によるタイプBの評

価とに区別している。合成標準不確かさの評価では，いずれのタイプの評価による不確かさも，分散（標

準不確かさの二乗）によって特徴付けて，同じ方法で処理することになっている。

この手順，及びその基礎となる付加的な仮定の詳細は，GUMに記載されている。

この規格の目的は，入力量の併行測定又は全測定操作による併行測定のいずれによって得られたかには

関係なく，上記b)を中心に，統計的手段による統計的不確かさの評価についての詳細を追加することであ

る。

この規格では，“測定対象物（artefact）”という用語を測定との関係においてしばしば用いる。この用語

を用いることによって，測定がバルク品目又は化学薬品などに対して行われるという一般的な説明になる。

4.2

チェック用標準

チェック用標準とは，次の特性をもつことが必要とされる標準である。

a) 定期的に測定できなければならない。

b) 生産品目に対して，組成及び形状が近似していなければならない。

c) 安定した人工物でなければならない。

d) 常に，測定プロセスで利用可能でなければならない。

理想的なチェック用標準は，標準がこれらの特性をもつことを条件として，該当する場合は生産品目か

らランダムに選択され，かつ，この目的のために確保されたものである。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

チェック用標準の使用例には，次のものが含まれる。

− 安定した測定対象物についての測定

− 校正実験から推定した，二つの参照標準の値の差

チェック用標準の測定値を解析する方法については，5.2.3で規定する。

この規格では，“チェック用標準”という用語を一般的な説明に用いる。例えば，バルク品目又は化学薬

品が使用されることもある。

4.3

不確かさの評価のステップ

4.3.1

不確かさの評価における第一歩は，試験品目について，測定結果を報告するための測定量を定義す

ることである。結果として生じる不確かさはこの定義によって左右されるため，測定量を明確に定義する

ように特に配慮することが望ましい。測定量の定義は，次のものが考えられる。

− ある瞬間における，空間のある1点における量

− ある瞬間における，特定の空間領域を平均した量

− ある期間全体にわたって平均した，空間のある1点における量

例えば，セラミック材料の試料の硬さに対応する測定量は，次の場合で（非常に）異なる。

a) 試料の特定の1点におけるもの

b) 試料全体にわたる平均とするもの

4.3.2

測定量の値が直接測定できる場合，標準不確かさの評価は，併行測定の数並びに併行測定を実施す

る環境条件及び作業上の条件によって左右される。また，参照標準に対する校正の不確かさのような，測

定を繰り返すために選択した条件では見つけることができないその他の不確かさの要因によっても左右さ

れる。他方，測定量の値が，直接測定することはできないが，間接的な量の測定から計算できる場合には，

様々な量を合成するためのモデル(又は関数関係)を定義しなければならない。この場合，測定量の値の標

準不確かさを評価するために，間接的な量の最適推定値の標準不確かさを評価する必要がある。

不確かさの評価で従うべきステップの概要は，次による。

a) タイプAの評価：

1) 出力量をYで表し，Yを繰返し測定できる場合は，次の偶然効果の分散成分の推定値を求めるため

に分散分析モデルを使用する。

− 試験品目に対する繰返し測定の結果のばらつき

− チェック用標準の測定のばらつき

− 実験計画に従って行った測定のばらつき

2) Yを直接繰返し測定できず，また，次のモデル

)

(

が知られていて，更に，入力量Xiを繰返し測定できる場合は，Xiの最適推定値xiの不確かさを評価

する。これによって，不確かさの伝ぱ（播）則を使用できる。

3) Y又はXiの測定を繰返しできない場合は，タイプBの評価を参照する。

b) タイプBの評価：各入力量の最適推定値の標準不確かさを評価する。

c) 測定結果の標準不確かさを得るために，タイプA及びタイプBの評価からの標準不確かさを合成する。

d) 拡張不確かさを計算する。

4.4

この規格における例

この規格にある例及び箇条8の詳細なケーススタディは，幾つかの不確かさの要因をもつ測定プロセス

の不確かさについて，その評価方法を説明することを目的としている。利用者は，これらの箇条で説明し

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

ている原則を，個別の用途に合わせて一般化することが望ましい。これらの例では，測定結果に対するか

たよりという形をとった，偶然効果及び系統効果の両方の効果を示す。ここでは，経時的に観察される不

確かさ，例えば，短期的な期間に対する不確かさ（併行精度），及び再現精度と同様に，日々の又は実験ご

との中間再現精度の方法に対する不確かさを定量化することに重点を置いている。利用者の目的のために

は，問題の測定プロセスにとって意味をなすような方法で定義することが望ましい。

不確かさの複数の要因を取り扱うための方策を明らかにするために，米国国立標準技術研究所（NIST）

の電気技術研究所からのデータを利用する。この測定値は，シリコンウエハの体積抵抗率（Ω・cm）であ

る。ウエハの表面のプローブによって抵抗を測定することが本質的に困難であること，及び測定量がASTM

試験方法で定義されていて，方法とは無関係に定義することができないという理由から，これらのデータ

が説明するために選ばれた。

実験の意図は，特殊な形で配線した4端子法を用いて認証を受けた，様々なレベルの抵抗率（Ω・cm）

におけるシリコンウエハの抵抗率測定の不確かさを評価することである。試験方法は，ASTM法F84であ

る。各ウエハについて報告されている抵抗率は，ウエハの中心部での6回の短期併行測定の平均値である。

不確かさのタイプAの評価

5.1

一般

5.1.1

一般的に，繰返しが可能な測定結果（GUM，3.1.4〜3.1.6参照）は，タイプAの評価に適したデー

タを提供できる。タイプAの評価は，例として，次の点に基づいて行うことができる。

− 結果を得るために必要な測定のプロセス又はそれに加えて行う，試験品目についての繰返し測定結果

− 実際の測定を行う前の，方法の妥当性評価時に行われる，適切な試験材料についての測定結果

− 適切とみなされる場合，測定方法の安定性をモニターするために一定期間にわたって繰返し測定され

た試験材料，すなわち，チェック用標準の測定結果

− 認証標準物質又は参照標準についての測定結果

− 影響する量の繰返しの観測及び識別（例えば，試験所内の環境条件の定期的又はランダムなモニタリ

ング，測定結果を計算するために使われる量の繰返し測定など）。

5.1.2

タイプAの評価は，偶然効果及び系統効果の双方に適用できる(GUM，3.2)。不確かさの評価が，

一連の測定結果の統計的解析に基づくものであることが唯一要求される。偶然効果と系統効果との区別は，

次のように行う。

− 偶然効果は，測定の単位（観察）ごとに変動するもので，補正を行わない。

− 系統効果は，短期間の幾つかの観察の間，基本的に一定であるとみなすことができるもので，少なく

とも理論的には，補正したり，結果から除くことができる。

系統効果と偶然効果との区別が困難な場合には，これらは関連する統計モデルの使用及び解釈の問題と

なる。一般的には，偶然効果と系統効果とを区別することはできない。

GUMでは，一般に，すべての系統効果を補正すること，すなわち，このような原因からの不確かさは

補正の不確かさだけとすることを推奨している。枝分かれ計画を用いた不確かさのタイプAの評価におけ

る時間の役割は5.2で規定する。測定の方法及び材料の不均質性による不確かさは，それぞれ5.3及び5.4

で検討する。測定の方法によるかたよりについての評価及び補正方法，並びにその不確かさの評価方法に

対する指針は，5.5で規定する。解析を行うに当たり，偶然効果と系統効果とのどちらが該当するかは，不

確かさの原因の報告値及び不確かさの内容への影響の仕方によって決まる。

あるタイプの測定機器について，そのタイプのすべての測定機器を代表するものとみなせるような機器

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

を数台もつ試験所を考えた場合，そのタイプの測定機器の中からランダムに選択して計測する場合の不確

かさをとりあげると，測定機器間の差は偶然効果と考えられる。

逆に，特定の1台（又は数台）の測定機器について不確かさを述べようとする場合，測定機器全体に対

する，その測定機器の系統効果が問題となる成分である。

5.2

不確かさのタイプAの評価における時間の役割

5.2.1

不確かさの時間依存性及び時間間隔の選択

多くの偶然効果は時間に依存し，しばしば環境変化を原因とする。次の三つのレベルの時間依存性が考

えられる。

a) 短期的変動（併行精度又は測定機器精度）

b) 中間的変動（日間の，オペレータ間の，又は機器間のもので，中間精度として知られる。）

c) 長期的変動［ラン間の変動，安定性（すべてのプロセスについて問題となるとはいえない。），又は中

間精度］

ここでの短期，長期の表現は，あくまで目安にすぎない。使用者は，その単位が分，時間又は日のいず

れであれ，その測定プロセスにとって重要な時間を定義することが必要である。

このアプローチをとる一つの理由は，現代の測定機器が短期的にはますます精度（併行測定）を上げて

いるものの，時間の経過とともに主に環境原因によって起こる変化は，測定プロセスにおける不確かさの

支配的原因となりうるからである。時間的に再現性がない測定結果については，不確かさを述べるのは適

切でないことがある。顧客は，測定が行われた日にち又は時節に関係なく，測定結果の不確かさを知る権

利をもつ。

多くの測定プロセスを説明するのには，2段階の時間的因子で十分である。新しい測定プロセス又は特

性が十分に理解されていないプロセスでは，3段階が必要になることがある。そのため3段枝分かれ計画

を検討するが，2段枝分かれ計画はその特別な場合に相当する。

4段階以上の枝分かれ計画は，この規格では検討しないが，ここで検討するアプローチの方法をそのよ

うな多段階計画まで拡張してもよい。JIS Z 8402-3を参照。

5.2.2

3段枝分かれ計画を用いた実験

5.2.2.1

経時的に現れるばらつきの原因の影響を調査する際，一般的には3段枝分かれ計画が望ましい。

データの収集及び解析は直接的に行い，通常は時間的因子を取り扱う場合には交互作用効果を推定する必

要はない。枝分かれ計画は，どの段階でも使用できる。不確かさの原因が十分に理解されておらず，また，

以前に調査したこともないような測定システムについては，3段が望ましい。

次に示す段階は，多くの測定システムの特性に基づくものであり，必要に応じて，特定の測定状況にあ

わせて適用する。

a) 段階1：測定の併行精度を得るために，短時間で行った測定

b) 段階2：日を変えて（又はその他の適切な時間経過後）行った測定

c) 段階3：月ごとに分けて行った一連の測定

これらの段階に関する記号の定義は，次による。

− 段階1：J (J > 1)一日の繰返し回数（併行条件での繰返し）

− 段階2：K (K > 1)一つのランの日数

− 段階3：L (L > 1)ランの回数

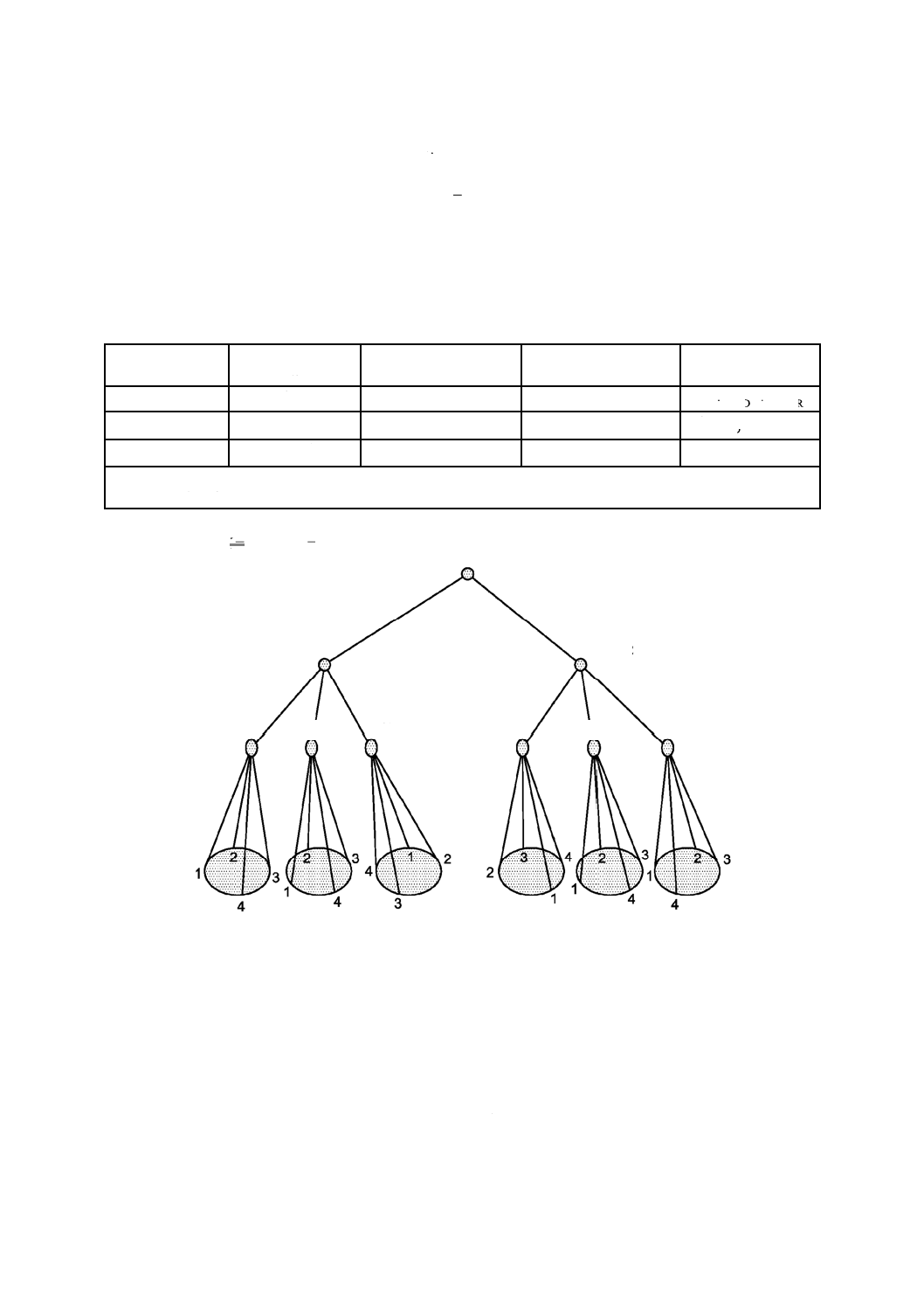
この基準によるデータの収集には，次のバランス型3段枝分かれ計画が望ましい。これは，測定プロセ

スにおける長期的変動を示すものである。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

lkj

ここで測定値Ylkj (l = 1，…，L； k = 1，...，K；j = 1，…，J )は，l番目のランでの，k番目の日の，j番

目の繰返しを表す。添字は，ラン，日及び繰返し中に変動する測定プロセスの偶然効果の項目を表す。こ

の実験の目的は，これらのばらつきの要因を定量化する分散成分を推定することにある。日及びランに対

する効果，δ及びγの分散成分をσD2及びσR2とし，測定誤差εの分散はσ2とする。これらの分散成分が，

標準不確かさを定める基礎となる。

表1−3段枝分かれ計画の分散分析表

要因

自由度

平方和

平均平方

平均平方の期待値

ラン

−

日（ラン内）

(−

D(R)

誤差

(−

変動の要因，平方和（SS）及び対応する自由度（ν）を，それぞれ，第1列，第3列及び第2列に示す。平方和
を対応する自由度で除した平均平方（MS）は，第4列に示してある。最終列は，平均平方の期待値である。

図1は，J = 4，K = 3及びL = 2の場合の概念図である。

図1−3段枝分かれ計画

5.2.2.2

類似する複数のゲージの値付けをしようとする場合には，この計画を，Q (Q > 1)のチェック用標

準（チェック用標準については，5.2.3参照）及びI (I > 1)のゲージについて繰り返すことができる。その

ような計画は，使いやすい又は計算しやすいという利点がある。特に，幾つかのチェック用標準について

情報が集められるので，各レベルでの繰返し回数を多くする必要はない。

測定は，1人のオペレータが行うことが望ましい。オペレータの違いが測定値に与える影響は，自動化

システムにおいては通常は考慮しなくてよい。ただし，線，端（エッジ），又はその他ものの形に関する判

断を伴う測定システムの場合は，オペレータ依存性が強くなる。オペレータ間で結果に相当な差が生じる

と考える理由がある場合は，計画の中の“ラン”を“オペレータ”に置き換えてもよい。同一の精度レベ

ラン1 ラン2

日1 日2 日3 日1 日2 日3

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

ルで測定を実施できるオペレータ群の中から，ランダムにL人の (L > 1)オペレータを選択する。（必要に

応じて，オペレータ間で精度比較ができることを検証するために，併行測定をするオペレータについて小

規模実験をする。）次に，指示どおり，データ収集及び解析をする。この場合，レベル3の標準偏差によっ

て，オペレータの効果を推定する。

各チェック用標準を測定するゲージについてはランダム化する。すなわち，最初のチェック用標準を選

択してゲージをランダム化し，第二のチェック用標準を選択してゲージをまたランダム化するというよう

に続ける。

チェック用標準及びゲージによる，J回の繰返しから得た各グループの平均及び標準偏差を求める。

この結果を，関連する環境要素の読取値及び重要な因子の特定とともに記録することが望ましい。こう

した情報を記録する方法としては，チェック用標準の測定ごとに，固定されたフィールド内の1行又は1

列情報をもつ一つのコンピュータファイルにまとめることが望ましい。表計算ソフトが，この目的に適し

ている。代表的な項目リストを，次に示す。

a) 年

b) 月

c) 日

d) オペレータ

e) 使用したチェック用標準

使用したゲージ

g) J回の繰返しの平均

h) J回の繰返しからの短期的標準偏差

自由度

環境要素の読取値（関連のある場合）

上のモデルから，自由度LK (J −1)の誤差の標準偏差を，確率的誤差に対する平均平方MSEを使って推

定し，次のように計算する。

(

)

(

∑

−

•

−

lkj

ただし，

∑

•

lkj

は，各グループにおけるJ回の繰返しの平均である。

自由度 L (K−1)の日の効果に対する平均平方MSD(R)は，次のように計算する。

(

D(R)

−

•

−

•

∑∑

ただし，

∑

•

•=

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

自由度 L−1のランの違いに対する平均平方MSRは，次のように計算する。

)

(

−

∑

•

ただし，

∑

•

•=

表1の分散分析表から，平方根記号の中の差が正の場合，日に対する標準偏差の推定量は，次のように

なる。

D(R)

−

また，ランに対する標準偏差の推定量は，次のようになる。

D(R)

−

負の場合は，

ˆσ若しくは

Rˆσはゼロ，又は両方をゼロとみなす。

2段枝分かれ計画では，測定プロセスの短期的及び日間変動についてデータを集めることもある。この

実験で収集したデータは，5.2.3でとりあげるチェック用標準で収集したものと似ている。チェック用標準

を複数使用する場合，“チェック用標準”の要因は3段枝分かれ実験の“ラン”の要因及びモデル並びに解

析が同じであるので，“チェック用標準”の要因は偶然要因とみなしてもよい。

5.2.3

二つのばらつきの段階を評価するためのチェック用標準

5.2.3.1

チェック用標準に関する手順

経時的な変化が現れるばらつき原因の影響を調査するためには，単一のチェック用標準に関する測定を

実施することが望ましい。データの収集及び解析は直接的に行い，時間に依存する誤差を扱う場合に交互

作用効果を推定することは一般に不要である。測定は二つの段階で行うが，多くの測定システムを特徴付

けるためには，これで十分である。次の段階は，多くの測定システムの特性に基づいているが，必要に応

じて，特定の測定状況に合わせることが望ましい。

− 段階1 測定値：ゲージの精度を推定するために短期間でとったもの

− 段階2 測定値：長期的変動を推定するために日を変えてとったもの

経時的にチェック用標準の測定をするスケジュール（1日1回，週2回，又はすべての測定条件のサン

プリングをするため適切とされる頻度）を決定して，それに従うことが望ましい。チェック用標準の測定

は，試験品目について報告されている値と同じようにすることが望ましい。例えば，報告値が相互に5分

間の間隔をおいて行った2回の繰返しの平均である場合，チェック用標準値は，同じ方法で実施した2回

の測定の平均であることが望ましい。この規則に対する例外が，1日最低J = 2回以上の繰返しが必要な場

合である。こうした冗長性がなければ，測定システムの短期間の精度を確認できない。

5.2.3.2

モデル

ここで検討する不確かさの要因を説明する統計的モデルは，バランス型2段枝分かれ計画である。

試験品目についての測定値はYkj (k = 1，…，K；j = 1，…，J )で表し，最初の添字は日を，また，2番目

の添字は繰返しを示す。添字付きの項は，それぞれ日，短い間隔で変動する測定プロセスの偶然誤差を表

している。実験の目的は，これら変動の要因を定量化する分散成分を推定することである。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

5.2.3.3

実験の実施の間隔

5.2.3.3で規定する二つの段階は，多くの測定システムの特性に基づくものであり，また，必要に応じて，

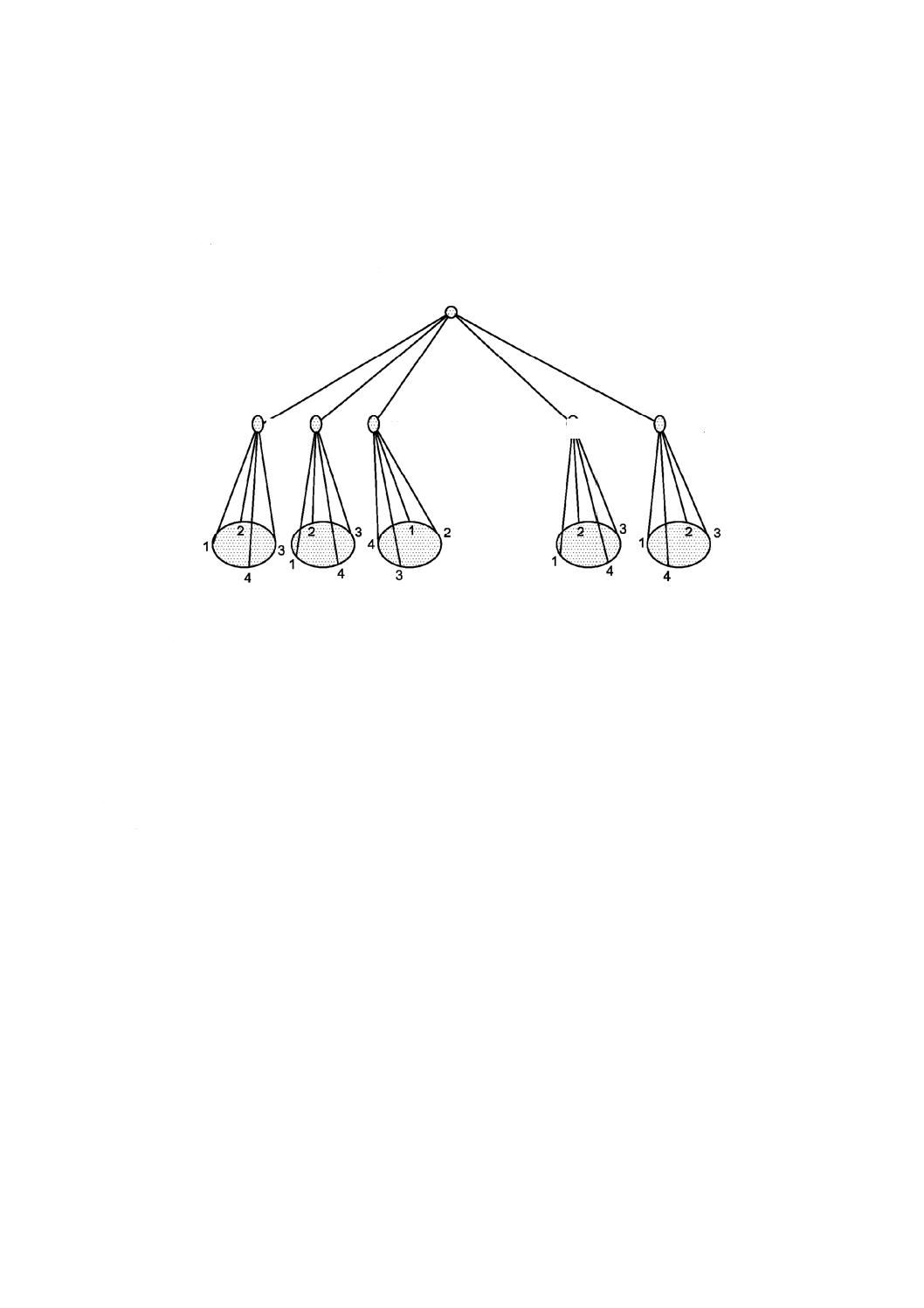
特定の測定状況に合わせることができる。代表的な計画例を図2に示す。各段階が次に表されるようなJ =

4回／日の繰返しの例である。

− 段階1：J (J > 1)回の短期繰返しによって，ゲージ精度をとらえる

− 段階2：K (K > 1)日（又はその他の適切な時間経過）

図2−2段枝分かれ計画

5.2.3.4

データ収集

図2に示すとおりに，繰返し測定が日間で行われるように，全体が正確に枝分かれ計画であることが重

要である。J回の繰返しの各グループについて，平均偏差及び標準偏差を，次の情報とともに記録すれば

十分である。

a) 年

b) 月

c) 日

d) オペレータ

e) 使用したチェック用標準

使用したゲージ

g) J回の繰返しの平均

h) J回の繰返しの併行標準偏差

自由度

環境要素の読取値（関連のある場合）

この2段枝分かれ計画の場合，表2の分散分析表を3段枝分かれ計画の分散分析表から求めることがで

きる。

日1 日2 日3 … 日K-1 日K

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表2−2段枝分かれ計画の分散分析表

原因

自由度

平方和

平均平方

平均平方の期待値

日

K−1

SSD

MSD

誤差

K(J−1)

SSE

MSE

自由度がK (J−1)である誤差の標準偏差は，次の式で計算する。

)

(

)

(

•

−

∑

ここに，

∑

•=

自由度がK−1である，日の効果に対する平均平方MSDは，次のようになる。

−

=∑

•

)

(

ここに，

∑

•

•=

平方根記号の中の差が正の場合，日間のばらつきを説明する標準偏差は，次のようになる。

MS−

負の場合，

σˆをゼロとする。

ここで対象としているような，従来から使われている推定量を使用する場合，分散成分の推定値がマイ

ナスになることがある。その他の推定量で負にならないものがあり，適切ならばその推定量を用いてもよ

い。

5.3

測定方法

5.3.1

不確かさのその他の要因

試験品目の測定は，通常，1日のうちに，一人のオペレータが，一つの測定機器などを用いて行う。不

確かさを用いて，試験所でのすべての測定の特性化をしようとする場合は，次の項目による違いを考慮に

入れることが望ましい。

− 測定機器

− オペレータ

− 形状

− その他

多くの場合，試験所における制御できない環境条件の影響は，一定期間にわたって求めた検査基準デー

タから推定できる。その不確かさの成分を計算する方法は，この規格の別の箇所で規定している。この章

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

では，特定の測定のため選んだオペレータ又は測定機器のような，制御可能な因子から生じた不確かさを

取り上げる。

なお，オペレータについては，時間依存タイプの実験又は測定方法に基づいて，1度だけ調査すること

が望ましい。十分に維持管理された試験所内における違いの要因例には，次のものがある。

− 測定機器を参照標準に対して直接校正できない，シリコンのシート抵抗のような誘導単位の測定にお

ける，測定機器間の違い

− 自動化されておらず，かつ，オペレータの見方に大きく依存する光学的測定における，オペレータ間

の違い

− 測定機器の幾何学的又は電気的な方法の違い

校正された測定機器は，校正の不確かさがタイプBの評価によって報告されることが多いため，通常は

この分類に入らず，試験所内の測定機器は校正の不確かさの範囲内で一致することが望ましい。定義され

た単位に対してその応答が直接校正されない測定機器は，タイプAの評価を受けることになる。特定のタ

イプの測定機器を用いる試験手順又は標準作業によって測定が規定されている状況にも，これを適用する。

ただし，例えば，分析化学におけるマトリックス効果のように，一部の系統効果は校正によって排除で

きないので，注意することが望ましい。

5.3.2

不確かさの背景の重要性

5.3.1の最初の部分で示す違いは，ランダムな差か，又はかたよりによる差として処理する。このアプロ

ーチは，主として，不確かさを報告する背景に依存している。例えば，測定機器の影響が重要な場合，一

つのアプローチは，試験所内の測定機器をいわば同一タイプの測定機器の無作為な試料としてみなし，測

定を行う特定の測定機器にかかわらず，すべての結果に適用する不確かさを見積もる。この場合，5.2.3の

2段枝分かれ計画を適用するが，ここで，第二の段階は，ランダムに選ばれた測定機器の影響である。も

う一つのアプローチは，特定の測定機器を用いた結果に適用する不確かさを評価することで，これは5.5

で系統誤差又はかたよりの解析としている。

次に，一つの要因に対する不確かさを評価するために，変量モデル二元配置計画を用いた簡単なアプロ

ーチを示す。

5.3.3

データの収集及び分散成分の計算

測定プロセスの測定装置による不確かさを評価するために，利用できる測定機器の中からI (I > 1)台の測

定機器を無作為に選ぶ。各測定機器について，Q (Q > 1)個の測定対象物に関する測定を行う。I×Qの測定

値が与えられると，測定機器間の差を示す標準偏差は，次のように各測定機器の平均値から計算され，自

由度はI−1となる。

)

(

inst

−

=∑

•

ここで，i番目の測定機器については，次のように表す。

∑

•=

，

∑

•

••=

5.3.4

変量効果の解析例

表3に，Q = 5のウエハ（138番，139番，140番，141番，142番）について，5個のプローブNo.（1，

281，283，2062，2362）を用いて得た抵抗率測定値（Ω・cm）の2元配置表を示す。5.5では，同じデータ

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

について，プローブNo. 2362のかたよりを解析する。それぞれのプローブの測定対象物にわたる平均値を

示す。プローブの（抵抗率測定値の平均値の）標準偏差は，自由度4で0.021 9 Ω・cmとなる。したがっ

て，Sinst = 0.021 9となる。

表3−5個のプローブを使用した5個のウエハの抵抗率測定値

単位 Ω・cm

プローブNo.

ウエハ識別番号

平均値

138

139

140

141

142

95.154 8

99.311 8

96.101 8

101.124 8

94.259 3

97.190 5

281

95.140 8

99.354 8

96.080 5

101.074 7

94.290 7

97.188 3

283

95.149 3

99.321 1

96.041 7

101.110 0

94.248 7

97.174 2

2062

95.112 5

99.283 1

96.049 2

101.057 4

94.252 0

97.150 8

2362

95.092 8

99.306 0

96.035 7

101.060 2

94.214 8

97.141 9

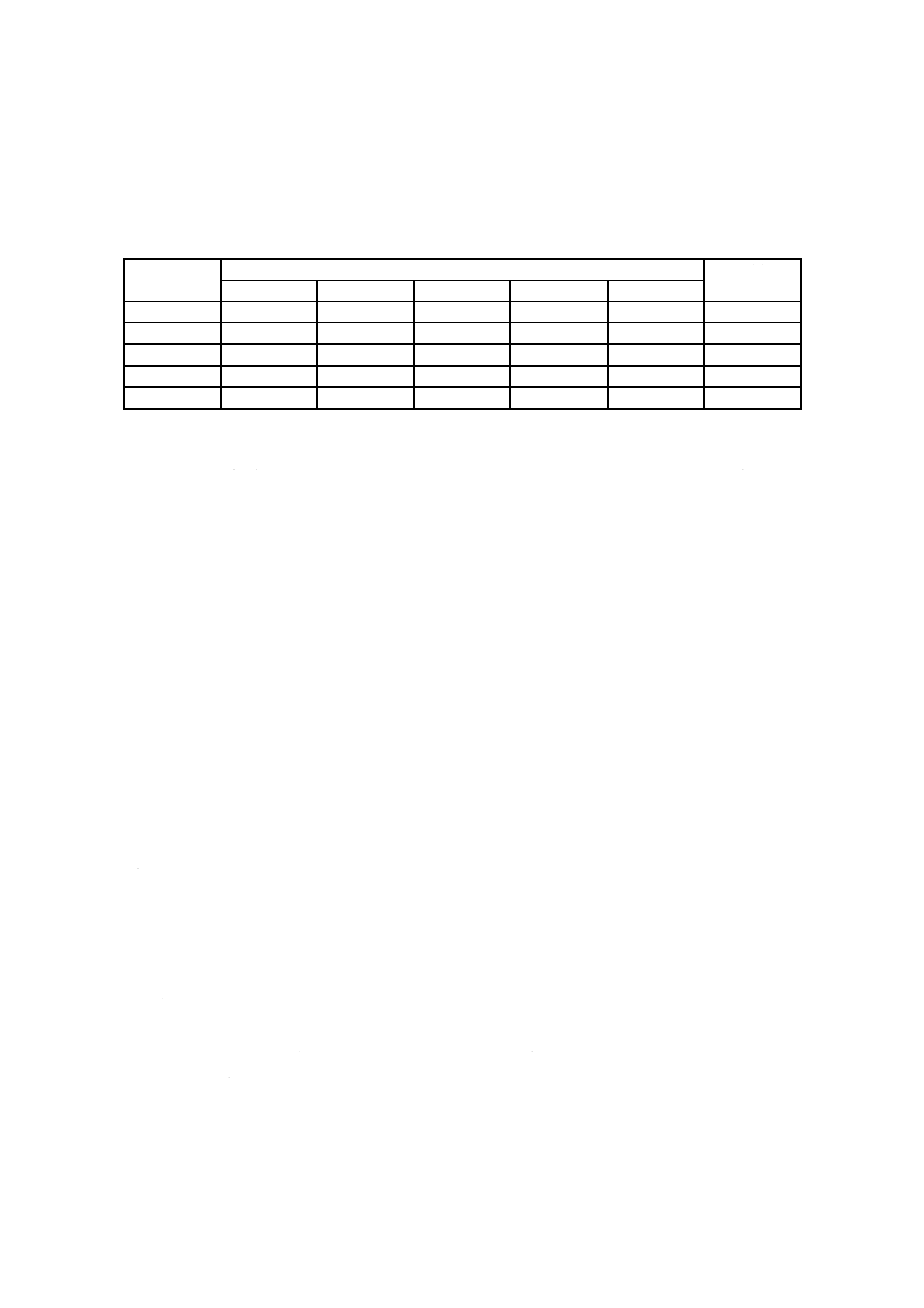
グラフ解析のために，測定値と各プローブの平均値との差を，各プローブについて，ウエハに対してプ

ロットし，プローブは個別のプロット記号によって表示した。このプロットでは，一部の測定機器が他の

測定機器に比べて常に読取値が高く又は低くなっているか，又はこの様子がプローブ全体を通じて一貫し

ているかを調べる。図3に示すグラフは表4（5.5.2.2参照）からとったもので，プローブ間に差があるこ

とを示しており，例えば，プローブNo.2062及びNo.2362は，他のプローブに比べて読取値が常に低くな

っている。

5.4

材料の不均質性

5.4.1

不均質性によって生じる問題点

人工物，電気素子，化学物質などは，特性化された量に比べて不均質となることがある。不均質性は，

次のような場合に不確かさの評価における一つの因子となる。

a) 人工物が単一の値によって特性付けられるが，その表面全体などにわたって不均質である場合

b) 一つの品目ロットに対して，ロットからの少数の試料で単一の値が割り当てられているが，そのロッ

トが試料ごとに不均質である場合

この状況は，不均質性が不確かさの主要な要因となることがある点で不都合である。測定プロセス自体

が非常に精密で，統計的に管理されている場合であっても，合成された不確かさが，材料の不均質性のた

めに，実際の目的には許容できないことがある。標準物質の均質性試験については，JIS Q 0035で規定し

ている。

5.4.2

ランダムな不均質性に関する方針

ランダムな不均質性は，偶然効果を定量化するための統計的方法を用いて評価する。不均質性の例とし

ては，目的の同位体に関して十分に均質化できない化学標準物質をあげることができる。同位体比は，ロ

ットから無作為に抽出した数本のボトルについて測定して求めなければならない。

5.4.3

データ収集及び不均質性の成分の計算

不均質性が測定結果に与える影響を特定し，かつ，定量化するための簡単な方法が，バランス型2段枝

分かれ計画である。K (K > 1)個の試験品目をロットから任意に抽出し，また，J (J > 1)回の測定を各試験品

について行う。測定値は，次のように表記される。

段階2の試験品目に関しては添字k = 1，…，Kを，また，段階1の試験品目内での測定の繰返しはj = 1，

…，Jとする。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

試験品目の不均質性による分散成分として定義されている，（試験品目間の）均質性の分散は，分散分析

の手法を用いて，5.2.3のように計算する，ここで，

∑∑

∑

•

−

item

2inh

)

(

)

(

ここに，

;

1∑

•=

;

1∑

•

••=

MSitemは，試験品目による平均平方である。

S 2inhは，材料の不均質性又は試験品目による分散成分の推定量である。

S 2inhが負の値の場合，不均質性の影響は統計的にゼロに等しいものとみなされ，不確かさにも寄与しな

い。すなわち，不均質性による不確かさは，次のように示すことができる。

)0,

(

max

inh

5.4.4

不均質性による不確かさの評価

不確かさの評価方法は，測定結果の用い方に依存する。通常，大きなバッチからの幾つかの試験品目に

ついて平均値を求め，その平均値をバッチ内の各試験品目に付与する場合に，不均質性は重要な意味をも

つ。測定結果がK個の異なる試験品目からの結果の平均として計算したものである場合，不均質性から生

じる平均値の標準不確かさ成分uinhは，Sinhから，次の式によって計算する。

max

inh

しかし，測定結果が，K個の異なった試験品目のデータの平均値として計算されたものであり，かつ，

バッチの残りの各品目それぞれに適用されるものである場合，バッチの残りの各品目それぞれに対する予

測間隔の不均質性から生じる標準不確かさ成分uinhは，予測区間（参考資料[5]参照）に基づいており，次

の式によって求める。

max

inh

5.4.5

系統的不均質性についての方針

系統的不均質性については，アプローチが多少異なる。例えば，粗さは，特定の粗さプロフィールをも

つように調製された50 mm平方の金属片の表面全体にわたって，系統的に変動する。認証する試験所は，

試験片上の数箇所で測定できるが，粗さを試験片上の位置の関数として特性化できる場合を除き，不均質

性を不確かさの要因として評価することが必要である。

こうした状況では，一つの方針として，試験片の表面全体について行った測定の平均として報告値を計

算し，また，平均からの外れとして不確かさを評価することが考えられる。不確かさの成分は，GUMで

示す不確かさのタイプBの評価の幾つかの方法のうちの一つで評価できる。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

5.5

測定の方法によるかたより

5.5.1

一般

統計的には，パラメータθを推定するために，推定量θˆのかたよりをθˆの予測値と真値θとの差として

定義する。すなわち，

θ−

]ˆ[

となる。真値θは未知なので，bも未知である。bの推定値が利用でき

れば，これを補正値として，bˆで表記する。補正は，基準値又はある種の平均値に関するものである。1

組の補正値，

ˆ,

,ˆ1Κ

が与えられていれば，推定量のかたよりを補正の平均値で次のように推定できる。

∑

補正値をランダムな値として取り扱う場合，補正値に関して正規分布のような確率分布を仮定できる。

補正値がゼロを中心としてまとまっている場合，補正値の確率分布の平均値が0であると仮定でき，こ

れを“ゼロ”補正と呼ぶことがある。この場合，θˆはθの，不偏推定量である。補正値が正規分布してい

るか，又は多数の補正値を利用できる場合，かたよりの不確かさは，補正値の試料平均の標準偏差によっ

て推定できる。分布についてあまり情報がない場合は，補正値

}

,ˆ

{

が，−aと aとの間で一様分

布していると仮定できる。この場合に，かたよりは0と推定される。量aは，次の式によって推定する。

−

}

min{

}

max{

かたよりの推定量bˆの標準偏差は，次の式によって推定する。

}

min{

}

max{

(

−

この規格において，計量学的に検討するかたよりの原因は，特定の測定方法を対象としている。試験品

目の測定は，通常，一人のオペレータが，1台の測定機器を用いて，同一日に行う。不確かさが，一つの

特定の方法における測定に関して用いられる場合であっても，次の要因に起因する有意差を考慮に入れる

必要がある。

a) 測定機器

b) オペレータ

c) 形状

d) その他

校正済みの測定機器は，校正の不確かさがタイプBの評価によって報告されることが多いので，この対

象には入らない。また，試験所内の測定機器は校正不確かさの範囲内で合致することが望ましい。定義さ

れた単位に対して応答が直接校正されていない測定機器は，タイプAの評価を受けたほうがよい。これは，

測定が特定の形式の測定機器を使用する試験手順又は標準作業によって定義されている状況である。

一つの方法による測定だけ，例えば，特定の一台の測定機器を用いる測定だけを検討する場合，又は不

確かさをより小さくする必要がある場合，例えば，測定機器間の差が問題となる場合，これらの場合には

測定機器をかたよりとして扱う。こうした状況では，特定の測定機器によるすべての測定値をその測定機

器に対する平均を基準として補正し，かつ，補正については不確かさのタイプAの評価をすることが一つ

の考え方である。この考え方は，試験所の測定機器が特定の形式のすべての測定機器からのランダムサン

プルである，という前提に基づいている。

しかしながら，例えば，二つの測定機器との間の比較しかできず，また，いずれも“かたよっていない”

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

かどうかが未知である場合を考えてみる。この状況では，平均が必ずしもかたよりのない結果をもたらす

とは限らないので，異なった考え方をする必要がある。測定機器間に有意な差がある場合（これは検定す

ることが望ましい。），ゼロ補正を適用して，補正による不確かさのタイプAの評価をすることが望ましい。

上記の検討は，かたよりについては考え得る状況が数多く存在すること，また，これらをケースバイケ

ースで処理することが望ましいことを指摘している。次の場合は，実験計画が必要である。

− データの収集

− かたよりの有無についての検定（図式的又は統計的）

− かたよりの推定

− 有意なかたよりによる不確かさの評価

この規格では，一般性を失うことなく，測定機器を唯一のかたよりの原因としている。まず，一つの測

定機器に対して測定モデルが一つある状況を考える。Y1，…，Ynを，単一の測定機器に基づく測定量の真

値θの独立した測定値であるとする。この測定機器を用いた多数の独立した測定値の平均を，μで表す。

したがって，

=μ

ここに，e1，….，enは，平均ゼロ及び分散σ 2で互いに独立な偶然誤差と仮定する。

θを推定するために，試料平均

∑

1を用いて，その平均値をその測定機器の結果として報告する。θ

の測定でYを用いることによって生じる補正又は誤差は，次のように分解できる。

)

(

−

ここに，

∑

また，かたよりは，

μ−

すなわち，

=θ

eという項はランダムな要素であり，bは系統的要素又は測定機器のかたよりの要素である。ランダム

な要素eの不確かさは，通常，正規分布を仮定して，u (e) = S/nで推定される。ここに，Sは Y 1，…，

Ynの試料標準偏差である。bの推定量であるbˆの不確かさは，科学的判断（不確かさのタイプBの評価）

又は統計的方法（不確かさのタイプAの評価）に基づいて評価する。単一測定機器の場合，bˆを平均がゼ

ロの分布を用いて，bˆの不確かさを定量化するのが便利である。bˆの平均が既知の量bであると考えられ

る場合は，各測定値Yiを推定量bによって補正してもよい。すなわち，YiをYi−bに置き換え，bˆがゼロ

に等しい平均をもつという仮定が制約条件とならないようにする。bの分布の形状は，正規分布又は一様

分布，若しくはその他の適切な分布をするとしてもよい。ここに，θの推定値としてのYの合成不確かさ

を，次の式によって計算する。

)

(

ここに，ubは，タイプA及び／又はタイプBの評価に基づいたbの不確かさである。これに対応する自

由度は，ウェルチ=サタスウェイト（Welch-Satterthwaite）の式を使って計算する。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

次にK個の測定機器で測定が行われる場合を考える。Yki (k = 1，…，K； i = 1，….，n)は，k番目の測

定機器を用いたi番目の独立な測定値である。対応する統計的モデルは，次のようになる。

=θ

ここに，bkは，k (k = 1，…，K )番目の測定機器に対応するかたよりであり，ekiは，偶然誤差である。

目的は，bk及びこの不確かさを推定することである。問題の解決策は，bkに関する仮定に依存し，5.5.2及

び5.5.3で検討している。5.5.4では，データが少ない場合のかたよりについて簡単に検討している。

5.5.2

一貫したかたより

5.5.2.1

一般

かたよりは，一貫したもの又は一貫しないものとして処理できる。かたよりが有意であり，かつ経時的

に安定であり，更に特定の測定機器について同一の大きさをもつ場合は，これを一貫したかたよりと呼び，

これが，繰返し実験によって確実に推定できる場合は補正することが望ましい。この場合，測定機器によ

るかたよりの程度又は大きさが，対象材料のすべてについて本質的に同じであると仮定する。

K個の測定機器を用い，n個の測定対象物について次の測定をすると仮定すると，

)

;

(

Yki

5.5.1にあげる統計的モデルは，次のようになる。

=θ

ここに，θは測定量Yの値，bkはk番目の測定機器のかたより，そしてekiは偶然誤差である。かたより

bkはランダムではなく一定の値とする。上記のモデル及び ∑

= 0という仮定から，

•

=θ

ここに，

∑

•=

i番目の測定対象物の場合，θは，

Y•で推定でき，また，k番目の測定機器によるi番目の測定対象物の

補正は，bˆki = Yki ‒

Y•となる。ここに，k番目の測定機器によるi番目の測定対象物の測定値は，K個のす

べての測定機器に対する平均によって補正する。上記のモデルから，k番目の測定機器に対するかたより

であるbkは，補正値の平均によって推定する。

)

(

)

(

••

•

−

∑

ここに，

∑

•

••=

k番目の測定機器による測定値に適用する補正値は，次の式による。

measured

corrected

−

k番目の測定機器に対するかたよりの不確かさ（又は補正の平均値の不確かさ）は，次の式による。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

()

(

)

(

)

∑

•

−

用途によっては，かたよりが有意なものかどうかを検定するために，統計的検定を行ってもよい。

5.5.2.2

一貫したかたよりの例

この例では，1台の計測機器で測定する例を検討しており，また，報告値は，この計測機器によるかた

よりについて補正される。任意の測定機器で測定する場合には，偶然効果の分析として取り扱われる。

表4においては，各ウエハに対する平均を各測定値から差し引いた。抵抗率測定（Ω・cm）は，5個の

シリコンウエハ（試験品目）のそれぞれについて，5個のプローブ（計測機器）を用いて実施した。表に

示す補正値は，各プローブの，他のプローブに対する差を表す，すなわち，k番目のプローブでi番目のウ
エハの場合，bˆki = Yki ‒

Y•となる。プローブNo.2362に対する値bˆ5i (i = 1，…，5)は不変であり，また，5

個のウエハでマイナスになっている。

表4−プローブ及びシリコンウエハに対する補正値(ki

bˆ)

単位 Ω・cm

プローブ

No.

プローブ
識別文字

ウエハ識別番号

138

139

140

141

142

0.024 76

−0.003 56

0.040 02

0.039 38

0.006 20

281

0.010 76

0.039 44

0.018 71

−0.010 72

0.037 61

283

0.019 26

0.005 74

−0.020 08

0.024 58

−0.004 39

2062

−0.017 54

−0.032 26

−0.012 58

−0.028 02

−0.001 10

2362

−0.037 25

−0.009 36

−0.026 08

−0.025 22

−0.038 30

プローブNo.2362の場合，

− かたよりは，

027

Ω

−

=∑

である。

− 補正値の標準偏差は，すべてのiに対して

011

5ˆ=

である。

− かたよりの標準偏差bˆ5（又は平均補正値）は，

005

011

5ˆ

に等しい。

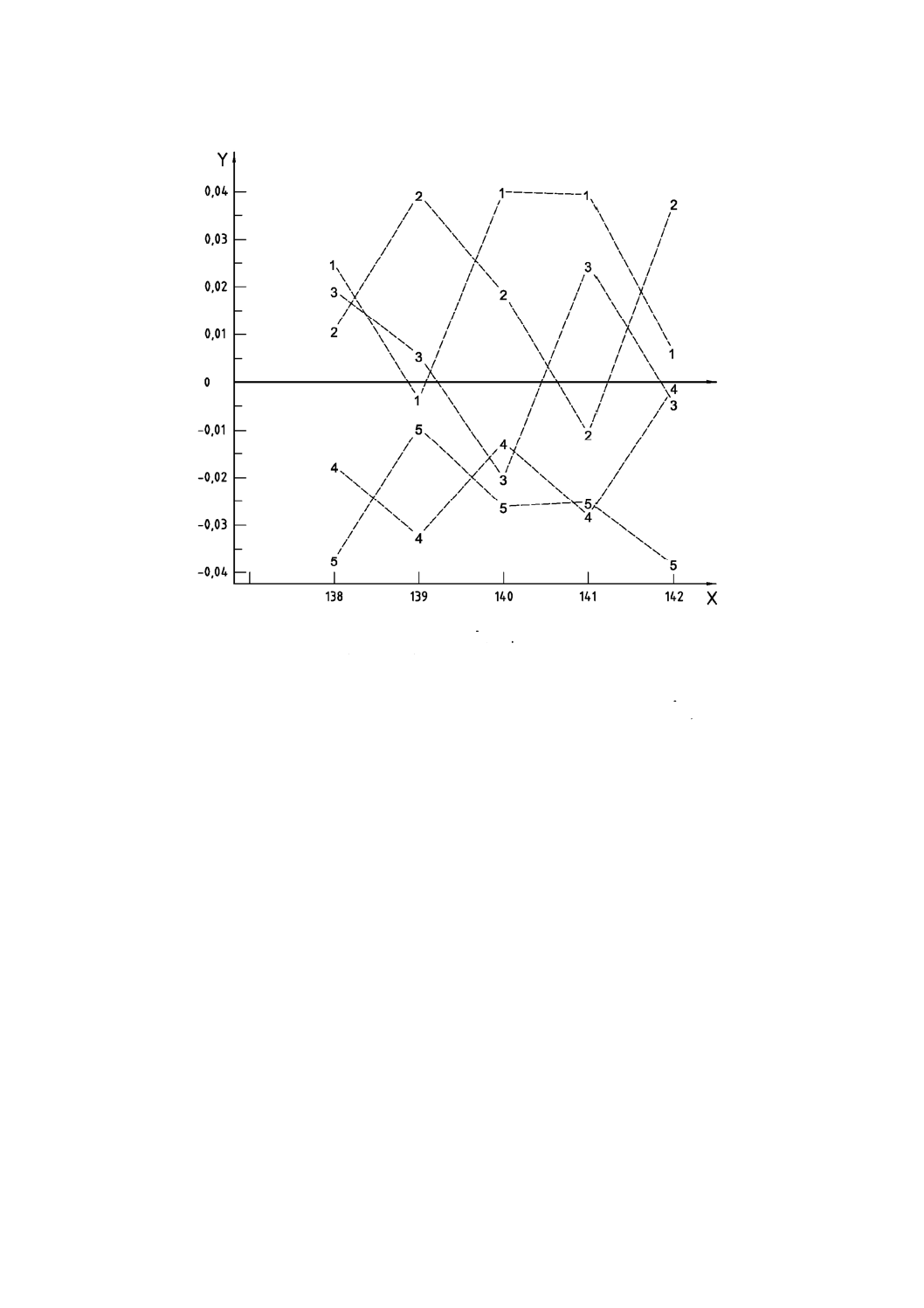
測定値と平均との間の差［すなわち，補正値(bˆki)］を，図3でプローブ識別文字によって示された各プ

ローブに対するウエハ識別番号を基準にプロットする。このグラフから，この測定プロセスで対象とする

計測機器であるプローブNo.2362（グラフ上の識別文字は5号）は，他のプローブと比較して，読取値が

常に低くなっていることが分かる。この様子は，間に2か月の期間をおいた2回のランでも一貫している。

プローブNo.2362には有意で一貫したかたよりがあるので，この計測機器（プローブ）による測定値は，

他の計測機器に対する平均かたよりによって補正することが望ましい。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

X軸：ウエハ識別番号

Y軸：

Ω

1，….，5

プローブの識別文字（表4参照）

注記この規格の図では対応国際規格に合わせて，小数点は“,”を用いた。

図3−シリコンウエハの識別番号に対してプロットした補正値(ki

bˆ)

5.5.3

一貫しないかたより

5.5.3.1

一般

かたよりが特定の計測機器，オペレータ又は測定方法に対して明らかにランダムな性質をもっている場

合，一貫しないかたよりと呼ぶ。かたよりの平均をゼロとすることができるが，それによって一般性を失

うことはない。ゼロでなければ，かたよりの推定値を測定値から差し引いて補正できる。この場合，かた

よりは経時的に符号又は大きさを変える。したがって，“ゼロ”補正を仮定できる。かたよりの不確かさは，

5.5.1の初めのところで検討したように，補正値の分布について，例えば，正規分布か又は一様分布なのか

を知ることで決まる。5.5.3.2に，“ゼロ”補正の例をあげる。その他のタイプの一貫しないかたよりを，

5.5.4に規定する。

5.5.3.2

一貫しないかたよりの例

5個のシリコンウエハ（試験品目）について，5個のプローブ（計測機器）を用いて抵抗率測定結果を得

る。表5は，測定対象物が5.5.2に示すすべてのプローブに基づいて計算した1 Ω･cmウエハの場合，ここ

で検討対象となるプローブNo.283の補正値又はかたよりを示す。2回のランの間に2か月間が経過してい

るが，平均補正値は，ラン1の場合はプラス，また，ラン2の場合はマイナスとなった。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表5−プローブNo.283のかたより

単位 Ω･cm

ウエハ識別番号

ラン1

ラン2

0.000 034 0

−0.000 184 1

−0.000 100 0

0.000 086 1

0.000 018 1

0.000 078 1

131

−0.000 070 1

0.000 158 0

208

−0.000 024 0

0.000 187 9

平均

−0.000 028 4

0.000 065 2

二つのランでの五つの補正値｛ki

bˆ，i = 1，2，3，4，5｝のそれぞれが正規分布していると仮定し，二つ

のランの平均値の差の検定（t検定）を行ったが，ラン1とラン2の平均値が同じであるという仮説が棄

却されなかった。そこで，両方のランの補正値を一緒にまとめると，自由度9のt値 = 0.501 6となり，有

意水準5 ％では平均値が0であるという仮説も棄却されない。プローブNo.283のかたよりの推定値は，

0.000 0184 Ω･cmで，プローブNo.283のかたよりの標準偏差は

283

ˆb

＝0.000 036 7 Ω･cmとなる。もう一つ

の方法として，補正値が±aの限度内のどこかに入るとする安全側の仮定がされ，このとき，5.5.1の初め
の公式を用いて，aの推定値a) = 0.000 227 3を得る。この場合，プローブNo.283のかたよりの推定値はゼ

ロになり，このかたよりの推定値の標準偏差は，次のようになる。

{

}

{

}

[

]

042

000

184

000

(

187

000

min

max

283

ˆ283

･

Ω

−

5.5.4

データが少ない場合のかたより

5.5.4.1

一般

この箇条では，現実にかたよりが存在するが，データが少なすぎるために，信頼性のあるかたよりの大

きさの推定ができない場合の取扱い方法の概要を示す。例えば，考え得る多くの測定プロセス方法のうち

の二つの差の検定では，補正を可能にするほど十分な信頼性をもったかたより推定値を導くことができず，

むしろ，測定プロセスに関わる問題点が明らかになる。このかたよりが有意の場合，これが一貫したかた

よりか又は一貫しないかたよりかによって戦略が決まる。

5.5.4.2

データが少ない場合のかたよりの例

単一ゲージの場合の配線設定の実験を，一例としてあげる。シリコンウエハの抵抗率を測定するための

4端子法による計測では，幾つかの方法で配線できる。ゲージ調査の間にすべての配線方法を試験するこ

とはできないので，潜在的問題点を特定する方法として，2種類の方法だけで測定を行った。

プローブNo.2062を2種類の方法で配線して，5個のウエハについて6日間（ウエハ39については2日

目を除く。）の測定を行った。同一の日に，2種類の方法で測定した測定値の差を補正値として扱い，また，

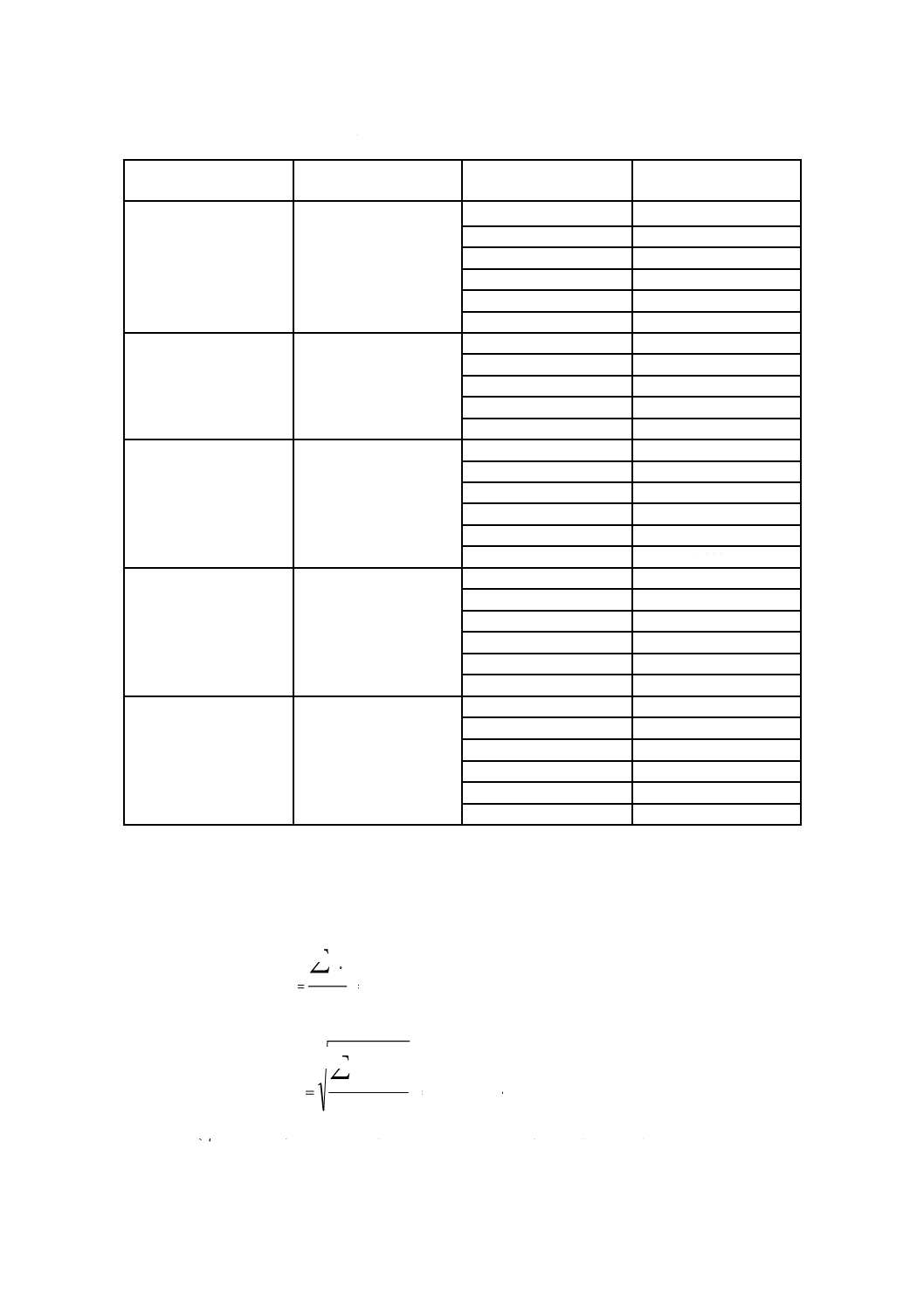
表6に示す。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表6−プローブNo.2062に対する配線方法の差

ウエハ

ウエア識別番号

日数

差

−0.010 8

−0.011 1

−0.006 2

0.002 0

0.001 8

0.000 2

−0.008 9

−0.004 0

−0.002 2

−0.001 2

−0.003 4

−0.001 6

−0.011 1

−0.005 9

−0.007 8

−0.000 7

0.000 6

103

−0.005 0

−0.014 0

−0.004 8

0.001 8

0.001 6

0.004 4

125

−0.005 6

−0.015 5

−0.001 0

−0.001 4

0.000 3

−0.001 7

二つの方法の差をプロットしたものが，図4である。この表から，差がほとんどマイナスになっている

ことが分かる。差の最大値及び最小値は，それぞれ，0.004 4及び−0.015 5である。方法によるかたより

は，差の平均値又は補正値で次のように推定する。

003

−

=∑

差の総数が29であることから，試料標準偏差に基づく配線のかたよりの不確かさは，次のようになる。

000

)ˆ

ˆ(

Ω

−

=∑

29の補正値

)

ˆ(ibについて，計算したt値 = −4.013 3となる。補正値の確率分布の平均がゼロであると

いう仮説は，棄却される。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

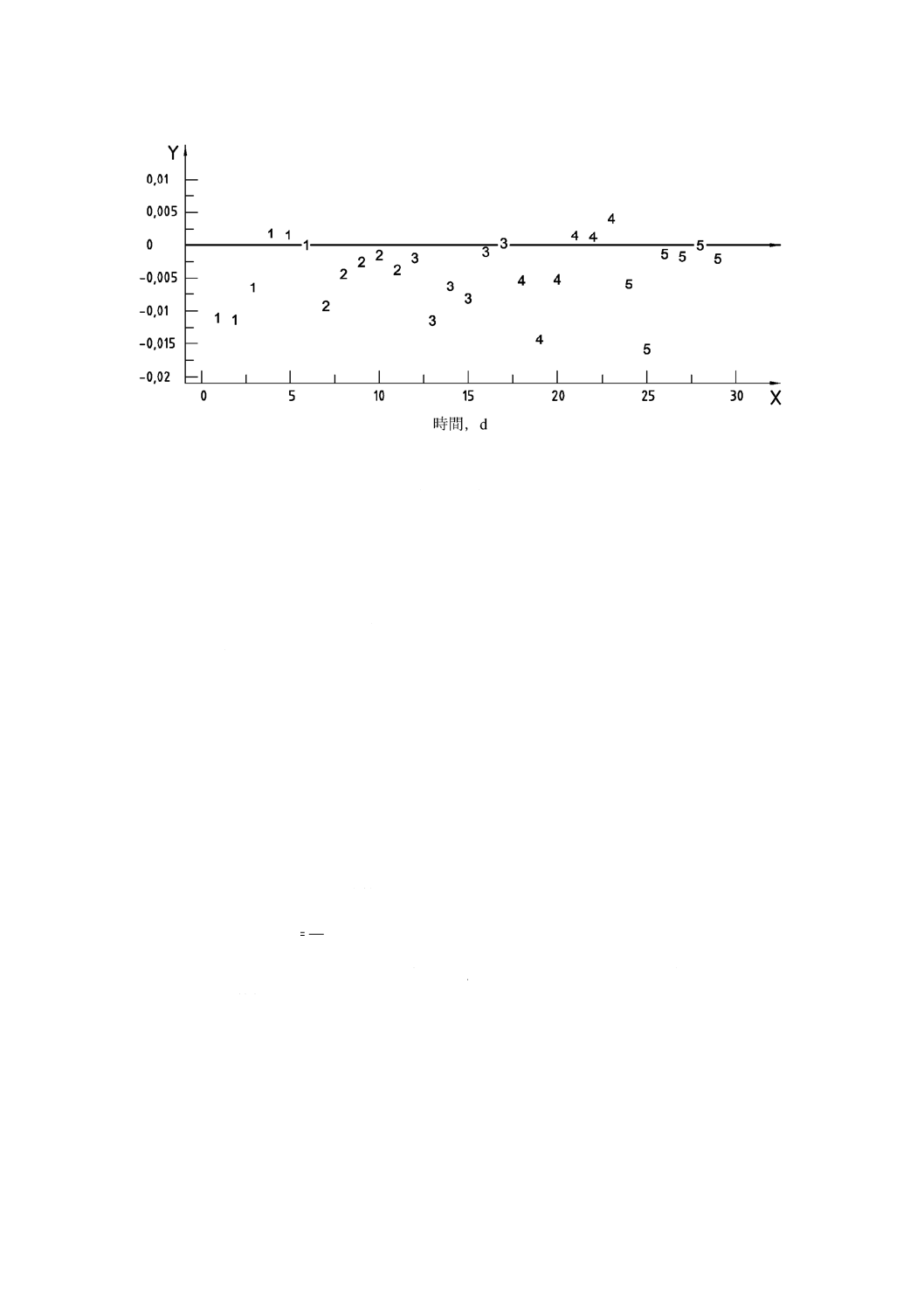
X軸：時間，d
Y軸：二つの配線構成の間の抵抗率の差，Ω･cm
1，….，5 ウエハの識別番号（表6参照）

図4−二つの配線方法の間の差−5個のウエハについて，

6日間，プローブNo.2062を使って実施された測定の一連の実験

不確かさのタイプBの評価

6.1

不確かさのタイプBの評価は，偶然効果及び系統効果の両者に適用する。これらの際立った特徴は，

不確かさ成分の計算がデータの統計的解析に基づいていないという点である。

タイプBの評価の実施に至る不確かさの要因の例には，次のようなものがある。

− 別の試験所で校正された参照標準

− 報告値の計算に使用された物理定数

− サンプリングできない環境効果

− 測定機器の構成／形態の調整不備

− 測定機器の不十分な分解能

6.2

参照標準に関する校正報告書，物理定数に対する不確かさの公表された報告書など，不確かさの要

因が文書化されている場合は，解析は容易である。不確かさは，通常，拡張不確かさUとして報告され，

次の公式を用いて，標準不確かさに換算される。

係数kが未知か又は文書化されていない場合は， k = 2とするのが安全である。個別の測定のプロセス

にとどまるが，統計的解析をするだけの十分なサンプリングができない不確かさの要因は，タイプBの評

価が必要になる。広く用いられている方法の一つが，次の項目によって，最悪のケースの効果を推定する

方法である。

− 経験

− 科学的判断

− 少数データ

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

6.3

身近な状況では，推定されたかたより又は補正値は，ある想定した統計分布から無作為抽出したも

のとみなされることができる。この場合，標準不確かさは，この分布の標準偏差とする。可能性のある統

計分布の中で，二つの分布について考える。

a) 一様分布端点±aが与えられ，−aと＋aとの間のすべての値が同程度に確からしい。

−a a

source=

対応する自由度は，aが十分に定量化されたものである場合，無限大とすることができる。その他

の場合は，自由度は，aが分かっている正確さを反映するように選択する。GUM，G 4.2を参照。

b) 三角分布三角分布では，同一端点をもつ一様分布の場合より標準不確かさは小さくなる。

−a a

source=

自由度は，通常，無限大とする。

不確かさの伝ぱ（播）

7.1

一般

7.1.1

不確かさの評価についてこれまで示したアプローチは，いわゆる，トップダウンアプローチである。

不確かさ成分は，直接，測定を繰返すことによって評価される。このアプローチを不確かさの伝ぱ（播）

則の利用と対比するために，方形の面積を，長さL及び幅Wの組の測定を繰り返すことによって推定する。

面積A，

A＝L×W

は，それぞれの繰返しから計算する。報告された面積の標準偏差は，繰返し求めた面積から直接推定する。

7.1.2

このアプローチは，次のような利点をもつ。

− 長さ及び幅の測定の間の共分散を適切に扱うことができる。

− ある範囲の測定条件の中で，また，十分な長時間で測定が行われる場合に現れる思いもよらない不確

かさの原因を適切に扱うことができる。

7.1.3

影響を与えるすべての効果を反映するような方法で，直接測定を繰り返すことができない場合があ

る。この場合，不確かさの伝ぱ（播）則の使用を検討できる(GUM)。このアプローチでは次のものを計算

する。

a) 長さの平均値と幅の平均値との積としての測定結果

b) “長さ”Lの標準不確かさ

c) “幅”Wの標準不確かさ

また，二つの変数の積に対する近似計算を用いて，二つの標準不確かさを，測定結果の一つの標準不確

かさに合成する。長さの測定値と幅の測定値との間に共分散がない場合，次に示す公式を用いる。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

≈

7.1.4

理想的な例では，この値は，面積測定値から直接得た値とそれほど差がないはずである。しかし，

状況によっては，次の理由から大きな差を示すことがある。

− 予測できなかった共分散

− 測定量の報告値に影響を与える乱れ

− 近似の誤差

一般に，不確かさの伝ぱ（播）則を，次のモデル，

)

(

すなわち，一つ又は複数の変数である測定値X，Z，….，の関数に適用すると，Yの標準偏差は，次の式

で与えられる。

∂∂

≈

ここに，

S： Xの標準不確かさ

S： Zの標準不確かさ

： X及びZの共分散

∂

∂： X，Z，...などの最適推定値であるx，z，...の点で評価した，

Xに関する関数fの偏微分値

7.1.5

測定を二つ一組で実施していない場合，共分散項を推定するのが困難になることがある。次のよう

な場合には，これらの項を公式から削除できる。

a) X，Zの測定値が独立な場合，その共分散項がゼロである。

b) 実際上，共分散項が十分なデータから推定されたものである場合，又はその決定について他の情報が

利用できる場合にだけ，共分散項を計算に含めることが望ましい。

一般に，Yが2個の分銅の質量の和であったり，2個のゲージブロックの端面間の長さの和であったり

などする場合には，校正して得られる試験項目の報告値はゼロでない共分散をもっているということを考

慮するのがよい。

7.2

一変数関数に関する公式

一変数の関数である報告値の標準偏差を，参考文献[6]から引用した表7に示す。報告値Yは，N個の測

定値の平均の，一変数の関数である。

7.3

二変数関数に関する公式

測定値の二変数の測定値の関数である報告値の標準偏差を，参考文献[6]から引用した表8に示す。報告

値Yは，N個の測定値の平均値の，二つの変数の関数である。標準偏差の係数を“感度係数”と呼ぶ。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表7−単一の変数の関数に対する標準偏差

Xの関数Y

Yの標準偏差の一次近似

備考

Xは，N個の独立測定値の平均

Sは，Xの標準偏差

1( X

)

In(X

Nが小さい場合，近似が悪くなり得る。

100

Xが正規分布していると仮定。

参考文献[7]参照。

表8−二つの変数の関数の標準偏差

X，Zの関数Y

Yの標準偏差

X及びZは，N個の測定値の平均である。

SはXの標準偏差

SはZの標準偏差

2XZ

はX，Zの共分散a)

−

)

(

)

(

注a) 推定値が信頼できる場合は，共分散項を含める。

事例−ゲージ調査からの不確かさのタイプAの評価

8.1

目的及び背景

この事例の目的は，複数の不確かさの原因をもつ測定プロセスについて，不確かさの評価を示すことで

ある。対象の測定は，シリコンウエハの抵抗率（Ω・cm）である。ここでは，この測定について示された

基準であるASTMのF84方法に従って，方法Aと呼ばれる特殊な方法に配線した4端子法を用いて校正

した，約100個のシリコンウエハの抵抗測定することについて，その不確かさを計算しようとするもので

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

ある。各ウエハの報告値は，ウエハ中心で，短時間で6回繰返し測定して得た値の平均値である。測定は，

測定可能な5個のNISTプローブの一つであるプローブNo.2362を用いて，アメリカ合衆国商務省国立標

準技術研究所（NIST）で実施した。

不確かさの評価では，次の時間に依存したばらつきの原因を考慮した。

a) ウエハ中心における測定の繰返し

b) 日間効果

c) ラン間の効果

さらに，次のかたよりの原因を考慮した。

− プローブNo.2362によるかたより

− 配線の方法Aによるかたより

8.2

データの収集及びチェック用標準

8.2.1

証明書用の測定それ自体は，日間及び長期的な効果について情報を与えることがないので，時間に

依存する不確かさ成分を推定するための主要な資料とはならない。三つの時間に依存する不確かさ成分を，

3段枝分かれ計画から推定した。

− J =ウエハの中心における5個の測定値

− K = 6日間

− L = 2のラン

3段枝分かれ計画に対するモデルは，次による。

lkj

＝

ここに，

,6,

,2.1

及び

8.2.2

この目的のためにウエハのロットからランダムに選択したM = 5個のウエハのそれぞれについて，

実験を繰り返した。これらのチェック用標準は，解析ではウエハ138，139，140，141及び142である。実

験はQ = 5個のプローブについても繰り返す。それらは，解析ではプローブNo.1，No.281，No.283，

No.2062，No.2362である。データには次のものが含まれる。

− ランの番号

− ウエハの識別

− 測定の月日

− オペレータ

− 温度

− ウエハ中心で五つの測定値の平均

− 五つの測定値からの短時間（併行精度）標準偏差

8.3

併行精度，日間及び長時間効果の解析

ウエハ識別番号に対して各プローブの併行精度標準偏差をプロットすることによって，プローブ

No.2362の精度を他のプローブと比較し，一致度を確認した。プローブNo.2362がラン1において最高の

精度（ばらつきの小ささ）を示したので，これを証明書用測定のために選択した。ただし，精度は，次に

示すように，不確かさに対する寄与分としては，唯一のものとも，最も重要なものともいえない。

ここでは，ウエハの効果を固定効果とする。ウエハによる交差的効果（二元配置的な直交する効果）を

伴う3段枝分かれ計画は混合モデルであり，5.2.2のモデルとは異なる。表9は，分散分析表である。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表9−ゲージ調査データの分散分析表

要因

自由度 ν

平均平方 MS

平均平方の期待値

ラン

198

009

MSR=

日（ラン内）

238

003

MSD(R)

5σ

σ+

誤差

804

000

MSE=

注記この例において，クロスオーバ効果（ウエハと実験との交互作用効果）は，考慮していない。こうした効果

は，一つの要因が他の原因に影響を及ぼす場合に考慮する。例えば，一方の薬剤の投与が他方の効果を抑制
するような状況で，2種類の薬剤の効果を調査する場合が該当する。

併行精度，日間及び繰返し効果の分散成分も得られる。

804

000

486

000

D(R)

−

198

000

D(R)

−

8.4

プローブのかたより

8.4.1

グラフ解析

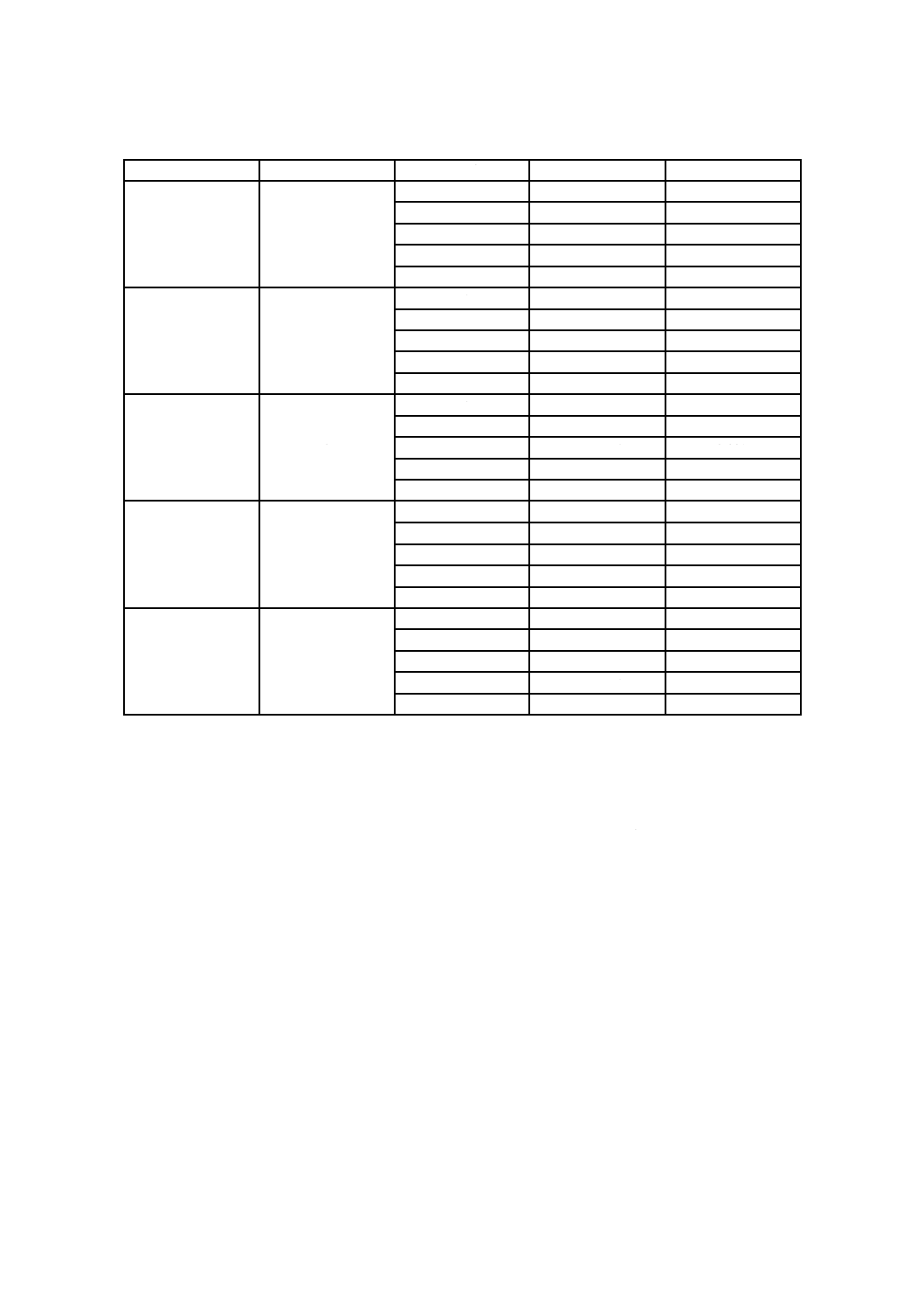
プローブの精度については，8.1で規定した。プローブのかたよりは，8.4で規定する。グラフ解析は，5

個のプローブの間の相対的なかたよりを明らかにする。各ウエハについて，各プローブに対するウエハ平

均からの差を，ウエハ識別番号に対してプロットする。グラフで示すように，プローブNo.2362（識別番

号5）は，他のプローブに対してかたよりを示す。すなわち，必ず低い値を示す。このかたよりは，プロ

ーブを用いると，より一層顕著になる（ラン2）。

プローブ識別番号

− 1 = No.1

− 2 = No.281

− 3 = No.283

− 4 = No.2062

− 5 = No.2362

8.4.2

定量解析

5個のプローブに対する補正値を，各ウエハの平均値からの差として表10に示す。個別のランにおいて，

5.5.2で定義するように，k = 1，2，3，4，5（プローブNo.1，281，283，2062，2362）及びi = 138，139，

140，141，142において，

•

−

である。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表10−5個のプローブに対するかたより

ウエハ

ウエハ識別番号

プローブNo.

ラン1

ラン2

138

0.024 8

−0.011 9

281

0.010 8

0.032 3

283

0.019 3

−0.025 8

2 062

−0.017 5

0.056 1

2 362

−0.037 2

−0.050 7

139

−0.003 6

−0.000 7

281

0.039 4

0.005 0

283

0.005 7

0.023 9

2 062

−0.032 3

0.037 3

2 362

−0.009 4

−0.065 7

140

0.040 0

0.010 9

281

0.018 7

0.010 6

283

−0.020 1

0.000 3

2 062

−0.012 6

0.018 2

2 362

−0.026 1

−0.039 8

141

0.039 4

0.032 4

281

−0.010 7

−0.003 7

283

0.024 6

−0.019 1

2 062

−0.028 0

0.043 6

2 362

−0.025 2

−0.053 4

142

0.006 2

0.009 3

281

0.037 6

0.017 4

283

−0.004 4

0.019 2

2 062

−0.001 1

0.000 8

2 362

−0.038 3

−0.046 9

8.4.3

プローブによるかたよりの扱い

精度が優れていることから，プローブNo.2362を認証プロセス用として選択したが，他のプローブに対

するかたよりが問題を引き起こしている。この問題を処理する可能性として，次の二つが考えられる。

a) プローブNo.2362で行ったすべての測定値をプローブの平均値について補正する。

b) 不確かさの評価において，プローブ間の差に対する標準偏差を含める。

調査対象のプローブがこの形式のプローブからのランダムなサンプルであると仮定できる場合は，a)の

方が優れた選択肢となる。単位（抵抗率）を試験方法によって定義する場合には，特にこれがあてはまる。

したがって，ここでは，プローブNo.2362の平均かたよりについてすべての測定値を補正し，不確かさの

タイプAの評価として，補正の標準偏差を求める。

表10から，ウエハごとのプローブNo.2362の補正値は表11になる。補正値は，すべてマイナスである。

場所での符号検定に基づいて，二つのランからの補正値は同じ母集団からのものとして処理した。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

表11−ウエハごとのプローブNo.2362に対するかたより

ウエハ

ラン1

ラン2

全体

138

‒ 0.037 2

‒ 0.050 7

139

‒ 0.009 4

‒ 0.065 7

140

‒ 0.026 1

‒ 0.039 8

141

‒ 0.025 2

‒ 0.053 4

142

‒ 0.038 3

‒ 0.046 9

平均
分散（10値）

‒ 0.027 2

‒ 0.051 3

‒ 0.039 3

0.000 261 8

標準偏差

0.016 18

プローブNo.2362のかたよりは，−0.039 3であると推定された。プローブNo.2362のかたよりの不確か

さは，次の式のようになる。

117

005

016

2362

8.5

配線のかたより

8.5.1

二つの方法で構成したプローブでの測定

多くの考え得る方法の中でも特定の方法である方法Aによって配線したプローブNo.2362で，証明書用

の測定を行った。ゲージ調査は，大きな外れを特定する方法として，二つの方法で配線したプローブ

No.2362を用いて実施した。配線方法に関する生データは，ここでは省略する。

8.5.2

グラフ解析

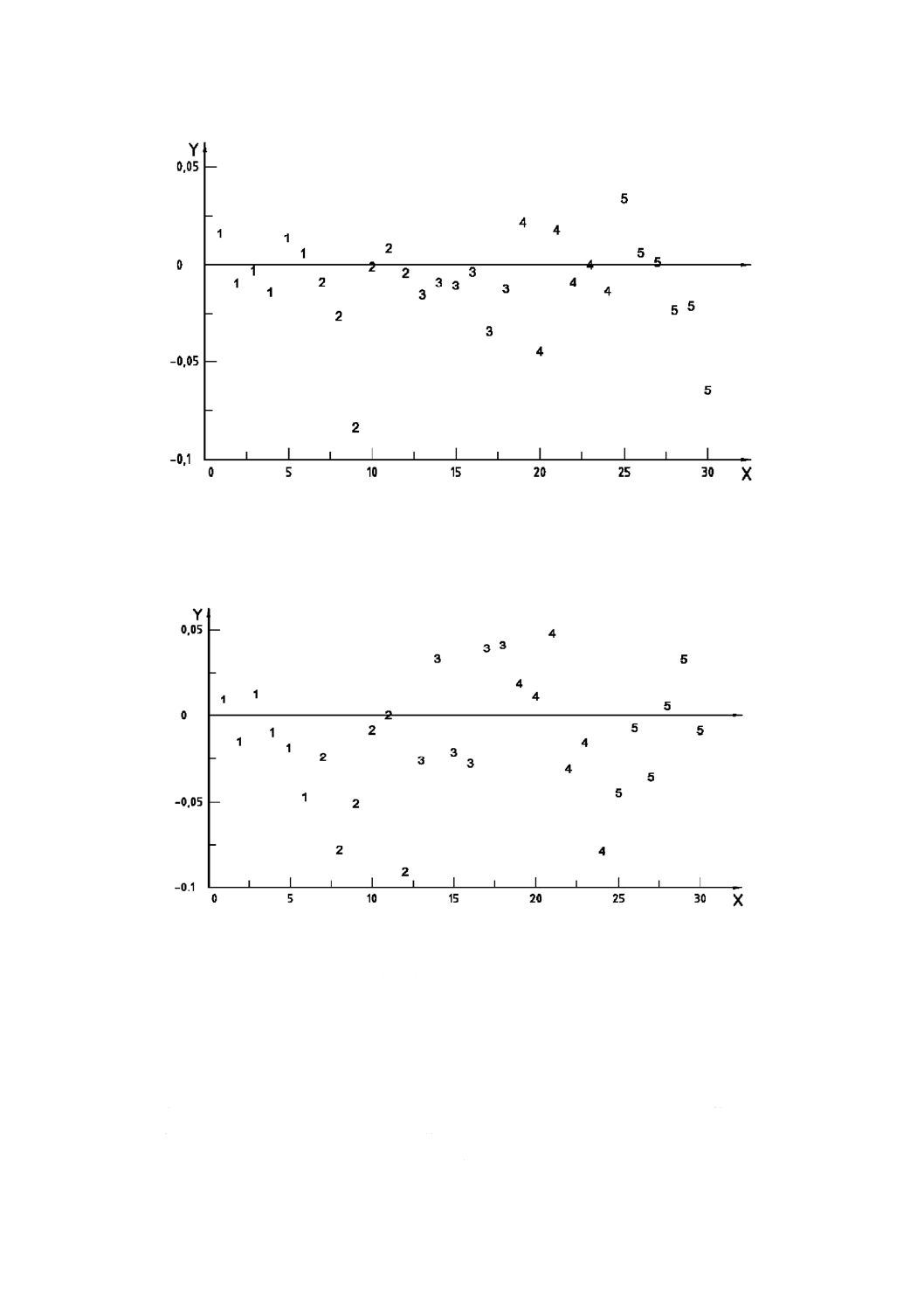
同じ日に実施した方法A及び方法Bでの測定値の間の差を，各ウエハについて，6日間のデータをプロ

ットした。図5は，約2か月の間隔をおいた2回のランを別々に表す。中心の線は，ゼロラインである。

データポイントは，このゼロラインの上下にかなりランダムに分散しており，プローブNo.2362について，

方法間の差がないことを示す。したがって，この原因による不確かさへの寄与は無視できるとみなす。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

する不確かさへの寄与は無視できる。

表12−二つの方法間の差

状態

平均

標準偏差

自由度

ラン1

−0.008 58

0.024 2

1.9

ラン2

−0.011 0

0.035 4

1.7

このように，方法間の差による不確かさSconfigはゼロに等しい（Sconfig = 0）。

8.6

不確かさの計算

8.6.1

一般

不確かさの値は，報告値によって変わることがある。この場合，各ウエハに対する証明書に記載される

抵抗率値は，1回のランで，1日間にウエハ中心部で行った6回の短期繰返しの平均値である。

箇条8のモデル，すなわち，

lkj

から，k日の，ランlにおける特定のウエハに対する値は，次のようになる。

•

8.6.2

不確かさのバジェット表

不確かさのバジェット表を，表13に示す。

表13−不確かさのバジェット表

要因

タイプ

分散

併行制度

804

000

日間

486

000

2D=

ラン間

198

000

2R=

プローブNo.2362

026

000

2probe=

配線方法

2config=

8.6.3

合成標準不確かさ

併行精度，日間，ラン及びプローブのかたよりを含む合成標準不確かさは，不確かさのバジェット表か

ら，次のように計算される。

038

2ˆ

2362=

8.6.4

有効自由度

ucの有効自由度は，ウェルチ=サタスウェイト（Welch-Satterthwaite）の公式によって近似的に求める。

8.1から合成標準不確かさは次のように書き換えることができる。

2ˆ

D(R)

2362

これらの不確かさ成分に対応する自由度は，それぞれ，44，10，1及び9である。ウェルチ=サタスウェ

イト（Welch-Satterthwaite）の公式による有効自由度は，次のようになる。

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

4ˆ

D(R)

eff

2362

≅

自由度が17で，確率レベルが0.95のとき，t表による限界値は2.11であり，したがって，拡張不確か

さは次のとおりになる。

082

Ω

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

附属書A

（規定）

記号

bˆ

k番目の測定機器に対するかたよりの推定量

誤差分散の推定量

2ˆk

k番目の測定機器に対するかたよりの分散の推定量

S2config

方法による分散の推定量

S2D

日の効果に対する分散要素の推定量

S2run

ランの効果に対する分散要素の推定量

平均平方

MSD

2段階枝分かれ計画における，日効果に対する平均平方

MSD(R)

3段階枝分かれ計画における，日効果に対する平均平方

MSE

確率誤差に対する平均平方

MSinh

試験品目における不均質係数に対する平均平方

MSinst

測定機器の係数に対する平均平方

MSitem

試験品目による平均平方

MSR

ランの効果に対する平均平方

平方和

SSD(R)

日の効果に対する平方和

SSE

確率誤差に対する平方和

SSR

ランの効果に対する平方和

繰り返しできる出力量

レベル2，例，日における係数の効果

確率誤差

レベル3，例，連における係数の効果

多数の測定値の真値又は平均値

不確かさに対する自由度

σ2

確率誤差の分散

日の効果に対する分散要素

ランの効果に対する分散要素

Z 8404-2：2008 (ISO/TS 21749：2005)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

参考文献

[1]

K. A. BROWNLEE. Statistical Theory and Methodology in Science and Engineering，John Wiley & Sons，Inc.，

New York，1960，p. 236

[2]

CARROLL CROARKIN and RUTH VARNER. Measurement Assurance for Dimensional Measurements on

Integrated-circuit Photomasks，NBS Technical Note 1164，U.S. Dept. Commerce，1982，44 pp

[3]

J. R. EHRSTEIN and M.C. CROARKIN. Standard Reference Materials: The Certification of 100 mm Diameter

Silicon Resitivity SRMs 2541 through 2547 Using Dual-Configuration Four-Point Probe Measurements，NIST

Special Publication 260-131，1998，Revised，84 pp

[4]

CHURCHILL EISENHART. Realistic Evaluation of the Precision and Accuracy of Instrument Calibration Systems

J Research National Bureau of Standards-C. Engineering and Instrumentation，67C (2)，1962，pp. 161-187

[5]

GERALD J. HAHN and WILLIAM Q. MEEKER. Statistical Intervals: A Guide for Practitioners，John Wiley &

Sons，Inc.，New York，1991，p. 61

[6]

HARRY KU. Notes on the Use of Propagation of uncertainty Formulas. J Research of National Bureau of

Standards-C. Engineering and Instrumentation，70C (4)，1966，pp. 263-273

[7]

SAMUEL KOTZ and NORMAN L. JOHNSON. Encyclopedia of Statistical Sciences，Vol. 2，John Wiley & Sons，

New York，1982，p. 29

[8]

MARY GIBBONS NATRELLA. Experimental Statistics，NBS Handbook 91，US Dept. Commerce，1963

[9]

STEPHEN WOLFRAM. Algebraic software， A System of Doing Mathematics by Computer，2nd edition，Addison

Wesley Publishing Co.，New York，1993

[10] ASTM Method F84-93，Standard Test Method for Measuring Resistivity of Silicon Wafers With an In-line

Four-Point Probe. Annual Book of ASTM Standards，10.05，West Conshohocken，PA 19428

[11] Measurement Systems Analysis Reference Manual. Chrysler Corp.，Ford Motor Corp.，General Motors Corp.，

2nd ed.，1995，120 pp

[12] Determining and Reporting Measurement Uncertainties，National Conference of Standards Laboratories

RP-12，1994，Suite 305B，1800 30th St.，Boulder，CO 80301

[13] International vocabulary of basic and general terms in metrology (VIM). BIPM，IEC，IFCC，ISO，IUPAC，

IUPAP，OIML，2nd ed.，1993，59 pp

[14] JIS Z 8404-1：測定の不確かさ−第1部：測定の不確かさの評価における併行精度，再現精度及び真

度の推定値の利用の指針