2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8403-1996
製品の品質特性−
規格値の決め方通則
Quality characteristics of products
−General rules for determination of specific values
1. 適用範囲 この規格は,出荷時の製品(1)の品質特性の規格値を要求条件と経済的観点との兼ね合いで
合理的に決める方法の,一般的な事項について規定する。
注(1) 商取引の対象となる品物で,ある一定の手段・工程を通じて製造されたものであり,半成品を
含む。
備考1. 個品に対する規格値は,最大許容値(規格上限値)・最小許容値(規格下限値)の両方(両方
限界,bilateral limits),又はいずれか一方(片側限界,unilateral limit)で示す。最大許容値及
び最小許容値を規格限界値といい,基準値と規格限界値との差が許容差である。
2. カタログ・取扱説明書に記載する仕様値(規格値)は,購入者及び社会の要求又は要望を考
慮して製造業者が定めるもので,この規格は適用しない。
3. この規格の引用規格を,次に示す。
JIS Z 8101 品質管理用語
JIS Z 8103 計測用語
2. 用語の定義及び記号 この規格で用いる主な用語の定義及び記号は,JIS Z 8101及びJIS Z 8103によ
るほか,次のとおりとする。
(1) 望小特性 (smaller-is-better characteristic) 理想的には0がよいとされ,負の値を取らず小さいほど良
い特性。規格値は最大許容値(⊿)で示す(すなわち,⊿以下)。
例 幾何偏差(真円度,平行度,位置度など),硬球の真球度,騒音レベル
(2) 普通特性 (nominal-is-best characteristic) 規格値が基準値 (m0) と,上の許容差(+⊿)及び下の許容
差(−⊿)とで(すなわち,m0±⊿で)示される特性。多くの品質特性はこれに属する。
備考 普通特性は,一般に基準値を望ましい値とするものであるので,望目特性と呼ぶこともある。
例 寸法(長さ,角度)
(3) 望大特性 (larger-is-better characteristic) 負の値を取らず,数値が大きいほど品質が良いとする特性。
規格値は最小許容値(⊿)で示す(すなわち,⊿以上)。
例 耐力,衝撃強さ
備考 率又は百分率で表す特性値のうち,0〜1(又は0〜100%)の範囲を超えない性質の特性値は,
望小特性・普通特性又は望大特性に変換する。
例 架橋度pを−10 log (1/ (p) −1) で変換する。
2
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(4) 生産者 製品を製造する者。
(5) 使用者 製品をその使用目的に沿って用いる者。
(6) 機能限界(⊿0) 製品が使用段階で機能しなくなる限界値。
(7) 平均損失 (A0) 使用段階で品質特性の実現値(以下,特性値という。)が機能限界を超えたときに発
生する損失の平均(金額)。
(8) 生産者側の損失 (A) 特性値が規格限界を超えたときに生産者側に発生する損失(金額)。
(9) 比例定数 (k) 経済的損失を表す定数であって,平均損失A0と機能限界⊿0の2乗とから,次の式で
求めた値。
普通特性又は望小特性の場合
2
0
0
Δ
A
k=
望大特性の場合
k=A0⊿02
3. 規格値の決め方
3.1
機能限界⊿0及び平均損失A0を決めるための考え方
3.1.1
製品の分類 使用状態に応じて,製品を次の三つに分類する。
(1) 最終製品 一般に最終製品として使用されるもの。
(2) 部品・半成品 最終製品に組み込まれるもの。
(3) 材料 (1)又は(2)の元の原材料・材料。
備考 (1),(2)又は(3)に応じて,⊿0及びA0が規定される。
3.1.2
最終製品の⊿0及びA0の決め方 最終製品の機能限界及び平均損失の決め方は,次による。
(1) 標準使用条件(例えば,取扱説明書に記載してある条件)における機能限界⊿0を求める。標準使用条
件での試験は1回だけでもよい。A0は市場で実際に機能しなかったときの製品単位量当たりの市場内
の費用の平均とする。この費用の中には使用者が受けた実害額・苦情処理費用を含める。
(2) 公的規制又はカタログによる規格値がある場合には,その規格値を機能限界⊿0とする。
また,リコール・苦情に対応するときのための製品単位量当たりの費用の平均をA0とする。
3.1.3
部品・半成品の⊿0及びA0の決め方 部品・半成品の機能限界及び平均損失の決め方は次による。
(1) 最終製品の特性値に部品・半成品の特性値が影響する場合には,部品・半成品の値によって最終製品
の特性値がその規格値を超える限界を機能限界⊿0とする。その場合,他の部品及び試験条件はすべて
標準使用条件で求める。最終製品がその規格値を超えたときの部品・半成品の費用の平均をA0とする。
(2) 部品・半成品が他の部品と関係なく,単独で市場でトラブルを起こす場合又は公的規制・カタログの
規格値がある場合は,3.1.2に準じて機能限界⊿0を求める。
また,A0も3.1.2に準じて求める。
3.1.4
材料の⊿0及びA0の決め方 材料の機能限界及び平均損失の決め方は次による。
(1) 出荷先が明白の場合,出荷先でトラブルを起こす限界が機能限界⊿0である。出荷先の素材・原料,ほ
かのすべての条件は標準使用条件として機能限界⊿0を求める。
また,A0は出荷先で機能限界を超えたときの損失である。
(2) 公的規制又はカタログの規格値が存在する場合には,それらの規格値を機能限界⊿0とする。市場で規
格値を満たさなかったことが分かって発生したリコール・苦情による製品単位量当たりの損失をA0
3
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とする。
3.2
規格値の決め方の手順 規格値の決め方の手順は,次による。
手順1 機能限界⊿0及び平均損失A0の推定 使用者の段階における機能限界⊿0及び平均損失A0を
推定する。
備考1. 多くの場合,機能限界⊿0及び平均損失A0は,概略の数値でもかまわない。
2.
普通特性で,基準値のプラス側とマイナス側とで機能限界⊿0及び平均損失A0が異
なるときには,両側で別々に求める。この場合,比例定数kが大きい方だけを用い
て,プラス側,マイナス側とも同じように損失を求めてもよい。
手順2 生産者側の損失Aの推定 特性値が規格限界を超えたことによって不合格になったときに,
生産者側に発生する損失の推定を次のように行う。
(1) 手直しが可能な場合には,手直し費用の平均とする。
(2) 手直しが不可能な場合には,製品の交換及び廃棄による損失の平均とする。
備考 生産者側の損失Aは,附属書1によって,あらかじめ,ある程度の最適化が行われて
いることが望ましい。
手順3 品質水準及び測定能力の検討 生産者側の損失Aの推定に当たって,規格値を設定する部品
に対してどの程度の品質水準で製造が可能なのか,又はそれらを判定するのに十分な測定能
力があるのかを附属書2及び附属書3によって検討する。その結果,能力が不十分な場合に
は改善を行う。
手順4 ⊿の計算 ⊿は次の式によって算出する。
普通特性又は望小特性の場合
0
0
Δ
A
A
Δ
×
=
望大特性の場合
0
0Δ
A
A
Δ
×
=
手順5 ⊿の検討 手順1,手順2及び手順3の結果を検討して,手順4で求めた規格値が工程能力
にそぐわないと考えられる場合には,次のようにAの値を変えて⊿の再計算を行う。
(1) 品質水準が十分である場合には,A及び⊿の値は再計算を行わない。
(2) 品質水準が不十分な場合には,不良率 (p) が求められる特性値については,次の式によ
って生産者側の損失Aの値を修正し,⊿の値を再計算する。
Aの修正値=
p
A
−
1
上記の検討を行っても,規格値を満たさず,これ以上の品質水準の改善が不可能な場
合には,全数検査を行うか,附属書2を参考にして材料変更・設計変更を行う。又は手
順4及び手順5の(2)で求めた⊿を暫定値として,必要に応じた制御などで対策を取る。
手順6 ⊿の決定 手順5の検討に基づいて⊿を決定する。
例1. 望小特性の場合:音響機器の軸受 高分子材料で作られた音響機器の軸受が金属部品に取り付
けられて作動する。この軸受の真円度が110μmを超えると回転むらが発生して,使用者の50%
がサービスステーションなどへ修理を依頼すると予測できる。そのとき修理費は5 000円である。
手順1 機能限界⊿0及び平均損失A0の推定
4
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
使用者段階 機能限界⊿0=110μm, 平均損失A0=5 000円
手順2 生産者側の損失Aの推定 生産者側の損失Aは部品購入原価などから700円となった。
手順4 最大許容値⊿の計算
⊿0=110μm,A0=5 000円,A=700円であるから
⊿=
110
000
5
700×
≒41 (μm)
手順6 最大許容値⊿の決定 以上から,真円度の最大許容値⊿は,きりがよい数値で40μm
とした。
例2. 望大特性の場合:手提げかばんのハンドル 手提げかばんのハンドルに金属部品を挿入して組
み立てる。このハンドルのはめあい強度が150N以下であると,使用中に不具合が生じて使用者
の50%が修理を依頼する。そのときの修理費は搬入・搬出などの費用を含め,5000円である。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階 機能限界⊿0=150N, 平均損失A0=5 000円
手順2 生産者側の損失Aの推定 生産者側の損失Aは部品購入原価などであり,140円であ
る。
手順4 最小許容値⊿の計算
⊿0=150N,A0=5 000円,A=140円であるから
⊿=
150
140
000
5
×
≒896 (N)
手順6 最小許容値⊿の決定 以上から,最小許容値⊿は,きりがよい数値で900Nとした。
5
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1 製品の品質とコストとのバランスの取り方
1. 適用範囲 この附属書は,製品の品質特性の規格値の決定に先立って実施する,製品の品質とコスト
とのバランスを取るための手法について規定する。
備考 製品の品質とコストとのバランスの取り方とは,選定可能な複数の製品構成要素又は材料があ
るとき,製品の品質特性の出荷後ばらつき(1)による使用者損失と入手コスト(2)との和である総
合損失 (LT) を最小にするように,複数の候補から一つを選定する方法をいう。
注(1) 出荷後の製品に発生する劣化・摩耗などに起因する時間的経過による品質特性のばらつき,及
び温度・湿度など環境条件の変化による品質特性のばらつき。
(2) 選定した候補を入手するのに必要な原価。
2. 用語の定義及び記号 この附属書で用いる主な用語の定義及び記号は,この規格の本体によるほか,
次による。
平均二乗誤差の和σT2 品質特性の出荷後ばらつきの平均二乗誤差の和。加工時の品質特性のばらつきは
含めない。
3. 製品の品質とコストのバランスの取り方の手順 特性値の規格値を満足する候補を幾つか選定し,そ
れぞれの出荷後ばらつきによる損失とその入手コストとの総和を比較し,総和がもっとも少ない候補を採
択する。その手順は次のとおりとする。
手順1 部品,要素,ユニットなどの製品構成要素又は材料の中から規格値を満足しそうな候補を幾
つか選定する。
手順2 選定された候補の入手コスト及び出荷後ばらつきに関する情報を入手する。
手順3 品質特性の区分に対応する損失関数を選定する。
(1) 望小特性又は普通特性の場合
損失
2
2
0
T
A
L
σ
Δ
=
ここに, σT2: 出荷後の特性値の理想値又は基準値からの偏差の二乗平均。
(2) 望大特性の場合
損失 L=A0⊿02σT2
ここに, σT2: 出荷後の特性値の逆数の二乗平均。
手順4 機能限界⊿0及び平均損失A0を求める。
手順5 選定された候補に対して平均二乗誤差の和σT2を予測する。
劣化・摩耗及び温度・湿度などによって品質特性が使用中変化するとすると,σT2は次のよ
うに計算する。
例えば,製品の出荷後,時間tにおける劣化によって変化した特性値をyd,摩耗によって
変化した特性値をya,環境変化(例えば,温度θ1からθ2までの)によって変化した特性値を
ynとすると
平均二乗誤差の和σT2=(劣化によるばらつきの平均二乗誤差)
6
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
+(摩耗によるばらつきの平均二乗誤差)
+(環境劣化によるばらつきの平均二乗誤差)
で求める。
(1) 望小特性の場合
∫
∫
∫
−
2
1
2
1
2
0
2
0
2
2
)
(
1
1
θ
θ
θ
θ
σ
dn
y
dt
y
dt
y
T
n
T
a
T
d
T
+
=
(2) 普通特性の場合
∫
∫
∫
−
−
−
−
2
1
2
0
1
2
0
2
0
0
2
0
2
)
(
)
(
1
)
(
1
)
(
1
θ
θ
θ
θ
σ
dn
m
y
dt
m
y
T
dt
m
y
T
n
T
a
T
d
T
+
=
となる。ただし,Tは設計寿命期間である。実際の計算ではT,yd,ya,及びynについて
特性変化曲線を求めて計算する。で求める。
(3) 望大特性の場合
平均二乗誤差の和σT2
=(劣化によって変化した特性値の逆数の二乗平均)
+(摩耗によって変化した特性値の逆数の二乗平均)
+(温度によって変化した特性値の逆数の二乗平均)
したがって,
∫
∫
∫
−
+
+
2
1
2
1
2
0
0
2
2
2
1
)
(
1
1
1
1
1
θ
θ
θ
θ
σ
dn
y
dt
y
T
dt
y
T
n
T
T
a
d
T=
となる。実際には,T,yd,ya,及びynについて特性変化曲線を求めて計算することにな
る。
手順6 平均二乗誤差の和σT2によるばらつきの損失の計算をする。
手順7 入手コストと平均二乗誤差の和σT2による損失とから総合損失LTを求め,経済性の比較を行
う。最も総合損失が小さい候補を採択する。
例1. 普通特性の例 ある精密機械に使用されるプーリを例にして説明する。このプーリの機能は,
外径に巻き付けたロープで直線運動する部品に一定速度を与えることにある。プーリの外径の
ばらつきは機能のばらつきに影響を与える。
手順1 設計で外径の基準値が48mmと決定された。プーリを加工する際の材質として幾つか
考えられる。その中からプラスチックの加工品3種類,アルミニウム加工品1種類,
焼結合金での加工品1種類の合計5種類を候補として選定する。
手順2 5種類の候補に関して出荷後ばらつきについてのデータ及びコストデータを入手す
る。設計上考えられる出荷後のばらつきは,外径の摩耗及び温度変化による熱膨張が
予測される。外径の摩耗については,ロープで移動部品を繰り返し引っ張るためにロ
ープの圧力と擦れによって摩耗が生じる。設計寿命回数時点で外径摩耗量のデータが
集められた。
また,熱膨張による外径変化を知るためにプーリの周囲温度変化の標準偏差及び熱
膨張係数のデータが集められた。附属書1表1が入手したデータである。
機械内部の温度のばらつきの標準偏差τは,7.5℃である。
手順3 ばらつきによる損失を計算する。この部品に与えられた特性が普通特性であることか

7
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ら,普通特性の損失関数を選定する。
2
2
0
0
T
A
L
σ
Δ
=
附属書1表1 各品種のばらつき及びコスト
候補(材料)
摩耗量 B (mm)
線膨張係数 b
コスト A
(設計寿命回数時点)
(10-6 ℃-1)
(円)
ABS成形品
0.050
100
100
ガラス入りポリカーボネート成形品
0.015
28
180
ポリアセタール成形品
0.030
81
130
アルミニウム切削品
0.009
23
250
焼結合金+切削品
0.010
12
310
手順4 機能限界⊿0及びそのときの使用者の平均損失A0の値を求める。プーリの半径が変化
すると移動部品の速度も変化し機能障害が発生する。外径が±0.28mm変化すると機能
障害が起きる。したがって,⊿0は0.28となる。顧客が使用しているとき,機能障害
が発生すると,部品の交換,修理が必要となる。部品費,技術料,日当を考えて合計
24 000円の費用が生じると予測される。したがって,A0は24 000円となる。
手順5 平均二乗誤差の和σT2を求める。この事例の場合には,摩耗による外径の変化及び温度
の変化によるばらつきが考えられる。したがって,摩耗劣化による平均二乗誤差σa2,
及び温度変化による平均二乗誤差σθ2を加えたものになる。
平均二乗誤差の和 σT2=σa2+σθ2
(1) 摩耗量の平均二乗誤差σa2は,外径の摩耗が使用回数に応じて直線的に変化すると
考えて求める。単位使用回数当たりの摩耗量β,設計寿命回数T,設計寿命回数時
点における摩耗量をBとすると,次のようになる。
∫T
a
B
T
dt
t
T0
2
2
2
2
2
3
3
)
(
1
=
=
=
β
β
σ
(2) 温度変化による外径の平均二乗誤差σθ2は,周囲の温度変化によって生じる。線膨
張係数bに機械内の温度変化の標準偏差τとプーリの半径rを乗じて求める。
σθ2=(bτr)2
手順6 損失を附属書1表1のデータをもとに求める。例えばABS成形品の場合は,摩耗によ
る外径変化は0.05と予測され,線膨張係数は0.0001/℃である。
また,機械内の温度変化の標準偏差τは7.5℃と予測されるので,ばらつきによる損
失は
2
2
0
T
A
L
σ
Δ
=
3.
354
)
24
5.7
1
000
.0(
3
05
.0
28
.0
000
24
2
2
2
=
=
×
×
+
(円)
となる。同様に他の候補を計算する。
手順7 ばらつきによる損失L及び入手コストAを合計した総合損失LTをそれぞれの候補につ
いて求めると,附属書1表2のようになる。

8
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1表2 損失コストの計算事例及び総合損失
単位 円
候補(材料)
損失コスト L
コストA
総合損失 LT
ABS成形品
354
100
454
ガラス入りポリカーボネート成形品
31
180
211
ポリアセタール成形品
157
130
287
アルミの切削品
14
250
264
焼結合金
12
310
322
計算結果から,最も総合損失が小さいのはガラス入りポリカーボネート成形品となる。
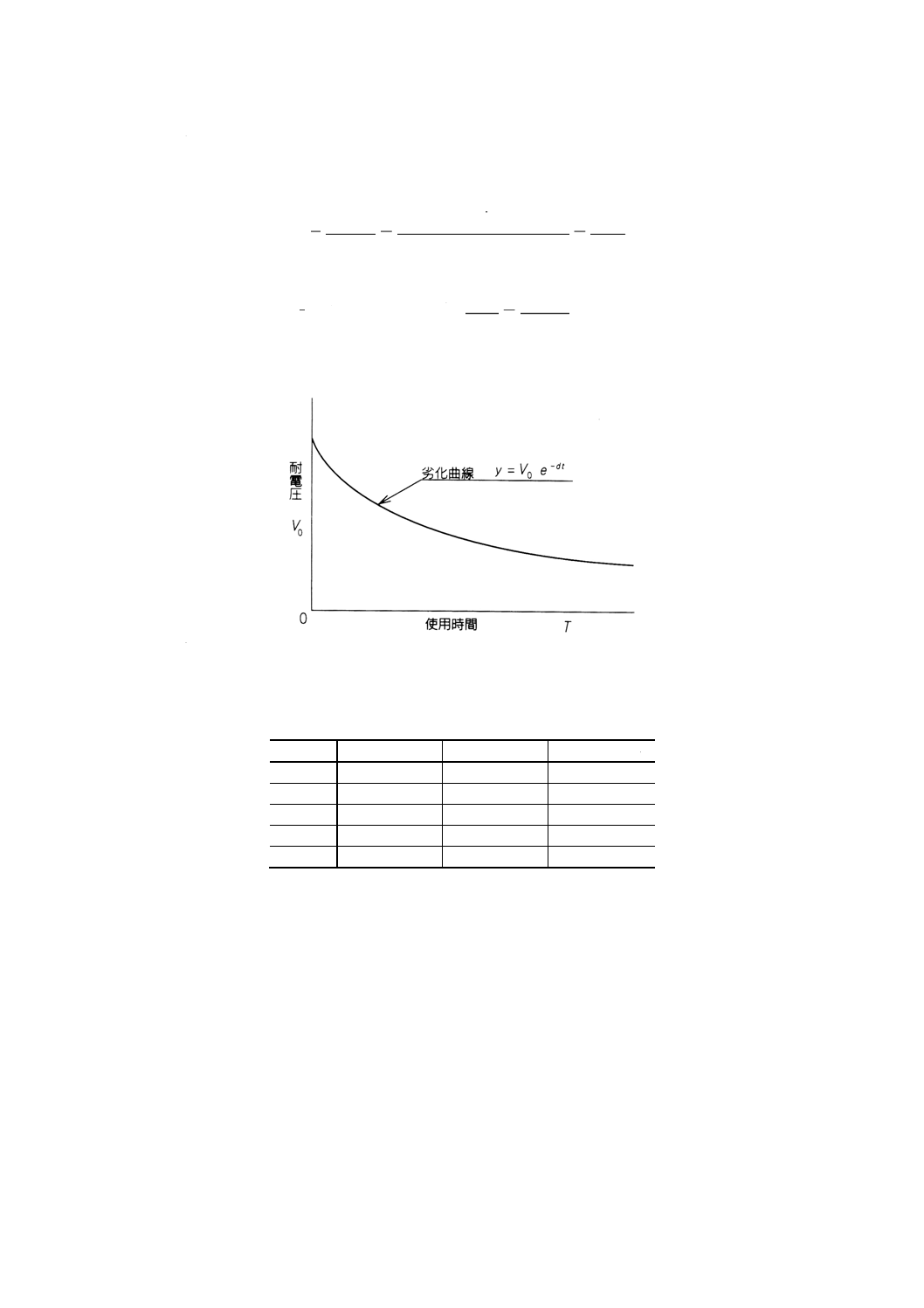
例2. 望大特性の例 出力+5Vの定電圧電源に使用するアルミニウム電解コンデンサの耐電圧に対
する計算を行う。耐電圧は高いほどよいので望大特性と考える。
手順1 入手可能なアルミニウム電解コンデンサの種類及び初期耐電圧特性は,附属書1表3
のようである。
附属書1表3 コンデンサの種類及耐電圧特性
候補
耐電圧 V0
5V印加時の劣化係数 d×10-5
コスト
(V)
(1/h)
(円)
A
16
2.230
100
B
25
1.530
120
C
50
0.852
195
D
63
0.701
230
E
100
0.475
305
手順2 選定されたコンデンサの耐電圧特性の変化を考える。使用中,耐電圧の劣化が考えら
れる。劣化係数は印加電圧と定格電圧との比に比例するとし,附属書1表3のように
予測した。
手順3 損失関数を選定する。この特性の場合には,耐電圧は高いほどよいことになるので,
望大特性の損失関数を選定する。
L=A0⊿02σT2
手順4 機能限界⊿0及び平均損失A0を求める。機能限界⊿0は,定格の出力電圧+5Vを加え
るのでこの値を用いる。耐電圧がこれより低下するとコンデンサが破壊すると考える。
平均損失A0については,コンデンサが破壊すると電源基板全体を交換しなければなら
ない。そのときの使用者の損失は,部品代を含めたサービス費用となる。その費用を
次のように見積もる。
部品代
定電圧電源プリント基板一式
3 000円
修理技術費
5 000円
その他諸経費
2 500円
合計
10 500円
手順5 平均二乗誤差の和σT2の式を求める。望大特性の平均二乗誤差の和σT2は,コンデンサ
の劣化耐電圧の逆数の二乗平均で求める。劣化係数d,総使用時間T,初期耐電圧を
V0とすると,次のようになる。
∫
∫
−
−
T
T
dT
dt
dt
T
e
T
dV
dt
e
T
V
dt
e
V
T
0
0
2
2
0
2
2
0
2
0
2
)1
(
2
1
1
1
1
=
=
=
σ
9
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順6 入手したデータを代入してばらつきによる損失を求める。例えば候補Aの場合を考え
る。初期耐電圧は16V,設計寿命期間Tを5年間とし,1日8時間使用すると考える。
設計寿命時間は9 600時間となる。平均二乗誤差の和σT2は,
1.
205
1
600
9
16
10
23
.2
2
1
2
1
2
5
600
9
10
23
.2
2
2
0
2
2
5
=
=
=
×
×
×
×
−
−
−
×
×
×
−
e
T
dV
edT
T
σ
となるので,ばらつきによる損失Lは次のようになる。
280
1
1.
205
500
262
1.
205
1
5
500
10
2
2
2
0
0
=
=
=
=
×
×
T
A
L
σ
Δ
同様に他の候補についても計算する。
附属書1図1 耐電圧の劣化
手順7 ばらつきによる損失L及び入手コストAの和を求め,総合コストLTとする。計算結果
を附属書1表4に示す。
附属書1表4 計算された総合損失
単位 円
候補
損失コスト L
コスト A
総合損失 LT
A
1280
100
1380
B
488
120
608
C
114
195
309
D
71
230
301
E
27
305
333
以上の結果から候補Dを選定すればよいことになる。
望小特性も同様な方法で,製品の品質とコストとのバランスを取るための検討をす
ることができる。
10
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2 品質水準の検討及び改善方法
1. 適用範囲 この附属書は,製品の品質特性の規格値に関連して,品質水準を検討し改善する方法につ
いて規定する。
2. 用語の定義 この附属書で用いる主な用語の定義及び記号は,規格の本体及び附属書1によるほか,
次のとおりとする。
(1) 動特性 あるシステムにおいて,出力を実現させるための入力信号と出力特性との間の関係をもとに
ばらつきを評価できる特性。これに対して,望小特性・普通特性・望大特性を静特性と呼ぶことがあ
る。例えば,測定器の出力,センサの出力,製品の寸法などである。
(2) 信号因子 システムの出力を変化させるための入力として取り上げたもの。
(3) 誤差因子 システムの特性のばらつきの原因となる条件の代表として取り上げたもの。
(4) SN比 (η) 動特性において、信号のパワーの雑音のパワーに対する比。ここでは,信号パワーを信
号因子の効果の大きさ又は雑音のパワーを誤差因子の効果の大きさとする。静特性の場合にも,便宜
的に平均値の効果又は雑音のパワーを用いてSN比を求めることができる。
(5) 現行の損失 (L1) 現状の品質水準から推定した損失。
(6) 許容最大損失 (L2) 規格限界に等しい特性値をもっている製品から推定した損失。
3. 品質水準の検討 設定された⊿の値と特性値の現状の平均二乗誤差VTとを損失で比較して,品質水準
の検討を次の手順で行う。
手順1 製品の特性値の現状の平均二乗誤差VTを,特性値yi (i=1,…,n) と基準値m0とから,次の
式によって算出する。
(1) 望小特性の場合
)
(
1
2
2
2
2
1
n
T
y
y
y
n
V
+
…
…
+
+
=
(2) 普通特性の場合
}
)
(
)
(
)
{(
1
2
0
2
0
2
2
0
1
m
y
m
y
m
y
n
V
n
T
−
+
…
…
+
−
+
−
=
(3) 望大特性の場合
+
…
…
+
+
2
2
2
21
1
1
1
1
n
T
y
y
y
n
V=
手順2 VTの値から求めた現行の損失L1及び許容最大損失L2を次の損失関数によって算出する。
(1) 望小特性の場合
T
V
A
L
2
0
0
1Δ
=
2
2
0
0
2
Δ
Δ
A
L=
11
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(2) 普通特性の場合
T
V
A
L
2
0
0
1Δ
=
2
2
0
0
2
Δ
Δ
A
L=
(3) 望大特性の場合
L1=A0∆02VT
L2=A0∆02
2
1
Δ
手順3 L1とL2との値を比較し,品質水準の判定を行う。例えば,次のように考えて判定する。
(1) L1がL2に比較して十分小さい場合には,品質水準は十分だと判定する。
(2) L1がL2に比較して大きい場合には,品質水準の改善を検討する。
(3) L1がL2に対して同等から21程度の間にある場合は,製品の価格と品質の改善の可能性の
度合いとを勘案して,品質水準の判定を行う。
(4) 品質水準の改善が不可能な場合には,生産者側の損失Aの値を変えて⊿を再検討する。
(5) ⊿の再検討が不可能な場合には,全数検査を行うか,材料変更又は設計変更を行う。
例1. 望小特性の例 音響機器の基板に使用している軸受の真円度の規格値が40μm,機能限界⊿0=
110μm,平均損失A0=5 000円である。
手順1 現在の製品について真円度を測定した。
データは
38.1 39.5 38.9 39.8 43.8 (μm)
であった。望小特性の平均二乗誤差VTを求める。
55
.
027
8
5
1
)
(
1
2
2
2
2
1
×
+
…
…
+
+
=
=
n
T
y
y
y
n
V
=1 605.51 (μm2)
手順2 現行の損失L1及び許容最大損失L2を求める。
51
.
05
16
110
000
5
2
2
0
0
1
×
=
=
T
V
A
LΔ
≒663.4 (円/個)
2
2
2
2
0
0
2
40
110
000
5
×
=
=
Δ
Δ
A
L
≒661.2 (円/個)
手順3 L1とL2を比較して,現在の工程の品質水準を判定する。ここでは現行の損失L1が許
容最大損失L2よりもやや大きいので,品質水準の改善を検討する。
例2. 望大特性の例 手提げかばんのハンドルのはめあい強度の規格値が900Nで,機能限界⊿0=
150N,平均損失A0=5 000円,生産者側の損失A=140円である。
手順1 現在の製品について,はめあい強度を測定した。
データは
1 355 1 229 1220 1 464 1 262 (N)
であった。望大特性の平均二乗誤差VTを求める。
5
1
1
1
1
1
2
2
2
21
=
=
+
…
…
+
+
n
T
y
y
y
n
V
×2.973 0×10−6=5.946 1×10-7 (N−2)
12
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順2 現行の損失L1及び許容最大損失L2を求める。
L1=A0∆02VT=5 000×1502×5.946 1×10−7≒66.9 (円/個)
L2=A0∆02
2
1
Δ=5 000×1502×
2
900
1
≒138.9 (円/個)
手順3 L1とL2とを比較して,現在の工程の品質水準を判定する。ここでは現行の損失L1が
許容最大損失L2よりも十分小さいとみなされるので,現在の製品の品質水準は適正と
判定する。
4. 品質水準の改善
4.1
品質水準の改善の方法 目的とする製品に対する品質水準の改善は,材料,加工機械,付属する機
械,加工条件,工程の管理方法などについて検討することによって行うが,従来の知見では十分に効果が
期待できない場合には,生産技術部門において,次の手順によって改善を検討する。
手順1 製品の特性値に影響を及ぼす加工条件などを取り上げて,その中から重要と推定した因子を
選択する。
手順2 取り上げた各因子に対して,許される範囲内のできるだけ広い範囲で2又は3水準を選ぶ。
手順3 加工者が設定できる因子を制御因子として直交配列表に割り付ける。各制御因子に対して加
工上のばらつきの原因となる条件を誤差因子として選ぶ。実際の加工において発生すると思
われる範囲内で誤差因子の水準を選ぶ。誤差因子を別の直交配列表に割り付ける。
備考 直交配列表としては混合型直交配列表,例えばL18,L36などが使われる。
手順4 制御因子と誤差因子とを組み合わせた実験計画によって実験を行う。
手順5 誤差因子を割り付けた直交配列表による実験のデータから,次の方法によって特性値の種類
に応じてSN比ηを求める。
(1) 動特性の場合 信号因子をMi (i=1,……,k) とする。
信号因子の各水準の繰り返し数をr0とし,yk1,yk2,……,ykr0の繰り返しのデータを
足し合わせてykと表示する。
0
2
2
12
2
11
r
k
y
y
y
ST
+
…
…
+
+
=
r=r0 (M12+M22+……+Mk2)
2
2
2
1
1
)
(
1
k
ky
M
y
M
y
M
r
S
+
…
…
+
+
=
β
1
0−
−
kr
S
S
V
T
e
β
=
e
e
V
V
S
r
)
(
1
−
β
η=
η (dB) =10 log η
(2) 望小特性の場合
)
(
1
1
2
2
2
21
n
y
y
y
n
+
…
…
+
+
=
η
η (dB) =10 log η
(3) 普通特性の場合
13
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ST=y12+y22+……+yn2
2
2
1
)
(
1
n
y
y
y
n
Sm
+
…
…
+
+
=
1
−
−
n
S
S
V
m
T
e=
e
e
m
V
V
S
n
)
(
1
−
=
η
η (dB) =l0 log η
(4) 望大特性の場合
+
…
…
+
+
2
2
2
2
1
1
1
1
1
1
n
y
y
y
n
=
η
η (dB) =10 log η
手順6 SN比を特性値として,制御因子を割り付けた直交配列表について,各因子の水準ごとのSN
比の和及び平均値を求める。
手順7 効果の大きいと認められる制御因子のSN比の一番大きい水準の組合せが最適成形条件とな
る。
手順8 最適成形条件における品質水準と改善前の品質水準とを比較し,SN比の利得 (dB) を求め
る。確認実験によって利得の再現性を確認する。
例1. 望小特性の場合 エッチング用レジストインキの品質水準が十分ではなく,これを改善するた
めに,エッチング後の外観の評点を特性値とした実験を行った。従来は,検査において,外観
の評点で“中”以下のものは不良品とされていた。
手順1 レジストインキの品質向上に役立つと思われる制御因子として,薬剤の種類,量など
を,附属書2表1のように設定した。
附属書2表1 制御因子及び水準の選択
因子
水準
1
2
3
A:ベースレンジの種類
A1
A2
−
B:アロニックスの種類
B1
B2
B3
C:ベースレンジの配合比
多い
中
少ない
D:顔料の種類(10部)
D1
D2
D3
E:添加剤Eの添加量
0部
2部
4部
F:添加剤Fの添加量
0部
0.2部
0.4部
G:開始剤の種類
G1
G2
G3
H:開始剤の添加量
2部
6部
10部
手順2 制御因子の水準値を附属書2表1のように設定した。誤差因子はエッチング用試料の
場所として3か所を取った。
手順3 附属書2表2のように,制御因子を直交配列表L18の各列に割り付けた。

14
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2表2 割付け及び実験結果
行番
因子及び列番
外観の判定
SN比
A
B
C
D
E
F
G
H
良
中
不良
η
1
2
3
4
5
6
7
8
(dB)
1
1
1
1
1
1
1
1
1
1
1
1
−2.3
2
1
1
2
2
2
2
2
2
3
0
0
12.0
3
1
1
3
3
3
3
3
3
1
2
0
1.6
4
1
2
1
1
2
2
3
3
2
1
0
4.3
5
1
2
2
2
3
3
1
1
1
1
1
−2.3
6
1
2
3
3
1
1
2
2
1
0
2
−4.3
7
1
3
1
2
1
3
2
3
0
3
0
0.0
8
1
3
2
3
2
1
3
1
1
0
2
−4.3
9
1
3
3
1
3
2
1
2
0
1
2
−4.8
10
2
1
1
3
3
2
2
1
0
1
2
−4.8
11
2
1
2
1
1
3
3
2
3
0
0
12.0
12
2
1
3
2
2
1
1
3
1
1
1
−2.3
13
2
2
1
2
3
1
3
2
3
0
0
12.0
14
2
2
2
3
1
2
1
3
3
0
0
12.0
15
2
2
3
1
2
3
2
1
0
3
0
0.0
16
2
3
1
3
2
3
1
2
2
0
1
−1.4
17
2
3
2
1
3
1
2
3
0
3
0
0.0
18
2
3
3
2
1
2
3
1
0
3
0
0.0
手順4 直交配列表L18の各行の条件の組合せでレジストインキを作成し,エッチングを行い,
試料を作製し,測定した。試料の3か所の外観を限度見本との比較によって,良,中,
不良の3段階に分け,データを取った。データは附属書2表2に示す。
手順5 良,中,不良の分類データに対し,0.25,1.00,2.00の評点を対応させた。この評点は
望小特性である。直交配列表の各行ごとに望小特性のSN比を求める。1行目のSN比
の計算は,次のようになる。
)
00
.2
00
.1
25
.0(
3
1
)
(
3
1
1
2
2
2
2
3
2
2
2
1
+
+
+
+
=
=
=
y
y
y
VTη
=1.687 5
η (dB) =10 log η=−2.3 (dB)
手順6 SN比η (dB) をデータとして,附属書2表3のように,直交配列表に割り付けた制御
因子の各水準ごとのSN比の和及び平均値を求める。
附属書2表3 因子の水準ごとの和及び平均値
因子
和
平均値
1
2
3
1
2
3
A
−0.1
27.5
−
−0.01
3.06
−
B
16.2
21.7
−10.5
2.70
3.62
−1.75
C
7.8
29.4
−9.8
1.30
4.90
−1.63
D
9.2
19.4
−1.2
1.53
3.23
−0.20
E
17.4
8.3
1.7
2.90
1.38
0.28
F
−1.2
18.7
9.9
−0.20
3.12
1.65
G
−1.1
2.9
25.6
−0.18
0.48
4.27
H
−13.7
25.5
15.6
−2.28
4.25
2.60
15
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順7 附属書2表3から,SN比の平均値の大きい水準の組合せである
A2B2C2D2E1F2G3H2
が最適条件になる。
手順8 エッチング後の外観に大きな効果をもつ要因は,A(ベースレジンの種類),B(アロ
ニックスの種類),C(ベースレジンの配合比),G(開始剤の種類)及びH(開始剤
の添加量)である。これらの条件を用いて,最適条件のSN比及び現状条件のSN比を,
次のように推定した。
なお,現状条件はA1B2C2D2E2F2G2H2である。
最適条件のSN比
)
(
)
(
)
(
)
(
)
(
dB)
(
2
3
2
2
2
η
η
η
η
η
η
η
−
+
−
+
−
+
−
+
−
+
H
G
C
B
A
=
=A2+B2+C2+G3+H2−4×η
=3.06+3.62+4.9+4.27+4.25−4×1.52
=14.02 (dB)
現状条件のSN比
)
(
)
(
)
(
)
(
)
(
dB)
(
2
2
2
2
1
η
η
η
η
η
η
η
−
+
−
+
−
+
−
+
−
+
H
G
C
B
A
=
=A1+B2+C2+G2+H2−4×η
=−0.01+3.62+4.9+0.48+4.25−4×1.52
=7.16 (dB)
利得の計算
最適条件のSN比と現状条件のSN比との差,すなわち,利得を求める。
利得=14.02−7.16=6.86 (dB)
6.86 (dB) の真数は4.85であるので,最適条件での分散は,現状条件の分散の
85
.4
1倍
に改善されることが分かった。たがって,最適条件での損失は,現状条件での損失の
85
.4
1になる。現状条件での損失が50万円であれば,最適条件での損失は約10万円と
なる。
確認実験によって,利得が再現することが確かめられた。
例2. 普通特性の場合 金型加工は3軸同時制御のNC工作機械で行っている。プラスチック製品の品
質向上のために,金型加工の工程能力の改善を目的にして実験を行った。金型加工では,設計
された曲面が正しく金型に生成されることが必要であるので,改善には動特性のSN比を用い
た。
手順1 工作機械の運転条件の中から,附属書2表4に示した因子を制御因子として取り上げ
た。
16
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2表4 制御因子及び水準の選定21
因子
水準
1
2
3
A:刃具
従来品*
新型
−
B:切込み量 (mm)
2
1
従来*
2倍
C:1刃当たりの送り量
C1
C2*
C3
D:回転速度 (rpm)
D1
D2*
D3
E:ピックフィード (mm)
2
1
従来*
2倍
F:送りのオーバライド
F1
F2*
F3
G:機械定数
G1
G2*
G3
注*
現状条件を示す。
手順2 制御因子の水準を,附属書2表4のように設定した。因子C,D,F,Gの水準は,従
来の設定条件を第2水準として,実行可能な限り大きく水準幅を取った。信号因子は,
加工曲面の特定の位置の高さの設計値(NC指令値)とし,高さの違う5か所の位置
を指定した。誤差因子は,N1=x軸方向,N2=y軸方向での加工の2水準とした。
手順3 附属書2表5のように,制御因子を直交配列表L18の各列に割り付けた。
誤差因子は直交配列表の外に割り付けた。
附属書2表5 割付け及び実験結果の解析で得られたSN比
行番
因子及び列番
SN比
A
B
C
D
E
F
G
η
1
2
3
4
5
6
7
(dB)
1
1
1
1
1
1
1
1
25.3
2
1
1
2
2
2
2
2
24.4
3
1
1
3
3
3
3
3
23.2
4
1
2
1
1
2
2
3
25.1
5
1
2
2
2
3
3
1
25.8
6
1
2
3
3
1
1
2
24.6
7
1
3
1
2
1
3
2
25.0
8
1
3
2
3
2
1
3
24.0
9
1
3
3
1
3
2
1
26.0
10
2
1
1
3
3
2
2
25.4
11
2
1
2
1
1
3
3
25.6
12
2
1
3
2
2
1
1
27.5
13
2
2
1
2
3
1
3
27.0
14
2
2
2
3
1
2
1
28.7
15
2
2
3
1
2
3
2
25.6
16
2
3
1
3
2
3
1
28.3
17
2
3
2
1
3
1
2
25.2
18
2
3
3
2
1
2
3
23.1
手順4 直交配列表L18の各条件の組合せのもとで,x軸方向,y軸方向の加工を行って試料を
作製し,信号因子として指定した5か所の高さを測定した。データは,曲面の基準面
からの高さである。直交配列表の第1行目のデータは,附属書2表6のとおりである。
附属書2表6 直交表L18の1行目の実験結果
誤差因子
信号

17
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
M1
M2
M3
M4
M5
−10.13
−3.56
3.44
9.83
30.00
N1
−10.10
−3.56
3.44
9.76
30.10
N2
−10.09
−3.50
3.42
9.76
29.99
計
−20.19
−7.06
6.86
19.52
60.09
手順5 手順4で求めたデータから,附属書2表5に示すように直交配列表の各行ごとに動特
性のSN比を求めた。直交配列表の1行目のSN比の計算は,次のようになる。データ
の繰返しr0は2である。
r=r0 (M12+M22+……+M52)
=2× [ (−10.13) 2+ (−3.56) 2+3.442+9.832+30.002]
=2 247.506
252
212
211
y
y
y
ST
…
…
+
+
=
=(−10.10)2+(−10.09)2+(−3.56)2+……+29.992
=2 248.197 0
[
]2
52
51
5
12
11
1
)
(
)
(
1
y
y
M
y
y
M
r
S
+
+
…
…
+
+
+
=
β
[
]2)
99
.
29
10
.
30
(
00
.
30
)
09
.
10
10
.
10
(
13
.
10
506
.
247
2
1
+
×
+
…
+
−
−
×
−
=
506
.
247
2
3
838
.
247
2
2
=
=2 248.170 6
Se=ST−Sβ
=2248.197 0−2248.170 6
=0.026 35
9
35
026
.0
=
Ve
=0.002 928
e
e
V
V
S
r
)
(
1
−
β
η=
928
002
.0
)
928
002
.0
6
170
.
248
2(
506
.
247
2
1
−
=
=341.64
η (dB) =10 1og η=25.3 (dB)
手順6 SN比η (dB) をデータとして,附属書2表7のように,直交配列表に割り付けた制御
因子の各水準ごとのSN比の和及び平均値を求める。
附属書2表7 制御因子の水準ごとの和及び平均値
因子
和
平均値
1
2
3
1
2
3
A
223.4
236.4
−
24.82
26.27
−
B
151.4
156.8
151.6
25.23
26.13
25.27

18
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C
156.1
153.7
150.0
26.02
25.62
25.00
D
152.8
152.8
154.2
25.47
25.47
25.70
E
152.3
154.9
152.6
25.38
25.82
25.43
F
153.6
152.7
153.5
25.60
25.45
25.58
G
161.6
150.2
148.0
26.93
25.03
24.67
手順7 附属書2表7から,SN比の平均値の大きい水準の組合せである
A2B2C1D3E2F1G1
が最適条件になる。
手順8 金型加工に大きな効果をもつ要因は,A(刃具),C(1刃当たりの送り量)及びG(機
械定数)である。これらの条件を含めて,自由度の和が全自由度の半分程度になるよ
うに効果の大きい要因を選んで,最適条件のSN比及び現状条件のSN比を,次のよう
に推定した。
なお,現状条件は,A1B2C2D2E2F2G2である。
最適条件のSN比
)
(
)
(
)
(
)
(
1
1
2
2
η
η
η
η
η
η
−
+
−
+
−
+
−
+
G
C
B
A
=
=A2+B2+C1+G1+−3×η
=26.27+26.13+26.10+27.02−3×25.57
=28.81 (dB)
現状条件のSN比
)
(
)
(
)
(
)
(
2
2
2
1
η
η
η
η
η
η
−
+
−
+
−
+
−
+
G
C
B
A
=
=A1+B2+C2+G2+−3×η
=24.82+26.13+25.62+25.03−3×25.57
=24.95 (dB)
利得の計算
最適条件のSN比と現状条件のSN比との差,すなわち,利得を求める。
利得=28.81−24.95=3.86 (dB)
3.86 (dB) の真数は2.43であるので最適条件での分散は,現状条件の分散の
43
.2
1倍に
改善されることが分かった。したがって,最適条件での損失は現状条件の損失の
43
.2
1に
なる。
確認実験によって,利得が再現することを確かめた。

19
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3 特性値の測定能力の検討及び改善方法
1. 適用範囲 この附属書は,製品の品質特性の規格値に関連して,測定能力の検討及び改善を行う方法
について規定する。
2. 用語の定義及び記号 この附属書で用いる主な用語の定義及び記号は,規格の本体,附属書1及び附
属書2によるほか,次のとおりとする。
(1) 測定コスト 対象となる測定器を用いて,定めた特性値を測定するのに要した時間と測定担当者の賃
金単価との積。
(2) 測定器のコスト 測定器の価格に,償却までの期間及び金利を考慮したもの。
3. 品質水準に占める測定誤差の影響の検討 利用できる標準の種類によって,次のいずれかの検討を行
う。
(1) 測定する量に対応し利用できる標準(直接的な標準)がある場合には,これを用いて4.1の手順によ
って,現状の測定の誤差を求め,加工の誤差と比較する。そのとき品質水準に占める測定の誤差の割
合が大きい場合には,測定方法の改善についての検討を行うが,従来の知見では十分な改善効果が期
待できない場合には,5.以下の手順によって改善を検討する。
(2) 直接的な標準が得られない場合には,4.2の手順によって測定系の要素の標準の誤差を求め,計測の
SN比を算出する。
4. SN比の求め方
4.1
直接的な標準がある場合の計測のSN比の求め方 直接的な標準がある場合には,測定器によって標
準を測定した読み値から,次の手順でSN比を求める。
手順1 対象となる測定方法の標準を信号因子とし,その種類及び水準を決定する。
手順2 測定方法の誤差原因と考えた誤差因子(1)を取り上げ,SN比を求めるための実験及び測定を行
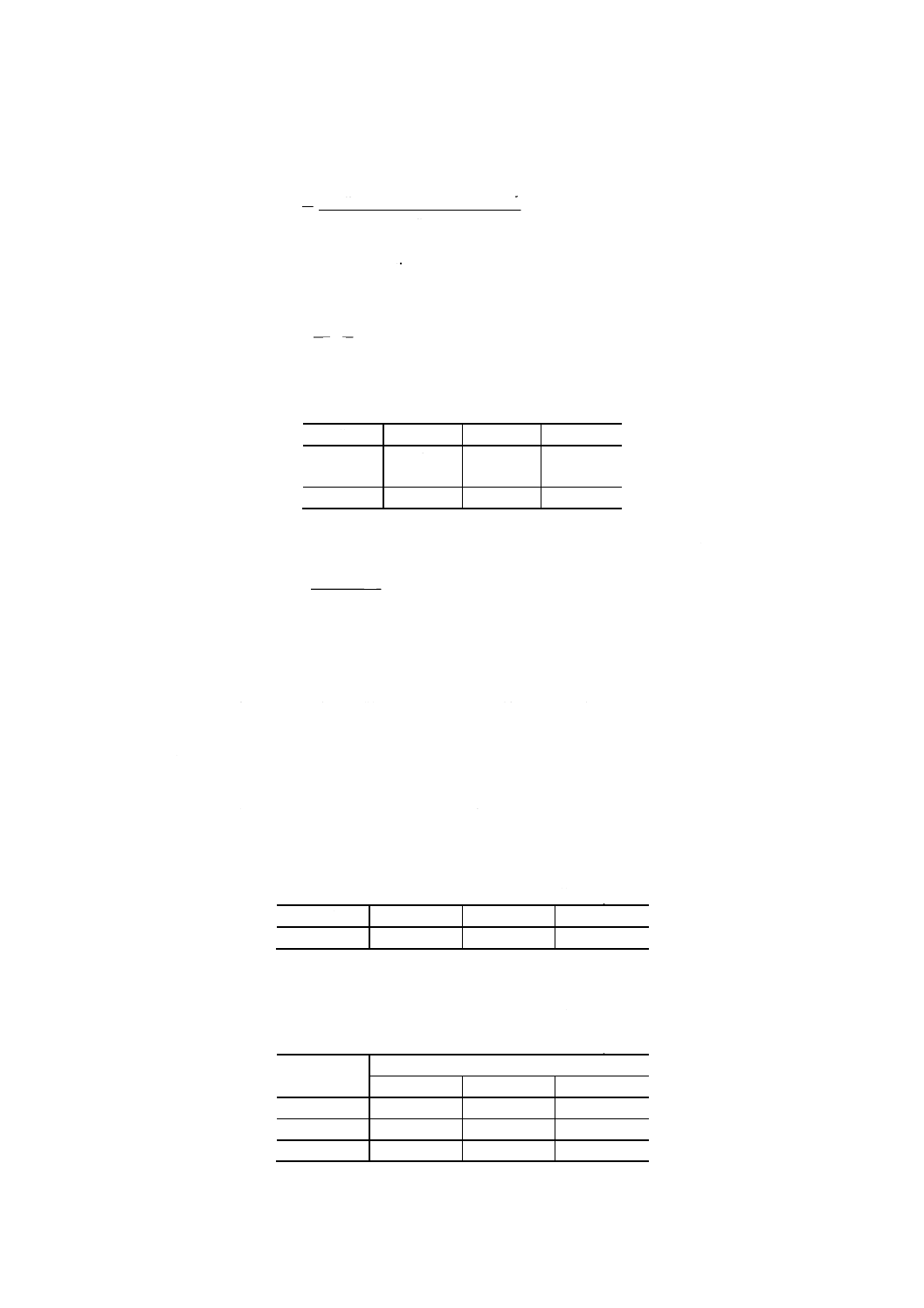
い,附属書3表1の測定データを得る。
注(1) 測定者,反復などがある。
附属書3表1 測定データ
反復
標準(信号因子)の水準
M1
M2
M3
…
Mk
R1
y11
y21
y31
…
yk1
R2
y12
y22
y32
…
yk2
・
…
・
…
・
…
Rr0
y1r0
y2r0
y3r0
…
ykr0
計
y1
y2
y3
…
yk
手順3 実験の結果について分散分析を行う。校正を比例式で行うとして,解析手順は次のとおりで
20
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ある。
r=r0 (M12+M22+……+Mk2)
r
y
M
y
M
y
M
S
k
k
2
2
2
1
1
)
(
+
…
…
+
+
=
β
2
2
12
211
0k
r
T
y
y
y
S
+
+
+
=
…
…
Se=ST−Sβ
1
0−
kr
S
V
e
e=
結果を附属書3表2の分散分析表にまとめる。
附属書3表2 分散分析表
要因
自由度
平方和
分散
β
1
Sβ
Vβ
e
kr0−1
Se
Ve
T
kr0
ST
−
手順4 誤差分散に対する信号因子の効果の大きさから,次の式を用いてSN比を算出する。
e
e
V
V
S
r
)
(
1
−
β
η=
測定の誤差分散は,次の式で求めることができる。
η
σ
1
2=
σ2は信号因子の次元で得られるので,特性値と同一の次元にするためには,β2を乗じる。
例 直接的な標準がある場合の例
触針式表面粗さ測定器 基準となる測定器で値を付けた粗さ試験片を用い,触針式表面粗さ測
定器を校正した場合について検討した。
手順1 信号因子として,標準の水準の選定を行う。
粗さ測定の標準として,その水準は附属書3表3のとおりである。
附属書3表3 粗さ標準の水準
単位 μmRa
水準
M1
M2
M3
表示値
1.2
3.2
4.1
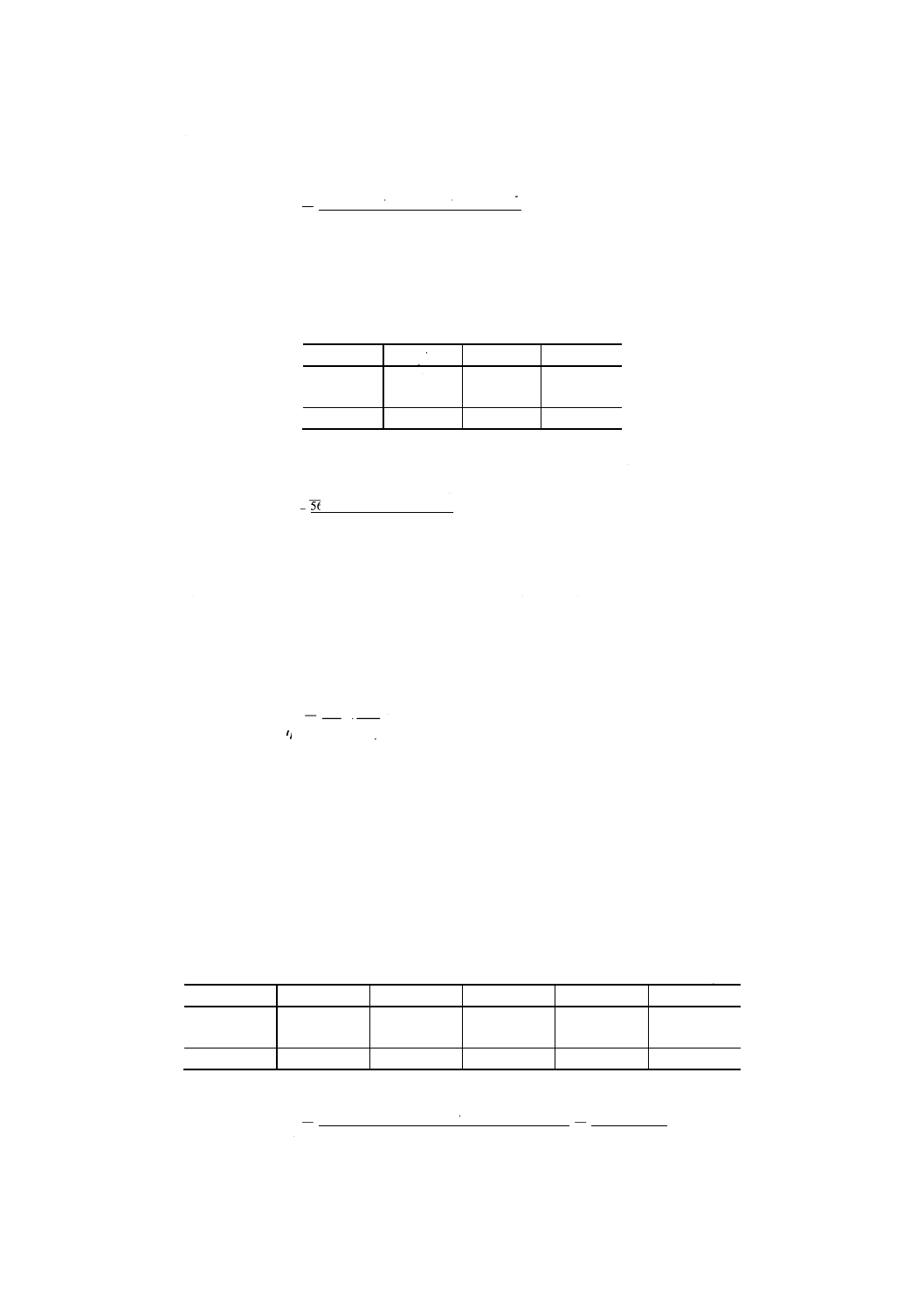
手順2 実験を行う。実験データを附属書3表4に示す。
附属書3表4 粗さ測定器の実験データ
単位 μmRa
反復
信号
M1
M2
M3
R1
1.1
3.3
3.8
R2
1.1
3.1
4.1
計
2.2
6.4
7.9
21
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順3 分散分析を行う。
r=2× (1.22+3.22+4.12) =56.98
98
.
56
)9.7
1.4
4.6
2.3
2.2
2.1(
2
×
+
×
+
×
=
β
S
=54.078
ST=54.17
Se=0.092
分散分析を行った結果は,附属書3表5のとおりである。
附属書3表5 粗さ測定データの分散分析表
要因
f
S
V
β
1
54.078
54.078
e
5
0.092
0.018
T
6
54.170
−
手順4 誤差分散に対する信号因子の効果の大きさからSN比を求める。
71
.
52
018
.0
)
018
.0
078
.
54
(
98
.
561
=
=
−
×
η
(μmRa)−2
4.2
直接的な標準はないが,測定系を構成する要素ごとにSN比が求められる場合 直接的な標準がな
い場合には,次の手順によってSN比を求める。
手順1 個々の要素の比率に対するSN比η01,η02……を求める。個々の要素のSN比を動特性のSN比
として求めた場合には,比率のSN比は信号の平均値の2乗m2を動特性のSN比にかけるこ
とで求められる。
手順2 個々の要素のSN比から,測定器を校正したときの比率のSN比η0を求める。
…
…
+
+
02
01
0
1
1
1
η
η
η=
例 測定系を構成する要素ごとにSN比が求められる場合の例
引張強さの誤差 要素の誤差の検討を行う。引張強さを求めるための要素として,力基準機
を標準として校正した力計,力計を用いて校正した引張試験機の荷重測定系及び試験片の断
面積を測定するためのマイクロメータを考える。
手順1 個々の要素の比率に対するSN比η01,η02……を求める。
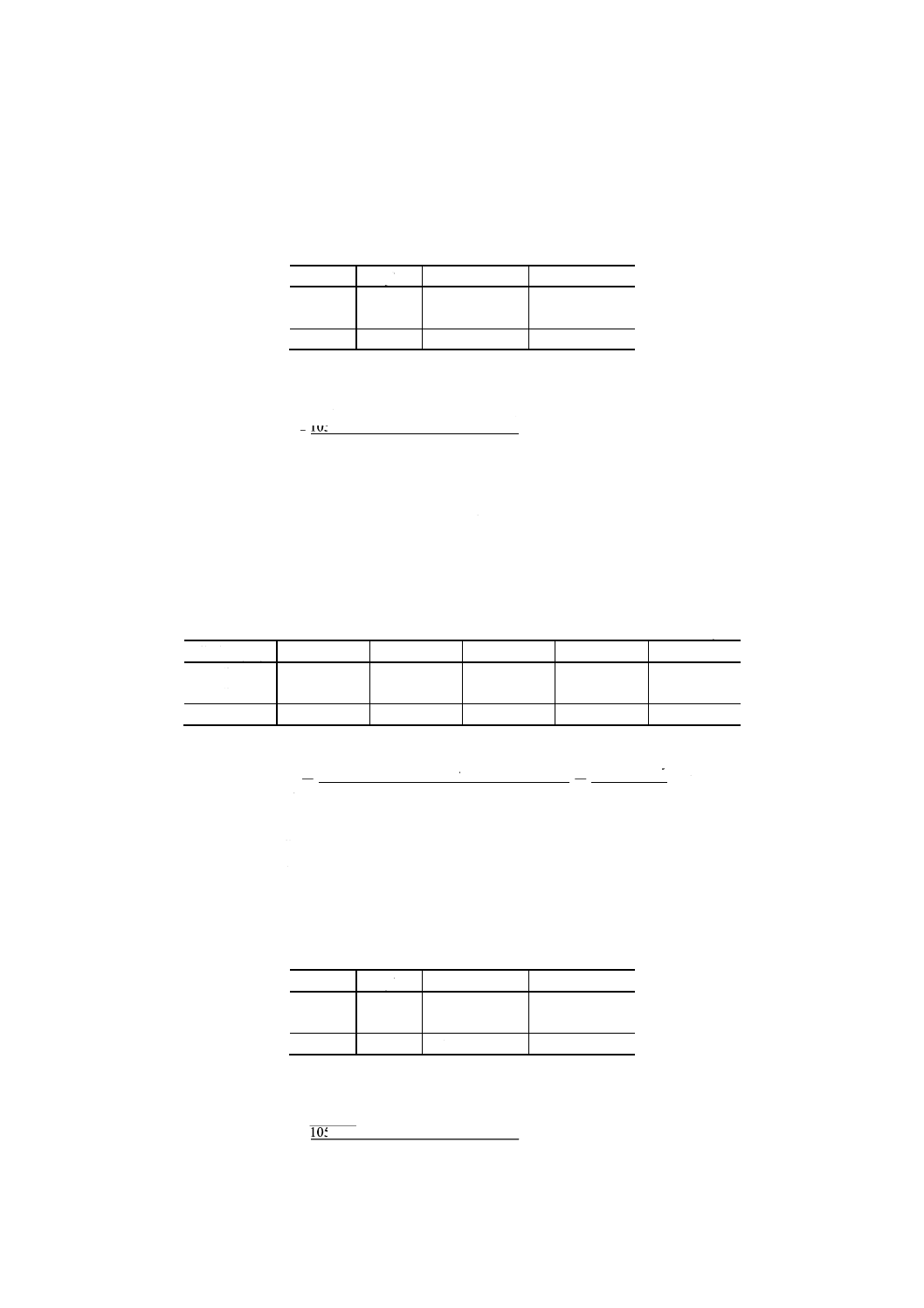
(1) 力計を力基準機を用いて校正したときのSN比 ゼロ点校正の後,附属書3表6
のデータを得て,このデータから比例式校正のSN比を求める。
附属書3表6 力計の測定結果
単位 μm
荷重 (kN)
0.98
1.96
2.94
3.92
4.90
反復R1
121.20
242.45
364.25
486.05
608.25
反復R2
121.30
242.50
364.30
486.10
608.35
計
242.50
484.95
728.55
972.15
1 216.60
r=2× (0.982+1.962+……+4.902) =105.644
644
.
105
257
.
102
13
644
.
105
)
60
.
216
1
90
.4
50
.
242
98
.0(
2
2
=
=
×
+
…
…
+
×
β
S
=1 624 977.647
ST=1 624 979.532
22
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Se=1.885
fe=10−1=9
Ve=0.209
分散分析を行った結果は,附属書3表7のとおりである。
附属書3表7 力計による測定データの分散分析表
要因
f
S
V
β
1
1 624 977.647
1 624 977.647
e
9
1.885
0.209
T
10
1 624 979.532
−
次の式によってSN比ηを算出する。
209
.0
)
209
.0
647
.
977
624
1(
644
.
1051
−
×
=
η
=73 596.399 (kN−2)
η (dB) =10 log η=48.67 (dB)
荷重の平均値m1に対する比率のSN比η01に変換する。
η01=ηm12=73 596.339×2.942=636 137.3
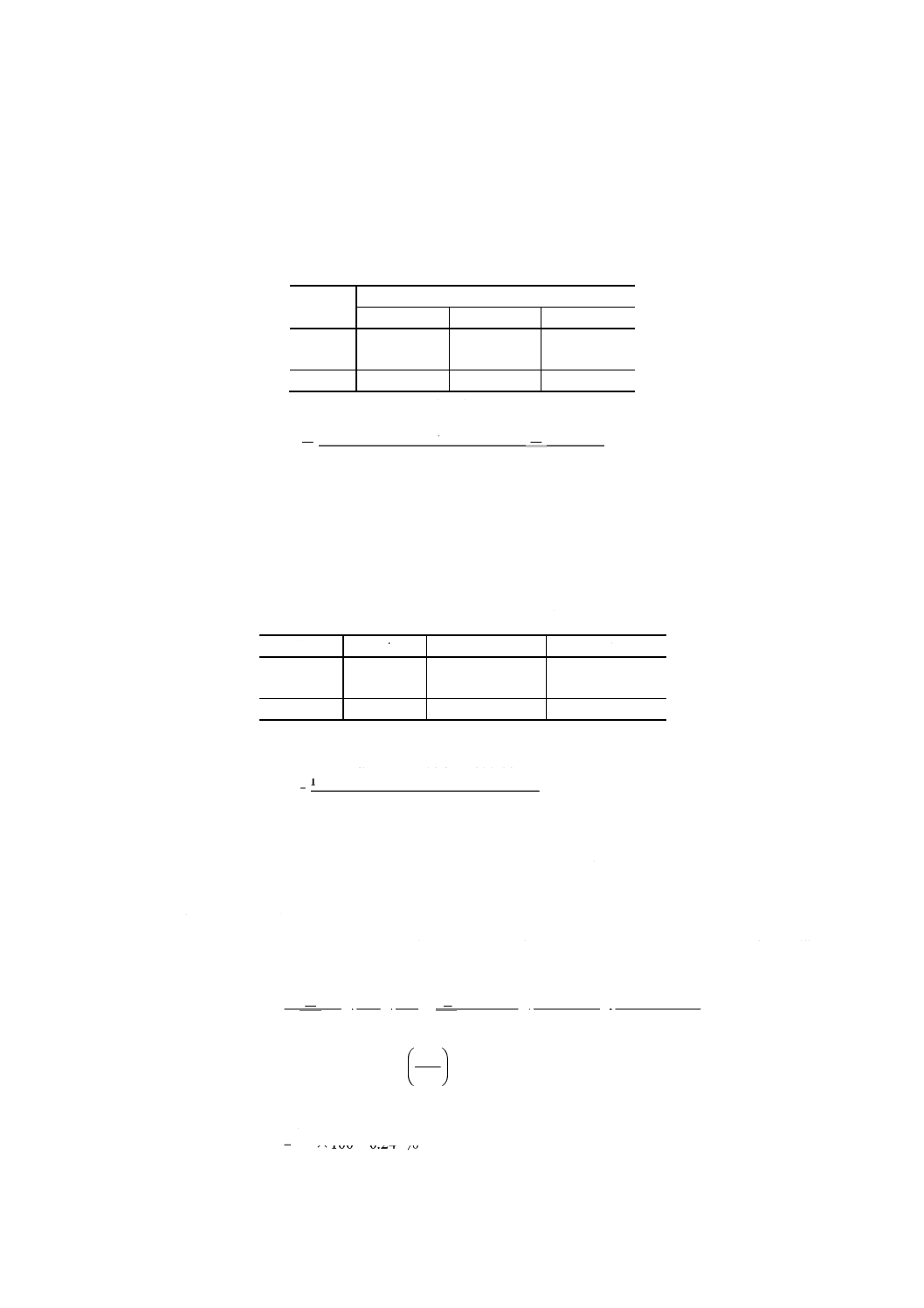
(2) 引張試験機の荷重を力計を用いて校正したときのSN比 (1)で校正した力計を用
いて試験機の荷重の校正を行うため,附属書3表8のデータを得た。
附属書3表8 引張試験機の荷重の測定結果
単位 μm
荷重 (kN)
0.98
1.96
2.94
3.92
4.90
反復 R1
120.70
241.20
362.80
485.00
606.90
反復 R2
120.80
241.80
363.05
485.35
607.00
計
241.50
483.00
725.85
970.35
1 213.90
r=2 (0.982+1.962+……,+4.902) =105.644
644
.
105
231
.
069
13
644
.
105
)
90
.
213
1
90
.4
50
.
241
98
.0(
2
2
=
=
×
+
…
…
+
×
β
S
=1 616 796.022
ST=1 616 801.185
Se=5.163
fe=10−1=9
Ve=0.574
分散分析を行った結果は,附属書3表9のとおりである。
附属書3表9 引張試験機の荷重データの分散分析表
要因
f
S
V
β
1
1 616 796.022
1 616 796.022
e
9
5.163
0.574
T
10
1 616 801.185
−
次の式によってSN比ηを算出する。
574
.0
)
574
.0
022
.
796
661
1(
644
.
1051
−
×
=
η
=26 662.345 (kN−2)
η (dB) =10 log η=44.26 (dB)
23
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
荷重の平均値m2に対する比率のSN比η02に変換する。
η02=ηm22=26 662.345×2.942=230 458.6
(3) マイクロメータをブロックゲージで比例式校正を行ったときのSN比 附属書3
表10のデータを得た。
附属書3表10 マイクロメータによる測定結果
単位 mm
反復
標準値
5.000
15.000
25.000
R1
5.001
15.003
25.008
R2
5.005
15.007
25.002
計
10.006
30.010
50.010
r=2 (52+152+252) =1 750
750
1
43
.
750
1
750
1
)
010
.
50
25
006
.
10
5(
2
2
=
=
×
+
…
…
+
×
β
S
=1 750.860 106
ST=1750.860 152
Se=4.6×10−5
fe=10−1=9
Ve=5.1×10−6
分散分析を行った結果は,附属書3表11のとおりである。
附属書3表11 マイクロメータによる測定データの分散分析表
要因
f
S
V
β
1
1 750.860 106 1 750.860 106
e
9
0.000 046 0.000 005 1
T
10
1 750.860 152
−
次の式によってSN比ηを算出する。
1
005
000
.0
)1
005
000
.0
106
860
.
750
1(
750
11
−
×
=
η
=196 174.8 (kN−2)
η (dB) =10 log η=52.93 (dB)
寸法の平均値m3に対する比率のSN比η03に変換する。
η03=ηm32=196 174.8×15.02=44 139 330.0
手順2 要素ごとのSN比から推定した試験機の総合的なSN比 単位をそろえるために比率
に直したSN比を用い,試料断面積の測定誤差を見積もるために,寸法測定は縦横そ
れぞれ1回の合計2回分を考慮する。
0.
330
139
44
2
6.
458
230
1
3.
137
636
1
2
1
1
1
1
03
2
0
01
0
+
+
×
+
+
=
=
η
η
η
η
=5.956 5×10−6≒
2
410
1
試料断面積の測定誤差は,
410
1×100=0.24 %
24
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
と推定された。
5. 測定方法の選択及び改善 同一測定対象について2種類以上の測定方法がある場合には,次の手順で
測定方法を選定する。
手順1 次によって測定誤差を明らかにする。
(1) 選択する測定方法を制御因子とし,その水準を明らかにする。
(2) 信号因子及び誤差因子並びにそれらの水準を定める。
(3) SN比を求めるための実験及び測定を行う。
(4) 分散分析を行い,SN比を求める。
(5) SN比の比較を行う。制御因子の水準別に測定の誤差を求める。
手順2 次によって測定誤差の経済性評価を行う。
(1) 比例定数を求める。
(2) 測定の誤差分散をσ2,そのときの目標値をm0とし,測定誤差による損失Lを求める。望
大特性の場合にも製造段階では目標値m0があると考え,比率のSN比ηを用いて,下側
許容限界について損失Lを求める。
望小特性又は普通特性の場合
L≒
2
2
0
0σ
Δ
A
望大特性の場合
L≒
η
η
2
0
2
0
0
2
0
2
0
)
(
)
(
m
Δ
m
A
m
Δ
m
A
0
×
−
×
−
=
(3) 測定にかかわる総損失L (T) を求める。
(4) 測定にかかわる1年間の損失を比較し,損失の最も小さい測定方法を求める。
例 製造業者1及び製造業者2の引張試験機がある。どちらを採用するかを決定したい場合の例。
手順1 測定の誤差を明らかにする。
(1) 制御因子の水準の決定
H1:製造業者1の引張試験機(容量4.9kN)
H2:製造業者2の引張試験機(容量9.8kN)
(2) 信号因子及び誤差因子の水準の選び方 使用される測定器の目盛の上下限の範囲
で小さい方から等間隔にM1,M2,M3を選ぶ。この例では,要素のSN比との統合
を考慮して,比率のSN比を用いる。
また,使用範囲をカバーするための標示因子,及び誤差の原因となる誤差因子
として,代表的なものを附属書3表12のように選ぶ。B及びCは標示因子,他は
誤差因子とする。

25
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3表12 引張試験機の測定誤差比較実験の因子及び水準の選定
因子
水準
1
2
3
A 室温
13℃
23℃
−
B 材料
PS
PP
POM
C 試験片の断面積
7.25mm2
14.7mm2
30.0mm2
D 引張速度
小
中
大
E 試験片取付け位置誤差
−hE
0
+hE
(3) 実験結果 附属書3表12の因子を直交配列表L18に割り付けて,実験を行った結
果は,附属書3表13のとおりである。特性値の単位は力の次元とするが,試験片
の寸法(断面積)のばらつきがあるので,試験片の断面積Cごとに平均断面積に
対して換算した値とする。
附属書3表13 割付け及び実験結果
単位 N
行番
因子
A
B
C
D
E
e
e
e
引張試験機(制御因子)
列番
1
2
3
4
5
6
7
8
H1
H2
1
1
1
1
1
1
1
1
1
426
455
2
1
1
2
2
2
2
2
2
851
894
3
1
1
3
3
3
3
3
3
1 680
1 702
4
1
2
1
1
2
2
3
3
264
273
5
1
2
2
2
3
3
1
1
538
567
6
1
2
3
3
1
1
2
2
1 108
1 206
7
1
3
1
2
1
3
2
3
501
510
8
1
3
2
3
2
1
3
1
1 053
1 085
9
1
3
3
1
3
2
1
2
2 031
2 090
10
2
1
1
3
3
2
2
1
464
459
11
2
1
2
1
1
3
3
2
774
740
12
2
1
3
2
2
1
1
3
1 580
1 561
13
2
2
1
2
3
1
3
2
269
270
14
2
2
2
3
1
2
1
3
514
535
15
2
2
3
1
2
3
2
1
982
1 012
16
2
3
1
3
2
3
1
2
487
470
17
2
3
2
1
3
1
2
3
941
954
18
2
3
3
2
1
2
3
1
2 053
2 122
(4) 分散分析を行いSN比を求める。断面積(因子C)を信号とした比例式のSN比を
求める。分散分析表は,附属書3表14のとおりである。
(a) H1:製造業者1の試験機のSN比
ST=4262+8512+……+2 0532=20 748 764
Bの水準ごとにCの線形式を求める。
B1:L1=M1C11+M2C12+M3C13
=7.25×890+14.7×1 625+30.0×3 260
=128 140
B2:L2=……=82 028.65
B3:L3=……=158 994.8
r=M12+M22+M32=7.252+14.72+30.02

26
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=1 168.652 5
5
652
.
168
1
6
4.
163
369
6
3
2
1
×
+
+
=
=
r
L
L
L
β
=52.648
r
L
L
L
S
6
)
(
2
3
2
1
+
+
=
β
=19 435 725.164 4
β
S
r
L
L
L
SB
−
+
+
2
2
3
2
2
2
1
=
=1 283 823.823 8
Se=ST-Sβ-SB=29 215.011 8
15
e
e
S
V=
=1 947.667 5
次の式によってSN比ηを算出する。
e
e
V
V
S
r
)
(
61
1
−
β
η=
=1.423 0=1.532 (dB)
(b) H2:製造業者2の試験機のSN比
ST=4552+8942+……+2 1222=21 771 115
Bの水準ごとにCの線形式を求める。
B1:L1=MlC11+M2C12+M3C13
=7.25×914+14.7×1 634+30.0×3 263
=128 536.3
B2:L2=……= 86 676.15
B3:L3=……=163 438.3
r=M12+M22+M32=7.252+14.72+30.02
=1 168.652 5
5
652
.
168
1
6
75
.
650
378
6
3
2
1
×
+
+
=
=
r
L
L
L
β
r
L
L
L
S
6
)
(
2
3
2
1
+
+
=
β
=20 447 536.87
β
β
S
r
L
L
L
S
−
+
+
2
2
3
2
2
2
1
=
=1 263 969.89
Se=ST-Sβ-SB=59 608.24
15
e
e
S
V=
=3 973.882 8
次の式によってSN比ηを算出する。
e
e
r
V
V
S
)
(
6
1
2
−
β
η=
=0.733 7=−1.345 (dB)
附属書3表14 分散分析表
要因
f
試験機H1
試験機H2
S
V
S
V
B
2
1 283 824
641 912
1 263 970
631 985

27
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Sβ
1
19 435 725
19 435 725
20 447 537
20 447 537
e
15
29 215
1 948
59 608
3 974
T
18
20 748 764
−
21 771 115
−
(5) SN比の比較を行う。断面積の平均値を乗じて,比率のSN比を求める。
H1のSN比η1=1.423 0=1.532 (dB)
比率のSN比η1=1.423 0×14.72=307.496 1
H2のSN比η2=0.733 7=−1.345 (dB)
比率のSN比η2=0.733 7×14.72=158.545 2
手順2 測定の誤差の経済性評価を行う。材料B2を用いた部品について検討する。特性値は望
大特性で,機能限界は⊿0=220N,そのときの平均損失A0=5 000円,現状の平均値を
基準値と考えてm0=830Nとする。
(1) 比例定数kを求める。
2
2
0
0
)
220
8301
(
000
5
)
(
−
−
=
=
0
Δ
m
A
k
=0.013 4(円/N2)
(2) 手順1の比例式校正を行ったときのSN比(比率のSN比)ηを用いて,測定の誤
差による損失を求める。望大特性であるから,測定の誤差による損失Lは次のと
おりである。
11
.
30
1
496
.
307
830
44
013
.0
)
(
2
1
2
0
2
0
0
1
=
=
=
×
×
−
η
m
Δ
m
A
L
0
(円/個)
40
.
58
2
545
.
158
830
44
013
.0
)
(
2
2
2
0
2
0
0
2
=
=
=
×
×
−
η
m
Δ
m
A
L
0
(円/個)
(3) 測定に関する総損失L (T) を求める。
ここでは1日の測定時間を4時間とした。
測定コスト=賃金×1日の測定時間×1年間の日数
=3 000×4(時間)×250=3 000 000(円)
測定器のコスト
H1:1 600 000円(1年間当たり:購入価格の21とした。)
H2:2 400 000円(1年間当たり:購入価格の21とした。)
1年間の生産個数
50万個
総損失
H1の試験機
L (T) 1 =1 600 000+3 000 000+30.11×500 000=19 655 000(円/年)
H2の試験機
L (T) 2=2 400 000+3 000 000+58.40×500 000=34 600 000(円/年)
(4) 測定に関する総損失を比較し,小さい方を採用する。
L (T) 2−L (T) 1=14 945 000(円/年)
引張試験機 (H1) の方が1年間当たり約1 495万円損失が少ない。

28
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6. 総合誤差の決定 最適な測定方法を選定したら,実物試料について測定を行う。このとき,標準を使
って測定器を校正したときの誤差と実物試料を測定したときの誤差とを加えたものが,最終的に総合誤差
となる。
例 H1の試験機の引張強さの総合誤差を求める。
各手順で求めたSN比を総合する。
100
1
496
.
307
1
10
5
956
.5
4
1
1
4
6
1
0
2
1
×
+
×
×
±
+
×
+
±
−
=
=
η
η
δ
δ
(%)
=±11.4(%)
ここで,
δ12: 標準の誤差。ただし,ここでは他の誤差に比較して非常に
小さいとして省略した。
η0: 要素ごとのSN比から推定した試験機の総合的なSN比[4.2
手順2参照]
η1: 実物の品物を測定したときのSN比[5.手順1(5)参照]
したがって,附属書3表12のA,D及びEを誤差因子とした条件範囲において,引張強さ(引
張試験機H1を用いて測定)の最終的な総合誤差は,平均値の約11.4%であり,平均値を50MPa
として誤差は約5.7MPaとなった。
関連規格 JIS K 7109 プラスチックの寸法許容差の決め方
29
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考 適用事例
この規格の理解の手助けとなるように,参考として各分野の適用事例を示す。
例1. 複写機の特性 複写機の濃度を1.2にする必要がある。市場の調査によれば濃度が低くなると顧
客が整備のサービスを依頼する。調査結果から0.4で顧客の半分がサービスを要求することが分
かっている。工場の出荷時に規格値を満足しなかった場合,最終工程で調整の作業が必要とな
る。そのときの費用は調整時間を賃率換算すると300円となる。
また,濃度が濃くなるとかぶり現象が生じるので,かぶり濃度の規格値も決める必要がある。
それぞれの出荷規格値を検討する。
(1) 普通特性:複写機濃度
手順1 機能限界⊿0及び平均損失A0の推定
サービスマンの経費
12 000円
サービス部品費
22 000円
合計
34 000円
使用者段階
機能限界 ⊿0=1.2−0.4=0.8
顧客のサービスに伴う費用 A0=34 000円
手順2 生産者側の損失Aの推定
生産者段階 調整時間による損失 A=300円
手順3 品質水準及び測定能力の検討
附属書1によって許容差設計の最適化を行っていたので品質水準は十分であると判
断した。このため,このまま許容差を算出することとした。
手順4 許容差⊿の計算
⊿0=0.8,A0=3 4000円,A=300円であるから
⊿=
0
A
A×⊿0=
000
34
300
×0.8≒0.075
手順5 許容差⊿の検討
工程能力を検討した結果,品質水準が十分であるため,このまま許容差⊿を決定す
る。
手順6 許容差⊿の決定
濃度は下がる方が顧客にとって問題が生じやすいので,下の許容差だけとし,許容
差⊿を大きい数値に丸めて0.1とした。
(2) 望小特性:複写機のかぶり濃度 濃度が濃くなると,非画像部にかぶり現象が生じるのでそ
の規格値も要求される。この場合の出荷検査規格についても検討する。
かぶりは少なければ少ないほどよいので,望小特性とする。市場の調査では0.03が機能限
界であった。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階
機能限界 ⊿0=0.03
30
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
顧客のサービスに伴う費用 A0=34 000円
手順2 生産者側の損失Aの推定
生産者段階
部品廃棄による損失 A=3 000円
手順4 最大許容値⊿の計算
⊿0=0.03,A0=34 000円,A=3 000円であるから
⊿=
0A
A×⊿0=
000
34
300
×0.03≒0.009
手順6 最大許容値⊿の決定 以上から,この製品の最大許容値⊿は,きりがよい数値で0.01
とした。
例2. 普通特性:マイクロスイッチの復帰力 マイクロスイッチを圧力スイッチなどのダイアフラム
に直接取り付けて使用している。マイクロスイッチの力とダイアフラムの力とをバランスさせ
る方法をとっており,復帰力が重要になることが多い。
復帰力が基準値から0.95N以上大きくなったり小さくなったりすると,組立品の特性値に影
響する。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階
組立品での機能限界 ⊿0=0.2N
平均損失 A0=1 000円
手順2 生産者側の損失Aの推定
生産者段階
部品交換及び調整のコストA=200円
手順4 許容差⊿の計算
⊿0=0.2N,A0=1 000円,A=200円であるから
⊿=
0A
A×⊿0=
000
1
200×0.2≒0.09 N
手順6 許容差⊿の決定 以上から,この製品の許容差⊿は,きりがよい数値で0.1Nとした。
例3. 望大特性:半導体デバイスDRAMのリフレッシュ周期 半導体デバイスの例として,小形コ
ンピュータに使用されている4M DRAMを取り上げる。DRAMにはいろいろの品質特性がある
が,その中でも主要特性の一つであるリフレッシュ周期tREFについて検討する。
リフレッシュ周期tREFとは,そのカタログの規格値の時間以内に機器側でリフレッシュ動作
をしないと,書き込まれたデータの保持が保証されないというものである。したがって,リフ
レッシュ周期tREFは望大特性である。
最小許容値を決めるに当たっての前提条件として,小形コンピュータ組立者側はDRAMのリ
フレッシュ周期tREFを,機器(小形コンピュータ)に組み込んだ状態で全数試験することによ
って,その不良品を除去していることとする。
この前提条件によって,小形コンピュータの最終使用者へはリフレッシュ周期tREFの初期特
性不良品が出荷されないので,機能限界⊿0及び平均損失A0については,小形コンピュータ組
立者段階だけを考慮すればよいことになる。
4M DRAMのリフレッシュ周期tREFのカタログの規格値は16msであり,この値未満になる
と小形コンピュータ組立者側が苦情をいうことができる。小形コンピュータの組立工程で不良
が発見されたときに,その診断,DRAM交換及び試験にかかる費用は24 000円であり,4M
DRAMの購入価格は1 200円である。
31
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順1 機能限界⊿0及び平均損失A0の推定
使用者(この場合は小形コンピュータ組立者)段階
機能限界⊿0=16ms
平均損失A0=24 000+1 200=25
200円
手順2 生産者側の損失Aの推定
使用者段階
破棄による損失A=1 200円
手順4 最小許容値⊿の計算
⊿0=16ms,A0=25 200円,A=1 200円であるから
⊿=
0A
A×⊿0=
200
1
2000
25
×16≒73.3 ms
手順6 最小許容値⊿の決定 以上から,リフレッシュ周期tREFの最小許容値を73msとした。
例4. 壁用吹付け塗料の特性 水性エマルジョンの壁用吹付け塗料は,使用時,水で希釈した塗料を
エアーガンで壁に吹き付ける。吹き付けた塗料がたれると壁面の美観が損なわれ,再施工など
が必要となる。粘度が高ければたれは少なくなるが,ガンで吹きにくくなるなどの弊害が出る。
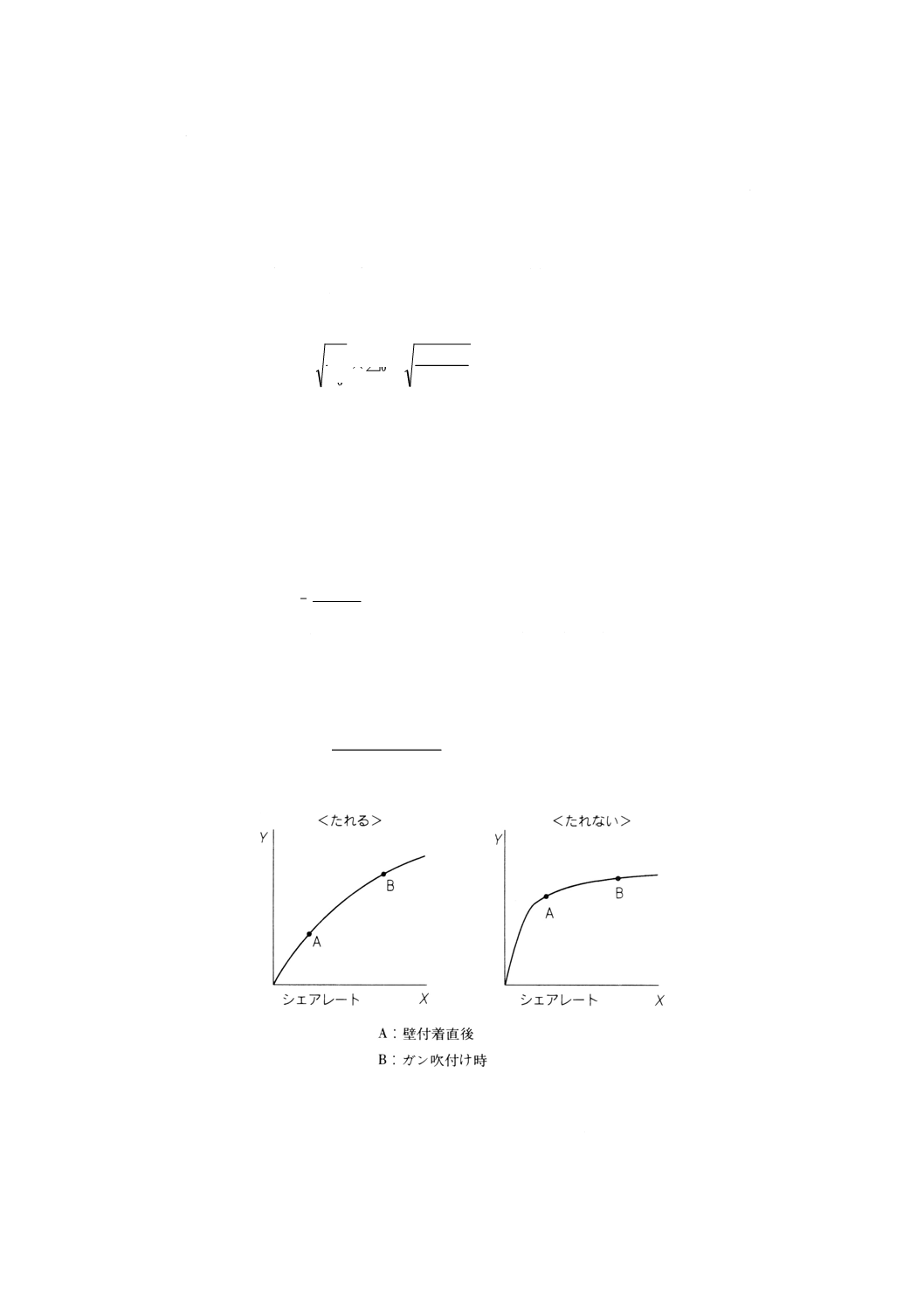
この塗料は,シェアレートによって粘度が変化する。この性状を利用して吹き付けやすくた
れない塗料にする(参考図1参照。)
たれやすさを示す尺度であるたれ性指数Fを次の式で定める。
A
A
B
Y
Y
Y
F
−
=
ここで,
YA: 低シェアレート(壁付着直後)のシェアストレス
YB: 高シェアレート(ガン吹付け時)のシェアストレス
であり,このたれ性指数Fは負の値とはならない望小特性である。
また,粘度は次の式で求められる。
粘度=
X
Y
シェアレート
シェアストレス
参考図1 シェアレート,シェアストレスとの関係
(1) 望小特性:壁用吹付け塗料のたれ性指数(受入側が受入検査をする場合) 作業現場にお
いて塗料をガンで吹き付けるときに,水で希釈するが,たれ性指数Fが大きくてたれやす
いと使用時(施工前)に不良として発見される場合が多い。検討の結果,たれ性指数Fが
8.5以上になると,使用者の50%が不良と考えることが分かっている。
32
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
また,苦情が発生したときの損失は,問題のあることが施工前に発見されるので苦情に
よって発生する費用は少ない。その費用の内容は,代替品運搬費20円/kg,苦情品処理費
40円/kg,施工手待ち労務費200円/kgが考えられ,合計260円/kgになる。工場におけ
る手直しのためのコストは,機能材料を追加して,再度の混練をすることとし,40円/kg
とした。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階 使用者の段階における機能限界 ⊿0=8.5
苦情発生時の費用 A0=260円/kg
手順2 生産者側の損失Aの推定
生産者段階 工場における手直しコスト A=40円/kg
手順4 最大許容値⊿の計算
⊿0=8.5,A0=260円/kg,A=40円/kgであるから
⊿=
0A
A×⊿0=
260
40×8.5≒3.33
手順6 最大許容値⊿の決定 以上から,この製品の最大許容値⊿は,きりがよい数値で
3.3とした。
(2) 望大特性:壁用吹付塗料の塗膜の付着強さ(受入側が受入検査をしない場合) たれ性の
ような使用時特性は多くの場合に,使用開始時(施工前)にその不良は分かるが,塗膜の
付着強さのような塗膜物性に関するものは使用後数日経過してから不良が発見され苦情と
なる。この場合の苦情発生による費用は使用前に不良が発見され苦情となる場合よりも大
きくなる。
塗膜の付着強さについて,塗装後に不良が発見され苦情となった場合を試算してみる。
機能限界は,⊿0=25N/cm2である。苦情発生時の費用は個人住宅1軒の再施工を想定す
る。足場費用,材料費用,施工労務費用を考慮し,A0=200万円とした。生産者段階の損
失はこの特性の不良の場合には,手直しでは対応できず,不良品を廃棄して新たに作るこ
とになるので,工場出荷価格を考えて
500kg/軒×500円/kg=25万円/軒
とした。
手順1 機能限界⊿0及び平均損失A0の推定
生産者段階 使用者の段階における機能限界 ⊿0=25N/cm2
苦情発生時の損失 A0=200万円/軒
手順2 生産者側の損失Aの推定
生産者段階 工場出荷価 A=25万円/軒
手順4 最小許容値⊿の計算
⊿0=25N/cm2,A0=200万円/軒,A=25万円/軒であるから
⊿=
A
A0×⊿0=
25
200×25≒7.07 N/cm2
手順6 最小許容値⊿の決定 以上から,最小許容値⊿は,きりがよい数値で70N/cm2と
した。
例5. 普通特性:プラスチック複合材料のフィラー含有率の許容差 プラスチックにフィラーとして
33
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ガラス繊維,炭素繊維などを混入した複合材料は,機械的特性が向上するので機構部品に用い
る。
フィラーの含有率が基準値より大きくなると,樹脂の流れ特性が低下し外観及び寸法に問題
を生じる。一方,基準値より小さい場合には,機械特性低下のため苦情が発生する。20wt%フ
ィラー入りの材料の場合に,この値は±5%付近にある。今,この複合材料の生産者における価
格を600円/kgとし,これを使用して作られた部品の単価を60円とする。ここで,部品の質
量は15gである。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階
機能限界 ⊿0=5%
平均損失 A0=4 000円/kg(60円/15g)
手順2 生産者側の損失Aの推定
生産者段階
破棄による損失 A:600円/kg
手順4 許容差⊿の計算
⊿0=5%,A0=4 000円/kg,A=600円/kgであるから
⊿=
0A
A×⊿0=
000
4
600×5≒1.9(%)
手順6 許容差⊿の決定 以上から,この複合材料の許容差⊿は,きりがよい数値で2%とし
た。
例6. 普通特性:ガラス繊維強化PCの分子量の許容差 カメラ外装に使用されているガラス繊維強
化PCの品質は,分子量で管理されている。分子量が基準値より高い場合には,成形したとき
に成形品の表面にガラス繊維が浮く傾向がある。逆に,分子量が低いと強度が低下する傾向が
ある。組立工程又は使用中に,割れ事故を起こすことがある。このため分子量の値の範囲の機
能限界は±3 000である。
今,ガラス繊維強化PCの生産者における価格を600円/kgとし,これを使用して作られる
製品の単価を100円とする。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階
機能限界 ⊿0=3 000
(分子量の単位)
平均損失 A0=5 000円/kg
(100円/製品1個20g)
手順2 生産者側の損失Aの推定
使用者段階
破棄による損失 A=600円/kg
手順4 許容差⊿の計算
⊿0=3 000,A0=5 000円/kg,A=600円/kgであるから
⊿=
0A
A×⊿0=
000
5
600×3 000≒1 039 (分子量の単位)
手順6 許容差⊿の決定 以上から,この用途の分子量の許容差⊿は,きりがよい数値で1 000
とした。
例7. 普通特性:衣料用布地の収縮率 衣料用布地の品質特性の一つである収縮率の機能限界はJIS
で±3%と決められている。収縮率が3%を超えるとその布地を使った製品の形態のくずれのた
め苦情が発生する。業者について調査を行った結果,検査段階において管理を行い,手直しを
することが明らかになった。
34
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
生産者の段階において不具合が生じた場合の費用は,再加工代に250円,検査に550円,包
装に425円が必要となる。したがって,Aは次のとおりである。
A=250+550+425=1 225円/反
一方,使用者段階においては縫製業者が収縮率±3%を超えた布地は手直しのため返品となり,
この費用は2 975円/反,さらに,使用者が再利用のために必要な時間を1時間とすれば,1
時間当たりの損失は4 800円となり,使用者(縫製業者)段階における平均損失A0は
A0=2 975+4 800=7 775円/反
と推定される。
手順1 機能限界⊿0及び平均損失A0の推定
使用者段階
機能限界 ⊿0=3%
平均損失 A0=7 775円/反
手順2 生産者側の損失Aの推定
使用者段階
手直しによる損失 A=1 225円/反
手順3 品質水準及び測定能力の検討
工程の品質水準を検討するため得たデータは,
0.94, 0.72, 0.53, 0.69, 1.02
であった。附属書2に従って,基準値を0と考える普通特性の平均二乗誤差VTを算出
する。
9
639
.0
)
02
.1
72
.0
94
.0(
5
1
)
(
1
2
2
2
2
2
2
2
1
=
=
=
+
…
…
+
+
×
+
…
…
+
+
n
T
y
y
y
n
V
(%2)
手順4 許容差⊿の計算
⊿0=3%,A0=7 775円,A=1 225円であるから
⊿=
0A
A×⊿0=
775
7
225
1
×3≒1.19(%)
手順5 許容差⊿の検討
L1=
T
V
Δ
A
2
0
0
×
23
775
7
×0.639 9≒553 (円/反)
ここでは,現行の損失L1が許容最大損失L2 (=A) よりも十分小さいとみなされるの
で,製品の品質水準は適正と判断する。
手順6 許容差⊿の決定 以上から,この収縮率の許容差⊿は,きりがよい数値で1%とした。
以上の例1.〜7.にその他の事例を加えて,この規格によって算出した⊿の例をまとめて参考表1に示す。
35
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考表1 各種部品の品質特性と決定した⊿の事例
特性値の種類
No.
品質特性
生産者側の
損失
A
機能限界
⊿0
平均損失
A0
この規格によっ
て算出した⊿値
⊿
望小特性
1.
プラスチック軸受の真円度
700円
110μm
5 000円
41μm
2.
テープレコーダ用カーボン
ファイバ入りプラスチック材フラ
イホイールの電気抵抗
200円
106Ω
6 000円
1.8×105Ω
3.
室内用送風機のファンのアンバラ
ンス
600円
1 000μm
l0 000円
245μm
4.
ドットプリンタのワイヤの先端部
の保持力
600円
0.5N
10 000円
0.12N
5.
壁用塗料たれ性指数
(受入検査がある場合)
40円/kg
8.5
260円/kg
3.3
普通特性
1.
動力伝達用シヤピンの強さ
(過負荷防止用)
2 000円
400N
100 000円
57N
2.
三角定規の直角部分の角度
1 500円
5′
4 000円
3′
3.
塩化ビニル被覆電線の硬さ
200円
6.0HRM
1 800円
2.0HRM
4.
チョークコイル取付け回転トルク
200円
4.0N-mm
5 000円
0.8N-mm
5.
半導体デバイスのDRAMのアクセ
スタイム
(上側)
1 200円
25 200円
+10ns
+2.2ns
(下側)
−50ns
−11ns
6.
複写機の濃度
(下側)
300円
0.8
34 000円
0.075
7.
マイクロスイッチの復帰力
200円
0.2N
1 000円
0.09N
8.
プラスチック複合材料のフィラー
含有率
600円/kg
5%
4 000円/kg
1.9%
9.
ガラス繊維強化PCの分子量
600円/kg
3 000
5 000円/kg
1 039
(分子量の単位)
10.
衣料用布地の収縮率
1 225円
3%
7 775円
1.19%
望大特性
1.
POM製回転軸の曲げ強さ
100円
10N
6 000円
77N
2.
ターンテーブルとスピンドルのは
めあい強度
150円
30N
7 000円
205N
3.
シャーシの圧入軸の抜け耐荷重
200円
15N
7 000円
89N
4.
タイミングベルト用プーリの溶着
強度
300円
40N
8 000円
207N
5.
接着剤の接着強度
9円/g
25MPa
15円/g
32MPa
6.
半導体デバイスDRAMのリフレッ
シュ周期
1 200円
16ms
25 200円
73.3ms
7.
手提げかばんのハンドル
140円
150N
5 000円
896N
8.
壁用吹付け塗料の塗膜の付着強さ
250 000円
25N/cm2
2 000 000円
70.7N/cm2
36
Z 8403-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Z 8403 原案作成委員会 構成表
氏名
所属
(委員長)
山 本 健太郎
明治大学
(委員)
天 野 徹
工業技術院標準部材料規格課
◎ 池 田 和 子
文化女子大学
◎ 小 池 昌 義
工業技術院計量研究所
◎ 秦 勝一郎
工業技術院計量研究所
福 田 収 一
東京都立科学技術大学
◎ 矢 野 宏
電気通信大学
◎ 岩 崎 浩一郎
ライオンエンジニアリング株式会社
上 野 憲 造
日産自動車株式会社
○ 唐 津 修
日本電信電話株式会社
田 口 玄 一 株式会社オーケン
◎ 塚 越 隆 啓
山武ハネウエル株式会社
◎ 土 倉 克 彦
ゼネカ株式会社
◎ 中 島 建 夫
東亞合成株式会社
◎ 二階堂 忠 信
日本電信電話株式会社
橋 本 政 弘
株式会社東芝
花 岡 英 夫
東京特殊電線株式会社
浜小路 正 博
日立金属株式会社
◎ 本 間 精 一
三菱エンジニアリングプラスチックス株式会社
◎ 矢 杉 井久雄
沖電気工業株式会社
◎ 吉 澤 正 孝
富士ゼロックス株式会社
(事務局)
◎ 若 園 叔 邦
財団法人日本規格協会
◎ 稲 葉 喜 彦
財団法人日本規格協会
備考 ◎印は分科会委員兼任
○印は分科会委員