(ISO 5725-6 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 8402 : 1991は廃止され,この規格に置き換えられる。
今回の制定では,1994年に第1版として発行されたISO 5725-6を基礎として用いた。
JIS Z 8402-6には,次に示す附属書がある。
附属書A(規定) JIS Z 8402で用いられる記号
JIS Z 8402 : 1999は,一般名称を“測定方法及び測定結果の精確さ(真度及び精度)”として,次の部
によって構成される。
第1部: 一般的な原理及び定義
(Part 1 : General principles and definitions)
第2部: 標準測定方法の併行精度及び再現精度を求めるための基本的方法
(Part 2 : Basic method for the determination of repeatability and reproducibility of a standard
measurement method)
第3部: 標準測定方法の中間精度
(Part 3 : Intermediate measures of the precision of a standard measurement method)
第4部: 標準測定方法の真度を求めるための基本的方法
(Part 4 : Basic methods for the determination of the trueness of a standard measurement method)
第5部: 標準測定方法の精度を求めるための代替法
(Part 5 : Alternative methods for the determination of the precision of a standard measurement
method)
第6部: 精確さに関する値の実用的な使い方
(Part 6 : Use in practice of accuracy values)
(ISO 5725-6 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
序文 ··································································································································· 4
1. 適用範囲 ························································································································ 4
2. 引用規格 ························································································································ 2
3. 定義 ······························································································································ 2
4. 許容差の求め方 ··············································································································· 2
4.1 併行許容差と再現許容差·································································································· 2
4.2 3個以上の値についての比較 ···························································································· 3
5. 測定結果の採択性をチェックし,最終報告値を求める方法 ······················································ 5
5.1 一般 ···························································································································· 5
5.2 併行条件で得た測定結果の採択性をチェックする方法 ··························································· 5
5.3 併行条件及び再現条件で得た測定結果の採択性をチェックする方法 ········································ 11
6. 試験室内の測定結果の安定性をチェックする方法 ································································· 13
6.1 背景 ··························································································································· 13
6.2 安定性をチェックする方法······························································································ 15
7. 試験室評価における併行標準偏差と再現標準偏差の利用 ························································ 28
7.1 評価方法 ····················································································································· 28
7.2 以前に評価されていない試験室による,ある測定方法の使用の評価 ········································ 29
7.3 以前に承認されている試験室についての継続評価 ································································ 32
8. 代替測定方法の比較 ········································································································ 37
8.1 代替測定方法の発端 ······································································································ 37
8.2 測定方法比較の目的 ······································································································ 37
8.3 方法Bが代替標準測定方法の候補である( ········································································ 38
8.4 精確さ評価実験 ············································································································ 38
8.5 方法Bは日常用の測定方法の候補である ··········································································· 44
附属書A(規定)JIS Z 8402で用いられる記号 ··········································································· 46
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8402-6 : 1999
(ISO 5725-6 : 1994)
測定方法及び測定結果の
精確さ(真度及び精度)−
第6部:精確さに関する値の実用的な使い方
Accuracy (trueness and precision) of measurement methods and results−
Part 6 : Use in practice of accuracy values
序文
この規格は,1994年に第1版として発行されたISO 5725-6 Acc racy (trueness and precision) of measurement
methods and results−Part6 : Use in practice of accuracy valuesを翻訳し,技術的内容及び規格票の様式を変更
することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
0.1
この規格では,測定方法の精確さを表すために“真度”と“精度”の二つの用語を用いている。“真
度”は,多数の測定結果の平均値と,真の値又は参照値との一致の程度を示すものである。“精度”は,測
定結果の間の一致の程度を示すものである。
0.2
“精度”を考える必要が生じるのは,同一と見なせる状況での,同一と見なせる試料について実施
される試験において,一般には同一の結果が得られないからである。これは,どのような測定の手順にお
いてもつきものの避けられない偶然誤差に基づく;すなわち,測定結果に影響する要因をすべて完全には
制御できないということである。実際に測定データの解釈においては,このばらつきを考慮しなければな
らない。例えば,測定結果とある定められた値との差は,避けられない偶然誤差の範囲内にあるかも知れ
ず,このような場合には,ある定められた値からの真の偏差は確定できない。同様に,二つのバッチ間の
測定結果の差が測定手順につきものの変動によるならば,バッチ間の本質的な差はわからないであろう。
0.3
この規格の第1部から第5部では,標準測定方法を用いて得られた測定値の精度(併行標準偏差及
び再現標準偏差に関して)と真度(かたよりのいろいろな成分に関して)の評価についての背景を論じ,
その方法を示した。しかし,このような評価は,その結果を実際に利用することがなければ無意味なもの
となるであろう。
0.4
測定方法の精確さが確立しているならば,この規格のこの部は,商取引の助けにする,試験室の作
業性を監視及び改善するというように,実用的心得に適用される。
1. 適用範囲
1.1
この規格のこの部の目的は,いろいろの実際の状況で,精確さに関するデータを使用する方法を,
a) 標準測定方法によって得られた測定結果の検討に用いられる併行許容差,再現許容差,及び他の許容
差を計算するための標準的な方法を示すこと;
2
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 併行条件又は再現条件で得られた測定結果の採択性をチェックする方法を定めること;
c) 試験室内での測定結果の安定性を評価する方法を述べ,試験室内での操作の“品質管理”の方法を定
めること;
d) 特定の試験室について,ある標準測定方法を満足に用い得るかどうかを評価する方法を述べること;
e) 代替測定方法を比較する方法を述べること;
によって示すことである。
1.2
この規格のこの部は,計量値の測定値が求められ,測定結果として1個の数値が得られるような測
定方法だけを対象とする。この1個の値は1組の観測値から計算によって求められたものであってもよい。
1.3
対象とする測定方法についての真度と精度の推定値は,この規格の第1部〜第5部に従って得られ
ていることを仮定する。
1.4
適用分野に関する付加的な情報がある場合には,それぞれの適用の項の初めに示す。
2. 引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,発効年を付記してあるものは,記載の年の版だけがこの規格の規定を構成するもので
あって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その最新版(追補
を含む。)を適用する。
JIS Q 0033 : 1997 認証標準物質の使い方
JIS Q 0035 : 1997 標準物質の認証−一般的及び統計学的原則
JIS Z 8101-1 統計−用語と記号−第1部 確率及び一般統計用語
JIS Z 8101-2 統計−用語と記号−第2部 統計的品質管理用語
JIS Z 8402-1 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第1部 一般的な原理及び定
義
JIS Z 8402-2 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第2部 標準測定方法の併行
精度及び再現精度を求めるための基本的方法
JIS Z 8402-3 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第3部 標準測定方法の中間
精度
JIS Z 8402-4 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第4部 標準測定方法の真度
を求めるための基本的方法
JIS Z 9021 : 1998 シューハート管理図
JIS Z 9325 : 1996 校正機関及び試験所の能力に関する一般要求事項
3. 定義
この規格の目的に合わせ,JIS Z 8101とJIS Z 8402-1において定義された用語を用いる。
この規格で用いる記号を附属書Aに示す。
4. 許容差の求め方
4.1
併行許容差と再現許容差
3
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.1.1
JIS Z 8402-2では,併行条件又は再現条件での測定に関する標準偏差を推定することに注意が向け
られている。しかし,試験室の通常業務では,2個以上の測定結果間に認められる差を検討すること必要
であり,この目的には標準偏差よりも,許容差のような尺度が必要となる。
4.1.2
ある量が,それぞれ標準偏差がσである独立なn個の推定値の和又は差であるならば,その標準偏
差はσnとなるだろう。再現許容差 (R) 又は併行許容差 (r) は2個の測定結果の差に対するものである
から,これに関連する標準偏差はσ2である。ふつうの統計的な取扱いでは,これらの2個の値の差の検
討に用いられる許容差は,この標準偏差のf倍,すなわちfσ2である。f(許容差の係数)の値は,許容
差の確率と想定している分布の形とに依存する。再現許容差と併行許容差では確率は95%と規定してあり,
この規格の解析では基礎となる分布をほぼ正規分布であると仮定している。正規分布では確率95%でのf
は1.96であるから,f2は2.77となる。この規格のこの部の目的は,統計家でない者が用いる,測定結果
を検討するための簡単な“大ざっぱなルール”を与えることであるから,f2の代わりに2.8という丸め
た値を用いることは合理的であろう。
4.1.3
前述のように,真の標準偏差の推定値は精度推定のプロセスから導かれるが,真の標準偏差は未知
のままである。したがって,統計的な習慣では,推定値をσよりもsで表すべきである。とはいえ,JIS Z
8402-1及びJIS Z 8402-2の手順が守られるならば,これらの推定値はかなりの数の測定結果に基づいてい
るはずで,標準偏差の真の値に近い最良の情報が得られているだろう。後述の他の適用では,もっと少な
いデータによる標準偏差の推定値に対して記号s(標準偏差の推定値)を用いる。したがって,記号σで完
全な精度評価実験から得られた値を表し,他の推定値 (s) との比較に用いられる真の標準偏差として扱う
のが最良であると思われる。
4.1.4
併行条件又は再現条件で得られた2個の測定結果を検討するときは,4.1.1〜4.1.3を考慮して,比
較は併行許容差r=2.8σr又はR=2.8σRに対してなされなければならない。
4.2
3個以上の値についての比較
4.2.1
一つの試験室での2組の測定結果
一つの試験室において併行条件で2組の測定を行い,第1の組でn1個の測定結果から平均1yを,第2
の組でn2個の測定結果から平均
2yを得たとき,
)
(
2
1
y
y−
の標準偏差は
+
2
1
2
1
1
n
n
r
σ
σ=
であり,|1y−
2y|に対する許容差は,確率95%で
+
2
1
2
1
2
1
8.2
n
n
CD
r
σ
=
である。
備考1. n1=n2=1ならば,予想されるとおり,上式はγ=2.8σrとなる。
4.2.2
二つの試験室での2組の測定結果
第1の試験室がn1個の測定結果から平均1yを,第2の試験室がn2個の測定結果から平均
2yを,どちら
も併行条件で得たときは,
)
(
2
1
y
y−
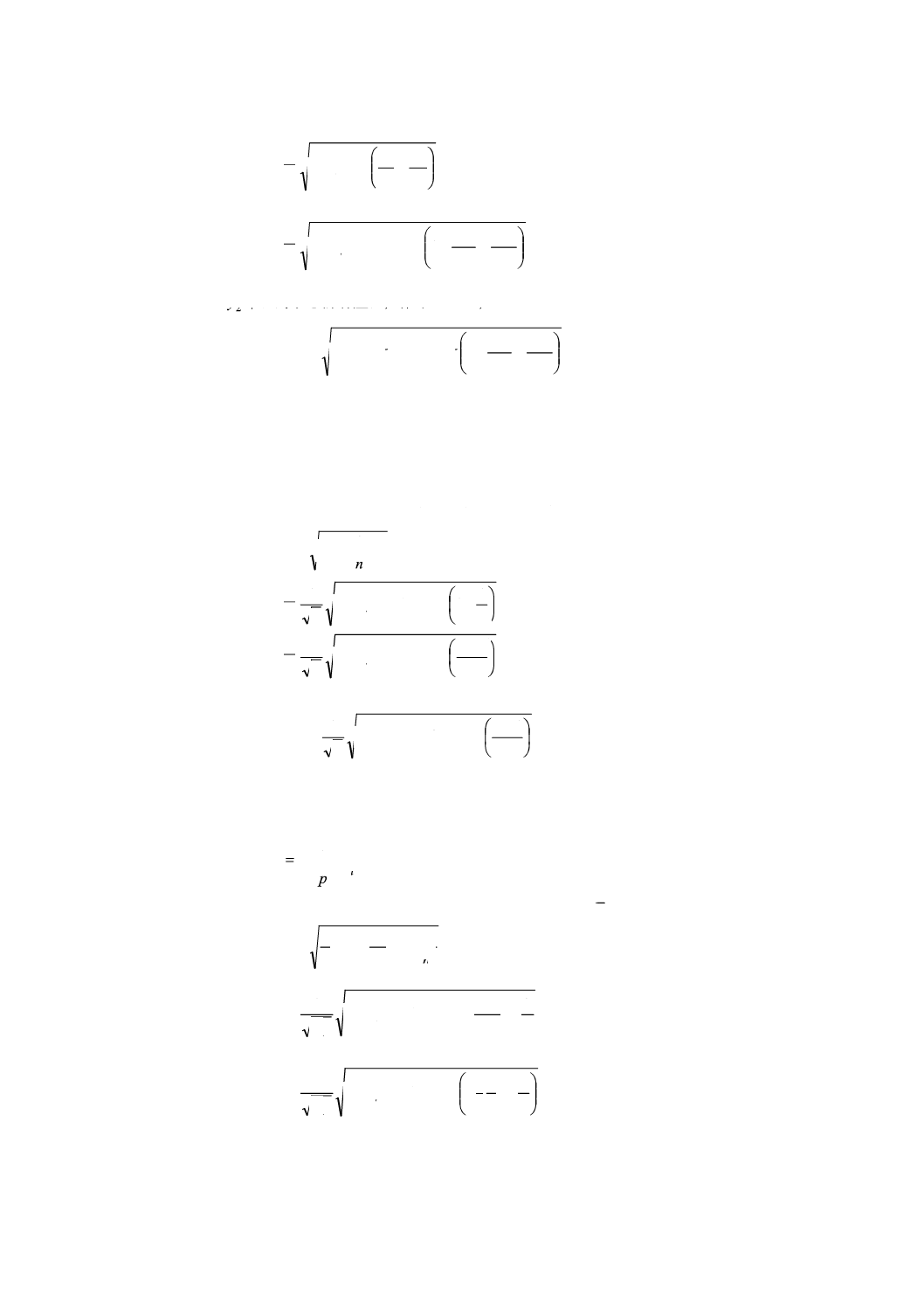
の標準偏差は
σ=
2
2
2L
2
1
2L
1
1
r
r
n
n
σ
σ
σ
σ
+
+
+
4
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=
+
+
2
1
2
2L
1
1
2
n
n
r
σ
σ
=
−
−
−
+
2
1
2
2
2L
2
1
2
1
1
2
)
(2
n
n
r
r
σ
σ
σ
であり,|1y−
2y|に対する許容差は,確率95%で,
CD=
−
−
−
2
1
2
2
2
1
2
1
1
)
8.2(
)
8.2(
n
n
r
R
σ
σ
である。
備考2. n1=n2=1ならば,予想されるとおり,上式はR=2.8σRとなる。
4.2.3
一つの試験室での参照値との比較
一つの試験室内で,n個の測定結果から平均yを得たとき,参照値μ0との比較は,その試験室に関する,
かたよりの試験室成分の情報がないならば, (y−μ0) の標準偏差
σ=
2
2L
1
r
nσ
σ+
=
−
−
+
n
r
r
1
1
2
)
(2
2
1
2
2
2L
σ
σ
σ
=
−
−
+
n
n
r
r
1
2
)
(2
2
1
2
2
2L
σ
σ
σ
を用いて行わなければならない。|y−μ0|に対する許容差は
CD=
−
−
n
n
r
R
1
)
8.2(
)
8.2(
2
1
2
2
σ
σ
である。
4.2.4
二つ以上の試験室での参照値との比較
p試験室が,ni個の測定結果から平均iyを(いずれも併行条件で)得て,総平均yを
y=
iy
pΣ
1
によって求め,この総平均を参照値μ0と比較しようとするときは, (y−μ0) の標準偏差は
σ=
i
rn
p
p
1
1
1
2
2
2L
Σ
σ
σ+
=
i
r
r
r
n
p
p
1
2
2
)
(2
2
1
2
2
2
2L
Σ
σ
σ
σ
σ
+
−
+
=
−
−
+
i
r
r
n
p
p
1
1
1
2
)
(2
2
1
2
2
2L
Σ
σ
σ
σ
であり,|y−μ0|に対する許容差は,確率95%で
5
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
CD=
−
−
i
r
R
n
p
p
1
1
1
)
8.2(
)
8.2(
2
1
2
2
Σ
σ
σ
である。
4.2.5
比較結果の引用
差の絶対値が上に示した適切な許容差を超えるときは,この差は疑わしいと考えなければならず,この
差を生じさせている全測定結果は疑わしいと考え,更に検討を加えなければならない。
5. 測定結果の採択性をチェックし,最終報告値を求める方法
5.1
一般
5.1.1
この節で述べるチェック方法は,標準化されている測定方法に従って測定を行い,その標準偏差σr
及びσRが既知である場合だけに適用することが望ましい。したがって,N個の測定結果の範囲が,4.に示
した適性な許容差を超えるときは,それらのN個の測定結果のうちの1個,2個又は全部が正常でないと
考えられる。正常でない測定結果の原因は,技術的に検討することが望ましい。しかし,商取引上の理由
で最終報告値として容認できる値を得ることが必要なこともあり,その場合には,測定結果をこの節の規
定に従って処理しなければならない。
5.1.2
この節は,測定結果が併行条件及び再現条件で得られており,用いられる確率が95%であることを
仮定して作成されている。しかし,中間条件(JIS Z 8402-3参照)で実施するときは,σrを適切な中間精
度の尺度に変える必要がある。
5.1.3
5.2の手順で最終報告値がメディアンになった場合には,そのデータを捨てるほうがよいかもしれ
ない。
5.2
併行条件で得た測定結果の採択性をチェックする方法
備考3. 5.2.2.1及び5.2.2.2で測定結果が高価又は安価であると言っているのは,金額上の意味だけでな
く,その測定が複雑であり,手間又は時間がかかるかどうかの意味で解釈してよい。
5.2.1
測定結果が1個の場合
実際の商取引で,測定結果が1個だけであることは稀である。測定結果が1個しかないときには,所与
の併行精度(の尺度)によって,測定結果の採択性を直接統計的に検定することは不可能である。その測
定結果が正しくないと少しでも疑われるならば,別の測定結果を得ることが望ましい。測定結果が2個得
られれば,後述のより普遍的な方法を実施できる。
5.2.2
測定結果が2個の場合
2個の測定結果は,併行条件で得ることが望ましい。次に,その2個の測定結果の差の絶対値を,併行
許容差r=2.8σrと比較すればよい。
5.2.2.1
測定結果を得ることが安価である場合
2個の測定結果の差の絶対値がrを超えないときは,両測定結果は採択可能であると考え,その最終報
告値は2個の測定結果の平均値とするとよい。差の絶対値がrを超えるならば,その試験室は更に2個の
測定結果を得ることが望ましい。
その4個の測定結果の範囲 (xmax−xmin) が,n=4に対する確率95%での許容範囲CR0.95 (4) 以下である
ならば,その4個の測定結果の平均値を最終報告値として報告するとよい。n=2〜40及びn=45〜100の
うちのいくつかの値についての許容範囲の係数f (n) を表1に示す。許容範囲は次の式によって算出する。
CR0.95 (n) =f (n) σr
6
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
その4個の測定結果の範囲がn=4に対する許容範囲を超えるならば,4個の測定結果のメディアンを最
終報告値として報告するとよい。
この手順は,図1に示すフローチャートにまとめられている。
5.2.2.2
測定結果を得ることが高価である場合
2個の測定結果の差の絶対値がrを超えないときは,両測定結果は採択可能であると考え,最終報告値
はその2個の測定結果の平均値とするとよい。差の絶対値がrを超えるならば,その試験室は更に1個の
測定結果を得ることが望ましい。
その3個の測定結果の範囲 (xmax−xmin) がn=3に対する許容範囲CR0.95 (3) 以下であるならば,その3
個の測定結果の平均値を最終報告値として報告するとよい。
その3個の測定結果の範囲がn=3に対する許容範囲より大きいならば,判定は次の二つの場合の一つに
しなければならない。
a) 別の測定結果を得ることが不可能である場合
その試験室はその3個の測定結果のメディアンを最終報告値として用いるとよい。
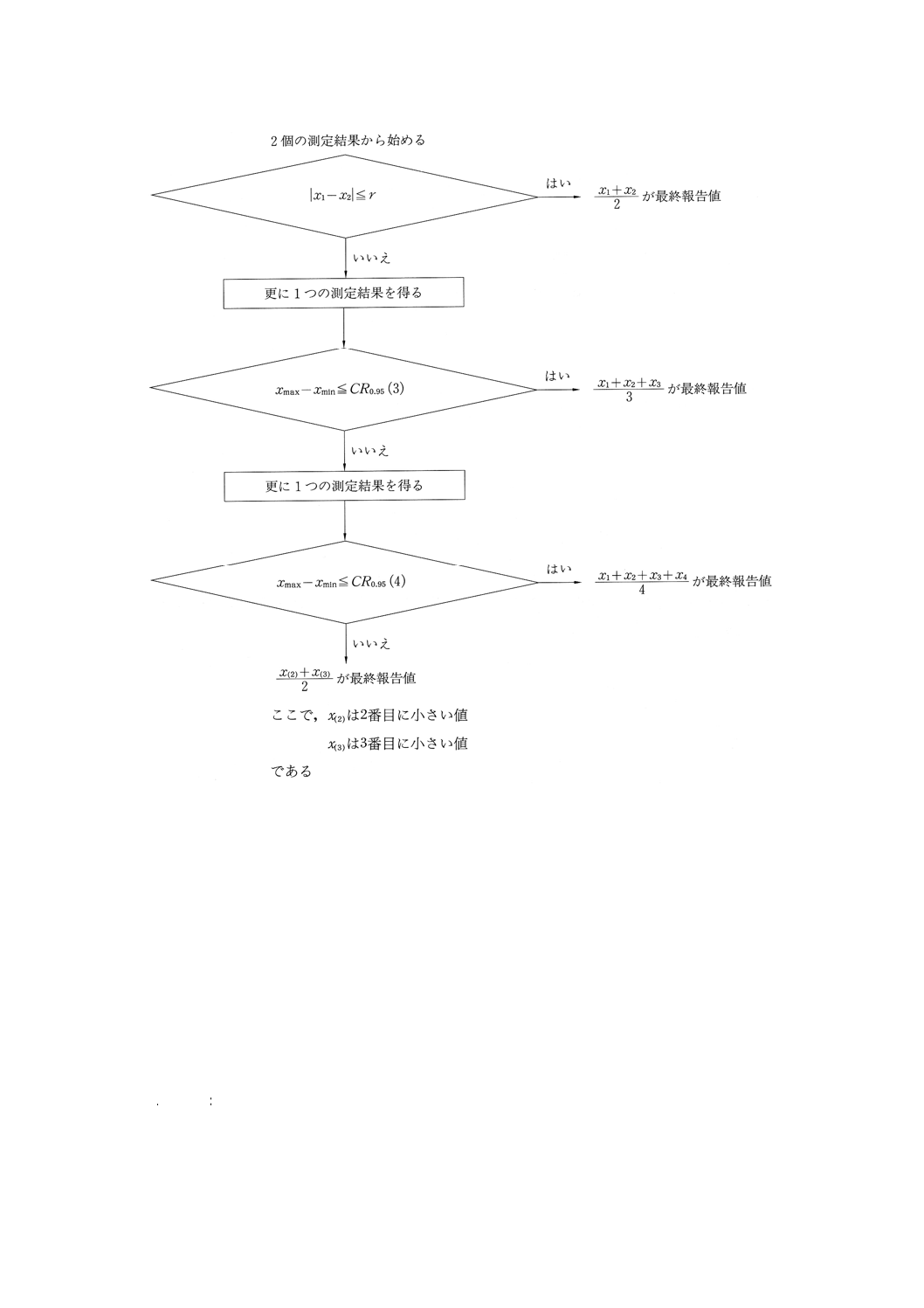
この手順は,図2に示すフローチャートにまとめられている。
b) 別の測定結果を得ることが可能である場合
その試験室は更にもう一つの測定結果を得ることが望ましい。その全体の4個の測定結果の範囲が
n=4に対する許容範囲CR0.95 (4) 以下であるときは,その4個の測定結果の平均値を最終報告値とし
て報告するとよい。その4個の測定結果の範囲がn=4に対する許容範囲より大きいならば,その試験
室はその4個の測定結果のメディアンを最終報告値として用いるとよい。
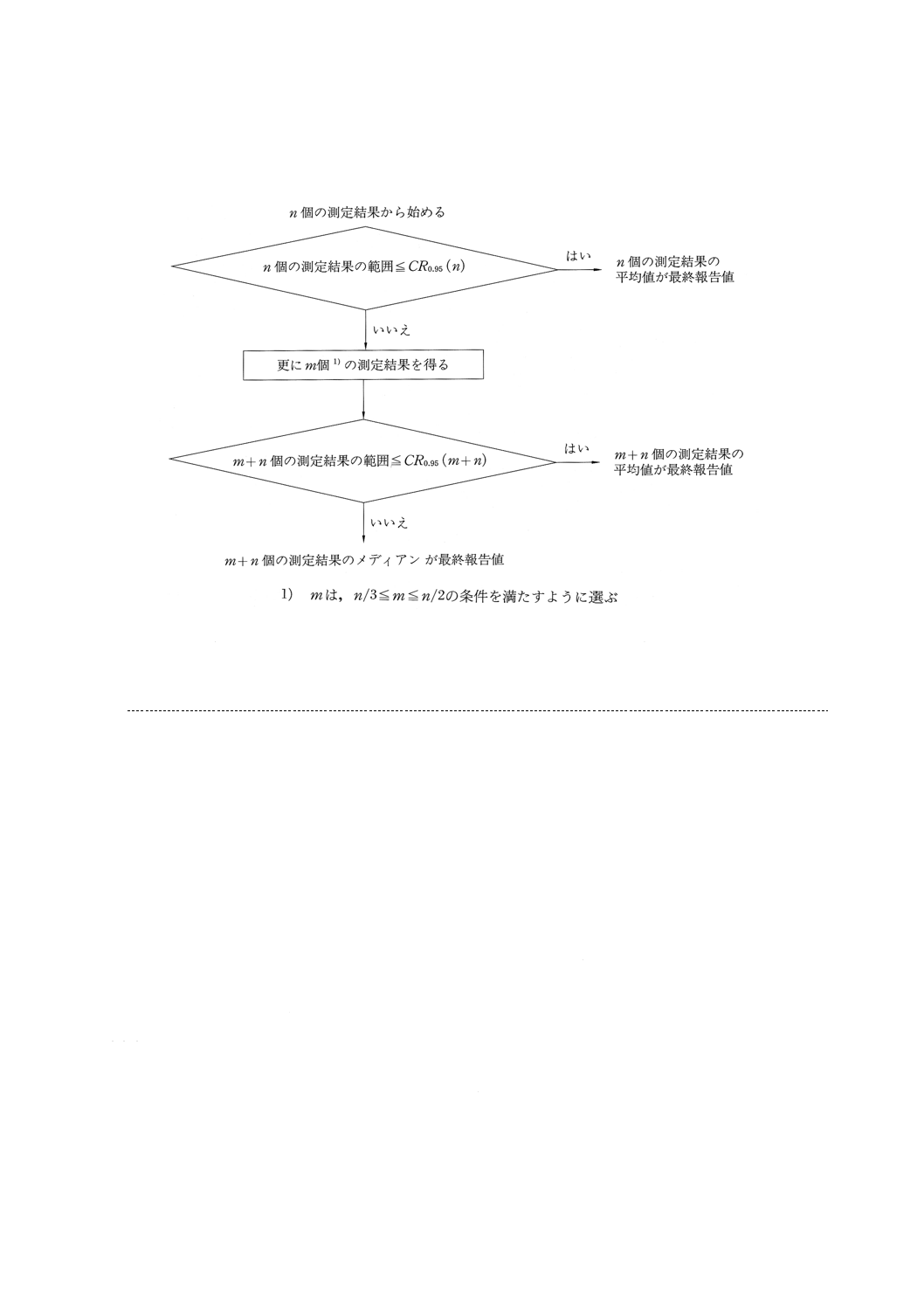
この手順は,図3に示すフローチャートにまとめられている。
5.2.3
測定結果が3個以上の場合
最初から3個以上の測定結果を得るのが実用的なこともある。併行条件でn≧3に対して最終報告値を得
る方法は,n=2の場合と似ている。
測定結果の範囲 (xmax−xmin) を,相当するnに対して表1から算出した許容範囲CR0.95 (n) と比較する。
その範囲が許容範囲を超えないときは,n個の測定結果の全部の平均値を最終報告値として用いる。
範囲が許容範囲CR0.95 (n) を超えるときは,図4〜6に示したA,B又はCの場合のうちの一つを,最終
報告値を得るために決めなければならない。
A及びBの場合は,測定結果を得ることが安価である場合と高価である場合とに対応している。Cの場
合は,最初の測定結果が5個以上で,個々の測定結果を得ることが安価であるとき,又は最初の測定結果
が4個以上で,個々の測定結果を得ることが高価であるときに推奨される代替法である。
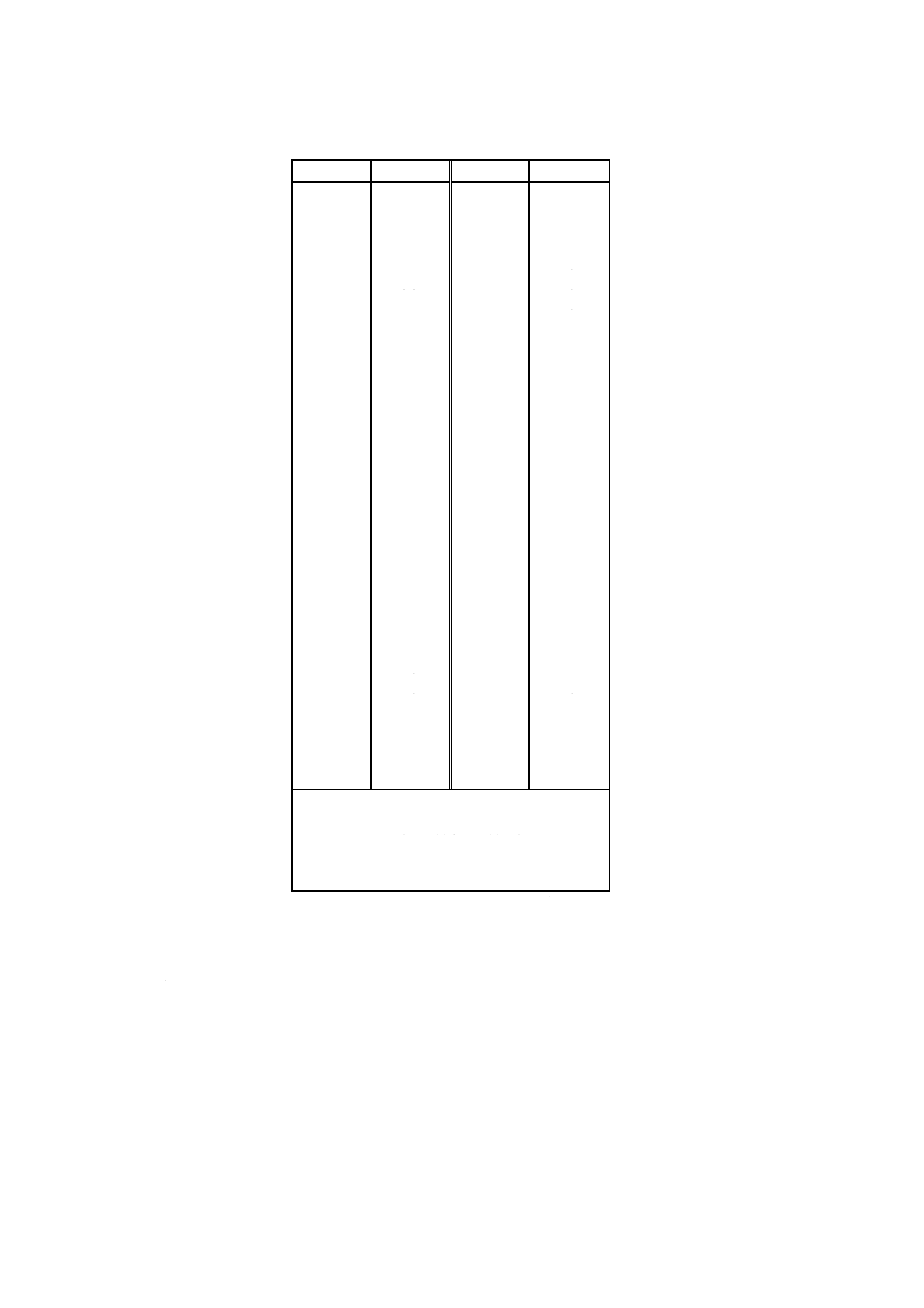
7
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1 許容範囲の係数 f (n)
n
f (n)
n
f (n)
2
2,8
25
5,2
3
3,3
26
5,2
4
3,6
27
5,2
5
3,9
28
5,3
6
4,0
29
5,3
7
4,2
30
5,3
8
4,3
31
5,3
9
4,4
32
5,3
10
4,5
33
5,4
11
4,6
34
5,4
12
4,6
35
5,4
13
4,7
36
5,4
14
4,7
37
5,4
15
4,8
38
5,5
16
4,8
39
5,5
17
4,9
40
5,5
18
4,9
45
5,6
19
5,0
50
5,6
20
5,0
60
5,8
21
5,0
70
5,9
22
5,1
80
5,9
23
5,1
90
6,0
24
5,1
100
6,1
備考 許容範囲の係数f (n) は,標準偏差がσの正
規分布からの大きさnのサンプルについ
て,サンプルの最大値・最小値をxmax,xmin
とするとき, (xmax−xmin) /σの分布の95%
分位点である。
参考 表の中では小数点としてコンマ (, ) を用いている。
安価な測定に対して,Aの場合とCの場合との違いは,Aの場合がn個の測定結果の追加を必要とする
のに,Cの場合はその半分以下しか必要でないことである。その判定は,nの大きさと測定の実施の容易
さとに依存するだろう。
高価な測定に対して,Bの場合とCの場合との違いは,Cの場合が測定結果の追加を要するのに,Bの
場合は追加を要しないことである。Bの場合は追加が許されないほど高価な場合にだけ考慮される。
8
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
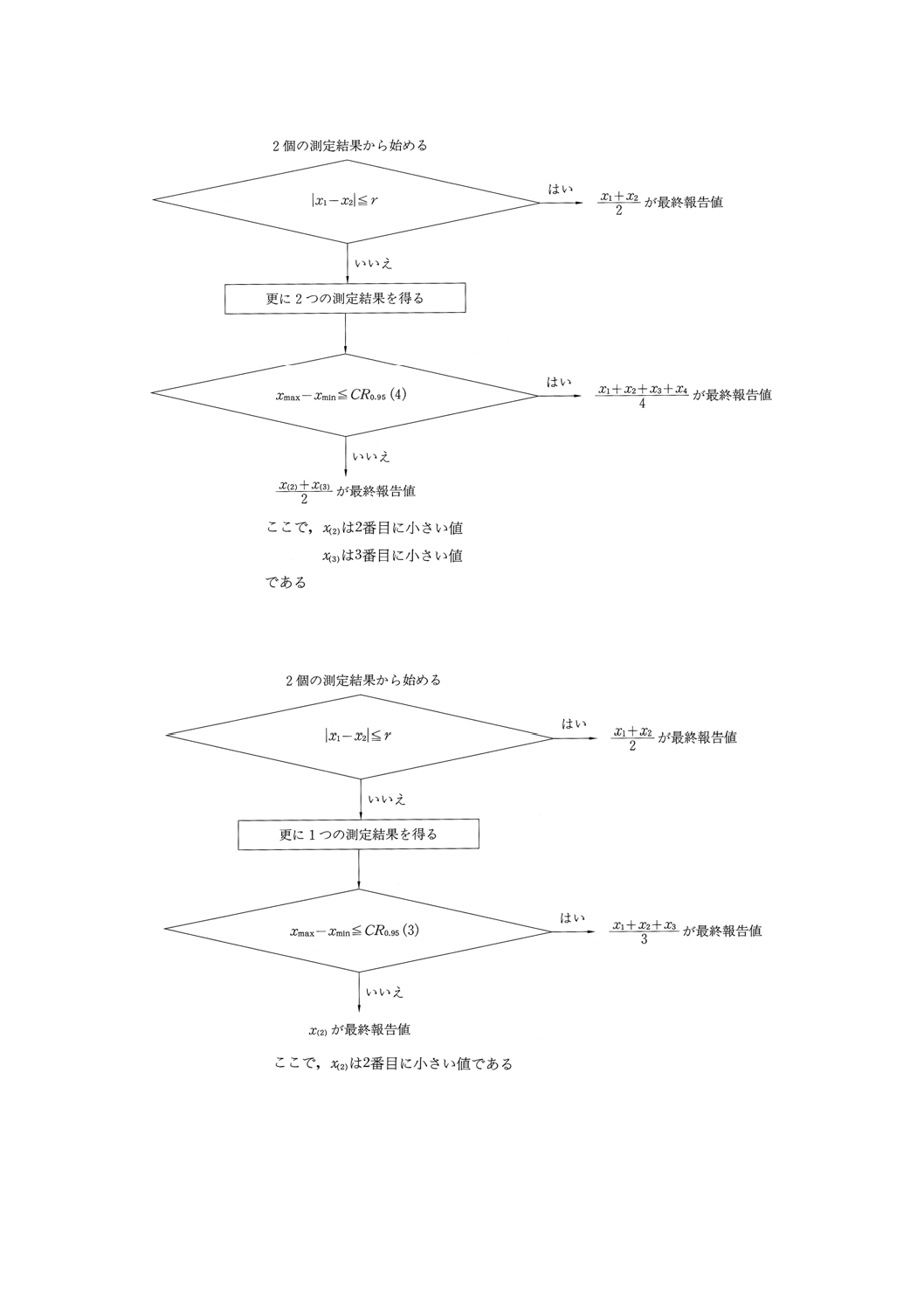
図1 2個の測定結果から始め,測定結果が安価であるとき,併行条件で得られた測定結果の採択性のチ
ェック方法:5.2.2.1の場合
図2 2個の測定結果から始め,測定結果が高価であるとき,併行条件で得られた測定結果の採択性のチ
ェック方法:5.2.2.2a)の場合
9
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3 2個の測定結果から始め,測定結果が高価であるとき,併行条件で得られた測定結果の採択性のチ
ェック方法:5.2.2.2b) の場合
5.2.4
Bの場合の例:高価な化学分析
高価な測定は化学分析にしばしば見られ,複雑で時間のかかる手順から構成され,1回の分析に2,3日
又はそれ以上を要する場合がこれにあたる。このような場合には,最初の分析で技術的に疑わしいデータ
や外れ値が出たとき,再分析を行うのは面倒で費用がかかる。したがって,ふつう最初から併行条件で3,
4個の測定結果を得て,Bの場合に従って最終報告値を求める。図5参照。
例えば,乾式試金法による鉱石中の金及び銀の定量にはいくつかの方法があるが,それらのすべてが高
価な特殊設備,熟練したオペレータ及び長い分析時間を必要とする。その全プロセスを完了するためには,
ふつう約2日間,鉱石が白金族金属や他の特殊な共存元素を含むならば,それ以上の時間が必要になる。
銅濃縮物について併行条件で金含有量として,次の測定結果を得た。
Au (g/t) : 11.0 11.0 10.8 10.5
これらの測定結果を,方法Bに従って処理する。
金及び銀の定量方法は,国際規格としては確立されていない。この金の定量で
10
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
σr=0.12 (g/t)
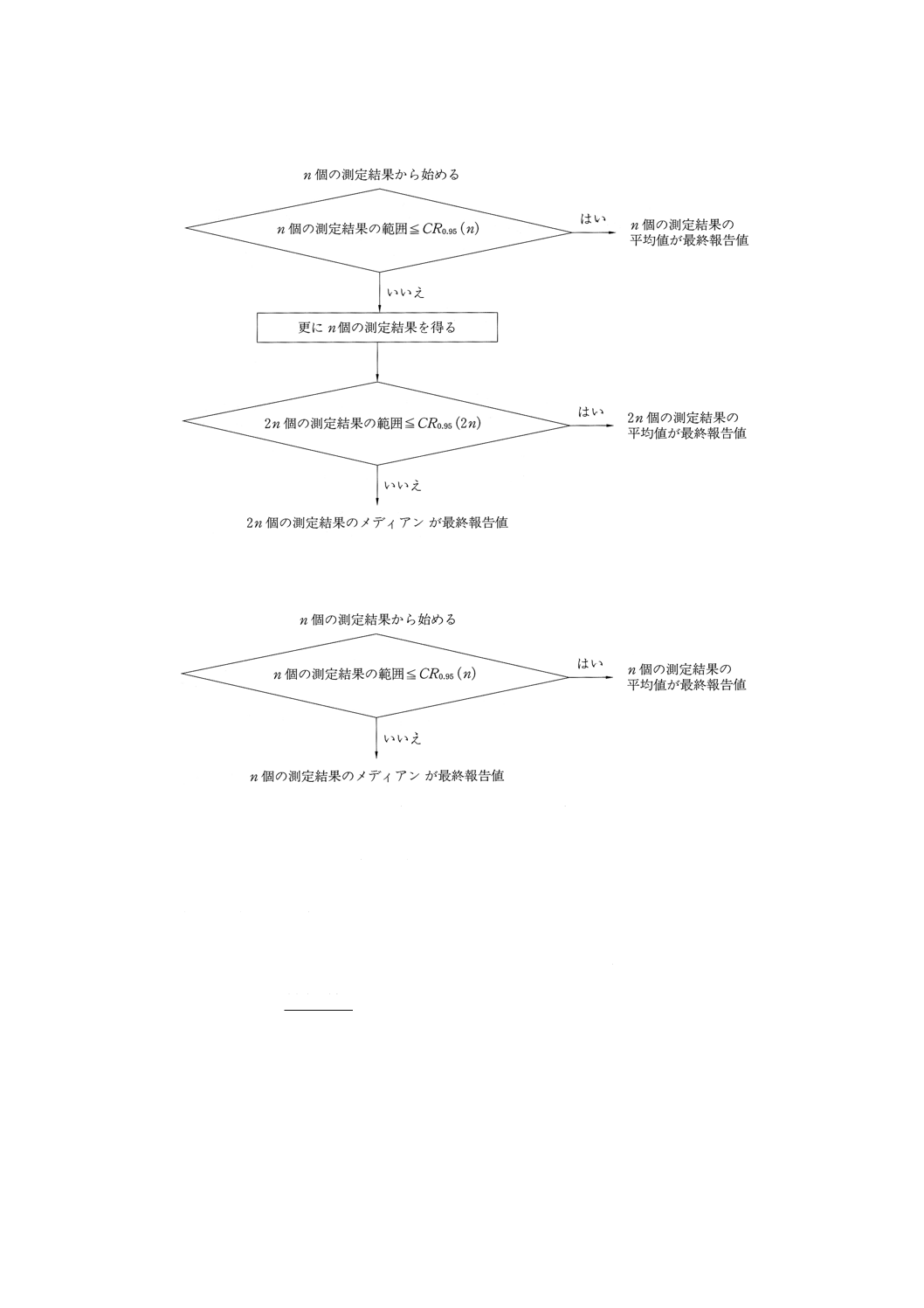
図4 n個の測定結果から始め,測定結果が安価であるとき,併行条件で得られた測定結果の採択性のチ
ェック方法:Aの場合
図5 n個の測定結果から始め,測定結果が高価であるとき,併行条件で得られた測定結果の採択性のチ
ェック方法:Bの場合
とすれば,表1から,f (4) =3.6であるから
CR0.95 (4) =3.6×0.12=0.43 (g/t)
となる。前述の4個の測定結果の範囲は
11.0−10.5=0.5
であり,CR0.95 (4) より大きいから,最終報告値は4個の測定結果のメディアン,すなわち
2
8.
10
0.
11 +
=10.9(g/t)
となる。
5.2.5
精度評価実験についての注意
5.2.2又は5.2.3に示した手順で,許容差を超える値をしばしば生じるならば,その試験室でのその測定
方法の精度,及び/又は精度評価実験を調査することが望ましい。
5.2.6
最終報告値の報告
11
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最終報告値だけを提示する場合には,次の2点を明記することが望ましい。
− 最終報告値の算出に用いた測定結果の数;
図6 測定結果が安価でn≧5個の測定結果から始めるとき,または測定結果が高価でn≧4個の測定結果
から始めるとき,併行条件で得られた測定結果の採択性のチェック方法:Cの場合
参考 高価な測定であって追加が許されn=3から始める場合には,図6(Cの場合)準用すればよい。
− 測定結果として,平均値とメディアンのどちらが用いられたか。
5.3
併行条件及び再現条件で得た測定結果の採択性をチェックする方法
5.3.1
一般
これらの方法は,2つの試験室が測定結果を得て,その測定結果又はその平均値の間に差がある場合を
扱う。再現標準偏差は,併行標準偏差と同様に,統計的検定手順の要素となる。
測定試料について測定結果を得るすべての場合に,測定結果を得るためと,再測定が必要になるときに
用いる予備のために,十分な試料を準備することが望ましい。この予備分がどのくらい必要であるかは,
測定方法とその複雑さとに依存する。とにかく,この予備の試料は,測定試料の品質の劣化又は有害な変
化から保護するために,注意深く保存することが望ましい。
測定試料は同一であることが望ましく,すなわち両試験室で試料調製手順の最終段階の試料を用いるこ
とが望ましい。
5.3.2
2つの試験室の測定結果間の一致性に関する統計的検定
5.3.2.1
それぞれの試験室の測定結果が1個の場合
それぞれの試験室の測定結果が1個の場合には,その2個の測定結果の差の絶対値を,許容差R=2.8σR
に対して検定すればよい。その2個の測定結果の差の絶対値がR以下ならば,その2個の測定結果は一致
していると考え,両者の平均値を最終報告値として用いてよい。
結果の差がRを超えているならば,測定方法の精度がよくないためなのか,及び/又は測定試料におけ
12
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る差に因るのか,を見つける必要がある。併行条件での精度を調べるために,それぞれの試験室が5.2.2
で示した手順に従って実行するとよい。
5.3.2.2
それぞれの試験室の測定結果が2個以上の場合
それぞれの試験室が5.2の手順に従って最終報告値を得ていることを仮定する。したがって,その2個
の最終報告値の採択性を考えることだけが必要である。試験室の最終報告値が一致しているかどうかを確
認するためには,その2個の最終報告値の差の絶対値を,次に示す許容差CD0.95に対して検定すればよい。
a) それぞれの最終報告値がn1及びn2個の測定結果の平均であるときのCD0.95:
CD0.95=
−
−
−
2
1
2
2
2
1
2
1
1
n
n
r
R
上式中でn1=n2=1ならば,Rは5.3.2.1で示した形 (R=2.8σR) になる。n1=n2=2ならば,式は簡
単に次のようになる。
CD0.95=
2
2
2
r
R−
b) それぞれの最終報告値がn1個の測定結果の平均値と,n2個の測定結果のメディアンであるときの
CD0.95:
CD0.95=
−
−
−
2
2
2
1
2
2
2
)}
(
{
2
1
1
n
n
c
n
r
R
ここで,c (n) は,メディアンの標準偏差の,平均値の標準偏差に対する比である。この値を表2に
示す。
c) それぞれの最終報告値がn1及びn2個の測定結果のメディアンであるときのCD0.95:
CD0.95=
−
−
−
2
2
2
1
2
1
2
2
2
)}
(
{
2
)}
(
{
1
n
n
c
n
n
c
r
R
c (n) の値は,表2を参照。
差が許容差を超えないときは,その2試験室の最終報告値は採択可能で,両者の総平均値を用いる
ことができる。差が許容差を超えるときは,5.3.3で概説する手順を守ることが望ましい。
表2 c (n) の値
測定結果の数,n
c (n)
1
1,000
2
1,000
3
1,160
4
1,092
5
1,197
6
1,135
7
1,214
8
1,160
9
1,223
10
1,176
11
1,228
12
1,187
13
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定結果の数,n
c (n)
13
1,232
14
1,196
15
1,235
16
1,202
17
1,237
18
1,207
19
1,239
20
1,212
参考 表の中では小数点としてコンマ (, ) を用いている。
5.3.3
2つの試験室の測定結果間の不一致の解決
2つの試験室の測定結果又は最終報告値間の不一致の原因として,以下が考えられる。
− 2つの試験室間の系統的な差,
− 測定試料の違い,又は
− σr及び/又はσRを求める際の誤差。
測定試料,及び/又は標準物質を交換できるときは,系統誤差の存在とその程度とを求めるために,そ
れぞれの試験室が相手方の測定試料を用いて測定結果を得ることが望ましい。もし測定試料を交換できな
いならば,各試験室は共通試料(できれば特性値既知の試料)について測定結果を得ることが望ましい。
特性値既知の試料を用いると,系統誤差の原因を片方の,又は両方の試験室に負わせることができる利点
がある。系統誤差の原因をその試験室に負わせるために特性値既知の試料を使用できない場合には,その
試験室の間で第三者の試験室へ委託することで合意に達することが望ましい。
測定試料に不一致があることが明らかなときは,両試験室は合同して共同サンプリングを行うか,第三
者機関を招いてサンプリングを行うことが望ましい。
5.3.4
仲裁
契約の当事者である2つの機関は,契約を結ぶとき又は紛争が起きたときに,仲裁手続に同意すること
が望ましい。
6. 試験室内の測定結果の安定性をチェックする方法
6.1
背景
6.1.1
品質管理の第一歩は化学分析,物理計測,官能評価などによる定量から始まる。これらの定量方法
によって得られた観測値には常に誤差が伴う。この誤差は
− サンプリング
− 試料調製
− 測定など
によるものに分けることができる。ただし,この節では測定による誤差,これは測定試料の試験片間の分
離できない変動も含まれるが,のみを取り上げる。
6.1.2
測定誤差はさらに
− 偶然原因による誤差(精度)と
− 系統原因による誤差(真度)
とに分けることができると考えられる。
14
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.1.3
ある測定方法を考えるとき,その方法の精度と真度が満足できる状態であることを期待するのは極
めて自然である。しかしながら,精度が満足できる状態であっても,真度が満足な状態である保証はない。
したがって,ある試験室内で測定結果の安定性をチェックしなければならないとき,精度と真度の両方を
チェックし,それぞれの望ましい状態での長期にわたる維持が必要とされる。
6.1.4
しかしながら,その測定方法に対して真の値が存在しないこともあり得る。又は,真の値が存在し
たとしても,標準物質を入手できないことにより測定結果の真度が調べられないこともある。これらの例
を表3に示す。
標準物質がないならば測定結果の真度をチェックすることは難しい。しかし,実際には,多くの場合に,
ある標準測定方法に(もしくは,適切な権威づけがされた方法に)厳密に徹底的に,しかも注意深く従い,
熟練したオペレータが設備の整った試験室で得た測定結果を,認証値の代わりに参照値として用いること
ができる。
6.1.5
この規格のこの部では,試験室内の測定結果の安定性をチェックするためにシューハート管理図
(JIS Z 9021参照)と累積和管理図を用いる。
精度又は真度が傾向的に変化するか,シフトする状況では,累積和管理図がシューハート管理図よりも
有効である。これに対して,突発変化が起こる状況ではシューハート管理図の代わりに累積和管理図を用
いる長所(有用性)はない。
真度に関しては傾向的な変化やシフトが起こりやすく,精度に関しては突発変化が起こりやすいので,
真度のチェックには累積和管理図を,精度のチェックにはシューハート管理図を奨める。
しかし,精度及び真度を同時にチェックするために,両方の管理図を併用することも効果的であると思
われる。
15
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3 測定結果の精確さ(真度と精度)をチェックするための真の値及び
重要なパラメータによる測定試料の特性値の分類
分類1)
例
特性値
標準物質2)の
入手の可否
精確さをチェックする
ための重要な母数3)
実用上に真の値として確立できる科学理論に基づ
いた理論値
安息香酸の化学組成
標準物質4)
∆とσW
理論的には真の値が存在するにもかかわらず,現
在の技術では実際に単一の真の値が確立すること
ができない。したがって,科学又は技術集団の主
催する共同実験研究に基づいた合意値を,取り決
めによる真の値として採用する。
a) 鉱石中の鉄の含有量
b) 黄鉄鉱中の硫黄の含有
量
標準物質
ない5)
∆とσW
σWとσL
国際的な,国立の,又は私的な機関によって確立
した標準とされる測定方法によって付与された値
を取り決めによる真の値として採用する。
a) ガソリンのオクタン価
b) コークスの強度
c) 熱可塑性プラスチック
のメルトフローレート
標準物質
なし6)
なし7)
∆とσW
σM/σW , σLとσW
σWとσL
1) JIS Z 8101-2参照
2) JIS Q 0035参照
3) ∆は試験室のかたより,σWは試験室内標準偏差,σLは試験室間標準偏差,σMは測定試料間標準偏差を示す。
4) それが純物質で安定していれば,測定試料そのものを標準物質として用いることができる。
5) 試料が不安定なために標準物質がつくれない。
6) 粒子径,形,組成が異なる硬くてもろい粒子からなる大量の試料が各測定に必要であり,これが破壊試験である
ため,標準物質がつくれない。
7) 参照値が測定方法そのものによって定義される。
6.1.6
チェックの実施は長期間にわたり,またオペレータと装置の変更を含むので,真の併行条件は適用
できない。したがって,このチェックにはJIS Z 8402-3に記述されている中間精度が用いられる。
6.2
安定性をチェックする方法
6.2.1
一般
6.2.1.1
試験室内の測定結果の安定性をチェックする状況には次の2つがある。
a) 工程管理のために使われる日常の測定結果に対して
b) 素材及び工業製品の価格決定のために使われる測定結果に対して
6.2.1.2
a)の場合に,精度がある望ましいレベルに維持されているかどうかを調べるためには,その試験
室内での長期にわたる測定結果から得た,少なくとも1因子が異なる中間標準偏差をチェックする必要が
ある(6.2.3の例2参照)。この場合,ふつうは中間精度をチェックするだけで十分である。なぜならば,
測定結果にかたよりがあったとしても,測定結果の変動が工程変動に比べて十分小さいならば工程変動の
管理は可能だからである。しかし,併行標準偏差をこの目的に用いるならば,感度が過大なために過剰な
反応を引き起こしてしまう可能性がある。したがって,この目的には適切に選定された中間標準偏差を用
いることが望まれる。
6.2.1.3
b)の場合に,真度及び精度がそれぞれの望ましいレベルに維持されているかを調べるために,精
度のチェックとともに真度のチェック(6.2.4の例3参照)も必要である。したがって,この場合には参照
値が必要となる。
6.2.1.4
ここに示す4つの例は以下の通り。
− 例1と例2は,併行精度や中間精度の安定性をシューハート管理図によってチェックする方法を示し
たものである。
16
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 例3と例4は,シューハート管理図や累積和管理図を用いて真度をチェックする方法を示したもので
ある。
6.2.2
例1:日常分析による併行標準偏差の安定性のチェック
6.2.2.1
背景
a) 測定方法
ISO 6352 : 1985, Ferronickel−Determination of nickel content−Dimethylglyoxime gravimetric method, に
規定されている方法によるニッケル含有量の測定
b) 出典
あるフェロニッケル製錬所の試験室における1985年9月の日報
c) 説明
フェロニッケル製錬所の試験室では,フェロニッケル製品の化学組成を求めるために化学分析を毎
日行っている。
同時に,その試験室で調製した私製標準物質を用いてニッケル測定結果の安定性のチェックを行っ
ている。上記のニッケル測定結果の安定性をチェックするために私製の標準物質の2つの試験片を併
行条件,すなわち同一オペレータが同一の装置で同時に分析するという条件の下で,分析を毎日行う。
私製標準物質の化学組成は次の通りである。
Ni 47.21%
Co 1.223%
Si 3.50%
Mn 0.015%
P 0.003%
S 0.001%
Cr 0.03%
Cu 0.038%
6.2.2.2
オリジナルデータ
併行条件の下で得た私製標準物質のニッケル含有量の日常分析測定結果を,表5にx1とx2として示す。
単位は質量パーセントである。
6.2.2.3
シューハート管理図による安定性のチェック
表5の測定結果にシューハート管理図(R管理図)(JIS Z 9021参照)を適用することにより,測定結果
の安定性をチェックし,併行標準偏差の大きさを評価する。中心線,管理限界(UCLとLCL)の計算に,
表4に示した係数を用いた。
備考4. 再現精度に使われる記号Rとの混乱を避けるため,JIS Z 9021のR管理図を以後は範囲管理
図とよぶ。
この例では,過去3ヵ月の測定結果から求められた併行標準偏差 (σr) が,範囲管理図の標準値として示
されているので,管理図は次のように計算される。
a) 中心線=d2σr=1.128×0.037 5=0.042 3
b) 処置限界
UCL=D2σr=3.686×0.037 5=0.138 2
LCL=なし
c) 警戒限界
UCL=D2 (2) σr=2.834×0.037 5=0.106 2
LCL=なし
併行標準偏差 (sr) の推定値は,以下のように導かれる。
w=|x1−x2|

17
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
sr=
2
2
30
1
i
d
/
w
d
/
30
/
w
=
∑
=0.055 3/1.128=0.049 0
各群は2つの試料からなり,範囲は30の群ごとに計算される。表5はこの計算用のワークシートである。
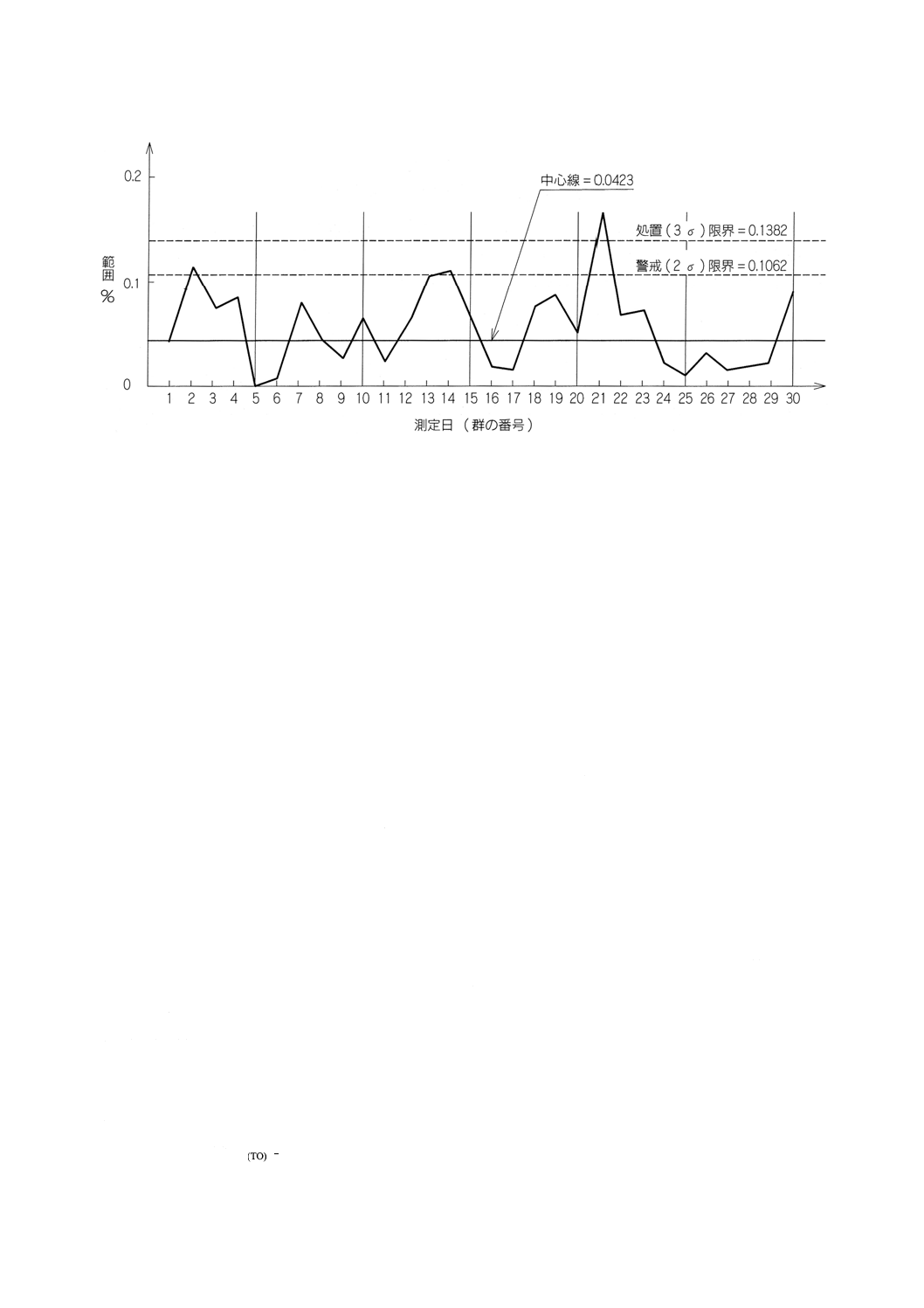
図7に管理限界を入れたデータのプロット例を示す。
図7に示した管理図は,1点が処置限界を超えており,また,連続する2点が警戒限界を超えているこ
とから,測定結果が安定していないことを示している。
表4 範囲管理図の計算用係数
中心線と処置限界の計算用の係数1)
警戒限界の計算用の係数2)
郡内の観測値の数 中心線の係数 処置限界の係数
警戒限界の係数
d2
D2
d3
D1 (2)
D2 (2)
2
1,128
3,686
0,853
−
2,834
3
1,693
4,358
0,888
−
3,469
4
2,059
4,698
0,880
0,299
3,819
5
2,326
4,918
0,864
0,598
4,054
1) これらの数値は,JIS Z 9021の表2から抜粋した。
2) 警戒限界の計算用の係数は,以下のようにして求められた。
D1 (2) =d2−2d3
D2 (2) =d2+2d3
参考 表の中では小数点としてコンマ (, ) を用いている。
18
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5 例1 (6.2.2) のための管理図用データシート
1.
品質特性
私製標準物質のニッケル含有量
2.
測定の単位
% (m/m)
3.
分析方法
ISO 6352
4.
期間
1985-09-01から1985-09-30頃
5.
試験室
フェロニッケル製錬所の現場の試験室 “A”
測定日(群の番号)
観測値
範囲
記事
x1
x2
w
1
47,379
47,333
0,046
2
47,261
47,148
0,113
警戒限界を超えた
3
47,270
47,195
0,075
4
47,370
47,287
0,083
5
47,288
47,284
0,004
6
47,254
47,247
0,007
7
47,239
47,160
0,079
8
47,239
47,193
0,046
9
47,378
47,354
0,024
10
47,331
47,267
0,064
11
47,255
47,278
0,023
12
47,313
47,255
0,058
13
47,274
47,167
0,107
警戒限界を超えた
14
47,313
47,205
0,108
警戒限界を超えた
15
47,296
47,231
0,065
16
47,264
47,247
0,017
17
47,238
47,253
0,015
18
47,181
47,255
0,074
19
47,327
47,240
0,087
20
47,358
47,308
0,050
21
47,295
47,133
0,162
処置限界を超えた
22
47,310
47,244
0,066
23
47,366
47,293
0,073
24
47,209
47,185
0,024
25
47,279
47,268
0,011
26
47,178
47,200
0,030
27
47,211
47,193
0,018
28
47,195
47,216
0,021
29
47,274
47,252
0,022
30
47,300
47,212
0,088
計
1,660
平均
0,055 3
w/d2=0,049 0
注
σr=0,037 5
a) 中心線=d2σr=1,128×0,037 5=0,042 3
b) 処置限界
UCL=D2σr=3,686×0,037 5=0,138 2
LCL=なし
c) 警戒限界
UCL=D2 (2) σr=2,834×0,037 5=0,106 2
LCL=なし
参考 表の中では小数点としてコンマ (, ) を用いている。
19
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図7 併行条件の下で得られた,私製標準物質のニッケル含有量 (%) の範囲管理図
6.2.3
例2:日常分析による,時間とオペレータの異なる中間標準偏差の安定性のチェック
6.2.3.1
背景
a) 測定方法
ISO 351 : 1984, Solid mineral−Determination of total sulfur−High temperature combustion methodに規定
されている方法による,質量パーセントで表された高炉用コークスの硫黄含有量の測定。
b) 出典
ある製鉄所の試験室における1985年8月の日報。
c) 説明
高炉用コークスを製造するコークス炉室から,毎日3直の各直ごとに各生産ロットから試料を採る。
そのとき,硫黄含有量 [% (m/m)] を求めるために,生産ロットごとに一つの測定試料が調製される。
6.2.3.2
オリジナルデータ
1985年8月におけるNo.1コークス炉室から採った試料の硫黄含有量 [% (m/m)] の品質管理分析用の測
定結果を表6に示す。ランダムに抽出された試料が,ある直のオペレータにより分析され (x1),その試料
を次の日に別の直のオペレータにより再度分析される (x2)。このようにして得た測定結果を毎日比較する。
6.2.3.3
シューハート管理図による安定性のチェック
表6の測定結果にシューハート管理図(範囲管理図)(JIS Z 9021参照)を適用することにより,測定結
果の安定性をチェックし,時間とオペレータの異なる中間標準偏差の大きさを評価する。
中心線,処置限界と警戒限界(UCLとLCL)の計算のための係数は6.2.2の例1を参照されたい。過去
3ケ月間の測定結果から求められた,時間とオペレータの異なる中間標準偏差,σI (TO),が範囲管理図の標
準値として示されているので,管理図は次のように計算される。
a) 中心線=1.128×0.013 3=0.015 0
b) 処置限界:
UCL=D2σI (TO) =3.686×0.013 3=0.049 0
LCL=なし
c) 警戒限界:
UCL=D2 (2) σI (TO) =2.834×0.013 3=0.037 8
20
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LCL=なし
中間標準偏差 (sI (TO)) の推定値は,以下の式から導出される。
W=|x1−x2|
si (TO) =
2
2
31
1
/
/
31
/
d
w
d
wi
=
∑
=0.014 2/1.128=0.012 6
各群は2つの試料からなり,範囲は31の群ごとに計算される。表6はこの計算用のワークシートである。
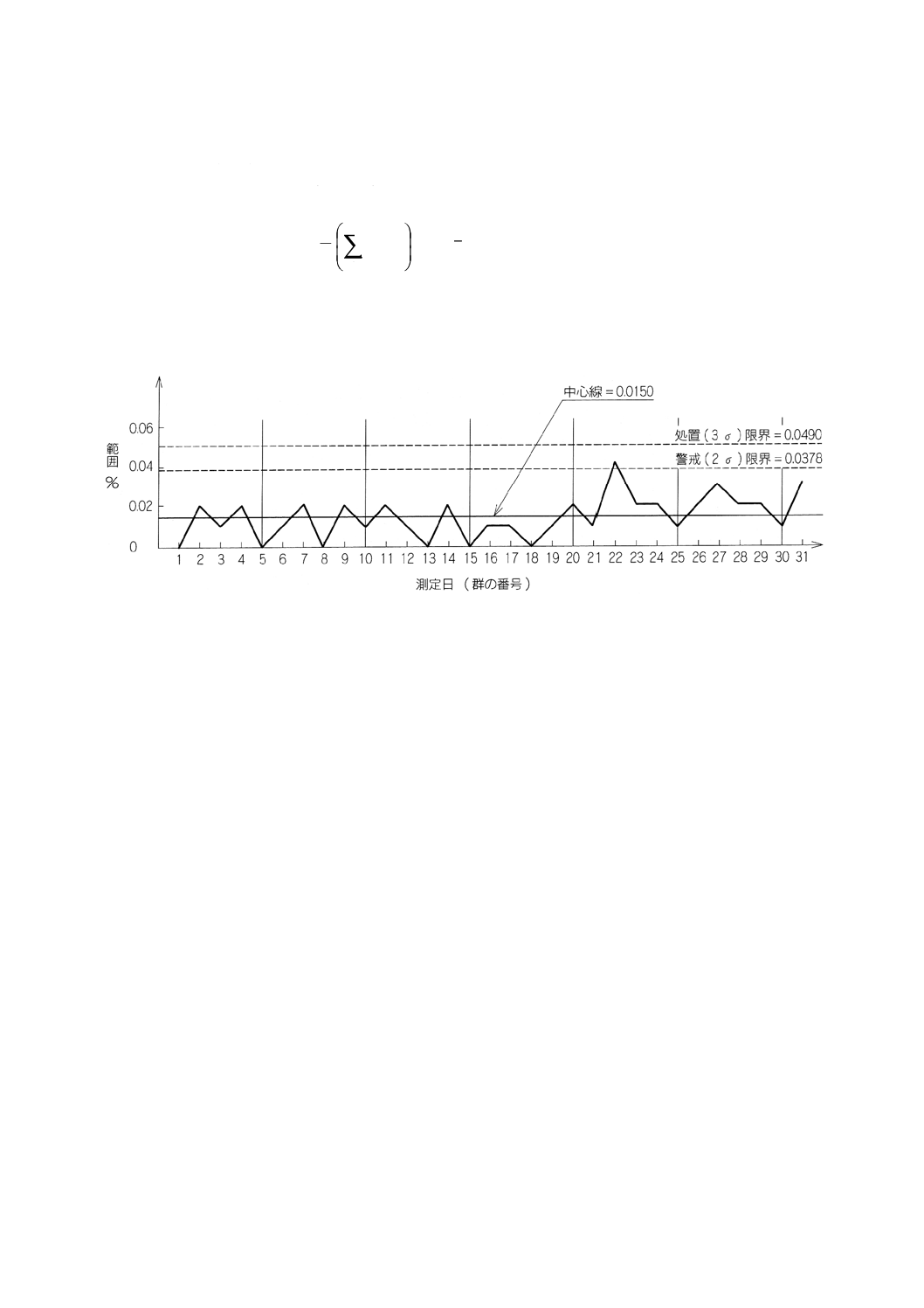
図8に管理限界を入れたデータのプロット例を示す。
図8に示した管理図は,測定結果が安定状態にないという徴候はみられない。
図8 時間とオペレータの異なる中間条件の下で得られた,高炉用コークス中の硫黄含有量 (%) の範囲管
理図
21
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表6 例2 (6.2.3) のための管理図用データシート
1. 品質特性
高炉用コークスの硫黄含有量
2. 測定の単位
% (m/m)
3. 分析方法
ISO 351
4. 期間
1985-08-01から1985-08-31頃
5. 試験室
製鉄所の現場の試験室 “B”
測定日(群の番号)
観測値
範囲
記事
x1
x2
w
1
0,56
0,56
0,00
2
0,48
0,50
0,02
3
0,57
0,58
0,01
4
0,60
0,58
0,02
5
0,58
0,58
0,00
6
0,50
0,49
0,01
7
0,56
0,58
0,02
8
0,56
0,56
0,00
9
0,48
0,46
0,02
10
0,54
0,53
0,01
11
0,55
0,57
0,02
12
0,46
0,45
0,01
13
0,58
0,58
0,00
14
0,54
0,56
0,02
15
0,56
0,56
0,00
16
0,57
0,58
0,01
17
0,46
0,45
0,01
18
0,56
0,56
0,00
19
0,56
0,57
0,01
20
0,57
0,55
0,02
21
0,44
0,45
0,01
22
0,59
0,55
0,04
警戒限界を超えた1)
23
0,55
0,57
0,02
24
0,58
0,56
0,02
25
0,46
0,45
0,01
26
0,60
0,58
0,02
27
0,59
0,56
0,03
28
0,54
0,56
0,02
29
0,47
0,49
0,02
30
0,59
0,58
0,01
31
0,49
0,52
0,03
計
16,84
16,72
0,44
平均
0,014 2
w/d2=0,0126
注
σI (TO) =0,013 3
x1:日常の分析
x2:翌日,別のオペレータによる2回目の分析
a) 中心線=d2σI (TO) =1,128×0,013 3=0,015 0
b) 処置限界
UCL=D2σI (TO) =3,686×0,013 3=0,049 0
LCL:なし
c) 警戒限界
UCL=D2 (2) σI (TO) =2,834×0,013 3=0,037 8
22
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LCL=なし
1) x2を求めたときの実際の温度が,規定値よりも低かった。
参考 表の中では小数点としてコンマ (, ) を用いている。
6.2.4
例3:日常分析の真度の安定性のチェック(1)
6.2.4.1
背景
a) 測定方法
ISO 1171 : 1981, Solid mineral fuels−Determination of ashに規定されている方法による質量パーセン
トで表された石炭の灰分含有量の測定
b) 出典
ある製鉄所の試験室における1985年6月の日報。
c) 説明
その製鉄所では,コークス炉室に石炭混合物が供給され,高炉用コークスを3直制で製造している。
コークス製品の品質を管理するため,ISO 1171に規定された方法により直ごとに石炭の灰分 [%
(m/m)] が分析される。時間とオペレータの異なる中間標準偏差の安定性のチェックは,例2(6.2.3)に
示した方法で行われている。
この例は,私製標準物質(灰分=10.29%)を使って日常分析による真度の安定性をチェックする方
法を示したものである。
6.2.4.2
オリジナルデータ
その標準物質が,3直のすべてのオペレータから毎日ランダムに指名された一人のオペレータによって1
回分析される。測定結果は表7にyとして示されている。
6.2.4.3
シューハート管理図による安定性のチェック
表7のデータにシューハート管理図を適用することにより,日常の分析の真度の安定性をチェックし,
そのかたよりの大きさを評価する。
この試験室では,日常分析が時間とオペレータの異なる中間条件の下で実施されているので,併行標準
偏差 (sr) を試験室内でのかたよりのチェックに使うことはできない。したがって,srを試験室から得た測
定結果の実際の精度とすることはできない。
時間とオペレータの異なる中間標準偏差,sI (TO),を得るために実験を行うよりも,簡便な方法として移
動範囲管理図を用いる。
表7の注に示した公式及び事前に得られたμとσI (TO) の値を用いて管理図を作成する。図9の管理図は,
かたよりと範囲の両方が非常に小さい期間と,測定結果が著しく安定性を欠いている期間を示しており,
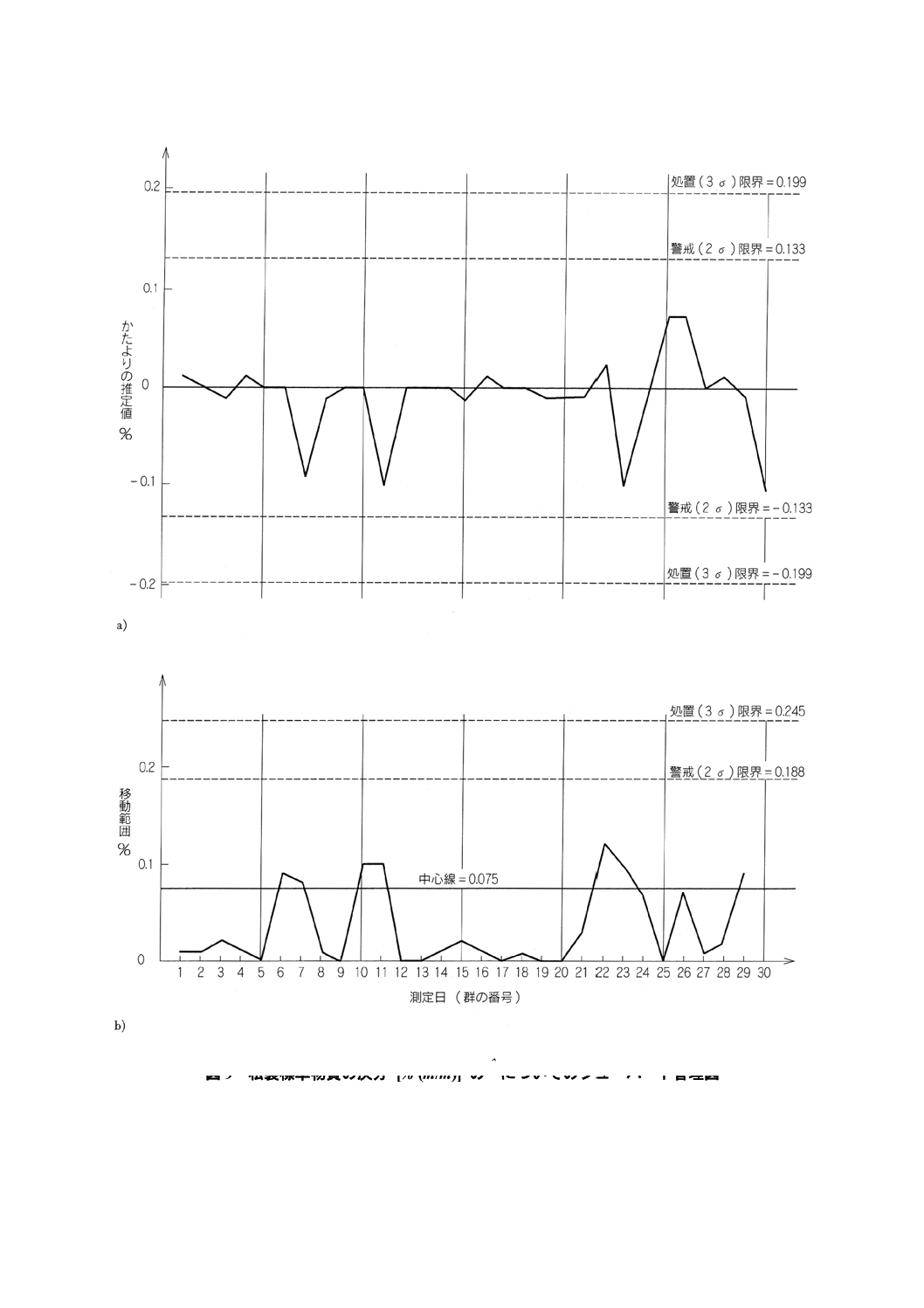
これらのパターンの理由を調査すべきであることを示している。
6.2.4.4
累積和管理図による安定状態のチェック
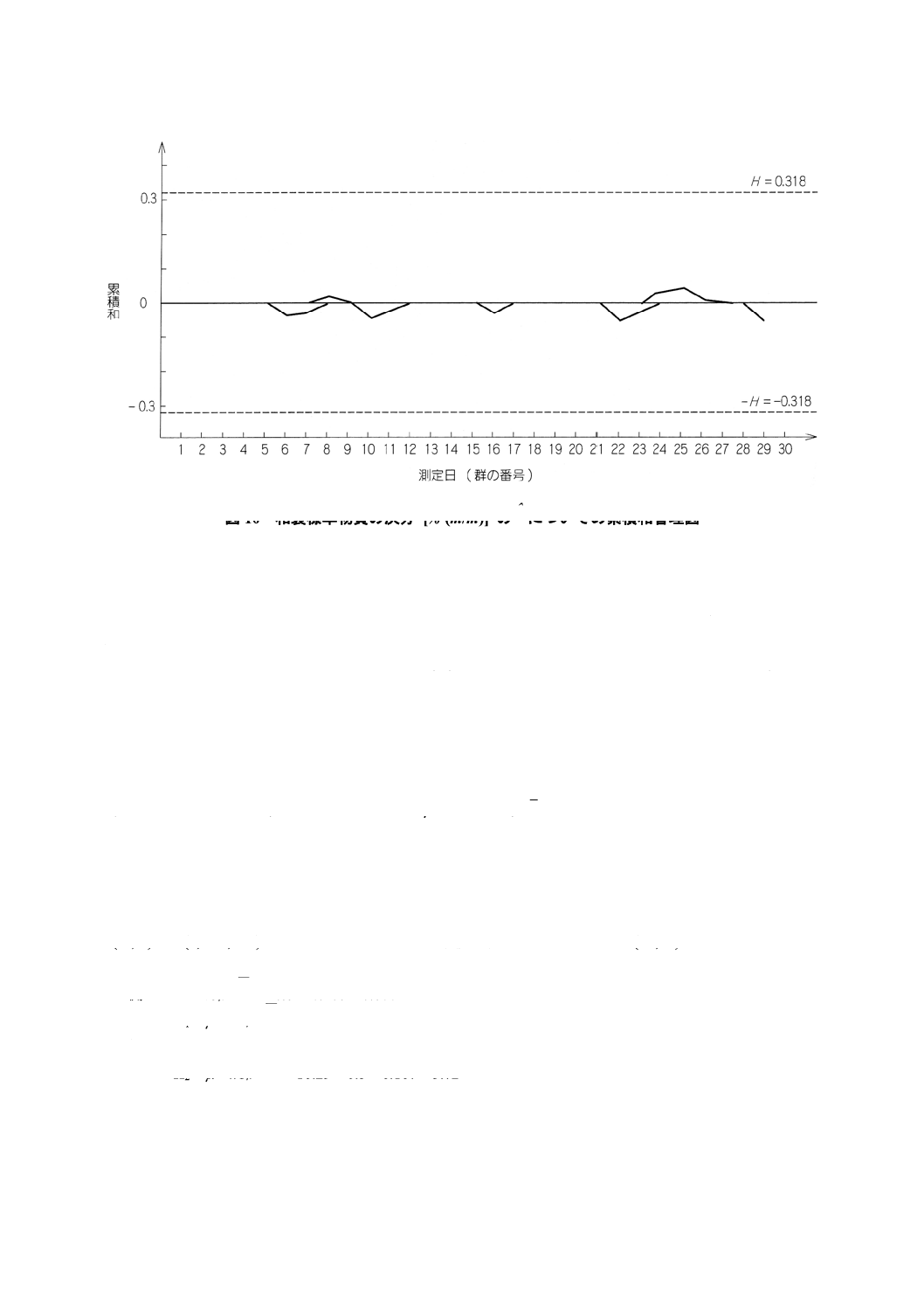
(h, k) = (4, 79 ; 0.5) としたときのδˆに対する累積和管理図の (H ; K) の計算を以下に示す(図10参照)。
上側: H=hσI (TO) =4.79×0.066 45=0.318
K1=μ+kσI (TO) =10.29+0.5×0.066 45=10.323
下側: −H=−0.318
K2=μ−kσI (TO) =10.29−0.5×0.066 45=10.257

23
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表7 例3(6.2.4)のための管理図用データシート
1. 品質特性
私製標準物質の灰分
2. 測定の単位 % (m/m)
3. 分析方法
ISO 1171
4. 期間
1985-06-01から1985-06-30頃
5. 試験室
製鉄所の現場の試験室 “C”
測定日(群の番号) 測定結果
かたよりの推定値
移動範囲
記事
y
δˆ
w
1
10,30
0,01
0,01
2
10,29
0,00
0,01
3
10,28
−0,01
0,02
4
10,30
0,01
0,01
5
10,29
0,00
0,00
6
10,29
0,00
0,09
7
10,20
−0,09
0,08
8
10,28
−0,01
0,01
9
10,29
0,00
0,00
10
10,29
0,00
0,10
11
10,19
−0,10
0,10
12
10,29
0,00
0,00
13
10,29
0,00
0,00
14
10,29
0,00
0,01
15
10,28
−0,01
0,02
16
10,30
0,01
0,01
17
10,29
0,00
0,00
18
10,29
0,00
0,01
19
10,28
−0,01
0,00
20
10,28
−0,01
0,00
21
10,28
−0,01
0,03
22
10,31
0,02
0,12
23
10,19
−0,10
0,10
24
10,29
0,00
0,07
25
10,36
0,07
0,00
26
10,36
0,07
0,07
27
10,29
0,00
0,01
28
10,30
0,01
0,02
29
10,28
−0,01
0,09
30
10,19
−0,10
計
308,44
−0,26
0,99
平均
−0,086 6
0,0341
w/d2=0,030 2
注
私製標準物質の灰分
μ=10,29
過去3ケ月の測定結果から求められた標準偏差
σI (TO) =0,066 45
かたよりの推定値
δˆ=y−μ
移動範囲
w=|δˆi−1−δˆi|
x−管理図
中心線=0
24
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
処置限界
UCL=+3σI (TO)=0,199 4
LCL=−3σI (TO)=−0,199 4
警戒限界
UCL=+2σI (TO)=0,132 9
LCL=−2σI (TO)=−0,132 9
移動範囲管理図
中心線=d2σI (TO) =1,128×0,066 45=0,074 96
処置限界
UCL=D2σI (TO)=3,686×0,066 45=0,245
LCL=なし
警戒限界
UCL=D2 (2) σI (TO)=2,834×0,066 45=0,188 3
LCL=なし
参考 表の中では小数点としてコンマ (, ) を用いている。
25
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図9 私製標準物質の灰分 [% (m/m)] のδˆについてのシューハート管理図
26
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図10 和製標準物質の灰分 [% (m/m)] のδˆについての累積和管理図
6.2.5
例4:日常分析の真度の安定性のチェック(2)
6.2.5.1
背景
a) 測定方法
Silver diethyldithiocarbamate-arsine evolution colorimetric法による亜鉛酸化物の砒素含有量の測定
b) 出典
Kanzelmeyer, J. H. “Quality Control for Analytical Methods”, ASTM Standardization News, October 1977,
Figure 2, p. 27.
6.2.5.2
オリジナルデータ
表8参照
6.2.5.3
シューハート管理図による安定性のチェック
表8の注に示した公式,及び事前に得られたμとσrを用い,xについてのシューハート管理図(図11参
照)をつくる。
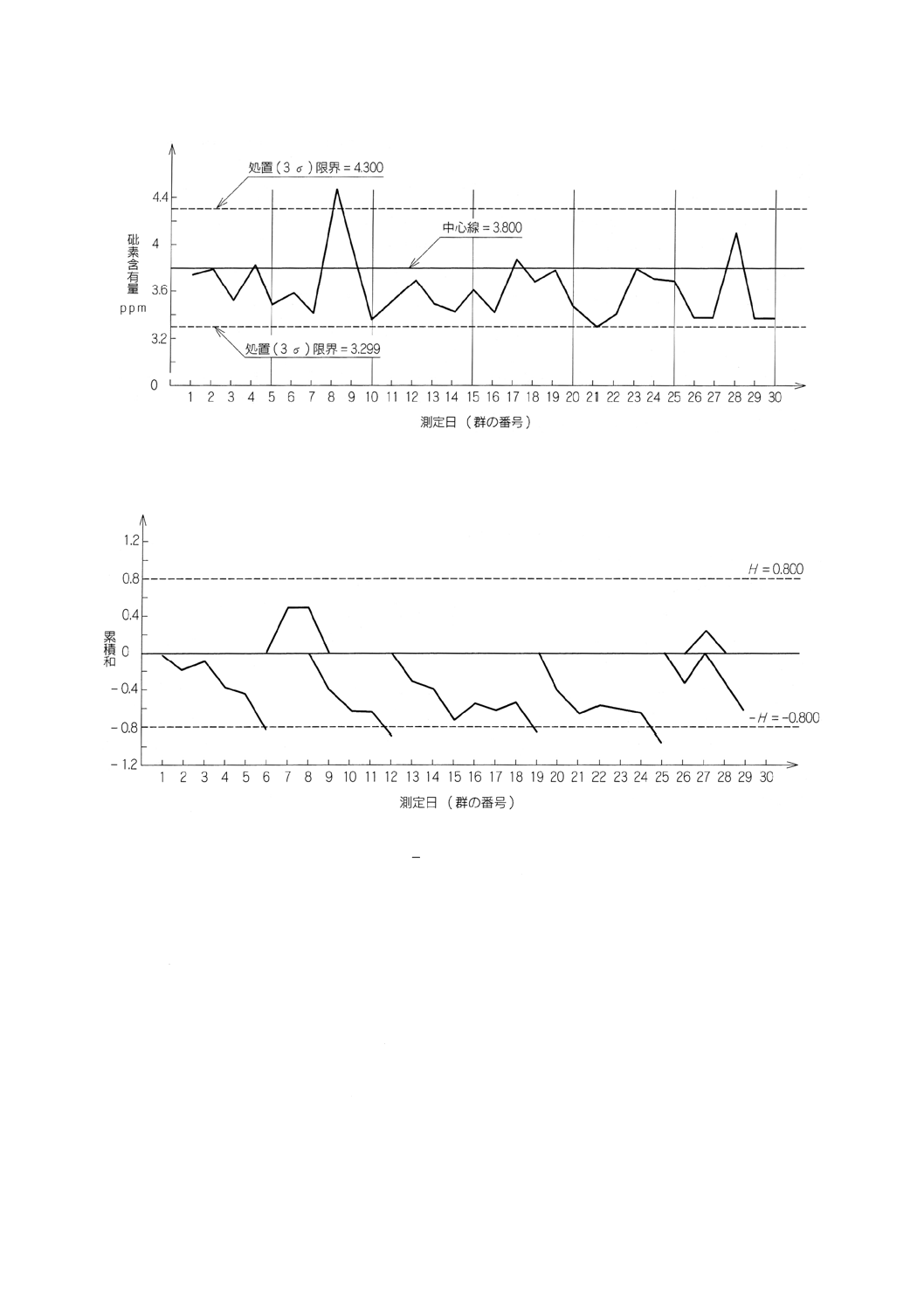
1点が処置限界を超え,7以上連続する測定結果が中心線の下側に2つあることから,管理図は測定結果
が安定していないことを示している。
6.2.5.4
累積和管理図による安定性のチェック
(h ; k) = (4, 79 ; 0.5) としたときのxに対する累積和管理図のパラメータ (H ; K) の計算を以下に示す
(図12参照)。
上側: H=hσr/n=4.79×0.167=0.800
K1=μ+kσr/n=3.800+0.5×0.167=3.88
下側: −H=−0.800
K2=μ−kσr/n=10.29−0.5×0.167=3.72

27
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表8 例4 (6.2.5) のためのx管理図用のデータシート
1.
品質特性
私製標準物質の砒素含有量
2.
測定の単位
ppm (m/m)
3.
分析方法
Silver diethyldithiocarbamate-arsine evolution colorimetric法
群の番号
観測値
記事
x1
x2
x
1
3,70
3,80
3,75
2
3,76
3,86
3,81
3
3,64
3,38
3,51
4
4,01
3,62
3,82
5
3,40
3,52
3,46
6
3,65
3,53
3,59
7
3,20
3,58
3,39
8
4,19
4,65
4,42
処置限界を超えた
9
3,97
3,77
3,87
10
2,95
3,69
3,32
11
3,43
3,55
3,49
12
3,85
3,53
3,69
13
3,77
3,17
3,47
14
3,19
3,60
3,40
15
3,75
3,45
3,60
16
3,55
3,25
3,40
17
3,98
3,76
3,87
18
3,56
3,78
3,67
19
3,54
4,02
3,78
20
3,35
3,55
3,45
21
3,37
3,25
3,31
22
3,42
3,42
3,42
23
3,71
3,87
3,79
24
3,77
3,62
3,70
25
3,82
3,58
3,70
26
3,73
3,02
3,38
27
3,48
3,28
3,38
28
4,01
4,19
4,10
29
3,63
3,11
3,37
30
3,51
3,23
3,37
計
108,28
平均
3,609
注
私製標準物質の砒素含有量
μ=3,80
過去の標準偏差
σr=0,236
x−管理図
中心線=3,80
処置限界
UCL=μ+3σr/n=4.300
LCL=μ−3σr/n=3.299
参考 表の中では小数点としてコンマ (, ) を用いている。
28
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図11 亜鉛酸化物のSilver diethyldithiocarbamate-arsine evolution colorimetric法による砒素(ひそ)含有
量の測定のxについてのシューハート管理図
図12 亜鉛酸化物のSilver diethyldithiocarbamate-arsine evolution colorimetric法による砒素(ひそ)含有
量の測定のxについての累積和管理図
7. 試験室評価における併行標準偏差と再現標準偏差の利用
7.1
評価方法
7.1.1
一般
ここでは,対象となる測定方法が一つで既に標準化されいろいろな試験室で用いられる場合の,試験室
の評価について述べる。従って,その測定方法の精度を併行標準偏差と再現標準偏差で推定することが可
能である。これらの値は,あらかじめ精度評価実験によって求められるものと仮定する。
測定方法のための標準物質が存在するか,又は参照試験室が存在するかによって,評価方式が3種類あ
る。標準物質が十分な測定水準に存在するならば,試験室が一つであっても評価を行うことができる。標
準物質が存在しない測定方法に関しては,そのような単純な評価は可能ではない。この場合には,対象の
試験室を,評価に関して高い水準にあることが広く認められている技術の優れた試験室と比較しなければ
29
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ならない。また試験室を継続的に評価するためには,しばしば多くの試験室を同時に評価しなければなら
ない。このような状況では,共同評価実験が有効である。
共同評価実験を行うことの目的は,それぞれの分析能力の改善を目指して各試験室の結果と他の試験室
の結果とを比較することである。
7.1.2
共同評価実験の定義の前提
測定方法の併行標準偏差は,試験室内での均一な条件の下で行われる測定の不確かさの尺度である。こ
の意味で,それは,JIS Z 8402-1に定義されている併行条件の下での室内精度を表現している。
標準物質が存在する場合のように,測定される特性について,真の値が存在し,かつ値が既知のときは,
試験室のかたよりは,直ちに求めることができる。真の値が未知のときは,かたよりを間接的に求めなけ
ればならない。一つの手段は,その試験室をかたより既知の試験室と比較することである。しかし,この
解決法は,その“参照”試験室の精度とかたよりに強く依存する。
共同評価実験の場合,再現精度は,異なる試験室間で得られた測定結果の一致の度合いを示している。
従って,それは各試験室のかたよりを評価するために用いることができる。共同評価実験で再現精度が求
められたとき,系統的な偏差の大きい試験室は,外れ値のように見えるであろう。
ここでは,測定方法の精度は,あらかじめ求められているものとする。すなわち,併行分散σr2,室間分
散σL2及び再現分散σR2は既知であることを意味している。
7.で述べる方法は,試験室のかたよりをチェックすることを主として意図している。6.で述べた方法は,
試験室の併行精度又は中間精度をチェックするために,より効果的である。
7.2
以前に評価されていない試験室による,ある測定方法の使用の評価
7.2.1
試験室の実施要領の評価
ある試験室の一般的な評価基準については,JIS Z 9325を参照のこと。試験室は,GLP(試験室のよい
実施要領,good laboratory practice)に従わなければならないし,満足できるような内部品質管理を行わな
ければならない。内部品質管理の方法は,すでに6.に述べた。
管理のこの部分は,各試験室の通常の作業状況についての査察に基づいているにすぎない。これは,特
別の測定試料の使用や他の試験室の参加を必要とせず,直ちに行うことができる。
対象となる試験室の,ある特定の測定方法の使用について定量的に評価するためには,管理実験を行う
必要がある。これは,その試験室内で標準物質(7.2.3参照)を使用するか,又は優れた試験室(7.2.4参照)
と比較することによって行うことができる。
7.2.2
管理実験に関する一般的な考慮
管理実験を計画するときには,次のような点を考慮すべきである。
a) 実験の測定水準の数 (q) をいくつにするか? この問題は,JIS Z 8402-1の6.3で考慮されている。
b) 各測定水準での反復数 (n) をいくつにするか?
共同評価実験の場合:
c) 参加試験室数 (p) はいくつになるか?
実験を計画するとき,JIS Z 8402-2の5.及び6.と同様に,JIS Z 8402-1の6.1を考慮に入れることが望ま
しい。
測定試料は,それが共同評価実験の試料であることが分からないようにして試験室に送らなければなら
ない。このようにすることで,その試料が特別な取扱いを受けず,試験室の通常の実施要領で取り扱われ
ることを保証するためである。
7.2.3
標準物質がある場合の測定方法
30
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.2.3.1
一般
7.2.3.1.1
標準物質が存在する場合には,評価は単一の試験室で行ってもよい。測定方法の精度が既知な
ので,室内精度の評価には併行標準偏差の既知の値を使用し,加えて測定結果と参照値を比較することで,
かたよりが求められる。
実験者が実験結果から高い確率で検出したいと望んでいる試験室間のかたよりの最小値として,検出可
能な試験室のかたより∆mを導入することが適切であることがある。
7.2.3.1.2
室内精度を評価するためには,試験室内で繰り返し測定を行う必要がある。
7.2.2に示した考慮の後に,q水準の測定試料が送られ,各測定水準ごとにn回の繰り返し測定が行われる。
結果の解析にはJIS Z 8402-2の7.に示されている方法を用いる。室内精度を評価するには,セル内標準偏
差srを既知の併行標準偏差σrと比較する。容認の基準は,
sr2/σr2<χ2 (1−α) (ν) /ν ···································································· (1)
である。ここでχ2 (1−α) (ν) は自由度ν=n−1のχ2分布の (1−α) 分位点である。特に断らない限り,有意水
準αは,0.05とする。
この不等式は,q個の測定水準のうち約95%について成立するはずである。普通qはそれほど大きくな
いので,このことは,基準(1)が,その試験室におけるq個の測定水準のすべてについて成立しなければな
らないことを意味している。
7.2.3.1.3
かたよりを評価するときは,各測定水準の平均値yを対応する参照値μと比較する。
n
n
s
s
s
n
s
s
r
R
r
y
)1
(
1
)
(
2
2
2
2L
2
−
−
+
=
=
······················································ (2)
なので容認の基準は,
|y−μ|<
n
n
r
R
1
2
2
2
−
−σ
σ
······················································· (3)
容認の基準(3)は,q個の測定水準のそれぞれについて適合しなければならない。
n=2のときは,基準(3)は簡単に
|y−μ|<
2
2
2
2
r
R
σ
σ−
····························································· (4)
となる。さらに検出可能なかたよりについては,容認の基準が
|y−μ|<∆m/2 ······································································· (5)
と導かれる。
7.2.3.2
例:コンクリート中のセメント含有量の定量
7.2.3.2.1
背景
セメント含有量はコンクリートの耐久性に影響を及ぼすので重要であり,コンクリートの仕様書にセメ
ント含有量の最小値が示されることがよくある。セメントの含有量は,セメントと骨材及びコンクリート
試料の試料中のカルシウム含有量の測定によって求められる。試験室の評価のために,セメント含有量既
知のコンクリート試料を調製することが可能である。
6つの試験室を評価するために,セメント含有量が425kg/m3の標準物質が調製された。各試験室で,そ
れぞれ2回の測定が行われた。
7.2.3.2.2
オリジナルデータ
表9参照。併行標準偏差と再現標準偏差の値は:
σr=16

31
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
σR=25
表9 コンクリートのセメント含有量
試験室i
観測値
y11
y12
1
406
431
2
443
455
3
387
431
4
502
486
5
434
456
6
352
399
7.2.3.2.3
セル平均と範囲の計算
表10参照。
表10 セル平均とセル範囲
試験室
セル平均
範囲
1
418.5
25
2
449
12
3
409
44
4
494
16
5
445
22
6
375.5
47
7.2.3.2.4
室内精度の評価
表10の範囲を,次式により併行標準偏差と比較する。
)
(
2
)
(
)
1(2
2
2
2
1
ν
χ
σ
α
−
−
≦
r
i
i
y
y
ここで,α=0.05,ν=1ならば,χ20.95 (1) =3.841である。
試験室No.6は,外れていることが判った。
(y6 ; 1−y6 ; 2)2=2 209;検定統計量の値=4.31
7.2.3.2.5
かたよりの評価
容認の基準の式(4)から
|y−425|<44.59
となる。
試験室No.4の検定統計量の値は
|y−425|=69
試験室No.6の検定統計量の値は
|y−425|=50.5
従って,これらの2つの試験室には,いずれも満足できないかたよりがある。
7.2.4
標準物質が存在しない測定方法
7.2.4.1
標準物質を入手できないので,評価は,技術の優れた試験室との比較によって行われなければな
らない。評価対象である新たな試験室についての信頼できる結論を得るために,十分な精度とかたよりで
業務を行っている試験室を見いだすことが重要である。
標準物質がある場合と同じように,2つの試験室間の検出可能なかたよりの差λを導入することが適切な
ことがある。それは実験者が,高い確率で検出したいと望んでいる,2つの試験室によって得られる結果

32
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の期待値間の差の最小値として定義される。
7.2.4.2
測定試料は,両方の試験室に7.2.3.1.2に述べたようにして送り,両方の試験室の室内精度も同様
に評価する。両方の試験室は,各測定水準で同じ個数 (n) の測定結果を得ることが望ましい。
7.2.4.3 測定方法のかたよりδを評価するときは,2つの試験室のそれぞれの測定水準で平均値を比較する。
一般に,n1を第1の試験室の測定結果の数とし,n2を第2の試験室の測定結果の数とすれば,
)2
1
(2
y
y
s
−
=
−
−
−
+
+
2
1
2
2
2
1
2
2L
2
1
2
1
1
2
1
1
2
n
n
n
n
r
R
r
σ
σ
σ
σ
=
················· (6)
なので,容認の基準は,
|
1y− 2y|
−
−
−
≤
2
1
2
2
2
1
2
1
1
2
2
n
n
r
Rσ
σ
···································· (7)
となる。容認の基準(7)は,q個の測定水準のそれぞれについて適合しなければならない。
n1=n2=2のときは,基準(7)は簡単に,
|
1y− 2y|
2
2
2
2
2
r
R
σ
σ−
≤
······················································ (8)
となる。
参考 基準(6)〜(8)で評価できるのは,試験室間のかたよりの差λであって,測定方法のかたよりδでは
ない。原国際規格のこの部分の冒頭の“測定方法のかたよりδを評価するとき”という記述は誤
まりで,“試験室間のかたよりの差λを評価するとき”が正しい。
また,ISO 5725-6では式(6)の左辺を誤って
)2(
)1(
(
2
y
y
s
−
と記述している。
7.3
以前に承認されている試験室についての継続評価
7.3.1
継続管理実験についての一般的な考慮
以前に承認されている試験室が,引き続き満足すべき技能を維持していることを保証するためには継続
評価が必要であり,訪問査察か,評価実験への参加のいずれかによって行うことが望ましい。どれくらい
の頻度で評価を行うべきかについては,さまざまな因子,例えば,技術的,経済的,及び安全性の因子が
寄与するため,特に定まったルールは決められていない。責任のある権威機関が,その状況に応じて評価
の頻度を決定すべきであろう。
継続評価は,同時に多くの試験室が評価されなければならない状況をしばしば引き起こす。この状況で
は,技術の優れた試験室との比較は奨められない。これは,最良の試験室であっても,その試験室自身も
チェックされなければならないためである。この状況では,共同評価実験を行うことが必要である。
7.3.2
試験室の実施要領の評価
試験室の実施要領の実態は7.2.1に述べた訪問査察によって評価される。
7.3.3
標準物質がある場合の測定方法
JIS Z 8402-4に述べられている方法を,試験室の継続評価に相応して適用することができる。
7.3.4
標準物質が存在しない測定方法
7.3.4.1
一般
7.3.4.1.1
標準物質を入手できないので,各試験室の評価は,複数の試験室が参加する共同評価実験に基
づいて行われる。
評価実験の計画は,精度実験の計画に非常によく似ているので,JIS Z 8402-1及びJIS Z 8402-2に記述
33
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
されている多くの検討すべき事項が適用される。その目的が,それぞれの試験室を個々に評価することで
あるので,測定水準ごとの反復数の選定は,7.2.2に述べた一つの試験室の状況と同様である。
その目的が評価であるため,参加する試験室の数が精度評価実験の場合よりも少なくてもよい。例えば,
国家を代表して参加する試験室に限って行われる実験などは,手続きから明らかであろう。参加試験室の
数の減少は,試験室間の系統的な偏差を減少することにはならない,ということが特に重要であり,この
ような場合に,外れ試験室を明らかにできないという危険性が増加するかもしれない。
7.3.4.1.2
7.2.2に示した考慮の後に,q個の測定水準の測定試料を,p個の試験室に送付し,各測定水準
でn回の測定が行われる。その結果を評価するときには,JIS Z 8402-2の7.に示されている方法を用いる。
これは欠測値や測定結果の追加が起こりうるために,セル内のデータ数が異なるかもしれないからである。
室内精度は,6.に述べたように,試験室ごとに評価される。
7.3.4.1.3 かたよりの総合評価については,各測定水準ごとに再現分散を計算する(JIS Z 8402-2, 7.5参照)。
sR2=sL2+sr2 ·············································································· (9)
ここで
n
s
y
y
n
p
s
r
p
i
i
i
/
)
(
1
1
2
1
2
2L
−
−
−∑
=
=
·············································· (10)
そして,
∑
p
i
in
p
n
1
1
=
=
············································································ (11)
である。
室間分散sL2は既知の室間分散σL2と比較される。
容認の基準は,
ν
ν
χ
σ
σ
α
)
()
1(2
2
2L
2
2L
−
+
+
≦
r
r
n
s
s
n
····························································· (12)
である。ここでχ2 (1−α) (ν) は自由度ν=p−1のχ2分布の (1−α) 分位点である。特に断らない限り,有意
水準αは,0.05とする。
もし,容認の基準(12)に適合するならば,室間分散sL2は容認でき,問題としている測定水準について,
すべての試験室が満足すべき精確な結果を得たと結論することができる。
基準が適合しないときには,グラッブズの検定統計量を計算することで,最も外れている結果を見つけ,
そこで問題となる試験室からの測定結果を除外し,残った (p−1) 試験室について再び分散を推定する。
もし修正した分散が,基準(12)を満足しているならば, (p−1) 試験室は承認される。そうでなければ,グ
ラッブズの検定の統計量を再計算し,必要ならばこの手順を数回繰り返す。JIS Z 8402-2に述べられたよ
うにグラッブズの検定は,繰り返して適用するのには適していない。従って,多くの外れ値があるときは,
全ての測定水準について,全てのデータを検査したほうがよい。もし,一つもしくは複数の試験室が,そ
れぞれ複数の測定水準で偏差が大きいときには,これらの試験室は大きすぎるかたよりを伴って測定作業
をしていると結論することができる。もし,その偏差が,一つの測定水準だけで見出されるならば,それ
はその測定試料の不規則性を調査するための十分な理由となる。もし,その偏差が,さまざまな試験室で,
又さまざまな測定水準で生じているならば,それらの偏差は,おそらく評価実験に欠陥があったことによ
るものであろう。そのときは,評価実験の一つ一つの部分について,可能ならば説明を見いだせるように,
34
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
詳しく調査することが必要である。
他の試験室から,(室内精度とかたよりのどちらか一方でも)外れて見える試験室には,実験の結果につ
いて知らせなければならないし,その試験室の実施要領を改善するために,その測定方法を調査しなけれ
ばならない。
7.3.4.1.4
引き続き行われる評価実験においては,特定の測定試料の測定で,試験室が異常によい精度を
示すことがないように,異なった測定試料を用いなければならない。その上,7.2.2で述べたように,測定
が,試験室の通常の実施要領で取り扱われることを保証するために,試料は,それが共同評価実験の試料
であることが分からないようにして送付しなければならない。
もしある評価実験の結果が,以前の評価実験の結果とかなり異なっているならば,この予期しない所見
についての可能な説明を見出すために,すべての入手可能な情報を分析することが重要である。
7.3.4.2
例:水のアルカリ度の分析
7.3.4.2.1
背景
水質の管理において,多くの試験室で水の化学分析が行われている。認可のためには,これらの試験室
は,繰り返して評価されなければならない。この例では,全アルカリ度の測定が考察されている。方法は
電位滴定である。この状況では標準物質は存在しないので,評価実験によって評価を行わなければならな
かった。
18試験室がこの実験に参加し,2つの測定水準について,各試験室でそれぞれの測定水準について2回
ずつの測定が行われた。
7.3.4.2.2
オリジナルデータ
表11参照。
表11 水のアルカリ度
試験室
測定水準
試験室
測定水準
1
2
1
2
1
2,040
5,250
10
2,170
5,520
2,040
5,300
2,200
5,330
2
2,100
5,460
11
1,980
4,990
2,110
5,460
1,940
5,020
3
2,070
5,240
12
2,120
5,340
2,070
5,200
2,110
5,330
4
2,070
5,308
13
2,160
5,330
2,090
5,292
2,150
5,420
5
2,740
5,850
14
2,050
5,330
2,610
5,850
2,070
5,330
6
2,086
5,305
15
2,070
5,387
2,182
5,325
2,056
5,335
7
2,128
5,296
16
2,010
5,210
2,076
5,346
2,030
5,330
8
2,060
5,340
17
2,066
5,300
2,080
5,340
2,070
5,280
9
2,060
5,310
18
2,060
5,300
2,080
5,300
2,070
5,280
参考 表の中では小数点としてコンマ (, ) を用いている。
7.3.4.2.3
セル平均と範囲の計算
セル平均を表12に,範囲を表13に示す。
35
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2つの測定水準に対する,既に確率された併行標準偏差と再現標準偏差の値は,
σr1=0.023 σr2=0.027 σR1=0.045 σR2=0.052
である。
表12 表11のセル平均
試験室
測定水準
1
2
1
2,040
5,275
2
2,105
5,460
3
2,070
5,220
4
2,080
5,300
5
2,675
5,850
6
2,134
5,315
7
2,102
5,321
8
2,070
5,340
9
2,070
5,305
10
2,185
5,425
11
1,960
5,005
12
2,115
5,335
13
2,155
5,375
14
2,060
5,330
15
2,063
5,361
16
2,020
5,270
17
2,068
5,290
18
2,065
5,290
表13 表11のセル範囲
試験室
測定水準
1
2
1
0,000
0,050
2
0,010
0,000
3
0,000
0,040
4
0,020
0,016
5
0,130
0,000
6
0,096
0,020
7
0,052
0,050
8
0,020
0,000
9
0,020
0,010
10
0,030
0,190
11
0,040
0,030
12
0,010
0,010
13
0,010
0,090
14
0,020
0,000
15
0,014
0,052
16
0,020
0,120
17
0,004
0,020
18
0,010
0,020
7.3.4.2.4
室内精度の評価
表13の範囲を次式により併行標準偏差と比較する。
wij2/2σrj2<χ2 (1−α) (ν) /ν
36
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
α=0.05およびν=1のとき,χ20.95 (ν) /ν=3.841である。
測定水準1については,次の試験室が外れていることが判る。
試験室5:w2=0.016 9
検定統計量の値=15.974
試験室6:w2=0.009 216
検定統計量の値=8.711
測定水準2については,次の試験室が外れていることが判る。
試験室10:w2=0.036 1
検定統計量の値=24.76
試験室13:w2=0.008 1
検定統計量の値=5.55
試験室16:w2=0.014 4
検定統計量の値=9.88
7.3.4.2.4
かたよりの評価
表12から,室間分散を次式により求める。
s2=
∑
+
−
−
p
i
r
i
i
s
s
n
y
y
n
p
1
2
2L
2)
(
1
1
=
=
測定水準1については,次の値が求められた。
nσL2+σr2=nσR2− (n−1) σr2=0.003 521
s2=0.044 36
検定統計量の値=12.60
α=0.05およびν=17のとき,χ20.95 (ν) /ν=1.623である。
もっとも大きく外れている値は試験室5のものである。
試験室5に対するグラッブズの検定統計量の値は,
G= (2.675−2.113 2) /0.148 9=3.77
この値とJIS Z 8402-2の9.のp=18に対する5%棄却限界値とを比較する。この棄却限界値は2.651であ
る。
試験室5の結果を除外して計算すると次のようになる。
s2=0.005 357
検定統計量の値=1.521
α=0.05及びν=16のとき,χ2 (1−α) (ν) /ν=1.644である。
結論は,“試験室5を除いたすべての試験室は測定水準1において十分に精確な結果を得ている”,とな
る。
測定水準2については,次の値が求められた。
nσL2+σr2=0.004 679
s2=0.050 34
検定統計量の値=10.758
α=005及びν=17のとき,χ2 (1−α) (ν) /ν=1.623である。
もっとも大きく外れている値は試験室5のものである。
試験室5に対するグラッブズの検定統計量の値は,
G= (5.85−5.337 0) /0.158 6=3.235
p=18に対する5%棄却限界値は2.651である。
試験室5の結果を除外して計算すると次のようになる。
s2=0.018 67
37
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定統計量の値=3.990
α=0.05及びν=16,χ2 (1−α) (ν) /ν=1.644
いまや,もっとも大きく外れている値は試験室11のものである。
試験室11に対するグラッブズの検定統計量の値は,
G= (5.005−5.306 9) /0.096 61=−3.125
p=17に対する5%棄却限界値は2.620である。
試験室11の結果を除外して計算すると次のようになる。
s2=0.007 00
検定統計量の値=1.496
α=0.05及びχ=15,χ2 (1−α) (ν) /ν=1.666
結論は“試験室5と試験室11を除いたすべての試験室は測定水準2において十分に精確な結果を得てい
る”,となる。
7.3.4.2.6
結論
評価実験によって,複数の試験室は,不満足な室内精度で測定作業をしていたことが明らかになった。
これらの試験室の番号は,5,6,10,13,16である。2つの試験室は,さらに1つ又は両方の測定水準で
有意なかたよりを示した。これらの番号は5と11である。これらの偏差の大きい全ての試験室には,その
結果について情報を与えることが望ましい。
8. 代替測定方法の比較
8.1
代替測定方法の発端
国際標準測定方法は,さまざまな要求事項を満たすための標準化の過程を経た測定方法である。これら
の要求事項の中には以下のものがある。
a) 国際的に取引される大部分の物質を含められるように,特性の広範囲な測定水準に適用可能でなけれ
ばならない。例えば,鉄鋼石中の総鉄含量を求める方法は,国際的に取引される鉄鉱石のできる限り
多くに適用可能でなければならない。
b) 装置,試薬及び人員は国際的基準で利用可能でなければならない。
c) 測定にかかる費用は容認できるものでなければならない。
d) 測定方法の精度と真度は,測定結果の利用者が容認できる程度でなければならない。
これらの方法は,ふつう日常作業に適用するには煩雑すぎるかもしれない妥協案である。試験室によっ
ては,独自の要求にはより簡便な方法で十分であると感じることもある。例えば,測定する大部分の試料
が,同じ供給源から来るもので,その特性の変化が比較的小さい場合には,より簡便で安価な方法で十分
であろう。
分野によっては歴史的理由のために,複数の測定方法が用いられるかもしれない。この場合には,一つ
の代替国際標準測定方法を定めることが望ましいであろう。
ここで述べられる比較は,1つの測定試料から得られる結果に基づいている。2つの測定方法の精度と真
度を比較するためには,測定試料を2つ以上用いるべきであると,強く推奨する。必要な測定試料の数は,
問題としている特性の測定水準の範囲や,試料中成分の変化に対する測定方法の感度などの種々の因子に
依存する。
8.2
測定方法比較の目的
38
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2.1
8.2では,一方(方法A)が国際標準測定方法又は国際標準測定方法の第一候補であるときの,2
つの方法の精度及び真度を比較するための手順を述べる。この比較は,2つの測定方法が異なる精度及び/
又は真度を有しているかについての証拠を与えるが,ある特定の適用のためにどちらかが他方より適して
いるということを奨めるものではない。この判定は,他の因子;例えば費用,装置が利用可能かなど,と
相まってなされることが望ましい。
8.2.2
8.2は主として次の適用のために規定される。
a) 国際標準測定方法の開発において,専門委員会は,どちらの候補方法が国際標準として採択するのに
適しているかを選択する問題に直面することがある。精度と真度は,この選択の根拠として用いる基
準の一つである。
b) ときには,代替標準測定方法の開発が必要であることが明らかになる。この方法の候補は,第一優先
の方法と同じぐらい精確であることが望ましい。この比較手順は,候補の測定方法が要求事項を満た
しているかを決めるのに役立つであろう。
c) ある試験室にとっては,測定する大部分の試料は同じ供給源から来る。これらの試料は一般的にほと
んど同じ組成を有している。この場合,国際標準測定方法を日常測定法として使用することは無益に
高価なものとなるかもしれない。このような試験室では,日常使用に,より簡便な方法を採用するこ
とが望ましいであろう。この方法は,既存の国際標準測定方法と同等の真度と精度をもった測定結果
をもたらすことが望ましい。
8.3
方法Bが代替標準測定方法の候補である(“標準測定方法”が未制定)
方法AとBの比較は,精度評価実験の結果に基づいて行わなければならない。方法Aが十分確立され
た標準測定方法である場合,方法Aの精度は比較の基準として用いることができる。方法A自体が標準測
定方法として開発中のものである場合,これも精度評価実験にかけるべきである。どちらの精度評価実験
も,JIS Z 8402-2に従って行わなければならない。
実験の目的は次の通りである。
a) 方法Bが方法Aと同じぐらいの精度があるかを求めること。実験結果は,方法Bと方法Aの精度の
尺度の比が規定値を超えるかについて検出できることが望ましい。
b) 同一試料を用いた両方法の精度評価実験での総平均の差が統計的に有意でないことを示すことによっ
て,又は認証標準物質を用いた方法Bの精度評価実験での総平均と認証値との差が統計的に有意でな
いことを示すことによって,方法Bの真度が方法Aの真度と同じであるかを求めること。加えて,2
つの方法の測定結果の期待値の差,又は各方法の測定結果の期待値と認証値の差が規定値を超えるか
について検出できることが望ましい。
8.4
精確さ評価実験
8.4.1
一般的な要求事項
精確さ評価実験は,JIS Z 8402-1に述べられている一般的な規定に従って行わなければならない。
両方の測定方法の手順は,参加試験室の誤解を避けるために,十分詳細に文書化されていなければなら
ない。評価実験の間,手順には何の変更も許されない。
その測定方法のユーザーとなる可能性のある試験室を母集団としたときに,参加試験室はその代表的な
サンプルでなければならない。
8.4.2
測定試料
測定方法の精度は,測定水準によって異なるのと同じように,測定試料のマトリックスの影響も受ける。
この場合,測定方法の精度の比較は同一試料を用いるときに最もうまく行われる。さらに,測定方法の真
39
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
度の比較は,同一試料を用いたときにのみ行うことができる。このため,各々の方法についての精確さ評
価実験を行う作業グループ間の連絡は,一人の共通の実施責任者を通じて行わなければならない。
測定試料の最も重要な要求事項は,均一であることである。すなわち,各試験室は同一試料を用いなけ
ればならない。測定試料内が不均一であると疑われる場合,測定用の試験片を採取する方法についての明
確な指図が手順書に記載されていなければならない。測定試料として,標準物質を用いると都合がよいこ
とがある。標準物質の均一性は保証されており,その測定方法で得られた結果は,標準物質の認証値と比
較することにより,かたよりとして考察できる。一般に標準物質が高価なことが欠点である。しかし多く
の場合には,標準物質の単位量を再分割することで解決される。測定試料として標準物質を用いる手順に
ついては,JIS Q 0033を参照せよ。
8.4.3
測定試料の数
使用する測定試料の数は,問題としている特性の測定水準の範囲,及び正確さの測定水準に対する依存
性によって異なる。多くの場合には,測定試料の数は,それに伴う作業量と必要な測定水準において利用
できる測定試料の量によって制限される。
8.4.4
試験室の数と測定回数
8.4.4.1
一般
二つの方法の試験室間共同実験の実施に必要な試験室の数と試験室あたりの測定回数は:
a) 二つの方法の精度;
b) 二つの方法の精度間の検出可能な比,ρ又はφ;これは二つの方法を用いた実験の結果から,実験者が
高い確率で検出したいと望んでいる精度の比の最小値であり,その精度が併行標準偏差で表される場
合の比をρで,その精度が室間平均平方の平方根で表される場合の比をφで表す;
c) 二つの方法間の検出可能なかたよりの差,λ;これは二つの方法で得られた結果の期待値間の差の最
小値である;
に依存する。
精度の推定値の比較に有意水準α=0.05を用いること,及び設定した標準偏差間の最小比,又はかたよ
り間の最小差を検出できない危険を,β=0.05とすることを推奨する。
これらのαとβの値によって,次式を検出可能な差に対して用いることができる。
λ=
B
B
2B
2LB
A
A
2A
2LA
/)
/
(
/)
/
(
4
p
n
p
n
r
r
σ
σ
σ
σ
+
+
+
····························· (13)
ここで,添え字のAとBは,それぞれ方法A及び方法Bを示す。
ほとんどの場合,方法Bの精度は未知である。この場合には方法Aの精度を代用として用いると,
λ=
B
B
2A
2LA
A
A
2A
2LA
/)
/
(
/)
/
(
4
p
n
p
n
r
r
σ
σ
σ
σ
+
+
+
···························· (14)
となる。
実験者は,式(13)や式(14)により,十分満足できる値が得られるまで,nA,nB,pA,pBの値を変えてみる
とよい。そのとき,精度の推定値を比較するのに適切な実験を行うために必要となるこれらのパラメータ
の値について,よく検討することが望ましい。
表14は,与えられたαとβの下での標準偏差の最小比を,自由度νAとνBの関数として示している。
併行標準偏差については
νA=pA (nA−1) 及びνB=pB (nB−1)
であり,室間平均平方については
40
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
νA=pA−1及びνB=pB−1
である。片方の方法の精度が十分に確立されている場合には,その自由度として表14では200を用いよ。
8.4.4.2
例:鉄鉱石中の鉄の定量
8.4.4.2.1
背景
鉄鉱石中の総鉄含量を定量するための2つの分析方法を詳細に調査する。これらは以下の通り同一精度
を有するものと仮定する。
σrA=σrB=0.1%Fe
σLA=σLB=0.2%Fe
8.4.4.2.2
要求事項
λ=0.4%Fe
ρ=φ=4
二つの方法の試験室間共同実験の実施に必要な試験室の最小数を,試験室数が同じで2回分析するとい
う仮定で計算する。すなわち,
pA=pB及びnA=nB=2
とする。
a) 真度の要求事項は:
0.4=4
B
A
p
p
/)2/
2.0
2.0(
/)2/
1.0
2.0(
2
2
2
2
+
+
+
である。よって
pA=pB=9
である。
b) 精度の要求事項は:
表14から,νA=νB=9によって,ρ=4又はφ=4となることが判る。
併行標準偏差の比較では,νA=pA及びνB=pBであるから,pA=pB=9である。
室間平均平方の比較では,νA=pA−1及びνB=pB−1であるから,pA=pB=10である。
8.4.4.2.3
結論
試験室間共同実験の実施に必要な参加試験室の最小数はそれぞれ10である。
8.4.5
測定試料の分配
試験室間共同実験の実施責任者は,測定試料の取得,調製,及び分配についての最終的な責任を負わな
ければならない。試料が良好な状態で参加試験室に受領され,試料が相違ないことが明確に確認されるこ
とを保証するために,予防措置を講じなければならない。参加試験室が,例えば,乾燥物換算であれば,
試料を秤量前に105℃でx時間乾燥する,などのように,同じ原則に基づいて試料を分析するよう指図し
なければならない。
8.4.6
参加試験室
参加試験室は,コーディネータの指図を実行するための組織化について責任を持つ担当者を選任しなけ
ればならない。担当者は適格な分析者でなければならない(研究員や“最上の”オペレータのような)著
しく熟練したスタッフは,標準偏差の非現実的に低い推定値を得ることを防ぐために,避けることが望ま
しい。選任された担当者は,併行条件の下で必要な回数の測定を行わなければならない。試験室は,指定
された期限内に測定結果をコーディネータに報告する義務がある。

41
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表14 α=0.05,β=0.05のときのρ (νA, νB, α, β) またはφ (νA, νB, α, β) の値
νB
νA
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
50
200
6 5,82 5,40 5,10 4,88 4,72 4,58 4,47 4,38 4,31 4,24 4,19 4,14 4,09 4,06 4,02 3,89 3,65 3,47
7 5,40 4,99 4,71 4,50 4,34 4,21 4,10 4,01 3,94 3,88 3,82 3,78 3,74 3,70 3,67 3,54 3,30 3,13
8 5,10 4,71 4,43 4,23 4,07 3,94 3,84 3,76 3,68 3,62 3,57 3,52 3,48 3,45 3,41 3,29 3,06 2,89
9 4,88 4,50 4,23 4,03 3,87 3,75 3,65 3,56 3,49 3,43 3,38 3,33 3,29 3,26 3,23 3,11 2,88 2,71
10 4,72 4,34 4,07 3,87 3,72 3,59 3,50 3,41 3,34 3,28 3,23 3,19 3,15 3,11 3,08 2,96 2,73 2,57
11 4,58 4,21 3,94 3,75 3,59 3,47 3,38 3,29 3,22 3,16 3,11 3,07 3,03 2,99 2,96 2,85 2,62 2,45
12 4,47 4,10 3,84 3,65 3,50 3,38 3,28 3,20 3,13 3,07 3,02 2,97 2,93 2,90 2,87 2,75 2,52 2,36
13 4,38 4,01 3,76 3,56 3,41 3,29 3,20 3,12 3,05 2,99 2,94 2,89 2,85 2,82 2,79 2,67 2,44 2,28
14 4,31 3,94 3,68 3,49 3,34 3,22 3,13 3,05 2,98 2,92 2,87 2,83 2,79 2,75 2,72 2,60 2,38 2,21
15 4,24 3,88 3,62 3,43 3,28 3,16 3,07 2,99 2,92 2,86 2,81 2,77 2,73 2,69 2,66 2,55 2,32 2,15
16 4,19 3,82 3,57 3,38 3,23 3,11 3,02 2,94 2,87 2,81 2,76 2,72 2,68 2,64 2,61 2,50 2,27 2,10
17 4,14 3,78 3,52 3,33 3,19 3,07 2,97 2,89 2,83 2,77 2,72 2,67 2,63 2,60 2,57 2,45 2,22 2,05
18 4,09 3,74 3,48 3,29 3,15 3,03 2,93 2,85 2,79 2,73 2,68 2,63 2,60 2,56 2,53 2,41 2,18 2,01
19 4,06 3,70 3,45 3,26 3,11 2,99 2,90 2,82 2,75 2,69 2,64 2,60 2,56 2,53 2,50 2,38 2,15 1,98
20 4,02 3,67 3,41 3,23 3,08 2,96 2,87 2,79 2,72 2,66 2,61 2,57 2,53 2,50 2,46 2,35 2,12 1,95
25 3,89 3,54 3,29 3,11 2,96 2,85 2,75 2,67 2,60 2,55 2,50 2,45 2,41 2,38 2,35 2,23 2,00 1,82
50 3,65 3,30 3,06 2,88 2,73 2,62 2,52 2,44 2,38 2,32 2,27 2,22 2,18 2,15 2,12 2,00 1,75 1,56
200 3,47 3,13 2,89 2,71 2,57 2,45 2,36 2,28 2,21 2,15 2,10 2,05 2,01 1,98 1,95 1,82 1,56 1,32
備考
1. ρ=
rA
B
σ
σr;vA=pA(nA−1);vB=pB(nB−1)
2. φ=
+
+
2A
2LA
A
2B
2
B
r
r
LB
n
n
σ
σ
σ
σ
;vA=pA−1;vB=pB−1
8.4.7
測定結果の収集
各方法の共同実験のコーディネータは,妥当な期間内に全ての測定結果を収集する義務がある。
測定結果が物理的に常軌を逸していないかを綿密に検討することはコーディネータの責務である。説明
可能な物理的原因による測定結果は,他の測定結果と同じ分布には属さない。
8.4.8
測定結果の評価
測定結果は,適格な統計解析者によって,JIS Z 8402-2に述べられている手順により評価されなければ
ならない。各測定試料について,次の値が計算される。
srA
方法Aの併行標準偏差の推定値
srB
方法Bの併行標準偏差の推定値
sRA
方法Aの再現標準偏差の推定値
sRB
方法Bの再現標準偏差の推定値
yA
方法Aの総平均
yB
方法Bの総平均
8.4.9
方法Aと方法Bの結果の比較
試験室間共同実験の実施の結果は,各測定水準ごとに比較しなければならない。方法Bは,特性の低い
測定水準側では,より精度が高い及び/又はかたよりがあるが,特性値の高い測定水準側ではより精度が
低い及び/又はかたよりがないということ,又はその反対が起こりうる。
8.4.9.1
グラフによる表示
各測定水準における生データのグラフ表示は望ましい。ときには,精度及び/又はかたよりに関して,
二つの測定方法の結果の差が明白なため,それ以上の統計的評価が不要なことがある。
42
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
全ての測定水準の精度と総平均のグラフ表示も望ましい。
8.4.9.2
精度の比較
8.4.9.2.1
方法Aは確立された標準測定方法である。
方法Aの精度は十分確立されている。
a) 室内精度
B
B
)
1(2
2A
2B
)
(
r
r
r
rs
ν
ν
χ
σ
α
−
≦
ならば,方法Bの室内精度が方法Aほどよくないという証拠はない。
B
B
)
1(2
2A
2B
)
(
r
r
r
rs
ν
ν
χ
σ
α
−
>
ならば,方法Bの室内精度が方法Aより劣っていると言える。
χ2 (1−α) (νrB) は自由度νrBのχ2分布の (1−α) 分位点であり,
νrB=pB (nB−1)
である。
b) 全体の精度
LB
LB
)
1(
2
2A
B
2A
2B
B
2B
)
(
)
/1
1(
)
/1
1(
ν
ν
χ
σ
σ
α
−
≤
−
−
−
−
r
R
r
R
n
s
n
s
ならば,方法Bの平均平方が方法Aほどよくないという証拠はない。
LB
LB
)
1(
2
2A
B
2A
2B
B
2B
)
(
)
/1
1(
)
/1
1(
ν
ν
χ
σ
σ
α
−
>
−
−
−
−
r
R
r
R
n
s
n
s
ならば,方法Bの平均平方が方法Aの平均平方ほどよくないと言える。
χ2 (1−α) (νLB) は自由度νLBのχ2分布の (1−α) 分位点であり,
νLB=pB−1
である。
8.4.9.2.2
どちらの方法も新しい標準測定方法の候補である。
a) 室内精度
Fr=
2A
2B
r
r
s
s
について,
Fα/2 (νrA, νrB) ≦Fr≦F (1−α/2) (νrA, νrB)
ならば,両者の室内精度が異なるという証拠はない。
Fr<Fα/2 (νrA, νrB)
ならば,方法Bの室内精度が方法Aより優れていると言える。
Fr>F (1−α/2) (νrB, νrA)
ならば,方法Bの室内精度が方法Aより劣っていると言える。
Fα/2 (νrA, νrB) とF (1−α/2) (νrA, νrB) は分子の自由度νrAと分母の自由度νrBのF分布のα/2及び (1−α/2)
分位点であり,
νrA=pA (nA−1)
νrB=pB (nB−1)
である。
43
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 全体の精度
2A
A
2A
2B
B
2B
)
/1
1(
)
/1
1(
r
R
r
R
R
s
n
s
s
n
s
F
−
−
−
−
=
について,
Fα/2 (νRB, νRA) ≦FR≦F (1−α/2) (νRB, νRA)
ならば,両者の室間精度が異なるという証拠はない。
FR<Fα/2 (νRB, νRA)
ならば,方法Bの全体の精度が方法Aより優れていると言える。
FR>F (1−α/2) (νRB, νRA)
ならば,方法Bの全体の精度が方法Aより劣っていると言える。
Fα/2 (νRB, νRA) 及びF (1−α/2) (νRB, νRA) は,分子の自由度νRBと分母の自由度νRAのF分布のα/2及び (1
−α/2) 分位点であり,
νLA=pA−1
νLB=pB−1
である。
備考5. F分布の (1−α/2) 分位点しか示していない表が多い。この場合に,α/2分位点は,次の関係
を用いて求めることができる。
Fα/2 (νrB, νrA) =1/F (1−α/2) (νrA, νrB)
Fα/2 (νRB, νRA) =1/F (1−α/2) (νRA, νRB)
8.4.9.3
真度の比較
8.4.9.3.1
平均値と標準物質の認証値の比較
各方法の総平均は,測定試料の一つとして用いられた標準物質の認証値と比較することができる。次の
検定が用いられる。
a)
|μ−y|≦2[
]
B
2B
B
2B
/
)
/1
1(
p
s
n
s
r
R
−
−
ならば,その方法の結果の総平均と,認証値の差は統計的に有意でない。
b)
|μ−y|>2[
]B
2B
B
2B
)
/1
1(
p
s
n
s
r
R
−
−
ならば,その方法の結果の総平均と,認証値の差は統計的に有意である。
この場合,次の2つの可能性がある。
1) |μ−y|≦δm/2
ならば,その測定方法に,許容できないほどのかたよりがあるという証拠はない。
2) |μ−y|>δm/2
ならば,その測定方法には,許容できないほどのかたよりがあると言える。
ここで,δmは,実験者が実験結果から高い確率で検出しようと望んでいる,その方法の結果の期待値と
標準物質の認証値の差の最小値である。
8.4.9.3.2
方法Aと方法Bの平均値の比較
a)
s
y
y
B
A−
≦2.0
ならば,方法Aと方法Bの平均値の差は統計的に有意でない。
44
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b)
s
y
y
B
A−
>2.0
ならば,方法Aと方法Bの平均値の差は統計的に有意である。
ここで
s=
2B
2A
s
s+
sA2= [s2RA− (1−1/nA) s2rA] /PA
sB2= [s2RB− (1−1/nB) s2rB] /PB
である。
この場合,次の2つの可能性がある。
1) |yA−yB|≦λ/2
ならば,2つの方法のかたよりの差が許容できないという証拠はない。
2) |yA−yB|>λ/2
ならば,2つの方法のかたよりの差は許容できないと言える。
ここで,λは,かたより間の検出可能な差である。
8.5
方法Bは日常用の測定方法の候補である
8.5.1
パラメータ
試験室の日常用の測定方法において問題となるパラメータは,長期平均μt,併行条件下の精度(併行標
準偏差σrで表される),及び中間精度(時間を変えた中間標準偏差σI (T) で表される)である。
これらのパラメータを推定するために,試験室は,参加試験室を“時間”で置き換えた試験室内評価実
験を行わなければならない(JIS Z 8402-3参照)。この試験室内評価実験を説明するのに用いる数学モデル
は,試験室間評価実験に用いるモデルにおいて添え字LをTで(試験室を時間で)で置き換えたものと同
じである。この場合,時間を変えた変動は,装置の校正,異なる試薬,異なる分析者,部屋の環境状態な
どのような試験室でよく生じるいろいろな変化に起因する変動を含む。それゆえ,試験室内評価実験は,
これらの変化が通常起り得る期間を押さえていることが望ましい。精度を比較するための手順は,8.4.9.3
に述べられているものと同じである。
かたよりは,それぞれの測定方法で認証標準物質を測定することによって求められる。ここでμ,は標
準物質の認証値である。
8.5.2
長期かたより試験
長期間の平均値
∑∑
tB
B
p
1
i
n
1
j
tB
B
ij
p
n
y
y
==
=
を計算する。ここで,iとjはそれぞれ長期(中間精度)及び短期(併行条件)測定に関する添え字であ
る。
a) |y−μt|≦2
tB
B
2B
2tB
/
n
p
s
s
r
+
ならば,長期平均と認証値の差は統計的に有意でない。
45
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) |y−μt|>2
tB
B
2B
2tB
/
n
p
s
s
r
+
ならば,長期平均と認証値の差は統計的に有意である。
この場合,次の2つの可能性がある。
1) |y−μt|≦δm/2
ならば,その方法の長期かたよりが許容できないという証拠はない。
2) |y−μt|>δm/2
ならば,その方法の長期かたよりが許容できないと言える。
ここで,δmは,実験者が事前に設定した検出可能な長期の差である。
46
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) JIS Z 8402で用いられる記号
a
関係式s=a+bmの切片
A
推定値の不確かさを計算するのに用いる係数
b
関係式s=a+bmの勾配
B
全平均と試験室の測定値の偏差を表す
成分(かたよりに占める試験室成分)
B0
Bの成分の中で中間精度条件の下では
変わらない,すべての要因
B (1), B (2),
など
Bの成分の中で中間精度条件で変化す
る要因
c
関係式logs=c+dlogmの切片
C, C', C''
検定統計量
Ccrit ,C′crit ,C''crit
統計的検定の棄却限界値
CDp
確率Pの許容差
CRp
確率Pの許容範囲
d
関係式logs=c+dlogmの勾配
e
測定値の成分中,すべての測定値に生
じている偶然誤差
f
許容範囲の係数
Fp (ν1,ν2)
分子の自由度ν1, 分母の自由度ν2のF分
布のp分位点
G
グラッブスの検定統計量
h
マンデルの試験室間一致性の検定統計量
k
マンデルの試験室内一致性の検定統計量
LCL
下側管理限界(処置限界または警戒限界)
m
試験特性の一般平均;水準
M
中間精度条件において考慮される因子の数
N
反復数
n
一つの試験室で一つの水準(すなわち,
セルごと)で得る測定値の数
p
共同実験に参加した試験室数
P
確率
q
共同実験における試験特性の水準数
r
併行精度限界値(許容差)
R
再現精度限界値(許容差)
RM
標準物質
s
標準偏差の推定値
sˆ
標準偏差の予測値
T
ある表示の総和
t
試験対象または群の数
UCL
上側管理限界(処置限界または警戒限界)
W
重み付き回帰式の計算で用いられる重み係数
w
一組の測定値の範囲
x
グラッブス検定に用いられるデータ
y
測定値
y
測定値の算術平均
y
測定値の全平均
α
有意水準
β
第二種の過誤の確率
γ
再現標準偏差と併行標準偏差の比 (σR/σr)
∆
試験室のかたより
Δˆ
⊿の推定値
δ
測定方法のかたより
δˆ
δの推定値
λ
二つの試験室または二つの測定方法間
のかたよりの検出可能な差
μ
試験特性の真値または参照値
ν
自由度
ρ
方法AとBの併行標準偏差間の検出可能な比
σ
標準偏差の真の値
τ
最終校正からの時間経緯に起因する変
動を表す測定値の成分
φ
方法AとBの試験室間平均平方の平方
根の検出可能な比
χ2p (ν)
自由度νのχ2分布におけるp分位点
添え字に用いる記号
C
校正法が異なることを示す
E
装置が異なることを示す
i
特定の試験室を示す添え字
I ( )
中間精度に関する添え字,かっこ内に
中間精度条件のタイプの識別子を記述
する
47
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
j
特定の水準に関する添え字 (JIS Z
8402-2) 分析の一群あるいは要因に関
する添え字 (JIS Z 8402-3)
k
試験室iにおける水準jのk番目の測定
値を示す添え字
L
試験室間を示す
m
検出可能なかたよりに関する添え字
M
試験試料間を示す
O
オペレーターが異なっていることを示す
P
確率
r
併行精度
R
再現精度
T
時間が異なることを示す
W
試験室内を示す
1, 2, 3…
測定値の得られた順序を示す
(1), (2), (3), … 測定値の大きさの順序を示す
48
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
規格原案作成委員会 構成表
氏名
所属
(委員長)
石 川 馨
東京大学
(幹事)
宮 津 隆
日本鋼管株式会社
岩 田 晶 夫
住友金属鉱山株式会社
内 沼 一 雄
日本石油株式会社
藤 森 利 美
東京大学
(委員)
石 井 清 次
工業技術院
神 森 大 彦
社団法人日本化学会
上 甲 子 郎
東京理科大学
横 山 毅
昭和電工株式会社
高 橋 梅太郎
海外貨物検査株式会社
窪 田 孝 昌
海外貨物検査株式会社
(事務局)
新 井 紀 弘
財団法人日本科学技術連盟
規格改正原案作成委員会 構成表
氏名
所属
(委員長)
宮 津 隆
西東京科学大学理工学部
(委員)
尾 島 善 一
東京理科大学理工学部
故 高 橋 梅太郎
元海外貨物検査株式会社
椿 広 計
慶應義塾大学理工学部
仁 科 健
名古屋工業大学工学部
西 島 保
東燃株式会社総合研究所
野 村 和 夫
東京ガス株式会社
番 場 章
三石テクノ株式会社
多 田 格 三
元株式会社東芝
藤 森 利 美
長崎大学経済学部
横 山 隆 壽
財団法人電力中央研究所狛江研究所
池 田 要
工業技術院標準部材料規格課
川 村 正 信
財団法人日本規格協会
黒 木 勝 也
財団法人日本規格協会
(事務局)
橋 本 進
財団法人日本規格協会
49
Z 8402-6 : 1999 (ISO 5725-6 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
品質管理分野国際整合化分科会
氏名
所属
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
○ 今 井 秀 孝
工業技術院計量研究所
○ 柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
日本電信電話株式会社
門 山 允
東京国際大学
○ 鹿 庭 なほ子
国立食品医薬品衛生研究所
兼 子 毅
武蔵工業大学工学部
○ 城 道 修
メルシャン株式会社
○ 椿 広 計
筑波大学社会工学系
○ 仁 科 健
名古屋工業大学工学部
野 澤 昌 弘
東京理科大学経営学部
三佐尾 武 雄
QCコンサルタント
○ 宮 津 隆
帝京科学大学理工学部
山 田 秀
東京都立科学技術大学工学部
横 尾 恒 雄
QCコンサルタント
大 嶋 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会
備考 ○印は許容差JIS原案作成WGの委員を兼ねる。