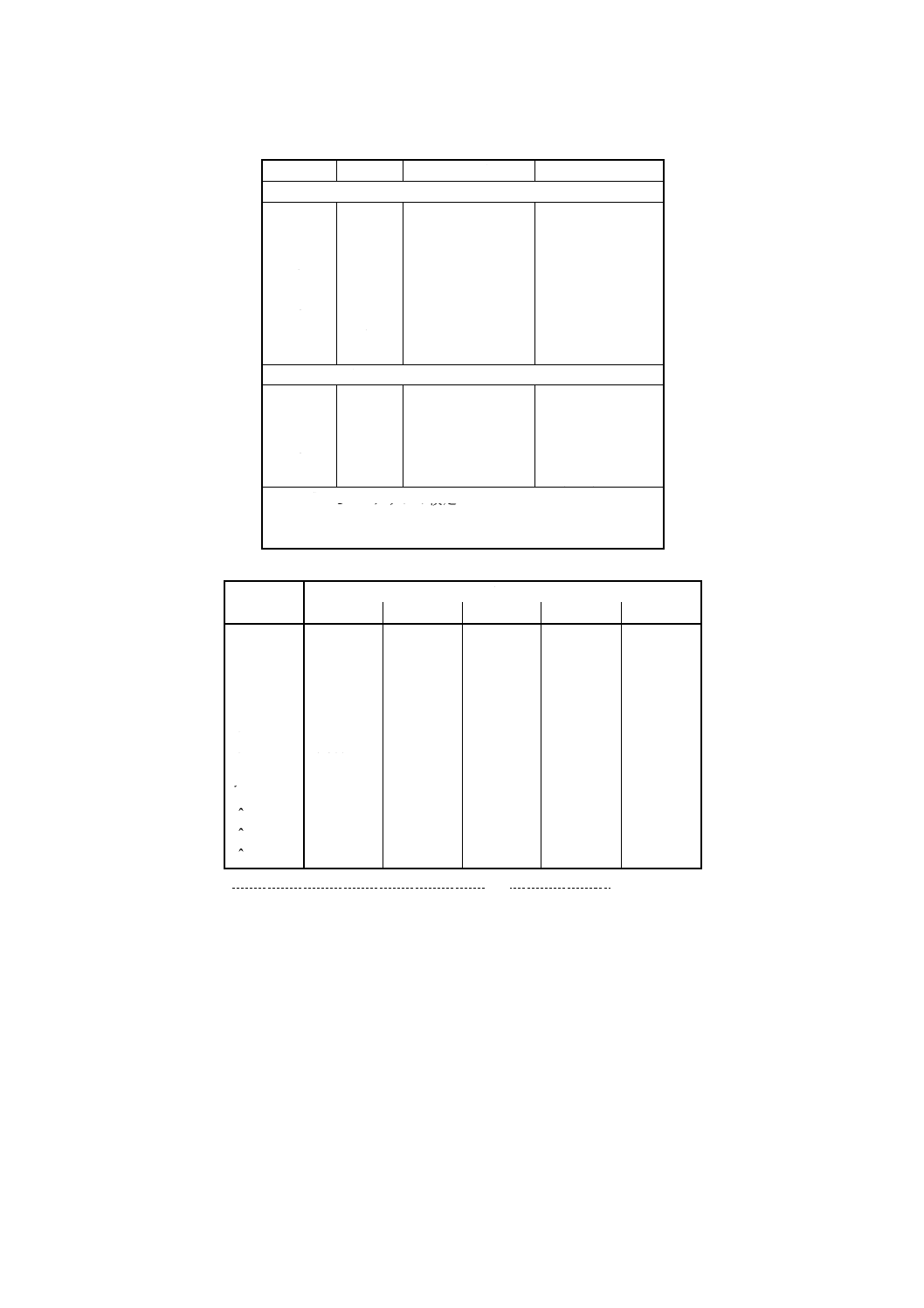(ISO 5725-4 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 8402 : 1991は廃止され,この規格に置き換えられる。
今回の制定では,1994年に第1版として発行されたISO 5725-4を基礎として用いた。
JIS Z 8402-4には,次に示す附属書がある。
附属書A(規定) JIS Z 8402で用いられる記号
附属書B(参考) 精確さ評価実験の例
附属書C(参考) 式の導出
附属書D(参考) 参考文献
JIS Z 8402 : 1999は,一般名称を“測定方法及び測定結果の精確さ(真度及び精度)”として,次の部に
よって構成される。
第1部: 一般的な原理及び定義
(Part 1 : General principles and definitions)
第2部: 標準測定方法の併行精度及び再現精度を求めるための基本的方法
(Part 2 : Basic method for the determination of repeatability and reproducibility of a standard
measurement method)
第3部: 標準測定方法の中間精度
(Part 3 : Intermediate measures of the precision of a standard measurement method)
第4部: 標準測定方法の真度を求めるための基本的方法
(Part 4 : Basic methods for the determination of the trueness of a standard measurement method)
第5部: 標準測定方法の精度を求めるための代替法
(Part 5 : Alternative methods for the determination of the precision of a standard measurement
method)
第6部: 精確さに関する値の実用的な使い方
(Part 6 : Use in practice of accuracy values)
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 2
2. 引用規格 ························································································································ 2
3. 定義 ······························································································································ 3
4. 共同実験による標準測定方法のかたよりの求め方 ·································································· 3
4.1 統計モデル ··················································································································· 3
4.2 標準物質に対する要求事項······························································································· 3
4.3 測定方法のかたよりの推定に際しての実験計画上の検討事項 ·················································· 4
4.4 JIS Z 8402-1,JIS Z 8402-2との相互参照 ·············································································· 4
4.5 必要な試験室数 ············································································································· 4
4.6 統計的評価 ··················································································································· 5
4.7 統計的評価の結果の解釈·································································································· 5
5. 標準測定方法による,一つの試験室の試験室かたよりの求め方 ················································ 7
5.1 実験の遂行 ··················································································································· 7
5.2 JIS Z 8402-1,JIS Z 8402-2との相互参照 ·············································································· 7
5.3 測定結果の数 ················································································································ 7
5.4 標準物質の選択 ············································································································· 8
5.5 統計的解析 ··················································································································· 8
6. パネルへの報告書とパネルによる決定事項 ··········································································· 9
6.1 統計解析者による報告書·································································································· 9
6.2 パネルによる決定事項····································································································· 9
7. 真度の値の利用 ··············································································································· 9
附属書A(規定) JIS Z 8402で用いられる記号 ········································································ 10
附属書B(参考) 精確さ評価実験の例 ··················································································· 13
B.1 実験の概要 ·················································································································· 13
B.2 精度の評価 ·················································································································· 13
B.3 真度の評価 ·················································································································· 14
B.4 更なる解析 ·················································································································· 14
附属書C(参考) 式の導出·································································································· 23
附属書D(参考) 参考文献 ································································································· 25
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8402-4 : 1999
(ISO 5725-4 : 1994)
測定方法及び測定結果の
精確さ(真度及び精度)−
第4部:標準測定方法の真度を求めるための基本的
方法
Accuracy (trueness and precision) of measurement methods and results−
Part 4 : Basic methods for the determination of the trueness
of a standard measurement method
序文 この規格は,1994年に第1版として発行されたISO 5725-4, Accuracy (trueness and precision) of
measurement methods and results−Part 4 : Basic methods for the determination of the trueness of a standard
measurement methodを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規格で
ある。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
0.1
この規格では,測定方法の精確さを表すために“真度”と“精度”の二つの用語を用いている。“真
度”は,多数の測定結果の平均値と,真の値又は参照値との一致の程度を示すものである。“精度”は,測
定結果の間の一致の程度を示すものである。
0.2
これらの量の一般的な考察はこの規格の第1部で示されており,この部では改めて記述しない。第1
部は基本的な定義と一般的な原理が示されているので,この部を含めて,他の部についても,第1部を合
わせて読まれることが望ましい。
0.3
測定方法の“真度”は,測定される特性についての真の値を考えることが可能なときには重要であ
る。測定方法によっては,真の値を厳密には知ることができなくても,測定される特性の参照値を得るこ
とができるかも知れない。例えば,適切な標準物質が得られる場合,又は他の測定方法との照合,もしく
は値が既知の試料を調製することによって参照値が確定できる場合である。測定方法の真度は,参照値と,
その測定によって得られる結果の測定水準とを比較することによって検討できる。真度は一般にかたより
の形で表現される。例えば,化学分析においては,測定方法が成分の全量を抽出できない場合,又は一つ
の成分が他の成分の定量を妨害する場合にかたよりが生じる。
0.4
真度では2つの尺度が重要であり,この規格のこの部ではその両方を共に考慮する。
a) 測定方法のかたより:測定方法によるかたよりが生じる場合,すなわち,いつ,どこで測定を行って
も同じかたよりが生じる可能性がある場合の,“測定方法のかたより(JIS Z 8402-1で定義)”の検討
が対象である。この検討には,JIS Z 8402-2に記述したように,多くの試験室が参加する大規模な実
験が必要となる。
2
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 試験室のかたより:単一試験室内の測定に“試験室のかたより(JIS Z 8402-1で定義)”が現れること
がある。試験室のかたよりを推定する実験の計画が提案された場合には,その推定値は実験を行った
ときにのみ有効であるということを認識すべきである。試験室のかたよりが変動していないことを示
すには,更に定期的な試験が必要である。このために,JIS Z 8402-6に記述されている方法を用いる
ことができる。
1. 適用範囲
1.1
この規格のこの部は,測定方法を適用する際に,測定方法のかたよりと試験室のかたよりを推定す
る基本的な方法を提供する。
1.2
ここでは,計量値の測定値が求められ,測定結果として一個の値が得られるような測定方法だけを
対象とする。この一個の値は一組の観測値から計算によって求められたものであってもよい。
1.3
同じように測定を行うために,測定方法が標準化されていることが重要である。その標準化された
方法によって全ての測定を実施する。
1.4
かたよりの値は,測定方法が正しい(真の)結果を与える能力の定量的推定値である。測定方法の
かたよりの値が,この方法で得られた測定結果と共に引用された場合には,かたよりの値もその測定結果
も同一の特性であり,全く同一の状況で測定されたことが想定される。
1.5
この規格のこの部は,参照値が,合意値(取り決めによる真の値)として確立し得る場合にのみ適
用可能である。例えば,測定標準や適切な標準物質によって,又は標準とされる測定方法 (reference
measurement method) を用いた測定結果を参照することによって,あるいは値が既知の試料を調製すること
によって,合意値が確立する場合である。
標準物質には,以下のようなものが上げられる:
a) 認証標準物質
b) 実験の目的のために既知の特性値を持つように作られた試料
c) かたよりが無視できるほど小さいことが知られている他の測定方法による測定で特性値が確定してい
る試料
1.6
この規格のこの部では,一度に一つの測定水準でかたよりを推定すれば十分な場合のみを考察する。
この部は,ある特性の測定のかたよりが,別の特性の測定水準の違いによって影響されるというような場
合には適用できない(すなわち,干渉は考えない)。2つの測定方法の真度の比較は,JIS Z 8402-6で検討
する。
備考1. この規格のこの部では,かたよりは,一度に一つの測定水準に対してのみ考えるので,測定
水準に対する添え字jは一貫して省くこととする。
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発効年を付記してあるものは,記載の年の版だけがこの規格の規定を構
成するものであって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その
最新版(追補を含む。)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部 確率及び一般統計用語
JIS Z 8101-2 統計−用語と記号−第2部 統計的品質管理用語
JIS Z 8402-1 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第1部 一般的な原理及び定
義
3
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Z 8402-2 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第2部 標準測定方法の併行
精度及び再現精度を求めるための基本的方法
3. 定義
この規格の目的に合わせ,JIS Z 8101とJIS Z 8402-1において定義された用語を用いる。
この規格で用いる記号を附属書Aに示す。
4. 共同実験による標準測定方法のかたよりの求め方
4.1
統計モデル
JIS Z 8402-1 : 1999の5.1の基本モデルにおいて,一般平均mを次のように置き換える。
m=μ+δ ·················································································· (1)
ただし,
μ: 測定された特性の参照値
δ: 測定方法のかたより。
モデルは次のようになる。
y=μ+δ+B+e ·········································································· (2)
式(2)は,δに興味のあるときに用いられる。ここで,Bはかたよりの試験室成分,すなわち,試験室間
変動を表現する測定結果の成分である。
試験室のかたより∆は,
∆=δ+B ·················································································· (3)
と与えられ,モデルは次のように書くこともできる。
y=μ+∆+e ·············································································· (4)
式(4)は,∆に興味があるときに用いる。
4.2
標準物質に対する要求事項
標準物質を用いる場合には,4.2.1と4.2.2に与えられた要求事項が満たされなければならない。標準物
質は均一でなくてはならない。
4.2.1
標準物質の選択
4.2.1.1
標準測定方法の適用を意図した,適切な測定水準で,標準物質の特性値(例えば濃度)は既知で
なければならない。標準測定方法のかたよりが,測定水準によって異なる場合もあるので,評価実験で,
特性値の複数の測定水準に対応する一連の標準物質を用いることが重要な場合もある。標準物質のマトリ
ックスは,標準測定方法の対象となる試料のマトリックス(例えば,石炭中の炭素,鉄鋼中の炭素)と可
能な限り類似したものを使うのが望ましい。
4.2.1.2
標準物質の量は,必要と考えられる場合には,若干の予備を含めた上で,全実験プログラムにと
って十分な量でなければならない。
4.2.1.3
可能な限り,標準物質は実験を通じて安定した特性をもっていることが望ましい。次に上げる3
つの場合がある。
a) 特性は安定している:事前の注意は不要。
b) 特性の認証値が保管状態によって影響されることがある:容器を開く前及び後では,容器の保管は,
認証文書に記載された方法で行うことが望ましい。
c) 特性が既知の率で変化する:特定の時間に対応する特性値を定義した参照値が与えられた認証文書が
4
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ある。
4.2.1.4
標準物質の不確かさによって表示される,認証値と真の値との起こり得る差異(JIS Q 0035参照)
は,ここで与える方法では考慮していない。
4.2.2
標準物質のチェックと配布
試料の配布に先立って,標準物質の単位を分割する場合,何らかの誤差が付随しないように注意深く行
わなければならない。試料分割に関する国際規格を参考にすることが望ましい。分配のための単位は,ラ
ンダムな選択によることが望ましい。測定プロセスが非破壊的ならば,共同実験のすべての試験室に同じ
標準物質を順に使用させることが可能であるが,こうすると実験の期間は長引くであろう。
4.3
測定方法のかたよりの推定に際しての実験計画上の検討事項
4.3.1
実験の目的は,測定方法のかたよりの大きさを推定すること,及び,この大きさが統計的に有意か
否かを判定することである。もし,かたよりが統計的に有意でないと分かれば,目的は,ある確率でこの
実験結果からは検出されない最大のかたよりの大きさを決定することとなる。
4.3.2
実験の計画は,JIS Z 8402-2 : 1999の4.1に示した精度評価実験の場合とほとんど同じである。相
違点は,
a) 参照値を用いるための付加的な要求事項があることと,
b) 参加試験室数及び,測定結果の数が4.5に示す要求事項を満たさなくてはならないこと
である。
4.4
JIS Z 8402-1,JIS Z 8402-2との相互参照
JIS Z 8402-1 : 1999の6.,JIS Z 8402-2の5.及び6.を適用する。この第4部に関連して第1部,第2部を
読む際には,“精度”または“併行精度と再現精度”のところに必要に応じて“真度”を挿入することが望
ましい。
4.5
必要な試験室数
試験室数及び各測定水準毎で必要な測定結果の数は互いに関連する。試験室の数については,JIS Z
8402-1 : 1999の6.3で論じられている。その数を決める指針を次に示す。
事前に定めたかたよりの大きさを,高い確率で(附属書C参照)検出することができる実験結果を得る
ためには,試験室数の最小値p,及び,測定結果の数nは,次の式を満たさなければならない。
84
.1
m
δ
σ≦
R
A
·············································································· (5)
ここで,
δmは,実験者が測定結果から検出したい事前に定めたかたよりの大
きさ,
σRは,測定方法の再現標準偏差,
で,Aはpとnの関数であり,次式で与えられる。
(
)
pn
n
A
2
2
1
1
96
.1
γ
γ
+
−
=
································································· (6)
ここで,
γ=σR/σr ··················································································· (7)
である。Aの値を表1に示す。
理想的には,試験室数と一試験室当たりの測定結果の繰り返し数は,事前に実験者がδmの値を定めた上
で,式(5)に記述された条件を満たすことが望ましい。しかしながら,現実的な理由によって,通常,試験
5
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
室数の選択は,資源の利用可能性とδmの値を満足な程度まで減少したいという希望との間の妥協点となる。
測定方法の再現性が乏しければ,かたよりの推定を高い確かさをもって達成することはできないであろう。
σRがσrより大きい(すなわち,γが1より大きい)ことはよくあるが,このときは1試験室1測定水準当
たりn=2より多くの測定結果を測定しても,得るものはほとんどない。
表1 測定方法のかたよりの推定値の不確かさを示す数値
p
γ=1
γ=2
γ=5
n=2 n=3 n=4 n=2 n=3 n=4 n=2 n=3 n=4
5 0,62 0,51 0,44 0,82 0,80 0,79 0,87 0,86 0,86
10 0,44 0,36 0,31 0,58 0,57 0,56 0,61 0,61 0,61
15 0,36 0,29 0,25 0,47 0,46 0,46 0,50 0,50 0,50
20 0,31 0,25 0,22 0,41 0,40 0,40 0,43 0,43 0,43
25 0,28 0,23 0,20 0,37 0,36 0,35 0,39 0,39 0,39
30 0,25 0,21 0,18 0,33 0,33 0,32 0,35 0,35 0,35
35 0,23 0,19 0,17 0,31 0,30 0,30 0,33 0,33 0,33
40 0,22 0,18 0,15 0,29 0,28 0,28 0,31 0,31 0,31
参考 表の中では小数点としてコンマ (, ) を用いている。
4.6
統計的評価
測定結果はJIS Z 8402-2に記されているように扱わなければならない。特に,外れ値が検出された場合
には,なぜそのような値が得られたのかを検討するために,参照値の適切さの見直しを含め,必要なすべ
ての手続きが実行されなければならない。
4.7
統計的評価の結果の解釈
4.7.1
精度のチェック
測定方法の精度は,sr(併行標準偏差の推定値)とsR(再現標準偏差の推定値)で表現される。式(8)〜
(10)では,各試験室ごとの測定結果の数 (n) が等しいことを仮定している。これが成立しない場合は,JIS
Z 8402-2に与えた対応する式を用いて,srとsRを算出するのがよい。
4.7.1.1
p試験室が参加した場合の併行分散の推定値sr2は,次のように計算される。
∑
=
p
i
i
r
s
p
s
1
2
2
1
=
··········································································· (8)
(
)
∑
=
−
−
n
k
i
ik
i
y
y
n
s
1
2
2
1
1
=
······························································ (9)
∑
=
n
k
ik
i
y
n
y
1
1
=
··········································································· (10)
ここで,si2,iyは,それぞれ,第i試験室で得られたn個の測定結果yikの分散
及び平均である。
試験室内分散に有意な差がないことを示すために,分散si2に対してJIS Z 8402-2に記載したコクランの
検定を適用しなくてはならない。外れ値の可能性をより徹底的に検討するために,JIS Z 8402-2に記載し
たマンデルのhプロット,kプロットも描かれることが望ましい。
標準測定方法の併行標準偏差がJIS Z 8402-2に準拠して事前に求められていないときには,srは,その
最良推定値と考えることができる。JIS Z 8402-2に準拠して,標準測定方法の併行標準偏差σrが求められ
6
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ていた場合には,sr2は,比
C=sr2/σr2 ················································································(11)
を計算して評価できる。検定統計量Cは,棄却限界値
Ccrit=χ2 (1−α) (v) /v
と比較される。ただし,χ2 (1−α) (v) は自由度v [=p−1)] のχ2分布の (1−α) 分位点である。特に断らない
限りαは0.05と仮定する。
a) C≦Ccritならば,sr2はσr2より有意には大きくない。
b) C>Ccritならば,sr2はσr2より有意に大きい。
前者の場合,併行標準偏差σrは測定方法のかたよりの評価に用いられる。後者の場合に,不一致の原因
を調べ,次の段階に進む前に可能ならば実験を繰り返すことが必要である。
4.7.1.2
p試験室が参加した場合の再現分散の推定値sR2は,次のように計算される。
2
2
1
2
1
1
1
1
r
p
i
i
R
s
n
y
y
p
s
−
+
−
−∑
=
=
············································ (12)
ここで,
∑
=
p
i
iy
p
y
1
1
=
············································································ (13)
である。
標準測定方法の再現標準偏差がJIS Z 8402-2に準拠して事前に求められていない場合,sRは,その最良
推定値と考えられよう。JIS Z 8402-2に準拠して再現標準偏差σR及び,併行標準偏差σrが決められている
場合には,sRは次の比を計算することで間接的に評価できる。
(
)
(
)
2
2
2
2
/1
1
/1
1
r
R
r
R
n
s
n
s
C
σ
σ
−
−
−
−
′=
····························································· (14)
検定統計量Cʼは棄却限界値
Cʼcrit=χ2 (1−α) (v) / v
と比較される。ただし,χ2 (1−α) (v) は自由度v [=p (n−1)] のχ2分布の (1−α) 分位点である。特に断らな
い限りαは0.05と仮定する。
a) Cʼ≦Cʼcritならば,sR2− (1−1/n) sr2は,σR2− (1−1/n) σr2より有意には大きくない。
b) Cʼ>Cʼcritならば,sR2− (1−1/n) sr2はσR2− (1−1/n) σr2より有意に大きい。
前者の場合,併行標準偏差σr及び再現標準偏差σRが測定方法の真度を評価するのに用いられる。後者の
場合,標準測定方法のかたよりの評価に先立って各試験室の測定状況の注意深い精査を行わなければなら
ない。ある試験室が要求されている装置を使わなかった場合もあれば,指定された条件に従わずに測定し
た場合もある。化学分析では,十分な管理がなされてないことによって,例えば,温度,湿度,不純物の
存在といった管理上の問題が生じる場合もある。結果として,期待される精度が実現するまで,実験を繰
り返さなければならないこともある。
4.7.2
標準測定方法のかたよりの推定
評価実験に参加した試験室によるかたよりの推定値は
μ
=−
y
δˆ
················································································ (15)
7
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
で与えられる。ただし,δˆは,正にも負にもなり得る。推定されたかたよりの絶対値がJIS Q 0035で定義
された不確かさの区間の幅の半分以下ならば,かたよりの証拠はない。
測定方法のかたよりの推定値の変動は,測定プロセスの結果として生じる変動に起因する。また,その
変動は,次のように計算される標準偏差によって次のように表現される。精度の値が既知の場合には,
(
)
p
n
r
R
2
2
ˆ
/1
1
σ
σ
σδ
−
−
=
·························································· (16)
精度の値が未知の場合には,
(
)
p
s
n
s
s
r
R
2
2
ˆ
/1
1−
−
=
δ
···························································· (17)
となる。
測定方法のかたよりの近似95%信頼区間は次のように計算することができる。
δˆ=AσR≦δ≦δˆ+AσR ······························································· (18)
ただし,Aは式(6)で与えられている。σRが未知の場合には,その推定値sRを代わりに用いなければならな
い。また,Aは,γ=sR/srを用いて計算しなくてはならない。
この信頼区間が0を含むならば,測定方法のかたよりは有意水準5%で有意ではないこととなり,0を含
まないならば有意ということになる。
5. 標準測定方法による,一つの試験室の試験室かたよりの求め方
以下で述べるように,試験室のかたよりを推定するために一つの試験室内で実験が行われることがある。
ここで,JIS Z 8402-2に準拠した精度評価実験によって,方法の併行標準偏差は確定しているものとする。
5.1
実験の遂行
実験は標準化された測定方法に厳密に従って行われなければならないし,測定は併行条件の下で行われ
なければならない。真度評価実施に先立って,当該試験室によって適用された標準測定方法の精度チェッ
クがなされていなければならない。このことは,標準測定方法の試験室内標準偏差と,公表されている併
行標準偏差とを比較することを意味する。
実験の計画は,JIS Z 8402-2に記述された精度評価実験において一つの試験室に要求された測定から構
成される。単一試験室に限定されている点を除いて,本質的な相違は参照値を用いることだけである。
試験室のかたよりを測ろうと試みる際,多くの労力をそのような実験に注ぐのは意味のない場合もある。
おそらく,定期的にJIS Z 8402-6に記述されたチェックを行う方が良いであろう。測定方法の併行精度が
良くなければ,試験室のかたよりの推定値が高い確かさを達成することは現実にはない。
5.2
JIS Z 8402-1,JIS Z 8402-2との相互参照
この第4部の内容に関連してJIS Z 8402-1及びJIS Z 8402-2を読む際には,“精度”または“併行精度及
び再現精度”のところに必要に応じて“真度”を挿入することが望ましい。JIS Z 8402-2における試験室
数はp=1となる。また,一人の人間が“実施責任者”と“監督者”の役割を兼ねるのが便利かもしれない。
5.3
測定結果の数
試験室のかたよりの推定値の不確かさは測定方法の併行精度と得られた測定結果の数に依存している。
実験結果によって,事前に設定したかたよりの大きさを高い確率(附属書C参照)で検出することを可能
にするためには,次の式が満たされなければならない。
8
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
84
.1
m
w
⊿
≦
r
Aσ
··········································································· (19)
ここで,
∆mは,実験者が事前に設定する実験結果から検出したい試験室のか
たよりの大きさ,
σrは,測定方法の併行標準偏差であり,
n
A
96
.1
w=
·············································································· (20)
である。
5.4
標準物質の選択
標準物質を用いる場合には,ここでも4.2.1に記述した要求事項が適用される。
5.5
統計的解析
5.5.1
試験室内標準偏差のチェック
n個の測定結果の平均値
wyと試験室内標準偏差σwの推定値swは次のように計算される。
∑
=
n
k
k
y
n
y
1
w
1
=
·········································································· (21)
(
)
∑
=
−
−
n
k
k
y
y
n
s
1
2
w
w
1
1
=
·························································· (22)
測定結果は,JIS Z 8402-2 : 1999の7.3.4に示されたグラッブズ検定により,外れ値が吟味されなければ
ならない。
標準測定方法の併行標準偏差σrが既知の場合には,swは,比
C”= (Sw/σr) 2 ········································································· (23)
を計算して評価できる。C”の値は,棄却限界値
C”crit=χ2 (1−α) (v) /v
と比較される。ただし,χ2 (1−α) (v) は自由度v= [=n−1] のχ2分布の (1−α) 分位点である。特に断らな
い限りαは0.05と仮定する。
a) C”≦C”critならば,swはσrより有意には大きくない。
b) C”>C”critならば,swはσrより有意に大きい。
前者の場合,併行標準偏差σrは試験室のかたよりの評価に用いられる。
後者の場合には,実験を繰り返して,全段階で標準測定方法が正しく行われていることを検証するかど
うかを,検討するのがよい。
5.5.2
試験室のかたよりの推定
試験室のかたより∆の推定値∆ˆは,次式で与えられる。
μ
=
−
∆
w
ˆ
y
·············································································· (24)
試験室のかたよりの推定値の変動は測定プロセスの結果として生じる変動に起因する。その変動は次の
ように計算される標準偏差によって表現される。併行標準偏差が既知の場合には,
n
r
σ
σ=
∆ˆ
················································································ (25)
9
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
併行標準偏差が未知の場合には,
n
s
S
w
ˆ=
∆
················································································ (26)
となる。
試験室のかたよりの95%信頼区間は次のように計算することができる。
∆ˆ−Awσr≦∆≦∆ˆ+Awσr ···························································· (27)
ただし,Awは式(20)で与えられている。σrが未知の場合には,その推定値srを代わりに用いなければな
らない。
この信頼区間が0を含むならば,試験室のかたよりは有意水準5%で有意ではないこととなり,0を含ま
ないならば有意ということになる。
試験室のかたよりはJIS Z 8402-6でも更に考察されている。
6. パネルへの報告書とパネルによる決定事項
6.1
統計解析者による報告書
統計解析が完了したら,統計解析者は報告を書き,パネルに提出しなければならない。この報告書には
以下の情報が与えられなければならない。
a) 測定方法の規定内容についてオペレータ及び/又は監督者から受理した所見にかかわる一切の報告;
b) 外れ試験室として除外された試験室に関わる一切の報告;
c) 発見された外れ値,及びこれらが説明付けられ,訂正されたか,又は除外されたかに関わる一切の報
告;
d) 適切な平均と精度に関する尺度の最終結果を示す表;
e) 標準測定方法が認められた標準に対して有意なかたよりを持つかどうかの声明書。もし,有意なかた
よりを持つのならば,各測定水準毎にかたよりの大きさの推定値を報告しなければならない。
6.2
パネルによる決定事項
パネルは統計解析者の報告について議論し,以下の質問に関する決定を下すことが望ましい。
a) 不整合な測定結果があるか? もしあれば,それは標準測定方法の記述の欠陥に起因するか?
b) 外れ試験室として除外された試験室に対し,どのような処置をとることが望ましいか?
c) 外れ試験室の結果及び/又は,オペレータ及び/又は監督者から受理した意見は,標準測定方法を改
善する必要性を示しているか? その場合,どのような改善が必要か?
d) 精確さ評価実験の結果は,測定方法を標準として採用することを正当化しているか? その公表に関
して,どのような処置をとるのか?
7. 真度の値の利用
JIS Z 8402-1 : 1999の7.を参照せよ。
10
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) JIS Z 8402で用いられる記号
a
関係式s=a+bmの切片
A
推定値の不確かさを計算するのに用いる係
数
b
関係式s=a+bmの勾配
B
全平均と試験室の測定値の偏差を表す成分
(かたよりに占める試験室成分)
B0
Bの成分の中で中間精度条件の下では変わ
らない,すべての要因
B(1), B(2), など Bの成分の中で中間精度条件で変化
する要因
c
関係式logs=c+dlogmの切片
C, Cʼ, C” 検定統計量
Ccrit, Cʼcrit, C”crit
統計的検定の棄却限界値
CDP
確率Pの許容差
CRP
確率Pの許容範囲
d
関係式logs=c+dlogmの勾配
e
測定値の成分中,すべての測定値に生じて
いる偶然誤差
f
許容範囲の係数
Fp (v1, v2) 分子の自由度v1,分母の自由度v2のF分
布のp分位点
G
グラッブスの検定統計量
h
マンデルの試験室間一致性の検定統計量
k
マンデルの試験室内一致性の検定統計量
LCL
下側管理限界(処置限界または警戒限界)
m
試験特性の一般平均;水準
M
中間精度条件において考慮される因子の数
N
反復数
n
一つの試験室で一つの水準(すなわち,セ
ルごと)で得る測定値の数
p
共同実験に参加した試験室数
P
確率
q
共同実験における試験特性の水準数
r
併行精度限界値(許容差)
R
再現精度限界値(許容差)
RM
標準物質
s
標準偏差の推定値
s)
標準偏差の予測値
T
ある表示の総和
t
試験対象または群の数
UCL
上側管理限界(処置限界または警戒限界)
W
重み付き回帰式の計算で用いられる重み係
数
w
一組の測定値の範囲
x
グラッブス検定に用いられるデータ
y
測定値
y
測定値の算術平均
y
測定値の全平均
α
有意水準
β
第二種の過誤の確率
γ
再現標準偏差と併行標準偏差の比 (σR/σr)
∆
試験室のかたより
∆ˆ
∆の推定値
δ
測定方法のかたより
δˆ
δの推定値
λ
二つの試験室または二つの測定方法間のか
たよりの検出可能な差
μ
試験特性の真値または参照値
v
自由度
ρ
方法AとBの併行標準偏差間の検出可能な
比
σ
標準偏差の真の値
τ
最終校正からの時間経緯に起因する変動を
表す測定値の成分
φ
方法AとBの試験室間平均平方の平方根の
検出可能な比
χ2p (v)
自由度vのχ2分布におけるp分位点
添え字に用いる記号
C
校正法が異なることを示す
E
装置が異なることを示す
i
特定の試験室を示す添え字
I ( )
中間精度に関する添え字,かっこ内に中間
精度条件のタイプの識別子を記述する
11
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
j
特定の水準に関する添え字 (JIS Z 8402-2)
分析の一群あるいは要因に関する添え字
(JIS Z 8402-3)
k
試験室iにおける水準jのk番目の測定値を
示す添え字
L
試験室間を示す
m
検出可能なかたよりに関する添え字
M
試験試料間を示す
O
オペレーターが異なっていることを示す
P
確率
r
併行精度
R
再現精度
T
時間が異なることを示す
W
試験室内を示す
1, 2, 3… 測定値の得られた順序を示す
(1), (2), (3), … 測定値の大きさの順序を示す

12
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考) 精確さ評価実験の例
B.1 実験の概要
鉄鉱石のマンガン含有量の原子吸収法による定量について,精確さ評価実験が,ISO/TC 102(鉄鉱石)
によって行われた。鉄鉱石試料として用いられたのは表B.1に示した参照値 (μ) をもつ5種の試験物質(測
定水準)である(表B.1の値は試験室には知らせなかった)。各試験室は,ランダムに選択された各測定水
準の測定用試料のびんを2本ずつ受け取り,各びん毎に2回分析を繰り返し実行した。2本ずつのびんを
用いるシステムの狙いは,びん間の変動が存在しないことを確認することである。分析は次のように行わ
れた。びん間の変動が存在しないことが確認された場合,4回の分析結果は併行条件における繰り返しと
見なし得る。分析の結果,びん間変動は有意でないことが示され,試料は均一と考えられた。こうして,
各試験室の測定結果は併行条件における繰り返しと見なすことができた。分析結果は表B.2に示した。5
種の試験物質(測定水準)の試験室平均と分散を表B.3に示す。
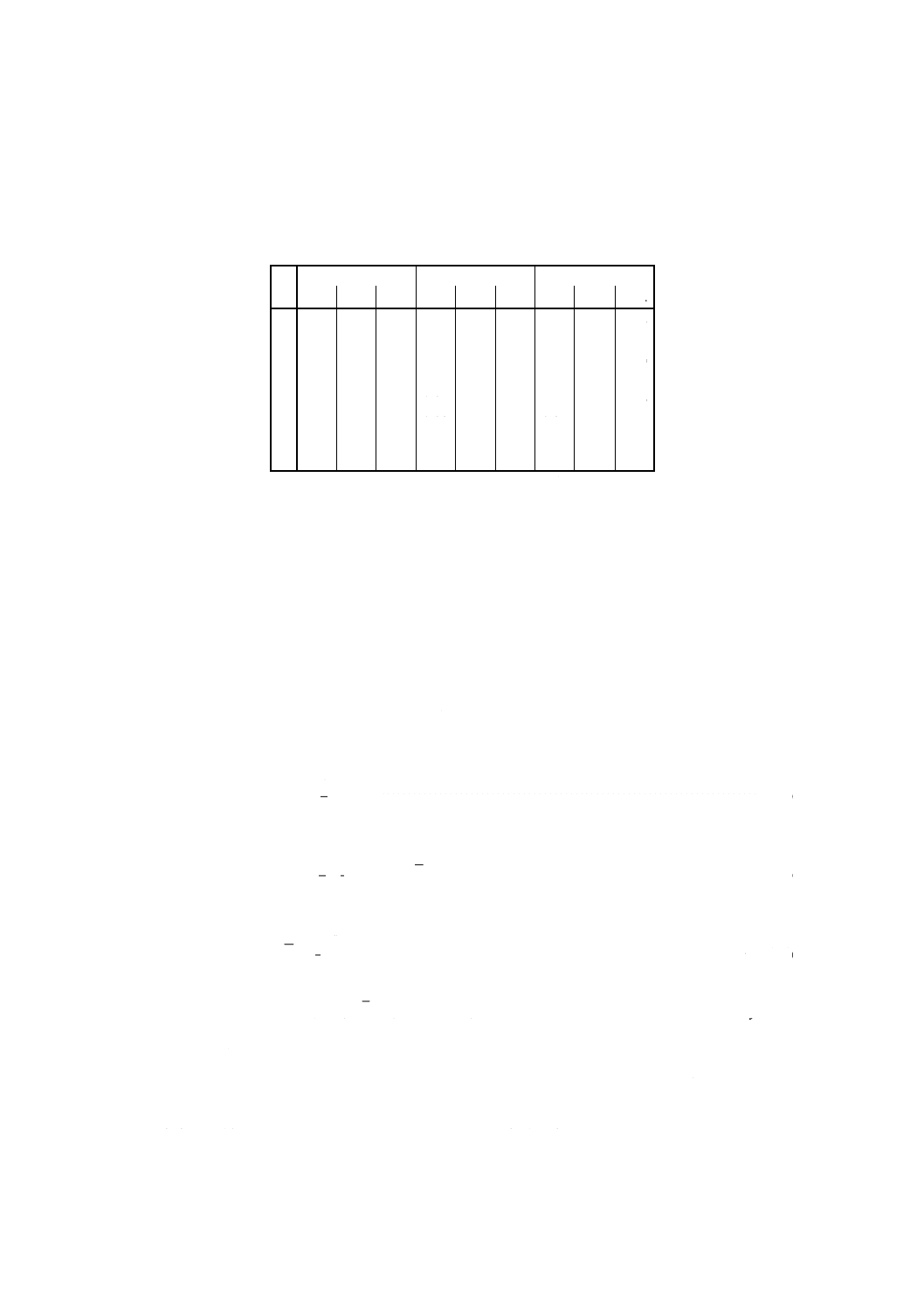
表B.1 鉄鉱石のマンガン含有量:参照値
測定水準
1
2
3
4
5
参照値μ (%Mn)
0,010 0
0,093 0
0,401 0
0,777 0
2,530 0
B.2 精度の評価
分析方法の精度を評価するために,データはJIS Z 8402-2に示された方法で分析された。各測定水準で
の測定結果は図B.1〜図B.5に示した。
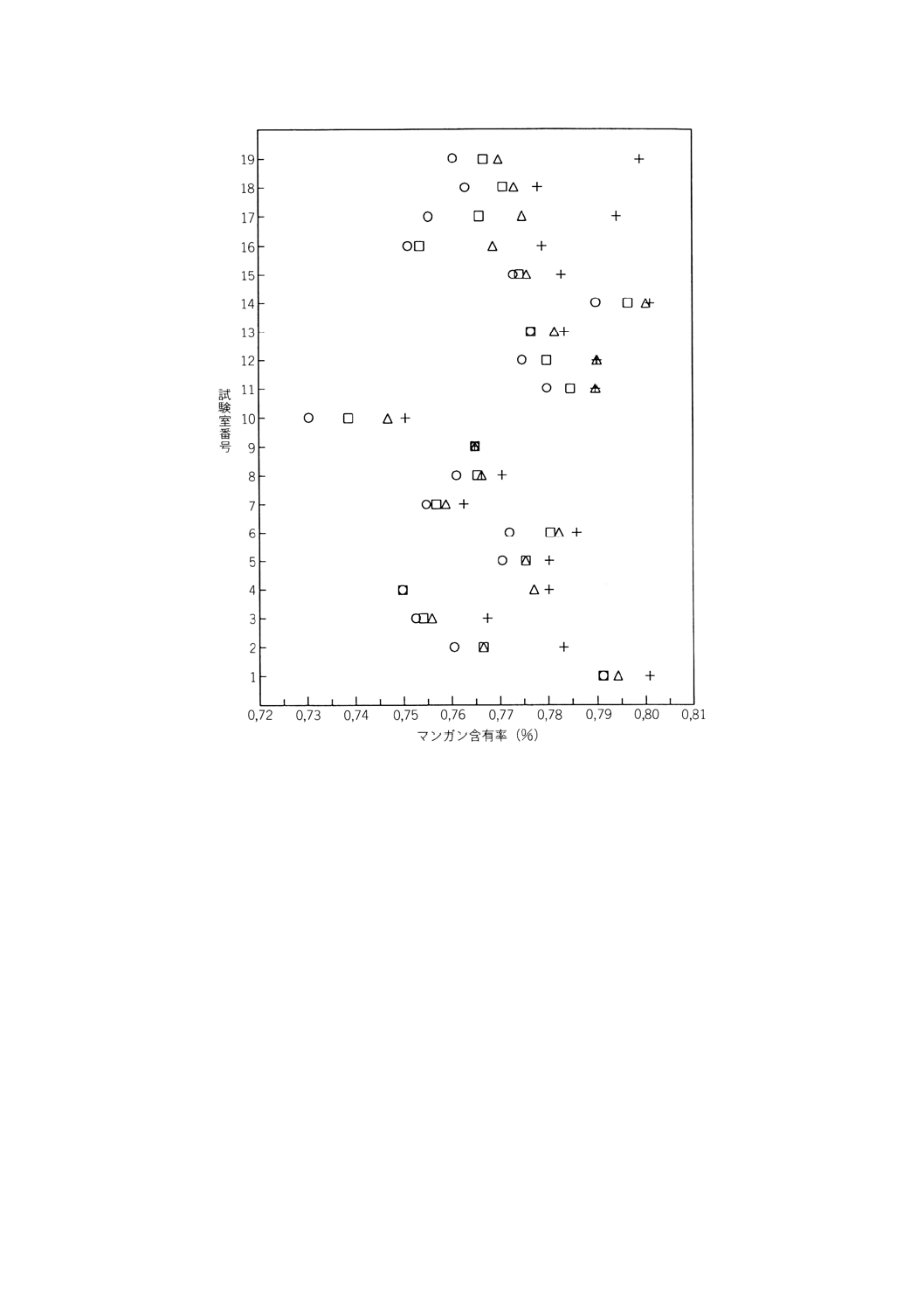
コクランの検定,およびグラッブズの検定に基づいて,外れ値が識別された。それらは,表B.4に示さ
れている。図B.1〜図B.5の枠で括られた点は測定結果が1%外れ値と識別されたものを示している。表
B.4によれば,7つの試験室からの結果が1%外れ値として識別されている。その中で,5つが2つの試験
室(試験室10,19)から生じている。1つの試験室の結果は5%外れ値として識別されているが,これも
同一の試験室(試験室10)から生じている。
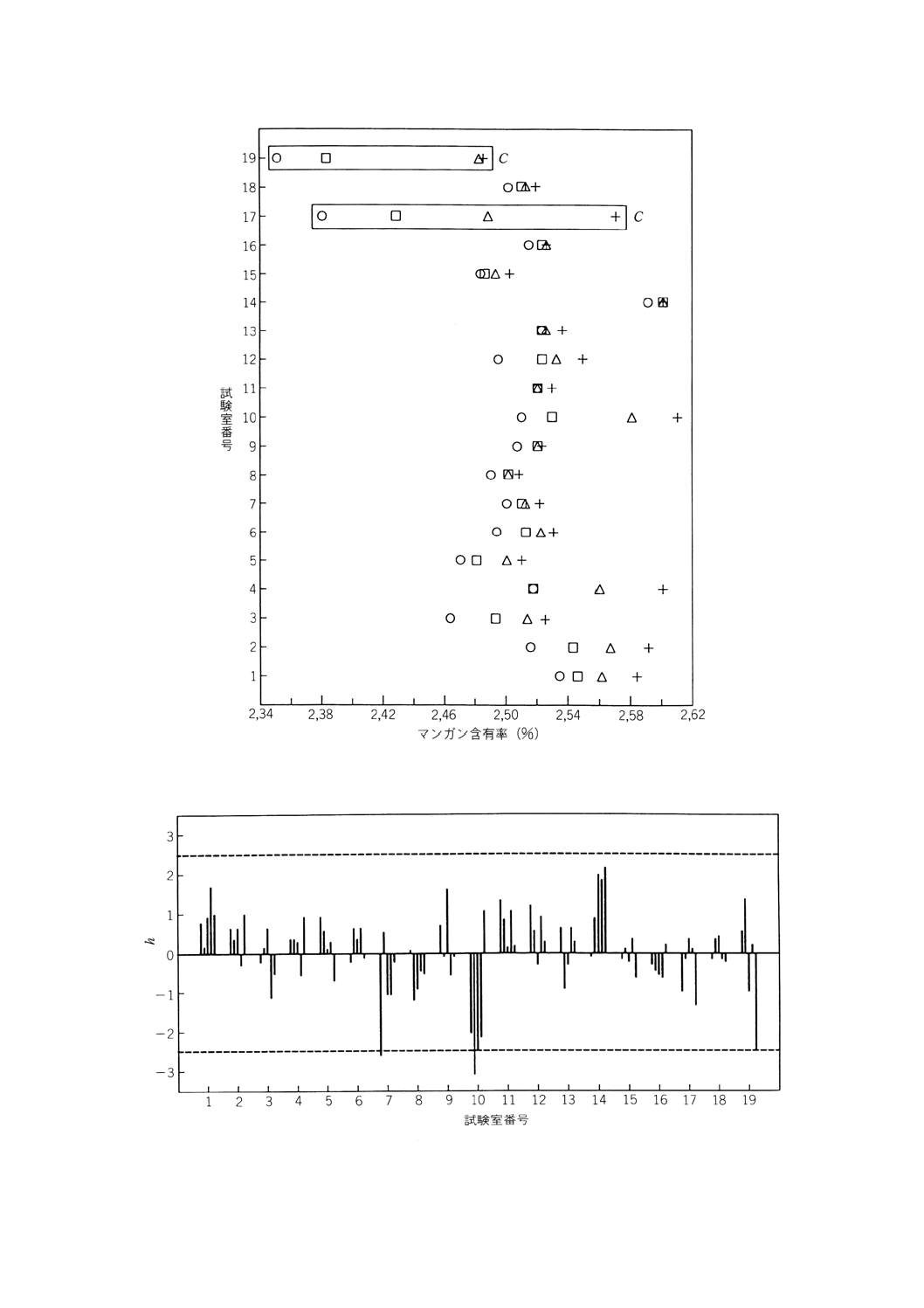
hとkの値を図B.6,図B.7に示す。hの値(図B.6)は明らかに試験室10が非常に低めの結果を得てい
ることを示している。その結果の2つ(測定水準2,3)が1%外れ値として識別されたのである。従って,
試験室10の結果をすべて除外することが決定された。これを,特別な注意の対象とし,この問題は解決さ
れるべきである。加えて,試験室7の測定水準1がグラッブズ検定により1%外れ値と識別され除外され
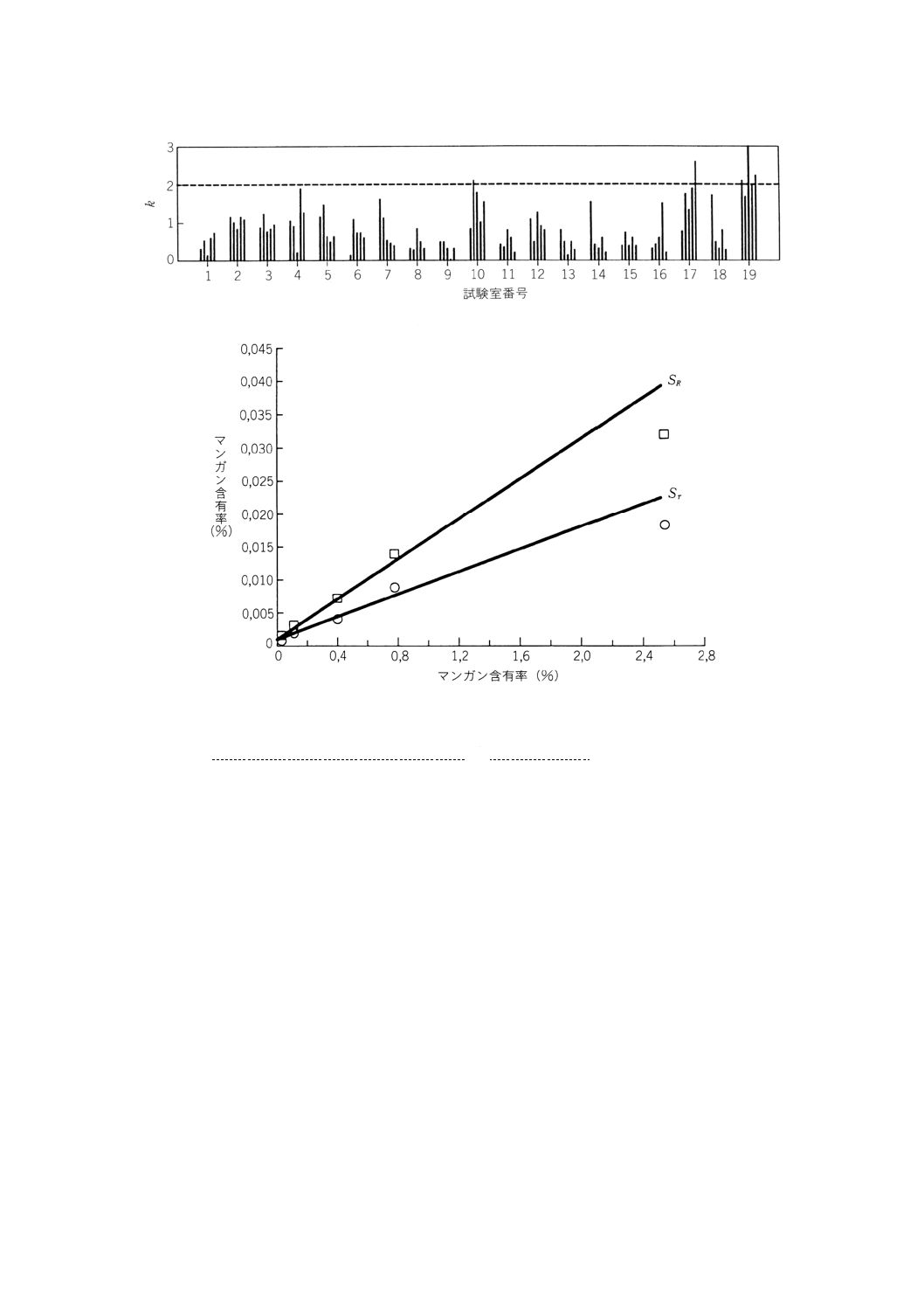
た。kの値(図B.7)は試験室10,17,19が他の試験室と比べて若干試験室内分散が大きい傾向があるこ
とを示している。ここで再び,これらの試験室を調べる,あるいは必要ならば測定方法の手順書を綿密に
するといった適切な処置がなされるべきである。解析に際して,コクランの検定で識別された1%外れ値
は除外することが決められた。すなわち,試験室19の測定水準3,5及び試験室17の測定水準5がそれに
該当する。
併行標準偏差,再現標準偏差はこれら除外したデータを含めずに計算された。この計算の結果は,表B.5
にまとめられ,測定水準毎に図B.8に描かれている。図B.8によれば,含有量の水準と精度の間の適切な
関係として,一次関数が妥当なように思われる。併行標準偏差及び再現標準偏差と含有量の水準との単回
帰式は次のようになる。
sr=0.000 579+0.008 85m
13
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
sR=0.000 737+0.015 57m
B.3 真度の評価
測定方法の真度は,式(18)を用いて測定方法のかたよりの95%信頼区間を計算し,それが0を含むか否
か(表B.5)で評価される。測定水準3,4,5では,信頼区間は0を含むので,この測定方法のかたより
はマンガンが高濃度の測定水準3,4,5では有意でないこととなる。測定水準1,2では信頼区間が0を含
まないので,かたよりはマンガンが低濃度の測定水準1,2では有意となる。
B.4 更なる解析
補助的解析,例えばyとμとの回帰分析を行えば,データから更なる情報を引き出せるであろう。
表B.2 鉄鉱石のマンガン含有量:分析の結果 (%Mn)
試験室
No.
びん
No.
測定水準
1
2
3
4
5
1
1
0,011 8 0,012 1 0,088 0 0,087 5 0,408
0,407
0,791
0,791
2,584
2,560
2
0,012 1 0,012 1 0,086 5 0,086 7 0,407
0,408
0,794
0,801
2,535
2,545
2
1
0,013 1 0,011 5 0,089 4 0,086 1 0,411
0,405
0,760
0,766
2,543
2,591
2
0,011 5 0,011 5 0,088 7 0,086 7 0,406
0,399
0,766
0,783
2,516
2,567
3
1
0,011 8 0,011 2 0,086 4 0,084 9 0,410
0,403
0,752
0,767
2,526
2,463
2
0,011 0 0,010 4 0,086 7 0,089 6 0,408
0,400
0,755
0,753
2,515
2,493
4
1
0,010 7 0,012 1 0,088 1 0,089 2 0,402
0,402
0,780
0,750
2,560
2,520
2
0,011 4 0,012 1 0,086 1 0,087 4 0,404
0,402
0,777
0,750
2,600
2,520
5
1
0,012 0 0,012 8 0,090 4 0,090 4 0,404
0,400
0,775
0,775
2,470
2,510
2
0,011 2 0,012 8 0,086 2 0,087 0 0,404
0,396
0,770
0,780
2,500
2,480
6
1
0,011 1 0,011 0 0,089 2 0,089 3 0,402
0,398
0,786
0,782
2,531
2,514
2
0,011 0 0,011 1 0,090 0 0,086 4 0,408
0,404
0,780
0,772
2,524
2,494
7
1
0,008 8 0,009 5 0,089 3 0,089 5 0,390
0,390
0,754
0,762
2,510
2,521
2
0,007 0 0,008 6 0,085 9 0,088 6 0,395
0,395
0,758
0,756
2,500
2,513
8
1
0,011 5 0,011 2 0,082 3 0,082 3 0,390
0,396
0,761
0,765
2,501
2,499
2
0,011 3 0,011 3 0,082 8 0,082 9 0,400
0,389
0,770
0,766
2,507
2,490
9
1
0,012 3 0,012 0 0,086 2 0,086 6 0,414
0,414
0,765
0,765
2,523
2,520
2
0,011 7 0,011 8 0,086 5 0,087 6 0,411
0,414
0,765
0,765
2,521
2,508
10
1
0,009 5 0,008 6 0,078 0 0,072 0 0,390
0,370
0,746
0,730
2,530
2,580
2
0,009 2 0,008 4 0,078 0 0,073 0 0,392
0,374
0,750
0,738
2,510
2,610
11
1
0,012 5 0,012 5 0,090 0 0,089 0 0,405
0,395
0,790
0,780
2,520
2,520
2
0,013 0 0,012 5 0,089 0 0,089 5 0,400
0,405
0,785
0,790
2,530
2,520
12
1
0,012 5 0,013 0 0,088 5 0,089 0 0,405
0,395
0,790
0,780
2,535
2,525
2
0,011 5 0,013 0 0,089 0 0,087 5 0,405
0,390
0,775
0,790
2,550
2,495
13
1
0,012 5 0,011 6 0,084 2 0,083 2 0,399
0,399
0,784
0,777
2,523
2,523
2
0,012 1 0,011 6 0,083 2 0,082 8 0,398
0,399
0,782
0,777
2,527
2,537
14
1
0,011 6 0,012 0 0,089 8 0,089 0 0,418
0,416
0,797
0,800
2,602
2,602
2
0,009 8 0,011 6 0,090 0 0,090 2 0,415
0,415
0,801
0,790
2,592
2,602
15
1
0,010 8 0,011 2 0,087 1 0,086 0 0,399
0,400
0,775
0,774
2,488
2,495
2
0,011 2 0,011 1 0,088 3 0,086 1 0,397
0,401
0,783
0,773
2,503
2,485
16
1
0,010 9 0,010 8 0,084 6 0,085 8 0,392
0,400
0,779
0,769
2,528
2,516
2
0,011 1 0,011 0 0,084 9 0,085 5 0,396
0,397
0,751
0,753
2,528
2,525
17
1
0,010 0 0,011 0 0,084 9 0,088 0 0,409
0,410
0,766
0,794
2,571
2,380
2
0,010 0 0,010 0 0,083 0 0,089 0 0,392
0,402
0,755
0,775
2,429
2,488
18
1
0,011 7 0,010 2 0,088 0 0,088 1 0,405
0,404
0,771
0,773
2,520
2,511
2
0,012 5 0,010 3 0,086 8 0,088 2 0,402
0,403
0,778
0,763
2,514
2,503
19
1
0,009 9 0,012 8 0,094 5 0,090 5 0,398
0,375
0,770
0,767
2,483
2,351
2
0,011 8 0,012 8 0,092 4 0,088 4 0,418
0,382
0,799
0,760
2,485
2,382
参考 表の中では,小数点としてコンマ (, ) を用いている。
14
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.3 鉄鉱石のマンガン含有量:試験室平均と試験室分散
試験室
No.
測定水準
1
2
3
4
5
試験室平均
1
0,012 03
0,087 18
0,407 50
0,794 25
2,556 00
2
0,011 90
0,087 73
0,405 25
0,768 75
2,554 25
3
0,011 10
0,086 90
0,405 25
0,756 75
2,499 25
4
0,011 58
0,087 70
0,402 50
0,764 25
2,550 00
5
0,012 20
0,088 50
0,401 00
0,775 00
2,490 00
6
0,011 05
0,088 73
0,403 00
0,780 00
2,515 75
7
0,008 48
0,088 33
0,392 50
0,757 50
2,511 00
8
0,011 33
0,082 58
0,393 75
0,765 50
2,499 25
9
0,011 95
0,086 73
0,413 25
0,765 00
2,518 00
10
0,008 93
0,075 25
0,381 50
0,741 00
2,557 50
11
0,012 63
0,089 38
0,401 25
0,786 25
2,522 50
12
0,012 50
0,088 50
0,398 75
0,783 75
2,526 25
13
0,011 95
0,083 35
0,398 75
0,780 00
2,527 50
14
0,011 25
0,089 75
0,416 00
0,797 00
2,599 50
15
0,011 08
0,086 88
0,399 25
0,776 25
2,492 75
16
0,010 95
0,085 20
0,396 25
0,763 00
2,524 25
17
0,010 25
0,086 23
0,403 25
0,772 50
2,467 00
18
0,011 18
0,087 78
0,403 50
0,771 25
2,512 00
19
0,011 83
0,091 45
0,393 25
0,774 00
2,425 25
試験室分散
1
0,225 0×10−7 0,489 2×10−6 0,333 3×10−6 0,222 5×10−4 0,454 0×10−3
2
0,640 0×10−6 0,248 2×10−5 0,242 5×10−4 0,982 5×10−4 0,103 4×10−2
3
0,333 3×10−6 0,386 0×10−5 0,209 2×10−4 0,482 5×10−4 0,772 2×10−3
4
0,449 2×10−6 0,168 7×10−5 0,100 0×10−5 0,272 2×10−3 0,146 7×10−2
5
0,586 7×10−6 0,492 0×10−5 0,146 7×10−4 0,166 7×10−4 0,333 3×10−3
6
0,333 3×10−8 0,252 9×10−5 0,173 3×10−4 0,346 7×10−4 0,258 9×10−3
7
0,111 6×10−5 0,276 3×10−5 0,833 3×10−5 0,116 7×10−4 0,753 3×10−4
8
0,158 3×10−7 0,102 5×10−6 0,269 2×10−4 0,136 7×10−4 0,495 8×10−4
9
0,700 0×10−7 0,369 2×10−6 0,225 0×10−5
0
0,460 0×10−4
10
0,262 5×10−6 0,102 5×10−4 0,123 7×10−3 0,786 7×10−4 0,209 2×10−2
11
0,625 0×10−7 0,229 2×10−6 0,229 2×10−4 0,229 2×10−4 0,250 0×10−4
12
0,500 0×10−6 0,500 0×10−6 0,562 5×10−4 0,562 5×10−4 0,539 6×10−3
13
0,190 0×10−6 0,356 7×10−6 0,250 0×10−6 0,126 7×10−4 0,436 7×10−4
14
0,970 0×10−6 0,276 7×10−6 0,200 0×10−5 0,246 7×10−4 0,250 0×10−4
15
0,358 3×10−7 0,114 9×10−5 0,291 7×10−5 0,209 2×10−4 0,642 5×10−4
16
0,166 7×10−7 0,300 0×10−6 0,109 2×10−4 0,178 7×10−3 0,322 5×10−4
17
0,250 0×10−6 0,766 9×10−5 0,689 2×10−4 0,272 3×10−3 0,675 7×10−2
18
0,124 9×10−5 0,429 2×10−6 0,166 7×10−5 0,389 2×10−4 0,500 0×10−4
19
0,186 9×10−5 0,680 3×10−5 0,364 9×10−3 0,295 3×10−3 0,476 3×10−2
参考 表の中では,小数点としてコンマ (, ) を用いている。
15
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.4 鉄鉱石のマンガン含有量:外れ値
測定水準
試験室
統計量の計算値1)
棄却限界値1)
1%外れ値一覧
1
7
G2=0,295
G2 (19) =0,339 8
10
2
10
G1=3,305
G1 (19) =2,968
3
19
C=0,474
C (4, 19) =0,276
10
C=0,305
C (4, 18) =0,288
4
−
−
−
5
17
C=0,358
C (4, 19) =0,276
19
C=0,393
C (4, 18) =0,288
5%外れ値一覧
1
−
−
−
2
−
−
−
3
−
−
−
4
−
−
−
5
10
C=0,284
C (4, 17) =0,250
1) C=コクランの検定
G1=一つの外れ値に関するグラッブズ検定
G2=片側2つの外れ値に関するグラッブズ検定
表B.5 鉄鉱石のマンガン含有量:併行標準偏差と再現標準偏差及び測定方法のかたよりの推定
測定水準
1
2
3
4
5
n
4
4
4
4
4
p
17
18
17
18
16
sr
0,000 65
0,001 43
0,004 07
0,008 95
0,018 15
sR
0,000 84
0,002 48
0,007 06
0,013 85
0,032 46
γ
1,29
1,73
1,73
1,54
1,79
A
0,352 8
0,399 9
0,411 7
0,383 0
0,428 7
AsR
0,000 296
0,000 991
0,002 906
0,005 301
0,013 916
y
0,011 6
0,087 4
0,402 4
0,773 9
2,524 9
μ
0,010 0
0,093 0
0,401 0
0,777 0
2,530 0
δˆ
0,001 6
−0,005 6
0,001 4
−0,003 1
−0,005 1
δˆ−AsR
0,001 3
−0,006 6
−0,001 5
−0,008 4
−0,019 0
δˆ+AsR
0,001 9
−0,004 6
0,004 3
0,002 2
0,008 8
参考 表の中では,小数点としてコンマ (, ) を用いている。
16
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 枠で囲んだ点は,片側2つの外れ値のためのグラッブズ検定 (G2) で1%
外れ値と識別されたもの
図B.1 鉄鉱石のマンガン含有量:測定水準1の測定結果
参考 図の中では,小数点としてコンマ (, ) を用いている。
17
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 枠で囲んだ点は,1つの外れ値のためのグラッブズ検定 (G1) で1%外れ
値と識別されたもの
図B.2 鉄鉱石のマンガン含有量:測定水準2の測定結果
参考 図の中では,小数点としてコンマ (, ) を用いている。
18
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 枠で囲んだ点は,コクランの検定 (C) で1%外れ値と識別されたもの
図B.3 鉄鉱石のマンガン含有量:測定水準3の測定結果
参考 図の中では,小数点としてコンマ (, ) を用いている。
19
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.4 鉄鉱石のマンガン含有量:測定水準4の測定結果
参考 図の中では,小数点としてコンマ (, ) を用いている。
20
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 枠で囲んだ点は,コクランの検定 (C) で1%外れ値と識別されたもの
図B.5 鉄鉱石のマンガン含有量:測定水準5の測定結果
参考 図の中では,小数点としてコンマ (, ) を用いている。
図B.6 鉄鉱石のマンガン含有量:試験室別に分けたhの値
21
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.7 鉄鉱石のマンガン含有量:試験室別に分けたkの値
図B.8 鉄鉱石のマンガン含有量:含有率水準mの一次関数としての
併行標準偏差と再現標準偏差
参考 図の中では,小数点としてコンマ (, ) を用いている。
22
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 式の導出
C.1 式(5),(6)(4.5参照)
試験室の数及び測定結果の数の最小値p,nは次の2つの条件を満たすよう計算する。
a) 検定によって,かたよりが0であることを確率1−α=0.95で検出できるのが望ましい。
b) 検定によって,事前に定めたかたよりの大きさδmを確率1−β=0.95で検出できるのが望ましい。
第1の条件は,実際に4.7.2で展開した。そこでは,測定方法のかたよりδの信頼区間を,かたよりが0
という帰無仮説 (H0 : δ=0) の,かたよりが0でないという対立仮説 (H1 : δ≠0) に対する統計的検定のた
めに用いている。
この検定と同等な方式は測定方法のかたよりの推定値の絶対値
|δˆ|=|y−μ|
を棄却限界値Kと比較することである。|δˆ|>Kならば,H0 (δ=0) を棄却し,|δˆ|≦Kならば,H0 (δ=0) を
棄却しない。Kは,H0が真のとき,それを棄却する確率が,選択した有意水準α=5%に等しくなくてはな
らないという要求事項に基づいて計算できる。
P (|δˆ|>K|δ=0) =α=0.05
P (|δˆ|≦K|δ=0) =1−α=0.95
()
()
−
−
δ
φ
δ
φ
ˆ
ˆ
V
K
V
K
=
()
1
ˆ
2
−
δ
φ
V
K
=
()
975
.0
ˆ=
δ
φ
V
K
()
960
.1
ˆ
975
.0
=
=u
V
K
δ
()
δˆ
960
.1
V
K=
······································································ (C.1)
ただし, φ ( ) は標準正規分布の累積分布関数
upは標準正規分布のp分位点,
V (δˆ) は測定方法のかたよりの推定値の分散
である。
V (δˆ) =V (y−μ) =V (y)
pn
p
r
L
2
2
σ
σ
+
=
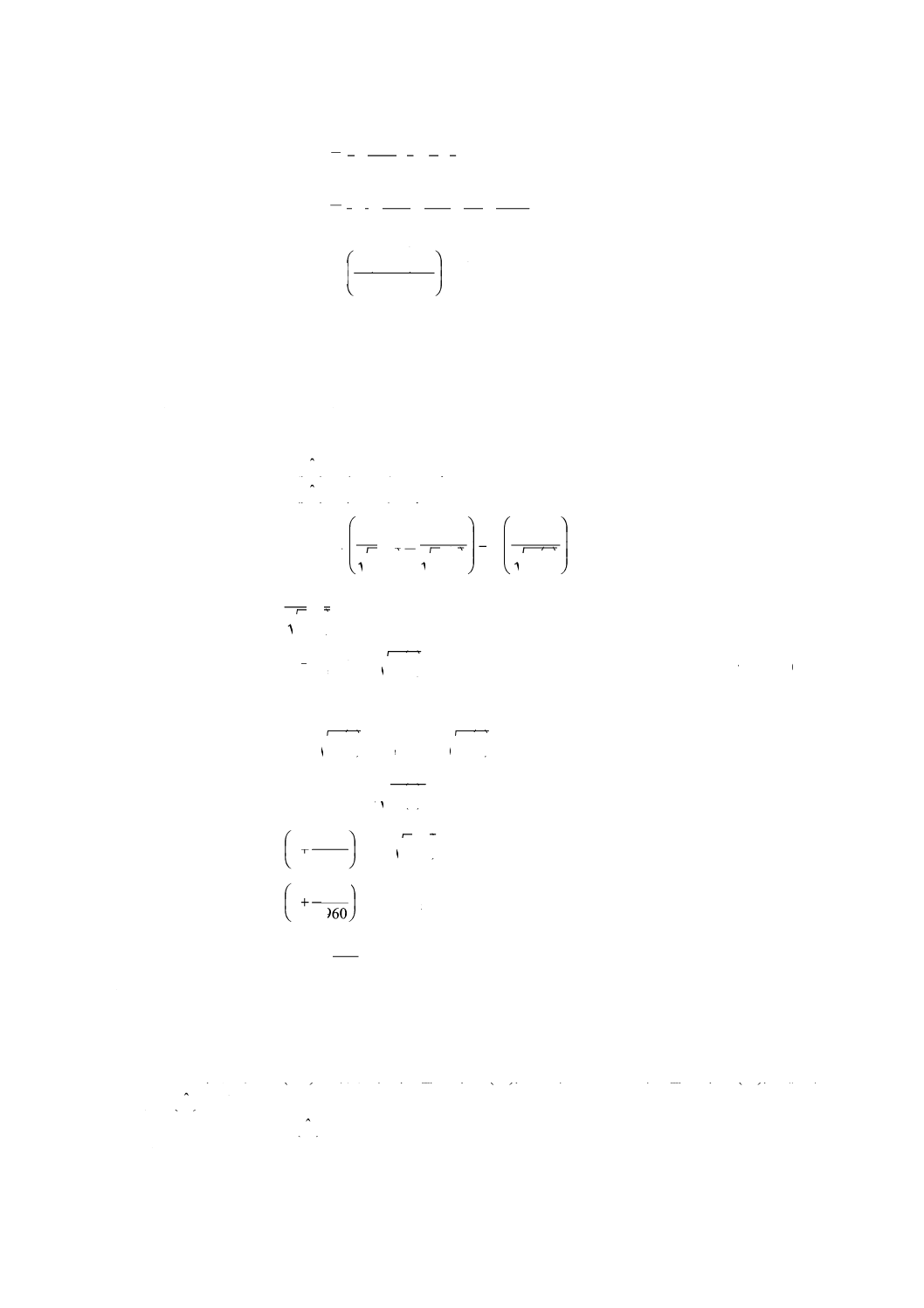
23
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
pn
p
r
r
R
2
2
2
σ
σ
σ
+
−
=
(
)
pn
n
R
R
R
2
2
2
2
2
/
/
γ
σ
γ
σ
σ
+
−
=
(
)
2
2
2
1
1
R
pn
n
σ
γ
γ
+
−
=
ただし, σL2は試験室間分散で
σR2=σL2+σr2
γ=σR/σr
である。
第2の条件は,検定によって事前に定めたかたよりの大きさδmを確率1−β=0.95で検出できるのが望ま
しいということである。すなわち,
P (|δˆ|>K|δ=δm) =1−β=0.95
P (|δˆ|≤K|δ=δm) =β=0.05
()
()
()
−
=
−
−
δ
δ
φ
δ
δ
δ
δ
δ
ˆ
ˆ
ˆ
ˆ
V
K
V
K
V
P
m
m
m≦
=
()
645
.1
ˆ
05
.0=−
=u
V
K
m
δ
δ
−
()
δ
δ
ˆ
645
.1
V
K
m−
=
······························································· (C.2)
である。Kについての2つの表現(C.1),(C.2)を等置すれば,
()
()
δ
δ
δ
ˆ
645
.1
ˆ
960
.1
V
V
m−
=
(
)()
m
V
δ
δ=
ˆ
645
.1
960
.1
+
()
m
V
δ
δ=
ˆ
960
.1
960
.1
645
.1
1
+
m
R
A
δ
σ=
+960
.1
645
.1
1
84
.1
m
R
A
δ
σ=
が得られる。
C.2 式(19),(20)(5.3参照)
これらの式は,前節の式(C.1)の導出で,δ,δm,δˆ,V (δˆ),Aを,それぞれ∆,∆m,∆ˆ,V (∆ˆ),Awに置
き換え,V (δˆ) の表現を
V (∆ˆ) =σr2/n
に置き換えることで,ただちに得られる。
24
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(参考) 参考文献
[1] JIS Z 8101-2 : 1999,統計−用語と記号−第2部 統計的品質管理用語
[2] JIS Z 8101-3 : 1999,統計−用語と記号−第3部 実験計画法用語
[3] JIS Z 8402-3 : 1999,測定方法及び測定結果の精確さ(真度及び精度)−第3部 標準測定方法の中間
精度
[4] JIS Z 8402-5 : −1),測定方法及び測定結果の精確さ(真度及び精度)−第5部 標準測定方法の精度
を求めるための代替法
[5] JIS Z 8402-6 : 1999,測定方法及び測定結果の精確さ(真度及び精度)−第6部 精確さに関する値の
実用的な使い方
[6] JIS Q 0033 : 1997,認証標準物質の使い方
[7] JIS Q 0035 : 1997,標準物質の認証−一般的及び統計学的原則
原案作成委員会 構成表
氏名
所属
(委員長)
石 川 馨
東京大学
(幹事)
宮 津 隆
日本鋼管株式会社
岩 田 晶 夫
住友金属鉱山株式会社
内 沼 一 雄
日本石油株式会社
藤 森 利 美
東京大学
(委員)
石 井 清 次
工業技術院
神 森 大 彦
社団法人日本化学会
上 甲 子 郎
東京理科大学
横 山 毅
昭和電工株式会社
高 橋 梅太郎
海外貨物検査株式会社
窪 田 孝 昌
海外貨物検査株式会社
(事務局)
新 井 紀 弘
財団法人日本科学技術連盟
改正原案作成委員会 構成表
氏名
所属
(委員長)
宮 津 隆
西東京科学大学理工学部
(委員)
尾 島 善 一
東京理科大学理工学部
故 高 橋 梅太郎
元海外貨物検査株式会社
椿 広 計
慶應義塾大学理工学部
仁 科 健
名古屋工業大学工学部
西 島 保
東燃株式会社総合研究所
野 村 和 夫
東京ガス株式会社
番 場 章
三石テクノ株式会社
多 田 格 三
元株式会社東芝
藤 森 利 美
長崎大学経済学部
横 山 隆 壽
財団法人電力中央研究所狛江研究所
池 田 要
工業技術院標準部材料規格課
川 村 正 信
財団法人日本規格協会
黒 木 勝 也
財団法人日本規格協会
(事務局)
橋 本 進
財団法人日本規格協会
1) 発行準備中
25
Z 8402-4 : 1999 (ISO 5725-4 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
品質管理分野国際整合化分科会
氏名
所属
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
○ 今 井 秀 孝
工業技術院計量研究所
○ 柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
日本電信電話株式会社
門 山 允
東京国際大学
○ 鹿 庭 なほ子
国立食品医薬品衛生研究所
兼 子 毅
武蔵工業大学工学部
○ 城 道 修
メルシャン株式会社
○ 椿 広 計
筑波大学社会工学系
○ 仁 科 健
名古屋工業大学工学部
野 澤 昌 弘
東京理科大学経営学部
三佐尾 武 雄
QCコンサルタント
○ 宮 津 隆
帝京科学大学理工学部
山 田 秀
東京都立科学技術大学工学部
横 尾 恒 雄
QCコンサルタント
大 嶋 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会
備考 ○印は許容差JIS原案作成WGの委員を兼ねる。