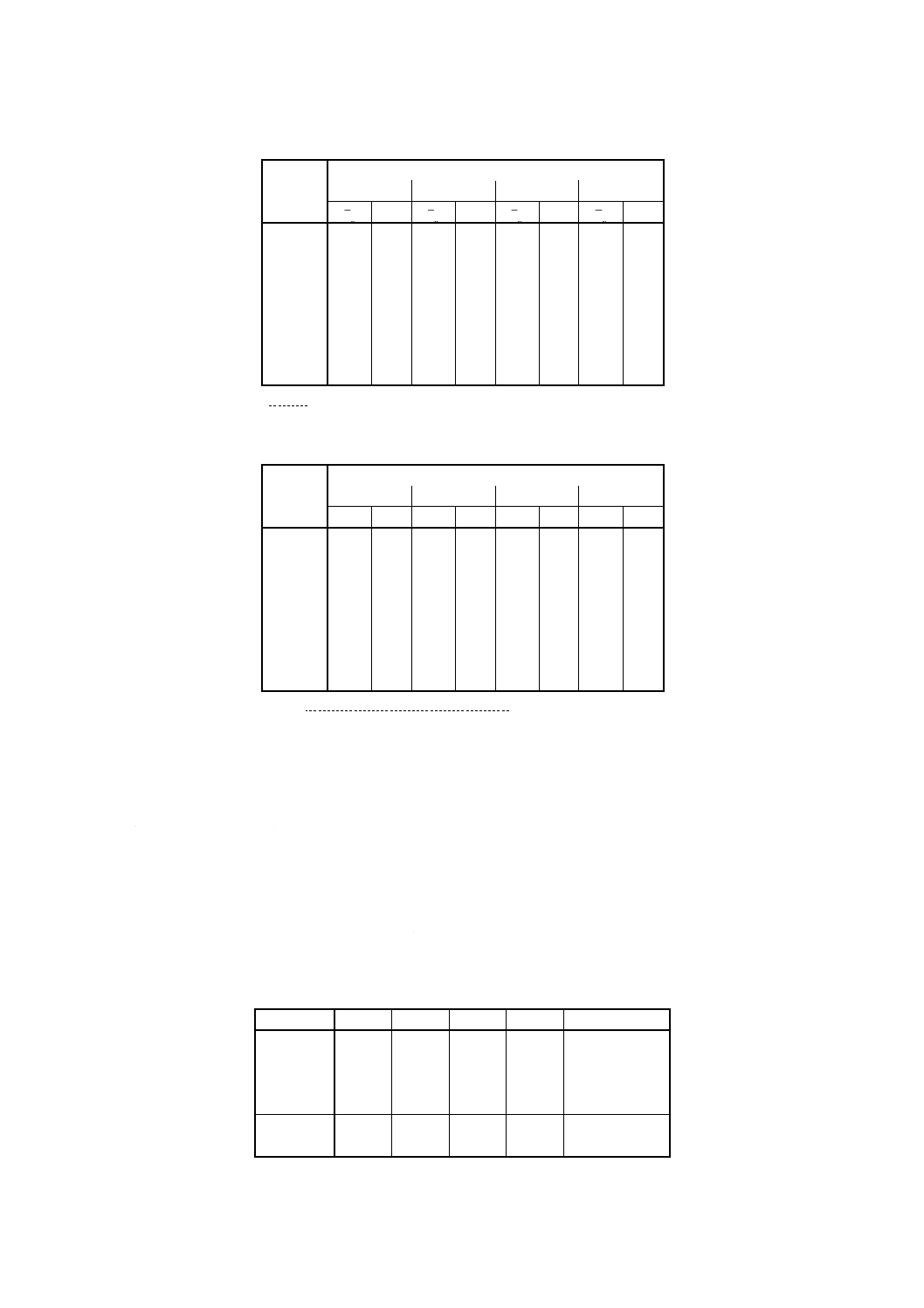Z 8402-2 : 1999 (ISO 5725-2 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 8402 : 1991は廃止され,この規格に置き換えられる。
今回の制定では,1994年に第1版として発行されたISO 5725-2を基礎として用いた。
JIS Z 8402-2には,次に示す附属書がある。
附属書A(規定) JIS Z 8402で用いられる記号
附属書B(参考) 精度評価実験の統計的解析の例
附属書C(参考) 参考文献
JIS Z 8402 : 1999は,一般名称を“測定方法及び測定結果の精確さ(真度及び精度)”として,次の部に
よって構成される。
第1部: 一般的な原理及び定義
(Part 1 : General principles and definitions)
第2部: 標準測定方法の併行精度及び再現精度を求めるための基本的方法
(Part 2 : Basic method for the determination of repeatability and reproducibility of a standard
measurement method)
第3部: 標準測定方法の中間精度
(Part 3 : Intermediate measures of the precision of a standard measurement method)
第4部: 標準測定方法の真度を求めるための基本的方法
(Part 4 : Basic methods for the determination of the trueness of a standard measurement method)
第5部: 標準測定方法の精度を求めるための代替法
(Part 5 : Alternative methods for the determination of the precision of a standard measurement
method)
第6部: 精確さに関する値の実用的な使い方
(Part 6 : Use in practice of accuracy values)
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 2
2. 引用規格 ························································································································ 2
3. 定義 ······························································································································ 3
4. 基本モデルにおけるパラメータの推定値 ·············································································· 3
5. 精度評価実験に必要な事項 ································································································ 3
5.1 実験の計画 ··················································································································· 3
5.2 参加試験室の募集 ·········································································································· 4
5.3 試料の調製 ··················································································································· 4
6. 精度試験の関係者 ············································································································ 6
6.1 パネル ························································································································· 6
6.2 統計解析者の役割 ·········································································································· 7
6.3 実施責任者の役割 ·········································································································· 7
6.4 監督者 ························································································································· 7
6.5 オペレータ ··················································································································· 8
7. 精度評価実験の統計的解析 ································································································ 8
7.1 前提となる基本事項 ······································································································· 8
7.2 測定結果のまとめと用いられる記号 ··················································································· 9
7.3 測定結果の一致性と外れ値についての調査 ········································································· 11
7.4 一般平均と分散の計算···································································································· 17
7.5 精度の値と測定水準mの関数関係の検討 ··········································································· 19
7.6 統計解析の段階的な手順································································································· 22
7.7 パネルへの報告書とパネルによる決定事項 ········································································· 26
8. 統計数値表 ···················································································································· 27
附属書A(規定) JIS Z 8402で用いられる記号 ········································································ 31
附属書B(参考) 精度評価実験の統計解析の例 ······································································· 34
B.1 例1:石炭中の硫黄分の定量(複数の測定水準,欠測値・外れ値がない場合) ························· 34
B.2 例2:ピッチの軟化点(複数の測定水準,欠測値がある場合) ·············································· 40
B.3 例3:クレオソート油の温度滴定(複数の測定水準,外れ値がある場合) ······························· 45
附属書C(参考) 参考文献·································································································· 51
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8402-2 : 1999
(ISO 5725-2 : 1994)
測定方法及び測定結果の
精確さ(真度及び精度)−
第2部:標準測定方法の併行精度及び
再現精度を求めるための基本的方法
Accuracy (trueness and precision) of measurement methods and results−
Part 2 : Basic method for the determination of repeatability
and reproducibility of a standard measurement method
序文
この規格は,1994年に第1版として発行されたISO 5725-2 Accuracy (trueness and precision) of measurement
methods and results−Part 2 : Basic method for the determination of repeatability and reproducibility of a standard
measurement methodを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規格で
ある。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
0.1
この規格では,測定方法の精確さを表すために“真度”と“精度”の二つの用語を用いている。“真
度”は,多数の測定結果の平均値と,真の値又は参照値との一致の程度を示すものである。“精度”は,測
定結果の間の一致の程度を示すものである。
0.2
これらの量の一般的な考察はこの規格の第1部で示されており,この部では改めて記述しない。第1
部は基本的な定義と一般的な原理が示されているので,この部を含めて,他の部についても,第1部を合
わせて読まれることが望ましい。
0.3
この規格のこの部は,併行標準偏差及び(室間)再現標準偏差によって標準測定方法の精度を推定
することだけを扱っている。状況によっては(分割法のような)別な種類の実験計画が,精度の推定に用
いられるが,それらをこの部では扱わない。それは,第5部の主題である。また,この部は二つの原則的
な精度以外の中間的な精度については,いかなる尺度についても考察していない。中間精度は第3部の主
題である。
0.4
状況によっては,精度を推定するために行われたある一つの実験で得られたデータが,真度の推定
にも用いられる。この部では真度の推定を考慮していない。真度の推定に関する事項はすべて第4部の主
題である。
2
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1. 適用範囲
1.1
JIS Z 8402のこの部は,
− 試験室間共同実験をとおして,測定方法の精度を定量的に推定するための実験を,計画する際に遵
守すべき一般的原理を詳述し,
− 測定方法の精度を推定するのに日常的に用いる基本的方法について,詳細かつ実用的な説明を提供
し,
− 精度を推定するための計画,実施及び測定結果の解析を行うに関係者に指針を提供する。
備考1. 基本的な方法の,特定の目的のための別な方法については,この規格の別の部に規定する。
附属書Bに,実験によって測定方法の精度を推定する実例を示す。
1.2
この規格のこの部は,計量値の測定値が求められ,測定結果として一個の値が得られるような測定
方法だけを対象とする。この一個の値は一組の観測値から計算によって求められたものであってもよい。
1.3
精度評価実験の計画及び実施において,第1部に規定したすべての原理が守られていることを前提
とする。この部で扱う基本的な方法は,個々の試験室で同じ水準の測定用試料を用いて同数個の測定結果
を分析する,すなわち,釣り合い型の(繰返し数の揃った)一様な水準の実験を用いている。この基本的
な方法は,すでに標準化されている測定方法及び多くの試験室で日常に使用されている測定方法に適用さ
れる。
備考2. 計算例は釣り合い型一様水準実験(繰返し数が一定の一元配置実験)の測定結果を示すため
のものである。しかし,一つの実験では,一つのセル当たり異なる繰返し数が報告されてお
り(不釣り合い型実験,繰返し数の異なる一元配置実験),別な実験ではいくつかのデータが
欠測している。この理由は,釣り合い型に計画された実験においても,不釣り合い型となる
可能性があるためである。外れ値や外れ値かもしれない値もまた考慮する必要がある。
1.4
この規格の第1部の5.に規定されている統計モデルは,分布が近似的に正規である測定結果の解釈
及び解析のために,適切な基礎と考える。
1.5
この部で既に述べたように,この部で取り扱う基本的な方法は,次の場合の測定方法の精度を(通
常的に)推定するために用いられる。すなわち,
a) この規格の第1部で定義されている併行標準偏差と(室間)再現標準偏差を求める必要がある場合,
b) 用いられる試料が均一であるか,または不均一性の影響が精度値に含められている場合,及び
c) 釣り合い型一様水準の実験計画を用いることが適当である場合に用いられる。
1.6
同じ方法を,まだ標準化されていない測定方法または日常使用されていない測定方法の精度を予備
推定する場合にも使うことができる。
2. 引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,発効年を付記してあるものは,記載の年の版だけがこの規格の規定を構成するもので
あって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その最新版(追補
を含む。)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部 確率及び一般統計用語
JIS Z 8101-2 統計−用語と記号−第2部 統計的品質管理用語
JIS Z 8402-1 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第1部 一般的な原理及び定
義
3
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3. 定義
この規格の目的に合わせ,JIS Z 8101とJIS Z 8402-1において定義された用語を用いる。
この規格で用いる記号を附属書Aに示す。
4. 基本モデルにおけるパラメータの推定値
4.1
この部に示す手順は,第1部の5.に示した統計モデルに基づいており,第1部の1.2に詳述されてい
る。特に,これらの手順は,第1部の5.の式(2)〜(6)に基礎をおいている。
このモデルは,
y=m+B+e
と表される。ここで,測定の対象となる試料について,
mは一般平均(期待値);
Bは併行条件の下でのかたよりの試験室成分;
eは併行条件の下で,一つ一つの測定に伴う偶然誤差
を示す。
4.2
第1部の式(2)〜(6)は,考察の対象となる母集団の真の標準偏差を表している。実際には,これらの
標準偏差の正しい値は未知であり,これらの精度の値は,考えられるすべての試験室(母集団)の数と比
べると少数の試験室(標本)から,かつ,それらの試験室内において考えられるすべての測定結果(母集
団)の数と比べると少数の測定結果(標本)から推定しなければならない。
4.3
実際の統計解析では,標準偏差の真の値σは未知であり,標本に基づく推定値で置き換えられるので,
記号σの代わりに,それが推定値であることを表すsを用いる。第1部の式(2)〜(6)に,これを行う必要が
あり,次のようになる。
sL2
は室間分散の推定値;
sw2
は室内分散の推定値;
sr2
は室内分散の推定値sw2の平均値であり,併行分散の推定値である;この平均値は,精確さ実
験に参加した試験室から外れ値を除いたすべての試験室から算出される。
sR2
は(室間)再現分散の推定値である。
sR2=sL2+sr2 ············································································ (1)
5. 精度評価実験に必要な事項
5.1
実験の計画
5.1.1
基本的な方法で用いる実験計画は以下の通りである。q種類の異なる測定水準を代表するq個のバ
ッチのサンプルを採り,p個所の試験室へ送付する。各々の試験室はq個の測定水準のそれぞれについて
併行条件の下で,正確にn個の測定結果を得るものとする。このような実験を釣り合い型一様水準実験
(balanced uniform-level experiment) とよぶ。
5.1.2
こうした測定実験は,以下に示すように,組織だって実施され,かつ手順書が示されねばならない。
a) 標準方法の規定に従って,必要とされる装置の予備点検を実施しなければならない。
b) 一つの測定水準に属する一組のn個の測定は,併行条件の下で実施しなければならない。すなわち,
同じオペレータが,同じ装置を用いて,短時間のうちに,測定方法に含まれていない限り装置の中間
校正をせずに,測定を実施しなければならない。
4
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
c) 併行条件の下で行う一組のn個の測定は,あたかも異なるn個の試料について測定を実施するかのよ
うに,独立して実施することが不可欠である。しかし,一般に,オペレータは,同一試料を測定して
いることを知ることになるが,この実験が実際の測定において結果にどのような違いが生じるかを明
らかにすることを目的としていることを,手順書のなかで強調しておくことが望ましい。この注意に
も関わらず,前の測定の結果が,引き続く後の測定の結果に影響する,従って,併行分散に影響を及
ぼす懸念があるときには,どの試料が,どの測定水準の繰返し試料であるかをオペレータにわからな
いようにコード化することによって,各々q種類の測定水準ごとにn個の独立した測定用試料を用い
ることを考慮することが望ましい。しかし,この手法は,測定の繰返しが併行条件下で実施されるこ
とを保証する点で問題を生じる。これが可能なのは,qn個のすべての測定が短時間のうちに実施でき
るような性質の測定に限られるであろう。
d) それぞれn回からなるq個のすべての組の測定が,厳密には短時間のうちに実施されなくともよい。
異なる組の測定が異なる日に実施されてもよい。
e) q種類の測定水準すべての測定は同一で唯一のオペレータが実施するとともに,どの測定水準につい
ても,一つの測定水準のn個の測定は,始めから終わりまで同一の装置を用いて実施しなければなら
ない。
f)
測定実験の途中でオペレータが実施不可能になったとき,オペレータ交替が,ある水準の一組のn個
の測定の途中でなく,q個の測定水準中の異なる組の間でなされるならば,他のオペレータが残りの
測定を完遂してもよい。この場合,いかなる変更もその結果とともに報告しなければならない。
g) 実験の終了の期限は,その期限内にすべての測定が完了するように設定しなければならない。このこ
とは,測定用試料を受けとった日から測定を実施する日までに許される経験時間を制限するために必
要であろう。
h) すべての測定用試料には,実験の名称と試料の識別用を明記したラベルを貼っておかねばならない。
5.1.3
オペレータは,5.1.2及びこの部の他の個所で単数形で(operatorとして)記述されている。測定に
よっては,実際には複数のオペレータから成るチームが実施し,一人一人のオペレータは操作のある特定
の部分を担当することがある。このような場合には,このチームを単数形の “the operator” と見なし,チ
ーム内の変更はいかなるものであっても異なるオペレータ,“a different operator” と見なさなければならな
い。
5.1.4
実際の取引の目的では,測定結果を適当に丸めてもよいが,精度評価実験においては,測定結果を
標準方法に規定されている桁数より少なくとも一桁多く報告しなければならない。もし,標準方法に桁数
の規定がないときには併行標準偏差の推定値の1/2より粗く丸めてはならない。精度がその測定水準mに
依存するときは,測定水準ごとに丸めの程度を変えることが必要となろう。
5.2
参加試験室の募集
5.2.1
試験室間共同実験に参加する試験室の募集に関する一般原則はこの規格の第1部の6.3に規定して
ある。必要な数の試験室の参加を募る際は,参加試験室の責任事項を明示しておかねばならない。適切な
募集用質問表の例を図1に示す。
5.2.2
この規格のこの部では,“試験室”とはオペレータ,装置及び試験場所(試験サイト)からなるも
のとする。したがって,一つのサイト(通常の意味では試験室)が,複数のオペレータと,各オペレータ
ごとに独立に測定を実施できる装置と場所を提供できる場合には,複数の“試験室”に相当する。
5.3
試料の調製
5
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.3.1
精度評価実験に用いる試料の選択について考慮を要する点は,この規格の第1部の6.4に述べられ
ている。
5.3.2
供給する試料の量を決める際は,測定結果を得る場合に起こる,試料の追加使用を必要とするかも
知れないような,偶発的な漏洩または誤差のために余分量を見込んで調製しておかなければならない。調
製する試料の全体量は,実験の実施と適切なストックをまかなうのに十分でなければならない。
5.3.3
いくつかの試験室に対しては,正式の測定結果を得る前に,標準測定方法に馴染むために,ある程
度の予備的な測定結果を得ることが必要かどうかを検討することが望ましい。必要な場合には,この目的
のために,(精度評価実験用の試料ではない)別の試料を供給すべきかどうかも検討することが望ましい。
5.3.4
ある試料を均一にしておく必要があるとき,均一化はその試料に最も適した方法で行わねばならな
い。測定に用いられる試料が均一でないとき,測定方法に規定されたように測定用試料を調製することが
重要である。その場合,各測定水準ごとに市販試料の一つのバッチから始めるのが望ましい。不安定な試
料の場合には,保存と取り扱いに関する特別な指示を規定しなければならない。
5.3.5
容器を開放すると(酸化,揮発性成分の操失,または試料の吸湿性などによって)試料が劣化する
恐れがある場合には,試験室及び測定水準ごとのn個の試料に別々の容器を用いなければならない。不安
定な試料の場合には,保存と取り扱いに関する特別な指示を規定しなければならない。測定が実施される
まで測定試料が同質であることを確実にするための注意が必要なこともある。また測定対象の試料が相対
密度または粒子サイズが異なる粉体混合物である場合には,輸送などによる振動の結果,分離することも
あるので何らかの注意が必要である。大気との反応が予想される場合には,試料を,脱気または不活性ガ
スを充填したアンプル中に封じるのもよい。食品または血液などのように腐敗しやすい試料の場合には,
解凍手順に関する詳しい指示書を添えて,凍結状態のまま,参加試験室に送る必要があろう。

6
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1 試験室共同実験のための募集用質問表
6. 精度試験の関係者
備考3. 試験室が異なれば,実際の測定の操作が同一であることは期待できない。したがって,本節
は,それぞれの状況を満たすように適切に修正して使用される指針として意図したものにす
ぎない。
6.1
パネル
6.1.1
パネルは測定方法とその適用に精通した専門家で構成することが望ましい。
6.1.2
パネルの任務は,
a) 実験を計画・調整すること;
b) 実験に求められる試験室数,測定水準の数及び測定の回数,並びに有効数字の桁数を決めること;
c) 統計解析の担当者を指名すること(6.2を参照);
d) 実施責任者を指名すること(6.3を参照);
e) 標準測定方法とともに試験室の監督者へ配布する指示書を検討すること;
f)
数名のオペレータに対し,その方法についての以前の勘を取り戻させるため,非公式に数回の測定を
行うのを認めるかどうかを決めること(こうした場合には正式な共同実験用試料で測定を行ってはな
らない);
7
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
g) 測定結果の統計的解析の完了時に,統計解析の報告書を議論する;
h) 併行標準偏差と(室間)再現標準偏差の値を最終的に設定すること;
i)
測定方法の規定,及び測定結果が外れ値として除外された試験室に関して,改善の処置が必要かどう
かを決めること,
である。
6.2
統計解析者の役割
パネルのメンバーのうち少なくとも一人は実験の統計的な計画と解析の経験があることが望ましい。統
計解析者の任務は,
a) 実験の計画に関する専門知識を役立てること;
b) データを解析すること;
c) 7.7に規定された指示に従ってパネルに提出する報告書を作成すること,
である。
6.3
実施責任者の役割
6.3.1
実験の実際上の実施組織は,単一の試験室に委託することが望ましい。その試験室の関係者の一人
が全責任を負うことが望ましい。その関係者を実施責任者と呼び,パネルが指名する。
6.3.2
実施責任者の任務は,
a) 必要数の試験室を募集し,確実に監督者が定められるようにすること;
b) 試料手配,試料調製ならびに試料送付を組織的に監督すること;測定水準ごとに,適切な量の試料が
予備ストックとして確保されること;
c) 5.1.2のa)〜h)の要点を網羅する手順指示書を起草し,監督者が意見または質問を出せるように,また,
選ばれたオペレータが通常の操作でこのような測定を行えることを確かめることができるように,十
分早期に前もって回付すること;
d) オペレータの作業記録としての用途にも,要求された有効桁数で監督者が測定結果を報告する用途に
も,適した記録書式を作成すること(この記録書式にオペレータの氏名,測定用試料の受理日付・測
定日付,装置の名称,及びその他あらゆる関連情報を含ませてもよい);
e) 測定の実施に関する試験室からの問合わせに対応すること;
f)
全体の日程が守られるように取り計らうこと;
g) データの記録書式を集めて統計解析の専門家に提出すること,
である。
6.4
監督者
6.4.1
それぞれの参加試験室における一人の関係者(監督者と呼ぶ。)が,実施責任者から送付された手
順指示書に従って測定の実施を組織立て,測定結果を報告することに責任を持つことが望ましい。
6.4.2
監督者の任務は,
a) 選ばれたオペレータが通常の操作でこのような測定を正常に遂行できることを確かめること;
b) 測定用試料を実施責任者の手順指示書どおりにオペレータに配布すること(及び必要ならば,習熟の
ための予備実験用の試料を準備すること);
c) 測定の実施を監督すること(監督者が実験の実施に参加してはならない);
d) オペレータが要求された回数の測定を確実に行うようにすること;
e) 測定が設定された日程どおりに確実に実施されるようにすること;
f)
所定の桁数で記録された測定結果,及び実験中に発生した異常事態と問題点,並びにオペレータの意
8
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
見を集めること,
である。
6.4.3
各試験室の監督者は,以下の情報を含む完全な報告書を作成することが望ましい。
a) 所定の記録書式に読めるように記入された,測定者自身の手による測定結果の原物,転記・タイプし
たものは不可(コンピュータまたは測定機器のプリントアウトでも構わない);
b) (もし,あれば)測定結果のもとになった,オペレータ自身の手によって所定の記録書式に読めるよ
うに記入された生の観測値又は読み値,転記・タイプしたものは不可;
c) オペレータによる,測定方法の規定に関する意見;
d) 測定中に生じた異常または障害に関する情報,オペレータの交替については測定ごとの担当オペレー
タ名を,欠測値については理由を含める;
e) 測定用試料を受理した日付;
f)
それぞれの測定用試料を測定した日付;
g) (意味がある場合には)使用した装置の情報;
h) あらゆる他の関連する情報。
6.5
オペレータ
6.5.1
すべての試験室で,正常に測定を行える代表として選ばれた,一人のオペレータによって測定が実
施されなければならない。
6.5.2
実験の目的は,標準測定方法にしたがって測定しているオペレータの一般的母集団から得られる精
度を明らかにすることであるので,一般的にはオペレータに,測定方法に規定されていない事項について
補足説明が与えられないことが望ましい。しかし,オペレータに,実験の実施目的が測定結果の実際の変
動の程度を見つけることであることを,納得させておき,オペレータの判断で一致していないと感じる測
定結果を捨てたり,またはやり直したりするようなことを避けることが望ましい。
6.5.3
一般的にはオペレータに,測定方法に規定されていない事項について補足説明が与えられないこと
が望ましいが,その規定に関して意見を述べるように,特に,その内容に含まれる指示事項が十分にわか
りやすく明白であるかどうかを述べるように,オペレータを促すことが望ましい。
6.5.4
オペレータの任務は,
a) 標準測定方法にしたがって測定を行うこと;
b) 実験中に発生した異常事態と問題点を報告すること;欠測値が一つ二つあっても,実験を損なうこと
はなく,かえって規定事項の不適切さを示すことになるので,測定結果を修正するよりは間違いを報
告した方がよい;
c) 規定の指示事項の適切さについて意見を述べること;これもまた規定事項の不適切さを示すことにな
るので,オペレータは指示どおりに実施することが不可能であった状況について報告することが望ま
しい,
である。
7. 精度評価実験の統計的解析
7.1
前提となる基本事項
7.1.1
データの解析は,統計の専門家によって解かれるべき統計の問題として考えることが望ましく,3
つの段階から成っている。
a) 外れ値や,それ以外の変則的な値を特定・処理し,モデルの適合性を検定するために,データを評価
9
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検討すること;
b) 測定水準ごとに精度と平均の予備的な値の計算を行うこと;
c) 精度と平均の最終的な値を設定すること。これには,解析により精度と測定水準との間に関数関係が
示唆される場合に,その関数形を求めることを含む。
7.1.2
この統計的解析では,最初に測定水準ごとに次の推定値を計算する。
− 併行分散
sr2
− 室間分散
sL2
− (室間)再現分散
sR2=sr2+sL2
− 平均値
m
7.1.3
この統計的解析には,外れ値に関する統計的検定の系統的な適用を含んでいる。極めて多様な検定
の方法がさまざまな文献に示されていて,かつ,この規格のこの部のために用いることができる。実用的
な理由で,7.3に述べるように,限られた数の検定方法だけを用いた。
7.2
測定結果のまとめと用いられる記号
7.2.1
セル
一つの試験室と一つの測定水準の組合せを,精度評価実験のセルと呼ぶ。理想的には,p個の試験室に
おけるq種類の測定水準の結果が,pq個のセルから成り,それぞれのセルは併行標準偏差と再現標準偏差
の計算に用いることができるn個の併行条件の測定結果を含む。しかし,このような理想的な状況は,必
ずしも,実際に得られるものではない。余計な繰返しによる過剰のデータにより,また欠測値や外れ値の
ために,理想状況からの乖離(かいり)が生ずる。
7.2.2
過剰のデータ
ときおり,ある試験室が,公式に規定した回数以上の測定を実施し,n個よりも多くの測定結果を報告
することがある。こうした場合には,その試験室の監督者は,その理由と,どれが正しいデータであるか
を報告しなければならない。すべて有効なデータであると言う回答であるときは,統計解析のために,そ
の測定結果から計画した個数のデータをランダムに選びだすことが望ましい。
7.2.3
欠測値
別な場合として,試料の損失または測定実施上の失敗などによって,測定結果のいくつかが欠測するこ
とがある。7.1で推奨する統計解析法は,全く空白のセルについては単純に無視することができ,部分的に
欠測しているセルは,標準的な計算手順に組み入れることができるというものである。
7.2.4
外れ値
これらは原測定結果,または,原測定結果から得られる表中に含まれるデータではあるが,同じ表にあ
る他のデータから著しく離れているため,それ以外のデータとは調和しないと考えられるものである。経
験的に,外れ値は必ずしも除外されるべきものではなく,かつ欠測値と同様な方法で考慮に入れねばなら
ないものである。
7.2.5
外れ試験室
一つの試験室において,複数の測定水準で,説明できない異常な測定結果が生じている場合には,その
試験室を外れ値と考えることができる。そのままにすると,その測定結果の水準が,大き過ぎる試験室内
分散,及び/または大き過ぎる系統誤差をもつことになろう。そのため,このような外れ試験室のデータ
の一部もしくは全部を捨てることが合理的であろう。
この規格のこの部には,疑わしい試験室を判定する統計的検定の方法を規定していない。この扱いにつ
いては,統計解析の専門家が決定の主たる責任をとることが望ましい。しかし,除外されたすべての試験
10
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
室について,将来の処置のために,パネルに報告しなければならない。
7.2.6
誤ったデータ
明白に誤りとわかるデータは,調査ののち,訂正するか,または,捨てることが望ましい。
7.2.7
釣り合い型一様水準の測定結果
理想的なケースでは,i (i=1, 2,…,p) で示すp個所の試験室で,j (j=1, 2,…,q) で示すq種類の測定水
準について,各々n回の繰り返し測定を行い,合計pqn個の測定結果が得られる。測定結果の欠測 (7.2.3),
外れ (7.2.4),試験室の外れ (7.2.5),または誤ったデータ (7.2.6) によって,理想的状況は,必ずしも達成
されない。7.2.8〜7.2.10に示す表記法及び7.4に示す手順は,こうした各件の下での繰返し数の異なる測定
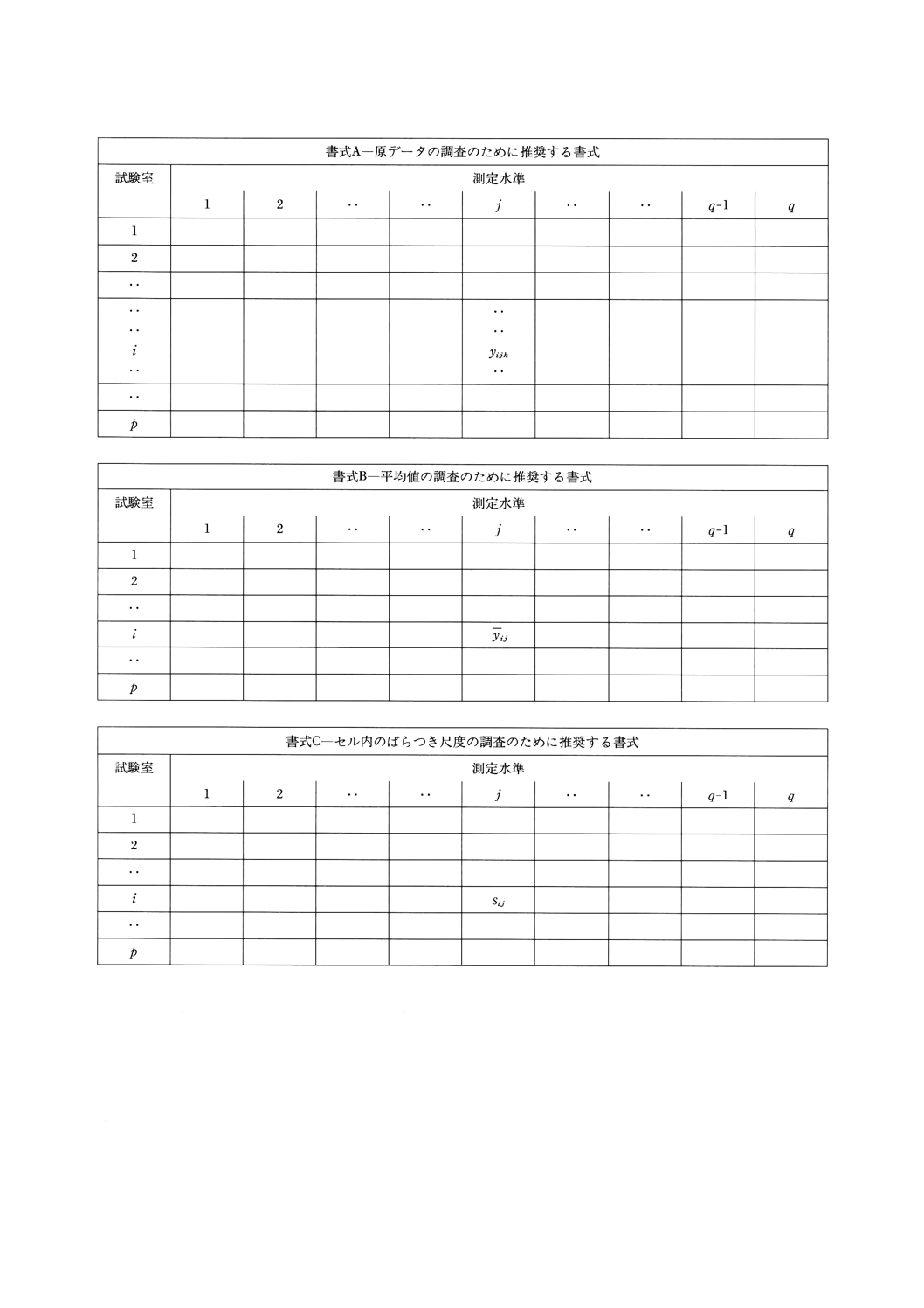
結果を考慮している。統計的解析のために推奨される書式の実例を図2に示す。以下の記述では,便宜的
にそれらを単に(図2)の書式A,B,及びCと呼ぶ。
7.2.8
原測定結果
図2の書式Aを参照のこと。ここで,
nijは,試験室iの測定水準jのセルの測定結果の数;
yijkは,これらの測定結果 (k=1, 2,…,nij) ;
pjは,(外れ値や誤った測定結果を除外後の)測定水準jで,測定結果を一つ以上報告している試験室
の数,
である。
7.2.9
セルの平均(図2の書式B)
これらは書式Aから以下のように導かれる。
ij
y=∑
=
jin
1
k
ijk
ij
y
n
1
······································································· (2)
このセルの平均値は,書式Aの測定結果より,一桁有効数字を増やして報告することが望ましい。
7.2.10 セル内のばらつきの尺度(図2の書式C)
これらは書式A(7.2.8参照)と書式B(7.2.9参照)から以下のように導かれる。
一般にはセル内標準偏差,
ijs=
∑
=
−
ij
n
k
ij
ijk
ij
y
y
n
1
2)
(
1
1
−
························································ (3)
または,以下の同等の式,
ijs=
−
−∑
∑
=
=
ij
ij
n
k
n
k
jk
i
ij
ijk
ij
y
n
y
n
1
2
1
2
1
)
(
1
1
············································ (4)
を用いる。
これらの式を用いて計算するときは,十分な桁数が保持されるように注意しなければならない;すなわ
ち,すべての中間の値は原データの少なくとも2倍の桁数まで計算されなければならない。
備考4
セルijが2っの測定結果だけからなる場合には,セル内標準偏差は
sij=|yij1−yij2|/2······································································ (5)
となる。
したがって,すべてのセルが2つの測定結果から成るときには,簡略化のため,標準
11
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
偏差の代わりに,測定結果の差の絶対値を用いることができる。
nijの値が1又は0のときは,書式Cの該当欄にダッシュ (−) を記入するとよい。
7.2.11 データの訂正または除外
データによっては,7.1.3,7.3.3及び7.3.4で述べた検定に基づき,訂正され,または除外されるものが
あるので,精度と平均の最終値を求めるために用いられるyijk,nij及びpjの値は,図2の書式A,B及びC
に記録された原測定結果について記述される値とは異なることがある。したがって,訂正や除外がある場
合の,精度と真度の最終値の報告には,どのデータが訂正,または,除外されたのかを必ず記述しなけれ
ばならない。
7.3
測定結果の一致性と外れ値についての調査
参考文献 [3] を参照すること。
12
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2 解析のために測定結果を調査するために推奨する書式
規定した多くの測定水準について集めたデータから,併行及び再現標準偏差が推定される。他のすべて
の試験室または値と不一致であるような試験室または値が存在すると,それらの推定値を変化させること
があり,そのような値に関して決定がなされなければならない。この目的のために二つの方法をここに示
す。
a) グラフィカルな一致性の検討方法
b) 数値的な外れ値の検定方法。
13
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.1
グラフィカルな一致性の検討方法
マンデル (Mandel) のh統計量及びk統計量と呼ばれる二つの尺度を用いる。これらは,測定方法のば
らつきを記述するだけでなく,試験室の評価にも役立つ。
7.3.1.1
試験室間の一致性の統計量hは,個々の試験室について,セル偏差(セル平均−その水準の総平
均)をセル平均の標準偏差で除して求められる。
∑
=
−
−
−
1
1
2)
(
)1
(
1
p
j
j
ij
j
j
ij
ij
y
y
p
y
y
h=
······················································· (6)
ここで,
ij
yは7.2.9を,ij
yは7.4.4を参照のこと。
それぞれのセルのhijの値は,試験室ごとに,各測定水準をグループにまとめて(これとは別に,測定水
準ごとに,各試験室をグループにまとめて)プロットする(図B.7参照)。
7.3.1.2
試験室内の一致性の統計量kは,個々の測定水準について,プールしたセル内標準偏差
j
ij
p
s
∑2
を計算し,ついで測定水準ごとに,個々の試験室について求める。
∑2ij
j
ij
ij
s
p
s
k=
··········································································· (7)
それぞれのセルのkijの値は,試験室ごとに,各測定水準をグループにまとめて,(これとは別に,測定
水準ごとに,各試験室をグループにまとめて)プロットする(図B.8参照)。
7.3.1.3
h及びkを図示した結果を検討することによって,特定の試験室が,他の結果と著しく異なる結
果のパターンを表しているかどうかが示されるであろう。これは,セル内分散が一貫して高いか又は低い
こと,及び/または,多くの水準を通じてセル平均が極端な値であることによってわかる。こういったこ
とが起きたなら,その試験室に連絡し,その挙動の原因を確かめる努力をすることが望ましい。この知見
に基づき,総計解析者は以下のことを行うことができるであろう:
a) とりあえず,その試験室のデータを保留にすること;
b) (可能ならば)その試験室に,測定のやり直しを依頼すること;
c) その試験室のデータを対象から除外すること。
7.3.1.4
hの値のプロットにはさまざまなパターンが現れる可能性がある。すべての試験室が,実験の,
さまざまな測定水準で正と負の両方のh値をとることがある。個々の試験室は,すべて正の値またはすべ
て負の値のh値をとる傾向もあり得るが,その場合,負の値の試験室の数は,正の値試験室の数とほぼ同
数である。こうしたパターンのうち二番目に述べたパターンは,共通の原因による試験室かたよりが存在
することを示している可能性があるが,こうしたパターンはいずれも異常なものでもなく,調査を必要と
するものでもない。一方,一試験室のすべてのh値の符号が正負の一種類だけであり,他のすべての試験
室のh値の符号がすべて反対の符号のときは,その理由を調べることが望ましい。同様に,ある一つの試
験室のh値が,極端な値であり,系統的に実験の測定水準に依存しているようであるなら,その理由を調
べることが望ましい。h値のプロットには,8.3(表6と7)で与えられる棄却限界値に対応する線が引か
れる。これらの棄却限界値の線は,データのパターンを検討する場合の指標として役立つものである。
14
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.1.5
ある試験室がk値の分布で,際だって大きな値が多く見られるようならば,その理由を調査する
ことが望ましい:これはその試験室の併行精度が他の試験室よりも劣っていることを示している。試験室
によっては,データの丸め過ぎや感度の低い測定のために,一様に小さいk値をもたらすことがある。k
値のプロットには,8.3(表6と7)で与えられる棄却限界値に対応する線が引かれる。これらの棄却限界
値の線は,データのパターンを検討する場合の指標として役立つものである。
7.3.1.6
試験室ごとのグループにまとめたh値またはk値のプロットから,ある一つの試験室が棄却限界
値の線に接近した数個のh値またはk値をもたらしていることが示される場合には,測定水準ごとのグル
ープにまとめ直したプロットを調べることが望ましい。試験室ごとのグループにまとめたプロットで大き
いと見てとれる値が,同じ測定水準の他の試験室と相応に一致していることがよくあるものである。その
値が他の試験室と際だって異なっている場合には,その理由を探すことが望ましい。
7.3.1.7
これらのh値とk値のグラフに加え,セル平均とセル範囲のヒストグラムは,別個の二つの母集
団の存在などを明らかにすることができる。ここで述べている方法の一般原理は一つの単峰型母集団を仮
定しているので,そのような場合は特別な処理が必要であろう。
7.3.2
数値的な外れ値の検定方法
7.3.2.1
外れ値を扱うために以下の慣例を推奨する。
a) 外れ値を識別するために,7.3.3及び7.3.4で推奨する検定方法を適用する。
− 検定統計量がその5%棄却限界値以下の場合には,その検定の対象を正常なものと認める。
− 検定統計量がその5%棄却限界値より大きく,1%棄却限界値以下の場合には,その検定の対象を
5%外れ値とよび,アスタリスクを一つ (*) 付して示す。
− 検定統計量がその1%棄却限界値を越える場合は,1%外れ値(または統計的外れ値)とよび,ア
スタリスクを二つ (**) 付して示す。
b) 次に,外れ値の原因が,技術的な誤り,例えば,
− 測定の実施における不注意による誤り
− 計算の誤り
− 測定結果を転記するときのちょっとした誤り
− 誤った試料の測定
などによって説明できるかどうかを調査する。
その誤りが,計算や転記のときの誤りならば,その外れ値と疑われた結果を正しい値に訂正するべ
きである。誤りが,誤った試料の測定によるのならば,その結果を正しいセルへ移すべきである。こ
うした訂正のあとで,もう一度外れ値について調べることが望ましい。技術的な誤りであって訂正で
きない結果は実験にふさわしくない“本物の”外れ値として除去することが望ましい。
c) 外れ値のうちで,はずれの説明が付いたものや,外れ試験室に属するものとして除外されたものの残
りがある場合,5%外れ値は正しいものとして,そのまま残し,1%外れ値は,統計解析者が妥当な理
由により残すと判断しない限り除外される。
d) あるセルのデータが,上の手順により,図2の書式Bで除外された場合には,図2の書式Cで対応す
るデータも除外されなければならない。逆の場合も同様である。
15
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.2.2
7.3.3と7.3.4に二つの異なった検定方法を示す。コクランの検定は室内変動の検定であり,最初
に適用することが望ましい。必要ならば,外れ値についての処置を取ったのち,検定を繰り返して適用す
ることが望ましい。もう一つの検定方法(グラッブズの検定)は,主目的が室間変動の検定であるが,(n
>2の場合には)コクランの検定で示唆された大きな室内変動が,そのセル内の唯一つの測定結果に帰因
するかの検定にも用いることができる。
7.3.3
コクラン (Cocbhran) の検定
7.3.3.1
この規格のこの部では,室内分散は試験室が異なっても,ほぼ一定であることを仮定している。
しかし経験によればこのとおりには必ずしもならないことがわかっているので,この検定の目的には,こ
の仮定の妥当性の検定も含まれている。この目的に用いることのできる検定方法は数種類あるが,コクラ
ンの検定が選ばれた。
7.3.3.2
同じ繰り返し数 (n) の測定結果から計算されたp個の標準偏差sについて,コクランの検定統計
量Cは,
∑
=
p
1
2
2max
i
i
S
S
C=
·············································································· (8)
である。ここで,smaxはp個の標準偏差の最大値である。
a) 検定統計量がその5%棄却限界値以下の場合には,その検定の対象を正常なものと認める。
b) 検定統計量がその5%棄却限界値より大きく,1%棄却限界値以下の場合には,その検定の対象を5%
外れ値とよび,アスタリスクを一つ (*) 付して示す。
c) 検定統計量がその1%棄却限界値を越える場合は,1%外れ値(または統計的外れ値)とよび,アスタ
リスクを二つ (**) 付して示す。
コクランの検定の棄却限界値を8.1(表4)に示す。
コクランの検定は図2の書式Cに,個々の測定水準ごとに適用しなければならない。
7.3.3.3
コクランの判定基準は,厳密には,すべての標準偏差が併行条件下で得られた同一個の(n個)
の測定結果から計算される場合に限られている。実際には,この数は,データの欠測または除外によって
変わりうる。しかしながら,この規格のこの部では,適切に組織化された実験においては,1セル当たり
の測定結果の数のばらつきはわずかであり,無視することができるので,大多数のセルの測定結果の数n
を用いてコクランの判定基準を適用してよい,と仮定している。
7.3.3.4
コクランの判定基準は一組の標準偏差のうち最大値のみを検定するものであり,外れ値の片側検
定である。いくつかの標準偏差があまりに小さいと,そのための分散の不均質が検定結果に現れることが
ある。しかしながら,原データの丸めの程度の影響を強く受けたために標準偏差が小さくなることがあり,
小さい標準偏差はあまり信頼できない。さらに,ある試験室が,他の試験室よりも高い精度を達成してい
ることを理由に,除外されることは合理的ではない。従ってコクランの判定基準は適切であると考えられ
る。
7.3.3.5
図2の書式Cでの有意性評価によって,ある試験室の標準偏差が,他の試験室の標準偏差と比べ
て,すべての,または大部分の測定水準で低い値であることが,明らかになることがある。これは,その
試験室が,他よりも低い併行標準偏差で測定している,言い換えると,よい技術および装置によるため,
標準測定方法を変更したため,あるいは標準測定方法を不正確に適用したためかもしれない。このような
場合には,パネルに報告することが望ましく,パネルはその事項についてさらに詳細な調査を行う価値が
あるかどうかを決定することが望ましい(この例は,B.1に記述した実験における試験室番号2である。)。
16
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.3.6
標準偏差の最大値が外れ値として判定されたなら,その値は除外し,残りについて再度コクラン
の検定を行うことが望ましい。この手順は繰り返し可能であるが,検定の前提となっている正規性が,近
似的にも十分でない場合には,除外過多になる場合がしばしばある。ここではコクランの検定の繰返し適
用を,単なる有用な手段として提案しているだけであり,それは複数の外れ値を同時に検定するための統
計的な方法がないためである。コクランの検定は,複数の外れ値のために考えられたものではないので,
結論を出す際には十分な注意を払うことが望ましい。特に,測定水準のうちの一つの水準だけで,2つま
たは3つの試験室が大きな標準偏差を示す場合には,コクランの検定の結論を注意して検討することが望
ましい。一方,一つの試験室が複数の測定水準で外れ値を出しているときは,この試験室の室内分散が異
常に大きいことを強く示していると考えてよく,その試験室のデータ全部を除外することが望ましい。
7.3.4
グラッブズ (Grubbs) の検定
7.3.4.1
外れ値が一つの場合
小さい順に並べたxi (i=1, 2,…,p) について,グラッブズの検定により,その最大値を外れ値かどうか
判定するには,グラッブズの検定統計量Gpを計算する。
s
x
x
G
p
p
/)
(
−
=
········································································ (9)
ここで,
∑
=
p
i
ix
p
x
1
1
=
··········································································· (10)
∑
=
−
−
p
i
ix
x
p
s
1
2)
(
1
1
=
····························································· (11)
である。
最小値が外れ値かどうかを判定するには,つぎの検定統計量を計算する。
s
x
x
G
)
(
1
1
−
=
a) 検定統計量がその5%棄却限界値以下の場合には,その検定の対象を正常なものと認める。
b) 検定統計量がその5%棄却限界値より大きく,1%棄却限界値以下の場合には,その検定の対象を5%
外れ値とよび,アスタリスクを一つ (*) 付して示す。
c) 検定統計量がその1%棄却限界値を越える場合は,1%外れ値(または統計的外れ値)とよび,アスタ
リスクを二つ (**) 付して示す。
7.3.4.2
外れ値が二つの場合
最大値と2番目に大きい値が外れ値かどうかを判定するためには,グラッブズの検定統計量Gを計算す
る。
20
2
,1
s
s
G
p
p−
=
········································································ (12)
ここで,
∑
=
−
p
i
ix
x
s
1
2
20
)
(
=
······································································ (13)
17
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
−
=
−
−
−
2
1
2
,1
2
,1
)
(
p
i
p
p
i
p
p
x
x
s
=
···························································· (14)
∑
−
=
−
−
2
1
,1
2
1
p
i
i
p
p
x
p
x
=
·································································· (15)
である。
逆に,最小値と2番目に小さい値を検定するためには,グラッブズの検定統計量Gは次のように計算さ
れる:
20
22,1
s
s
G=
············································································ (16)
ここで,
∑
=
−
p
i
ix
x
s
3
2
2,1
22,1
)
(
=
·································································· (17)
∑
=
−
p
i
ix
p
x
3
2,1
2
1
=
····································································· (18)
である。
グラッブズの検定の棄却限界値を8.2(表5)に示す。
7.3.4.3
グラッブズの検定の適用
精度評価実験を解析する場合に,グラッブズの検定を以下の場合に適用することができる。
a) ある測定水準jにおける,セル平均値(図2の書式B)への適用。
このときには,
ij
iy
x=
及び
p=pj
である。ここで,jは,(測定の水準を表しているので)一定値である。
一つの測定水準のデータに対して,外れ値が一つの場合のグラッブズの検定を,7.3.4.1に従ってセ
ル平均値に適用する。この検定で,セル平均値が外れ値であることが示されるなら,それを除外し,
セル平均の反対側の極値に対して(すなわち,最大値が外れ値であるなら,その最大値を除外し,最
小値に対して),グラッブズの検定を繰り返すが,この場合には,7.3.4.2に記述した外れ値が片側の二
つの場合のグラッブズの検定は適用しない。もし最初のグラッブズの検定が最大値と最小値をともに
外れ値と見なさないときには,7.3.4.2で示した外れ値が二つの場合の検定を適用する。
b) コクランの検定で,セル内の標準偏差が疑わしいと示唆されたセル内の測定結果への適用。
7.4
一般平均と分散の計算
7.4.1
統計解析の方法
この規格のこの部で採用された統計解析の方法は,個々の測定水準mと精度を別々に推定するものであ
る。計算結果は個々の測定水準jごとに表に示す。
7.4.2
基本データ
18
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
計算に必要な基本データは図2に示す三つの表,
− 表Aには原測定結果が,
− 表Bにはセル内の平均値が,
− 表Cにはセル内のばらつきの尺度が,
示されている。
7.4.3
空でないセル
7.3.2.1のd)に記述した規則に従い,計算に用いられる空でないセルの数は,それぞれの測定水準につい
て,常に表BとCで同じになる。データの欠測により,表Aに測定結果が一つだけのセルがある場合に
は,例外が生じ,表Cは空のセルになるが,表Bは空でない。こうした場合,
a) その単独の測定結果を除外して,表B及び表Cをともに空のセルとする
b) 除外することが情報の不本意な損失になると考えるのならば,表Cの該当欄にダッシュ (−) を記入
する
ことが可能である。
空でないセルの数は,測定水準が異なると異なり,故にpjの添字jが相違する。
7.4.4
一般平均mの計算
測定水準jについて,一般平均は,
∑
∑
=
=
p
i
ij
p
i
ij
ij
j
j
n
y
n
y
m
1
1
^
=
=
·································································· (19)
となる。
7.4.5
分散の計算
個々の測定水準ごとに三つの分散を計算する。これは,併行分散,室間分散と(室間)再現分散である。
7.4.5.1
併行分散は,
∑
∑
=
=
−
−
p
i
ij
p
i
ij
ij
rj
n
s
n
s
1
1
2
2
)1
(
)1
(
=
··································································· (20)
である。
7.4.5.2
室間分散は,
j
rj
dj
j
n
s
s
s
2
2
2L
−
=
·········································································· (21)
である。ここで,
∑
∑
∑
=
=
−
−
−
−
p
i
p
i
p
i
ij
j
ij
ij
j
ij
ij
dj
n
y
y
n
p
y
y
n
p
s
1
1
1
2
2
2
2
)
(
)
(
1
1
)
(
1
1
=
=
·············· (22)
19
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−
−∑
∑
∑
=
=
=
p
i
p
i
ij
p
i
ij
ij
j
n
n
n
p
n
1
1
1
2
1
1
=
························································· (23)
である。
これらの計算手順は附属書BのB.1及びB.3に例で説明される。
7.4.5.3
すべてのnijについて,nij=n=2が成立する特別な場合は,より簡単な式,
∑
=
−
p
i
ij
ij
rj
y
y
p
s
1
2
2
1
2
)
(
2
1
=
∑
=
−
−
−
p
i
rj
j
ij
j
s
y
y
p
s
1
2
2
2L
2
)
(
1
1
=
を用いてよい。
これらはB.2の例で説明される。
7.4.5.4
確率変数であるために,この計算で得られる2Lj
sが負の値になる場合には,それを0とすること
が望ましい。
7.4.5.5
(室間)再現精度は,
2L
2
2R
j
rj
j
s
s
s
+
=
·········································································· (24)
である。
7.4.6
分散のmへの従属性
次に,精度がmに従属しているかを検討することが望ましい。従属している場合には関係を表す関数を
求めることが望ましい。
7.5
精度の値と測定水準mの関数関係の検討
7.5.1
精度とmとの間に規則的な関数関係が存在するとは限らない。試料の不均質性が測定結果の変動
の不可分な要素になっている場合には,この不均質性が,測定水準mの規則的な関数である場合にのみ,
関数関係が存在することになる。組成が異なり,かつ異なる生産プロセスによる固体試料の場合,規則的
な関数関係の成立は全く不確かである。以下の手順を適用する前に,この点を解決しておくことが望まし
い。そうでない場合は,実験の対象となった個々の試料について,精度の値を別々に推定しなければなら
ないであろう。
7.5.2
7.5.3〜7.5.9では,論拠と手順を,簡潔さのために併行標準偏差についてのみ記述するが,これは
併行標準偏差と(室間)再現標準偏差の両者に適用される。ここで考察する関数関係は3種類だけである。
I
: sr=bm
(原点を通る直線)
II : sr=a+bm
(正の切片をもつ直線)
III : lgsr=c+dlgm(又はsr=Cmd);d≦1
(指数的な関数関係)
たいていの場合,この関数関係の一つが満足なあてはめをもたらすことが期待できる。そうでない場合
には,統計解析者は,これに代わる解を求めることが望ましい。混乱を避けるためには,式中に現れるa,
b,c,C及びdには,併行条件の場合ならばar,br,…,再現条件ならばaR,bR…と添え字をつけて区別す

20
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
るが,ここでは表記の簡略化のために省略している。srも測定水準jを表す添え字だけを残して簡単にs
とした。
7.5.3
関数関係IとIIIはm=0のときs=0となるため,一般にd>0である。これは実験上の観点からは
受容できないように見える。報告するときには,精度のデータは試験室間共同実験を行った測定水準の範
囲内でのみ適用できることを明示しておくことが望ましい。
7.5.4
a=0かつd=1のとき,3種類の関数はすべて同じになる。したがって,aが0の近傍にあり,ま
たdが1の近傍にあるときには,これらの関数のうちの二つまたは三つとも実用上同程度に適合する。そ
のような場合には,以下の単純な原則を満たすので,関数Iを選ぶことが好ましい。
“二つの測定結果が (100b) %以上異なるときは,疑わしいと考えられる。”
統計的に表現すると,これは変動係数 (100s/m) が,あらゆる測定水準で一定であることを意味してい
る。
7.5.5
j
m
^に対するsjのプロット,またはlg
j
m
^に対するlg sjのプロットで,その点の組が無理なく直線近
傍に存在することがわかる場合には,手で引いた線で十分な解となり得る;しかし,別な理由で,数値的
なあてはめが好ましいときは,関数関係IとIIは7.5.6の手順による,関数IIIは7.5.8の手順によることを
推奨する。
7.5.6
統計学的には,直線へのあてはめは,
j
m
^及びsjが推定値であるため誤差を伴うという事実により
複雑になる。しかし,傾きbは通常小さい(0.1のオーダー,又はそれ以下)ので,
j
m
^の誤差はほとんど
影響せずsjの推定の誤差が支配的である。
7.5.6.1
sの標準誤差はsjの予測値 (ŝj) に比例するため,回帰直線の良好な推定には加重回帰が必要であ
る。
重みは1/(ŝj)2に比例する。ここではŝj測定水準jにおける併行標準偏差の予測値である。しかし,ŝjは計
算されているパラメータに依存している。
残差の重み付き最小二乗法で推定値を求める数学的に正しい手順は複雑になるであろう。実用的には十
分であることが証明されている手順を以下に推奨する。
7.5.6.2
1/(ŝNj)2に等しい重みWjを用いる。ここでN=0,1,2,…は逐次反復の回を表す。計算式は,
∑
j
j
W
T=
1
∑
j
j
jm
W
T
^
2=
∑
j
j
jm
W
T
2
^
3=
∑
j
j
js
W
T=
4
である。このとき,関数関係I (s=bm) の場合,bの値はT5/T3で与えられる。関数関係II (S=a+bm) の
場合,
−
−
2
2
3
1
5
2
4
3
T
T
T
T
T
T
T
a=
····································································· (25)
21
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−
−
2
2
3
1
4
2
5
1
T
T
T
T
T
T
T
b=
····································································· (26)
となる。
7.5.6.3
関数関係Iの場合,重みWj=1/(ŝj)2にŝj=b^j
mを代入すると,次のように表現は簡単になる:
q
m
s
b
j
j
j
∑
)
/
(
^
=
······································································ (27)
しかも反復は不要である。
7.5.6.4
関数関係IIの場合,7.4で得られたsの最初の値が初期値ŝojである。これを計算に用いると
W0j=1/(ŝ0j)2 (j=1, 2,…,q)
であり,7.5.6.2に従ってa1及びb1を計算する。
これから
ŝ1j=a1+b1^j
m
が求められる。次にW1j=1/(ŝ1j)2として計算を繰り返すと
ŝ2j=a2+b2
j
m^
となる。
これらの式から得られるW2j=1/(ŝ2j)2を用いて,再度,同じ手順を繰り返すこともできるが,意味のない
変化が生じるだけである。W0jからW1へステップは重みのなかの大きな誤差を排除するのに有効であり,
ŝ2jに関する式は,最終のものと考えることが望ましい。
7.5.7
lg sの標準誤差はsに依存せず,lg
^
j
mに対するlg sの重みなしの回帰が適当である。
7.5.8
関数関係IIIの場合,計算式は
∑
j
m
T
j
^
1
lg
=
∑
j
m
T
2
j
^
2
)
(lg
=
∑
j
js
T
lg
3=
)
lg
(
)
(lg
2
j
^
4∑
j
js
m
T=
となる。したがって,
−
−
21
2
4
1
3
2
T
qT
T
T
T
T
c=
····································································· (28)
−
−
2
1
2
3
1
4
T
qT
T
T
qT
d=
······································································ (29)
である。

22
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.5.9
同じデータについて,関数関係I,II及びIIIをあてはめた例を7.5.9.1〜7.5.9.3に示す。データは計
算手順を説明する目的だけのためにB.3の事例から取ったものである。このデータはB.3でさらに議論す
る。
7.5.9.1
関数関係Iをあてはめた例を表1に示す。
表1 関数関係I : s=bm
j
m
3,94
8,28
14,18
15,59
20,41
sj
0,092
0,179
0,127
0,337
0,393
j
jm
s
^
/
0,023 4
0,021 6
0,008 9
0,021 6
0,019 3
q
m
s
b
j
j
j
∑
^)
/
(
=
019
,0
5
8
0094
,0
=
s=bm
0,075
0,157
0,269
0,296
0,388
参考 表の中では小数点としてコンマ (, ) を用いている。
7.5.9.2
関数関係IIをあてはめた例を表2に示す(
^
j
m,sjは7.5.9.1に示したものである)。
表2 関数関係II : s=a+bm
W0j
118
31
62
8,8
6,5
s1=0,058+0,009 0m
ŝ1j
0,093
0,132
0,185
0,197
0,240
W1j
116
57
29
26
17
s2=0,030+0,0156m
ŝ2j
0,092
0,159
0,251
0,273
0,348
W2j
118
40
16
13
8
s3=0,032+0,0154m
ŝ3j1)
0,093
0,160
0,251
0,273
0,348
備考 重みの値は有意ではない;有効数字は2桁で十分である。
1) s2からの差は無視できる。
参考 表の中では小数点としてコンマ (, ) を用いている。
7.5.9.3
関数関係IIIをあてはめた例を表3に示す。
表3 関数関係III : lgs=c+dlgm
lg
^
j
m
+0,595
+0,918
+1,152
+1,193
+1,310
lgs0j
−1,036
−0,747
−0,896
−0,472
−0,406
lgs=−1,506 5+0,772 lgm
又はs=0,031m0.77
s
0,089
0,158
0,239
0,257
0,316
参考 表の中では小数点としてコンマ(, )を用いている。
7.6
統計解析の段階的な手順
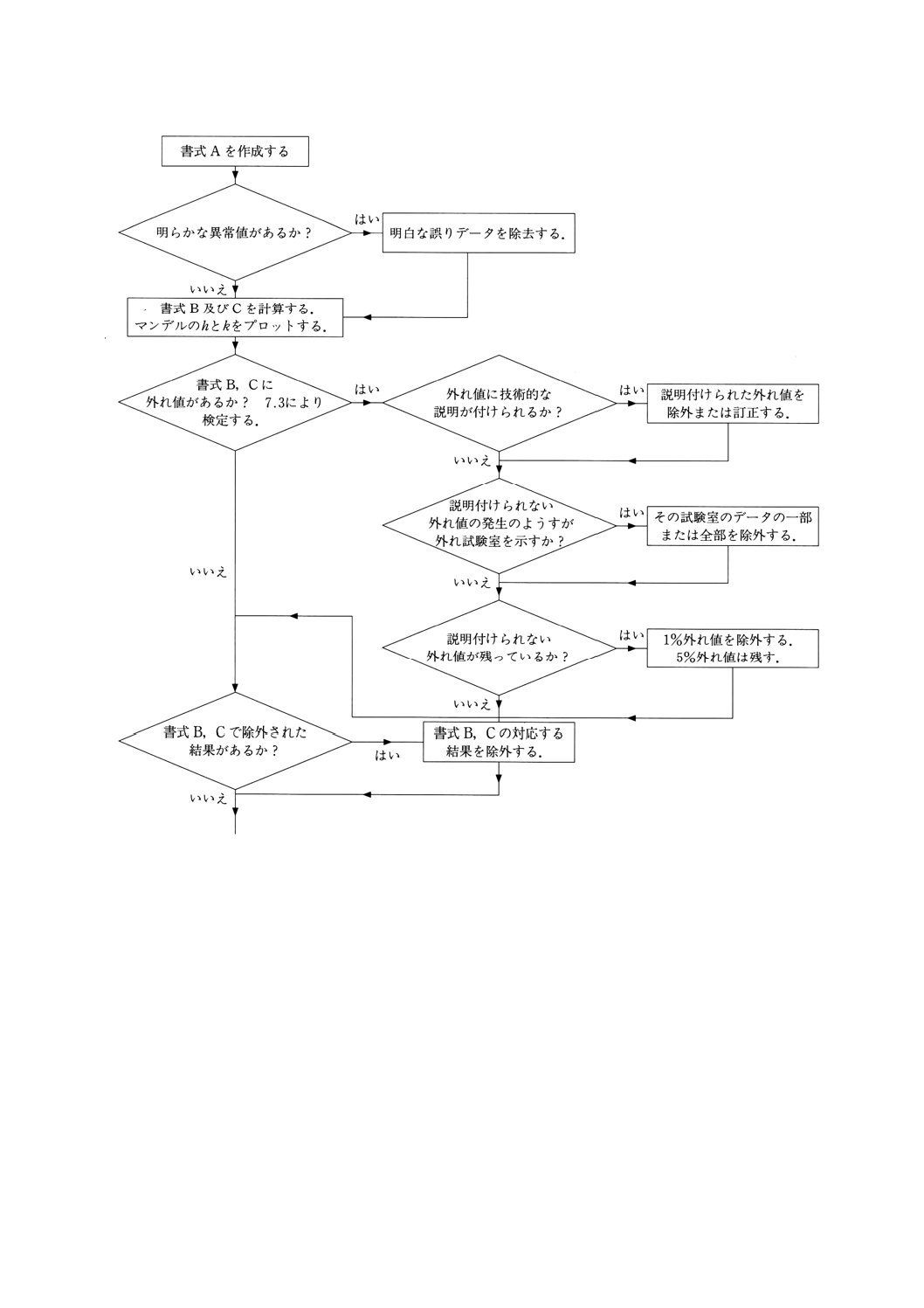
備考5. 7.6に記述する手順を図3に段階的に示す。
7.6.1
得られたすべての測定結果を一つの書式,図2の書式A(7.2参照)に集める。i=1,2,…,p(デ
ータを提供したp個所の試験室を表す。)のp行,j=1,2,…,q(昇順に並べたq個の測定水準を表す)
のq列の配列にしてあるこの書式を推奨する。
一様水準の実験では,書式Aのセル内の測定結果を区別する必要はないので,いかなる順に並べても差
し支えない。
23
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.6.2
書式Aについて明らかな異常を調査し,必要ならば,誤りが明らかなデータ(例えば,装置の測
定範囲を越えたデータや技術的理由であり得ないデータ)を除去し,パネルに報告する。ある特定の試験
室,または特定のセルの測定結果が,他のデータと整合してないことが一見して明らかな場合がよくある。
このような明らかに不整合なデータは,即座に除去することが望ましく,このことを,将来の考察のため
にパネルに報告されねばならない(7.7.1参照)。
7.6.3
必要ならば7.6.2にしたがって訂正の後,書式Aから,セル平均値の書式Bとセル内ばらつきの尺
度の書式Cを計算する。
書式Aで測定結果が一つだけのセルがあれば,7.4.3の選択肢の一つを採用する。
7.6.4
7.3.1に記述したマンデルのhとkのプロットを作成し,データの一致性を調べる。これらのプロ
ットは以後のデータ解析のために,データの妥当性や外れ値,外れ試験室の可能性を示唆するであろう。
しかし,この段階ではいかなる決定的な処置をとらずに,7.6.5〜7.6.9の手順が完了するまで保留とする。
7.6.5
書式B及び書式Cについて(図2参照),測定水準ごとに外れ値の有無を点検する[7.3.2.1のa)
を参照]。7.3で述べた統計的検定をすべての疑わしい値に適用し,5%外れ値にアスタリスク一つ,1%外
れ値にはアスタリスク二つを付ける。外れ値がない場合には,7.6.6〜7.6.10の手順を無視し,直ちに7.6.11
の手順に進む。
7.6.6
外れ値について,何か技術的な説明があるか,又は説明がありそうかを調べ,可能ならば,その説
明を実証する。十分に説明が付いた外れ値は,必要に応じ,訂正または除去し,これに応じた訂正を書式
BとCに適用する。説明が付けられない外れ値が残らなければ,7.6.7〜7.6.10の手順を無視し,直ちに7.6.11
の手順に進む。
備考6. 外れ値が数多く存在する場合,これは分散の非一様性や試験室間の差異が大きいことを
示しているかもしれず,測定方法の適切さに問題があるかもしれない。このことはパネ
ルに報告することが望ましい。
7.6.7
書式Bまたは書式Cの中の,説明されていない外れ値の発生のようすが,外れ試験室(7.2.5参照)
の存在を示唆していないならば,7.6.8の手順を無視して,直ちに7.6.9の手順に進む。
7.6.8
その試験室が外れ試験室であるという疑いに対する根拠が,その試験室のデータの全部あるいは一
部を除外することを十分に正当化するに足ると考えられるならば,それらのデータを除外し,パネルに報
告する。
試験室のデータの全部あるいは一部を除外するかどうかの決定は解析を行っている統計解析者の責任で
あるが,将来の検討のために必ずパネルに報告しなければならない。
7.6.9
説明がつかず,又は外れ試験室に帰因しない外れ値が残る場合には,1%外れ値は除外するが,5%
外れ値は正しいものとしてそのまま残す。
24
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3 統計解析の主要手順のフローダイヤグラム
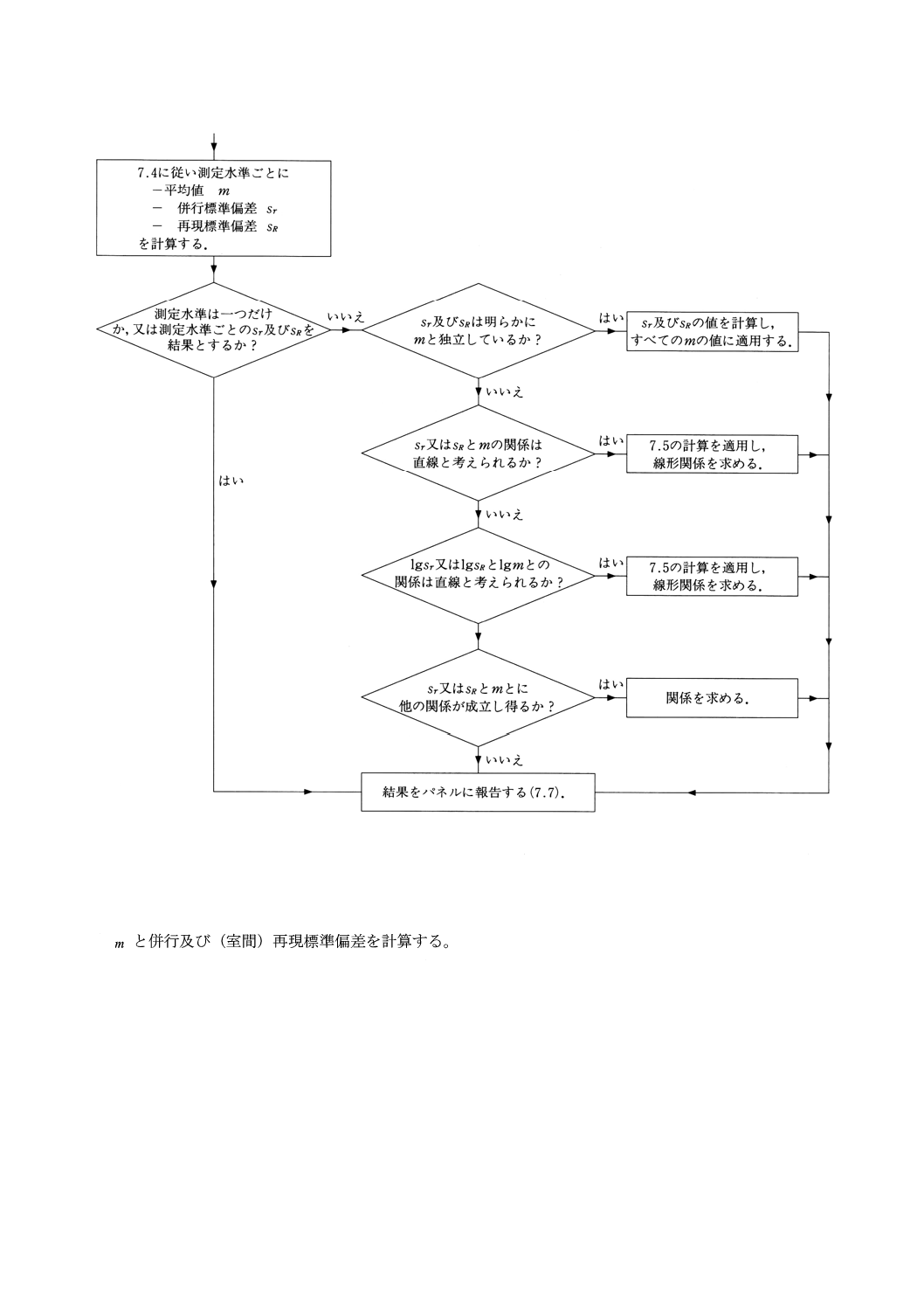
25
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3 統計解析の主要手順のフローダイヤグラム(続き)
7.6.10 これまでの手順で,書式Bに空のセルが生じたならば,書式Cの対応するセルも空にする。逆も
同様である。
7.6.11 書式B及びCで正しいものとして残された結果から,7.4に示した手順で,測定水準ごとに,平均
値
j
m^と併行及び(室間)再現標準偏差を計算する。
7.6.12 一つの測定水準だけで行われた実験や,併行及び(室間)再現標準偏差を測定水準の関数ではなく,
測定水準ごとに設定することが望ましい(7.5.1参照)と判断された場合には,7.6.13〜7.6.17の手順を無視
し,直ちに7.6.19に進む。
備考7. 以下の7.6.13〜7.6.17の手順はsr及びsRに対して別々に適用されるが,簡略化のため,sr
について詳述する。

26
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.6.13 sjを
j
m^に対しプロットし,このプロットからsがmに従属しているかどうかを判断する。sがmに
従属すると考えられる場合は7.6.14の手順を無視し,7.6.14の手順に進む。疑わしい場合には両方の場合
について計算し,パネルに決定させる。この問題を解くために適切で有用な統計的な検定方法は存在しな
いが,測定方法に習熟した技術専門家は,決定を下すのに十分な経験を積んでいることが望ましい。
7.6.14 併行標準偏差の最終の値として,∑
r
j
q
s
s=
1
を用いる。手順7.6.15〜7.6.18を無視して,直ちに手順7.6.19
に進む。
7.6.15 7.6.13のプロットからsとmとの関係が直線によって表されるかどうかを判断し,直線の場合には,
関数関係I (s=bm),または関数関係II (s=a+bm) のどちらが適切かを判定する(7.5.2を参照)。手順7.5.6
によりパラメータb,または二つのパラメータaとbを求める。この直線関係が満足いくものと考えられ
るなら,手順7.6.16を無視して直ちに手順7.6.17に進む。そうでない場合は7.6.16に進む。
7.6.16 lgsjをlg
j
m^に対しプロットし,このプロットからlgsとlgmとの関係が無理なく直線で表されるか
どうかを判定する。これが妥当と考えられるなら7.5.8に示した手順により,関数III (lgs=c+dlgm) をあ
てはめる。
7.6.17 手順7.6.15または7.6.16で満足のいく関数関係が成立したならば,与えられたmの値に対する関
係から得られる滑らかな値をsr(またはsR)の最終の値とする。手順7.6.18を無視し,手順7.6.19に進む。
7.6.18 手順7.6.15と7.6.16のいずれでも満足いく関係が得られなかった場合には,統計解析者はsとm
との間に何か別な関係が成立し得るかどうか,またはその代わりに,データがあまりに不規則なため関数
関係の成立はあり得ないと考えられるかどうかを判断する。
7.6.19 基本データと統計解析から得られた結果及び結論を示す報告書を作成し,これをパネルへ提出する。
7.3.1のグラフィカルな表現は結果の一致やばらつきを示すのに有用であろう。
7.7
パネルへの報告書とパネルによる決定事項
7.7.1
統計解析者による報告書
統計解析が完了したのち,統計解析者は報告書を書き,パネルへ提出することが望ましい。この報告書
には以下の情報が与えられていることが望ましい。
a) 測定方法の規定内容についてオペレータ及び/または監督者から受理した所見に関わる一切の報告;
b) 手順7.6.2及び7.6.8で外れ試験室として除外された試験室に関わる一切の報告;
c) 発見された外れ値,及びこれらが説明付けられ,訂正されたか,または除外されたかに関わる一切の
報告;
d)
j
m^,sr及びsRに関する最終書式,並びに手順7.6.13,7.6.15または7.6.16で到達した結論に関わる報
告と,これらの手順で推奨されたプロットによる説明;
e) 統計解析で用いた書式A,B及びC(図2),付録にするのもよい。
7.7.2
パネルのとるべき決定
パネルはこの報告書を議論し,以下の質問に関して決定を下すことが望ましい。
a) 不整合な測定結果,外れ値があるか?もしあれば,それは標準測定方法の記述の欠陥に起因するか?
b) 外れ試験室として除外された試験室に対し,どのような処置をとることが望ましいか?
c) 外れ試験室の結果及び/または,オペレータ及び/または監督者から受理した意見は,標準測定方法
を改善する必要性を示しているか?その場合,どのような改善が必要か?
d) 精度評価実験の結果は併行標準偏差及び(室間)再現精度の値の決定を正当化するか?その場合,そ
の値はいくらで,どのような形で公表し,かつその精度データの適用範囲は?
7.7.3
完全な報告書
27
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
精度評価実験の実施の理由と組織化について記述する報告書は,統計解析者による報告,及び合意に達
した結論を含め,パネルの承認を受けるために実行委員により作成されることが望ましい。一致性やばら
つきに関する多少の図解表示は多くの場合,有用である。報告書は,精度評価試験を承認する責任を持つ
組織・機関及び他の関係組織・機関に回付することが望ましい。
8. 統計数値表
8.1
コクランの検定の棄却限界値(7.3.3を参照)を表4に示す。
8.2
グラッブズの検定の棄却限界値(7.3.4を参照)を表5に示す。
外れ値が一つの場合のグラッブズの検定では,表の1%及び5%より大きい値となったものが,それぞれ
5%外れ値及び1%外れ値である。
外れ値が二つの場合のグラッブズの検定では,表の1%及び5%より小さい値となったものが,それぞれ
5%外れ値及び1%外れ値である。
8.3
マンデルのh及びh統計量(7.3.1を参照)に関する指標の値を表6及び表7に示す。
表4 コクランの検定の棄却限界値
p
n=2
n=3
n=4
n=5
n=6
1%
5%
1%
5%
1%
5%
1%
5%
1%
5%
2
−
−
0,995
0,975
0,979
0,939
0,959
0,906
0,937
0,877
3 0,993
0,967
0,942
0,871
0,883
0,798
0,834
0,746
0,793
0,707
4 0,968
0,906
0,864
0,768
0,781
0,684
0,721
0,629
0,676
0,590
5 0,928
0,841
0,788
0,684
0,696
0,598
0,633
0,544
0,588
0,506
6 0,883
0,781
0,722
0,616
0,626
0,532
0,564
0,480
0,520
0,445
7 0,838
0,727
0,664
0,561
0,568
0,480
0,508
0,431
0,466
0,397
8 0,794
0,680
0,615
0,516
0,521
0,438
0,463
0,391
0,423
0,360
9 0,754
0,638
0,573
0,478
0,481
0,403
0,425
0,358
0,387
0,329
10
0,718
0,602
0,536
0,445
0,447
0,373
0,393
0,331
0,357
0,303
11
0,684
0,570
0,504
0,417
0,418
0,348
0,366
0,308
0,332
0,281
12
0,653
0,541
0,475
0,392
0,392
0,326
0,343
0,288
0,310
0,262
13
0,624
0,515
0,450
0,371
0,369
0,307
0,322
0,271
0,291
0,243
14
0,599
0,492
0,427
0,352
0,349
0,291
0,304
0,255
0,274
0,232
15
0,575
0,471
0,407
0,335
0,332
0,276
0,288
0,242
0,259
0,220
16
0,553
0,452
0,388
0,319
0,316
0,262
0,274
0,230
0,246
0,208
17
0,532
0,434
0,372
0,305
0,301
0,250
0,261
0,219
0,234
0,198
18
0,514
0,418
0,356
0,293
0,288
0,240
0,249
0,209
0,223
0,189
19
0,496
0,403
0,343
0,281
0,276
0,230
0,238
0,200
0,214
0,181
20
0,480
0,389
0,330
0,270
0,265
0,220
0,229
0,192
0,205
0,174
21
0,465
0,377
0,318
0,261
0,255
0,212
0,220
0,185
0,197
0,167
22
0,450
0,365
0,307
0,252
0,246
0,204
0,212
0,178
0,189
0,160
23
0,437
0,354
0,297
0,243
0,238
0,197
0,204
0,172
0,182
0,155
24
0,425
0,343
0,287
0,235
0,230
0,191
0,197
0,166
0,176
0,149
25
0,413
0,334
0,278
0,228
0,222
0,185
0,190
0,160
0,170
0,144
26
0,402
0,325
0,270
0,221
0,215
0,179
0,184
0,155
0,164
0,140
27
0,391
0,316
0,262
0,215
0,209
0,173
0,179
0,150
0,159
0,135
28
0,382
0,308
0,255
0,209
0,202
0,168
0,173
0,146
0,154
0,131
29
0,372
0,300
0,248
0,203
0,196
0,164
0,168
0,142
0,150
0,127
30
0,363
0,293
0,241
0,198
0,191
0,159
0,164
0,138
0,145
0,124
31
0,355
0,286
0,235
0,193
0,186
0,155
0,159
0,134
0,141
0,120
32
0,347
0,280
0,229
0,188
0,181
0,151
0,155
0,131
0,138
0,117
28
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p
n=2
n=3
n=4
n=5
n=6
1%
5%
1%
5%
1%
5%
1%
5%
1%
5%
33
0,339
0,273
0,224
0,184
0,177
0,147
0,151
0,127
0,134
0,114
34
0,332
0,267
0,218
0,179
0,172
0,144
0,147
0,124
0,131
0,111
35
0,325
0,262
0,213
0,175
0,168
0,140
0,144
0,121
0,127
0,108
36
0,318
0,256
0,208
0,172
0,165
0,137
0,140
0,118
0,124
0,106
37
0,312
0,251
0,204
0,168
0,161
0,134
0,137
0,116
0,121
0,103
38
0,306
0,246
0,200
0,164
0,157
0,131
0,134
0,113
0,119
0,101
39
0,300
0,242
0,196
0,161
0,154
0,129
0,131
0,111
0,116
0,099
40
0,294
0,237
0,192
0,158
0,151
0,126
0,128
0,108
0,114
0,097
p=与えられた測定水準での試験室の数
n=セルあたりの測定結果の数(7.3.3.3参照)
参考 表の中では小数点としてコンマ (, ) を用いている。
表5 グラッブズの検定の棄却限界値
p
外れ値が一つの場合
外れ値が二つの場合
1%
5%
1%
5%
3
1,155
1,155
−
−
4
1,496
1,481
0,000 0
0,000 2
5
1,764
1,715
0,001 8
0,009 0
6
1,973
1,887
0,011 6
0,034 9
7
2,139
2,020
0,030 8
0,070 8
8
2,274
2,126
0,056 3
0,110 1
9
2,387
2,215
0,085 1
0,149 2
10
2,482
2,290
0,115 0
0,186 4
11
2,564
2,355
0,144 8
0,221 3
12
2,636
2,412
0,173 8
0,253 7
13
2,699
2,462
0,201 6
0,283 6
14
2,755
2,507
0,228 0
0,311 2
15
2,806
2,549
0,253 0
0,336 7
16
2,852
2,585
0,276 7
0,360 3
17
2,894
2,620
0,299 0
0,382 2
18
2,932
2,651
0,320 0
0,402 5
19
2,968
2,681
0,339 8
0,421 4
20
3,001
2,709
0,358 5
0,439 1
21
3,031
2,733
0,376 1
0,455 6
22
3,060
2,758
0,392 7
0,471 1
23
3,087
2,781
0,408 5
0,485 7
24
3,112
2,802
0,423 4
0,499 4
25
3,135
2,822
0,437 6
0,512 3
26
3,157
2,841
0,451 0
0,524 5
27
3,178
2,859
0,463 8
0,536 0
28
3,199
2,876
0,475 9
0,547 0
29
3,218
2,893
0,487 5
0,557 4
30
3,236
2,908
0,498 5
0,567 2
31
3,253
2,924
0,509 1
0,576 6
32
3,270
2,938
0,519 2
0,585 6
33
3,286
2,952
0,528 8
0,594 1
34
3,301
2,965
0,538 1
0,602 3
35
3,316
2,979
0,546 9
0,610 1
36
3,330
2,991
0,555 4
0,617 5
37
3,343
3,003
0,563 6
0,624 7
29
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p
外れ値が一つの場合
外れ値が二つの場合
1%
5%
1%
5%
38
3,356
3,014
0,571 4
0,631 6
39
3,369
3,025
0,578 9
0,638 2
40
3,381
3,036
0,586 2
0,644 5
アメリカ統計学会から許可を得て,附属書Cの参考
文献[4]から転載。
p=与えられた水準での試験室の数
参考 外れ値が一つの場合,表の値よりも大きければ有意。外れ値が二つの場合,表の値よりも小さ
ければ有意。
なお,表の中では小数点としてコンマ(, )を用いている。
表6 有意水準1%におけるマンデルの
h及びk統計量に関する指標の値
p
h
k
n
2
3
4
5
6
7
8
9
10
3 1,15 1,71 1,64 1,58 1,53 1,49 1,46 1,43 1,41 1,39
4 1,49 1,91 1,77 1,67 1,60 1,55 1,51 1,48 1,45 1,43
5 1,72 2,05 1,85 1,73 1,65 1,59 1,55 1,51 1,48 1,46
6 1,87 2,14 1,90 1,77 1,68 1,62 1,57 1,53 1,50 1,47
7 1,98 2,20 1,94 1,79 1,70 1,63 1,58 1,54 1,51 1,48
8 2,06 2,25 1,97 1,81 1,71 1,65 1,59 1,55 1,52 1,49
9 2,13 2,29 1,99 1,82 1,73 1,66 1,60 1,56 1,53 1,50
10 2,18 2,32 2,00 1,84 1,74 1,66 1,61 1,57 1,53 1,50
11 2,22 2,34 2,01 1,85 1,74 1,67 1,62 1,57 1,54 1,51
12 2,25 2,36 2,02 1,85 1,75 1,68 1,62 1,58 1,54 1,51
13 2,27 2,38 2,03 1,86 1,76 1,68 1,63 1,58 1,55 1,52
14 2,30 2,39 2,04 1,87 1,76 1,69 1,63 1,58 1,55 1,52
15 2,32 2,41 2,05 1,87 1,76 1,69 1,63 1,59 1,55 1,52
16 2,33 2,42 2,05 1,88 1,77 1,69 1,63 1,59 1,55 1,52
17 2,35 2,44 2,06 1,88 1,77 1,69 1,64 1,59 1,55 1,52
18 2,36 2,44 2,06 1,88 1,77 1,70 1,64 1,59 1,56 1,52
19 2,37 2,44 2,07 1,89 1,78 1,70 1,64 1,59 1,56 1,53
20 2,39 2,45 2,07 1,89 1,78 1,70 1,64 1,60 1,56 1,53
21 2,39 2,46 2,07 1,89 1,78 1,70 1,64 1,60 1,56 1,53
22 2,40 2,46 2,08 1,90 1,78 1,70 1,65 1,60 1,56 1,53
23 2,41 2,47 2,08 1,90 1,78 1,71 1,65 1,60 1,56 1,53
24 2,42 2,47 2,08 1,90 1,79 1,71 1,65 1,60 1,56 1,53
25 2,42 2,47 2,08 1,90 1,79 1,71 1,65 1,60 1,56 1,53
26 2,43 2,48 2,09 1,90 1,79 1,71 1,65 1,60 1,56 1,53
27 2,44 2,48 2,09 1,90 1,79 1,71 1,65 1,60 1,56 1,53
28 2,44 2,49 2,09 1,91 1,79 1,71 1,65 1,60 1,57 1,53
29 2,45 2,49 2,09 1,91 1,79 1,71 1,65 1,60 1,57 1,53
30 2,45 2,49 2,10 1,91 1,79 1,71 1,65 1,61 1,57 1,53
p=与えられた測定水準における試験室の数
n=その測定水準での個々の試験室内の繰り返し数
備考 Dr J. Mandelにより作成,氏の許可のもとに掲載
参考 表の中では小数点としてコンマ (, ) を用いている。
30
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表7 有意水準5%におけるマンデルの
h及びk統計量に関する指標の値
p
h
k
n
2
3
4
5
6
7
8
9
10
3 1,15 1,65 1,53 1,45 1,40 1,37 1,34 1,32 1,30 1,29
4 1,42 1,76 1,59 1,50 1,44 1,40 1,37 1,35 1,33 1,31
5 1,57 1,81 1,62 1,53 1,46 1,42 1,39 1,36 1,34 1,32
6 1,66 1,85 1,64 1,54 1,48 1,43 1,40 1,37 1,35 1,33
7 1,71 1,87 1,66 1,55 1,49 1,44 1,41 1,38 1,36 1,34
8 1,75 1,88 1,67 1,56 1,50 1,45 1,41 1,38 1,36 1,34
9 1,78 1,90 1,68 1,57 1,50 1,45 1,42 1,39 1,36 1,35
10 1,80 1,90 1,68 1,57 1,50 1,46 1,42 1,39 1,37 1,35
11 1,82 1,91 1,69 1,58 1,51 1,46 1,42 1,39 1,37 1,35
12 1,83 1,92 1,69 1,58 1,51 1,46 1,42 1,40 1,37 1,35
13 1,84 1,92 1,69 1,58 1,51 1,46 1,43 1,40 1,37 1,35
14 1,85 1,92 1,70 1,59 1,52 1,47 1,43 1,40 1,37 1,35
15 1,86 1,93 1,70 1,59 1,52 1,47 1,43 1,40 1,38 1,36
16 1,86 1,93 1,70 1,59 1,52 1,47 1,43 1,40 1,38 1,36
17 1,87 1,93 1,70 1,59 1,52 1,47 1,43 1,40 1,38 1,36
18 1,88 1,93 1,71 1,59 1,52 1,47 1,43 1,40 1,38 1,36
19 1,88 1,93 1,71 1,59 1,52 1,47 1,43 1,40 1,38 1,36
20 1,89 1,94 1,71 1,59 1,52 1,47 1,43 1,40 1,38 1,36
21 1,89 1,94 1,71 1,60 1,52 1,47 1,44 1,41 1,38 1,36
22 1,89 1,94 1,71 1,60 1,52 1,47 1,44 1,41 1,38 1,36
23 1,90 1,94 1,71 1,60 1,53 1,47 1,44 1,41 1,38 1,36
24 1,90 1,94 1,71 1,60 1,53 1,48 1,44 1,41 1,38 1,38
25 1,90 1,94 1,71 1,60 1,53 1,48 1,44 1,41 1,38 1,36
26 1,90 1,94 1,71 1,60 1,53 1,48 1,44 1,41 1,38 1,36
27 1,91 1,94 1,71 1,60 1,53 1,48 1,44 1,41 1,38 1,36
28 1,91 1,94 1,71 1,60 1,53 1,48 1,44 1,41 1,38 1,36
29 1,91 1,94 1,72 1,60 1,53 1,48 1,44 1,41 1,38 1,36
30 1,91 1,94 1,72 1,60 1,53 1,48 1,44 1,41 1,38 1,36
p=与えられた測定水準における試験室の数
n=その測定水準での個々の試験室内の繰り返し数
備考 Dr J. Mandelにより作成,氏の許可のもとに掲載
参考 表の中では小数点としてコンマ (, ) を用いている。
31
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) JIS Z 8402で用いられる記号
a
関係式s=a+bmの切片
A
推定値の不確かさを計算するのに用い
る係数
b
関係式s=a+bmの勾配
B
全平均と試験室の測定値の偏差を表す
成分(かたよりに占める試験室成分)
B0
Bの成分の中で中間精度条件の下では
変わらない,すべての要因
B(1),B(2),など Bの成分の中で中間精度条件で
変化する要因
c
関係式logs=c+dlogmの切片
C,C',C” 検定統計量
Ccrit,C'crit,C”crit
統計的検定の棄却限界値
CDP
確率Pの許容差
CRP
確率Pの許容範囲
d
関係式logs=c+dlogmの勾配
e
測定値の成分中,すべての測定値に生
じている偶然誤差
f
許容範囲の係数
FP (υ1, υ2)
分子の自由度υ1,分母の自由度υ2
のF分布のp分位点
G
グラッブスの検定統計量
h
マンデルの試験室間一致性の検定統計
量
k
マンデルの試験室内一致性の検定統計
量
LCL
下側管理限界(処置限界または警戒限
界)
m
試験特性の一般平均;水準
M
中間精度条件において考慮される因子
の数
N
反復数
n
一つの試験室で一つの水準(すなわち,
セルごと)で得る測定値の数
p
共同実験に参加した試験室数
P
確率
q
共同実験における試験特性の水準数
r
併行精度限界値(許容差)
R
再現精度限界値(許容差)
RM
標準物質
s
標準偏差の推定値
ŝ
標準偏差の予測値
T
ある表示の総和
t
試験対象または群の数
UCL
上側管理限界(処置限界または警戒限
界)
W
重み付き回帰式の計算で用いられる重
み係数
w
一組の測定値の範囲
x
グラッブス検定に用いられるデータ
y
測定値
y
測定値の算術平均
y
測定値の全平均
α
有意水準
β
第二種の過誤の確率
γ
再現標準偏差と併行標準偏差の比
(σR/σr)
⊿
試験室のかたより
^
Δ
⊿の推定値
δ
測定方法のかたより
^
δ
δの推定値
λ
二つの試験室または二つの測定方法間
のかたよりの検出可能な差
μ
試験特性の真値または参照値
υ
自由度
ρ
方法AとBの併行標準偏差間の検出可
能な比
σ
標準偏差の真の値
τ
最終校正からの時間経緯に起因する変
動を表す測定値の成分
φ
方法AとBの試験室間平均平方の平方
根の検出可能な比
χ2p (υ)
自由度υのχ2分布におけるp分位点
32
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
添え字に用いる記号
C
校正法が異なることを示す
E
装置が異なることを示す
i
特定の試験室を示す添え字
I( )
中間精度に関する添え字,かっこ内に
中間精度条件のタイプの識別子を記述
する
j
特定の水準に関する添え字(JIS Z
8402-2)
分析の一群あるいは要因に関する添え
字(JIS Z 8402-3)
k
試験室iにおける水準jのk番目の測定
値を示す添え字
L
試験室間を示す
m
検出可能なかたよりに関する添え字
M
試験試料間を示す
O
オペレーターが異なっていることを示
す
P
確率
r
併行精度
R
再現精度
T
時間が異なることを示す
W
試験室内を示す
1, 2, 3
…
測定値の得られた順序を示す
(1), (2), (3), … 測定値の大きさの順序を示す
33
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考) 精度評価実験の統計解析の例
B.1
例1:石炭中の硫黄分の定量(複数の測定水準,欠測値・外れ値がない場合)
B.1.1 背景
a) 測定方法
質量パーセントで表現された測定結果が得られる石炭中の硫黄分の定量。
b) 出典
Tomkins, S. S., Industrial and Engineering Chemistry[附属書Cの引用文献 [6] を参照]
c) 説明
8試験室が出典に記載された標準測定方法に従って分析を行い,この実験に参加した。試験室1は4
個の測定結果を報告し,試験室5は4ないし5個を報告した。その他は全て3回の測定を行った。
d) グラフによる提示
マンデルのh,kをプロットすべきであるが,この例題では重要なことがほとんどないので,別のグ
ラフによる提示にスペースを譲ることとし,hとkは除外した。マンデルのプロットはB.3の例で完
全に図示し,議論される。
B.1.2 オリジナルデータ
これらのデータは質量% [% (m/m)] を単位として表B.1に,図2の書式A(7.2.8参照)の形式で示され,
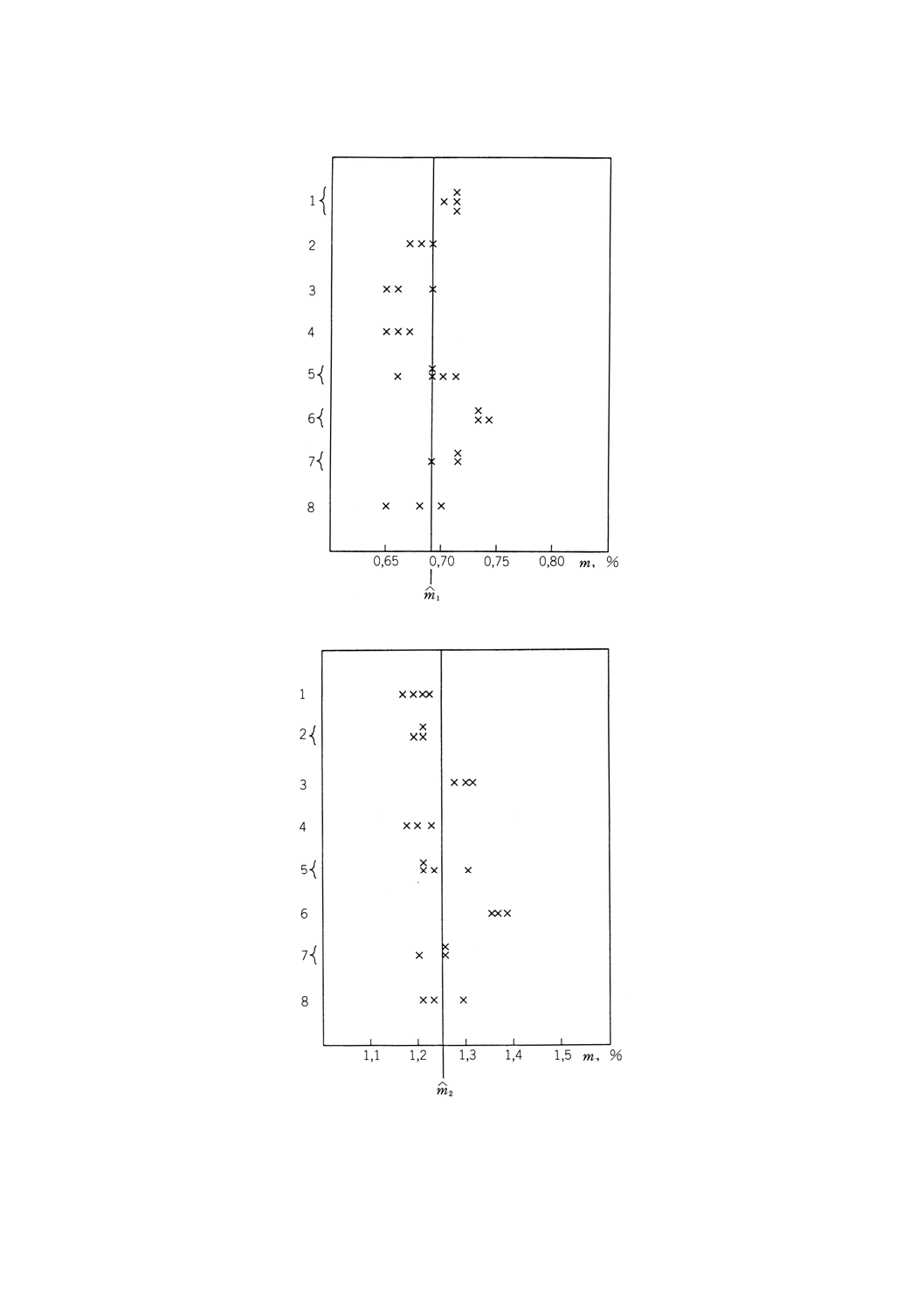
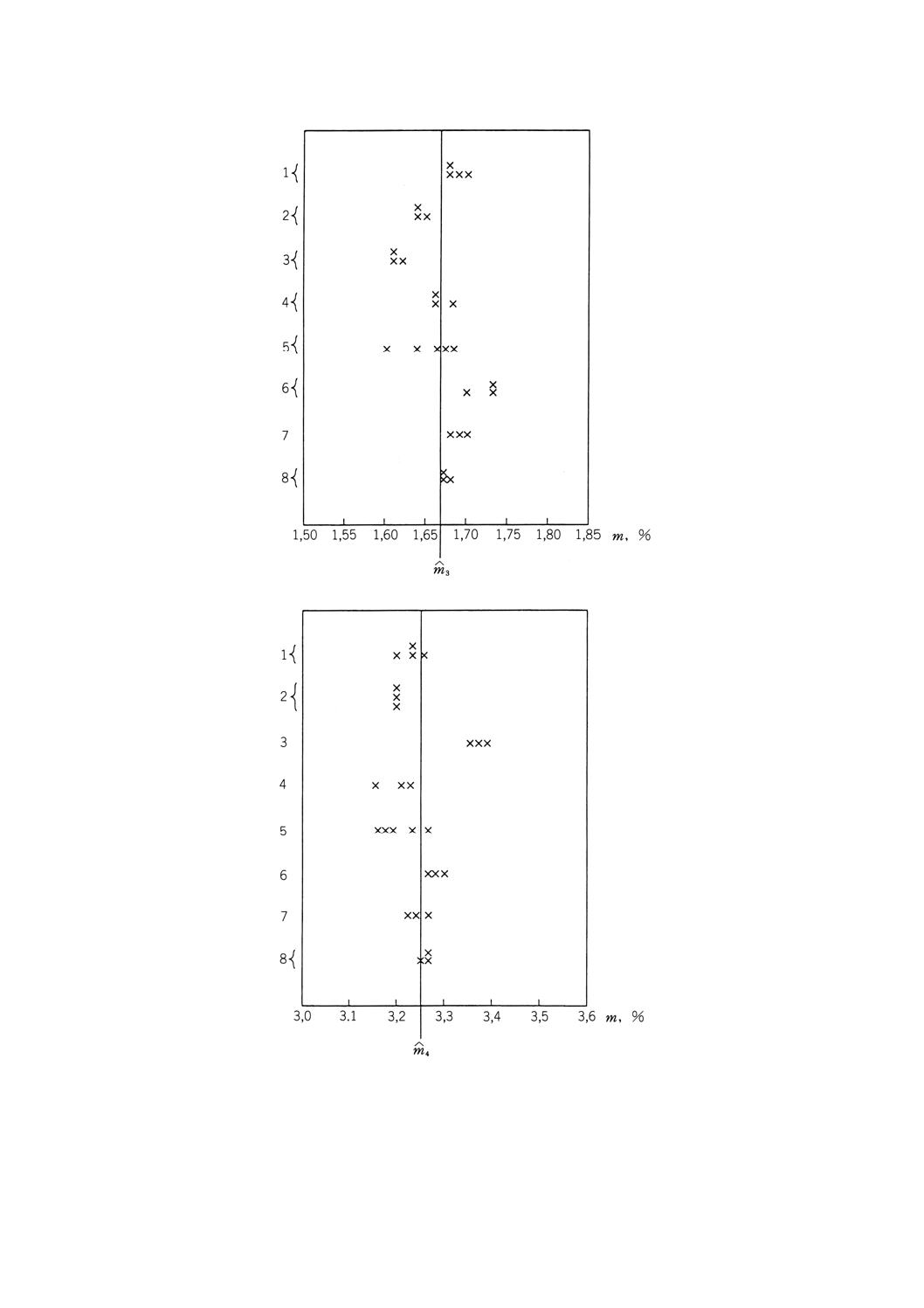
特に問題はない。これらのデータのグラフによる提示は図B.1〜B.4に示されている。
B.1.3 セル平均値
)
(ij
yの計算
セル平均値は質量%[%(m/m)]を単位として表B.2に,図2の書式B(7.2.9参照)の形式で示されている。
B.1.4 標準偏差(sij)の計算
標準偏差は質量% [% (m/m)] を単位として表B.3に,図2の書式C(7.2.10参照)の形式で示されている。
表B.1 オリジナルデータ:石炭中の硫黄分
試験室i
測定水準j
1
2
3
4
1
0,71
1,20
1,68
3,26
0,71
1,18
1,70
3,26
0,70
1,23
1,68
3,20
0,71
1,21
1,69
3,24
2
0,69
1,22
1,64
3,20
0,67
1,21
1,64
3,20
0,68
1,22
1,65
3,20
3
0,66
1,28
1,61
3,37
0,65
1,31
1,61
3,36
0,69
1,30
1,62
3,38
4
0,67
1,23
1,68
3,16
0,65
1,18
1,66
3,22
0,66
1,20
1,66
3,23
5
0,70
1,31
1,64
3,20
0,69
1,22
1,67
3,19
0,66
1,22
1,60
3,18
0,71
1,24
1,66
3,27
0,69
−
1,68
3,24

34
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試験室i
測定水準j
1
2
3
4
6
0,73
1,39
1,70
3,27
0,74
1,36
1,73
3,31
0,73
1,37
1,73
3,29
7
0,71
1,20
1,69
3,27
0,71
1,26
1,70
3,24
0,69
1,26
1,68
3,23
8
0,70
1,24
1,67
3,25
0,65
1,22
1,68
3,26
0,68
1,30
1,67
3,26
参考 表の中では小数点としてコンマ
(, ) を用いている。
備考8
表B.1に引用されている実験では,試験室に何回の測定を行うべきかが指示されておらず,
最少実験回数が示されているのみであった。この規格のこの部で推薦されている手順によれ
ば,試験室1と5に対して,全てのセルの測定結果をちょうど3個に減らすために,ランダムに
データを選ぶべきであった。しかしながら,異なった数の測定結果に対する計算手順を述べ
るために,この例ではすべての結果を捨てないで残すこととした。読者が,
j
m
^,sr,sRの値
に,比較的小さな影響しか与えないということを確かめたいと思うならば,データのランダ
ム選択を行って各セルの測定結果を全て3に減らすとよい。
35
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.1 石炭中の硫黄分 測定水準1
図B.2 石炭中の硫黄分 測定水準2
36
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.3 石炭中の硫黄分 測定水準3
図B.4 石炭中の硫黄分 測定水準4
37
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.2 セル平均:石炭中の硫黄分
試験室i
測定水準j
1
2
3
4
ij
y
nij
ij
y
nij
ij
y
nij
ij
y
nij
1
0,708
4
1,205
4
1,688
4
3,240
4
2
0,680
3
1,217
3
1,643
3
3,200
3
3
0,667
3
1,297
3
1,613
3
3,370
3
4
0,660
3
1,203
3
1,667
3
3,203
3
5
0,690
5
1,248
4
1,650
5
3,216
5
6
0,733
3
1,373
3
1,720
3
3,290
3
7
0,703
3
1,240
3
1,690
3
3,247
3
8
0,677
3
1,253
3
1,673
3
3,257
3
参考 表の中では小数点としてコンマ(, )を用いている。
表B.3 標準偏差:石炭中の硫黄分
試験室i
測定水準j
1
2
3
4
sij
nij
sij
nij
sij
nij
sij
nij
1
0,005
4
0,021
4
0,010
4
0,028
4
2
0,010
3
0,006
3
0,006
3
0,000
3
3
0,021
3
0,015
3
0,006
3
0,010
3
4
0,010
3
0,025
3
0,012
3
0,038
3
5
0,019
5
0,043
4
0,032
5
0,038
5
6
0,006
3
0,015
3
0,017
3
0,020
3
7
0,012
3
0,035
3
0,010
3
0,021
3
8
0,025
3
0,042
3
0,006
3
0,006
3
参考 表の中では小数点としてコンマ (, ) を用いている。
B.1.5 一致性と外れ値の精査
n=3,p=8試験室の場合のコクランの検定では,棄却限界値は5%のとき0.516,1%のとき0.615である。
測定水準1では,sの最大値は試験室8で:Σs2=0.001 82;検定統計値=0.347
測定水準2では,sの最大値は試験室5で:Σs2=0.006 36;検定統計値=0.287
測定水準3では,sの最大値は試験室5で:Σs2=0.001 72;検定統計値=0.598
測定水準4では,sの最大値は試験室4で:Σs2=0.004 63;検定統計値=0.310
この結果は測定水準3のセルが一つだけ5%外れ値で,1%外れ値がないことを意味している。この5%
外れ値はその後の計算では捨てないで残している。グラッブズの検定セルの平均値に適用し,その結果は
表B.4に示してある。片側1個の外れ値は存在しない。上側2個の検定で,測定水準2では,試験室3と
6が,5%外れ値となる。これらの値も解析では捨てないで残してある。
表B.4 セル平均へのグラッブズ検定の適用
測定水準
下側1個 上側1個 下側2個 上側2個
検定のタイプ
1
1,24
1,80
0,539
0,298
グラッブズの
検定統計量の値
2
0,91
2,09
0,699
0,108
3
1,67
1,58
0,378
0,459
4
0,94
2,09
0,678
0,132
5%外れ値
2,126
2,126
0,110 1
0,110 1
グラッブズの
棄却限界値
1%外れ値
2,274
2,274
0,056 3
0,056 3
38
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.1.6
j
m
^,srj,sRjの計算
7.4.4及び7.4.5で定義した分散は,次のように計算される。測定水準1を例とすると,
試験室の数 p=8
∑
642
.
18
1
=
=
i
iy
n
T
∑
7
883
.
12
)
(
2
2
=
=
i
iy
n
T
∑
27
3
=
=
in
T
∑
95
2
4
=
=
in
T
∑
−
411
004
.0
)1
(
2
5
=
=
i
i
s
n
T
2
232
000
.0
3
5
2
=
=
p
T
T
sr
−
3
460
000
.0
)1
(
)1
(
4
2
3
3
2
3
2
1
3
2
2
L
=
=
−
−
−
−
−
T
T
p
T
s
p
T
T
T
T
s
r
sR2=sL2+sr2=0.000 692 5
44
690
.0
3
1
^
=
=TT
m
sr=0.015 24
sR=0.026 32
測定水準2,3,4の計算も,同じように行うことができ,その結果は表B.5に示されている。
表B.5
j
m
^,srj,sRjの計算値:石炭中の硫黄分
測定水準j
pj
^
m
srj
sRj
1
8
0,690
0,015
0,026
2
8
1,252
0,029
0,061
3
8
1,667
0,017
0,035
4
8
3,250
0,026
0,058
B.1.7 精度のmへの従属性
表B.5のデータを検討してみたところでは,いかなる従属性も見いだされないので,平均値を用いるこ
とができる。
B.1.8 結論
次のように呈示すべきである。
測定方法の精度は単位を質量パーセントとして,
併行標準偏差sr=0.022
再現標準偏差sR=0.045
である。この値は,0.69% (m/m) から3.25% (m/m) の範囲に適用することができるであろう。この精度は8
試験室が参加し,この範囲をカバーする一様水準実験によって求められたものである。この実験では,4

39
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
個の外れ値が検出されたが,それらは捨てないで計算に含められている。
B.2
例2:ピッチの軟化点(複数の測定水準,欠測値がある場合)
B.2.1 背景
a) 測定方法
ピッチの軟化点の環球法による測定
b) 出典
タール及びその製品の標準試験法;ピッチセクション;方法番号No.PT3中性グリセリンを用いる
方法(附属書Cの引用文献 [5])
c) 試料
ピッチの市販品バッチから選ばれたもので,引用文献 [5] のピッチセクションの“試料”の章の規
定に従って,採取,調製された。
d) 説明
これは温度特性 (℃) の測定である。16試験室が参加した。通常の市販製品の範囲をカバーするた
めに,約87.5℃,92.5℃,97.5℃,102.5℃の4個の試料を測定することを意図していたが,測定水準2
については,平均温度約96℃で,測定水準3と類似の不適切な試料が選定されてしまった。試験室5
では,測定水準2に対して,一回目に測定方法を不正確に適用したため,二回目の測定に必要な試料
が残らなかった。試験室8では,測定水準1の試料がなかった(測定水準4の試料が2つあった。)。
e) グラフによる提示
マンデルのh,k統計量をプロットすべきであるが,この例もまた,他のグラフを提示するために省
略した。マンデルのプロットはB.3の例で完全に図示し,議論される。
B.2.2 オリジナルデータ
これらのデータは℃を単位として表B.6に,図2の書式A(7.2.8参照)の形式で示されている。
B.2.3 セル平均値
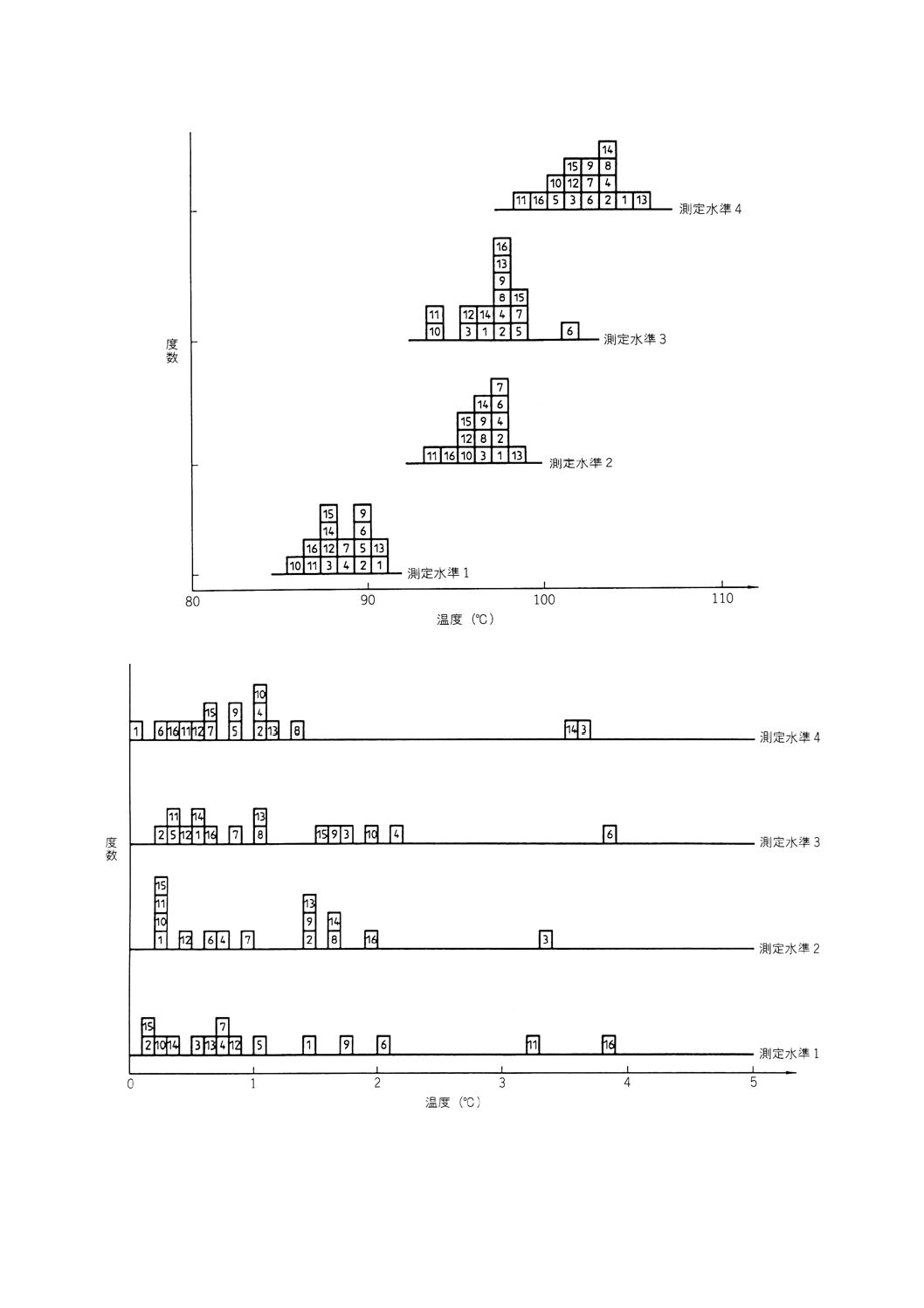
これらの値は℃を単位として表B.7に,図2の書式B(7.2.9参照)の形式で示されている。
このグラフは図B.5に示されている。
B.2.4 セル内の差の絶対値
この実験においてはセルごとの測定結果が2個であるので,その差の絶対値はデータのばらつきを示す
のに用いることができる。これらの差の絶対値は℃を単位として表B.8に,図2の書式C(7.2.10参照)
の形式で示されている。
このグラフは図B.6に示されている。
表B.6 オリジナルデータ:ピッチの軟化点 (℃)
試験室i
測定水準j
1
2
3
4
1
91,0
97,0
96,5
104,0
89,6
97,2
97,0
104,0
2
89,7
98,5
97,2
102,6
89,8
97,2
97,0
103,6
3
88,0
97,8
94,2
103,0
87,5
94,5
95,8
99,5
40
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試験室i
測定水準j
1
2
3
4
4
89,2
96,8
96,0
102,5
88,5
97,5
98,0
103,5
5
89,0
97,2
98,2
101,0
90,0
−
98,5
100,2
6
88,5
97,8
99,5
102,2
90,5
97,2
103,2
102,0
7
88,9
96,6
98,2
102,8
88,2
97,5
99,0
102,2
8
−
96,0
98,4
102,6
−
97,5
97,4
103,9
9
90,1
95,5
98,2
102,8
88,4
96,8
96,7
102,0
10
86,0
95,2
94,8
99,8
85,8
95,0
93,0
100,8
11
87,6
93,2
93,6
98,2
84,4
93,4
93,9
97,8
12
88,2
95,8
95,8
101,7
87,4
95,4
95,4
101,2
13
91,0
98,2
98,0
104,5
90,4
99,5
97,0
105,6
14
87,5
97,0
97,1
105,2
87,8
95,5
96,6
101,8
15
87,5
95,0
97,8
101,5
87,6
95,2
99,2
100,9
16
88,8
95,0
97,2
99,5
85,0
93,2
97,8
99,8
備考 明らかな外れ値はない。
参考 表の中では小数点としてコンマ (, ) を
用いている。
表B.7 セル平均:ピッチの軟化点(℃)
試験室i
測定水準j
1
2
3
4
1
90,30
97,10
96,75
104,00
2
89,75
97,85
97,10
103,10
3
87,75
96,15
95,00
101,25
4
88,85
97,15
97,00
103,00
5
89,50
−
98,35
100,60
6
89,50
97,50
101,35
102,10
7
88,55
97,05
98,60
102,50
8
−
96,75
97,90
103,25
9
89,25
96,15
97,45
102,40
10
85,90
95,10
93,90
100,30
11
86,00
93,30
93,75
98,00
12
87,80
95,60
95,60
101,45
13
90,70
98,85
97,50
105,05
14
87,65
96,25
96,85
103,50
15
87,55
95,10
98,50
101,20
41
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試験室i
測定水準j
1
2
3
4
16
86,90
94,10
97,50
99,65
備考 i=5,j=2の要素は欠測である。(7.4.3参
照)
参考 表の中では小数点としてコンマ (, ) を
用いている。
表B.8 セル内の差の絶対値:ピッチの軟化点 (℃)
試験室i
測定水準j
1
2
3
4
1
1,4
0,2
0,5
0,0
2
0,1
1,3
0,2
1,0
3
0,5
3,3
1,6
3,5
4
0,7
0,7
2,0
1,0
5
1,0
−
0,3
0,8
6
2,0
0,6
3,7
0,2
7
0,7
0,9
0,8
0,6
8
−
1,5
1,0
1,3
9
1,7
1,3
1,5
0,8
10
0,2
0,2
1,8
1,0
11
3,2
0,2
0,3
0,4
12
0,8
0,4
0,4
0,5
13
0,6
1,3
1,0
1,1
14
0,3
1,5
0,5
3,4
15
0,1
0,2
1,4
0,6
16
3,8
1,8
0,6
0,3
参考 表の中では小数点としてコンマ (, ) を
用いている。
42
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.5 ピッチの軟化点:セル平均
図B.6 ピッチの軟化点:セル内の差の絶対値
B.2.5 一致性と外れ値の精査
43
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
コクランの検定を適用した検定統計量の値を,表B.9に示す。
n=2のときの,p=15及びp=16に対する有意水準5%の棄却限界値はそれぞれ0.471及び0.452である。
外れ値はない。
セル平均に対するグラッブズ検定を行った。片側1個の外れ値も,片側2個の外れ値もなかった。
表B.9 コクランの検定統計量Cの値
水準j
1
2
3
4
C
0,391 (15)
0,424 (15)
0,434 (16)
0,380 (16)
備考 試験室の数をかっこ内に示す。
表B.10 セル平均へのグラッブズ検定の適用
測定水準;n
下側1個 上側1個 下側2個 上側2個
検定のタイプ
1;15
1,69
1,56
0,546
0,662
グラッブズの
検定統計量の値
2;15
2,04
1,77
0,478
0,646
3;16
1,76
2,27
0,548
0,566
4;16
2,22
1,74
0,500
0,672
5%外れ値
グラッブズの
棄却限界値
n=15
2,549
2,549
0,336 7
0,336 7
n=16
2,585
2,585
0,360 3
0,360 3
1%外れ値
n=15
2,806
2,806
0,253 0
0,253 0
n=16
2,852
2,852
0,276 7
0,276 7
B.2.6
j
m
^,srj,sRjの計算
7.4.4と7.4.5に従って計算した。
測定水準1を例とすると,次のように計算される。計算の便宜のためにすべてのデータから80.00を差
し引いてある。セル内の繰返し数n=2のときの方法を用いた。
試験室の数
p=15
繰返しの数
n=2
∑
0
950
.
125
1
=
=
iy
T
∑
5
977
.
087
1
)
(
2
2
=
=
iy
T
∑
−
0
910
.
36
)
(
2
2
1
3
=
=
i
i
y
y
T
3
230
.1
2
3
2
=
=p
T
sr
5
557
.1
2
)1
(
T
T
2
2
1
2
2
L
=
−
=
rs
p
p
p
s
−
−
sR2=sL2+sr2=2.787 8
p
T
m
1
^=
(80.00を加えて)=88.396 6
sr=1.109 2
sR=1.669 7

44
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
すべての測定水準の結果は表B.11に示されている。
表B.11
j
m
^,srj,sRjの計算値:ピッチの軟化点
測定水準j
Pj
j
m
^(℃)
srj
sRj
1
15
88,40
1,109
1,670
2
15
96,27
0,925
1,597
3
16
97,07
0,993
2,010
4
16
101,96
1,004
1,915
B.2.7 精度のmへの従属性
表B.11をざっと調べたところ,再現精度を除いて明らかな従属性は見つからない。mの全ての範囲にわ
たる精度の変化が仮にあったとしても,小さずきて有意とは考えられない。さらに,mの値の範囲が小さ
いこと,及び測定の性質からみて,mの値に従属性を期待することは難しい。通常の市販製品をカバーす
るようなこの範囲では,精度はmに従属しないと結論するのが,安全であるように思われる。そこで,併
行標準偏差,再現標準偏差の最終値として,平均値を採択することができるであろう。
B.2.8 結論
実用としては,この測定方法の精度の値は試料の測定水準に対して独立であると考えられ,それらは,
併行標準偏差
sr=1.0℃
再現標準偏差
sR : 1.8℃
となる。
B.3 例3:クレオソート油の温度滴定(複数の測定水準,外れ値がある場合)
B.3.1 背景
a) 出典
タール及びその製品の標準試験方法;クレオソートセクション;方法番号No.Co.18(附属書Cの引
用文献 [5])
b) 試料
クレオソート油の市販品バッチから選ばれたもので,引用文献 [5] のクレオソート油セクションの
“試料”の章の規定に従って,採取,調製された。
c) 説明
これは温度滴定を含む化学分析の標準方法で,測定結果は質量パーセントで表わされる。9試験室
が参加し,5種の試料を2回繰り返して測定した。測定試料は一般的に商業上で利用される範囲をカ
バーするよう,概ねの測定水準が4,8,12,16,20 [% (m/m)] になるように選ばれた。通常の方法で
は,測定結果は小数点以下一桁まで記録することになっているが,この実験ではオペレータに小数点
以下二桁まで求めるように指示した。
B.3.2 オリジナルデータ
これらデータは質量パーセントを単位として表B.12に,図2の書式A(7.2.8参照)の形式で示されて
いる。試験室1の結果はすべて高く,他の試験室の結果よりも著しく高い測定水準があった。試験室6の
測定水準5における二番目の値は疑わしい;この値は測定水準4の値とした方がもっとよく合うかも知れ
ない。これらの点についてはB.3.5でさらに検討する。
B.3.3 セル平均値
これらの値は質量パーセントを単位として表B.13に,図2の書式B(7.2.9参照)の形式で示されてい

45
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
表B.12 オリジナルデータ:クレオソート油の温度滴定
試験室i
測定水準j
1
2
3
4
5
1
4,44
4,39
9,34
9,34
17,40
16,90
19,23
19,23
24,28
24,00
2
4,03
4,23
8,42
8,33
14,42
14,50
16,06
16,22
20,40
19,91
3
3,70
3,70
7,60
7,40
13,60
13,60
14,50
15,10
19,30
19,70
4
4,10
4,10
8,93
8,80
14,60
14,20
15,60
15,50
20,30
20,30
5
3,97
4,04
7,89
8,12
13,73
13,92
15,54
15,78
20,53
20,88
6
3,75
4,03
8,76
9,24
13,90
14,06
16,42
16,58
18,56
16,58
7
3,70
3,80
8,00
8,30
14,10
14,20
14,90
16,00
19,70
20,50
8
3,91
3,90
8,04
8,07
14,84
14,84
15,41
15,22
21,10
20,78
9
4,02
4,07
8,44
8,17
14,24
14,10
15,14
15,44
20,71
21,66
参考 表の中では小数点としてコンマ (, ) を用いている。
表B.13 セル平均:クレオソート油の温度滴定
試験室i
測定水準j
1
2
3
4
5
1
4,415
9,340
17,150** 19,230** 24,140*
2
4,130
8,375
14,460
16,140
20,155
3
3,700
7,500
13,600
14,800
19,500
4
4,100
8,865
14,400
15,550
20,300
5
4,005
8,005
13,825
15,660
20,705
6
3,890
9,000
13,980
16,500
17,570
7
3,750
8,150
14,150
15,450
20,100
8
3,905
8,055
14,840
15,315
20,940
9
4,045
8,305
14,170
15,290
21,185
*
5%外れ値を示す。
** 1%外れ値を示す。
参考 表の中では小数点としてコンマ (, ) を用いている。
表B.14 セルの範囲:クレオソート油の温度滴定
試験室i
測定水準j
1
2
3
4
5
1
0,05
0,00
0,50
0,00
0,28
2
0,20
0,09
0,08
0,16
0,49
3
0,00
0,20
0,00
0,60
0,40
4
0,00
0,13
0,40
0,10
0,00
5
0,07
0,23
0,19
0,24
0,35
6
0,28
0,48
0,16
0,16
1,98*
7
0,10
0,30
0,10
1,10*
0,80
8
0,01
0,03
0,00
0,19
0,32
9
0,05
0,27
0,14
0,30
0,95
*
5%外れ値を示す。
参考 表の中では小数点としてコンマ(, )を用いている。
B.3.4 セル内の差の絶対値
これらの値は質量パーセントを単位として表B.14に,図2の書式C(7.2.10参照)の形式で示されてい
46
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
B.3.5 一致性と外れ値の精査
マンデルのh,kの一致性の統計量(7.3.1参照)の計算結果を図B.7とB.8に示す。水平な線は,8.3か
ら得られるマンデルの指標の値に対応している。
hのプロット(図B.7)は,明らかに試験室1がどの測定水準についても,他の全ての試験室の値よりも
ずっと高い値であることを示している。この結果は試験室共同実験を実施している委員会の側に注意を喚
起すべきであることを意味している。もし,これらの測定結果に対する説明が見つからないならば,委員
会は,特別な,場合によっては統計的でない考慮にも基づいて,精度の値の計算に,この試験室を含める
か,除外するかを,委員会として決定すべきであろう。
kのプロット(図B.8)は,試験室6と7で繰り返した測定結果間にかなり大きなばらつきがあることを
示している。しかしながら,これらの測定結果は,説明の可能性を調べるための検討以上に,何らかの特
殊な処置,また,仮にそのような処置が必要であるとしても,これらの測定結果の補正処置を必要とする
ほどには,深刻なものではないように思われる。
コクランの検定の適用によって,次の結果を得る。
測定水準4では差の絶対値1.10から検定統計量の値は1.102/1.814 9=0.667となる。
測定水準5では差の絶対値1.98から検定統計量の値は1.982/6.166 3=0.636となる。
p=9のとき,コクランの検定の棄却限界値は5%で0.638,1%で0.754である。
測定水準4における1.10という値は明らかに外れ値であり,測定水準5における1.98という値は,また,
外れ値といってもよいほど5%の棄却限界値に近い。これらの二つの値は他の全ての値とかなり離れてお
り,コクランの検定統計量で用いられる分母を大きくするので,この2つの値をどちらも外れ値と見なし,
アスタリスク(*)がつけられる。しかしながら,この2つの値についての証拠は,マンデルのkプロット
(図B.8)もこれらの値に対して疑いを示しているものの,これらを除外できるほど充分ではない。
グラッブズの検定をセル平均について適用した結果を表B.15に示す。
片側1個のグラッブズ検定で,測定水準3及び4にそれぞれ1個の外れ値があることを示しているので,
片側2個のグラッブズ検定は適用していない(7.3.4参照)。
測定水準3と4で試験室1のセル平均は外れ値であることが判る。この試験室の測定水準5のセル平均
もまた高い。このことはマンデルのhプロット(図B.7)によっても明瞭に示されている。
さらに,問い合わせた結果,試験室6で測定水準5の少なくとも1つの試料は測定水準4のものと間違
っているかも知れないことが判った。このセルの差の絶対値もまた疑わしいので,このセルの測定結果は
除外しなければならないかも知れない。このセルの値がなくなったので,試験室1の測定水準5の測定結
果は,今では決定的に疑わしい。
この結果から,どの試料が測定されたか不明であるために,試験室6の測定水準5の測定結果を二つと
も除外すること,そして,外れ試験室であるため,試験室1のすべての測定結果を除外することが決まっ
た。
これらの測定結果を除いて,測定水準4におけるコクラン検定の統計量を8試験室に対する棄却限界値
(5%水準で0.680)と比較したが,もはや外れ値はなかった。
B.3.6
j
m
^,srj,sRjの計算
試験室1の全測定結果と試験室6の測定水準5の測定結果を除外し,7.4.4と7.4.5に従って,
j
m
^,srj,
sRjを計算し,質量パーセントを単位として表B.16に示す。
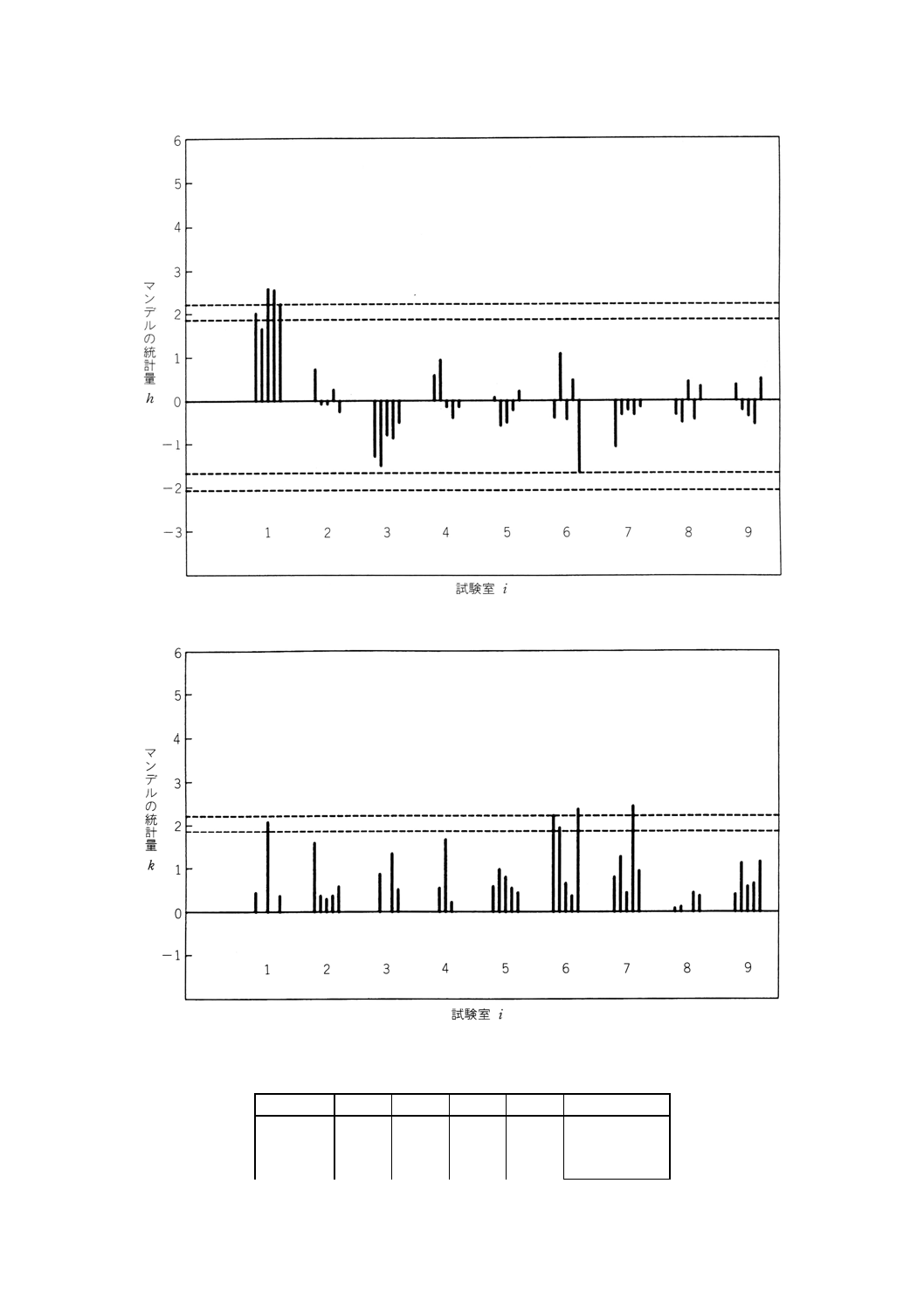
47
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.7 クレオソート油の滴定:マンデルの室間一致性の統計量h
図B.8 クレオソート油の滴定:マンデルの室内一致性の統計量k
表B.15 セル平均へのグラツブズ検定の適用
測定水準
下側1個 上側1個 下側2個 上側2個
検定のタイプ
1
1,36
1,95
0,502
0,356
グラッブズの
検定統計量の値
2
1,57
1,64
0,540
0,395
3
0,86
2,50
−
−
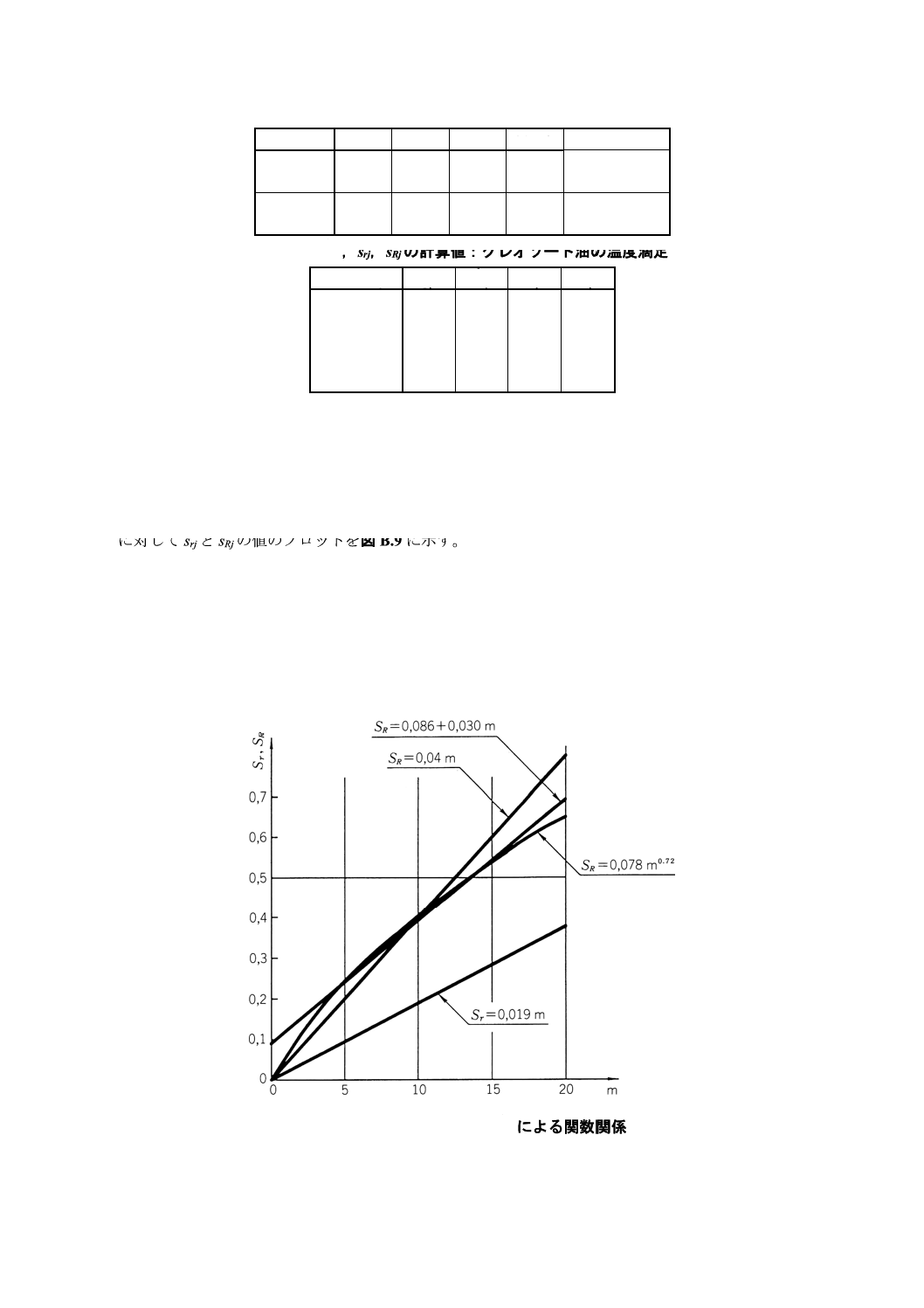
48
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定水準
下側1個 上側1個 下側2個 上側2個
検定のタイプ
4
0,91
2,47
−
−
5
1,70
2,10
0,501
0,318
5%外れ値
2,215
2,215
0,149 2
0,149 2
グラッブズの
棄却限界値
1%外れ値
2,387
2,387
0,085 1
0,085 1
表B.16
j
m
^,srj,sRjの計算値:クレオソート油の温度滴定
測定水準j
pj
j
m
^
srj
sRj
1
8
3,94
0,092
0,171
2
8
8,28
0,179
0,498
3
8
14,18
0,127
0,400
4
8
15,59
0,337
0,579
5
7
20,41
0,393
0,637
B.3.7 精度のmに対する従属性
表B.16から,標準偏差は,mの値が高くなるにつれて増加する傾向にあることは明らかであるように思
われる。それで,ある種の関数関係を設定できるという可能性がある。この見解は,この測定方法に詳し
い化学者による,精度は測定水準に対して独立ではない傾向がある,という見解によって支持された。
関数関係のあてはめの実際の計算は,7.5.9でsrについて詳細に記述されているため,ここでは示さない。
j
m
^に対してsrjとsRjの値のプロットを図B.9に示す。
図B.9から明らかに測定水準3の値はひどく外れているが,いかなる代わりの方法(7.5.2参照)によっ
ても改善されない。
併行精度については原点を通る直線が適切であるように思われる。
再現精度については3本の線が全てデータに適合しているが,関数関係IIIが最もよく適合している。
クレオソート油の標準測定方法に対する要求事項に精通した人ならば,最も適切な関係を選ぶことがで
きるかも知れない。
図B.9 表B.16のsrjとsRjの
j
m
^による関数関係
B.3.8 精度の最終の値
49
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
適当に丸めた最終の値は次のようになる。
併行標準偏差
sr=0.019m
再現標準偏差
sR=0.086+0.030m又は
sR=0.078m0.72
B.3.9 結論
B.3.8のsRの2つの計算式のどちらが望ましいかということについては,統計的な理由はない。パネル
が,どちらを用いるかを決めるべきであろう。
試験室1が外れ試験室となった理由は研究すべきである。
このことから,かなり不満足な精度実験であったように思われる。9試験室のうちの1つは外れ試験室
として除外されなければならなかったし,正しくない試料を供給された試験室もあった。測定水準3の試
料の値は,測定水準2と4の中間の値ではなく,測定水準4とほぼ同じ値であり,間違って選ばれたよう
である。そのうえ,測定水準3の試料は,他の試料と性質が異なっているようにみえる,多分,均質性が
高かったのであろう。複数の測定水準の試料を選定することを含め,より注意を払って実験をやり直すこ
とは,意義があることであろう。
50
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 参考文献
[1] JIS Q 0033 : 1997, 認証標準物質の使い方
[2] JIS Q 0035 : 1997, 標準物質の認証−一般的及び統計学的原則
[3] ASTM E691-87, Standard Practice for Conducting an Interlaboratory Study to Determine the Precision of a
Test Method. American Society for Testing and Materials, Philadelphia, PA, USA
[4] Grubbs, F.E. and Beck, G. Extension of sample sizes and percentage points for significance tests of outlying
observations. Technometrics, 14,1972, pp.847-854.
[5] “Standard Methods for Testing Tar and its Products” . 7th Ed. Standardisation of Tar Products Tests Committee,
1979
[6] Tomkins, S.S. Industrial and Engineering Chemistry (Analytical Edition), 14, 1942, pp.141-145.
[7] Grubbs, F.E. Procedures for detecting outlying observations in samples. Technometrics, 14, 1969, pp.1-21.
[8] JIS Z 8101-2 : 1999, 統計−用語と記号−第2部 統計的品質管理用語
[9] JIS Z 8101-3 : 1999, 統計−用語と記号−第3部 実験計画法用語
[10] JIS Z 8402-3 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第3部 標準測定方法の中
間精度
[11] JIS Z 8402-4 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第4部 標準測定方法の真
度を求めるための基本的方法
[12] JIS Z 8402-5 : −1), 測定方法及び測定結果の精確さ(真度及び精度)−第5部 標準測定方法の精
度を求めるための代替法
[13] JIS Z 8402-6 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第6部 精確さに関する値
の実用的な使い方
1) 発行準備中
51
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
原案作成委員会 構成表
氏名
所属
(委員長)
石 川 馨
東京大学
(幹事)
宮 津 隆
日本鋼管株式会社
岩 田 晶 夫
住友金属鉱山株式会社
内 沼 一 雄
日本石油株式会社
藤 森 利 美
東京大学
(委員)
石 井 清 次
工業技術院
神 森 大 彦
社団法人日本化学会
上 甲 子 郎
東京理科大学
横 山 毅
昭和電工株式会社
高 橋 梅太郎
海外貨物検査株式会社
窪 田 孝 昌
海外貨物検査株式会社
(事務局)
新 井 紀 弘
財団法人日本科学技術連盟
改正原案作成委員会 構成表
氏名
所属
(委員長)
宮 津 隆
西東京科学大学理工学部
(委員)
尾 島 善 一
東京理科大学理工学部
故 高 橋 梅太郎
元海外貨物検査株式会社
椿 広 計
慶應義塾大学理工学部
仁 科 健
名古屋工業大学工学部
西 島 保
東燃株式会社総合研究所
野 村 和 夫
東京ガス株式会社
番 場 章
三石テクノ株式会社
多 田 格 三
元株式会社東芝
藤 森 利 美
長崎大学経済学部
横 山 隆 壽
財団法人電力中央研究所狛江研究所
池 田 要
工業技術院標準部材料規格課
川 村 正 信
財団法人日本規格協会
黒 木 勝 也
財団法人日本規格協会
(事務局)
橋 本 進
財団法人日本規格協会
52
Z 8402-2 : 1999 (ISO 5725-2 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
品質管理分野国際整合化分科会
氏名
所属
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
○ 今 井 秀 孝
工業技術院計量研究所
○ 柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
日本電信電話株式会社
門 山 允
東京国際大学
○ 鹿 庭 なほ子
国立食品医薬品衛生研究所
兼 子 毅
武蔵工業大学工学部
○ 城 道 修
メルシャン株式会社
○ 椿 広 計
筑波大学社会工学系
○ 仁 科 健
名古屋工業大学工学部
野 澤 昌 弘
東京理科大学経営学部
三佐尾 武 雄
QCコンサルタント
○ 宮 津 隆
帝京科学大学理工学部
山 田 秀
東京都立科学技術大学工学部
横 尾 恒 雄
QCコンサルタント
大 嶋 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会
備考 ○印は許容差JIS原案作成WGの委員を兼ねる。