Z 8402-1 : 1999 (ISO 5725-1 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 8402 : 1991は廃止され,この規格に置き換えられる。
今回の制定では,1994年に第1版として発行されたISO 5725-1を基礎として用いた。
JIS Z 8402-1には,次に示す附属書がある。
附属書A(規定) JIS Z 8402で用いられる記号
附属書B(規定) 精度の尺度の不確かさに関する図
附属書C(参考) 参考文献
JIS Z 8402 : 1999は,一般名称を“測定方法及び測定結果の精確さ(真度及び精度)”として,次の部に
よって構成される。
第1部:
一般的な原理及び定義
(Part 1 : General principles and definitions)
第2部:
標準測定方法の併行精度及び再現精度を求めるための基本的方法
(Part 2 : Basic method for the determination of repeatability and reproducibility of a standard
measurement method)
第3部:
標準測定方法の中間精度
(Part 3 : Intermediate measures of the precision of a standard measurement method)
第4部:
標準測定方法の真度を求めるための基本的方法
(Part 4 : Basic methods for the determination of the trueness of a standard measurement
method)
第5部:
標準測定方法の精度を求めるための代替法
(Part 5 : Alternative methods for the determination of the precision of a standard measurement
method)
第6部:
精確さに関する値の実用的な使い方
(Part 6 : Use in practice of accuracy values)
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 2
2. 引用規格 ························································································································ 3
3. 定義 ······························································································································ 3
4. 精確さ評価実験に関する定義の実際的な意味 ········································································ 6
4.1 標準測定方法 ················································································································ 6
4.2 精確さ評価実験 ············································································································· 6
4.3 同一試料(同一と見なせるような状態の測定試料) ······························································ 7
4.4 短い時間間隔 ················································································································ 7
4.5 参加試験室 4.5.1 ············································································································ 7
4.6 測定条件 ······················································································································ 8
5. 統計モデル ····················································································································· 8
5.1 基本モデル ··················································································································· 8
5.2 基本モデルと精度との関係······························································································ 10
5.3 拡張モデル ·················································································································· 10
6. 精確さを推定する際の実験計画において考慮すべき事項 ························································ 10
6.1 精確さ評価実験の立案···································································································· 10
6.2 標準測定方法 ··············································································································· 10
6.3 精確さ評価実験のための試験室の選定 ··············································································· 11
6.4 精確さ評価実験に用いる試料の選択 ·················································································· 15
7. 精確さ(真度と精度)に関する値の利用方法 ······································································· 16
7.1 真度と精度の公表 ········································································································· 16
7.2 真度と精度の値の実際的な利用 ························································································ 17
附属書A(規定)JIS Z 8402で用いられる記号 ··········································································· 18
附属書B(規定)精度の尺度の不確かさに関する図 ···································································· 21
附属書C(参考)参考文献····································································································· 23
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8402-1 : 1999
(ISO 5725-1 : 1994)
測定方法及び測定結果の
精確さ(真度及び精度)−
第1部:一般的な原理及び定義
Accuracy (trueness and precision) of measurement methods and results-
Part 1 : General principles and definitions
序文 この規格は,1994年に第1版として発行されたISO 5725-1, Accuracy (trueness and precision) of
measurement methods and results−Part 1 : General principles and definitionsを翻訳し,技術的内容及び規格票の
様式を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
0.1
この規格では,測定方法の精確さを表すために“真度”と“精度”の二つの用語を用いている。“真
度”は,多数の測定結果の平均値と,真の値又は参照値との一致の程度を示すものである。“精度”は,測
定結果の間の一致の程度を示すものである。
0.2
“精度”を考える必要が生じるのは,同一と見なせる状況での,同一と見なせる試料について実施
される試験において,一般には同一の結果が得られないからである。これは,どのような測定の手順にお
いてもつきものの避けられない偶然誤差に基づく;すなわち測定結果に影響する要因をすべて完全には制
御できないということである。実際に測定データの解釈においては,このばらつきを考慮しなければなら
ない。例えば,測定結果とある定められた値との差は,避けられない偶然誤差の範囲内にあるかも知れず,
このような場合には,ある定められた値からの真の偏差は確定できない。同様に,二つのバッチ間の測定
結果の差が測定手順につきものの変動によるならば,バッチ間の本質的な差はわからないであろう。
0.3
同一と見なせる試料間の変動は別として,同じ測定方法による測定結果をばらつかせる多くの異な
る因子には,つぎのようなものがある。
a) オペレータ
b) 使用した装置
c) 装置の校正
d) 環境(温度,湿度,空気の汚染,など)
e) 個々の測定間の経過時間
異なるオペレータ及び/又は異なる装置によって得られた(測定結果間の)変動は,同一のオペレータ
が同じ装置を用いて短い時間間隔のうちに実施して得られた(測定結果間の)変動よりも大きいのが常で
ある。
2
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0.4
測定の繰返しによる変動に対する一般用語は精度である。多くの実際の場合に,併行条件と再現条
件と名付けられた二つの精度の条件が必要であり,測定方法のばらつきを記述するのに役に立つというこ
とが知られている。併行条件のもとでは,上にあげたa)〜e)の因子は一定で変動には寄与しないが,一方,
再現条件下では,これらは変化して測定結果の変動に影響する。したがって,併行精度と再現精度は精度
の両極であり,前者は最小,後者は最大の変動を表す。a)〜e)の一つ以上の因子が変動し得るときには,
これら二つの両極の精度の状況の間に中間条件を考えることができて,ある定められた状況のもとでは,
この中間条件が用いられる。精度は,通常の場合,標準偏差の形で表現される。
0.5
測定方法の“真度”は,測定される特性についての真の値を考えることが可能なときには重要であ
る。測定方法によっては,真の値を厳密には知ることができなくても,測定される特性の参照値を得るこ
とができるかも知れない。例えば,適切な標準物質が得られる場合,又は他の測定方法との照合,もしく
は値が既知の試料を調製することによって参照値が確定できる場合である。測定方法の真度は,参照値と,
その測定によって得られる結果の水準とを比較することによって検討できる。真度は一般にかたよりの形
で表現される。例えば,化学分析においては,測定方法が成分の全量を抽出できない場合,又は一つの成
分が他の成分の定量を妨害する場合にかたよりが生じる。
0.6
“精確さ (accuracy)”という用語は,この規格においては,真度と精度の両方を表すために使われて
いる。
“accuracy” はかつては,現在は真度と名付けられている一つの要素だけのために使われていたが,これ
は系統効果だけでなく,偶然効果による参照値からの総合的なへだたりを含めるべきであるということが,
多くの人々にわかるようになってきた。
“かたより (bias)”は,極めて長い間,統計的事項として扱われてきており,それが(医師,弁護士な
どの)専門的職業の人々の間で思想的反発を生じていたが,“真度 (trueness)”という用語を用いることに
より,積極的な見方が強調されるようになった。
1. 適用範囲
1.1
この規格の目的は次のとおりである:
a) 測定方法及び測定結果の精確さ(真度及び精度)を評価するとき,応用するときに理解しておくべき
一般的な原則の概略を述べること,及び実験によって種々の尺度の実用的な推定を行う方法を提示す
ること(この規格の第1部);
b) 実験によって測定方法の精度の二つの両極の値を推定する基本的な方法を規定すること(この規格の
第2部);
c) 適用するときの条件を与えて中間精度を得る手順,及び中間精度を推定する方法を規定すること(こ
の規格の第3部);
d) 測定方法の真度を求めるための基本的な方法を規定すること(この規格の第4部);
e) この規格の第2部及びこの規格の第4部に示されている測定方法の精度及び真度を求める基本的な方
法に対して,ある特定の状況下で用いるいくつかの代替法を規定すること(この規格の第5部);
f)
真度及び精度のいくつかの実用的な適用について記述すること(この規格の第6部)
1.2
この規格のこの部は,計量値の測定値が求められ,測定結果として1個の値が得られるような測定
方法だけを対象とする。この1個の値は1組の観測値から計算によって求められたものであってもよい。
この部は,測定方法の正確な値を与える能力(真度),又は,得られた値を再現する能力(精度)の定量
的表現について定義する。したがって,全く同じものが,全く同じように測定され,測定プロセスは管理
3
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
状態にあるということが前提になっている。
この規格のこの部は,いかなる不均質性についても適切な考慮が払われている限り,製品又は天然産の
液体,粉体,固体など非常に広い範囲の物質に対して適用してよい。
2. 引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,発効年を付記してあるものは,記載の年の版だけがこの規格の規定を構成するもので
あって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その最新版(追補
を含む。)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部 確率及び一般統計用語
JIS Z 8101-2 統計−用語と記号−第2部 統計的品質管理用語
JIS Z 8402-2 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第2部 標準測定方法の併行
精度及び再現精度を求めるための基本的方法
JIS Z 8402-3 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第3部 標準測定方法の中間
精度
JIS Z 8402-4 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第4部 標準測定方法の真度
を求めるための基本的方法
3. 定義
この規格の目的に合わせ,以下の定義を用いる。
いくつかの定義は,JIS Z 8101からの引用である。
この規格で用いる記号附属書Aに示す。
参考 この規格は原案段階では“測定方法”にtest methodという用語を,“測定結果”にtest resultと
いう用語を用いていた。その後(1985年),testは統計的検定 (statistical test) と紛らわしいとい
う指摘を受けて,“測定方法”と“測定結果”をそれぞれmeasurement method, measurement result
に変更することになった。規格の表題もこの変更を受けて,measurement methods and resultsに
変更された。この変更は規格本体の中で徹底されておらず,測定結果 (test result),測定水準
(level of test) などの用語が残っている。この翻訳に,この混乱を持ち込まぬように配慮し,で
きる限り“測定”と訳すことにした。
3.1
観測値,測定値 (observed value) :1回の測定結果として得られる特性の値。 [JIS Z 8101-1]
3.2
測定結果,試験値 (test result) :規定された測定方法の実施によって得られる特性の値。
備考1. 測定方法には,何個の観測値を取るのか,及びそれらの平均,又は複数個の観測値の適切な
関数(例えば,メディアンや標準偏差など)のいずれを測定結果とするのかを規定するのが
よい。また気体体積の標準状態への換算のような,補正が規定されることがある。したがっ
て,複数の観測値から計算された結果が一個の測定結果になり得る。単純な場合には,単一
の観測値そのものが測定結果となる。
[JIS Z 8101-2]
3.3
精度評価実験の測定(試料の)水準 (level of the test in a precision experiment) :測定の対象である
一つの試料 (material),又は一つの試験片についての,すべての試験室の測定結果の一般平均。
3.4
精度評価実験のセル (cell in a precision experiment) :一つの試験室で,一つの測定水準で得られた
複数個の測定結果。
4
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.5
(採択された)参照値 (accepted reference value) :次のようにして得られた,比較のために容認さ
れた標準として役立つ値。
a) 科学的原理に基づく理論値又は確定値。
b) ある国家,又は国際機関の実験研究に基づく付与値,又は認証値。
c) 科学又は技術集団の主催する共同実験研究に基づく合意値,又は認証値。
d) a),b),c)のいずれにも拠ることができないときは,その量の期待値,すなわちその測定値の母集団の
平均値。
[JIS Z 8101-2]
3.6
精確さ (accuracy) :個々の測定結果と採択された参照値との一致の程度。
備考2. 一連の測定結果について考える場合には,精確さ,ばらつきの成分と各測定結果に共通する
系統誤差,すなわち,かたよりの成分との両方の成分で構成される。
[JIS Z 8101-2]
3.7
真度,正確さ (trueness) :十分多数の測定結果から得られた平均値と,採択された参照値との一致
の程度。
備考3. ふつう真度はかたよりによって表される。
備考4. “trueness” (真度)はこれまで “accuracy of the mean” (平均値の正確さ)と表現されていた。
この表現は推奨しない。
[JIS Z 8101-2]
参考 “十分多数の測定結果 (a large series of test results) から得られた平均値”は,測定結果の期待値
の意味である。
3.8
かたより (bias) :測定結果の期待値と,採択された参照値との差。
備考5. かたよりは,偶然誤差と対照される系統誤差の全体である。かたよりに寄与する系統誤差は,
一つ以上あることもある。大きなかたよりは,採択された参照値からの大きな系統的な差を
もたらす。
[JIS Z 8101-2]
参考 正負の符号を問題にする場合には,“測定結果の期待値から採択された参照値を引いた値”をか
たよりとする。
3.9
試験室のかたより (laboratory bias) :ある試験室で得られた測定結果の期待値と,採択された参照
値との差。
3.10 測定方法のかたより (bias of the measurement method) :ある測定方法によって(すべての試験室で)
得られる測定結果の期待値と採択された参照値との差。
備考6. 操作上の例であるが,ある化合物の硫黄分の測定を目的とする測定方法で,硫黄の完全な抽
出が行えない場合には,測定方法が負の値のかたよりを持つことになる。同一の方法を用い
る多数の試験室の測定結果の平均値の,採択された参照値からの隔たりによって,測定方法
のかたよりを評価する。測定水準が異なれば,測定方法のかたよりも変化することがある。
3.11 かたよりの試験室成分 (laboratory component of bias) :試験室のかたよりと,測定方法のかたより
との差。
備考7. かたよりの試験室成分は,その試験室と用いられた測定条件に特有のものであり,測定水準
が異なれば,その値も異なることがある。
備考8. かたよりの試験室成分は,測定結果の全平均に関係し,真の値又は採択された参照値に関係
しない。
3.12 精度 (precision) :定められた条件の下で繰り返された独立な測定結果の間の一致の程度。
備考9. 精度は偶然誤差の分布のみに依存し,真の値や特定の値には関係しない。
備考10. ふつう精度はその悪さ (imprecision) によって表現され,測定結果の標準偏差として計算され
5
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。標準偏差が大きいと,精度が低いという。
備考11. “独立な測定結果”とは,同一もしくは類似した測定対象物の過去の結果の影響を受けない
測定結果のことをいう。精度の大きさは繰返しに関して定められた条件に依存する。併行条
件,再現条件は繰返しに関する両極の条件である。
[JIS Z 8101-2]
参考 “独立な測定結果”は同一試料に対する測定結果であることが「定められた条件」の中で示さ
れる。
3.13 併行精度,繰返し精度 (repeatability) :併行条件による測定結果の精度。
[JIS Z 8101-2]
3.14 併行条件 (repeatability conditions) :同一と見なせるような測定試料について,同じ方法を用い,同
じ試験室で,同じオペレータが,同じ装置を用いて,短時間のうちに独立な測定結果を得る測定の条件。
[JIS Z 8101-2]
3.15 併行標準偏差 (repeatability standard deviation) :併行条件で得られた測定結果の標準偏差。
備考12. 併行標準偏差は,併行条件の下での測定結果の分布のばらつきの尺度である。
備考13. 同じように併行分散,併行変動係数も定義され,併行条件の下での測定結果の分布のばらつ
きの尺度として用いられる。
[JIS Z 8101-2]
3.16 併行許容差 (repeatability limit) :併行条件で得られた二つの測定結果の差の絶対値が,その値以下
になることが95%の確率で期待される値。
備考14. 記号にrを用いる。
[JIS Z 8101-2]
参考 3.13「併行精度」は概念を,3.15「併行標準偏差」は尺度を,3.16「併行許容差」は比較の基準
として用いられる限界をそれぞれ表し,用語を使い分けている。概念を表す場合にrepeatability
を「繰返し性」と呼ぶことがある。
3.17 (室間)再現精度 (reproducibility) :再現条件による測定結果の精度。
[JIS Z 8101-2]
3.18
(室間)再現条件 (reproducibility conditions) :同一と見なせるような測定試料について,同じ
方法を用い,異なる試験室で,異なるオペレータが,異なる装置を用いて,独立な測定結果を得る測定の
条件。
[JIS Z 8101-2]
3.19 (室間)再現標準偏差 (reproducibility standard deviation) :再現条件で得られた測定結果の標準偏
差。
備考15. 再現標準偏差は,再現条件の下での測定結果の分布のばらつきの尺度である。
備考16. 同じように(室間)再現分散,(室間)再現変動係数も定義され,再現条件の下での測定結果
の分布のばらつきの尺度として用いられる。
[JIS Z 8101-2]
3.20 (室間)再現許容差 (reproducibility limit) :再現条件で得られた二つの測定結果の差の絶対値が,
その値以下になることが95%の確率で期待される値。
備考17. 記号にRを用いる。
[JIS Z 8101-2]
参考 3.17「再現精度」は概念を3.19「再現標準偏差」は尺度を,3.20「再現許容差」は比較の基準と
して用いられる限界をそれぞれ表し,用語を使い分けている。概念を表す場合にreproducibility
を「再現性」とよぶことがある。
3.21 外れ値,異常値 (outlier) :一組の値のうち,他の値と不整合な値。
備考18. この規格の第2部に,真度と精度の評価実験で外れ値を識別するための統計的検定法と有意水
準が定められている。
3.22 共同評価実験 (collaborative assessment experiment) :同一試料,同じ標準測定方法による,各試験
室の測定能力を評価するための多施設共同実験。
6
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考 同一試料は,4.3で規定されている。
備考19. 3.16と3.20の定義は,測定結果が連続量(計量値)である場合に適用される。測定結果が離散
量(計数値)であるか,または丸められた値である場合は,上に定義された併行許容差と再
現許容差とは,二つの測定結果の差の絶対値が,その値以下になることが95%以上の確率で
期待される値の最小値となる。
備考20. 3.8から3.11,3.15,3.16,3.19及び3.20の定義は,実際には値が未知である理論値を定義の文
に含んでいる。実際には,再現標準偏差,併行標準偏差,及びかたよりの値は(この規格の
第2部と第4部に示される)実験で求められるが,これらは統計的に表現するとそれぞれの推
定値であり,誤差を含んでいる。したがって許容差r及びRの確率は正確には95%にならな
いことがある。多数の試験室が精度評価実験に参加するならば,この確率は95%に近くなる
が,参加試験室数が30未満であると95%からかなり逸脱するおそれがある。これは避けられ
ないが,これらの許容差の本来の目的は,測定結果の差がその測定方法に固有の確率的な不
確かさに基づくのか否かを判定する道具として用いることであるから,実際上の有用性を深
刻に損なうことはない。併行許容差rや再現許容差Rを超える測定結果の差は,疑わしいと
する。
参考 3.6から3.10の定義文に含まれる「採択された参照値」は「真の値」とすべきである。「真度」,
「かたより」は概念上,真の値から測られなければならない。すなわち真の値から測られた「真
度」,「かたより」は“真の”「真度」,「かたより」である。また,3.6から3.10の定義のような
参照値から測られた「真度」,「かたより」は「真度」,「かたより」の“推定値”である。実際
に用いられる値は推定値であるが,推定値でもって概念を定義することは適切ではない。例え
ば「かたよりのない測定方法」と「かたよりの推定値が0である測定方法」では表現される意
味が異なってくる。また推定値は推定の技術に依存するため,推定値を用いた定義は技術の進
歩に対して一貫性を持たないという問題もある。
備考21. 記号rとRは既に他の目的で一般に使われている。すなわちJIS Z 8101-1では,rは相関係数
の記号として,R(やW)は一連の観測値の範囲の記号として推奨されている。しかしこれ
らの記号が規格の中で用いられ,誤解を招くおそれがある場合には併行許容差rや再現許容
差Rと言葉を補って用いられれば,混乱を生じることはない。
4. 精確さ評価実験に関する定義の実際的な意味
4.1
標準測定方法
4.1.1
同じように測定を行うために,測定方法を標準化しておかなければならない。その標準化された方
法によって全ての測定を実施する。これは測定がどのように実施されるかについて,十分詳細に記載した
文書があることを意味しており,測定試料がどのように採取・調製されるかについての記述も含まれてい
ることが望ましい。
4.1.2
文書化された測定方法があるということは,その測定方法を確立することに責任を持つ機関がある
ということを意味している。
備考22. 標準測定方法は6.2においてさらに詳細に規定される。
4.2
精確さ評価実験
4.2.1
精確さ(真度及び精度)の値は,その目的のために特に設立された専門パネルの下で組織された参
加試験室によって報告された一連の測定結果から求められることが望ましい。
7
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
そのような共同実験は「精確さ評価実験」と呼ばれる。精確さ評価実験を限定された目的に応じて「精
度評価実験」又は「真度評価実験」と呼んでもよい。その目的が真度を求めることならば,精度評価実験
は事前に完了しているか又は同時に実施されなければならない。
実験で得られた精確さの推定値は,その標準測定方法によって実施される測定に対してのみ有効である
ことを常に表記することが望ましい。
4.2.2 精確さ評価実験は,しばしば標準測定方法の適切さを実用的に評価する試験と考えることができる。
標準化の主な目的の一つは,使用者(試験室)間の違いをできるだけ除去することであり,精確さ評価実
験によって得られたデータは,この目的がどの程度効果的に達成されているかを表している。試験室内分
散(第7節参照)や試験室平均に際立った違いがあれば,標準測定方法がまだ十分に詳細でなく,改善で
きることを意味しているかもしれない。その場合,このことを追加検討の要求とともに規格作成機関へ報
告することが望ましい。
4.3
同一試料(同一と見なせるような状態の測定試料)
4.3.1
精確さ評価実験では,規定された製品の規定された試料又は試験片は異なった場所,異なった国,
あるいは異なった大陸であっても,実験本部から多数の試験室に送付される。これらの試験室における測
定が,同一と見なせるような状態の試料で実施されなければならないと述べている併行条件の定義 (3.14)
は,測定が実際に行われる時期について言及している。これを達成するため,2つの異なった条件を満足
しなければならない。
a) サンプルはそれぞれの試験室に発送されたときほぼ同一とみなせるような状態でなければならない。
b) それらは輸送中及び実際に測定が実施されるまでの期間が異なった時間間隔に対して,上記の状態が
保たれなければならない。
精確さ評価実験を計画・実施するとき,両方の条件は注意深く守られなければならない。
備考23. 試料の選択は6.4でさらに詳細に規定する。
4.4
短い時間間隔
4.4.1
併行条件の定義 (3.14) によれば,併行精度を求めるための測定は操作条件が一定のもとになされ
なければならない;すなわち,測定が実施されている間,0.3で列挙したような因子が一定であることが望
ましい。特に,個々の測定ごとに必須でないかぎり,測定の間装置を再校正しないことが望ましい。実際,
併行条件下での測定は,一定であることを常に保証できない環境的因子のような,これらの因子の変化を
最小にするため,可能な限り短い時間間隔で実施することが望ましい。
4.4.2
測定間の時間間隔に影響するかもしれない第2の考慮すべき事項もある。それは,測定結果が独立
であると仮定することである。もし以前の結果が次の測定結果に影響する(併行分散の推定値が減少する)
ことが懸念されるならば,同一のものであるとオペレータに分からない様に別の番号をつけた試料を用意
する必要があるかもしれない。これらの試料が測定される順番に関する指示書が出され,おそらく,その
順番は全ての「同一」試料が一緒に測定されないようにランダム化されているであろう。これは,その一
連の測定が短時間に全て完了するような性質の測定でないかぎり,繰り返し測定にかかる時間が短い時間
間隔の目的を損なうことになることを意味しているかもしれない。常識に勝るものはない。
4.5
参加試験室
4.5.1
この規格の第1部の基本的な仮定は,標準測定方法において併行精度は,標準手順を適用している
すべての試験室では少なくとも近似的には等しく,その結果すべての試験室に適用できる共通で平均的な
併行標準偏差の値を設定しうる,ということである。一方,併行条件の下で一連の測定を実施することに
よって,どの試験室でもその測定方法についての各々の併行標準偏差を推定し,共通の標準の値に対して
8
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
それをチェックすることが可能である。この手順はこの規格の第6部において扱う。
4.5.2
理論上,3.8〜3.20に定義された値は,その測定方法を実施するすべての試験室に対して適用され
る。実際には,これらは試験室の母集団からのサンプル(試験室)について求められている。このサンプ
ル(試験室)の選択の詳細は6.3に述べる。6.3で指示している試験室の数及び実施される測定の回数が守
られていれば,真度及び精度の推定値は満足できるはずである。しかし,その後参加している試験室が,
標準測定方法を使用するすべての試験室の真の代表ではなかったり,あるいは代表しなくなったことが明
らかになった場合には,測定をやり直さなければならない。
参考 試験室全体を母集団として,共同実験に参加した試験室をサンプルとよんでいる。
4.6
測定条件
4.6.1
試験室内で得られる観測値のばらつきに寄与する因子は0.3に列挙されている。環境条件の変化及
び測定間の装置の再校正による影響を含む異なった時間に行われる測定では,それらの因子は,時間,オ
ペレータ,及び装置として与えられるかもしれない。併行条件の下では,すべての因子を一定に保って測
定が実施され,再現条件の下では,異なった試験室で測定が実施される。試験室が異なると,すべての因
子が異なるだけでなく,試験室の管理及び維持,測定の安定性のチェックなどの差異による付加的な影響
も異なる。
4.6.2
同一の試験室内で測定が実施されるが,時間,オペレータ,装置のうち,一つ以上の因子が変化す
る中間条件を考慮することは場合によっては有効であろう。測定方法の精度の設定において,適切な測定
条件(すなわち,前述の3つの因子を一定とするか否かなど)を定めることは非常に重要である。
なお,一つの因子に起因する変化の大きさは測定方法に依存するであろう。例えば化学分析においては,
オペレータ及び時間の因子が支配的であり,同様に微量分析では装置及び環境が,物理試験では装置及び
校正が支配的であろう。
5. 統計モデル
5.1
基本モデル
測定方法の精確さ(真度と精度)を推定するために,測定結果yを(1)式に示す3つの成分の和として仮
定しておくことは有用である。
y=m+B+e ·············································································· (1)
ここで,試験の対象となる試料について,
mは一般平均(期待値);
Bは併行条件の下でのかたよりの試験室成分;
eは併行条件の下で,一つ一つの測定に伴う偶然誤差
を示す。
5.1.1
一般平均m
5.1.1.1 一般平均mは測定水準(測定試料の水準)を表す。ある化学成分の異なった純度の試料,又は異
なった試料(例えば,異なったタイプの鉄鋼)は異なった測定水準に対応する。多くの技術的な状況にお
いて,測定水準は測定方法ごとに定められるものであり,(測定方法に依存しない)真の値の概念は当ては
まらない。しかし,滴定される溶液の真の濃度のように,測定の真の値μの概念が成り立つ状況もあり得
る。測定水準mは必ずしも真の値μに等しいとは限らない。
9
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.1.1.2 同じ測定方法によって得た測定結果の差を調べるとき,測定方法のかたよりは差に影響しないし,
無視することができる。しかし,契約や仕様の要求事項が測定(試料の)水準mではなく,真の値μによ
って規定されている場合に規定された値と測定結果とを比較するとき,又は,異なった測定方法を用いて
得た測定結果を比較するとき,測定方法のかたよりを考慮しなければならない。もし真の値が存在し,満
足な標準物質があるならば,この規格の第4部に示されているように,測定方法のかたよりを求めること
が望ましい。
5.1.2
かたよりの試験室成分B
5.1.2.1
かたよりの試験室成分Bは,併行条件のもとで行った一連の測定を通じて一定であるが,異なっ
た条件下で行われた測定においては違った値をとると考えられる。測定結果が常に特定の2つの試験室間
で比較されるとき,ある精確さ評価実験を通じて求められた個々の試験室のかたよりから,又は,その試
験室間で独自の実験を行うことによって,試験室間の相対的なかたよりを求めておくことが必要である。
しかし,任意の2つの試験室間の相違に関して一般的な結論を得るためには,又は,固有のかたよりがま
だ求められていない2つの試験室間の比較をするときには,かたよりの試験室成分を分布としてとらえて
おく必要がある。このことが,再現精度の概念が存在する理由である。この規格の第2部に与えられた手
順は,かたよりの試験室成分が近似的に正規分布に従うことを仮定して作られているが,実際には,ひと
やまの分布であるならばほとんどの分布に対して利用できる。
5.1.2.2
Bの分散は室間分散と呼ばれ,
var (B) =σL2 ············································································· (2)
と表現される。ここで,σL2はオペレータ間と装置間の変動を含む。
この規格の第2部に記述された基本的な精度評価実験では,これらの成分は分離されていない。この規
格の第3部では,Bの偶然成分のうちのいくつかの成分の大きさを求める方法が与えられている。
5.1.2.3
一般に,Bは偶然成分と系統成分の和として解釈することができる。ここではBを構成する要因
を網羅的に挙げることは試みないが,それらは異なった気象条件,製造上の公差内での装置のばらつき,
オペレータが異なった環境で訓練を受けたことによる技術の違いも含む。
5.1.3
誤差項e
5.1.3.1
誤差項eは一つ一つの測定結果に含まれる偶然誤差を表す。この規格のこの部で与えられる手順
は,確率変数としての誤差の分布が近似的に正規分布に従うことを仮定して設定されているが,実際には,
ひとやまの分布であるならばほとんどの分布に対して利用できる。
5.1.3.2
ある1つの試験室内での併行条件における分散を室内分散と呼び,
var (e) =σW2 ············································································· (3)
と表現する。
5.1.3.3
オペレータの技能レベルの違いなどによって,室内分散σW2は試験室間で違いがあることが考え
られる。しかし,この規格のこの部では,試験室間の室内分散の違いが小さくなるように,測定方法が適
切に標準化され,すべての試験室がその標準化された測定方法を用いることによって,試験室が異なって
も共通な室内分散となることが正当化されていると仮定する。この共通な値を併行分散と呼び,式(4)によ
って表現する。この値はそれぞれの室内分散の平均値によって推定される。
()
2
2
var
w
r
eσ
σ
=
=
······································································ (4)
式(4)に表現した平均値は,精確さ評価実験に参加した試験室から外れ値を除いたすべての試験室から算
出される。
10
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2
基本モデルと精度との関係
5.2.1
5.1で述べた基本モデルを採用したとき,併行分散は誤差項eの分散として直接求められる。しか
し,再現分散は併行分散と5.1.2.2に述べた室間分散の和になる。
5.2.2
精度として次の2つの量が必要とされる。
併行標準偏差
()e
r
var
=
σ
············································································· (5)
及び,再現標準偏差
2
2
r
L
R
σ
σ
σ
+
=
········································································ (6)
は精度として必要とされる2つの量である。
5.3
拡張モデル
必要に応じて基本モデルを拡張したモデルが利用される。拡張モデルはこの規格の関連する部に記述さ
れる。
6. 精確さを推定する際の実験計画において考慮すべき事項
6.1
精確さ評価実験の立案
6.1.1
標準測定方法の精度及び/または真度を推定するための実験に関する実施計画は,その標準測定方
法及びその適用に精通した専門家のパネルが立案することが望ましい。パネルのメンバーのうち少なくと
も一人は,統計的実験計画と解析の経験者であることが望ましい。
6.1.2
実験を計画する際には以下の案件を考慮する。
a) 適切な標準測定方法があるか?
b) 共同実験のために,いくつの試験室を募集するか?
c) どのように試験室を募集し,かつ,試験室に対する要求事項は何か?
d) 実際の測定水準はどの範囲か?
e) 実験で用いる水準数はいくつにするか?
f)
これらの水準を代表する適切な試料は何か,かっ,それらをどのように調製するか?
g) 反復回数を何回とするか?
h) すべての測定を完了するための日程をどう規定するか?
i)
5.1の基本モデルは適切か,又は,そのモデルの変更を考慮するか? 同一の試料が,すべての試験室
において,同じ状態で測定されることを保証するために,特別な留意事項が必要か?
これらの案件は6.2〜6.4で考察する。
6.2
標準測定方法
対象とする測定方法は,4.1で述べたように,標準化されていなければならない。こうした測定方法は,
頑健であること,すなわち,手順上のわずかな違いが結果に予想外の大幅な変化をもたらさないことが必
要である。もし,このことが起こり得るようなら,適切な予防措置又は警告がなされなければならない。
これに加え,標準測定方法を開発する過程で,かたよりを除外又は低減するために,あらゆる努力を払う
ことが望ましい。
同様な実験手順は,すでに確立されている標準測定方法及び新しく標準化された測定方法両者の真度及
び精度を求めるために用いることができる。後者の場合,試験室が経験を積むに従い真度及び精度が変わ
11
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ることがあるため,得られた結果は予備的な推定値とみなすことが望ましい。
測定方法を記述した文書は曖昧でなく完全なものでなければならない。その測定方法は,手順に係わる
環境条件,試薬及び装置,設備の予備点検,並びに測定用試料の調製に関するすべての不可欠な操作を含
み,妥当なものがあれば,オペレータが利用できる他の手順書を引用することが望ましい。測定結果の計
算方法及び表示方法は,報告する有効数字の桁数を含め,正確に規定しておくことが望ましい。
6.3
精確さ評価実験のための試験室の選定
6.3.1
試験室の選択
統計的観点からは,精確さを推定するためのどんな実験に参加する試験室も,その測定方法を使用する
すべての試験室の中から,ランダムに選ばれることが望ましい。志願した試験室だけで行うことは現実の
姿を表していないかもしれない。しかし,例えば参加する試験室が異なる大陸に,又は異なる気候の地域
に散在していることが必要であるという要求事項など,他の実際的な要件も,代表性のパターンに影響を
及ぼすかもしれない。
参加する試験室が,その方法を標準化する過程で特別な経験を積んできた試験室ばかりで構成されるこ
とは望ましくない。また,熟練者によって到達できるその方法の精確さを示すために,専門化した“標準”
試験室で構成することも望ましくない。
試験室間共同実験に参加を募るべき試験室の数と各測定(試料の)水準において各々の試験室に要求さ
れる測定結果の個数とは,相互に依存している。どれくらいの数が望ましいかを決定するための指針は,
6.3.2〜6.3.4で示される。
6.3.2
精度の推定に必要な試験室の数
6.3.2.1
第5節の式(2)〜(6)で記号σで表される種々の量は真の標準偏差であるがその値は未知であり,精
度評価実験の目的はそれらを推定することにある。真の標準偏差 (σ) の推定値 (s) を得るとき,推定値 (s)
が存在すると期待できるσのまわりの範囲に関する結論を導くことができる。これは,カイ二乗分布と,
推定値sを算出するもとになった結果の個数とを用いることによって解ける,よく知られた統計的問題で
ある。しばしば用いられる式は:
P
A
s
A
P
=
+
<
−
<
−
σ
σ
······························································· (7)
である。Aはしばしばパーセントで表され,それによって,推定された標準偏差 (s) が,真の標準偏差 (σ)
の±A以内にあることが,特定の確率Pで期待できることを意味している。
参考 私たちが馴染んだ統計学では,通常得られた標本分散から真の分散に関する推定を行い,本書
のように真の分散から標本分散について推定することはあまり行わない。真の標準偏差σが特
定の確率Pで存在すると期待できる範囲は,標準偏差の推定値sから次式を用いて推定するこ
とができる:
P
A
s
A
s
P
P
P
=
≤
≤
2
1
ν
σ
ν
······················································ 参考(1)
ここで,AP1及ひAP2はそれぞれ自由度υのχ2分布のP1及びP2分位点である。但し,このと
きP1−P2=Pである。
式参考(1)から次のようにして本文の式(7)を導くことかできる。
すなわち,式参考(1)の [ ] 内の式の各辺をsで割ると

12
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
P
P
A
s
A
ν
σ
ν
≤
≤
上記の式の各辺の逆数をとると
ν
σ
ν
2
1
P
P
A
s
A
≥
≥
上記の式の各辺から1をひくと
1
1
2
1
−
≥
−
≥
−
ν
σ
σ
ν
P
P
A
s
A
ここで,
A
AP
=
−1
1
ν
,
A
AP
−
=
−1
2
ν
とおけば本文の式(7)の左辺の [ ] 内の式と等しくなる。
故に,
ν
2
2
1
=
+
P
P
A
A
P1−P2=P
を満たすP1,P2を選択すればσに対称の不確かさの信頼区間を求めることができる。
6.3.2.2
測定水準が一つの場合,併行標準偏差の不確かさは,試験室の数 (p) 及び各試験室内の測定結果
の個数 (n) に依存することになるだろう。再現標準偏差の不確かさは二つの標準偏差[式(6)参照]から求
めるので,手順はもっと複雑となる。もうひとつの係数γ,即ち:
γ=σR/σr ··················································································· (8)
で表される再現標準偏差の併行標準偏差に対する比が必要である。
6.3.2.3
確率水準Pを95%と仮定するならば,Aの値を求める近似式が作成されて以下に示されている。
これらの式は,募集する試験室数を設計し,各測定水準において各々の試験室に必要な測定結果の個数を
決定する目的を持っている。これらの式は,信頼限界を与えているわけではないので,信頼限界を計算す
るために解析段階で用いることは望ましくない。式は以下の通りである。
併行精度では,
(
)1
2
1
96
.1
−
=
=
n
p
A
A
r
······························································· (9)
であり,再現精度では,
(
)
[
](
)(
)
(
)p
p
n
p
n
n
p
A
A
R
1
2
1
1
1
1
96
.1
2
4
2
2
−
−
−
+
−
+
=
=
γ
γ
···································· (10)
である。
備考24. 自由度ν及び期待値がσ2である標本分散は,近似的に分散2σ4/νの正規分布をするとみなせる
であろう。式(9)及び(10)は,σr及びσRの推定に伴った分散についてのこのような前提の下で
導かれた。この近似の妥当性は正確な計算によって確認された。
13
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.2.4
γの値は未知であるが,しばしば測定方法を標準化する過程で得られた試験室内及び試験室間標
準偏差の予備的な推定値が利用できる。種々の試験室数 (P) 及び試験室当たりの結果の個数 (n) が与えら
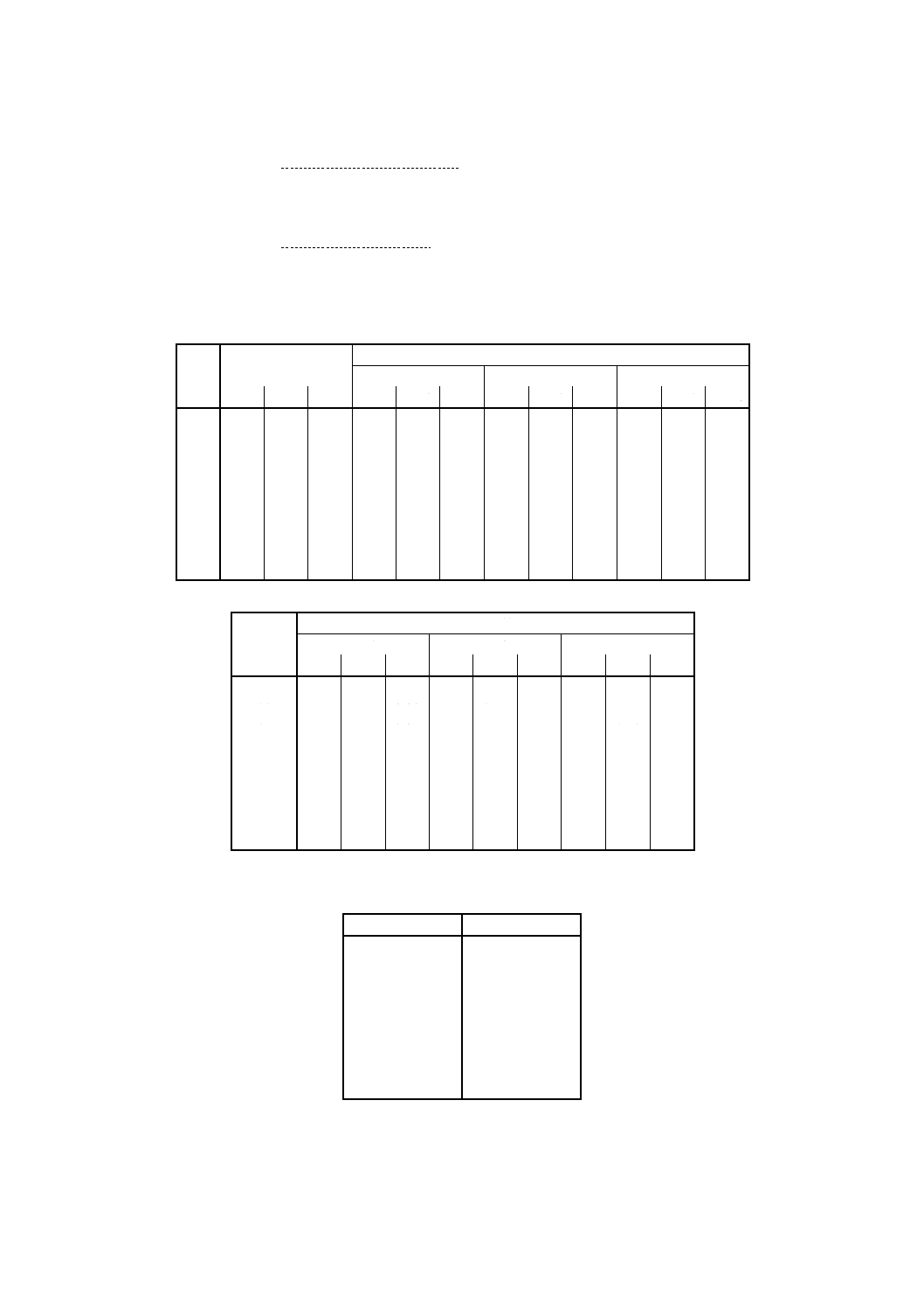
れたときの,併行標準偏差及び再現標準偏差の不確かさの正確な値が表1に示され,また,附属書Bに図
で示されている。
6.3.3
かたよりの推定に必要な試験室数
6.3.3.1
測定方法のかたよりδは,次によって推定できる:
μ
δ
−
=y
ˆ
················································································ (11)
ここで,
y: 実験の特定の水準において,全試験室から得られた全測定結果の
総平均
μ: 参照値
この推定値の不確かさは,次式で表すことができる。
[
]
95
.0
ˆ
=
+
<
<
−
R
R
A
A
P
σ
δ
δ
σ
δ
·················································· (12)
この式は,真の測定方法のかたよりからAσR以内に,0.95の確率で推定値があるであろうということを
示している。係数γ[式(8)参照]の形で表すと次のようになる。
(
)
pn
n
A
2
2
1
1
96
.1
γ
γ
+
−
=
································································ (13)
Aの値は表2に示されている。
6.3.3.2
ある実験時におけるある試験室のかたより∆は,以下によって推定されるであろう。
μ
−
=
∆
y
ˆ
··············································································· (14)
ここで,
y: 実験の特定の水準における当該試験室で得られた全測定結果の
算術平均
μ: 参照値
この推定値の不確かさは,次式で表される。
[
]
95
.0
ˆ
=
+
∆
<
∆
<
−
∆
r
w
r
w
A
A
P
σ
σ
················································· (15)
この式は,真の試験室のかたよりからAwσr以内に,0.95の確率で推定値があるであろうということを示
している。ここで,試験室内不確かさは以下の通りである。
n
Aw
96
.1
=
·············································································· (16)
Awの値は表3に示されている。
参考 6.3.2.1の参考と同様,通常は得られた標本平均から真の平均に関する推定を行い,本書のよう
に真の平均から標本平均について推定することはあまり行わない。真の測定方法のかたよりδ
が特定の確率Pで存在すると期待できる範囲は,測定方法のかたよりの推定値δから次式を用
いて推定することができる:
[
]P
A
A
P
r
r
=
+
<
<
−
σ
δ
δ
σ
δ
ˆ
ˆ
··················································· 参考(2)
式参考(2)の [ ] 内の式の各辺から(
δ
δ+
ˆ
)をひくと
14
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
r
r
A
A
σ
δ
δ
σ
δ
+
−
<
−
<
−
−
ˆ
上記の式の各辺に−1をかけると
r
r
A
A
σ
δ
δ
σ
δ
−
>
>
+
ˆ
となり,本文の式(12)の左辺の [ ] 内の式と等しくなる。
本文の式(15)についても,同様のことがいえる。
表1 併行標準偏差及び再現標準偏差の推定値の不確かさの値
試験
室数
p
Ar
AR
γ=1
γ=2
γ=3
n=2 n=3 n=4 n=2 n=3 n=4 n=2 n=3 n=4 n=2 n=3 n=4
5
10
15
20
25
30
35
40
0.62
0.44
0.36
0.31
0.28
0.25
0.23
0.22
0.44
0.31
0.25
0.22
0.20
0.18
0.17
0.16
0.36
0.25
0.21
0.18
0.16
0.15
0.14
0.13
0.46
0.32
0.26
0.22
0.20
0.18
0.17
0.16
0.37
0.26
0.21
0.18
0.16
0.15
0.14
0.13
0.32
0.22
0.18
0.16
0.14
0.13
0.12
0.11
0.61
0.41
0.33
0.28
0.25
0.23
0.21
0.20
0.58
0.39
0.31
0.27
0.24
0.22
0.20
0.19
0.57
0.38
0.30
0.26
0.23
0.21
0.19
0.18
0.68
0.45
0.36
0.31
0.28
0.25
0.23
0.22
0.67
0.45
0.36
0.31
0.28
0.25
0.23
0.22
0.67
0.45
0.36
0.31
0.27
0.25
0.23
0.22
表2 測定方法のかたよりの推定値の不確かさAの値
試験室数
p
Aの値
γ=1
γ=2
γ=5
n=2 n=3 n=4 n=2 n=3 n=4 n=2 n=3 n=4
5
10
15
20
25
30
35
40
0.62
0.44
0.36
0.31
0.28
0.25
0.23
0.22
0.51
0.36
0.29
0.25
0.23
0.21
0.19
0.18
0.44
0.31
0.25
0.22
0.20
0.18
0.17
0.15
0.82
0.58
0.47
0.41
0.37
0.33
0.31
0.29
0.80
0.57
0.46
0.40
0.36
0.33
0.30
0.28
0.79
0.56
0.46
0.40
0.35
0.32
0.30
0.28
0.87
0.61
0.50
0.43
0.39
0.35
0.33
0.31
0.86
0.61
0.50
0.43
0.39
0.35
0.33
0.31
0.86
0.61
0.50
0.43
0.39
0.35
0.33
0.31
表3 試験室内かたよりの推定値の不確かさAwの値
測定結果の数n
Awの値
5
0.88
10
0.62
15
0.51
20
0.44
25
0.39
30
0.36
35
0.33
40
0.31
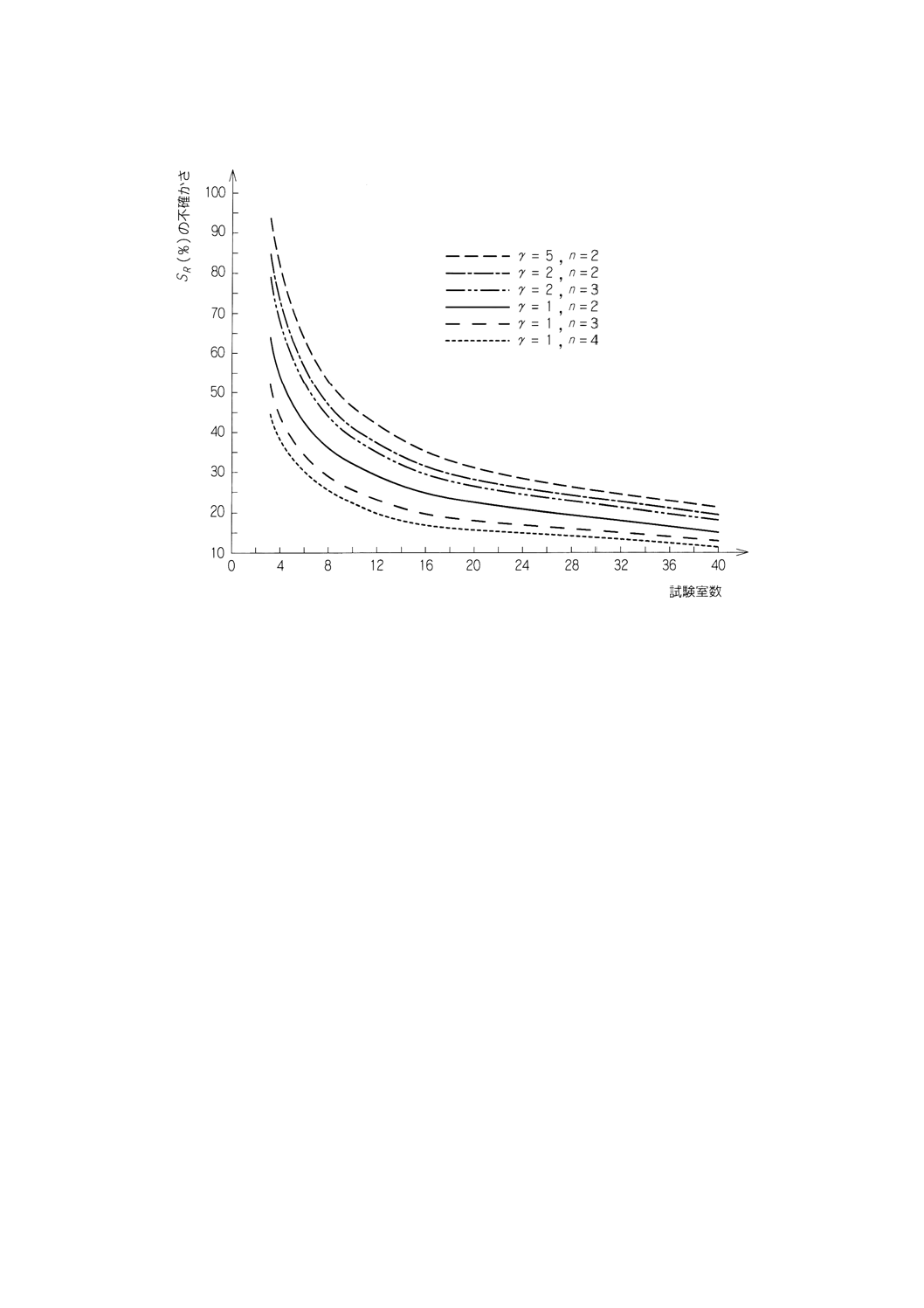
6.3.4
試験室選択における暗黙の了解
試験室数の選択は,利用可能な人的,財政的,時間的などの資源と,個々の推定値の不確かさを満足で
きる水準にまで下げたいという願望との間の妥協となるであろう。附属書Bにおける図B.1及びB.2を見
15
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ると,もし精度評価実験に少数の試験室 (
5
≈
p
) しか参加しないならば,併行標準偏差及び再現標準偏差
は,それらの真の値からかなり逸脱していることもあり得るということが,またpが20を越えるときには,
試験室数が2,3増加しても,これらの推定値の不確かさは僅かしか減少しない,ということが分かる。8
〜15のpを選択することが普通である。σLがσrよりも大きい(すなわち,γが2より大きい)場合には,
そしてそのような場合はしばしばであるが,1水準1試験室当たりn=2より多い測定結果を得ても,成果
はほとんどない。
6.4
精確さ評価実験に用いる試料の選択
6.4.1
測定方法の精確さを求めるための実験に用いる試料は,その測定方法が通常用いられると期待され
る範囲を十分に代表していることが望ましい。一般的に,5つの異なる試料は精確さを適切に確定するの
に十分広範囲な水準を与える。改良が必要であると考えられ,さらに精確さ評価実験が予定される新規に
開発された測定方法の最初の検討においては,より少ない試料数でも差し支えないであろう。
6.4.2
測定によって変化しない単位体を測定しなければならない場合,少なくとも原理的には,同一の1
セットの測定対象物を複数の試験室において測定することができる。しかし,このことはしばしば異なる
国や異なる大陸の遠く離れた試験室に同一の1セットの測定対象物を回送することを必要とし,そのとき
は,輸送中の損失や損傷という大きな危除を伴う。もし異なる測定対象物を異なる試験室で用いるときに
は,実際に目的に照らして,それらが同一と見なせることを保証できるように選択しなければならない。
6.4.3
異なる水準を代表する試料を選択するに当たり,試料送付の準備をする前に試料が十分均質化され
ているか,又は精確さの値に試料の不均質の影響を含ませるべきかを検討することが望ましい。
6.4.4
金属,ゴム,織物のような均質化できない固体試料を測定しなければならないときで,さらに同一
の試験片について測定を繰り返すことができないときは,測定試料の不均質性は測定精度の主要な成分を
構成し,もはや同一と見なされる試料という概念は有効ではない。それでも精度評価実験を実施すること
は可能であるが,得られた精度値は用いたその試料にのみ有効であり,そういうものとして引用されるこ
とが望ましい。求めた精度のより普遍的な使い方は,異なる時期,又は異なる製造者で製造された試料を
測定したときの精度の値が,有意に変わらないということを示すことができるときにのみ受け入れられる。
このことはこの規格において考慮されているよりもさらに入念な実験が必要とされるかもしれない。
6.4.5
一般に,破壊試験を必要とする場合,測定を行う試料の違いから生じる測定結果のばらつきへの寄
与は,測定方法そのもののばらつきに比べて無視できるか,さもなければ測定方法のばらつきの固有の部
分を構成し,まさに精度の成分である。
6.4.6
測定中の試料が経時的に変化するときは,このことを考慮に入れて実験全体のタイムスケールを選
ぶことが望ましい。ある場合には試料を測定する日時を指定することが適切かもしれない。
6.4.7
以上では,測定試料の試験室への移送に関連して,異なる試験室における測定について述べている。
しかし,油貯蔵庫の場合のように,ある種の測定試料は移送できない。そのような場合は,異なる試験室
で測定するということはその試験場所に各オペレータを装置と共に送り込むことを意味する。他の場合に
は,川の水流のように,測定する量が過渡的又は変動的であるかもしれない。このときはできるだけ同一
条件で何回かの測定を行うという配慮をしなければならない。指針となる原則は,同一の測定を繰り返す
能力を決めることが常にその目的でなければならない。
6.4.8
測定方法の精度値設定の前提条件は,精度が測定試料に依存しないか,又は予想できるかたちで依
存するということである。ある測定方法では,一つ以上の定義可能なクラス(品質区分)の測定試料に関
してのみその精度を引用することができる。そのようなデータは他に適用するときの精度に対しては大ま
かな基準となるにすぎない。精度は測定水準に密接に関係するということはよくあるが,そのとき,精度

16
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の設定には精度と水準の関係を確立させるということが含まれる。それゆえ,標準測定方法の精度値を公
表する際,精度評価実験に用いる試料について,適用可能な範囲を併せて明確に記載することが推奨され
る。
6.4.9
真度評価のためには,少なくとも用いた試料の内一つは参照値を有していることが望ましい。もし
真度が水準によって変化しそうであれば,いくつかの水準において参照値を有する試料が必要となる。
7. 精確さ(真度と精度)に関する値の利用方法
7.1
真度と精度の公表
7.1.1
精度評価実験で,3.14及び3.18で述べた条件下での併行標準偏差及び再現標準偏差の推定値を得
るのが目的であれば,5.1の基本モデルを使用すべきである。これらの標準偏差を推定する適切な方法はこ
の規格の第2部に述べられており,又代替法がこの規格の第5部に述べられるであろう。中間精度の推定
値を得るのが目的であれば,この規格の第3部に示した代替モデルと代替法を使用しなければならない。
7.1.2
測定方法のかたよりが求められたときは,常にかたよりを求めた標準となるものについての文書を
添えて公表することが望ましい。かたよりが測定(試料)の水準によって変化するときは,水準,求めら
れたかたより及びそれに使用した標準を表にして公表することが望ましい。
7.1.3
真度又は精度を推定するために共同実験が行われた時は,参加した各試験室は実験で求められた全
平均値に対しての試験室のかたより成分を知らされるのが望ましい。そして,そのかたよりの値はその後
類似した実験を行うときは価値のあるものだが,校正を行う目的で使用すべきではない。
7.1.4
すべての標準測定方法の併行標準偏差及び再現標準偏差はこの規格の第2部〜第4部に従って決め
られなくてはならない。その標準測定方法の一部に「精度」という項目を設けて報告するのが望ましい。
同じ項目に併行許容差及び再現許容差(r及びR)を記述してもよい。精度が測定(試料)の水準によって
変わらないときは,各々(r及びR)につき1つの平均値を示せばよい。精度が試験の水準によって変わる
ときは表4に示した形式で示し,かつ数式で表現してもよい。中間精度も同様の方法で報告するのが望ま
しい。
表4 標準偏差の報告例
(試験の)範囲又は水準
併行標準偏差
sr
再現標準偏差
sR
〜
〜
〜
7.1.5
報告値のみでなく併行及び再現条件の定義(3.14と3.18)を,「精度」の節に記述しなくてはなら
ない。中間精度の結果が得られている時にはどの要因(時間,オペレータ,装置)が変わったのかを述べ
る点に注意を払うのが望ましい。併行許容差及び再現許容差を述べるときは,二つの試験値の差と確率95%
に関連させた記述を加えることが望ましい。次に示すような記述の仕方を推奨する。
同一と見なせる試料で同じオペレータが同じ装置を使って可能な限り短い時間間隔で試験して得られた
2つの測定結果の差が併行許容差 (r) を越えるのは,規定の操作を間違いなく行っていれば平均して20回
に1回以下であろう。
同一と見なせる試料で2つの試験室で得られた測定結果の差が再現許容差 (R) を越えるのは,規定の操
作を間違いなく行っていれば平均して20回に1回以下であろう。
測定結果を得るのに使用した測定方法の規格の節 (clause) の番号を引用したり他の方法で,測定結果の
17
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定義を明確にすること。
7.1.6
通常,“精度”の項の終わりの部分に,精確さに関する実験について簡単に記述するのが望ましい。
次に示すような記述の仕方を推奨する。
精確さ(真度と精度)はJIS Z 8402−(部):(年)に従って, (p) 試験所と (q) の測定水準で評価され
た。 ( ) カ所の試験室のデータは,外れ値を含んでいた。外れ値は併行標準偏差及び再現標準偏差の計
算から除外した。
真度又は精度が(測定する)試料に影響するときは特に,精確さ評価実験に使用された試料についての
記述を加えておくべきである。
7.2
真度と精度の値の実際的な利用
真度と精度の利用の詳細はこの規格の第6部に述べられている。いくつかの例を次に示す。
7.2.1
測定結果の判定
製品規格では併行条件で得られる繰返しの測定値が要求されることがある。そのような場合には,測定
結果を確認し,それが許容できない場合どんな対策がとられるべきかを決めるために併行標準偏差が使わ
れる。売手と買い手が同一試料を測定しその結果が異なるときは,その差異がその方法に予想された大き
さであるかどうかを判断するために併行及び再現標準偏差が使われることがある。
7.2.2
室内の測定結果の安定性判定
日常的に標準物質を複数回測定することにより,その測定値のかたよりと併行精度の両方についてその
試験室の結果の安定性を確認するとともに,試験室の能力を証明することができる。
7.2.3
試験室の測定能力の評価
試験室の認定制度はますます広く普及しつつある。測定方法の真度と精度に関する知識の普及によって,
標準物質を使ったり共同実験を行うことによって対象試験室のかたよりと併行精度を評価できるようにな
った。
7.2.4
他の測定方法との比較
同じ特性について測定する2つの方法があり,1つは他の方法に比べ簡単でコストのかからない方法だ
が一般には使用されていないとする。この場合,限定された範囲の試料については,真度と精度がそのコ
ストのかからない方法を使用してよいかどうかを判定する基準になるかもしれない。
18
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定)
JIS Z 8402で用いられる記号
a
関係式s=a+bmの切片
A
推定値の不確かさを計算するのに用いる係数
b
関係式s=a+bmの勾配
B
全平均と試験室の測定値の偏差を表す成分
(かたよりに占める試験室成分)
B0
Bの成分の中で中間精度条件の下では変わらない,
すべての要因
B(1),B(2),など
Bの成分の中で中間精度条件で変化する要因
c
関係式logs=c+dlogmの切片
C,C',C''
検定統計量
Ccrit,C'crit,C''crit
統計的検定の棄却限界値
CDp
確率Pの許容差
CRp
確率Pの許容範囲
d
関係式logs=c+dlogmの勾配
e
測定値の成分中,すべての測定値に生じている偶然
誤差
f
許容範囲の係数
Fp (ν1,ν2)
分子の自由度ν1,分母の自由度ν2のF分布のp分位
点
G
グラッブスの検定統計量
h
マンデルの試験室間一致性の検定統計量
k
マンデルの試験室内一致性の検定統計量
LCL
下側管理限界(処置限界または警戒限界)
m
試験特性の一般平均;水準
M
中間精度条件において考慮される因子の数
N
反復数
n
一つの試験室で一つの水準(すなわち,セルごと)
で得る測定値の数
p
共同実験に参加した試験室数
P
確率
q
共同実験における試験特性の水準数
r
併行精度限界値(許容差)
R
再現精度限界値(許容差)
RM
標準物質
s
標準偏差の推定値
sˆ
標準偏差の予測値
T
ある表示の総和
t
試験対象または群の数
UCL
上側管理限界(処置限界または警戒限界)
W
重み付き回帰式の計算で用いられる重み係数
w
一組の測定値の範囲
x
グラッブス検定に用いられるデータ
y
測定値
y
測定値の算術平均
y
測定値の全平均
α
有意水準
β
第二種の過誤の確率
γ
再現標準偏差と併行標準偏差の比 (σR/σr)
∆
試験室のかたより
∆ˆ
∆の推定値
δ
測定方法のかたより
δˆ
δの推定値
λ
二つの試験室または二つの測定方法間のかたよりの
検出可能な差
μ
試験特性の真値または参照値
ν
自由度
ρ
方法AとBの併行標準偏差間の検出可能な比
σ
標準偏差の真の値
τ
最終校正からの時間経緯に起因する変動を表す測定
値の成分
φ
方法AとBの試験室間平均平方の平方根の検出可能
な比
χ2p (ν)
自由度νのχ2分布におけるp分位点
添え字に用いる記号
C
校正法が異なることを示す
E
装置が異なることを示す
i
特定の試験室を示す添え字
I ( )
中間精度に関する添え字,かっこ内に中間精度条件
のタイプの識別子を記述する
j
特定の水準に関する添え字 (JIS Z 8402-2)
19
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
分析の一群あるいは要因に関する添え字
(JIS Z 8402-3)
k
試験室iにおける水準jのk番目の測定値を示す添
え字
L
試験室間を示す
m
検出可能なかたよりに関する添え字
M
試験試料間を示す
O
オペレーターが異なっていることを示す
P
確率
r
併行精度
R
再現精度
T
時間が異なることを示す
W
試験室内を示す
1,2,3…
測定値の得られた順序を示す
(1),(2),(3),…
測定値の大きさの順序を示す
20
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(規定)
精度の尺度の不確かさに関する図
図B.1 srの真の値からの乖離量(信頼率95%)
21
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.2 sRの真の値からの乖離量(信頼率95%)
22
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考)
参考文献
[1] JIS Z 8101-2 : 1999,統計−用語と記号−第2部 統計的品質管理用語
[2] JIS Z 8101-3 : 1999,統計−用語と記号−第3部 実験計画法
[3] JIS Z 8402-5 : −1),測定方法及び測定結果の精確さ(真度及び精度)−第5部 標準測定方法の精度
を求めるための代替法
[4] JIS Z 8402-6 : 1999,測定方法及び測定結果の精確さ(真度及び精度)−第6部 精確さに関する値の
実用的な使い方
[5] JIS Q 0033 : 1997,認証標準物質の使い方
[6] JIS Q 0035 : 1997,標準物質の認証−一般的及び統計学的原則
規格原案作成委員会 構成表
氏名
所属
(委員長)
石 川 馨
東京大学
(幹事)
宮 津 隆
日本鋼管株式会社
岩 田 晶 夫
住友金属鉱山株式会社
内 沼 一 雄
日本石油株式会社
藤 森 利 美
東京大学
(委員)
石 井 清 次
工業技術院
神 森 大 彦
社団法人日本化学会
上 甲 子 郎
東京理科大学
横 山 毅
昭和電工株式会社
高 橋 梅太郎
海外貨物検査株式会社
窪 田 孝 昌
海外貨物検査株式会社
(事務局)
新 井 紀 弘
財団法人日本科学技術連盟
規格改正原案作成委員会 構成表
氏名
所属
(委員長)
宮 津 隆
西東京科学大学理工学部
(委員)
尾 島 善 一
東京理科大学理工学部
故 高 橋 梅太郎
元海外貨物検査株式会社
椿 広 計
慶應義塾大学理工学部
仁 科 健
名古屋工業大学工学部
西 島 保
東燃株式会社総合研究所
野 村 和 夫
東京ガス株式会社
番 場 章
三石テクノ株式会社
23
Z 8402-1 : 1999 (ISO 5725-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
多 田 格 三
元株式会社東芝
藤 森 利 美
長崎大学経済学部
横 山 隆 壽
財団法人電力中央研究所狛江研究所
池 田 要
工業技術院標準部材料規格課
川 村 正 信
財団法人日本規格協会
黒 木 勝 也
財団法人日本規格協会
(事務局)
橋 本 進
財団法人日本規格協会
品質管理分野国際整合化分科会
氏名
所属
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
○ 今 井 秀 孝
工業技術院計量研究所
○ 柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
日本電信電話株式会社
門 山 允
東京国際大学
○ 鹿 庭 なほ子
国立食品医薬品衛生研究所
兼 子 毅
武蔵工業大学工学部
○ 城 道 修
メルシャン株式会社
○ 椿 広 計
筑波大学社会工学系
○ 仁 科 健
名古屋工業大学工学部
野 澤 昌 弘
東京理科大学経営学部
三佐尾 武 雄
QCコンサルタント
○ 宮 津 隆
帝京科学大学理工学部
山 田 秀
東京都立科学技術大学工学部
横 尾 恒 雄
QCコンサルタント
大 嶋 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会
備考 ○印は許容差JIS原案作成WGの委員を兼ねる。




