Z 8000-1:2014
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
0.1 量 ······························································································································· 1
0.2 単位 ···························································································································· 2
0.3 単位の値の実現 ············································································································· 2
0.4 表の配列 ······················································································································ 3
1 適用範囲 ························································································································· 3
2 引用規格 ························································································································· 3
3 用語及び定義 ··················································································································· 3
4 量································································································································· 13
4.1 量の概念 ····················································································································· 13
4.2 量の種類−量演算 ········································································································· 13
4.3 量の体系−基本量及び組立量··························································································· 14
4.4 普遍定数及び実験的定数 ································································································ 14
4.5 量方程式における一定乗数······························································································ 14
4.6 国際量体系(ISQ) ······································································································· 15
5 次元······························································································································ 15
6 単位······························································································································ 16
6.1 単位及び数値 ··············································································································· 16
6.2 数学的演算 ·················································································································· 16
6.3 量方程式及び数値方程式 ································································································ 17
6.4 一貫性のある単位系 ······································································································ 17
6.5 国際単位系(SI) ·········································································································· 18
7 印刷に関する規則 ············································································································ 23
7.1 量記号 ························································································································ 23
7.2 単位の名称及び記号 ······································································································ 25
7.3 数 ······························································································································ 27
7.4 化学元素及び核種 ········································································································· 29
7.5 ギリシャ語アルファベット······························································································ 30
附属書A(規定)物理量の名称に用いる用語 ············································································ 31
附属書B(規定)数の丸め方 ································································································· 35
附属書C(規定)対数量及びその単位 ····················································································· 36
附属書D(参考)量及び単位の分野における国際機関································································· 38
参考文献 ···························································································································· 39
附属書JA(参考)JISと対応国際規格との対比表 ······································································ 40
Z 8000-1:2014
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人日本規格協会(JSA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
これによって,JIS Z 8202-0:2000及びJIS Z 8203:2000は廃止され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 8000の規格群には,次に示す部編成がある。
JIS Z 8000-1 第1部:一般
JIS Z 8000-3 第3部:空間及び時間
JIS Z 8000-4 第4部:力学
JIS Z 8000-5 第5部:熱力学
JIS Z 8000-6 第6部:電磁気
JIS Z 8000-7 第7部:光
JIS Z 8000-8 第8部:音
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格
JIS
Z 8000-1:2014
量及び単位−第1部:一般
Quantities and units-Part 1: General
序文
この規格は,2009年に第1版として発行されたISO 80000-1を基とし,技術的内容を変更して作成した
日本工業規格である。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。変更の一
覧表にその説明を付けて,附属書JAに示す。
0.1
量
量体系及び単位系の表現法には,相互に矛盾がなければ異なる方法が存在してよい。どの方法を用いる
かは,あくまで取決めによって合意される。この規格では,国際度量衡総会(CGPM: Conference General de
Poids et Mesures)が単位系として採用した国際単位系(SI: Systeme International dʼUnites)の基礎となった
方法を示した。
ここで使用されている量及び量の間の関係は,物理科学の全域にわたってほぼ普遍的に受け入れられて
いるものである。それらは今日,大多数の科学の教科書に記載されており,全ての科学者及び技術者によ
く知られている。
注記 CGS-ESU系1),CGS-EMU系1) 及びガウス系での電磁気単位の場合,定義される量体系に相違
がある。CGS-ESU系では,電気定数ε0(真空の誘電率,permittivity of vacuum)は1,すなわち
無次元として定義されており,CGS-EMU系では,磁気定数μ0(真空の透磁率,permeability of
vacuum)は1,すなわち無次元として定義されているが,対照的に国際量体系(ISQ)では,そ
れらは無次元ではない。ガウス系は,CGS-ESU系及びCGS-EMU系に関連しており,同じ混乱
がある。
力学において,一般にニュートンの運動の法則は,F=c・maと表す。古い技術体系である
MKS単位系2) ではc=1/gnであり,gnは自由落下の標準加速度である。国際量体系(ISQ)で
は,c=1である。
注1) CGS:センチメートル−グラム−秒,ESU:静電単位,EMU:電磁単位
2) MKS:メートル−キログラム−秒
量及び量の間の関係は,本質的にその数は無限であり,新しい分野の科学及び技術の発展に伴って進化
し続けている。したがって,この規格にこれらの量及び量の間の関係を全て規定することは不可能である。
代わりに,より一般的に使用される量及び量の間の関係を規定している。
特定の専門分野で活動している規格利用者が,関心をもっている量が,この規格又はその他の規格に規
定されていないと気付く可能性がある。しかし,これらの規格利用者が,関心をもっている量を,この規
格に規定されている,よりよく知られている例に関係付けることができれば,規格利用者が関心をもって
2
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
いる量を定義することへの妨げとはならないであろう。
関心のある量の値を表現するために使用される単位の大部分は,量体系という概念が開発されるずっと
以前から開発及び使用されていたが,単に物理科学の方程式である量の間の関係は,重要である。なぜな
ら,いずれの単位系においても,単位間の関係は重要な役割を果たし,これらは対応する量の関係から開
発されたものだからである。
SIの単位の基礎として使用されている量,及びそれらの間の関係は,国際量体系(ISQ)と命名されて
いる。この名称は,現在の調和がとれたシリーズの元になっている旧JIS Z 8202規格群の中では使用され
なかった。しかし,ISQという名称は,2007年に発行されたISO/IEC Guide 99,及び2006年に発行され
たSI文書第8版[8] でも使用されている。共に,この新しい量及び単位シリーズの一貫性を確実にするため
であった。それらが発行された時点で,既にこの新しい版では新しい用語が使用されるであろうというこ
とが発表されていた。しかし,ISQは,近代科学及び技術の全てが基づく,本質的に無限で持続的に進化
及び拡大している量体系,及び方程式に割り当てられた単に便利な表示に過ぎないということを認識する
ことが望ましい。ISQは,旧JIS Z 8202規格群において,この体系のために使用された表現である“SIの
基礎となる量体系”の省略表示である。
なお,この規格で扱う量及び単位の分野における国際機関の名称については,附属書Dに参考として記
載している。
0.2
単位
一組の基本量に対応する一組の基本単位を定義し,次に,基本量から組立量を定義している関係を用い
て,基本単位のべき乗の積の形で組立単位を定義することによって単位系が確立されている。この規格及
びSIには,七つの基本量及び基本単位がある。基本量は,長さ,質量,時間,電流,熱力学温度,物質量
及び光度であり,対応する基本単位はそれぞれ,メートル,キログラム,秒,アンペア,ケルビン,モル
及びカンデラである。これらの基本単位の定義及びそれらの実現方法は,SIの中心をなしている。これは,
国際度量衡委員会(CIPM: Comite International des Poids et Mesures)の下の諮問委員会が責任を負って担当
している。この基本単位の現在の定義及びその実現方法は,SI文書[8] に記載されている。SI文書の原本は,
国際度量衡局(BIPM: Bureau International des Poids et Mesures)によって発行されている。基本量は,この
ように明確な定義をもつ基本単位とは対照的に,運用上定められている場合を除いて,単に慣習によって
選ばれ,明確に定義されている訳ではない。
0.3
単位の値の実現
単位の値を実現するということは,単位と同一種類のある量の値を,単位の値と比較するために測定を
行う場合,単位の定義を用いることである。これは,科学において量の値の測定を行うに当たっての本質
的手段である。基本単位の値の実現は,特に重要である。組立単位の値の実現は,原則として基本単位の
実現に従う。
単位の値の実用的実現のための多くの異なる方法があっても差し支えなく,また,科学の進歩に伴って
新しい方法が開発されても差し支えない。物理法則に矛盾しないいずれの方法も,どのSI単位の実現のた
めにも使用することができる。
なお,単位の実現のために,実験的方法を見直すことは多くの場合有益であり,CIPMではSI文書の一
部に記載されているような方法を推奨している。
3
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0.4
表の配列
この規格群においては,ISQのサブセットである量,及びそれらの間の関係は,左側のページに記載し
ており,SIの単位(及びその他の幾つかの単位)は,右側のページに記載している。幾つかの追加の量及
び単位も同様に,それぞれ左右のページに記載している。量の項目番号は,pp-nn.sの形で記載している
(pp:規格群の部番号,nn又はnn.s:細分番号)。単位の項目番号は,pp-nn.lの形で記載している(pp:
規格群の部番号,nn:細分番号,l:細別文字)。
1
適用範囲
この規格は,量,量体系,単位,量記号及び単位記号並びに一貫性のある単位系[特に国際量体系(ISQ)
及び国際単位系(SI)]に関する定義及び一般的な事項について規定する。ただし,順序尺度量(ordinal
quantities)及び名義的性質(nominal properties)は除く。
この規格は,広く科学及び技術の分野での使用並びにJIS Z 8000規格群の手引とすることを意図してい
る。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 80000-1:2009,Quantities and units−Part 1: General(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8401 数値の丸め方
ISO/IEC Guide 99,International vocabulary of metrology−Basic and general concepts and associated terms
(VIM)
注記 なお,上記のISO/IEC Guide 99については,TS Z 0032として発行されている。
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
注記 この箇条で規定している定義の内容は,ISO/IEC Guide 99の規定内容と同一であるが幾つかの
注記及び例は修正している。
3.1
量(quantity)
数と計量参照(reference)との組合せとして表すことができる大きさをもつ,現象,物体又は物質の性
質。
注記1 一般的概念の“量”は,次の表に示すように,幾つかのレベルの特定の概念に分けることが
できる。表の左側は,“量”の基にある特定の概念を示している。これらは,右側の欄の個々
の量に対する一般的概念である。

4
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
長さ,l
半径,r
円Aの半径,rA又はr(A)
波長,λ
ナトリウムのD線の波長,λD又はλ(Na; D)
エネルギー,E
運動エネルギー,T
任意の系の粒子iの運動エネルギー,Ti
熱,Q
水の試料iの蒸発熱,Qi
電荷,Q
陽子の電荷,e
電気抵抗,R
任意の回路の抵抗器iの電気抵抗,Ri
対象Bの物質量濃度,cB
ワイン試料iのエタノールの物質量濃度,ci(C2H5OH)
対象Bの個数濃度,CB
血液試料i中の赤血球の個数濃度,C(Erys; Bi)
ロックウェルCスケール硬さ,HRC
鉄鋼試料iのロックウェルCスケール硬さ,HRCi
注記2 計量参照(reference)は,測定単位,測定手順,標準物質又はこれらの組合せのいずれかで
ある。量の大きさについては,3.19を参照。
注記3 量を表す記号は,量及び単位を規定するJIS Z 8000及びISO/IEC 80000規格群に規定されて
いる。量を表す記号は,斜体文字で記載する。一つの任意の記号は,異なる量を示すことが
できる。
注記4 ここに定義する量は,スカラーである。ただし,その要素が量であるベクトル又はテンソル
も量とみなされる。
注記5 “量”の概念は,一般に,例えば“物理量”,“化学量”及び“生物量”,又は“基本量”及び
“組立量”に分けてよい。
注記6 この3.1は,ISO/IEC Guide 99の定義1.1に従っている。ただし,注記の一つを削除した。
注記7 物理量には,係数,因子,変数,比,定数などの名称を使用して区別するものがあるが,そ
の命名方法に関する一般的な指針については,附属書Aに規定している。
3.2
量の種類(kind of quantity)
相互に比較可能な量に共通の側面。
注記1 量の種類は,“種類”と省略することもある。例えば,同じ種類の量。
注記2 “量の種類”に従って“量”を区分することは,ある程度任意である。
例1 直径,円周及び波長の量は,一般に同じ種類の量,つまり,長さという種類の量と
考えられている。
例2 熱,運動エネルギー及び位置エネルギーの量は,一般に同じ種類の量,つまり,エ
ネルギーという量の種類と考えられている。
注記3 任意の量体系内における同じ種類の量は,同一の量の次元をもつ。ただし,同一次元の量は,
必ずしも同じ種類とは限らない。
例3 量である力のモーメント及びエネルギーは,ともに同一の次元をもつが,慣習によ
って,同じ種類の量とはみなさない。熱容量及びエントロピー,並びに対象の数,
相対浸透率及び質量分率の場合も同様である。
注記4 この3.2は,ISO/IEC Guide 99の定義1.2に従っている。ただし,注記1を追加した。
3.3
量体系(system of quantities)
量の集合で,これらの量を関係付ける矛盾のない方程式の集合を合わせもつもの。
注記1 ロックウェルCスケール硬さのような順序尺度量(3.26参照),及び光の色のような名義的
性質(3.30参照)は,経験的関係だけを通して他の量と関係付けられるため,通常は量体系
5
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の一部とはみなさない。
注記2 この3.3は,ISO/IEC Guide 99の定義1.3に従っている。ただし,注記1を変更した。
3.4
基本量(base quantity)
慣習的に選択された任意の量体系の部分集合に含まれる量であって,その部分集合の中のいずれの量も,
その部分集合内の他の量では表現できないもの。
注記1 この定義でいう部分集合を,“基本量の集合”と呼ぶ。
例 ISQにおける基本量の集合は,3.6に示す。
注記2 基本量は,他の基本量のべき乗の積として表現することができないので,互いに独立である
ものとみなす。
注記3 “対象の数(number of entities)”は,どの量体系でも基本量とみなすことができる。
注記4 この3.4は,ISO/IEC Guide 99の定義1.4に従っている。ただし,定義は若干異なる。
3.5
組立量(derived quantity)
ある量体系の中で,その体系の基本量によって定義される量。
例 長さ及び質量を基本量にもつ量体系では,密度は質量と体積(長さの3乗)との商で定義される
組立量である。
注記 この3.5は,ISO/IEC Guide 99の定義1.5に従っている。ただし,例は若干異なる。
3.6
国際量体系,ISQ(International System of Quantities)
七つの基本量(長さ,質量,時間,電流,熱力学温度,物質量及び光度)を基本とする量体系。
注記1 この量体系は,量及び単位を規定するJIS Z 8000及びISO/IEC 80000規格群に記載されてい
る。
注記2 国際単位系(SI)(3.16参照)は,ISQに基づいている。
注記3 この3.6は,ISO/IEC Guide 99の定義1.6に従っている。ただし,注記1は若干異なる。
3.7
量の次元(quantity dimension,dimension of a quantity),次元(dimension)
数値因子を除外し,基本量のべき乗の積として表した量と,量体系の基本量との関係。
例1 ISQでは,力の量の次元をdim F=LMT−2と表記する。
例2 同じ量体系で,dim ρB=ML−3は構成要素Bの質量濃度の量の次元であり,ML−3は,密度ρの
量の次元でもある。
例3 自由落下の局所加速度がgである場所における長さlの質点振り子の周期Tは,次の式で求め
られる。
g
l
T
π
2
=
又は
()l
C
T
g
=
ただし,()
g
g
π
2
=
C
したがって,dim C(g)=T・L−1/2
注記1 次元のべき乗は,指数をべき乗した次元である。各次元は,基本量の次元である。
注記2 基本量の次元の記号は,大文字の直立体(ローマン体)一文字で表す。ある組立量の次元の
6
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
取決めによる記号表現は,組立量の定義に従って,基本量の次元のべき乗となる。量Qの次
元は,dim Qと表記される。
注記3 量の次元を組み立てるときには,そのスカラー,ベクトル又はテンソルの特性は考慮に入れ
ない。
注記4 任意の量体系では,
− 同じ種類の量は同じ量の次元をもち,
− 量の次元の異なる量は常に種類の異なる量であるが,
− 同じ量の次元をもつ量は同じ種類である必要はない。
注記5 ISQで基本量の次元を表す記号は,次のとおりである。
基本量
次元
長さ
L
質量
M
時間
T
電流
I
熱力学温度
Θ
物質量
N
光度
J
したがって,量Qの次元は,Q=LαMβTγIδΘεNζJηと表記される。ここに,次元指数と名付け
られた指数は,正,負又はゼロである。基本量の指数が0の場合には,その基本量の次元は
記載せず,指数が1の場合には,その基本量の次元を示す指数は記載しない。全ての指数が
0のときは,3.8を参照。
注記6 この3.7は,ISO/IEC Guide 99の定義1.7に従っている。ただし,例2,例3及び注記5は異
なる。
3.8
次元1の量(quantity of dimension one),無次元量(dimensionless quantity)
その量の次元において,基本量に対応する次元の全ての指数が0である量。
注記1 一般に“無次元量”という用語が使用されており,ここでは歴史的理由からこれを踏襲する。
これは,このような量の次元の記号表現で,全ての指数が0であるという事実に由来する。
“次元1の量”という用語は,そのような量では次元の記号表現が記号1であるという取決
めを反映している(箇条5を参照)。この次元は数ではなく,次元の乗算のための単位元であ
る。
注記2 次元が1である量の測定単位及び値は数であるが,このような量は単なる数よりも多くの情
報を伝える。
注記3 次元1のある幾つかの量は,同じ種類の二つの量の比として定義される。一貫性のある組立
単位は,数の1(記号1)である。
例1 平面角,立体角,屈折率,相対浸透率,質量分率,摩擦係数,マッハ数
注記4 対象の数は,次元1の量である。
例2 コイルの巻数,任意の試料中の分子の数,量子系のエネルギーレベルの縮退
注記5 この3.8は,ISO/IEC Guide 99の定義1.8に従っている。ただし,注記1及び注記3は異な
る。
7
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.9
測定の単位(unit of measurement),測定単位(measurement unit),単位(unit)
二つの量の比を数として表現するために,他のいかなる同じ種類の量とも比較できる実数スカラー量で,
取決めによって定義し,採用するもの。
注記1 測定単位は,取決めによって割り当てられる名称及び記号で指定される。
注記2 同一次元の量の測定単位は,その量が同じ種類のものでなくても,同一の名称及び記号で指
定してよい。例えば,ジュール毎ケルビン及びJ/Kは,熱容量の測定単位及びエントロピー
の測定単位の両方についての,それぞれ名称及び記号であるが,両者は一般に同じ種類の量
とはみなされない。しかし,特別な測定単位名は,特定の種類の量だけに使用が限定されて
いる場合がある。例えば,測定単位“毎秒”(1/s)は,周波数に使用する場合はヘルツ(Hz)
であり,放射能の意味として使用する場合はベクレル(Bq)である。もう一つの例として,
ジュール(J)はエネルギーの単位として使用されるが,力のモーメント,すなわち,ニュー
トンメートル(N・m)の単位としては決して使用されない。
注記3 次元1の量の測定単位は数である。場合によって,これらの測定単位は,例えば,ラジアン,
ステラジアン及びデシベルのような特別な名称が与えられるか,又は10−3に等しいミリモル
毎モル,及び10−9に等しいマイクログラム毎キログラムのような商によって表現される。
注記4 ある任意の量の場合,短い用語の“単位”は,“質量単位”又は“質量の単位”のように量の
名称と組み合わせることがある。
注記5 この3.9は,ISO/IEC Guide 99の定義1.9に従っている。ただし,定義文及び注記2は若干
異なる。
3.10
基本単位(base unit)
取決めによって採用された基本量の測定単位。
注記1 一貫性のある各単位系では,基本量ごとにただ一つの基本単位が存在する。
例1 SIでは,メートルが長さの基本単位である。CGS系では,センチメートルが長さの
基本単位である。
注記2 基本単位は,同一次元の組立量に用いてもよい。
例2 雨量は,単位面積当たりの体積と定義するとき,SIにおいて一貫性のある組立単位
としてのメートルを用いる。
注記3 対象の数では,数の1,記号1を任意の単位系の基本単位とみなすことができる。3.4の注記
3と比較。
注記4 この3.10は,ISO/IEC Guide 99の定義1.10に従っている。ただし,注記2は若干異なる。
また,注記3に追記がある。
3.11
組立単位(derived unit)
組立量の測定単位。
例 メートル毎秒(m/s)及びセンチメートル毎秒(cm/s)は,SIにおける速さの組立単位である。キ
ロメートル毎時(km/h)は,SI以外の速さの測定単位であるが,SIと併用して用いる単位として
受け入れられている。1海里毎時に相当するノットは,SI以外の速さの測定単位である。
(ISO/IEC Guide 99の定義1.11参照)
8
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.12
一貫性のある組立単位(coherent derived unit)
任意の量体系及び選択した基本単位の集合で,1以外の係数を含まない,基本単位のべき乗の積となる
組立単位。
注記1 基本単位のべき乗は,ある指数でべき乗した基本単位である。
注記2 特定の量体系及び所定の基本単位の集合に関してだけ,一貫性を決定することができる。
例1 メートル,秒及びモルが基本単位であるならば,メートル毎秒は,速度を量方程式
v=dr/dtで定義するとき,速度の一貫性のある組立単位となり,また,モル毎立方
メートルは,物質量濃度を量方程式c=n/Vで定義するとき,物質量濃度の一貫性の
ある組立単位となる。キロメートル毎時及びノットは,組立単位の例として示した
ように(3.11参照),このような量体系では一貫性のある組立単位ではない。
注記3 組立単位は,一つの量体系では一貫性があるが,別の量体系では一貫性がない場合がある。
例2 センチメートル毎秒は,CGS単位系では一貫性のある速さの単位であるが,SIでは
一貫性のある組立単位ではない。
注記4 任意の単位系で次元が1である全ての組立量の一貫性のある組立単位は,数の1,記号1で
ある。測定単位1の名称及び記号は,通常は明記しない。
(ISO/IEC Guide 99の定義1.12参照)
3.13
単位系(system of units)
任意の量体系において,任意の規則に従って定義される,それらの倍量及び分量を含む基本単位及び組
立単位の集合。
(ISO/IEC Guide 99の定義1.13参照)
3.14
一貫性のある単位系(coherent system of units)
任意の量体系に基づいた,各組立量の測定単位が一貫性のある組立単位である単位系。
例 一貫性のあるSI単位の集合及びその単位の間の関係。
注記1 単位系は,ある量体系と採用した基本単位とに関してだけ一貫性をもつことができる。
注記2 一貫性のある単位系では,数値方程式は,数値因子を含めて,対応する量方程式と同じ形式
をもつ。3.25の数値方程式の例を参照。
注記3 この3.14は,ISO/IEC Guide 99の定義1.14に従っている。ただし,注記2は異なる。
3.15
体系外の測定単位(off-system measurement unit),体系外の単位(off-system unit)
任意の単位系に属していない測定単位。
例1 電子ボルト[≈ 1.602 18×10−19 J 3)]は,SIに関してはエネルギーの体系外の測定単位である。
注3) 国際規格では,“≈”を使用することになっているが,我が国では“≒”を用いてもよ
い。
例2 日,時,分は,SIに関しては時間の体系外の測定単位である。
注記 この3.15は,ISO/IEC Guide 99の定義1.15に従っている。ただし,例1は異なる。
3.16
国際単位系,SI(International System of Units)

9
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
国際度量衡総会(CGPM)によって採択された,一連の接頭語並びにその名称及び記号を含めた単位の
名称及び記号,並びにそれらの使用規則を含む,ISQに基づく単位系。
注記1 SIは,ISQの七つの基本量並びに表1に掲げる対応する基本単位の名称及び記号に基づいて
いる(6.5.2参照)。
注記2 SIの基本単位及び一貫性のあるSI組立単位は,“一貫性のあるSI単位の集合”という一貫性
のある集合を形成する。
注記3 国際単位系の詳細な解説及び説明については,国際度量衡局(BIPM)が発行し,BIPMのウ
ェブサイトから入手可能な最新版のSI小冊子第8版を参照。
注記4 量の演算では,“対象の数”という量は,基本単位1,記号1とする基本量とみなすことが多
い。
注記5 単位の倍量及び単位の分量を表すSI接頭語については,6.5.4を参照。
注記6 この3.16は,ISO/IEC Guide 99の定義1.16に従っている。ただし,注記1及び注記5は異
なる。
3.17
単位の倍量(multiple of a unit)
任意の測定単位に1より大きい整数を乗じて得られる測定単位。
例1 キロメートルは,メートルの10進の倍量である。
例2 時間は,秒の非10進の倍量である。
注記1 SI接頭語を,SI基本単位及びSI組立単位の10進の倍量で示す場合を,6.5.4に示す。
注記2 SI接頭語は,厳密に10のべき乗を指し,2のべき乗を指すときに用いてはならない。例えば,
1 024ビット(210ビット)を表すときは1キロビットではなく,1キビビット(1 Kibit)を使
用することが望ましい。
2進の倍量用の接頭語は,次のとおりである。
倍量
値
接頭語
名称
記号
(210)8
1 208 925 819 614 629 174 706 176 ヨビ
Yi
(210)7
1 180 591 620 717 411 303 424 ゼビ
Zi
(210)6
1 152 921 504 606 846 976 エクスビ
Ei
(210)5
1 125 899 906 842 624 ペビ
Pi
(210)4
1 099 511 627 776 テビ
Ti
(210)3
1 073 741 824 ギビ
Gi
(210)2
1 048 576 メビ
Mi
(210)1
1 024 キビ
Ki
出典:IEC 80000-13:2008
注記3 この3.17は,ISO/IEC Guide 99の定義1.17に従っている。ただし,注記1及び注記2は異
なる。
3.18
単位の分量(submultiple of a unit)
任意の測定単位を1より大きい整数で除して得られる測定単位。
例1 ミリメートルは,メートルの10進の分量である。
例2 平面角で,秒は分の非10進の分量である。
10
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 SI接頭語を,SI基本単位及びSI組立単位の10進の分量で示す場合を,6.5.4に示す。
(ISO/IEC Guide 99の定義1.18参照)
3.19
量の値(quantity value,value of a quantity),値(value)
量の大きさを表現する,数と計量参照との組合せ。
例1 ある棒の長さ:5.34 m又は534 cm
例2 ある物体の質量:0.152 kg又は152 g
例3 ある円弧の曲率:112 m−1
例4 ある試料のセルシウス温度:−5 ℃
例5 ある回路素子のある周波数におけるインピーダンス,ここにjは虚数単位:(7+3j) Ω
例6 あるガラス試料の屈折率:1.32
例7 ある試料のロックウェルCスケール硬さ:43.5 HRC
例8 ある銅試料中のカドミウム質量分率:3 μg/kg又は3×10−9
例9 水中の鉛イオンの質量モル濃度:1.76 μmol/kg
例10 あるヒトの血しょう(漿)試料中のルトロピンの物質量濃度(WHO国際規格80/552):5.0 IU/l
(“IU/l”は,WHO国際単位毎リットル)
注記1 計量参照の種類に応じて,量の値は,次のいずれかとなる。
− 数と測定単位との積(例1,例2,例3,例4,例5,例8及び例9参照):
次元1の量については,一般に,測定単位1は表示しない(例6及び例8参照)。
− 測定手順に対する数と計量参照(reference)との組合せ(例7参照)
− 数と標準物質との組合せ(例10参照)
注記2 数は複素数の場合がある(例5参照)。
注記3 量の値は複数の方法で表現することができる(例1,例2及び例8参照)。
注記4 ベクトル量又はテンソル量の場合は,各要素が量の値をもつ。
例
ある粒子に働く力[例えば,直交座標系成分(Cartesian components)で表す力]
は,次の式で表す。
(Fx, Fy, Fz)=(−31.5, 43.2, 17.0) N
ここで,(−31.5, 43.2, 17.0)は数値ベクトルであり,N(ニュートン)は単位又は
各成分を量で表すと次のとおり。
(Fx, Fy, Fz)=(−31.5 N, 43.2 N, 17.0 N)
注記5 この3.19は,ISO/IEC Guide 99の定義1.19に従っている。ただし,例10及び注記4は異な
る。
3.20
量の数値(numerical quantity value,numerical value of a quantity),数値(numerical value)
計量参照の役目を果たす数以外の,量の値の表記中の数。
注記1 次元1の量の場合,計量参照は数である測定単位であり,これは量の数値の一部とはみなさ
ない。
例1 3 mmol/molに等しい物質量分率の場合,量の数値は3であり,単位はミリモル毎モ
ル(mmol/mol)である。単位のミリモル毎モル(mmol/mol)は,数値としては0.001
であるが,この数0.001は量の数値の一部ではなく,量の数値は3のままである。
11
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記2 測定単位をもつ量(すなわち,順序尺度量以外の量)の場合,量Qの数値{Q}は,{Q}=Q/[Q]
と表記することが多い。ここで,[Q]は単位を表す。
例2 量の値が5.721 kgの場合,量の数値は{m}=(5.721 kg)/kg=5.721である。同じ量の
値は5 721 gと表すことができるが,この場合,量の数値は{m}=(5 721 g)/g=5 721
である。3.19参照。
注記3 この3.20は,ISO/IEC Guide 99の定義1.20に従っている。ただし,注記2は異なる。
3.21
量演算(quantity calculus)
順序尺度量以外の量に適用する,数学の規則及び操作の集合。
注記 量方程式は,測定単位の選び方によらず同一の表式となる一方で,数値方程式はそうではない
ため,誤解を避ける上で量の四則演算及び量方程式の使用が強く推奨される(3.22,3.25,4.2
及び6.3も参照)。
(ISO/IEC Guide 99の定義1.21参照)
3.22
量方程式(quantity equation)
任意の量体系における,量の間の測定単位の選び方によらない,数学的関係。
例1 Q1,Q2及びQ3がそれぞれ別の量を表し,ζが数値である場合は,Q1=ζ Q2 Q3となる。
例2 T=(1/2) mv2
ここに,
T: 運動エネルギー
v: 質量mの特定の粒子の速さ
例3 n=It/F
ここに,
F: ファラデー定数
n: 1価の成分の物質量
I: 電流
t: 電気分解の継続時間
(ISO/IEC Guide 99の定義1.22参照)
3.23
単位方程式(unit equation)
基本単位,一貫性のある組立単位,又は他の測定単位の間の数学的関係。
例1 3.22の例1の量において,[Q1],[Q2]及び[Q3]がそれぞれQ1,Q2及びQ3の測定単位を表す場合,
これらの測定単位が,ある一貫性のある単位系に含まれていれば,[Q1]=[Q2][Q3]である。
例2 J :=kg m2 s−2 4)
ここに,
J: ジュール
kg: キログラム
m: メートル
s: 秒
(記号“:=”は,ISO 80000-2の2-7.3に示すように,“定義上として等しい”ことを示す。)
注4) 国際規格では,“:=”を用いることになっているが,我が国では“=”又は“≡”を用
いてもよい。また,この規格では,“:=”を全て“=”で表した。
例3 1 km/h=(1/3.6) m/s
注記 この3.23は,ISO/IEC Guide 99の定義1.23に従っている。ただし,例2は異なる。
12
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.24
単位間の換算率(conversion factor between units)
同じ種類の量を表す二つの測定単位の比。
例1 km/m=1 000であるから,1 km=1 000 m
注記 測定単位は,異なる単位系に属することがある。
例2 h/s=3 600であるから,1 h=3 600 s
例3 (km/h)/(m/s)=(1/3.6)であるから,1 km/h=(1/3.6) m/s
(ISO/IEC Guide 99の定義1.24参照)
3.25
数値方程式(numerical value equation),数量値方程式(numerical quantity value equation)
任意の量方程式において,特定の測定単位を用いた場合の,数量値間の数学的関係。
例1 3.22の例1の量で,{Q1},{Q2}及び{Q3}がそれぞれQ1,Q2及びQ3の数値を表す場合,これら
が基本単位又はある一貫性のある組立単位のいずれか又は両方で表されていれば,{Q1}=
ζ{Q2}{Q3}である。
例2 ある粒子の運動エネルギーを表す量方程式T=(1/2) mv2で,m=2 kg,v=3 m/sであれば,{T}
=(1/2)×2×32は,Tがジュールを単位とする数値9であることを示す数値方程式である。
注記1 この3.25は,ISO/IEC Guide 99の定義1.25に従っている。
注記2 量方程式は,測定単位の選び方によらず同一の表式となる一方で,数値方程式はそうではな
いため,誤解を避ける上で量の四則演算及び量方程式の使用が強く推奨される(3.22及び6.3
参照)。
3.26
順序尺度量(ordinal quantity)
量の間には代数演算関係が存在しないが,同じ種類の量がほかにあるときに,大きさに従い全体の順序
関係を確立することができる,取決めによる測定手順によって定義できる量。
例1 ロックウェルCスケール硬さ
例2 石油燃料のオクタン価
例3 リヒタースケール(Richter scale)による地震強度
例4 0から5までのスケールによる腹痛の主観的レベル
注記1 順序尺度量は,経験的関係だけを示すものであり,測定単位も量の次元ももたない。順序尺
度量の差及び比に物理的な意味はない。
注記2 順序尺度量は,順序尺度量の値の目盛(3.28参照)に従って決められる。
(ISO/IEC Guide 99の定義1.26参照)
3.27
測定目盛(quantity-value scale,measurement scale)
大きさに従ってその種類の量のランク付けに使用する,任意の種類の量の値の順序集合。
例1 セルシウス温度目盛
例2 時間目盛
例3 ロックウェルCスケール硬さ目盛
注記 この3.27は,ISO/IEC Guide 99の定義1.27に従っている。
13
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.28
順序尺度量の値の目盛(ordinal quantity-value scale,ordinal value scale)
順序尺度量の値の測定目盛。
例1 ロックウェルCスケール硬さ目盛
例2 石油燃料のオクタン価目盛
注記1 順序尺度量の値の目盛は,測定手順に従った測定によって確立されることがある。
注記2 この3.28は,ISO/IEC Guide 99の定義1.28に従っている。
3.29
取決めによる参照目盛(conventional reference scale)
正式な合意によって定義される測定目盛。
(ISO/IEC Guide 99の定義1.29参照)
3.30
名義的性質(nominal property)
定量的に示すことができない,現象,物体又は物質の特性。
例1 人間の性別
例2 塗料見本の色
例3 化学分野でのスポット(斑点:spot)試験の色
例4 JISで規定する2文字の国名コード
例5 ポリペプチドにおけるアミノ酸の配列
注記1 名義的性質は,英数字コード又は他の手段を用いた語句で表現することができる値をもつ。
注記2 “名義的性質の値”を,量の公称値と混同してはならない。量の公称値は,この規格では使
用していない。
注記3 この3.30は,ISO/IEC Guide 99の定義1.30に従っている。ただし,注記2は異なる。
4
量
4.1
量の概念
この規格では,現象,物質又は物体の量的な表記に用いる量を取り扱う。
測定目盛(ビューフォート風力階級,リヒタースケール,色度の目盛など)に従って配列された,又は
慣行的な試験(例えば,硬さ及び耐食性)の結果のような順序尺度量は取り扱わない。また,人間の性別,
JISで規定する2文字の国名コード又は通貨のような名義的性質についても同様に取り扱わない。
4.2
量の種類−量演算
量は,相互に比較できる量の種類に分類することができる。直径,距離,高さ,波長などが,一般には
長さという一つの種類を構成する。相互に比較できる量は,“同じ種類の量”という。
次に示すように,順序尺度量以外の量は数学的操作を行うことができる。
2個以上の量は,相互に比較できる量の同一の種類に属していない限り,加えたり減じたりすることは
できない。したがって,方程式における等号の両側の量も,同一の種類でなければならない。
量は,代数の規則に従って互いに乗除演算されることによって,新しい量になる。
量の加算,減算,乗算及び除算という数学的演算を厳密に行うことは,量演算という。量演算において
は,代数的表現は量又は数であることが望ましい。
14
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.3
量の体系−基本量及び組立量
量は,自然法則を表現する又は新しい量を定義する方程式によって関係付けられる。量の間の各方程式
は,量方程式という。
異なる種類の幾つかの量を相互に独立したものと考えるのが便利である。それらの量を基本量と呼ぶ。
基本量を用いて方程式によって定義又は表現することができる他の量を組立量と呼ぶ。
どの量を幾つ基本量とみなすかは,選択の問題である。また,組立量を定義するためにどの方程式を使
用するかも,選択の問題である。量の間を結ぶ,矛盾のない方程式の集合を量体系と呼ぶ。
4.4
普遍定数及び実験的定数
幾つかの量は,全ての状況下で一定であるとみなされるものがある。そのような量は,普遍定数又は基
礎物理定数という。
例1 プランク定数h=6.626 068 96 (33)×10−34 J・s [CODATA 2006]
例2 ファラデー定数F=96 458.339 9 (24) C/mol [CODATA 2006]
ほかの量は,ある状況下で一定であるかもしれないが,ほかに依存する。それらの値は,一般には測定
によって得られる。それらを実験的定数と呼ぶ。
例3 数個の質点振り子のある観測点における長さl及び周期Tの測定値は,次の量方程式で表す。
l
C
T=
ここに,
C: 場所に依存する実験的定数
理論によれば,Cは次のように表される。
g
π
2
=
C
ここに,
g: その地点での自由落下の加速度であり,別の実験的定数
4.5
量方程式における一定乗数
量方程式は,一定乗数を含むことがある。これらの乗数は,その方程式に含まれる量の定義,すなわち,
選択された量の体系に依存する。そのような乗数が,純粋の数値である場合,これを数値因子と呼ぶ。
例1 CGS系においては,長さ,質量,及び時間が三つの基本量である。その体系においては,古典
力学における粒子の運動エネルギーは,次の方程式で表される。
2
2
1v
m
T=
ここに,
T: 運動エネルギー
m: 質量
v: 速さ
ISQでも同じ関係が成り立つ。
一つの乗数に,いくつかの普遍定数が含まれている場合もある。
例2 ISQにおいて,電荷に関するクーロンの法則は,次の方程式で表される。
2
2
1
0
π
4
1
r
q
q
F
ε
=
ここに,
F: 力
q1及びq2: 二つの電荷
r: 距離
ε0: 普遍定数,すなわち,電気定数
一つの乗数に,いくつかの取決め合意値が含まれている場合もある。
例3 現在は使われていないMKS系では,長さ,質量及び時間が三つの基本量である。その体系で
15
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は,ニュートンの運動の法則は,次の方程式で表される。
ma
F
n
1
g
=
ここに,
F: 力
m: 質量
a: 加速度
gn: 取決めによる量の値,すなわち,CGPM 1901によって採用さ
れた自由落下の標準加速度
(この体系においては,力と質量とは同じ次元をもつ。)
一定乗数のうち数値因子でないものは,しばしば係数と呼ばれる。
4.6
国際量体系(ISQ)
JIS Z 8000及びISO/IEC 80000規格群に規定されている,特別に選択された乗数を含む基本量及び量方
程式を,国際量体系と定義する(全ての言語でISQと表示する。)。組立量は,量方程式によって基本単位
を用いて定義することができる。ISQには,長さ,質量,時間,電流,熱力学温度,物質量及び光度とい
う七つの基本量がある。
5
次元
量の体系においては,いかなる量Qも方程式を用い,基本量で表現することができる。表現は,複数の
項の和からなることもある。これらの項は,いずれもある選ばれた集合からの基本量A,B,C,…,とき
には数値因子ξのべき乗との積として,ξAαBβCγ…という形式で表記できる。この場合,指数の集合である
α,β,γ,…は,各項について同じである。
量Qの次元(3.7参照)は,次元の積,
dim Q=AαBβCγ…
と表される。
ここに,A,B,C,…は,それぞれ基本量A,B,C,…の次元を表し,α,β,γ,…は次元指数という。
これらの次元指数の全てが0である量は,次元の積A0B0C0…=1(ここに記号1は,対応する次元を表
す。)をもつ。そのような量は,次元1の量と呼ばれ,数として表される。
注記 歴史的な理由から,次元1の量は,“無次元量”ともいう。3.8の注記1参照。
ISQにおいて,長さ,質量,時間,電流,熱力学温度,物質量及び光度という七つの基本量に基づく基
本量の次元は,それぞれ,L,M,T,I,Θ,N及びJによって表される。したがって,ISQにおいては,
量Qの次元は,一般に次のようになる。
dim Q=LαMβTγIδΘεNζJη
例 量
次元
速さ
LT−1
周波数
T−1
力
LMT−2
エネルギー
L2MT−2
エントロピー
L2MT−2Θ−1
電位
L2MT−3I
磁束
L2MT−2I−1
照度
L−2J
16
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
モルエントロピー
L2MT−2Θ−1N−1
効率
1
6
単位
6.1
単位及び数値
ある種類からの一つの量の具体的な例を,単位(3.9参照)という基準量として選べば,同じ種類の他の
いかなる量も,この単位によって,この単位と一つの数の積として表すことができる。この数は,この単
位で表した量の数値という。
例1 ナトリウム線の中の1本の波長は,次による。
λ ≈ 5.896×10−7 m
ここに,
λ: 量である波長の記号
m: 長さの単位メートルの記号
5.896×10−7: メートルで表記した波長の数値
量及び単位の公式の扱い方は,次の式による。
Q={Q} · [Q]
ここに,
Q: 量の記号
[Q]: 単位の記号
{Q}: 単位[Q]で表した量Qの数値の記号
ベクトル及びテンソルに対しては,各成分は上記のように表すことができる量である。ベクトル及びテ
ンソルは,それぞれ単位を乗じた数値ベクトル及び数値テンソルとしても表現することができる。
ある量を,最初の単位のk倍である他の単位で表すならば,新しい数値は,最初の数値の1/k倍となる。
なぜなら,数値と単位の積である量は,単位には影響されない。
例2 例1において,波長の単位を,メートルから,メートルの10−9倍であるナノメートルに変える
と,メートルで表記された量の数値の109倍の数値が得られることになる。
ここに, λ ≈ 5.896×10−7 m=5.896×10−7×109 nm=589.6 nm
量自体と,特定の単位で表した量の数値との間の区別をすることが重要である。特定の単位で表した量
の数値は,例えば{λ}nmのように,量記号を括弧(波括弧)で囲み,単位を下付添字として示すことによっ
ても表すことができる。しかし,数値は,単位に対する量の比として,明確に表記することが望ましい。
例3 λ/nm ≈ 589.6
この表記方法は,グラフ及び表の欄の見出しに使用することを推奨する。
6.2
数学的演算
二つの量,Q1及びQ2の積及び商については,次の式が成立する。
{}{}[][]
2
1
2
1
2
1
Q
Q
Q
Q
Q
Q
=
{}{}[]
[]
2
1
2
1
2
1
Q
Q
Q
Q
Q
Q
=
ここに,
積{Q1} {Q2}: 量Q1Q2の数値{Q1Q2}
積[Q1] [Q2]: 量Q1Q2の単位[Q1Q2]
同様に,
商{Q1}/{Q2}: 量Q1/Q2の数値{Q1/Q2}
商[Q1]/[Q2]: 量Q1/Q2の単位[Q1/Q2]
[Q1] [Q2],[Q1]/[Q2]などの単位は,複合単位という。
例1 等速運動中の粒子の速さvは,次の式で示される。
v=l/t
17
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
l: 時間tの間に移動する距離である。
したがって,粒子が継続時間t=2 sの間に距離l=6 mを進むと,速さvは次の式のとおりと
なる。
v=l/t=(6 m)/(2 s)=3 m/s
注記1 A/Bとして定義される量は,“BによるAの商”又は“A毎B”というが,“A毎単位B”では
ない。
{Q1Q2}={Q1} {Q2}などのような数値間の方程式は,数値方程式という。[Q1Q2]=[Q1] [Q2]などのような
単位間の方程式は,単位方程式という。
指数関数,対数関数,三角関数などの引数は,数,数値,又は量の次元1の組合せである(箇条5参照)。
注記2 この箇条及びこの箇条以降にみられる対数関数の利用に当たっては,附属書Cに留意事項を
規定している。
例2 exp (E/kT), ln (p/kPa), sin (π/3), cos (ωt+α)
同じ種類の二つの量の比と,その比のある種の関数,例えば,その比の対数とは,同じ物理的状況を記
しているが,異なる量である。
例3 p/p0及びln(p/p0)は,異なる量である。数学においては,ln(p/p0)=ln p−ln p0であるが,pが圧力
を表す量演算においては,ln p及びln p0は意味をもたないことに留意しなければならない。
6.3
量方程式及び数値方程式
これまで紹介された三つの方程式,すなわち,量方程式,数値方程式,及び単位方程式は,科学及び技
術の分野において使用されている。一般には,量方程式及び数値方程式が使用される。単位方程式は,用
いられることは少ない。数値方程式(及び単位方程式)の表式は,単位の選び方に依存する。一方,量方
程式の表式は,この選び方によらないという利点をもつ。したがって,量方程式の使用が通常は好まれ,
強く推奨される。
例 一つの簡単な量方程式は,6.2に記載した,次の式である。
v=l/t
例えば,速さ,距離,及び継続時間の単位として,それぞれキロメートル毎時(km/h),メー
トル(m),及び秒(s)を使用すれば,次の数値方程式が得られる。
{v}km/h=3.6 {l}m/{t}s
ここに, {v}km/h=v/(km/h)
この数値方程式中にある数の3.6は,選ばれた特定の単位によるものである。これと異なる単
位の選択をすれば,この数値因子は一般に異なるものとなる(6.1参照)。
数値方程式においては,数値因子は使用される単位の選び方に関係するので,そのような方程式におい
ては,下付き添字を省略しないことが望ましい。下付き添字を使用しない場合,同じ文脈中に単位を明確
に示さなければならない。
6.4
一貫性のある単位系
単位を任意に選ぶこともできるが,各量に対する単位を独立して選択すると,数値方程式に余分な数値
因子が出現する。
しかし,数値方程式が数値因子も含み,選択された量体系において,対応する方程式と全く同一の形式
をもつように単位系を選ぶことが可能であり,また,実用上もより便利である。そのような単位系を確立
するには,まず,各基本量に対するただ一つの単位を定義する。基本量の単位は,基本単位と呼ぶ。次に,
全ての組立量の単位が,量体系における方程式に従って,基本単位を用いて表現される。組立量の単位は,
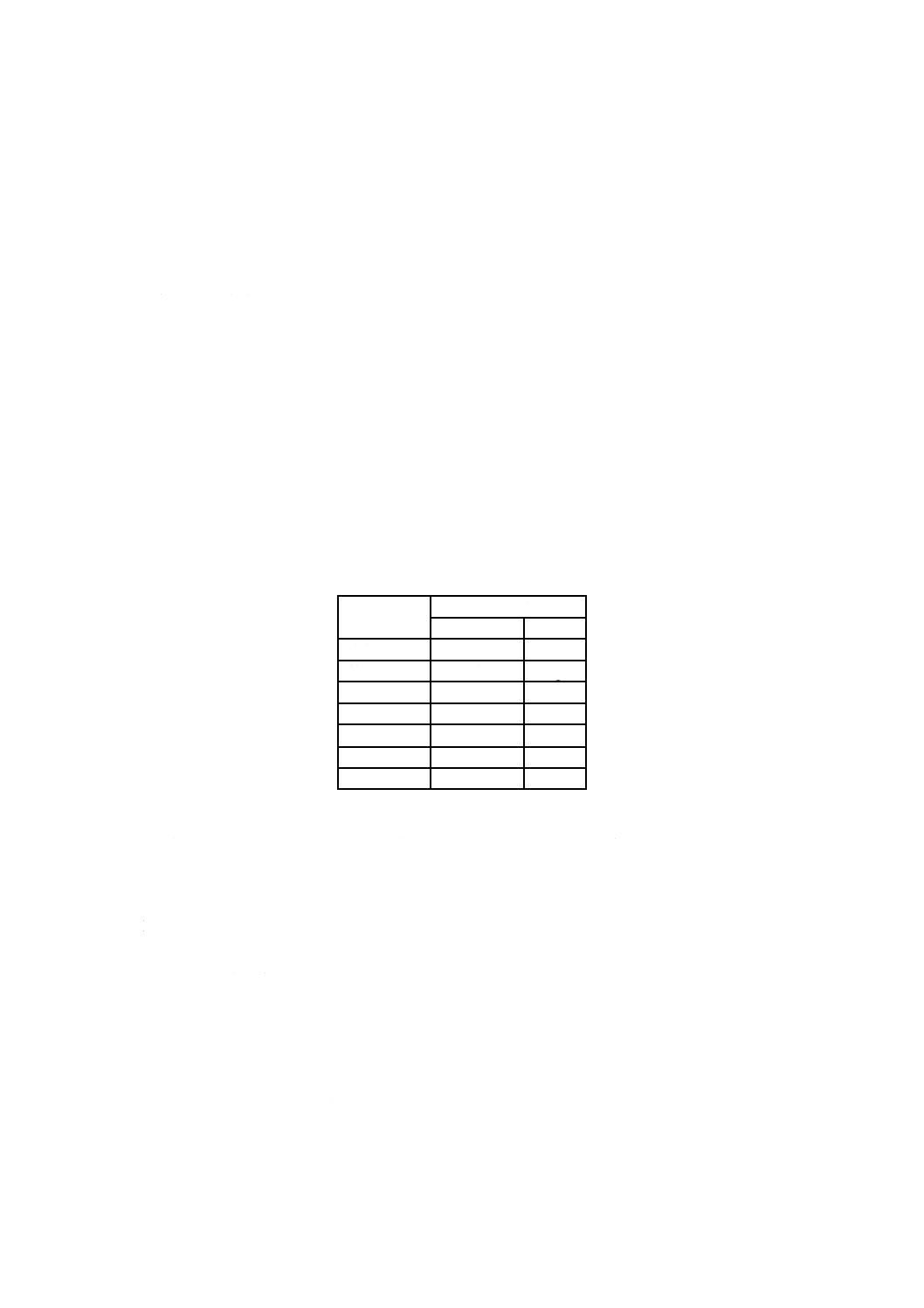
18
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
組立単位と呼ぶ。この方法で定義される単位系は,当該の方程式を含む量体系に関して,一貫性があると
いう。
一貫性のある単位系において,各単位の表現は,その量の次元に対応する。すなわち,単位の表現は,
量の次元における基本次元の記号を,対応する基本単位の記号に置き換えることによって得られる。特に,
次元1の量には,単位1(記号1)が付与される。そのような一貫性のある単位系においては,基本単位を
用いた組立単位の表記で,1以外の数値因子が表れることはない。
6.5
国際単位系(SI)
6.5.1
一般
全ての言語でSIと表示される国際単位系は,第11回国際度量衡総会(CGPM: Conférence Générale des
Poids et Mesures)[1960]で採択された。SIは,ISQに関して一貫性のある単位系である。
SIは,次からなる。
− 基本単位
− 組立単位
これらは,ともに一貫性のあるSI単位系を形成する。
6.5.2
SI基本単位
七つのSI基本単位を,表1に示す。
表1−ISQ基本量のためのSI基本単位
ISQ基本量
SI基本単位
名称
記号
長さ
メートル
m
質量
キログラム
kg
時間
秒
s
電流
アンペア
A
熱力学温度
ケルビン
K
物質量
モル
mol
光度
カンデラ
cd
6.5.3
SI組立単位
SI基本単位による一貫性のあるSI組立単位の表記は,次の形式的な置換えによって,対応するISQ組
立量の次元の積から得ることができる。
L → m
Θ → K
M → kg
N → mol
T → s
J → cd
I → A
1 → 1
これらの置き換えは,可逆的である。したがって,ISQ組立量の次元は,基本単位による一貫性がある
SI組立単位から得ることができる。
例1
量
七つのSI基本単位によって表記されるSI単位の記号
速さ
m/s
周波数
s−1
力
kg・m/s2
エネルギー
kg・m2/s2
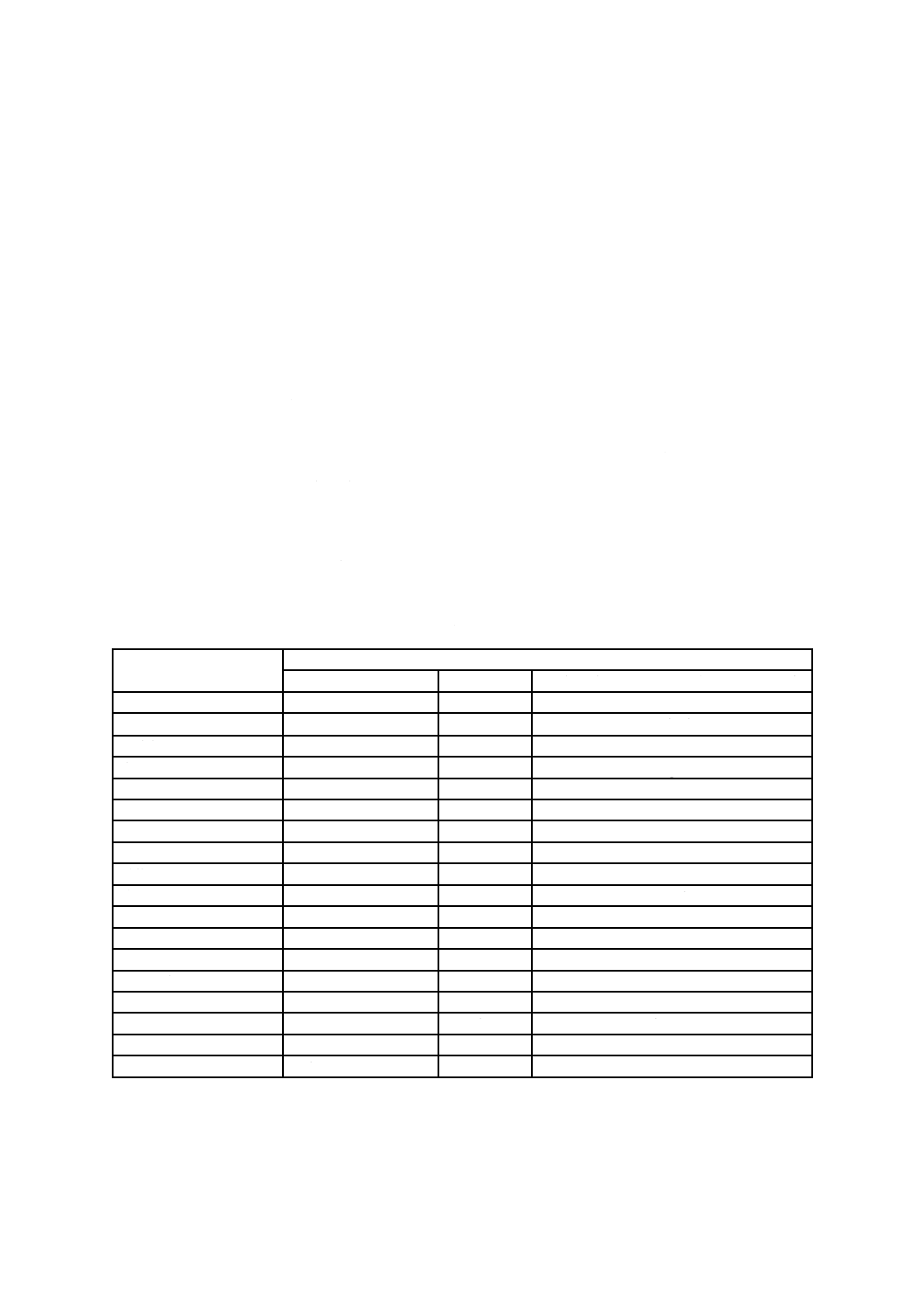
19
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
エントロピー
kg・m2/(s2・K)
電位
kg・m2/(s3・A)
磁束
kg・m2/(s2・A)
光子照度
s−1/m2
モルエントロピー kg・m2/(s2・K・mol)
効率
1
単位は,量の特別な場合であり,したがって,量方程式において使用することができる一方で,次元は
使用することができない。次元及び単位のいずれも,1以外のいかなる数値因子も含まない。各単位は大
きさをもつが,次元は大きさをもたない。次元は量体系に対応するが,単位は量体系と一貫性のある特定
の単位系に対応する。
SI組立単位の中には,固有の名称及び記号をもつものがある。CGPMによって承認されたものを表2及
び表3に示す。
単位の複雑な組合せでは,固有の名称及び記号を使用することが有利な場合が多い。
例2 組立単位ジュール,1 J=1 m2・kg/s2,を用いて,モルエントロピーの記号は次で表しても差し支
えない。
J/(K・mol)
組立単位ボルト,1 V=1 m2・kg/(s3・A)を用いて,磁束の記号は次で表しても差し支えない。
V・s
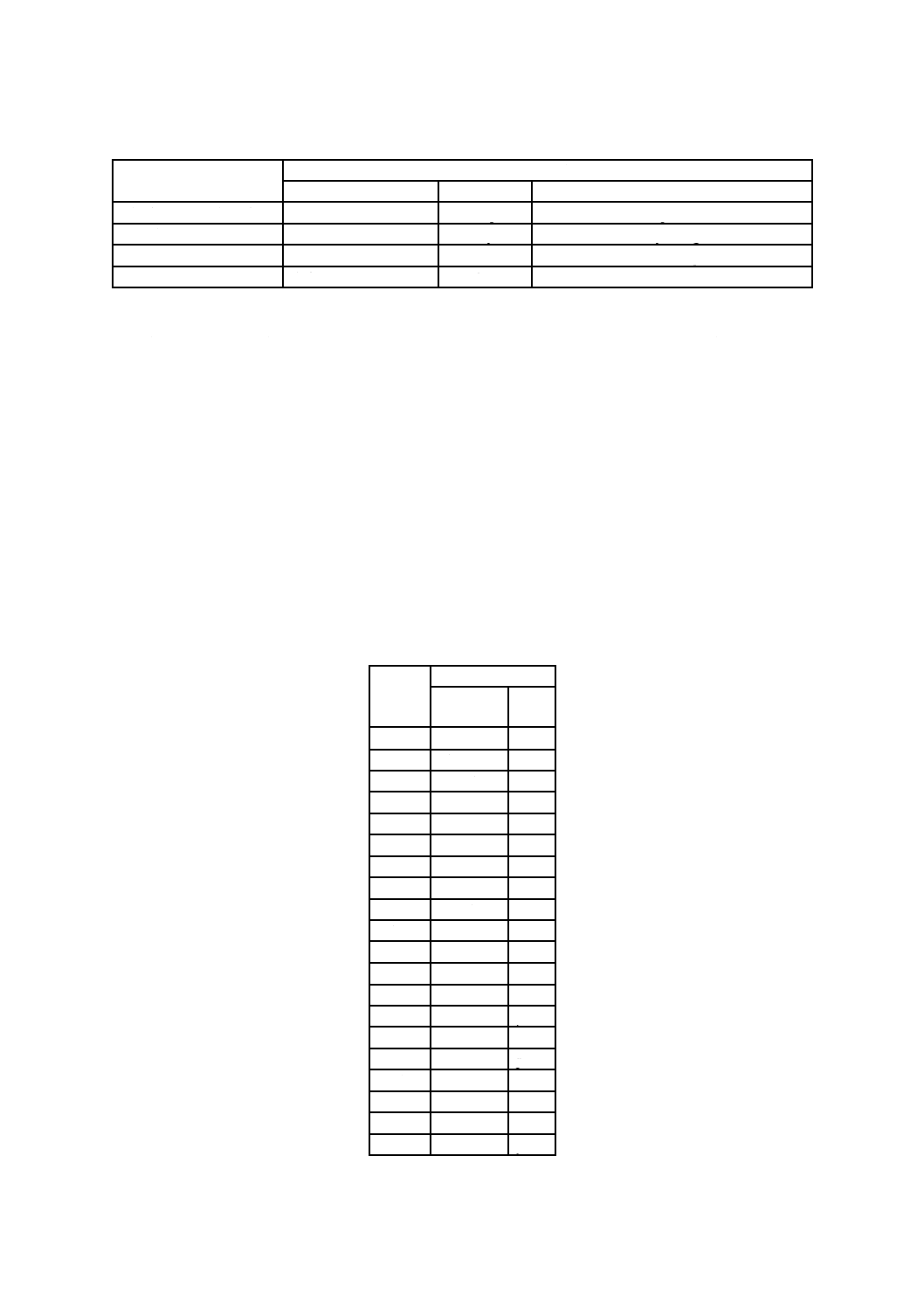
表2−固有の名称及び記号をもつSI組立単位
ISQ組立量
SI組立単位
固有の名称
固有の記号
SI基本単位及びSI組立単位による表し方
平面角
ラジアン
rad
rad=m/m=1
立体角
ステラジアン
sr
sr=m2/m2=1
周波数
ヘルツ
Hz
Hz=s−1
力
ニュートン
N
N=kg・m/s2
圧力,応力
パスカル
Pa
Pa=N/m2
エネルギー
ジュール
J
J=N・m
電力
ワット
W
W=J/s
電荷
クーロン
C
C=A・s
電位
ボルト
V
V=W/A
静電容量
ファラド
F
F=C/V
電気抵抗
オーム
Ω
Ω=V/A
電気コンダクタンス
ジーメンス
S
S=Ω−1
磁束
ウエーバ
Wb
Wb=V・s
磁束密度
テスラ
T
T=Wb/m2
インダクタンス
ヘンリー
H
H=Wb/A
セルシウス温度
セルシウス度
℃
℃=K
光束
ルーメン
lm
lm=cd・sr
照度
ルクス
lx
lx=lm/m2
20
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3−人の健康保護のために認められる固有の名称及び記号をもつSI組立単位
ISQ組立量
SI組立単位
固有の名称
固有の記号
SI基本単位及びSI組立単位による表し方
(放射性核種の)放射能 ベクレル
Bq
Bq=s−1
吸収線量
グレイ
Gy
Gy=J/kg
線量当量
シーベルト
Sv
Sv=J/kg
酵素活性
カタール
kat
kat=mol/s
SI組立単位は,場合によってはSI基本単位と同一であることに留意することが望ましい。例えば,雨
量は,単位面積当たりの体積として与えられる。これは組立量であり,したがって,組立単位で表される。
一貫性のあるSI組立単位としては,立方メートル毎平方メートル(m3/m2=m)で,SI基本単位であるメ
ートルに等しい。
単位1(記号1)は,一般にSI組立単位である。例えば,摩擦係数に対するSI組立単位は,ニュートン
毎ニュートンで1に等しい(N/N=1)。しかし,計数値に対する単位1,例えば,原子中の陽子の数を考慮
してみる。ここでは,計数値は,基本量として考えられる。なぜなら,それは他のいかなる基本量を用い
ても表現することができないからである。したがって,この場合,CGPMはまだそれをSI基本単位として
採用していないが,単位1(記号1)は,基本単位としても考えられる。
6.5.4
SI接頭語
大きな桁の又は小さな桁の数値を避けるため,一貫性のあるSI単位の10進の倍量及び分量群を,表4
に示す接頭語とともに構成する。これらのSI倍量単位及びSI分量単位は,ISQに関して一貫性がない。
表4−SI接頭語
倍量
又は
分量
接頭語
名称
記号
1024
ヨタ
Y
1021
ゼタ
Z
1018
エクサ
E
1015
ペタ
P
1012
テラ
T
109
ギガ
G
106
メガ
M
103
キロ
k
102
ヘクト
h
101
デカ
da
10−1
デシ
d
10−2
センチ
c
10−3
ミリ
m
10−6
マイクロ
μ
10−9
ナノ
n
10−12
ピコ
p
10−15
フェムト
f
10−18
アト
a
10−21
ゼプト
z
10−24
ヨクト
y
21
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
接頭語記号は,その接頭語が直接付着する単一の単位記号と組み合わされ,単位の10進の倍量及び分量
(正又は負のべき乗)の新しい記号を形成するものとみなされる。また,他の単位記号と組み合わせて複
合単位のための記号を構成することもできる。
例1 1 cm3=(10−2 m)3=10−6 m3
1 μs−1=(10−6 s)−1=106 s−1
1 Ω/km=1 Ω/(103 m)=10−3 Ω/m
複合した接頭語は,用いてはならない。
例2 10−9 mに対して,nm(ナノメートル)と記載するが,mμmとはしない。
注記1 歴史的理由から,質量のSI基本単位の名称であるキログラムは,SI接頭語“キロ”を含んで
いる。キログラムの10進の倍量及び分量の単位の名称は,分量のグラム(g)という語に接
頭語を加えて,例えば,ミリグラム(mg)とするが,マイクロ・キログラム(μkg)とはし
ない。
SI基本単位である質量のために,接頭語のない新しい名称を採用することが提案されてい
る。同時に,分量であるグラムにも,SIとともに使用される追加の単位として,分量である
立方デシメートル(dm3)と等しいリットル(l),及び倍量であるメガグラム(Mg)と等し
いトン(t)と同じ地位が与えられることが望ましい。これが承認されるならば,現在リット
ル及びセンチリットルが使用されているように,グラム及びキログラムを引き続き使用する
ことができる。
SI接頭語は,正確に10の整数乗を示す。それらは,2進法の倍量を示すために用いてはならない。2進
法の倍量の接頭語は,3.17に示す。これら倍量の起源及び由来については,IEC 80000-13:2008の箇条4
を参照する。
例3 1 kbit=1 000 bit
1 Kibit=1 024 bit
注記2 SI接頭語は,ISO通貨コードにも使用される。例えば,
1 kEUR=1 000 EUR(欧州ユーロ)
1 kGBP=1 000 GBP(英国ポンド)
1 MUSD=1 000 000 USD(USドル)
1 GSEK=1 000 000 000 SEK(スウェーデン・クローナ)
6.5.5
単位1
次元1の量に対する一貫性があるSI単位は,単位1(記号1)である。そのような量を数値的に表す場
合には,一般に記号としての単位1は明示しない。
例1 巻き線における巻き数N=25×1=25
しかし,このような量の中の特定のものでは,単位1が固有の名称及び記号をもつものもあり,この単
位は状況に応じて使用する。
例2 平面角 α=0.52 rad=0.52
立体角 Ω=2.3 sr=2.3
場の量のレベル LF=12 Np=12(表5参照)
このような固有の名称及び記号を,同一の次元をもっているが種類が異なる量の区別を容易にするため
に,組立単位のための表示において用いても差し支えない。
例3 角速度,ω=17 rad/s
光子束,Φ=37×106 s−1

22
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
減衰係数,α=0.83 Np/m
曲率,κ=0.34 m−1
単位1のための固有の名称及び記号は,SI接頭語と組み合わせても差し支えないが,単位1そのもの,
又は記号1は,SI接頭語と組み合わせてはならない。代わりに,数値を10のべき乗によって表しても差
し支えない。
注記 接頭語と組み合わせることができる,単位1及び記号1のための固有の名称及び記号を一般的
使用のために採用することが提案されている。
場合によっては,1 %=0.01の場合に,パーセント(%)が一貫性のある単位1の分量として使用される。
例4 反射率r=83 %=0.83
また,パーミル(‰)も,1 ‰=0.001のとき,一貫性のある単位1の分量として使用される。
単位“パーセント”も“パーミル”も数であるから,例えば質量パーセント,体積パーセントなどと称
することは意味がない。したがって,%(m/m)又は(V/V)というような付加情報は,記号%に付けては
ならない。7.2も参照。質量分率を表す好ましい方法は,例えば,“Bの質量分率はwB=0.78である”又は
“Bの質量分率はwB=78 %である”である。さらに,“パーセンテージ”という用語は,量の名称におい
ては用いてはならない。なぜなら,誤解を招くからである。仮に質量分率が0.78=78 %の場合,パーセン
テージを78とするか,それとも78 %=0.78とするのか分からない。その代わりに,“分率”という,曖昧
ではない用語を使用する。質量分率及び体積分率は,また,μg/g=10−6又はml/m3=10−9という形式で表
すこともできる。
ppm,pphm,ppb,pptなどのような略号は,言語によるので,不明瞭であるため,用いてはならない。
代わりに,10のべき乗の使用が望ましい。
6.5.6
その他の単位
SI単位と併用するために存続が必要なものとして,CIPMによって認められているSI以外の特定の単位
がある。これらの単位を表5及び表6に示す。
表5−SI単位と併用してよい単位
量
単位
名称
記号
定義c)
時間
分
時
日
min
h
d
1 min =60 s
1 h =60 min
1 d =24 h
平面角
度
分
秒
°
′
″
1°=(π/180) rad
1′=(1/60)°
1″=(1/60)′
体積
リットル
l,L a)
1 l =1 dm3
質量
トン
t
1 t =1 000 kg
レベル
ネーパb)
ベル
Np b)
B
1 Np=ln e=1
1 B =(1/2) ln 10 Np≈1.151 293
注a) JISでは,リットルの二つの記号は同等とする。CGPMでは,リットル記号“l”は,フォン
トによってはアラビア数字の“1”と混同する危険があるために小文字及び大文字の二つ
の記号“l”及び“L”を承認している。ISO及びIECは,原記号である小文字の“l”だけ
を使用する。なぜならそれは,人物の正式名から引き出された単位ではないからである。
b) 単位ネーパ(Np)は,SIと一貫性があるが,CGPMによってSI単位としてまだ採用され
ていない。レベルは,ISQにおいて対数を用いて定義される。
c) 定義欄に記載の“=”は,対応国際規格では“:=”とされており,左辺が右辺によって定
義されていることを示している。しかし,我が国ではこの記号は用いられないことから
上記の表記を採用した。

23
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表6−SI単位と併用してよい単位で,そのSI単位による値は実験的に得られる単位
量
単位
名称
記号
定義
エネルギー
電子ボルト
eV
真空中で,1ボルトの電位差を通過する電子によって得
られる運動エネルギーである。
1 eV=1.602 176 487 (40)×10−19 J
[CODATA 2006]
質量
ダルトンa)
Da a)
基底状態で静止状態の核種12Cの原子の質量の1/12
1 Da=1.660 538 782 (83)×10−27 kg
[CODATA 2006]
長さ
天文単位
ua
太陽と地球の間の距離の平均値にほぼ等しい慣行的値
1 ua=1.495 978 706 91 (6)×1011 m
注a) ダルトンは,以前は統一原子質量単位(u)と呼ばれていた。
一時的にSIと併用することが必要なものとして,CIPMによって認められているSI以外の特定の単位も
ある。それらは,適切であれば,JIS Z 8000及びISO/IEC 80000規格群の他の部の単位のページ(右側の
ページ)の換算率及び説明欄に示されている。
無効電力に対するバール(var),(1var=1 V・A)のように,特別な目的のための幾つかの単位が,ISO,
IEC又はOIMLによって採用されている。
原子単位,CGS単位,英国単位,米国単位など,ほかにも多くの単位が存在する。原子単位を除いて,
そのような全ての単位の使用は反対されている。
物理量値を表すためには,アラビア数字及び国際単位記号を用いる。
7
印刷に関する規則
7.1
量記号
7.1.1
一般
量記号は,一般的にラテン語又はギリシャ語のアルファベットの一文字であるが,場合によっては添字
又はその他の修飾用符号を付けることができる。しかし,マッハ数(Ma)のような特性数のための記号は,
アルファベット2文字で表し,1文字目は常に大文字とする。そのような2文字からなる記号が積の中の
因子として表れる場合には,他の記号から離すことを推奨する。
これらの量記号は,本文の他の部分で使用されている書体とは関係なく,常に斜体で印刷する。
量記号は,例えば,文章の末尾におけるような通常の句読点以外は,記号の後に終止符を付けない。
ベクトル量及びテンソル量の表記法は,ISO 80000-2による。
量記号は,JIS Z 8000及びISO/IEC 80000規格群に示す。
量記号を印刷するための斜体文字についての推奨フォントはない。
7.1.2
添字
与えられた文脈中で,異なる量が同一の文字記号をもつとき,又は一つの量に対して,異なる用途若し
くは値が対象となるときは,添字の使用によって区別をすることができる。
添字の印刷については,次の原則を適用する。
a) 物理量又は順序数のような数学的変数を表す添字は,斜体で印刷する。
b) その他の,例えば単語又は数を表す添字は,ローマン体(直立体)で印刷する。
24
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例
斜体添字
直立体添字
Cp
(p: 圧力)
Cg (g: 気体)
Ci
(i: 順序数)
c3 (3: 第3番目)
Σn an ωn (n: 順序数)
gn (n: 標準状態)
Fx
(x: x成分)
μr
(r: 相対的)
gik
(i,k: 順序数)
Sm (m: モル)
Iλ
(λ: 波長)
T1/2 (1/2: 2分の1)
注記 常用添字のリストについては,IEC 60027-1を参照する。
7.1.3
量記号の合成
量記号が二つ以上の量の積として組み合わされるときには,この組合せは,次のいずれかの方法によっ
て表す。
ab,a b,a · b,a×b
注記1 ある分野,例えば,ベクトル演算においては,a · bとa×bとは区別する。
一つの量を他の量で除するときには,次のいずれかの方法によって表す。
1
1
−
−
b
a
b
a
b
a
b
a
,
,
,
aとb−1との間のスペースなしにab−1とはしない。なぜなら,(ab)−1として誤って解釈されるかもしれ
ないからである。
注記2 斜線(/)は,斜体文字(l)と容易に混同する。除算には,横線を用いることが望ましい。
この方法は,分子及び分母,又はその双方がそれ自体 積又は商であるような場合にも拡大
適用できる。
そのような組合せにおいては,曖昧さを避けるために,括弧を使用しない限り,乗算記号又は除算記号
を同一の行中で斜線(/)の後ろには付けない。
例1
1
−
=
=
c
ab
c
ab
c
ab
(
)c
b
a
bc
a
c
b
a
=
=
,ただし,a/b/cとはしない。
bc
ad
d
c
b
a
=
(
)
c
b
a
bc
a =
,ただし,a/b · cとはしない。
斜線は,分子及び分母が加算又は減算を行う場合には,曖昧さを避けるために,必要なときには括弧を
使用することを条件として,使用することができる。乗算及び除算は,複合数式においては加算及び減算
に優先するべき乗は,乗算及び除算並びに単項演算に優先する。例えば,−a2は−(a2)に等しいが,(−a)2
には等しくない。
例2 (a+b) (c+d),括弧は必要である。
a+b · c+d=a+(b · c)+d,括弧は必要ではない。
(a+b)/(c+d),括弧は必要である。
a+b/c+d=a+(b/c)+d,括弧は必要ではない。
25
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
“+”,“−”,“±”,“×”,“・”などの2項演算子(斜線“/”を除く。),及び“=”,“<”,“≦”など
の関係を表すほとんどの記号の両側には,スペースが必要である。しかし,単項演算子“+(プラス)”及
び“−(マイナス)”の後にはスペースは入れない。
注記3 我が国では,上記に示す記号の両側にはスペースは入れなくともよい。
括弧は,他の数学的演算記号の使用による曖昧さをなくすためにも使用できる。
例3 ln x+y=(ln x)+y,ただし,ln(x+y)とはしない。
この例では演算の順序を変えることによって,曖昧さをなくすことができる。
科学技術分野での使用に推奨されるその他の数学符号及び記号は,ISO 80000-2に示す。
数式又は方程式においては,量記号を使用し,量の名称又は省略形を用いてはならない。
例4 “速度は距離を継続時間で除したものに等しい”又は“v=l/t”と記載するが,“速度=距離/
継続時間”又は“v=l割るt”とは記載しない。
7.1.4
量の表示
量の表現において,単位記号は数値の後に置き,数値と単位記号との間にスペースをあける。この規則
は,パーセント(%)及びパーミル(‰)の単位にも適用されることに留意する。この規則に従い,セル
シウス温度を表す場合,セルシウス度を示す“℃”の記号の前にスペースを開けなければならないことに
も留意する。
この規則に対する唯一の例外は,平面角に対する度,分,及び秒の単位であり,この場合には,数値と
単位記号との間にスペースを入れない。
表す量が量の和又は差であるときには,数値をまとめるために括弧を使用し,共通の単位記号を全数値
の後に付けるか,又はその表示は量の表示の和又は差として表さなければならない。
例1 l=12 m−7 m=(12−7) m=5 m,ただし,12−7 mとはしない。
t=23.6 ℃,ただし,t=23.6°Cとはしない。
U=230×(1+5 %) V=230×1.05 V ≈ 242 V,ただし,U=230 V+5 %とはしない。
量の名称を式に組み入れない。斜体や添え字付の量の名称及びその省略形は用いない。
例2
ρ=Vmを,
体積
質量
密度=
と書いてはならない。
7.2
単位の名称及び記号
7.2.1
一般
単位の記号は,本文の他の部分で使用されている書体とは関係なく,常にローマン体(直立体)で印刷
する。単位記号は,複数でも変形せず,“.”を付けずに表記する。
大半の単位の記号は,ラテン語又はギリシャ語のアルファベットの一つ以上の文字で構成され,単位の
名称が人名によるときのその最初の文字を大文字で記載することを除き,これらの文字は小文字で記載す
る。
なお,“℃”のように指数の位置に符号が付いた単位記号は例外である。
例1 V
ボルト
s
秒
Sh
シャノン
mol
モル
Ω
オーム
26
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
μm
マイクロメートル
単位記号の最初の文字を大文字で記載するこの規則は,言語によって異なる単位名称には適用されない。
単位に国際的に用いる記号が存在する場合には,その他のものではなく,これを使用しなければならな
い。
量の特別な性質又は関与した測定状況に関する情報を示す手段として,単位記号にどんな修飾記号であ
っても付加することは認められない。
例2 Umax=500 V,(U=500 Vmaxとはしない。)
Pmech=750 W,(P=750 Wmechとはしない。)
wB=0.76=76 %,[0.76 (m/m)又は76 % (m/m)とはしない。]
単位の表示には,単位記号及び数学記号以外を含めない。
例3 含水量は170 kg/m3と記載するが,170 kg H2O/m3とは記載しない。
単位の記号を印刷するローマン体(直立体)についての推奨フォントはない。
7.2.2
単位記号の合成
二つ以上の単位の乗算法によって複合単位を構成するとき,この単位は,次のうちのいずれかの方法で
表す。
N・m,Nm
注記 後者の方式は,単位記号の一つが接頭語記号と同一であるときに特別の注意を払うことを条件
に,スペース抜きで表すことができる,すなわちNmと表しても差し支えない。これは,メー
トル及びミリとしてのm,並びにテスラ及びテラとしてのTの場合である。
例 mNは,ミリニュートンを意味し,メートルニュートンではない。
一つの単位を他の単位で除すことによって,複合単位が形成されたときは,この単位は,次のうちの一
つの方法で表す。
1
1
s
m
s
m
s
m
s
m
−
−
・
べき乗は,乗算及び除算に優先する。曖昧さを避けるために,括弧が挿入されない限り,乗算記号又は
除算記号は,同一の行中で斜線(/)の後ろに付けてはならない。複雑な場合においては,マイナスのべき
乗又は水平バーを用いても差し支えない。
7.2.3
接頭語
接頭語記号は,本文の他の部分で使用されている書体とは関係なく,ローマン体(直立体)で,接頭語
記号と単位記号との間をあけずに印刷する。
接頭語を印刷するローマン体についての推奨フォントはない。
7.2.4
複合単位の名称
二つの単位の積の名称は,スペースを入れない二つの名称の連結である。
例1 ニュートンメートル
単位のn乗の名称は,その名称の後に“n乗”を付ける。ただし,2乗及び3乗は,それぞれ,“平方”
及び“立方”と表現しても差し支えない。
例2 メートル4乗
平方パスカル秒
二つの単位の商の名称は,二つの名称の間に“毎”という言葉を挿入する。複合名称には,二つ以上の
“毎”を使用してよい。
27
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例3 メートル毎秒
ジュール毎キログラム毎ケルビン
7.2.5
複合単位の英文名称(参考)
英語では,二つの単位の積の名称は,スペースによって分けられた二つの名称の連結である。
例1 newton metre
単位のn乗の名称は,その名称の後に“n乗”を付ける。ただし,2乗及び3乗は,それぞれ,“平方”
及び“立方”と表現しても差し支えない。
例2 second to the power minus one
metre per second squared
二つの単位の商の名称は,二つの名称の間に“毎”という言葉を挿入することによって形成される。複
合名称には,二つ以上の“毎”を括弧なしで含んではならない。
例3 metre per second
joule per kilogram kelvin
しかし,joule per kilogram per kelvinとは書かない。
7.3
数
7.3.1
一般
数字は,本文の他の部分で使用されている書体とは関係なく,ローマン体(直立体)で印刷する。
数字を印刷するローマン体についての推奨フォントはない。
大きい桁の数の読取りを容易にするため,数字は小数点記号から左右に3桁のグループに分離してもよ
い。3桁より大きいグループにはしない。分離する場合には,小スペースを挿入する。決して,点,コン
マ又はその他の手段によって分けてはならない。
例1 1 234.5678ではなく1 234.567 8,また,0.5678ではなく0.567 8と書く。
小数点がない場合には,右端から左へと数える。
例2 数の“1 234”においては,下線数字が右端である。
3桁のグループへの分離は,例えばこの規格のように,参照番号として使用される順序数に対しては,
適用しない。
西暦年を書くときにはスペースを入れない(例 1935)。
数(又は量)の前の正符号又は負符号(“同一の符号”又は“符号の変更”を示すために使用される。)
は単項演算子であり,数との間にはスペースを入れない(例3参照)。しかし,例4のような演算に対して
は,正又は負の符号の両側にスペースがなければならない。7.1.3を参照する。また,=,<,>のような
関係を示す符号の両側にはスペースを設ける。
例3 セルシウス温度 −7 ℃から+5 ℃まで
例4 5 + 2,5 − 3,n ± 1.6,D < 2 mm,> 5 mm
注記 我が国では,例4のような場合符号の両側にスペースは入れなくともよい。
7.3.2
小数点の記号
小数点の記号は,下付きの点とする。一つの文書内は一貫して,同一の小数点記号を使用する(注記2
参照)。
数の大きさ(絶対値)が1より小さい場合には,小数点の記号の前に0を付ける。
例 0.567 8
注記1 ISO/IEC Directives, Part 2,Rules for the structure and drafting of International Standardsによれば,
28
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
国際規格において小数点の記号は,下付きのコンマである。
注記2 国際度量衡総会(CGPM: Conférence Général des Poids et Mesures)は,2003年の会議において,
次の決議を全会一致で採択した。
“小数点記号は,下付きの点又は下付きのコンマのいずれかでなければならない。”
実際にどちらを用いるかは,当該言語における慣習的使用法による。英語で書かれたほと
んどの文書においては,小数点には点が,またフランス語(及びその他の多くの欧州の言語)
で書かれたほとんどの文書においては,小数点にはコンマが使用されることが多い。ただし,
技術的分野によっては,小数点にはコンマが常に使用される。
7.3.3
数の乗算及び除算
数の乗算の記号は,積算記号(×)又は中点(・)である。積算記号又は中点の両側にはスペースを置
く(7.1.3参照)。積算記号(×)又は中点(・)は,数及び数値の乗算及びベクトル積及びデカルト座標
積を示すことに使用する。中点(・)は,ベクトルのスカラー積などを示すことに使用する。また,スカ
ラー積又は複合単位を示すことにも使用される。文字記号の積を表す場合にも適している。
注記 我が国では,積算記号又は中点の両側にスペースは入れなくともよい。
例1 l=2.5×103 m
例2 A=80 mm×25 mm
数の乗算記号全般については,ISO 80000-2:2009の2-9.5に規定されている。また,ISO 80000-2:2009に
は,ベクトル積,スカラー積及びデカルト座標積の例が記載されている。
場合によっては,乗算記号を省略する[例 4c−5d,6ab,7(a+b),3 ln 2]。
小数点の記号として点が使用される場合は,数字間の乗算の記号として中点ではなく積算記号を使用す
ることが望ましい。コンマが小数点記号として使用される場合は,数字間の乗算の記号として積算記号及
び中点の両方を用いても差し支えない。
例3 4 711.32×0.351 2 4 711,32 · 0,351 2 4 711,32×0,351 2
一つの数の他の数による除算は,次の方法のうちの一つで示される。
1
1
−
−
b
a
b
a
b
a
b
a
,
,
,
10の負のべき乗を除き,数字の負の指数は避ける。
例4 10−3はよいが,3−3は避ける。
これらの手順は,分数の分子若しくは分母又はそれら双方自体が積又は商である場合にも拡張すること
ができる。そのような組合せにおいては,曖昧さを避けるために括弧が挿入されない限り,斜線(/)の後
には,同一行内では乗算記号又は除算記号を付けてはならない。
7.3.4
誤差及び不確かさ
詳細の情報なしにある数が与えられたとき,最後の桁は1と等しい丸めの幅を用いて丸められているも
のと,一般には解釈される(附属書B参照)。したがって,例えば,数401 008は,401 008.0±0.5という
二つの値の間の値,すなわち,401 007.5と401 008.5の間の値を表すものと一般には推定される。この場
合,数401 008における最大の誤差は0.5である。しかし,適用例によっては,丸めは単に最後の幾つかの
数字を切り捨てることによって行われる。例えば,401 008.91は,小数点以下が切り捨てられた場合,401 008
となる。そのような切り捨ての場合,数401 008は401 008.0と401 009.0との間の値を表し,誤差は0と
1との間にある。同様に,数40.100 8は,40.100 75と40.100 85との間の値,又はときには40.100 80と40.100
90との間の値を表すものと,一般には推定される。
29
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最後の桁の誤差範囲内にその数が入ると考えられる場合,その数の桁を有効桁と呼ぶ。
数401 000の場合,401は三つの有効桁を含むが,右の三つの0が有効であるのか,又は単に大きさを示
すために使用されているのかは分からない。その区別を次の方法で示すことが望ましい。
401×103,
3有効桁
401.0×103,
4有効桁
401.00×103,
5有効桁
401.000×103, 6有効桁
小数点記号の後の全ての数字は,有効であるとみなす。
量の数値は,多くの場合,付随した標準不確かさとともに与えられる。その量の分散が正規分布と仮定
できる場合には,数値とその不確かさを,次の方法で表現しても差し支えない。
l=a(b) m
ここに,
l: メートル単位で表した長さ(m)
a: 数値
b: aの最小有効桁で表した標準不確かさ(ISO/IEC Guide 99参照)
例 l=23.478 2(32) m
ここに,
l: メートル単位で表した長さ(m)
23.478 2: 数値
32: 0.003 2に相当する標準不確かさ
注記1 不確かさは,(23.478 2±0.003 2) mという方法で表現されることがある。しかし,これは数学
的観点からは誤りである。23.478 2±0.003 2は,23.481 4又は23.475 0を意味するが,これら
二つの値の間の全ての値を意味するものではない。ISO/IEC Guide 98-3:2008の7.2.2の注記
には“この±の様式は従来から高い信頼区間に対応する区間を示すのに用いられ,拡張不確
かさと混同することがあるため,可能ならば避けるのが望ましい。”と記載されている。
工学的な許容誤差の文脈では,23.478 2±0.003 2は23.478 2の周囲に対照的に分散する
0.006 4 (2×0.003 2)の幅をもった区間(上限23.481 4,下限23.475 0)を意味し,したがって,
上下限を含む,その区間の全ての値が対象となることに留意する。
注記2 数の記載に際した数の小さな桁の丸め方については,附属書Bを参照する。
7.4
化学元素及び核種
化学元素の記号は,この記号の部分以外の本文に使われる書体とは関係なく,ローマン体(直立体)で
表す。記号は,ラテン語のアルファベットの1文字又は2文字で構成される。最初の文字は大文字で,次
の文字がある場合は,小文字である。この記号の後には,例えば,文章の末尾におけるような通常の句読
点以外は,ピリオドを打たない。
例1 H He C Ca
全化学元素記号の一覧表は,ISO 80000-9に規定されている。
核種又は分子を特定する上付き又は下付きの添字は,次に示す意味及び位置をもつ。
核種の核粒子数(質量数)は,左の上付き添字で示す。例えば,
14N
分子内の核種の原子数は,右の下付き添字で示す。例えば,
14N2
注記 原子数が1と等しい場合,原子数は記載しない。例えば,H2O
陽子数(原子番号)は,左の下付き添字で示す。例えば,
30
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
64Gd
イオン化状態及び電子励起状態は,右の上付き添字で示す。核励起状態は,左の上付き添字で核種の質
量数の次に記号“*”を添えて示すが,準安定核種の場合には,核種の質量数の次に文字m(ローマン体)
を添えて示す。
例2 イオン化状態:Na+,PO43−又は(PO4)3−
電子励起状態:He*
核励起状態:137*Xe 準安定核種の場合には,133mXe
7.5
ギリシャ語アルファベット
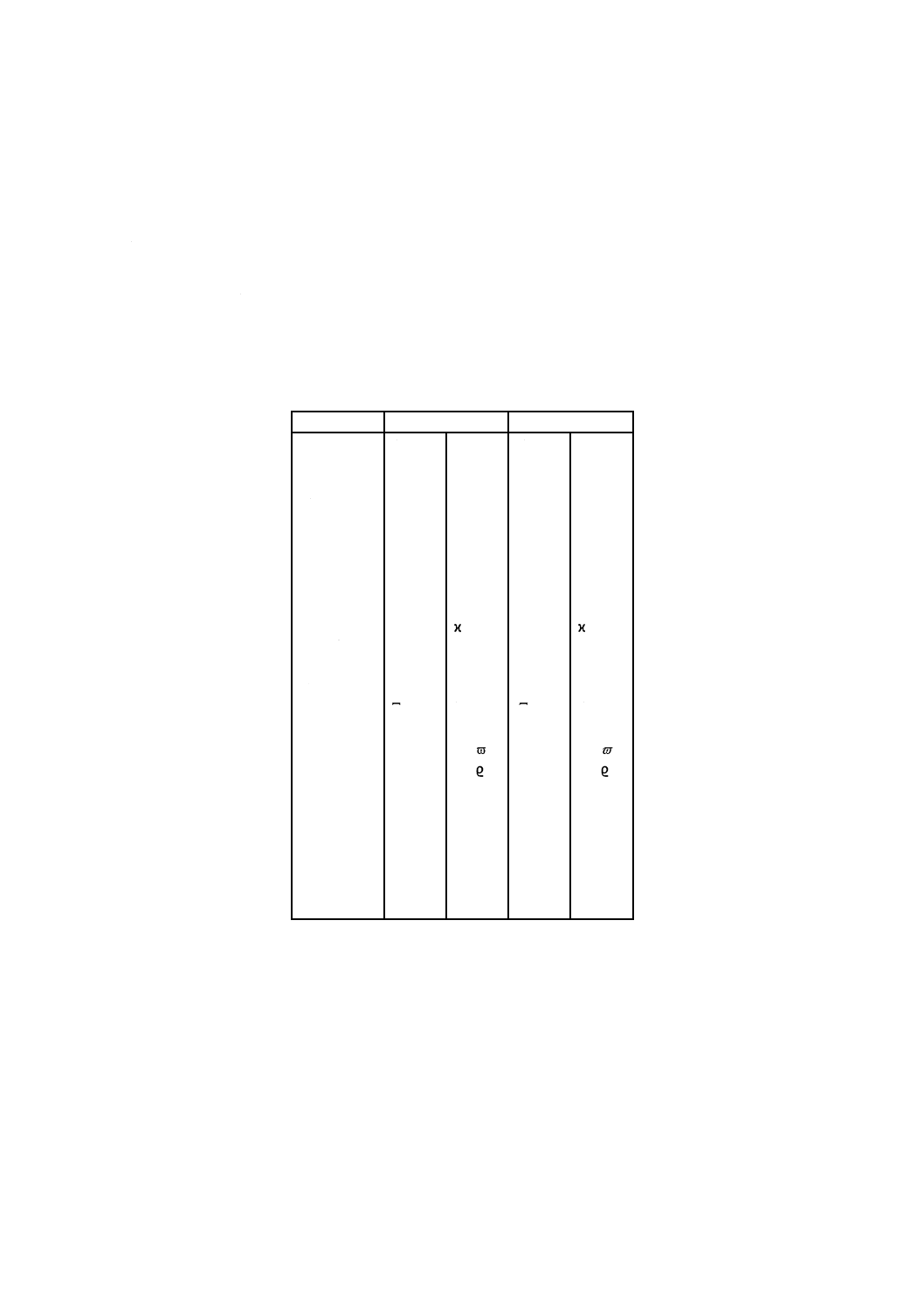
ギリシャ語のアルファベットの文字は,表7による。
表7−ギリシャ文字
名称
直立体
斜体
アルファ
Α
α
Α
α
ベータ
Β
β
Β
β
ガンマ
Γ
γ
Γ
γ
デルタ
∆
δ
∆
δ
エプシロン
Ε
ε,є
Ε
ε,є
ジータ
Ζ
ζ
Ζ
ζ
イータ
Η
η
Η
η
シータ
Θ
ϑ,θ
Θ
ϑ,θ
イオタ
Ι
ι
Ι
ι
カッパ
Κ
,κ
Κ
,κ
ラムダ
Λ
λ
Λ
λ
ミュー
Μ
μ
Μ
μ
ニュー
Ν
ν
Ν
ν
クサイ
Ξ
ξ
Ξ
ξ
オミクロン
Ο
ο
Ο
ο
パイ
Π
π,
Π
π,
ロー
Ρ
ρ,
Ρ
ρ,
シグマ
Σ
σ
Σ
σ
タウ
Τ
τ
Τ
τ
ユプシロン
Υ
υ
Υ
υ
ファイ
Φ
ϕ,φ
Φ
ϕ,φ
カイ
Χ
χ
Χ
χ
プサイ
Ψ
ψ
Ψ
ψ
オメガ
Ω
ω
Ω
ω
31
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
物理量の名称に用いる用語
A.1 一般
ある量に特定の名称がない場合には,その名称は,通常,係数(coefficient),因子(factor),変数(parameter),
比(ratio),定数(constant)などの用語と組み合わせて構成する。同様に,比(specific),密度(density),
モル(molar),濃度(concentration)などの用語が,他の関連量又は組立量を表すために,物理量の名称に
加えられる。新たに適切な記号を選択するときには,物理量の命名方法にも何らかの指針が必要であろう。
厳格な規則を提示したり,又は種々の科学分野に用いられている比較的頻繁にみられる混用を排除する
ことは,この附属書の意図ではない。しかし,新しい量に名称を付けるときに,この原則に従うことが望
ましい。さらに,従来の用語を見直す場合には,この原則からの逸脱を厳格に調査するのがよい。
量自体は,常にそれを表現している単位から独立しているので,量の名称には対応する単位の名称を反
映してはならない。
注記1 この附属書の例の大半は,現存の実例からの引用であり,推奨を意図するものではない。
注記2 用語の名前は言語に大きく依存するため,これらの推奨は主に英語に適用する。
A.2 係数(coefficient),因子(factor)
A.2.1 もし,特定の条件下で,ある量Aが他の量Bに比例するならば,この関係は乗法のA=k・Bによっ
て表す。この式における乗数である量kは,係数(coefficient)又は因子(factor)ということが多い。
A.2.2 係数(coefficient)という用語は,二つの量A及びBが異なる次元をもつときに使用するのがよい。
例1 ホール係数(Hall coefficient):AH EH=AH(B×J)
線膨張係数(linear expansion coefficient):αl dl/l=αl dT
拡散係数(diffusion coefficient):D J=−D grad n
注記 モジュラス(modulus)という用語が係数(coefficient)という用語の代わりに用いられること
もある。
例2 弾性係数(modulus of elasticity):E σ=Eε
A.2.3 因子(factor)という用語は,二つの量A及びBが同一の次元をもつときに使用するのがよい。
例 結合因子(coupling factor):k Lmn=k(LmLn)1/2
品質因子(quality factor):Q |X|=QR
摩擦因子(friction factor):μ F=μFn
注記 我が国では,“摩擦係数”が慣用的に用いられている。
A.3 変数(parameter),数(number),比(ratio)
A.3.1 方程式において起こる量の組合せは,新しい量を構成すると見られることがある。そのような量を,
変数(parameter)ということがある。
例 グリューナイゼン定数(Grüneisen parameter):γ γ=αV/(kcV ρ)
A.3.2 輸送現象の記載における次元1の量の組合せの中には,特性数(characteristic number)というもの
があり,その名称には数(number)という用語を付ける。
32
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例 レイノルズ数(Reynolds number):Re Re=ρυ/η
プラントル数(Prandtl number):Pr Pr=ηcp/λ
A.3.3 二つの量の次元1の商は,比(ratio)ということが多い。
例1 熱容量比(heat capacity ratio):γ γ=Cp/CV
熱拡散比(thermal diffusion ratio):kT kT=DT/D
易動度比(mobility ratio):b b=μ−/μ+
“分率”(fraction)という用語が,1より小さい比(ratio)の代わりに使用されることがある。
例2 Bの物質量分率(amount-of-substance fraction of B):xB xB=nB/n
パッキングフラクション(packing fraction):f f=Δr/A
率(index)という用語が,比(ratio)の代わりに使用されることがある。この用法を拡大することは推
奨できない。
例3 屈折率(比)(refractive index):n n=c0/c
A.4 レベル(level)
量Qとその量の基準値Q0との比の対数は,レベル(level)という。
例 工率の量のレベル(level of a power quantity):Lp Lp=ln(P/P0)
A.5 定数(constant)
A.5.1 あらゆる条件の下において同一の値をもつと考えられる量は,普遍定数(universal constant)又は
基礎物理定数(fundamental physical constant)という。その名称が特別に存在しない場合には,その名称に
は定数(constant)という用語を明示的に含む。
例 万有引力定数(gravitational constant):G
プランク定数(Planck constant):h
A.5.2 特定の物質について,あらゆる条件の下において同一の値をもつ量は,物質定数(constant of matter)
という。ここでも,特別な名称がないことを前提として,その量の名称には,定数(constant)という用語
を含む。
例 壊変定数(decay constant for a particular nuclide):λ
A.5.3 特定の条件の下においてだけ同一の値を維持する,又は数学的計算によって導かれるその他の量
に,定数(constant)という用語を含む名称が与えられることがある。この用法を拡大することは推奨しな
い。
例 平衡定数[equilibrium constant for a chemical reaction (which varies with temperature)]:Kp
マーデルンク定数(Madelung constant for a particular lattice):α
A.6 一般的に使用される用語
A.6.1 ある量を質量で除したものを表すために,比(specific)という形容詞が,その量の名称に付けら
れる。
例 比熱容量(specific heat capacity):c c=C/m
比体積(specific volume):v v=V/m
比エントロピー(specific entropy):s s=S/m
比放射能(specific activity):a a=A/m
33
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 比(specific)という形容詞の代わりに,質量(mass)又は量(massic)という形容詞が用いら
れることがある。
A.6.2 密度(density)という用語又は体積(volumic)という形容詞は,ある量を体積で除したものを表
すためにその量の名称に付けられる。A.6.3及びA.6.4も参照する。
例 密度(density,ただしmass density又はvolumic massと呼ぶこともある。):ρ ρ=m/V
電荷密度,体積電荷(electric charge density又はvolumic electric charge):ρ ρ=Q/V
エネルギー密度(energy density又はvolumic energy):e e=E/V
体積分子(粒子)数,分子(粒子)数密度(number density又はvolumic number):n n=N/V
A.6.3 表面密度(surface … density)という用語又は面(の)(areic)という形容詞は,ある量を面積で除
したものを表すためにその量の名称に付けられる。また,面(area)という用語が用いられることもある。
例1 面密度(areic mass又はsurface mass density):ρA ρA=m/A
表面電荷密度(areic electric charge又はsurface electric density):ρA ρA=Q/A
密度(density)という用語又は面(の)(areic)という形容詞は,束又は流れを表す量を断面積で除した
ものを表すために,その量の名称に付けられる。A.6.2も参照する。
例2 熱流密度(density of heat flow rate又はareic heat flow rate):q q=Φ/A
電流密度(electric current density又はareic electric current):J J=I/A
磁束密度(magnetic flux density又はareic magnetic flux):B B=Φ/A
A.6.4 線密度(linear … density)という用語又は線(の)(linear又はlineic)という形容詞が,ある量を
長さで除したものを表すために,その量の名称に付けられる。また,線(line)という用語が用いられるこ
ともある。
例1 線密度(linear mass density又はlineic mass):ρl ρl=m/l
線(linear)という用語は,類似する量の間の識別のために,量の名称に付けられることもある。
例2 平均線飛程(mean linear range):R R=ΣRi/n
平均質量飛程(mean mass range):Rρ Rρ=Rρ
線膨張係数(linear expansion coefficient):αl αl=l−1dl/dT
体膨張係数(cubic expansion coefficient):αV αV=V−1dV/dT
線減弱係数,(線減衰係数)(linear attenuation coefficient):μ μ=−J−1dJ/dx
質量減衰係数,(質量減弱係数)(mass attenuation coefficient):μm μm=μ/ρ
A.6.5 モル(molar)という形容詞は,ある量を物質量で除したものを表すために,その量の名称に付け
られる。
例 モル体積(molar volume):Vm Vm=V/n
モル内部エネルギー(molar internal energy):Um Um=U/n
モル質量(molar mass):M M=m/n
注記 しかし,モル(molar)という用語は,新たな量の名称を付与するに当たって,対応する単位(こ
の場合はモル)を反映してはならないという原則に違反する。A.1も参照する。
A.6.6 濃度(concentration)という用語が,混合成分中の特にある成分のある量を全体積で除したものを
表すために,その量の名称に付けられる。
例 物質Bのモル濃度(amount-of-substance concentration of B):cB cB=nB/V
物質Bの分子数濃度(molecular concentration of B):CB CB=NB/V
物質Bの質量濃度(mass concentration of B):ρB ρB=mB/V
34
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
分光濃度(spectral concentration)という用語は,分光分布関数を表すために使用される。
35
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(規定)
数の丸め方
B.1
数の丸め方
数の丸め方は,JIS Z 8401による。
注記 この規格の対応国際規格であるISO 80000-1の附属書Bで規定された内容は,JIS Z 8401で規
定された内容と同等である。
36
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(規定)
対数量及びその単位
C.1 一般
対数量は,対数関数を用いて定義された量である。定義が完全であるためには,対数の基数が指定され
なければならない。
対数の引数の出所によって,対数量は次のように分類される。
a) 二つの同じ種類の量の比の対数によって定義される対数比
b) 引数が数として明確に与えられている対数量,例えば,対数情報理論量
c) 他の対数量
一つの引数に対し,いかなる指定の基数による対数も,対象としている物理的状況について,引数その
ものが与える情報と同一の情報を与える。異なる基数で定義された量は,互いに比例しているが,異なる
値をもっており,したがって異なる量である。一つの応用分野においては,同一の基数による対数だけが
使用されなければならない。
C.2 対数工率平方根の量(場の量)
工率平方根の量は,それが線形システムに作用するとき,その量の平方が工率に比例する量である。こ
の量は以前,対数量に関して場の量と呼ばれていたが,この名前は他の意味(位置ベクトルrによる量)
をもつため,今ではあまり使用されなくなった。
正弦関数的に時間変化する場の量に対しては,二乗平均値の平方根が対数の引数である。
非正弦関数的な場の量に対しては,適切に指定された時間間隔での二乗平均値の平方根が使用される。
周期量に対しては,適切な時間間隔が1サイクルである。
例えば,電気通信,音響効果など,正弦関数的場の量に対しては,複素表示が頻繁に使用される。複素
量比の対数は,自然対数を用いて有効に,そして自然対数を用いてだけ記すことができる。他の多くの数
学的関係及び演算も,自然対数を用いる場合,より単純となる。これが,ISQにおいて自然対数が使用さ
れる理由である。自然対数を用いた場合,単位ネーパ(Np)は,SIと一貫性のある単位となるが,まだ
CGPMによってSI単位として採用されていない。
理論計算においては,位相角としてのラジアン(rad)及び振幅比としてのネーパ(Np)は,当然複素表
示及び自然対数となる。
しかし,歴史的理由から,ベル(B),及びその約数デシベル(dB)は,位相ではなく振幅比だけが検討
される応用において非常に一般的である。ベルは,10進法の対数に基づいている。
C.3 対数工率の量
工率に比例する量は,工率の量という。多くの場合,エネルギー関連の量も,この文脈の中で工率の量
という。工率の量は,対応する場の量の平方に比例するとき,因子1/2が対数工率の量の定義に含まれて
いるため,対数量の数値は同一である。
37
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.4 対数情報理論量
情報理論においては,三つの異なる基数の対数が使用される。その対数の三つの基数は,2,e及び10
である。対応する量の単位は,それぞれ,シャノンは“Sh”,情報の自然単位は“nat”,ハートレーは“Hart”
である。
38
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
量及び単位の分野における国際機関
D.1 JCGM
JCGMは,計量関連国際ガイドに関する合同委員会である。JCGMは,八つの国際機関(BIPM,IEC,
IFCC,ILAC,ISO,IUPAC,IUPAP及びOIML)の国際合同委員会である。JCGMは,測定における不確
かさの表現のガイド(GUM),及び国際計量計測用語(VIM)の改訂・整備を行う。JCGMの事務局は,
BIPMが務めている。
D.2 CGPM−CIPM−BIPM
CGPMは,加盟国全ての代表で構成される国際度量衡総会である。CIPMは,国際度量衡委員会であり,
CGPMの監督の下に業務を行う。BIPMは,国際度量衡局であり,CIPMの監督の下に業務を行う。
D.3 IEC−IEC/TC 25
IECは,国際電気標準会議である。IEC/TC 25は,量及び単位に関する第25専門委員会である。
D.4 IFCC
IFCCは,国際臨床化学連合である。
D.5 ILAC
ILACは,国際試験所認定協力機構である。
D.6 ISO−ISO/TC 12
ISOは,国際標準化機構である。ISO/TC 12は,量及び単位に関する第12専門委員会である。
D.7 IUPAC
IUPACは,国際純正・応用化学連合である。
D.8 IUPAP
IUPAPは,国際純粋・応用物理学連合である。
D.9 OIML−CGML−CIML−BIML
OIMLは,国際法定計量機関である。この機関の組織体は,国際法定計量会議(OIML総会)(CGML),
国際法定計量委員会(CIML),及び国際法定計量事務局(BIML)である。
39
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] ISO 80000-2,Quantities and units−Part 2: Mathematical signs and symbols to be used in the natural sciences
and technology
[2] ISO 80000-9,Quantities and units−Part 9: Physical chemistry and molecular physics
[3] ISO/IEC Directives, Part 2, 2004, Rules for the structure and drafting of International Standards
[4] ISO/IEC Guide 98-3:2008,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
[5] IEC 60027-1,Letter symbols to be used in electrical technology−Part 1: General
[6] IEC 60027-2,Letter symbols to be used in electrical technology−Part 2: Telecommunications and electronics
[7] IEC 80000-13,Quantities and units−Part 13: Information science and technology
[8] 国際文書第8版(2006)/日本語版国際単位系(SI)
(電子版:http://www.webstore.jsa.or.jp/lib/lib.asp?fn=/standard/std07̲10.htm)
[9] CODATA Recommended Values of the Fundamental Physical Constants: 2006,(基礎物理定数表)
[10] TS Z 0032 国際計量計測用語−基本及び一般概念並びに関連用語(VIM)
40
Z 8000-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
JISと対応国際規格との対比表
JIS Z 8000-1:2014 量及び単位−第1部:一般
ISO 80000-1:2009 Quantities and units−Part 1: General
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごと
の評価及びその内容
(V)JISと国際規格との技術的差異
の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
7.2.4 複合
単位の名称
複合単位の名称につい
て規定
−
−
追加
JISでは日本語表記が必要なため追
加した。
ISOへの改正提案はしない。
7.2.5 複合
単位の英文
名称(参考)
−
7.2.4
JISと同じ
変更
ISOの英文表記を参考として記載し
た。
ISOへの改正提案はしない。
−
−
7.2.5
英語及びフランス語にお
ける量の名称及び単位の
名称のつづり
削除
JISとしては英語及びフランス語は
必要ないため削除した。
ISOへの改正提案はしない。
附属書B
(規定)
数の丸め方を規定
Anne
x B
JISとほぼ同じ
変更
JISでは,JIS Z 8401を引用した。
JIS Z 8401とAnnex Bとは同一内容
であり,実質的な技術的差異はな
い。
JIS Z 8401が広く引用されている
ためJISを廃止せず,引用するこ
ととした。技術的差異はないため,
ISOへの改正提案はしない。
JISと国際規格との対応の程度の全体評価:ISO 80000-1:2009,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 削除 ················ 国際規格の規定項目又は規定内容を削除している。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
4
0
Z
8
0
0
0
-1
:
2
0
1
4
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。