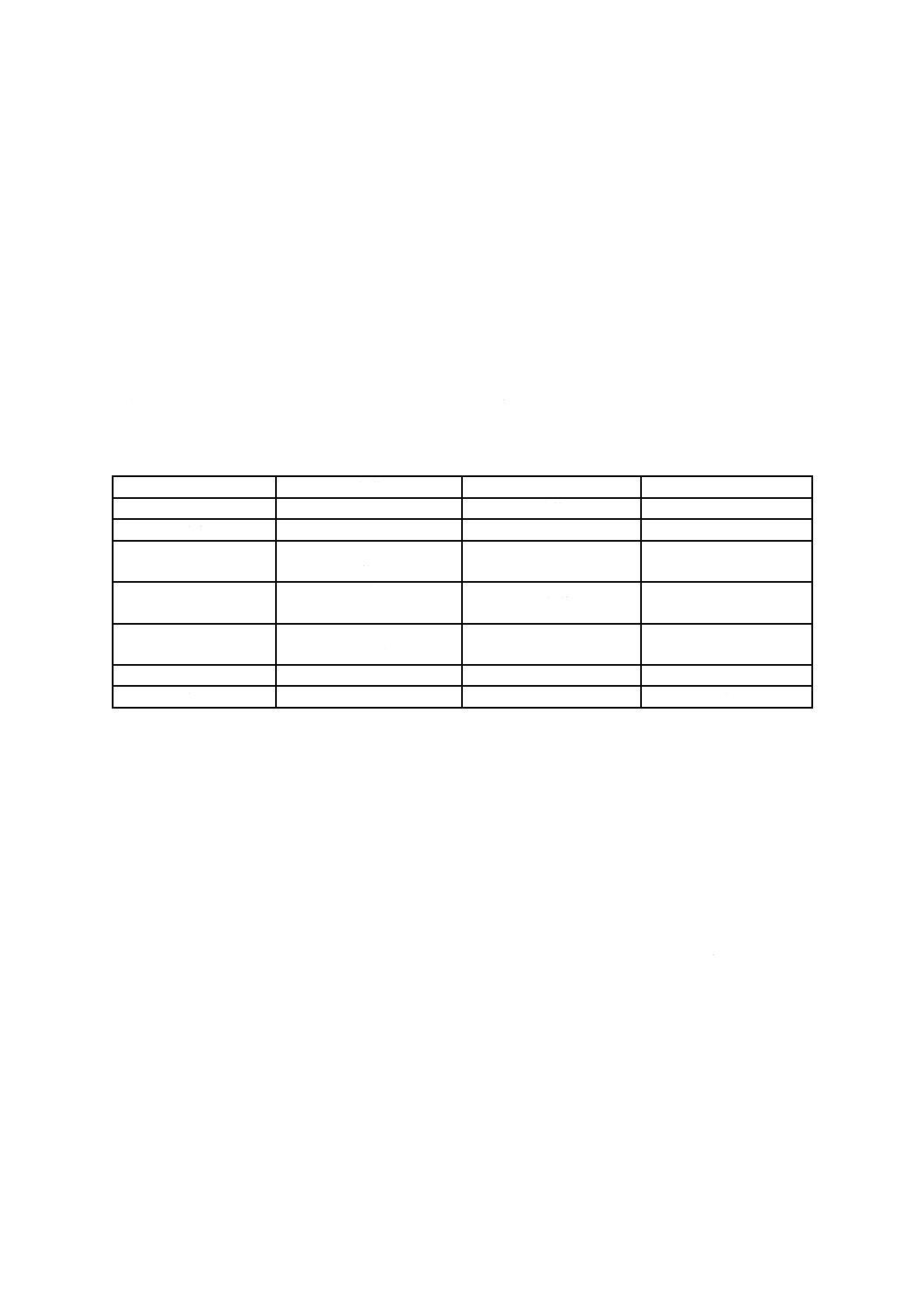K 7170:2008 (ISO 17282:2004)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,日本プラスチック工業連盟 (JPIF) 及び財団
法人日本規格協会 (JSA) から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工
業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
K 7170:2008 (ISO 17282:2004)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 2
2. 引用規格 ························································································································ 2
3. 記号 ······························································································································ 4
3.1 試験変数 ······················································································································ 4
3.2 応力解析のための材料特性······························································································· 5
3.3 破壊特性 ······················································································································ 6
3.4 成形加工シミュレーション用材料の特性 ············································································· 6
4. 設計に必要なデータ ········································································································· 7
4.1 一般 ···························································································································· 7
4.2 熱機械的性能の設計 ······································································································· 7
4.3 成形工程解析用設計 ······································································································ 11
5. 設計データの決定 ··········································································································· 14
5.1 一般 ··························································································································· 14
5.2 機械的性能用設計のためのデータの取得 ············································································ 14
5.3 加工設計用データの取得 ································································································ 18
附属書A(参考)プラスチック成形品への有限要素解析法の適用例 ··············································· 20
附属書B(参考)プラスチック加工シミュレーション解析の適用 ·················································· 49
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 7170:2008
(ISO 17282:2004)
プラスチック−
設計データの取得及び提示のための指針
Plastics-Guide to the acquisition and presentation of design data
序文 この規格は,2004年に第1版として発行されたISO 17282,Plastics−Guide to the acquisition and
presentation of design dataを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規
格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
プラスチック及びその複合材料は,鋼鉄及びアルミニウムのような従来からある素材と競合して,荷重
に耐える用途への使用が増加している。これらの用途では,要求にかなった設計によって,部品の使用上
の安全限界について信頼できる知見をもつことが重要である。様々な条件の下でプラスチックの性能予測
を可能とする方法にコンピュータによる方式があり,この方法は,継続的に改良されている。これらの条
件には,使用時の荷重及び環境における機械的性能だけではなく,部品を製造するときの溶融ポリマーの
流動が含まれる。
荷重がかかる用途のプラスチックを効果的に設計するためには,特性に及ぼす時間,温度,速度及び環
境の影響を考慮した包括的なデータが必要である。プラスチックに関するデータを測定し,提示する規格
には,JIS K 7140-1,JIS K 7140-2,JIS K 7141-1,JIS K 7141-2及びJIS K 7141-3がある。
これらの規格の目的は,材料の選択方法を支援するために,異なった出所からの異なった材料に関して
比較可能なデータを測定できるようにすることにある。膨大な量のデータが,これらの規格によって規定
され,規格の本来の目的ではないものの,一部のデータには,設計に用いてよいものもある。しかし多く
の用途では,追加のデータ又は代わりのデータが必要となる。
この指針の目的は,プラスチックの設計に必要なデータを具体的に明らかにすることによって,データ
提示に関する既存の規格の利用価値を高めることである。データのどれを選択するかは,利用できる設計
用コンピュータ方式の要求事項によって決まる。データを測定するための望ましい試験方法,試験片及び
試験条件を,5.に示す。幾つかの特性については,試験方法及び試験片が日本工業規格又はISO規格で
まだ利用できるようになっていない。将来規格化される可能性のある適切なデータ取得の方法を,表12
及び表13の注に参考として示す。
この指針は,コンピュータによる設計に必要なプラスチックの特性データが容易に利用できるように,
用いるコンピュータ方式に整合したデータベースの開発を支援することを目的としている。特性によって
は,設計解析に必要な形での情報を提示するために,データの解析及び解釈が必要となる。データ解析の
ための幾つかの方法を,附属書A及び附属書Bに示す。
2
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1. 適用範囲 この規格は,プラスチックの設計に用いるデータの取得及び提示の指針について規定する。
この規格は,設計に用いるコンピュータ方式に必要なデータの取得に重点を置き,また,部品製造時の溶
融樹脂の流動解析に必要なデータ,及び実使用時の部品の機械的特性を予測するために必要なデータが含
まれる。データの要求事項には,充てん材入プラスチック,非充てんプラスチック,短繊維強化材料及び
長繊維強化材料に関する設計が含まれる。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
(修正している),NEQ(同等でない)とする。
ISO 17282 : 2004,Plastics−Guide to the acquisition and presentation of design data (IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで発効年又は発行年を付記してあるものは,記載の年の版だけがこの規格の
規定を構成するものであって,その後の改正版・追補には適用しない。発効年又は発行年を付記していな
い引用規格は,その最新版(追補を含む。)を適用する。
JIS K 7108 プラスチック―薬品環境応力き裂の試験方法―定引張応力法
備考 ISO 6252 : 1992,Plastics−Determination of environmental stress cracking (ESC)−
Constant-tensile-stress methodが,この規格と一致している。
JIS K 7112 プラスチック―非発泡プラスチックの密度及び比重の測定方法
備考 ISO 1183 : 1987,Plastics−Methods for determining the density and relative density of non-cellular
plasticsからの引用事項は,この規格の該当事項と同等である。
参考 ISO 1183は,ISO1183-1 : 2004,ISO1183-2 : 2004,及びISO1183-3 : 1999の3部に編成され
た。
JIS K 7115 プラスチック―クリープ特性の試験方法―第1部:引張クリープ
備考 ISO 899-1 : 1993,Plastics−Determination of creep behaviour−Part 1 : Tensile creepからの引用事
項は,この規格の該当事項と同等である。
参考 ISO 899-1は,2003年に改正された。
JIS K 7139 プラスチック―多目的試験片
備考 ISO 3167 : 1993,Plastics−Multipurpose test specimensが,この規格と一致している。
参考 ISO 3167は,2002年に改正された。
JIS K 7140-1 プラスチック―比較可能なシングルポイントデータの取得及び提示―第1部:成形材
料
備考 ISO 10350-1 : 2007,Plastics−Acquisition and presentation of comparable single-point data−Part 1 :
Moulding materialsがこの規格と一致している。
JIS K 7140-2 プラスチック―比較可能なシングルポイントデータの取得及び提示―第2部:長繊維
強化プラスチック
備考 ISO 10350-2 : 2001,Plastics−Acquisition and presentation of comparable single-point data−Part 2 :
Long-fibre-reinforced plasticsがこの規格と一致している。
JIS K 7141-1 プラスチック―比較可能なマルチポイントデータの取得及び提示―第1部:機械的特
性
備考 ISO 11403-1 : 2001,Plastics−Acquisition and presentation of comparable multipoint data−
3
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Part 1 : Mechanical propertiesが,この規格と一致している。
JIS K 7141-2 プラスチック―比較可能なマルチポイントデータの取得及び提示―第2部:熱特性及
び加工特性
備考 ISO 11403-2 : 2004,Plastics−Acquisition and presentation of comparable multipoint data−
Part 2 : Thermal and processing propertiesが,この規格と一致している。
JIS K 7141-3 プラスチック―比較可能なマルチポイントデータの取得と提示―第3部:特性への環
境影響
備考 ISO 11403-3 : 1999,Plastics−Acquisition and presentation of comparable multipoint data−
Part 3 : Environmental influences on propertiesが,この規格と一致している。
JIS K 7152-3 プラスチック―熱可塑性プラスチック材料の射出成形試験片―第3部:小形角板
備考 ISO 294-3 : 2002,Plastics−Injection moulding of test specimens of thermoplastic materials−Part
3 : Small platesが,この規格と一致している。
JIS K 7162 プラスチック―引張特性の試験方法 第2部:型成形,押出成形及び注型プラスチック
の試験条件
備考 ISO 527-2 : 1993,Plastics−Determination of tensile properties−Part 2 : Test conditions for
moulding and extrusion plasticsが,この規格と一致している。
JIS K 7199 プラスチック―キャピラリーレオメータ及びスリットダイレオメータによるプラスチッ
クの流れ特性試験方法
備考 ISO 11443 : 1995,Plastics−Determination of the fluidity of plastics using capillary and slit-die
rheometers が,この規格と一致している。
JIS K 7244-2 プラスチック―動的機械特性の試験方法―第2部:ねじり振子法
備考 ISO 6721-2 : 1994,Plastics−Determination of dynamic mechanical properties−Part 2 :
Torsion-pendulum methodが,この規格と一致している。
JIS K 7244-3 プラスチック―動的機械特性の試験方法―第3部:曲げ振動−共振曲線法
備考 ISO 6721-3 : 1994,Plastics−Determination of dynamic mechanical properties−Part 3 : Flexural
vibration−Resonance-curve methodが,この規格と一致している。
JIS K 7244-4 プラスチック―動的機械特性の試験方法―第4部:引張振動―非共振法
備考 ISO 6721-4 : 1994,Plastics−Determination of dynamic mechanical properties−Part 4 : Tensile
vibration−Non-resonance methodが,この規格と一致している。
JIS K 7244-5 プラスチック―動的機械特性の試験方法―第5部:曲げ振動―非共振法
備考 ISO 6721-5 : 1996,Plastics−Determination of dynamic mechanical properties−Part 5 : Flexural
vibration−Non-resonance methodが,この規格と一致している。
ISO 61,Plastics−Determination of apparent density of moulding material that cannot be poured from a
specified funnel
ISO 294-4,Plastics−Injection moulding of test specimens of thermoplastic materials−Part 4 : Determination
of moulding shrinkage
ISO 294-5,Plastics−Injection moulding of test specimens of thermoplastic materials−Part 5 : Preparation of
standard specimens for investigating anisotropy
ISO 527-4,Plastics−Determination of tensile properties−Part 4 : Test conditions for isotropic and orthotropic
fibre-reinforced plastic composites
4
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ISO 527-5,Plastics−Determination of tensile properties−Part 5 : Test conditions for unidirectional
fibre-reinforced plastic composites
ISO 2577,Plastics−Thermosetting moulding materials−Determination of shrinkage
ISO 6721-7,Plastics−Determination of dynamic mechanical properties−Part 7 : Torsional vibration−
Non-resonance method
ISO 6721-10,Plastics−Determination of dynamic mechanical properties−Part 10 : Complex shear viscosity
using a parallel-plate oscillatory rheometer
ISO 11357-2,Plastics−Differential scanning calorimetry (DSC)−Part 2 : Determination of glass transition
temperature
ISO 11357-3,Plastics−Differential scanning calorimetry (DSC)−Part 3 : Determination of temperature and
enthalpy of melting and crystallization
ISO 11357-4,Plastics−Differential scanning calorimetry (DSC)−Part 4 : Determination of specific heat
capacity
ISO 11357-5,Plastics−Differential scanning calorimetry (DSC)−Part 5 : Determination of
characteristic reaction-curve temperatures and times,enthalpy of reaction and degree of conversion
ISO 11357-7,Plastics−Differential scanning calorimetry (DSC)−Part 7 : Determination of
crystallization kinetics
ISO 11359-2,Plastics−Thermomechanical analysis (TMA)−Part 2 : Determination of coefficient of linear
thermal expansion and glass transition temperature
ISO 15310,Fibre-reinforced plastic composites−Determination of the in-plane shear modulus by the plate
twist method
ISO 17744,Plastics−Determination of specific volume as a function of temperature and pressure (pvT
diagram)−Piston apparatus method
3. 記号
3.1
試験変数
ε
引張ひずみ
備考
工学ひずみが約0.1を超える場合,工学ひずみの代わりに真ひずみ [loge (1+ε)] を用いる。
工学ひずみが0.1以下の場合は,工学ひずみと真ひずみとの間には,有意差はない。
参考
“真ひずみ”は,我が国では,“自然ひずみ”,“公称ひずみ”又は“対数ひずみ”と呼ぶ
ことがある。
ε&
引張ひずみ速度
p
ε
引張ひずみの塑性成分
備考
これは,非線形挙動を記述するための弾塑性モデルに用いられる。
γ
せん断ひずみ
γ&
せん断ひずみ速度
p
γ&
せん断ひずみの塑性成分
t
時間
σ
応力
T
温度
5
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
f
周波数
ch
化学的環境
N
疲労試験の破壊までの繰返し数
R
疲労試験において最大応力に対する最小応力の比
T&
温度変化速度
p
圧力
CH
p
保圧時の金型内圧力(キャビティ圧力)
Ht
保圧時間
h
試験片厚さ
sv
滑り速度
3.2
応力解析のための材料特性(表2及び表3参照)
E
定速引張試験の引張弾性率
n
pE
,
E
横方向等方性材料において,繊維の定方向配向の方向又は分子の定方向配向の方向と同
じ方向の引張弾性率(
p
E)及びこれと直角方向の引張弾性率(
n
E)
参考 横方向等方性材料とは,一方向強化高分子材料などで異方性材料とも呼ばれる。次の横方向性
材料も同じ。
p
G
横方向等方性材料に定方向配向の方向に応力をかけたときのせん断弾性率
D
引張クリープコンプライアンス
R
E
引張応力緩和弾性率
n
pD
,
D
横方向等方性材料において,定方向配向と同じ方向の引張クリープコンプライアンス(
p
D)
及びこれと直角方向の引張クリープコンプライアンス(
n
D)
E
,
E
′′
′
引張貯蔵弾性率及び引張損失弾性率
G
,
G
′′
′
せん断貯蔵弾性率及びせん断損失弾性率
T
σ
真の引張降伏応力[表12の注(4)参照]
λ
静水圧感度パラメータ[表12の注(6)参照]
Tn
Tpσ
σ,
横方向等方性材料において,定方向配向と同じ方向に負荷を与えたときの引張降伏応力(
Tp
σ)
及びこれと直角方向に負荷を与えたときの引張降伏応力(
Tn
σ)
[表12の注(4)及び注(9)参照]
Sn
Spσ
σ,
横方向等方性材料において,定方向配向と同じ方向に負荷を与えたときのせん断降伏応力(
Sp
σ)
及びこれと直角方向に負荷を与えたときのせん断降伏応力(
Sn
σ)
[表12の注(9)参照]
ν
ポアソン比
e
ν
ポアソン比の弾性成分
p
ν
ポアソン比の塑性成分であって,試験片に引張応力を与えたときの,軸方向ひずみの塑性成分に
対する,軸と直角方向ひずみの塑性成分との比のマイナス。[表12の注(5)参照]
pn
ν
定方向配向と同じ方向の一軸応力で求めた異方性材料のポアソン比
ψ
流動パラメータ
α
線膨張係数
n
pα
α, 横方向等方性材料において,定方向配向と同じ方向の線膨張係数(
p
α)及びこれと直角方向の線
膨張係数(
n
α)
6
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
pc
比熱
3.3
破壊特性(表4参照)
u
σ
定速引張試験の引張強さ
un
upσ
σ,
横方向等方性材料において,定方向配向と同じ方向に負荷を与えたときの引張強さ(
up
σ)及び
これと直角方向に負荷を与えたときの引張強さ(
un
σ)
u
ε
定速引張試験時の破壊ひずみ
un
upε
ε,
横方向等方性材料において,定方向配向と同じ方向に負荷を与えたときの破壊ひずみ(
up
ε)及
びこれと直角方向に負荷を与えたときの破壊ひずみ(
un
ε)
c
σ
引張クリープ破壊強さ
cn
cpσ
σ,
横方向等方性材料において,定方向配向と同じ方向に負荷を与えたときのクリープ破壊強さ
(
cp
σ)及びこれと直角方向に負荷を与えたときのクリープ破壊強さ(
cn
σ)
f
σ
引張疲れ強さ
fn
fpσ
σ,
横方向等方性材料において,定方向配向と同じ方向に負荷を与えたときの引張疲れ強さ
(
fp
σ)及びこれと直角方向に負荷を与えたときの引張疲れ強さ(
fn
σ)
3.4
成形加工シミュレーション用材料の特性(表3,表4及び表5参照)
η
溶融粘度
eu
η
一軸伸張粘度
eb
η
二軸伸張粘度
reactive
η
反応系の粘度
1
N
第一法線応力差
Β
ρ
かさ密度
m
ρ
溶融密度
S
ρ
固体の密度
reacted
ρ
反応後の密度
κ
熱伝導率
m
κ
溶融樹脂の熱伝導率
pc
比熱
pm
c
溶融樹脂の比熱
sT
固化温度であって,金型充てんシミュレーション・ソフトウェアによって定義される基準温度。
ej
T
製品突出し温度であって,金型充てんシミュレーション・ソフトウェアによって定義される基準
温度。
v
比容積
r
ΔH
反応熱
ind
t
等温誘導時間
gel
α
ゲル化度
R&
反応速度
s
bμ
μ,
動摩擦係数であって,バレルの金属面と樹脂の動摩擦係数(
b
μ)及びスクリューの金属面と樹
脂との動摩擦係数(
s
μ)
m
T
溶融温度
gT
ガラス転移温度
7
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
CT
結晶化温度
f
ΔH
融解エンタルピ
C
ΔH
結晶化エンタルピ
X
結晶化度
X&
結晶化速度
Mp
S
定方向配向に平行な成形収縮率
Mn
S
定方向配向に直角の成形収縮率
pn
ν
定方向配向と同じ方向に与えた一軸応力下で求めた横方向等方性材料のポアソン比
np
ν
定方向配向と直角方向に与えた応力下及び定方向配向と同じ方向で測定した横ひずみとから求
めた横方向等方性材料のポアソン比
参考 附属書BのB.2.3に記載されているように,この値は,
n
pE
,
E
及び
pn
ν値から求めるソフトウエ
アによる計算値である。
p
G
定方向配向の方向に応力を加えたときの横方向等方性材料のせん断弾性率
p
α
異方性材料の定方向配向の方向に平行な線膨張係数
n
α
異方性材料の定方向配向の方向に直角の線膨張係数
4. 設計に必要なデータ
4.1
一般 この規格で取り扱う設計用データは,次の二つのグループに分類する。
− 熱機械的性能の解析用データ(4.2参照)
− 成形工程の解析用データ(4.3参照)
4.2
熱機械的性能の設計
4.2.1 設計の工程 部品(成形品)の機械的性能の設計工程では,二つの作業が必要となる。一番目は,
実用荷重での成形品の応力−ひずみ分布の解析である。二番目は,解析で予測される最大応力,最大ひず
み又は最大変位と,材料の破壊基準値又は成形品の使用条件を基にした最大許容値との比較である。成形
品の寸法及び形状を選定するために,安全限界を超えない範囲で,これらの作業を繰り返す。これらの二
つの作業に必要なデータの要求事項は異なる。
応力解析用のデータに必要な事項は,実際の,しかるべき荷重条件下で応力とひずみとを関係付ける構
成則によって求める。有効な構成関係が得られるかどうかは,次の要因による。
− 機械的挙動,すなわち材料が等方性であるか,異方性であるか,非晶性を示すか,又はゴム的挙動を
示すかどうか。
− 発生するひずみの程度。ひずみが小さい場合は,線形粘弾性又は線形弾性挙動とみなすが,ひずみが
大きい場合は,応力とひずみとの関係は非線形挙動となる。
− 与えた荷重又は変位及びその温度の履歴。プラスチックは粘弾性を示すので,その特性は,時間,周
波数及びひずみ速度に依存する。そのため衝撃のような短時間荷重への応答は,長時間かかる負荷荷
重への応答とは著しく異なる。
有限要素解析(FEA)は,複雑な形状の製品の応力,ひずみ及び温度の分布を計算するはん用的な方法
である。このことから,応力解析を実施する上で必要な,ここに規定するデータの要求事項は,プラスチ
ックに適し,利用できる材料モデルを用いて指針化されている。正確な計算であるかどうかは,実際に存
在する構成関係に裏付けられた,解析用材料モデルを用いているかどうかにかかっている。
成形品の許容使用限界は,成形品そのもの又はもととなるプラスチック材料に依存する。材料の安全使
8
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
用限界は,一般的には応力又はひずみの極限値で表現され,更に温度,湿度,加工条件,過酷な雰囲気の
有無及び荷重履歴のような多くの要因に依存することになる。クラック発生による破壊の場合は,追加の
特性データが必要となる。
4.2.2
熱機械的性能のための設計データ 熱機械的性能を設計するために必要なデータは,応力解析を実
施するデータ及び材料破壊を予測するデータからなる。原理的には,これらのデータ要求事項は,その材
料の詳細な特性及び当該用途での使用条件によって決まる。しかし,実際には,設計者は,設計解析を技
術的に扱いやすく経済的負担がかからないようにするために,材料の挙動又は使用条件を近似することで
種々の簡略化をすることがある。これによって,要求されるデータ及び実際に使用されるデータが影響を
受ける。
設計者の観点から云えば,材料挙動の最も簡単な例は,等方性,線形及び温度依存性のない弾性材料で
ある。しかし,4.2.1で規定するように,プラスチックは,異方性,非線形,温度依存性の粘弾性又は可塑
性の側面をもっている。ある特定の側面が設計上の問題に関係している場合は,設計者がより簡単な形式
のモデルを仮定することで複雑な解析を避けるとともに,“有効な”材料特性を使用することでこの側面を
補うことができる。例としては,線形解析で割線弾性率又は接線弾性率を用いて非線形性を表す,弾性解
析で長期クリープ弾性率を用いて粘弾性を表す,“平均的な”特性値又は“代表的な” 特性値を用いて,
異方性及び温度依存性代替をすることが挙げられる。しかし,より単純な(近似の)表示形式を用いても
よいが,適切で“有効な”特性を選択するためには,通常より複雑な形式の挙動のためのデータが必要と
なる。
設計の問題点には,成形品形状の仕様(形,寸法など)及び使用条件(例えば,荷重及び他の拘束条件)
を含める。FEAソフトウェアは,複雑な状況を扱うことができるが,設計者は,設計計算を簡易化するた
めに,成形品の形状を理想化し,また使用条件を近似してもよい[例えば,応力とひずみとを別々に計算
(ただし後者のひずみの計算にだけ材料特性を必要とする)できる“静定”状況を作り出すことによって]。
同様に設計者は,近似的な設計計算(例えば,“擬似弾性”と仮定して)を用いてもよい。これらの理想化
及び仮定によって,設計予測が不正確になるが,これを,用いた設計データ(しかるべきデータを選ぶ必
要はあるものの)の品質のせいにしてはならない。
設計解析の重要点は,適切な材料モデルの選定にある。この選定によって,材料設計データに必然的な
要求項目が決まり,また,どの様なモデルを選定するかは,とりわけ使用する荷重の種類に依存する。こ
の荷重には,例えば次のようなものがある。
− 荷重時間が重要な変数となる,クリープ又は応力緩和を伴う長期荷重
− 振動数が重要な変数となる,例えば減衰振動のような周期的荷重
− ひずみ速度が重要な変数となる,例えば衝突のような高速荷重
9
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 1 典型的な使用条件,材料挙動及びモデル形式
使用条件
重要変数
材料挙動の形式
モデル形式(下欄参照)
より単純な条件
−
弾性
A,B
弾塑性
C
長期荷重
時間
粘弾性又は粘塑性
C1,D1,E1
周期的荷重
周波数
C2,D2,E2
高速荷重
ひずみ速度
C3,D3,E3
モデル形式:
A: 線形弾性は,少なくとも最初の解析には,最も簡単で最も普通に用いる材料モデルである。
B: 非線形亜弾性モデルによって,非線形挙動のひずみレベル下の近似解析が得られる。超弾性モデルは,エラスト
マー材料に利用可能であるが,この規格では考慮しない。
C: 金属用弾塑性モデルは,ほとんどのFEAソフトウェアの利用が可能で,非線形の条件及び三次元応力の条件を扱
うことができる。フォン・ミーゼス(von Mises)降伏則に基づくこれらモデルは,プラスチックには用いられて
こなかったかもしれない。また,ここでは,静水圧に敏感な降伏基準のより一般的な形式[線形ドラッガー・プ
ラガー(Drucker-Prager)モデル]を,考慮する。弾塑性モデルの幾つかのバージョンでは,弾性,塑性及び時間,
周波数又は速度の影響を混ぜ合わせている。これらの後者の形式のモデル(C1,C2及びC3)をこの表に示して
いるが,この規格では,C3だけを考慮する。
D: 線形粘弾性は,微小ひずみ挙動に限定されるが,時間,周波数又は速度のいずれが重要な使用変数であるかによ
って,3種類の異なる形式のモデル(D1,D2,D3)にデータを使用できる。
E: 一般的な使用条件での非線形粘弾性モデルは,利用可能な形式のものがないが,特別の条件下で使用できるモデ
ルが存在する。これらは,等時曲線に基づくクリープ形式(E1),大振幅振動のための有限線形形式(E2)及び速
度依存形式(E3)を含むが,後者の二形式(E2,E3)は,これ以上この規格では言及しない。
既に述べたように,応力解析には,等方性特性又は異方性特性,線形挙動又は非線形挙動,及び温度の
影響を考慮する必要がある。したがって,明らかに,基本的に材料特性が必要となる多くの組合せがあり,
最も重要な組合せに焦点を合わせることが必要である。このことを,表1に示す形式モデルに関連して論
じている。
これらのモデル形式を更に考慮することで,熱機械性能の設計に必要なデータを特定することできる。
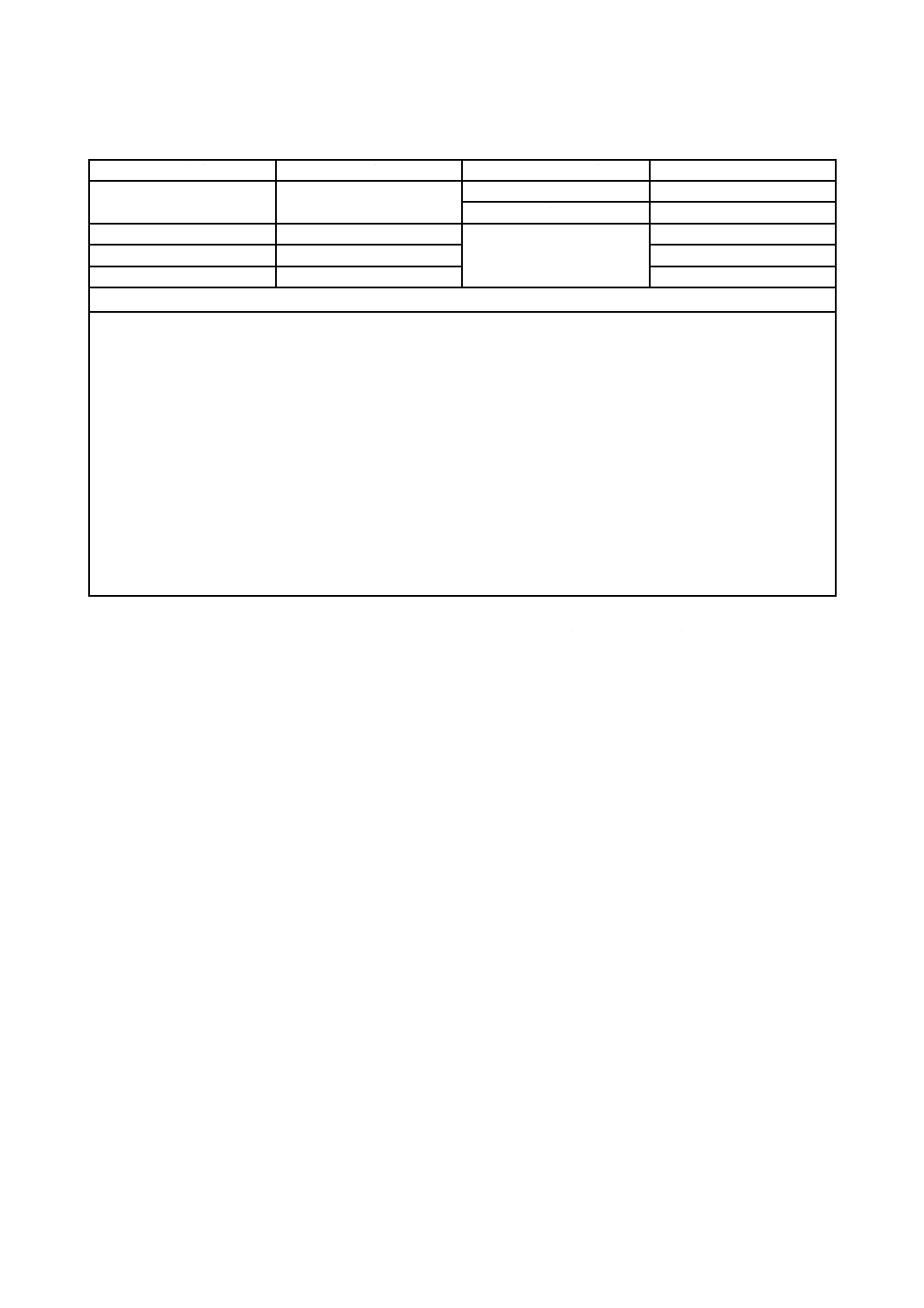
等方性材料については,これらデータを,表2に要約している。異方性材料については,材料の方向の特
性の変化を示す追加データが必要となる。最も単純な状況は,応力が平面に限定され,厚さ方向の応力が
無視できる平板又はパネル状の成形品に荷重を加える場合である。表3は,これを想定している。プラス
チックについては,複数の軸方向に応力がかかり,荷重履歴が定まらない場合,材料がいつ破裂するかを
求めるための基準は,確立されていない。異なる荷重履歴を与えたときの引張試験から得られる極限値を,
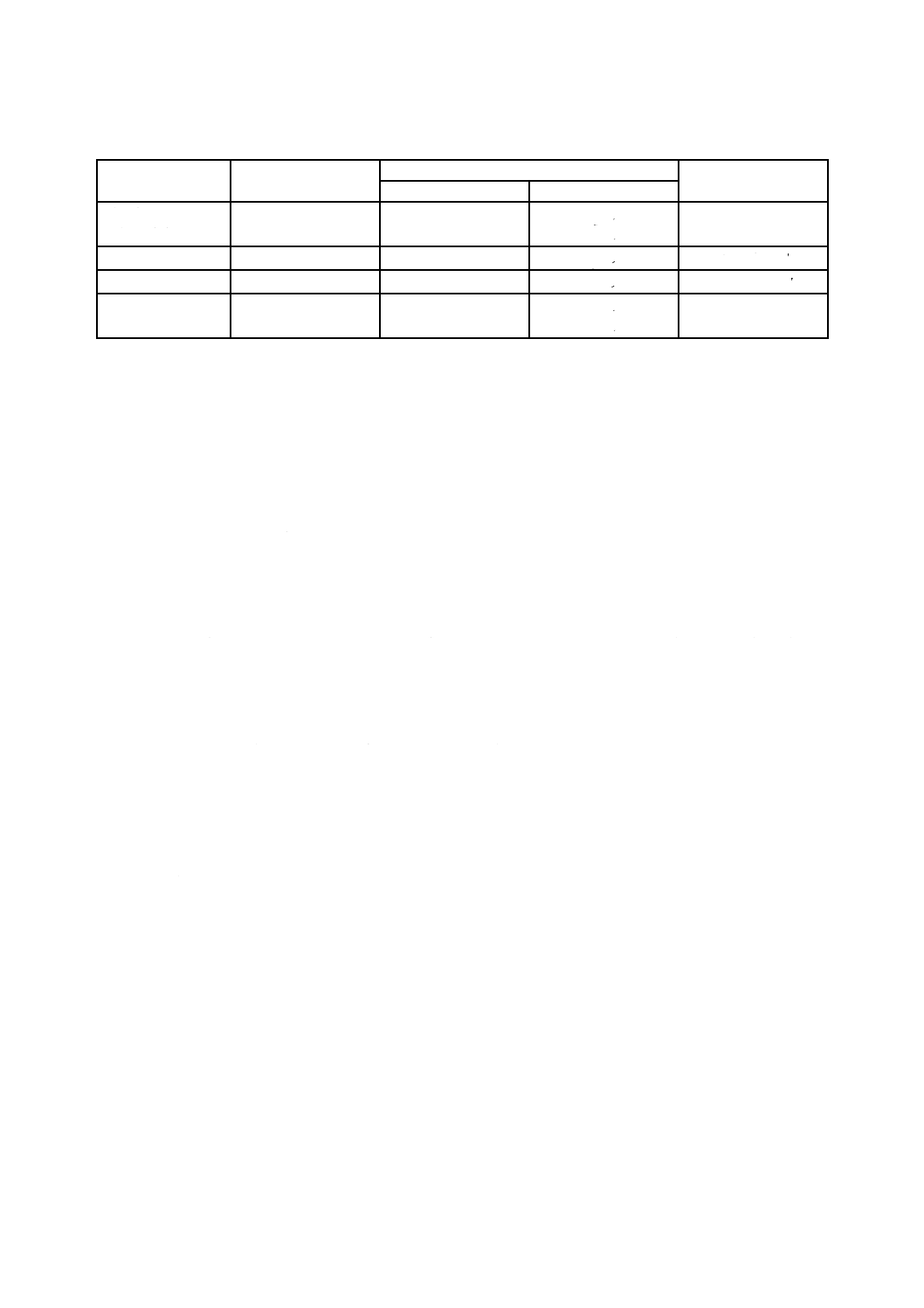
表4に示す。この表で用いる記号は,3.による。
材料挙動が実質的に等方性かつ線形弾性である場合には,表2のモデルAに示すデータがすべてである。
挙動がより複雑であるが,等方性線形弾性解析を実行する場合には,他のモデルによるデータが,“有効な”
特性を選択するのに必要となるかもしれない。例えば,モデルD及びEのデータによって,粘弾性の影響
を表すために有効な特性が得られ,モデルC及びEのデータは,非線形に処理するために有効な特性を選
択するのに用いることができ,また表3のデータは,横方向等方性の効果をみるために有効な特性を選択
するのに用いることができる。設計解析のために,これらの要素をすべて考慮する場合には,モデルC,
D及びE並びに表3のデータが独自に必要となる(ただし,表3の備考を参照)。

10
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 2 応力解析に必要なデータ(等方性材料)
挙動
モデル形式
特性
変数
線形弾性
A
ν
,
E
T
非線形弾性
B
ν
,
E
σ
T
T
,
ε
非線形(弾塑性)
C
e
,ν
E
T
σ
ψ
ν
λ
,
,
p
T
T
,
p
ε
T
,
p
ε
線形粘弾性
D1
D2
D3
ν
,
E
,
D
R
ν
,
G
,
G
E
,
E
)
は
(
′′
′
′′
′
又
ρ
ν
,
E
t ,T
f,T
T
ε&,T
非線形粘弾性
E1
ν
,
D
ν
,
R
E
T
,
,
tσ
T
,
,
tε
速度依存弾塑性
C3
e
,ν
E
T
σ
ψ
ν
λ
,
,
p
ε&,T
T
,
,
p
pε
ε&
T
,
,
p
pε
ε&
表 3 応力解析に必要なデータ(横方向等方性材料)
挙動
モデル形式
特性
変数
線形弾性
A
p
pn
n
p
G
,
,
E
,
E
ν
T
非線形(弾塑性)
C
p
pn
n
p
G
E
E
,
,
,
ν
Tn
Tpσ
ε,
Sn
Spσ
σ,
T
T
,
p
ε
T
,
p
ε
線形粘弾性
D1
Dp ,Dn
t,T
非線形粘弾性
E1
Dp ,Dn
T
t
,
,σ
速度依存弾塑性
C3
p
pn
n
p
G
E
E
,
,
,
ν
Tn
Tpσ
σ,
Sn
Spσ
σ,
ε&,T
T
,
,
p
pε
ε&
T
,
,
p
pγ
ε&
備考 横方向等方性材料に関する上記モデル及びデータ要求事項は,等方性材料に比べて
明らかに複雑であり,線形弾性の場合以外は,有効な特性を選定する目的を除くと
使われることはまれである。
ある状況下では,表2及び表3に示す特性データに追加が必要となる。荷重時に温度変化のある場合の
解析では,熱膨張係数α(異方性材料ではαp及びαn)が必要となる。荷重による加速度が大きく,慣性
力を無視できない場合は,材料の密度ρが,必要である。ひずみが大きく,ひずみ速度が速い場合,プラ
スチック材料に内部発熱が生じ,その影響を予測しなければならないため,比熱
pcのデータも必要となる。
さらに,吸水量に敏感な材料の場合には,その用途に見合った湿度に状態調節した材料のデータが必要
である。
11
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 4 異なる荷重履歴の引張試験によって生じる応力及びひずみの極限値
荷重条件
モデル形式
特性
変数
等方性
異方性
単純条件
定伸び速度
A,B,C
u
uε
σ,
up
upε
σ,
un
unε
σ,
T
長期荷重
D1,E1
c
σ
cn
cpσ
σ,
t ,ch ,T
周期的荷重
D2
f
σ
fn
fpσ
σ,
N , R ,T
高速荷重
C3
u
uε
σ,
up
upε
σ,
un
unε
σ,
ε&,T
プラスチックの破壊特性は,様々な劣化過程によって引き起こされる材料の分子構造又は結晶構造の,
長期間での変化に敏感であることに注意を要する。特筆すべきものとしては,高温暴露による,物理的老
化(自由体積の緩和),熱劣化,及び太陽光暴露による紫外線劣化がある。
4.3
成形工程解析用設計
4.3.1
成形工程のシミュレーション プラスチック成形品の成形に用いる各種加工方法の中で,射出成形
は,実用上最も普及している方法である。それだけに,射出成形工程のシミュレーションのためのコンピ
ューター支援エンジニアリング(CAE)ツールは,入手可能なソフトウェアの数及びその洗練度合いの点
でより進んでいる。最近,押出成形,ブロー成形及び熱成形のような他の加工方法のシミュレーションの
ためにCAEツールの開発が盛んとなっている。
4.3.2
射出成形シミュレーション用データ 射出成形シミュレーション用ソフトウェアは,多くのソフト
ウェア供給者から入手可能である。一般に,これらのソフトウェアのほとんどは,三次元の温度分布を反
映した二次元の解析を提供するものである。完全な三次元のシミュレーションを可能とする機能が強化さ
れたソフトウェアが,ごく最近導入されている。これらの二つのシミュレーションソフトウェアは,成形
品形状の厳密な定義を必要とし,溶融高分子の流動挙動を説明するために様々な粘度モデルを利用するこ
とから,本質的にかなり複雑となり,更に,これらのソフトウェアを使うためには,専門知識が必要であ
る。そのような厳密な解析の必要性を克服するために,単純な二次元のシミュレーションのソフトウェア
が,幾つか現在市場に出ている。
これらの方法の主目的は,成形品の製造を最適化するために,充てん工程及び保圧工程をシミュレーシ
ョンすることにある。射出成形シミュレーションには,主として次の3つのタイプがある。
− 金型キャビティに充てんすることができるかどうかを決め,必要な圧力を評価するための単純な金型
充てん解析
− 加工条件を最適化するため,又はゲートの数,適切なゲートの寸法,ゲートの位置などの成形品及び
金型要素設計を評価するために行う,金型充てん,保圧及び冷却の高度な解析
− 許容差を満たし,かつ,製造された成形品の寸法安定性を予測する収縮及びそりの解析
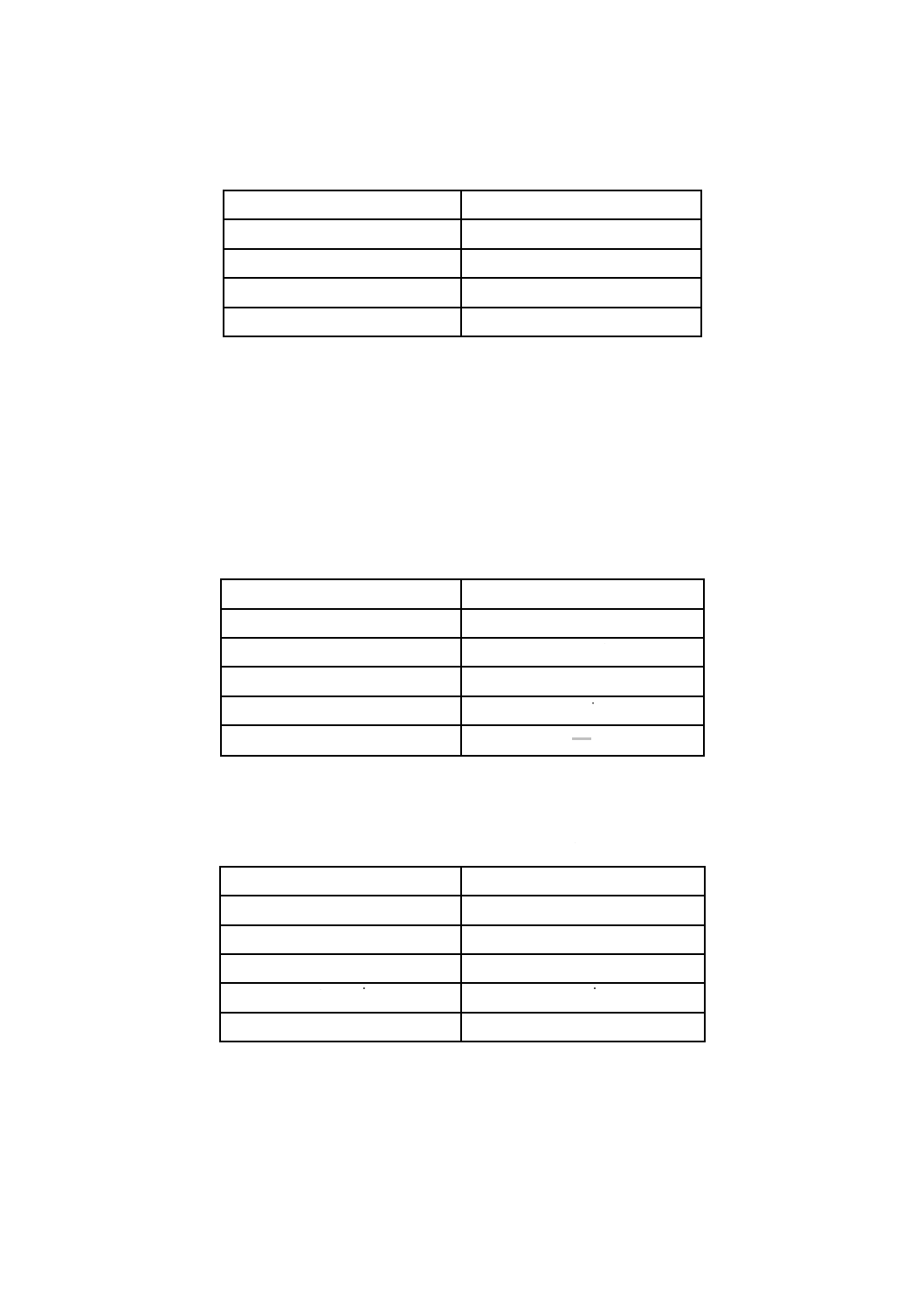
単純な金型充てんシミュレーションのために必要な材料特性を,表5に示す。
12
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5 射出成形のシミュレーションに必要なデータ−
熱可塑性プラスチック及び熱可塑性エラストマーの単純な金型充てん解析
特性
変数
η
T,γ&
ρm
―
km ,cpm
―
Ts ,Tej
―
ソフトウェアパッケージによっては,固化温度Tsの代わりに,“非流動温度”又は“転移温度”も,基
準とすることがある。またTejが必要かどうかもソフトウェアパッケージによる。充てん,保圧及び冷却工
程の高度な解析のために必要な材料特性を表6及び表7に示す。材料特性の要件は,熱可塑性プラスチッ
クス用と熱可塑性エラストマー用とは基本的には同じである。熱硬化性などの反応性材料の場合,主な違
いは,反応動力学データを含むこと及び溶融粘度データの代わりに反応性樹脂粘度データを用いることで
ある。
表6 射出成形シミュレーションに必要なデータ−
熱可塑性プラスチック及び熱可塑性エラストマーの金型充てん,保圧及び冷却の高度な解析
特性
変数
η
T,γ&,p
V
p,T,T&
k ,cp
T
Ts
p,T&
Tej
―
既存の適切なデータがないときは,粘度の圧力依存性,熱伝導率及び比熱の温度依存性は,解析に含め
ない。
表7 成形シミュレーションに必要なデータ−
熱硬化性を含む反応性材料の金型充てん,保圧及び冷却の高度な解析
特性
変数
ηreactive
T,t,γ&
ρreacted
−
k ,cp
T
ΔHr ,R&
T,T&
αgel
―
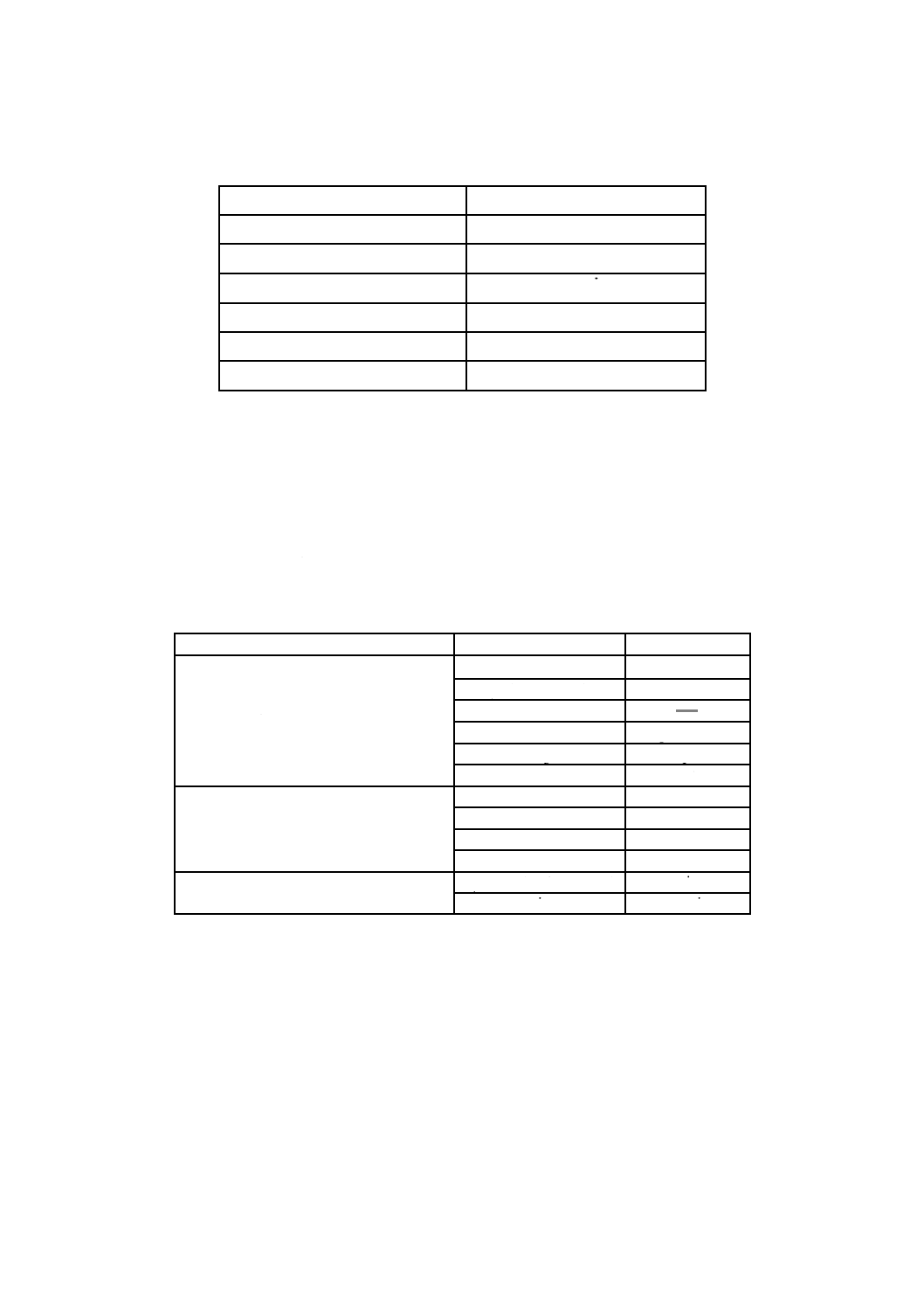
収縮及び反りの解析に必要な材料特性を,表8に示す。
13
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表8 射出成形シミュレーションに必要なデータ−
収縮・反りの解析用の追加データ
特性
変数
SMp,SMn
h,pcH
X(準結晶性材料)
T
X&(準結晶性材料)
T,T&
Ep,En
T
pn
ν,
np
ν,Gp
―
αp,αn
T
4.3.3
押出成形シミュレーション用データ 押出成形のシミュレーションには,一般的に,固体輸送,バ
レル内のポリマーの溶融挙動,ダイ内の溶融流動及び押出物の冷却の要件を含む。既存のCAEソフトウェ
アは,溶融ポリマーの流動挙動の特徴を表すために異なった複数の粘度モデルを採用し(附属書B参照),
様々な単純化仮定を行っている。単純化仮定は,一般的には,伸長流動の寄与を無視するもので,これに
よって,単軸の伸長粘度及び第一法線応力差データの必要性がなくなる。
これらの解析を取り入れて押出成形シミュレーションに必要な特性を,表9に示す。
表9 押出成形シミュレーションに必要な特性
解析のタイプ
特性
変数
固体輸送及びポリマーの溶融
Tm,
f
ΔH(準結晶性材料)
―
Tg (非晶性材料)
―
ρm,ρs
―
μb,μs
p,T,vs
ρB
p
k,cp
T
ダイ内の溶融流動
ρm
―
km,cpm
T
η,N1
T,γ&
ηeu
T,t,ε&
押出物の冷却
Tc,
C
ΔH(準結晶性材料)
T&
X&
T,T&
実用上は,正確さの低下を許容するならば,k及びcpの温度依存性は,しばしば無視される。
4.3.4
ブロー成形,熱成形,押出ブロー成形及びインフレーションフィルム成形のシミュレーション用デ
ータ
射出ブロー成形及び熱成形の工程には,軟化状態でのプリフォーム又はシートの変形過程があり,一方,
押出ブロー成形及びインフレーションフィルム成形の工程には,溶融状態での変形過程がある。これらの
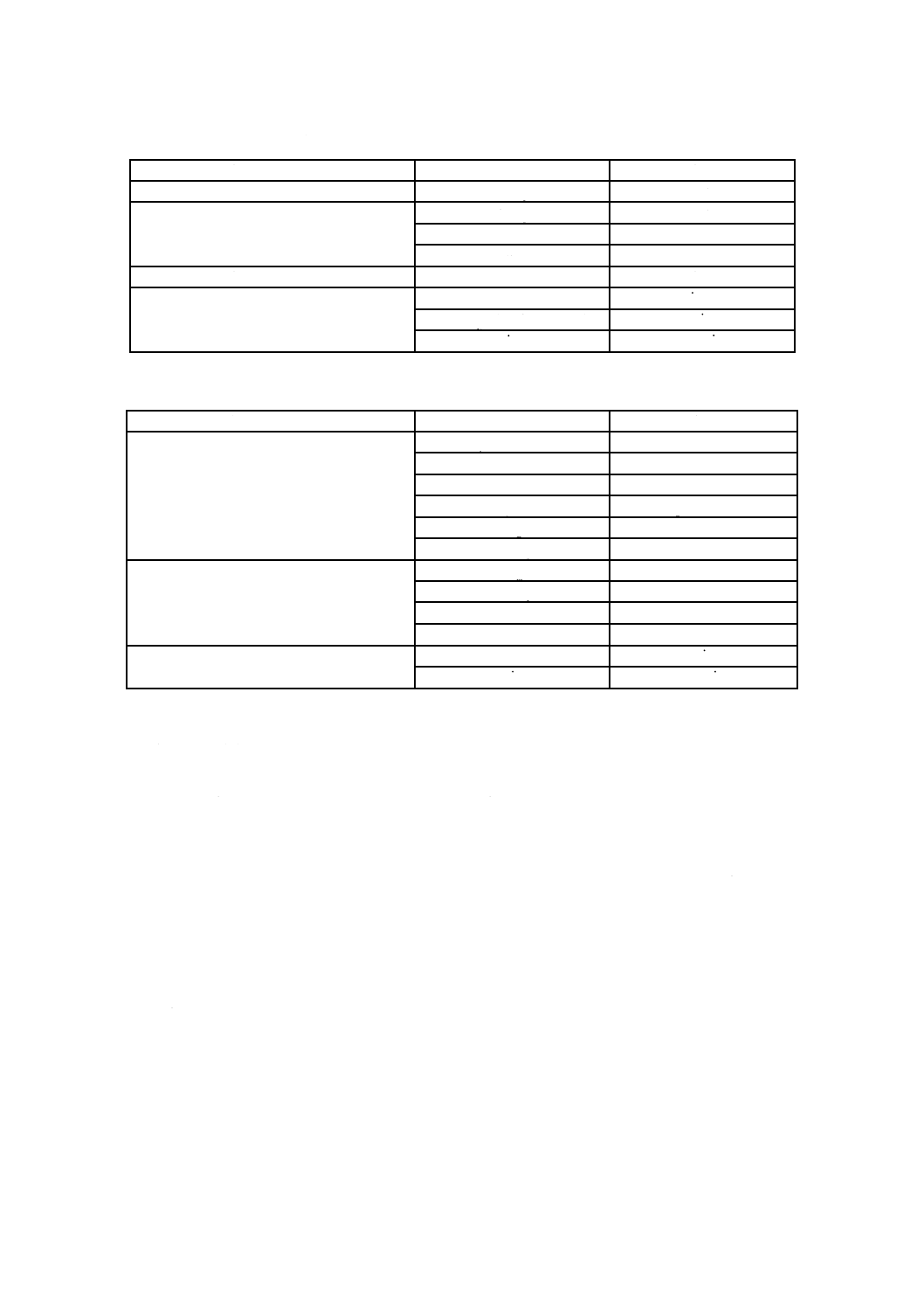
シミュレーションに必要な材料特性を,表10及び表11に示す。
14
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表10 射出ブロー成形及び熱成形のシミュレーションに必要な材料特性
解析のタイプ
特性
変数
プリフォーム又はシートの再加熱
k,cp
T
軟化した材料の変形
k,cp
T
N1
T,γ&
ηeb
T,t,ε&
解析のタイプ
特性
変数
成形品の固化
Ts (非晶性材料)
T&,p
Tc,
C
ΔH(準結晶性材料)
T&
X&
T,T&
表11 押出ブロー成形及びインフレーションフィルム成形のシミュレーションに必要な材料特性
解析のタイプ
特性
変数
バレル内のポリマーの溶融
Tm,
f
ΔH(準結晶性材料)
−
Tg(非晶性材料)
−
ρm
−
μb,μs
p,T,vs
ρB
P
k ,cp
T
ダイ内の溶融物の流れ
ρm
−
k ,cp
T
η,N1
T,γ&
ηeu ,ηeb
T,t ,ε&
押出成形品の冷却
Tc ,
c
ΔH(準結晶性材料)
T&
X&
T,T&
5. 設計データの決定
5.1
一般 この箇条では,表2〜表11に示した特性を求めるために,望ましい試験方法を規定する。ま
た,各々の特性データの取得に用いる望ましい標準試験片及び試験条件も規定する。5.2では,機械的性能
の設計に必要なデータを,5.3では,工程解析に必要なデータを扱う。
データ測定用のJIS又はISOがない特性値については,表の注に,問題なく使われている装置及び試験
片を参照として示す。これらの方法は,将来の規格開発の対象となる可能性がある。
5.2
機械的性能用設計のためのデータの取得 表2,表3及び表4に示される機械的特性データを求める
ための推奨試験方法を,表12に示す。
JIS又はISOに基づく方法では,規定を十分に満足する条件下で作製した標準試験片を用いる。これら
試験片の内部構造が,設計する成形品と通常異なることに注意する必要がある。これらの構造の違いが特
性値にどの程度影響するかは,その特性,成形方法及び成形条件並びに成形品の形状による。設計に用い
る試験片データをより妥当なものにする方法は,まだ確立されてない。
備考 ISO TC61の作業グループは,射出成形による平板形状の追加の標準試験片を作製するための
適切な金型設計を検討中である(ISO 294-5参照)。
平板の,金型内の溶融物の流れ方向及び直角方向から切り出した試験片を試験することによって,分子
配向又は繊維配向に起因する特性の上下限の範囲を得ることは可能であろう。これらの範囲内で特性値を
適切に選択するためには,成形品の物性を支配する部位における流動状態の知見が必要と思われる。
短繊維強化プラスチック製品の引張弾性率の異方性は,成形品中の繊維配向の作用を計算する流動シミ
15
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ュレーションソフトウェアによって評価できる可能性がある。繊維特性及びマトリックス特性に関する知
見は,他のパラメータと同様に必要である。弾性挙動を評価するとき,このアプローチの重要な特徴は,
成形品の厚さ方向で変動する特性に基づいて情報が得られることにある。しかし,概して,どのような予
側方法を用いても,得られた特性値又は性能値には,不確かさがある。
設計に用いる個別の試験データの精度も,材料特性のロットごとのばらつきによって影響される。設計
用データの精度は,異なる複数ロットのデータの統計解析によって向上させることができる。
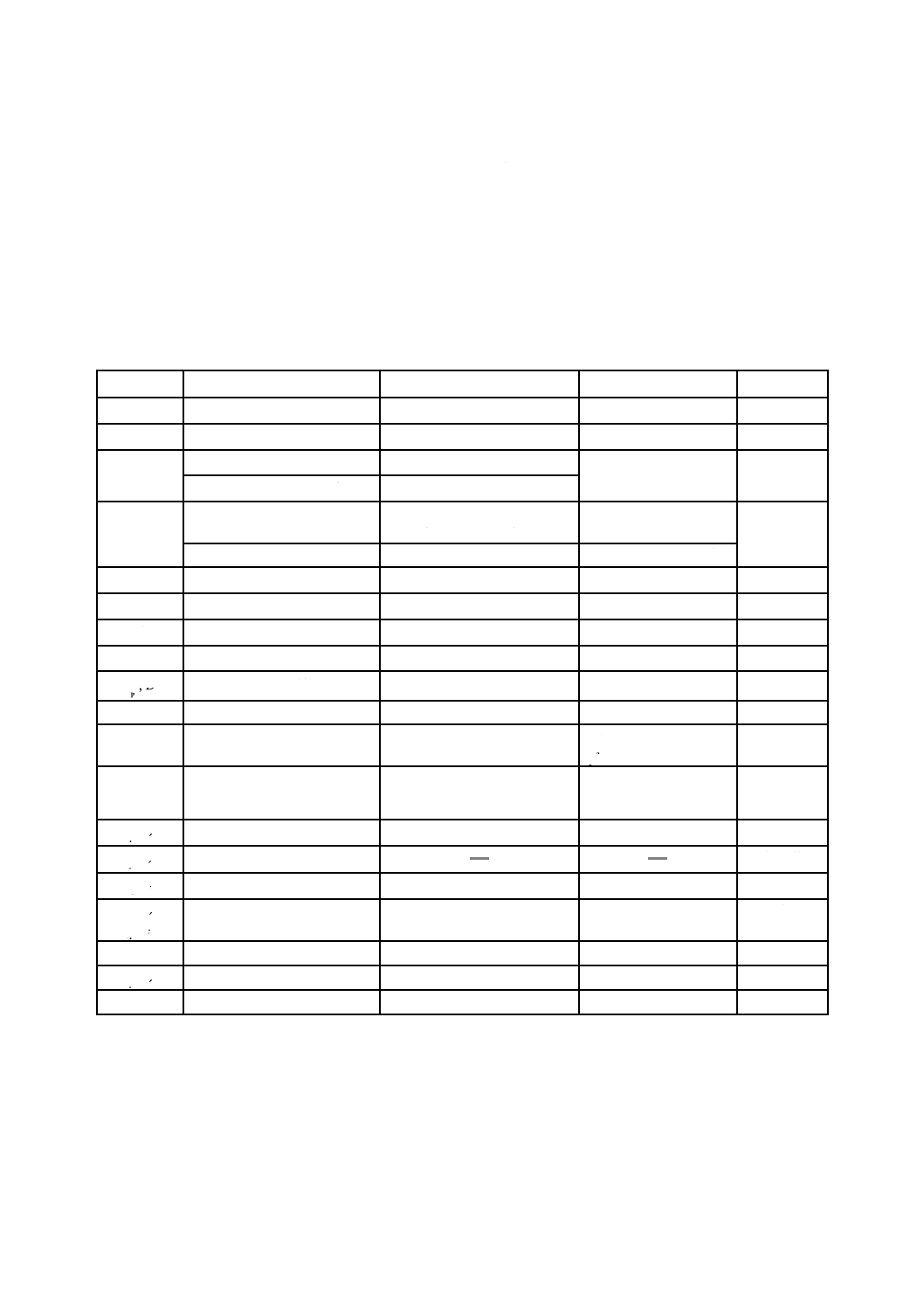
試験片データにこれらの制限はあるが,表12の試験方法は,設計データの取得に妥当なものである。
表12 機械的性能設計用に必要なデータの取得のために望ましい試験方法
特性
試験方法
試験片
推奨される試験条件
注番号
E
JIS K 7162
JIS K 7139
JIS K 7141-1
(1)
ν
JIS K 7162
JIS K 7139
―
(2)
pn
n
p
ν
,
E
,
E
JIS K 7162
ISO 294-5 平板から切り出す。
JIS K 7141-1
(3)
ISO 527-4又はISO 527-5
ISO 527の関連の部を参照
Gp
ISO 6721-7
JIS K 7152-3又はISO 294-5平
板から切り出す。
JIS K 7141-1
ISO 15310
150 mm角の平板
JIS K 7141-1の温度
σT
JIS K 7162
ダンベル形引張試験片
JIS K 7141-1
(4)
p
ν
JIS K 7162
JIS K 7139
―
(5)
λ
せん断又は圧縮試験
―
―
(6)
D
JIS K 7115
JIS K 7139
JIS K 7141-1
n
P,D
D
JIS K 7115
ISO 294-5 平板から切り出す。
JIS K 7141-1
(3)
ER
ISO規格はない
―
―
(7)
E
E
′′
′,
JIS K 7244-4又はJIS K 7244-5 JIS K 7152-3又はISO 294-5平
板から切り出す。
T : JIS K 7141-1による
f : 0.05,0.5,5,50 Hz
(8)
G
G
′′
′,
ISO 6721-7
JIS K 7152-3又はISO 294-5
同上
(8)
平板から切り出す。
Tn
Tpσ
σ,
JIS K 7162
ISO 294-5 平板から切り出す。
JIS K 7141-1
(9),(4)及び(3)
Sn
Spσ
σ,
ISO規格はない
―
―
(9),(10)
u
uε
σ,
JIS K 7162
ダンベル形引張試験片
JIS K 7141-1
un
upσ
σ,
un
upε
ε,
JIS K 7162
ISO 294-5 平板から切り出す。
JIS K 7141-1
(3)
c
σ
JIS K 7108
JIS K 7139
cn
cpσ
σ,
JIS K 7108
ISO 294-5 平板から切り出す。
(3)
f
σ
―
―
―
―

16
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 12 機械的性能設計用に必要なデータの取得のために望ましい試験方法(続き)
注(1) JIS K 7141-1では,異なる出所のデータを比較できるように,標準温度での弾性率の値を提示することが有益
であると考えられる場合,用いる標準温度を規定している。弾性率は,ひずみ速度の増加によって増大するし,
その速度依存性は,温度によって変化し,緩和領域の中心に近い温度ほど大きくなるだろう。ひずみ速度によ
る弾性率変化の測定は,1×10-5〜1×10-1 s-1の範囲で行われるのが慣例である。より高速度でのひずみの測定
は,従来の引張試験機では,困難である[ただし,注(4)参照]。高速度でのデータ取得は,低い温度での測定
又は高周波動的機械的データの相関から得られる。
長期間,力が負荷される用途(荷重時間>0.5 h)では,クリープ弾性率値は,引張クリープ試験で得られた
値を用いるのが望ましい。
(2) ポアソン比を求めるための横ひずみの測定は,JIS又はISOには記載されていない。単軸引張り応力下での,
試験片の幅変化を測定するため,トランスデューサーが必要である。この目的には,横方向伸び率計が,利用
可能である。ポアソン比は,温度及びひずみ速度によって変化する,弾性率と同様に,その変化は,緩和領域
で最も明確となる。ポアソン比は,ひずみでも変化する[注(5)参照]。
(3) 適切な形状の試験片を,成形シートの,定配向の配向方向及び直角方向から切り出す。射出成形材料の場合,
特性は,成形条件,金型の形状及びおそらく金型内の位置に依存する。ISO 294-5は,高い異方性をもつ平板
試験片を作製できる金型の寸法及び形状を規定している。高い異方性となる最適な成形品厚さは,1 mm近辺
である。平板の最適な長さ及び幅は,約80 mmであり,機械加工によって作製する多目的試験片(JIS K 7162
の1BA形)の半分の大きさである。この試験片形状を用いて,破壊特性も求めることができる。もし,破壊
のかなり下(前)のひずみデータだけが必要な場合,60 mm角の平板(JIS K 7152-3)から切り出した,端面
並行の試験片で測定してもよいが,試験片が短いために,結果の確度が低くなることに注意を要する。
(4) 弾塑性モデルで,非線形挙動は,塑性変形に起因すると考えられる。σTの最低値は,応力−ひずみ曲線での
湾曲(非線形)の開始点と一致する。したがって,σTの値は,塑性ひずみによって変わり,データは,“応力
−ひずみ”曲線の測定から導き出される(A.4参照)。“応力−ひずみ”データは,一般的には温度及びひずみ
速度の測定範囲に渡って必要となる(A.5参照)。高ひずみ速度のデータは,衝撃性能の予測のために必要であ
るが,ひずみの高速試験の測定は,JIS又はISOに,今のところ規定されていない。ひずみ値は,機械の追従
性及び試験片中の不均一なひずみを補正すれば,クロスヘッドの変位の測定から導き出せる。高速の試験用に
は,小形引張試験片の使用が望ましい。 中程度の速度での測定を外挿して,高速のデータを得ることも考え
られるが,いまだ実証された方法はない。
長期間力が負荷される(荷重時間>0.5 h)用途では,σTの値は,引張クリープ試験から得られる,等時間隔
の応力−ひずみ曲線から得るのが望ましい。
(5) 塑性成分のポアソン比
p
νは,挙動が非直線性となるひずみの大きな箇所の,軸方向及び直角方向のひずみの
同時測定から導かれる。ポアソン比は,弾塑性モデルの流れパラメータを求めるために使われる。直角方向の
ひずみ測定は,公称(工学)応力の測定から,真の応力値を導き出すためにも用いられる。A.4中の式(A.6),
(A.7),(A.8)及び(A.9)は,関連するパラメータの相互関係を示す。
(6) λ量は,弾塑性材料モデルの降伏基準に用いられ,降伏挙動に関する,応力の静水力学成分の影響の尺度であ
る。それは,単軸圧縮と単軸引張りの降伏応力の比に等しく,引張り応力−ひずみデータ及び圧縮又はせん断
応力−ひずみ曲線の測定から導くことができる。圧縮下のデータ取得には,試験片の座屈を防止するために精
巧な器具が必要である。座屈防止のためより短く,より厚い試験片を用いることは,試験片に横方向応力の増
加を招くことになる。したがって,JIS K 7181は,この目的のためには適していない。せん断応力−ひずみデ
ータは,単純に荷重を加えた,ノッチ付き短冊試験片[ロシペスク(losipescu)法]又はノッチ付きの平板[ア
ルカン(Arcan)法]から得ることができる。せん断ひずみは,繊維強化試験片の場合,ひずみゲージで測定
できるが,非強化プラスチック用には,目的に合致した伸長計を使用することが望ましい。
プラスチック用に提案された降伏点基準式(A.4参照)は,次のとおりである。

17
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 12 機械的性能設計用に必要なデータの取得のために望ましい試験方法(続き)
(
)
1
2
T
2
1)
(
2
1
3
1/2
J
JD
λ
λ
λ
λ
σ
−
+
+
=
)
3
(2
3
S
T
S
T
C
σ
σ
σ
σ
σ
λ
=
=
ここに,J1及びJ2D:応力変数であり,かつ,応力成分の関数
C
σ:引張降伏応力
T
σと同じ相当塑性ひずみ時の圧縮降伏応力
S
σ:引張降伏応力
T
σと同じ相当塑性ひずみ時のせん断降伏応力
λ=1になるこれらの材料用には,上式は,フォン・ミーゼスの降伏基準に変える。
(7) JIS又はISOには,応力緩和弾性率の測定を規定しているものはない。試験片及び伸長計は,クリープデータ
を取得するために用いたものと同じである。一定の変位が試験片に与えられ,時間による負荷の減少を記録す
る。応力緩和関数ER(t) は,一定ひずみに対する時間依存応力の比によって与えられる。個別の時間の応力緩
和弾性率は,緩和領域から外れた時間及び温度では,その時間でのクリープコンプライアンスの逆数にほぼ等
しい。通常,クリープデータの応力緩和データへの変換には,クリープ特性全般の知識が必要である。
(8) 動的特性を測定する市販の装置は多い。これらは,温度スキャンが比較的早く完了できるよう,小さな試験片
を採用している。小さな試験片では,得られる弾性率値に有意な誤差を発生することがある。これらの試験中
の誤差の原因に関する情報及び修正方法に関する手引は,JIS K 7244の各部を参照することが望ましい。
(9) ひずみの関数としてのこれら特性は,異方性材料の弾塑性モデルの適用に関してだけ必要である。
(10) JIS又はISOは,存在しないが,各種材料のせん断における応力−ひずみ曲線を得るためにロシペスク又はア
ルカンの試験方法が,用いられている。繊維強化プラスチックの場合は,ひずみゲージがせん断ひずみを求め
るのに用いられている。非強化プラスチック用では,目的に合致した伸長計とすることが望ましい。
18
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
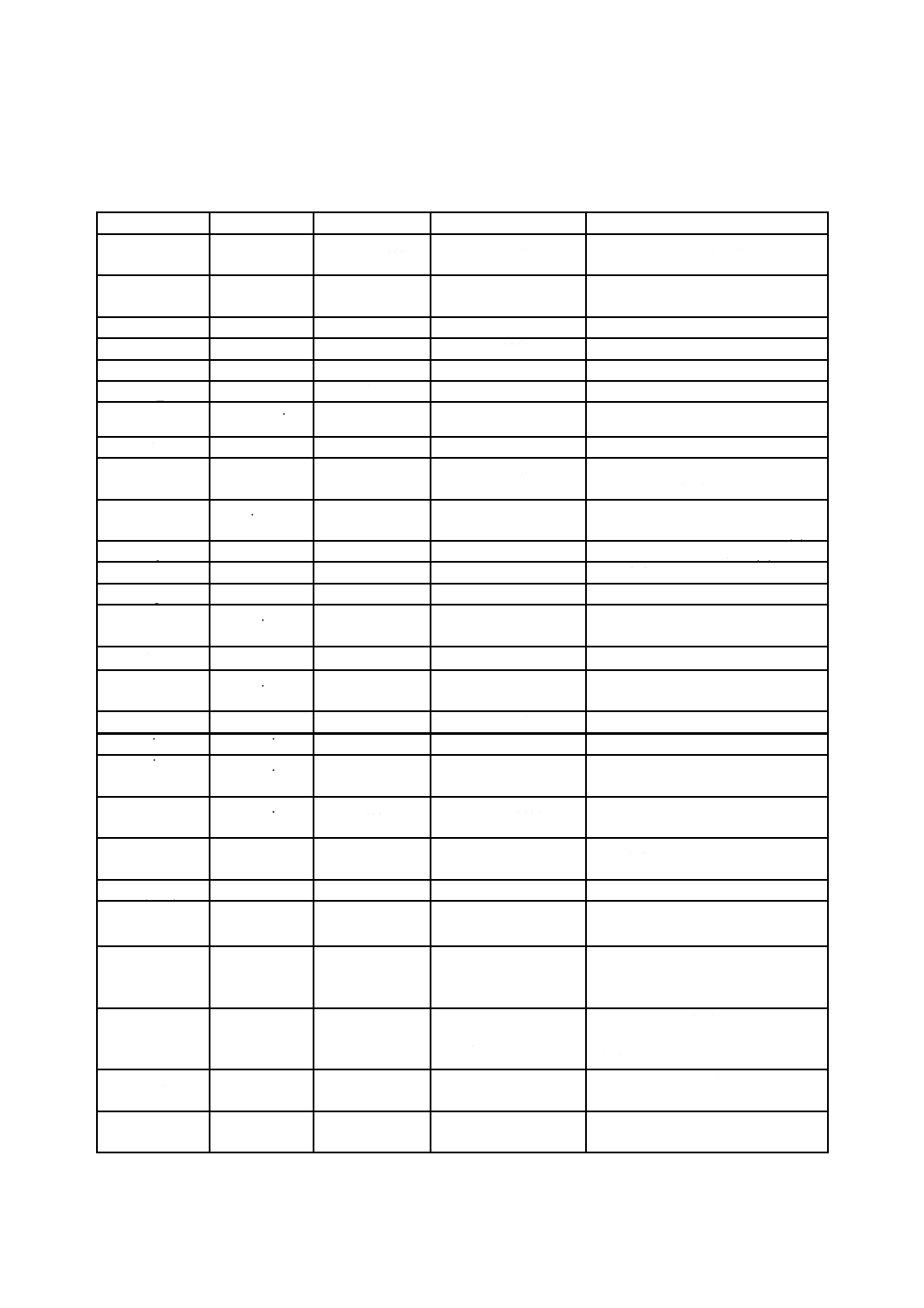
5.3
加工設計用データの取得 表13は,表5〜表11に示した,加工シミュレーションに必要なデータを
求めるための推奨事項である。
表13 加工設計用に必要なデータの取得のために望ましい試験方法
特性
変数
試験方法
試験片
推奨試験条件
η
(熱可塑性)
T,γ&,p
JIS K 7199
原材料
JIS K 7141-2及び注(1)参照
ηreactive
(熱硬化性)
T,t,γ&
注(2)及び注(3)
原材料
ηeu
T,t,ε&
注(4)
原材料
ηeb
T,t,ε&
注(5)
原材料
N1
T,γ&
注(6)
原材料
ρm
注(7)
原材料
v
p,T,T&
ISO 17744
射出成形試験片
注(8)及び注(9)
k
T
注(10)
原材料
cp
T
ISO 11357-4
原材料
冷却速度:10 ℃/min
JIS K 7141-2参照
Ts
T&,p
ISO 11357-3
注(11)
原材料
冷却速度:10 ℃/min,50 ℃/min,
100 ℃/min及び200 ℃/min 注(12)
Tej
―
ISO 11357-3
原材料
冷却速度:10 ℃/min 注(12)
Tm
―
ISO 11357-3
原材料
加熱速度:10 ℃/min
Tg
―
ISO 11357-2
原材料
冷却速度:10 ℃/min
Tc
T&
ISO 11357-3
原材料
冷却速度:10 ℃/min,50 ℃/min,
100 ℃/min及び200 ℃/min
f
ΔH
―
ISO 11357-3
原材料
加熱速度:10 ℃/min
c
ΔH
T&
ISO 11357-3
原材料
冷却速度:10 ℃/min,50 ℃/min,
100 ℃/min及び200 ℃/min
X
T
ISO 11357-7
原材料
冷却速度:10 ℃/min
X&
T,T&
ISO 11357-7
原材料
―
R&
(熱硬化性)
T,T&
ISO 11357-5
未硬化材料
―
f
ΔH
(熱硬化性)
T,T&
ISO 11357-5
未硬化材料
―
αgel
(熱硬化性)
―
ISO 11357-5
未硬化材料
加熱速度:10 ℃/min 注(13)
ρ(reacted)
―
JIS K 7112
硬化した材料
―
αp及びαn
T
ISO 11359-2
試験片は,JIS K 7152-3
平板から切り出す。
JIS K 7141-2参照
SMp及びSMn
(熱可塑性)
h,pCH
ISO 294-4
60 mm×60 mm平板
(JIS K 7152-3参照)
1 mm,1.5 mm及び2 mm厚さ;
キャビティー圧力25 MPa,50 MPa
及び100 MPa
SMp及びSMn
(熱硬化性)
h,pCH
ISO 2577
60 mm×60 mm平板
(JIS K 7152-3参照)
1 mm,1.5 mm及び2 mm厚さ;
キャビティー圧力 25 MPa,50 MPa
及び100 MPa
Ep及びEn
T
JIS K 7162
試験片は,ISO 294-5
平板から切り出す。
試験温度 23 ℃; 1 mm/min;
0.05 ~ 0.25 % ひずみ範囲
νpn及びνnp
―
JIS K 7162
試験片は,ISO 294-5
平板から切り出す。
試験温度 23 ℃; 1 mm/min;
0.1 ~ 0.5 %ひずみ範囲注(14)
19
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 13 加工設計用に必要なデータの取得のために望ましい試験方法(続き)
特性
変数
試験方法
試験片
推奨試験条件
Gp
(成形材料)
―
JIS K 7244-2
又はISO 6721-7
JIS K 7139を用いるか
又はISO 294-5から切
り出す。
JIS K 7141-1参照
Gp
(繊維強化
プラスチック)
―
ISO 15310
150 mm角平板
―
μ,μs
p,T, vs
注(15)
―
―
pB
p
注(16)
―
―
注(1) 粘度の圧力依存性は,薄壁成形品の成形に関係するが,その測定については,粘度測定のどの試験規格にも規
定されていない。したがって,ほとんどの解析において,粘度の圧力依存性は無視される。
(2) 反応系の粘度の測定の場合,JIS K 7199に基づいたスリットダイレオメータを用いるとよい。代わりに,ISO
6721-10に基づいた平行板粘度計を用いてもよい。
(3) 反応系の粘度のせん断速度依存性の測定には,動的メカニカルレオメータを用いるとよい。
(4) この規格の制定時には,ポリマー溶融物の単軸伸張粘度測定のための規格はないが,メイスナー(Meissner)の
装置,ゴッターフェルト・レオテン(Gottfert Rheoten)伸張粘度計,又はローザンド・プレシジョン社(Rosand
precision Ltd.)の7形機*を使って,測定できる。加工範囲内の3点の温度で,単軸伸張粘度を測定することが
望ましい。
注*
これらは商業的に利用できる製品の一例である。この情報は,この規格の利用者の便宜のために記載するもの
であって,JISがこの商品を推奨するものではない。
(5) フィルム膨張方式による新しい装置の開発が,IKV(Institut für Kunststoffverarbeitung)社によって報告されては
いるが,現在のところ,ポリマー溶融物の二軸伸張粘度測定に関する試験規格はない。代わりに,メイソナー
の装置が,二軸伸張粘度を測定するためにも使われている。加工範囲内の3点の温度で,二軸伸張粘度を測定
することが望ましい。
(6) 限られた範囲のせん断速度での第一法線応力差を求めるには,ISO 6721-10に基づいた平行板粘度計が望まし
い。測定データは,JIS K 7141-2と同じ条件で求める必要がある。
(7) 溶融密度は,MFRとMVRとの比によって求めることができるが,pvTデータによると,より正確な値が,求
められる。溶融密度は,成形温度領域の真ん中に相当する温度で測定することが望ましい。
(8) 測定は,1MPaでの評価も含め,40 MPa,80 MPa,120 MPa,160 MPa及び200 MPaで,2.5 ℃/minの冷却速度
で行うことが望ましい。
(9) 準結晶性樹脂の場合,冷却速度の効果は,結晶化温度及び比重(又は密度)のずれに顕著に表れる。そのずれ
は,示差走査熱量計(DSC)で定量した,結晶化温度及び結晶化度の変化の補正によって予測できる。
(10) 熱伝導率を求めるには,最高推奨成形温度から23 ℃への冷却によって測定する非定常熱線法が望ましい。
(11) 加圧DSCは,固化温度の圧力依存性を求めるために用いることができるが,現在,この試験方法を記載した規
格はない。
(12) 固化温度及び突き出し温度は,金型充てんのシミュレーションソフトウェアに定義しているように,DSC測定
から得られる参照温度である。これらの,圧力が作用する値の測定は,現在では,一般的でない[注(11) 参照]。
(13) ゲル化転化率は,幾つかの昇温速度における未硬化材料のDSC解析から,カマル(Kamal)モデルを用いて計
算し,マカスコ(Macasko)モデルでのスリットダイレオメータのデータと組み合わせる。αgelは,粘度が無限
大になるときのゲル化転換率である。
(14) ポアソン比νpnは,応力−ひずみ曲線の直線部分で測定する。ポアソン比νnpは,次の式で計算できる。
νnp=νpnEn/Ep
(15) 動摩擦係数を求める試験規格は,現在ない。バレル及びスクリュの表面粗さは,これらのパラメータの代入値
として考慮する。一般的に,μbは,滑らかなバレルには0.3,粗いバレルには0.45及び溝付バレルには1.0が,
代入値となる。同様に,μsは,平滑なスクリュ表面では0.25及び腐食したスクリュ表面では0.35が,代入値
となる。
(16) 成形材料のかさ密度を測定する試験規格は,現在ない。粉末状成形材料の見掛密度を求めるのには,ISO 61の
試験方法を用いることは可能である。
20
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(参考)プラスチック成形品への有限要素解析法の適用例
この附属書は,本体に関連する事柄を補足するもので,規定の一部ではない。
A.1 成形品形状及び荷重条件 この附属書では,異なる荷重状況にあるプラスチック成形品の応力及びひ
ずみ分布の計算によって,有限要素法の適用について説明する。複数タイプの材料挙動の範囲を考慮する。
有限要素解析(FEA)で使用される様々な材料モデルに必要とされるパラメータを,実験データからどの
ようにして導くことができるのかを示すことが目的である。ここでは,必要最小限の説明としており,よ
り詳細な情報は,技術文献及びFEAソフトウェアのユーザ・マニュアルを参照することが望ましい。
考慮する適用内容を,表A.1に示す。
表A.1 考慮する有限要素解析の適用
箇条
挙動
荷重
モデル形式
A.2
線形弾性
静的
A
A.3
非線形弾性
静的
B
A.4
非線形
(弾塑性)
静的
C
A.5
非線形
(速度依存塑性)
衝撃的
C3
A.6
非線形粘弾性
(時間依存塑性)
クリープ
E1又は(C1)
A.7
線形粘弾性
動的
D2
A.8
異方性線形弾性
静的
A
A.2〜A.6では,一つの成形品形状及び荷重条件に対して,異なる材料モデルの適用を考慮する。その成
形品は,外周近くのリングに単純に支持された,円板で,図A.1に示すように,その中心に荷重が負荷さ
れる。選択した寸法は,ISO 6603-2に示すパンクチャー衝撃テスト用の寸法と一致している。その規格で
推奨する厚さ2 mmに替えて,厚さ3 mmの試験片となっていることに注意する。試験片の要素メッシュ
を,図A.2に示すが,荷重装置及び支持体は,円板に比較し無限剛体とみなし線状メッシュで記述する。
A.2 線形弾性材料モデルの適用
このモデルでは,応力及びひずみ成分は,すべてのひずみレベルで線形関係であると仮定する。しかし
ながら,中央の大変位によってもたらされる円板の形状変化を見越した,幾何学的な非線形性は,解析に
考慮されている。本体の表2によると,このモデルの要求データは,引張弾性率E及びポアソン比νであ
る。本体の表12に示すように,これらは,JIS K 7162に規定の手順に従った引張試験から求められる。こ
の解析において,荷重速度又は荷重を加える時間に対する特性の依存性は,解析に考慮されていないが,
用途に特有な,ひずみ速度又は荷重を加える時間で測定したデータを用いることで,関連する誤差を最小
にすることができる。
プロピレン−エチレン共重合体の,10 mm/分の一定の引張りひずみ速度で測定した引張試験結果を,図
A.3に示す。これは,弾性ひずみ速度2×10-3 s-1に相当する。線形挙動の限界である,ひずみ領域が0.01
までのデータから,引張弾性率1.6 GPa及びポアソン比0.39の値を得た。これらの値を用いて,平板中央
21
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の変位に接する半球状の接触点で生じる力の変化を得るために,有限要素解析が用いられている。図A.4
には,これを,非線形解析(A.4参照)から導かれた結果と比較して示す。図A.5に,中央の変形4 mmの
ときの半径方向の引張ひずみ成分の分布を示す。平板の一部領域では,ひずみ量が線形挙動限界を超えて
いるが,これは,非線形挙動モデルを基にした曲線からの,図A.4の予測曲線とのずれに一致している。
有効なヤング率値を,適切な高ひずみでの引張応力−ひずみ曲線の割線傾きから選ぶことによって,線
形弾性解析と,高変形での非線形解析とが,ほぼ一致するようにできる。しかしながら,適切なひずみの
選定方法が明確でなく,また,中央のより小さい変位での予測確度が低下するであろう。
A.3 非線形弾性材料モデルの適用 平板のひずみレベルが線形挙動限界を超えるような変位になると,線
形弾性解析の誤差は,しだいに顕著となる。図A.3の応力−ひずみ曲線で非線形性をある程度認める擬似
弾性モデルを用いることで,より確度の高い予測ができる。このモデルの要求データを,表A.2に示す。
表A.2 図A.3のプロピレン−エチレン共重合体のデータから得られた
擬似弾性モデルのための要求データ
ε
ET
νT
I1
I2
I3
− 0.06
− 0.04
− 0.02
− 0.01
0
0.01
0.02
0.04
0.06
0.08
0.1
0.2
0.075
0.252
0.818
1.200
1.600
1.200
0.818
0.252
0.075
0.013
0.003
0.001
0.459
0.457
0.455
0.433
0.390
0.433
0.455
0.327
0.221
0.176
0.157
0.122
−1.570 × 10 −2
−6.032 × 10 −3
−2.768 × 10 −3
−1.754 × 10 −3
0.0
1.754 × 10 −3
2.768 × 10 −3
6.032 × 10 −3
1.570 × 10 −2
2.880 × 10 −2
4.216 × 10 −2
1.163 × 10 −1
2.168 × 10 −3
1.070 × 10 −3
2.704 × 10 −4
6.546 × 10 −5
0.0
6.546 × 10 −5
2.704 × 10 −4
1.070 × 10 −3
2.168 × 10 −3
3.441 × 10 −3
4.948 × 10 −3
1.499 × 10 −2
− 2.944 × 10 −5
− 1.154 × 10 −5
− 1.485 × 10 −6
− 1.700 × 10 −7
0.0
1.700 × 10 −7
1.485 × 10 −6
1.154 × 10 −5
2.944 × 10 −5
5.243 × 10 −5
8.364 × 10 −5
3.501 × 10 −4
ETは,引張ひずみεの関数として得られる引張弾性率の正接値で,応力−ひずみ曲線のひずみεでの傾
きと同等である。νTは,ポアソン比の正接値で,ひずみεでの縦ひずみに対する横ひずみのプロットの傾
きと同等である。I1,I2及びI3は,ひずみ不変量で,次のように引張ひずみεと関連する。
(
)
(
)
=
=
=
3
2
3
2
2
2
2
1
1
ε
ν
ν
νε
ε
ν
I
I
I
-
-
······························································ (A.1)
ここに,I1,I2及びI3の値は,ひずみεが線形領域にあるときのものであり,
ET及びνTはそれぞれ線形弾性値E及びνeである。
図A.6の力−変位曲線は,このモデルによって予測した。図A.7は,中央の変位4 mmにおける,引張
ひずみ成分の等高線図を示す。
A.4 弾塑性モデルの適用
A.4.1 弾塑性モデル及び降伏基準 擬似弾性モデルによって達成できる確度の限界は,よく分かっていな
いが,高ひずみ及び多軸応力条件下では,このモデルは信頼できないように思われる。弾塑性モデルは,
22
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これらの条件下で,より正確かもしれない,ただし,金属及びその他の一部材料の変形解析に開発されて
きたこと及びプラスチックへの適用は,まだこれからの研究課題であることに注意を要する。応力−ひず
み曲線の非線形性は,塑性変形によると解釈され,湾曲を開始するところの応力が,第一降伏点とみなさ
れる(プラスチック材料に使われる用語では,これと対照的に,非線形変形は,大きく回復可能なところ,
降伏点は,応力−ひずみ曲線のピークのところとある。)。その後のひずみによる応力増加は,ひずみ硬化
として解釈される。このひずみ領域では,総ひずみには,弾性及び塑性成分の両方を含むと考えられ,そ
の後,このモデルによると,回復困難な状態となる。この理由から,弾塑性モデルは,荷重の逆転を含む
ような状況のプラスチックに適用することは,期待できない。
総変形に対する塑性の寄与を記述するために,その材料の降伏及び塑性ひずみ硬化を特徴付けるパラメ
ータの知識が必要である。降伏パラメータは,材料の降伏基準によって定義され,引張応力−ひずみ曲線
の形は,ひずみ硬化挙動を決定する。
一般に,金属の降伏は,与えられた応力のせん断成分だけに依存すると仮定される。この場合,降伏基
準はフォン・ミーゼス式によって与えられる。
2
1
2D
T
3J
=
σ
···································································· (A.2)
ここに,J2Dが,有効せん断応力であり,与えられた応力の成分の関数である。
主応力σ1,σ2及びσ3の成分で示すと,
(
)(
)
(
)
[
]
2
2
2
1
3
3
2
2
1
D
2
6
1
σ
σ
σ
σ
σ
σ
−
−
−
+
+
=
J
·································· (A.3)
式(A.2)では,σTは,一軸引張降伏応力であり,ひずみ硬化材料では,ひずみの塑性成分によって増
加する。σTの決定法及びその塑性ひずみ依存性は,次の細分箇条で説明する。
フォン・ミーゼスの降伏基準は,限られた種類のプラスチック材料の降伏挙動を適切に説明する。一般
的に,降伏は,応力のせん断及び静水(等方)成分の両方に敏感で,式(A.2)を修正した方が,より適切
となる。静水成分J1と降伏応力とが線形関係と見なした最も簡単な式(A.2)の修正は,次のようになる。
(
)
(
)
1
2
1
2
1
2
1
3
2D
T
J
J
λ
λ
λ
λ
σ
+
+
+
=
················································ (A.4)
この場合,
3
2
1
1
+
+
=
σ
σ
σ
J
·································································· (A.5)
パラメータλは,応力の静水成分に対する降伏挙動感度の尺度である。λ=1のとき,式(A.4)は,式
(A.2)となる。式(A.4)は,幾つかのFEAソフトウェアに使用され,土壌などのずれを説明するために
開発された線形ドラッガープラガー(Drucker-Prager)モデルと同じである。静水応力感度の異なる形の他
のモデルとして,モアーコロンボ(Mohr-Coulomb)及び指数ドラッガープラガーモデルがある。
A.4.2 材料パラメータの由来 弾塑性材料モデル(タイプC)に必要なデータを,表A.2に列記し,本体
表12の注(4),(5)及び(6)に簡潔に説明した。
小ひずみの場合の引張弾性率E及びポアソン比νeの値は,一般に弾性挙動の特性を表すため及びひずみ
の弾性成分を求めるために用いる。この目的のために,ポアソン比に代わってせん断弾性率を使用するこ
とがあり得るが,ポアソン比は,Eを求める試験で測定することができるので,ここではポアソン比とす
る(本体表12参照)。また,横ひずみの測定値を非線形領域に拡張できるならば,使用可能な真応力が,
23
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定(工学)値から計算される。
有限要素解析では,真の塑性ひずみに対する真の引張降伏応力の依存性データが必要である。この関数
の求め方を図A.3及び図A.8に図示する。図A.3では,測定した応力−ひずみ曲線(工学応力と呼ばれる)
及びひずみによるポアソン比の変化の関係を示す。弾塑性モデルでは,線形挙動限界は,塑性変形の開始
点を示し,よって第一降伏応力を示す。前記の曲線上のすべての応力は,工学引張降伏応力σYである。
σYの値が,ポアソン比がνのときのひずみεと対応するならば,εでの真の引張降伏応力は,次の式によ
って得られる。
(
)2
Y
T
νε
σ
σ
-
1
=
··································································· (A.6)
この関数を図A.3にプロットした。
式(A.6)は,一般的に,ひずみが0.1を超えたときに,真応力値を用いることが望ましいことを示して
いる。
弾塑性モデルにおいて,図A.3の非線形領域に対応するひずみεは,弾性成分及び塑性成分の合計とみ
なされる。任意のひずみレベルでは,これらの成分は,真ひずみにちがいなく,真の塑性ひずみ
(
)
p
+
1
loge
ε
は,次の式によって得られる。
(
)
(
)ET
1
log
1
log
e
p
e
σ
ε
ε
-
+
=
+
··················································· (A.7)
このときのσTは,工学引張ひずみεでの真の降伏応力である。一般に約0.1以上のひずみでは,工学ひ
ずみよりも真ひずみを使う必要があることが見てとれる。
図A.8は,図A.3のデータから導かれた真の塑性ひずみに対する真の降伏応力のプロットを示す。
このモデルのための本体表2の残りのパラメータは,λ,
p
ν及びψである。もしフォン・ミーゼスの降
伏基準を妥当と仮定すると,これらのパラメータは次の値となる。
λ=1
p
ν=0.5
ψ=0
したがって,測定の必要がなくなる。フォン・ミーゼスの降伏基準は,引張ひずみの増加に伴いポアソ
ン比の値が,0.5に近づく材料に有効であるようだ。しかしながら,多くのプラスチック,とりわけ多相系
では,ひび割れ又は空洞化が影響する塑性変形機構によって,ひずみに対応したポアソン比の減少を示す。
この降伏メカニズムの兆候は,図A.3に示されるようにポアソン比の減少が示唆している。これらの材料
の降伏状況は,式(A.4)で与えられているような圧力に敏感な基準でよりよく示されている。せん断又は
圧縮といった異なる応力状態下の追加試験からλを求める手順が報告されている。
流動パラメータψの推定は,ポアソン比の塑性成分
p
ν の測定値(図A.8参照)から次の式を用いて得る
ことができる。
)
(
)
(
p
p
1
2
2
1
3
tan
ν
ν
ψ
+
=
-
································································ (A.8)
ここに,
p
νは,横ひずみの測定値εt及び次の式によって算出する。
+
+
+
−
=
)
(
)
(
p
e
e
t
e
p
1
log
1
log
T
ε
σ
ν
ε
ν
E
········································ (A.9)
24
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.4.3 FE解析の比較 図A.9及び図A.10に,円板の中心に荷重を負荷した場合の,力−変位曲線及びひ
ずみ分布の計算値を示す。これらには,二つの材料モデルが使用されている。一つは,フォン・ミーゼス
基準[式(A.2)]に基づくもので,図A.3及び図A.8に示されるデータから導かれる弾性率,ポアソン比
の弾性成分及びひずみ硬化関数σT(εp)の材料パラメータを必要とする。もう一方のモデルは,λ=1.5
及びψ=30゜の値でのフォン・ミーゼスモデルに用いられているものと同じ引張試験データとともに静水
学的応力に敏感な降伏基準[式(A.4)]を採用している。ひずみのパターン及び力−変位曲線は,似てい
るが,各モデルによって予測される最大ひずみレベルには大きな差があることが見てとれる。
A.4.4 箇条A.4の要約 引張試験の応力−ひずみ曲線は,弾塑性解析に必要な基本的データである。これ
らのデータから,塑性ひずみに対する引張降伏応力のプロットが得られる。これが利用可能な唯一の材料
特性の情報ならば,小ひずみにおけるポアソン比の現実的値は,推測しなければならず,そして,フォン・
ミーゼスの降伏則は,仮定しなければならない。
大ひずみまでのポアソン比測定も可能ならば,真の引張降伏応力が,計算可能である。0.1を超えるひず
みが発生する場合にだけ,これらの値が必要となる。これらの場合には,真の塑性ひずみ値も使用するこ
とが望ましい。
圧縮又はせん断のような追加の応力状態での応力−ひずみ曲線は,応力の静水学的成分に敏感な降伏基
準を用いる必要性を調査するために必要とされる。そのような降伏基準は,ドラッガープラガーモデル及
びモアーコロンボ材料モデルで採用されている。これらモデルの静水学的感受性パラメータは,二つの応
力−ひずみ曲線から得ることができる。
ここで考慮する適用例では,現実的な降伏基準を用いて計算した力−変位曲線は,フォン・ミーゼス推
定によって得られたものと同様であった。しかしながら,円板中の最大ひずみ値は,大きく異なっていた。
もし,ひずみの臨界レベルに基づく破壊基準と組み合わせた解析を用いていたとすれば,この違いは重大
かもしれない。
A.5 ひずみ速度依存の材料特性と弾塑性モデルの適用 プラスチックの変形挙動は,荷重負荷速度に敏
感である。応力−ひずみデータは,ひずみ速度に依存し,それ故,用いるクロスヘッドの速度に依存する。
幾つかのFE解析ソフトウェアを用いて,速度依存の材料特性によって弾塑性解析を行うことになる。そ
の場合,入力データは,ある範囲でひずみ速度を一定にして測定した複数の応力−ひずみ曲線を利用して
求める。プロピレン−エチレン共重合体のそのデータを,図A.11に示す。中央部のくびれた試験片を用い
るので,ひずみ速度は,試験中約二倍に増加する。記録された値は,塑性ひずみ速度であり,試験の初期
段階に対応する弾性ひずみ速度よりも大きい。塑性ひずみ[σT(εp)]に対する降伏応力の曲線は,各
ひずみ速度での降伏応力をプロットすることによって得た。速度による引張弾性率の小さな変動も観察さ
れた。
異なる速度で変形したときの,図A.1の円板の中央に荷重を負荷した変位に対する力を予測するために,
これらのデータを用いて,動的解析を行った。慣性の寄与を含めることができるよう,円板及び衝撃子の
密度の値も必要である。A.4での圧力敏感性の降伏基準は,ひずみ速度には依存しないと仮定してλ=1.5
及びψ=30゜の値を用いた。明確なソルバーコード(プログラム著作物の登録分類コード)のソフトウエ
アを解析に用いた。種々の荷重負荷速度での結果を,図A.12に示す。
25
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.6 非線形クリープモデルの適用 プラスチックのクリープは,付加した応力σ0に応答して起こるポリマ
ー分子構造の時間依存変化である緩和過程に起因する。材料に生じるクリープ変形は,時間依存ひずみε
(t)によって特徴付けられ,式(A.10)から導かれるクリープコンプライアンス関数である。
()
()
0
σ
εt
t
D
=
··································································· (A.10)
クリープ挙動は,引張クリープ実験で多く検討されており,その場合,D(t),ε(t)及びσ0は,それぞれ
引張コンプライアンス,引張ひずみ及び引張応力と関係がある。多くの数学的関数が,モデル実験結果に
用いられてきた。式(A.11)の関数は,各々のガラス転移温度より十分低い温度で,プラスチックによく
用いられている。
()
()n
t
D
t
D
τ
exp
0
=
····························································· (A.11)
パラメータτは,クリープ過程での平均遅延時間(遅延時間は,パラメータnの大きさと関係する分布
をもつ)である。D0は,弾性コンプライアンスであり,適切なひずみ速度で測定した弾性率の逆数に等し
い。
式(A.11)のパラメータτは,一定と仮定されるので,この式には,材料の物理的エージング(物理的
経時変化)は,考慮していない。物理的エージングは,成形温度から徐々に冷却されるにしたがい,ポリ
マー構造がゆっくりと再組織化することとに関係している。これらの変化によって,クリープ時間でパラ
メータτが累進的な増加を引き起こす分子の運動性が,長期間にわたって減少する。
これは,材料の経時及びエージング速度が知られていればモデル化できる長いクリープ時間でのクリー
プ関数に変化を生じさせる。
小さなクリープ応力の場合,パラメータτは応力の大きさに依存せず,かつ,クリープ挙動は線形とな
る。より高い応力の場合,図A.13のPVCで得た実験データに示すように,クリープ曲線は,より短い時
間側へシフトする。このシフトは,結果的に平均遅延時間τの減少につながる高応力を加えることによっ
て,分子の運動性が増加したものと説明される。非線形クリープ挙動の上昇は,この運動性の高まりによ
るものである。運動性の増加は一時的であり,荷重を加えた後の,物理的エージングの増加と近似な荷重
のもと,経時的にτは,比較的速く増加する。τの応力及び時間の依存性のモデル化並びにそれらがどの
ようにクリープ変形に影響するかについては,今後の研究課題である。
ここで検討する適用例に対しては,クリープコンプライアンスの物理的エージングの影響は無視する。
この状態の場合,図A.13のクリープデータは,次の式(A.12)のように簡単な指数法則によって,適切に
モデル化できる。
()
()
[
]
n
t
D
t
D
τ
+
=
1
0
····························································· (A.12)
パラメータD0 ,τ及びnの値は,実験データに最も適合するように選択した。この適合性を,図A.13
に示す。D0及びnの値は,各曲線で同じである。パラメータτは,各応力レベルで異なるが,クリープ時
間では,一定と仮定する。式(A.11)又は式(A.12)が,実験結果を正確に表示できないのは,この物理
的エージングの無視が,原因である。τの応力依存性は,与える応力によって高さが変わるポテンシャル
障壁を横切る分子遷移に関するアイリング(Eyring)の式を基にした次の関係式で,適切に表せる。
(
)
0
0
sinh
σ
σ
τ
×
=
a
A
·································································· (A.13)
ここに,A及びaは,材料パラメータである。

26
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.13中のデータの適合性を得るために用いる式(A.12)及び(A.13)中のパラメータの値を,表A.3
に示す。
表A.3 PVCのクリープモデルに用いられる式(A.12)及び(A.13)の中のパラメータの値
D0,
n
A
a
GPa-1
s・MPa-1
MPa-1
0.305
0.28
4.2×106
0.3
荷重を付加したときの材料の物理的経時時間による,表A.3のA及びaの値,よって遅延時間τ,は,
注意する価値がある。図A.13のPVCデータの場合,PVCのガラス転移温度から急冷した後の試験片に,
クリープ応力を240時間付加した。低い応力(6 MPa以下)では,試験中に試験片は,著しくエージング
し,式(A.12)は,クリープデータからそれる。クリープ試験開始時に試験片がかなり古いならば,パラ
メータτは,既により大きくなってしまっており,試験中のτの変化は,少なくなる。適度に大きなτを
用いる限り,式(A.12)は,実験データによくあてはまる。より古い材料に高応力をかけた効果は,負荷
時のτの値をやはり減少させるが,その後クリープ時間の経過とともに,再び増加する。これは,図A.13
に図示したように,式(A.12)のクリープデータから同様なずれを生じさせる。
式(A.12)及び(A.13)は,単軸な引張応力下のクリープを示したものである。しかしながら,式(A.12)
を多軸のクリープ応力状態に適用するため一般化でき,その式を次に示す。
()
()
[
]
n
t
S
t
τ
σ
ε
+
=
1
l
k
ijkl
ij
························································ (A.14)
(
)
σ
σ
τ
×
=
a
A
sinh
································································· (A.15)
テンソル式(A.14)は,時間依存ひずみεij (t)の成分を,弾性コンプライアンステンソルSijklによる,付
加応力σkl の成分と関連づけている。等方性材料の場合,コンプライアンステンソルの成分は,後出の式
(A.20)に示すように,通常は,引張弾性率及びポアソン比の二つの材料特性によって表現できる。
パラメータσは,有効応力で,応力によるτの減少が,応力の大きさはもちろん,応力の状態にも依存
するという観測結果を示している。これは,単軸圧縮下のクリープ試験の解析によって,所定の応力レベ
ルに対するτの減少が,同じ単軸引張応力下よりも著しく少ないことによって説明される。すなわち,τ
の減少の主要原因は,応力のせん断成分ではあるが,静力学成分にも影響を受けるということを示唆して
いる。式(A.4)で示す,プラスチックの降伏に関する静力学的応力の影響によって類推し,次のようなσ
の式が考えられている。
(
)
(
)
1
2
1
2D
1
1
3
J
2
J
2
β
β
β
β
σ
−
+
+
=
············································· (A.16)
J1及びJ2Dは,クリープ応力マトリックスの不変量であり,式(A.3)及び式(A.5)で定義する。引張
下及び圧縮下のPVCの非線形クリープデータの解析から,β=2を得た。
式(A.14)と式(A.15)のクリープ関数は,クリープを時間依存弾性として扱っている。時間依存項も,
応力の大きさによって影響を受けるので,非線形挙動をモデル化する。有限要素解析ソフトウェアの非線
形クリープは,一般的に時間依存塑性によってモデル化する。これらのモデルは,金属材料のクリープに
広く適用できるが,プラスチックで観察される挙動を表すこと及び式(A.14)で示すことに用いる前に,
若干の評価判断が,必要である。
時間依存塑性モデルでは,全ひずみは,弾性成分と塑性成分との合計で,時間依存性及びそれによるク
リープは,塑性成分に起因する。クリープひずみ速度の一般的な様式は,せん断及び膨張(体積)変形機
27
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
構から発生する寄与の合計であると考える。クリープひずみε&ijのテンソル成分のひずみ速度は,次の式
(A.17)による。
()
ij
sw
ij
s
ij
δ
ε
σ
ε
ε
&
&
&
+
∂∂
=
q
t
························································ (A.17)
ここに,s
ε& 及びsw
ε&は,それぞれせん断及び体積的変形によるひずみ速度へ
の寄与である。パラメータqは,
2
1
D
2
3J
[式(A.2)参照]の代わりに用
い,有効応力であり,また,
j
i=の場合δij=1,
j
i≠の場合はδij=0である。
次の式(A.18)のような関係がある。
(
)
ij
m
ij
ij
2
3
δ
σ
σ
σ
−
=
∂
∂
q
q
·························································· (A.18)
ここに,σm は平均応力であり,J1/3[式(A.5)参照]に等しい。
よって,式(A.17)は,次のように表すことができる。
()
ij
s
m
sw
ij
s
ij
2
3
2
3
ε
ε
σ
ε
σ
ε
ε
&
&
&
&
&
−
+
=
q
q
t
·············································· (A.19)
ここに,PVCのクリープ関数に戻ると,式(A.14)は,次のように表す
ことができる。
()(
)
[
]
()
[
]
n
ij
m
0
ij
0
ij
1
3
1
τ
δ
σ
ν
σ
ν
ε
t
D
D
t
+
−
+
=
································· (A.20)
ここに,νは,ポアソン比であり,クリープ時間で一定と仮定する。
微分すると,次のようになる。
()
(
)
[
]
1
n
ij
m
0
ij
0
ij
3
1
−
−
+
=
t
D
D
n
t
n
δ
σ
ν
σ
ν
τ
ε&
····································· (A.21)
もし,次の式(A.22)の関係を満たせば,式(A.19)と同じになる。
(
)
(
)
1
0
m
sw
1
0
=
s
2
1
1
−
−
−
=
+
n
n
n
n
t
D
n
t
D
n
3
2q
ν
τ
σ
ε
ν
τ
ε
&
&
及び
·············· (A.22)
さらに,式(A.16)の記号を,応力不変量q及びσmに変えると,次のようになる。
(
)
(
)
β
σ
β
β
β
σ
2
1
3
2
1
m
−
+
+
=
q
····················································· (A.23)
このように,時間依存塑性モデル[式(A.17)]のs
ε&及び
sw
ε&は,材料パラメータn,τ,ν及びD0の
情報から求められ,クリープ応力は,q及びσmによって特定する。
ここでは,式(A.19)及び式(A.22)に基づくクリープモデルを,図A.1に示した円板試験片のクリー
プ荷重下の変形を求めるために,有限要素解析ソフトウェアーに用いている。クリープ挙動が,式(A.20)
及び式(A.23)によって特徴付けられるPVCを,材料として用いた。これらの式の中の材料パラメータの
28
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
値は,表A.3に記載し,β=2及びν=0.35とする。半球状の接触点に200 Nの力を加えた。荷重付加時
間による,中央の変形量の計算結果を,図A.14 a) に示す。クリープ解析の初め近く(t=102 s)及び終わ
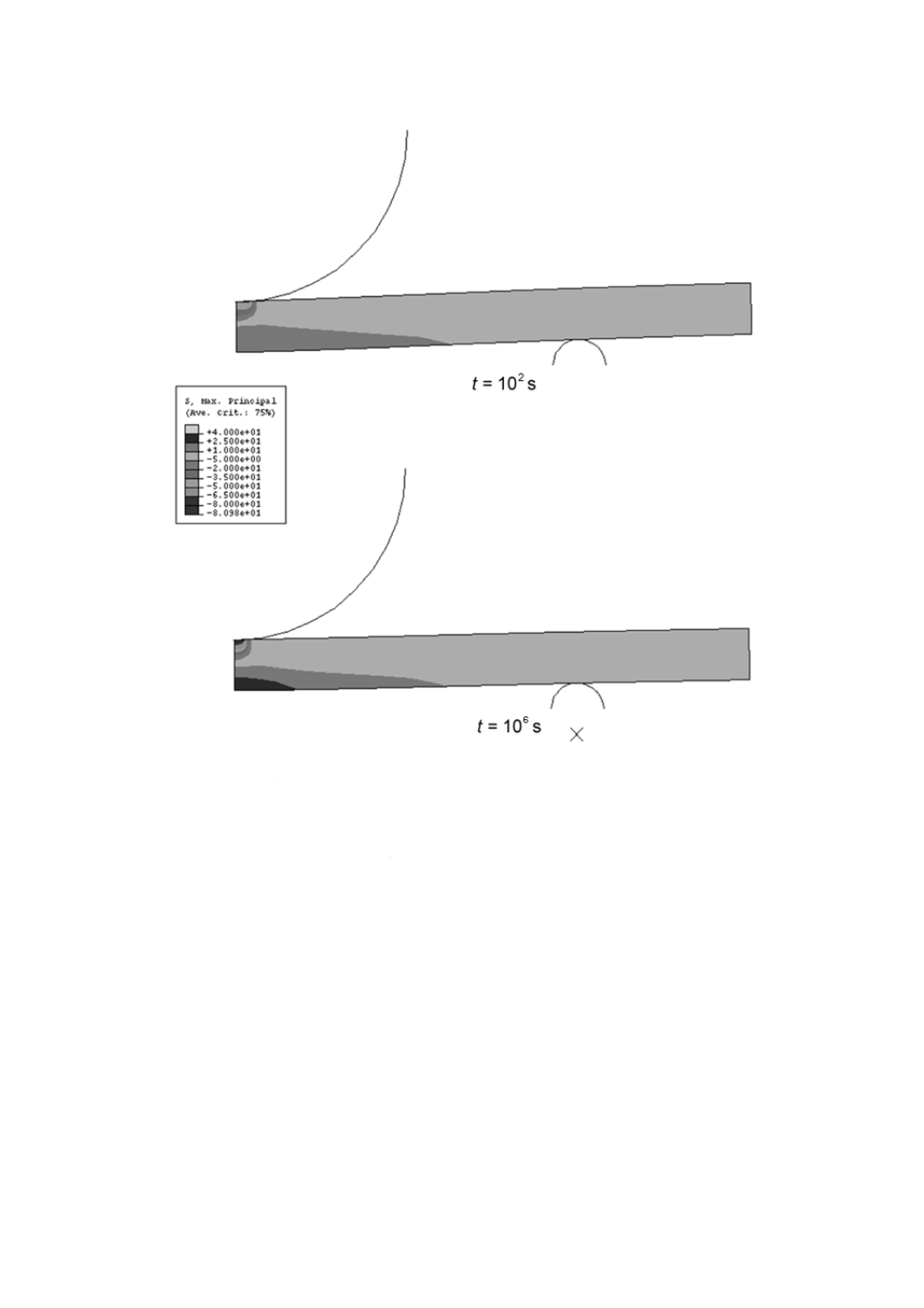
り(t=106 s)の最大主応力の等高線を,図A.14 b) に示す。試験片内の応力分布が時間によって変化し,
高応力領域では,応力レベルが緩和することが分かる。これに伴って,ひずみ分布の計算結果は,荷重付
加時間によって,ひずみレベルの全般的増加を示した。
比較のため,線形粘弾性挙動での解析も,検討した。ここでは,緩和時間τは,図A.13のグラフ曲線の
12 MPaに概略対応する4×106 sの値で一定と仮定した。この解析では,円板の全領域の弾性率は,応力の
大きさ又は状態には関係なく,同じ割合で減少する。ひずみ分布は,時間とともに増加するが,非線形ク
リープ解析とは対照的に,応力分布は一定のままであった。荷重付加時間による,中央の変位及びひずみ
分布の変化の計算結果もまた,非線形解析で得られた結果と著しく異なっていた。
A.7 線形粘弾性材料モデルの適用 この例証では,構成要素への共鳴振動の励起による周期的な荷重付加
に対する単純成分の応答を計算するのに,有限要素解析を用いる。低周波共振モードの振動数及び相対振
幅を求める。ここで考慮する適用の場合,推進力は,関連する振動数領域に渡り,10 kNの一定振幅をも
つと仮定する,とはいえ,もし力の分布が既知であるならば,励起振動数の任意の分布への応答は,計算
できると思われる。
この適用の構成要素は,その周囲が,非常に堅い土台に固定された,薄肉の半球状のシェルである。解
析に用いるシェルの寸法及びメッシュを図A.15に示す。土台によって構成要素に周期的な力を付加し,ま
た力の方向は,土台面に垂直であるとみなす。シェル中のひずみは,その材料の線形粘弾性領域内にいつ
もあり,その力は,十分に小さいとみなされる。
解析のために必要な最小限のデータ(本体の表2参照)は,材料の,動的引張弾性率の貯蔵成分及び損
失成分である各々E′及びE′′,ポアソン比ν並びにポリマーの密度ρの値である。厳密には,ポアソン比
は複雑な量であるが,しかし,一般的には,これを実数とみなすことに起因する確度の損失は,無視でき
る程度だろう。最も簡単な解析では,単一振動数及び適切な温度でのE′及びE′′のデータが必要であり,
かつ,特性は,振動数に依存しないと仮定する。
振動数が,ポリマーの緩和領域内にあるとき,関連振動数領域で測定したデータを用いることによって,
もっと正確な予測ができる。
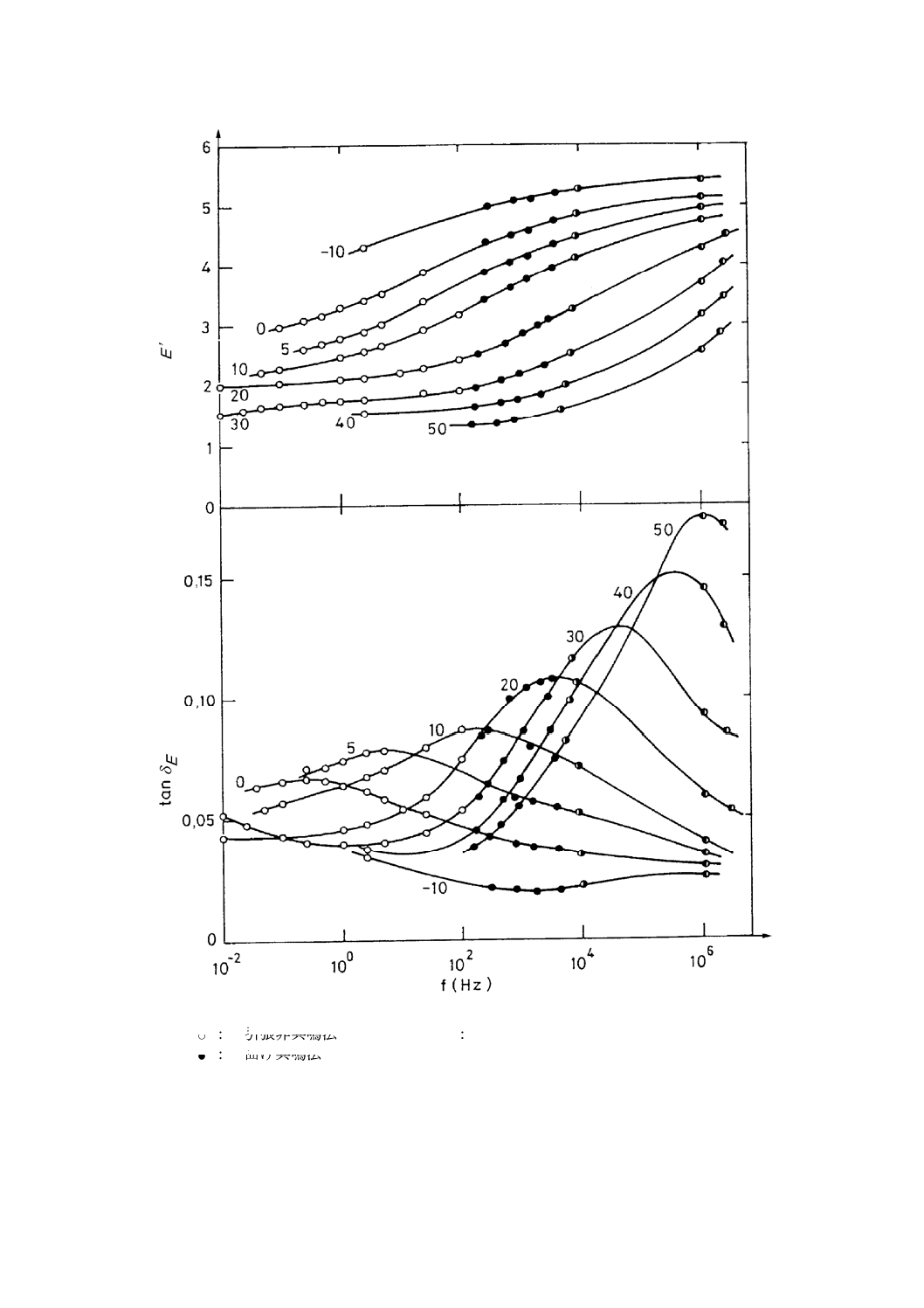
ポリプロピレンホモポリマーの広範囲な動的特性値を,図A.16に示す。すなわち,−10 ℃から50 ℃
の間の温度別の,広範囲の振動数領域におけるE′及びtanδE=E′/E′′を示している。これらの結果は,多
様な動力学的試験方法を用いて得たものである。100 Hzまでの低振動数でのデータは,引張振動非共振法
(JIS K 7244-4参照)を用いて得た。100 Hzと5 kHzとの間は,曲げ振動共振曲線法(JIS K 7244-3参照)
を用いて得た。試験片が,縦の共振モードの振動をするようにした,この改良方法は,10 kHzまでのデー
タの測定を可能にした。超音波伝ぱ法(ISO 6721-8参照)は,1 MHzから5 MHzの領域の特性を測定する
ために用いた。
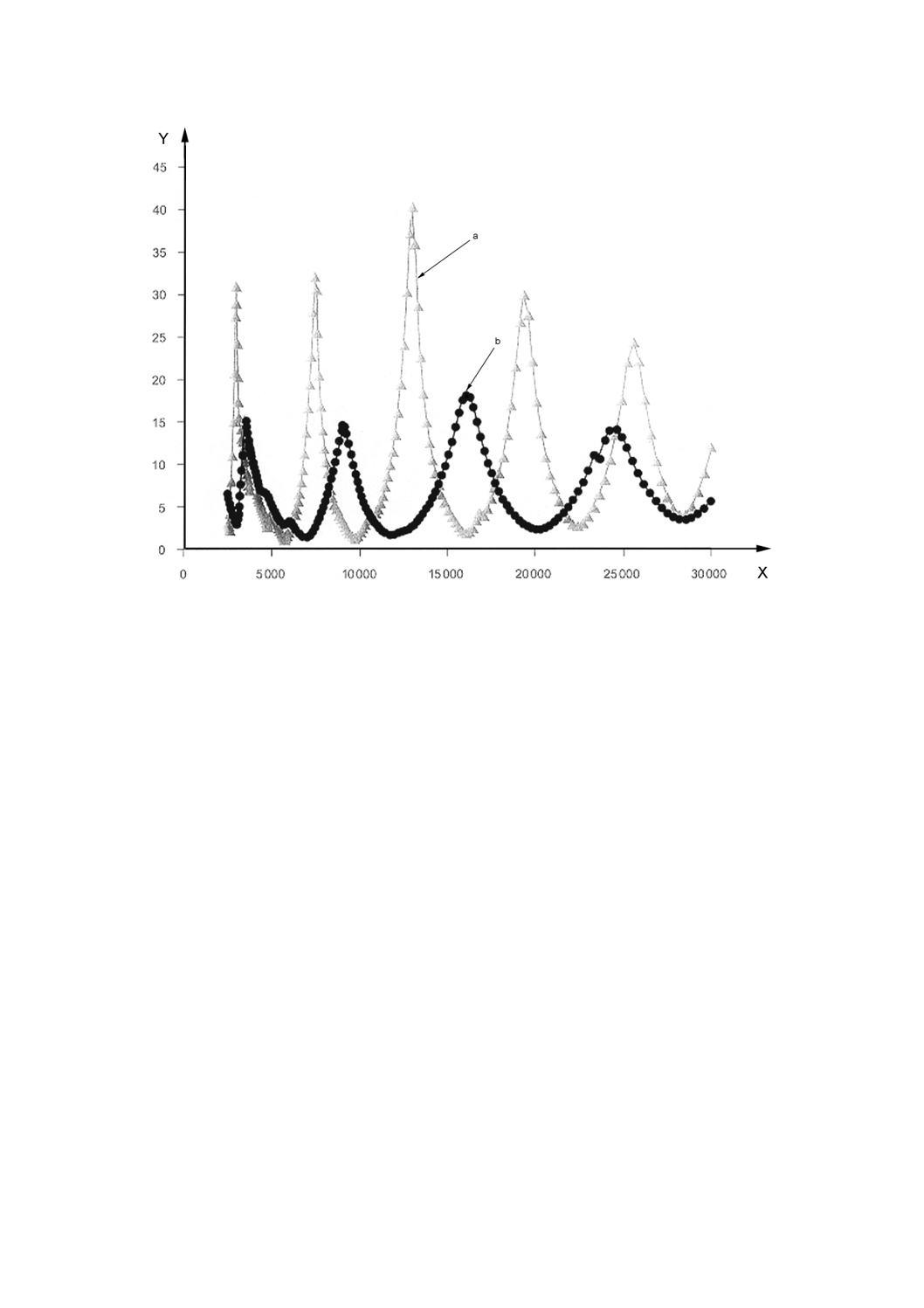
温度20 ℃でのポリプロピレンのシェルの共振モード振動数及び振幅の計算結果を,図A.17に示す。図
A.17の曲線aは,10 Hzの単一振動数で求めたE′及びE′′を用いて得た。ここでは,特性は,振動数に依
存しないと仮定する。比較のために,図A.16の20 ℃,振動数領域0.1 Hz〜100 Hz間でのE′及びE′′のデ
ータを用いて予側した応答を,図A.17の曲線bに示す。
図A.16に示す広範囲のデータを求めるには,多様な試験方法を必要とするが,各特性の振動数及び温度
の依存性を同等と仮定すると,はるかに少ない測定値からこれらのデータをたいがい導ける。このように,
29
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
広範囲の振動数領域のデータは,狭い振動数領域だが,広い温度範囲で求めた“E′−振動数データ”の重
ね合せによって得る。図A.16の緩和機構は,ポリマー非晶相中のガラス−ゴムへの相転移を特定し,通常,
時間−温度の重ね合せによるWLF式が,この転移の動態を説明する。実際,tanδE (引張損失係数)に
おけるピークの振動数は,平均緩和時間の温度依存性によるWLF式を満足する。しかしながら,図A.16
の損失係数曲線の幅は,温度の上昇によって狭くなっている。これは,この緩和過程における緩和時間の
分布が,温度によって変化することを暗示している。結論として,振動数に対するE′の曲線の形は,温度
と共に変化し,またこれが,時間−温度の重ね合せを用いて予測した特性値の確度の限界であろう。
A.8 非等方性弾性モデルの適用 この箇条では,単軸引張応力下での積層品中央の孔周りの応力分布を得
るために,非等方性線形弾性解析を用いる。この積層品は,一定方向に,連続繊維で強化されたプラスチ
ックの8層で構成されている。座標軸及び積層品寸法を,図A.18に示す。X軸は,与える応力の方向であ
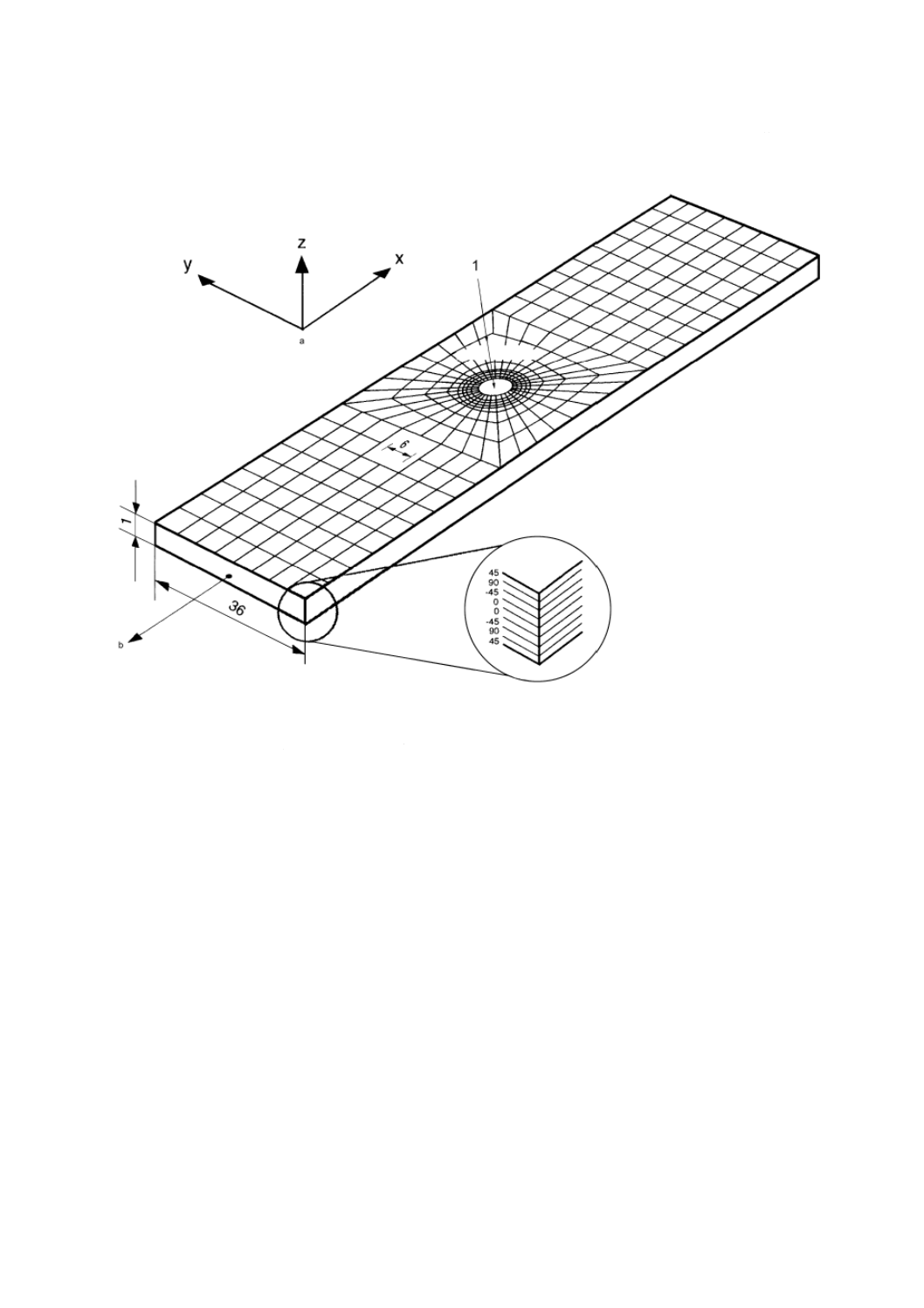
る。各層の繊維の配向は,繊維軸とX軸からなる角度で区別し,図の拡大部分に示す。
各層の座標軸は,1軸が,繊維の配向方向に沿っていることで規定する。この軸に直角な平面の特性は,
等方性と仮定する。3軸は,積層品の厚さ貫通方向(z軸)と一致させる。
解析の中で,孔の周りの材料が,平面応力状態とみなせるように,荷重の導入と関連した拘束は,円板
の各末端に集中すると仮定する。これは,積層品に,厚さ方向(z軸)に沿った応力の構成要素は,ない
ことを暗示している。
直角方向等方性の仮説のために,単層の弾性非等方性を特徴付けるため,五個の独自の材料パラメータ
が,必要である。通常この目的に用いる五個の特性を,表A.4に示す。E1及びE2は,各々繊維配向の方向
及び直角方向の引張弾性率である。G12及びG23は,各々繊維軸を含んだ平面及びこの軸に直角な平面のせ
ん断弾性率であり,ν12は,繊維軸方向に与えた応力に対するポアソン比である。表A.4の中で,これら
のパラメータは,表A.3及び本体の3.2で規定した特性値Ep,En,Gp及びνpnと同一である。
炭素繊維強化エポキシ樹脂用に測定した値も,表A.4に示す。繊維が,単一方向に配置した圧縮成形板
から切り出した試験片で,特性値を求めた。引張特性及びポアソン比は,ISO 527-5を用いて測定し,せ
ん断弾性率G12は,ISO 15310を用いて測定した。平面応力の状態が,積層品及び各層中に存在するので,
直角方向のせん断弾性率G23の認識は,この解析には必要ない。これらの特性もまたISO 6721-8に規定の
超音波伝ぱ法を用いて求めることができることは,注意に値する。
その規格の現行版は,等方性材料を扱っており,また非等方性材料に対して必要なデータ解析は,記載
がない。
表A.4 直角方向等方性の炭素繊維強化エポキシ樹脂の材料特性
E1=Ep
E2=En
G12=Gp
ν12=νpn
G23
(GPa)
(GPa)
(GPa)
135
10
5.3
0.3
−
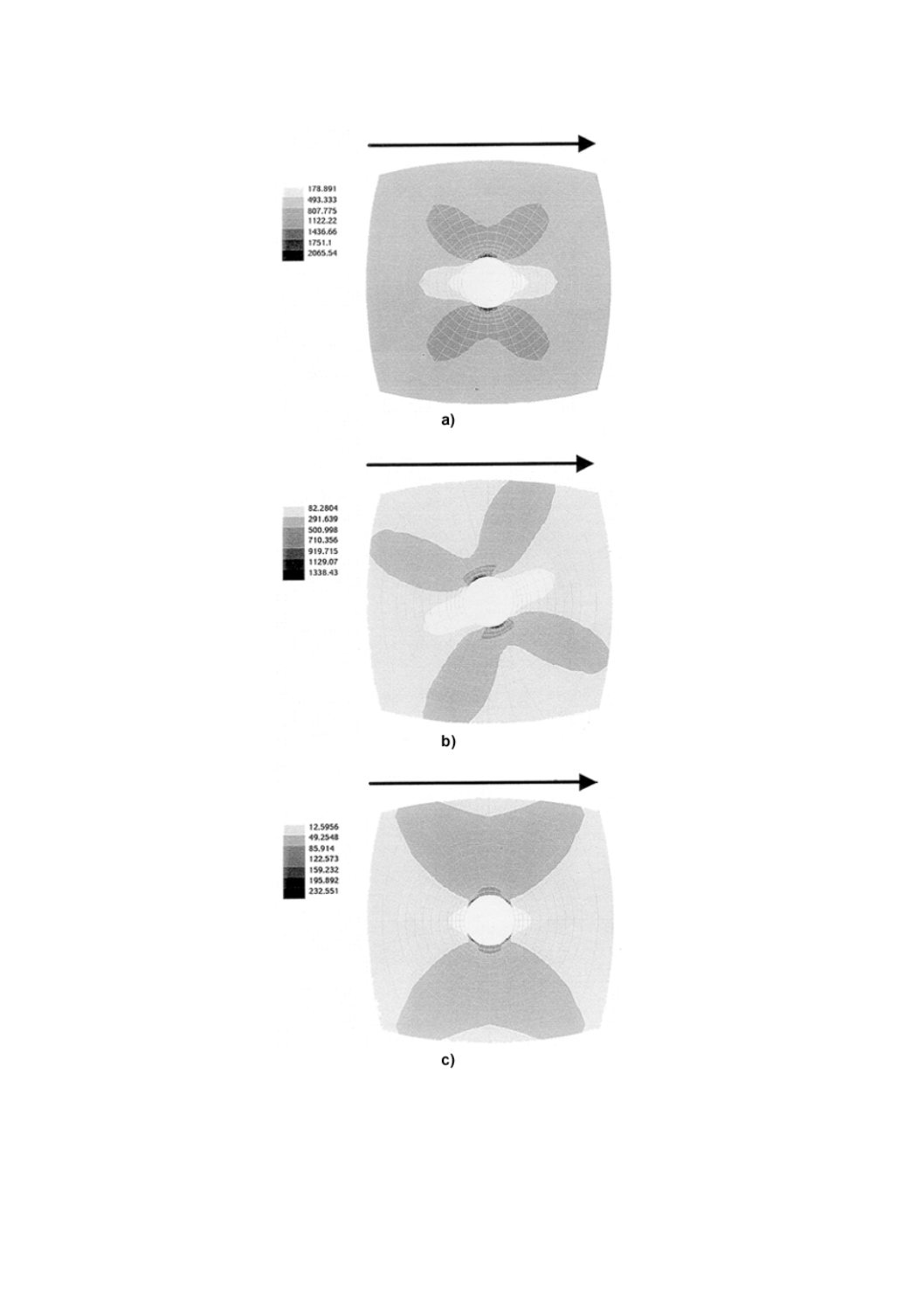
140 MPaの応力を与えて発生した各層中の最大主応力の分布を計算するために,有限要素解析が用いら
れてきた。最大主応力の等高線図を,図A.19に示す。これらの応力の最大値は,積層品中の破壊の開始を
予測するために,個々の層の多軸破壊基準を用いる妥当性を調査するために用いられてきた。
関連規格 ISO 6721-8 Plastics―Determination of dynamic mechanical properties―Part 8 : Longitudinal and
shear vibration―Wave-propagation method
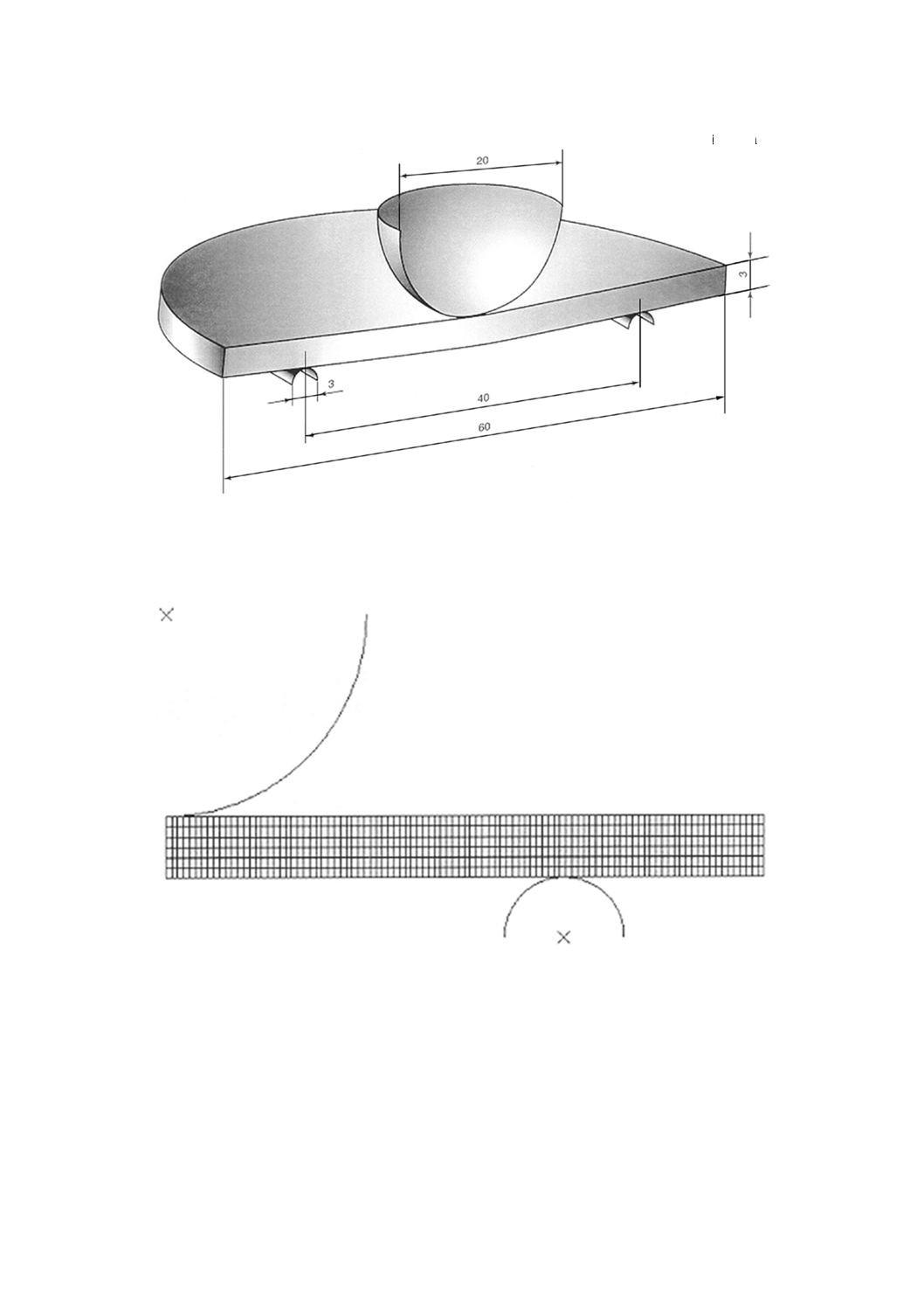
単位 mm
30
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
図A.1 有限要素解析による異なる材料モデル適用の実例用
円板状試験片及び荷重の配置図
図A.2 有限要素解析用メッシュ線図
31
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
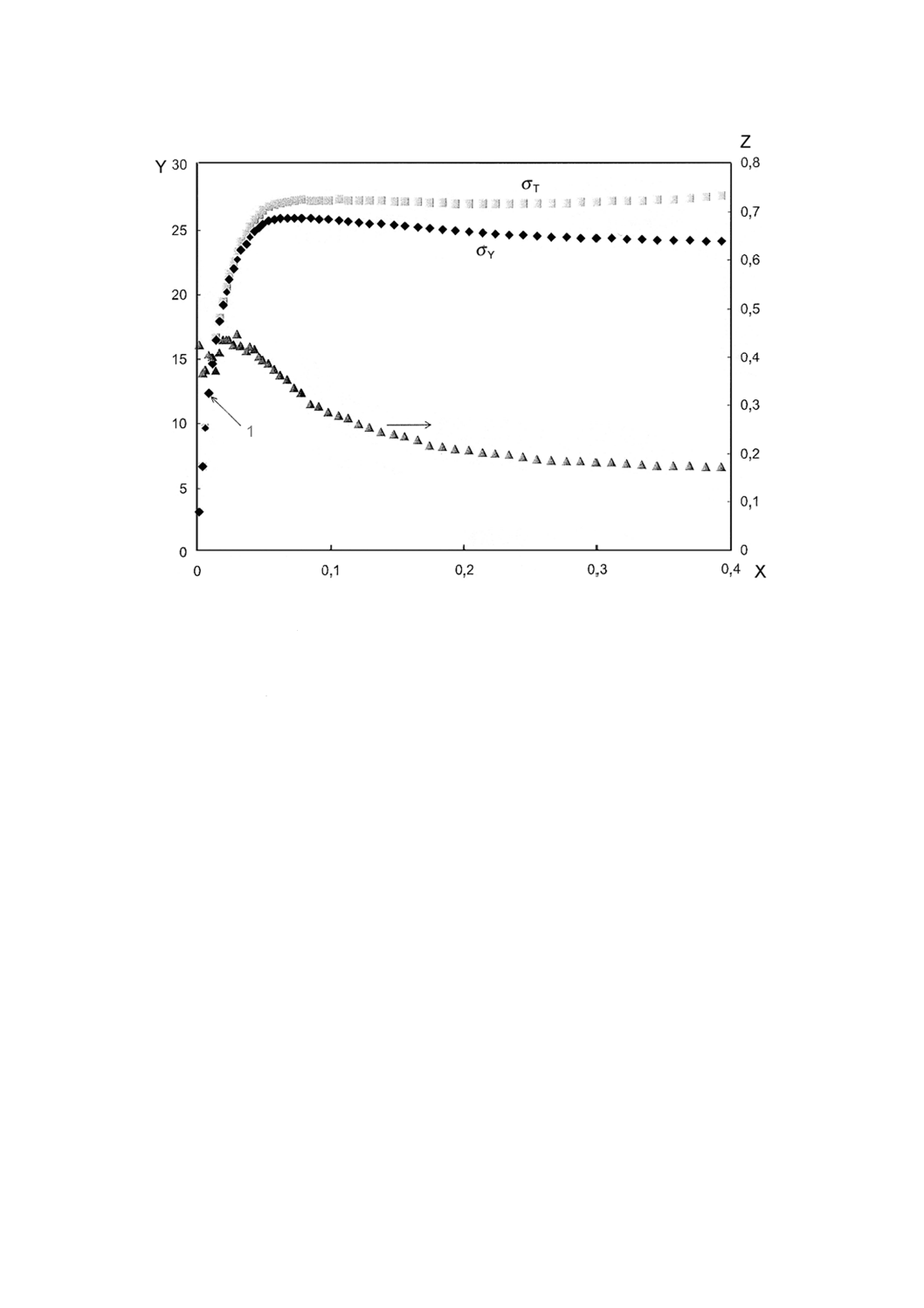
X : 真ひずみ
Y : 応力,MPa
Z : ポアソン比
σT: 真の応力
σY: 工学応力
1 : 第1降伏点
備考 真の引張応力は,式(A.6)を用いて,これらの結果から計算した。
図A.3
プロピレン−エチレン共重合体の引張ひずみに対する工学応力及びポアソン比
の測定値
32
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X: 要素変位,mm
Y: 力,kN
1: 弾性解析
2: フォン・ミーゼス及びドラッガープラガー解析
図A.4 線形弾性解析を用いて得られた,中央の節点変位で計算した力の変化
−非線形解析に基づく計算との比較 (図A.9参照)
33
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.5 線形弾性解析を用いて予測した,中央での節点変位4 mmの時の
半径方向の引張ひずみの等高線図
34
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
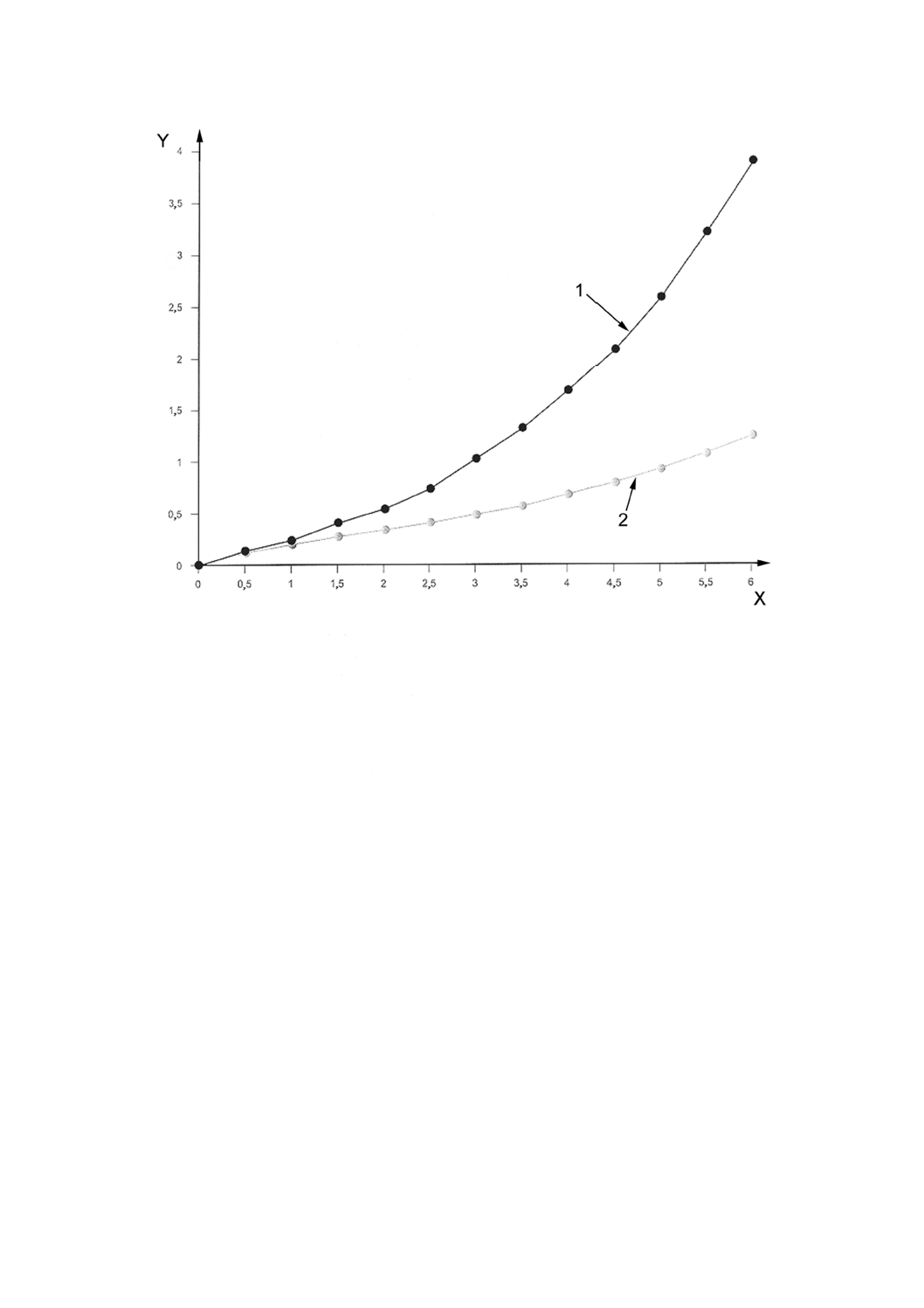
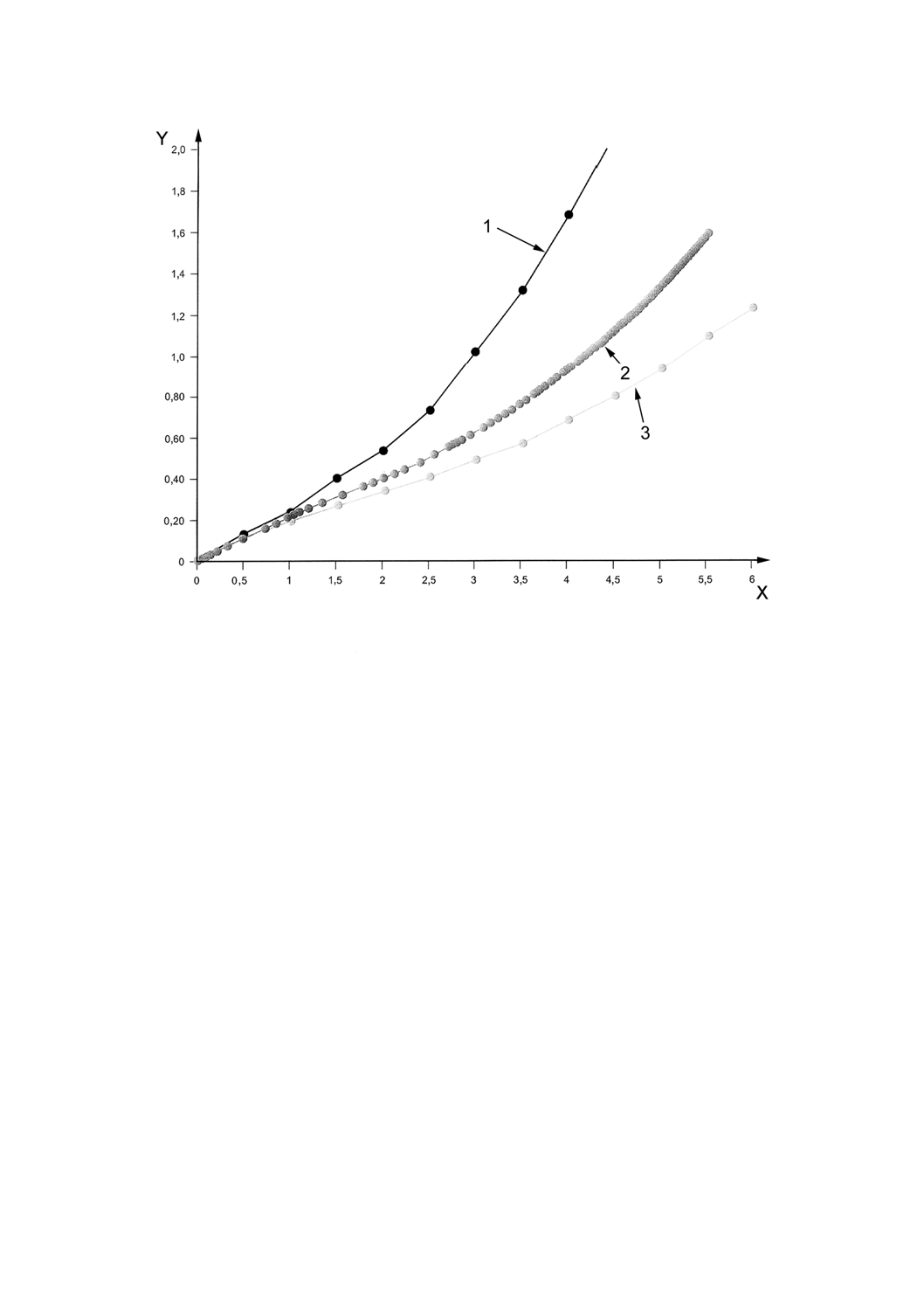
X: 要素変位,mm
Y: 力,kN
1: 弾性解析
2: 疑似弾性解析
3: フォン・ミーゼス解析
図A.6 非線形,弾性解析を用いて予測した中央の節点変位に対する力の変化
35
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
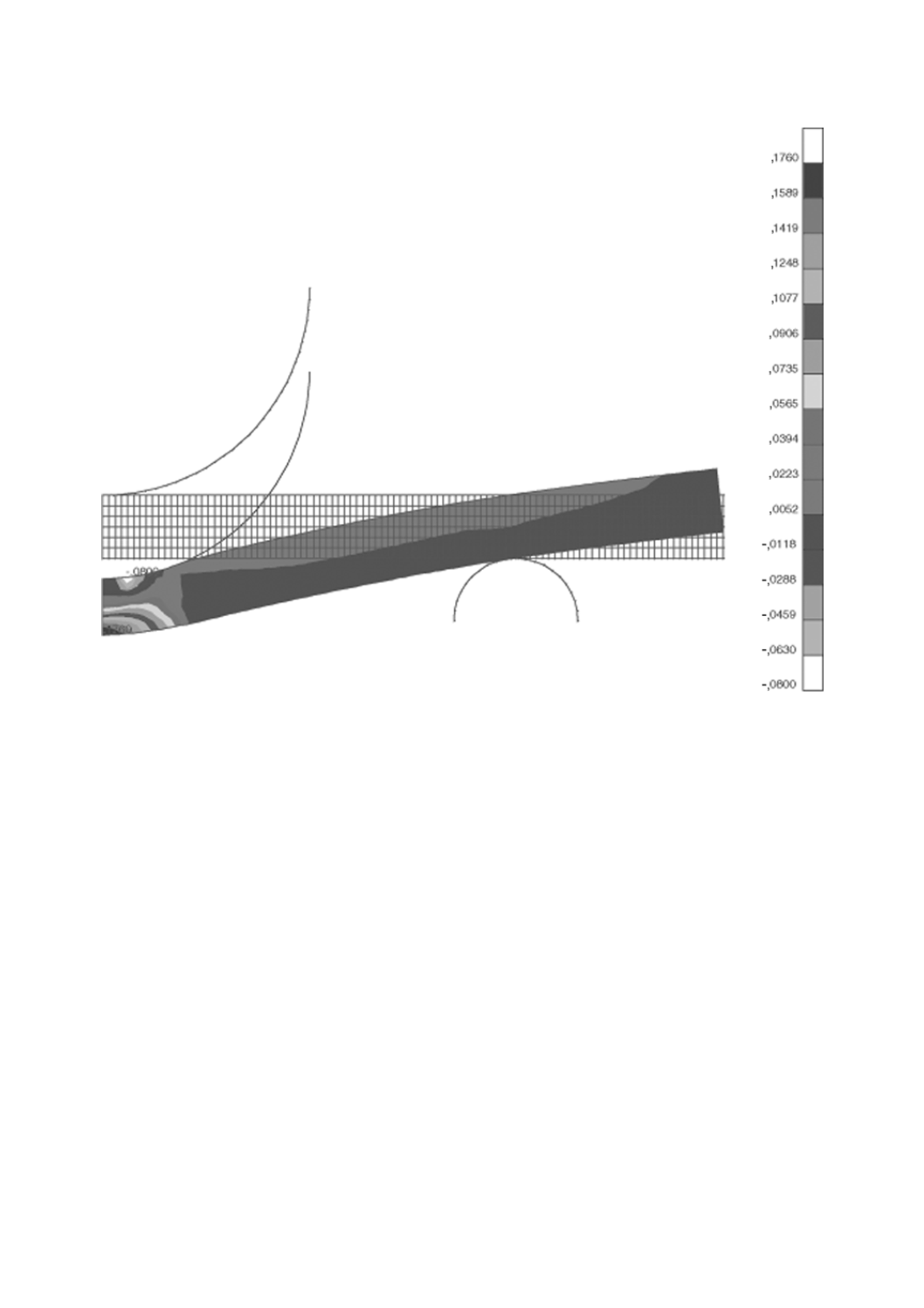
図A.7 非線形弾性解析を用いて予測した中央での節点変位4 mmのときの
半径方向の引張ひずみの等高線図
36
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
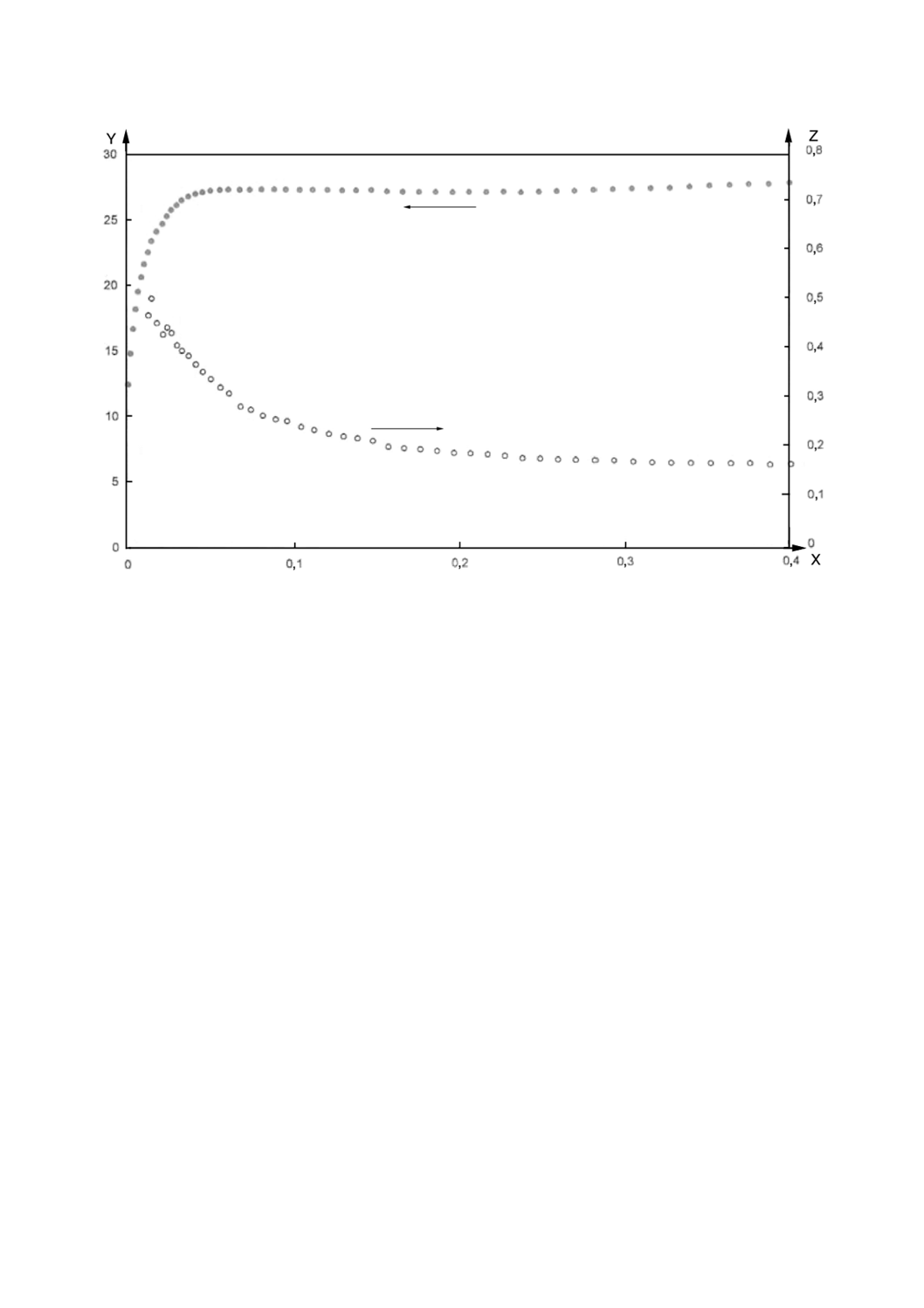
X: 真ひずみの塑性成分
Y: 真の降伏応力,MPa
Z: 真のポアソン比の塑性成分
図A.8 図A.3のデータから得られたプロピレン−エチレン共重合体の真ひずみの
塑性成分に対する真の降伏応力,及び真のポアソン比の塑性成分
[式(A.7)及び(A.9)を参照]
37
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
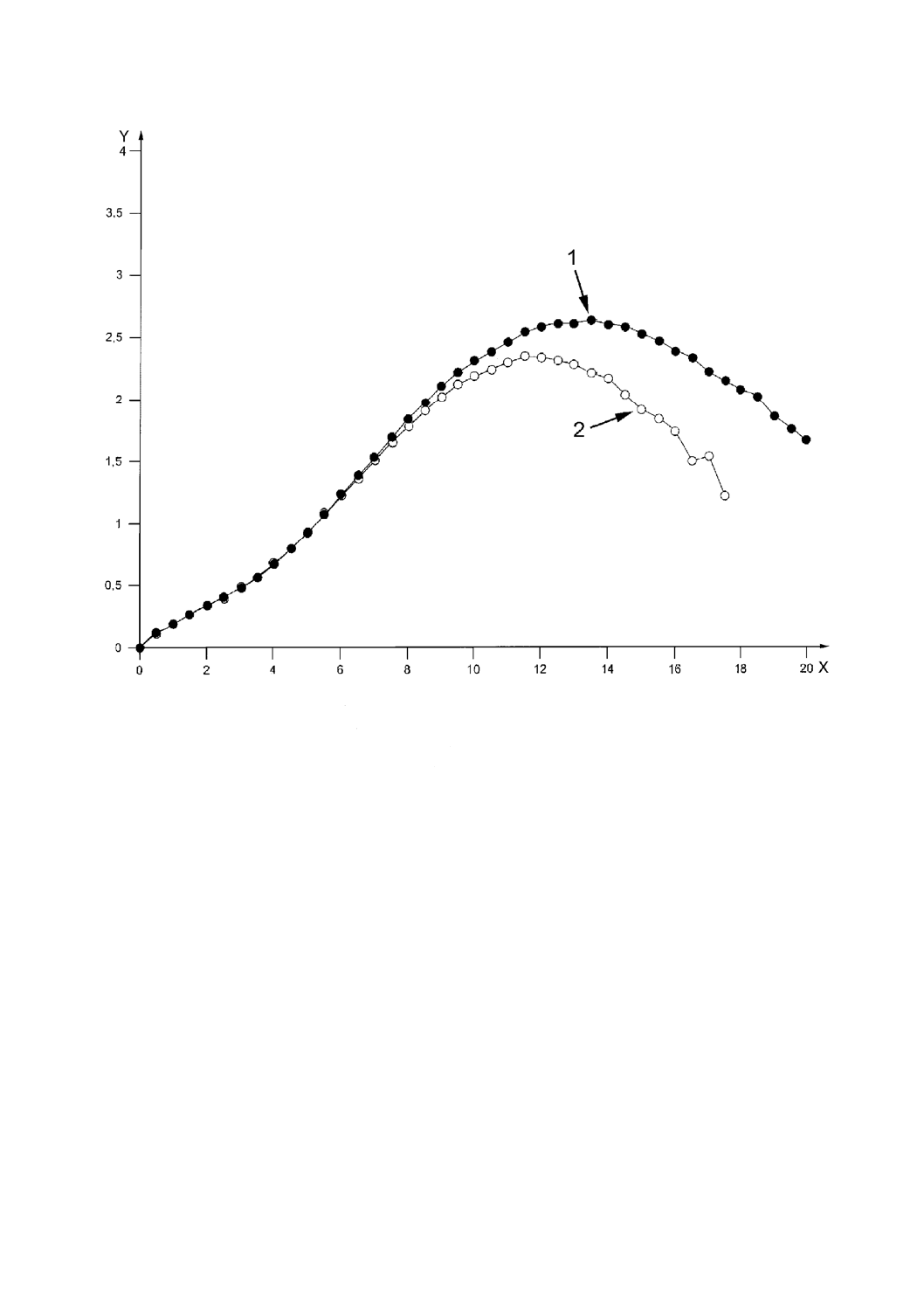
X: 要素変位,mm
Y: 力,kN
1: ドラッガープラガー解析
2: フォン・ミーゼス解析
図A.9 フォン・ミーゼスモデル及び線形ドラッガープラガーモデルを用いて計算した
“力−変位曲線”
38
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
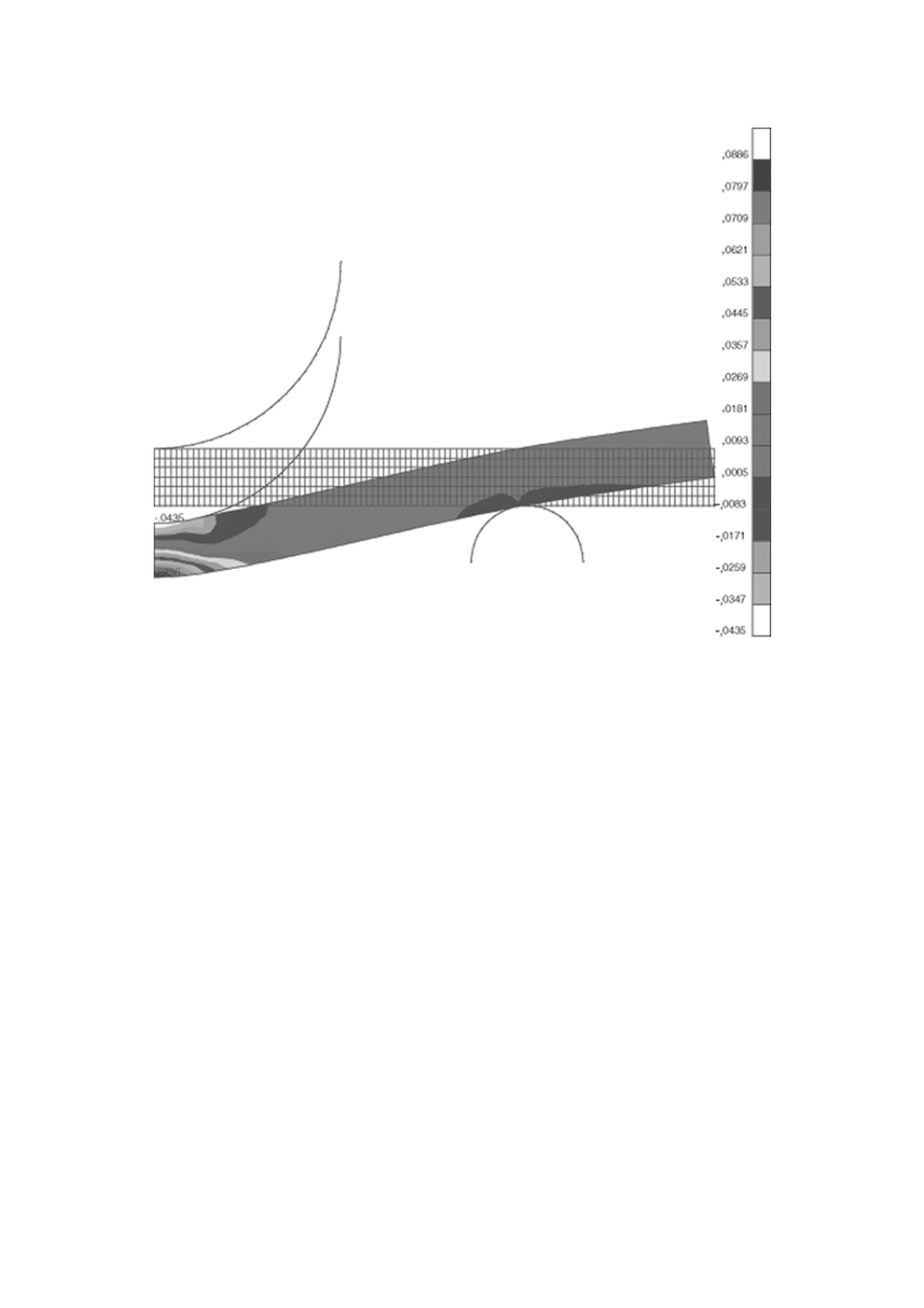
a) フォン・ミーゼスモデル
b) 線形ドラッガープラガーモデル
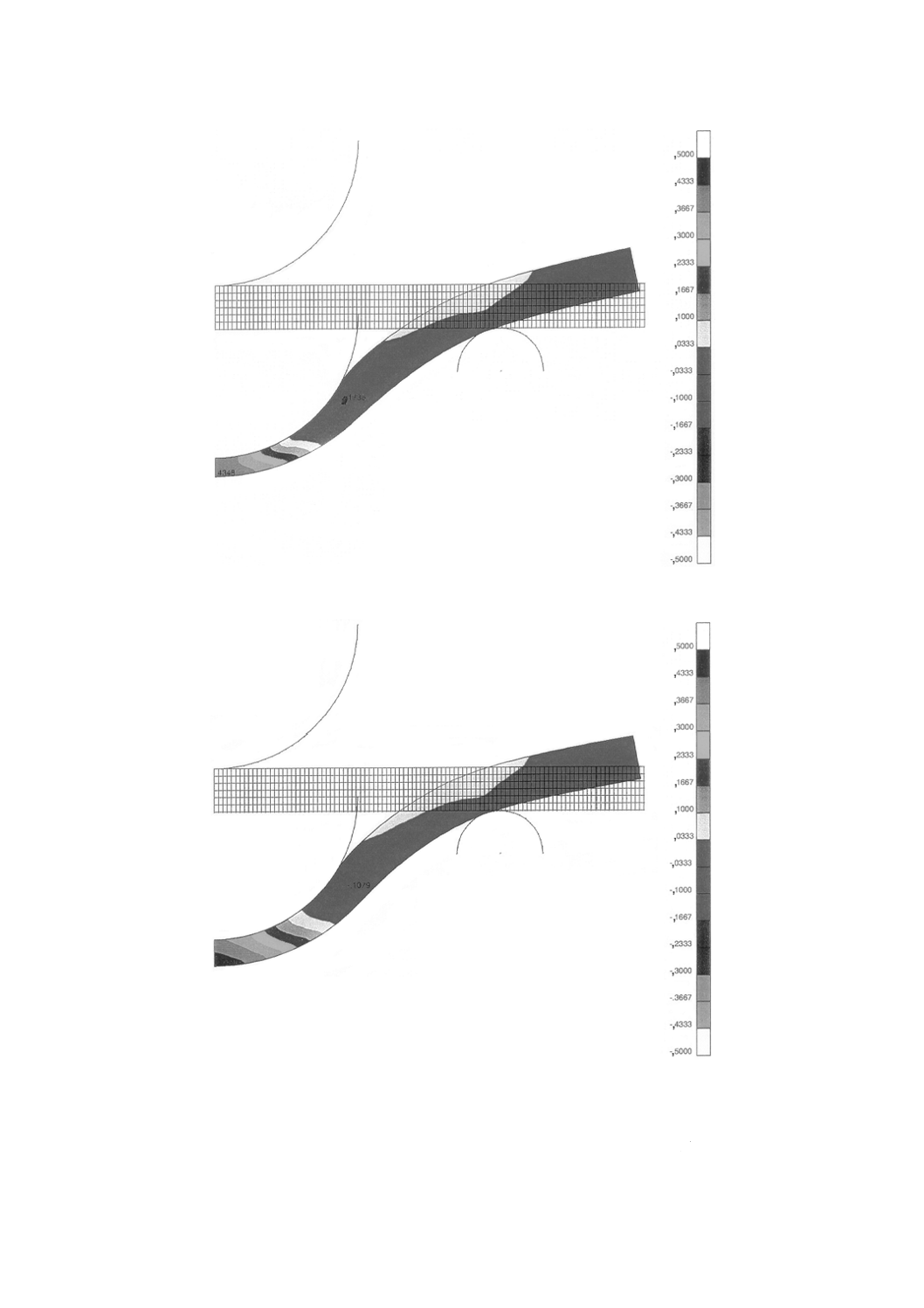
図A.10 フォン・ミーゼスモデルa) 及び 線形ドラッガープラガーモデルb) を用いて
計算した,中央での節点変位12 mmのときの半径方向の引張ひずみの等高線図

39
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X: ひずみ
Y: 応力,MPa
備考 各曲線に表示した値は,ひずみの塑性成分の値である。
図A.11 異なるひずみ速度及び23 ℃張力で測定したプロピレン−
エチレン共重合体の真の応力−ひずみ曲線
40
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
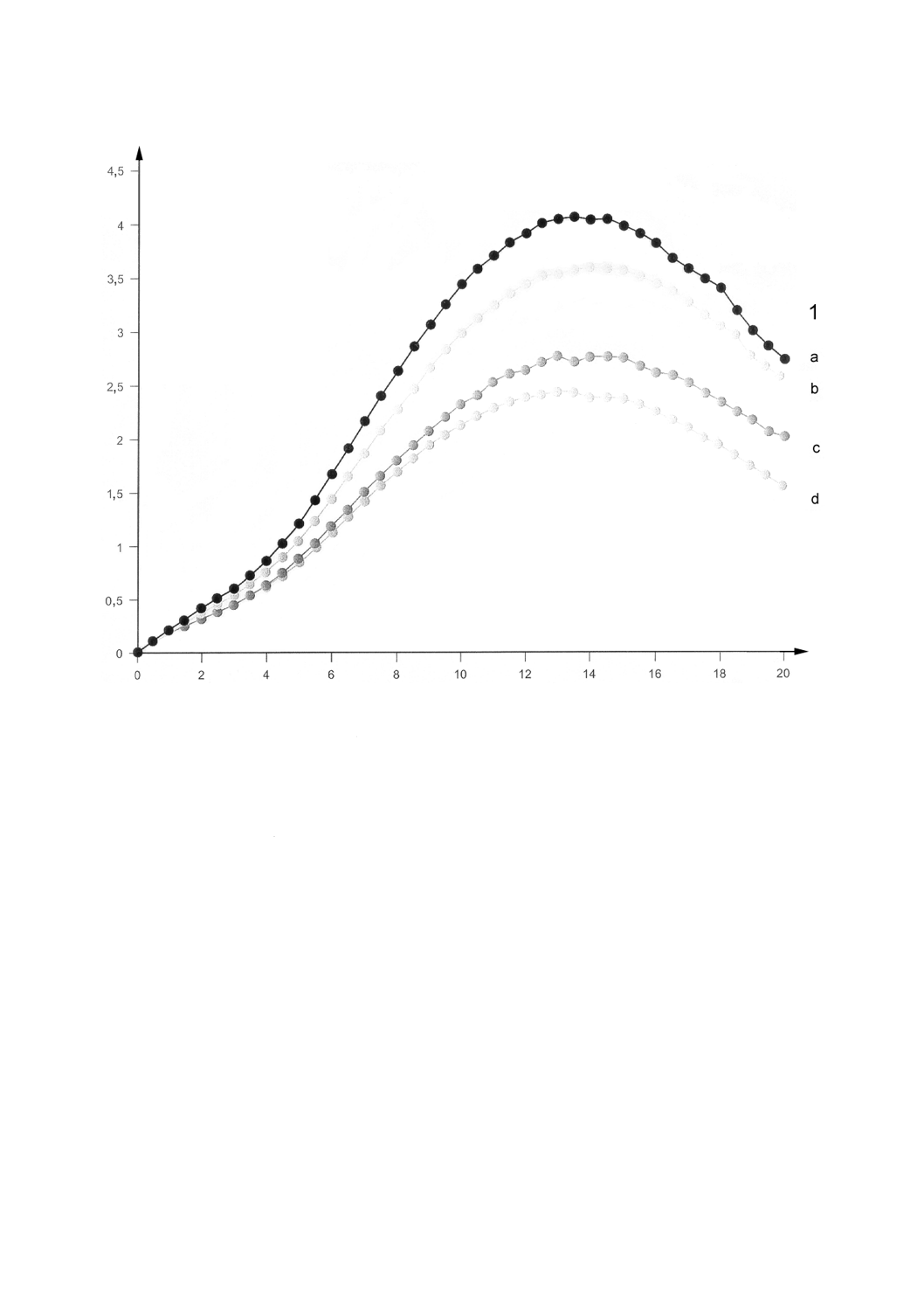
X: 要素変位,mm
Y: 力,kN
1: 試験速度
a: 1 m/s
b: 0.1 m/s
c: 0.01 m/s
d: 1 mm/s
図A.12 図A.11及び線形ドラッガープラガーモデルに示した速度依存の材料特性を
用いて,負荷速度の範囲に対して計算した力−変位曲線
41
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X: 時間,s
Y: 引張コンプライアンス,GPa−1
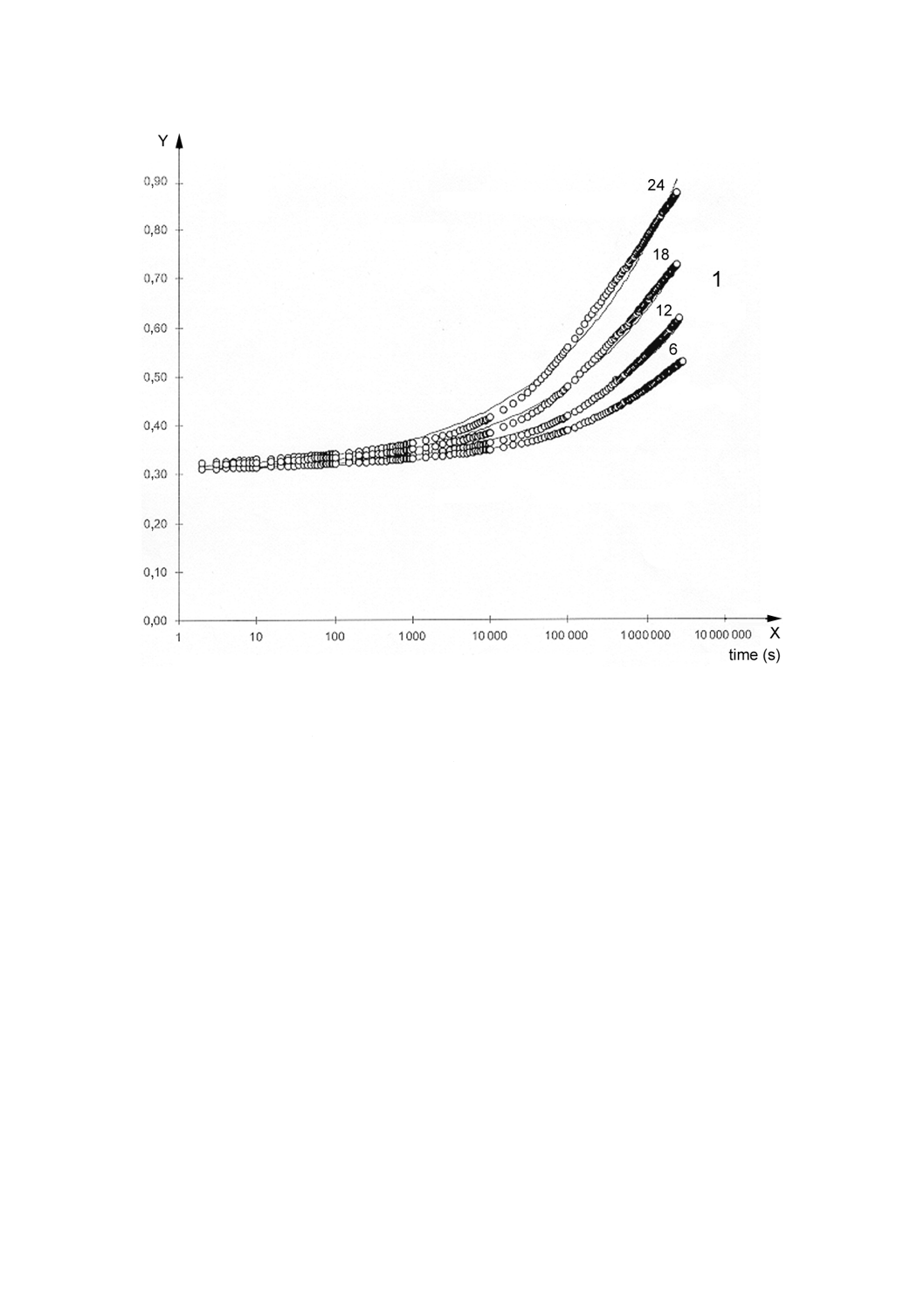
1: 負荷応力,MPa
備考 クリープ挙動は,応力緩和効果を無視した式(A.12)及び(A.13)を用いて表される。
図A.13 種々の負荷応力レベルでのPVCに対する引張クリープコンプライアンス曲線
42
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
t: 時間,s
d: 変位,mm
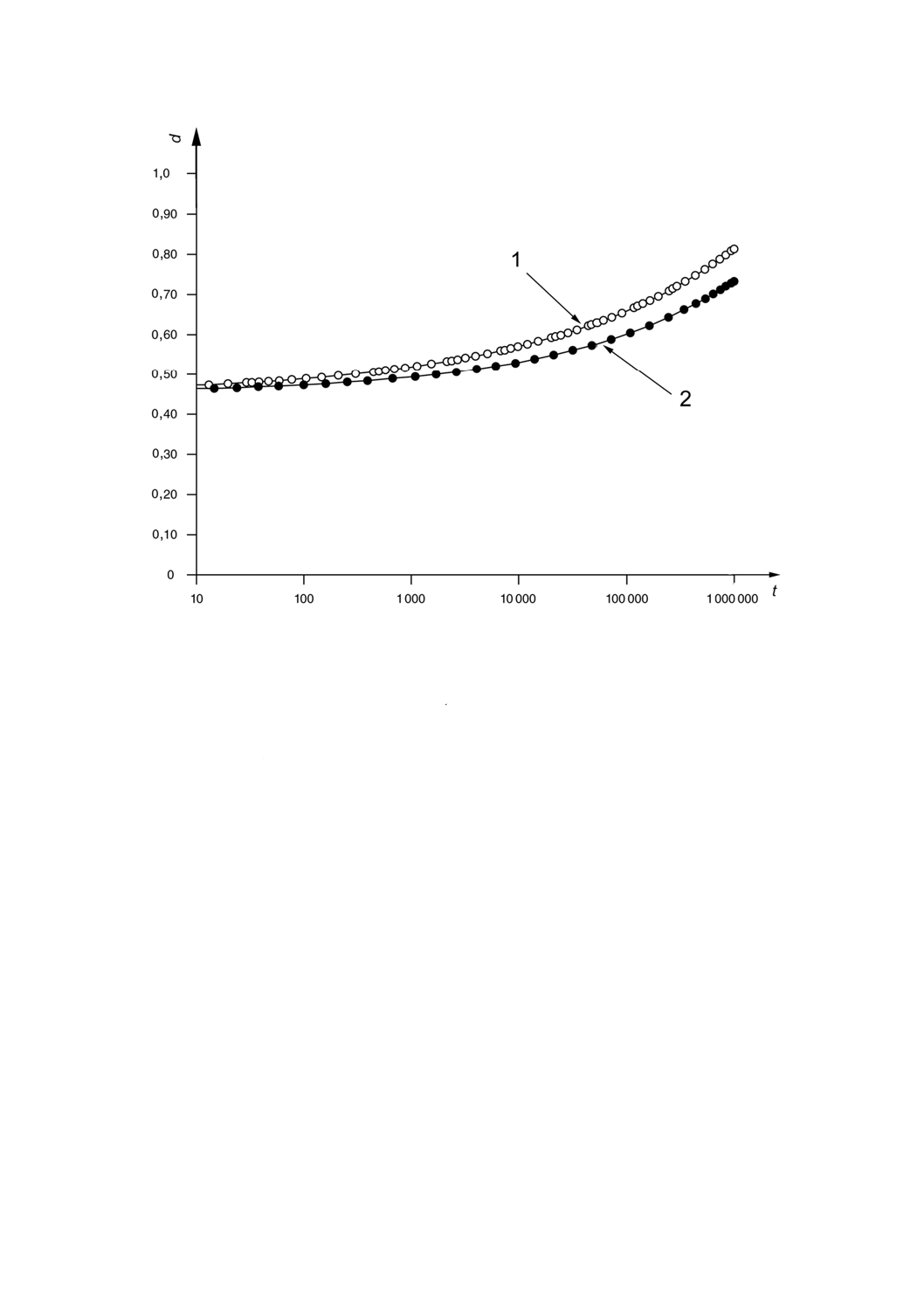
1: 非線形解析
2: 線形解析,r = 4×10 6 s
図A.14 a) クリープ時間t に対する板の中央での節点変位d の増加の計算値
43
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
t: クリープ時間,s
備考 応力目盛は,MPaである。
図A.14 b) クリープ時間tに対する最大主応力の分布の変化
44
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
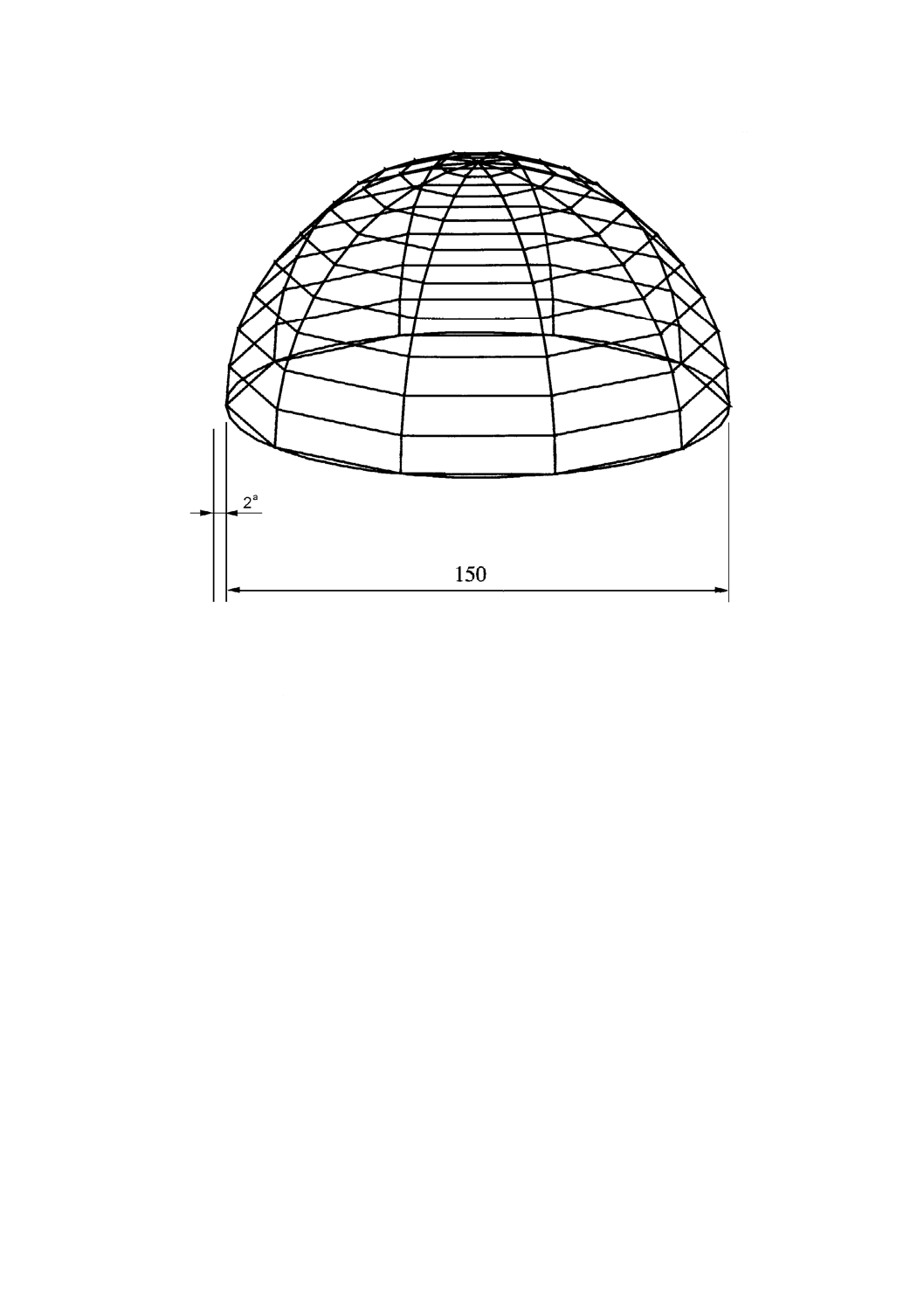
単位 mm
a: 壁の厚さ
図A.15 粘弾性材料の半球状のシェルの共鳴周波数を計算するために用いる
有限要素メッシュ及び寸法
45
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
○ : 引張非共鳴法
f : 周波数,Hz
● : 曲げ共鳴法
E′ : 引張貯蔵弾性率,GPa
◑: 超音波パルス技術法
tanδE: 引張損失係数
◐: 縦共鳴法
図A.16 各曲線上の温度(℃)でのポリプロピレンに対するE′及びtanδEの周波数依存性
46
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X: 周波数,Hz
Y: 速度振幅,mm/s
a: 基部波節速度,単一周波数でのデータ;曲線は,単一周波数
10Hzで,図A.16からの動的特性データを用いて得た。
b: 基部波節速度,周波数依存性データ;曲線は,全周波数帯の
データを用いて得た。
図A.17 図A.15に示す半球状のシェルの共鳴モデルの速度振幅及び周波数
単位 mm
47
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
1: 中央の孔
a: 層分割方向の軸
b: 負荷応力
図A.18 有限要素解析用積層品の層及びメッシュ線図
48
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a: 負荷応力の方向
図A.19 積層材料上の遠隔応力140 MPaによって生じた
各層の最大主応力(MPa)の等高線図
a
a
a
0°層
45°層
90°層

49
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考)プラスチック加工シミュレーション解析の適用
この附属書は,本体に関連する事柄を補足するもので,規定の一部ではない。
B.1 概要 この附属書では,プラスチックの種々の加工シミュレーションソフトウェアの適用を,本体の
4.3で定義した適切な材料データを使っての例証を示す。考慮した適用例を,表B.1に示す。
表B.1 加工シミュレーション解析の適用
項目番号
加工方法
解析タイプ
B.2.1
B.2.2
B.2.3
射出成形
熱可塑性プラスチックの金型充てん簡易解析
熱可塑性プラスチックの金型充てん,保圧及び冷却の高度な解析
熱可塑性プラスチックの成形収縮/反り解析例
B.3.1
B.3.2
B.3.3
押出成形
押出機中の樹脂の溶融状態
コートハンガーダイ中の溶融流動シミュレーション
異型押出しダイ中の溶融流動シミュレーション
商業ベースの加工シミュレーションソフトウェアでは,溶融樹脂の流動挙動を説明するため,広範で多
様な粘度モデルの選択ができることを注意することが重要である。書式,特に,これらの粘度モデルに用
いる変数及びモデル係数の記号は,周知の参考文献に基づくそれらとほとんど違いはないようである。一
般的に,各ソフトウェアは,適切な曲線近似手法によって,実験に基づく溶融せん断粘度データから選択
した粘度モデル用の適切な係数を求めるモジュールも含んでいる。
射出成形シミュレーションソフトウェア用の最も一般的な粘度モデルを,表B.2に示す。一次モデルは,
一般的に,単純な二次元解析を用いる。実際の粘度データの入力条件は,ソフトウェアによって異なる可
能性がある。例えば,Moldflowソフトウェア(1)では,一次モデル用粘度データの入力形式は,三個の係数
(粘度係数,せん断係数及び温度係数)又は三つのデータポイントのセットのいずれかの形式とし,そこ
からソフトウェア専用の曲線近似モジュールによってモデル係数A,B及びCが計算される。
1
1
1,
η
γ及び
&
T
2
2
2,
η
γ及び
&
T
3
3
3,
η
γ及び
&
T
注(1) Moldflowは,商業的に入手できる製品の一例である。この情報は,この規格利用者の便宜のた
めに記載するものであって,JISがこの商品を推奨するものではない。
同様に,2次モデルの場合も,粘度データの入力形式は,次のような二次粘度マトリックスか,又は六
個の多項式係数のセットのいずれかの形式とすることができる。
温度(℃)
せん断速度(1/s) 粘度(Pa・s)
Tm−20
1 000
η1
Tm
100
η2
Tm
1 000
η3
Tm
10 000
η4
Tm+20
100
η5
Tm+20
1 000
η6
50
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.2 射出成形シミュレーションソフトウェアに用いる一般的粘度モデル
シミュレーション
ソフトウェアのモデル
粘度モデル
記号の説明
一次モデル
CT
e
A
B
γ
η
&
=
A 粘度係数
B せん断速度係数
C 温度係数
二次モデル
(
)
(
)
(
)
2
6
5
2
4
3
2
1
ln
ln
ln
ln
T
A
T
A
A
T
A
A
A
+
+
+
+
+
=
γ
γ
γ
η
&
&
&
A1 モデル係数
A2 モデル係数
A3 モデル係数,1/℃
A4 モデル係数
A5 モデル係数,1/℃
A6 モデル係数,1/(℃)2
クロス/アレニウス
(Cross/Arrhenius)
モデル
(
)
[
]
n
p
T
Te
Be
−
+
=
1
0
/
*
/
1
b
τ
γ
η
η
β
&
ηo ゼロせん断粘度,Pa・s
n 累乗の指数
τ* シェアシンニング(shear thinning)を生
じ始めるせん断応力レベル,Pa
Tb 温度感度係数,K
B ゼロせん断粘度係数,Pa・s
β ηoの圧力依存係数,1/Pa
p 圧力,Pa
クロス/WLF
(Cross/WLF)モデル
(
)
(
)
[
]
{
}
(
)
[
]
n
T
T
A
T
T
A
e
D
−
+
−
+
−
−
=
1
0
r
2
r
1
1
*
/
1
/
τ
γ
η
η
&
ここに,Tr=D2+D3 p
ηo ゼロせん断粘度, Pa・s
n 累乗の指数
τ* シェアシンニングを生じ始めるせん断応
力レベル,Pa
Tr 基準温度,℃
D1 定数,Pa・s
D2 圧力ゼロ時のガラス転移温度,℃
D3 圧力感度係数,℃/Pa
A1 粘度の温度感度係数
A2 定数,℃
p 圧力,Pa
備考 すべてのモデル用,η=粘度(Pa・s),γ&= せん断速度(1/s),T=温度(℃),e:ネイピア数(自然対数の
底)
押出を含む成形工程用のシミュレーションソフトウェアに用いる最も一般的な粘度モデルを表B.3にま
とめる。実際は,累乗則及び対数多項式モデルを簡単な解析に用い,一方,高度な解析には,カロ(Carreau)
及びクロスモデルを用いる。カロモデルの簡略方式では,せん断速度が無限大に近づくとき,粘度(η∞)
はゼロになると仮定する。

51
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.3 押出成形シミュレーションソフトウェアに用いる最も一般的粘度モデル
シミュレーション
ソフトウェアのモデル
粘度モデル
記号の説明
ニュートン流体モデル
(
)
r
T
T
b
Ae
−
−
=
η
A 定数,Pa・s
b 温度感度係数,1/℃
Tr 基準温度,℃
べき法則モデル
(
)
1
r
−
−
−
=
n
T
T
b
Ae
γ
η
&
A 定数,Pa・s
b 温度感度係数,1/℃
Tr 基準温度,℃
n 累乗の指数
対数多項式モデル
(
)
(
)
(
)
(
)
(
)(
)
γ
γ
γ
η
&
&
&
ln
ln
ln
ln
r
6
2
r
5
r
4
2
3
2
1
T
T
a
T
T
a
T
T
a
a
a
a
−
+
−
+
−
+
+
+
=
Tr 基準温度,℃
a1 モデル係数
a2 モデル係数
a3 モデル係数
a4 モデル係数,1/℃
a5 モデル係数,1/(℃)2
a6 モデル係数,1/℃
クロスモデル
(
)
[
]
n
−
+
=
1
0
0
*
/
1
τ
γ
η
η
η
&
ηo ゼロせん断粘度,Pa・s
τ* シェアシンニングを生じ始めるせん断応力
レベル,Pa
n 累乗則の指数
カロモデル
簡略法式
(
)
(
)
(
)
[
](
)a
n
a
T
T
b
T
T
b
re
Ae
/
1
r
r
1
−
−
−
−
−
+
=
γ
η
&
(
)
[
](
)2
/
1
2
0
1
n
−
+
=
γ
λ
η
η
&
ηo ゼロせん断粘度,Pa・s
A モデル定数,Pa・s
b 温度感度係数,1/℃
Tr 基準温度,℃
a 定数
r 定数,s
n 累乗の指数
λ シェアシンニングを生じ始めのせん断速度
に関連するパラメータ,s
備考 すべてのモデル用,η=粘度(Pa・s),γ&=せん断速度(1/s),T=温度(℃),e:ネイピア数(自然対数の底)
高度な,金型充てん,保圧及び冷却解析用に,pvT挙動の特徴を表すために,射出成形シミュレーショ
ンソフトウェアでは,よく知られたモデルを用いている。測定したpvTデータを,シミュレーションソフ
トウェアに適合させるために用いるモデルを,表B.4に示す。
Moldflow(1)シミュレーションソフトウェアへのpvTデータ入力用の一般的様式は,材料のpvT挙動の特
徴を表す,十三個の標準点のセットである。準結晶性材料では,Tgより低い温度領域に七個の標準点を,
Tgより高い温度領域に四個の標準点を,残り二個の標準点は,境界点に,選択する。他方非晶性材料では,
十個だけの標準点,すなわちTgよりも高い温度領域及び低い温度領域で各々四個の標準点を,また境界点
に残り二個の標準点を用いる。これら十三個の標準点は,温度及び圧力の適切な領域(ISO/DIS 17744に
よる)にわたって測定したpvTデータの二領域モデル式での最適合化によって求める。

52
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.4 射出成形シミュレーションソフトウェアで用いる一般的pvTモデル
シミュレーション
ソフトウェアのモデル
pvT モデル
記号の説明
二領域タイト(Tait)
モデル
[C-mould (2) ソフトウェ
アで使用]
(
)
()
()
[
]
{
}
( )p
T
v
T
B
p
T
v
p
T
v
t,
/
1
ln
0894
.0
1
,
0
+
+
−
=
ここに,もしT > Tt(p)なら,
(
)
()
(
)
(
)
0
,
t
m
4
3m
5
2m
1m
0
5
=
=
−
+
=
−
−
p
T
v
e
b
T
B
b
T
b
b
v
b
T
b
また,もしT < Tt (p)なら,
(
)
()
(
)
(
)
(
)
p
b
b
T
b
b
T
b
e
b
p
T
v
e
b
T
B
b
T
b
b
v
9
5
8
5
7
t
S
4
S
3
5
S
2
S
1
0
,
−
−
−
−
=
=
−
+
=
v
比容積,m3/kg
T
温度,℃
p
圧力,Pa
Tt(p) 転移温度,℃
Tt(p)=b5+b6 p
b1m,b1s タイト係数,m3/kg
b2m,b2s タイト係数,m3/kg・K
b3m,b3s タイト係数,Pa
b4m,b4s タイト係数,1/K
b5 タイト係数,K
b6 タイト係数,K/Pa
b7 タイト係数,m3/kg
b8 タイト係数,1/K
b9 タイト係数,1/Pa
二分野モデル
[Moldflow (1) ソフトウェ
アで使用]
結晶性材料:
・低温領域(Tg未満)
・高温領域(Tgより上)
・境界式
非晶性材料:
・低温領域(Tg未満)
・高温領域(Tgより上)
p
a
T
a
e
a
P
a
T
a
P
a
a
v
7
5
3
2
4
1
6
−
+
+
+
+
=
P
b
T
b
P
b
b
v
+
+
+
=
3
2
4
1
T
c
c
P
2
1+
=
P
a
T
a
P
a
a
v
+
+
+
=
3
2
4
1
P
b
T
b
P
b
b
v
+
+
+
=
3
2
4
1
ai=タイト係数
bi=タイト係数
ci=タイト係数
他の記号は,二領域タイトモデル
と同じ。
注(2) C-mouldは,商業的に入手できる製品の一例である。この情報は,この規格利用者の便宜のために記載
するものであって,JISがこの商品を推奨するものではない。
B.2 射出成形工程のシミュレーション 成形工程シミュレーション用の材料データの影響を実例で説明
するために,本体の4.3.2で規定した各案件を別々に熟考することが重要である。
B.2.1 熱可塑性プラスチックの簡単な金型充てん解析の実例 熱可塑性プラスチックの簡単な金型充て
ん解析に,材料データを用いる実例を説明するために,図B.1に示す,単一構成形状の“自動車のドアパ
ネル”を選択する。実例の成形品の大きさ及びランナーシステムは,現在の自動車部品の実寸法にぴった
りと一致している。特に,部品の厚さは,2.25 mmであり,またランナーシステムは,直径16 mmのホッ
トランナー,直径で5 〜10 mmのテーパ状のスプルー,及びゲートの入口厚さ4 mmから結合部厚さ1.5 mm
53
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に変化するファンゲートである。
成形品及びランナーシステムの有限要素メッシュを,胴及びはりの構成要素を用いて作成する(図B.2
参照)。“自動車のドアパネル”に選定する材料は,充てん材なしのポリプロピレン(PP)である。このPP
材料の簡単な金型充てん解析に必要な,入力材料データは,次による。
ρm
=728 kg/m3
cpm
=3 400 J/kg℃
km
=0.169 W/m℃
Tr
=130 ℃
備考 この実例に用いるC-mould(2)シミュレーションソフトウェアでは,Ts及びTejの代わりに転移温
度Trが,必要である。
ISO/DIS 11443に従って溶融せん断粘度データを測定し,また材料の粘度は,クロス/アレニウスモデ
ルで表す。
簡単な金型充てん解析は,C-mould(2)シミュレーションソフトウェアを用いて行う。見掛粘度データを
用いるのに対応し,修正なし,ラビノビッチ(Rabinowitsch)修正だけ(非ニュートン流体挙動の修正),
及びラビノビッチ及びバーグレィ(Rabinowitsch/Bagley)修正(接合損失のために)の三つのケースを考
える。
粘度データに対するクロス/アレニウスモデルの係数は,次による;
ケースi 見かけ粘度データ n =0.251 22
τ*
=51 845 Pa
B
=0.012 998 Pa・s
Tb
=5 498.5 K
β
=0 Pa-1
ケースii ラビノビッチ修正あり n=0.252 08
τ*だけ =43 216 Pa
B
=0.014 934 Pa・s
Tb
=5 396.3 K
β
=0 Pa-1
ケースiii ラビノビッチ及びバーグレィ修正あり n=0.226 98
τ*修正 =45 319 Pa
B
=0.009 970 8 Pa・s
Tb
=5 549.7 K
β
=0 Pa-1
三つのケースに対する,異なる温度での“粘度―せん断速度”データを図B.3に示す。
充てん段階のシミュレーションには,次のような加工条件を用いる。
− 溶融温度 :240 ℃
− 金型温度 :30 ℃
− 充てん時間:4 s
54
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
相対的な射出速度プロフィールは,充てん中一定に保ち,充てん/保圧切り替えは,97 %容量に設定した。
一連のショートショット実験の溶融先端部の進み具合の観察結果となんの修正もなし(ケースiに相当)
に数値的シミュレーションした結果との比較を図B.4に示すが,この比較は,溶融先端の描写に関して,
数値的シミュレーションと実験との間には,よい相関があることを証明している。
三つのケースの圧力分布への修正の影響を,図B.5から図B.7に示す。最大射出圧力(これは,最終部
品の外観及び機械的品質はもちろん,成形機の大きさの決定にも重要な因子である)に関する差は,注意
に値する。ケースi(修正なし)とケースiii(完全な修正あり)との間で観察される最大射出圧力の17 %
の差は,成形シミュレーションの最終結果及び結果的に最終部品の特性の予測に関して,明らかに粘度デ
ータの修正を考慮することの重要性を実証している。
B.2.2 熱可塑性プラスチックの金型充てん,保圧及び冷却の高度な解析の実例 熱可塑性プラスチックの
金型充てん,保圧及び冷却の高度な解析への材料データの活用は,自動車のロッカーカバー(エンジンの
カムカバー)(図B.8参照)で例示する。部品の大きさは,総容量953.5 cm3に相当する。部品の寸法は,
500 mm×250 mm×100 mmであり,全体的厚さは3.0 mmで,一方局部的厚さは,1.5 mm(リブ部)〜2.5 mm
(フランジ部)の間にある。
金型充てんの高度なシミュレーション解析の場合,シミュレーションソフトウェアとしてMoldflow(1)
のMF/flowモジュールを選定する。ロッカーカバー用の選定材料は,ミンロン[Minlon(3)]EFE6053で,
ガラス繊維24 %及び無機フィラー16 %入りのPA 66の銘柄である。金型充てん,保圧及び冷却の高度な解
析に必要な材料の入力データ(本体表6参照)は,次による。
cpm=2 554 J/kg℃
km=0.271 4 W/m℃
備考 高度な充てん解析に入力するcp及びkは,一般的に温度の関数(本体の表6参照)としての値
を必要とするが,簡略化し,溶融状態に相当する単一の値をこの実例では用いる。
Ts=235 ℃
Tej=203 ℃
注(3) Minlon®は,デュポン(DuPont)によって供給される製品の商標である。この情報は,この規
格利用者の便宜のために与えられるものであって,JISがこの商品を推奨するものではない。
ISO/DIS 11443によって溶融せん断粘度データを測定し,材料粘度を表すために,二次モデルを選択す
る。この材料の二次粘度マトリックス入力値は,次による。
温度(℃)
せん断速度(1/s) 粘度(Pa・s)
275
1 000
285.6
295
100
279.8
295
1 000
147.6
295
10 000
48.3
315
100
130.2
315
1 000
76.8
保圧段階の溶融樹脂の圧縮性を説明するために必要なpvTデータを得るために,13個の標準データ点入
力値を次に示す。
55
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
温度(℃)
圧力(MPa)
比容積(m3/kg)
0.0
0
0.000 667 25
0.0
160
0.000 654 27
20.0
0
0.000 671 84
20.0
160
0.000 656 71
245.2
0
0.000 733 82
252.1
80
0.000 713 06
256.3
160
0.000 697 84
261.0
0
0.000 759 58
269.9
160
0.000 715 00
270.0
0
0.000 762 97
270.0
160
0.000 715 01
310.0
0
0.000 778 03
310.0
160
0.000 724 09
シミュレーションに用いる加工条件は,次による。
溶融温度:295 ℃
金型温度:90 ℃
射出時間:2.5 s
流量 :377 cm3/s
82 容量%充てん時,射出圧力は,100 MPaに達する。この段階で,射出圧力を一定に保つ,その結果と
して,3.0秒後100容量%充てん時に流動速度は,32.5 %減少する。
直径2.0 mm及び長さ2.0 mmの各々同じ寸法の二つのゲートをもつ,等距離ランナー系での充てん解析
の結果を,図B.9〜図B.12に示す。ランナー及びゲート間での初期圧力降下は,20 MPaと計算された。せ
ん断発熱によって,流動最前部の温度は,295 ℃(溶融温度)から302.8 ℃(図B.11も参照)まで上昇し,
ほぼ8 ℃の温度上昇である。したがって,遅い射出速度を用いることは,明白な選択のように見えるが,
その場合,固化層厚さの量は,射出時間3.0秒で得られる72 %よりもずっと多く増加するだろう(図B.12
参照)。そして,固化層が最も大きくなるため,その空間部分の充てんは,困難になるはずである。
保圧解析では,保圧は,充てん終了時の100 MPaから4秒間で60 MPaまで直線的に低下した,次の1 秒
間で0 MPaとなり,全保圧時間は,5 秒であった。図B.13及び図B.14に計算結果を示す。保圧時間5 秒
間でのモデル要素の各圧力分布を図B.13に示し,一方,図B.14に保圧終了時の固化層厚さの量を%で示
す。厚いいくつかの部分には,その中央層に依然として溶融材料があるが,およそのカバー部は,ほぼ完
全に固化しているので,5秒後に更に保圧する意味がないことは,明白である。このような結果は,保圧
を解除する時を求めるのに有効である。
冷却解析は,保圧時間5秒,冷却時間25秒及び型開き時間5秒と仮定した充てん解析の結果に基づいて
いる。この部品のために設計した,直径10 mmの三つの冷却回路を,図B.8に示す。冷却回路は,P20鋼
又は類似の熱伝導率の材料によるキャビティの内部に配置されると仮定する。各々の回路の水の流量は,
10 L/min,入口温度は80 ℃,この場合,推定平均キャビティ温度は,90 ℃と見込まれる。要素の中央層
に近い部分の最大温度を,図B.15に示す。12 mm及び8 mm厚さのランナーは,明らかに最高温度である
ことが見ることができる。冷却25 秒後,カバー中の最高温度は,カバーの四つの孔の5 mm厚さの輪部
で,依然として約220 ℃である。成形品突出しピンの位置にもよるが,突出し力によるカバーの過度の変
56
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
形を避けるために,長めの冷却時間が妥当かもしれない。冷却時間25秒後の厚さ全体の平均温度を,図
B.16に,またモデル要素の表面と裏面との間の温度差を,図B.17に示す。図B.17の中で,赤い部分は,
表面温度が,より高温,また青い部分は,裏面温度が,より高温である。これらの部分をよく冷却するこ
とは,サイクルタイムの短縮のみならず,突出し時の温度がより均一になるためにそりが少なくなる結果
となる。
B.2.3 熱可塑性プラスチックの収縮/反り解析の実例 Moldflow(1)シミュレーションソフトウェアの収
縮/反り解析モジュールのMF/shrink及びMF/warpを用いて,B.2.2に示したのと同じ自動車ロッカーカバ
ーで,収縮/反り解析への材料データの活用を例示する。
MF/shrinkモジュールは,溶融温度,金型温度,射出速度及び保圧時のキャビティ圧力のようなキーとな
る成形変数四十個の組合せを含んだ計画実験で,Moldflow(1)が,測定した収縮係数を用いる。測定した収
縮値から,金型内の溶融樹脂の冷却のように,材料の収縮に影響する各主要因子からの寄与を考慮する関
係を用いて,収縮係数を求める。
SMp=a1M(SpvT)+a2M(結晶化)+a3M(金型拘束)+a4M(配向)+a5
SMn=b1M(SpvT)+b2M(結晶化)+b3M(金型拘束)+b4M(配向)+b5
ここに,
SMp: 材料の配向方向に平行な収縮成分
SMn: 材料の配向方向に垂直な収縮成分
SpvT: 材料のpvT特性に起因する体積収縮
Mi : ( )内に示す因子による収縮を表す係数
ai : 収縮モデルに平行な収縮係数
bi : 収縮モデルに垂直な収縮係数
この実証に用いる材料Minlon (3) EFE6053(ガラス繊維24 %及び無機フィラー16 %入りのPA 66銘柄)
での,収縮/反り解析(本体の表8参照)用の材料入力データは,次による。
Ep
=8 250 MPa
En
=6 000 MPa
νpn
=0.35
νnt
=0.48(Ep,En及びνpn値からソフトウェアによる計算値)
Gp
=2 472 MPa(Ep,En及びνpn値からソフトウェアによる計算値)
a5
=0.003 4(SMp=0.34 %に対応する)
b5
=0.011(SMn=1.1 %に対応する)
高充てん材料のように配向の収縮に与える影響が,他の係数と比べて,著しく大きいことを考慮して,
溶融樹脂が固化するまでの圧力及び温度変化による体積変化,結晶化又は金型拘束に関連する他のすべて
の収縮係数を,0.0に設定する。さらに,離型時にキャビティは,均一な表面温度であると仮定する。
変形を計算する参照面の定義として(変形ゼロ,境界条件),次のような拘束条件を設定した。
− X軸変形(すなわち,長手方向の収縮),ゲートに近くの,長手の端のコーナに一点
− Y軸変形(すなわち,幅方向の収縮),長手の端のコーナに二点
− Z軸変形(すなわち,天面の反り),長手の端及びゲートの短面辺のコーナに三点
収縮/反り解析の結果を,図B.18及び図B.19に示す。図B.18では,ロッカーカバー長手の端までの計
算した収縮は,材料の流れ方向の収縮特性(SMp)0.34 %なのに対し,0.46 %であることを示している。図
B.19では,計算したそり変位は,3.2 mmである結果となっている(固定の三つのコーナに対するコーナ4
の変位)。
57
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.3 押出成形工程のシミュレーション ここでの実例は,シート押出しで通常用いられるコートハンガー
ダイ及び異形押出しで用いる異型ダイの二つの異なるタイプのダイ中の樹脂溶融流動のシミュレーション
に,関連材料データを用いて,実証することを意図している。
B.3.1 押出機中の樹脂の溶融解析の実証 シート,フィルム又は異型などの押出形状自身には関係なく,
第一段階は,押出機の中での樹脂の溶融解析である。その解析には,次の三段階がある。
a) 等温熱移動を伴うドラグ誘導樹脂固体輸送
b) 樹脂の溶融
c) 均一溶融体の等温非圧縮流動
押出機中の樹脂溶融解析の実例のため,はん用形状の90 mm径スクリュー(三つのゾーン及び単軸一定
フライトからなるL/Dが24のスクリュー)及び同径の滑らかなバレルをもつ押出機を選定する。材料は,
PE-LD樹脂を選定する。材料投入温度は,30 ℃に,また,回転速度は,80 min−1(rpm) に設定する。シミ
ュレーションには,EXTRUCAD(4)3.0ソフトウェアを用いる。
解析に必要な材料の入力データ(本体の表9参照)は,次による。
Tm
=110 ℃
ΔHf
=129 785 J/kg
ρb
=595 kg/m3
ρs
=919 kg/m3
ρm
=775 kg/m3
Cpm
=2 600 J/kg℃
Cps
=2 595 J/kg℃
km
=0.18 W/m℃
μb
=0.3(滑らかなバレルを仮定)
μs
=0.25(滑らかなスクリュー表面を仮定)
備考 動的摩擦係数μb及びμsは,通常測定困難である。バレル及びスクリューの表面粗さは,しばし
ば,これらのパラメータの値として考える。μbの値は,慣例として,滑らかなバレルに対して
0.3を,粗いバレルに対して0.45を,また溝付バレルに対して1.00を用いる。同様に,滑らかな
スクリュー表面に対して0.25を,また腐食したスクリュー表面に対して0.35をμsの規定値とし
て用いる。
注(4) EXTRUCADは,PolyDynamicsによって供給される製品の商標である。この情報は,この規格
の利用者の便宜のために記載するものであって,JISがこの商品を推奨するものではない。同
じ結果になることが示せれば,これと同等の他のものを用いてもよい。
溶融せん断粘度η(T,γ&)をカロモデル(伸長流動の寄与を考慮していない。)によって表す。このPE-LD
樹脂用のカロの係数は,次による。
A
=6 500 Pa.s
b
=0.018 1 /℃
r
=1 s
a
=2
n
=0.48
Tr
=180 ℃
58
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
流動解析には,与えた質量流量に対する押出機長さに沿った,内部温度,圧力及びせん断応力の分布,
並びにバレルと材料との間の可塑化エネルギーを評価することができる有限差分法計算が含まれる。図
B.20は,スクリュー長に沿って計算した内部温度を例示する。一方,スクリュー長に沿った平均圧力及び
せん断応力分布を,図B.21及び図B.22にそれぞれ示す。バレルと材料間の計算総可塑化エネルギーの分
布を,図B.23に示す。
B.3.2 シート押出工程解析の実例−コートハンガーダイ中の溶融樹脂流動シミュレーション シート押
出工程の解析は,前記のB.3.1で用いたPE-LD材料によって例示する。押出機中の溶融樹脂解析は,B.3.1
に示したものと同じである。ダイの中の樹脂の溶融流動シミュレーションのために,コートハンガーダイ
をこの解析に用いる。このシミュレーションでは,FLATCAD(5)3.0ソフトウェアを選定する。
ダイ内の有限差分法計算は,与えた質量流量に対するダイ中の内部温度,圧力及び平均滞留時間の分布
の評価を可能とする。その結果を図B.24〜図B.26に示す。
注(5) FLATCAD及びPROFILECADはPolyDynamicsによって供給される製品の商標である。この情
報は,この規格の利用者の便宜のために記載するものであって,JISがこの商品を推奨するも
のではない。同じ結果になることが示せれば,これと同等の他のものを用いてもよい。
B.3.3 異型押出工程解析の実例−異型ダイ中の溶融樹脂流動シミュレーション 異型押出し工程の解析
を,PROFILECAD (5) 3.0ソフトウェアを用い,単純なT型異型ダイで例示する。はん用形状の90 mm径
スクリュー(三つのゾーン及び単軸一定フライトからなるL/Dが24のスクリュー)及び同径の滑らかな
バレルをもつ押出機を選定する。選定材料は,PVC樹脂である。材料投入温度は30 ℃に,またスクリュ
ー回転速度は100 min-1(rpm) に設定する。押出機中の溶融樹脂流動解析に必要な材料入力データ(本体の
表9参照)は,次による。
Tm
=190 ℃
ΔHf
=0 J/kg (非晶性材料)
ρb
=530 kg/m3
ρs
=1 340 kg/m3
ρm
=1 050 kg/m3
Cpm
=2 200 J/kg℃
Cps
=2 320 J/kg℃
km
=0.182 W/m℃
μb
=0.3(滑らかなバレルを仮定)
μs
=0.25(滑らかなスクリュー表面を仮定)
備考 バレル及びスクリューの表面粗さは,しばしば,これらのパラメータの値として考える。μbの値
は,慣例として,滑らかなバレルに対して0.3を,粗いバレルに対して0.45を,また溝付バレル
に対して1.00を用いる。同様に,滑らかなスクリュー表面に対して0.25を,また腐食したスクリ
ュー表面に対して0.35をμsの規定値として用いる。
PVCに対数多項式粘度モデルを用い,モデルの係数の入力データは,次による。
59
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a1
=11.784
a2
=−0.639 1
a3
=−1.127 44 E-02
a4
=−1.834 49 E-02 ℃-1
a5
=8.784 48 E-06 ℃-2
a6
=9.665 12 E-04 ℃-1
Tr
=0 ℃
溶融樹脂解析は,既にB.3.1に示しているので,ここでは,異型ダイの中の樹脂の溶融シミュレーショ
ンだけを例示する。有限差分法計算は,与えた質量流量に対するダイ中の全応力,せん断速度及び粘度の
分布の評価を可能にする。計算の結果を図B.27〜図B.29に示す。
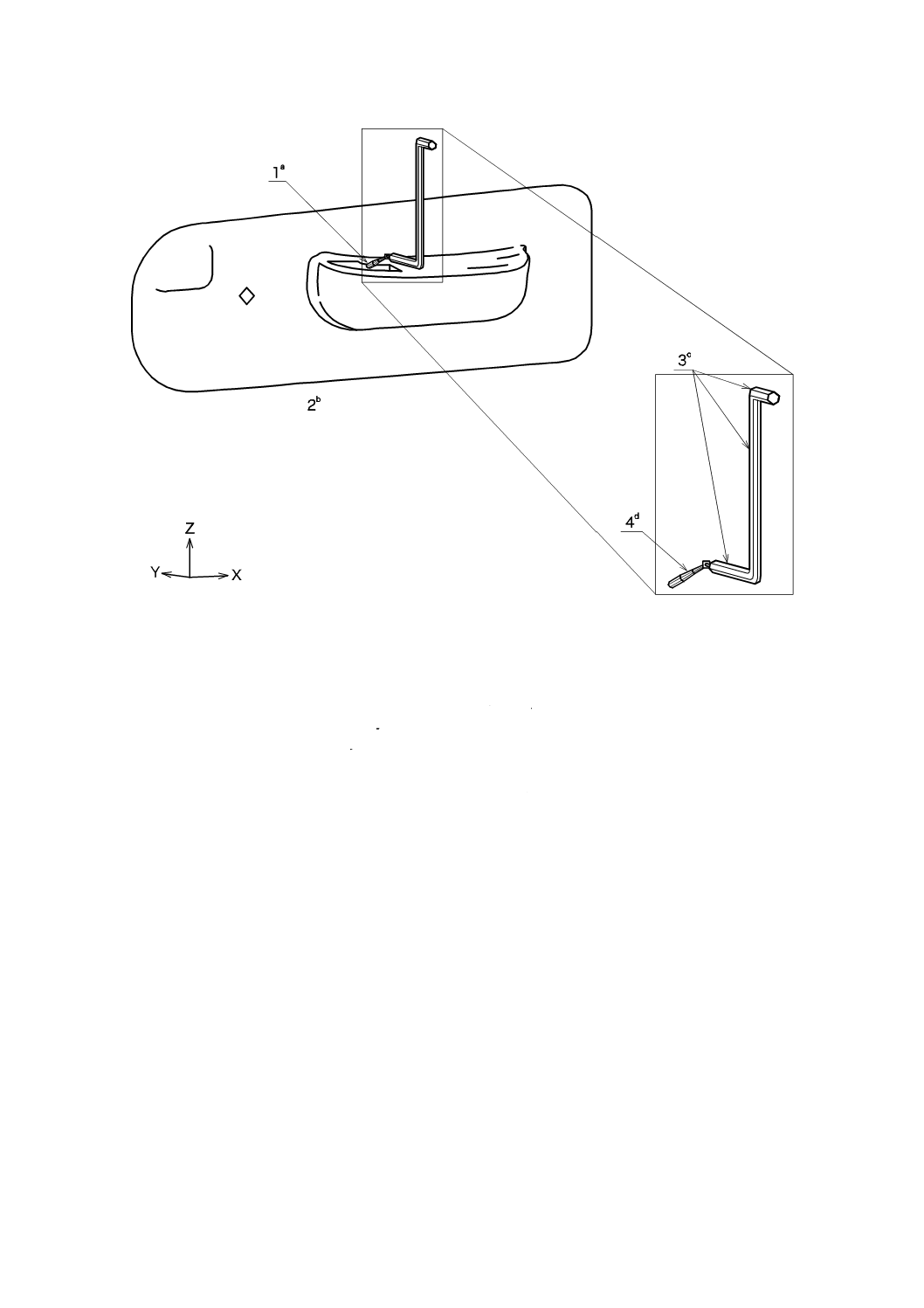
60
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1: ファンゲート
2: 基部
3: ホットランナ
4: スプルー
a: 入口厚さ=4 mm,出口厚さ=1.5 mm
b: 厚さ=2.25 mm
c: 径=16 mm
d: 径=5〜10 mm
図B.1 自動車ドアパネルの配置及びランナーシステム
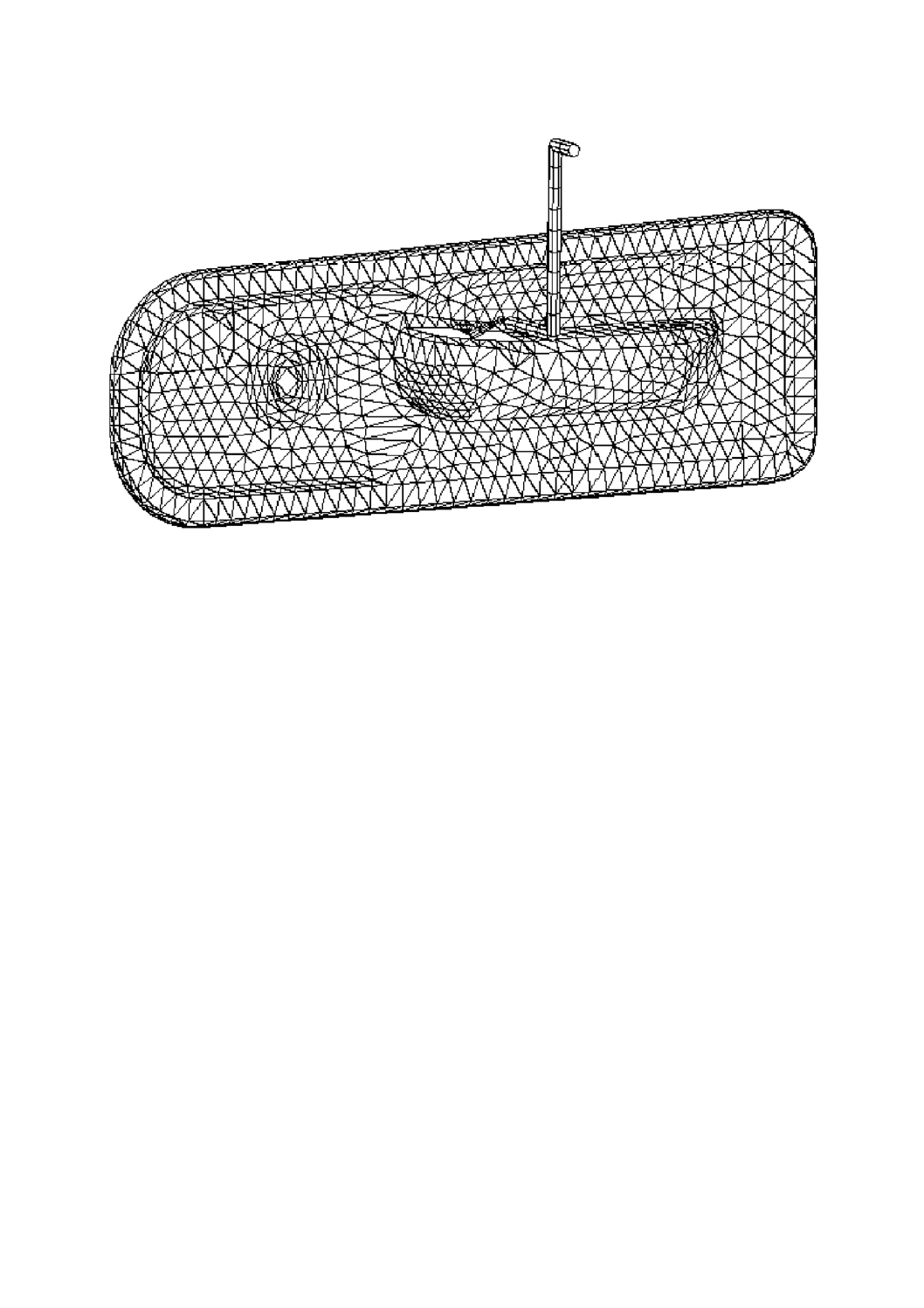
61
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.2 金型充てん簡易解析に用いる自動車ドアパネルの有限要素メッシュ
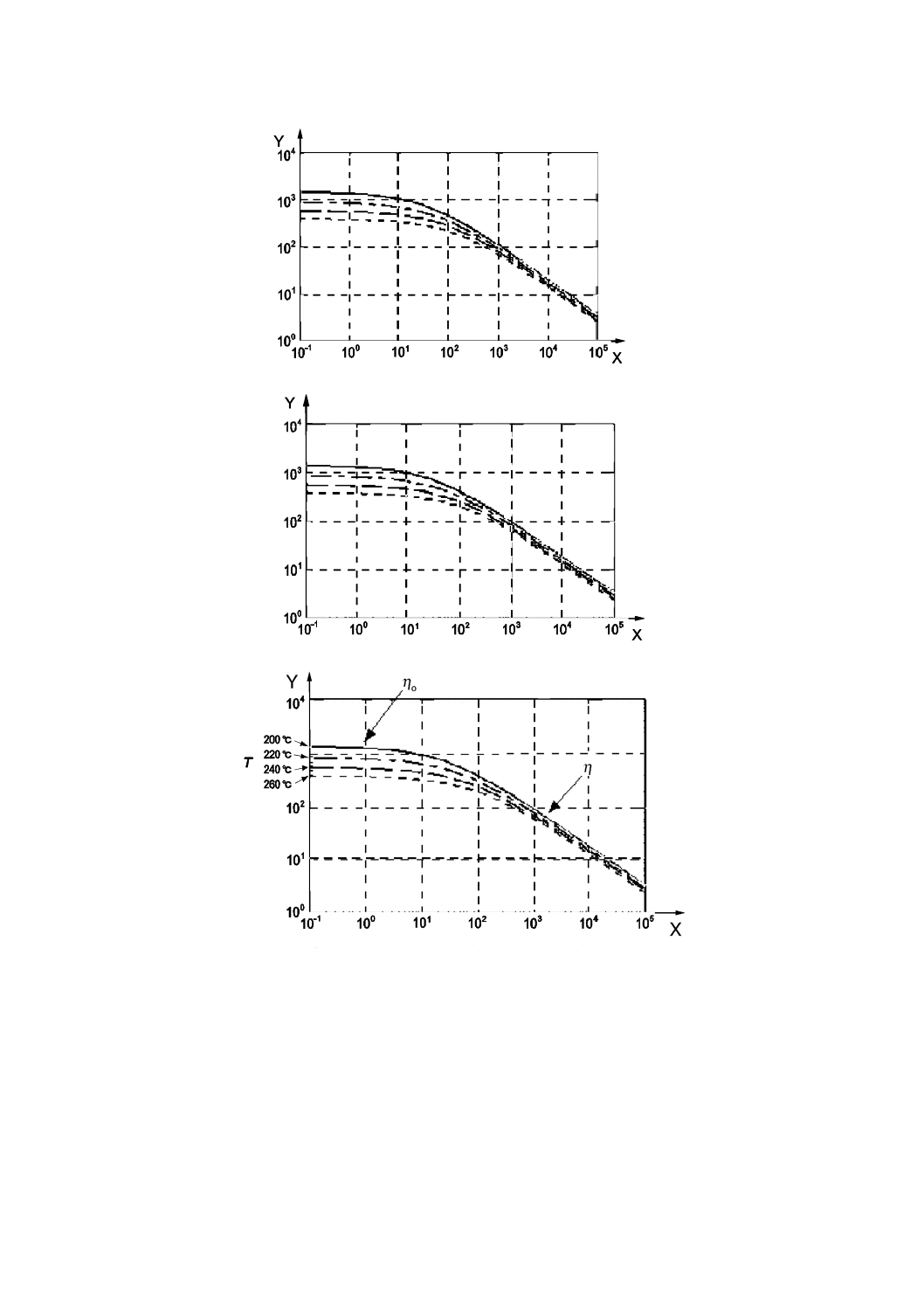
62
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 見掛粘度
b) 補正粘度−ラビノビッチ
c) 補正粘度−ラビノビッチ及びバーグレィ
X: せん断速度,1/s
Y: 粘度,Pa・s
T: 溶融温度,℃
ηo: ゼロせん断粘度(ニュートン流体についての数値)
η: せん断速度依存パラメータ(直線部の傾斜から求める)
図B.3 三つのケースの異なる温度における粘度−せん断速度データの代表例
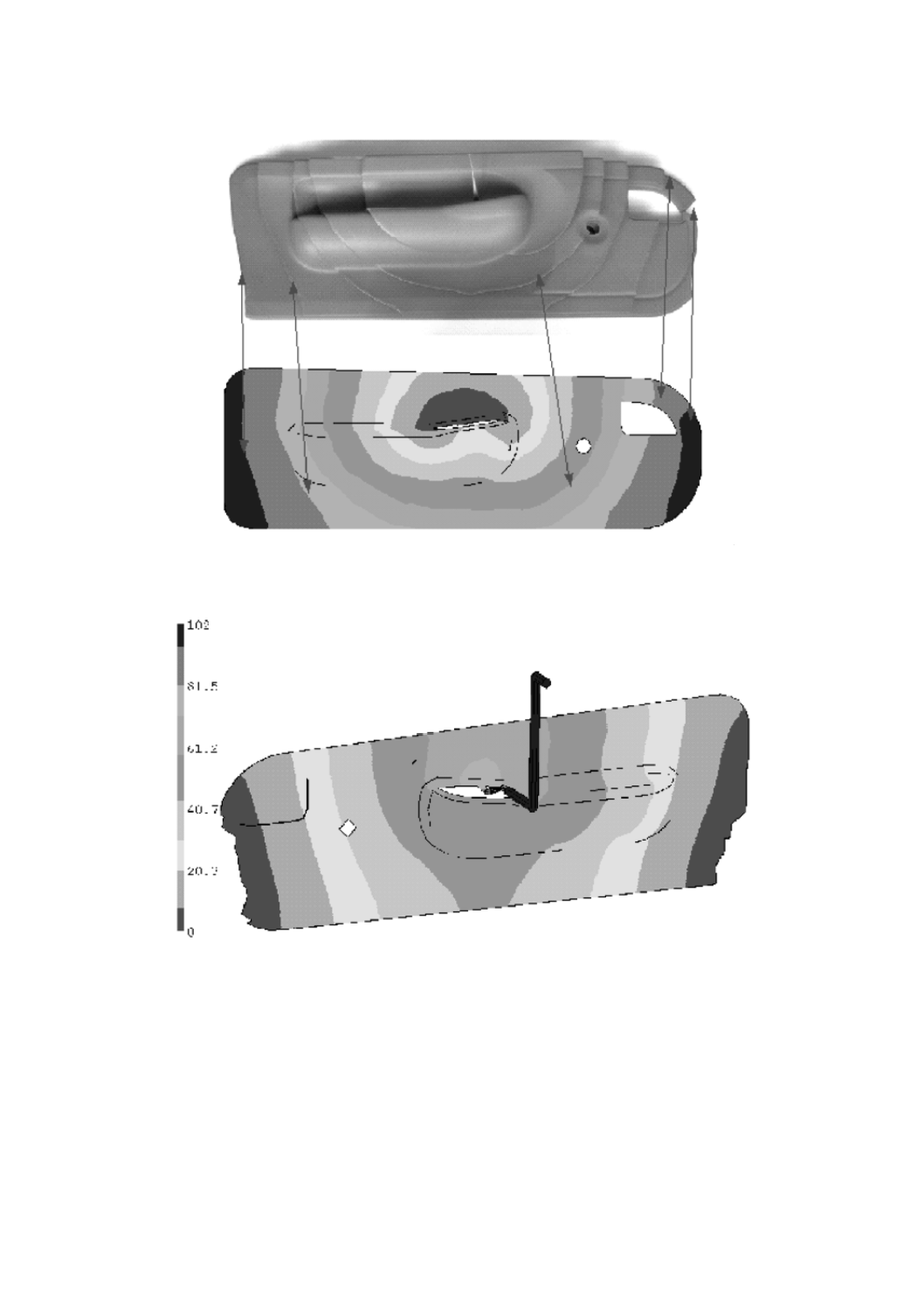
63
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.4 実験室的なショートショット成形品と溶融樹脂最前部の進み具合の数値計算した
シミュレーション結果との比較
見掛粘度;Pmax=105 MPa
図B.5 ケースⅰ(見掛粘度を使用)における充てん末期段階の圧力分布
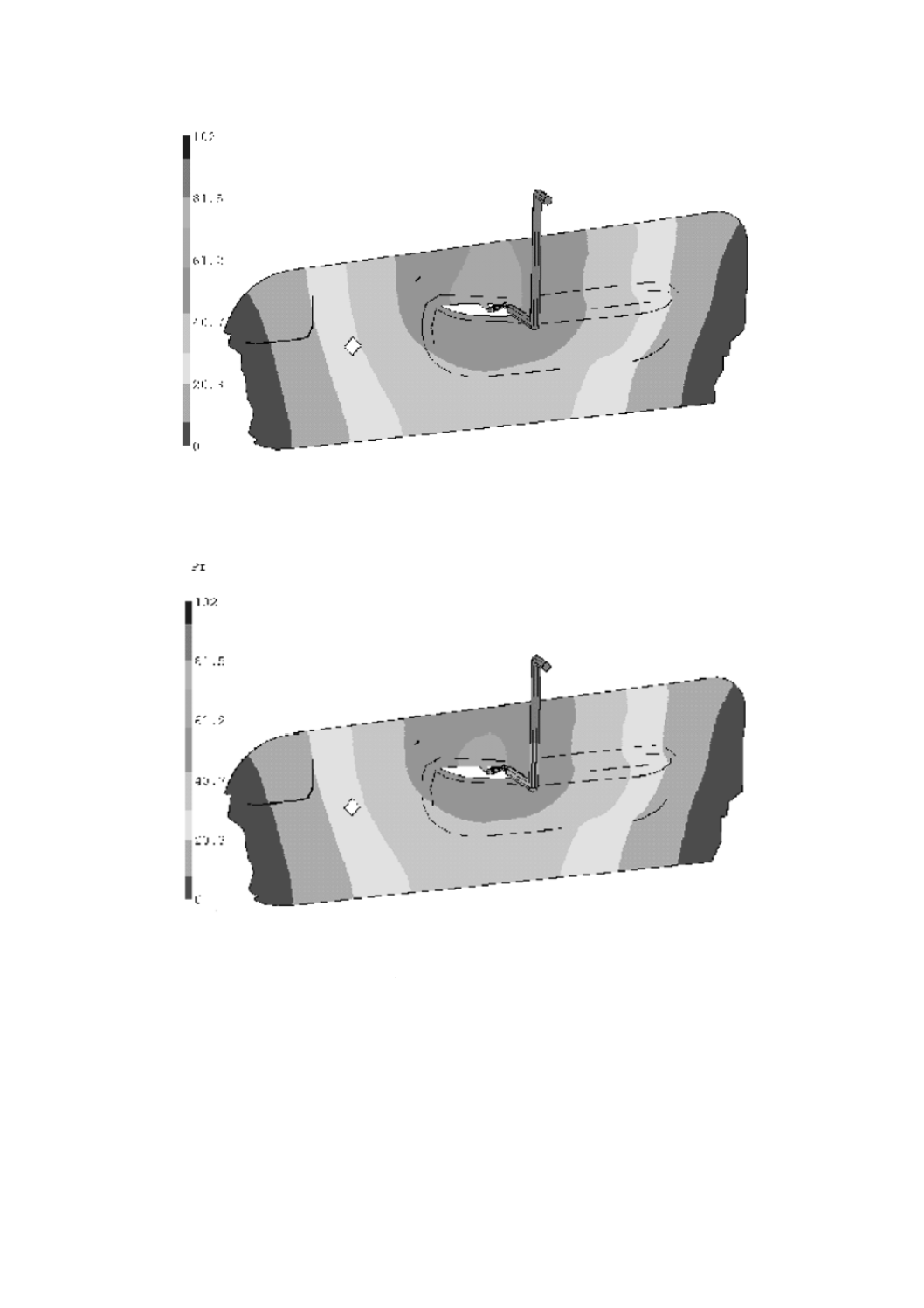
64
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
修正粘度−レビノビッチ;Pmax=93 MPa(−11 %)
図B.6 ケースⅱ(レビノビッチ修正の補正粘度を使用)における充てん末期段階の圧力分布
補正粘度(レビノビッチ−バーグレィ);Pmax=87 MPa(−17 %)
図B.7 ケースⅲ(レビノビッチ−バーグレィの補正粘度を使用)における充てん末期段階の圧力分布
65
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.8 ロッカーカバーモデルの有限要素メッシュ及び冷却ラインの図
図B.9 計算した溶融樹脂最前部の位置

66
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.10 充てん末期(すなわち保圧開始時)の圧力分布
図B.11 ロッカーカバーの溶融樹脂流動最前部の計算温度
67
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.12 充てん末期の固化層の計算厚さ(%)
図B.13 保圧中の計算(最大)圧力

68
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.14 保圧末期(保圧5秒後)における固化層の計算厚さ(%)
図B.15 冷却25秒後の厚さ方向の計算最大温度
69
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.16 冷却25秒後の厚さ方向の計算平均温度図
図B.17 冷却25秒後の表面と裏面の計算温度差
70
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.18 ロッカーカバーのX軸方向の計算変形
図B.19 ロッカーカバーのZ軸方向(反り)計算変形
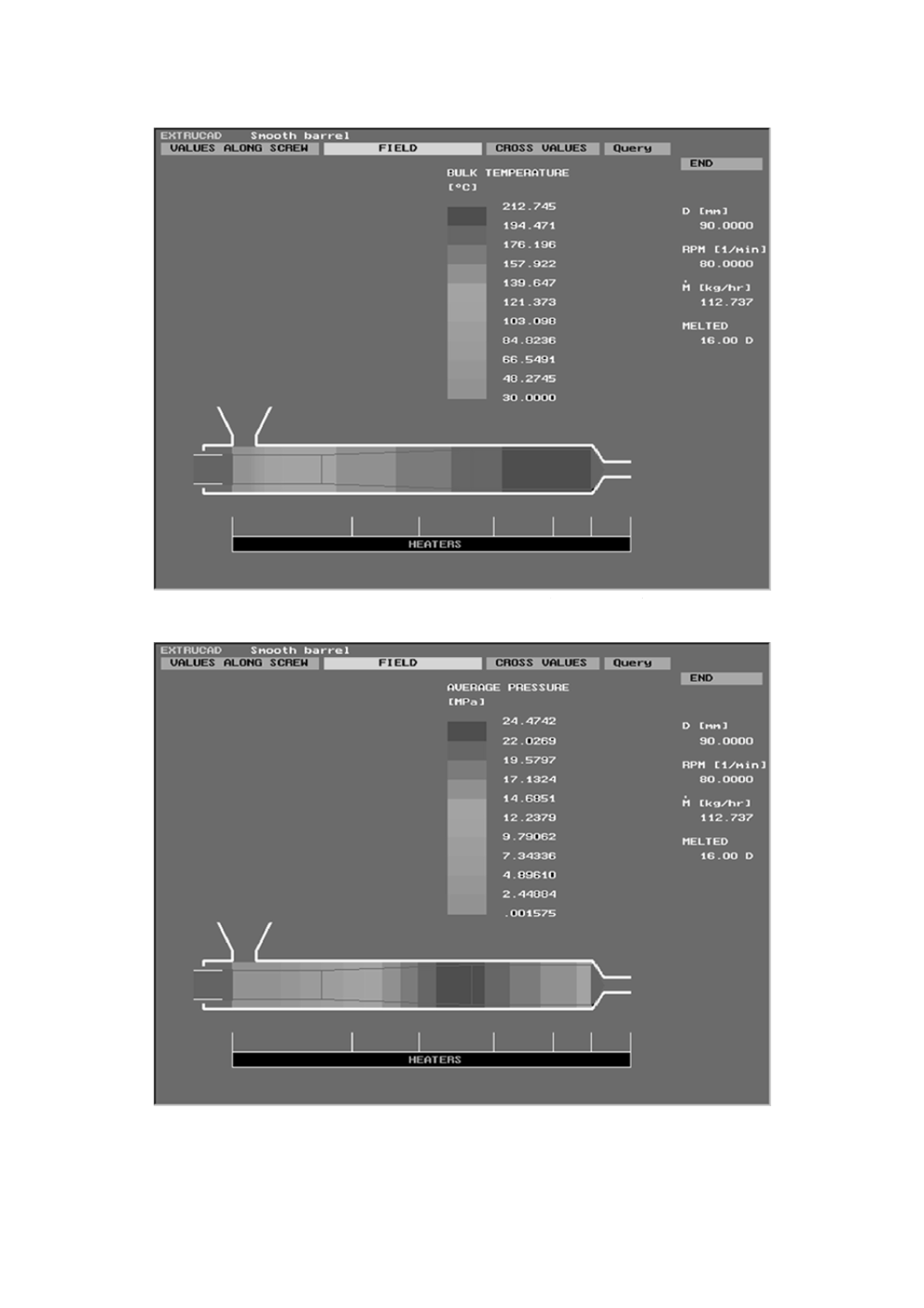
71
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.20 スクリューの長さに沿った計算内部温度分布
図B.21 スクリューの長さに沿った計算平均圧力分布
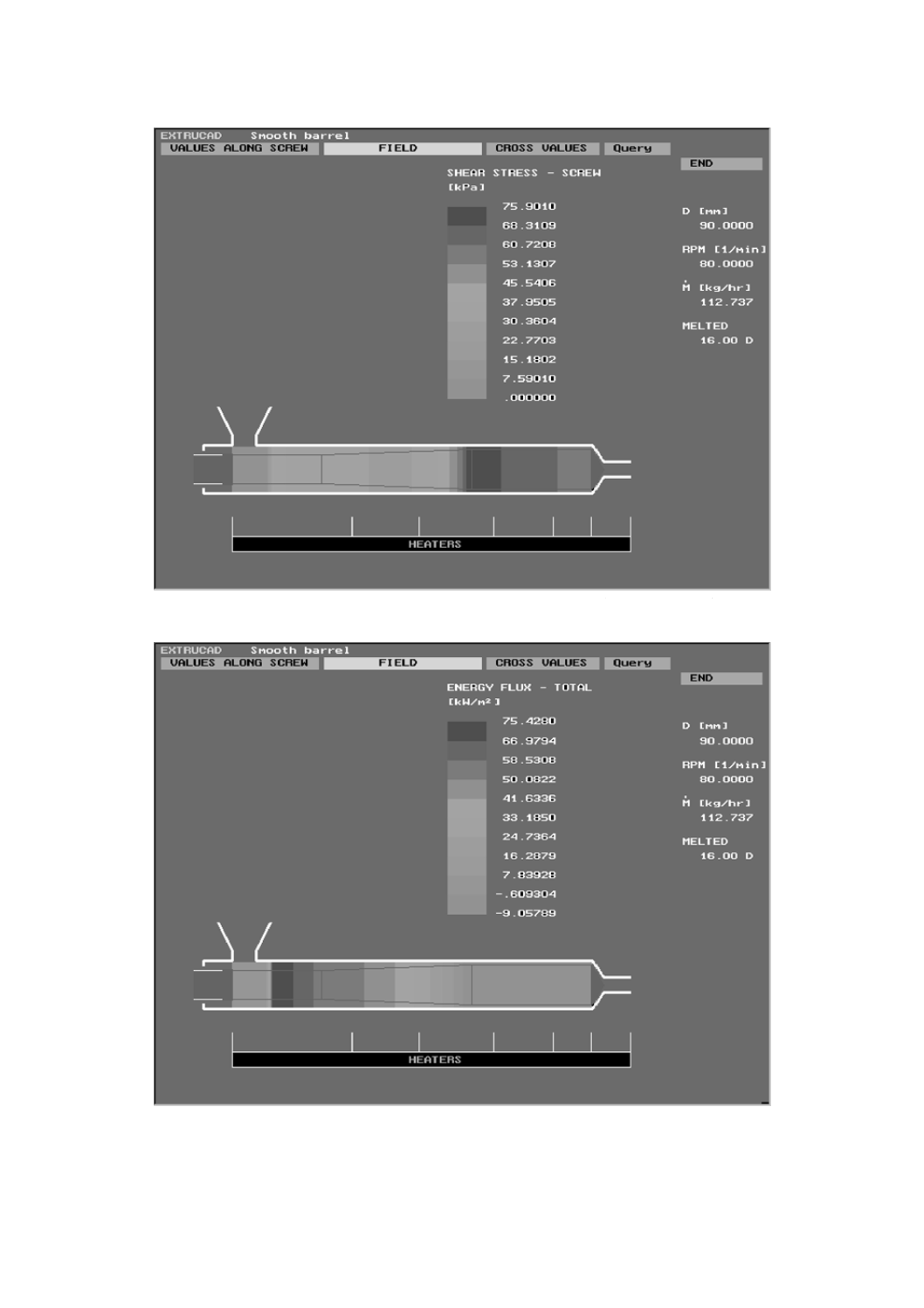
72
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.22 スクリューの長さに沿ったスクリュー表面の計算せん断応力分布
図B.23 スクリューの長さ方向に沿ったバレルと材料間の計算可塑化エネルギー分布
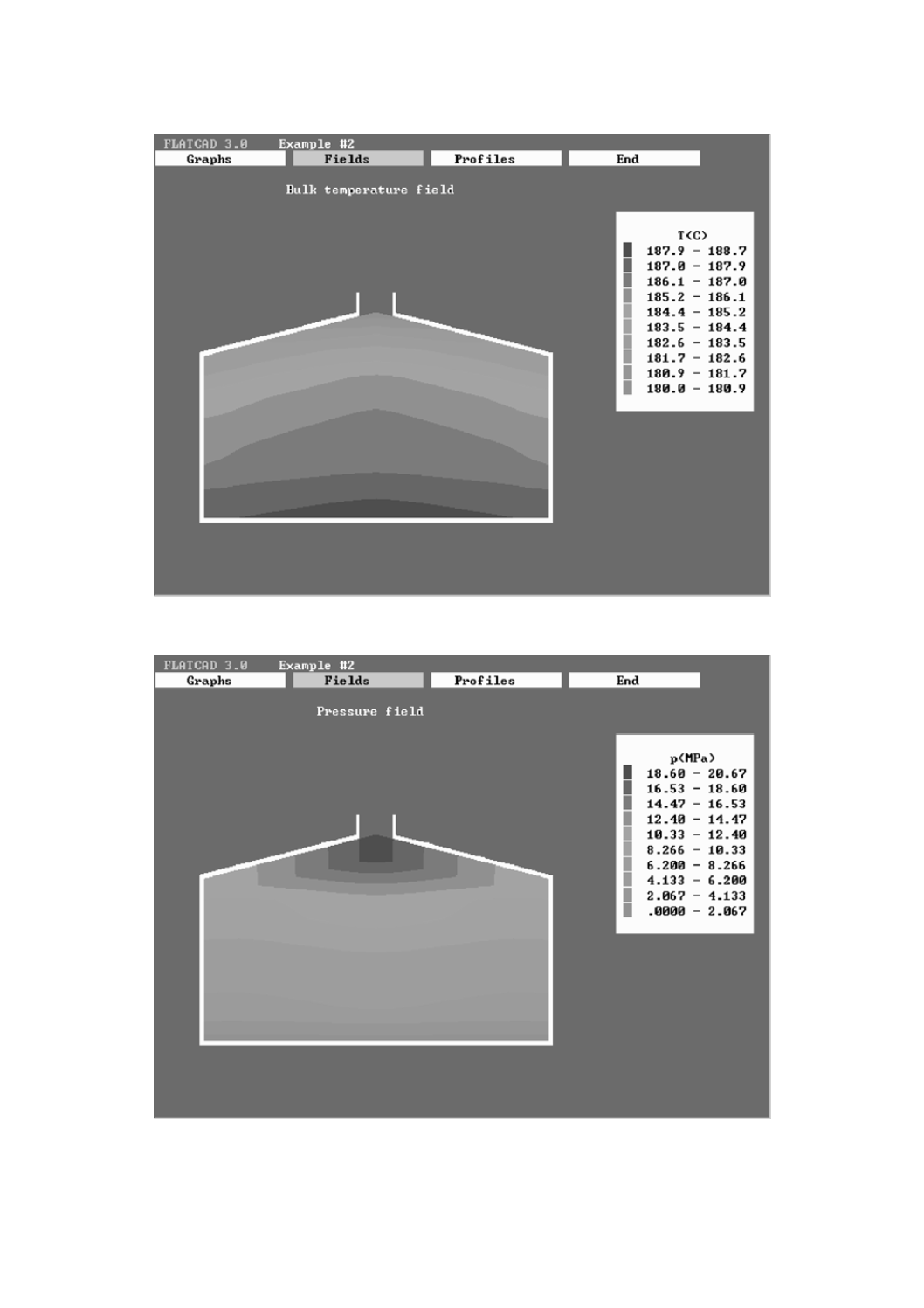
73
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.24 コートハンガーダイの計算内部温度分布
図B.25 コートハンガーダイ内部の計算圧力分布

74
K 7170:2008 (ISO 17282:2004)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.26 コートハンガーダイ内部の計算平均滞留時間分布
図B.27 異型押出しダイ内部の計算総応力分布

75
K 7170:2008 (ISO 17282:2004)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.28 異型押出しダイ内部の計算せん断速度分布
図B.29 異型押出しダイ内部の計算速度分布