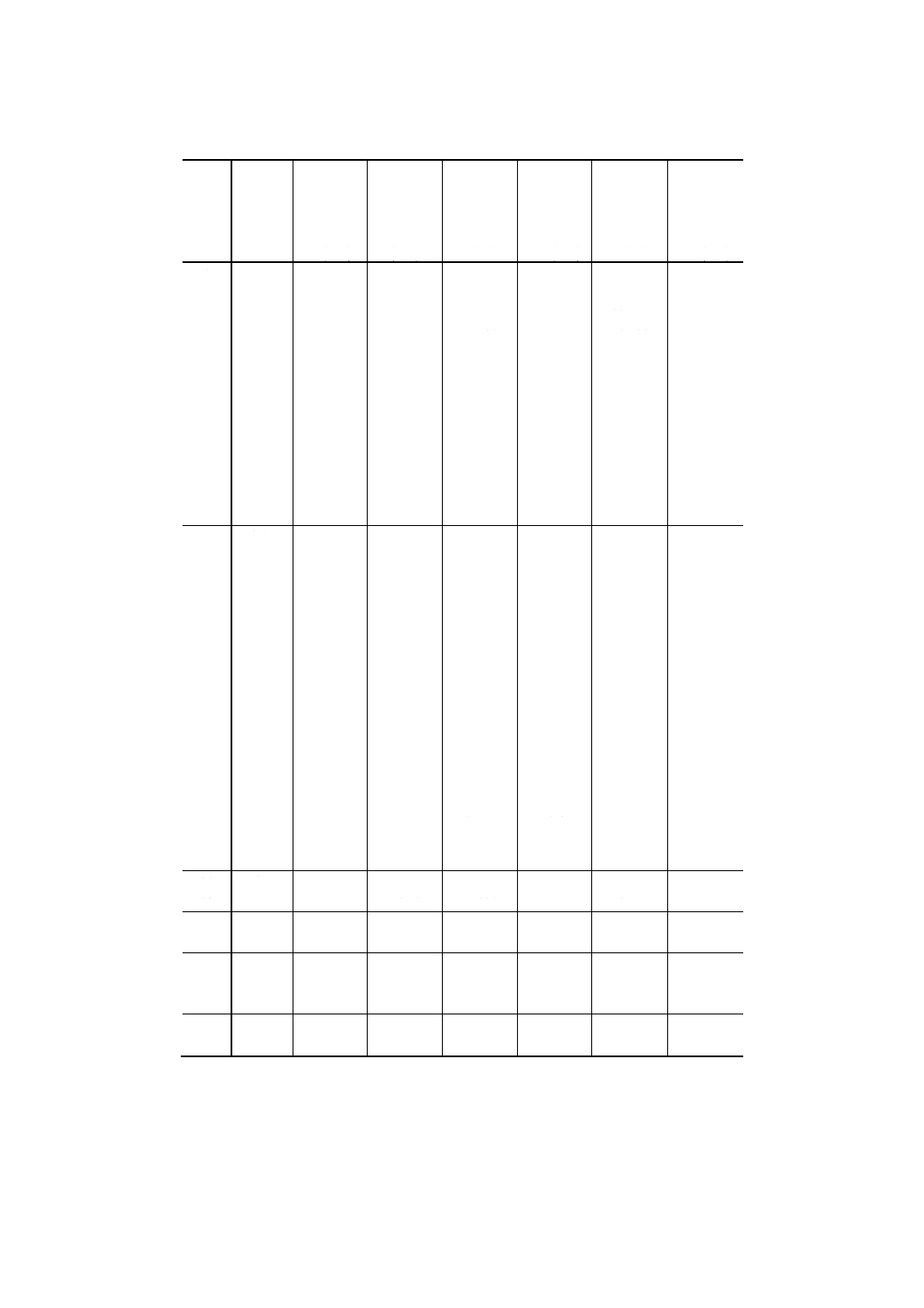2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 7109-1986
プラスチックの寸法許容差の決め方
General Tolerancing Rules for Plastics Dimensions
1. 適用範囲 この規格は,プラスチックの合理的な寸法許容差を定める方法の,一般的な事項について
規定する。
2. 用語の意味及び記号 この規格で用いる主な用語の意味及び記号は,次のとおりとする。
(1) プラスチック 高分子物質を主原料として人工的に有用に形作った固体。ただし,繊維・ゴム・塗料・
接着剤などを除外する。
(2) 基準値 (m) 組立者が図面に示したプラスチックの基準の寸法。
(3) 許容差 (⊿) 基準値と規定された限界値との差。
(4) 生産者 プラスチックを製造する者。
(5) 組立者 プラスチックを使った製品を製造する者。
(6) 使用者 組立者の製品を使う者。
(7) 許容限界値 (⊿0) プラスチックの寸法が基準値と異なって使用者又は組立者の段階で不具合を生じ
る場合に寸法に許容される限界値と基準値との差。
(8) 平均損失 (A0) 寸法が許容限界値を超えたときに発生する損失の平均。
(9) 生産者側の損失 (A) 組立者が生産者から購入する場合の価格(購入原価の推定値)。
(10) 比例定数 (k) 経済的損失を表す定数。平均損失A0を許容限界値⊿0の2乗で除した値。
2
0
0
⊿
A
k=
(11) 選定許容限界値(1) (⊿0) 使用者と組立者の比例定数kのうち大きいほうのkの許容限界値。
(12) 選定平均損失(2) (A0) 使用者と組立者の比例定数kのうち大きいほうのkの平均損失。
注(1) 許容限界値と記号が同じであるが,使い方で区別する。
(2) 平均損失と記号が同じであるが,使い方で区別する。
3. 許容差の求め方
3.1
選定許容限界値⊿0及び選定平均損失A0の求め方 次の手順によって求める。
(1) 使用者の段階における許容限界値⊿0及び平均損失A0を推定する。
(2) 組立者の段階における許容限界値⊿0及び平均損失A0を推定する。
(3) (1)及び(2)の比例定数kを求める。
(4) 二つのkの値を比較し,kの値の大きいほうの許容限界値⊿0及び平均損失A0を選択する。
備考 1. 許容限界値⊿0及び平均損失A0は,おおよその値でもかまわない場合が多い。
2. 許容限界値⊿0及び平均損失A0が寸法のプラス側とマイナス側で異なるときは両側で別々に
2
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
求める。この場合kが大きいほうだけを用いて,プラス側,マイナス側とも同じように損失
を求めてもよい。
例:音響製品に使用しているプラスチック部品の例
(1) 部品の寸法と基準値との差が0.15mmを超えたとき,音のひずみのため使用者の半数が製品
を修理すると仮定し,使用者段階における許容限界値⊿0を0.15mmと推定する。
この製品の修理料を3 000円,使用者が修理のため店頭に搬入,搬出するための時間を1
時間として,使用者の段階での時間損失を3 000円(この値は,それぞれの場合に応じて算
出する。)とすれば,使用者段階における平均損失A0は
)
(
000
6
000
3
000
3
0
円
=
+
=
A
と推定される。
(2) 組立て段階において,プラスチック部品の寸法と基準値との差が0.07mmを超えると,組立
てができないか又は製品としての性能が得られないとすれば,組立者の段階における許容限
界値⊿0は0.07mmと推定される。
組立者の段階において,組み立てた後で不良品が発見された場合,部品代として200円(購
入原価),手直しに要する時間を5分として,ここでの時間損失を1時間当たり3 000円(こ
の値はそれぞれの場合に応じて算出する。)とすれば,組立者の段階における平均損失A0は
)
(
450
60
5
000
3
200
0
円
=
×
+
=
A
と推定される。
(3) 使用者及び組立者の段階における比例定数kを求める。
使用者:
667
266
15
.0
000
6
)1(
2=
=
k
組立者:
91837
07
.0
450
)2(
2=
=
k
(4) 比例定数kの値を比較する。
)2(
)1(
k
k
>
であるから選定許容限界値及び選定平均損失として,使用者の段階における許容限界値⊿0
及び平均損失A0を選択する。
)
(
15
.0
0
mm
=
⊿
)
(
000
6
0
円
=
A
3.2
生産者側の損失Aの推定 組立者が生産者から購入する購入原価の推定を行う。
例:音響製品に使用しているプラスチック部品の購入原価を,ここでは200円と見積る。
)
(
200
0
円
=
A
3.3
加工能力及び計測能力の検討 生産者側の損失Aの推定に当たり,許容差を設定する部品に対して
どの程度の精度で加工が可能なのか,また,それらを判定するのに十分な計測能力があるのかを附属書1
及び附属書2に基づき検討する。その結果,能力が不十分な場合には改善を行う。
3.4
許容差⊿の計算 許容差⊿を次の式によって計算する。
3
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0
0
⊿
⊿
A
A
=
例:⊿0=0.15 (mm) ,A0=6 000(円),A=200(円)の場合
)
(
027
.0
15
.0
000
6
200
mm
=
×
=
⊿
3.5
許容差⊿の検討 3.2,3.3及び3.4の結果を検討して無理があると思われれば,Aの値を変えて⊿の
再計算を行う。
(1) 加工能力が十分で不良率が適正な場合は,A及び⊿の値は再計算を行わない。
例:⊿=0.027 (mm) に決定する。
(2) 加工能力が不十分で,不良率 (p) が大きすぎる場合は,次の式によって生産者側の損失Aの値を修正
し,⊿の値を再計算する。
p
A
−
1
例:A=200(円),p=0.3の場合
)
(
7.
285
7.0
200
3.0
1
200
円
=
=
−
)
(
033
.0
15
.0
000
6
7.
285
mm
=
×
=
⊿
(3) 上記の検討を行っても加工能力の改善が不可能で許容差が満たされない場合には,全数検査をする。
3.6
許容差の決定 3.5の検討に基づいて許容差を決定する。
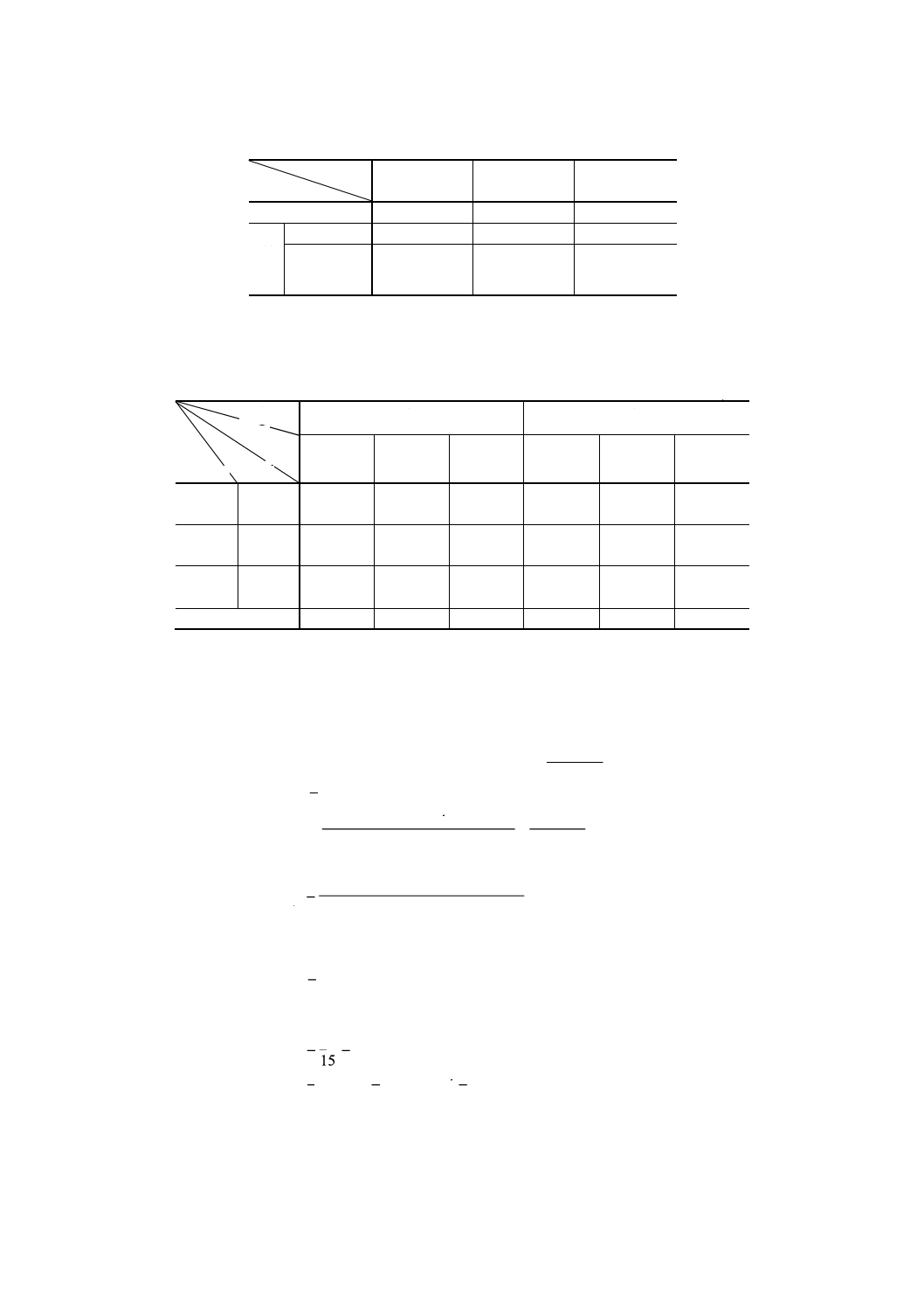
参考 参考表に,各種部品の基準寸法,使用者の段階における平均損失A0,生産者側の損失A,使用
者の段階における許容限界値⊿0及び本規格によって求めた許容差⊿の関係を使用者側の比例
定数kの大きかった場合について示す。
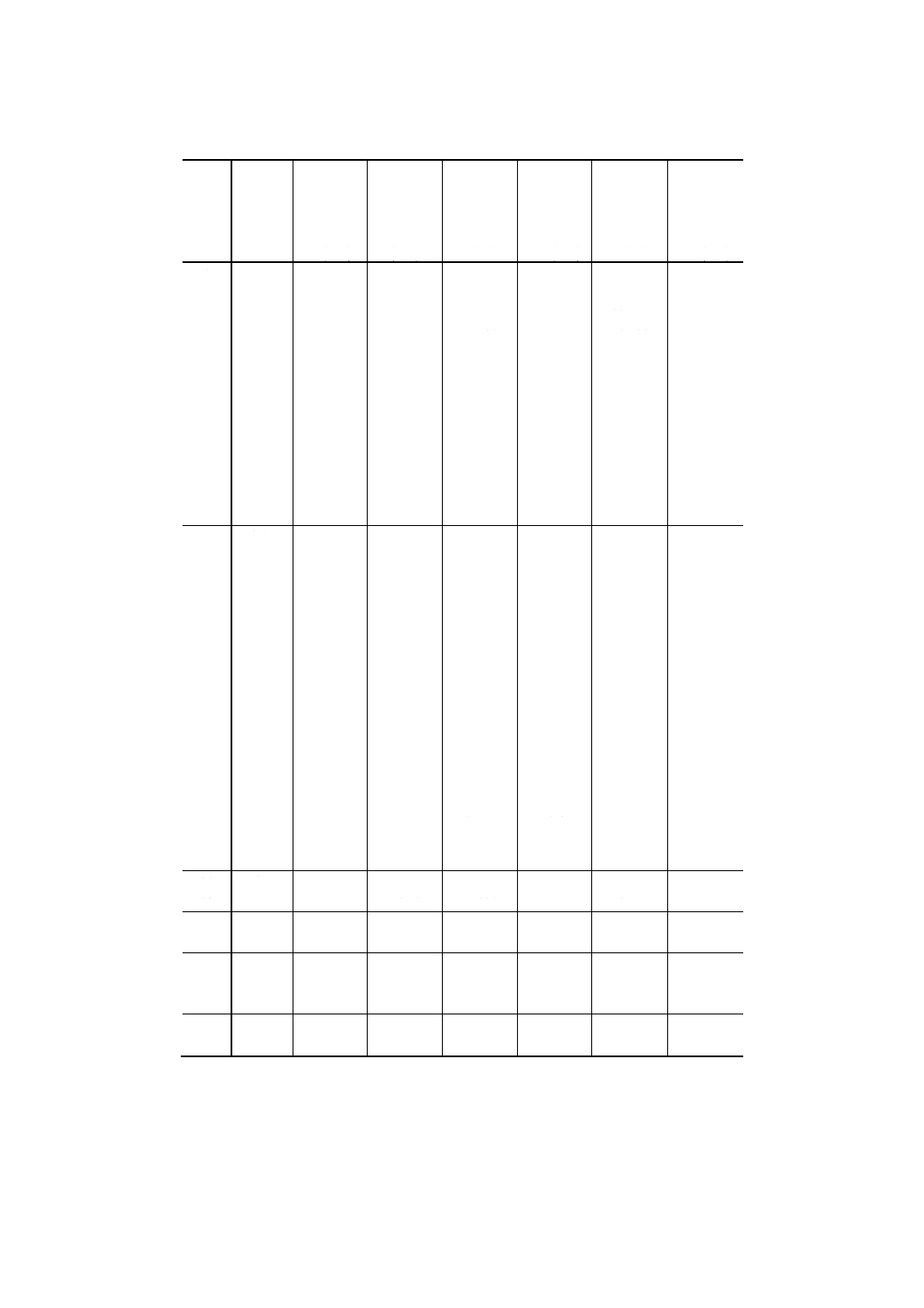
4
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考表
No.
機能
基準値
組立者側
が決めた
許容差
生産者側
の損失
使用者の
段階にお
ける許容
限界値
使用者の
段階にお
ける平均
損失
本規格に
よって求
めた許容
差
m (mm)
(mm)
A(円)
⊿0 (mm)
A0(円)
⊿ (mm)
1
外径
3.95
0.040
30
0.11
5 000
0.009
2
5.40
0.020
6
0.04
100
0.018
3
6.00
0.100
300
0.18
10 000
0.028
4
6.00
0.050
10
0.10
1 500
0.008
5
6.11
0.015
30
0.08
5 000
0.006
6
6.30
0.050
55
0.15
10 000
0.011
7
30.00
0.040
5
0.15
1 500
0.009
8
30.00
0.200
500
0.30
2 000
0.150
9
38.50
0.120
400
1.00
15 000
0.163
10
39.15
0.100
600
0.13
2 000
0.071
11
41.30
0.035
250
0.15
6 000
0.031
12
60.00
0.025
30
0.08
5 000
0.006
13
120.00
0.150
25
0.23
20 000
0.026
14
内径
2.00
0.015
100
0.08
1 500
0.021
15
2.00
0.015
60
0.05
2 000
0.009
16
3.00
0.010
150
0.05
5 000
0.009
17
3.00
0.040
30
0.30
5 000
0.023
18
4.00
0.025
200
0.05
1 500
0.016
19
4.00
0.015
15
0.05
5 000
0.003
20
4.90
0.010
500
0.03
2 000
0.015
21
6.00
0.015
100
0.05
3 500
0.009
22
6.05
0.030
50
0.13
9 000
0.010
23
7.90
0.050
100
0.08
1 000
0.025
24
9.00
0.030
76
0.06
1 000
0.017
25
10.00
0.018
50
0.03
6 000
0.003
26
18.00
0.015
4 000
0.08
5 500
0.068
27
31.75
0.150
40
0.30
2 000
0.042
28
46.00
0.013
1 500
0.05
6 000
0.023
29
56.80
0.025
120
0.09
5 000
0.014
30
65.00
0.150
300
0.50
8 000
0.097
31
幅
39.00
0.05
40
0.26
3 000
0.030
32
302.00
0.50
100
0.08
1 000
0.025
33
長さ
8.80
0.025
2 000
0.20
5 000
0.126
34
100.00
0.05
10
0.10
500
0.014
35
ピッチ
23.00
0.02
25
0.04
1 000
0.024
36
45.00
0.05
160
0.15
1 600
0.047
37
69.80
0.01
300
0.30
10 000
0.050
38
振れ
0.00
0.05
100
0.10
3 000
0.018
39
0.00
0.10
300
0.15
3 000
0.047
5
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1 加工能力の検討及び改善方法
1. 適用範囲 この附属書は,プラスチックの寸法許容差に関連して,成形加工能力の検討及び加工能力
の改善方法について規定する。
2. 用語の意味及び記号 この附属書で用いる主な用語の意味は,本文によるほか,次のとおりとする。
SN比(η) 信号パワーの雑音パワーに対する比。ここでは,信号パワーを平均値又は信号因子の効果
の大きさ,雑音パワーを誤差因子の効果の大きさとする。
3. 品質と加工能力の検討 許容差⊿と寸法のばらつきσとを比較して成形加工能力の検討を次の手順で
行う。
手順1
プラスチックの寸法の基準値mに対するばらつきの大きさσをプラスチックの寸法yと基準
値mの差の2乗の平均の平方根として,次のように表す。
の平均
2)
(
m
y−
=
σ
手順2
σの値は,現状の技術水準又は4.の加工能力改善のための実験などから求める。
手順3
σの値から工程能力指数 (Cp) を求める。
σ
3
⊿
=
p
C
手順4
求めたCpの値から,加工能力の判定を行う。例えば,次のように考えて判定する。
(1) Cpの値が十分大きい場合は加工能力は十分だと判定する。
(2) Cpの値が小さい場合は加工能力の改善を検討する。
(3) 加工能力の改善が不可能な場合は生産者側の損失Aの値を変えて許容差⊿の再検討をする。
(4) 許容差⊿の再検討が不可能な場合は全数検査を行う。
例:音響製品に使用しているプラスチック部品の許容差⊿が0.027mmの場合。
手順1, 2
σの値は,現状の技術水準から0.015mmと推定する。
手順3
6.0
015
.0
3
027
.0
=
×
=
p
C
手順4
例えば,工程能力が適当かどうかを判断するためにCp=0.8を一つの目安とすると,
この例では0.8より小さいので加工能力の改善を検討する。
4. 加工能力の改善 目的とする製品に対する加工能力の改善は,材料,加工機,附属する機械,加工条
件などについて検討することによって行うが,従来の知見では十分に効果が期待できない場合は以下の手
順によって改善を検討する。
手順1
プラスチックの寸法に影響を及ぼすと考えられる加工条件などを取り上げて,その中から重
要と思われる因子を選択する。
手順2
取り上げた各因子に対して,許される範囲内の広い範囲で数水準を選ぶ。
手順3
制御因子を多元配置又は直交配列表に割り付ける。各制御因子に対して加工上のばらつきの
原因となる条件を誤差因子として選ぶ。実際の加工において発生すると思われる範囲内で誤
6
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
差因子の水準を選ぶ。誤差因子を別の多元配置又は直交配列表に割り付ける。
手順4
制御因子と誤差因子を組み合わせた実験計画によって実験を行う。
手順5
誤差因子を割り付けた多元配置又は直交配列表について分散分析を行い,SN比を求める。
手順6
SN比を特性値として,制御因子を割り付けた多元配置又は直交配列表について各水準ごとの
SN比の和を求め,分散分析を行う。
手順7
効果の大きいと認められる制御因子についてSN比の一番大きい組合せが最適成形条件とな
る。
手順8
最適成形条件における加工能力を求め,改善前の加工能力と比較検討する。
例:現状の加工能力が低いため,成形条件を変えて最適条件を求め加工能力の向上を図る実験。
手順1
加工能力の向上に役立つと思われる制御因子として,金型温度,樹脂温度,射出速度,
冷却時間を選んだ。
手順2
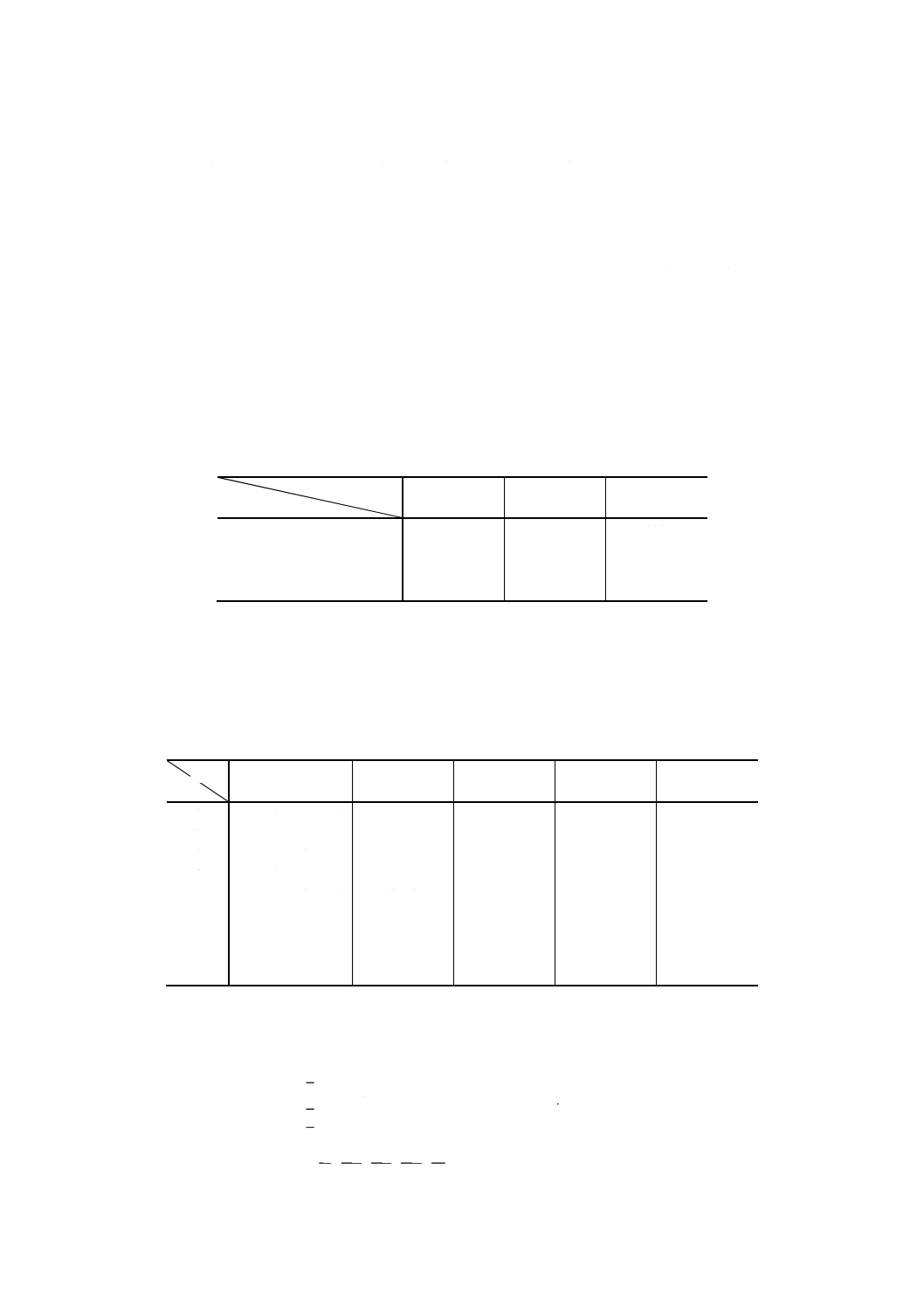
各制御因子の水準を次のように選んだ。
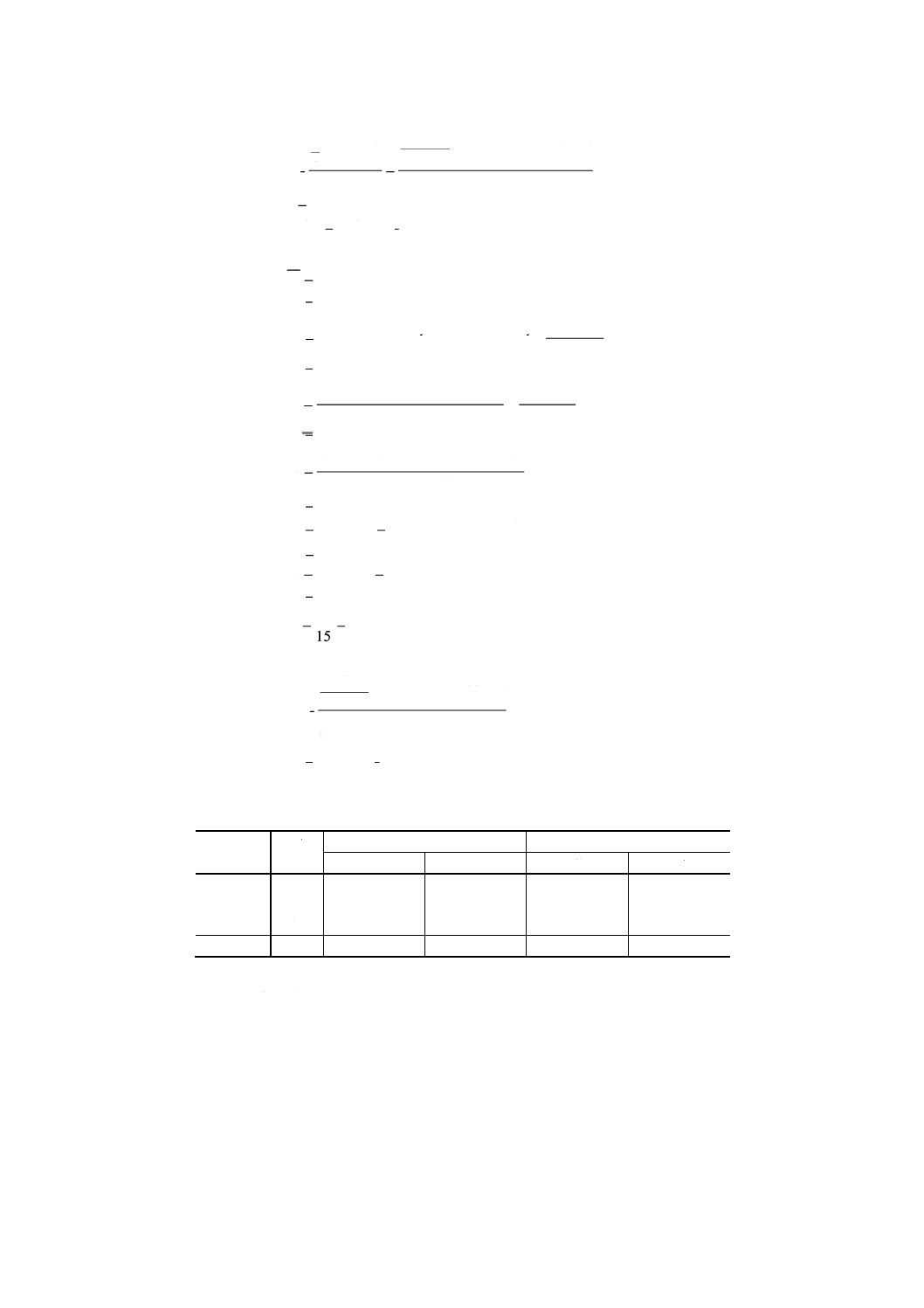
附属書1表1 因子と水準
水準
制御因子
1
2
3
A:金型温度 (℃)
60
80
100
B:樹脂温度 (℃)
190
205
220
C:射出速度 (mm/s)
12
24
36
D:冷却時間 (s)
5
15
25
手順3, 4 制御因子をL9の直交配列表に割り付けて加工実験を行い,立ち上がりの10ショット
ごとに試料を採取し,プラスチック部品の外径を測定した。ここでは,ショット間の
ばらつきを誤差因子とした。得られたデータは,次のとおりである。
附属書1表2 各条件におけるデータ
単位 mm
因子
No.
A
B
C
D
y1
y2
y3
y4
1
1
1
1
1
39.010
39.028
39.042
39.063
2
1
2
2
2
39.150
39.161
39.170
39.180
3
1
3
3
3
39.202
39.242
39.249
39.261
4
2
1
2
3
39.020
39.030
39.058
39.066
5
2
2
3
1
39.161
39.181
39.194
39.219
6
2
3
1
2
39.135
39.140
39.145
39.162
7
3
1
3
2
39.086
39.098
39.100
39.108
8
3
2
1
3
39.040
39.056
39.060
39.075
9
3
3
2
1
39.136
39.141
39.152
39.155
手順5
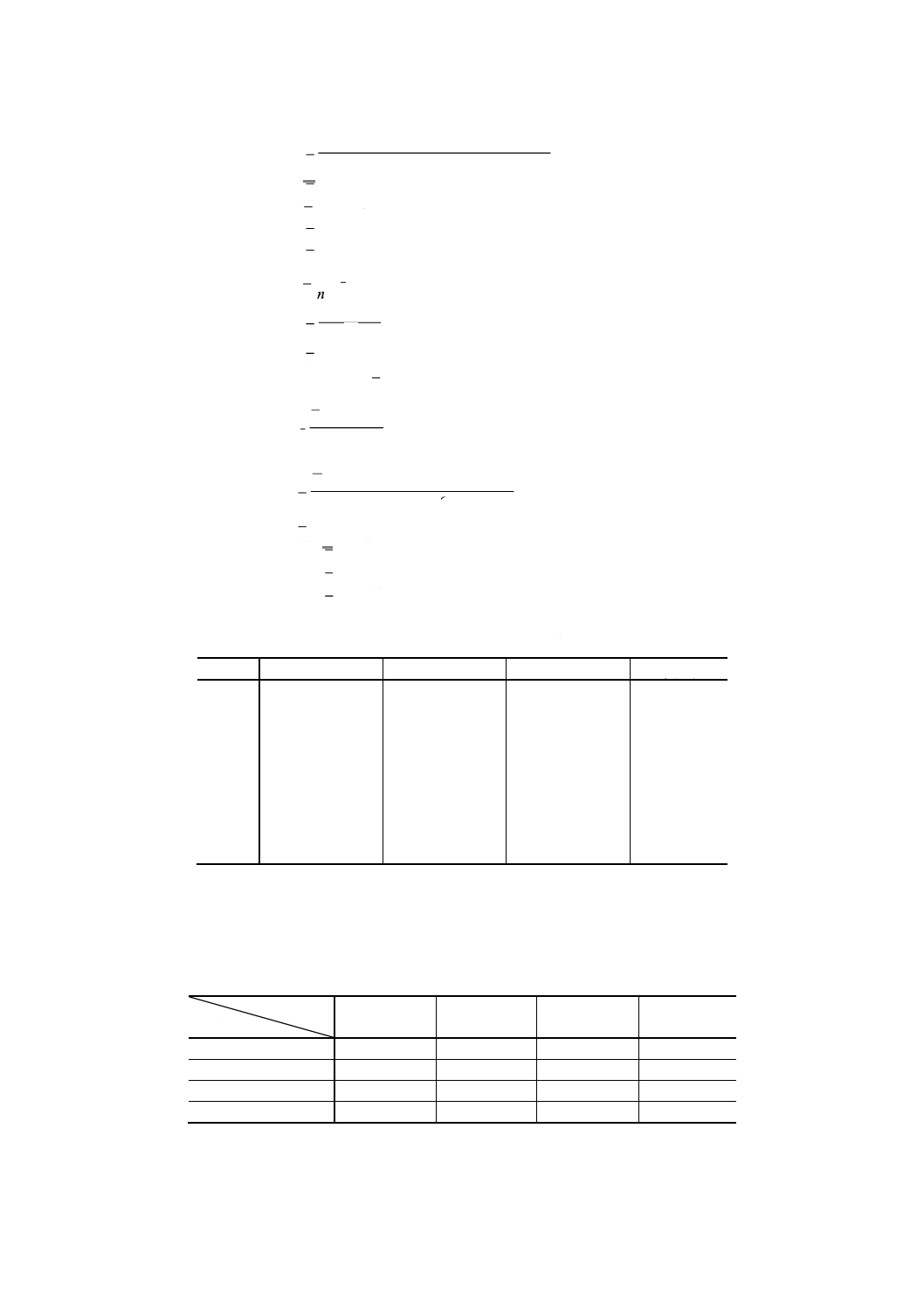
No.1〜No.9のデータをそれぞれ分散分析し,SN比η (dB) を求める。No.1の計算例は
次のようになる。
2
4
2
3
2
2
2
1
y
y
y
y
ST
+
+
+
=
2
2
2
2
063
.
39
042
.
39
028
.
39
010
.
39
+
+
+
=
617
160
.
095
6
=
n
y
y
y
y
Sm
2
4
3
2
1
)
(
+
+
+
=
7
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
)
063
.
39
042
.
39
028
.
39
010
.
39
(
2
+
+
+
=
112
159
.
095
6
=
m
T
e
S
S
S
−
=
112
159
.
095
6
617
160
.
095
6
−
=
505
001
.0
=
1
−
=nS
V
e
e
1
4
505
001
.0
−
=
6
501
000
.0
=
4
)
(
=
有効除数
r
e
e
m
V
V
S
r
)
(
1
−
=
η
6
501
000
.0
)6
501
000
.0
112
159
.
095
6(
4
1
−
×
=
858
037
3
=
η
η
log
10
)
(
=
dB
858
037
3
log
10
=
)
(
8.
64
dB
=
同様にしてNo.9までの計算を行う。
附属書1表3 分散分析の結果及びSN比
No.
ST
Sm
Ve
η (dB)
1
6 095.160 617
6 095.159 112
0.000 501 6
64.8
2
6 135.667 721
6 135.667 230
0.000 163 6
69.7
3
6 158.641 490
6 158.639 529
0.000 653 7
63.7
4
6 097.581 020
6 097.579 569
0.000 483 7
65.0
5
6 143.034 279
6 143.032 506
0.000 590 9
64.1
6
6 129.481 094
6 129.480 681
0.000 137 7
70.5
7
6 114.614 664
6 114.614 416
0.000 082 7
72.7
8
6 102.031 961
6 102.031 340
0.000 206 9
68.7
9
6 129.637 506
6 129.637 264
0.000 080 7
72.8
手順6
SN比η (dB) を特性値として分散分析を行う。附属書1表2の因子の組合せを用いて
求めた,各制御因子及び水準ごとのSN比の和は,次のようになる。
附属書1表4 各水準ごとのSN比の和
単位 dB
水準
制御因子
1
2
3
計
A:金型温度
198.2
199.6
214.2
612.0
B:樹脂温度
202.5
202.5
207.0
612.0
C:射出速度
204.0
207.5
200.5
612.0
D:冷却時間
201.7
212.9
197.4
612.0
8
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
n
CF
2
9
3
2
1
)
(
η
η
η
η
+
+
+
+
=
Λ
Λ
Λ
Λ
9
)8.
72
7.
68
7.
72
5.
70
1.
64
0.
65
7.
63
7.
69
8.
64
(
2
+
+
+
+
+
+
+
+
=
166
4
=
CF
ST
−
+
+
+
+
=
)
(
2
9
2
3
2
2
2
1
η
η
η
η
Λ
Λ
Λ
Λ
7.
107
=
CF
SA
−
+
+
+
+
+
+
+
+
×
=
]
)
(
)
(
)
[(
3
1
2
9
8
7
2
6
5
4
2
3
2
1
η
η
η
η
η
η
η
η
η
CF
−
+
+
×
=
)
2.
214
6.
199
2.
198
(
3
1
2
2
2
34
.
52
=
CF
SB
−
+
+
+
+
+
+
+
+
×
=
]
)
(
)
(
)
[(
3
1
2
9
6
3
2
8
5
2
2
7
4
1
η
η
η
η
η
η
η
η
η
CF
−
+
+
×
=
)
0.
207
5.
202
5.
202
(
3
1
2
2
2
50
.4
=
CF
SC
−
+
+
+
+
+
+
+
+
×
=
]
)
(
)
(
)
[(
3
1
2
7
5
3
2
9
4
2
2
8
6
1
η
η
η
η
η
η
η
η
η
CF
−
+
+
×
=
)
5.
200
5.
207
0.
204
(
3
1
2
2
2
17
.8
=
CF
SD
−
+
+
+
+
+
+
+
+
×
=
]
)
(
)
(
)
[(
3
1
2
8
4
3
2
7
6
2
2
9
5
1
η
η
η
η
η
η
η
η
η
CF
−
+
+
×
=
)
4.
197
9.
212
7.
201
(
3
1
2
2
2
69
.
42
=
附属書1表5 SN比η (dB) の分散分析結果
因子
f
S
V
A:金型温度
2
52.34
26.17
B:樹脂温度
2
4.50
2.25
C:射出速度
2
8.17
4.08
D:冷却時間
2
42.69
21.34
計
8
107.70
手順7
附属書1表5の分散分析の結果から金型温度と冷却時間の効果が大きいことが分かる。
最適成形条件は,効果の大きかった因子の水準の中からSN比の値が最も大きいもの
を選んだ組合せである。附属書1表4から,金型温度Aでは第3水準の和214.2dB,
冷却時間Dでは第2水準の和212.9dBが最も大きな値である。この場合の成形条件は,
金型温度100℃,冷却時間15秒である。
手順8
最適成形条件におけるSN比η (dB) の値は,金型温度Aの第3水準及び冷却時間Dの
第2水準の場合のSN比の平均値
3A及び
2
Dを用いて次の式から推定する。
9
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)
(
)
(
)
(
2
3
η
η
η
η
−
+
−
+
=
D
A
dB
η
−
+
=
2
3
D
A
9
0.
612
3
9.
212
3
2.
214
−
+
=
)
(4.
74
dB
=
この値を用いて次の式から標準偏差σを求める。基準値mは,39.100mmである。
10
)
(
10
dB
m
η
σ=
10
4.
74
10
1.
39
=
)
(5
007
.0
mm
=
CPの値は,
5
007
.0
3
027
.0
×
=
p
C
2.1
=
となり,改善された加工能力は,求められた許容差に対して十分であると判定する。
10
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2 寸法計測能力の検討及び改善方法
1. 適用範囲 プラスチックの寸法許容差に関連して,計測能力の検討及び改善を行う方法について規定
する。
2. 用語及び記号の意味 この附属書で用いる主な用語の意味及び記号は,本文によるほか次のとおりと
する。
(1) 計測コスト 対象となる計測器を用いて,定められた寸法を測定するのに要した時間と,計測担当者
の賃金単価との積。
(2) 計測器のコスト 計測器の価格に,償却までの期間と金利を考慮したもの。
(3) SN比 信号パワーの雑音パワーに対する比。ここでは,信号パワーを計測対象の量の効果の大きさ,
雑音パワーを誤差因子の効果の大きさとする。
3. 計測の誤差と加工の誤差の比較 現状の計測の誤差を求めて加工の誤差と比較する。計測の誤差の占
める割合が大きい場合は,計測方法の改善についての検討を行うが,従来の知見では十分な効果が期待で
きない場合は,以下の手順によって改善を検討する。
4. 標準を計測した場合の計測のSN比を求める 計測器によって標準を測定した読み値から,以下の手
順でSN比を求める。
手順1
対象となる計測方法の標準の種類とその水準を決定する。
手順2
計測方法の誤差原因と考えられる誤差因子(1)を取り上げ,SN比を求めるための実験及び測定
を行い,附属書2表1のデータを得る。
注(1) 測定者,反復などがある。
附属書2表1 測定データ
標準
反復
M1
M2
M3…………Mk
R1
y11
y12
y13…………y1k
R2
y21
y22
y23…………y2k
・
・
・
・…………・
・
・
・
・…………・
Rr0
yr01
yr02
yr03………yr0k
計
y1
y2
y3………yk
手順3
実験の結果について分散分析を行う。解析手順は以下のとおりである。
k
M
M
M
M
k
Λ
Λ
+
+
=
2
1
]
)
(
)
(
)
[(
2
2
2
2
1
0
M
M
M
M
M
M
r
r
k−
+
+
−
+
−
=
Λ
Λ
r
y
M
M
y
M
M
y
M
M
S
k
k
2
2
2
1
1
]
)
(
)
(
)
[(
−
+
+
−
+
−
=
Λ
Λ
β
11
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
k
y
y
y
y
y
S
k
r
k
r
T
2
0
11
2
0
2
12
2
11
)
(
+
+
−
+
+
+
=
Λ
Λ
Λ
Λ
β
S
S
S
T
e
−
=
2
0−
=krS
V
e
e
結果を附属書2表2の分散分析表にまとめる。
附属書2表2 分散分析表
要因
f
S
V
β
1
Sβ
Vβ
e
kr0−2
Se
Ve
計
kr0−1
ST
手順4
誤差分散に対する信号の効果の大きさからSN比を求める。
例:プラスチック用低測定力マイクロメータを用いて,標準(ブロックゲージ)を計測した場合につ
いて検討した。
手順1 標準の水準の選定を行う。
寸法測定の標準としてブロックゲージを選び,その水準は附属書2表3のとおりである。
附属書2表3 標準の寸法の表示値
単位μm
水準
M1
M2
M3
寸法
5 000
15 000
25 000
手順2 実験を行う。
誤差因子として測定の反復を選び,実験を行った結果は附属書2表4のとおりである。
附属書2表4 測定結果
単位μm
標準
反復
Ml
M2
M3
R1
5 001
15 003
25 008
R2
5 005
15 007
25 002
計
10 006
30 010
50 010
手順3 分散分析を行う。
00
.
000
15
3
/)
000
25
000
15
000
5(
=
+
+
=
M
00
.
000
000
400
]
000
10
)
000
10
[(
2
2
2
=
+
−
=
r
00
.
000
000
400
)
010
50
000
10
006
10
000
10
(
2
×
+
×
−
=
β
S
004
080
400
=
00
.
039
080
400
6
026
90
002
25
005
5
001
5
2
2
2
2
=
−
+
+
+
=
Λ
Λ
T
S
00
.
35
00
.
004
080
400
00
.
039
080
400
=
−
=
e
S
分散分析を行った結果は,附属書2表5のとおりである。
12
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2表5 分散分析表
要因
f
S
V
β
1
400 080 004.00
400 080 004.00
e
4
35.00
8.75
計
5
400 080 039.00
手順4 誤差分散に対する信号の効果の大きさからSN比を求める。
e
e
V
V
S
r
)
(
1
−
=
β
η
75
.8
)
75
.8
004
080
400
(
000
000
400
1
−
×
=
7
113
.0
=
5. 測定方法の選択と改善 同一測定対象について2種類以上の測定方法がある場合には,次の手順で測
定方法を選定する。
手順1 計測の誤差を明らかにする。
(1) 制御因子とその水準を明らかにする。
(2) 信号因子及び誤差因子とその水準を定める。
(3) SN比を求めるための実験及び測定を行う。
(4) 分散分析を行い,SN比を求める。
(5) SN比を特性値とした分散分析を行う。
(6) 制御因子の水準別に計測の誤差を求める。
手順2 計測の誤差の経済性評価を行う。
(1) 比例定数kを求める。
(2) 計測の誤差による損失Lを求める。
(3) 計測にかかわる総損失L (T) を求める。
(4) 計測にかかわる1年間の損失を比較し,損失の最も小さい計測方法を求める。
例:プラスチック部品の寸法測定器として普通のマイクロメータとプラスチック用マイクロメータが
ある。どちらを採用するか決定したい場合。
手順1 計測の誤差を明らかにする。
(1) 制御因子の水準の決定。
A1:普通のマイクロメータ
A2:プラスチック用マイクロメータ
(2) 信号因子と誤差因子の水準の決定。
信号因子と誤差因子の水準を附属書2表6に示した。この場合,信号因子の間
隔h=130 (μm) はおおよその値である。
13
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2表6 信号因子と誤差因子の水準
水準
因子
1
2
3
信号因子 M (mm)
19.930
20.060
20.190
誤
差
因
子
測定者 B
1
2
3
反復 R
1
2
−
(3) 実験結果 附属書2表6に従った実験を行った結果は,附属書2表7のとおりである。
附属書2表7 実験結果
単位 μm
制御因子
信号
因子
測定者 反復
A1
A2
M1
M2
M3
M1
M2
M3
B1
R1
19 937
20 074
20 188
19 941
20 072
20 201
R2
19 927
20 062
20 185
19 953
20 071
20 203
B2
R1
19 935
20 069
20 204
19 943
20 078
20 203
R2
19 928
20 059
20 193
19 948
20 073
20 200
B3
R1
19 944
20 073
20 207
19 946
20 074
20 204
R2
19 930
20 065
20 195
19 941
20 071
20 202
計
119 601
120 402
121 172
119 672
120 439
121 213
(4) 分散分析を行いSN比を求める。信号因子がおおよその値であるから,回帰からの残差Mres
はSeに含めない。
(a) A1:普通のマイクロメータのSN比
18
175
361
195
20
927
19
937
19
2
2
2
2
−
+
+
+
=
Λ
Λ
T
S
67
.
465
206
=
18
175
361
6
172
121
402
120
601
119
2
2
2
2
−
+
+
=
M
S
78
.
696
205
=
00
.
800
202
)
130
172
121
130
601
119
(
2
×
+
×
−
=
β
S
08
.
670
205
=
08
.
670
205
78
.
696
205
−
=
−
=
β
S
S
S
M
Mres
70
.
26
=
78
.
696
205
67
.
465
206
−
=
−
=
M
T
e
S
S
S
89
.
768
=
26
.
51
15=
=
e
e
S
V
00
.
800
202
130
2
6
2
2
2
0
=
×
×
=
×
=
h
r
r
SN比
14
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
26
.
51
)
26
.
51
08
.
670
205
(
800
202
1
)
(
1
−
×
=
−
=
e
e
V
V
S
r
β
η
8
019
.0
=
)
(
03
.
17
log
10
)
(
dB
dB
−
=
=
η
η
(b) A2:プラスチック用マイクロメータのSN比
00
.
060
20
=
M
00
.
800
202
=
r
18
324
361
202
20
953
19
941
19
2
2
2
2
−
+
+
+
=
Λ
Λ
T
S
50
.
046
198
=
18
324
361
6
213
121
439
120
672
19
2
2
2
2
−
+
+
=
M
S
40
.
891
197
=
00
.
800
202
)
130
313
121
130
672
119
(
2
×
+
×
−
=
β
S
10
.
890
197
=
1.
890
197
4.
891
197
−
=
−
=
β
S
S
S
M
Mres
30
.1
=
4.
891
197
5.
046
198
−
=
−
=
M
T
e
S
S
S
10
.
155
=
33
.
10
15=
=
e
e
S
V
SN比
33
.
10
)
33
.
10
10
.
197890
(
202800
1
−
×
=
η
0945
.0
=
)
(
24
.
10
log
10
)
(
dB
dB
−
=
=
η
η
分散分析を行った結果は,附属書2表8のとおりである。
附属書2表8 分散分析表
要因
f
A1
A2
S
V
S
V
β
1
205 670.08
205 670.08
197 890.10
197 890.10
Mres
1
26.70
26.70
1.30
1.30
e
15
768.89
51.26
155.10
10.33
計
17
206 465.67
198 046.50
(5) SN比の比較を行う。
A1のSN比 η1=0.019 8=−17.03 (dB)
A2のSN比 η2=0.094 5=−10.24 (dB)
以上よりA2のほうがSN比が高い。
手順2 計測の誤差の経済性評価を行う。
(1) 比例定数kを求める。
15
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
40
10
)
(
=
=
寸法許容差
しした場合の費用
品物を不合格又は手直
k
25
006
.0
=
(2) 計測の誤差による損失を求める。
A1のマイクロメータL1=kσ12=0.006 25×51.26
=0.320(円/個)
A2のマイクロメータL2=kσ22=0.006 25×10.33
=0.065(円/個)
(3) 計測にかかわる総損失を求める。
ここでは1日の測定時間を41時間とした。
計測コスト=賃金×1日の測定時間×1年間の日数
=3 000×41(時間)×250=187 500(円)
計測器のコスト A1: 10 000円(1年間当たり:購入価格の21とした)
A2: 15 000円(1年間当たり:購入価格の21とした)
1年間の生産個数 135万個
総損失L (T) 1=10 000+187 500+0.320×1 350 000
=629 500(円/年)
L (T) 2=15 000+187 500+0.065×1 350 000
=290 250(円/年)
(4) 計測にかかわる総損失を比較し,小さいほうを採用する。
L (T) 1−L (T) 2=339250(円/年)
1年間当たりプラスチック用マイクロメータ (A2) のほうが約34万円損失が少ない。
6. 総合した誤差の決定 最適な計測方法を選定したら,実物の成形品の計測を行う。このとき,標準を
使って計測器を校正したときの誤差,実物成形品を計測した誤差を加えたものが最終的に総合した誤差と
なる。
例:プラスチック用マイクロメータの総合した誤差を求める。
各手順で求めた誤差を総合する。
+
×
+
±
=
2
1
21
1
1
4
η
η
δ
δ
+
×
±
=
5
094
.0
1
7
113
.0
1
4
)
(
8.8
m
μ
±
=
ここに,
η1: 標準を測定した場合のSN比
η2: 実際の品物を測定した場合のSN比
δ1: 標準の誤差(ここでは小さいので考慮に入れない。)
プラスチック用マイクロメータの最終的な総合誤差は,約±9μmであった。
16
K 7109-1986
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS原案作成委員会 構成表
氏名
所属
(委員長)
田 口 玄 一
財団法人日本規格協会
(幹事)
矢 野 宏
工業技術院計量研究所
(委員)
岩 崎 健 彦
五合化学株式会社
小 出 遵 一
日立化成工業株式会社
富 島 明
山武ハネウエル株式会社
斉 藤 敏 郎
住友重機械株式会社
杉 山 昭
株式会社山城精機製作所
本 間 精 一
三菱瓦斯化学株式会社
高 野 菊 雄
ポリプラスチックス株式会社
内 田 一 信
池上金型工業株式会社
中 村 哲 夫
株式会社三豊製作所
土 倉 克 彦
アイワ株式会社
渋 沢 清 和
株式会社リコー
矢 野 宏
工業技術院計量研究所
鴨 下 隆 志
工業技術院計量研究所
今 津 好 昭
東京都立工業技術センター
川 村 正 信
財団法人日本規格協会
田 口 玄 一
財団法人日本規格協会
山 本 健太郎
明治大学
中 軸 美智雄
通商産業省基礎産業局
山 田 次 雄
工業技術院標準部
熊 田 和 雄
社団法人日本合成樹脂技術協会
松 川 俊 雄
埼玉県商工部
松 田 次 郎
工業技術院計量研究所
オブザーバー
庄 司 隆 一
工業技術院標準部
さらに審議を効率的に進めるために次の分科会を組織した。
氏名
所属
今 津 好 昭
東京都立工業技術センター
鴨 下 隆 志
工業技術院計量研究所
川 村 正 信
財団法人日本規格協会
熊 田 和 雄
社団法人日本合成樹脂技術協会
渋 沢 清 和
株式会社リコー
松 川 俊 雄
埼玉県商工部
松 田 次 郎
工業技術院計量研究所
矢 野 宏
工業技術院計量研究所
山 田 次 雄
工業技術院標準部
オブザーバー
庄 司 隆 一
工業技術院標準部
また,解説の執筆は次のメンバーによる。
氏名
所属
今 津 好 昭
東京都立工業技術センター
鴨 下 隆 志
工業技術院計量研究所
田 口 玄 一
財団法人日本規格協会
松 川 俊 雄
埼玉県商工部
松 田 次 郎
工業技術院計量研究所
矢 野 宏
工業技術院計量研究所