K 6394:2007
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,日本ゴム工業会
(JRMA)/財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を改正すべきとの申出が
あり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS K 6394:1998は改正され,この規格に置き換えられる。
改正に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO 4664-1:2005,Rubber,vulcanized or
thermoplastic−Determination of dynamic properties−Part 1: General guidanceを基礎として用いた。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
JIS K 6394には,次に示す附属書がある。
附属書1(参考)動的性質の計算方法の例
附属書2(参考)JISと対応する国際規格との対比表
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義及び記号 ·················································································································· 2
4. 動的性質の一般事項 ········································································································· 8
4.1 一般事項 ······················································································································ 8
4.2 試験の用途 ··················································································································· 9
4.3 試験の分類 ··················································································································· 9
4.4 試験装置選定の留意点 ···································································································· 9
4.5 動的運動 ····················································································································· 10
4.6 周波数と温度との換算 ··································································································· 13
5. 試験装置 ······················································································································· 14
5.1 試験装置の概要 ············································································································ 14
5.2 試験装置の校正 ············································································································ 15
6. 試験片 ·························································································································· 16
6.1 試験片の形状及び寸法 ··································································································· 16
6.2 試験片の採取・作製 ······································································································ 16
6.3 試験片の数 ·················································································································· 16
6.4 試験片の厚さ及び直径又は幅の測定 ·················································································· 16
7. 試験方法 ······················································································································· 16
7.1 試験条件 ····················································································································· 16
7.2 操作方法 ····················································································································· 20
8. 試験結果のまとめ方 ········································································································ 21
8.1 強制振動非共振方法 ······································································································ 21
8.2 自由振動方法 ··············································································································· 22
8.3 応力及びひずみと形状要素との関係 ·················································································· 22
9. 記録 ····························································································································· 23
附属書1(参考)動的性質の計算方法の例 ················································································ 25
附属書2(参考)JISと対応する国際規格との対比表 ·································································· 27
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 6394:2007
加硫ゴム及び熱可塑性ゴム−
動的性質の求め方−一般指針
Rubber, vulcanized or thermoplastic−
Determination of dynamic properties−General guidance
序文 この規格は,2005年に第1版として発行されたISO 4664-1,Rubber,vulcanized or thermoplastic−
Determination of dynamic properties−Part 1: General guidanceを翻訳し,技術的内容を変更して作成した日本
工業規格である。
なお,この規格で側線又は点線の下線を施してある箇所は,原国際規格を変更している事項である。変
更の一覧表をその説明を付けて,附属書2(参考)に示す。
警告 この規格の利用者は,通常の実験室の作業に精通しているものとする。この規格は,その使用に
関連して起こるすべての安全上の問題を取り扱おうとするものではない。この規格の利用者は,
各自の責任において安全及び健康に対する適切な措置をとらなければならない。
1. 適用範囲 この規格は,加硫ゴム及び熱可塑性ゴム(製品も含む。)の自由振動方法及び強制振動方法
による動的性質の求め方の一般指針について規定する。ただし,反発弾性及び繰り返しによる疲労試験に
ついては適用しない。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
(修正している),NEQ(同等でない)とする。
ISO 4664-1:2005,Rubber,vulcanized or thermoplastic−Determination of dynamic properties−Part 1:
General guidance (MOD)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発行年を付記してあるものは,記載の年の版だけがこの規格の規定を構
成するものであって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その
最新版(追補を含む。)を適用する。
JIS B 7507 ノギス
JIS K 6200 ゴム用語
JIS K 6250 ゴム−物理試験方法通則
備考 ISO 23529:2004,Rubber−General procedures for preparing and conditioning test pieces for physical
test methodsからの引用事項は,この規格の該当事項と同等である。
JIS K 6254 加硫ゴム及び熱可塑性ゴム−低変形における応力・ひずみ特性の求め方
2
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 ISO 7743:2004,Rubber,vulcanized or thermoplastic−Determination of compression stress-strain
propertiesからの引用事項は,この規格の該当事項と同等である。
JIS K 6272 ゴム−引張,曲げ及び圧縮試験機(定速)−仕様
備考 ISO 5893:2002,Rubber and plastics test equipment−Tensile,flexural and compression types
(constant rate of traverse)−Specificationからの引用事項は,この規格の該当事項と同等である。
ISO 4663:1986,Rubber−Determination of dynamic behaviour of vulcanizates at low frequencies−Torsion
pendulum method
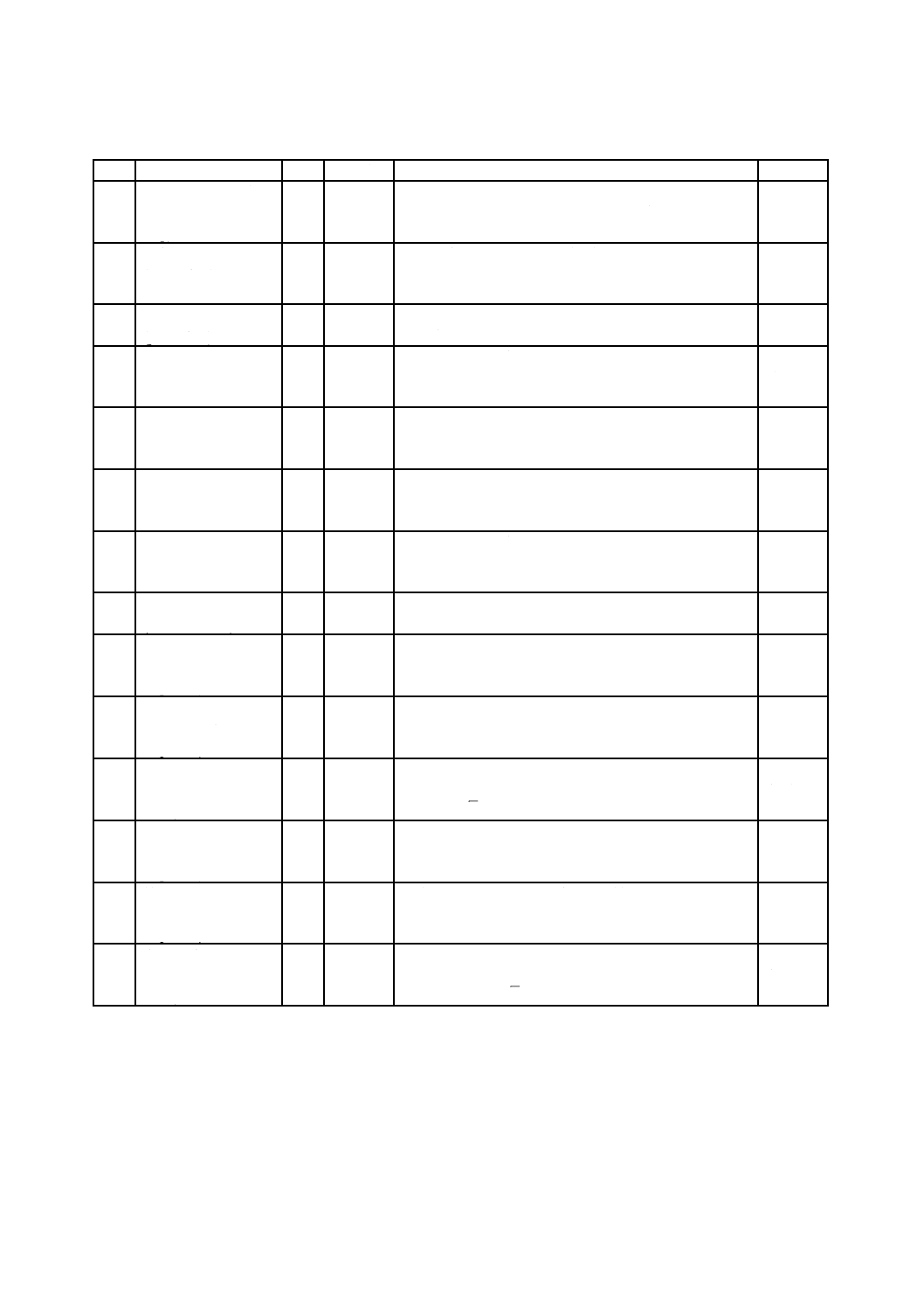
3. 定義及び記号 この規格で用いる主な用語の定義及び記号は,JIS K 6200によるほか,表1,表2,表
3,表4,参考図1,図1,図2及び図3による。
3
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 1 周期的変形に用いる用語
番号
用語
記号 基本単位
定義
備考
1
ヒステリシス曲線
(mechanical hysteresis
loop)
−
−
試験片に周期的変形を与えたときに示される連続した
応力―ひずみ又は荷重―たわみの閉曲線
参考図1
参照
2
エネルギー損失
(energy loss)
−
J/m3
周期的変形の周期ごとに単位体積当たりに失われる力
学的エネルギーで,ヒステリシス曲線の面積に相当す
る。
3
パワー損失
(power loss)
−
W/m3
周期的変形時に熱に変化したパワーで,エネルギー損失
と周波数との積
4
平均荷重
(mean load)
−
N
荷重―たわみ曲線における荷重の平均値
参考図1
及び図1
参照
5
平均応力
(mean stress)
−
Pa
応力―ひずみ曲線における応力の平均値
参考図1
及び図1
参照
6
平均たわみ
(mean deflection)
−
m
荷重―たわみ曲線におけるたわみの平均値
参考図1
及び図1
参照
7
平均ひずみ
(mean strain)
−
−
応力―ひずみ曲線におけるひずみの平均値
参考図1
及び図1
参照
8
平均弾性係数
(mean modulus)
−
Pa
平均応力と平均ひずみとの比
9
最大荷重振幅
(maximum load
amplitude)
F0
N
平均荷重を基準とした片振幅の最大値
参考図1
参照
10
最大応力振幅
(maximum stress
amplitude)
τ0
Pa
平均応力を基準とした片振幅の最大値
参考図1
参照
11
実効応力
(root-mean-square
stress)
−
Pa
1サイクルにおける応力の二乗の時間平均値の平方根
(実効応力は,対称な正弦波応力に対してはその最大応
力振幅を2で除して得られる。)
参考図1
参照
12
最大たわみ振幅
(maximum deflection
amplitude)
x0
m
平均たわみを基準とした片振幅の最大値
参考図1
参照
13
最大ひずみ振幅
(maximum strain
amplitude)
γ0
−
平均ひずみを基準とした片振幅の最大値
参考図1
参照
14
実効ひずみ
(root-mean-square
strain)
−
−
1サイクルにおけるひずみの二乗の時間平均値の平方根
(実効ひずみは,対称な正弦波ひずみに対してはその最
大ひずみ振幅を2で除して得られる。)
参考図1
参照
4
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 2 正弦波振動に用いる用語
番号
用語
記号 基本単位
定義
備考
1
ばね定数
(spring constant)
K
N/m
変形と同位相の荷重をたわみで除した値
2
貯蔵せん断弾性係数
(elastic shear modulus
又は
storage shear modulus)
G′
Pa
せん断ひずみと同位相のせん断応力を,せん断ひずみで
除した値
δ
γ
τ
cos
*
0
G
G
=
′
=′
3
損失せん断弾性係数
(loss shear modulus)
G′′
Pa
せん断ひずみと
rad
2
π
位相がずれたせん断応力を,せん
断ひずみで除した値
δ
γ
τ
sin
*
0
G
G
=
′′
=
′′
4
複素せん断弾性係数
(complex shear
modulus)
G*
Pa
せん断応力とせん断ひずみとの比で,それぞれの複素数
によってベクトルで示される。
G
i
G
*
G
′′
+′
=
5
絶対せん断弾性係数
(absolute shear
modulus)
|G*| Pa
複素せん断弾性係数の絶対値
2
2G
G
*
G
′′
+
′
=
6
貯蔵たて弾性係数
(storage normal
modulus, elastic
normal modulus
又はelastic Youngʼs
modulus)
E′
Pa
ひずみと同位相の応力を,ひずみで除した値
δ
γ
τ
cos
*
0
E
E
=
′
=
′
7
損失たて弾性係数
(loss normal modulus
又はloss Youngʼs
modulus)
E′′
Pa
ひずみと
rad
2
π
位相がずれた応力を,ひずみで除した値
δ
γ
τ
sin
*
0
E
E
=
′′
=
′′
8
複素たて弾性係数
(complex normal
modulus又はcomplex
Youngʼs modulus
E*
Pa
応力とひずみとの比で,それぞれの複素数によってベク
トルで示される。
E
i
E
*
E
′′
+′
=
9
絶対たて弾性係数
(absolute normal
modulus)
|E*| Pa
複素たて弾性係数の絶対値
2
2E
E
*
E
′′
+
′
=
10
貯蔵ばね定数,又は
動的ばね定数
(storage spring
constant又はdynamic
spring constant)
K′
N/m
たわみと同位相の荷重を,たわみで除した値
δ
cos
*
0
K
x
F
K
=
′
=
′
11
損失ばね定数
(loss spring constant)
K′′ N/m
たわみと
rad
2
π
位相がずれた荷重を,たわみで除した値
δ
sin
*
0
K
x
F
K
=
′′
=
′′
12
複素ばね定数
(complex spring
constant)
K*
N/m
荷重とたわみとの比で,それぞれの複素数のベクトルで
示される。
K
i
K
*
K
′′
+
′
=
5
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 2 正弦波振動に用いる用語(続き)
番号
用語
記号 基本単位
定義
備考
13
絶対ばね定数
(absolute spring
constant)
|K*| N/m
複素ばね定数の絶対値
2
2
*
K
K
K
′′
+
′
=
14
損失正接
(tangent of the loss
angle)
tan δ −
損失弾性係数と貯蔵弾性係数との比
せん断
G
G
′
′′
=
δ
tan
引張・圧縮
E
E
′
′′
=
δ
tan
15
損失係数
(loss factor)
Lf
−
損失ばね定数と貯蔵ばね定数との比
K
K
Lf
′
′′
=
16
損失角
(loss angle)
δ
rad
ひずみと応力又はたわみと荷重の位相角で,そのtanは
損失正接又は損失係数となる。
表 3 周期的変形で用いられるその他の用語
番号
用語
記号 基本単位
定義
備考
1
対数減衰率
(logarithmic
decrement)
Λ
−
正弦波の減衰振動において,連続した振幅の比の自然対
数
2
減衰比
(damping ratio)
u
−
実際の減衰と臨界減衰との比
減衰比は対数減衰率の関数として表される。
=
+
=
−
π
π
π
2
tan
sin
2
1
2
1
2
Λ
Λ
Λ
u
3
減衰係数
(damping constant)
c
N・s/m
加えた力のうちで変形と
rad
2
π
位相がずれた成分を,変
形速度で除した値
δ
ω
sin
*
1K
c =
ここに,
f
π
ω2
=
4
伝達率
(transmissibility)
Vτ
−
(
)
(
)2
2
2
2
tan
1
tan
1
δ
ω
ω
δ
τ
+
−
+
=
n
V
ここに,
m
'
K
n=
ω
δ
cos
*
'K
K=
6
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 4 記号
記号
基本単位
記号の説明
対応英語
A
m2
試験片の断面積
test piece cross-sectional area
a(T)
−
WLF式のシフトファクタ
Williams,Landel,Ferry(WLF) shift factor
α
rad
ねじれ角
angle of twist
b
m
試験片の幅
test piece width
c
N・s/m
減衰係数
damping constant
C
−
熱容量
heat capasity
γ
−
ひずみ
strain
γ0
−
最大ひずみ振幅
maximum strain amplitude
δ
rad
損失角
loss angle
E
Pa
たて弾性係数又はヤング率
normal modulus又はYoungʼs modulus
Ec
Pa
弾性係数(圧縮法)
effective Youngʼs modulus
E′
Pa
貯蔵たて弾性係数
storage normal modulus
E′′
Pa
損失たて弾性係数
loss normal modulus
E*
Pa
複素たて弾性係数
complex normal modulus又はcomplex Youngʼs modulus
|E*|
Pa
絶対たて弾性係数
absolute normal modulus
F
N
荷重
load
F0
N
最大荷重振幅
maximum load amplitude
F
Hz
周波数
frequency
G
Pa
せん断弾性係数
shear modulus
G′
Pa
貯蔵せん断弾性係数
storage shear modulus
G′′
Pa
損失せん断弾性係数
loss shear modulus
G*
Pa
複素せん断弾性係数
complex shear modulus
|G*|
Pa
絶対せん断弾性係数
absolute shear modulus
h
m
試験片の厚さ
test piece thickness
K
N/m
ばね定数
spring constant
K′
N/m
貯蔵ばね定数
storage spring constant
K′′
N/m
損失ばね定数
loss spring constant
K*
N/m
複素ばね定数
complex spring constant
|K*|
N/m
絶対ばね定数
absolute spring constant
k
−
ゴムの硬さで決まる係数
numerical factor
kl
−
ねじりにおける形状係数
shape factor in torsion
Lf
−
損失係数
loss factor
l
m
試験片の有効長さ(つかみ具間距離)
test piece length
λ
−
伸張率
extension ratio
Λ
−
対数減衰率
logarithmic decrement
M′
Pa
貯蔵弾性係数
storage modulus
M′′
Pa
損失弾性係数
loss modulus
M*
Pa
複素弾性係数
complex modulus
|M*|
Pa
絶対弾性係数
absolute complex modulus
m
kg
質量
mass
ρ
Mg/m3
ゴムの密度
rubber density
Q
N・m
トルク
torque
S
−
形状係数
shape factor
T
K
試験温度
test temperature
Tg
K
低周波数におけるガラス転移温度
low frequency glass transition temperature
7
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 4 記号(続き)
記号
基本単位
記号の説明
対応英語
T0
K
基準温度
reference temperature
t
s
時間
time
tanδ
−
損失正接
tangent of the loss angle
τ
Pa
応力
stress
τ0
Pa
最大応力振幅
maximum stress amplitude
τ ′
Pa
ひずみと同位相の応力
in phase stress
τ ′′
Pa
ひずみと
rad
2
π
位相がずれた応力
out of phase stress
u
−
減衰比
damping ratio
Vτ
−
伝達率
transmissibillity
ω
rad/s
角周波数
angular frequency
x
m
たわみ
displacement
x0
m
最大たわみ振幅
maximum displacement amplitude
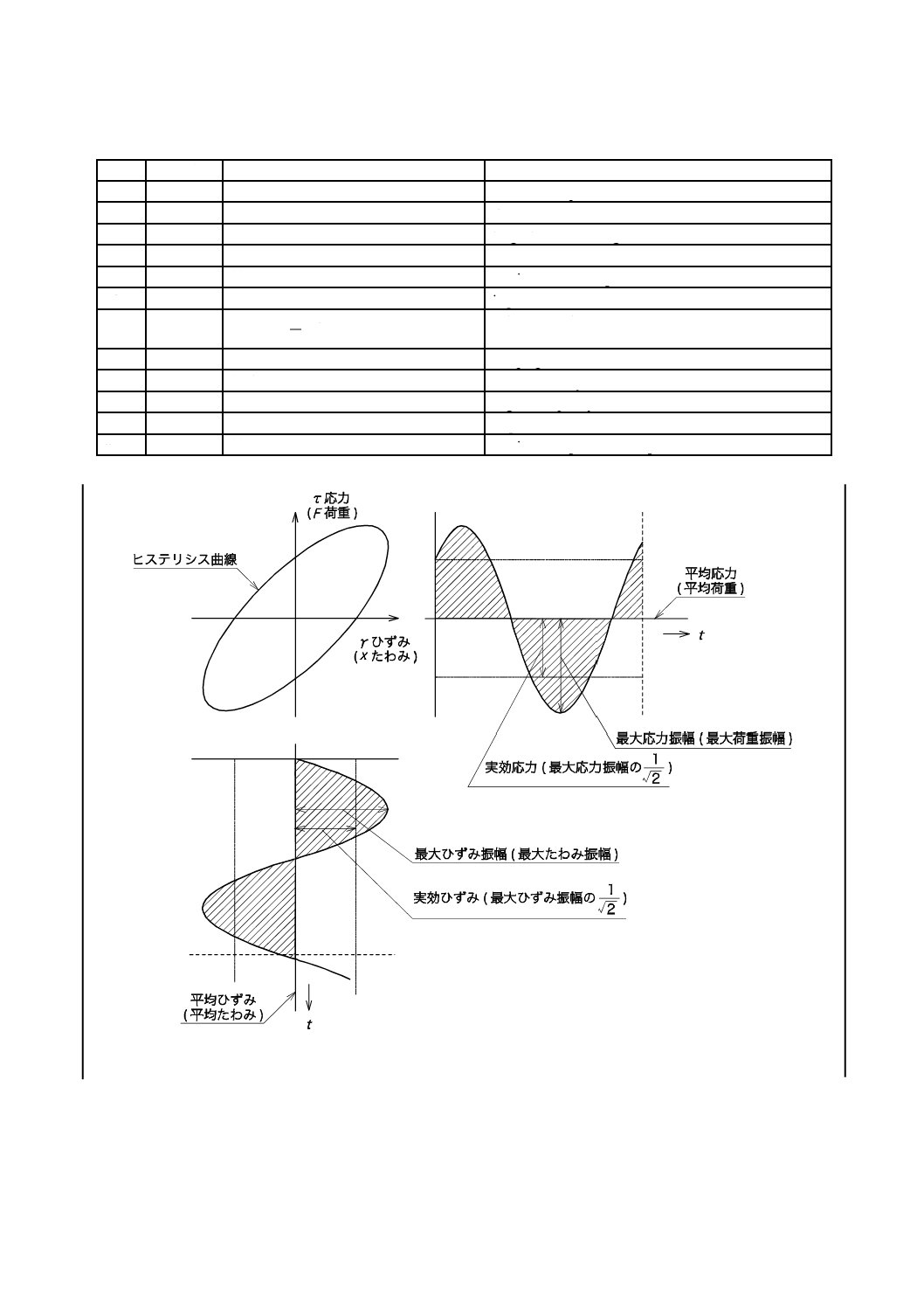
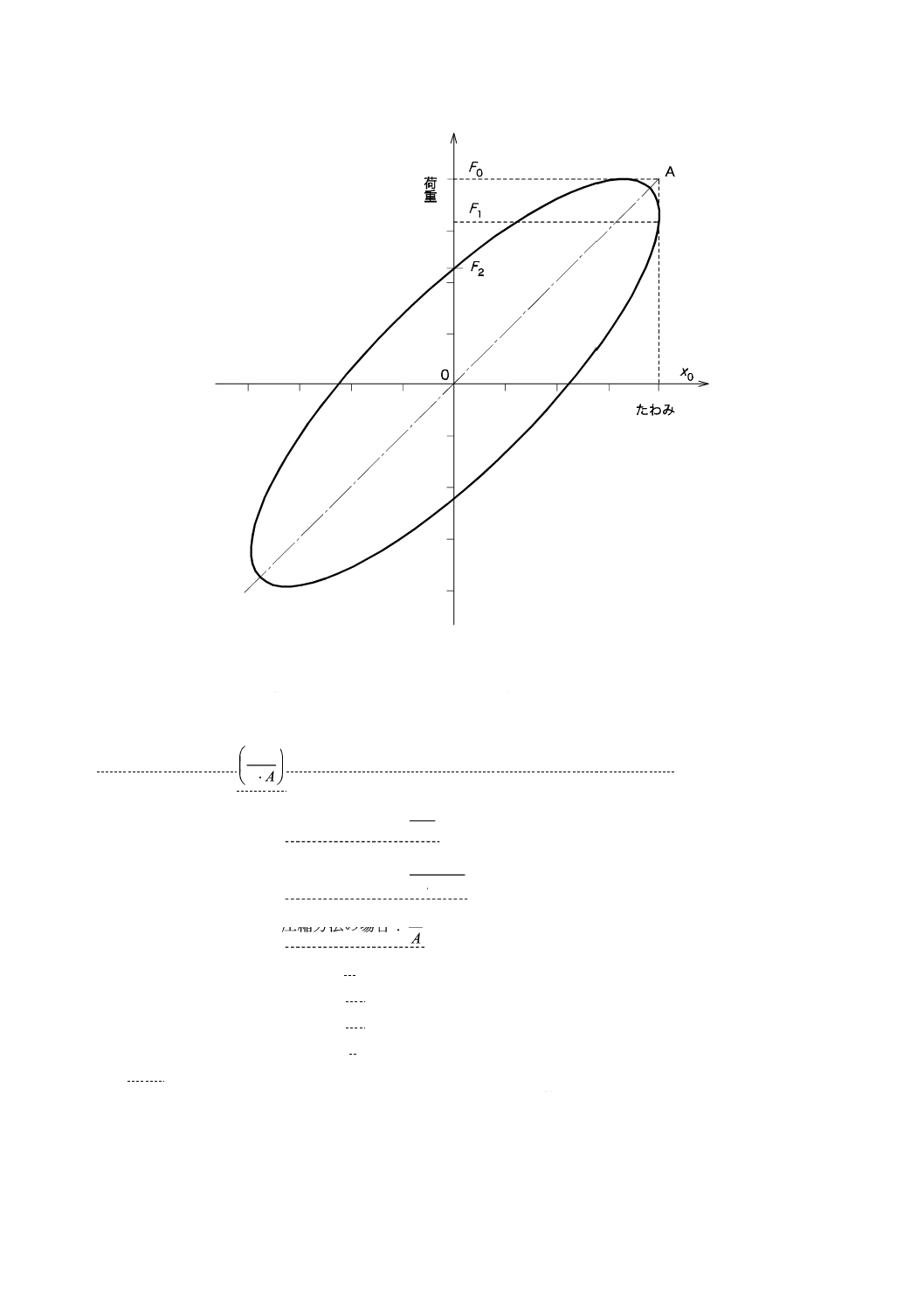
参考図 1 対称な正弦波波形のときの応力とひずみとの関係
8
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考1. ヒステリシス曲線がひずんだときの平均応力と平均ひずみとは,それぞれの波形の山と谷とが作る面
積の釣合いが取れたところで求める。
2. 正弦波運動では,ヒステリシス曲線はだ(楕)円形となる。
なお,静的ひずみを付加した試験では,与えた静的ひずみの大きさによって動的な弾性係数が変化
するために静的ひずみの値を付記する。
図 1 波形がひずんだときの応力とひずみの関係
4. 動的性質の一般事項
4.1
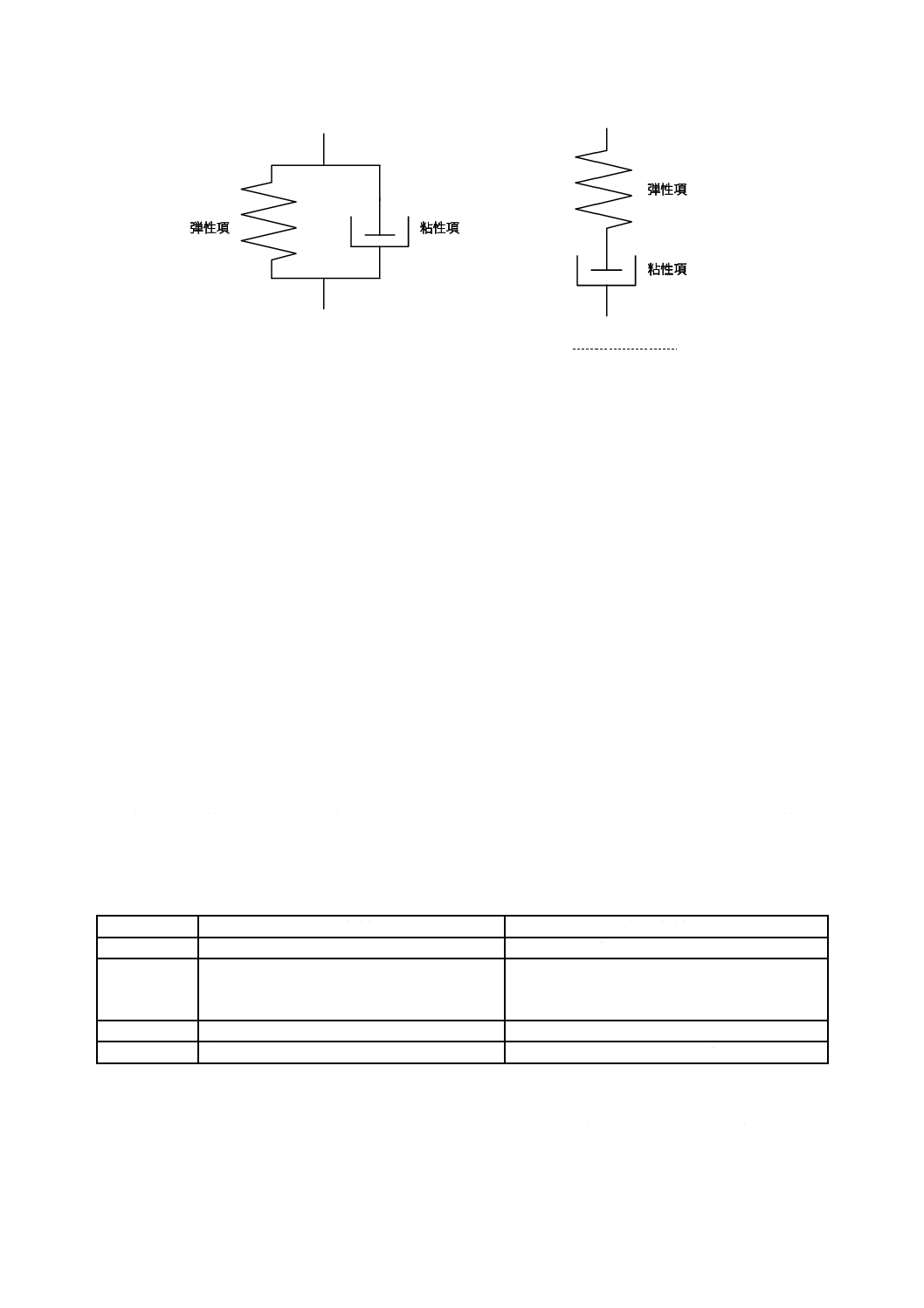
一般事項 物質の変形は,力を加えない限り発生しない。加硫ゴム及び熱可塑性ゴムは,金属など
の弾性体とは異なり粘弾性体である。粘弾性体の動的性質を説明する場合には,図2に示したVoigt−Kelvin
モデル又はMaxwellモデルで,弾性項(ばね)と粘性項(ダッシュポット)との二つの成分に分けると便
利である。粘弾性体は,粘性項の影響によって,荷重,応力などの刺激を与えると,それに対するたわみ,
ひずみなどの変形の応答に時間的な遅れ(位相差)が発生する(4.5.1参照)。したがって,衝撃,振動な
どのエネルギーを減衰させる性質をもっている。加硫ゴム及び熱可塑性ゴムの動的性質は,これらの刺激
及び応答の関係を定量的に表した物理的性質であるといえる。
参考 参考文献:J. D. Ferry,Viscoelastic Properties of Polymers,John Wiley and Sons (1983)
9
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) Voigt−Kelvinモデル
b) Maxwellモデル
図 2 ゴムの力学モデル
4.2
試験の用途 動的性質試験は,材料の特性,設計資料,製品性能などを比較及び評価するために用
いられる。動的性質試験結果は,ひずみ,応力,周波数,試験温度,試験片の形状などに対する依存性が
大きく,試験装置の能力,ヒステリシス曲線の直線性,試験片の内部発熱などの影響によって制約される
場合がある。したがって,結果を比較する場合には,これらの項目を特定化し調整する必要がある。
重要なことは,データを得るための条件及び装置が試験目的に合致していなければならないことである。
小形試験装置のような材料特性を評価するのに適切な装置は,設計資料のデータ採取又は製品特性を測定
するための,周波数,振幅,変形方法などの試験条件で測定を行うことができない場合がある。
4.3
試験の分類 動的性質試験は,試験の用途,振動方法,変形方法などによって選定され,次のよう
に分類される。
a) 振動方法による分類 振動方法には,振動を外部入力によって与え維持させる強制振動方法と,試験
片を固定し,振幅を系の内部摩擦によって減衰させる自由振動方法との2種類の方法がある。さらに,
強制振動方法には,非共振方法と共振方法との2種類の方法がある。
b) 変形方法による分類 変形方法には,圧縮方法,せん断方法,引張方法,曲げ方法及びねじり方法が
ある。
c) 試験装置による分類 試験装置は,試験の用途,振動方法,変形方法,試験片の種類などによって選
定し,実用的には,強制振動方法を用いた大形試験装置及び小形試験装置が一般的である。動的性質
試験の試験装置による分類は,表5による。
表 5 動的性質試験の分類
試験装置
小形試験装置
大形試験装置
試験の目的
材料特性の比較及び評価
設計資料及び製品性能の比較並びに評価
振動方法
強制振動非共振方法
強制振動非共振方法
強制振動共振方法
自由振動方法
変形方法
引張方法,曲げ方法,圧縮方法及びせん断方法 圧縮方法,引張方法,ねじり方法及びせん断方法
試験片の形状 短冊状,円柱状,角柱状
円柱状,角柱状,円すい状及び製品
4.4
試験装置選定の留意点 試験装置選定に当たっての試験方法が与える長所及び短所は,次による。
a) 一般的にせん断方法は,他の変形方法と比較し,応力−ひずみ曲線が大きなひずみまで線形となる。
しかし,試験片は,金属板との組合せが必要となる。
10
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 圧縮方法は,実用条件の再現,特に製品試験に有効であるが,一般的に大きな負荷容量を必要とし,
試験片の形状要素の考慮が必要である。
c) 曲げ方法,ねじり方法及び引張方法は,負荷容量は小さく試験片が簡単に作製できるが,応力の絶対
値を測定するためにはやや不十分である。
d) 設計資料を採取するには,せん断方法で強制振動非共振方法を用いるとよい。
e) 負荷容量が大きく高価な試験装置は,ひずみ振幅が大きいせん断方法,圧縮方法及び製品試験に用い
るために必要である。
f)
材料特性の比較及び評価には,変形方法はあまり重要ではなく,負荷容量の大きな試験装置も必要な
い。周波数,温度及びひずみが自動走査できる試験装置が有効である。
g) 自由振動方法は,通常ねじり方法を用いた低周波数及び低ひずみ振幅の場合に制限される。
h) 強制振動共振方法は,通常曲げ方法に適用され,周波数及び振幅の依存性を測定できない。
4.5
動的運動
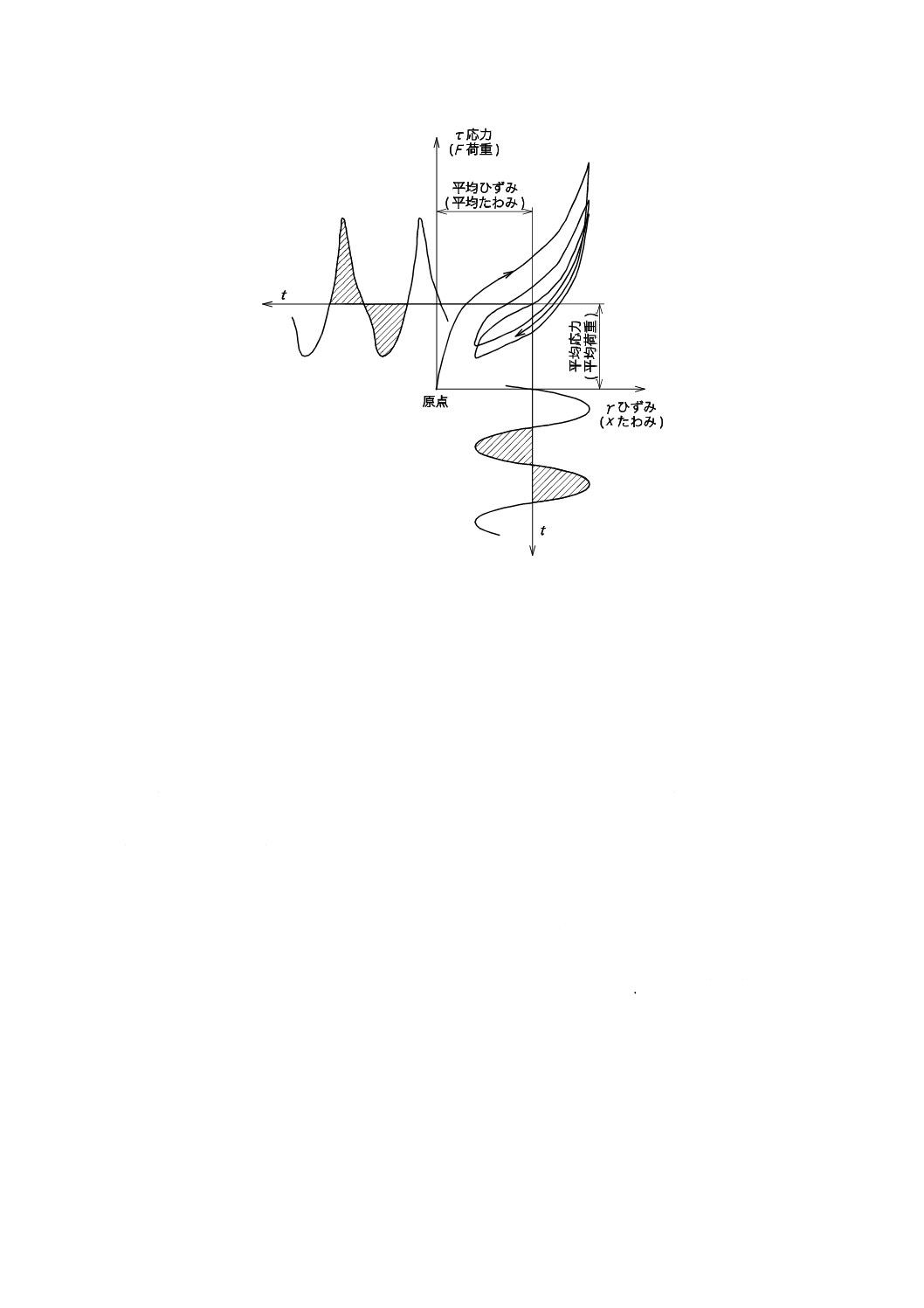
4.5.1
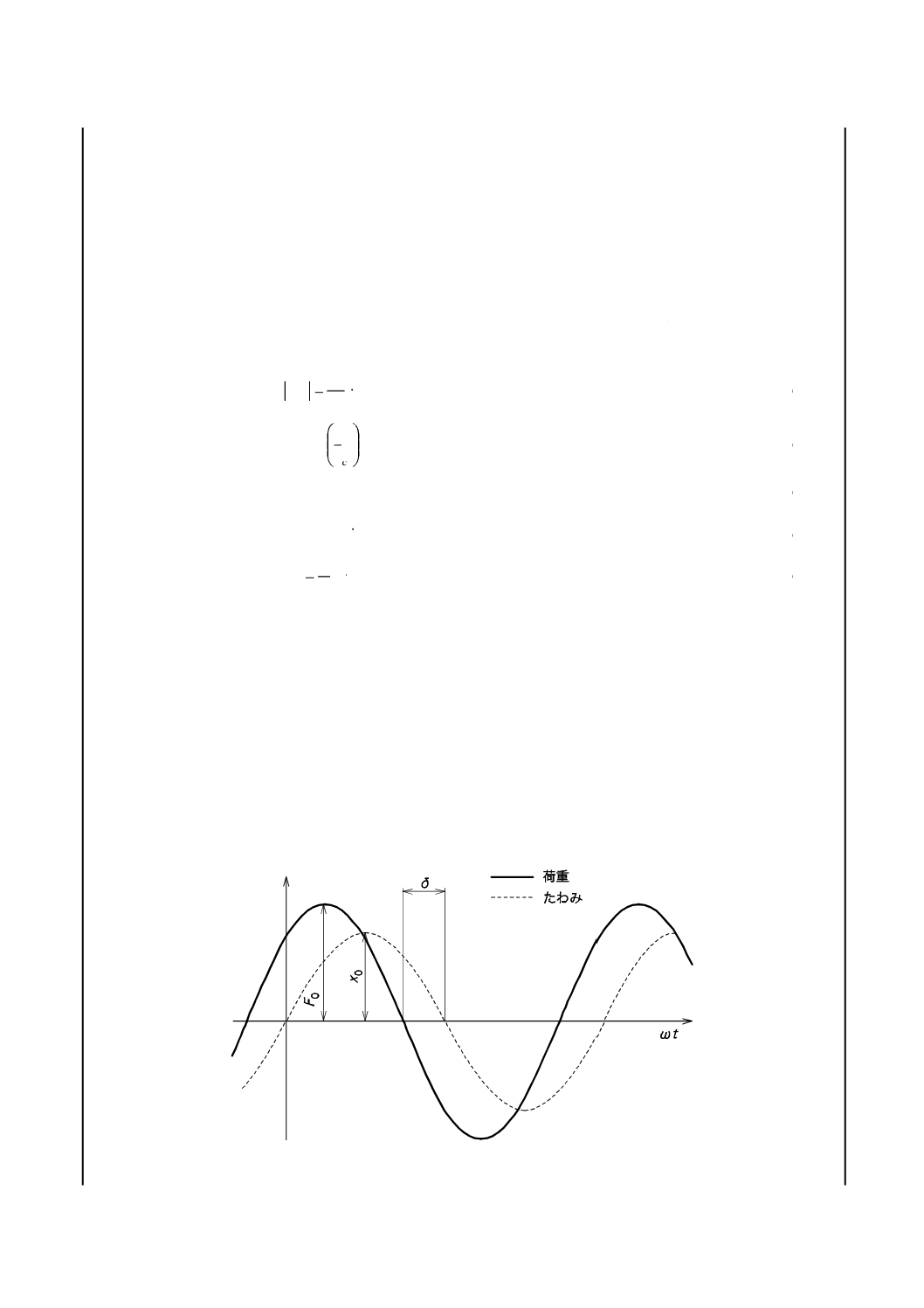
強制振動方法 試験片に正弦波振動を加えた場合の応力及びひずみの時間波形は,図3のとおりで
ある。
図 3 応力及びひずみの時間波形
なお,ひずみは,式(1)によって求める。
t
sin
0
ω
γ
γ=
············································································· (1)
ここに,
γ: ひずみ
γ0: 最大ひずみ振幅
ω: 角周波数(rad/s)
t: 時間(s)
11
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
また,そのときの応力は,ひずみと位相が異なって損失角δ だけ進んでおり,式(2)によって求める。
(
)
δ
ω
τ
τ
+
=
t
sin
0
······································································· (2)
ここに,
τ: 応力(Pa)
τ0: 最大応力振幅(Pa)
δ: 損失角(rad)
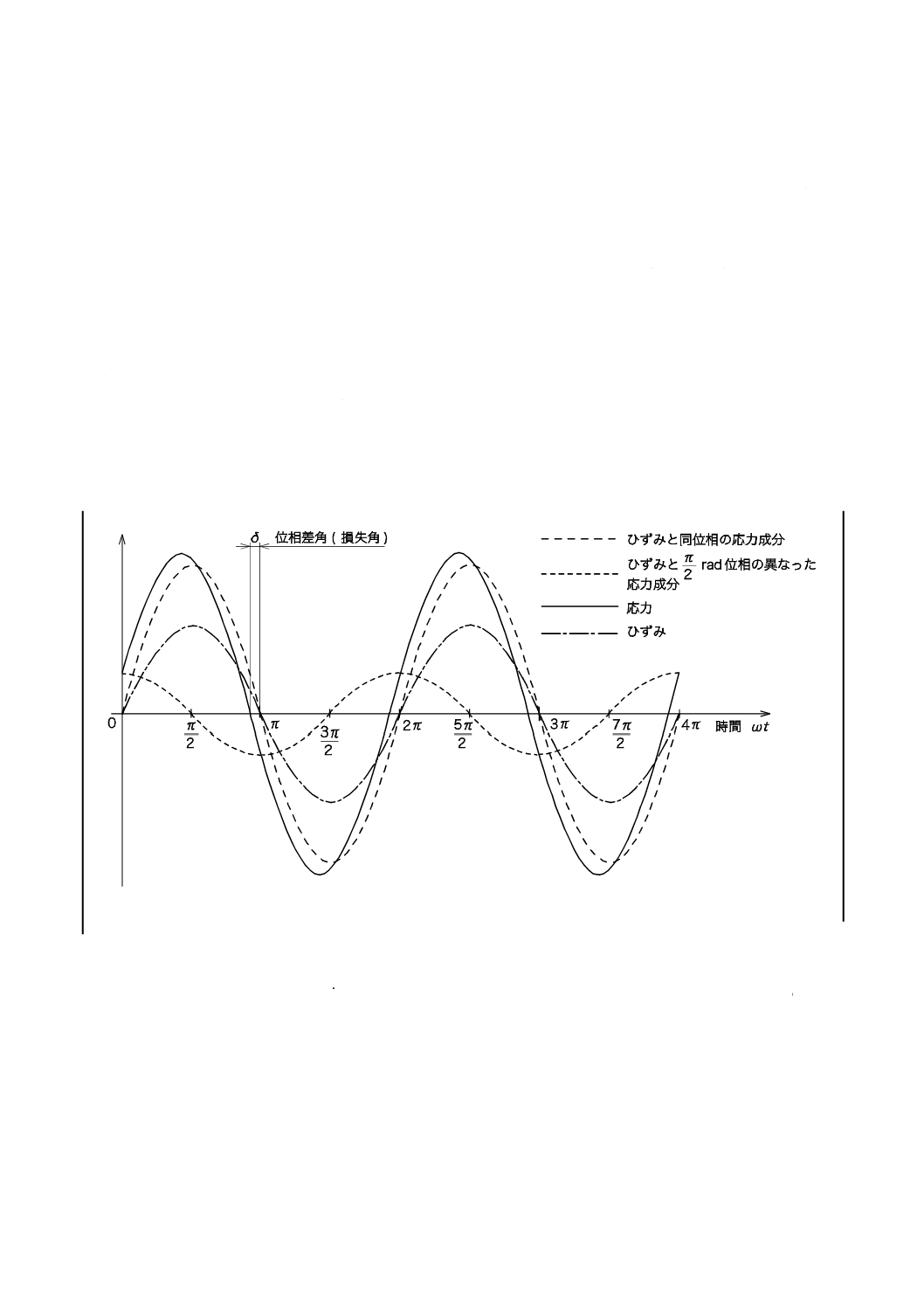
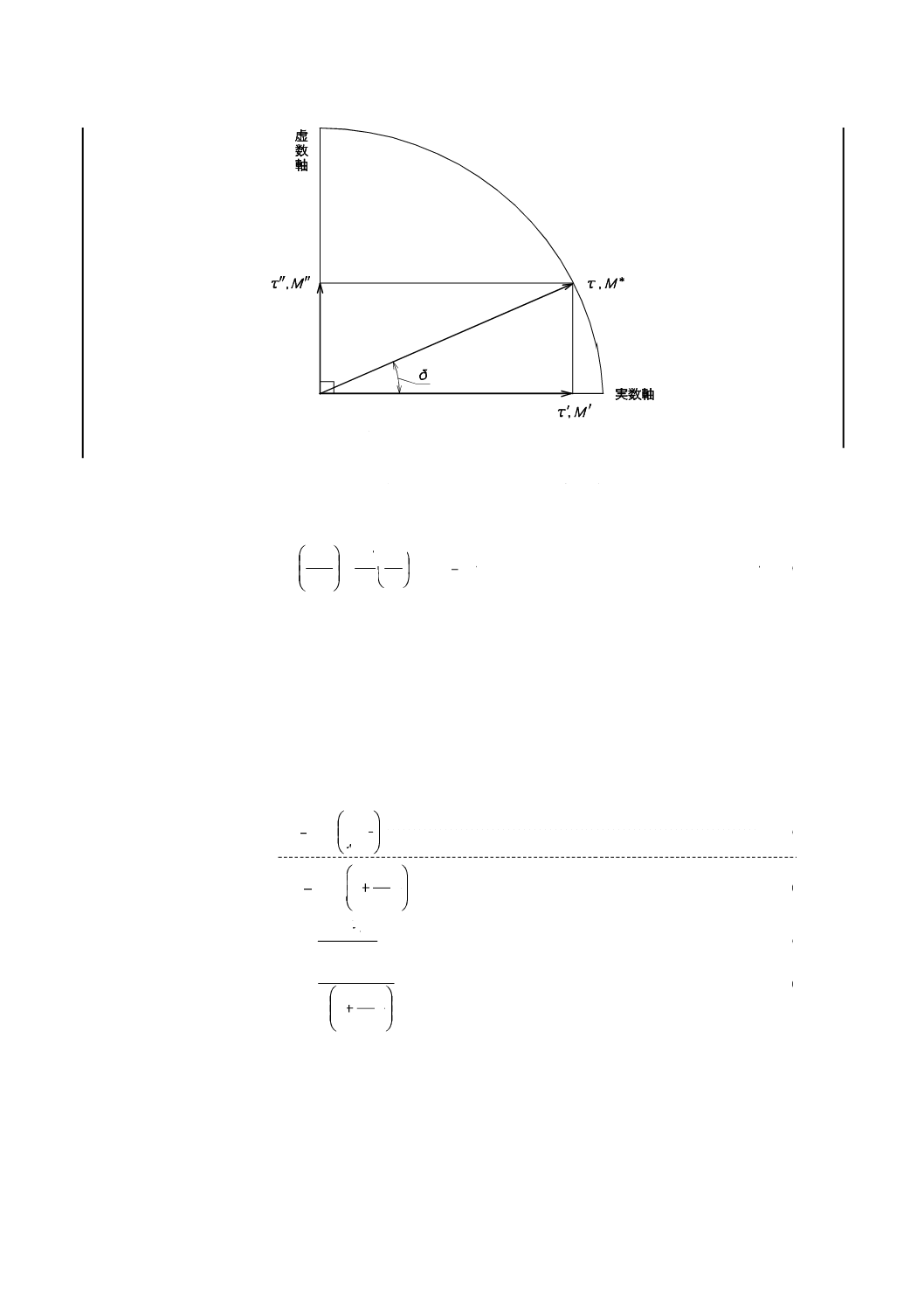
動的性質は,参考図2のような平面上のベクトルを用いて考えると便利である。式(2)の応力τ は,式(1)
のひずみ γ と同位相の応力ベクトルτ ′と
rad
2
π
位相の異なった応力のベクトルτ ′′に分解できる。したが
って,複素弾性係数M*は,貯蔵弾性係数M′と虚数単位(
1
−)とを乗じた損失弾性係数M′′の和として,式
(3)で示される。損失弾性係数に虚数単位を乗じることは,貯蔵弾性係数に対して位相を
rad
2
π
進めたこと
を意味している。
M
i
M
*
M
′′
+′
=
·········································································· (3)
ここに,
M*: 複素弾性係数(Pa)
M′: 貯蔵弾性係数(Pa)
M′′: 損失弾性係数(Pa)
i: 虚数単位=
1
−
貯蔵弾性係数及び損失弾性係数は,式(4)及び式(5)によって求める。
δ
δ
γ
τ
γ
τ
cos
*
cos
0
0
0
M
M
=
=
′
=
′
······················································· (4)
δ
δ
γ
τ
γ
τ
sin
*
sin
0
0
0
M
M
=
=
′′
=
′′
······················································· (5)
ここに, τ′: ひずみと同位相の応力(Pa)
τ′′: ひずみと
rad
2
π
位相の異なった応力(Pa)
複素弾性係数の大きさを表す絶対弾性係数は,式(6)によって求める。
()(
)2
2
M
M
*
M
′′
+
′
=
································································· (6)
ここに, |M*|: 絶対弾性係数(Pa)
また,動的運動によって損失したエネルギー量を表す損失正接は,式(7)によって求める。
M
M
′
′′
=
δ
tan
··············································································· (7)
ここに, tan δ: 損失正接
12
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図 2 複素平面上のベクトルで表した動的性質
4.5.2
自由振動方法 加硫ゴム及び熱可塑性ゴムと質量との系を考え自由に振動させたときの運動方程
式は,式(8)になる。
0
2
2
=
′
+
′′
+
x
K
dt
dx
K
dt
x
d
m
ω
························································· (8)
ここに,
K′: 貯蔵ばね定数(N/m)
K′′: 損失ばね定数(N/m)
m: 質量(kg)
x: たわみ(m)
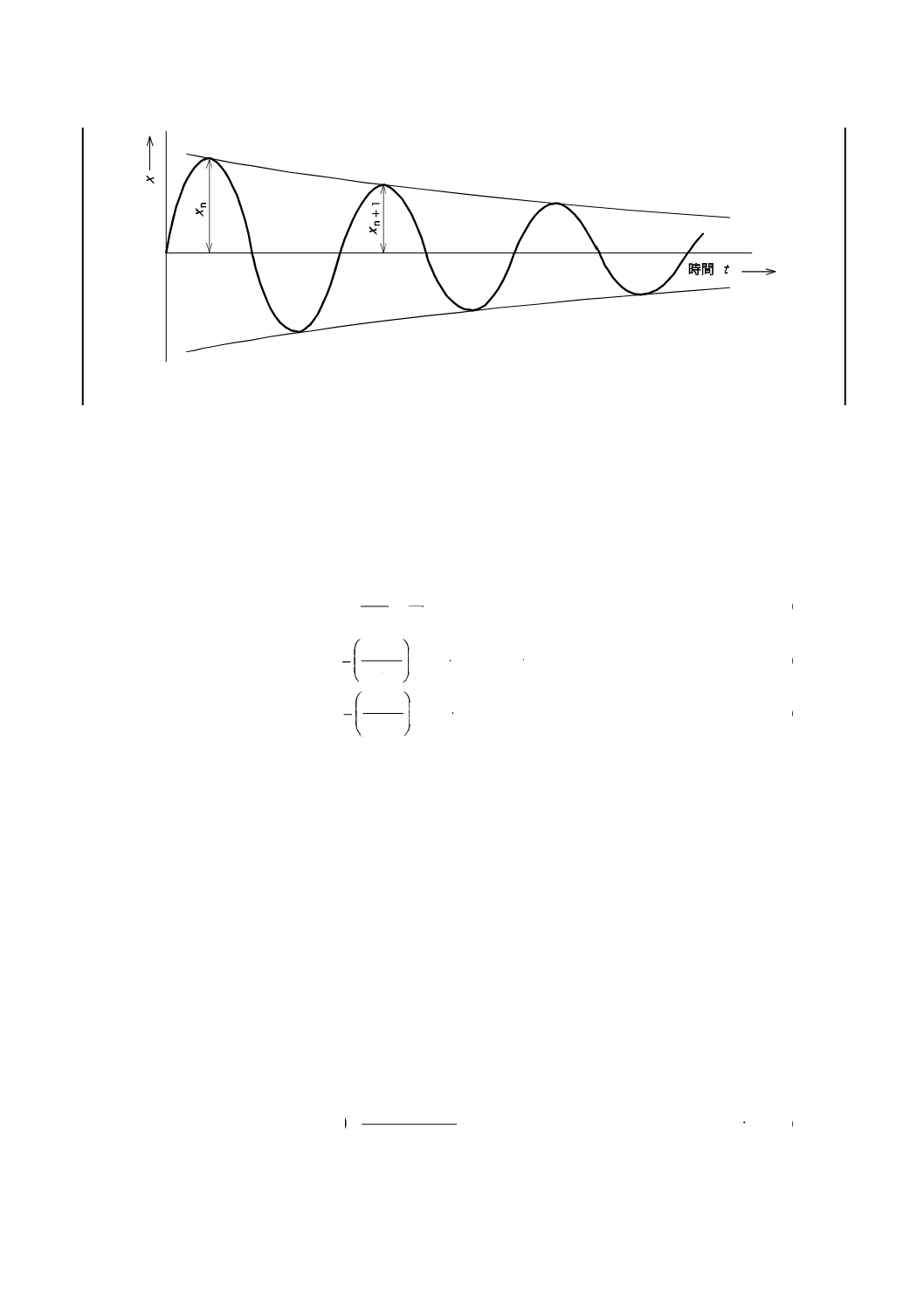
自由振動方法は,参考図3に示す減衰振動の波形を考え,振幅が徐々に減少することから,振幅の減衰
の自然対数をとり対数減衰率を式(9)によって求め,貯蔵ばね定数,損失ばね定数及び損失係数は,式(10)
〜(12)によって求める。
=
+1
log
n
n
ex
x
Λ
·········································································· (9)
+
=
′
2
2
2
4
1
π
Λ
ω
m
K
··································································· (10)
π
Λ
ω
=
′′
2
m
K
··········································································(11)
+
=
2
2
4
1
π
Λ
π
Λ
f
L
····································································· (12)
ここに,
Λ: 対数減衰率
n: 振動の回数
xn: 周期n時の振幅(m)
xn+1: 周期n+1時の振幅(m)
Lf: 損失係数
13
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図 3 自由振動方法のときの時間波形
4.6
周波数と温度との換算 広範囲にわたる周波数及び温度の試験が要求される場合には,試験装置の
能力によっては測定領域外となり試験ができない場合がある。この場合,低温度時の弾性係数と高周波数
時の弾性係数とに同じような変化が見られることから,この温度と周波数との相互依存性を利用した換算
方法がある。周波数の換算は,WLF (Williams,Landel,Ferry)の実験式(13)を用いてWLFのシフトファク
タa(T)を求めることによってできる。また,換算した周波数における換算弾性係数は,式(14)及び式(15)
で試験温度を変化させ左辺を求め,同じ式によって求める。
()
(
)
(
)
0
2
0
1
10
log
T
T
C
T
T
C
T
a
−
+
−
−
=
···························································· (13)
(
)
[
]
0
0
0
)
(
,
T
T
a
f
M
T
T
T
f
M
,
′
=
′
ρ
ρ
·············································· (14)
(
)
[
]
0
0
0
)
(
,
T
T
a
f
M
T
T
T
f
M
,
′′
=
′′
ρ
ρ
············································· (15)
ここに,
a(T): WLFのシフトファクタ
T: 試験温度(K)
T0: 基準温度(K)
C1,C2: 物質係数
M′ (f,T): 実験貯蔵弾性係数(Pa)
M′′ (f,T): 実験損失弾性係数(Pa)
M′ [f・a(T),T0]: 換算貯蔵弾性係数(Pa)
M′′ [f・a(T),T0]: 換算損失弾性係数(Pa)
f: 実験周波数(Hz)
f・a(T): 換算周波数(Hz)
ρ: 試験温度でのゴムの密度(Mg/m3)
ρ0: 基準温度でのゴムの密度(Mg/m3)
WLFの式は,概算値を求める場合には,基準温度にガラス転移温度を,C1に17.44を,C2に51.6を代
入し,式(16)によって求める。
()
(
)
(
)
g
g
T
T
T
T
T
a
−
+
−
−
=
6.
51
44
.
17
log10
························································ (16)
ここに, Tg: 低周波数におけるガラス転移温度(K)
14
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
以上の換算方法は,充てん剤又は結晶化領域によって制限があり注意が必要である。温度及び周波数が
広範囲にわたるため得られた換算が適切でないとき,また,実験値に対して一けた以上の温度及び周波数
の換算を行うことは,信頼性を低下させる場合があるので十分な注意が必要である。
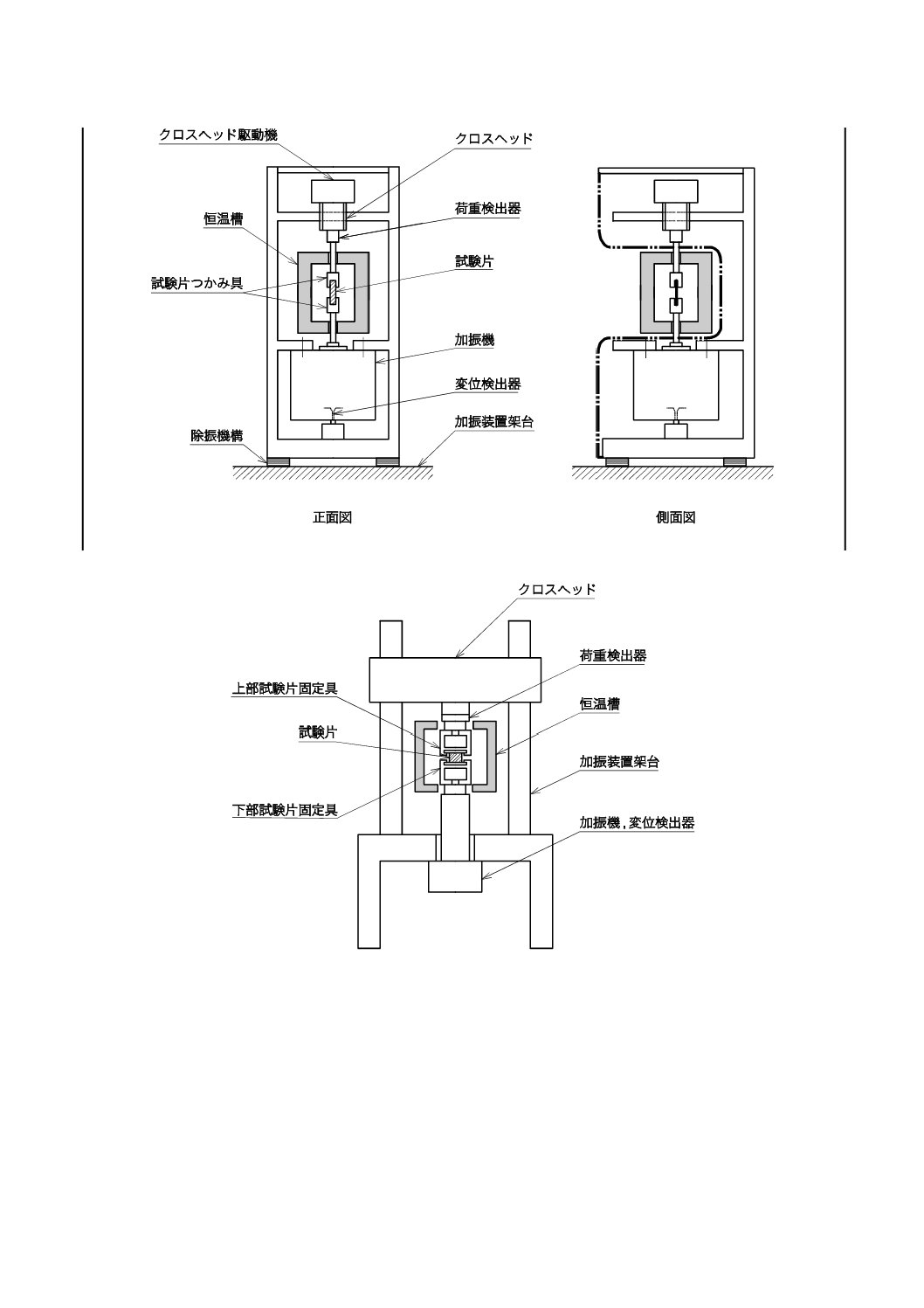
5. 試験装置
5.1
試験装置の概要 試験装置の基本構成は,次による。
なお,強制振動非共振方法を用いたときの,大形試験装置及び小形試験装置の例を,図4及び図5に示
す。また,自由振動方法の試験装置の基本構成は,ISO 4663による。
a) 加振装置架台 加振装置架台は,加振による共振の影響をなくすため,堅固な構造のものを用いるも
のとする。
b) 加振機 加振機は,定常的に安定したたわみ振幅を試験片に与えることができるものとする。また,
加振機から試験片へ伝達される振動は,高調波が10 %を超えない正弦波振動とする。
c) クロスヘッド クロスヘッドは,加振機の反力を受け止め,かつ,荷重検出器に加振機の反力による
振動及び加振装置各部からの振動を伝達させない構造のものとする。
d) 検出器 検出器は,荷重,たわみ,周波数,温度などの実験パラメータが測定できるものとする。
参考 荷重検出器の剛性は,1 μm/定格出力以上のものとする。
なお,剛性を満足できない場合には,荷重検出器のたわみを適切な方法で補正する。
e) 試験片つかみ具又は固定具 試験片つかみ具又は固定具は,試験片の変形方法及び試験装置によって
異なるが,いずれの場合も試験条件範囲で試験片が滑らずに振動を伝達できるものとする。
f)
恒温槽 試験室の標準温度以外に規定された温度で試験を行う場合には,恒温槽を用いる。恒温槽は,
試験片を試験温度に維持できるものとする。
g) 制御回路部 制御回路部は,周波数の発振制御,恒温槽の温度制御,荷重又はたわみを負荷する制御
回路によって構成される。
h) データ処理部 データ処理部は,各検出器からの出力を受け取り,各データの処理,演算及び作図に
よる解析ができるものが望ましい。
i)
試験片寸法測定器 試験片寸法測定器は,JIS K 6250の10.(寸法測定方法)による。
15
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 4 小形試験装置の例
図 5 大形試験装置の例
5.2
試験装置の校正 試験装置の校正は,装置の各パラメータごとに実施し,それぞれの許容差は,表6
による。
なお,静的たわみ及び静的荷重の校正は,JIS K 6272による。

16
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 6 装置の各パラメータの許容差
パラメータ
たわみ
荷重
周波数
温度
試験片寸法
許容差
±1 %
±1 %
±2 %
±1 ℃
±1 %
ねじり振り子を用いた自由振動方法の場合には,試験片つり下げ具の復元力,つり下げ具及びディスク
の減衰に対する補正も行う。
6. 試験片
6.1
試験片の形状及び寸法 試験片の形状及び寸法は,変形方法の種類及び試験装置の容量によって異
なるので,それぞれの試験方法による,試験片の形状及び寸法は,表7,表8及び7.1.7による。金属板と
の加硫接着を施した試験片は,金属板の厚さを成形前に測定しておくことで,ゴムの厚さを事前に推定し
ておく必要がある。
6.2
試験片の採取・作製 試験片の採取・作製は,JIS K 6250の8.(試験片の採取・作製)によって,
成形しても加硫シートから作製してもよい。せん断方法及び圧縮方法の試験片は,成形で作製することが
望ましい。せん断方法及び圧縮方法でゴムと金属板とを接着する場合には,加硫接着又は成形後薄膜の接
着剤でゴムと金属板とを接着してもよい。
なお,試験片は,製品の一部から切り出し又はバフ掛けによって採取してもよく,必要に応じて最終製
品を用いてもよい。
6.3
試験片の数 試験片の数は,3個以上が望ましい。
6.4
試験片の厚さ及び直径又は幅の測定 試験片の厚さ(1)及び直径又は幅(2)の測定は,JIS K 6250の10.
(寸法測定方法)による。
なお,金属板と組み合わせた試験片は,JIS B 7507に規定するノギス又はこれと同等以上の精度をもつ
ものを用いて測定する。
注(1) 厚さは,数箇所測定し,その中央値とする。金属板と組み合わせた試験片は,金属板間を測定
する。
(2) 直径又は幅は,試験片厚さ方向中央部を数箇所測定し,その中央値とする。
7. 試験方法
7.1
試験条件
7.1.1
試験室の標準状態 試験室の標準状態は,JIS K 6250の6.(試験室の標準条件)による。
7.1.2
試験片の保管 試験片の保管は,JIS K 6250の7.(試料及び試験片の保管)による。
7.1.3
試験片の状態調節 試験片の状態調節は,次による。
a) 熱的状態調節 試験片は,試験前にJIS K 6250の9.(試験片の状態調節)を行うものとする。次に試
験温度で平衡に達するまで十分な時間調節を行う。特に試験温度が高温の場合には,この温度調節は,
試験片が劣化するため,必要以上長い時間行ってはならない。試験片の温度調節時間は,試験片の大
きさに関係し,JIS K 6250の附属書Aによる。
b) 機械的状態調節 充てん剤入りのゴムの動的性質は,ひずみ及び温度に対する依存性が大きい。再現
性のよい結果を得るためには,試験片を事前に機械的調節をする必要がある。機械的状態調節は,試
験で用いる最大ひずみ及び試験温度で最低6回行い,平衡状態をとるために試験開始まで12時間放置
する。
17
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
なお,平均ひずみを加えて試験を行う場合には,放置時間中,試験片に試験で用いる平均ひずみを
加えておくことが望ましい。
この機械的状態調節は,自由振動方法のような小さなひずみしか与えない場合には,省略してもよ
い。
7.1.4 試験ひずみの一般事項 充てん剤を多く配合したゴムの動的性質は,ひずみに対する依存性を示す。
一般的に,試験ひずみは,実際使用時のひずみに相当するように選定するが,試験装置の能力,応力−ひ
ずみ曲線の直線性及び内部発熱の影響によって制限される。推奨する試験ひずみは,表7,表8及び7.1.7
による。
一連の試験において,これらのひずみ振幅すべてが要求されるわけではない。どれか一つのひずみ振幅
が使われた場合,その値が試験目的に合致していなければならない。
実際は,試験装置の感度によっては,与えるひずみの下限側が制限されたり,高周波数域及びガラス転
移温度付近では,与えるひずみの上限側が制限される場合がある。実際の使用時に製品は,静的ひずみと
動的ひずみとを同時に受けることがあり,静的ひずみは,必ずしも同じ変形方法とは限らない。このよう
な条件に対して適切な結果を得るためには,動的ひずみを静的ひずみに重複させて与えてもよい。この方
法は,主に製品試験に適用され,通常は圧縮用試験片に適用される。
7.1.5
試験周波数及び試験温度の一般事項 試験ひずみと同様に加硫ゴム及び熱可塑性ゴムは,周波数及
び温度に対する依存性をもつ。この依存性は,特に転移点付近では大きく見られる。したがって,実際の
使用に適した周波数及び温度を選択する必要がある。材料の比較及び評価を行う場合には,広範囲の周波
数及び温度における測定が要求される場合がある。推奨する試験周波数及び試験温度は,表7,表8及び
7.1.7による。
7.1.6
強制振動非共振方法を用いたときの試験片及び試験条件 強制振動非共振方法を用いたときの試
験片及び試験条件は,次による。
18
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
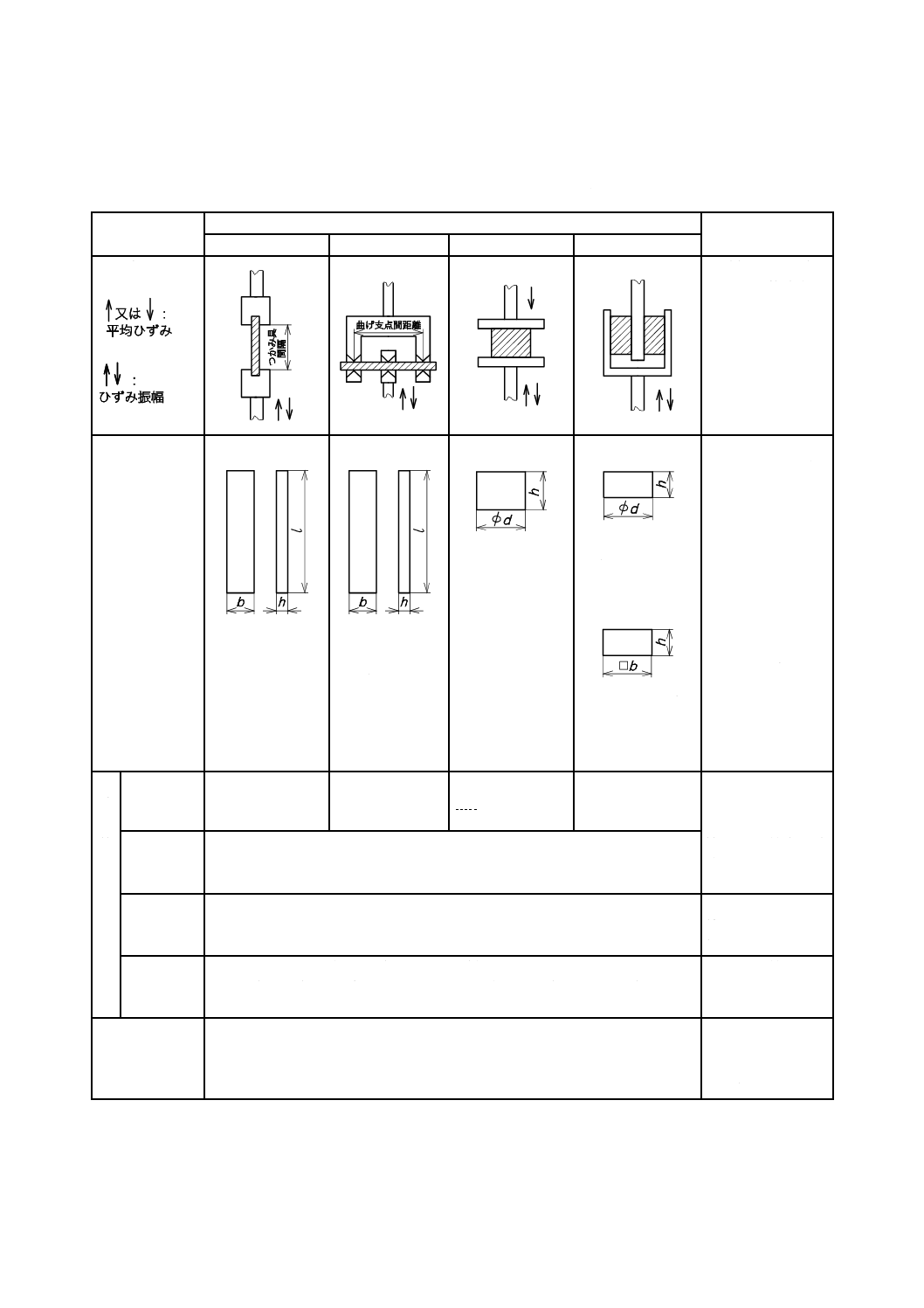
a) 小形試験装置 小形試験装置を用いたときの試験片及び試験条件は,表7による。
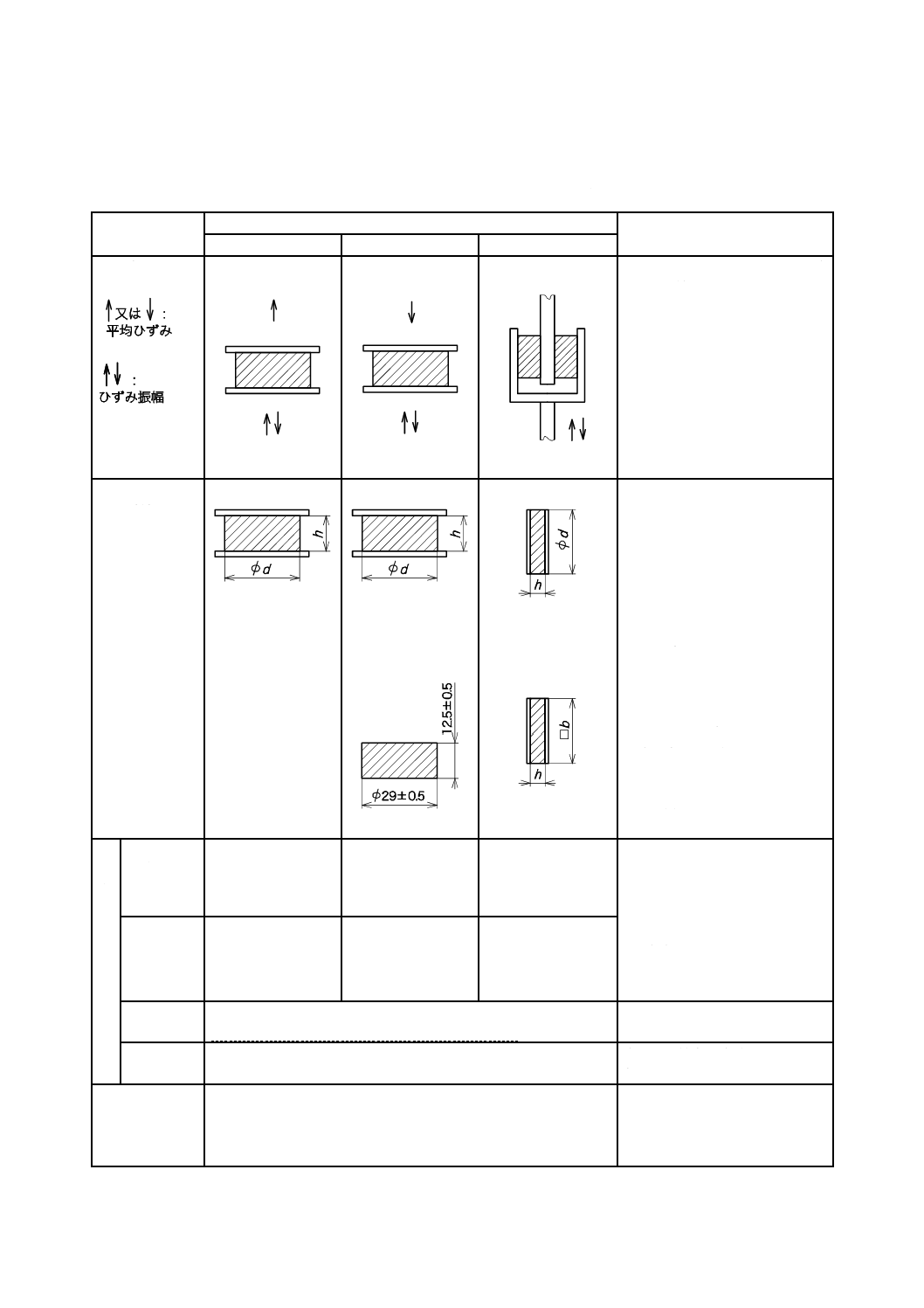
表 7 小形試験装置を用いたときの試験片及び試験条件
変形方法
備考
引張方法
曲げ方法
圧縮方法
せん断方法
試験方法
曲げ方法は,通常ゴ
ム−繊維複合体な
どの弾性率が高く
比較的曲げにくい
材料に適用される。
試験片の形状
及び寸法
短冊状
つかみ具間隔は,
幅(b)の2.5倍から
5倍とする。
h=1〜3 mm
b=4〜12 mm
つかみ具間隔
=20〜60 mm
短冊状
曲げ支点間距離
は,厚さ(h)の16
倍が望ましい。
h=1〜3 mm
b=4〜12 mm
円柱状
h:d≒1:1.5
h=1〜5 mm
円柱状
h:d=1:4以上
h≦12 mm
角柱状
h:b=1:4以上
h≦12 mm
試験片の寸法は,引
張方法及び曲げ方
法の場合,厚さ,幅
及びつかみ具間距
離又は曲げ支点間
距離を測定し,圧縮
方法及びせん断方
法の場合,厚さ及び
幅又は直径を測定
する。各寸法は,±
1 %以内で測定で
きなければならな
い。
試
験
条
件
平均ひずみ
%
1〜10
0
1〜10
0
与える条件が装置
パラメータに依存
する場合がある。
検出器の最大許容
差は,±1 %以内が
望ましい。
ひずみ振幅
%
±0.5,±1,±2
ひずみを走査するひずみ特性を測定してもよい。
周波数
Hz
1,5,10,15,30,50,100,150,200
周波数を走査する周波数特性を測定してもよい。
周波数の最大許容
差は,±2 %以内が
望ましい。
試験温度
℃
JIS K 6250の11.2(試験温度及び試験湿度)から選択
特性が急激に変化する転移点付近では,より細かい温度が必要な場合がある。
温度を走査する温度特性を測定してもよい。
検出器の最大許容
差は,±1 ℃以内が
望ましい。
結果の評価に
必要な項目
|M*|,M′,M′′,tan δ
温度,ひずみ,周波
数を走査した場合,
結果をグラフで表
す場合がある。
19
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 大形試験装置 大形試験装置を用いたときの試験片及び試験条件は,表8による。
表 8 大形試験装置を用いたときの試験片及び試験条件
変形方法
備考
引張方法
圧縮方法
せん断方法
試験方法
大形試験装置による試験の場合
には,圧縮方法又は引張方法より
も,応力とひずみとの関係に直線
性があり,ヒステリシス曲線が完
全だ円に近くなるせん断方法が
望ましい。
この場合,通常曲げの影響を避け
るため2個の試験片を組み合わせ
て用いる。
この代替えでねじりせん断方法
を用いてもよい。
試験片の形状
及び寸法
金具付円柱状
h:d≒1:1.5
金具付円柱状
h:d≒1:1.5
円柱状
単位 mm
金具付円柱状
h:d=1:4以上
h≦12 mm
金具付角柱状
h:b=1:4以上
h≦12 mm
試験片の厚さ及び直径又は幅は,
±1 %以内で測定できなければ
ならない。
試験片の形状及び寸法は,試験装
置の形式及び容量によって,左記
条件を満足するように選択する。
金具付試験片は,適切な接着剤を
使用してゴムと金具とを接着し
なければならない。
圧縮方法の円柱状試験片は,JIS
K 6254に規定する大形試験片を
用いる。
ねじりせん断方法の円すいせん
断試験片は,直径が約35 mmで,
円すいの角度が5°未満,円すい
とプレートとの角度が3°未満の
ものを用いる。
試
験
条
件
平均ひずみ
%
5〜20
10
0
検出器の最大許容差は,±1 %以
内が望ましい。
試験片に加える平均ひずみ及び
ひずみ振幅は,左記条件に合うよ
う求められた平均たわみ及びた
わみ振幅を用いる。
なお,ひずみを走査するひずみ特
性を測定してもよい。
ひずみ振幅
%
±0.2〜±10
±2,±5
±1,±3,±6,
±10,±15
周波数
Hz
1,5,10,15,30,50,100,150,200
周波数を走査する周波数特性を測定してもよい。
周波数の最大許容差は,±2 %以
内が望ましい。
試験温度
℃
JIS K 6250の11.2(試験温度及び試験湿度)から選択する。
検出器の最大許容差は,±1 ℃以
内が望ましい。
結果の評価に
必要な項目
|M*|,M′,M′′,tan δ
試験結果は,弾性係数及び損失正
接の代わりに,|K*|,K ′,K ′′,Lf
などのばね定数及び損失係数を
求めてもよい。
20
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.1.7
自由振動方法を用いたときの試験片及び試験条件 自由振動方法を用いたときの試験片及び試験
条件は,次による。
a) 試験片の形状及び寸法 試験片の形状及び寸法は,厚さが1〜3 mm,幅が4〜12 mm(厚さとの最大
比が10以下)で,つかみ具間隔が幅の10倍以上(最大が120 mm)となるような長さの短冊状試験
片を用いる。試験片の厚さ,幅及びつかみ具間隔は,±1 %の精度で測定しなければならない。
b) 試験条件 試験条件は,ひずみ振幅が最大0.5 %,周波数が0.1〜10 Hzで,試験温度はJIS K 6250の
11.2(試験温度及び試験湿度)から選択する。
7.2
操作方法 強制振動非共振方法を用いたときの操作方法は,次による。
a) 試験片をつかみ具又は固定具に取り付ける。正弦波振動は,試験片を正しく取り付けたときだけに得
られるため,試験片の取付けは特に重要である。試験片にたわみ,ゆがみなどが生じないように注意
しなければならない。また,試験片を正しく取り付けるために,トルクレンチ,トルクドライバなど
を用いて正常な状態に取り付けなければならない。
b) 試験を行うに当たって,温度特性を測定するときは,低温から高温の順で,周波数特性を測定すると
きは,低周波数から高周波数の順で,ひずみ特性を測定するときは,小ひずみから大ひずみの順で測
定しなければならない。
c) 試験室の標準温度以外の温度で試験を行う場合には,恒温槽を試験温度に設定し,試験片が試験温度
に達するまで十分な時間放置する。
d) 試験片に平均ひずみ又は平均たわみを与え,その後,ひずみ振幅又はたわみ振幅及び試験周波数で振
動を与える。
なお,振幅を安定させるために,最低6回の予備加振を与える(3)。
注(3) 試験片の内部発熱を防ぐために,加振後1分以内に試験を開始することが望ましい。
なお,低振幅及び低周波数での試験の場合,周期が維持される時間は制限する必要はない。
e) 振幅が安定した状態で(4),応力(荷重)及びひずみ(たわみ)の時間波形,又は応力(荷重)−ひず
み(たわみ)のヒステリシス曲線,最大応力(荷重)振幅,最大ひずみ(たわみ)振幅,損失角など
を記録又は採取し,データ解析装置又は作図された記録から試験結果を計算する。
注(4) 大振幅及び高周波数で試験をする場合には,特に試験片が発熱するので,試験時間を短くす
る必要がある。特に転移点付近では,注意が必要となる。試験片の温度上昇は,式(17)で示
した1周期当たりの単位容積当たりのエネルギー損失を用いることによって予測できる。
2
0
*
sin
γ
δ
π
M
········································································ (17)
したがって,試験片の熱損失がない場合には,式(18)によって温度上昇を求めることがで
きる。
c
f
M
2
0
*
sin
γ
δ
π
····································································· (18)
ここに, c: 単位容積当たりの熱容量(MJ/m3 ℃)
(通常は,代表的に1.7 MJ/m3 ℃を用いる。)
試験中,温度上昇に影響を与える時間依存性の変化が起こる場合には,その結果から外挿
し,試験温度に相当する動的性質を求めることができる。また,製品試験の場合には,平衡
温度に達するまで試験を継続することがよい場合がある。

21
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8. 試験結果のまとめ方
8.1
強制振動非共振方法 強制振動非共振方法を用いた場合の動的性質は,一般的に絶対ばね定数,貯
蔵ばね定数,損失ばね定数又はこれらに対応する弾性係数,及び損失係数又は損失正接が必要である。こ
れらは,周波数,振幅又は温度の関数として,表又は図で表すと便利である。
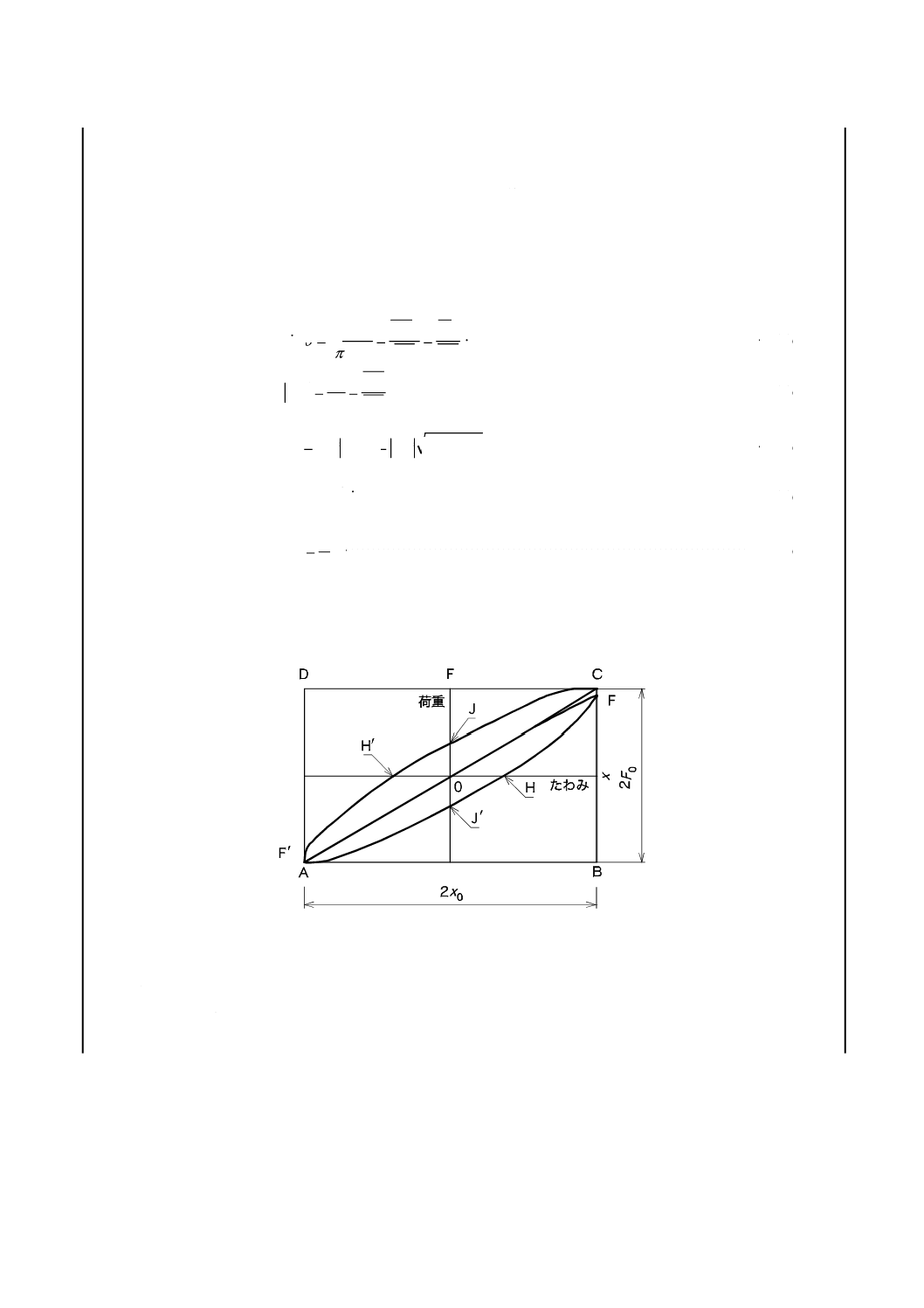
なお,動的性質の結果の求め方の一例は,図6に示したヒステリシス曲線から導くことができる。しか
し,充てん剤を配合したゴム及び大振幅で試験をしたときは,この曲線に非線形挙動が見られ,ヒステリ
シス曲線がだ円とはならず,結果の計算が複雑になる。
図6は,せん断試験片を用いた動的性質試験で得られた荷重−たわみ曲線を示す。静的たわみが付加さ
れているときは,荷重軸とたわみ軸とが交差する点は,ゼロとはならない。したがって,ここに示した荷
重−たわみ曲線は,動的成分だけである。
なお,ゴムでは挙動に線形性があるときに,図6に示したとおりヒステリシス曲線はだ円形となる。
この場合,絶対せん断弾性係数は,式(19)によって求める。
0
0
0
0
2
x
F
A
h
*
G
=
=γτ
··································································· (19)
ここに, F0: 最大荷重振幅(N)
x0: 最大たわみ振幅(m)
A: 試験片の断面積(m2)
h: 試験片の厚さ(m)
したがって,
0
0
x
Fは,定義した長方形の対角線となり,直線0Aの傾きとして表される。
なお,貯蔵せん断弾性係数及び損失せん断弾性係数は,それぞれ,式(20)及び(21)によって求め,更に損
失正接は,式(22)によって求める。
0
1
2
cos
*
x
F
A
h
G
G
=
=
′
δ
····························································· (20)
0
2
2
sin
*
x
F
A
h
G
G
=
=′′
δ
······························································ (21)
G
G
′
′′
=
δ
tan
············································································· (22)
また,損失角は,ヒステリシス曲線で囲まれた面積を用いて,式(23)から求めることもできる。この方
法は,平均損失角δ の値が得られるので,線形性がなくだ円形とならないときに近似できる。
0
0
sin
x
F
=π
δ
だ円の面積 ···································································· (23)
22
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 6 荷重−たわみのヒステリシス曲線
なお,この求め方は,変形方法にせん断方法を用いた場合である。したがって,試験片2個を一組とし
て試験を行うため2で除した式となっている。他の変形方法を用いる場合の動的性質は,せん断方法で用
いた試験片の形状項
A
h
2
を,それぞれ,次に示した形状項に置き換えて求める。
引張方法の場合:
h
b
l
曲げ方法の場合:
3
3
16
h
b
l
圧縮方法の場合:Ah
ここに, A: 試験片の断面積(m2)
b: 試験片の幅(m)
h: 試験片の厚さ(m)
l: 試験片の有効長さ(つかみ具間距離)(m)
参考 具体的な計算方法の例は,附属書1参照。
8.2
自由振動方法 自由振動方法を用いた場合の動的性質の計算は,4.5.2及び8.3によって求める。
8.3
応力及びひずみと形状要素との関係 動的性質試験における,応力及びひずみと形状要素との関係
は,それぞれ次による。
23
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 引張方法及び圧縮方法の場合 引張方法及び圧縮方法の場合の応力とひずみとの関係は,式(24)によ
る。
(
)
2
3
−
−
=
λ
λ
τE
········································································· (24)
ここに,
τ: 応力(Pa)
E: たて弾性係数(Pa)
λ: 伸長比
ただし,試験片と試験片固定具との接する面に接着剤を用いたとき及び金具付きの試験片を用いた
ときの圧縮方法の場合には,式(25)によって求める。
(
)
2
2
1
kS
E
Ec
+
=
······································································ (25)
ここに, Ec:
k:
弾性係数(圧縮法)(Pa)
ゴムの硬さで決まる係数
S: 圧縮における形状係数
b) せん断方法の場合 せん断方法の場合の応力とひずみとの関係は,式(26)による。
γ
τG
=
················································································· (26)
せん断試験の場合は,式(26)のとおり応力とひずみとに比例関係があるため,形状要素を考慮する
必要はない。
c) ねじり方法の場合 ISO 4663に従ったねじり方法の場合には,短冊状試験片を用い,応力とひずみと
の関係は,式(27)になる。
l
a
G
h
b
k
Q
l
=
3
··································································· (27)
ここに,
Q: トルク(N・m)
kl: ねじりにおける形状係数
a: ねじれ角(rad)
b: 試験片の幅(m)
h: 試験片の厚さ(m)
G: せん断弾性係数(Pa)
l: 試験片の有効長さ(つかみ具間距離)(m)
9. 記録 試験成績には,次の事項を記録する。
a) 適用規格番号
b) 試験片の詳細
1) 試料及び試験片の素性の記述
2) 採取・作製方法を含んだ試験片の詳細
3) 試験片の形状及び寸法
c) 試験条件
1) 形式,駆動,測定システムなどを含んだ試験装置の詳細
2) 機械的状態調節方法及び熱的状態調節方法の手順
3) 試験片の数
24
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4) 変形方法
5) 平均ひずみ,ひずみ振幅,試験周波数,試験温度などの試験条件
6) 一点測定以外の場合,試験の順序(温度特性,周波数特性,ひずみ特性などを測定した場合)
7) この規格と異なる方法を用いた場合,その内容
8) 計算方法に用いた手順
d) 試験結果
e) 試験年月日
f)
その他必要事項
25
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1(参考)動的性質の計算方法の例
この附属書は,動的性質の計算方法の例について記載するものであり,規定の一部ではない。
1. 荷重及びたわみの時間波形による方法 荷重及びたわみの時間波形を用いる方法は,記録した波形か
ら最大荷重,最大たわみ,周期及び位相差(時間)を求め(附属書1図1参照),絶対ばね定数,損失角,
貯蔵ばね定数及び損失ばね定数を,式(1)〜(5)によって求める。
0
0
x
F
*
K =
················································································· (1)
=
ct
t
∆
π
δ2
·············································································· (2)
δ
cos
*
K
K=
′
··········································································· (3)
δ
sin
*
K
K=
′′
··········································································· (4)
K
K
Lf
′
′′
=
·················································································· (5)
ここに,
tc: 波形1周期の時間,又は長さ
Δt: 損失角(位相差)の時間,又は長さ
|K*|: 絶対ばね定数(N/m)
K′: 貯蔵ばね定数(N/m)
K′′: 損失ばね定数(N/m)
δ: 損失角(rad)
Lf: 損失係数
F0: 最大荷重振幅(N)
x0: 最大たわみ振幅(m)
附属書1図 1 荷重及びたわみの時間波形
26
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2. 荷重−たわみのヒステリシス曲線による方法 荷重−たわみのヒステリシス曲線による動的性質の計
算は,記録した曲線に外接し,荷重軸,たわみ軸に平行な辺からなる長方形ABCDを描く(附属書1図2
参照),この長方形の面積と荷重−たわみのヒステリシス曲線とで囲まれた部分の面積を求める(この面積
は相対値でもよい。)。又は荷重−たわみのヒステリシス曲線で囲まれた部分の面積の代わりに,附属書1
図2におけるHH'又はJJ'の長さと,AB又はBCの長さとの比を求め,式(6)によって損失角の正弦を求め
る。次に,絶対ばね定数,貯蔵ばね定数,損失ばね定数及び損失係数を,式(7)〜(10)によって求める。
BC
J
J
AB
H
H
W
W
′
=
′
=
=π∆
δ2
sin
··························································· (6)
AB
BC
x
F
*
K
=
=
0
0
········································································· (7)
δ
δ
2
sin
1
*
cos
*
−
=
=
′
K
K
K
······················································ (8)
δ
sin
*
K
K=
′′
··········································································· (9)
K
K
Lf
′
′′
=
················································································ (10)
ここに,
W: 長方形ABCDの面積の1/2
∆W: 荷重−たわみ曲線で囲まれた部分の面積
附属書1図 2 荷重−たわみ曲線
3. データ処理機による方法 データ処理機による方法は,荷重及びたわみの時間波形から求める方法,
ヒステリシス曲線から求める方法,荷重及びたわみの時間波形を基にフーリエ変換を利用した方法などが
ある。
27
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
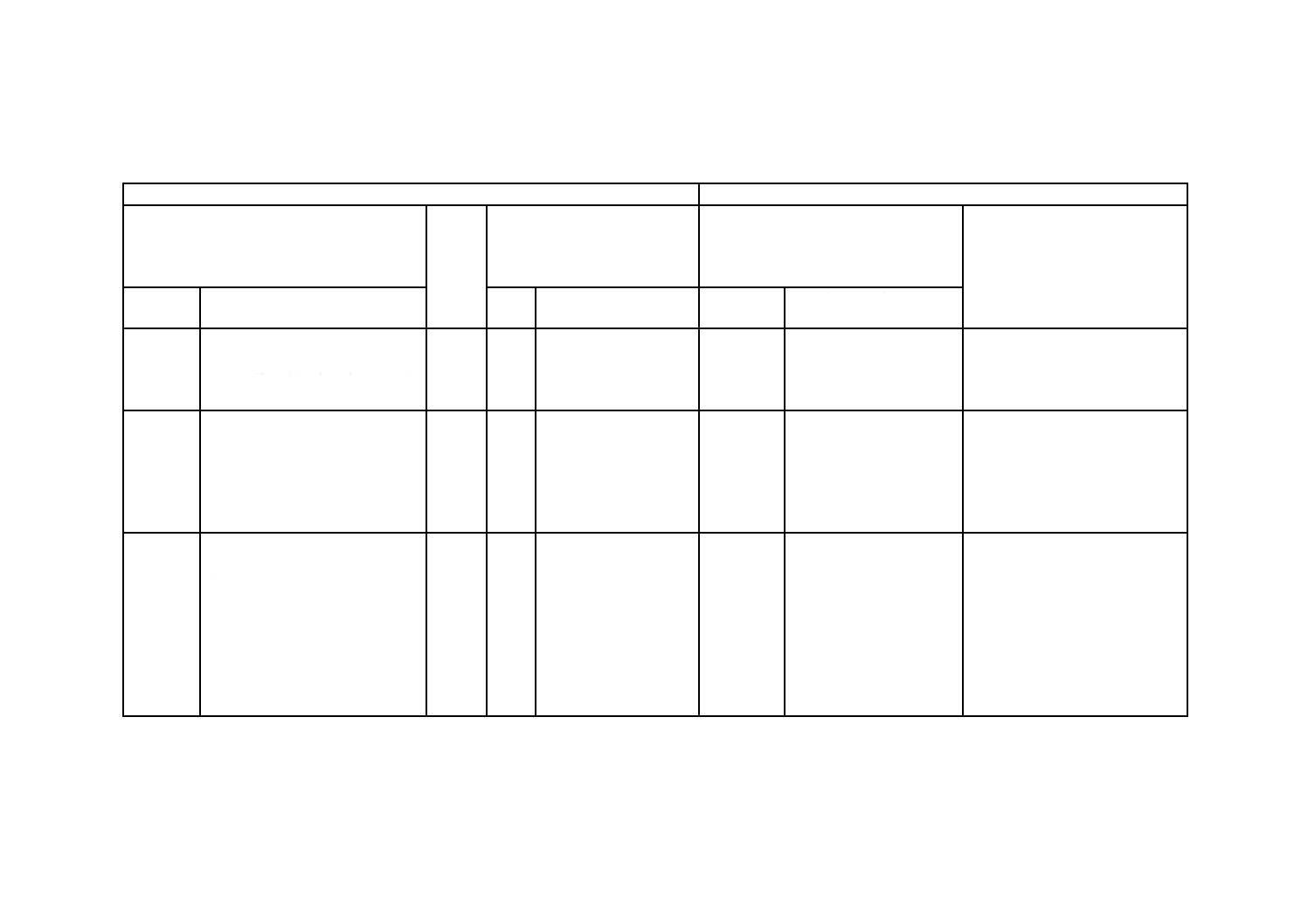
附属書2(参考)JISと対応する国際規格との対比表
JIS K 6394:2007 加硫ゴム及び熱可塑性ゴム−動的性質の求め方−一般指針
ISO 4664-1:2005 加硫ゴム及び熱可塑性ゴム−動的性質の求め方−ガイド
(Ⅰ) JISの規定
(Ⅱ) 国
際規格
番号
(Ⅲ) 国際規格の規定
(Ⅳ) JISと国際規格との技術的差異の項
目ごとの評価及びその内容
表示箇所:本体及び附属書
表示方法:点線の下線又は実線の側線
(Ⅴ) JISと国際規格との技術的差異
の理由及び今後の対策
項目
番号
内容
項目
番号
内容
項目ごと
の評価
技術的差異の内容
1. 適用範
囲
加硫ゴム及び熱可塑性ゴムの自
由振動方法及び強制振動方法に
よる動的性質の求め方の一般指
針について規定。
ISO
4664
1
JISと同じ。
IDT
−
−
2. 引用規
格
JIS B 7507
JIS K 6200
JIS K 6250
JIS K 6254
JIS K 6272
ISO 4663
2
−
−
ISO 23529
ISO 7743
ISO 5893
ISO 4663
MOD/追加
MOD/追加
IDT
IDT
IDT
IDT
ノギスのJISを追加。
用語のJISを追加。
−
−
−
−
分かりやすくするための追加で,
実質的な差異はない。
−
−
−
−
3. 定義及
び記号
主な用語の定義を規定。
表1 周期的変形に用いる用語
表2 正弦波振動に用いる用語
表3 周期的変形で用いられるそ
の他の用語
表4 記号
3
3.1
3.2
3.3
4
用語及び定義
周期的変形に用いる用
語
正弦波振動に用いる用
語
周期的変形で用いられ
るその他の用語
記号
MOD/追加
IDT
IDT
IDT
IDT
用語のJISを追加。
−
−
−
−
分かりやすくするための追加で,
実質的な差異はない。
−
−
−
−
2
7
K
6
3
9
4
:
2
0
0
7
28
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(Ⅰ) JISの規定
(Ⅱ) 国
際規格
番号
(Ⅲ) 国際規格の規定
(Ⅳ) JISと国際規格との技術的差異の項
目ごとの評価及びその内容
表示箇所:本体及び附属書
表示方法:点線の下線又は実線の側線
(Ⅴ) JISと国際規格との技術的差異
の理由及び今後の対策
項目
番号
内容
項目
番号
内容
項目ごと
の評価
技術的差異の内容
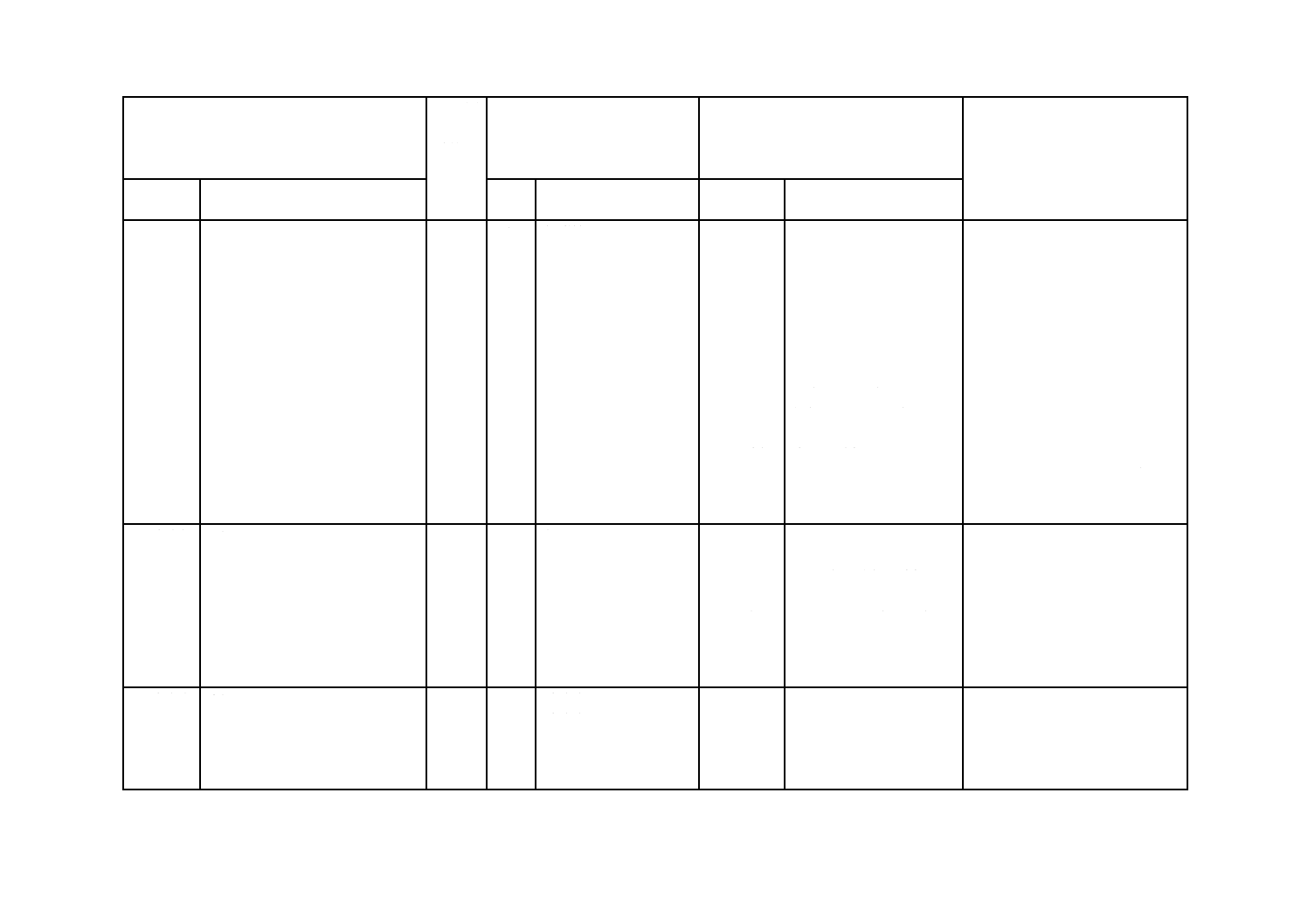
4. 動的性
質の一般
事項
4.1
一般事項
4.2
試験の用途
4.3
試験の分類
4.4
試験装置選定の留意点
4.5
動的運動
4.5.1
強制振動方法
4.5.2
自由振動方法
4.6
周波数と温度との換算
5.1
5.2
5.3
5.4
5.5.1
5.5.2
5.6
粘弾性
動的試験の用途
動的試験の分類
試験装置選定の留意点
強制振動方法
自由振動方法
周波数と温度との換算
MOD/追加
IDT
IDT
IDT
MOD/追加
MOD/追加
IDT
図2 b) Maxwellモデルを
追加。
−
−
−
図3 応力及びひずみの時
間波形に,ひずみと同位相
の応力とひずみとπ/2rad
位相の異なった応力とを
追加。
式(9)を追加。
−
分かりやすくするための追加で,
実質的な差異はない。
−
−
−
分かりやすくするための追加で,
実質的な差異はない。
自由振動方法の概念を説明する
ために必要であり,ISO規格への
追加を提案する。
−
5. 試験装
置
5.1
試験装置の概要
5.2
試験装置の校正
6
7
装置
校正
MOD/追加
MOD/変更
IDT
a) 加振装置架台を追加。
c) クロスヘッドを追加。
g) 制御回路部を追加。
h) データ処理部を追加。
図4を現状に合わせ変更。
−
これらは,分かりやすくするため
の追加で,実質的な差異はない。
試験装置の向きだけの変更で,実
質的な差異はない。
−
6. 試験片 6.1
試験片の形状及び寸法
6.2
試験片の採取・作製
6.3
試験片の数
6.4
試験片の厚さ及び直径又は
幅の測定
8.2
8.1
8.3
−
試験片の寸法
試験片の準備
試験片の数
−
IDT
IDT
IDT
MOD/追加
−
試験片の寸法測定方法を
追加。
−
分かりやすくするための追加で,
実質的な差異はない。
2
8
K
6
3
9
4
:
2
0
0
7
29
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(Ⅰ) JISの規定
(Ⅱ) 国
際規格
番号
(Ⅲ) 国際規格の規定
(Ⅳ) JISと国際規格との技術的差異の項
目ごとの評価及びその内容
表示箇所:本体及び附属書
表示方法:点線の下線又は実線の側線
(Ⅴ) JISと国際規格との技術的差異
の理由及び今後の対策
項目
番号
内容
項目
番号
内容
項目ごと
の評価
技術的差異の内容
7. 試験方
法
7.1.1
試験室の標準状態
7.1.2
試験片の保管
7.1.3
試験片の状態調節
7.1.4
試験ひずみの一般事項
7.1.5
試験周波数及び試験温度
の一般事項
7.1.6
強制振動非共振方法を用
いたときの試験片及び試
験条件
7.1.7
自由振動方法を用いたと
きの試験片及び試験条件
7.2
操作方法
9.1
9.1
9.2
9.3
8.4.1
8.4.2
8.5
8.6
8.7
10
保管
保管
温度
機械的調節
ひずみ
周波数及び温度
小形試験装置
大形試験装置
自由振動方法を用いた
動的試験
試験方法
IDT
IDT
IDT
IDT
IDT
IDT
MOD/追加
MOD/削除
MOD/追加
IDT
MOD/追加
−
引張方法のつかみ具間距
離を追加。
圧縮方法の平均ひずみに
幅をもたせた。
周波数特性の測定をして
もよいことを追加
ひずみ振幅の推奨値を削
除。
ひずみ特性を追加。
−
試験片の取付け方法の詳
細を追加。
−
これらは,ISO規格の規定では試
験ができない場合があり,重要な
事項であることからISO規格へ
の追加を提案する。
重要な事項でありISO規格への
追加を提案する。
推奨試験条件が重複しておりISO
規格の明らかな間違いであり削
除した。
重要な事項でありISO規格への
追加を提案する。
−
分かりやすくするための追加で,
実質的な差異はない。
2
9
K
6
3
9
4
:
2
0
0
7
30
K 6394:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(Ⅰ) JISの規定
(Ⅱ) 国
際規格
番号
(Ⅲ) 国際規格の規定
(Ⅳ) JISと国際規格との技術的差異の項
目ごとの評価及びその内容
表示箇所:本体及び附属書
表示方法:点線の下線又は実線の側線
(Ⅴ) JISと国際規格との技術的差異
の理由及び今後の対策
項目
番号
内容
項目
番号
内容
項目ごと
の評価
技術的差異の内容
8. 試験結
果のまと
め方
8.1
強制振動非共振方法
8.2
自由振動方法
8.3
応力及びひずみと形状要素
との関係
11.1
11.2
11.3
11.4
要求項目
強制振動
自由振動
応力及びひずみと形状
要素との関係
IDT
MOD/追加
IDT
IDT
−
式(20)及び(21)に計算方法
の追加。
せん断方法以外のときの
結果の求め方を追加。
−
−
−
分かりやすくするための追加で,
実質的な差異はない。
−
−
9. 記録
12
記録
MOD/追加
その他必要事項を追加
分かりやすくするための追加で,
実質的な差異はない。
附属書1
(参考)
動的性質の計算方法の例
−
−
−
MOD/追加
−
動的性質の理論式を基に,実際の
実験によって求められたパラメ
ータから導く一般的な計算方法
を参考として記載。
JISと国際規格との対応の程度の全体評価:MOD
備考1. 項目ごとの評価欄の記号の意味は,次のとおりである。
― IDT ·················· 技術的差異がない。
― MOD/削除 ········· 国際規格の規定項目又は規定内容を削除している。
― MOD/追加 ········· 国際規格にない規定項目又は規定内容を追加している。
― MOD/変更 ········· 国際規格にない規定内容を変更している。
2. JISと国際規格との対応の程度の全体評価欄の記号の意味は,次のとおりである。
― MOD ················ 国際規格を修正している。
3
0
K
6
3
9
4
:
2
0
0
7





















