Z 9041-4 : 1999 (ISO 3494 : 1976)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。
今回の制定は,国際規格に整合させるために,ISO 3494 : 1976を基礎として用いた。
JIS Z 9041 : 1999は一般名称を“データの統計的な解釈方法”として,次の各部によって構成される。
第1部:データの統計的記述
第2部:平均と分散に関する検定方法と推定方法
第3部:割合に関する検定方法と推定方法
第4部:平均と分散に関する検定方法の検出力

Z 9041-4 : 1999 (ISO 3494 : 1976)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
第1章:比較検定
−一般的注意 ······················································································································· 1
−歴史的いきさつ ················································································································· 2
平均
箇条
比較検定
分散 参照されるJIS Z 9041-2の書式
1.
与えられた値と平均との比較
既知
A
……………………
3
2.
与えられた値と平均との比較
未知
Aʼ
……………………
4
3.
二つの平均の比較
既知
C
……………………
6
4.
二つの平均の比較
未知
Cʼ
……………………
8
分散
箇条
比較検定
参照されるJIS Z 9041-2の書式
5.
与えられた値と平均との比較
E
…………………………… 11
6.
二つの平均の比較
G
…………………………… 12
第2章:各種曲線
−各種曲線の参照関係 ········································································································· 14
−各種の検出力曲線 ············································································································ 14
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9041-4 : 1999
(ISO 3494 : 1976)
データの統計的な解釈方法−
第4部:平均と分散に関する
検定方法の検出力
Statistical interpretation of data−
Part 4 : Power of tests relating to means and variances
序文
この規格は,1976年に第1版として発行されたISO 3494,Statistical interpretation of data−Power of tests
relating to means and variancesを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工
業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
第1章:比較検定
一般的注意
1) この規格は,“JIS Z 9041-2,データの統計的解釈−平均と分散に関する検定方法と推定方法”の続き
に当たる規格である。
この規格の適用の条件は,JIS Z 9041-2の中で述べられている。すなわち,ここで検討する検定法
は,測定変数が各母集団で正規分布すると仮定されるとき妥当である。JIS Z 9041-2は,第1種の危
険(又は有意水準)だけに関心をおいている。この規格は,第2種の危険と検定の検出力についての
判断の仕方を提言する。
2) JIS Z 9041-2では,第1種の危険について次のように述べている。すなわち,両側検定のときは帰無
仮説(検定される仮説)が真のときにその仮説を棄却する確率であり,片側検定のときはこの確率の
最大値である。帰無仮説を棄却しないことは,現実的には,帰無仮説を受容することになる。しかし,
帰無仮説を棄却しないことは,その仮説が真であることを意味するものではない。
それに対応して,第2種の危険(βと表す)は,帰無仮説が偽のときにそれを棄却しない確率であ
る。この第2種の誤りについての確率の補数(1−β)が,検定の“検出力”である(この一般的注意
の後の“歴史的いきさつ”参照)。
3) 第1種の危険の値は,その危険によって起こる結果に応じて消費者が選択する(通常α=0.05又はα=
0.01が採用される)のに比べ,第2種の危険は,真の仮説(帰無仮説H0が偽であること),すなわち,
帰無仮説に対する対立仮説に依存している。例えば,ある母集団の平均と与えられた値μ0とを比較す
る場合,ある特定の対立仮説は,母集団平均の値がμ≠μ0,すなわち,偏差μ−μ0≠0であることに相
当する。
2
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4) 検定のOC曲線とは,第2種の危険の値βを,対立仮説を定義するパラメータの関数として表した曲線
である。βは,第1種の危険に選んだ値,サンプルサイズ,検定の性質(両側検定か片側検定か)な
どにも依存している。平均値の比較においては,βは母集団の標準偏差にも依存する。この値が未知
のとき,危険率βは正確には分からない。
5) OC曲線は,次の問題に対処する。
a) 問題1:与えられた対立仮説と与えられたサンプルサイズについて,帰無仮説を棄却しない確率β(第
2種の危険)を決定する。
b) 問題2:与えられた対立仮説と与えられたβについて,選択すべきサンプルサイズを決定する。
曲線のセットが一つあれば両方の問題に対処することができるが,実用的な応用を容易にするため,2
種類のセットが示される。
− 図1.1〜14.1,α=0.05又はα=0.01と,各種サンプルサイズについて,対立仮説の関数として危険β
を与える。
− 図1.2〜14.2,α=0.05又はα=0.01と,各種の危険βの値について,対立仮説の関数として選択すべ
きサンプルサイズを与える。
6) 仮説の検定や曲線による統計量の解釈の実用上の意義に注意する。例えばμ=μ0(又はμ1=μ2)のよう
な仮説を検定するとき,μとμ0とがあまり大きくは違わない(又はμ1とμ2とがあまり大きくは違わな
い)ことを,ほとんど誤ることなしに結論できるかどうかを知ることが一般的に望まれる。また,検
定に対する第1種の危険についてα=0.05又はα=0.01の値を選択することは,ある程度し(恣)意的
なものである。ゆえに,できる限りα=0.05とα=0.01の両方の第1種の危険の値を用い,値がμ0に近
い(又は差D=μ1−μ2の値が0に近い)ときどのような検定結果になるのか調べてみること,また,
この状況で,OC曲線を用いていろいろな対立仮説に対する危険βを評価することは有用であろう。
7) この規格の第2章で与えられる曲線セットは,以下の6つの節で記述され議論される。これら節は,
JIS Z 9041-2中の書式に対応している。
各種の曲線セットと,解決される問題,この規格とJIS Z 9041-2の書式などの間の詳細な対応は,
各図の上部に示される。
参考 JIS Z 9041-2データの統計的解釈−第2部:平均と分散に関する検定方法と推定方法からの引
用事項は,ISO 2602 : 1980 Statistical interpretation of test results−Estimation of the mean−
Confidence interval, ISO 2854 : 1976 Statistical interpretation of data−Techniques of estimation and
tests relating to means and variances, ISO 3301 : 1975 Statistical interpretation of data−Comparison of
two means in the case of paired observationsの該当事項と同等である。
歴史的いきさつ
“第1種の危険”と“第2種の危険”の概念は,J. NeymanとE. S. Pearsonによって,1928年に発表さ
れた論文によって導入された。その後,著者らは第2種の誤りに関して,確率の補数の方が利用者にとっ
て一般により理解しやすい概念であると考えた。帰無仮説(検定している仮説)に対して特定した対立仮
説を有意として検出する性質から,彼らはそれを検定の“検出力”と呼んだ。これがいま論じている“検
出力”であり,与えられた帰無仮説からの偏差を検出する確率である。この確率を,彼らはβという記号
で表した。
“検出力”という用語を,改めて導入する必要はない。そのような確率についてより簡単に語ることが
できる。すなわち,あるサンプルに対し有意水準αで統計的検定を行い,母集団のパラメータλが,少なく
ともある与えられた量だけある特定の値λ0とは異なることを(実際にそのような差があるとき)検出する
3
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
確率,又はλとλ0との比が,少なくともある与えられた数値になることを検出する確率である。
おそらくは,アメリカ合衆国の統計学の産業応用の利用者によって,表記法の変更が導入された。これ
は,βで表される“消費者の危険”を“生産者の危険α”と同時に考慮することを望んだためである。
JIS Z 8101,統計−用語と記号では,第2種の危険に“β”という記号が採用された。それゆえ,この規
格中でも同じ意義で採用されてきた。しかしながら,統計学の文献中で両方の意味でβが利用されており,
また,疑いなく今後も使い続けられるであろうことから,各利用例について,どちらの意味で用いられて
いるかを調べておくべきであろう。
1. 与えられた値と平均との比較(分散既知)
JIS Z 9041-2の書式A参照。
1.1
記法
n = サンプルサイズ
μ = 母集団平均
μ0 = 与えられた値
σ = 母集団における標準偏差
1.2
検定される仮説
両側検定に関して,帰無仮説はμ=μ0であり,それに対応する対立仮説はμ≠μ0である。
片側検定のときには,帰無仮説は次のどちらかである。
a) μ≦μ0,対応する対立仮説はμ>μ0
b) μ≧μ0,対応する対立仮説はμ<μ0
1.3
問題1 : nを与えて,危険βを決定する
様々なμの値に対して,対立仮説はパラメータλ(0<λ<∞)によって次のように定義される。
a)
σ
μ
μ
λ
0
−
=
n
(両側検定)対立仮説μ≠μ0
b)
σ
μ
μ
λ
)
(
0
−
=n
(片側検定μ≦μ0)対立仮説μ>μ0
c)
σ
μ
μ
λ
)
(
0
−
−
=
n
(片側検定μ≧μ0)対立仮説μ<μ0
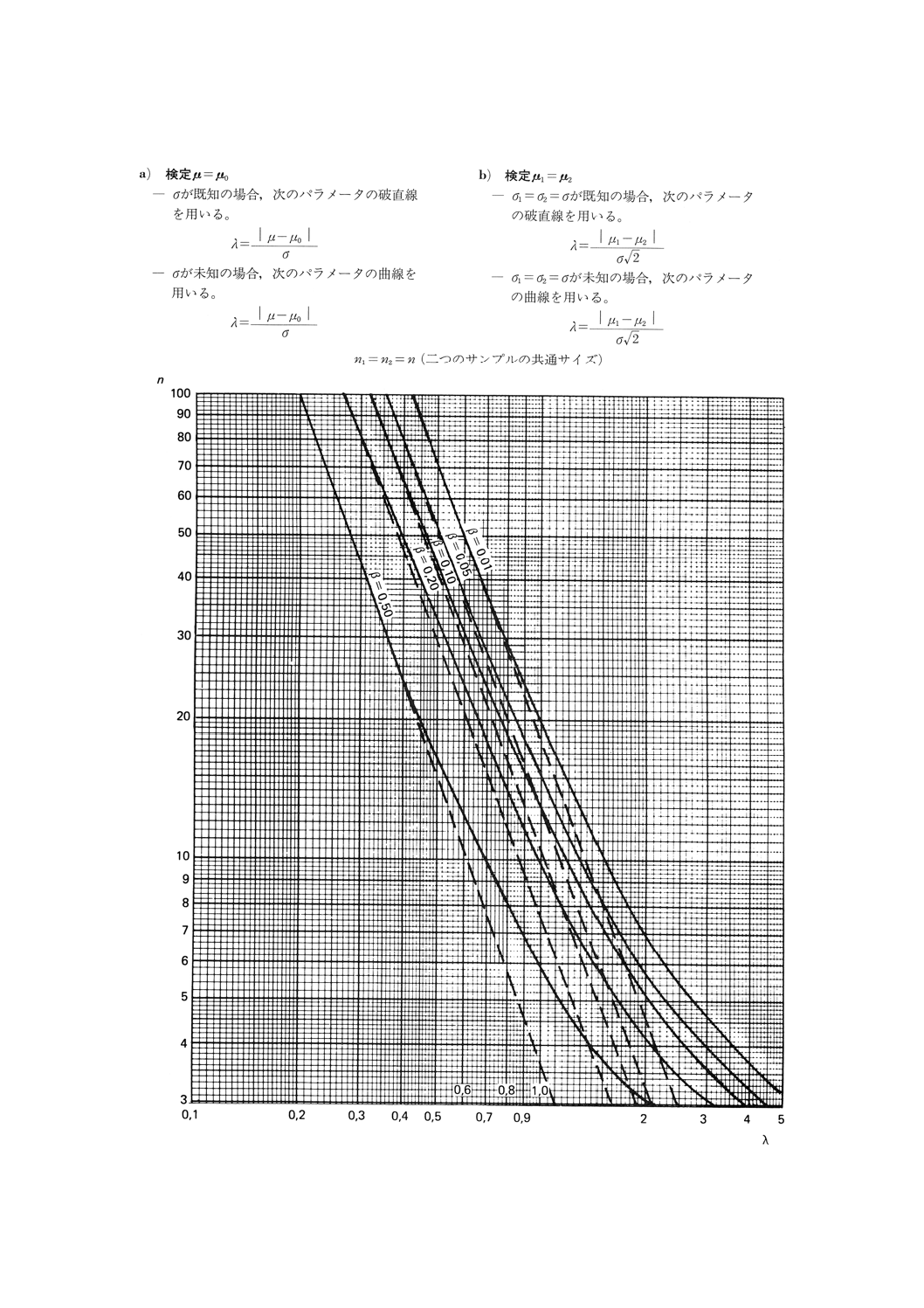
状況に応じて,次の図を参照する。
図1.1(両側検定)第1種の危険α=0.05
図2.1(両側検定)第1種の危険α=0.01
図3.1(片側検定)第1種の危険α=0.05
図4.1(片側検定)第1種の危険α=0.01
βは,適当な検定のν=∞の曲線上で,横軸λに対応する点の縦軸座標値である。
1.4
問題2 : βを与えて,サンプルサイズnを決定する
様々なμの値について,対立仮説はパラメータλ(0<λ<∞)によって次のように定義される。
a)
σ
μ
μ
λ
0
−
=
(両側検定)対立仮説μ≠μ0
b)
σ
μ
μ
λ
0
−
=
(片側検定μ≦μ0)対立仮説μ>μ0
c)
σ
μ
μ
λ
0
−
=
(片側検定μ≧μ0)対立仮説μ<μ0
状況に応じて,次の図を参照する。
図1.2(両側検定)第1種の危険α=0.05
図2.2(両側検定)第1種の危険α=0.01
図3.2(片側検定)第1種の危険α=0.05
4
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4.2(片側検定)第1種の危険α=0.01
nは,与えられたβの値に対応する直線(破線)上で横軸λに対応する点の縦軸座標値である。
1.5
例
ある綿糸の生産者は,配送する各ロットごとに,平均破壊負荷(Nで測定)が最低でもμ0=2.30に等し
いことを保証する。消費者は,ロットの様々な糸巻きからとりだした一定の長さの糸について,JIS Z 9041-2
に記述されている片側検定によって仮説μ≧μ0=2.30が棄却されないときだけ,そのロットの受入れに同意
する。このときの検定の第1種の危険は,α=0.05である(ゆえに,ここでaは,“生産者の危険”である。)。
消費者の経験的知識によれば,ロットによって平均は異なるかもしれないが,一つのロット内の破壊負
荷のばらつきは標準偏差σ=0.33で,実際上一定である。
1.5.1
消費者は,ロット当たりn=10の糸巻きを選択することを想定し,実際の平均破壊負荷がμ=2.10
であるとき,仮説μ≧2.30を棄却しない(ゆえに,そのロットを受け入れる)確率を知りたいと希望した。
参照すべき図は,図3.1である。μ=2.10に対応するλは,次のようになる。
92
.1
33
.0
)
10
.2
30
.2(
10
)
(
0
=
−
=
−
−
=
σ
μ
μ
λ
n
ν=∞の直線によれば,100βの値は36である。すなわち,β=0.36又は36%である。
1.5.2
1.5.1で消費者によって考えられたβの値は大きすぎるので,彼はμ=2.10のとき危険βを0.10(又は
10%)に減らすために十分なサイズのサンプルを選ぶことにした。
参照すべき図は,図3.2である。μ=2.10に対するパラメータλの値は,次のようになる。
61
.0
33
.0
10
.2
30
.2
0
=
−
=
−
−
=
σ
μ
μ
λ
β=0.10の直線(破線)で読み取ったnの値は,n=22である。
2. 与えられた値と平均との比較(分散未知)
JIS Z 9041-2の書式A'を参照。
重要な付記
第2種の危険βは,母集団における標準偏差の真の値σに依存するが,それは未知である。そこで,σの
大きさの程度が分かるとき,βは近似的に知ることができる。妥当な事前情報がないときには,σの代わり
にサンプルから推定した推定量sを用いることになるであろう。
OC曲線から読み取った値が,標準偏差σの誤差によって影響されることを考慮すべきであると強く勧め
る。σが少数のサンプルから推定されたときは,非常に不正確になるかもしれない。このような場合,σの
推定誤差の影響を考慮して,σの信頼限界の範囲内にsをおくことも酌量できる。この信頼限界は,JIS Z
9041-2の書式Fの方法によって計算される。
2.1
記法
n = サンプルサイズ
μ = 母集団平均
μ0 = 与えられた値
σ = 母集団における標準偏差(これは近似値によって置き換えられる)
ν = n−1
2.2
検定される仮説
両側検定の場合,帰無仮説はμ=μ0であり,対立仮説はμ≠μ0に対応する。
5
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
片側検定の場合,帰無仮説は次のいずれかである。
a) μ≦μ0,対立仮説はμ>μ0に対応する;
b) μ≧μ0,対立仮説はμ<μ0に対応する。
2.3
問題1 : nを与えて,危険βを決定する
様々なμの値に対応して,対立仮説はパラメータλ(0<λ<∞)によって次のように定義される。
a)
σ
μ
μ
λ
0
−
=n
(両側検疋)対立仮説μ≠μ0
b)
σ
μ
μ
λ
)
(
0
−
=n
(片側検定μ≦μ0)対立仮説μ>μ0
c)
σ
μ
μ
λ
)
(
0
−
−
=
n
(片側検定μ≧μ0)対立仮説μ<μ0
状況に応じて,次の図を参照する。
図1.1(両側検定)第1種の危険α=0.05
図2.1(両側検定)第1種の危険α=0.01
図3.1(片側検定)第1種の危険α=0.05
図4.1(片側検定)第1種の危険α=0.01
βは,適切な図のν=n−1の曲線上の横軸λに対応する点の縦軸座標値である。
2.4
問題2 : βを与えて,サンプルサイズnを決定する
様々なμの値について,対立仮説はパラメータλ(0<λ<∞)によって次のように定義される。
a)
σ
μ
μ
λ
0
−
=
(両側検定)対立仮説μ≠μ0
b)
σ
μ
μ
λ
0
−
=
(片側検定μ≦μ0)対立仮説μ>μ0
c)
σ
μ
μ
λ
0
−
−
=
(片側検定μ≧μ0)対立仮説μ<μ0
nは,与えられたβの値に対応する曲線上の横軸λに対応する点の縦軸座標値である。
2.5
例
この例は,1.5の例と同じであるが,消費者は破壊負荷の標準偏差の正確な値を知らない。しかしながら,
経験上,標準偏差は次の限界内に収まるであろうことを知っている。
σI=0.30 σs=0.45
2.5.1
消費者は,ロット当たりn=10の糸巻きを選択すると想定し,実際の平均破壊負荷はμ=2.10とい
う想定の下で,仮説μ≧2.30を棄却しない(すなわち,ロットを受け入れる)確率を知りたいと望んだ1)。
参照すべき図は,図3.1である。σの両端の値に対応するλの値は,次のようになる。
1.2
30
.0
)
10
.2
30
.2(
10
I
=
−
=
λ
4.1
45
.0
)
10
.2
30
.2(
10
S
=
−
=
λ
対応する100β%のν=9の(補間によって読み取った)値は,
βI=0.40(又は40%)
βS=0.64(又は64%)
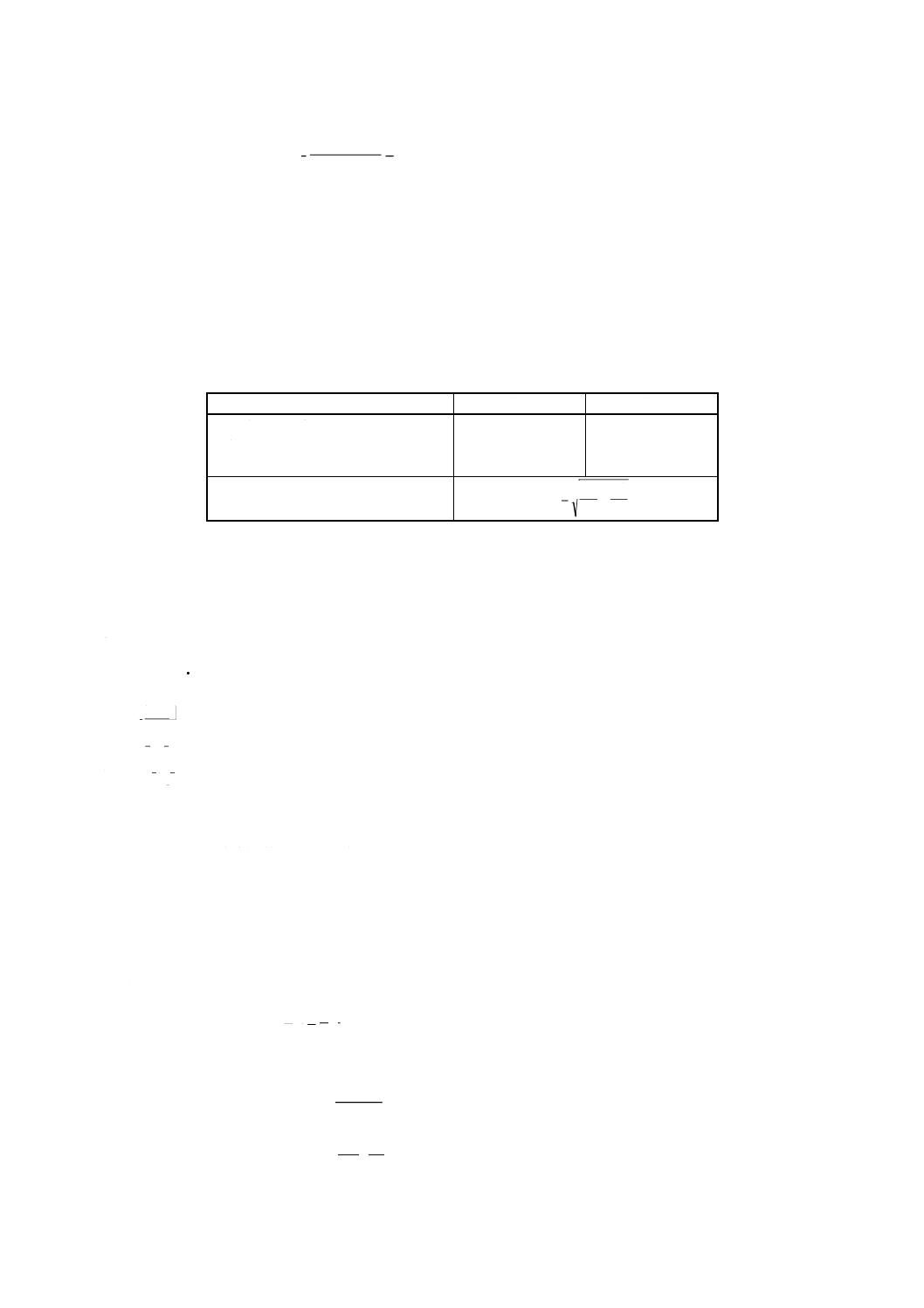
2.5.2
消費者は,最も不利な仮説(σ=σS=0.45)の下で,μ=2.10のときβが0.10(又は10%)を超えな
いことを望んだ。
参照すべき図は,図3.2であり,β=0.10の曲線と次の値を調べる。
1)
つまり,有意水準α=0.05のStudent検定を用いたとき,μ=2.10という値がμ0=2.30より有意に小
さいと判断されない確率である。
6
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
44
.0
45
.0
10
.2
30
.2
=
−
=
λ
β=0.10とλ=0.44とから,nは45程度であることが分かる。
もし,ロットを幾つか調べて,標準偏差が安定していることが分かったなら,σはより精度よく推定で
きる。このとき,生産者と消費者の保証を維持しながら,その後のロットから取るサンプルサイズを少な
くすることができるであろう。
3. 二つの対応のない測定の平均の比較(分散既知)
JIS Z 9041-2の書式Cを参照。
3.1
記法
母集団1
母集団2
サンプルサイズ
n1
n2
平均
μ1
μ2
分散
21
σ
22
σ
二つのサンプルの平均の差の標準偏差
2
22
1
21
n
n
D
σ
σ
σ
+
=
3.2
検定する仮説
両側検定では,帰無仮説はμ1=μ2であり,対立仮説はμ1≠μ2に対応する。
片側検定では,帰無仮説は次のどちらかになる。
a) μ1≦μ2対応する対立仮説はμ1>μ2
b) μ1≧μ2対応する対立仮説はμ1<μ2
3.3
問題1 : n1とn2とを与えて,危険βを決定する
差μ1−μ2の様々な値に対して,対立仮説は,パラメータλ(0<λ<∞)によって次のように定義される。
a)
D
σ
μ
μ
λ
2
1−
=
(両側検定)対立仮説μ1≠μ2
b)
D
σ
μ
μ
λ
2
1−
=
(片側検定μ1≦μ2)対立仮説μ1>μ2
c)
D
σ
μ
μ
λ
2
1−
−
=
(片側検定μ1≧μ2)対立仮説μ1<μ2
状況に応じて,次の図を参照する。
図1.1(両側検定)第1種の危険α=0.05
図2.1(両側検定)第1種の危険α=0.01
図3.1(片側検定)第1種の危険α=0.05
図4.1(片側検定)第1種の危険α=0.01
βは,適切な図中の曲線ν=∞上で横軸λに対応する点の縦軸座標値である。
二つのサンプルの合計サイズが固定されているとき,n1+n2=2nとして,最良の効率(すなわちβ最小の
状況)は次のとき得られる。
2
2
1
1
σ
σ
n
n=
ゆえに,
2
1
1
1
2
σ
σ
σ
+
=n
n
2
1
2
2
2
σ
σ
σ
+
=n
n
7
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
2
1
2
σ
σ
μ
μ
λ
+
−
=
n
(σ1=σ2=σの場合,
σ
μ
μ
λ
2
1
2
−
=
n
)
3.4
問題2 : βを与えて,サンプルサイズn1とn2とを決定する
状況に応じて図1.1,2.1,3.1,4.1を利用して,ν=∞の曲線によって一般的な場合の標記の問題を解く
ことができる。座標値βは,この曲線中の横軸λの点に対応する。 (n1, n2) の組合せはすべて次の条件を満
たしている。
2
2
1
2
22
1
21
−
=
+
λ
μ
μ
σ
σ
n
n
最も経済的な(n1+n2最小)サンプルは,次のような条件を満たす。
2
2
1
1
σ
σ
n
n=
ゆえに,
n1=σ1 (σ1+σ2)
2
2
1
−μ
μ
λ
n2=σ2 (σ1+σ2)
2
2
1
−μ
μ
λ
−
=
=
=
=
2
2
1
2
1
2
1
2
μ
μ
λσ
σ
σ
σ
n
n
の場合,
σ1=σ2=σ,n1=n2=nという特殊な場合では,パラメータλ(0<λ<∞)による対立仮説を,様々な差
μ1−μ2について,次のようにより適切に定義される。
a)
2
2
1
σ
μ
μ
λ
−
=
(両側検定)対立仮説μ1≠μ2
b)
2
2
1
σ
μ
μ
λ
−
=
(片側検定μ1≦μ2)対立仮説μ1>μ2
c)
2
1
2
σ
μ
μ
λ
−
=
(片側検定μ1≧μ2)対立仮説μ1<μ2
状況に応じて,次の図を用いる。
図1.2(両側検定)第1種の危険α=0.05
図2.2(両側検定)第1種の危険α=0.01
図3.2(片側検定)第1種の危険α=0.05
図4.2(片側検定)第1種の危険α=0.01
nは,与えられた値βに対応する直線(破線)上で,横軸λに対応する点の縦軸座標値である。
3.5
例
ある綿糸の生産者が,製造工程を変更した。しかし,彼の宣言によると,平均破壊負荷は同じまま(μ1
=μ2)である。μ1は旧工程に対応し,μ2は新工程に対応する。
消費者は,新しい過程を受け入れる用意がある。しかし,生産者の宣言を確認したいと希望している。
そのため,与えられた長さの糸をいろいろな糸巻きから取り,JIS Z 9041-2に記述されているようにして
μ1=μ2の仮説を両側検定する。このときの第1種の危険をα=0.05とする(ゆえに,αはここで“生産者の
8
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
危険”である。)。
この生産者の製品のすべてについて破壊負荷のばらつきは実質的に一定であり,標準偏差σ=0.33で特
徴づけられることを,消費者は経験から知っている。
3.5.1
消費者は,二つの製造工程それぞれのロットから10個の糸巻きを選択し,実際は|μ1−μ2|が0.30
に等しいときμ1=μ2の仮説を棄却しない(すなわち,新しい製造工程のロットを受け入れる)確率を知り
たいと望んでいる。
参照すべき図は,図1.1であり,パラメータは,次のようになる。
D
σ
μ
μ
λ
2
1−
=
|μ1−μ2|=0.30
6
147
.0
33
.0
10
2
2
2
22
1
21
=
×
=
=
+
=
σ
σ
σ
σ
n
n
n
D
03
.2
6
147
.0
30
.0
=
=
λ
曲線ν=∞によると,100βの値は47,すなわち,β=0.47又は47%である。
3.5.2
消費者によって検討されたこの値は大きすぎるので,μ1−μ2=0.30のとき危険βを0.10 (10%) まで
小さくさせるために,十分に大きいサンプルのサイズを選択することにした。
参照すべき図は,図1.2であり,パラメータは,次のようになる。
64
.0
2
33
.0
30
.0
2
2
1
=
=
−
=σμ
μ
λ
β=0.10の直線(破線)から読み取られたnの値は,n=26である。
4. 二つの対応のない測定の平均の比較(分散は未知であるが等しいと仮定される)
JIS Z 9041-2の書式C'参照。
重要な付記
第2種の危険βは,二つの母集団の標準偏差の真の値σに依存するが,それは未知である。ゆえに,βは,
近似的にだけ,また,σの大体の大きさが分かるときだけ知ることができる。有効な事前情報がないとき
には,σのかわりにサンプルから得られた推定値sを使うことになる。
OC曲線から読み取った値が,標準偏差σの誤差によって影響されることを考慮すべきであると強く勧め
る。σが少数のサンプルから推定されたときは,非常に不正確になるかもしれない。このような場合,σの
推定誤差の影響を考慮して,σの信頼限界の範囲内にsをおくことも酌量できる。この信頼限界は,JIS Z
9041-2の書式Fの方法によって計算される。
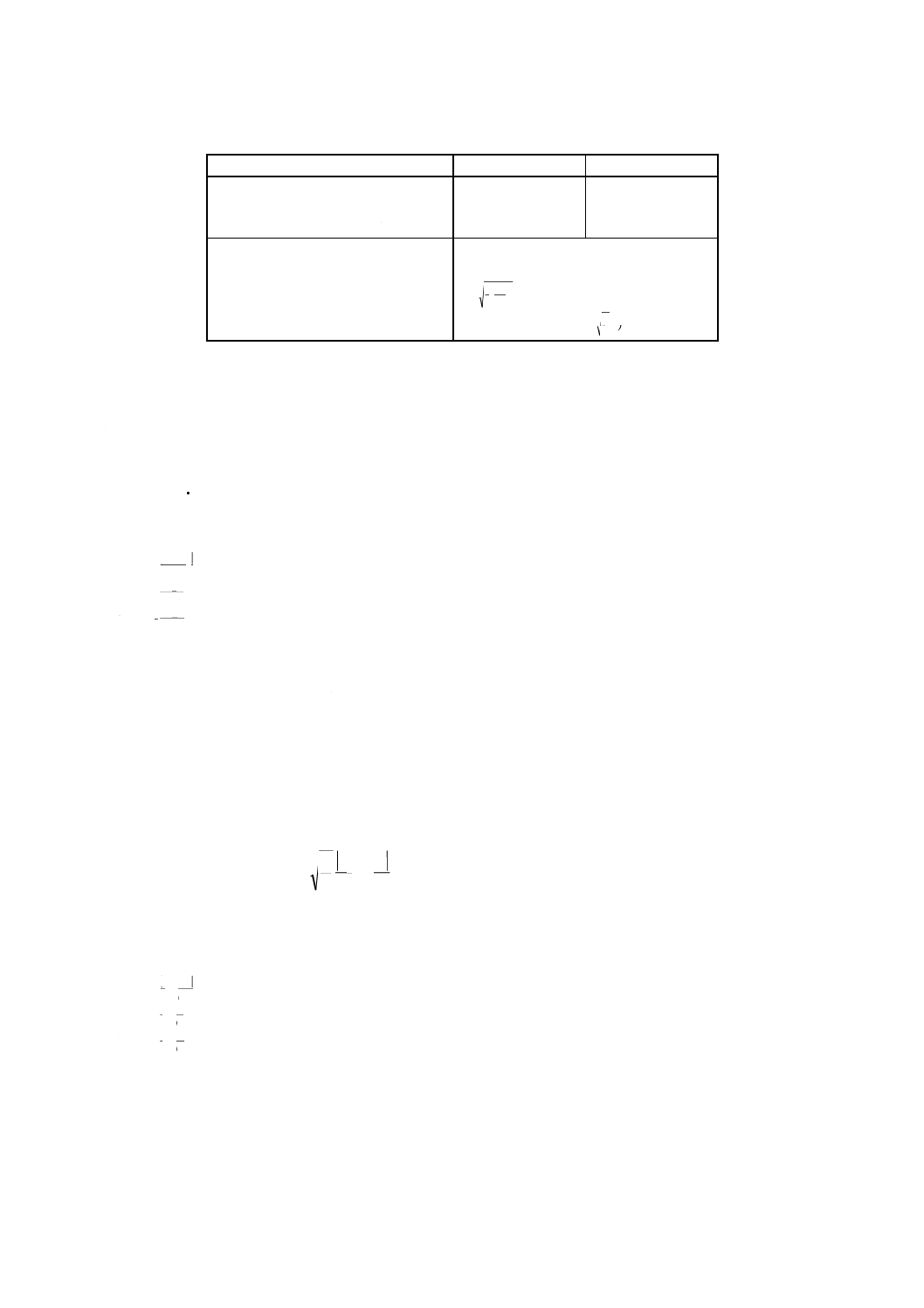
4.1
記法
9
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
母集団1
母集団2
サンプルサイズ
n1
n2
平均
μ1
μ2
分散(これは近似値で置き換えられる)
σ2
σ2
自由度の数
ν=n1+n2−2
[n1=n2=nのとき2 (n−1) ]
二つのサンプルの平均の差の標準偏差
σ
σ
2
1
2
1
n
n
n
n
D
+
=
(n1=n2=nのとき
σ
n
2)
4.2
検定される仮説
両側検定の場合,帰無仮説はμ1=μ2であり,対立仮説はμ1≠μ2になる。
片側検定の場合には,帰無仮説は次のいずれかである。
a) μ1≦μ2,対立仮説はμ1>μ2
b) μ1≧μ2,対立仮説はμ1<μ2
4.3
問題1 : n1とn2とを与えて,危険βを決定する
平均の差μ1−μ2の様々な値に対応して,対立仮説は,パラメータλ(0<λ<∞)によって次のように定
義される。
a)
D
σ
μ
μ
λ
2
1−
=
(両側検定)対立仮説μ1≠μ2
b)
D
σ
μ
μ
λ
2
1−
=
(片側検定μ1≦μ2)対立仮説μ1>μ2
c)
D
σ
μ
μ
λ
1
2−
=
(片側検定μ1≧μ2)対立仮説μ1<μ2
状況に応じて,次の図を参照する。
図1.1(両側検定)第1種の危険α=0.05
図2.1(両側検定)第1種の危険α=0.01
図3.1(片側検定)第1種の危険α=0.05
図4.1(片側検定)第1種の危険α=0.01
βは,適切な図のλ=n1+n2−2の曲線上で横軸λに対応する点の縦軸座標値である。
二つのサンプルの合計サイズだけが固定されていて,n1+n2=2nのとき(βを最小にする),n1=n2=nを
求めることに関心がある。その場合は,次のようにする。
σ
μ
μ
λ
2
1
2
−
=
n
4.4
問題2:βを与えて,サンプルの共通のサイズnを決定する
平均の差μ1−μ2の様々な値に対応して,対立仮説は,パラメータλ(0<λ<∞)によって次のように定
義される。
a)
2
2
1
σ
μ
μ
λ
−
=
(両側検定)対立仮説、μ1≠μ2
b)
2
2
1
σ
μ
μ
λ
−
=
(片側検定μ1≦μ2)対立仮説μ1>μ2
c)
2
1
2
σ
μ
μ
λ
−
=
(片側検定μ1≧μ2)対立仮説μ1<μ2
状況に応じて,次の図を参照する。
図1.2(両側検定)第1種の危険α=0.05
図2.2(両側検定)第1種の危険α=0.01
図3.2(片側検定)第1種の危険α=0.05
10
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4.2(片側検定)第1種の危険α=0.01
nは,与えられた値βに対応する曲線上で横軸λに対応する点の縦軸座標値である。
4.5
例
この例は,消費者は破壊負荷の標準偏差の正確な値を知らないことを除いて,3.5と同様である。しかし,
二つのロットの標準偏差は等しくなる(σ1=σ2)ことについて強い見込みがあることが分かっている。
4.5.1
この消費者は,二つの製造工程のロットから10個の糸巻きを選択し,実際は|μ1−μ2|が0.30に
等しいとき,帰無仮説μ1=μ2が棄却されない(ゆえに,新しい製造工程を受け入れる)確率を知りたいと
思った2)。
二つのサンプルについて実行された測定値は,次のような結果になった:
a) 1番目のロット:1x=2.176Σ (x1−1x)2=1.256 3
b) 2番目のロット:
2x=2.520Σ (x2− 2x)2=1.389 7
二つの平方和の差異は大変小さいので,先に示した仮説
21
σ=
22
σは完全に適合する(JIS Z 9041-2の書式
Gを参照)。
二つのロットの共通分散σ2の推定値は,次のようになる。
0
147
.0
18
0
646
.2
2
10
10
7
389
.1
3
256
.1
2
=
=
−
+
+
=
s
信頼係数1−α=0.95でのσ2の上限は,次のようになる(JIS Z 9041-2の書式F参照)。
8
281
.0
39
.9
0
646
.2
)
18
(
0
646
.2
205
.0
2
=
=
=x
s
σ
ゆえに,σが次の値を超えることはほとんどない。
53
.0
8
281
.0
=
=
s
σ
参照すべき図は,図1.1であり,次のようになる。
27
.1
53
.0
30
.0
2
10
2
2
1
=
×
=
−
=
s
s
n
σ
μ
μ
λ
ν=18の場合,対応する100βの値は(補間によって)80に近いことが読み取れる。すなわち,第2種の
危険の上限は,約0.80 (80%) である。
4.5.2
この消費者は,最も不利な仮説(σ=σs=0.53)の下で,|μ1−μ2|=0.30のときにβが0.20 (20%) を
超えないことを望んだ。
参照すべきは,図1.2の曲線β=0.20であり,次のようになる。
4.0
2
53
.0
30
.0
2
2
1
=
=
−
=
s
σ
μ
μ
λ
β=0.20でλ=0.4のとき,n=49と読み取れる。
2×50=100個の測定値を用いれば,σについて極めて正確な推定値が得られ,それを根拠として,対立
仮説がμ1−μ2=0.30のときの第2種の危険の大体の値が,図1.1から読み取れる。
2)
つまり,有意水準α=0.05のStudent検定を用いたとき,|μ1−μ2|=0.30の差を検出できない確率
である。
11
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5. 分散又は標準偏差と与えられた値との比較
JIS Z 9041-2の書式E参照。
5.1
記法
n = サンプルサイズ
σ2 = 母集団の分散(σ=母集団の標準偏差)
20
σ = 分散の与えられた値(σ0=標準偏差の与えられた値)
5.2
検定される仮説
両側検定の場合,帰無仮説はσ2=
20
σ(σ=σ0)であり,対立仮説はσ2≠
20
σ(σ≠σ0)である。
片側検定の場合は,帰無仮説は次のいずれかである。
a) σ2≦
20
σ(σ≦σ0),対立仮説はσ2>
20
σ(σ>σ0)
b) σ2≧
20
σ(σ≧σ0),対立仮説はσ2<
20
σ(σ<σ0)
いずれの場合においても,対立仮説は,次のパラメータによって定義される。
λ:σ/σ0
0<λ<∞ :両側検定の場合
1<λ<∞ :片側検定σ2≦<
20
σ(σ≦σ0)の場合
0<λ<1 :片側検定σ2≧<
20
σ(σ≧σ0)の場合
5.3
問題1:nを与えて,危険βを決定する
状況に応じて,次の図を参照する。
図5.1(両側検定)第1種の危険α=0.05
図6.1(両側検定)第1種の危険α=0−01
図7.1(片側検定σ2≦<
20
σ)第1種の危険α=0.05
図8.1(片側検定σ2≦<
20
σ)第1種の危険α:0.01
図9.1(片側検定σ2≧<
20
σ)第1種の危険α=0.05
図10.1(片側検定σ2≧<
20
σ)第1種の危険α=0.01
βは,適当な図の曲線 (n) 上で横軸λに対応する点の縦軸座標値である。
5.4
問題2:βを与えて,サンプルサイズnを決定する
状況に応じて,次の図を参照する。
図5.2(両側検定)第1種の危険α=0.05
図6.2(両側検定)第1種の危険α=0.01
図7.2(片側検定σ2≦<
20
σ)第1種の危険α:0.05
図8.2(片側検定σ2≦<
20
σ)第1種の危険α=0.01
図9.2(片側検定σ2≧<
20
σ)第1種の危険α=0.05
図10.2(片側検定σ2≧<
20
σ)第1種の危険α=0.01
nは,βの与えられた値に対応する曲線上で横軸λに対応する点の縦軸座標値である。
5.5
例
ある綿糸の生産者は,綿糸の破壊負荷のばらつきが減少したということで製造工程の品質を改善できた
と宣言した。以前のばらつきは,標準偏差でσ0=0.45(<
20
σ=0.202 5)であった。
ある消費者は,本当に品質が改善されているなら,その改善に対してより多くの価格を支払う用意があ
る。しかし,実際には改善されていないときに改善があったと判断してしまう危険を少なくしたいと希望
している。彼は,JIS Z 9041-2に記述されているような片側検定σ2≧
20
σ=0.202 5(σ≧0.45)を実行するこ
12
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とにした。このときの第1種の危険をα=0.05とした(ゆえに,ここでαは“生産者の危険”である。)。
5.5.1
この消費者は,新工程のロットからn=12の糸巻きを選択したと想定し,真の標準偏差がσ=0.30
まで実際に減少していたときに,仮説σ≧0.45を棄却できない(ゆえに,改善したと判断できない)確率
を知りたいと希望した。
参照すべき図は,図9.1であり,このときのパラメータλの値は,次のようになる。
67
.0
45
.0
30
.0
0
=
=
=σσ
λ
n=12の曲線によれば,100βの値はおよそ51,すなわち,β=0.51 (51%) である。
5.5.2
この消費者は,いま問題になっている改善が実際に有効であっても,それを明らかにできない危険
が大きいことを認識した。そこで,σ=0.30のときにβの値を0.10 (10%) まで減少させるのに十分なほど大
きなサンプルサイズを選択することにした。
参照すべき図は,図9.2である。
β=0.10,λ=0.67としたとき,n=29となることが分かる。
6. 二つの分散又は二つの標準偏差の比較
JIS Z 9041-2の書式G参照。
この場合のOC曲線は,二つのサンプルのサイズが等しいという特別な場合だけに与えられる。
6.1
記法
第1群の母集団の分散:
21
σ(標準偏差σ1)
第2群の母集団の分散:
22
σ(標準偏差σ2)
第1群のサンプルサイズ:n1=n
第2群のサンプルサイズ:n2=n
6.2
検定される仮説
両側検定の場合,帰無仮説は
21
σ=
22
σ(σ1=σ2)であり,対立仮説は
21
σ≠
22
σ(σ1≠σ2)に対応する。こ
れらの仮説は,次のパラメータによって定義される。
λ=σ2/σ1(対立仮説がσ1<σ2のとき) (1<λ<∞)
λ=σ1/σ2(対立仮説がσ1>σ2のとき)
片側検定の場合は,帰無仮説は次のいずれかである。
a)
21
σ≦
22
σ(σ1≦σ2),対応する対立仮説は
21
σ>
22
σ(σ1>σ2)であり,パラメータλ=σ1/σ(1<λ<∞)
によって定義される。
b)
21
σ≧
22
σ(σ1≧σ2),対応する対立仮説は
21
σ<
22
σ(σ1<σ2)であり,パラメータλ=σ2/σ1(1<λ<∞)
によって定義される。
6.3
問題1:nを与えて,βを決定する
状況に応じて,次の図を参照する。
図11.1(両側検定)第1種の危険α=0.05
図12.1(両側検定)第1種の危険α=0.01
図13.1(片側検定)第1種の危険α=0.05
図14.1(片側検定)第1種の危険α=0.01
βは,適当な図の曲線 (n) 上で横軸λに対応する点の縦軸座標値である。
6.4
問題2:βを与えて,サンプルサイズnを決定する
13
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
状況に応じて,次の図を参照する。
図11.2(両側検定)第1種の危険α=0.05
図12.2(両側検定)第1種の危険α=0.01
図13.2(片側検定)第1種の危険α=0.05
図14.2(片側検定)第1種の危険α=0.01
nは,βの与えられた値に対応する曲線上で,横軸λに対応する点の縦軸座標値である。
6.5
例
ある綿糸の生産者は,消費者に2種類のロットを提示した。1番のロットは(生産者の言によれば),破
壊負荷のばらつきが小さく,ゆえに,少し高価である。
ある消費者は,ばらつきが本当に小さいなら1番のロットを選択する用意がある。また,真のばらつき
がσ1≧σ2であるときに,σ1<σ2であると判断してしまう確率を小さくしたいと希望した。彼は,JIS Z 9041-2
に記述されている方法に従って,片側検定
21
σ≧
22
σ(σ1≧σ2)を第1種の危険α=0.05で実行することにし
た(ゆえに,αはここでは“消費者の危険”である。)。
6.5.1
この消費者は,各ロットからn=20の糸巻きを選んだと想定し,真のばらつきがσ1=32σ2であった
ときに,仮説σ1≧σ2が棄却されない(ゆえに,1番のロットの方が2番のロットよりもばらつきが小さい
とはいえない)確率を知りたいと希望した。
参照すべき図は,図13.1であり,このときのパラメータλの値は,次のようになる。
5.1
1
2=
=σ
σ
λ
n=20のとき,100βに対応する値は48,すなわち,β=0.48 (48%) であることが(補間によって)読み
取れる。
6.5.2
この消費者は,いま問題になっている改善が実際に有効であっても,それを明らかにできない危険
が大きいことを認識した。そこで彼は,σ1/σ2=2/3のとき,βの値を0.10 (10%) にまで減少させるのに十分
なほど大きなサンプルを各ロットから選択することにした。
参照すべき図は図13.2である。
β=0.10,λ=1.5のとき,n=55と読み取ることができる。

14
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
第2章:各種曲線
各種曲線の参照関係
対応する
第1章の節
参照する
JIS Z 9041-2
の書式
検定
第1種の危険
α
各種曲線の対応
問題1 1)
問題2 2)
平均値の比較
1.
A
μ=μ0:σ概知
2.
A'
μ=μ0:σ未知
0.05
1.1
1.2
3.
C
μ1=μ2:σ1,σ2既知
0.01
2.1
2.2
4.
C'
μ1=μ2:σ1=σ2未知
1.
A
μ≦μ0,μ≧μ0:σ概知
2.
A'
μ≦μ0,μ≧μ0:σ未知
0.05
3.1
3.2
3.
C
μ1≦μ2,μ1≧μ2:σ1,σ2既知
0.01
4.1
4.2
4.
C'
μ1≦μ2,μ1≧μ2:σ1=σ2未知
分散又は標準偏差と与えられた値との比較
5.
E
σ2=
20
σ
0.05
5.1
5.2
0.01
6.1
6.2
σ2≦
20
σ
0.05
7.1
7.2
0.01
8.1
8.2
σ2≧
20
σ
0.05
9.1
9.2
0.01
10.1
10.2
二つの分散の比較,又は二つの標準偏差の比
較
6.
G
21
σ=
22
σ
0.05
11.1
11.2
0.01
12.1
12.2
21
σ≦
22
σ:
21
σ≧
22
σ
0.05
13.1
13.2
0.01
14.1
14.2
注1) サンプルサイズを与えて,βを決定する。
2) βを与えて,取るべきサンプルサイズを決定する。
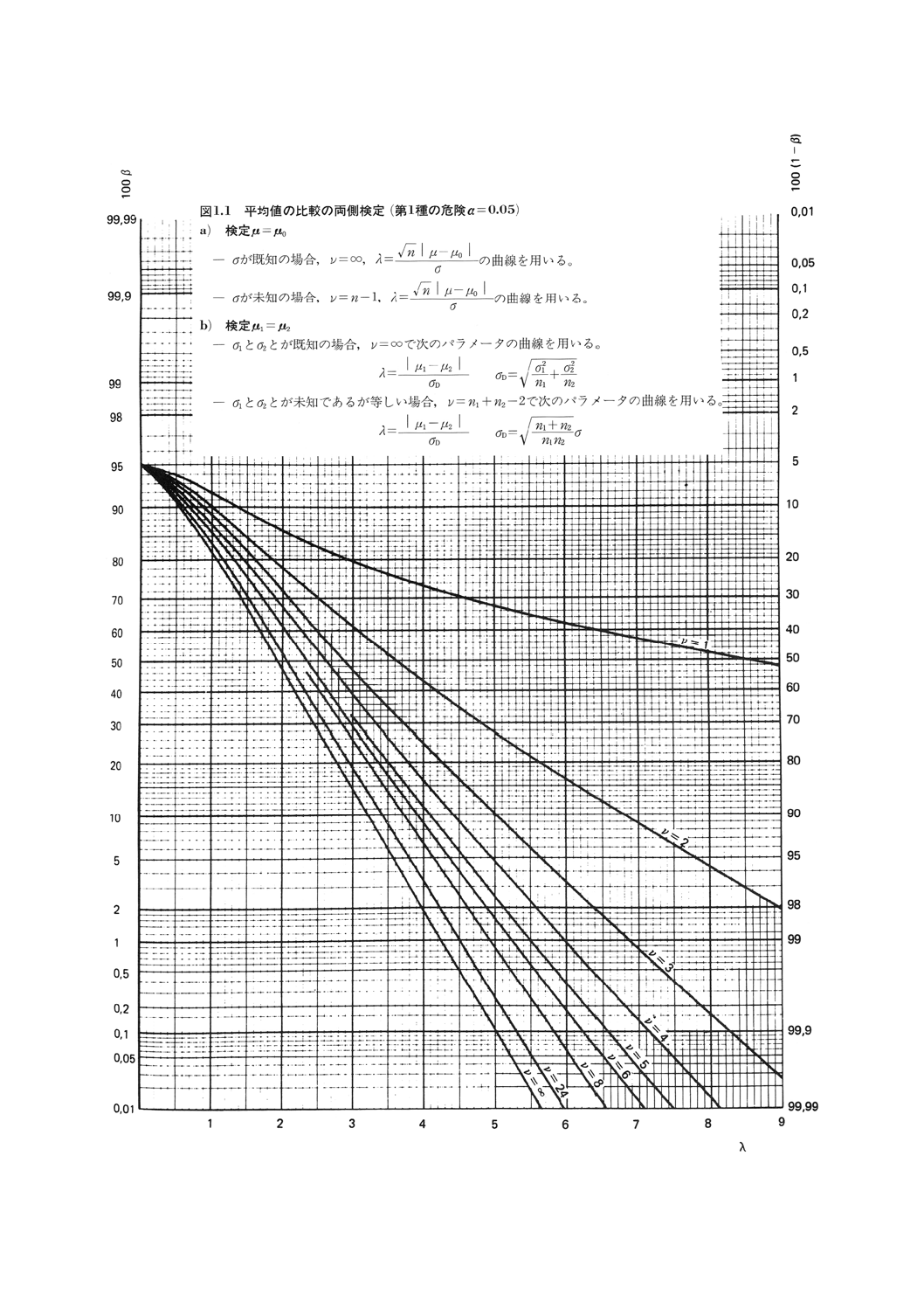
各種の検出力曲線
各種曲線
尺度
横軸
縦軸
1.1, 2.1, 3.1, 4.1, 7.1, 8.1, 11.1, 12.1, 13.1, 14.1
線形
正規
7.2, 8.2, 11.2, 12.2, 13.2, 14.2
線形
対数
9.1, 10.1
対数
正規
1.2, 2.2, 3.2, 4.2, 9.2, 10.2
対数
対数
5.1, 6.1
対数(λ<1について) 正規
線形(λ>1について) 正規
5.2, 6.2
対数(λ<1について) 対数
線形(λ>1について) 対数
15
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
16
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1.2 平均値の比較の両側検定(第1種の危険α=0.05)
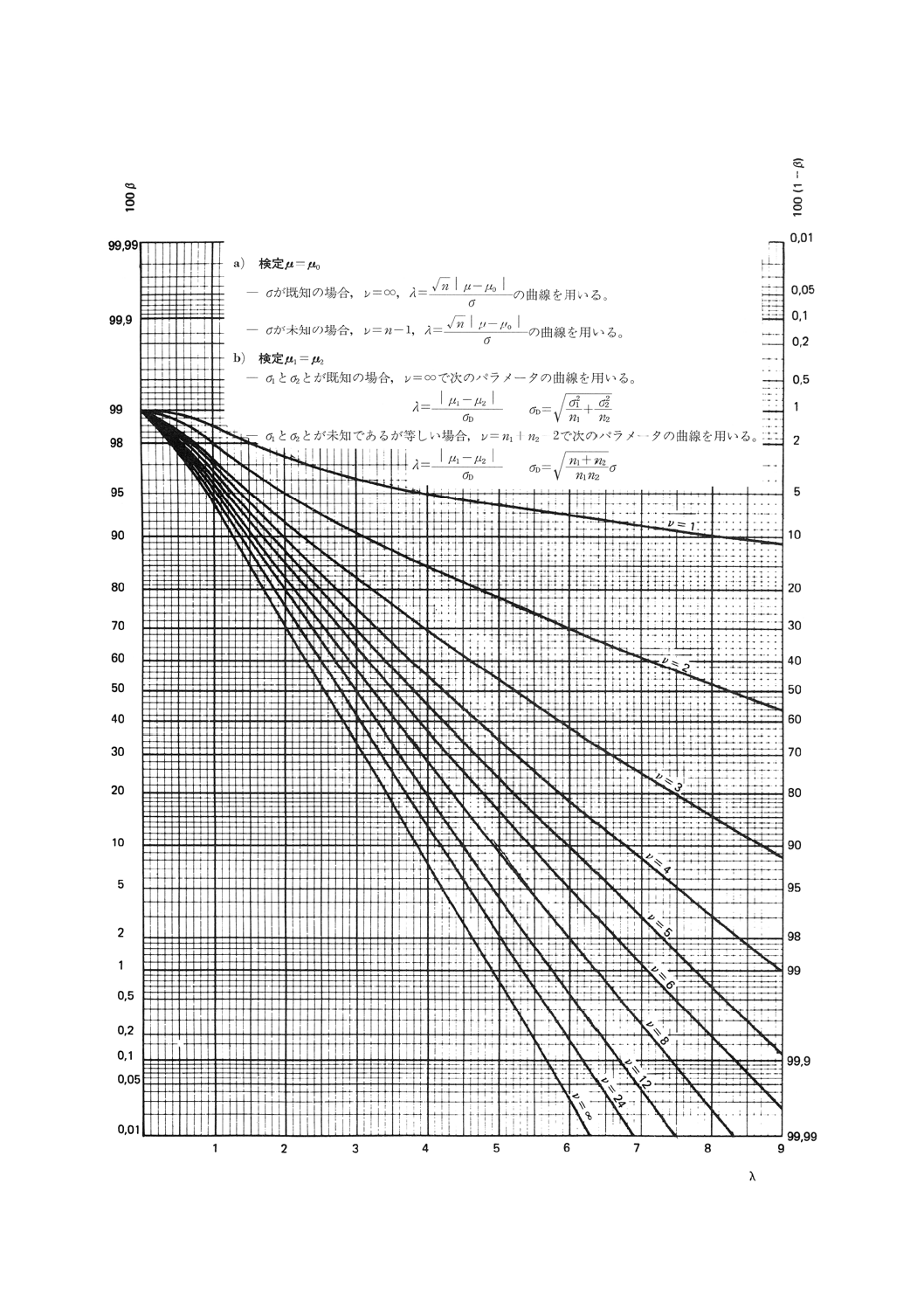
17
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2.1 平均値の比較の両側検定(第1種の危険α=0.01)
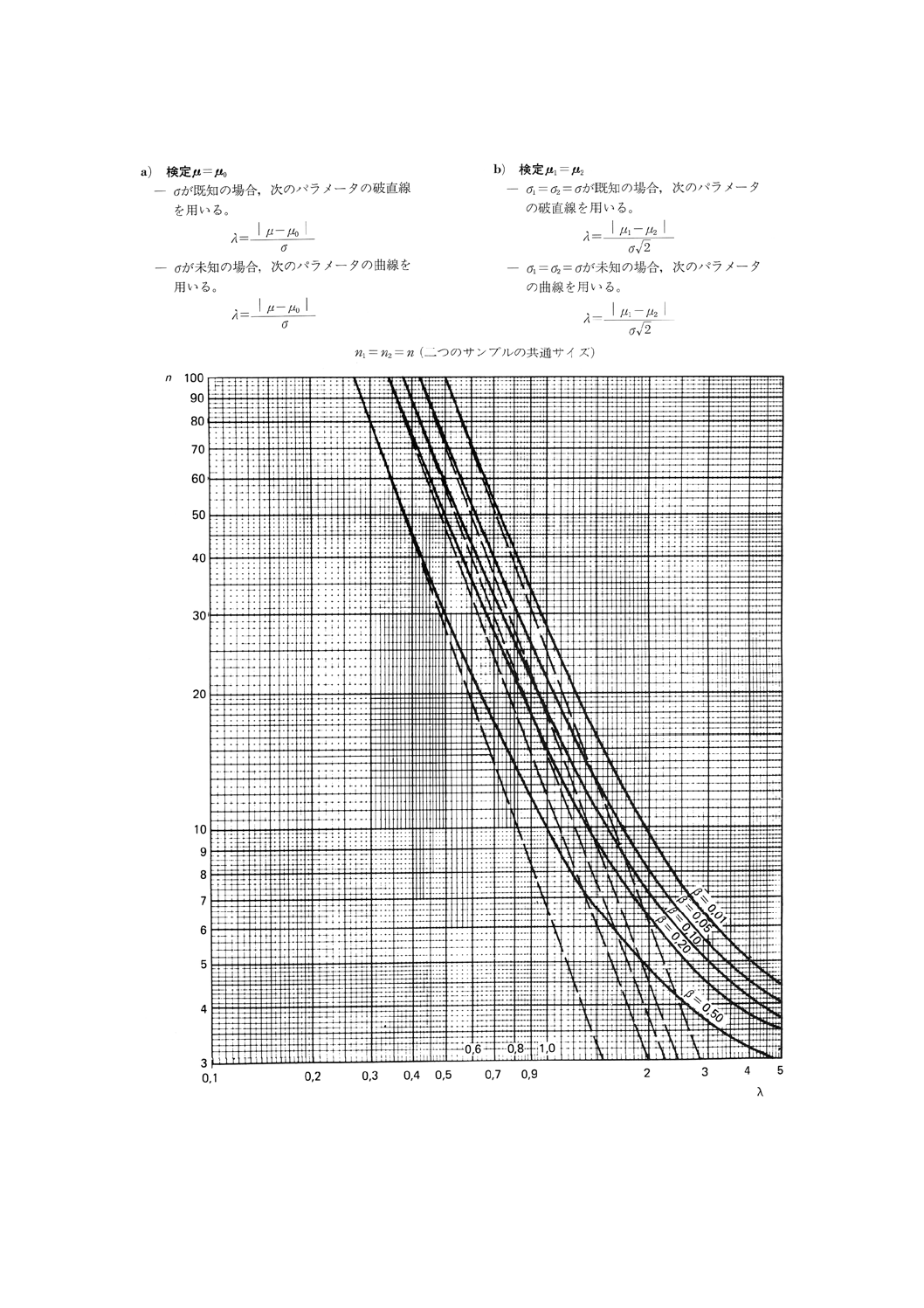
18
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2.2 平均値の比較の両側検定(第1種の危険α=0.01)
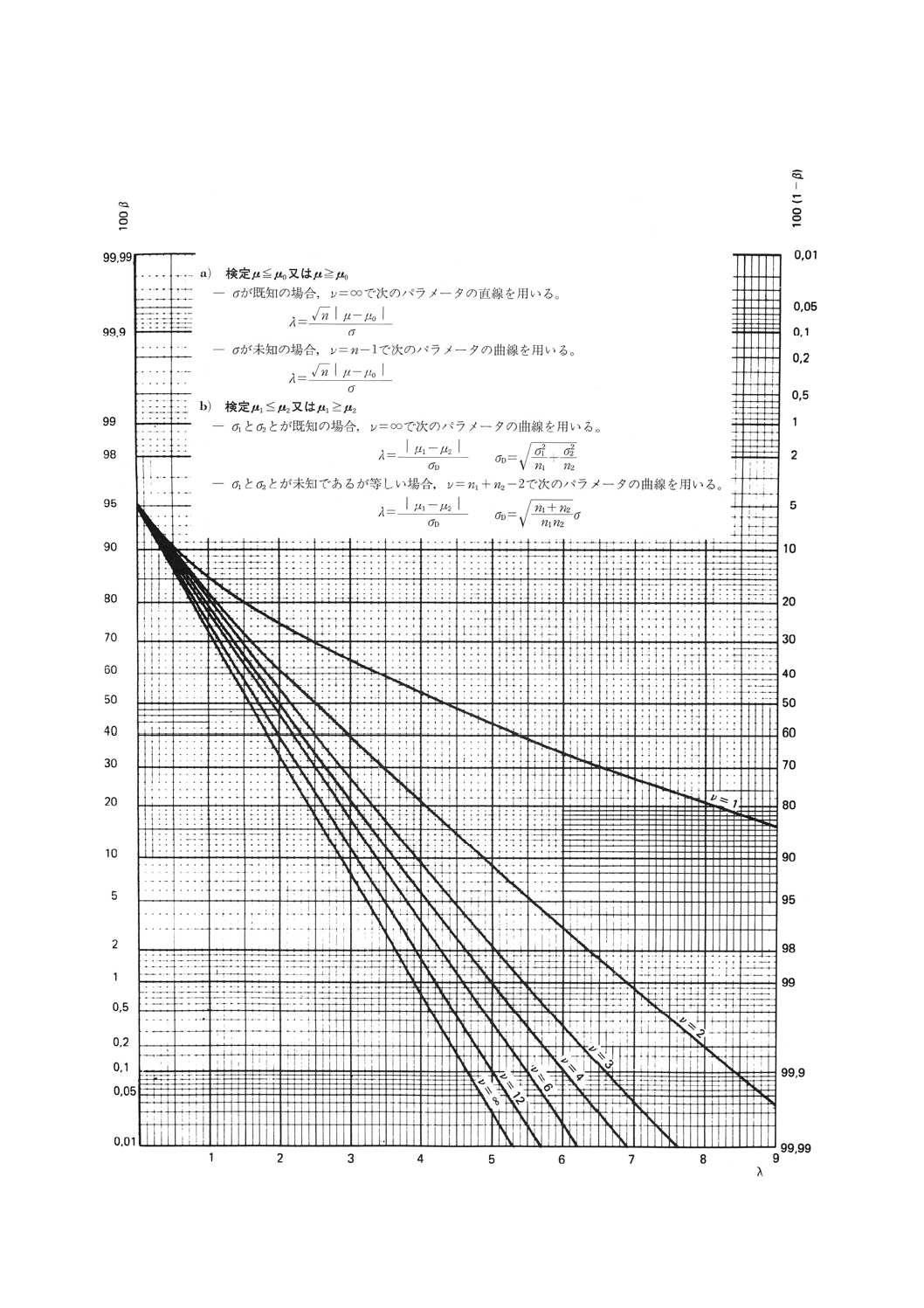
19
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3.1 平均値の比較の片側検定(第1種の危険α=0.05)
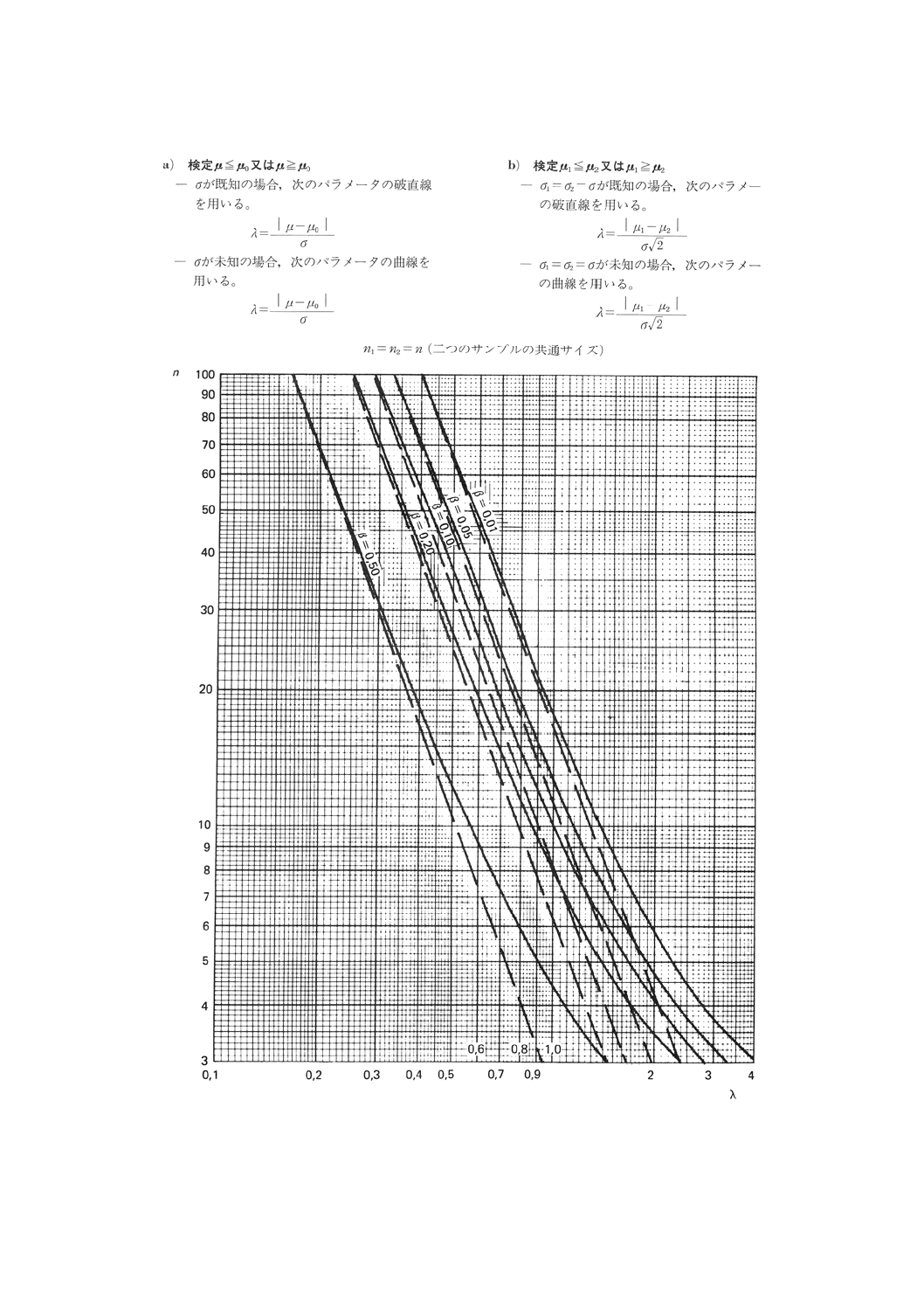
20
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3.2 平均値の比較の片側検定(第1種の危険α=0.05)
21
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
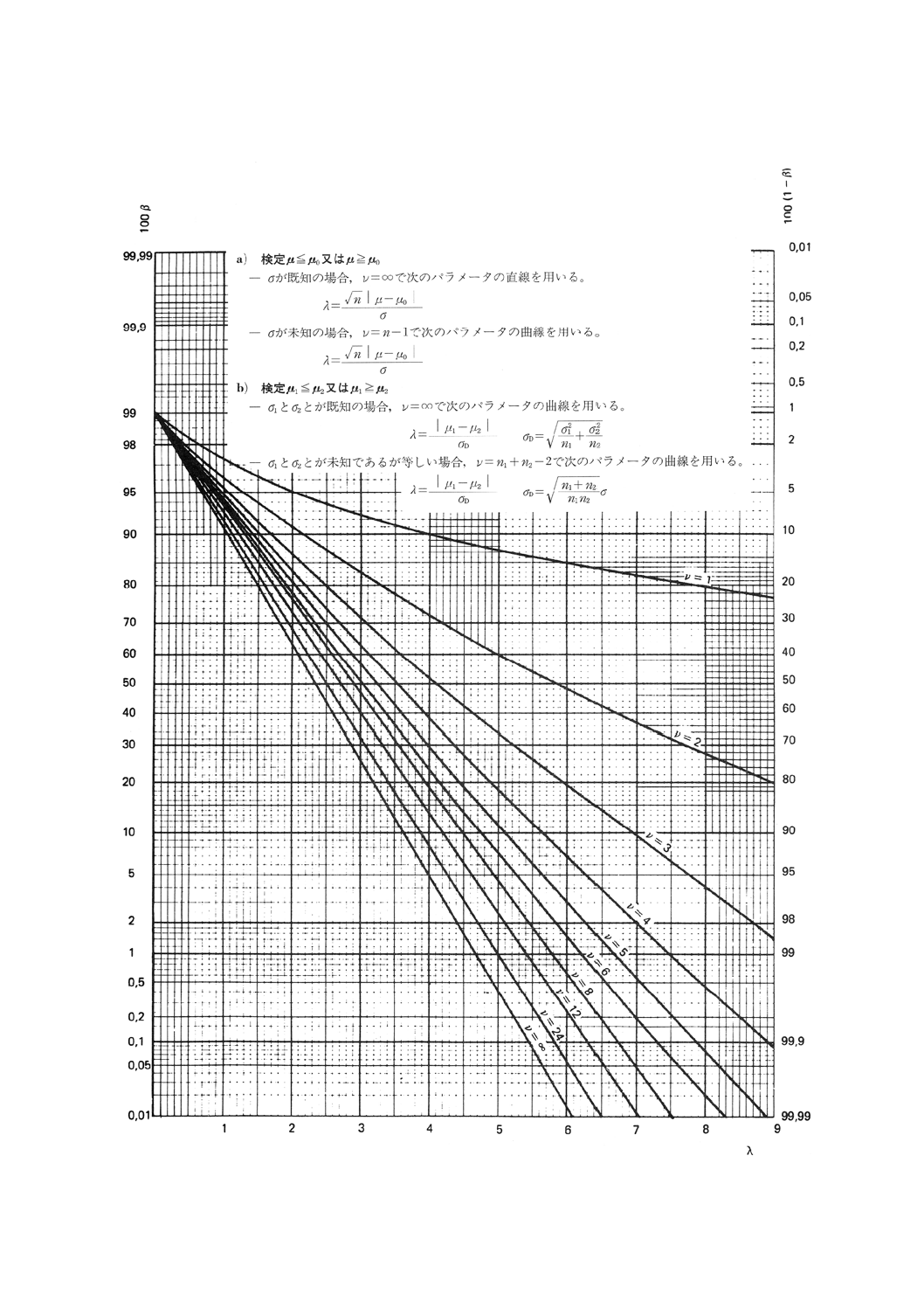
図4.1 平均値の比較の片側検定(第1種の危険α=0.01)
22
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
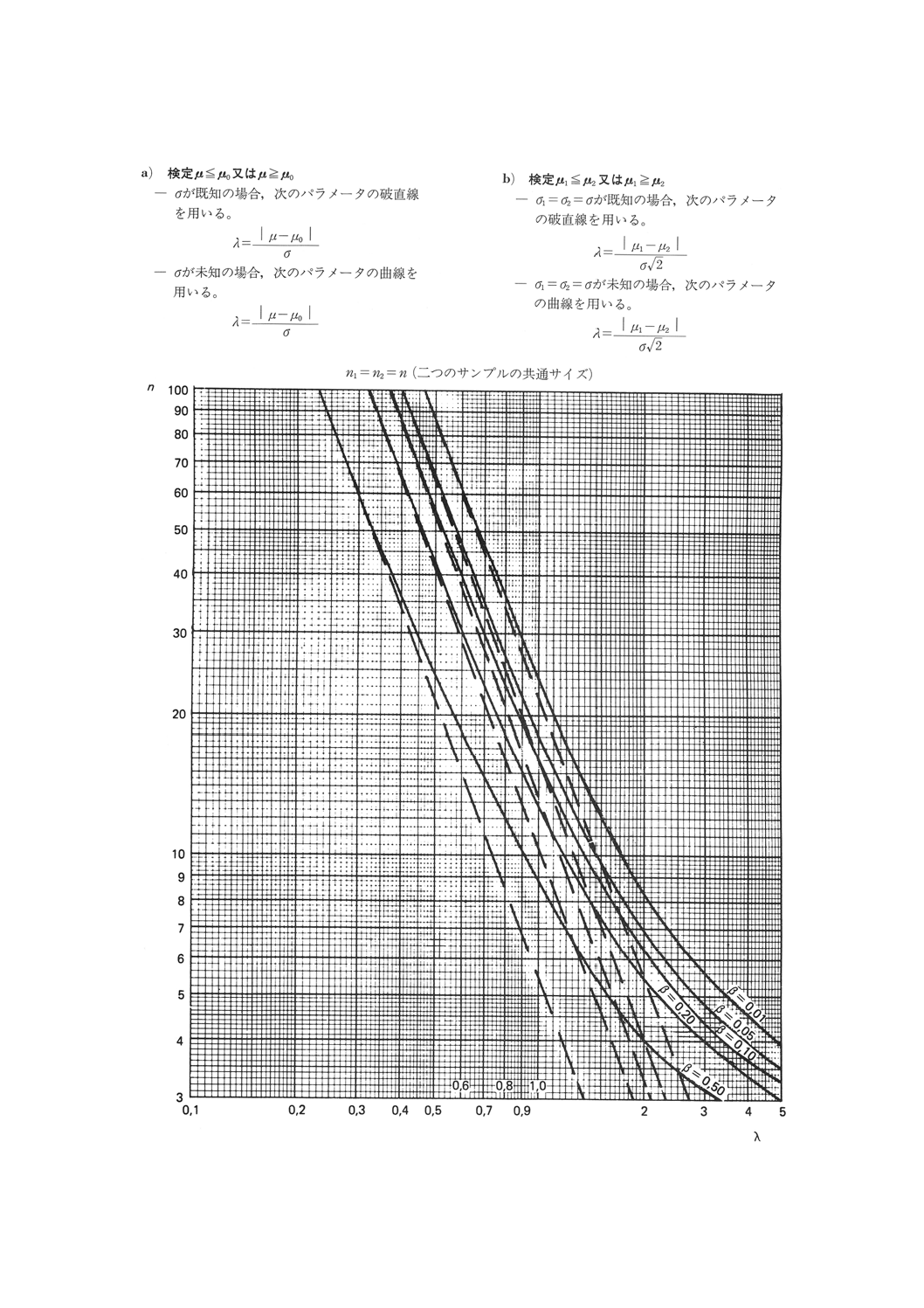
図4.2 平均値の比較の片側検定(第1種の危険α=0.01)
23
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
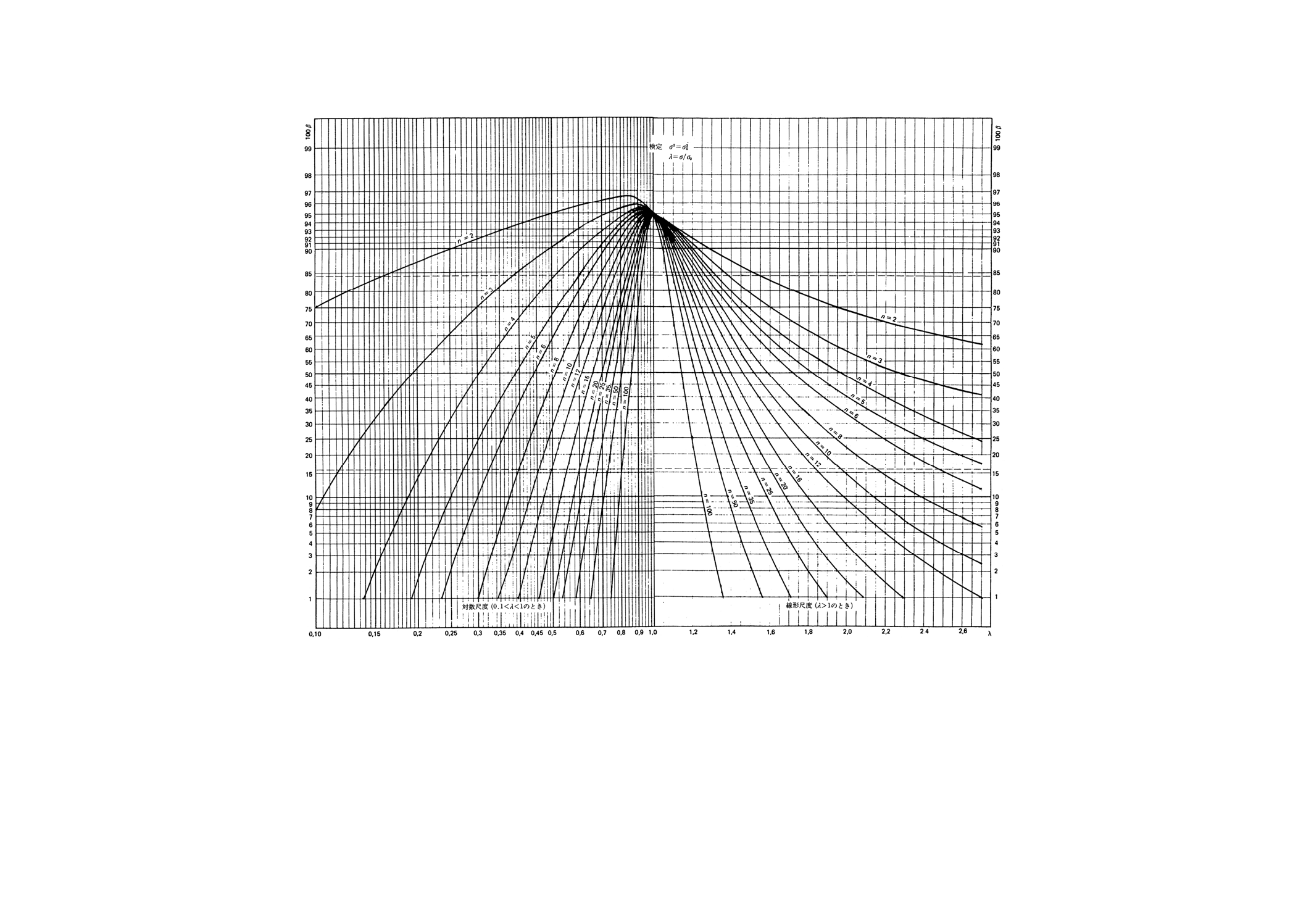
図5.1 分散と与えられた値との比較の両側検定(第1種の危険α=0.05)
24
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
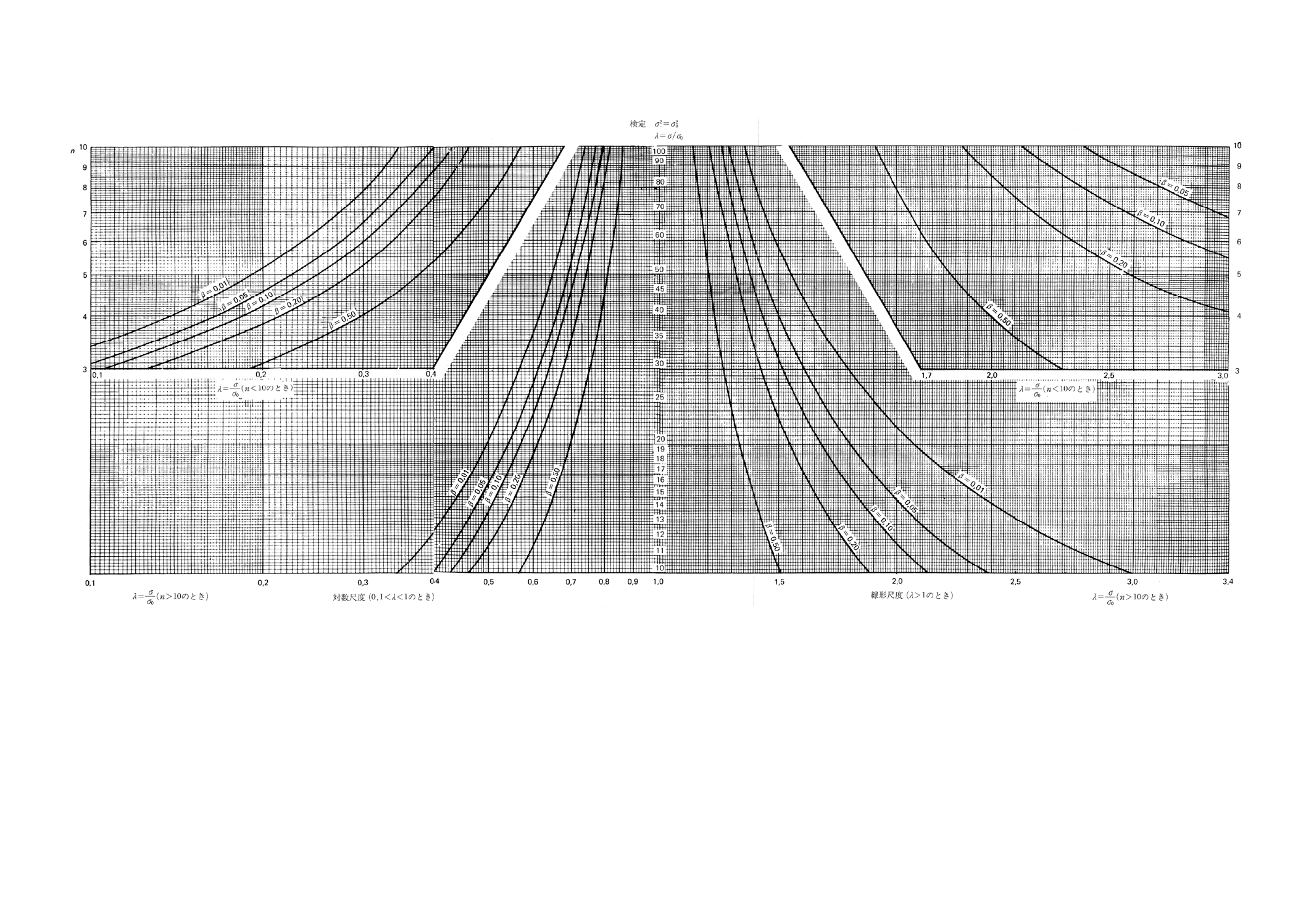
図5.2 分散と与えられた値との比較の両側検定(第1種の危険α=0.05)
25
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
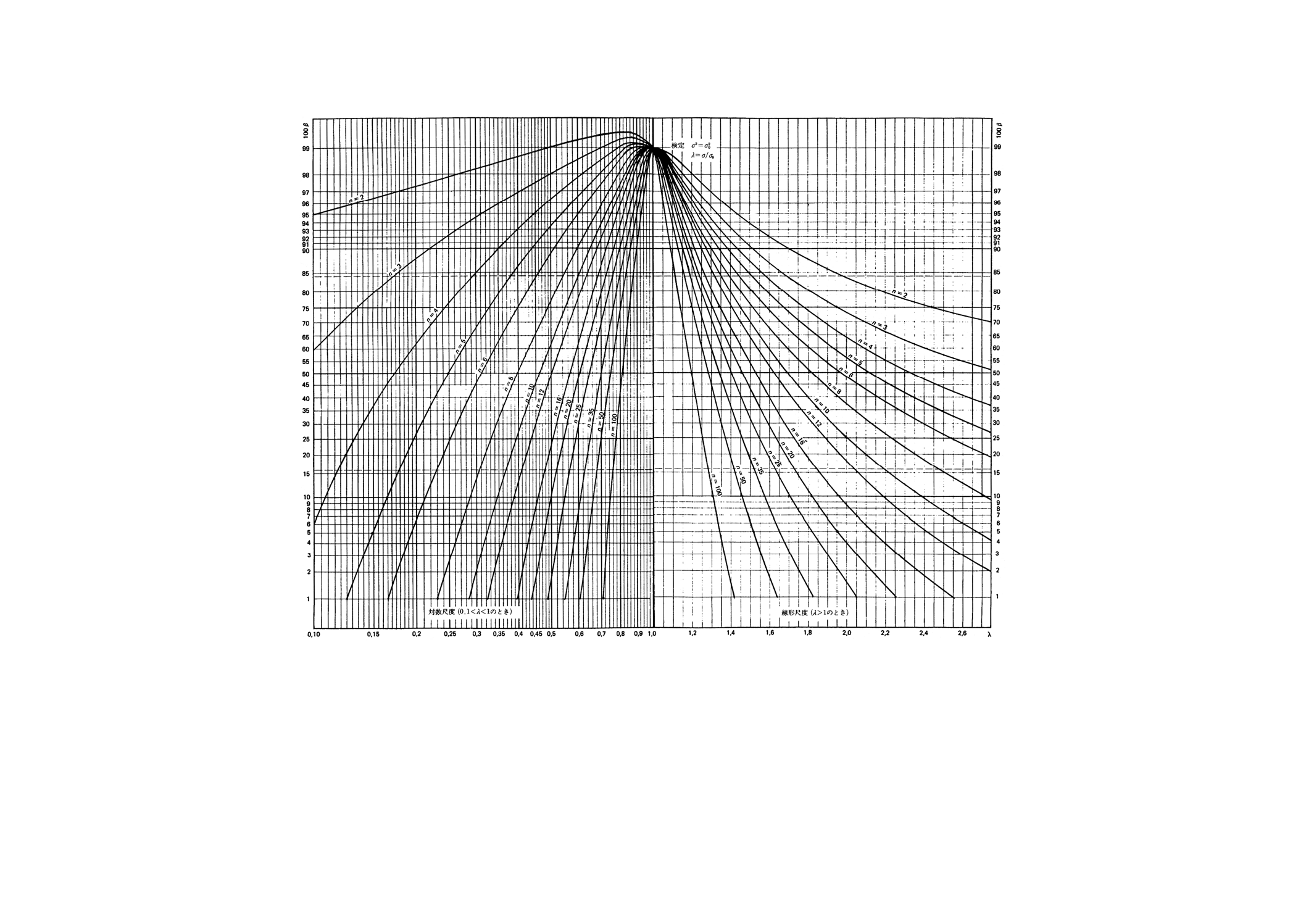
図6.1 分散と与えられた値との比較の両側検定(第1種の危険α=0.01)
26
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
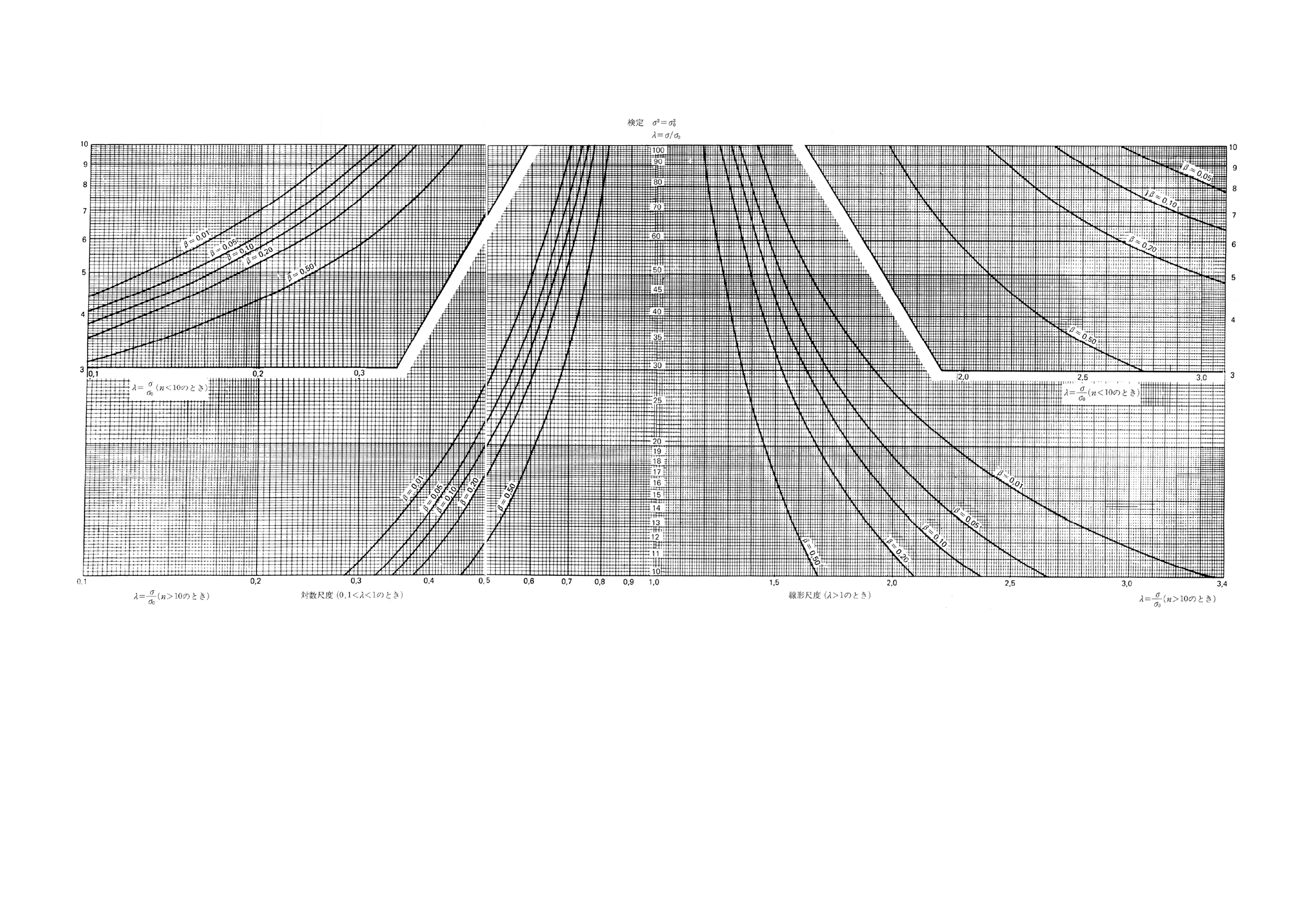
図6.2 分散と与えられた値との比較の両側検定(第1種の危険α=0.01)
27
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
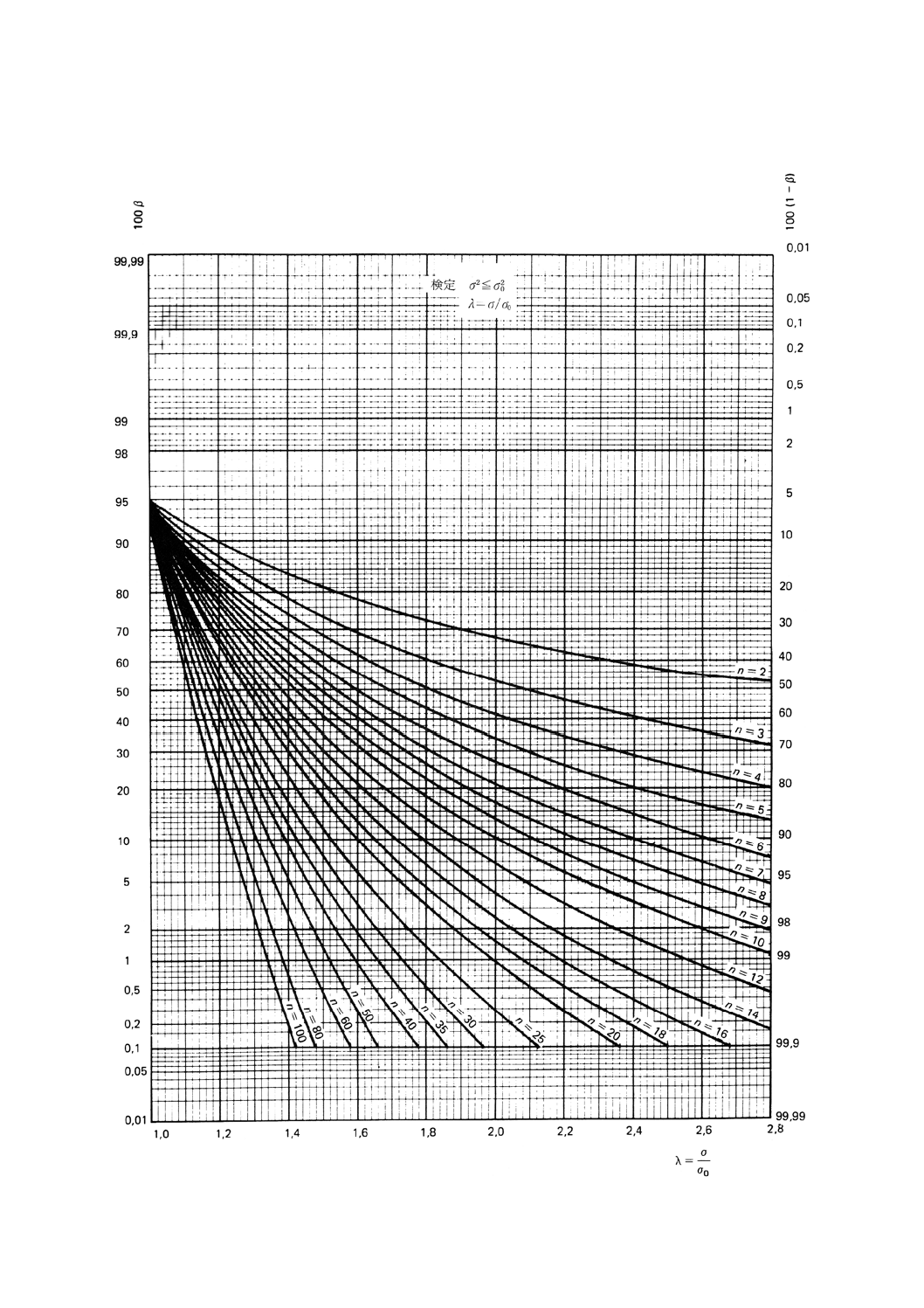
図7.1 分散と与えられた値との比較の片側検定(第1種の危険α=0.05)
2
8
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
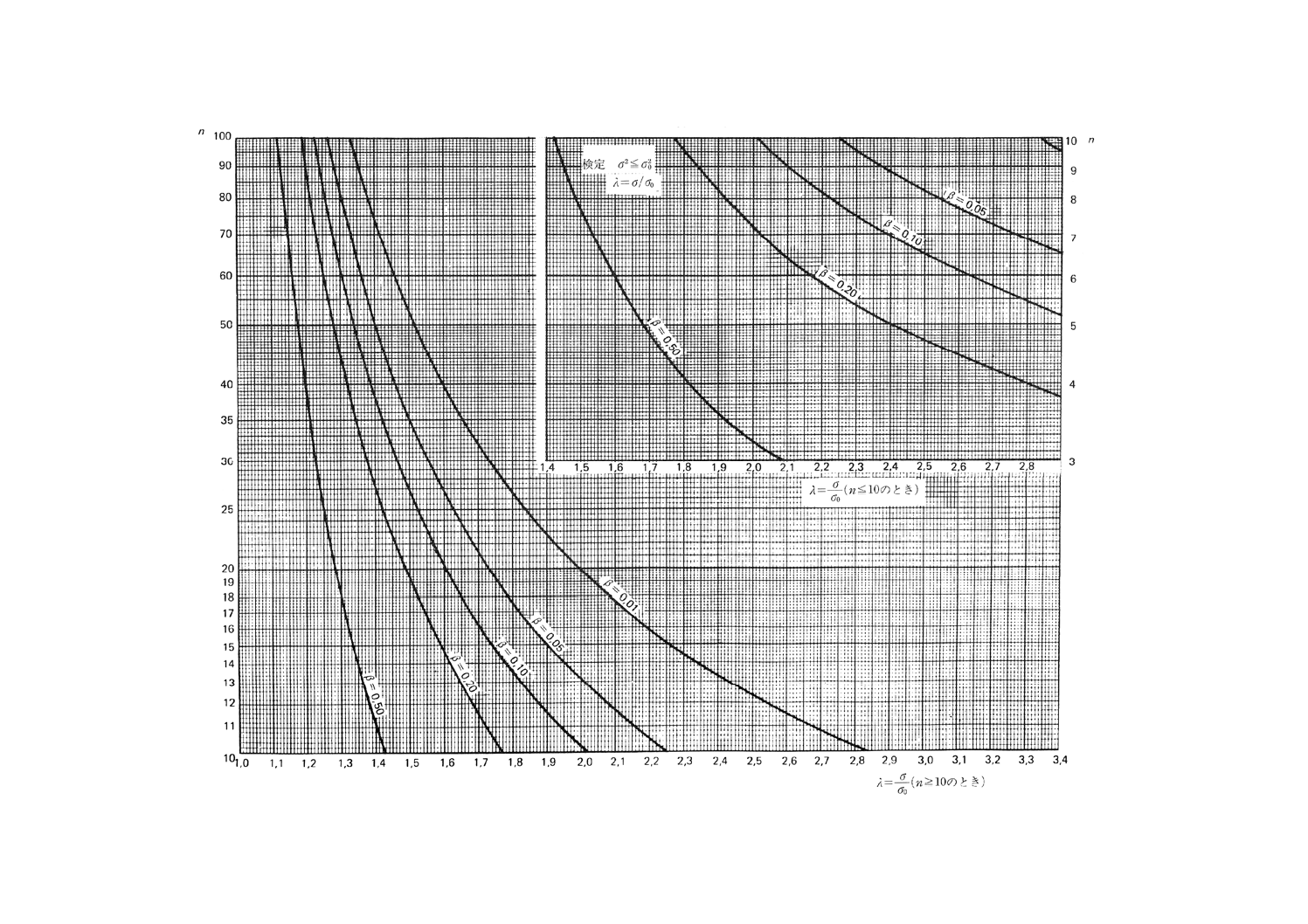
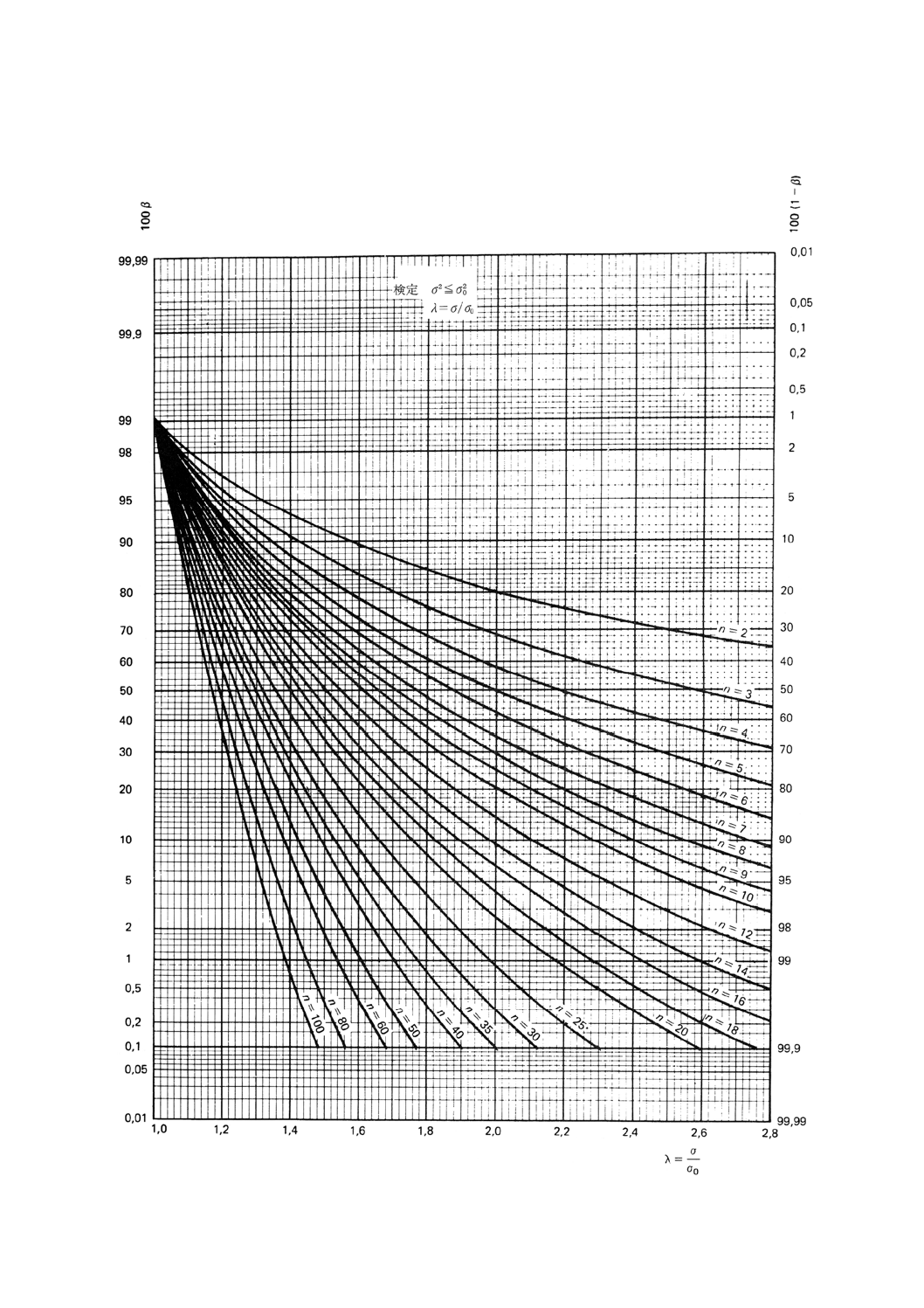
図7.2 分散と与えられた値との比較の片側検定(第1種の危険α=0.05)
29
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図8.1 分散と与えられた値との比較の片側検定(第1種の危険α=0.01)
3
0
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
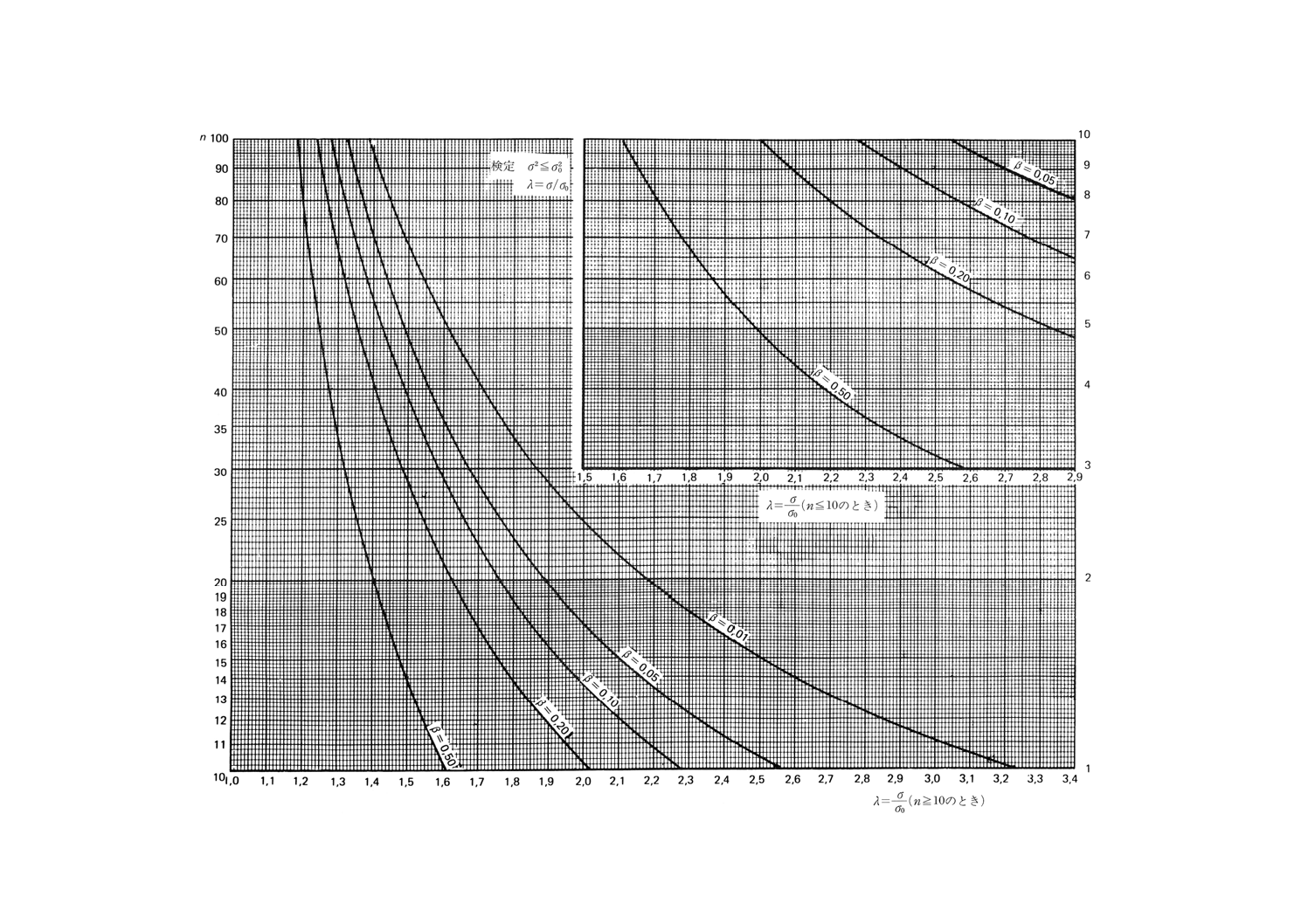
図8.2 分散と与えられた値との比較の片側検定(第1種の危険α=0.01)
31
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図9.1 分散と与えられた値との比較の片側検定(第1種の危険α=0.05)
3
2
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
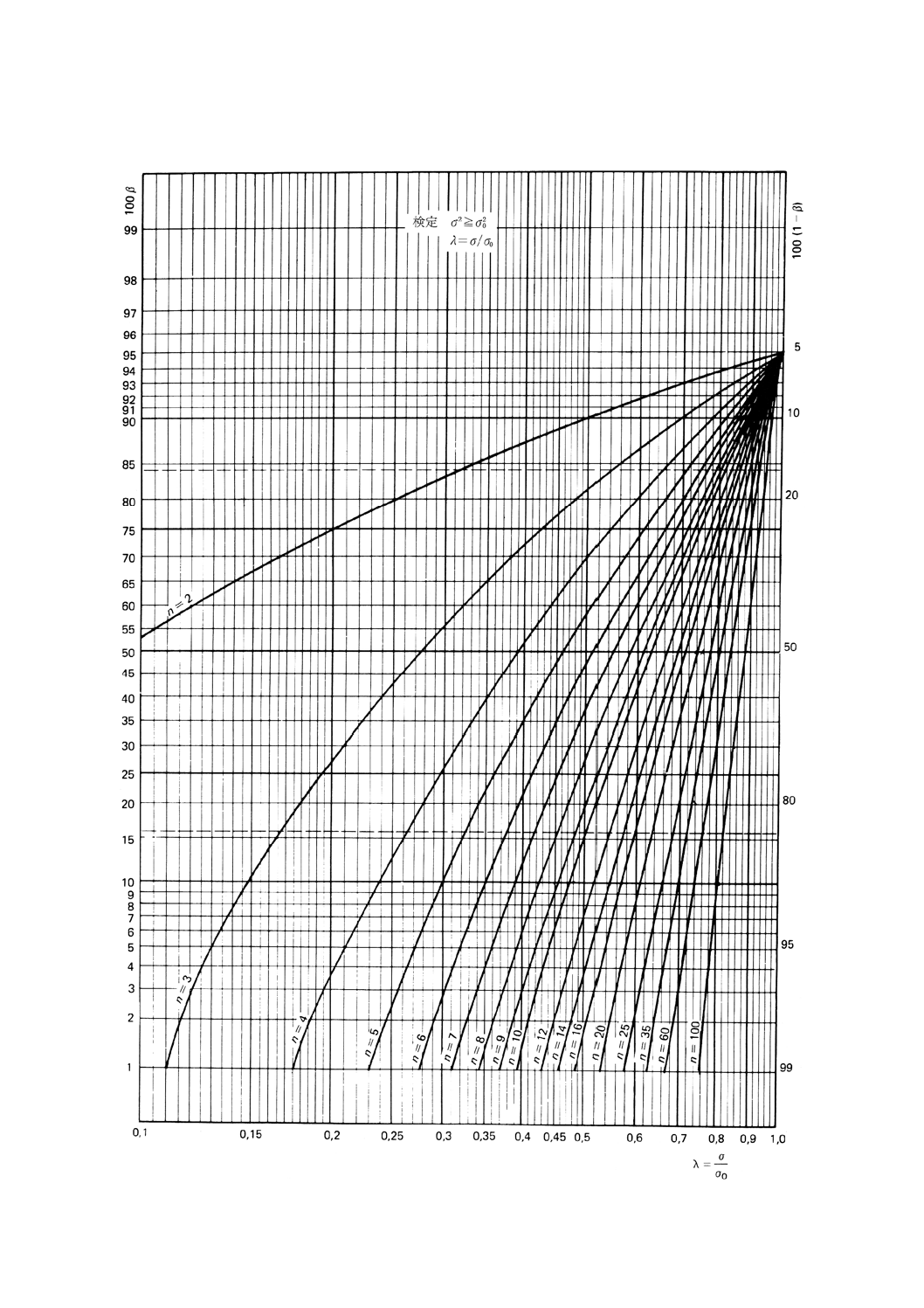
図9.2 分散と与えられた値との比較の片側検定(第1種の危険α=0.05)
33
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
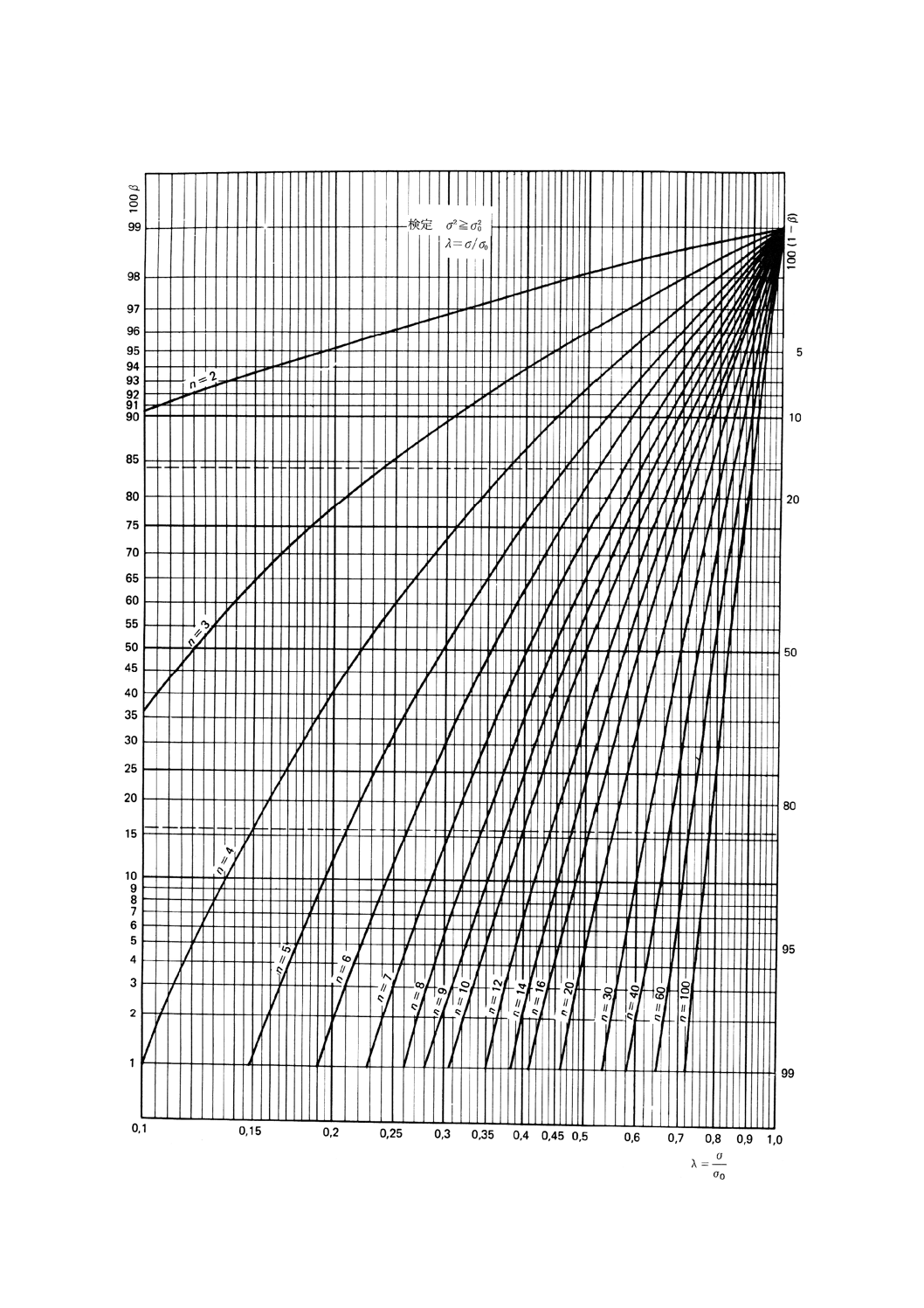
図10.1 分散と与えられた値との比較の片側検定(第1種の危険α=0.01)
3
4
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
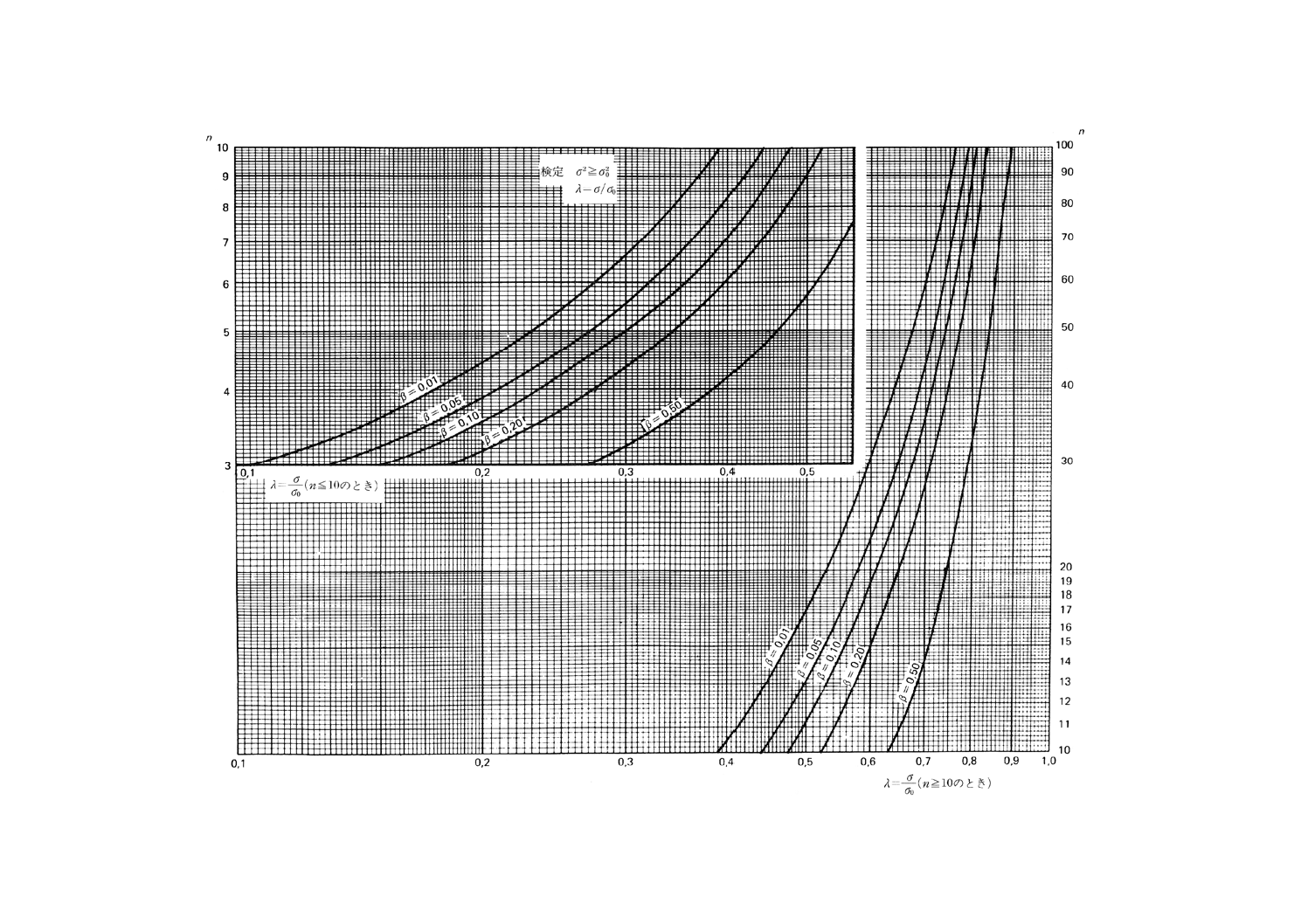
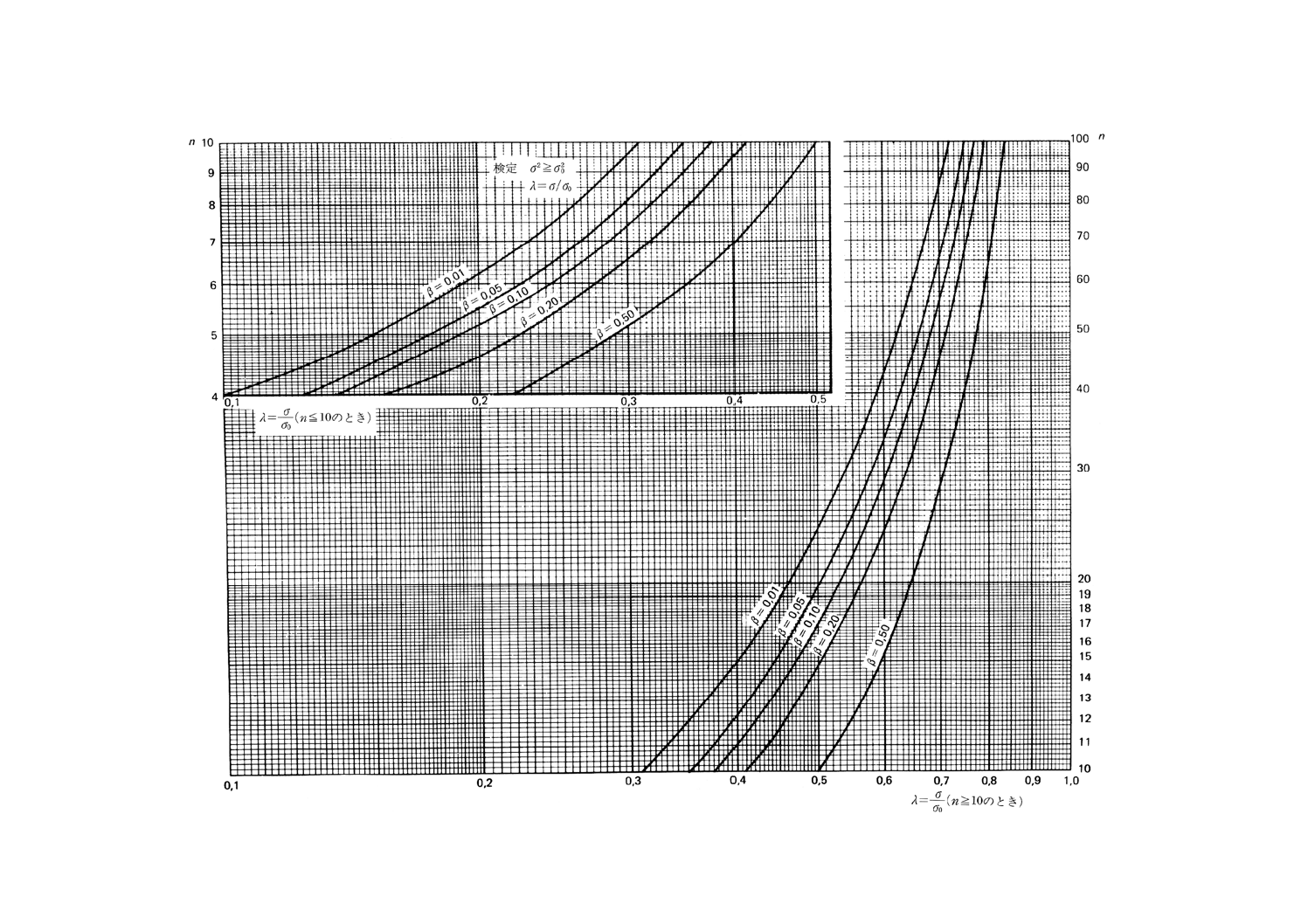
図10.2 分散と与えられた値との比較の片側検定(第1種の危険α=0.01)
35
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
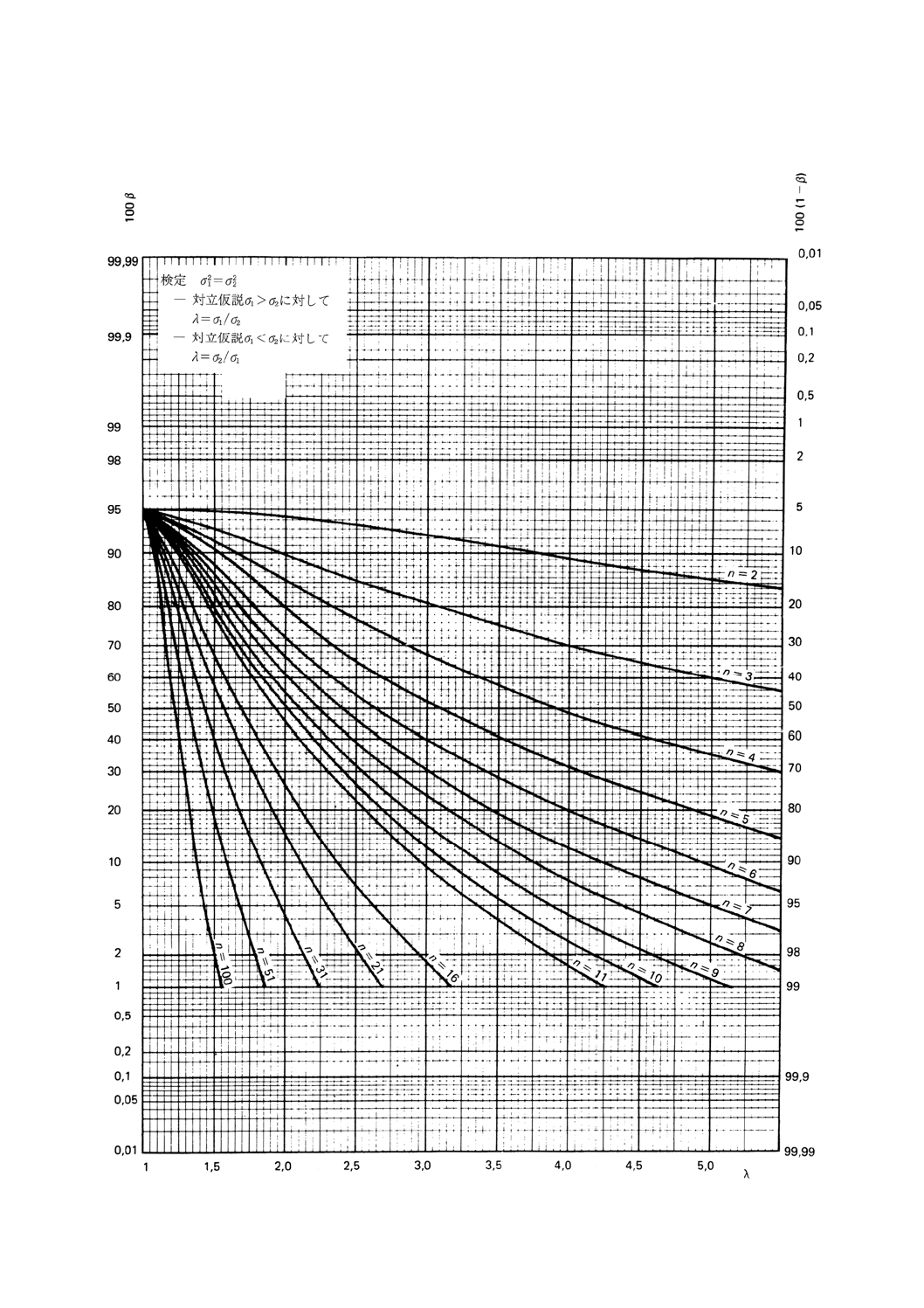
図11.1 二つの分散の比較の両側検定(第1種の危険α=0.05)
3
6
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
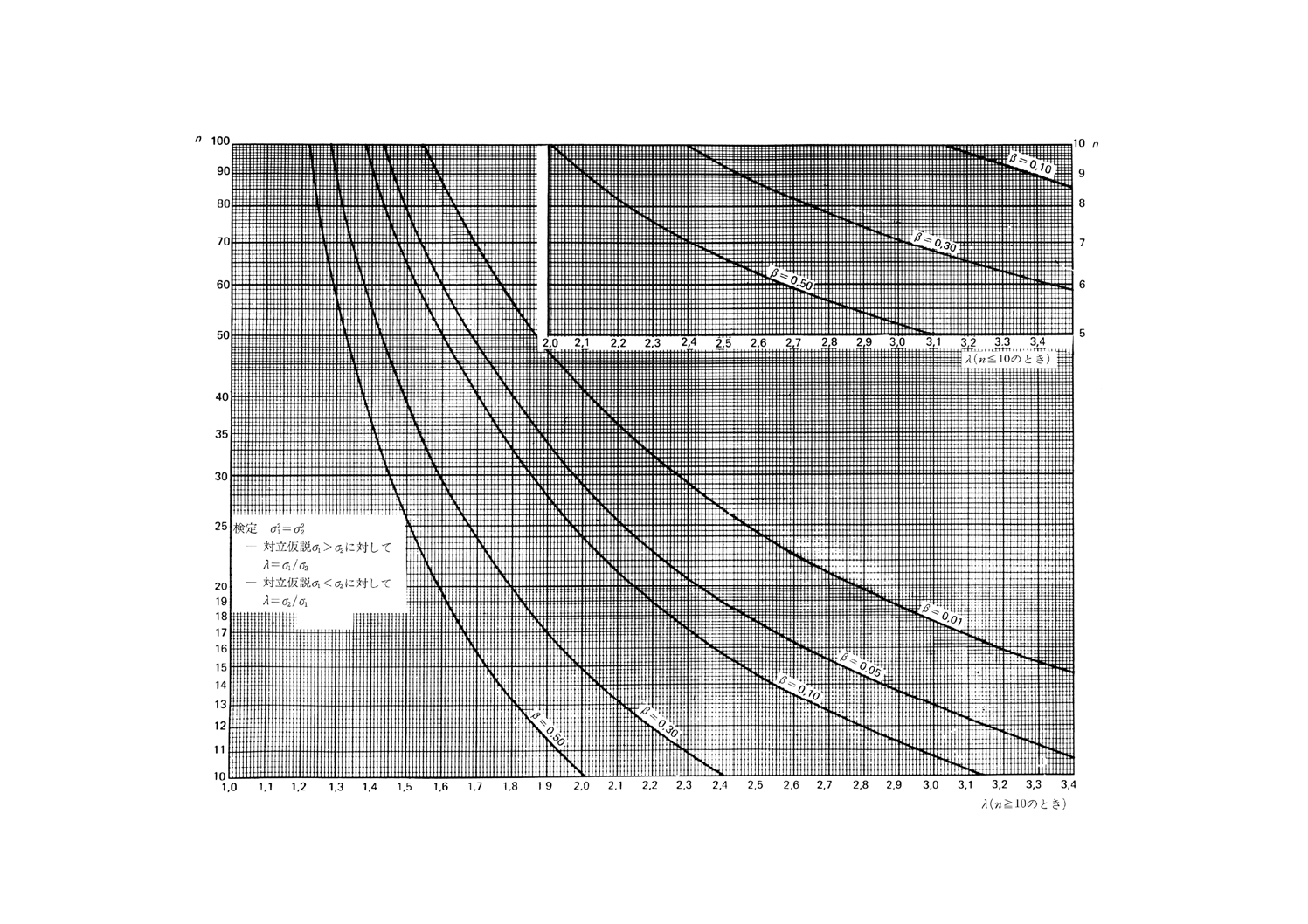
図11.2 二つの分散の比較の両側検定(第1種の危険α=0.05)
37
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
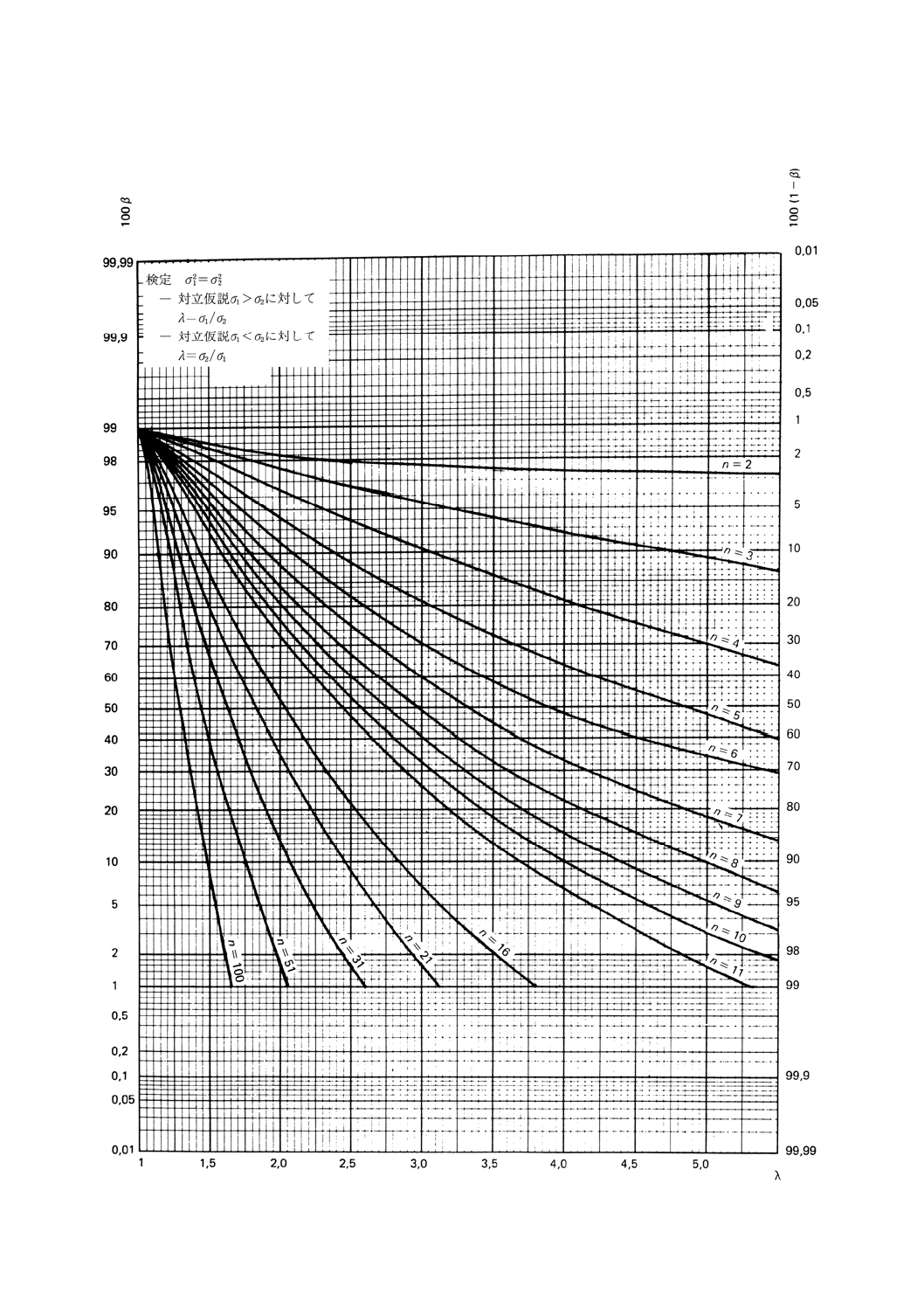
図12.1 二つの分散の比較の両側検定(第1種の危険α=0.01)
3
8
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
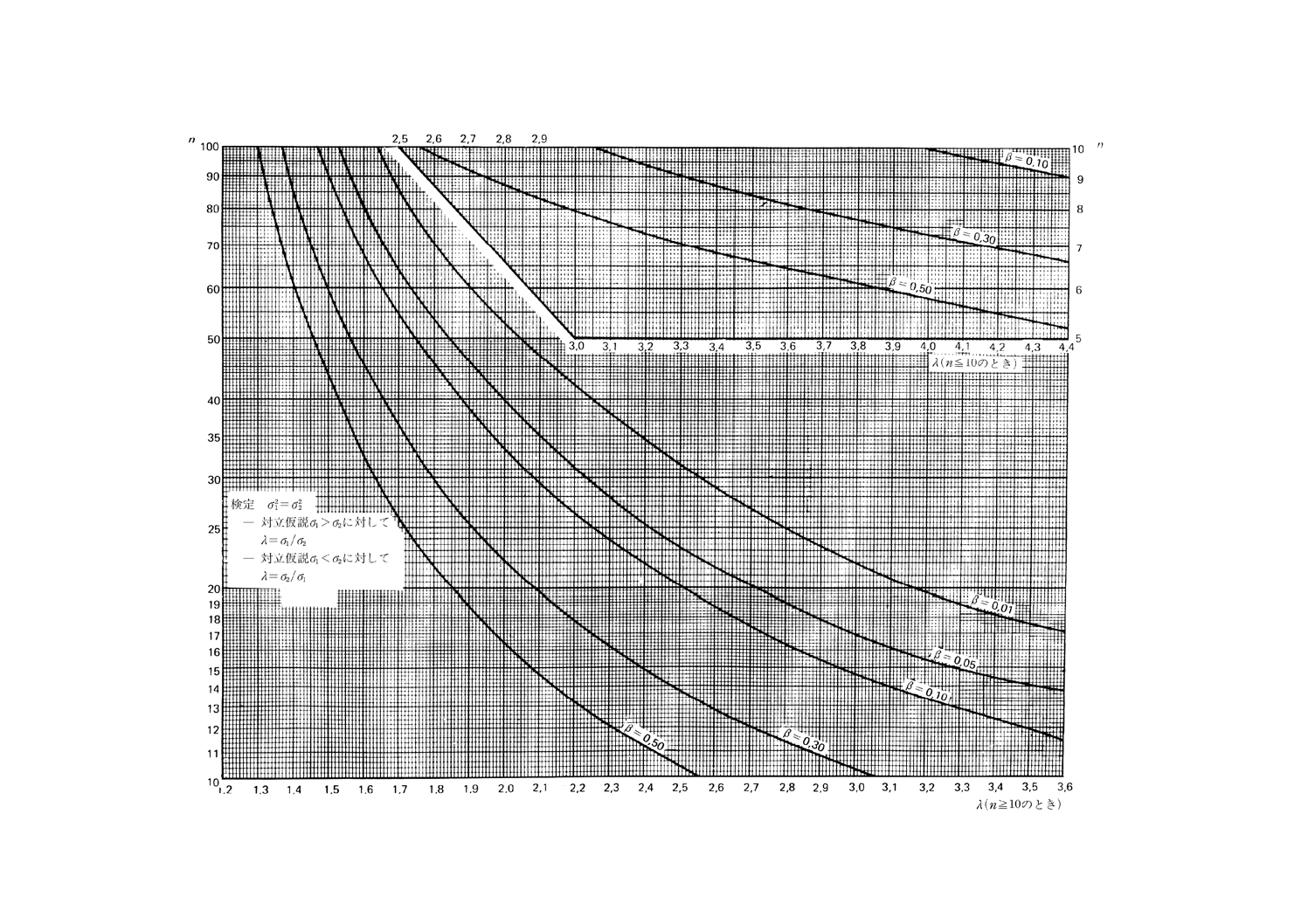
図12.2 二つの分散の比較の両側検定(第1種の危険α=0.01)
39
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
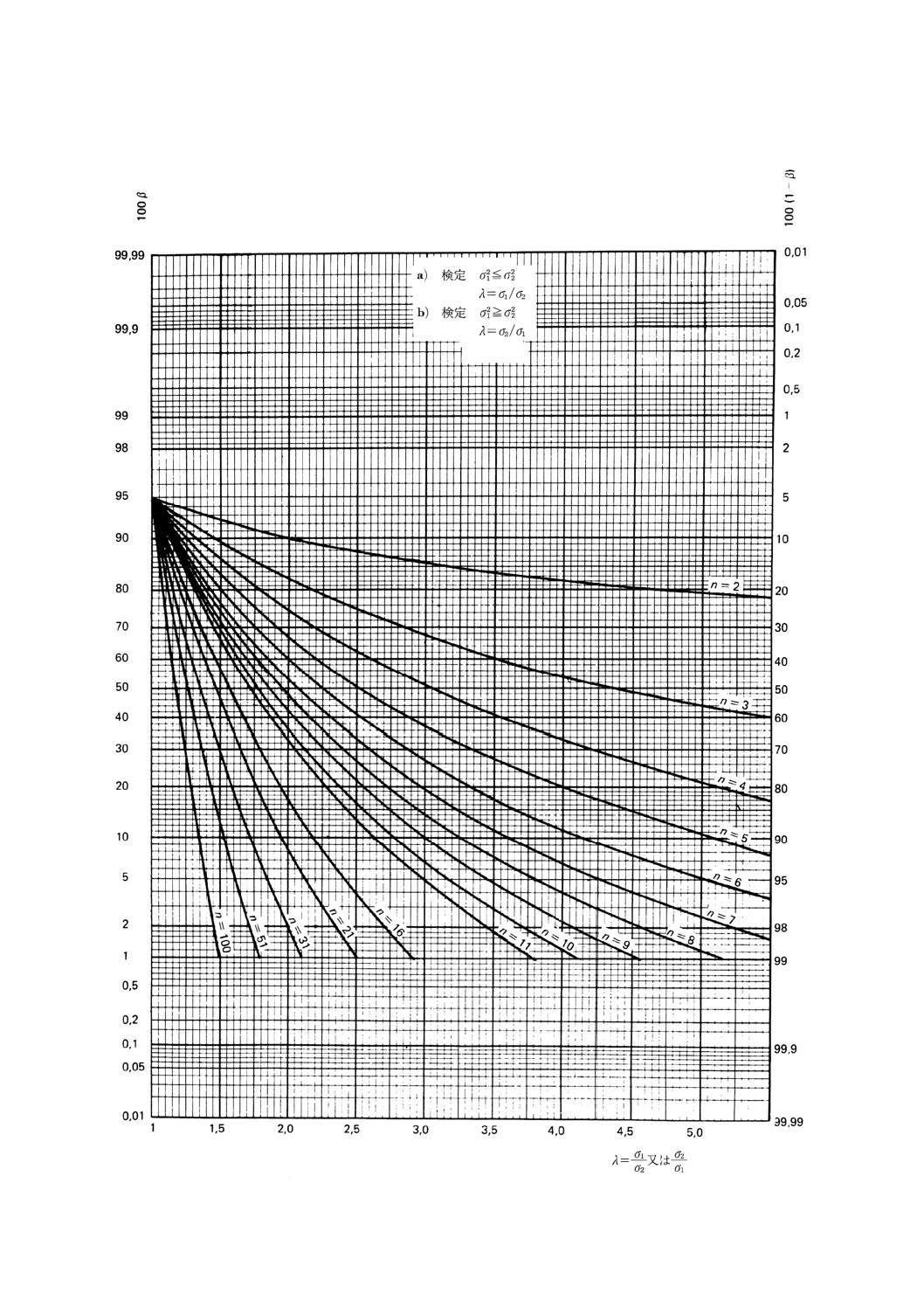
図13.1 二つの分散の比較の片側検定(第1種の危険α=0.05)
4
0
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
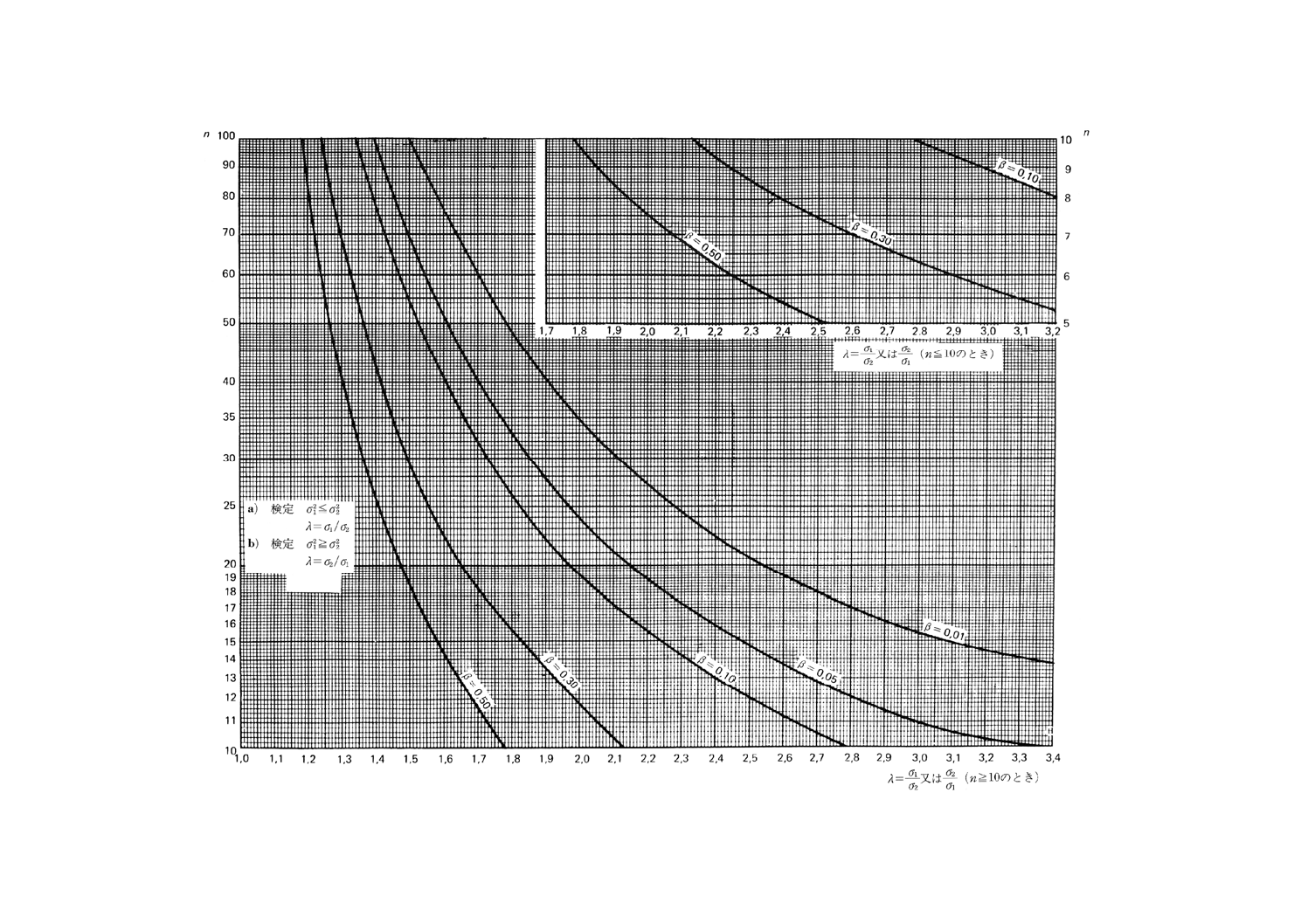
図13.2 二つの分散の比較の片側検定(第1種の危険α=0.05)
41
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
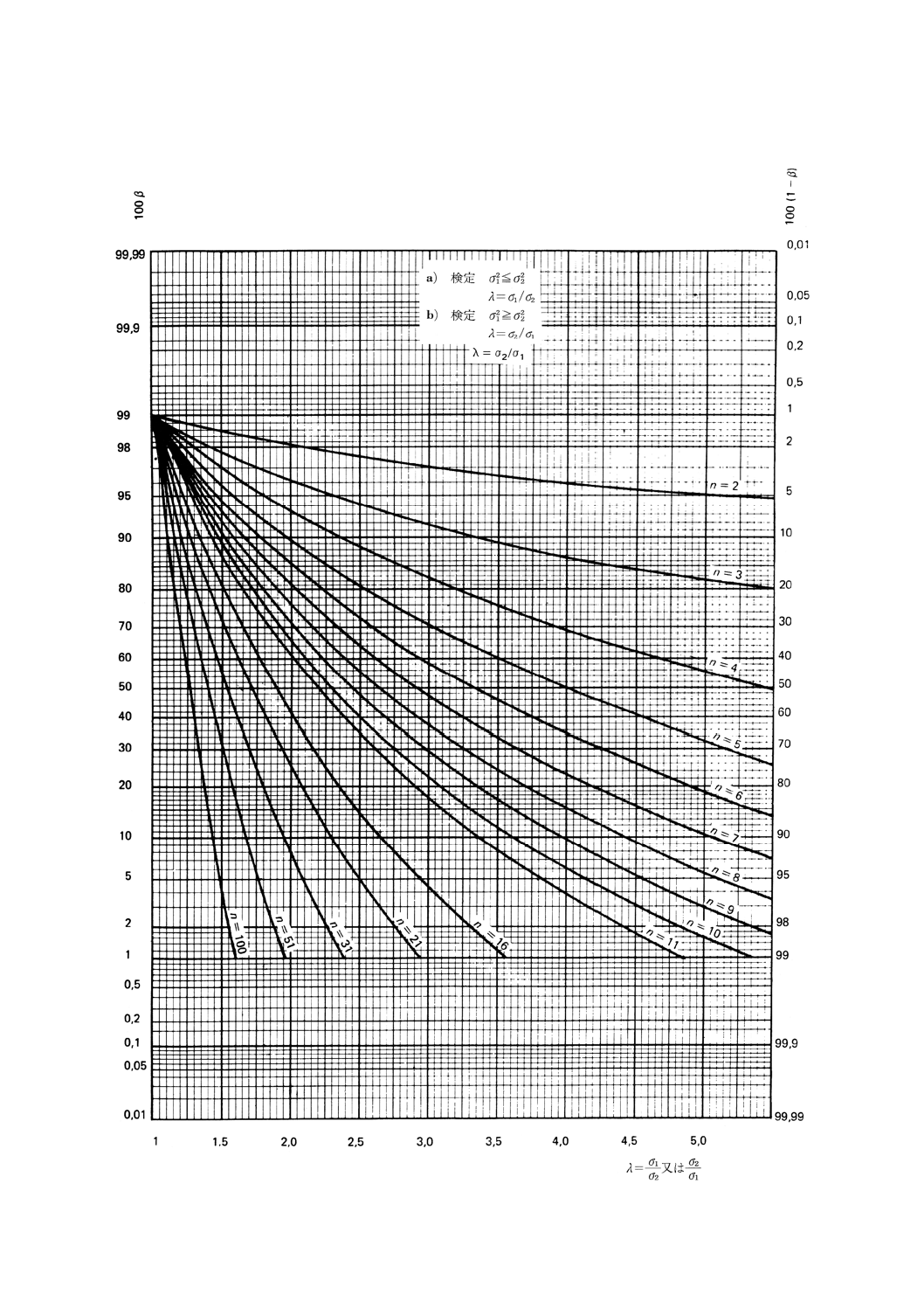
図14.1 二つの分散の比較の片側検定(第1種の危険α=0.01)

4
2
Z
9
0
4
1
-4
:
1
9
9
9
(I
S
O
3
4
9
4
:
1
9
7
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図14.2 二つの分散の比較の片側検定(第1種の危険α=0.01)
43
Z 9041-4 : 1999 (ISO 3494 : 1976)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
品質管理分野国際整合化分科会
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
今 井 秀 孝
工業技術院計量研究所
柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
QCコンサルタント
門 山 允
元東京国際大学(故人)
兼 子 毅
武蔵工業大学
◎ 椿 広 計
筑波大学社会工学系
仁 科 健
名古屋工業大学工学部
○ 野 澤 昌 弘
東京理科大学経営学部
三佐雄 武 雄
QCコンサルタント
宮 津 隆
帝京科学大学理工学部
○ 山 田 秀
東京理科大学工学部
○ 岸 本 淳 司
株式会社SASインスティチュートジャパン
横 尾 恒 雄
QCコンサルタント
大 島 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会































