Z 8828:2019 (ISO 22412:2017)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義··················································································································· 2
4 記号及び単位··················································································································· 3
5 測定原理························································································································· 4
6 装置······························································································································· 4
7 試料作製························································································································· 6
7.1 概要 ···························································································································· 6
7.2 限界濃度 ······················································································································ 7
7.3 適切な濃度の確認 ·········································································································· 7
8 測定手順························································································································· 8
9 結果の算出方法················································································································ 9
9.1 概要 ···························································································································· 9
9.2 相関関数解析 ··············································································································· 10
9.3 周波数解析法 ··············································································································· 11
10 測定系の適格性確認及び測定結果の評価 ············································································ 11
10.1 測定系の適格性確認 ····································································································· 11
10.2 測定結果の評価 ··········································································································· 12
10.3 測定の精度及び測定結果の不確かさ ················································································ 13
11 測定結果の報告 ············································································································· 13
附属書A(参考)理論的背景 ································································································· 15
附属書B(参考)考えられる測定誤差の概要及びその影響を最小にする方法 ·································· 22
附属書C(参考)オンライン測定 ··························································································· 25
附属書D(参考)推奨する試料調製方法 ·················································································· 26
参考文献 ···························································································································· 30
Z 8828:2019 (ISO 22412:2017)
(2)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
粉体工業技術協会(APPIE)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業
規格を改正すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業
規格である。これによって,JIS Z 8828:2013は改正されこの規格に置き換えられ,また,JIS Z 8826:2005
は廃止され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本工業規格 JIS
Z 8828:2019
(ISO 22412:2017)
粒子径解析−動的光散乱法
Particle size analysis-Dynamic light scattering (DLS)
序文
この規格は,2017年に第2版として発行されたISO 22412を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,主に液中に分散したサブミクロンの粒子,エマルション又は気泡の平均流体力学径及び粒
子径分布の測定に動的光散乱(DLS)法を用いる方法について規定する。DLS法は,準弾性光散乱(QELS)
法又は光子相関(PCS)法とも呼ばれる。
なお,PCS法とは,DLS法の測定手法の一つである。
この規格は,粒子の希薄懸濁液から濃厚懸濁液まで幅広い測定条件に適用できる。濃厚懸濁液でのDLS
法の測定原理は,希薄懸濁液の場合と基本的に同じである。しかしながら,濃厚懸濁液の測定では,特別
な装置構成及び試料調製が必要となる。高粒子濃度では,粒子間相互作用及び多重散乱の影響が大きくな
り,希薄懸濁液の場合と異なる見かけの粒子径が求まることになる。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 22412:2017,Particle size analysis−Dynamic light scattering (DLS)(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8819-1 粒子径測定結果の表現−第1部:図示方法
注記 対応国際規格:ISO 9276-1,Representation of results of particle size analysis−Part 1: Graphical
representation
JIS Z 8819-2 粒子径測定結果の表現−第2部:粒子径分布からの平均粒子径又は平均粒子直径及びモ
ーメントの計算
注記 対応国際規格:ISO 9276-2,Representation of results of particle size analysis−Part 2: Calculation
of average particle sizes/diameters and moments from particle size distributions
2
Z 8828:2019 (ISO 22412:2017)
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
注記1 粉体の粒子特性評価に関する用語は,JIS Z 8890を参照。
注記2 ISO及びIECでは標準化で用いる用語集を整備し,次のアドレスに記載されている。
− IECの用語はhttp://www.electropedia.org/で参照できる。
− ISOのオンライン参照アドレスはhttp://www.iso.org/obpである。
3.1
粒子(particle)
物理的境界をもった小さな物体(ISO 26824の1.1参照)。
注記1 物理的な境界は,界面とも記載される。
注記2 粒子は一つの塊として運動する。
3.2
平均流体力学径,
DLS
x
(average hydrodynamic diameter)
基礎となる粒子径分布の代表値に対応する流体力学直径。
注記1 平均粒子径は,粒子径分布の計算なしに直接的に決定するか,又は計算機で求めた光強度基
準,体積基準及び個数基準の粒子径分布から若しくは近似(変換)した頻度関数から計算す
る。
注記2 キュムラント法では散乱光強度基準の調和平均径を与え,場合によっては“z平均径”と呼
ぶ。
注記3 算術平均径,幾何平均粒子径又は調和平均粒子径は,JIS Z 8819-2によって粒子径分布から
計算できる。
注記4 頻度関数(線形座標系)又は変換した頻度関数(対数座標系)から計算した値は,大きく異
なるかもしれない(JIS Z 8819-1参照)。
注記5
DLS
x
は,粒子形状及び散乱ベクトル(すなわち,観察角度,レーザ波長及び分散媒の屈折率)
にも依存する。
3.3
多分散指数,PI(polydispersity index)
粒子径分布の広がりを示す無次元指標。
注記 単分散で球形の試験試料に対する典型的なPIの値は,0.07より小さい。
3.4
散乱体積(scattering volume)
入射レーザ光,及び受光器で受光される散乱光で定義される体積。
3.5
散乱光強度(scattered intensity)
散乱体積中の粒子によって散乱された光の強度。
3.6
カウントレート,IS(count rate)
単位時間当たりの光子パルス数。光電流(photocurrent)ともいう。
注記 散乱光強度に比例する光検出器で測定された電流でもある。
3
Z 8828:2019 (ISO 22412:2017)
3.7
妥当性評価(validation)
標準物質を用いて測定したときに,測定手順が全ての項目で規定どおりであることの確認。
なお,正確さの推定には,認証標準物質を用いる。
3.8
標準物質,RM(reference material)
一つ以上の特定の目的に関連し,計測過程で意図された用途に合致するように作製され,十分に均質で
安定な物質(ISO Guide 30:2015の2.1.1,修正)。
3.9
認証標準物質,CRM(certified reference material)
一つ以上の特定の目的のために計量的に有効な方法で測定された物質で,特定の特性値及びそれに関連
した不確かさ並びに計量的なトレーサビリティを示した認証値をもつ(ISO Guide 30:2015の2.1.2,修正)。
3.10
適格性確認(qualification)
標準物質を用いて測定したときに,装置がその仕様どおりに動作していることの確認。
4
記号及び単位
C(Γ)
減衰定数又は特性周波数の正規化した分布関数
無次元
DT
並進拡散係数
m2/s
Dc
協同拡散係数
m2/s
Ds
自己拡散係数
m2/s
f
周波数f=ω/(2 π)
Hz
g(1)(τ)
正規化された散乱光電場の相関関数
無次元
G(2)(τ)
散乱光強度の相関関数
任意の単位
G(Γj)
正規化された減衰定数Γjの分布関数
任意の単位
IS
散乱光強度,カウントレート,又は光電流
任意の単位
I0
入射光強度
任意の単位
M
ヒストグラムの区分数
無次元
n
分散媒の屈折率
無次元
P(ω)
パワースペクトル
任意の単位
PI
多分散指数
無次元
ΔQint,i
粒子径区分i,すなわち,粒子径範囲xi−1<x≦xiでの散乱光強度基準の粒子量。
無次元
x
この規格では粒子の流体力学的直径
nm
DLS
x
流体力学的平均径
nm
Γ
散乱光強度基準における減衰定数又は特性周波数分布の平均値
s−1
Γmax
ヒストグラム法での最大減衰定数
s−1
Γmin
ヒストグラム法での最小減衰定数
s−1
η
分散媒の粘度
mPa·s
θ
散乱角
°
λ0
レーザ光の真空中での波長
nm
4
Z 8828:2019 (ISO 22412:2017)
μ2
散乱光強度基準粒子径分布をキュムラント展開したときの2次の係数
s−2
ρ
粒子密度
g/cm3
τ
相関時間
s
q
散乱ベクトルの絶対値
nm−1
φ
粒子の体積分率
無次元
ω
角周波数
rad/s
5
測定原理
流体中に懸濁する粒子は,懸濁する流体分子との相互作用の結果として,ブラウン運動をしている。ブ
ラウン運動に関するストークス−アインシュタインの理論[1]では,非常に低い濃度の平滑な表面をもつ球
の運動は,粒子の大きさとともに,懸濁流体の粘度及び温度によって決まる。したがって,既知の温度及
び粘度の流体中における粒子の運動の測定から,粒子の大きさを決定することができる。
DLS法[2]〜[6]では,粒子の運動を光学的に検出する。懸濁粒子は,可干渉な単色光によって照射される。
運動する懸濁粒子からの散乱光には,粒子の位置の時間的変動で生じた光の変動位相(時間変動位相)が
含まれている。散乱光の時間変動位相は,入射光の位相とのずれか,又は入射光の中心周波数からの周波
数のずれのいずれかと考えることができる。長時間の測定によって,ランダムな粒子の運動は,光学的な
位相のずれか,又は周波数のずれの分布を形成する。これらのずれは,粒子群からの散乱光(ホモダイン
又は自己ビートモード)か,又は入射光の一部を参照光(ヘテロダイン)として用いることで求められる。
装置構成によらず,粒子からの受信した光学的な信号は,粒子の散乱効率に関係し,したがって,散乱光
強度基準である。
この方法で評価される粒子の大きさの上限は,粒子の沈降によって決まり,粒子密度によるが,一般的
には10 μm以下である。
DLS法は,静置している懸濁液に対して開発された。流れと観測軸(方向)とを直交する様に選択する
場合,流動する試料も適切な手法,及び装置構成によって測定できる(附属書C)。
種々の拡散モード,粒子間相互作用,多重散乱及び蛍光は,DLS測定による見掛けの粒子径の算出に本
質的な影響を与える。附属書B参照。
6
装置
一般的な装置は,次の要素から構成される。
6.1
レーザ 粒子に照射される可干渉性の単色光で,照射及び検出方向によって決まる面に対して直交
する電場成分に分極している(垂直偏光)。どのようなレーザも使用可能である。例えば,ガスレーザ(He-Ne
レーザ,Arレーザ),固体レーザ,半導体励起固体レーザ,及び半導体レーザ。
6.2
光学系 散乱体積に入射するレーザを集光するため,及び散乱光を検出するために使用するレンズ
及び部品。光ファイバは,しばしば検出系及び光伝送用の光学系の一部として使用される。
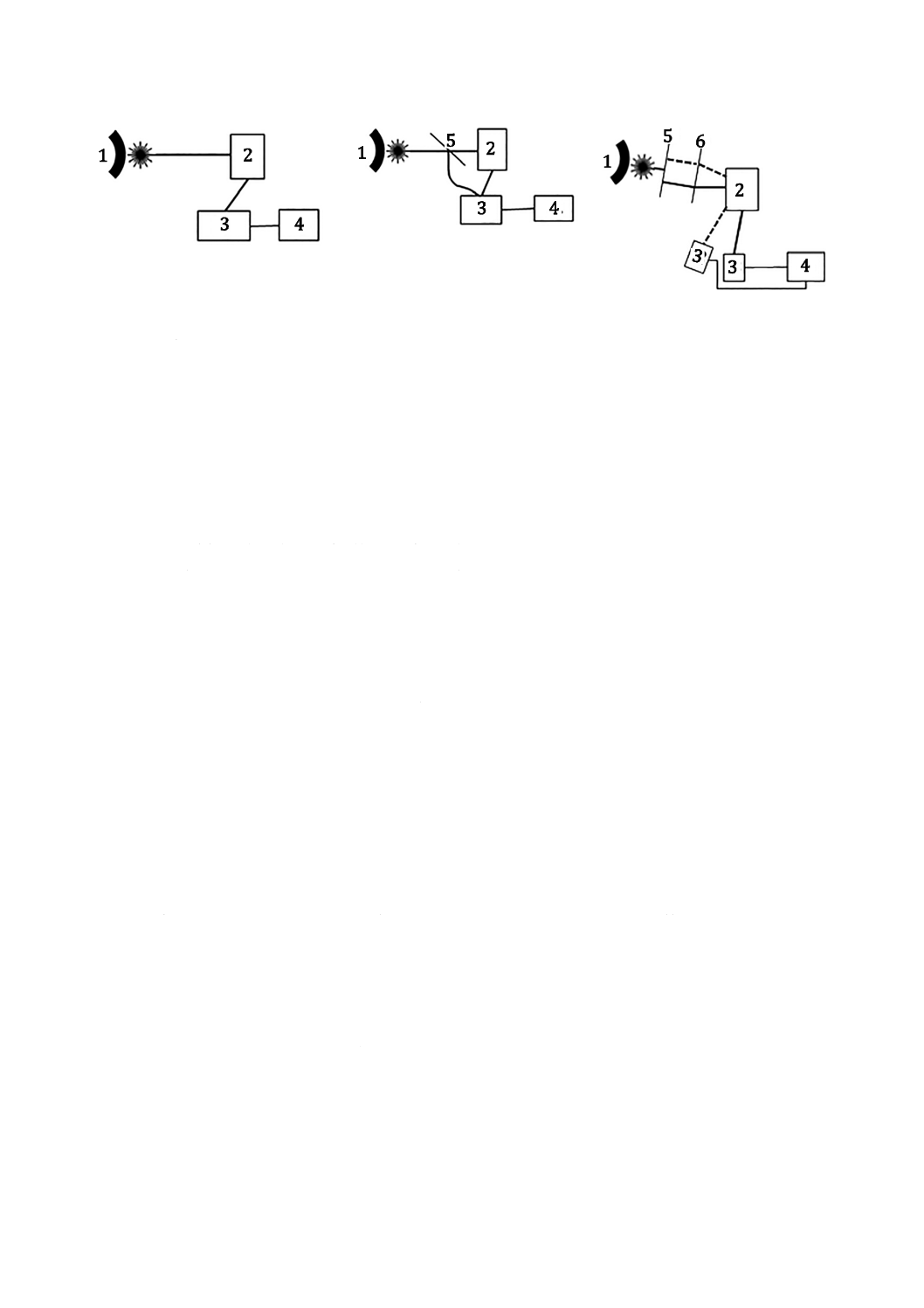
可干渉な光を使用すると,散乱光と参照光とが干渉し,散乱光の周波数のずれが測定できる。図1のa)
及びb)に示す参照光に対する二つの方法が一般的に用いられている。
5
Z 8828:2019 (ISO 22412:2017)
a) ホモダイン法
b) ヘテロダイン法
c) 交差相関法
(ホモダイン法同時検出法)
1
レーザ
2
試料
3
検出器
4
相関器又はスペクトルアナライザ
5
ビームスプリッタ
6
レンズ
図1−DLS法の一般的な光学系配置
− ホモダイン法(自己ビート法ともいう。)[図1 a)]では,粒子群からの散乱光を検出器で混合するこ
とで,周波数のずれ(又は位相差)の測定が可能になる。
− ヘテロダイン法[図1 b)]では,散乱光は,入射光の一部と混合される。シフトを起こしていない入
射光は,周波数のずれ(又は位相差)の測定に対する参照光となる。
注記 DLS法では“ヘテロダイン”は,同一光源からの光の散乱光と非散乱(散乱していない)光
との混合と理解されている。DLS法のヘテロダイン法の定義は,例えば,光学干渉法での定
義とは異なる。
− 交差相関法[図1 c)]では,二つのホモダイン法による測定が次のように同時に実施される。二つの
散乱ベクトルの大きさと散乱体積は一致するが,対応する散乱ベクトルは一致しない。そのため,こ
の二つのレーザ光は対応する散乱光のゆらぎパターンを生じる。しかし,それらのゆらぎの相関は理
想的ではない。なぜならば,一方の検出器はもう一方からの散乱光も検出し,多重散乱は全く相関が
ないからである。上記の二つの事象は,単にバックグラウンド成分を増加させるだけであって,時間
依存の信号成分に影響を与えることはない。
6.3
試料ホルダ 試料温度の変動を±0.3 ℃に制御可能なもの。試料温度に関する正確な情報は種々の計
算に必要であるが,どの温度に調整するかは問題ではない。
6.4
光検出器 捕捉された散乱光の強度に比例する出力をもつもの。光電子増倍管又は(アバランシェ)
光ダイオードが一般的に使用される。検出器は,どのような角度でも設置可能である。データ収集は,線
形又は対数間隔で行う。
6.5
信号処理ユニット 時間的に変動する散乱光強度の信号の取り込み,及び入力信号の自己相関関数,
交差相関関数,又はパワースペクトルの出力が可能なもの。この出力は,線形,対数,又は両者を組み合
わせた形で作動するハード的な及び/又はソフト的な相関器によって行われる。
この出力は,懸濁粒子の粒子径を代表する特性周波数又は時間変動位相の分布を含んでいる。検出され
る光子の到達時間には分布がある。このことは,入射光強度が一定であっても,散乱光の信号が変動する
ことを意味する。変動する散乱光強度信号は,これまでに得られた信号に重ねられる。相関分析では,相
関性のない信号は一定であるが,拡散する粒子に関係する信号は指数的に減少する。スペクトル解析では,
6
Z 8828:2019 (ISO 22412:2017)
相関性のない信号は,直流成分又はゼロ周波数項で表される。時間変動成分から,DLSの理論を用いて粒
子径分布を決定する。
6.6
計算ユニット 粒子径及び/又は粒子径分布を得るための信号処理が可能なもの。信号処理ユニッ
トとしての機能を併せもつ計算ユニットもある。
− 自己相関解析による計算では,粒子径分布を決めることなく平均粒子径が求められる。しかし,粒子
径分布の算出も可能である。
− 周波数解析による計算では,信号のパワースペクトルを用いて粒子径分布を算出する。
− 交差相関法による計算では,多重散乱の影響を定量化及び最小化することができる。したがって,高
い粒子濃度まで利用可能になる(しかしながら,粒子間相互作用の影響を除くことはできない。)。こ
の方法の欠点は,より複雑な光学系を必要とする点である。
6.7
装置の設置場所 清浄な環境で,過剰な電気ノイズ及び機械的振動がなく,日光が直接当たらない
環境である場所。有機溶剤を懸濁媒に用いる場合,健康及び安全面に関する国内の規制に従い,作業空間
の換気を十分に行う。頻繁な光学系の調整を避けるため,装置は堅固なテーブル又はベンチに設置する。
警告 DLS装置は,眼球に永久的な損傷を与える低出力又は中出力レーザを備えている。レーザビー
ムの光路又は反射光を,決して直接のぞき込んではならない。レーザが動作している場合,高
い反射率の物体がレーザビームの光路内に置かれていないことを確認する。
レーザ放射の安全性に関する国内法規を遵守しなければならない。
7
試料作製
7.1
概要
分散媒中に粒子を十分分散させた試料を用いることが望ましい。超音波,ろ過などの分散手順は,結果
に影響を与えるため,その分散手順を報告しなければならない。分散媒は,次の要件を満たす。
a) 測定波長域で十分に透明で(吸収がなく),蛍光を発しない。
b) 粒子状の不純物を含まない。
c) 粒子状物質の溶解,膨潤又は凝集が起きない。
d) 粒子状物質とは十分に異なる既知の屈折率をもつ。
e) 使用される測定温度範囲において,粘度は±2 %の範囲で既知である。
注記 平均粒子径
DLS
x
は,粘度ηに直接,逆比例するので,DLS
x
の不確かさは常にηの不確かさよ
り大きい。
f)
バックグラウンドの散乱は,装置の取扱説明書に記載された値より,低い(これは,分散媒だけでの
カウントレート,及び測定部に試料又は溶媒が存在しない場合のカウントレートを測定することで確
認できる。前者の場合,少なくとも試料より1桁少ないことが推奨され,一方,後者では,装置のバ
ックグラウンド値以下であることが望まれる。)。
二重層の形成は,流体力学径に重大な影響を及ぼす。拡散二重層又は電気二重層を圧縮できるほど高い
イオン強度をもつ分散媒を用いると,DLSによる測定結果と電子顕微鏡による測定結果との間でよりよい
一致が得られる。伝導度を1 mS/cmにすれば,通常,流体力学径と顕微鏡で測定した径とは一致するよう
になる。特に,二重層を圧縮する方法は,微小な粒子で有効である。
水が分散媒として多く用いられる。新しくイオン交換され,ろ過(孔径0.2 μmのろ材)された水を用い
ることが推奨される。二重層厚さを減少させるために,イオン性の添加物(すなわち,濃度10 mmol/L=
0.6 g/Lの塩化ナトリウム)を添加してもよい。しかしながら,イオン強度の調整が試料を不安定にしない
7
Z 8828:2019 (ISO 22412:2017)
か,又は添加物が試料と反応しないかを,あらかじめ検討しておく必要がある(塩素イオンと銀イオンと
の関係など)。
7.2
限界濃度
DLSの測定範囲における粒子濃度の下限は,粒子径,検出器の感度などの因子の他に,測定体積中にあ
る粒子の数によって決まる。
懸濁粒子を含む試料からの散乱光強度(カウントレート又はISとして表現される。)は,分散媒だけの
場合に得られる信号の10倍以上であることが望ましい。散乱光強度比が10より小さい場合,粒子の質量
分率が低いか,又は粒子径分布が非常に広いかのいずれかであり,結果のばらつきが大きく,精度も低く
なる。
報告されている粒子径に影響を与えることなく測定できる分散粒子の最大濃度は,粒子間相互作用及び
多重散乱によって決まる。濃度限界は希釈によって経験的に決めることが望ましい(附属書B参照)。
7.3
適切な濃度の確認
装置が異なると,異なる光学観測角及び光学配置が採用されている。ここに示す目視及び確認の方法は
一般的なものであるが,特定の装置の操作に対しても適用できる。
次のような目視及び確認を推奨する。
a) 試料を装置に設置する前に目視で検査する。低濃度の試料はほとんど透明である。高濃度では,乳白
又は不透明である。
b) 試料は事前に装置に入れ,試料の温度を確実に一定値にする。カウントレート又は信号値を確認する。
次のいずれかの操作によって,カウントレート又は信号値を調整できる。
− 受光検出器の開口を変える(検出器の可干渉度も変える。)。
− 受光検出器のゲインを調整する。
− レーザ光源に印加する電力を調整(限定的な調整)する。
− 減光フィルタをレーザ光源の前又は検出器の前に用いる。
c) 自己相関法による相関関数解析を用いる装置では,適切に設定された相関計を用いて,切片値1)が装
置メーカによって定められた値より大きいかを確認する。その値が低いことは,調整の悪い光学系,
多重散乱,又は散乱光の非常に弱い試料による。非常に弱い散乱光しか得られない試料では,検出器
の開口を広げる必要があるが,可干渉性が失われるので注意が必要である。大きい粒子に関しては,
適切な粒子数を含むように測定体積を増やす必要があることがある。測定体積の増加も切片値を減少
させる原因となる。予想より低い切片値は,試料の吸収及び蛍光に起因することもある。今まで示し
た要因の全てが切片値を減少させるので,原因を明確にするためには更なる試験を必要とする。
注1) 相関時間0における値
d) 異なる粒子濃度で実施された測定結果は,測定の不確かさの範囲内で一致することが望ましい。濃度
の増加に伴って粒子径が減少することは,かなりの量の多重散乱,及び希釈剤と元の分散液との粘度
の違いによって起こる分散液の粘度変化及び/又は粒子の協同拡散(附属書B参照)を示唆している。
異なる粒子濃度での測定結果は,無限希釈への外挿法によって粒子径を推定することにも利用される。
直径が500 nmより小さい粒子で体積分率φ=10−5〜10−4の試料は,上の要求事項(適切な粒子濃度
条件)を満たしている。多分散粒子及び/又は粒子径が大きい粒子の場合には,受光検出器の制限視
野又は入射レーザ光のビーム径を大きくし,散乱体積を大きくしなければ,全ての要求事項を満たす
濃度を見い出せないこともある。このような場合,測定される切片値は,要求事項c)を満たさなくな
ることがある。1 μm以上の粒子では,要求事項c)及びd)は,特殊な場合にだけ成立する。
8
Z 8828:2019 (ISO 22412:2017)
全ての試料調製方法(分散媒,粒子濃度及び分散手順)は,記録することが望ましい(推奨する試料調
製方法を,附属書Dに示す。)。
8
測定手順
測定手順は,次による。
a) 装置の電源を入れ,暖気運転をする。通常,レーザの強度が安定し,試料ホルダが規定の温度に達す
るまで15分間〜30分間が必要である。
注記 多くの場合,測定した温度での溶媒の粘度が既知であるので,温度を調整することよりも一
定の温度で測定することが重要である。
b) 分散媒だけを満たした測定セルに由来する散乱光のカウントレート又は信号値が低く,粒子の混入を
示す激しいゆらぎがないことを確認したほうがよい。カウントレート又は信号値が高いと,セル壁面
の汚れ又は不均一性の可能性がある。バックグラウンド除去を行う装置の場合,使用する分散媒のバ
ックグラウンド信号を測定し,保存する。
c) 試料を目視し,粒子,糸くず,繊維,その他の異物の存在の有無を確認する。異物がある場合には,
試料調製をやり直す。
d) 適切かつ清浄な測定セルに必要量の試料を入れる。使い捨て(例えば,プラスチック製)又は再利用
可能な(例えば,光学測定用ガラス製又は石英製)測定セルとする。使い捨てプラスチックセルと比
較して,ガラスセルは,セルを通った光が散乱するとき,光の屈折が少なく,そのため実際の観察角
度が検出器と入射光との間の幾何学的角度と等しくなるという利点をもつ。測定セルの材質は,分散
媒及び粒子に対して化学的に安定でなければならない。試料の注入前に,フィルタでろ過した脱イオ
ン水又は非水系の分散液を測定する場合はその溶媒でセルを洗浄する。不純物が残る場合には,穏和
な界面活性剤又は光学セル用の洗浄剤を使用してもよい。ろ過した脱イオン水で数回セルをすすいで,
残った界面活性剤を取り除く。セルを逆さにして,水分を取り除く。セルに蓋をして,必要なときま
で清浄に保管する。
水及び溶媒をろ過するフィルタの孔径は,目的に応じて適切なものを使用する。理想的には,測定
する最も小さい粒子より小さい孔径が望ましい。
ガラスセルの代わりに使い捨てのプラスチックセル[例えば,ポリメタクリル酸メチル(PMMA)
製又はポリスチレン製]を使用することもできる。プラスチックセルの壁面はきず付きやすく,ガラ
ス又は石英の光学品質には及ばない。そのため,使い捨てプラスチック製セルは弱い散乱光の試料に
は用いないほうがよく,壁面のダストを除去するための洗浄は,懸濁溶媒でのすすぎ及び/又は粒子
を含まない気流を用いるのがよい。セルの面を素手で触ったり,又はセル表面をきず付ける材質(光
学用ペーパー又はティシュペーパーを含む。)で拭いたりしないように注意する。
試料を入れたセルを装置に入れる又は測定プローブを試料に入れる。温度が一定になるまで待つ。
温度は既知で,測定中の温度変化は±0.5 ℃であることが望ましい。
セル内に温度センサをもたない装置のための別の方法は,室温を測定し,その室温±0.3 ℃に試料
ホルダを調整する。試料の温度が室温になるまで待ち,試料ホルダに挿入後,直ちに測定する,又は
装置の試料ホルダの温度から±0.3 ℃に温度調整した浴槽内で試料を入れたセルを同じ温度になるま
で放置する。この場合,装置に挿入する前にセルの外側を乾燥させる。
試料の温度が試料ホルダの温度と一致していないと,水に分散した試料の粒子径の不確かさは,1 ℃
当たり約2 %である。
9
Z 8828:2019 (ISO 22412:2017)
注記 1 mLの試料の入った測定セルの温度を3 ℃変えるには,約10分間必要である。
e) 測定試料に気泡がないことを確認する。また,セルの壁面に気泡が付着していないことを確認する。
f)
試料番号及び測定日時,1回当たりの測定時間,測定回数,測定温度,測定中の温度変化,溶媒の屈
折率及び粘度,粒子濃度(既知の場合),希釈率,レーザ光の波長,散乱角を記録する。
g) 試料の平均散乱光強度を確認する。
ホモダイン光学系では,平均散乱光強度は,製造メーカによって指定された範囲内で受光検出器の
感度を調整しながら,可干渉性を維持するために減光フィルタを使った光量調整又は検出開口を最小
化することによって調整することが望ましい。試料からの散乱光強度は,分散媒だけからの強度の10
倍以上であることが望ましい。
ヘテロダイン光学系では,参照光信号は試料の散乱光信号より大きいこと(参照光信号と散乱光信
号との比は10:1程度)が望ましい。参照光を制限することで,散乱光が相対的に強くなるようにする
ことが望ましい。
h) カウントレート又は信号値に大きく急激な変動が見られるときは,試料への異物混入を示すので,測
定を続けないほうがよい。
i)
相関関数が単調減少しない場合又はパワースペクトルがローレンツ型でない場合は,測定を続けない
ほうがよい。
j)
キュムラント法を使って,測定ごとの平均粒子径
DLS
x
及び多分散指数PIを記録する。
k) 平均粒子径に粒子濃度依存性が見られた場合には,無限希釈濃度へ外挿して得た値(又は最低濃度で
の測定値)を採用する。粒子と溶媒との相互作用を変えないために,希釈は粒子を含まず,同じ濃度
の塩及び界面活性剤並びに同じpHの溶媒を用いて行う。
ここで規定した事項を確認すれば,多重散乱の影響を最小化することができる。しかし,特に粒子
径が100 nm未満で体積分率が0.01より大きい場合,粒子間相互作用が平均粒子径の推定に影響する
ことがある。このため,未知の分散系に対しては,粒子濃度比が2倍以上となる2種類以上の粒子濃
度に対して測定するのがよい。
l)
測定終了時には,試料中に顕著な沈殿物が認められないことを目視によって確認する,又は複数の連
続した測定結果に傾向がないかを調べる。沈殿物が見られた場合には,少量であり測定の正確さへの
影響が許容できるものであるか,又は試料がDLS測定に適さないものであるかを判断する。
9
結果の算出方法
9.1
概要
DLS法は,低分解能手法である。したがって,粒子径分布において狭い間隔のピークを分離することは
できない。低分解能は,質量中位径から離れた粒子径では,より大きな不確かさをもつことも意味する。
DLS法によって得られる本来の信号は,散乱光強度基準である。多くの装置は,散乱光強度基準の結果
から体積又は個数基準に計算できる。多くの手法では,散乱光強度基準の粒子径分布Qintに対して平滑化
がなされており,不確かさをもたらす。全ての手法に影響する二つ目の問題は,粒子径に対する散乱光強
度の大きな非線形依存性である。このため,散乱光強度基準の分布を体積又は個数基準の分布に変換する
ことはあまり推奨できず,個数基準の分布(特に,Qintの平滑化を含む手法)は推奨できない。
DLS法による粒子径分布の決定は,例えば,レーザ回折・散乱法(光の回折)及び顕微鏡法(電子の透
過)とは異なる物理特性に基づくため,得られる粒子径分布は異なることがある。
減衰定数又は特性周波数の分布C(Γ)は,レーザ光波長,偏光状態及び散乱角θに依存するので,試料の
10
Z 8828:2019 (ISO 22412:2017)
平均粒子径及び多分散指数は,それらの値に依存する。
粒子径分布を計算するためのアルゴリズムが複数存在する。これらのアルゴリズムは,同一の試料に対
してしばしば異なった分布を与える。そのため,粒子径分布とともに,アルゴリズム及び計算条件を記録
することが重要である。この箇条では,現時点で十分に議論されたアルゴリズムを要約する。理論的背景
についての更なる情報を,附属書Aに記載しており,簡単な概要は参考文献[7]を参照。
9.2
相関関数解析
9.2.1
キュムラント法
キュムラント法では,指数関数的に減衰する多くの関数の集合体を一つの指数関数に近似し,多項式に
展開する。粒子径分布を記述する二つのパラメータ,すなわち,平均粒子径
DLS
x
及び多分散指数PIがい
わゆる“キュムラント法”として得られる。
キュムラント法において相関関数から
DLS
x
及びPIへの計算は,勾配法,ガウス・ニュートン法又はレ
ーベンバーグ・マーカート法を用いた相関関数の非線形最小二乗フィッティングによって行われる。DLS
x
及びPIは,相関関数の対数に線形最小二乗フィッティングによっても得られる。データの対数を取る操作
が,データ点の重み付けに影響するので,各データ点に適切な統計的重み付けをとって対数を取る。統計
誤差は相関計のチャンネル間で等しいかもしれないが,データ点の重みは同じでない。キュムラント法か
ら得られる
DLS
x
及びPIは散乱光強度基準である。
9.2.2
分布計算アルゴリズム
これらのアルゴリズムでは,多成分指数関数フィッティングを相関関数に適用することで,粒子懸濁液
又は分子溶液の拡散係数の分布を計算する。これらのアルゴリズムの出力は,粒子径分布であり,必要で
あれば平均粒子径を決定することもできる。
9.2.2.1
非負拘束付き最小二乗(NNLS)法
非負拘束付き最小二乗法は,相関関数の指数減衰に代数的なフィッティングを行う。変更可能なパラメ
ータは幾つもあるが,二つの重要なパラメータは,“重み付け手法”,及び“アルファパラメータ”又は“正
則化”である。DLS法におけるデータの重み付けは,ベースラインのノイズに対して,重要な相関関数の
僅かな変化を際立たせるために用いられる。データの重み付けがない場合,ベースラインのノイズが,不
適切なピークの存在又は誤ったデータ解釈につながる。
正則化又はアルファパラメータは,結果として得られる粒子径分布内の“とがり”の許容程度を調整す
る。相関関数のデコンボリューションは,逆ラプラス変換を用いて最終的に固有関数を線形結合に単純化
する。この手法の注意点は,固有値が小さいとき,僅かなノイズが解の数を極端に増加させる。そのため,
不良設定問題といわれている。この問題を解決するために,分布解の一次導関数として安定化項が,一連
の固有関数に加えられる。
アルファパラメータは,この安定化項に適用される乗数(比例定数)で,解の導関数の強調程度として
定義される。大きいアルファ値(0.1)は,解のとがりを制限し,滑らかな粒子径分布が得られる。小さな
アルファ値(0.000 01)は,重み付け及び導関数の重要性を減少させ,結果として,よりとがった分布を生
じる。そのため,アルファパラメータは,測定した相関関数におけるノイズレベルの大きさの推定値とし
て大まかに説明される。理想的又は最適なアルファパラメータはなく,適切な値は解析される試料に依存
する。多分散性が低く,強い散乱光の粒子に関しては,アルファパラメータを小さくすると,散乱光基準
の粒子径分布の分解能が向上することがある。
9.2.2.2
コンティン法
コンティン法は,自由度の数を減少させ,平滑化した解を得るために,固有関数解析と組み合わせた制
11
Z 8828:2019 (ISO 22412:2017)
約付き正則化NNLS法を使用している。
コンティン法では,複数解が得られるため,データと矛盾しない最小のすそ広がりの分布を選択する。
減衰率が2倍以上ならば,減衰率の分離が可能である。
得るべき分布についての予想が必要である。例えば,推定分布範囲,データポイント数などの拘束条件
を指定する必要がある。正則化パラメータは,F検定及び信頼水準に基づいて自動的に決定される。
9.2.2.3
ヒストグラム法
ヒストグラム法は,解が得られるまでΓ(Γ=DTq2)の分布が繰返し処理される反復法の1種である。解
析プログラムにおいて,初期のΓの分布値は同じ値をもつヒストグラムである。このアルゴリズムは,測
定データと一致するようにヒストグラム値を繰り返し変更する。
ヒストグラム法は,Γの区分数Mが可変であるという利点がある。これは,観察データが正確でないと
きは,M数を減らすことができる。G(Γj)並びにヒストグラムの始まり及び終わりに対応するΓmin及びΓmax
の初期値は重要ではない。誤差の限度が測定結果の統計誤差内になるとフィッティングは終了する。得ら
れる分布は,幅が広く,かつ,分布が滑らかになる傾向にある。
9.2.2.4
その他のアルゴリズム
NNLS法に基づいて指数和の正規化[14]を行うL-Curve[12][13]の他にも多くのアルゴリズム及びプログラム
[15][16]が存在する。一般に,こうしたアルゴリズムの違いは,与えられた一連の機器及び測定条件に対して
最適化するため,NNLS法での変数(例えば,“正規化”又はアルファパラメータ,及び実行される重み付
け手順)の最適化方法に対する違いである。
9.3
周波数解析法
周波数解析法は,検出器からの信号を規則的な間隔で,解析に必要な最も高い周波数でサンプリングす
る。サンプリングした値は,高速フーリエ変換(FFT)を用いてパワースペクトルに変換する。
演算方法の基本は,最適な粒子径分布が得られるまで,あらかじめ選んでおいた粒子径及び周波数チャ
ンネルから得られたパワースペクトルを反復計算でフィッティングすることにある。例えば,1 nmから
6 500 nmまでの粒子径範囲では,16 000 Hzまでの線形パワースペクトルが必要である。パワースペクトル
は,80の対数間隔のチャンネルに変換される。粒子径チャンネルも対数間隔に変換される。こうして得ら
れた分布から,平均粒子径,PI及び他の数値が計算できる。
− ステップ1 粒子径チャンネル1〜Nは,対数間隔で定義される。周波数チャンネル1〜Nは同じ対数
間隔で定義され,測定した線形パワースペクトルは対数チャンネルに変換される。
− ステップ2 式(A.25)を用いてN個の周波数チャンネルの応答を計算し,粒子径分布の第1回目の近
似値を得る。
− ステップ3 計算から求めた値と測定した値とを比較して,近似粒子径分布を補正する。
ステップ2からステップ3までは,計算値と測定値との誤差が最小になるまで繰り返し,最適な粒子径
分布を得る。代表的には,1 nm〜6 500 nmで80の粒子径チャンネルが使用される。反復デコンボリュー
ション結果から,全てが等しい散乱強度の重みをもつ粒子径チャンネルを横軸とした,JIS Z 8819-1に合
致した粒子径分布が得られる。
10 測定系の適格性確認及び測定結果の評価
10.1 測定系の適格性確認
DLSによる粒子径測定は,第一原理に基づく絶対的測定法のため,校正用粒子を用いた粒子径の校正作
業は,必要ではない。SIトレーサビリティを保証するために,測定結果を得るために必要な数値,すなわ
12
Z 8828:2019 (ISO 22412:2017)
ち,測定変数(測定温度,レーザ波長,散乱角など)は,校正されたトレーサブルな手法で測定し,決定
することが望ましい。装置の設置後にCRM粒子の分散液で装置の性能を検証することが望ましい。さら
に,設置後定期的に又は装置性能が疑わしい場合にも検証することが望ましい。
機器の性能は,機器を設置直後及びその後定期的に,CRM粒子の懸濁液を使用して確認することができ
る。
適格性の確認が不合格の場合,使用したCRM粒子懸濁液,試験試料の調製,又は装置に問題がある。
同じ算出アルゴリズムを用いたDLS法で値付けされたCRM粒子を使用することが望ましい。理想的に
は,CRM粒子の化学的特性及び形態は,試験試料と可能な限り一致することが望ましい。
別の方法として,CV値(=標準偏差/平均粒子直径)が5 %のような狭い粒子径分布をもち,DLS又
は電子顕微鏡で値付けされた平均粒子径をもつポリスチレンラテックスのCRMを使用することができる。
潜在的な偏りを評価するために,CRM粒子の平均値の不確かさは,測定の不確かさに対する許容差を合
成し,拡張不確かさを得るために2倍にすることが望ましい。認証値と5回測定の平均値との絶対値差は,
この拡張不確かさよりも小さい値でなければならない。
直径約100 nmの粒子懸濁液の場合では,5回連続測定の標準偏差は2 %未満でなければならない。PI値
は,0.1未満でなければならない。測定の不確かさの許容差は1.5 %とされている。
例 認証平均値が102 nm±3 nmのポリスチレンラテックスCRM(拡張不確かさk=2)を5回測定し
た。5回測定の平均値は105.9 nm,標準偏差は1.4 nmであった。許容可能な偏り及び精度の確認
は,次による[26]。
1) CRMの拡張不確かさから標準不確かさへの変換は,認証書に記載された包含係数kで拡張不
確かさを除す:uCRM=3 nm/2=1.5 nm
2) 測定平均値の測定の不確かさの許容差を計算する。測定値が100 nmに近い場合,1.5 %の許
容差を使用する:umeas=1.5 %×105.9 nm=1.6 nm
3) 拡張不確かさUを求めるために,1)と2)との結果の二乗和及び包含係数kの値2を乗じる。
nm
4.4
1.6
1.5
2
2
2
2
meas
2
CRM
2
=
+
=
+
=
u
u
U
4) 測定平均値と認証値との絶対値差は,105.9 nm−102 nm=3.9 nmである。
この差がUよりも小さいので,測定値は偏りに関する試験を満足している。
5) 5回測定の相対標準偏差は1.3 %であり,したがって,要求されている2 %よりも小さい。
10.2 測定結果の評価
10.2.1 妥当な測定結果は,次の条件を満たすことが望ましい。
a) 最小粒子径に対応する減衰時間より小さい時間間隔で測定する限り,粒子径分布は測定時間間隔に依
存しない。
b) 粒子径分布のピーク位置は,選択した粒子径範囲に依存していない。
c) 選択した粒子径範囲の端にピークが存在しない。
d) 粒子の物理的特性及び化学的特性が妥当であり,矛盾していない。
e) 他の粒子径測定法の結果と比較して妥当である。
10.2.2 自己相関法で測定する場合,次の方法で相関関数の切片の最大値を求めることができる。
a) 可能で,かつ,必要な場合,Bmax値が得られる集光開口を選択する。
注記 Bmaxの定義を附属書Aに示す。
b) 7.3のc)及びd)の要求を満たす少なくとも2種類の異なる濃度のポリスチレンラテックスの懸濁液(直
13
Z 8828:2019 (ISO 22412:2017)
径約100 nm)によって,切片Bを決定する(附属書A参照)。
B値が系統的に粒子濃度に依存している場合,無限希釈に結果を外挿する。
10.3 測定の精度及び測定結果の不確かさ
達成可能な精度は,試料の特性及び評価アルゴリズムに依存している。一般に,均質で単分散の試料で
得られた結果は,多分散の試料で得られた結果よりも変動は少ない。
− 繰返し性 直径50 nm〜200 nmの単分散試料では,
DLS
x
の相対標準偏差は2 %未満であることが望ま
しい。
注記 同一の試験所内であっても,測定ごと,測定者ごと,機器ごと,場所ごとなどの更なる変動
要因がある。
− 再現性 直径50 nm〜200 nmの単分散試料では,5 %の試験所間標準偏差が達成可能である。
− 真度 DLS法で得られた結果は,散乱角及び評価アルゴリズムを含む多くの要因に依存しているた
め,多分散試料の測定結果は,測定装置及び使用した算出方法の設定に固有なものである。粒子が球
形の単分散である場合は,測定の不確かさに対する真度の下限寄与を見積もることができる[17]。
各測定結果の測定値の不確かさは,少なくとも繰返し性及び再現性の寄与を含むことが望ましい。
11 測定結果の報告
測定結果の報告は,少なくとも次の情報を含まなければならない[k)〜r)については,JIS Q 17025参照。]。
a) 平均粒子径
DLS
x
,及びその不確かさ
b) 試料の多分散性指標(例えば,多分散指数PI)
c) 平均値を求めるために測定した測定回数
d)
DLS
x
及びPIの平均値が濃度依存性を示す場合,それらの値として無限希釈の外挿値又は最低濃度で
得られた値を使用する。
e) 試料を特定するために必要な全ての情報(粒子形状及び均質性の詳細を含む。)。
f)
試験所又は他の機関で使用されているサンプリング計画及び手法の出典。それらは,妥当性評価又は
結果の応用に関連している。
g) 使用した計算アルゴリズム。使用した計算アルゴリズムがこの規格に記載されていれば,その名称を
記載する。また,平均又は代表値の種類(算術,幾何又は調和平均値,中央値及びモード値),スケー
ルの種類(線形又は対数),及び測定粒子径範囲を示す。
h) 懸濁液の条件
− 分散液及びそのろ過手順(該当する場合)
− 粒子の濃度(既知の場合)
− 分散剤及びその濃度
− 超音波処理条件:時間,周波数及び印加電力(該当する場合)を含む分散手順
− 懸濁液の粘度及び屈折率
i)
測定条件
− 測定した実際の濃度(既知の場合)
− 測定期間
− 試料の温度
j)
この規格で規定していない,又は追加的なものとみなされる全ての詳細な操作,及び結果に影響を及
ぼすと考えられる詳細な事柄。
14
Z 8828:2019 (ISO 22412:2017)
k) 表題(例えば,“試験結果報告書”)
l)
試験機関の名称及び住所,測定が行われた場所(試験機関の住所と異なる場合)
m) 試験報告書固有の識別番号(シリアル番号など),及びページが試験報告書の一部として認識されるよ
うにするための各ページの標識,並びに試験報告書の終わりが明確になる標識。
n) 顧客の名前及び住所
o) 測定する品目の説明,条件及び明確な識別情報
p) 妥当性の評価及び結果の利用に対して重要になる場合,試験試料の受領日及び試験の実施日。
q) 測定報告書を承認する者の氏名,職能及び署名,又は同等の人物証明。
r) 必要な場合,試験又は校正した項目が測定結果に関係する影響項目。
s)
全ての関連する評価及び測定パラメータ。これらは,試験報告書に必ずしも追加する必要はない。
15
Z 8828:2019 (ISO 22412:2017)
附属書A
(参考)
理論的背景
A.1 相関関数解析
A.1.1 自己相関法及び交差相関法
典型的なDLS測定では,狭い帯域の単色かつ可干渉性の光源,すなわち,単一な波長λ0をもつレーザ
光を粒子懸濁液に照射する。分散粒子によって散乱された光を,入射光に対して角度θの位置で干渉させ
て検出する。分散粒子は連続的にブラウン運動しているため,観測される散乱光強度I(t)は,時間に関し
て変動している。したがって,これらの散乱光強度ゆらぎの時間関数を解析することによって,分散粒子
の運動に関する情報が得られる。相関解析における時間解析は,式(A.1)で与えられる散乱光強度の時間自
己相関関数G(2)(τ)が求まる相関計を使用する。
G(2)(τ)=〈I(τ)・I(t+τ)〉 ······························································ (A.1)
この相関関数は,時間差(相関時間)τだけに依存し,G(2)(τ)の計数を始める絶対時間tには依存しない。
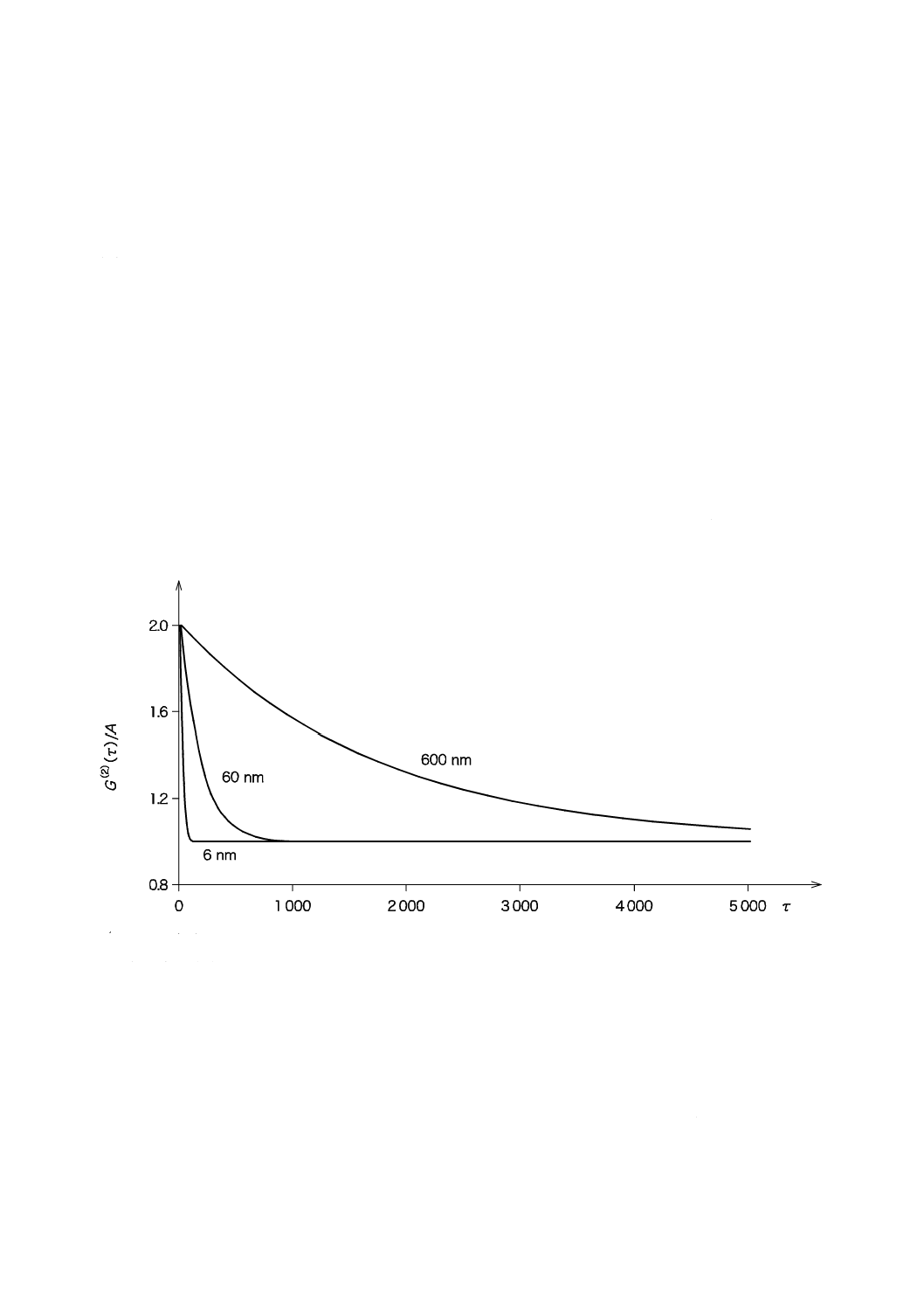
式(A.1)中の記号〈 〉は,様々な時間tに対するI(t)I(t+τ)の平均値を示す。図A.1に,自己相関関数の一
例を示す。
A:ベースライン
G(2)(τ):自己相関関数(任意の単位)
τ:相関時間(μs)
図A.1−正規化された自己相関関数
交差相関の場合は,単色かつ可干渉性の2本のレーザ光の焦点を粒子懸濁液中に合わせる。2本の光線
は,粒子懸濁液中で相互に交わる。2本のレーザ光の重なりあった部分が,測定体積を形成する。粒子に
よって散乱された光を,特定の散乱角度において2個の検出器を用いて検出する。このように,二つの独
立した散乱測定を,同じ測定体積中において行う。このことによって,測定結果から多重散乱の影響が減
少する。
16
Z 8828:2019 (ISO 22412:2017)
交差相関は,幾つかの取り合わせが可能で,例えば,異なる散乱角度を使用する,異なるレーザ波長を
使用する,などが挙げられる。これらは,散乱ベクトルが同じである限り,同じ方法で評価可能である。
測定された交差相関関数は,図A.1に示した自己相関関数とよく似ている。
測定体積V中においてブラウン運動している多数の単分散粒子に対して,本質的にG(2)(τ)は式(A.2)に示
す時間差τの指数減衰関数となる。
G(2)(τ)=A[1+Bexp(−2Γτ)] ························································ (A.2)
ここで,
A:原理的に,時間に依存しない定数で,散乱光強度の時間平均<I>の2乗に比例し,この規格内では
“ベースライン”と呼ぶ。
B:B≦1である装置因子と考えることができる(この規格内では,相関関数の切片として規定する。)。
減衰定数Γは,式(A.3)に与えるように,ブラウン運動している均質な球状粒子の並進拡散係数DTと関
連がある。
Γ=DTq2 ················································································ (A.3)
ここで,qは,式(A.4)で与えられる散乱ベクトルの大きさである。
( )2
sin
4π
0
θ
λ
n
q=
······································································ (A.4)
散乱ベクトルq
は,入射波ベクトルk i及び散乱波ベクトルk sの間の差ベクトルq
(=k s−k i)によって定義す
る。k
i及びk
s双方の大きさは2πn/λ0に等しく,nは懸濁液の屈折率を表している。
DLS法に関して注意すべきことは,粒子径ではなく,拡散係数を測定していることである。粒子径は,
拡散係数を粒子径に関係付けることによって決定されているに過ぎない。粘度ηの媒体中に分散した相互
作用のない球形粒子に対して,並進拡散係数は,式(A.5)に与えるストークス−アインシュタイン式によっ
て粒子直径xと関係付けられる。
ηx
kT
D
3π
T=
············································································ (A.5)
ここで,kはボルツマン定数,Tは絶対温度である。
粒子濃度についてこの規格に定めた条件に従えば,測定体積中の粒子数ゆらぎ,多重散乱及び粒子間相
互作用が,粒子径に与える偏りの影響を除くか又は少なくとも最小限にすることができる。粒子数ゆらぎ
による偏りを最小化するために,この規格では,測定体積中に最低でも1 000個の粒子が存在することを
推奨する。
最低1 000粒子という判断基準は,単分散粒子にだけに適用できる。多分散粒子では,散乱体積中に
DLS
x
より粒子径の小さな粒子が多数存在している必要がある。
以上の数式は,原理的には,均質な球形粒子にその使用が限られている。非球形かつ不均質な粒子に対
しても,並進及び回転の両方の過程が存在するが,これらの数式を用いて測定及び解析が行える。この場
合,式(A.1)〜式(A.3),及び式(A.14)は,見かけの球相当径を定める式となる。
多分散試料の場合では,実際には,式(A.2)は式(A.6)となる。
+
=
2
(1)
(2)
)
(
1
)
(
τ
g
B
A
τ
G
························································· (A.6)
ここで,電場の自己相関関数g(1)(τ)は,式(A.7)に示す正規化された減衰定数の分布関数C(Γ)に関係付け
られる。
17
Z 8828:2019 (ISO 22412:2017)
∫∞
=0
(1)
)d
)exp(
(
)
(
Γ
Γτ
Γ
C
τ
g
−
······················································ (A.7)
ただし,
∫∞
=
0
1
)d
(
Γ
Γ
C
········································································· (A.8)
である。式(A.8)において,C(Γ)dΓは減衰定数がΓからΓ+dΓまでの範囲にある粒子からの散乱光強度の
分率に比例する。
次のような幾つかの種類の多分散性によって,減衰定数に分布が生じる場合がある。
1) 粒子径の多分散性。すなわち,全ての粒子が同じ形状及び組成をもち,例えば,均質で等方的な球
状であるが,個々の粒子の一次元的な大きさだけが異なるとき。
2) 形状の多分散性。すなわち,粒子の形が異なり,例えば,球状,円盤状及び棒状の混合物であるが,
体積及び組成は等しいとき。
3) 不均質かつ異方性をもつ物質である。すなわち,粒子間で幾つかの物質の存在割合が異なっている
場合,例えば,均質な球に積層球が混じっているとき。
4) 以上に示した複数の多分散性において考えられる全ての組合せ。
DLS法による粒子径測定を適用するときには,1)の多分散性だけを仮定する。
この規格では,減衰定数の分布は次の二つの変数によって規定する。
a) 式(A.9)で定義される平均化された減衰定数Γ
∫∞
=0
)d
(
Γ
Γ
ΓC
Γ
····································································· (A.9)
b) 無次元の多分散指数PI,すなわち,式(A.10)で定義される分布の広さの指標
2
2
PI
Γ
μ
=
··············································································(A.10)
ここで,μ2は式(A.11)によって算出する。
(
)
Γ
Γ
C
Γ
Γ
μ
)d
(
0
2
2∫∞
=
−
··························································· (A.11)
減衰定数が,平均Γ及び標準偏差σのガウス分布,すなわち,式(A.12)
(
)
=
2
2
2
exp
2π
1
)
(
σ
Γ
Γ
σ
Γ
C
−
−
···················································(A.12)
である場合は,PIはΓ及びσを用いて式(A.13)で表せる。
2
2
2
2
2
PI
Γ
σ
Γ
μ=
=
·····································································(A.13)
ストークス−アインシュタインの式で定義される粒子径は,緩和時間に逆比例するので[式(A.3)及び式
(A.5)参照],式(A.9)は,この規格における平均粒子径
DLS
x
を定義することにも使用できる。
[
]
=∫∞
x
x
Γ
C
x
x
1
d
)
(
1
1
0
DLS
·························································(A.14)
式(A.14)中のC[Γ(x)]d(1/x)は粒子径がxからx+dxの範囲にある粒子からの散乱光強度の分率を表してい
るので,平均粒子径
DLS
x
は式(A.14)で定義するように,散乱光強度の調和平均粒子径である。
この平均粒子径は一般に,質量平均粒子径とは異なる値であり,さらに,より大きな値となる点である
18
Z 8828:2019 (ISO 22412:2017)
ことに注意を要する。加えて,例えば,(小角)レーザ光散乱又は回折によって決定する平均粒子径とも異
なる。
さらに,注意すべき点として,ある粒子径分布に関して,C(Γ)はレーザの波長及び偏光状態,並びに散
乱角θに依存する[式(A.3)及び式(A.4)参照]。そのため,同じ試料であっても,DLS
x
及びPIも,これらの
要因に依存して変化する。30 nm以下の粒子径分布測定においては,(粒子径が波長に対して十分小さいた
め)DLS
x
及びPIはレーザ波長(及び散乱角)に対して明確な依存性を示さない。
A.1.2 キュムラント法
キュムラント法では,式(A.7)中の係数exp(−Γτ)を平均値exp(−Γτ)の周りで多項式に展開する。式(A.6)
の3次以降を切り捨てると,この多項式は,式(A.15)に近似できる。
(
)
[
]
2
2
(2)
2
exp
1
)
(
τ
μ
τ
Γ
B
A
τ
G
+
+
≈
−
··············································(A.15)
この式は,平均減衰定数Γ,μ2及び平均粒子径
DLS
x
,並びに多分散指数PIを決定する基本式となる。
線形回帰を行うため,式(A.15)を,式(A.16)又は式(A.17)に変形する。
[
]
2
2
2
2
ln
2
1
)
(
ln
2
1
)
(
τ
μ
τ
Γ
AB
A
Γ
G
τ
y
+
≅
=
−
−
··································(A.16)
()
(
)
m
j
τ
a
τ
a
a
τ
y
j
j
j
1,2,3...
2
2
1
0
=
+
=
−
··········································(A.17)
ここで,j:相関計の遅延チャンネルの番号
ベースラインAは,次の二つの方法で決定される。測定全期間中のカウントレートの総和の時間平均か
ら,又は相関時間τ>>25/ΓにおけるG2(τ)の推定値から求めることができる。ベースラインAを両方法で
推定し,その大きい方の値を採用することを推奨する。しかしながら,この二つの推定値差が,小さい方
の数値の10−3倍より大きい場合には,これ以上の解析を行ってはならない。
解析の対象とするyj=y(τj)の範囲は,[G2(τj)−A]値の範囲が[G2(τ1)−A]>[G2(τj)−A]>[G2(τ1)−A]/100を満
足し,かつ,少なくとも一つの[G2(τj)−A]は,[G2(τ1)−A]/50より小さい。解析対象範囲の[G2(τj)−A]は,全
て正である。そうでない場合,これ以上の解析を行ってはならない。この範囲に入るyjの値の数mは,20
以上である。
式(A.18)で与えられる値sが最小となるように,パラメータa0,a1及びa2を最小二乗法によって決定す
ることで,y(τj)を式(A.15)によって近似できる。
(
)
(
)2
2
2
1
0
1
2
1
0
,
,
j
j
m
j
j
τ
a
τ
a
a
y
w
a
a
a
s
+
=∑
=
−
−
······································(A.18)
式(A.18)中のwjは正規化された重み係数であり,生データG2(τj)がy(τj)に非線形変換されることを意味す
る。
平均粒子径
DLS
x
は,a1から式(A.19)によって求める。
19
Z 8828:2019 (ISO 22412:2017)
(
)2
0
1
DLS
2
sin
4π
3π
1
=
λ
θ
n
η
kT
a
x
····················································(A.19)
ここに,
k: ボルツマン定数
T: 絶対温度
η: 分散媒の粘度
n: 分散媒の屈折率
θ: 散乱角
λ0: レーザ光の真空中での波長
多分散指数PIは,a1及びa2から式(A.20)によって求める。
PI=2a2/a12 ············································································(A.20)
切片Bの値は,a0及びAから式(A.21)によって求める。
B=[exp(2a0)]/A ······································································(A.21)
この値は,与えられた実験条件において得られる最大値Bmaxと比較する。B/Bmax<0.8となれば,自己相
関関数の測定結果を破棄する。
近似計算の残差は,式(A.22)によって与えられ,近似の指標として用いることができる。
s/(m−4) ···············································································(A.22)
ここに,
s: 式(A.18)で計算されるフィッティングの残差
m: データ数
球形単分散粒子では,残差は0.8以下になることが望ましい。球形単分散粒子以外は,一般的に規則性
が存在しないので目的に応じた残差を指標とすることが望ましい。
A.2 周波数解析
周波数解析では,散乱光の検出器からの出力は,デジタル高速フーリエ変換(FFT)で処理される。FFT
では,周波数パワースペクトルが計算される。単分散系において,パワースペクトルP(ω)は,ヘテロダイ
ン光検出器で検出された変動信号から式(A.23)で与えられる(参考文献[18]参照)。
()
20
2
0
S
R
2
ω
ω
ω
I
I
ω
P
+
=
·····························································(A.23)
ここに,
IR: 入射光強度
IS: 散乱光強度
ω0: 特性周波数
ω: 角周波数
ホモダイン法では,パワースペクトルの振幅は散乱光強度の2乗IS2に比例し,散乱光強度の2乗値は,
試料濃度に比例する。この検出方法では,散乱していない入射光は散乱光と混じり合っていないと仮定し
ている。すなわち,I0≪〈IS〉の条件が成立すると仮定している。このことは迷光及びヘテロダイン光混合
がなく,検出方法が純粋なホモダインであることを示している。また,検出器にノイズがなく,測定セル
又は光学素子からの迷光又は散乱光がないことも仮定している。
ヘテロダイン法では,入射レーザ光の一部を検出した散乱光と混合する。ヘテロダイン検出のパワース
ペクトルにはホモダインの成分が常に含まれる。パワースペクトルを純粋なヘテロダインとして取り扱う
には,ホモダイン成分をヘテロダイン成分より十分に小さくしなければならない。I0≫〈IS〉のときにヘテ
ロダインとなる。高濃度,すなわち,〈IS〉が大きい場合でも,I0≫〈IS〉となるようにする。両成分が混
合した場合は,ヘテロダインでの特性周波数ω0のパワースペクトルとホモダインでの特性周波数2ω0のパ
20
Z 8828:2019 (ISO 22412:2017)
ワースペクトルとが組み合わさったパワースペクトルとなる。特性周波数ω0は,式(A.24)で与えられるよ
うに,粒子径xに反比例し,パワースペクトルの半値幅となる。
( )2
sin
3
16π
1
2
2
0
θ
η
λ
kT
x
ω=
···························································(A.24)
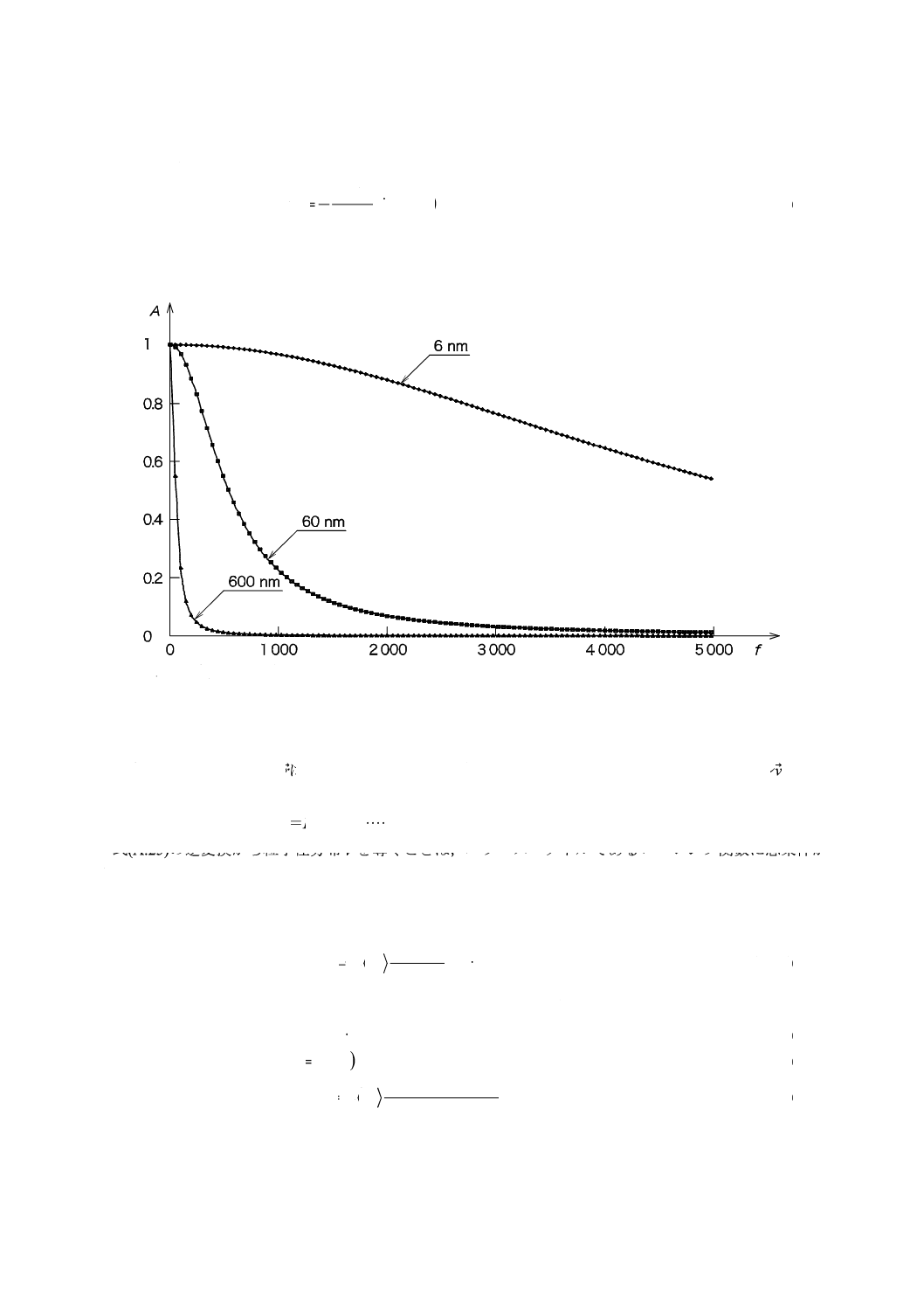
図A.2に,ヘテロダイン法でのパワースペクトルを示す。粒子径が特性周波数に反比例することが明ら
かである。
A:強度,任意の単位
f:周波数,Hz
図A.2−ヘテロダイン法におけるいろいろな粒子のパワースペクトル
測定された応答ベクトルr
は,ローレンツ行列Lに体積で重み付けられた粒子径分布のベクトルv
を乗じ
ることで得られる[式(A.25)]。粒子径分布は,個々の粒子の応答の重み付き総和である。
r
=L・v
·················································································(A.25)
式(A.25)の逆変換から粒子径分布vρを導くことは,パワースペクトルであるローレンツ関数に悪条件が
含まれるため,困難である。
多分散系のヘテロダイン法では,周波数微分値の積で正規化されたパワースペクトルは,特性周波数の
分布関数と式(A.26)で示すように関係付けられる。
()
ω
ω
ω
ω
I
I
ω
ω
P
d
2
d
20
2
0
S
0
+
=
······················································(A.26)
式(A.27)及び式(A.28)を用いて,周波数(座標)を対数座標に変換することで式(A.29)を得る。
()
ω
xln
=
··············································································(A.27)
()
0
0
lnω
x=
···········································································(A.28)
()
x
e
e
I
I
x
x
P
x
x
x
x
d
1
d
)
(
)
(
S
0
0
0
−
−
−
+
=
············································(A.29)
対数変数に変換すると,単一粒子径に対するパワースペクトルの形は同一で,対数周波数軸を移動させ
ただけである。粒子径分布をもつ場合,対数周波数軸でのパワースペクトル強度は,粒子径分布に対応す
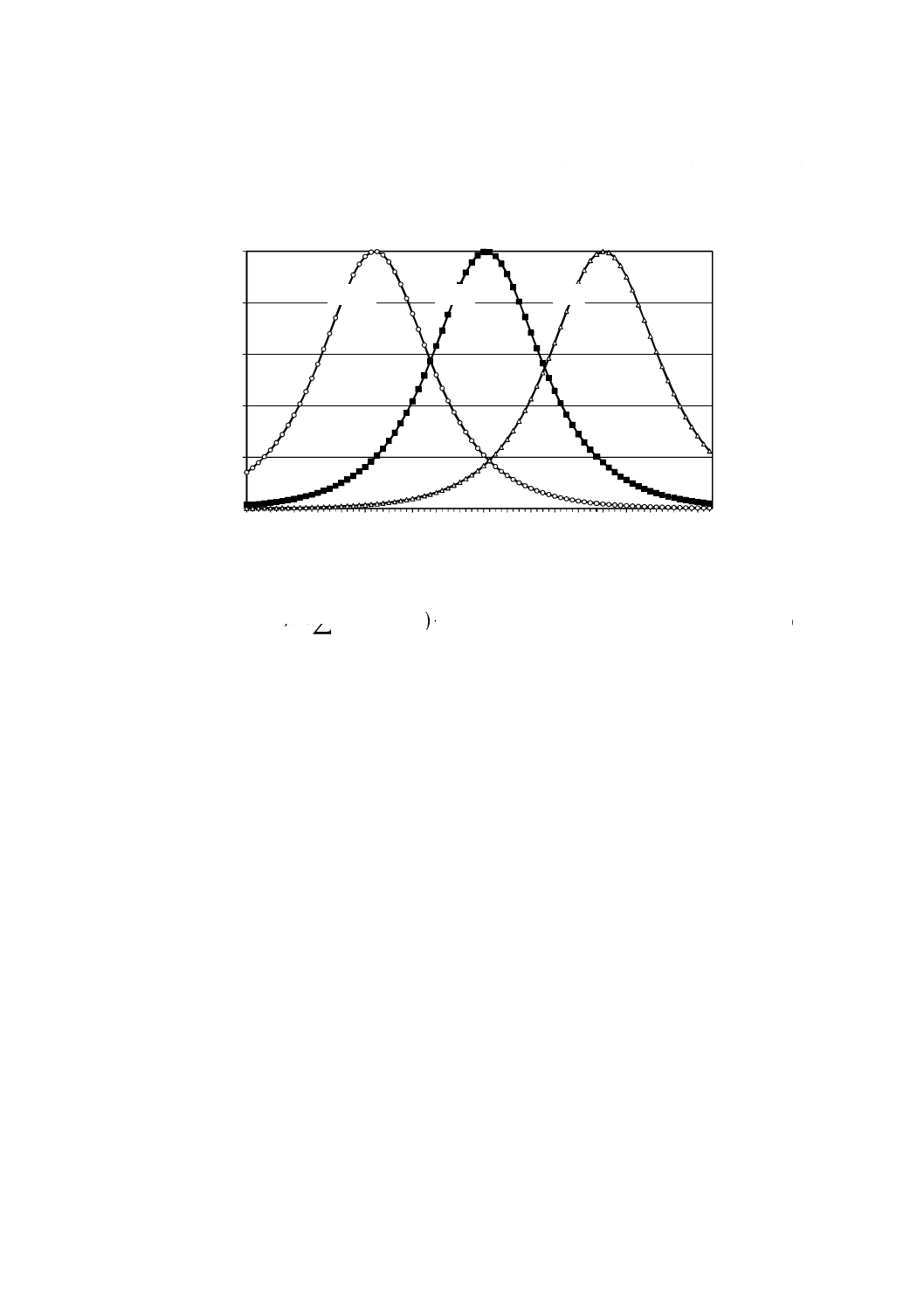
21
Z 8828:2019 (ISO 22412:2017)
る応答行列が寄与した強度分布をもつ。応答関数の強度は,粒子径の6乗に比例する散乱光強度とノイズ
との重みをもっている。図A.3に,大きさの異なる三つの粒子の応答関数を示す。応答関数は,対数軸特
性周波数ω0でピークをもつ。式(A.25)の行列は,式(A.30)中の応答関数Rのコンボリューションになる。
図A.3−対数座標軸パワースペクトル
(
)()
n
n
m
n
x
v
x
x
R
r∑
=
−
·····························································(A.30)
対数座標軸周波数パワースペクトル[式(A.30)]の逆変換は,式(A.25)の逆変換と比較して非常に単純に
なっており,線形反復法を使用することで粒子径分布に変換することが可能である[19]。
0.0
0.2
0.4
0.6
0.8
1.0
1
5
9
1317212529333741454953576165697377
強
度
対数間隔周波数チャンネル
対数座標軸パワースペクトル
600 nm
60 nm
6 nm
22
Z 8828:2019 (ISO 22412:2017)
附属書B
(参考)
考えられる測定誤差の概要及びその影響を最小にする方法
B.1
概要
様々な要因が,DLSの結果に影響を与える可能性がある。この附属書は,有効な結果を得るために,幾
つかの影響とそれらを最小にする方法について記載している。
B.2
高濃度懸濁液の測定
B.2.1 概要
未知試料を測定する場合,見掛けの測定粒子径に濃度の影響が現れる限界試料濃度を予想することは不
可能である。そのため,試料濃度を数桁変化させて測定を行う方法を推奨する。高濃度試料では,多重散
乱,粒子間相互作用及び他の影響(例えば,非球形効果)が測定した粒子径に影響を与える可能性がある。
この場合,これらの影響のない粒子径を求めるには,見掛けの測定粒子径を無限希釈試料濃度へ外挿する
方法が必要である。品質管理的には特定の試料と分散剤との組合せに対して許容できる最大試料濃度を決
定するのがよい。したがって,使用する装置で初めての試料を測定する場合,こうした妥当性確認の手順
を行う必要がある。試料を希釈することによって,試料の化学的又は電気二重層の広がりの変化から,粒
子径が変わる可能性があることに注意しなければならない。しかし,見掛けの粒子径が,適切な濃度まで
希釈して測定した結果と一致しなくても,決めた限界試料濃度でストークス−アインシュタインの式から
計算した見掛けの粒子径は,品質管理の目的に使用することができる。
粒子間相互作用及び多重散乱による影響を避けるために,幾つかの濃度で測定を行い,系統的な濃度依
存性が認められる場合は,得られた結果を無限希釈に外挿することが推奨される。
B.2.2 多重散乱
DLS測定では,粒子で1回だけ散乱した光が測定されると仮定している。高濃度では,ある粒子で散乱
された光が検出器に到達する前に,別の粒子で再び散乱される。これは,さらなる位相因子が追加され,
光強度変動のスペクトルを広げることを意味する。粒子が速く動くように観察されるため,小さな直径の
粒子として検出される。
この多重散乱の影響を最小にするため,幾つかの方法が用いられる。
一つの方法は,入射及び散乱の光路長を最小にする光学系を採用することである。後方散乱光学系を含
めて,試料内に最小光路長を形成する幾つかの方法がある。後方散乱光学系は,設計上光路長を短くする
ことができる。長い光路長では不透明になる試料でも,短い光路長では多重散乱を無視することができる。
別の方法は交差相関法を用いることであり,原理的に多重散乱の影響を除去する。実際には多重散乱の
影響を最小にするにすぎず,除去はしていない。その結果,単一の散乱光が測定できなくなる程の高濃度
が測定の上限濃度となる。後方散乱光学系と同様,光路長を短くするとより高濃度まで測定できる。
B.2.3 粒子間相互作用
拡散係数から流体力学的直径に変換する式は,個々の粒子の運動が,相互に他の粒子の影響を受けない
と仮定している。低濃度では,通常この条件が満たされるが,高濃度では,DLSによって測定された粒子
径は正しい粒子径とは異なる。粒子間相互作用が明確に現れるのは,大きな多分散性,複数のピーク,及
びより大きな見掛けの粒子径が出現する場合である。
23
Z 8828:2019 (ISO 22412:2017)
高濃度試料の場合,DLS法では個々の粒子の拡散係数ではなく,多数の粒子集合体の拡散を測定する。
すなわち,粒子径,粒子濃度,散乱角及びレーザ波長に依存する2種類の拡散係数に分類できる。散乱ベ
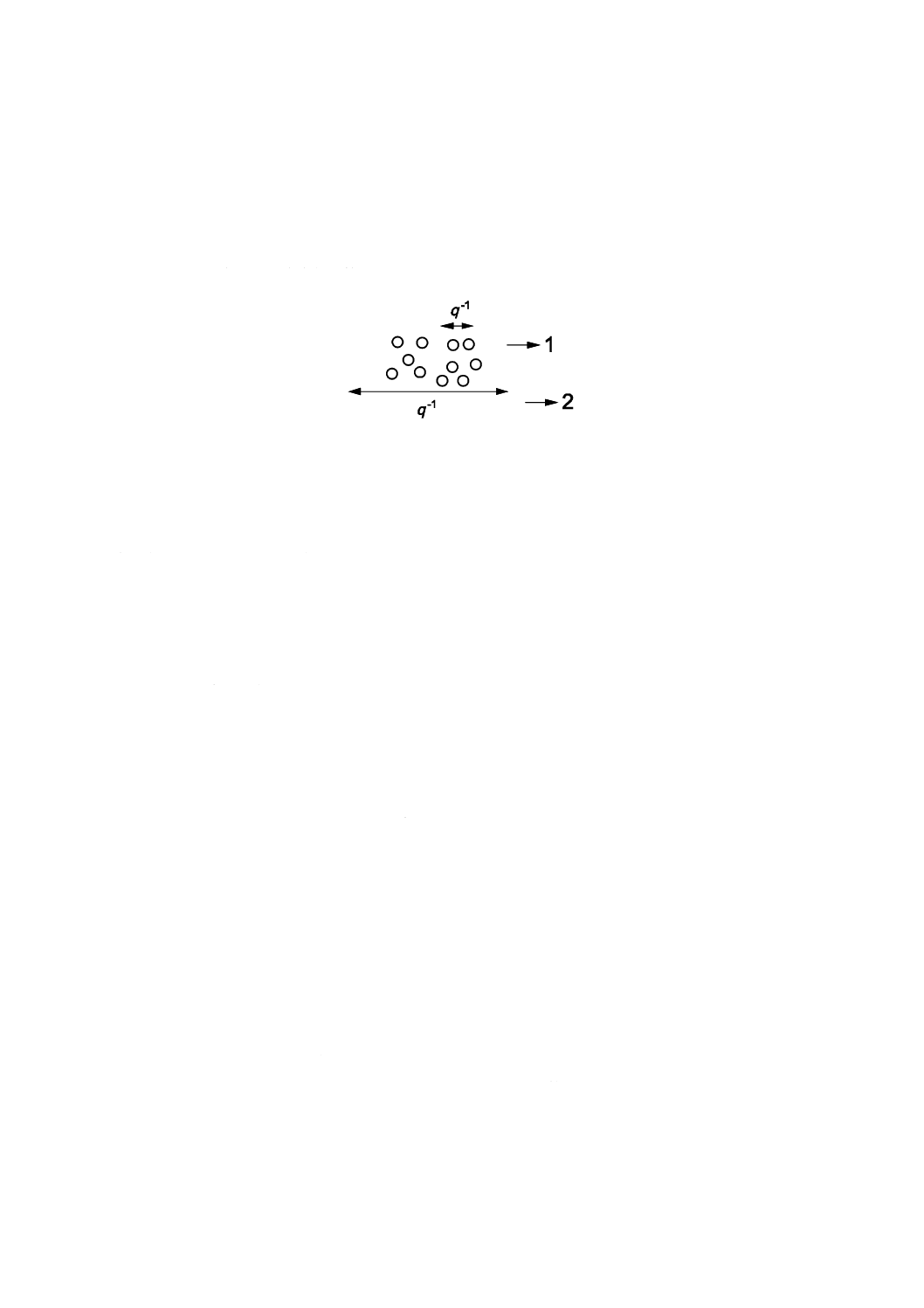
クトルの逆数q−1と平均粒子間距離hとの比によって,いずれの状態の拡散が求まるかが決まる(図B.1
参照)。
q−1<h/(2π)の場合,多くの粒子が分散する状態で,個々の粒子の自己拡散がDLS法によって測定される。
q−1>h/(2π)の場合,粒子集合体の協同拡散が測定される。
1
自己拡散
2
協同拡散
図B.1−拡散に及ぼす平均粒子間距離と散乱ベクトルの逆数との比の影響
両方の状態は,自己拡散係数DS及び協同拡散係数DCという拡散係数で表現する。両方の拡散係数は,
濃度依存性をもつが,その依存性は異なる。
したがって,希薄分散液試料の場合,各粒子の自己拡散係数が観測される。粒子濃度が増加した場合及
び/又は比較的大きな粒子で,平均粒子間距離が,散乱ベクトルより小さくなる場合,自己拡散の代わり
に粒子の協同拡散が観察される。
その結果,測定した拡散係数から,ストークス−アインシュタインの式を用いて計算した見掛けの粒子
径は,粒子の濃度に依存する。
上記の説明では,特に並進拡散係数を求めるためにストークス−アインシュタインの式を使用すること
は,球形粒子だけに適用できる。非球形粒子の場合,測定された拡散係数は,並進及び回転の拡散係数の
重ね合わせになることに注意する必要がある。
要約すると,拡散に重要な影響を与える粒子間相互作用力は,純粋な流体力学的抵抗から粒子の表面電
位によって生じる静電気反発力及びファンデルワールス引力までの幾つかの相互作用がある。さらに,こ
うした相互作用が同時に起こる可能性もある。したがって,粒子間相互作用が存在する状態で測定した拡
散係数は,個々の粒子の特性を表すのではなく,粒子懸濁液全体の粒子特性を表している。
粒子間相互作用の影響の現れ方は,系特有である。長距離相互作用は,低粒子濃度でも大きな影響を与
えるが,まれには,高粒子濃度でも粒子が相互作用の影響を受けずに拡散する場合がある。しかし,個々
の粒子及び流体システムにおいて,粒子間相互作用が問題となる粒子濃度があり,正しい粒子径を求める
ためには,希釈が必要になる限界粒子濃度が存在する。
さらに,異なる希釈程度で試料を測定することで,多重散乱の有無を調べることもできる。
B.2.4 制限拡散
制限拡散とは,他の粒子の存在が粒子の自由な拡散を妨げる現象である。一例としてポリマーネットワ
ーク中の粒子の拡散が挙げられる。高試料濃度における粒子径計算に溶媒粘度を用いた場合,又は平均粒
子径の濃度依存性が試料の見掛け粘度の濃度依存性と同じ場合には,多峰性(粒子径頻度分布図でピーク
を複数回観察できる。)又は多分散性は変化しないが,粒子径は大粒子径側へ移動する現象が現れる。
24
Z 8828:2019 (ISO 22412:2017)
B.3
沈降
DLS法が妥当な結果をもたらすためには,沈降速度は拡散速度よりもはるかに遅い必要がある。この条
件が満たされているかは,相関曲線を見ることで確認でき,ランダムなブラウン運動の場合には,単調な
減衰を示す。高い頻度で相関関数が増加することは,非ランダム運動,すなわち粒子の沈降を示す。
相関関数の安定的な減衰状態は,試料の分散安定性が手早く確認できる指標でもある。
B.4
粒子数の変動
測定体積中の粒子数は一定である必要がある。これは,大きな粒子又は低濃度の試料を測定する場合に
は当てはまらない。相関関数の切片が1以上及び高い頻度で相関関数が増加することは,自己相関関数の
設定中に粒子数が変動していることを示す(これは他の測定条件の設定と異なる場合がある。)。
B.5
粗大粒子及びダスト
短い時間間隔(例えば,0.1秒間間隔)で計測した散乱強度の時間平均信号(カウントレート)において,
高いカウントレートの大きな変動が計測された場合,大きな粒子の存在を示しており,試料中に僅かに存
在する粗大粒子の沈降又は粉じんの混入の可能性を示している。試料を通過するレーザ光中に輝点が出現
する場合も,一般に粗大粒子の存在を示す。粗大粒子が粉じんの混入によるものである場合,分散媒を使
用前に更に清浄化(ろ過及び/又は蒸留)する。これらの粗大粒子が元の試料の一部であると結論付けら
れた場合,ユーザーは広い粒子径分布に起因する精度の低い結果を受け入れるか,又はろ液若しくは上澄
み液を再度測定するかである。どのような処理を行っても試験報告書に記載する必要がある。
B.6
異なる拡散
非球形粒子は,散乱光強度のゆらぎに対する回転拡散成分及び平行移動拡散成分の両方に寄与する。そ
れぞれの割合は,計測角度に依存する。報告された流体力学的直径は,これらの拡散成分に依存する可能
性がある[20]。
B.7
蛍光
蛍光粒子は,入射光の一部を吸収し,より長波長の光を再放射する。この再放射された光が検出器の感
度波長内である場合,無相関の信号量を増加させる。狭帯域バンドパスフィルタは,この影響を最小に抑
えるのに使用できる。
25
Z 8828:2019 (ISO 22412:2017)
附属書C
(参考)
オンライン測定
一般に,DLS法は静止状態の試料に適用する。流れは,粒子に余分な動きを加えるため,測定される見
掛けの拡散係数に付随的な寄与を与える可能性がある。この基本的な問題があるにもかかわらず,オンラ
イン測定可能なDLS装置が市販されており,意味ある値を測定した実施例が報告されている。オンライン
システムを使用する場合,次の問題を考慮する必要がある。
− 大きな粒子は付随的な動きとして,バルク流れの影響を最も受けやすく,相関関数の減衰が速くなる。
したがって,信頼性の高い測定可能な最大粒子径が制限される。
− 乱れのある流れ,又はセル壁面近傍の流れの一般的な状態である乱流は,その流れの影響を計算でき
ない場合がある。
− 定常状態ではない状態[例えば,フィールド フロー フラクショネーション(FFF)で観察されるよ
うな粒子数の変動]では,粒子数の少ない状態での測定結果(例えば,FFF溶出信号の散乱強度分布
のすそ近く)は,粒子数の多い状態での測定結果(例えば,FFF溶出信号分布の中心付近)と比べて
信頼性が低くなる。
− 定常状態から逸脱する状況では,粒子濃度の変化が影響を与える場合もある。
− 粒子移動による問題は,多分散試料で一層顕著になる。
− 試料は非常に希薄であることが多いので,散乱強度の弱い散乱体の測定も影響を受ける可能性がある。
流れ系で測定したい者には,これらの潜在的な影響が測定結果の精度に及ぼさない保証を得るために,
材料,粒子径範囲及び粒子濃度範囲について,オンラインシステムの妥当性を慎重に確認することを求め
る。すなわち,オンラインシステム(可能ならば分画採取後も)と静的システムの結果とを比較すること
を強く推奨する。
26
Z 8828:2019 (ISO 22412:2017)
附属書D
(参考)
推奨する試料調製方法
D.1 一般
試料の調製は,溶媒の清浄化,セル洗浄,溶液及び懸濁液の調製の三つの手順がある。はじめの二つの
手順(溶媒の清浄化及びセル洗浄)について,この附属書で詳細を記載する。最後の手順(溶液及び懸濁
液の調製)は,それぞれの試料に依存するため,D.5に一般的な指針を記載する。D.6にはポリスチレンラ
テックス粒子の水懸濁の調製を詳細に記載する。
DLS法測定における主要な問題の一つはダストである。ダストとは,測定に好ましくない影響を与える
散乱体に付けられた一般名である。ダストの存在は,平均粒子径の結果に重大な偏りを与える。
ダストは,ろ過,蒸留又は遠心分離によって溶媒から除去できる。ろ過は,安価な使い捨てフィルタを
利用できるため,最も簡便な方法である。しかし,液体の脱イオン化又は微量な不純物を除去するために
は,蒸留が必要になることもある。ろ過膜との相互作用によって,ろ過を用いることができない場合には,
遠心分離によってダストを除去する。この場合,遠心分離した後の上澄みを測定セルに移す。
次の箇条では,溶媒を清浄化するための方法を幾つか記載する。最初に最も簡単な方法から試し,用途
に合った最適な方法を選ぶのがよい。分散した粒子を変化させずに,ダストを含まない試料を調製するこ
とができれば,この附属書に記載した以外の方法を用いて差し支えない。
D.2 ろ過
D.2.1 水
少量の水のろ過には,直径25 mm,孔径0.2 μmの使い捨てろ紙を取り付けた容積20 mLの注射器を利
用する。ルアーロック付きの注射器を選ぶ。注射針が必要な場合は,孔径が大きなもの(18ゲージ)を使
用する。小さな口径の針先から水を噴霧すると,水が液滴となり,表面積が増加するため,空気中の多く
のダストが液中に取り込まれる。水を静かに流出させるようにし,噴霧してはならない。
ろ過の初期段階では,ろ紙が目詰まりするような粗い粒子を除去するために,注射器及び注射針を数回
洗浄し,粒子を洗い流す。可能ならば,ろ過した溶媒に粒子として混入する残留物(ポリマーコーティン
グ剤など)が付着していないろ紙を使用する。不可能ならば,このような残留物を除去するため,使用前
にろ紙を数回洗浄する。水が多くのダストを含む場合は,予備ろ過も検討する。予備ろ過は,孔径の小さ
なろ紙の寿命を長くする。
大量の液体をろ過するときには,大きなろ過面積をもつ孔径0.2 μmのろ紙を装塡した直径47 mm又は
より大きな直径のろ紙ホルダを使用する。ろ紙ホルダを水供給口に接続する。ろ紙上に付着した粒子を除
去するため,最低20 mLの水をろ紙に通す。これは,ろ紙表面の残留物を洗い落とす一方で,ろ紙の寿命
も低下させる。ろ過の間は,空気とろ液との接触面積が大きくならないように,ろ液をセル又は希釈容器
に注ぐ。
D.2.2 有機溶媒
使用する溶媒が,プラスチック製のろ紙ホルダ及びろ紙材質に影響を与えないならば,水に対して示し
たD.2.1と同じ浄化方法を用いる。影響を与えるならば,ステンレス製のろ紙ホルダ及び使用する溶媒に
適した材質のろ紙を用いる。溶媒に適したろ紙の選択指針は,ろ紙の製造メーカから入手できる。
27
Z 8828:2019 (ISO 22412:2017)
少量の溶媒をろ過するときには,ガラス製の注射器に接続された直径13 mm又は25 mmのステンレス
製のろ紙ホルダ及びろ紙を使用する。また,溶媒に溶解しない材質のOリングを選ばなければならない。
ろ紙に孔をあけないように,先の平らなピンセットを用いてろ紙を取り扱う。
D.3 清浄化
D.3.1 水
残留イオンは,散乱体(粒子)に化学的及び相互作用的な影響を与える場合がある。イオンは,試料を
安定化する場合もあるが,凝集を引き起こす場合もある。粒子形状の変化が拡散係数に影響する場合は,
結果として,DLS法による測定結果に影響する。
市販の純水製造装置も利用が可能である。これらの装置は,イオンを除去し,微量な有機物を吸着し,
0.2 μmの粒子までろ過できる交換式のカートリッジで構成されている。この装置は,簡便に利用でき,小
型,安全で,かつ,維持管理が簡単である。
別の方法として,イオン交換カートリッジ,沸騰フラスコ,凝縮器,容器及び孔径0.2 μmのろ紙を順に
接続し,これに水を通して浄化する方法がある。イオン交換カートリッジ入口までの配管,及び冷却水の
配管に用いるポリ塩化ビニル(PVC)製のチューブを除いて,全てポリテトラフルオロエチレン(PTFE)
製チューブを使用する。いずれの接続部にもグリースを使用してはならない。
組立後は,測定試料を調製するときに使用する純水を得る前に,装置に数リットルの純水を流し,捨て
る。
D.3.2 有機溶媒
非極性溶媒では,通常,脱イオンカラムは不要である。プラスチック製のろ紙ホルダを47 mmのPTFE
製ホルダに,ろ紙を溶媒に対して適切なものに交換する。溶媒に接触するPVC製の配管を,全てPTFE製
に交換(第2候補はふっ素樹脂ゴム)する。可燃性の溶媒を蒸留するときには十分に注意する。
D.4 測定セルの洗浄
D.4.1 一般
必要なセル洗浄の程度は測定条件に依存する。個別に包装された使い捨ての清浄なセルを用いる場合は
一番簡単な方法は,ろ過された圧縮空気でダストを吹き飛ばすだけである。セルの先端部分をもち,光が
通過する部分に指紋を付けてはならない。
D.4.2 洗剤及び水
厳密なセルの洗浄方法を,次に示す。簡単な方法から試していき,用途に合った最適な方法を選択する。
精製水でセルを十分すすぐ。セルの内側及び外側を,研磨剤を含まない洗剤で洗う。このとき,僅か数μm
の引っかききずが問題となるため,ブラシは使用せず,洗剤と水とをセルに入れ,セルを勢いよく振る。
さらに十分に洗浄するには,希薄な洗剤水で満たした小型の超音波洗浄槽(出力40 W程度)にセルを
浸し,数分間,超音波洗浄を行う。可能ならば加熱する。セルにきずが付くのを避けるため,セルどうし
及びセルと洗浄槽の壁とが当たらないようにする。超音波洗浄槽の洗浄液は,こまめに交換する。
精製水で十分に洗浄する。セルを逆さまにして乾燥させるか,セルの内側にダストが付着しないように
カバーを掛ける,又は粒子が存在していないHEPAフィルタ付きベンチ内でセルを清浄にし,その清浄な
状態を保つ。
D.4.3 酸
試料粒子がときどきセル壁面に吸着することがある。また,油滴,微生物などが付着して,洗剤及び水
28
Z 8828:2019 (ISO 22412:2017)
だけでは完全に洗浄できないことがある。セルに付着した水が一様に乾燥しない場合,及びセルから水が
一様な液膜となって流れない場合は,次の洗浄処理を考慮する。
濃硫酸にセルを1時間浸す。PTFEで被覆されたピンセットを用いて,セルを取り出す。精製水ですす
ぎ,洗剤液で超音波洗浄を行った後,ろ過した水で数回すすぐ。カバーを掛けて乾燥する。
ラテックス試料が残ったまま乾燥させると,ガラス又は石英セル表面に強固な膜ができることがある。
この膜の除去にも,濃硫酸による洗浄が極めて有効である。
D.5 溶液及び懸濁液の調製
最も重要なことは,全て(セル及びその蓋,希釈瓶及びその蓋,分注用のピペット又は注射器,緩衝液,
界面活性剤溶液調製用のガラス器具など)を精製及びろ過した溶媒ですすぐことである。また,緩衝液及
び界面活性剤溶液は,精製及びろ過した溶媒で調製する。
使い捨てのプラスチック製ピペットからダストを除去するには,通常は圧縮空気を使うだけで十分であ
るが,カバーを掛けずに放置したため油及びダストが付着したガラス製ピペットに対しては,この方法で
は不十分である。
ダストの再混入を防止するために,試料調製の最終段階で使用する溶媒が,室内の空気と接触する機会
を最小にする。室内空気との接触を可能な限り避けるため,直接接続して溶媒を供給する。光を散乱する
バクテリアが増殖するため,ろ過水は,長時間保存してはならない。可能であれば,少量の新鮮な溶液を
毎日調製するか,不可能な場合は,使用前にろ過する。
可能ならば,フラスコ,瓶又はセル中に溶液を噴霧することを避ける。溶媒が,清浄で滑らかな表面を
つたって流れるようにすると,再混入するダストを減らすことができる。
一度調製した試料は,決して強く振ってはならない。試料を振るとダストを含む空気が取り込まれると
ともに,空気が溶液に溶け込む。目に見えない小さな気泡は,測定したい試料粒子よりも,大きな散乱を
与える。試料をゆっくりと回すのが最善である。濃縮された試料の液滴に希釈液を加える方が,希釈液に
液滴を滴下するより,一様な濃度の試料液を迅速に作ることができる。
分子溶液を作るときには,専門の文献を参考にする。光を散乱し,誤った結果を導き出すゲル及びその
他の超分子には注意する必要がある。
粒子が凝集したままで,あきらかに均一な懸濁液にならない場合は,数滴のエタノールを試料に滴下し
てぬらした後,水に分散させる。
界面活性剤は過剰に使用しない。臨界ミセル濃度(一般的には体積分率10−4〜10−5 %)を超えると,界
面活性剤は凝集を促進する場合がある。
D.6 ラテックス懸濁液の調製
DLS法の測定を初めて行う場合は,電子顕微鏡又はDLS法で測定された粒子径が約100 nmで,粒子径
分布が狭いポリスチレンラテックス粒子を選ぶとよい。この試料の水懸濁液はよく光を散乱するため,装
置の調整にも用いることができる。また,最大切片Bmaxを決定することもできる[7.3 c)参照]。
このようなポリスチレン粒子は,数種類,市販されている。購入後,1年以上経過した試料は,使用し
てはならない。これらのラテックス試料は,製造元が推奨する温度で密閉容器中に保存する。
塩化ナトリウム濃度10 mmol/L(=0.6 g/L)の溶液200 mLを調製する。使い捨ての孔径0.2 μmのろ紙
でこの溶液をろ過する。ろ過した溶液で,容積25 mLの容器及びねじ込み式の蓋,又は使用する試料セル
及びその蓋を十分にすすぐ。これらには使用するまでカバーを掛ける。
29
Z 8828:2019 (ISO 22412:2017)
注記 電解質は,試料に影響を及ぼす可能性がある。例えば,塩化ナトリウムは銀イオンを沈殿させ
る。
市販のラテックス試料は,プラスチック製の容器に入っており,通常は界面活性剤が含まれている。ラ
テックス試料の濃度は,通常,質量分率1〜10 %の範囲にある。この場合,試料作製用容器へ4滴滴下し,
ろ過した10 mmol/Lの塩化ナトリウム溶液を約20 mL加える。この結果,得られる試料は,少し濁った状
態で,5 mWのHe-Neレーザでの測定に適する。レーザが高出力の場合には,ラテックス試料を1滴だけ
滴下するか,若しくは2段階で希釈を行う。
希釈瓶中の試料に対し,10秒間程度の発振と数秒間の静止とを繰り返し,合計約2分間の超音波処理を
施す。
測定セルをすすぐ。D.4.2で示した洗剤と水とを用いた方法を適用する。いかなる研磨剤も使用してはな
らない。測定セルを精製水で十分すすいだ後,ろ過した水ですすぐ。セルの蓋をすすぐ。試料を容器から
セルの中へ静かに注ぎ,蓋をする。
セルの外側がぬれている場合には,試料ホルダへセルを装塡する前に乾かす。すりきずが付くようなタ
オルでセルを拭いてはならない。セルを吸着紙で軽くたたいて乾かす,又は吸着紙,できれば光学ガラス
用の吸着紙の上で,セルをゆっくりと回して水分を拭う。
レーザ光が可視光であるならば,箇条8に従い,レーザポインタ及び装置自体のレーザ光路にセルを置
く。光散乱による明瞭な光線が観察されることが望ましい。光線が太く不明瞭である場合,試料は濃すぎ
るため希釈する。光線が極端に薄く不明瞭な場合,すなわち,ろ過水中とほぼ同程度であれば試料が薄す
ぎるため,ラテックスを添加する。不規則な強い散乱光が容易に観測される場合は,希釈瓶及び水を更に
注意深く洗浄・清浄化して,新しい試料を調製する。
30
Z 8828:2019 (ISO 22412:2017)
参考文献
[1] Einstein A Investigations on the theory of the Brownian movement. In: Fürth R., ed. Cowper, A.D., translator.
Methuen, London, 1926. 124 p
[2] Pecora R Doppler shifts in light scattering from pure liquids and polymer solutions. J. Chem. Phys. 1967,
40,1604-1614
[3] Xu R Particle characterization: Light scattering methods. Kluwer Academic Publishers. Powder Technology
Series, Dordrecht, 2000, Vol. 13
[4] Pecora R ed. Dynamic light scattering: Applications of photon correlation spectroscopy. Plenum, New York,
1985
[5] Chu B Laser light scattering: Basic principles and practice. Academic Press, Boston, Second Edition, 1991,
343 pp. [Reprinted by Dover, Mineola, NY, 2007]
[6] Brown W. ed. Dynamic light scattering, the method and some applications. Clarendon, Oxford, 1993. 735 pp.
(Monographs on the physics and chemistry of materials: No. 49)
[7] Johnson R. M., & Brown W. An overview of current methods of analysing QLS data. (1970) In: Harding, S.E.,
Satelle, D. B, Bloomfield, V. A (eds). Laser Light Scattering in Biochemistry. The Royal Society of Chemistry,
Cambridge, 1992 ISBN 0-85186-486-4
[8] Provencher S.W. A constrained regularization method for inverting data represented by linear algebraic or
integral equations. Comput. Phys. Commun. 1982, 27, 213-227
[9] Provencher S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear
algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229-242
[10] Provencher S.W. Inverse problems in polymer characterization: Direct analysis of polydispersity with photon
correlation spectroscopy. Makromol. Chem. 1979, 180, 201-209
[11] Foord R., Jakeman E., Oliver J., P ike E. R, Blagrove R. J., Wood E., Peacocke A.R. Determination of diffusion
coefficients of haemocyanin at low concentration by intensity fluctuation spectroscopy of scattered laser light.
Nature, 1970, 227,242-245
[12] Hansen P.C., & OʼLeary D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems.
SIAM J. Sci. Comput. 1993, 14, pp. 1487-1503
[13] Ruf H. Effects of experimental errors in dynamic light scattering data on the results from regularized inversions.
Progr Colloid Polym Sci. 2000, 115, 255-258
[14] Jakes J. Regularized Positive Exponential Sum (REPES) Program−A Way of Inverting Laplace Transform
Data Obtained by Dynamic Light Scattering, Collect. Czech. Chem. Commun. 1995, 60, 1781-1797
[15] Lawson C.L., & Hanson R .J. Solving Least Squares Problems. Prentice-Hall, Englewood Cliffs, N.J., 1974:
reprinted by SIAM -Society for Industrial & Applied Mathematics, Philadelphia 1995. ISBN
978-0-89871-356-5
[16] Twomey S. Introduction to the mathematics of inversion of remote sensing and indirect measurements. Dover
Publications, Mineola, 1997. ISBN 0486694518
[17] Takahashi K., Kato H., Saito T., Matsuyama S., Kinugasa S. Precise Measurement of the Size of Nanoparticles
by Dynamic Light Scattering with Uncertainty Analysis. Part. Part. Systems Charact. 2008, 25, 31-38)
31
Z 8828:2019 (ISO 22412:2017)
[18] Berne B. J., & P ecora R. Dynamic light scattering with applications to chemistry, biology, and physics. Wiley,
New York, 1976, 376 pp. [Reprinted by Dover, Mineola, NY, 2000]
[19] Trainer M.N., Wilcock W.L., Ence B.M. (March 1992) Method and Apparatus for Measuring Small Particle
Size Distributions. US Patent No. 5094532
[20] Kätzel U., Vorbau M., Stintz M., Gottschalk-Gaudig T., Barthel H. D ynamic L ight Scattering for the
Characterization of Polydisperse Fractal Systems: II. Relation between Structure and DLS Results. Part. Part.
Systems Charact. 25, 2008, 19-30
[21] ISO Guide 30:2015,Reference materials−Selected terms and definitions
[22] JIS Z 8890 粉体の粒子特性評価−用語
注記 対応国際規格:ISO 26824:2013,Particle characterization of particulate systems−Vocabulary
[23] JIS Q 17025 試験所及び校正機関の能力に関する一般要求事項
注記 対応国際規格:ISO/IEC 17025,General requirements for the competence of testing and calibration
laboratories
[24] Varenne F., Botton J., M erlet C., Beck-Broichsitter M., Legrand F.X., Vauthier C. Standardization and
validation of a protocol of size measurements by dynamic light scattering for monodispersed stable
nanomaterial characterization, Colloid. Surface. A 486,2015, 124-138
[25] Braun A., Couteau O., Franks K., Kestens V., Roebben G., Lamberty A., Linsinger T.P.J. Validation of dynamic
light scattering and centrifugal liquid sedimentation methods for nanoparticle characterisation, Adv. Powder
Techol. 22 (2011) 766-770
[26] Linsinger T. ERM-Application Note 1: Comparison of a measurement result with the certified value, European
Communities 2005, https:// ec .europa .eu/ jrc/ sites/ default/ files/ erm application note 1 en .pdf




