Z 8819-2:2019 (ISO 9276-2:2014)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 記号及び定義 ··················································································································· 2
4 モーメント表記法 ············································································································· 3
4.0 一般 ···························································································································· 3
4.1 モーメント表記法によるモーメントの定義 ·········································································· 4
4.2 モーメント表記法による平均粒子径の定義 ·········································································· 4
4.3 粒子径分布からのモーメント及び平均粒子径の計算 ······························································ 6
4.4 粒子径分布の分散及び標準偏差 ························································································ 8
4.5 対数正規分布でのモーメント及び平均粒子径の計算 ······························································ 9
4.6 比表面積及びザウター径の計算 ························································································ 9
5 モーメント比表記法 ·········································································································· 9
5.0 一般 ···························································································································· 9
5.1 モーメント比表記法によるモーメントの定義 ······································································· 9
5.2 モーメント比表記法による平均粒子径の定義 ······································································ 10
5.3 粒子径分布からの平均粒子径の計算·················································································· 11
5.4 粒子径分布の分散及び標準偏差 ······················································································· 12
5.5 種々の平均粒子径の関係 ································································································ 13
5.6 比表面積及びザウター径の計算 ······················································································· 13
6 モーメント表記法とモーメント比表記法との関係 ·································································· 14
7 計算された粒子径分布のパラメータの正確さ ········································································ 15
附属書A(参考)体積基準分布のヒストグラムから各種の平均粒子径及び
標準偏差を求める計算例(モーメント表記法) ··································································· 16
附属書B(参考)体積基準分布のヒストグラムから各種の平均粒子径及び
標準偏差を求める計算例(モーメント比表記法) ································································ 18
附属書C(参考)粒子径分布パラメータの計算の正確さ ····························································· 21
参考文献 ···························································································································· 23
Z 8819-2:2019 (ISO 9276-2:2014)
(2)
まえがき
この規格は,産業標準化法第16条において準用する同法第12条第1項の規定に基づき,一般社団法人
日本粉体工業技術協会(APPIE)及び一般財団法人日本規格協会(JSA)から,産業標準原案を添えて日本
産業規格を改正すべきとの申出があり,日本産業標準調査会の審議を経て,経済産業大臣が改正した日本
産業規格である。これによって,JIS Z 8819-2:2001は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
注記 工業標準化法に基づき行われた申出,日本工業標準調査会の審議等の手続は,不正競争防止法
等の一部を改正する法律附則第9条により,産業標準化法第12条第1項の申出,日本産業標準
調査会の審議等の手続を経たものとみなされる。
日本産業規格 JIS
Z 8819-2:2019
(ISO 9276-2:2014)
粒子径測定結果の表現−第2部:粒子径分布からの
平均粒子径及びモーメントの計算
Representation of results of particle size analysis-
Part 2: Calculation of average particle sizes/diameters and
moments from particle size distributions
序文
この規格は,2014年に第2版として発行されたISO 9276-2を基に,技術的内容及び構成を変更するこ
となく作成した日本産業規格である。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。
粒子径測定は粒子状物質の特性評価に多く用いられている。粉体強度,流動性,溶解速度,懸濁液の安
定性などの粒子状物質の物理特性と粒子径とを関係付けることが特性評価の目的である。粒子径分布をも
つ物質に対しては,物理特性を適切に表現できるパラメータを用いることが重要である。例えば個数,表
面積又は体積で重み付けられた平均粒子径である。
この規格は,粒子径分布の平均及び標準偏差を求めるためにモーメントを利用する二つの方法を規定し
ている。
一番目のモーメント表記法特有の利点は,モーメント及び平均粒子径によって粒子径分布を特徴付ける
ことである。モーメント表記法は,物理学,特に機械工学の手法に基づく重み付けを扱っており,個数基
準の分布から求められる算術平均をその一部として含む[1],[2]。
二番目のモーメント比表記法は,個数基準の分布に基づいているが,他の測定基準への変換も含む[3],
[4]。
重要なことは,モーメント表記法とモーメント比表記法とで定義される平均粒子径の下付添字の意味が
異なることである。二つの表記法は簡単な関係でつながっており,その関係は箇条6に記載されている。
両表記法は,いわゆる特性関数及びプロセス関数に対する製品及びプロセスの物理的特性を適切に表現
できる平均粒子径の導出及び/又は選択に適している。用いられる平均粒子径としては,関係する製品又
はプロセスの物理的特性と因果関係をもつことが望まれる。
粒子特性評価は,非常に広い科学の専門分野と関連している。用いられる粒子径分布に関する表記法は,
工業分野及び応用に依存してきた。そのため,共通に適する表記法はまだ見いだされていない。
また,ある粒子径範囲での光散乱のように,粒子径に対する依存性として,単純な指数則を仮定して求
めた平均粒子径では表現できない特性もある[5]。
1
適用範囲
この規格は,与えられた粒子径分布から種々のモーメント,平均粒子径及び標準偏差を計算するための

2
Z 8819-2:2019 (ISO 9276-2:2014)
関連する方程式及び用語に関して,利用されるモーメント表記法及びモーメント比表記法の二つの表記法
について規定する。粒子径分布は,ヒストグラムとして与えられても,又は解析的な関数として与えられ
ても構わない。
粒子の形状にかかわらず,相当径をその粒子の粒子径とみなす。ただし,ここでは,粒子形状係数は考
慮しない。粒子径の測定結果は測定原理に依存するため,測定手法について報告書に記載することが重要
になる。測定される粒子サンプルは,対象とする粉体の母集団を代表するものと考える。
両表記法について,ヒストグラムデータから平均粒子径及び標準偏差を求める計算例を附属書に示す。
平均粒子径の正確さは,不完全な分布から求めるときに低下することがある。また,粒子径区間の数が
極めて少ない場合にも,正確さが低下することがある。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 9276-2:2014,Representation of results of particle size analysis−Part 2: Calculation of average
particle sizes/diameters and moments from particle size distributions(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この引用
規格は,記載の年の版を適用し,その後の改正版(追補を含む。)は適用しない。
ISO 9276-3:2008,Representation of results of particle size analysis−Part 3: Adjustment of an experimental
curve to a reference model
3
記号及び定義
この規格で用いる主な記号及び定義は,次による。
二つの表記法を明確に区別するため,必要に応じて異なる記号をモーメント表記法(M)及びモーメン
ト比表記法(M-R)において使用する。両表記法に対して,具体的な平均粒子径の用語を,対応する箇条
(箇条4及び箇条5)にそれぞれ記載する。
記号
定義
M表記法
M-R表記法
i
i
上側粒子径がxi(M)又は中点がDi(M-R)となる粒子径区間の番号
k
−
粒子径xのべき指数
m
m
粒子径区間の数
r
r
測定基準(粒子量の分布を測定する基準を表す指数)
注記 測定次元ともいう(JIS Z 8890)[17]。
r=0,個数基準
r=1,長さ基準
r=2,表面積基準又は投影面積基準(ここでは両者を面積基準と呼ぶ。)
r=3,体積基準又は質量基準
Mk,r
−
サンプルにおける分布qr(x)のk-次モーメント
mk,r
−
サンプルにおける分布qr(x)のk-次の中心モーメント
−
Mp
個数基準粒子径分布のp-次モーメント
−
mp
個数基準粒子径分布のp-次の中心モーメント
−
N
サンプル中の全粒子数

3
Z 8819-2:2019 (ISO 9276-2:2014)
記号
定義
M表記法
M-R表記法
−
O
平均粒子径の次数(O=p+q)
−
p,q
モーメント比表記法におけるDのべき指数又はべき指数を示す下付添字
qr(x)
qr(D)
測定基準rの相対粒子量分布密度(以下では,分布密度という。)
注記 JIS Z 8819-1では,頻度と呼んでいる。
Eq
−
r,i
−
i番目の粒子径区間幅Δxiにおける分布密度の平均
Qr(x)
Qr(D)
測定基準rの積算分布
ΔQr,i
ΔQr,i
積算分布の差分,すなわち,i番目の粒子径区間幅Δxiに含まれる相対粒子量
注記 ΔQr,iは,対応国際規格では定義されていないが,対応国際規格の5.3の式(54)及び
式(55)に誤りがあり修正したため,追加した。
sr
sr
分布qr(x)及びqr(D)の標準偏差
sg
sg
幾何標準偏差
s
s
対数正規分布の標準偏差(s=ln sg)
S
S
表面積
SV
SV
比表面積(粒子実体積当たりの表面積)
V
V
粒子体積
EV
−
−
平均粒子体積
x
D
粒子径,相当球の直径
xi
−
i番目の粒子径区間の上側粒子径
xi−1
−
i番目の粒子径区間の下側粒子径
Ex
−
i
Di
i番目の粒子径区間の中点(粒子径区間の上側粒子径,下側粒子径の算術平均などで与
えられる。)
注記
Ex
−
iは,対応国際規格では定義されていないが,対応国際規格の4.2.4の式(18),4.3.2
の式(27)及び式(30)で用いられているため,追加した。
xmin
−
与えられた粒子径分布において,それ以下には粒子が存在しない粒子径
xmax
−
与えられた粒子径分布において,それ以上には粒子が存在しない粒子径
Ex
−
k,r
ED
−
p,q
平均粒子径(一般的表示)
Ex
−
k,0
−
算術平均粒子径
Ex
−
k,r
−
重み付き平均粒子径
Ex
−
geo,r
ED
−
p,p
幾何平均粒子径
注記 対応国際規格では,別の行に記載されているが,同じ定義のため,まとめた。
Ex
−
har,r
−
調和平均粒子径
x50,3
−
体積基準積算分布の中位径
xp,r
−
測定基準rの分布におけるp-パーセンタイル値
注記 対応国際規格では,定義されていないが,対応国際規格の4.4の式(42)及び式(44)
で用いられているため,追加した。
Δxi=xi−xi−1
−
i番目の粒子径区間の幅
4
モーメント表記法
4.0
一般
モーメントは,粒子径分布の平均径及び標準偏差の一般的な定義になる。大きな母集団から抽出された
有限な数の粒子からなるランダムサンプル(標本)は,母集団の粒子径分布のモーメントを推定するのに
用いる。標本値から未知の母集団の数値(母数)を推測することを推定と呼ぶ。粒子径測定は常に,離散
的なサンプルを扱う。また,幾つかの離散的な粒子径区間を用いる。そこで,この規格では標本のモーメ
ントを扱う。
4
Z 8819-2:2019 (ISO 9276-2:2014)
4.1
モーメント表記法によるモーメントの定義
分布密度のk-次モーメント[1]は,式(1)の積分によって定義する。
∫
=
max
min
d)
(
,
x
x
r
k
r
k
x
x
q
x
M
···································································· (1)
ここに, Mk,r: モーメント
k: 粒子径xのべき指数
r: 分布密度の測定基準
r=0の場合のq0(x)は個数基準分布密度となり,r=3の場合のq3(x)は体積又は質量基準分布密度となる。
積分の上下限が最大粒子径(xmax)及び最小粒子径(xmin)の場合,式(1)は完全モーメントを表す。
特別な場合として,M0,rは,次の式(2)のように常に1になる。
1
)
(
)
(
d)
(
d)
(
min
max
0
,0
max
min
max
min
=
−
=
=
=
∫
∫
x
Q
x
Q
x
x
q
x
x
q
x
M
r
r
x
x
r
x
x
r
r
····················· (2)
ここに,積算分布は,次の式(3)による。
∫
=
i
x
x
r
i
r
x
x
q
x
Q
min
d)
(
)
(
····································································· (3)
次の式(4)のように,式(1)の積分範囲が,粒子が存在する範囲内に含まれる任意の二つの粒子径xi−1とxi
との間の場合を不完全モーメントという。
∫
−
=
−
i
i
x
x
r
k
i
i
r
k
x
x
q
x
x
x
M
1
d)
(
)
,
(
1
,
·························································· (4)
ここに,xmin<xi−1<xi<xmax
注記 式(4)は,“粒子が存在する範囲内に含まれる任意の二つの粒子径xi−1とxiとの間”で与えられ
る不完全モーメントの定義になるが,この規格で扱う他のモーメントは全て完全モーメントに
なる。
式(1)及び式(4)で表されるモーメントのほかに,分布密度qr(x)の,いわゆるk-次の中心モーメントmk,r
を求めることができる。これを,重み付き平均粒子径
Ex
−
k,rまわりのモーメントという[式(11)参照]。
k-次の中心モーメントは,次の式(5)の定義による。
∫
−
=
max
min
d)
(
)
(
,1
,
x
x
r
k
r
r
k
x
x
q
x
x
m
··························································· (5)
4.2
モーメント表記法による平均粒子径の定義
4.2.0
一般
全ての平均粒子径は,次の式(6)によって定義する。
k
r
k
r
k
M
x
,
,=
············································································ (6)
下付添字のk及びrに用いた数値に応じて,定義される平均粒子径が異なる。式(6)で求められる平均粒
子径は,かなり異なる可能性があるので,下付添字のk及びrを常に明記することが望ましい。
平均粒子径には,算術平均粒子径及び重み付き平均粒子径の二つのグループがある。

5
Z 8819-2:2019 (ISO 9276-2:2014)
4.2.1
モーメント表記法による平均粒子径
Ex
−
k,rに関する用語
表1に,平均粒子径の用語を示す。
表1−平均粒子径
Ex
−
k,rに関する用語
記号
用語
Ex
−
1,0
個数基準算術平均長さ径(個数平均径)
Ex
−
2,0
個数基準算術平均面積径(平均面積径)
Ex
−
3,0
個数基準算術平均体積径(平均体積径)
Ex
−
1,1
重み付き長さ基準平均径(長さ平均径)
Ex
−
1,2
重み付き面積基準平均径(体面積平均径),ザウター径
Ex
−
1,3
重み付き体積基準平均径(体積平均径)
4.2.2
算術平均粒子径
算術平均粒子径は,個数基準分布密度q0(x)から求められ,次の式(7)の定義による。
k
k
k
M
x
0,
0,=
············································································ (7)
顕微鏡(画像法)による個々の粒子の計数は,個数基準の分布(r=0)から平均を求める代表的な例に
なる。
算術平均粒子径には,次のものがある[2]。
個数基準算術平均長さ径(個数平均径):
0,1
0,1
M
x
=
····································· (8)
個数基準算術平均面積径(平均面積径,又は平均表面積径[6]):
2
0,2
0,2
M
x
=
··· (9)
個数基準算術平均体積径(平均体積径[6]):
3
0,3
0,3
M
x
=
···························· (10)
4.2.3
重み付き平均粒子径
重み付き平均粒子径は,次の式(11)の定義による。
k
r
k
r
k
M
x
,
,=
············································································(11)
ふるい分け前後におけるふるいのひょう量(ふるい分け法)は,質量基準の分布(r=3)から平均を求
める代表例になる。重み付き平均粒子径は,分布qr(x)の粒子径軸(横軸)上の重心を表している。式(12)
〜式(15)で与えられる重み付き平均粒子径がよく用いられる。
個数基準分布密度q0(x)の重み付き平均粒子径は,個数基準算術平均長さ径[式(8)]に等しく,次による。
個数基準算術平均長さ径(個数平均径[6]):
Ex
−
1,0=M1,0 ····················· (12)
長さ基準分布密度q1(x)の重み付き平均粒子径は,次による。
重み付き長さ基準平均径(長さ平均径[6]):
Ex
−
1,1=M1,1 ····················· (13)
面積基準分布密度q2(x)の重み付き平均粒子径は,次による。
重み付き面積基準平均径(体面積平均径[6]):
Ex
−
1,2=M1,2 ·················· (14)
体積基準分布密度q3(x)の重み付き平均粒子径は,次による。
重み付き体積基準平均径(体積平均径[6]):
Ex
−
1,3=M1,3 ····················· (15)
4.2.4
幾何平均粒子径
n個の数値の和をnで除して計算される算術平均の代わりに,幾何平均は,n個の積のn乗根として与え
られる。対数値による計算では,n個の対数値の和をnで除すと幾何平均の対数が求まる。算術平均は幾
何平均より大きく,その差は分布幅が広がるに従って大きくなる。
式(6)でkを0に近づけた極限は,幾何平均粒子径を与える(モーメント比表記法におけるp=qに対す
る導出[3]を参照)。
r-基準分布の幾何平均粒子径は,連続分布に対して次の式(16)の定義による。

6
Z 8819-2:2019 (ISO 9276-2:2014)
r
x
x
r
r
x
x
x
q
x
x
,
geo
,0
max
min
d)
(
)
(ln
exp
=
=
∫
················································ (16)
また,対数による表現は,次の式(17)による。
∫
=
=
max
min
d)
(
)
(ln
ln
ln
,
geo
,0
x
x
r
r
r
x
x
q
x
x
x
················································ (17)
ヒストグラムのデータの場合,r-基準分布の幾何平均粒子径は,次の式(18)のように求められる。
r
m
i
i
r
i
m
i
i
i
r
i
r
x
Q
x
x
q
x
x
,
geo
1
,
1
,
,0
Δ
)
(ln
exp
Δ
)
(ln
exp
=
=
=
∑
∑
=
=
·················· (18)
ここに,
Ex
−
i: 粒子径区間iの中点
ΔQr,i: 粒子径区間幅Δxiに含まれる相対粒子量
注記 粒子径分布が対数正規分布で近似できる場合(ISO 9276-5),幾何平均粒子径は分布の中央値(中
位径)と一致する。
4.2.5
調和平均粒子径
n個の数値の逆数を算術平均した値の逆数を,調和平均と呼ぶ[7]。調和平均は幾何平均より小さく,標
本の分散が大きいほど両者の差が大きくなる。r-基準分布の調和平均粒子径は,次の式(19)で与えられる。
r
x
x
r
r
M
x
x
q
x
x
,1
,
har
1
d)
(
1
1
max
min
−
=
=
∫
····················································· (19)
ヒストグラムからは,次の式(20)のように求めることができる。
∑
∑
=
=
=
=
m
i
i
r
i
m
i
i
i
r
i
r
Q
x
x
q
x
x
1
,
1
,
,
har
Δ
1
1
Δ
1
1
·············································· (20)
4.3
粒子径分布からのモーメント及び平均粒子径の計算
4.3.1
個数又は体積基準分布からのMk,r及び平均粒子径の計算
実際の操作では,測定データは個数基準分布密度q0(x)又は体積基準分布密度q3(x)で与えられることが多
い。4.2で定義された各平均粒子径は,式(21)によって求めることができる[1]。
k
r
r
k
k
r
r
k
k
r
k
r
k
M
M
M
M
M
x
3,3
3,3
0,
0,
,
,
−
−
+
+
=
=
=
············································ (21)
式(21)から次の関係が導かれる。
kM
M
M
x
3,3
3,1
0,2
0,2
−
−
=
=
····························································· (22)
3
3,3
3
0,3
0,3
1
−
=
=
M
M
x
····························································· (23)
7
Z 8819-2:2019 (ISO 9276-2:2014)
3,2
3,1
0,1
0,2
1,1
1,1
−
−
=
=
=
M
M
M
M
M
x
·························································· (24)
3,1
0,2
0,3
2,1
2,1
1
−
=
=
=
M
M
M
M
x
························································· (25)
0,3
0,4
3,1
3,1
M
M
M
x
=
=
···································································· (26)
式(21)〜式(26)によると,平均粒子径を計算する場合,次のモーメントが必要になる。
個数基準分布密度q0(x):M1,0,M2,0,M3,0,M4,0
体積基準分布密度q3(x):M1,3,M−1,3,M−2,3,M−3,3
式(21)は,任意の測定基準の平均粒子径又はモーメントが,個数基準の二つのモーメントの比として表
されることを示している。この比がモーメント比表記法の主な関係として用いられる。
4.3.2
ヒストグラムで与えられた粒子径分布からのMk,rの計算
分布密度がヒストグラムで与えられる場合,粒子径区間Δxi=xi−xi−1で分布密度は一定になる。したが
って,式(1)は,次の式(27)のように書き換えられる。
∑
∫
=
=
=
m
i
i
i
r
k
i
x
x
r
k
r
k
x
q
x
x
x
q
x
M
1
,
,
Δ
)
(
d)
(
max
min
············································ (27)
ここに,
1
,
,
Δ
−
−
=
i
i
i
r
i
r
x
x
Q
q
········································································· (28)
式(28)によって,式(29)となる。
∑
∫
=
=
=
m
i
i
r
k
i
x
x
r
k
r
k
Q
x
x
x
q
x
M
1
,
,
Δ
d)
(
max
min
················································· (29)
粒子径区間における近似的な平均
Ex
−
ikは,各粒子径区間における算術平均として与えることができる。
k
i
i
k
i
x
x
x
+
=
−
2
1
····································································· (30)
算術平均のほかに,幾何平均又は積分平均のような平均があるが,これらに特別な優位性があるわけで
はない。全ての粒子径分布に対して優位性のある粒子径区間における平均の設定方法がないことは,幾つ
かの研究によって示されている[8]。
ヒストグラムは元々離散的だが,これに基づくモーメント及び平均径の計算値の不確かさは2 %〜6 %に
なる。ただし,これは,粒子径区間幅,及び各粒子径区間幅に入る粒子量の不確かさに依存する。より多
くの粒子径区間に対する測定によって測定結果の粒子径分解能を向上させる方法は,ISO 9276-3に規定さ
れている。
次のモーメントM1,0,M2,0,M3,0,M4,0,M1,3,M−1,3,M−2,3及びM−3,3は,式(31)〜式(38)で求めることが
できる。
∑
∑
=
=
=
=
m
i
i
i
m
i
i
i
i
Q
x
x
q
x
M
1
,0
1
1
,0
1
0,1
Δ
Δ
·················································· (31)
8
Z 8819-2:2019 (ISO 9276-2:2014)
∑
∑
=
=
=
=
m
i
i
i
m
i
i
i
i
Q
x
x
q
x
M
1
,0
2
1
,0
2
0,2
Δ
Δ
················································· (32)
∑
∑
=
=
=
=
m
i
i
i
m
i
i
i
i
Q
x
x
q
x
M
1
,0
3
1
,0
3
0,3
Δ
Δ
·················································· (33)
∑
∑
=
=
=
=
m
i
i
i
m
i
i
i
i
Q
x
x
q
x
M
1
,0
4
1
,0
4
0,4
Δ
Δ
················································· (34)
∑
∑
=
=
=
=
m
i
i
i
m
i
i
i
i
Q
x
x
q
x
M
1
,3
1
1
,3
1
3,1
Δ
Δ
·················································· (35)
∑
∑
=
=
−
=
=
m
i
i
i
m
i
i
i
i
,
Q
x
x
q
x
M
1
,3
1
1
,3
1
3
1
Δ
1
Δ
1
················································ (36)
∑
∑
=
=
−
=
=
m
i
i
i
m
i
i
i
i
,
Q
x
x
q
x
M
1
,3
2
1
,3
2
3
2
Δ
1
Δ
1
·············································· (37)
∑
∑
=
=
−
=
=
m
i
i
i
m
i
i
i
i
,
Q
x
x
q
x
M
1
,3
3
1
,3
3
3
3
Δ
1
Δ
1
··············································· (38)
4.4
粒子径分布の分散及び標準偏差
粒子径分布の広がりは標準偏差srを平方した分散で表される。分布qr(x)の分散sr2は,次の式(39)によっ
て定義される。
∫
−
=
max
min
d)
(
)
(
2
,1
2
x
x
r
r
r
x
x
q
x
x
s
···························································· (39)
モーメントを用いると,分散は,次の式(40)で求めることができる[3]。
2
,1
,2
,2
2
)
(
r
r
r
r
M
M
m
s
−
=
=
··························································· (40)
ヒストグラムの場合には,次の式(41)による。
2
1
,
1
1
,
2
2
1
,
1
1
,
2
2
Δ
Δ
Δ
Δ
−
=
−
=
∑
∑
∑
∑
=
=
=
=
m
i
i
r
i
m
i
i
r
i
m
i
i
i
r
i
m
i
i
i
r
i
r
Q
x
Q
x
x
q
x
x
q
x
s
·········· (41)
sr2の計算例を,附属書Aに示す。
対数正規分布qr(x)に対して,標準偏差sは,次の式(42)で求めることができる。
s=ln(x84,r/x50,r)=ln(x50,r/x16,r) ························································ (42)
ここに,
xp,r: r-基準分布のp-パーセンタイル値
幾何標準偏差sgは,次の式(43)による。
sg=exp(s) ··············································································· (43)
したがって,次の式(44)の関係が得られる。

9
Z 8819-2:2019 (ISO 9276-2:2014)
sg=x84,r/x50,r=x50,r/x16,r ································································ (44)
4.5
対数正規分布でのモーメント及び平均粒子径の計算
対数正規分布の分布密度qr(x)でのk-次モーメントに関して,次の式(45)の関係が成立する。
)
5.0
ln
exp(
)
5.0
exp(
2
2
,
50
2
2
,
50
,
s
k
x
k
s
k
x
M
r
kr
r
k
+
=
=
···························· (45)
一連の平均粒子径は,式(45)で与えられるk-次モーメントのk乗根として,又は分布の中位径(幾何平
均)x50,r及び標準偏差から次の式(46)で求めることができる。
)
5.0
exp(ln
)
5.0
exp(
2
,
50
2
,
50
,
ks
x
ks
x
x
r
r
r
k
+
=
=
·································· (46)
対数正規分布の中位径x50,rは,幾何平均径
Ex
−
0,rと一致する。
4.6
比表面積及びザウター径の計算
比表面積(粒子実体積当たりの表面積)SVは,面積基準平均径,すなわち,ザウター径
Ex
−
1,2の逆数に比
例する[式(14)]。
2,1
V
6
x
S=
··············································································· (47)
適切な測定基準の分布から得られるモーメントを用いてSVを求めることができる。式(25)によると,SV
は,表面積,個数又は体積基準分布に基づいて次の式(48)で与えられる。
3,1
0,3
0,2
2,1
V
6
6
6
−
=
=
=
M
M
M
M
S
······················································· (48)
非球形粒子の場合,形状係数を導入する。
5
モーメント比表記法
5.0
一般
モーメントは,粒子径分布の平均径及び標準偏差の一般的な定義になる。大きな母集団から抽出された
有限な数の粒子からなるランダムサンプル(標本)は,母集団の粒子径分布のモーメントを推定するのに
用いる。標本値から未知の母集団の数値(母数)を推測することを推定と呼ぶ。粒子径測定は常に,離散
的なサンプルを扱う。また,幾つかの離散的な粒子径区間を用いる。そこで,この規格では標本のモーメ
ントを扱う。
5.1
モーメント比表記法によるモーメントの定義
モーメントとしては,単にモーメントと呼ばれる粒子径軸の原点まわりのモーメント,及び算術平均粒
子径まわりのモーメントの,2種類の異なるモーメントが用いられる。
サンプルの個数基準分布に基づくp-次モーメントMpは,次の式(49)による。
∑
−
=
i
p
i
i
p
D
n
N
M
1
·································································· (49)
ここに,
∑
=
i
in
N
: 測定された全粒子数
Di: i番目の粒子径区間の中点[式(30)に対するコメント参照]
ni: i番目の粒子径区間に含まれる粒子数(粒子径区間の個数
基準分布密度に基づく頻度)
算術平均径になる粒子径xの1次モーメントM1は,通常,
ED
−と表記される。2次モーメント及び3次モ
ーメントはそれぞれ,サンプル粒子群の平均粒子表面積及び平均粒子体積に比例する。
平均粒子径
ED
−まわりのp-次モーメント(中心モーメント)mpは,次の式(50)による。
10
Z 8819-2:2019 (ISO 9276-2:2014)
∑
−
=
−
i
p
i
i
p
D
D
n
N
m
)
(
1
···························································· (50)
粒子径Dの中心モーメントは,平均値との差に関係し,その代表的な例として,サンプル分散m2が上
げられる。
5.2
モーメント比表記法による平均粒子径の定義
5.2.0
一般
サンプル粒子の平均粒子径
ED
−
p,qは,個数基準分布密度に基づく粒子径のp-次モーメントとq-次モーメン
トとの比の1/(p−q)乗で定義される[5]。
)
(
)
/(
1
,
q
p
M
M
D
q
p
q
p
q
p
≠
=
−
························································· (51)
式(49)を用いて式(51)は,次の式(52)のように書き直すことができる。
)
(
)
/(
1
,
q
p
D
n
D
n
D
q
p
i
qi
i
i
p
i
i
q
p
≠
=
−
∑
∑
··················································· (52)
pとqとが等しい場合,次の式(53)が成り立つ。
)
(
ln
exp
,
q
p
D
n
D
D
n
D
i
p
i
i
i
i
p
i
i
p
p
=
=
∑
∑
············································· (53)
べき指数p及びqの値に制限はない。選択される平均粒子径は,関係する具体的な製品又はプロセス特
性との間に因果関係があることが望ましい[4],[10]。
5.2.1
モーメント比表記法による平均粒子径
ED
−
p,qに関する用語
表2に,M-R表記による平均粒子径の用語を示す[9]。

11
Z 8819-2:2019 (ISO 9276-2:2014)
表2−平均粒子径
ED
−
p,qに関する用語
記号
用語
ED
−
−3,0
調和平均体積径
ED
−
−2,1
長さ基準調和平均体積径
ED
−
−1,2
面積基準調和平均体積径
ED
−
−2,0
調和平均面積径
ED
−
−1,1
長さ基準調和平均面積径
ED
−
−1,0
調和平均径
ED
−
0,0
幾何平均径
ED
−
1,1
長さ基準幾何平均径
ED
−
2,2
面積基準幾何平均径
ED
−
3,3
体積基準幾何平均径
ED
−
1,0
個数基準算術平均長さ径(個数平均径)
ED
−
2,1
重み付き長さ基準平均径(長さ平均径)
ED
−
3,2
重み付き面積基準平均径(体面積平均径),ザウター径
ED
−
4,3
重み付き体積基準平均径(体積平均径)
ED
−
2,0
個数基準算術平均面積径(平均面積径)
ED
−
3,1
重み付き長さ基準平均面積径
ED
−
4,2
重み付き面積基準平均面積径
ED
−
5,3
重み付き体積基準平均面積径
ED
−
3,0
個数基準算術平均体積径(平均体積径)
ED
−
4,1
重み付き長さ基準平均体積径
ED
−
5,2
重み付き面積基準平均体積径
ED
−
6,3
重み付き体積基準平均体積径
5.2.2
幾何平均粒子径
表2に示すように,一連の平均粒子径
ED
−
p,pは幾何平均粒子径となる[9]。その例として,写真から画像法
によってクラス分けして求めた気泡径分布の面積基準幾何平均径
ED
−
2,2がある。
5.2.3
調和平均粒子径
表2に示すように,pが負の一連の平均粒子径
ED
−
p,qは調和平均粒子径となる[9]。理論的な例として,粒
子まわりの熱移動がある[4]。
5.3
粒子径分布からの平均粒子径の計算
サンプルの平均粒子径
ED
−
p,qは,任意の測定基準の粒子径分布から式(52)及び式(53)に類似した次の式(54)
及び式(55)によって推定することができる。
)
(
Δ
Δ
1
,
,
,
q
p
D
Q
D
Q
D
q
p
r
qi
m
i
i
r
r
p
i
m
i
i
r
q
p
≠
=
−
−
−
∑
∑
············································ (54)
及び
)
(
Δ
ln
Δ
exp
,
,
,
q
p
D
Q
D
D
Q
D
r
p
i
m
i
i
r
i
r
p
i
m
i
i
r
p
p
=
=
−
−
∑
∑
······································· (55)
12
Z 8819-2:2019 (ISO 9276-2:2014)
ここに, ΔQ r,i: i番目の粒子径区間に含まれる粒子量
Di: i番目の粒子径区間の中点
r: 測定基準で,0,1,2又は3。すなわち,個数,長さ,面積
及び体積(又は質量)にそれぞれ対応する
m: 粒子径区間の数
ΔQr,iが正規化された量の必要はないが,総和=1とすることで正規化できる。式(54)及び式(55)は,r=0
及びni=ΔQ0,iの場合(個数基準分布),式(52)及び式(53)とよく似た形になる。
ヒストグラムは元々離散的なので,これに基づくモーメント及び平均径の計算値の不確かさは1 %〜5 %
となる。ただし,これは,粒子径区間幅,及び各粒子径区間幅に入る粒子量の不確かさに依存する。その
他の多くの情報は,箇条7に記載されている。
注記 式(54)及び式(55)で対応国際規格に誤りがあり,ΔQ r,iと記載すべきところをqr(Di)としている。
この規格では,正しい記号ΔQ r,iに置き換え,箇条3に追加した。
5.4
粒子径分布の分散及び標準偏差
個数基準分布(r=0)の分散になる中心モーメントm2は,次の式(56)のように定義される。
∑
−
=
−
i
i
i
D
D
n
N
m
2
0,1
1
2
)
(
························································· (56)
m2は母集団の粒子径分布の分散(標準偏差の平方)σ2より常に過小評価されるため,母分散に対する不
偏分散s2を得るには,m2にN/(N−1)を乗じる。すなわち,サンプルの粒子径の分散s02は,式(57)から求め
ることができる。
1
)
(
1
2
0,1
2
20
−
−
=
−
=
∑
N
D
D
n
m
N
N
s
i
i
i
················································· (57)
標準偏差s0は,次の式(58)による。
1
20,1
2
0
−
−
=∑
N
D
N
D
n
s
i
i
i
····························································· (58)
式(58)は,次の式(59)のように書き直すことができる。
20,1
20,2
0
D
D
c
s
−
=
···································································· (59)
ここに,
)1
(
−
=
N
N
c
········································································ (60)
実用上,N≫100であればc ≈ 1となるので,次の式(61)でs0を求めることができる。
20,1
20,2
0
D
D
s
−
≈
····································································· (61)
式(61)は,個数基準分布(r=0)で成り立つ。一般的に,どんな基準の分布に対しても標準偏差srは,
次の式(62)によって求めることができるが,srは不偏標準偏差ではない[3]。
2
,
1
2
,
2
r
r
r
r
r
D
D
s
+
+
−
≈
································································ (62)
sr2の計算例を,附属書Bに示す。
粒子径分布が対数正規分布である場合の母標準偏差σは,次のサンプル標準偏差sによって推定できる。

13
Z 8819-2:2019 (ISO 9276-2:2014)
[
]
1
)
ln(
2
0,0
−
=∑
N
D
D
n
s
i
i
i
··························································· (63)
ここで,σ及びsは,対数に変換された粒子径Dの標準偏差になることに注意する。
式(62)の類推から,どのような対数正規分布に対する標準偏差sも,次の式(64)から求めることができる
が,sは不偏統計量ではない。
[
]
∑
∑
=
i
ri
i
i
r
r
i
ri
i
D
n
D
D
D
n
s
2
,)
ln(
························································ (64)
粒子径測定では,次の量sgを幾何標準偏差という[3]。
sg=exp(s) ··············································································· (65)
ただし,それは真の意味の標準偏差ではない。
5.5
種々の平均粒子径の関係
平均粒子径の間には,次の式(66)及び式(67)の関係がある[5]。
ED
−
p,0≦
ED
−
m,0 (p≦m) ··································································· (66)
ED
−
p−1,q−1≦
ED
−
p,q ········································································· (67)
粒子径分布がより均一になるに従い,種々の平均粒子径の違いは小さくなる。等号は,全ての粒子径が
等しい場合(単分散)に成り立つ。
他方,関連する幾つかの平均粒子径に対して次の式(68)の関係がある。
qq
pp
q
p
q
p
D
D
D
0,
0,
,)
(
=
−
······························································ (68)
例えば,p=3,q=2の場合,
20,2
30,3
2,3
D
D
D
=
になる。
次の式(69)のように,簡単な対称関係が与えられる。
ED
−
p,q≡
ED
−
q,p ··············································································· (69)
下付添字pとqとの和Oを,平均径
ED
−
p,qの次数という。
O=p+q ················································································ (70)
対数正規分布の場合,平均粒子径の間に次の式(71)の関係がある。
ED
−
p,q=
ED
−
0,0exp[(p+q)s2/2] ···························································· (71)
例えば,標準偏差s=0.7,平均径
ED
−
p,qの次数O(=p+q)が6でサンプルサイズN=180の場合,又はs=
1.0,O=10でN=1 450の場合,式(71)の計算精度(相対誤差)は約2 %になる。小さな標準偏差で,小さ
な次数O,又は大きなサンプルサイズNの場合には,平均粒子径
ED
−
p,qの計算精度は良くなる。
式(71)は,対数正規分布の場合に次数Oが同じならば平均径は同じ値になることを示している。式(71)
から,次の式(72)の関係を得る。
ED
−
p,q=
ED
−
3,3exp[(p+q−6)s2/2] ························································ (72)
5.6
比表面積及びザウター径の計算
比表面積(粒子実体積当たりの表面積)SVは,面積基準平均径(ザウター径)
ED
−
3,2に逆比例し,次の式
(73)で与えられる。
2,3
V
6
D
S=
·············································································· (73)
非球形粒子の場合,形状係数を導入する。

14
Z 8819-2:2019 (ISO 9276-2:2014)
6
モーメント表記法とモーメント比表記法との関係
M表記又はM-R表記のいずれが適するかは応用分野による。両方法では,箇条3〜箇条5に示されてい
るように記号及び用語が異なる。しかし,計算法は類似している。両表記法での平均粒子径
Ex
−
k,rと
ED
−
p,qと
の間には,次の式(74)で与えられる関係がある。
ED
−
p,q=
ED
−
k+r,r=
Ex
−
k,r(q=r及びp=k+r) ·········································· (74)
k=0は,幾何平均粒子径
Ex
−
0,rを与える。この関係は,文献[5]の
ED
−
q,qと同様な方法で導出できる。
式(74)の例として,粒子実体積当たりの表面積に関する平均径,すなわち,ザウター径
ED
−
3,2=
Ex
−
1,2がある。
3,1
0,2
0,3
2,1
2,1
)2
3
/(
1
2
3
2,3
1
−
−
=
=
=
=
=∑∑
M
M
M
M
x
D
n
D
n
D
i
i
i
i
i
i
························· (75)
個数分布での表記ではq=r=0及びp=k+0になり,二つの表記法は一致する。すなわち,
)
/(
1
,
q
p
i
qi
i
i
p
i
i
q
p
D
n
D
n
D
−
=∑∑
···························································· (52)
注記1 対応国際規格では,この式の番号を(49)としているが,誤りのため正しい番号(52)に置き換え
た。
及び
k
r
r
k
k
r
k
r
k
M
M
M
x
0,
0,
,
,
+
=
=
···························································· (21)
注記2 対応国際規格では,この式の番号を(61)としているが,誤りのため正しい番号(21)に置き換え
た。
になるので,次の式(8)〜式(10)の関係が得られる。
0,1
0,1
0,1
M
x
D
=
=
··················································································· (8)
2
0,2
0,2
0,2
M
x
D
=
=
··············································································· (9)
3
0,3
0,3
0,3
M
x
D
=
=
·············································································· (10)
個数分布ではない場合には,式(74)は,例えば,次の式(24)及び式(26)のようになる。
3,2
3,1
0,1
0,2
1,1
1,1
1,2
−
−
=
=
=
=
M
M
M
M
M
x
D
················································· (24)
0,3
0,4
3,1
3,1
3,4
M
M
M
x
D
=
=
=
··························································· (26)
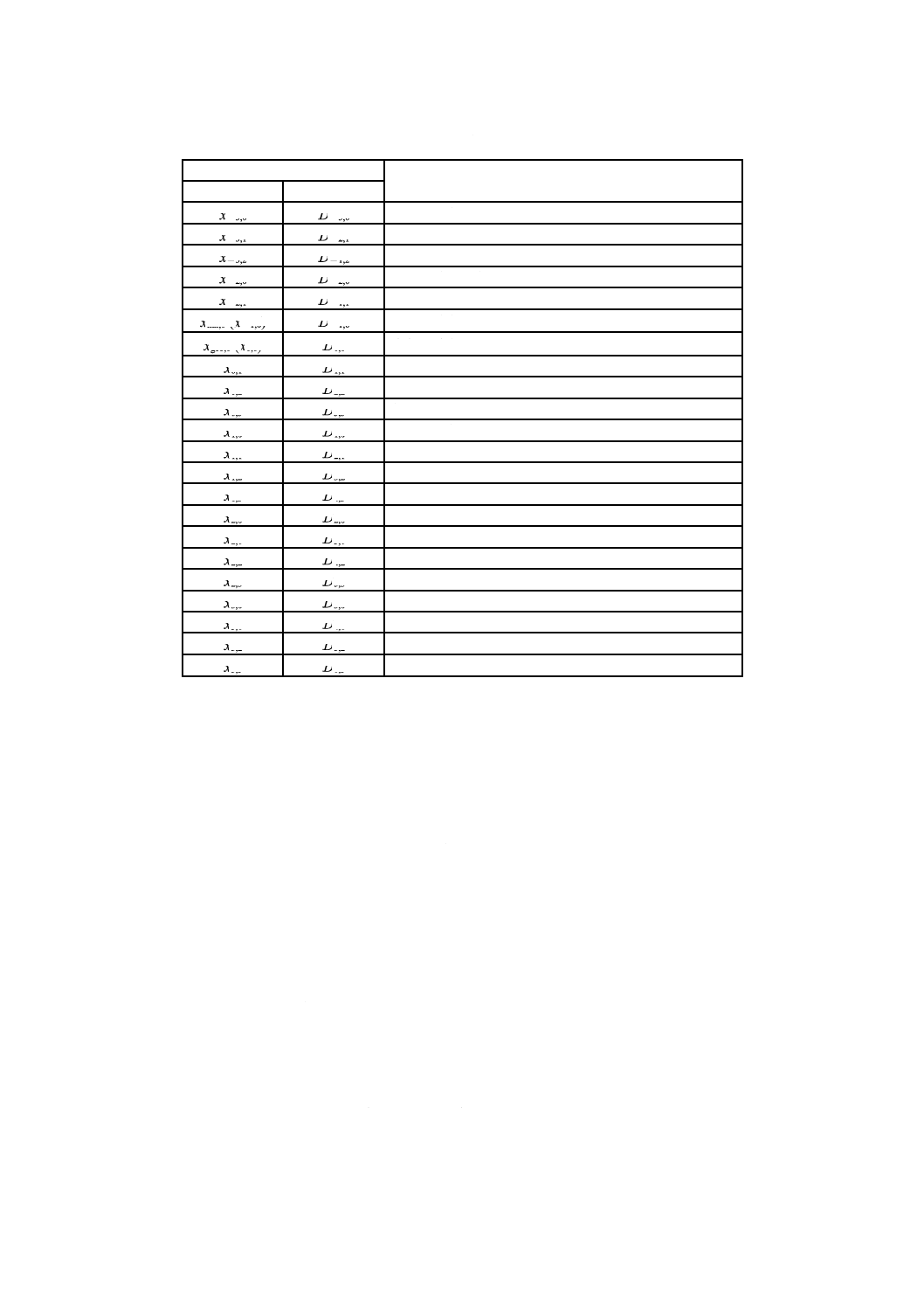
5.2.1に記載したモーメント比表記法の記号と4.2.1に記載したモーメント表記法の記号との比較を,表3
に示す。
15
Z 8819-2:2019 (ISO 9276-2:2014)
表3−平均粒子径の用語及び対応する各表記法の記号
記号
用語
M表記法
M-R表記法
Ex
−
−3,0
ED
−
−3,0
調和平均体積径
Ex
−
−3,1
ED
−
−2,1
長さ基準調和平均体積径
Ex
−
−3,2
ED
−
−1,2
面積基準調和平均体積径
Ex
−
−2,0
ED
−
−2,0
調和平均面積径
Ex
−
−2,1
ED
−
−1,1
長さ基準調和平均面積径
Ex
−
har,0 (
Ex
−
−1,0)
ED
−
−1,0
調和平均径
Ex
−
geo,0 (
Ex
−
0,0)
ED
−
0,0
幾何平均径
Ex
−
0,1
ED
−
1,1
長さ基準幾何平均径
Ex
−
0,2
ED
−
2,2
面積基準幾何平均径
Ex
−
0,3
ED
−
3,3
体積基準幾何平均径
Ex
−
1,0
ED
−
1,0
個数基準算術平均長さ径(個数平均径)
Ex
−
1,1
ED
−
2,1
重み付き長さ基準平均径(長さ平均径)
Ex
−
1,2
ED
−
3,2
重み付き面積基準平均径(体面積平均径),ザウター径
Ex
−
1,3
ED
−
4,3
重み付き体積基準平均径(体積平均径)
Ex
−
2,0
ED
−
2,0
個数基準算術平均面積径(平均面積径)
Ex
−
2,1
ED
−
3,1
重み付き長さ基準平均面積径
Ex
−
2,2
ED
−
4,2
重み付き面積基準平均面積径
Ex
−
2,3
ED
−
5,3
重み付き体積基準平均面積径
Ex
−
3,0
ED
−
3,0
個数基準算術平均体積径(平均体積径)
Ex
−
3,1
ED
−
4,1
重み付き長さ基準平均体積径
Ex
−
3,2
ED
−
5,2
重み付き面積基準平均体積径
Ex
−
3,3
ED
−
6,3
重み付き体積基準平均体積径
7
計算された粒子径分布のパラメータの正確さ
異なる方法で粒子径分布が測定された場合,粒子径分布及びその特性値の違いは有意になる場合がある。
例えば,異なる方法で得られた結果を比較する場合,平均径,パーセンタイル値などの粒子径分布のパ
ラメータを,測定した粒子径分布の基準から他の基準に変換する必要がある。体積基準分布を個数基準に
変換する場合である。数学的には,代表的な場合に1 %以内の正確さで変換される。しかしながら,実際
にはパラメータの誤差は次の要因によって著しく増加する。
− 粒子径分布が上下端のいずれかで僅かに切り取られている場合(例えば,測定基準による分率で0.05 %
〜0.3 %)。しばしば,限られた測定による精密さ又はデコンボリューションの問題から誤差は増加す
る。
− 粒子径分布の上端に本来含まれる粒子が,測定された粒子径分布にはほとんど含まれていない場合。
上端の量の不確かさは大きい。
− 試料に不均一な物質が存在する,又は測定量から粒子径分布に変換するときに不適切なモデルを用い
たことによって,粒子径分布に見せかけのピークが見られる場合。
− 幅の広い粒子径分布において分布の基準(測定基準r)を大きく変える場合。体積基準を表面積基準
にする場合の誤差は,体積から個数に変換する場合に比べて小さい。
− 広い粒子径区間にほとんど粒子が含まれない場合。
− 有意な測定誤差がある場合。
さらに,多くの説明及び例を,附属書Cに示す。
16
Z 8819-2:2019 (ISO 9276-2:2014)
附属書A
(参考)
体積基準分布のヒストグラムから各種の平均粒子径及び
標準偏差を求める計算例(モーメント表記法)
次の計算例で用いられる体積基準積算分布は,対数正規分布に従うとする(ISO 9276-5参照)。
−
=
2
3,0
3
)
ln(
5.0
exp
π
2
1
)
(
s
x
x
s
x
x
q
········································ (A.1)
ここに,
Ex
−
0,3: 体積基準分布の幾何平均径。この場合,
Ex
−
0,3の値は中位径x50,3
に等しい
s: 標準偏差(粒子径の対数値の標準偏差)
幾何標準偏差sgは,次の式(A.2)で与えられる。
sg=exp(s) ·············································································· (A.2)
体積基準分布を,幾何平均径
Ex
−
0,3=5.0 μm及び幾何標準偏差sg=1.648 7に相当する標準偏差s=0.50と
仮定して計算した数値を,表A.1に示す。便宜上,一連の粒子径区間の境界は,式(A.3-1)及び式(A.3-2)の
ようにR5シリーズ及びR10シリーズで与えられている(実際には区間数は概して多い。)。
R5シリーズの場合,
585
.1
10
5
1
=
=
−
i
i
x
x
·····································(A.3-1)
R10シリーズの場合,
259
.1
10
10
1
=
=
−
i
i
x
x
···································(A.3-2)
分布の最大値を,25.0 μmと仮定する。この境界以上の粒子で分布から除かれる体積分率は,0.000 64に
なる。また,R5シリーズの1番目の区間の境界下限値になる0.995 µmでも分布は切り捨てられる。その
境界以下で除かれる粒子の体積分率は,0.000 62になる。除かれる粒子の体積分率は,全体で0.001 26に
なる。
表A.1にあるxi,Q3,i,Δxi,ΔQ3,i,正規化されたΔQ3,i及び
Eq
−
3,iの各数値(R5シリーズの場合)を用いて
式(35)〜式(38)で与えられるモーメントが計算される。Q3,iの値は,Excel 1)の関数LOGNORMDIST(平均,
標準偏差)によって計算したもので,分布の両端を切り捨てたことによる正規化をしていないことに注意
する。
Q3,i=LOGNORMDIST[xi, ln(
Ex
−
0,3),s]=LOGNORMDIST(xi, 1.609 44, 0.5)···· (A.4)
注1) Excelは,Microsoftが供給する製品の商品名である。この文書を利用する人の利便性のために
この情報を提供するもので,この製品をこの規格が推奨するものではない。同様な結果が得ら
れるならば,相当する製品を使用することができる。
モーメントの解析値は,式(1)に対数正規分布を代入し,xmin=0からxmax=∞までの間で積分した値にな
る。すなわち,分布は切り捨てされていない。
求められたモーメントの値を,表A.2に示す。列2には,解析的に求めた式から計算された四つのモー
メントの値を示す。列3及び列5にはそれぞれ,R5シリーズ及びR10シリーズに対して数値計算で求め
た値を示す。
表A.1に示す正規化されたΔQ3,iの値は,列3及び列5の数値を計算するために用いられる。計算値は,

17
Z 8819-2:2019 (ISO 9276-2:2014)
列2に示される値と僅かに異なる。しかし,列4及び列6に示される偏差のように,5 %〜6 %の範囲内で
両者は一致している。
注記 体積基準の粒子径分布に対数正規分布を仮定した場合のk-次モーメントは,次の式(A.5)になる。
)2/
exp(
2
2
3,0
3,
σ
k
x
M
k
k=
···························································· (A.5)
式(22)〜式(26)を考慮して表A.2のモーメントによって求めた平均粒子径を,表A.3に示す。
体積基準分布の分散s32は,表A.1の列2及び列3,並びに列7又は列8のデータを用いて式(41)によっ
て求めることができる。粒子径区間の中点は,表A.1の列2及び列3にある各粒子径区間の境界値の算術
平均になる。分散s32は10.081になり,標準偏差s3は3.175になる。
表A.1−モーメントの計算に用いる対数正規分布の基礎データ(R5シリーズ)
i
xi(µm)
xi−1(µm)
Q3,i
Δxi(µm)
ΔQ3,i
ΔQ3,i(正規化)
Eq
−
3,i(µm−1)
−
0.995
−
0.000 6
−
−
−
−
1
1.577
0.995
0.010 5
0.582
0.009 9
0.009 9
0.017 0
2
2.500
1.577
0.082 8
0.923
0.072 3
0.072 4
0.078 4
3
3.962
2.500
0.320 9
1.462
0.238 0
0.238 3
0.163 0
4
6.280
3.962
0.675 7
2.317
0.354 8
0.355 3
0.153 3
5
9.953
6.280
0.915 7
3.673
0.240 0
0.240 2
0.065 4
6
15.774
9.953
0.989 2
5.821
0.073 5
0.073 5
0.012 6
7
25.000
15.774
0.999 4
9.226
0.010 1
0.010 1
0.001 1
表A.2−モーメントの解析値と計算値との比較
解析値
R5シリーズ
R10シリーズ
計算値
偏差(%)
計算値
偏差(%)
M1,3(µm)
5.666
5.854
3.3
5.703
0.7
M−1,3(µm−1)
0.226 6
0.222 2
−2.0
0.225
−0.6
M−2,3(µm−2)
0.065 9
0.063 9
−3.1
0.064 9
−1.7
M−3,3(µm−3)
0.024 6
0.023 4
−5.1
0.023 6
−4.3
表A.3−平均粒子径の解析値と計算値との比較
解析値
R5シリーズ
R10シリーズ
計算値
偏差(%)
計算値
偏差(%)
Ex
−
1,0(µm)
2.676
2.731
2.1
2.751
2.8
Ex
−
2,0(µm)
3.033
3.082
1.6
3.090
1.9
Ex
−
3,0(µm)
3.436
3.496
1.7
3.487
1.5
Ex
−
1,1(µm)
3.436
3.477
1.2
3.472
1.0
Ex
−
1,2(µm)
4.412
4.501
2.0
4.441
0.7
Ex
−
1,3(µm)
5.666
5.854
3.3
5.703
0.7
表A.3に示される解析値とR5シリーズ及びR10シリーズを用いた計算値との間の差は小さい。原理的
には,R5シリーズより偏差の小さいR10シリーズを用いることが望まれ,そのことは,
Ex
−
1,2及び
Ex
−
1,3の値
によって明らかに確認できる。その結果は,R10シリーズのような狭い粒子径区間は,R5シリーズのよう
な広い粒子径区間より推奨されることを意味する。正確さに関するその他の情報は箇条7に与えられてい
る。

18
Z 8819-2:2019 (ISO 9276-2:2014)
附属書B
(参考)
体積基準分布のヒストグラムから各種の平均粒子径及び
標準偏差を求める計算例(モーメント比表記法)
次の計算例で用いられる体積基準積算分布は,対数正規分布に従うとする(ISO 9276-5参照)。
−
=
2
3,3
3
)
ln(
5.0
exp
π
2
1
)
(
s
D
D
s
D
D
q
····································· (B.1)
ここに,
ED
−
3,3: 体積基準幾何平均径
s: 標準偏差(粒子径の対数値の標準偏差)
幾何標準偏差sgは,次の式(B.2)で与えられる。
sg=exp(s) ·············································································· (B.2)
体積基準分布を,幾何平均径
ED
−
3,3=5 μm及び幾何標準偏差sg=1.648 7に相当する標準偏差s=0.50と仮
定して計算した数値を,表B.1に示す。便宜上,一連の粒子径区間の境界は,式(B.3-1)及び式(B.3-2)のよ
うにR5シリーズ及びR10シリーズで与えられている(実際には区間数は概して多い。)。
R5シリーズの場合,
585
.1
10
5
1
=
=
−
i
i
x
x
····································· (B.3-1)
R10シリーズの場合,
259
.1
10
10
1
=
=
−
i
i
x
x
··································· (B.3-2)
分布の最大値を,25.0 μmと仮定する。この境界以上の粒子で分布から除かれる体積分率は,0.000 64に
なる。また,R5シリーズにおける1番目の区間の境界下限値になる0.995 µmでも分布は切り捨てられる。
その境界以下で除かれる粒子の体積分率は,0.000 62になる。除かれる粒子の体積分率は,全体で0.001 26
になる。
Excel 1)の関数LOGNORMDIST(平均,標準偏差)によって積算体積分率∑
i
i
iD
n
3の値は計算され,表
B.1の列4に示されている。
)5.0,
44
609
.1,
(T
LOGNORMDIS
]
),
ln(
,
[T
LOGNORMDIS
up
3,3
up
3
i
i
i
i
i
D
s
D
D
D
n
=
=
∑
···· (B.4)
ここに, Dupi: i番目の粒子径区間の上側境界(列3)
表B.2の値は,表B.1のデータを用いて求められた。正規化された分布に基づいていないこれらの値を
用いて,式(52)及び式(53)によって平均粒子径を求めた。体積基準分布は対数正規分布で与えられているの
で,いかなる平均粒子径の解析値も,与えられている
ED
−
3,3及びsの値を式(72)に代入することで求めるこ
とができる。
表B.3に求められた平均粒子径を示す。解析値とR10シリーズ及びR5シリーズで求めた値との差は小
さい。原理的には,R5シリーズより偏差の小さいR10シリーズを用いることが望まれ,そのことは,
ED
−
3,2
及び
ED
−
4,3の値によって明らかに確認できる。

19
Z 8819-2:2019 (ISO 9276-2:2014)
表B.1−対数正規分布による体積分布(R5シリーズ)
区間番号
中点Di
(µm)
粒子径範囲
(µm)
積算分率
∑
i
i
iD
n
3
頻度分率
3i
iD
n
1
1.286
0.995以上 1.577未満
0.010 52
0.009 90
2
2.039
1.577以上 2.500未満
0.082 83
0.072 31
3
3.231
2.500以上 3.962未満
0.320 87
0.238 04
4
5.121
3.962以上 6.280未満
0.675 72
0.354 85
5
8.116
6.280以上 9.953未満
0.915 71
0.239 99
6
12.863
9.953以上 15.774未満
0.989 21
0.073 50
7
20.387
15.774以上 25.000未満
0.999 36
0.010 14
表B.2−平均粒子径及び幾何標準偏差を計算するためのデータ
中点Di
(µm)
分率
niDi3
ni
(×100)
nilnDi
(×100)
niDi
(×100)
niDi2
(×100)
niDi3lnDi
(×100)
niDi4
(×100)
2
3,3)]
[ln(
D
D
n
i
i
(×100)
1.286
0.009 90
0.464 9
0.117 1
0.598 1
0.769 3
0.249 2
1.272 9
1.895 2
2.039
0.072 31
0.853 4
0.607 9
1.739 8
3.546 9
5.150 7
14.741 9
6.165 3
3.231
0.238 04
0.705 7
0.827 6
2.280 1
7.367 2
27.918 5
76.914 8
5.099 7
5.121
0.354 85
0.264 2
0.431 6
1.353 1
6.929 4
57.959 4
181.718 4
0.000 2
8.116
0.239 99
0.044 9
0.094 0
0.364 3
2.956 9
50.250 7
194.781 0
5.038 1
12.863
0.073 50
0.003 5
0.008 8
0.044 4
0.571 4
18.774 8
94.545 9
6.203 5
20.387
0.010 14
0.000 1
0.000 4
0.002 4
0.049 7
3.057 7
20.676 3
1.929 2
合計
0.998 73
2.336 7
2.087 3
6.382 3
22.190 9
163.361 0
584.651 2
26.331 2
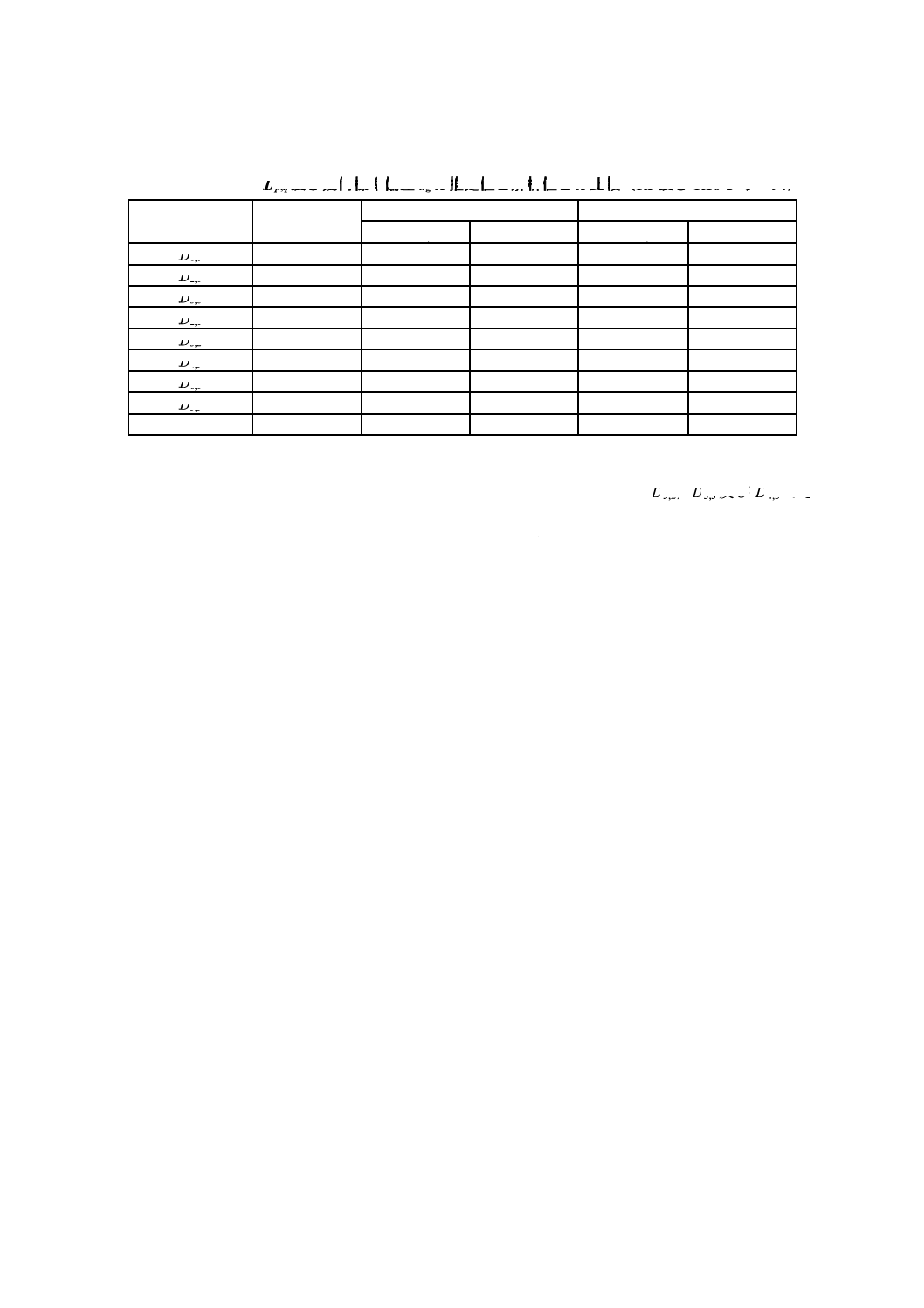
平均粒子径及び標準偏差の推定値は,表B.2の一番下の行にある合計を用いて計算することができる。
ED
−
1,0=6.382 3/2.336 7=2.731[列5及び列3,式(52)]
ED
−
2,0=(22.190 9/2.336 7)1/2=3.082[列6及び列3,式(52)]
ED
−
3,0=(99.873/2.336 7)1/3=3.496[列2及び列3,式(52)]
ED
−
2,1=22.190 9/6.382 3=3.477[列6及び列5,式(52)]
ED
−
3,2=99.873/22.190 9=4.501[列2及び列6,式(52)]
ED
−
4,3=584.651 2/99.873=5.854[列8及び列2,式(52)]
ED
−
5,3=(44.293 7/0.998 73)1/2=6.660[列2,式(52),ただし,∑
=
7
1
3
i
i
iD
n
=44.293 7]
ED
−
0,0=exp (2.087 3/2.336 7)=2.443[列4及び列3,式(53)]
ED
−
3,3=exp (163.361 0/99.873)=5.133[列7及び列2,式(53)]
sg=exp(s)=[
])
100
73
998
.0(
2
331
.
26
×
=exp (0.513 47)=1.671 1[列9及び列2,式(64)及び式(65),サン
プルサイズは大きいと仮定する(N≫100)]。
s0=
2
2
731
.2
082
.3
−
=1.427[上記
ED
−
2,0及び
ED
−
1,0,式(61),サンプルサイズは大きいと仮定する(N≫100)]。
ED
−
5,3及び
ED
−
4,3の値はそれぞれ,6.660及び5.854になり,式(62)に従って体積基準分布の標準偏差s3を計
算する場合に必要になる。これらの値から,s3=3.176,分散s32=10.086となる。
幾何平均径
ED
−
0,0は,対数幾何標準偏差s=ln(sg)=ln(1.671 1)=0.513 5,及び
ED
−
3,3=5.133の各値を式(72)
に代入して計算することができる。
ED
−
0,0=5.133×exp[(0+0−6)×0.513 52/2)]=2.327
この値は,
ED
−
0,0を式(53)から計算した値,2.443に対して約5 %異なる。しかし,その解析値に対する偏
20
Z 8819-2:2019 (ISO 9276-2:2014)
差は−1.5 %になる。推定値と対応する解析値との比較は,表B.3に与えられる。
表B.3−平均粒子径
ED
−
p,q及び幾何標準偏差sgの推定値と解析値との比較(R5及びR10シリーズ)
平均径及び標準
偏差の測定基準
解析値(µm)
R5シリーズ
R10シリーズ
推定値(µm)
偏差(%)
推定値(µm)
偏差(%)
ED
−
1,0
2.676
2.731
2.06
2.751
2.77
ED
−
2,0
3.033
3.082
1.62
3.090
1.90
ED
−
3,0
3.436
3.496
1.74
3.487
1.48
ED
−
2,1
3.436
3.477
1.18
3.472
1.03
ED
−
3,2
4.412
4.501
2.00
4.441
0.65
ED
−
4,3
5.666
5.854
3.32
5.703
0.66
ED
−
0,0
2.362
2.443
3.44
2.466
4.44
ED
−
3,3
5.000
5.133
2.66
5.033
0.66
sg
1.648 7
1.583 7
−3.94
1.579 0
−4.23
表B.3に示されるR5シリーズ及びR10シリーズを用いた計算値と解析値との差は,小さい。原理的に
は,R5シリーズより偏差の小さいR10シリーズを用いることが望まれ,特に,
ED
−
3,2,
ED
−
3,3及び
ED
−
4,3でその
ことが確認できる。その結果は,R10シリーズのような狭い粒子径区間は,R5のような広い粒子径区間よ
り推奨されることを意味する。正確さに関する他の情報は,箇条7に与えられている。
21
Z 8819-2:2019 (ISO 9276-2:2014)
附属書C
(参考)
粒子径分布パラメータの計算の正確さ
広い粒子径分布の場合,測定基準の変換によって分布は大きくシフトするので,分布の範囲は重要にな
る。例えば,ISO 9276-5によれば対数正規分布の中位径は,次の式(C.1)の関係にある。
ln(D50,3)=ln(D50,2)+s2=ln(D50,1)+2s2=ln(D50,0)+3s2 ························ (C.1)
ここに, s=ln sg: 対数正規分布の標準偏差
sg: 対数正規分布の幾何標準偏差
同様な関係式は,その他の分布の特徴パラメータに対しても成立する。例えば,分布がより広い場合に
は(すなわち,sが大きな場合),D50,3からD50,0へのシフトが大きいことを式(C.1)は示している。測定さ
れた体積基準粒子径分布の幅が広い(又は中くらいの幅の)場合に,粒子径分布の下端の僅かな範囲に無
視できない粒子数が含まれることを計算することができる。例えば,s=0.7(D90,3/D10,3=6.0に相当)の対
数正規分布において,粒子径分布の下端部の体積分率0.05 %は,個数分率では12 %に相当する。したがっ
て,下端部の体積分率0.05 %のカットオフは,個数分率で12 %の細粒のロスを意味する。同様に,測定さ
れた個数基準粒子径分布の幅が広い(又は中くらいの幅の)場合には,粒子径分布の上端部の少ない個数
が相当する粒子体積は無視できない。
粒子径区間幅が広いことは,多くの粒子が同じ粒子径として扱われることを意味するため,広い粒子径
区間に少ない数の粒子が含まれる場合には,測定された粒子径分布の粒子径区間の幅に対して注意が必要
になる。したがって,粒子径分布の測定基準を変えることで大きな不確かさが生じる。例えば,附属書A
及び附属書BのR5シリーズのデータには,約4 %に上る偏りがある。
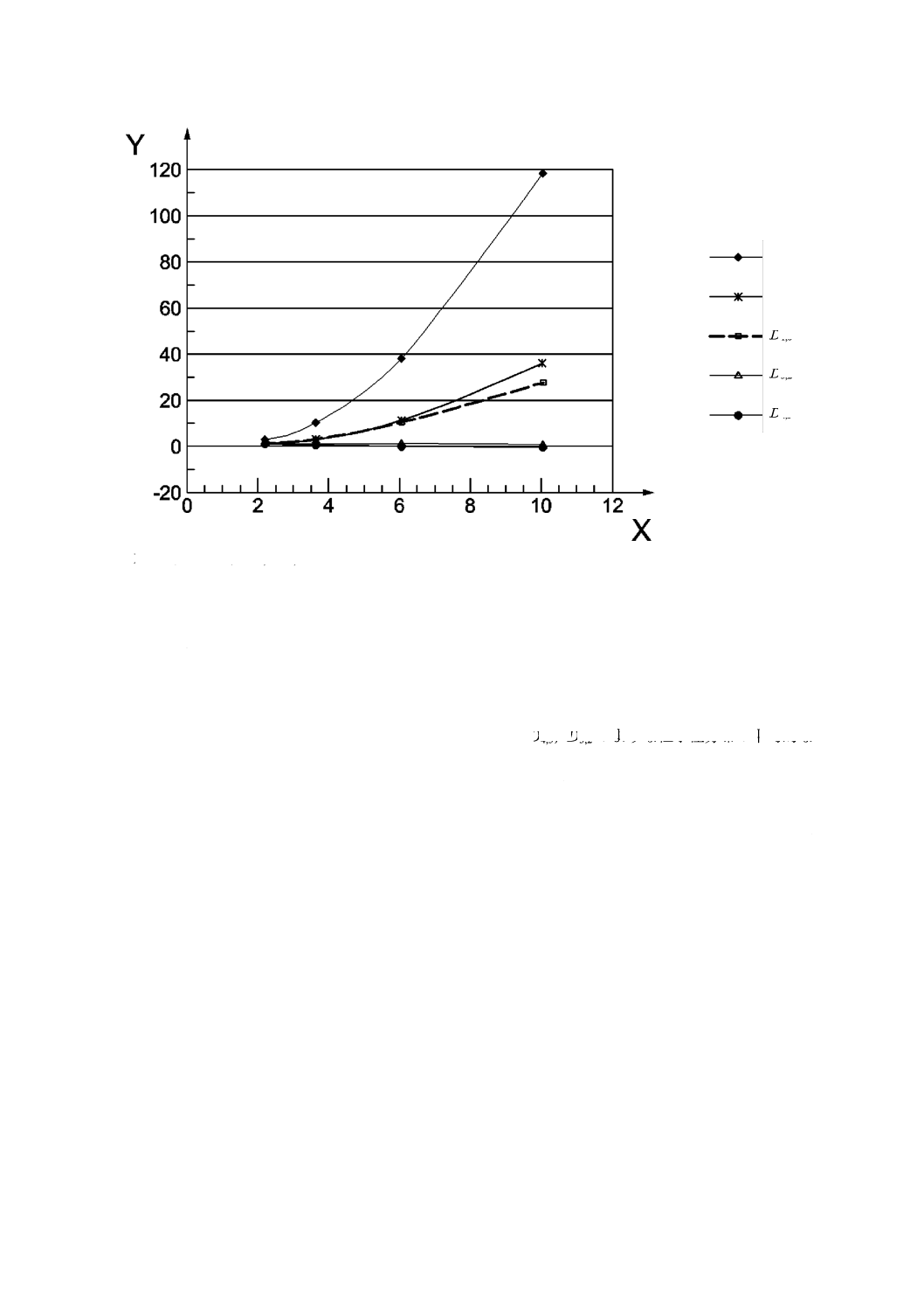
例として図C.1に,異なる分布幅をもつD50,3=5 μmである体積基準の対数正規分布に対して求めた種々
の分布パラメータの偏差を示す。理論的な分布の上端部及び下端部をそれぞれ,体積分率で0.05 %を切り
捨てた。粒子径区間をR20シリーズに設定した。R20シリーズでは,区間の比は101/20=1.122になる(ISO
565)。
22
Z 8819-2:2019 (ISO 9276-2:2014)
X :分布の幅,D90,3/D10,3
Y :偏差,%
図C.1−分布パラメータの計算値に対する分布幅の影響
図C.1のデータは,比D90,3/D10,3がおおよそ3.5より小さい場合,切り捨てていない分布における理論値
に対する変換の偏差は,10 %以下になることを示している。さらに,その値が測定された分布の端に対応
する(この場合には体積基準分布の下端。)分布幅が広くなるに従い,計算される粒子径分布のパラメータ
に対する偏差は大きくなることを図C.1は示している。また,
ED
−
4,3,
ED
−
3,2のような粒子径分布の平均的なパ
ラメータの測定値と理論値との偏差は1 %以下になることが明確に示されている。ただし,全てのパラメ
ータは,分布の切捨てがない場合に偏りが1 %以下になるように計算されることに注意する。
R5シリーズの分解能(ステップ幅101/5=1.585)を上記と同様の対数正規分布に用いた場合,粒子径区
間幅の影響も示されている。例えば,粒子径区間の中点を境界値の算術平均とすると,D50,3は5.132 μm(偏
り2.6 %)になる。他方,幾何平均では,正しい値5.0 μmが得られる。もちろん,中点の与え方は,分布
の粒子径区間の設定に依存する。
平均粒子径及び分布の特徴パラメータの計算精度は,次のような場合に変換によって大きく低下する可
能性がある。
− 粒子径分布が広い。
− 分布が切り捨てられている。
− 測定基準(r)の変換がかなり大きい。
高い正確さが必要な場合には,Excel 1)などを用いて,シミュレーションによって潜在的な偏差を検討す
ることを推奨する。
D10,0
D50,0
ED
−
1,0
ED
−
3,2
ED
−
4,3
23
Z 8819-2:2019 (ISO 9276-2:2014)
参考文献
[1] LESCHONSKI, K.: “Representation and Evaluation of Particle Size Analysis Data”, Particle Characterisation,
1, 89-95 (1984)
[2] STINTZ, M.: “Representation of Results of Particle Size Analysis−Calculation of Average Particle
Sizes/Diameters and Moments from Particle Size distributions”, World Congress on Particle Technology 4,
21.-25.07., Sydney, Proceedings, Int. Number 661 (2002)
[3] ALDERLIESTEN, M.: “Mean Particle Diameters. Part I: Evaluation of Definition Systems”, Part. Part. Syst.
Charact., 7, 233-241 (1990)
[4] ALDERLIESTEN, M.: “Mean Particle Diameters From Statistical Definition to Physical Understanding”,
Thesis, Delft University of Technology (2008)
[5] MASUDA, H. and IINOYA, K.: “Mean Particle Diameter in an Analysis of a Particulate Process”, Memoiries
of the Faculty of Engineering, Kyoto University, Vol. 34, Part 4, Kyoto (1972)
[6] HEYWOOD, H.: “The Scope of Particle Size Analysis and Standardization. The Institution of Chemical
Engineers”, Suppl. Trans. Inst. Chem. Engineers, 25, 14-24 (1947)
[7] HERDAN, G.: “Small Particle Statistics”, pp. 32-33, Butterworths, London (1960)
[8] ALDERLIESTEN, M.: “Mean Particle Diameters. Part III: An Empirical Evaluation of Integration and
Summation Methods for Estimating Mean Particle Diameters from Histogram Data”, Part. Part. Syst. Charact.,
19, 373-386 (2002)
[9] ALDERLIESTEN, M.: “Mean Particle Diameters. Part II: Standardization of Nomenclature”, Part. Part. Syst.
Charact., 8, 237-241 (1991)
[10] MUGELE, R. A. and EVANS, H. D.: “Droplet Size Distribution in Sprays”, Ind. Eng. Chem., 43, 1317-1324
(1951)
[11] RUMPF, H. and EBERT, K. F.: “Darstellung von Kornverteilungen und Berechnung der spezifischen
Oberfläche”, Chem. lng. Tech., 36, 523-537 (1964)
[12] MERKUS, H.: “Particle Size Measurements; Fundamentals, Practice, Quality”, Particle Technology Series,
Springer Netherlands (2009)
[13] ISO 565,Test sieves−Metal wire cloth, perforated metal plate and electroformed sheet−Nominal sizes of
openings
[14] ISO 3534-1:2006,Statistics−Vocabulary and symbols−Part 1: General statistical terms and terms used in
probability
[15] ISO 9276-5,Representation of results of particle size analysis−Part 5: Methods of calculation relating to
particle size analyses using logarithmic normal probability distribution
[16] JIS Z 8819-1 粒子径測定結果の表現−第1部:図示方法
[17] JIS Z 8890:2017 粉体の粒子特性評価−用語
[18] 粉体工学会編,粉体工学ハンドブック,朝倉書店(2014)













