JISZ8819-1:1999 粒子径測定結果の表現

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

日本工業規格 JIS

Z 8819-1 : 1999

(ISO 9276-1 : 1998)

粒子径測定結果の表現−

第1部：図示方法

Representation of results of particle size analysis−

Part 1 : Graphical representation

序文この規格は，1998年に第1版として発行されたISO 9276-1, Representation of results of particle size

analysis−Part 1 : Graphical representationを翻訳し，技術的内容を変更することなく作成した日本工業規格で

ある。

1. 適用範囲この規格は，粒子径測定結果を表すためのヒストグラム，頻度分布及び積算分布の図示方

法を規定する。さらに，用語の標準化を図るとともに，測定データから前述の各種の分布を得るための計

算手順についても規定する。

この規格は，固体，液体及び気泡粒子のすべての粒子径範囲の測定結果の図示に対して適用する。

2. 引用規格次に掲げる規格は，この規格に引用されることによって，この規格の規定の一部を構成す

る。この引用規格は，その最新版（追補を含む。）を適用する。

ISO 565 : 1990 Test sieves−Metal wire cloth, perforated metal plate and electroformed sheet−Nominal

sizes of openings

参考 ISO 565の内容は，“JIS Z 8801 : 1994試験用ふるい”に含まれる。

3. 記号

3.1

一般この規格では，xを粒子径又は球形粒子の直径を表現する記号として使用する。しかし，dも

これらを表現する記号として広く使用されているので，xの代わりに使用してもよい。

x又はd以外の記号は，粒子径を表す記号として使用しないほうがよい。

3.2

記号の説明

粒子径，球の直径（3.1参照）

（下付き添字）上限xiを含む粒子径区間を表す数：△xi＝xi−xi−1

全粒子区間数

q0 (x)

個数基準頻度

q1 (x)

長さ基準頻度

q2 (x)

面積又は投影面積基準頻度

q3 (x)

体積又は質量基準頻度

qr (x)

頻度（一般的表現）

Z 8819-1 : 1999 (ISO 9276-1 : 1998)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

qr* (ln x)

対数を横軸とする頻度

qr (x)

ヒストグラム（一般的表現）

qr, i (x)

粒子径区間△xiの平均頻度：qr, i (x) ＝q (△xi) ＝qr (xi-1, xi)

Q0 (x)

個数基準積算分率

Q1 (x)

長さ基準積算分率

Q2 (x)

面積又は投影面積基準積算分率

Q3 (x)

体積又は質量基準積算分率

Qr (x)

積算分率（一般的表現）

Qr, i

積算分率：Qr, i＝Qr (xi)

△Qr, i

粒子径区間△xiでの積算分率の増分：△Qr, i＝△Qr (xi-1, xi) ＝Qr (xi) −Qr (xi-1)

粒子径，球の直径（3.1参照）

xmin

それ以下では存在しない粒子の径

xmax

それ以上では存在しない粒子の径

粒子径区間の最大粒子径

xi-1

粒子径区間の最小粒子径

△xi

粒子径区間の幅：△xi＝xi−xi-1

変換された座標：ξ＝ξ (x)

（下付き添字，添字i参照）

4. 粒子径，測定値及び測定基準

4.1

一般粒子径測定データを図示するとき，独立変数，すなわち粒子の大きさを特徴付ける物理量を

横軸に，従属変数，すなわち測定値と測定の基準を特徴付ける量を縦軸にプロットする（図1参照）。

図1 粒子径測定結果の表現に用いる座標系

4.2

粒子径粒子径の表現に関しては，3.1を参照する。

粒子径の測定は，異なった物理量の測定結果に基づいて行うので，粒子径を定義する絶対的な方法はな

い。実際に測定される粒子物性によらず，粒子径は一次元の大きさとして表現される。この規格では，粒

子径は同一物性の球の直径として定義する。これは球相当径として知られているものである。相当径の計

算の根拠となった物理量は，適切な下付き添字で表現するものとする。

例えば， xs：表面積相当径

xv：体積相当径

Z 8819-1 : 1999 (ISO 9276-1 : 1998)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

また，粒子径は，ふるいの目開き又は画像解析によって得られるフェレー径のような統計的粒子径など，

他の定義も可能である。

4.3

測定値及び測定基準測定値及び測定基準は，従属変数に対して，次の記号を用いることによって

区別する。測定値には，次の2種類がある。

Q：積算分率

q：頻度

測定値は次のいずれかの基準で測定され，測定基準は一般的に下付き添字γで表示するか，次のいずれか

の数値で表示する。

個数：r＝0

長さ：r＝1

面積：r＝2

体積又は質量：r＝3

頻度と積算分率に用いられる記号を，表1に示す。

表1 分布に対する記号

測定基準

記号

頻度

積算分率

個数

q0 (x)

Q0 (x)

長さ

q1 (x)

Q1 (x)

面積

q2 (x)

Q2 (x)

体積又は質量

q3 (x)

Q3 (x)

一般的表現

qr (x)

Qr (x)

5. グラフ表示粒子径測定結果の例を，図2〜4に示す。

5.1

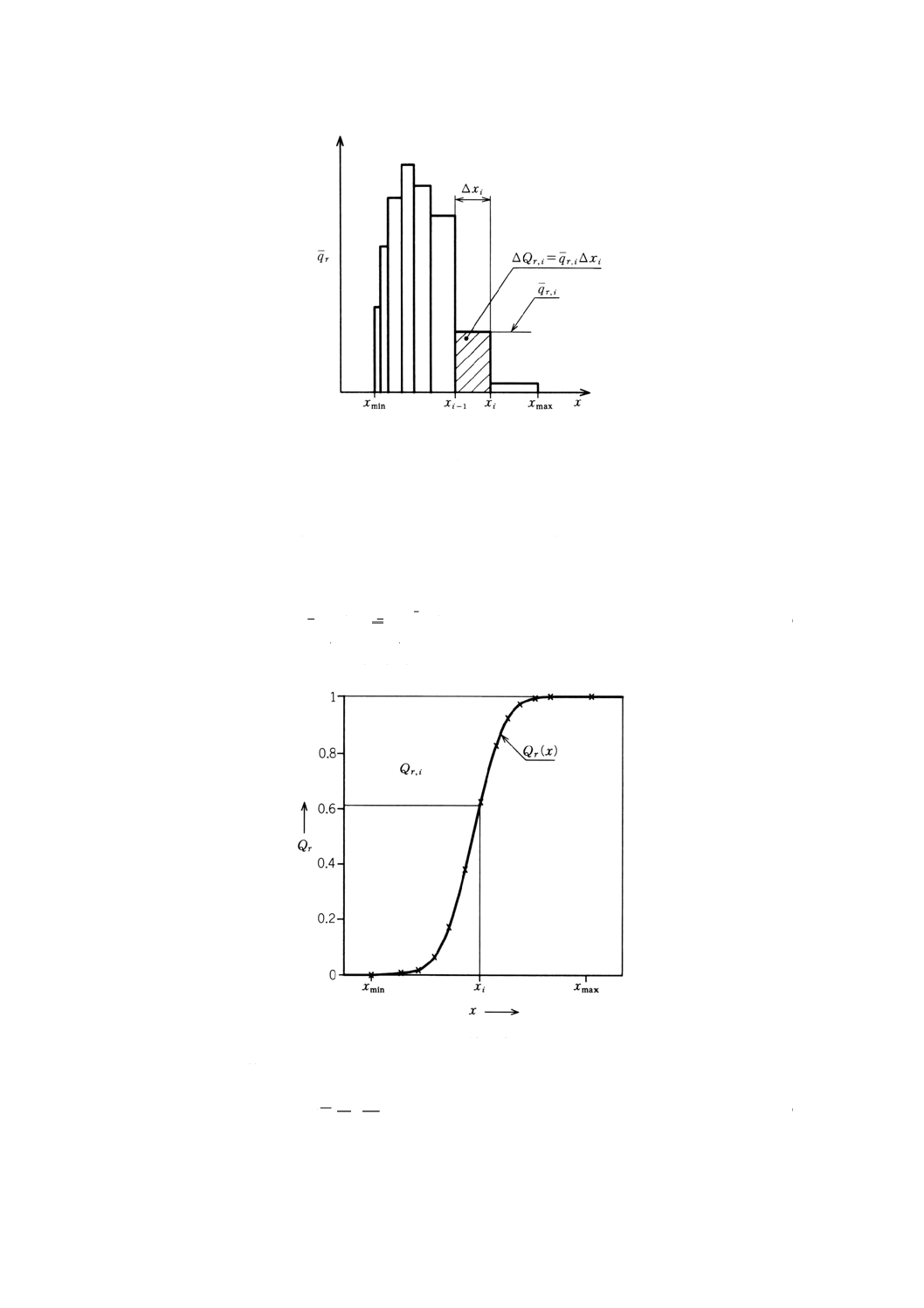
ヒストグラムqr (x) 図2に頻度qr (x) を正規化したヒストグラムqr (x) を示す。ヒストグラムは一

連の長方形の柱で構成されており，各長方形の柱の面積は，分率△Qr, iを表している。

ここに，

△Qr, i＝△Qr (xi-1, xi) ＝qr (xi-1, xi) △xi ············································ (1)

又は，

(

)

(

)

∆

−

＝

··········································· (2)

すべての分率△Qr, iの和は，ヒストグラムqr (x) で形成される領域の面積に等しく，100%又は1となる

ように正規化する。したがって，式(3)の関係が成立する。

100

＝

∑

∆

······················································ (3)

Z 8819-1 : 1999 (ISO 9276-1 : 1998)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

図2 頻度分布関数

)

のヒストグラム

5.2

積算分率図3に正規化された積算分率Qr (x) の例を示す。ヒストグラムのデータから積算分率を

計算する場合には，図3に示すように，個々の点Qr, i＝Qr (xi) だけが得られる。

個々の点の値Qr (xi) は，xiと等しいか，それ以下の粒子の分率として定義される。この分布の連続曲線

は，適切な内挿法によって計算でき，第一次近似は，隣接点を直線で結ぶことによって得られる。

正規化された積算分布の適用範囲は，0と1，すなわち0と100%の間である。

∑

∆

＝

··························································· (4)

ここに， 1≦v≦i≦n

図3 積算分布

5.3

頻度qr (x) 積算分率Qr (x) が微分可能とすると，頻度の連続関数は，式(5)のように得られる。

()

＝

·········································································· (5)

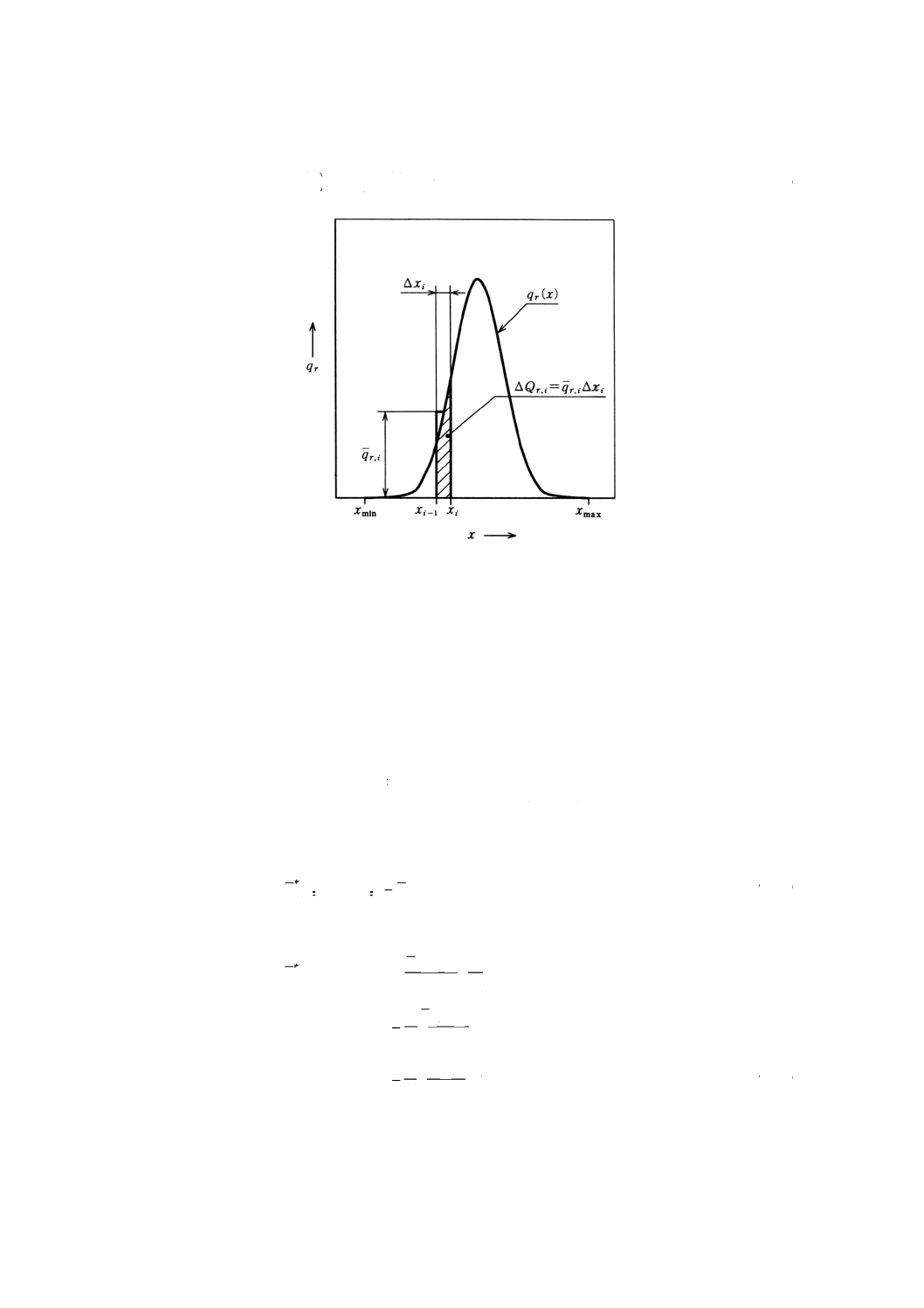
図4にqr (x) を示す。

Z 8819-1 : 1999 (ISO 9276-1 : 1998)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

逆に，積算分率Qr (x) は，頻度qr (x) を積分することによって得られる。

()

∫ixx

min

ｄ

＝

································································· (6)

図4 頻度分布

6. 横軸を対数とする積算及び頻度分布の図表示ある粒子径分布においては，最小粒子径 (xmin) と最大

粒子径 (xmax) の間で数けたにも及ぶため，データを普通方眼紙上にプロットするのは適切でないことがあ

る。このような場合，結果を横軸を対数とした方眼紙上にプロットする。

6.1

横軸を対数とする積算分布横軸が対数の方眼紙にプロットするとき，積算分率Qr, i，すなわち積算

分布の縦軸は変わらない。これに伴い，積算分布曲線の形は変わるが，ある粒子径以下の積算値は変わら

ない。したがって，式(7)の関係が成り立つ。

Qr (x) ＝Qr (ln x) ········································································ (7)

6.2

横軸を対数とする頻度分布ヒストグラムの頻度の値q*r, i＝q*r (xi−1, xi) は，頻度分布曲線の下の面

積が変わらないように，式(8)によって再計算しなければならない。特に，全面積は横軸をどのように変換

しようが1又は100%になる。

(

)

(

)

∆

−

······················································ (8)

ここに， ξは，xの任意の関数である。

したがって，横軸を対数とする場合，頻度分布を得るには次式の変換が必要である。

(

)

(

)

−

∆

(

)

−

∆

(

)

−

∆

························································ (9)

式(9)は，自然対数を常用対数としても成り立つ。

Z 8819-1 : 1999 (ISO 9276-1 : 1998)

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

附属書A（参考）粒子径解析結果の図示例

ふるいによって得られた次のデータを基にして，この規格の適用方法について記述したもので，規定の

一部ではない。

表A.1 ふるいで得られたデータからのヒストグラムと積算分布の計算

△Q3, i

△xi

q3, i＝

△Q3, i/△xi

1/mm

Q3, i

q*3, i

0.063

0.000 0

0.09

0.001 0

0.027

0.037 0

0.001 0

0.002 8

0.125

0.000 9

0.035

0.025 7

0.001 9

0.002 7

0.18

0.001 6

0.055

0.029 1

0.003 5

0.004 4

0.25

0.002 5

0.07

0.035 7

0.006 0

0.007 6

0.355

0.005 0

0.105

0.047 6

0.011 0

0.014 3

0.5

0.011 0

0.145

0.075 9

0.022 0

0.032 1

0.71

0.018 0

0.21

0.085 7

0.040 0

0.051 3

0.037 0

0.29

0.127 6

0.077 0

0.108 0

1.4

0.061 0

0.4

0.152 5

0.138 0

0.181 3

0.102 0

0.6

0.170 0

0.240 0

0.286 0

2.8

0.160 0

0.8

0.200 0

0.400 0

0.475 5

0.210 0

1.2

0.175 0

0.610 0

0.588 8

5.6

0.240 0

1.6

0.150 0

0.850 0

0.713 3

0.125 0

2.4

0.052 1

0.975 0

0.350 5

11.2

0.024 0

3.2

0.007 5

0.999 0

0.071 3

0.001 0

4.8

0.000 2

1.000 0

0.002 8

表の欄2のxiの値は，JIS Z 8801に規定する試験用ふるいの目開きである。

連続する二つのふるい間の粒子の質量は，ひょう（秤）量によって求めた。また，相対質量△Q3, iは，

各粒子径区間△xiごとに，欄3に示す。

粒子径区間△xiは，△xi＝xi−xi−1で計算し，欄4に示す。

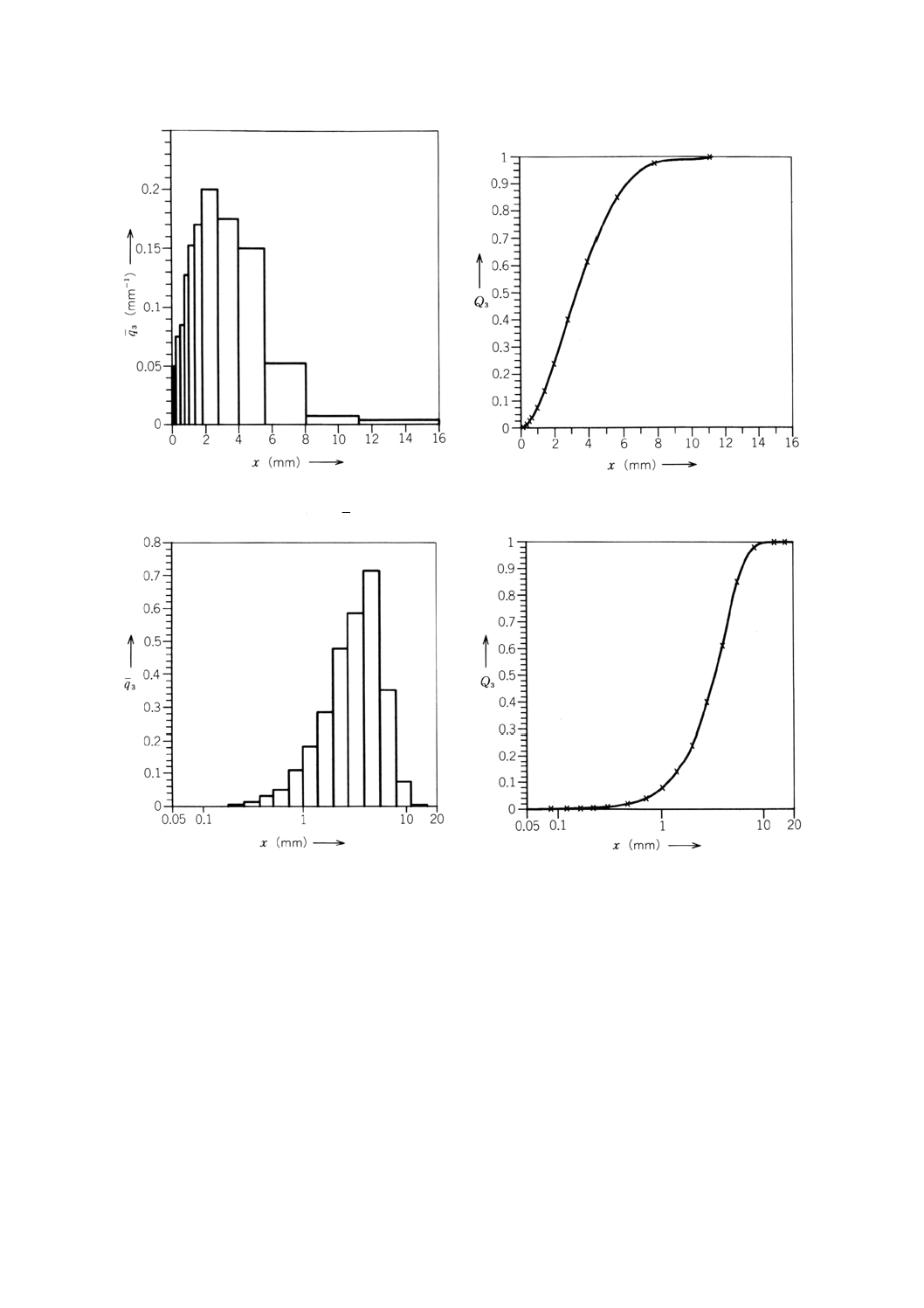
ヒストグラムの縦軸q3, i（欄5参照）は，式(2)を用いて計算した。q3 (x) 及びQ3 (x) を図A.1及び図

A.2に示す。

q*3, iは，式(9)によって計算（欄7参照）し，q*3, i (1n x) とQ3 (1n x) を図A.3及び図A.4に示す。