Z 8462-6:2018 (ISO 11843-6:2013)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 2
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 3
4 測定系及びデータ処理 ······································································································· 3
5 近似による計算 ················································································································ 3
5.1 正規分布に基づく限界値 ································································································· 3
5.2 応答変数の限界値の求め方 ······························································································ 4
5.3 検出能力が十分か否かの判定基準······················································································ 5
5.4 検出能力が十分か否かの判定基準の確認············································································· 5
6 検出能力の評価結果の報告 ································································································· 6
7 測定結果の報告 ················································································································ 7
附属書A(参考)この規格で用いる記号 ··················································································· 8
附属書B(参考)ポアソン分布を正規分布によって近似する場合の期待値及び分散の推定 ·················· 9
附属書C(参考)近似の正確さ ······························································································ 10
附属書D(参考)検出器のチャンネル数の選択 ········································································· 14
附属書E(参考)計算例 ······································································································· 15
Z 8462-6:2018 (ISO 11843-6:2013)
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人日本規格協会(JSA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 8462の規格群には,次に示す部編成がある。
JIS Z 8462-1 第1部:用語及び定義
JIS Z 8462-2 第2部:検量線が直線である場合の方法
JIS Z 8462-3 第3部:検量線がない場合に応答変数の限界値を求める方法
JIS Z 8462-4 第4部:与えられた値が検出可能か否かの判定方法
JIS Z 8462-5 第5部:検量線が線形及び非線形である場合の方法
JIS Z 8462-6 第6部:測定値がポアソン分布に従う場合の限界値及び検出可能な最小値を正規分布近
似によって求める方法
JIS Z 8462-7 第7部:分析機器ノイズの確率論的性質に基づく方法
日本工業規格 JIS
Z 8462-6:2018
(ISO 11843-6:2013)
測定方法の検出能力−第6部:測定値が
ポアソン分布に従う場合の限界値及び検出可能な
最小値を正規分布近似によって求める方法
Capability of detection-Part 6: Methodology for the determination of
the critical value and the minimum detectable value in
Poisson distributed measurements by normal approximations
序文
この規格は,2013年に第1版として発行されたISO 11843-6を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
多くの測定機器で信号の検出にパルス計測法が用いられている。X線回折装置(XRD),蛍光X線分析
装置(XRF),光電子分光装置(XPS),オージェ電子分光装置(AES),2次イオン質量分析装置(SIMS),
又はガスクロマトグラフ質量分析装置(GCMS)のような,X線,電子及びイオンを分光する検出器がこ
の種の測定機器に該当する。ここで取り扱われる信号は,ランダムかつ不規則な間隔で発生し,統計学的
にはポアソン分布を示すと理解されているので,検出可能な最小値を求める方法論は,統計学的原則に従
い構築することができる。
信号の検出可能な最小値の決定は,実際の作業において重要になることがある。“信号は明らかに検出さ
れていない”か,又は“信号はバックグラウンドノイズレベルとは十分に異なっている”[1]-[8]かを判定す
るときの判断基準となる。例えば,有害物質又は半導体物質の表面汚染の測定のときに有用となる。RoHS
指令(電気・電子機器における特定有害物資の使用制限)では,EU市場で取引されている電気・電子製
品に6種類の有害物質[六価クロム,鉛,水銀,カドミウム,難燃物質であるポリ臭化ビフェニール(PBB)
及びポリ臭化ジフェニルエーテル(PBDE)]の使用が禁止されている。これらの測定では,蛍光X線分析
法(XRF)及びガスクロマトグラフ質量分析法(GCMS)を使用する。また,環境物質又は建材中に存在
する,アスベスト類の有害性レベル及び結晶性シリカの測定には,X線回折装置(XRD)を使用する。
検出可能な最小値を求める方法は化学分析の分野で広く利用されているが,その分野ではパルス計測は
使用されていない。パルス計測分野では,検出可能な最小値を求める方法を確立することが要請されてい
る[9]。
この規格は,国際純正・応用化学連合(IUPAC: International Union of Pure and Applied Chemistry)によっ
て合意されたISO 11843規格群に基づくものであり,これらに整合させるためポアソン分布を正規分布に
よって近似している。分散,応答変数の限界値,検出能力基準及び最小検出能力レベルの算出には,汎用
的な近似法を用いる[10]。
2
Z 8462-6:2018 (ISO 11843-6:2013)
この規格では,確率を次のとおり定義している。
− 測定対象系が基底状態にあるとき,これが基底状態にないものと誤って判定する確率をαとする。
− 状態変数の値が検出可能な最小値(xd)に等しいときに,これが基底状態にあるものと誤って判定す
る確率をβとする。
この規格は,JIS Z 8462-1,JIS Z 8462-3及びJIS Z 8462-4に準拠している。
1
適用範囲
この規格は,測定値がポアソン分布に従う測定において,応答変数の限界値及び検出可能な最小値の求
め方について規定する。この規格は,バックグラウンドノイズ及び信号の両方がポアソン分布に従う場合
に適用できる。また,JIS Z 8462-3及びJIS Z 8462-4に整合させるため,ポアソン分布は汎用的な正規分
布による近似方法を用いる。
正規分布による近似からの最小値とポアソン分布からの算出値との比較を附属書Cに示す。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 11843-6:2013,Capability of detection−Part 6: Methodology for the determination of the critical
value and the minimum detectable value in Poisson distributed measurements by normal
approximations(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Q 0030 標準物質に関連して用いられる用語及び定義
注記 対応国際規格:ISO Guide 30,Reference materials−Selected terms and definitions(IDT)
JIS Z 8101-1 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: General statistical terms
and terms used in probability(IDT)
JIS Z 8101-2 統計−用語及び記号−第2部:統計の応用
注記 対応国際規格:ISO 3534-2,Statistics−Vocabulary and symbols−Part 2: Applied statistics(IDT)
JIS Z 8462-1 測定方法の検出能力−第1部:用語及び定義
注記 対応国際規格:ISO 11843-1,Capability of detection−Part 1: Terms and definitions(IDT)
JIS Z 8462-2 測定方法の検出能力−第2部:検量線が直線である場合の方法
注記 対応国際規格:ISO 11843-2,Capability of detection−Part 2: Methodology in the linear calibration
case(IDT)
JIS Z 8462-3 測定方法の検出能力−第3部:検量線がない場合に応答変数の限界値を求める方法
注記 対応国際規格:ISO 11843-3,Capability of detection−Part 3: Methodology for determination of the
critical value for the response variable when no calibration data are used(IDT)
JIS Z 8462-4 測定方法の検出能力−第4部:与えられた値が検出可能か否かの判定方法
注記 対応国際規格:ISO 11843-4,Capability of detection−Part 4: Methodology for comparing the
minimum detectable value with a given value(IDT)
3
Z 8462-6:2018 (ISO 11843-6:2013)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS Z 8101-1,JIS Z 8101-2,JIS Z 8462-1〜JIS Z 8462-4及びJIS
Q 0030による。この規格で用いる記号は,附属書Aを参照する。
4
測定系及びデータ処理
測定の条件は,通常,実験的な組立てによって測定値がポアソン分布に従う場合に限定する。測定され
るパルス数は観測されるスペクトルの測定時間及び測定の幅が増えれば増加する。これら時間及び幅は明
確に記述し,かつ測定中に変更してはならない。検出可能な最小値の信頼性を損なわずに求めるために,
次の制約事項を遵守する。
a) 信号及びバックグラウンドノイズは,ポアソン分布に従う。数値は総測定値の平均値を採用する。
b) 生データは,平滑化処理のような加工又は処理をしてはならない。
c) 測定時間:複数回の短い測定時間よりも長い測定時間を採用する方が望ましい。例えば,測定時間100
ミリ秒の測定を10回行うより測定時間1秒の測定1回の方がよい。ポアソン分布の正規分布による近
似は,より数値の大きい平均値において信頼性が高い。
d) 測定回数:ここで用いる数値は平均値だけであるため,繰り返して測定する必要がある。検出能力も
測定回数とともに高くなる。
e) 検出器のチャンネル数:設定するチャンネル領域は,隣接するピークのチャンネル領域に重複しては
ならない。また,バックグラウンドノイズの測定に用いるチャンネル数と試料スペクトルの測定に用
いるチャンネル数とは同数でなければならない(附属書D参照)。
f)
ピーク幅:一つのピークを対象にするときは,半値全幅(FWHM; Full Width at Half Maximum)を用い
ることが望ましい。ピークトップとピークの裾のノイズ領域とで測定することが望ましい。適切な半
値全幅(FWHM)はあらかじめ標準試料によって求めておく。バックグラウンドノイズの測定に用い
るチャンネル数と試料スペクトルの測定に用いるチャンネル数とは同数にしなければならないので,
ピークの半値全幅に相当するチャンネル数をバックグラウンドノイズの測定におけるチャンネル数に
も採用しなければならない。
g) 追加的要因は,次による。
1) 測定装置は,正常に稼働していなければならない。検出器は,直線性の良い計数領域で動作してい
なければならない。
2) 縦軸及び横軸の両応答性は,校正していなければならない。
3) ノイズではないと明確に確認できない信号は,測定の対象としない。
4) 測定中の試料の変質は,無視できる程度に小さくなければならない。
5) 対象とする成分の少なくとも一つの信号又はピークを観測していなければならない。
5
近似による計算
5.1
正規分布に基づく限界値
測定された信号が意味あるものか否かの判断は,実測定値の平均値
g
yと適切に選択されたycとを比較
することによって可能となる。yc値は,限界値と呼ばれ,次の式(1)を満たす。
(
)
α
x
y
y
P
≦
0
c
g
=
>
···································································· (1)
ここで,確率Pは測定系が基底状態(x=0)にあり,かつ,αはあらかじめ選択した値であるという条
4
Z 8462-6:2018 (ISO 11843-6:2013)
件で計算する。式(1)は,式(2)の条件の下,
g
y>ycである確率を示す。
K
J
σ
z
y
y
α
1
1
b
1
b
c
+
±
=
−
······························································· (2)
ここに, z1−α: 1−αとなる信頼水準における標準正規分布の(1−α)に対応す
る分位点
σb: 基底状態の応答の実際の測定条件における標準偏差値
by: 基底状態に対して実際に測定した応答変数の平均値
J: 基底状態(ブランクサンプル)の値を表す標準物質の測定の
繰返し回数
K: 実際の状態(試験サンプル)の測定の繰返し回数
式(2)中の“±”の符号は,状態変数の増加とともに応答変数が増加する場合に“+”を用い,“−”の
符号はこの逆の場合に用いる。
限界値の定義は,JIS Z 8462-1及びJIS Z 8462-2に従う。実際の状態及び基底状態における測定値に対
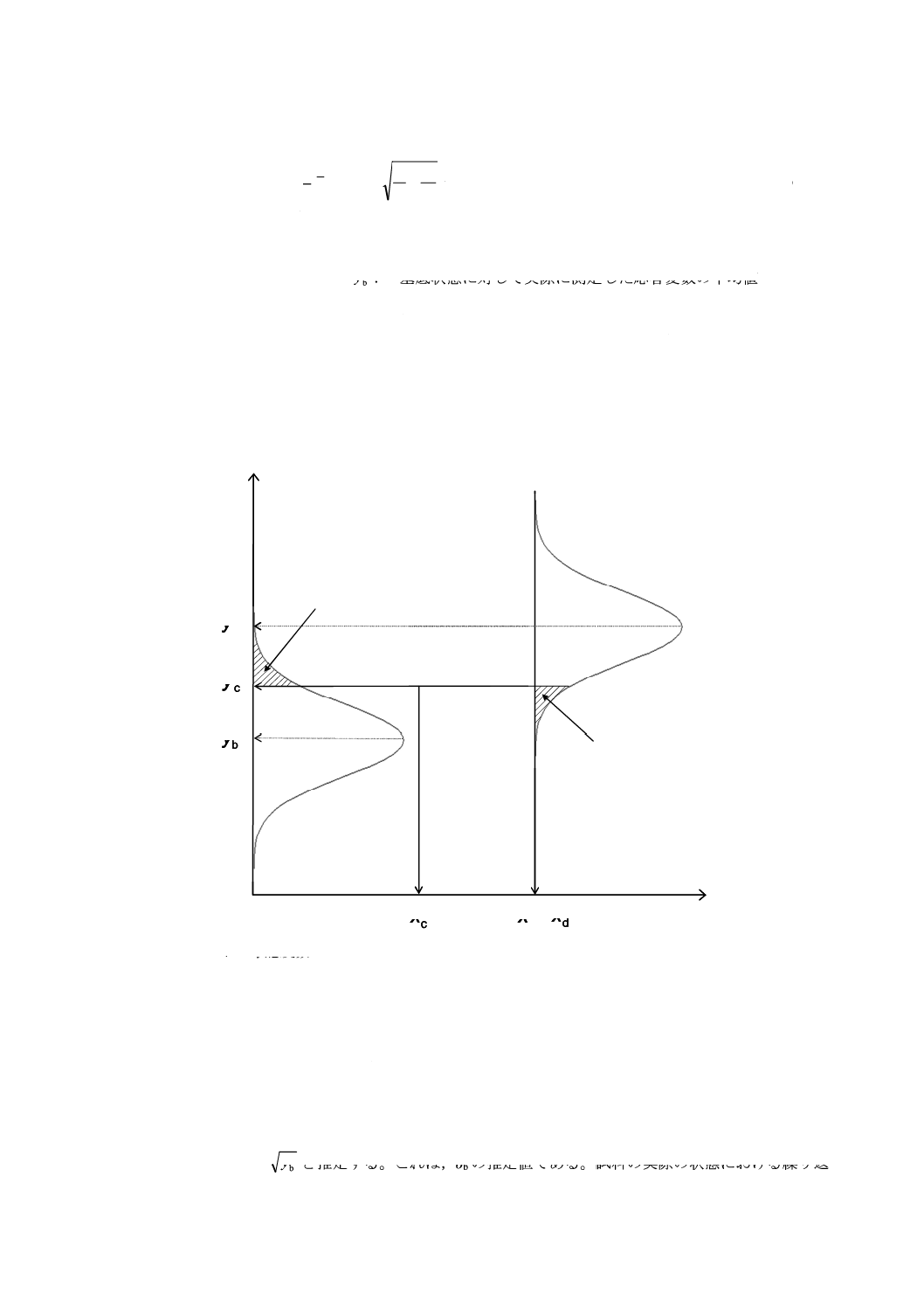
する関係を図1に示す。
X
,
gx
cy
dx
by
gy
cx
0
α
β
X
,
gx
cy
dx
by
gy
cx
0
α
β
X: 状態変数
Y: 応答変数
α: 第1種の誤りが起こる確率
β: 第2種の誤りが起こる確率
注記 xdは,xgより小さいか又は等しい。
図1−限界値と実際の状態及び基底状態における測定値との相対的な位置を示す概念図
5.2
応答変数の限界値の求め方
応答変数が十分に大きな平均値をもちポアソン分布に従う場合,基底状態において繰り返し測定する応
答変数の標準偏差値を,
byと推定する。これは,σbの推定値である。試料の実際の状態における繰り返
Y
X
g
g

5
Z 8462-6:2018 (ISO 11843-6:2013)
し測定する応答変数の標準偏差値は
gyとなり,σg(附属書Bを参照)の推定値となる。
ポアソン分布に従う応答変数の限界値ycは正規分布で近似でき,一般的に式(3)で表すことができる。
K
J
y
z
y
K
J
σ
z
y
y
α
α
1
1
1
1
b
1
b
b
1
b
c
+
+
≈
+
+
=
−
−
································ (3)
ここに,
by: 基底状態で測定した実際の応答変数の平均値
5.3
検出能力が十分か否かの判定基準
測定方法が十分な検出能力をもつか否かの判定基準は,限界値以上の確率(すなわち,検出能力)が特
定の信頼水準(1−β)以上となることである。この判定基準を満たせば,検出可能な最小値xdは,状態変
数値xgより小さいか又は等しい。これによって検出可能な最小値は,正しくない判定が行われる確率βに
よって応答変数ηg(応答変数の期待値)に等しいと定義する。また,確率βが示す状態は,測定する信号
は存在せず,かつ,バックグラウンドノイズだけが存在する状態にあり,第2種の誤りが起きていると判
定する。
xg値に対応する応答変数の標準偏差がσgである場合,(1−β)より大きいか又は等しいという確率の判
定基準は不等式(4)によって設定し,この不等式によって不等式(5)及び不等式(6)を導き出す。
2
g
2
b
1
c
g
1
1
σ
K
σ
J
z
y
η
β
+
+
−
≧
·························································· (4)
式(2)及び式(3)で定義したように,ycを
K
J
σ
z
η
y
α
1
1
b
1
b
c
+
+
=
−
に置き換えれば,
2
g
2
b
1
b
1
b
g
1
1
1
1
σ
K
σ
J
z
K
J
σ
z
η
η
β
α
+
+
+
−
−
−
≧
······································ (5)
ここに,
α: 第1種の誤りが起こる確率
β: 第2種の誤りが起こる確率
ηb: 基底状態の実際の測定条件における応答変数の期待値
ηg: 状態変数xgに対応する試料の実際の測定条件における応答変
数の期待値
β=α及びK=Jとすれば,判定基準は単純化され,
+
+
−
−
2
g
2
b
b
1
b
g
2
1
σ
σ
σ
J
z
η
η
α
≧
················································ (6)
となる。また,σbを5.2のように推定値
byで置換し,同様にσgを推定値
gy(附属書Bを参照)で置換
する場合には,判定基準は不等式(7)となる。
(
)
g
b
b
1
b
g
2
1
y
y
y
J
z
η
η
α
+
+
−
−
≧
················································· (7)
注記 この方法を検証する場合,検出能力はJIS Z 8462-4と同様に,通常,K=J=1として決定する。
5.4
検出能力が十分か否かの判定基準の確認
応答変数の標準偏差及び期待値は,通常,未知であるため,不等式(6)によって示される妥当性の確認は,
実験データを当てはめることによって行う。単純化された判定基準としての不等式(6)の左辺は未知であり,
一方右辺は既知である。
左辺の(ηg−ηb)信頼区間は,基底状態及び状態変数xgに対応する試料をN回繰り返して測定した値に
よって表すことができる。
(ηg−ηb)の100(1−α) (%)信頼区間は,不等式(8)となる。

6
Z 8462-6:2018 (ISO 11843-6:2013)
2
g
2
b
)2
1(
b
g
b
g
2
g
2
b
)2
1(
b
g
1
1
)
(
1
1
)
(
σ
N
σ
N
z
y
y
η
η
σ
N
σ
N
z
y
y
α/
α/
+
+
−
−
+
−
−
−
−
≦
≦
···· (8)
ここに, z(1−α/2): 正規分布における100(1−α/2) %点
注記 式(8)は,推定に関する一般論について記述している。
検出能力の十分な判定基準の確認には片側検定を用いる。(ηg−ηb)の下側100(1−α) %片側信頼区間は,
不等式(9)となる。
2
g
2
b
)
(1
b
g
b
g
1
1
)
(
σ
N
σ
N
z
y
y
η
η
α
+
−
−
−
−
≧
··········································· (9)
ここに,
N: 検出能力の検証のために用いるそれぞれの標準物質の測定回
数
gy: 状態変数xgに対応する試料の実際の測定における応答変数の
平均値
ηb: 基底状態の実際の測定条件における応答変数の期待値
ηg: 状態変数xgに対応する試料の実際の測定条件における応答変
数の期待値
不等式(9)で等号が成立する場合を,不等式(6)と比較することによって不等式(10)を得る。
+
+
+
−
−
=
−
−
−
2
g
2
b
b
)
1(
2
g
2
b
)
1(
b
g
b
g
2
1
1
1
)
(
σ
σ
σ
J
z
σ
N
σ
N
z
y
y
η
η
α
α
≧
···· (10)
(ηg−ηb)に対する信頼限界T0の近似的な100(1−α) %値は,σb及びσgを式(3)及び不等式(7)で定義して
いるように,
by及び
gyにそれぞれ置き換えると,式(11)によって算出できる。
g
b
)
1(
b
g
0
1
)
(
y
y
N
z
y
y
T
α
+
−
−
=
−
··················································(11)
低値側の信頼限界T0が式(7)を満たせば,検出可能な応答値
gyの最小値は,最小の検出可能な応答値yd
より小さいか又は同等であると結論できる。よって,xdはxgより小さいか又は同等である。また,比較的
大きなNに対し,低値側の信頼限界を与える式(11)は信頼性が高くなる。
注記 附属書Eに箇条5に関する計算例を示す。
6
検出能力の評価結果の報告
検出能力の評価は,通常,測定方法の使用開始前の妥当性確認の一部として行う。その評価結果として,
次の事項を報告する。
a) 参照状態の値xgを含む,標準物質についての情報
b) それぞれの参照状態の繰返し回数N
c) 平均値
by及び gy
d) 選択したα,β,J及びKの値
e) 推定値を代入した式(7)の判定基準の左辺及び右辺,すなわち(
gy−by)又は(β=α,K=J)とした場合の
(ηg−ηb)及び低値側の許容限界値である
+
+
−
2
g
2
b
b
1
2
1
σ
σ
σ
J
zα
f)
検出能力に関する結論
g) 必要であれば,対象とするバックグラウンド値及び検出可能な最小値。この値は,式(10)においてN
を無限大,Jを1とする場合に得られる。
7
Z 8462-6:2018 (ISO 11843-6:2013)
7
測定結果の報告
状態変数の応答を表す観測値を報告する。観測値を仮説検定に用いたが,観測値を単に検定の限界値と
なる上限値又は最小検出下限値として報告してはならない。適用した限界値,及び可能な場合,検出可能
な最小値も報告する。
8
Z 8462-6:2018 (ISO 11843-6:2013)
附属書A
(参考)
この規格で用いる記号
X:
状態変数
Y:
応答変数
J:
基底状態(ブランクサンプル)の値を表す標準物質の測定の繰返し回数
K:
実際の状態(試験サンプル)の測定の繰返し回数
N:
検出能力の評価における各標準物質の測定回数
x:
状態変数の値
y:
応答変数の値
yc:
JIS Z 8462-1及びJIS Z 8462-3に規定する応答変数の限界値
xc:
状態変数の限界値
xg:
検出可能な最小値よりも大きいか否かを検定するために与えた値
xd:
状態変数の検出可能な最小値
σb:
実際の測定条件における基底状態に対する応答の標準偏差
σg:
実際の測定条件における状態変数がxgの試料に対する応答変数の標準偏差
ηb:
実際の測定条件における基底状態に対する応答変数の期待値
ηg:
実際の測定条件における状態変数がxgに等しい試料に対する応答変数の期待値
by:
基底状態に対して実際に測定した応答変数の平均値
gy:
状態変数がxgの試料に対して実際に測定した応答変数の平均値
yd:
値がxdの状態変数に対応する,検出可能な最小の応答値
λ:
ポアソン分布に従う事象の発生数の期待値
α:
第1種の誤りが起こる確率
β:
第2種の誤りが起こる確率
1−α: 基底状態における信頼水準
1−β: 実際の状態における信頼水準
z1−α:
標準正規分布の(1−α)分位点
z1−β:
標準正規分布の(1−β)分位点
T0:
下側信頼限界
9
Z 8462-6:2018 (ISO 11843-6:2013)
附属書B
(参考)
ポアソン分布を正規分布によって近似する場合の期待値及び分散の推定
ポアソン分布の確率質量関数をp(y, λ)とする。これは次の式(B.1)によって表す。
λ
y
y
λ
y,λ
p
−
=
e
!
)
(
······································································· (B.1)
ここに,
λ: ある時間内に起こる事象の発生数の期待値
y: その時間内に実際に起きた事象の数
確率変数Yは母数λのポアソン分布に従うので,この確率変数の期待値及び分散はともにλに等しい。
すなわち,E(Y)=λ及びVar(Y)=λが成立する。ただ一つの母数λが,推定する対象である。J回の独立
な測定に基づくこの推定は,次の式(B.2)によって行う。
J
y
y
λ
J
i∑
=
=
=
1
i
)
········································································ (B.2)
ポアソン分布を正規分布によって近似する場合,確率変数Yは正規分布N(λ, λ)に従う確率変数Zで置き
換えることができる。
10
Z 8462-6:2018 (ISO 11843-6:2013)
附属書C
(参考)
近似の正確さ
この附属書では,従来の正規分布による近似から算出する検出可能な最小値を,ポアソン分布から直接
算出する値と比較する。これによって,近似の正確さが値の大きさに応じてどのように変化するかが分か
る。
ポアソン分布から直接導かれる検出可能な最小値は,次の手順によって計算する。
ポアソン分布に従う変数の和もポアソン分布に従うが,それらの差はポアソン分布にはならない。
この差を正確に表すには,次の確率質量関数を使用する。測定のバックグラウンドノイズに対応する,
基底状態での応答変数yb,及び実際の状態に対応する応答変数の値ydは,帰無仮説の下では,同じ母集団
から得られる二つの標本を表す。これは,ys=|yb−yd|として,確率質量分関数式(C.1)から求めることを意
味する。
[]
[
]
)
2(
)!
(!
Pr
s
s
s
2
1
s
)
(
2
s
θ
I
e
y
j
j
θ
e
y
y
θ
y
j
y
j
j
θ
−
∞
=
−
−
+
−
=
−
=
∑
························· (C.1)
Iy(・)は,第1種の変形ベッセル関数である。対立仮説の下では,確率質量関数は式(C.2)から求める。
[]
[
]
(
)
2
1
2
2
1
)
(
1
s
2
1
)
(
s
2
)!
(!
Pr
s
s
2
1
s
s
2
1
θ
θ
I
θ
θ
e
y
j
j
θ
θ
e
y
y
/
y
θ
θ
y
j
y
j
j
θ
θ
=
−
=
+
−
∞
=
−
−
+
−
∑
(C.2)
実際の状態に対する検出可能な最小の応答値は,これら二つの式から導くことができる。
一方,近似的に得られる検出可能な最小の応答値は,式(7),及び測定の繰返し数Nを無限大としたとき
の式(11)から算出できる。
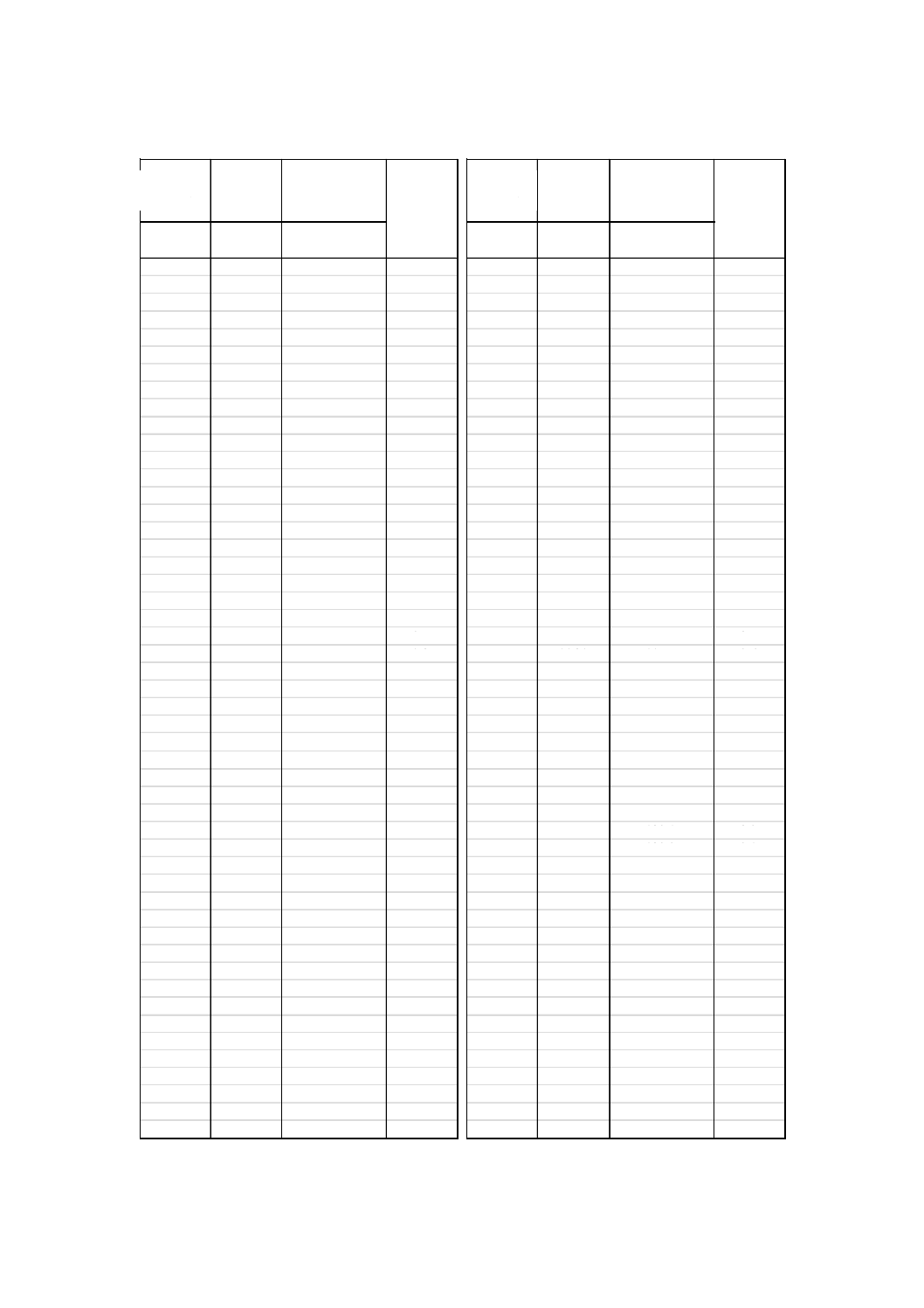
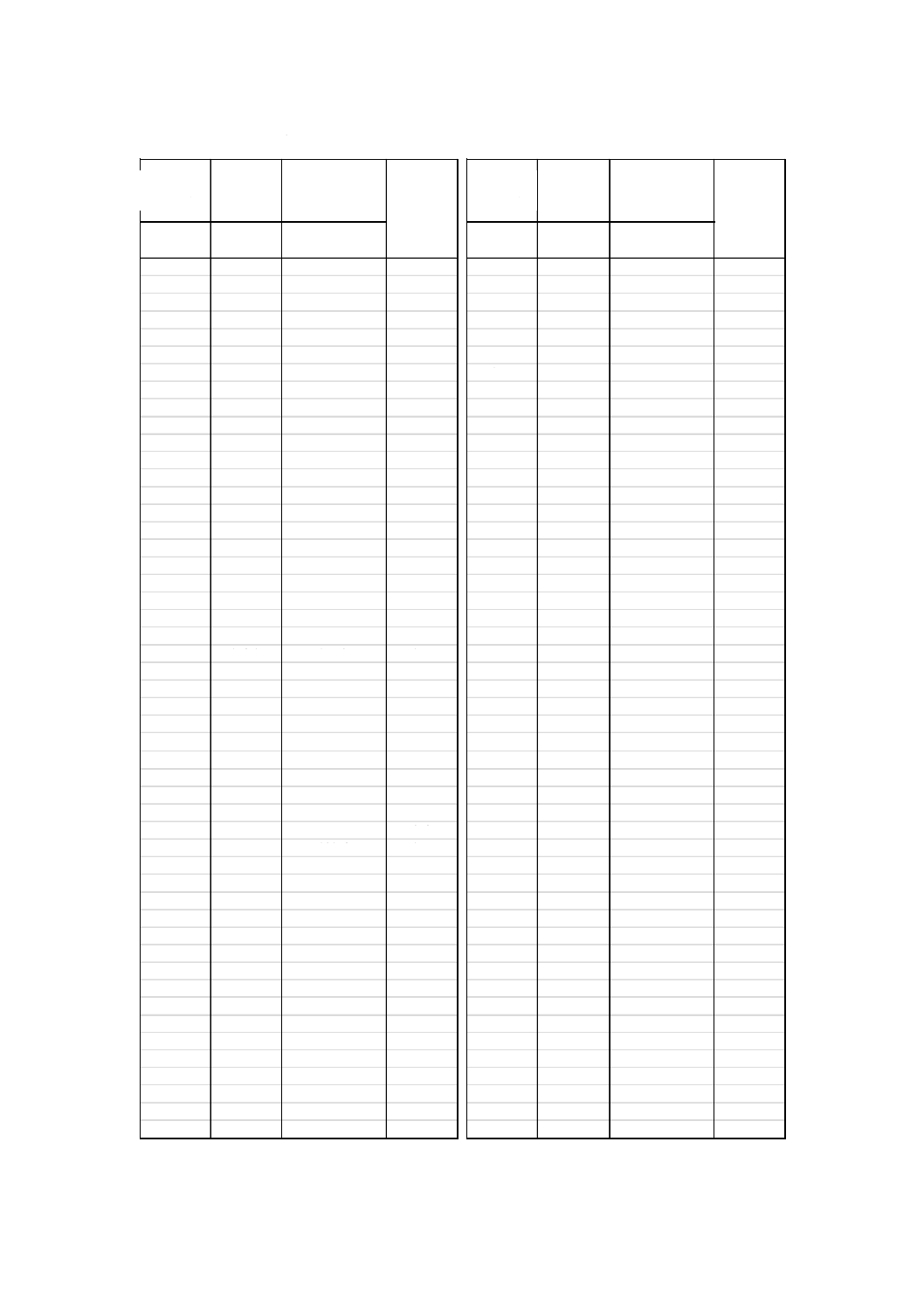
表C.1には,基底状態に対応するybの値を1〜200に変化させたときの検出可能な最小値を,ポアソン
分布による直接計算[11]からの差とともに示す。
ポアソン分布による直接計算と正規分布近似による計算とはかなりよく一致しており,広い範囲にわた
ってその差は1以内にある。
応答変数の検出可能な最小値を5 %以下の正確さで求めようとする場合は,バックグラウンドの値が18
以上になるように,測定条件を設定する。
11
Z 8462-6:2018 (ISO 11843-6:2013)
表C.1−ポアソン分布による値と正規分布近似による値との差
バックグラ
ンド
ポアソン分
布
正規分布
yb
yd
yd
1
8.2
8.4
-0.1
2
11.3
11.3
0.0
3
14.1
13.8
0.3
4
17.1
16.0
1.0
5
18.9
18.1
0.8
6
20.8
20.1
0.7
7
22.2
22.0
0.2
8
24.7
23.9
0.9
9
26.1
25.7
0.4
10
27.4
27.4
0.0
11
29.9
29.1
0.7
12
31.2
30.8
0.3
13
32.5
32.5
0.0
14
34.9
34.1
0.7
15
36.1
35.7
0.4
16
37.4
37.3
0.1
17
39.8
38.9
0.9
18
41.0
40.4
0.6
19
42.3
42.0
0.3
20
43.5
43.5
0.0
21
45.8
45.0
0.8
22
47.1
46.5
0.5
23
48.3
48.0
0.3
24
49.5
49.5
0.0
25
51.8
51.0
0.8
26
53.0
52.4
0.6
27
54.2
53.9
0.3
28
55.4
55.3
0.1
29
57.7
56.8
1.0
30
58.9
58.2
0.7
31
60.1
59.6
0.5
32
61.3
61.0
0.3
33
62.5
62.4
0.0
34
64.7
63.8
0.9
35
65.9
65.2
0.7
36
67.1
66.6
0.5
37
68.3
68.0
0.3
38
69.5
69.4
0.1
39
71.7
70.8
1.0
40
72.9
72.1
0.8
41
74.1
73.5
0.6
42
75.2
74.9
0.4
43
76.4
76.2
0.2
44
77.5
77.6
0.0
45
79.8
78.9
0.9
46
80.9
80.3
0.7
47
82.1
81.6
0.5
48
83.3
82.9
0.3
49
84.4
84.3
0.1
50
85.6
85.6
0.0
差
バックグラ
ンド
ポアソン分
布
正規分布
yb
yd
yd
51
87.8
86.9
0.9
52
88.9
88.3
0.7
53
90.1
89.6
0.5
54
91.2
90.9
0.3
55
92.4
92.2
0.2
56
93.5
93.5
0.0
57
95.7
94.8
0.9
58
96.9
96.1
0.8
59
98.0
97.4
0.6
60
99.2
98.7
0.4
61
100.3
100.0
0.3
62
101.5
101.3
0.1
63
102.6
102.6
0.0
64
104.8
103.9
0.9
65
105.9
105.2
0.7
66
107.1
106.5
0.6
67
108.2
107.8
0.4
68
109.3
109.1
0.3
69
110.5
110.4
0.1
70
111.6
111.6
0.0
71
113.8
112.9
0.9
72
114.9
114.2
0.7
73
116.0
115.5
0.6
74
117.2
116.7
0.4
75
118.3
118.0
0.3
76
119.4
119.3
0.2
77
120.5
120.5
0.0
78
122.7
121.8
0.9
79
123.9
123.1
0.8
80
125.0
124.3
0.7
81
126.1
125.6
0.5
82
127.2
126.8
0.4
83
128.3
128.1
0.2
84
129.5
129.3
0.1
85
130.6
130.6
0.0
86
132.8
131.9
0.9
87
133.9
133.1
0.8
88
135.0
134.3
0.6
89
136.1
135.6
0.5
90
137.2
136.8
0.4
91
138.3
138.1
0.3
92
139.5
139.3
0.1
93
140.6
140.6
0.0
94
142.7
141.8
0.9
95
143.9
143.1
0.8
96
145.0
144.3
0.7
97
146.1
145.5
0.6
98
147.2
146.8
0.4
99
148.3
148.0
0.3
100
149.4
149.2
0.2
差
yb
yd
yd
yb
yd
yd
バックグラ
ウンド
バックグラ
ウンド
12
Z 8462-6:2018 (ISO 11843-6:2013)
表C.1−ポアソン分布による値と正規分布近似による値との差(続き)
バックグラ
ンド
ポアソン分
布
正規分布
yb
yd
yd
101
150.5
150.5
0.1
102
151.6
151.7
-0.1
103
153.8
152.9
0.9
104
154.9
154.2
0.7
105
156.0
155.4
0.6
106
157.1
156.6
0.5
107
158.2
157.8
0.4
108
159.3
159.1
0.3
109
160.4
160.3
0.2
110
161.5
161.5
0.0
111
163.7
162.7
1.0
112
164.8
163.9
0.9
113
165.9
165.2
0.7
114
167.0
166.4
0.6
115
168.1
167.6
0.5
116
169.2
168.8
0.4
117
170.3
170.0
0.3
118
171.4
171.2
0.2
119
172.5
172.5
0.1
120
173.6
173.7
0.0
121
175.8
174.9
0.9
122
176.9
176.1
0.8
123
178.0
177.3
0.7
124
179.1
178.5
0.6
125
180.2
179.7
0.4
126
181.3
180.9
0.3
127
182.4
182.1
0.2
128
183.5
183.3
0.1
129
184.6
184.5
0.0
130
186.7
185.8
1.0
131
187.8
187.0
0.9
132
188.9
188.2
0.8
133
190.0
189.4
0.6
134
191.1
190.6
0.5
135
192.2
191.8
0.4
136
193.3
193.0
0.3
137
194.4
194.2
0.2
138
195.5
195.4
0.1
139
196.6
196.6
0.0
140
198.7
197.8
1.0
141
199.8
198.9
0.9
142
200.9
200.1
0.8
143
202.0
201.3
0.6
144
203.1
202.5
0.6
145
204.2
203.7
0.5
146
205.3
204.9
0.3
147
206.4
206.1
0.2
148
207.5
207.3
0.1
149
208.6
208.5
0.1
150
209.6
209.7
0.0
差
バックグラ
ンド
ポアソン分
布
正規分布
yb
yd
yd
151
211.8
210.9
0.9
152
212.9
212.1
0.8
153
214.0
213.3
0.7
154
215.0
214.4
0.6
155
216.1
215.6
0.5
156
217.2
216.8
0.4
157
218.3
218.0
0.3
158
219.4
219.2
0.2
159
220.5
220.4
0.1
160
221.6
221.6
0.0
161
223.7
222.7
1.0
162
224.8
223.9
0.9
163
225.9
225.1
0.8
164
227.0
226.3
0.7
165
228.1
227.5
0.6
166
229.1
228.6
0.5
167
230.2
229.8
0.4
168
231.3
231.0
0.3
169
232.4
232.2
0.2
170
233.5
233.4
0.1
171
234.6
234.5
0.0
172
236.7
235.7
1.0
173
237.8
236.9
0.9
174
238.9
238.1
0.8
175
240.0
239.3
0.7
176
241.0
240.4
0.6
177
242.1
241.6
0.5
178
243.2
242.8
0.4
179
244.3
244.0
0.3
180
245.4
245.1
0.2
181
246.5
246.3
0.2
182
247.5
247.5
0.1
183
248.6
248.6
0.0
184
250.7
249.8
0.9
185
251.8
251.0
0.8
186
252.9
252.2
0.8
187
254.0
253.3
0.7
188
255.1
254.5
0.6
189
256.2
255.7
0.5
190
257.2
256.8
0.4
191
258.3
258.0
0.3
192
259.4
259.2
0.2
193
260.5
260.3
0.1
194
261.6
261.5
0.1
195
262.6
262.7
0.0
196
264.8
263.8
0.9
197
265.8
265.0
0.8
198
266.9
266.2
0.7
199
268.0
267.3
0.7
200
269.1
268.5
0.6
差
yb
yd
yd
yb
yd
yd
バックグラ
ウンド
バックグラ
ウンド
13
Z 8462-6:2018 (ISO 11843-6:2013)
0
5
10
15
20
25
30
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
X
Y
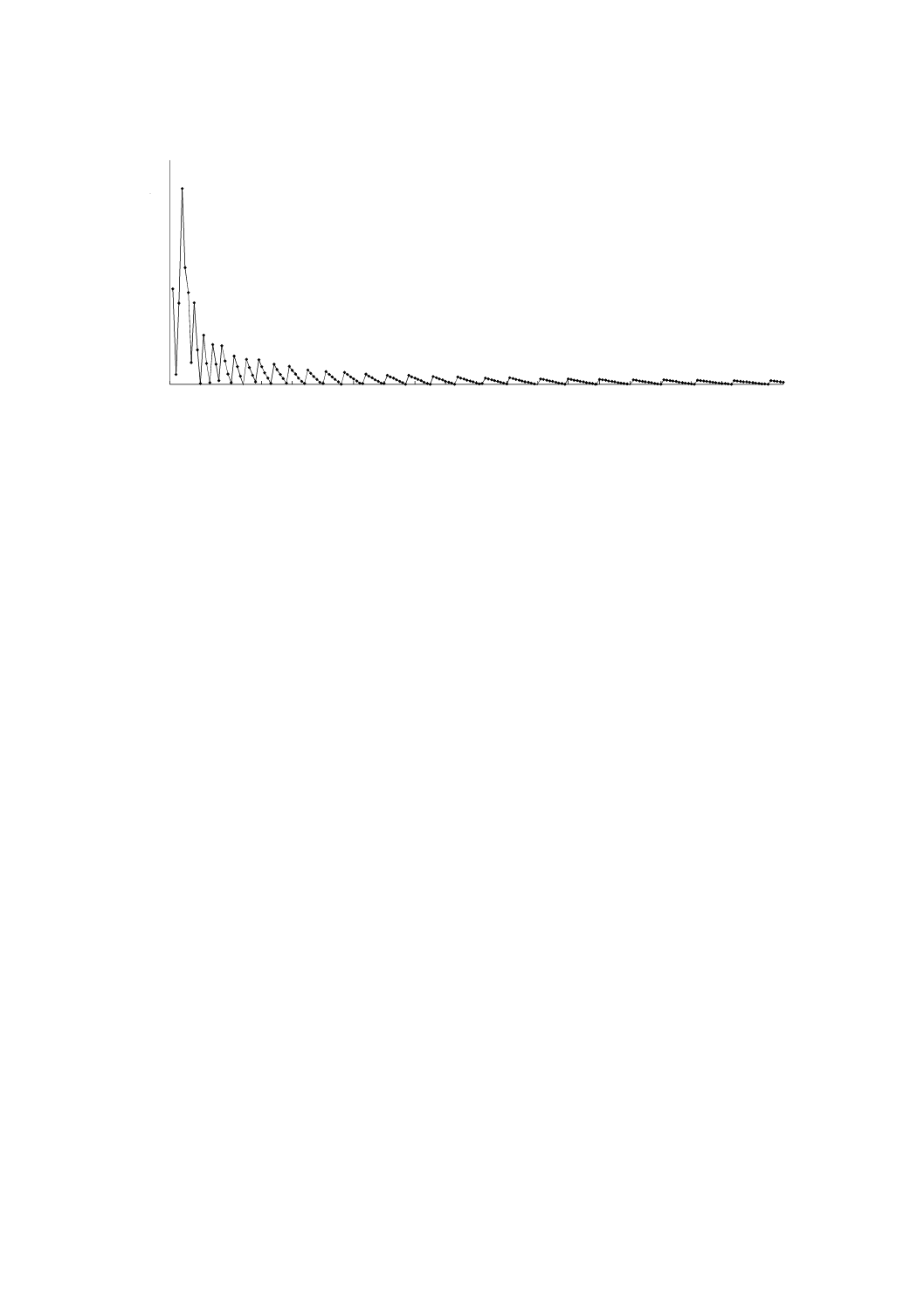
X: バックグラウンド値(表C.1のyb)
Y: 百分率で表した相対差(%)
図C.1−バックグラウンドの値に対するポアソン分布の値と正規分布近似による値との差の百分率変化
14
Z 8462-6:2018 (ISO 11843-6:2013)
附属書D
(参考)
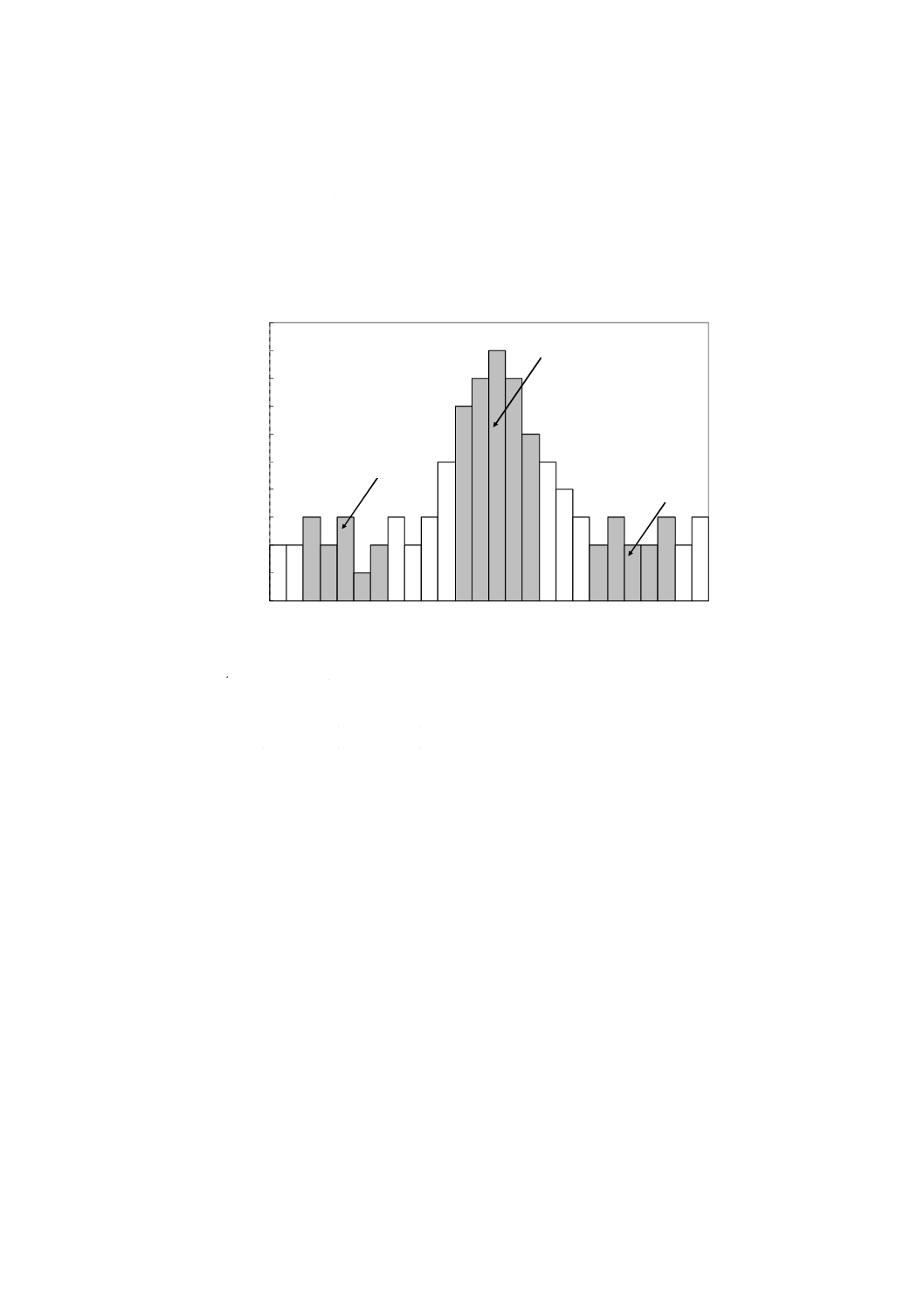
検出器のチャンネル数の選択
対象となる範囲は,測定のために選択した検出器のチャンネル数によって決まる。ピークの重なり合い
がないこと,並びにバックグラウンド及び試料の測定領域のチャンネル数は同数にすることが重要である。
0
1
2
3
4
5
6
7
8
9
10
1
3
5
7
9
1113151719212325
S
B1
B2
Y
X
X: チャンネル数
Y: 相対的強度(カウント数)
S: 信号の測定範囲
B1:左のバックグラウンド領域
B2:右のバックグラウンド領域
図D.1−信号の測定範囲の特定
B1
B2
15
Z 8462-6:2018 (ISO 11843-6:2013)
附属書E
(参考)
計算例
E.1
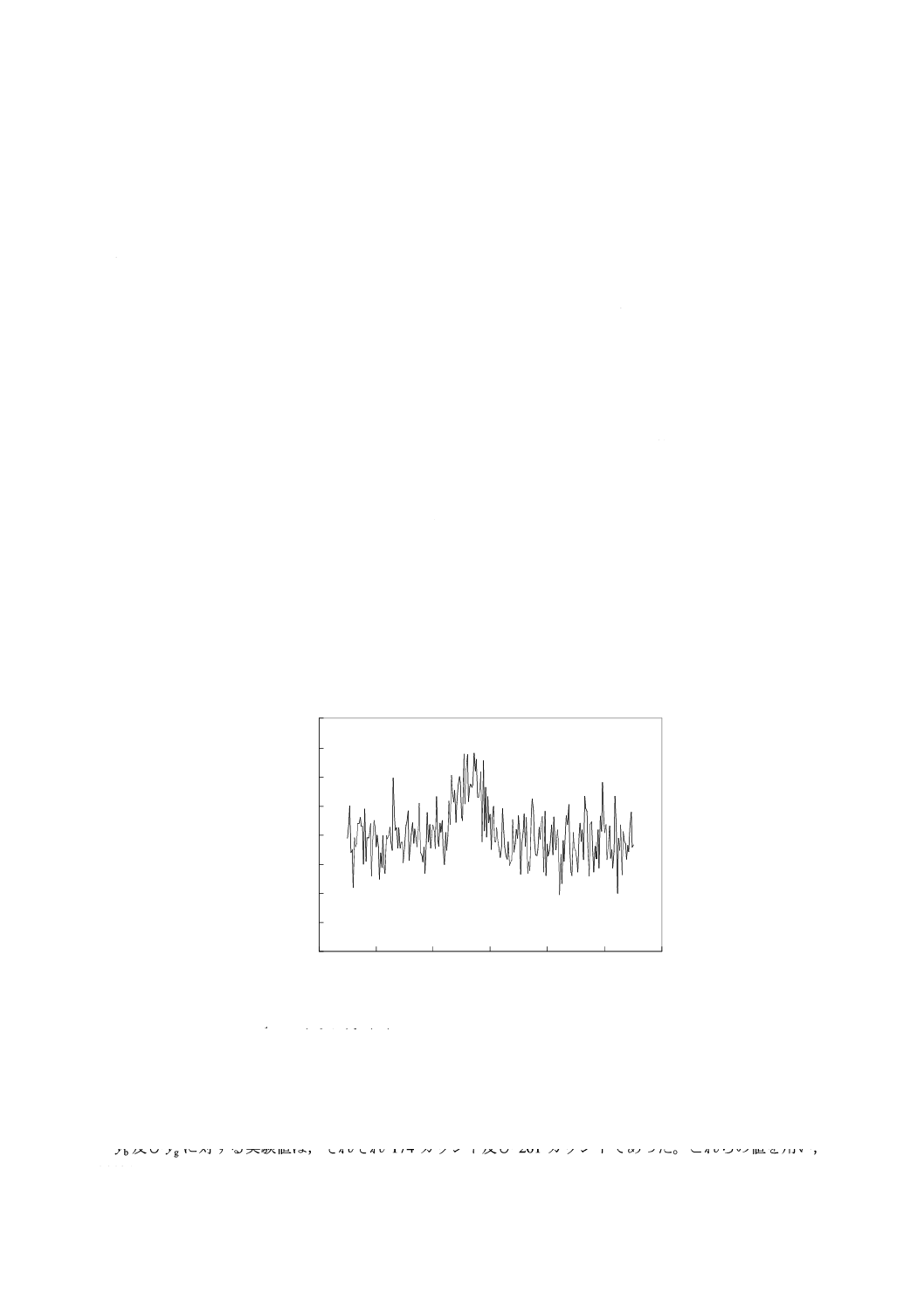
例1:X線回折法による有害物質の測定
有害物質であるアスベストのクリソタイルは,X線回折装置によって検出することができる。0.10 mg
のクリソタイルを精ひょう(秤)した後,純水に分散し,ろ(濾)紙上に補集後,分析した。
分析した量は濃度0.10 %(0.1 mg/100 mg)であり,建材に使用が認められる規制の上限値である。濃度
xb=0であるブランク試料の濃度及び濃度xgの未知試料に対して,繰り返し5回の測定を行った。アスベ
ストであるクリソタイルを,粉末X線回折装置(XRD)によってブラッグ角2θで走査した結果を,図E.1
に示す。
繰り返し5回行った測定によって,検出能力をK=J=1,α=β=0.05として計算した。
測定条件
測定装置
:X線回折装置
X線源
:ターゲット銅(Cu),波長0.154 nmの単色Kアルファ線
出力
:40 kV,40 mA
チャンネル幅
:ブラッグ角2θで0.02度
走チャンネル数
:23(バックグラウンドノイズ領域及びピーク領域の両領域で)
測定回数
:5
チャンネルごとの積算時間
:0.2 s
半値幅(FWHM)
:ブラッグ角2θで46度
0
2
4
6
8
10
12
14
16
10
11
12
13
14
15
16
Y
X
X:ブラッグ角(2θ)
Y:相対強度(カウント)
図E.1−アスベストであるクリソタイルのX線回折図
E.1.1 統計的解析
by及び
gyに対する実験値は,それぞれ174カウント及び261カウントであった。これらの値を用い,
低値側95 %信頼限界を式(11)に従い計算する。

16
Z 8462-6:2018 (ISO 11843-6:2013)
7
71
261
174
5
1
645
1
)
174
261
(
1
)
(
g
b
)
1(
b
g
.
.
y
y
N
z
y
y
α
=
+
×
−
−
=
+
−
−
−
この値は,式(6)及び式(7)を用いた次の式よりも大きい。
(
)
0
65
261
174
174
2
1
1
645
1
2
1
2
g
2
b
b
1
.
.
σ
σ
σ
J
zα
=
+
+
×
=
+
+
−
したがって,少なくとも95 %の信頼度によって0.1 %のクリソタイルは存在していると結論できる。
E.1.2 アスベストの検出可能な最小値の推定
建材中のアスベストの検出可能な最小濃度を同条件を用いて推定することができる。検出可能な最小検
出濃度は,測定回数を増やすことによって低くすることができる。測定回数を無限大まで増加させると,
次の式に示すようにぎりぎりの検出可能な濃度の最小値を得ることができる。
+
+
=
+
−
−
−
−
2
d
2
b
b
1
d
b
)
1(
b
d
2
1
)
(
σ
σ
σ
z
y
y
N
z
y
y
α
α
(
)
d
b
b
1
d
b
)
1(
b
d
2
1
)
(
y
y
y
z
y
y
z
y
y
α
α
+
+
=
+
∞
−
−
−
−
(
)
d
d
174
174
2
645
1
174
y
.
y
+
+
×
×
=
−
上記の式から,238カウントが応答変数
dyの検出可能な最小値として得られ,これから1カウント当た
りの質量分率(%)で表したアスベストの検出可能な最小濃度が次のように計算できる。
0.1 %/(261−174)カウント=1.15×10−3 %/カウント
アスベストのクリソタイルの検出可能な限界最小濃度は,次の計算によって求める。
1.15×10−3 %×(238−174)カウント=0.074 %
アスベストのクリソタイルの推定される検出可能な最小濃度は,0.074 %となる。
E.2
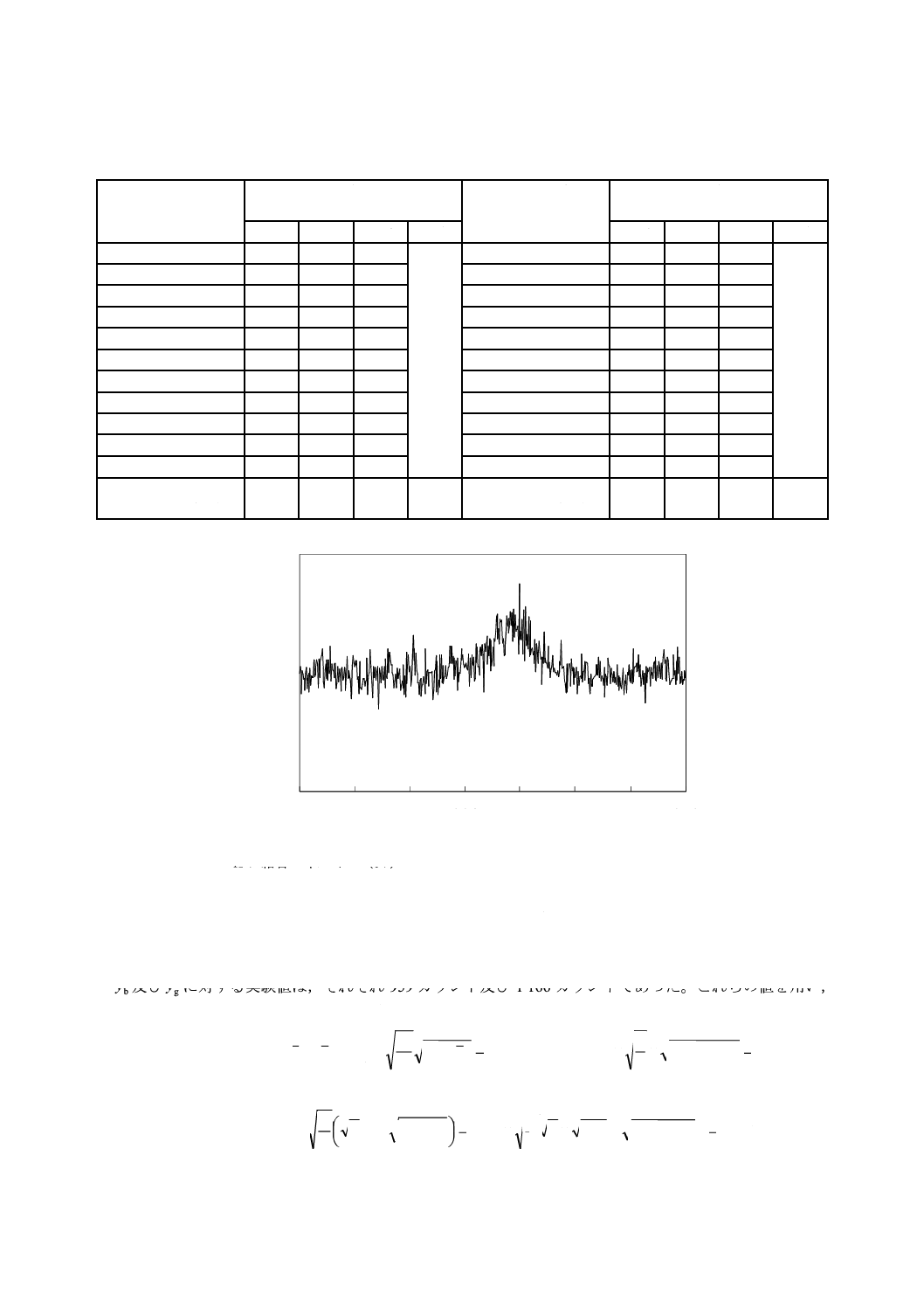
例2:XPS(X線光電子分光法)によるシリコンウエハ上の汚染測定
シリコンウエハ表面上の有機物汚染は,XPS測定から得られる炭素1 s電子軌道の結合エネルギーを用
いて測定する。
同一試料上で測定されたスペクトルにおいて,xb=0であるブランク部位に相当するスペクトル領域及
び濃度xgである汚染部位に相当するピーク領域の二つの領域を繰り返し3回測定し,その値を表E.1に示
す。また,併せて,炭素1 sのXPSスペクトルを図E.2に示す。
繰り返し3回行った測定によって,K=J=1及びα=β=0.05に対する検出能力を計算した。
測定条件
測定装置
:X線光電子スペクトルメータ
X線源
:アルミニウムの単色化Kアルファ線
出力
:0.9 W
チャンネル幅
:0.025 eV
走チャンネル数
:11(バックグラウンドノイズ領域及びピーク領域の両領域)
測定回数
:3回
チャンネルごとの積算時間
:100 ms
17
Z 8462-6:2018 (ISO 11843-6:2013)
表E.1−試料及びブランクの測定値
単位 カウント
バックグラウンド
ノイズ
測定値
ピーク領域
測定値
(eV)
n=1
n=2
n=3
平均
(eV)
n=1
n=2
n=3
平均
291.85
102
78
81
283.98
111
98
113
291.83
99
77
87
283.95
98
103
111
291.80
96
64
88
283.93
107
103
128
291.78
112
85
72
283.90
99
104
91
291.75
100
86
90
283.88
111
95
109
291.73
99
88
63
283.85
108
131
110
291.70
109
81
76
283.83
103
95
87
291.68
95
76
98
283.80
121
115
118
291.65
91
79
75
283.78
97
116
91
291.63
107
90
78
283.75
102
103
102
291.60
92
90
72
283.73
118
95
105
yi(チャンネルごとの
カウント数の合計)
1102
894
880
959
yi(チャンネルごとの
カウント数の合計)
1175
1158
1165
1 166
40
50
60
70
80
90
100
110
120
130
140
278
280
282
284
286
288
290
292
X
Y
X: 結合エネルギー(eV)
Y: 相対的強度(カウント)
図E.2−炭素1 sのXPSスペクトル
E.2.1 統計的解析
by及び
gyに対する実験値は,それぞれ959カウント及び1 166カウントであった。これらの値を用い,
低値側95 %信頼限界を式(10)によって計算する。
2
163
166
1
959
3
1
645
1
)
959
166
1(
1
)
(
g
b
)
1(
b
g
.
.
y
y
N
z
y
y
α
=
+
×
×
−
−
=
+
−
−
−
この値は,不等式(6)を用いた次の式よりも大きい。
(
)
9
147
166
1
959
959
2
1
1
645
1
2
1
2
g
2
b
b
1
.
.
σ
σ
σ
J
zα
=
+
+
×
×
=
+
+
−
したがって,少なくとも95 %の信頼度によって,シリコンウエハは炭化水素によって汚染されていると
18
Z 8462-6:2018 (ISO 11843-6:2013)
結論できる。
E.2.2 近似による検出可能な炭化水素濃度の最小値の推定
シリコンウエハ表面の汚染炭化水素の検出可能な最小値の推定は,全元素成分の測定カウント数及び使
用した装置の感度係数から行うことができる。
参考文献
[1] H. Kaiser, Die berechnung der nachweisempfindlichkeit, Spectrochimica Acta, 3, 40-67, 1947
[2] L. A. Currie and G. Svehla, Limits for qualitative detection and quantitative determination. Application to
radiochemistry, Anal. Chem., 40, 586-593, 1968
[3] Daniel MacDougall, Warren B. Crummett, Guidelines for data acquisition and data quality evaluation in
environmental chemistry, Anal. Chem., 52, 2242-2249, 1980
[4] L.A.Currie, The Limitations of Models and Measurements as Revealed Through Chemometric
Intercomparison, J. Res. NBS, 90, 409-422, 1985
[5] L. A. Currie, G. Svehla, Nomenclature for the presentation of results of chemical analysis (IUPAC
Recommendations 1994), Pure Appl. Chem., 66, 595-608, 1994
[6] L. A. Currie, Nomenclature in evaluation of analytical methods including detection and quantification
capabilities (IUPAC Recommendations 1995), Pure Appl. Chem., 67, 1699-1724, 1995
[7] L. A. Currie, Detection: International update, and some emerging dilemmas involving calibration, the blank,
and multiple detection decisions, Chemo. Intell. Lab. Syst., 37, 151-181, 1997
[8] ISO/IEC Guide 98-3,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
[9] D. R. Baer, Improving surface-analysis methods for characterization of advanced materials by development
of standards, reference data, and interlaboratory comparisons, Surf. Interface Anal., 39, 283-293, 2007
[10] Y. Furukawa, M. Iwasaki and A. Tanaka, A practical method for determining minimum detectable values in
pulse-counting measurements, Anal. Sci., 26, 259-265, 2010
[11] Yusuke Tsutsumi, Hironobu Kawamura, Tomomichi Suzuki, The estimation of detection capability for
Poisson distributed measurements, ANQ Congress, Ho Chi Minh City, 2011
[12] ISO 5479:1997,Statistical interpretation of data−Tests for departure from the normal distribution
[13] ISO 5725-2:1994,Accuracy (trueness and precision) of measurement methods and results−Part 2: Basic
method for the determination of repeatability and reproducibility of a standard measurement method









