Z 8462-5:2011 (ISO 11843-5:2008)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 3
4 正味状態変数の精度プロファイル ························································································ 5
5 正味状態変数の限界値及び検出可能な最小値 ········································································· 6
5.1 一般 ···························································································································· 6
5.2 確率αに関する計算 ······································································································· 6
5.3 確率βに関する計算 ······································································································· 7
5.4 微分による方法 ············································································································· 7
6 例·································································································································· 7
6.1 一般 ···························································································································· 7
6.2 不確かさの伝ぱ(播)則 ································································································· 8
6.3 モデルフィッティング ··································································································· 10
6.4 競合ELISAへの応用 ····································································································· 10
附属書A(規定)この規格で用いる記号及び省略形 ··································································· 12
附属書B(参考)式(9)の導出 ································································································· 13
附属書C(参考)式(13)の導出 ······························································································· 14
参考文献 ···························································································································· 15
Z 8462-5:2011 (ISO 11843-5:2008)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人日本規格協会(JSA)から,工業標
準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業
大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 8462の規格群には,次に示す部編成がある。
JIS Z 8462-1 第1部:用語及び定義
JIS Z 8462-2 第2部:検量線が直線である場合の方法
JIS Z 8462-3 第3部:検量線がない場合に応答変数の限界値を求める方法
JIS Z 8462-4 第4部:与えられた値が検出可能か否かの判定方法
JIS Z 8462-5 第5部:検量線が線形及び非線形である場合の方法
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格
JIS
Z 8462-5:2011
(ISO 11843-5:2008)
測定方法の検出能力−
第5部:検量線が線形及び非線形である場合の方法
Capability of detection-Part 5: Methodology in the linear and
non-linear calibration cases
序文
この規格は,2008年に第1版として発行されたISO 11843-5を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
線形及び非線形の検量線(校正関数)は,実用的に常用される。この規格は,測定方法の検出能力とい
う観点から,検量線よりもむしろ正味状態変数の確率分布に着目することによって,両者を同等に扱う。
この規格は,正味状態変数の標準偏差又は変動係数を,正味状態変数の連続な関数として作成する方法を
規定している。この連続なプロットは,精度プロファイルと呼ばれ,観測された応答変数から作成される。
精度プロファイルの幾つかの例がこの規格で示されている。
確率α及び確率β,並びに線形の検量線が必要であるというJIS Z 8462-2:2003の基本的な概念は,この
規格においても保持されている。基底状態と検出可能な変数値との区間には,線形の検量線が適用される。
この点においては,JIS Z 8462-2:2003との適合性は確保されている。
線形の検量線で特徴付けられる分析法と,非線形の検量線で特徴付けられる分析法とを比べる場合には,
この規格が推奨される。線形の検量線の場合は,JIS Z 8462-2:2003及びこの規格の両方が利用可能である。
線形の検量線の場合は,応答変数の精度プロファイルと正味状態変数の精度プロファイルとは同じである
から,応答変数の精度プロファイルだけを使うJIS Z 8462-2:2003は,応答変数及び正味状態変数の両方の
精度プロファイルを適用するこの規格と同じ結果を与える。
1
適用範囲
この規格は,次の基本的方法について規定する。この規格は,検量線(校正関数)が線形及び非線形の
両方の場合に適用できる。
− 応答変数に関する精度プロファイル,すなわち,応答変数の標準偏差(SD)又は変動係数(CV)を
正味状態変数の関数として記述する。
− この精度プロファイルを検量線に関連させて正味状態変数に対する精度プロファイルに変換する。
− この正味状態変数に対する精度プロファイルを使って,正味状態変数の限界値及び検出可能な最小値
を推定する。
この規格で規定する方法は,JIS Z 8462-2:2003が適用できない様々なタイプの測定装置において,物質
が検出できるかどうかを調べるときに有用である。適用可能な測定の例としては,環境中にあるダイオキ
2
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
シン,農薬,ホルモン様化学物質などの残留性有機汚染物質(persistent organic pollutants,POPs)の競合
ELISA(enzyme-linked immunosorbent assay,エライザ)による分析,ヒトに発熱を誘発する菌体内毒素の
試験などがある。
正味状態変数の限界値及び検出可能な最小値の定義及び適用性は,JIS Z 8462-1:2001及びJIS Z
8462-2:2003に規定している。この規格は,JIS Z 8462-2:2003の概念を非線形の場合に拡張したものである。
限界値xc及び検出可能な最小値xdは,正味状態変数の単位として与えられている。xc及びxdが応答変数
の分布に基づいて定義されていれば,それらの定義には,応答変数を正味状態変数に変換するための検量
線を含む。この規格は,検量線の形とは別に,xc及びxdを正味状態変数の分布に基づいて定義する。その
結果として,検量線の形が線形又は非線形であることにかかわらず,この定義は有効である。
検量線は,連続で微分可能であり,かつ,単調増加又は単調減少でなければならない。
また,標準偏差(SD)又は変動係数(CV)が検出可能な最小値の近傍だけで既知の場合にも,適用で
きる。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 11843-5:2008,Capability of detection−Part 5:Methodology in the linear and non-linear calibration
cases(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: Probability and general
statistical terms(MOD)
JIS Z 8101-2 統計−用語と記号−第2部:統計的品質管理用語
注記 対応国際規格:ISO 3534-2,Statistics−Vocabulary and symbols−Part 2: Statistical quality control
(MOD)
JIS Z 8101-3:1999 統計−用語と記号−第3部:実験計画法
注記 対応国際規格:ISO 3534-3:1999,Statistics−Vocabulary and symbols−Part 3: Design of
experiments(IDT)
JIS Z 8402-1 測定方法及び測定結果の精確さ(真度及び精度)−第1部:一般的な原理及び定義
注記 対応国際規格:ISO 5725-1,Accuracy (trueness and precision) of measurement methods and results
−Part 1: General principles and definitions(IDT)
JIS Z 8462-1:2001 測定方法の検出能力−第1部:用語及び定義
注記 対応国際規格:ISO 11843-1:1997,Capability of detection−Part 1: Terms and definitions(IDT)
JIS Z 8462-2:2003 測定方法の検出能力−第2部:検量線が直線である場合の方法
注記 対応国際規格:ISO 11843-2:2000,Capability of detection−Part 2: Methodology in the linear
calibration case(IDT)
3
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS Z 8101-1,JIS Z 8101-2,JIS Z 8101-3:1999,JIS Z 8402-1,
JIS Z 8462-1:2001及びJIS Z 8462-2:2003によるほか,次による。
なお,この規格で用いられる記号及び省略形を附属書Aに示す。
3.1
正味状態変数の限界値,xc(critical value of the net state variable)
その値を超えると,あらかじめ定められた確率αで,観測した測定対象系が基底状態(ブランク状態)
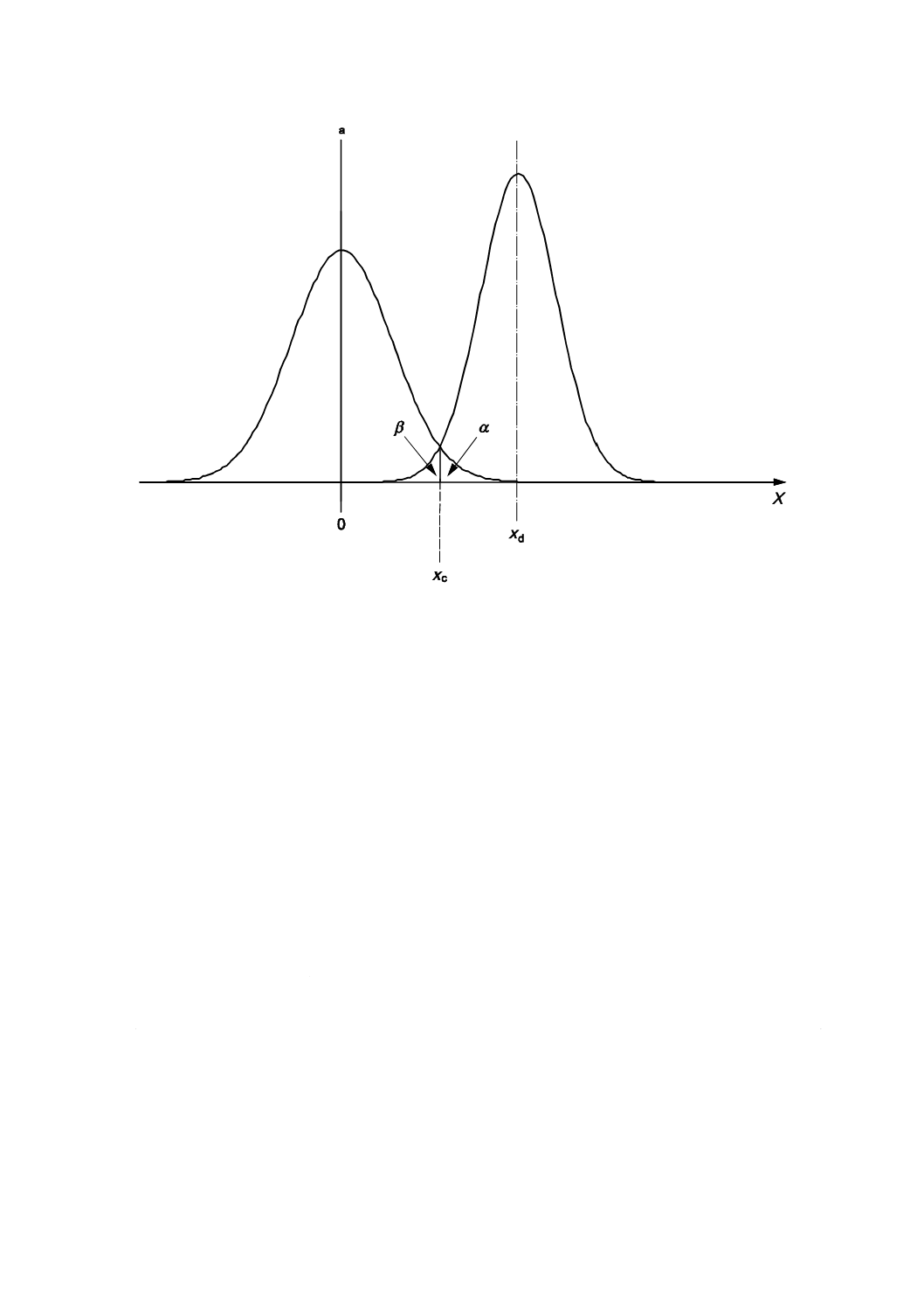
ではないと判定される正味状態変数Xの値(JIS Z 8462-1:2001の10.参照)。図1を参照。
3.2
検出可能な最小正味状態変数値,xd(minimum detectable value of the net state variable)
確率(1−β)で測定対象系が基底状態(ブランク状態)にないと判定される,実際の状態における正味
状態変数Xの値(JIS Z 8462-1:2001の11.参照)。図1を参照。
3.3
精度(precision)
<測定方法の検出能力> 観測された応答変数の標準偏差(SD),又は検量線から推定された正味状態
変数の標準偏差(SD)。
注記1 精度として適切ならば,標準偏差(SD)の代わりに変動係数(CV)を用いてもよい。
注記2 この規格では,精度は併行条件(JIS Z 8101-2参照)に基づいて定義されている。
注記3 多くの場合,従来の用語を踏襲するという慣例によって,この規格では,非精密及び非精密
プロファイルよりも,むしろ精度及び精度プロファイルを使用している。
注記4 < >の記号は,一つの用語が複数の概念を表す場合に,それぞれの概念が関係する主題又
は分野を表示して対象を限定し,区別するために用いる。
4
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
xc 正味状態変数の限界値
xd 検出可能な最小正味状態変数値
X
正味状態変数
α
X=0における第1種の過誤の確率
β
X=xdにおける第2種の過誤の確率
a
確率密度
注記 JIS Z 8462-1:2001の図1は,応答変数の分布及び非線形の検量線を図示している。この規格の図1では,JIS Z
8462-1:2001に示されている応答変数の分布から検量線の傾きを用いて変換された正味状態変数の分布を示す。
図1−基底状態X=0(左)及びxdの状態(右)において推定された正味状態変数の分布
3.4
精度プロファイル(precision profile)
<測定方法の検出能力> 応答変数又は正味状態変数の,標準偏差又は変動係数であり,正味状態変数
の関数で表した数学的記述。
3.5
応答変数,Y(response variable)
実験の結果を表す変数(JIS Z 8101-3:1999の1.2参照)。
注記1 この一般的な定義は,JIS Z 8462シリーズの目的に応じた限定的な表現,すなわち,“状態変
数Zの直接的に観測可能な代用物”と解釈できる。
注記2 応答変数Yは,分析のどのような段階においても確率変数であり,検量線によって変換され
た場合,その精度プロファイルは,正味状態変数の標準偏差σX(X)又は正味状態変数の変動係
数ρX(X)として表される。
5
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.6
応答変数の精度プロファイル(precision profile of response variable)
化学分析工程におけるピペット操作及び測定機器のベースラインノイズのようなランダム性に起因する
不確かさに基づくが,測定機器の不完全さとしてしばしば解釈できるような系統誤差に起因する不確かさ
には基づかない連続プロット。
3.7
正味状態変数,X(net state variable)
状態変数Zと基底状態(ブランク状態)におけるその値z0との差(JIS Z 8462-1:2001の4.参照)。
注記 正味状態変数Xは,検量線が作成される段階においては決定論的な変数であるが,σX(X)又は
ρX(X)として表される正味状態変数の精度プロファイルは,応答変数のランダム性から導かれる。
4
正味状態変数の精度プロファイル
実験的又は理論的な理由によって,精度(SD又はCV)は,正味状態変数Xよりも,むしろ応答変数Y
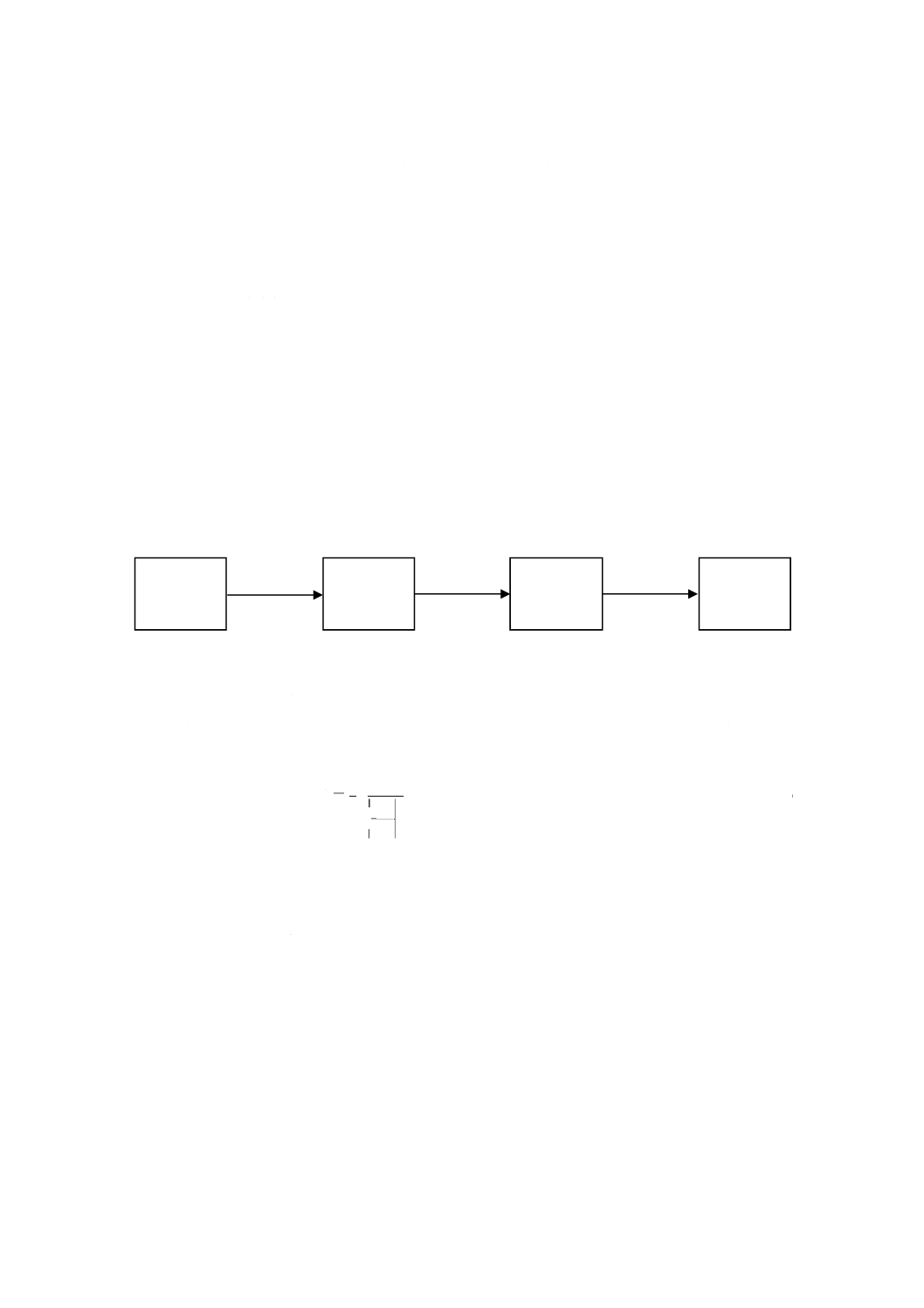
に結び付けられる。ゆえに,Yの全ての値は,対応するXの値に変換する必要があり,図2に示すように,
精度も同様に変換する必要がある(参考文献[1]及び[2]参照)。
図2−応答変数から正味状態変数への不確かさの変換
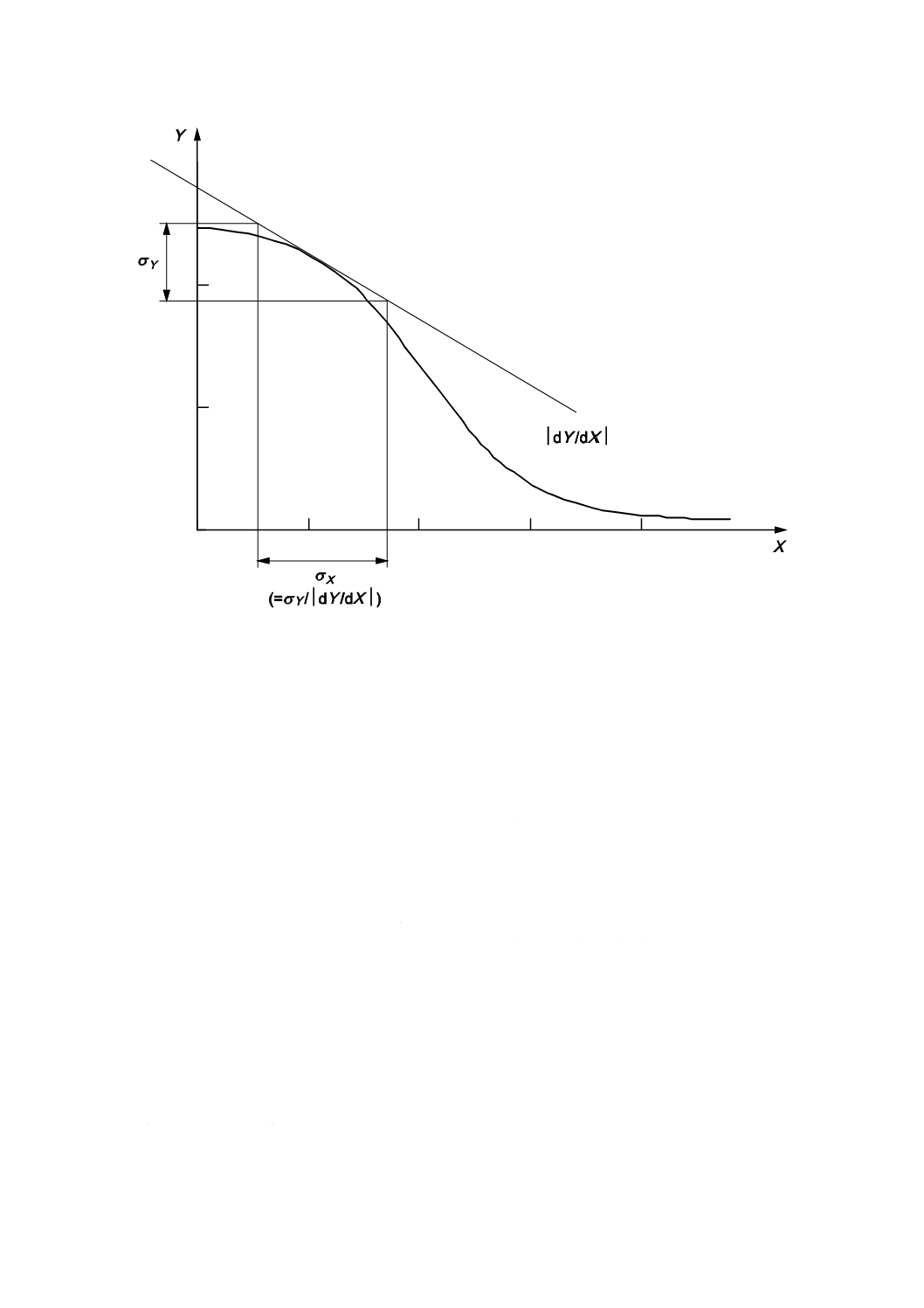
図3に示すように,検量線の微分の絶対値|dY/dX|を用いれば,応答変数のSD,σY(X)は,正味状態変数の
SD,σXに変換できる。すなわち,σX(X)=σY(X)/|dY/dX|である。また,XのCV,ρX(X)への変換は,次のよう
に定式化される。
X
Y
X
Y
X
X
Y
X
d
d
)
(
)
(
ρ
ρ
=
····································································· (1)
ρY(X)がXの関数として与えられれば,求める量ρX(X)は,式(1)を同様に利用して,Xの関数として記述
できる。絶対値|dY/dX|を使えば,この規格は,単調に減少する検量線にも適用できる。
注記1 検量線が原点を通る直線(Y=aX)である場合,正味状態変数の精度プロファイルρX(X)は,
応答変数の精度プロファイルρY(X)と等しい。Y=aXであれば,Y/X=|dY/dX|=aとなる。
注記2 式(1)は,X=0においては定義されないが,正味状態変数のSD,σX(X) [=ρY(X)Y/|dY/dX|]が有
限である限り,変動係数,ρX(X)は,Xが0に近づくに従って無限大に発散することになる。
YのCV
ρY(X)
×Y
/|dY/dX|
/X
YのSD
σY(X)
XのSD
σX(X)
XのCV
ρX(X)
6
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3−検量線の微分の絶対値,|dY/dX|を用いた応答変数のSD,σYの正味状態変数のSD,σXへの変換
5
正味状態変数の限界値及び検出可能な最小値
5.1
一般
次に示す全ての定義は,正味状態変数の確率分布に基づいている。
限界値xcは,次によって定義する。
xc=kcσX(0) ················································································ (2)
ここに,
kc: 確率αに対応した係数
σX(0): X=0の場合のSD
関係式σX(0)=σY(0)/|dY/dX|が使われた場合,式(2)は,xc=kcσY(0)/|dY/dX|と記述できる。検出可能な最小値
xdは,次によって定義する。
xd=xc+kdσX (xd) ········································································· (3)
ここに,
kd: 確率βに対応した係数
σX(xd): X=xdの場合のSD(図1参照)
精度プロファイルσX(X)(3.4参照)は,限界値xc及び検出可能な最小値xdのいずれの場合も決定するた
めに必要である。
注記1 正味状態変数が正規分布に従っている場合,確率α=β=5 %に対応する係数は,kc=kd=1.65
である。
注記2 σX(X)が一定であり,[σX(X)=σX]及びkc=kd=1.65という仮定の下では,式(2)及び式(3)は,xc
=1.65 σX及びxd=3.30 σXと簡単に記述できる。
5.2
確率αに関する計算
X=0の場合のSD,つまりσX(0)をσX(xd)の代わりに使うと,xc及びxdの定義は,次の式によって定義す
7
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
xc=kcσX(0) ················································································ (4)
xd=(kc+kd)σX(0) ········································································· (5)
この場合,式(4)は式(2)と同じであり,確率αは一般的な定義に等しい。しかし,確率βは,初期のβと
は異なることがある。この計算においては,全範囲にわたる精度プロファイルσX(X )は必要ではない。
注記 σX(X)が一定であり,[σX(X)=σX]及びkc=kd=1.65であるという仮定の下では,式(4)及び式(5)は,
xc=1.65 σX及びxd=3.30 σXと簡単に記述できる。
5.3
確率βに関する計算
σX(xd)が,5.1にあるσX(0)の代わりに使われた場合,xc及びxdは,次の式によって定義する。
xc=kcσX(xd) ··············································································· (6)
xd=(kc+kd)σX(xd) ········································································ (7)
この場合,確率βは一般的な定義に等しいが,確率αは初期のαとは異なることがある。
注記 σX(X)が一定であり,[σX(X)=σX]及びkc=kd=1.65であるという仮定の下では,式(6)及び式(7)は,
xc=1.65σX及びxd=3.30σXと簡単に記述できる。
5.4
微分による方法
5.3の定義は,この項で扱う微分法に適用できるという特別な利点がある。式(7)は,次のように表す。
ρX (xd)=σX (xd)/ xd=1/(kc+kd) ························································· (8)
この式は,X=xdにおける正味状態変数のCVを表している。式(8)の一つの利点は,検出可能な最小値
xdが,正味状態変数のCVが1/(kc+kd)×100 %となるときの正味状態変数として決定できることにある。
連続な精度プロファイルσX(X )は,xc及びxdを求めるために必要である。
検量線の片対数プロット(Y vs. lgX)の傾き,dY/d lgXは,正味状態変数Xに依存して変化するが,その
傾きは,検出可能な最小値において特別な値を取る。
)
(
)
(
303
.2
lg
d
d
d
d
c
d
x
σ
k
k
X
Y
Y
x
X
×
+
=
=
·················································· (9)
ここで,左辺は,X=xd (ln 10=2.303)における微分の絶対値,|dY/d lgX|を表している。この式は,検量線
の一般的な性質を表し,検量線の形(線形又は非線形)にかかわらず成り立つ。式(9)の導出を附属書Bに
示す。
注記1 kc=kd=1.65の場合,式(8)は,σX(X)=1/3.30=30 %と記述できる。xdは,CVが30 %となるX
として確定できる。
注記2 kc=kd=1.65の場合,式(9)は,次のように表す。
132
.0
)
(
lg
d
d
d
d
x
σ
X
Y
Y
x
X
=
=
·································································· (10)
ここで,定数0.132は,1/(3.3×2.303)である。
6
例
6.1
一般
6.2及び6.3は,応答変数のSD又はCVとして表された精度プロファイル(3.4参照)を推定する方法に
焦点を絞る。目的の量σX(X)は,箇条4に示すように,応答変数のSD又はCVの連続曲線から変換できる。
6.4の例は,競合ELISA(エライザ)への微分による方法の適用である。6.4においては,競合ELISAの
8
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検量線は,通常,非線形であるが,検出可能な最小値の周囲においては,線形の仮定が有効であることが
示される。
6.2
不確かさの伝ぱ(播)則
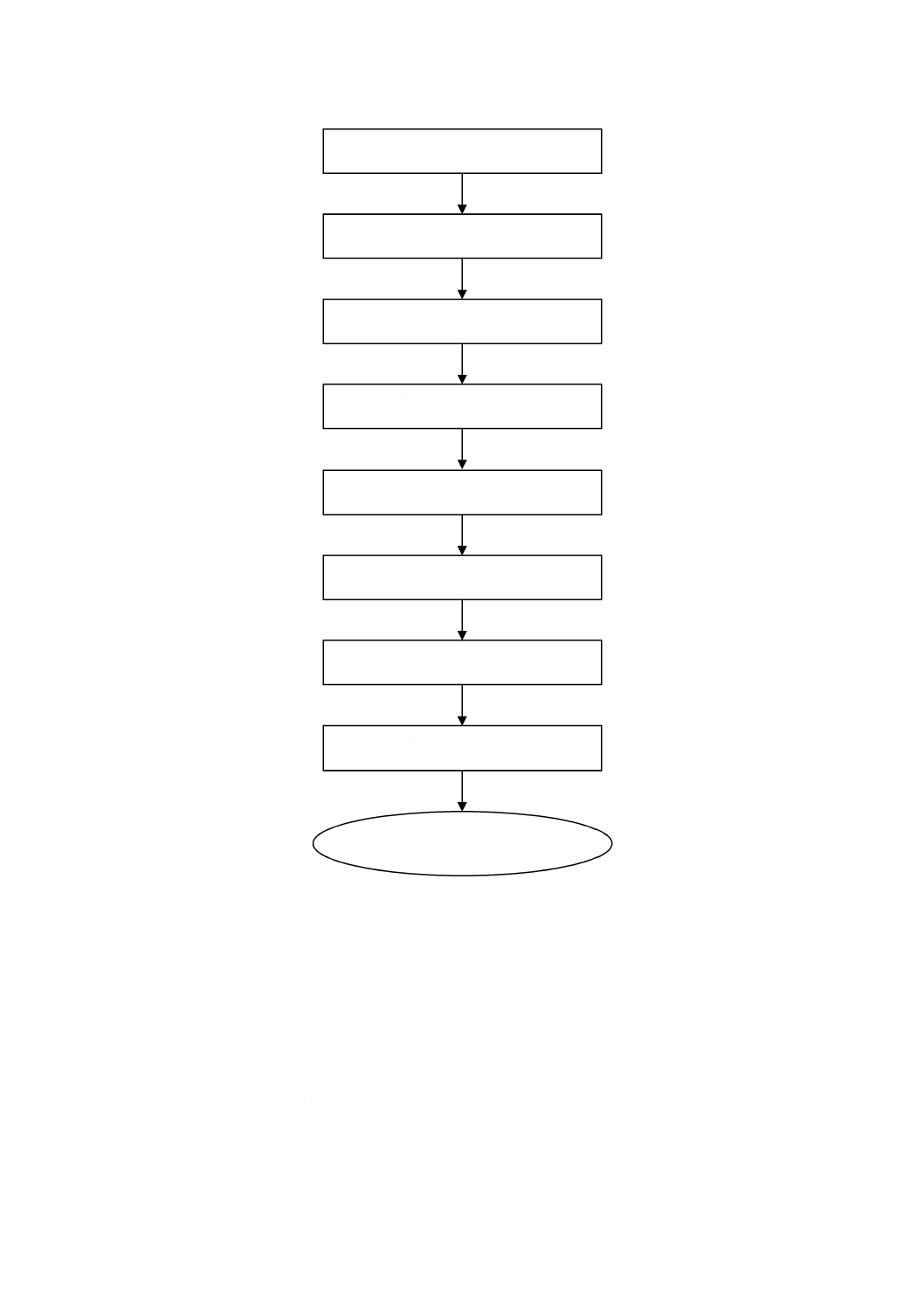
17α-ヒドロキシプロゲステロンの競合ELISAを例に挙げる。この化学分析系の実験手順を図4に示す。
この分析は,96ウェル(穴)のマイクロプレートで行われる。検量線はマイクロプレートごとに作成され,
サンプル(分析試料)の実際の化学分析は,同一マイクロプレート中の異なったウェルで行われる。ここ
では,プレート内不確かさが検討される。
この競合ELISAの不確かさは,基本的にはサンプルと標識抗原との競合反応に起因する。応答変数Y(こ
こでは,吸光度測定値)は,マイクロプレートのウェルの表面に固定された抗体(抗血清)と結合する標
識抗原の量に比例する(参考文献[1]参照)。
B
G
X
G
Y
+
∝
ここに,
X: サンプルの量(正味状態変数)
G: 標識抗原の量
B: 抗体の量
不確かさの伝ぱ(播)則(参考文献[3]参照)をこの化学分析の手順に応用することによって,応答変数
YのCVの2乗が次のように導かれる(参考文献[1]参照)。
2
2
2
2
2
2
2
2
)
(
)
(
)
(
+
Y
σ
r
r
r
r
G
X
X
X
W
S
B
X
G
Y
+
+
+
+
+
=
ρ
································(11)
ここに,
X: サンプルの量(正味状態変数)
Y: 吸光度測定値(応答変数)。検量線の式で置き換えるこ
とができる。
G: 標識抗原の量(0.1 μg/L)
rX: 分注したサンプルの体積のCV(0.9 %)
rG: 分注した標識抗原の体積のCV(0.9 %)
rB: 分注した抗血清の体積のCV(1.9 %)
rS: (2/3)×[分注した発色性基質溶液の体積のCV
(0.6 %)]。2/3は,ピペットの容量誤差をマイクロプレ
ートのウェルの表面で起こる色素生成の誤差に変換す
るために使われる係数である。
σW: マイクロプレートのウェル間の吸光度のSD(0.002
absorbance)。プレート内不確かさである限り,一定であ
る。
化学分析の目的成分量の精度σX(X)は,図2に示すように,式(11)から計算できる。
9
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4−競合ELISAの実験手順
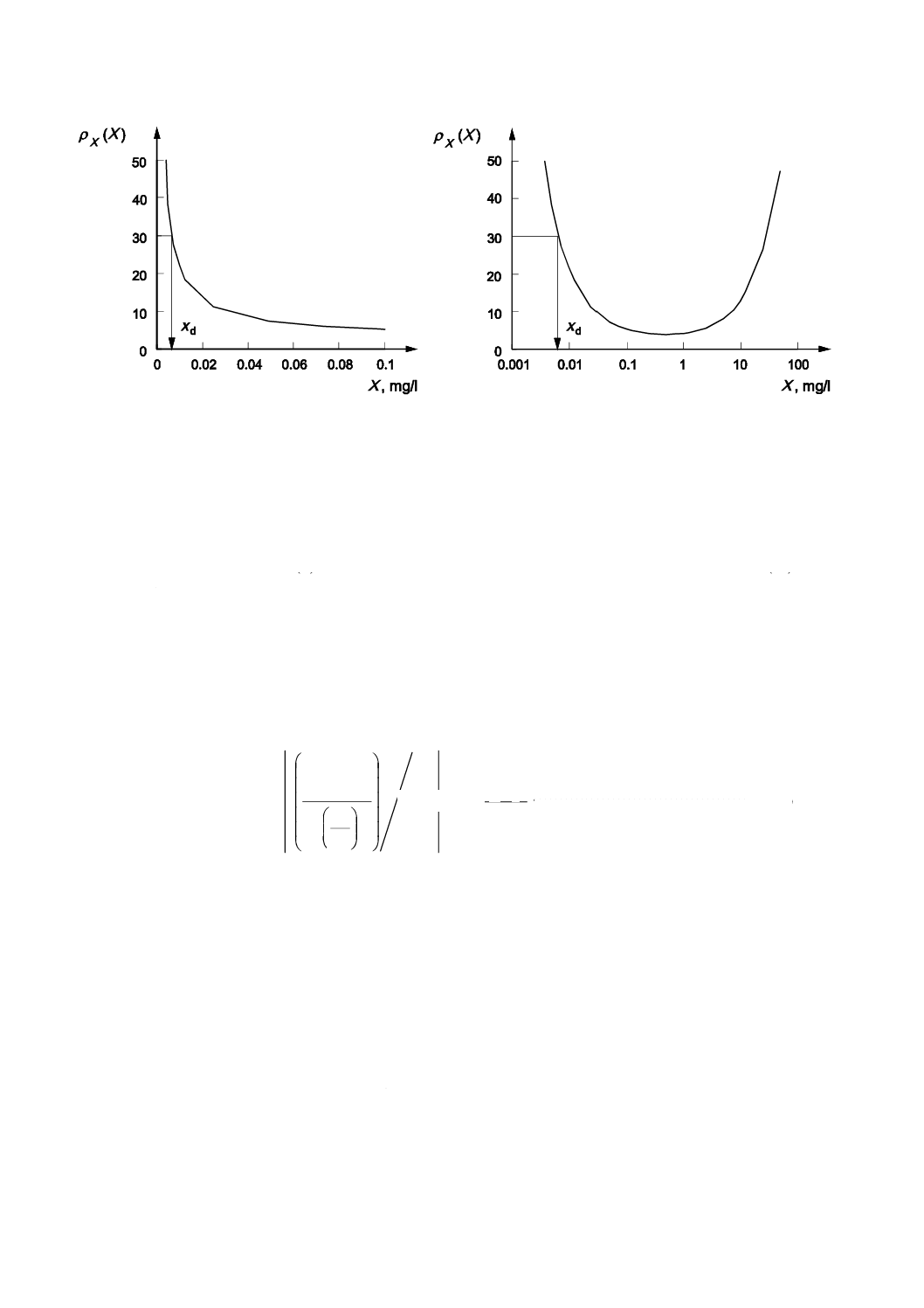
この例の精度プロファイルρX(X)は,図5に示す。CV,ρX(X)は,式(11)から上で述べたパラメータを用
いて計算され,百分率で表示される。5.3の定義が採用されれば,検出可能な最小値xdは,精度プロファ
イルの図上で決定される(図5の矢印を参照)。30 %CVの意味は,5.4の注記1に示す。
精度プロファイルは,標準スケールと片対数スケールとでは,同じ検出可能な最小値を与える。図5 b)
は,X=0の点とこの点とにおけるCV値を除いている。しかし,このことが理論上も実践上も問題にはな
らない理由は,この規格では,検出可能な最小値を求めるために,検出可能な最小値の近傍だけ精度プロ
ファイルとしてのCV値を要求するからである。
サンプルの分注,50 µL
標識抗原の分注,50 µL
反応停止液の分注,100 µL
抗血清の分注,50 µL
洗浄及びタッピング
インキュベーション
30分の放置
基質の分注,100 µL
吸光度測定値
10
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 標準スケール
b) 片対数スケール
図5−17α-ヒドロキシプロゲステロンの競合ELISAにおける正味状態変数のCV,
ρX(X)(精度プロファイル)及び検出可能な最小値xdの標準スケール及び片対数スケールの表示
6.3
モデルフィッティング
免疫測定法では,応答変数の分散は,次の指数モデルで近似できる(参考文献[2]参照)。
σY(X)2∝Yj ··············································································· (12)
ここで,σY (X)は,応答変数YのSDを表す。j=0の場合,この分散は,一定である。j=1の場合,この
分散は,応答変数に比例する。j=2の場合,応答変数のCV,ρY (X)は,一定である。この比例定数は,最
小2乗法から決定できる。
6.4
競合ELISAへの応用
競合ELISAにおいては,B/B0と示される標準化された検量線がしばしば用いられ,式(10)は,次のよう
に記述する(参考文献[4]参照)。
132
.0
)
(
lg
d
1
1
d
d
2
d
1
x
ρ
X
C
X
Y
x
X
C
=
=
+
············································ (13)
ここで,ρY (xd)は,xdにおける応答変数のCVである。この導出を附属書Cに示す。
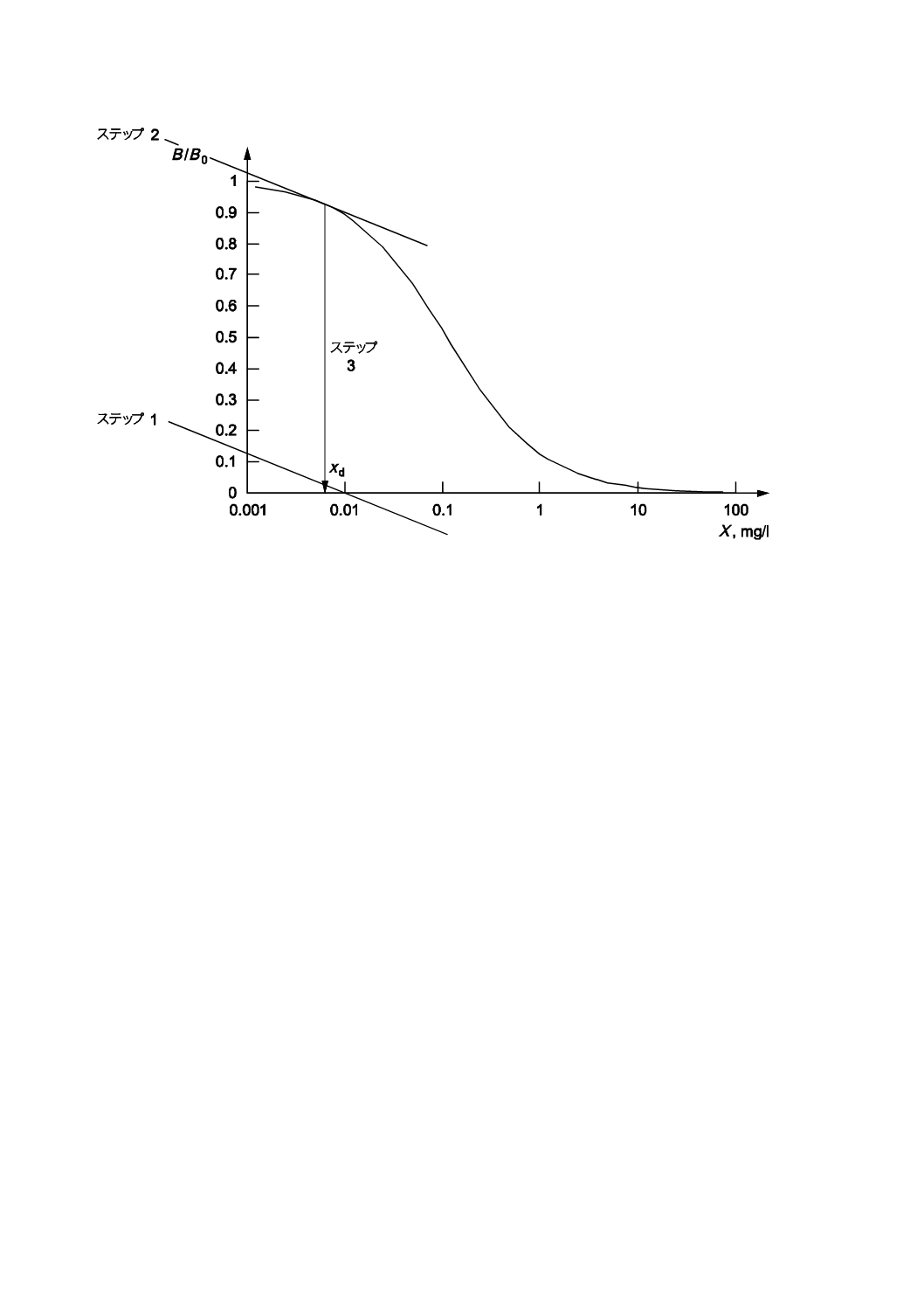
正味状態変数の検出可能な最小値は,式(13)で記述する傾きから求める。図6は,17α-ヒドロキシプロ
ゲステロンの競合ELISA(6.2の例と同じ。)における片対数B/B0曲線を示す。低サンプル濃度において,
1.9 %及び観測された応答変数のCVを近似として用いれば[〜〜ρY (xd)],式(13)は,0.15(=0.019/0.132)を
与える。
xdの作図による推定は,次のように記述する(図6参照)。
− ステップ1:式(13)によって計算された傾きをもつ直線を,左下隅の目盛を使って作図する。
− ステップ2:ステップ1の直線と同じ傾きをもち,かつ,B/B0に接する直線を引く。
− ステップ3:その接点からX軸へ垂線を下ろす。
この垂線とX軸との交点がxdに対応する。この方法は,6.2の例とほとんど同じ結果を与える(図5と
図6とを比較参照)。
11
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 ステップ1,ステップ2及びステップ3は,6.4に記してある。
図6−17α-ヒドロキシプロゲステロンの競合ELISAにおけるB/B0曲線の片対数プロット
12
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
この規格で用いる記号及び省略形
SD
標準偏差
CV
変動係数(標準偏差を平均値で除したもの)
POP
残留性有機汚染物質
ELISA
エライザ,enzyme-linked immunosorbent assay(酵素結合免疫吸着法ともいう。)
X
正味状態変数
Y
応答変数
xc
正味状態変数の限界値
xd
検出可能な最小正味状態変数
kc
確率αに対応した係数
kd
確率βに対応した係数
α
X=0における第1種の過誤の確率
β
X=xdにおける第2種の過誤の確率
σY(X)
Xの関数としての応答変数のSD
ρY(X)
Xの関数としての応答変数のCV
σX(X)
Xの関数としての正味状態変数のSD
ρX(X)
Xの関数としての正味状態変数のCV
|dY/dX|
検量線の微分の絶対値
B/B0
任意の容量における測定値と容量0における測定値との比
13
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
式(9)の導出
変換方程式[式(1)]は,xdの定義式[式(7)]を以下のように展開することに利用できる。
X
Y
X
σ
X
σ
Y
X
d
d
)
(
)
(
=
d
d
d
ln
d
d
)
(
)
(
1
ln
d
d
)
(
)
(
d
d
)
(
)
(
d
d
d
c
d
d
d
c
d
d
c
d
x
X
Y
x
X
Y
x
X
Y
X
Y
x
x
σ
k
k
x
X
Y
x
σ
k
k
X
Y
x
σ
k
k
x
=
=
=
+
=
+
=
+
=
×
×
×
ここで,微分の絶対値は,検量線の傾きが負の場合に利用できる。未知変数xdは,次のように上の式か
ら削除することができる。
)
(
)
(
ln
d
d
d
d
c
d
x
σ
k
k
X
Y
Y
x
X
×
+
=
=
実用目的のために行われる自然対数から常用対数への変換(ln X=2.303 lgX )によって,目的の式[式
(9)]が導かれる。参考文献[4]も参照。
14
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
式(13)の導出
競合ELISAにおいては,検量線は,通常パラメータ4個のロジスティック関数として表される。
3
2
3
0
1
1
C
C
X
C
C
Y
C+
+
−
=
そして,その標準形は,B/B0として知られている。
1
2
0
1
1
C
C
X
B
B
+
=
ここでは,C0,C1,C2及びC3は,実際の検量線データへの最小2乗フィッティングによって決定され
る係数である。式(10)は,次のように関係式dY=(C0−C3)dB/B0から誘導される。
132
.0
)
(
)
(
lg
d
d
3
0
0
C
C
X
σ
X
B
B
Y
−
=
係数C0は,ブランクサンプル(X=0)に対する最も大きな応答変数を表し,C3は,濃度無限大(X=∞)
で最も小さい応答変数を表すので,σY(X)/(C0−C3)は,近似的にσY(X)/C0と等しくなる。ρY(X)を次のように
定義する。
0
3
0
)
(
)
(
)
(
C
X
C
C
X
X
Y
Y
Y
σ
σ
ρ
≈
−
=
ここで,σY(X)/C0は,ブランクに対する応答変数のCV,ρY(0)を意味する。最後の二つの式から,式(13)
は誘導される。参考文献[4]も参照。
15
Z 8462-5:2011 (ISO 11843-5:2008)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] Y. Hayashi. R. Matsuda. T. Maitani. K. Imai. W. Nishimura. K. Ito and M. Maeda. Precision. limit of detection
and range of quantitation in competitive ELISA. Anal. Chem.. 76(5):1295-1301. 2004.
[2] R. A. Dudley. P. Edwards. R. P. Ekins. D. J. Finney. I. G. M. McKenzie. G. M. Raab. D. Rodbard. and R. P. C.
Rodgers. Guidelines for immunoassay data processing. Clin. Chem.. 31(8):1264-1271. 1985.
[3] ISO. Guide to the expression of uncertainty in measurement. 1995.
[4] Y. Hayashi. R. Matsuda. K. Ito. W. Nishimura. K. Imai and M. Maeda. Detection limit estimated from slope of
calibration curve: An application to competitive Elisa. Anal. Sci.. 21:167-169. 2005.





