Z 8404-1:2018 (ISO 21748:2017)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 2
2 引用規格························································································································· 3
3 用語及び定義 ··················································································································· 3
4 記号······························································································································· 6
5 原則······························································································································· 8
5.1 個々の測定結果及び測定プロセスのパフォーマンス ······························································ 8
5.2 再現性データの適用性 ···································································································· 8
5.3 統計的モデルの基本式 ···································································································· 8
5.4 繰返し性データ ············································································································· 9
6 併行精度,再現精度及び真度の推定値を用いた不確かさの評価 ················································· 9
6.1 測定の不確かさの評価の手順 ··························································································· 9
6.2 予想される精度と現実の精度との差·················································································· 10
7 測定方法のパフォーマンス値の,特定の測定プロセスでの測定結果への適用可能性の確認 ············ 10
7.1 一般 ··························································································································· 10
7.2 かたよりの試験所成分の管理状態の検証············································································ 10
7.3 併行精度の検証 ············································································································ 13
7.4 パフォーマンスの継続的検証 ·························································································· 13
8 試験品の的確性の確認 ······································································································ 13
8.1 一般 ··························································································································· 13
8.2 サンプリング ··············································································································· 14
8.3 試料の調製及び前処理 ··································································································· 14
8.4 試験品の種類の変更 ······································································································ 14
8.5 応答レベルによる不確かさの変化····················································································· 14
9 追加要因の検討 ··············································································································· 15
10 合成標準不確かさの一般的表現 ························································································ 15
11 共同実験データに基づく不確かさのバジェット表································································· 16
12 合成された測定結果に対する不確かさの評価 ······································································ 17
13 不確かさ情報の表現 ······································································································· 17
13.1 一般的な表現 ·············································································································· 17
13.2 包含係数の選択 ··········································································································· 18
14 測定方法のパフォーマンス値と不確かさの値との比較 ·························································· 18
14.1 比較のための基本となる仮定 ························································································· 18
14.2 比較手順 ···················································································································· 19
14.3 差異の原因 ················································································································· 19
Z 8404-1:2018 (ISO 21748:2017) 目次
(2)
ページ
附属書A(参考)不確かさ評価への二つのアプローチ ································································ 20
附属書B(参考)実験による不確かさ評価················································································ 25
附属書C(参考)不確かさ評価の例 ························································································ 26
参考文献 ···························································································································· 36
Z 8404-1:2018 (ISO 21748:2017)
(3)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般財団法人日本
規格協会(JSA)から,工業標準原案を具して日本工業規格を改正すべきとの申出があり,日本工業標準
調査会の審議を経て,経済産業大臣が改正した日本工業規格である。これによって,JIS Z 8404-1:2006は
改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 8404の規格群には,次の示す部編成がある。
JIS Z 8404-1 第1部:測定の不確かさの評価における併行精度,再現精度及び真度の推定値の利用の
指針
JIS Z 8404-2 第2部:測定の不確かさの評価における繰返し測定及び枝分かれ実験の利用の指針
日本工業規格 JIS
Z 8404-1:2018
(ISO 21748:2017)
測定の不確かさ−第1部:測定の不確かさの
評価における併行精度,再現精度及び真度の
推定値の利用の指針
Measurement uncertainty-Part 1: Guidance for the use of repeatability,
reproducibility and trueness estimates in measurement uncertainty
evaluation
序文
この規格は,2017年に第2版として発行されたISO 21748を基に,技術的内容及び規格票の様式を変更
することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。また,実線
の下線を施してある箇所は,対応国際規格でイタリックで強調されている事項である。
測定結果の不確かさについての知識は,その測定結果の解釈のために不可欠である。不確かさの定量的
評価を行わない限り,観測された,測定結果の差が実験のばらつき以上のものを反映しているか,試験品
目が仕様に従っているか,又は限界値を定めた法律に抵触しているかを判断することができない。不確か
さに関する情報がなければ,測定結果を誤って解釈するおそれがある。そのような根拠に基づいて誤った
判断を下せば,産業界に不必要な出費が生じたり,法律による不当な訴追がなされたり,健康上の又は社
会的な悪影響が生じたりするなどの結果を引き起こす危険性がある。
JIS Q 17025の認定及び関連システムに基づいて運営される試験所は,測定結果及び試験結果の不確かさ
を評価し,適宜,不確かさを報告することを求められる。ISO/IEC Guide98-3:2008として発行されている
“測定における不確かさの表現のガイド(GUM)”は,広く採用されている標準的な方法である。ただし,
これは,測定プロセスのモデルが利用できる場合に適用されるものである。一方,非常に多くの標準的な
試験方法は,JIS Z 8402-2:1999に基づく共同実験の対象となっている。この規格は,これらの試験方法に
よる結果の不確かさを評価するための,適切で経済的な方法論を示す。この方法論は,共同実験によって
得られた試験方法のパフォーマンスのデータを考慮しており,GUMの原則に完全に適合するものである。
この規格で用いる不確かさの一般的なアプローチ(評価方法)には,次のことが必要である。
− JIS Z 8402-2:1999に基づく共同実験によって得られた,使用する試験方法の併行精度,再現精度及び
真度の推定値を,使用する試験方法に関する公開情報から入手できること。これらは,試験方法の真
度に付随する不確かさの評価値とともに,試験所内及び試験所間の分散成分の推定値を提供する。
− 試験所は,実証されたパフォーマンスに沿った試験方法がその試験所で実施されていることを,自ら
のかたより及び精度を調べて確認できること。これによって,公開されたデータが試験所の測定結果
に対して適用可能であることが確認できる。
2
Z 8404-1:2018 (ISO 21748:2017)
− 共同実験において適切には取り入れられなかった測定結果への影響が同定され,これらの効果に起因
する測定結果のばらつきが定量化されていること。
不確かさの評価は,GUMで規定された方法に従って,該当する分散の推定値を合成することによって
行われる。このような推定値は,他の寄与成分とともに,不確かさ又はある場合には最終的に報告される
不確かさの評価において役に立つ。
不確かさの評価において再現精度の値を使用するという一般的な原則は,“トップダウン”アプローチと
呼ばれることがある。
試験方法を十分に理解しているかどうかの確認として,共同実験によって得られた試験結果のばらつき
を,GUMの手順を用いて得た測定の不確かさと比較することは有用である。こうした比較は,共同実験
のデータを用いて同じパラメータを推定する一貫した方法論があれば,より有効である。
1
適用範囲
この規格は,次の事項を実施するときの指針を示す。
− JIS Z 8402-2:1999に従って実施した共同実験によって得られたデータを利用する測定の不確かさの評
価。
− 共同実験による結果と,不確かさの伝ぱ(播)則を用いて得られた測定の不確かさとの比較(箇条14
参照)。
JIS Z 8402-3:1999は,中間精度を検討するために拡張モデルを提供している。この規格で示す一般的な
方法をそのような拡張モデルの使用に適用することはできるが,拡張モデルを使用する不確かさの評価は,
この規格では対象としていない。
この規格は,測定結果に付随した不確かさを求めることが必要となる,全ての測定及び試験の分野にお
いて適用可能である。
この規格は,再現精度のデータが存在しないときの併行精度のデータの利用には触れていない。
この規格は,認識された,無視できない系統効果が補正されていることを前提としている。補正は,測
定方法の一部として数値上の補正をすること,又は系統効果の原因を調査し,除去することによって行う。
この規格に示す推奨事項は,主として指針を提供するためのものである。ここに示す推奨事項は,多く
の目的に対して有効な不確かさの評価方法であるが,その他の適切な評価方法を採用してもよい。
一般に,この規格で,測定結果,測定方法及び測定プロセスに関して示すことは,試験結果,試験方法
及び試験プロセスにも同様に適用されるものとみなされる。また,逆も成り立つ。したがって,多くの場
合,“測定”を“試験”に,又は“試験”を“測定”に置き換えて読むことができる。さらに,単に“結果”,
“方法”,“プロセス”と表記されているときに,その前に“測定”及び/又は“試験”を付け加えて読む
ことができる。
注記1 附属書Cに不確かさ評価の例を示す。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 21748:2017,Guidance for the use of repeatability,reproducibility and trueness estimates in
measurement uncertainty evaluation(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
3
Z 8404-1:2018 (ISO 21748:2017)
2
引用規格
この規格に引用規格はない。
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
注記 “中間精度条件”については,JIS Z 8402-3:1999を参照。
3.1
かたより(bias)
試験結果又は測定結果の期待値と真の値との差。
注記1 かたよりは,偶然誤差と対比される系統誤差の全体である。かたよりに寄与する系統誤差は,
一つ以上あることもある。真の値からの大きな系統的なずれがあると,大きなかたよりとな
る。
注記2 測定器のかたよりは,通常,表示値の誤差を適切な回数の繰返し測定について平均すること
によって推定される。指示値の誤差は,“測定器の指示値から相当する入力量の真の値を引い
た値”である。
注記3 現実には,合意された参照値が真の値の代用となる。
(JIS Z 8101-2:2015の3.3.2参照)。
3.2
合成標準不確かさ(combined standard uncertainty)
測定結果を幾つかの他の量の値から求めるときの,測定結果の標準不確かさ。これは,これらの各量の
変化に応じて測定結果がどれだけ変わるかによって重み付けした,これらの各量の分散又は共分散の和の
正の平方根に等しい。
(ISO/IEC Guide 98-3:2008の2.3.4参照)。
3.3
包含係数(coverage factor)
拡張不確かさ(3.4)を求めるために,合成標準不確かさ(3.2)に乗じる数として用いる数値係数。
注記 包含係数kは,代表的には2〜3の範囲にある。
(ISO/IEC Guide 98-3:2008の2.3.6参照)。
3.4
拡張不確かさ(expanded uncertainty)
測定結果の周りの,合理的に測定対象量に結び付けられ得る値の分布の大部分を含むと期待される区間
を定める量。
注記1 この部分の割合は,区間の包含確率又は信頼の水準と考えてもよい。
注記2 拡張不確かさによって定める区間に特定の信頼の水準を割り当てるには,測定結果及びその
合成標準不確かさ(3.2)が特徴付ける確率分布に関する明示的又は暗示的仮定を必要とする。
このような仮定が正当化できる程度においてだけ,この区間に付随する信頼の水準を知るこ
とができる。
注記3 参考文献[20]の段落5では,拡張不確かさを,総合不確かさ(overall uncertainty)と呼んでい
る。
(ISO/IEC Guide 98-3:2008の2.3.5参照)
4
Z 8404-1:2018 (ISO 21748:2017)
3.5
精度,精密度,精密さ(precision)
定められた条件の下で繰り返された独立した試験結果と測定結果との間の一致の程度。
注記1 精度は偶然誤差の分布だけに依存し,真の値又は特定の値には関係しない。
注記2 通常,精度は,その悪さ(imprecision)によって表現され,試験結果又は測定結果の標準偏
差として計算される。標準偏差が大きいと,精度が悪い(又は精度が低い)という。
注記3 精度の定量的尺度は,規定された条件に大きく依存する。併行条件(3.7)及び再現条件(3.10)
は,両極端の規定された条件である。
(JIS Z 8101-2:2015の3.3.4参照)。
3.6
併行精度,繰返し精度,繰返し性(repeatability)
併行条件(3.7)下での精度(3.5)。
注記 併行精度は,結果のばらつきの大きさで定量的に表現できる。
(JIS Z 8101-2:2015の3.3.5参照)。
3.7
併行条件(repeatability conditions)
同一試験又は測定アイテムについて,同じ方法を用い,同じ試験施設又は測定施設で,同じオペレータ
が,同じ装置を用いて,短時間のうちに独立した試験結果又は測定結果を得る繰返しの条件。
注記 併行条件は,次を含む。
− 同一の測定操作又は試験操作
− 同一のオペレータ
− 同一条件で使用される同一の測定装置又は試験装置
− 同一の場所
− 短時間内での繰返し
(JIS Z 8101-2:2015の3.3.6参照)。
3.8
併行標準偏差(repeatability standard deviation)
併行条件(3.7)下で得られた試験結果又は測定結果の標準偏差。
注記1 これは,併行条件下での試験結果又は測定結果の分布のばらつきの尺度である。
注記2 同様に,“併行分散(repeatability variance)”及び“併行変動係数(repeatability coefficient of
variation)”も定義され,併行条件下での試験結果又は測定結果のばらつきの尺度として用い
られる。
(JIS Z 8101-2:2015の3.3.7参照)。
3.9
再現精度,再現性(reproducibility)
再現条件(3.10)下での精度(3.5)。
注記1 再現精度は,結果のばらつきの大きさで定量的に表現できる。
注記2 結果は,通常,かたよりを補正した結果であると理解されている。
(JIS Z 8101-2:2015の3.3.10参照)。
5
Z 8404-1:2018 (ISO 21748:2017)
3.10
再現条件(reproducibility conditions)
同一の試験又は測定アイテムについて,同じ方法を用い,異なる試験施設又は測定施設で,異なるオペ
レータが,異なる装置を用いて,独立した試験結果又は測定結果を得る繰返しの条件。
(JIS Z 8101-2:2015の3.3.11参照)。
3.11
再現標準偏差(reproducibility standard deviation)
再現条件(3.10)下で得られた試験結果又は測定結果の標準偏差。
注記1 これは,再現条件下での試験結果又は測定結果の分布のばらつきの尺度である。
注記2 同様に,“再現分散(reproducibility variance)”及び“再現変動係数(reproducibility coefficient of
variation)”が定義され,再現条件下での試験又は測定結果のばらつきの尺度として用いられ
る。
(JIS Z 8101-2:2015の3.3.12参照)。
3.12
標準不確かさ(standard uncertainty)
標準偏差で表す,測定結果の不確かさ(3.14)。
(ISO/IEC Guide 98-3:2008の2.3.1参照)。
3.13
真度(trueness)
試験結果又は測定結果の期待値と真の値との一致の程度。
注記1 真度の尺度は,通常,かたより(3.1)で表現される。
注記2 真度は,しばしば“平均値の精確さ”といわれる。しかし,この用語は推奨されない。
注記3 現実には,合意された参照値が真の値の代用となる。
(JIS Z 8101-2:2015の3.3.3参照)。
3.14
不確かさ(uncertainty)
測定結果に付随した,合理的に測定対象量に結び付けられ得る値のばらつきを特徴付けるパラメータ。
注記1 このパラメータは,例えば,標準偏差(又はそのある倍数)であっても,又は信頼の水準を
明示した区間の半分の値であってもよい。
注記2 測定の不確かさは一般に多くの成分を含む。これらの成分の一部は一連の測定結果の統計分
布によって推定することができ,また,実験標準偏差によって特徴付けられる。その他の成
分は,それらもまた標準偏差によって特徴付けられるが,経験又は他の情報に基づいて確率
分布を想定して評価する。
注記3 測定結果は測定対象量の値の最良推定値であること,並びに補正及び参照標準に付随する成
分のような系統効果によって生じる成分も含めた全ての不確かさの成分は,ばらつきに寄与
することを考えている。
(ISO/IEC Guide 98-3:2008の2.2.3参照)。
3.15
不確かさのバジェット表(uncertainty budget)
不確かさ(3.14)の原因及びそれらに伴う標準不確かさの一覧表であり,測定結果に付随した合成標準
6
Z 8404-1:2018 (ISO 21748:2017)
不確かさ(3.2)の評価のためにまとめたもの。
注記1 この一覧表は,感度係数(結果に影響する量が単位量変化したときの結果の変化),各標準不
確かさの自由度,タイプA評価又はタイプB評価による各標準不確かさの評価方法などの追
加情報を含むことが多い(ISO/IEC Guide 98-3参照)。
注記2 ISO/IEC Guide 99:2007では,次のように定義されている。
2.33 不確かさバジェット(uncertainty budget)
測定不確かさ,その測定不確かさの成分,並びに,それらの計算及び合成に関する表明(statement)。
注記 不確かさバジェットには,測定モデル,推定値と測定モデルの量に付随する測定不確かさ,
共分散,適用した確率密度関数のタイプ,自由度,測定不確かさの評価のタイプ及び包含
係数を含めることが望ましい。ただし,この訳は仮訳である。
4
記号
a
実験式
bm
a
sR
+
=
ˆ
における切片を示す定数
B
かたよりの試験所成分
b
実験式
bm
a
sR
+
=
ˆ
における傾きを示す係数
c
実験式
d
Rcm
s=
ˆ
における係数
ci
感度係数
ix
y∂
∂/
d
実験式
d
Rcm
s=
ˆ
式における指数を示す定数
e
併行条件下での偶然誤差
k
包含係数
l
試験所番号
m
複数の測定結果の平均値
N
合成標準不確かさの計算に含まれる寄与成分の数
n'
合成標準不確かさの計算において,共同実験のデータに追加される寄与成分の数
nl
認証標準物質を用いた共同実験における,試験所lによる測定の繰返し回数
nr
測定の回数
p
試験所の数
Q
十分大きなバッチから取った試験品の数
q
共同実験において,合意によって付与された値の数
rij
xiとxjとの相関係数
sb
標準偏差で表したグループ間分散成分
sD
かたより管理の確認に使用する標準物質の繰返し測定によって得られた結果の推定標準偏差又は実
験標準偏差
sinh
試料の不均質性に付随する標準偏差
sl
併行精度の確認における,試験所lの自由度vlをもつ併行標準偏差の推定値
sL
試験所間標準偏差の推定値
Lˆs
sLが応答に依存するときの,かたよりの試験所成分Bの標準偏差の調整後の推定値
sr
試験所内標準偏差の推定値(併行条件下での偶然誤差eの推定標準偏差)
rs′
要因効果が応答に依存するときの,試験所内標準偏差の調整後の推定値
sR
再現標準偏差の推定値
7
Z 8404-1:2018 (ISO 21748:2017)
Rs′
試験所の繰返し標準偏差に対する調整をした後の再現標準偏差の推定値
Rsˆ
要因効果が応答に依存するときの,実験的モデルから計算した再現標準偏差の調整後の推定値
sw
繰返し又はその他の繰返し性の実験によって得られた試験所内標準偏差の推定値
δˆs
共同実験によって求めた,かたよりδˆの推定標準偏差
()
y
Δ
s
基準方法による値又は合意によって付与された値と日常の方法による値との比較における差の試験
所間標準偏差
u)ˆ(δ 認証値μˆをもつ参照計測標準又は参照標準物質の測定によるδの推定の不確かさに起因するδの不
確かさ
u)ˆ(μ 認証値μˆの不確かさ
u(xi) 入力量xiの不確かさ
u(y)
yの合成標準不確かさ
ui(y) yの合成標準不確かさに対する値xiの寄与成分
u(yi) 測定結果又は付与された値yiの合成標準不確かさ
u(Y)
測定結果Y=f(y1, y2, ...)の合成標準不確かさ
uinh
試料の不均質性に付随する不確かさ
U
拡張不確かさ(合成標準不確かさのk倍)
U(y) yの拡張不確かさ[U(y)=ku(y)]
xi
測定結果の計算における,i番目の入力量の値
ix′
i番目の入力量の,公称値xからの偏差
Y
他の測定結果yiの関数で表された測定結果
yi
複数の方法間又は共同実験における付与された値と合意によって付与された値との比較において,
基準方法によって得られた試験品iの結果
iyˆ
方法間の比較において,日常の試験方法によって得られた試験品iの結果
Δ
試験所のかたより
Δl
試験所lのかたよりの推定値(試験所の平均値mから認証値μˆを減じた値)
y
Δ
日常の測定方法について,基準方法又は合意によって付与された値との比較における,試験所のか
たよりの平均値
δ
測定方法に固有のかたより
δˆ
推定された又は測定されたかたより
μ
理想的な結果の未知の期待値(真の値)
μˆ
標準物質の認証値(参照値)
σ0
技能試験での標準偏差
σD
かたより管理の確認に使用する標準物質の繰返し測定から得た測定結果の標準偏差の真の値
σL
試験所間標準偏差(Bの標準偏差)
σr
試験所内標準偏差(eの標準偏差)
σw
グループ内標準偏差
σw0
十分なパフォーマンスを得るために必要な標準偏差(JIS Q 0033参照)
veff
測定結果yiの標準偏差又は不確かさに付随する有効自由度
vi
不確かさへのi番目の寄与成分に付随する自由度
vl
繰返し性の確認のおける,試験所lの推定標準偏差slに付随する自由度
8
Z 8404-1:2018 (ISO 21748:2017)
注記 対応国際規格では不確かさに関わる表現に不適切なところが残っているが,この規格では特に
注記なしで適切に修正した。
5
原則
5.1
個々の測定結果及び測定プロセスのパフォーマンス
5.1.1
測定の不確かさは,個々の測定結果に関するものである。これに対し,併行精度,再現精度及びか
たよりは,測定又は試験プロセスのパフォーマンスに関するものである。測定又は試験プロセスとは,JIS
Z 8402規格群に基づく共同実験において,実験に参加した全ての試験所によって用いられた単一の測定方
法である。この規格では,測定方法は,ISO/IEC Guide 99:2007の2.6で定義されているように,一つの詳
細な手順の形で規定されていることを前提としている。また,測定又は試験方法のパフォーマンスに関す
る共同実験の検討から導き出したプロセスのパフォーマンスに関する数値は,同じプロセスによって得ら
れる個々の測定結果の全てに当てはまることを暗黙の前提としている。この前提が成り立つためには,測
定プロセスに関する適切な品質管理及び品質保証のデータの形での裏付けが必要である(箇条7参照)。
5.1.2
後に示すように,個々の試験品での違いを更に考慮する必要がある場合もあるが,この点を念頭に
置いたうえで,既によく調べられていて完成度の高い測定プロセスについては,個々の試験品に関して個
別的で詳細な不確かさの検討を行う必要はない。
5.2
再現性データの適用性
この規格は,次の二つの原則に基づいている。
− 第一に,共同実験によって得られた再現標準偏差は,測定の不確かさ評価のための有効な根拠である
(A.2.1参照)。
− 第二に,共同実験の枠組みにおいて検討対象でなかった要因の効果については,無視できることを実
証するか,そうでなければ,明確な形で考慮しなければならない。後者の場合は,共同実験に用いら
れた基本モデルを拡張することを意味する(A.2.3参照)。
5.3
統計的モデルの基本式
5.3.1
この規格の基礎となる統計的モデルは,式(1)による。
∑
+
′
+
+
+
=
e
x
c
B
y
i
i
δ
μ
························································· (1)
ここに,
y: 適切な関数から計算された測定結果
μ: 理想的な結果の(未知の)期待値
δ: 測定方法に固有のかたより
B: かたよりの試験所成分
x'i: xiの公称値からの偏差
ci: 感度係数。これは
ix
y∂
∂
に等しい。
e: 併行条件下での偶然誤差
B及びeは,分散がそれぞれ
2
L
σ,
2
r
σの正規分布に従うと仮定する。これらの項は,共同実験のデータ
の解析のためにJIS Z 8402-2:1999において用いられたモデルを構成している。
方法のかたよりδ,試験所のかたよりB,及び偶然誤差eのそれぞれに対して得られた標準偏差は,共
同実験の条件下におけるばらつきの全体的な指標であるので,残りの和∑
′i
ix
c
は,δ,B又はeに含まれた
偏差以外の偏差x'iについて取る。すなわち,この和を取ることは,共同実験の過程では実施しなかった操
作の影響を組み込む方法となる。
9
Z 8404-1:2018 (ISO 21748:2017)
こうした操作の例を,次に示す。
a) 試験品の調製。通常は,試験品ごとに行うが,共同実験の場合には,試料配布に先立って実施されて
いる。
b) 日常のサブサンプリングの効果。共同実験の対象となる試験品については,通常,共同実験の前に均
質化を行っている。偏差x'iは,期待値ゼロ及び分散u2(xi)の正規分布に従うものと仮定している。
このモデルの論理的根拠を,附属書Aに示す。
注記 一般に,誤差は測定結果と参照値との差と定義される。GUMでは,“誤差”(一つの値)と“不
確かさ”(複数の値のばらつき)とを明確に区別している。ただし,不確かさの評価では,偶然
効果に起因するばらつきを明確にし,これらを明示的にモデルに含めることが重要である。式
(1)のように,期待値ゼロの“誤差項”を含めることによって,この目的を実現できる。
5.3.2
式(1)のモデルが与えられると,測定結果の不確かさu(y)は,式(2)によって評価することができる。
2
2
2
2
L
2
2
)
(
)ˆ(
)
(
r
i
i
s
x
u
c
s
u
y
u
+
+
+
=
∑
δ
················································· (2)
ここに,
2
Ls: Bの推定分散
2
rs: eの推定分散
)ˆ(δ
u
: δの標準不確かさ。これは認証値μˆをもつ参照計測標準
又は参照標準物質の測定によるδの推定の不確かさに相
当する。
)
(ix
u
: x′iの標準不確かさ
再現標準偏差Rsは
2
2
L
2
r
R
s
s
s
+
=
であるので,
2
2
L
rs
s+
は
2
Rsで置き換えることができ,式(2)は式(3)となる。
∑
+
+
=
)
(
)ˆ
(
)
(
2
2
2
2
2
i
i
R
x
u
c
s
u
y
u
δ
······················································ (3)
5.4
繰返し性データ
この規格では,繰返し性データは,主に精度に対する確認の目的で用いる。この確認は,他の検討と併
せて,ある特定の試験所が,共同実験によって得られた再現精度のデータ及び真度のデータを,自身の不
確かさ評価に使えるかどうかを調べるためのものである。また,繰返し性データは,不確かさの再現性成
分の計算にも用いる(7.3及び箇条11参照)。
6
併行精度,再現精度及び真度の推定値を用いた不確かさの評価
6.1
測定の不確かさの評価の手順
この規格の基礎となる原則(箇条5参照)から導かれる測定の不確かさを評価する手順は,次による。
a) 使用する測定方法に関して公開されている情報から,その方法の併行精度,再現精度及び真度の推定
値を入手する。
b) その試験所の測定のかたよりが,a)において入手した推定値から予想される範囲内にあるか否かを確
認する。
c) 現在の測定で実現されている精度が,a)において入手した併行精度及び再現精度の推定値から予想さ
れる範囲内にあるか否かを確認する。
d) a)で推定値を参照した共同実験では適切に考慮されていない測定に対する影響があるかどうかを明確
10
Z 8404-1:2018 (ISO 21748:2017)
にし,それぞれの影響の感度係数と不確かさとを考慮して,これらの効果によって生じると思われる
測定結果のばらつきを定量化する。
e) かたより及び精度がb)及びc)において確認したような管理状態にある場合は,再現精度の推定値[a)]
に,真度に付随する不確かさ[a)及びb)]及び追加された成分の影響[d)]を合成して,合成標準不
確かさを求める。
これらの各手順については,箇条7〜箇条11で詳しく示す。
注記 かたよりが管理状態にない場合は,この規格では,プロセスを管理状態に置くための是正措置
を講じることを前提としている。
6.2
予想される精度と現実の精度との差
現実の精度が6.1 a)で推定値を参照した共同実験から予想されるものとは異なる場合は,それに伴う不
確かさへの寄与を調整することが望ましい。精度が応答の大きさに比例するという,よくある場合につい
ては,8.5において,再現精度の推定値の調整の仕方を示す。
7
測定方法のパフォーマンス値の,特定の測定プロセスでの測定結果への適用可能性の確認
7.1
一般
共同実験の結果から,測定方法のパフォーマンスの指標(sR,sr)が得られ,場合によっては,測定方法
のかたよりの推定値も得られる。これらは,測定方法のパフォーマンスに関する“仕様”を構成する。特
定の目的のためにその測定方法を採用するときに,試験所は,通常,この“仕様”を満たしていることを
示す必要がある。多くの場合,これは,併行精度が管理状態にあること(7.3参照)及びかたよりの試験所
成分が管理状態にあること(7.2参照)を実証するための検討,並びに継続的なパフォーマンス確認[品質
管理及び品質保証(7.4参照)]によって達成できる。
7.2
かたよりの試験所成分の管理状態の検証
7.2.1
一般
7.2.1.1
試験所は,ある測定方法を導入するに当たり,かたよりが管理状態であること,すなわち,かた
よりの試験所成分が共同実験から予想される範囲内にあることを実証することが望ましい。次の説明にお
いては,日常的に試験される試料の値にできるだけ近い参照値をもつ試料を使って,かたよりの確認が行
われていることを前提としている。かたよりの確認に使用される試料の参照値が,日常的に試験される試
料の値からかけ離れている場合には,8.4及び8.5に従って,得られた不確かさへの寄与を調整することが
望ましい。
7.2.1.2
かたよりの試験所成分の確認は,一般に,試験所の測定結果と何らかの参照値との比較であり,
Bの推定である。式(2)はBの変動に伴う不確かさがsLで表されることを示しており,sL自体はsRに含ま
れる。ただし,かたよりの確認自体に不確かさがあるので,この確認に付随する不確かさは,原則として,
その測定方法を使って将来得られる結果の不確かさを増大させる。このため,かたよりの確認に付随する
不確かさは,sRに比べて小さいこと(理想的には0.2 sR未満)が重要であり,以下の指針は,かたよりの
確認に付随する不確かさが無視できることを前提としている。これが実際に成立し,かつ,かたよりの試
験所成分が予想より大きいという証拠が見付からない場合には,式(3)を修正せずに適用できる。かたより
の確認に付随する不確かさが大きい場合には,式(3)に基づいて評価する不確かさを大きくすることが賢明
である。例えば,不確かさのバジェット表(3.15参照)に項目を追加する。
共同実験における真度の調査から,その測定方法に無視できないかたよりがあることが判明している場
合には,試験所のかたよりを評価するとき,判明しているその測定方法のかたよりを考慮に入れることが

11
Z 8404-1:2018 (ISO 21748:2017)
望ましい。例えば,その測定結果に判明している補正を加える。
7.2.2
かたよりの試験所成分が管理状態にあることを実証する方法
7.2.2.1
一般
かたよりの管理は,例えば,次の方法のいずれかによって実証することができる。この規格では,一貫
性をもたせるため,全てのかたよりの検定において同一の一般的な基準を使用する。もちろん,より厳格
な検定を行ってもよい。
7.2.2.2
認証標準物質又は計測標準の利用
試験所lは,併行条件下で認証標準物質又は計測標準の参照標準に対するnl回の繰返し測定を行い,こ
の参照標準について,試験所lのかたよりの推定値Δl(試験所の平均値mから認証値μˆを減じた値に等し
い。)を求める。実行可能ならば,不確かさが
ln
s2w
<0.2sRとなるようにnlを選択することが望ましい。
一般に,ここで用いられる参照標準は,測定方法の真度を評価するときに用いられた認証標準物質又は計
測標準と同じではない。さらに,Δlは,一般にBとは等しくない。記号の表記はこの規格に合わせ変更し
ているが,JIS Q 0033:2002に従って,式(4)が成立している場合,測定プロセスは管理状態にあると判断す
る。
D
2σ
<
lΔ
·················································································· (4)
式(4)のσDは,式(5)で与えられるsDで推定する。
ln
s
s
s
2
w
2
L
2
D
+
=
·············································································· (5)
ここに,
nl: 試験所lによる測定の繰返し回数
sw: nl回の繰返し測定又はその他の併行実験から求めた試験
所内標準偏差
sL: 共同実験によって得られた試験所間標準偏差
式(4)の基準を満たしていることは,かたよりの試験所成分Bが共同実験によって得られたデータの母集
団に含まれることの裏付けと考えられる。ここで,認証標準物質又は計測標準は,校正用標準としてでは
なく,独立した確認用物質又は管理用物質として使用されていることに注意する。
注記1 試験所は,2より小さい係数を用いるか,又は別のより感度の高いかたよりに対する検定を
実施することによって,式(4)より厳格な基準を任意に採用してもよい。
注記2 この手順では,参照値の不確かさは,σDと比べて小さいと仮定している。
7.2.2.3
不確かさが既知の基準試験方法との比較
試験所lは,基準試験方法と試験所で用いている日常の試験方法との両方を用いて,適切な数nl個の試
験品を試験し,nl対の値(yi,
iyˆ)を得る。ここで,yiは試験品“i”に対して基準試験方法によって得た
結果であり,
iyˆは試験品“i”に対して日常の試験方法によって得た値である。次に,試験所は,かたより
の平均値
y
Δを式(6)から,また,yiと
iyˆとの差の標準偏差()
y
Δ
s
を式(7)によって計算する。
)
ˆ(
1
1
i
i
n
i
l
y
y
y
n
Δ
l
−
=∑
=
······································································ (6)
()
(
)
∑
=
−
−
=
l
i
n
i
y
y
l
y
Δ
Δ
n
Δ
s
1
2
1
1
·························································· (7)
12
Z 8404-1:2018 (ISO 21748:2017)
ここに,
i
i
y
y
y
Δi
−
=ˆ
実行可能ならば,標準偏差が
()
l
yn
Δ
s
/
2
<0.2sRとなるようにnlを選ぶ。式(4)及び式(5)の場合と同様に,
l
yn
Δ
s
s
s
)/
(
2
2
L
2
D
+
=
であるとして,
y
Δ<0.2sDのとき,測定プロセスは適正に稼動していると考えられる。
この場合には,式(3)を変更せずに用いる。
注記1 試験所は,2より小さい包含係数を用いるか,又は別のより感度の高いかたよりに対する検
定を実施することによって,
y
Δ<0.2sDより厳格な基準を任意に採用してもよい。
注記2 この手順では,参照法に付随する標準不確かさはσDに比べて小さいこと,及び偏差
i
i
y
y
y
Δi
−
=ˆ
は分散が近似的に一定とみなせる母集団からのものであることを仮定している。
7.2.2.4
同じ方法を使用する他の試験所との比較
試験所lが,かたよりを推定することができる別の共同実験(例えば,JIS Q 17043において定義されて
いるような技能試験)に参加している場合には,そのデータをかたよりの管理状態の確認に利用してもよ
い。次の二つのシナリオが考えられる。
a) その共同実験が,独立に付与された値及び不確かさをもつ計測標準又は標準物質について試験を行っ
た場合。この場合,7.2.2.2の手順がそのまま適用できる。
b) その共同試験によって,y1,y2,Κ,yqのq(≧1)個の値が合意によって付与された場合。この場合,
試験所は,その試験結果が
1ˆy, 2ˆy,Κ,
q
yˆであったとき,かたよりの平均値Δyを式(8)によって,ま
た,付与された値との差の標準偏差s(Δy)を式(9)にょって計算する。
(
)
∑
=
−
=
q
i
i
i
y
y
y
q
Δ
1
ˆ
1
······································································ (8)
()
(
)
∑
=
−
−
=
q
i
y
yi
y
Δ
Δ
q
Δ
s
1
2
1
1
·························································· (9)
ここに,
i
i
y
y
y
Δi
−
=ˆ
q
Δ
s
s
s
y)/
(
2
2
L
2
D
+
=
として,
y
Δ<2sDであれば,その試験所の測定プロセスは適切に稼動していると考え
られる。この場合,式(3)を変更せずに用いてよい。
注記1 この手順では,付与された値はqよりも多数回の測定結果に基づいており,そのため,付与
された値の不確かさは無視できること,かつ,偏差Δyiは分散が近似的に一定とみなせる母集
団からのものであることを仮定している。
技能試験では,付与された値yiとの差をとり,技能試験の標準偏差σ0で除すことによって,回答された
結果
iyˆを,z-スコア
(
)
0
/
ˆ
σ
i
i
i
y
y
z
−
=
に変換する場合(JIS Q 17043:2011参照)がある。z-スコアが使われ,
技能試験の標準偏差がその測定方法のsR以下である場合,q個の付与された値から得られるz-スコアの平
均値が
q
2
±
の範囲内にあることが,その試験所のかたよりが管理状態にあることの十分な証拠となる。
これは,計算上は便利であり,注記1に示す等分散の仮定にあまり影響されない。ただし,この基準は,
通常,7.2.2.4の記載に比べ厳格になることに留意する。試験所は,より厳格な基準を採用することは自由
であるが(注記2参照),厳格な同等性のためには7.2.2.4に記載した計算は必要である。
注記2 試験所は,7.2.2.4の記載より厳格な基準を採用することは自由である。
13
Z 8404-1:2018 (ISO 21748:2017)
7.2.3 有意なかたよりの試験所成分が検出された場合
適用範囲で示したとおり,この規格は,かたよりの試験所成分が管理状態にあることが実証可能である
場合にだけ適用できる。過大なかたよりが検出された場合,測定を行う前に,そのかたよりを必要な範囲
内に収めるための措置を講じなければならない。こうした措置とは,通常,かたよりの原因を調査して除
去することである。
7.3
併行精度の検証
7.3.1
試験所lは,その試験所の併行精度が共同実験によって得られた併行標準偏差と整合していること
を示すことが望ましい。整合性の実証のために,一つ又は複数の適切な試験試料を繰り返し分析し,(必要
に応じて結果をプールして)自由度vlの併行標準偏差slを得る。slの値を,必要であれば信頼度95 %のF
検定を用い,共同実験によって得られた併行標準偏差srと比較する。実行可能ならば,νl≧15を満たす十
分な回数の繰返しを行うことが望ましい。
7.3.2
slがsrより有意に大きいことが判明した場合,その試験所は,原因を特定し是正するか,又はこの
規格を使って計算される全ての不確かさの評価において,srの代わりにslを使用することが望ましい。こ
の場合,
2
2
L
r
R
s
s
s
+
=
は,
2
2
L
l
R
s
s
s
+
=
′
によって置き換えられるため,再現標準偏差の推定値sRの増加を
招くことに特に注意する。ここで,s′Rは再現標準偏差の調整後の推定値である。逆に,slがsrより有意に
小さい場合,その試験所は,srの代わりにslを用いて不確かさの評価値を小さくしてもよい。
精度の検討では,どのような場合でも,データが予想外の傾向をもたないことを確認し,標準偏差swが
様々な試験品に対して一定かどうかを確認することが重要である。標準偏差swが一定でない場合には,異
なるクラスの試験品のそれぞれについて,精度を別個に評価するか,又はその依存性についての(8.5のよ
うな)一般的なモデルを導き出すのがよい。
注記 特定の精度の値が必要な場合,JIS Q 0033:2002に,必要な精度の値をσwoとして
=
wo
w
2
c
σ
s
x
に
基づく検定の詳細が記載されている。
7.4
パフォーマンスの継続的検証
かたより及び精度の事前推定に加えて,試験所は,その測定手順がその管理状態に維持されていること
を確認するために必要な手段を講じることが望ましい。特に,次のことが必要である。
− かたより及び精度の定期的確認を含む適切な測定の品質管理。これらの確認には,適正で安定した均
質な試験品又は材料を使用するのがよい。管理図の使用を強く推奨する(JIS Z 8402-5:2002及びJIS Z
8402-6:1999参照)。
− 適切な品質システムの中で活動する,十分に訓練を受けた適任の要員の配置を含む,測定の品質の保
証手段。
管理図を使用している場合に,一定期間にわたって行われた品質管理用の測定の標準偏差は,精度及び
かたよりが適切に管理されている場合,通常,7.3.2で算出されたs'Rの値より小さい。
8
試験品の的確性の確認
8.1
一般
共同実験,又はJIS Z 8402-2:1999及びJIS Z 8402-3:1999に基づく中間精度の推定においては,均質な材
料又は少ない種類の試験品について測定するのが普通であり,また,事前に調製された材料を配布するの
が一般的な方法である。一方で,日常の試験品は多様であったり,試験に先立って追加の処理が必要とな
14
Z 8404-1:2018 (ISO 21748:2017)
ることがある。例えば,環境試験試料の場合,共同実験の目的のために,乾燥し,細かく粉砕され,均質
化されたものが提供されることが多いが,日常の試験における試料は,湿っていて,不均質で,分割の仕
方も粗い。したがって,こうした差異を調べ,必要に応じて考慮することが必要である。
8.2
サンプリング
8.2.1
サンプリングプロセス
共同実験にサンプリング処理を含むことはまれであるが,試験所内で使用する方法にサブサンプリング
を含む場合,又は日常的に使用する試験手順が少量の試料からバルクの特性を評価する場合には,サンプ
リングの効果を調べることが望ましい。ISO 11648-1又は特定の目的に適したその他の規格でサンプリン
グに関する文書を参考にするとよい。
8.2.2
不均質性
不均質性は均質性試験によって実験的に調べることができる。この均質性試験では,通常,複数の試験
品の繰返し測定の試験結果に対する分散分析(ANOVA)から分散の推定値を求めることができ,試験品間
成分である分散
2
inh
sが不均質性の効果を表す。(所定の均質化を行った後でも)試験材料が有意に不均質で
あることが判明した場合は,この分散の推定値をそのまま標準不確かさとする(すなわち,
inh
inh
s
u=
)こ
とが望ましい。状況によっては,特に,大きいバッチから抜き取ったQ個の試験試料に対する不均質性の
標準偏差及び試験結果の平均値を同一バッチの他の試験試料に適用する状況においては,不確かさの寄与
は予測区間に基づいて決められる[すなわち,
(
)Q
Q
s
u
1
inh
inh
+
=
]。また,サンプリングプロセスに関す
る知識及びサンプリング分布に関する適切な仮定を用いることによって,不均質性の効果を理論的に推定
することも可能である。
8.3
試料の調製及び前処理
多くの共同実験においては,試料は配布される前に均質化され,更に安定化されることがある。しかし,
試験所内で適用される試料に対する特定の前処理手順が及ぼす効果を調べ,考慮することが必要である。
一般に,こうした調査は,近似的に又は正確に定められた特性をもつ材料について調べることで,測定結
果に対してその手順が及ぼす効果を明らかにする。この効果は,ばらつき又は系統効果の変化として現れ
る。その効果がばらつきを増すものと想定される場合には,不確かさのバジェット表に適切な項を加える
ことによって,ばらつきの有意な変化を考慮に入れることが望ましい。有意な系統効果として現れる場合
には,その効果に対する上限値を設けるのが最も簡便である。GUMの推奨に従って,この上限値をく(矩)
形分布又はその他の適切な有限対称分布の限界値であるとみなし,その分布の半値幅を適切な係数で除す
ことによって,標準不確かさを評価する。
8.4
試験品の種類の変更
共同実験において用いた試験品と比べて種類又は組成が異なることに起因して生じた不確かさが問題と
なる場合,それを調査することが望ましい。一般に,こうした効果は,バルク特性に起因する立証された
効果を基に予測し,GUMの基本アプローチを使って不確かさを評価するか,試験品の種類又は組成を系
統的に又は偶然的に変化させることによって調べることが望ましい(附属書B参照)。
8.5
応答レベルによる不確かさの変化
8.5.1
sRの調整
ある特定の測定に関して,不確かさの一部又は大部分の寄与が測定対象量の値に依存することがある。
JIS Z 8402-2:1999では,特定の正の値m(応答という。)に対する再現標準偏差が,次のモデルのいずれか
によって表されるような,三つの単純なケースを考察している。
15
Z 8404-1:2018 (ISO 21748:2017)
bm
sR=
ˆ
················································································· (10)
bm
a
sR
+
=
ˆ
··············································································(11)
d
R
cm
s=
ˆ
················································································ (12)
ここに,
Rsˆ: 近似モデルから計算される調整後の再現標準偏差
a,b,c及びd: 異なる平均値mをもつ5個以上の試験品に対する実
験から求めた係数(a,b及びcは正の数)
式(10)〜式(12)のいずれかを適用するとき,適切なモデルを用いて計算した再現精度の推定値に基づいて
標準不確かさを求めることが望ましい。
7.3の手順を適用する場合,Rsˆにも併行精度の項srの調整後の寄与を反映させることが望ましい。多く
の目的に対しては,Rsˆに対する単純な比例変化で十分である,すなわち,
(
)
2
w
2
2
2
s
s
s
s
bm
a
s
L
l
L
R
+
+
+
=
′
····························································· (13)
ここで,Rs′は7.3と同じ意味である。
8.5.2
不確かさに対する他の寄与の変化
一般に,不確かさに対する寄与が,予測可能な形で測定結果の値(応答)によって変化する場合には,
これに応じてyの標準不確かさも調整することが望ましい。
注記 不確かさに対する多くの寄与がyに厳密に比例する場合には,全ての重要な効果をyに対する
積の形の効果に換算して表し,全ての標準不確かさを相対標準偏差の形で表すのが便利である
ことが多い。
9
追加要因の検討
箇条8では,共同実験と日常の試験との間で異なると思われる主な要因について考察した。ある特定の
場合には,それ以外の効果が作用することがあり得る。これは,共同実験の中で制御変数が偶然又は故意
に一定であったか,又は日常の試験においてとり得る条件の範囲が共同実験の条件の範囲内に適切に含ま
れていなかったことに起因する。
共同実験の中で一定に保たれていた,又は要因又は変化が不十分であった要因による効果を,他の実験
によるばらつきから,又は確立した理論からの推論を用いて,別に評価することが望ましい。これらの効
果が無視できない場合には,これらの要因に付随した不確かさを評価し,記録し,通常の方法[すなわち,
式(3)の伝ぱ(播)則]に従って他の寄与と合成することが望ましい。
10 合成標準不確かさの一般的表現
箇条8で示した要因を考慮して,
2
R
sの代わりに調整した推定値
2ˆR
sを使用する必要性を考えると,式(3)
は,測定結果yの合成標準不確かさu (y)を評価するための一般的表現である式(14)となる。
[
]
∑′=
+
+
=
n
i
i
i
R
x
u
c
u
s
y
u
1
2
2
2
2
2
)
(
)ˆ(
ˆ
)
(
δ
·················································· (14)
ここで, )ˆ(δ
u
は,式(15)によって求める。式(A.8)も参照。

16
Z 8404-1:2018 (ISO 21748:2017)
()
()μ
u
p
s
n
s
μ
u
s
u
r
R
δ
ˆ
)
/1
1(
ˆ
)ˆ(
2
2
2
2
2ˆ
+
−
−
=
+
=
δ
··································· (15)
ここに,
p: 試験所の数
n: 各試験所における繰返し測定回数
)ˆ(μ
u
: 共同実験でかたよりを推定するために用いた認証値μˆ
の標準不確かさ
変数u(B)が式(14)に現れないのは,Bの標準不確かさsLが既に
2ˆR
sに含まれているためである。添え字“i”
は,箇条8及び箇条9において確認した効果を含んでいる(これらには,1からn'までの連続する見出し
番号を割り当てると仮定する。)。全ての効果及び不確かさがsRと比べて小さい場合,ほとんどの現実的な
目的では,明らかにこれらを無視できる。例えば,0.2 sR未満の標準不確かさは,全体の不確かさの評価に
おいては0.02 sR未満の変化量となる。
注記1 8.5.2の注記に記載したように,全ての不確かさへの寄与を相対標準偏差又はパーセントの形
で表現する場合,式(14)及び式(15)は相対値に適用することができ,得られる不確かさu(y)も
相対標準偏差又はパーセントの形で表現される。
注記2 測定方法のかたよりが無視できるほど小さく,共同実験と同じ手順が試験品の測定に適用さ
れている場合,合成標準不確かさはu(y)=sRとなる。
11 共同実験データに基づく不確かさのバジェット表
この規格は,基本的に,測定又は試験の結果に対して式(3)の一つのモデルだけを仮定している。このモ
デルへの継続的信頼性を裏付けるために必要な証拠は,様々な情報源から求めることができるが,関連す
る試験に付随する不確かさが無視できる場合は,式(3)を用いる。ただし,式(3)の形が少し変わるような状
況も存在する。特に,再現精度又は併行精度の項が応答に依存する場合がそうである。対象となる範囲に
わたって,不確かさが応答と独立な場合は,不確かさのバジェット表は表1のようになり,不確かさが応
答に依存する場合は,表2のようになる。
表1−応答から独立した不確かさの寄与
効果
yの標準不確かさa)
コメント
δ
)ˆ
(δ
u
この項は,共同実験にかたよりに対する補正が組み込ま
れ,かつ,不確かさが無視できない場合にだけ含まれる。
B
sL
表2参照。
e
sr
試験品の測定において,その方法b)のnr回の繰返しの平
均値が使われた場合,eの標準不確かさは
r
r
n
sˆ
となる。
xi
()
i
ix
u
c
箇条8及び附属書Bを参照。
注a) これらの標準不確かさの単位はyと同じである。また,それらを相対値で表してもよい(箇条10の注記
参照)。
b) 方法自体が繰返しを指示する場合がある。nrはこうした繰返しを含めた方法全体を繰り返す回数を表す。

17
Z 8404-1:2018 (ISO 21748:2017)
表2−応答に依存する不確かさの寄与
効果
yの標準不確かさa) b)
コメント
δ
)ˆ
(
ˆ
δ
δu
y
∂
∂
この項は,共同実験にかたよりに対する補正が組み込まれ,か
つ,不確かさが無視できない場合にだけ含まれる(補正が単純
な加減算ではない場合に対応するために,微分係数が含まれ
る。)。
B
m
b
a
s
L
L
Lˆ
+
=
式(11)と同様に,aL及びbLは,sLと平均値mとの間に仮定され
る直線関係の係数である。
この形式が適用可能なのは,sLのmに対する依存性が確認され
ている場合に限る。依存性が確認されていない場合は,表1の
B及びeに付随する合成推定値を使用する。
e
m
b
a
s
r
r
r
+
=
ˆ
式(11)と同様に,ar及びbrは,srと平均値mとの間に仮定され
る直線関係の係数である。
試験品の測定において,その方法c)のnr回の繰返しの平均値が
使われた場合,erの標準不確かさは
r
r
n
s
となる。
この形式が適用可能なのは,srのmに対する依存性が確認され
ている場合に限る。依存性が確認されていない場合は,表1の
B及びeに付随する合成推定値を使用する。
B,e
bm
sR=
ˆ
又は
bm
a
sR
+
=
ˆ
又は
d
R
cm
s=
ˆ
式(10),式(11)及び式(12)で示したとおり,a及びbはsRと平均
値mとの間の確認された適正な関係の係数である。
mに対するsL及びsrそれぞれの依存性が確認されていない場合
は,B及びeそれぞれの標準偏差の推定値(表1参照)の代わ
りに,その合成推定値を使用することが望ましい。
xi
()
i
i
x
u
c
箇条8及び附属書B参照。
注a) これらの標準不確かさの単位はyと同じである(箇条10の注記参照)。
b) ここでは,式(11)の形の単純な直線依存性を想定している。
c) 方法それ自体が繰返しを指示する場合がある。nrはこうした繰返しを含めた方法全体を繰り返す回数を表す。
12 合成された測定結果に対する不確かさの評価
12.1 “合成された結果”Yは,そのそれぞれの試験が共同実験によって調査されている,幾つかの異な
る試験結果yiから得る。例えば,“食肉成分”の計算では,一般に,窒素定量から計算したたんぱく質含
有量と,それぞれ異なる標準的な方法によって測定した脂肪及び水分含有量とを合成する。
12.2 寄与する個々の試験結果yiの標準不確かさu(yi)は,この規格に示す原則を用いて求めるか,適宜,
式(A.1)又は式(A.2)を用いて直接求める。入力値yiが独立である場合,測定結果Y=g(y1, y2, ...)の合成標準
不確かさu(Y)は,式(16)で表す。
[
]2
)
(
)
(
∑
=
i
i
iy
u
c
Y
u
································································ (16)
入力値yiが独立でない場合は,GUM[式(A.2)を使用]を参照して,相関関係について十分考慮するこ
とが望ましい。
13 不確かさ情報の表現
13.1 一般的な表現
GUMの原則に従えば,不確かさは,合成標準不確かさu(y)又は拡張不確かさU(y)=ku(y)[ここで,k
は包含係数(13.2参照)]として表す。また,相対値で不確かさを表現すると便利なことがある。例えば,
18
Z 8404-1:2018 (ISO 21748:2017)
変動係数,又は報告された結果に対する割合で表した相対拡張不確かさの例がある。
13.2 包含係数の選択
13.2.1 一般
拡張不確かさを評価するとき,包含係数kを選択するに当たっては,次の事項を考慮することが重要で
ある。
13.2.2 望ましい信頼の水準
多くの現実的な目的の場合には,信頼の水準が約95 %になるように,拡張不確かさを求めることが望ま
しい。ただし,信頼の水準の選択は,適用の重大性,誤った結果が及ぼす影響などの要因によって左右さ
れる。kの選択において,これらの要因を,適用に関連する指針及び法的要求事項と共に,十分に考慮す
ることが望ましい。
13.2.3 評価値の自由度
13.2.3.1 約95 %の信頼の水準が要求され,かつ,不確かさに対する支配的な寄与成分の自由度が大きい
(>10)という,多くの現実的な目的の場合には,k=2を選択することによって,起こり得る値の範囲を
示す十分に信頼できる指標が得られる。しかし,特に,式(14)における一つ以上の有意な項の推定値の自
由度が7未満である場合には,過小評価につながることがある。
13.2.3.2 自由度ν1をもつ一つの項ui(y)が支配的である場合[表示レベルで,ui(y)≧0.7u(y)]では,通常,
u(y)の有効自由度veffをviとすればよい。
13.2.3.3 複数の重要な項がほぼ同じ大きさであり,いずれも限られた自由度(すなわち,vi≪10)である
場合には,ウエルチ-サタスウェイトの式[式(17)]を使って有効自由度veffを求める。
()
()
∑
=
=
N
i
i
i
ν
y
u
ν
y
u
1
4
ff
e
4
····································································· (17)
kの値は,必要とされる信頼の水準と自由度veffに対するt分布の両側検定値を用いて,veffから選択する。
一般に,veffが整数値でないときは,小数点以下を切り捨てるのが最も安全である。
注記 測定及び試験の多くの分野では,統計的外れ値の頻度は正規分布からの期待値と比べてかなり
高いことがあるため,その分布についての十分な知識をもたずに高い信頼の水準(>95 %)に
外挿して推定するときには,極めて慎重な配慮が必要である。
14 測定方法のパフォーマンス値と不確かさの値との比較
14.1 比較のための基本となる仮定
この規格に基づく測定の不確かさの評価は,主に再現精度又は中間精度の推定値に基づいており,これ
らの精度推定値が得られた共同実験の間一定に保たれていた要因に十分に配慮した合成標準不確かさを与
える。得られた合成標準不確かさu(y)は,原則として,測定プロセスの詳細な数学的モデルから得られる
標準不確かさと等しくなるはずである。利用可能であれば,この二つの異なる評価値の比較をすることは,
二つの評価値の信頼性に対する有効な検定をすることに相当する。14.2に示す検定手順によるのがよい。
ただし,この手順は,次の二つの重要な仮定に基づいていることに注意する必要がある。
− 第一に,有効自由度veffをもつ合成標準不確かさu(y)をどのように評価したとしても,それは,自由度
n−1をもつ標準偏差sの分布に従う[すなわち,
)
)(
1
(
2
2σ
s
n−
は,自由度n−1のx2分布に従う。]。
この仮定によって,通常のF検定が利用できる。ただし,合成標準不確かさには,様々な分布形を
19
Z 8404-1:2018 (ISO 21748:2017)
もち,様々な大きさの分散をもつ項に付随する不確かさが含まれるため,検定は示唆的なものとして
取り扱い,適用された信頼の水準は十分慎重に見ることが望ましい。
− 第二に,比較する二つの合成標準不確かさの評価は,完全に独立している。しかし,幾つかの要因は
両方の評価値に共通しているであろうから,現実には独立しているとは考えにくい。一つの捉え難い
効果に,不確かさに関わる判断が既知の試験所間パフォーマンス値の影響を受けているという傾向が
ある。この効果を避けるために十分な注意を払っていると仮定している。複数の重要な要因が二つの
合成標準不確かさの評価に共通する場合,一つの場合よりもはるかに高い頻度で,二つの評価値は類
似するであろう。このような場合,次に示す比較によって有意差が発見できないからといって,その
比較結果を測定モデルの信頼性を示す強力な証拠であるとみなさないほうがよい。
14.2 比較手順
有効自由度がそれぞれν1及びν2である二つの評価値u(y)1及びu(y)2を,次のように比較する。ただし,
二つのうち値が大きい方をu(y)1,信頼の水準α(例えば,信頼率95 %に対してはα=0.05)とする。
a)
[
]2
2
1
)
(
)
(
y
u
y
u
F=
を計算する。
b) 上側棄却限界値Fcrit=F(α/2,ν1,ν2)を調べるか,又はソフトウェアから値を得る。上側及び下側の限
界値が与えられている場合は,常に1より大きい上側の限界値を選ぶ。
c) F>Fcritの場合,u(y)1はu(y)2よりも有意に大きいと考えることが望ましい。
14.3 差異の原因
合成標準不確かさの評価値の間に有意差が生じるには様々な理由があり得る。その中には,次のような
ものを含む。
− 試験所間での真の能力の違い
− 測定に及ぼす重要な効果の全ては含まれてはいないという,モデルの不完全さ
− 合成標準不確かさに対する重要な要因の過大評価又は過小評価
20
Z 8404-1:2018 (ISO 21748:2017)
附属書A
(参考)
不確かさ評価への二つのアプローチ
A.1 GUMのアプローチ
“測定における不確かさの表現のガイド(GUM)”は,ある測定プロセスのモデルから得られた測定結
果yに付随する測定の不確かさを評価するための方法を定めている。GUMの方法論は,国際度量衡局
(BIPM)の勧告[20]に基づいている。この勧告は,第一に,不確かさの成分は,一連の観測値の統計的解
析(“タイプA評価”),又はその他の手段(“タイプB評価”)によって評価されると認識している。その
他の手段には,例えば,公表された標準物質又は計測標準の不確かさのデータを利用する,必要に応じて
専門的判断を利用するなどがある。それぞれの成分を,評価の方法を問わず,標準偏差の形で表し,必要
に応じて合成する。
BIPMの勧告を取り入れたGUMの実施は,
)
...,
,
,
(
2
1
N
x
x
x
f
y=
の形の測定モデルで始まる。これは,測
定結果yを入力量xiに関係付けるものである。GUMでは,入力量が独立している場合の不確かさu(y)を,
式(A.1)に示すように求めている。
()
()
∑
=
=
N
i
i
i
x
u
c
y
u
1
2
2
································································· (A.1)
ここに,
ci:
i
i
x
y
c
∂
∂
=
から決定した感度係数,xiによるyの偏
微分
u(xi)及びu(y): xi及びyそれぞれの標準不確かさ(すなわち,標準
偏差で表した測定の不確かさ)
入力量が独立でない場合,式(A.2)に示すように,関係は更に複雑になる。
()
()
(
)
∑
∑∑
=
=
≠
=
+
=
N
i
N
i
N
j
i
j
j
i
j
i
i
i
x
x
u
c
c
x
u
c
y
u
1
1
,1
2
2
,
······································· (A.2)
ここに,
u(xi, xj): xiとxjとの間の共分散
ci及びcj: 式(A.1)で説明した感度係数
実際には,共分散は,式(A.3)に示すように,相関係数rijに関連していることが多い。
ij
j
i
j
i
r
x
u
x
u
x
x
u
)
(
)
(
)
,
(
=
······························································ (A.3)
ここに,−1≦rij≦1
測定モデルに著しい非線形が含まれる場合,式(A.1)を,より高次の項を含むように拡張する。非線形の
問題は,GUMに詳しく説明されている。
式(A.1)〜式(A.3)を用いて合成標準不確かさu(y)を計算した後,u(y)に包含係数kを乗じることによって,
拡張不確かさを計算する。包含係数は,u(y)を評価したときの自由度を基に選択することができる。これ
については,箇条13参照。
一般に,GUMの方法において,入力量は,測定されるか,又は付与されることが暗黙の了解となって
21
Z 8404-1:2018 (ISO 21748:2017)
いる。測定可能な量という点で容易に定義できない影響(例えば,測定者による影響)が生じた場合には,
その影響を考慮に入れた別の標準不確かさ成分を求めるか,又は別の変数を式
)
...,
,
,
(
2
1
N
x
x
x
f
に含めると
便利である。
このアプローチは,個々の入力量に焦点を当てているため,不確かさ評価の“ボトムアップ”アプロー
チと呼ばれることがある。
u(y)の物理的解釈が,完全に直接的に行えるというわけではない。u(y)には専門的判断によって評価され
る項が含まれることがあるため,u(y)は“確信の程度”を表現した関数であると考えるのが適切であろう。
実際には,この関数は観測できる場合とできない場合とがある。ただし,u(y)の計算が,最終的に,全て
の入力変数は想定された分布に従ってランダムに変化すると仮定して得られる標準偏差に帰結するという
ことによって,より直接的な物理的解釈が与えられる。通常,これは,全ての入力量がランダムに変化し
得るという条件の下で,観測可能であり,また,測定可能である。
A.2 共同実験アプローチ
A.2.1 基本モデル
共同実験の計画,構成及び統計的処理については,JIS Z 8402規格群に規定されている。共同実験デー
タの統計的処理の前提となる最も単純なモデル(JIS Z 8402規格群と同一の記号を使用している。)を,式
(A.4)に示す。
e
B
m
y
+
+
=
·········································································· (A.4)
ここに,
m: yの期待値
B: 併行条件下でのかたよりの試験所成分。標準偏差σLの正規分布
に従うと仮定する。
e: 併行条件下での偶然誤差。標準偏差σWの正規分布に従うと仮
定する。
さらに,Bとeとには相関関係がないものと仮定する。
この単純なモデルに式(A.1)を適用して,一つの測定結果yに対して式(A.5)を求める。
)
(
)
(
)
(
2
2
2
e
u
B
u
y
u
+
=
································································ (A.5)
σL2及びσW2は,それぞれB及びeの分散である。これらは,試験所間の共同実験で得られた試験所間分
散sL2及び併行条件下での分散sr2によって推定される。これによって,u(B)=sL及びu(e)=srを用いて,こ
の測定結果に付随する合成標準不確かさu(y)を与える式(A.6)が求められる。
2
2
L
2
)
(
rs
s
y
u
+
=
········································································ (A.6)
JIS Z 8402-2:1999と比較すると,式(A.6)は,まさしく再現標準偏差の推定値sRである。このアプローチ
は,測定方法全体のパフォーマンスに注目しているため,“トップダウン”アプローチと呼ばれることがあ
る。
各試験所は,測定対象量の値に対する試験所の最良推定値yであると仮定して,mの推定値を式
...)
,
,
(
2
1x
x
f
y=
から計算していることに注意する。仮に,
...)
,
,
(
2
1x
x
f
y=
が測定システムの振る舞いを表す
完全な測定モデルであるとすると,sL及びsrによって表されるばらつきは,量x1, ..., xnのばらつきから生
じると考えられる。再現精度の条件の下で全ての大きな影響を与える量がランダムにばらつく場合,上に
22
Z 8404-1:2018 (ISO 21748:2017)
示したu(y)の物理的解釈を考慮して,式(A.6)のu(y)は,式(A.1)又は式(A.2)によって表されるu(y)の評価値
であることが分かる。
したがって,この規格がよりどころとする第一の原則は,共同実験によって得られた再現標準偏差は,
測定の不確かさ評価のための有効な根拠であるという点である。
A.2.2 真度のデータの組込み
一般に,真度は,確立された参照値に対するかたよりとして測定される。幾つかの共同実験において,
特定の測定系[通常は国際単位系(SI)]における測定方法の真度は,その測定系の単位で表した参照値μˆ
をもつ認証標準物質(CRM)又は計測標準を用いた実験によって検証される(JIS Z 8402-4:1999参照)。
ここで得られる統計モデルは,式(A.7)で表される。
e
B
μ
y
+
+
+
=
δ
ˆ
······································································ (A.7)
ここに,
μˆ: 参照値
δ: 測定方法のかたより
共同実験によって,推定された測定方法のかたよりδˆを得ることができる。これは,式(A.8)によって推
定される標準偏差をもつ。
(
)
p
s
n
s
s
r
R
2
2
ˆ
1
1−
−
=
δ
································································ (A.8)
ここに,
p: 試験所の数
n: 各試験所における繰返し回数
このかたよりに付随する標準不確かさ
)ˆ
(δ
u
は,式(A.9)から求められる。
)ˆ
(
)ˆ
(
2
2
ˆ
2
μ
δ
δu
s
u
+
=
··································································· (A.9)
ここに,
)ˆ(μ
u
: 共同実験における真度推定に用いられた参照値μˆの標
準不確かさ
共同実験によって推定されたかたよりが試験所の結果の計算に含まれる場合,それが無視できないもの
であれば,推定されたかたよりに付随する不確かさを不確かさのバジェット表に含めることが望ましい。
A.2.3 その他の効果−合成モデル
実際には,もちろん,sR及び
)ˆ
(δ
u
に,測定結果を左右する全ての効果のばらつきが含まれるわけではな
い。共同実験の性質上,重要な要因が抜けることがあったり,偶然又は意図的に一部の要因が欠けていた
り,過小評価されていたりする。この規格がよりどころとする第二の原則は,共同実験の枠組みにおいて
検討対象でなかった要因の効果については,無視できることを実証するか,又は明確な形で考慮するとい
う点である。
これは,yの推定値を求めるために必要な,公称値xiからの偏差x'iの効果を検討し,その効果の近似的
な直線性を想定することによって,簡単に達成される。この合成モデルは,式(A.10)で表す。
e
x
c
B
y
i
i+
′
+
+
+
=
∑
δ
μˆ
·························································(A.10)
23
Z 8404-1:2018 (ISO 21748:2017)
ここに,和Σに含める項は,B,δ及びeに含めた効果を除く全ての効果を網羅する。
こうした効果の例としては,サンプリングの影響,試験品の調製,及び個々の試験品の組成又はタイプ
のばらつきが挙げられる。厳密にいえば,これは,最も一般的なモデルを線形化した形である。GUMが
示すとおり,必要に応じて,より高次の項又は相関項を正確に取り入れることが可能である。
x'iの中心化(xiから公称値を減じる操作)はu(xi)に影響を及ぼさないこと,すなわち,u(x'i)=u(xi)であ
るという点に着目すると,式(A.10)から推定されるyの標準不確かさは,式(A.11)によって求められる。
)
(
)ˆ(
)
(
2
2
2
2
2
L
2
i
i
r
x
u
c
u
s
s
y
u
∑
+
+
+
=
δ
············································· (A.11)
ここに,和Σに含める項は,他の項で扱わない効果に限定される。
測定方法のパフォーマンス評価という枠組みにおいて,中間精度条件も式(A.10)で表せるといってよい
が,中間精度条件の下では,再現条件の下よりもランダムに変化する変数が少なくなるため,和Σに含め
たほうがよい変数の数は,それに対応して増える。ただし,一般的には,和Σをとる対象となる効果を適
切に選択すれば,式(A.10)は全ての精度条件に適用される。当然,sr及びsLの項がゼロで,全体的かたよ
りの不確かさが決められないという極端なケースでは,式(A.11)は,式(A.1)と同じになる。
次の二つの推論が存在する。
− 第一に,共同実験によって得られた定量的なデータが,検討中の試験結果に対して適用可能であるこ
とを立証することが必要である。
− 第二に,共同実験のデータが適切であるとしても,有効な不確かさを評価するために,追加される効
果[式(A.10)におけるx'i]を十分考慮するための更なる共同実験及び配慮が必要となる場合がある。
追加される効果を配慮するに当たっては,式(A.1)の適用が想定される。
最後に,この規格は,JIS Z 8402規格群で示す手順によって得られた併行精度,再現精度及び真度のデ
ータを検討することで,測定の不確かさの評価が確実に行えることを主張するに当たり,JIS Z 8402規格
群と同じ前提を用いている。
a) 再現精度のデータを使用する場合,全ての試験所のパフォーマンスが同様であると仮定する。特に,
使用された試験品に関する試験所の併行精度は同じであり,かたよりの試験所成分[式(A.10)におい
てはBの項で表される。]は,共同実験においてサンプリングされたものと同じ母集団からサンプリ
ングされたものである。
b) 共同実験において配付された試験物質は,均質であり,かつ,安定している。
A.3 アプローチの間の関係
A.1及びA.2の説明では,二つの明らかに異なる不確かさ評価のアプローチを示した。一方の極限にお
いて,GUMのアプローチは,数学的モデルの入力量に付随する分散に基づき,不確かさを分散の形で評
価する。他方の極限において,再現性実験の間,同じ影響量が典型的に変化するとすれば,観測したばら
つきは同じ不確かさの直接的な推定になっているという事実を利用している。実際には,異なるアプロー
チによって求めた不確かさの値は,次のことを含む様々な要因によって異なる。
a) 不完全な数学モデル(例えば,未知の効果の存在)
b) 再現性実験における,全ての影響量の不完全な,又は非典型的なばらつき
したがって,二つの異なる評価値の比較は測定モデルの完全性の評価として有効である。ただし,GUM
24
Z 8404-1:2018 (ISO 21748:2017)
のアプローチにおいてさえ,実験併行精度又はその他の精度の推定値が,不確かさへの異なった寄与とし
て取り込まれることが多いという点に注意が必要である。同様に,再現性を評価する前に,個々の効果に
ついて,少なくとも有意性が確認されるか,又は定量化されるのが普通である。したがって,実際的な不
確かさの評価は,しばしば,双方の極限の要素を用いている。
測定結果の解釈の一助として不確かさの値を結果とともに与える場合,各アプローチの不備を是正する
ことが重要である。実際のところ,モデルが不完全である可能性は,保守的な評価を行うこと,すなわち,
モデルの不確かさに追加的な配慮を加えることによって,解決される。この規格においては,入力量のば
らつきが不十分である可能性は,追加される効果を評価することによって解決される。これは,“トップダ
ウン”アプローチ及び“ボトムアップ”アプローチの要素を合成したハイブリッドアプローチを意味する。
25
Z 8404-1:2018 (ISO 21748:2017)
附属書B
(参考)
実験による不確かさ評価
B.1
感度係数推定のための実践的手順
入力量xiがその区間全体にわたって連続的に変化する可能性がある場合には,その変化の効果を直接検
討すると便利である。xiに対し結果がほぼ直線的に変化すると想定した場合の単純な手順を,次に示す。
a) 変数xiが変化する区間を選択する。その区間は,最良推定値(又は測定方法によって特定された値)
を中心とすることが望ましい。
b) xiの5以上のそれぞれの水準において,測定手順全体(又は,そのうちのxiの影響を受ける部分)を
実行する。必要に応じて繰り返す。
c) xiを横軸,測定結果を縦軸として,線形モデルを結果に当てはめる。
d) こうして得た直線の傾きは,式(A.1)又は式(14)における感度係数ciである。
このアプローチは,異なる試験品に対して異なる感度係数を示すことがある。これは,特定の品目又は
試験品の種類の総合的な検討においては利点となり得る。ただし,感度係数を幅広い事例に適用する場合
には,様々な試験品目が十分類似性のある挙動を示すことの検証が重要である。
B.2
偶然効果による不確かさを評価するための簡単な手順
入力量xjが,不連続である場合,又は容易に制御できない場合には,それに付随する不確かさを,変数
をランダムに変化させる実験の結果を解析することによって導き出すことができる。例えば,環境分析に
おいて,土壌の種類は分析結果に予想外の影響を与える可能性がある。偶然誤差が目的成分の量の大きさ
に対しほぼ独立している場合,実証された値が入手できる,又は既知の変化を引き起こす一連の試験品を
使うことによって,そのような変動に起因する誤差のばらつきを検証することが可能である。
一般的な手順を,次に示す。
a) 代表として選択した試験品に対して,全体の測定を実行する。そこでは,併行精度条件下で,それぞ
れの試験品について同じ回数の測定を繰り返す。
b) それぞれの観測値について,既知の値との差を計算する。
c) (目的の量によって分類された)測定結果に対して分散分析を行い,得られた平方和を用いて,群内
分散の推定値
2
w
s及び群間分散の推定値
2
bsを求める。xjの変動に起因する標準不確かさu(xj)は,sbに等
しい。
注記 異なる試験品又は試験品の種類が,検討しているその量に対して異なった影響を示す場合(す
なわち,その量と試験品の種類とに交互作用がある場合),その交互作用は,sbの値を大きくす
る。こうした状況の詳しい扱いは,この規格の適用範囲外である。
26
Z 8404-1:2018 (ISO 21748:2017)
附属書C
(参考)
不確かさ評価の例
C.1 自動車排気ガス中の一酸化炭素(CO)の測定
C.1.1 導入
乗用車は,発売前に型式試験を受け,その車種のエンジン及び一酸化炭素汚染ガスの排気システムから
の排気に関する法的要求事項への適合を確認する試験(適合性試験)が義務付けられている。認可の上限
値は,2.2 g/kmである。試験方法は,参考文献[21]に示されている。同指令には,次のような仕様がある。
− 走行サイクル(Euro96)は,速度(km/h),時間(秒)及び連動ギアの関数として与えられている。サ
イクル実行のため,試験対象の車両を規定のローラーベンチに載せる。
− 測定機器は,規定の一酸化炭素(CO)分析装置である。
− 環境は,規定の汚染監視室で管理する。
− 要員は,規定の教育訓練を受けている。
このような適合性試験は,自動車製造業者の生産施設にある試験所又は独立の試験所において実施する
ことが可能である。
C.1.2 共同実験のデータ
こうした試験方法を採用し,日常に使用する前に,その試験方法による試験結果に対して(さらに,試
験結果の不確かさに対して)影響を及ぼす要因又は原因を評価しておくことが必要である。様々な試験所
において実施された実験に基づいて,評価が行われる。試験方法を管理するためは,JIS Z 8402-2に従っ
て共同実験が計画され,実施される。この共同実験の目的は,決められた複数の試験所において日常に使
用した場合の,その試験方法の精度を推定することにある。精度の推定は,共同実験で収集したデータを,
JIS Z 8402-2に従って統計的に解析することによって行われる。共同実験は,各参加試験所が測定実施に
必要な全てのプロセスを行い,関係する全ての影響要因を考慮に入れる形で実施される。
このような共同実験によって,試験所の併行精度に大きな差がないこと,及び試験方法の併行標準偏差
は0.22 g/kmと推定し得ることが実証された。また,試験方法の再現性標準偏差は,0.28 g/kmと推定でき
る。
C.1.3 かたよりの管理
真度の評価(標準に対するかたよりの管理)には,方法論的及び技術的な問題がある。標準物質という
意味での“標準車両”は存在しない。したがって,真度は,使われる試験システムの校正によって管理し
なければならない。例えば,CO分析装置の校正は,標準ガスによって行うことができる。また,ローラ
ーベンチの校正は,時間,長さ,速度,加速度などの量について行うことが可能である。様々な速度にお
ける排出率に関する知識及びこれに類する情報から,これらの校正に付随する不確かさは,測定結果の不
確かさの大きな要因にならないことが確認されている(すなわち,全ての計算で求めた不確かさは,再現
標準偏差をはるかに下回る。)。したがって,かたよりは,適切な管理下にあると考えられる。
C.1.4 精度
ある試験所による複数回の試験走行の結果,併行標準偏差は約0.20 g/kmであることが実証された。こ
れは,共同試験で確認された併行精度の範囲内である。したがって,精度は良好な管理下にあると考えら
れる。
27
Z 8404-1:2018 (ISO 21748:2017)
C.1.5 試験品の妥当性
この試験方法の適用範囲は,それが“乗用車”に属する全ての車両に適していることを明らかにしてい
る。ほとんどの車両は適合性を比較的容易に達成しており,低い排気レベルでは不確かさが小さい傾向に
あるが,規制限界に近いレベルでは不確かさが重要となる。したがって,規制限界に近いレベルで評価さ
れた不確かさは,低い一酸化炭素(CO)排出レベルについては,合理的でやや保守的な推定であると判断
された。試験の結果,ある車両が規制限界を大きく超える排気ガスを排出したことが判明した場合,限界
値との比較が重要な意味をもつときは,更なる不確かさの検討が必要であろうという点に注意する。ただ
し,実際には,そのような車両が,改良を加えずに販売されることはあり得ない。
C.1.6 不確かさの評価
過去の検討によって,その試験所内でかたより及び精度が適切に管理されていることが実証され,共同
実験で行われなかった作業については他の要因が発生していなかったことから,標準不確かさの評価に再
現標準偏差を使用し,約95 %の信頼の水準を与える包含係数k=2とすれば,拡張不確かさはU=0.56 g/km
となる。
注記 適合性試験の分野における不確かさに関する結果の解釈については,ISO 10576-1[12]で検討され
ている。
C.2 食肉成分の定量
C.2.1 導入
食肉製品は,食肉成分が正確に表示されることを確実にするように規制されている。食肉成分は,窒素
含有量(総たんぱく質に換算)と脂肪含有量との組合せとして定量される。この例では,各要因が主とし
て箇条12で示した再現性の推定値に起因する場合に,不確かさの様々な要因を合成するための原則を示す。
C.2.2〜C.2.6の例は,参考文献[23]〜[26]に基づいている。
C.2.2 基本式
総食肉成分含有量wmeatは,式(C.1)で求める。
fat
pro
meat
w
w
w
+
=
······································································ (C.1)
ここに,
wpro: 質量百分率で表した総食肉たんぱく質含有量
wfat: 質量百分率で表した総脂肪含有量
総食肉たんぱく質含有量wproは,式(C.2)で求める。
N
mN
pro
100
f
w
w
=
···································································· (C.2)
ここに,
fN: その材料に固有の窒素係数
wmN: 総食肉窒素含有量
この場合,wmNは,ケルダール分析法で定量された総窒素含有量に等しい。
C.2.3 食肉成分含有量の定量における実験手順
食肉成分の定量に必要な実験手順は,次による。
a) 総脂肪含有量wfatを定量する。
b) ケルダール法によって,総食肉窒素含有量wmNを定量する(複数回の測定の平均値)。
c) 窒素係数fNを用いて,総食肉タンパク質含有量wproを計算する[式(C.2)]。
d) 総食肉成分含有量wmeatを計算する[式(C.1)]
28
Z 8404-1:2018 (ISO 21748:2017)
C.2.4 不確かさの成分
検討が必要な不確かさの成分は,C.2.3に挙げたそれぞれの量に付随するものである。最も重要なものは,
wmeatの約90質量%を構成するwproに関係する。wproに付随する最大の不確かさ成分は,次の要因によって
生じる。
a) 材料に関する知識が不十分なことによって生じる,係数fNの不確かさ
b) 分析間及び長時間にわたる詳細な分析の間での,分析方法の再現性の変化
c) 分析方法のかたよりに付随する不確かさ
d) 総脂肪含有量wfatの不確かさ
注記 不確かさa),b)及びc)は,それぞれ試料,試験所及び分析方法に関連する。全体の不確かさを
評価するときは,手順の個々の段階についての検討と共に,これら三つの要因をそれぞれの段
階で検討するとよい。
C.2.5 不確かさ成分の評価
C.2.5.1 fNの不確かさ
fNの不確かさは,公表された値の範囲から評価できる。参考文献[23]は,幅広い調査に基づいて,牛肉
の窒素係数が食肉の様々な産地及び切断部位によって大きく変化するという結果を示している。さらに参
考文献[23]は,fNについて観察された標準偏差が0.052であること,より幅広い試料の種類については相対
標準偏差が0.014であることを認めている。
注記 参考文献[23]での窒素係数の測定にはケルダール法を用いているため,ここでの目的に直接適
用可能である。
C.2.5.2 wtNの不確かさ
二つの共同実験[24][25]における情報から,再現性又は測定方法の実施における誤差から生じる不確かさの
評価が可能となる。共同実験の条件を詳しく検証したところ,第一に,共同実験が,優秀な能力ある代表
的な試験所によって,幅広い試料の種類について実施されていること,第二に,再現標準偏差sRが窒素レ
ベルと高い相関にあること,が明らかになった。両方の共同実験において,それぞれの標準偏差はwtNに
ほぼ比例しており,再現標準偏差での最も当てはめのよい式はsR=0.021wtN,同時に,併行標準偏差では
sr=0.018wtN,試験所間標準偏差ではsL=0.011wtN,であることが示された。
この方法は,それぞれ,2回の測定を行い平均値をとるように規定している。このため,単一の測定結
果の併行精度の推定値である併行分散は,試験所において二つの結果を平均していることを考慮して,2
で除さなければならない(表1のsrに関するコメントを参照)。したがって,総窒素含有量に付随する標
準不確かさu(wtN)は,式(C.3)のようになる。
tN
2
2
tN
2
2
L
tN
tN
017
.0
2
018
.0
011
.0
2
)
(
w
w
s
s
w
w
u
r
=
+
=
+
=
···················· (C.3)
式(C.3)は,試験方法の実施における妥当な変動に起因する,wtNの不確かさの最良評価値である。
併行精度の値は,個々の試験所の精度を受け入れるかどうかの合否判定をするための基準としても使用
できる。この判定方法は,試験所の二つの測定結果の差が95 %信頼区間(1.96
2
rs
にほぼ等しい)の外
にある場合は,結果を不合格とするのが望ましいと規定している。この確認によって,分析を行う試験所
の試験所内精度が共同実験において求められた精度に適合していることを調べる。
注記 この確認を時間をおいて繰り返したとき,約5 %を超える頻度で外れる場合は,精度が十分な

29
Z 8404-1:2018 (ISO 21748:2017)
管理下にない可能性があるため,手順を改善する措置が必要になる。
また,分析方法における未知のかたよりによって生じたwtNの不確かさに対しても,何らかの考慮をす
る必要がある。信頼できる標準物質がない場合は,基本的に異なる原理に基づく別の分析方法と比較して,
かたよりを求めるのが一般的である。様々な試料の種類について,ケルダール法と全窒素燃焼法とを比較
したところ,0.01 wtNの差が実証された。これは,JIS Q 0033:2002が規定する基準2σD[式(4)参照]の範
囲内であることから,かたよりに付随する不確かさは,再現精度において十分考慮されていることが確認
された。
C.2.5.3 wfatの不確かさ
脂肪分析に関する別の共同実験のデータ[26]は,再現標準偏差値を0.02 wfatと推定している。ここでも,
分析は2回行われ,その差が適切な併行精度の限界の範囲内である場合に限って結果が認められ,それに
よって,試験所の精度が管理されていることが確認される。脂肪の定量に適した標準物質についての事前
の検証作業によって,かたよりに付随する不確かさは再現精度の数値によって十分考慮されていることが
確認されている。
C.2.6 合成標準不確かさ
表C.1には,上記の数値を用いて計算した個々の値及び不確かさを示す。
表C.1−食肉成分に関する不確かさのバジェット表
量
xiの値
%(質量)
u(xi)
u(xi)/ xi
総脂肪含有量,wfat
5.50
0.110
0.020
総食肉窒素含有量,wmN
3.29
0.056
0.017
窒素係数,fN
3.65
0.052
0.014
総食肉たんぱく質含有量,wpro
90.1
90.1× 0.022 = 1.98
022
.0
014
.0
017
.0
2
2
=
+
総食肉成分含有量,wmeat
95.6
98
.1
110
.0
98
.1
2
2
=
+
0.021
約95 %の信頼の水準が求められている。これは,合成標準不確かさに包含係数k=2を乗じ,(二桁に丸
めると)約95 %の信頼の水準の総食肉成分含有量の拡張不確かさU=4.0 %が得られる。すなわち,wmeat
=95.6±4.0 %となる。
注記 “総食肉成分含有量”は,製品によって,100 %を超えることがある。
C.3 AOAC法(990.12)による一般生菌数の測定の不確かさ
C.3.1 導入
この測定方法は,食品の微生物活性の検査のための微生物学的方法[27]である。この方法では,乾燥培地
と水溶性ゲルの細菌培養プレートを用いる。培養プレートに,1プレート当たり試料をそれぞれ1.0 mlず
つ加え,約20 cm2の生育面に広げる。プレートで培養した菌のコロニを数える。測定対象量は,観測され
るコロニ形成単位の数である。カウントがゼロをとらない場合は,通常,log10(カウント),すなわち,コ
ロニ形成単位(CFU)のカウント数を底が10の対数で報告する。殻類,小麦,野菜の3種類の食品につい
て不確かさ評価を行う。
この例は,米国試験所認定協会の許諾を得て,参考文献[28]に公表されたデータに基づいている。参考
文献[27]も参照。
30
Z 8404-1:2018 (ISO 21748:2017)
C.3.2 共同実験のデータ
この測定方法は,汚染レベルが異なる六つの食品について,食品一つ当たり2試料,1試料につき2回
の繰返し測定を行う12試験所の共同実験によって検証された。データ解析はJIS Z 8402-2:1999によって
行われ,この検証実験には,正確な分取量(共同実験においては,一定量の試料が提供された。)に関する
ステップ以外の,試験プロセスの全てのステップが含まれていた。表C.2には,不確かさの評価が必要な
三つの食品について報告された併行相対標準偏差及び再現相対標準偏差の推定値を百分率で示した。
表C.2−生菌数に関する共同実験データ
食品
再現相対標準偏差
%
併行相対標準偏差
%
えび
11.1
9.8
野菜
9.2
6.3
小麦粉
5.8
5.3
併行精度と再現精度のデータは全て,得られたlog10(カウント)値の平均値に対する相対標準偏差で表
されている。このことは,応答レベルにほぼ比例するばらつきを示し,相対標準偏差はほぼ一定である,
この特定の測定方法に対して便利である。
C.3.3 かたよりの管理
かたよりの試験所成分が予想される範囲内にあることを確認するため,試験所と参照試験所との比較実
験を行った。野菜及びえびの結果は,常に10 %未満であった(
x
Δl
1.0
<
に対応,ここで,xは関係する測
定結果の平均値)。小麦粉試料については,5 %のかい離であった(
lΔ≦0.05xに対応)。これらの偏差は,
明らかに再現標準偏差と整合しており,かたよりの試験所成分は許容できるものと判断される。
C.3.4 精度の管理
試験所内ばらつきが予想される範囲内であることを確認するため,10回の繰返しによって併行相対標準
偏差の推定値を求める。全ての食品の併行相対標準偏差は5 %以内である(sl≦0.05x)。したがって,併行
精度が許容できるだけでなく,7.3.2に示したとおり,より小さい調整された再現精度を計算することがで
きる。調整された再現相対標準偏差を表C.3に示す。
表C.3−調整された再現相対標準偏差
食品
再現相対標準偏差
%
試験所間相対標準
偏差
%
併行相対標準偏差
%
調整された
再現相対標準偏差
%
えび
11.1
5.2
5.0
7.2
野菜
9.2
6.7
5.0
8.4
小麦粉
5.8
2.4
5.0
5.5
C.3.5 試験品目の妥当性の確認
C.3.5.1 試料調製及び前処理
共同実験ではサンプリングのステップを除いている。この追加の不確かさ成分を考慮すると,試料調製
(サブサンプリング,ひょう量)のステップは(専門家の意見によれば)合成標準不確かさに,更に3.0 %
の寄与があると見積もられている。この成分の寄与は,表C.4に含めた。
31
Z 8404-1:2018 (ISO 21748:2017)
C.3.5.2 応答レベルに伴う不確かさの変化
再現性,繰返し性,追加の試料調製ステップの寄与は,生菌数にほぼ比例すると考えられている。この
ことは,式(10)の形の基本モデルを示唆している。すなわち,係数bを調整された再現相対標準偏差と等
しいとおくこと,及び追加のサンプリングの寄与を比例的な寄与として扱うということである,このこと
は,上で述べたように,全ての不確かさの寄与を相対値の形で示すという,簡単なアプローチと等価であ
る。
C.3.6 合成標準不確かさ
合成標準不確かさ(相対標準偏差で表した)は,それぞれの食品について表C.4に示すように計算され
る。
表C.4−調整された再現相対標準偏差
食品
試験所間相対標準偏差
%
併行相対標準偏差
%
試料調製の標準不確
かさへの寄与
%
合成標準不確かさu(y)
(相対標準偏差)
%
えび
5.2
5.0
3.0
7.8
野菜
6.7
5.0
3.0
8.9
小麦粉
2.4
5.0
3.0
6.4
C.3.7 拡張不確かさ
拡張不確かさは,約95 %の信頼の水準を与えるように,包含係数2を用いて計算される。それによると,
えび,野菜及び小麦粉について,拡張不確かさは,[観測されたlog10(カウント)の百分率として]それ
ぞれ15.6 %,17.8 %及び12.8 %となる。
C.3.8 補足
一般生菌数の結果は,通常log10(カウント)でまとめられる。ただし,個々の試験品目については,コ
ロニ形成単位の拡張不確かさの区間で報告することがしばしば有用である。これは,C.3.7に示すように,
log10(カウント)に対する拡張不確かさを計算して,それをコロニ形成単位に変換するのがよい。このこ
とを値が150 CFUの試験品に対する拡張不確かさの区間の計算で説明する。関連する計算を表C.5にまと
める。
表C.5−調整された再現相対標準偏差
食品
標準不確かさ
(相対標準偏差)
拡張不確かさ(U)
(CFUカウント
の百分率)
150 CFUの対
数(log10)
対数(log10)
での拡張不確
かさ
CFUカウントの
対数(log10)の不
確かさ区間
最終的な
CFUカウン
トの不確かさ
区間
えび
7.8
15.6
2.176 1
0.339 5
1.836 6〜2.515 6
68〜328
野菜
8.9
17.8
2.176 1
0.387 3
1.788 8〜2.563 4
61〜366
小麦粉
6.4
12.8
2.176 1
0.278 5
1.897 6〜2.454 6
79〜285
C.4 粗繊維の定量の不確かさ
C.4.1 導入
この測定方法は,動物飼料中の粗繊維の定量のために用いられる。粗繊維は,酸にもアルカリにも溶解
しない,脂肪を含まない有機物の量と定義される。動物飼料中の繊維の含有量は,典型的には質量分率で
32
Z 8404-1:2018 (ISO 21748:2017)
2 %から12 %の間である。
C.4.2 繊維濃度の計算
繊維濃度Cfibreは,試料の質量での百分率(すなわち,百分率で表した質量分率であり,この例では単に
“%”と表す。)として,次の式によって計算される。
(
)(
)100
s
ba
bd
sa
sd
fibre
×
−
−
−
m
m
m
m
m
C
················································ (C.4)
ここに,
ms: 試料の質量(およそ1 gが分析に供される。)(g)
msd: 恒量になるまで乾燥した試料とるつぼの質量(g)
msa: 灰化後の試料とるつぼの質量(g)
mbd: 恒量になるまで乾燥した空試験のるつぼの質量(g)
mba: 灰化後の空試験のるつぼの質量(g)
注記 空試験は,空のるつぼを用い,測定方法の全てのステージを行う。
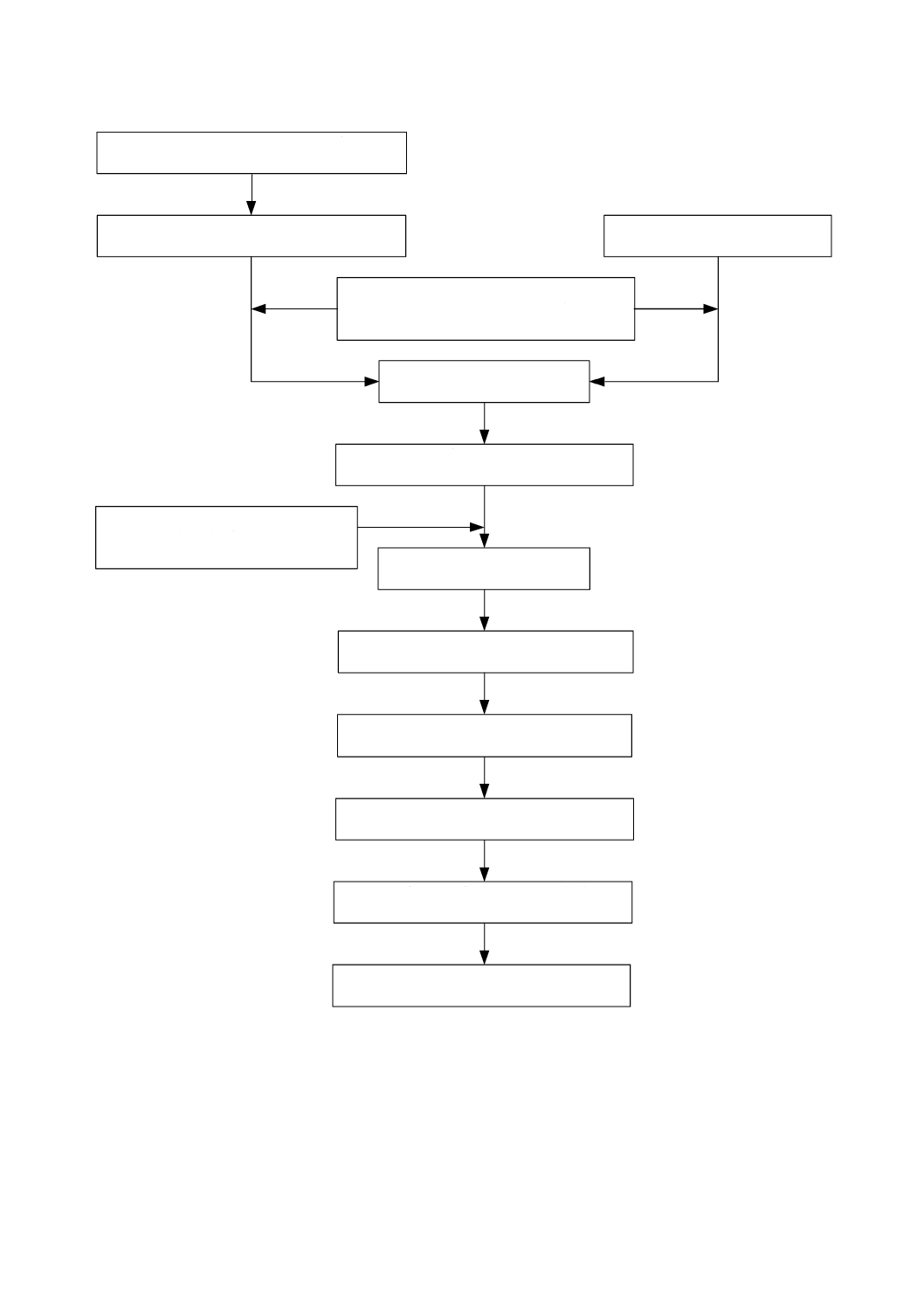
測定方法の主な手順を表した流れ図を図C.1に示す。
C.4.3 共同実験のデータ
この方法については,JIS Z 8402-2:1999に従った共同実験が行われた。この共同実験において,代表的
な繊維濃度及び脂質濃度をもつ,五つの異なる飼料が分析された。参加者は,試料の粉砕を含む,この方
法の全ての手順を実施した。得られた繰返し性と再現性の推定値を表C.6に示す。
表C.6−粗繊維の共同実験データ
試験試料
繊維含有量の平均値
%
再現標準偏差(sR)
%
再現相対標準偏差
併行標準偏差(sr)
%
A
2.3
0.293
0.127
0.198
B
12.1
0.563
0.0465
0.358
C
5.4
0.390
0.0722
0.264
D
3.4
0.347
0.102
0.232
E
10.1
0.575
0.0569
0.391
C.4.4 かたよりの制御
かたよりの試験所成分が予想される範囲内であるかを確認するために,試験所は,当該の分析方法で認
証された(測定対象量は特定の分析方法に対する参照によって定義されるため,このことは必須である。)
標準物質を用いて分析を行った。認証値は,93 g/kg±14 g/kg(9.3 %)である。試験所による分析結果は
9.16 %であり,これに対応した試験所のかたよりはΔl=−0.14 %となる。これは,およそ9 %レベルでの
再現標準偏差から予想される範囲内に十分入っている。認証値の標準不確かさは,7 g/kg(質量分率0.7 %)
であり,表C.6にある同様の繊維レベルでの再現標準偏差と比較して小さい。従って,試験所のかたより
は,許容できるものであると判断できる。
C.4.5 精度の管理
試験所における方法の検証の一部として,共同実験で用いられた幾つかの試料と同じような繊維濃度を
もつ飼料を用いて繰返し性(バッチのばらつき内)の実験が行われた。結果を表C.7にまとめた。表C.6
と比較すると,試験所は,共同実験のばらつきと同様のばらつきを得ている。
33
Z 8404-1:2018 (ISO 21748:2017)
表C.7−粗繊維の試験試料における繰返し性のデータ
試験試料
繊維含有量の平均値
%
併行標準偏差(sr)
%
F
3.0
0.198
G
5.5
0.264
H
12.0
0.358
C.4.6 応答レベルによる不確かさの変化
表C.6の併行標準偏差及び再現性標準偏差は,明らかに,粗繊維の濃度レベルに応じて増加している。
ただし,再現相対標準偏差の傾向が単純な比例モデルでは不適切である場合もある。このようなときに,
その試験所は,ある繊維レベルの不確かさを,共同実験における類似の繊維レベルで得られた再現性を基
に選ぶことができる。例えば,2.5 %(質量分率)以下の繊維レベルについては,0.29 %(質量分率)の再
現標準偏差を表C.6から選ぶ。
C.4.7 追加される要因
試験所は,他の影響量が通常の試験試料の測定結果に及ぼす影響について,実験及び検討を実施してい
た。それらに基づく不確かさの評価の結果を表C.8に示す。恒量にするための乾燥以外は,要因のいずれ
も有意ではない。測定プロセスのこの部分に付随する不確かさは,試験所による恒量操作の仕様によって
得られた。すなわち,標準分析方法は恒量について規定しておらず,試験所は,乾燥時間を延ばした場合
に質量の差が0.002 g以内に収まるように,乾燥時間を選択していた。推定される最大の変動値を3で除
すことによって得られた不確かさとして,1 gの試料を用いて分析した場合,0.115 %(質量分率)が得ら
れる。
表C.8−粗繊維の定量における影響量の効果
不確かさの要因
値
標準不確かさ 付随する不確か
さを併行標準偏
差で表したもの
%
情報源
試料の質量
1.0 g
0.000 20 g
0.000 20
校正証明書
酸の濃度
−
−
0.000 30
酸濃度による繊維量変化の公表データ
アルカリの濃度
−
−
0.000 48
アルカリ濃度による繊維量変化の公表デー
タ
酸分解の時間
−
−
0.009 0
分解時間による繊維量変化の公表データ
アルカリ分解の時間
−
−
0.007 2
分解時間による繊維量変化の公表データ
恒量にするための乾燥
−
0.001 15 g
−
試験所における仕様
灰化の温度及び時間
−
無視できる
−
公表データ。灰化温度及び時間を変えても有
意な変化はない。
空試験の間の灰化後の減量
−
無視できる
−
実験による検証
C.4.8 合成標準不確かさ
恒量にするための乾燥に伴う不確かさは粗繊維の繊維レベルに比例するわけではないため,不確かさの
評価に単純な比例モデルを適用することはできない。その代わりに,粗繊維の典型的な繊維レベルにおい
て不確かさの評価を行うことが便利である。代表的な繊維レベルについて推定された不確かさを表C.9に
示す。

34
Z 8404-1:2018 (ISO 21748:2017)
表C.9−調整された再現相対標準偏差
繊維量レベル
%
再現標準偏差(sR)
%
追加された試料乾燥の
寄与
%
合成標準不確かさu(y)
%
2.5以下
0.293
0.115
0.31
2.5〜5
0.390
0.115
0.41
5〜10
0.575
0.115
0.59
C.4.9 拡張不確かさ
拡張不確かさを,約95 %の信頼の水準を与える包含係数2を用いて計算すると,表C.9に示すように,
幾つかの繊維量レベルにおいて,それぞれ0.6 %,0.8 %,1.2 %が得られる。
35
Z 8404-1:2018 (ISO 21748:2017)
図C.1−粗繊維の分析手順
粗繊維量を百分率で計算
1 mmのふるいを通過するように試料を
粉砕
試料1 gをるつぼに入れてひょう(秤)量
空試験のるつぼのひょう量
ろ過助剤,消泡剤を加えた後,沸騰した
硫酸(H2SO4)150 mlを添加
30分間,激しく煮沸
ろ過,沸騰水30 mlで3回洗浄
消泡剤を加えた後,沸騰した水酸化
カリウム(KOH)溶液150 mlを添加
30分間,激しく煮沸
ろ過,沸騰水30 mlで3回洗浄
真空引き,アセトン25 mlで3回洗浄
恒量になるまで130 ℃で乾燥
475 ℃〜500 ℃で灰化,ひょう量
36
Z 8404-1:2018 (ISO 21748:2017)
参考文献
[1] JIS Z 8101-1:2015 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: General statistical terms
and terms used in probability
[2] JIS Z 8101-2:2015 統計−用語及び記号−第2部:統計の応用
注記 対応国際規格:ISO 3534-2,Statistics−Vocabulary and symbols−Part 2: Applied statistics
[3] JIS Z 8101-3 統計−用語と記号−第3部:実験計画法
注記 対応国際規格:ISO 3534-3,Statistics−Vocabulary and symbols−Part 3: Design of experiments
[4] JIS Z 8402-1:1999 測定方法及び測定結果の精確さ(真度及び精度)−第1部:一般的な原理及び定
義
注記 対応国際規格:ISO 5725-1,Accuracy (trueness and precision) of measurement methods and results
−Part 1: General principles and definitions
[5] JIS Z 8402-2:1999 測定方法及び測定結果の精確さ(真度及び精度)−第2部:標準測定方法の併行
精度及び再現精度を求めるための基本的方法
注記 対応国際規格:ISO 5725-2,Accuracy (trueness and precision) of measurement methods and results
−Part 2: Basic method for the determination of repeatability and reproducibility of a standard
measurement method
[6] JIS Z 8402-3:1999 測定方法及び測定結果の精確さ(真度及び精度)−第3部:標準測定方法の中間
精度
注記 対応国際規格:ISO 5725-3,Accuracy (trueness and precision) of measurement methods and results
−Part 3: Intermediate measures of the precision of a standard measurement method
[7] JIS Z 8402-4:1999 測定方法及び測定結果の精確さ(真度及び精度)−第4部:標準測定方法の真度
を求めるための基本的方法
注記 対応国際規格:ISO 5725-4,Accuracy (trueness and precision) of measurement methods and results
−Part 4: Basic methods for the determination of the trueness of a standard measurement method
[8] JIS Z 8402-5:2002 測定方法及び測定結果の精確さ(真度及び精度)−第5部:標準測定方法の精度
を求めるための代替法
注記 対応国際規格:ISO 5725-5,Accuracy (trueness and precision) of measurement methods and results
−Part 5: Alternative methods for the determination of the precision of a standard measurement
method
[9] JIS Z 8402-6:1999 測定方法及び測定結果の精確さ(真度及び精度)−第6部:精確さに関する値の
実用的な使い方
注記 対応国際規格:ISO 5725-6,Accuracy (trueness and precision) of measurement methods and results
−Part 6: Use in practice of accuracy values
[10] JIS Z 9020-4:2018 管理図−第4部:累積和管理図
注記 対応国際規格:ISO 7870-4,Control charts−Part 4: Cumulative sum charts
[11] JIS Z 9020-2:2016 管理図−第2部:シューハート管理図
注記 対応国際規格:ISO 7870-2,Control charts−Part 2: Shewhart control charts
37
Z 8404-1:2018 (ISO 21748:2017)
[12] ISO 10576-1,Statistical methods−Guidelines for the evaluation of conformity with specified requirements−
Part 1: General principles
[13] ISO 11648 (all parts),Statistical aspects of sampling from bulk materials
[14] JIS Q 0033:2002 認証標準物質の使い方
注記 対応国際規格:ISO Guide 33,Reference materials−Good practice in using reference materials
[15] JIS Q 17025:2005 試験所及び校正機関の能力に関する一般要求事項
注記 対応国際規格:ISO/IEC 17025,General requirements for the competence of testing and calibration
laboratories
[16] ISO/IEC Guide 98-3:2008,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
[17] ISO/IEC Guide 99:2007,International vocabulary of metrology−Basic and general concepts and associated
terms (VIM)
[18] JIS Q 17043:2011 適合性評価−技能試験に対する一般要求事項
注記 対応国際規格:ISO/IEC 17043,Conformity assessment−General requirements for proficiency
testing
[19] AFNOR FD X07-021(1999年10月),Normes fondamentales−Métrologie et applications de la statistique−
Aide à la démarche pour l'estimation et l'utilisation de l'incertitude des mesures et des résultats d'essais
[20] Recommendation INC-1(1980), BIPM
[21] European Directive 70/220,自動車排出ガスの大気汚染対策
[22] Kaarls, Procès-verbaux du Comité International des Poids et Mesures, 49, BIPM, 1981, pp A.1-A.12
[23] Analytical Methods Committee. Analyst (Lond.) . 1993, 118 p. 1217
[24] Shure, B., Corrao, P.A., Glover, A. and Malinowski, A.J. J. AOAC Int 1982., 65 p. 1339
[25] King-Brink, M. and Sebranek, J.G. J., AOAC Int. 1993, 76p. 787
[26] Breese Jones, D. US Department of Agriculture Circular No. 183 (August 1931)
[27] Official Methods of Analysis, AOAC Int. Gaithersburg, MD, Twentieth Edition, 2016
[28] A2LA Guidance Document G108−Guidelines for Estimating Uncertainty for Microbiological Counting
Methods. American Association for Laboratory Accreditation, 2014