Z 8402-5:2002 (ISO 5725-5:1998)
(1)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人 日本規格協会(JSA)から,工業標
準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業
大臣が制定した日本工業規格である。
制定に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO 5725-5:1998,Accuracy (trueness
and precision) of measurement methods and results―Part 5:Alternative methods for the determination of the
precision of a standard measurement methodを基礎として用いた。
JIS Z 8402-5には,次に示す附属書がある。
附属書A(規定)JIS Z 8402で用いられる記号
附属書B(参考)アルゴリズムA及びSで用いられる係数の誘導
附属書C(参考)ロバストな解析に使用する式の誘導
附属書D(参考)参考文献
JIS Z 8402は,一般名称を“測定方法及び測定結果の精確さ(真度及び精度)”として,次の部によって
構成される。
第1部:一般的な原理及び定義
(Part 1:General principles and definitions)
第2部:標準測定方法の併行精度及び再現精度を求めるための基本的方法
(Part 2:Basic method for the determination of repeatability and reproducibility of a standard
measurement method)
第3部:標準測定方法の中間精度
(Part 3:Intermediate measures of the precision of a standard measurement method)
第4部:標準測定方法の真度を求めるための基本的方法
(Part 4:Basic methods for the determination of the trueness of a standard measurement method)
第5部:標準測定方法の精度を求めるための代替法
(Part 5:Alternative methods for the determination of the precision of a standard measurement
method)
第6部:精確さに関する値の実用的な使い方
(Part 6:Use in practice of accuracy values)
Z 8402-5:2002 (ISO 5725-5:1998)
(2)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 2
2. 引用規格 ························································································································ 2
3. 定義 ······························································································································ 3
4. 水準分割計画 ·················································································································· 3
4.1 水準分割計画の適用 ······································································································· 3
4.2 水準分割計画のレイアウト······························································································· 4
4.3 水準分割実験の構成 ······································································································· 4
4.4 統計的モデル ················································································································ 5
4.5 水準分割実験データの統計的解析······················································································ 6
4.6 データの一致性と外れ値の吟味························································································· 7
4.7 水準分割実験結果の報告 ································································································· 8
4.8 例1:水準分割実験―たんぱく質の定量 ············································································· 8
5. 不均質物質に関する計画 ·································································································· 14
5.1 不均質物質に関する計画の適用························································································ 14
5.2 不均質物質に対する実験計画のレイアウト ········································································· 16
5.3 不均質物質の実験の構成 ································································································ 16
5.4 不均質物質の実験の統計モデル························································································ 17
5.5 不均質物質の実験データの統計解析 ·················································································· 18
5.6 データの一致性と外れ値の精査························································································ 21
5.7 不均質物質の実験結果の報告··························································································· 22
5.8 例2:不均質物質の実験 ································································································· 22
5.9 不均質物質の計画における一般的計算公式 ········································································· 29
5.10 例3:一般公式の適用 ··································································································· 31
6. ロバストなデータ解析方法 ······························································································· 34
6.1 ロバストなデータ解析方法の適用····················································································· 34
6.2 ロバストな解析:アルゴリズムA ····················································································· 36
6.3 ロバストな解析:アルゴリズムS ····················································································· 37
6.4 公式:水準を分割しない計画の一つの測定水準に関するロバストな解析 ·································· 38
6.5 例4:水準を分割しない計画の一つの測定水準に関するロバストな解析 ··································· 39
6.6 公式:水準分割計画の一つの測定水準に対するロバストな解析 ·············································· 43
6.7 例5:水準分割計画の一つの測定水準に対するロバストな解析 ··············································· 43
6.8 公式:不均質物質の実験のある一つの測定水準に対するロバストな解析 ·································· 46
6.9 例6:不均質物質の実験のある一つの測定水準に対するロバストな解析 ··································· 46
附属書A(規定)JIS Z 8402で用いられる記号 ·········································································· 50
Z 8402-5:2002 (ISO 5725-5:1998) 目次
(3)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
附属書B(参考)アルゴリズムA及びSで用いられる係数の誘導 ················································· 53
附属書C(参考)ロバストな解析に使用する式の誘導································································· 55
附属書D(参考)参考文献 ···································································································· 56
解 説 ······························································································································· 57
Z 8402-5:2002 (ISO 5725-5:1998)
(4)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
白 紙
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8402-5:2002
(ISO 5725-5:1998)
測定方法及び測定結果の精確さ(真度及び精度)―
第5部:標準測定方法の精度を求めるための代替法
Accuracy (trueness and precision) of measurement methods and results―
Part 5:Alternative methods for the determination of the precision of a
standard measurement method
序文 この規格は,1998年に第1版として発行されたISO 5725-5,Accuracy (trueness and precision) of
measurement methods and results―Part 5:Alternative methods for the determination of the precision of a standard
measurement methodを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規格で
ある。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
0.1 この規格のこの部では,測定方法の精確さを表すために,“真度”と“精度”の二つの用語を用いて
いる。“真度”は,多数の測定結果の平均値と,真の値又は参照値との一致の程度を示すものである。“精
度”は測定結果の間の一致の程度を示すものである。
0.2 これらの量の一般的な考察はこの規格の第1部で示されており,この部では改めて記述しない。第1
部は基本的な定義と一般的な原理が示されているので,この部と第1部を併せて読まれることが望ましい。
0.3 この規格の第2部は,試験室間共同実験によって標準的な精度,すなわち,併行標準偏差及び再現標
準偏差を推定する方法を対象とし,水準を分割しない計画によってこれを行う基本的方法を規定している。
この規格のこの部は,この基本的方法に対する代替方法を規定するものである。
a) 基本的方法では,同じオペレータによる一つのサンプルの測定結果が,同一サンプルの次の測定結果
に影響する可能性があり,その結果,併行精度及び再現精度の標準偏差の推定値がかたよりをもつ危
険性がある。この危険性が重大であると考えられる場合は,これを軽減するため,この規格のこの部
に規定する水準分割計画による方が好ましい。
b) 基本的方法では,実験に使用する同一試料のサンプルを多数用意しなければならない。不均質物質の
場合はこれが不可能であるため,基本的方法では,再現標準偏差の推定値がサンプル間のばらつきに
よって大きくなる。この規格のこの部の不均質物質に関する計画は,サンプル間のばらつきについて
基本的方法では得られない情報を提供する。この方法によってサンプル間のばらつきを除去した再現
精度の推定値を計算することができるであろう。
c) 基本的方法では,外れ値の検定を実施して,併行精度及び再現精度の標準偏差の計算から除外すべき
データを特定する必要がある。外れ値を除外すれば,併行精度及び再現精度の標準偏差の推定値が大
きく変わることがあり,実際に外れ値の検定を行う場合,除外すべきデータはデータ解析者の判断に
よって決定しなければならないときがある。この規格のこの部は,外れ値の検定によってデータを除
2
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
外することなく,外れ値を含むデータから併行精度及び再現精度の標準偏差を計算することができて,
結果がデータ解析者の判断に左右されないロバストなデータ解析方法を規定する。
参考1. 統計的解析では,外れ値の存在など,データ解析上の前提条件が崩れた場合に,その影響の
受けにくさをロバストネス(頑健性)と呼ぶ。この規格では“ロバストな”という言葉を,
“外れ値の影響を受けにくい”いう意味で用いている。
2. “水準を分割しない計画”を,JIS Z 8402-2では“一様水準実験”(1.3の備考2.,1.5,5.1.1,
7.2.7,7.6.1,B.1.8)と称した。また,JIS Z 8402-2の0.3において述べた“(分割法のような)
別な種類の実験計画”は,この部で扱う“水準分割計画”を意味している。
1. 適用範囲 JIS Z 8402のこの部は,
− 標準測定方法の併行標準偏差及び再現標準偏差を求めるための基本的方法に対する代替方法,すなわ
ち,水準分割計画及び不均質物質に関する計画の詳細
− 計算からデータを除外するための外れ値の検定を行うことなく精度評価実験の結果を解析するロバス
トな方法,特にその詳細な適用方法
を規定する。
この規格のこの部は,JIS Z 8402-2の基本的計画よりも場合によっては価値がある代替計画を規定し,
かつ,JIS Z 8402-2の方法よりもデータ解析者の判断に対する依存度合いが小さい併行標準偏差及び再現
標準偏差の推定値を与えるロバストな解析方法を規定することによって,JIS Z 8402-2を補完するもので
ある。
参考 この規格では“ロバストな”という言葉を,“外れ値の影響を受けにくい”という意味で用いて
いる。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
(修正している),NEQ(同等でない)とする。
ISO 5725-5:1998,Accuracy (trueness and precision) of measurement methods and results―Part 5:
Alternative methods for the determination of the precision of a standard measurement method
(IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発効年を付記してあるものは,記載の年の版だけがこの規格の規定を構
成するものであって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その
最新版(追補を含む。)を適用する。
JIS Z 8101-1 統計―用語と記号―第1部:確率及び一般統計用語
備考 ISO 3534-1:1993 Statistics―Vocabulary and symbols―Part 1:Probability and general statistical
termsからの引用事項は,この規格の該当事項と同等である。
JIS Z 8101-2 統計―用語と記号―第2部:統計的品質管理用語
備考 ISO 3534-2:1993 Statistics―Vocabulary and symbols―Part 2:Statistical quality controlからの
引用事項は,この規格の該当事項と同等である。
JIS Z 8101-3 統計―用語と記号―第3部:実験計画法
備考 ISO/FDIS 3534-3:1999 Statistics―Vocabulary and symbols―Part 3:Design of experimentsが,
3
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この規格と一致している。
JIS Z 8402-1:1999 測定方法及び測定結果の精確さ (真度及び精度)―第1部:一般的な原理及び定
義
備考 ISO 5725-1:1994 Accuracy (trueness and precision) of measurement methods and results―
Part 1:General principles and definitionsが,この規格と一致している。
JIS Z 8402-2:1999 測定方法及び測定結果の精確さ (真度及び精度)―第2部:標準測定方法の併行
精度及び再現精度を求めるための基本的方法
備考 ISO 5725-2:1994 Accuracy (trueness and precision) of measurement methods and results―
Part 2:Basic method for the determination of repeatability and reproducibility of a standard
measurement methodが,この規格と一致している。
3. 定義 この規格の目的に合わせ,JIS Z 8101-1,JIS Z 8101-2及びJIS Z 8402-1に定義された用語を
用いる。
この規格で用いる記号を,附属書Aに示す。
4. 水準分割計画
4.1
水準分割計画の適用
4.1.1
この規格の第2部で述べた水準を分割しない計画(一様水準実験)では,各参加試験室が,各測定
水準について同一試料を2回以上測定しなければならない。この計画では,一つめの測定結果が,同一試
料の次の測定結果に影響してしまうことをオペレータが容認するおそれがある。その場合には精度評価実
験の結果はゆがめられる。すなわち,併行標準偏差σrの推定値は小さくなり,試験室間標準偏差σLの推
定値は大きくなる。水準分割計画では,各参加試験室が,各測定水準について,2個の類似した試料から
採ったサンプルのそれぞれを与えられ,オペレータは両者が同一ではないことを告げられるが,サンプル
の違いの程度については告げられないものとする。このため水準分割計画は,一つめのサンプルの測定結
果がもう一つのサンプルの測定結果に影響をおよぼす危険性を減らして,標準測定方法の併行標準偏差及
び再現標準偏差を求める方法といえる。
4.1.2
水準分割実験の一つの測定水準で得たデータを用いて,片方のサンプルのデータに対して類似した
もう一方のサンプルのデータをプロットすることによってグラフを描くことができる。例を図1に示す。
このようなグラフは,試験室の中でほかと比べてかたよりが大きな試験室を特定することに役立つ。これ
は,大きい試験室のかたよりの原因を追及し,その是正措置をとる場合に役立つ。
4.1.3
測定方法の併行標準偏差及び再現標準偏差は,一般にサンプルの測定水準に依存する。例えば,測
定結果が化学分析によって得たある成分の含有率である場合,その成分の含有率が増加すれば,併行標準
偏差及び再現標準偏差も大きくなるのが普通である。水準分割実験では,ある実験水準で使用する二つの
類似試料は,同じような併行標準偏差及び再現標準偏差を与えることが期待される程度に類似していなけ
ればならない。水準分割計画では,ある実験水準に使用する二つのサンプルがほぼ同一水準の測定結果を
与えれば十分であり,二つのサンプルが大きく異なるように計画しても得るところはない。
化学分析においては,対象とする成分を含むマトリックスが精度に影響することが多い。したがって,
水準分割実験では,各測定水準について類似したマトリックスの二つのサンプルが必要である。十分類似
したサンプルは,対象成分を少量添加することによって得られることがある。サンプルが天然物又は工業
製品の場合,水準分割実験に使用するために十分類似したサンプルを得ることが困難な場合がある。この
4
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
場合は,同一製品の二つのバッチを使用することが一つの解決策であろう。忘れてならないのは,水準分
割実験においてサンプルを選択する目的は,オペレータに同一であることを期待させないサンプルを提供
することである。
4.2
水準分割計画のレイアウト
4.2.1
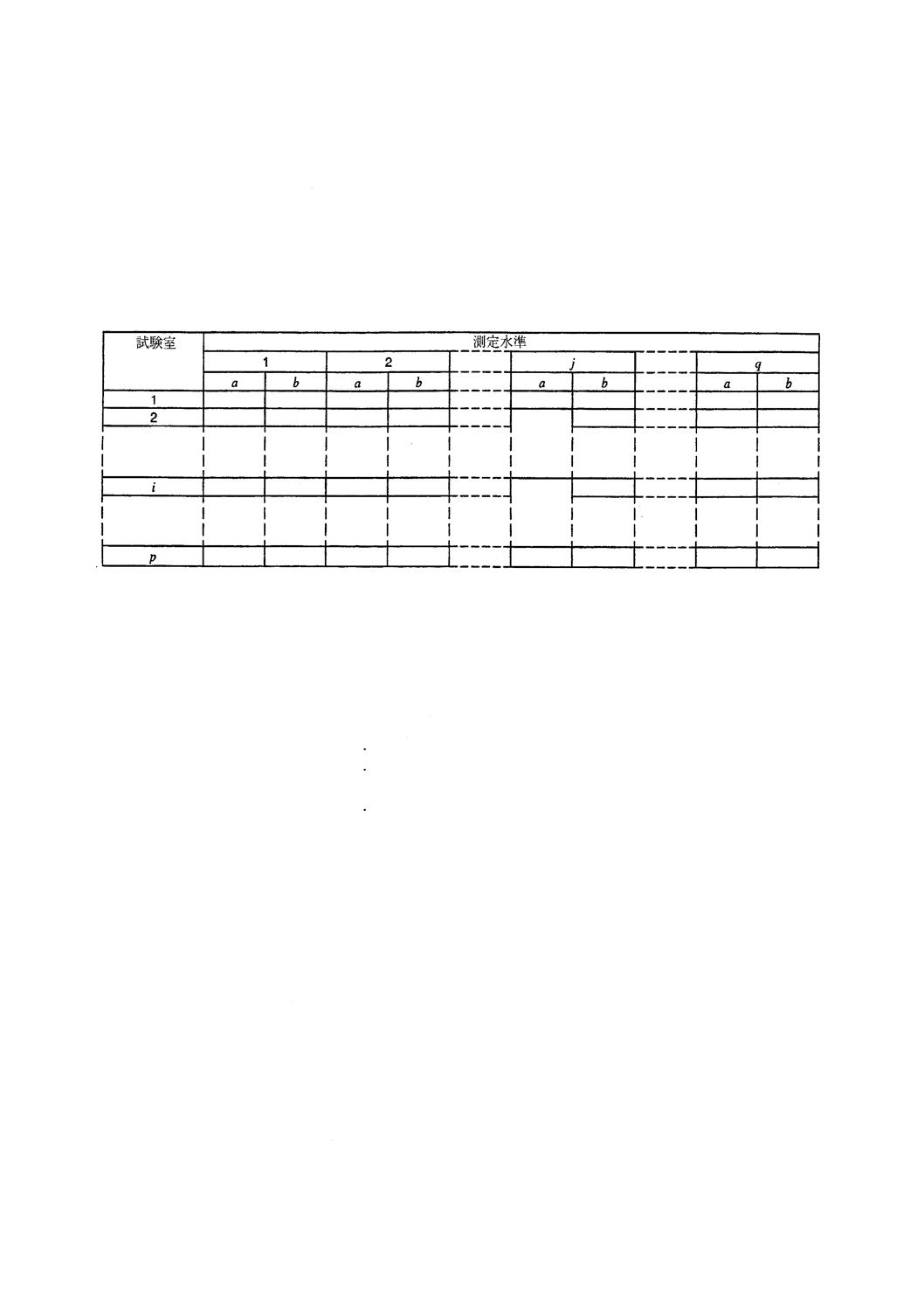
表1に水準分割計画のレイアウトを示す。
p箇所の各参加試験室はq個の測定水準ごとに二つのサンプルを測定する。
ある測定水準の二つのサンプルをa及びbで表し,aは一方の試料から採ったサンプルを,bはもう一方
の類似試料のサンプルを意味する。
4.2.2
水準分割実験のデータを
yijk
で表すが,ここで,
添字iは試験室を意味し(i=1,2,...,p)。
添字jは測定水準を意味し( j=1,2,...,q)。
添字kはサンプルを意味する(k=a又はb)。
4.3
水準分割実験の構成
4.3.1
水準分割実験の計画に当たっては,JIS Z 8402-1の6.の記述を参照されたい。
JIS Z 8402-1の6.3には,実験に参加する試験室数を求めるための式(一般にAで表される値を含む式)
が多数示されている。水準分割実験においてこれに対応する式は,次のとおりである。
備考 これらの式はJIS Z 8402-1 6.3.2.2.の備考24. に示す方法によって導いた。
併行標準偏差及び再現標準偏差の推定値の不確かさを評価するため,次の値を計算する。
併行精度については
Ar=1.96
)]
(
/[
1
2
1
−
p
······························································· (1)
であり,γ=σR /σrとおくとき再現精度については
AR=1.96
)]
(
}/[
)]
(
{[
1
8
1
1
2
1
4
2
2
−
p
γ
+
−
γ
+
····································· (2)
である。
繰返し数nが2の場合,JIS Z 8402-1のpが,ここではp−1になることがあるという点を除けば,JIS Z
8402-1の式(9)及び式(10)は上の式(1)及び式(2)と同じであることが分かる。この差は小さいので,JIS Z
8402-1の表1,図B.1及び図B.2を用いて,水準分割実験における併行標準偏差及び再現標準偏差の推定
値の不確かさを評価することができる。
水準分割実験において,測定方法のかたよりの推定値の不確かさを評価するため,n=2としてJIS Z
8402-1の式(13)で定義される値Aを計算し(又はJIS Z 8402-1の表2を用いて),その値をJIS Z 8402-1
の規定に従って利用する。
水準分割実験において,試験室のかたよりの推定値の不確かさを評価するため,n=2としてJIS Z 8402-1
の式(16)で定義される値AWを計算する。水準分割実験における繰返し回数は実際には2であるから,繰
返し数を増やすことによって試験室のかたよりの推定値の不確かさを小さくすることはできない(この不
確かさを小さくする必要がある場合は,水準を分割しない計画を適用するのがよい)。
4.3.2
水準分割実験の構成の詳細については,JIS Z 8402-2の5.及び6.の規定によるものとする。JIS Z
8402-2に示されている繰返し数nは,水準分割計画における水準の分割数(すなわち2)としてもよい。
5
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
サンプルaからのサンプルを参加試験室にランダムに割り当て,次に改めてランダムにサンプルbから
のサンプルを参加試験室に割り当てる。
水準分割実験においては,データ報告の際に,統計の専門家にとって,各測定水準についてサンプルa
から得られた結果と,サンプルbから得られた結果を区別できるようになっている必要がある。(2種の)
サンプルにそれが可能となるようにラベル付けをするが,このことが参加試験室に分からないように注意
をする。
表 1 水準分割計画のデータ照合用の推奨様式
4.4
統計的モデル
4.4.1
この規格のこの部において使用する基本モデルは,JIS Z 8402-1 5.の式(1)によって与えられる。
JIS Z 8402-1 5.では,測定方法の精確さ(真度と精度)を推定する場合,各測定結果を三つの成分の和で
あると仮定することが有用であると述べている。
ijk
ij
j
ijk
e
B
m
y
+
+
=
······································································ (3)
ここで,それぞれの測定サンプルについて,
mj : 測定水準 j=1,...,qにおける一般平均(期待値)
Bij : 試験室 i=1,...,p,測定水準 j=1,...,qにおける併行条件の
下でのかたよりの試験室成分
eijk : 試験室i,測定水準jにおける併行条件の下での測定結果 k=
1,...,nに伴う偶然誤差
である。
4.4.2
水準分割実験の場合,このモデルは次の式で表される。
ijk
ij
jk
ijk
e
B
m
y
+
+
=
····································································· (4)
4.4.1の式(3)と唯一異なる点は,mjkに添字kが追加され,これが,式(4)の一般平均が測定水準jにおけ
るa又はbのどちらのサンプル(k=1又は2)についてのものかを表す。
Bijに添字kが存在しないことは,試験室iにおけるかたよりが,個々の測定水準においてはサンプルが
a,bのいずれであるかに依存しないことを表す。これが二つのサンプルが類似していることが重要である
ことの理由である。
参考 以下ではaのサンプルについてはk=1ではなくk=aと,bのサンプルについてはk=bと表し
ている。
4.4.3
セル平均値を次のとおり定義する。
2
)/
(
ijb
ija
ij
y
y
y
+
=
······································································ (5)
更に,セル差を,次のとおり定義する。
6
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ijb
ija
ij
y
y
D
−
=
············································································ (6)
4.4.4
水準分割実験の水準jにおける一般平均を,次のとおり定義する。
2
)/
(
jb
ja
j
m
m
m
+
=
····································································· (7)
4.5
水準分割実験データの統計的解析
4.5.1
データを表1に示した表に記入する。試験室と測定水準の各組合せをこの表における“セル”とい
い,各セルには2個のデータyijaとyijbが入る。
セル差Dijを計算してこれを表2に示した表に記入する。この解析方法では,各セル差を,
a−b
のように計算し,値が負の場合にはマイナス記号をつけることが必要である。
セル平均値yijを計算してこれを表3に示した表に記入する。
4.5.2
表1のセルで測定結果が欠けている場合(例えば,サンプルを損なった,又は,後述の外れ値の検
定結果に従ってデータを除外した場合),対応する表2及び表3のセルはともに空白とする。
4.5.3
実験の各測定水準jについて,表2のj列におけるセル差の平均値Djと標準偏差sDjを計算する。
∑
p
D
D
ij
j=
··········································································· (8)
∑
)
(
)
(
1
2
−
−
=
p
D
D
s
j
ij
Dj
························································· (9)
ここで,Σは試験室i=1,...,pについての総計を表す。
表2に空白のセルがある場合,pは表2のj列の空白でないセルの個数となり,総計も空白でないセル
について計算する。
4.5.4
実験の各測定水準jについて,次の式を用いて表3のj列におけるセル平均値の平均値yjと標準偏
差syjを計算する。
∑
p
y
y
ij
j=
·········································································· (10)
∑
)
(
)
(
1
2
−
−
=
p
y
y
s
j
ij
yj
··························································(11)
ここで,Σは試験室i=1,...,pについての総計を表す。
表3に空白のセルがある場合,pは表3のj列の空白でないセルの個数となり,総計も空白でないセル
について計算する。
4.5.5
表2,表3及び4.5.3と4.5.4において計算した統計量を用いて,4.6の方法によってデータの一致
性と外れ値について吟味する。除外されるデータがあれば,統計量を計算し直す。
4.5.6
次の式を用いて,併行標準偏差srjと再現標準偏差sRjを計算する。
2
Dj
rjs
s=
·········································································· (12)
2
2
2
2
rj
yj
Rj
s
s
s
+
=
····································································· (13)
4.5.7
srjとsRjが平均値yjに依存するか否かを調べ,もし依存する場合は,JIS Z 8402-2 7.5の方法によ
って関数関係を求める。
表 2 水準分割計画のセル差の表の推奨様式

7
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 3 水準分割計画のセル平均値の表の推奨様式
4.6
データの一致性と外れ値の吟味
4.6.1
JIS Z 8402-2 7.3.1の方法によって,h統計量を用いてデータの一致性を吟味する。
セル差の一致性をチェックするため,次の式でh統計量を計算する。
Dj
j
ij
ij
s
D
D
h
)
(
−
=
···································································· (14)
セル平均値の一致性をチェックするため,次の式でh統計量を計算する。
yj
j
ij
ij
s
y
y
h
)
(−
=
····································································· (15)
データの一致性を欠く試験室を明らかにするため,図2及び図3に示すとおり,各試験室ごとにこれら
二つの統計量を測定水準の順に打点する。そのグラフの解釈方法の詳細については,JIS Z 8402-2 7.3.1
で十分に述べている。ある試験室の併行精度がほかの試験室に比べて全般的に悪い場合は,セル差につい
てのグラフにh統計量が大きいものが異常に多数現れる。ある試験室における測定結果が全般的にかたよ
っている場合は,セル平均値のグラフに,h統計量のほとんどが一つの方向に現れる。いずれの場合も,
該当する試験室については,実態を調査して結果を実験の組織者へ報告するよう要請すべきである。
4.6.2
JIS Z 8402-2 7.3.4に述べるグラッブズ(Grubbs)の検定を行って,外れ値を吟味する。
セル差の外れ値を検定するため,表2の各列の値について,順番にグラッブズの検定を行う。
セル平均値の外れ値を調べるため,表3の各列の値について,順番にグラッブズの検定を行う。
これらの検定結果の解釈方法については,JIS Z 8402-2 7.3.2で十分に述べている。これらの検定は,
実験の報告においてほかのデータからあまりにもかけ離れているため,併行標準偏差及び再現標準偏差の
8
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
計算にその値を含めると,計算結果が大きく影響を受ける可能性があるデータを特定するために行う。一
般に1 %外れ値とみなされるデータは計算から除外し,5 %外れ値とみなされるデータは,除外すべき特段
の理由がない限り,計算に含める。検定の結果,表2若しくは表3のいずれか一方において,あるデータ
を併行標準偏差及び再現標準偏差の計算から除外すべきであると判定されたら,これら二つのうちのもう
一方の表における対応する値も計算から除外する。
4.7
水準分割実験結果の報告
4.7.1
JIS Z 8402-2 7.7は,
− 統計的解析結果のパネルへの報告
− パネルが行うべき決定
− 報告全体の準備
についての助言を与える。
4.7.2
JIS Z 8402-2 7.1において,標準測定方法の併行標準偏差及び再現標準偏差に関する表示の様式
を推奨する。
4.8
例1:水準分割実験―たんぱく質の定量
4.8.1
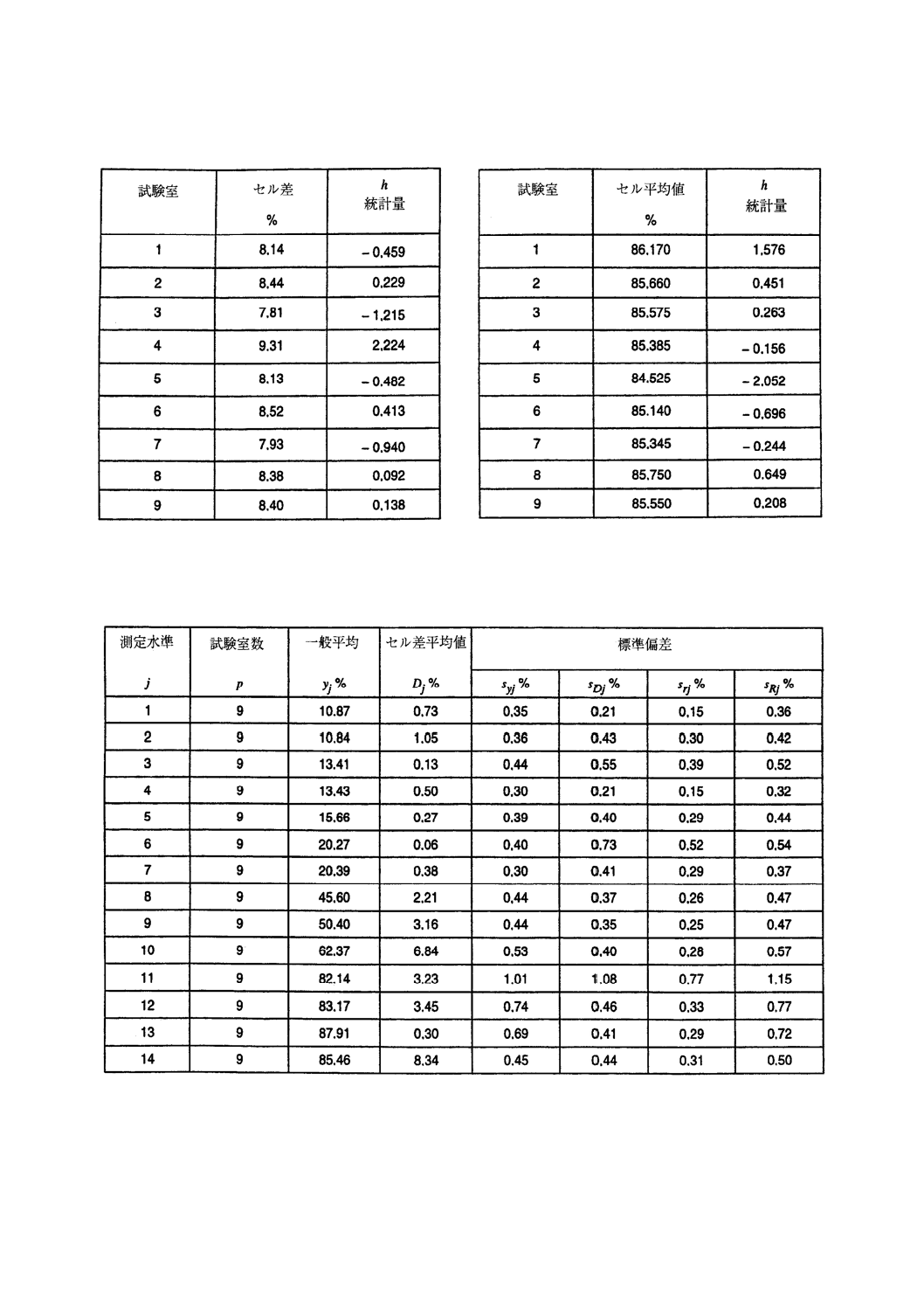
表4は,飼料中のたんぱく質含有率を燃焼して定量する実験[5]のデータである。9か所の試験室が
参加し,実験は14の測定水準について行った。各測定水準について,ほぼ同じ量のたんぱく質を含む2
種の飼料を用いた。
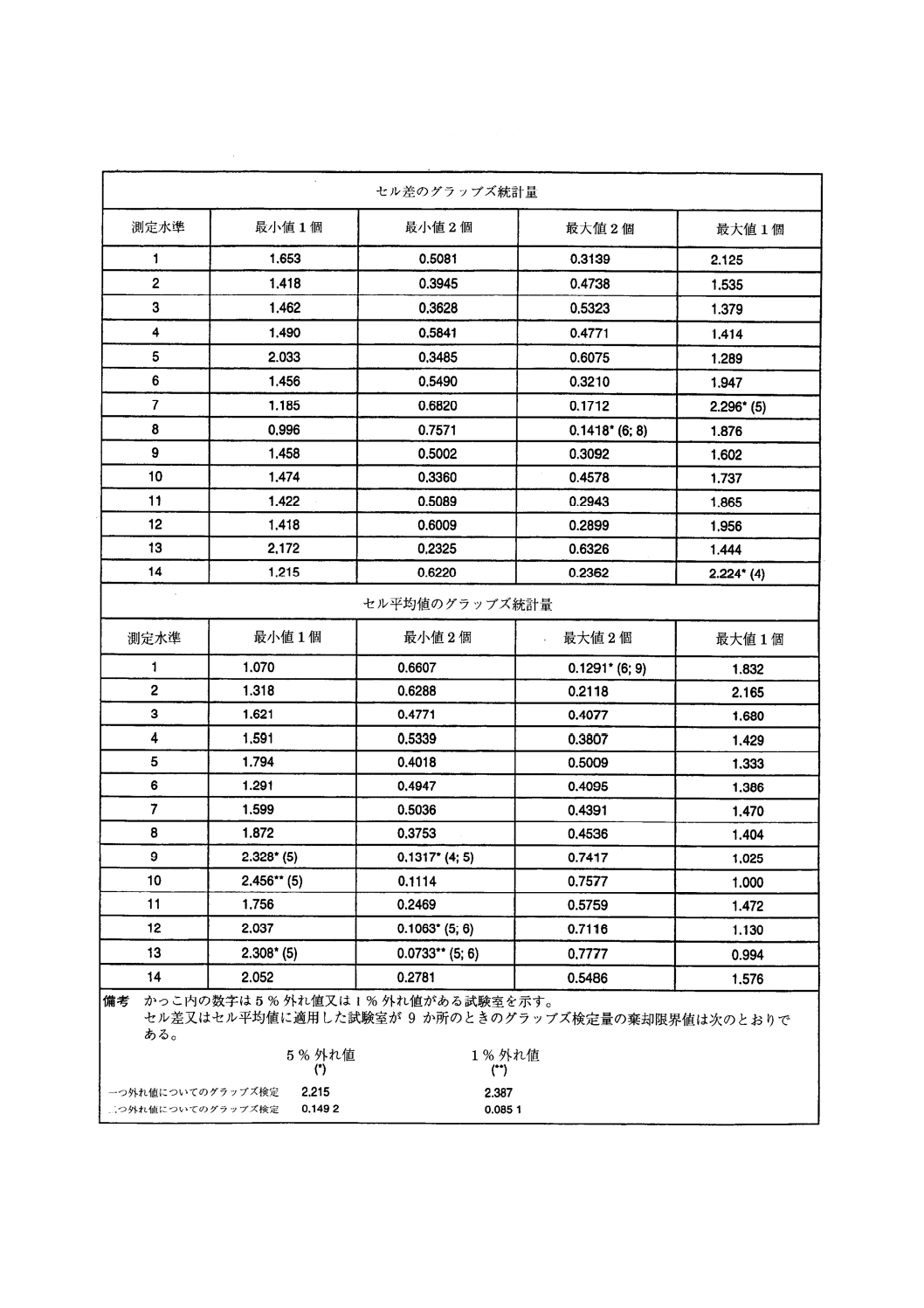
4.8.2
表5及び表6は,この実験の測定水準14( j=14)だけについて4.5.1の方法で計算したセル平均
値とセル差を示す。
4.5.3の式(8)及び式(9)を用いると,表5のセル差から次の値が得られ,
D14=8.34 %
sD14=0.436 1 %
表6の平均値に4.5.4の式(10)及び式(11)を適用すると,次の値が得られ,
y14=85.46 %
sy14=0.453 4 %
したがって,4.5.6の式(12)及び式(13)を用いて,次の併行標準偏差及び再現標準偏差を得る。
sr14=0.31 %
sR14=0.50 %
表7にほかの測定水準に関する計算結果を示す。
4.8.3
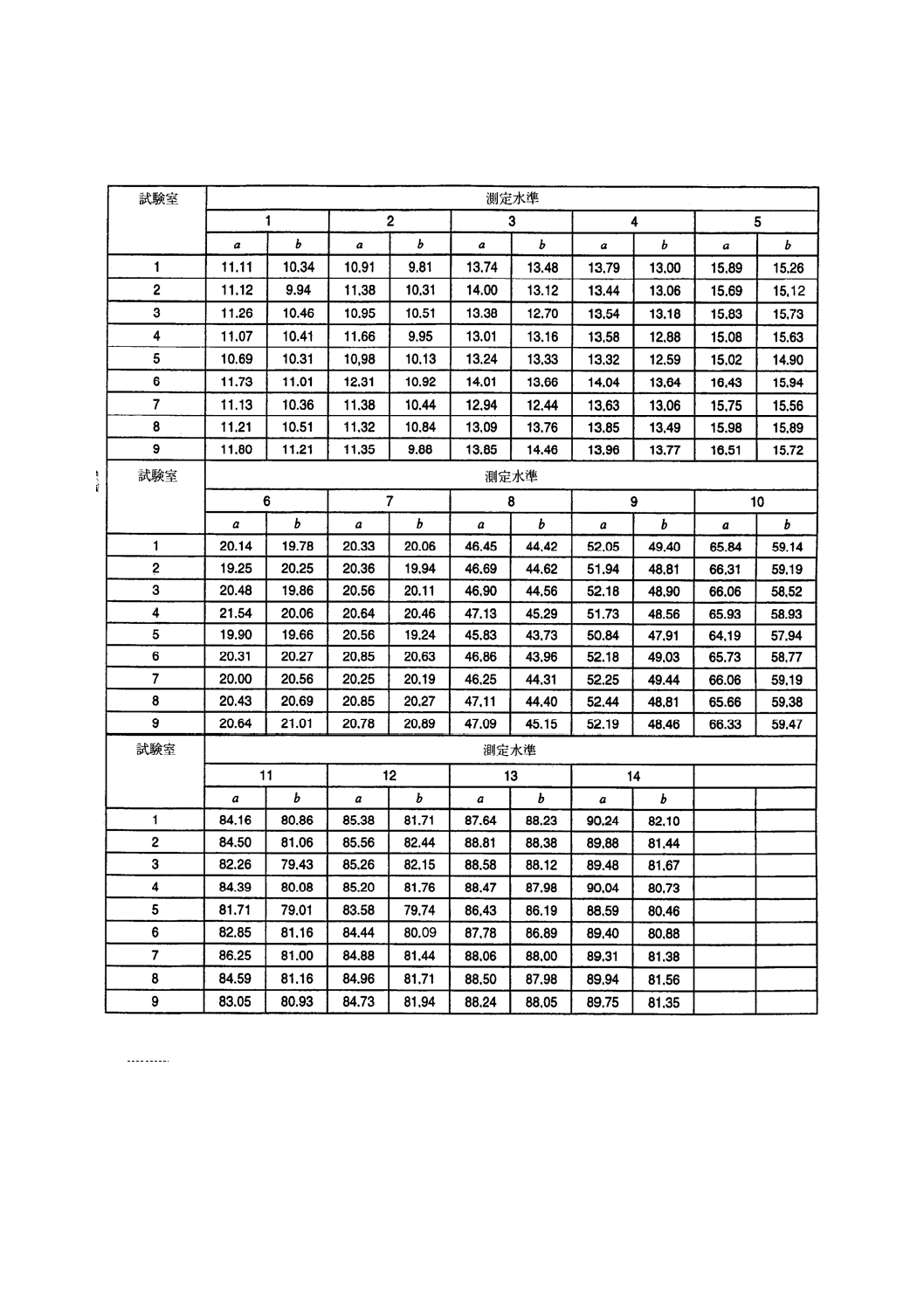
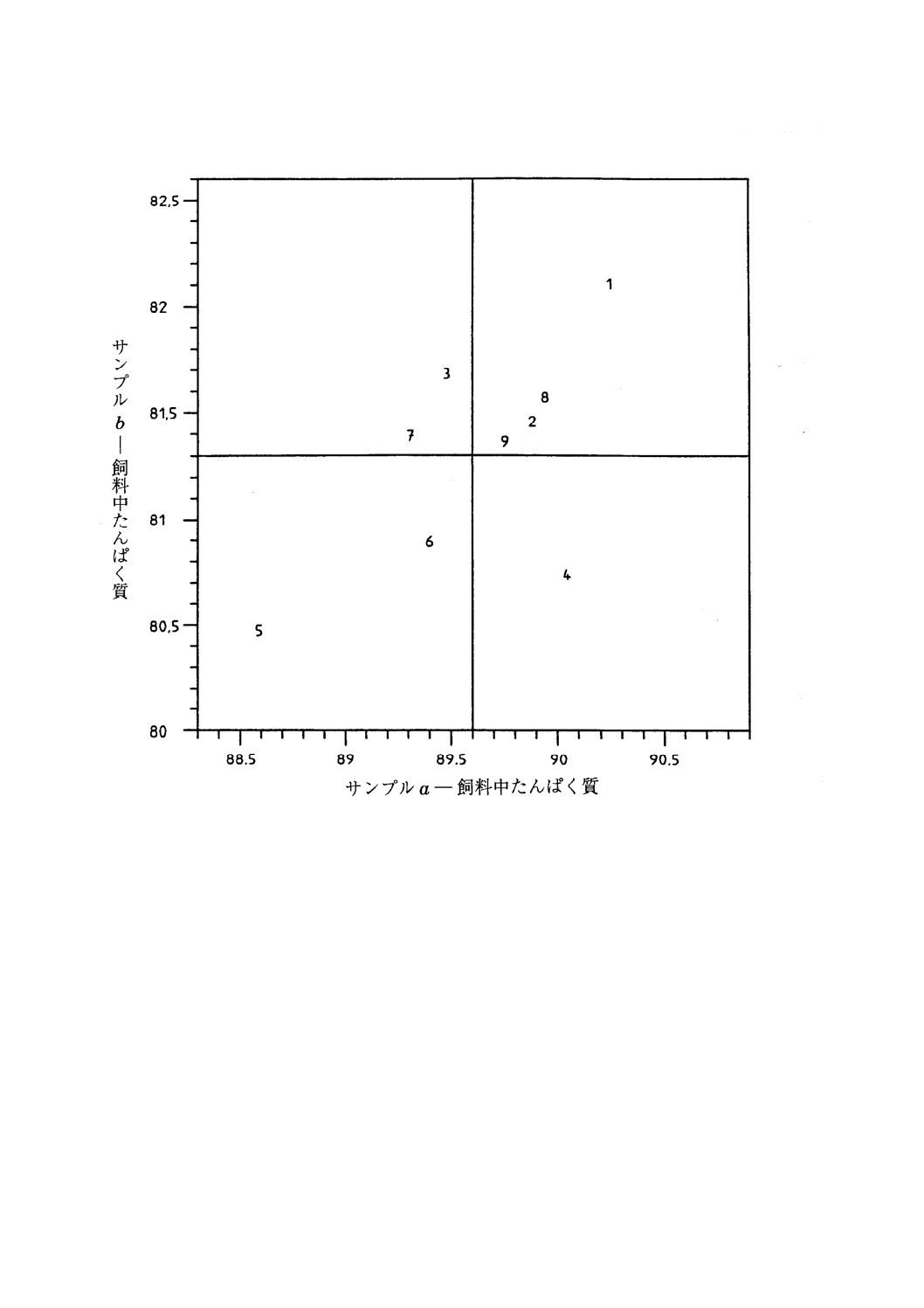
図1は,測定水準14に関して表4のサンプルaの測定結果を,対応するサンプルbの測定結果と
対比してプロットしたユーデン・プロットである。グラフの左下隅に試験室5の点があり,右上隅に試験
室1の点がある。これは,サンプルa及びbに関して,試験室5のデータには一貫して負のかたよりがあ
り,試験室1のデータには一貫して正のかたよりがあることを示す。図1のように水準分割計画のデータ
をプロットする場合,このようなパターンが観察されることはよくある。図1はまた,試験室4の測定結
果が,二つのサンプルの同一性を示す直線からいくらか離れていて普通でないことを示す。その他の試験
室は,グラフの中央部においてグループを構成している。したがって,図1からは,三つの試験室のかた
よりの原因を調査すべきであることが分かる。
備考 ユーデン・プロットの解釈方法の詳細については,参考文献[7]及び[8]を参照されたい。
4.8.4
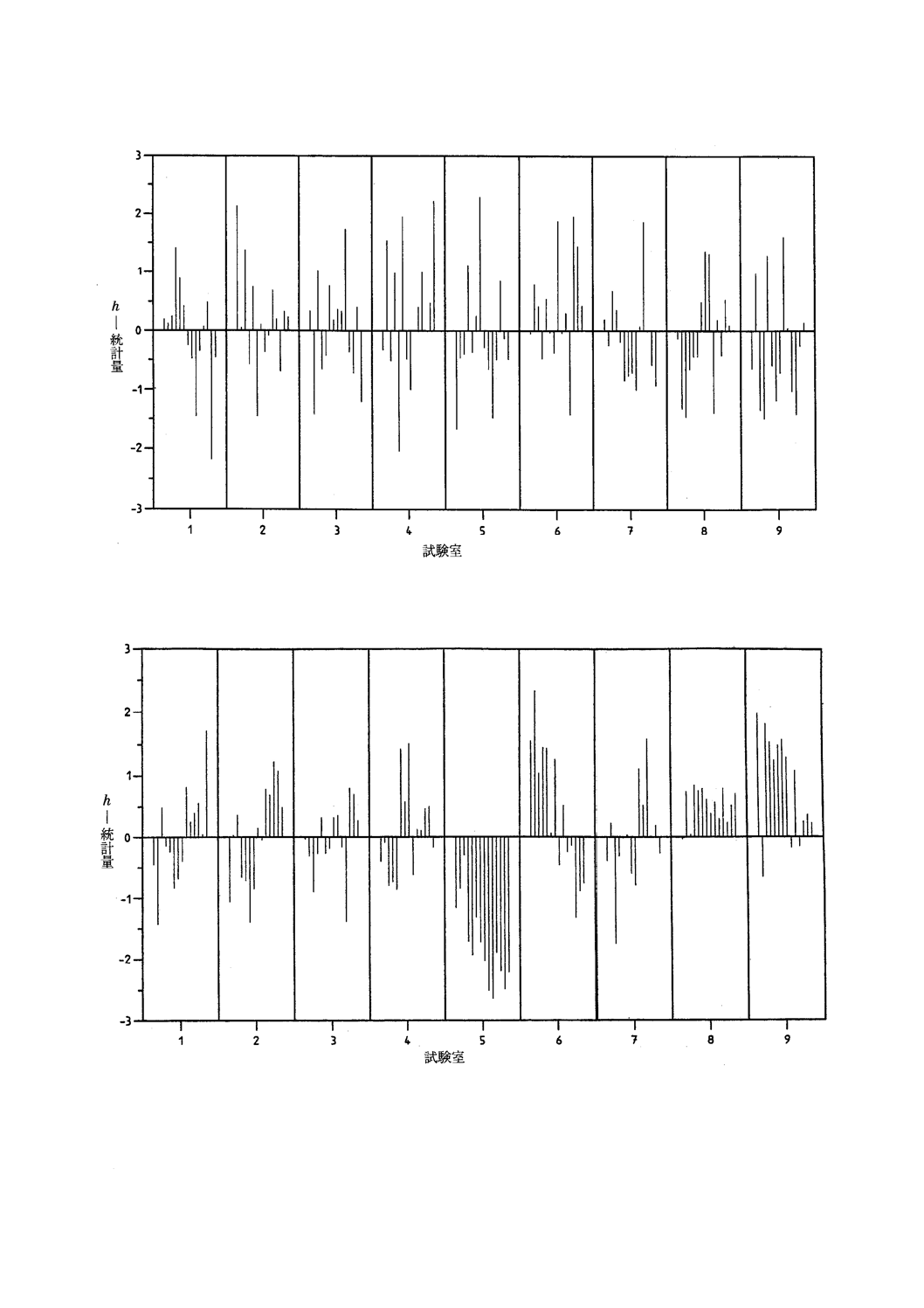
表5及び表6には,4.6.1の方法で計算した測定水準14だけのh統計量の値を示す。全測定水準の
値は図2及び図3にプロットした。
9
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3において,セル平均値のh統計量から,試験室5の全測定水準におけるh統計量が負の値をとって
いるため試験室5のデータには一貫して負のかたよりがあることが分かる。同じ図において,試験室8及
び9のh統計量はほとんどすべて正で,これは試験室8及び9のデータには一貫して正のかたより(ただ
し試験室5の負のかたよりより小さいかたより)があることを示す。また,試験室1,2,6のh統計量に
は,各試験室における測定水準によって異なるかたよりがある。このような試験室と測定水準の交互作用
は,試験室かたよりの原因について手掛かりを与えるであろう。
図2には注目すべきパターンは存在しない。
4.8.5
表8にグラッブズの統計量の値を示す。この検定からも試験室5のデータは疑わしいことが分かる。
4.8.6
統計の専門家は,データの解析を進める前に,ここで試験室5の疑わしいデータについて可能性の
ある原因の追及を開始すべきである。原因が特定されない場合は,併行標準偏差及び再現標準偏差の計算
から試験室5の全データを除外することが考えられる。そして,併行標準偏差及び再現標準偏差と一般平
均の間の可能性のある関数関係を検討して解析を進めることになるであろう。これによって生じる問題は
すべてJIS Z 8402-2で既に扱っているため,ここでは検討しないこととする。
10
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 4 例1:飼料中のたんぱく質の定量(質量%)
参考 表4で原国際規格では,測定水準5,試験室2,サンプルbのデータ“15.12”を“15.10”と,
測定水準12,試験室6,サンプルbのデータ“80.09”を“80.90”と,誤記している。
11
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 5 例1:測定水準14のセル差 表 6 例1:測定水準14のセル平均値
参考 表6で,“セル平均値”を原国際規格では“セル差”と誤記している。
表 7 例1:表4の全14測定水準データから計算した平均値,セル差平均値及び標準偏差の値
12
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 8 例1:グラッブズ統計量の値
参考 表8で,測定水準10の“最小値2個”と“最大値2個”の欄は,原国際規格では誤って空欄に
している。
13
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 質量 %
図 1 例1:測定水準14のデータ
14
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 2 例1:セル差一致性のチェック(試験室別)
図 3 例1:セル平均値一致性のチェック(試験室別)
5. 不均質物質に関する計画
5.1
不均質物質に関する計画の適用
15
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.1.1
材質が不均質な物質の例として皮革がある。皮革はどの二つをとっても同じではない。1枚の皮革
の中でも材質は場所によって大きく異なる。皮革に適用される試験方法に,BS 3144[3]の引張強さ試験があ
る。この試験は,亜鈴形状の試験片を用いる。BS 3144は1枚の皮革から切り出す試験片の数と,切り出
す位置及び方向を指定する。したがって,皮革試験のための“サンプル”とは当然皮革1枚のことをいう。
JIS Z 8402-2に規定する水準を分割しない計画に基づき,各試験室へ測定水準ごとに皮革を1枚送付して
精度評価実験を行い,各皮革について測定結果を二つ得る場合,皮革間の変動が試験室間の変動に加わり,
再現標準偏差を大きくするであろう。これに対し,各試験室へ測定水準ごとに皮革を2枚送付し,各皮革
について測定結果を二つずつ得る場合,そのデータを用いて,皮革間の変動を推定し,皮革間変動を除外
した測定方法の再現標準偏差を計算することができる。
5.1.2
材質が不均質な物質のもう一つの例は砂(例えば,コンクリートに配合される砂)である。砂は,
風力又は水力の作用によって,様々な粒度の粒子が層を成してたい(堆)積する。したがって,砂を使用す
るときは粒度分布が必ず関心事となる。コンクリートに配合する場合,砂の粒度分布はふるい試験(例え
ば,BS 812-103[1])によって測定する。砂を測定する場合,製品から大口試料を採取し,その中から幾つ
かの試験用サンプルを採取する。一般に大口試料は10 kgであり,試験用サンプルは約200 gである。砂自
体に不均質性があるため,同一製品であっても大口試料の間には必ず違いがある。したがって,皮革の場
合と同じく,各試験室へ各測定水準ごとに大口試料を1袋送付して水準を分割しない実験を行えば,大口
試料間の違いによって測定方法の再現標準偏差の計算値が大きくなるであろう。これに対し,各試験室へ
各測定水準ごとに大口試料を2袋送付すれば,サンプル間のばらつきを除外した再現標準偏差の値を計算
することができる。
5.1.3
5.1.1及び5.1.2の例から,不均質物質のもつもう一つの特徴が明らかになる。物質が均質でないた
め,試験片の製作や試験用サンプルの調製がばらつきの重要な要因となり得る。したがって,皮革の場合
は,皮革から試験片を切り出すプロセスが引張強さの測定値に大きく影響することがある。砂のふるい試
験の場合は,大口試料から試験用サンプルを取り出すプロセスが,一般に測定方法がもつばらつきの主た
る要因となる。精度評価実験の試験片や試験用サンプルを(同一“試料”を作ろうとして)通常使用する
方法とは異なる方法で準備すると,実験から得た併行標準偏差及び再現標準偏差の値は,実際に経験する
ばらつきを表すことにはならないであろう。ある場合には(例えば,技能試験,又は測定方法の開発過程
で精度評価実験を行う場合),できる限り物質のばらつきを除去するように工夫した特別なプロセス(又は
方法)によって,同一“試料”を作ることが好ましいこともある。しかしながら,精度評価実験の目的が
実際に経験されるばらつきを見出だすこと(例えば,売り手と買い手が同一製品のサンプルを測定する場
合)であれば,測定方法の精度のなかにサンプルの不均質性によるばらつきを含める必要がある。また,
実験に際して,個々の測定はほかの測定と互いに独立して行い,独立性が確保されるよう注意しなければ
ならない。例えば,試験片を準備する場合,ある段階で試験片を数個同時に処理すると,その独立性が失
われ,その段階において発生するかたよりやばらつきが,これらの一緒に処理した試験片の測定結果すべ
てに共通に影響してしまう。
5.1.4
この項において述べる不均質物質についての実験計画によって,JIS Z 8402-2に規定する水準を分
割しない計画では得られない,サンプル間の差違に関する情報を得ることができる。新たな情報を得るた
めには当然コストがかかる。すなわち,ここに提案する計画では測定すべきサンプル数が多くなる。しか
し,この新たな情報にこそ価値がある。5.1.1で議論した皮革の例では,皮革間の差違に関する情報によっ
て,コンサインメントの質を評価するために測定すべき皮革の枚数を決定し,また個々の皮革の試験片を
少なくして皮革を多数回測定するか,又は皮革を少数にして個々の皮革から取る試験片を多くして測定す
16
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
るかを決定することができる。5.1.2で議論した砂の例では,大口試料間の差違に関する情報によって,大
口試料の採取方法が適切であるか,又は改善を要するかを決定することができる。
5.1.5
この項で述べる実験計画は,枝分れとして配置した三つの要因に関する実験に適用することができ
る。三つの要因とは,枝分れの最上位の“試験室”,次の水準の“試験室内サンプル”,及び最下位の“サ
ンプル内測定結果”である。実際によく用いられるもう一つのケースは,“試験室”を最上位,“試験室内
測定結果”を次の水準,“測定結果内定量”を最下位にする3要因枝分れである。あとのケースとしては,
精度評価実験に参加する試験室が,それぞれ均質物質のサンプルを一つずつ送付され,各サンプルについ
て測定を2回(又はそれ以上)行い(すなわち,“測定結果内測定結果”),かつ,各測定においては多数回
定量を行い,測定結果がその定量値の平均値として計算される(すなわち,“試験室内定量”)ような場合
である。5.5,5.6及び5.9の式はこのような実験で得たデータに適用されるが,併行標準偏差及び再現標準
偏差は,ここに述べる方法とは若干異なる方法で計算しなければならない(5.5.5の備考2. 参照)。平均値
としての測定結果を求めるための定量値の数は,併行標準偏差及び再現標準偏差の値に影響する。したが
って,その回数も指定しなければならない。
5.2
不均質物質に対する実験計画のレイアウト
5.2.1
表9に不均質物質についての実験計画のレイアウトを示す。
この表は簡単に参加試験室p'箇所が,測定水準q個についてそれぞれ2個のサンプルを与えられ,各サ
ンプルについて測定結果を二つ得ることにしている。したがって,実験の各セルには測定結果が四つ(サ
ンプル2個のそれぞれに測定結果が2個)存在することになる。
この簡単な計画を一般化して,各測定水準ごとに各試験室へサンプルを3個以上与えるか,又はサンプ
ルごとに測定結果を三つ以上得ることも可能である。一般化した計画に要する計算は,サンプルごとの測
定結果が2個で,各水準各試験室ごとのサンプルが2個の場合よりもはるかに複雑になる。しかしながら,
一般化した計画の原理は簡単な計画の原理と同じである。したがって,ここでは,簡単な計画のための計
算について詳述する。5.9において,一般化した計画における併行精度及び再現精度の標準偏差の計算式を
示し,5.10にその適用例を掲げる。
5.2.2
不均質物質についての計画から得られたデータを,次の記号で表す。
yijtk
ここで,
添字iは試験室を表す(i=1,2,...,p'),
添字jは水準を表す(j=1,2,...,q),
添字tはサンプルを表す(t=1,2,...,g),
添字kは測定結果を表す(k=1,2,...,n)。
簡単な計画ではg=2及びn=2である。一般化した計画では,g又はn,又はその両者が2より大きい。
備考 JIS Z 8402-1及びJIS Z 8402-2において,pは参加試験室数として用い,かつ,コクラン検定
の棄却限界値の表におけるpとして使用する。水準を分割しない実験においては,これら二つ
の数は同じである。不均質物質についての実験計画においては,コクラン検定のpは試験室数
の倍数になることがある。したがって,ここではp'を参加試験室数とし,pをコクラン検定で
用いる。
5.3
不均質物質の実験の構成
5.3.1
不均質物質の実験の計画に当たっては,JIS Z 8402-1の6.の規定を参照されたい。そのほかに,各
測定水準で各試験室に対して準備すべきサンプル数を考えなければならないが,コストを考慮して通常2
17
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
個が適当であろう。
JIS Z 8402-1 6.及び附属書Bの式,表及び図を用いて,参加試験室数,サンプル数及び繰返し数を選
択することができるが,5.3.2〜5.3.5に規定する修正が必要である。
5.3.2
不均質物質の実験から得た併行標準偏差について,その推定値の不確かさは,JIS Z 8402-1の式(9)
によって定義した値の代わりに,JIS Z 8402-1 6.3で述べられた次の値Arで評価することができる。
)]
(
[
1
'
2
1
96
.1
−
n
g
p
Ar=
························································· (16)
また,この式はJIS Z 8402-1の式(9)のpをp'×gで置き替えることによっても得ることができる。した
がって,JIS Z 8402-1の図B.1及び表1にp=p'×gを適用すれば,図B.1と表1のAr欄の併行精度の値を
使用することができる。各試験室の各測定水準についてサンプルを2個(g=2)準備する簡単な計画では,
JIS Z 8402-1の表又は図にp=2p'を適用されたい。
備考 上のArの式(及び次のARの式)は,すべてJIS Z 8402-1の備考24.に示す方法で導いた。
5.3.3
不均質物質の実験から得た再現標準偏差について,その推定値の不確かさは,JIS Z 8402-1の式
(10)によって定義した値の代わりに,JIS Z 8402-1の6.3で述べられた次の値ARで評価することができる。
)
(
)
(
4
3
2
1
2
96
.1
γ
+
+
=
D
D
D
AR
················································· (17)
ここで,
D1=[(γ2−1)+(φ2/g)+1/(ng)]/(p'−1)
D2=[(φ2/g)+1/(ng)]2/[p'(g−1)]
D3=1/[p'g(n−1)]
φ=σH /σr
(σHは5.4.1において定義)
γ=σR /σr ·········································································· (18)
φとγの値は,測定方法標準化の過程において得た標準偏差σH,σR及びσrの予備的推定値から求める
ことができる。
参考 原国際規格では式(17)及び式(18)において,記号のフォントが不統一であったので訂正した。
また,D1の式で原規格では1/ngと誤っていたのを1/(ng)に訂正し,D2の式で原規格では(1/ng)
と誤っていたのを1/(ng)に訂正した。
5.3.4
不均質物質の実験計画の更に詳細については,JIS Z 8402-2 5.及び6.の記述を参照されたい。
JIS Z 8402-2の5.1.2では,“n回のひとまとまりの試験”又は“n個のひとまとまりの測定値”に関する
要件(例えば,n回のひとまとまりの試験は併行条件の下で行うこと)を規定している。不均質物質の実
験においては,これらの要件はセル内のひとまとまりのg×n個の試験,すなわち,一つの測定水準の一つ
の試験室内での試験すべてに適用される。
不均質物質の実験において,各測定水準について準備すべきサンプル数はp'×g(すなわち,簡単なg=
2の場合は2p')である。これらのサンプルp'×g個は参加試験室へランダムに割り付けなければならない。
5.4
不均質物質の実験の統計モデル
5.4.1
この規格のこの部において使用する基本的モデルは,4.4.1の式(3)で表される。不均質物質の実験
については,このモデルを次のように拡張する。
ijtk
ijt
ij
j
ijtk
e
H
B
m
y
+
+
+
=
····························································· (19)
m,B及びe項の意味は4.4.1の式(3)の場合と同じである。式(19)にはそのほかにHijt項がある。この項
はサンプル間変動を表し,添字tは試験室内のサンプルを表す(その他の添字の意味については5.2.5を参
18
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
照されたい)。
サンプル間変動はランダムであり,試験室には依存せず,実験の測定水準に依存すると仮定するのが合
理的である。したがって,Hijtの期待値はゼロであり,その分散は次の式で表されるものとする。
2
var
Hj
ijt
H
σ
=
)
(
······································································· (20)
5.4.2
通常のケース,すなわち,個々の試験室のサンプル数が2個,1サンプル当たりの測定結果が2個
の場合(g=n=2),次の値を定義する。
a) 試験室i,測定水準j,サンプルt(t=1又は2)についてのサンプル平均及び測定結果間範囲
2
2
1
)
(
ijt
ijt
ijt
y
y
y
+
=
··································································· (21)
2
1
ijt
ijt
ijt
y
y
w
−
=
······································································· (22)
b) 試験室i及び測定水準jについてのセル平均及びサンプル間範囲
2
2
1
)
(
ij
ij
ij
y
y
y
+
=
····································································· (23)
2
1
ij
ij
ij
y
y
w
−
=
········································································· (24)
c) 測定水準jについて一般平均及びセル平均値の標準偏差
∑
=
q
j
ij
j
p
y
y
1
'
=
·········································································· (25)
)
(
)
(
1
'
1
2
−
−
=
p
y
y
s
q
j
j
ij
yj
∑
=
······················································· (26)
ここに,総計は試験室i=1,2,...,p'について行う。
5.5
不均質物質の実験データの統計解析
5.5.1
ここでは,通常のケース,すなわち,各試験室での各測定水準についてサンプルを2個準備し,各
サンプルについて測定結果を2個得る場合について詳述する(一般的なケースについては5.9及び5.10に
おいて検討する)。
データを表9に記入する。この表で試験室と測定水準の各組合せが“セル”を構成する。各セルにはデ
ータが四つある。
5.4.2の式(21)から式(26)までを用い
a) 測定結果間範囲を計算して表10に記入する。
b) サンプル間範囲を計算して表11に記入する。
c) セル平均値を計算して表12に記入する。
範囲は正の値として記入する(すなわち,符号を無視する)。
19
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
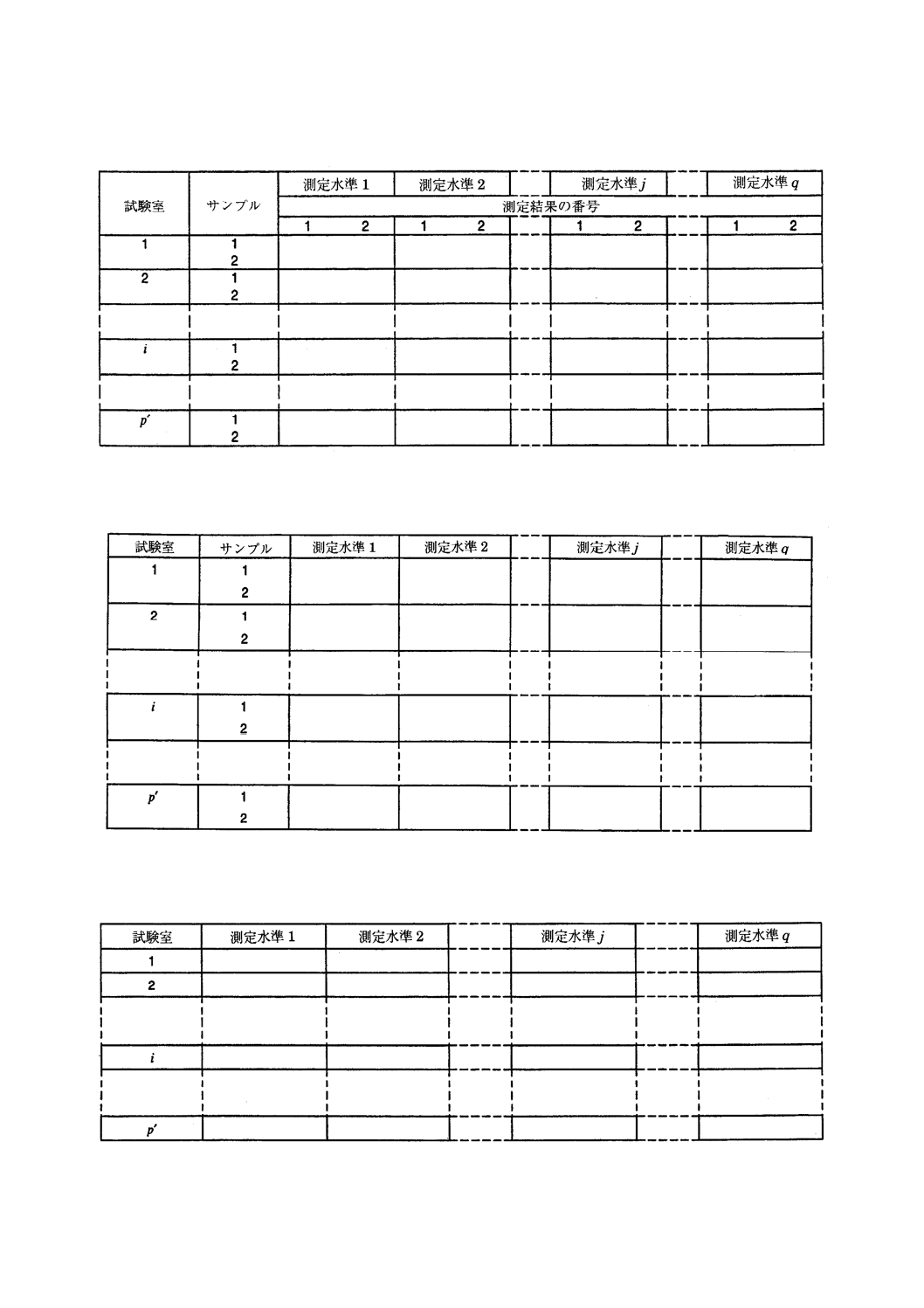
表 9 不均質物質の計画でのデータの照合用の推奨様式
表 10 不均質物質の計画での測定結果間範囲の表の推奨様式
表 11 不均質物質の計画でのサンプル間範囲の表の推奨様式

20
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 12 不均質物質の計画でのセル平均値の表の推奨様式
5.5.2
表9に測定結果が3個以下しか存在しないセルがある場合(例えば,サンプルを損なったり,後述
の外れ値の検定の結果データを除外した場合)は,
a) 後述の一般的なケースの式を使用するか,又は
b) そのセルのデータはすべて無視する。
a)の方が好ましい。b)はデータが無駄になるが簡単な式を使用することができる。
5.5.3
実験の各測定水準について次の値を計算する。
a) 表10の欄jの測定結果間範囲の平方和(試験室p'箇所及びサンプル2個の数値の和)
∑∑
=
=
'
1
2
1
2
p
i
t
ijt
rj
w
SS=
······································································· (27)
b) 表11の欄jのサンプル間範囲の平方和(試験室p'箇所の数値の和)
∑
=
'
1
2
p
i
ij
Hj
w
SS=
··········································································· (28)
c) 5.4.2の式(25)及び式(26)を用いた表12の欄jのセル平均値の平均値と標準偏差
5.5.4
表10,表11及び表12と,5.5.3において計算した統計量を用いて,5.6の方法によってデータの一
致性と外れ値を調査する。合格しないデータがあれば再度統計量を計算する。
5.5.5
次の式を用いて,併行標準偏差srjと再現標準偏差sRjを計算する。
)
(
'
4
2
p
SS
s
rj
rj=
······································································· (29)
)
(
)
(
'
4
2
2
p
SS
SS
s
s
Hj
rj
yj
Rj
−
+
=
······················································· (30)
ただし,
rj
Rjs
s<
················································································· (31)
となる場合は,sRjを
rj
Rjs
s=
················································································· (32)
とする。
次の式で,サンプル間変動の標準偏差の推定値を計算する。
)
(
)
(
'
8
'
2
2
p
SS
p
SS
s
rj
Hj
Hj
−
=
······················································· (33)
備考1. 有意性検定を行って,サンプル間変動が統計的に有意であるか否かを調べることもできる。
21
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
しかしながら,これはここでの解析に要求される検定ではない。特に,このような検定を行
ってサンプル間変動を無視できるとし,各セルの測定結果がすべて同一サンプルから得られ
たものとして取り扱う解析は正しくない。このような手順は,併行標準偏差の推定にかたよ
りを導入することになる。サンプル間変動が統計的に有意でないということは,サンプル間
変動が無視できる証拠ではないからである。
2. 5.1.5で述べたケース(三つの要因が“試験室”,“試験室内測定結果”及び“測定結果内定量”
の場合)においては,併行標準偏差及び再現標準偏差は,次の式で計算する。
)
(
'
2
2
p
SS
s
Hj
rj=
)
(
'
4
2
2
p
SS
s
s
Hj
yj
Rj
+
=
これらの式は,測定結果を2回の定量の平均値として計算する場合に適用する。
5.5.6
srjとsRjが一般平均yjに依存するか否かを調べ,もし依存する場合は,JIS Z 8402-2の7.5の方法に
よって関数関係を求める。
5.6
データの一致性と外れ値の精査
5.6.1
JIS Z 8402-2の7.3.1の方法によって,h及びk統計量を用いてデータの一致性を調べる。
セル平均値の一致性をチェックするため,次の式でh統計量を計算する。
yj
j
ij
ij
s
y
y
h
)
(−
=
····································································· (34)
測定値が一致性を欠く試験室を明らかにするため,各試験室ごとにこれらの統計量を測定水準の順序で
プロットする。
サンプル範囲の一致性をチェックするため,次の式でk統計量を計算する。
'p
SS
w
k
Hj
ij
ij=
·································································· (35)
測定値が一致性を欠く試験室を明らかにするため,各試験室ごとにこれらの統計量を測定水準の順序で
プロットする。
測定結果間範囲の一致性をチェックするため,次の式でk統計量を計算する。
'
2p
SS
w
k
rj
ijt
ijt=
································································ (36)
測定値が一致性を欠く試験室を明らかにするため,各試験室ごとにこれらの統計量を測定水準の順序で
プロットする。
これらのグラフの解釈方法の詳細については,JIS Z 8402-2の7.3.1を参照されたい。ある試験室の測定
結果が全般的にかたよっている場合は,セル平均値のグラフにおいて,h統計値のほとんどが大きい値と
なり,かつ,同一方向に現れる。ある試験室が一つの測定水準での測定を併行条件で行わず,外来要因に
よってサンプル間変動が大きくなる場合,サンプル間範囲のグラフには,通常大きなk統計量が現れる。
ある試験室の併行精度がよくない場合,測定結果間範囲に基づくグラフには,通常大きなk統計量が現れ
る。
5.6.2
JIS Z 8402-2 7.3.3及び7.3.4のコクラン検定及びグラッブズ検定を行って,外れ値を調べる。
測定結果間範囲における外れ値を調べるため,各測定水準jについて次の式のコクラン統計量を計算す
る。
rj
SS
w
C
2
max
=
········································································ (37)
ここに,wmaxは測定水準jにおける測定結果間範囲wjitの最大値である。
22
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Z 8402-2の8.1の棄却限界値の表を使用する場合,一番左の列に示すpが2p'に相当する行にあるn
=2に相当する列の値を用いる。
サンプル間範囲における外れ値を調べるため,各測定水準jについて,次の式のコクランの統計量を計
算する。
HJ
SS
w
C
2
max
=
········································································ (38)
ここに,wmaxは測定水準jにおけるサンプル間範囲wjiの最大値である。
JIS Z 8402-2の棄却限界値の表を使用する場合,一番左の列に示すpがp'に相当する行にあるn=2に相
当する列の値を用いる。
セル平均値における外れ値を調べるため,JIS Z 8402-2の7.3.4の方法で,各測定水準jについて,セル
平均値からグラッブズ統計量を計算する(ここでは,JIS Z 8402-2のsを,5.4.2の式(26)によって定義さ
れるsyjと読み替える)。
これらの検定の解釈方法の詳細については,JIS Z 8402-2の7.3.2を参照されたい。不均質物質の実験で
は,これらの検定は次の手順で行う。まず測定結果間範囲についてコクランの検定を行う。この検定の結
果,ある測定結果範囲が1 %外れ値となり,これを除外すべきであると決定された場合は,1 %外れ値とな
った範囲を与えている測定結果二つを,併行標準偏差及び再現標準偏差の計算から除外する(ただし,セ
ル内のほかの測定結果は保持するものとする)。次にサンプル間範囲についてコクランの検定を行う。最後
にセル平均値についてグラッブズの検定を行う。あるサンプル間範囲が1 %外れ値であると決定されたか,
又はあるセル平均値が1 %外れ値であると決定され,この1 %外れ値を与える測定結果を除外すべきであ
ると決定した場合は,該当するセルの測定結果を,すべて併行標準偏差及び再現標準偏差の計算から除外
する。
5.7
不均質物質の実験結果の報告 4.7において述べたことがらは,不均質物質の実験にも当てはまる。
5.8
例2:不均質物質の実験
5.8.1
滑走路及び高速道路の表面を構成する材料(セメント結合又はアスファルト結合)に使用される骨
材は,ぬれと凍結に耐えなければならない。この性能を測定する方法の一つが硫酸マグネシウム安定性試
験[2]である。この試験では,骨材の試験用サンプルを飽和硫酸マグネシウム溶液に浸したのち乾燥させる
サイクルを多数回繰り返す。この試験は,10.0 mmふるいを透過しない骨材について行う。この処理によ
って粒子が劣化するので,試験の最後に骨材を10.0 mmふるいにかけて,これを透過する質量比率を測定
する。その値が大きい場合(10から20 %を超える場合)は,骨材の安定性が悪いことになる。
5.8.2
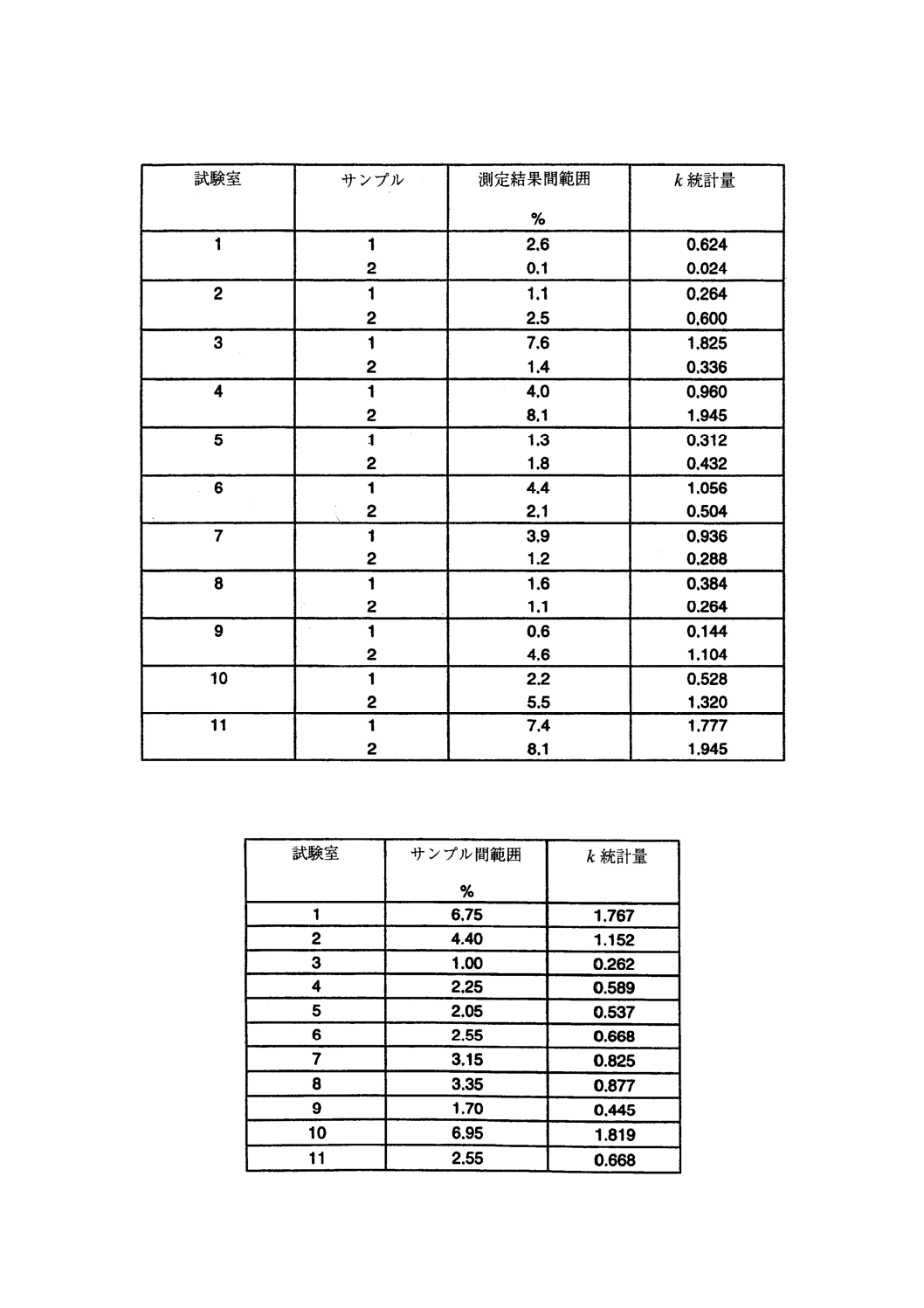
表13は,骨材の8サンプル対を試験室11か所へ送り,各サンプルについて硫酸マグネシウム安定
性測定結果を二つ得た実験のデータを示す。サンプルは質量が約100 kgであり,(これらは,多数の別種
の試験にも供され),この試験用サンプルの質量は約350gであった。
5.8.3
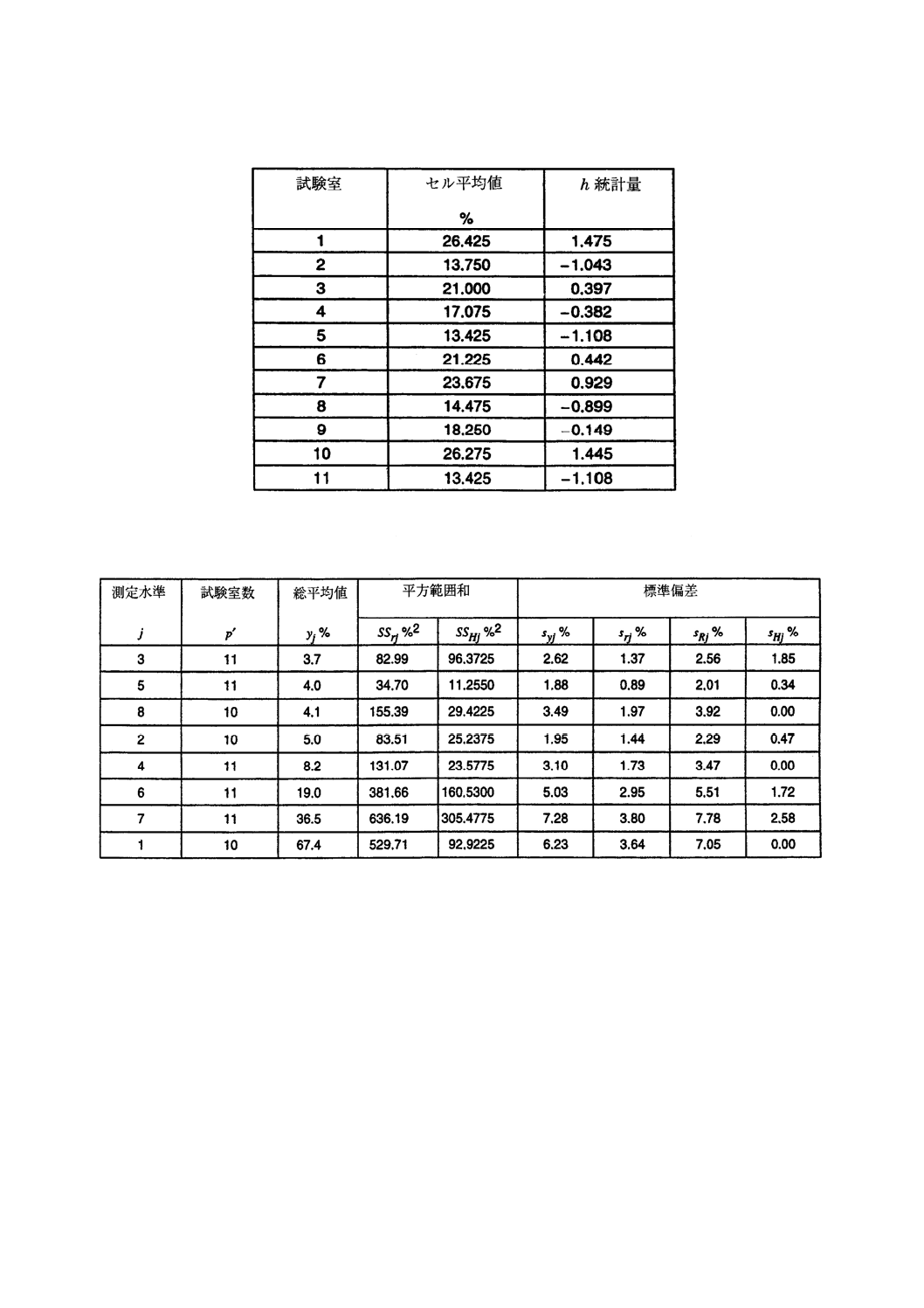
表14,表15及び表16は,実験の測定水準6について,5.4.2の式(21)から式(24)までを用いて計
算した測定結果間範囲,サンプル間範囲及びセル平均値を示す。
5.5.3の式(27)及び式(28)を用いると,表14の測定結果間範囲及び表15のサンプル間範囲から次の値を
得る。
SSr6=381.66 (%)2
SSH6=160.530 0 (%)2
5.4.2の式(25)及び式(26)を表16のセル平均値に適用すると,次の値を得る。
y6=19.0 % (一般平均)
sy6=5.03 %
したがって,5.5.5の式(29)から式(33)までを用いると,併行標準偏差及び再現標準偏差と,サンプル間
23
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
変動の精度に関する標準偏差は,次の値となる。
sr6=2.95 % sR6=5.51 % sH6=1.72 %
表17にほかの測定水準の計算結果を掲げた。
5.8.4
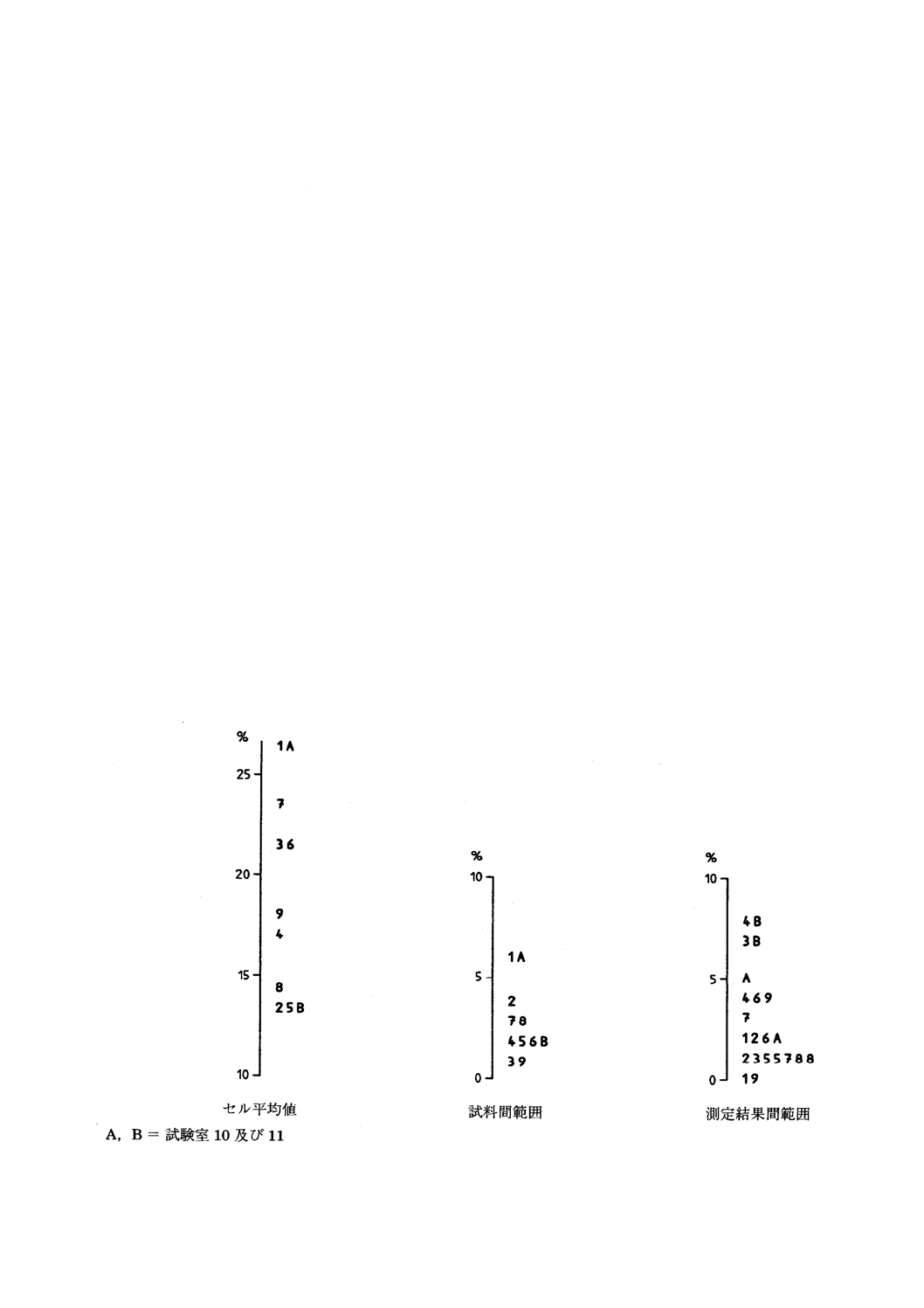
図4は,測定水準6について測定結果間範囲,サンプル間範囲及びセル平均値のヒストグラムを示
す。このタイプのグラフは,種々の要因(異なる測定結果,サンプル及び試験室)から発生するばらつき
について,理解しやすい全体像を提供する。図4は,この実験の測定水準6では,セル平均値が大きく変
動していることを示す。したがって,この測定方法を適用する場合,水準によっては,売り手と買い手の
間で測定結果が食い違い,紛糾する可能性がある。一方,サンプル間範囲は測定結果間範囲より小さい。
これは,測定水準6ではサンプル間変動が有意でないことを示唆している。
5.8.5
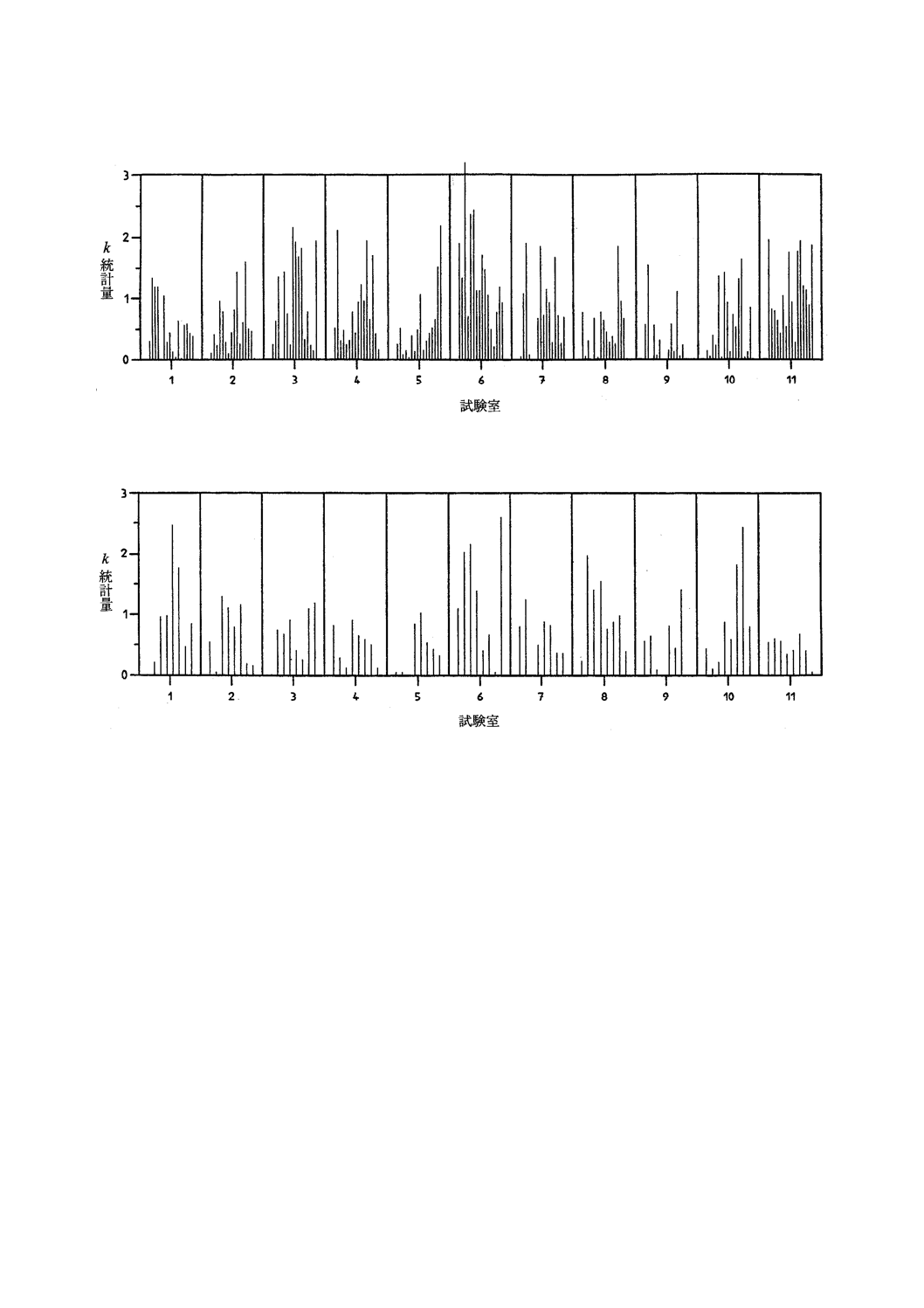
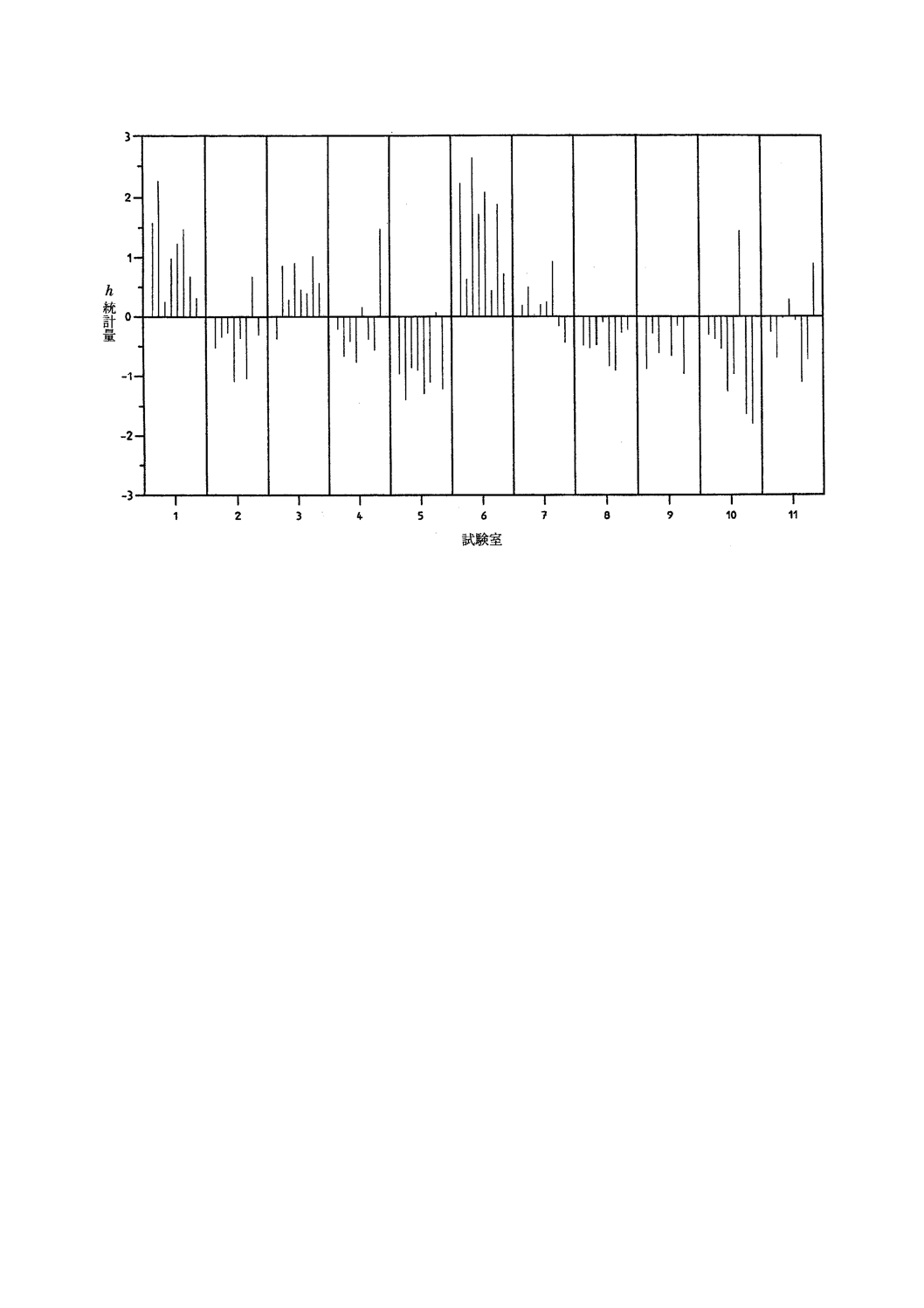
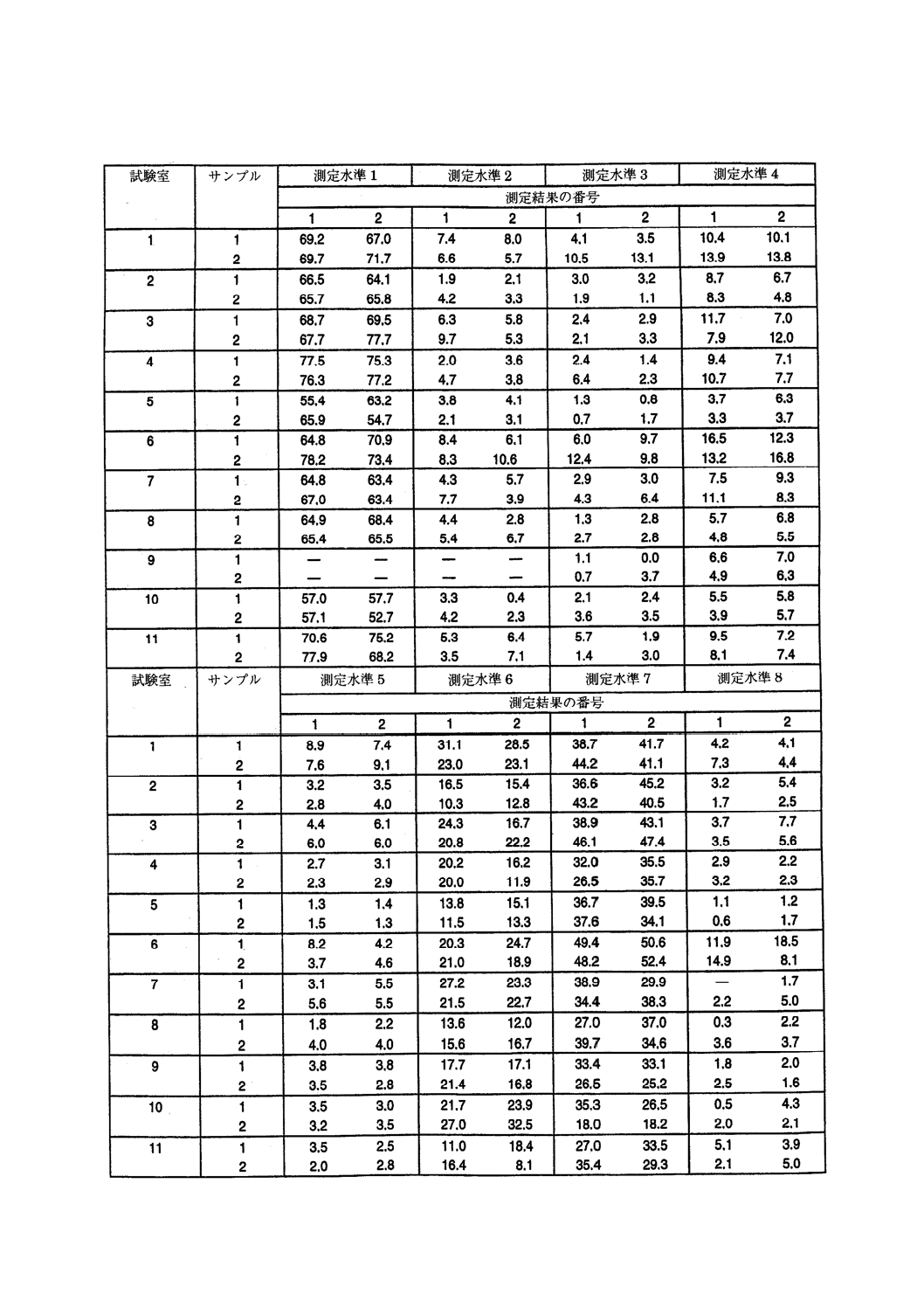
表14,表15及び表16はまた,測定水準6について,5.6.1において計算したh及びk統計量の値
を示している。図5から図7までに全測定水準について値をプロットした。これらの図では,表17に示す
とおり測定水準を一般平均が増加する順序で配列した。図5によれば,試験室6では測定結果間範囲のk
統計量が大きくなる値が数個ある。これは,この試験室の併行精度がほかの試験室よりも悪いことを意味
する。図6によれば,試験室3か所(1,6及び10)において,サンプル間範囲のk統計量が大きくなって
いる。このことは,これらの試験室が大口試料から試験片を準備する際に,勧告された手順を遵守しなか
った可能性を示唆する。図7によれば,ほとんどの試験室において,h統計量が一貫して負であるか,又
は正である(ここでも試験室1,6及び10が最大値を記録している)。これは,ほとんどの試験室に一貫し
たかたよりがあり,測定方法が適切に規定されていないことを意味する明確な証拠である。
5.8.6
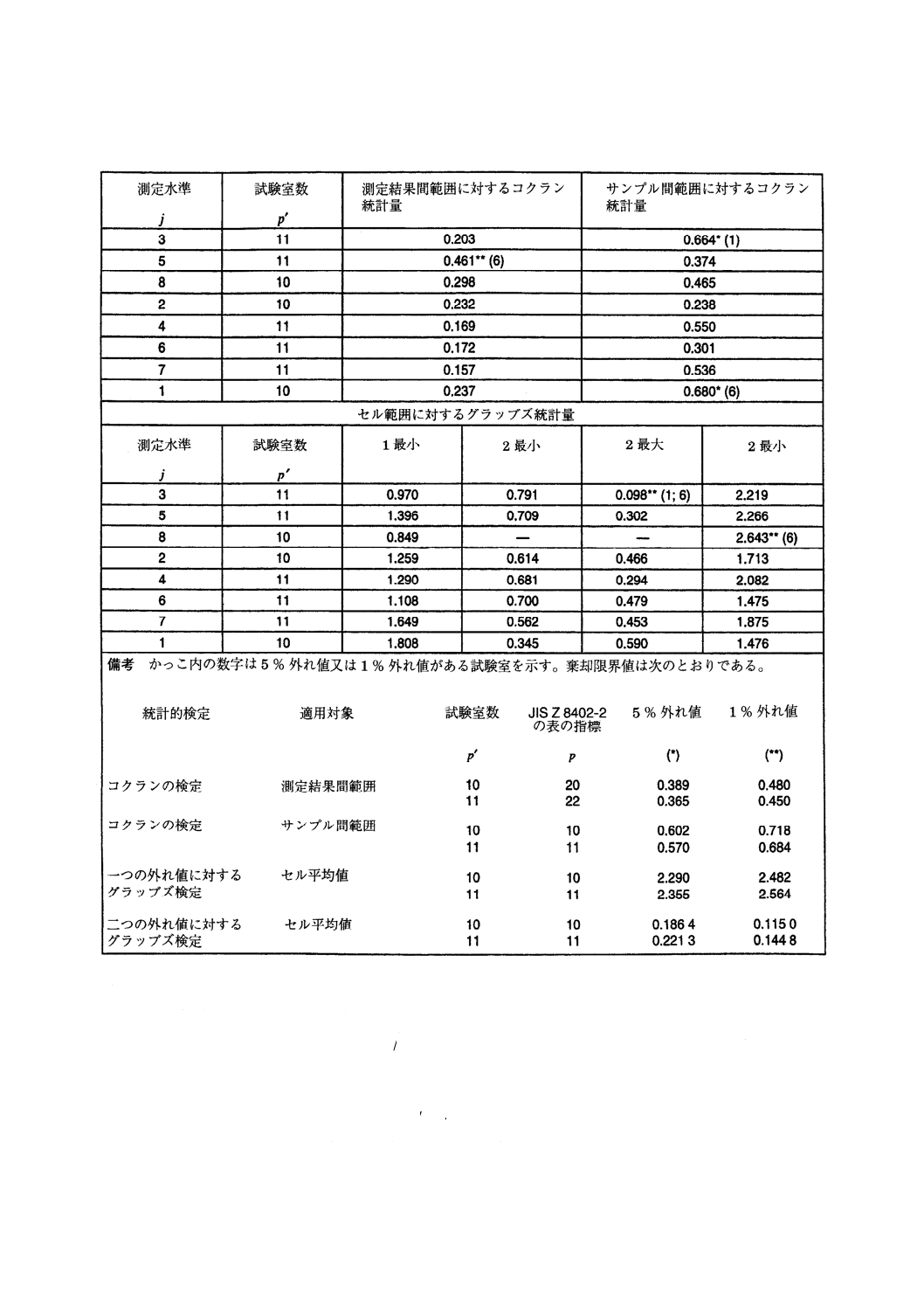
データに,5.6.2のコクラン検定とグラッブズ検定を適用すると,表18に示す結果を得る。ここで
は,1 %外れ値が二つ特定される。ほかの情報が存在しないので,1 %外れ値を示すデータは除外して計算
を繰り返す。こうすることで,JIS Z 8402-2で検討した水準を分割しない計画の場合と同じ方法で,関数
関係を調べて解析を継続することができる。
図 4 例2:測定水準6について表14,表15及び表16から得た範囲及び平均値のヒストグラム
24
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 5 例2:測定結果間範囲の一致性のチェック(試験室別)
図 6 例2:試料間範囲の一致性のチェック(試験室別)
25
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 7 例2:セル平均値の一致性のチェック(試験室別)
26
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 13 例2:硫酸マグネシウム安定性(%)
27
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 14 例2:測定水準6における測定結果間範囲
表 15 例2:測定水準6におけるサンプル間範囲
28
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 16 例2:測定水準6におけるセル範囲
表 17 例2:表13の全8測定水準データから計算した平均値,平方範囲和及び標準偏差の値
29
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 18 コクラン及びグラッブズ統計量の値
5.9
不均質物質の計画における一般的計算公式 各水準jについて,次の統計量を計算する。
a) 一般平均(i,t及びkに関する総計)
∑∑∑
j
ijtk
j
n
y
m=
································································ (39)
ここに,njは総計に含まれる測定結果数である。
b) 各iに関する試験室効果(t及びkに関する総計)
∑∑
ij
j
ijtk
ij
n
m
y
B
)
(
−
=
···························································· (40)
=(試験室平均値)―(一般平均)
30
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,nijは総計に含まれる測定結果数である。
c) 各i及びtに関するサンプル効果(kに関する総計)
∑
ijt
ij
j
ijtk
ijt
n
B
m
y
H
)
(
−
−
=
························································ (41)
=(サンプル平均値)−(試験室平均値)
ここに,nijtは総計に含まれる測定結果数である。
d) 各i,t及びkに関する残差
ijt
ij
j
ijtk
ijtk
H
B
m
y
z
−
−
−
=
···························································· (42)
=(測定結果)−(サンプル平均値)
e) サンプルに関する平方和(iに関する総計)
∑
2ij
ij
Lj
B
n
SS=
········································································ (43)
f) サンプルに関する平方和(i及びtの両方に関する総計)
∑∑
2ijt
ijt
Hj
H
n
SS=
··································································· (44)
g) 併行精度に関する平方和(i,t及びkに関する総計)
∑∑∑
2ijtk
rj
z
SS=
···································································· (45)
h) 自由度
1
'−
=
j
Ljp
v
j
j
Hj
p
g
v
'
−
=
··········································································· (46)
j
j
rj
g
n
v
−
=
ここに,
p'jは少なくとも測定結果を1個報告した試験室数である。
gjは少なくとも測定結果が1個報告されたサンプル数である。
njは測定結果全体の個数である。
i) 各iに関する係数(tに関する総計)
∑ijt
ij
n
n=
············································································· (47)
∑
2ijt
ij
n
K=
············································································· (48)
j) 係数(iに関する総計)
∑
2ij
j
n
K=
············································································· (49)
∑
ij
j
K
K=
'
············································································ (50)
∑
ij
ij
j
n
K
K=
''
········································································ (51)
k) 次の公式による併行標準偏差srj,サンプル間標準偏差sHj,試験室間標準偏差sLj,及び再現標準偏差
sR
rj
rj
rj
v
SS
s=
2
·········································································· (52)
31
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)
(
]
[
''
2
2
j
j
rj
Hj
Hj
Hj
K
n
s
v
SS
s
−
−
=
×
···················································· (53)
)
(
]
)
(
[
j
j
j
rj
Lj
Hj
j
j
j
Lj
Lj
n
K
n
s
v
s
n
K
K
SS
s
−
−
−
−
=
2
2
'
''
2
×
×
························ (54)
2
2
2
Lj
rj
Rj
s
s
s
+
=
··········································································· (55)
備考 上の計算式はScheffé(シェフェ)[4]の統計理論によって導いた。
5.10 例3:一般公式の適用
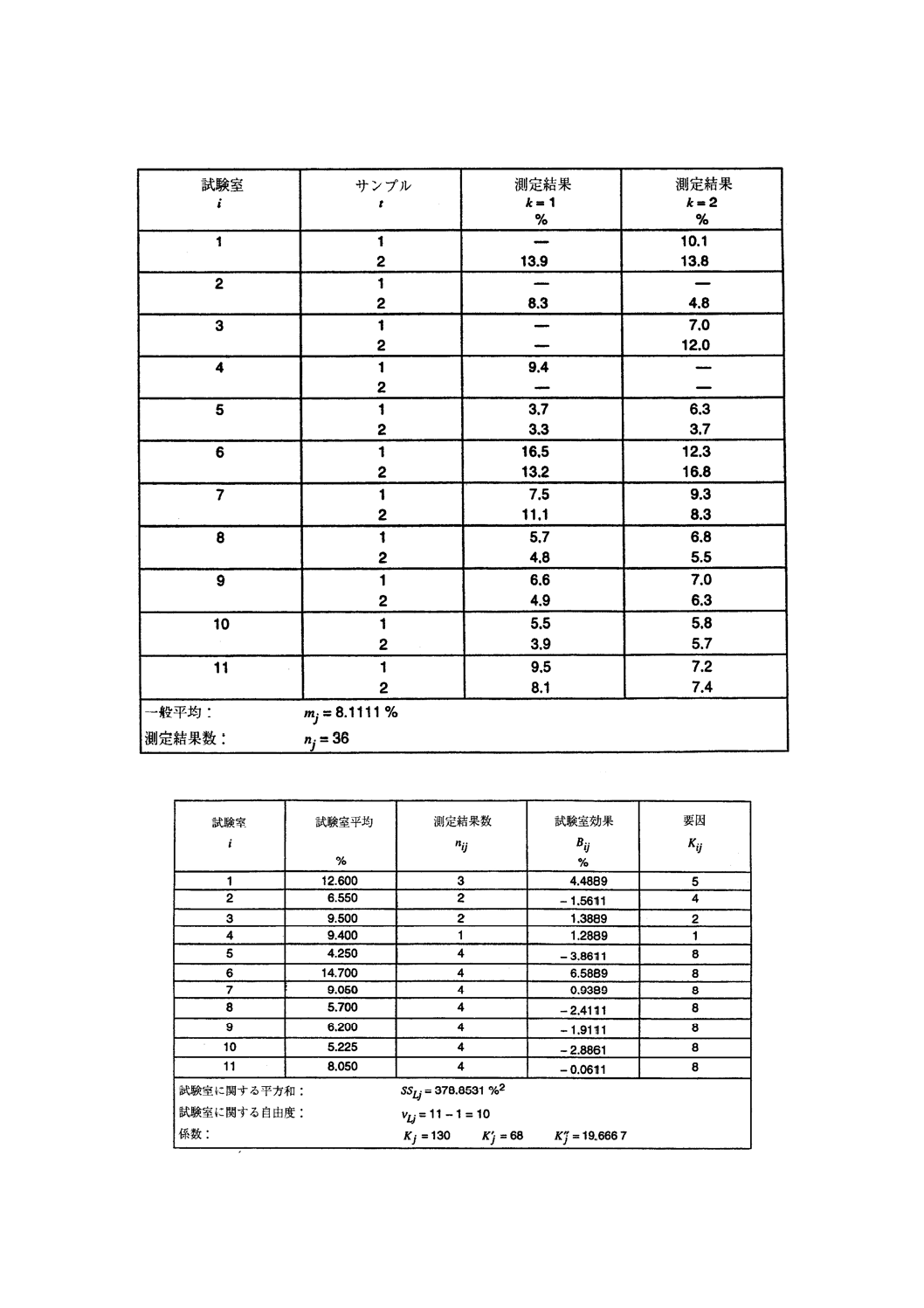
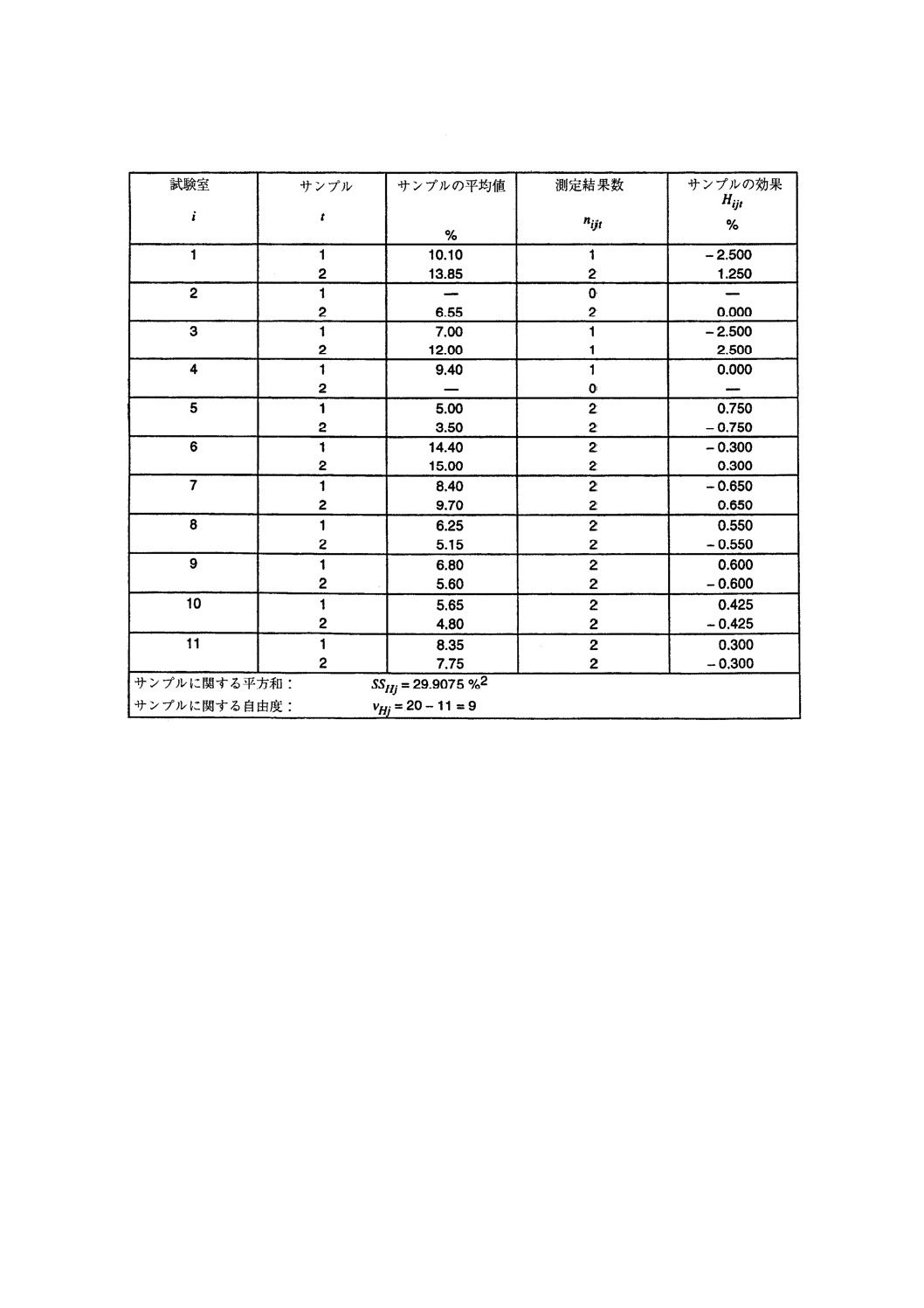
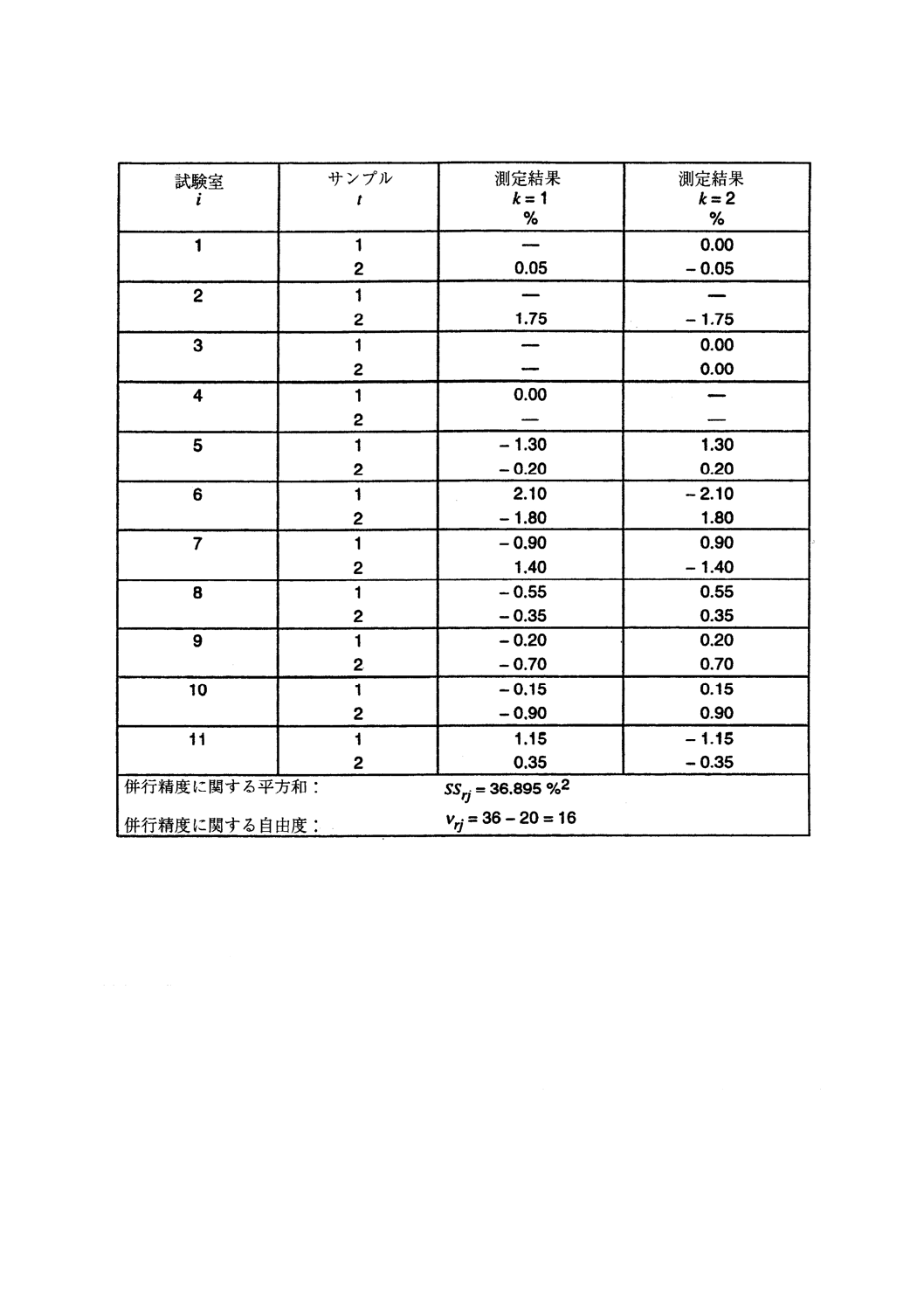
5.10.1 例2の測定水準4のデータを用い,かつ,測定結果の一部が欠落したものを一般公式の適用例とし
て示す(表19参照)。5.9に掲げた公式から表19の一般平均と,表20,表21及び表22の平方和,自由度
及び要因を得る。
5.10.2 5.9のステップk)の式(52)及び式(55)を適用して,次の値を得る。
2
2
16
0
895
.
36
%
=
=
rj
rj
rj
v
SS
s
したがって
%
52
.1
=
rj
s
及び
2
2
''
2
2
667
.
19
36
5185
.1
9
9075
.
29
%
)
(
]
[
)
(
]
[
−
−
=
−
−
=
×
×
j
j
rj
Hj
Hj
Hj
K
n
s
v
SS
s
したがって
%
75
.0
=
Hj
s
及び
)
(
]
)
(
[
)
(
]
)
(
[
36
130
36
5185
.1
10
7487
.0
36
68
6667
.
19
8531
.
378
2
2
2
2
'
''
2
−
−
−
−
=
−
−
−
−
=
×
×
×
×
j
j
j
rj
Lj
Hj
j
j
j
Lj
Lj
n
K
n
s
v
s
n
K
K
SS
s
したがって
%
27
.3
=
Lj
s
及び
%
61
.3
27
.3
52
.1
2
2
=
+
=
Rj
s
32
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 19 例3:測定水準4における硫酸マグネシウム安定性
表 20 例3:試験室に関する平方和の計算
33
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 21 例3:サンプルに関する平方和の計算
34
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 22 例3:併行精度平方和の計算
6. ロバストなデータ解析方法
参考 この規格では“ロバストな”という言葉を,“外れ値の影響を受けにくい”という意味で用いて
いる。
6.1
ロバストなデータ解析方法の適用
6.1.1
JIS Z 8402-2は,精度評価実験のデータについて外れ値の検定を2種類(コクラン検定及びグラッ
ブズ検定)行うことと,これらの検定の片方又は両方で,統計量が有意水準1 %で棄却限界値を超えるよ
うなデータを除外することを推奨している(そのデータを保持すべき相当の理由がある場合を除く。)。実
際は,この手順を踏むことは容易でないことが多い。4.8の例1の外れ値の検定結果(表8参照)を考えて
みると,試験室5では,グラッブズ検定によって確かに1 %外れ値であると分類できる水準10のセル平均
値はただ1個であるが,そのほかにも5 %外れ値が3個ある。図3は,この試験室では何かが不備であるこ
とを強く示唆している。この場合,試験室5については次のいずれを選択するかを決定しなければならな
35
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い。
a) データをすべて保持する。
b) 水準10のデータだけを除去する。
c) データをすべて除去する。
この決定は,併行標準偏差及び再現標準偏差の計算値に決定的な影響をおよぼすであろう。精度評価実
験のデータを解析する場合,データが5 %外れ値と1 %外れ値の間にあることをよく経験する。したがっ
て,計算結果が影響を受けるような判断を強いられることがあるが,これは好ましいことではないであろ
う。この項で述べるロバストな方法では,計算結果に影響を与えるような判断を要せずしてデータを解析
することができる。したがって,精度評価実験の結果に外れ値があると予想される場合は,ロバストな方
法を適用することが望ましい。
6.1.2
JIS Z 8402-1の5.で議論したモデルには,測定方法を用いるすべての試験室に共通の併行標準偏差
を決定してもよいという仮定がある。実際は,試験室の中にはほかと比べて併行精度が悪いところもある。
例えば,5.8の例2の実験の図5では,試験室6は明らかに試験室9よりも併行精度がはるかに悪い。した
がって,この場合,試験室がすべて同等の併行精度を達成するという仮定が正しいとは思われない。ある
測定方法をはじめて精度評価実験に適用したか,又はその測定方法に経験が浅い参加者の中には,併行精
度が悪い参加者もいるであろう。ロバストな方法を適用することが特に妥当であるのはこのような場合で
ある。
6.1.3
精度評価実験のデータを解析する場合,ロバストな方法[6]を適用する目的は,外れ値の影響を受け
ないようにして,併行標準偏差及び再現標準偏差を計算することである。実験の参加者を質の良いデータ
の提供者と質の劣るデータの提供者に分類できるなら,ロバストな方法は,質の良いデータに対して有効
な併行標準偏差及び再現標準偏差の値をもたらし,(質の劣るデータが多量に存在しない限り)質の劣るデ
ータの影響を受けない。
6.1.4
ロバストなデータ解析方法の適用は,精度評価実験の計画,組織及び実施には影響しない。ロバス
トな方法を適用するか,又は1 %外れ値の排除を伴う方法を適用するかは統計の専門家が決定し,その決
定をパネルへ報告するのがよい。ロバストな方法を適用する場合,JIS Z 8402-2又はJIS Z 8402-5に述べ
たデータの外れ値の検定及び一致性チェックを行い,1 %外れ値の原因又はh及びk統計量のパターンに
ついて検討するのがよい。しかしながら,この検定及びチェックの結果としてデータを除去すべきではな
い。
6.1.5
h及びk統計量の分母は,JIS Z 8402-2の計算方法によって,報告されたデータから計算した標準
偏差である。もしデータに外れ値がある場合,分母が大きくなり,統計量のグラフをゆがめる効果がある
であろう。例えば,ある試験室が,ある水準について,ほかの外れ値よりもはるかに異常であるセル平均
値の外れ値を与えるなら,その水準のh統計量グラフにおいて極端に大きなh統計量が現れるであろう。
これに対し,ほかのすべての試験室については,例えその水準について外れ値を出した試験室が一部あっ
たとしても,そのh統計量は小さいであろう。h統計量の計算において総平均を使用すれば同じような効
果がある。h及びt統計量の分母として標準偏差のロバストな推定値を使用し,h統計量の計算に総平均の
ロバストな推定値を使用すれば,このひず(歪)みを防止することができる。そのため,このようなロバ
ストな値を使用することを推奨する。
6.1.6
精度実験のデータから,次の二つの統計量を計算することができる。
a) セル平均,これから試験室間変動の値を与える標準偏差を計算することができる。
b) セル内の標準偏差又は範囲(すなわち,水準分割計画における差),この組合せで試験室内変動の値を
36
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
得る。
ここで述べるロバストな方法は,セル平均値,標準偏差,範囲又は差を置き替えるものではないが,こ
れらを組み合わせて併行標準偏差及び再現標準偏差を計算する統計量を得るための代替法を提供する。
例えば,JIS Z 8402-2で検討した水準を分割しない計画において,一つの測定水準から得られたデータ
を解析する第1段階は,各セルの測定結果の平均値と標準偏差を計算することである。その後,セル平均
値を用いて試験室間ばらつきの尺度となる標準偏差を計算する。この項のロバストな方法を用いるときに
は,この計算に“アルゴリズムA”を適用するが,グラッブズ検定の結果によってセル平均値を計算から
除外することはしない。また,セル標準偏差をプールしておいて併行精度標準偏差の推定値を得る。ロバ
ストな解析ではこれを“アルゴリズムS”を用いて行うが,コクラン検定の結果によってセル標準偏差を
除外することはしない。いずれの方法(JIS Z 8402-2の方法又はこの項の方法)の場合も,これらの二つ
の値を用いて,同じように併行標準偏差及び再現標準偏差を計算する。
更に複雑な例は,JIS Z 8402-3の附属書Cにある6要因スタッガード型枝分れ計画である。この計画の
第1段階では,各試験室(各水準)について,実験で調査した各種要因によるばらつきの情報をもつデー
タの平均値,yi(1),…,yi(5)と,一連の範囲wi(1),…,wi(5)を計算する。ここに述べるロバストな方法を用
いてデータを解析するため,セル平均値に“アルゴリズムA”を適用し,一連の範囲に順番に“アルゴリ
ズムS”を適用する。次にこのような計算によって得た統計量を用いて,JIS Z 8402-3の解析方法を適用
する場合と同じく,併行,中間及び再現標準偏差の推定値を得る。
6.1.7
この規格のこの部に含まれるロバストな方法は,この規格の第2,3,4及び第5部にある実験計画
すべてに適用することが可能であり,かつ,必要な計算が比較的簡単であるため,ここに採用した。しか
しながら,ロバストな方法は,セル平均値,セル標準偏差及びセル範囲をロバストな形で組み合わせる手
段を提供するものであることに注意する必要がある。この方法は個々の測定結果をロバストな形で組み合
わせるものではない。すなわち,この方法は,セル平均値とセル標準偏差からスタートする。セルの測定
結果をロバストな形で組み合わせるロバスト法も存在するが,実際に適用する場合は更に複雑になるであ
ろう。
6.2
ロバストな解析:アルゴリズムA
6.2.1
このアルゴリズムは,適用するデータの平均値と標準偏差のロバストな値を得る。これを次の値の
求め方に適用する。
a) すべての計画におけるセル平均値
b) 水準分割計画におけるセル間差
6.2.2
データp個を増加する順序にならべて,次の記号で表す。
x1,x2,…,xi,…,xp
これらのデータのロバストな平均値とロバストな標準偏差をx*とs*で表す。
6.2.3
x*とs*の初期値を計算する。すなわち,
x*=xiのメディアン(i=1,2,...,p) ······································· (56)
s*=1.483×|xi−x*|のメディアン(i=1,2,...,p) ······················· (57)
6.2.4
次の方法でx*とs*の値を更新する。
次の値を計算する。
*
5.1s
=
ϕ
··············································································· (58)
各xi(i=1,2,...,p)について,次の値を計算する。
37
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ϕ
ϕ
ϕ
ϕ
)
(そのほかの場合
の場合
+
>
+
の場合
−
<
−
=
i
i
i
i
x
x
x
x
x
x
x
x
*
*
*
*
*
,
,
·············································· (59)
次の式で新しいx*とs*の値を計算する。
∑
=
p
i
ip
x
x
1
*
*=
··········································································· (60)
∑
=
−
−
p
i
i
p
x
x
s
1
2
*
*
*
1
134
.1
)
(
)
(
=
··················································· (61)
6.2.5
x*とs*のロバストな推定値は反復計算によって得られる。すなわち,反復によってx*とs*の推定値
がほとんど変化しなくなるまで6.2.4の計算を繰り返す。これはコンピュータのプログラムで簡単に実現
できる方法である。
6.2.6
計算を手作業で行う場合,6.2.4の式(60)と式(61)を次のように書き変えれば,反復計算を伴わな
い簡単な方法が得られる。
)
(
)
(
U
L
*
L
U
*
5.1
'
u
u
p
s
u
u
x
x
−
−
−
+
=
×
··········································· (62)
])
(
)
(
)
([
)
(
)
(
)
(
U
L
U
L
U
L
2
2
2
U
L
2
*
4
5.1
134
.1
1
'
1
u
u
p
u
u
pu
pu
p
s
u
u
p
s
−
−
−
+
−
−
−
−
−
=
×
···························· (63)
ここに
uLは
ϕ
−
<*x
xi
となるデータxiの個数
uUは
ϕ
+
>*x
xi
となるデータxiの個数
x'とs'は,
ϕ
≤
*x
xi−
となる(p−uL−uU)個のデータxiの平均値と標準偏差
である。
uLとuUが既知の場合は,これらの式で直接x*及びs*を計算することができる。解を得る一つの方法は,
x*との差が1.5s*より大きいデータの実際の個数が,x*とs*を計算するために用いたuL及びuUの値に等しく
なる有効な答えが得られるまで,系統的に種々の可能性(すなわち,uL=0とuU=0,uL=0とuU=1,uL
=1とuU=0,uL=1とuU=1など)を試してみることである。実際は,図4に示すようなヒストグラムを
用いて,x*との差が1.5s*より大きい可能性がある値を特定すれば,多数のケースを評価しなくても答えを
得ることができるであろう。
もう一つの方法は,反復計算によって概略の答えを得たあと,式(62)及び式(63)を解き,正確な答えを
得ることである。次の例ではこの方法を適用する。
6.3
ロバストな解析:アルゴリズムS
6.3.1
このアルゴリズムは,すべての計画において試験室内標準偏差(又は試験室内範囲)に適用する。
このアルゴリズムでは,適用した標準偏差又は範囲についてプールしたロバストな値を得る。
6.3.2
データp個を増加する順序にならべて,次の記号で表す。
w1,w2,…,wi,…,wp
これらの値は範囲又は標準偏差である。
プールしたロバストな値をw*で表し,各wiに関する自由度をνで表す(wiが範囲のときはν=1,wiが
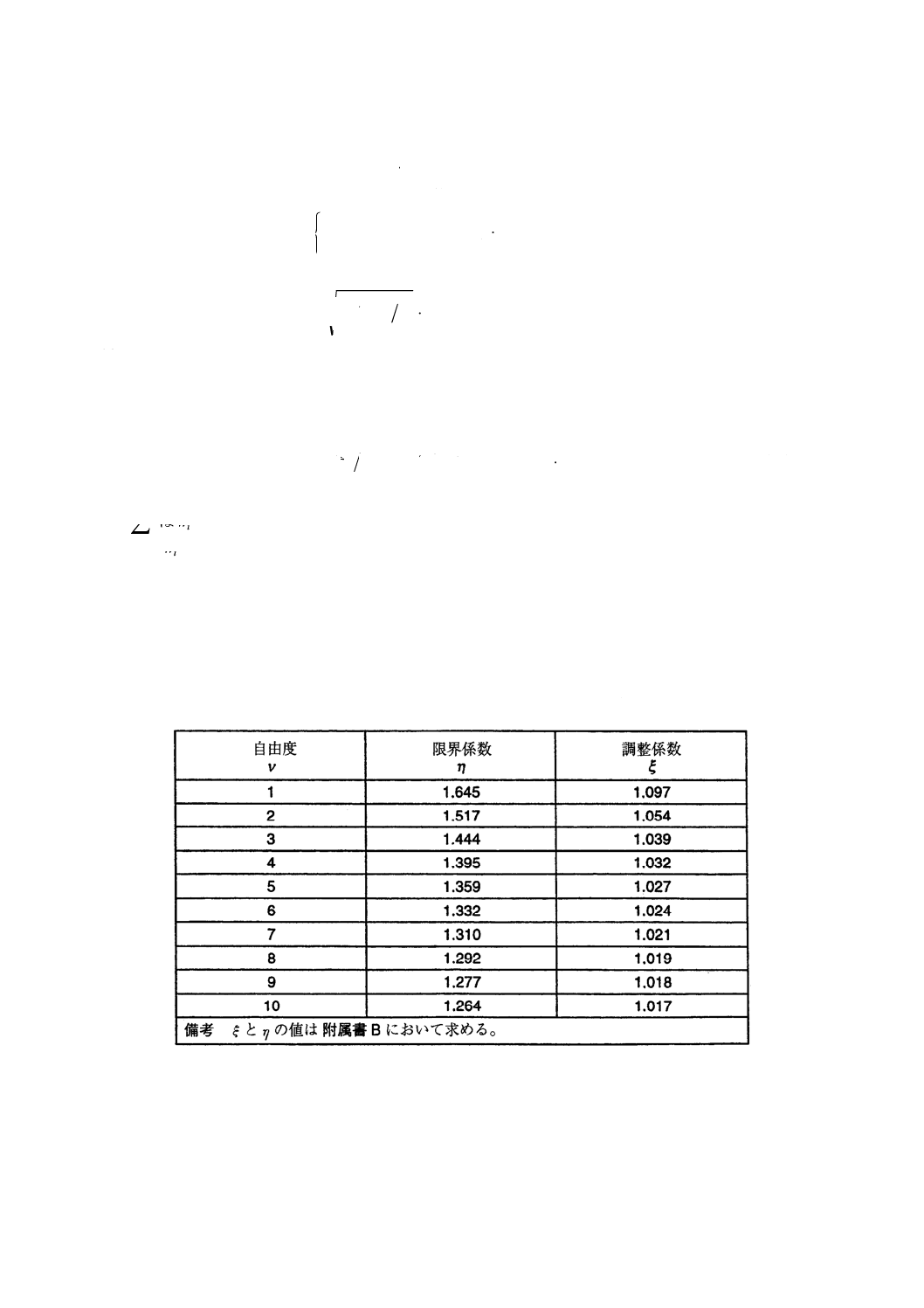
n個の結果の標準偏差のときはν=n−1)。表23からアルゴリズムに必要なξとηの値を得る。
6.3.3
w*の初期値を以下のように計算する。
w*=wiのメディアン(i=1,2,...,p) ······································ (64)
6.3.4
次の方法でw*の値を更新する。
38
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
次の値を計算する。
ψ=η×w* ············································································ (65)
各wi(i=1,2,...,p)について,次の値を計算する。
>
)
,
,
*
それ以外の場合
ψの場合
ψ
=
(
i
i
i
w
w
w
··················································· (66)
次の式で新しいw*の値を計算する。
∑
=
p
i
i
p
w
w
1
2
*
*
)
(
=ξ
································································· (67)
6.3.5
ロバストな推定値w*は反復計算によって得られる。すなわち,反復によって推定値w*が変化しな
くなるまで6.3.4の計算を繰り返す。これはコンピュータのプログラムで簡単に実現できる方法である。
6.3.6
計算を手作業で行う場合は,6.2.6に述べた方法に類似していて,反復計算を伴わない簡単な方法
がある。このため6.3.4の式(67)を,次のように書き変える。
]
)
(
)
(
[
]
[
)
(
∑
×
×
2
*
U
2
*
2
2
*
'
w
u
w
p
w
i
η
+
ξ
=
······································· (68)
ここに,
∑'は
ψ
≤
iw
となるwiについての和
uUは
ψ
>
iw
となるwiの個数
である。
この式は,η×w*より大きいwiの個数がuUに等しくなるまで,順番にuU=0,uU=1,uU=2などと置
いていけば解くことができる。実際は,図4に示すようなヒストグラムを用いて,範囲がη×w*を超える
可能性がある値を特定すれば,多数のケースを評価しなくても答えを得ることができるであろう。
次の例で用いる方法では,反復法によって概略の答えを得たあと,式(68)を解いて正確な答えを得る。
表 23 ロバストな解析に必要な係数:アルゴリズムS
6.4
公式:水準を分割しない計画の一つの測定水準に関するロバストな解析
6.4.1
水準を分割しない計画の場合,ある水準の併行標準偏差srのロバストな推定値は,その水準のセル
範囲又はセル標準偏差にアルゴリズムSを適用し,6.3.4の式(67)からロバストな値w*を求めることによ
って得られる。セル標準偏差にアルゴリズムSを適用すると,
39
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
*
w
sr=
·················································································· (69)
となる。
セルごとに測定結果が二つある場合は,アルゴリズムSをセル範囲に適用し,
2
*
w
sr=
··········································································· (70)
となる。
6.4.2
ある水準のセル平均値の標準偏差sdのロバストな推定値は,そのセル平均値にアルゴリズムAを
適用し,6.2.4の式(61)からロバストな値s*を求めることによって得られ,
sd=s* ··················································································· (71)
を用いる。
6.4.3
次に,次の式から試験室間標準偏差sLを得ることができる。
sL=
)
(
n
s
s
r
d
2
2−
····································································· (72)
ここに,nはセル当たり測定結果の数である。
平方根の中の値が負の場合は,
sL=0 ···················································································· (73)
とする。
次の式でその水準の再現標準偏差を計算する。
sR=
2
2
rs
s+
L
········································································· (74)
6.5
例4:水準を分割しない計画の一つの測定水準に関するロバストな解析
6.5.1
JIS Z 8402-2の例3は,データが外れ値を含む水準を分割しない計画の例である。その例の水準5
では,試験室1がグラッブズの検定によってほぼ5 %外れ値となるセル平均値を与え,試験室6がコクラ
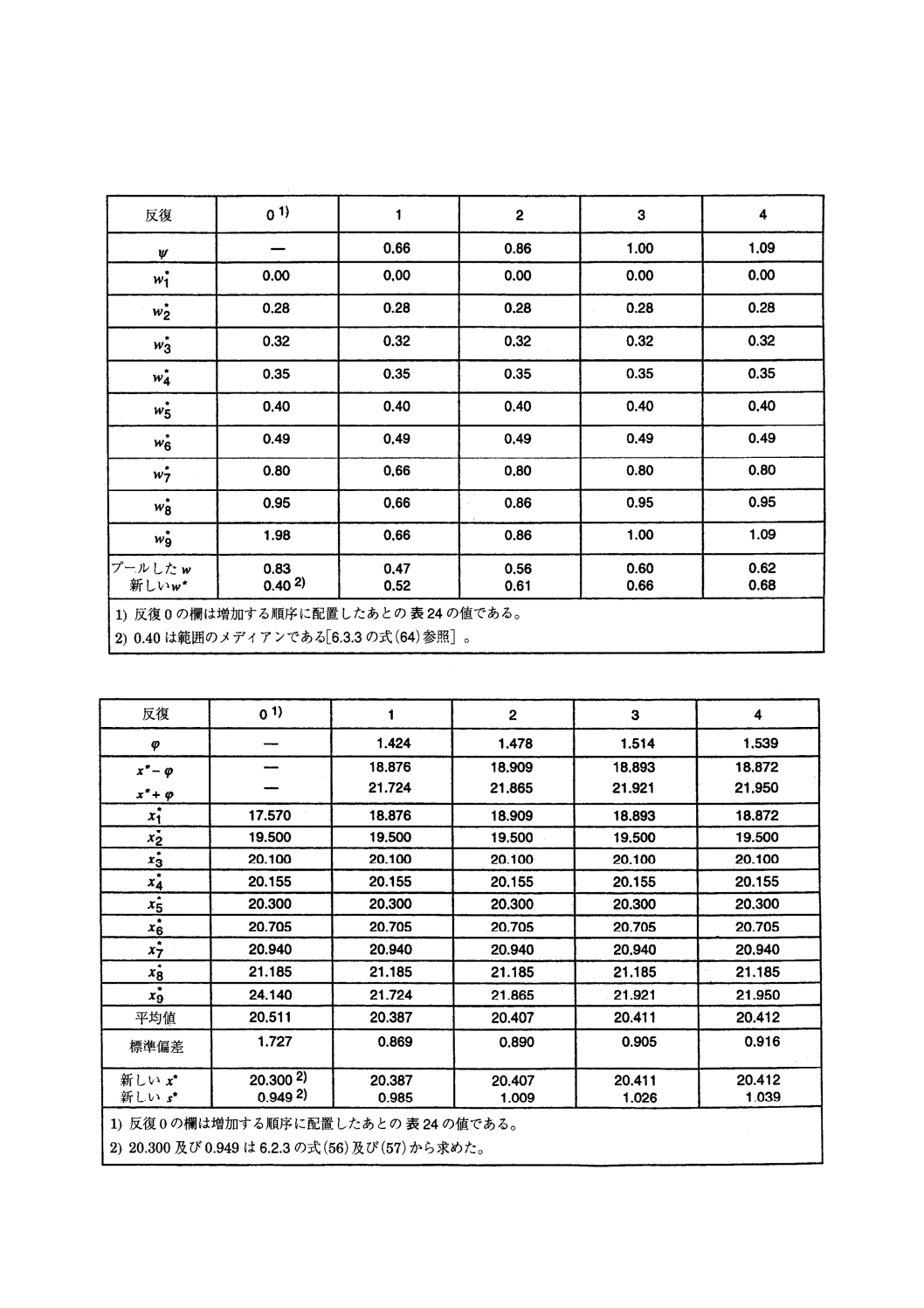
ンの検定によってほぼ5 %外れ値となるセル範囲を与えるため,特に興味深い。表24にこれらのデータを
再掲載した。
6.5.2
全試験室のデータを保持した場合,JIS Z 8402-2の7.4の公式を用いて,併行標準偏差及び再現標
準偏差を推定することができ,次の結果を与える。
p=9
m=20.511
sr=0.585
sd=1.727
sL=1.677
sR=1.776
6.5.3
しかし,データ解析者が,JIS Z 8402-2に従い,この実験のほかの測定水準の情報に基づき,試験
室6が試験したサンプルの同一性に疑問を抱き,試験室1及び6のデータを計算から除外するように判断
した場合には,次の結果を与える。
p=7
m=20.412
sr=0.393
sd=0.573
40
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
sL=0.501
sR=0.637
この二つの試験室のデータを除外するという決定は,明らかに併行標準偏差及び再現標準偏差の推定値
に大きな影響を及ぼしている。
6.5.4
解析の第1のステップは,併行標準偏差のロバストな推定値を得ることである。表25に示すよう
にセル範囲を増加する順序に並べ替えれば,都合よく計算を行うことができる。反復計算を行うアルゴリ
ズムSを適用することで,この表に示す結果が得られる。この例では,各セル範囲の自由度はν=1であ
るので,ξ=1.097,η=1.645となる。表に示すように反復計算を4回行えば,ロバストな値はw*≒0.7
となり,ただ一つのセル範囲(w*9=1.98)だけがψより大きい。コンピュータで計算を行えば,w*の値が
あまり変わらなくなるまで反復計算を続けることが可能であろう。
次の方法で直接,解を得ることもできる。6.3.6の式(68)に,
uU=1
∑
=
p
i
i
p
w
1
2
*
5
249
.0
'
=
)
(
を代入すると,
9
645
.1
097
.1
5
249
.0
097
.1
2
*
2
2
*
)
(
)
(
w
w
×
×
+
=
となり,次の解が得られる(仮定uU=1が正しい場合)。
w*=0.69 %(クレオソート含有率)
この値からψ=1.645×0.69=1.14となり,仮定したとおりw*9だけがψより大きく,更にw*9を1.14で
置き替えると,w*=0.63×1.097=0.69を再び与え,解が妥当であることが確認される。
したがって,併行標準偏差の推定値は,次のとおりである。
sr=
2
69
.0
=0.49 %(クレオソート含有率)
この値は6.5.2及び6.5.3において求めた二つの推定値の間にある。
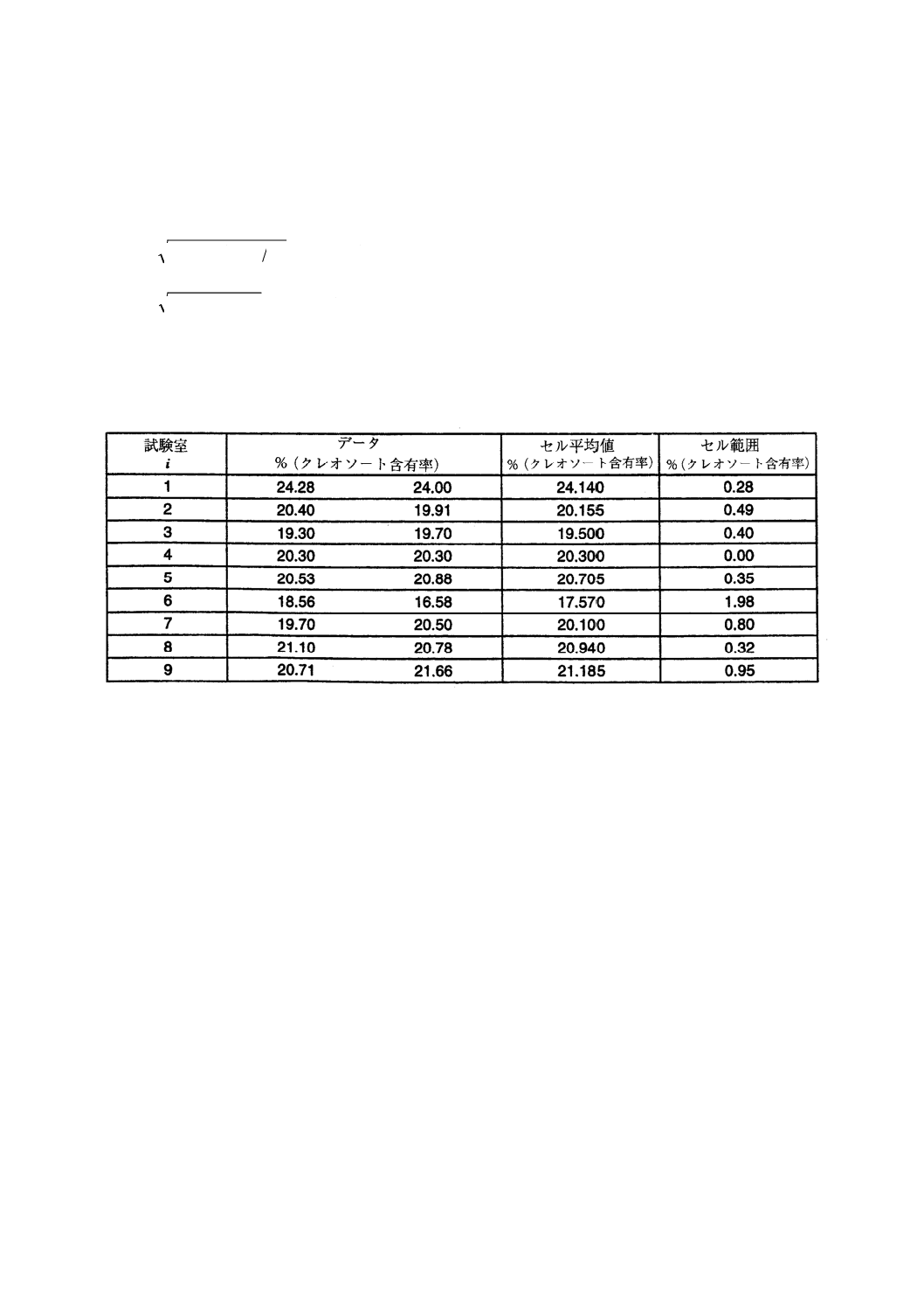
6.5.5
解析の次のステップは,セル平均値の標準偏差のロバストな推定値を得ることである。セル平均値
にアルゴリズムAを適用して表26に示す結果を得るが,ここではセル平均値を増加する順序に並べ替え
てある。表のとおり反復計算を4回行えば,ロバストな値はx*=20.412及びs*≒1.1であり,二つの両極端
の平均値(x*1=17.570,x*9=24.140)だけが,x*との差がϕより大きい。コンピュータで計算を行えば,x*
とs*の値があまり変わらなくなるまで反復計算を続けることが可能であろう。
手作業で計算を行う場合,データ解析者は6.2.6で述べられている直接的な方法を用いて,次の値を試し
てみるのがよい。
uL=uU=1
この結果,次の値を得る。
412
.
20
'=
x
及び
573
.0
'=
s
% (クレオソート含有率)
したがって,6.2.6の式(62)及び式(63)から,
]
)
(
[
)
(
)
(
7
4
9
9
5.1
134
.1
8
573
.0
6
*
2
2
2
2
−
+
−
=×
s
となり,
s*=1.070 % (クレオソート含有率)
及び,
x*=x'=20.412 % (クレオソート含有率)
を得る。
41
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
このs*の値からϕ=1.605となり(仮定したとおりx*1とx*9だけが,x*=20.412からϕ以上離れている),
x*1を18.807,x*9を22.017で置き替えると,新しい値としてx*=20.412とs*=0.944×1.134=1.070を再び
与え,解が妥当であることが確認される。
したがって,試験室間の標準偏差の推定値は,6.4.3の式(72)から,
sL=
)
(
2
49
.0
070
.1
2
2−
=1.012 % (クレオソート含有率)となり,再現標準偏差の推定値は,6.4.3
の式(74)から,
sR=
2
2
49
.0
012
.1
+
=1.124 % (クレオソート含有率)
となる。
この値も,6.5.2及び6.5.3において求めた二つの推定値の間にある。
表 24 例4:クレオソート・オイルの温度滴定
42
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 25 例4:セル範囲へのアルゴリズムSの適用[クレオソート含有率(%)]
(ν=1;ξ=1.097;η=1.645)
表 26 例4:セル平均値へのアルゴリズムAの適用[クレオソート含有率(%)]
43
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.6
公式:水準分割計画の一つの測定水準に対するロバストな解析
6.6.1
水準分割計画の場合,ある測定水準における併行標準偏差のロバストな推定値srは,その測定水準
のセル間差にアルゴリズムAを適用し,式(61)からロバストな値s*を求め,次の式でsrを計算することに
よって得られる。
2
*s
sr=
············································································· (75)
6.6.2
ある測定水準におけるセル平均値の標準偏差のロバストな推定値syは,その測定水準のセル平均値
に再度アルゴリズムAを適用し,式(61)からロバストな値s*を求め,次の式でsyを計算することによって
得られる。
sy=s* ··················································································· (76)
その後,4.5.6の公式を用いてその水準の再現標準偏差の推定値を計算することができる。
6.7
例5:水準分割計画の一つの測定水準に対するロバストな解析
6.7.1
4.8の例1のデータは,多数の5 %外れ値及び一つの1 %外れ値を含んでいる(表8参照)。また,
図3は,試験室5の結果に一貫して負のかたよりがあることを示している。これらの異常なデータの原因
が特定できない場合,異常なデータがあるか否か,あるとすればどのデータを併行標準偏差及び再現標準
偏差の計算から除外するかを判断しなければならないが,これは困難である。ここでは,測定水準14のデ
ータ(表4参照)を用いて,ロバストな解析から得られる結果を示す。
6.7.2
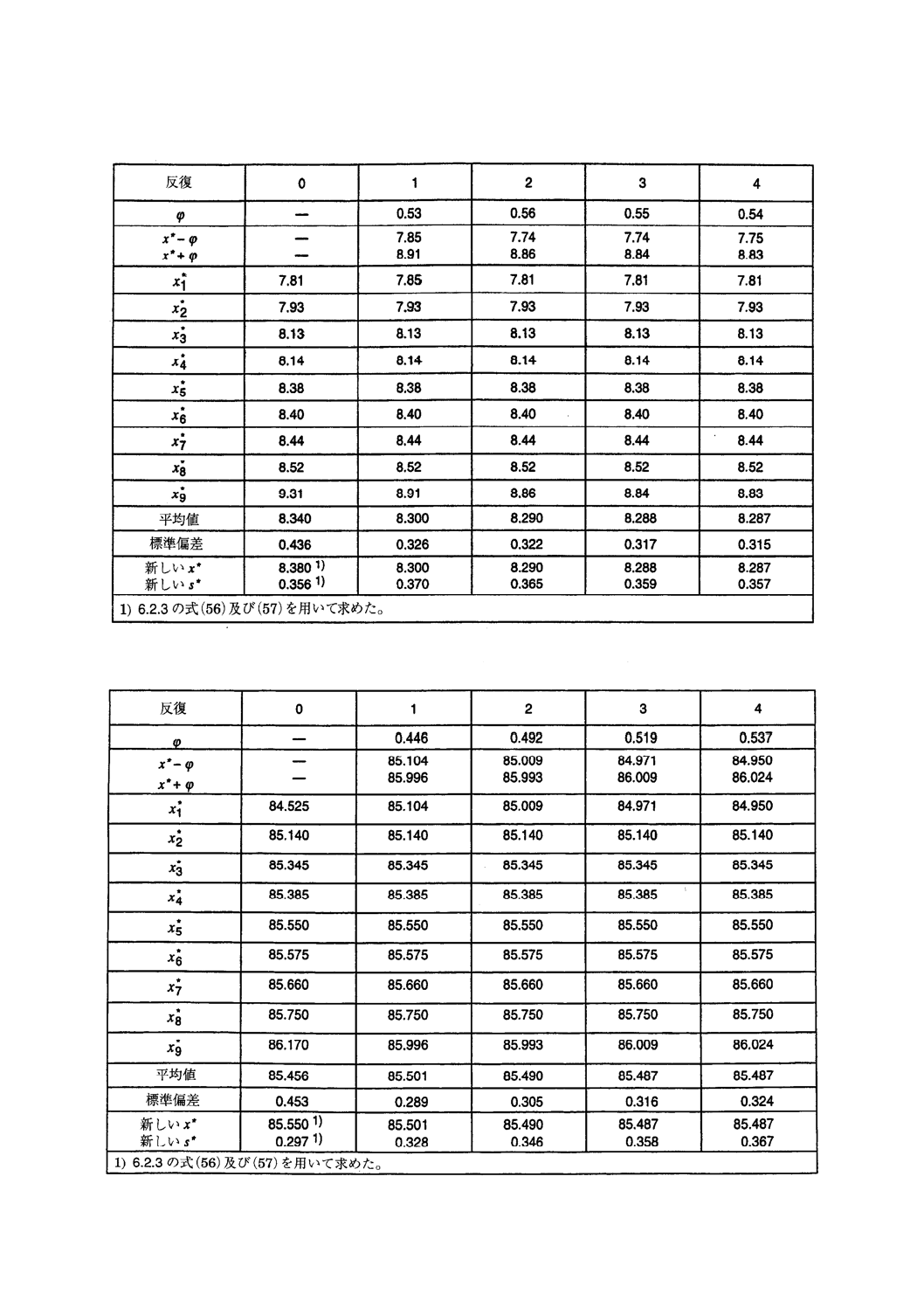
併行標準偏差のロバストな推定値を得るため,セル間差(表5)にアルゴリズムAを適用する。す
ると,表27の結果を得るが,表27ではセル差を増加する順序に並べ替えた。表のように反復計算を4回
行うと,ロバストな値はx*≒8.29とs*≒0.36となり,x*9だけがx*との差がϕより大きいことが分かる。
6.2.6の方法においてuL=0及びuU=1と置くと
x'=8.219及びs'=0.257 % (たんぱく質含有率)
となるため,6.2.6の式(62)及び式(63)は,次のように書き変えることができる。
x*=8.219+1.5×s*/8
及び
(s*)2=7×(0.257)2/[8/1.1342−1.52(0+9−0)/8]
その結果,
s*=0.354 % (たんぱく質含有率)
また,6.6.1の式(75)から
sr=0.354/2=0.250 % (たんぱく質含有率)
セル間差のロバストな平均値は
x*=8.219+1.5×0.354/8=8.285 % (たんぱく質含有率)
これらのx*及びs*の値を用いると
ϕ=1.5×0.354=0.531
したがって,
x*−ϕ=7.754 及びx*+ϕ=8.816 % (たんぱく質含有率)
x*及びs*の計算において,x*9だけがこれらの限界値の範囲外にあると仮定した。その仮定が正しいことが
確認され,有効な答えが得られた。
6.7.3
セル平均値(表6)にアルゴリズムAを適用すると表28の結果を得る。表28ではセル平均値を増
加する順序に並べ替えた。この状態は表26の場合に類似しており,ここでは,x*1とx*9が,x*との差がϕ
より大きくなっていて,x*はx*2からx*8までの平均値,すなわち,85.486へ収束しつつある。再度6.2.6の
44
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
方法を用い,かつ,uL=uU=1と置くと,x*2からx*8までの平均値と標準偏差は
x'=85.486及びs'=0.209
となる。
したがって,6.2.6の式(63)を用いて,次の式からs*を求めることができ,
(s*)2=6×(0.209)2/[8/1.1342−1.52(9+9−4)/7]
その結果,
s*=0.390 % (たんぱく質含有率)
が得られる。
ここで,6.2.2の式(62)から
x*=85.486 % (たんぱく質含有率)
が得られる。
この答えが有効であることをチェックするためϕの値を計算する。
ϕ=1.5×0.390=0.585
及び
x*−ϕ=84.901及びx*+ϕ=86.071 % (たんぱく質含有率)
仮定したとおり,x*1とx*9だけがこれらの限界値の外側にある。
6.6.2の式(76)を用いて再現精度標準偏差を求めると
sy=0.390 % (たんぱく質含有率)
また,4.5.6の式(13)から
sR=0.410 % (たんぱく質含有率)
したがって,この例では,ロバストな方法によって,報告されたデータをすべて用いた場合(表7)より
もやや小さい推定値sr及びsRが得られる。
45
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 27 例5:セル差へのアルゴリズムAの適用(たんぱく質質量%)
表 28 例5:セル平均値へのアルゴリズムAの適用(たんぱく質質量%)
46
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.8
公式:不均質物質の実験のある一つの測定水準に対するロバストな解析
6.8.1
不均質物質の計画において,試験室p' 箇所それぞれに各測定水準のサンプルを2個準備し,各サ
ンプルについて測定結果を二つ得るという簡単な計画の場合,併行標準偏差及び再現標準偏差のロバスト
な推定値は,次のようにアルゴリズムA及びSを3回適用することによって得られる。
a) 測定結果間範囲にアルゴリズムSを適用して,6.3.4の式(67)からロバストな値w*を求め,次の式に
代入する。
SSr=2p'(w*)2 ········································································· (77)
b) サンプル間範囲にアルゴリズムSを適用して,式(67)からロバストな値w*をもう一つ求め,次の式に
代入する。
SSH=p'(w*)2 ·········································································· (78)
c) セル平均値にアルゴリズムAを適用して,6.2.4の式(61)からロバストな値s*を求め,次の式に代入す
る。
sy=s* ··················································································· (79)
これらの計算は,次の例に示すとおり,第1欄に範囲又は平均値を増加する順序に配置した表形式で行
えば便利であろう。
6.8.2
そのあと,5.5の公式を用いて,併行標準偏差及び再現標準偏差と,サンプル間変動を与える標準
偏差sHの推定値を計算する。
6.9
例6:不均質物質の実験のある一つの測定水準に対するロバストな解析
6.9.1
5.8の例2の水準6のデータには外れ値が含まれていない。したがって,そのデータを用いて,こ
の場合にロバストな解析によって得られる結果を示す。
6.9.2
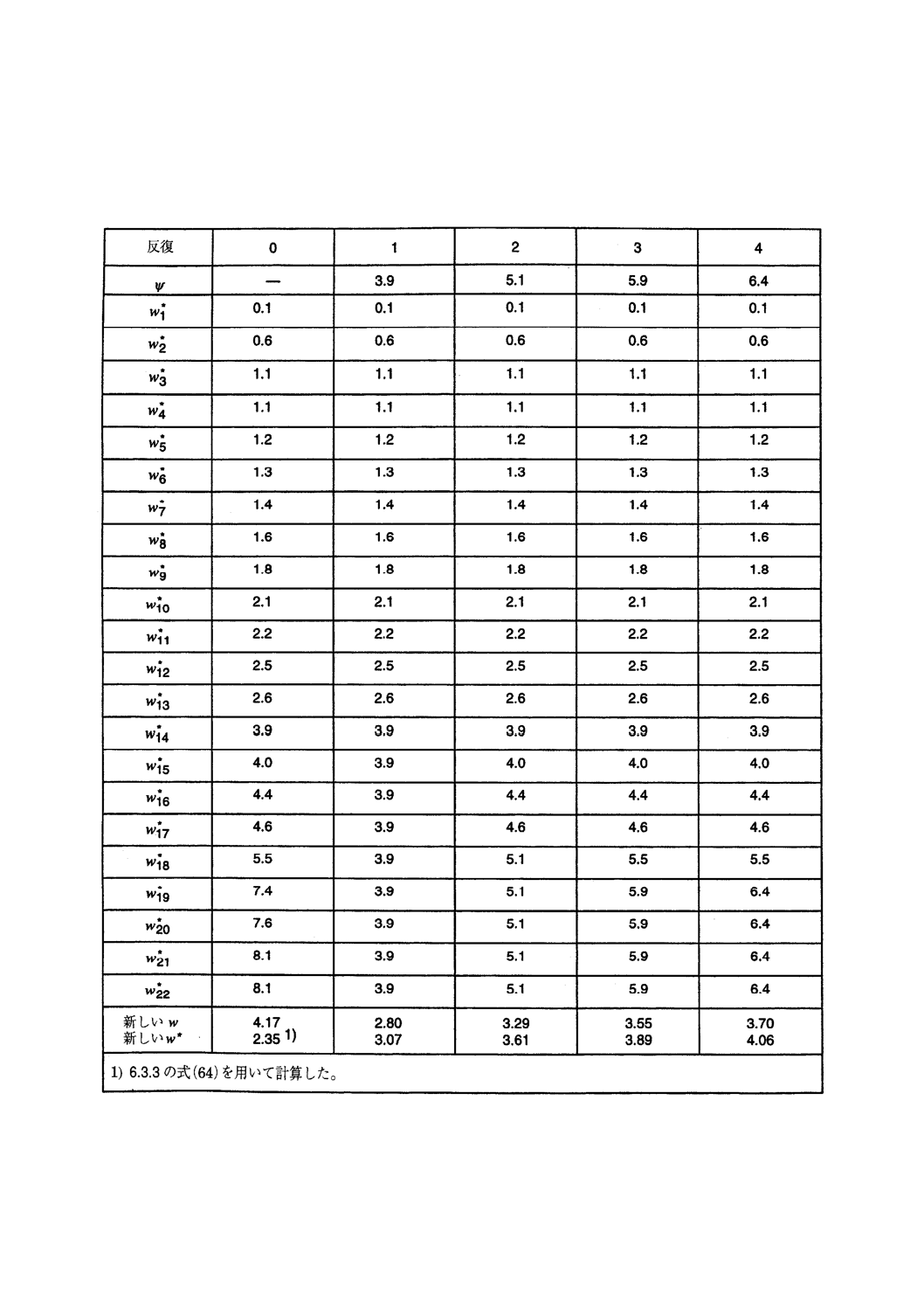
測定結果間範囲(表14)にアルゴリズムSを適用すると表29の結果を得る。ここでは自由度ν=
1であり,したがって,η=1.645,ξ=1.097及びデータ個数p=2p'=22である。表の反復計算4回の結
果,ロバストな値はw*≒4.5であり,w*19からw*22までがψより大きい。6.3.6に定義したΣ'とuUは,この
場合は次の値となる。
uU=4
∑
p
wi
2
*
'
)
(
=137.92/22=6.269 1
したがって,6.3.6の式(68)から次の式を得る。
(w*)2=1.0972×6.269 1+4(1.097×1.645w*)2/22
その結果,次の値を得る。
w*=4.30 %
このw*の値によってψ=7.1であり,w*19からw*22までの値四つがψより大きいことが分かり,したが
って,この値はw*の有効な解である。
6.8.1の式(77)から
SSr=22×4.302=406.78 %2
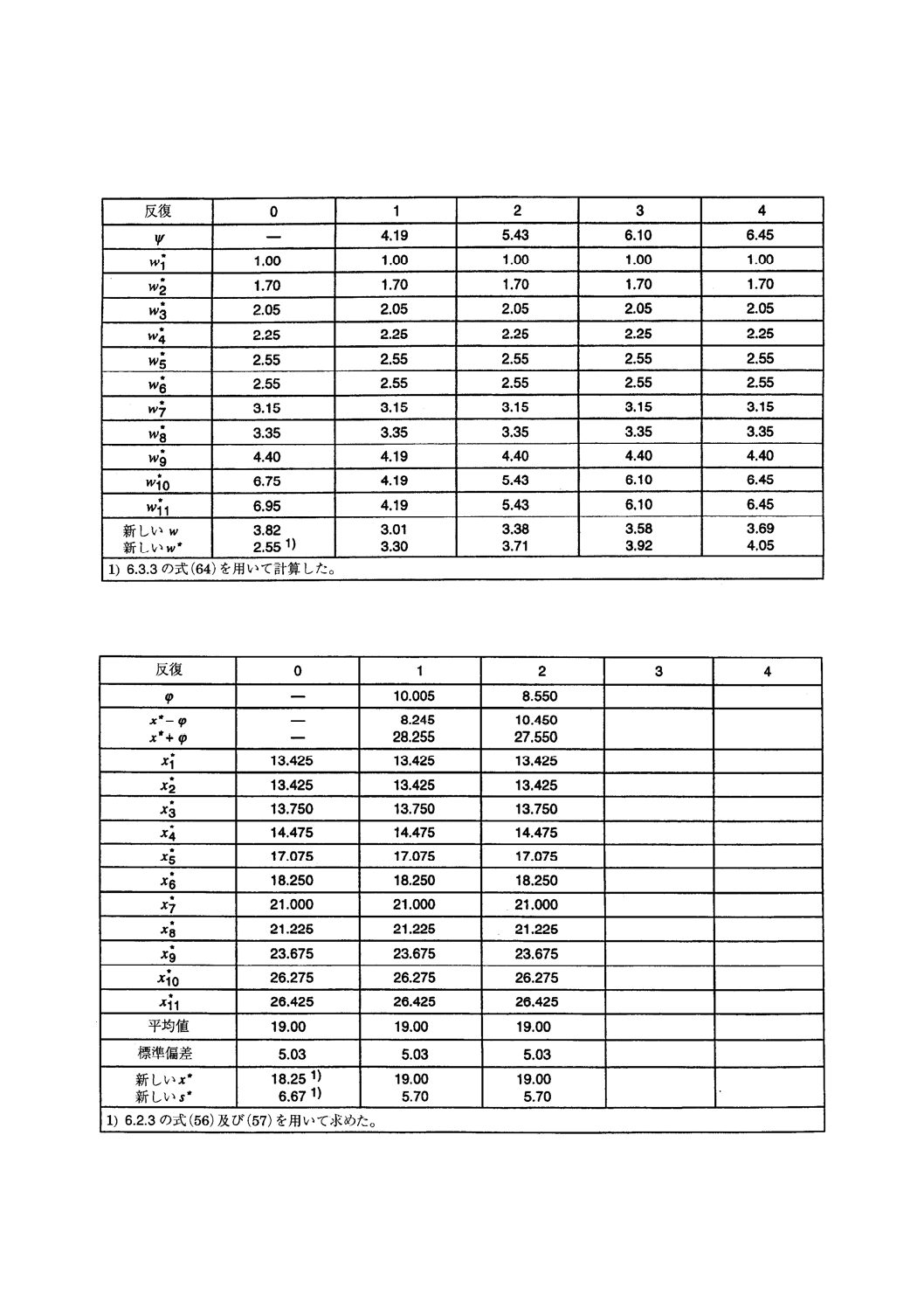
6.9.3
サンプル間範囲(表15)へアルゴリズムSを再度適用すると表30の結果を得る。表の反復計算4
回の結果,ロバストな値はw*≒4.0であり,w*10とw*11がψより大きいことが分かる。6.3.6に定義したΣ'
とuUは,この場合は次の値となる。
uU=2
∑
′p
wi
2
*
'
)
(
=66.665/11=6.060 5
したがって,6.3.3の式(68)から次の式を得る。
47
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(w*)2=1.0972×6.060 5+2(1.097×1.645w*)2/11
その結果,次の値を得る。
w*=4.23 %
残念ながら,この値はψ=1.645×4.23=6.96に対応し,w*10及びw*11はこの値を超えないため,この値
は有効な解ではない。このことは,uU=1又はuU=0でなければ正しい解が得られないことを示唆してい
る。
uU=1とすると,
∑
′p
wi
2
*
'
)
(
=112.227 5/11=10.202 5
したがって,式(68)から次の式を得る。
(w*)2=1.0972×10.202 5+(1.097×1.645w*)2/11
その結果,次の値を得る。
w*=4.18 %
この場合ψ=1.645×4.18=6.88である。この値を超えるのはw*11だけであるため,この値は有効な解で
あることが分かる。
6.8.1の式(78)を用いると,次の値を得る。
SSH=11×4.182=192.20 %2
6.9.4
セル平均値(表16)にアルゴリズムAを適用して表31に示す結果を得る。計算を2回反復すると
値が収束し,s*=5.70となる(x*からの差がϕより大きいx*iの値は存在しない)。
6.8.1の式(79)から次の値を得る。
sy=5.70 %
6.9.5
6.9.2,6.9.3及び6.9.4において得た結果を組み合わせると,5.5.5の式(29)及び式(33)から
sr2=406.78/44 %2
sR2=5.702+(406.78−192.20)/44 %2
sH2=192.20/22−406.78/88 %2
したがって,
sr=3.04 %
sR=6.11 %
sH=2.03 %
したがって,この例では,ロバストな方法によって,報告されたデータ(5.8.3及び表17)をすべて用い
た場合よりも少し大きな推定値sr,sR及びsHを得た。
48
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 29 例6:測定結果範囲へのアルゴリズムSの適用
(ν=1;ξ=1.097;η=1.645)
49
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 30 例6:サンプル間範囲(%)へのアルゴリズムSの適用
(ν=1;ξ=1.097;η=1.645)
表 31 例6:セル平均値(%)へのアルゴリズムAの適用
50
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) JIS Z 8402で用いられる記号
a
関係式s=a+bmの切片
A
推定値の不確かさを計算するのに用いる係数
b
関係式s=a+bmのこう配
B
全平均と試験室の測定値の偏差を表す成分(かたよりに占める試験室成分)
B0
Bの成分の中で中間精度条件の下では変わらない,すべての要因
B(1),B(2),など Bの成分の中で中間精度条件で変化する要因
c
関係式log s=c+d log mの切片
C,C',C''
検定統計量
Ccrit,C'crit,C''crit 統計的検定の棄却限界値
CDP
確率Pの許容差
CRP
確率Pの許容範囲
d
関係式log s=c+d log mのこう(勾)配
e
測定値の成分中,すべての測定値に生じている偶然誤差
f
許容範囲の係数
Fp(ν1,ν2)
分子の自由度ν1,分母の自由度ν2のF分布のp分位点
G
グラッブスの検定統計量
h
マンデルの試験室間一致性の検定統計量
k
マンデルの試験室内一致性の検定統計量
LCL
下側管理限界(処置限界又は警戒限界)
m
試験特性の一般平均;水準
M
中間精度条件において考慮される因子の数
n
一つの試験室で一つの水準(すなわち,セルごと)で得る測定値の数
N
反復数
p
共同実験に参加した試験室数
P
確率
q
共同実験における試験特性の水準数
r
併行精度限界値(許容差)
R
再現精度限界値(許容差)
RM
標準物質
s
標準偏差の推定値
sˆ
標準偏差の予測値
t
試験対象又は群の数
T
ある表示の総和
UCL
上側管理限界(処置限界又は警戒限界)
w
一組の測定値の範囲
W
重み付き回帰式の計算で用いられる重み係数
x
グラッブス検定に用いられるデータ
51
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
y
測定値
y
測定値の算術平均
y
測定値の全平均
α
第二種の過誤の確率
γ
再現標準偏差と併行標準偏差の比(σR /σr)
δ
測定方法のかたより
δˆ
δの推定値
Δ
試験室のかたより
Δˆ
Δの推定値
λ
二つの試験室又は二つの測定方法間のかたよりの検出可能な差
μ
試験特性の真値又は参照値
ν
自由度
ρ
方法AとBの併行標準偏差間の検出可能な比
σ
標準偏差の真の値
τ
最終校正からの時間経緯に起因する変動を表す測定値の成分
φ
方法AとBの試験室間平均平方の平方根の検出可能な比
χ2p(ν)
自由度νのχ2分布におけるp分位点
添え字に用いる記号
C
校正法が異なることを示す
E
装置が異なることを示す
i
特定の試験室を示す添え字
I()
中間精度に関する添え字,かっこ内に中間精度条件のタイプの識別子を記述する。
j
特定の水準に関する添え字(JIS Z 8402-2)
分析の一群又は要因に関する添え字(JIS Z 8402-3)
k
試験室iにおける水準jのk番目の測定値を示す添え字
L
試験室間を示す
m
検出可能なかたよりに関する添え字
M
試験試料間を示す
O
オペレータが異なっていることを示す
P
確率
r
併行精度
R
再現精度
T
時間が異なることを示す
W
試験室内を示す
1,2,3,...
測定値の得られた順序を示す
(1),(2),(3),... 測定値の大きさの順序を示す
JIS Z 8402-5において追加使用する記号及び略語
D
水準分割実験におけるセル内差
52
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
g
試験室において一つの測定水準でテストする試料数
H
サンプルの偶然誤差を表す測定結果の成分
K
セル内測定結果数によって決まる係数
p'
共同試験室実験に参加する試験室数
SS
平方和
uL
ロバストな解析における下限より小さいデータ数
uU
ロバストな解析における上限より大きいデータ数
z
残差
Φ
標準偏差の比
ϕ
ロバストな解析に使用する限界(アルゴリズムA)
η
ロバストな解析に使用する限界係数(アルゴリズムS)
ψ
ロバストな解析に使用する限界(アルゴリズムS)
ζ
ロバストな解析に使用する調整係数(アルゴリズムS)
JIS Z 8402-5で下付き添字として追加使用する記号
a,b
水準分割実験のサンプルの識別子
t
試験室i水準jのサンプルの識別子
H
サンプル間
JIS Z 8402-5で上付き添え字として追加使用する記号
*
ロバストな推定値
53
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考) アルゴリズムA及びSで用いられる係数の誘導
B.1 はじめに Royal Society of Chemistry(英国王立化学協会)のAnalytical Methods Committee(分析方法
委員会)[参考文献[6]参照]は,精度評価実験のデータを解析するロバストな方法を提案した。この規格の
この部の“アルゴリズムA”は,その協会の論文から誘導した。また,アルゴリズムAにおいてs*を計算
するための係数1.134もその論文から引用した(これは,この論文においてc=1.5の場合の
θ
/1
の値で
ある)。
“アルゴリズムS”は,参考文献[6]の手順に類似したアルゴリズムであり,各試験室が測定水準ごとに
測定値をn=2個報告する特別の場合に相当する。この方法は,ロバストな解析を三つ以上の因子が存在す
る精度評価実験(例えばこの規格のこの部の5.の不均質物質の計画,及びJIS Z 8402-3のスタッガード型
枝分れ計画)に適用する場合に便利である。
次にアルゴリズムSに使用する係数を誘導する。
B.2 この附属書において使用する記号
σ
真の標準偏差
s
σの推定値として用いる標準偏差
ν
sの自由度
ω
ν+2
ξ
アルゴリズムSの調整係数
η
アルゴリズムSの限界係数
χν2
自由度νのカイ二乗分布に従う確率変数
>
≤
σの場合
η
σ
φ
σの場合
η
=
s
s
s
s*
B.3 限界係数η及び調整係数ξの導出
調整係数ξとは,(s*)2がσ2の不偏推定値を与えるようs*を調整するための値をいう。
すなわち,
E{(ξ×s*)2}=σ2 ·································································· (B.1)
である。これは次のように表される。
E{ν(s*/σ)2}=ν/ξ2 ···························································· (B.2)
ここに{ }内の値はν(s/σ)2,すなわち,カイ二乗変量χν2に緊密に関連している。
カイ二乗変量χν2の確率密度関数は,
f(x)=e−x/2x(ν/2−1)2−ν/2/Γ(ν/2) ·············································· (B.3)
である。したがって,限界
ησ
≤
s
は
2
2νη
σ
ν
≤
)
/
(s
と同じであるため,
x
x
f
x
x
xf
s
E
d
d
2
2
2
0
2
*
)
(
)
(
}
)
(
{
∫
∫
∞
νη
νη
νη
+
=
σ
ν
······································· (B.4)
である。
(B.4)の右辺の第2項は
54
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)
(
)
(
ησ
=νη
νη
νη
ν
>
>
×
×
s
P
x
P
2
2
2
2
······································· (B.5)
である。アルゴリズムSについては,ησがsの分布の上側10 %点となるよう限界係数ηを選択する。
したがって,
1.0
=
ησ)
(>
s
P
····································································· (B.6)
である。
Biometrika Tables(バイオメトリカの統計数値表)のカイ二乗分布表から,この規格のこの部の表23の
ηの値を得る。式(B.5)及び式(B.6)は,式(B.4)の右辺の第2項の値が0.1νη2であることを示す。ηはs
の自由度に依存することに注意されたい。
式(B.4)の右辺の第1項は,次のように書ける。
(
)x
Γ
x
xex
d
2
2
2
1
2
0
2
2
ν
ν
ν
νη
−
−
−
∫
ω=ν+2の場合,ガンマ関数にはよく知られた次の性質がある。
)
(
)
(
)
(
)
(
2
2
1
2
2
ν
ν
=
+
ν
=
ω
Γ
Γ
Γ
×
したがって,この式の第1項は,次のように書き換えられる。
z
x
P
x
Γ
x
ex
×
×
<
∫
=ν
νη
=ν
ω
ν
ω
νη
ω
−
−
ω
−
)
(
)
(
2
2
0
2
1
2
2
d
2
2
2
················ (B.7)
その結果,与えられた自由度νに対して,上述の方法でηを計算し,Biometrika Tables(バイオメトリカ
の統計数値表)のカイ二乗分布表を再度使用してzを求め,式(B.4)の右辺の二つの項を求めることができ
る。
式(B.2),式(B.5),式(B.6),及び式(B.7)を式(B.4)に代入すると
2
2
1.0νη
+
=ν
ξ
ν
z
×
又は
2
1.0
1
η
+
ξ=
z
··································································· (B.8)
となる。
この値を用いて,この規格のこの部の表23の調整係数ξを得ることができる。
55
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) ロバストな解析に使用する式の誘導
参考 この規格では“ロバストな”という言葉を,“外れ値の影響を受けにくい”という意味で用いて
いる。
6.2.6に述べた方法によって,式(62)及び式(63)を用いて平均値と標準偏差のロバストな値を計算する。
この式二つは,6.2.4(アルゴリズムA)の式(60)及び式(61)から次のようにして導かれる。
6.2.4及び6.2.6の記号を用いると
∑
p
x
x
i*
*=
········································································· (C.1)
∑
)
(
U
L
'
'
u
u
p
x
x
i
−
−
=
····························································· (C.2)
及び
)
(
)
(
1
'
'
'
U
L
2
−
−
−
−
=
u
u
p
x
x
s
i
∑
············································· (C.3)
である。
ここに,∑'は,
ϕ
≤
*i
ix
x−
となる
)
(
U
Lu
u
p
−
−
個のデータxiに関する総和を表す。
したがって,式(C.1)は,次のように書き表される。
∑∑
×
×
×
)
(
(
)
*
*
U
*
L
*
*
5.1
5.1
*
'
s
x
u
s
x
u
x
x
x
p
i
i
+
+
−
+
=
=
したがって,
*
U
L
U
L
*
U
L
'
s
u
u
x
u
u
p
x
u
u
p
×
×
×
)
(
)
(
)
(
−
+
−
−
=
−
−
となる。これから次の式を得る。
)
(
)
(
U
L
*
L
U
*
5.1
'
u
u
p
s
u
u
x
x
−
−
−
+
=
············································ (C.4)
これは6.2.6の式(62)である。
式(61)から式(63)を導くため,式(61)の中において,総和項を次のように展開する。
∑
∑
×
2
*
U
L
2
*
2
*
*
5.1
'
)
)
(
)
(
)
(
(
s
u
u
x
x
x
x
i
i
+
+
−
=
−
···································· (C.5)
式(C.4)を用いて,総和項のx*にこれを代入してまとめると
∑
∑
×
)
(
)
(
)
(
)
(
)
(
U
L
U
L
U
L
2
*
2
2
*
*
4
5.1
'
'
u
u
p
u
u
pu
pu
s
x
x
x
x
i
i
−
−
−
+
+
−
=
−
·········· (C.6)
となる。
式(C.3)の'sの定義を用いて,これを次のように書き変える。
∑
×
×
)
(
)
(
)
(
)
(
)
(
)
(
U
L
U
L
U
L
2
*
2
U
L
2
*
*
4
5.1
'
1
u
u
p
u
u
pu
pu
s
s
u
u
p
x
xi
−
−
−
+
+
−
−
−
=
−
················································ (C.7)
式(C.7)を式(61)に代入して式(63)を得る。
56
Z 8402-5:2002 (ISO 5725-5:1998)
著作権法により無断での複製,転載等は禁止されております。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(参考) 参考文献
[1] BS 812-103:1985, Testing aggregates―Part 103:Methods for determination of particle size distribution.
British Standard Institution.
参考 BS 812-103に相当する国内規格としてJIS A 1102:1999“骨材のふるい分け試験方法”がある。
[2] BS 812-121:1989, Testing aggregates―Part 121:Methods for determination of soundness. British Standard
Institution.
[3] BS 3144:1968, Methods of sampling and physical testing of leather. British Standard Institution.
参考 BS 3144に相当する国内規格としてJIS K 6550:1994“革試験方法”がある。
[4] Scheffe, H. The analysis of variance. Wiley, New York, 1959.
[5] Sweeney, Generic Combustion Method for Determination of Crude Protein in Feeds:Collaborative Study.
Journal of the Association of Offical Analytical Chemists, 72, 1989, pp. 770-774.
参考 ISO 5725-5:1998では,[5]の論文名が“An inter-laboratory study of the determination of protein
by combustion in feeds”と誤って記述されているため,上記の正しい論文名を記述した。
[6] Analytical Methods Committee, Robust statistics―How not to reject outliers. Part 1:Basic concepts. Part 2:
Inter-laboratory trials, The Analyst, 114, 1989, pp. 1693-1697 (part 1), pp. 1699-1702 (part 2). Royal
Society of Chemistry, London.
参考 ISO 5725-5:1998では,[6]のページ番号が誤って“pp. 1653-1697 (part 1)”と記述されてい
ため,正しいページ番号を記載した。
[7] Youden, W. J. The Youden plot. Industrial Quality Control, 15, 1959, pp. 133-137.
[8] Mandel, J. and Lashof, T. W. Interpretation and Generalization of Youdenʼs Two-Sample Diagram. Journal of
Quality Technology, 6, 1974, pp. 22-36.
日本工業標準調査会標準部会 基本技術専門委員会 構成表
氏名
所属
(委員会長) 今 井 秀 孝
独立行政法人産業技術総合研究所
(委員)
大 井 みさほ
東京学芸大学名誉教授
尾 島 善 一
東京理科大学理工学部
加 藤 久 明
日本デザイン学会
小松原 仁
財団法人日本色彩研究所
橘 秀 樹
東京大学生産技術研究所第5部
田 森 行 男
財団法人日本品質保証機構
徳 岡 直 静
慶應義塾大学理工学部
藤 咲 浩 二
社団法人日本産業機械工業会
前 原 郷 治
社団法人日本鉄鋼連盟
村 上 陽 一
社団法人日本電機工業会
山 村 修 蔵
財団法人日本規格協会
























