Z 8402-3 : 1999 (ISO 5725-3 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 8402 : 1991は廃止され,この規格に置き換えられる。
今回の制定では,1994年に第1版として発行されたISO 5725-3を基礎として用いた。
JIS Z 8402-3には,次に示す附属書がある。
附属書A(規定) JIS Z 8402で用いられる記号
附属書B(規定) 完全枝分れ実験の分散分析
附属書C(規定) スタッガード型枝分れ実験の分散分析
附属書D(参考) 中間精度評価実験の統計解析の例
附属書E(参考) 参考文献
JIS Z 8402 : 1999は,一般名称を“測定方法及び測定結果の精確さ(真度及び精度)”として,次の部に
よって構成される。
第1部: 一般的な原理及び定義
(Part 1 : General principles and definitions)
第2部: 標準測定方法の併行精度及び再現精度を求めるための基本的方法
(Part 2 : Basic method for the determination of repeatability and reproducibility of a standard
measurement method)
第3部: 標準測定方法の中間精度
(Part 3 : Intermediate measures of the precision of a standard measurement method)
第4部: 標準測定方法の真度を求めるための基本的方法
(Part 4 : Basic methods for the determination of the trueness of a standard measurement method)
第5部: 標準測定方法の精度を求めるための代替法
(Part 5 : Alternative methods for the determination of the precision of a standard measurement
method)
第6部: 精確さに関する値の実用的な使い方
(Part 6 : Use in practice of accuracy values)
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 3
2. 引用規格 ························································································································ 3
3. 定義 ······························································································································ 4
4. 一般的な要求事項 ············································································································ 4
5. 重要な因子 ····················································································································· 4
6. 統計モデル ····················································································································· 5
6.1 基本モデル ··················································································································· 5
6.2 一般平均m ··················································································································· 5
6.3 項B····························································································································· 6
6.4 項B0,B(1),B(2),など ································································································· 6
6.5 誤差項e ······················································································································· 7
7. 測定条件の選択 ··············································································································· 7
8. 試験室内評価実験と中間精度の解析 ···················································································· 8
8.1 最も単純な方法 ············································································································· 8
8.2 別な方法 ······················································································································ 8
8.3 測定条件の最終結果に与える影響 ······················································································ 9
9. 試験室間共同実験と中間精度の解析 ···················································································· 9
9.1 基礎になる仮定 ············································································································· 9
9.2 最も単純な方法 ············································································································ 10
9.3 枝分れ実験 ·················································································································· 10
9.4 完全枝分れ実験 ············································································································ 10
9.5 スタッガード型枝分れ実験······························································································ 11
9.6 枝分れ実験における因子の割り付け ·················································································· 11
9.7 枝分れ実験とJIS Z 8402-2に示した手順との比較 ································································· 11
9.8 完全枝分れ実験とスタッガード型枝分れ実験との比較 ·························································· 12
附属書A (規定) JIS Z 8402で用いられる記号 ······································································ 13
附属書B(規定) 完全枝分れ実験の分散分析 ·········································································· 16
B.1 3因子完全枝分れ実験 ···································································································· 16
B.2 4因子完全枝分れ実験 ···································································································· 17
附属書C(規定) スタッガード型枝分れ実験の分散分析 ··························································· 19
C.1 3因子スタッガード型枝分れ実験 ····················································································· 19
C.2 4因子スタッガード型枝分れ実験 ····················································································· 20
C.3 5因子スタッガード型枝分れ実験 ····················································································· 21
C.4 6因子スタッガード型枝分れ実験 ····················································································· 22
附属書D(参考) 中間精度評価実験の統計解析の例 ································································· 24
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.1 例1:特定の試験室内での特定の測定水準における,[時間+オペレータ]の異なる中間標準偏差,
sI(TO) を求める ····················································································································· 23
D.2 例2:試験室間共同実験によって,時間の異なる中間標準偏差を求める ·································· 24
附属書E(参考) 参考文献 ·································································································· 31
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8402-3 : 1999
(ISO 5725-3 : 1994)
測定方法及び測定結果の
精確さ(真度及び精度)−
第3部:標準測定方法の中間精度
Accuracy (trueness and precision) of measurement methods and results−
Part 3 : Intermediate measures of the precision
of a standard measurement method
序文
この規格は,1994年に第1版として発行されたISO 5725-3, Accuracy (trueness and precision) of measurement
methods and results−Part 3 : Intermediate measures of the precision of a standard measurement methodを翻訳し,
技術的内容及び規格票の様式を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
0.1
この規格では,測定方法の精確さを表すために“真度”と“精度”の二つの用語を用いている。“真
度”は,多数の測定結果の平均値と,真の値又は参照値との一致の程度を示すものである。“精度”は,測
定結果の間の一致の程度を示すものである。
0.2
これらの量の一般的な考察はこの規格の第1部で示されており,ここでは改めて記述しない。第1
部は基本的な定義と一般的な原理が示されているので,この部を含めて,他の部についても,第1部を合
わせて読まれることが望ましいということを強調したい。
0.3
同一と見なせる試料間の変動は別として,同じ測定方法による測定結果をばらつかせる多くの異な
る因子には,つぎのようなものがある。
a) オペレータ
b) 使用した装置
c) 装置の校正
d) 環境(温度,湿度,空気の汚染,など)
e) 試薬のバッチ
f)
個々の測定間の経過時間
異なるオペレータ及び/又は異なる装置によって得られた(測定結果間の)変動は,同一のオペレータ
が同一装置を用いて短い時間間隔のうちに実施して得られた(測定結果間の)変動よりも大きいのが常で
ある。
2
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0.4
多くの実際の場合に,併行条件と再現条件と名付けられた二つの精度の条件が必要であり,測定方
法のばらつきを記述するのに役に立つということが知られている。併行条件の下では,0.3にあげたa)〜f)
の因子は一定で変動には寄与しないが,一方,再現条件下では,これらは変化して測定結果の変動に影響
する。したがって,併行精度と再現精度は精度の両極であり,前者は最小,後者は最大の変動を表す。a)
〜f)の一つ以上の因子が変動し得るときには,これら二つの両極の精度の状況の間に中間条件を考えるこ
とができて,ある定められた状況の下では,この中間条件が用いられる。
精度は,通常の場合,標準偏差の形で表現される。
0.5
この規格のこの部は測定方法の中間精度に焦点をあてて述べている。この精度が中間と呼ばれるの
は,その大きさが,測定方法の精度の二つの両極の値である併行標準偏差及び再現標準偏差の間になるか
らである。
このような中間精度の必要性を説明するためには,製造工場に付属する現代の試験室の業務,例えば,
異なる装置を用いて異なるオペレータによって測定が行われる三交代制の作業システム,を考えてみれば
よい。このとき,オペレータや装置は測定結果のばらつきに寄与する因子である。測定方法の精度を評価
する際にはこれらの因子も考慮する必要がある。
0.6
この規格のこの部で定義する中間精度が有用となるのは,主として,これらを推定することが,試
験室内で用いられる測定方法を,開発し,標準化し,または管理することを目的とする手続きの一部とな
っているときである。これらの精度は特別に計画された試験室間の共同研究によっても推定できるが,1.3
及び9.1に示す理由で,その解釈と適用には注意が必要である。
0.7
測定方法の精度に最も影響を与える4つの因子は次のものである:
a) 時間:連続して行われる測定間の時間間隔が,短いかそれとも長いか。
b) 校正:連続して行われる測定群の間で,使用する装置が再校正をされるかそれともされないか。
c) オペレータ:連続して行われる測定が,同一オペレータによって行われるか異なるオペレータによっ
て行われるか。
d) 装置:測定で,同一装置(同じバッチの試薬)が用いられるか又は異なる装置(異なるバッチの試薬)
が用いられるか。
0.8
そのため,試験室内での測定の条件変化(時間,校正,オペレータ,及び装置)を考慮に入れるた
めに,以下のM因子異なる中間条件 (M=1,2,3,4) を,導入するのがよい。
a) M=1:4つの因子のうち,1個の因子だけが異なる;
b) M=2:4つの因子のうち,2個の因子が異なる;
c) M=3:4つの因子のうち,3個の因子が異なる;
d) M=4:4つの因子の,すべてが異なる。
異なる中間条件による異なる中間標準偏差は,カッコの中に対応する条件を列挙したsI ( ) で表される。
例えば,sI(TO)は時間 (T) とオペレータ (O) を変えたときの中間標準偏差である。
0.9
中間条件の下で得られた測定値では,0.7に掲げた一つ以上の因子が変化する。併行条件の下ではこ
れらの因子は一定とみなされている。
併行条件の下で得られる測定結果の標準偏差は,中間条件の下で得られる測定結果の標準偏差より一般
的に小さい。化学分析では,一般的に,中間条件の下での標準偏差は併行条件の下での標準偏差の2ない
し3倍程度であろう。もちろん,これは再現標準偏差を上まわることはないはずである。
例えば,銅鉱石中の銅の定量において,35の試験室による共同実験では,電解重量法とNa2S2O3滴定法
のいずれにおいても,1因子異なる(オペレータと装置は同一で,時間が異なる)中間条件の下での標準
3
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
偏差は,併行条件の下での標準偏差の1.5倍であった。
1. 適用範囲
1.1
この規格のこの部は,一つの試験室内で測定の条件(時間,校正,オペレータ,及び装置)が変わ
ることによる4つの中間精度について詳細を述べる。これらの中間精度は,特定の試験室内での実験又は
試験室間共同実験によって確定することができる。
更に,この規格のこの部では,
a) 中間精度の定義の意味を詳述し;
b) 実際的な状況での中間精度の推定値の解釈と適用における手引きとを示し;
c) 中間精度の推定誤差については一切規定せず;
d) 測定方法自体の真度の求め方には係わらないで,真度と測定条件との関連を詳述する。
1.2
この規格のこの部は,計量値の測定値が求められ,測定結果として一個の値が得られるような測定
方法だけを対象とする。この一個の値は一組の観測値から計算によって求められたものであってもよい。
1.3
これらの中間精度を求めることの本質は,これらの精度が,測定方法の定められた条件の下で測定
結果を再現する能力の尺度になるということである。
1.4
この規格のこの部で説明する統計的方法は,中間精度に関してより正確な情報を得るために,“類似
している”測定条件からの情報を併合できるという前提に依存している。この前提は,“類似している”と
いう主張が本当に“類似している”限り強力な前提である。しかし,試験室間共同研究で中間精度が推定
されるときには,このような前提を維持することはかなり難しい。例えば,異なる試験室からの情報を併
合することが無意味にならないように,“時間”や“オペレータ”のような効果が試験室を越えて“類似し
ている”ようにコントロールすることは,大変困難である。このように,中間精度に関する試験室間共同
研究の結果を使用するには注意を要する。一試験室内での研究もこの前提に立っているが,その場合には,
ある因子の実際の影響をコントロールし,把握することは分析者の及ぶ範囲内であるので,より現実的で
ある。
1.5
試験室内で中間精度を推定し,確認するために,この規格のこの部で述べられている方法以外にも,
例えば管理図(JIS Z 8402-6を参照)のような技法がある。この規格のこの部に示されている方法だけが,
試験室内における中間精度の推定をするための唯一のアプローチではない。
備考1. この規格のこの部は,枝分かれ実験のような実験計画を引用している。基本的情報は附属書
B及びCに示されている。この領域の他の参考文献を附属書Eに示す。
2. 引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,発効年を付記してあるものは,記載の年の版だけがこの規格の規定を構成するもので
あって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その最新版(追補
を含む。)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部 確率及び一般統計用語
JIS Z 8101-2 統計−用語と記号−第2部 統計的品質管理用語
JIS Z 8402-1 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第1部 一般的な原理及び定
義

4
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Z 8402-2 : 1999 測定方法及び測定結果の精確さ(真度及び精度)−第2部 標準測定方法の併行
精度及び再現精度を求めるための基本的方法。
JIS Q 0033 : 1997 認証標準物質の使い方
JIS Q 0035 : 1997 標準物質の認証−一般的及び統計学的原則
3. 定義
この規格の目的に合わせ,JIS Z 8101とJIS Z 8402-1において定義された用語を用いる。
この規格で用いる記号を附属書Aに示す。
4. 一般的な要求事項
同じように測定を行うために,測定方法を標準化しておかなければならない。一つの試験室内で行われ
る実験,試験室間共同実験,のどちらの場合でも,実験を構成するすべての測定が,その標準化された方
法によって実施されなければならない。
5. 重要な因子
5.1
試験室内における測定条件において,主として4つの因子(時間,校正,オペレータ,及び装置)
が測定のばらつきに寄与すると考えられる(表1を参照)。
表1 4つの重要な因子とその状態
因子
試験室内の測定条件
状態1(同じ)
状態2(異なる)
時間
同じときに行われた測定
時間を変えて行われた測定
校正
測定の間には校正は行わない
測定の間に校正が行われる
オペレータ
同一オペレータ
異なるオペレータ
装置
再校正を行わない同一装置
異なる装置
5.2
“同じときに行われた測定”とは,環境条件などの不変性を常に保証できるとは限らない条件の変
動を最小とするために,できる限り短時間の内に行われた測定も含む。“時間を変えて行われた測定”とは,
長い時間間隔で実施された測定のことで,環境条件の違いの影響を含んでいるであろう。
5.3
測定結果を求めるために不可欠な部分として,その測定方法自体に含まれるいかなる校正も,ここ
で述べる“校正”にはあてはまらない。“校正”とは,試験室内で一連の測定と測定の間に定期的に行われ
る校正の手順を意味する。
5.4
ある種の作業では,実際には“オペレータ”は複数のオペレータから成るチームで一人一人のオペ
レータは手順の特定の部分を担当していることがある。このような場合には,このチームを一人のオペレ
ータと見なし,メンバーやチーム内での役務分担などのいかなる変更も,異なる“オペレータ”と見なす
ことが望ましい。
5.5
“装置”は,実際には装置の組み合わせであることが多く,いかなる主要な構成要素の交換も異な
る装置と見なすことが望ましい。何が主要な構成要素であるかということについては,常識にゆだねる。
温度計の交換は主要な構成要素と考えられるかもしれないが,水浴にほんの少し異なる容器を用いること
は僅かな相違と考えられよう。試薬のバッチを変えることは主要な構成要素と考えることが望ましい。校
正することによりこのような変化が生じたならば,異なる“装置”又は再校正と考えることができる。
5
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.6
併行条件の下では4つのすべての因子が表1の状態1である。中間条件では1つ以上の因子が表1
の状態2であり,“M因子異なる精度条件”と記述する。ここで,Mは状態2における因子の数である。
再現条件の下では,結果は異なる試験室で得られるので,4つのすべての因子が状態2にあるばかりでな
く,試験室の運営や維持,オペレータの一般的な訓練の水準,測定結果の安定性と点検などが試験室間で
異なることに伴う付加的な効果も存在する。
5.7
M因子異なる中間条件の下では,下付添え字によって,どの因子が表1に示す状態2にあるのかを
規定する必要がある。例えば,
− 時間が異なる中間標準偏差,sI(T);
− 校正が異なる中間標準偏差,sI(C);
− オペレータが異なる中間標準偏差,sI(O);
− [時間+オペレータ]が異なる中間標準偏差,sI(TO);
− [時間+オペレータ+装置]が異なる中間標準偏差,sI(TOE);
− 他の多くの条件が同様の形式で規定できる。
6. 統計モデル
6.1
基本モデル
測定方法の精確さ(真度と精度)を推定するために,測定結果yを(1)式に示す3つの成分の和として仮
定しておくことは有用である。
y=m+B+e ·············································································· (1)
ここで, 試験の対象となる試料について,
mは一般平均(期待値);
Bは併行条件の下でのかたよりの試験室成分;
eは併行条件の下で,一つ一つの測定に伴う偶然誤差
を示す。これらの成分のそれぞれに関する議論と,基本モデルの拡張に関する議論を以下に述べる。
6.2
一般平均m
6.2.1
一般平均mは測定結果全体の平均である。試験室間共同実験(JIS Z 8402-2参照)で得られたm
の値は,“真の値”と測定方法にのみ依存し,それぞれの測定が実施された試験室,用いられた装置,実施
したオペレータ,測定の日時には依存しない。試料を特定したときの一般平均は“測定水準”とよばれる。
例えば,ある化学成分の純度の異なった試料,又は異なった試料(例えば,異なったタイプの鉄鋼)は異
なった測定水準に対応する。
滴定される溶液の真の濃度のように,真の値μの概念は意味を持つ状況は多い。測定水準mはふつう真
の値μと等しくなく,その差 (m−μ) は“測定方法のかたより”とよばれる。
状況によっては,測定水準は測定方法に依存して規定され,測定方法と独立な真の値の概念を適用でき
ない。例えば鉄鋼のヴィッカース硬度やコークスのマイカムインデックスがこの範疇に含まれる。とはい
え,一般にこの測定方法のかたよりをδ(真の値が存在しないときはδ=0)で表す。このとき一般平均m
は
m=μ+δ ·················································································· (2)
となる。
備考2. かたよりの項δに関する議論と真度評価実験の説明をJIS Z 8402-4に示す。
6
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.2.2
同じ測定方法によって得た測定結果の差を調べるとき,測定方法のかたよりは差に影響しないし,
無視することができる。しかし,契約や仕様の要求事項が測定(試料の)水準mではなく,真の値μによ
って規定されている場合に規定された値と測定結果とを比較するとき,又は,異なった測定方法を用いて
得た測定結果を比較するとき,測定方法のかたよりを考慮しなければならない。
6.3
項B
6.3.1
Bは,いくつかの原因によって生じるその試験室に起因するmからの偏差を表す項で,一つ一つの
測定結果に発生する偶然誤差eとは関係しない。一つの試験室での併行条件の下ではBは一定値と考えら
れ,“かたよりの試験室成分”とよばれる。
6.3.2
とはいえ日常的に一つの試験方法を用いる場合には,Bの値が,オペレータ,用いられた装置,環
境(温度,湿度,大気汚染など),などの相違に起因する多数の影響から成り立っていることが分かる。統
計モデル[式(1)]は次のように書き直すことができる。
y=m+B0+B(1)+B(2)+…+e ························································· (3)
または
y=μ+δ+B0+B(1)+B(2)+…+e ····················································· (4)
ここでBは変量B0,B(1),B(2)…から成り立ち,多数の中間精度因子を表す。
実際には,研究の目的や,測定方法の感度を考慮することによって,このモデルでどの項まで用いるか
が決まる。多くの場合には簡略化した形で充分である。
6.4
項B0,B(1),B(2),など
6.4.1
併行条件の下では,これらの項はすべて一定値となり,測定結果のかたよりに加わる。中間条件の
下では,B(1),B(2)などは因子の変量効果としてさまざまな値を取る(表1の状態2)のに対して,B0は因
子の定数効果としてそのままの値を取る(表1の状態1)。B(1),B(2)などは,もはやかたよりには寄与しな
いが,中間標準偏差を増大させるため,中間標準偏差は併行標準偏差よりも大きくなる。
6.4.2
オペレータの違いの影響には,測定する際の個人的な習慣(例えば,目盛りの読み方など)が含ま
れる。これらの違いのいくつかは,測定方法の標準化,特に技術の明瞭で精確な記述,によって除去され
ることが望ましい。一人のオペレータによって得られた測定結果にはかたよりが含まれるが,このかたよ
りは常に一定値になるのではなく(例えば,かたよりの大きさは,その人のその日の精神的・肉体的条件
によって変化するので),かたよりを正しく補正したり,校正することはできない。このようなかたよりは,
明瞭な操作マニュアルと訓練によって減少させるのが望ましい。このような状況ではオペレータの違いの
影響は変量的なものと考えることができる。
6.4.3
装置の違いの影響には,設置場所の違いの影響,特にインジケーターの変動などが含まれる。装置
の違いの影響には,正しい校正によって修正することができるものがある。系統的な原因による装置の間
の差は,校正によって修正されるのがよく,その手順は標準測定方法に含めることが望ましい。試薬のバ
ッチの変化などは,そのように処理するほうがよい。この目的には参照値が必要で,JIS Q 0033とJIS Q
0035が参考になる。標準物質を用いて校正している場合,装置の違いの影響は変量効果と考えることがで
きる。
6.4.4
時間による影響は環境的な違い,例えば室温,湿度などの違い,によるものであろう。環境条件の
標準化でこれらの影響を減らすように試みるのがよい。
7
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.5
オペレータの習熟や疲労の影響はオペレータと時間の交互作用と考えられる。装置の性能が,開始
時と数時間を経た後と異なることがあるが,これは装置と時間の交互作用の例である。オペレータの母集
団が小さく,さらに装置の母集団も小さいならば,これらの因子の影響は変量効果ではなく,それぞれ母
数効果として評価してもよい。
6.4.6
JIS Z 8402-2に示された手順は,かたよりの試験室成分の分布が近似的に正規分布であることを仮
定して設定されているが,実際には単峰な分布であればほとんどの分布に対して適用できる。Bの分散は
室間分散とよばれ
Var (B) =σL2············································································· (5)
と表される。しかし,これにはオペレータ,装置,時間,環境,の違いの影響も含まれる。枝分れ実験で
オペレータ,装置,測定時刻,環境,などを変えて行った精度評価実験からは,中間精度の分散を計算す
ることができる。Var (B) は,試験室,オペレータ,測定日,環境などの独立な寄与から成るものと考え
ることができて,
Var (B) =Var (B0) +Var (B(1)) +Var (B(2)) +… ······························· (6)
となる。それぞれの分散は,
Var (B0) =σ(0)2,Var (B(1)) =σ(1)2,Var (B(2)) =σ(2)2,など ··················· (7)
で表される。
Var (B) は実際にはsL2で推定され,適切な実験計画によって同様の中間精度の推定値が求められる。
6.5
誤差項e
6.5.1 誤差項eは一つ一つの測定結果に含まれる偶然誤差を表す。この規格のこの部で与えられる手順は,
確率変数としての誤差の分布が近似的に正規分布にしたがうことを仮定して設定されているが,実際には,
ひとやまの分布であるならばほとんどの分布に対して利用できる。
6.5.2
ある一つの試験室の分散を室内分散とよび,
Var (e) =σw2 ············································································· (8)
と表現する。
6.5.3
オペレータの技能レベルの違いなどによって,室内分散σw2は試験室間で違いがあることが考えら
れる。しかし,この規格のこの部では,試験室間の室内分散の違いが小さくなるように,測定方法が適切
に標準化され,すべての試験室がその標準化された測定方法を用いることによって,試験室が異なっても
共通な室内分散となることが正当化されていると仮定する。この共通な値を併行分散とよび,式(9)によっ
て表現する。この値はそれぞれの室内分散の平均値によって推定される。
)
(
2
e
Var
r=
σ
·············································································· (9)
式(9)に表現した平均値は,精確さ評価実験に参加した試験室から外れ値を除いたすべての試験室から算
出される。
7. 測定条件の選択
7.1
測定方法を用いる際,一つの試験室において考えられる多くの測定条件には,
a) 併行条件(4つの因子を一定に保つ。)
b) 1つの因子だけを変える,いろいろな中間条件
c) 2つの因子を変える,いろいろな中間条件
d) 3つの因子を変える,いろいろな中間条件
8
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
e) 4つの因子をすべて変える中間条件
がある。測定方法の規格に,併行標準偏差は必ず示されなければならないけれども,考え得る精度をすべ
て示すことは必要ではない(,さらには現実的ではない)。中間精度に関しては,一般的な実際の商取引
で,普通に起こり得る条件が示されるべきで,それに適した中間精度を一つ,その測定条件の詳細な記述
とともに規定すれば充分である。測定条件で変化させる因子は注意して定めるべきである。特に時間を変
化させた中間条件ならば,引き続く測定の間の実際的な平均時間間隔を示すのがよい。
7.2
標準化された測定方法は可能な限りかたよりが小さく,測定方法に固有のかたよりは技術的な方法
で処理されていると仮定する。それゆえ,この規格のこの部では測定条件によってもたらされるかたより
だけを扱う。
7.3
測定条件の因子(時間,校正,オペレータ,装置)を併行条件から変化させること(すなわち表1
の状態1から状態2への移行)は,測定結果のばらつきを一般に増加させる。しかしながら,多数の測定
結果の平均値の期待値は,併行条件よりも,一般にかたよりが小さくなる。中間条件で標準偏差が大きく
なることは,単一の測定結果の代わりに複数の測定結果の平均値を最終結果とすることで,一般に克服さ
れる。
7.4
大部分の試験室での実際的な考慮,すなわち測定の最終結果に要求される精度(標準偏差)と測定
実施コストによって,変化させる因子の数と,測定方法の標準化の際に変化させられる因子の選択とが決
まるものである。
8. 試験室内評価実験と中間精度の解析
8.1
最も単純な方法
一試験室内で中間精度を推定する最も単純な方法は,一つの試料(破壊試験の場合には,一組の同一と
見なしうる試料)について,一つ一つの測定ごとに因子を変化させてn回測定を行うことである。nは15
以上が推奨される。これが達成されない場合には,中間精度を推定するこの方法は他の推定の手順と比べ
て十分なものといえない。解析方法は単純であるが,時間を変えた中間精度を求めるために同一試料を日
を変えて毎日測定する場合や,測定の間の校正の影響を調べる場合には一般に有用である。
n回の測定結果のk番目をykとし,yでn回の測定結果の平均値を表すとき,測定番号kを横軸にした
(
)y
yk−
のグラフは,外れ値を識別するのによい。より正式な外れ値の検定は,グラッブズ検定を適用す
るもので,JIS Z 8402-2 : 1999の7.3.4に示されている。
M因子異なる中間標準偏差の推定値は
∑
=
−
−
=
n
k
k
I
y
y
n
s
1
2
)
(
)
(
1
1
·························································· (10)
で与えられ,中間条件を示す記号をかっこ内に示すとよい。
8.2
別な方法
8.2.1
全部の測定をn個の測定結果からなるt群のグループに分けて行う方法がある。例えば,一つの試
験室内でt種類の試料を一組にして測定し,中間条件での因子を変化させ,再びt種類の試料を測定する。
この手順を各試料についてn個の測定結果を得るまで繰り返す。各群のn個の測定結果は同一の試料(破
壊試験の場合には,一組の同一と見なしうる試料)について得られなければならないが,全試料が同一試
料であることは重要ではない。M因子異なる中間標準偏差として同じ値を適用できると考えられる区間に,
t種類の試料の測定水準がすべて含まれることのみが必要である。t (n−1) の値は15以上が推奨される。
9
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例 あるオペレータがt種類の試料のそれぞれについて一つずつ測定結果を得て,つぎに別のオペレ
ータがこれを繰り返し,場合によってはさらに別のオペレータが,というように続けていき,sI (0)
の推定値を計算することができる。
8.2.2
j番目の試料についてのk番目の測定結果をyjkとし,jyでj番目の試料についてのn回の測定結果
の平均値を表すとき,試料測定番号jを横軸にした
)
(
j
jk
y
y−
のグラフは,外れ値を識別するのによい。
より正式な外れ値の検定は,グラッブズ検定を適用するもので,JIS Z 8402-2 : 1999の7.3.4に示されてお
り,それぞれの群を別々に対象にしても,tn個の全測定結果をまとめて対象にしても,適用することがで
きる。
M因子異なる中間標準偏差の推定値s1 ( ) は,
∑
∑
=
=
−
−
=
n
k
j
jk
t
j
I
y
y
n
t
s
1
2
1
)
(
)
(
)1
(
1
··············································· (11)
で与えられる。n=2の場合(すなわち各試料について測定結果が二つのとき)には,この式は,
∑
=
−
=
t
j
j
j
I
y
y
t
s
1
2
2
1
)
(
)
(
2
1
·························································· (12)
と簡単になる。
8.3
測定条件の最終結果に与える影響
8.3.1
時間,校正,オペレータ,装置の組合せのうち,一つの因子が変わっただけでもyの期待値は変化
する。これは平均値の有用性の一つの限界である。化学分析や物理試験において,yは最終結果として報
告される。原材料の取引では,この最終結果はしばしばその原材料の品質評価に用いられ,製品の価格に
大きな影響を与える。
例 石炭の国際商取引では,コンサインメントの大きさは70 000tを超えることがよくあり,その灰分
の値は最終的にはわずか1gの測定試料から決定される。灰分1%の相違につき石炭1tあたりUSD
1.5に相当すると契約に明記してあると,化学天秤による灰の秤量で1mgの違いが灰分0.1%,す
なわち石炭1tあたりUSD 0.15に当たるため,コンサインメント全体ではUSD 10 500(0.1×1.5
×70 000なので)になってしまう。
参考 USDはアメリカ合衆国の通貨単位(ドル,$)の正式な表記である。
8.3.2
結果として化学分析や物理試験の最終結果は充分に正しく,信頼性が高く,特に普遍的で再現性が
あるべきである。特定のオペレータ,装置,時間の条件の下でのみ保証される最終結果は,商取引の目的
には充分にふさわしいとはいえないであろう。
9. 試験室間共同実験と中間精度の解析
9.1
基礎になる仮定
試験室間共同実験による中間精度の推定は,ある特定の因子の効果が全試験室で同じである,すなわち,
例えば一つの試験室でオペレータを変えることが,他の試験室でオペレータを変えることと同じ効果であ
り,時間の違いによるばらつきは全試験室で同じであるといった仮定に拠っている。もしこの仮定が満た
されないならば,中間精度の概念が意味をなさないばかりか,この後の項で提案する中間精度を推定する
技法も意味を持たない。全試験室の情報を併合するために必要な,仮定の検討のためには,外れ値に対す
10
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る慎重な配慮(必ずしも外れ値を棄てなくてよい)が払われなければならない。外れ値を検出する一つの
強力な技法は,因子の種々の水準や実験に参加した各試験室の関数として,測定値を図示することである。
9.2
最も単純な方法
q水準の試料をpヵ所の試験室に送付し,それぞれの試験室でq水準についてn回ずつの測定の間,中
間精度の因子を変えて測定した場合の解析は,併行標準偏差の代わりに中間標準偏差が推定されることを
除けば,JIS Z 8402-2で説明した計算と同じ方法になる。
9.3
枝分れ実験
中間精度を推定する方法として,さらにより精巧な実験を実施することもある。このような方法には完
全枝分れ実験やスタッガード型枝分れ実験(これらの用語の定義はJIS Z 8101-3参照)がある。枝分れ実
験を採用することの利点は,一回の試験室間共同実験で一度に,併行及び再現標準偏差だけでなく一つ以
上の中間標準偏差を推定することが可能であることである。しかしながら,これらは9.8で説明するよう
にある種の注意を払わなければならない。
9.4
完全枝分れ実験
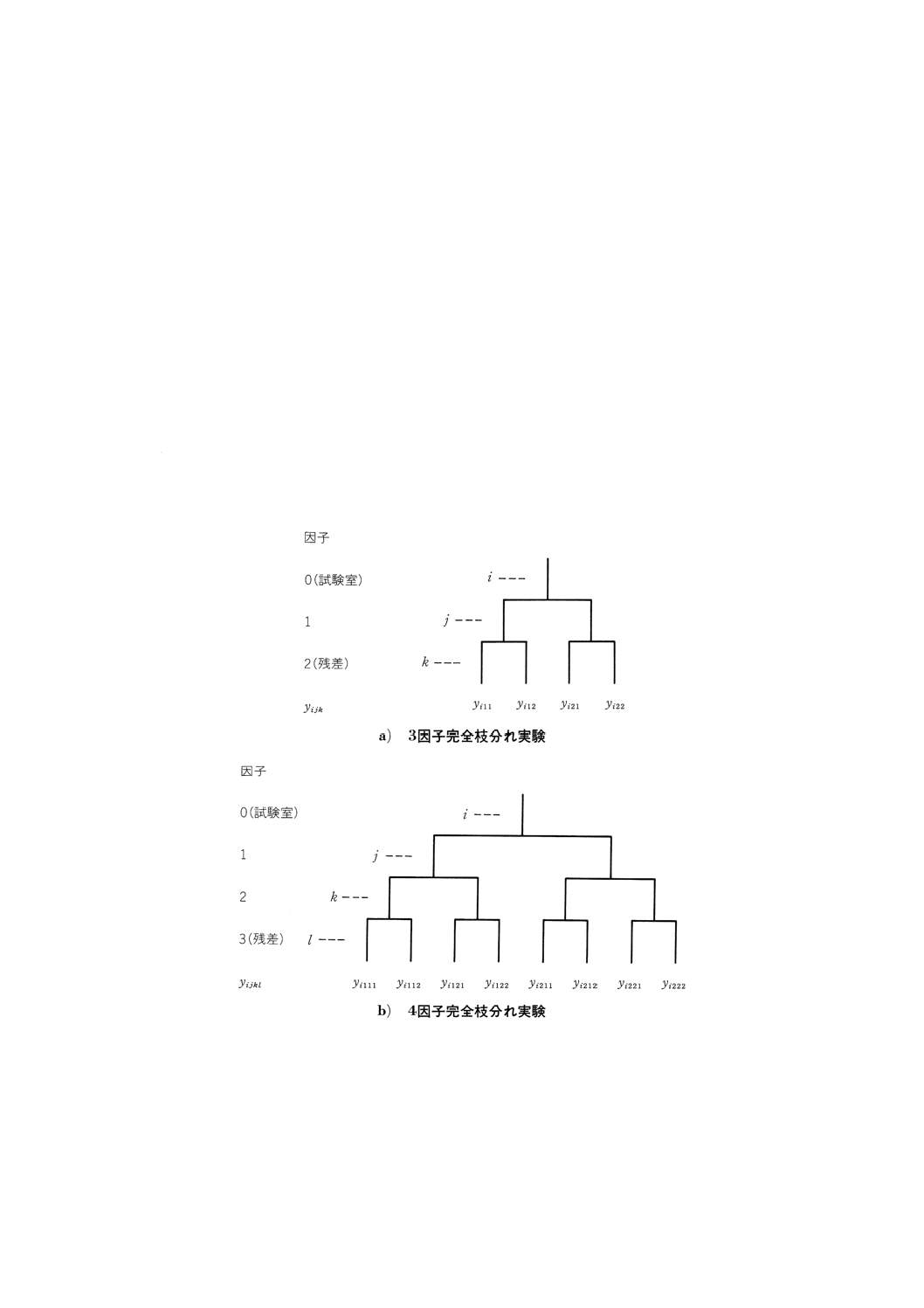
ある測定水準での,完全枝分れ実験の図式的な配置を図1に示す。
図1 3因子及び4因子完全枝分れ実験の配置図
いくつかの試験室で共同して3因子完全枝分れ実験を実施すると,併行及び再現標準偏差と同時に中間
精度を一つ得ることができる。すなわちσ(0),σ(1)とσrを推定することができる。同様に4因子完全枝分れ
実験は二つの中間精度,すなわちσ(0),σ(1),σ(2)とσrを推定するために用いることができる。
3因子完全枝分れ実験の図1a)におけるデータyの下付添え字i,j,kは,例えばそれぞれ試験室,実験

11
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日,併行条件での繰返しを表している。
4因子完全枝分れ実験の図1b)におけるデータyの下付添え字i,j,k,lは,例えばそれぞれ試験室,実
験日,オペレータ,併行条件での繰返しを表している。
n因子完全枝分れ実験の解析は“分散分析 (ANOVA) ”という統計技法を用いて,各測定水準ごとに別々
に行われる。詳細を附属書Bに示す。
9.5
スタッガード型枝分れ実験
ある測定水準での,スタッガード型枝分れ実験の図式的な配置を図2に示す。
3因子のスタッガード型枝分れ実験ではそれぞれの試験室iごとに測定結果が3つ必要である。測定結
果yi1とyi2は併行条件の下で得て,yi 3を例えば時間の異なる中間条件(この場合yi1とyi2を得た日とは異
なる日にyi3を得ることになる)のように,M因子異なる中間条件 (M=1,2,3) の下で得る。
図2 スタッガード型枝分れ実験の配置図
4因子のスタッガード型枝分れ実験では,yi4を,さらにもう一つ因子を変えた中間条件,例えば別な日
に別なオペレータで測定することにより,時間とオペレータの異なる中間条件の下で得る。
n因子スタッガード型枝分れ実験の解析も“分散分析 (ANOVA)”という統計技法を用い,測定のそれぞ
れの段階に適用される。詳細を附属書Cに示す。
9.6
枝分れ実験における因子の割り付け
枝分れ実験における因子について,最も系統的な影響(すなわち,最も多くの測定結果に共通の影響)
を与える因子に最高のランク (0,1,…) を,最も偶然的な影響を与える因子に最低のランクを割り当て,
最低ランクの因子は残差変動と考えられる。例えば,図1b)と図2に示したような4因子の実験では,因
子0は試験室,因子1はオペレータ,因子2は測定が行われる日,因子3は繰返しとすればよい。完全枝
分れ実験はその対称性の理由で,この点は重要でないかもしれない。
9.7
枝分れ実験とJIS Z 8402-2に示した手順との比較
JIS Z 8402-2に示した手順は,測定試料の水準ごとに別々に解析されるので,まさしく2因子完全枝分
れ実験であり,併行及び再現標準偏差の二つの標準偏差が求められる。因子0は試験室で,因子1が繰返
しである。もしこの実験計画に,各試験室の二人のオペレータが併行条件でそれぞれ二つの測定結果を得
るというように,因子を一つ追加すると,併行及び再現標準偏差に加えて,オペレータの異なる中間標準
偏差が求められる。この代わりに,各試験室でオペレータを変えずに日を変えて併行条件での測定を繰り
返すならば,この3因子完全枝分れ実験により,時間の異なる中間標準偏差を求められる。各試験室で二
人のオペレータがそれぞれ二つの測定結果を得て,別な日にもう一度同じように測定を実施するというよ
12
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
うに,さらに因子を追加すると,併行標準偏差,再現標準偏差,オペレータの異なる中間標準偏差,時間
の異なる中間標準偏差,オペレータと時間の異なる中間標準偏差を求めることができる。
9.8
完全枝分れ実験とスタッガード型枝分れ実験との比較
n因子完全枝分れ実験ではそれぞれの試験室で2n−1個の測定結果が必要であるが,これは試験室にとっ
て過大な要求になることがある。これがスタッガード型枝分れ実験の主たる論拠となっている。この実験
計画は,解析が少し複雑になり,測定結果の数が少ないために各標準偏差の推定値の不確かさが増大する
けれども,同じ個数の標準偏差を求めるためにより少ない個数の測定結果で足りる。
13
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A (規定) JIS Z 8402で用いられる記号
a
関係式s=a+bmの切片
A
推定値の不確かさを計算するのに用いる係数
b
関係式s=a+bmの勾配
B
全平均と試験室の測定値の偏差を表す成分(かた
よりに占める試験室成分)
B0
Bの成分の中で中間精度条件の下では変わらな
い,すべての要因
B(1),B(2),など Bの成分の中で中間精度条件で変化する要
因
c
関係式logs=c+dlogmの切片
C,Cʼ,C” 検定統計量
Ccrit,Cʼcrit,C”crit 統計的検定の棄却限界値
CDP
確率Pの許容差
CRP
確率Pの許容範囲
d
関係式logs=c+dlogmの勾配
e
測定値の成分中,すべての測定値に生じている偶
然誤差
f
許容範囲の係数
Fp(v1, v2)
分子の自由度v1,分母の自由度v2のF分布のp
分位点
G
グラッブスの検定統計量
h
マンデルの試験室間一致性の検定統計量
k
マンデルの試験室内一致性の検定統計量
LCL
下側管理限界(処置限界または警戒限界)
m
試験特性の一般平均;水準
M
中間精度条件において考慮される因子の数
N
反復数
n
一つの試験室で一つの水準(すなわち,セルごと)
で得る測定値の数
p
共同実験に参加した試験室数
P
確率
q
共同実験における試験特性の水準数
r
併行精度限界値(許容差)
R
再現精度限界値(許容差)
RM
標準物質
s
標準偏差の推定値
s)
標準偏差の予測値
T
ある表示の総和
t
試験対象または群の数
UCL
上側管理限界(処置限界または警戒限界)
W
重み付き回帰式の計算で用いられる重み係数
w
一組の測定値の範囲
x
グラッブス検定に用いられるデータ
y
測定値
y
測定値の算術平均
y
測定値の全平均
α
有意水準
β
第二種の過誤の確率
γ
再現標準偏差と併行標準偏差の比(σR/σr)
∆
試験室のかたより
Δ)
∆の推定値
δ
測定方法のかたより
δ)
δの推定値
λ
二つの試験室または二つの測定方法間のかたよ
りの検出可能な差
μ
試験特性の真値または参照値
v
自由度
ρ
方法AとBの併行標準偏差間の検出可能な比
σ
標準偏差の真の値
τ
最終校正からの時間経緯に起因する変動を表す
測定値の成分
φ
方法AとBの試験室間平均平方の平方根の検出
可能な比
χ2p(v)
自由度vのχ2分布におけるp分位点
添え字に用いる記号
C
校正法が異なることを示す
E
装置が異なることを示す
i
特定の試験室を示す添え字
I ( )
中間精度に関する添え字,かっこ内に中間精度条
件のタイプの識別子を記述する
14
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
j
特定の水準に関する添え字 (JIS Z 8402-2) 分析
の一群あるいは要因に関する添え字 (JIS Z
8402-3)
k
試験室iにおける水準jのk番目の測定値を示す
添え字
L
試験室間を示す
m
検出可能なかたよりに関する添え字
M
試験試料間を示す
O
オペレーターが異なっていることを示す
P
確率
r
併行精度
R
再現精度
T
時間が異なることを示す
W
試験室内を示す
1,2,3…
測定値の得られた順序を示す
(1),(2),(3),…
測定値の大きさの順序を示す
15
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(規定) 完全枝分れ実験の分散分析
この附属書に記述されている分散分析は,試験室間共同実験では測定水準ごとに別々に用いられなけれ
ばならない。簡単にするために,データの添え字のうち,測定水準を表す添え字は省いてある。添え字j
は,この規格の他のパートでは測定水準として用いられているが,この部では因子1(因子0は試験室)
を表すために用いられていることに留意して欲しい。
JIS Z 8402-2 : 1999の7.3に記述されている方法は,データの一致性と外れ値をチェックするために用い
られるべきである。この附属書に記述されている実験計画では,どこかの試験室の測定結果に欠測値があ
る場合の正しい解析は大変複雑になる。ある試験室の測定結果を外れ値であると判断した場合は,その試
験室の(影響を受ける測定水準の)全てのデータを解析の対象から除外することが望ましい。
B.1 3因子完全枝分れ実験
実験で得られたデータをyijkで表す。この場合の平均値及び範囲を以下に示す。
)
(
2
1
2
1
ij
ij
ij
y
y
y
+
=
)
(
2
1
2
1
i
i
i
y
y
y
+
=
∑
=
i
iy
p
y
1
2
1
)1(
ij
ij
ij
y
y
w
−
=
2
1
)2(
i
i
i
y
y
w
−
=
ここでpは共同実験に参加した試験室の数である。
総平方和SSTは次のように分解される。
∑∑∑
+
+
=
−
=
i
j
k
e
ijk
SS
SS
SS
y
y
SST
1
0
)
(
2
ここで
∑∑∑
∑
∑
−
=
−
=
−
=
i
j
k
i
i
i
i
i
y
y
y
y
y
y
SS
2
2
2
2
)
(4
)
(
4
)
(
4
)
(
0
∑∑∑
∑
∑
∑
=
−
=
−
=
i
j
k
i
i
i
j
ij
i
ij
w
y
y
y
y
SS
2)2(
2
2
)
(
2
)
(
1
∑∑∑
∑∑
=
−
=
i
j
k
i
j
ij
ij
ijk
w
y
y
SSe
2
)1(
2
2
1
)
(
である。
平方和SS0,SS1,SSeの自由度はそれぞれp−1,p,2pであるので,分散分析表は表B.1に示すように
構成される。
表B.1 3因子完全枝分れ実験の分散分析表
要因 平方和
自由度
平均平方
平均平方の期待値
0
SS0
p−1
MS0=SS0/ (p−1)
σr2+2σ(1)2+4σ(0)2
1
SS1
p
MS1=SS1/p
σr2+2σ(1)2
残差 SSe
2p
MSe=SSe/ (2p)
σr2
計
SST
4p−1
σ(0)2,σ(1)2,σr2の不偏推定値s(0)2,s(1)2,sr2はそれぞれ平均平方MS0,MS1,MSeから次のように求める
ことができる。
16
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)1
0
(
4
1
2
)0
(
MS
MS
s
−
=
)
1
(
2
1
2
)1(
MSe
MS
s
−
=
sr2=MSe
併行分散,1因子異なる中間分散,再現分散の推定値は,それぞれ次のようになる。
sr2
sI(1)2=sr2+s(1)2
sR2=sr2+s(1)2+s(0)2
B.2 4因子完全枝分れ実験
実験で得られたデータをyijklで表す。この場合の平均値及び範囲を以下に示す。
)
(
2
1
2
1
ijk
ijk
ijk
y
y
y
+
=
2
1
)1(
ijk
ijk
ijk
y
y
w
−
=
)
(
2
1
2
1
ij
ij
ij
y
y
y
+
=
2
1
)2(
ij
ij
ij
y
y
w
−
=
)
(
2
1
2
1
i
i
i
y
y
y
+
=
2
1
)3(
i
i
i
y
y
w
−
=
∑
=
i
iy
p
y
1
ここでpは共同実験に参加した試験室の数である。
総平方和SSTは次のように分解される。
∑∑∑∑
+
+
+
=
−
=
i
j
k
e
l
ijkl
SS
SS
SS
SS
y
y
SST
2
1
0
)
(
2
ここで
∑∑∑
∑
∑
=
=
−
=
i
j
k
i
i
l
i
y
p
y
y
y
SS
2
2
2
)
(
8
)
(
8
)
(
0
∑∑∑
∑
∑
∑
∑
=
−
=
−
=
i
j
k
i
i
i
j
i
ij
l
i
ij
w
y
y
y
y
SS
2)3(
2
2
2
)
(
4
)
(
1
∑∑∑
∑
∑∑
∑∑
∑
=
−
=
−
=
i
j
k
i
i
j
ij
j
k
ij
ijk
l
ij
ijk
w
y
y
y
y
SS
2)2(
2
2
)
(
2
)
(
2
∑∑∑
∑∑∑
∑
=
−
=
i
j
k
i
j
k
ijk
l
ijk
ijkl
w
y
y
SSe
2
)1(
2
2
1
)
(
である。
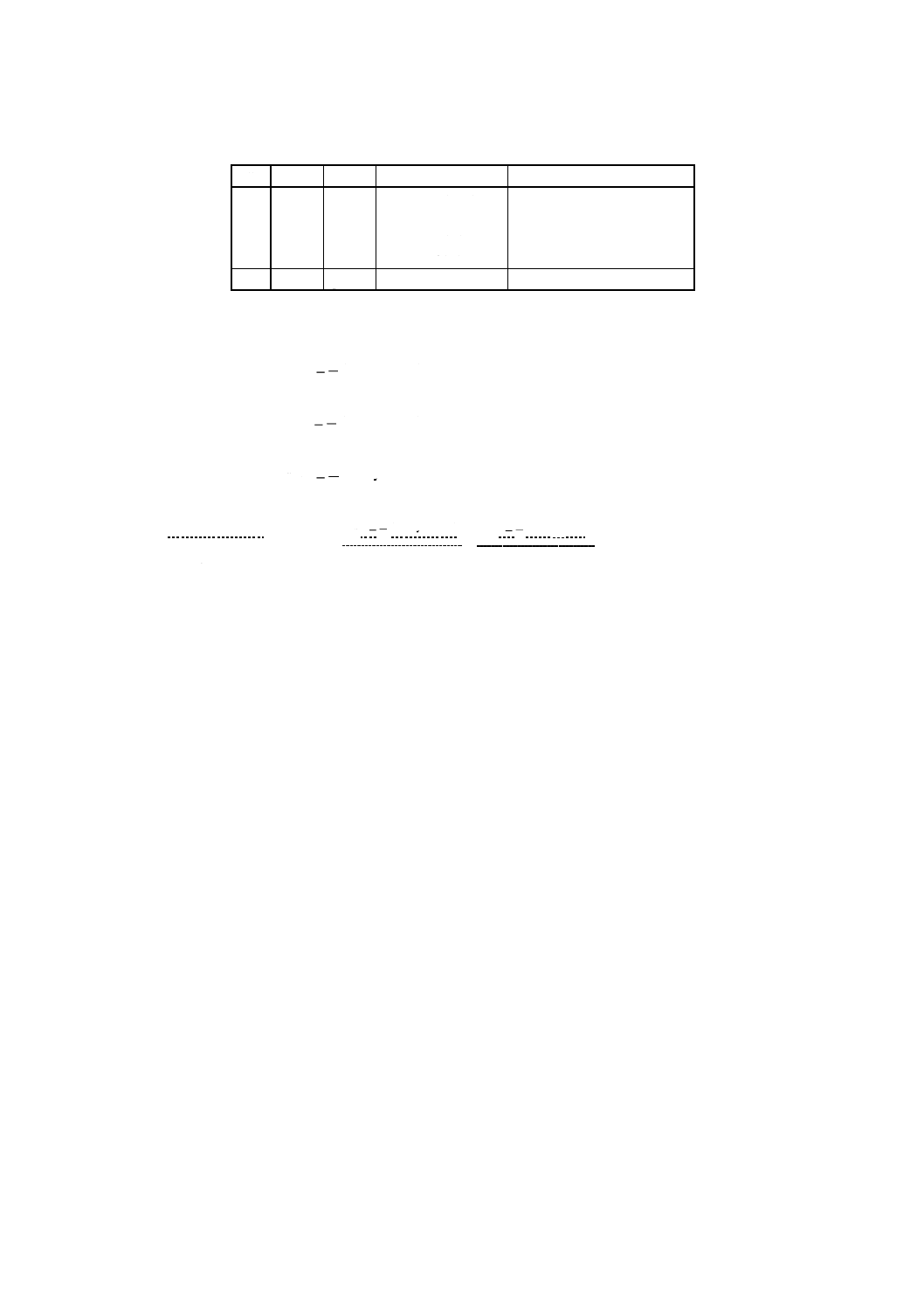
平方和SS0,SS1,SS2,SSeの自由度はそれぞれp−1,p,2p,4pであるので,分散分析表は表B.2に
示すように構成される。
17
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.2 4因子完全枝分れ実験の分散分析表
要因 平方和
自由度
平均平方
平均平方の期待値
0
SS0
p−1
MS0=SS0/ (p−1)
σr2+2σ(2)2+4σ(1)2+8σ(0)2
1
SS1
p
MS1=SS1/p
σr2+2σ(2)2+4σ(1)2
2
SS2
2p
MS2=SS2/ (2p)
σr2+2σ(2)2
残差 SSe
4p
MSe=SSe/ (4p)
σr2
計
SST
8p−1
σ(0)2,σ(1)2,σ(2)2,σr2の不偏推定値s(0)2,s(1)2,s(2)2,sr2はそれぞれ平均平方MS0,MS1,MS2,MSeから
次のように求めることができる。
)1
0
(
8
1
2
)0
(
MS
MS
s
−
=
)2
1
(
4
1
2
)1(
MS
MS
s
−
=
)
2
(
2
1
2
)
2
(
MSe
MS
s
−
=
参考 ISO 5725-3 : 1994では,
)1
2
(
4
1
2
)1(
MS
MS
s
−
=
,
)
1
(
2
1
2
)
2
(
MSe
MS
s
−
=
と誤って記載されている。
sr2=MSe
併行分散,1因子異なる中間分散,2因子異なる中間分散,再現分散の推定値は,それぞれ次のようにな
る。
sr2
sI(1)2=sr2+s(2)2
sI(2)2=sr2+s(2)2+s(1)2
sR2=sr2+s(2)2+s(1)2+s(0)2
18
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(規定) スタッガード型枝分れ実験の分散分析
この附属書に記述されている分散分析は,試験室間共同実験では測定水準ごとに別々に用いられなけれ
ばならない。簡単にするために,データの添え字のうち,測定水準を表す添え字は省いてある。添え字j
は,この規格の他のパートでは測定水準として用いられているが,この部では試験室内の繰返しに対して
用いられていることに留意して欲しい。
JIS Z 8402-2 : 1999の7.3に記述されている方法は,データの一致性と外れ値をチェックするために用い
られるべきである。この附属書に記述されている実験計画では,どこかの試験室の測定結果に欠測値があ
る場合の正確な解析は大変複雑になる。ある試験室の測定結果を外れ値であると判断した場合は,その試
験室の(影響を受ける測定水準の)全てのデータを解析の対象から除外することが望ましい。
C.1 3因子スタッガード型枝分れ実験
第i試験室での実験で得られたデータをyij (j=1,2,3) で表す。この場合の平均値及び範囲を以下に示
す。
)
(
2
1
2
1
)1(
i
i
i
y
y
y
+
=
2
1
)1(
i
i
i
y
y
w
−
=
)
(
3
1
3
2
1
)
2
(
i
i
i
i
y
y
y
y
+
+
=
3
)1(
)2(
i
i
i
y
y
w
−
=
∑
=
i
iy
p
y
)
2
(
1
ここでpは共同実験に参加した試験室の数である。
総平方和SSTは次のように分解される。
∑∑
+
+
=
−
=
i
j
ij
SSe
SS
SS
y
y
SST
1
0
)
(
2
ここで
∑
−
=
i
i
y
p
y
SS
2
2
)2(
)
(
3
)
(
3
0
∑
=
i
i
SS
2
)2
(
3
2
1
ω
∑
=
i
i
SSe
2
)1(
2
1
ω
である。
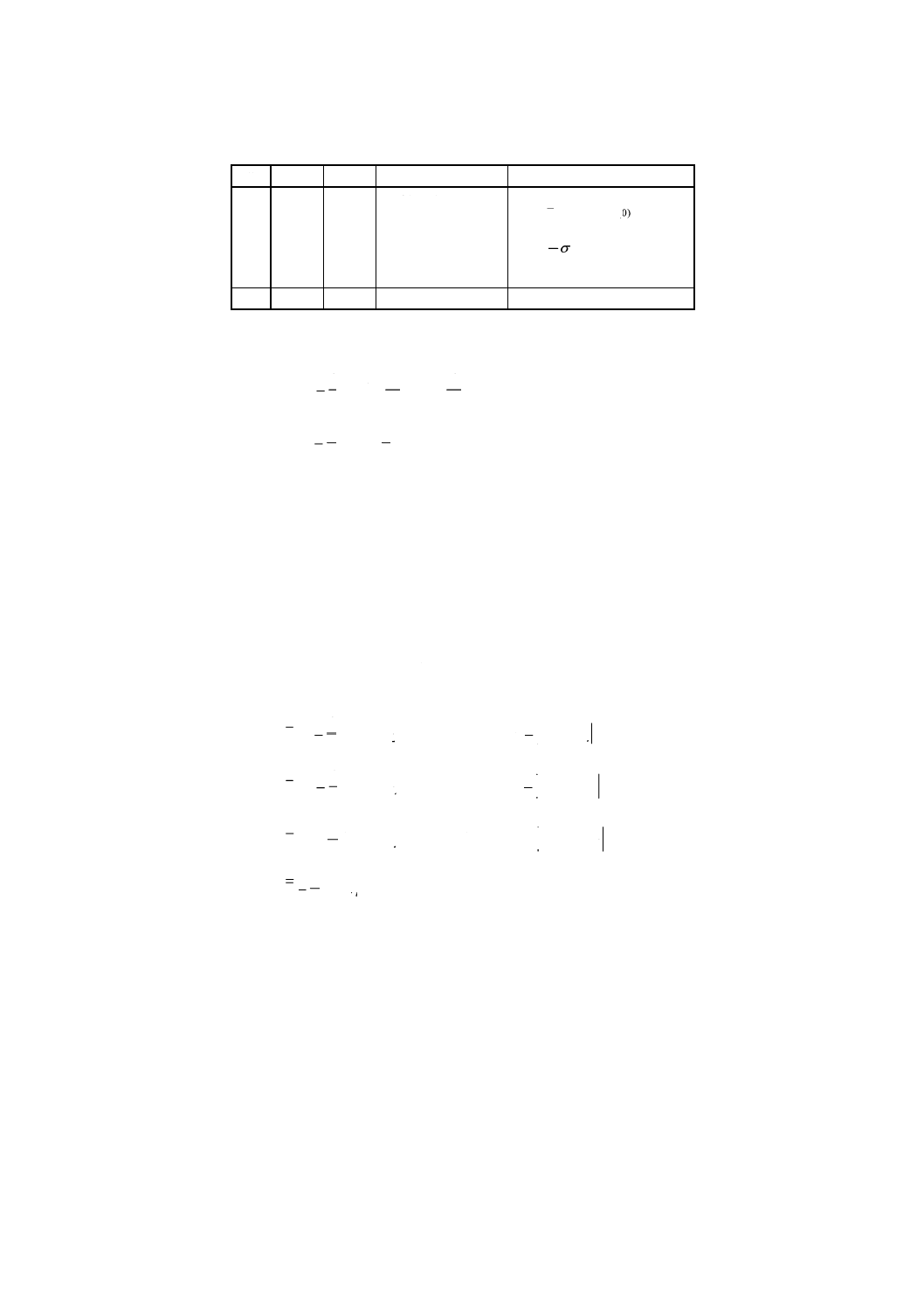
平方和SS0,SS1,SSeの自由度はそれぞれp−1,p,pであるので,分散分析表は表C.1に示すように
構成される。
19
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.1 3因子スタッガード型枝分れ実験の分散分析表
要因 平方和
自由度
平均平方
平均平方の期待値
0
SS0
p−1
SS0/ (p−1)
2)0(
2
)1(
2
3
3
5
σ
σ
σ
+
+
r
1
SS1
p
SS1/p
2
)1(
2
3
4σ
σ+
r
残差 SSe
p
SSe/p
σr2
計
SST
3p−1
σ(0)2,σ(1)2,σr2の不偏推定値s(0)2,s(1)2,sr2はそれぞれ平均平方MS0,MS1,MSeから次のように求める
ことができる。
MSe
MS
MS
s
12
1
1
12
5
0
3
1
2
)0
(
+
−
=
MSe
MS
s
4
3
1
4
3
2
)1(
−
=
sr2=MSe
併行分散,1因子異なる中間分散,再現分散の推定値は,それぞれ次のようになる。
sr2
sI(1)2=sr2+s(1)2
sR2=sr2+s(1)2+s(0)2
C.2 4因子スタッガード型枝分れ実験
第i試験室での実験で得られたデータをyij (j=1,2,3,4) で表す。この場合の平均値及び範囲を以下
に示す。
)
(
2
1
2
1
)1(
i
i
i
y
y
y
+
=
2
1
)1(
i
i
i
y
y
w
−
=
)
(
3
1
3
2
1
)
2
(
i
i
i
i
y
y
y
y
+
+
=
3
)1(
)2(
i
i
i
y
y
w
−
=
)
(
4
1
4
3
2
1
)3
(
i
i
i
i
i
y
y
y
y
y
+
+
+
=
4
)2(
)3(
i
i
i
y
y
w
−
=
∑
=
i
iy
p
y
)3
(
1
ここでpは共同実験に参加した試験室の数である。
分散分析表は表C.2に示すように構成される。

20
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.2 4因子スタッガード型枝分れ実験の分散分析表
要因
平方和
自由度
平均平方
平均平方の期待値
0
∑
−
i
i
y
p
y
2
2
)3(
)
(
4
)
(
4
p−1
SS0/ (p−1)
2
)0(
2
)1(
2
)2(
2
4
2
5
2
3
σ
σ
σ
σ
+
+
+
r
1
∑
i
i
w
2
)3(
4
3
p
SS1/p
2
)1(
2
)2(
2
2
3
6
7
σ
σ
σ
+
+
r
2
∑
i
i
w
2
)2
(
3
2
p
SS2/p
2
)2(
2
3
4σ
σ+
r
残差 ∑
i
i
w
2
)1(
2
1
p
SSe/p
σr2
計
∑∑
−
i
j
ij
y
y
2)
(
4p−1
参考 ISO 5725-3 : 1994では.要因0の平方和が∑
−
i
i
y
p
y
2
2
)2
(
)
(
4
)
(
4
と誤って記載され
ている。
C.3 5因子スタッガード型枝分れ実験
第i試験室での実験で得られたデータをyij (j=1,2,3,4,) で表す。この場合の平均値及び範囲を以
下に示す。
)
(
2
1
2
1
)1(
i
i
i
y
y
y
+
=
2
1
)1(
i
i
i
y
y
w
−
=
)
(
3
1
3
2
1
)
2
(
i
i
i
i
y
y
y
y
+
+
=
3
)1(
)2(
i
i
i
y
y
w
−
=
)
(
4
1
4
3
2
1
)3
(
i
i
i
i
i
y
y
y
y
y
+
+
+
=
4
)2(
)3(
i
i
i
y
y
w
−
=
)
(
5
1
5
4
3
2
1
)4
(
i
i
i
i
i
i
y
y
y
y
y
y
+
+
+
+
=
5
)3(
)4(
i
i
i
y
y
w
−
=
∑
=
i
iy
p
y
)
4
(
1
ここでpは共同実験に参加した試験室の数である。
21
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
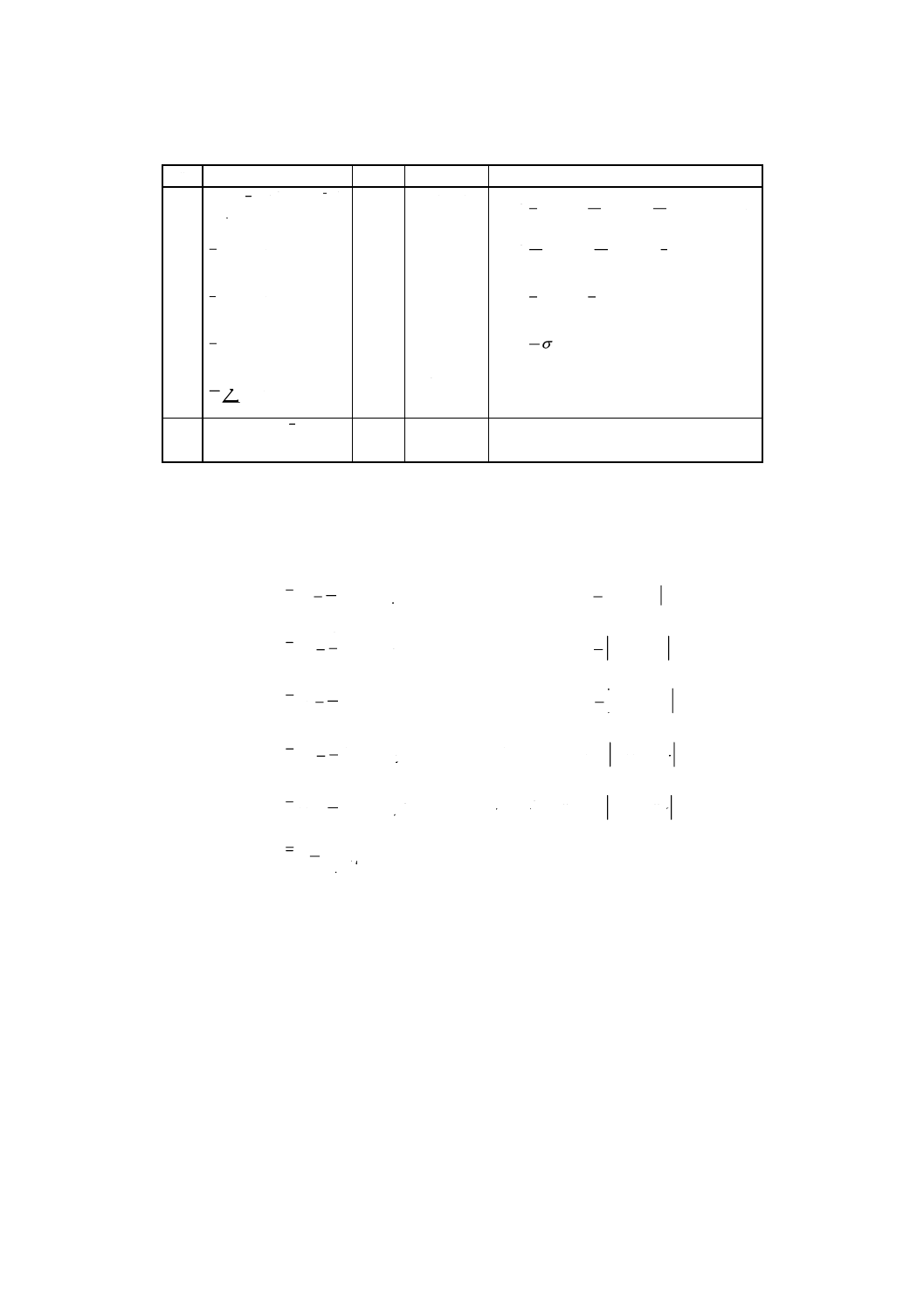
表C.3 5因子スタッガード型枝分れ実験の分散分析表
要因
平方和
自由度
平均平方
平均平方の期待値
0
∑
−
i
i
y
p
y
2
2
)4
(
)
(
5
)
(
5
p−1
SS0/ (p−1)
2
)
0
(
2
)1(
2
)2
(
2
)3(
2
5
5
17
5
11
5
7
σ
σ
σ
σ
σ
+
+
+
+
r
1
∑
i
i
w
2
)4
(
5
4
p
SS1/p
2
)1(
2
)2
(
2
)3
(
2
5
8
10
13
10
11
σ
σ
σ
σ
+
+
+
r
2
∑
i
i
w
2
)3(
4
3
p
SS2/p
2
)2
(
2
)3(
2
2
3
6
7
σ
σ
σ
+
+
r
3
∑
i
i
w
2
)2
(
3
2
p
SS3/p
2
)3
(
2
3
4σ
σ+
r
残差 ∑
i
i
w
2
)1(
2
1
p
SSe/p
σr2
計
∑∑
−
i
j
ij
y
y
2)
(
5p−1
分散分析表は表C.3に示すように構成される。
C.4 6因子スタッガード型枝分れ実験
第i試験室での実験で得られたデータをyij (j=1,2,3,4,5,6) で表す。この場合の平均値及び範囲を
以下に示す。
)
(
2
1
2
1
)1(
i
i
i
y
y
y
+
=
2
1
)1(
i
i
i
y
y
w
−
=
)
(
3
1
3
2
1
)
2
(
i
i
i
i
y
y
y
y
+
+
=
3
)1(
)2(
i
i
i
y
y
w
−
=
)
(
4
1
4
3
2
1
)3
(
i
i
i
i
i
y
y
y
y
y
+
+
+
=
4
)2(
)3(
i
i
i
y
y
w
−
=
)
(
5
1
5
4
3
2
1
)4
(
i
i
i
i
i
i
y
y
y
y
y
y
+
+
+
+
=
5
)3(
)4(
i
i
i
y
y
w
−
=
)
(
6
1
6
5
4
3
2
1
)5
(
i
i
i
i
i
i
i
y
y
y
y
y
y
y
+
+
+
+
+
=
6
)4(
)5(
i
i
i
y
y
w
−
=
∑
=
i
iy
p
y
)5
(
1
ここでpは共同実験に参加した試験室の数である。
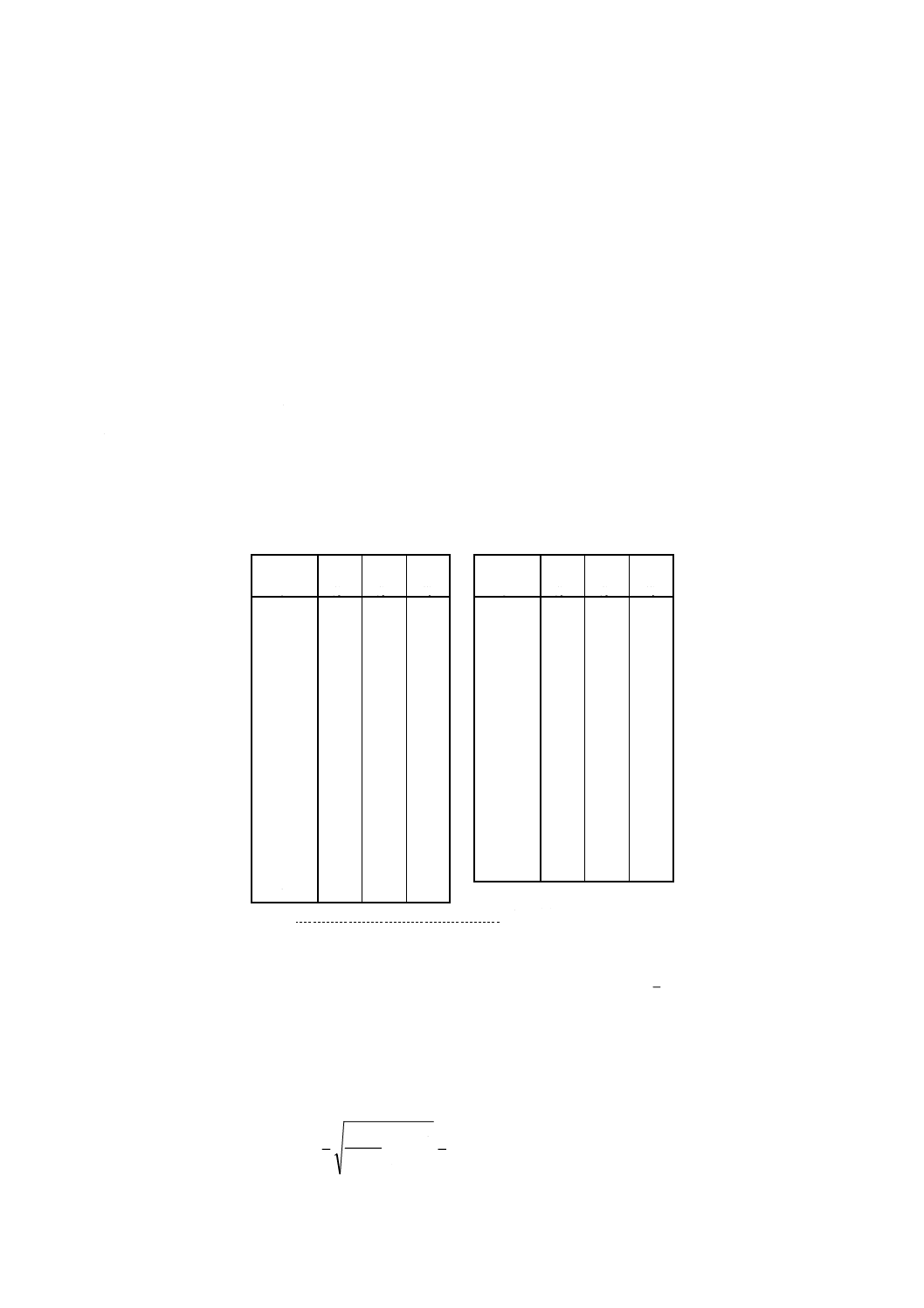
分散分析表は表C.4に示すように構成される。

22
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.4 6因子スタッガード型枝分れ実験の分散分析表
要因
平方和
自由度
平均平方
平均平方の期待値
0
∑
−
i
i
y
p
y
2
2
)5
(
)
(
6
)
(
6
p−1
SS0/ (p−1)
2)0(
2)1(
2)2(
2)3(
2)4(
2
6
3
13
3
2
3
4
σ
σ
σ
σ
σ
σ
+
+
+
+
+
r
1
∑
i
i
w
2
)5
(
6
5
p
SS1/p
2
)1(
2
)
2
(
2
)3
(
2
)4
(
2
3
5
5
7
5
6
15
16
σ
σ
σ
σ
σ
+
+
+
+
r
2
∑
i
i
w
2
)4
(
5
4
p
SS2/p
2
)1(
2
)2
(
2
)3
(
2
5
8
10
13
10
11
σ
σ
σ
σ
+
+
+
r
3
∑
i
i
w
2
)3(
4
3
p
SS3/p
2
)2
(
2
)3(
2
2
3
6
7
σ
σ
σ
+
+
r
4
∑
i
i
w
2
)2
(
3
2
p
SS4/p
2
)3
(
2
3
4σ
σ+
r
残差
∑
i
i
w
2
)1(
2
1
p
SSe/p
σr2
計
∑∑
−
i
j
ij
y
y
2)
(
6p−1
23
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(参考) 中間精度評価実験の統計解析の例
D.1 例1:特定の試験室内での特定の測定水準における,[時間+オペレータ]の異なる中間標準偏差,sI(TO)
を求める
D.1.1 背景
a) 測定方法
鉄鋼中の炭素含有量を真空発光分光分析法によって定量し,測定結果を質量パーセントで表す。
b) 出典
1984年11月のある製鉄所の日報。
c) 実験計画
特定の試験室において,毎日の分析試料からランダムに選択されたサンプルを,翌日オペレータを
変えてもう一度分析する。一ヶ月でこのようなデータの29組が得られた(表D.1参照)。
表D.1 オリジナルデータ−炭素の含有量,% (m/m)
試料番号 1回目 2回目 範囲
j
yj1
yj2
wj
1
0,130
0,127
0,003
2
0,140
0,132
0,008
3
0,078
0,080
0,002
4
0,110
0,113
0,003
5
0,126
0,128
0,002
6
0,036
0,032
0,004
7
0,050
0,047
0,003
8
0,143
0,140
0,003
9
0,091
0,089
0,002
10
0,040
0,030
0,010
11
0,110
0,113
0,003
12
0,142
0,145
0,003
13
0,143
0,150
0,007
14
0,169
0,165
0,004
15
0,169
0,173
0,004
試料番号 1回目 2回目 範囲
j
yj1
yj2
wj
16
0,149
0,144
0,005
17
0,044
0,044
0,000
18
0,127
0,122
0,005
19
0,050
0,048
0,002
20
0,042
0,146
0,104
21
0,150
0,145
0,005
22
0,135
0,133
0,002
23
0,044
0,045
0,001
24
0,100
0,161
0,061
25
0,132
0,131
0,001
26
0,047
0,045
0,002
27
0,168
0,165
0,003
28
0,092
0,088
0,004
29
0,041
0,043
0,002
参考 表の中では小数点としてコンマ (, ) を用いている。
D.1.2 解析
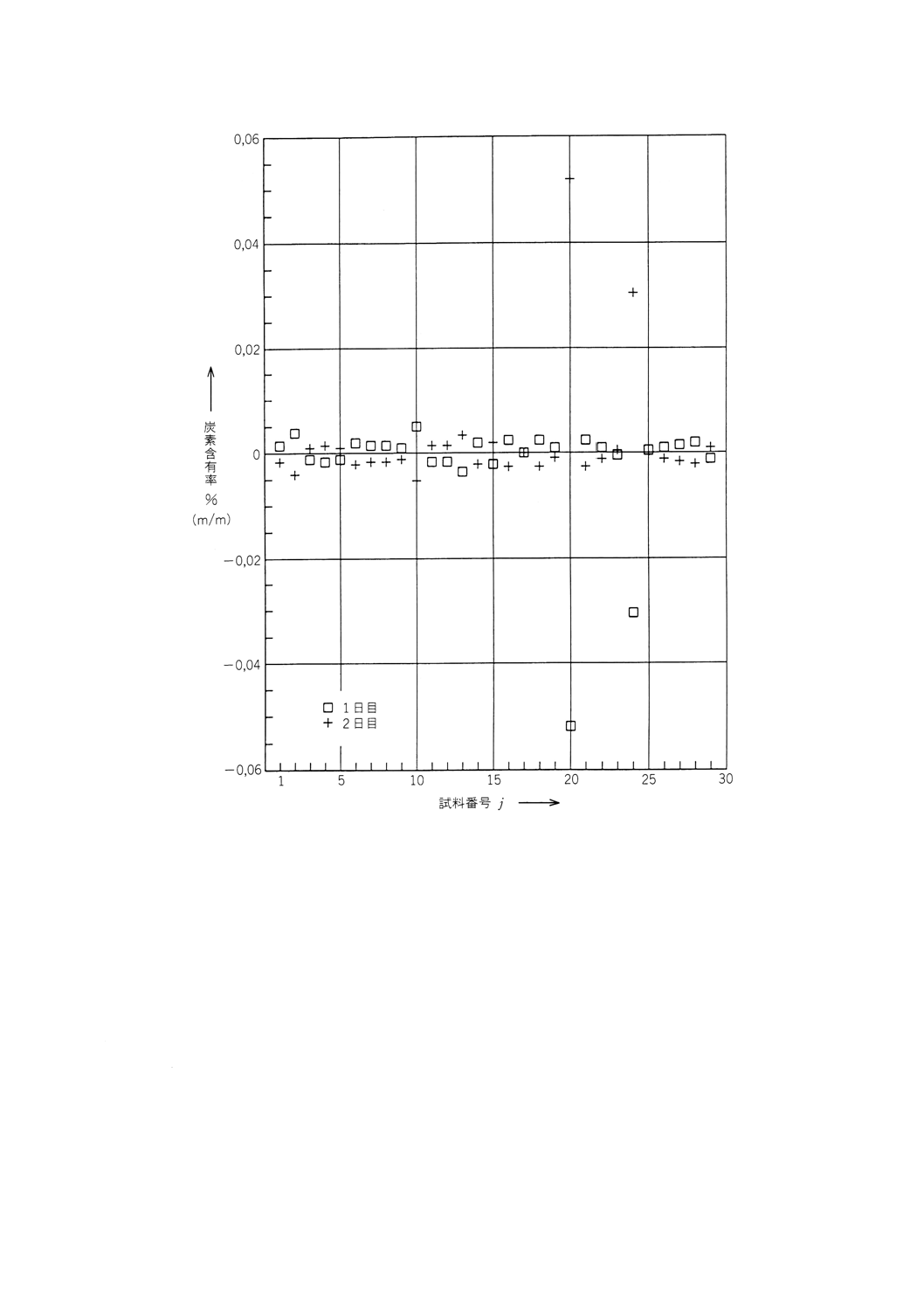
データyj1,yj2及び範囲wj=|yj1−yj2|を表D.1に示す。8.2に示された手順に従って解析する。
データ[サンプル番号jに対する2回分の測定値の平均値からの偏差,
)
(
j
jk
y
y−
]のプロットを図D.1
に示す。このプロット及びコクランの検定を適用した結果は,20番と24番のサンプルの範囲が外れ値で
あることを示している。これら2個のサンプルについての両日の測定値の間には大きな差があり,これは
主としてデータの記録時の間違いによるものと思われる。これら2つのサンプルの値は[時間+オペレー
タ]の異なる中間標準偏差,sI(TO),の計算からは除外した。sI(TO) は式(12)に従って次のように計算される。
3
27
1
2
)
(
10
87
.2
27
2
1
−
=
×
=
×
=
∑
j
j
TO
i
w
s
24
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.1 鉄鋼中の炭素の含有量−サンプル番号に
対する2つ測定値の平均からの偏差
D.2 例2:試験室間共同実験によって,時間の異なる中間標準偏差を求める
D.2.1 背景
a) 測定方法
実験の指示に記載されている原子吸光法による鉄鋼中のバナジウムの定量。測定結果を質量パーセ
ントで表す。
b) 出典
ISO/TC 17,鉄鋼/SC1(化学成分の定量法)。1985年5月に実施された実験。
c) 実験計画
3因子スタッガード型枝分れ実験が行われ,実験に含まれる6個の各測定水準について,20の試験
室が,各々,併行条件の下で1日の内に得られた2つの測定結果と,次の日に更にもう一つ得られた
25
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定結果を報告した。どの試験室においても,すべての測定は同一の装置を用いて同一のオペレータ
によって行われた。
D.2.2 解析
6つの測定水準すべてのデータを表D.2に表示する。
分散分析は1つの測定水準だけ,すなわち,測定水準1について示す。
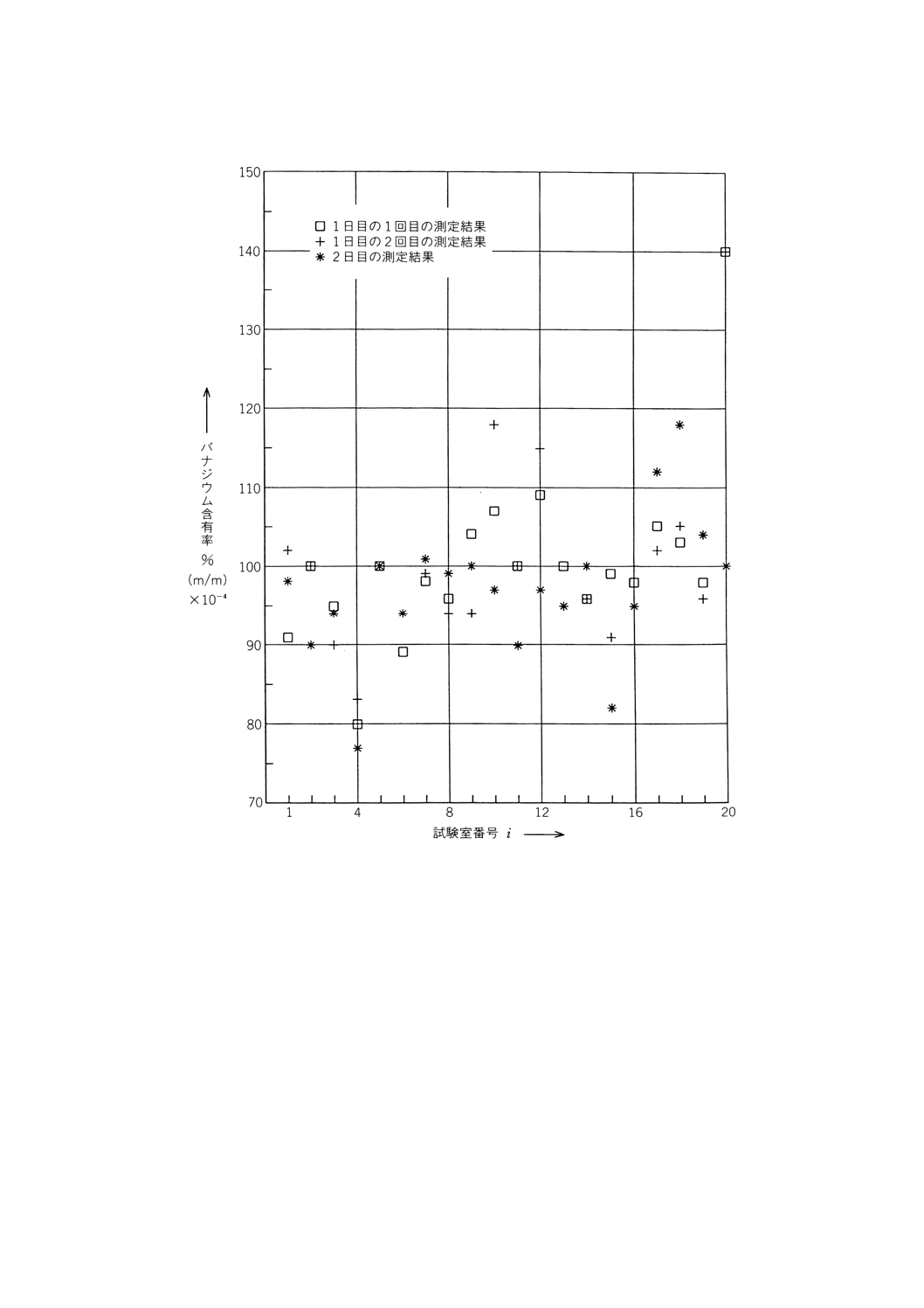
データのプロット(試験室番号iについての1日目及び2日目の測定結果)を図D.2に示す。このプロ
ットは試験室20が外れ試験室であることを示している。2日目の測定結果と1日目の平均値とには大きな
差があり,これは他の試験室の測定結果と比べて非常に大きい。この試験室のデータは精度の計算からは
はずした。
附属書CのC.1に従って,wi(1),wi(2)及び
)2(iy
を計算し,結果を表D.3に示す。
wi(1),wi(2)及び
)2(iy
の平方和及び平均値yは次のように計算される。
6
2)1(
10
52
.5
−
×
=
∑
i
i
w
6
2)2(
10
44
.
12
−
×
=
∑
i
i
w
6
2
)2(
10
16
.
832
1
)
(
−
×
=
∑
i
iy
25
798
009
.0
19
1
)2
(
=
=∑
i
iy
y
これらの値から平方和SS0,SS1及びSSeが得られ,分散分析表を表D.4に示す。
試験室間の分散の不偏推定値s(0)2,試験室内の日間分散の不偏推定値s(1)2及び併行分散の推定値sr2は以
下のようにして得られる。
s(0)2=0.278×10−6
s(1)2=0.218×10−6
sr2=0.145×10−6
再現標準偏差sR,時間を変えた中間標準偏差sI(T)及び併行標準偏差srは以下のようにして求まる。
3
2)0(
2)1(
2
10
801
.0
−
×
=
+
+
=
s
s
s
s
r
R
3
2)1(
2
)
(
10
603
.0
−
×
=
+
=
s
s
s
r
T
I
3
2
10
381
.0
−
×
=
=
r
r
s
s
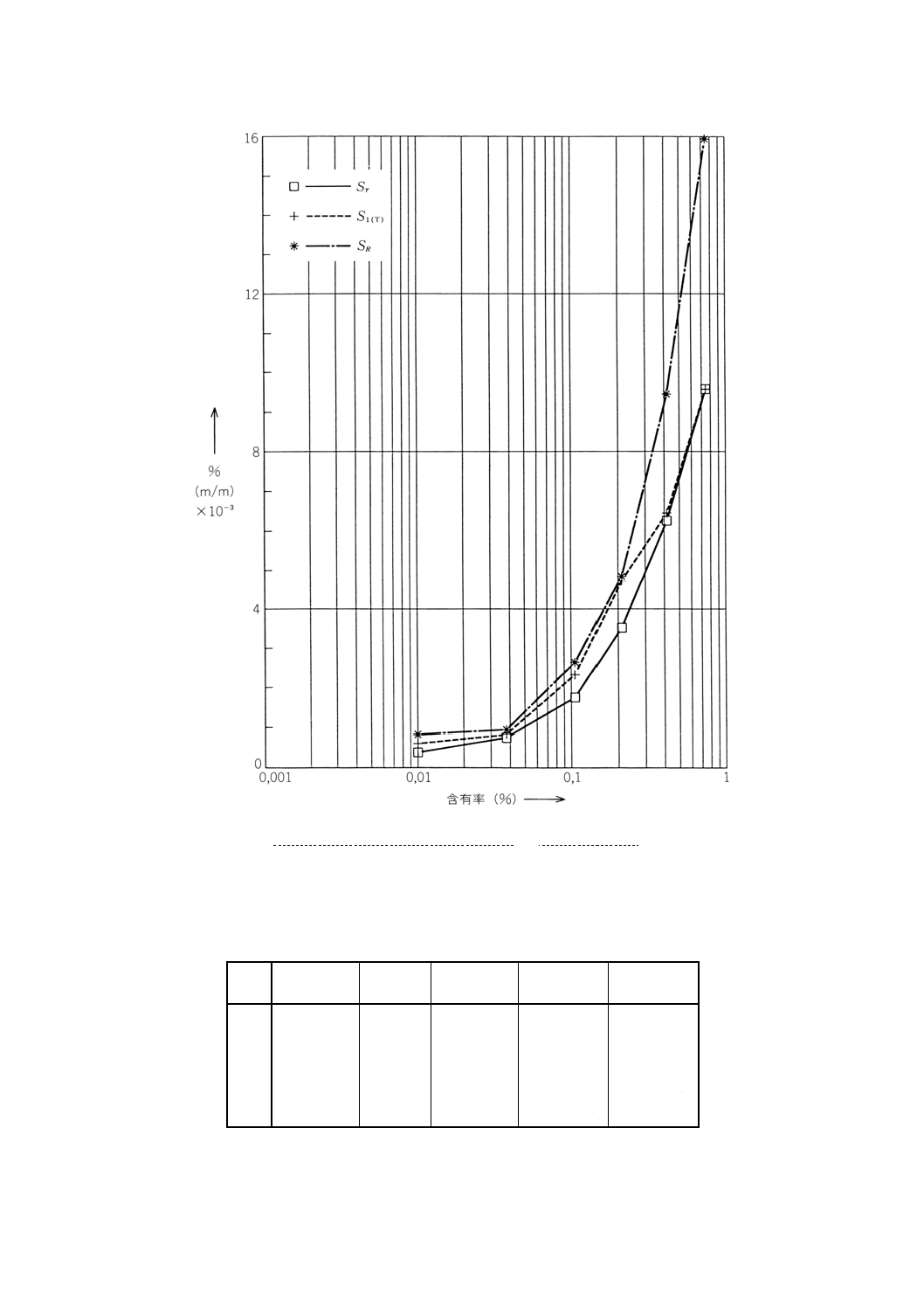
これらのバナジウム含有量の6つの測定水準の標準偏差の値を表D.5にまとめ,図D.3に示す。
2
6
Z
8
4
0
2
-3
:
1
9
9
9
(I
S
O
5
7
2
5
-3
:
1
9
9
4
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
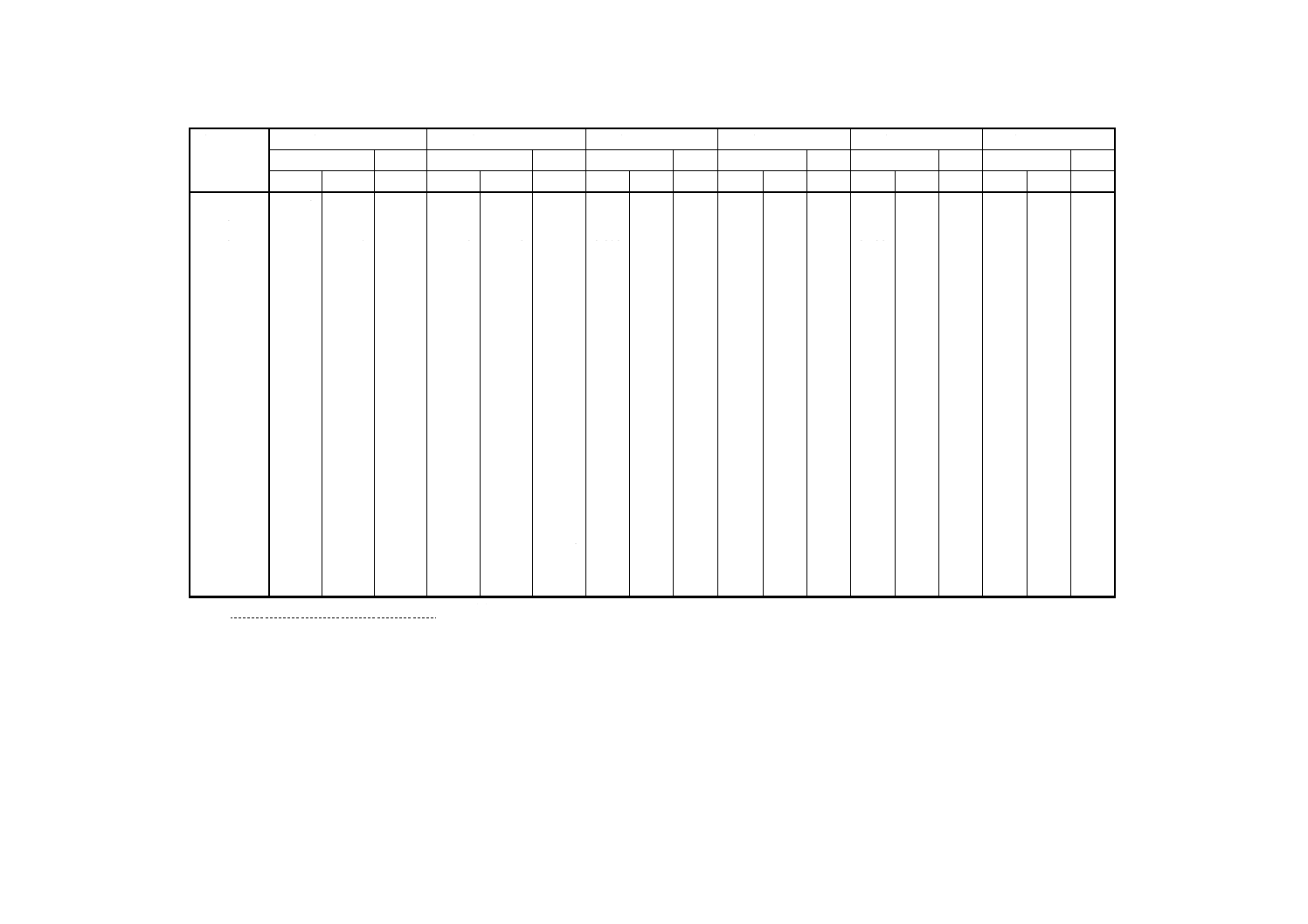
表D.2 オリジナルデータ−バナジウム含有率,% (m/m)
試験室番号
測定水準1 (0,01%)
測定水準2 (0,04%)
測定水準3 (0,1%)
測定水準4 (0,2%)
測定水準5 (0,5%)
測定水準6 (0,75%)
i
1日目
2日目
1日目
2日目
1日目
2日目
1日目
2日目
1日目
2日目
1日目
2日目
yi1
yi2
yi3
yi1
yi2
yi3
yi1
yi2
yi3
yi1
yi2
yi3
yi1
yi2
yi3
yi1
yi2
yi3
1
0,009 1 0,010 2 0,009 8 0,038 2 0,038 8 0,038 5
0,101
0,103
0,102
0,214
0,211
0,210
0,514
0,510
0,513
0,755
0,753
0,751
2
0,010 0 0,010 0 0,009 0 0,041 0 0,041 0 0,039 0
0,111
0,111
0,108
0,220
0,220
0,215
0,520
0,540
0,540
0,800
0,755
0,750
3
0,009 5 0,009 0 0,009 4 0,039 0 0,038 0 0,037 0
0,108
0,110
0,107
0,213
0,215
0,215
0,500
0,514
0,504
0,738
0,730
0,724
4
0,008 0 0,008 3 0,007 7 0,037 4 0,036 1 0,038 2
0,109
0,106
0,104
0,214
0,222
0,201
0,519
0,518
0,518
0,744
0,742
0,732
5
0,010 0 0,010 0 0,010 0 0,035 0 0,037 0 0,037 0
0,103
0,103
0,110
0,210
0,210
0,205
0,495
0,500
0,512
0,743
0,753
0,750
6
0,008 9 0,009 4 0,009 4 0,036 8 0,036 8 0,037 7
0,106
0,106
0,108
0,232
0,240
0,221
0,526
0,532
0,513
0,733
0,740
0,746
7
0,009 8 0,009 9 0,010 1 0,037 6 0,038 0 0,038 4
0,107
0,105
0,108
0,215
0,215
0,216
0,521
0,519
0,526
0,754
0,756
0,756
8
0,009 6 0,009 4 0,009 9 0,037 9 0,036 6 0,037 9
0,108
0,107
0,108
0,193
0,195
0,210
0,507
0,493
0,511
0,732
0,729
0,732
9
0,010 4 0,009 4 0,010 0 0,036 5 0,037 0 0,036 7
0,104
0,106
0,105
0,211
0,205
0,213
0,509
0,515
0,515
0,734
0,738
0,747
10
0,010 7 0,011 8
0,009 7 0,037 0 0,037 5 0,038 0
0,105
0,110
0,105
0,210
0,220
0,225
0,520
0,520
0,525
0,760
0,760
0,765
11
0,010 0 0,010 0 0,009 0 0,038 0 0,038 0 0,037 5
0,102
0,102
0,102
0,213
0,211
0,214
0,513
0,516
0,514
0,746
0,748
0,746
12
0,010 9 0,011 5
0,009 7 0,039 0 0,039 0 0,039 0
0,101
0,108
0,105
0,208
0,215
0,210
0,509
0,528
0,510
0,758
0,748
0,750
13
0,010 0 0,009 5 0,009 5 0,037 5 0,037 5 0,037 5
0,103
0,104
0,108
0,212
0,222
0,215
0,510
0,520
0,505
0,735
0,755
0,750
14
0,009 6 0,009 6 0,010 0 0,037 4 0,037 4 0,038 9
0,104
0,106
0,110
0,218
0,218
0,212
0,520
0,528
0,522
0,740
0,735
0,742
15
0,009 9 0,009 1 0,008 2 0,038 1 0,037 5 0,039 2
0,109
0,106
0,107
0,214
0,210
0,211
0,510
0,510
0,515
0,749
0,729
0,744
16
0,009 8 0,010 0 0,009 5 0,037 3 0,037 7 0,039 7
0,105
0,105
0,104
0,215
0,212
0,218
0,519
0,517
0,531
0,754
0,751
0,759
17
0,010 5 0,010 2
0,011 2
0,038 9 0,038 2 0,037 3
0,107
0,108
0,104
0,214
0,210
0,209
0,517
0,515
0,514
0,735
0,728
0,741
18
0,010 3 0,010 5
0,011 8
0,038 2 0,038 0 0,037 4
0,103
0,104
0,103
0,224
0,218
0,217
0,515
0,514
0,517
0,788
0,798
0,787
19
0,009 8 0,009 6 0,010 4 0,038 3 0,037 5 0,036 6
0,110
0,109
0,104
0,217
0,215
0,215
0,530
0,525
0,520
0,755
0,745
0,740
20
0,014 0 0,014 0 0,010 0 0,037 0 0,040 8 0,036 9
0,104
0,106
0,107
0,214
0,214
0,203
0,518
0,518
0,481
0,730
0,737
0,658
参考 表の中では小数点としてコンマ (, ) を用いている。
27
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.2 鉄鋼中のバナジウム含有率−試験室番号に対する
測定水準1の1日目及び2日目の測定結果
28
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.3 wi(1),wi(2)及び
)2(iy
の値
試験室番号
i
wi (1)
wi (2)
)2(iy
1
0,001 1
0,000 15
0,009 700
2
0,000 0
0,001 00
0,009 667
3
0,000 5
0,000 15
0,009 300
4
0,000 3
0,000 45
0,008 000
5
0,000 0
0,000 00
0,010 000
6
0,000 5
0,000 25
0,009 233
7
0,000 1
0,000 25
0,009 933
8
0,000 2
0,000 40
0,009 633
9
0,001 0
0,000 10
0,009 933
10
0,001 1
0,001 55
0,010 733
11
0,000 0
0,001 00
0,009 667
12
0,000 6
0,001 50
0,010 700
13
0,000 5
0,000 25
0,009 667
14
0,000 0
0,000 40
0,009 733
15
0,000 8
0,001 30
0,009 067
16
0,000 2
0,000 40
0,009 767
17
0,000 3
0,000 85
0,010 633
18
0,000 2
0,001 40
0,010 867
19
0,000 2
0,000 70
0,009 933
参考 表の中では小数点としてコンマ (, ) を用い
ている。
表D.4 分散分析表−バナジウム含有量
要因
平方和
自由度
平均平方
平均平方の期待値
0(試験室) 24,16×10−6
18
1,342×10−6
2)0(
2)1(
2
3
3
5
σ
σ
σ
+
+
r
1(日)
8,29×10−6
19
0,436×10−6
2
)1(
2
3
4σ
σ+
r
残差
2,76×10−6
19
0,145×10−6 σr2
計
35,21×10−6
56
29
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考 表の中では小数点としてコンマ (, ) を用いている。
図D.3 鉄鋼中のバナジウム含有率−含有率の関数で表した併行標準偏差sr,
時間の異なる中間標準偏差sI(T) 及び再現標準偏差sR
表D.5 6つの測定水準の鉄鋼中バナジウム含有率のsr,sI(T) 及びsRの値
測定
水準
外れ試験室
の番号
平均 (%)
sr (%)
sI (T) (%)
sR (%)
1
20
0,009 8
0,381×10−3
0,603×10−3
0,801×10−3
2
2
0,037 8
0,820×10−3
0,902×10−3
0,954×10−3
3
−
0,105 9
1,739×10−3
2,305×10−3
2,650×10−3
4
6と8
0,213 8
3,524×10−3
4,710×10−3
4,826×10−3
5
20
0,516 4
6,237×10−3
6,436×10−3
9,412×10−3
6
20
0,748 4
9,545×10−3
9,545×10−3
15,962×10−3
30
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E(参考) 参考文献
[1] JIS Z 8101-2 : 1999,統計−用語と記号−第2部 統計的品質管理用語
[2] JIS Z 8101-3 : 1999,統計−用語と記号−第3部 実験計画法用語
[3] JIS Z 8402-4 : 1999,測定方法及び測定結果の精確さ(真度及び精度)−第4部 標準測定方法の真度
を求めるための基本的方法
[4] JIS Z 8402-5 : 1), 測定方法及び測定結果の精確さ(真度及び精度)−第5部 標準測定方法の精度を
求めるための代替法
[5] JIS Z 8402-6 : 1999, 測定方法及び測定結果の精確さ(真度及び精度)−第6部 精確さに関する値の
実用的な使い方
[6] Winer, B. J. Statistical principles in experimental design. McGraw-Hill, 1962.
[7] Snedecor, G. W. and Cochran, W. G. Statistical methods. Iowa University Press, 1967.
1) 発行準備中
31
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
原案作成委員会 構成表
氏名
所属
(委員長)
石 川 馨
東京大学
(幹事)
宮 津 隆
日本鋼管株式会社
岩 田 晶 夫
住友金属鉱山株式会社
内 沼 一 雄
日本石油株式会社
藤 森 利 美
東京大学
(委員)
石 井 清 次
工業技術院
神 森 大 彦
社団法人日本化学会
上 甲 子 郎
東京理科大学
横 山 毅
昭和電工株式会社
高 橋 梅太郎
海外貨物検査株式会社
窪 田 孝 昌
海外貨物検査株式会社
(事務局)
新 井 紀 弘
財団法人日本科学技術連盟
改正原案作成委員会 構成表
氏名
所属
(委員長)
宮 津 隆
西東京科学大学理工学部
(委員)
尾 島 善 一
東京理科大学理工学部
故 高 橋 梅太郎
元海外貨物検査株式会社
椿 広 計
慶應義塾大学理工学部
仁 科 健
名古屋工業大学工学部
西 島 保
東燃株式会社総合研究所
野 村 和 夫
東京ガス株式会社
番 場 章
三石テクノ株式会社
多 田 格 三
元株式会社東芝
藤 森 利 美
長崎大学経済学部
横 山 隆 壽
財団法人電力中央研究所狛江研究所
池 田 要
工業技術院標準部材料規格課
川 村 正 信
財団法人日本規格協会
黒 木 勝 也
財団法人日本規格協会
(事務局)
橋 本 進
財団法人日本規格協会
32
Z 8402-3 : 1999 (ISO 5725-3 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
品質管理分野国際整合化分科会
氏名
所属
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
○ 今 井 秀 孝
工業技術院計量研究所
○ 柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
日本電信電話株式会社
門 山 允
東京国際大学
○ 鹿 庭 なほ子
国立食品医薬品衛生研究所
兼 子 穀
武蔵工業大学工学部
○ 城 道 修
メルシャン株式会社
○ 椿 広 計
筑波大学社会工学系
○ 仁 科 健
名古屋工業大学工学部
野 澤 昌 弘
東京理科大学経営学部
三佐尾 武 雄
QCコンサルタント
○ 宮 津 隆
帝京科学大学理工学部
山 田 秀
東京都立科学技術大学工学部
横 尾 恒 雄
QCコンサルタント
大 嶋 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会
備考 ○印は許容差JIS原案作成WGの委員を兼ねる。














