Z 8101-1：2015 (ISO 3534-1：2006) 

（1） 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

目 次 

ページ 

序文 ··································································································································· 1 

適用範囲 ····························································································································· 2 

1 一般統計用語 ··················································································································· 2 

2 確率で用いられる用語 ······································································································ 24 

附属書A（参考）記号 ·········································································································· 51 

附属書B（参考）統計に関するコンセプトダイアグラム ······························································ 53 

附属書C（参考）確率に関するコンセプトダイアグラム ····························································· 59 

附属書D（参考）用語の開発に用いた方法論 ············································································ 63 

参考文献 ···························································································································· 67 

Z 8101-1：2015 (ISO 3534-1：2006) 

（2） 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

まえがき 

この規格は，工業標準化法第14条によって準用する第12条第1項の規定に基づき，一般財団法人日本

規格協会（JSA）から，工業標準原案を具して日本工業規格を改正すべきとの申出があり，日本工業標準

調査会の審議を経て，経済産業大臣が改正した日本工業規格である。 

これによって，JIS Z 8101-1:1999は改正され，この規格に置き換えられた。 

この規格は，著作権法で保護対象となっている著作物である。 

この規格の一部が，特許権，出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意

を喚起する。経済産業大臣及び日本工業標準調査会は，このような特許権，出願公開後の特許出願及び実

用新案権に関わる確認について，責任はもたない。 

JIS Z 8101（統計−用語及び記号）の規格群には，次に示す部編成がある。 

JIS Z 8101-1 第1部：一般統計用語及び確率で用いられる用語 

JIS Z 8101-2 第2部：統計の応用 

JIS Z 8101-3 第3部：実験計画法（予定） 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

日本工業規格          JIS 

Z 8101-1：2015 

(ISO 3534-1：2006) 

統計−用語及び記号− 

第1部：一般統計用語及び確率で用いられる用語 

Statistics-Vocabulary and symbols-Part 1: General statistical terms and 

terms used in probability 

序文 

この規格は，2006年に第2版として発行（及び2007年にその修正版として発行）されたISO 3534-1を

基に，技術的内容及び対応国際規格の構成を変更することなく作成した日本工業規格である。 

なお，この規格で点線の下線を施してある参考事項は，対応国際規格にはない事項である。 

この規格とJIS Z 8101-2とは相互に矛盾しないことを意図している。それぞれの規格で用いる数学のレ

ベルは，用語定義が一貫性をもち，正しく簡潔であるために必要な最低限にとどめている。確率及び統計

で用いられる用語に関するこの規格は，基本的であり，その必要性のためやや高度なレベルの数学によっ

て表現されている。統計の応用に関するJIS Z 8101-2又は他のISO/TC 69の規格（及び対応するJIS）の

ユーザがこの規格の用語の定義を参照することを考慮して，用語によってはあまり専門的でない表現で記

述した注記及び例による説明を加えてある。これらの略式の説明は正式な定義の代用にはならないが，実

用的で専門家でない人向けの概念的な規定であり，用語規格の多様なユーザのニーズに応えるであろう。

JIS Z 8101-2又はJIS Z 8402の規格群のような規格に普段から接しているような実際的なユーザにとって

は，注記及び例によってこの規格がより理解しやすくなる。 

確率及び統計に関して明確で合理性のある完全な用語集は，統計的方法の規格を開発し，活用する上で，

不可欠である。この規格に示された用語の定義は，統計的な規格の開発者にとって曖昧さをなくすために，

十分に正確で数学的にも洗練されていなければならない。それぞれの応用の領域，前後の関係，及び概念

のより詳細な説明は，当然ではあるが確率及び統計の入門的な教科書にも記述されている。 

コンセプトダイアグラムを附属書（参考）に次のそれぞれの用語のグループについて示した。 

1) 一般統計用語（附属書B） 

2) 確率で用いられる用語（附属書C）。 

一般統計用語については，6種類のダイアグラムで，確率で用いられる用語については4種類のダイアグ

ラムである。コンセプトの間のつながりを示すために複数のダイアグラムに重複して現れる用語もある。

附属書Dにコンセプトダイアグラム及びその解釈について簡単な説明を記述した。 

これらのダイアグラムによって様々な用語の間の関係を図示することが，この規格の今回の改正におい

て役立った。これらのダイアグラムは，この規格を他の言語に翻訳するときにも有用であろう。 

この規格の全体に関する注意として，特に断らない限り，用語の定義は1次元（1変量）の場合につい

ての規定である。ここでこのように規定しておくことで，多くの用語の定義で “1次元の場合である”と

記述することを繰り返す必要性を回避した。 

2 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

適用範囲 

この規格は，他のJISの作成で用いられる一般統計用語及び確率で用いられる用語について規定する。 

さらに，一部の用語について記号も規定する。 

用語は，次のように区分する。 

a) 一般統計用語（箇条1） 

b) 確率で用いられる用語（箇条2） 

附属書Aに，この規格で用いることが推奨されている記号を示す。 

附属書B及び附属書Cに，この規格の見出し語をその関係によって配置したコンセプトダイアグラムを

示す。 

注記 この規格の対応国際規格及びその対応の程度を表す記号を，次に示す。 

ISO 3534-1:2006，Statistics−Vocabulary and symbols−Part 1: General statistical terms and terms used 

in probability（IDT） 

なお，対応の程度を表す記号“IDT”は，ISO/IEC Guide 21-1に基づき，“一致している”こ

とを示す。 

1 

一般統計用語 

1.1 

母集団 ぼしゅうだん（population） 

検討の対象となるアイテムの全体。 

注記1 母集団は，実在して有限な場合，実在して無限の場合，又は完全に仮想的な場合がある。特

に，標本調査では，しばしば“有限母集団”という用語が用いられる。同様に，連続的なも

のからのサンプリングでは“無限母集団”という用語が用いられる。箇条2では，母集団は，

確率に関する文脈で，標本空間（2.1）として扱われる。 

注記2 母集団を仮想的に考えることによって，様々な仮定のもとでまだとられていないデータの性

質を検討することができる。したがって，母集団を仮想的に考えることは，統計調査の計画

の段階，特に，適切なサンプルサイズの決定に有用である。仮想的な母集団は，有限でも無

限でもよい。仮想的な母集団は，推測統計では特に有用な概念であり，統計を用いる研究に

おいて証拠の強さを評価するときに役立つ。 

注記3 母集団の性質を記述することによって，調査研究の状況を説明することができる。例えば，

もし，三つの村が人口学的な研究又は健康に関する研究のために選ばれるなら，母集団はこ

れらの選ばれた村の住人から構成される。一方，もし，ある特定の地域の全ての村の中から

三つの村がランダムに選ばれるのなら，母集団はその地域の住人全体から構成される。 

1.2 

サンプリング単位，抽出単位 さんぷりんぐたんい，ちゅうしゅつたんい（sampling unit） 

母集団（1.1）を実質的に最小単位に分割したものの一つ。 

注記1 状況に応じて，興味のある最小の単位は，個人，世帯，学校区域，行政単位などがある。 

注記2 本来は一度のサンプリング操作で採られる量又はものを意味し，ものを指す場合は単位体と

呼ぶこともある。 

1.3 

サンプル，標本，試料 さんぷる，ひょうほん，しりょう（sample） 

3 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

一つ以上のサンプリング単位（1.2）からなる母集団（1.1）の部分集合。 

注記1 サンプリング単位は，対象とする母集団に応じて定まり，アイテム，数値，又は抽象的なも

のでもよい。 

注記2 JIS Z 8101-2におけるサンプルの定義には，有限母集団からランダムサンプルを採取すると

きに本質的な役割を果たすサンプリングフレームの例が含まれている。 

1.4 

観測値，測定値 かんそくち，そくていち（observed value） 

サンプル（1.3）の一つの構成要素のある側面に関して得られた値。 

注記1 “実現値”及び“データ”はよく用いられる同義語である。英語ではデータの単数形は，デ

ータム（datum）である。 

注記2 この定義は，観測値がどのように発生したか，又は，その値がどのように得られたのかを規

定していない。その値は確率変数（2.10）の一つの実現値を表しているかもしれないが，常

にそうであるとは限らない。当該の観測値は，後で行われる統計解析の対象となる複数の観

測値の一つの場合もある。所定の実現値の集合を観測する確率の決定問題として扱う場合に

限り，統計的メカニズムが関係し，かつ，本質的なものになる。観測値の要約を計算したり，

グラフによる描写をしたりするには，その種の統計的前提は必ずしも必要ではない。観測値

の解析のこの種の予備的段階をデータ分析と呼ぶこともある。 

注記3 注記2で予備的段階として位置付けられているデータ分析は，探索的データ解析に含まれる。

注記2の趣旨は，検証的データ解析の場合にだけ統計的に厳格な取扱いが要求されることで

ある。 

1.5 

記述統計 きじゅつとうけい（descriptive statistics） 

観測値（1.4）をグラフ，数値，又はその他の要約手段を用いて描写すること。 

例1 数値的要約には，平均（1.15），範囲（1.10），標準偏差（1.17）などを求めることが含まれる。 

例2 グラフを用いた要約の例は，箱ひげ図，ダイアグラム，Q-Qプロット，正規確率プロット，散

布図，多変量散布図，ヒストグラムなどである。 

1.6 

ランダムサンプル，無作為標本 らんだむさんぷる，むさくいひょうほん（random sample） 

ランダムな選択方法によって選ばれたサンプル（1.3）。 

注記1 この定義は，無限母集団も許容しており，JIS Z 8101-2の定義よりも制約的ではない。 

注記2 n個のサンプリング単位からなるサンプルが有限な標本空間（2.1）から選ばれるとき，n個

のサンプリング単位の可能な各組合せは，特定の抽出確率（2.5）をもつ。標本調査の計画に

当たっては，可能な全ての組合せに対して，この特定の確率を前もって計算しておく場合が

ある。 

注記3 有限標本空間からの標本調査に対しては，様々なサンプリング計画によって，ランダムサン

プルを得ることができる。例えば，層別ランダムサンプリング，系統ランダムサンプリング，

集落サンプリング，補助変数の大きさに比例した抽出確率を用いるサンプリング，その他多

くの方法がある。 

注記4 この定義は，一般的に，実際の観測値（1.4）を指すこととなる。これらの観測値は確率変数

（2.10）の実現値と考えることができる。すなわち，それぞれの観測値は一つの確率変数に

4 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

対応する。推定量（1.12），統計的検定（1.48）のための検定統計量，又は信頼区間（1.28）

がランダムサンプルから導かれるときは，この定義は，これらの確率変数の実際の観測値で

はなくて，このサンプルを抽象化した確率変数に対応するものとなる。 

注記5 無限母集団からのランダムサンプルは，しばしば，標本空間からの繰返し抽出によって生成

され，注記4で述べた定義の解釈を用いれば，独立，同一分布に従う確率変数からなるサン

プルを導く。 

1.7 

単純ランダムサンプル，単純無作為標本 たんじゅんらんだむさんぷる，たんじゅんむさくいひょうほん

（simple random sample） 

＜有限母集団＞ある与えられた大きさをもつ部分集合が，全て等確率で選ばれるようなランダムサンプ

ル（1.6）。 

注記1 この定義は，表現はわずかに異なるが，JIS Z 8101-2による定義と整合する。 

注記2 ＜ ＞の記号は，一つの用語が複数の概念を表す場合に，それぞれの概念に関係する主題又

は分野を表示して対象を限定し，区別するために用いる。 

1.8 

統計量 とうけいりょう（statistic） 

確率変数（2.10）だけで規定された関数。 

注記1 統計量は，1.6の注記4で述べた意味でランダムサンプル（1.6）に含まれる確率変数の関数

である。 

注記2 注記1に関連して，{X1，X2，…，Xn} が未知の平均（2.35）μ ，及び未知の標準偏差（2.37）

σ をもつ正規分布（2.50）からのランダムサンプルなら，(X1＋X2＋…＋Xn)/nで表される標本

平均（1.15）は統計量である。一方，[(X1＋X2＋…＋Xn)/n]−μは，母数（2.9）を含むので統

計量ではない。 

注記3 ここで与えられた定義は，数理統計学の中に見いだされる取扱いに対応した技術的定義であ

る。英語ではstatistic（統計量）の複数形，すなわちstatisticsは統計学を指すこともあり，そ

の場合はISO/TC 69の国際規格で記載されている解析活動を含む技術的分野を意味する。 

1.9 

順序統計量 じゅんじょとうけいりょう（order statistic） 

確率変数（2.10）を非減少な順序に並べることによって得られる統計量（1.8）。 

例 標本の観測値が9，13，7，6，13，7，19，6，10，7であるとする。順序統計量の観測値は，6，6，

7，7，7，9，10，13，13，19となる。これらの値は，X(1) からX(10) までの実現値と考えることが

できる。 

注記1 ランダムサンプル（1.6）の観測値（1.4）を {x1，x2，…，xn} とし，非減少な順序に並べて

x(1) ≦ … ≦ x(k) ≦ … ≦ x(n) と表す。そのとき，(x(1)，…，x(k)，…，x(n)) は順序統計量 (X(1)，

…，X(k)，…，X(n)) の観測値であり，x(k) はk番目の順序統計量の観測値である。 

注記2 実際的観点では，データセットに対して順序統計量を得ることは，注記1で記述したように

形式的にデータをソートすることと同じである。そのとき，データセットをソートすること

によって，この後の幾つかの定義で与えられるように，それ自体が有用な要約統計量になる。 

なお，この規格では非減少な又は非増加な順序に並べかえることをソートするという。 

注記3 標本の値を非減少な順序に順位付ければ，順序統計量は，その順位に対応する標本の値を意

5 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

味する。上に示した例のように，まだ観測されていない確率変数をソートするよりも，観測

された標本の値（確率変数の実現値）をソートするほうが理解しやすい。しかしながら，非

減少な順序に並び替えられたランダムサンプル（1.6）からの確率変数を考慮することは可能

である。例えば，n個の確率変数の最大値はその実現値を得る前に検討可能である。 

注記4 個々の順序統計量は，確率変数だけで規定された関数なので統計量である。この関数は，確

率変数を並べ替えた集合における位置又は順位を特定する。 

注記5 離散型確率変数及び桁数の少ない実現値の場合には，同じ値をもつデータ（タイデータ）の

取扱いの問題が生じる。“非減少な順序”という言葉は，“上昇順”という言葉よりも，問題

によってはより正確な言い回しとして用いられる。複数個の同じ値のデータは，その個数分

だけ記録に残し，一つの値にまとめてはならないことは重要である。上記の例では，6，6の

二つの実現値が同じ値のデータである。 

注記6 順序付けは，確率変数の絶対値に基づくのではなく，符号付きで行う。 

注記7 順序統計量の全体の集合は，n次元の確率変数になる。ここで，nは標本における観測値の個

数である。 

注記8 n次元の順序統計量の各成分も順序統計量と呼ばれるが，その場合には，標本内の順序を示

す数字を下付の括弧内に表す。 

注記9 最小値，最大値，及びサンプルサイズが奇数の場合の標本メディアン（1.13）は，順序統計

量の例である。例えば，サンプルサイズが11のとき，X(1) は最小値，X(11) は最大値であり，

X(6) は標本メディアンである。 

1.10 

範囲，サンプルレンジ はんい，さんぷるれんじ（sample range） 

最大の順序統計量（1.9）から最小の順序統計量を引いた量。 

例 1.9の例を引き続き考えると，範囲の観測値は19−6＝13である。 

注記1 統計的工程管理では，範囲は，時間的に推移する工程のばらつきを監視するためにしばしば

用いられる。特に，サンプルサイズが比較的小さい場合に用いられる。 

注記2 統計量であることを強調するときには，標本範囲と呼ぶこともある。 

注記3 混乱が生じなければ，サンプルを省略してレンジと呼んでもよい。 

1.11 

ミッドレンジ，中点値 みっどれんじ，ちゅうてんち（mid-range） 

最小及び最大の順序統計量（1.9）の平均（1.15）。 

例 1.9に示した例の数値を用いると，ミッドレンジの観測値は， (6＋19)/2＝12.5である。 

注記 ミッドレンジを用いると，小さなデータセットの中心位置を迅速に簡便に評価できる。 

1.12 

推定量 すいていりょう（estimator） 
θˆ 

母集団のパラメータθの推定（1.36）に用いられる統計量（1.8）。 

注記1 母集団の平均（2.35）（μと表す。）を推定する標本平均（1.15）は母平均の推定量である。正

規分布（2.50）などのような分布（2.11）に対して母集団の平均μに対する“自然な”推定量

は標本平均である。 

注記2 母集団の性質［例えば，1変量分布（2.16）のモード（2.27）など］を推定する際，適切な推

6 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

定量は，分布の母数の推定量の関数であったり，ランダムサンプル（1.6）の複雑な関数であ

ったりする。 

注記3 “推定量”という言葉は，ここでは広い意味で用いられている。それは，母数の点推定量と

いう意味も，区間推定の意味も含んでおり，更に予測（しばしば予測量と呼ばれることもあ

る。）の意味も含んでいる。推定量は，カーネル推定量及び他の特別な目的をもつ統計量も含

んでいる。より詳細な議論を1.36の注記に示す。 

1.13 

（標本）メディアン，中央値，中位数 （ひょうほん）めでぃあん，ちゅうおうち，ちゅういすう（sample 

median） 

サンプルサイズ（JIS Z 8101-2，1.2.26を参照）nが奇数なら，[(n＋1)/2] 番目の順序統計量（1.9）。サン

プルサイズnが偶数なら，(n/2) 番目と [(n/2)＋1] 番目との順序統計量の和を2で割った量。 

例 1.9の例で考えると，8が標本メディアンの実現値である。この場合（サンプルサイズは，偶数の

10）には，5番目及び6番目の値がそれぞれ7及び9なので，それらの平均は8になる。厳密に

は標本メディアンは確率変数として定義されているが，実務上は“標本メディアンは8である”

という形式で報告される。 

注記1 サンプルサイズnのランダムサンプル（1.6）に対して，1からnまで非減少な順序で並べら

れた確率変数（2.10）において，サンプルサイズnが奇数なら標本メディアンは， (n＋1)/2

番目の確率変数である。また，サンプルサイズnが偶数なら，標本メディアンは， (n/2) 番

目の確率変数と (n/2＋1) 番目の確率変数との算術平均である。対応国際規格では，この注記

において“(n/2＋1) 番目”を“(n＋1)/2番目”と誤記している。 

注記2 概念的には，まだ観測されていない確率変数を順番に並べることは不可能と見えるかもしれ

ない。しかし，観測された後に並び替えることまでを織り込んだものが順序統計量であると

理解すればよい。実際，観測値を得たら，値を並び替えて，順序統計量の実現値を得る。こ

れらの実現値がランダムサンプルから構成した順序統計量と解釈できる。 

注記3 標本メディアンは，サンプルの半分ずつがそれぞれ上側と下側とにあるという意味で，分布

の中心位置の推定量となる。 

注記4 実務上，標本メディアンは，データセットの中の非常に極端な値に影響されにくい推定量を

与えるという意味で有用である。例えば，収入金額のメディアン及び住宅価格のメディアン

は，要約値としてしばしば報告される。 

注記5 混乱が生じなければ，“標本”を省略してもよい。 

1.14 

k次の標本モーメント，k次の標本積率 kじのひょうほんもーめんと，kじのひょうほんせきりつ（sample 

moment of order k） 

E(X k) 

ランダムサンプル（1.6）における確率変数（2.10）のk乗の和を標本（1.3）における観測値の個数で割

った量。 

注記1 サンプルサイズがnのランダムサンプル，すなわち，{X1，X2，…，Xn} に対して，k次の標

本モーメントE(X k) は， 

7 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

∑

=

n

i

k

i

X

n

1

1

である。 

ここでは，E(X k) と    とを同一視するような記述になっているが，通常の記号法では，

前者は期待値をとった後なので定数であり，かつ，後者は確率変数なので，両者の同一視は

できない。したがって，この記号法E(X k) を使用することは避けたほうがよい。 

注記2 さらに，この概念を“原点のまわりの”k次の標本モーメントと呼ぶことがある。 

注記3 1次の標本モーメントは，次に定義される標本平均（1.15）である。 

注記4 定義は任意のkに対して与えられているが，実際上よく用いられるのは，k＝1の場合［標本

平均（1.15）］，k＝2の場合［標本分散（1.16）及び標本標準偏差（1.17）に関連］，k＝3の場

合［標本ゆがみ（1.20）に関連］，及びk＝4の場合［標本とがり（1.21）に関連］である。 

注記5 E(X k)の“E”は，確率変数Xの“期待値”に由来している。 

注記6 “（原点まわりの）標本k次モーメント”とも呼んでもよい。 

注記7 混乱が生じなければ，“標本”を省略してもよい。 

1.15 

（標本）平均，算術平均 （ひょうほん）へいきん，さんじゅつへいきん（sample mean，average，arithmetic 

mean） 

ランダムサンプル（1.6）における確率変数（2.10）の和を，和をとった個数で割った量。 

例 1.9の例を考えると，標本平均の実現値は9.7である。これは，観測値の合計97をそのサンプル

サイズ10で割って求めた値である。 

注記1 統計量として考えると，標本平均は，1.8の注記3で述べた意味でランダムサンプルにおける

確率変数の関数である。この意味での推定量と，ランダムサンプルの観測値（1.4）から計算

された標本平均の数値とを区別しなければならない。 

注記2 統計量として考えた標本平均は，母集団の平均（2.35）の推定量としてしばしば用いられる。

よく使われる同義語は算術平均である。 

注記3 サンプルサイズnのランダムサンプル，すなわち，{X1，X2，…，Xn} に対して，標本平均は， 

∑

=

=

n

i

i

X

n

X

1

1

である。 

注記4 標本平均は，1次の標本モーメントと考えることができる。 

注記5 サンプルサイズが2のときには，標本平均，標本メディアン（1.13），及びミッドレンジ（1.11）

は一致する。 

注記6 混乱が生じなければ，“標本”を省略してもよい。 

1.16 

（標本）分散，不偏分散 （ひょうほん）ぶんさん，ふへんぶんさん（sample variance） 

S2 

ランダムサンプル（1.6）における確率変数（2.10）からそれらの標本平均（1.15）を引いた偏差の2乗

和を，サンプルサイズ−1で割った量。 

∑

=

n

i

k

i

X

n

1

1

8 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例 1.9の数値例を引き続き考えて計算すると，標本分散は17.57となる。観測された標本平均からの

偏差の2乗和は158.10で，サンプルサイズは10なので，10−1＝9となる。158.10を9で割れば

よい。 

注記1 統計量（1.8）として考えると，標本分散S2は，ランダムサンプルにおける確率変数の関数で

ある。統計量の意味でのこの推定量（1.12）と，ランダムサンプルの観測値（1.4）から計算

された標本分散の数値とを区別しなければならない。この数値結果は，経験標本分散，又は

観測された標本分散と呼ばれ，普通s 2と表される。 

注記2 サンプルサイズnのランダムサンプル，すなわち，{X1，X2，…，Xn} に対して，標本平均を

Xと表すとき，標本分散は，次の式による。 

∑

=

−

−

=

n

i

i

X

X

n

S

1

2

2

)

(

1

1

注記3 標本分散は，標本平均からの確率変数（2.10）の偏差の2乗の“ほとんど”平均である（分

母においてnではなくn−1を用いることだけが異なる。）。n−1を用いることによって，標

本分散は母集団の分散（2.36）の不偏推定量（1.34）となる。これが不偏分散の由来である。 

注記4 n−1は，自由度（2.54）として知られている量である。 

注記5 標本分散は，中心化標本確率変数の2次の標本モーメントとみなすことができる。対応国際

規格では“中心化標本確率変数”を“標準化標本確率変数（1.19）”と誤記している。この規

格では与えられていないが，“中心化標本確率変数”は“確率変数からその標本平均を引いた

量”と定義される。 

注記6 混乱が生じなければ，“標本”を省略してもよい。 

1.17 

（標本）標準偏差 （ひょうほん）ひょうじゅんへんさ（sample standard deviation） 

S 

標本分散（1.16）の非負の平方根。 

例 1.9の数値例を用いると，標本分散の観測値が17.57なので，標本標準偏差の観測値は4.192とな

る。ここで，データに基づいて途中の桁をより多く保持して計算すると4.191になる。 

注記1 実務的には，標本標準偏差は，標準偏差（2.37）を推定するために用いられる。Sは確率変数

（2.10）であり，ランダムサンプル（1.6）からの実現値ではないことを再度強調しておく。 

注記2 標本標準偏差は，分布（2.11）のばらつきの指標である。 

注記3 混乱が生じなければ，“標本”を省略してもよい。 

1.18 

（標本）変動係数 （ひょうほん）へんどうけいすう（sample coefficient of variation） 

標本標準偏差（1.17）を標本平均（1.15）で割った量。 

注記1 変動係数（2.38）と同様，この統計量は，正の値しかとらない母集団のときに用いられる。

変動係数は，通常，パーセントで表示される。ばらつきが平均に比例して増加する場合に，

変動係数は有用である。 

注記2 標本変動係数を“相対標準偏差”と呼ぶことは薦められない。 

注記3 混乱が生じなければ，“標本”を省略してもよい。 

9 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

1.19 

標準化（された）標本確率変数，規準化（された）標本確率変数 ひょうじゅんか（された）ひょうほん

かくりつへんすう，きじゅんか（された）ひょうほんかくりつへんすう（standardized sample random variable） 

確率変数（2.10）からその標本平均（1.15）を引いて，標本標準偏差（1.17）で割った量。 

例 1.9の例では，標本平均の観測値は9.7であり，標本標準偏差の観測値は4.191（対応国際規格は

4.192と誤記）であった。したがって，標準化標本確率変数の観測値は，次のとおりである（小数

点2桁まで示す。）。 

−0.17，  0.79， −0.64， −0.88，  0.79， −0.64，  2.22， −0.88， 

 0.07， −0.64 

注記1 標準化標本確率変数は，理論的に対応する標準化確率変数（2.33）と区別しなければならな

い。標準化の意図は，解釈及び比較を容易にするために，確率変数を，平均が0，標準偏差

が1となるように変換することである。 

注記2 標準化された観測値は，その平均の観測値が0，標準偏差の観測値が1になる。 

注記3 混乱が生じなければ，“標本”を省略してもよい。 

1.20 

（標本）ゆがみ，（標本）ひずみ （ひょうほん）ゆがみ，（ひょうほん）ひずみ（sample coefficient of skewness） 

ランダムサンプル（1.6）からの標準化標本確率変数（1.19）の3乗の算術平均。 

例 1.9の数値例を用いると，標本ゆがみの観測値は0.971 88となる。この例のようにサンプルサイズ

が10程度では標本ゆがみは非常にばらつきが大きくなるので，用いる場合には注意が必要である。

注記1に示した別の公式（2番目の公式）を用いた場合には，計算結果は1.349 83となる。 

注記1 定義に対応する公式は，次のとおりである。 

3

1

1∑

=

−

n

i

i

S

X

X

n

幾つかの統計解析パッケージではかたより（1.33）を修正するために，次の標本ゆがみの公

式を用いている。 

∑

=

−

−

n

i

i

Z

n

n

n

1

3

)2

)(

1

(

ここに， 

S

X

X

Z

i

i

−

=

である。サンプルサイズが大きい場合には，二つの推定値の違いは無視できるレベルである。

かたよりのある推定値に対するかたよりのない推定値との比は，それぞれn＝10に対して

1.389，n＝100に対して1.031， n＝1 000に対して1.003である。 

注記2 ゆがみは分布の非対称性を表す。この統計量の値が0に近ければ，母集団分布は近似的に対

称である。一方，0でなければ，分布の中心の片側に極端な値をもつ分布が対応する可能性

がある。データのゆがみは標本平均（1.15）と標本メディアン（1.13）との値の食い違いにも

反映される。プラスにゆがんだデータは右に裾を引いており，幾つかの極端に大きな観測値

の存在の可能性を示唆する。同様に，マイナスにゆがんだデータは左に裾を引いており，幾

10 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

つかの極端に小さな観測値の存在の可能性を示唆する。 

注記3 標本ゆがみは，標準化標本確率変数（1.19）の3次の標本モーメントと考えることができる。 

注記4 ゆがみ（歪み）ひずみ（歪み）をわいど（歪度）ともいう。 

注記5 混乱が生じなければ，“標本”を省略してもよい。 

1.21 

（標本）とがり （ひょうほん）とがり（sample coefficient of kurtosis） 

ランダムサンプル（1.6）からの標準化標本確率変数（1.19）の4乗の算術平均。 

例 1.9の数値例を用いると，標本とがりの観測値は2.674 19となる。この例のようにサンプルサイズ

が10程度では標本とがりは非常にばらつきが大きくなるので，用いる場合には注意が必要である。

統計解析パッケージでは標本とがりの計算において様々な調整を用いている（2.40の注記3を参

照）。注記1に示した別の公式を用いた場合には，計算結果は1.497 23（対応国際規格では0.436 05

と誤記）となる。これらの二つの値，2.674 19及び1.497 23（対応国際規格では0.436 05と誤記）

は，直接的には比較できない。比較するために，2.674 19−3（正規分布のとがりの値3と比較の

ため）を求めると−0.325 81となる。この値は，1.497 23とはかなり異なっている。（対応国際規

格では1.497 23を0.436 05と誤記したため，“この値は0.436 05と近似的に比較できる程度とな

る。”と誤記している。） 

注記1 定義に対応する公式は，次のとおりである。 

4

1

1∑

=

−

n

i

i

S

X

X

n

幾つかの統計解析パッケージでは，かたより（1.33）を修正するため，及び正規分布のとが

り（その値は3）からの違いを示すために，次の公式を用いている。 

∑

=

−

−

−

−

−

−

−

+

n

i

i

n

n

n

Z

n

n

n

n

n

1

2

4

)3

)(

2

(

)1

(3

)3

)(

2

)(

1

(

)1

(

ここに， 

S

X

X

Z

i

i

−

=

である。上記の公式の第2項は，nが大きければ近似的に3になる。しばしば，とがりは，

正規分布との比較を強調するために2.40で定義された値から3を引き去って報告される。実

務家は，統計解析パッケージを用いるのであれば，この調整がなされているかどうかに注意

することが必要である。 

注記2 とがりは，（単峰の）分布の裾の重さに関連する。正規分布（2.50）の場合には，標本とがり

の実現値は，データのばらつきに依存するが，近似的に3になる。実務的に，正規分布のと

がりは，ベンチマーク又は規準の値となる。3より小さなとがりをもつ分布（2.11）は正規分

布よりも裾が軽く，3より大きなとがりをもつ分布は正規分布より裾が重い。 

注記3 とがりの観測値が3よりもはるかに大きいときには，母集団分布が正規分布よりも本質的に

重い裾をもつ可能性がある。別な母集団の観測値，又は値を誤記した観測値がサンプルに混

入した可能性もある。この議論は，対称な分布を前提にしたものである。 

注記4 標本とがりは，標準化標本確率変数の4次の標本モーメントと考えることができる。 

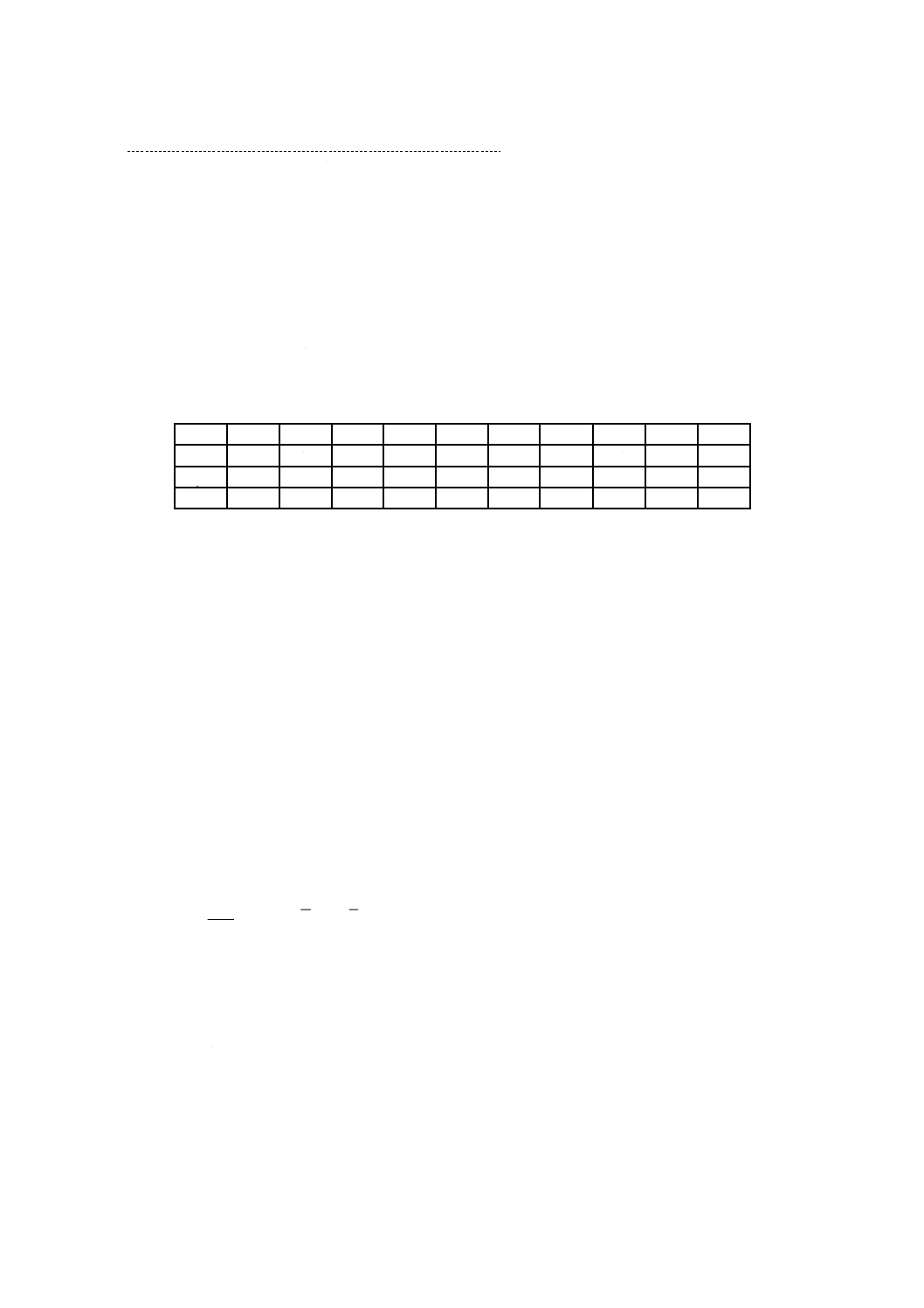
11 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記5 とがり（尖り）をせんど（尖度）ともいう。 

注記6 混乱が生じなければ，“標本”を省略してもよい。 

1.22 

（標本）共分散，不偏共分散 （ひょうほん）きょうぶんさん，ふへんきょうぶんさん（sample covariance） 

SXY 

対になっているランダムサンプル（1.6）において，それぞれの確率変数（2.10）からそれぞれの標本平

均（1.15）を引いた偏差の積の和を，サンプルサイズ−1で割った量（サンプルサイズは，対の数）。 

例1 次に示す三つの確率変数X，Y，Zの10組の観測値（x，y，z）を用いた数値例を考える。この

例では，x及びyだけを用いる。 

表1−例1のための測定結果 

i 

1 

2 

3 

4 

5 

6 

7 

8 

9 

10 

x 

38 

41 

24 

60 

41 

51 

58 

50 

65 

33 

y 

73 

74 

43 

107 

65 

73 

99 

72 

100 

48 

z 

34 

31 

40 

28 

35 

28 

32 

27 

27 

31 

Xに対する標本平均の観測値は46.1，Yに対する標本平均の観測値は75.4である。標本共分

散は，次のようになる。 

[(38−46.1)×(73−75.4)＋(41−46.1)×(74−75.4)＋…＋(33−46.1)×(48−75.4)]/9＝257.178 

例2 表1について，y及びzだけを考える。Zに対する標本平均の観測値は，31.3である。標本共分

散は，次のようになる。 

[(73−75.4)×(34−31.3)＋(74−75.4)×(31−31.3)＋…＋(48−75.4)×(31−31.3)]/9＝−54.356 

［対応国際規格では，上式の第2項を，(74−75.4)×(74−31.3) と誤記している。］ 

注記1 統計量（1.8）として考えると，標本共分散は，1.6の注記3で与えた意味で，大きさnのラ

ンダムサンプルからの確率変数の対 [(X1，Y1)，(X2，Y2)，…，(Xn，Yn)] の関数である。統計

量の意味での推定量（1.12）は，ランダムサンプルにおけるサンプリング単位（1.2） [(x1，

y1)，(x2，y2)，…，(xn，yn)] の対の観測値から計算された標本共分散の数値と区別する必要が

ある。この数値は，経験標本共分散，又は観測された標本共分散と呼ばれる。 

注記2 標本共分散SXYは，次の式で与えられる。 

∑

=

−

−

−

n

i

i

i

Y

Y

X

X

n

1

)

)(

(

1

1

注記3 n−1を用いるのは，母集団の共分散（2.43）の不偏推定量（1.34）となるようにするためで

ある。 

注記4 表1の例は三つの変数からなるが，定義では二つの変数の対を用いる。実際には，多変数が

存在する状況にしばしば直面する。 

注記5 混乱が生じなければ，“標本”を省略してもよい。 

1.23 

（標本）相関係数 （ひょうほん）そうかんけいすう（sample correlation coefficient） 

rxy 

12 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

標本共分散（1.22）を対応する標本標準偏差（1.17）の積で割った量。 

例1 1.22の例1の続きを考える。Xに対する標本標準偏差の観測値は12.948，Yに対する標本標準

偏差の観測値は21.329である。したがって，（XとYとの）標本相関係数の観測値は，次のよ

うになる。 

257.178/(12.948×21.329)＝0.931 2 

例2 1.22の例2の続きを考える。Yに対する標本標準偏差の観測値は21.329，Zに対する標本標準

偏差の観測値は4.165である。したがって，（YとZとの）標本相関係数の観測値は，次のよう

になる。 

−54.356/(21.329×4.165)＝−0.612 

注記1 標本相関係数の計算は，次の数式で表される。 

∑

∑

∑

=

=

=

−

−

−

−

n

i

i

n

i

i

n

i

i

i

Y

Y

X

X

Y

Y

X

X

1

2

1

2

1

)

(

)

(

)

)(

(

この表現は，標本共分散と標本分散の積の平方根との比と同値である。しばしば，標本相関

係数を表すためにrxyの記号が用いられる。標本相関係数の観測値は，実現値 (x1，y1)，(x2，

y2)，…，(xn，yn) に基づいて計算される。 

注記2 標本相関係数の観測値は [−1，1] に値をとる。1に近い場合は，強い正の相関を意味する。

−1に近い場合，強い負の相関を意味する。標本相関係数は二つの変数の間の直線関係の程

度を示し，値が1又は−1に近いときには直線関係が強いことを，値が0に近いときは直線

関係が弱いことを示す。 

注記3 混乱が生じなければ，“標本”を省略してもよい。 

1.24 

標準誤差 ひょうじゅんごさ（standard error） 

θ

σˆ 

推定量（1.12）θˆの標準偏差（2.37）。 

例 標本平均（1.15）は母集団の平均（2.35）の推定量であり，一つの確率変数（2.10）の標準偏差が

σなら，標本平均の標準誤差は

n

σ

である。ここで，nはサンプルサイズである。標準誤差の

推定量は

n

S

であり，Sは標本標準偏差（1.17）である。 

注記1 実務上，標準誤差は，推定量の標準偏差の自然な推定値を与える。 

注記2 “非標準”誤差という反対語はない。標準誤差は，“推定量の標準偏差”という表現の省略形

と見ることができる。実務的には，普通，標準誤差は，標本平均の標準偏差を暗黙に意味し

ている。標本平均の標準誤差には，記号として

X

σを用いる。 

1.25 

区間推定 くかんすいてい（interval estimator） 

上側限界を与える統計量（1.8）と下側限界を与える統計量とで囲まれた区間。 

注記1 端点の一つが＋∞，−∞又は母数の自然な限界値の場合もある。例えば，0は母集団の分散

（2.36）の区間推定に対する自然な下側の限界値である。そのような場合には，通常，片側

区間として表示される。 

13 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記2 区間推定は，母数（2.9）の推定（1.36）と結び付けて行われる。区間推定では，サンプリン

グを繰り返すという条件の下で，又はほかの確率的な意味において，名目の比率で母数を含

むと考えられる。 

注記3 よく用いられている三つのタイプの区間推定は，母数に対する信頼区間（1.28），将来の観測

値に対する予測区間（1.30），及び分布（2.11）の一定比率以上を含む統計的許容区間（1.26）

である。 

1.26 

統計的許容区間 とうけいてききょようくかん（statistical tolerance interval） 

ランダムサンプル（1.6）から決定され，所定の信頼率で，その母集団（1.1）の定められた割合を少な

くとも含むような区間。 

注記 ここでいう信頼率は，このような区間を多数回構成したとき，その母集団の一定以上の割合が

含まれる比率である。 

1.27 

統計的許容限界 とうけいてききょようげんかい（statistical tolerance limit） 

統計的許容区間（1.26）の端点を表す統計量（1.8）。 

注記1 統計的許容限界には，次の二つの場合がある。 

− 片側統計的許容区間（片方の端点が無限大か，又は確率変数の取り得る自然な境界値に

なっている。）の場合には，上側又は下側統計的許容限界のいずれかをもつ。 

− 両側統計的許容区間の場合には，上側及び下側の両方の統計的許容限界をもつ。 

確率変数の取り得る自然な境界値が片側限界の限界となることもある。 

注記2 JIS Z 8101-2の“3.1.6 specified tolerance（許容差）”と混同してはならない。 

1.28 

（両側）信頼区間 （りょうがわ）しんらいくかん（confidence interval） 

母数（2.9）θの区間推定（1.25）で，統計量（1.8）T0，T1がP[T0 < θ < T1] ≧ 1−α を満たす区間 (T0，

T1)。 

注記1 区間の信頼率は，同一条件による多数回の繰り返しで得られたランダムサンプル（1.6）から

の信頼区間が，母数の真値を含む場合の比率である。信頼区間は，観測された信頼区間が母

数の真値を含む確率（2.5）を意味するものではない（真値は，観測された信頼区間に含まれ

るか，含まれないかのいずれかである。）。 

注記2 母数θの任意の値に対して，不等式P[T0 < θ < T1] ≧ 1−α が成立するとき，この100(1−

α) %を信頼率又は信頼係数と呼ぶ。これは信頼区間の性能を表している。ここで，αは一般

に小さな数とし，信頼率は95 %又は99 %とすることがよくある。適用する分野によっては，

信頼率として90 %なども用いられる。 

1.29 

片側信頼区間 かたがわしんらいくかん（one-sided confidence interval） 

片方の端点が，＋∞，−∞，又は自然な境界値となっている信頼区間（1.28）。 

注記1 1.28の定義で，T0を−∞とするか，又はT1を＋∞にした場合である。片側信頼区間は，興味

の中心が厳密に片方に限定されている状況で用いられる。例えば，携帯電話の安全性に関す

る音量の試験では，所定の安全条件の下で発生する音量の上限を示すので，上側信頼限界が

関心事となる場合が多い。一方，構造力学的な試験では，機械が故障する力の下側信頼限界

14 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

が関心事となる場合が多い。 

注記2 片側信頼区間のもう一つの場合は，母数が0のような自然な境界をもつ場合に生じる。ポア

ソン分布（2.47）を用いて，顧客からの苦情回数をモデル化する場合には，0が下側の境界値

となる。他の例としては，電子部品の信頼度の信頼区間は，(0.98，1) となる場合が多い。こ

こで，1は自然な上側の境界値である。 

1.30 

予測区間 よそくくかん（prediction interval） 

連続値の母集団（1.1）から追加的にランダムサンプル（1.6）を抽出したときに，少なくとも与えられ

た個数より多くの個数が，所定の信頼率で含まれることが主張可能な変量値の範囲。 

注記 予測区間を算出した観測値と同様な状況で，通常，新たに得られる1個の値を観測する場合に

関心がある。このほかにも，実際的な状況としては回帰分析の場合がある。ここでは，独立変

数の与えられた領域に対して予測区間を構成する。 

1.31 

推定値 すいていち（estimate） 

推定量（1.12）の観測値（1.4）。 

注記 推定値は，観測値から得られた数値を指す。仮想した確率分布（2.11）の母数（2.9）の推定（1.36）

の場合は，推定量は母数の推定のための統計量（1.8）を指し，推定値は観測値を用いて得られ

た結果を指す。単一の値を計算したことを強調する場合には点推定値と呼び，区間推定の場合

には区間推定値と呼ぶ。 

1.32 

推定誤差 すいていごさ（error of estimation） 

推定値（1.31）から母数（2.9）又は推定しようとした母集団の特性を引いたもの。 

注記1 母集団の特性は，単一若しくは複数の母数の関数，又は確率分布（2.11）に関連する別の量

の場合もある。 

注記2 推定量の誤差の原因となるのは，サンプリング，測定の不確かさ，丸めなどが考えられる。

推定量の誤差は，実質的には，関心事がどの程度分かっているかの性能を実務家に示すもの

である。推定量の誤差の主要な原因を明らかにすることは，品質改善活動の重要な要素であ

る。 

1.33 

かたより（bias） 

推定誤差（1.32）の期待値（2.12）。 

注記1 この定義は，JIS Z 8101-2（3.3.2）並びにTS Z 0032：2012（4.20）と異なっている。ここで

は1.34の注記で示すような一般的な意味で用いられている。対応国際規格では，“VIM:1993

（5.25及び5.28）”と表記しているが，VIM: 1993（5.25）［及びVIM: 1984（5.28）］と表記す

るのが正しい。VIMは改訂されてISO/IEC Guide 99：2007（TS Z 0032：2012が一致してい

る。）となり，当該箇条は4.20となった。 

注記2 かたよりの存在は，実務的にも不幸な結果を招く可能性がある。例えば，かたよりのために

素材強度の過小な推定がおきれば，機器の予期せぬ故障が生じる可能性がある。標本調査で

は，かたよりは，政策の選択において誤った決定を導く場合があろう。 

注記3 “かたより”を“偏り”と表記してもよい。 

15 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

1.34 

不偏推定量 ふへんすいていりょう（unbiased estimator） 

かたより（1.33）が0となる推定量（1.12）。 

例1 平均（2.35）μ，標準偏差（2.37）σの正規分布（2.50）に従うn個の独立な確率変数（2.10）の

ランダムサンプル（1.6）の場合，標本平均（1.15）X及び標本分散（1.16）S 2は，それぞれ平

均μ及び分散（2.36）σ 2の不偏推定量となる。 

例2 1.37の注記1で述べているように分散σ 2のさいゆう（最尤）推定量（1.35）は，分母をn−1

ではなく，nとしているので，かたよりのある推定量である。分母にn−1を用いる標本分散の

平方根は，標本標準偏差（1.17）として，応用上よく用いられているが，これは母標準偏差（2.37）

のかたよりのある推定量となることに注意が必要である。 

例3 対をなすn個の独立な確率変数が，（母）共分散（2.43）ρ σX σY（対応国際規格は，ρ σXYと誤記）

の同一な2変量正規分布（2.65）からのランダムサンプルである場合には，その標本共分散（1.22）

は，母共分散の不偏推定量となる。そのさいゆう（最尤）推定量は，分母をn−1ではなく，n

としているので，かたよりがある。 

注記 推定量にかたよりがないことは，平均的には推定量が正しい値を与えているという意味で望ま

しいことである。不偏推定量が，母集団の母数の“最適な”推定量を探索する際の，有用な初

期値を与えることは確かである。ここで示した定義は，統計理論的な性質に関するものである。 

日常的には，実務家は，日々の応用において研究にかたよりが生じないように努めている。

例えば，ランダムサンプルが，確実に関心のある母集団を代表するものとするといったことで

ある。 

1.35 

さいゆう（最尤）推定量 さいゆうすいていりょう（maximum likelihood estimator） 

ゆうど（尤度）関数（1.38）が，最大，又は上限とみなし得る母数（2.9）の値を推定量（1.12）とした

もの。 

注記1 さいゆう（最尤）推定は，分布（2.11）が［例えば，正規分布（2.50），ガンマ分布（2.56），

ワイブル分布（2.63）などと］特定されている場合に，その母数の推定値を得る方法として

定評がある。さいゆう（最尤）推定量は，（例えば，単調変換で不変となるといった）統計的

に望ましい性質を持っており，多くの状況で選択すべき推定方法を与える。さいゆう（最尤）

推定量にかたより（1.33）があるときには，単純な補正を行うことがある。1.34の例2で述

べたように，正規分布の分散（2.36）のさいゆう（最尤）推定量にはかたよりがあるが，そ

のかたよりは，分母をnではなく，n−1にすることで補正できる。そのような場合に生じる

かたよりの大きさは，標本の大きさを大きくすれば，減少する。 

注記2 略語MLEが，状況に応じて，さいゆう（最尤）推定量及びさいゆう（最尤）推定のいずれ

にも用いられる。 

1.36 

推定 すいてい（estimation） 

母集団（1.1）から抽出したランダムサンプル（1.6）に基づいて，その母集団を統計的に描写する手続

き。 

注記1 推定には，ある推定量（1.12）から具体的な推定値（1.31）を得る手続きがある。 

注記2 推定は，点推定，区間推定，又は母集団の性質の推定を含むかなり広い状況で用いられると

16 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

理解されている。 

注記3 多くの場合，統計的な描写とは，想定したモデルの単一又は複数のパラメータ（2.9）の推定

又は母数の関数の推定を指す。より一般的な，母集団の描写は，それに特化したものとは限

らず，例えば，自然災害の被害に関連する統計を指す（死傷者数，被害損失，及び農作物の

被害の全ては，防災対策上で推定したいものであろう。）。 

注記4 想定したモデルがデータの描写としては不適切であることが，記述統計（1.5）を考察するこ

とで示唆される場合もある。例えば，当該モデルのデータへの適合度指標が，それを示唆す

ることもあろう。そのような場合には，他のモデルを考えて，推定プロセスを続ける。 

1.37 

さいゆう（最尤）推定 さいゆうすいてい（maximum likelihood estimation） 

さいゆう（最尤）推定量（1.35）に基づく，推定（1.36）。 

注記1 正規分布（2.50）の場合，標本平均（1.15）は母数（2.9）μ のさいゆう（最尤）推定量（1.35）

であるが，標本分散（1.16）の分母をn−1ではなくて，nにしたものが母数σ 2のさいゆう（最

尤）推定量である。通常は，σ 2の不偏推定量（1.34）になるので，分母にn−1を用いること

が多い。 

注記2 さいゆう（最尤）推定は，ゆうど（尤度）関数からの推定量（1.12）の導出そのものを指す

ことがある。 

注記3 さいゆう（最尤）推定を行う場合には，推定量の明示的な数式表現ができる場合もあるが，

そうでない場合には，さいゆう（最尤）推定値を求めるのに連立方程式の解を得る反復計算

が必要となる状況もある。 

注記4 略語MLEが，状況に応じて，さいゆう（最尤）推定量及びさいゆう（最尤）推定のいずれ

にも用いられる。 

1.38 

ゆうど（尤度）関数 ゆうどかんすう（likelihood function） 

確率密度関数（2.26）又は確率質量関数（2.24）を観測値（1.4）で評価し，分布族（2.8）の母数（2.9）

の関数とみなしたもの。 

例1 非常に大きな母集団（1.1）から10個のアイテムがランダムに選択された状況を考えてみよう。

この中で3個のアイテムが特定の性質をもっていたことが分かった。この標本から当該特性を

もっている母比率は，0.3（3/10）という直感的な推定値（1.31）が得られる。2項分布（2.46）

に基づくモデルを用いると，ゆうど（尤度）関数（nを10，xを3に固定し，確率質量関数をp

の関数とみなしたもの）は，p＝0.3で最大となり，直感と一致する。 

［さらに，このことは，この2項分布（2.46）の確率質量関数120 p3 (1−p)7をpを横軸にし

てプロットすると検証できる。］ 

例2 標準偏差（2.37）既知の正規分布（2.50）では，ゆうど（尤度）関数が最大となるμ が標本平均

と一致することを一般的に示すことができる。 

注記1 対応国際規格で“確率質量関数”が抜けているのは誤りである。 

注記2 例2では標準偏差が既知としているが，標準偏差が未知の正規分布でも，ゆうど（尤度）関

数が最大となるμ が標本平均と一致する。 

1.39 

プロファイルゆうど（尤度）関数 ぷろふぁいるゆうどかんすう（profile likelihood function） 

17 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

ゆうど（尤度）関数（1.38）を単一の母数（2.9）の関数として表現するために，当該母数以外の全ての

母数をゆうど（尤度）関数が最大となるように定めたときのゆうど（尤度）関数。 

注記 母数をθ1，θ2，…，θpとし，ゆうど（尤度）関数をl (θ1，θ2，…，θp) とした場合，単一の母数

をθ1としたときのプロファイルゆうど（尤度）関数l1(θ1) は，次のように表される。 

)

,

,

,

(

max

)

(

2

1

,

,

1

1

2

p

l

l

p

θ

θ

θ

θ

θ

θ

Λ

Λ

=

1.40 

仮説 かせつ（hypothesis） 

H 

母集団（1.1）についての主張。 

注記 母集団に関する主張には，通常，ある分布族（2.8）の単一又は複数の母数（2.9）に関するもの，

又は分布族自体に関するものがある。 

1.41 

帰無仮説 きむかせつ（null hypothesis） 

H0 

統計的検定（1.48）によって検定される仮説（1.40） 

例1 平均（2.35）及び標準偏差（2.37）ともに未知の同一正規分布（2.50）に従う独立な確率変数（2.10）

からのランダムサンプル（1.6）で，平均μ に関する帰無仮説を，平均がμ 0以下となるという

ものとする場合があり，このことは，通常，H0 : μ ≦ μ 0と書く。（対応国際規格で用いられて

いる不等号付きの帰無仮説H0 : μ ≦μ 0については，様々な議論がある。） 

例2 母集団（1.1）に関する統計モデルが，正規分布であるという帰無仮説もあり得る。このタイプ

の帰無仮説では，平均と標準偏差は特定しない。 

例3 母集団に関する統計モデルが，対称分布であるという帰無仮説もあり得る。このタイプの帰無

仮説では，分布形を特定しない。 

注記1 帰無仮説は，実現可能な確率分布の集合の部分集合を明確に示したものである。 

注記2 この定義は，対立仮説（1.42）及び統計的検定（1.48）と一緒に考えた方がよい。なぜならば，

仮説検定を適切に応用しようとすれば，これら全ての要素が必要となるからである。 

注記3 実際には，帰無仮説を実証することは決してできない。むしろ，与えられた状況が，帰無仮

説を棄却するには，評価が不十分と考えられる場合があるだけである。元来，仮説検定を行

うのは，取り扱おうとしている問題に関する対立仮説を，仮説検定結果が支持することを期

待しているからである。 

注記4 帰無仮説を棄却できないということは，帰無仮説の妥当性を“証明”したことではなく，む

しろ，帰無仮説を否定する十分な証拠がなかったと考えることができる。この場合は，帰無

仮説が実際に正しい（若しくは帰無仮説に極めて近い），又は帰無仮説からの逸脱を検出する

にはサンプルサイズが不十分である，のいずれかである。 

注記5 本来の関心が帰無仮説に集中している場合もある。その場合でも，帰無仮説からの逸脱の可

能性は，関心事となろう。帰無仮説に対する評価を適切なものとするためには，サンプルサ

イズ，及び所定の逸脱又は対立仮説の検出力に正当な配慮を行う必要がある。 

注記6 帰無仮説を棄却できない場合とは異なり，対立仮説を採択することは，関心のある予想が支

持されたという意味で，明確な結果である。“帰無仮説を棄却し，対立仮説を支持する”とい

18 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

う結論は，“今回は，帰無仮説が棄却できなかった”といった結論よりは，曖昧さが少ない結

論である。 

注記7 帰無仮説は，帰無仮説の評価に対応する検定統計量（1.52）を構成するときの基礎となる。 

注記8 帰無仮説は，H0で示されることが多い（Hの添え字は，英語ではオー又はノート“nought”

と発音されることもあるが，ゼロを用いる。）。 

注記9 帰無仮説で指定される部分集合は，可能ならば，主張が検討したい予想と排反するように選

択するのがよい。1.48の注記2，及び1.49の例を参照されたい。（この部分集合の設定に関し

て様々な議論がある。） 

1.42 

対立仮説 たいりつかせつ（alternative hypothesis） 

HA，H1 

帰無仮説（1.41）が成り立たないときに，許容される確率分布（2.11）の全ての集合又は部分集合の選択

に関する主張。 

例1 1.41の例1の帰無仮説に対する対立仮説は，平均（2.35）が指定された値より大きくなること

であり，このことは，HA : μ > μ 0と書く。 

例2 1.41の例2の帰無仮説に対する対立仮説は，母集団に関する統計モデルが，正規分布ではない

というものである。 

例3 1.41の例3の帰無仮説に対する対立仮説は，母集団に関する統計モデルが，非対称分布である

というものである。このタイプの対立仮説では，非対称な分布形を特定しない。 

注記1 対立仮説は，帰無仮説の補集合である。定義に基づくと補集合の部分集合であってもよい。 

注記2 対立仮説は，H1又はHAで示すことができ，この両者のどちらかが好まれるということはな

い。 

注記3 対立仮説は，帰無仮説と相反する主張である。対応する検定統計量（1.52）を，帰無仮説か

対立仮説かを決定するのに用いる。 

注記4 対立仮説は，帰無仮説及び統計的検定（1.48）と一緒に考えた方がよい。 

注記5 対立仮説を採択することは，関心のある予想が支持されたという意味で，帰無仮説が棄却で

きなかったことに比べて，明確な結果である。 

1.43 

単純仮説 たんじゅんかせつ（simple hypothesis） 

分布族（2.8）の単一の分布を特定している仮説（1.40）。 

注記1 単一の確率分布（2.11）だけから構成される単純仮説には，帰無仮説（1.41）の場合もあれば，

対立仮説（1.42）の場合もある。 

注記2 平均（2.35）未知，標準偏差（2.37）既知の同一の正規分布（2.50）に従う独立な確率変数（2.10）

からのランダムサンプル（1.6）の場合，μに関する単純仮説は，その平均が，所与の値μ0に

等しいことである。これは，一般に，H0 : μ＝μ0と書く。 

注記3 単純仮説は確率分布（2.11）を完全に特定する。 

1.44 

複合仮説 ふくごうかせつ（composite hypothesis） 

分布族（2.8）の複数の分布（2.11）を特定している仮説（1.40）。 

例1 1.41と1.42の例で与えられた帰無仮説（1.41）及び対立仮説（1.42）は，全て複合仮説の例で

19 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

ある。 

例2 1.48の例3のケース3は，単純仮説である。例4の帰無仮説も単純仮説である。1.48のその他

の仮説は，複合仮説である。 

注記 複数の確率分布（2.11）から構成される複合仮説には，帰無仮説（1.41）の場合もあれば，対立

仮説（1.42）の場合もある。 

1.45 

有意水準 ゆういすいじゅん（significance level） 

α 

＜統計的検定＞帰無仮説（1.41）が真のときに，それを棄却する確率（2.5）の上限値。 

注記1 帰無仮説が単純仮説（1.43）の場合には，帰無仮説が真のときにそれを棄却する確率は一つ

の値にしかならない。 

注記2 ＜ ＞の記号は，一つの用語が複数の概念を表す場合に，それぞれの概念に関係する主題又

は分野を表示して対象を限定し，区別するために用いる。 

1.46 

第1種の誤り，第1種の過誤 だいいっしゅのあやまり，だいいっしゅのかご（Type I error） 

帰無仮説（1.41）が真のときに，それを棄却すること。 

注記1 実際，第1種の誤りは，正しくない決定である。したがって，このような正しくない決定を

行う確率（2.5）は，可能な限り小さなものにとどめることが望ましい。第1種の過誤の確率

を0にしようとすれば，帰無仮説を棄却することは絶対できない。すなわち，証拠のいかん

にかかわらず，帰無仮説を棄却しないという常に同じ決定がなされる。 

注記2 結果の離散性から，事前に設定した有意水準の公称値，例えば，0.05が達成できない状況が

ある（例えば，2項分布の母数pの検定の場合）。 

注記3 “あわてものの誤り”ということがある。 

1.47 

第2種の誤り，第2種の過誤 だいにしゅのあやまり，だいにしゅのかご（Type II error） 

帰無仮説が真でないときに，帰無仮説（1.41）を棄却できないこと。 

注記1 実際，第2種の誤りは，正しくない決定である。したがって，このような正しくない決定を

行う確率（2.5）は，可能な限り小さなものにとどめることが望ましい。サンプルサイズが十

分でないために帰無仮説からの逸脱を示すことができず，第2種の誤りが生じることが多い。 

注記2 “ぼんやりものの誤り”ということがある。 

1.48 

（統計的）検定，統計的仮説検定，有意性検定 （とうけいてき）けんてい，とうけいてきかせつけんて

い，ゆういせいけんてい（statistical test，significance test） 

帰無仮説（1.41）を棄却して対立仮説（1.42）を支持できるかどうかを決定する手続き。 

例1 例として，実際に，連続確率変数（2.29）が，−∞から＋∞の値をとり得るものとし，更に真

の確率分布が正規分布（2.50）ではないという疑いがあれば，仮説は，次のように策定される。 

− 考慮すべき全対象は，−∞から＋∞の値をとり得るすべての連続確率分布（2.23）である。 

− 真の確率分布は，正規分布ではないことが予想されている。 

− 帰無仮説は，真の確率分布が正規分布となることである。 

− 対立仮説は，真の確率分布が正規分布ではないということである。 

20 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例2 確率変数が標準偏差（2.37）既知の正規分布に従う場合で，母平均 μ が所与のμ 0から逸脱して

いることが疑われるならば，仮説は，次の例のケース3に従って策定される。 

例3 この例では，統計的検定で可能な三つのケースについて考察する。 

ケース1 工程平均が平均の目標値μ 0より高いと予想されている。この予想は，次のような仮

説を導く。 

帰無仮説： H0：μ ≦ μ 0 

対立仮説： H1：μ ＞ μ 0 

帰無仮説を不等号なしでH0：μ ＝ μ 0と表すことも多い。 

ケース2 工程平均が平均の目標値μ 0より低いと予想されている。この予想は，次のような仮

説を導く。 

帰無仮説： H0：μ ≧ μ 0 

対立仮説： H1：μ ＜ μ 0 

帰無仮説を不等号なしでH0：μ ＝ μ 0と表すことも多い。 

ケース3 工程平均が平均の目標値（対応国際規格は，“平均の目標値”を工程平均と誤記）と

異なると予想されているが，いずれの方向にずれているかは特定されていない。この予想は，

次のような仮説を導く。 

帰無仮説： H0：μ ＝ μ 0 

対立仮説： H1：μ ≠ μ 0 

これら三つの場合は，全て対立仮説が基準となる状態からのどの方向に逸脱しているかとい

う予想に基づき，仮説が策定されている。 

例4 この例では，ロット1，ロット2の各不良率p1，p2（0 ≦ p1 ≦ 1，0 ≦ p2 ≦ 1）を考察の対象

とする。二つのロットは異なるので，ロットの不良率も異なると予想されている。この予想は，

次のような仮説を導く。 

帰無仮説： H0：p1 ＝ p2 

対立仮説： H1：p1 ≠ p2 

注記1 統計的検定は，サンプルからの観測値を用いて，真の確率分布が帰無仮説と対立仮説のいず

れに属するかを決めるための手続きであり，ある前提条件のもとで妥当となる。 

注記2 統計的検定を行う前に，最初に利用できる情報に基づき確率分布の可能な集合を決める。次

に，検討すべき予想に整合する確率分布を特定し，対立仮説を構成する。最後に，帰無仮説

を対立仮説と相反するものとして定式化する。可能な確率分布の集合，すなわち，帰無仮説

や対立仮説は，多くの場合，関連する母数の値の集合を用いて定められる。 

注記3 決定は，サンプルからの観測値に基づいて行われる。したがって，帰無仮説が正しいときに

それを棄却する第1種の誤り（1.46）と，対立仮説が正しいにもかかわらず，帰無仮説を棄

却することができない第2種の誤り（1.47）といった誤りが生じることがある。 

注記4 例3のケース1及びケース2が，片側検定の例である。ケース3が両側検定の例である。片

側か両側かは，対立仮説に対応する母数 μ の領域を考えることで定まる。より一般的には，

片側検定及び両側検定は，選択した検定統計量の棄却域で決められる。すなわち，検定統計

量には，対立仮説を支持する棄却域が付随する。しかし，棄却域がいつでも，ケース1，ケ

ース2，及びケース3のような母数空間の単純な記述に直接関連するとは限らない。 

注記5 統計的検定の背後にある前提への注意は不可欠であり，これを怠れば統計的検定の結果は妥

21 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

当性を欠くものになることがある。前提が誤って想定されていても推論の結果が安定してい

るような統計的検定はロバストであると呼ばれる。平均に関する一標本t検定は，正規分布

でない分布に対しても非常にロバストとなる例である。分散均一性に関するバートレットの

検定は，あまりロバストでない方法の例であり，分散が実際には均一な分布の場合でも，等

分散性の仮説を過度に棄却する傾向がある。 

1.49 

p値，有意確率 ぴーち，ゆういかくりつ（p-value） 

検定統計量（1.52）の観測値に対して，その値を含み，その値よりも帰無仮説（1.41）を支持すること

にならない検定統計量が得られる確率（2.5）。この確率を計算するためには帰無仮説が成立しているとい

う前提条件が必要である。 

例 1.9で紹介した数値例を考察する。例として，これらの値は，母平均が公称12.5であると期待さ

れている工程からの観測値であると仮定しよう。さらに，この工程の技術者は，これまでの経験

から工程平均がこの公称値より一貫して低い値であったと感じているとしよう。検討が行われ，

大きさ10のランダムサンプルが採取され，1.9に示したような観測結果が得られたとする。適切

な仮説は， 

帰無仮説： H0：μ ≧ 12.5 

対立仮説： H1：μ ＜ 12.5 

である。標本平均が9.7ということは，予想どおりの方向であるが，この予想を支持するのに足

るほど十分に12.5からずれているのであろうか？この例では，検定統計量（1.52）は−2.112 6（対

応国際規格は，−1.976 4と誤記）であり，対応するp値は0.031 9（対応国際規格は，0.040と誤

記）である。これは，検定統計量の値が−2.112 6（対応国際規格は，−1.976 4と誤記）以下と観

測される確率は，真の工程平均が実際に12.5の場合には，100回中4回よりも少ないことを意味

する。この場合，事前に有意水準を0.05に設定していたなら，帰無仮説を棄却し，対立仮説を支

持することになる。 

この問題に，別の定式化がなされていたと仮定しよう。工程は目標値である12.5から外れてい

るが，その方向は特定できないと考えてみよう。この状況は，次の仮説を導く。 

帰無仮説： H0：μ ＝12.5 

対立仮説： H1：μ ≠12.5 

ランダムサンプルとして同一のデータが与えられたとすれば，検定統計量も−2.112 6（対応国

際規格は，−1.976 4と誤記）と等しい値になる。この対立仮説に対して，関心のある質問は，“こ

のような極端な検定統計量の値又はそれ以上に極端な値が観測される確率はどのくらいか？”と

いうものになる。この場合，関連する二つの領域があり，検定統計量の値が−2.112 6（対応国際

規格は，−1.976 4と誤記）以下の領域と，2.112 6（対応国際規格は，1.976 4と誤記）以上の領域

である。t検定統計量がこれらの領域に属する確率は0.063 8（対応国際規格は，0.080と誤記）で

ある（片側のp値の倍である）。検定統計量の値が，これよりも極端な値として観測されるのは

100回中7回よりも少ない（対応国際規格は，100回に8回であると誤記）。したがって，帰無仮

説は有意水準0.05では棄却されない。 

注記1 例えば，もしp値が0.029となれば，検定統計量がこれより極端な値をとる可能性は，帰無

仮説の下で，100回に3回よりも小さいこととなる。これは，かなり小さなp値なので，こ

の情報を基に，帰無仮説を棄却したいと思うであろう。より形式的には，有意水準を0.05と

22 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

設定されていた場合には，0.05より小さいp値0.029ならば，確かに帰無仮説は棄却される。 

注記2 p値は，有意確率と呼ばれることがある。これを応用上，固定値として設定される有意水準

（1.45）と混同するのは望ましくない。 

1.50 

（検定の）検出力 （けんていの）けんしゅつりょく（power of a test） 

1から第2種の誤り（1.47）の確率（2.5）を引いたもの。 

注記1 確率分布族（2.8）の未知母数（2.9）の特定の値に対する検出力は，当該母数値において計算

される帰無仮説（1.41）の棄却確率に等しい。 

注記2 実際に検定を行う多くの場合では，サンプルサイズが大きくなることによって検出力も増大

する。いい換えれば，対立仮説（1.42）が正しい場合，帰無仮説を棄却する確率が，サンプ

ルサイズが大きくなるにつれて大きくなる。したがって，第2種の誤りの確率は，減少する。 

注記3 検定を行う状況では，サンプルサイズが極端に大きくなれば，帰無仮説からの小さな逸脱も

検出し，帰無仮説を棄却できることが望ましい。いい換えれば，サンプルサイズが無限に大

きくなる場合，検出力は1に近づくことが望ましい。このような検定は，一致性をもつと呼

ばれる。二つの検定を検出力に関して比較する場合，同じ帰無仮説及び対立仮説に対して，

有意水準も同じならば，検出力の高い検定の方が有効であるとみなす。一致性及び有効性に

ついては，より正式な数学的な記述もあるが，それらは，この規格の適用範囲を超えている

（様々な統計学辞典又は数理統計学の教科書を参照されたい。）。 

1.51 

検出力曲線 けんしゅつりょくきょくせん（power curve） 

検出力（1.50）を分布族（2.8）の母数（2.9）の関数として表した値の集合。 

注記 関連する用語“OC曲線”（JIS Z 8101-2の4.5.1）参照。 

1.52 

検定統計量 けんていとうけいりょう（test statistic） 

検定（1.48）に関連して用いる統計量（1.8）。 

注記 検定統計量は，考察の対象とする確率分布（2.11）が帰無仮説（1.41）又は対立仮説（1.42）に

整合的であるか否かを評価するのに用いる。 

1.53 

グラフを用いた記述統計 ぐらふをもちいたきじゅつとうけい（graphical descriptive statistics） 

図的な表現による記述統計（1.5）。 

注記 一般に多くの数値を管理可能な少数のものに要約する，又は視覚化に適した方法にそれらの数

値を表現することが記述統計のねらいである。グラフを用いた要約の例には，ボックスプロッ

ト，確率プロット，Q-Qプロット，正規確率プロット，散布図，多変量散布図，及びヒストグ

ラム（1.61）がある。 

1.54 

数値を用いた記述統計 すうちをもちいたきじゅつとうけい（numerical descriptive statistics） 

数値で表現された記述統計（1.5）。 

注記 数値を用いた記述統計には，平均（1.15），範囲（1.10），標準偏差（1.17），四分位範囲などが

ある。 

23 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

1.55 

級，クラス きゅう，くらす（classes） 

注記 全ての級を集めたものは網羅的かつ互いに排反であると想定する。数直線は，−∞と＋∞との

間の全ての実数を意味する。 

1.55.1 

級，クラス きゅう，くらす（class） 

＜質的特性＞サンプル（1.3）におけるアイテムの部分集合。 

注記 ＜ ＞の記号は，一つの用語が複数の概念を表す場合に，それぞれの概念に関係する主題又は

分野を表示して対象を限定し，区別するために用いる。 

1.55.2 

級，クラス きゅう，くらす（class） 

＜順序特性＞順序尺度上のカテゴリーの一つ又は近接する複数のカテゴリーをまとめたもの。 

1.55.3 

級，クラス きゅう，くらす（class） 

＜量的特性＞数直線上の区間。 

1.56 

級の限界，級の境界，クラスの限界，クラスの境界 きゅうのげんかい，きゅうのきょうかい，くらすの

げんかい，くらすのきょうかい（class limits，class boundaries） 

＜量的特性＞級（1.55）の上限及び下限を定義する値。 

注記 この定義は，量的特性の級の限界を示したものである。 

1.57 

級の中点，級の中心，クラスの中点，クラスの中心 きゅうのちゅうてん，きゅうのちゅうしん，くらす

のちゅうてん，くらすのちゅうしん（mid-point of class） 

＜量的特性＞級の限界（1.56）における上限と下限との平均（1.15）。 

注記 級の中点は，ヒストグラムの関連でクラスマークとしても知られる。 

1.58 

級の幅，クラスの幅 きゅうのはば，くらすのはば（class width） 

＜量的特性＞級（1.55）の上限から下限を引いた値。 

1.59 

度数，頻度 どすう，ひんど（frequency） 

特定の級（1.55）で，物事が生じる回数，又は観測値（1.4）が含まれる個数。 

1.60 

度数分布，頻度分布 どすうぶんぷ，ひんどぶんぷ（frequency distribution） 

級（1.55）と物事が生じた回数との関係性，又は級と観測値（1.4）の個数との関係性。 

1.61 

ヒストグラム ひすとぐらむ（histogram） 

底辺の長さが級の幅（1.58）に等しく，その面積が級の度数に比例する近接する長方形からなる度数分

布（1.60）のグラフ表現。 

注記1 級の幅が不均一な場合には，注意が必要である。級の幅が不均一な場合には，級の面積を級

の度数に比例させるとよい。 

24 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記2 全ての級の幅を等しくし，長方形の高さを級の度数に比例させるのが一般的である。 

1.62 

棒グラフ ぼうぐらふ（bar chart） 

一定の幅で，高さが度数（1.59）に比例する長方形からなる，名義尺度の度数分布（1.60）のグラフ表現。 

注記1 長方形は見かけの美観を求めて三次元画像として描かれることがあるが，これは何ら追加情

報をもたらさないので勧められない。棒グラフの場合，長方形は近接させる必要はない。 

注記2 ヒストグラムと棒グラフとの違いは，利用可能なソフトウェアがここで与えた定義に従うと

は限らないため，次第に曖昧になりつつある。 

1.63 

累積度数，累積頻度 るいせきどすう，るいせきひんど（cumulative frequency） 

指定された級の上限までの総度数（1.59）。 

注記1 この定義は，級の限界（1.56）に対応する値に対してだけ適用可能である。 

注記2 累積度数を“経験分布関数”と呼ぶことがある。 

1.64 

相対度数，相対頻度 そうたいどすう，そうたいひんど（relative frequency） 

度数（1.59）を物事が生じた総数又は観測値（1.4）の総数で割ったもの。 

1.65 

累積相対度数，累積相対頻度 るいせきそうたいどすう，るいせきそうたいひんど（cumulative relative 

frequency） 

累積度数（1.63）を物事が生じた総数又は観測値（1.4）の総数で割ったもの。 

2 

確率で用いられる用語 

2.1 

標本空間 ひょうほんくうかん（sample space） 

Ω 

起こり得る全ての結果の集合。 

例1 消費者が購入したバッテリーが故障するまでの時間を考える。もし，初めて使用するときに故

障しているのであれば故障するまでの時間は0である。もし，バッテリーがしばらくの間機能

するならば，故障するまでの時間は何時間かになる。したがって，標本空間は｛初めてバッテ

リーを使おうとしたとき，すでに故障している｝と｛x時間後（x > 0）にバッテリーが故障す

る｝という結果からなる。この例は，この章を通じて用いられる。特に，2.68で徹底した議論

がなされている。 

例2 一つの箱に1，2，3，4，5，6，7，8，9，10のラベルが付けられた10個の抵抗が入っている。

もし，この抵抗の集まりから二つの抵抗がランダムに非復元抽出されたとすると，標本空間は

次の45通りの結果からなる：(1，2)，(1，3)，(1，4)，(1，5)，(1，6)，(1，7)，(1，8)，(1，9)，

(1，10)，(2，3)，(2，4)，(2，5)，(2，6)，(2，7)，(2，8)，(2，9)，(2，10)，(3，4)，(3，5)，(3，

6)，(3，7)，(3，8)，(3，9)，(3，10)，(4，5)，(4，6)，(4，7)，(4，8)，(4，9)，(4，10)，(5，6)，

(5，7)，(5，8)，(5，9)，(5，10)，(6，7)，(6，8)，(6，9)，(6，10)，(7，8)，(7，9)，(7，10)，

(8，9)，(8，10)，(9，10)。ここで，事象 (1，2) は (2，1) と同じとみなし，抵抗が選ばれる順

序は問題としていない。もし，順序を問題とするならば，標本空間は合計90通りの結果からな

25 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

る。 

例3 先の例で復元抽出を行ったとすると，10個の事象 (1，1)，(2，2)，(3，3)，(4，4)，(5，5)，(6，

6)，(7，7)，(8，8)，(9，9) 及び (10，10) を追加しなければならない。順序を問題としない場

合は，標本空間は55通りの結果からなる。順序を問題とする場合では，標本空間は100通りの

結果からなる。 

注記1 結果は，現実の実験から生じることも，完全に仮想的な実験から生じることもあり得る。そ

の集合は，リストに示されたものであったり，正の整数 {1，2，3，…} のような可算集合で

あったり，又は数直線であったりする。 

注記2 標本空間は，確率空間（2.68）の三つ組の第1要素である。 

2.2 

事象 じしょう（event） 

A 

標本空間（2.1）の部分集合。 

例1 2.1の例1において，{0}，(0，2)，{5.7}，[7，＋∞) は事象の例であり，初めから故障している

バッテリー，初めのうちは働くが2時間未満に故障するバッテリー，ちょうど5.7時間で故障

するバッテリー，及び7時間未満では故障していないバッテリーに対応している。{0} 及び 

{5.7} は，それぞれただ一つの値を含む集合である。(0，2) は，数直線上の一つの開区間であ

る。[7，＋∞) は，数直線上の左側が閉じた無限区間である。 

例2 2.1の例2に引き続き，順序を考慮しない非復元抽出だけ考える。一つの起こり得る事象は，｛抵

抗1又は2の少なくとも一個が標本に含まれている｝で定まる事象Aである。この事象は，17

個の結果 (1，2)，(1，3)，(1，4)，(1，5)，(1，6)，(1，7)，(1，8)，(1，9)，(1，10)，(2，3)，(2，

4)，(2，5)，(2，6)，(2，7)，(2，8)，(2，9) 及び (2，10) からなる。別の事象Bとして，｛抵抗

8，9，10のどれも標本に含まれない｝を考える。この事象は，21個の結果 (1，2)，(1，3)，(1，

4)，(1，5)，(1，6)，(1，7)，(2，3)，(2，4)，(2，5)，(2，6)，(2，7)，(3，4)，(3，5)，(3，6)，

(3，7)，(4，5)，(4，6)，(4，7)，(5，6)，(5，7)，及び(6，7) からなる。 

例3 例2の続きで，事象AとBとの共通部分（すなわち，抵抗1及び2の少なくとも一つが標本に

含まれ，かつ，抵抗8，9，及び10のどれも含まれない事象）は，次の11の結果からなる。(1，

2)，(1，3)，(1，4)，(1，5)，(1，6)，(1，7)，(2，3)，(2，4)，(2，5)，(2，6)，(2，7)。 

事象AとBとの和は，次の27の結果，(1，2)，(1，3)，(1，4)，(1，5)，(1，6)，(1，7)，(1，

8)，(1，9)，(1，10)，(2，3)，(2，4)，(2，5)，(2，6)，(2，7)，(2，8)，(2，9)，(2，10)，(3，4)，

(3，5)，(3，6)，(3，7)，(4，5)，(4，6)，(4，7)，(5，6)，(5，7)， (6，7) からなる。 

事象AとBとの和（すなわち，抵抗1及び2の少なくとも一つが標本に含まれるか，又は抵

抗8，9及び10のどれも含まれない事象）に含まれる結果の数は27であり，それは17＋21−

11である。つまり，事象Aに含まれる結果の数と事象Bに含まれる結果の数との和から共通部

分に含まれる結果の数を引いたものが，事象AとBとの和に含まれる結果の数である。 

注記 事象及び実験の結果が与えられたとき，その結果がその事象に属するとき，その事象は起こっ

たといわれる。実際の事象は，事象のσ加法族（2.69）に属することとなる。このシグマ加法

族は，確率空間（2.68）の三つ組の第2要素である。ポーカー，ルーレットなどといった賭け

において事象は，自然に生じる。そこでは，一つの事象に属する結果の数を決定することで賭

けのオッズが決まる。 

26 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2.3 

余事象 よじしょう（complementary event） 

AC 

所与の事象（2.2）を標本空間（2.1）から除いたもの。 

例1 2.1のバッテリーの例1において，事象 {0} の余事象は，事象 (0，＋∞) である。同じことだ

が，バッテリーが初めから機能しない事象の余事象は，バッテリーが初めは機能する事象であ

る。同様に，事象 [0，3) はバッテリーが初めから機能しなかったか，機能してもそれが3時

間未満であった場合に対応するが，この事象の余事象は [3，＋∞) であり，バッテリーが3時

間後も働き，寿命がそれより長い場合に対応する。 

例2 2.2の例2の続き。事象Bの中の結果の数は，B＝｛標本が抵抗8，9，10の少なくとも一つを

含む｝の余事象を考えることで容易に見つけることができる。この事象は，7＋8＋9＝24個の

結果，(1，8)，(2，8)，(3，8)，(4，8)，(5，8)，(6，8)，(7，8)，(1，9)，(2，9)，(3，9)，(4，9)，

(5，9)，(6，9)，(7，9)，(8，9)，(1，10)，(2，10)，(3，10)，(4，10)，(5，10)，(6，10)，(7，10)，

(8，10)，(9，10) を含む。この例では，全標本空間は45個の結果を含むから，事象Bは，45

−24＝21個の結果［すなわち，(1，2)，(1，3)，(1，4)，(1，5)，(1，6)，(1，7)，(2，3)，(2，

4)，(2，5)，(2，6)，(2，7)，(3，4)，(3，5)，(3，6)，(3，7)，(4，5)，(4，6)，(4，7)，(5，6)，

(5，7)，(6，7)］を含む。 

注記1 余事象は，標本空間における所与の事象の補集合である。 

注記2 余事象も事象の一つである。 

注記3 事象Aに対してAの余事象は，通常ACの記号で表される。 

注記4 事象の確率そのものよりも余事象の確率を計算するほうが容易であることが多い。例えば，1

パーセントの不良品を含む1 000個のアイテムからランダムに10個のアイテムを選ぶとき少

なくとも一つの不良品が見つかる事象を書き下ろそうとすると，結果は，ばく（莫）大な数

になる。この事象の余事象（一つの不良も発見されない。）は，ずっと扱いやすい。 

2.4 

独立事象 どくりつじしょう（independent events） 

共通部分の確率（2.5）がそれぞれの確率の積となる事象（2.2）の対。 

例1 赤色のさいころ及び白色のさいころを投げる状況を考える。36通りの可能な目の出方は，どれ

も等しく1/36の確率が割り当てられているとする。Diを赤及び白のさいころの出た目の数の和

がiになる事象とする。Wを白のさいころの出た目の数が1である事象とする。事象D7とW

とは独立であるが，i＝2，3，4，5，6に対して事象DiとWとは独立ではない。独立でない事

象の対は，従属事象と呼ばれる。 

例2 応用の場面で，独立及び従属事象はごく普通に現れる。事象又は出来事が従属である場合，関

連している事象の結果を知ることは大変有益である。例えば，心臓手術を受けようとしている

人に対して，成功の見込みは，喫煙歴又はその他の危険因子をもっている人の場合は，大変異

なったものになる可能性がある。このように，喫煙及び侵襲的な手術による死は，従属関係が

あり得る。これに対比して，この人が何曜日に生まれたかは，死と独立であろう。信頼性工学

では，故障原因に共通点がある構成要素の寿命は独立ではない。原子炉の燃料棒にひびが入る

確率はおそらく小さいが，一本の燃料棒にひびが入っているという条件のもとでは隣接した棒

にひびが入っている確率はおおむね増加するだろう。 

27 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例3 2.2の例2の続きで，標本抽出が単純ランダムサンプリングで行われ，全ての結果が同じ確率

1/45で起こるとする。このとき，P(A)＝17/45＝0.377 8，P(B)＝21/45＝0.466 7，P(AかつB)＝11/45

＝0.244 4である。しかし，積P(A)×P(B)＝(17/45)×(21/45)＝0.176 3であって，これは0.244 4

とは異なるので，事象AとBとは独立ではない。 

注記 この定義は，二つの事象に対して与えられたが，一般化される。事象A及びBに対して，独立

性の条件は，P(A∩B)＝P(A)P(B) である。三つの事象A，B，Cが独立であるためには， 

P(A∩B∩C)＝P(A)P(B)P(C) 

P(A∩B)＝P(A)P(B) 

P(A∩C)＝P(A)P(C) 及び 

P(B∩C)＝P(B)P(C) 

が成り立たなければならない。 

一般に，三つ以上の事象に対して，A1，A2，…，Anが独立であるとは，これらの事象の部分

族（A1，A2，…，Anから幾つか選んだもの）の共通部分の確率がそれぞれの事象の積に等しく，

それがあらゆる部分族ごとに成立することである。全ての事象対が独立だが三つの事象は独立

でないような（すなわち，対独立だが完全には独立ではない。）例を作ることができる。 

2.5 

（事象Aの）確率 （じしょうAの）かくりつ［probability (of an event A)］ 

P(A) 

事象（2.2）に割り当てられる閉区間 [0，1] の中の実数。 

例 2.1の例2の続きで，事象の確率はそれを構成する全ての結果に対する確率を足し合わせることで

得られる。もし，全ての45通りの結果が等確率で起こるならば，おのおの確率は1/45になる。

事象の確率は，結果の個数を数え，その個数を45で割ることで得られる。 

注記1 確率測度（2.70）は，標本空間の全ての事象に対する実数の割り当て方を提供している。実

数を割り当てる。ある一つの事象を取り上げたとき，確率測度による確率の割当てはその事

象に確率を与える。いい換えれば，確率測度は，全ての事象に対する割当てを完全に与え，

一方，確率は一つの事象に対する特定の割当てを表している。 

注記2 この定義では，確率とは特定の事象に対する確率を意味する。確率は，事象の長期にわたる

生起の相対頻度，又は起こりやすさに関する確信の度合いに関連付けられることもある。事
象Aの確率は，普通P(A)で表される。スクリプト文字

を用いた

(A)という記号は，確率

空間（2.68）の形式を表に出して考えなければならない状況で用いられる。 

2.6 

条件付き確率 じょうけんつきかくりつ（conditional probability） 

P(A | B) 

事象A及び事象Bの共通部分の確率（2.5）をBの確率で割ったもの。 

例1 2.1の例1において，｛バッテリーが少なくとも3時間持続する｝という事象（2.2）A，すなわ

ち [3，＋∞) を考える。事象Bを｛バッテリーが初めに機能する｝すなわち (0，＋∞) とする。

Bを与えたもとでのAの条件付き確率は，初めに機能するバッテリーだけを扱っていることを

考慮に入れている。 

例2 2.1の例2の続きで，非復元抽出ならば，抵抗2が1回目に選ばれたとすると，2回目に選ばれ

る確率は0である。もし，抵抗が選ばれる確率が全て等しいとすると，抵抗2が1回目に選ば

28 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

れなければ，2回目に選ばれる条件付き確率は0.111 1 (＝1/9) である。 

例3 2.1の例2の続き。復元抽出で，各回に全ての抵抗が選ばれる確率が全て等しいならば，抵抗2

が1回目に選ばれるかそうでないかにかかわらず，2回目に抵抗2が選ばれる条件付き確率は

0.1である。したがって，1回目と2回目との結果は，独立事象である。 

注記1 事象Bの確率は，正である必要がある。 

注記2 “BのもとでのA（A given B）”は，より詳しくは“事象Bが起こったという条件のもとでの

事象A”という。条件付き確率の記号の縦線は，“…の条件のもとで”と読まれる。 

注記3 事象Bのもとでの事象Aの条件付き確率が事象Aの確率に等しいならば，事象Aと事象B

とは独立である。いい換えれば，Bが生起したことを知っても，Aの確率は変化しない。 

2.7 

（確率変数Xの）分布関数 （かくりつへんすうXの）ぶんぷかんすう［distribution function (of a random 

variable X)］ 

F(x) 

事象（2.2）(−∞，x] の確率（2.5）を与えるxの関数。 

注記1 区間 (−∞，x] は，x以下の全ての値の集合である。 

注記2 分布関数は，確率変数（2.10）の確率分布（2.11）を完全に記述する。離散型及び連続型の確

率分布の分類だけでなく確率変数の分類も分布関数の分類に基づいている。 

注記3 確率変数は実数値又は順序の付いたk個の実数の組であるので，xも実数又は順序のついたk

個の実数の組であることが定義に暗に含まれている。多変量分布（2.17）に対する分布関数

は，その多変量分布に従う確率変数が特定の値以下である確率（2.5）を与える。多変量分布

関数を表現する記法は，F(x1，x2，…，xn)＝P[X1 ≦ x1，X2 ≦ x2，…，Xn ≦ xn] である。また，

分布関数は，非減少である。1変量では，分布関数はF(x)＝P[X ≦ x] となり，確率変数Xが

x以下の値をとる事象の確率を与える。 

注記4 通常，分布関数は，離散分布（2.22）関数と連続分布（2.23）関数とに類別されるが，その他

の可能性もある。2.1のバッテリーの例を思い出すと，次のような分布関数の例がある。 

0 

x < 0の場合 

F(x)＝ 

0.1 

x＝0の場合 

0.1＋0.9[1−exp(−x)] 

x > 0の場合 

この分布関数の定め方からバッテリーの寿命は，非負である。バッテリーが初めから機能し

ない確率は，10 %ある。その後は，バッテリーの寿命は，平均寿命1時間の指数分布（2.58）

である。 

注記5 分布関数は，しばしばcdf（cumulative distribution function，累積分布関数）と略記される。 

2.8 

（確率）分布族 （かくりつ）ぶんぷぞく（family of distributions） 

確率分布（2.11）の集合。 

注記1 確率分布を区別するとき，確率分布のパラメータ（2.9）がインデックスとしてよく用いられ

る。 

注記2 確率分布の平均（2.35）及び／又は分散（2.36）が，しばしば分布族のインデックスとして用

いられ，又は分布族を表すのに三つ以上のパラメータが必要な場合はその一部として用いら

れる。平均及び分散は，分布族の明示的なパラメータであるとは限らず，パラメータの関数

29 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

の場合もある。 

2.9 

パラメータ，母数 ぱらめーた，ぼすう（parameter） 

分布族（2.8）のインデックス。 

注記1 パラメータは，1次元のこともあり，多次元のこともある。 

注記2 分布族の平均に直接対応付けられるパラメータを位置母数（ロケーションパラメータ）と呼

ぶことがある。標準偏差（2.37），又はそれに比例するパラメータを尺度母数（スケールパラ

メータ）と呼ぶことがある。位置母数でも尺度母数でもないパラメータを，形状母数（シェ

イプパラメータ）と呼ぶことがある。 

2.10 

確率変数，変量 かくりつへんすう，へんりょう（random variable） 

標本空間（2.1）の上で定義された，k次元実ベクトル値関数。 

例 2.1のバッテリーの例では，標本空間の事象は，言葉で記述されていた（バッテリーが初めから故

障している，バッテリーは初めのうち働き，x時間後に故障する。）。このような事象は，数学的

に扱いにくいので，それぞれの事象に（一つの実数である。）バッテリーが故障する時間を対応さ

せることは自然である。確率変数が値0をとるならば，そのような結果は，初期故障に対応する

と理解される。確率変数が正の値をとるならば，バッテリーは，初め機能し，その後ある時間に

故障したと理解される。確率変数による表現をすれば，“バッテリーがその補償期間，例えば，6

時間，を超えても機能する確率は幾らか”といった問いに答えることができる。 

注記1 k次元実ベクトルは，順序のあるk個の実数の組 (x1，x2，…，xk) を意味する。より一般的

には，順序のあるk個の実数の組は，k次元の行ベクトル又は列ベクトルで表される。 

注記2 確率変数には，次元があり，それをkで表す。k＝1であれば，確率変数は，1次元又は1変

量であるといわれる。k > 1の場合，確率変数は多次元であるといわれる。英語では，k次元

をk-dimensionalと表記する。 

注記3 1次元確率変数は，確率空間（2.68）の構成要素である標本空間（2.1）の上で定義された実

数値関数である。 

注記4 順序のある実数の対を値とする確率変数は，2次元であるといわれる。この定義は，k個の数

の組の場合にも拡張される。 

注記5 k次元確率変数の第j要素は，k個の組の第j要素だけに対応する確率変数である。k次元確

率変数の第j要素は，その要素の値に基づいて事象（2.2）が定まる確率空間に対応する。 

注記6 確率変数（random variable）のことを変量（variate）ということもある。 

2.11 

確率分布，分布 かくりつぶんぷ，ぶんぷ（probability distribution，distribution） 

確率変数（2.10）によって誘導される確率測度（2.70）。 

例 2.1のバッテリーの例の続き。バッテリーの寿命の分布は，特定の値が起こる確率を完全に定める。

所与のバッテリーの寿命が幾らであるかはっきりせず，（試験の前には）バッテリーが初めに機能

するかどうかさえもわからない。不確かな結果の確率的な性質を確率分布は完全に定める。2.7

の注記4では，分布関数によって具体的に確率分布が表現された。 

注記1 分布関数（2.7），存在するならば確率密度関数（2.26），特性関数など，数多くの数学的に同

等な分布の表現がある。難しさは様々であるが，これらの表現を用いると確率変数が与えら

30 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

れた範囲の値をとる確率を求めることができる。 

注記2 確率変数は標本空間上で定義されている実数値関数であるから，確率変数は確率1で実数値

をとる。バッテリーの例においては，P[X ≧ 0]＝1である。多くの場合に，基礎にある確率

測度よりも，確率変数及びその表現の一つを直接扱うほうがずっと容易である。しかしなが

ら，一つの表現から別の表現に変える場合でも，確率測度によって一貫性が保たれている。 

注記3 ただ一つの成分からなる確率変数は，1次元分布又は1変量分布に従うといわれる。確率変

数に二つの成分がある場合，それは2次元分布又は2変量分布に従うといい，二つより多く

の成分がある場合，確率変数は多次元分布又は多変量分布に従うという。 

2.12 

期待値 きたいち（expectation） 

確率変数（2.10）の関数の確率測度（2.70）に関する標本空間（2.1）上の積分。 

注記1 確率変数Xの関数g(X) の期待値は，E[g(X)] と表され， 

E[g(X)]＝

∫

∫

=

k

R

Ω

x

F

x

g

P

X

g

)

(

d)

(

d)

(

と計算される。 

ここに，F(x) は，対応する分布関数である。 

注記2 E[g(X)] の“E”は，確率変数g(X) の“期待値（expected value，expectation）”に由来する。E

は，確率変数を実数へ，上記の計算式で対応させる作用素又は関数とみなすことができる。 

注記3 E[g(X)] に対して二種類の積分が与えられている。1番目は標本空間上の積分であり，概念に

訴えるものであるが，事象そのものは（例えば，言葉で与えられていたりすると）扱いにく

いので，実用的ではない。2番目の積分は，Rk上の計算を表しており，より実用的である。 

注記4 実際的な多くの場合，上の積分は見覚えのある形になる。例としては，g(x)＝xrとするとr次

のモーメント（2.34）になり，g(x)＝xとすると平均（2.35），g(x)＝[x−E(X)]2とすると分散（2.36）

になる。 

注記5 この定義は，前の例及び注記のように1次元に限定されるものではない。多次元の場合に関

しては，2.43参照。 

注記6 離散確率変数（2.28）に対して，注記1の積分は，総和記号で置き換えられる。例は，2.35

にある。 

2.13 

p分位点，100pパーセント点，p分位数，100pパーセンタイル pぶんいてん，100pぱーせんとてん，p

ぶんいすう，100pぱーせんたいる（p-quantile，p-fractile，100p-percentile） 

Xp，xp 

0 < p < 1なるpに対して，分布関数（2.7）F(x) がp以上になるx全体の下限。 

例1 確率質量関数が表2で与えられる2項分布（2.46）を考える。この数値はパラメータn＝6，p

＝0.3の2項分布に対応している。この場合に幾つかのp分位点を挙げると，次のようになる。 

x0.1＝0 

x0.25＝1 

x0.5＝2 

x0.75＝3 

x0.90＝3 

31 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

x0.95＝4 

x0.99＝5 

x0.999＝5 

2項分布は離散的なので，p分位点は整数になる。 

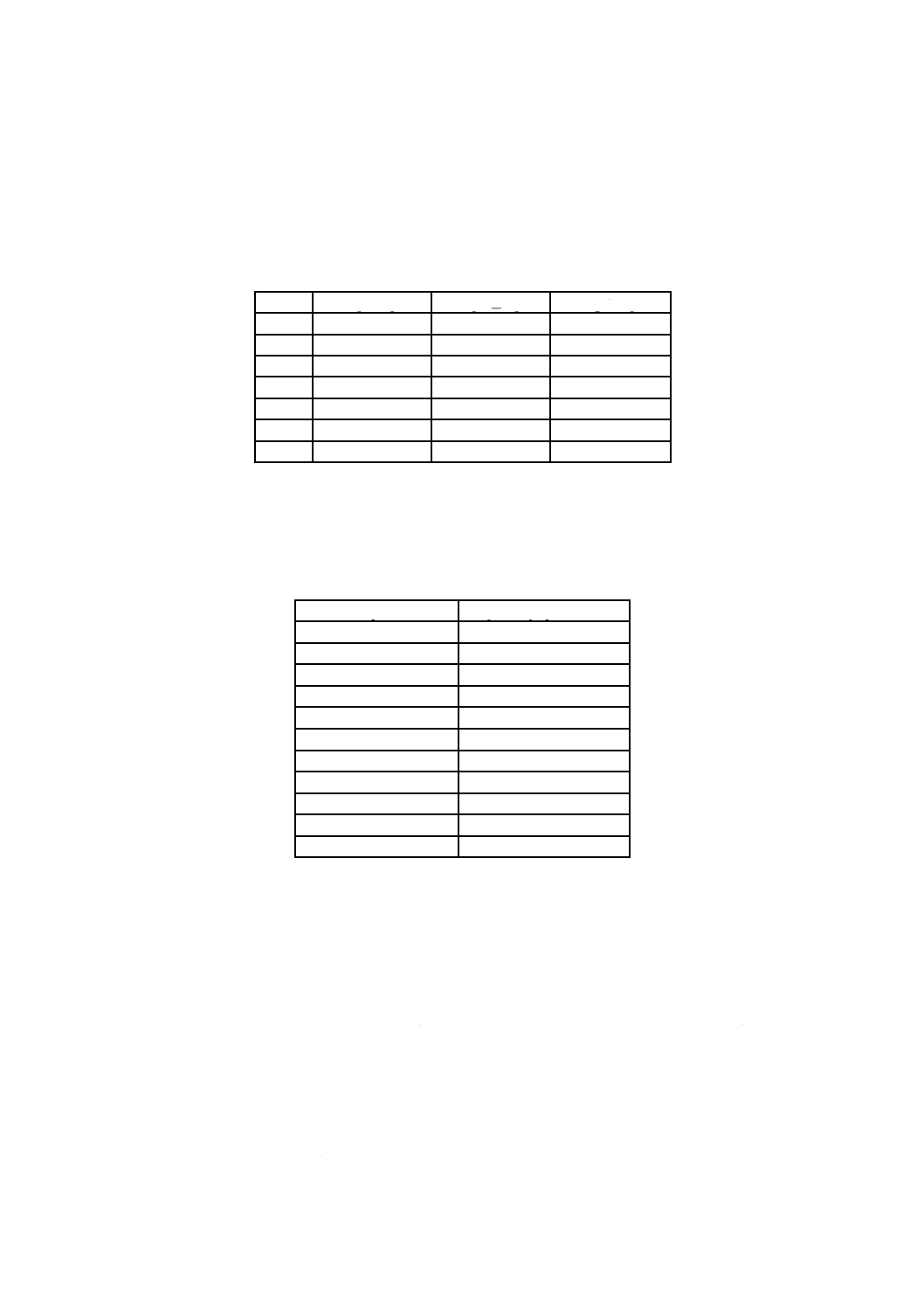
表2−2項分布の例 

X 

P[X＝x] 

P[X ≦ x] 

P[X > x] 

0 

0.117 649 

0.117 649 

0.882 351 

1 

0.302 526 

0.420 175 

0.579 825 

2 

0.324 135 

0.744 310 

0.255 690 

3 

0.185 220 

0.929 530 

0.070 470 

4 

0.059 535 

0.989 065 

0.010 935 

5 

0.010 206 

0.999 271 

0.000 729 

6 

0.000 729 

1.000 000 

0.000 000 

例2 標準正規分布（2.51）を考え，その分布関数から値を選んで表3に与える。幾つかのp分位点

は，次のとおりである。 

表3−標準正規分布の例 

p 

P[X ≦ x]＝pとなるx 

0.1 

−1.282 

0.25 

−0.674 

0.5 

0.000 

0.75 

0.674 

0.841 344 75 

1.000 

0.9 

1.282 

0.95 

1.645 

0.975 

1.960 

0.99 

2.326 

0.995 

2.576 

0.999 

3.090 

Xの分布は連続だから，第2列の見出しは，P[X < x]＝pとなるx，としてもよい。 

注記1 連続分布（2.23）に対して，p＝0.5の場合0.5分位点はメディアン（2.14）に一致する。pが

0.25に対しては，0.25分位点は下側四分位点として知られる。連続分布においては，分布の

25 %は0.25分位点より下にあり，また75 %は0.25分位点より上にある。pが0.75に対して

は，0.75分位点は上側四分位点として知られている。 

注記2 一般に，分布の100p %はp分位点より下にあり，分布の100(1−p) %はp分位点より上にあ

る。離散分布に対しては，この定義以外にも別な定義が用いられることがあるので，一般に

メディアンの定義を満たす値が複数あり，困難が伴う。 

注記3 Fが連続で狭義の単調増加であれば，p分位点はF(x)＝pの解である。 

注記4 分布関数がある区間において，定数でありpに等しければ，その区間に属する全ての値をF

のp分位点とする定義もある。 

32 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記5 p分位点は，1変量分布（2.16）に対して定義される。 

注記6 検定の棄却限界値に用いる，上側100pパーセント点は100(1−p) パーセント点である。両側

100pパーセント点は，100(1−p/2) パーセント点である。 

注記7 上側，下側の代わりに“上位”，“下位”と呼ぶこともある。 

2.14 

メディアン，中央値 めでぃあん，ちゅうおうち（median） 

0.5分位点（2.13）。 

例 2.7の注記4のバッテリーの例において，メディアンは，0.1＋0.9[1−exp(−x)]＝0.5の解であって，

0.587 8である。 

注記1 メディアンは，最もよく使われるp分位点（2.13）の一つである。連続1変量分布（2.16）の

メディアンは，母集団（1.1）の半分がそれ以上，半分がそれ以下となるようなものである。 

注記2 メディアンは，1変量分布（2.16）に対して定義される。 

注記3 母集団のメディアンであることを強調して，母メディアン，又は母中央値と呼んでもよい。 

2.15 

四分位点 しぶんいてん（quartile） 

0.25分位点（2.13）又は0.75分位点。 

例 2.14のバッテリーの例で，0.25分位点は0.182 3であり0.75分位点は1.280 9である。 

注記1 0.25分位点は下側四分位点として，0.75分位点は上側四分位点として知られている。 

注記2 四分位点は，1変量分布（2.16）に対して定義される。 

注記3 母集団の四分位点であることを強調して，母四分位点と呼んでもよい。 

2.16 

1変量確率分布，1変量分布 いちへんりょうかくりつぶんぷ，いちへんりょうぶんぷ（univariate probability 

distribution，univariate distribution） 

単一の確率変数（2.10）の確率分布（2.11）。 

注記 1変量確率分布は，1次元の分布である。2項分布（2.46），ポアソン分布（2.47），正規分布（2.50），

ガンマ分布（2.56），t分布（2.53），ワイブル分布（2.63）及びベータ分布（2.59）は，1変量確

率分布の例である。 

2.17 

多変量確率分布，多変量分布 たへんりょうかくりつぶんぷ，たへんりょうぶんぷ（multivariate probability 

distribution，multivariate distribution） 

複数の確率変数（2.10）の確率分布（2.11）。 

注記1 二つの確率変数の確率分布は，より限定的な表現として“多変量”の代わりに“2変量”が

用いられることが多い。序文に述べたように確率変数が一つである場合の確率分布を明示的

に1次元，又は1変量分布（2.16）と呼ぶ。このために，特に断りがない限り1変量である

ことが仮定されていることが多い。 

注記2 多変量分布は，同時分布又は結合分布と呼ばれることもある。 

注記3 多項分布（2.45），2変量正規分布（2.65），多変量正規分布（2.64）などは，この規格に挙げ

られた多変量分布の例である。 

2.18 

周辺確率分布，周辺分布 しゅうへんかくりつぶんぷ，しゅうへんぶんぷ（marginal probability distribution，

33 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

marginal distribution） 

確率変数（2.10）の成分の空でない真部分集合の確率分布（2.11）。 

例1 三つの確率変数X，Y，Zの確率分布には，二つの確率変数，すなわち，(X，Y)，(X，Z)，(Y，

Z) についての周辺分布が三つと，一つの確率変数，すなわち，X，Y，Zについての周辺分布が

三つ存在する。 

例2 2変量正規分布（2.65）に従う確率変数の対 (X，Y) では，確率変数Xの周辺分布も確率変数Y

の周辺分布も，ともに正規分布（2.50）である。 

例3 多項分布（2.45）では，k > 3ならば (X1，X2) の分布は周辺分布となる。X1，X2，…，Xkのそれ

ぞれの分布もまた周辺分布となる。この周辺分布は，それぞれ2項分布（2.46）である。 

注記1 k次元の同時分布について，k1 < kであるk1個の確率変数からなる部分集合の確率分布は，周

辺分布の一例である。 

注記2 確率密度関数（2.26）で表された連続（2.23）多変量確率分布（2.17）の場合，その周辺確率

分布の確率密度関数は，周辺分布の対象でない確率変数についてその全定義域においてもと

の確率密度関数を積分することによって求められる。 

注記3 確率質量関数（2.24）で表された離散（2.22）多変量確率分布（2.17）の場合，その周辺確率

分布の確率質量関数は，周辺分布の対象でない確率変数についてその全定義域においてもと

の確率質量関数の和をとることによって求められる。 

2.19 

条件付き確率分布，条件付き分布 じょうけんつきかくりつぶんぷ，じょうけんつきぶんぷ（conditional 

probability distribution，conditional distribution） 

標本空間（2.1）の空でない真部分集合内に限定され，その部分集合内の全確率が1になるように補正さ

れた確率分布（2.11）。 

例1 2.7 注記4のバッテリーの例で，初めからバッテリーが機能している場合のバッテリーの寿命

の条件付き分布は指数分布（2.58）である。 

例2 2変量正規分布（2.65）で，X＝xのもとでのYの条件付き分布は，Xを知ったときYへの影響

を反映している。 

例3 フロリダにおける年間のハリケーン被害の保険損害額の分布を表す確率変数Xを考える。この

分布は，ハリケーン被害が全くない年もあることから保険損害額がゼロであるという確率も正

である。興味の対象が，ハリケーン被害が実際にあった年に限定した条件付き分布であること

もある。 

注記1 二つの確率変数X及びYの分布について，Xについての条件付き分布とYについての条件付

き分布とが考えられる。Y＝yを条件付けられたXの分布は“Y＝yのもとでのXの条件付き

分布”と表記され，X＝xを条件付けられたYの分布は“X＝xのもとでのYの条件付き分布”

と表記される。 

注記2 周辺分布（2.18）は，条件付けられていない分布とみなすことができる。 

注記3 上の例1は，1変量分布が他の1変量分布の値によって調整されることを説明していて，こ

の場合，条件付き分布は，元の分布と異なる分布になる。これに対して，故障分布が指数分

布の場合，最初の10時間に故障が起きなかったという条件のもとでの将来の故障の分布は，

元の分布と同一のパラメータの指数分布になる。 

注記4 ある種の結果が起きえないという状況での離散分布は，条件付き分布になる。例えば，り（罹）

34 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

病者中の固形がん患者数のモデルでは，0をとらず，正の値［腫瘍のない患者はり（罹）病

の定義外であるため］だけに条件付けられたポアソン分布が用いられる。 

注記5 条件付き分布とは，標本空間を特定の部分集合に限定することを意味する。(X，Y) が2変量

正規分布（2.65）に従うとき，(X，Y) について [0，1]×[0，1] の領域だけに結果が生起する

ことが与えられたもとで，(X，Y) の条件付き分布に興味があるかもしれない。他にはX2＋

Y2 ≦ rが与えられたときの (X，Y) の条件付き分布も考えられる。この状況は，例えば，部

品の公差がこの領域に対応し，公差を満たしている部品の性能に更に興味があるという状況

である。 

2.20 

回帰曲線 かいききょくせん（regression curve） 

確率変数（2.10）Yについて，確率変数Xの値がxと与えられたときの条件付き確率分布（2.19）に基づ

くYの期待値（2.12）の値の集まり。 

注記1 ここで，(X，Y) が2変量分布（2.17の注記1参照）に従うというもとで回帰曲線が定義され

る。したがって，回帰曲線は，Yが確率変数でない説明変数の集まりと関連付けられる回帰

分析とは概念が異なる。 

注記2 (X，Y) が2変量正規分布に従う場合では，回帰曲線は直線となり，回帰直線と呼ばれる。 

2.21 

回帰曲面 かいききょくめん（regression surface） 

確率変数（2.10）Yについて，二つの確率変数X1，X2の値がx1，x2と与えられたときの条件付き確率分

布（2.19）に基づくYの期待値（2.12）の値の集まり。 

注記1 ここで，2.20と同様に，(Y，X1，X2) が多変量分布（2.17）に従うというもとで回帰曲面が定

義される。したがって，回帰曲線と同様に，回帰曲面は，回帰分析及び応答曲面探索の方法

論とは概念が異なる。 

注記2 (Y，X1，X2) が3変量正規分布に従う場合，回帰曲面は平面となり，回帰平面と呼ばれる。 

2.22 

離散確率分布，離散分布 りさんかくりつぶんぷ，りさんぶんぷ（discrete probability distribution，discrete 

distribution） 

標本空間（2.1）Ωが有限又は可算無限である確率分布（2.11）。 

例 この規格での離散分布の例には，多項分布（2.45），2項分布（2.46），ポアソン分布（2.47），超幾

何分布（2.48），及び負の2項分布（2.49）がある。 

注記1 “離散”とは，標本空間が有限のリストとなること，又は標本空間が，例えば，欠点の数が

0，1，2，…のように，先がどのように続くかが明らかな無限のリストになっていることであ

る。また，2項分布は有限の標本空間 {0，1，2，…，n} に対応するが，ポアソン分布は可

算無限の標本空間 {0，1，2，…} に対応する。 

注記2 合否抜取検査における計数値データには，離散分布が用いられる。 

注記3 離散分布の分布関数（2.7）は，離散的な値をとる。 

2.23 

連続確率分布，連続分布 れんぞくかくりつぶんぷ，れんぞくぶんぷ（continuous probability distribution，

continuous distribution） 

xにおける分布関数（2.7）が，非負の関数の−∞からxまでの積分で表される確率分布（2.11）。 

35 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例 連続分布が生じる状況には，工業分野での応用で見いだされる計量値データが用いられる状況の

ほとんどが相当する。 

注記1 連続分布の例には，正規分布（2.50），標準正規分布（2.51），t分布（2.53），F分布（2.55），

ガンマ分布（2.56），カイ2乗分布（2.57），指数分布（2.58），ベータ分布（2.59），一様分布

（2.60），タイプI極値分布（2.61），タイプII極値分布（2.62），タイプIII極値分布（2.63），

対数正規分布（2.52）などがある。 

注記2 この定義における非負の関数は，確率密度関数（2.26）である。したがって，分布関数がい

たるところ微分可能であると主張することは非常に制限的である。しかしながら，実際的に

は多くのよく用いられている連続分布は分布関数の導関数が，対応する確率密度関数になる

という性質をもっている。 

注記3 合否抜取検査における計量値データには，連続分布が用いられる。 

2.24 

確率質量関数，確率関数 かくりつしつりょうかんすう，かくりつかんすう（probability mass function） 

＜離散分布＞確率変数（2.10）が個々の値に等しくなる確率（2.5）を与える関数。 

例1 三つの正しいコインを投げたとき，表のでる枚数を確率変数Xとすると，確率質量関数は， 

P(X＝0)＝1/8 

P(X＝1)＝3/8 

P(X＝2)＝3/8 

P(X＝3)＝1/8 

である。 

例2 応用のときによく登場する離散分布（2.22）の定義のために，多様な確率質量関数が与えられ

る。1変量離散分布として，2項分布（2.46），ポアソン分布（2.47），超幾何分布（2.48）及び

負の2項分布（2.49）がある。多変量離散分布の例として，多項分布（2.45）がある。 

注記1 Xが確率変数，xiが実現値，piでその確率を表すとき，P(X＝xi)＝piで確率質量関数が与えら

れる。 

注記2 2.13の例1のp分位点で2項分布（2.46）の確率質量関数が導入された。 

注記3 ＜ ＞の記号は，一つの用語が複数の概念を表す場合に，それぞれの概念に関係する主題又

は分野を表示して対象を限定し，区別するために用いる。 

2.25 

確率（質量）関数のモード かくりつ（しつりょう）かんすうのもーど（mode of probability mass function） 

確率質量関数（2.24）が局所的最大値をとる値。 

例 n＝6，p＝1/3の2項分布（2.46）は，単峰でモードは2（対応国際規格では，モードは3と誤記）

である。 

注記 離散分布（2.22）は，モードが一つのときに単峰，二つのときに二峰，三つ以上のときに多峰

である。 

2.26 

確率密度関数，密度関数 かくりつみつどかんすう，みつどかんすう（probability density function） 

f (x) 

連続分布（2.23）のxにおける分布関数（2.7）が，−∞からxまでの積分によって表されるときの非負

の被積分関数。 

36 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例1 応用の場面でよく登場する連続分布の定義のために，多様な確率密度関数が与えられる。連続

分布として，正規分布（2.50），標準正規分布（2.51），t分布（2.53），F分布（2.55），ガンマ分

布（2.56），カイ2乗分布（2.57），指数分布（2.58），ベータ分布（2.59），一様分布（2.60），多

変量正規分布（2.64），及び2変量正規分布（2.65）がある。 

例2 分布関数が0 ≦ x ≦ 1の範囲でF(x)＝3x2−2x3と定義されるとき，対応する確率密度関数は， 

0 ≦ x ≦ 1の範囲でf(x)＝6x(1−x) である。 

例3 2.1（より適切には，2.7の注記4を参照）のバッテリーの例で，初めから故障している確率が

正のため，この分布関数に対応する確率密度関数は，存在しない。しかし，バッテリーが初め

は機能していたという条件付き分布の確率密度関数は，x > 0の範囲でf(x)＝exp(−x) である。

これは，指数分布である。 

注記1 分布関数Fが連続微分可能であれば，確率密度関数は， 

f(x)＝dF(x)/dx 

である。 

注記2 xに対してf(x) を図示すると，対称，とがっている，裾が重い，単峰，二峰などといった描

写ができる。ヒストグラムに対して，当てはめたf(x)を重ねて示すと，データと当てはめた

分布との一致の程度を視覚的に評価できる。 

注記3 確率密度関数の一般的な略字は，pdfである。 

2.27 

（確率）密度関数のモード （かくりつ）みつどかんすうのもーど（mode of probability density function） 

確率密度関数（2.26）が局所的に最大値をとる値。 

注記1 連続分布（2.23）は，その確率密度関数のモードが一つのときに単峰，二つのときに二峰，

三つ以上のときに多峰である。 

注記2 分布の全てのモードが連結集合をなすときも単峰という。 

2.28 

離散確率変数 りさんかくりつへんすう（discrete random variable） 

離散分布（2.22）に従う確率変数（2.10）。 

注記 この規格で考慮されている離散確率変数として，2項分布（2.46），ポアソン分布（2.47），超幾

何分布（2.48），多項分布（2.45）などに従う確率変数がある。 

2.29 

連続確率変数 れんぞくかくりつへんすう（continuous random variable） 

連続分布（2.23）に従う確率変数（2.10）。 

注記 この規格で考慮されている連続確率変数として，正規分布（2.50），標準正規分布（2.51），t分

布（2.53），F分布（2.55），ガンマ分布（2.56），カイ2乗分布（2.57），指数分布（2.58），ベー

タ分布（2.59），一様分布（2.60），タイプI極値分布（2.61），タイプII極値分布（2.62），タイ

プIII極値分布（2.63），対数正規分布（2.52），多変量正規分布（2.64），2変量正規分布（2.65）

などに従う確率変数がある。 

2.30 

中心化（された）確率分布，中心確率分布 ちゅうしんか（された）かくりつぶんぷ，ちゅうしんかくり

つぶんぷ（centred probability distribution） 

中心化確率変数（2.31）の確率分布（2.11）。 

37 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2.31 

中心化（された）確率変数，中心確率変数 ちゅうしんか（された）かくりつへんすう，ちゅうしんかく

りつへんすう（centred random variable） 

確率変数（2.10）からその母平均（2.35）を差し引いた確率変数。 

注記1 中心化確率変数の母平均は 0に等しい。 

注記2 この用語は母平均の存在する確率変数だけに適用される。例えば，自由度が1のt分布（2.53）

には母平均が存在しない。 

注記3 確率変数Xの母平均（2.35）がμ のとき，対応する中心化確率変数はX−μ であり，その母平

均は0に等しい。 

2.32 

標準化（された）確率分布，標準確率分布 ひょうじゅんか（された）かくりつぶんぷ，ひょうじゅんか

くりつぶんぷ（standardized probability distribution） 

標準化確率変数（2.33）の確率分布（2.11）。 

2.33 

標準化（された）確率変数，標準確率変数 ひょうじゅんか（された）かくりつへんすう，ひょうじゅん

かくりつへんすう（standardized random variable） 

母標準偏差（2.37）が1である中心化確率変数（2.31）。 

注記1 確率変数（2.10）は，その母平均が0で母標準偏差が1であるならば，そのまま標準化確率

変数である。区間が (−30.5，30.5) の一様分布（2.60）は母平均0，母標準偏差1である。標

準正規分布（2.51）は，もちろん標準化された確率分布である。 

注記2 確率変数Xの分布（2.11）で，母平均（2.35）がμ，母標準偏差がσ であれば，この標準化確

率変数は， (X−μ )/σ である。 

2.34 

r次のモーメント，r次の積率 rじのもーめんと，rじのせきりつ（moment of order r，rth moment） 

確率変数（2.10）のr乗の期待値（2.12）。 

例 確率密度関数（2.26）がx > 0の範囲でf(x)＝exp(−x) である確率変数を考える。このとき部分積

分によって，E(X)＝1，E(X2)＝2，E(X3)＝6，E(X4)＝24であり，一般にE(X r)＝r! となる。これは

指数分布（2.58）の例である。 

注記1 離散の1変量の場合の公式は，取り得る値の個数が有限でn個のとき， 

∑

=

=

n

i

i

r

i

r

x

p

x

X

E

1

)

(

)

(

で，また，取り得る値の個数が可算無限大のとき， 

∑

∞

=

=

1

)

(

)

(

i

i

r

i

r

x

p

x

X

E

である。連続の1変量の場合の公式は， 

∫∞∞

−

=

x

x

f

x

X

E

r

r

d)

(

)

(

である。 

38 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記2 k次元の確率変数の場合には，r乗は成分ごとに適用する。 

注記3 ここに規定されたモーメントは，確率変数Xのべき乗を用いている。より一般的に，X−μ 又

は(X−μ )/σ のr次のモーメントを考えることができる。 

2.35 平均 へいきん（means） 

2.35.1 

母平均，平均，1次のモーメント ぼへいきん，へいきん，いちじのもーめんと（mean，moment of order r

＝1） 

μ 

＜連続分布＞確率密度関数（2.26）f (x)とxとの積の数直線上での積分，すなわち，rが1のときのr次

モーメント。 

例1 連続確率変数（2.29）Xの確率密度関数が0 ≦ x ≦ 1の範囲でf(x)＝6x(1−x) であるとする。

このときXの母平均は， 

(

)

∫

=

−

1

0

2

5.0

d

1

6

x

x

x

である。 

例2 2.1及び2.7のバッテリーの例で，分布の離散部分の平均は0で，その確率が0.1，また，連続

部分の平均は1で，その確率が0.9なので，全体での母平均は0.9である。この分布は，連続分

布と離散分布とが混合した分布である。 

注記1 連続分布（2.23）の母平均は，E(X) の記号で表され， 

∫∞∞

−

=

x

x

xf

X

E

d)

(

)

(

で計算される。 

注記2 全ての確率変数（2.10）に母平均が存在するわけではない。例えば，確率密度関数がf(x)＝[π(1

＋x2)]−1で定義される確率変数Xは，E(X) に対応する積分が発散する。 

注記3 ＜ ＞の記号は，一つの用語が複数の概念を表す場合に，それぞれの概念に関係する主題又

は分野を表示して対象を限定し，区別するために用いる。 

2.35.2 

母平均，平均 ぼへいきん，へいきん（mean） 

μ 

＜離散分布＞確率質量関数（2.24）p(xi) とxiとの積の総和。 

例1 離散確率変数（2.28）Xで三つの正しいコインを投げたときの表のでる回数を表すとする。こ

の確率質量関数は， 

P(X＝0)＝1/8 

P(X＝1)＝3/8 

P(X＝2)＝3/8 

P(X＝3)＝1/8 

である。したがって，Xの母平均は， 

0(1/8)＋1(3/8)＋2(3/8)＋3(1/8)＝12/8＝1.5 

である。 

例2 2.35.1の例2を参照。 

39 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記 離散分布（2.22）の母平均は，E(X) の記号で表され，取り得る値の個数がnのとき， 

∑

=

=

n

i

i

ix

p

x

X

E

1

)

(

)

(

で，また，取り得る値の個数が可算無限大のとき， 

∑

∞

=

=

1

)

(

)

(

i

i

ix

p

x

X

E

で計算される。 

2.36 

母分散，分散 ぼぶんさん，ぶんさん（variance） 

V 

確率変数（2.10）の中心化確率分布（2.30）におけるrが2のときのr次モーメント（2.34）。 

例1 2.24の例での離散確率変数（2.28）の母分散は， 

∑

=

=

=

−

3

0

2

75

.0

)

(

)5.1

(

i

i

i

x

X

P

x

である。 

例2 2.26の例での連続確率変数（2.29）の母分散は 

05

.0

d)

1(

6

)5.0

(

1

0

2

=

−

−

∫

x

x

x

x

である。 

例3 2.1のバッテリーの例を引き続き考える。一般に，Xの分散がE(X 2)−[E(X)]2で求められる。2.35.1

の例2（対応国際規格では，2.35の例3と誤記）から，E(X)＝0.9である。また，同様の議論に

よって，E(X 2)は，1.8であることが分かる。この結果Xの分散は，1.8−(0.9)2で0.99である。 

注記 母分散の定義は，いい換えると，確率変数とその母平均（2.35）との差の2乗の期待値（2.12）

となる。確率変数Xの分散をV(X) の記号で表す，すなわち，V(X)＝E{[X−E(X)]2} である。 

2.37 

母標準偏差，標準偏差 ぼひょうじゅんへんさ，ひょうじゅんへんさ（standard deviation） 

σ 

母分散（2.36）の非負の平方根。 

例 2.1及び2.7のバッテリーの例で，母標準偏差は0.995である。 

2.38 

母変動係数，変動係数 ぼへんどうけいすう，へんどうけいすう（coefficient of variation） 

CV 

＜正値の確率変数＞母標準偏差（2.37）を母平均（2.35）で割ったもの。 

例 2.1及び2.7のバッテリーの例で，母変動係数は，     なので1.105 54（対応国際規格では，

0.99/0.995なので0.994 97と誤記）である。 

注記1 変動係数は，パーセントで表されることが一般的である。 

注記2 これまで使われていた“相対標準偏差”よりも，変動係数という用語を用いるべきである。 

9.0

99

.0

40 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記3 ＜ ＞の記号は，一つの用語が複数の概念を表す場合に，それぞれの概念に関係する主題又

は分野を表示して対象を限定し，区別するために用いる。 

2.39 

（母）ゆがみ，（母）ひずみ （ぼ）ゆがみ，（ぼ）ひずみ（coefficient of skewness） 

γ1 

確率変数（2.10）の標準化確率分布（2.32）についての3次モーメント（2.34）。 

例 2.1及び2.7のバッテリーの例は，連続分布と離散分布の混合した分布である，2.34の例の結果か

ら， 

E(X)＝0.1(0)＋0.9(1)＝0.9 

E(X2)＝0.1(02)＋0.9(2)＝1.8 

E(X3)＝0.1(03)＋0.9(6)＝5.4 

E(X4)＝0.1(04)＋0.9(24)＝21.6 

である。ゆがみを計算するために，公式E{[X−E(X)]3}＝E(X3)−3 E(X)E(X2)＋2 [E(X)]3と，2.37か

ら標準偏差が0.995となることを用いる。この結果，ゆがみは， [5.4−3(0.9)(1.8)＋2(0.9)3]/(0.995)3

＝2.028（対応国際規格は，1.998と誤記）となる。 

注記1 (X−μ )/σ の3乗の期待値（2.12），すなわちE[(X−μ )3/σ3] は，同値な定義である。 

注記2 ゆがみは，分布（2.11）の対称性の尺度であり，

1βという記号が用いられることがある。

ゆがみは，負の値をとることもあるが，その場合でも，この記号  を用いる。対称な分布

では，ゆがみは，（必要なモーメントが存在するとして）0に等しい。ゆがみが0の分布の例

として，正規分布（2.50），α ＝β のときのベータ分布（2.59），必要なモーメントが存在する

ときのt分布（2.53）などがある。 

注記3 ゆがみ（歪み），ひずみ（歪み）をわいど（歪度）とも呼ぶ。 

注記4 混乱が生じなければ，“母”を省略してもよい。 

2.40  

（母）とがり （ぼ）とがり（coefficient of kurtosis） 

β2 

確率変数（2.10）の標準化確率分布（2.32）についての4次モーメント（2.34）。 

例 2.1及び2.7のバッテリーの例でとがりを計算するために，公式 

E{[X−E(X)]4}＝E(X4)− 4 E(X)E(X3)＋ 6 [E(X) ]2E(X2)−3 [E(X)]4 

を用いる。この結果，とがりは 

[21.6−4(0.9)(5.4)＋6(0.9)2(2)−3(0.9)4]/(0.995)4＝9.12 

となる。（対応国際規格では，9.12を8.94と誤記） 

注記1 (X−μ )/σ の4乗の期待値（2.12），すなわちE[(X−μ )4/σ 4] は，同値な定義である。 

注記2 とがりは，分布（2.11）の裾の重さの尺度である。一様分布（2.60）のとがりは1.8，正規分

布（2.50）のとがりは3，指数分布（2.58）のとがりは9である。 

注記3 報告されたとがりを検討する場合，この定義によって計算される値から3（正規分布のとが

り）を引いてあることがあるので，注意が必要である。この意味で，γ2(＝β2−3) という記号

が用いられることがある。 

注記4 とがり（尖り）をせんど（尖度）とも呼ぶ。 

注記5 混乱が生じなければ，“母”を省略してもよい。 

1β

41 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2.41 

（r，s）次の同時モーメント （r，s）じのどうじもーめんと（joint moment of orders r and s） 

同時確率分布（2.11）について，一つの確率変数（2.10）のr乗ともう一つの確率変数のs乗との積の平

均（2.35）。 

2.42 

（r，s）次の同時中心モーメント （r，s）じのどうじちゅうしんもーめんと（joint central moment of orders 

r and s） 

同時確率分布（2.11）について，一つの中心化確率変数（2.31）のr乗ともう一つの中心化確率変数のs

乗との積の平均（2.35）。 

2.43 

（母）共分散 （ぼ）きょうぶんさん（covariance） 

σXY 

同時確率分布（2.11）について，二つの中心化確率変数（2.31）の積の平均（2.35）。 

注記1 共分散は，二つの確率変数の（1，1）次の同時中心モーメント（2.42）である。 

注記2 E(X)＝μX，E(Y)＝μY のとき，共分散は， 

E[(X−μX)(Y−μY)] 

の式で表される。 

2.44 

母相関係数，相関係数 ぼそうかんけいすう，そうかんけいすう（correlation coefficient） 

同時確率分布（2.11）について，二つの標準化確率変数（2.33）の積の平均（2.35）。 

注記 相関係数は，単に相関と呼ばれることがある。しかしながら，この用法は，二つの変数の関係

性としての相関と重なるので注意が必要である。 

2.45 

多項分布 たこうぶんぷ（multinomial distribution） 

確率質量関数（2.24）が 

(

)

k

x

k

x

x

k

k

k

p

p

p

x

x

x

n

x

X

x

X

x

X

P

Κ

Λ

Λ

2

1

2

1

2

1

2

2

1

1

!

!

!

!

,

,

,

=

=

=

=

ここに，x1，x2，…，xkはx1＋x2＋…＋xk ＝nを満たす非負の整数 

で表される離散分布（2.22）。ただし， 

kは2以上の整数， 

パラメータpi (i＝1，2，…，k) は，pi > 0でp1＋p2＋…＋pk＝1 

を満たす。 

注記 多項分布は，それぞれの試行において互いに排反なk個の事象のいずれかが起き，一連の試行

を通じてそれぞれの事象の確率が不変なとき，n回の独立な試行におけるそれぞれ事象の起こ

る回数の確率を与える。 

2.46 

2項分布 にこうぶんぷ（binomial distribution） 

確率質量関数（2.24）が 

42 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

(

)

(

)

(

)

x

n

x

p

p

x

n

x

n

x

X

P

−

−

−

=

=

1

!

!

!

，x＝0，1，2，…，n 

で表される離散分布（2.22）。ただし，nは，n＝1，2，…であり，パラメータpは，0 < p < 1である。 

例 2.24の例1で説明に用いた確率質量関数は，パラメータn＝3，p＝0.5の2項分布に相当すると考

えることができる。 

注記1 2項分布は，本質的に，多項分布（2.45）においてk＝2とした場合である。 

注記2 2項分布は，それぞれの試行において互いに排反な2個の事象（2.2）のいずれかが起き，一

連の試行を通じて，それぞれの事象の確率（2.5）が不変なとき，n回の独立な試行における

それぞれの事象の起こる回数の確率を与える。 

注記3 2項分布の母平均（2.35）は，npに等しい。2項分布の母分散（2.36）は，np(1−p) に等しい。 

注記4 2項分布の確率質量関数は，2項係数の記号 

(

)!

!

!

x

n

x

n

x

n

−

=

を用いて表してもよい。 

2.47 

ポアソン分布 ぽあそんぶんぷ（Poisson distribution） 

確率質量関数（2.24）が， 

(

)

λ

λ

−

=

=

e

!

x

x

X

P

x

，x＝0，1，2，… 

と表される離散分布（2.22）。ただし，パラメータλは，λ> 0である。 

注記1 2項分布（2.46）においてnp→λとなるように，n→∞，p→0とすればパラメータλのポアソ

ン分布になる。 

注記2 ポアソン分布の母平均（2.35）及び母分散（2.36）は，ともにパラメータλに等しい。 

注記3 ある単位時間における事象の起こり方が，ある条件（例えば，故障率が時刻と無関係である。）

を満たしているとき，ポアソン分布の確率質量関数（2.24）は，単位時間中の事象の生起回

数に関する確率を与える。 

2.48 

超幾何分布 ちょうきかぶんぷ（hypergeometric distribution） 

確率質量関数（2.24）が， 

(

)

(

)

(

)

(

)(

)

(

)

−

+

−

−

−

−

−

=

=

!

!

!

!

!

!

!

!

!

n

N

n

N

x

n

M

N

x

n

M

N

x

M

x

M

x

X

P

ここに，xは，max(0，M−N＋n) ≦ x ≦ min(M，n) を満たす整数， 

で表される離散分布（2.22）。ただし， 

N＝1，2，… 

M＝0，1，2，…，N−1 

n＝1，2，…，N 

である。対応国際規格では，xの範囲の下限をmax(0，M−N) と誤記している。 

注記1 大きさNの母集団（又はロット）にマークの付いたものがM個あるとする。その母集団から

43 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

非復元抽出されたサンプルサイズnの単純ランダムサンプル（1.7）に含まれるマークの付い

たものの数は超幾何分布（2.11）になる。 

注記2 超幾何分布を理解するのに表4を参照するとよい。 

表4−超幾何分布の一般的な例 

全体のアイテム数 

マーク付きアイテム数 

マークなしアイテム数 

母集団 

N 

M 

N−M 

サンプル内 

N 

x 

n−x 

サンプル外 

N−n 

M−x 

N−n−M＋x 

注記3 nがNと比べて小さい場合，超幾何分布は試行回数n，成功確率p＝M/Nの2項分布で近似さ

れる。 

注記4 超幾何分布の母平均（2.35）は， (nM)/Nである。超幾何分布の母分散（2.36）は， 

1

1

−

−

−

N

n

N

N

M

N

M

n

である。 

2.49 

負の2項分布 ふのにこうぶんぷ（negative binomial distribution） 

確率質量関数（2.24）が， 

(

)(

)

(

)

(

)x

c

p

p

c

x

x

c

x

X

P

−

−

−

+

=

=

1

!

1

!

!

1

，x＝0，1，2，… 

で表される離散分布（2.22）。ただし，パラメータcとpは，c > 0と0 < p < 1である。対応国際規格では，

xの範囲の上限をnと誤記しているが，上限はない（上限＝＋∞）。 

注記1 パラメータcが1の負の2項分布は幾何分布である。幾何分布の確率質量関数は，ある事象

（2.2）が生起する確率（2.5）をpとしたとき，その事象（2.2）がx＋1回目に初めて生じる

確率を表す。 

注記2 確率質量関数を， 

(

)

{

}x

c

p

p

x

c

x

X

P

−

−

−

=

=

1

)

(

のように表記してもよい。負の2項分布という名称は，この確率質量関数から名付けられた。

対応国際規格では，確率質量関数の右の部分 {−(1−p)}xを (1−p) xと誤記している。 

注記3 パラメータcが1以上の整数値をとるとき，定義どおりの確率質量関数は“パスカル分布”

と呼ばれる。その場合の確率質量関数は，確率（2.5）pの事象（2.2）の生起する回数がx＋c

試行目にちょうどc回に達する確率をあたえる。 

注記4 負の2項分布の母平均（2.35）は，c(1− p)/pである。負の2項分布の母分散（2.36）は，c(1

− p)/p2である。 

2.50 

正規分布，ガウス分布 せいきぶんぷ，がうすぶんぷ（normal distribution，Gaussian distribution） 

確率密度関数（2.26）が， 

44 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

()

(

)

2

2

2

e

2

1

σ

μ

π

σ

−

=

x

x

f

−

，−∞ < x < ＋∞ 

で表される連続分布（2.23）。ただし，パラメータμ及びσは，−∞ < μ < ＋∞，σ > 0である。 

注記1 正規分布は統計的方法では，最もよく用いられる確率分布（2.11）の一つである。確率密度

関数の形状から，俗に（西洋の）釣鐘型の分布と呼ばれている。正規分布は確率現象を表す

モデルであるだけではなく，標本平均（1.15）の分布の極限でもある。また，実験の妥当性

を評価するために，統計的方法において参照用の分布としてもよく用いられている。 

注記2 正規分布で，位置母数μは母平均（2.35）であり，尺度母数σは母標準偏差（2.37）である。 

2.51 

標準正規分布 ひょうじゅんせいきぶんぷ（standardized normal distribution，standardized Gaussian 

distribution） 

μ＝0，σ＝1の正規分布（2.50）。 

注記 標準正規分布の確率密度関数（2.26）は， 

()

2

2

e

2

1

x

x

f

−

π

=

，−∞ < x < ＋∞ 

で表される。一般の数値表では，様々なxの値に対して，標準正規分布の確率密度関数の積分

値を正規分布表として与えている。 

2.52 

対数正規分布 たいすうせいきぶんぷ（lognormal distribution） 

確率密度関数（2.26）が， 

()

(

)

2

2

2

In

e

2

1

σ

μ

π

σ

−

−

=

x

x

x

f

，x > 0 

で表される連続分布（2.23）。ただし，パラメータμ及びσは，−∞ < μ < ＋∞とσ > 0である。 

注記1 Yが母平均（2.35）μ，母標準偏差（2.37）σの正規分布（2.50）に従うとき，X＝exp(Y) で変

換されるXは定義に示された確率密度関数をもつ対数正規分布に従う。逆に，Xが定義に示

された確率密度関数をもつ対数正規分布に従うとき，ln(X) は母平均μ，母標準偏差σの正規

分布に従う。 

注記2 対数正規分布の母平均は，exp[μ＋(σ2/2)] である。対数正規分布の母分散は，exp(2μ＋σ2)×

[exp(σ2)−1] である。これは，対数正規分布の母平均と母分散が正規分布のパラメータμとσ2

の関数であることを意味している。 

注記3 対数正規分布とワイブル分布（2.63）は，信頼性工学の分野でよく用いられる。 

2.53 

t分布，スチューデント分布 てぃーぶんぷ，すちゅーでんとぶんぷ（t distribution，Studentʼs distribution） 

確率密度関数（2.26）が， 

()

(

)

[

]

(

)

(

)2

1

2

1

2

2

1

+

−

+

×

Γ

+

Γ

=

v

v

t

v

v

v

t

f

π

，−∞ < t < ＋∞ 

で表される連続分布（2.23）。ただし，パラメータvは，正の整数である。 

45 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記1 母標準偏差をデータから推定した場合に，標本平均（1.15）の評価するためにt分布はよく用

いられている。母平均がある特定の値に等しいかどうかの判定は，t統計量と自由度n−1の

t分布とを比較で可能となる。 

注記2 分子は標準正規分布（2.51）に従う確率変数，分母は分子と独立にカイ2乗分布（2.57）に従

う確率変数を自由度で割って正の平方根をとったものである分数を考えたとき，その分数は

t分布に従う。パラメータvは，自由度（2.54）と呼ばれる。 

注記3 ガンマ関数は，2.56で定義されている。 

2.54 

自由度 じゆうど（degrees of freedom） 

v 

和における項の数からそれらの項に対する制約式の数を引いたもの。 

注記 この概念は，分散（2.36）の推定量（1.12）の分母にn−1を用いる理由のところで既に記述さ

れている。自由度の数はパラメータを修正するのに使われる。自由度という用語は，JIS Z 8101-3

で広く用いられており，自由度で割った平方和を平均平方と定義している。 

2.55 

F分布 えふぶんぷ（F distribution） 

確率密度関数（2.26）が， 

()

(

)

[

]

(

)(

)()

()

(

)

(

)(

)2

2

1

1

2

2

2

2

1

2

1

2

1

2

1

1

2

1

2

2

2

v

v

v

v

v

v

x

v

x

v

v

v

v

v

v

x

f

+

−

+

Γ

Γ

+

Γ

=

，x > 0 

で表される連続分布（2.23）。ただし，パラメータv1，v2は正の整数であり，ガンマ関数は2.56で定義され

ている。 

注記1 F分布は，母分散（2.36）の比を評価するための参照用の分布である。 

注記2 独立な二つのχ 2分布（2.57）に従う確率変数をそれぞれの自由度（2.54）で割ったものの比

は分子の自由度ν1，分母の自由度ν2のF分布に従う。 

2.56 

ガンマ分布 がんまぶんぷ（gamma distribution） 

確率密度関数（2.26）が， 

()

()

α

βα

β

α

Γ

=

−

−

x

x

x

f

e

1

，x > 0 

で表される連続分布（2.23）。ただし，パラメータα及びβは，α > 0及びβ > 0である。 

注記1 ガンマ分布は，信頼性工学における故障時間の分布として用いられる。指数分布（2.58）は，

ガンマ分布の特殊な場合である。また，故障率が時間とともに増加するモデルもガンマ分布

で表現できる。 

注記2 ガンマ関数の定義は， 

()∫∞

−

−

=

Γ

0

1

d

e

x

x

x

α

α

，α > 0 

である。αが整数のとき，Γ(α)＝(α−1)! である。 

注記3 ガンマ分布の母平均（2.35）は，αβである。ガンマ分布の母分散（2.36）は，αβ2である。 

2.57 

カイ2乗分布，χ 2分布 かいにじょうぶんぷ（chi-squared distribution，χ 2 distribution） 

46 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

確率密度関数（2.26）が， 

()

( )2

2

e

2

2

1

2

v

x

x

f

v

x

v

Γ

=

−

−

，x > 0 

で表される連続分布（2.23）。ただし，νは，v > 0である。 

注記1 データが正規分布（2.50）に従い，母標準偏差（2.37）σが既知である場合，統計量nS 2/σ 2

は自由度n−1のカイ2乗分布に従う。この結果からσ 2の信頼区間を構成できる。また，カ

イ2乗分布は適合度検定の参照用の分布としても用いられる。 

注記2 カイ2乗分布はガンマ分布（2.56）のパラメータをα＝v/2，β＝2とした場合に当たる。この

パラメータvは，自由度（2.54）と呼ばれる。 

注記3 カイ2乗分布の母平均（2.35）はvであり，母分散（2.36）は2vである。 

2.58 

指数分布 しすうぶんぷ（exponential distribution） 

確率密度関数（2.26）が， 

()

β

β

x

x

f

−

−

=

e

1

，x > 0 

で表される連続分布（2.23）。ただし，パラメータβは，β > 0である。 

注記1 信頼性工学において，指数分布は非経年変化性又は無記憶性を表すための基本的なモデルで

ある。 

注記2 指数分布はガンマ分布（2.56）のパラメータαを1とした場合に当たり，また，カイ2乗分

布（2.57）のパラメータvを2とした場合にも当たる。 

注記3 指数分布の母平均（2.35）はβであり，母分散（2.36）はβ 2である。 

2.59 

ベータ分布 べーたぶんぷ（beta distribution） 

確率密度関数（2.26）が， 

()

(

)

()()

(

)

1

11

−

−

−

Γ

Γ

+

Γ

=

β

α

β

α

β

α

x

x

x

f

，0 ≦ x ≦ 1 

で表される連続分布（2.23）。ただし，パラメータα及びβは，α > 0及びβ > 0である。 

注記 ベータ分布の確率密度関数は，様々な形状（単峰型，J型，U型）をとる。ベータ分布は，比

率に関係する不確かさのモデルとして用いられる。例えば，ハリケーン保険のハリケーン被害

のモデル化において，ある与えられた風速に対する建造物の損傷率は，家屋によって異なるが，

その平均損傷率は0.40であるとする。母平均が0.40であるベータ分布は，建造物に対する損傷

率のモデルとして用いることができる。 

2.60 

一様分布 いちようぶんぷ（uniform distribution，rectangular distribution） 

確率密度関数（2.26）が， 

()

a

b

x

f

−

=

1

，a ≦ x ≦ b 

で表される連続分布（2.23）。 

注記1 a＝0，b＝1の一様分布は典型的な乱数生成のもととなる分布である。 

47 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

注記2 一様分布の母平均（2.35）は，(a＋b)/2であり，母分散（2.36）は (b−a)2/12である。 

注記3 a＝0，b＝1の一様分布は，ベータ分布のパラメータをα＝1，β＝1とした場合に当たる。 

2.61 

タイプI極値分布，グンベル分布，二重指数分布 たいぷいちきょくちぶんぷ，ぐんべるぶんぷ，にじゅ

うしすうぶんぷ（type I extreme value distribution，Gumbel distribution） 

分布関数（2.7）が， 

()

(

)b

a

x

x

F

−

−

−

=

e

e

，−∞ < x < ＋∞ 

で表される連続分布（2.23）。ただし，パラメータa及びbは，−∞ < a <＋∞及びb > 0である。 

注記 極値分布は一番端の順序統計量（1.9）X(1) 及びX(n) の参照用の分布を与える。nを十分に大き

くしたとき，その極限分布は3通りの可能性しかなく，2.61，2.62及び2.63で示された三つの

タイプの極値分布のどれかである。 

2.62 

タイプII極値分布，フレシェ分布 たいぷにきょくちぶんぷ，ふれしぇぶんぷ（type II extreme value 

distribution，Fréchet distribution） 

分布関数（2.7）が， 

()

k

b

a

x

x

F

−

−

−

=e

，x > a 

で表される連続分布（2.23）。パラメータa，b及びkは，−∞ < a <＋∞，b > 0，k > 0である。 

2.63 

タイプIII極値分布，ワイブル分布 たいぷさんきょくちぶんぷ，わいぶるぶんぷ（type III extreme value 

distribution，Weibull distribution） 

分布関数（2.7）が， 

()

k

b

a

x

x

F

−

−

−

=

e

1

，x > a 

で表される連続分布（2.23）。パラメータa，b及びkは，−∞ < a <＋∞，b > 0，k > 0である。 

注記1 最大値，最小値の分布の極限がとり得る三つの分布のうちの一つである。ワイブル分布は様々

な応用分野，とりわけ信頼性工学で重要な分布である。ワイブル分布は多種多様なデータに

対する適合性の良いことが経験的に知られている。 

注記2 パラメータaは，データのとり得る値の下限であるという意味での位置母数である。パラメ

ータbは，尺度母数［ワイブル分布の標準偏差（2.37）に関係している。］である。パラメー

タkは形状母数である。 

注記3 k＝1のワイブル分布は，指数分布である。ワイブル分布においてa＝0とし，xを1/k乗すれ

ば，指数分布を得ることができる。レイリー分布はワイブル分布のパラメータをa＝0，k＝2

とした場合に当たる。 

2.64 

多変量正規分布 たへんりょうせいきぶんぷ（multivariate normal distribution） 

確率密度関数（2.26）が， 

(

)

(

)

2

2/1

2/

1

e

)

2(

)

(

μ

μ

−

Σ

−

−

−

−

−

=

x

x

x

T

Σ

f

n

π

，各xの要素xiは−∞ < xi < ＋∞ 

48 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

で表される連続分布（2.23）。ただし，μはn次元パラメータベクトル，Σはパラメータを要素とするn×n

対称行列で，正値定符号行列である。太字はn次元ベクトルを示す。対応国際規格では，確率密度関数の

中で (2π)−n /2|Σ |−1/2を (2π)− π/2|Σ |−n /2と誤記している。 

注記 多変量正規分布の周辺分布（2.18）は，いずれも正規分布である。しかし，多変量正規分布の

ほかに周辺分布が正規分布となる多変量分布は数多く存在する。 

2.65 

2変量正規分布 にへんりょうせいきぶんぷ（bivariate normal distribution） 

確率密度関数（2.26）が， 

(

)

−

+

−

−

−

−

−

−

−

=

2

2

2

2

2

)

1(2

1

exp

1

2

1

,

y

y

y

y

x

x

x

x

y

x

y

y

x

x

y

x

f

σ

μ

σ

μ

σ

μ

ρ

σ

μ

ρ

ρ

σ

πσ

−∞ < x，y <＋∞ 

で表される連続分布（2.23）。ただし，μx，μyは，−∞ < μx，μy <＋∞であり，σx，σy，ρは，σx，σy >0，|ρ| < 

1である。 

注記1 上記の確率密度関数（2.26）をもつ確率変数の組 (X，Y) について，X及びYの母平均，母分

散は，E(X)＝μx，E(Y)＝μy，V(X)＝σx2，V(Y)＝σy2であり，X及びYの母相関係数（2.44）はρ

である。 

注記2 この2変量正規分布の周辺分布は，正規分布になる。Y＝yという条件付きのXの分布は，X

＝xという条件付きのYの分布も同様であるが，正規分布になる。 

2.66 

標準2変量正規分布 ひょうじゅんにへんりょうせいきぶんぷ（standardized bivariate normal distribution） 

標準正規分布（2.51）を周辺分布にもつ2変量正規分布（2.65）。 

2.67 

標本分布，サンプリング分布 ひょうほんぶんぷ，さんぷりんぐぶんぷ（sampling distribution） 

統計量の分布。 

注記 標本分布の例は，2.53の注記2，2.55の注記1及び2.57の注記1に示されている。 

2.68 

確率空間 かくりつくうかん（probability space） 
（Ω，ℵ，

） 

標本空間（2.1），σ集合体（2.69），確率測度（2.70）の三つ組。 

例1 単純な場合として，標本空間が工場である日に作られた全ての製品105個からなるとする。σ

集合体は標本空間の全ての部分集合からなる。書き下すと，空集合，｛製品1｝，｛製品2｝，…，

｛製品105｝，｛製品1，製品2｝，…，｛105個すべての製品｝である。例えば，一つの事象に属

する製品数を全製品数で割った比率で確率測度を定義することができる。その場合，事象｛製

品4，製品27，製品92｝は，3/105という確率をもつ。 

例2 二つ目の例として，バッテリーの寿命を取り上げる。バッテリー購入時に既に故障していた場

合，寿命を0時間とする。バッテリーが機能していたとすると，その寿命は指数分布（2.58）

のようなある確率分布（2.11）に従う。このとき観測される寿命値に，離散データ（既に故障

しているバッテリーの割合）及び連続データ（寿命値）の2種類が混在する。この例を簡単に

するために，全ての寿命時間は調査期間より短いと仮定し，連続値であるということを仮定し

49 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

ている。実際には，右又は左打切りデータ（例えば，寿命時間が少なくとも5時間であると分

かっている場合，寿命時間が3時間から3.5時間の間である場合など）が含まれる可能性があ

り，その場合にこの構造の有用性が明らかとなる。標本空間は，半直線（0以上の実数）から

なる。σ集合体は [0，x) の形の区間の全て及び集合 {0} を含んでいる。さらに，σ集合体は

可算個のこれらの集合の和と，可算個のこれらの集合の共通部分の全てを含む。確率測度は，

各集合に対して確率を与える。σ集合体には，バッテリーが既に故障しているという事象，及

びバッテリーがある正の寿命値をもつという事象も含まれる。寿命時間に関連する計算の詳細

は，別に示した。 

2.69 

σ集合体，σ加法族 しぐましゅうごうたい，しぐまかほうぞく（sigma algebra of events，σ-algebra，sigma 

field，σ-field） 

ℵ 

次の性質をもつ事象（2.2）の集合。 

a) Ω は，ℵに属する。 

b) ある事象がℵに属するならば，その余事象（2.3）もまたℵに属する。 

c) 事象列 {Ai} がℵに含まれるならば，和集合Υ∞=1

i

iA及び共通部分Ι∞=1

i

iAもℵに属する。 

例1 標本空間が整数の集合であるならば，σ集合体を整数の全ての部分集合からなる集合とするこ

とができる。 

例2 標本空間が実数の集合であるならば，σ集合体を数直線上の区間に対応する全ての集合，並び

にそれらの有限個又は可算無限個の和集合及び共通部分を含むようにとることができる。この

例は，k次元“区間”を考えることによってより高次元へ拡張することが可能である。特に，2

次元において，区間の集合は実数s，tの全てに対して {(x，y) : x < s，y < t} で定義される領域

からなる。 

注記1 σ集合体は，集合を要素としてもつ集合である。性質a) で述べたように，全ての可能な結果

の集合であるΩ は，σ集合体に含まれる。 

注記2 性質c) にはσ集合体の（高々可算無限個の）部分集合を集めるという集合演算が含まれ，可

算個のこれらの集合の和と可算個のこれらの集合の共通部分のいずれもまたσ集合体に属す

ることを意味している。 

注記3 性質c) は有限個の集合の和，及び共通部分をとる演算についても閉じている（演算結果がσ

集合体に属する）ことを示している。σ集合体の記号σは，ℵが集合の可算無限回の演算で

さえも閉じていることを強調するために用いられる。 

注記4 対応国際規格では，a) で，“  は  に属する”と誤記している。 

2.70 

確率測度 かくりつそくど（probability measure） 

次の条件a)，b) を満たすσ集合体上で定義される非負関数。 

a) 

(Ω)＝1 

ただし，Ω は標本空間（2.1）， 

ℵ

ℵ

50 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

b) (

)

()

∑∞=

∞

=

=

1

1

i

i

i

i

A

A

Υ

ただし，{Ai} は互いに排反な事象（2.2）列。 

例 2.1のバッテリー寿命の例の続きで，バッテリーが1時間未満で故障するという事象を考えよう。

この事象は，｛初めから機能しない｝及び｛初めは機能するが1時間未満で故障する｝という二つ

の排反な事象からなる。これを {0} 及び (0，1) のように表しても等価である。{0} の確率測度

は，初めから機能しないバッテリーの割合である。集合 (0，1) の確率測度は，ある特定の故障

時間を表す連続確率分布［例えば，指数分布（2.58）］によって定まる。 

注記1 確率測度は，σ集合体中の各事象に対して閉区間 [0，1] 内のある値を与える。絶対生起する

ことのない事象に値0を，必ず生じる事象に1を与える。特に，確率測度は空集合に0を与

え，標本空間（全事象）に1を与える。 

注記2 性質b) は，任意の二つの事象の共通部分に要素がないとき和集合の確率測度は個々の事象

に対する確率測度の和であることを意味している。このことは，事象の数が可算無限個であ

る場合にも成り立つ。 

注記3 確率空間の三つ組は，確率変数を介して効果的に関係付けられる。確率変数（2.10）の像集

合内の事象に対する確率（2.5）は，標本空間内の対応する事象の確率から導かれる。確率変

数の像集合内の事象は，確率変数の像集合上へ確率変数によって移される標本空間内のもと

の事象の確率が割り当てられる。 

注記4 確率変数の像集合は実数の集合，又はn次元実ベクトルの集合である（像集合とは，写像で

ある確率変数によって対応付けられた集合である。）。 

51 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書A 

（参考） 

記号 

記号 

用語 

英語 

箇条 

A 

事象 

event 

2.2 

Ac 

余事象 

complementary event 

2.3 

ℵ 

σ 集合体，σ 加法族 

sigma algebra of events， 

σ-algebra，sigma field, σ-field 

2.69 

α 

有意水準 

significance level 

1.45 

α，λ，μ，β， 
σ，ρ，γ， 
p，N，M，c， 
ν，a，b，k 

パラメータ 

parameter 

2.9 

β2 

（母）とがり 

coefficient of kurtosis 

2.40 

E(X k) 

k次の標本モーメント 

sample moment of order k 

1.14 

E[g(X)] 

期待値 

expectation of the function g of a 
random variable X 

2.12 

F(x) 

分布関数 

distribution function 

2.7 

f (x) 

確率密度関数 

probability density function 

2.26 

γ1 

（母）ひずみ 

coefficient of skewness 

2.39 

H 

仮説 

hypothesis 

1.40 

H0 

帰無仮説 

null hypothesis 

1.41 

HA，H1 

対立仮説 

alternative hypothesis 

1.42 

k 

次元の数 

dimension 

k，r，s 

モーメントの次数 

order of a moment 

1.14，2.34，
2.41，2.42 

μ 

平均 

mean 

2.35 

ν 

自由度 

degrees of freedom 

2.54 

n 

サンプルサイズ 

sample size 

Ω 

標本空間 

sample space 

2.1 

(Ω，ℵ，

) 

確率空間 

probability space 

2.68 

P(A) 

事象Aの確率 

probability of an event A 

2.5 

P(A | B) 

条件付き確率 

conditional probability of A given B 

2.6 

確率測度 

probability measure 

2.70 

rxy 

標本相関係数 

sample correlation coefficient 

1.23 

s 

標本標準偏差の実現値 

observed value of a sample standard 
deviation 

S 

標本標準偏差 

sample standard deviation 

1.17 

S2 

標本分散，不偏分散 

sample variance 

1.16 

SXY 

標本共分散 

sample covariance 

1.22 

σ 

母標準偏差，標準偏差 

standard deviation 

2.37 

σ 2 

母分散，分散 

variance 

2.36 

σXY 

（母）共分散 

covariance 

2.43 

52 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

記号 

用語 

英語 

箇条 

θ

σˆ 

標準誤差 

standard error 

1.24 

X

σ 

標本平均の標準誤差 

standard error of the sample mean 

θ 

分布のパラメータ 

parameter of a distribution 

θˆ 

推定量 

estimator 

1.12 

V(X) 

母分散，分散 

variance of a random variable X 

2.36 

X(i) 

順序統計量 

ith order statistic 

1.9 

x, y, z 

観測値，測定値 

observed value 

1.4 

X, Y, Z, T 

確率変数，変量 

random variable 

2.10 

Xp, xp 

p分位点，100pパーセント点 

p-quantile 
p-fractile 

100p-percentile 

2.13 

X, x 

標本平均，平均，算術平均 

average, sample mean 

1.15 

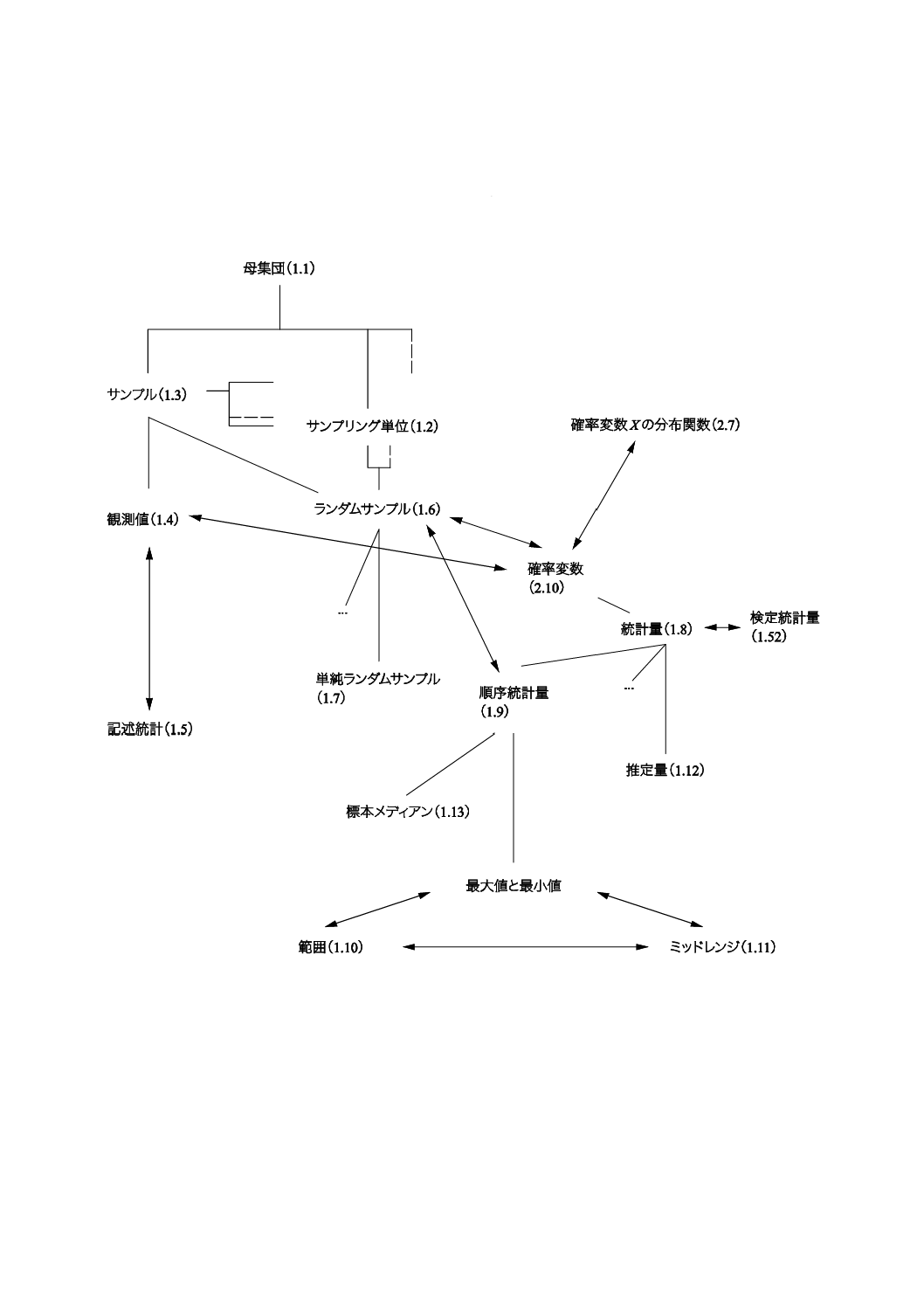
53 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書B 

（参考） 

統計に関するコンセプトダイアグラム 

図B.1−母集団及びサンプルに関するコンセプトダイアグラム 

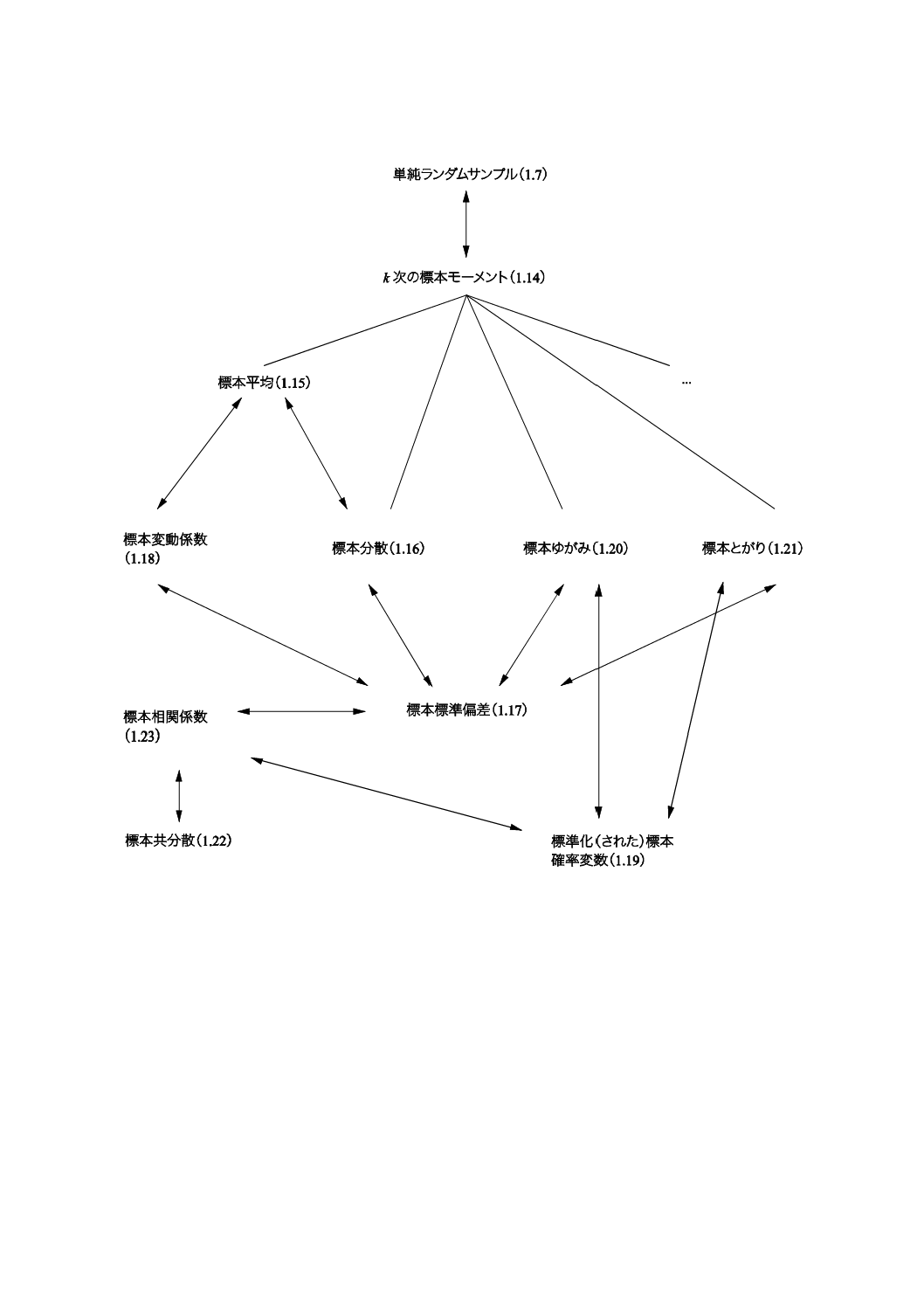
54 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図B.2−サンプルモーメントに関するコンセプトダイアグラム 

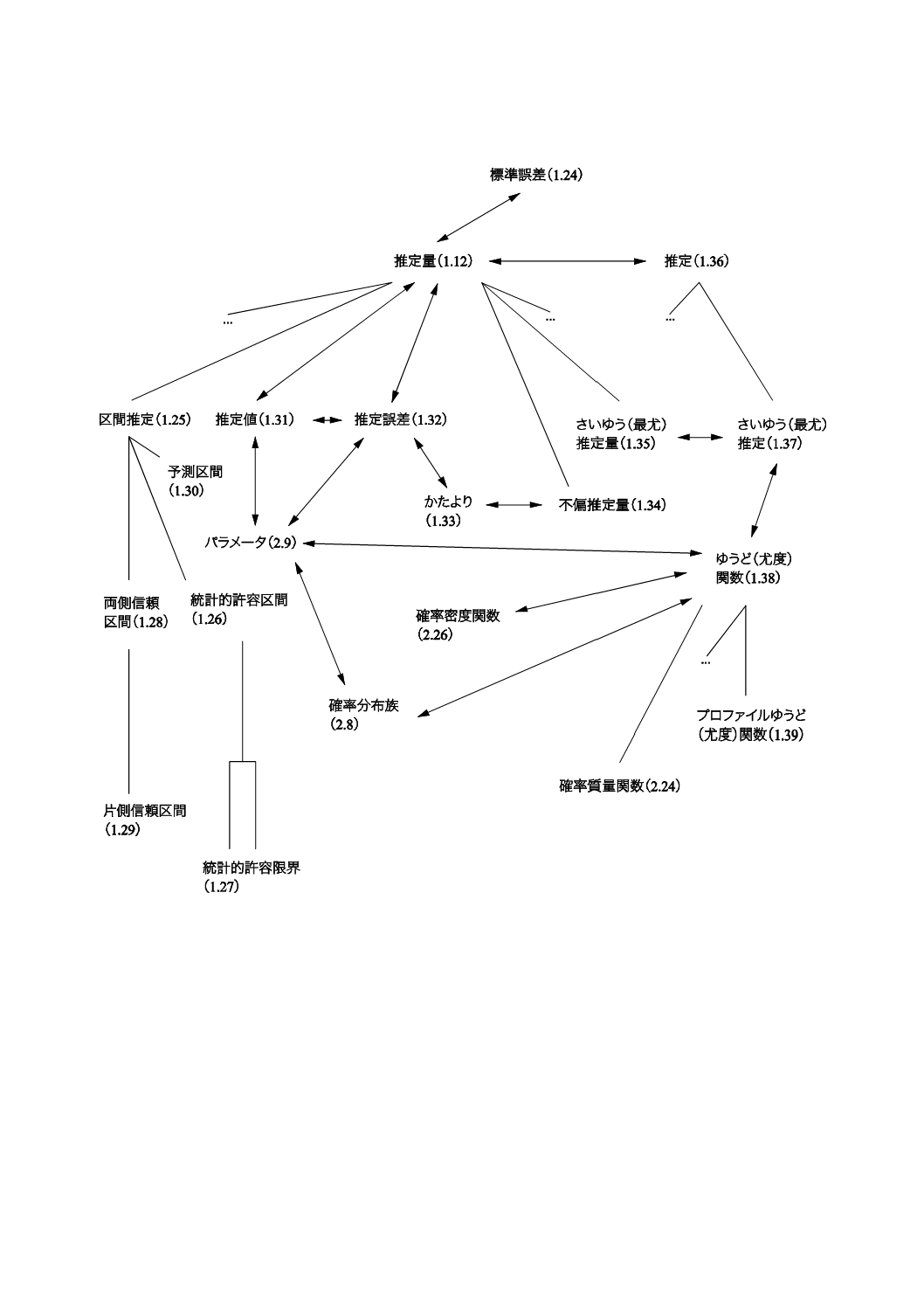
55 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図B.3−推定に関するコンセプトダイアグラム 

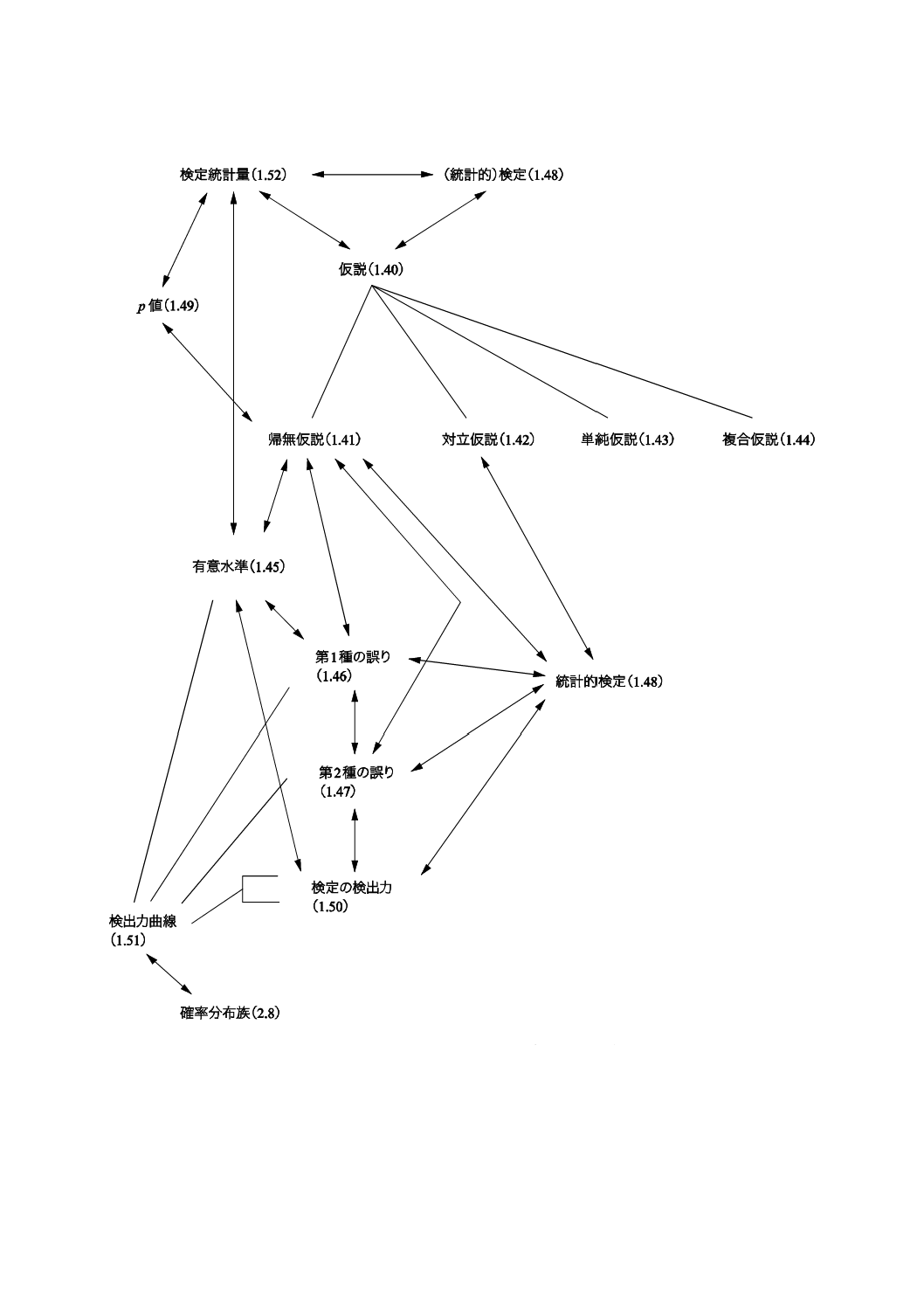
56 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図B.4−統計的検定に関するコンセプトダイアグラム 

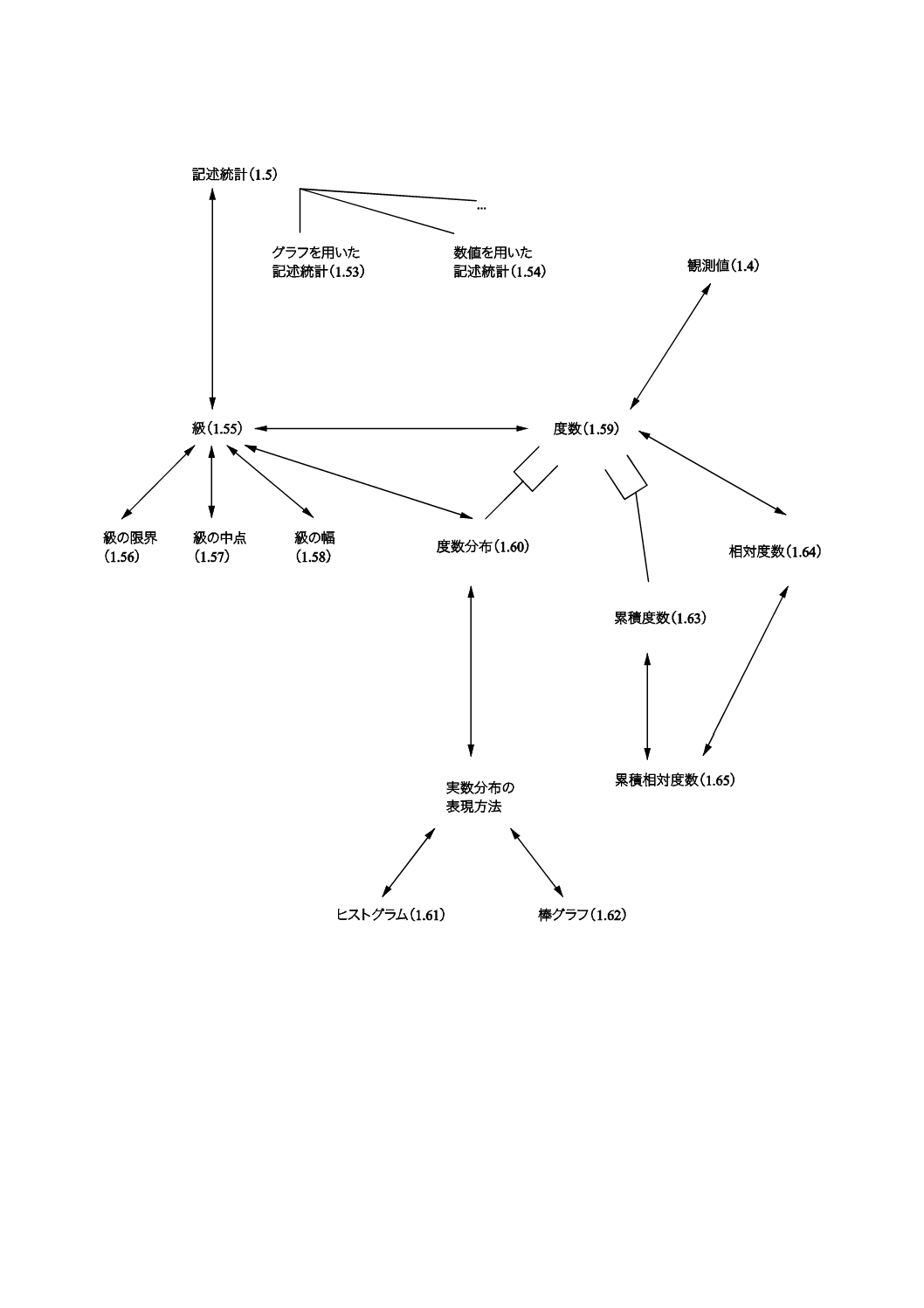
57 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図B.5−度数分布及び級に関するコンセプトダイアグラム 

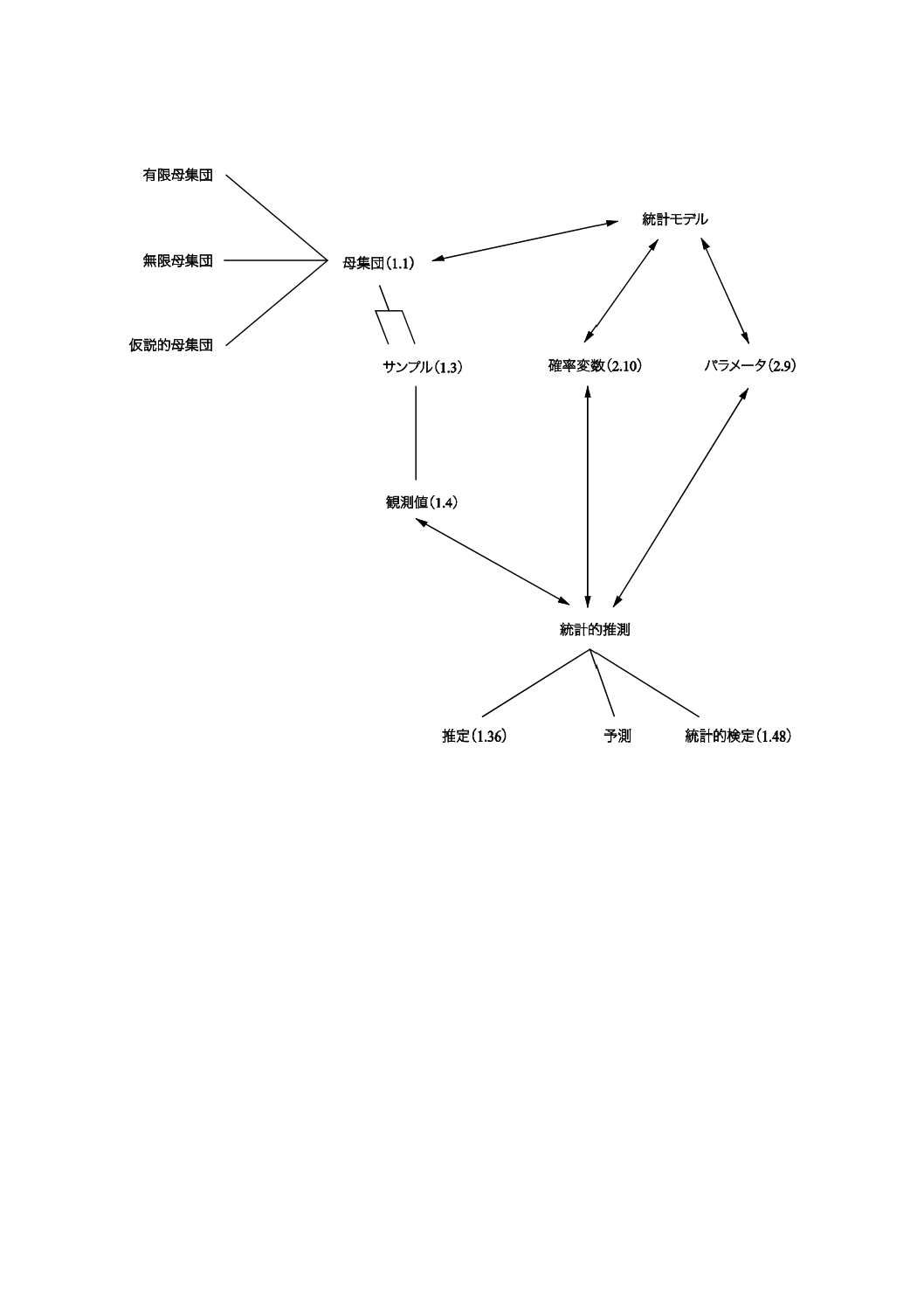
58 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図B.6−統計的推測に関するコンセプトダイアグラム 

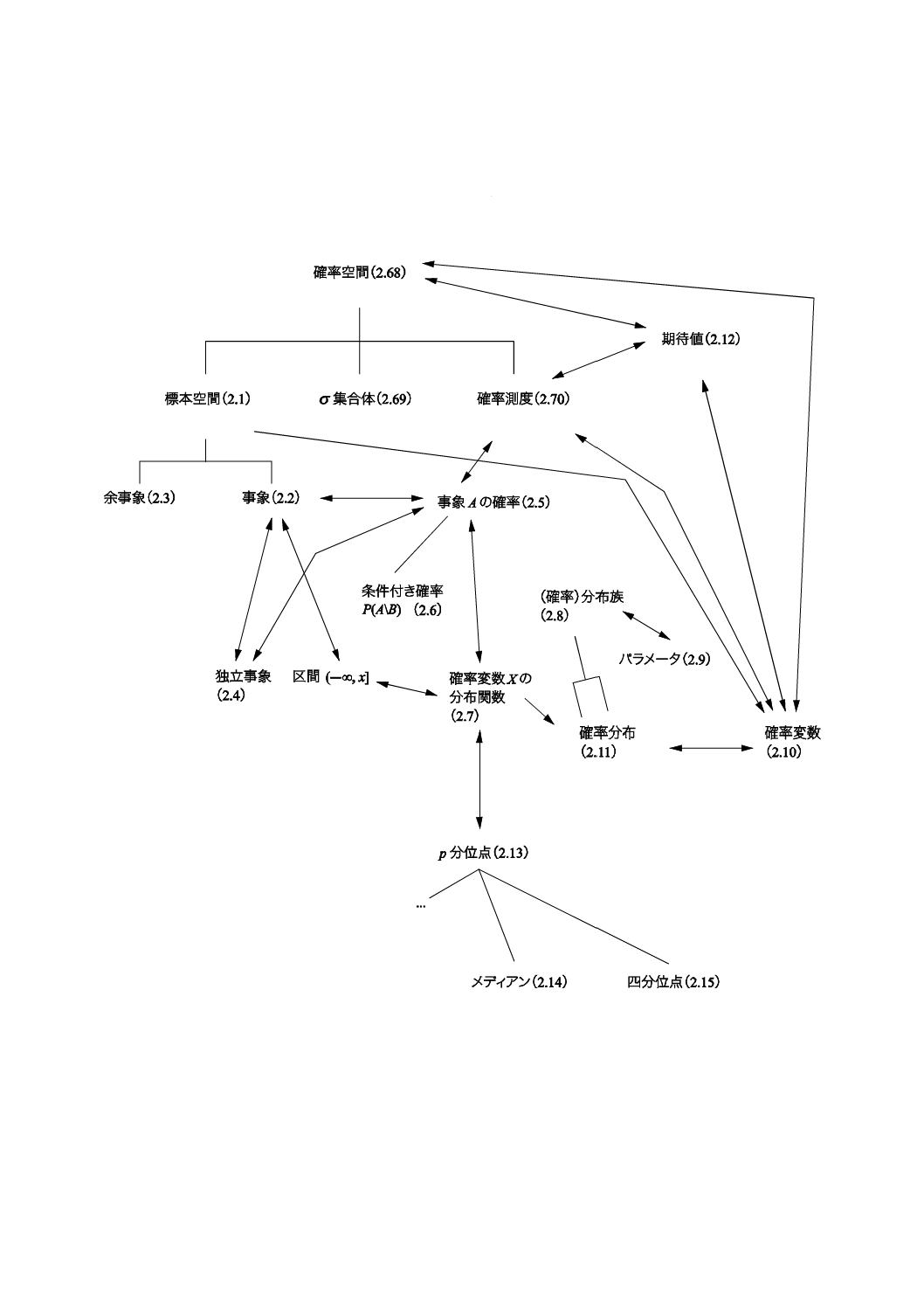
59 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書C 
（参考） 

確率に関するコンセプトダイアグラム 

図C.1−確率の基本に関するコンセプトダイアグラム 

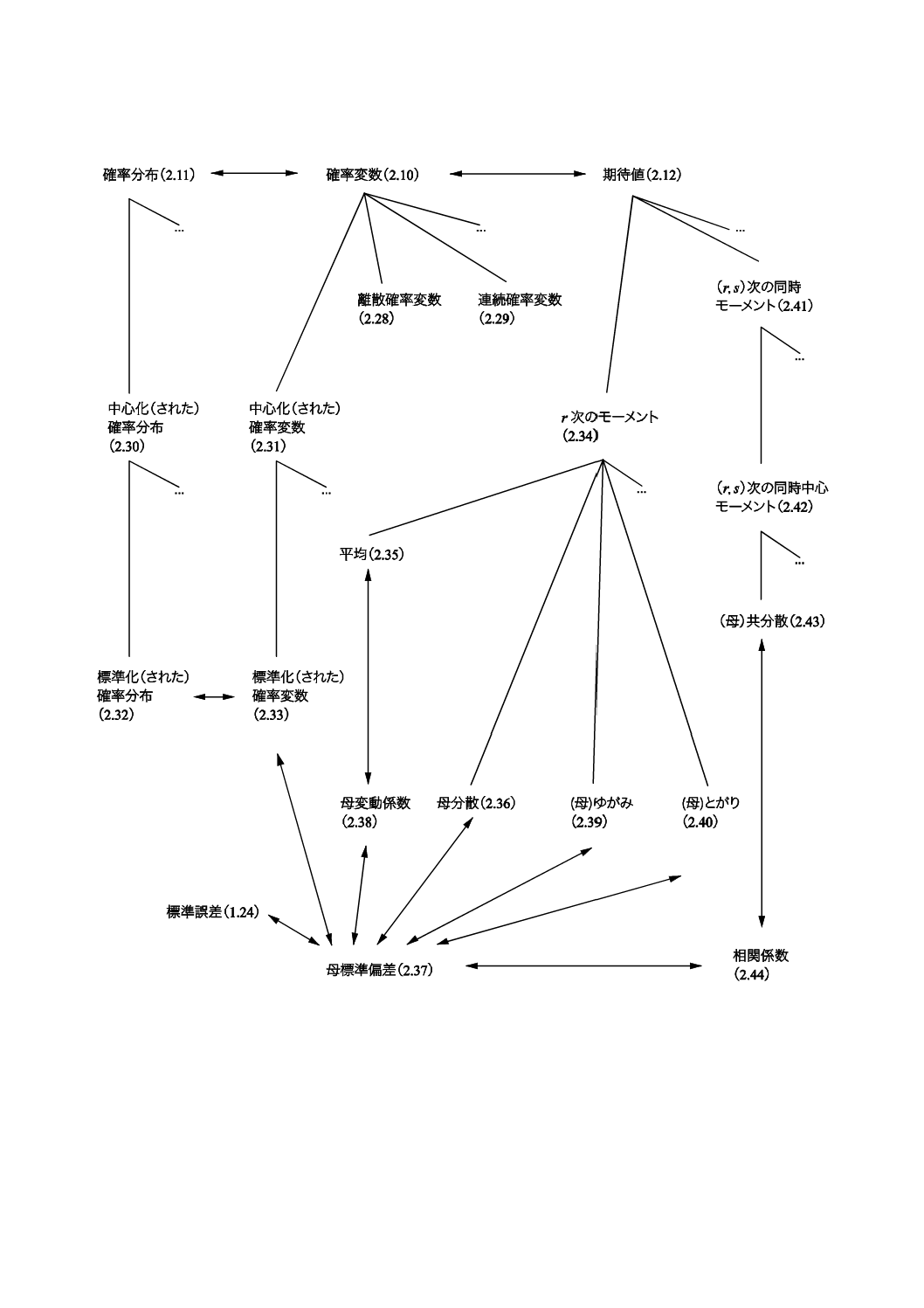
60 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図C.2−モーメントに関するコンセプトダイアグラム 

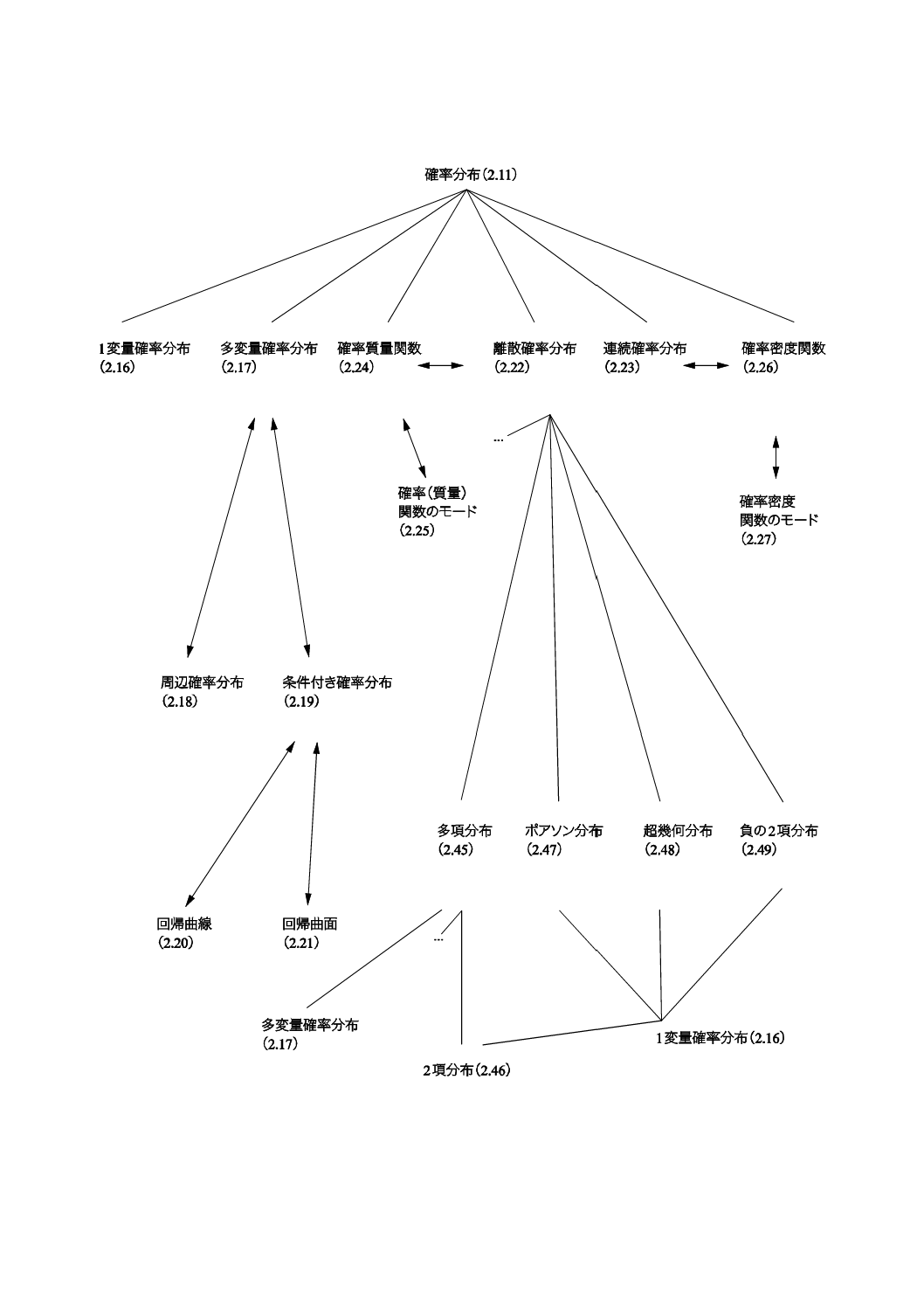
61 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図C.3−確率分布に関するコンセプトダイアグラム 

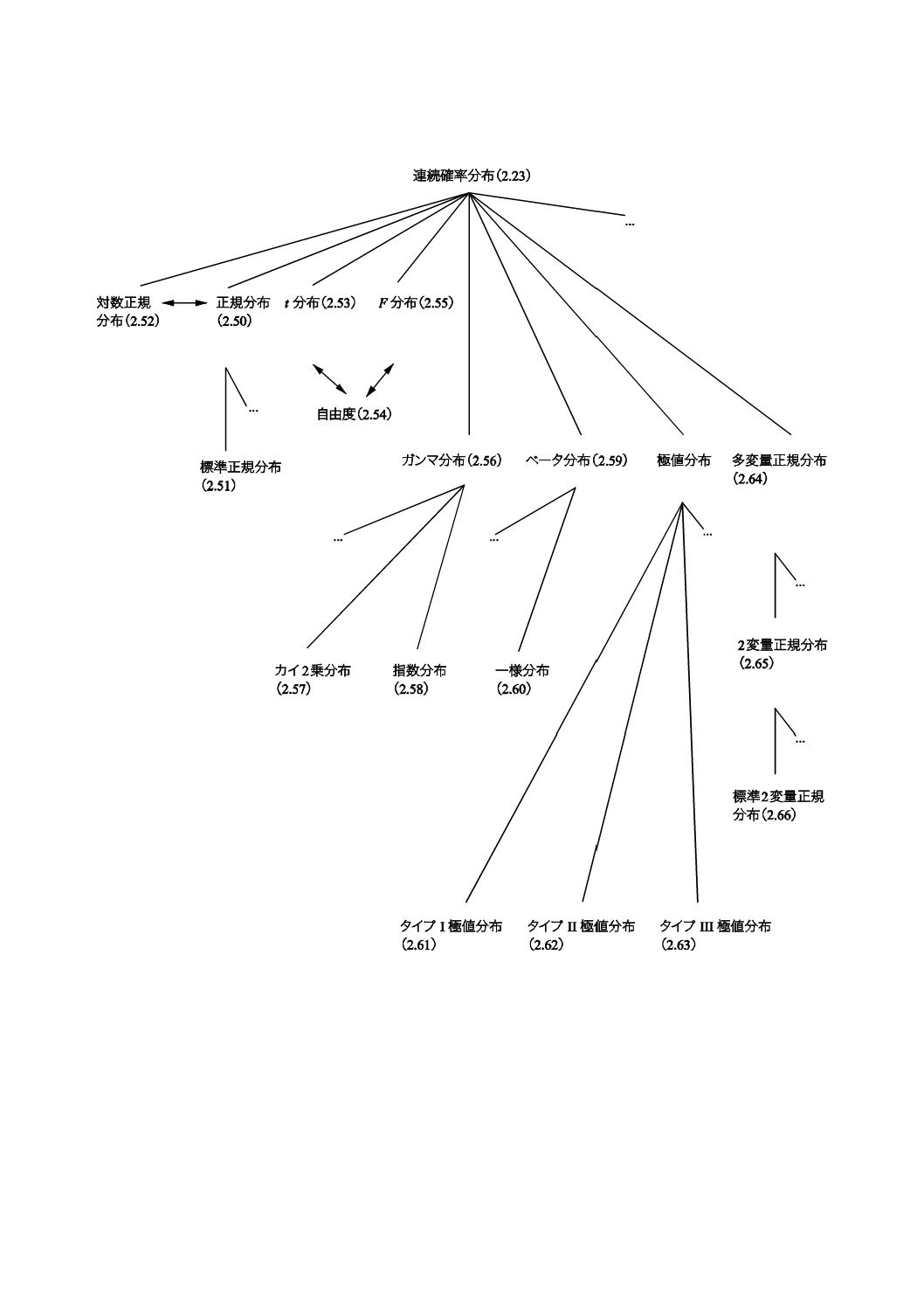
62 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図C.4−連続分布に関するコンセプトダイアグラム 

63 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書D 
（参考） 

用語の開発に用いた方法論 

D.1 序文 

JISを普遍的に適用するためには，統計的方法の規格を使用する可能性のある全ての利用者にとって，

分かりやすく，相互に矛盾のない，調和のとれた用語が用いられていることが要求される。 

概念というものは互いに独立してはいないので，統計的方法の分野で用いられる概念の相互関係を分析

し，概念の体系として整理することは，相互に矛盾のない用語を作成する上で不可欠である。このような

分析がこの規格の原案作成に際して行われた。原案作成作業で用いられたコンセプトダイアグラムは参考

として有用と考え，D.4に採録した。 

D.2 見出し語の内容及び置換えルール 

概念は，言語間の変換の単位となる（一つの言語の中での変形を含む。例えば，米語，英語など）。それ

ぞれの言語ごとに，その言語における概念を普遍的に分かりやすくするための最適な用語の選択，すなわ

ち翻訳に対する文学的ではない方法が選択される。 

ある定義は，概念を明確にするために本質的な特性だけを記述することによって行われる。重要ではあ

るが，その説明に本質的ではない概念に関する情報は，その定義の参考に記述される。 

用語をその定義で置き換えるとき，小さな構文上の変更は行うにしても，文章の意味が変わることは望

ましくない。このような置き換えは，定義の正確さをチェックする簡単な方法である。しかし，定義が多

くの用語を含み，意味が複雑な場合には，置き換えは一度に一つ又は多くとも二つにとどめないとうまく

いかない。用語の全文を置き換えることは，構文的に実現が難しくなり，また，意味を伝える助けになら

ないであろう。 

D.3 概念の相互関係及び図示 

D.3.1 一般 

概念間の相互関係は“種”の特性の階層構造に基づくので，用語の定義作業において，概念の最も容易

な記述は，その“種”に名前を付けること，及びその親の概念又は兄弟の概念とを区別する特性を記述す

ることによって行える。 

この附属書に示された概念間の相互関係には，三つの基本形がある。それは一般的関係（D.3.2），部分

的関係（D.3.3）及び連関的関係（D.3.4）である。 

D.3.2 一般的関係 

階層内の下位概念は，上位概念の全ての特性を受け継ぎ，また，上位（親）の概念及び同位（兄弟）の

概念と区別する特性についての記述を含む。例えば，“春夏秋冬”と“季節”との関係である。 

一般的関係は，矢印なしの扇又は樹形図で示される（図D.1参照）。 

64 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図D.1−一般的関係の図示 

D.3.3 部分的関係 

階層内の下位概念が，上位概念の構成部分を形成する。例えば，“春夏秋冬”は，“年”という概念の部

分として定義してもよい。これに対し，“晴天”（夏の一つの特性）を“年”の部分として定義するのは不

適切である。 

部分的関係は矢印なしのレーキ（熊手）の記号で示される（図D.2参照）。単数の部分は一本の直線で，

複数の部分は二重線で示される。 

図D.2−部分的関係の図示 

D.3.4 連関的関係 

連関的関係は，一般的関係及び部分的関係で示したように簡単には記述できないが，概念の体系の中で，

一つの概念及び他の概念の関係の性質を明確にするために役立つ。例えば，原因及び結果，活動及び位置，

活動及び結果，道具及び機能，材料，製品などである。 

連関的関係は，両端に矢印のある直線で示される（図D.3参照）。 

図D.3−連関的関係の図示 

D.4 コンセプトダイアグラム（概念体系図） 

図B.1〜B.5までは，この規格の箇条1によって定義される用語のコンセプトダイアグラムである。図

B.6は，図B.1〜B.5の中に既に登場する特定の用語の関係を示す，追加のコンセプトダイアグラムである。

図C.1〜C.4は，この規格の箇条2で定義される用語の概念図である。幾つかの用語は，複数のコンセプト

ダイアグラムに登場し，それが図をつな（繋）げる役目をしている。その用語は，以下の表のとおりであ

る。 

65 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図B.1 母集団及びサンプルに関する概念 

記述統計（1.5） 

図B.5 

単純ランダムサンプル（1.7） 

図B.2 

推定量（1.12） 

図B.3 

検定統計量（1.52） 

図B.4 

確率変数（2.10） 

図C.1，C.2 

分布関数（2.7） 

図C.1 

図B.2 サンプルモーメントに関する概念 

単純ランダムサンプル（1.7） 

図B.1 

図B.3 推定に関する概念 

推定量（1.12） 

図B.1 

パラメータ（2.9） 

図C.1 

確率分布族（2.8） 

図B.4，C.1 

確率密度関数（2.26） 

図C.3 

確率質量関数（2.24） 

図C.3 

図B.4 統計的検定に関する概念 

検定統計量（1.52） 

図B.1 

確率密度関数（2.26） 

図B.3，C.3 

確率質量関数（2.24） 

図B.3，C.3 

確率分布族（2.8） 

図B.3，C.1 

図B.5 度数分布及び級に関する概念 

記述統計（1.5） 

図B.1 

図B.6 統計的推測に関する概念 

母集団（1.1） 

図B.1 

サンプル（1.3） 

図B.1 

観測値（1.4） 

図B.1，B.5 

推定（1.36） 

図B.3 

統計的検定（1.48） 

図B.4 

パラメータ（2.9） 

図B.3，C.1 

確率変数（2.10） 

図B.1，C.1，C.2 

図C.1 確率の基本に関する概念 

確率変数（2.10） 

図B.1，C.2 

確率分布（2.11） 

図C.2，C.3 

確率分布族（2.8） 

図B.3，B.4 

分布関数（2.7） 

図B.1 

パラメータ（2.9） 

図B.3 

図C.2 モーメントに関する概念 

確率変数（2.10） 

図B.1，C.1 

確率分布（2.11） 

図C.1，C.3 

66 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

図C.3 確率分布に関する概念 

確率分布（2.11） 

図C.1，C.2 

確率質量関数（2.24） 

図B.3，B.4 

連続確率分布（2.23） 

図C.4 

1変量確率分布（2.16） 

図C.4 

多変量確率分布（2.17） 

図C.4 

図C.4 連続分布に関する概念 

1変量確率分布（2.16） 

図C.3 

多変量確率分布（2.17） 

図C.3 

連続確率分布（2.23） 

図C.3 

図C.4に関して，正規分布，t分布，F分布，標準正規分布，ガンマ分布，ベータ分布，カイ2乗分布，

指数分布，一様分布，タイプI極値分布，タイプII極値分布，及びタイプIII極値分布は，1変量確率分布

の例として示されている。また，多変量正規分布，2変量正規分布，及び標準2変量正規分布は，多変量

確率分布の例として示されている。1変量確率分布（2.16）及び多変量確率分布（2.17）を概念図に入れる

と，あまりにも煩雑になるので含めていない。 

67 

Z 8101-1：2015 (ISO 3534-1：2006) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

参考文献 

[1] ISO 31-11:1992，Quantities and units−Part 11: Mathematical signs ans symbols for use in the physical 

sciences and technology 

[2] JIS Z 8101-2 統計−用語及び記号−第2部：統計の応用 

注記 対応国際規格：ISO 3534-2:2006，Statistics−Vocabulary and symbols−Part 2: Applied statistics（IDT） 

[3] JIS Z 8402（全ての部） 測定方法及び測定結果の精確さ（真度及び精度） 

注記 対応国際規格：ISO 5725 (all parts)，Accuracy (trueness and precision) of measurement methods and 

results（IDT） 

[4] TS Z 0032：2012 国際計量計測用語−基本及び一般概念並びに関連用語（VIM） 

注記 対応国際規格：ISO/IEC Guide 99，International vocabulary of metrology−Basic and general concepts 

and associated terms (VIM)（IDT）