X 7254:2008
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
0 適用範囲 ························································································································· 1
1 導入······························································································································· 1
2 抽象構文 ························································································································· 2
2.1 オントロジ ··················································································································· 3
2.2 事実 ···························································································································· 5
2.3 公理 ···························································································································· 6
3 直接モデル論的意味論 ······································································································ 11
3.1 語い(彙)及び解釈 ······································································································ 11
3.2 埋込み構成要素の解釈 ··································································································· 12
3.3 公理及び事実の解釈 ······································································································ 13
3.4 オントロジの解釈 ········································································································· 14
4 RDFグラフへの写像 ········································································································ 15
4.1 RDFグラフへの翻訳(変換) ·························································································· 16
4.2 RDFグラフ形式でのOWL DLオントロジ及びOWL Liteオントロジの定義 ····························· 21
5 RDFに互換なモデル論的意味論 ························································································· 22
5.1 OWL及びRDFの世界 ··································································································· 23
5.2 OWL解釈 ··················································································································· 23
5.3 OWL Full ···················································································································· 28
5.4 OWL DL ····················································································································· 29
附属書A(参考)証明 ·········································································································· 31
附属書B(参考)例 ············································································································· 45
附属書C(参考)原勧告における最終審議案からの変更······························································ 48
附属書D(参考)語い(彙)の索引 ························································································ 54
附属書E(参考)原勧告の貢献者···························································································· 56
附属書F(規定)文献 ··········································································································· 57
X 7254:2008
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人日本規格協会(JSA)から工業標準原
案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣
が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
原勧告の標題及びまえがきの翻訳
OWL ウェブオントロジ言語−意味論及び抽象構文
W3C勧告 2004年2月10日
この版の掲載場所
http://www.w3.org/TR/2004/REC-owl-semantics-20040210/
最新版の掲載場所
http://www.w3.org/TR/owl-semantics/
以前の版の掲載場所
http://www.w3.org/TR/2003/PR-owl-semantics-20031215/
編者
Peter F. Patel-Schneider, Bell Labs Research, Lucent Technologies
Patrick Hayes, IHMC, University of West Florida
Ian Horrocks, Department of Computer Science, University of Manchester
この勧告についての正誤表は,http://www.w3.org/2001/sw/WebOnt/errata#owl-semanticsを参照し
てもらいたい。正誤表は,規定としての修正も含まれるかもしれない。
この文書は,一つのHTMLファイルの形式 (http://www.w3.org/TR/owl-absyn/semantics-all.html)
でも入手できる。ただし,これは規定とはしない。
翻訳 (http://www.w3.org/2003/03/Translations/byTechnology?technology=owl-semantics) も参照し
てもらいたい。
著作権 © 2004 W3C®(MIT,INRIA,慶應義塾)が,すべての権利を保有する。免責,商標,
文書の使用及びソフトウェアの使用許諾に関するW3Cの規則を適用する。
X 7254:2008
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
要約
この勧告は,W3Cのウェブオントロジ作業グループが設計したウェブオントロジ言語OWLに
ついて,OWLの部分言語であるOWL DL及びOWL Liteの両方に関する高水準の抽象構文を規定
する。この抽象構文で書かれたOWLオントロジに形式的な意味を与えるために,モデル論的意
味論を与える。さらに,OWL Fullに対応するRDFグラフとしてのOWLオントロジに関する形
式的な意味を与えるために,RDF意味論の拡張になる形式でのモデル論的意味論も与える。抽象
構文からRDFグラフへの写像を与えることによって,(部分言語の範囲になる)抽象構文で記述
できるOWLオントロジに関しては,二つのモデル理論は,同じ結果を与えることが示される。
この文書の状態
この文書は,W3Cの勧告である。この勧告は,W3C会員企業及び関連する団体によって閲読
されており,技術統括責任者によってW3C勧告として承認されている。これは安定した文書で
あり,参考資料として使用してよく,他の文書から引用規定として引用してもよい。W3Cはこの
勧告を制定することによって,この規定への注目を喚起し,広い普及を促進するという役割を果
たす。この結果,Webの機能及び相互運用性が高まる。
この文書は,OWL,Web Ontology Language,についてのW3C勧告の六つの部の一つである。
この文書は,ウェブオントロジ作業グループによって,W3C セマンティックウェブ活動(活動
表明はhttp://www.w3.org/2001/sw/Activityを,グループ規約は
http://www.w3.org/2001/sw/WebOnt/charterを参照してもらいたい。)の一部として,2004年2月10
日公開のために開発された。
この勧告の以前の版で示されたOWLの原案は,広く審議され,作業グループの技術要件を満
たしている。作業グループは,受け取ったコメントすべてを議論し,必要に応じて変更を行った。
勧告案からのこの文書への変更は,変更記録(附属書C参照)に詳細に示されている。
この勧告についてのコメントは,public-webont-comments@w3.org に報告してもらいたい。コメ
ントの一覧は,http://lists.w3.org/Archives/Public/public-webont-comments/で入手できる。関係する
技術の一般的な議論は,www-rdf-logic@w3.orgで行って欲しい。議論の一覧は,
http://lists.w3.org/Archives/Public/www-rdf-logic/で入手できる。
実装の一覧は,http://www.w3.org/2001/sw/WebOnt/implsで入手できる。
W3Cは,この作業に関係する特許開示の一覧を管理している。
http://www.w3.org/2001/sw/WebOnt/disclを参照してもらいたい。
“この文書の状態”は,この文書が公開された時点での状態を示している。他の文書がこの文
書を置き換えることもある。現在のW3Cの公開文書の一覧及びこの勧告の最新版は,
http://www.w3.org/TR/においてW3C技術報告索引で見つけることができる。
X 7254:2008
(4)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
白 紙
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
X 7254:2008
OWLウェブオントロジ言語−意味論及び抽象構文
OWL Web Ontology Language−Semantics and Abstract Syntax
序文
この規格は,2004年2月にWorld Wide Web Consortium (W3C) から公表されたOWL Web Ontology
Language Semantics and Abstract Syntaxを翻訳し,技術的内容を変更することなく作成した日本工業規格で
ある。
オントロジとは,文書における語の意味や語の間の関係を規定する枠組みであり,それを記述する言語
としてOWL (Web Ontology Language)が開発された。
OWLウェブオントロジ言語に関して,W3Cの勧告が6件公表されており,この規格は,OWL Web
Ontology Language Semantics and Abstract Syntax W3C Recommendation 10 February 2004に対応するものであ
る。
なお,その他の勧告は次のとおりである。
・OWL Web Ontology Language Overview W3C Recommendation 10 February 2004
・OWL Web Ontology Language Guide W3C Recommendation 10 February 2004
・OWL Web Ontology Language Reference W3C Recommendation 10 February 2004
・OWL Web Ontology Language Use Cases and Requirements W3C Recommendation 10 February 2004
・OWL Web Ontology Language Test Cases W3C Recommendation 10 February 2004
この規格を理解するために,[Overview],[Guide],[Reference]を参考にすることを推奨する。またこの3
件はTSとして日本語で公表されており,それぞれTS X 7251: 2006,TS X 7252: 2006,TS X 7253: 2006で
ある。
なお,この規格で点線の下線を施してある箇所は,原勧告(W3C勧告)にはない事項である。
0
適用範囲
この規格は,W3Cのウェブオントロジ作業グループが設計したウェブオントロジ言語OWLについて,
OWLの部分言語であるOWL DL及びOWL Liteの両方に関する高水準の抽象構文を規定する。この抽象構
文で書かれたOWLオントロジに形式的な意味を与えるために,モデル論的意味論を与える。さらに,OWL
Fullに対応するRDFグラフとしてのOWLオントロジに関する形式的な意味を与えるために,RDF意味論
の拡張になる形式でのモデル論的意味論も与える。抽象構文からRDFグラフへの写像を与えることによっ
て,(部分言語の範囲になる)抽象構文で記述できるOWLオントロジに関しては,二つのモデル理論が,
同じ結果を与えることが示される。
1
導入
この箇条は,規定ではない。
2
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この規格は,ウェブオントロジ言語OWLの規定文書だが,規定以外も含む一連のOWL技術文書群の
一部になっている。その中の規定ではないOWL 概要[OWL Overview]は,その技術文書群を構成する様々
な文書のそれぞれを示し,それらが互いにどのように整合するかを示す。
注記 外部文書への参照は,原勧告では[OWL Overview]といった記述から参照箇所にリンクされてい
る。ただし,この規格では被参照箇所へのリンクは記載しない。代わりに,附属書Fの対応す
る項目を参照する。
この規格は,W3Cのウェブオントロジ作業グループ (WebOnt) が作成したウェブオントロジ言語OWL
の複数の表現形式の,幾つかの相互に関連する規定を含む。最初に箇条2は,OWL Lite及びOWL DLの
両方に関して,高水準の抽象構文を規定する。OWL Liteは,OWLの部分集合である。OWL DLは,OWL
を使用する上でLiteよりは充実した表現形式をもつが,OWLオントロジの構成方法にまだ幾つか制限が
ある。これらの制限を取り除いたものが,OWL Fullと呼ばれるOWL言語の完全版であって,これはRDF
と同じ抽象構文をもつ。OWLに関する規定の交換構文は,RDF/XML [RDF Syntax]とする。OWL 機能一
覧[OWL Reference]は,RDF構文をOWLでどのように使用するかを示す。OWL抽象構文からRDFグラフ
[RDF Concepts]への写像は,箇条4で与える。
この規格は,OWLの二つの形式的な意味論を含む。これらの意味論のうち,一つは箇条3で定義する。
これは,抽象構文で書かれたOWLオントロジの直接的であって,標準的なモデル論的意味論とする。も
う一つは,箇条5で定義する。これは,RDF意味論[RDF Semantics]の語い(彙)の拡張であって,RDFグ
ラフの形式でOWLオントロジの意味論を与える。この第二の意味論には二つの版がある。一つは,先ほ
どの直接的な意味論に,より強く対応している。したがってOWL DLの意味論になる。もう一つは,クラ
スを個体として取り扱う必要がある場合において,又は抽象構文で扱うことができないその他の状況にお
いて使用できる。したがってOWL Fullの意味論になる。これらの二つの版は,実際極めて類似しており,
議論の領域の分割の方法だけが異なる。
附属書Aでは,二つの意味論,直接的意味論及びRDFS互換意味論が,OWL個体,OWLクラス,OWL
特性,RDF,RDFS及びOWL構造語い(彙)を区別する抽象OWLオントロジに対応するOWLオントロ
ジに関しては,同じ結果をもつことを証明する。附属書Aでは,OWL FullのためのRDFS互換意味論の
論理的帰結が,OWL DLのためのRDFS互換意味論のすべての論理的帰結を含むことの証明の概略も与え
る。最後に,附属書Bにおいて,この規格で定義した様々な概念の幾つかの例を与える。
この規格は,OWLの技術的詳細に興味をもつ人が読むことを念頭においている。特に,OWLの知識を
もたない読者を意図したものではない。それらの読者は,まず,OWL 手引[OWL Guide]を読むことが望ま
しい。OWLの構文解析プログラム及びその他の構文論的ツールの開発者は,特に箇条2及び箇条4に興
味をもつと思われる。OWLの推論プログラム及びその他の意味論的ツールの開発者は,特に,箇条3及
び箇条5に興味をもつと思われる。
2
抽象構文
箇条2におけるOWLの構文は,OWLの交換構文を抽象化したものなので,その言語への導入及び評価
が容易となっている。この特別な構文は,フレームというシステムに似た表現形式をもっていて,クラス
又は特性に関する情報の集まりを,一つの大きな構文の構成要素で提供する。ほとんどの記述論理のよう
に数多くの原子的な塊に分割することはないし,RDFグラフ [RDF Concepts]としてOWLを記述する場合
のように更に多くの三つ組に分割することもない。ここで使用する構文は,抽象構文のためのものとして
も,どちらかといえば非形式的といえるものになっており,一般に,ある構成要素の引数は,順序がその

3
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
構成要素の意味に影響しない場合はいつでも,順序付けがなされていないと考える。
この規格では,抽象構文は,XML[XML]で使われているEBNF記法に非常によく似た拡張BNFによっ
て規定する。終端記号は,引用符で囲む。非終端記号は,引用符で囲まない。代替要素は,縦線(|)で区
切られるか,又は別の生成規則で提供される。高々1回出現する構成要素は,角括弧([…])で囲む(0回
を含む)。何回も出現する構成要素は,波括弧({…})で囲む。生成規則の中では,空白を無視する。
抽象構文の中の名前は,RDF URI参照[RDF Concepts]とする。これらの名前は,多くの場合,表1の名
前空間の一つを使用して,修飾された名前に短縮される。
表1−名前空間の一覧
名前空間の名前
名前空間
rdf
http://www.w3.org/1999/02/22-rdf-syntax-ns#
rdfs
http://www.w3.org/2000/01/rdf-schema#
xsd
http://www.w3.org/2001/XMLSchema#
owl
http://www.w3.org/2002/07/owl#
抽象構文の各構成要素の意味は,導入のときに,非形式的に示す。これらの構成要素の形式的意味は,
モデル論的意味論によって,箇条3で提供される。
利用者によってはOWLのような表現力の強い言語の全機能が重要になることは広く認識されているが,
それが,それらの言語の全機能を提供するソフトウェアツール群の支援を試みるグループの気勢をそいで
いることも分かっている。より実装しやすい目標を与えるために,OWL Lite[OWL Overview]と呼ばれる,
より小規模な言語を定義した。このより小規模の言語は,ウェブ応用を支援するために重要だがRDFスキ
ーマ[RDF Schema]では欠落している機能を提供するために設計された。しかし,OWL DLもOWL Liteも
RDFスキーマのすべての機能を提供するわけではないことに注意する。抽象構文は,(OWL Lite抽象構文
と呼ばれる)このより小規模の言語に対しても表現されるし,(OWL DL抽象構文と呼ばれる)OWLのよ
り充実した表現形式に対しても表現される。
この規格の抽象構文は,OWLの交換構文ほど一般的ではない。特に,自己参照をする構文構造を構築
することは許されていない。さらに,クラス,特性及び個体が互いに素な集まりを形成する場合に使うこ
とを意図している。これらは,大まかにいえば,OWLの推論を決定可能とするために要求される制限に
なっている。したがって,この抽象構文は,OWL DLのための構文と考えるのがよい。
注記 OWL Lite及びOWL DLは,SHIF(D)及びSHION(D)として知られる記述論理に強く対応してお
り,データ型の取扱い方法に限界がある。OWL Liteの抽象構文は,SHIF(D)と関連する共通的
で明示的な構成子の多くを含まないが,その表現力は残されている。
2.1
オントロジ
抽象構文におけるOWLオントロジ (ontology) には,注釈 (annotation),公理 (axiom) 及び事実 (fact) の
列が含まれる。OWLオントロジは,名前をもつことができる。OWLオントロジに関する注釈を使用する
ことで,原作者及び他のオントロジへの取込み参照を含む,オントロジと関連した他の情報を記録できる。
OWLオントロジの主な内容は,その公理及び事実で表現され,それによって,そのオントロジのクラス,
特性及び個体に関する情報が提供される。
ontology ::= 'Ontology(' [ ontologyID ] { directive } ')'
directive ::= 'Annotation(' ontologyPropertyID ontologyID ')'
| 'Annotation(' annotationPropertyID URIreference ')'
| 'Annotation(' annotationPropertyID dataLiteral ')'
4
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
| 'Annotation(' annotationPropertyID individual ')'
| axiom
| fact
オントロジの名前を抽象構文で使用するのは,ウェブ上でのオントロジの公開と関連付けられた意味を
与えるためとする。したがって,抽象構文中のオントロジの名前は,それを入手できるURI(統一資源識
別子)となることを意図している。ただし,これはOWLの形式的な意味の一部ではない。 取込み注釈は,
事実上,ウェブ文書を検索し,それをオントロジとして扱うための指示になる。しかし,文書が欠落して
いたり,入手不可能であったり,時間的に変化するなどのウェブの多くの局面は,OWL規定の範囲外と
する。つまり,ここで意味することは,URIが,あるOWLオントロジに引用できるということだけとす
る。この規格の複数の箇所で,取込みを,このように理想化した操作的な意味で使用する。
オントロジは,クラス (class),特性 (property) 及び個体 (individual) に関する情報を組み込んでいる。
それらは,各々URI参照 (URIreference) である識別子 (ID) をもつことができる。これらの識別子の中に
は,公理を与える必要があるものもある。詳細については,2.3に示す。
datatypeID ::= URIreference
classID ::= URIreference
individualID ::= URIreference
ontologyID ::= URIreference
datavaluedPropertyID ::= URIreference
individualvaluedPropertyID ::= URIreference
annotationPropertyID ::= URIreference
ontologyPropertyID ::= URIreference
一つのURI参照は,一つのオントロジにおいて,datatypeIDとなりclassIDとなることはできない。一つ
のURI参照は,一つのオントロジにおいて,datavaluedPropertyID,individualvaluedPropertyID,
annotationPropertyID又はontologyPropertyIDの,二つ以上になることもできない。しかし,一つのURI参
照は,クラス又はデータ型の識別子であって,同時に個体の識別子又は特性の識別子となることはできる。
最もそのようなオントロジは,OWL DLのRDFグラフには変換できない。
OWLでは,データ型は,そのデータ型の値空間であるデータ値の集合を示す。クラスは個体の集合を
示す。特性は,個体を他の情報に関連付ける。特性は,4個の互いに素な群,すなわちデータ値特性
(data-valued property),個体値特性 (individual-valued property),注釈特性 (annotation property) 及びオントロ
ジ特性 (ontology property) に分けられる。データ値特性は,個体をデータ値に関連付ける。個体値特性は,
個体を他の個体に関連付ける。注釈特性は,個体,クラス名,特性名及びオントロジ名に注釈を付けるた
めに使用される。オントロジ特性は,オントロジを他のオントロジに関連付ける。特にこの特性は,他の
オントロジから情報を取り込むために使用される。個体識別子は,資源を参照するために使用され,デー
タリテラルはデータ値を参照するために使用される。
OWLには,二つの組込みのクラスが存在し,それらは両者とも,OWL名前空間のURI参照,すなわち,
http://www.w3.org/2002/07/owl#で始まる名前を使用する。この規格では,OWLの組込みクラスに対して,
名前空間名owlを使用する。この規格全体を通して,修飾された名前をURI参照の短縮形として使用する。
識別子owl:Thingをもつクラスは,すべての個体のクラスとする。識別子owl:Nothingをもつクラスは,空
のクラスとする。いずれのクラスもOWL Liteの一部とする。
次のXMLスキーマデータ型[XML Schema Datatypes]は,データ型に対するXMLスキーマの正準URI参
5
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
照http://www.w3.org/2001/XMLSchema#nameによって,組込みデータ型としてOWLでの使用が可能となる。
この場合のnameは,データ型xsd:string, xsd:boolean, xsd:decimal, xsd:float, xsd:double, xsd:dateTime, xsd:time,
xsd:date, xsd:gYearMonth, xsd:gYear, xsd:gMonthDay, xsd:gDay, xsd: gMonth, xsd:hexBinary, xsd:base64Binary,
xsd:anyURI, xsd:normalizedString, xsd:token, xsd:language, xsd:NMTOKEN, xsd:Name, xsd:NCName, xsd:integer,
xsd:nonPositiveInteger, xsd:negativeInteger, xsd:long, xsd:int, xsd:short, xsd:byte, xsd:nonNegativeInteger,
xsd:unsignedLong, xsd:unsignedInt, xsd:unsignedShort, xsd:unsignedByte及びxsd:positiveIntegerの局所名とする。
これら以外のXMLスキーマの組込みデータ型は,OWLにとって問題がある。これについては,RDF意味
論[RDF Semanticsの5.1]に示されている。RDFに組込みのデータ型であるrdf:XMLLiteralも,OWLの組込
みデータ型とする。XMLスキーマでは,URI参照からXMLスキーマデータ型へたどるための標準的な方
法がないので,OWLでは,利用者定義のXMLスキーマデータ型を使用するための標準的な方法は存在し
ない。
OWLでは,組込みの注釈特性が複数存在する。すなわち,owl:versionInfo, rdfs:label, rdfs:comment,
rdfs:seeAlso及びrdfs:isDefinedByがこれにあたる。RDFにおけるそれらの定義との整合性を保つために,
rdfs:label及びrdfs:commentだけが,データリテラルとともに使用できる。
組込みのオントロジ特性も複数存在する。すなわち,owl:imports,owl:priorVersion,
owl:backwardCompatibleWith及び owl:incompatibleWithがこれにあたる。owl:importsを使用するオントロジ
注釈には,対象のオントロジを取り込むという特別な効果がある。
OWL構成要素の多くは,注釈 (annotation) を使用するが,注釈指示と同様に,それらは,構成要素の一
部と関連付けられる情報を記録するために使われる。
annotation ::= 'annotation(' annotationPropertyID URIreference ')'
| 'annotation(' annotationPropertyID dataLiteral ')'
| 'annotation(' annotationPropertyID individual ')'
2.2
事実
OWL抽象構文には,2種類の事実 (fact) が存在する。
第1の種類の事実は,個体 (individual) が属するクラス,並びにその個体の特性及び値 (value) の形式
で,特定の個体に関する情報を言明する。個体は,その個体を示し,その個体を参照するために使用でき
るindividualIDをもつことができる。しかし,個体は,individualIDを必ずしももつ必要はない。これらの
個体はとく(匿)名(RDF用語では空白)であって,直接に他の箇所から参照することができない。次に
示す構文は,rdf:nodeIDを使用していないことを除けばRDF/XML構文[RDF Syntax]に類似している。
fact ::= individual
individual ::= 'Individual(' [ individualID ] { annotation } { 'type(' type ')' } { value } ')'
value ::= 'value(' individualvaluedPropertyID individualID ')'
| 'value(' individualvaluedPropertyID individual ')'
| 'value(' datavaluedPropertyID dataLiteral ')'
事実は,型 (type) となることができるものを除き,OWL Lite抽象構文及びOWL DL抽象構文において
同じとする。OWL Liteでは,型となることができるのは,クラスID (classID) 又はOWL Lite制限 (restriction)
とする(2.3.1.2参照)。
type ::= classID
| restriction
OWL DL抽象構文では,型となることができるのは,一般的な記述 (description) であって,これには,
6
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
クラスID及びOWL Lite制限だけでなく他の構成要素も含まれる。
type ::= description
抽象構文のデータリテラル (data literal) は,型なしリテラル (plain literal) 又は型付きリテラル (typed
literal) のいずれかとする。型なしリテラルは,RDF 型なしリテラル [RDF Concepts]の場合と同様に,正
規形CのUnicode文字列及び任意選択の言語タグ (language tag) から構成される。型付きリテラルは,RDF
型付きリテラル [RDF Concepts]の場合と同様に,字句表現(lexical representation,BNFではlexicalForm)
及びURI参照から構成される。
dataLiteral ::= typedLiteral | plainLiteral
typedLiteral ::= lexicalForm '^^' URIreference
plainLiteral ::= lexicalForm | lexicalForm '@' languageTag
lexicalForm ::= RDFと同様に正規形CのUnicode文字列
languageTag ::= RDFと同様にXML言語タグ
注記 記法“^^”及び“@”は,原勧告では“'”が付いておらず終端記号ではないように見えるが,
これは明らかな編集上の誤りであって,終端記号と思われる。実際,[RDF Semantics]にその用
例がある。その意味は,“^^”が“その後に型にあたるものを記述”,“@”が“その後に言語タ
グを記述”となっている。明らかな編集上の誤りなので,この規格では,“'”を付けて修正し
た。
第2の種類の事実は,複数の個体識別子が同一のものに,又はどの二つをとってもそれぞれ異なるもの
にするために使用する。
fact ::= 'SameIndividual(' individualID individualID {individualID} ')'
| 'DifferentIndividuals(' individualID individualID {individualID} ')'
2.3
公理
OWL Lite抽象構文とOWL DL抽象構文との最も大きな相違は,公理に現れる。公理は,クラス及び特
性に関する情報を提供するために使われる。OWL Liteは,OWL DLに比べ小規模な言語であるため,最初
に2.3.1で,OWL Liteの公理を規定する。OWL DL公理は,2.3.2で解説する。OWL DLの公理は,OWL Lite
公理を特殊例として含んでいる。
公理を使用することによって,クラス及び特性の識別子を,それらの特徴の部分的な規定又は完全な規
定のいずれかと関連付け,クラス及び特性に関する他の情報を提供することができる。以前は公理は定義
と呼ばれていたが,常識的な用語の使用では公理は必ずしも定義ではないので,より中立的な名前が選択
された。
ここで使用する構文は,幾つかのフレーム(というシステムの)処理系で使用される構文にある程度類
似させている。OWL Liteの各クラス公理は,より一般的なクラスの集まり,及び制限構成要素の形式での
局所的な特性制限の集まりを含む。制限構成要素は,特性の局所的な値域,何個の値を使用できるか,及
び/又は要求される値の集まりを提供する。ここでいうクラスとは,これらのより一般的なクラスと制限
との共通部分と等価か,又はその部分集合かのいずれかとする。OWL DL抽象構文では,クラス公理は,
記述の集まりを含む。この集まりは,より一般的なクラス,制限,個体の集合及び記述のブール結合とな
り得る。クラスは,列挙によっても指定できる。等価又は互いに素とすることもできる。
特性は,他の特性と等価にすること又は他の特性の下位特性にすることができる。特性は,関数特性,
逆関数特性,対称特性又は推移特性とすることができる。さらに,大域的な定義域及び値域を与えられる
ことができる。しかし,特性に関するほとんどの情報は,より自然に制限の中で表現され,それによって,
7
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
局所的な値域及びメンバ数情報を指定することができる。
クラスID又はデータ型IDとして使用されるURI参照は,区別されなければならないので,公理を必要
とする。ただし,組込みOWL クラス,データ型及びrdfs:Literalを除く。一つのクラス又はデータ型に対
して,公理が二つ以上存在してもよい。抽象構文オントロジで使用される特性は,データ値特性,個体値
特性又は注釈特性のいずれかとして分類されなければならない。そこでこの目的のために,特性も少なく
とも一つの公理を必要とする。あるオントロジが別のオントロジを取り込む場合,取り込まれたオントロ
ジ(及び再帰的にそれが取り込むあらゆるオントロジ)の公理をこれらの目的のために,使用することが
できる。
2.3.1
OWL Liteの公理
2.3.1.1
OWL Liteのクラス公理
OWL Liteでは,クラスの公理 (axiom) は,あるクラスがその上位 (super) クラスの集まりと OWL Lite
制限との和集合に厳密に等価である(次のBNFでmodalityがcompleteの場合)か,和集合の下位クラス
となる(次のBNFでmodalityがpartialの場合)かを言明するのに使われる。クラスの使用が非推奨
(deprecated) であることを示すこともできる。
axiom ::= 'Class(' classID ['Deprecated'] modality { annotation } { super } ')'
modality ::= 'complete' | 'partial'
super ::= classID | restriction
OWL Liteでは,二つ以上のクラスが等価(equivalent)であると言明することができる。
axiom ::= 'EquivalentClasses(' classID classID { classID } ')'
データ型 (datatype) 公理はもっと簡単であって,データ型ID (datatype ID) が一つのデータ型のIDであ
ることを示し,そのデータ型の注釈を与えるためだけに役立つ。
axiom ::= 'Datatype(' datatypeID ['Deprecated'] { annotation } )'
2.3.1.2
OWL Liteの制限
OWL Liteのクラス公理では,制限 (restriction) を使用して,クラスの特性に局所的な制約を課す。次の
BNFで,制限のallValuesFrom部分のそれぞれは,クラスの個体に対する特性のすべての値が指定したク
ラス又はデータ型に属さなければならないという制約を課す。someValuesFrom部分のそれぞれは,指定し
たクラス又はデータ型に属する特性には,少なくとも値が一つ存在しなければならないという制約を課す。
このcardinality(メンバ数)部分は,クラスの各個体に対する特性について,どのくらい多くの異なる値
が存在するかを示す。OWL Liteでは,許容されるメンバ数は,0及び1とする。
どの特性が制限の中にcardinality(メンバ数)の部分をもつことができるかに関する制約については,
2.3.1.3を参照してもらいたい。
restriction ::= 'restriction(' datavaluedPropertyID dataRestrictionComponent ')'
| 'restriction(' individualvaluedPropertyID individualRestrictionComponent ')'
dataRestrictionComponent ::= 'allValuesFrom(' dataRange ')'
| 'someValuesFrom(' dataRange ')'
| cardinality
individualRestrictionComponent ::= 'allValuesFrom(' classID ')'
| 'someValuesFrom(' classID ')'
| cardinality
cardinality ::= 'minCardinality(0)' | 'minCardinality(1)'
8
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
| 'maxCardinality(0)' | 'maxCardinality(1)'
| 'cardinality(0)' | 'cardinality(1)'
2.3.1.3
OWL Liteの特性公理
特性 (property) も,フレームに似た構文を使って指定する。データ値特性 (data-valued property) は,個
体を整数などのデータ値に関連付ける。個体値特性 (individual-valued property) は個体を他の個体に関連付
ける。これらの2種類の特性に上位特性 (super-property) を与えることができ,特性階層の構築が可能と
なる。個体値特性をデータ値特性の上位特性にしたり,又はその逆とすることは,意味がない。データ値
特性及び個体値特性に,定義域 (domain) 及び値域 (range) を与えることもできる。特性の定義域は,RDFS
と同様に,どの個体が,その特性を述部としてもつ言明において主語となり得るかを指定する。OWL Lite
では,特性の定義域はクラスとする。複数の定義域の存在が可能であり,その場合には,それらすべての
定義域に属する個体だけが主語となることができる。特性の値域は,どの個体又はデータ値が,その特性
を述部としてもつ言明の目的語となり得るかを指定する。ここでも,複数の値域が可能であって,その場
合,それらすべての値域に属する個体又はデータ値だけが目的語となることができる。OWL Liteでは,個
体値特性の値域はクラスとし,データ値特性の値域はデータ型とする。
データ値特性を関数 (functional) 又は部分関数 (partial functional) として指定することができる。この場
合,特性における一つの個体に対して,あるデータ値との関係は一つ以下しかあり得ない。個体値特性を
別の特性の逆特性 (inverse) に指定することができる。個体値特性は,対称的 (symmetric),部分関数的
(partial functional),部分逆関数的 (partial inverse-functional) 又は推移的 (transitive) と指定することもでき
る。
OWL Liteでは,すべての特性がメンバ数の制限をもつことができるわけではないし,関数的又は逆関数
的として指定できるわけでもない。これは,推論の決定可能性を維持することによる。個体値特性は,次
の四つの条件のいずれかを満たす場合に,複合的とする。
a) 関数的又は逆関数的として指定されている場合。
b) それを使用するメンバ数の制限が存在する場合。
c) 複合的な逆関数的な特性が存在する場合。
d) 複合的な上位特性が存在する場合。
複合特性を推移的として指定することはできない。
注釈特性 (annotation property) 及びオントロジ特性 (ontology property) は,データ値特性及び個体値特性
よりもはるかに単純になっている。それらに関する公理の中での唯一の情報は,注釈となる。
axiom ::= 'DatatypeProperty(' datavaluedPropertyID ['Deprecated'] { annotation }
{ 'super(' datavaluedPropertyID ')' } ['Functional']
{ 'domain(' classID' ')' } { 'range(' dataRange ')' } ')'
| 'ObjectProperty(' individualvaluedPropertyID ['Deprecated'] { annotation }
{ 'super(' individualvaluedPropertyID ')' }
[ 'inverseOf(' individualvaluedPropertyID ')' ] [ 'Symmetric' ]
[ 'Functional' | 'InverseFunctional' | 'Functional' 'InverseFunctional' | 'Transitive' ]
{ 'domain(' classID ')' } { 'range(' classID ')' } ')'
| 'AnnotationProperty(' annotationPropertyID { annotation } ')'
| 'OntologyProperty(' ontologyPropertyID { annotation } ')'
dataRange ::= datatypeID | 'rdfs:Literal'
9
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
次の公理は,複数の特性を等価 (equivalent) にするか,又は一つの特性を別の特性の下位特性
(sub-property) とする。
axiom ::= 'EquivalentProperties(' datavaluedPropertyID datavaluedPropertyID { datavaluedPropertyID } ')'
| 'SubPropertyOf(' datavaluedPropertyID datavaluedPropertyID ')'
| 'EquivalentProperties(' individualvaluedPropertyID individualvaluedPropertyID
{ individualvaluedPropertyID } ')'
| 'SubPropertyOf(' individualvaluedPropertyID individualvaluedPropertyID ')'
2.3.2
OWL DLの公理
2.3.2.1
OWL DLのクラス公理
OWL DLの抽象構文には,OWL Liteのクラス公理のより一般的な版が存在する。そこでは,上位クラス,
より一般的な制限,及びそれらのブール結合(実際には,集合演算)を使用できる。これらの構成要素を,
合わせて記述 (description) と呼ぶ。
axiom ::= 'Class(' classID ['Deprecated'] modality { annotation } { description } ')'
modality ::= 'complete' | 'partial'
OWL DL 抽象構文では,クラスを指定した個体の集合から厳密に構成することもできる。これは,次に
よる。
axiom ::= 'EnumeratedClass(' classID ['Deprecated'] { annotation } { individualID } ')'
最後に,OWL DL抽象構文では,記述の集まりがどの二つを取ってもそれぞれ互いに素となる (disjoint),
同じインスタンスをもつ (equivalent),又はある記述が別の記述の下位クラス (subclass) になるのを要求す
ることを可能とする。これらの公理のうち,最後の二つは,注釈 (annotation) が欠落していることを除き,
最初の種類のクラス公理を一般化することに注意してもらいたい。
axiom ::= 'DisjointClasses(' description description { description } ')'
| 'EquivalentClasses(' description { description } ')'
| 'SubClassOf(' description description ')'
OWL DLでは,EquivalentClasses構成要素の中で,記述を一つだけもつことができる。これによって,
オントロジは,何とも関連付けられない記述を含むことができる。これは,意味論上有用ではないが,オ
ントロジの最適とはいえない編集を許容する。
データ型 (datatype) 公理は,OWL Liteの場合と同様とする。
axiom ::= 'Datatype(' datatypeID ['Deprecated'] { annotation } )'
2.3.2.2
OWL DLの記述
OWL DL抽象構文の記述 (description) は,クラス識別子 (class identifier) 及び制限 (restriction) を含む。
記述は,他の記述のブール組合せ(実際には,集合演算)及び個体の集合となることもある。
description ::= classID
| restriction
| 'unionOf(' { description } ')'
| 'intersectionOf(' { description } ')'
| 'complementOf(' description ')'
| 'oneOf(' { individualID } ')'
2.3.2.3
OWL DLの制限
OWL DL抽象構文の制限 (restriction) は,OWL Liteの制限を一般化する。すなわち,OWL Liteではクラ
10
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
スだけが使用できる箇所において,記述を使用可能にし,データ型 (datatype) だけでなくデータ値 (data
value) の集合を使用可能にする。データ型及びデータ値の集合の組合せをデータ値域 (data range) と呼ぶ。
OWL DL抽象構文では,クラスの特性 (property) について値を与えることもできる。さらに,メンバ数
(cardinality) が,0及び1だけに限定されることはない。
restriction ::= 'restriction(' datavaluedPropertyID dataRestrictionComponent { dataRestrictionComponent } ')'
| 'restriction(' individualvaluedPropertyID individualRestrictionComponent
{ individualRestrictionComponent } ')'
dataRestrictionComponent ::= 'allValuesFrom(' dataRange ')'
| 'someValuesFrom(' dataRange ')'
| 'value(' dataLiteral ')'
| cardinality
individualRestrictionComponent ::= 'allValuesFrom(' description ')'
| 'someValuesFrom(' description ')'
| 'value(' individualID ')'
| cardinality
cardinality ::= 'minCardinality(' non-negative-integer ')'
| 'maxCardinality(' non-negative-integer ')'
| 'cardinality(' non-negative-integer ')'
データ値域 (data range) は,データ値特性の値域として用いられるとともに,OWL DL抽象構文の他の
場所でも使用される。データ値域は,データ型 (datatype) 又はデータ値の集合のいずれかとする。
dataRange ::= datatypeID | 'rdfs:Literal'
| 'oneOf(' { dataLiteral } ')'
OWL Liteにおいては,制限でどの特性がメンバ数構成要素をもつことができるかの制約が存在する。こ
の制約は,OWL DLにも同様に存在する。
2.3.2.4
OWL DLの特性公理
OWL DL抽象構文の特性公理 (property axiom) は,定義域及び値域においてクラスの代わりに記述
(description) を,値域においてデータ型の代わりにデータ値域を使用可能とすることによって,OWL Lite
の特性公理を一般化する。
axiom ::= 'DatatypeProperty(' datavaluedPropertyID ['Deprecated'] { annotation }
{ 'super(' datavaluedPropertyID ')'} ['Functional']
{ 'domain(' description ')' } { 'range(' dataRange ')' } ')'
| 'ObjectProperty(' individualvaluedPropertyID ['Deprecated'] { annotation }
{ 'super(' individualvaluedPropertyID ')' }
[ 'inverseOf(' individualvaluedPropertyID ')' ] [ 'Symmetric' ]
[ 'Functional' | 'InverseFunctional' | 'Functional' 'InverseFunctional' | 'Transitive' ]
{ 'domain(' description ')' } { 'range(' description ')' } ')'
| 'AnnotationProperty(' annotationPropertyID { annotation } ')'
| 'OntologyProperty(' ontologyPropertyID { annotation } ')'
どの特性を関数的 (functional) 又は逆関数的 (inverse-functional) と指定できるかについての制約は,同
様にOWL DLにも存在する。
11
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
OWL Liteの場合と同様に,次の公理は,複数の特性 (property) を等価 (equivalent) にするか,又はある
特性を別の特性の下位特性 (sub-property) とする。
axiom ::= 'EquivalentProperties(' datavaluedPropertyID datavaluedPropertyID { datavaluedPropertyID } ')'
| 'SubPropertyOf(' datavaluedPropertyID datavaluedPropertyID ')'
| 'EquivalentProperties(' individualvaluedPropertyID individualvaluedPropertyID
{ individualvaluedPropertyID } ')'
| 'SubPropertyOf(' individualvaluedPropertyID individualvaluedPropertyID ')'
3
直接モデル論的意味論
OWLのこのモデル論的意味論は,OWL DLの抽象構文のオントロジ(すなわち,OWL Liteの抽象構文
を含んでいる。)から,直接的に,標準的なモデル理論へ到達する。この意味論は,RDFS意味論の語い(彙)
拡張になっている箇条5の意味論よりも単純といえる。
3.1
語い(彙)及び解釈
意味論を語い(彙)の概念から始める。OWLオントロジを検討するとき,その語い(彙)は,そのオ
ントロジ内のすべてのURI参照及びリテラルと,そのオントロジによって取り込まれるオントロジとを含
まなければならない。しかし,それに加えて,他のURL参照及びリテラルも含めることができる。
3.1では,VOPを,組込みのOWLオントロジ特性へのURI参照とする。
定義
OWL語い(彙)Vは,リテラルVLの集合及びVC, VD, VI, VDP, VIP, VAP及びVOの七つのURI
参照の集合から構成される。どの語い(彙)においても,VC及びVDは互いに素であって,VDP, VIP,
VAP及びVOPは,どの二つを取ってもそれぞれ互いに素とする。語い(彙)のクラス名の集合で
あるVCは,owl:Thing及びowl:Nothingを含む。語い(彙)のデータ型の名前の集合であるVDは,
組込みのOWLデータ型へのURI参照及びrdfs:Literalを含む。語い(彙)の注釈特性の名前の集
合であるVAPは,owl:versionInfo, rdfs:label, rdfs:comment, rdfs:seeAlso及びrdfs:isDefinedByを含む。
語い(彙)の個体値特性の名前の集合であるVIP,語い(彙)のデータ値特性の名前の集合であ
るVDP,語い(彙)の個体の名前の集合であるVI,語い(彙)のオントロジの名前の集合である
VOは,特に必す(須)の要素をもたない。
定義終
定義
RDFの場合と同様に,データ型dは,Unicode文字列の集合である字句空間L(d),値空間V(d)
及び語い(彙)空間から値空間への全域写像 (total mapping) L2V(d) によって特徴付けられる。
定義終
定義
データ型写像Dは,URI参照から,データ型への部分写像 (partial mapping) とする。これは,
xsd:string及びxsd:integerを適切なXMLスキーマデータ型に写像する。
注記 データ型写像は,その他の組込みのOWLデータ型のためのデータ型を含んでもよい。そ
れ以外のデータ型も含んでもよいが,OWL構文においてこれらのデータ型が何であるかを
知らせるための規定は存在しない。
定義終
定義
12
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Dをデータ型写像とする。語い(彙)VL, VC, VD, VI, VDP, VIP, VAP, VOをもつDに関する抽象OWL
解釈は,I = <R, EC, ER, L, S, LV>という形式の組とする。ここで,Pをべき集合演算子とすると,
各要素は次による。
a) Iの資源Rは,空でない集合とする。
b) Iのリテラル値LVは,Rの部分集合とする。LVは,Unicode文字列の集合,Unicode文字
列と言語タグとの対の集合,及びDの中の各データ型に対する値空間を含む。
c) EC : VC → P(O)
d) EC : VD → P(LV)
e) ER : VDP → P(O×LV)
f)
ER : VIP → P(O×O)
g) ER : VAP ∪ { rdf:type } → P(R×R)
h) ER : VOP → P(R×R)
i)
L : TL → LV,ここで,TLは,VL中の型付きリテラルの集合とする。
j)
S : VI ∪ VC ∪ VD ∪ VDP ∪ VIP ∪ VAP ∪ VO ∪ { owl:Ontology, owl:DeprecatedClass,
owl:DeprecatedProperty } → R
k) S(VI) ⊆ O
l)
EC(owl:Thing) = O ⊆ R,ここで,Oは空でなく,LVと互いに素とする。
m) EC(owl:Nothing) = { }
n) EC(rdfs:Literal) = LV
o) D(d') = dならばEC(d') = V(d)とする。
p) D(d') = dならばL("v"^^d') ∈V(d) とする。
q) D(d') = d,かつ,v ∈L(d)ならばL("v"^^d') = L2V(d)(v)とする。
r) D(d') = d,かつ,v ∉L(d)ならばL("v"^^d') ∈ R - LVとする
定義終
ECは,OWLクラス及びデータ型として使われるURI参照に対する意味を与える。ERは,OWL特性と
して使われるURI参照に対する意味を与える。特性rdf:typeは,非推奨 (deprecation) に対する意味を与え
るために注釈特性に追加されている。表3の記述を参照してもらいたい。Lは,型付きリテラルに対して
意味を与える。Sは,OWL個体を示すために使われるURI参照に対して意味を与え,注釈に対して意味
を与えるのに役立つ。整形式ではないリテラルに課されたすべての要件を満たすことができる解釈は存在
しないことに注意してもらいたい。この“整形式でない”とは,1.5^^xsd:integerなど,字句の形式がその
データ型に対して妥当ではないものをいう。
Sは,VLの中の型なしリテラルに対して,(実質上)それ自体に写像することによって,拡張される。
すなわち,言語タグをもたない型なしリテラルlに対しては,S("l") = lとし,言語タグをもつ型なしリテ
ラルlに対して,S("l"@t) = <l,t> とする。Sは,型付きリテラルlに対しては,S(l) = L(l)とするように,L
を使って型付きリテラルへ拡張される。
3.2
埋込み構成要素の解釈
ECは,表2のとおりに,記述,データ領域,個体,値及び注釈の構文構成要素に拡張される。
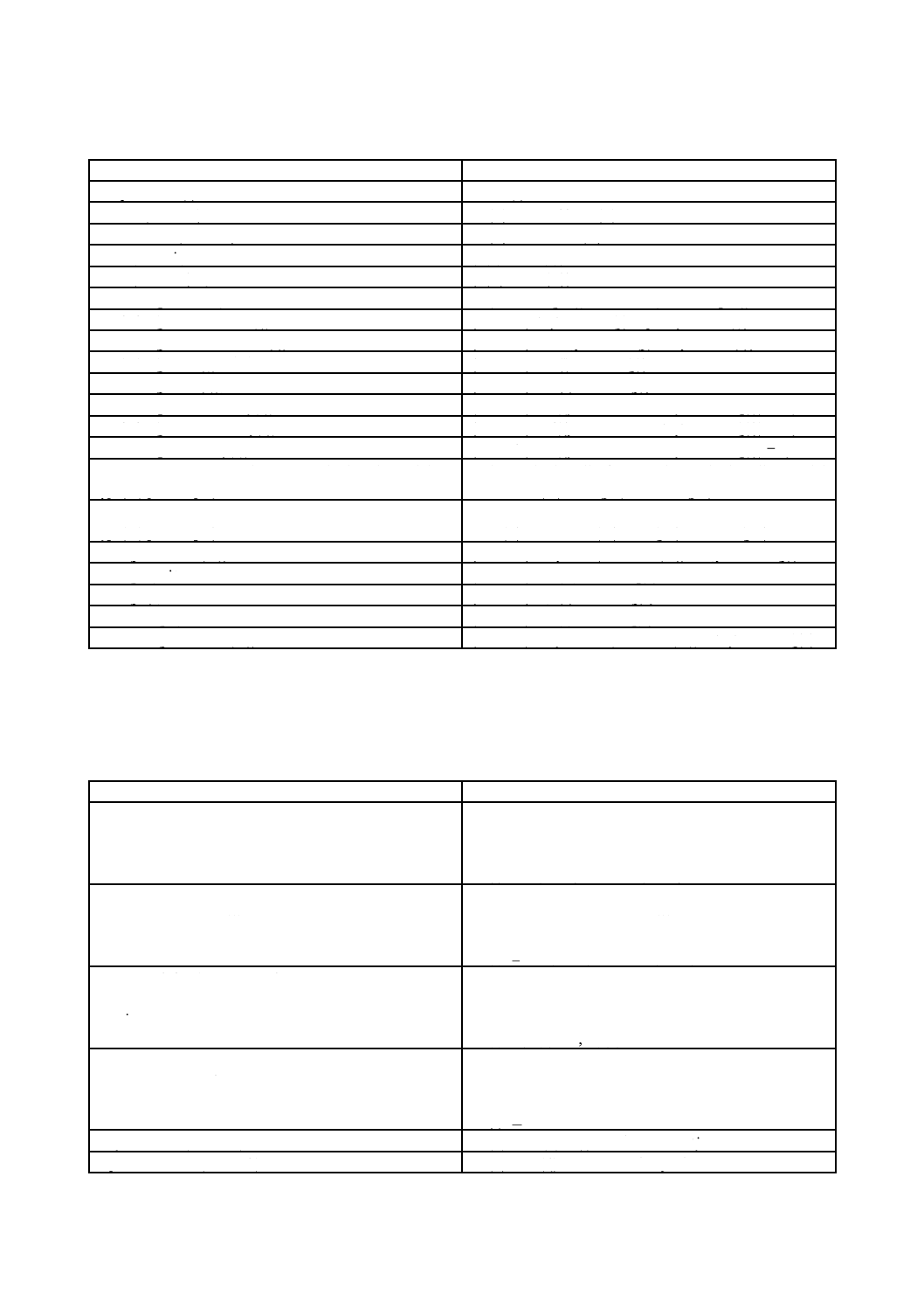
13
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−EC拡張表
抽象構文
解釈(ECの値)
complementOf(c)
O - EC(c)
unionOf(c1 … cn)
EC(c1) ∪ … ∪ EC(cn)
intersectionOf(c1 … cn)
EC(c1) ∩ … ∩ EC(cn)
oneOf(i1 … in), ijは個体IDとする
{S(i1), …, S(in)}
oneOf(v1 … vn), vjはリテラルとする
{S(v1), …, S(vn)}
restriction(p x1 … xn), n > 1とする
EC(restriction(p x1)) ∩…∩EC(restriction(p xn))
restriction(p allValuesFrom(r))
{x ∈ O | <x,y> ∈ ER(p) implies y ∈ EC(r)}
restriction(p someValuesFrom(e))
{x ∈ O | ∃ <x,y> ∈ ER(p) ∧ y ∈ EC(e)}
restriction(p value(i)), i個体IDとする
{x ∈ O | <x,S(i)> ∈ ER(p)}
restriction(p value(v)),vはリテラルとする
{x ∈ O | <x,S(v)> ∈ ER(p)}
restriction(p minCardinality(n))
{x ∈ O | card({y ∈ O∪LV : <x,y> ∈ ER(p)}) ≧n}
restriction(p maxCardinality(n))
{x ∈ O | card({y ∈ O∪LV : <x,y> ∈ ER(p)}) ≦n}
restriction(p cardinality(n))
{x ∈ O | card({y ∈ O∪LV : <x,y> ∈ ER(p)}) = n}
Individual(annotation(p1 o1) … annotation(pk ok) type(c1) …
type(cm) pv1 … pvn)
EC(annotation(p1 o1)) ∩ … EC(annotation(pk ok)) ∩ EC(c1)
∩ … ∩ EC(cm) ∩ EC(pv1) ∩…∩ EC(pvn)
Individual(i annotation(p1 o1) … annotation(pk ok) type(c1) …
type(cm) pv1 … pvn)
{S(i)} ∩ EC(annotation(p1 o1)) ∩ … EC(annotation(pk ok))
∩ EC(c1) ∩ … ∩ EC(cm) ∩ EC(pv1) ∩…∩ EC(pvn)
value(p Individual(…))
{x ∈ O | ∃ y∈EC(Individual(…)) : <x,y> ∈ ER(p)}
value(p id) , idは個体IDとする
{x ∈ O | <x,S(id)> ∈ ER(p) }
value(p v) , vはリテラルとする
{x ∈ O | <x,S(v)> ∈ ER(p) }
annotation(p o) , oはURI参照とする
{x ∈ R | <x,S(o)> ∈ ER(p) }
annotation(p Individual(…))
{x ∈ R | ∃ y ∈ EC(Individual(…)) : <x,y> ∈ ER(p) }
3.3
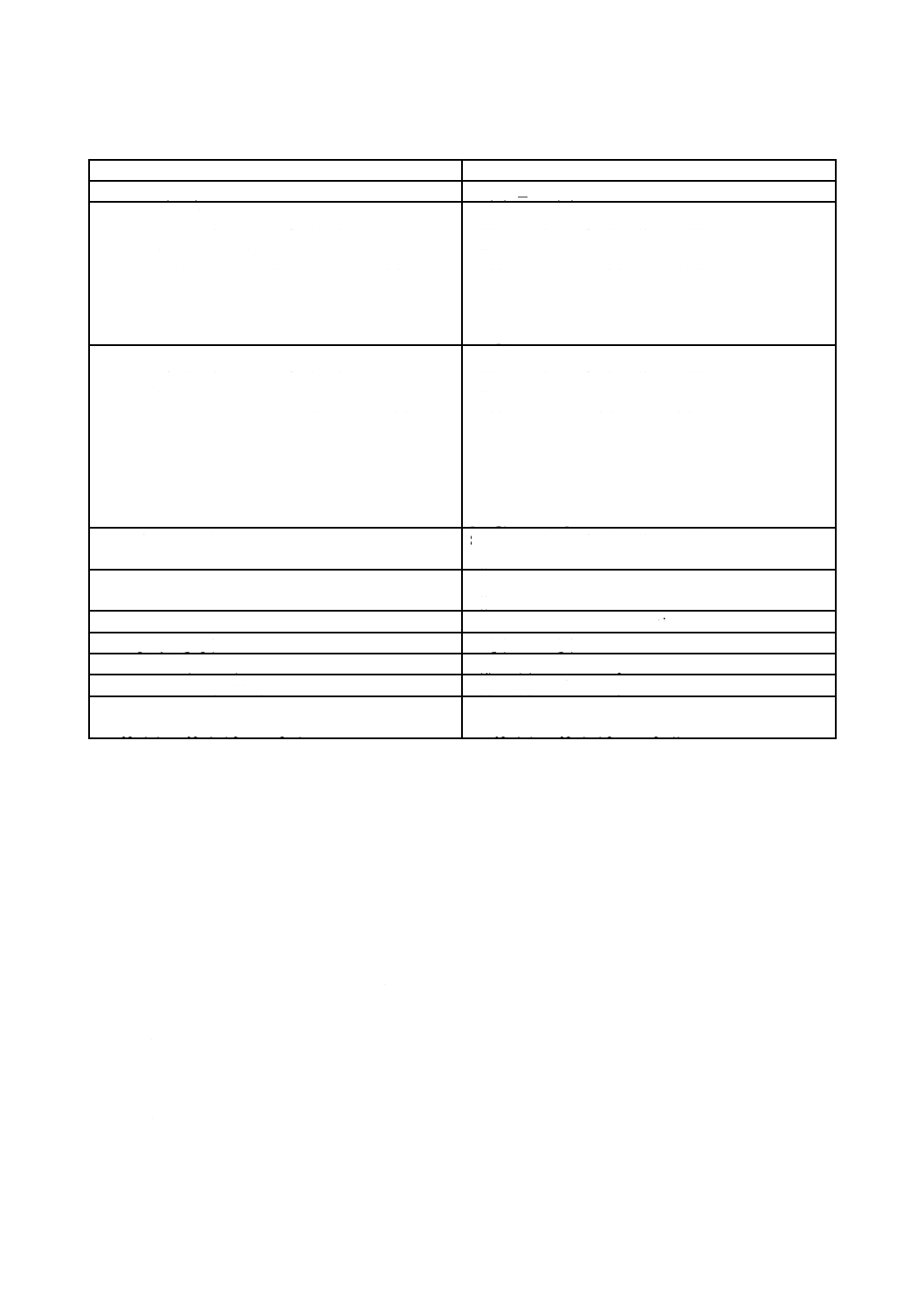
公理及び事実の解釈
抽象OWL解釈Iは,表3に示すとおりに,OWLの公理及び事実を充足する。表3では,公理及び事実
の任意選択の部分を角括弧([…])で囲み,それと対応する任意選択の条件も角括弧で囲んでいる。
表3−公理及び事実の解釈
指示
解釈における条件
Class(c [Deprecated] complete
annotation(p1 o1) … annotation(pk ok)
descr1 … descrn)
[ <S(c),S(owl:DeprecatedClass)> ∈ ER(rdf:type) ]
S(c) ∈ EC(annotation(p1 o1)) … S(c) ∈ EC(annotation(pk
ok))
EC(c) = EC(descr1) ∩…∩ EC(descrn)
Class(c [Deprecated] partial
annotation(p1 o1) … annotation(pk ok)
descr1 … descrn)
[ <S(c),S(owl:DeprecatedClass)> ∈ ER(rdf:type) ]
S(c) ∈ EC(annotation(p1 o1)) … S(c) ∈ EC(annotation(pk
ok))
EC(c) ⊆ EC(descr1) ∩…∩ EC(descrn)
EnumeratedClass(c [Deprecated]
annotation(p1 o1) … annotation(pk ok)
i1 … in)
[ <S(c),S(owl:DeprecatedClass)> ∈ ER(rdf:type) ]
S(c) ∈ EC(annotation(p1 o1)) … S(c) ∈ EC(annotation(pk
ok))
EC(c) = { S(i1), …, S(in) }
Datatype(c [Deprecated]
annotation(p1 o1) … annotation(pk ok) )
[ <S(c),S(owl:DeprecatedClass)> ∈ ER(rdf:type) ]
S(c) ∈ EC(annotation(p1 o1)) … S(c) ∈ EC(annotation(pk
ok))
EC(c) ⊆ LV
DisjointClasses(d1 … dn)
EC(di) ∩ EC(dj) = { } ただし 1 ≦i < j ≦n
EquivalentClasses(d1 … dn)
EC(di) = EC(dj) ただし 1 ≦i < j ≦n
14
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3−公理及び事実の解釈(続き)
指示
解釈における条件
SubClassOf(d1 d2)
EC(d1) ⊆ EC(d2)
DatatypeProperty(p [Deprecated]
annotation(p1 o1) … annotation(pk ok)
super(s1) … super(sn)
domain(d1) … domain(dn) range(r1) … range(rn)
[Functional])
[ <S(c),S(owl:DeprecatedProperty)> ∈ ER(rdf:type) ]
S(p) ∈ EC(annotation(p1 o1)) … S(p) ∈ EC(annotation(pk
ok))
ER(p) ⊆ O×LV ∩ ER(s1) ∩…∩ ER(sn) ∩
EC(d1)×LV ∩…∩ EC(dn)×LV ∩
O×EC(r1) ∩…∩ O×EC(rn)
[ER(p)は関数的]
ObjectProperty(p [Deprecated]
annotation(p1 o1) … annotation(pk ok)
super(s1) … super(sn)
domain(d1) … domain(dn) range(r1) … range(rn)
[inverse(i)] [Symmetric]
[Functional] [ InverseFunctional]
[Transitive])
[ <S(c),S(owl:DeprecatedProperty)> ∈ ER(rdf:type)]
S(p) ∈ EC(annotation(p1 o1)) … S(p) ∈ EC(annotation(pk
ok))
ER(p) ⊆ O×O ∩ ER(s1) ∩…∩ ER(sn) ∩
EC(d1)×O ∩…∩ EC(dn)×O ∩
O×EC(r1) ∩…∩ O×EC(rn)
[ER(p)はER(i)の逆] [ER(p)は対称的]
[ER(p)は関数的] [ER(p)は逆関数的]
[ER(p)は推移的]
AnnotationProperty(p annotation(p1 o1) … annotation(pk ok)) S(p) ∈ EC(annotation(p1 o1)) … S(p) ∈ EC(annotation(pk
ok))
OntologyProperty(p annotation(p1 o1) … annotation(pk ok))
S(p) ∈ EC(annotation(p1 o1)) … S(p) ∈ EC(annotation(pk
ok))
EquivalentProperties(p1 … pn)
ER(pi) = ER(pj) ただし 1 ≦i < j ≦n
SubPropertyOf(p1 p2)
ER(p1) ⊆ ER(p2)
SameIndividual(i1 … in)
S(ij) = S(ik) ただし 1 ≦j < k ≦n
DifferentIndividuals(i1 … in)
S(ij) ≠ S(ik) ただし 1 ≦j < k ≦n
Individual([i] annotation(p1 o1) … annotation(pk ok)
type(c1) … type(cm) pv1 … pvn)
EC(Individual([i] annotation(p1 o1) … annotation(pk ok)
type(c1) … type(cm) pv1 … pvn)) は空でない
3.4
オントロジの解釈
箇条2によって,OWLオントロジは,注釈をもつことができる。注釈は,それ自体の意味論条件を必
要とする。この局所的な意味に加えて,owl:imports注釈は別のOWLオントロジの内容も現在のオントロ
ジに取り込む。取り込まれたオントロジがある場合には,その名前は,取込み構成要素の引数とする。こ
の取込みの取扱いは,ウェブの場合とは分離している。OWLオントロジで名前を使用する意図は,その
名前をウェブ上のオントロジの位置とすることだが,これは,この規格の範囲外とする。
定義
Dをデータ型写像とする。次のすべての場合及びその場合に限り,VL,VC,VD,VI,VDP,VIP,
VAP及びVOから構成される語い(彙)をもつDに関して,抽象OWL解釈Iは,OWLオントロジO
を充足する。
a) クラス ID(データ型ID,個体ID,データ値特性ID,個体値特性ID,注釈特性ID,注釈ID
又はオントロジID)として使われるOの各URI参照が,VC(それぞれ,VD,VI,VDP,VIP,
VAP又はVO)に属する場合。
b) O中の各リテラルがVLに属する場合。
c) オントロジ注釈を除き,IがOの各指示を充足する場合。
15
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) <o,S(owl:Ontology)> ∈ ER(rdf:type) となる何らかのo ∈ R が存在し,Annotation(p v) という
形式のオントロジ注釈のそれぞれについて,<o,S(v)> ∈ ER(p) が成立し,かつ,Oが名前n
をもつならば,S(n) = o となる場合。
e) Iが,Oのowl:imports注釈指示で言及している各オントロジを充足する場合。
定義終
定義
抽象OWLのオントロジと,公理及び事実との集まりは,データ型写像Dに関して何らかの解釈
Iが存在し,Iがその集まりの中の各オントロジと,公理及び事実とを充足する場合に限り,Dに関
して無矛盾とする。
定義終
定義
抽象OWLのオントロジと公理及び事実との集まりOは,Oの各々のオントロジと公理及び事実
とを充足するデータ型写像Dに関する各解釈が,抽象OWLオントロジ又は公理若しくは事実O'
をも充足する場合,写像Dに関して,O'を 論理的帰結とする。
定義終
4
RDFグラフへの写像
箇条4では,箇条2で示したOWL DL及びOWL Liteの抽象構文から,OWLの交換構文,すなわち,
RDF/XML [RDF Syntax]への写像を与える。この写像及びその逆写像は,抽象構文と交換構文との間の関係
を与える。箇条5及びA.1では,この写像がOWL DLオントロジの意味を保存することを示している。4.2
では,抽象構文オントロジからの写像の結果であるRDFグラフとして,OWLの部分言語であるOWL DL
及びOWL Liteを定義する。
OWLの交換構文は,RDF/XML [RDF Syntax]であって,これは,OWL 機能一覧[OWL Reference]で規定
されている。さらに,RDF/XMLで記述されたOWLオントロジの意味は,そのRDF/XML文書のRDF構
文解析の結果であるRDFグラフ [RDF Concepts]だけから決定される。したがって,抽象構文形式のOWL
オントロジを交換構文に翻訳するには,それぞれの指示を三つ組の集まりに変換するのは一つの方法にな
る。OWL Liteの構成要素はすべて,完全な抽象構文の構成要素の特殊例なので,OWL DL変換だけを示す。
OWL DLは,抽象構文全体にわたって定義される意味論と,RDFグラフの部分集合から構成される具象
構文とをもつ。そのため,特定の抽象構文オントロジを,特定のRDF/XML文書及びそれらに対応するグ
ラフに関連付ける必要がある。箇条4は,抽象構文オントロジと複数のRDFグラフとの間の多対多関係を
定義する。これを行うために,非決定的な写像規則の集合を使う。すなわち,意味論を特定のRDFグラフ
に適用するためには,写像規則に従ってそのグラフと対応する抽象構文オントロジの一つを見い出し,意
味論をその抽象オントロジに適用する必要がある。この写像は,特定の抽象オントロジに対応するRDF
グラフがどれも同じ意味をもつように設計されている。同様に,特定の抽象構文に対応するRDFグラフが
どれも同じ意味をもつようにも設計されている。さらに,対応する抽象構文の形式をもたないRDFグラフ
にこの処理を適用することはできないので,この写像規則は,RDF/XMLで記述されたOWL DLを構文的
に特徴付けるグラフの集合を暗黙に定義する。
ここで使う三つ組の構文は,RDF意味論[RDF Semantics]で使うものと同じになっている。ただし,この
規格では,修飾された名前を使用できるものとする。RDF意味論で詳細に記述されているとおり,この構
文を標準的な構文に変換するには,標準OWL名前空間を使用して,名前空間名を局所名に連結すること
16
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
によって,RDFの標準的な方法で,修飾された名前をURI参照に展開するだけでよい。
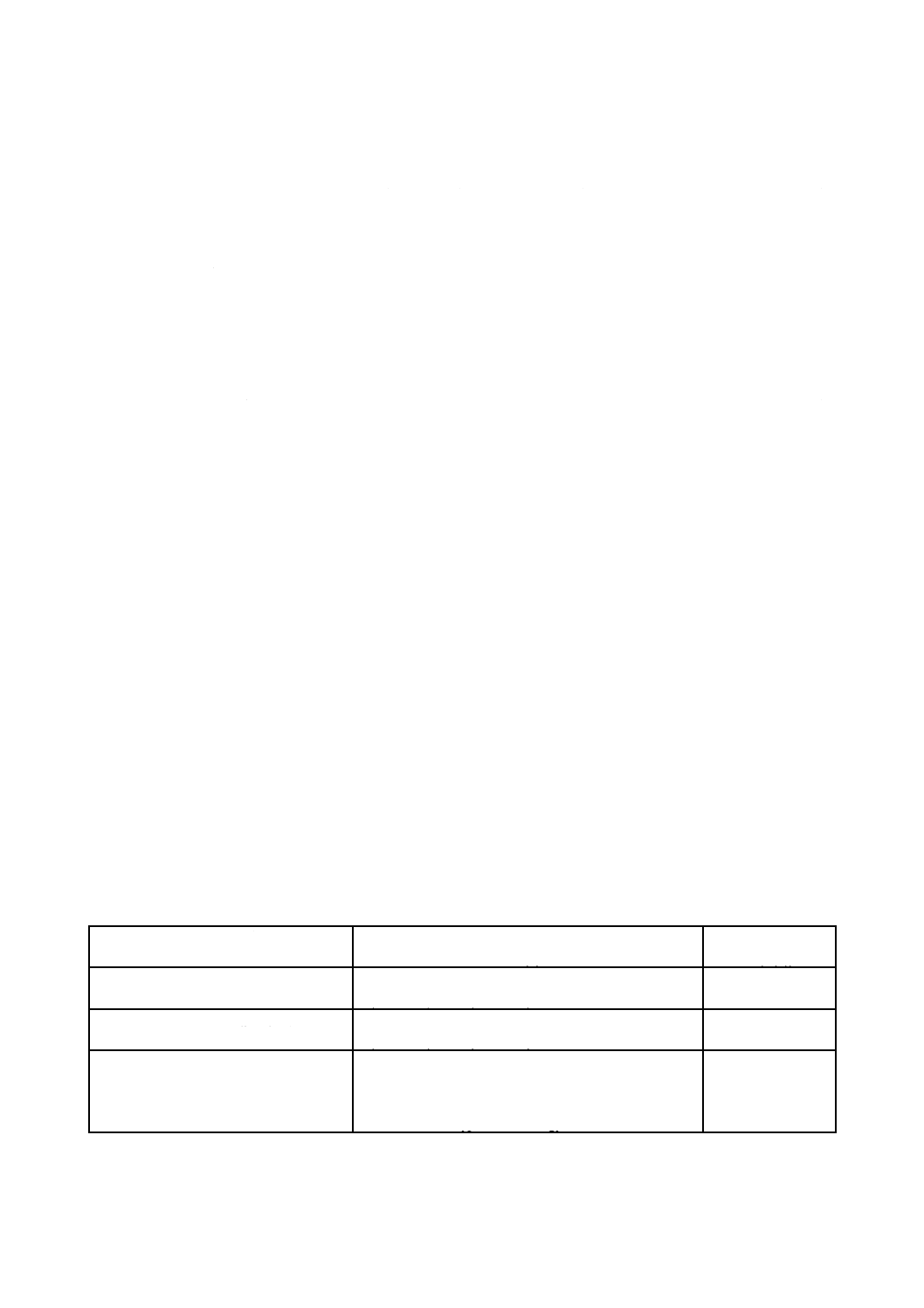
4.1
RDFグラフへの翻訳(変換)
RDFグラフへの翻訳のための表4の変換表は,抽象構文をOWL交換構文,すなわちRDFグラフに変換
する変換規則を与える。幾つかの場合,特に,DifferentIndividuals構成要素については,異なる変換規則も
存在する。これらの場合では,いずれかの規則を選択することができ,その結果,非決定的な変換となる。
他の幾つかの場合,特に,クラス公理及び特性公理については,生成されてもよいし生成されなくてもよ
い三つ組が存在する。これらの三つ組は,[opt] の印をつけることによって示される。さらに,幾つかの場
合では,二つの三つ組のうち,一つを生成しなければならないこともある。これは,その二つの三つ組を
ORで分けることによって示される。これらの非決定性によって,更に多くのRDFを生成することが可能
となる。
表4の左列は,抽象構文 (S) の一つの要素とする。中央の列は,その要素の三つ組((T(S)))への変換
を表す。右列は,変換の主ノード(M(T(S)))に対する識別子を表し,指示の一部として出現できる構文上
の構成要素に対応するものとする。構成要素の繰返しは,description1 … descriptionnのように,省略記号(…)
を使って列挙する。この形式によって,構文で使用できるnのすべての値について,変換を簡単に規定す
ることができる。抽象構文の(角括弧で囲まれる)任意選択の部分は,変換の(角括弧で囲まれる)任意
選択の部分になる。さらに,組込みのOWLデータ型, 組込みのOWLクラス, 組込みのOWL注釈特性,
及び組込みのOWLオントロジ特性のいずれについても,その変換の最初のrdf:type三つ組又はそのいかな
る公理も任意選択であるものとする。
表4には,指示に対する変換もあれば,指示の一部に対する変換もある。最後の変換は,列に関するも
のだが,これは抽象構文の一部ではない。この最後の変換は,他の幾つかの変換を更に簡潔にし,読みや
すくするために使う。
多くの指示に対しては,これらの変換規則は,他の変換規則を使う,その指示の構成要素の変換を要求
する。構成要素の変換が,三つ組(任意選択の三つ組でもよい。)の主語,述語又は目的語として使われる
ときには,その構成要素の変換は生成規則の一部であって(ただし,変換は生成規則ごとに一回だけとす
る。),その変換の主ノードは三つ組の中で使用されるのが望ましい。
ここでの無名ノード識別子は,各変換に対して局所的として考えられなければならない。すなわち,あ
る変換規則のそれぞれの呼出しには,異なる識別子を使用するのがよい。名前をもたないオントロジは,
主ノードを無名ノードとしている。名前をもつオントロジは,その名前を主ノードとして使う。いずれの
場合も,このノードは,表4ではOで表される。
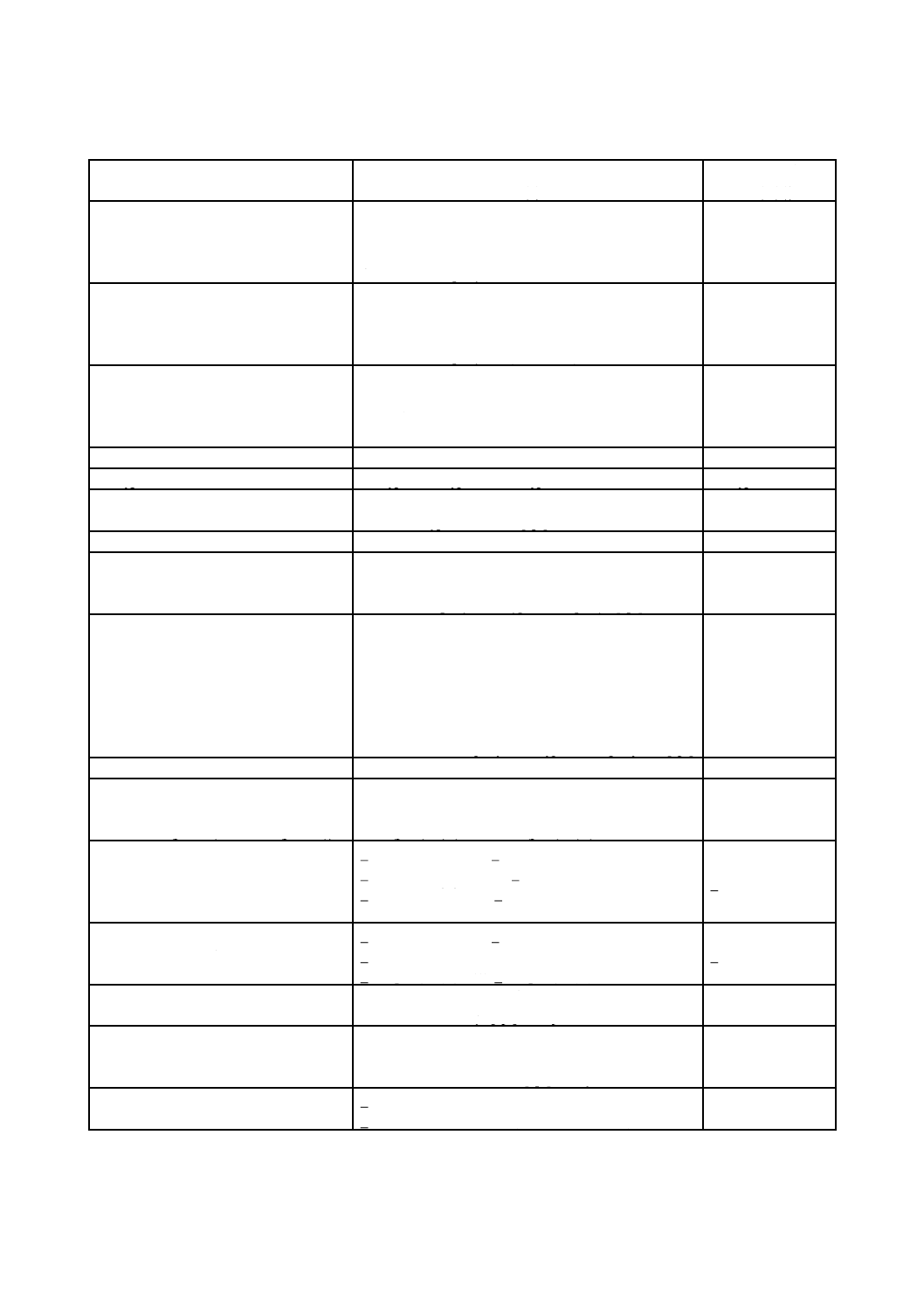
表4−三つ組への変換
抽象構文及び列
S
変換
T(S)
主ノード
M(T(S))
Ontology(O directive1 … directiven)
O rdf:type owl:Ontology .
T(directive1) … T(directiven)
Ontology(directive1 … directiven)
O rdf:type owl:Ontology .
T(directive1) … T(directiven)
Annotation(ontologyPropertyID
URIreference)
OntologyPropertyID rdf:type
owl:OntologyProperty .
O ontologyPropertyID URIreference .
URIreferencerdf:type owl:Ontology .
17
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−三つ組への変換(続き)
抽象構文及び列
S
変換
T(S)
主ノード
M(T(S))
Annotation(annotationPropertyID
URIreference)
annotationPropertyID rdf:type
owl:AnnotationProperty .
annotationPropertyID rdf:type rdf:Property . [opt]
O annotationPropertyID URIreference .
Annotation(annotationPropertyID
dataLiteral)
annotationPropertyID rdf:type
owl:AnnotationProperty .
annotationPropertyID rdf:type rdf:Property . [opt]
O annotationPropertyID T(dataLiteral) .
Annotation(annotationPropertyID
individual)
annotationPropertyID rdf:type
owl:AnnotationProperty .
annotationPropertyID rdf:type rdf:Property . [opt]
O annotationPropertyID T(individual) .
rdfs:Literal
rdfs:Literal
datatypeID
datatypeID rdf:type rdfs:Datatype .
datatypeID
classID
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
classID
individualID
individualID
datavaluedPropertyID
datavaluedPropertyID rdf:type
owl:DatatypeProperty .
datavaluedPropertyID rdf:type rdf:Property . [opt]
datavaluedPropertyI
D
individualvaluedPropertyID
individualvaluedPropertyID rdf:type
owl:ObjectProperty .
[individualvaluedPropertyIDを
owl:InverseFunctionalProperty,owl:TransitiveProperty,
又はowl:SymmetricPropertyとして型付けするオントロ
ジの変換中に三つ組が存在するならば,opt]
individualvaluedPropertyID rdf:type rdf:Property . [opt]
individualvaluedPro
pertyID
dataLiteral
dataLiteral
dataLiteral
Individual(iID annotation1 … annotationm
type(type1)… type(typen)
value(pID1 v1) … value(pIDk vk))
iID T(annotation1) … iID T(annotationm)
iID rdf:type T(type1) . … iID rdf:type T(typen) .
iID T(pID1) T(v1) . … iID T(pIDk) T(vk) .
iID
Individual(annotation1 … annotationm
type(type1)…type(typen)
value(pID1 v1) … value(pIDk vk))
(少なくとも一つの型をもつ)
̲:x T(annotation1) … ̲:x T(annotationm)
̲:x rdf:type T(type1) . … ̲:x rdf:type T(typen) .
̲:x T(pID1) T(v1) . … ̲:x T(pIDk) T(vk) .
̲:x
Individual(annotation1 … annotationm
value(pID1 v1) … value(pIDk vk))
̲:x T(annotation1) … ̲:x T(annotationm)
̲:x rdf:type owl:Thing .
̲:x T(pID1) T(v1) . … ̲:x T(pIDk) T(vk) .
̲:x
SameIndividual(iID1 … iIDn)
iIDi owl:sameAs iIDi+1 . 1≦i<n
iIDi owl:sameAs iIDj . [opt] 1≦i≠j≦n
DifferentIndividuals(iID1 … iIDn)
iIDi owl:differentFrom iIDj . OR
iIDj owl:differentFrom iIDi . 1≦i<j≦n
iIDj owl:differentFrom iIDi . [opt] 1≦i≠j≦n
DifferentIndividuals(iID1 … iIDn)
̲:x rdf:type owl:AllDifferent .
̲:x owl:distinctMembers T(SEQ iID1 … iIDn) .

18
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−三つ組への変換(続き)
抽象構文及び列
S
変換
T(S)
主ノード
M(T(S))
Class(classID [Deprecated] partial
annotation1 … annotationm
description1 … descriptionn)
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
[classID rdf:type owl:DeprecatedClass .]
classID T(annotation1) … classID T(annotationm)
classID rdfs:subClassOf T(description1) . …
classID rdfs:subClassOf T(descriptionn) .
Class(classID [Deprecated] complete
annotation1 … annotationm
description1 … descriptionn)
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
[classID rdf:type owl:DeprecatedClass .]
classID T(annotation1) … classID T(annotationm)
classID owl:intersectionOf T(SEQ description1…
descriptionn) .
Class(classID [Deprecated] complete
annotation1 … annotationm
description)
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
[classID rdf:type owl:DeprecatedClass .]
classID T(annotation1) … classID T(annotationm)
classID owl:equivalentClass T(description) .
Class(classID [Deprecated] complete
annotation1 … annotationm
unionOf(description1 …
descriptionn))
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
[classID rdf:type owl:DeprecatedClass .]
classID T(annotation1) … classID T(annotationm)
classID owl:unionOf T(SEQ description1…
descriptionn) .
Class(classID [Deprecated] complete
annotation1 … annotationm
complementOf(description))
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
[classID rdf:type owl:DeprecatedClass .]
classID T(annotation1) … classID T(annotationm)
classID owl:complementOf T(description) .
EnumeratedClass(classID [Deprecated]
annotation1 … annotationm
iID1 … iIDn)
classID rdf:type owl:Class .
classID rdf:type rdfs:Class . [opt]
[classID rdf:type owl:DeprecatedClass .]
classID T(annotation1) … classID T(annotationm) .
classID owl:oneOf T(SEQ iID1…iIDn) .
DisjointClasses(description1 …
descriptionn)
T(descriptioni) owl:disjointWith T(descriptionj) . OR
T(descriptionj) owl:disjointWith T(descriptioni) .
1≦i<j≦n
T(descriptioni) owl:disjointWith T(descriptionj) . [opt] 1≦
i≠j≦n
EquivalentClasses(description1 …
descriptionn)
T(descriptioni) owl:equivalentClass
T(descriptionj) .
Gのすべての<i,j>に対して。ここで,Gは,無向グラ
フとして解釈したときに,{1,...,n}の連結グラフを形成
するような {1,...,n}x{1,...,n}上の対の集合とする。
SubClassOf(description1 description2)
T(description1) rdfs:subClassOf T(description2) .
19
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−三つ組への変換(続き)
抽象構文及び列
S
変換
T(S)
主ノード
M(T(S))
Datatype(datatypeID [Deprecated]
annotation1 … annotationm )
datatypeID rdf:type rdfs:Datatype .
datatypeID rdf:type rdfs:Class . [opt]
[datatypeID rdf:type owl:DeprecatedClass .]
datatypeID T(annotation1) … datatypeID
T(annotationm)
unionOf(description1 … descriptionn)
̲:x rdf:type owl:Class .
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:unionOf T(SEQ description1…
descriptionn) .
̲:x
intersectionOf(description1 …
descriptionn)
̲:x rdf:type owl:Class .
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:intersectionOf T(SEQ description1…
descriptionn) .
̲:x
complementOf(description)
̲:x rdf:type owl:Class .
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:complementOf T(description) .
̲:x
oneOf(iID1 … iIDn)
̲:x rdf:type owl:Class .
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:oneOf T(SEQ iID1…iIDn) .
̲:x
oneOf(v1 … vn)
̲:x rdf:type owl:DataRange .
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:oneOf T(SEQ v1 … vn) .
̲:x
restriction(ID component1 … componentn)
(少なくとも二つの構成要素をもつ)
̲:x rdf:type owl:Class .
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:intersectionOf
T(SEQ(restriction(ID component1) …
restriction(ID componentn))) .
̲:x
restriction(ID allValuesFrom(range))
̲:x rdf:type owl:Restriction .
̲:x rdf:type owl:Class . [opt]
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:onProperty T(ID) .
̲:x owl:allValuesFrom T(range) .
̲:x
restriction(ID someValuesFrom(required))
̲:x rdf:type owl:Restriction .
̲:x rdf:type owl:Class . [opt]
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:onProperty T(ID) .
̲:x owl:someValuesFrom T(required) .
̲:x
restriction(ID value(value))
̲:x rdf:type owl:Restriction .
̲:x rdf:type owl:Class . [opt]
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:onProperty T(ID) .
̲:x owl:hasValue T(value) .
̲:x
restriction(ID minCardinality(min))
̲:x rdf:type owl:Restriction .
̲:x rdf:type owl:Class . [opt]
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:onProperty T(ID) .
̲:x owl:minCardinality
"min"^^xsd:nonNegativeInteger .
̲:x
20
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−三つ組への変換(続き)
抽象構文及び列
S
変換
T(S)
主ノード
M(T(S))
restriction(ID maxCardinality(max))
̲:x rdf:type owl:Restriction .
̲:x rdf:type owl:Class . [opt]
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:onProperty T(ID) .
̲:x owl:maxCardinality
"max"^^xsd:nonNegativeInteger .
̲:x
restriction(ID cardinality(card))
̲:x rdf:type owl:Restriction .
̲:x rdf:type owl:Class . [opt]
̲:x rdf:type rdfs:Class . [opt]
̲:x owl:onProperty T(ID) .
̲:x owl:cardinality
"card"^^xsd:nonNegativeInteger .
̲:x
DatatypeProperty(ID [Deprecated]
annotation1 … annotationm
super(super1)… super(supern)
domain(domain1)…
domain(domaink)
range(range1)…
range(rangeh)
[Functional])
ID rdf:type owl:DatatypeProperty .
ID rdf:type rdf:Property . [opt]
[ID rdf:type owl:DeprecatedProperty .]
ID T(annotation1) … ID T(annotationm)
ID rdfs:subPropertyOf T(super1) . …
ID rdfs:subPropertyOf T(supern) .
ID rdfs:domainT(domain1) . …
ID rdfs:domainT(domaink) .
ID rdfs:range T(range1) . …
ID rdfs:range T(rangeh) .
[ID rdf:type owl:FunctionalProperty . ]
ObjectProperty(ID [Deprecated]
annotation1 … annotationm
super(super1)… super(supern)
domain(domain1)…
domain(domaink)
range(range1)…
range(rangeh)
[inverseOf(inverse)]
[Functional |
InverseFunctional |
Transitive])
[Symmetric]
ID rdf:type owl:ObjectProperty .
[最後の三つの三つ組のうち,一つが含まれている
ならば,opt]
ID rdf:type rdf:Property . [opt]
[ID rdf:type owl:DeprecatedProperty .]
ID T(annotation1) … ID T(annotationm)
ID rdfs:subPropertyOf T(super1) . …
ID rdfs:subPropertyOf T(supern) .
ID rdfs:domainT(domain1) . …
ID rdfs:domainT(domaink) .
ID rdfs:range T(range1) . …
ID rdfs:range T(rangeh) .
[ID owl:inverseOf T(inverse) .]
[ID rdf:type owl:FunctionalProperty . ]
[ID rdf:type owl:InverseFunctionalProperty . ]
[ID rdf:type owl:TransitiveProperty . ]
[ID rdf:type owl:SymmetricProperty . ]
AnnotationProperty(ID
annotation1 … annotationm)
ID rdf:type owl:AnnotationProperty .
ID rdf:type rdf:Property . [opt]
ID T(annotation1) … ID T(annotationm)
OntologyProperty(ID
annotation1 … annotationm)
ID rdf:type owl:OntologyProperty .
ID rdf:type rdf:Property . [opt]
ID T(annotation1) … ID T(annotationm)
EquivalentProperties(dvpID1 …
dvpIDn)
T(dvpIDi) owl:equivalentProperty T(dvpIDi+1) .
1≦i<n
21
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−三つ組への変換(続き)
抽象構文及び列
S
変換
T(S)
主ノード
M(T(S))
SubPropertyOf(dvpID1 dvpID2)
T(dvpID1) rdfs:subPropertyOf T(dvpID2) .
EquivalentProperties(ivpID1 … ivpIDn)
T(ivpIDi) owl:equivalentProperty T(ivpIDi+1) . 1≦i<n
SubPropertyOf(ivpID1 ivpID2)
T(ivpID1) rdfs:subPropertyOf T(ivpID2) .
annotation(annotationPropertyID
URIreference)
annotationPropertyID URIreference .
annotationPropertyID rdf:type
owl:AnnotationProperty .
annotationPropertyID rdf:type rdf:Property . [opt]
annotation(annotationPropertyID
dataLiteral)
annotationPropertyID T(dataLiteral) .
annotationPropertyID rdf:type
owl:AnnotationProperty .
annotationPropertyID rdf:type rdf:Property . [opt]
annotation(annotationPropertyID
individual)
annotationPropertyID T(individual) .
annotationPropertyID rdf:type
owl:AnnotationProperty .
annotationPropertyID rdf:type rdf:Property . [opt]
SEQ
rdf:nil
SEQ item1…itemn
̲:l1 rdf:type rdf:List . [opt]
̲:l1 rdf:first T(item1) . ̲:l1 rdf:rest ̲:l2 .
…
̲:ln rdf:type rdf:List . [opt]
̲:ln rdf:first T(itemn) . ̲:ln rdf:rest rdf:nil .
̲:l1
前述の予約語い(彙)を使用しない複数のOWL抽象オントロジが,同等のRDFグラフに写像できるの
で,この変換は単射ではない。しかし,これが起こり得る唯一の場合は,複数のDisjointClass公理が,一
つの大きなDisjointClass公理と同じ効果をもつといったように,複数の構成要素が同じ意味をもつ場合に
なる。単射を望むならば,正準逆変換を定義することもできる。
4.2
RDFグラフ形式でのOWL DLオントロジ及びOWL Liteオントロジの定義
RDFグラフの形式でOWL Liteオントロジ及びOWL DLオントロジを検討する場合,OWLのクラス,
特性又は個体として,ある語い(彙)を使用してはならないことに注意を払わなければならない。この注
意を払わない場合,(RDF又はOWL規定における)この語い(彙)の組込み定義又は使用は,OWLオン
トロジにおける情報を増大させることになってしまう。この分類に属するRDF語い(彙)は少ない。これ
は,rdf:subjectなどの幾つかのRDF語い(彙)がRDF規定によって意味をほとんど提供されないか,又は
全く提供されないためであって,その使用方法が,RDF規定が提供するいかなる意味にも無矛盾の場合に
は,問題を起こさないことによる。
定義
使用してはならないRDFからの語い(彙)は,rdf:type, rdf:Property, rdf:nil, rdf:List, rdf:first, rdf:rest,
rdfs:domain, rdfs:range, rdfs:Resource, rdfs:Datatype, rdfs:Class, rdfs:subClassOf, rdfs:subPropertyOf,
rdfs:member, rdfs:Container及び rdfs:ContainerMembershipPropertyとする。使用してはならないOWLか
らの語い(彙)は owl:AllDifferent, owl:allValuesFrom, owl:AnnotationProperty, owl:cardinality, owl:Class,
owl:complementOf, owl:DataRange, owl:DatatypeProperty, owl:DeprecatedClass, owl:DeprecatedProperty,
owl:differentFrom, owl:disjointWith, owl:distinctMembers, owl:equivalentClass, owl:equivalentProperty,
owl:FunctionalProperty, owl:hasValue, owl:intersectionOf, owl:InverseFunctionalProperty, owl:inverseOf,
22
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
owl:maxCardinality, owl:minCardinality, owl:ObjectProperty, owl:oneOf, owl:onProperty, owl:Ontology,
owl:OntologyProperty,
owl:Restriction,
owl:sameAs,
owl:someValuesFrom,
owl:SymmetricProperty,
owl:TransitiveProperty,及びowl:unionOfとする。使用してはならない語い(彙)とは,使用してはな
らないRDFからの語い(彙)と使用してはならないOWLからの語い(彙)との和集合とする。
定義終
定義
クラス固有の語い(彙)とは,rdf:Statement, rdf:Seq, rdf:Bag及びrdf:Altとする。データ型固有の語
い(彙)とは,組込みのOWLデータ型とする。特性固有の語い(彙)とは,rdf:subject, rdf:predicate,
rdf:object及びすべてのコンテナの所属関係特性,すなわち,rdf:̲1, rdf:̲2, …などとする。
定義終
定義
抽象構文形式におけるOWL DLオントロジと公理及び事実との集まりOは,次の場合には,分離
された語い(彙)をもつ。
a) Oの中の複数のオントロジが,全体として,クラスID,データ型ID,個体ID,個体値特性ID,
データ値特性ID,注釈特性ID,オントロジ特性ID又はオントロジIDのうち二つ以上のものと
して,いかなるURI参照も使わない場合。
b) Oの中の複数のオントロジが,全体として,すべての個体IDに型を与える場合。
c) Oの中のオントロジが,注釈の値としての場合を除き,クラスIDとしてクラス固有の語い(彙)
だけを使用し,データ型IDとしてデータ型固有の語い(彙)だけを使用し,データ域ではrdfs:Literal
だけを使用し,datavaluedPropertyID,individualvaluedProperty ID又はannotationProperty IDとして
特性固有の語い(彙)だけを使用し,クラスIDとして組込みクラスだけを使用し,データ型ID
として組込みデータ型だけを使用し,annotationProperty IDとして組込み注釈特性だけを使用し,
ontologyProperty IDとして組込みオントロジ特性だけを使用し,いかなる使用してはならない語
い(彙)にも言及しない場合。
定義終
定義
RDFグラフが,分離された語い(彙)をもつ抽象構文形式において,OWL DLオントロジと公理及
び事実との集まりの,表4の三つ組への変換の結果と等価となる場合(これをもう少し緩めることは
後で示す。),そのRDFグラフは,RDFグラフ形式のOWL DLオントロジという。あるRDFグラフが
RDFグラフ形式のOWL DLオントロジかどうかを決定する目的のために,メンバ数制限において,符
号化されたデータ値が非負整数である範囲で,"1"^^xsd:integerといった構成を明示的に使用できる。
定義終
定義
Oの内容が,抽象構文形式のOWL Liteオントロジ又は公理若しくは事実であることを除いて,一
つ目の定義のとおりとなる場合,RDFグラフは,RDFグラフ形式のOWL Liteオントロジという。
定義終
5
RDFに互換なモデル論的意味論
この箇条で示すOWLのモデル論的意味論は,RDF意味論[RDF Semantics]で定義された意味論の拡張で
あって,OWLによるRDFの意味論の拡張を定義する。
23
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 箇条5で定義されるOWL DLの意味論と,箇条3で定義される直接モデル論的意味論とは,強
く対応している。5.4の定理1及び定理2を参照してもらいたい。しかし,これら二つの形式の
間で,何らかの競合が生じた場合は,直接モデル論的意味論を優先する。
5.1
OWL及びRDFの世界
OWL語い(彙)のすべては,“OWL世界”(この規格が規定するもの)で定義されている。これは,RDF
世界([RDF Semantics],[RDF Concepts],[RDF Syntax]などが規定するもの)の一部を,OWL個体,OWL
クラス及びOWL特性の三つに分割したものとする。owl:Thingのクラス拡張は,OWL世界の個体を構成
する。owl:Classのクラス拡張は,OWL世界のクラスを構成する。owl:ObjectProperty, owl:DatatypeProperty,
owl:AnnotationProperty及び owl:OntologyPropertyのクラス拡張の和集合は,OWL世界の特性を構成する。
OWLの使用においては,二つの異なる表現形式が存在する。OWL Fullと呼ばれる,制限の少ない表現
形式では,OWL世界の三つの部分は,それらのRDFにおける対応部分,すなわちrdfs:Resource, rdfs:Class
及びrdf:Propertyのクラスの外延(オブジェクト,又はオブジェクトと値との対の集合)で識別される。
OWL Fullでは,RDFの場合と同様に,OWL世界の要素は,同時に個体にもクラスにもなることが可能で
あって,実際には,個体,クラス及び特性のいずれにもなることができる。OWL DLと呼ばれる制限の多
い表現形式では,三つの部分はRDFにおける対応部分とは異なっており,しかも,どの二つを取っても互
いに素となっている。さらに制限の多いOWL DL表現形式は,論理的帰結の決定可能性を確保するために,
ある種の表現力を犠牲にしている。OWLの両方の表現形式は,DAML+OILのモデル論的意味論をRDF意
味論へ単純に変換するだけでは欠落してしまう論理的帰結を提供する。
二つの表現形式の主な相違点は,実質的には,URI参照が実際にOWL世界の適切な部分に確実に存在
することを必す(須)とするかどうかにある。OWL Fullでは,これに注意を払う必要はない。OWL DLで
は,使用されるURI参照の多くに局所化のための情報を提供しなければならない。これらの局所化の仮定
は,OWL Fullでは自明に真とし,OWL DLと密接に対応するOWL抽象構文を使用するときには,無視す
ることもできる。しかし,OWL DLを三つ組で記述する場合は,語い(彙)のどの要素がOWL世界のど
の部分に属するかに細心の注意を払わなければならない。
箇条5の全体を通して,OWL語い(彙)は,組込みのクラス,組込みの注釈特性及び組込みのオント
ロジ特性と,使用してはならないOWLからの語い(彙)とからなる。
5.2
OWL解釈
OWL DLの意味論とOWL Fullの意味論とは非常に似ている。そのため,それらの意味論の共通部分を
始めに示し,その後,相違点を示す。
RDF意味論[RDF Semantics]によれば,RDF及びRDFSの語い(彙)を含むURI参照及びリテラルの集
合Vと,データ型写像Dとに対し,VのD解釈は,I = < RI, PI, EXTI, SI, LI, LVI >の組としている。ここで,
RIは,議論の領域すなわち世界,つまり,VにおけるURI参照及びリテラルの指示対象を含む空でない集
合とする。PIは,RIの部分集合であって,Iの特性とする。EXTIは,特性に意味を与えるために使用され,
PIからP(RI×RI) への写像とする。SIは,VにおけるURI参照から,RIにおけるそれらの指示対象への写
像とする。LIは,Vにおける型付きリテラルから,RIにおけるそれらの指示対象への写像とする。LVIは,
RIの部分集合であって,少なくとも,Unicode文字列の集合,Unicode文字列と言語タグとの対の集合,及
びDにおける各データ型の値空間を含む。CIはクラスの集合であって,CI = { x ∈RI | <x,SI(rdfs:Class)> ∈
EXTI(SI(rdf:type)) }と定義される。CEXTIはCIからP(RI)への写像であって,CEXTI(c) = { x∈RI | <x,c>∈
EXTI(SI(rdf:type)) }と定義される。D解釈は,その詳細はRDF意味論で定義されているとおりだが,他の
幾つかの条件を満たさなければならない。例えば,EXTI(SI(rdfs:subClassOf))は,推移的な関係でなければ
24
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ならず,すべてのデータ型のクラスの外延は,LVIの部分集合でなければならない。
定義
Dをrdf:XMLLiteral,xsd:integer及びxsd:stringのデータ型を含むデータ型写像とする。語い(彙)V
がRDF及びRDFS語い(彙)並びにOWL語い(彙)を取り込む場合,VのOWL 解釈,I = < RI, PI, EXTI,
SI, LI, LVI >は,5.2のすべての制約を充足するVのD解釈とする。
定義終
注記 抽象構文の記述を構成するOWL語い(彙)の要素は,他の意味論における関係に対応するOWL
語い(彙)の要素とは取り扱いが異なる。前者は,意味論の必要条件 (only-if) 及び包括原理を
もつが,後者は,意味論の必要十分条件 (if-and-only-if) をもつ。前者の意味論の必要条件は,
意味論の矛盾及びその他の意味論に関する問題を避けるために必要とされる。前者に対する包
括原理及び後者に対する意味論の必要十分条件は,有益な論理的帰結が妥当であるために必要
とされる。
5.2.1
OWL世界の部分及び構文上の分類に関する条件
OWL世界の部分及び構文上の分類に関する条件は,表5による。
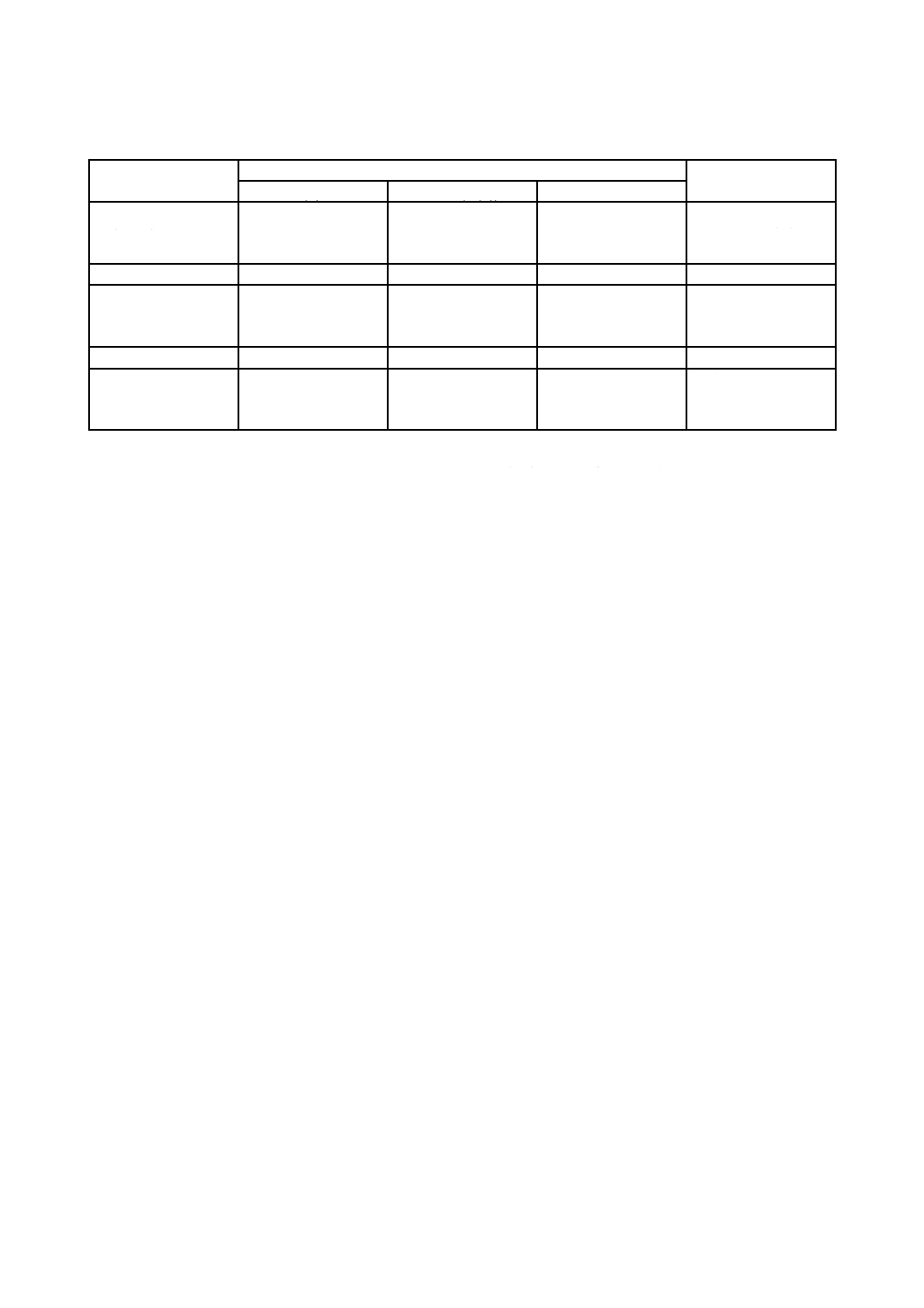
表5−OWL世界の部分及び構文上の分類に関する条件
If E is
then
備考
SI(E)∈
CEXTI(SI(E))=
and
owl:Class
CI
IOC
IOC⊆CI
これはIOCをOWLク
ラスの集合として定
義している。
rdfs:Datatype
IDC
IDC⊆CI
これはIDCをOWLデ
ータ型の集合として
定義している。
owl:Restriction
CI
IOR
IOR⊆IOC
これはIORをOWL制
限の集合として定義
している。
owl:Thing
IOC
IOT
IOT⊆RI and IOT ≠φ
これはIOTをOWL個
体の集合として定義
している。
owl:Nothing
IOC
{}
rdfs:Literal
IDC
LVI
LVI⊆RI
owl:ObjectProperty
CI
IOOP
IOOP⊆PI
これはIOOPをOWL
個体値特性の集合と
して定義している。
owl:DatatypeProperty
CI
IODP
IODP⊆PI
これはIODPをOWL
データ型特性の集合
として定義している。
owl:AnnotationPropert
y
CI
IOAP
IOAP⊆PI
これはIOAPをOWL
注釈特性の集合とし
て定義している。
owl:OntologyProperty
CI
IOXP
IOXP⊆PI
これはIOXPをOWL
オントロジ特性の集
合として定義してい
る。
25
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5−OWL世界の部分及び構文上の分類に関する条件(続き)
If E is
then
備考
SI(E)∈
CEXTI(SI(E))=
and
owl:Ontology
CI
IX
これはIXをOWLオ
ントロジの集合とし
て定義している。
owl:AllDifferent
CI
IAD
rdf:List
IL
IL⊆RI
これはILをOWLリ
ストの集合として定
義している。
rdf:nil
IL
"l"^^d
CEXTI(SI(d))
SI("l"^^d) ∈ LVI
型付きリテラルは
OWLでは正常に使用
できる。
5.2.2
OWL組込み構文クラス及び特性
I(owl:FunctionalProperty), I(owl:InverseFunctionalProperty), I(owl:SymmetricProperty),
I(owl:TransitiveProperty), I(owl:DeprecatedClass)及びI(owl:DeprecatedProperty)は,CIに属する。
I(owl:equivalentClass), I(owl:disjointWith), I(owl:equivalentProperty), I(owl:inverseOf), I(owl:sameAs),
I(owl:differentFrom), I(owl:complementOf), I(owl:unionOf), I(owl:intersectionOf), I(owl:oneOf),
I(owl:allValuesFrom), I(owl:onProperty), I(owl:someValuesFrom), I(owl:hasValue), I(owl:minCardinality),
I(owl:maxCardinality), I(owl:cardinality)及びI(owl:distinctMembers)は,すべてPIに属する。
I(owl:versionInfo), I(rdfs:label), I(rdfs:comment), I(rdfs:seeAlso)及びI(rdfs:isDefinedBy)は,すべてIOAPに属
する。I(owl:imports), I(owl:priorVersion), I(owl:backwardCompatibleWith)及びI(owl:incompatibleWith)は,すべ
てIOXPに属する。
5.2.3
OWLクラス,データ型及び特性の特徴
OWLクラス,データ型及び特性の特徴は,表6による。

26
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表6−OWLクラス,データ型及び特性の特徴
IF E is
then if e∈CEXTI(SI(E)) then
備考
owl:Class
CEXTI(e)⊆IOT
OWLクラスのインスタンスはOWL
個体である
rdfs:Datatype
CEXTI(e)⊆LVI
owl:DataRange
CEXTI(e)⊆LVI
OWLデータ値域は特殊なデータ型と
する。
owl:ObjectProperty
EXTI(e)⊆IOT×IOT
個体値特性の値は OWL個体とする。
owl:DatatypeProperty
EXTI(e)⊆IOT×LVI
データ型特性の値はリテラル値とす
る。
owl:AnnotationProperty
EXTI(e)⊆IOT×(IOT∪LVI)
注釈特性の値は若干の制約を受ける。
owl:OntologyProperty
EXTI(e)⊆IX×IX
オントロジ特性はオントロジを他の
オントロジに関連付ける。
If E is
then c∈CEXTI(SI(E)) iff c∈IOOP∪
IODP and
備考
owl:FunctionalProperty
<x,y1>, <x,y2> ∈ EXTI(c) implies y1 =
y2
個体値特性もデータ型特性も関数特
性となり得る。
If E is
then c∈CEXTI(SI(E)) iff c∈IOOP
and
備考
owl:InverseFunctionalProperty
<x1,y>, <x2,y>∈EXTI(c) implies x1 = x2
逆関数特性となり得るのは個体値特
性だけとする。
owl:SymmetricProperty
<x,y> ∈ EXTI(c) implies <y, x>∈
EXTI(c)
対称特性となり得るのは個体値特性
だけとする。
owl:TransitiveProperty
<x,y>, <y,z>∈EXTI(c) implies <x,z>∈
EXTI(c)
推移特性となり得るのは個体値特性
だけとする。
5.2.4
rdfs:subClassOf, rdfs:subPropertyOf, rdfs:domain及び rdfs:range のif-and-only-if条件
rdfs:subClassOf, rdfs:subPropertyOf, rdfs:domain及び rdfs:rangeのif-and-only-if条件は,表7による。
表7−rdfs:subClassOf, rdfs:subPropertyOf, rdfs:domain及びrdfs:rangeのif-and-only-if条件
If E is
then for
<x,y>∈EXTI(SI(E)) if-and-only-if
rdfs:subClassOf
x,y∈IOC
CEXTI(x) ⊆ CEXTI(y)
rdfs:subPropertyOf
x,y∈IOOP
EXTI(x) ⊆ EXTI(y)
rdfs:subPropertyOf
x,y∈IODP
EXTI(x) ⊆ EXTI(y)
rdfs:domain
x∈IOOP∪IODP,y∈IOC
<z,w>∈EXTI(x) implies z∈CEXTI(y)
rdfs:range
x∈IOOP∪IODP,y∈IOC∪IDC
<w,z>∈EXTI(x) implies z∈CEXTI(y)
5.2.5
等価性に関連付けされるOWL語い(彙)の特徴
等価性に関連付けされるOWL語い(彙)の特徴は,表8による。
表8−等価性に関連付けされるOWL語い(彙)の特徴
If E is
then <x,y>∈EXTI(SI(E)) if-and-only-if
owl:equivalentClass
x,y∈IOC and CEXTI(x)=CEXTI(y)
owl:disjointWith
x,y∈IOC and CEXTI(x)∩CEXTI(y)={}
owl:equivalentProperty
x,y∈IOOP∪IODP and EXTI(x) = EXTI(y)
owl:inverseOf
x,y∈IOOP and <u,v>∈EXTI(x) if-and-only-if <v,u>∈EXTI(y)
owl:sameAs
x = y
owl:differentFrom
x ≠ y
5.2.6
ブール結合及び集合に関連付けされるOWL語い(彙)の条件
ブール結合及び集合に関連付けされるOWL語い(彙)の条件は,表9による。
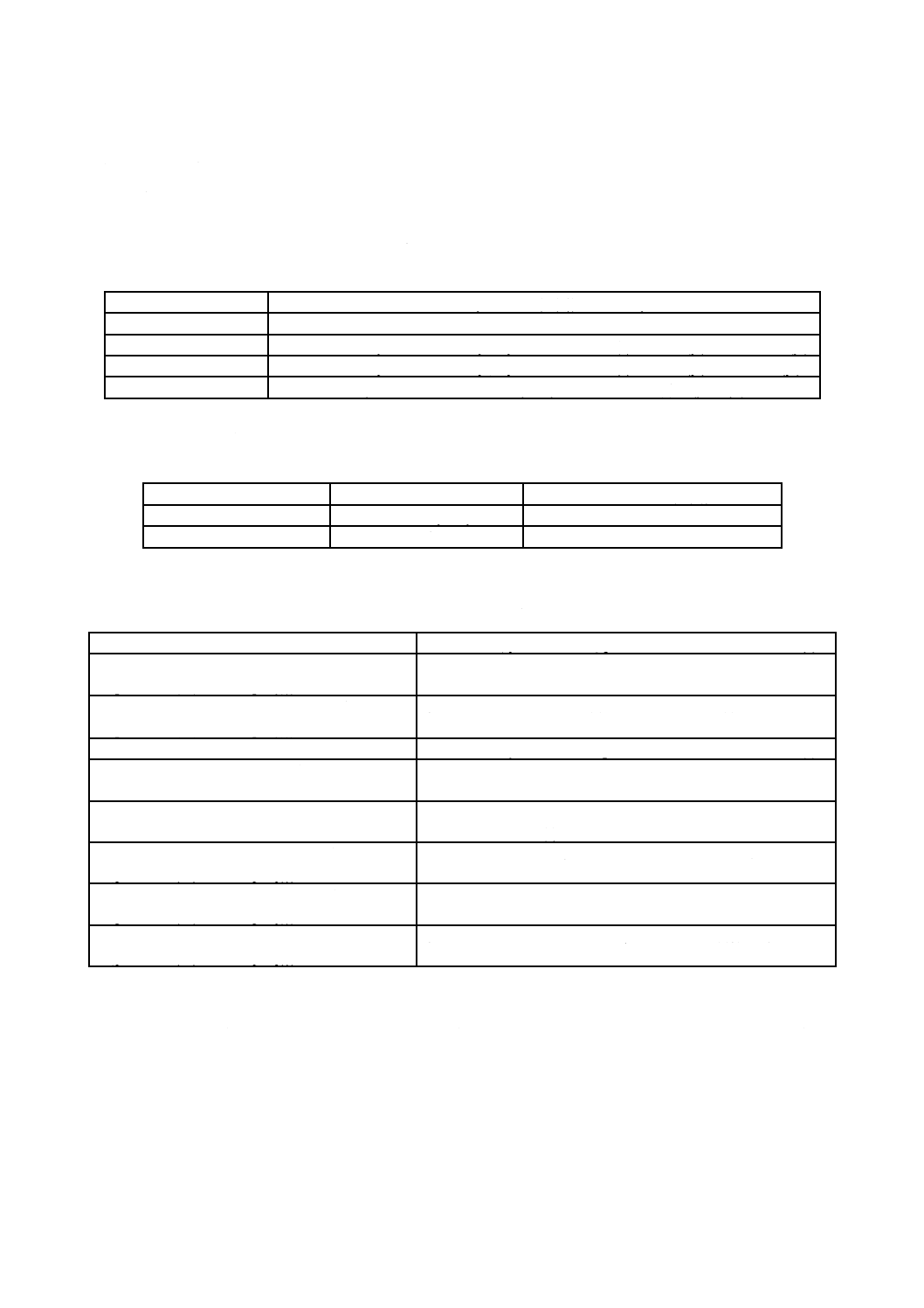
27
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
l1をC上の列y1,…,ynとすると,これは次と同値になる。
a) n=0 の場合,l1=SI(rdf:nil)
b) n>0 の場合。l1∈IL and ∃ l2, …, ln ∈ IL,ただし次の条件を満たす。
<l1,y1>∈EXTI(SI(rdf:first)), y1∈C, <l1,l2>∈EXTI(SI(rdf:rest)), …,
<ln,yn>∈EXTI(SI(rdf:first)), yn∈C, and <ln,SI(rdf:nil)>∈EXTI(SI(rdf:rest)).
表9−ブール結合及び集合に関連付けされるOWL語い(彙)の条件
If E is
then <x,y>∈EXTI(SI(E)) if-and-only-if
owl:complementOf
x,y∈ IOC,かつ,CEXTI(x)=IOT-CEXTI(y)
owl:unionOf
x∈IOC,かつ,yはIOC上の列y1,…yn,かつ,CEXTI(x) = CEXTI(y1)∪…∪CEXTI(yn)
owl:intersectionOf
x∈IOC,かつ,yはIOC上の列y1,…yn,かつ,CEXTI(x) = CEXTI(y1)∩…∩CEXTI(yn)
owl:oneOf
x∈CI,かつ,yはIOT又はLVI上の列y1,…yn,かつ,CEXTI(x) = {y1,..., yn}
5.2.7
owl:oneOfの追加条件
owl:oneOfの追加条件は,表10による。
表10−owl:oneOfの追加条件
If E is
and
then if <x,l>∈EXTI(SI(E))のthen
owl:oneOf
IはLVI上の列 y1,…yn
x∈IDC
owl:oneOf
IはIOT上の列 y1,…yn
x∈IOC
5.2.8
OWL制限の条件
OWL制限の条件は,表11による。
表11−OWL制限の条件
If
then x∈IOR, y∈IOC∪IDC, p∈IOOP∪IODP,and CEXTI(x) =
<x,y>∈EXTI(SI(owl:allValuesFrom))) ∧
<x,p>∈EXTI(SI(owl:onProperty)))
{u∈IOT | <u,v>∈EXTI(p) implies v∈CEXTI(y)}
<x,y>∈EXTI(SI(owl:someValuesFrom))) ∧
<x,p>∈EXTI(SI(owl:onProperty)))
{u∈IOT | ∃ <u,v>∈EXTI(p) ただし v∈CEXTI(y) }
If
then x∈IOR, y∈IOT∪LVI , p∈IOOP∪IODP,and CEXTI(x) =
<x,y>∈EXTI(SI(owl:hasValue))) ∧
<x,p>∈EXTI(SI(owl:onProperty)))
{u∈IOT | <u, y>∈EXTI(p) }
If
then x∈IOR, y∈LVI,yが負ではない整数であって,p∈IOOP∪
IODP,and CEXTI(x) =
<x,y>∈EXTI(SI(owl:minCardinality))) ∧
<x,p>∈EXTI(SI(owl:onProperty)))
{u∈IOT | card({v ∈ IOT ∪ LV : <u,v>∈EXTI(p)}) ≧y }
<x,y>∈EXTI(SI(owl:maxCardinality))) ∧
<x,p>∈EXTI(SI(owl:onProperty)))
{u∈IOT | card({v ∈ IOT ∪ LV : <u,v>∈EXTI(p)}) ≦y }
<x,y>∈EXTI(SI(owl:cardinality))) ∧
<x,p>∈EXTI(SI(owl:onProperty)))
{u∈IOT | card({v ∈ IOT ∪ LV : <u,v>∈EXTI(p)}) = y }
5.2.9
包括条件(原理)
包括条件(原理)は,表12による。最初の二つの包括条件は,幾つかのOWL構成要素で使用される有
限な長さの列の存在を必す(須)とする。三番目の包括条件は,owl:AllDifferentのインスタンスの存在を
必す(須)とする。残りの包括条件は,適切なOWLの記述及びデータ値域の存在を必す(須)とする。
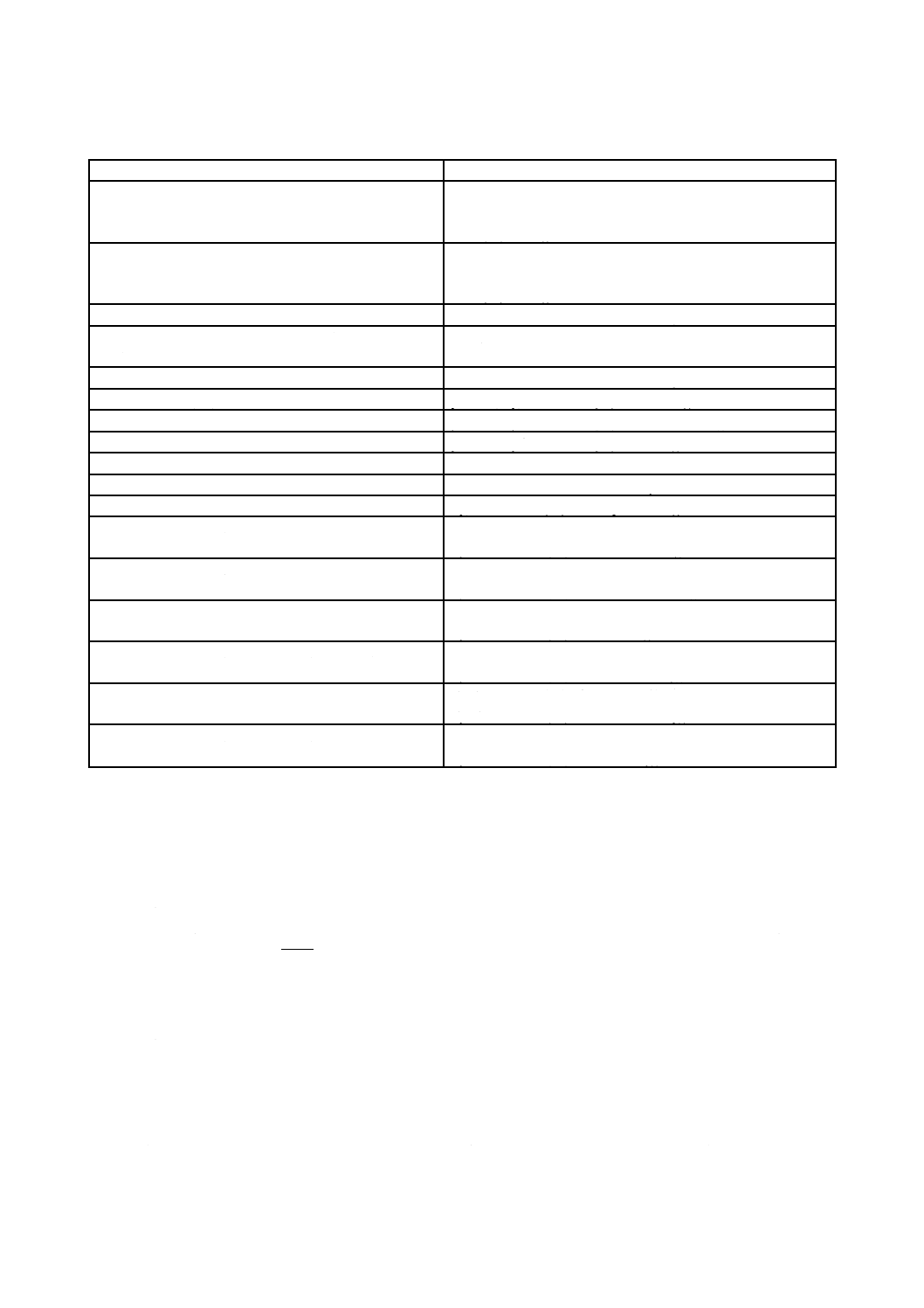
28
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表12−包括条件(原理)
If there exists
then there exists l1,…,ln ∈ILwith
x1, …, xn ∈ IOC
<l1,x1> ∈ EXTI(SI(rdf:first)), <l1,l2> ∈ EXTI(SI(rdf:rest)), …
<ln,xn>
∈
EXTI(SI(rdf:first)),
<ln,SI(rdf:nil)>
∈
EXTI(SI(rdf:rest))
x1, …, xn ∈ IOT∪LVI
<l1,x1> ∈ EXTI(SI(rdf:first)), <l1,l2> ∈ EXTI(SI(rdf:rest)), …
<ln,xn>
∈
EXTI(SI(rdf:first)),
<ln,SI(rdf:nil)>
∈
EXTI(SI(rdf:rest))
If there exists
then there exists y with
IOT上の列I=x1,…,xn ただし xi≠xj で 1≦i<j≦n につ
いて
y∈IAD, <y,l>∈EXTI(SI(owl:distinctMembers))
If there exists
then there exists y with
IOC上の列I=x1,…,xn
y∈IOC, <y,l> ∈ EXTI(SI(owl:unionOf))
IOC上の列I=x1,…,xn
y∈IOC, <y,l> ∈ EXTI(SI(owl:intersectionOf))
IOT上の列I=x1,…,xn
y∈IOC, <y,l> ∈ EXTI(SI(owl:oneOf))
LVI上の列I=x1,…,xn
y∈IDC, <y,l> ∈ EXTI(SI(owl:oneOf))
If there exists
then there exists y ∈IOC with
x ∈ IOC
<y,x> ∈ EXTI(SI(owl:complementOf))
x ∈ IOOP∪IODP ∧ w ∈ IOC ∪ IDC
<y,x> ∈ EXTI(SI(owl:onProperty)) ∧
<y,w> ∈ EXTI(SI(owl:allValuesFrom))
x ∈ IOOP∪IODP ∧ w ∈ IOC ∪ IDC
<y,x> ∈ EXTI(SI(owl:onProperty)) ∧
<y,w> ∈ EXTI(SI(owl:someValuesFrom))
x ∈ IOOP∪IODP ∧ w ∈ IOT ∪ LVI
<y,x> ∈ EXTI(SI(owl:onProperty)) ∧
<y,w> ∈ EXTI(SI(owl:hasValue))
x ∈ IOOP∪IODP ∧ w ∈ LVI ∧ wは非負整数
<y,x> ∈ EXTI(SI(owl:onProperty)) ∧
<y,w> ∈ EXTI(SI(owl:minCardinality))
x ∈ IOOP∪IODP ∧ w ∈ LVI ∧ wは非負整数
<y,x> ∈ EXTI(SI(owl:onProperty)) ∧
<y,w> ∈ EXTI(SI(owl:maxCardinality))
x ∈ IOOP∪IODP ∧ w ∈ LVI ∧ wは非負整数
<y,x> ∈ EXTI(SI(owl:onProperty)) ∧
<y,w> ∈ EXTI(SI(owl:cardinality))
5.3
OWL Full
OWL Fullは,OWL世界の一部を強制的にRDFの類似部分と一致させる条件を用いて,共通条件を拡張
する。これらの新しい条件は,共通条件と強く相互作用している。例えば,OWL Fullでは,IOTは,RDF
における議論の領域全体となるので,リストに関する2番目の包括条件(表12の内容の2行目)は,リス
トのリストを含むいかなる種類のリストをも生成する。
定義
語い(彙)VのOWL Full 解釈は,次の条件を充足するOWL解釈とする。OWL解釈は,データ型
写像に関してなされることを思い出してもらいたい。
IOT = RI,IOOP = PI,IOC = CI
定義終
定義
KをRDFグラフの集まりとする。x owl:imports uという形式のKのあらゆる要素のすべての三つ組
について,uにおいてアクセス可能なRDF/XML文書をRDFグラフへ取り込むRDF処理の結果であ
るグラフをKが含む場合及びその場合に限り,Kは取込み閉包とする。RDFグラフの集まりの取込み
閉包とは,その集まり内の(すべての)グラフを含むRDFグラフの最小の取込み閉包された集まりと
29
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
する。
定義終
定義
K及びQをRDFグラフの集まりとし,Dをデータ型写像とする。RDF語い(彙)及びRDFS語い
(彙)並びにOWL 語い(彙)を含むいかなる語い(彙)VのDについてのすべてのOWL Full解釈
が,KのすべてのRDFグラフを充足し,QのすべてのRDFグラフも充足する場合及びその場合に限
り,Dに関して,Kは QをOWL Fullとして論理的に帰結する。KのすべてのRDFグラフを充足する
何らかのOWL Full解釈が存在する場合及びその場合に限り,KはOWL Full無矛盾とする。
定義終
5.4
OWL DL
OWL DLは,議論の領域を複数の互いに素な部分に分けて,5.2の条件を拡張する。この違いは二つの
結果をもたらす。まず,議論の領域のOWL部分は,述語(クラス及び特性)と個体とが互いに素となる
標準的な一階論理となる。次に,OWL DL解釈のOWL部分を,特定の表現力をもつ記述論理に対する記
述論理解釈として見ることができる。
定義
語い(彙)VのOWL DL 解釈は,次の条件を充足するOWL解釈とする。OWL解釈がデータ型写
像に関してなされることを思い出してもらいたい。
a) LVI, IOT, IOC, IDC, IOOP, IODP, IOAP, IOXP, IL及びIXは,すべてどの二つを取っても互いに
素となる。
b) vを,使用してはならない語い(彙)(4.2参照)とすると
SI(v) ∈ RI - (LVI∪IOT∪IOC∪IDC∪IOOP∪IODP∪IOAP∪IOXP∪IL∪IX)
定義終
OWL DLの論理的帰結は,OWL Fullの論理的帰結と同様に定義される。
定義
K及びQをRDFグラフの集まりとし,Dをデータ型写像とする。RDF及びRDFS語い(彙)並び
にOWL 語い(彙)を含むいかなる語い(彙)VのDについてのすべてのOWL DL解釈が,Kのすべ
てのRDFグラフを充足し,QのすべてのRDFグラフも充足する場合及びその場合に限り,Dに関し
て,Kは QをOWL DLとして論理的に帰結する。KのすべてのRDFグラフを充足する何らかのOWL
DL解釈が存在する場合及びその場合に限り,KはOWL DL無矛盾とする。
定義終
直接モデル論的意味論とOWL DL意味論とは強く対応している。しかし,いかなる競合が起こった場合
でも,直接モデル論的意味論を優先する。箇条5の最初にある注記を参照してもらいたい。原則的には,
この抽象構文で書くことができるオントロジが他のオントロジを直接モデル論的意味論で論理的に帰結す
る場合は,それを正確にOWL DLとしても論理的に帰結する。例えば,概念,特性及び個体が干渉しない
ようにするためには,語い(彙)を分割しなければならないし,取込みが同様に動作するように調整しな
ければならない。
この対応が妥当であるためには,特定の名前をもつ抽象構文のオントロジと,そのURIでウェブから入
手できる文書との間に何らかのつながりがなければならない。このつながりは,ここでは,意味論の範囲
外なので,個別に調整されなければならない。同様に,このつながりは,ウェブの一時的で移動的な局面
を無視しているため,ウェブの理想化にすぎない。
30
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定義
Tを抽象構文から4.1のRDFグラフへの写像とする。Oを抽象構文形式におけるOWL DLオントロ
ジと公理及び事実との集まりとする。いかなるURI uについても,Oのあらゆるオントロジにおける
取込み指示において,uにおいてウェブ上でアクセスできる文書のRDF構文解析が結果的にKが名前
uをもつOにおけるオントロジであるT(K)となる場合及びその場合に限り,Oは取込み閉包という。
定義終
定理1
O及びO'を,抽象構文形式におけるOWL DLオントロジと公理及び事実との集まりとする。ここで,
O及びO'は取込み閉包であって,それらの和集合は分離された語い(彙)(4.2参照)をもつとする。
また,xsd:string及びxsd:integerを適切なXMLスキーマデータ型に写像し,rdf:XMLLiteralに対する
RDF写像を含むデータ型写像Dを仮定する。Oの翻訳(4.1参照)がDについてO'の翻訳をOWL DL
として論理的に帰結する場合及びその場合に限り,Dに関して,OはO'を論理的に帰結する。
定理1終
この証明は,A.1に示す。
この定理によって,次の簡単な結論が導かれる。xsd:string及びxsd:integerを適切なXMLスキーマデー
タ型に写像し,rdf:XMLLiteralのRDF写像を含むデータ型写像Dを仮定すると,Oの翻訳がDに関して無
矛盾である場合及びその場合に限り,OはDに関して無矛盾とする。
OWL DLとしての論理的帰結とOWL Fullとしての論理的帰結との間にも対応が存在する。
定理2
O及びO'を抽象構文形式におけるOWL DLオントロジと公理並びに事実との集まりとする。ここで,
O及びO'は取込み閉包であって,それらの和集合は分離された語い(彙)(4.2参照)をもつとする。
xsd:string及びxsd:integerを適切なXMLスキーマデータ型に写像し,rdf:XMLLiteralのRDF写像を含
むデータ型写像Dを仮定する。Oの翻訳がDに関するO'の翻訳をOWL DLとして論理的に帰結する
場合,Oの翻訳は,Dに関するO'の翻訳をOWL Fullとして論理的に帰結する。
定理2終
証明の概略は,A.2で示す。
31
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
証明
この附属書は,規定の一部ではない。
この附属書では,箇条5の定理の証明を示す。
前提
附属書Aを通して,Dは,すべての組込みOWLデータ型及びrdf:XMLLiteralのデータ型を含むデータ
型写像(3.1参照)とする。Tは,抽象OWLオントロジから4.1のRDFグラフへの写像とする。VBは,
組込みOWL語い(彙)とする。同様に,語い(彙)の中の型なしリテラルには言及しない。
前提終
注記 附属書Aを通して,すべての解釈はデータ型写像Dに関して行われる。したがって,すべての
結果がDに関して意味をもつ。構成の自明な詳細は省略していることがある。
A.1 抽象OWLとOWL DLとの対応
A.1では,二つの意味論が,あるOWLオントロジに関して対応することを示す。二つの意味論とは,附
属書Aで直接モデル理論と呼ぶ箇条3の抽象OWLオントロジの直接モデル理論,及び附属書AでOWL DL
モデル理論と呼ぶ箇条5のOWL DL意味論である。
定義
Dを前提に示すとおりに仮定する場合,分離されたOWL語い(彙)(4.2参照)は,更に形式化されて
URI参照V'となる。V'は,使用してはならない語い(彙)(4.2参照)とは互いに素であって,互いに素な
区画に分割される。これは,V' = VO + VC + VD + VI + VOP + VDP + VAP + VXPと書ける。そして,組込
みのOWLクラスはVCに属し,URI参照,Dのすべてのデータ型名及びrdfs:LiteralはVDに属し,OWL
組込み注釈特性はVAPに属し,OWL組込みオントロジ特性はVXPに属する。
定義終
定義
分離されたOWL語い(彙),V' = VO + VC + VD + VI + VOP + VDP + VAP + VXPの翻訳を,T(V')と書く。
T(V')は,次の形式の三つ組すべてから構成される。
a) v ∈VOに対してはv rdf:type owl:Ontology
b) v ∈VCに対してはv rdf:type owl:Class
c) v ∈VDに対してはv rdf:type rdfs:Datatype
d) v ∈VIに対してはv rdf:type owl:Thing
e) v ∈VOPに対してはv rdf:type owl:ObjectProperty
f) v ∈VDPに対してはv rdf:type owl:DatatypeProperty
g) v ∈VAPに対してはv rdf:type owl:AnnotationProperty
h) v ∈VXPに対してはv rdf:type owl:OntologyProperty
定義終
定義
分離された語い(彙)(箇条4参照)をもつ抽象構文形式のOWL DLオントロジと公理及び事実との集
32
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まりO(箇条2参照)は,分離された語い(彙)の新しい概念V = VO + VC + VD + VI + VOP + VDP + VAP
+ VXPを用いて,次のとおりに形式化される。
a) オントロジ名として使用されるすべてのURI参照はVOから選択され,クラスIDはVCから選択さ
れ,データ型IDはVDから選択され,個体IDはVIから選択され,個体値特性IDはVOPから選択
され,データ値特性IDはVDPから選択され,注釈特性IDはVAPから選択され,オントロジ特性ID
はVXPから選択される。
注記 原勧告では,a)の最初の行の“VO”が“VA”となっていたが,オントロジ名なので“VO”の
間違いと思われる。
b) 個体IDとして使用されるすべてのURI参照は,Oにおけるあるオントロジの型を提供される。
c) Oのオントロジと公理及び事実とは,クラスIDとして,クラス固有の語い(彙)だけを使用し,デ
ータ型IDとして,データ型固有の語い(彙)だけを使用し,データ値特性ID,個体値特性ID,注釈
特性ID又はオントロジ特性IDとして,特性固有の語い(彙)だけを使用し,使用してはならない語
い(彙)には言及しない。
定義終
これらの前提において,(5.4の定理1と等価な)証明する定理は次のとおり。
定理1(A.1.5の定理と同じ)
O及びO'を,取込み閉包である抽象構文形式の,OWL DLオントロジと公理及び事実との集まりとする。
ただし,それらの和集合が分離された語い(彙)をもつとする。このとき,T(O)がT(O')をOWL DLとし
て論理的に帰結する場合及びその場合に限り,OはO'を直接的に論理的に帰結する。
定理1終
A.1.1 記述の対応
補助定理1
V' = VO + VC + VD + VI + VOP + VDP + VAP + VXPを分離されたOWL語い(彙)とする。V = VO ∪ VC
∪ VD ∪ VI ∪ VOP ∪ VDP ∪ VAP ∪ VXP ∪ VBとする。I' = <R,EC,ER,L,S,LV>をV'の直接的解釈
とする。I = <RI,PI,EXTI,SI,LI,LVI> を,LVI = LVとなる,T(V')を充足するVのOWL DLの解釈とする。CEXTI
には通常の意味をもたせ(5.2の最初を参照),構文上のあらゆる構成要素をその指示対象に写像するよう
に,通常どおり,Iを上乗せする。さらに,次が成り立つとする。
a) R = RI
b) v∈VC∪VDに対してEC(v)=CEXTI(SI(v))
c) v∈VOP∪VDP∪VAP∪VXPに対してER(v)=EXTI(SI(v))
d) x ∈ Rに対して< x, S(owl:DeprecatedClass) > ∈ ER(rdf:type) iff < x, SI(owl:DeprecatedClass) > ∈
EXTI(SI(rdf:type))
e) x ∈ Rに対して< x, S(owl:DeprecatedProperty) > ∈ ER(rdf:type) iff < x, SI(owl:DeprecatedProperty) > ∈
EXTI(SI(rdf:type))
注記 原勧告のd)及びe)にはEXTI(SI(rdf:type))の前に∈が抜けていた。この規格ではこれを追加した。
f)
型付きデータリテラルdに対してL(d)=LI(d)
g) v ∈ VI ∪ VC ∪ VD ∪ VOP ∪ VDP ∪ VAP ∪ VXP ∪ VO に対してS(v)=SI(v)
このとき,V'上の任意の抽象OWL記述又はデータ値域であるdに対して,次が成立する。
a) Iは,T(d)を直接的に充足する。
b) AをT(d)のすべての空ノードからRIへの写像とし,I+AがT(d)をOWL DLとして充足する場合は,い
33
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
かなるAに対しても次が成立する。
1) CEXTI(I+A(M(T(d)))) = EC(d)
2) dが記述の場合I+A(M(T(d)))∈CEXTI(SI(owl:Class))
3) dがデータ値域の場合I+A(M(T(d)))∈CEXTI(SI(rdfs:Datatype))
証明
この補助定理の証明は,構造的帰納法による。証明を通じて,IOT = CEXTI(I(owl:Thing)), IOC =
CEXTI(I(owl:Class)), IDC = CEXTI(I(rdfs:Datatype)), IOOP = CEXTI(I(owl:ObjectProperty)), IODP =
CEXTI(I(owl:DatatypeProperty)),及び IL = CEXTI(I(rdf:List))とする。
帰納法が成立するためには,下位構成要素をもつあらゆる記述又はデータ値域dに対して, T(d)が,そ
の下位構成要素のそれぞれについて,他の下位構成要素からの三つ組と空ノードを共有しない三つ組を含
むことを示す必要がある。これは,Tの規則から簡単に検証できる。
p∈VOPの場合,Iは p∈IOOPを充足する。IはOWL DL解釈なので,Iは <p,I(owl:Thing)>∈
EXTI(I(rdfs:domain)) 及び <p,I(owl:Thing)>∈EXTI(I(rdfs:range))を充足する。したがって,IはT(p)を充足す
る。p∈VDPの場合も同様である。
注記 以下,補助定理1の証明の終わりまでは,構造的帰納法に従って,基礎となる場合と帰納的な
場合とを分けて示す。
a) 基礎となる場合
1) owl:Thing及びowl:Nothingを含むv ∈VCの場合
v∈VCであってIはT(V)を充足するので,I(v)∈CEXTI(I(owl:Class))となる。IはOWL DLの解釈
なので CEXTI(I(v))⊆IOTとなり,<I(v),I(owl:Thing)>∈EXTI(I(rdfs:subClassOf))となる。したがって,
IはT(v)をOWL DLとして充足する。M(T(v))はvなので,CEXTI(I(M(T(v))))=EC(v)となる。よって,
これらから,I(v)∈IOCとなる。
2) rdfs:Literalを含む v ∈VDの場合
v∈VDであってIがT(V)を充足するので,I(v)∈CEXTI(I(rdfs:Datatype))となる。IはOWL DLの
解釈なので CEXTI(I(v))⊆LVIとなり,<I(v),I(rdfs:Literal)>∈EXTI(I(rdfs:subClassOf))となる。したが
って,IはRDF互換なので,T(v)を充足する。M(T(v))はvなので,CEXTI(I(M(T(v))))=EC(v)となる。
よって,これらから,I(v)∈IDCとなる。
3) d=oneOf(i1…in)の場合。ただし,ijは個体IDとする。
1≦j≦n についてij∈VIであって,IがT(V)を充足するので,I(ij)∈IOTとなる。次に,列に対す
る二つ目の包括原理は,IOT上で列I(i1),…,I(in)となるl∈ILの存在を必す(須)とする。IOT上で列
I(i1),…,I(in)となるいかなるIに対しても,oneOfの包括原理は,<y,l> ∈ EXTI(I(owl:oneOf))となるy
∈CEXTI(I(rdfs:Class))の存在を必す(須)とする。さらに,oneOfの三つ目の性質から,y∈IOCと
なる。したがって,IはT(d)を充足する。T(d)を充足するいかなるI+Aに対しても,
CEXTI(I+A(M(T(d)))) = {I(i1),…,I(in)} = EC(d)となる。よって,I+A(M(T(d)))∈IOCとなる。
4) d=oneOf(v1…vn)の場合。ただし,viはデータリテラルとする。
I(vj)∈LVIなので,列に対する二つ目の包括原理は,LVI上で列I(v1),…,I(vn)となるl∈ILの存在を
必す(須)とする。LVI上で列I(v1),…,I(vn)となるいかなるIに対しても,oneOfの包括原理は,<y,l>
∈ EXTI(IS(owl:oneOf))となるy∈CEXTI(I(rdfs:Class))の存在を必す(須)とする。さらに,oneOfの
二つ目の性質から,y∈IOCとなる。したがって,IはT(d)を充足する。T(d)を充足するいかなるI+A
に対しても,CEXTI(I+A(M(T(d)))) = {I(i1),…,I(in)} = EC(d)となる。よって,I+A(M(T(d)))∈IDCとな
34
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
5) d=restriction(p value(i))及びp∈VOP∪VDPであってiが個体IDの場合
p∈VOP∪VDPなので,この証明の最初の方の結果からIはT(p)を充足する。IはT(V')を充足す
るので,I(p)∈IOOP∪IODPとなる。さらに,i∈VIであってIがT(V')を充足するので,I(i)∈IOTと
なる。制限についての包括原理によって,IはT(d)を充足する。I+AがT(d)を充足するいかなるA
についても,CEXTI(I+A(M(T(d)))) = { x∈IOT | <x,I(i)> ∈EXTI(p) } = { x∈R | <x,S(i)> ∈ER(p) } =
EC(d)となる。よって,I+A(M(T(d)))∈IOCとなる。
6) d=restriction(p value(i))及びp∈VOP∪VDPであってiが型付けされたデータ値の場合
同様に証明できる。
7) d=restriction(p minCardinality(n))及びp∈VOP∪VDPであってnが負ではない整数の場合
同様に証明できる。
8) d=restriction(p maxCardinality(n))及びp∈VOP∪VDPであってnが負ではない整数の場合
同様に証明できる。
9) d=restriction(p Cardinality(n))及び,p∈VOP∪VDPであってnが負ではない整数の場合
同様に証明できる。
b) 帰納的な場合
1) d=complementOf(d')の場合
帰納法の仮定によって,IはT(d')を充足する。d'は記述なので,帰納法の仮定によって,ある写像
Aが存在し,このAが,T(d')のすべての空ノードを定義域の要素に写像し,I+AがT(d')を充足し,
I+A(M(T(d'))) = EC(d')及びI+A(M(T(d')))∈IOCを満たす。次に,complementOfに対する包括原理は,
I+Aが <y,e>∈EXTI(I(owl:complementOf))を充足するy∈IOCの存在を必す(須)とし,それによっ
てIはT(d)を充足する。T(d)を充足するいかなるI+Aに対しても,CEXTI(I+A(M(T(d)))) =
IOT-CEXTI(I+A(M(T(d)))) = R-EC(d') = EC(d)となる。よって,I+A(M(T(d)))∈IOCとなる。
2) d = unionOf(d1 … dn)の場合
帰納法の仮定から,Iは,1≦i≦nについてdiを充足する。したがって,ある写像Aiが存在し,
T(di)のすべての空ノードを定義域の要素に写像し,I+AiがT(di)を充足する。T(di)の空ノードは,i
≠jのとき, T(dj)の空ノードとは互いに素なので,I+A1+…+Anは,したがってIは,T(di)∪…∪T(dn)
を充足する。各diは記述なので,帰納法の仮定によって,I+A1+…+An(M(T(di)))∈IOCとなる。列に
対する最初の包括原理は,IOC上で列I+A1+…+An(M(T(d1))),…, I+A1+…+An(M(T(dn)))となるl∈IL
の存在を必す(須)とする。さらに,unionOfの包括原理は,<y,l>∈EXTI(I(owl:unionOf))となるy
∈IOCの存在を必す(須)とするので,IはT(d)を充足する。
T(d)を充足するいかなるI+Aに対しても,I+AはT(di)を充足し,それによって,CEXTI(I+A(di)) =
EC(di)となる。そのために,CEXTI(I+A(M(T(d)))) = CEXTI(I+A(d1))∪…∪CEXTI(I+A(dn)) = EC(d1)∪
…∪EC(dn) = EC(d)となる。よって,I(M(T(d)))∈IOCとなる。
3) d = intersectionOf(d1 … dn)の場合
同様に証明できる。
4) d = restriction(p x1 x2 … xn)の場合
p∈VOP∪VDPなので,この証明の最初の方の結果からIはT(p)を充足する。帰納法の仮定から,
Iは,1≦i≦nについてrestriction(p xi)を充足する。したがって,ある写像Aiが存在し,T(restriction(p
xi))のすべての空ノードを定義域の要素に写像し,I+AiがT(restriction(p xi))を充足する。T(restriction(p
35
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
xi))の空ノードは,i≠jのとき,T(restriction(p xj))の空ノードとは互いに素なので,I+A1+…+Anは,
したがってIは,T(restriction(p x1 … xn))を充足する。各restriction(p xi)は記述なので,帰納法の仮
定によって,M(T(restriction(p xi)))∈IOCとなる。列に対する最初の包括原理は,IOC上で列I+A1+
…+An(M(T(restriction(p xi)))),…, I+A1+…+An(M(T(restriction(p xi))))となるl∈ILの存在を必す(須)と
する。さらに,intersectionOfの包括原理は,<y,l>∈EXTI(I(owl:intersectionOf))となるy∈IOCの存在
を必す(須)とする。したがって,IがT(d)を充足する。
T(d)を充足するいかなるI+Aに対しても,I+AはT(di)を充足する。したがってCEXTI(I+A(di)) =
EC(di))となる。そのために,CEXTI(I+A(M(T(d)))) = CEXTI(I+A(restriction(p xi)))∩…∩
CEXTI(I+A(restriction(p xn))) = EC(restriction(p xi))∩…∩EC(restriction(p xi)) = EC(d) となる。よって,
I(M(T(d)))∈IOCとなる。
5) d = restriction(p allValuesFrom(d'))及びp∈VOP∪VDPであってd'が記述の場合
p∈VOP∪VDPなので,この証明の最初の方の結果からIはT(p)を充足する。帰納法の仮定によ
って,IはT(d')を充足する。Aを,T(d')のすべての空ノードを定義域の要素に写像し,I+AがT(d')
を充足する写像であるとする。するとd'は記述なので,帰納法の仮定によって,いかなるAに対し
ても,I+A(M(T(d'))) = EC(d')及びI+A(M(T(d')))∈IOCとなる。p∈VOP∪VDPであって,IがT(V')
を充足するので,I(p)∈IOOP∪IODPとなる。さらに,allValuesFrom制限の包括原理は,IがT(d)を
充足することを示す方法で,IがT(d')又はT(p)には存在しないT(d)の三つ組を充足することを必す
(須)とする。
T(d)を充足するいかなるI+Aに対しても,CEXTI(I+A(M(T(d)))) = {x∈IOT | ∀ y∈IOT : <x,y>∈
EXTI(p) implies y∈CEXTI(M(T(d'))) } = {x∈R | ∀ y∈R : <x,y>∈ER(p) implies y∈EC(d') } = EC(d)と
なる。よって,I+A(M(T(d)))∈IOCとなる。
6) d = restriction(p someValuesFrom(d))及びp∈VOP∪VDPであってd'が記述の場合
同様に証明できる。
7) d = restriction(p allValuesFrom(d))及びp∈VOP∪VDPであってd'がデータ値域の場合
同様に証明できる。
8) d = restriction(p someValuesFrom(d))及びp∈VOP∪VDPであってd'がデータ値域の場合
同様に証明できる。
証明終
補助定理1終
補助定理1.1
V', V, I'及びIを補助定理1の場合と同じとする。dをV'上のIndividual(…)形式の抽象OWL個体構成要
素とする。Aを,T(d)のすべての空ノードをRIに写像し,I+AがT(d)をOWL DLとして充足する写像の場
合,いかなるAに対しても,I+A(M(T(d)))∈EC(d)となる。同様に,いかなるr∈EC(d)に対しても,写像A
が存在し,AはI+A(M(T(d))) = rとなるように,T(d)のすべての空ノードをRIに写像する。
証明
簡単な帰納的な論証によって,I+A(M(T(d)))がEC(d)のすべての要件を満たさなければならないことが示
される。他の帰納的な論証によって,下位構成要素の空ノードの非共有に依存して,各r∈EC(d)に対し,
I+A(M(T(d))) = rとなるAが存在することが示される。
証明終
補助定理1.1終
36
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.1.2 指示の対応
補助定理1.9
V', V, I'及びIを補助定理1の場合と同じとする。FをV'上のOWL指示とし,annotation(p x)形式の注釈
をもつとする。Fがクラス又は特性の公理の場合,nをそのクラス又は特性の名前とする。Fが個体の公理
の場合,nをT(F)の主ノードとする。すると,AをT(F)のすべての空ノードからRIへの写像の場合,いか
なるAに対しても,I'がその注釈から帰結する条件を直接的に充足するとき及びそのときに限り,I+Aは,
その注釈から帰結する三つ組をOWL DLとして充足する。
証明
URI参照への注釈については,意味論条件及び翻訳の三つ組を検査することによって,この補助定理を
簡単に証明できる。Individual(...)の注釈については,補助定理1.1の使用も必要となる。
証明終
補助定理1.9終
補助定理2
V', V, I'及びIを補助定理1の場合と同じとする。FをV'上のOWL指示とする。すると,I'がFを充足す
る場合及びその場合に限り,IはT(F)を充足する。
証明
この証明の主要部分は,指示に関する構造的帰納法になる。注釈は多くの指示で現れるが,全く同様に
作用するので,注釈は補助定理1.9を用いるだけでよい。したがって,この証明の残りの部分では,注釈
を無視する。非推奨も同じ方法で取り扱うことができるので,この証明の残りの部分では同様に非推奨も
無視する。
a) F = Class(foo complete d1 … dn)の場合
d=intersectionOf(d1 … dn)とおく。このdは記述なので,IはT(d)を充足する。同様に,AをT(d)の
空ノードの写像とし,I+AがT(d)を充足する場合は,いかなるAに対してもCEXTI(I+A(M(T(d)))) =
EC(d)となる。したがって,dのいかなる下位記述であるd'に対しても,CEXTI(I+A(M(T(d')))) = EC(d')
及びI+A(M(T(d')))∈IOCとなる。したがって,AをT(d)の空ノードの写像とし,I+AがT(d)を充足す
る場合,CEXTI(I+A(M(T(d)))) = EC(d)及びI+A(M(T(d)))∈IOCとなる。さらに,dの下位記述である各
d'については,CEXTI(I+A(M(T(d')))) = EC(d')及びI+A(M(T(d')))∈IOCとなる。
I'がFを充足する場合,EC(foo) = EC(d)となる。上記によって,何らかのAが存在し,
CEXTI(I+A(M(T(d)))) = EC(d) = EC(foo) = CEXTI(I(foo))及びI+A(M(T(d)))∈IOCとなる。IがT(V)を充
足するので,I(foo)∈IOCとなり,したがって,<I(foo),I+A(M(T(d)))> ∈ EXTI(I(owl:equivalentClass))
となる。さらに,I(owl:intersectionOf)の意味論条件によって,<I(foo),I+A(M(T(SEQ d1 … dn)))> ∈
EXTI(I(owl:intersectionOf))となる。
dがintersectionOf(d1)の形式の場合,CEXTI(I+A(M(T(d1)))) = EC(d1) = EC(d) = EC(foo)及び
I+A(M(T(d1)))∈IOCとなる。そのために,I(owl:equivalentClass)の意味論条件によって,
<I(foo),I+A(M(T(d1)))> ∈ EXTI(I(owl:equivalentClass))となる。d1がcomplementOf(d'1)の形式の場合,IOT
- CEXTI(I+A(M(T(d'1)))) = CEXTI(I+A(M(T(d1)))) = EC(d1) = EC(d) = EC(foo),かつ,I+A(M(T(d'1)))∈IOC
となる。そのために,I(owl:complementOf)の意味論条件によって, <I(foo),I+A(M(T(d'1)))> ∈
EXTI(I(owl:complementOf))となる。d1が unionOf(d11 … d1m)の形式の場合,CEXTI(I+A(M(T(d11)))) ∪
… ∪ CEXTI(I+A(M(T(d1m)))) = CEXTI(I+A(M(T(d1)))) = EC(d1) = EC(d) = EC(foo)及び1≦j≦mについて
I+A(M(T(d1j)))∈IOCとなる。そのために,I(owl:unionOf)の意味論条件によって,<I(foo),I+A(M(T(SEQ
37
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d11 … d1m)))> ∈ EXTI(I(owl:unionOf))となる。
よって,可能な各T(F)について,IはT(F)を充足する。
IがT(F)を充足する場合,Iは,T(intersectionOf(d1 … dn))を充足する。したがって,上記述のとお
り,何らかのAが存在し,<I(foo),I+A(M(T(d)))> ∈ EXTI(I(owl:equivalentClass))となる。したがって,
EC(d) = CEXTI(I+A(M(T(d)))) = CEXTI(I(foo)) = EC(foo)となる。よって,I'はFを満たす。
b) F = Class(foo partial d1 … dn)の場合
d=intersectionOf(d1 … dn)とおく。このdはV'上のdが記述なので,IはT(d)を充足する。同様に,
AをT(d)の空ノードの写像とし,I+AがT(d)を充足する場合は,いかなるAに対しても,
CEXTI(I+A(M(T(d)))) = EC(d) となる。したがって,1≦i≦nに対して,CEXTI(I+A(M(T(di)))) = EC(di)
となる。そのために,AをT(d)の空ノードの写像とし,I+AがT(d)を充足する場合,1≦i≦nに対して,
CEXTI(I+A(M(T(di)))) = EC(di)及びI+A(M(T(di))∈IOCとなる。
I'がFを充足する場合,1≦i≦nに対して,EC(foo) ⊆EC(di) となる。上記によって,あるAが存在
し,CEXTI(I+A(M(T(di)))) = EC(di) ⊇ EC(foo) = CEXTI(I(foo))及びI+A(M(T(di))∈IOCとなる。IがT(V)
を充足するので,I(foo)∈IOCとなる。したがって,1≦i≦nに対して,<I(foo),I+A(M(T(di)))> ∈
EXTI(I(rdfs:subClassOf))となる。よって,IはT(F)を充足する。
IがT(F)を充足する場合,1≦i≦nに対して,Iは T(di)を充足する。したがって,1≦i≦nに対して,
上記によって,あるAが存在し,<I(foo),I+A(M(T(di)))> ∈ EXTI(I(rdfs:subClassOf))となる。したがっ
て,1≦i≦nに対して,EC(d) = CEXTI(I+A(M(T(di)))) ⊇ CEXTI(I(foo)) = EC(foo)となる。よって,I'は
Fを充足する。
c) F = EnumeratedClass(foo i1 … in)の場合
d=oneOf(i1 … in)とおく。このdはV'上の記述なので,IはT(d)を充足する。同様に,AをT(d)の空
ノードの写像とし,I+AがT(d)を充足する場合は,EC(d) = CEXTI(I+A(M(T(d)))) = {SI(M(T(i1))), …
SI(M(T(in)))}となる。同様に,1≦j≦nに対して,SI(M(T(ij)) ∈IOTとなる。
I'がFを充足する場合,EC(foo) = EC(d)となる。上記によって,あるAが存在し,CEXTI(I+A(M(T(d))))
= EC(d) = EC(foo) = CEXTI(I(foo))及びI+A(M(T(d))∈IOCとなる。ここで,eをI+A(M(T(SEQ i1 … in)))
とする。すると,I(owl:oneOf)の意味論条件によって,<I(foo),e> ∈ EXTI(I(owl:oneOf))となる。よっ
て,IはT(F)を充足する。
IがT(F)を充足する場合,Iは,T(SEQ i1 … in)を充足する。したがって,上記によって,あるAが
存在し,<I(foo),I+A(M(T(SEQ i1 … in)))> ∈ EXTI(I(owl:oneOf))となる。したがって, {SI(M(T(i1))), …,
SI(M(T(in)))} = CEXTI(I(foo)) = EC(foo) となる。よって,I'はFを充足する。
d) F = Datatype(foo)の場合
ここで示す必要があるのは,fooの型付けだけだが,これはクラスの場合と同様に示すことができ
る。
e) F= DisjointClasses(d1 … dn)の場合
di はV'上の記述なので,IはT(di)を充足する。同様に,AをT(di)の空ノードの写像とし,I+Aが
T(di)を充足する場合は,いかなるAについてもCEXTI(I+A(M(T(di)))) = EC(di)となる。
IがT(F)を充足する場合,1≦i≦nに対して,あるAiが存在し,1≦i<j≦nのそれぞれについて,I
が <I+Ai(M(T(di))),I+Aj(M(T(dj)))> ∈EXTI(I(owl:disjointWith))を充足する。したがって,i≠jに対して,
EC(di)∩EC(dj) = {}となる。よって,I'はFを充足する。
I'がFを充足する場合,i≠jに対して,EC(di)∩EC(dj) = {}となる。いかなるAi及びAjに対しても,
38
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
上記のとおり,i≠jについて,<I+Ai+Aj(M(T(di))),I+Ai+Aj(M(T(dj)))> ∈EXTI(I(owl:disjointWith))となる。
各iについて,少なくとも一つのAiが存在し,T(dj)の空ノードはすべて互いに素なので,I+A1+…+An
は T(DisjointClasses(d1 … dn))を充足する。よって,IはT(F)を充足する。
f)
F = EquivalentClasses(d1 … dn)の場合
同様に証明できる。
g) F = SubClassOf(d1 d2)の場合
大体同様に証明できる。
h) F = ObjectProperty(p super(s1) … super(sn) domain(d1) … domain(dm) range(r1) … range(rk) [inverse(i)]
[Symmetric] [Functional] [InverseFunctional] [OneToOne] [Transitive])の場合
1≦i≦mに対してdiはV'上の記述なので,IはT(di)を充足する。同様に,AをT(di)の空ノードの写
像とし,I+AがT(di)を充足する場合,いかなるAに対しても,CEXTI(I+A(M(T(di)))) = EC(di)となる。
1≦i≦kに対するriも同様となる。
I'がFを充足する場合,p∈VOPなので,IはI(p)∈IOOPを充足する。IはOWL DLの解釈なので,
Iは <I(p),I(owl:Thing)>∈EXTI(I(rdfs:domain)) 及び<I(p),I(owl:Thing)>∈EXTI(I(rdfs:range))を充足する。
同様に,1≦i≦nに対して,ER(p)⊆ER(si)となるので,EXTI(I(p))=ER(p)⊆ER(si)=EXTI(I(si))であって,
Iは <I(p),I(si)>∈EXTI(I(rdfs:subPropertyOf))を充足する。次に,1≦i≦mに対して,ER(p)⊆EC(di)×R
となるので,<z,w>∈ER(p)はz∈EC(di)がいえ,I+AがT(di)を充足するいかなるAに対しても,<z,w>
∈EXTI(p)は z∈CEXTI(I+A(M(T(di))))がいえる。したがって,<I(p),I+A(M(T(di)))>∈EXTI(I(rdfs:domain))
となる。1≦i≦kに対するriも同様となる。
I'がFを充足し,inverse(i)がFに属する場合,ER(p)及びER(i)は逆関係となる。したがって,<v,u>
∈ER(i)の場合及びその場合に限り,<u,v>∈ER(p)となる。したがって,<v,u>∈EXTI(i)の場合及びその
場合に限り,<u,v>∈EXTI(p)となり,Iは<I(p),I(i)>∈EXTI(I(owl:inverseOf))を充足する。I'がFを充足
するし,SymmetricがFに属する場合,ER(p)は対称的となる。したがって,<x,y>∈ER(p)の場合,<y,x>
∈ER(p)となり,それによって,<x,y>∈EXTI(p)の場合,<y, x>∈EXTI(p)となる。よって,Iは p∈
CEXTI(I(owl:Symmetric))を充足する。Functional,InverseFunctional及びTransitiveについても同様とな
る。よって,I'がFを充足する場合,IはT(F)を充足する。
IがT(F)を充足する場合,1≦i≦nに対して,<I(p),I(si)>∈EXTI(I(rdfs:subPropertyOf))なので,
ER(p)=EXTI(I(p)) ⊆ EXTI(I(si))=ER(si)となる。同様に,1≦i≦mに対して,I+AがT(di)を充足するA
について,<I(p),I+A(M(T(di)))>∈EXTI(I(rdfs:domain))なので,<z,w>∈EXTI(p)はz∈
CEXTI(I+A(M(T(di))))がいえる。したがって,<z,w>∈ER(p)はz∈EC(di)がいえ, ER(p)⊆EC(di)×Rと
なる。1≦i≦kに対するriも同様となる。
IがT(F)を充足する,inverse(i)がFに属する場合,Iは <I(p),I(i)>∈EXTI(I(owl:inverseOf))を充足する。
したがって,<v,u>∈EXTI(i)の場合及びその場合に限り,<u,v>∈EXTI(p)となる。したがって,<v,u>
∈ER(i)の場合及びその場合に限り,<u,v>∈ER(p)となり,ER(p)及びER(i)が逆関係になる。IがFを
充足し,SymmetricがFに属する場合,Iはp∈CEXTI(I(owl:Symmetric))を充足する。したがって,<x,y>
∈EXTI(p)の場合,<y, x>∈EXTI(p)となる。よって,<x,y>∈ER(p)の場合,<y,x>∈ER(p)となり,ER(p)
は対称的となる。Functional, InverseFunctional及びTransitiveについても同様となる。よって,IがT(F)
を充足する場合,I'はFを充足する。
i)
F = DatatypeProperty(p super(s1) … super(sn) domain(d1) … domain(dm) range(r1) … range(rl) [Functional])
の場合
39
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
同様に証明できるが,より簡単である。
j)
F = AnnotationProperty(p domain(d1) … domain(dm))の場合
同様に証明できるが,より一層簡単である。
k) F = OntologyProperty(p domain(d1) … domain(dm))の場合
同様に証明できるが,より一層簡単である。
l)
F = EquivalentProperties(p1 … pn), ただし,pi∈VOPの場合
pi∈VOPであって,IがT(V')を充足するので,I(pi)∈IOOPとなる。IがT(F)を充足する場合,1≦i<j
≦nのそれぞれに対して,<I(pi),I(pj)>∈EXTI(I(owl:equivalentProperty))となる。そのために,1≦i<j≦n
のそれぞれに対して,EXTI(pi) = EXTI(pj)となり,1≦i<j≦nのそれぞれに対して,ER(pi) = ER(pj)とな
り,I'はFを充足する。
I'がFを充足する場合,1≦i<j≦nのそれぞれに対して,ER(pi) = ER(pj)となる。そのために,1≦i<j
≦nのそれぞれに対して,EXTI(pi) = EXTI(pj)となる。OWL DLにおけるowl:equivalentPropertyの定義
によって,1≦i<j≦nのそれぞれに対して,<I(pi),I(pj)>∈EXTI(I(owl:equivalentProperty))となる。よって,
IはT(F)を充足する。
m) F = SubPropertyOf(p1 p2)の場合
大体同様に証明できるが,より簡単である。
n) F = SameIndividual(i1 … in)の場合
SamePropertyAsの場合と同様に証明できる。
o) F = DifferentIndividuals(i1 … in)の場合
SamePropertyAsの場合と同様に証明できる。
p) F = Individual([i] type(t1) … type(tn) value(p1 v1) … value(pn vn))の場合
IがT(F)を充足する場合,写像Aが存在し,AはT(F)の各空ノード写像とし,I+AがT(F)を充足す
る。T(F)を簡単に検査することによって,次のことが判明する。すなわち,Aの写像と, Fの中の個
体IDに対する写像(固体すべてはIOTに属している。)とを加えたものによって,I'がFを充足する
ことが分かる。
I'がFを充足する場合,Fの中の各個体構成要素について,Fにおいて型関係及び関係を真にするR
の要素が存在しなければならない。T(F)の三つ組は次の3種類に分かれる。
1) owl:Thingに対する型関係。これは,上の要素がRに属するので,Iで真となる。
2) OWLの記述との型関係。これは,補助定理1によって,I'で真となるので,Iで真となる。
3) OWLの特性関係。これは,Iで真となるので,I'で真となる。
これらによって,IはT(F)を充足する。
証明終
補助定理2終
A.1.3 RDF意味論から直接的意味論への対応
補助定理3
V' = VO + VC + VD + VI + VOP + VDP + VAP + VXPを分離されたOWL語い(彙)とする。V = VO ∪ VC
∪ VD ∪ VI ∪ VOP ∪ VDP ∪ VAP ∪ VXP ∪ VBとする。このとき,T(V')を充足する,Vのすべ
てのOWL DLの解釈I = <RI,PI,EXTI,SI,LI,LVI>に対して,V'の直接的な解釈I'が存在し,Oが,語い(彙)
V'をもつOWL抽象オントロジと公理及び事実との集まりであって,取込み閉包となる場合,そのあらゆ
るOに対して,IがT(O)をOWL DLとして充足するとき及びそのときに限り,I'は直接的にOを充足する。
40
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
証明
CEXTIを,通常のとおり,Iから定義されるとする。要求される直接的解釈は,I' = < RI, EC, ER, L, S, LVI
>であって,次の条件を満たす。
a) v∈VC∪VDに対して,EC(v) = CEXTI(SI(v))となる。
b) v∈VOP∪VDP∪VAP∪VXPに対して,ER(v) = EXTI(SI(v))となる。
c) x∈Rに対して,< x, SI(owl:DeprecatedClass) > EXTI(SI(rdf:type))である場合及びその場合に限り,< x,
S(owl:DeprecatedClass) > ∈ER(rdf:type)となる。
d) x∈Rに対して,< x, SI(owl:DeprecatedProperty) > EXTI(SI(rdf:type))である場合及びその場合に限り,<
x,S(owl:DeprecatedProperty)> ∈ER(rdf:type)となる。
注記 原勧告のc)及びd)には,EXTI(SI(rdf:type)の前に∈が抜けていた。この規格ではこれを追加した。
e) 型付きリテラルdに対して,L(d) = LI(d)となる。
f)
v∈VI ∪ VC ∪ VD ∪ VOP ∪ VDP ∪ VAP ∪ VXP ∪ VOに対して,S(v) = SI(v)となる。
注記 原勧告のf)は,最初のvがnになっていた。vが正しいので,この規格ではvに統一した。
V', V, I'及びIは,補助定理2の要件を満たしている。したがって,V'上のあらゆる指示Dに対して,I'
がDを充足する場合及びその場合に限り,IはT(D)を充足する。
Oは取込み閉包なので,Oは,T(O)に取り込まれるすべてのオントロジを含み,取込み指示の取込み部
分も同様に扱われる。ある抽象オントロジを充足することは,その指示を充足することであって,ある抽
象オントロジの翻訳を充足することは,すべての三つ組を充足することになる。そのために,I'がKを直
接的に充足する場合及びその場合に限り,IはT(K)をOWL DLとして充足する。
証明終
補助定理3終
A.1.4 直接的意味論からRDF意味論への対応
補助定理4
V' = VO + VC + VD + VI + VOP + VDP + VAP + VXPを分離されたOWL語い(彙)とする。V = VO ∪ VC
∪ VD ∪ VI ∪ VOP ∪ VDP ∪ VAP ∪ VXP ∪ VBとする。このとき,V'のすべての直接的解釈I' = <
U, EC, ER, L, S, LV >に対して,T(V')を充足するVのOWL DL解釈Iが存在し,Oが,語い(彙)V'をもつ
OWL抽象オントロジと公理及び事実との集まりであって,取込み閉包となる場合,そのあらゆるOに対
して,IがT(O)をOWL DLとして充足するとき及びそのときに限り,I'は直接的にOを充足する。
証明
I = < RI, PI, EXTI, SI, L, LVI >を次のとおり構成する。
a) IOCをV'上のすべてのOWL記述とし,これにクラス固有の語い(彙)を追加する。
IDCをV'上のすべてのOWLデータ値域とする。
IOP = VOP ∪ VDP ∪ VAP ∪ VXPとし,これに特性固有の語い(彙)を追加する。
IX = VOとする。
ILをrdf:nilとし,これにU上,IOC上及びLV上の有限の列を追加する。
IADをrdf:nilとし,これにU上の有限の列を追加する。
IVを使用してはならない語い(彙)とし,ここからrdf:nilを除く。
b) RIをU, IOC, IDC, IOP, IX, IL, IAD及びIVの互いに素となる和集合(非交和)とする。
c) PIをIOP ∪ IVとする。
d) LVI = LVとする。
41
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
n∈VIに対して,SI(n) = S(n)とする。
n∈V-VIに対して,SI(n) = nとする。
e) c∈IOCに対して,定義されている場合は,CEXTI(c)=EC(c)とし,それ以外の場合は{}とする。
d∈IDCに対して,CEXTI(d)=EC(d)とする。
x∈U∪IL∪IAD∪IOP∪IXに対して,CEXTI(x)={}とする。
f)
CEXTI(SI(rdf:type)) = {}とする。
CEXTI(SI(rdf:Property)) = PIとする。
CEXTI(SI(rdf:List)) = ILとする。
CEXTI(SI(rdf:XMLLiteral))はRDF XMLリテラル値とする。
CEXTI(SI(rdf:first))= CEXTI(SI(rdf:rest)) = CEXTI(SI(rdfs:domain)) = CEXTI(SI(rdfs:range)) = {}とする。
CEXTI(SI(rdfs:Resource)) = RIとする。
CEXTI(SI(rdfs:Literal)) = LVIとする。
CEXTI(SI(rdfs:Datatype)) = Dとする。
CEXTI(SI(rdfs:Class)) = IOC ∪ IVとする。
CEXTI(SI(rdfs:subClassOf)) = CEXTI(SI(rdfs:subPropertyOf)) = CEXTI(SI(rdfs:member)) = {} とする。
CEXTI(SI(rdfs:Container)) = CEXTI(SI(rdf:Seq)) ∪ CEXTI(SI(rdf:Bag)) ∪ CEXTI(SI(rdf:Alt)) とする。
CEXTI(SI(rdfs:ContainerMembershipProperty))はRDFのコンテナのメンバ関係特性とする。
g) r∈IOPに対して,定義されている場合は,EXTI(r)=ER(r)とし,それ以外の場合は,{}とする。
h) EXTI(SI(rdf:type))は,CEXTIによって決定される。
EXTI(SI(rdf:Property)) = EXTI(SI(rdf:List)) = EXTI(SI(rdf:XMLLiteral)) = {} とする。
x∈IL及びyがその最初の要素の場合及びその場合に限り,<x,y> ∈ EXTI(rdf:first) とする。
x∈IL及びyがその最初の要素を除いたものの場合及びその場合に限り,<x,y> ∈EXTI(rdf:rest)とする。
EXTI(SI(rdfs:domain)) = { <x,y> : x∈IOP y∈IOC ∧ ∀ w, <w,z> ∈EXTI(x) implies w ∈CEXTI(y)} と
する。
EXTI(SI(rdfs:range)) = { <x,y> : x∈OP y∈IOC ∧ ∀ z, <w,z> ∈EXTI(x) implies z ∈CEXTI(y)とする。
EXTI(SI(rdfs:Resource)) = EXTI(SI(rdfs:Literal)) = EXTI(SI(rdfs:Datatype)) = EXTI(SI(rdfs:Class)) = {} とす
る。
EXTI(SI(rdfs:subClassOf)) = { <x,y> : x,y∈IOC ∧ CEXTI(x) ⊆CEXTI(y) } とする。
EXTI(SI(rdfs:subPropertyOf)) = { <x,y> : x,y∈OP ∧ EXTI(x) ⊆EXTI(y) } とする。
EXTI(SI(rdfs:member))は,(RDFの)コンテナのメンバ関係特性の外延の和集合とする。
EXTI(SI(rdfs:Container)) = EXTI(SI(rdfs:ContainerMembershipProperty)) = {}
i)
owl:allValuesFrom, owl:cardinality, owl:hasValue, owl:maxCardinality, owl:minCardinality, owl:onProperty及
び owl:someValuesFromの外延は,必要に応じて,それらの各部分にIOC及びIDCの要素を結合する
ものとする。それらのクラスの外延はすべて空とする。
j)
owl:complementOf, owl:intersectionOf, owl:oneOf及びowl:unionOfの外延は,必要に応じて,それらの意
味論条件を正しく成立させるものとする。それらのクラスの外延はすべて空とする。これらの外延の
修正は,その過程において何の繰返しも引き起こさないので,これは,ここでは,簡単に実行できる。
k) CEXTI(SI(owl:AnnotationProperty)) = VAPとする。
CEXTI(SI(owl:OntologyProperty)) = VXPとする。
CEXTI(SI(owl:Class)) = IOCとする。
42
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
CEXTI(SI(owl:DatatypeProperty)) = VDPとする。
CEXTI(SI(owl:FunctionalProperty)) は,その外延が部分関数的となるVOP∪VDP の要素とする。
CEXTI(SI(owl:InverseFunctionalProperty))は,その外延が逆部分関数的となるVOPの要素とする。
CEXTI(SI(owl:ObjectProperty)) = VOPとする。
CEXTI(SI(owl:Ontology)) = VOとする。
CEXTI(SI(owl:Restriction))は,OWLの制限であるIOCの要素とする。
CEXTI(SI(owl:SymmetricProperty))は,その外延が対称的となるVOPの要素とする。
CEXTI(SI(owl:TransitiveProperty))は,その外延が推移的となるVOPの要素とする。
EXTI(SI(owl:AnnotationProperty)) = EXTI(SI(owl:OntologyProperty)) = EXTI(SI(owl:Class)) =
EXTI(SI(owl:DatatypeProperty)) = EXTI(SI(owl:FunctionalProperty)) =
EXTI(SI(owl:InverseFunctionalProperty)) = EXTI(SI(owl:ObjectProperty)) = EXTI(SI(owl:Ontology)) =
EXTI(SI(owl:Restriction)) = EXTI(SI(owl:SymmetricProperty)) = EXTI(SI(owl:TransitiveProperty)) = {} とす
る。
l)
CEXTI(SI(owl:AllDifferent))は,owl:distinctMembers特性をもつIADの要素から構成される。
EXTI(SI(owl:differentFrom))は,Uにおける非同等関係とする。
EXTI(SI(owl:disjointWith)) は,互いに素なクラスの外延をもつIOCのメンバを関連付ける。
EXTI(SI(owl:distinctMembers))は,IADの要素をILにおけるそれらの複写に関連付けるが,これは他と
異なる個体の列の場合に限られる。
EXTI(SI(owl:equivalentClass))は,同じクラスの外延をもつIOCのメンバを関連付ける。
EXTI(SI(owl:equivalentProperty))は,同じ外延をもつIOP∪IDPのメンバを関連付ける。
EXTI(SI(owl:inverseOf))は,外延が互いの逆となるIOPのメンバを関連付ける。
EXTI(SI(owl:sameAs))は,Uにおける同等関係とする。
EXTI(SI(owl:AllDifferent)) = CEXTI(SI(owl:differentFrom)) = CEXTI(SI(owl:disjointWith)) =
CEXTI(SI(owl:distinctMembers)) = CEXTI(SI(owl:equivalentClass)) = CEXTI(SI(owl:equivalentProperty)) =
CEXTI(SI(owl:inverseOf)) = CEXTI(SI(owl:sameAs)) = {} とする。
m) CEXTI(SI(owl:DeprecatedClass)) = { x ∈ IOC∪IDC : <x,S(owl:DeprecatedClass)>∈ER(rdf:type) }
CEXTI(SI(owl:DeprecatedProperty)) = { x ∈ IOOP∪IODP : <x,S(owl:DeprecatedProperty)>∈
ER(rdf:type) } とする。
EXTI(SI(owl:DeprecatedClass)) = EXTI(SI(owl:DeprecatedProperty)) = {} とする。
これらによって,OWL DLにおけるクラスの外延の条件が,クラスに対応するOWL抽象構文の構成要
素の条件と合致するので,Iは,OWL DLの解釈となる。
V', V, I'及びIは,補助定理2の要件を満たすので,V'上のいかなる指示Dについても,I'がDを充足す
る場合及びその場合に限り,IはT(D)を充足する。
Oが取込み閉包なので,Oは,T(O)に取り込まれるすべてのオントロジを含む。取込み指示の取込み部
分も同様に取り扱われる。ある抽象オントロジを充足するということは,その指示を充足することであっ
て,ある抽象オントロジの翻訳を充足するということは,そのすべての三つ組を充足することである。そ
のために,I'がKを直接的に充足する場合及びその場合に限り,IはT(K)をOWL DLとして充足する。
証明終
補助定理4終
A.1.5 対応定理
43
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定理1
O及びO'を,取込み閉包である抽象構文形式の,OWL DLオントロジと公理及び事実との集まりとする。
ただし,それらの和集合が分離された語い(彙)V'をもち,V'のすべてのURI参照がOで使用されるとす
る。このとき,T(O)がT(O')をOWL DLとして論理的に帰結する場合及びその場合に限り,OはO'を直接
的に論理的に帰結する。
定理1終
その結果,V'の中の各URI参照はOで使用されるので,IはT(V')を充足する。
定理1の証明
OがO'を論理的に帰結すると仮定する。IをT(O)を充足するOWL DLの解釈とする。その場合,補助定
理3によって,何らかの直接的解釈I'が存在し,次の条件を満たす。すなわち,V'上のいかなる抽象OWL
オントロジ又は公理若しくは事実についても,I'がXを充足する場合及びその場合に限り,IがT(X)を充
足する。したがって,I'は,Oの各オントロジを充足する。OはO'を論理的に帰結するので,I'はO'を充足
する。そのために,IはT(O')を充足する。よって,T(K)及びT(V')はT(Q)をOWL DLとして論理的に帰結
する。
T(O)がT(O')をOWL DLとして論理的に帰結すると仮定する。I'を,Kを充足する直接的解釈とする。そ
の場合,補助定理4によって,何らかのOWL DLの解釈 Iが存在し,次の条件を満たす。すなわち,V'
上のいかなる抽象OWLオントロジXについても,I'がXを充足する場合及びその場合に限り,IはT(X)
を充足する。したがって,IはT(O)を充足する。T(O)がT(O')をOWL DLとして論理的に帰結するので,I
はT(O')を充足する。そのために,I'はO'を充足する。よって,OはO'を論理的に帰結する。
定理1の証明終
A.2 OWL DLとOWL Fullとの対応
A.2では,OWL DLとOWL Fullとの関係についての証明の概要を示す。この証明は,完成していない。
この証明を完結させるには,大きな努力が必要かもしれない。また,対応関係の詳細を幾つか変更する必
要があるかもしれない。
KをRDFグラフとする。KのOWLの解釈は,KのD解釈であるOWL解釈となる(5.2参照)。
補助定理5
Vを分離された語い(彙)とする。その場合,すべてのOWLの解釈Iについて,5.3の場合と同様に,
OWL DLの解釈I'が存在し,次の条件を満たす。すなわち,Kを,分離された語い(彙)Vをもつ抽象構
文形式のOWLオントロジとする場合,いかなるKに対しても,I'がT(K)のOWL DLの解釈となるとき及
びそのときに限り,IはT(K)のOWLの解釈となる。
証明概要
すべてのOWL DLの解釈はOWLの解釈なので,逆方向は明らかである。
I = < RI, EXTI, SI, LI >をT(K)を充足するOWLの解釈とする。I' = < RI', EXTI', SI', LI' > をT(K)を充足する
OWL解釈とする。RI' = CEXTI(I(owl:Thing)) + CEXTI(I(owl:DatatypeProperty)) + CEXTI(I(owl:ObjectProperty))
+ CEXTI(I(owl:Class)) + CEXTI(I(rdf:List)) + RIとする。この場合,+ は互いに素な和集合,すなわち非交和
とする。複写の様々な役割を分離するために,EXTI'を定義する。語い(彙)を適切な複写に写像するため
に,SI'を定義する。Kが分離された語い(彙)をもつので,これはうまく機能する。そのために,役割に
従って,Iを分けることができ,EXTIに,不適切な関係は存在しない。要するに,RI'の最初の構成要素は
OWLの個体になり,RI'の2番目の構成要素はOWLのデータ型特性になり,RI'の3番目の構成要素はOWL
44
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の個体値特性になり,RI'の4番目の構成要素はOWLのクラスになり,RI'の5番目の構成要素はRDFのリ
ストになり,RI'の6番目の構成要素はその他すべてのものになる。
注記 原勧告では,RI'の第2項はObjectProperty となっていたが,これは,その後の説明の意味内容
からすると,DatatypePropertyの誤りと思われる。
証明概要終
補助定理5終
定理2
O及びO'を,抽象構文形式におけるOWL DLオントロジと公理及び事実との集まりとし,それらは取込
み閉包とする。ただし,それらの和集合は,分離された語い(彙)(4.2参照)をもつとする。その場合,
Oの翻訳がO'の翻訳をOWL DLとして論理的に帰結する場合,Oの翻訳は,O'の翻訳をOWL Fullとして
論理的に帰結する。
証明
補助定理5及びすべてのOWL Fullの解釈が,OWLの解釈であることを根拠とする。
注記 ただし,“及びその場合に限り”だと,真とはならない。
証明終
定理2終
45
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
例
この附属書は,規定の一部ではない。
この附属書は,この規格以外のOWLの規定で開発された概念との関連を例として示す。
B.1
抽象構文からRDFグラフへの写像の例
箇条4の変換規則の例を示す。次のオントロジの変換を検討する。
Ontology(ex:ontology
DatatypeProperty(ex:name)
ObjectProperty(ex:author)
Class(ex:Book)
Class(ex:Person)
Individual(type(ex:Book)
value(ex:author Individual(type(ex:Person) value(ex:name "Fred"^^xsd:string)))))
このオントロジは,次のとおりに変換できる。
ex:ontology rdf:type owl:Ontology .
ex:name rdf:type owl:DatatypeProperty .
ex:author rdf:type owl:ObjectProperty .
ex:Book rdf:type owl:Class .
ex:Person rdf:type owl:Class .
̲:x rdf:type ex:Book .
̲:x ex:author ̲:x1 .
̲:x1 rdf:type ex:Person .
̲:x1 ex:name "Fred"^^xsd:string .
さらに,次のオントロジを検討する。
Ontology(ex:ontology2
Class(ex:Person)
Class(ex:Student)
ObjectProperty(ex:enrolledIn)
Class(ex:Student complete ex:Person
restriction(ex:enrolledIn allValuesFrom(ex:School) minCardinality(1))))
このオントロジは,次のとおりに変換できる。
ex:ontology2 rdf:type owl:Ontology .
ex:enrolledIn rdf:type owl:ObjectProperty .
ex:Person rdf:type owl:Class .
46
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ex:School rdf:type owl:Class .
ex:Student rdf:type owl:Class .
ex:Student owl:equivalentClass ̲:x .
̲:x owl:intersectionOf ̲:l1 .
̲:l1 rdf:first ex:Person .
̲:l1 rdf:rest ̲:l2 .
̲:l2 rdf:first ̲:lr .
̲:l2 rdf:rest rdf:nil .
̲:lr owl:intersectionOf ̲:lr1 .
̲:lr1 rdf:first ̲:r1 .
̲:lr1 rdf:rest ̲:lr2 .
̲:lr2 rdf:first ̲:r2 .
̲:lr2 rdf:rest rdf:nil .
̲:r1 rdf:type owl:Restriction .
̲:r1 owl:onProperty ex:enrolledIn .
̲:r1 owl:allValuesFrom ex:School .
̲:r2 rdf:type owl:Restriction .
̲:r2 owl:onProperty ex:enrolledIn .
̲:r2 owl:minCardinality "1"^^xsd:nonNegativeInteger .
B.2
OWL DL及びOWL Fullにおける論理的帰結の例
OWL DLは,語い(彙)が議論の領域の適切な部分に属することを示すことができる限り,期待される
論理的帰結を提供する。次に例を示す。
John friend Susan .
この記述は,次をOWL DLとして論理的に帰結しない。
John rdf:type owl:Thing .
Susan rdf:type owl:Thing .
friend rdf:type owl:ObjectProperty .
次の制限の結論付けを可能とするためには,上の三つの三つ組を追加する必要がある。
John rdf:type ̲:x .
̲:x owl:onProperty friend .
̲:x owl:minCardinality "1"^^xsd:nonNegativeInteger .
しかし,一度この特別な情報を追加すると,繰返しをもつ記述を含む論理的帰結を除き,すべての自然
な論理的帰結を導くことができる。次に例を示す。
John rdf:type owl:Thing .
47
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
friend rdf:type owl:ObjectProperty .
John rdf:type ̲:x .
̲:x owl:onProperty friend .
̲:x owl:maxCardinality "0"^^xsd:nonNegativeInteger .
この記述は,次を論理的に帰結しない。
John rdf:type ̲:y .
̲:y owl:onProperty friend .
̲:y owl:allValuesFrom ̲:y .
これは,これらの繰返し記述について,包括原理が存在しないことによる。OWL DLは,自然な論理的
帰結を保持しながら,矛盾を形成しないために,このような包括原理を欠落させている。
OWL DLでは,次の形式の三つ組すべてから構成される,局所化の表明を行う特定の集合を追加するこ
とによって,構文が分離されたいかなる知識ベースにおいても,欠落している局所化を修復することがで
きる。
<individual> rdf:type owl:Thing .
<class> rdf:type owl:Class .
<oproperty> rdf:type owl:ObjectProperty .
<dtproperty> rdf:type owl:DatatypeProperty .
このような表明のすべてをOWL DLの知識ベースに追加した結果を,その知識ベースの局所化と呼ぶ。
OWL Fullは,期待されるとおりの論理的帰結を提供し,語い(彙)に型付け情報を与える必要はない。
次に例を示す。
John friend Susan .
この記述は,次をOWL Fullとして論理的に帰結する。
John rdf:type ̲:x .
̲:x owl:onProperty friend .
̲:x owl:minCardinality "1"^^xsd:nonNegativeInteger .
48
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
原勧告における最終審議案からの変更
この附属書は,規定の一部ではない。
この附属書は,この規格の元になったW3C勧告の最終審議案からの変更について,参考となる記述を
提供している。最終審議案後に行われたW3C勧告への重要な変更はすべて,最終審議案後の幾つかの編
集上の変更とともに,この附属書の中に示されている。
C.1 最終審議案後の重要な変更
C.1では,OWLの規定を修正する,W3C勧告への最終審議案後の変更に関する情報を提供する。
[2003年4月10日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Apr/0046.htmlへの対応として,owl:Class,
owl:Restriction, owl:ObjectProperty, owl:DatatypeProperty, owl:AnnotationProperty, owl:OntologyProperty,
owl:Ontology, owl:AllDifferent, owl:FunctionalProperty, owl:InverseFunctionalProperty, owl:SymmetricProperty
及びowl:TransitivePropertyを 5.2のCIに追加した。これらのうち,幾つかは既に推論可能であった。
[2003年4月10日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Apr/0046.htmlに関連して,owl:distinctMembersを
5.2のRIに追加した。
注記 5.2.2に“及びI(owl:distinctMembers)は,すべてPIに属する”とある。おそらく,RIはPIの間違
いと思われる。
[2003年4月15日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Apr/0064.htmlへの対応として,
owl:OntologyPropertyを4.2の使用してはならないOWL語い(彙)の使用してはならない語い(彙)に
追加した。
[2003年5月5日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0017.htmlに記録されているとおり,
owl:NothingをOWL Liteに追加するという2003年5月1日のウェブオントロジ作業グループの決定によ
って,owl:Nothingの導入を変更し,そのように示した。owl:Nothingの索引も更新された。
[2003年5月9日]
内部の無矛盾性を改善するために,4.1の注釈特性について,任意選択のrdf:Property型を追加した。
[2003年5月30日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0402.htmlに記録されているとおり,
EquivalentClassesの写像を修正するという2003年5月29日のウェブオントロジ作業グループの決定に
よって,http://lists.w3.org/Archives/Public/www-webont-wg/2003Apr/0003.html及び
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0052.htmlへの対応として,
EquivalentClasses(d1 ... dn)の写像規則を変更して,Gにおけるすべての <i,j> に対して,T(di)
owl:equivalentTo T(dj)とした。この場合,Gは{1,...,n}上の対の集合であって,無向グラフとして解釈され
た場合に,{1,...,n}に対する連結グラフを形成する。
49
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[2003年5月30日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0402.htmlに記録されているとおり,オント
ロジ特性の公理を追加するという2003年5月29日のウェブオントロジ作業グループの決定によって,
2.3.1.3及び2.3.2.4のOWL Lite及びOWL DL抽象構文にオントロジ特性の公理を追加した。また,3.3
のオントロジ特性公理の直接的意味論条件を追加し,4.1のオントロジ特性公理の写像も追加した。補助
定理2及び補助定理3の証明を修正した。
[2003年5月30日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0402.htmlに記録されているとおり,
owl:intersectionOf及び関連する箇所の意味論を内包的な意味論から外延的な意味論へ変更するという
2003年5月29日のウェブオントロジ作業グループの決定によって,5.2のowl:intersectionOf, owl:unionOf,
owl:complementOf及びowl:oneOfの意味論条件を修正した。補助定理1の証明に変更を加える必要はな
かった。補助定理4及び補助定理2の証明を修正した。
[2003年6月2日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jun/0004.htmlのJeremy Carrolの意見への対応と
して,4.1において,型をもたないとく(匿)名の個体に関する写像規則を若干変更した。
[2003年6月4日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jun/0011.htmlへの対応として,2.3.1.3,2.3.2.3及
び4.1において,データ型及びrdfs:Literalの取扱いを若干変更した。
[2003年6月4日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0050.htmlのowlsas-rdf-equivalent-class
に関する項目への対応として,3.4のオントロジ注釈の取扱いを変更した。
[2003年6月5日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jun/0004.htmlのJeremy Carrollの意見への対応と
して,直接的意味論を修正し,OWLの個体ではない定義域要素を許可した。これらの定義域要素は,
クラス,特性及びオントロジの注釈に意味を与えるために使用される。3.1,3.2,3.3及びA.1において,
変更が加えられた。
[2003年6月26日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jun/0364.htmlに記録されているとおり,
owl:sameIndividualAsをowl:sameAsに置き換えるという2003年6月26日のウェブオントロジ作業グル
ープの決定によって,2.2,3.3,4.1,4.2,5.2及びA.1に変更を加えた。
[2003年6月30日]
Jeremy Carollが通知したowl:hasValueの意味論条件の不具合を修正し,5.2において,特性から個体又
はデータ値への値に対する条件を変更した。
[2003年7月23日]
rdfs:subClassOf及びrdfs:subPropertyOfの必要十分条件を必要条件に変更するという,最終審議案後の
RDF意味論への重要な変更への対応として,OWLのクラス上のrdfs:subClassOf,並びにOWLの個体値
特性及びOWLのデータ型特性上のrdfs:subPropertyOfについて,必要十分条件を5.2に追加した。
[2003年7月23日]
集まりに対する型付けの三つ組を削除する(ただし,適用可能な規定は知られていない。)というRDF
構文の三つ組への写像についての重要な変更への対応として,4.1のリスト資源の型付けを任意選択にし
50
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
た。同様に,B.1の例を変更した。
C.2 最終審議案後の編集上の変更
C.2では,最終審議案後のW3C勧告への編集上の変更,すなわち,OWLの規定に影響を与えない変更
に関して情報を提供する。
[2003年4月9日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0023.htmlの2の項目への対応として,
2.3の“特性についてのほとんどの情報”を“特性に関するほとんどの情報”に変更した。
[2003年4月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0029.htmlの1の項目への対応として,
“XMLスキーマでは,URI参照からXMLスキーマデータ型へたどるための標準的な方法がないので,
OWLでは,利用者定義のXMLスキーマデータ型を使用するための標準的な方法は存在しない。”とい
う文を箇条2の使用可能なXMLスキーマデータ型の議論に追加した。
[2003年4月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0029.htmlの2.1の項目への対応とし
て,3.1において,“特性rdf:typeは,非推奨 (deprecation) に対する意味を与えるために注釈特性に追加
されている。表3の記述を参照してもらいたい。”という文を“ERは,OWL特性として使われるURI
参照に対する意味を与える。”という文の後に追加した。
[2003年4月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0029.htmlの2.3の項目への対応とし
て,3.1において,“データ型理論は,xsd:string及びxsd:integerのデータ型を含まなければならない。デ
ータ型理論は,他のOWLでの使用が適切である組込みXMLスキーマデータ型のデータ型を含んでもよ
い。同様に他のデータ型を含んでもよいが,OWL構文には,これらのデータ型が何であるかを伝える
ための準備はない。”という文をデータ型の定義の直後に追加した。
注記 これは更に変更されたらしく,実際には,“データ型写像は,その他の組込みのOWLデータ型
のためのデータ型を含んでもよい。それ以外のデータ型も含んでもよいが,OWL構文において
これらのデータ型が何であるかを知らせるための規定は存在しない。”という文が,データ型の
定義の直後に追加されている。
[2003年4月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0029.htmlの2.5の項目への対応とし
て,3.2において,“注釈”をECが拡張されるリストに追加した。
[2003年5月9日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0050.htmlの
owlsas-rdf-datatype-denotationに関する項目への対応として,2.1から“RDFの場合と同様”という句を削
除した。
[2003年5月9日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0050.htmlの
owlsas-rdf-equivalent-classに関する項目への対応として,2.3.2.1において,記述をただ一つだけもつ
EquivalentClassesが認められる理由についての説明を追加した。
[2003年5月9日]
51
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0050.htmlへの対応として,3.2の複数
のxを取る制限に関する意味論条件において,“n>1とする”を追加した。
[2003年5月9日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0050.htmlへの対応として,2.3.2.2で
“クラス識別子及び制限を含む”,及び5.2で“記述を構成するOWL語い(彙)の要素”に変更した。
[2003年5月13日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0180.htmlへの対応として,附属書Aの目次
のリンクを修正した。
注記 “附属書Aの目次のリンク”は,JISとしての規格には存在しない。
[2003年5月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0030.htmlへの対応として,箇条4の
最初に新しい段落を追加した。
[2003年5月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0057.htmlへの対応として,2.1の最初
近くの抽象構文におけるOWLオントロジに関する言い回しを幾つか変更した。
[2003年5月14日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0057.htmlへの対応として,4.1の変換
にリンクのアンカを追加した。
注記 “リンク”は,JISとしての規格には存在しない。
[2003年5月14日]
オントロジ名に関するある議論への対応として,2.1のオントロジ名の目的に関する議論を変更した。
[2003年5月22日]
Jeff Heflinからの通知http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0302.htmlへの対応と
して,5.3及び5.4において,ソフトウェアツールが取込み閉包の間の論理的帰結を決定するのが望まし
い効果にコメントを追加した(ただし,2003年5月27日に削除されている。)。
[2003年5月22日]
5.3及び附属書Aの“ウェブとの無矛盾”を“取込み閉包”に変更した。
[2003年5月26日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003May/0335.htmlへの対応として,3.4,5.3及び5.4
の定義において,幾つかのの“if(場合)”を“iff(場合及びその場合に限り)”に変更した。完全な定
義は,“if(場合)”を使用して書かれることが多いので,これは編集上の変更である。
[2003年5月30日]
補助定理4の証明において,誤字を修正した。
[2003年6月4日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0029.htmlの2.2及び2.3の項目への対
応として,rdfs:Literal及びrdf:XMLLiteralの状態を 箇条2,2.1及び4.2で明確にしている。
[2003年6月19日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jun/0257.htmlへの対応として,A.2の定理2の証
明の後に注記を置く変更を行い,この定理の逆は真ではないという注記をつけた。
[2003年6月19日]
52
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0055.htmlへの対応として,4.1の三つ
組への変換に関する文を多少変更した。
[2003年6月19日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jun/0264.htmlへの対応として,ウェブオントロジ
作業グループによる他の規定に関する導入の資料を箇条1に追加した。
[2003年6月24日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003May/0069.htmlへの対応として,既存の記
述論理との対応に関する注記を,箇条2に追加した。
[2003年7月22日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Jul/0011.html及び
http://lists.w3.org/Archives/Public/public-webont-comments/2003Jul/0041.htmlへの対応として,箇条2及び
5.2において,“オブジェクト”を使用していた複数の箇所を“個体”又は“個体値”に変更し,5.2に他
の編集上の変更を加えた。
[2003年7月23日]
ソフトウェアツールへのあらゆる参照を削除するために,3.1及び2.1において,データ型の取扱いに
関して,いい回しを変更した。
[2003年7月25日]
http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0064.htmlへの対応として,すべての
箇条について,参考又は規定の種類別に明示的に表示を行った。
[2003年7月25日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jul/0296.htmlへの対応として,箇条1から,二つ
のモデル理論の間の関係に関するコメントを削除した。
[2003年8月6日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Jul/0015.htmlへの対応として,A.2の
owl:IndividualPropertyをowl:ObjectPropertyに変更した。
[2003年8月6日]
2.1に応じて,http://lists.w3.org/Archives/Public/public-webont-comments/2003Apr/0064.htmlの取扱いに関
して,2.3.1.3及び2.3.2.3のrdfs:Literalの前後に引用符を追加し,これは終端記号であって,非終端記号
ではないことを示した。
C.3 勧告候補後の重要な変更
C.3では,OWLの規定に変更を加える勧告候補後のW3Cの規定への変更について情報を提供する。
[2003年9月18日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Sep/0156.htmlへの対応として,4.1において,型
付けする三つ組が他の何らかの生成規則から生成される場合,IndividualvaluedPropertyID生成の型の三
つ組を任意選択にした。
[2003年10月3日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Sep/0177.htmlへの対応として,抽象構文から三つ
組への写像を増補して,オントロジ外の公理及び事実の集まりが三つ組形式のOWL DLを生成できるも
のとし,オントロジが注釈をもたない場合は,とく(匿)名のオントロジに関する型の三つ組を任意選
53
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
択とした。直接モデル理論における論理的帰結の定義を更新して,オントロジ外の公理及び事実の集ま
りの上の論理的帰結が成立することを可能にした。3.4,4.2及び5.4に変更を加えた。附属書Aの証明
の多くが,軽微な変更を必要とした。
[2003年11月6日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Oct/0167.htmlの提案への対応として,及び作業グ
ループの決定http://lists.w3.org/Archives/Public/www-webont-wg/2003Nov/0000.htmlに従って,3.1の
EC(owl:Thing)が非空でなくてはならず,5.2のIOTが非空でなくてはならないという条件を追加した。
[2003年11月29日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Nov/0064.html及び
http://lists.w3.org/Archives/Public/www-webont-wg/2003Nov/0132.htmlへの対応として,5.2を変更して,RDF
意味論[RDF Semantics]の最新版に従ってデータ型を取り扱うものとした。
[2003年11月29日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Nov/0064.htmlへの対応として,注記を箇条5の
最初の辺りに追加し,5.4にこの注記への参照を追加した。これによって,直接モデル論的意味論がOWL
DL意味論に優先することを明示的に言明した。
C.4 勧告候補後の編集上の変更
C.4では,勧告候補後のW3Cの規定への編集上の変更,すなわち,OWLの規定に影響しない変更に関
する情報を提供する。
[2003年11月29日]
http://lists.w3.org/Archives/Public/www-webont-wg/2003Nov/0132.htmlへの対応として,箇条2,箇条3,
箇条4及び箇条5に幾つかの編集上の変更を加えた。
[2003年12月3日]
さらに,http://lists.w3.org/Archives/Public/www-webont-wg/2003Nov/0132.html及び次の議論への対応と
して,箇条3,箇条5及び附属書Aに幾つかの編集上の変更を加えた。
C.5 勧告案からの変更
C.5では,勧告案後のW3Cの規定の変更に関する情報を提供する。
[2003年12月21日]
誤植の修正を行った。複数の箇所のRecommentationをRecommendationに変更した。
[2004年1月29日]
http://lists.w3.org/Archives/Public/www-webont-wg/2004Jan/0021.htmlへの対応として,4.2の分離された
語い(彙)の定義を明らかにした。
[2004年1月29日]
http://www.ilrt.bris.ac.uk/discovery/chatlogs/webont/2004-01-29#T17-08-44への対応として,RDFに互換な
データ型写像が必然的にrdf:XMLLiteralのデータ型を含むことを 5.2のRDFに互換なOWLの解釈の定
義で明らかにした。
54
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
語い(彙)の索引
この附属書は,規定の一部ではない。
表D.1は,RDF及びRDFSの語い(彙)の幾つかの要素及びOWLの語い(彙)の各要素についての情
報への参照先を提供する(一番左の列を除く。)。最初の列は,箇条2の抽象構文の語い(彙)要素の主要
な定義を示している。2列目は,OWL Liteの抽象構文における,語い(彙)要素の主要な定義先を示す。
3列目は,箇条3の直接的意味論における,語い(彙)要素の主要な定義先を示す。4列目は,箇条4にお
ける,語い(彙)要素についての,抽象構文から三つ組への翻訳の主要部分の記述先を示す。5列目は,
箇条5における,RDFSに互換な意味論の語い(彙)要素の主要な定義先を示す。
注記 表D.1のうち,原勧告に次の明らかな編集上の誤りがあった。この規格では修正した。
a) owl:AnnotationProperty,owl:OntologyProperty及びrdfs:Literalの抽象OWL DL構文及び抽象
OWL Lite構文の参照が反対になっていた。
b) owl:equivalentProperty及びrdfs:subPropertyOfの抽象OWL DL構文の参照が2.3.1.3になっ
ていた。
表D.1−語い(彙)用語
語い(彙)用語
抽象OWL DL
構文
抽象OWL Lite
構文
直接的意味論
三つ組への写像
RDFSに互換な
意味論
owl:AllDifferent
4.1
5.2
owl:allValuesFrom 2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:AnnotationPro
perty
2.3.2.4
2.3.1.3
3.2
4.1
5.2
owl:backwardCom
patibleWith
2.1
2.1
4.1
owl:cardinality
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:Class
2.3.2.1
2.3.1.1
3.3
4.1
5.2
owl:complementOf 2.3.2.2
3.2
4.1
5.2
owl:DatatypePrope
rty
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:DeprecatedCla
ss
2.3.2.1
2.3.1.1
3.3
4.1
5.2
owl:DeprecatedPro
perty
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:DataRange
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:differentFrom 2.2
2.2
3.3
4.1
5.2
owl:disjointWith
2.3.2.1
3.3
4.1
5.2
owl:distinctMembe
rs
4.1
5.2
owl:equivalentClas
s
2.3.2.1
2.3.1.1
3.3
4.1
5.2
owl:equivalentPro
perty
2.3.2.4
2.3.1.3
3.3
4.1
5.2
55
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.1−語い(彙)用語(続き)
語い(彙)用語
抽象OWL DL
構文
抽象OWL Lite
構文
直接的意味論
三つ組への写像
RDFSに互換な
意味論
owl:FunctionalPro
perty
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:hasValue
2.3.2.3
3.2
4.1
5.2
owl:imports
2.1
2.1
3.4
4.1
5.4
owl:incompatible
With
2.1
2.1
4.1
owl:intersectionOf 2.3.2.2
3.2
4.1
5.2
owl:InverseFunctio
nalProperty
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:inverseOf
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:maxCardinalit
y
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:minCardinalit
y
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:Nothing
2.1
2.1
3.2
4.1
5.2
owl:ObjectPropert
y
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:oneOf
2.3.2.2
3.2
4.1
5.2
owl:onProperty
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:Ontology
2.1
2.1
3.4
4.1
5.2
owl:OntologyProp
erty
2.3.2.4
2.3.1.3
3.2
4.1
5.2
owl:priorVersion
2.1
2.1
4.1
owl:Restriction
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:sameAs
2.2
2.2
3.3
4.1
5.2
owl:someValuesFr
om
2.3.2.3
2.3.1.2
3.2
4.1
5.2
owl:SymmetricPro
perty
2.3.2.4
2.3.1.3
3.3
4.1
4.2
owl:Thing
2.1
2.1
3.2
4.1
5.2
owl:TransitiveProp
erty
2.3.2.4
2.3.1.3
3.3
4.1
5.2
owl:unionOf
2.3.2.2
3.2
4.1
5.2
owl:versionInfo
2.1
2.1
4.1
rdf:List
4.1
5.2
rdf:nil
4.1
5.2
rdf:type
2.2
2.2
3.3
4.1
rdfs:comment
2.1
2.1
4.1
rdfs:Datatype
4.1
5.2
rdfs:domain
2.3.2.4
2.3.1.3
3.3
4.1
5.2
rdfs:label
2.1
2.1
4.1
rdfs:Literal
2.3.2.3
2.3.1.3
4.1
4.1
5.2
rdfs:range
2.3.2.4
2.3.1.3
3.3
4.1
5.2
rdfs:subClassOf
2.3.2.1
2.3.1.1
3.3
4.1
5.2
rdfs:subPropertyOf 2.3.2.4
2.3.1.3
3.3
4.1
5.2
56
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(参考)
原勧告の貢献者
この附属書は,規定の一部ではない。
Joint US/EU ad hoc Agent Markup Language Committeeは,OWLの直接的な先駆けであるDAML+OILを開
発した。DAML+OILに含まれる概念の多くは,OWLにも含まれるのだが,これらの概念は,Ontology
Inference Layer (OIL) にも存在している。
この規格の原勧告は,全体として,ウェブオントロジ作業グループ内で議論を積み重ねた結果である。
この作業グループの参加者を,次に示す。
Yasser alSafadi, Jean-François Baget, James Barnette, Sean Bechhofer, Jonathan Borden, Frederik Brysse,
Stephen Buswell, Jeremy Carroll, Dan Connolly, Peter Crowther, Jonathan Dale, Jos De Roo, David De Roure, Mike
Dean, Larry Eshelman, Jérôme Euzenat, Tim Finin, Nicholas Gibbins, Sandro Hawke, Patrick Hayes, Jeff Heflin,
Ziv Hellman, James Hendler, Bernard Horan, Masahiro Hori, Ian Horrocks, Jane Hunter, Francesco Iannuzzelli,
Rüdiger Klein, Natasha Kravtsova, Ora Lassila, Massimo Marchiori, Deborah McGuinness, Enrico Motta, Leo Obrst,
Mehrdad Omidvari, Martin Pike, Marwan Sabbouh, Guus Schreiber, Noboru Shimizu, Michael Sintek, Michael K.
Smith, John Stanton, Lynn Andrea Stein, Herman ter Horst, David Trastour, Frank van Harmelen, Bernard Vatant,
Raphael Volz, Evan Wallace, Christopher Welty, Charles White,及びJohn Yanosy.
57
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書F
(規定)
文献
F.1
引用規定(規定)
[RDF Concepts]
Resource Description Framework (RDF): Concepts and Abstract Syntax, Graham Klyne and Jeremy J. Carroll,
Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/ .
注記 最新版は,http://www.w3.org/TR/rdf-concepts/で入手可能。
[RDF Semantics]
RDF Semantics, Patrick Hayes, Editor, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-mt-20040210/ .
注記 最新版は,http://www.w3.org/TR/rdf-mt/で入手可能。
[RDF Syntax]
RDF/XML Syntax Specification (Revised), Dave Beckett, Editor, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-syntax-grammar-20040210/ .
注記 最新版は,http://www.w3.org/TR/rdf-syntax-grammar/で入手可能。
[RDF Tests]
RDF Test Cases, Jan Grant and Dave Beckett, Editors, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-testcases-20040210/ .
注記 最新版は,http://www.w3.org/TR/rdf-testcases/で入手可能。
[XML]
JIS X 4159:2005 拡張可能なマーク付け言語(XML)1.0
注記 Extensible Markup Language (XML) 1.0 (Third Edition), W3C Recommendation 04 February
2004が,この規格に一致している。最新版は,http://www.w3.org/TR/REC-xml/で入手可能。
[XML Schema Datatypes]
XML Schema Part 2: Datatypes. Paul V. Biron and Ashok Malhotra, eds. W3C Recommendation 02 May 2001.
注記 最新版は,http://www.w3.org/TR/xmlschema-2/で入手可能。
F.2
参考文献(参考)
[DAML+OIL]
DAML+OIL (March 2001) Reference Description. Dan Connolly, Frank van Harmelen, Ian Horrocks, Deborah L.
McGuinness, Peter F. Patel-Schneider, and Lynn Andrea Stein. W3C Note 18 December 2001.
注記 最新版は,http://www.w3.org/TR/daml+oil-referenceで入手可能。
[OWL Guide]
OWL Web Ontology Language Guide, Michael K. Smith, Chris Welty, and Deborah L. McGuinness, Editors,
W3C Recommendation, 10 February 2004, http://www.w3.org/TR/2004/REC-owl-guide-20040210/ .
注記 TS X 7252:2006 OWLウェブオントロジ言語−手引,が,この規定に一致している。最新
版は,http://www.w3.org/TR/owl-guide/で入手可能。
58
X 7254:2008
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[OWL Issues]
Web Ontology Issue Status. Michael K. Smith, ed. 27 June 2003.
[OWL Overview]
OWL Web Ontology Language Overview, Deborah L. McGuinness and Frank van Harmelen, Editors, W3C
Recommendation, 10 February 2004, http://www.w3.org/TR/2004/REC-owl-features-20040210/ .
注記 TS X 7251:2006,OWLウェブオントロジ言語−概要,が,この規定に一致している。最新
版は,http://www.w3.org/TR/owl-features/で入手可能。
[OWL Reference]
OWL Web Ontology Language Reference, Mike Dean and Guus Schreiber, Editors, W3C Recommendation, 10
February 2004, http://www.w3.org/TR/2004/REC-owl-ref-20040210/ .
注記 TS X 7253:2006,OWLウェブオントロジ言語−機能一覧,が,この規定に一致している。
最新版は,http://www.w3.org/TR/owl-ref/で入手可能。
[RDF Syntax]
RDF/XML Syntax Specification (Revised), Dave Beckett, Editor, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-syntax-grammar-20040210/ .
注記 最新版は,http://www.w3.org/TR/rdf-syntax-grammar/で入手可能。
[RDF Vocabulary]
RDF Vocabulary Description Language 1.0: RDF Schema, Dan Brickley and R. V. Guha, Editors, W3C
Recommendation, 10 February 2004, http://www.w3.org/TR/2004/REC-rdf-schema-20040210/ .
注記 最新版は,http://www.w3.org/TR/rdf-schema/で入手可能。















