X 7123:2012 (ISO 19123:2005)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 2
2 適合性···························································································································· 2
3 引用規格························································································································· 3
4 用語,定義,略語及び表記法 ······························································································ 4
4.1 用語及び定義 ················································································································ 4
4.2 略語 ···························································································································· 8
4.3 表記法 ························································································································· 9
5 被覆の基本特性 ················································································································ 9
5.1 被覆に関する背景知識 ···································································································· 9
5.2 被覆スキーマ ··············································································································· 11
5.3 CV̲Coverage ··············································································································· 11
5.4 CV̲DomainObject ········································································································· 14
5.5 CV̲AttributeValues ······································································································· 14
5.6 CV̲CommonPointRule ··································································································· 14
5.7 CV̲DiscreteCoverage ····································································································· 15
5.8 CV̲GeometryValuePair ·································································································· 16
5.9 CV̲ContinuousCoverage ································································································· 17
5.10 CV̲ValueObject ·········································································································· 18
5.11 CV̲InterpolationMethod ······························································································· 18
5.12 CV̲ContinuousCoverageの下位クラス············································································· 18
6 離散被覆························································································································ 19
6.1 離散被覆の型 ··············································································································· 19
6.2 CV̲DiscretePointCoverage ······························································································ 20
6.3 CV̲PointValuePair ········································································································ 21
6.4 CV̲DiscreteGridPointCoverage ························································································ 21
6.5 CV̲GridPointValuePair ·································································································· 22
6.6 CV̲DiscreteCurveCoverage ····························································································· 22
6.7 CV̲CurveValuePair ······································································································· 23
6.8 CV̲DiscreteSurfaceCoverage ··························································································· 23
6.9 CV̲SurfaceValuePair ····································································································· 24
6.10 CV̲DiscreteSolidCoverage ····························································································· 24
6.11 CV̲SolidValuePair ······································································································· 25
7 ティーセンポリゴン被覆 ··································································································· 25
7.1 ティーセンポリゴンネットワーク····················································································· 25
X 7123:2012 (ISO 19123:2005) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
7.2 CV̲ThiessenPolygonCoverage ·························································································· 26
7.3 CV̲ThiessenValuePolygon ······························································································· 27
8 四辺形グリッド被覆 ········································································································· 28
8.1 一般 ··························································································································· 28
8.2 四辺形グリッド幾何 ······································································································ 28
8.3 CV̲Grid ····················································································································· 31
8.4 CV̲GridEnvelope ·········································································································· 32
8.5 CV̲GridPoint··············································································································· 32
8.6 CV̲GridCoordinate ······································································································· 32
8.7 CV̲GridCell ················································································································ 33
8.8 CV̲Footprint ··············································································································· 33
8.9 CV̲RectifiedGrid ·········································································································· 34
8.10 CV̲ReferenceableGrid ·································································································· 34
8.11 CV̲ContinousQuadrilateralGridCoverage ········································································· 35
8.12 CV̲GridValueCell········································································································ 37
8.13 CV̲GridPointValuePair ································································································ 37
8.14 CV̲GridValuesMatrix ··································································································· 37
8.15 CV̲SequenceRule ········································································································ 38
8.16 CV̲SequenceType ········································································································ 38
9 六角形グリッド被覆 ········································································································· 38
9.1 一般 ··························································································································· 38
9.2 CV̲HexagonalGridCoverage ···························································································· 39
9.3 CV̲GridValuesMatrix ···································································································· 40
9.4 CV̲ValueHexagon ········································································································· 41
10 不規則三角網(TIN)被覆 ······························································································· 41
10.1 一般 ·························································································································· 41
10.2 CV̲TINCoverage ········································································································· 42
10.3 CV̲ValueTriangle ········································································································ 43
11 分割曲線被覆 ················································································································ 43
11.1 一般 ·························································································································· 43
11.2 CV̲SegmentedCurveCoverage ························································································ 44
11.3 CV̲ValueCurve ··········································································································· 44
11.4 CV̲ValueSegment ········································································································ 45
11.5 評価 ·························································································································· 45
附属書A(規定)抽象試験項目群 ··························································································· 47
附属書B(参考)UML表記法 ································································································ 50
附属書C(参考)内挿法 ······································································································· 55
附属書D(参考)順次列挙 ···································································································· 58
参考文献 ···························································································································· 63
X 7123:2012 (ISO 19123:2005)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,公益財団法人日本測量調査技術協会(APA)
から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経
て,経済産業大臣及び国土交通大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣,国土交通大臣及び日本工業標準調査会は,このような特許権,出願公開後の
特許出願及び実用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格
JIS
X 7123:2012
(ISO 19123:2005)
地理情報−被覆の幾何及び関数のためのスキーマ
Geographic information-Schema for coverage geometry and functions
序文
この規格は,2005年に第1版として発行されたISO 19123を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。この規格は,ISO/TC 211が関与する種々の地理情報規格を基とした日
本工業規格(以下,地理情報規格シリーズという。)の一つである。
地理情報規格シリーズは,地球上の位置と直接的又は間接的に関連付けられたオブジェクト又は現象に
関する情報処理技術のための規格であり,河川,道路などに関する様々なデータを電子化し,各種情報処
理の高度化及び効率化に適用される。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
地理的事象は,離散及び連続の二つの大まかな種類に分けられる。離散事象は,比較的明確に定義され
た境界又は空間的な広がりをもつ認識可能な対象である。離散事象の例としては,建物,河川,測量三角
点などがある。連続事象は,空間上で変化し,特定できる広がりをもたない。連続事象の例としては,気
温,地質,標高などがある。連続事象の値又は記述は,空間(及び場合によっては時間)における特定の
位置においてだけ意味をもつ。例えば,温度は,測定されたものであっても,他の場所から内挿されたも
のであっても,定義された場所でだけ特定の値を取る。
これらの概念は,相互に排除し合うものではない。事実,地形に含まれる多くの要素は,離散事象とも
連続事象ともみなすことができる。例えば,河川は離散実体だが,流速及び水質の指標は,場所によって
変化する。同様に,高速道路は地物としても事故又は交通流量を測定する観測の集まりとしても考えるこ
とができ,農地は空間オブジェクトとしても期間内に得られた収穫量の測定値の集合としてもみなすこと
ができる。
歴史的に,地理情報は,ベクトルデータ及びラスタデータと呼ばれる二つの基本的な種類で扱われてき
た。
“ベクトルデータ”は,離散事象に対応し,個々のデータは,地物として表現される。実世界における
離散事象の空間特性は,一つ以上の幾何プリミティブ(点,曲線,曲面及び立体)によって表現される。
離散事象のその他の特性は,地物属性として記録される。通常,一つの地物は,一組の属性値と関連付け
られる。JIS X 7107は,幾何プリミティブ及び位相プリミティブによって地物を記述するためのスキーマ
を規定している。
一方,“ラスタデータ”は,空間上で連続的に変化するような実世界の事象に対応する。このデータは,
それぞれが規則的に並んだ点又はセルの一つの要素と関連付けられた値の集合からなる。ラスタデータは,
通常,点の間又はセル内の空間位置に対して値を内挿するための方法と関連付けられている。このデータ
構造は,空間に対して連続的に変化する事物の表現に使用可能な唯一のものではないため,この規格では,
空間位置に直接値を割り当てるようなデータ表現に対して,Open Geospatial ConsortiumのAbstract
2
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Specification [1]から採用した“被覆”という用語を用いる。被覆は,空間定義域,時間定義域又は時空間定
義域から属性の値域への関数である。被覆は,定義域内の位置を,データ型が定義する値のレコードと関
連付ける。
この規格で被覆は,地物の下位型とみなす。被覆は,各属性型に対して複数の値をもつ地物で,地物の
幾何表現に含まれる個々の直接位置が各属性型に対して一つの値をもつ。
離散事象の概念と連続事象の概念とが相互に排除し合うものでないのと同様,これらの離散地物又は被
覆としての表現も,相互に排除し合わない。このため,同じ事象を,離散地物としても被覆としても表現
してもよい。都市は,その名称,領域,総人口など個々の属性に対して一つの値を返すような離散地物と
みなすこともできる。また,都市地物は,市内の各位置について,人口密度,地価,大気環境指標などの
値を返すような被覆として表現することもできる。
その上,被覆は,共通の属性をもつ離散地物の集まりから導き出すことができる。その場合,それぞれ
の位置における被覆の値は,その位置に存在する地物の属性値となる。反対に,離散地物の集まりは,被
覆から導き出すことができる。その場合,それぞれの離散地物は,特定の属性値及び関連付けられた位置
の集合で構成される。
なお,対応国際規格は,2008年にISO/TC 211において行われた定期見直し投票の結果,今後改正して
いくことが決まっている。
1
適用範囲
この規格は,被覆の空間特性に対する概念スキーマを定義する。被覆は,空間定義域,時間定義域又は
時空間定義域を,その定義域の全ての地理的位置に対して共通な地物属性型をもつ地物属性値に写像する
ことを可能にする。定義域は,一つの時間次元と三つまでの空間次元とによって定義することができる座
標空間における直接位置の集まりからなる。被覆の例として,ラスタ,不規則三角網,点被覆及びポリゴ
ン被覆がある。被覆は,幾つかの応用分野(例えば,リモートセンシング,気象学,並びに水深,標高,
土壌及び植生の地図作成)で普及しているデータ構造である。この規格では,被覆の定義域と,関連付け
られた属性の値域との間の関係を定義する。空間定義域の特性を定義するのに対して,属性の値域の特性
はこの規格には含まない。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 19123:2005,Geographic information−Schema for coverage geometry and functions(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
適合性
この規格は,複数の被覆オブジェクト型のインタフェースを規定する。さらに,これらのインタフェー
スとは独立して,被覆データの交換も規定する。そのため,二つの適合性クラスの集合を規定する。一つ
はインタフェースの実装のため,もう一つは被覆データの交換のための適合クラスの集合である。それぞ
れの集合は,この規格で規定したそれぞれの被覆型のための適合性クラスを含む(表1参照)。

3
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−適合性クラス
適合性クラス
細分箇条
単純被覆インタフェース
A.1.1
離散被覆インタフェース
A.1.2
ティーセンポリゴン被覆インタフェース
A.1.3
四辺形グリッド被覆インタフェース
A.1.4
六角形グリッド被覆インタフェース
A.1.5
TIN(不規則三角網)被覆インタフェース
A.1.6
分割曲線被覆インタフェース
A.1.7
離散被覆交換
A.2.1
ティーセンポリゴン被覆交換
A.2.2
四辺形グリッド被覆交換
A.2.3
六角形グリッド被覆交換
A.2.4
TIN(不規則三角網)被覆交換
A.2.5
分割曲線被覆交換
A.2.6
一般に,インタフェース適合性クラス群は,関係するクラスの全ての属性,関連及び操作の実装を必要
とする。この集合は,全ての被覆型の評価のための単純なインタフェースに対する一つの適合性クラス
(A.1.1参照)を含むが,被覆の内部構造を明らかにするものではない。集合の残りは,被覆の内部構造に
関する追加情報を明らかにする,特定の被覆型へのインタフェースに対する適合性クラス群である。
交換適合性クラス群は,関係するクラスの属性及び関連の実装だけを必要とする。
附属書Aの抽象試験項目群は,この規格に適合するために必要な実装要件を示す。表1は,各適合性ク
ラスについて適用される抽象試験項目群の細分箇条一覧である。
3
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,記載の年の版を適用し,その後の改正版(追補を含む。)は適用しない。
JIS X 7107:2005 地理情報−空間スキーマ
注記 対応国際規格:ISO 19107:2003,Geographic information−Spatial schema(IDT)
JIS X 7108:2004 地理情報−時間スキーマ
注記 対応国際規格:ISO 19108:2002,Geographic information−Temporal schema(IDT)
JIS X 7109:2009 地理情報−応用スキーマのための規則
注記 対応国際規格:ISO 19109:2005,Geographic information−Rules for application schema(IDT)
JIS X 7111:2004 地理情報−座標による空間参照
注記 対応国際規格:ISO 19111:2003,Geographic information−Spatial referencing by coordinates(IDT)
JIS X 7115:2005 地理情報−メタデータ
注記 対応国際規格:ISO 19115:2003,Geographic information−Metadata(MOD)
ISO/TS 19103:2005,Geographic information−Conceptual schema language
4
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
用語,定義,略語及び表記法
4.1
用語及び定義
この規格で用いる主な用語及び定義は,次による。
4.1.1
連続被覆(continuous coverage)
同一の地物属性について,一つの空間オブジェクト,時間オブジェクト又は時空間オブジェクトの定義
域の中にある様々な直接位置に対し,様々な値を返す被覆。
注記 連続被覆の時空間定義域は,その空間及び/又は時間の範囲という意味では通常は有界だが,
それは無限個の直接位置に分けることができる。
4.1.2
凸包(convex hull)
与えられた幾何オブジェクトを含む最小の凸集合。
(Dictionary of Computing:1996[2]の定義を変更した。)
4.1.3
凸集合(convex set)
幾何集合の中にある任意の二つの直接位置を結ぶ直線分上の任意の直接位置が,その幾何集合に含まれ
るような幾何集合。
(Dictionary of Computing:1996[2]参照)
4.1.4
座標(coordinate)
n次元空間内の点の位置を示すためのn個の数値の列。
(JIS X 7111参照)
4.1.5
座標次元(coordinate dimension)
座標系における位置を記述するために必要な計測数又は軸の数。
(JIS X 7107参照)
4.1.6
座標参照系(coordinate reference system)
原子によって実世界に関連付けた座標系。
(JIS X 7111参照)
4.1.7
被覆(coverage)
空間定義域,時間定義域又は時空間定義域内の各々の直接位置に対して,決められた値域からの値を返
す関数として機能する地物。
例 被覆の例としては,ラスタ画像,ポリゴンオーバレイ,数値標高行列などがある。
注記 すなわち,被覆は,各属性型に対して複数の値をもつ地物で,地物の幾何表現における個々の
直接位置が各属性型に対して一つの値をもつものである。
4.1.8
被覆幾何(coverage geometry)
座標によって記述した被覆の定義域の形状。
5
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.1.9
曲線(curve)
直線の連続な像を表現する一次元の幾何プリミティブ。
(JIS X 7107参照)
注記 曲線の境界は,その両端の点の集合である。
4.1.10
ドローネ三角網(Delaunay triangulation)
三角形のネットワークで,その中の任意の三角形の3頂点を通る円(外接円)が内部に他のいかなる三
角形の頂点も含まないようなもの。
4.1.11
直接位置(direct position)
座標参照系の中で一つの座標によって記述された位置。
(JIS X 7107参照)
4.1.12
離散被覆(discrete coverage)
一つの空間オブジェクト,時間オブジェクト又は時空間オブジェクトの定義域の中にある全ての直接位
置に対し,同一の地物属性の値を返す被覆。
注記 離散被覆の定義域は,空間オブジェクト,時間オブジェクト又は時空間オブジェクトの有限集
合で構成される。
4.1.13
領域,定義域(domain)
明確に定義された集合。
(ISO/TS 19103参照)
注記 定義域は,演算子及び関数の定義域及び値域を定義するために用いる。
4.1.14
評価(evaluation)
(被覆)被覆の定義域内にある直接位置における被覆の値を決定すること。
4.1.15
地物(feature)
実世界の現象の抽象概念。
(ISO 19101参照)
4.1.16
地物属性(feature attribute)
地物の特性。
(ISO 19101参照)
4.1.17
関数(function)
ある領域[この関数の定義域(source, domain)]の各要素を,別の領域[この関数の値域(target, co-domain,
range)]の一意な要素に関連付ける規則。
(JIS X 7107参照)
6
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.1.18
幾何オブジェクト(geometric object)
幾何集合を表す空間オブジェクト。
(JIS X 7107参照)
4.1.19
幾何プリミティブ(geometric primitive)
単一の連結で均質な空間の要素を表す幾何オブジェクト。
(JIS X 7107参照)
4.1.20
幾何集合(geometric set)
直接位置の集合。
(JIS X 7107参照)
4.1.21
幾何値オブジェクト(geometry value object)
幾何値対の集合で構成されるオブジェクト。
4.1.22
幾何値対(geometry value pair)
空間オブジェクト,時間オブジェクト又は時空間オブジェクトと幾何属性値のレコードとで構成される
順序対。
4.1.23
グリッド(grid)
複数の曲線からなる集合二つ以上から構成されるネットワークで,各集合の要素となる曲線が,他の集
合の要素となる曲線と一定の規則で交差するもの。
注記1 六角形グリッド(9.1参照)の場合を除き,曲線は,空間をグリッドセルに分割する。
注記2 三次元空間及び時空間について考えるときは,上の定義及び注記1の“曲線”を“曲面”(又
は “超曲面”)と読み替えるとよい。
注記3 JIS X 7107では,用語gridの日本語訳を“格子”としていた。
4.1.24
グリッド点(grid point)
グリッドにおいて二つ以上の曲線が交差する点。
4.1.25
逆評価(inverse evaluation)
(被覆)与えられた地物属性値に対応するオブジェクトの集合を,被覆の定義域から選び出すこと。
4.1.26
点(point)
位置を表現する零次元の幾何プリミティブ。
(JIS X 7107参照)
注記 点の境界は,空集合である。
4.1.27
点被覆(point coverage)
7
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
点で構成される定義域をもつ被覆。
4.1.28
ポリゴン被覆(polygon coverage)
ポリゴンで構成される定義域をもつ被覆。
4.1.29
値域(range)
(被覆)関数によって,被覆の定義域の要素と関連付けられた地物属性値の集合。
4.1.30
ラスタ(raster)
ディスプレイ装置上の表示パターンであって,平行な走査線から構成され,通常は長方形のもの。
注記 ラスタは,グリッドの一種である。
4.1.31
レコード(record)
有限の,名前をもつ,相互に関連性のあるアイテム(オブジェクト又は値)の集まり。
(JIS X 7107参照)
注記 論理的には,レコードは<名称,アイテム>の対の集合である。
4.1.32
偏位修正グリッド(rectified grid)
グリッドであって,そのグリッド座標と外部座標参照系座標との間にアフィン変換関係が成立している
もの。
注記 座標参照系が原子によって地球と関連付けられている場合,グリッドは幾何偏位修正グリッド
である。
4.1.33
参照可能グリッド(referenceable grid)
グリッド座標値を,外部座標参照系の座標値に換算できる変換と関連付けられたグリッド。
注記 座標参照系が原子によって地球と関連付けられている場合,グリッドは対地参照可能グリッド
である。
4.1.34
立体(solid)
三次元ユークリッド空間のある領域の連続な像を表す三次元の幾何プリミティブ。
(JIS X 7107参照)
注記 立体は,三つのパラメタをもつ直接位置の集合によって局所的に実現することができる。立体
の境界は,その立体の限界を構成する,向きを付けられた閉曲面の集合である。
4.1.35
空間オブジェクト(spatial object)
地物の空間特性を表現するために用いるオブジェクト。
(JIS X 7107参照)
4.1.36
時空間定義域(spatiotemporal domain)
(被覆)時空間オブジェクトで構成される定義域。
8
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 連続被覆の時空間定義域は,時空間オブジェクトの集まりとの関連で定義される直接位置の集
合から構成される。
4.1.37
時空間オブジェクト(spatiotemporal object)
空間及び時間の直接位置の集合を表すオブジェクト。
4.1.38
曲面(surface)
局所的に平面領域の連続な像を表す二次元の幾何プリミティブ。
(JIS X 7107参照)
注記 曲面の境界は,曲面の限界の輪郭を描く向きをもつ閉曲線である。
4.1.39
モザイク分割(tessellation)
空間の,元の空間と同一次元をもち互いに隣接する部分空間の集合への分割。
注記 合同で規則的なポリゴン又は多面体で構成されるモザイク分割は,規則的なモザイク分割であ
る。規則的だが,合同でないポリゴン又は多面体で構成されるモザイク分割は,準規則的なモ
ザイク分割である。その他は,不規則なモザイク分割である。
例 モザイク分割の例を,図11,図13,図20及び図22に示す。
4.1.40
ティーセンポリゴン(Thiessen polygon)
平面上の点の集合の中の一つの点を含み,その集合の中の他のいかなる点よりもこの点に近い,全ての
直接位置を含むようなポリゴン。
注記 ティーセンポリゴンの例を,図11に示す。
4.1.41
位相次元(topological dimension)
幾何オブジェクト内の直接位置を他の位置と区別するのに必要な自由変数の最小の数。
(JIS X 7107参照)
4.1.42
不規則三角網(triangulated irregular network)
三角形で構成されるモザイク分割。
4.1.43
ベクトル(vector)
方向及び大きさをもつ量。
注記 もし線分の長さ及び方向がベクトルの大きさと方向とに等しいならば,この線分はベクトルを
表す。ベクトルデータという用語は,地物の空間的な構成を,方向をもつ線分の集合として表
現するデータを指す。
4.2
略語
GIS
地理情報システム(Geographic Information System)
TIN
不規則三角網(Triangulated Irregular Network)
UML 統一モデル化言語(Unified Modelling Language)

9
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.3
表記法
この規格で規定する概念スキーマは,ISO/TS 19103に従い,統一モデル化言語(UML)[4]を用いている。
附属書Bは,この規格で用いるUML表記法を示す。
このスキーマで使われている複数のモデル要素は,ISO/TC 211によって作成された他の国際規格で定義
されている。ISO/TC 211内での申し合わせによって,UMLクラスの名称は,基本データ型のクラスを除
き,クラスを定義している規格及びUMLパッケージを識別する二文字の接頭語が付く。この規格で定義
するUMLクラスは,二文字接頭語としてCVをもつ。表2は,この規格で用いているUMLクラスが定義
されている他の規格及びパッケージの一覧である。
表2−この規格外で定義されているUMLクラスの情報源
接頭語
JIS
パッケージ
EX
JIS X 7115
Extent
GF
JIS X 7109
General Feature Model
GM
JIS X 7107
Geometry
SC
JIS X 7111
Spatial Coordinates
TM
JIS X 7108
Temporal Schema
5
被覆の基本特性
5.1
被覆に関する背景知識
5.1.1
一般
被覆は,有界な空間(被覆の定義域)内の位置を地物属性値群(被覆の値域)に関連付ける地物である。
言い換えれば,被覆は地物であり関数でもある。被覆の例としては,ラスタ画像,ポリゴンオーバレイ,
数値標高行列などがある。
被覆は,単一の地物を表しても,地物の集合を表してもよい。
5.1.2
被覆の定義域
被覆の定義域は,直接位置によって記述される幾何オブジェクトの集合である。被覆の定義域は,その
幾何オブジェクト集合に対する凸包内の全ての直接位置に拡張してもよい。直接位置は,空間又は時間の
座標参照系と関連付けられている。一般に用いられる定義域には,点集合,グリッド,閉じた長方形の集
まり及びその他の幾何オブジェクトの集まりがある。幾何オブジェクトは,定義域を余すところなく分割
してもよく,それによってグリッド又はTINのようなモザイク分割を形成する。点集合及びその他の互い
に隣接しない幾何オブジェクトの集合は,モザイク分割を形成しない。被覆の下位型を,それぞれの定義
域に応じて定義してもよい。
被覆の定義域は,それが存在する空間の座標次元と,それが含む幾何オブジェクトの位相次元との両方
において様々である。明らかに,定義域を構成する幾何オブジェクトは,定義域の座標次元よりも大きな
位相次元をもつことができない。座標次元3の定義域は,点,曲線,曲面又は立体で構成されてもよいが,
座標次元2の定義域は,点,曲線又は曲面でしか構成されない。JIS X 7107は,地物の記述に用いるため
の多くの幾何オブジェクト(UMLクラスGM̲Objectの下位型)を定義している。これらの幾何オブジェ
クトの多くは,被覆のための定義域の定義に用いることができる。また,JIS X 7108は,
TM̲GeometricPrimitiveを定義しているが,それらは,被覆の定義域の定義に用いてもよい。
一般的には,ある被覆の定義域を構成する幾何オブジェクトは共通部分をもたないが,この規格は,重
なり合う幾何オブジェクトを含む被覆の定義域を許容する。
10
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.1.3
被覆の値域
被覆の値域は,地物属性値の集合である。被覆の値域は,有限集合又は無限集合のいずれでもよい。被
覆は,定義域を共有し互いに関連した多くの関数をモデル化することが多い。このため,この値集合(被
覆の値域)は,共通のスキーマをもつレコードの集まりとして表現される。
例 ある被覆は,ある郡における直接位置のそれぞれに対して,その地点における当日昼の温度,気
圧,湿度及び風速を割り当てることがある。この被覆は,その郡における個々の直接位置を四つ
の項目をもつレコードに写像する。
地物属性値は,どのようなデータ型に属していてもよい。しかし,連続被覆の評価は,通常,数値又は
ベクトルにだけ適用可能な内挿法によって実装される。他のデータ型は,ほとんど常に離散被覆と関連付
けられる。
被覆の値域の中のあるレコードが与えられたとき,逆評価とは,特定の属性値と関連付けられた幾何オ
ブジェクトの集合を計算して提示することである。逆評価は,単一の地物属性値と関連付けられた多くの
幾何オブジェクトを返してもよい。
例 逆評価は,標高被覆から等高線を抽出したり,画像から分類した地域を抽出したりするのに用い
る。
5.1.4
離散被覆及び連続被覆
被覆には,二つの型がある。離散被覆は,幾何オブジェクトの有限個の集まり及びこれらの幾何オブジ
ェクトに含まれる直接位置で構成される定義域をもつ。離散被覆は,個々の幾何オブジェクトを地物属性
値の単一のレコードに写像する。幾何オブジェクト及びそれに関連するレコードは,一つの幾何値対を形
成する。このため,離散被覆は連続被覆とは異なり,離散関数又は階段関数となる。離散関数は,幾つか
の(入力,出力)対として明示的に列挙できる。離散被覆は,独立変数及び従属変数の順序対の集まりと
して表現してもよい。独立変数は幾何オブジェクトであり,従属変数は地物属性値である。
例 各々のポリゴンがもつ土壌型を探すため,ポリゴンの集合に写像する被覆は,離散被覆の一例で
ある。
連続被覆は,座標空間における直接位置の集合で構成される定義域をもつ。連続被覆は,直接位置を値
のレコードに写像する。
例 千代田区の直接位置を当日正午の気温に写像する被覆を考える。この被覆の定義域及び値域は,
無限個の異なる値を取ってもよい。この連続被覆は,一群の気象観測所で観測された温度値を保
持する離散被覆と関連付けられることになる。
連続被覆は,空間としては有界であるものの無限集合を成す直接位置と,直接位置を地物属性値に関係
付ける数学関数とで構成してもよい。これを解析被覆と呼ぶ。
例 地価と都市中心からの相対位置とを関連付ける統計的傾向面は,連続被覆の一例である。
より多くの場合,連続被覆の定義域は,幾何オブジェクトの有限個の集まりで特定され,その和集合又
は凸包内の直接位置で構成される。ほとんどの場合,連続被覆は,その評価の基礎として用いられる基準
値の集合を提供する離散被覆とも関連付けられる。他の直接位置における連続被覆の評価は,この基準集
合の幾何値対を内挿することで実行される。これは,この基準集合に含まれる幾何オブジェクトから構成
された追加的な幾何オブジェクトに依存することが多く,これらの追加的なオブジェクトは,基準のオブ
ジェクトよりも高い位相次元であることが一般的である。この規格では,このようなオブジェクトを幾何
値オブジェクトと呼ぶ。幾何値オブジェクトは,幾何値対の集合の幾何オブジェクトから構成された幾何
オブジェクトであり,その幾何値対は,幾何値オブジェクトの内部の直接位置に対する被覆の評価の基準
11
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を提供する。
例 不規則三角網の評価には,隣接する三つの点値対で構成される三角形からの内挿が必要である。
5.2
被覆スキーマ
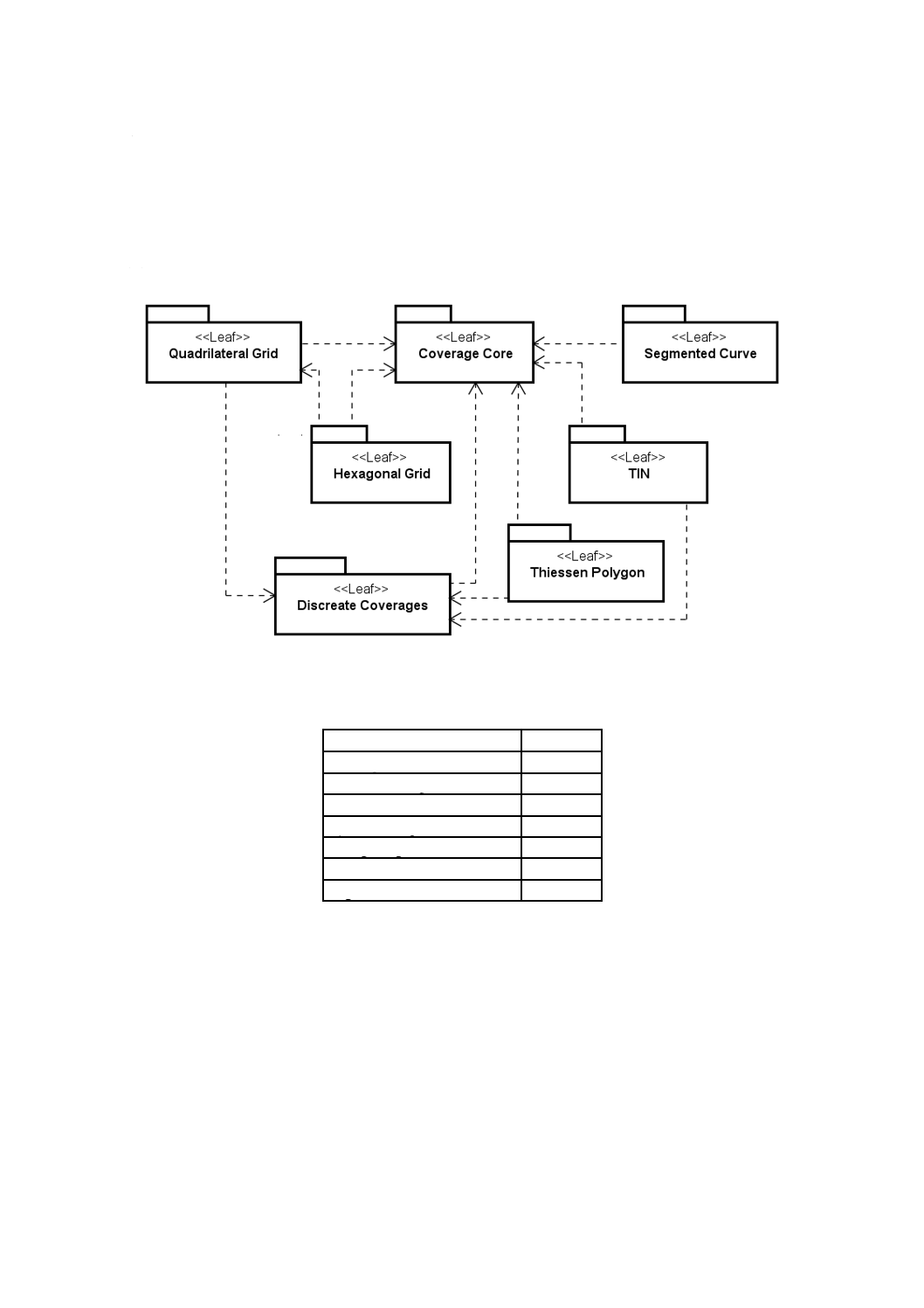
被覆スキーマは,図1のようなパッケージ間依存関係をもった七つのパッケージで構成される。ここで
はCoverage Core(被覆中核)パッケージを記述し,その他のパッケージは,表3のとおり,それぞれ箇条
6〜箇条11に示す。
図1−被覆スキーマのパッケージ群
表3−被覆幾何パッケージの記述
パッケージ
箇条
Coverage core
5
Discrete coverages
6
Thiessen polygon
7
Quadrilateral grid
8
Hexagonal grid
9
TIN
10
Segmented curve
11
5.3
CV̲Coverage
5.3.1
一般
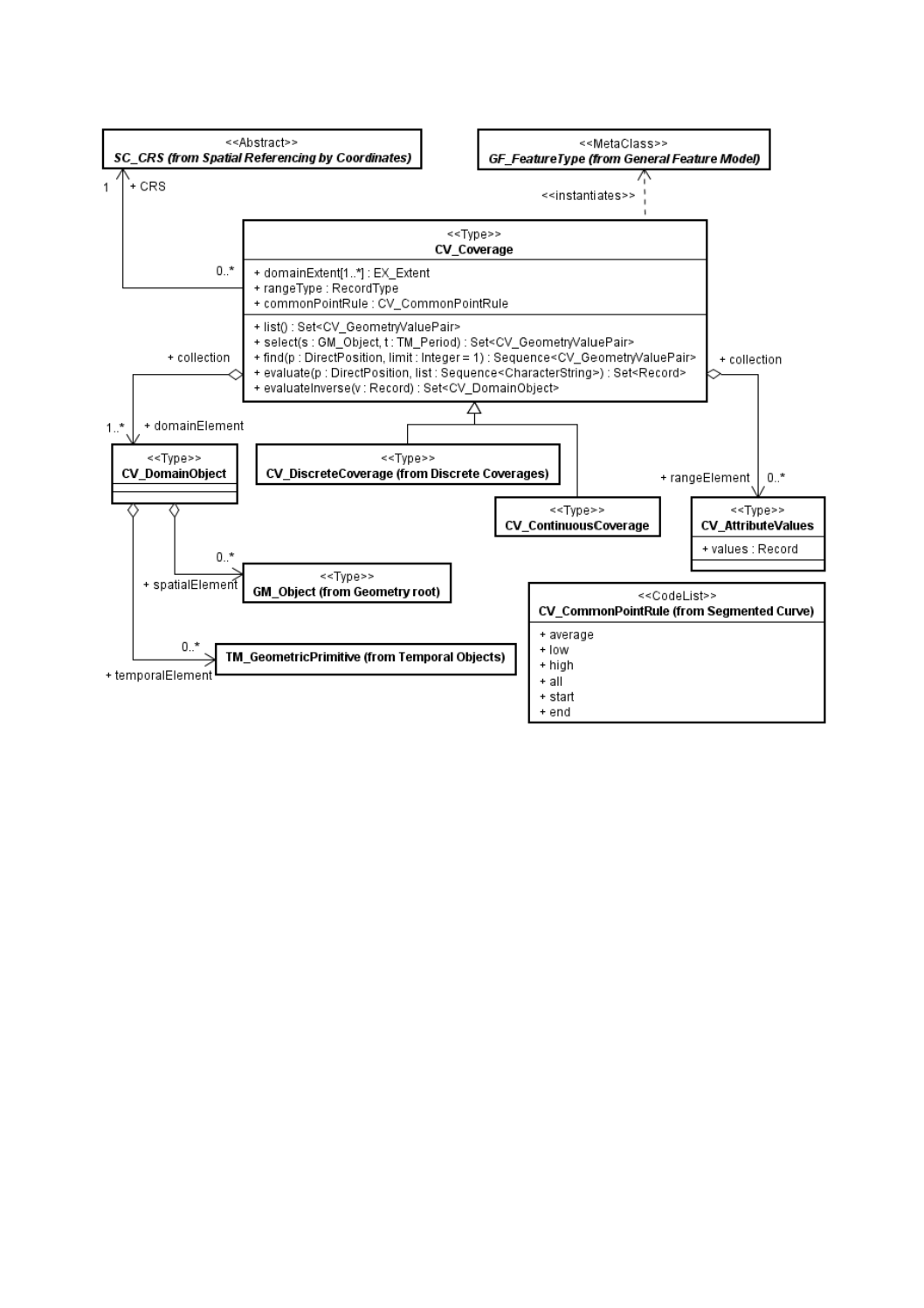
CV̲Coverage(被覆)クラス(図2参照)は,メタクラスGF̲FeatureType(JIS X 7109参照)のインス
タンスの一つである。CV̲Coverageは,三つの属性,五つの操作及び三つの関連をもつ。
5.3.2
domainExtent
domainExtent[1..*]: EX̲Extent(定義域範囲)属性は,被覆の定義域の範囲を含む。EX̲Extent(範囲)デ
ータ型は,JIS X 7115で定義する。範囲は,空間,時間及び時空間のいずれかで規定される。
5.3.3
rangeType
rangeType: RecordType(値域型)属性は,被覆の値域を記述する。データ型RecordTypeは,ISO/TS 19103
で定義する。これは,属性名とデータ型との対の一覧で構成される。最も一般的な形式のrangeTypeは単
12
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
純な一覧であるが,より複雑な構造体を記述するために再帰的にRecordTypeを用いることができる。具体
的な被覆のrangeTypeは,応用スキーマで規定する。
5.3.4
commonPointRule
commonPointRule: CV̲CommonPointRule(共通点規則)属性は,CV̲DomainObject又はCV̲ValueObject
のいずれかの幾何オブジェクトについて,幾何オブジェクト間の境界又は複数の重なり合う幾何オブジェ
クトの境界内に該当する位置におけるCV̲Coverageの評価に用いる手続を特定する。
CV̲CommonPointRuleデータ型は,5.6で定義する。
5.3.5
list
list(): Set <CV̲GeometryValuePair>(一覧)操作は,CV̲Coverageの定義域中の各CV̲DomainObjectとそ
れぞれの地物属性値のレコードとの対を含んだCV̲GeometryValuePair(5.8参照)の辞書を返す。解析被
覆の場合には,この操作は空集合を返す。
5.3.6
select
select (s: GM̲Object, t: TM̲Period): Set <CV̲GeometryValuePair>(選択)操作は,GM̲Object及びTM̲Period
を入力として受け取り,そのGM̲Object及びTM̲Periodの範囲内に存在するCV̲DomainObjectを含む
CV̲GeometryValuePairの集合を返す。sがNULLの場合,この操作はtの範囲内のCV̲DomainObjectを含
む全てのCV̲GeometryValuePairを返す。tがNULLの場合,この操作はsの範囲内のCV̲DomainObjectを
含む全てのCV̲GeometryValuePairを返す。解析被覆の場合には,この操作は空集合を返す。
5.3.7
find
find (p: DirectPosition, limit: Integer = 1): Sequence <CV̲GeometryValuePair>(探索)操作は,DirectPosition
を入力として受け取り,DirectPositionからの距離が最も近いCV̲DomainObject及びそのCV̲DomainObject
とDirectPositionとの距離を含む,CV̲GeometryValuePairの列を返す。この列は,DirectPositionに最も近い
CV̲DomainObjectを含むRecordで始まり,DirectPositionからの距離の順に並ぶ。この列の長さ(返される
CV̲GeometryValuePairの数)は,limitパラメタで指定した数以下でなければならない。既定では,単一の
CV̲GeometryValuePairを返す。この操作は,列の最後のCV̲DomainObjectが列に含まれていない他の
CV̲DomainObjectのいずれかとDirectPositionからの距離が等しい場合には警告を返す。解析被覆の場合に
は,この操作は空集合を返す。
注記 この操作は,被覆の定義域が被覆の範囲を分割しつくしていない場合に有用である。このよう
な場合であっても,返される列の最初の要素は,入力DirectPositionを含むCV̲GeometryValuePair
であってもよい。
5.3.8
evaluate
evaluate (p: DirectPosition, list: Sequence <CharacterString>): Set <Record>(評価)操作は,DirectPositionを
入力として受け取り,その直接位置に対応する地物属性値のRecordの集合を返す。listパラメタは,それ
ぞれがrangeTypeのフィールドを識別する地物属性名の列である。listがNULLの場合,操作はrangeType
のフィールドのそれぞれに対して値を返す。そうでない場合,listに含まれるフィールドのそれぞれに対し
て値を返す。DirectPositionデータ型はJIS X 7107で定義し,Recordデータ型はISO/TS 19103で定義する。
与えられた直接位置が被覆の定義域内にない場合,エラーメッセージを生成する。DirectPositionの入力が,
定義域中の複数の幾何オブジェクト内に含まれる場合,操作はcommonPointRule属性の値に従って計算さ
れた地物属性値のレコードを返す。
注記 通常,この操作は地物属性値のレコードを一つ返す。
13
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2−CV̲Coverage
5.3.9
evaluateInverse
evaluateInverse (v : Record): Set <CV̲DomainObject>(逆評価)操作は,地物属性値のRecordを入力とし
て受け取り,CV̲DomainObjectの集合を返す。通常,これはRecordの入力値と等しい値に関連付けられた
DomainのCV̲DomainObjectの集合となる。しかし,この操作は,応用スキーマで指定したとおりに,こ
の定義域のCV̲DomainObjectから導き出された他のCV̲DomainObjectを返してもよい。
例 evaluateInverse操作は,CV̲GridCoverageのCV̲GridPointと関連付けられた地物属性値から導き
出された等高線の集合を返すことがある。
5.3.10 CoordinateReferenceSystem
CoordinateReferenceSystem(座標参照系)関連は,このCV̲Coverageをその定義域中のオブジェクトを
参照するための座標参照系に連結する。SC̲CRSクラスは,JIS X 7111で規定する。
CoordinateReferenceSystem関連におけるCRS関連役割の多重度は1であり,それゆえ,同じ値域をもって
いても異なる座標参照系で定義された定義域をもつ被覆は,異なる被覆である。
5.3.11 Domain
Domain(定義域)関連は,このCV̲Coverageを定義域のCV̲DomainObjectの集合に連結する。
CoordinateReferenceSystem
Domain
SpatialComposition
TemporalComposition
range
14
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.3.12 Range
Range(値域)関連は,このCV̲Coverageをその値域のCV̲AttributeValuesの集合に連結する。CV̲Coverage
の値域は,同種のレコードの集まりでなければならない。すなわち,値域は,定義域全体で一定の次元を
もち,そのレコードの各フィールドは定義域全体で同一の属性型の値を示す。
注記 この規格では,Domain関連及びRange関連をどのように実装するかは規定しない。該当するデ
ータはリアルタイムに生成されても,永続的な局所記憶に保持されていても,又は遠隔位置か
ら電子的に提供されてもよい。
5.4
CV̲DomainObject
5.4.1
一般
CV̲DomainObject(定義域オブジェクト)は,CV̲Coverageの定義域の要素を表す。これ
(CV̲DomainObject)は,JIS X 7107が規定するGM̲Object,JIS X 7108が規定するGM̲GeometricPrimitive
並びにその他の規格が規定する空間オブジェクト及び時空間オブジェクト(この規格が規定する
CV̲GridPointを含む。)のどのような組合せを含んでもよい。
5.4.2
SpatialComposition
SpatialComposition(空間合成)関連は,CV̲DomainObjectを,それを構成するGM̲Objectの集合に関連
付ける。
5.4.3
TemporalComposition
TemporalComposition(時間合成)関連は,CV̲DomainObjectを,それを構成するTM̲GeometricPrimitive
の集合に関連付ける。
5.5
CV̲AttributeValues
5.5.1
一般
CV̲AttributeValues(属性値)は,CV̲Coverageの値域の要素を表す。
5.5.2
values
values(値)属性は,CV̲Coverage.rangeType(5.3.3参照)で規定したとおり,各属性に対して一つの値
を含むRecordである。
例 (標高のような)単一(スカラ)値をもつ被覆。(電磁気スペクトルの様々な部分の輝度のような)
全てが同じ方法で定義された一連の(配列又はテンソル)値をもつ被覆。
5.5.3
Range
Range(値域)関連は,CV̲AttributeValuesの集合を,その集合を値域としてもつCV̲Coverageに連結す
る(5.3.12参照)。
離散被覆の場合,CV̲Coverage.rangeElementは,多重度がCV̲Coverage.domainElementと同じである。
すなわち,CV̲DomainObjectの各インスタンスに一つのCV̲AttributeValuesのインスタンスが存在する。
通常,評価操作が用いる値が保持されている。
連続被覆の場合,各CV̲DomainObjectに対して無限個のCV̲AttributeValuesのインスタンスが存在する。
幾つかのインスタンスが評価操作に対する入力として保持されることもあるが,ほとんどの場合,その操
作の必要に応じて生成される。
5.6
CV̲CommonPointRule
CV̲CommonPointRule(共通点規則)は,evaluate操作に対するDirectPositionの入力が複数の幾何オブジ
ェクト内に該当するような場合を扱うための方法を識別する符号リストである。これらの規則の解釈は,
離散被覆と連続被覆とで異なる。離散被覆の場合,各CV̲GeometryValuePairはそれぞれの属性に一つの値
15
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を提供する。規則は,DirectPositionを含むCV̲GeometryValuePairの集合と関連付けられた値の集合に適用
される。連続被覆の場合,各属性に対する値がDirectPositionを含む各CV̲ValueObjectに対して内挿され
なければならない。したがって,規則は各属性に対して内挿された値の集合に適用されなければならない。
符号及びその意味は,次のとおりである。
a) average−地物属性値の平均を返す。
b) low−最小の地物属性値を用いる。
c) high−最大の地物属性値を用いる。
d) all−DirectPositionの入力に対して定まる全ての地物属性値を返す。
e) start−二番目のCV̲ValueSegmentのstartValueを用いる。
f)
end−最初のCV̲ValueSegmentのendValueを用いる。
注記 符号“start”及び“end”は,分割曲線被覆にだけ適用される。
5.7
CV̲DiscreteCoverage
5.7.1
一般
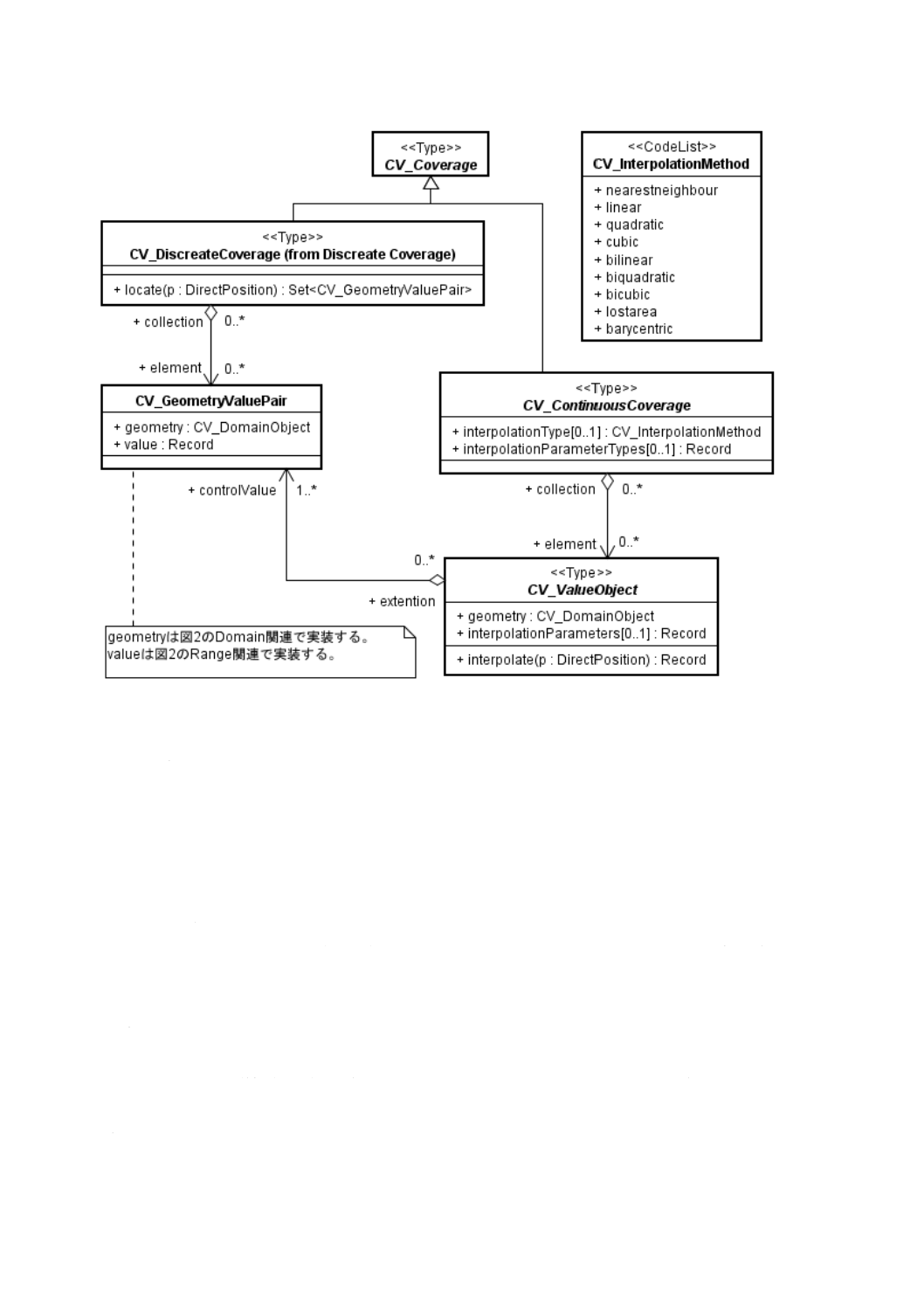
図3は,CV̲Coverageの主な下位クラスを示す。CV̲DiscreteCoverage(離散被覆)は,定義域の一つの
CV̲DomainObject内のあらゆる直接位置に対して同じ地物属性値のレコードを返す下位クラスである。
CV̲DiscreteCoverageの下位クラスについては,箇条6で規定する。
5.7.2
locate
locate (p: DirectPosition): Set <CV̲GeometryValuePair>(場所取得)操作は,DirectPositionを入力として受
け取り,このDirectPositionを含むCV̲DomainObjectをもつCV̲GeometryValuePairの集合を返す。
DirectPositionがこのCV̲DiscreteCoverageの定義域の中のいずれのCV̲DomainObject上にもない場合,こ
の操作はNULL値を返す。
5.7.3
evaluate
CV̲Coverageから継承したevaluate (p: DirectPosition, list: Sequence <CharacterString>): Set <Record>(評価)
操作は,DirectPositionを入力として受け取り,このDirectPositionを含むCV̲DomainObjectをもつ
CV̲GeometryValuePairを見つけ,地物属性値のレコードの集合を返す。通常,入力されるDirectPositionは
唯一のCV̲GeometryValuePair内にだけ含まれ,この操作はそのCV̲GeometryValuePairと関連付けられた
地物属性値のレコードを返す。DirectPositionが二つのCV̲GeometryValuePair間の境界上又は複数の重なり
合うCV̲GeometryValuePair内にある場合,この操作はcommonPointRule属性の値に従って導き出された地
物属性値のレコードを返す。DirectPositionがこのCV̲DiscreteCoverageの定義域の中のいずれの
CV̲DomainObject上にもない場合,この操作はNULL値を返す。
5.7.4
evaluateInverse
CV̲Coverageから継承したevaluateInverse (v: Record): Set <CV̲DomainObject>(逆評価)操作は,地物属
性値のRecordを入力として受け取り,入力レコードと値が等しいCV̲GeometryValuePairを見つけ,それ
らに属するCV̲DomainObjectの集合を返す。このCV̲DiscreteCoverageに関連付けられたいずれの
CV̲GeometryValuePairも入力されたRecordと値が等しくない場合には,NULL値を返す。
注記 逆評価は,事実上,レコードの値の性質などを考慮し,個別の操作として応用スキーマなどで
規定するのが望ましい。
5.7.5
CoverageFunction
CoverageFunction(被覆機能)関連は,CV̲DiscreteCoverageをそれに含まれるCV̲GeometryValuePairの
集合に連結する。この関連は,任意選択である。
16
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3−CV̲Coverageの下位クラス
5.8
CV̲GeometryValuePair
5.8.1
一般
CV̲GeometryValuePair(幾何値対)クラスは,離散被覆の関係を定義する集合の要素を記述する。この
クラスの各構成要素は,二つの部分で構成されている。すなわち,それが属する被覆の定義域の定義域オ
ブジェクト,及びそれが属する被覆の値域の地物属性値のレコードである。CV̲GeometryValuePairは
evaluate操作の実行時に生成されてもよく,永続する必要はない。CV̲GeometryValuePairは,地物属性値
のレコードを定義域オブジェクトの特定の下位型との対に制限するものとして下位クラス化される。
5.8.2
geometry
geometry: CV̲DomainObject(幾何)属性は,このCV̲GeometryValuePairの構成要素である
CV̲DomainObjectを保持する。
5.8.3
value
value: Record(値)属性は,このCV̲DomainObjectと関連付けられた地物属性値のレコードを保持する。
5.8.4
CoverageFunction
CoverageFunction(被覆機能)関連は,このCV̲GeometryValuePairをそれが構成要素になっている
CV̲DiscreteCoverageに連結する。
5.8.5
Control
Control(基準)関連は,離散被覆の場合には空になる。これについては,CV̲ValueObject(5.10.5参照)
CoverageFunction
Control
CoverageFunction
17
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の部分で規定する。
5.9
CV̲ContinuousCoverage
5.9.1
一般
CV̲ContinuousCoverage(連続被覆)は,定義域内にある全ての直接位置に対して個別の地物属性値のレ
コードを返すCV̲Coverageの下位クラスである。
5.9.2
interpolationType
interpolationType [0..1]: CV̲InterpolationMethod(内挿型)属性は,CV̲ValueObject内の任意の直接位置に
おける地物属性値を導き出すために用いる内挿法を識別する符号である。属性の有無は任意選択であり,
解析被覆(内挿によるものではなく数学的関数を用いて直接位置を属性値に写像するもの)については,
値は必要ではない。
5.9.3
interpolationParameterTypes
多くの内挿法は,内挿関数への入力として被覆の値域内の値だけを使用するが,追加的なパラメタを必
要とする方法も存在する。任意選択のinterpolationParameterTypes(内挿パラメタ型)属性は,interpolationType
によって識別された内挿法を用いるのに必要なパラメタの型を指定する。RecordTypeデータ型は,ISO/TS
19103で規定する。これは,名前及びデータ型の辞書である。
5.9.4
locate
locate (p: DirectPosition): Set <CV̲ValueObject>(場所取得)操作は,DirectPositionを入力として受け取り,
このDirectPositionを含むCV̲ValueObjectの集合を返す。DirectPositionがこのCV̲DiscreteCoverageの定義
域の中のいずれのCV̲ValueObject内にもない場合には,NULL値を返す。
5.9.5
select
select(選択)操作は,CV̲Coverage(5.3.6参照)から継承される。CV̲ContinuousCoverageの場合には,
このCV̲ContinuousCoverageを構成するCV̲ValueObjectに関連付けられたCV̲GeometryValuePairに属して
いるCV̲DomainObjectを返す。
5.9.6
evaluate
CV̲Coverageから継承したevaluate (p: DirectPosition, list:Sequence <CharacterString>): Set <Record>(評価)
操作は,DirectPositionを入力として受け取り,この直接位置における地物属性値のレコードを返す。評価
法の多くは,CV̲ValueObjectの内部又は周辺での内挿を行う。通常,入力されるDirectPositionは唯一の
CV̲ValueObject内にだけ含まれ,この操作は,そのCV̲ValueObject内に内挿された地物属性値のレコード
を返す。DirectPositionが二つのCV̲ValueObject間の境界上又は複数の重なり合うCV̲ValueObject内にあ
る場合,この操作はcommonPointRule属性の値に従って導き出された地物属性値のレコードを返す。
DirectPositionがいずれのCV̲ValueObject上にもない場合は,NULL値を返す。
5.9.7
evaluateInverse
CV̲Coverageから継承したevaluateInverse (v: Record): Set <CV̲DomainObject>(逆評価)操作は,地物属
性値のRecordを入力として受け取り,入力レコードと値が等しいCV̲GeometryValuePairを見つけ,それ
らに属するCV̲DomainObjectの集合を返す。通常,このCV̲ContinuousCoverageを構成するCV̲ValueObject
に関連付けられたCV̲GeometryValuePairに属しているCV̲DomainObjectを返す。しかし,この操作は,
応用スキーマで指定したとおりに,この定義域のCV̲DomainObjectから導き出された他の
CV̲DomainObjectを返してもよい。CV̲DiscreteCoverageに関連付けられたいずれのCV̲GeometryValuePair
も入力されたRecordと等しい値をもたない場合,この操作はNULL値を返す。
例 evaluateInverse操作は,CV̲GridCoverageのCV̲GridPointと関連付けられた地物属性値から導き
18
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
出された等高線の集合を返すことができる。
5.9.8
CoverageFunction
CoverageFunction(被覆機能)関連は,このCV̲ContinuousCoverageを,それを構成するCV̲ValueObject
の集合に連結する。この関連は任意選択で,解析被覆はCV̲ValueObjectを必要としない。
5.10 CV̲ValueObject
5.10.1 一般
CV̲ValueObject(値付きオブジェクト)は,CV̲ContinuousCoverage内に地物属性値を内挿するための基
礎を提供する。CV̲ValueObjectは,evaluate操作の実行時に生成されてもよく,永続する必要はない。
5.10.2 geometry
geometry:CV̲DomainObject(幾何)属性は,このCV̲ValueObject及びControl関連によって連結される
CV̲GeometryValuePairのCV̲DomainObjectから構成されるCV̲DomainObjectである。
5.10.3 interpolationParameters
任意選択のinterpolationParameter:Record(内挿パラメタ)属性は,interpolate操作の実行に必要なパラメ
タの値をCV̲ContinuousCoverageのinterpolationParameterTypes属性で指定したとおりに保持する。
5.10.4 interpolate
interpolate (p: DirectPosition): Record(内挿)操作は,DirectPositionを入力として受け取り,その
DirectPositionに対して算出された地物属性値のレコードを返す。
5.10.5 Control
Control(基準)関連は,このCV̲ValueObjectを,CV̲ValueObjectを構築するための,及びこの
CV̲ValueObject内のDirectPositionに対してCV̲ContinuousCoverageを評価するための,基礎を提供する
CV̲GeometryValuePairの集合に連結する。
5.10.6 CoverageFunction
CoverageFunction(被覆機能)関連は,このCV̲ValueObjectをそれが要素となっている
CV̲ContinuousCoverageに連結する。
5.11 CV̲InterpolationMethod
CV̲InterpolationMethod(内挿法)は,連続被覆の評価に用いられる内挿法を識別する符号リストである。
個々の内挿法の解説については,附属書Cを参照。内挿法には,nearestneighbour,linear,quadratic,cubic,
bilinear,biquadratic,bicubic,lostarea,barycetricなどがある。
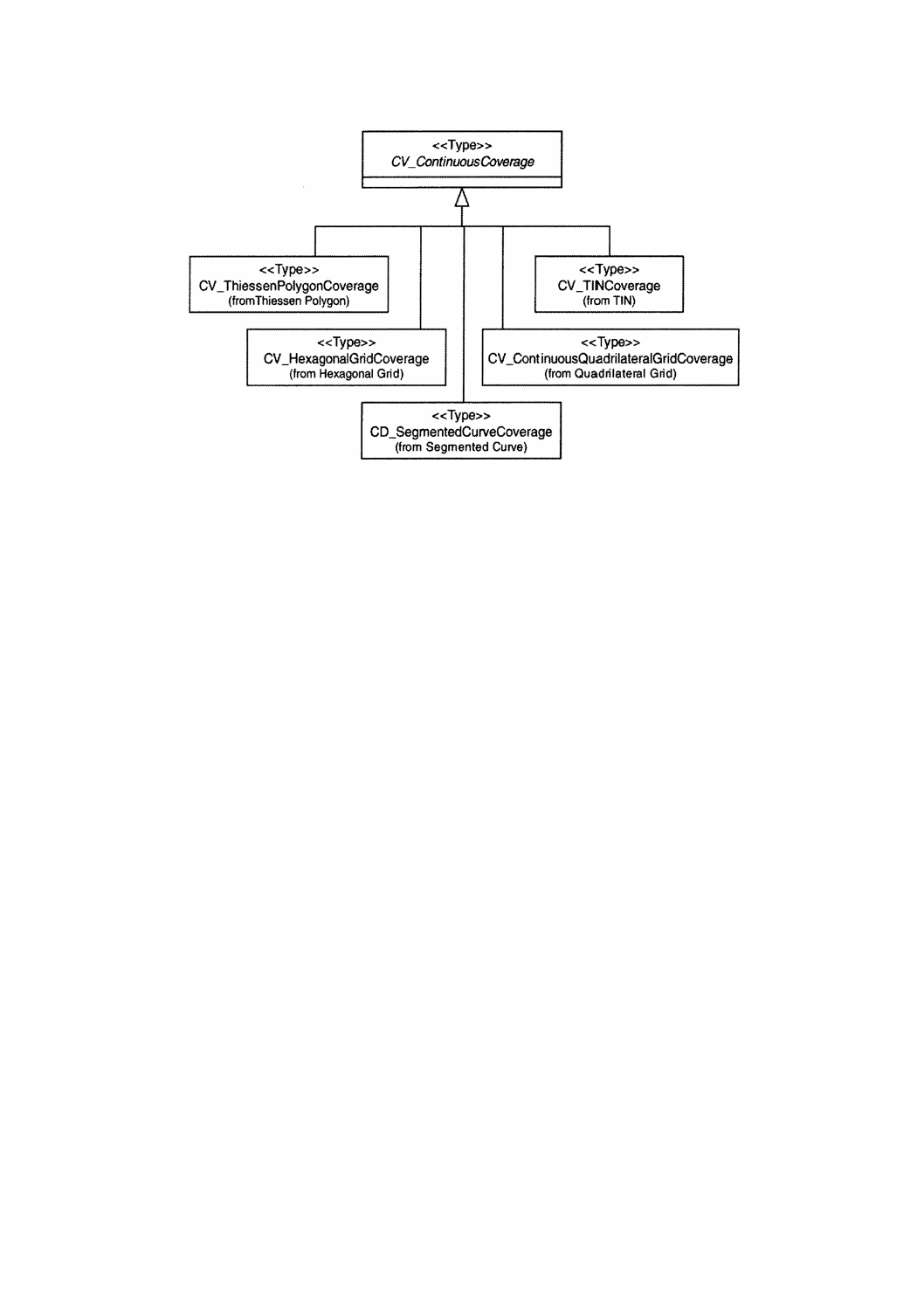
5.12 CV̲ContinuousCoverageの下位クラス
この規格は,CV̲ContinuousCoverageの五つの下位クラスのためのスキーマを規定する(図4参照)。
CV̲ThiessenPolygonCoverage
は箇条
7,CV̲ContinuousQuadrilateralGridCoverage
は箇条
8,
CV̲HexagonalGridCoverageは箇条9,CV̲TINCoverageは箇条10,CV̲SegmentedCurveCoverageは箇条11
でそれぞれ規定する。
19
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4−連続被覆
6
離散被覆
6.1
離散被覆の型
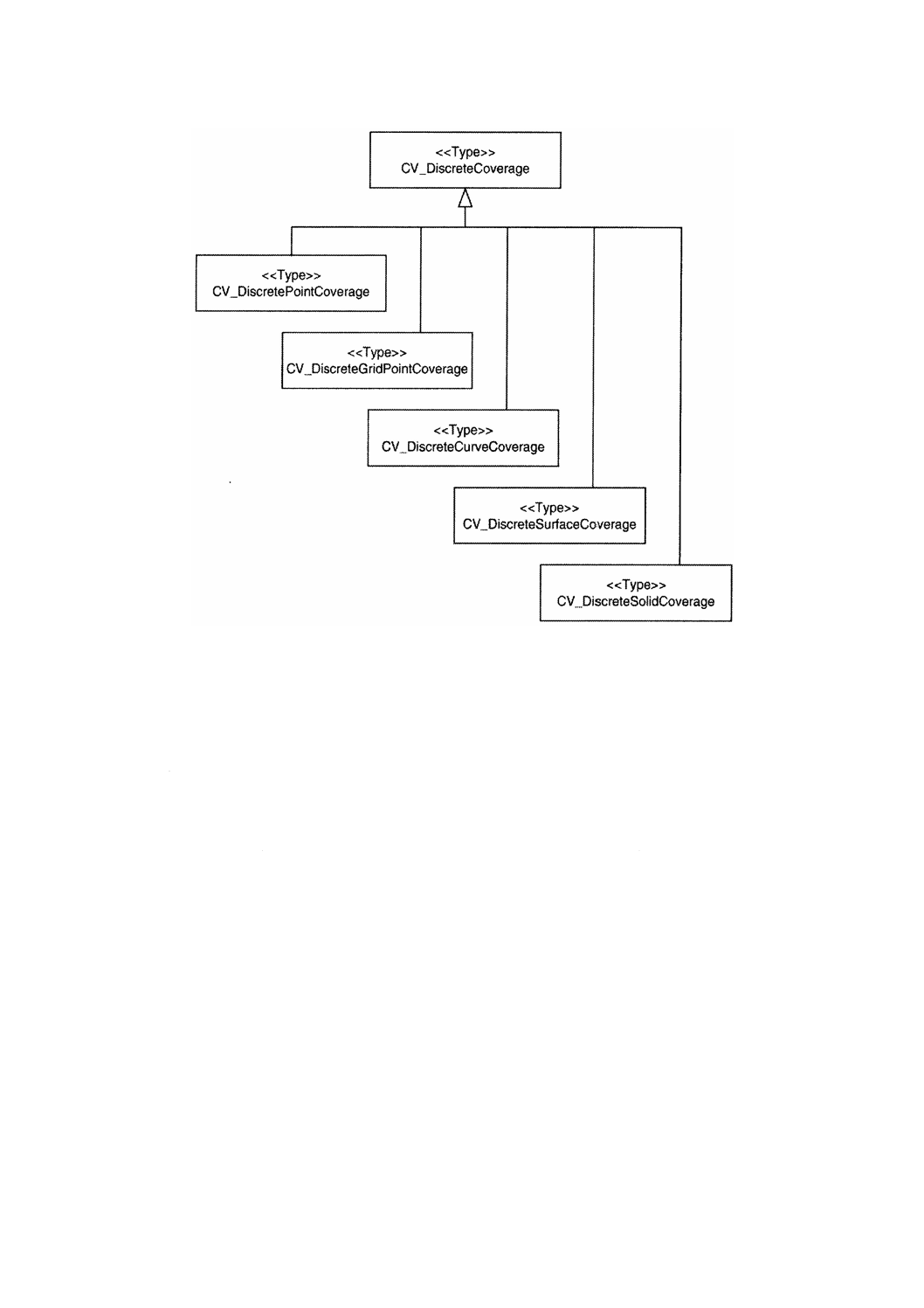
CV̲DiscreteCoverage(離散被覆)の定義域は,幾何オブジェクトの集まりからなる。CV̲DiscreteCoverage
は,空間定義域に含まれる幾何オブジェクト型に基づいて下位クラス化される(図5参照)。
CV̲DiscreteCoverageのそれぞれの下位クラスは,CV̲GeometryValuePairの特定の下位クラスと関連付けら
れている。二つのクラスの下位クラスは,親クラスで規定する属性及び操作,並びに親のクラス間の関連
を継承するが,後述する制約をも併せもつ(6.2.2,6.4.2,6.6.2,6.8.2及び6.10.2参照)。
20
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図5−離散被覆の型
この上位クラスは抽象クラスではないため,この上位クラスのインスタンスは,CV̲GeometryValuePair
の混合型で構成してもよい。
6.2
CV̲DiscretePointCoverage
6.2.1
一般
離散点被覆は,点で構成される有限の定義域であることが特徴である。一般にこの定義域は,不規則に
分布した点の集合である。しかし,離散点被覆の主な用途は,その離散点被覆の点の間を内挿することに
よって評価を行う連続被覆関数に基礎を提供することである。ほとんどの内挿アルゴリズムは,点の間の
空間関係の構造化パターンに依存する。この場合,離散点被覆の空間定義域に含まれる点が規則的な方法
で配置しているか,又は連続被覆の空間定義域が離散点被覆の点に対して規則的な方法で分割されている
ことが必要である。グリッド被覆(箇条8及び箇条9参照)は最初の方法を採用しており,ティーセンポ
リゴン被覆(箇条7参照)及びTIN被覆(箇条10参照)は二つ目の方法を採用している。
例 水路測深の集合は,離散点被覆である。
21
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
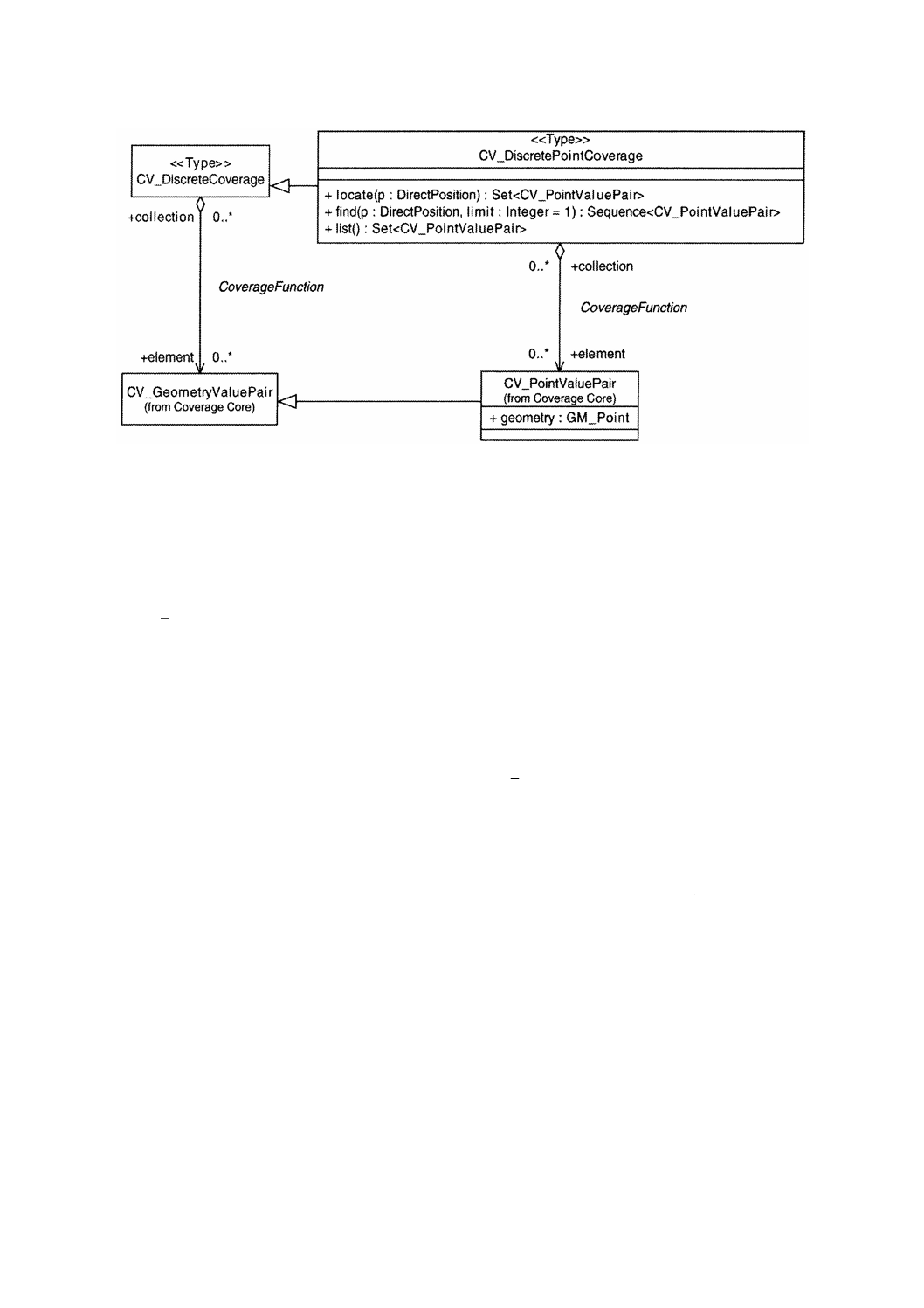
図6−CV̲DiscretePointCoverage
6.2.2
継承する関連及び操作
CV̲DiscretePointCoverage(離散点被覆:図6参照)は,関連するCV̲GeometryValuePair及び各操作が返
すCV̲GeometryValuePairをCV̲PointValuePairに限定する制約とともに,CoverageFunction関連並びにlocate,
find及びlist操作をCV̲DiscreteCoverage(5.7参照)から継承する。
6.3
CV̲PointValuePair
CV̲PointValuePair(点値対)は,幾何属性の値としてGM̲PointをもつCV̲GeometryValuePairの下位型
である。
6.4
CV̲DiscreteGridPointCoverage
6.4.1
一般
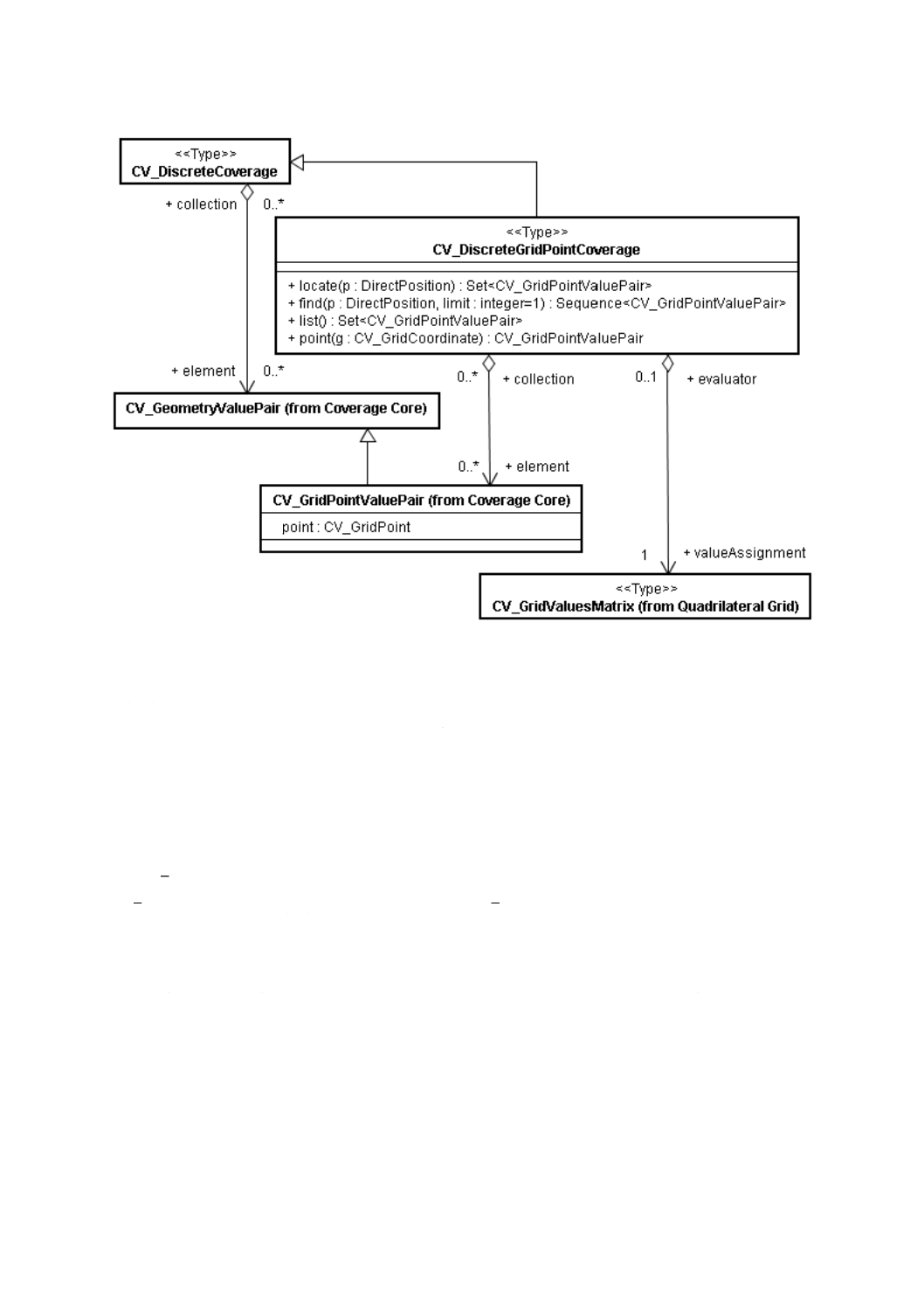
CV̲DiscreteGridPointCoverage(離散グリッド点被覆:図7参照)の定義域は,CV̲GridValuesMatrix(8.14
参照)を通じて地物属性値のレコードと関連付けられたCV̲GridPoint(8.5参照)の集合である。
6.4.2
継承する関連及び操作
CV̲DiscreteGridPointCoverage(図7参照)は,関連するCV̲GeometryValuePair及び各操作が返す
CV̲GeometryValuePairをCV̲GridPointValuePairに限定する制約とともに, CoverageFunction関連並びに
locate,find及びlist操作をCV̲DiscreteCoverageから継承する。elementがPointFunction関連を通じて
CV̲GridValuesMatixから生成されるため,CoverageFunction関連はこのような場合に導き出されるものと
して示されている。継承したevaluate及びevaluateInverse操作は,CV̲GeometryValuePairに値を与えるた
めにCV̲GridValuesMatrixを使用する。
22
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図7−CV̲DiscreteGridPointCoverage
6.4.3
point
point (g: CV̲GridCoordinate): CV̲GridPointValuePair(点取得)操作は,グリッド座標を入力として受け取
り,関連付けられたCV̲GridValuesMatrixのデータを用いてこのグリッド位置に関連付けられた
CV̲GridPointValuePairを生成して返す。
6.4.4
PointFunction
PointFunction(点関数)関連は,CV̲DiscreteGridPointCoverageを,それを評価するCV̲GridValuesMatrix
に連結する。
6.5
CV̲GridPointValuePair
CV̲GridPointValuePair(グリッド点値対)は,CV̲GridPointをその幾何属性の値としてもつ
CV̲GeometryValuePairの下位型である。
6.6
CV̲DiscreteCurveCoverage
6.6.1
一般
離散曲線被覆は,曲線で構成される有限の空間定義域によって特徴付ける。この曲線は,道路,鉄道,
河川などの地物を表していることが多い。これらは,ネットワークの要素となることがある。
例 路線番号,名称,舗装幅,舗装材料の種類などを道路網の各部分に割り当てる被覆。
6.6.2
継承する操作及び関連
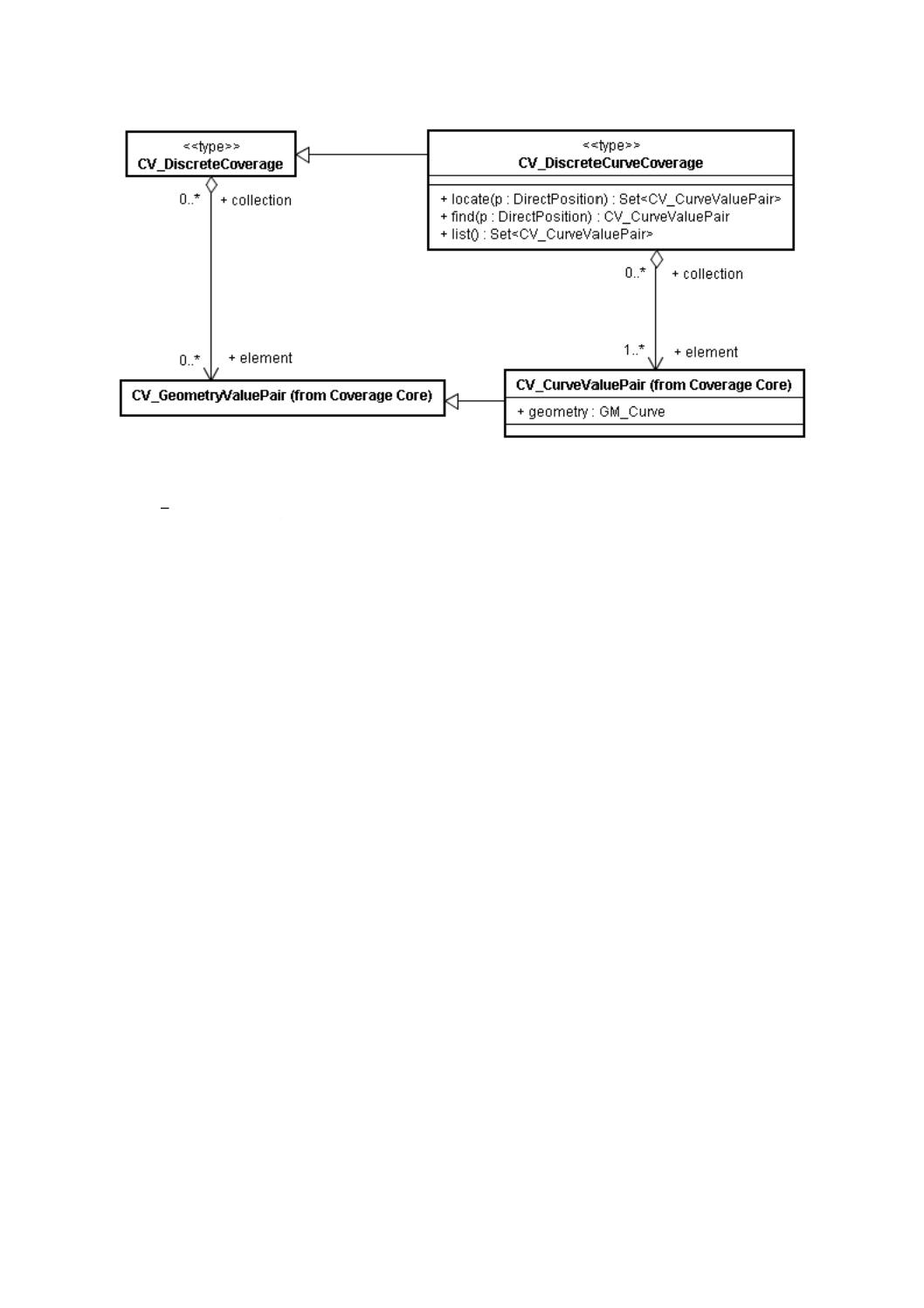
CV̲DiscreteCurveCoverage(離散曲線被覆:図8参照)は,関連するCV̲GeometryValuePair及び各操作
が返すCV̲GeometryValuePairをCV̲CurveValuePairに限定する制約とともに,CoverageFunction関連並び
にlocate,find,list,evaluate及びevaluateInverse操作をCV̲DiscreteCoverageから継承する。
CoverageFunction
/CoverageFunction
PointFunction
+
23
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図8−CV̲DiscreteCurveCoverage
6.7
CV̲CurveValuePair
CV̲CurveValuePair(曲線値対)は,幾何属性の値としてGM̲CurveをもつCV̲GeometryValuePairの下
位型である。
6.8
CV̲DiscreteSurfaceCoverage
6.8.1
一般
離散曲面被覆は,定義域が曲面の集まりで構成される被覆である。多くの場合,被覆の定義域を構成す
るこの曲面群は,相互排他的に被覆の範囲を余すところなく分割する。曲面又はその境界は,どのような
形状であってもよい。被覆の構成要素である曲面の境界は,多くの場合,自然現象に相応し極めて不規則
である。
例 土壌の種類を表す被覆は,典型的には,不規則な境界をもつ曲面で構成される空間定義域をもつ。
どのようなポリゴンの集合も離散曲面被覆の空間定義域として使用できる。合同なポリゴンで構成され
る空間定義域は,極めて一般的である。これらの定義域は,合同な長方形又は正六角形で構成されること
が多い。このモザイク分割のような幾何については,四辺形グリッド(8.2参照)又は六角形グリッド(9.1
参照)を使用して記述してもよい。離散曲面被覆の空間定義域は,TIN(箇条10参照)を構成する三角形,
又はティーセンポリゴンネットワーク(7.1参照)のポリゴンからなっていてもよい。
CoverageFunction
CoverageFunction
24
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
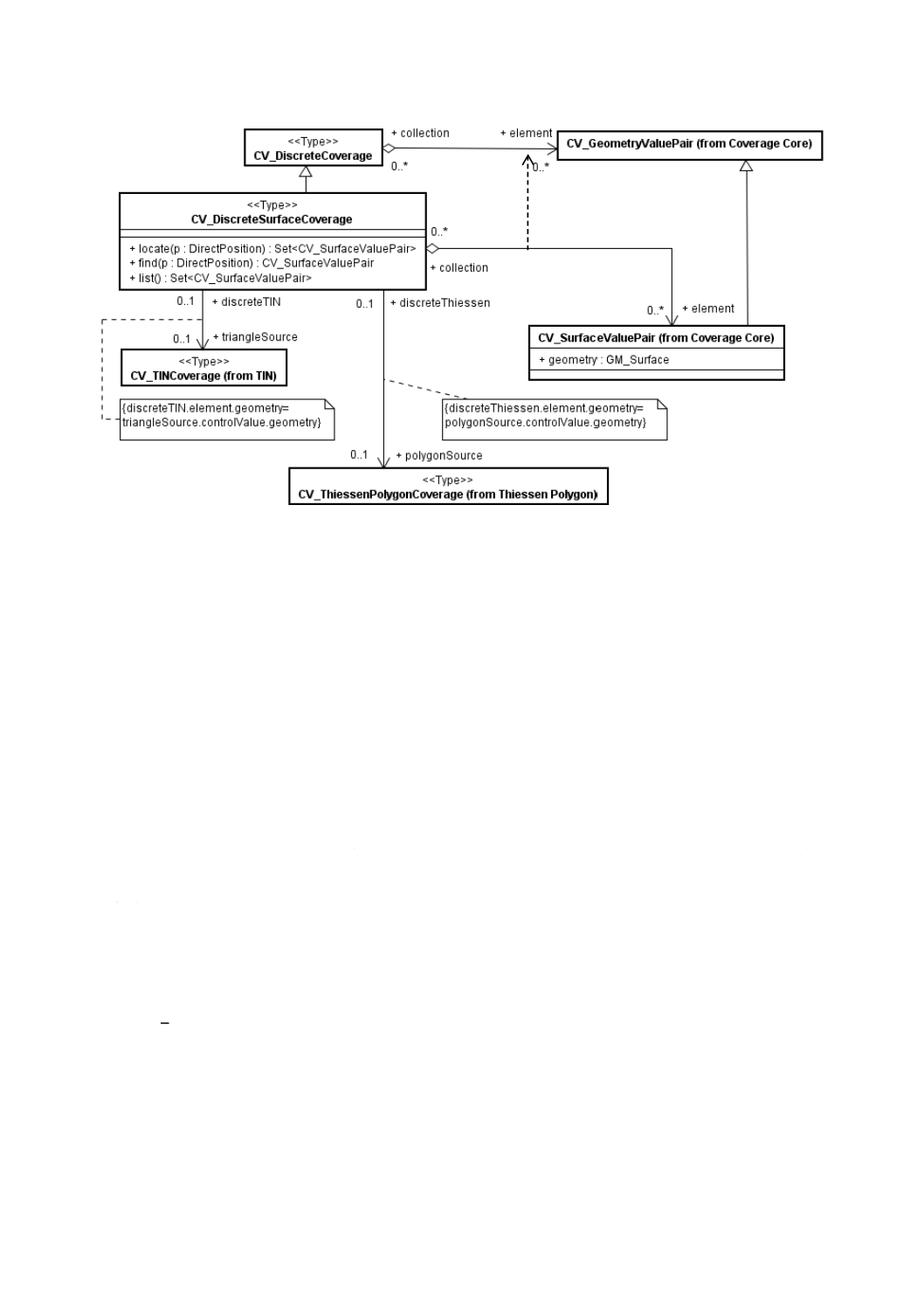
図9−CV̲DiscreteSurfaceCoverage
6.8.2
継承する操作及び関連
CV̲DiscreteSurfaceCoverage(離散曲面被覆:図9参照)は,関連するCV̲GeometryValuePair及び各操作
が返すCV̲GeometryValuePairをCV̲SurfaceValuePairに限定する制約とともに,CoverageFunction関連並び
にlocate,find,list,evaluate及びevaluateInverse操作をCV̲DiscreteCoverageから継承する。
6.8.3
TINBase
TINBase(TIN基底)関連は,CV̲DiscreteSurfaceCoverageをCV̲TINCoverage(10.2参照)に連結する
ために使用する。
制約
discreteTIN.element.geometry = triangleSource.controlValue.geometry
は,CV̲DiscreteSurfaceCoverageの空間定義域がCV̲TINCoverageに属する三角形で構成されることを示す。
6.8.4
ThiessenBase
ThiessenBase(ティーセン基底)関連は,CV̲DiscreteSurfaceCoverageをCV̲ThiessenPolygonCoverage(7.2
参照)に連結するために使用する。
制約
discreteThiessen.element.geometry = polygonSource.controlValue.geometry
は,CV̲DiscreteSurfaceCoverageの空間定義域がCV̲ThiessenPolygonCoverageに属するポリゴンで構成され
ることを示す。
6.9
CV̲SurfaceValuePair
CV̲SurfaceValuePair(曲面値対)は,幾何属性の値としてGM̲SurfaceをもつCV̲GeometryValuePairの
下位型である。
6.10 CV̲DiscreteSolidCoverage
6.10.1 一般
離散立体被覆は,立体の集まりで構成される定義域をもつ被覆である。立体又はその境界は,どのよう
な形状であってもよい。一般に,被覆の定義域を構成する立体は,互いに重なり合わず,かつ,被覆の範
CoverageFunction
CoverageFunction
TINBase
ThiessenBase
25
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
囲を余すところなく分割するが,これは要求ではない。
例 都市地域における建物は,建物名,住所,床面積,現住者数などの属性をそれぞれもつ,連結し
ていないGM̲Solidの集合として表現することができる。
曲面の場合(5.8参照)と同様に,離散立体被覆の空間定義域は,被覆の範囲を規則的又は準規則的なモ
ザイク分割にしてもよい。このモザイク分割は,グリッドセルの集合が被覆の空間定義域になるような三
次元グリッドによって定義することができる。
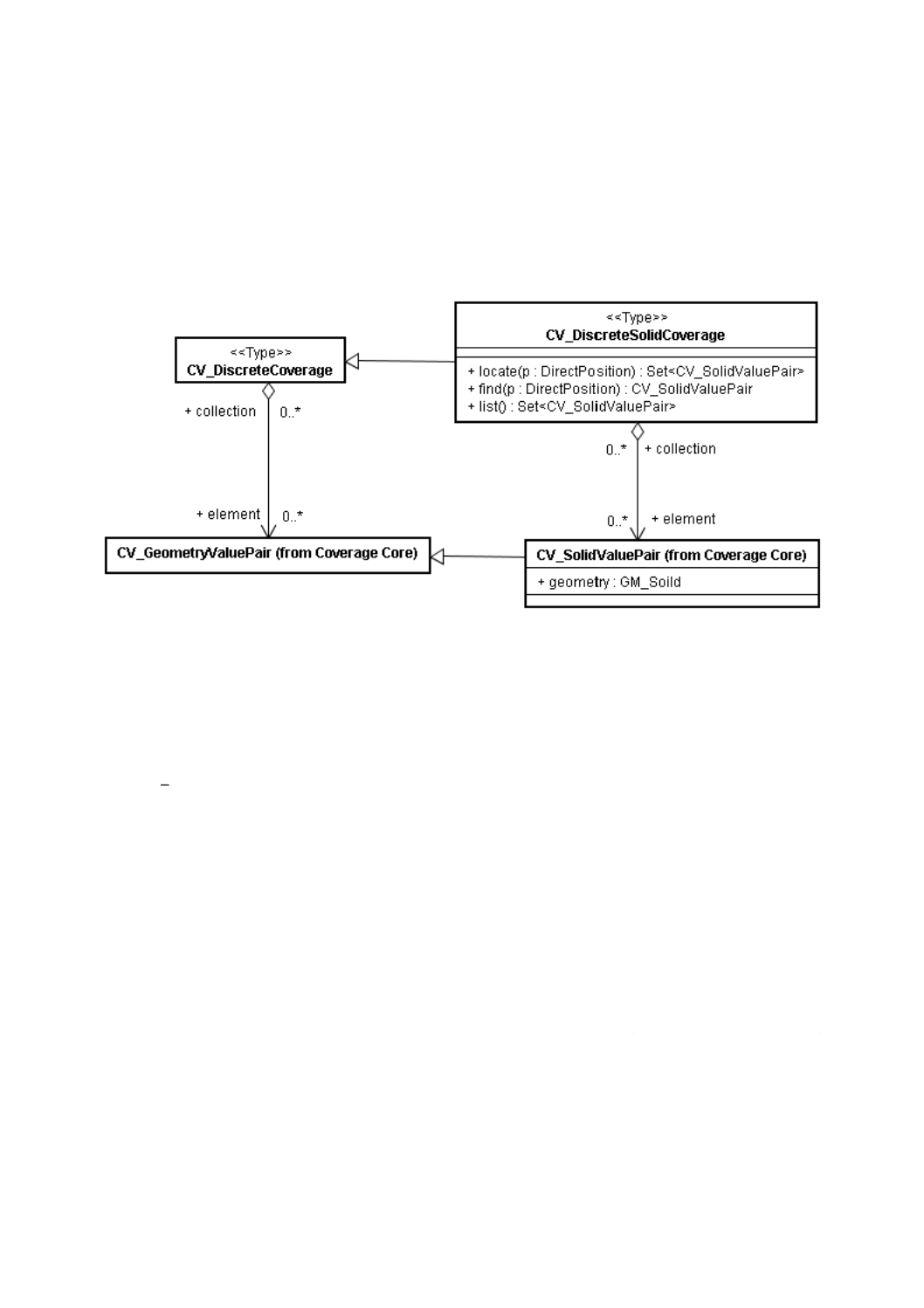
図10−CV̲DiscreteSolidCoverage
6.10.2 継承する操作及び関連
CV̲DiscreteSolidCoverage(離散立体被覆:図10参照)は,関連するCV̲GeometryValuePair及び各操作
が返すCV̲GeometryValuePairをCV̲SolidValuePairに限定する制約とともに,CoverageFunction関連並びに
locate,find,list,evaluate及びevaluateInverse操作をCV̲DiscreteCoverageから継承する。
6.11 CV̲SolidValuePair
CV̲SolidValuePair(立体値対)は,GM̲Solidを幾何属性の値としてもつCV̲GeometryValuePairの下位
型である。
7
ティーセンポリゴン被覆
7.1
ティーセンポリゴンネットワーク
平面上にある点の有限な集まりは,点の集まりと同数のポリゴンの集まりとに平面を分割できる。ティ
ーセンポリゴンは定義集合の点の一つから生成され,定義集合の全ての点の中で,選んだ点が最も近くな
るような直接位置の集合によって形成される。この指定された点は,生成されたポリゴンの中心と呼ばれ
る。隣り合うポリゴン間の境界は,それぞれの中心を結ぶ線の垂直二等分線である。各ポリゴンは,その
エッジの各々を唯一の他のポリゴンと共有する。各ポリゴンは,定義集合に含まれる点を必ず一つだけ含
む。ティーセンポリゴンは,ボロノイ図又は近接集合という名でも呼ばれている。
CoverageFunction
CoverageFunction
26
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
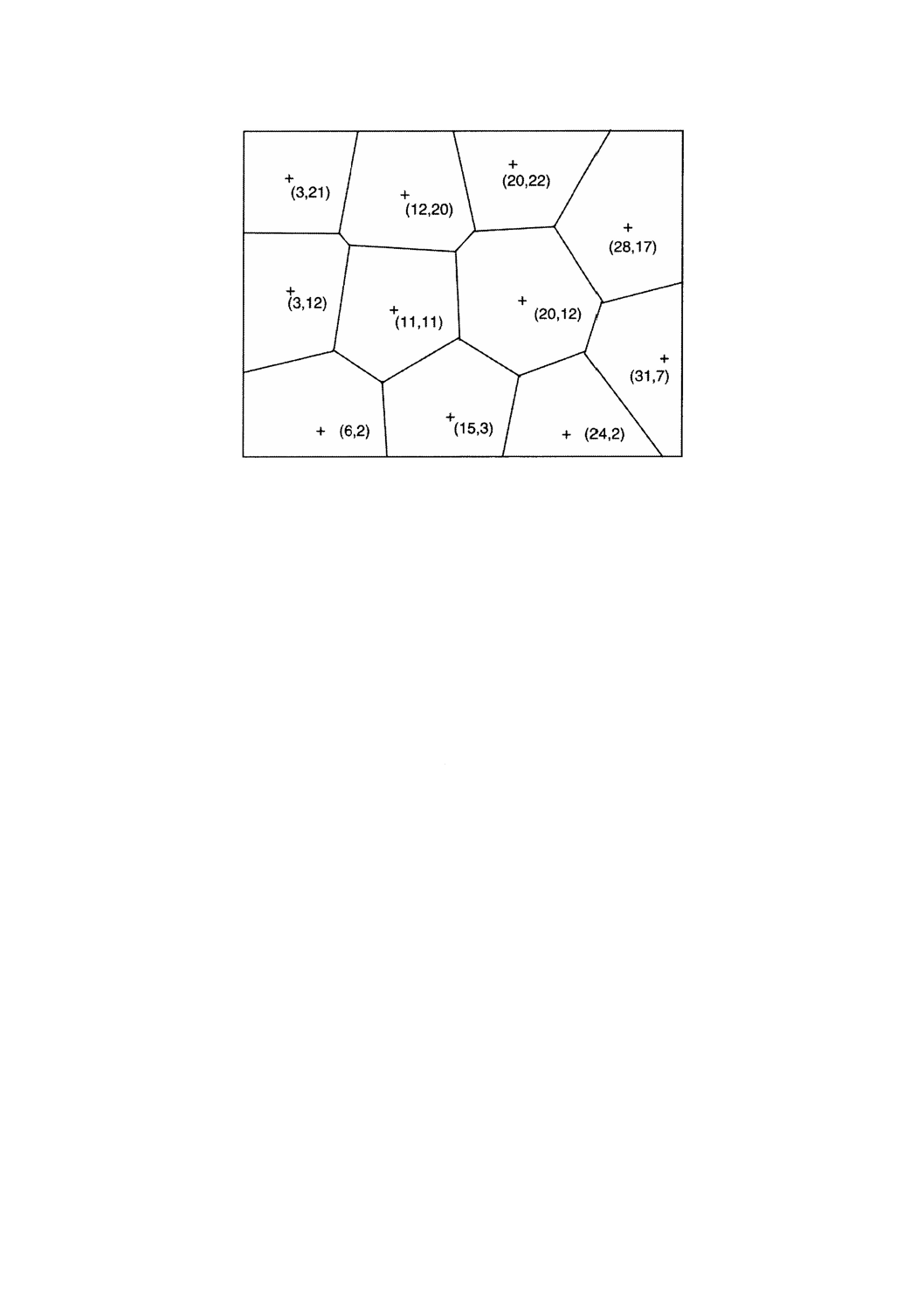
図11−中心の(x,y)座標を示したティーセンポリゴンネットワークの例
ティーセンポリゴンネットワーク(図11参照)は,ティーセンポリゴンを使った二次元空間のモザイク
分割である。ティーセンポリゴンネットワークは,ポリゴン中心からポリゴン内部の直接位置への地物属
性値の内挿を可能にする構造を提供する。
例 図11は,点の集まり(x,y)座標の,各点間に引かれる線の垂直二等分線及び結果として生じる
ポリゴンを表す。
7.2
CV̲ThiessenPolygonCoverage
7.2.1
一般
CV̲ThiessenPolygonCoverage(ティーセンポリゴン被覆:図12参照)は,離散点と値との対の集合によ
って構成されるティーセンポリゴンネットワーク内にある直接位置で被覆を評価する。評価は,入力位置
を囲むCV̲ThiessenValuePolygonの中心の間の内挿に基づく。
7.2.2
clipArea
clipArea: GM̲Surface(抽出範囲)属性は,CV̲ThiessenPolygonNetworkの範囲を記述する。その範囲の
境界によって,ティーセンポリゴンネットワークの最も外側のポリゴンの境界を決定する。そうすればテ
ィーセンポリゴンネットワークが無限に広がることがない。
7.2.3
interpolationType
継承されたinterpolationType: CV̲InterpolationMethod = “lost area”(内挿型)属性は,被覆の評価で使用す
る内挿法を定める。最も一般的な内挿法は,“lostarea”(喪失領域:C.9参照)及び“nearestneighbour”(最
近隣:C.2参照)である。喪失領域内挿は,CV̲ThiessenValuePolygon内の個々の直接位置に対して異なる
地物属性値のRecordを返す。一方,最近隣内挿は,CV̲ThiessenValuePolygon内の全ての直接位置に対し,
そのCV̲ThiessenPolygonの中心となるCV̲PointValuePairに関連付けられているRecordを返す。すなわち,
最近隣内挿を使用するCV̲ThiessenPolygonCoverageは,離散曲面被覆のように振る舞う。
7.2.4
locate
locate (p: DirectPosition): CV̲ThiessenValuePolygon(場所取得)操作は,CV̲ThiesenValuePolygonを返す
という制約の下でCV̲ContinuousCoverageから継承される。この操作は,DirectPositionを入力として受け
取り,このDirectPositionを含むCV̲ThiessenValuePolygonを返す。
27
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
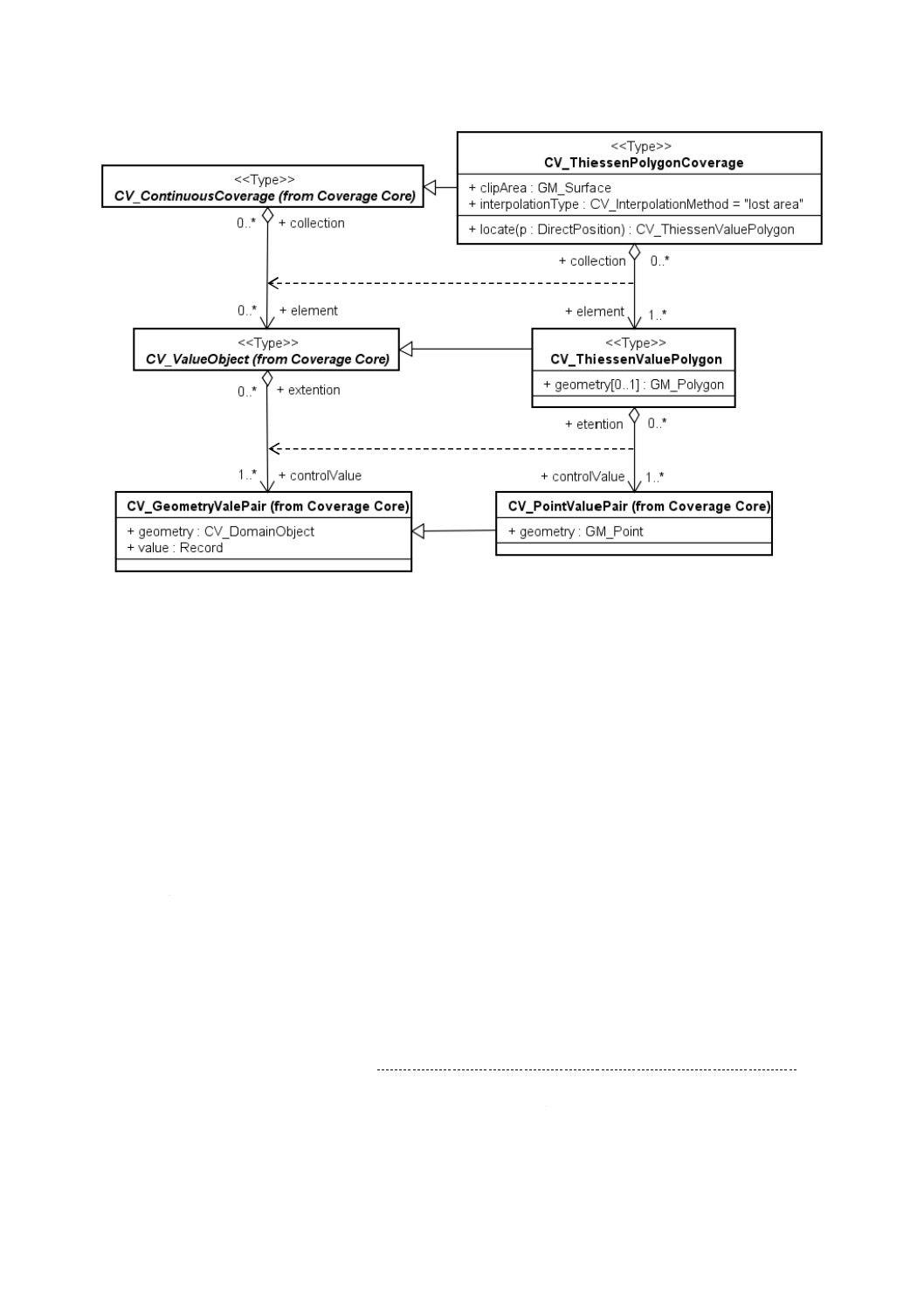
図12−CV̲ThiessenPolygonCoverage
7.2.5
evaluate
evaluate (p: DirectPosition, list: Sequence <CharacterString>): Set <Record>(評価)操作は,CV̲Coverageか
ら継承される。CV̲ThiessenPolygonCoverageの評価には,二つの段階がある。最初の段階では,入力され
たDirectPositionを含むCV̲ThiessenValuePolygonを見つけ,次の段階では,その周囲の
CV̲ThiessenValuePolygonの中心におけるCV̲PointValuePairから,そのDirectPositionにおける地物属性値
を内挿する。
7.2.6
CoverageFunction
CoverageFunction(被覆機能)関連は,このCV̲ThiessenPolygonCoverageを,それを構成する
CV̲ThiessenValuePolygonに連結する。
7.3
CV̲ThiessenValuePolygon
7.3.1
一般
CV̲ThiessenValuePolygon(値付きティーセンポリゴン)は,CV̲ValueObjectの下位クラスである。個々
のCV̲ThiessenValuePolygonは,CV̲ThiessenPolygonCoverageの評価時に生成されてもよく,永続する必要
はない。
7.3.2
geometry
geometry: GM̲Polygon(幾何)属性は,Control関連によって識別されたCV̲PointValuePairを中心とする
ティーセンポリゴンの幾何を保持する。この属性は,使用する内挿法によってはもたなくてもよい。
7.3.3
Control
Control(基準)関連は,CV̲ThiessenValuePolygonを,それ自身の中心におけるCV̲PointValuePairに連
結する。
CoverageFunction
Control
CoverageFunction
Control
28
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8
四辺形グリッド被覆
8.1
一般
グリッド被覆は,定義域の系統立ったモザイク分割を用いる。このようなモザイク分割の主な利点は,
定義域の要素の順序立った列挙法を与えることで,データの保存及びアクセスを効率化できることである。
このモザイク分割は,データがいかに取得されたか又はいかにそのモデルにおいて計算されたかを示すこ
とができる。グリッド被覆の定義域は,グリッド点の集合であり,連続グリッド被覆の場合,その凸包を
含む。
注記 この箇条8に基づき四辺形グリッド被覆データを実装する場合,実装が困難な箇所がある。こ
れらは,対応国際規格の改正で修正する。
8.2
四辺形グリッド幾何
注記 “四辺形グリッド幾何”としたが,8.2.1及び8.2.2では,二次元での四辺形グリッドだけでな
く,三次元での六面体グリッドなども扱う。
8.2.1
一般
グリッドは,複数の曲線からなる集合の二つ以上から構成されるネットワークで,各集合の要素となる
曲線が,他の集合の要素となる曲線と一定の規則で交差するものである。曲線はグリッド線,それらが交
わる点はグリッド点,グリッド線の間の空間はグリッドセルと呼ぶ。
一般に,グリッド線は直線であり,グリッド空間に対して各次元のグリッド線の集合が一つ存在する。
このとき,グリッドセルは,平行四辺形(正方形及び長方形を含む。)又は平行六面体である。このような
グリッドは,二つ以上の等間隔の平行な線の集合で構成されるネットワークとなり,そこでは,各集合の
要素が,他の集合の要素と直交する(図13参照)。このネットワークは,グリッドの次元と同数の軸の集
合をもつ。また,ネットワークは,それぞれの軸と平行なグリッド線の集合を一つもつ。グリッドの規模
は,整数の列で記述され,それぞれの整数は,一つの軸と平行な線の総数となる。二次元におけるグリッ
ド線の全ての交点には,グリッド点が存在する。グリッドの軸は,グリッド座標を定義するための基礎を
提供し,座標は,座標値0をもつことで識別される原点からの軸上の距離で計測される。グリッド点のグ
リッド座標は,整数である。関連している地物属性値レコードをグリッド点に関連させるための順序付け
規則を提供するためには,軸を特定する必要がある。
図13−例−7×7の二次元直交グリッド
注記 二次元グリッドの次元(軸)は,列及び行と呼ばれることが多い。
グリッドは,外部座標参照系によって定義される。これには,外部座標参照系におけるグリッドの原点
の位置,グリッド軸の方向及びグリッド線間の間隔の尺度に関する追加情報が必要である。空間が均一で
29
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
あれば,グリッド座標系と外部座標参照系との間にはアフィン関係があり,このグリッド(図14参照)
は,偏位修正グリッドと呼ばれる。加えて,外部座標参照系が原子によって地球と関連している場合,グ
リッドは,地球偏位修正グリッドとなる。偏位修正グリッドのグリッド線は,直交する必要はない。グリ
ッド線間の間隔は,それぞれの軸に沿って一定になるが,全ての軸で同じ間隔にする必要はない。重要な
点は,グリッド座標を外部座標参照系の座標に変換することがアフィン変換になることである。
注記1 偏位修正という言葉は,画像空間から他の座標参照系への変換ということを意味している。
しかし,この形態のグリッドは,地球を基礎にした座標系で最初に定義され,画像以外の資
料からデータを集めるための基礎として使用されることが多い。
注記2 グリッド座標系は,JIS X 7111で規定する施工座標参照系のインスタンスの一つである。そ
の原子は,一つ以上の地上基準点の集合である。
符号の意味
X,Y,Z 三次元空間を定める軸
V1,V2
オフセットベクトル
O
グリッドの原点
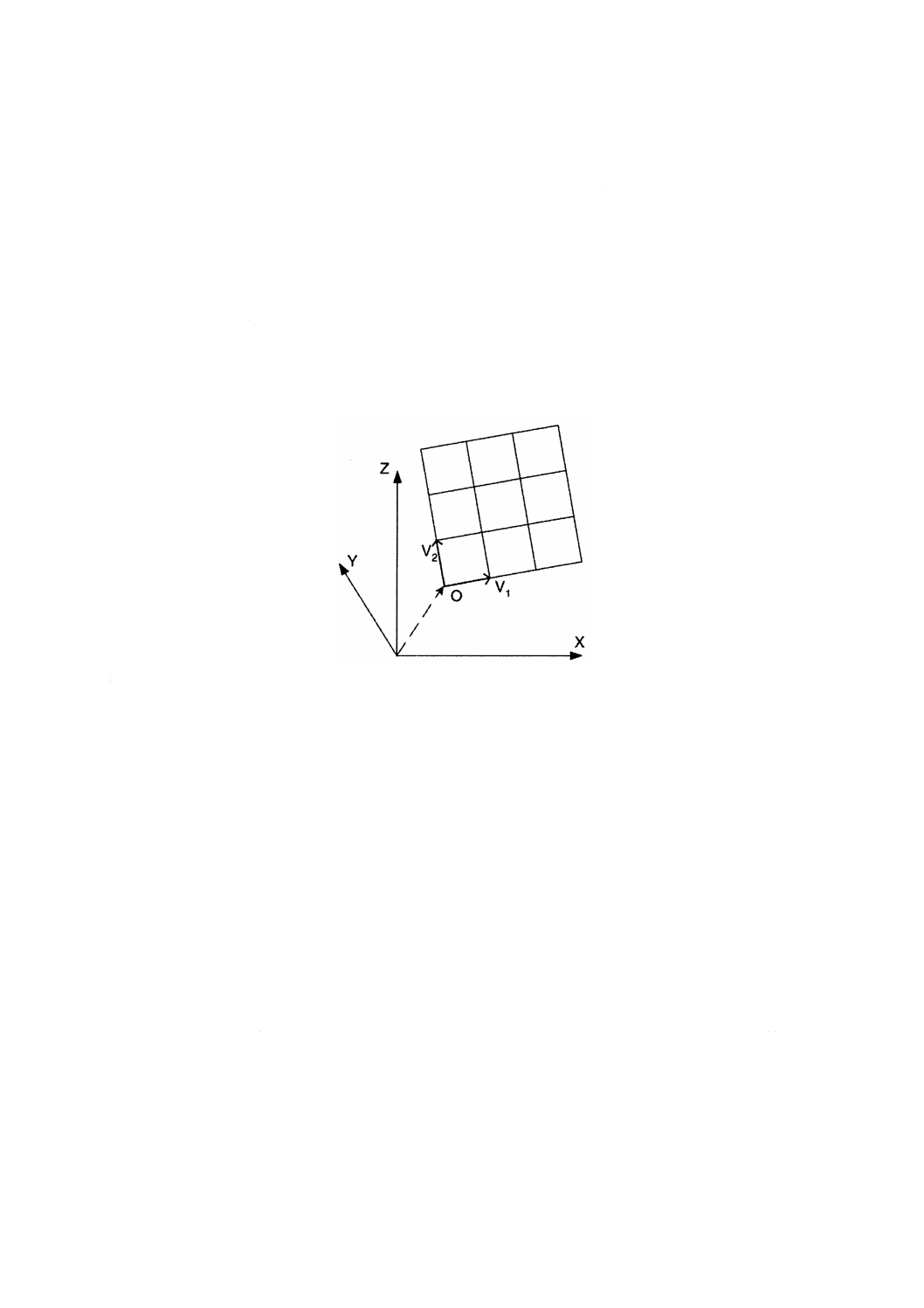
図14−偏位修正グリッドの幾何
例 図14は,X,Y及びZ軸によって定められる三次元空間における二次元グリッドを示している。
グリッドの原点は,Oである。V1及びV2で示された二つのオフセットベクトルは,グリッド軸
の方向及びグリッド線間の間隔を規定する。このグリッド点の座標は,O+aV1+bV2である。
グリッドと外部座標参照系との関係が,その座標参照系における原点,方向,間隔だけでグリッドを特
定できるようなもの(偏位修正グリッド)ではないときにも,グリッド座標を座標参照系の座標に変換す
ることは可能である。この変換は,式の形で行われる必要はなく,グリッド位置を外部座標参照系の座標
へ関係付ける表であってもよい。このようなグリッドは,参照可能グリッドとして分類される。外部座標
参照系が原子によって地球と関連している場合,グリッドは,対地参照可能グリッドとなる。参照可能グ
リッドは,グリッドに含まれる全ての点の位置を空間参照系の中で決定することができるような情報と関
連付けられているが,座標参照系の中の点の位置をグリッド自身の属性から導き出すことのできる偏位修
正グリッドとは異なり,その座標の位置は,グリッド座標から直接得られるわけではない。参照可能グリ
ッドと関連付けられた情報から作られる変換は,座標参照系の中でのグリッドを作成するが,そのグリッ
ドのグリッド線は,直線である必要も直交する必要もなく,グリッドセルは,異なる形状及び大きさであ
ってもよい。
30
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2.2
セル構造
用語“セル”は,グリッド関連で,二つの概念を指している。一つはデータの収集及び描画の視点から
重要であり,もう一つはグリッド被覆評価の視点から重要である。この用語の曖昧さが,グリッド被覆の
評価又は描画に際して,位置決めの誤りをしばしばひき起こす。
グリッド点に関連付けられた地物属性値は,グリッド点によって表現される標本点の周辺の小さな空間
の中で計測されたか又は観測された現実世界の特性を表現する。これらの点を結ぶグリッド線は,グリッ
ドセルの集合を形成する。一般的な単純な仮定は,標本空間が標本点の間を等分割するということである。
したがって,標本空間は,最初のセルの集合と合同な,各々のセルがその中心にグリッド点をもつように
ずらされた二つ目のセルの集合によって示される。グリッド被覆の評価は,グリッド点の間の内挿に基づ
き,すなわち,標本点を表すグリッド点を結ぶグリッド線を境界とするグリッドセルの中での内挿に基づ
く。
符号の意味
a,b,c,d
グリッド点
A,B,C,D セル(点線を境界とする。)
U
グリッドセル(実線を境界とする。)
X
グリッドセル内の直接位置
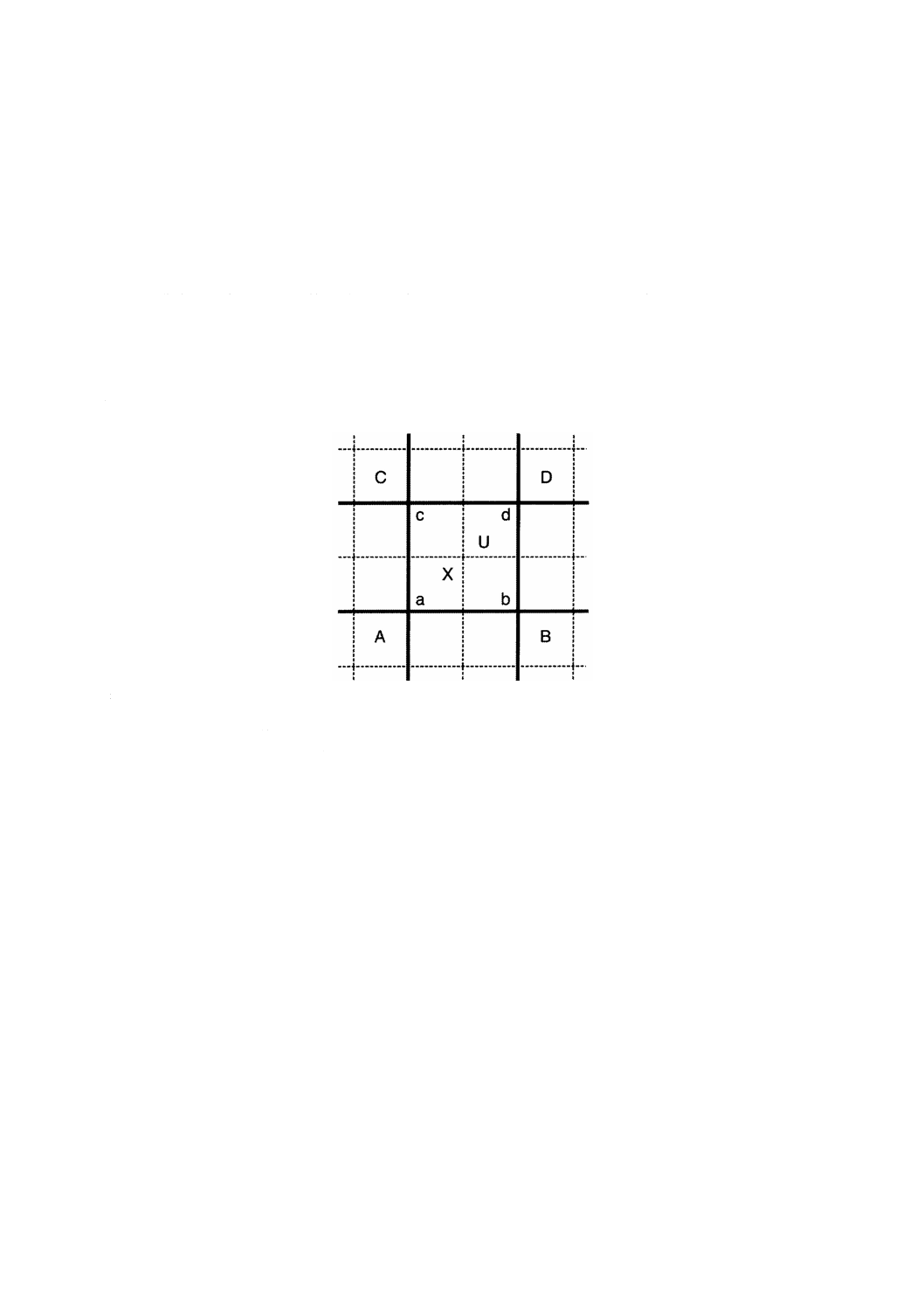
図15−グリッドセル構造
例 図15は,実線の交点が,標本点の集合に対応するグリッド点集合(a,b,c,d)を表す。点線は,
これらのグリッド点に関連付けられた標本区域を表すセル(A,B,C,D)の境界である。この
例では,標本区域はグリッドセルをずらしたものとなっているが,常にそうでなければならない
ということはない。グリッドセルU(実線を境界とする。)内の任意の直接位置Xにおける評価
は,a,b,c及びd(並びにセル外の追加グリッド点を含む。)からの内挿に基づく。
この規格では,グリッドセルという用語は,グリッド点を結ぶグリッド線を境界とするセルを指す。標
本区域という用語は,標本点を囲む観測又は計測された空間を指す。フットプリントという用語は,ある
座標参照系における標本区域の表現を指す。
処理,描画などでグリッドデータを扱うとき,標本空間の大きさ及び形状が標本点の空間分布の単純な
関数であり,グリッドセル及び標本セルが合同であると想定することが多い。
実際には,標本空間の大きさ及び形状は,属性値の測定又は計算に用いられる方法によって決定される。
最も単純な場合は,標本空間が標本点である場合である。多くの場合,標本空間は,標本点を囲む円板,
球又は超球である。センサデータの場合,標本空間の大きさ及び形状は,センサモデル及び標本点に対す

31
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
るその位置の関数であり,非常に複雑であることもある。隣り合う標本空間は境界線を共にしてもよく,
又は重なり合っても空隙があってもよい。
標本空間の大きさ及び形状への影響に加え,測定技術は,標本空間への観測値又は測定値の適用性にも
影響する。多くの場合,記録された値は標本空間の平均値を表すと想定される。実際には,標本空間の要
素が結果に一様に貢献するわけではないので,標本空間内の位置の関数で重み付けされた加重平均である
と考えた方がよい。標本空間の特性を扱うのに特化した内挿法を設計してもよい。
グリッド座標と外部座標参照系との間の変換(例えば補正)が,標本空間の表現をゆが(歪)め,内挿
誤差を引き起こすこともある。
8.3
CV̲Grid
8.3.1
一般
クラスCV̲Grid(グリッド:図16参照)は,四辺形グリッドの幾何特性を含む。
図16−CV̲Grid
8.3.2
dimension
dimension: Integer(次元)属性は,グリッドの次元を表す。
8.3.3
axisNames
axisNames: Sequence <CharacterString>(軸名)属性は,グリッド軸の名前を一覧表示する。
8.3.4
extent
任意選択のextent: CV̲GridEnvelope(範囲)属性は,グリッド点の座標の範囲を指定する。
8.3.5
Organization
Organization(構成)関連は,CV̲Gridを,グリッド線の交点にあるCV̲GridPointの集合に連結する。
EvaluationStructure
Organization
Reference
SampleSpace
Location
32
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.3.6
EvaluationStructure
EvaluationStructure(評価構造)関連は,CV̲Gridを,グリッド線によって示されるCV̲GridCellの集合
に連結する。
8.3.7
下位クラス
CV̲Gridは,二つに区分された三つの下位クラスをもつ(図17参照)。Positioning区分には,グリッド
座標を外部座標参照系に関連付ける情報をもつCV̲RectifiedGrid(8.9参照)及びCV̲ReferenceableGrid(8.10
参照)を含む。Valuation区分には,この値域からの値を各グリッド点に割り当てるための情報をもつ
CV̲GridValuesMatrix(8.14参照)を含む。
CV̲Gridは抽象クラスではないため,CV̲Gridのインスタンスは,その下位クラスのインスタンスでな
くてもよい。この区分は,下位クラスCV̲GridValuesMatrixのインスタンスが,同時に,下位クラス
CV̲RectifiedGrid又はCV̲ReferenceableGridのいずれのインスタンスであってもよいことを示す。
8.4
CV̲GridEnvelope
8.4.1
一般
CV̲GridEnvelope(グリッド包被:図16参照)は,CV̲Gridの対角となる隅のグリッド座標値を示すデ
ータ型である。CV̲GridEnvelopeは,二つの属性(low及びhigh)をもつ。
8.4.1.1
low
low: CV̲GridCoordinate(最小値)属性は,CV̲Gridの中にある全てのグリッド点の最小座標値である。
8.4.1.2
high
high: CV̲GridCoordinate(最大値)属性は,CV̲Gridの中にある全てのグリッド点の最大座標値である。
8.5
CV̲GridPoint
8.5.1
一般
CV̲GridPoint(グリッド点)は,グリッド線の交点を表すクラスである。
8.5.2
gridCoord
gridCoord:CV̲GridCoordinate(グリッド座標)属性は,CV̲Gridの中のCV̲GridPointの場所を特定する
グリッド座標を保持する。
8.5.3
Organization
Organization(構成)関連は,CV̲GridPointを,それが要素となるCV̲Gridに連結する。
8.5.4
Location
Location(場所)関連は,CV̲GridPointを,それが隅になっているCV̲GridCellの集合に連結する。こ
の関連のCV̲GridPoint終端の多重度は,あらゆる次元のグリッドに対応できるよう,上限が設定されてい
ない。四辺形グリッドでは,corner(隅)の多重度は1以上である。
8.5.5
Reference
Reference(参照)関連は,CV̲GridPointを,外部座標参照系におけるその表現であるGM̲Pointに結び
付けてもよい。
8.5.6
SampleSpace
SampleSpace(標本空間)関連は,CV̲GridPointをCV̲GridPointに関連付けられた外部座標参照系にお
ける標本空間を表すCV̲Footprintに結び付けてもよい。SampleSpace関連の多重度によって,CV̲Footprint
に対する複数の外部座標参照系を可能としている。
8.6
CV̲GridCoordinate
8.6.1
一般
33
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
CV̲GridCoordinate(グリッド座標)は,CV̲GridPointのグリッド座標を保持するためのデータ型である。
8.6.2
coordValues
coordValues: Sequence <Integer>(座標値)属性は,グリッドの各次元の一つの整数値を保持する。これ
らの座標値の順序付けは,CV̲Grid.axisNamesの要素の順序と同じでなければならない。一つの座標の値
は,特定の軸の方向でグリッドの原点からのオフセットの数と同じでなければならない。
8.7
CV̲GridCell
8.7.1
一般
CV̲GridCell(グリッドセル)は,CV̲Gridのグリッド線によって描く。その隅は,境界となるグリッド
線の交点でCV̲GridPointと関連付けられている。
8.7.2
Location
Location(場所)関連は,CV̲GridCellを,その隅でCV̲GridPointの集合に連結する。
8.7.3
EvaluationStructure
EvaluationStructure(評価構造)関連は,CV̲GridCellを,それが要素となっているCV̲Gridに連結する。
8.8
CV̲Footprint
8.8.1
一般
CV̲Footprint(フットプリント)は,外部座標参照系におけるグリッドの標本区域である。
8.8.2
geometry
geometry: GM̲Object(幾何)属性は,GM̲Object.CRS(JIS X 7107参照)によって識別される座標参照
系内のCV̲Footprintの幾何属性を記述する。
8.8.3
SampleSpace
SampleSpace(標本空間)関連は,CV̲Footprintを,それが対応するCV̲GridPointに連結する。
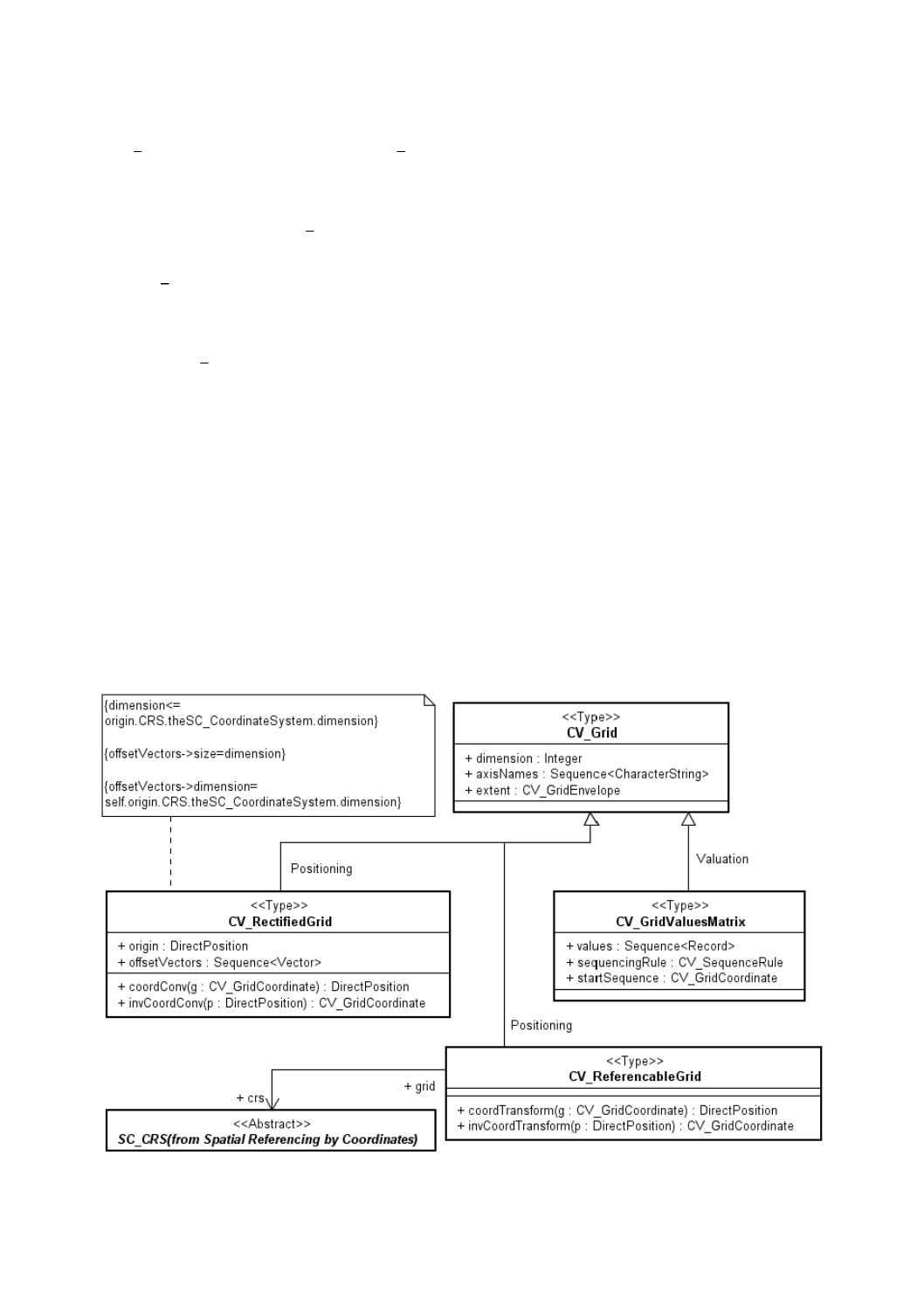
図17−CV̲Gridの下位クラス
CoordinateReferenceSystem
34
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.9
CV̲RectifiedGrid
8.9.1
一般
偏位修正グリッドについては,次の二つを外部座標参照系で定義する(図14参照)。
− グリッド原点
− グリッド軸の方向とグリッド線間の間隔とを指定するオフセットベクトル群
CV̲RectifiedGrid(偏位修正グリッド:図17参照)クラスは,偏位修正グリッドの追加的な幾何特性を
含む。
8.9.2
origin
origin: DirectPosition(原点)属性は,外部座標参照系の中に偏位修正グリッドの原点を配置するための
直接位置である。この座標参照系は,DirectPositionとJIS X 7111で規定するSC̲CRSクラスとの間の
CoordinateReferenceSystem(JIS X 7107で規定)関連によって識別される。
8.9.3
offsetVectors
offsetVectors: Sequence<Vector>(オフセットベクトル)属性は,それぞれの方向でグリッドの間隔を決定
するオフセットベクトルの列である。これらのベクトルは,外部座標参照系に基づいて定義される。デー
タ型Vectorは,ISO/TS 19103で規定する。
8.9.4
coordConv
coordConv (g: CV̲GridCoordinate): DirectPosition(座標換算)操作は,CV̲GridCoordinateを入力として受
け取り,DirectPositionを返す。この操作は,アフィン変換においてorigin属性及びoffsetVectors属性の値
を使用する。これは,JIS X 7111で定義する座標換算操作である。
8.9.5
invCoordConv
invCoordConv (p: DirectPosition): CV̲GridCoordinate(逆座標換算)操作は,DirectPositionを入力として受
け取り,最も近いCV̲GridPointのCV̲GridCoordinateを返す。この操作は,アフィン変換においてorigin
属性及びoffsetVectors属性の値を使用する。これは,JIS X 7111で定義する座標換算操作である。
8.9.6
制約
制約は,次による。
a) {dimension <= origin.CRS.theSC̲CoordinateSystem.dimension} グリッド次元は,原点であるGM̲Point
のCoordinate Reference System関連によって識別された座標参照系の次元以下でなければならない。
b) {offsetVectors -> size = dimension} オフセットベクトルの数は,グリッド次元と同じでなければならな
い。
c) {offsetVectors -> dimension = self.origin.CRS.theSC̲CoordinateSystem.dimension} オフセットベクトル
の次元は,座標参照系の次元と同じでなければならない。
8.10 CV̲ReferenceableGrid
8.10.1 一般
CV̲ReferenceableGrid(参照可能グリッド)は,二つの操作coordTransform及びinvCoordTransformを提
供する。
8.10.1.1 coordTransform
coordTransform (g: CV̲GridCoordinate): DirectPosition(座標変換)操作は,CV̲GridCoordinateを入力とし
て受け取り,CoordinateReferenceSystem(8.10.2参照)関連によって識別された座標参照系における
DirectPositionを返す。これは,JIS X 7111で定義する座標変換操作である。
8.10.1.2 invCoordTransform
35
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
invCoordTransform (p: DirectPosition): CV̲GridCoordinate(逆座標変換)操作は,CoordinateReferenceSystem
(8.10.2参照)によって識別された座標参照系におけるDirectPositionを入力として受け取り,最も近い
CV̲GridPointのCV̲GridCoordinateを返す。これは,JIS X 7111で定義する座標変換操作である。
8.10.2 CoordinateReferenceSystem
CoordinateReferenceSystem(座標参照系)関連は,CV̲ReferenceableGridを,それが参照可能である座標
参照系に連結する。この関連はgridからcrsに誘導可能でなければならないが,反対方向では誘導可能で
なくてもよい。
8.11 CV̲ContinousQuadrilateralGridCoverage
8.11.1 一般
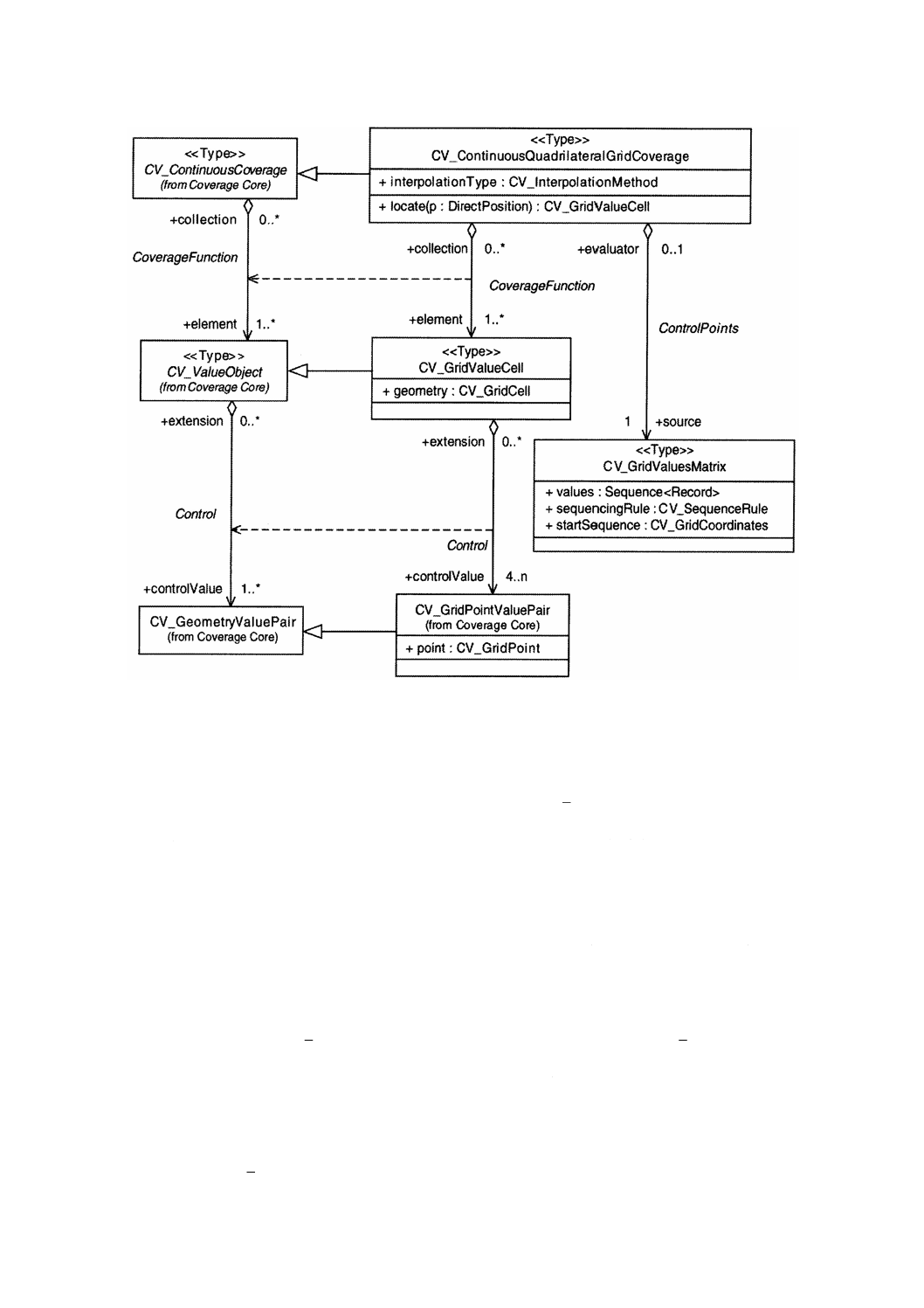
CV̲ContinuousQuadrilateralGridCoverage(連続四辺形グリッド被覆:図18参照)は,CV̲GridValuesMatrix
(8.14参照)に基づいて機能するCV̲ContinuousCoverageの下位クラスである。
CV̲ContinuousQuadrilateralGridCoverageの定義域は,CV̲GridValuesMatrixによって定義されたグリッド点
の集まりの凸包である。CV̲ContinuousQuadrilateralGridCoverageの評価は,CV̲GridValuesMatrixによって
与えられたCV̲GridPointの凸包の中にある直接位置で地物属性値を生成する。一般的な考え方は,セルの
各隅のグリッド点を用いた内挿を行うことによって,それぞれのグリッドセルの内部の直接位置へ属性値
定義を拡張することである。
8.11.2 interpolationType
継承されたinterpolationType:CV̲InterpolationMethod = bilinear(内挿型)属性は,evaluate操作によって使
用される内挿法を識別する。
36
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図18−CV̲ContinuousQuadrilateralGridCoverage
8.11.3 locate
locate (p: DirectPosition): CV̲GridValueCell(場所取得)操作は,CV̲ContinuousCoverageから継承され,
DirectPositionを入力として受け取り,このDirectPositionを含むCV̲GridValueCellを返す。
8.11.4 evaluate
evaluate (p: DirectPosition, list: Sequence <CharacterString>): Set <Record>(評価)操作は,CV̲Coverageか
ら継承される。CV̲ContinuousQuadrilateralGridCoverageの評価には,二つの段階がある。最初の段階は,
CV̲QuadrilateralGridCoverage.sourceの指すCV̲GridValuesMatrix(8.14参照)からの情報を用いて,入力
DirectPositionを含むCV̲GridValueCellを生成することである。次の段階は,CV̲GridValueCellの隅におけ
るCV̲GridPointValuePairからDirectPositionにおける地物属性値を内挿することである。内挿法の中には
[例えば,双三次内挿(C.8参照)],DirectPositionを含むCV̲GridValueCellの外側のCV̲GridPointValuePair
を使う必要がある。
注記 最近隣内挿は,CV̲GridValueCellの中にある全ての直接位置に対し,CV̲GridValueCellの最も
近い隅でCV̲GridPointValuePairと関連するRecordを返す。すなわち,最近隣内挿を使用する
CV̲ContinuousQuadrilateralGridCoverageは,離散曲面被覆の役割を果たすことになる。
8.11.5 ControlPoints
ControlPoints(基準点)関連は,このCV̲ContinuousQuadrilateralGridCoverageを,evaluate操作に対して
データを提供するCV̲GridValuesMatrixに連結する。この関連はevaluatorからsourceに誘導可能でなけれ
37
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ばならないが,反対方向では誘導可能でなくてもよい。
8.11.6 CoverageFunction
CoverageFunction(被覆機能)関連は,CV̲ContinuousQuadrilateralGridCoverageを,evaluate操作を提供
するための構造を与えるCV̲GridValueCellの集合に連結する。
8.12 CV̲GridValueCell
8.12.1 一般
CV̲GridValueCell(グリッド値セル)は,CV̲ContinuousQuadrilateralGridCoverageにおける内挿を提供す
るCV̲ValueObjectの下位クラスである。CV̲GridValueCellは,CV̲GridCellによって定義された幾何構造
をもつCV̲GridPointValuePairの集まりである。
8.12.2 geometry
geometry:CV̲GridCell(幾何)属性は,CV̲GridCell内のDirectPositionにおける地物属性値の内挿を提供
するCV̲GridPointValuePairについて,その構造を定義するCV̲GridCellを保持する。
8.12.3 Control
Control(基準)関連は,CV̲GridValueCellを,その隅でCV̲GridPointValuePair(8.13参照)に連結する。
8.13 CV̲GridPointValuePair
8.13.1 一般
CV̲GridPointValuePair(グリッド点値対)は,CV̲GridPoint及び地物属性値Recordで構成される
CV̲GeometryValuePairの下位クラスである。
8.13.2 point
point: CV̲GridPoint(点)属性は,CV̲GridPointValuePairの幾何構成要素である。これは,CV̲Gridから
継承されたOrganization関連を通じてCV̲GridValuesMatrixに連結するCV̲GridPointの一つである。
8.13.3 value
value: Record(値)属性は,CV̲GridValuesMatrixの列valuesから引き出されたCV̲GridPointValuePairの
構成要素である。
8.14 CV̲GridValuesMatrix
8.14.1 一般
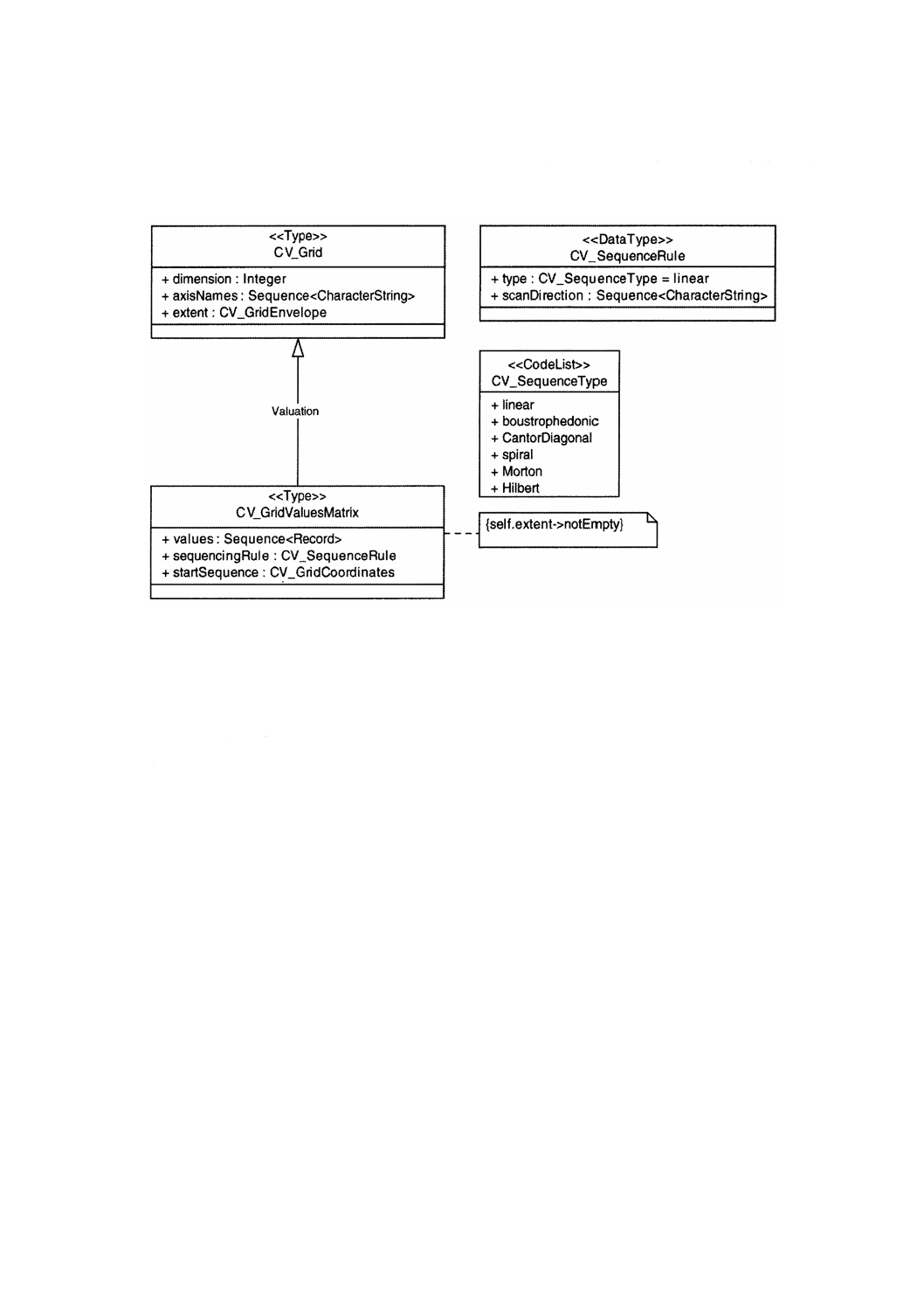
CV̲GridValuesMatrix(グリッド値行列:図19参照)は,地物属性値をグリッド幾何と結合するCV̲Grid
の下位クラスである。CV̲GridValuesMatrixは,三つの属性,values,sequencingRule及びstartSequenceを
もつ。CV̲GridValuesMatrixは,地物属性値のレコードをグリッド点に割り当てるためのアルゴリズムを指
定する順序付け規則と関連付けられたレコードの列を保持する。
8.14.1.1 values
values: Sequence<Record>(値)属性は,N個の地物属性値レコードの列となり,この場合のNは,extent
によって指定されるグリッドの要素体集合の中にあるグリッド点の数である。
8.14.1.2 sequencingRule
sequencingRule: CV̲SequenceRule(順序規則)属性は,グリッド点を,列valuesの要素との関連に対応
して順序付けるための方法を記述する。
8.14.1.3 startSequence
startSequence: CV̲GridCoordinate(開始順序)属性は,グリッド点がvalues列の中にある最初のレコード
と関連付けていることを表す。
38
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.14.2 制約
制約{self.extent -> notEmpty = True}は,継承されたextent属性(8.3.4では,任意選択として定義した。)
に対して値を提供しなければならないことを示す。
図19−CV̲GridValuesMatrix
8.15 CV̲SequenceRule
8.15.1 一般
CV̲SequenceRule(順序規則)は,地物属性値のレコードの列の中にある位置に,グリッド座標を写像
するための情報を含むデータ型である。
8.15.2 type
type: CV̲SequenceType(型)属性は,使用する順序付け方法の型を識別する。既定値は,“linear”であ
る。
8.15.3 scanDirection
scanDirection: Sequence <CharacterString>(走査方向)属性は,符号付きaxisNameのリストであり,地物
属性値のレコードの列内にある位置に写像されるグリッド点の順序を示す。地物属性値の交互配置が可能
であるため,追加要素がこのリストに含まれることもある。走査方向に関する詳細な情報については,D.1
を参照。順次列挙の方法には,linear,boustrophedonic,CantorDiagonal,spiral,Morton,Hilbertなどがあ
る。
8.16 CV̲SequenceType
CV̲SequenceType(順序型)は,グリッド点の順次列挙のための方法を識別する符号リストである。順
次列挙のための方法は,附属書Dに示す。
9
六角形グリッド被覆
9.1
一般
被覆は,正六角形で構成されるモザイクに基づくことがある。このようなモザイクは,通常,六角形グ

39
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
リッドと呼ぶ。実際,このようなモザイクを形成する正六角形の集合の中心は,四辺形グリッドのグリッ
ド点に相当する(図20参照)。この四辺形グリッドは,長さが同じで,方向が60°開いている二つのオフ
セットベクトルによって偏位修正グリッドとして表すこともできる。オフセットベクトルの長さをSとす
ると,六角形の一辺の長さは,L = S tan 30°となる。このことは,被覆範囲の中にある値がグリッド値行
列(8.14参照)として格納できること,及び順序規則(8.15参照)を通じてアクセスできるということを
意味している。六角形は,四辺形グリッドのグリッド点の周囲に生成されたティーセンポリゴンとなる。
注記 直交しない長さの等しい二つのオフセットベクトルによって記述される全ての二次元の偏位修
正グリッドのグリッド点から生成されたティーセンポリゴンの集合は,合同な六角形の集合と
なる。この六角形は,もし二つのオフセットベクトルの方向が正確に60°開いていなければ,
正六角形ではない六角形になる。
図20−六角形グリッド
9.2
CV̲HexagonalGridCoverage
9.2.1
一般
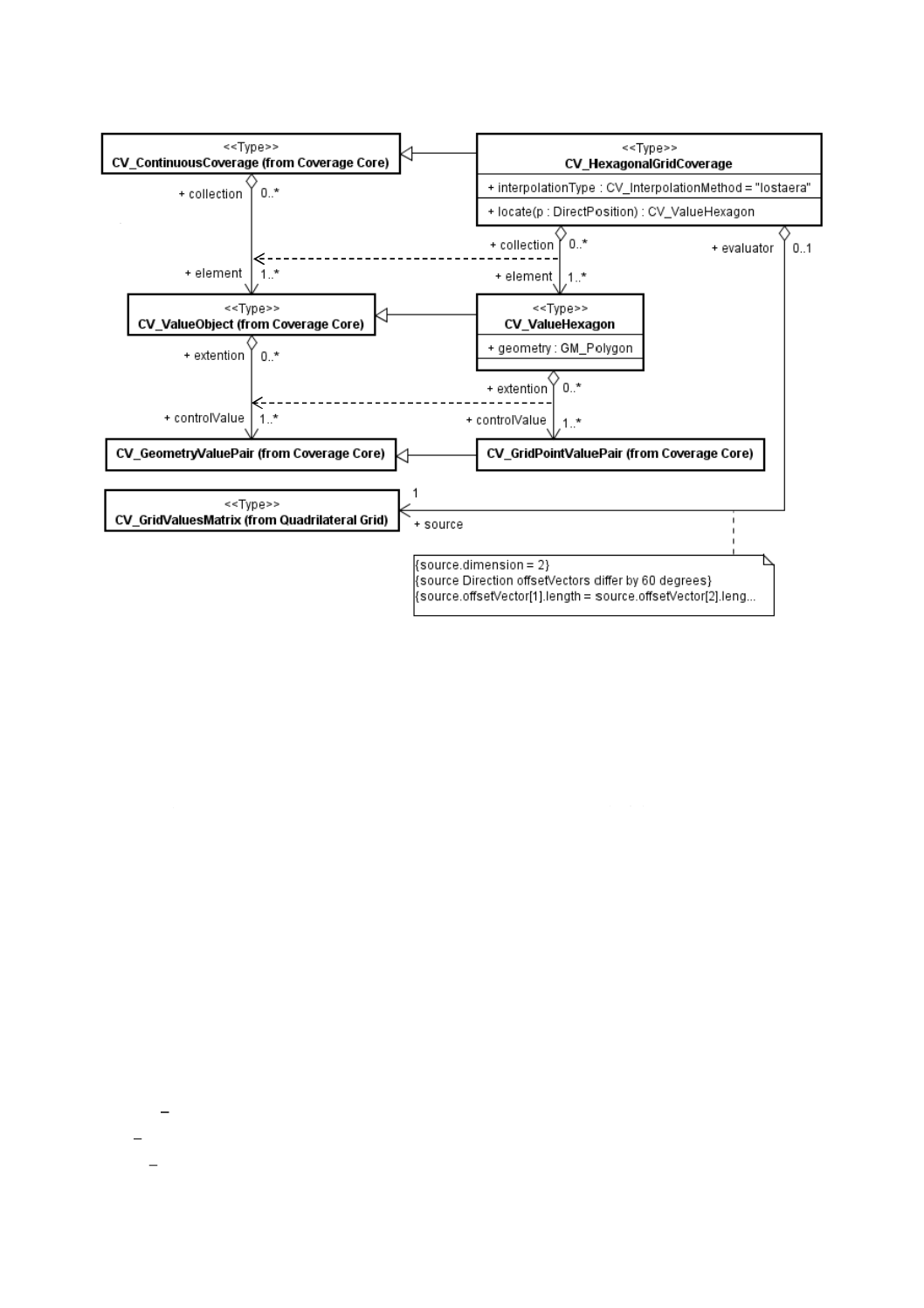
CV̲HexagonalGridCoverage(六角形グリッド被覆:図21参照)は,グリッド点の集合を中心とする六角
形のネットワークの中にある直接位置で被覆を評価する。評価は,入力位置の周辺にあるCV̲ValueHexagon
の中心間の内挿法に基づく。
9.2.2
interpolationType
継承されるinterpolationType: CV̲InterpolationMethod = “lostarea”(内挿型)属性は,被覆の評価で使用す
る内挿法を識別する。最も一般的な内挿法は,“lostarea”(喪失領域:C.9参照)及び“nearestneighbour”(最
近隣:C.2参照)である。喪失領域内挿は,CV̲ValueHexagonの中にある個々の直接位置に対して,異な
る地物属性値のRecordを返すことができる。一方,最近隣内挿は,CV̲ValueHexagonの中にある全ての直
接位置に対し,CV̲ValueHexagonの中心でCV̲GridPointValuePairと関連付けられたRecordを返す。すな
わち,最近隣内挿を使うCV̲HexagonalGridCoverageは,離散曲面被覆のように振る舞う。
40
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図21−CV̲HexagonalGridCoverage
9.2.3
locate
locate (p: DirectPosition): CV̲ValueHexagon(場所取得)操作は,CV̲ValueHexagonを返す制約とともに,
CV̲ContinuousCoverageから継承される。この操作は,DirectPositionを入力として受け取り,この
DirectPositionを含むCV̲ValueHexagonを返す。
9.2.4
evaluate
evaluate (p: DirectPosition, list: Sequence <CharacterString>): Set <Record>(評価)操作は,CV̲Coverageか
ら継承される。CV̲HexagonalGridCoverageの評価には,二つの段階がある。最初の段階は,入力DirectPosition
を含むCV̲ValueHexagonを見つけることであり,次の段階は,そのCV̲ValueHexagonを取り囲む幾つか
CV̲ValueHexagonの中心でのCV̲GridPointValuePairからDirectPositionでの地物属性値を内挿することで
ある。
9.2.5
CoverageFunction
CoverageFunction(被覆機能)関連は,CV̲HexagonaGridCoverageを,それを構成しているCV̲ValueHexagon
の集合に関連付ける。
9.2.6
ControlPoints
ControlPoints(基準点)関連は,CV̲HexagonalGridCoverageを,それを評価するCV̲GridValuesMatrixに
関連付ける。
9.3
CV̲GridValuesMatrix
CV̲GridValuesMatrix(グリッド値行列)は8.14に規定しているが,次の四つの制約によって特記される。
a) CV̲RectifiedGridである。
CoverageFunction
CoverageFunction
Control
Control
ControlPoints
41
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) {source.dimension = 2} 継承されるdimension属性の値は2である。
c) {source Direction of offsetVectors differ by 60 degrees} offsetVectorの方向が60°開いている。
d) {source.offsetVector[1].length = source.offsetVector[2].length} offsetVector同士の長さが同じである。
9.4
CV̲ValueHexagon
9.4.1
一般
CV̲ValueHexagon(六角形値)は,CV̲ValueObjectの下位型である。
9.4.2
geometry
geometry:GM̲Polygon(幾何)属性は,Control関連によって識別されたCV̲GridPointValuePairを中心と
するCV̲ValueHexagonの幾何を保持する。
9.4.3
Control
Control(基準)関連は,CV̲ValueHexagonを,その中心でCV̲GridPointValuePairに関連付ける。
10 不規則三角網(TIN)被覆
10.1 一般
TINの基本的な考え方は,平面上の離散点被覆の定義域と同様の点の凸包を,重なり合わない一意の三
角形の集合へと,分割することである。ドローネ三角形分割法は,三角形の頂点角がなるべく等しくなる
ような形状をもち,個々の三角形の外接円が,その三角形の頂点以外の離散点被覆の点を含まないような
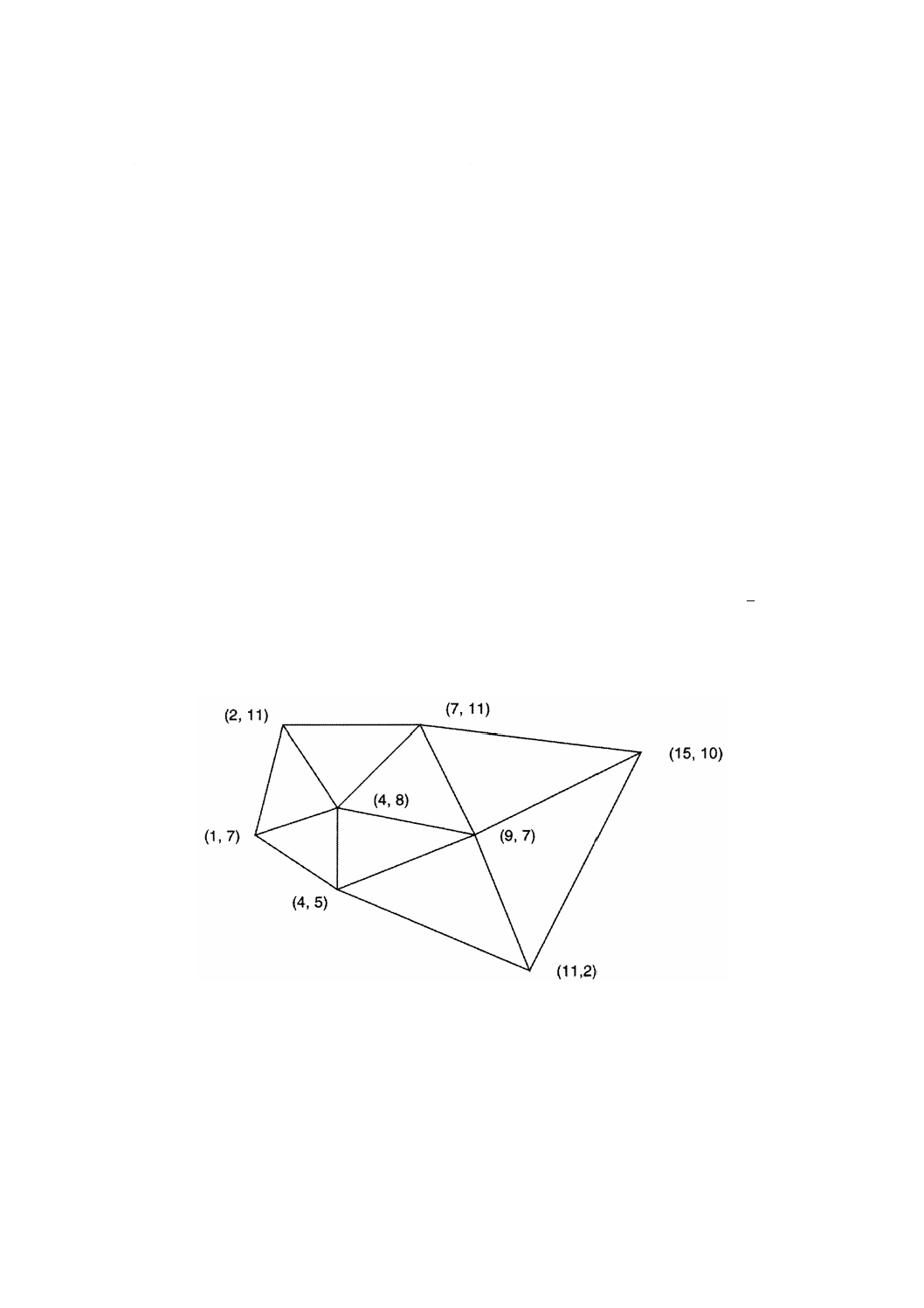
三角形で構成されるTINモザイク分割を作成するために広く使われている(図22参照)。GM̲Tin(JIS X
7107参照)は,ドローネ三角形分割について記述している。
注記 ティーセンポリゴン被覆において,隣接するティーセンポリゴンの中心点同士を全て結ぶとド
ローネ三角分割となる。
図22−(x,y)座標を示した不規則三角網の例
42
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
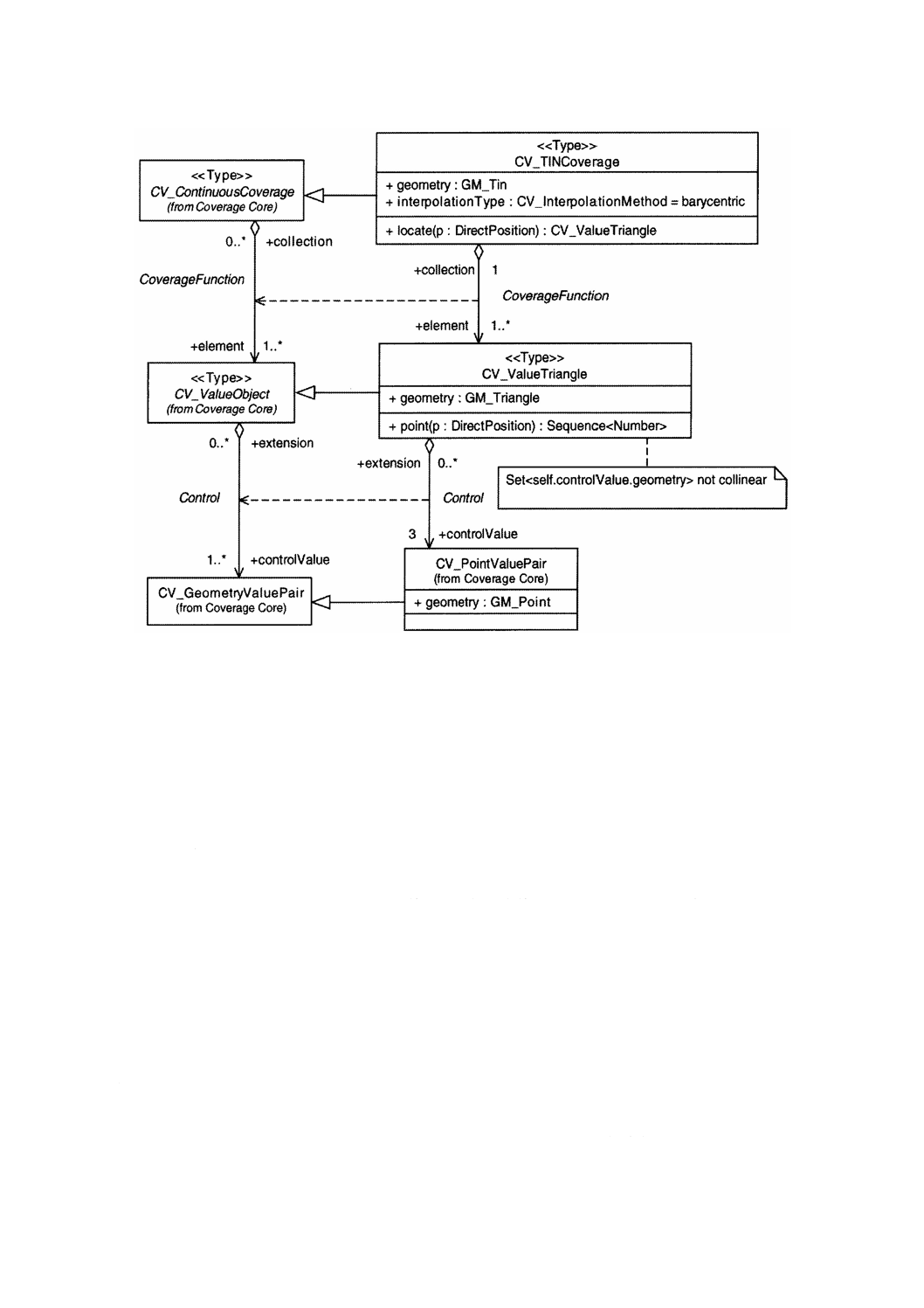
図23−CV̲TINCoverage
10.2 CV̲TINCoverage
10.2.1 一般
CV̲TINCoverage(TIN被覆:図23参照)は,GM̲Tinによって特徴付けられるCV̲ContinuousCoverage
の下位型である。その地物属性値は,それぞれの隅で与えられる地物属性値のレコードを使い,モザイク
内にあるそれぞれの三角形の中で内挿を行うことによって計算する。すなわち,この地物属性値は,
CV̲ValueTriangleの操作によって作成する。
10.2.2 geometry
geometry: GM̲Tin(幾何)属性は,被覆評価のための構造を提供する不規則三角網を保持する。GM̲Tin
(JIS X 7107参照)は,三角形における抑止線及び傾斜変換線を用いるための機能を含む。
10.2.3 interpolationType
継承されるinterpolationType: CV̲InterpolationMethod = “barycentric”(内挿型)属性は,被覆評価で使用す
る内挿法を規定する。最も一般的な内挿法は,“barycentric”(重心:C.10参照)である。
10.2.4 locate
locate (p: DirectPosition): CV̲ValueTriangle(場所取得)操作は,CV̲ValueTriangleを返す制約とともに,
CV̲ContinuousCoverageから継承される。この操作は,直接位置を入力として受け取り,この直接位置が
存在するCV̲ValueTriangleを,CV̲ValueTriangleの隅に割り当てられた地物属性値のRecordとともに返す。
10.2.5 evaluate
evaluate (p: DirectPosition, list: Sequence <CharacterString>): Set <Record>(評価)操作は,CV̲Coverageか
ら継承される。CV̲TINCoverageの評価には,二つの段階がある。最初の段階は,入力DirectPositionを含
43
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
むCV̲ValueTriangleを見つけることであり,次の段階は,CV̲ValueTriangleの頂点で,CV̲PointValuePair
から地物属性値のDirectPositionを内挿することである。
10.2.6 CoverageFunction
CoverageFunction(被覆機能)関連は,CV̲TINCoverageを,それを構成するCV̲ValueTriangleに関連付
ける。
10.3 CV̲ValueTriangle
10.3.1 一般
CV̲ValueTriangle(三角形値)は,GM̲Pointが同一直線上ではない三つのCV̲PointValuePairで構成され
るCV̲ValueObjectの下位型である。CV̲ValueTriangleは,被覆の内挿に使用される。
10.3.2 geometry
geometry:GM̲Triangle(幾何)属性は,その頂点で三つのCV̲PointValuePairの相対位置を定義する
GM̲Triangleを保持する。
注記 ここで保持するGM̲Triangleと,上位クラスCV̲TINCoverageの属性としてもつGM̲Tin が,
GM̲TriangularSurface の下位クラスとして継承したGM̲Triangleとは,同じものをもつことに
なる。
10.3.3 point
point (p: DirectPosition): Sequence <Number>(点)操作は,CV̲ValueTriangleの中にある直接位置を受け
取り,その位置の重心座標を数値の列として返す。
10.3.4 Control
Control(基準)関連は,CV̲ValueTriangleを,その頂点である三つのCV̲PointValuePairに関連付ける。
10.3.5 制約
集合<self.controlValue.geometry>は,同一直線上にはない。関連するCV̲PointValuePairの中にある三つの
GM̲Pointも同一直線上にはない。
11 分割曲線被覆
11.1 一般
分割曲線被覆は,例えばネットワークの構成要素のように,曲線に沿って連続的又は不連続的に変化す
る事象をモデル化するために使用する。分割曲線被覆の定義域は,曲線の集合によって記述され,その集
合の中の全ての曲線の直接位置を含む。
曲線を弧長でパラメタ化すると,曲線上での直接位置間の内挿が単純になる。曲線に沿って不連続的に
変化する事象の表現には,連続的に変化する幾つかの部分に曲線を分割する操作が必要となる。そのよう
な分割も,弧長でパラメタ化することによって単純化される。GM̲Curve(JIS X 7107参照)は,弧長によ
るパラメタ化を提供する。特に,操作:
GM̲GenericCurve.paramForPoint (p:DirectPosition):Set <Distance>, DirectPosition(点パラメタ取得)
は,GM̲Curveの始点から入力DirectPositionまでの,弧長の距離を返す。
44
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
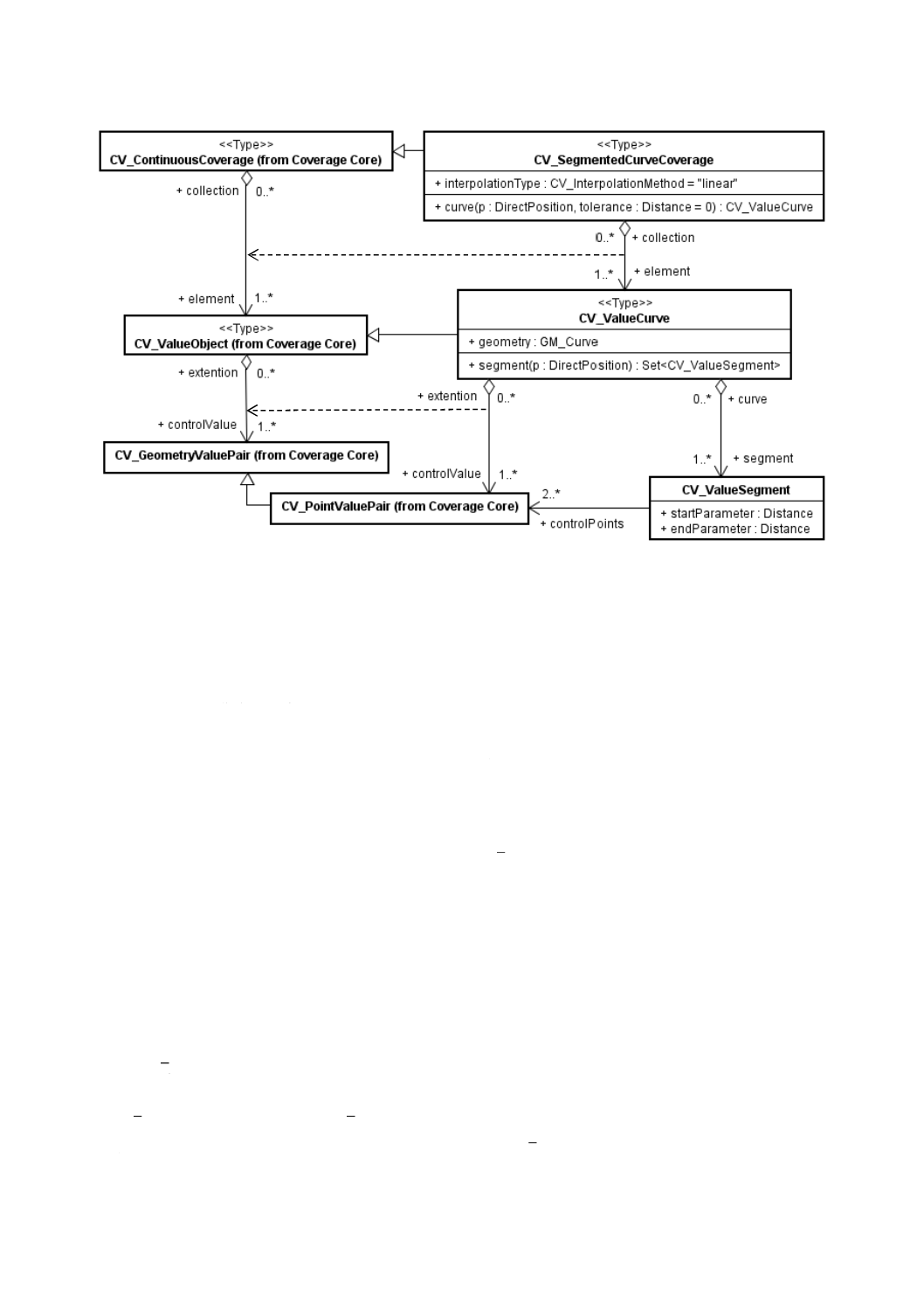
図24−分割曲線被覆
11.2 CV̲SegmentedCurveCoverage
11.2.1 一般
CV̲SegmentedCurveCoverage(分割曲線被覆:図24参照)は,GM̲Curveで構成される定義域上で操作
を行う。CV̲SegmentedCurveCoverageは,それぞれが地物属性値をGM̲Curve上の位置に写像する
CV̲ValueCurveの集合で構成する。
11.2.2 interpolationType
継承されるinterpolationType: CV̲InterpolationMethod = “linear”(内挿型)属性は,被覆の評価で使用する
内挿法を識別する。既定値は,“linear”(線形)であるが,応用スキーマで他の内挿法を定義してもよい。
11.2.3 curve
curve (position: DirectPosition, tolerance: Distance = 0): CV̲ValueCurve(曲線)操作は,DirectPositionを入
力として受け取り,そのDirectPositionに最も近いCV̲ValueCurveを返す。この操作は,DirectPositionが,
CV̲SegmentedCurveCoverageの中のどの一つのCV̲ValueCurveに対しても接近していない(すなわち,
toleranceパラメタによって規定された距離以内でない)場合,エラーメッセージを返す。torelanceの既定
値は,0である。
11.2.4 CoverageFunction
CoverageFunction(被覆機能)関連は,CV̲SegmentedCurveCoverageを,それを構成するCV̲ValueCurves
に関連付ける。
11.3 CV̲ValueCurve
11.3.1 一般
CV̲ValueCurve(曲線値)は,GM̲Curve,及びその曲線上にある全ての位置で地物属性値を決定する追
加情報から構成される。CV̲ValueCurveは,JIS X 7107のGM̲Curveで定義する弧長パラメタ化の操作に
依存する。
CoverageFunction
Control
Control
CoverageFunction
Segmentation
Control
45
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11.3.2 geometry
geometry: GM̲Curve(幾何)属性は,このCV̲ValueCurveの基本となるGM̲Curveである。
11.3.3 segment
segment (position: DirectPosition): Set <CV̲ValueSegment>(分割値)操作は,DirectPositionを入力として
受け取り,そのDirectPositionに最も近いCV̲ValueSegmentの集合を返す。この操作は,GM̲Curveで定義
するparamForPoint操作を呼び出し,入力DirectPositionに対応するDistanceパラメタを得る。paramForPoint
は,入力DirectPositionに最も近いGM̲Curve上の位置のためのパラメタ値を返す。場合によっては,
paramForPointは,複数のパラメタ値を返すことがある。segment操作は,通常,一つのCV̲ValueSegment
を返す。この操作が,一つのCV̲ValueSegmentを返すのではないのは,次の三つの場合である。
a) CV̲ValueCurveが単純ではない場合。入力DirectPositionに最も近いこの曲線上の位置が,自己交差の
点となる。paramForPointは,二つ以上のパラメタ値を返す。この場合,segment操作は例外を返す。
b) CV̲ValueCurve上に,入力DirectPositionから同じ最小距離となる二つ以上の位置がある場合。
paramForPoint操作は,二つ以上のパラメタ値を返す。この場合,segment操作は例外を返す。
c) 入力DirectPositionに最も近いCV̲ValueCurve上の位置が,一つのCV̲ValueSegmentの終点,及び次
のCV̲ValueSegmentの始点に当たる場合。この場合,操作は両方のCV̲ValueSegmentを返す。
11.3.4 Segmentation
Segmentation(分割)関連は,CV̲ValueCurveを,それを構成するCV̲ValueSegmentの列に関連付ける。
11.3.5 Control
Control(基準)関連は,CV̲ValueCurveを,CV̲ValueCurveに沿った内挿のための制御値を与える二つ
又はそれ以上のCV̲PointValuePairの集合に関連付ける。
11.4 CV̲ValueSegment
11.4.1 一般
CV̲ValueSegment(分割値)の境界は,その親クラスCV̲ValueCurveの基本となるGM̲Curveの弧長パ
ラメタの二つの値によって規定する。
11.4.2 startParameter
startParameter: Distance(始点パラメタ)属性は,CV̲ValueSegmentの始点となる親曲線の弧長パラメタ
値である。
11.4.3 endParameter
endParameter: Distance(終点パラメタ)属性は,CV̲ValueSegmentの終点となる親曲線の弧長パラメタ値
である。
11.4.4 Control
Control(基準)関連は,CV̲ValueSegmentを,内挿のための制御値を与えるCV̲PointValuePairに関連付
ける。線形内挿は,最低二つの制御値を必要とし,通常,それらは,CV̲ValueSegmentの始点及び終点に
おける制御値である。より高い次数の関数による内挿を提供するには,追加的な制御値が必要となる。
11.5 評価
CV̲SegmentedCurveCoverageは,CV̲Coverageからevaluate (p: DirectPosition, list: Sequence
<CharacterString>): Set <Record>操作を継承する。CV̲SegmentedCurveCoverageの評価には,幾つかの段階
がある。
1) curve操作を呼び出し,入力DirectPositionを含むCV̲ValueCurveを見つける。
2) CV̲ValueCurve.segment操作を呼び出し,入力DirectPositionを含むCV̲ValueSegmentを見つける。
46
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3) CV̲ValueCurve.segmentが,一つのCV̲ValueSegmentを返した場合,指定されたinterpolationTypeを使
用して関連するcontrolValueから地物属性値を計算する。
4) CV̲ValueCurve.segmentが,一対の隣接するCV̲ValueSegmentを返した場合,CV̲Coverageから継承
されるcommonPointRule属性によって規定された規則に従って地物属性値を計算する。
47
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
抽象試験項目群
A.1
被覆インタフェースのための抽象試験
A.1.1 単純被覆インタフェース
単純被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,domainExtent属性,evaluate操作,Domain関連,Range
関連及びCoordinateReferenceSystem関連をもつCV̲Coverageをインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 5.3及び5.4
d) 試験種類 機能
A.1.2 離散被覆インタフェース
離散被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1の全ての要件を満たすと同時に,locate操作,find
操作,list操作,及びCoverageFunction関連をもつ,CV̲DiscreteCoverageとその下位型とをインスタ
ンス化することを検証し,さらに,geometry属性及びvalue属性をもつCV̲GeometryValuePairクラス
をインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1,5.7,5.8及び箇条6
d) 試験種類 機能
A.1.3 ティーセンポリゴン被覆インタフェース
ティーセンポリゴン被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1の全ての要件を満たすと同時に,規定される属性,
操作,関連及び制約条件をもつCV̲ThiessenPolygonCoverageクラス及びCV̲ThiessenValuePolygonク
ラスをインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1及び箇条7
d) 試験種類 機能
A.1.4 四辺形グリッド被覆インタフェース
四辺形グリッド被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1の全ての要件を満たすと同時に,規定される属性,
操作,関連及び制約条件をもつCV̲Grid,CV̲GridPoint,CV̲GridCell,CV̲GridValuesMatrix,
CV̲GridPointValuePair,CV̲DiscreteGridPointCoverage,CV̲ContinuousGridCoverage
及び
CV̲GridValueCellの各クラスをインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1及び箇条8
d) 試験種類 機能
A.1.5 六角形グリッド被覆インタフェース
48
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
六角形グリッド被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1の全ての要件を満たすと同時に,規定される属性,
操作,関連及び制約条件をもつCV̲HexagonalGridCoverage,CV̲ValueHexagon,CV̲Grid,
CV̲RectifiedGrid,CV̲GridValuesMatrix及びCV̲GridPointValuePairの各クラスをインスタンス化する
ことを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1,8.3〜8.13及び箇条9
d) 試験種類 機能
A.1.6 TIN被覆インタフェース
TIN被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1の全ての要件を満たすと同時に,規定される属性,
操作,関連及び制約条件をもつCV̲TINCoverage及びCV̲ValueTriangleの各クラスをインスタンス化
することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1及び箇条10
d) 試験種類 機能
A.1.7 分割曲線被覆インタフェース
分割曲線被覆インタフェース試験の構成は,次による。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1の全ての要件を満たすと同時に,規定される属性,
操作,関連及び制約条件をもつCV̲SegmentedCurveCoverage,CV̲ValueCurve及びCV̲ValueSegment
の各クラスをインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1及び箇条11
d) 試験種類 機能
A.2
被覆交換のための抽象試験
A.2.1 離散被覆交換
離散被覆交換試験の構成は,次による。
a) 試験目的 交換スキーマが,CV̲DiscreteCoverage又はその下位型の一つの被覆について,必須の属性
及び関連を正しく実装することを検証する。
b) 試験方法 交換スキーマの文書を検査する。
c) 参照 箇条5及び箇条6
d) 試験種類 機能
A.2.2 ティーセンポリゴン被覆交換
ティーセンポリゴン被覆交換試験の構成は,次による。
a) 試験目的 交換スキーマが,CV̲ThiessenPolygonCoverageの必須の属性及び関連を正しく実装するこ
とを検証する。
b) 試験方法 交換スキーマの文書を検査する。
c) 参照 箇条7
d) 試験種類 機能
49
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.2.3 四辺形グリッド被覆交換
四辺形グリッド被覆交換試験の構成は,次による。
a) 試験目的 交換スキーマが,CV̲ContinuousQuadrilateralGridCoverageの必須の属性及び関連を正しく
実装することを検証する。
b) 試験方法 交換スキーマの文書を検査する。
c) 参照 箇条8
d) 試験種類 機能
A.2.4 六角形グリッド被覆交換
六角形グリッド被覆交換試験の構成は,次による。
a) 試験目的 交換スキーマが,CV̲HexagonalGridCoverageの必須の属性及び関連を正しく実装すること
を検証する。
b) 試験方法 交換スキーマの文書を検査する。
c) 参照 箇条9
d) 試験種類 機能
A.2.5 TIN被覆交換
TIN被覆交換試験の構成は,次による。
a) 試験目的 交換スキーマが,CV̲TINCoverageの必須の属性及び関連を正しく実装することを検証す
る。
b) 試験方法 交換スキーマの文書を検査する。
c) 参照 箇条10
d) 試験種類 機能
A.2.6 分割曲線被覆交換
分割曲線被覆交換試験の構成は,次による。
a) 試験目的 交換スキーマが,CV̲SegmentedCurveCoverageの必須の属性及び関連を正しく実装するこ
とを検証する。
b) 試験方法 交換スキーマの文書を検査する。
c) 参照 箇条11
d) 試験種類 機能

50
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
UML表記法
B.1
一般
この附属書では,この規格のUML図で用いられるUML表記法について簡単に説明する。
B.2
クラス
UMLクラス(図B.1参照)は,モデル化されるシステム内の概念を表す。UMLクラスは,同じ属性,
操作,方法,関係及び意味を共有するオブジェクト集合の記述である。クラスは,水平線で区切られた三
つの区画をもつ実線輪郭の長方形で表す。一段目の名前区画には,クラス名及びクラスのその他の一般的
特性(ステレオタイプなど)を記述する。二段目の区画には,属性の一覧を記述する。三段目の区画には,
操作の一覧を記述する。図を簡素化するために,属性区画及び操作区画を省略してもよい。ただし,省略
しても,属性又は操作がないことを意味するわけではない。
英字でクラス図を記述する場合は,ISO/TS 19103の規定によれば,クラス名には空白を含んではならず,
名前における個々の語の最初の文字は,大文字でなければならない。
図B.1−UMLクラス
B.3
ステレオタイプ
ステレオタイプは意味を拡張するもので,既存の型及びクラスの構造を拡張するものではない。この規
格で使用するクラスのステレオタイプを,次に示す。
<<DataType>> 識別性(独立した存在及び副作用の可能性)を欠く値集合の記述子。データ型には,あ
らかじめ定義された基本的な型及び使用者が定義できる型がある。DataTypeは,操作をほとんど又は全く
もたず,伝送,保存,符号化又は永続保存のために他のクラスの抽象状態を保持することを主な目的とす
るクラスである。
<<Enumeration>> そのインスタンスが,名前付けしたリテラル値の一覧を形成するデータ型。列挙する
名前及びそのリテラル値の両方を宣言する。列挙は,クラス内で取り得る,明確に定義された値の短いリ
ストを意味する。典型的な例は,二つ(又は三つ)の取ることが可能な値,すなわち,TRUE,FALSE(及
びNULL)だけをもつ真偽値型である。ほとんどの列挙は,他に特に規定がない場合,整数の順次集合と
して符号化される。実際の符号化は,通常,プログラム言語コンパイラにとってだけ有用である。
ISO/TS 19103で定義する<<CodeList>>は,辞書型のキーとして文字列値を用い,文字列型の値を返す柔
軟な列挙であり,例えば,Dictionary<String, String>がある。符号リストは,取ることが可能な値の長いリ
{Constraint}
51
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ストを表現するのに有用である。リストの要素が完全に知られている場合,列挙を使用しなければならな
い。要素の起こりそうな値しか分からない場合は,符号リストを使用しなければならない。列挙された符
号リストは,JIS X 0304などの規格に従って符号化してもよい。符号リストは,その値が使用者の目に触
れる可能性が高いため,覚えやすいものであることが多い。実装によって様々な符号化体系を使うことも
あるが,他の符号化体系への変換テーブルが用意されていることが多い。
<<Type>>は,JIS X 4170で定義するクラスのステレオタイプである。Typeは,オブジェクトの物理的実
装を定義することなく,オブジェクトの定義域を,そのオブジェクトに適用できる操作とともに規定する
ために使用する。Typeは,属性及び関連をもつことができる。この属性及び関連は,型の操作の振る舞い
を規定する目的でだけ定義され,状態データの実際の実装は表さない。
B.4
属性
属性は,クラスのオブジェクトに共通する特性を表す。属性は,属性の特性を記述する要素に構文解析
することができるテキスト文字列によって指定する。
visibility name [multiplicity]: type-expression = initial-value
visibilityは,public(“+”で示される。)又はprivate(“-”で示される。)を取り得る。
nameは,文字列である。英字でクラス図を記述する場合は,ISO/TS 19103の規定によれば,属性名に
は空白を含んではならず,属性名の最初の文字は小文字でなければならず,属性名における最初の語に続
く個々の語の最初の文字は大文字でなければならない。
multiplicityは,クラスのインスタンスが所定の属性についてもつことができる値の数を指定する。
multiplicityの表記法は,B.10に示す。
type-expressionは,属性のデータ型を識別する。
initial-valueは,属性の初期値を指定する。
B.5
操作
操作は,オブジェクトから要求され得るサービスを表す。操作は,操作の特性を記述する要素に構文解
析することができるテキスト文字列によって指定する。
visibility name (parameter-list): return-type-expression {property-string}
visibilityは,public(“+”で示される。)又はprivate(“-”で示される。)を取り得る。
nameは,文字列である。英字でクラス図を記述する場合は,ISO/TS 19103の規定によれば,操作名に
は空白を含んではならず,操作名の最初の文字は小文字でなければならず,操作名における最初の語に続
く個々の語の最初の文字は大文字でなければならない。
parameter-listは,それぞれがパラメタ名及びデータ型によって記述されるパラメタの一覧である。他に
特に規定がなければ,これらは入力パラメタとする。
出力パラメタreturn-type-expressionは,操作が返す値のデータ型を識別する。
{property-string}は,要素に適用する特性値を示す任意のフィールドである。
B.6
制約
制約は,意味論的条件又は制約を指定する。JIS X 4170は制約を記述するためのオブジェクト制約言語
を規定しているが,任意の形式的表記法又は自然言語を用いて制約を記述してもよい。制約は,波括弧{ }
内のテキスト文字列として示す。制約は,制約を適用する要素の近くに配置する。要素の表記法がテキス
52
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ト文字列(属性など)である場合,制約文字列が波括弧内の要素テキスト文字列に続いてもよい。リスト
内の要素として含まれる制約は,リスト内の次の制約要素又はリストの端までの,リスト内の後続要素全
てに適用する。
B.7
注記
注記には,テキスト情報を含む。注記は,点線によって0個以上のモデル要素に付加し,右上隅の“隅
が曲がった”長方形として示す。注記は,注釈又は制約を記述するために使用してもよい。
B.8
関連
関連(図B.2参照)は,クラスのインスタンス間の意味論的な結び付きを指定する,クラス間の関係で
ある。関連は,クラス長方形同士を結ぶ実線で表す。関連の名前を,実線の近く(ただし,実線の端付近
ではない。)に文字列を配置して表してもよい。英字でクラス図を記述する場合は,ISO/TS 19103の規定
によれば,関連名には空白を含んではならず,名前における個々の語の最初の文字は大文字でなければな
らない。関連の端には,多重度及び役割名を含め,クラスに関する情報を付加する。
図B.2−UML関連
B.9
役割名
関連の端に付加する役割名は,関連の他方の端のクラスに対するそのクラスの役割を指定する。図B.2
では,roleAlphaは,Alphaという名前のクラスがBetaという名前のクラスに対してもつ役割を示す。役割
名は,文字列で表す。英字でクラス図を記述する場合は,ISO/TS 19103の規定によれば,役割名には空白
を含んではならず,役割名の最初の文字は小文字でなければならず,役割名における最初の語に続く個々
の語の最初の文字は大文字でなければならない。
B.10 多重度
多重度は,関連の他方の端におけるクラスと関連付けてもよいクラスのインスタンス数を指定する。図
B.3に示した値は,全て有効である。これらの値の意味を,次に示す。
− Alphaの0個又は一つのインスタンスをBetaの一つのインスタンスと関連付けてもよい。
− Betaの0個又は一つ以上のインスタンスをAlphaの一つのインスタンスと関連付けてもよい。
− Gammaの一つのインスタンスだけ,Deltaの一つのインスタンスと関連付けてもよい。
− Deltaのn個のインスタンスをGammaの一つのインスタンスと関連付けてもよい(nは整数)。
− Phiのインスタンスと関連付けてもよいEpsilonのインスタンスの数は,n1〜n2の範囲であってもよい
(n1及びn2は整数)。
− Phiのn個以上のインスタンスをEpsilonの一つのインスタンスと関連付けてもよい。
AssociationName
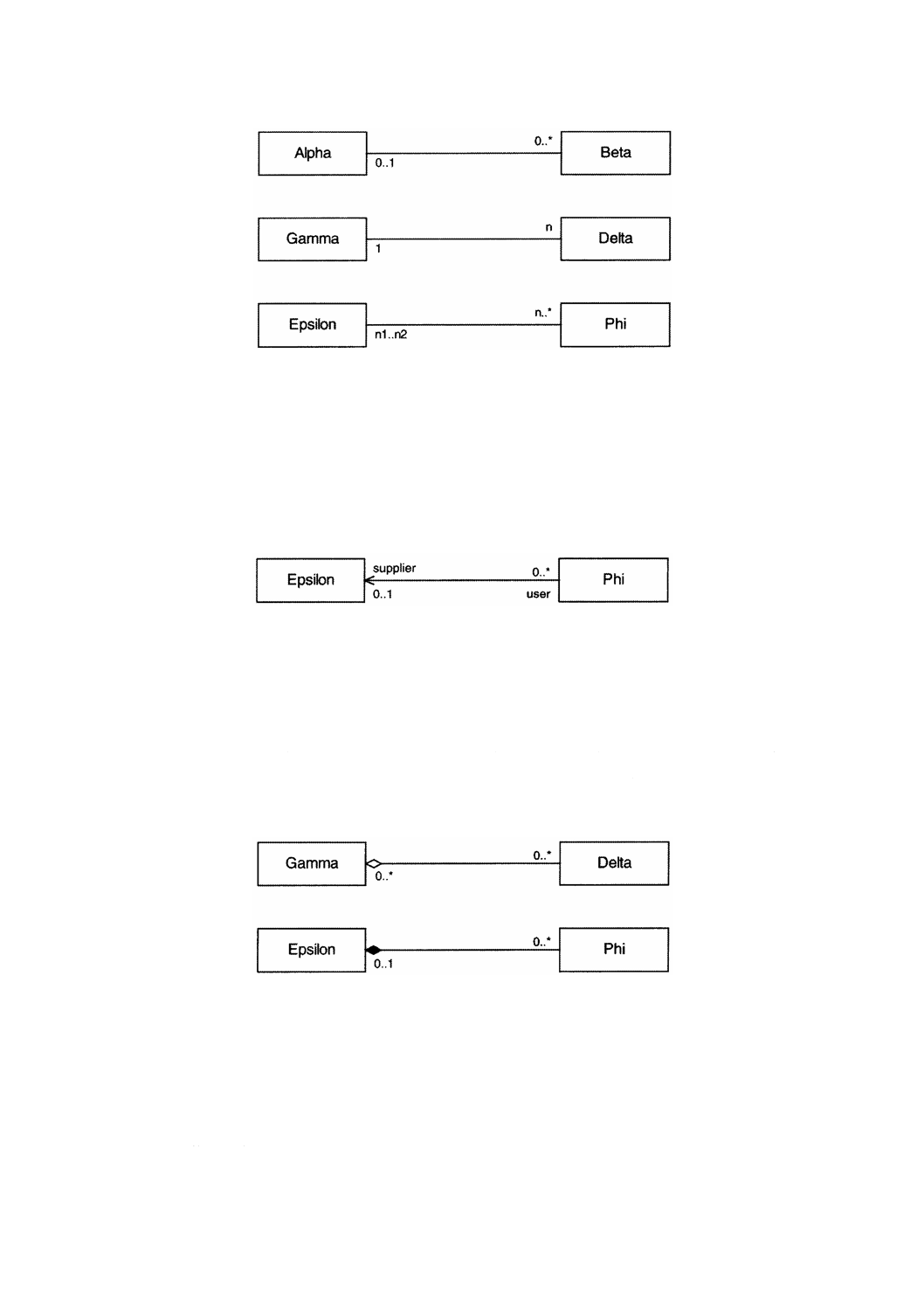
53
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.3−UMLの多重度
B.11 誘導可能性
矢印を関連経路の端に付けて,矢印が付けられたクラスへ誘導可能であることを示してもよい。例え
ば,図B.4では,使用者から供給者へ関連が誘導可能となる。これは,クラスPhiのインスタンスは,ク
ラスEpsilonのインスタンスが保持する情報にアクセスできることを意味する。例えば,Epsilonを指定す
る操作は,Phiの属性値を使用することができる。
図B.4−UMLの誘導可能性
B.12 集成
関連を使用して,クラス間の集成関係又は合成関係を示してもよい。関連の端にある白いひし形は,そ
の端におけるクラスが,関連の他方の端におけるクラスのインスタンスの集成であることを示す。例えば,
図B.5のGammaという名前のクラスは,Deltaという名前のクラスの0個以上のインスタンスの集成であ
る。集成は,弱い合成とみなされる。集成の構成要素は集成から独立して存在することができ,複数の集
成の構成要素になることができる。
図B.5−集成及び合成
B.13 合成
関連の端にある黒いひし形は,その端におけるクラスが,関連の他方の端におけるクラスのインスタン
スから構成されていることを示す。例えば,図B.5のEpsilonという名前のクラスは,Phiという名前のク
ラスの0個以上のインスタンスから構成される。合成の構成要素は,合成クラスから独立して存在するこ
とはできず,複数の合成クラスの構成要素になることもできない。
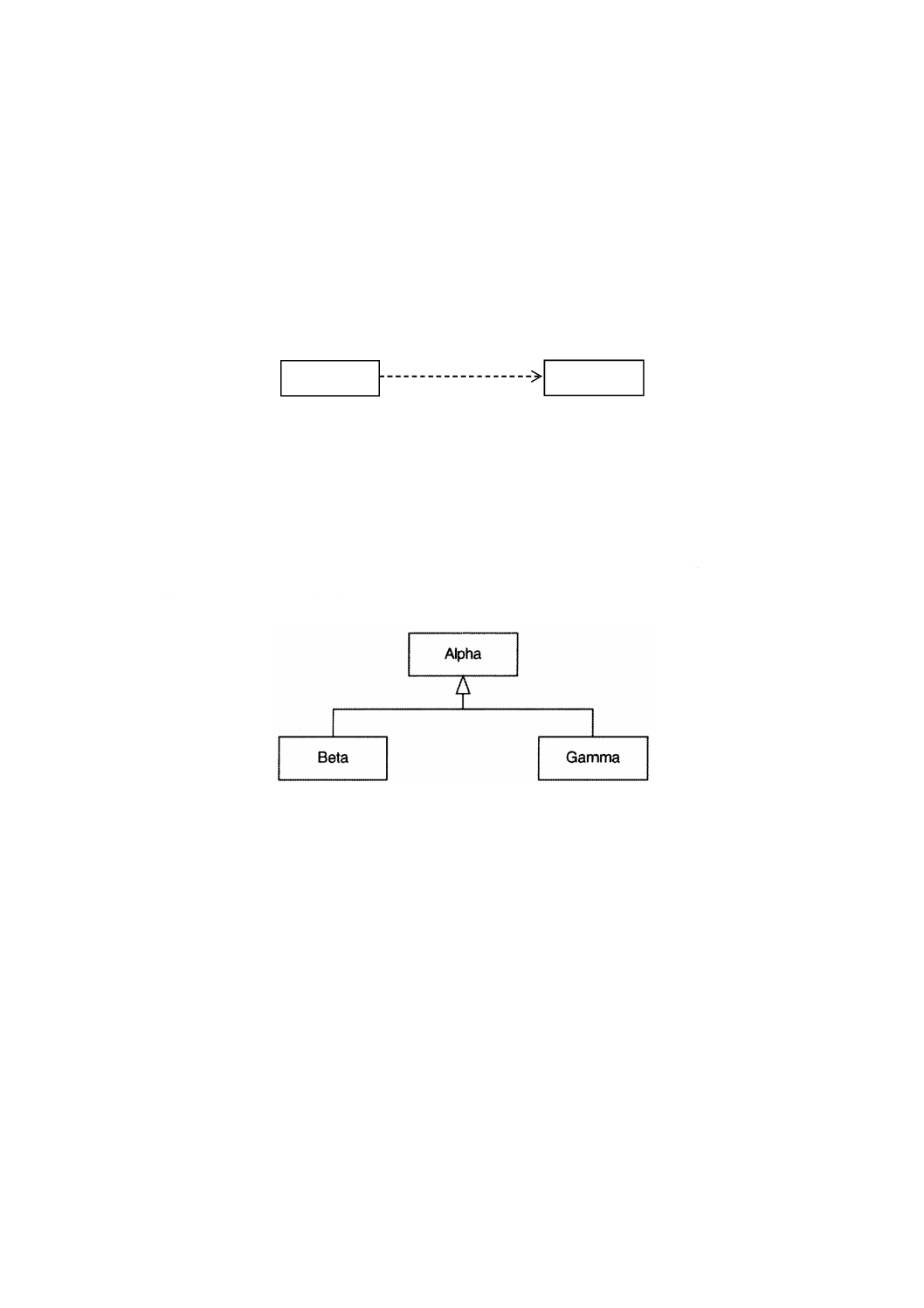
54
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.14 依存関係
依存関係は,一つ以上の要素の実装又は機能にとって,一つ以上の他の要素の存在が必要であるという
ことを示す。依存関係は,二つのモデル要素(又は二つのモデル要素集合)間の意味論的関係を示す。依
存関係はモデル要素自体を関係付けるものであり,その意味に対するインスタンス集合を必要としない。
依存関係は,二つのモデル要素間に引かれた点線矢印として示される。矢印の末端のモデル要素(従属者)
は,矢印の先端のモデル要素(供給者)に依存する。依存関係の種類は,<<import>>,<<refine>>,<<use>>
などギュメ(“<<”及び“>>”)内のキーワードで示してもよい。図B.6の例では,EpsilonがPhiに対する
<<use>>依存関係をもつ。
図B.6−依存関係
B.15 汎化
JIS X 4170では,汎化(図B.7参照)は,より一般的な要素とより具体的な要素との間の分類関係とし
て定義する。より具体的な要素は,より一般的な要素と完全に整合しており,追加情報を含む。より一般
的な要素が許可されている場合,より具体的な要素のインスタンスを用いてもよい。汎化は,子(下位ク
ラスなど,より具体的な要素)から親(上位クラスなど,より一般的な要素)への実線経路として示し,
より一般的な要素に接するこの経路の末端には大きな白抜きの三角形を付ける。
図B.7−UMLの汎化
Epsilon
Phi
<<use>>
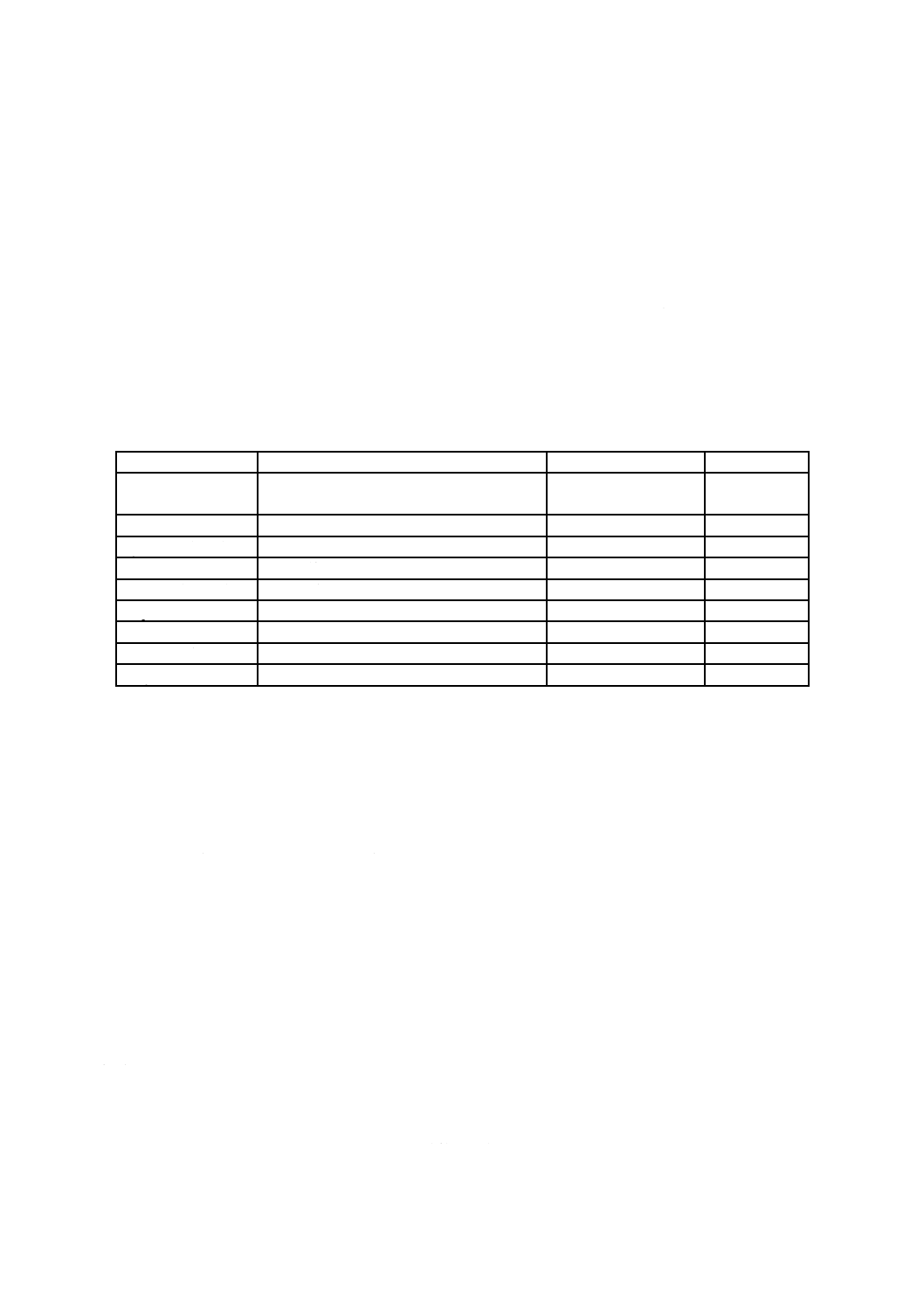
55
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
内挿法
C.1
一般
連続被覆の評価には,この連続被覆への基準として与えられた離散被覆の定義域において,幾何オブジ
ェクトと関連付けられた既知の地物属性値及び地物属性値の間の内挿が含まれる。符号リスト
CV̲InterpolationMethod(5.9.2参照)には,九つの内挿法が含まれる。いずれも,指定された幾何構成の文
脈で使用する(表C.1参照)。CV̲InterpolationMethodは符号リストであるため,応用スキーマにおいて追
加の内挿法を指定するように拡張してもよい。
表C.1−内挿法
方法
被覆型
値オブジェクトの次元
箇条
Nearest
Neighbour
(最近隣)
全て
全て
C.2
Linear(線形)
分割曲線
1
C.3
Quadratic(二次)
分割曲線
1
C.4
Cubic(三次)
分割曲線
1
C.5
Bilinear(双一次)
四辺形グリッド
2
C.6
Biquadratic(双二次) 四辺形グリッド
2
C.7
Bicubic(双三次)
四辺形グリッド
2
C.8
Lost Area(喪失領域) ティーセンポリゴン,六角形グリッド
2
C.9
Barycetric(重心)
TIN
2
C.10
C.2
最近隣内挿
最近隣内挿は,任意の被覆に適用することができる。この内挿は,被覆の定義域の中で最も近い定義域
オブジェクトと関連した地物属性値を直接位置に割り付けることによって,この直接位置で地物属性値を
生成する。最近隣内挿は,離散被覆を,被覆の定義域における定義域オブジェクトの凸包に対して定義さ
れた階段関数に拡張する。最近隣内挿は,この規格で記述されている中で,名目尺度値又は順序尺度値を
もつ属性の内挿に使用可能な唯一の内挿法である。
C.3
線形内挿
線形内挿は,値曲線に沿って行われる内挿で広く使用する(11.3参照)。この内挿は,地物属性値が値区
分に沿った距離に比例して変化するという想定に基づく。
v=a+bx
線形内挿は,二つの点値対を結ぶ線分に沿って地物属性値を内挿するために使用することもある。また,
位置がアーク長パラメタの値によって記述される場合,あらゆる形態の曲線上にある位置で地物属性値を
内挿するために使用することができる。
二つの点値対(ps, vs)及び(pt, vt)があり,psが値区分の始点,ptが値区分の終点,vsとvtとがこれらの点に
対応する地物属性値である場合,直接位置piと対応する地物属性値viは,次のようになる。
vi=vs+(vt−vs)[( pi−ps)/( pt−ps)]
56
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 離散点被覆の場合,階段関数の“階段”は,被覆の定義域における点の集合によって生成され
たティーセンポリゴンとなる。
C.4
二次内挿
二次内挿も,曲線上での内挿に使用する。この内挿は,地物属性値が値区分に沿った距離の二次関数と
して変化するという想定に基づく。
v=a+bx+cx2
ここで,aは値区分の始点における地物属性値であり,vは曲線上の始点からx離れた位置の地物属性値
となる。基準値を与えてこの関数の係数を計算するには,三つの点値対が必要となる。
C.5
三次内挿
三次内挿も,曲線上での内挿に使用する。この内挿は,地物属性値が値区分に沿った距離の三次関数と
して変化するという想定に基づく。
v=a+bx+cx2+dx3
ここで,aは値区分の始点における地物属性値であり,vは曲線上の始点からx離れた位置の地物属性値
となる。基準値を与えてこの関数の係数を計算するには,四つの点値対が必要となる。
C.6
双一次内挿
双一次内挿は,四辺形グリッド内の直接位置で地物属性値を内挿するために使用する。この内挿は,地
物属性値がグリッドセル内の位置の双一次関数として変化するという想定に基づく。
v=a+bx+cy+dxy
頂点がV,V+V1,V+V2,及びV+V1+V2であって,それぞれの頂点における地物属性値がv1,v2,v3
及びv4であるグリッドセル(ここで,V1及びV2はグリッドのオフセットベクトル)に含まれる直接位置p
があるとする。ここで,i及びjは一意の数字であり,0≦i<1,0≦j<1,p=V+iV1+jV2であるとする。
この場合,pにおける地物属性値は,次のとおりである。
v=(1−i)(1−j)v1+i(1−j)v2+j(1−i)v3+ijv4
注記 未偏位修正グリッドでは,V1及びV2は,単位ベクトル(0,1)及び(1,0)になる。
C.7
双二次内挿
双二次内挿も,四辺形グリッド内の直接位置で地物属性値を計算するために使用する。この内挿は,地
物属性値がグリッドセル内の位置の双二次関数として変化するという想定に基づく。
v=a+bx+cy+dx2+exy+fy2+gx2y+hxy2+ix2y2
双二次内挿の実装のためのアルゴリズムに関する議論は,参考文献[6]を参照。
C.8
双三次内挿
双三次内挿も,四辺形グリッド内の直接位置で地物属性値を計算するために使用する。この内挿は,地
物属性値がグリッドセル内の位置の双三次関数として変化するという想定に基づく。
v=a0+a1x+a2y+a3x2+a4xy+a5y2+a6x2y+a7xy2+a8x2y2+a9x3+a10y3+a11x3y
+a12xy3+a13x3y2+a14x2y3+a15x3y3
双三次内挿の実装のためのアルゴリズムに関する議論は,参考文献[8]を参照。
57
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.9
喪失領域内挿
喪失領域内挿は,離散点被覆を,点被覆の定義域の凸包で定義した連続関数fに拡張する。
その場合,{p1, p2, …, pn}は,点被覆の定義域とし,{T1, T2, …, Tn}は,集合{p1, p2, …, pn}によって生成
されたティーセンポリゴンとする。
qが{p1, p2, …, pn}の凸包内の直接位置であるようなf (q)を計算する場合を考える。まず,{p1, p2, …, pn}
によって生成されたティーセンポリゴンを形成し,集合{p1, p2, …, pn}にqを追加し,n+1点の集合{p1, p2,
…, pn, q}に対応するティーセンポリゴンを形成する。qを含むポリゴンが,qを含む新しいポリゴンに対し
て“領域を喪失する”ような形で二つのポリゴンが隣接するという点を除き,二つのポリゴン集合は一致
する。
喪失領域内挿は,加重平均を形成し,それぞれの地物属性値は,qでポリゴンが新しいポリゴンに対し
て失った領域の程度に従って,pでの地物属性値を導く。より正式には,次のようになる。
a) 離散点被覆が点値対{(p1, v1), (p2, v2), …, (pn, vn)}によって特徴付けられると仮定する。
b) {p1, p2, …, pn, q}によって形成されたティーセンポリゴン集合の中で,qを含むポリゴンと隣接するの
は{T1, T2, …, Tk}である。
c) {p1, p2, …, pn}によって生成された集合から導かれた対応するティーセンポリゴンは,{T'1, T'2, …, T'k}
である。
d) i番目のポリゴンによって失われる面積は,T 'i−Tiである。
e) 失われた面積の合計は∑
)
(
i
iT
T'−
であり,その合計は,1〜kの間の全てのiにわたる(すなわち,合
計は,qを含むティーセンポリゴンに対して面積を失った全てのポリゴンにわたる。)。
なお,この合計は,pを含むティーセンポリゴンの領域と一致することに注意する必要がある。
f) qで内挿された地物属性値は,次のようになる。
(
)
[
]∑
∑
×
)
(
)
(
i
i
i
i
i
T
T'
T
T'
v
q
f
−
−
=
ここで,合計は同じ範囲i=1, …, k全体にわたる。
C.10 重心内挿
今,P,Q,Rが三角形の頂点であると仮定する。この三角形内にある任意の直接位置Sに対し,0≦i≦1,
0≦j≦1,0≦k≦1,及びi+j+k=1であるような一意な三つの数i,j及びkがある。この場合,次の方程
式が成り立つ。
S=iP+jQ+kR
この場合,数(i, j, k)は,Sの重心座標である。
CV̲PointValuePair (p1, v1),(p2, v2),及び(p3, v3)で構成する値三角形があり,直接位置Sがその内部にある
とすると,Sの重心座標は,S=ip1+jp2+kp3であるような(i, j, k)となり,Sでの地物属性値は,v=iv1+jv2
+kv3となる。
注記 “重心”という名称は,上述の方程式を使うとき,Sは,頂点P,Q,Rにそれぞれi,j及びk
という大きさの点質量をもつ三角形の重心となるという事実に由来している。質量を三つの隅
に割り当てるため,重心は,この三角形の中にある全ての直接位置を占めることができる。詳
細は,参考文献[5]を参照。
58
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
順次列挙
D.1
一般
順次列挙は,属性値レコードをグリッド点に割り当てる順序を指定する。CV̲SequenceType(8.16参照)
は,順次化の方法の型を識別するための符号リストを提供する。この附属書では,これらの型について詳
しく説明する。
グリッド座標値を単純な方法で増加(又は減少)させることを基礎とする順次化規則は幾つか存在する。
また,より複雑な空間充塡曲線も使用することができる。空間充塡曲線は,空間を規則的な方法で次第に
再分割し,再分割によって生まれた要素を一定の規則に従って結び付けることによって生成する。これら
は,グリッドの生成に使用できるほか,別々に定義されたグリッドの中でグリッド点又はグリッドセルに
順序付けを割り当てるときにも使用可能である。空間充塡曲線は,単純な座標値増加方法よりも,不規則
な形状をもつグリッド又は大きさが変化するセルでの順次化に適している。
いずれの場合にも,グリッドセルの順序付けは,一つのグリッド軸に沿って座標を増やしていくことに
よって開始する。この過程のある時点で,二番目のグリッド軸に沿って座標を増やす作業を開始し,その
後三番目のグリッド軸,更にそれ以降のグリッド軸でも同様の作業を開始し,最終的に全てのグリッド軸
の方向へと進展していく。この附属書に掲載する図は,その例である。属性CV̲SequenceRule.scanDirection
(8.15.3参照)は,走査を行う順序を識別する符号付き軸名の一覧を提供する。この一覧には,地物属性
値の交互配置を支援するための追加要素を含むことがある(交互配置に関する詳細な議論については,D.8
を参照。)。
順序列の中でグリッドセルの隣接する対が最大限に連結されているとき,その順序付けは連続であると
いう。グリッドセルの隣接する対が連結されていても最大限には連結されていないとき,その順序付けは
半連続であるという。セルの隣接する対が連結されていないとき,非連続であるという。
例 二次元の場合,一つのセルは,少なくとも一つの隅を共有するような八つのセルと連結している。
このセルは,一つの辺と二つの隅とを共有する四つのセルと最大限に連結している。三次元の場
合,セルは,面を共有するセルと最大限に連結している。
注記 この附属書に掲載する例図では,走査線の連続部分を実線で,非連続部分を破線で示す。
D.2
線形走査
線形(linear)走査(図D.1参照)では,地物属性値のレコードが,scanDirectionの一覧に入っている最
初のグリッド軸と平行な一本のグリッド線に沿う隣接するグリッド点に割り当てられる。その列の走査が
完了すると,地物属性値レコードの割当ては,最初のグリッド線と平行な次のグリッド線に移り,二番目
の軸と平行にグリッド線からグリッド線へと移っていく。グリッドが三次元の場合,順序付け過程は,一
つの平面にある全てのグリッド点に地物属性値レコードを割り付け,一つの平面が完了すると,他の平面
に移行し,その後グリッドの三番目の軸と平行に平面から平面へと移行し,完了する。この過程は,任意
の数の軸に拡張することができる。線形走査は,一つのグリッド線に沿うときだけ連続である。
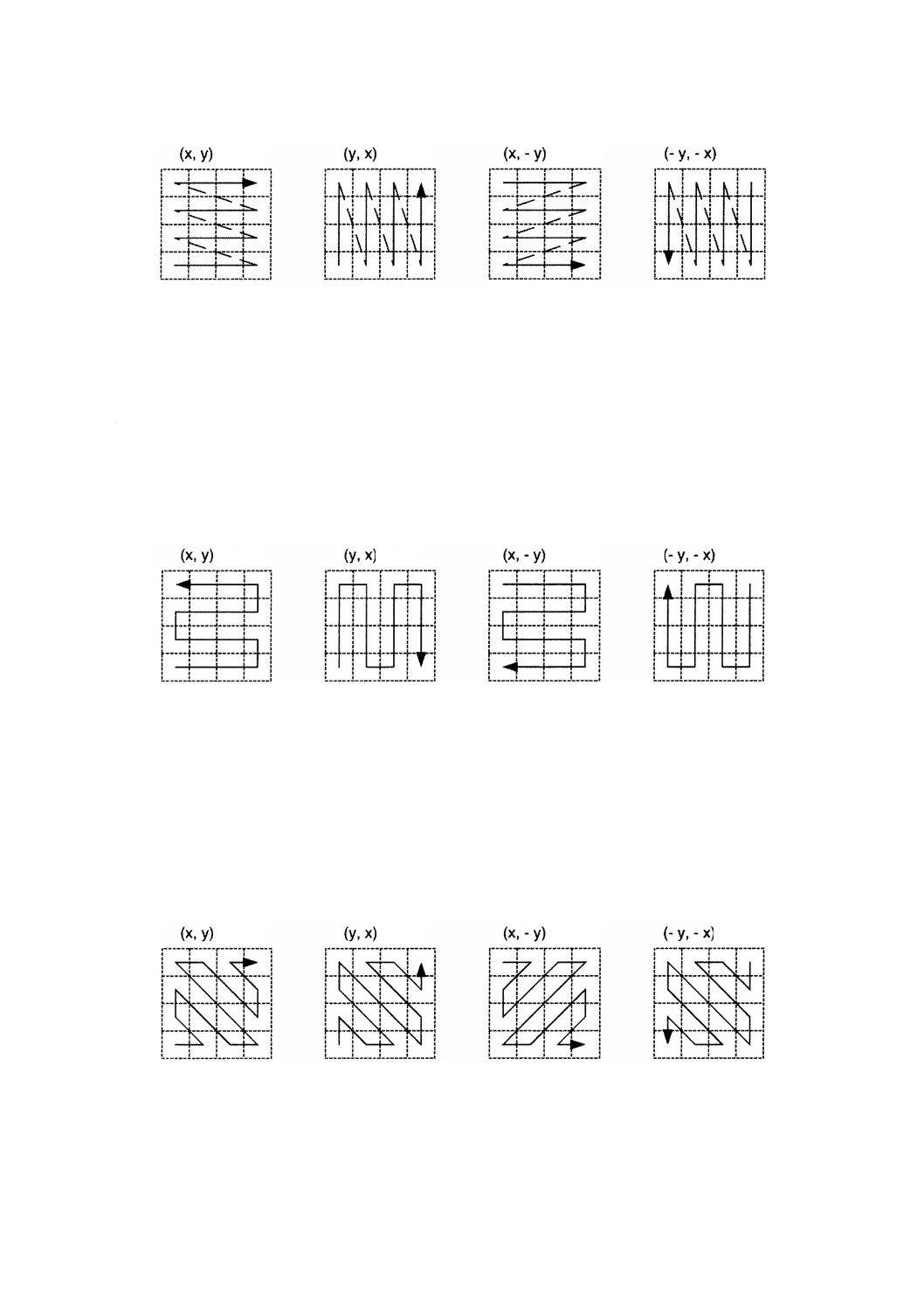
59
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 二次元グリッドの軸は,“行”(水平)及び“列”(垂直)と呼ばれることが多い。この場合,(x,y)順での走
査は,行走査又は行重視走査と呼ばれることもある。
図D.1−二次元グリッドにおける線形走査の例
D.3
牛耕走査
線形走査の一種で,牛耕(boustrophedonic)走査又はバイトオフセット走査と呼ばれるこの方式は,グ
リッド行が変わるたびに走査の方向が逆向きになる(図D.2参照)。三次元グリッドの場合も,面が変わる
と走査の方向が逆になる。牛耕走査は,連続である。
図D.2−二次元グリッドにおける牛耕走査の例
D.4
カントール対角線走査
カントール対角線(Cantor Diagonal)走査は,ジグザグ走査とも呼ばれており,グリッドの平行な対角
線に沿って方向を入れ替えながらグリッド点を順序付ける(図D.3参照)。走査パターンは,最初のステッ
プの方向に影響される。線形走査と同様,カントール対角線走査も,連続する平面で同じ走査パターンを
繰り返すことによって,三つ以上の次元のグリッドに拡張することができる。カントール対角線走査は,
一つの平面で半連続となる。
図D.3−二次元グリッドにおけるカントール対角線走査の例
順
順
順
順
順
順
順
順
順
順
順
順
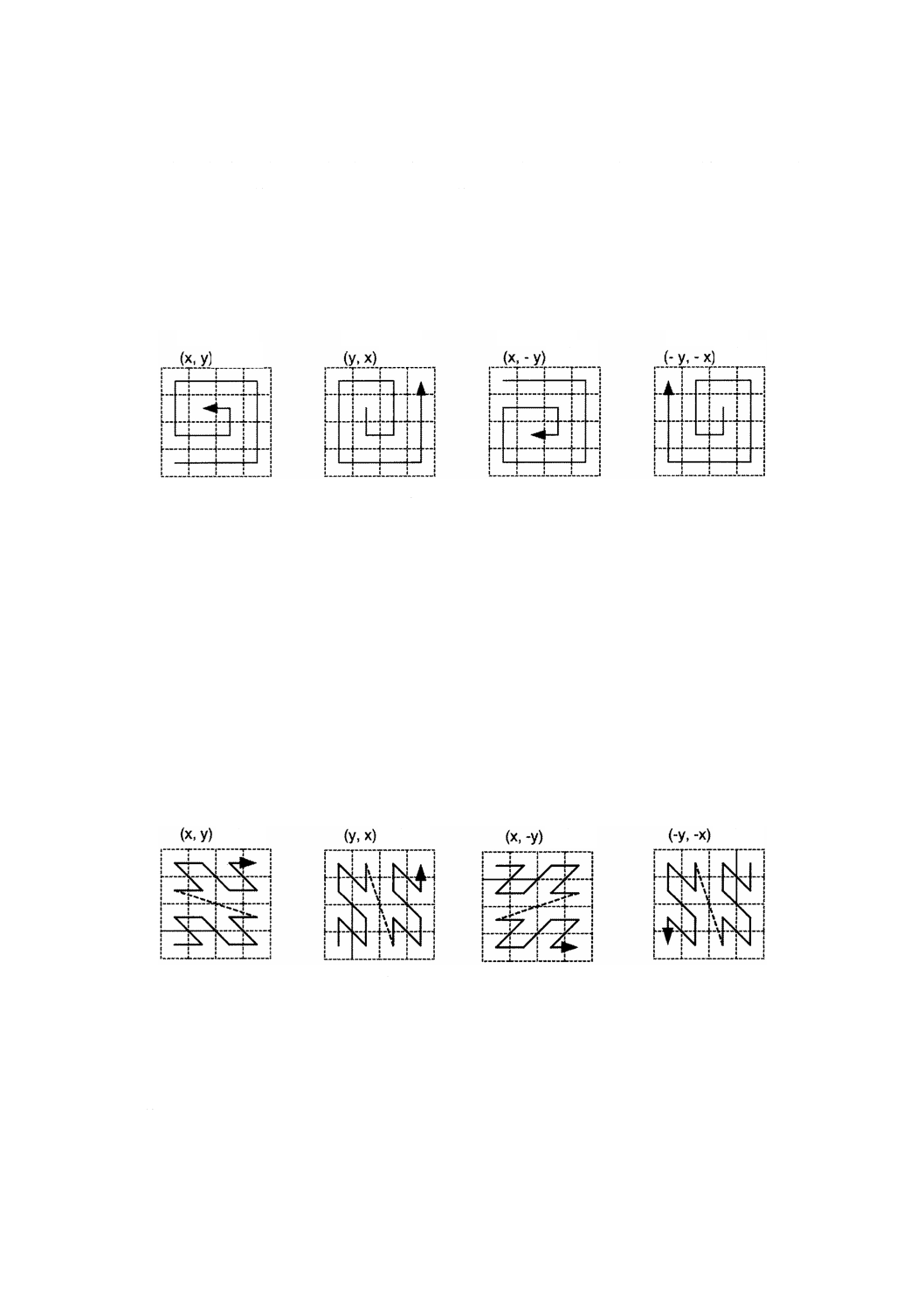
60
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.5
らせん走査
らせん(spiral)走査(図D.4参照)は,グリッドの中心(外向きらせん),又は隅(内向きらせん)の
いずれかから始まる。線形走査又はカントール対角線走査と同様,らせん走査も,隣接する平面でこの走
査パターンを繰り返すことによって,三つ以上の次元のグリッドに拡張することができる。らせん走査は,
いずれの平面でも連続するが,二次元以上のグリッドでの連続性は,平面が変わるたびに内向きと外向き
とを入れ替えることによってだけ維持される。
図D.4−二次元グリッドにおけるらせん走査の例
D.6
モートン順序付け
モートン(Morton)順序付けは,空間を次々と四分割し,四分割されたものを,図D.5で示すようなZ
パターンで順序付けることによって生成される空間充塡曲線を基にする。それぞれのグリッド点に対する
順序付け指標は,グリッド座標を2進数に変換し,得られる値のビットを交互配置することで計算できる。
CV̲SequenceRule.scanDirectionによって指定したグリッド軸の一覧がある場合,一本の軸に対応する座標
のビットは,一覧の次の軸に対応する座標のビットよりも位取りが低い。モートン順序付けは,任意の次
元に拡張することができる。また,モートン順序付けは,非連続である。
注記 曲線の形状は,四分区間の初期順序付けによって形成されるため,モートン順序付けは,Z順
序付けとも呼ばれている。
図D.5−二次元グリッドにおけるモートン順序付けの例
モートン順序付け技法によって生成されるグリッドは,正方形になり,各方向におけるその大きさは,2
の累乗の倍数になる。しかし,指標生成のためのビット交互配置技法は,不規則な形状又は異なる大きさ
のグリッドセルをもつようなグリッドを含め(図D.6参照),あらゆるグリッドのグリッド点を順序付ける
ために使用できる。
内向き
内向き
外向き
外向き
順
順
順
順
順
順
順
順
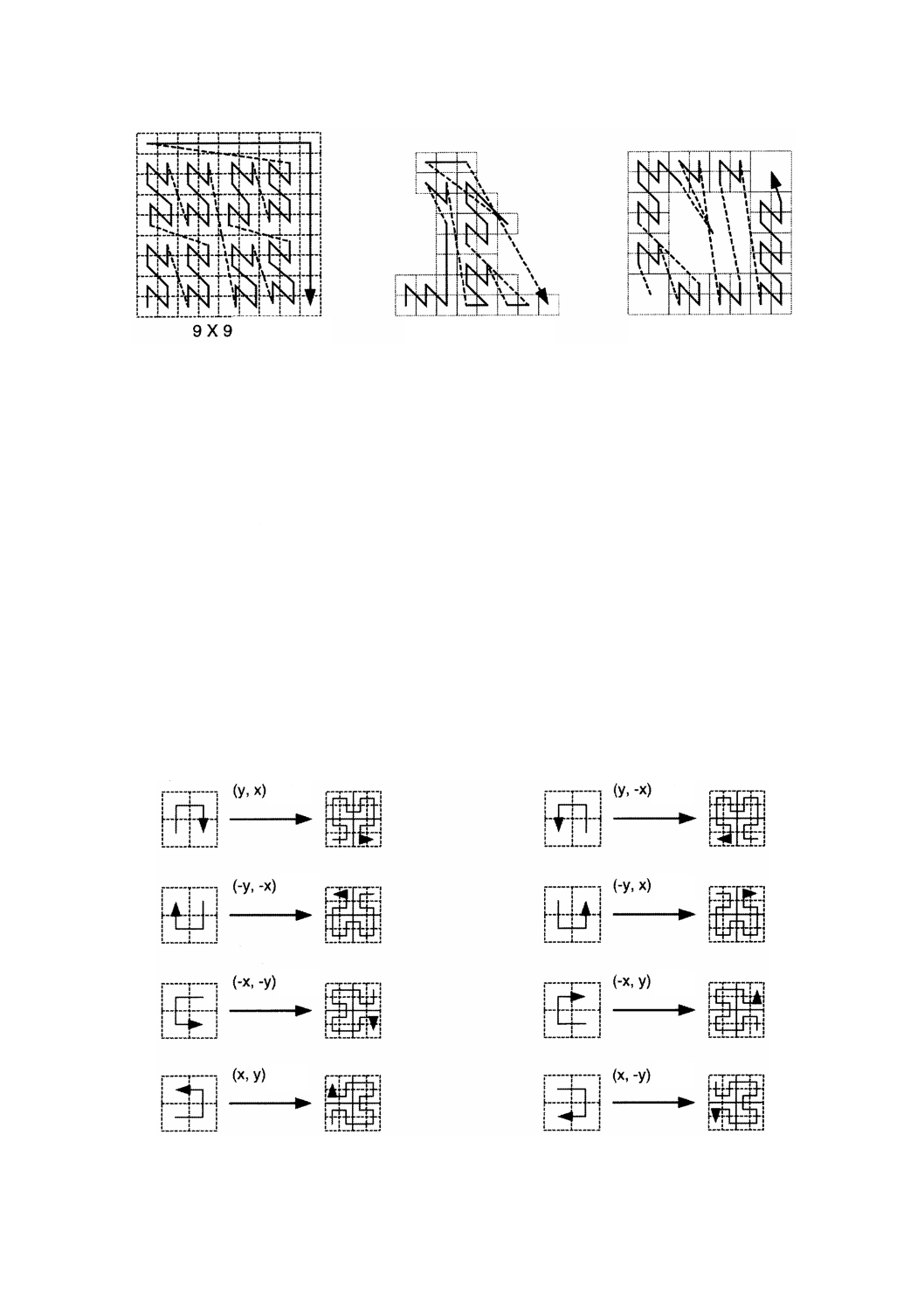
61
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.6−不規則なグリッドにおけるモートン順序付けの例
D.7
ヒルベルト順序付け
モートン順序付けと同様,ヒルベルト(Hilbert)順序付けも,空間を次々と四分割することによって生
成される空間充塡曲線を基にするが,分割の初期パターンに違いがある。分割を進めるとき,曲線の一部
を異なるパターンに置き換える作業が含まれる(図D.7参照)が,これがモートン順序付けのような一つ
のパターンの単純な置換えとは異なる。ヒルベルト順序付けのパターンには,二つの集合がある。図の左
側の列は,走査方向が同じ(両方ともプラス又は両方ともマイナス)向きのパターンの集合である。一方,
右側の列は,走査方向が反対(一方はプラス,他方はマイナス)の向きのパターンの集合である。ヒルベ
ルト曲線は,同じ集合のパターンから構成され,その集合では,全てのパターンを使用する。
注記 四分割区間の最初の期順序付けの曲線の形にちな(因)んで,ヒルベルト順序付けは,π順序
付けとも呼ばれる。
順序付け指標の操作は,モートン順序付けよりも,ヒルベルト順序付けに対応するものの方が入り組ん
でいる。二次元の場合に対応するアルゴリズム(図D.8参照)は,参考文献[7]及び[8]に記述されている。三
次元ヒルベルト曲線は,参考文献[9]で論じられている。ヒルベルト順序付けは,連続である。
図D.7−ヒルベルト曲線を生成するための置き換えパターン
グリッド
不規則な形状
大きさの異なるセル
順
順
順
順
順
順
順
順
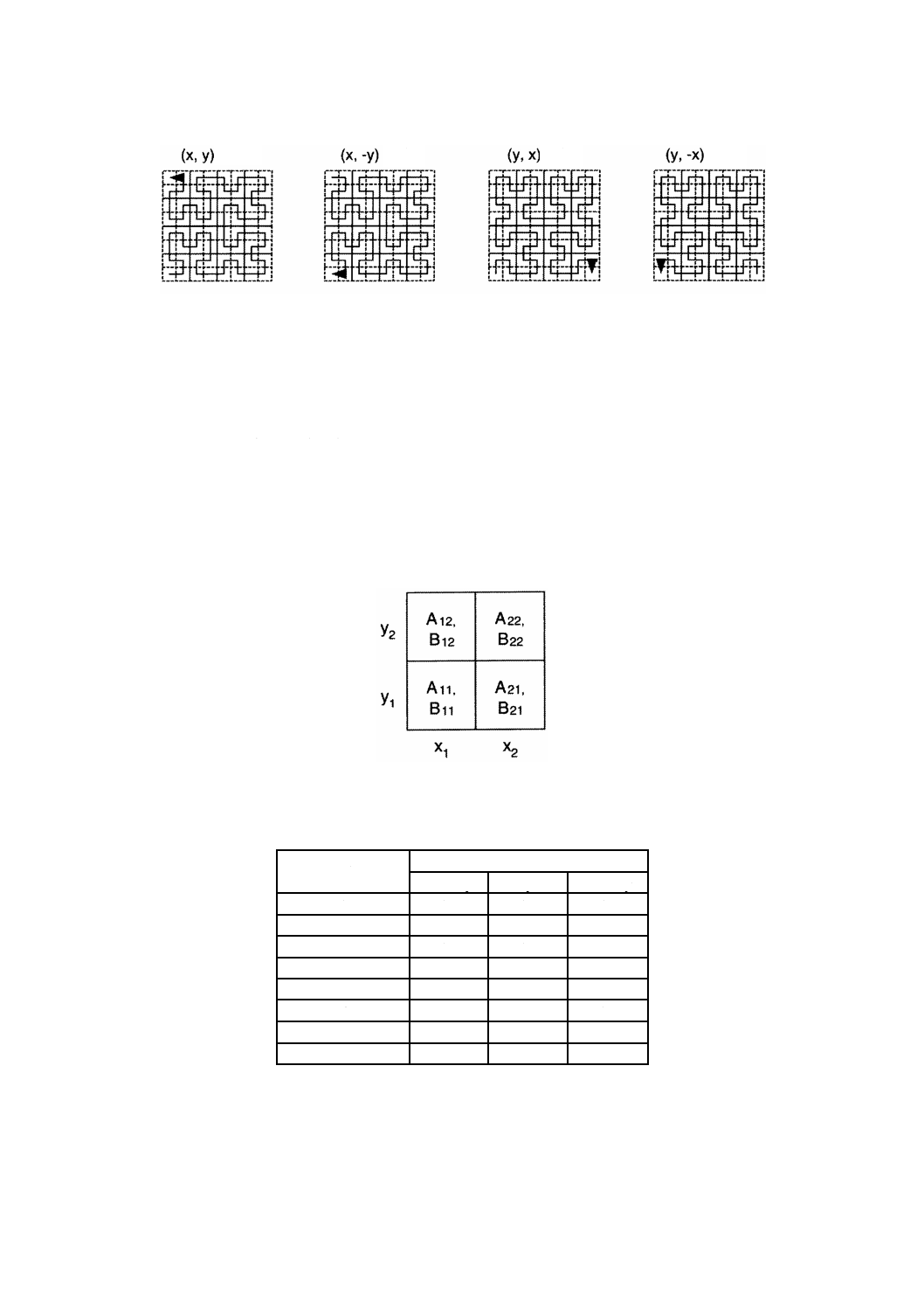
62
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.8−二次元グリッドにおけるヒルベルト順序付けの例
D.8
地物属性値の交互配置
グリッド被覆の範囲が,複数の地物属性を含んでいる場合,それらの地物属性値は,その一覧の中に様々
な方法で交互配置される。このような交互配置は,その範囲に対応する要素を,CV̲SequenceRuleの属性
scanDirectionが与える軸の一覧に含めることで記述できる。属性のレコードに対する指標は,座標と同じ
やり方で増加させられる。
例 図D.9に示した2×2のグリッドについて考える。このグリッドは,A及びBという二つの属性
の値域(r)をもつ。線形走査が,まずx方向にプラス,その後y方向にプラスという形で進む場
合,走査順序を選び,表D.1で示すような各種の方法で地物属性値を呼び出すことができる。
図D.9−二つの属性の範囲をもつ二次元グリッドの例
表D.1−交互配置の例
順序
走査方向
r,x,y
x,y,r
x,r,y
1
A11
A11
A11
2
B11
A21
A21
3
A21
A12
B11
4
B21
A22
B21
5
A12
B11
A12
6
B12
B21
A22
7
A22
B12
B12
8
B22
B22
B22
順
順
順
順
63
X 7123:2012 (ISO 19123:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] Open Geospatial Consortium, The OpenGIS Specification: Abstract Specification, Wayland, Massachusetts,
1999. Available at http://www.opengeospatial.org/specs/
[2] Dictionary of Computing, Fourth Edition, Oxford University Press, 1996
[3] ISO 19101:2002, Geographic information−Reference model
[4] JIS X 4170:2009 オープン分散処理−統一モデル化言語(UML)1.4.2版
注記 対応国際規格:ISO/IEC 19501:2005, Information technology−Open Distributed Processing−
Unified Modeling Language (UML) Version 1.4.2(IDT)
[5] HILTON, P. J. and WYLIE, S., Homology Theory, an Introduction to Algebraic Topology, Cambridge
University Press, 1960
[6] KIDNER, D.B., Higher-order interpolation of regular grid digital elevation models, International Journal of
Remote Sensing Vol. 24, No. 14, July 2003, pp. 2981-2987
[7] LAURINI, R. and THOMPSON, D., Fundamentals of Spatial Information Systems, Academic Press, 1992
[8] GOODCHILD, M. F. and GRANDFIELD, A. W., Optimizing Raster Storage: An Examination of Four
Alternatives, Auto-Carto 6, 1983
[9] GILBER, W., A Cube-filling Hilbert Curve, Mathematical Intelligencer 6(3), 1984
[10] JIS X 0304:2011 国名コード
注記 対応国際規格:ISO 3166-1:2006, Codes for the representation of names of countries and their
subdivisions−Part 1: Country codes(IDT)