X 7107:2005 (ISO 19107:2003)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人 日本測量調査技術協会(APA)から,
工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経
済産業大臣及び国土交通大臣が制定した日本工業規格である。
制定に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO 19107:2003,Geographic
information―Spatial schemaを基礎として用いた。
この規格の一部が,技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願公開後の
実用新案登録出願に抵触する可能性があることに注意を喚起する。経済産業大臣,国土交通大臣及び日本
工業標準調査会は,このような技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願
公開後の実用新案登録出願にかかわる確認について,責任はもたない。
JIS X 7107には,次に示す附属書がある。
附属書A(規定)抽象試験項目群
附属書B(参考)用語とその定義の概念による編成
附属書C(参考)空間スキーマ概念の事例
附属書D(参考)応用スキーマの例
附属書E(参考)参考文献
X 7107:2005 (ISO 19107:2003)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 2
2. 適合性 ··························································································································· 2
2.1 一般 ···························································································································· 2
2.2 適合分類 ······················································································································ 4
3. 引用規格 ························································································································ 4
4. 定義 ······························································································································ 5
5. 記号,表記法及び略語 ····································································································· 12
5.1 表現及び表記 ··············································································································· 12
5.1.1 統一モデリング言語(UML:Unified Modeling Language)の概念 ········································ 12
5.1.2 属性,操作及び関連 ···································································································· 12
5.1.3 ステレオタイプ ·········································································································· 15
5.1.4 データ型及びコレクション型 ························································································ 16
5.1.5 強代替性 ··················································································································· 18
5.2 構成 ··························································································································· 18
5.3 略語 ··························································································································· 20
6. Geometryパッケージ ······································································································ 20
6.1 意味 ··························································································································· 20
6.2 Geometry rootパッケージ ······························································································· 23
6.2.1 意味 ························································································································· 23
6.2.2 GM̲Object ················································································································ 23
6.3 Geometric primitiveパッケージ ························································································ 30
6.3.1 意味 ························································································································· 30
6.3.2 GM̲Boundary ············································································································ 30
6.3.3 GM̲ComplexBoundary ································································································ 31
6.3.4 GM̲PrimitiveBoundary ································································································ 31
6.3.5 GM̲CurveBoundary ···································································································· 31
6.3.6 GM̲Ring ·················································································································· 31
6.3.7 GM̲SurfaceBoundary ·································································································· 32
6.3.8 GM̲Shell ·················································································································· 32
6.3.9 GM̲SolidBoundary ····································································································· 32
6.3.10 GM̲Primitive ··········································································································· 33
6.3.11 GM̲Point ················································································································ 35
6.3.12 Bearing ··················································································································· 36
6.3.13 GM̲OrientablePrimitive ····························································································· 37
X 7107:2005 (ISO 19107:2003)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.14 GM̲OrientableCurve ································································································· 38
6.3.15 GM̲OrientableSurface ······························································································· 39
6.3.16 GM̲Curve ··············································································································· 39
6.3.17 GM̲Surface ············································································································· 41
6.3.18 GM̲Solid ················································································································ 42
6.4 Coordinate geometryパッケージ······················································································· 43
6.4.1 DirectPosition ············································································································· 43
6.4.2 GM̲PointRef ············································································································· 44
6.4.3 GM̲Envelope ············································································································· 44
6.4.4 TransfineteSet<DirectPosition> ······················································································· 45
6.4.5 GM̲Position ·············································································································· 45
6.4.6 GM̲PointArray及びGM̲PointGrid ··············································································· 45
6.4.7 GM̲GenericCurve ······································································································ 45
6.4.8 GM̲CurveInterpolation································································································ 48
6.4.9 GM̲CurveSegment······································································································ 49
6.4.10 GM̲LineString ········································································································· 51
6.4.11 GM̲LineSegment ······································································································ 51
6.4.12 GM̲GeodesicString ···································································································· 52
6.4.13 GM̲Geodesic ··········································································································· 52
6.4.14 GM̲ArcString ·········································································································· 52
6.4.15 GM̲Arc ·················································································································· 54
6.4.16 GM̲Circle ··············································································································· 55
6.4.17 GM̲ArcStringByBulge ································································································ 55
6.4.18 GM̲ArcByBulge ······································································································· 56
6.4.19 GM̲Conic ··············································································································· 57
6.4.20 GM̲Placement ·········································································································· 58
6.4.21 GM̲AffinePlacement ·································································································· 59
6.4.22 GM̲Clothoid ············································································································ 59
6.4.23 GM̲OffsetCurve ······································································································· 60
6.4.24 GM̲Knot ················································································································ 61
6.4.25 GM̲NotType ············································································································ 61
6.4.26 GM̲SplineCurve ······································································································· 62
6.4.27 GM̲PolynomialSpline································································································· 62
6.4.28 GM̲CubicSpline ······································································································· 62
6.4.29 GM̲SplineCurveForm ································································································ 63
6.4.30 GM̲BSplineCurve ····································································································· 63
6.4.31 GM̲Bezier ··············································································································· 64
6.4.32 GM̲SurfaceInterpolation ···························································································· 64
6.4.33 GM̲GenericSurface ··································································································· 65
6.4.34 GM̲SurfacePatch ······································································································ 67
X 7107:2005 (ISO 19107:2003)
(4)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.35 GM̲PolyhedralSurface ······························································································· 68
6.4.36 GM̲Polygon ············································································································· 68
6.4.37 GM̲TriangulatedSurface ····························································································· 70
6.4.38 GM̲Triangle ············································································································ 70
6.4.39 GM̲Tin ·················································································································· 70
6.4.40 GM̲ParametricCurveSurface ······················································································· 72
6.4.41 GM̲GriddedSurface ·································································································· 75
6.4.42 GM̲Cone ················································································································ 75
6.4.43 GM̲Cylinder ············································································································ 75
6.4.44 GM̲Sphere ·············································································································· 75
6.4.45 GM̲BilinearGrid······································································································· 76
6.4.46 GM̲BicubicGrid ······································································································· 76
6.4.47 GM̲BSplineSurfaceForm ···························································································· 76
6.4.48 GM̲BSplineSurface ··································································································· 77
6.5 Geometric aggregateパッケージ ······················································································· 77
6.5.1 意味 ························································································································· 77
6.5.2 GM̲Aggregate ··········································································································· 77
6.5.3 GM̲MultiPrimitive ····································································································· 78
6.5.4 GM̲MultiPoint ·········································································································· 78
6.5.5 GM̲MultiCurve ········································································································· 79
6.5.6 GM̲MultiSurface········································································································ 79
6.5.7 GM̲MultiSolid ··········································································································· 79
6.6 Geometric complexパッケージ ························································································· 79
6.6.1 意味 ························································································································· 79
6.6.2 GM̲Complex ············································································································· 80
6.6.3 GM̲Composite ··········································································································· 82
6.6.4 GM̲CompositePoint ···································································································· 83
6.6.5 GM̲CompositeCurve ··································································································· 83
6.6.6 GM̲CompositeSurface ································································································· 84
6.6.7 GM̲CompositeSolid ···································································································· 85
7. Topologyパッケージ ······································································································· 85
7.1 意味 ··························································································································· 85
7.2 Topology rootパッケージ ································································································ 87
7.2.1 意味 ························································································································· 87
7.2.2 TP̲Object ················································································································· 89
7.3 Topological primitiveパッケージ ······················································································ 91
7.3.1 意味 ························································································································· 92
7.3.2 TP̲Boundary ············································································································· 92
7.3.3 TP̲ComplexBoundary·································································································· 92
7.3.4 TP̲PrimitiveBoundary ································································································· 92
X 7107:2005 (ISO 19107:2003)
(5)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.5 TP̲EdgeBoundary······································································································· 93
7.3.6 TP̲FaceBoundary ······································································································· 93
7.3.7 TP̲SolidBoundary······································································································· 94
7.3.8 TP̲Ring ···················································································································· 94
7.3.9 TP̲Shell ··················································································································· 94
7.3.10 TP̲Primitive ············································································································ 94
7.3.11 TP̲DirectedTopo ······································································································· 96
7.3.12 TP̲Node ·················································································································· 99
7.3.13 TP̲DirectedNode ······································································································ 100
7.3.14 TP̲Edge ················································································································· 100
7.3.15 TP̲DirectedEdge ······································································································ 101
7.3.16 TP̲Face ················································································································· 101
7.3.17 TP̲DirectedFace ······································································································ 102
7.3.18 TP̲Solid ················································································································· 103
7.3.19 TP̲DirectedSolid ······································································································ 103
7.3.20 TP̲Expression ········································································································· 104
7.4 Topological complexパッケージ ······················································································· 106
7.4.1 意味 ························································································································ 106
7.4.2 TP̲Complex ············································································································· 106
8. 派生位相関係 ················································································································ 107
8.1 一般 ·························································································································· 108
8.2 ブール値演算子及び集合演算子 ······················································································ 108
8.2.1 ブール値演算子の形式 ································································································ 108
8.2.2 ブール値関係 ············································································································ 109
8.2.3 集合操作との関係 ······································································································ 109
8.3 エーゲンホーファ演算子 ······························································································· 109
8.3.1 エーゲンホーファ演算子の形式 ···················································································· 109
8.3.2 エーゲンホーファ関係 ································································································ 110
8.3.3 集合操作との関係 ······································································································ 110
8.4 完全位相演算子 ··········································································································· 110
8.4.1 完全位相演算子の形式 ································································································ 110
8.4.2 完全位相関係 ············································································································ 110
8.5 組合せ ······················································································································· 110
附属書A(規定)抽象試験項目群 ·························································································· 111
A.1 幾何プリミティブ ········································································································ 111
A.2 幾何複体 ···················································································································· 113
A.3 位相複体 ···················································································································· 115
A.4 幾何実現を伴う位相複体 ······························································································· 117
A.5 ブール値演算子 ··········································································································· 119
附属書B(参考)用語とその定義の概念による編成 ··································································· 121
X 7107:2005 (ISO 19107:2003)
(6)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.1 目的 ·························································································································· 121
B.2 全般的な用語 ·············································································································· 121
B.3 コレクション型とその関連用語 ······················································································ 121
B.4 モデル化の用語 ··········································································································· 122
B.5 位置の用語 ················································································································· 122
B.6 幾何の用語 ················································································································· 122
B.7 位相の用語 ················································································································· 125
B.8 幾何及び位相複体の関係性 ···························································································· 128
附属書C(参考)空間スキーマ概念の事例 ·············································································· 129
C.1 幾何 ·························································································································· 129
附属書D(参考)応用スキーマの例 ······················································································· 136
D.1 背景 ·························································································································· 136
D.2 単純位相 ···················································································································· 136
D.3 地物位相 ···················································································································· 139
D.4 MiniTopo(最小位相プロファイル) ··············································································· 140
附属書E(参考)参考文献 ··································································································· 147
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
X 7107:2005
(ISO 19107:2003)
地理情報―空間スキーマ
Geographic information―Spatial schema
序文 この規格は,2003年に第1版として発行されたISO 19107 Geographic information―Spatial schemaを
翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規格である。この規格は,
ISO/TC211が関与する種々の地理情報規格を基とした日本工業規格(以下,地理情報規格群という。)の
一つである。
地理情報規格群は,地球上の位置と直接的又は間接的に関連付けられたオブジェクト又は現象に関する
情報処理技術のための規格であり,河川,道路などに関する様々なデータを電子化し,各種情報処理の高
度化,効率化に適用される。
なお,この規格で,点線の下線を施してある箇所は,原国際規格にない事項である。
この規格は,地理的な事物の空間的特性を記述し操作するための概念スキーマを提供する。この領域に
おける規格化は,地理情報にかかわる他の規格の基礎となるものである。
事物とは現実世界の現象を抽象化したものであり,その中で地球上の場所との関連付けをもつものが地
物である。ベクトルデータは幾何プリミティブ及び位相プリミティブからなり,それらを個別に又は組み
合わせて用いることによって,地物の空間的特性を表現するオブジェクトを構成する。ラスタデータは,
対象となる範囲を空間のモザイクのように隙間なく覆う小単位に分割し,各小単位に属性値を割当てたも
のである。この規格では,ベクトルデータのみを取り扱う。
この規格で定義するモデルでは,空間的特性を,幾何オブジェクト(GM̲Object)又は位相オブジェク
ト(TP̲Object)として付与された値を持つ,一つ以上の空間属性によって記述している。幾何は,次元,
位置,大きさ,形状及び向きを含む地物の空間的特性について,座標や数学的関数による定量的な記述方
法を提供する。オブジェクトの幾何の記述に用いられる数学的関数は,空間位置の定義に用いる座標参照
系の型に依存している。幾何は,地理情報をある測地参照系又は座標系から他のものへと変換した時に,
その情報の中で唯一変化する特性である。
位相は,例えば地理データをある座標系から別の系に変換する時のように,空間を伸縮させる連続的な
変形に対しても不変であるような幾何形状の特性を扱う。地理情報の中では,n次元グラフの連結性とい
う,グラフの連続的な変換のもとでも不変な性質を記述するために,位相を用いる。計算位相幾何は,基
礎をなす幾何から導出できる幾何プリミティブの連結性に関する情報を提供する。
空間演算子は,空間オブジェクトの使用,問合せ,生成,修正又は削除を行う関数及び手続きである。
この規格は,これらの演算子の定義と実装のための規定を作成するためにその分類体系を定義する。その
目的は,次のとおりである。
a)
様々な実装が既知の正確度及び解像度の制限内で同等な結果を生成することを保証できるよう,曖
昧さを排して空間演算子を定義すること。
2
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b)
適合システムの基礎を形成する標準的な演算の集合を定義する際にこれらの定義を用い,それによ
って実装者のための実証実験と適合性検証の基準として機能すること。
c)
地理データの問合せ及び操作では,基本的な演算子を組み合わせて使用されることが想定されるた
め,これを許容する演算子の代数を定義すること。
空間的特性についての概念スキーマを規格化することよって,応用システム間で地理情報を共有する能
力を向上させることができる。地理情報システム及び地理情報ソフトウェア開発者並びに地理情報の利用
者は,このスキーマを使用して,互いに整合して理解可能な空間データ構造を提供することができる。
1. 適用範囲 この規格は,地物(feature)の空間特性を記述するための概念スキーマと,これらのスキ
ーマに合致する空間演算の集合について規定する。ここでは,三次元までのベクトルの幾何と位相を扱っ
ており,3軸までの座標空間に埋め込まれた三次元までの位相次元における空間(幾何及び位相)オブジ
ェクトについて,地理情報のアクセス,問合せ,管理,処理及びデータ交換に用いる標準化した空間演算
を規定する。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide21に基づき,IDT(一致している),MOD(修
正している),NEQ(同等でない)とする。
ISO 19107:2003,Geographic information―Spatial schema (IDT)
2. 適合性
2.1
一般 この規格の6.及び7.では,統一モデリング言語(UML:Unified Modeling Language)を使用し
て記述した,地物の空間特性を記述するための概念スキーマを提供している。このスキーマは,応用スキ
ーマ,プロファイル及び実装仕様で使用しなければならない概念クラスを定義する。この規格は,外部に
対して明らかにしたインタフェースだけに関係し,次のような現実の状況に対してそのインタフェース仕
様を満たすことが必要とされる以外には,内在する実装には何の制限も与えない。
− COM,CORBAなどの技術を用いたソフトウェアサービスへのインタフェース
− SQLなどの技術を用いたデータベースへのインタフェース
− ISO 19118で規定した符号化法を使用したデータ交換
ほとんどの応用システムは,この概念スキーマで記述した特性のすべてを必要とするわけではない。こ
のため,この箇条では,データ構造を定義する上で必要最小限の範囲から完全なオブジェクト実装まで,
要求に幅がある各応用システムに対応した適合クラスの集合を定義する。様々な方法で実装できるUML
の型の集合がこの柔軟性を制御する。UMLでデザインしたオブジェクトの実装において一般的なように,
オブジェクトの機能を完全に定義した実装は,選択した適合分類の型で定義されたすべての操作を実装し
なければならない。一部若しくはすべての操作を外部の“独立関数”に依存するか,又は全く依存しない
ことを選択した実装は,すべての操作に対応する必要はないが,メンバ変数で定義されることによって選
択されたUML型のそれぞれの型の状態を記録するのに必要なデータ型には常に対応しなければならない。
“比ゆ(喩)的には同一”だが技術的には異なる実体に対して,共通の名称を使用してよい。この規格に
おけるUMLモデルは抽象型を定義し,応用スキーマは概念クラスを定義し,各種ソフトウェアシステム
は実装クラス又はデータ構造を定義し,符号化(ISO 19118)によるXMLは実体のタグを定義する。これら
はすべてが同じ情報内容を参照する。より深いレベルでは実装したデジタルの実体には重要な技術的相違
があっても,同一の名前を同一の情報内容の表現に利用可能にするのは困難ではない。このことによって,
3
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
UMLモデルの型を応用スキーマで直接使用することができる。
応用スキーマに対して,幾何又は位相オブジェクトの型を定義する39の適合性選択肢を定める。それら
を三つの基準で分類する。
最初の二つの基準(データの複雑さ及び次元)は,与えられた適合性選択肢に適合する応用スキーマが
実装しなければならない空間スキーマの定義する型を定める。実装するオブジェクト型の次元を定義する
際,応用スキーマで実装しようとする曲線又は曲面の補間型を指定することが必要となる。一次元のオブ
ジェクトを含む応用スキーマの曲線実装では,“線形”補間手法を含めなければならない。一次元のオブジ
ェクトを含む応用スキーマには,常に,任意の曲線を必要に応じて折れ線として近似し,データをより単
純なスキーマに変換できる仕組みを含めなければならない。二次元のオブジェクトを含む応用スキーマの
曲面実装には,常に,“平面”補間手法を含めなければならない。その応用スキーマには,常に,任意の曲
面を必要に応じて曲面分の集合として近似し,データをより単純なスキーマに変換できる仕組みを含めな
ければならない。曲線と曲面との補間手法の追加は任意選択であるが,実装する場合には,この規格に規
定する定義に従わなければならない。
三つ目の基準(機能の複雑さ)は,これらの型の要素(属性,関連役割,及び操作)で実装しなければ
ならないものを定める。これらのスキーマの中で最も限定したものは,データ型だけを定義するものであ
り,データ又は演算パラメタをサービス提供者へ引き渡す際に使用してもよい。
最初の基準は,データの複雑さの階層とする。四つの階層を次に示す。
− 幾何プリミティブ
− 幾何複体
− 位相複体
− 幾何実現を伴う位相複体
備考 一般に“スパゲッティ”データと呼ばれるデータのスキーマは,幾何プリミティブの構造化さ
れていない集合だけを使用する。幾何のそれぞれの構成要素に対する単一の定義が必要な場合
には,スキーマには幾何複体を導入する。同一の幾何複体内のプリミティブは境界だけを共有
する。スキーマに明示的な位相情報が必要な場合には,幾何複体を拡張して位相複体の構造を
含めるようにする。複体に含まれるオブジェクトの型は複体の次元によって決まる。一般に“チ
ェーンノード”位相と呼ばれるものは,一次元の位相複体である。一般に地図の二次元環境に
おいて“完全位相”と呼ばれるものは,二次元の座標系の幾何オブジェクトによって実現され
る二次元の位相複体である。
第二の基準は次元とする。単純な幾何に対する階層は,次の四つとする。
− 零次元オブジェクト
− 零次元及び一次元オブジェクト
− 零次元,一次元及び二次元オブジェクト
− 零次元,一次元,二次元及び三次元オブジェクト
ただし,零次元複体は零次元幾何プリミティブの集合以上に有益な情報を提供しないので,複体につい
ては一次元,二次元及び三次元までだけ適合性クラスを定義する。
第三の基準は,機能の複雑さの階層とする。この階層は,次の三つとする。
− データ型だけ
− 単純操作
− 完全操作

4
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この規格の8.は,幾何及び位相オブジェクト同士の位相的な関係を得るために使用する,三つのグルー
プのブール演算子を定義する。この規格は,これらの演算子を実装する応用スキーマのために,四つの適
合性クラスを定義する。
2.2
適合分類 この規格に適合するためには,実装は,規定の適合性クラスについて附属書Aの抽象試
験項目群(ATS:Abstract Test Suite)の要求を満たさなければならない。表1から表5までは,それぞれの
適合性クラスに適用されるATSの箇条を示す。
表 1 幾何プリミティブの適合性クラス
次元 データ型 単純操作 完全操作
0
A.1.1.1
A.1.2.1
A.1.3.1
1
A.1.1.2
A.1.2.2
A.1.3.2
2
A.1.1.3
A.1.2.3
A.1.3.3
3
A.1.1.4
A.1.2.4
A.1.3.4
表 2 幾何複体の適合性クラス
次元 データ型 単純操作 完全操作
1
A.2.1.1
A.2.2.1
A.2.3.1
2
A.2.1.2
A.2.2.2
A.2.3.2
3
A.2.1.3
A.2.2.3
A.2.3.3
表 3 位相複体の適合性クラス
次元 データ型 単純操作 完全操作
1
A.3.1.1
A.3.2.1
A.3.3.1
2
A.3.1.2
A.3.2.2
A.3.3.2
3
A.3.1.3
A.3.2.3
A.3.3.3
表 4 幾何実現を伴う位相複体の適合性クラス
次元 データ型 単純操作 完全操作
1
A.4.1.1
A.4.2.1
A.4.3.1
2
A.4.1.2
A.4.2.2
A.4.3.2
3
A.4.1.3
A.4.2.3
A.4.3.3
表 5 ブール演算子の適合性クラス
集合演算子
A.5.1
エーゲンホーファ演算子
A.5.2
完全位相演算子
A.5.3
すべての演算子
A.5.4
3. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発行年を付記してあるものは,記載の年の版だけがこの規格の規定を構
成するものであって,その後の改正版・追補には適用しない。発行年を付記していない引用規格は,その
最新版(追補を含む。)を適用する。
JIS X 7111 地理情報―座標による空間参照
備考 ISO 19111 Geographic information―Spatial referencing by coordinatesが,この規格と一致してい
5
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
ISO 19109(1) Geographic information―Rules for application schema
ISO/IEC 11404:1996 Information technology―Programming languages, their environments and system
software interfaces―Language-independent datatype
注(1) 未発行
4. 定義 この規格で用いる主な定義は,次による。
参考 附属書Bでは,用語をその概念上の関係によって体系化している。
4.1
応用(application) 利用者の要求に応えるために行われるデータの操作及び処理(ISO 19101)。
4.2
応用スキーマ(application schema) 一つ以上の応用システムによって要求されるデータのための
概念スキーマ(ISO 19101)。
4.3
多重集合(bag) 繰返しのある,関連する項目(オブジェクト又は値)の,有限非順序な集まり。
備考 論理的には,多重集合は,<項目,項数> の対の集合である。
4.4
境界(boundary) 実体の広がりの限界を示す集合。
備考 境界が最もよく使用されるのは,集合が点の集まり又はこれらの点を表すオブジェクトの集ま
りであるような幾何に関する記述においてである。他の分野では,この用語を,実体とその論
議領域での余事象との遷移領域を比ゆ(喩)的に記述するために使用する。
4.5
バッファ(buffer) 指定された幾何オブジェクトから与えられた距離以内のすべての直接位置を含
む幾何オブジェクト。
4.6
環状列(circular sequence) 論理的な開始点をもたないために,それ自身のどのような循環的なシ
フトとも同一になり,結果として最後の項目が順列の最初の項目に先行するとみなされる列。
4.7
クラス(class) 同じ属性,操作,メソッド,関係及び意味を共有するオブジェクトの集合の記述
(ISO TS 19103(2))。
注(2) 未発行
備考 クラスは,その環境に対して提供する操作の集まりを規定するために,インタフェースの集合
を使用してもよい。この用語は,最初にオブジェクト指向プログラミングの一般的な理論の中
でこの用法で使用され,後にUMLにおいても同じ意味で使用するものとして採用された。
4.8
閉包(closure) 位相オブジェクト又は幾何オブジェクトの内部と境界との和集合。
4.9
双対境界(coboundary) ある位相オブジェクトに対応して,その位相オブジェクトを境界として
もつ,より高い位相次元の位相プリミティブの集合。
備考 ノードがエッジの境界に存在する場合,このエッジは,そのノードの双対境界上にある。この
二つの関係のいずれか一つに関連付けられた任意の方向パラメタは,もう一方の関係に対して
も関連付けられる。これは,ノードがエッジの終点ノードである(正の有向エッジの終端とし
て定義される)場合,そのノードの正の方向(正の有向ノードとして定義される)が双対境界
上にエッジをもつようにするためである(図35参照)。
4.10 合成曲線(composite curve) 列の各曲線が(最初のものを除き)直前の曲線の終点から開始する
ような曲線の列。
備考 合成曲線は,直接位置の集合として,曲線のすべての性質をもつ。
4.11 合成立体(composite solid) 共有された境界曲面に沿って互いに隣接する立体の連結した集合。
備考 合成立体は,直接位置の集合として,立体のすべての性質をもつ。
6
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.12 合成曲面(composite surface) 共有された境界曲線に沿って互いに隣接する曲面の連結な集合。
備考 合成曲面は,直接位置の集合として,曲面のすべての性質をもつ。
4.13 計算幾何(computational geometry) 幾何演算を実装するための,幾何表現に関する操作及び計算。
例 計算幾何演算は,幾何包含若しくは交差の試験,凸包若しくはバッファ領域の計算又は幾何オブ
ジェクト間の最短経路探索を含む。
4.14 計算位相幾何(computational topology) 通常,計算幾何において実行される位相オブジェクトの
演算の支援,拡張又は定義を行う位相的な概念,構造及び代数。
4.15 連結(connected) オブジェクトの任意の二つの直接位置がそのオブジェクト内に完全に含まれる
曲線上に配置できることを意味する幾何オブジェクトの性質。
備考 位相オブジェクトは,幾何実現が連結である場合にだけ,連結である。これは,位相幾何学の
定理から導かれるので,定義には含まない。
4.16 連結ノード(connected node) 一つ以上のエッジが開始又は終了するノード。
4.17 凸包(convex hull) 与えられた幾何オブジェクトを含む最小の凸集合[Dictionary of Computing (7)]。
備考 “最小”とは集合論的に最小のことであり,計量的な意味をもつものではない。この定義は“そ
の幾何オブジェクトを含むすべての凸集合の積集合”と言い換えることもできる。
4.18 凸集合(convex set) 自分自身が含む任意の二つの直接位置について,それらを結ぶ直線分上の任
意の直接位置をも含むような幾何集合[Dictionary of Computing (7)]。
備考 凸集合は,“単連結”である。すなわち内部に穴をもたない。通常は,適切な次元のユークリッ
ド球と位相同形とみなしてよい。また,球の表面は,測地的には測地線を直線とみなせば凸と
考えることができる。
4.19 座標(coordinate) n次元空間内の点の位置を示すn個の数値の列(JIS X 7111)。
備考 座標参照系では,それらの数値には単位を付与しなければならない。
4.20 座標次元(coordinate dimension) ある座標系における位置を記述するために必要な計測値又は座
標軸の数。
4.21 座標参照系(coordinate reference system) 原子(datum)によって地球に関連付けられた座標系(JIS
X 7111)。
4.22 座標系(coordinate system) 点にどのように座標を割り当てるかを規定するための数学的規則の集
合(JIS X 7111)。
4.23 曲線(curve) 直線の連続な像を表現する一次元の幾何プリミティブ。
備考 曲線の境界は,その両端の点の集合である。曲線が閉路の場合,二つの端は同一であり,その
曲線は(位相的に閉じている場合には),境界をもたないとみなす。最初の点を始点,最後のも
のを終点と呼ぶ。“直線の連続的な像”という定義文の語句によって,曲線の連結性が保証され
る。位相幾何学の定理は,連結している集合の連続的な像は連結であることを規定している。
4.24 曲線分(curve segment) 一定の内挿及び定義の方法を用いて曲線の連続した部分を表現するため
に用いる一次元の幾何オブジェクト。
備考 単一の曲線分によって表現される幾何集合は,一つの曲線と等しい。
4.25 輪体(cycle) 境界をもたない空間オブジェクト。
備考 輪体は境界の構成要素[殻(shell)及び輪(ring)を参照]を記述するために使用する。輪体は,そ
れ自身の上で閉じているため境界をもたないが,有界である(すなわち,範囲は無限ではない)。
例えば,円周又は球面は,境界をもたないが有界である。
7
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.26 直接位置(direct position) 座標参照系の中で一つの座標によって記述された位置。
4.27 有向エッジ(directed edge) エッジとその向きの一つとの間の関連を表す有向位相オブジェクト。
備考 有向エッジは,そのエッジと向きが一致しているものは + という向きを,そうでなければ ‒
という向きをもつとする。有向エッジは,位相幾何においては同一のエッジの右側(-)と左側
(+)とを区別する場合,同一のエッジの始点ノード(-)と終点ノード(+)とを区別するため
に,そして計算位相幾何においてはこれらの概念を表現するために用いる。
4.28 有向フェイス(directed face) フェイスとその向きの一つとの間の関連を表す有向位相オブジェク
ト。
備考 有向フェイスの外部境界を構成する有向エッジの向きは,この有向フェイスの正の側からみて,
正の向きが決まる。位相立体の境界を示す有向フェイスの向きは,この位相立体から離れる方
向を指す。隣接する位相立体では,それらが共有する境界には異なる向きを付けることになる
が,これは,隣接するフェイスとそれらが共有するエッジとの間の同種の関連と整合している。
有向フェイスは,双対境界関係においてフェイスとエッジとの間の空間的な関係を保持するた
めに用いる。
4.29 有向ノード(directed node) ノードとその向きの一つとの間の関連を表す有向位相オブジェクト。
備考 有向ノードは,双対境界関係においてエッジとノードとの間の空間的な関連を保持するために
用いる。一つのエッジに関するノードの向きは,そのエッジの終点ノードでは“+”,始点ノー
ドでは“-”になる。これは,“ベクトル=終点−始点”というベクトルの概念と整合している。
4.30 有向位相立体(directed solid) 位相立体とその向きの一つとの間の関連を表す有向位相オブジェク
ト。
備考 有向位相立体は,双対境界関係においてフェイスと位相立体との間の空間的な関係を保持する
ために用いる。一つのフェイスに関する位相立体の向きは,そのフェイスの上方法線が位相立
体の外側へ向く場合には“+”,内側に向く場合は“-”である。これは,立体の境界となる曲面
に対して“上方=外側”という概念と整合する。
4.31 有向位相オブジェクト(directed topological object) 位相プリミティブとその向きの一つとの間の
論理的な関連を表す位相オブジェクト。
4.32 領域,定義域(domain) 明確に定義された集合(ISO TS 19103)。
備考 領域は,演算子及び関数の定義域と値域とを定義するのに用いる。
4.33 エッジ(edge) 一次元の位相プリミティブ。
備考 エッジの幾何実現は曲線である。エッジの境界は,位相複体の中でこのエッジと関連付けられ
た一つ又は二つのノードの集合である。
4.34 エッジノードグラフ(edge-node graph) ある位相複体内に埋め込まれているグラフで,その複体
内のすべてのエッジとそれに連結したノードからなるもの。
備考 エッジノードグラフは,それが埋め込まれている複体の部分複体である。
4.35 終点ノード(end node) エッジを含む位相複体の有効な幾何実現において,そのエッジを実現す
る曲線の終点に対応する,このエッジの境界のノード。
4.36 終点(end point) 曲線の最後の点。
4.37 外部(exterior) 全体集合とある集合の閉包との差集合。
備考 外部の概念は,位相複体及び幾何複体の両方に適用できる。
4.38 フェイス(face) 二次元の位相プリミティブ。
8
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 フェイスの幾何実現は曲面である。フェイスの境界は,境界関係をとおしてフェイスに関連付
けられる同じ位相複体内の有向エッジの集合である。これらは,輪の形に揃えることができる。
4.39 地物(feature) 実世界の現象の抽象概念(ISO 19101)。
備考 地物は,型又はインスタンスとして現れる。型又はインスタンスの一方だけを意味するときに
は,地物型又は地物インスタンスという用語を使うことが望ましい。
参考 地物は元来地上の自然物及び人工物の概念を指す用語であるが,この規格では,それ以外の実
世界に現れる物事を抽象化した概念も指す。
4.40 地物属性(feature attribute) 地物の特性(ISO 19101)。
備考 地物属性は,それに関連付けられた名前,データ型及び値の定義域をもつ。地物インスタンス
の地物属性は,加えてその定義域から選ばれた属性値をもつ。
4.41 関数(function) ある領域[この関数の定義域(source, domain)]の各要素を,別の領域[この関数
の値域(target, co-domain, range)]の一意な要素に関連付ける規則。
4.42 地理情報(geographic information) 地球に関係した場所と暗示的又は明示的に関連付けられた現
象に関する情報。
4.43 幾何集成(geometric aggregate) 内部構造をもたない幾何オブジェクトの集まり。
備考 要素間の空間関係に関する推定は,行えない。
参考 UMLにおけるaggregateには,“縮める”という概念は含まず,“集めて一つにまとめる”とい
う意味なので,ここでは集約ではなく集成とする。
4.44 幾何境界(geometric boundary) 幾何オブジェクトの範囲を限定する,より低い幾何次元の幾何プ
リミティブの集合によって表現される境界。
4.45 幾何複体(geometric complex) 互いに素な幾何プリミティブの集合で,各幾何プリミティブの境
界を,その集合の中の,より低い次元の幾何プリミティブの和集合として表すことができるようなもの。
備考 集合の中の幾何プリミティブは,複数の幾何プリミティブの内部に存在するような直接位置が
ないという意味で互いに素である。集合は,境界演算のもとで閉じているが,これは,幾何複
体の各要素について,その要素の境界を表す幾何プリミティブの集まり(これも幾何複体とな
る。)が存在することを意味する。既に述べたように,点(幾何の唯一の零次元プリミティブオ
ブジェクト型)の境界は空集合である。したがって,最も高い次元の幾何プリミティブが立体
(三次元)の場合,この定義の境界演算を次々と適用していくと,高々3ステップ後には終結
する。また,任意のオブジェクトの境界は輪体となる。
4.46 幾何次元(geometric dimension) 幾何集合の中のどの直接位置も,その直接位置を内部に含みn
次元ユークリッド空間Rnと相似(同形)な部分集合と関連付けることができるような数nの最大値。
備考 曲線は,実数直線の一部の連続写像であるので,1の幾何次元をもつ。曲面は,その全体をR2
に写像することはできないが,各点位置の周りには微小な近傍があってそれがR2の単位円の内
部に(連続関数によって)写像されることがわかることから,二次元である。この規格では,
主要な曲面分(GM̲SurfacePatchのインスタンス)のほとんどは,それを定義する内挿の方法
によってR2の一部に写像される。
4.47 幾何オブジェクト(geometric object) 幾何集合を表す空間オブジェクト。
備考 幾何オブジェクトは,幾何プリミティブ,幾何プリミティブの集まり又は単一の実体として扱
われる幾何複体からなる。幾何オブジェクトは,地物又は地物の重要な部分の空間表現に用い
てよい。
9
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.48 幾何プリミティブ(geometric primitive) 単一の連結で均質な空間の要素を表す幾何オブジェクト。
備考 幾何プリミティブは,幾何構成についての情報を表す不可分なオブジェクトである。点,曲線,
曲面及び立体は幾何プリミティブである。
4.49 幾何実現(geometric realization) 位相複体の位相プリミティブに一対一対応した幾何プリミティ
ブをもつ幾何複体。その二つの複体の境界関係は一致する。
備考 この実現では,位相プリミティブは,対応する幾何プリミティブの内部を表現するものとみな
す。合成したものは閉じている。
4.50 幾何集合(geometric set) 直接位置の集合。
備考 この集合は,ほとんどの場合無限集合である。
4.51 グラフ(graph) 一部がエッジによって結合されているノードの集合。
備考 地理情報システムでは,グラフは,二つのノードに結合するエッジを複数もつことができ,同
じノードを両端にもつエッジをもつこともできる。
4.52 準同形(homomorphism) 一方から他方への構造を保存する関数をもつ二つの領域(二つの複体の
ような)の間の関係。
備考 準同形は逆関数を必要としない点で同形と異なる。同形には,本質的には互いに逆関数の関係
にあたる二つの準同形がある。連続関数は,“位相的な特性”を保存するので位相準同形である。
位相複体の幾何実現への写像は,境界の概念を保存する。したがって,一つの準同形である。
4.53 インスタンス(instance) クラスを実現するオブジェクト。
4.54 内部(interior) 幾何オブジェクト上にありその境界上にはないすべての直接位置の集合。
備考 位相オブジェクトの内部は,その任意の幾何実現の内部の準同形の像である。これは,位相幾
何学の定理から導かれるので,ここでの定義には含めない。
4.55 孤立ノード(isolated node) どのエッジとも関係しないノード。
4.56 同形(isomorphism) 二つの領域の一方から他方への一対一で構造を保存する関数が存在して,そ
れら二つの関数をどの順序で合成しても恒等関数に一致するような,二つの領域(二つの複体のような)
の間の関係。
備考 要素が一対一に対応し,その対応で次元及び境界が保存される場合,幾何複体は,位相複体に
同形である。
4.57 近傍(neighbourhood) 指定された直接位置を内部に含み,その直接位置から指定された距離以内
のすべての直接位置を含む幾何集合。
4.58 ノード(node) 零次元の位相プリミティブ。
備考 ノードの境界は,空集合である。
4.59 オブジェクト(object) 状態と振る舞いとをカプセル化した,明確に定義された境界及び識別をも
つ実体(UML Semantics [19])。
備考 この用語は,最初にオブジェクト指向プログラミングの一般理論の中でこの用法で使用され,
後にUMLの中で同じ意味で使用するものとして採用された。オブジェクトはクラスのインス
タンスである。属性と関係とが状態を表す。操作,メソッド及び状態機構は,振る舞いを表す。
4.60 平面位相複体(planar topological complex) 二次元ユークリッド空間に埋め込むことができる幾何
実現をもつ位相複体。
4.61 点(point) 位置を表現する零次元の幾何プリミティブ。
備考 点の境界は,空集合である。
10
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.62 レコード(record) 有限の,名前をもつ,相互に関連性のある項目(オブジェクト又は値)の集
まり。
備考 論理的に,レコードは <名称,項目> の対の集合となる。
4.63 輪(ring) 輪体である単純曲線。
備考 輪は二次元及び三次元座標系における曲面の境界の要素を記述するために用いる。
4.64 列(sequence) 繰返しを許した,関連する項目(オブジェクト又は値)の,有限で順序をもつ集
まり。
備考 論理的には,列は <項目,相対位置> の対の集合である。この規格では,括弧で列を区切り,
列の要素をコンマで分けるLISP構文を用いる。
4.65 集合(set) 繰返しを許さない,関連する項目(オブジェクト又は値)の,有限で順序をもたない
集まり。
4.66 殻(shell) 輪体である単純曲面。
備考 殻は,三次元座標系における立体の境界の要素を記述するために用いる。
4.67 単純(simple) 内部が等方的(すべての点が同形な近傍をもつ。)で,したがって,至るところ適
切な次元のユークリッド座標空間の開部分集合に局所的に同形である,という幾何オブジェクトの特性。
備考 これは,内部の直接位置がいかなる種類の自己交差にも関与しないことを意味する。
4.68 立体(solid) 三次元ユークリッド空間のある領域の連続な像を表す三次元の幾何プリミティブ。
備考 立体は,直接位置の三つのパラメタをもつ集合によって局所的に実現することができる。立体
の境界は,その立体の限界を包含する,向きをもつ閉曲面の集合である。
4.69 空間オブジェクト(spatial object) 地物の空間特性を表現するために用いるオブジェクト。
4.70 空間演算子(spatial operator) その定義域又は値域に最低一つの空間パラメタをもつ関数又は手
続。
備考 空間オブジェクトに対するすべてのUML操作は,この規格の8.の問合せ演算子もそうである
ように,空間演算子として分類することができる。
4.71 始点ノード(start node) エッジを含む位相複体の有効な幾何実現において,そのエッジを実現す
る曲線の始点に対応する,このエッジの境界のノード。
4.72 始点(start point) 曲線の最初の点。
4.73 強代替性(strong substitutability) あるクラス,型又はインタフェースを継承又は実現した下位ク
ラスの任意のインスタンスを,その原型のインスタンスの代わりとして任意の状況において用いることの
できる能力。
備考 代替性の弱い形式は,暗黙の代替を行う状況に様々な制限を設ける。
4.74 部分複体(subcomplex) すべての要素が,より大きな複体の一部でもあるような複体。
備考 幾何複体及び位相複体の定義が要求するのは,境界演算について閉じることだけであることか
ら,特定の次元又はそれ以下の任意のプリミティブの集合は,常に元のより大きな複体の部分
複体になる。したがって,任意の完全平面位相複体は,部分複体であるエッジノードグラフを
含む。
4.75 曲面(surface) 局所的に平面領域の連続な像を表す二次元の幾何プリミティブ。
備考 曲面の境界は,曲面の限界の輪郭を描く向きをもつ閉曲線である。球面又はn次元トーラス(n
次元“把”をもつ位相球面)と同形である曲面は,境界をもたない。このような曲面を輪体と
呼ぶ。
11
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.76 曲面分(surface patch) 一定の内挿及び定義方法を用いて曲面の連続した部分を表す二次元の連結
な幾何オブジェクト。
4.77 位相境界(topological boundary) 位相オブジェクトの範囲を制限する,より低い位相次元の向き
をもった位相プリミティブの集合で表される境界。
備考 位相複体の境界は,この位相複体の幾何実現の境界と整合する。
4.78 位相複体(topological complex) 境界演算について閉じている位相プリミティブの集まり。
備考 境界演算について閉じているとは,位相プリミティブが位相複体に含まれる場合には,その境
界オブジェクトもまたこの位相複体に含まれることを意味する。
4.79 位相次元(topological dimension) 幾何オブジェクト内の直接位置を他の位置と区別するのに必要
な自由変数の最小の数。
備考 上の自由変数は,多くの場合局地座標系として考えることができる。三次元座標空間におい
て,uとvとを実数,Aを平面上の任意の点,X及びYを平面の二つの接ベクトルとすると,
平面はP(u,v) = A + u X + v Yと書き表すことができる。この平面の位置はuとvとによって(こ
こでは至る所を)識別できるので,平面は二次元であり,(u,v)はこの平面上の点の座標とな
る。一般の曲面では,通常は,至る所を普遍的に識別するのは不可能である。曲面上の点を曲
面の接平面上へ射影すると,接点の微小近傍の局所同形を通常得ることができる。曲面に対す
るこの“局所座標”系は,曲面が二次元位相オブジェクトであるための要件を満たす。
この規格は空間座標だけを取り扱うので,任意の三次元オブジェクトは座標に依存してその
位相次元を定めることができる。四次元モデル(時空間)では,接空間が三次元までのオブジ
ェクトの位相次元を定めるという重要な役割も果たす。
4.80 位相式(topological expression) 多変量多項式のように演算される,向きをもつ位相プリミティブ
の集まり。
備考 位相式は,計算位相幾何の多くの計算で使用する。
4.81 位相オブジェクト(topological object) 連続した変換のもとでも変わらない空間特性を表す空間オ
ブジェクト。
備考 位相オブジェクトは,位相プリミティブ,位相プリミティブの集まり又は位相複体である。
4.82 位相プリミティブ(topological primitive) 単独の不可分な要素を表す位相オブジェクト。
備考 位相プリミティブは幾何実現における同じ次元の幾何プリミティブの内部に相当する。
4.83 位相立体(topological solid) 三次元の位相プリミティブ。
備考 位相立体の境界は有向フェイスの集合からなる。
4.84 全域フェイス(universal face) 二次元複体中の非有界フェイス。
備考 全域フェイスは,通常どのような地物の一部でもなく,データ集合の非有界の部分を表すため
に用いる。通常,この内部境界(それは外部境界をもたない。)をデータ集合によって表された
地図の外部境界とみなす。この規格は,全域フェイスを特別扱いしないが,応用スキーマでは
そうすることが有効な場合もある。
4.85 全域位相立体(universal solid) 三次元複体中の非有界位相立体。
備考 全域位相立体は,三次元において全域フェイスに相当するものであり,通常はどのような地物
の一部でもない。
4.86 ベクトル幾何(vector geometry) 構成的な幾何プリミティブの使用による幾何の表現。
12
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5. 記号,表記法及び略語
5.1
表現及び表記
5.1.1
統一モデリング言語(UML:Unified Modeling Language)の概念 この規格では,概念スキーマ
は,統一モデリング言語(以下,UMLという。)を使用して表現する。
UMLクラスは,同じ属性,操作,メソッド,関係及び意味を共有するオブジェクトの集合の記述である。
パラメタ化されたクラスは,共通の操作,メソッド及び関係をもつクラスの集合を単独で記述するもので
あり,属性の正確な構造及び操作の振る舞いはパラメタの集合によって制御され変化する。例えば,パラ
メタ化クラスの実現(インスタンス化されたクラスと呼ぶ。)において,整数のパラメタをある属性配列の
大きさを決定するために使用することがある。
この規格では,幾何又は位相の要素を幾つかの方法を織り交ぜてモデル化しているが,このことは実装
における制約とはみなさないほうがよい。属性は,データとして直接実装するか,又は値を取得及び設定
するための“取得”操作及び“設定”操作の対として実装してもよい。この規格のほとんどの図式は,単
一のクラスに焦点を当て,その属性,操作及び重要な関係を示した“構造図”である。その他の図式は,
クラスの関係の概要を示している。UMLは,すべての図式の中ですべての関係を示す事は要求しておらず,
幾つかの図式では単純さを保つために自明な関係については省略している。例えば,GM̲Objectは
Set<GM̲Object>と明らかな関係があるが,GM̲Objectの図式には明示的に示していない。
5.1.2
属性,操作及び関連 属性及び操作は,UML Notation Guide (UML記法ガイド18) に合致した
UML図として表現する。
属性のUML表記は,次の形式をとる。
Attribute-declaration :== “«” stereotype “»” visibility name multiplicity “ : ”
type = initial-value {property, …}
multiplicity :== “[” cardinality-range,… “]”
cardinality-range :== begin-value {“..” end-value}
操作のUML記法,は次の形式をとる。
Operation :== “«” stereotype “»” visibility name “(” parameterlist “)”
“ : ” [return-type], … {“{” property{=value}, …“}”},…
parameterlist :== [direction] parameter-name “ : ” type [“=” default-value]
上の構文の変数部分は,次のとおりとする。
a) stereotype(ステレオタイプ) 定義された属性又は操作のタグを使用する(次を参照)。
b) visibility(可視性) パブリック(+),プライベート(-)又はプロテクテッド(#)の値は,この属
性又は操作に対するオブジェクト外部からの可視性を示す。visibilityが“/”を含む場合,この属性は,
このモデルの他の部分から導出する。
c) name(名前) 属性又は操作の名称。
d) multiplicity(多重度) この属性がもつことのできる値の数であり,他で特に指定されないかぎり一
つの集合として構成するとみなされる。これは,“[..]”というUMLの記法を用いる以外は,ISO/IEC
11404の“size”の機構と一貫性を保った拡張とする。概念の一貫性を維持するために,この規格では,
ISO/IEC 11404の“size”の下位型として用いるときでも,単一の(UMLに従った)多重度の構文を
用いる。
e) begin-value(開始値) 有効な多重度を表す任意の整数。終了値が続かない場合は,開始値だけを可
能な多重度に加える。
13
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
f)
end-value(終了値) 先行する開始値より大きな値をとる整数又は無限又は非有界な基数範囲を表す
“n”。“a..b”はa <= j <= bとなる任意の整数jを意味する。[a..a]は,[a]と同じ意味とみなす。
g) parameterlist(パラメタリスト) パラメタ宣言のコンマ区切りリスト。
h) parameter-name(パラメタ名) 操作のパラメタの名前。通常は,定義される操作の中でのパラメタ
の役割を示す。操作の構文構造及び属性の構文構造は,操作にパラメタリストを含むことを除いて,
同じであることに注意しなければならない。
i)
direction (入出力方向) “in”(入力:値は呼出し前に設定され操作に影響を与える。),“out”(出
力:値は操作中に設定され,呼出し側はその値に操作完了後にアクセスする。)又は“inout”(入出力:
値は呼出し前に設定され操作に影響を与え,操作は呼出し側が操作完了後にアクセスできる値に再設
定する。)の値をとる,このパラメタの入出力方向の選択指示。パラメタの既定の入出力方向は“in”
とする。
j)
type(型) 先行するパラメタ又は属性のオブジェクト又は値の型。
k) default-value(既定値) 呼出し側が指定しなかった場合の入力又は入出力パラメタの値。コンスト
ラクタが設定しなかった場合のオブジェクトの属性の値。
l)
return-type(戻り値の型) 操作の戻り値又はオブジェクトの型で,本質的に操作の型となる。
m) property(プロパティ) NOT NULL又はUNIQUEのような属性又は操作に関する付加的な情報。
“{size = [0..n]}”のように,プロパティ名とそれに続く値とで構成してもよい(プロパティの下位型
としての解釈については,ISO/IEC 11404参照。)。
n) ... 先行する記述を何度でも繰り返してよい。
o) initial-value(初期値) コンストラクタが,そのパラメタリストによって明確に上書きしない限り,
新しいオブジェクトを構築するときに用いる属性の既定の値。
この規格では,オブジェクト制約言語(OCL:Object Constraint Language)の表記法を軽微な変更を行っ
て使用する。“ocl”接頭辞は,多くの演算子では削除している。これは不要であり紛らわしいためで,特
にこれらの演算子をISO TS 19103の基本型の箇条で接頭辞無しで使用しているためである。“::”はその後
に続く部分に対する名前空間を示す決定演算子とする。OCLでは多くの場合,名前空間はその操作を定義
しているクラスになるが,クラスを定義しているパッケージの名前を含んでもよい。この規格では,すべ
ての名前空間は,クラス識別子であり,次の二つの形式のうちのいずれかを取る。
class-identifier :== class-name | package-name::class- identifier
type :== class-identifier
誤解される恐れ又は強調の必要性がないかぎり,パッケージ名は含まない。この規格では,すべてのク
ラス名は,モデル内で一意な名称を,2文字のパッケージ識別接頭辞の後に下線“̲”でつないだ形式をと
る。これによって,型及びクラス名のパッケージ名決定の必要性を除いている。この規格のプロファイル
は,できる限りこの規定に従うことが望ましい。属性,役割名及び操作は,次のように記述する。
attribute-name {multiplicity} : attribute-type
{association-name “::”}role-name {multiplicity} “ : ” attribute-type
{type-1“::”}operation-name(name-2 “ : ” type-2, name-3 “ : ” type-3, … )
“ : ” return-type
役割は,多重度が1でない場合,役割値を集合として構成するものとする。役割値を他の方式で構成す
る必要がある場合,次のように,ISO/IEC 11404に従ったサイズを多重度として与えた適当なパラメタ化
コレクションクラスをattribute-type (属性型)として使用することが望ましい。
14
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
boundary : CircularSequence<GM̲OrientableCurve> {size = [1..n]}
(C++で用いるような)オブジェクト指向の演算子の記法では,次のメソッド宣言のように,最初のパ
ラメタを操作の前に置く。
return-type type-1::operation(type-2, type-3 … )
このようなメソッドは,“type-1”オブジェクトの名前空間が有効な場合にだけ有効であるという意味で,
利用できる名前空間を限定している。さらに,呼出しの間は,“type-1”型の暗黙のパラメタを使用してよ
い。OCLではこのオブジェクトを“self”と記述し,C++では“this”と記述する。非オブジェクト指向言
語又はオブジェクト言語の独立関数では,操作の関数記法は,最初のパラメタを区別せずに,次のように
記述する。
operation(name-1 : type-1, name-2 : type-2, name-3 : type-3 …) : return-type, …
これらの記法は(強調を除き)同等とし,この規格のプロファイルではいずれを使用してもよい。
これらの操作の定義は,“操作の署名(シグニチャ)”又は“プロトコル”と呼ぶ。これは操作と呼出し
機構とを分離する。UMLでは,正式な記法はプロトコルを定義し,それらに関連する操作はOCL制約を
記載できる関連文書内で略式に定義されるだけである。
属性を(取得操作と設定操作との対である)操作の型として考える見方では,この用語を属性“署名(シ
グニチャ)”を含むように拡張してよい。署名(シグニチャ)の定義は,操作の名前,戻り値の型並びにパ
ラメタの名前及び型を含む。メソッド又は属性は,通常は型をその下位型と置き換える以外は元の署名(シ
グニチャ)と同一の署名(シグニチャ)をもつような新しいメソッドを提供することで上書きしてよい。
署名(シグニチャ)の再利用を“多態性”と呼ぶ。クラス継承から発生する多態性は“構造的”多態性と
呼ぶ。意味上の類似性から発生する多態性は“自然な”多態性又は“一般的”多態性と呼ぶ。例えば,幾
何及び位相クラスにおける“境界”を得る共通のプロトコルは,位相の定義に基づいた操作上の制約から
発生する自然な多態性である。これは,二つのパッケージが共通のスーパークラスを原型として共有して
いないため,構造的多態性ではない。クラス継承の階層がオブジェクトの意味に基づくとすると,構造的
多態性は自然な多態性となる。意味上の類似性に依存しない多態性は“臨時”多態性とする。例えば,数
字の間に置かれる加算を示す“+”及び文字列クラスの結合を示す“+”の利用は,臨時多態性である。臨
時多態性は,意味的に紛らわしく,したがってこの規格では使用せず,この規格のプロファイルでも避け
ることが望ましい。
多くの操作は,すべてのパラメタを読み取り専用(direction = “in”)として渡し,オブジェクトの唯一
の変更又は生成は,設定操作による戻り値の型を利用して行うという,関数の形式で定義している。イン
タフェースの記述において,“this”という修飾は,呼び出しているオブジェクトのインタフェースの実体
を示す。OCLでは,このオブジェクトは“self”として参照する。オブジェクトを他のオブジェクトのメ
ソッドにパラメタとして渡す場合,それは“渡された”オブジェクトとして参照する。
クラス1
クラス2
Relation
widget
gadget
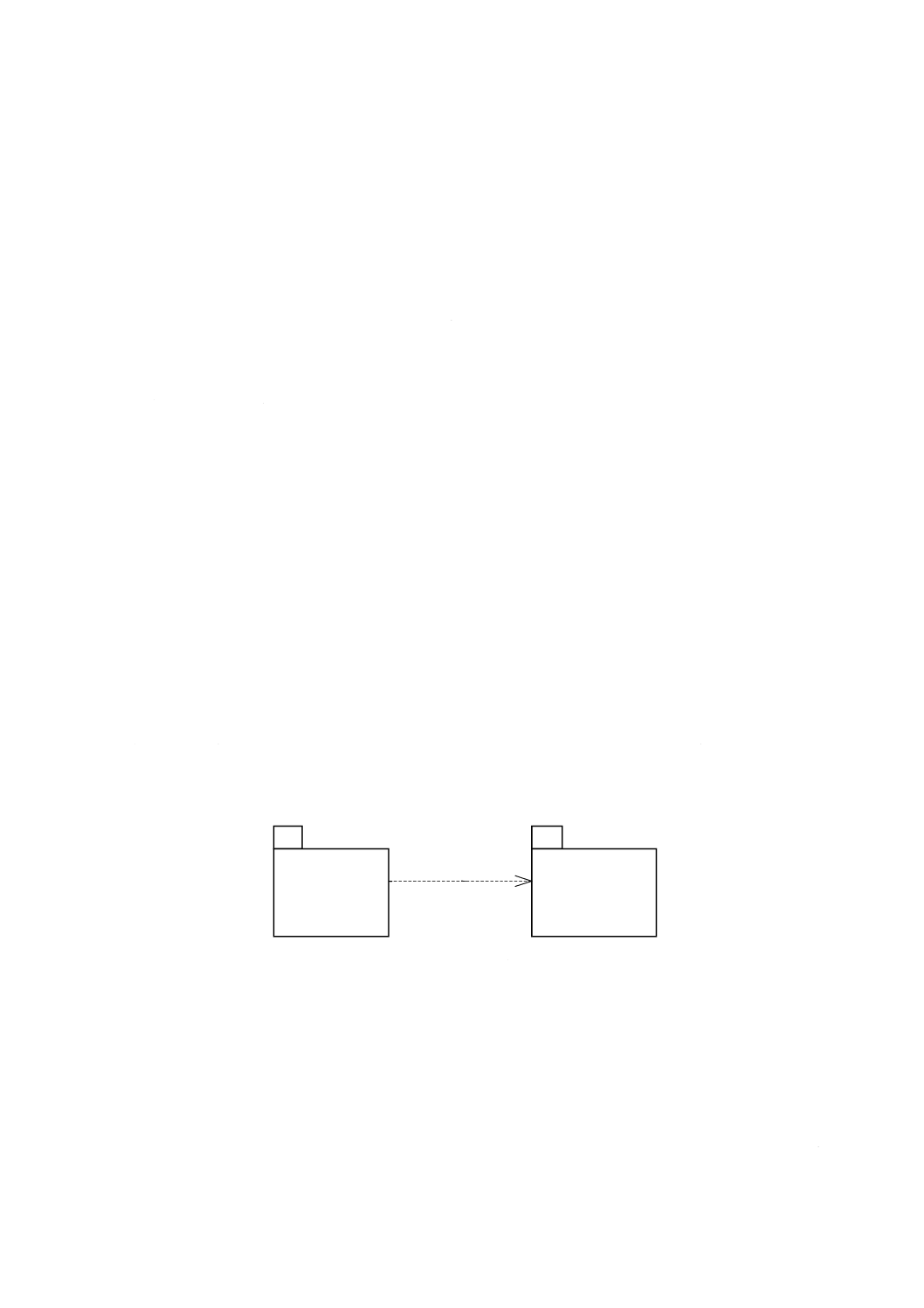
図 1 UMLにおける関連の表記例
モデルの各関連には関連名を付け,関連に参加する各クラスには役割名を付ける。図1の図式の場合,
“クラス1”は“クラス2”と“Relation”という名前で関連し,この二つのクラスを実装する場合には,
15
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
通常,次に示すようにこの関係の役割の名前をつけた“属性”として他方のクラスへの参照をもたせる。
Class1::gadget : Set<Class2> // 多対多の強連結
Class2::widget : Set<Class1>
又は,
Class1::gadget [1..n] : Class2 // 多対多の強連結
Class2::widget [1..n] : Class1
Class2の役割名は,Class2を指すClass1中の変数名として使用することに注意しなければならない。コ
レクションの型は,役割の並べ方の種類によって決める。
Class1::gadget : Sequence<Class2> // 多対多で順序をもつ強連結
Class2::widget : Set<Class1>
多くの役割はSet(非順序関係)又はSequence(順序関係)のいずれかに一致する。役割には,順番が
自然な開始位置をもたない環状列になるものもある。以降の規格の特定の部分ではこの記法を使用してい
るが,これは関連の特定の実装を示すものではない。相手のクラスが関連の存在に依存しない弱連結につ
いては,次のようにパラメタ化クラスReference< > を使用する。
Class1::gadget [1..n] : Reference<Class2>
// 弱連結
Class2::widget [1..n] : Class1
// 強連結
5.1.3
ステレオタイプ UMLモデルのほとんどの実体の記述には,オブジェクト名の近くにギュメ(“«”
及び“»”)で囲んで記述する“ステレオタイプ”を使用してよい。ステレオタイプは,UMLを拡張してモ
デルにその要素の記述を加えることに使用する。この規格では次に示すステレオタイプを使用する。
参考 上の文中の“ギュメ”はフランス語における引用符である。ギュメは,ISO/IEC 8859-1,ISO10646
/JIS X 0221,JIS X 0213などの符号化文字集合に含まれている文字だが,JIS X 0208などには
含まれていないので,環境によってはギュメを表記できない場合も多いと予想される。ギュメ
を表記できない環境でステレオタイプを記述する場合,これらを代替する文字としてJIS X
0208の“≪”(2区67点:非常に大きい)及び“≫”(2区68点:非常に小さい)を使用して
もよい。
a) «Interface»(インタフェース) このクラスは,直接インスタンス化せず,操作の署名(シグニチャ)
の抽象コレクションとして使用する。«Interface» クラスは,操作の構造的多態性のための参照クラス
を定義するために使用する。幾つかのプログラム言語では,このようなクラスをvirtual(仮想)又は
abstract(抽象)と呼ぶ。UMLの規格では,«Interface» クラスから可視となる属性又は関連をそのク
ラスに含んではいけない。Interfaceから不可視となる関連についてはそのInterfaceを加えてよい。言
い換えると,(Interface以外の)クラスは,そのクラスからたどれるがInterfaceからはたどれないよう
な,Interfaceへの関連をもってよい。応用スキーマでこの規格と同様に使用する場合には,この規格
のInterfaceと同じ名前の実装クラスを作成することは,応用スキーマでの論理的な矛盾を引き起こす。
b) «Type»(型) このクラスは,直接インスタンス化せず,操作,属性及び関係の各署名(シグニチャ)
の抽象コレクションとして使用する。«Type» クラスは,属性及び関連を含む構造的多態性のための参
照クラスを定義するために使用する。属性及び関連の実際の内部構成は実装に依存する。これらの要
素の構成は不明なので,UMLでは «Type» クラスにはメソッド(操作の実装)を一切含んではならな
い。応用スキーマ内でこの規格と同様に使用する場合には,この規格のTypeと同じ名前の実装クラス
は,そのTypeがAbstract (UMLの記号表記法では,名前をイタリック体で示す。)でない限り作成
してよい。
16
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
c) «Abstract»(抽象) このクラス(UMLではクラス名をイタリック体で表記することでも表す。)は,
メソッドを含んでよいこと以外は «Type» と同様とする。このクラスは,追加されたメソッドを含む
構造的多態性のための基底クラスを定義する。応用スキーマ内でこの規格と同様に使用する場合には,
この規格のAbstractクラスと同じ名前の実装クラスを作成することは,応用スキーマでの論理的な矛
盾を引き起こす。
d) «Data type»(データ型) このクラスは,直接インスタンス化してよく,基本的に分類又は振る舞い
の記述を禁止してデータをカプセル化するのに使用する。«Data type» は,それ自身を識別せず,他の
クラスの属性,強い集成(aggregate)の対象クラスなどとして,ある種のコンテナに強く集成しなけれ
ばならない。«Data type» 型は,弱い集成の対象として使用してはならず,Reference< > パラメタ化ク
ラスで使用してもいけない。
e) «Union»(共用) 所属する属性として列挙した幾つかの選択肢のいずれか一つからなる型。これは
多くのプログラム言語における識別共用体に類似する。ポインタを用いる幾つかの言語では,これは
識別属性によって決定される適切な型に型変換可能な“void”ポインタを必要とする。
f)
«Leaf»(終端) 下位パッケージを含まず,オブジェクトクラス及びインタフェースの定義だけを含
むパッケージに適用する。技術的な要求事項ではないが,この規格は,すべてのオブジェクトの定義
を終端パッケージに配置した後,より大きな非終端パッケージに体系化する。
g) «CodeList»(符号リスト) 列挙型(enumeration)と同様に幾つかの値の内の一つをとるが,その目
的は異なっていて,符号リストを次第に拡張してよい。ほとんどの符号リストは,数値として格納す
るが,文字列を使用する実装もある。この規格では,符号リストが文字列符号をもつものとして定義
しているが,これは,実装の詳細によって決まるものであり,純粋な数値符号を用いてもよい。
5.1.4 データ型及びコレクション型 コレクション型は,この規格に一致したものでなければならないが,
そのインタフェースについてはすべてを具体化する必要はない。これらの型は,UML図に含まれてはいな
いが,時としてオブジェクト制約言語(OCL)の記述で暗に使用されている(ISO TS 19103参照)。
これらのインタフェースの中では有限集合を使用することが最も一般的である。“T”を型とすると,
“T”型のオブジェクトのすべての有限非順序集合を構成して,新たにインスタンス化するクラス型を
“Set<T>”と記述する。実装環境は,しばしば配列のような幾つかの一般的なコレクション型を提供して
いるが,ここで,それらの型に対するはん用インタフェースを規定しようとするものではない。ISO TS
19103にはこれらの型のインタフェース定義の例が含まれている。この規格は,論理的に同等だが特定の
実装環境に備わった型の使用を制限するものではない。基本クラス型と,これらのコレクション型のよう
なパラメタ化型で,この規格で使用するものを次に示す。
a) TransfiniteSet<T>(Tの超限集合) 値にだけ限定した,場合によっては無限の集合。例えば,整数
及び実数は,超限集合である。これは実際には数学における集合の通常の定義だが,プログラム言語
では集合という用語を有限集合の意味に限定している。
b) Set<T>(Tの集合) 有限集合。オブジェクト型のために使用する。各オブジェクトは,集合の中に
一つしかないものとみなす。各オブジェクトは,複数の集合の要素となりうるので,必ずしも強い集
成ではない。他で示していない限り,この規格ではSetを弱い集成(Set<Reference<T>>)の意味で使
用する。
c) Bag<T>(Tの多重集合) 各オブジェクトが集合の中に複数存在してよい,有限非順序集合。論理的
には pair<ocject : T, count : Integer> (Tのオブジェクトと整数型の回数との対)の集合と考えてよ
い。
17
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) Sequence<T>(Tの列) 値を繰り返してよいオブジェクトの有限順序集合。論理的にはoffsetを列の
中のオブジェクトの位置としてpair<object : T, offset : Integer> (Tのオブジェクトと整数型の相対位
置との対)の集合と考えてよい。実装によって,相対位置は1,0又は任意の位置から数えてよい。各
対をオブジェクト上に射影するとBagができる。重複を削除するとSetになる。
e) CircularSequence<T>(Tの環状列) そのすべての巡回シフトを同一とみなした,自身に巻き戻るよ
うな列。これは,相対位置の巡回シフトによって区別される以外は,Sequenceと同等なクラスとみな
す。
f)
Reference<T>(Tの参照) C++におけるポインタ,SQL99(従来のSQL3)のREF及びJavaのクラ
ス変数に相当する,クラスTの識別可能なオブジェクトへの参照。この規格のクラスの定義文では,
弱い関連は,適切なクラスへの参照として表現する。強い集成は,属性と同じ方法で表現する。
g) Number(数),Float(浮動小数点数),Integer(整数),Real(実数) 通常は,その環境のプログラ
ム言語のプリミティブとしてインスタンス化されるような,様々な単純な値の型。ISO TS 19103を参
照。
h) Length(長さ),Area(面積),Distance(距離) メートル,エーカーなどの特定の単位と関連させ
て使用する,様々なスカラ値(ISO TS 19103参照)。
備考 プログラム形式による関連の表現では,UMLに対するコード生成としてもっとも一般的な規約
を使用している。関連役割は,その関連の役割の対象となるクラスをTとすると,Reference<T>
型のメンバ名として使用している。あいまいさが残る場合には,関連名をその役割の名前空間
として,関連名::役割名 : Reference<対象クラス>のように使用している。当然,関連の参照側
のクラスを使用して,参照側クラス::役割名 : Reference<対象クラス>のようにも表現している。
関連が強い集成の場合,参照を論理的に取り去り,参照側クラス::役割名 : 対象クラスと表現
してよい。強い集成で単方向の関連は,その意味がメンバ属性と論理的に一致する。関連を使
用するか,又は役割に類似した属性を使用するかは,UMLで異なる設計を生み出す原因の一つ
になっている。いったんコード生成を行うと,UMLにおける関連についての情報(及び,欠落
する他のすべての情報)の復元は,役割に類似した属性の対による往復化処理と同じになる。
データ型には,ISO/IEC 11404 の用語とわずかに異なった,ISO TS 19103で定義されたRecord型の単
純なインスタンスのものもある。ISO/IEC 11404の規定は,パラメタリストと混乱する可能性があるので,
この規格ではわずかに変更した構文[外側の丸括弧“( )”を“< >”で置き換える。]を使用する。
Record Type :== “<” field-name “ : ” type [= default-value],… “>”
Record Instance :== “<” field-name “ : ” field-value,… “>”
この,戻り値として複数の型をもつ構文は,中括弧を省略している以外はこのRecordの構文と一致する
ことに注意する。この規格では,単独で使用する場合は,このRecordの構文を使用するが,無名型として
レコードに類似した構造を返す操作を定めるときには,UMLの標準的な戻り値が複数の型の構文を使用す
る。
この規格で定義した操作の幾つかは,そのとり得る値としてNULL及びEMPTYを使用する。NULLは
求める値が未定義であることを示す。この規格では,すべてのNULL値は,同一であるとみなす。オブジ
ェクトの要求にNULLが返された場合,指定した基準に合致するオブジェクトがなかったものとする。
EMPTYは,要求された集合が要素を含まないことを示し,いずれの型の集合にも変換可能なオブジェク
トを参照する。強い型の集成をもつプログラミングシステムと異なり,この規格では,唯一の空集合が存
在し,それを表すオブジェクト同士は,同一であるという数学的な反復定義を使用する。空であること以
18
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
外には,このような集合は固有の情報を欠くので,文脈によってはNULL値とEMPTY集合とは等しいも
のとみなす。
5.1.5
強代替性 この規格は,実装プロファイル及び転送スキーマは強代替性を用いて構築されるものと
みなしている。これは応用スキーマを設計する様々な局面で,プロファイルの構築者は,あるクラスがこ
のスキーマで定義されたクラスに必要なデータ,操作,関連を満たすのであれば,本来のクラスの代わり
にそれを使用してもよいということを示す。この代替性の実装の方法は規定しないので,実装環境の特徴
に応じて様々な方法を使用してよい。これは,特にデータ型に依存した性質をもつ転送の規格についても
いえる。転送する集合における各実体は,それがデータだけからなる表現形式であることから,この規格
で定義したクラスとの関係を希薄なものだけとすることが可能である。この技術を最大に利用してクラス
に関連した下位クラスを定義することが,代替性としてもっとも有効な手段である。
この前提として,“is type of”(〜の型である)階層としての下位クラス化の意味を厳守することを必要
とする。クラスの個々のインスタンスは,そのクラスの上位型として定義されたすべての集合のメンバで
なければならない。したがって,たとえ下位型がその上位型より複雑であるという概念に直観的に反する
としても,円をだ(楕)円の下位型であると定義してもよいが,その逆を定義してはならない。
5.2
構成 この規格の後続の箇条は,UMLパッケージという観点でまとめている。パッケージは,関係
する型及びインタフェースの集合であり,ソフトウェアシステムの設計に関する一貫したコンポネントを
形成する。パッケージは,しばしばシステムの他のパッケージが提供するサービスを呼び出すので,通常,
完全なシステムを形成することはない。クライアントとして働くあるパッケージがサーバとして働く別の
パッケージを使用して必要なサービスを供給する場合,クライアントパッケージは,サーバパッケージに
依存するという。この依存性は,パッケージ中のオブジェクトクラスがサーバパッケージの定義する別の
オブジェクトにアクセスするときに発生する。純粋にクライアント又はサーバになることは,地理情報に
おける幾何についてはまれなことなので,この規格ではこれらのステレオタイプを使用しない。依存クラ
スは要求を伝えることのできる関連を通してサーバと関連付けられるので,大部分のオブジェクトクラス
の依存性は,オブジェクトクラスの関連から発生する。異なるパッケージ間にあるオブジェクト間のさま
ざまな依存性は,パッケージ間の一つの依存性として反映しなければならない。このパッケージ依存性は,
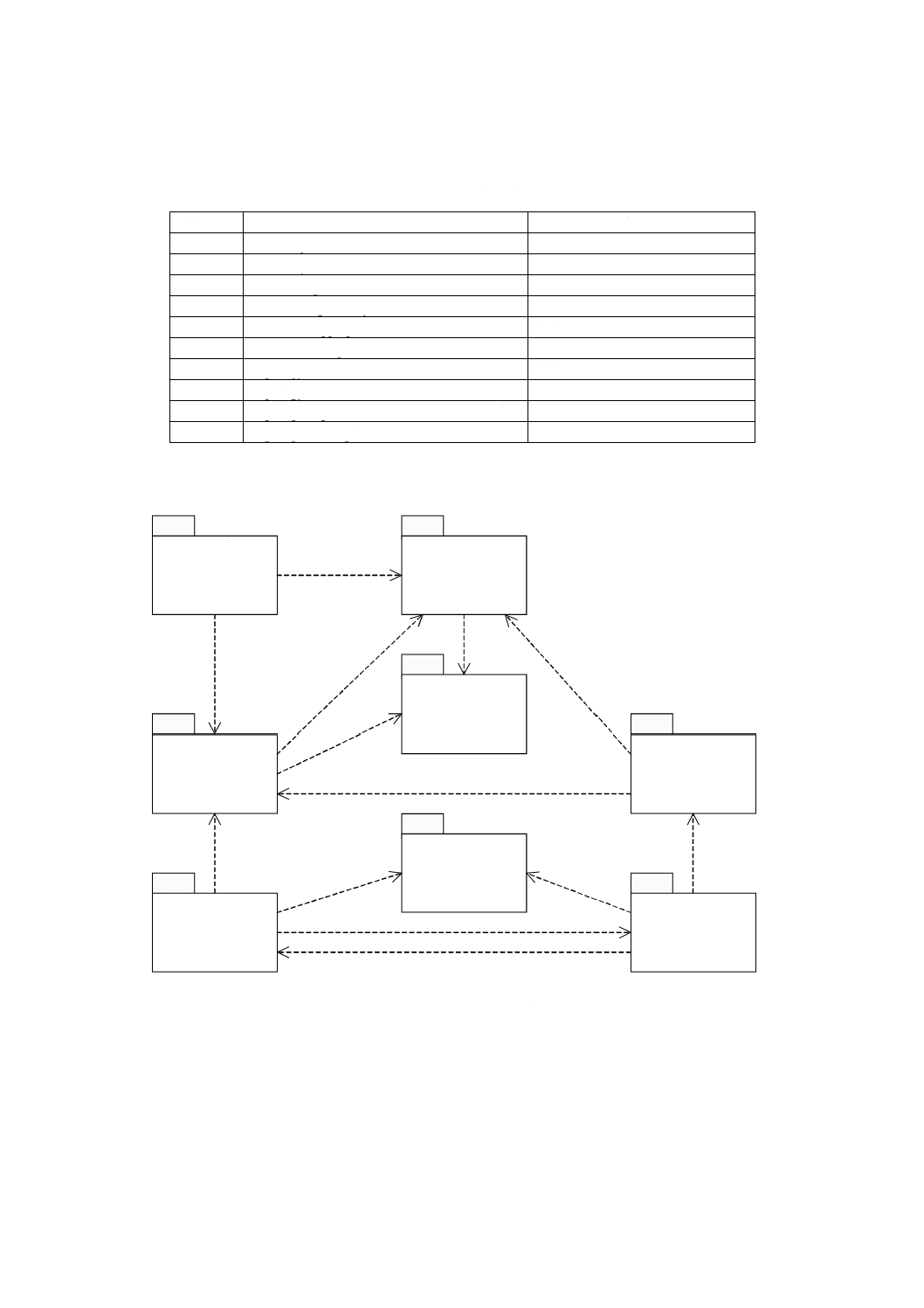
図2の図形記法を用いたパッケージ図式で示す。
«クライアント»
従属パッケージ
«サーバ»
独立パッケージ
図 2 UMLのパッケージ依存性の例
このクライアントサーバの関係によって,パッケージ間の依存性は,実用的な応用スキーマの基準を定
義する。この規格で定義する任意のパッケージの実装を含む応用スキーマは,依存したすべてのクラスの
実装も含まなければならない。
表6は,この規格で規定するパッケージの要約を示す。6.と7.で定めるパッケージは,規定とする。そ
れらは,規格に適合したシステムの外部インタフェースの基礎を形成する応用スキーマに幾何及び位相の
構成要素を提供する。JIS X 7111のSpatial referencing by Coordinatesパッケージ及びISO TS 19103のBasic
19
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Typesパッケージのような他の規格から,追加のパッケージを参照する。これらは,空間スキーマ機能を
完全で読みやすい図として示すために,必要な範囲でここに転載している。
表 6 パッケージ及びクラス
箇条番号 パッケージ名
パッケージに含まれる主なクラス
6.
Geometry (幾何)
幾何のクラス
6.2
Geometry Root (幾何基底)
幾何の基底クラス
6.3
Geometric primitive (幾何プリミティブ)
幾何プリミティブ
6.4
Coordinate geometry (座標幾何)
座標幾何クラス
6.5
Geometric aggregates (幾何集成)
集成
6.6
Geometric complex (幾何複体)
幾何複体及び合成体
7.
Topology (位相)
位相のクラス
7.2
Topology root (位相基底)
位相の基底クラス
7.3
Topological primitive (位相プリミティブ) 位相プリミティブ
7.4
Topological complexes (位相複体)
位相複体
図3は,この規格の規定の箇条における終端パッケージを示す。
«Leaf»
Geometric
aggregates
(from Geometry)
«Leaf»
Geometry root
(from Geometry)
«Leaf»
Coordinate
geometry
(from Geometry)
«Leaf»
Geometric
primitive
(from Geometry)
«Leaf»
Topological
primitive
(from Topology)
«Leaf»
Topological
complex
(from Topology)
«Leaf»
Geometric
complex
(from Geometry)
«Leaf»
Topology root
(from Topology)
図 3 規定のUMLパッケージの依存性
備考 本文中の例は,この規格に示す事項を理解するのに最も適した位置にあり,またそれ自体,し
ばしば後の箇条で規定する他の事項を暗に先行引用することがある。例えば,GM̲Envelopeの
解説にはGM̲LineStringの先行引用を含む。ほとんどの場合は,先行引用した事項(型,操作
又は属性)は,しばしば意味を豊かにし,共通して使用される用語に密接に関係するので,分
かりやすくなる。読者が紛らわしいと思う場合は,概要をつかむために実例を飛ばして文書全
20
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
体を読み,それから例を交えて再度詳しく読むのがよい。
5.3
略語
ATS 抽象試験項目群(Abstract Test Suiteの略称)
API 応用プログラムインタフェース
C++ C言語を基本としてオブジェクト指向に拡張したプログラム言語
LISP リスト処理(LISt Processing)を基本とするプログラム言語
規格はCommon LISPと呼ぶ。
MBR 最小境界長方形領域(Minimum Bounding Regionの略称)
OCL オブジェクト制約言語(Object Constraint Languageの略称)
SQL 3 SQL 99の開発時における一般的な名称
SQL 99 オブジェクト指向データ型拡張機構を含んでいる,1999年に採択されたSQL言語の規定
TIN 不規則三角網(Triangulated Irregular Networkの略称)
UML 統一モデリング言語(Unified Modelling Languageの略称)
2D 二次元
3D 三次元
6. Geometryパッケージ
6.1
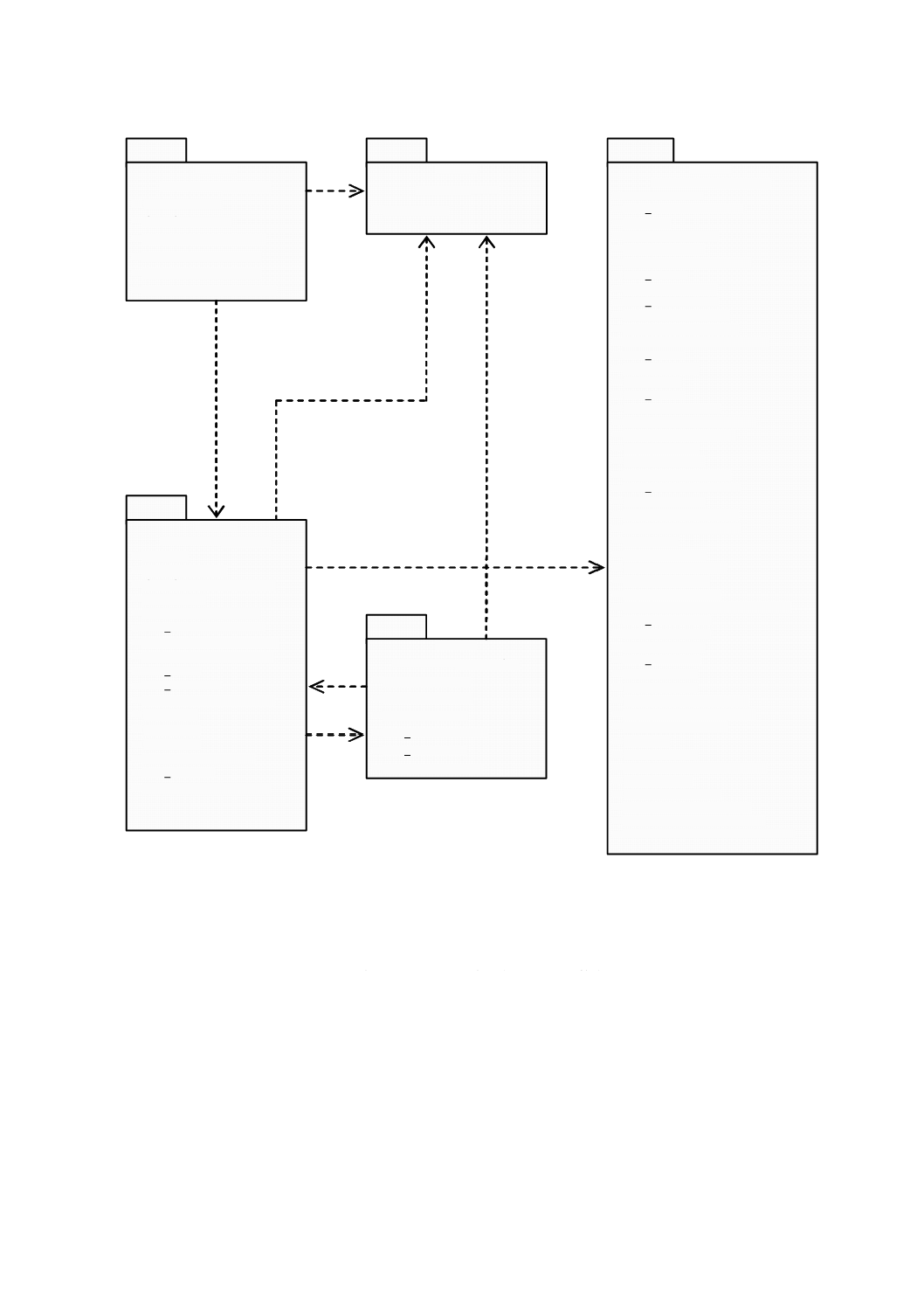
意味 Geometry(幾何)パッケージ(図4)は座標幾何としての様々なクラスを含む。すべてのクラ
スは,基底クラスであるGM̲Objectを通じて座標参照系への任意選択の関連を継承する。この規格で定義
するインタフェースをとおして示したすべての直接位置は,それを用いる幾何オブジェクトの空間参照系
に属していなければならない。幾何複体,幾何合成体又は幾何集成のすべての要素は,同じ座標参照系に
関連しなければならない。GM̲Objectのインスタンスが座標参照系を指定した他の(GM̲Aggregate又は
GM̲Complexのような)GM̲Objectに集成される場合,これらの要素は,他の指定がないかぎり同じ座標
参照系にあるものとみなす。
21
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 4 Geometryパッケージ:クラス内容及び内部依存性
幾何パッケージは,基本的な幾何オブジェクト,幾何集成体及び幾何複体を示す内部パッケージをもち,
それらは,単純な集成(aggregate)より精巧な内部構造をもつ。図4は,幾何パッケージ間の依存性及び各
パッケージにおけるクラスの一覧を示す。
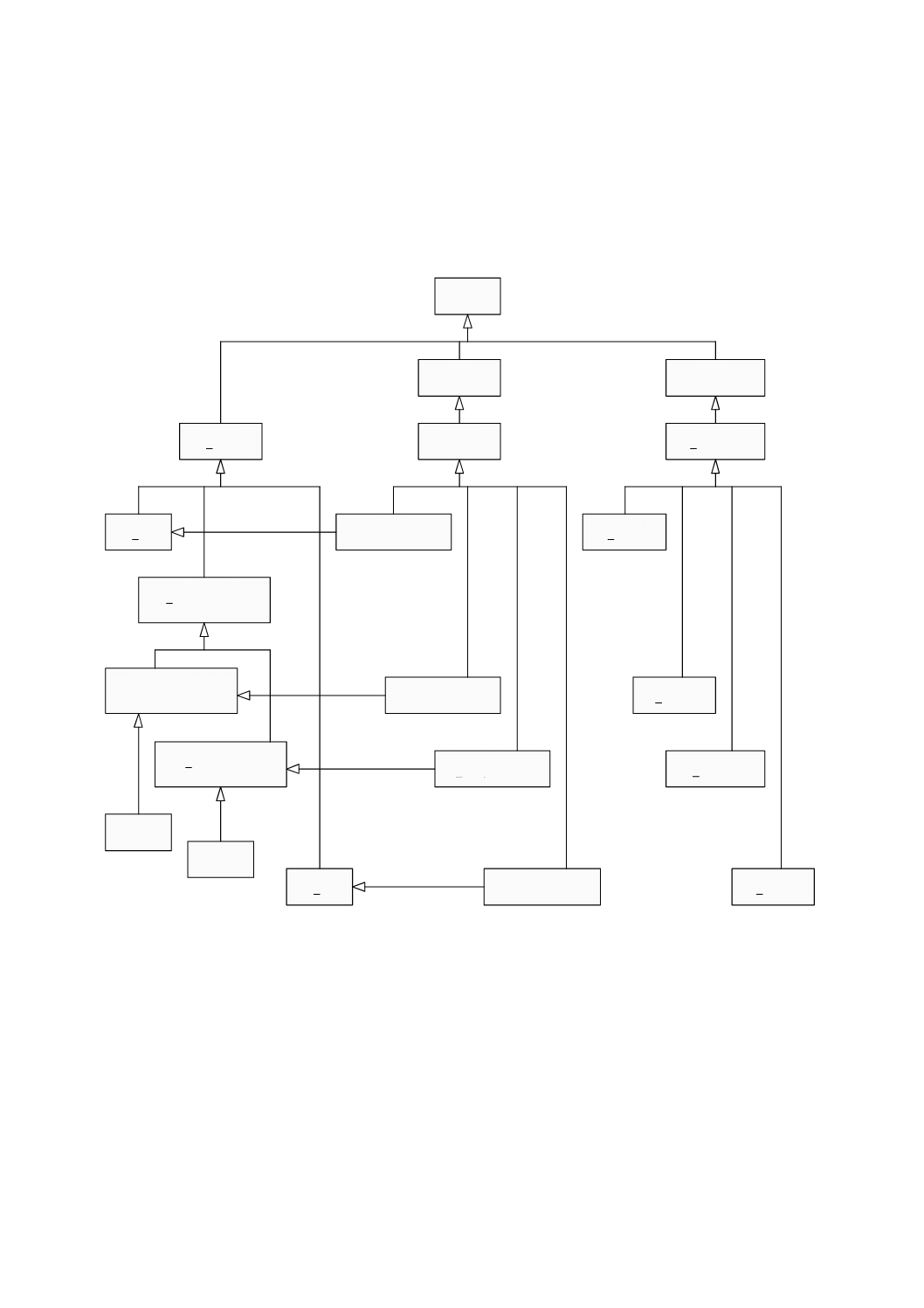
幾何パッケージで定義する基本的なクラスを図5に示す。GM̲Objectの意味を継承するすべてのオブジ
ェクトは,直接位置の集合として振る舞う。その振る舞いはそれが含む直接位置によって決まる。
GM̲Primitiveの下位のオブジェクトは,開集合,すなわちその境界上の点を含まない。曲線はその端点を
含まず,曲面はその境界曲線を含まず,立体は境界曲面を含まない。GM̲Complexの下位のオブジェクト
は,閉集合,すなわちその境界上の点を含む。このことは明らかにあいまいさの原因になる。プリミティ
«Leaf»
Geometric complex
+ GM̲Complex
+ GM̲Composite
+ GM̲CompositeCurve
+ GM̲CompositePoint
+ GM̲CompositeSolid
+ GM̲CompositeSurface
«Leaf»
Coordinate geometry
+ DirectPosition
+ GM̲AffinePlacement
+ GM̲Arc
+ GM̲ArcByBulge
+ GM̲ArcString
+ GM̲ArcStringByBulge
+ GM̲Bezier
+ GM̲BicubicGrid
+ GM̲BilinearGrid
+ GM̲BSplineCurve
+ GM̲BSplineSurface
+ GM̲BSplineSurfaceForm
+ GM̲Circle
+ GM̲Clothoid
+ GM̲Cone
+ GM̲Conic
+ GM̲CubicSpline
+ GM̲CurveInterpolation
+ GM̲CurveSegment
+ GM̲Cylinder
+ GM̲Envelope
+ GM̲GenericCurve
+ GM̲GenericSurface
+ GM̲Geodesic
+ GM̲GeodesicString
+ GM̲GriddedSurface
+ GM̲Knot
+ GM̲KnotType
+ GM̲LineSegment
+ GM̲LineString
+ GM̲OffsetCurve
+ GM̲ParametricCurveSurface
+ GM̲Placement
+ GM̲PointArray
+ GM̲PointGrid
+ GM̲PointRef
+ GM̲Position
+ GM̲Polygon
+ GM̲PolynomialSpline
+ GM̲PolyhedralSurface
+ GM̲SurfacePatch
+ GM̲Tin
+ GM̲Triangle
+ GM̲TriangulatedSurface
+ GM̲Sphere
+ GM̲SplineCurve
+ GM̲SplineCurveForm
+ GM̲SurfaceInterpolation
+ TransfiniteSet<DirectPosition>
«Leaf»
Geometric primitive
+ Bearing
+ GM̲Boundary
+ GM̲ComplexBoundary
+ GM̲Curve
+ GM̲CurveBoundary
+ GM̲OrientableCurve
+ GM̲OrientablePrimitive
+ GM̲OrientableSurface
+ GM̲Point
+ GM̲Primitive
+ GM̲PrimitiveBoundary
+ GM̲Ring
+ GM̲Shell
+ GM̲Solid
+ GM̲SolidBoundary
+ GM̲Surface
+ GM̲SurfaceBoundary
«Leaf»
Geometric aggregates
+ GM̲Aggregate
+ GM̲MultiCurve
+ GM̲MultiPoint
+ GM̲MultiPrimitive
+ GM̲MultiSolid
+ GM̲MultiSurface
«Leaf»
Geometry root
+ GM̲Object
22
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ブとしての線の表現はその端点を参照する必要があるが,直接位置の集合としてはこれらの点を含まない。
複体としての線の表現もその端点を参照するが,同時に端点を直接位置の集合として含む。これは,同一
のデジタル表現がプリミティブとしてアクセスするか,複体としてアクセスするかによって若干異なる意
味をもつことを示す。
図 5 特化関係をもつ幾何基本クラス
この意味的な違いはGM̲CompositeCurve(合成曲線)において最も顕著である。合成曲線は,その幾何
形状が複数の曲線プリミティブとしても表現され得るような地物の表現に用いる。地図学の観点からする
と,この二つの表現には違いはない。しかし,位相幾何学の観点では,これらは異なる。両者の区別を
GM̲CompositeCurveとGM̲OrientableCurveとの間の継承関係として継承関係図(図5参照)に示す。
GM̲CompositeCurve (6.6.5参照)は本来,閉GM̲Objectに意味付けられているが,GM̲Primitiveの操作
(6.3.10参照)の下では開GM̲Objectとしても振る舞う。このオブジェクトのインタフェースプロトコル
«Type»
GM̲Object
«Type»
GM̲Complex
«Type»
GM̲Composite
«Type»
GM̲Primitive
«Type»
GM̲Aggregate
«Type»
GM̲MultiPrimitive
«Type»
GM̲Point
«Type»
GM̲OrientableCurve
(from Geometric primitive)
«Type»
GM̲OrientablePrimitive
(from Geometric primitive)
«Type»
GM̲Curve
«Type»
GM̲OrientableSurface
(from Geometric primitive)
«Type»
GM̲Surface
«Type»
GM̲Solid
«Type»
GM̲CompositePoint
«Type»
GM̲CompositeCurve
«Type»
GM̲CompositeSurface
«Type»
GM̲CompositeSolid
«Type»
GM̲MultiPoint
«Type»
GM̲MultiCurve
«Type»
GM̲MultiSurface
«Type»
GM̲MultiSolid
23
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
が位相幾何の細部に依存する場合には,最初にその区別を必要とするときにGM̲PrimitiveとGM̲Complex
とのいずれの継承かを識別しなければならない。これらのプロトコルは,GM̲Objectで定義されている同
一の操作から継承した場合でも,その意味を継承する継承木の枝に依存して異なる振る舞いをする。実装
プロファイルの作成者はこれを考慮して,意味的な不調和を起こすような実現関係には代理の仕組みを用
いてよい。このような手続は,多重継承が許されないか又は仮想的なメソッド結合が制限されているよう
なシステムのオブジェクト指向プログラミング及びデータベースで必要となる。
6.2
Geometry rootパッケージ
6.2.1
意味 幾何オブジェクトは,座標幾何と座標参照系とを組み合せたものとする。すべての操作にお
いて,すべての幾何計算は,最初にアクセスした幾何オブジェクト(通常は,操作を呼出す対象となった
オブジェクト。)の座標参照系の中で行わなければならない。操作の返すオブジェクトは,他で明確に宣言
されない限り,計算に用いた座標参照系になければならない。この箇条で定義するインタフェースプロト
コルは,基本的に集合論に従っている。一般に,幾何オブジェクトは,DirectPosition (直接位置)で表さ
れる幾何の点の集合とする(6.4.1参照)。幾何オブジェクトを,オブジェクトとしてインスタンス化した
ものをGM̲Objectとする。値として用いる幾何の点を,オブジェクトとしてインスタンス化したものを
DirectPositionとする。GM̲Objectに定義している一般的な集合論の操作は,それより下位のクラス階層に
おいては,境界のDirectPositionを集合の要素として含むか否かによって違いが生じてくる。GM̲Primitive
の下位型は境界点を含まず,GM̲Complexの下位型は境界点を含む。
GM̲Object及びGM̲Primitiveは,応用スキーマのオブジェクト又はデータ構造として直接インスタンス
化してはならないという意味で純粋な抽象クラスとする。これらのクラスのインスタンスは,GM̲Point,
GM̲Curve又はGM̲Surfaceのような非抽象下位型のうちの一つのインスタンスでなければならない。これ
はGM̲Complexには当てはまらない。GM̲Complexは応用スキーマによって直接にインスタンス化でき,
GM̲Compositeの非抽象下位クラスのうちの一つのインスタンスでなくてもよい。この規格では
GM̲Complexは明示的に実装しないが,応用スキーマがこの規格に適合したクラスライブラリ
に”GM̲Complex”と呼ばれる具象クラスを含むことは有効とする。応用スキーマの名前空間はこの規格の
名前空間と異なるものであり,このような見かけ上の名前の論理的な乱用は有効であることを考慮しなけ
ればならない。このことは,この規格の抽象クラスについては適用しない。抽象クラスは,実装に直接対
応することが論理的には不可能である。抽象クラスのコンストラクタは,抽象型の直接の論理的なインス
タンスではなく,その型の具象下位クラスのインスタンスを生成する。
“抽象”に関するこのような解釈は,UMLで一般に用いられるものより厳密であるが,ここでは応用ス
キーマ開発者に対する指針として適切である。
6.2.2
GM̲Object
6.2.2.1
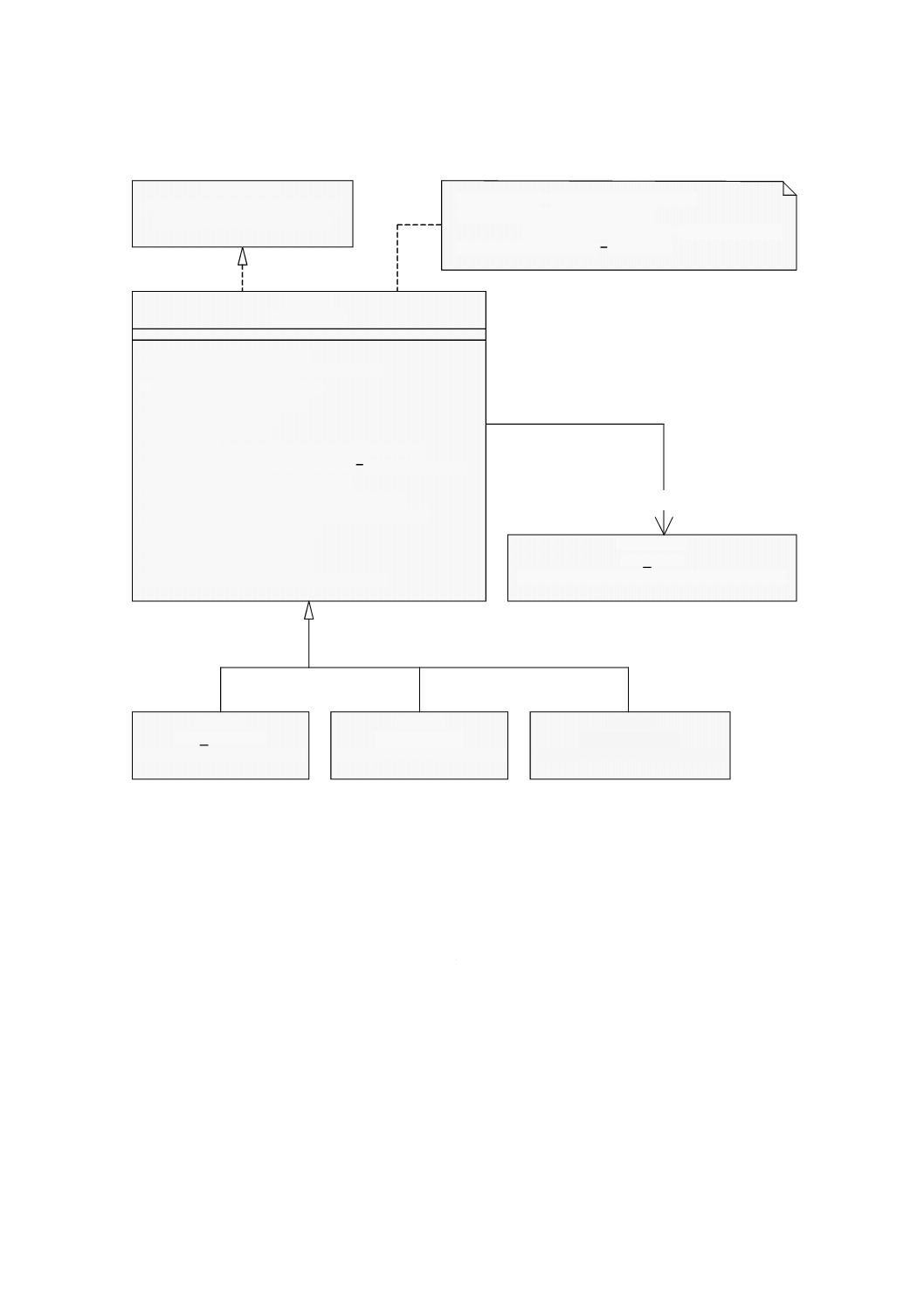
意味 GM̲Object(幾何オブジェクト)(図6参照)は,幾何オブジェクトの分類の基底クラスで,
地理的に参照されるすべての幾何オブジェクトに共通なインタフェースを定める。GM̲Objectのインスタ
ンスは,特定の座標参照系における直接位置の集合とする。GM̲Objectは,直接位置の集合に対する集合
操作インタフェース(TransfiniteSet<DirectPosition>)をもつ,点の無限集合とみなす。無限コレクション
クラスは,直接実装できないので,GM̲Objectインタフェースに従って包含を調べる真偽試験を提供しな
ければならない。この規格は,ベクトル幾何クラスに限定しているが,将来の作業においてもGM̲Object
を変更することなく基底クラスとして使用してよい。
備考 型としてのGM̲Objectは,データ型として明確な初期状態又は初期値表現をもたない。
GM̲Objectをインスタンス化した下位クラスは,明確な初期状態又は初期値表現をもつ。
24
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.2.2.2
mbRegion “mbRegion”(最小境界長方形領域取得)操作は,それぞれの応用システムが様々な
方法での実装を選択できるよう,ここでは単にインタフェースとして定める。この操作は,その座標参照
系においてこのGM̲Objectを含む領域を返す。既定の操作は,“GM̲Object::envelope”操作が返すものと
同じ空間集合を表す,適切なGM̲Objectの下位クラスのインスタンスを返す。mbRegionは,最小境界長
方形(MBR又は包被)以外の範囲を用いたインデックス方法を提供するような場合に最も一般的に用いら
れる。
GM̲Object::mbRegion() : GM̲Object
非ベクトル幾何表現は,この規格で定義する型ではないが,ここで返すGM̲Objectとして使用してよい。
6.2.2.3
representativePoint “representativePoint”(代表点取得)操作は,様々な方法で実装できるよう,
ここでは単にインタフェースとして定める。これは,このGM̲Object上に存在する点の値(DirectPosition)
を返す。“GM̲Object::centroid”操作の返す点がオブジェクト上に存在すればその点のDirectPositionを用い
ることを既定の方法としてよい。
GM̲Object::representativePoint() : DirectPosition
representativePointの他の用途として,画像表示を行うシステムでラベルを配置するために用いてよい。
記号及び文字の配置の定義は,この規格の適用範囲外とする。
6.2.2.4
boundary “boundary”(境界取得)操作は,このGM̲Objectの境界上のすべての直接位置を含
んだGM̲Objectの有限集合を返す。これらのオブジェクトの集まりは,適宜,さらに内部構造をもち,
GM̲Complexの下位型であるGM̲Boundaryデータ型の下位クラスとして表現する。戻り値のGM̲Object
の有限集合には,このGM̲Objectと同じ座標参照系を使用する。GM̲ObjectがGM̲Complexに含まれる
場合は,このGM̲Complexは,戻り値の境界GM̲Objectを含む。GM̲ObjectがどのGM̲Complexにも所
属しない場合,境界GM̲Objectを操作の結果として生成してよい。
GM̲Object::boundary() : GM̲Boundary
戻り値の集合の構成は,GM̲Objectの型に依存する。後に規定するGM̲Objectの各下位クラスは,その
境界集合の構成をより厳密に規定する。
境界の要素は元の要素より次元が小さくなければならない。
-- 境界のすべてのオブジェクトは,元のGM̲Objectに比べ,次元が1以上小さい。
boundary->select(dimension) <= self.dimension ‒ 1
25
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Interface»
TransfiniteSet<DirectPosition>
(from Coordinate geometry)
«Type»
GM̲Object
+ mbRegion() : GM̲Object
+ representativePoint() : DirectPosition
+ boundary() : GM̲Boundary
+ closure() : GM̲Complex
+ isSimple() : Boolean
+ isCycle() : Boolean
+ distance(geometry : GM̲Object) : Distance
+ dimension(point : DirectPosition = NULL) : Integer
+ coordinateDimension() : Integer
+ maximalComplex() : Set<GM̲Complex>
+ transform(newCRS : SC̲CRS) : GM̲Object
+ envelope() : GM̲Envelope
+ centroid() : DirectPosition
+ convexHull() : GM̲Object
+ buffer(radius : Distance) : GM̲Object
{dimension() > boundary().dimension}
{boundary().notEmpty() implies
boundary().dimension() = dimension() -1}
{boundary().isEmpty() = isCycle()}
«Abstract»
SC̲CRS
(from Spatial Referencing by Coordinates)
+object
0..n
{Reference}
0..1
+CRS
Coordinate Reference System
«Type»
GM̲Primitive
(from Geometric primitive)
«Type»
GM̲Complex
(from Geometric complex)
«Type»
GM̲Aggregate
(from Geometric aggregates)
図 6 GM̲Object
6.2.2.5
closure “closure”(閉包取得)操作は,このGM̲Objectとその境界上のすべての点を含んだ
GM̲Objectとの有限集合(オブジェクトとその境界との和集合)を返す。これらのオブジェクトの集まり
は,さらに適切な内部構造をもつ。戻り値のGM̲Objectの有限集合には,このGM̲Objectと同じ座標参
照系を用いる。もしGM̲ObjectがGM̲Complexに含まれる場合には,このGM̲Complexは戻り値の境界
GM̲Objectを含む。GM̲ObjectがどのGM̲Complexにも含まれない場合には,境界GM̲Objectを操作の
結果として生成してよい。
GM̲Object::closure() : GM̲Complex
6.2.2.6
isSimple “isSimple”(単純判定)操作は,GM̲Objectが内部に自己交差又は自己接触する点が
ない場合,TRUEを返す。数学的な形式論では,オブジェクト内部のすべての点が距離近傍をもち,その
近傍とオブジェクトとの共通集合がn次元球と同形であることを示す。ここでnは,このGM̲Objectの次
元とする。
26
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲Object::isSimple() : Boolean
ほとんどの座標幾何は,その位相次元のユークリッド空間の領域において,直接又は間接に関数によっ
て表現されるので,単純性に関する最も簡単な試験は,一対一で双連続(双方向で連続)な関数が存在す
るか否かを調べる方法である。このような関数は,位相同形となる。この試験は,“閉じた”オブジェクト
(すなわち,isCycle操作がTRUEになるオブジェクト)には機能しない。
GM̲Complexには単純なGM̲Objectしか含んではならないが,“スパゲッティ”データ集合の中ではし
ばしば単純でないGM̲Objectが含まれる。
備考 “スパゲッティ”は,通常は,使用する前に“きれいに”しなければならないような,許容水
準を超えたデータの幾何的な異常及び矛盾を示す,軽べつした(無礼な)用語である。このよ
うな矛盾は,次の異常型(これらに限定されるわけではない)の一部又はすべてを含む。
1)a 過短線は,他の線と交差すべき線で,短すぎてそれと交差する点との間にすき間を残したも
のである。これを(道路同士がブロック一枚の厚さの壁で隔てられている場合のような)地
物が実際に“接近”している場合と区別するのは,しばしば困難である。この問題は,特に
過短線が曲面又はポリゴンの境界を閉じるのに失敗する場合に扱いが難しい。これは多くの
場合,縮尺の小さすぎる図を使用し,線の終点を“留め”るのに失敗したデジタイズ作業を
示す。
2)b 過長線は,他の線と交差して終わる線で,長すぎて交差する点の向こう側にわずかにはみ出
た線を残したものである。これは多くの場合,縮尺の小さすぎる図を用い,線の終点を視覚
的に“留め”ようとしたデジタイズ作業を示す。
3)c 端環線は,他の線と交差して終わる線で,長すぎて戻り交差する点の向こう側にわずかには
み出た環状の線を残したものである。これは多くの場合,縮尺の小さすぎる図を用い,線を
はみ出た後に“留め”たデジタイズ作業を示す。
4)d 裂片及びすき間は,同一の幾何を表現すべき複数の線で,一致せずに二つの面の境界間に重
複する地域(裂片)及びすき間を残したものである。この問題は,自然地物の実際の幾何が
単に下手なデジタイズ作業による裂片及びすき間に似ているため,入り組んだ小川の地域を
扱う際にとりわけ困難となる。これは多くの場合,共通のデータベースに統合された(しか
し正しく融合されなかった)複数の情報源が同一のデータに対して存在することを示す。
“スパゲッティ”の本当の問題は,問題を訂正するための試行錯誤が(手作業であれ自動であれ),多く
の場合新たに様々な事実誤認を引き起こすことである。これは幾何に関する深刻な品質の問題である。
6.2.2.7
isCycle “isCycle”(輪体判定)操作は,位相的な単純化(GM̲Aggregateの下位クラスのような,
非構造的な集成の要素間の重複部分を取り除くこと)によってこのGM̲Objectの境界要素がなくなる場合,
TRUEを返す。この条件は,“閉曲線”の“閉”の代わりに参照する。これは,“閉”という語に二つの異
なる両立しない定義があるため,混乱の原因となる。輪体という語を用いるのはまれ(一般には代数的位
相幾何学の分野に限られる。)だが,混乱の原因を低減できる。本質的に,オブジェクトは,あるユークリ
ッド空間の領域の境界となる幾何オブジェクトと同形な場合,輪体となる。したがって点は,その境界が
空であるため輪体である。曲線は,同じ始終点をもつ円と同形の場合,輪体となる。曲面は,球面又はト
ーラスのいずれかと同形の場合,輪体となる。有限の大きさの立体は,三次元空間では決して輪体とはな
らない。
GM̲Object::isCycle(): Boolean
例 次の
OCL
は,境界取得操作を用いて
GM̲Object
を生成し,さらに
27
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TransfiniteSet<DirectPosition>::isEmpty() 操作を用いてその境界が空集合であるかを判定する。
GM̲Object:
isCycle() = boundary().isEmpty()
6.2.2.8
distance “distance”(距離取得)操作は,このGM̲Objectと他のGM̲Objectとの間の距離を返
す。この距離は,二つのGM̲Objectの各点のすべての対の距離の集合の最大下界として定義する。距離の
値は,メートルなどの距離単位に関連付けた負でない数とする。必要に応じて,二番目の幾何オブジェク
トは,距離を計算する前に最初のオブジェクトと同じ座標参照系に変換する。
GM̲Object::distance(geometry : GM̲Object) : Distance
幾何オブジェクトが重複又は接触する場合,その間の距離は0とする。このような場合に負の距離を用
いる実装も流通しているが,このような方法は実装の一貫性を損ない,理論的にも機能しない。
距離にはISO TS 19103で定義する計量データ型の単位のいずれかを使用する。
備考 距離計算における参照系の役割は重要である。一般に,点の間(すなわち,幾何オブジェクト
の間)で定義してよい距離として,少なくとも地図距離,測地距離及び地形距離の3種類があ
る。
地図距離は,(縮尺を考慮にいれた地図上のような)座標投影での位置によって定義した点間距
離である。地図距離は,縮尺関数が良質な導関数をもつ場合,通常は,小さな範囲で正確であ
る。
測地距離は,座標参照系が用いる地表モデルの表面に沿った,2点間の最短曲線の長さで定義
した距離である。測地距離は,範囲の広い領域に対してうまく機能し,地球の曲率を考慮する。
これは,特に航空及び航海に便利だが,航程線距離(方位が一定の曲線)と測地線距離とを区
別するよう注意が必要である。
地形距離は,局所的な垂直変位(測高)を考慮したものである。地形距離は,測地距離又は地
図距離のいずれに基づいてもよい。
6.2.2.9
dimension “dimension”(次元取得)操作は,このGM̲Objectに固有の次元を返す。その値は座
標次元以下でなければならない。幾何オブジェクトの集合の次元は,その部品の次元で最大のものとする。
点は零次元,曲線は一次元,曲面は二次元,立体は三次元とする。局所的には,幾何オブジェクトのある
点における次元は,その点の幾何オブジェクト上の局所近傍となる任意の座標近傍の次元となる。次元は,
このGM̲Objectの内部にある複数のDirectPositionに対してだけ,明確に定義される。渡されたDirectPosition
がNULLであるときは,この操作は,このGM̲Object中のすべてのDirectPositionの次元のなかで,最も
大きな次元を返さなければならない。
GM̲Object::dimension(point : DirectPosition = NULL) : Integer
6.2.2.10 coordinateDimension “coodinateDimension”(座標次元取得)操作は,このGM̲Objectを定義す
る座標の次元を返す。この次元は,このGM̲Objectの座標参照系の座標の次元と同じでなければならない。
GM̲Object::coordinateDimension(): Integer
6.2.2.11 maximalComplex プリミティブの集合としてのGM̲Complexは,元の複体の“上位複体”とし
て参照される,別のより大きなGM̲Complexに集合として含まれてよい。そのようなより大きい上位複体
がない場合,そのGM̲Complexは,極大とする。“maximalComplex”(極大複体取得)操作は,この
GM̲Objectが含まれる極大GM̲Complexの集合を返す。
GM̲Object::maximalComplex() : Set<GM̲Complex>
使用する応用スキーマがGM̲Complexを含まない場合,この操作は,NULL値を返す。
28
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 極大複体の通常の意味では,GM̲Primitiveは,それを強集成する複数の極大複体に含まれては
ならない。これは,絶対ではなく,実装の意味に依存し,GM̲PrimitiveとGM̲Complexとの間
の関係は,多対多となってよい。プログラム作成の観点から見ると,これは,維持が困難な(だ
が不可能ではない。)動的構造ではあるが,静的な問合せだけの構造としては,同じ幾何オブジ
ェクトを要素とする二つの表現に固有の冗長なデータを最小化することにかなり有効である。
6.2.2.12 transform “transform”(変換取得)操作は,このGM̲Objectを,指定した座標参照系にその変
換精度以内で座標変換した新しいGM̲Objectを返す。
GM̲Object::transform(newCRS : SC̲CRS) : GM̲Object
6.2.2.13 envelope “envelope”(包被取得)操作は,このGM̲Objectの最小境界長方形を返す。この包被
は,このGM̲ObjectのDirectPositionがとる各座標値の最小値から最大値までの範囲を示す座標領域とす
る。包被の最も単純な表現は,一つ目にはすべての直交座標のそれぞれの最小値を,二つ目には最大値を
もつ二つのDirectPositionからなる。ただし,これら二つの位置は,このオブジェクトの座標参照系の有効
範囲外になる場合もある。ここでは,この操作は応用システムが様々な方法の実装を選択できるようイン
タフェースとして定める。
GM̲Object::envelope() : GM̲Envelope
6.2.2.14 centroid “centroid”(図心取得)操作は,このGM̲Objectの数学的な図心を返す。結果は,オ
ブジェクト上にあるとは限らない。異なる種類のプリミティブの集まりの場合,次元が最大となるプリミ
ティブだけを考慮して図心を求める。例えば,複数の曲面の図心を計算するには,面積で加重した平均を
求める。曲線は,面積をもたないのでこの平均には影響しない。
GM̲Object::centroid() : DirectPosition
備考 この位置は,オブジェクトの座標参照系の有効範囲の外側となる場合があるが,ほとんどの座
標参照系の有効範囲が凸であるため,その可能性は低い。このような稀有な状況が起こりうる
場合,実装は適切に対処しなければならない。
6.2.2.15 convexHull “convexHull”(凸包取得)操作は,このGM̲Objectの凸包を表すGM̲Objectを返
す。
GM̲Object::convexHull() : GM̲Object
備考 このGM̲Objectは,部分的にオブジェクトの座標参照系の有効範囲の外側となる場合があるが,
ほとんどの座標参照系の有効範囲が凸であるため,その可能性は低い。このような稀有な状況
が起こりうる場合,実装は適切に対処しなければならない。
凸の定義には“線”又は“最短の曲線”を使用する必要があるため,様々な座標系を使用してオブジェ
クトに様々な種類の凸包を定めてよい。それぞれの実装はこのあいまいさを適切に解決しなければならな
い。二つの妥当な座標系において,一方の座標系のオブジェクトの凸包は,もう一方の座標系において同
じオブジェクトの凸包を変換した像によって非常によく近似される。
6.2.2.16 buffer “buffer”(バッファ取得)操作は,このGM̲Objectからの距離がパラメタに指定した値
以下となるようなすべての点を含むGM̲Objectを返す。戻り値のGM̲Objectは,元のGM̲Objectと同じ
参照系を用いる。戻り値のGM̲Objectの次元は,通常は座標次元と同じとなる。すなわち,戻り値の
GM̲Objectは二次元空間上ではGM̲Surfaceの集合となり,三次元空間上ではGM̲Solidの集合となる。し
かし,応用システムは,これと異なるよう定義してもよい。
GM̲Object::buffer(radius : Distance) : GM̲Object
備考 このGM̲Objectは,部分的にオブジェクトの座標参照系の有効範囲の外側となる場合がある。
29
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
このような状況が起こりうる場合,実装は適切に対処しなければならない。
6.2.2.17 Coordinate Reference System関連 “Coordinate Reference System::CRS”(座標参照系)関連は,
このGM̲Objectと,DirectPositionにおける座標に使用する座標参照系とを関連付ける。この関連が空の場
合,このGM̲Objectは,それを包含する他のGM̲ObjectのSC̲CRSを使用する。
GM̲Object::CRS[0,1] : SC̲CRS
備考 この関連が空となるような最も一般的な例は,極大GM̲Complexの下位複体及び要素である。
GM̲Complexは,そのSC̲CRSをすべてのGM̲Primitive要素及びすべてのGM̲Complex下位
複体に及ぼしてよい。この関連は,GM̲ObjectからSC̲CRSの方向にだけ有効とする。これは,
データ集合中の座標参照系オブジェクトが,それを使用するGM̲Objectの一覧を保持しないこ
とを示す。
6.2.2.18 TransfiniteSetの実現による操作
6.2.2.18.1 GM̲Objectは,次の操作をTransfiniteSet<DirectPosition>インタフェース(ISO TS 19103)に基
づいて実現する。
6.2.2.18.2 contains ブール値を返す“contains”(包含判定)操作は,GM̲Objectが他のGM̲Object又は
座標(DirectPosition)で指定した一点を包含する場合にTRUEを返す。この操作は,
TransfiniteSet<DirectPosition>::containsのインスタンス化を目的とする。
GM̲Object::contains(pointSet : GM̲Object) : Boolean
// 部分集合演算子
GM̲Object::contains(point : DirectPosition) : Boolean // 要素包含演算子
指定したGM̲Objectが単独のGM̲Pointの場合,この操作は,このGM̲Objectの点のDirectPositionに
対して行った,集合要素に含まれるか否かの試験と一致する。点と他の幾何オブジェクトとは同一の基底
(GM̲Object)を共有するため,通常は,点の包含とGM̲Objectの集合の包含とを区別する必要はない。
次は,基本的な集合論の公理をOCLで表現したものを示す。
GM̲Object:
contains(that : GM̲Object) and that.contains(other : GM̲Object)
implies contains(other)
contains(that : GM̲Object) and that.contains(p : DirectPosition)
implies contains(p)
contains(point : GM̲Point) implies contains(point.position)
備考 “contains”は集合論における厳密な意味での包含であり,次元に関する制約を受けない。
GM̲Complex中のGM̲Primitiveが包含する他のプリミティブは,次元が2以上低いものに限る
(6.3.10.4参照)。
6.2.2.18.3 intersects ブール値を返す“intersects”(交差判定)操作は,このGM̲Objectが他のGM̲Object
と交差する場合にTRUEを返す。この操作は,TransfiniteSet<DirectPosition>::intersectsのインスタンス化を
目的とする。
GM̲Object::intersects(pointSet : GM̲Object) : Boolean
GM̲Complex中では,GM̲Primitive同士は,互いに交差しない。一般に,位相構造データは交差の情報
を得るために共有した幾何オブジェクトを使用する。
備考 この交差は,DirectPositionについての集合論における厳密な意味での共通な包含関係である。
GM̲Primitiveを開集合(境界を包含しない)とみなすので,共通の端点を共有する二つの
(GM̲Primitiveとしての)GM̲Curveは,交差しない。GM̲Complexを閉集合(境界を包含す
30
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る)とみなすので,共通の端点を共有する二つの(GM̲Complexとしての)GM̲CompositeCurve
は,交差する。
6.2.2.18.4 equals ブール値を返す“equals”(同値判定)操作は,GM̲Objectが他のGM̲Objectと等しい
場合にTRUEを返す。この操作は,TransfiniteSet<DirectPosition>::equalsのインスタンス化を目的とする。
GM̲Object::equals(pointSet : GM̲Object) : Boolean
二つの異なるGM̲Objectは,それに関連付けられた座標参照系で有効な範囲のすべてのDirectPosition
に対して,そのGM̲Object::contains操作の試験が同じ真偽値を返す場合,等しいものとする。
備考 直接位置の無限集合は試験できないため,同値の内部実装は,二つの異なる表現の間の同一性
を試験しなければならない。この試験は,座標系の解像度又はデータの精度によって制限して
よい。応用スキーマは,元のGM̲Objectと指定したGM̲Objectが同じ次元をもち,二つの
GM̲Objectのすべての直接位置が相手の直接位置から許容誤差距離以内にある場合に真を返す
ような,許容誤差を定めてよい。
6.2.2.18.5 union “union”(和集合取得)操作は,このGM̲Objectと指定したGM̲Objectとの集合論に
おける和集合を返す。
この操作はTransfiniteSet<DirectPosition>::unionのインスタンス化を目的とする。
GM̲Object::union(pointSet : GM̲Object) : GM̲Object
6.2.2.18.6 intersection “inersection”(積集合取得)操作は,このGM̲Objectと指定したGM̲Objectとの
集合論における積集合を返す。
この操作はTransfiniteSet<DirectPosition>::intersectionのインスタンス化を目的とする。
GM̲Object::intersection(pointSet : GM̲Object) : GM̲Object
6.2.2.18.7 difference “difference”(差集合取得)操作は,このGM̲Objectと指定したGM̲Objectとの集
合論における差集合を返す。
この操作はTransfiniteSet<DirectPosition>:: difference のインスタンス化を目的とする。
GM̲Object::difference(pointSet : GM̲Object) : GM̲Object
備考 difference操作は左右対称ではなく,通常A.difference(B)はB.difference(A)に等しくない。
6.2.2.18.8 symmetricDifference “symmetricDifference”(対称差集合取得)操作はこのGM̲Objectと指定
したGM̲Objectとの集合論における対称差集合を返す。この操作はTransfiniteSet<DirectPosition>::
symmetricDifference のインスタンス化を目的としたものである。
GM̲Object::symmetricDifference(pointSet : GM̲Object) : GM̲Object
6.3
Geometric primitiveパッケージ
6.3.1
意味 Geometric primitive(幾何プリミティブ)パッケージは,あらゆる幾何プリミティブ及びそ
れらの境界を記述するために使用されるデータに対応するための型を含む。
6.3.2
GM̲Boundary 幾何オブジェクトの境界を表すデータに使用するすべての型の抽象基底クラスを
GM̲Boundary(幾何境界)(図7参照)とする。GM̲Objectの任意の下位クラスは,GM̲Object::boundary
操作による境界の表現にGM̲Boundaryの下位クラスを使用する。幾何の本来の特性によって境界オブジ
ェクトは,輪体となる。
備考 GM̲Boundaryに対して“幾何境界”と表記しているように,幾何と位相に同様の定義があり,
区別が必要な場合にはそれぞれを付加して明示している。
GM̲Boundary:
{isCycle() = TRUE}
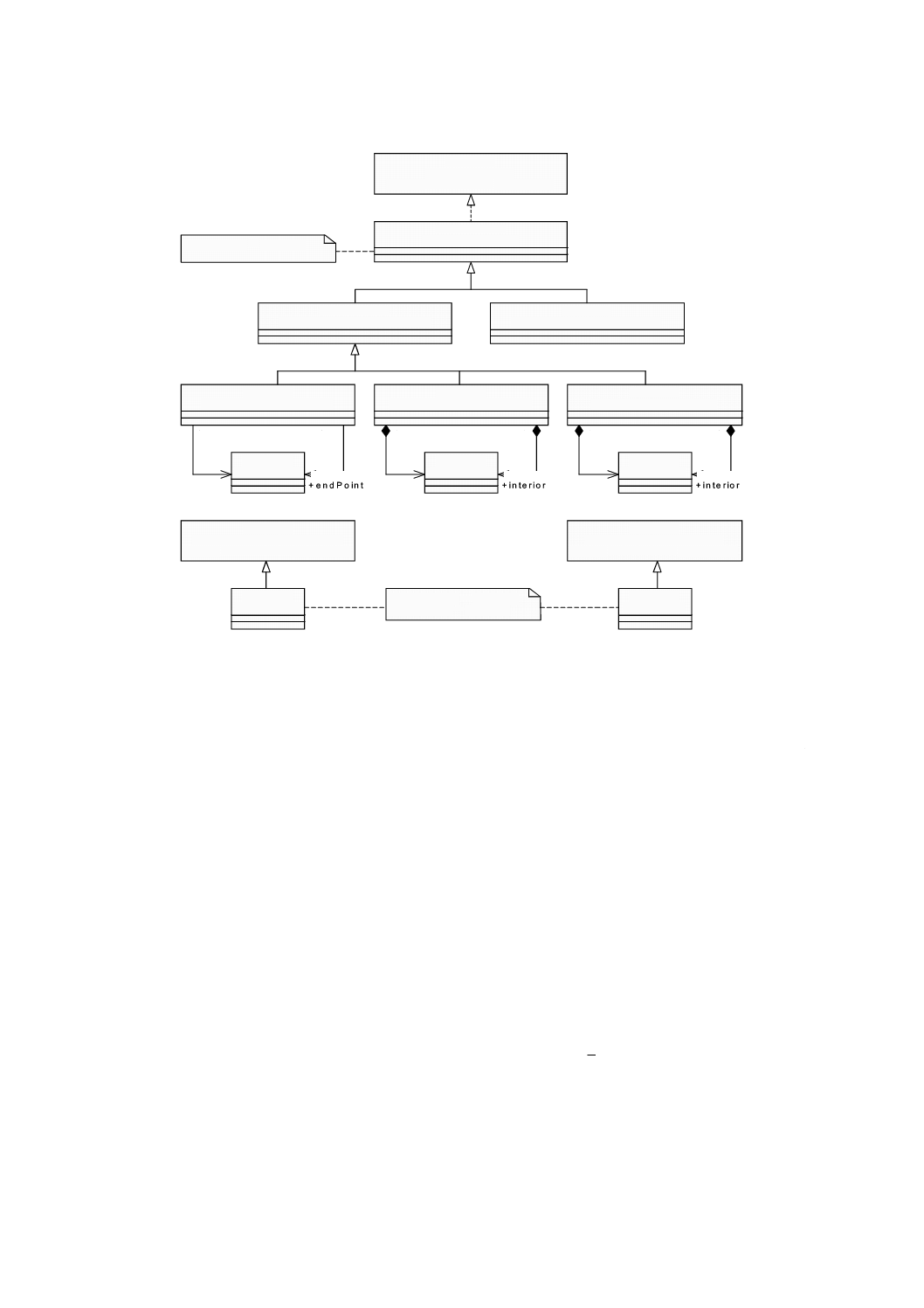
31
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲Complex
(from Geometric complex)
«Abstract»
GM̲Boundary
{isCycle() = TRUE}
«Type»
GM̲ComplexBoundary
«Abstract»
GM̲PrimitiveBoundary
«Type»
GM̲CurveBoundary
«Type»
GM̲SurfaceBoundary
«Type»
GM̲SolidBoundary
«Type»
GM̲Point
«Type»
GM̲Ring
«Type»
GM̲Shell
1
+startPoint
0..n
0..1
+exterior
0..1
+exterior
1
+endPoint
0..n
+interior
0..n
+interior
0..n
1
1
1
1
{isSimple() = TRUE}
{isCycle() = TRUE}
«Type»
GM̲CompositeSurface
(from Geometric complex)
«Type»
GM̲CompositeCurve
(from Geometric complex)
«Type»
GM̲Shell
«Type»
GM̲Ring
図 7 GM̲Boundary
6.3.3
GM̲ComplexBoundary GM̲Complexオブジェクトに対する境界取得操作は,プリミティブの集
まりで,元のオブジェクトより次元が一つ小さいGM̲Complexとなる,GM̲ComplexBoundary(幾何複体
境界)を返す。
6.3.4
GM̲PrimitiveBoundary GM̲PrimitiveBoundary(幾何プリミティブ境界)抽象クラスは,
GM̲Primitiveの下位型の境界操作が返す様々な型の基底となる。点は,境界をもたないため,その境界に
は特別な下位クラスは必要としない。
6.3.5
GM̲CurveBoundary
6.3.5.1
意味 GM̲Curveの境界はGM̲CurveBoundary(曲線境界)として表現する。
6.3.5.2
startPoint,endPoint GM̲CurveBoundaryは,二つのGM̲Pointの参照を含む。
GM̲CurveBoundary::startPoint : Reference<GM̲Point>;
GM̲CurveBoundary::endPoint : Reference<GM̲Point>;
6.3.6
GM̲Ring GM̲Ring(幾何輪)は,GM̲SurfaceBoundaryの単連結要素を表現するのに使用する。
これは,輪体(境界が空のオブジェクト)として連結した幾つかのGM̲OrientableCurveへの参照で構成す
る。
GM̲Ringは,列の各GM̲OrientableCurveの終点が次のGM̲OrientableCuveの始点となる点で,
GM̲CompositeCurveと類似した構造をもつ。列は,円形であるため,この法則は常に成り立つ。各輪は,
すべての境界と同様に輪体で単純とする。
32
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲Ring:
{isSimple() = TRUE}
{isCycle() = TRUE}
6.3.7
GM̲SurfaceBoundary
6.3.7.1
意味 GM̲Surfaceの境界は,GM̲SurfaceBoundary(曲面境界)として表現する。
6.3.7.2
exterior及びinterior GM̲SurfaceBoundaryは,その境界の様々な要素に対応する,幾つかの
GM̲Ringで構成する。通常の二次元の場合,これらの輪のいずれか一つを外部(exterior)境界として区別す
る。一般的な多様体では外部境界を常に指定する必要はなく,その場合すべての境界を内部(interior)境界
として関連し,外部を空とする。
GM̲SurfaceBoundary::exterior[0,1] : GM̲Ring;
GM̲SurfaceBoundary::interior[0..n] : GM̲Ring;
備考 ここでの外部と内部の使用は,幾何オブジェクトの“内部”及び“外部”の定義を指すもので
はない。これらの用語は,一般的な用法として用いており,オブジェクトの内部であるという
概念に対して,容器の内部であるという,同じ言語構文を用いた言語的隠喩を反映したもので
ある。通常の数学の用語では,外部境界とはジョルダンの分割定理(ジョルダンの曲線定理の
二次元からの拡張)で使用されるものである。外部境界は,無限の空間から曲面(又は三次元
の立体)を分離する。内部境界は,他の有界オブジェクトからオブジェクトを直接分離する。
外部の一意性は,非有界空間の一意性による。基本的に,ジョルダンの分割定理は,輪又は殻
の挿入がそれぞれ二次元又は三次元空間を有界部分と非有界部分とに分離することを示す。こ
れは,より大きい次元でも同様だが,この規格では,最大でも三次元までに制限する。
例1. 基礎多様体が無限円柱である場合,この円柱の二つの横断面による切断は,切断面間のコンパ
クトな曲面及び二つの部分の分離した非有界円柱を定義する。この場合,いずれかの切断を合
理的に外部と呼ぶこともできる。このような多義的な場合,この規格ではすべての境界を“内
部”集合として示すこととする。外部境界の一意性が保証されるのは,二次元平面E2上だけで
ある。
例2. 球面の赤道をとって1メートルのバッファを生成すると,二つの同形の境界要素をもつ曲面が
得られる。これらのうちのいずれかを外部として区別する公平な方法はない。
6.3.8
GM̲Shell GM̲Shell(幾何殻)は,GM̲SolidBoundaryの単連結要素を表現するのに使用する。こ
れは,位相輪体(境界が空のオブジェクト)として連結した幾つかのGM̲OrientableSurfaceへの参照で構
成する。GM̲Ringとは異なり,GM̲Shellの要素に,は自然な順序はない。GM̲Ringと同様にGM̲Shell
は,単純とする。
GM̲Shell:
{isSimple() = TRUE}
{isCycle() = TRUE}
6.3.9
GM̲SolidBoundary
6.3.9.1
意味 GM̲Solidの境界は,GM̲SolidBoundary(立体境界)として表現する。
6.3.9.2
exterior及びinterior GM̲SolidBoundaryは,GM̲SurfaceBoundaryと類似する。通常の三次元ユ
ークリッド空間では,一つの殻を外部(exterior)境界として区別する。より一般的な場合には,常にそうす
る必要はない。
GM̲SolidBoundary::exterior[0,1] : GM̲Shell;
33
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲SolidBoundary::interior[0..n] : GM̲Shell;
備考 外部殻をもたない立体は,有限の立体の“補集合”を定義するために使用してよい。このよう
な無限立体は,内部(interior)境界だけをもつ。この規格を四次元ユークリッド空間まで拡張し
たり三次元コンパクト多様体を(おそらく地理情報の範ちゅうを超えて)使用するような場合,
外部境界をもたない有界立体を新たに例示することができる。
6.3.10 GM̲Primitive
6.3.10.1 意味 GM̲Primitive(幾何プリミティブ)(図8)は幾何プリミティブの抽象基底クラスとする。
この主な目的は,各次元のプリミティブを一まとめにして基本的な“boundary”操作を定義することであ
る。幾何プリミティブ(GM̲Primitive)は,システム内で更に他のプリミティブに分解することのできな
いような,幾何オブジェクトとする。曲線及び曲面は,それぞれが複数の曲線分及び曲面分で構成されて
はいるが,幾何プリミティブに含まれる。この合成は,強い集成とし,曲線分及び曲面分は,プリミティ
ブ以外の部分では用いてはならない。
備考 大部分の幾何プリミティブは,何度でも限りなく分解できる。線分に中点を与えることによっ
て,その線分は,二つの独立した線分に分割できる。曲面に沿った曲線を与えることによって,
その曲面は,それぞれが曲面となる二つの部分に分割できる。このため,プリミティブを“不
可分”とする一般的な定義は,不可分となる唯一の幾何オブジェクトが点であるという幾何学
モデルにおいては理にかなったこととはいえない。
地物の記述に用いる幾何オブジェクトは幾何プリミティブの集まりとする。幾何プリミティブの集まり
は,幾何複体であってもよく,そうでなくてもよい。幾何複体は,境界取得操作による閉包又は相互に排
他的な構成部分による閉包などのさらなる操作ももつ。
GM̲Primitive及びGM̲Complexは,操作,属性及び関連の点で大部分の意味が共通する。この例外とし
て,GM̲Primitiveは(境界が空となるGM̲Pointの自明な場合を除き)その境界を含まないが,GM̲Complex
はすべての場合においてその境界を含む。これは,GM̲Primitive及びGM̲Complexの両方としてGM̲Object
の操作を実装するインスタンス化されたオブジェクトについて,集合論的な各操作は,その名前の解決方
法によってその意味を決めることを示す。具体的には,GM̲CompositeCurveのような特定のオブジェクト
は,GM̲Primitive::contains (端点に対してFALSEを返す。)とGM̲Complex::contains(端点に対してTRUE
を返す。)とは異なる。さらに,そのオブジェクトをGM̲Primitiveの値及びGM̲Complexの値に型変換し
た場合には,この二つの値は,GM̲Objectとして等しくなくてよい。
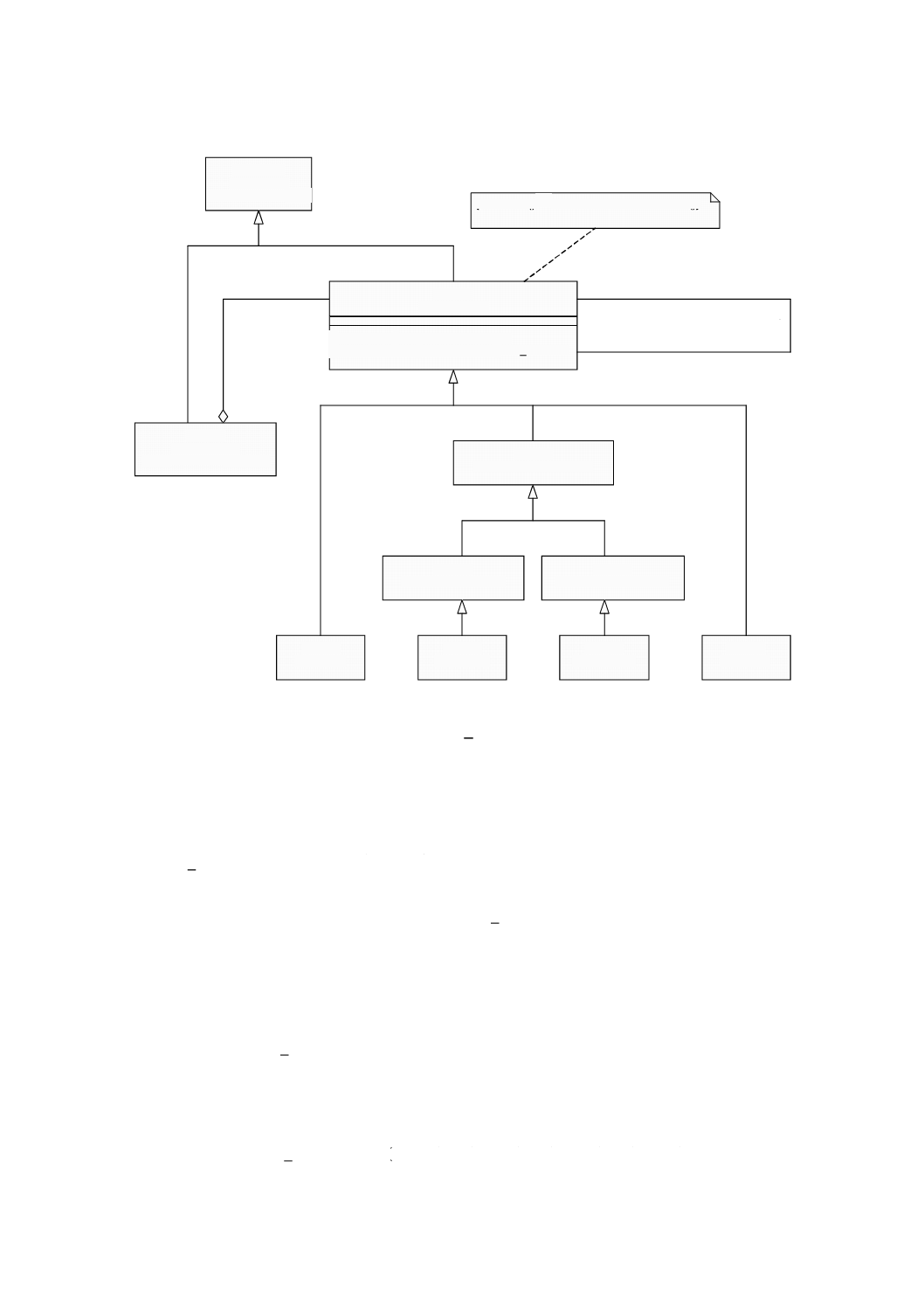
34
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
{dimension() >= cotainedPrimitive.dimension()}
<<Type>>
GM̲Object
(from Geometry root)
«Type»
GM̲Complex
(from Geometric complex)
Complex
+complex
0..n
1..n
+element
«Type»
GM̲Primitive
+ boundary() : GM̲PrimitiveBoundary
+ GM̲Primitive(e : GM̲Envelope) : GM̲Primitive
«Type»
GM̲Solid
«Type»
GM̲Surface
«Type»
GM̲Curve
«Type»
GM̲Point
«Type»
GM̲OrientableSurface
«Type»
GM̲OrientableCurve
«Type»
GM̲OrientablePrimitive
+containedPrimitive
0..n
0..n
+containingPrimitive
Interior to
図 8 GM̲Primitive
6.3.10.2 boundary “boundary”(境界取得)操作は,GM̲Primitiveの境界をGM̲Primitiveの集合として
返す。これは,GM̲Objectの操作を特化したもので,戻り値である集合のクラスを制約しない。GM̲Primitive
の境界集合の構成は,プリミティブの型に依存する。
GM̲Primitive::boundary() : GM̲PrimitiveBoundary
6.3.10.3 GM̲Primitive(コンストラクタ) 問合せ操作では,よくGM̲Envelopeを用いるため,GM̲Object
を返す型変換操作をもたなければならない。GM̲Primitiveのコンストラクタがこれを提供する。
GM̲Primitive::GM̲Primitive(env : GM̲Envelope) : GM̲Primitive.
備考 この操作の実際の戻り値は,座標参照系の次元及び包被の範囲によって決める。二次元のシス
テムで返すプリミティブ(包被が点又は線に畳み込めない限り)は,GM̲Surfaceとする。三次
元のシステムの場合,通常の戻り値はGM̲Solidとする。
例 GM̲EnvelopeがそのSC̲CRS (空間参照系)オブジェクトの有効領域に完全に含まれている場合,
その関連するGM̲Primitiveは,各頂点の座標値を組合せた凸包となる。例えば,二次元上のある
包被を次のように定義する(ここではSC̲CRSは,広域変数として無視する。)。
env : GM̲Envelope = <lowerCorner = (x1,y1), upperCorner = (x2,y2)>
次に,各座標要素を組み換えて,ポリゴンを構成する一連の頂点を作成する。
multi̲point : GM̲MultiPoint = { (x1,y1), (x1,y2), (x2,y1), (x2,y2) }
35
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここで,multi̲pointにGM̲Objectで定義された凸包関数を用いるとポリゴンを得る。
multi̲point.convexHull () -> polygon : GM̲Surface
二次元のポリゴンの範囲は,その境界によって全体が定義される(ポリゴンを構成する曲面分
は,平面で,内部の制御点を必要としない。)。境界については,二次元のGM̲Surfaceを表現す
るためのデータ型がある。
polygon.boundary -> ring : GM̲Ring = { string : GM̲Linestring
= <(x1,y1), (x1,y2), (x2,y2), (x2,y1), (x1,y1)> }
よって,GM̲SurfaceBoundaryのレコードは,次のようになる(凸集合には“interior”の穴はな
い。)。
boundary : GM̲SurfaceBoundary = < exterior = ring, interior = { } >
これらの各型の正確な定義は,対応する箇条による。
6.3.10.4 Interior to関連 “Interior to”(内包)関連は,定義が互いに一致するGM̲Primitive同士を関連
付ける。これは,応用システムがSet<DirectPosition>の解釈及びそれに関連する計算幾何を置き換え,一つ
のGM̲Primitiveを他のそれの内包(interior to)として宣言することを認める。
この関連は,GM̲Complexに含まれるGM̲Primitiveについて,ほとんどの場合,境界の情報で十分なた
め,通常は,空となる。
GM̲Primitive::coincidentSubelement [0..n] : Reference<GM̲Primitive>
GM̲Primitive::superElement [0..n] : Reference<GM̲Primitive>
この関連はGM̲Objectに定義した集合論の操作とdimension操作とによって制約される。
GM̲Primitive:
superElement->includes(p: GM̲Primitive) = GM̲Object::contains(p)
dimension() >= coincidentSubelement.dimension()
備考 この関連は,二つのGM̲Primitiveが互いに近接しない場合には用いてはならない。これは,応
用システムが固有で不可避な丸め,切捨て,その他計算機による計算に特有の数学的な問題を
補正できるようにするためのものである。
6.3.10.5 Complex関連 GM̲Primitiveは,幾つかのGM̲Complex(幾何複体)に含まれていてよい(6.6.2
参照)。この関連は,この(プリミティブから複体への)方向にたどれなくてもよく,それは,応用スキー
マで定める。
GM̲Primitive::complex [0..n] : Reference<GM̲Complex>
6.3.11 GM̲Point
6.3.11.1 意味 GM̲Point(点)(図9参照)は,ただ一つの点からなる幾何オブジェクトを表す基本的な
データの型とする。
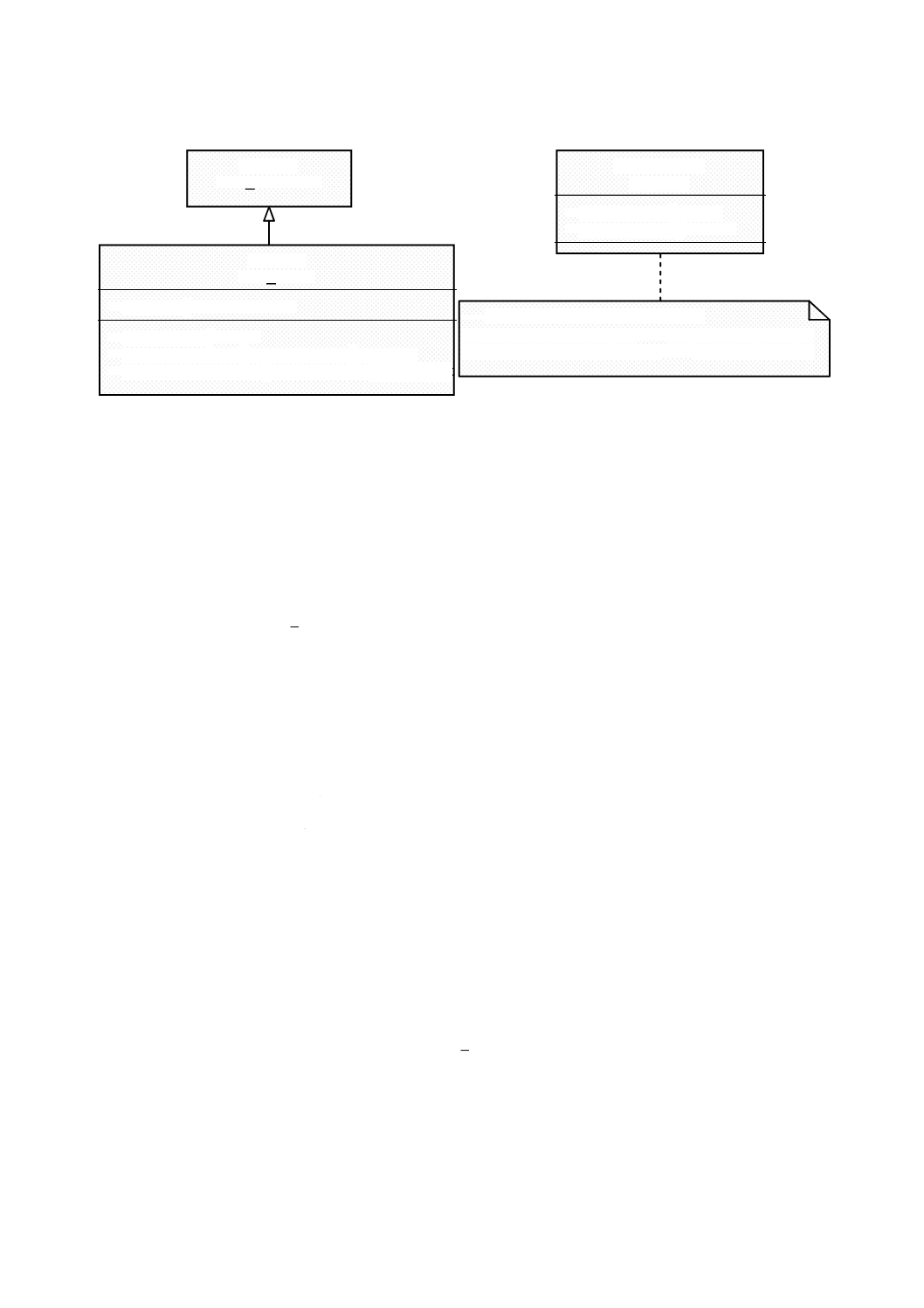
36
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲Primitive
«Type»
GM̲Point
+ position : DirectPosition
+ boundary() : NULL
+ bearing(toPoint : GM̲Position) : Bearing
+ GM̲Point(position : GM̲Position) : GM̲Point
«DataType»
Bearing
+ angle[0,1,2] : Angle
+ direction[0,1] : Vector
-- 少なくとも片方の値は空でない。
{angle.isEmpty() implies Not direction.isEmpty()}
{direction.isEmpty() implies Not angle.isEmpty()}
図 9 GM̲Point
6.3.11.2 position “position”(位置)属性は,このGM̲PointのDirectPositionとする。
GM̲Point::position : DirectPosition
GM̲Pointは,それが定義している幾何を表現する上でGM̲Positionを使うことができないGM̲Primitive
の唯一の下位クラスとする。GM̲Positionは,DirectPositionであるか,又はGM̲Point(それからDirectPosition
を取得できる。)の参照とする。GM̲Pointがこの手法を用いるのを禁止することによって,無限の回帰参
照を防止する。応用システムは,この論理上の問題を防ぐために他の方法を使用してもよい。
備考 多くの場合,GM̲Pointの状態は,その位置属性によって完全に決まる。この唯一の例外は,記
号表記のような付加的な非幾何情報を提供するためにGM̲Pointを下位クラス化する場合とす
る。
6.3.11.3 boundary “boundary”(境界取得)操作は,GM̲Objectの境界取得操作を特化した操作で,空
集合を示すEMPTY値を返す。
GM̲Point::boundary() : EMPTY
6.3.11.4 bearing “bearing”(方向角取得)操作は,このGM̲Pointと指定したGM̲Positionとの間の曲線
の(このGM̲Point上での)接線の方向を返す。
GM̲Point::bearing(toPoint : GM̲Position) : Bearing
方向を定義するための曲線に用いる型はGM̲Pointを定義するSC̲CRSによって異なる。例えば,メル
カトル図法では,曲線は,等角航路になる。三次元の地心座標系では,曲線は用いるジオイド又はだ(楕)
円体の表面に沿って2点を結ぶ測地線であってもよい。この関数に対応する実装は,用いる曲線の性質を
規定しなければならない。
備考 “Vector”型は,ISO TS 19103で定義する一般的なデータ型である。
6.3.11.5 GM̲Point(コンストラクタ) GM̲Pointコンストラクタは,指定した位置にGM̲Pointを生成
する。
GM̲Point::GM̲Point(position : GM̲Position) : GM̲Point
6.3.12 Bearing
6.3.12.1 意味 Bearing(方向角データ)は,座標参照系における方向を表現するのに使用するデータ型と
する。これは,二次元の座標参照系では“真北から計測した角度”又はその方向の二次元の点ベクトルを
用いて実現する。三次元の座標参照系では,二つの角度又は任意の三次元ベクトルを使用してよい。角度
の集合及びベクトルの両方を用いる場合には,それらは互いに一貫性がなければならない。
37
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.12.2 angle 二次元の座標系で通常使用されるこの形式のBearingは,その第一のangle(方位角)を参
照曲面の接平面に平行に第一座標軸(通常は,北)から反時計回りに計測する。二つの角度(angle)を指定
する場合,第二のanlge(仰角)は,通常,参照曲面の接平面に平行な局所平面に対して上方(正の角度)
又は下方(負の角度)の角度を表現する。
Bearing::angle [0,1,2] : Angle
6.3.12.3 direction 三次元の座標系で通常使用されるこの形式のBearingは,direction(方向)をその座標
系の任意のベクトルとして表現する。
Bearing::direction [0,1] : Vector
6.3.13 GM̲OrientablePrimitive
6.3.13.1 意味 有向プリミティブ(orientable primitive)(図10参照)は,その内部の局所座標系(多様体遷
移)に関して反対向きの新しい幾何オブジェクトを作成できるプリミティブとする。曲線の場合,その向
きは,曲線をたどる方向を反映し,すなわち,そのようなパラメタ化を意味する。境界曲線として用いる
場合,囲まれる曲面は,有向曲線の“左”にあるものとする。曲面の場合,その向きは,局所座標系が右
手系となるような“上”の方向又は右手系を形成するZ軸を満たす方向を向いた曲面を反映する。境界曲
面として用いる場合,囲まれる立体は,その曲面の“下”にあるものとする。点及び立体の向きは,三次
元空間では幾何の直接的な解釈が存在しない。
GM̲OrientablePrimitive(有向幾何プリミティブ)オブジェクトは,本質的に,このプリミティブと参照
したオブジェクトとの向きが一致するか一致しないかを判定する“orientation”反転可能フラグ(“+”又は
“-”のいずれか)をもった,幾何プリミティブへの参照とする。
備考 “正”のプリミティブを有向プリミティブの下位クラスとする理由は幾つかある。第一の理由
は,下位クラス化の意味による。下位クラス化は,“is type of”(〜の型である)階層とみなさ
れる。この視点から見れば,“正”のプリミティブは,単純に,正の向きをもつ有向プリミティ
ブである。もし逆の見方をして,有向プリミティブが“正”のプリミティブの下位クラスとし
た場合,下位クラス化の論理によって,“負”のプリミティブは,“正”のプリミティブと同じ
種類の幾何の記述を保持しなければならないこととなる。唯一可能な方法は,Geometry root(幾
何基底)パッケージにおいて“負”のプリミティブをその反対のオブジェクトを参照するもの
として分離することである。これは,下位クラス化の木を大きく複雑化する。オブジェクト数
を最少にして論理的な複雑さを避けるために,正の向きのプリミティブは,自己参照とし(か
つ対応するプリミティブの下位型のインスタンスとする。),負の向きのプリミティブはそうで
はないとする。
有向プリミティブは,(向きを示す)符号及び基本幾何プリミティブ(曲線又は曲面)によって示すこと
がある。符号データ型はISO TS 19103で定義したものを使用する。“c”を曲線とすると,“<+,c>”は正
の有向曲線となり,“<-,c>”は負の有向曲線となる。ほとんどの場合,レコードのための構文の“< , >”
を省いても混乱は起こらないので,“<+,c>”を“+c”又は単に“c”と,また“<-,c>”を“-c”と,そ
れぞれ書いてもよい。曲線が正しく一列に並ぶ場合,次のように曲線の空間計算を実行することができる。
c及びdは,GM̲OrientableCurveで,c.endPoint = d.startPointとすると
( c + d ) ==: GM̲CompositeCurve = < c,d >
6.3.13.2 orientation 有向プリミティブの“orientation”(向き属性)は,このオブジェクトが表現する向
きが二つのうちのいずれであるかを決定する。
GM̲OrientablePrimitive::orientation : Sign
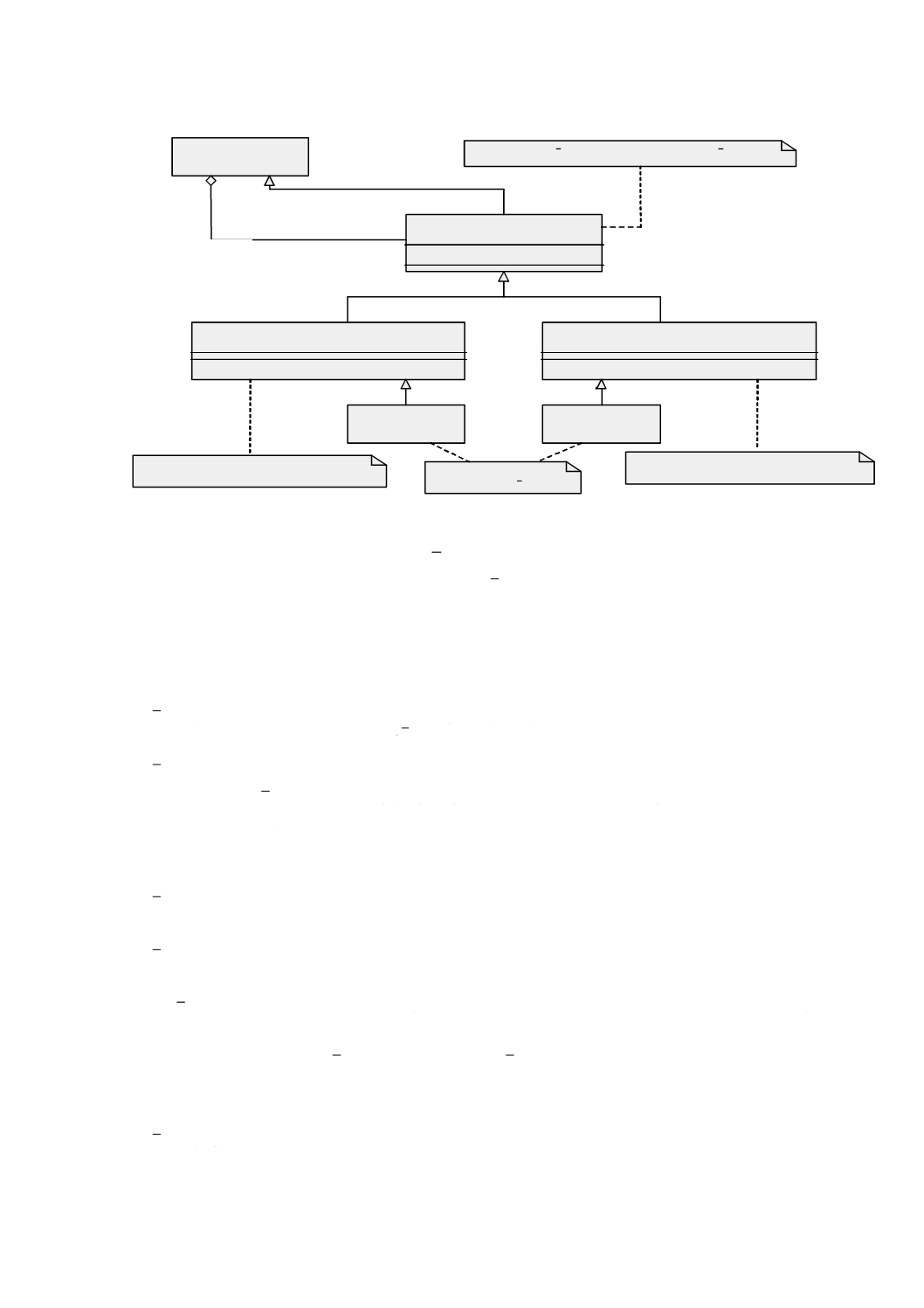
38
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲Primitive
+primitive
1
Oriented
«Type»
GM̲OrientablePrimitive
+ orientation : Sign
0,2
+proxy
«Type»
GM̲OrientableCurve
+ boundary() : GM̲CurveBoundary
«Type»
GM̲OrientableSurface
+ boundary() : GM̲SurfaceBoundary
«Type»
GM̲Curve
«Type»
GM̲Surface
{(orientation = "+") implies (primitive = self )}
{primitive.isTypeOf(GM̲Curve)}
{primitive = self}
{orientation = "+"}
{primitive.isTypeOf(GM̲Surface)}
図 10 GM̲OrientablePrimitive
6.3.13.3 Oriented関連 一次元又は二次元の各GM̲Primitiveは,それぞれ異なる向きの二つの
GM̲OrientablePrimitiveへの関連をもつ。
GM̲Primitive::proxy [0,2] : Reference<GM̲OrientablePrimitive>;
GM̲OrientablePrimitive::primitive [1] : Reference<GM̲Primitive>;
曲線及び曲面には,それぞれの幾何オブジェクトに対してちょうど二つの有向プリミティブがある。
GM̲Primitive:
(proxy->notEmpty) = (dimension = 1 or dimension = 2);
GM̲OrientablePrimitive:
a, b :GM̲OrientablePrimitive
((a.primitive = b.primitive) and (a.orientation = b.orientation)) implies a = b;
向きが“+”(正)の場合,GM̲OrientablePrimitiveは,対応するGM̲Curve又はGM̲Surfaceでなければ
ならない。
GM̲OrientableCurve:
orientation = “+” implies self.isTypeOf(GM̲Curve);
GM̲OrientableSurface:
orientation = “+” implies self.isTypeOf(GM̲Surface);
6.3.14 GM̲OrientableCurve
6.3.14.1 意味 GM̲OrientableCurve(有向曲線)は,GM̲OrientablePrimitiveから継承した向き及び曲線か
らなる。向きが“+”の場合,GM̲OrientableCurveは,GM̲Curveでなければならない。向きが“-”の場
合,GM̲OrientableCurveは,曲線上の通過方向と逆向きにパラメタ化されたもう一つのGM̲Curveに関連
をもたなければならない。
GM̲OrientableCurve:
{Orientation = "+" implies primitive = self};
39
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
{Orientation = "-" implies
primitive.parameterization(length()-s) = parameterization(s)};
6.3.14.2 boundary “boundary”(境界取得)操作は,GM̲Object及びGM̲Primitiveで定義した境界取得
操作を特化した操作とする。境界取得操作は,曲線の始点及び終点からなる点の順序対を返す。曲線が閉
じている場合,境界は空とする。GM̲CurveBoundaryデータ型は,曲線の境界の構造を単純化するために
定義している(6.3.5参照)。
GM̲OrientableCurve::boundary() : GM̲CurveBoundary
6.3.15 GM̲OrientableSurface
6.3.15.1 意味 GM̲OrientableSurface(有向曲面)は,GM̲OrientablePrimitiveから継承した向き及び曲線
からなる。向きが“+”の場合,GM̲OrientableSurfaceは,GM̲Surfaceでなければならない。向きが“-”
の場合,GM̲OrientableSurfaceは,“曲面の上方”を意味するupNormalがこのGM̲OrientableSurfaceの方
向と逆向きとなるような,GM̲Surfaceを参照しなければならない(6.4.33.2参照)。
GM̲OrientableSurface:
{Orientation = "+" implies primitive = self};
{(Orientation = "-" and TransfiniteSet::contains(p :
DirectPosition))
implies (primitive.upNormal(p) = - self.upNormal(p))};
6.3.15.2 boundary “boundary”(境界取得)操作は,GM̲Objectで定義した境界取得操作を,
GM̲OrientableSurfaceに対応した戻り値の型をもつものとして特化したものとする。この操作は,この
GM̲Surfaceの範囲を限定するGM̲OrientableCurveの環状列の集合を返す。これらの曲線は,この
GM̲Surfaceの各境界要素をそれぞれ一つの曲線環状列として構成する。
GM̲OrientableSurface::boundary() : GM̲SurfaceBoundary;
“exterior”境界を明確に定義しない場合,GM̲SurfaceBoundaryのすべての輪は“interior”境界として列
挙されなければならない。
備考 曲面の外部境界の概念は,二次元平面においてだけ有効とする。有界な筒は,二つの境界要素
をもち,そのどちらも論理的に外部とすることはできない。したがって,三次元では,すべて
の場合を満たすような“外部”についての有効な定義はない。
6.3.16 GM̲Curve
6.3.16.1 意味 GM̲Curve(曲線)(図11参照)は,GM̲OrientablePrimitiveを通じてGM̲Primitiveから派
生した下位型とする。これは,一次元幾何の基本的な要素となる。曲線は開区間の連続な像で,これによ
って,tを実パラメタ,Enをn(通常は,座標参照系によって決定される二又は三)次元ユークリッド空間
としてc(t):(a,b)→Enとするようなパラメタ化関数で表現できる。同一の曲線の像を同一の方向に描く,
e(t) = c(a + t(b-a)):(0,1)→Enといった正の伸縮又は線形転位のような他のパラメタ化表現はこの曲線に対す
る等しい表現とする。単純化のため,GM̲Curveは弧長によってパラメタ化することとし,これにしたが
ってGM̲GenericCurve (6.4.7参照)から継承するパラメタ化操作は0から曲線の長さまでの間のパラメ
タの値で有効となる。
曲線は,その座標系の下で連続かつ連結で可測な長さをもつ。この曲線の向きは,パラメタ化表現によ
って決定し,このパラメタ化表現の導関数を近似する接方向関数と一致し,常に“前”方向を指向する。
c(t):(a,b)→Enで定義される曲線の逆向きのパラメタ化表現はs(t) = c(a + b - t) :(a,b)→Enの形式の関数で定
義してよい。
一つの曲線は,一つ以上の曲線分からなる。曲線の各曲線分は,異なる内挿法を用いて定義してよい。
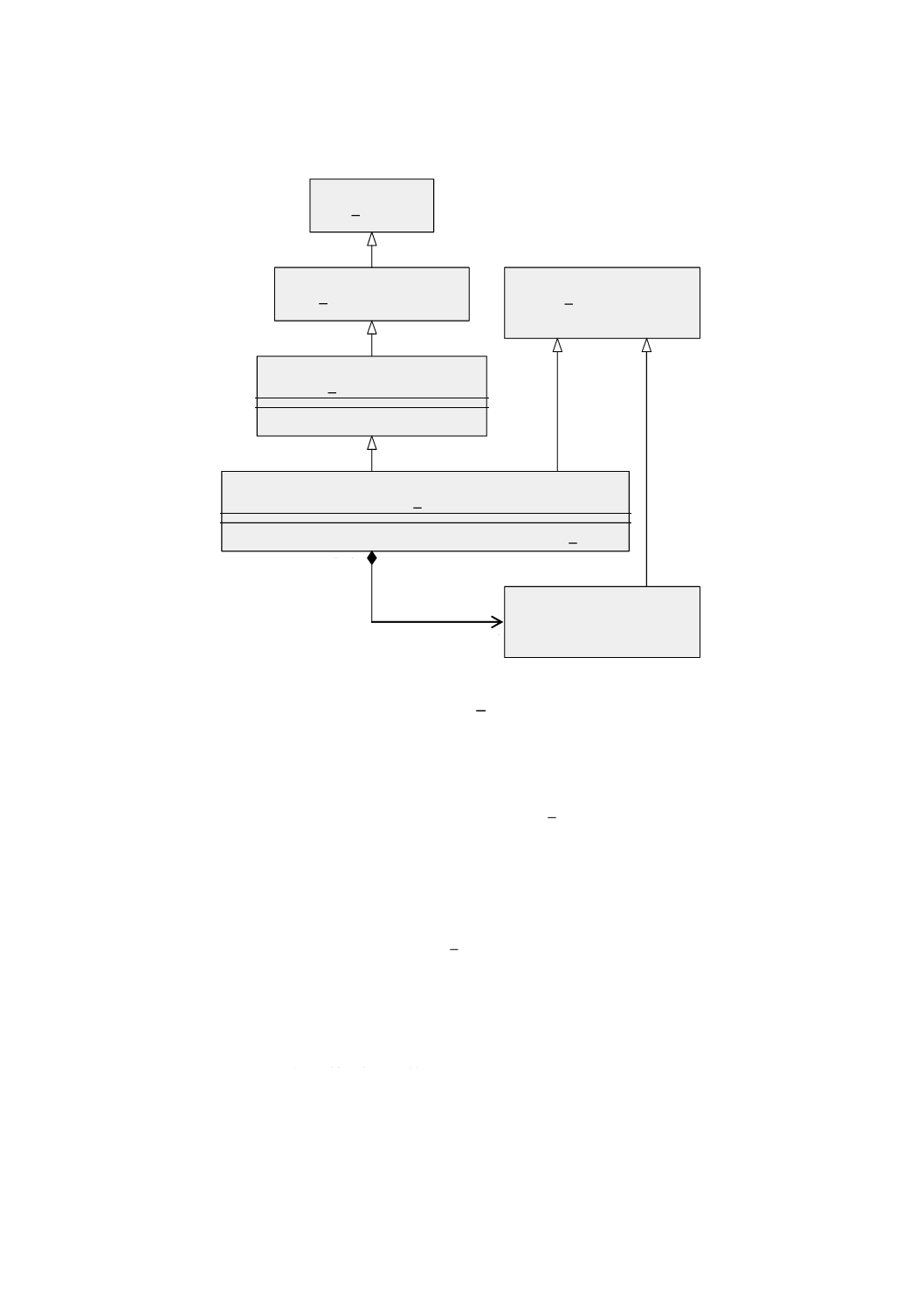
40
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
曲線分は,最後を除き,その終点が一連の曲線分の次の曲線分の始点と互いに連結する。
«Type»
GM̲Primitive
«Type»
GM̲OrientablePrimitive
«Type»
GM̲OrientableCurve
+ boundary() : GM̲CurveBoundary
«Type»
GM̲Curve
+ GM̲Curve(segment[1..n] : GM̲CurveSegment) : GM̲Curve
«Interface»
GM̲GenericCurve
(from Coordinate Geometry)
«Abstract»
GM̲CurveSegment
(from Coordinate Geometry)
1..n
+segment
{Sequence}
Segmentation
0..1
+curve
図 11 GM̲Curve
6.3.16.2 GM̲Curve(コンストラクタ) GM̲Curveのコンストラクタは,終点及び始点に対応関係をも
つ一連のGM̲CurveSegmentをとり,GM̲Curveを生成する。
GM̲Curve::GM̲Curve(segment[1..n] : GM̲CurveSegment) : GM̲Curve
6.3.16.3 Segmentation関連 “Segmentation”(分割)関連は,それぞれが曲線の一部分に沿った点の直接
位置を定義するような,GM̲Curveの一連の構成要素(GM̲CurveSegment)を示す。GM̲CurveSegmentの
順番は,GM̲Curveを描くのに用いる順番とする。
GM̲Curve::segment [1..n] : GM̲CurveSegment
GM̲CurveSegment::curve [0,1] : Reference<GM̲Curve>
特定のパラメタ区間に対してGM̲CurveとGM̲CurveSegmentとは一致する。
GM̲CurveSegment:
{curve.startParam() <= self.startParam()};
{curve.endParam() >= self.endParam()};
{self.startParam() < self.endParam()};
{s : Distance (startParam() <= s <= endParam())
implies (curve.parameterization(s) = self.parameterization(s)));
備考 この規格では,曲線分は,曲線の文脈以外では現れず,したがってこの関連での“curve”役割
41
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の多重度は“1”となるが,これは,この方法以外で曲線分を用いる妨げとなる。そこで,この
規格には影響しないので,多重度を“0..1”とすることで,他の規格がこれに基づいて,より制
限しない方法で曲線分を用いることができるようにする。
6.3.17 GM̲Surface
6.3.17.1 意味 GM̲Surface(曲面)(図12参照)は,GM̲Primitiveの下位クラスとし,二次元の幾何の基
本的な要素とする。メビウスの輪のような向きをもてない曲面は許されない。曲面の向きは,上向きの法
線を選択することによって“上”方向を選択し,曲面が輪体でない場合には,外部境界が反時計回りとな
ることからその上方向が判断できる。曲面の方向性の反転は,各境界要素の曲線の方向性を反転させ,曲
面の概念的な“上”及び“下”の方向を交換する。曲面が立体の境界となる場合,“上”の方向は,通常は
外側とする。境界をもたない閉曲面の場合,上の方向は,その曲面分の上方向とし,それらは互いに一致
しなければならない。これに含まれるGM̲SurfacePatchはGM̲Surfaceの内部構造を定める。
備考 GM̲Surfaceに求められる“妥当性”の条件は,向きについての制約だけである。
6.3.17.2 GM̲Surface(コンストラクタ) 一つ目の形式のGM̲Surfaceのコンストラクタは,辺と辺とに
対応関係をもつ一連のGM̲SurfacePatchをとり,GM̲Surfaceを生成する。
GM̲Surface::GM̲Surface(patch[0..n] : GM̲SurfacePatch) : GM̲Surface
二つ目の形式は,常に二次元座標空間で機能することが保証され,GM̲SurfaceBoundaryを構成する
GM̲Curveの集まりとして境界を指定することによって,GM̲Surfaceを構築する。三次元座標空間では,
このコンストラクタの二つ目の形式は,すべての境界を定義するGM̲Curveのインスタンスが,曲面内部
を定義する共通面上にある(単一の面上に存在する)ことを必要とする。
GM̲Surface::GM̲Surface(bdy : GM̲SurfaceBoundary) : GM̲Surface
6.3.17.3 Segmentation関連 “Segmentation”(分割)関連は,GM̲Surfaceを形成する互いに繋がった
GM̲SurfacePatchの集合と関係付ける。内挿法に応じて,曲面分の集合は,意味をもった追加的な構造を
必要としてもよい。一般に,曲面分の形状は,応用スキーマで定義しなければならない。
GM̲Surface::patch [1..n] : GM̲SurfacePatch
GM̲SurfacePatch::surface [0,1] : Reference<GM̲Surface>
GM̲Surface.coordinateDimensionが2の場合,GM̲Surface全体は境界からの線型補間によって定義され
る一つの論理的な曲面分になる。
備考 この規格では,曲面分は,曲面の文脈以外には現れないため,この関連での“surface”役割の
多重度は“1”とすることになるが,それは,この方法以外で曲面分を使用する妨げとなる。多
重度を“0..1”とすることによって,この規格には影響を与えず,また,他の規格がこれに基づ
いてより制限のない方法で曲面分を使用することができるようになる。
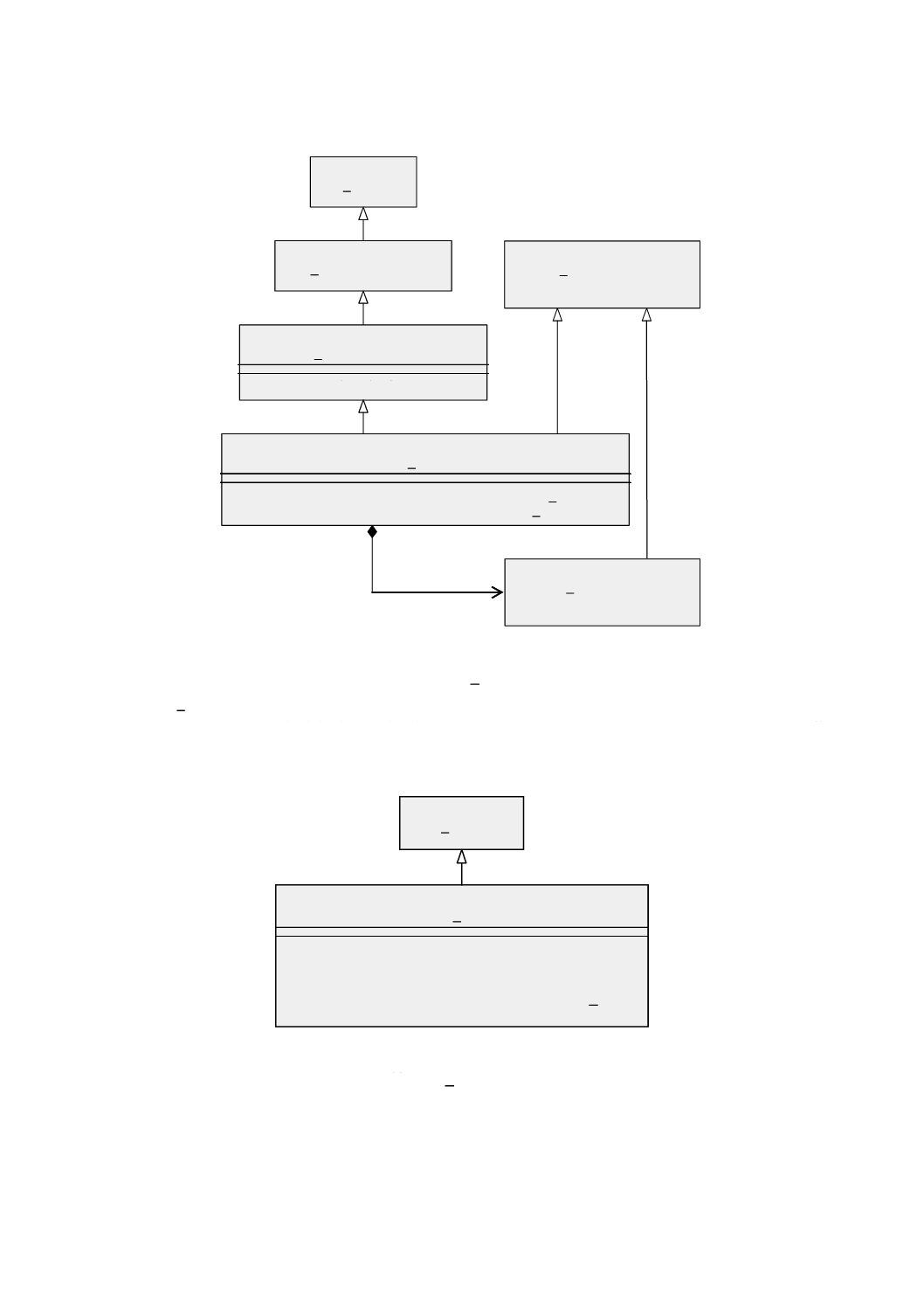
42
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲Primitive
«Type»
GM̲OrientablePrimitive
«Type»
GM̲OrientableSurface
+ boundary() : GM̲SurfaceBoundary
«Type»
GM̲Surface
+ GM̲Surface(patch[1..*] : GM̲SurfacePatch) : GM̲Surface
+ GM̲Surface(bdy : GM̲SurfaceBoundary) : GM̲Surface
«Interface»
GM̲GenericSurface
(from Coordinate Geometry)
«Abstract»
GM̲SurfacePatch
(from Coordinate Geometry)
1..n
+patch
Segmentation
0..1
+surface
図 12 GM̲Surface
6.3.18 GM̲Solid
6.3.18.1 意味 GM̲Solid(立体)(図13参照)はGM̲Primitiveの下位クラスとし,三次元幾何の基本的
な要素とする。立体の範囲は,境界面によって定義する。
«Type»
GM̲Solid
+ boundary() : GM̲SolidBoundary
+ area() : Area
+ volume() : Volume
+ GM̲Solid(boundary : GM̲SolidBoundary) : GM̲Solid
«Type»
GM̲Primitive
図 13 GM̲Solid (立体)
43
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.18.2 boundary “boundary”(境界取得)操作は,GM̲Object及びGM̲Primitiveで定義する境界取得
操作を対応した戻り値の型をもつよう特化したものとする。これは,このGM̲Solidの範囲を限定する
GM̲Surfaceの集合の列を返す。これらの曲面は,GM̲Solidの境界要素のそれぞれに一つの曲面集合を構
成する。これらの殻は,それぞれ輪体(境界のない合成閉曲面)とする。
GM̲Solid::boundary() : GM̲SolidBoundary
備考 立体の外部殻は,その存在する座標空間が常に三次元のユークリッド空間であるという理由だ
けで定義する。一般に,有界な三次元多様体中の立体は,識別可能な外部境界をもたない。
“exterior”境界が明確に定義されていない場合,GM̲SolidBoundaryのすべての殻は,“interior”境界と
して列挙されなければならない。
立体の境界となるGM̲OrientableSurfaceは,外側を向く。すなわち,各GM̲Surfaceの向きによって定
義された“上”が,立体の内部から離れる方向を向く。
合成曲面としての各GM̲Shellは,輪体となる(6.2.2.7参照)。
6.3.18.3 area “area”(表面積取得)操作は,立体の境界要素のすべての曲面の面積の合計を返す。
GM̲Solid::area() : Area
Set<GM̲Surface>クラスは,集合の要素の面積を累積する“area”という“列演算”をもつ。これを用い
て,GM̲Solidについて次のように表すことができる。
GM̲Solid:
area() = boundary().area()
6.3.18.4 volume “volume”(体積取得)操作は,このGM̲Solidの体積を返す。これは,外部境界殻の内
部の体積から各内部境界殻の内部の体積の合計を引いたものとする。
GM̲Solid::volume() : Volume
6.3.18.5 GM̲Solid(コンストラクタ) この規格では,座標参照系を三次元までに制限しているため,
あらゆる立体は,その境界で定義できる。GM̲Solidの既定のコンストラクタは,適切に構造化され,
GM̲SolidBoundaryを構成するGM̲Shellの集合から生成する。
GM̲Solid::GM̲Solid(boundary : GM̲SolidBoundary) : GM̲Solid
6.4
Coordinate geometryパッケージ
6.4.1
DirectPosition
6.4.1.1
意味 DirectPosition(直接位置)オブジェクトデータ型(図14参照)は,ある空間参照系上の位
置の座標を保持する。この空間参照系は,JIS X 7111で定義する。DirectPositionは,データ型として,た
いていはJIS X 7111のSC̲CRSへの参照をもった(GM̲Objectsのような)より大きなオブジェクトに含
まれる。このため,DirectPosition::cordinateReferenceSystemの値は,対象となるDirectPositionがこのよう
なSC̲CRSへの参照をもつ,より大きなオブジェクトに含まれている場合には,NULLのままとしてよい。
この場合,DirectPosition::cordinateReferenceSystemは,暗黙でそれを含むオブジェクトのSC̲CRSの値をと
るものとして扱う。
6.4.1.2
coordinate “coordinate”(座標)属性は,この位置の座標を指定した参照系で保持するNumber
の列とする。
DirectPosition::coordinate : Sequence<Number>
6.4.1.3
dimension “dimension”(次元)属性は,座標列の長さ(項数)とする。これは,参照系によっ
て決まる。
/ DirectPosition::dimension : Integer = (coordinate.length)
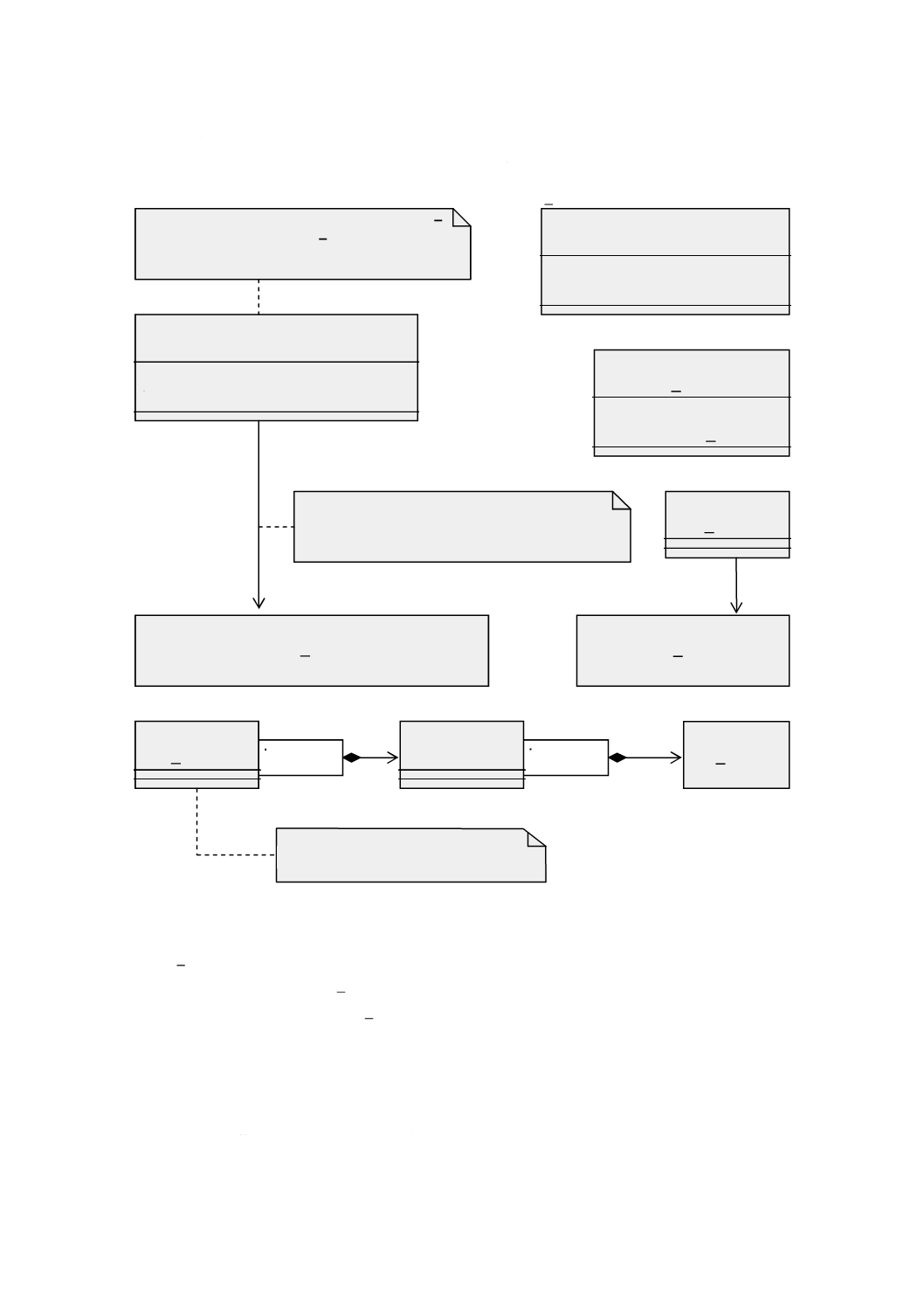
44
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.1.4
coordinateReferenceSystem “coordinateReferenceSystem”(座標参照系)関連役割は,その座標
を定めている座標系とする。SC̲CRS型はJIS X 7111で規定する。
DirectPosition::cordinateReferenceSystem [0,1] :JIS X 7111::SC̲CRS
«DataType»
DirectPosition
+ coordinate : Sequence<Number>
/+ dimension : Integer
«DataType»
GM̲PointRef
{coordinateReferenceSystem.dimension =
coordinate.size =
dimension}
0..n
+directPosition
«DataType»
GM̲Envelope
+ upperCorner : DirectPosition
+ lowerCorner : DirectPosition
«Union»
GM̲Position
+ direct : DirectPosition
+ indirect : GM̲PointRef
関連が存在しない場合のCRSは,例えばこの
直接位置をもつGM̲ObjectのCRSなどのように,
このデータ型の名前空間によって決定される。
0..1
+coordinateReferenceSystem
«Abstract»
SC̲CRS
(from Spatial Referencing by Coordinates)
«Type»
GM̲Point
(from Geometric primitive)
+point
1
i : Integer
«DataType»
GM̲PointGrid
i : Integer
«DataType»
GM̲PointArray
«Union»
GM̲Position
+row
1..n
+column
1..n
row, column.の個数は,定数
0..n
row, column.の個数は,定数 である。
図 14 DirectPosition
6.4.2
GM̲PointRef GM̲PointRef(点参照データ)は,存在する点を参照するために使用する。これは
テンプレートクラスReference<GM̲Point>をインスタンス化したものとする。
GM̲PointRef::point : Reference<GM̲Point>
6.4.3
GM̲Envelope
6.4.3.1
意味 GM̲Envelope(包被データ)は,多くの場合,最小境界直方体又は長方形として用いられ
る。GM̲Envelopeは,次元の値に関係なく二つの直接位置(点座標)として明確に表現できる。GM̲Envelope
の符号化には,この二つの点を符号化するだけでよい。これは,この規格のすべてのデータ型と矛盾する
ことはなく,その状態をその公開アクセス可能な属性によって表す。
45
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.3.2
upperCorner GM̲Envelopeの“upperCorner”(上端属性)は,各次元の座標値がそれぞれその
GM̲Envelopeのすべての点における座標値の最大値からなる座標位置とする。
GM̲Envelope::upperCorner : DirectPosition
6.4.3.3
lowerCorner GM̲Envelopeの“lowerCorner”(下端属性)は,各次元の座標値がそれぞれその
GM̲Envelopeのすべての点における座標値の最小値からなる座標位置とする。
GM̲Envelope::lowerCorner : DirectPosition
6.4.4
TransfineteSet<DirectPosition> 幾何オブジェクトの機能の多くは,その幾何オブジェクトを潜在
的にDirectPositionの無限集合とみなしたものから派生する(図6参照)。TransfineteSet<T>(超限集合)パ
ラメタ化クラスは,ISO TS 19103で定義する。
6.4.5
GM̲Position GM̲Position(位置)データ型は,DirectPosition,又はDirectPositionを取得する対
象のGM̲Pointへの参照のいずれかで構成される共用型とする。このデータ型を用いると,座標として直
接的(directの形式)又はGM̲Pointへの参照として間接的(indirectの形式)のいずれかの方法で位置を
識別できる。
GM̲Position::direct [0,1] : DirectPosition
GM̲Position::indirect [0,1] : GM̲PointRef
GM̲Position:
{direct.isNull = indirect.isNotNull}
6.4.6
GM̲PointArray及びGM̲PointGrid この規格の幾何構成物の多くは,列又は格子(長さが等し
い列の列)を構成する参照点を用いる必要がある。
GM̲PointArray::column[1..n] : GM̲Position
GM̲PointGrid::row[1..n] : GM̲PointArray
6.4.7
GM̲GenericCurve
6.4.7.1
意味 GM̲Curve及びGM̲CurveSegmentは,いずれも曲線幾何形状の一部分を表現するため,幾
つかの操作の署名(シグニチャ)を共有する。これらは,GM̲GenericCurve(一般曲線)インタフェース
クラス(図15参照)で定義する。
6.4.7.2
startPoint及びendPoint “startPoint”(始点取得)操作及び“endPoint”(終点取得)操作は,そ
れぞれGM̲GenericCurve上の最初の点及び最後の点のDirectPositionを返す。これは,GM̲Primitiveの境
界取得操作と異なり,これら二つの点を表現するオブジェクトではなく,その値だけを返す。
GM̲GenericCurve::startPoint() : DirectPosition
GM̲GenericCurve::endPoint() : DirectPosition
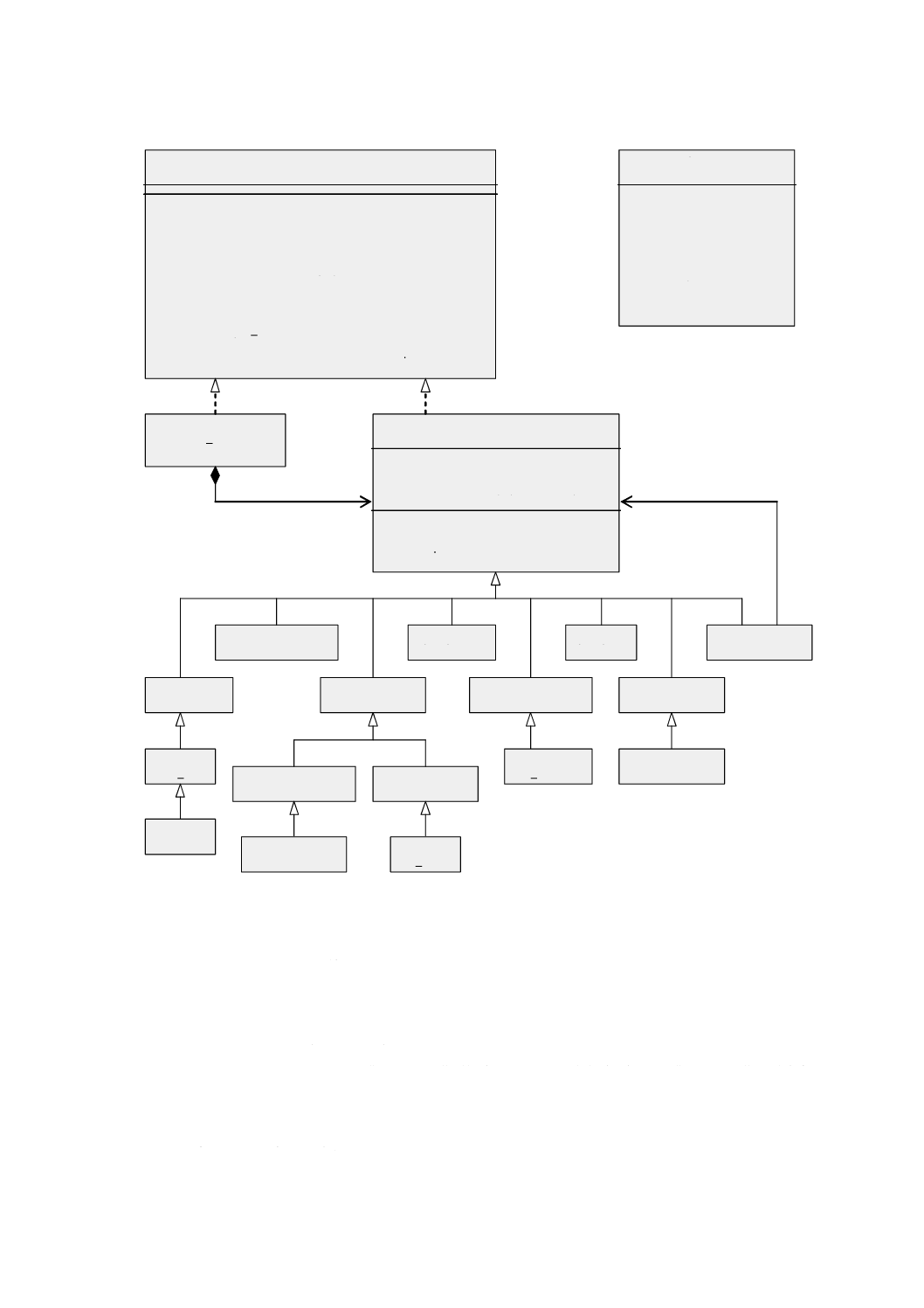
46
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Interface»
GM̲GenericCurve
+ startPoint() : DirectPosition
+ endPoint() : DirectPosition
+ param( s : Distance) : DirectPosition
+ tangent( s : Distance) : Vector
+ startParam() : Distance
+ endParam() : Distance
+ paramForPoint( p : DirectPosition) : Set< Distance>, DirectPosition
+ constrParam( cp : Real) : DirectPosition
+ startConstrParam() : Real
+ endConstrParam() : Real
+ length( point1 : GM̲Position: point2 : GM̲Position) : Length
+ length( cparam1 : Real, cparam2 : Real) : Length
+ asLineString( spacing : Distance, offset : Distance) : GM̲LineString
«Type»
GM̲Curve
(from Geometric primitive)
«Abstruct»
GM̲CurveSegment
+ interpolation : GM̲CurveInterpolation = "linear"
+ numDeri vativesAtStart[ 0, 1] : Integer = 0
+ numDerivativesAtEnd[ 0,1] : Integer = 0
+ numDerivativeInterior[ 0, 1] : Integer = 0
+ samplePoint() : GM̲PointArray
+ boundary() : GM̲CurveBoundary
+ reverse() : GM̲CurveSegment
0..1
+curve
{Sequence} 1..n
+segment
Segmentation
«CodeList»
GM̲CurveInterpolation
+ linear
+ geodesic
+ circularArc3Points
+ circularArc2PointWithBulge
+ elliptical
+ clothoid
+ conic
+ polynomialSpline
+ cubicSpline
+ rationalSpline
«Type»
GM̲ArcString
«Type»
GM̲ArcStringByBulge
«Type»
GM̲SplineCurve
«Type»
GM̲Clothoid
«Type»
GM̲GeodesicString
«Type»
GM̲Conic
«Type»
GM̲LineString
«Type»
GM̲OffsetCurve
«Type»
GM̲Arc
«Type»
GM̲Circle
«Type»
GM̲Geodesic
«Type»
GM̲PolynomialSpline
«Type»
GM̲BSplineCurve
«Type»
GM̲CubicSpline
«Type»
GM̲Bezier
«Type»
GM̲LineSegment
0..n
1
+baseCurve
図 15 曲線分クラス
6.4.7.3
tangent “tangent”(接線取得)操作は,指定したパラメタ値においてこのGM̲GenericCurveに
接する接ベクトルを返す。このベクトルは,パラメタ化した曲線の微分を近似する。この接ベクトルは,
弧長によるパラメタ化に従って求められた(長さ1.0の)単位ベクトルとする。
GM̲GenericCurve::tangent(s : Distance) : Vector
6.4.7.4
startParam及びendParam “startParam”(始点パラメタ取得)操作及び“endParam” (終点パ
ラメタ取得)操作は,それぞれ,startPoint及びendPointに対応するパラメタを示す。
GM̲GenericCurve::startParam() : Distance
GM̲GenericCurve::endParam() : Distance
47
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲GenericCurve:
{parameterization(startParam()) = startPoint()};
{parameterization(endParam()) = endPoint()};
{length() = endParam() - startParam()}
GM̲Curveの始点及び終点のパラメタは,常にそれぞれ0と曲線の弧長でなければならない。GM̲Curve
中のGM̲CurveSegment(曲線分)では,個々のGM̲CurveSegmentの始点及び終点のパラメタは,Segmentation
関連(6.3.16.3参照)において,その曲線分の開始点及び終了点となるそれぞれの位置におけるGM̲Curve
のパラメタと等しく,したがって,最初を除くすべての曲線分のstartParamは,その直前の曲線分の
endParamに等しい。GM̲GenericCurveを他の目的に使用する場合,二つのパラメタがそのGM̲GenericCurve
の弧長の分だけ異なるような制約がなければならない。
6.4.7.5
paramForPoint “paramForPoint”(点パラメタ取得)操作は,指定したDirectPositionにおける
このGM̲GenericCurveのパラメタを返す。DirectPositionが曲線上にない場合,曲線上の最も近い点を使用
する。
GM̲GenericCurve::paramForPoint(p : DirectPosition) : Set<Distance>, DirectPosition
最も近いDirectPositionとは,“p”の実質の値として用いられるものとし,すなわち,“p”として指定し
た座標に最も近いGM̲GenericCurve上の点とする。曲線が単純な場合,返される集合には,距離を一つだ
け含む。指定した“p”からの最小距離が等しいDirectPositionがGM̲GenericCurve上に複数ある場合,戻
り値として取り得る応答のうちの一つを任意に選んでよい。
6.4.7.6
param “param”(パラメタ取得)操作は,曲線を実数区間の連続な像としてパラメタ化し表現
したものとする。この操作は指定した距離におけるGM̲GenericCurve上のDirectPositionを返す。パラメタ
化は,始点のパラメタに,弧長,すなわち始点からGM̲GenericCurveに沿って計測した距離を加えたもの
とする。
GM̲GenericCurve::param(s : Distance) : DirectPosition
6.4.7.7
startConstrParam及びendConstrParam “startConstrParam”(始点構造パラメタ取得)操作及び
“endConstrParam”(終点構造パラメタ取得)操作は,それぞれstartPoint及びendPointに対しての構造パ
ラメタ化に使用するパラメタを示す。
GM̲GenericCurve::startConstrParam() : Real
GM̲GenericCurve::endConstrParam() : Real
GM̲GenericCurve:
constrParam(startConstrParam()) = startPoint();
constrParam(endConstrParam()) = endPoint();
startConstrParamは,endConstrParamより小さいという条件はないが,パラメタ化は狭義単調(狭義単調
増加又は狭義単調減少)でなければならない。
備考 構造パラメタは,多くの場合操作を容易にするために定められ,既定のパラメタ化である弧長
距離に対して単純な関係をもつことはまれである。通常,幾何構造物はプログラマが合理的と
考える構造パラメタを使用し,弧長パラメタは要求時に計算される。
6.4.7.8
constrParam “constrParam”(構造パラメタ変換)操作は,パラメタが曲線の弧長を表現すると
いう制約及びGM̲Curveとその要素のGM̲CurveSegmentとの間の制約をもたない,曲線の実数区間の連
続な像としての代替的な表現とする。この操作は,基となる曲線の構造式を表現する際に最も一般的に用
いられ,特に曲線を使用してパラメタ化曲面を構成する場合に有効となる。
48
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲GenericCurve::constrParam(cp : Real) : DirectPosition
6.4.7.9
length ある曲線幾何の弧長は,座標参照系における弧長の計測数値とする。弧長は,距離の累
積であるから,その戻り値には計測している距離に適した単位を使用しなければならない。“length”(弧長
取得)操作は,2点間の曲線に添った距離を返す。二つの引数は,それぞれ始点及び終点を既定値にもつ。
2点のいずれかが曲線上の点でない場合,その点を曲線上のもっとも近いDirectPositionに投影した後に距
離を計算しなければならない。曲線が単純でなく,2点のいずれかを複数回通過している場合,その距離
はこのGM̲Curve上の2点間の極小の距離とする。
GM̲GenericCurve::length(point1 : GM̲Position = startPoint(),
point2 : GM̲Position = endPoint()
) : Length
この操作の第2の形式は,パラメタ化及びconstrParam操作で使用する変数同士で直接変換できるよう,
構造距離に対して直接使用する。
GM̲GenericCurve::length(cparam1 : Real = startConstrParam(),
cparam2 : Real = endConstrParam()
) : Length
既定のパラメタ化によって定まる直接位置間の距離は,単純にパラメタの差とする。また,length関数
は,構造パラメタから弧長パラメタへの変換を可能にする。
If p = length(startConstrParam, p2) + startParam
then parameterization(p) = constrParam(p2)
6.4.7.10 asLineString “asLineString”(折れ線取得)関数は,制御点(曲線分の端)がこの曲線上にある
ような折れ線(直線分の列)を生成する。(0でない)“spacing”(最大間隔)を指定した場合,生成した曲
線に沿った制御点間の距離は“spacing”を超えてはならない。(0でない)“offset”(最大相対距離)を指
定した場合,生成した曲線上の任意の点と元の曲線との間の距離は“offset”を超えてはならない。両方の
引数を指定した場合,両方の制限を適用する。曲線の元の制御点が曲線上に存在する場合,それらは,返
したGM̲LineStringのcontrolPointsに含まなければならない。いずれの引数も0の場合,返される折れ線
は,元の曲線の制御点から生成しなければならない。
GM̲GenericCurve::asLineString(spacing : Distance = 0, offset : Distance = 0)
: GM̲LineString
備考 この関数は,画面表示のような単純な動作のために曲線の直線近似を生成するのに有用である。
これは,しばしば“描画曲線”として参照する。この目的で,“offset”の方式は,曲線に対し
て対象となる表示装置に適した最小限の表現を保持するのに有効である。この関数は,また,
制御点を変換することによって,ある座標参照系から他の座標参照系への曲線の変換に備える
のにも有用である。この場合,“spacing”の方式がより適している。曲線がどのように構築さ
れているかについて,より詳しい情報がない場合,両方の引数を既定値の0とするのは地理的
な解釈にも幾何的な解釈にも有用ではない。
6.4.8
GM̲CurveInterpolation GM̲CurveInterpolation(曲線内挿法符号リスト)は,応用スキーマにお
いて内挿法の識別として用いてよい符号のリストとする。符号リストであるため,GM̲CurveInterpolation
の取り得る値を制限しない。GM̲CurveInterpolationの下位型は,下位クラス化によって直接的に生成する
ことも,内挿法及びそれに対応するcontrolParametersレコードへの関連を指定することで間接的に生成す
ることもできる。“内挿”として明確になっている意味には次のものが含まれるが,これらに限定されるも
のではない。
a) 線形(linear) この内挿法はcontrolPointの連続する各対の間を結ぶ直線上のDirectPositionを返す。
49
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 測地(geodesic) この内挿法はcontrolPointの連続する各対の間を結ぶ測地線上のDirectPositionを返
す。測地線は長さが最小になる曲線とする。測地は,そのGM̲CurveSegmentを含むGM̲Curveの座
標参照系によって決定する。
c) 3点円弧(circularArc3Points) この内挿法は,controlPointの連続した3点の組ごとに,2点目の制
御点がこの制御点列の始めからの偶数番目となり,1点目から2点目を通り3点目に至る円弧上の
DirectPositionを返す。制御点列は,奇数の要素をもたなければならない。
備考 3点が同一直線上にある場合,この円弧は,直線分となる。
d) 2点間膨らみ円弧(circularArc2PointWithBulge) この内挿法は,controlPointの連続する各対ごと
に,対応する制御パラメタが弦の中点から弧の中点までのオフセットを左方向が正で右方向が負とな
るよう定めた,1点目から2点目に至る弧上のDirectPositionを返す。この形式は,限定的な定義手法
を用いているため,二次元でだけ使用する。
e) だ(楕)円弧(elliptical) この内挿法は,controlPointの連続する4点の組ごとに,1点目から順番に
間の点を通って4点目に至るだ(楕)円弧上のDirectPositionを返す。
備考 4点が同一直線上にある場合,この弧は,直線分となる。4点が同一円周上にある場合,この
弧は,円弧となる。
f)
クロソイド型(clothoid) 角状らせん又はクロソイドによる内挿法を用いる。
g) 円すい弧型(conic) だ(楕)円弧と同様にして,5点の連続したcontrolPointを用いて円すい曲線の断
面を決定する。
h) 多項式スプライン型(polynomialSpline) 折れ線と同様の形式のcontrolPointを使用し,それらを多
項式スプライン関数によってつなぐ。通常,連続性の次数には,多項式に使用した次数を使用する。
i)
三次スプライン型(cubicSpline) controlPointは始点の接線方向及び3次多項式スプラインの形式の
3次多項式を使用して内挿する。
j)
有理スプライン型(rationalSpline) 折れ線と同様の形式のcontrolPointを使用し,それらを有理(多
項式の商)スプライン関数によってつなぐ。通常,連続性の次数には,多項式に使用した次数を使用
する。
この一覧は符号リストとして実装し,実際の値は,上の文字列と異なってよい。
GM̲CurveInterpolation::
linear
geodesic
circularArc3Points
circularArc2PointWithBulge
elliptical
clothoid
conic
polynomialSpline
cubicSpline
rationalSpline
6.4.9
GM̲CurveSegment
6.4.9.1
意味 GM̲CurveSegment(曲線分抽象)はGM̲Curveの等質な部分を定義する。GM̲CurveSegment
は,最大でも一つのGM̲Curveに属する。
50
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.9.2
interpolation “interpolation”(内挿法)属性は,この曲線分に使用する曲線内挿法を指定する。
この内挿法は,このGM̲CurveSergmentの位置を決定するための制御点及び制御パラメタを使用する。
GM̲CurveSegment::interpolation : GM̲CurveInterpolation
6.4.9.3
numDerivatives “numDerivativesAtStart”(始点連続性級数)属性及び“numDerivativesAtEnd”(始
点連続性級数)属性は,この曲線分とその前後の曲線分との間の連続性の種類を定義し,最初の属性は直
前の曲線分との,第2の属性は直後の曲線分との連続性を扱う。曲線中の最初及び最後の曲線分では,こ
れらの値のうち適切なほうを無視する。“numDerivativesInterior”(内部連続性級数)属性は,曲線の内部で
保証される連続性の種類を定義する。既定値である“0”は,単純な連続を意味し,これは満たさなければ
ならない最低水準の連続性とする。この水準は,数学の文献では,“C0”として表されるものである。1の
値は,関数とその一次導関数が対応する端点同士で連続する,“C1”級の連続を意味する。任意の整数n
の値は,関数とそのn次までの導関数が連続する,“Cn”級の連続を意味する。
GM̲CurveSegment::numDerivativesAtStart [0,1]: Integer = 0;
GM̲CurveSegment::numDerivativesInterior [0,1]: Integer = 0;
GM̲CurveSegment::numDerivativesAtEnd [0,1]: Integer = 0;
備考 これらの値は,基本的な曲線の定義が限定されているシステム上でだけ,適切に使用すること
ができる。例えば,折れ線とその線分とでは,線分の端点で内部角を調整するような予備の制
御パラメタが存在しないので,C0より上の連続性に対応できない。一方,スプライン関数の場
合,端の曲線分がC1級又はそれ以上の連続性に対応するよう導関数の値を調整するため,しば
しば自由な次数を追加としてもつ。
6.4.9.4
samplePoint “samplePoint”(標本点取得)操作は,GM̲CurveSegment上にある点の値の順序配
列(GM̲PointArray)を返す。多くの場合,それらは,曲線分の構成に使用した制御点に関係した点とな
る。
GM̲CurveSegment::samplePoint() : GM̲PointArray
備考 曲線分のcontrolPointは,その形状を制御するために使用し,常にその曲線分上に存在している
わけではない。例えば,スプライン曲線の場合,曲線分は,幾つかのcontrolPointのベクトルの
重み付け和として表現する。それぞれの重み付け関数は,曲線上の点が対応するcontrolPoint
に最も接近して通過する区間におおむね対応する構造パラメタの区間内に最大値をもつ。これ
らの点は,重み付け関数の最大値における曲線の値で,曲線分の標本点となる。
6.4.9.5
boundary GM̲CurveSegmentの“boundary”(境界取得)操作は,GM̲CurveSegmentの端点が既
存のGM̲Pointを必要とせず,境界が一時的に生成したGM̲Pointを含んでよいことを除き,GM̲Curveの
境界取得操作と同様に操作する。
GM̲CurveSegment::boundary() : GM̲CurveBoundary
備考 上記のGM̲CurveBoundaryは,ほとんど常に二つの離れた位置となるが,GM̲Curveのように
GM̲CurveSegment自身も輪体となることができる。曲線分を集成(aggregate)したGM̲Curveの
startPoint及びendPointを除いて,境界に使用するすべての点が一時的である(戻り値として生
成される)ような状況はもっともありがちである。GM̲CurveがGM̲Complexの一部である場
合,これら二つの位置(GM̲CurveのstartPoint及びendPoint)は,同じGM̲Complexに含まれ
るGM̲Pointで表す。
6.4.9.6
reverse GM̲CurveSegmentの“reverse”(反転取得)操作は,単純に曲線分のパラメタ化の方向
性を反転させる。
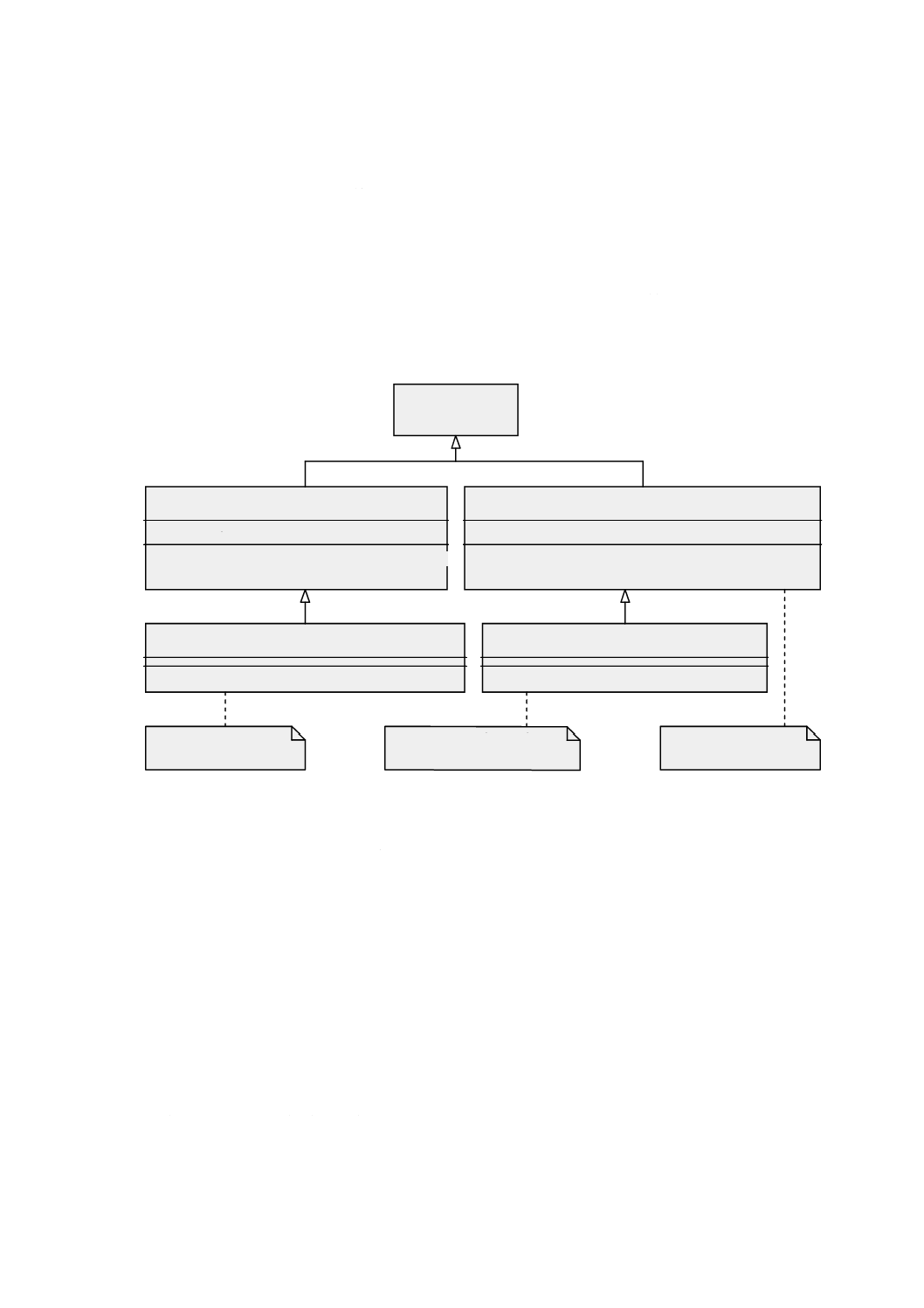
51
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲CurveSegment::reverse() : GM̲CurveSegment
6.4.10 GM̲LineString
6.4.10.1 意味 GM̲LineString(折れ線)(図16参照)は,おのおのがGM̲LineSegment (6.4.11参照)の
ようにパラメタ化した直線分の列からなる。このクラスは,本質的には,記憶領域を大幅に節約しつつ,
Sequence<GM̲LineSegments>を単一のオブジェクトに組み合せる。
6.4.10.2 controlPoint GM̲LineStringの“controlPoint”(制御点)属性は,曲線を直線的に内挿するような
位置の列とする。この列の1点目はそのGM̲LineStringのstartPointとし,列の最後の点はGM̲LineString
のendPointとする。
GM̲LineString::controlPoint : GM̲PointArray
«Abstract»
GM̲CurveSegment
«Type»
GM̲LineString
+ controlPoint : GM̲PointArray
+ GM̲LineString(points[2..n] : GM̲Position) : GM̲LineString
+ asGM̲LineSegment() : Sequence<GM̲LineSegment>
«Type»
GM̲GeodesicString
+ controlPoint : GM̲PointArray
+ GM̲GeodesicString(points[2..n] : GM̲Position) : GM̲GeodesicString
+ asGM̲Geodesic() : Sequence<GM̲Geodesic>
«Type»
GM̲LineSegment
+ GM̲LineSegment(point[2] : GM̲Position) : GM̲LineSegment
«Type»
GM̲Geodesic
+ GM̲Geodesic(point [2] : GM̲Position) : GM̲Geodesic
--controlPoint列のすべての
点は,双線型とする。
--controlPoint列のすべての点は,
同一の測地線上に存在する。
{interpolation = "geodesic"}
図 16 直線,弧及び測地線による内挿法
6.4.10.3 GM̲LineString(コンストラクタ) “GM̲LineString”のコンストラクタは,点の列をとり,そ
れらの点をcontrolPointとするGM̲LineStringを構築する。
GM̲LineStringのコンストラクタは2点以上の位置をとり,それらを結ぶ適切な折れ線を生成する。
GM̲LineString::GM̲LineString(points[2..n] : GM̲Position) : GM̲LineString
6.4.10.4 asGM̲LineSegment “asGM̲LineSegment”(線分型変換)操作は,折れ線を,それと等価な線
分の列に分解する。
GM̲LineString::asGM̲LineSegment() : Sequence<GM̲LineSegment>
6.4.11 GM̲LineSegment
6.4.11.1 意味 GM̲LineSegment(線分)は直線で結ばれた二つの異なるDirectPosition (startPoint及び
endPoint)からなる。したがって,そのinterpolation属性は,“linear”でなければならない。
GM̲GenericCurve::parameterization = c(s)の既定値は,次のようになる。
(L : Distance) = endParam ‒ startParam
c(s) = ControlPoint[1] + ((s-startParam)/L) * (ControlPoint[2] - ControlPoint[1])
52
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
controlPoint配列の他のすべての点は,この直線上になければならない。GM̲LineSegmentの制御点は,
すべてその始点と終点との間の直線上になければならない。これらの2点の間には,他の位置を直線的に
内挿してよい。
備考 構造パラメタtが 0≦t≦1.0 となる線形内挿法で, c(0) = c.startPoint()及びc(1) = c.endPoint()と
すると次が成り立つ。
t
c
t
c
t
c
)1(
)
1
)(
0(
)
(
+
−
=
6.4.11.2 GM̲LineSegment(コンストラクタ) “GM̲LineSegment”のコンストラクタは,二つの位置を
とり,それらを結ぶ適切な線分を生成する。コンストラクタは,クラススコープをもつ。
GM̲LineSegment::GM̲LineSegment(point[2] : GM̲Position) : GM̲LineSegment
6.4.12 GM̲GeodesicString
6.4.12.1 意味 GM̲GeodesicString(測地線列)は,測地線分の列からなる。このクラスは,本質的には,
記憶領域を大幅に節約しつつ,Sequence<GM̲Geodesic>を単一のオブジェクトに組み合わせる。
6.4.12.2 controlPoint GM̲GeodesicStringの“controlPoint”(制御点)属性は,このGM̲GeodesicStringを
用いている座標参照系のジオイド面又はだ(楕)円体面による測地線を使用して内挿した位置の列である。
これらの点の構成は,GM̲LineString (6.4.10.2参照)と同じとする。
GM̲GeodesicString::controlPoint : GM̲PointArray
GM̲GeodesicStringの内挿法は“geodesic”とする。
GM̲GeodesicString::interpolation : GM̲CurveInterpolation = “geodesic”
6.4.12.3 GM̲GeodesicString(コンストラクタ) “GM̲GeodesicString”のコンストラクタは複数の位置
をとり,使用している座標参照系のジオイド面又はだ(楕)円体面によって定義される測地線を用いて内挿
を行い,それらを結ぶ適切な測地線列を生成する。
GM̲GeodesicString::GM̲GeodesicString(points[2..n]:GM̲Position):GeodesicString
6.4.12.4 asGM̲Geodesic “asGM̲Geodesic”(測地線型変換)操作は,測地線列を等価な測地線分の列に
分解する。
GM̲GeodesicString::asGM̲Geodesic() : Sequence<GM̲Geodesic>
6.4.13 GM̲Geodesic
6.4.13.1 意味 GM̲Geodesic(測地線)は,測地曲線で結ばれた二つの異なる位置からなる。GM̲Geodesic
の制御点は,すべてが始点と終点との間を結んだ測地線上になければならない。それら2点の間では,座
標参照系が使用するだ(楕)円体又はジオイドモデルによって定義した測地曲線を他の位置の内挿に使用し
てよい。そのcontrolPointの他のすべての点はこの測地線上になければならない。
6.4.13.2 interpolation GM̲Geodesicの“interpolation”(内挿法属性)は“geodesic”とする。
GM̲Geodesic::interpolation : GM̲CurveInterpolation = “geodesic”
6.4.13.3 GM̲Geodesic(コンストラクタ) GM̲Geodesicのコンストラクタは,二つの位置をとり,それ
らを結ぶ適切な測地線を生成する。コンストラクタは,クラススコープをもつ。
GM̲Geodesic:: GM̲Geodesic(point[2] : GM̲Position) : GM̲Geodesic
6.4.14 GM̲ArcString
6.4.14.1 意味 GM̲ArcString(弧列)(図17)は,内挿法に円弧を使用することを除いてGM̲LineString
と同様とする。円弧の決定には,3点が必要であるため,controlPointは,各弧の始点,始点と終点との間
のある点及び各弧の終点という三つのGM̲Positionの集合の,点の重複を含んだ列として扱う。各弧の終
点は,次の弧の始点となるため,controlPointの列では重複点のGM̲Positionは,繰り返さない。
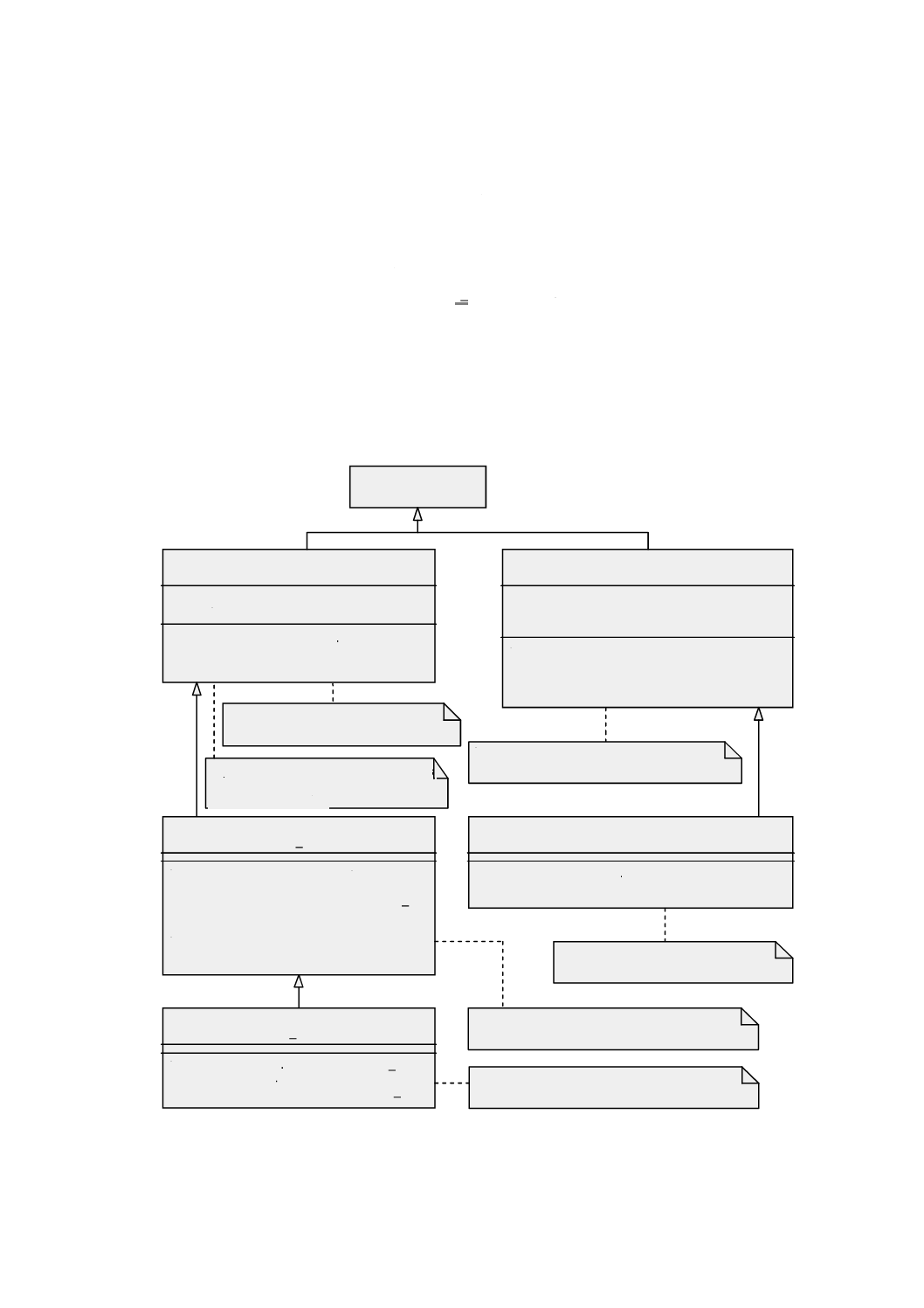
53
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.14.2 numArc “numArc”(弧数)属性はこの列における円弧の数とする。内挿法は,三つの位置の重
複を含んだ集合が必要なため,弧の数はcontrolPointの数を決定する。
GM̲ArcString::numArc : Integer = ((controlPoint.length ‒ 1)/2)
6.4.14.3 controlPoint “controlPoint”(制御点)属性は,この列における弧を制御するために使用する点
の列とする。この列の最初の三つのGM̲Positionは,最初の弧を決定する。奇数番目で始まる三つの連続
したGM̲Positionは,いずれもこの列の別個の弧を決定する。
GM̲ArcString::controlPoint : GM̲PointArray {size = 2 * numArc + 1}
6.4.14.4 interpolation GM̲ArcStringの“interpolation”(内挿法)属性は,“circularArc3Points”とする。
GM̲ArcString::interpolation : GM̲CurveInterpolation = “circularArc3Points”
6.4.14.5 GM̲ArcString (コンストラクタ) GM̲ArcStringのコンストラクタは,GM̲Positionで定義し
た点の列をとり,それらを結ぶ3点弧の列を生成する。弧列の性質から,列は,必ず奇数個の位置を含む。
GM̲ArcString::GM̲ArcSting( point[3,5,7...] : GM̲Position): GM̲ArcString
-- controlPoint列のすべての点は同一の円上にある
«Abstract»
GM̲CurveSegment
«Type»
GM̲ArcString
+ numArc : Integer
+ control Point : GM̲PointArray
+ GM̲ArcString(point[3, 5, 7,..] : GM̲Position)
: GM̲ArcString
+ asGM̲Arc() : Sequence<GM̲Arc>
«Type»
GM̲ArcStringByBulge
+ bulge : Sequence<Real>
+ numArc : Integer
+ normal : Sequence<Vector>
+ GM̲ArcStringByBulge(point[2..n] : GM̲Position,
bulge[1..n] : Real, normal[1..n] : Vector)
: GM̲ArcStringByBulge
+ asGM̲ArcString() : GM̲ArcString
{interpolation = "circularArc3Points"}
{controlPoint.count = 2 * numArc + 1}
{interpolation = "circularArc2PointWithBulge"}
{bulge.count = normal.count = numArc}
«Type»
GM̲Arc
+ GM̲Arc(point[3] : GM̲Position) : GM̲Arc
+ GM̲Arc(point[2] : GM̲Position, bulge : Real,
normal : Vector) : GM̲Arc
+ center() : DirectPosition
+ radius() : Distance
+ startOfArc() : Bearing
+ endOfArc() : Bearing
«Type»
GM̲ArcByBulge
+ GM̲ArcByBulge(point[2] : GM̲Position, bulge : Real,
normal : Vector) : GM̲ArcByBulge
--すべての円弧は同一の円上にある
«Type»
GM̲Circle
+ GM̲Circle(point[3] : GM̲Position) : GM̲Circle
+ GM̲Circle(center : GM̲Position,
radius : Distance) : GM̲Circle
-- controlPoint列の始点と終点とは同一である
-- 原国際規格では属性名がcontrolPoints
となっているが,本文の記述と整合させるた
めcontrolPointとした。
図 17 弧
54
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.14.6 asGM̲Arc “asGM̲Arc”(弧型変換)操作は,この弧列と幾何的に等しい弧の列を生成する。
GM̲ArcString::asGM̲Arc() : Sequence<GM̲Arc>
6.4.15 GM̲Arc
6.4.15.1 意味 GM̲Arc(弧)は,3点で定義され,その3点によって決まる円の,1点目から始まり2
点目を通って3点目に至る弧からなる。3点が同一直線上にある場合,弧は3点折れ線となり,中心,半
径,始角及び終角の値を返すことはできない。
備考 モデル上では,GM̲Arcは,ただ一つの弧から成り立つ単純な弧列としてGM̲ArcStringの下位
クラスとなる。これは,しばしば上位クラスよりその下位クラスが(追加的なメソッド及び属
性を伴って)複雑になると考えられるという意味で直観的でないかもしれない。GM̲Arcは,
より少ないデータしかもたないためGM̲ArcStringより単純ではあるが,それが“中心”,“始角”
及び“終角”といった幾何情報を返すことができるという点ではより複雑になる。この追加計
算の複雑さのため,この方法での下位クラス化が必要となる。加えて,“is type of”(〜の型で
ある)の意味は,この方向だけに作用する。
その最も単純な表現において,GM̲ArcのcontrolPoint列中の3点は,弧の始点,始点でも終点でもない
弧上の点,及びGM̲Arcの終点の順になければならない。
GM̲Arc::controlPoint : GM̲PointArray = < startPoint : GM̲Position,
midPoint : GM̲Position,
endPoint : GM̲Position>
追加の点を与える場合,すべての点は,制御点配列における同一直線上にない3点によって定義される
円周上になければならない。すべての点は,同一の円周上になければならず,controlPoint配列において弧
上でそれらが発生する順に指定しなければならない。
備考 controlPoint列の中央のGM̲Positionを示す“midPoint”(中点)という用語は,GM̲Positionが
円弧の幾何的中点であることを要求するものではない。このことは,このGM̲Positionにとっ
て計算上の安定性の見地から最良の選択ではあるが,数学的作用に絶対必要というわけではな
い。
6.4.15.2 GM̲Arc(コンストラクタ) “GM̲Arc”のコンストラクタは,三つの位置をとり,対応する
弧を生成する。
GM̲Arc::GM̲Arc(point[3] : GM̲Position): GM̲Arc
GM̲Arcのコンストラクタの二つ目は,二つの位置並びに弧の中点から弦の中点への差を表現する距離
及び方向をとり,対応する弧を形成する。
GM̲Arc::GM̲Arc(point[2] : GM̲Position, bulge : Real, normal : Vector) : GM̲Arc
得られる弧の中点は,次のように与えられる:
midPoint = ((startPoint + endPoint)/2.0) + bulge*normal
二次元座標参照系では,bulge (膨らみ幅)は符号をもち,normal(法線)は弧の始終点間の線分(弧
の弦)に直交し,左を向くものとする。
例 2点をP0 = (x0,y0) 及び P1 = (x1,y1) とし,膨らみをbとすると,P0からP1への方向ベクトル
は,次の式で与えられる:
55
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
0
1
2
0
1
0
1
0
1
1
0
)
(
)
(
)
,
(
)
,
(
y
y
x
x
y
y
x
x
u
u
u
−
+
−
−
−
=
=
ρ
{v
u ,} が右手系局所座標系を満たすためには,二つのベクトルは,ベクトルの内積が0,外積が1でな
ければならない。このことから,この対を満たす左向きの法線は,次のとおりとする。
)
,
(
)
,
(
0
1
1
0
u
u
v
v
v
−
=
=
弦の中点から膨らみの分だけ移動した円弧の中点は,次のとおりとする:
v
b
P
P
m
+
+
=
2
1
0
これは,b > 0 の場合左向き,b < 0 の場合右向きとする。
6.4.15.3 center “center”(中心点取得)操作は,この弧を含む円の中心を直接位置として計算する。返
されるDirectPositionの座標参照系は,GM̲Arcの座標参照系と同じものでよい。幾つかの極端な(特に元
の弧が非常に大きい半径を有する)場合,計算されたDirectPositionは,GM̲Arcで用いた座標参照系の有
効な定義域の外であってもよい。応用スキーマは,そのような場合の適切な動作方針を選んでよい。
GM̲Arc::center() : DirectPosition
6.4.15.4 radius “radius”(半径取得)操作は,この弧を含む円の半径を計算する。
GM̲Arc::radius() : Distance
6.4.15.5 startOfArc “startOfArc”(弧開始方向取得)操作は,この弧を含む円の中心から弧の始点への
線の方向を計算する。二次元の場合これは始角となる。三次元の場合,法線の方向角は,弧が参照円と平
行であることを示す。そうでない場合,方向は,高さの情報を含まなければならない。
GM̲Arc::startArc() : Bearing
6.4.15.6 endOfArc “endOfArc”(弧終了方向取得)操作は,この弧を含む円の中心から弧の終点への線
の方向を計算する。二次元の場合これは終角となる。三次元の場合,法線の方向角は弧が参照円と平行で
あることを示す。そうでない場合,方向は,高さの情報を含まなければならない。
GM̲Arc::endOfArc() : Bearing
6.4.16 GM̲Circle GM̲Arc(円)と同様だが,完全な円を形成するよう閉じたもの。“start”及び“end”
の方向は等しく,示された最初のcontrolPointの方向とする。
備考 これには,さらに少なくとも同一直線上にない異なる三つの点を明確に定義する必要がある。
弧は,最初の点に出会うまで単純に延長される。
6.4.17 GM̲ArcStringByBulge
6.4.17.1 意味 弧の変種であるGM̲ArcStringByBulge(膨らみ弧列)は,構成要素のGM̲Arcの二つ目の
コンストラクタのパラメタをそのまま保持し,標準的な弧の他の属性については再計算する。controlPoint
列はGM̲ArcStringの列と類似しているが,中点のGM̲Positionは計算で求められるためため不必要とする。
制御点列は,各弧の始点及び終点からなる。
6.4.17.2 bulge 膨らみとは,各弧の中点の変位量を制御する。“bulge”(膨らみ)属性は,各弧の中点の
変位方向を決定する法線に対する実数の倍率とする。膨らみは,制御点配列の隣接点の各対に必要なため,
膨らみ列の長さは制御点配列の長さより1だけ小さい。
GM̲ArcByBulge::bulge : Sequence<Real>
膨らみは,単に法線に対する倍率であるため,距離としては扱わず,変位の距離の単位は,その座標参
56
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
照系のベクトルのlength関数によって決まる。この規格の例では,しばしば法線をユークリッドの単位ベ
クトルとして扱うが,その長さを座標参照系で用いる距離公式の一つに依存するよう定めてもよく,定め
なくてもよい。
結果として生成される弧の中点は,次のとおりになる。
midPoint = ((startPoint + endPoint)/2.0) + bulge*normal
6.4.17.3 numArc “numArc”(弧数)属性は,この列の円弧の数とする。内挿法は二つの位置の重複のあ
る集合が必要なため,弧の数はcontrolPointの数を決定する。
GM̲ArcStringByBulge:numArc : Integer = ((controlPoint.length ‐ 1))
6.4.17.4 normal “normal”(法線)属性は,弧の始点と終点とを結ぶ線である弧の弦に対する法線ベク
トル(垂線)とする。二次元座標系では,法線は,二つの方向しかなく,しばしば弦の線から左向き角を
示す正号又は右方向を示す負号を伴った長さを示す符号付き実数で表す。三次元では法線は弧のstartPoint
とendPointに沿った弧の面を決定する。
法線は,通常,単位ベクトルだが,これは絶対に要求されるわけではない。法線が0ベクトルの場合,
幾何オブジェクトは二つの端点間の直線と等しくなる。法線列の長さは膨らみ列の長さと正確に等しく,
制御点列の長さより1だけ小さい。
GM̲ArcByBulge::normal : Sequence<Vector>
備考 “midPoint”(中点)派生属性を,“bulge”(膨らみ)属性及び“normal”(法線)属性によって
決定された弧の中点として定義してよい。
/ GM̲ArcByBulge::midPoint : Sequence<GM̲Position>
midpoint(n) = (controlPoint(n) + contolPoint(n))/2.0) + bulge*normal
各controlPoint対にそれに関連した中点を配置すると,結果としてこのGM̲ArcStringByBulgeと幾何的
に同値な(3点内挿法を用いた)GM̲ArcStringの制御点の有効な集合が得られる。
6.4.17.5 interpolation GM̲ArcStringByBulgeの“interpolation”(内挿法)属性は,常に
“circularArc2PointWithBulge”とする。
6.4.17.6 GM̲ArcStringByBulge(コンストラクタ) コンストラクタは膨らみの表現をオブジェクトの内
部で保持することを除き,GM̲Arcの二つ目のコンストラクタに等しい。
GM̲ArcByBulge::GM̲ArcByBulge(point[2..n] : GM̲Position, bulge[1..n] : Real,
normal[1..n] : Vector ) : GM̲ArcStringByBulge
得られる弧の中点は,次のとおりとなる:
midPoint(n) = ((point(n) + point(n+1))/2.0) + (bulge * normal)
6.4.17.7 asGM̲ArcString 各GM̲ArcStringByBulgeは,“asGM̲ArcString”(弧列型変換)操作を使用して
基本となるGM̲ArcStringとして再変換できる。
GM̲ArcStringByBulge::asGM̲ArcString() : GM̲ArcString;
6.4.18 GM̲ArcByBulge
6.4.18.1 意味 GM̲ArcByBulge(膨らみ弧)は,GM̲ArcStringByBulge(6.4.17参照)を制約したものと
する。GM̲ArcByBulgeのインスタンスは,すべての制御点を同一の円上にもつ。
6.4.18.2 GM̲ArcByBulge(コンストラクタ) コンストラクタは,膨らみの表現が保持されることを除
きGM̲Arcの二つ目のコンストラクタに等しい。
GM̲ArcByBulge::GM̲ArcByBulge(point[2] : GM̲Position, bulge : Real,
normal : Vector ) : GM̲ArcByBulge
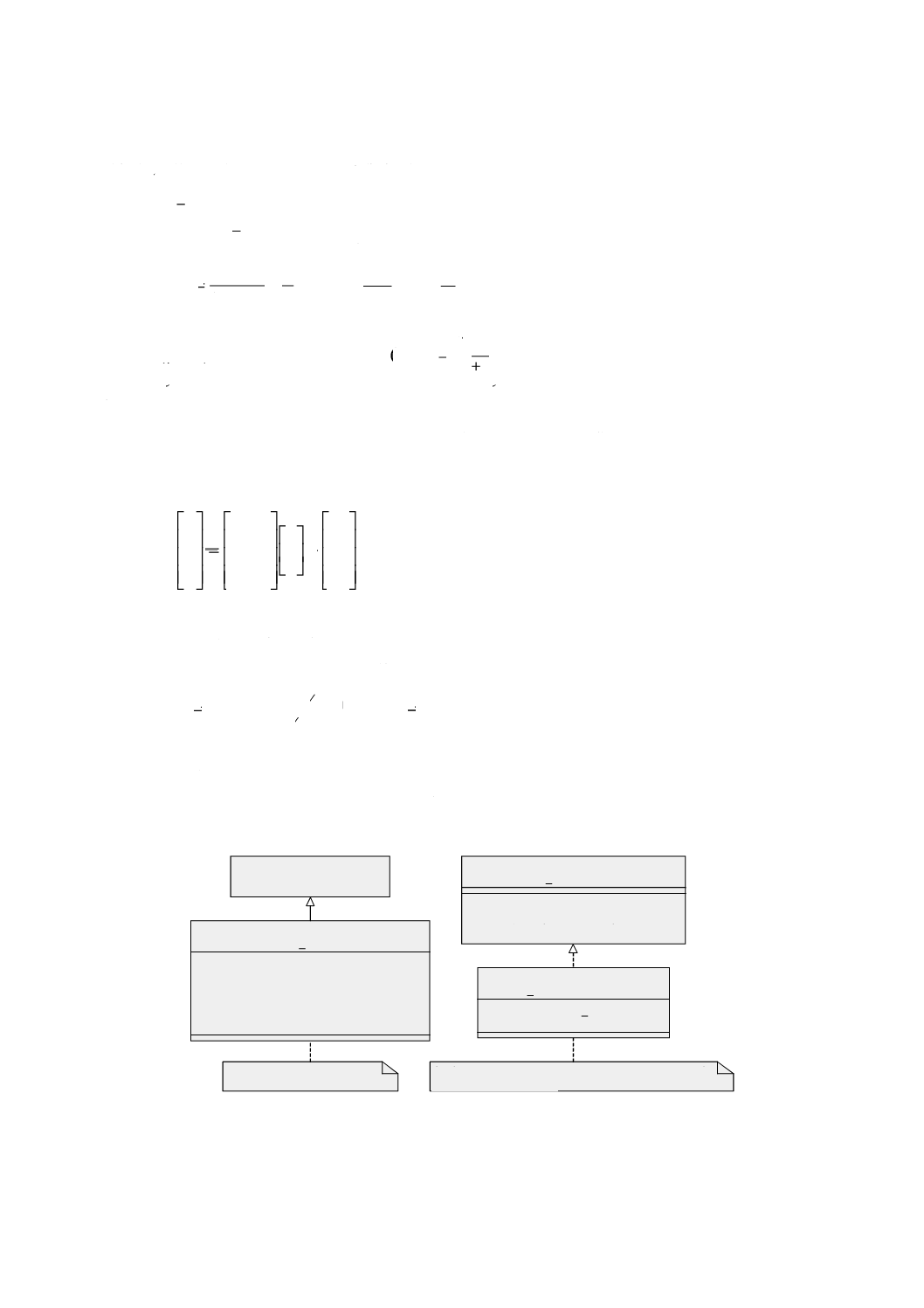
57
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
得られる弧の中点は,次のとおりとなる:
Midpoint = ((startPoint + endPoint)/2.0) + (bulge * normal)
6.4.19 GM̲Conic
6.4.19.1 意味 GM̲Conic(円すい曲線)型(図18参照)は,あらゆる一般的な円すい曲線を表現する。
すべての円すい切断曲線は,極座標 (ρ, ϕ) を使用して次のように標準的に表現される。
()
ϕ
ρ
cos
1e
P
+
=
for
2
2
π
ϕ
π
≤
≤
−
ここで“P”は半通径,“e”は離心率とする。この式は,極(原点)における焦点及びこの焦点に最も
近い極軸(ϕ = 0)の方向の(極座標表示で (
)(
)
(
)
0 ,
1
,
e
P+
=
ϕ
ρ
となる)頂点をもつ円すい曲線を定める。
この式でe = 0の場合は円,0 < e < 1の場合はだ(楕)円,e = 1の場合は放物線,e > 1の場合は双曲線の分
枝の一つとなる。
これらの一般的な円すい曲線は,通常の座標変換 u = ρ cos( ϕ ) 及び v = ρ sin( ϕ ) によって二次元直交
パラメタ空間 (u,v) に写像することができる。さらに,これを次式によって定義したアフィン変換 (u,v) →
(x,y,z) によって三次元座標参照系に変換することができる。
+
=
0
0
0
z
y
x
v
u
v
v
v
u
u
u
z
y
x
z
y
x
z
y
x
ここで,ϕ は,構造パラメタとして用いることができる。 (x0,y0,z0)で指定したDirectPositionは,局
所座標空間 (u,v) の原点の写像となる。
一方,原点を次の式によって円すい曲線の頂点に移してもよい。
(
)e
P
u
+
−
=
1
)
cos(
'
ϕ
ρ
及び
)
sin(
'
ϕ
ρ
=
v
これによって,vは構造パラメタとして使用することができる(GM̲GenericCurveの定義については
6.4.7.7による。)。
一般に,離心率及びPが共に小さい円すい曲線では,最初に示した“中心”表現を使用する。離心率又
はPが大きい円すい曲線では,二つ目に示した“線型”表現を用いる傾向がある。
«Abstruct»
GM̲CurveSegment
«Type»
GM̲Conic
+ position : GM̲AffinePlacement
+ shifted : Boolean
+ eccentricity : Real
+ semiLatusRectum : Real
+ startConstrParam : Real
+ endConstrParam : Real
«Interface»
GM̲Placement
+ inDimension() : Integer
+ outDimesion() : Integer
+ transform(in : Vector) : Vector
«Type»
GM̲AffinePlacement
+ location : GM̲Position
+ refDirection[1..n] : Vector
{interpolation = "conic"}
{refDirection->dimension = outDimension}
{refDirection.count = inDimension}
図 18 円すい曲線及び配置
58
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.19.2 position “position”(位置)属性は,パラメタ空間による円すい曲線を,GM̲Objectの座標参照
系に対応した円すい曲線の対象となる空間参照系の座標空間へ写像するアフィン変換オブジェクトとする。
このアフィン変換は,前の箇条の式で与えられる。
GM̲Conic::position : GM̲AffinePlacement
6.4.19.3 shifted “shifted”(平行移動)属性は,(u,v)を平行移動せずにアフィン変換を使用した場合に
FALSEとし,平行移動したパラメタ(u',v')にアフィン変換を使用した場合にはTRUEとする。これは,パ
ラメタ空間の原点にあるのが円すい曲線の焦点と頂点とのいずれかを制御する。
GM̲Conic::shifted : Boolean
6.4.19.4 eccentricity “eccentricity”(離心率)属性は,前記の定義式で使用する離心率パラメタ“e”の
値とする。これは,曲線の全体的な形状を制御し,曲線が円,だ(楕)円,放物線又は双曲線のいずれにな
るかを決定する。
GM̲Conic::eccentricity : Real
6.4.19.5 semiLatusRectum “semiLatusRectum”(半通径)属性は,前記の定義式で使用するパラメタ“P”
の値とする。これは,円すい曲線がその各焦点においてどの程度広がっているかを制御する。
GM̲Conic::semiLatusRectum : Real
6.4.19.6 startConstrParam,endConstrParam “startConstrParam”(始点構造パラメタ)属性及び
“endConstrParam”(終点構造パラメタ)属性は,6.4.19.1で定めた構造パラメタ化で使用される,startPoint
及びendPointにそれぞれ対応したパラメタを示す。
GM̲Conic::startConstrParam : Real
GM̲Conic::endConstrParam : Real
GM̲Conic:
constrParam(startConstrParam) = startPoint();
constrParam(endConstrParam) = endPoint();
前提としてstartConstrParamがendConstrParamよりも小さいとは限らないが,このパラメタ化は,狭義
単調(狭義単調増加又は狭義単調減少)でなければならない。
6.4.20 GM̲Placement
6.4.20.1 意味 配置(placement)は,ある標準的な幾何構造を取り出し,それを地理的空間に配置する。
これは,構造パラメタ空間から使用している座標参照系の座標空間への変換を定義する。この規格では,
式におけるパラメタ空間は二次元では(u,v),三次元では(u,v,w)として示す。この規格では,式におけ
る座標参照系の位置は,二次元では(x,y),三次元では(x,y,z)として示す。
6.4.20.2 inDimension “inDimension()”(入力次元取得)操作は,入力パラメタ空間の次元を返す。
GM̲Placement::inDimension() : Integer
6.4.20.3 outDimension “outDimension()”(出力次元取得)操作は,出力座標参照系の次元を返す。
GM̲Placement::outDimension() : Integer
備考 通常,outDimension(座標参照系の次元)は,inDimensionより大きい。そうでない場合,この
変換は,おそらく異常で,より小さい次元のパラメタ空間からの単純な変換で置き換えてよい。
6.4.20.4 transform “transform”(変換)操作は,パラメタ座標点を出力直交空間における座標点に写像
する。
GM̲Placement::transform(in :Vector {size = inDimension()}) : Vector {size = outDimension()}
59
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.21 GM̲AffinePlacement
6.4.21.1 意味 GM̲AffinePlacement(アフィン配置)は,パラメタ空間から対象の座標空間への線形変換
として定義する。二次元の直交パラメタ空間(u,v)を三次元座標参照系(x,y,z)に変換する場合,次に規
定するアフィン変換(u,v) → (x,y,z)を使用する。
+
=
0
0
0
z
y
x
v
u
v
v
v
u
u
u
z
y
x
z
y
x
z
y
x
この際,この式の定めるGM̲AffinePlacement::locationは,(u,v)における原点に対する像の位置となる
直接位置(x0,y0,z0)とする。二つの参照ベクトル(ux,uy,uz)及び(vx,vy,vz)は(u,v)の原点における単位基
底ベクトルに対する像の方向とする。
6.4.21.2 location “location”(所在)属性は,パラメタ空間原点に対する像を示す。これは6.4.21.1の式
におけるベクトル(x0,y0,z0)とする。
GM̲AffinePlacement::location : GM̲Position
6.4.21.3 refDirection “refDirection”(基準方向)属性は,パラメタ空間の座標基底ベクトルに対する像
の方向を与える。これらは,上記の式における行列の列とする。与えられる方向ベクトルの数は,
inDimensionと一致する。方向ベクトルの次元は,outDimensionと一致する。
GM̲AffinePlacement::refDirection [inDimension] : Vector {size = outDimension}
6.4.22 GM̲Clothoid
6.4.22.1 意味 GM̲Clothoid(クロソイド)(図19参照)は,曲率が長さに対する固定関数となる平面曲
線とするクロソイド(又はらせん)を実装する。座標系を適切に選択すると,クロソイドは次のようにフ
レネル積分で表現できる。
∫
=
t
d
A
t
x
0
2
)
2
cos(
)
(
τ
τ
及び
∫
=
t
d
A
t
y
0
2
)
2
sin(
)(
τ
τ
クロソイド曲線及び区間クロソイド曲線のより詳しい特性についての文献は,16)による。
この幾何は,主に直線・円弧又は円弧・円弧の型の曲線間の移行曲線として使用する。この曲線型によ
って前述の曲線型の間でのC2級連続移行を実現することができる。クロソイドの式の1例は,Aを定数,
Rを曲線に沿った可変曲率半径及びtを曲線に沿ったフレネル積分で得られる長さとして,A2 = R×tとす
る。
6.4.22.2 refLocation “refLocation”(基準所在)属性はフレネル積分によって定義した曲線をこのオブジ
ェクトの座標参照系に配置するアフィン写像とする。
GM̲Clothoid::refLocation : GM̲AffinePlacement
6.4.22.3 scaleFactor “scaleFactor”(縮尺率)属性は6.4.22.1の式のAの値を与える。
GM̲Clothoid::scaleFactor : Number
6.4.22.4 startParameter “startParameter”(開始パラメタ)属性は,この曲線分の始点となる変曲点から
の弧長距離とする。これはフレネル積分で使用する“t”の下限とし,この曲線分の始点における構造パラ
メタの値とする。“startParameter”は,正負のいずれにもなりうる。パラメタ“t”は,構造パラメタとし
て振る舞う(6.4.7.8参照)。
GM̲Clothoid::startParameter : Real
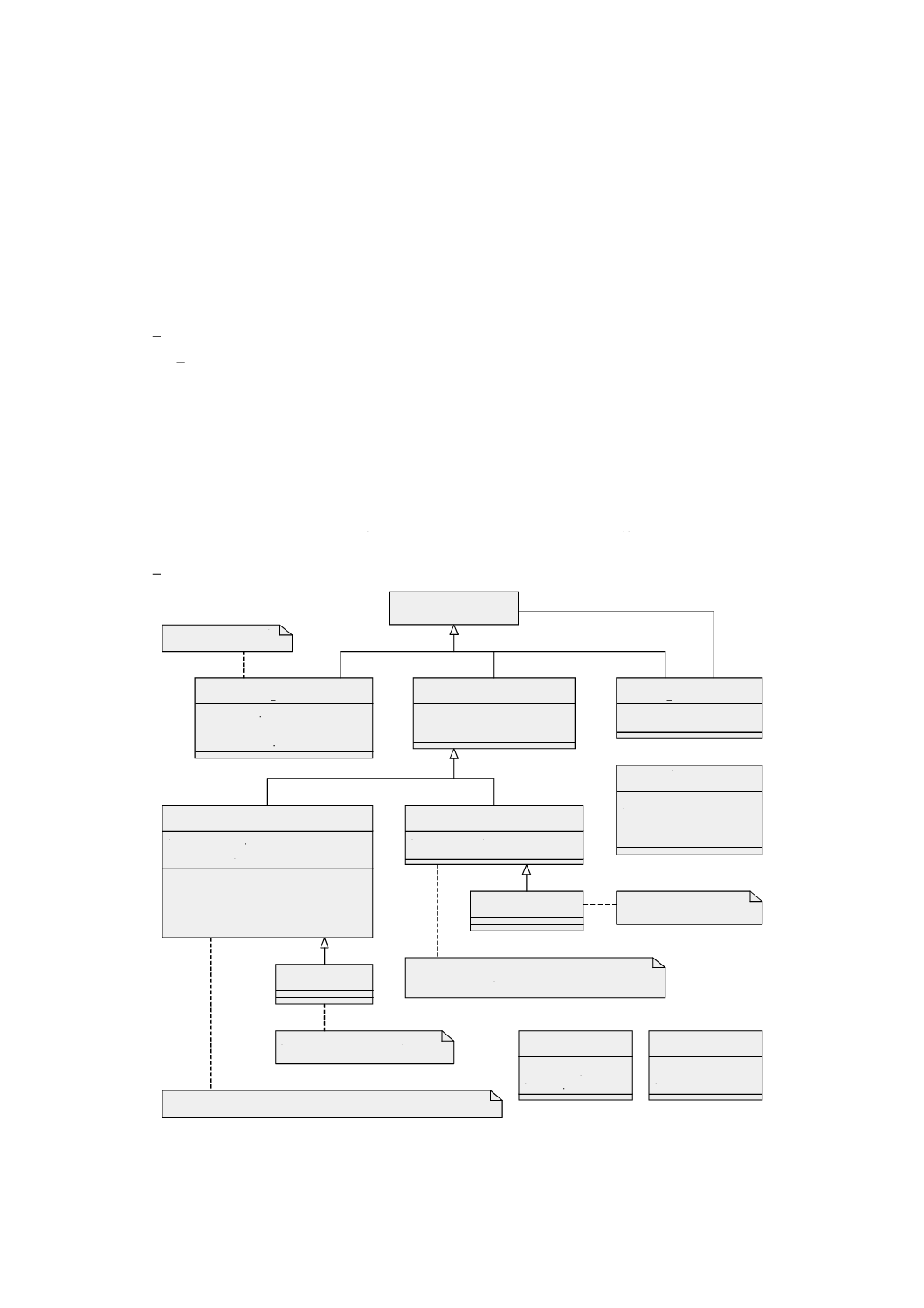
60
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 0.0(零)がstartConstrParamとendConstrParamとの間にある場合,この曲線はクロソイドの変
曲点を通り,二階微分ベクトルによって得られる曲率半径の方向は接線ベクトルに対する方向
を変える。パラメタ“t”に対する“長さ”という用語は,パラメタ空間でだけ有効であり,配
置後の弧長との関係及び曲線の座標参照系との関係は規定しない。
6.4.22.5 endParameter “endParameter”(終了パラメタ)属性は,この曲線分の終点となる変曲点からの
弧長距離である。これはフレネル積分で使用する“t”の上限であり,この曲線分の終点における構造パラ
メタである。“endConstrParam”は正負のいずれにもなりうる。
GM̲Clothoid:: endParameter : Real
6.4.23 GM̲OffsetCurve
6.4.23.1 意味 変位曲線(offset curve)は,基準曲線から一定の距離にある曲線とする。これは,定義か
ら変位した曲線を構築する簡易で単純な代替手段として用いる。
6.4.23.2 baseCurve “baseCurve”(基準曲線)属性は,この曲線が変位として定義されている曲線への参
照である。
GM̲OffsetCurve::baseCurve : Reference<GM̲Curve>
6.4.23.3 distance “distance”(距離)属性は,生成した変位曲線における基準曲線からの距離とする。二
次元座標系では正のdistanceは基準曲線の左側とし,負のdistanceは基準曲線の右側とする。
GM̲OffsetCurve::distance : Length
«DataType»
GM̲Knot
+ value : Real
+ multiplicity : Integer
+ weight : Real
«CodeList»
GM̲KnotType
+ uniform
+ quasiUniform
+ piecewiseBezier
«Abstruct»
GM̲CurveSegment
«Type»
GM̲SplineCurve
+ degree : Integer
+ knot : Sequence<GM̲Knot>
+ controlPoints : GM̲PointArray
«Type»
GM̲Clothoid
+ refLocation : GM̲AffinePlacement
+ scaleFactor : Number
+ startParameter : Real
+ endParameter : Real
«Type»
GM̲ OffsetCurve
+ distance : Length
+ refDirection[0..1] : Vector
«Type»
GM̲BSplineCurve
+ curveForm[0,1] : GM̲SplineCurveForm
+ knotSpec[0,1] : GM̲KnotType
+ isPolynomial : Boolean
+ GM̲BSplineCurve(
deg : Integer,
pts : GM̲PointArray,
k[0,1] : Sequence<GM̲Knot>,
ks[0,1] : GM̲KnotType
) : GM̲BSplineCurve
«Type»
GM̲PolynomialSpline
+ vectorAtStart : Sequence<Vector>
+ vectorAtEnd : Sequence<Vector>
«Type»
GM̲Bezier
«Type»
GM̲CubicSpline
+ baseCurve
1
1..n
«CodeList»
GM̲SplineCurveForm
+ polylineForm
+ circularArc
+ ellipticArc
+ parabolicArc
+ hyperbolicArc
{interpolation = clothoid}
{degree > 0}
{interpolation = "polynomialSpline"}
{vectorAtEnd. count = vectorAtStart. count = degree - 2 }
{degree = 3}
{interpolation = "cubicSpline"}
{(interpolation = "polynomialSpline") OR (interpolation = "rationalSpline)}
{degree = controlPoint.count - 1}
{interpolation = "polynomial"}
図 19 スプライン及び特殊曲線

61
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.23.4 refDirection “refDirection”(基準方向)属性は,基準曲線からの変位曲線のベクトル方向を定
義するのに使用する。これは,座標系が二次元でdistanceが正又は負の値をもちうる場合,省略できる。
この場合,distanceは,基準曲線の接線に対して左側(正のdistance)又は右側(負のdistance)を定義す
る。
三次元において,基準曲線はすべての点で明確に定義された接線方向をもつ。基準曲線“c”上の任意の
点(パラメタ)における変位曲線は,次の方向に存在する。
t
v
s
ρ
ρ
ρ
×
=
ただし
()
.
on
refDirecti
c
v=
ρ
かつ
()
.tangent
c
t=
ρ
変位方向を矛盾なく定めるためには,vρは,曲線上のすべての点でtρと同じ又は反対の方向であっては
ならない。
GM̲OffsetCurve::refDirection : Vector
refDirectionの規定値は,地理的意味で曲線の上方を示す高さに対する局所座標軸ベクトルとする。
備考 refDirectionが局所高度軸(“上方指示”)の正の接線の場合,変位ベクトルは上方から曲線の左
方を指す。
6.4.24 GM̲Knot
6.4.24.1 意味 GM̲Knot(ノットデータ)は,スプライン曲線及びスプライン曲面のための構造パラメタ
空間を制御するのに使用する。各ノット列は,スプラインのパラメタ空間の一つの次元に対して使用され
る。このため,曲面スプラインでは,パラメタ (u,v) のそれぞれの値となる二つのノット列が存在する。
片方をi番目,もう一方をj番目のパラメタは,元のノット列からのパラメタをそれぞれ (ui) 及び (vj) と
表すと (ui,vj) となる。スプライン曲線及びスプライン曲面の各ノットは,GM̲Knotを使用して記述する。
6.4.24.2 value “value”(値)属性は,スプラインのノットにおけるパラメタの値とする。ノットの列は
非減少列とする。すなわち,列における各ノットの値は,直前のノットの値と等しいかより大きくなけれ
ばならない。等しいノットを連続して用いる場合,通常は,多重度を用いて処理する。
GM̲Knot::value : Real
6.4.24.3 multiplicity “multiplicity”(多重度)属性は,スプラインの定義に使用する(重みが等しい)ノ
ットの多重度とする。
GM̲Knot::multiplicity : Integer
6.4.24.4 weight “weight”(重み)属性は,スプラインのこのノットに使用する平均の重みの値とする。
GM̲Knot::weight : Real
6.4.25 GM̲NotType Bスプラインが一様であるとは,すべてのノットの多重度が1で,先行するノット
と正定数だけが異なる場合をいう。Bスプラインが疑似一様であるとは,すべてのノットが,両端では多
重度が(degree + 1)かつ他の場所では多重度が1で,先行するノットと正定数だけが異なる場合をいう。こ
のGM̲NotType(ノット)符号リストは,様々なスプラインのパラメタ空間におけるノットの分布を記述
するのに使用する。これは,次の値をとってよい。
− uniform :ノットの形状が一様Bスプラインを満たす。
− quasiUniform :ノットの形状が擬似一様Bスプラインを満たす。
− piecewiseBezier :ノットの形状が区間ベジェ曲線を満たす。
GM̲KnotType::
uniform
62
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
quasiUniform
piecewiseBezier
6.4.26 GM̲SplineCurve
6.4.26.1 意味 GM̲SplineCurve(スプライン曲線)(図19)は,多項式又は有理式のいずれかの形式のス
プラインを使用するGM̲CurveSegmentの下位型に対する基底型として振る舞う。
6.4.26.2 knot “knot” (ノット)属性は,スプライン基底関数を定義するのに使用する異なるノットの
列とする。ノットデータ型がノットの多重度に関する情報を保持することに注意する。
GM̲SplineCurve::knot : Sequence<GM̲Knot>
6.4.26.3 degree “degree”(次数)属性は,このGM̲PolynomialSplineの内挿に使用する多項式の次数と
する。
GM̲SplineCurve::degree : Integer
6.4.26.4 controlPoints “controlPoints”(制御点)属性はこのGM̲SplineCurveの内挿に使用する点の配列
とする。
GM̲SplineCurve::controlPoints : GM̲PointArray
6.4.27 GM̲PolynomialSpline
6.4.27.1 意味 n次多項式スプライン(polynominal spline)は,定義多項式が切り替わる制御点において
Cn-1級連続性を保持するような,n次多項式をつなげたものとして定義する。この連続性の水準は
“numDerivativesInterior”属性によって制御する。パラメタは,その曲線分の始点及び終点に,多項式の
(degree - 2)次までの導関数と同じだけの方向を含む。GM̲LineStringは,一次多項式スプラインと等し
い。これはそのcontrolPointに単純な連続性(C0級)をもつが,導関数の情報は必要としない(degree - 2 =
-1)。
備考 多項式スプラインとBスプライン(基底スプライン)との主な相違点は,多項式スプラインは,
自身の制御点を通過し,制御点と標本点配列とが一致することである。
6.4.27.2 interpolation GM̲PolynomialSplineの内挿法は,“polynomialSpline”とする。
GM̲PolynomialSpline::
interpolation : GM̲InterpolationMethod = “polynomialSpline”
6.4.27.3 vectorAtStart “vectorAtStart”(始点ベクトル)属性は,このGM̲PolynomialSplineにおいて内
挿に使用する最初の(degree - 2)次までの導関数に使用するスプラインの始点での値とする。
GM̲PolynomialSpline::vectorAtStart : Sequence<Vector> {size = degree - 2}
6.4.27.4 vectorAtEnd “vectorAtEnd”(終点ベクトル)属性は,このGM̲PolynomialSplineにおいて内挿
に使用する最後の(degree - 2)次までの導関数に使用するスプラインの終点での値とする。
GM̲PolynomialSpline::vectorAtEnd :Sequence<Vector> {size = degree - 2}
6.4.28 GM̲CubicSpline 三次スプライン(cubic spline)は,折れ線と同様に曲線分の列であるが,各々
の曲線分は,その定義関数を伴う。三次スプラインは,三次多項式による区間内挿を定義する制御点及び
導関数パラメタの集合を用いる。折れ線とは異なり,弧長によってパラメタ化したものも多項式である必
要はない。スプラインには,この規格で使用する二つのパラメタ化は,定義式による表現(構造パラメタ)
及びGM̲GenericCurveの要件を満たす弧長による再パラメタ化表現とする。
曲線を記述する関数はC2級,すなわち,すべての点で一次及び二次導関数をもち,定められた順に
controlPointを通過しなければならない。制御点間の曲線分は,三次多項式によって定義する。多項式は,
制御点において一次及び二次導関数ベクトルがいずれの側からも同一となるように切り替わる。制御パラ
63
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
メタレコードは,vectorAtStart及びvectorAtEndを含まなければならない。それらは, n = controlPoint.count
とするとそれぞれ controlPoint[1]及びcontrolPoint[n] における単位接ベクトルとなる。
“vectorAtStart”及び“vectorAtEnd”は,その列がそれぞれ単一の接ベクトルとなるよう制約される。
GM̲CubicSpline::vectorAtStart : Vector
// “degree ‒ 2” は 1
GM̲CubicSpline::vectorAtEnd : Vector
// “degree ‒ 2” は 1
備考 三次多項式の実際の実装は様々だが,このように生成した曲線の一意性が保証される。実装例
に関しては,2),10),12),18)及び19)による。
GM̲CubiclSplineの内挿法は“cubicSpline”とする。
GM̲CubicSpline::interpolation : GM̲InterpolationMethod = “cubicSpline”
GM̲CubiclSplineの次数は,“3”とする。
GM̲CubicSpline::degree : Integer = “3”
6.4.29 GM̲SplineCurveForm このGM̲SplineCurveForm(スプライン曲線形式)符号リストは,特定の
Bスプラインにより近似してよい曲線を示すために使用する。これは,次の値をとってよい。
− polylineForm :一次Bスプライン(折れ線)によって表される線分の連結した列。
− circularArc :円弧又は円。
− ellipticArc :だ(楕)円弧又はだ(楕)円。
− parabolicArc :放物線の有界な弧。
− hyperbolicArc :双曲線の一方の枝の有界な弧
GM̲SplineCurveForm::
polylineForm
circularArc
ellipticalArc
parabolicArc
hyperbolicArc
6.4.30 GM̲BSplineCurve
6.4.30.1 意味 Bスプライン(図19参照)は制御点及び基底関数によって記述された区間パラメタ多項
式曲線又は区間パラメタ有理曲線である。ノットにおける重みが等しい場合には,多項式スプラインとな
る。そうでない場合には,有理関数スプラインとなる。“isPolynomial”真偽値が真の場合,重みはすべて
1とする。Bスプライン曲線が区間ベジェ曲線であるとは,内部ノットが多重度1ではなく“degree”をも
ち,それ以外の疑似一様の要件を満たすことをいう。この下位型では,ノットは 0.0 で始まり,その間隔
は 1.0 となる。個々の多重度が (degree + 1)となる 0.0 及び 1.0 の二つのノットだけをもつ区間ベジェ
曲線は,単純ベジェ曲線に等しい。
6.4.30.2 degree “degree”(次数)属性は,基底関数の代数的次数とする。
GM̲BSplineCurve::degree : Integer
6.4.30.3 curveForm “curveForm”(曲線形式)属性は,このスプラインを使用して近似しようとする本
来の曲線がいずれの型かを識別するために使用する。これは,参考情報であり,本来の意図をとらえるた
めに使用される。このような近似を意図していない場合,この属性の値は,NULLとする。
GM̲BSplineCurve::curveForm : GM̲SplineCurveForm
6.4.30.4 knotSpec “knotSpec”(ノット仕様)属性は,このスプラインの定義に使用するノット分布の型
を定める。これは,参考情報とし,構成関数の違いに応じて設定される。
64
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
GM̲BSplineCurve::knotSpec[0,1] : GM̲KnotType
6.4.30.5 isPolynomial “isPolynomial”(多項式判定)属性は,多項式スプラインの場合“True”とする。
GM̲BSplineCurve::isPolynomial : Boolean
6.4.30.6 GM̲BSplineCurve(コンストラクタ) “GM̲BSplineCurve”クラスのコンストラクタは,6.4.30.2
〜6.4.30.5の属性値に対応する情報を得て,Bスプライン曲線を構築する。knotSpecが存在しない場合,
knotTypeはuniformとし,ノットは均等に配置され,最初と最後とを除き,多重度は1とする。両端にお
いてノットは,multiplicity = degree + 1とする。knotTypeがuniformの場合,それらを指定する必要はない。
GM̲BSplineCurve::GM̲BSplineCurve(deg : Integer, pts : GM̲PointArray, k [0,1] :
Sequence<GM̲Knot>, ks [0,1] : GM̲KnotType) : GM̲BSplineCurve
備考 Bスプライン曲線がuniformで次数が1の場合,Bスプラインは,折れ線(GM̲LineString)に等
しい。knotTypeが“piecewiseBezier”の場合,ノットは既定値として均等に配置し,最初と最
後とを除き,次数に等しい多重度をもつ。両端においてノットの多重度は,次数に1を加えた
ものとなる。
6.4.31 GM̲Bezier GM̲Bezier(ベジェ)は,内挿のためにベジェ多項式又はバーンスタイン多項式を使
用する多項式スプラインとする。長さnの制御点配列は,曲線分全体を定義するn次多項式曲線を生成す
る。これらの曲線は,次のベジェ多項式又はバーンスタイン多項式と呼ぶ一連の基底関数に基づき定義す
る。
(
)
i
n
i
i
n
t
t
i
n
t
J
−
−
=
1
)
(
,
ただし i = 0, 1, 2 … n で
(
)!
!
!
i
n
i
n
i
n
−
=
“n + 1”の制御点P0, P1...Pnの集合は,次の式によって曲線分を決定する:
∑
=
=
n
i
i
n
i
t
J
P
t
c
0
,
)
(
)
(ρ
ただし t ∈ [0,1].
この曲線分の標本点は,各多項式 (i/n) の最大値で定義される曲線の値とする:
=
n
i
c
Si
ρ
ただし i = 0, 1, 2 … n
備考 n = 1の場合,次の二つの重み関数となる:
(
)
)
1(
1
0
1
)(
1
0
0,1
t
t
t
t
J
−
=
−
=
及び
(
)
t
t
t
t
J
=
−
=
−1
1
1
1,1
1
1
1
)(
P0及びP1によって,曲線分は,次のようになる:
1
0
)
1(
)
(
tP
P
t
t
c
+
−
=
ρ
ただし, t ∈ [0,1].
言い換えると,n = 1の場合,ベジェ多項式は,単純な線分と幾何的に等しい。
6.4.32 GM̲SurfaceInterpolation GM̲SurfaceInterpolation(曲面内挿法符号リスト)(図20)は,応用ス
キーマが指定する内挿法を識別するのに使用してよい符号リストとする。“interpolation”の有効な値は,
次を含むが,これらに制限されるわけではない。
a) なし(none) この曲面の内部は,指定されない。この曲面は,座標参照系の定義する基準面に従う
ものと仮定する。
b) 平面(planar) この内挿法は,単一の平面上の点を返す。この場合の境界は,この平面上に含まれ
65
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
c) 球面(spherical),だ(楕)円体面(elliptical)及び円すい面(conic) この曲面は,球面,だ(楕)円体
面又は円すい面の一部とする。
d) 不規則三角網(tin) 制御点は,隣接する複数の三角形を構成し,それぞれが小平面分を形成する。
e) パラメタ曲線(parametricCurve) 制御点は,二次元格子を構成し,格子の各ますは曲線の族で定義
される曲面で補間される。
f)
多項式スプライン(polynomialSpline) 制御点は,不規則な二次元格子を構成し,格子の各ますは多
項式スプライン関数で補間される。
g) 有理スプライン(rationalSpline) 制御点は,不規則な二次元格子を構成し,格子の各ますは有理(多
項式商)スプライン関数で補間される。
h) 三角形スプライン(triangulatedSpline) 制御点は,隣接した複数の三角形を構成し,それぞれが多
項式スプライン関数で補間される。
使用されている内挿法に複数の表現が適合する場合,最も制限の厳しいものを使用する。
GM̲SurfaceInterpolation::
none
planar
spherical
elliptical
conic
tin
parametricCurve
polynomial
polynomialSpline
rationalSpline
triangualtedSpline
6.4.33 GM̲GenericSurface
6.4.33.1 意味 GM̲Surface及びGM̲SurfacePatchは,いずれも区切った幾何曲面を表し,そのため幾つか
の操作を共有する。これらは,GM̲GenericSurface(一般曲面)インタフェース(図20参照)で定義する。
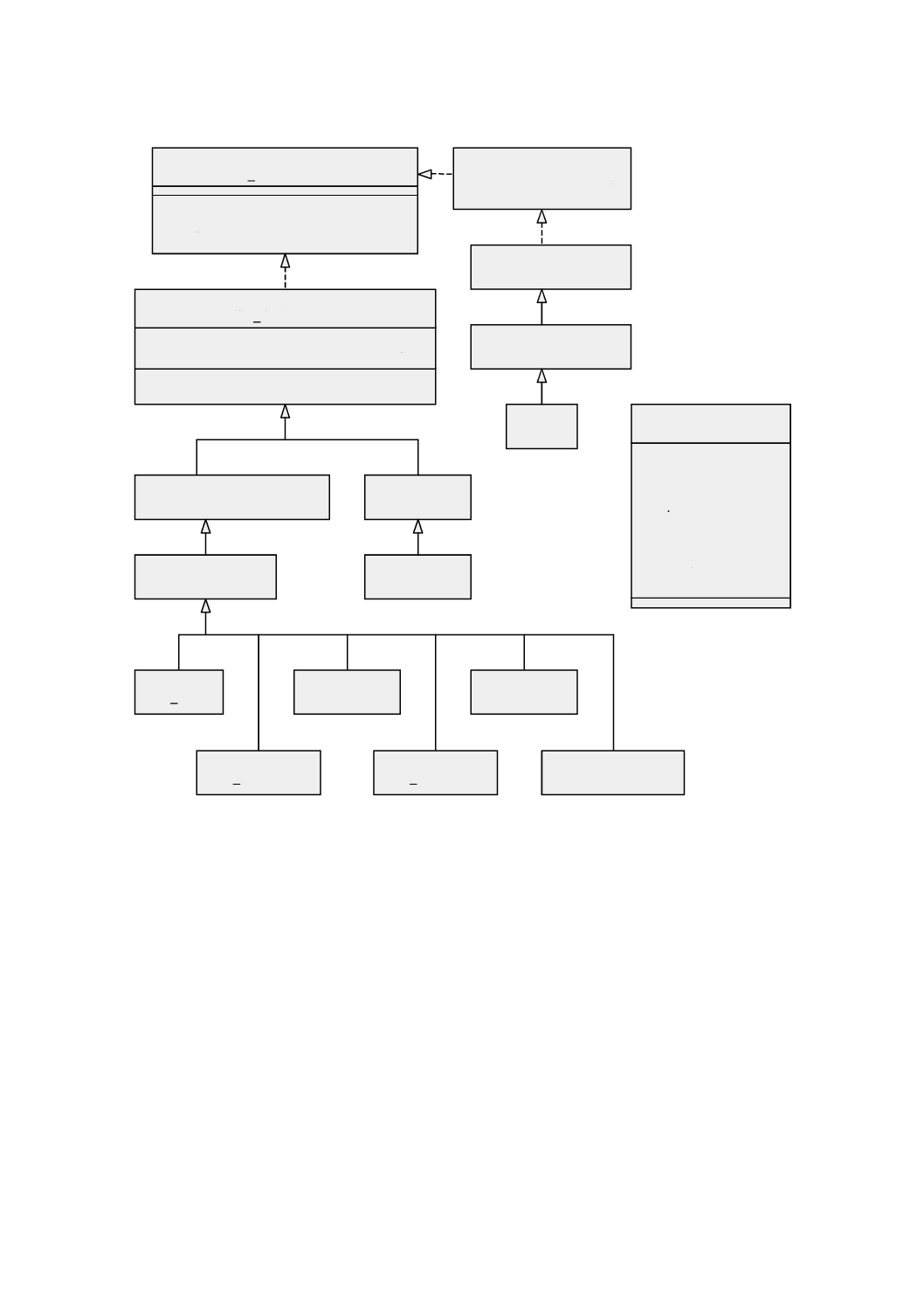
66
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Interface»
GM̲GenericSurface
+ upNormal(point : DirectPosition) : Vector
+ perimeter() : Length
+ area() : Area
«Abstract»
GM̲SurfacePatch
+ interpolation : GM̲SurfaceInterpolation = "planar"
+ numDerivativesOnBoundary[0, 1] : Integer = 0
+ boundary() : GM̲SurfaceBoundary
«Type»
GM̲ParametricCurveSurface
«Type»
GM̲Polygon
«Type»
GM̲Triangle
«Type»
GM̲GriddedSurface
«Type»
GM̲Cone
«Type»
GM̲BicubicGrid
«Type»
GM̲Cylinder
«Type»
GM̲BilinearGrid
«Type»
GM̲Sphere
«Type»
GM̲BSplineSurface
«Type»
GM̲Surface
(from Geometric primitive)
«Type»
GM̲PolyhedralSurface
«Type»
GM̲TriangulatedSurface
«Type»
GM̲Tin
«CodeList»
GM̲SurfaceInterpolation
+ none
+ planar
+ spherical
+ elliptical
+ conic
+ tin
+ parametricCurve
+ polynomialSpline
+ rationalSpline
+ triangulatedSpline
図 20 曲面分(Surface patches)
6.4.33.2 upNormal “upNormal”(上方法線取得)操作は,GM̲GenericSurface上にあるDirectPositionを
とり,その点においてGM̲GenericSurfaceと直交するベクトルを返す。
GM̲GenericSurface::upNormal(point : DirectPosition) : Vector
上向きの法線は,常に境界と矛盾しない方法で上を指す。これは,曲面のupNormalが示す側から見た
場合に曲面の外側境界が反時計周りであることを意味する。内部境界は時計回りとする。曲面のupNormal
が示す側は“top”として参照する。“upNormal”操作は連続で,法線の長さは常に1.0となる。
備考 立体の境界に沿ったupNormalは,常に立体から離れる方向を指す。これには,立体内の空白
を扱う上で意味論的な小さな問題があり,upNormalは(数学的一貫性のため)言語的には空白
の内部となる空白領域の中心を指すことになる。ここでの混乱は, “立体の内部”及び“コン
テナの内部”の表現でほとんどの言語が使用する基本的な言語上の比喩が,位相の視点とは矛
盾して“内部”という語を用いることである。岩石の“内部”の空洞は,岩石の実体を構成す
る固体素材と同じように岩石の中にあるわけではない。また,カップの“内部”のコーヒーは,
67
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
カップの“内部”の陶磁ガラス質と同じように内部にあるわけではない。文化に由来するこの
ような比ゆ(喩)の使用は,すべての言語に渡って一貫してはいないであろうし,そのうち幾
つかはこれらの二つの異なる概念に異なった表現を使用するかもしれない。この規格では(位
相)数学に由来し言語上中立な概念である“内部”を使用する。
6.4.33.3 perimeter “perimeter”(周囲長取得)操作は,このGM̲GenericSurfaceのすべての境界要素の長
さの合計を返す。perimeterはlengthと同様に距離の累積(積分)であるため,その戻り値は距離の測定に
適した参照系のものとする。
GM̲GenericSurface::perimeter() : Length
備考 perimeter は,すべての境界要素の長さの合計として定義する。曲線又は曲線の集まりの長さは
常に正であり,異常な曲線を除いて零とはならない。これは曲面の穴も総周囲長を増すように
加えることを意味する。
6.4.33.4 area 二次元幾何オブジェクトの面積は,その曲面面積の(距離の平方単位の)数値計測結果と
する。面積は二つの距離の積の累積(積分)であるため,その戻り値は,平方メートル(m2)のような平
方距離の測定に適切した計測単位によらなければならない。“area”(面積取得)操作は,この
GM̲GenericSurfaceの面積を返す。
GM̲GenericSurface::area() : Area
戻り値には,座標参照系と曲面の形状との両方を考慮しなければならない。
備考 曲面の定義はDirectPositionの集合と一致し,曲面の穴は総面積には影響しない。通常のグリー
ンの定理(又はより一般的なストークスの定理)による積分を使用する場合,曲面の穴の周囲
の積分は,曲面分の外側に対する積分から差し引かれている。
6.4.34 GM̲SurfacePatch
6.4.34.1 意味 GM̲SurfacePatch(曲面分)(図20参照)はGM̲Surfaceの共通の性質をもった部分を定義
する。“Segmentation”関連の多重度(図12参照)はそれぞれのGM̲SurfacePatchは最大でも一つの
GM̲Surfaceにだけ含まれることを規定している。
6.4.34.2 interpolation “interpolation”(内挿法)属性はこのGM̲SurfacePatchに使用する曲面内挿法を決
定する。この方法は,このGM̲SurfacePatchの位置を決定するために様々な下位クラスで定義される制御
点と制御パラメタを使用する。
GM̲SurfacePatch::Interpolation : GM̲SurfaceInterpolation
6.4.34.3 numDerivativesOnBoundary “numDerivativesOnBoundary”(境界連続性)属性列は,境界曲線
を共有する隣接曲面分とこの曲面分との間の連続性の型を規定する。この値の列は,曲面分の
GM̲GenericCurve::boundaryが返すGM̲SurfaceBoundaryのGM̲Ringに対応する。既定値の“0”は,必す
(須)な最小限の水準の連続性である単純な連続性を意味する。この水準は,数学の表現では“C0級”と
呼ばれる。“1”の値は,適切な端点で連続で微分可能な関数を意味する“C1級”連続を表す。任意の整数
“n”の値はn回微分可能を意味する“Cn級”連続を表す。
GM̲SurfacePatch::numDerivativesOnBoundary[0..n] : Integer
6.4.34.4 boundary “boundary”(境界取得)操作は,GM̲SurfaceBoundaryとしてのGM̲Ringを構成する
GM̲OrientableCurveで表現したこのGM̲SurfacePatchの境界を返す。
GM̲SurfacePatch::boundary() : GM̲SurfaceBoundary
備考 この操作の意味は,ここで使用する曲線が必ずしも永続的に存在するGM̲OrientableCurveのイ
ンスタンスではないことを除いて,GM̲Surface::boundaryと同じものである。このGM̲Curve
68
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
のデータ型の値は,一時的に存在するものも有効とする。通常の場合,GM̲SurfacePatchはそ
の集成(aggregate)であるGM̲Surfaceと境界の一部を共有し,それ以外の部分の境界は,(必ず
しも異ならない。)GM̲SurfacePatchと共有する。附属書Cでは,立体の例(C.1.3.1参照)は,
それ自身が折りたたまれて位相柱を形成している単独の曲面分を,立体境界を形成する二つの
正方形端片とともに使用している。この場合,最初の曲面分は,両端の蓋のそれぞれと一つの
境界曲線分を共有し,他の境界曲線分を自分自身と共有する。
6.4.35 GM̲PolyhedralSurface
6.4.35.1 意味 GM̲PolyhedralSurface(多面体面)(図21参照)は,共通な境界曲線に沿って結合したポ
リゴン曲面(GM̲Polygon)で構成されるGM̲Surfaceとする。これは,もちうる曲面分の型を制約する点
だけがGM̲Surfaceと異なる。
6.4.35.2 GM̲PolyhedralSurface(コンストラクタ) “GM̲PolyhedralSurface”のコンストラクタは,面
となるGM̲Polygonをとり,必要な集成を生成する。
GM̲PolyhedralSurface::GM̲PolyhedralSurace(tiles[1..n]: GM̲Polygon ) : GM̲PolyhedralSurface
6.4.35.3 patch “patch”(曲面分)関連役割は,この曲面とその個々の面とからなるポリゴンとを関連さ
せる。それは,空であってはならない。
GM̲PolyhedralSurface::patch[0..n] : Reference<GM̲Polygon>
GM̲PolyhedralSurface::patch[0,n] : Reference<GM̲Polygon>
6.4.36 GM̲Polygon
6.4.36.1 意味 GM̲Polygon(ポリゴン)(図21参照)は,境界曲線の集合で定義された曲面分で,それ
らの曲線に接する基本的な曲面とする。特に定めない場合,曲線は同一平面上にあり,ポリゴンはその内
部に平面内挿法を使用するものとする。
6.4.36.2 boundary “boundary”(境界)属性は,このGM̲Polygonの境界となるGM̲SurfaceBoundaryを
保持する。
GM̲Polygon::boundary : GM̲SurfaceBoundary
備考 曲面分の境界は,それを含んでいるGM̲Surfaceと同じGM̲Complexである必要はない。
GM̲Surfaceの内部に含まれる(二つの曲面分の共通境界として振る舞う。)曲線は,GM̲Surface
を含むいずれのGM̲Complexの一部でもない。それらは,純粋にデータの構成によるものであ
り,GM̲Complexの接続性を定義するGM̲CurveとGM̲Surfaceとの間のどのような位相関係
も表すものではない。
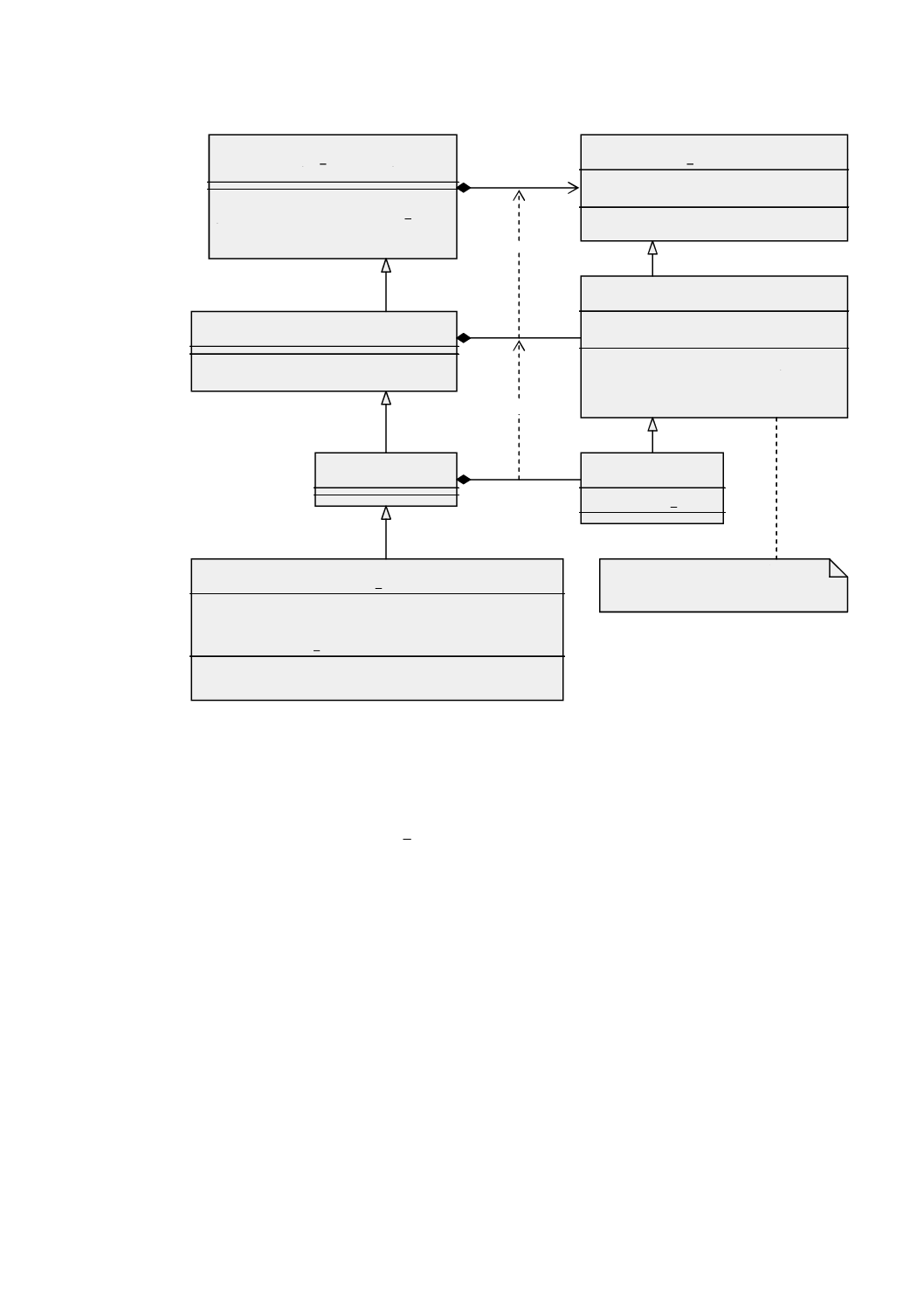
69
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲Surface
(from Geometric primitive)
+ GM̲Surface(patch[1..n] : GM̲SurfacePatch)
: GM̲Surface
+ GM̲Surface(bdy : GM̲SurfaceBoundary)
: GM̲Surface
«Abstract»
GM̲SurfacePatch
+ interpolation : GM̲ SurfaceInterpolation = "planar"
+ numDerivativesOnBoundary[0, 1] : Integer = 0
+ boundary() : GM̲SurfaceBoundary
«Type»
GM̲PolyhedralSurface
+ GM̲PolyhedralSurface(tiles[1..n] : GM̲Polygon)
: GM̲PolyhedralSurface
«Type»
GM̲Polygon
+ boundary : GM̲SurfaceBoundary
+ spanningSurface[0, 1] : GM̲Surface
+ GM̲Polygon(boundary : GM̲SurfaceBondary)
: GM̲Polygon
+ GM̲Polygon(boundary : GM̲SurfaceBondary,
spanSurf : GM̲Surface) : GM̲Polygon
«Type»
GM̲TriangulatedSurface
«Type»
GM̲Triangle
+ corners[3] : GM̲Position
«Type»
GM̲Tin
+ stopLines : Set<GM̲LineString>
+ breakLines : Set<GM̲LineString>
+ maxLength : Distance
+ controlPoint[3..n] : GM̲Position
+ GM̲Tin(post : Set<GM̲Position>, stopLines : Set<GM̲LineString>,
breakLines : Set<GM̲LineString>, maxLength : Number) : GM̲Tin
-- 補間曲面は,曲線を含まなければならない
{spanningSurface.NotEmpty implies
spanningSurface.contains(boundary)}
subset
subset
0..1
+ surface
0..1
+ surface
0..1
+ surface
1..n
+ patch
1..n
+ patch
1..n
+ patch
Segmentation
図 21 ポリゴン曲面(Polygonal surface)
6.4.36.3 spanningSurface 任意で設定される補間曲面(spanning surface)は,ポリゴンの内部を補間する
方法を提供する。
GM̲Polygon::spanningSurface[0,1] : GM̲Surface
備考 補間曲面はポリゴン境界と交わる境界要素をもたず,曲面の一部分のポリゴンの境界曲線によ
って明確に指定すべきである。最も一般的な補間曲面は,標高モデルである。これは,この規
格で直接表現できないが,その役割にしばしば不規則三角網又は格子曲面を用いる。
6.4.36.4 GM̲Polygon(コンストラクタ) GM̲Polygonの最初の形式のコンストラクタは,同一平面上の
GM̲PositionをcontrolPointとして使用して定義した(GM̲SurfaceBoundaryで構成される)境界曲線の集合
から直接GM̲Polygonを生成する。
GM̲Polygon::GM̲Polygon(boundary : GM̲SurfaceBondary) : GM̲Polygon
備考 GM̲SurfaceBoundaryの外側の意味は,生成した平面ポリゴンの平面での外側と一致する。
GM̲Polygonの第2の形式のコンストラクタは,補間曲面上のGM̲Polygonを生成する。
GM̲SurfaceBoundaryで使用している合成曲線が使用する内挿法の型については制約しないが,正しく処理
するためには,それらすべてが“spanningSurface”上になければならない。
GM̲Polygon(boundary : GM̲SurfaceBondary, spanSurf : GM̲Surface) : GM̲Polygon
備考 この作業では境界要素が適切に方向付けられていることが重要となる。球のような有界多様体
70
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
では,しばしば,向きが適切に用いられないことによって,あいまいさの原因となる。
6.4.37 GM̲TriangulatedSurface GM̲TriangulatedSurface(三角網曲面)(図21参照)は,複数の三角形
(GM̲Triangle)だけから構成したGM̲PolyhedralSurfaceとする。その三角形網の生成方法は制約されない。
6.4.38 GM̲Triangle GM̲Triangle(三角形)は三つの頂点で定義した平面上のGM̲Polygonとする。こ
のため,GM̲Triangleは次の形式のコンストラクタの結果として得られる。
GM̲Polygon(GM̲LineString(<P1,P2,P3,P1>))
ここで,P1,P2及びP3 は三つのGM̲Positionとする。GM̲Triangleには穴はない。GM̲Triangleは
GM̲TriangulatedSurfaceを構成するために用いる。
備考 三角形の点はc1 + c2 + c3 = 1.0となる三つの負でない数字c1,c2及びc3からなる重心座標の集合
を定義することによって,その頂点の式で位置付けることができる。このとき,三角形の各点
Pはある重心座標の集合で示すことができる。
3
3
2
2
1
1
P
c
P
c
P
c
P
+
+
=
6.4.39 GM̲Tin
6.4.39.1 意味 GM̲Tin(不規則三角網)(図21参照)はドローネ・アルゴリズム又はこれに抑止線,傾
斜変換線及び三角形の最大辺長に対する考慮を補った同様のアルゴリズム(図22参照)を使用した
GM̲TriangulatedSurfaceとする。これらの網はこの修正にもかかわらず,網の各三角形に対してその頂点を
通過する円はその内部に他の三角形の頂点を含まないという,ドローネの基準を満たす。
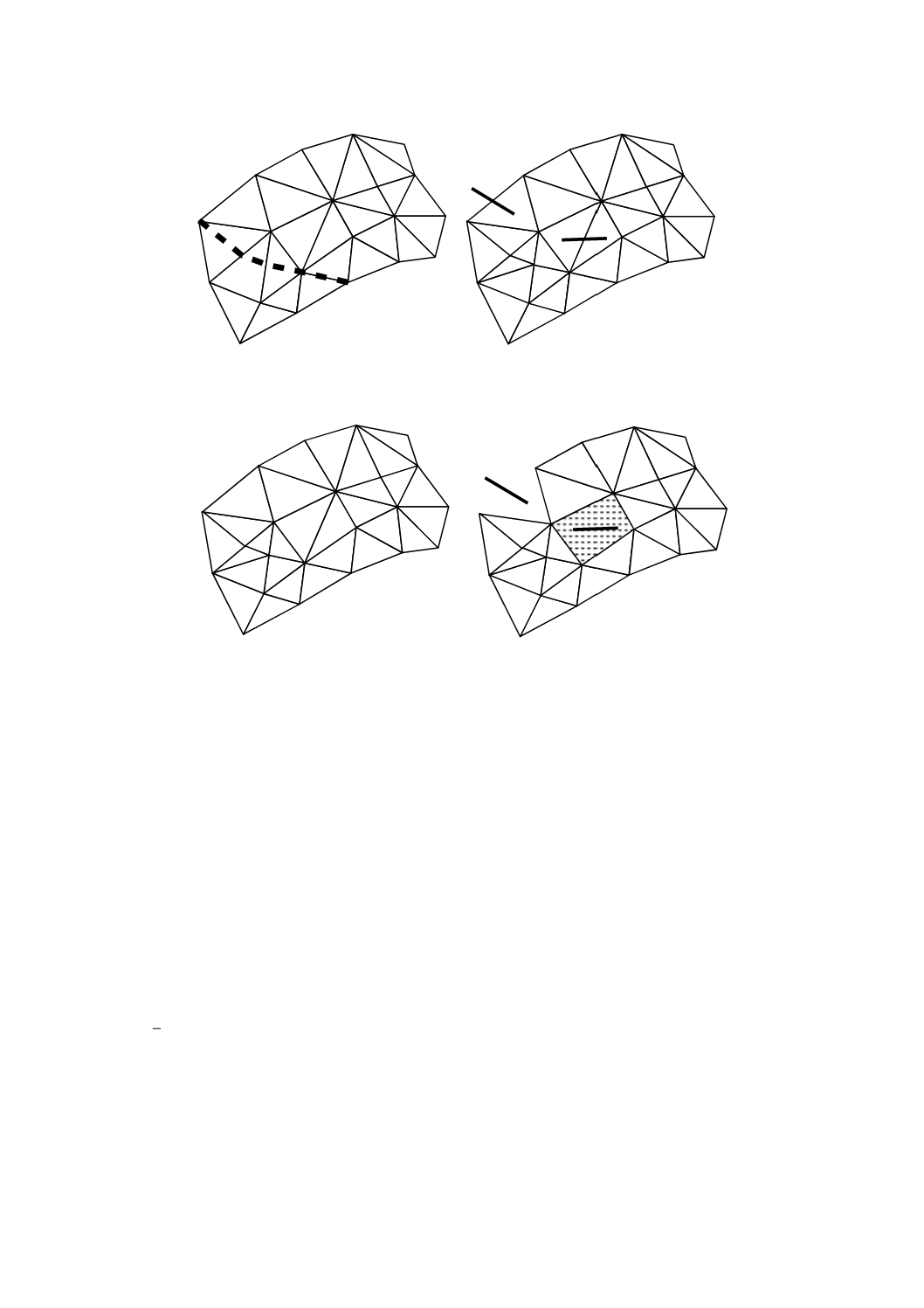
71
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
傾斜分割線を用いない
最初の(ドローネ)三角形分割
傾斜分割線を用いた
再三角形分割
追加の抑止線
穴及び境界変更を引き起こす
抑止線を用いた再三角形分割
図 22 不規則三角網の生成 (TIN construction)
6.4.39.2 stopLines stopline(抑止線)は,曲面の連続性又は正則性に局所的に問題がある部分の線であ
る。これらの異常な領域では抑止線と交わる三角形は不規則三角網曲面から取り除き,曲面の穴として残
すものとする。交差が曲面の境界三角形上で発生した場合,結果として曲面の境界は変化する。“stopLines”
(抑止線)属性はすべての異常な曲線分を線分の集合として含む。
GM̲Tin::stopLines : Set<GM̲LineString>
6.4.39.3 breakLines breakline(傾斜変換線)は,曲面の局所的な稜線又は(流水線のような)谷線を表
す,曲面の形の決定的な本質の線とする。Delaunayの基準を満たさない場合であっても,不規則三角網は,
これらを構成する曲線分を含まなければならない。“breakLines”(傾斜変換線)属性はこれらの決定的曲線
分を線分の集合として含む。
GM̲Tin::breakLines : Set<GM̲LineString>
6.4.39.4 maxLength データが適切な計算の保証に十分な密度をもたない曲面の領域は,その辺の長さに
基づいた三角形の保持基準を追加することによって取り除く。最大辺長(maxLength)を超える三角形の
辺については,その辺に隣接する三角形を曲面から削除する。
GM̲Tin::maxLength : Distance
72
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.39.5 controlPoint 不規則三角網の三角形の頂点は,しばしばポスト(標柱)として参照される。
“controlPoint”(制御点)属性は,この不規則三角網のポストとして用いるGM̲Positionの集合を含む。そ
れぞれの不規則三角網は,三角形を含むため,最低でも三つのポストがなければならない。これらの点の
順序は,表現する曲面には影響しない。応用スキーマは,controlPointから不規則三角網の再構築を容易に
するために制御点の順序に基づいた情報を付け加えてもよい。
GM̲Tin::controlPoint[3..n] : GM̲Position
備考 不規則三角網の制御点は,多くの場合“ポスト(標柱)”と呼ばれる。
6.4.39.6 GM̲Tin(コンストラクタ) この限定されたDelaunay網のコンストラクタは,三角形の頂点(ポ
スト),傾斜変換線,抑止線及び三角形の最大辺長を必要とする。
GM̲Tin::GM̲Tin(post : Set<GM̲Position>, stopLines : Set<GM̲LineString>,
breakLines : Set<GM̲LineString>, maxLength : Number): GM̲Tin
6.4.40 GM̲ParametricCurveSurface
6.4.40.1 意味 このパラメタ化曲線による曲面を形成する曲面分GM̲ParametricCurveSurface(パラメタ化曲線
面)(図23)は,曲線のすべてが連続な族で次の形式の構成関数で与えられる。
surface(s,t): [a,b]×[c,d] -> DirectPosition
パラメタのいずれかの値を固定することによって,曲線の単一パラメタの族を得る。
ct(s) = cs(t) = surface(s,t)
GM̲ParametricCurveSurface(図23)の関数は,これら二つの曲線の族を表す。一つ目は“水平”の横断
面ct(s)を示し,二つ目は“垂直”の横断面cs(t)を示す。水平及び垂直の用語は,パラメタ空間を参照する
もので,座標参照系における曲線が水平であったり垂直であったりする必要はない。表6.1は,これらの
曲面曲線の型の対で可能なものの幾つかを一覧する(これらと同じ曲面に対して別の表現も可能である。)。
曲面のパラメタ式の二つの導関数i及びjは,次の式で与えられる。
)
,
(
)
(
t
s
surface
s
s
c
ds
d
ds
dsurface
t
∂∂
=
=
≡
i
)
,
(
)
(
t
s
surface
t
t
c
dt
d
dt
dsurface
s
∂∂
=
=
≡
j
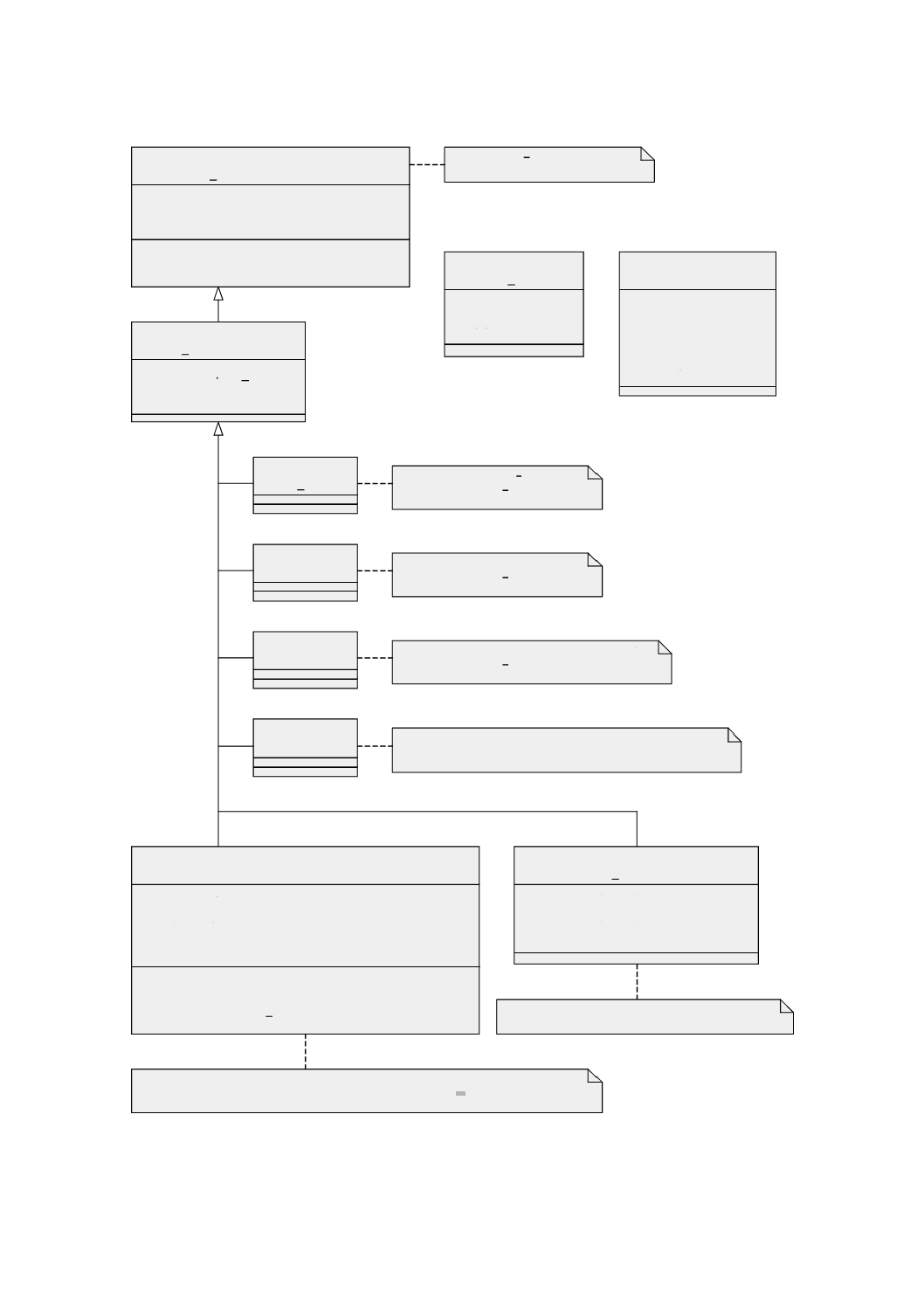
73
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲BicubicGrid
+ horiVectorAtStart : Sequence<Vector>
+ horiVectorAtEnd : Sequence<Vector>
+ vertVectorAtStart : Sequence<Vector>
+ vertVectorAtEnd : Sequence<Vector>
«Type»
GM̲BilinearGrid
«Type»
GM̲Knot
+ value : Real
+ multiplicity : Integer
+ weight : Real
«CodeList»
GM̲BSplineSurfaceForm
+ planar
+ cylindrical
+ conical
+ spherical
+ toroidal
+ unspecified
«Type»
GM̲ParametricCurveSurface
+ horizontalCurveType : GM̲CurveInterpolation
+ verticalCurveType : GM̲CurveInterpolation
+ horizontalCurve(t : Real) : GM̲Curve
+ verticalCurve(s : Real ) : GM̲Curve
+ surface(s : Real, t : Real) : DirectPosition
«Type»
GM̲GriddedSurface
+ controlPoint : GM̲PointGrid
/+ rows : Integer
/+ columns : Integer
«Type»
GM̲Cone
«Type»
GM̲Cylinder
«Type»
GM̲Sphere
{interpolation = "parametricCurve"}
{horizontalCurveType = "conic"}
{verticalCurveType = "linear"}
{horizontalCurveType = "conic"}
{verticalCurveType = "linear"}
{horizontalCurveType = "circularArc3Points"}
{verticalCurveType = "circularArc3Points"}
{horizontalCurveType = verticalCurveType = "cubicSpline"}
{numDerivativesOnBoundary = 2}
{horizontalCurveType = verticalCurveType = "linear"}
«Type»
GM̲BSplineSurface
+ degree[1, 2] : Integer
+ knot[2] : Sequence<GM̲Knot>
+ knotSpec : GM̲KnotType
+ surfaceForm : GM̲BSplineSurfaceForm
+ isPolynomial : Boolean
+ GM̲SplineSurface(pts : GM̲PointGrid,
deg[1, 2] : Integer, k[0, 2] : Sequence<GM̲Knot>,
ks[0, 1] : GM̲ KnotType) : GM̲BSplineSurface
{horizontalCurveType = "polynomialSpine" OR horizontalCurveType = "rationalSpine"}
{verticalCurveType = "polynomialSpine" OR verticalCurveType = "rationalSpine"}
図 23 GM̲ParametricCurveSurface(パラメタ化曲線曲面)及びその下位型
74
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
曲面のupNormalの既定値は,これらの二つの曲線の導関数のベクトルが両方とも零でない場合,それ
らの外積となる。
k = i×j
座標系が二次元の場合,ベクトルkが“上方向”の高度ベクトルを供給することによって局所座標系を
拡張する。この場合,基底ベクトル (i,j) は,右手系でなければならない,すなわち,iからjへの方向
角は180゜以下でなければならない。これは <i,j> によって与えられる局所座標軸の右手系“動枠”を与
える。動枠は,幾何オブジェクトから,そのオブジェクト局所接空間の基底への連続関数として定義する。
曲線に対して,これは,局所接線である曲線の導関数となる。局面に対して,これは,局所接線対となる。
パラメタ化曲線は,自然な動枠をもち,この箇条で定義した方法で曲面のupNormalを定義するのに使用
する。
備考 明示的な動枠の存在は,“有向”な多様体を定義する。連続なupNormalの存在が曲面が向き付
け可能であることを示すのはこのためである。メビウスの輪又はクラインの壷のような向き付
け不可能な曲面は,直感的に理解しがたい。6.3.17.1は,この規格に合致する応用スキーマでこ
れらを使用することを禁止する。クラインの壷を構成するには三次元空間では足りず,特異な
表現ができる四次元空間が必要となる。
表 7 パラメタ化曲線曲面の様々な型
曲面型
水平曲線型
垂直曲線型
GM̲Cylinder
円,半径固定
直線分
GM̲Cone
円,半径減少
直線分
GM̲Sphere
定数緯度円
定数経度円
GM̲BilinearGrid
折れ線
折れ線
GM̲BicubicGrid
三次スプライン
三次スプライン
6.4.40.2 horizontalCurveType “horizontalCurveType”(水平曲線)属性は,パラメタ“s”に対応した,
曲面を水平に横断する曲面曲線の型を示す。
GM̲ParametricCurveSurface::horizontalCurveType : GM̲CurveInterpolation
6.4.40.3 verticalCurveType “verticalCurveType”(垂直曲線)属性は,パラメタ“t”に対応した,曲面を
垂直に横断する曲面曲線の型を示す。
GM̲ParametricCurveSurface::verticalCurveType : GM̲CurveInterpolation
6.4.40.4 horizontalCurve “horizontalCurve”(水平曲線取得)操作は,パラメタ“s”に対応した,曲面
を水平に横断する曲線を生成する。この曲線は,バラメタ“t”を定数として保持する。
GM̲ParametricCurveSurface::horizontalCurve(t : Real) : GM̲Curve
備考 この関数又は対応する垂直曲線取得関数が返すGM̲Curveは,通常,この曲面を含む
GM̲Complexのいずれの一部でもない。これらは,たいてい一時的な値である。この例外は,
パラメタ空間の両端で発生することがある。曲面を維持するパラメタ空間の境界は,対象曲面
の境界に正規に写像される。
6.4.40.5 verticalCurve “verticalCurve”(垂直曲線取得)操作は,パラメタ“t”に対応した,曲面を垂直
に横断する曲線を生成する。この曲線は,バラメタ“s”を定数として保持する。
GM̲ParametricCurveSurface::verticalCurve(s : Real) : GM̲Curve
6.4.40.6 surface “surface”(曲面上位置取得)操作は,垂直及び水平の両方向で曲面を横断する。
GM̲ParametricCurveSurface::surface(s : Real, t : Real) : DirectPosition
75
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.41 GM̲GriddedSurface
6.4.41.1 意味 GM̲GriddedSurface(格子曲面)(図23参照)は,パラメタ空間の四辺形格子を用いて定
義したGM̲ParametricCurveSurfaceとする。この格子の行は水平曲面曲線の制御点となり,列は垂直曲面曲
線の制御点となる。この動作条件は,パラメタ座標の対(s,t)に対するもので,整数値の各相対位置に対し
て水平曲線が計算され,“s”で評価される。これは,制御点列を次のように定義する。
<cn(s) : s = 1 … columns>
この列から“s”に対して垂直曲線を計算し,“t”で評価する。ほとんどの場合,計算の順序(水平−垂
直か,又は垂直−水平か)による違いはない。違いがある場合,水平−垂直の順序を使用する。
備考 格子曲面は,ほとんどの場合,二次元スプラインである。この場合,各パラメタの重み関数は,
計算順序を重要でないものとする。
∑∑
=
=
=row
i
columns
j
j
i
j
t
i
s
P
t
w
s
w
t
s
surface
0
0
,
)
(
)
(
),
(
ρ ただし,
j
iP,ρはi行j列の制御点とする。
論理的には,どのような曲線内挿法型の対であってもGM̲GriddedSurfaceの下位型を導き出すことがで
きる。次からの箇条は,この方法で表現できる曲面で,最も共通的に用いるものを幾つか定義する。
6.4.41.2 controlPoint “controlPoint”(制御点)属性は,行優先形式で与えられる制御点の二重インデッ
クス列とする。
GM̲GriddedSurface::controlPoint : GM̲PointGrid
備考 格子の形状について,前提条件はない。例えば,位置は二・五次元曲面の効果をもつ必要はな
く,連続する点はすべての点の縦座標が等しくてもよい。又は,いずれか一方又は両方の曲線
が閉じていてもよい。
6.4.41.3 rows “rows”(行数)派生属性は,パラメタ格子の行数を与える。
GM̲GriddedSurface::rows : Integer = controlPoint->row.count : Integer
6.4.41.4 columns “columns”(列数)派生属性は,パラメタ格子の列数を与える。
GM̲GriddedSurface::rows : Integer = controlPoint->row->column.count : Integer
6.4.42 GM̲Cone GM̲Cone(円すい)は,controlPointが線形に変化する円すい断面の群として与えられ
るGM̲GriddedSurfaceとする。
備考 すべての定義位置が一致する5点だ(楕)円は点となる。したがって切り出されただ(楕)円円すい
は,2×5の制御点の集合<<P1,P1,P1,P1,P1>,<P2,P3,P4,P5,P6>>で与えられる。P1
は,円すいの頂点となる。P2,P3,P4,P5及びP6は円すいの底面のだ(楕)円の周上の異なる
5点となる。水平曲線がだ(楕)円ではなく円の場合,この円すいは,<<P1,P1,P1>,<P2,P3,
P4>>を使用して構築できる。
6.4.43 GM̲Cylinder GM̲Cylinder(円柱)は,平行線の集合に沿って位置が変化する円の群として与え
られ,これを横切る断面の水平曲線が一定の形状を保持するような,GM̲GriddedSurfaceとする。
備考 6.4.42の備考と同様の動作条件があり,GM̲Cylinderは,<<P1,P2,P3>,<P4,P5,P6>>の形
式の制御点で与えられる二つの円で指定できる。
6.4.44 GM̲Sphere GM̲Sphere(球面)は,球の軸に沿って線形に位置が変化し,その半径が中心角の余
弦関数に比例して変化するような,円の群として与えられるGM̲GriddedSurfaceとする。水平な円は緯度
が一定の線に類似し,垂直な円弧は一定の経度の線に類似する。
備考 制御点が経度及び緯度が増加する順に並んでいる場合,球面のupNormalは,外側に向く法線
76
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
になる。
例 単位を度とする緯度及び経度の格子集合(u, v)は,次のとおりに取るものとする。
(-90, -180)
(-90, -90)
(-90, 0)
(-90, 90)
(-90, 180)
(-45, -180)
(-45, -90)
(-45, 0)
(-45, 90)
(-45, 180)
(0, -180)
(0, -90)
(0, 0)
(0, 90)
(0, 180)
(45, -180)
(45, -90)
(45, 0)
(45, -90)
(45, 180)
(90, -180)
(90, -90)
(90, 0)
(90, -90)
(90, 180)
また,これらの点を次の一般式を用いて三次元に写像する(ここでRは求める球面の半径とする。)。
z = R sin u
x = (R cos u) (sin v)
y = (R cos u) (cos v)
このとき,半径R,中心を (0, 0) とする球面を格子曲面として得る。制御点の最初の行全
体及び最後の行全体は,それぞれ北極点及び南極点となる三次元ユークリッド空間の単独の点
に写像され,各水平曲線が幾何輪体を形成するよう自身に戻って閉じることに注意する。これ
は,距離に関して(有限の長さで)有界であり,位相に対して境界のない(境界をもたず輪体
となる。)曲面を与える。
6.4.45 GM̲BilinearGrid GM̲BilinearGrid(双線形格子)は,水平曲線及び垂直曲線に折れ線を用いる
GM̲GriddedSurfaceとする。
備考 各格子方眼は,分割曲面で必ずしも平面ではないので,これはポリゴン曲面ではない。
6.4.46 GM̲BicubicGrid
6.4.46.1 意味 GM̲BicubicGrid(双三次多項式格子)は,水平曲線及び垂直曲線に三次多項式スプライン
を用いるGM̲GriddedSurfaceとする。
備考 スプラインの最初の接線は,追加された制御点の行(及び列)の対でしばしば代用される。
6.4.46.2 horiVectorAtEnd,horiVectorAtStart,vertVectorAtEnd及びvertVectorAtStart 水平曲線及び垂
直曲線は,その完全な定義に最初及び最後の接線ベクトルを必要とする。四つの属性がこれらの値を供給
する。
GM̲BicubicGrid::horiVectorAtEnd : Sequence<Vector>;
GM̲BicubicGrid::horiVectorAtStart : Sequence<Vector>;
GM̲BicubicGrid::vertVectorAtEnd : Sequence<Vector>;
GM̲BicubicGrid::vertVectorAtStart : Sequence<Vector>;
6.4.47 GM̲BSplineSurfaceForm “GM̲BsplineSurfaceForm”(Bスプライン曲面形式)符号リストは
GM̲BsplineSurfaceの表す特定の幾何形式を示すために使用し,次の値をとり得る。
− planar (平面形)は,各パラメタが一次の,Bスプライン曲面で表される平面の有界部分。
− cylindrical (円柱形)は,Bスプライン曲面で表される円筒面の有界部分。
− conical (円すい形)は,Bスプライン曲面で表される真円の円すい面の有界部分。
− spherical (球面形)は,Bスプライン曲面で表される完全な球又はその有界部分。
− toroidal (トーラス形)は,Bスプライン曲面で表されるトーラス又はその部分。
− unspecified (不定形)は,特定の曲面を指定しない。
GM̲BSplineSurfaceForm::
plane
cylindrical
77
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
conical
spherical
toroidal
unspecified
6.4.48 GM̲BSplineSurface
6.4.48.1 意味 GM̲BSplineSurface(Bスプライン曲面)は,制御点,基底関数及び場合によっては重みで
表現される有理式又は多項式パラメタ曲面とする。重みがすべて等しい場合,スプラインは,区間多項式
になる。それらが等しくない場合,スプラインは,区間有理式になる。“isPolynomial”真偽値がTRUEの
場合,重みはすべて1とする。
6.4.48.2 degree “degree”(次数)属性は,第一及び第二パラメタの基底関数の代数次数とする。値が一
つしか与えられない場合,二つの次数は,等しいものとする。
GM̲BSplineSurface::degree [1,2] : Integer
6.4.48.3 surfaceForm “surfaceForm”(曲面形式)属性は,このスプラインが近似する曲面の特定の型を
識別するために用いる。これは,参考情報とし,本来の意図をとらえるために用いる。どのような近似も
意図していない場合,この属性の値は,NULLとする。
GM̲ BSplineSurface::surfaceForm : GM̲BSplineSurfaceForm
6.4.48.4 knot “knot”(ノット)属性は,二つのパラメタのBスプライン基底関数を定義するのに用いる
異なるノットの二つの列とする。knotデータ型は,knotの多重度の情報を保持することに注意する。
GM̲BSplineSurface::knot [2] : Sequence<GM̲Knot>
6.4.48.5 knotSpec “knotSpec”(ノット仕様)属性は,このスプラインの定義で用いるknotの配置の型
を与える。これは参考情報とし,構造関数の違いによって定める。
GM̲BSplineSurface::knotSpec[0,1] : GM̲KnotType
6.4.48.6 isPolynomial “isPolynomial”(多項式判定)属性は,多項式スプラインの場合“True”とする。
GM̲BSplineSurface::isPolynomial : Boolean
6.4.48.7 GM̲BSplineSurface(コンストラクタ) “GM̲BsplineSurface”クラスのコンストラクタは,6.4.48.2
〜6.4.48.6の属性で記述される附属情報をとり,Bスプライン曲面を生成する。knotSpecを指定しない場合,
knotTypeはuniformとし,ノットは等間隔で最初及び最後を除き multiplicity = 1 とする。ノットの両端は,
multiplicity = degree + 1 とする。knotTypeがuniformの場合,これらを指定する必要はない。
GM̲BSplineSurface::GM̲BSplineSurface(pts : Sequence<GM̲PointArray>,
deg[1,2] : Integer,k[0,2] : Sequence<GM̲Knot>,
ks[0,1] : GM̲KnotType) : GM̲BSplineSurface
6.5
Geometric aggregateパッケージ
6.5.1
意味 幾何オブジェクトの任意の集成(aggregation)を作成することができる。これは,付加的な内
部構造をもつ必要はなく,ある特定の型の幾何部分を“集める”ために使用する。この点において,集成
は6.6で定義する“合成”及び“複体”と異なる。これらの集成に対する操作は,その要素のクラス操作
から派生した累積操作とする。応用システムは,石油備蓄基地,果樹園などを表現する点の集まりのよう
な,複数の幾何オブジェクトを表現に使用するような地物に対して集成を使用してよい。
6.5.2
GM̲Aggregate

78
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.5.2.1
意味 GM̲Aggregate(幾何集成)(図24参照)は,幾何オブジェクトを集成する。これらは,し
ばしば方向変更の必要があるので,曲線参照及び曲面参照は,GM̲Curve及びGM̲Surfaceを直接指すので
はなくGM̲OrientableCurve及びGM̲OrientableSurfaceを指す。
多くの幾何オブジェクトは,それぞれ別の地物に含まれるため,強集成のコレクションとして保持する
ことができない。そのため,この箇条で定めるコレクションはすべて弱集成であり,幾何オブジェクトを
含むものに対しては参照を用いる。さまざまな参照オブジェクト間の型関係は,次以降に示す。
備考 GM̲OrientablePrimitiveの下位クラスは,参照オブジェクトがそのオブジェクトの特定の方向に
連結できるものとして扱う。
6.5.2.2
element “element”(要素)関連役割は,このGM̲Aggregateに含まれるGM̲Objectの集合とす
る。GM̲Aggegateの下位クラスでは,要素は,GM̲Primitiveの特定の型に限定される。
GM̲Aggregate::element : Set<GM̲ObjectRef>
6.5.2.3
fromSet “fromSet”(集合集成化)操作は,GM̲Objectの集合からGM̲Aggregateを生成するコ
ンストラクタとする。
GM̲Aggregate::fromSet(set : Set<GM̲Object>) : GM̲Aggregate
6.5.3
GM̲MultiPrimitive GM̲MultiPrimitive(多プリミティブ)は,すべてのプリミティブの集成に対
する基底クラスとする。“element”関連役割は,このGM̲MultiPrimitiveに含まれるGM̲Primitiveの集合
とする。ここでの属性宣言は,GM̲Aggregateにおける属性宣言をこの型の集成にGM̲Primitiveだけが含
まれるよう特化する。
GM̲MultiPrimitive::element : Set<GM̲Primitive>
«Type»
GM̲Object
(from Geometry root)
«Type»
GM̲Aggregate
+ fromSet(set : Set<GM̲Object>) : GM̲Aggregate
«Type»
GM̲MultiPrimitive
«Type»
GM̲Object
(from Geometry root)
«Type»
GM̲MultiPoint
/+ position : Set<DirectPosition>
«Type»
GM̲MultiCurve
/+ length : Length
«Type»
GM̲MultiSurface
/+ area : Area
/+ perimeter : Length
«Type»
GM̲MultiSolid
/+ volume : Volume
/+ area : Area
{element.subTypeOf(GM̲Point)}
{element.subTypeOf(GM̲OrientableCurve)}
{element.subTypeOf(GM̲OrientableSurface)}
{element.subTypeOf(GM̲Solid)}
{element.subTypeOf(GM̲Primitive)}
+ element
0..n
図 24 GM̲Aggregate
6.5.4
GM̲MultiPoint
79
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.5.4.1
意味 GM̲MultiPoint(多点)は,点だけを含む集成クラスとする。“element”関連役割は,この
GM̲MultiPointに含まれるGM̲Pointの集合とする。
GM̲MultiPoint::element : Set<GM̲Point>
6.5.4.2
position “position”(位置)派生属性は,このGM̲MultiPointに含まれるGM̲PointのDirectPosition
の集合とする。
GM̲MultiPoint::position : Set<DirectPosition>
6.5.5
GM̲MultiCurve
6.5.5.1
意味 GM̲MultiCurve(多曲線)は,GM̲OrientableCurveのインスタンスだけを含む集成クラス
とする。“element”関連役割は,このGM̲MultiCurveに含まれるGM̲OrientableCurveの集合とする。
GM̲MultiCurve::element : Set<GM̲OrientableCurve>
6.5.5.2
length “length”(弧長)派生属性は,このGM̲MultiCurveに含まれるすべてのGM̲Curveの長
さの累計とする。
GM̲MultiCurve::length : Length
6.5.6
GM̲MultiSurface
6.5.6.1
意味 GM̲MultiSurface(多曲面)は,GM̲OrientableSurfaceのインスタンスだけを含む集成クラ
スとする。“element”関連役割は,このGM̲MultiSurfaceに含まれるGM̲OrientableSurfaceの集合とする。
GM̲MultiSurface::element : Set<GM̲OrientableSurface>
6.5.6.2
area “area”(面積)派生属性は,このGM̲MultiSurfaceに含まれるすべてのGM̲Surfaceの面
積の累計とする。
GM̲MultiSurface::area : Area
6.5.6.3
perimeter “perimeter”(周囲長)派生属性は,このGM̲MultiSurfaceに含まれるすべての
GM̲Surfaceの周長を累計したものとする。
GM̲MultiSurface::perimeter : Length
6.5.7
GM̲MultiSolid
6.5.7.1
意味 GM̲MultiSolid(多立体)は,立体だけを含む集成クラスとする。“element”関連役割はこ
のGM̲MultiSolidに含まれるGM̲Solidの集合とする。
GM̲MultiSolid::element : Set<GM̲Solid>
6.5.7.2
volume “volume”(体積)派生属性は,このGM̲MultiSolidに含まれるすべてのGM̲Solidの体
積の累計とする。
GM̲MultiSolid::volume : Volume
6.5.7.3
area “area”(表面積)派生属性は,このGM̲MultiSolidに含まれるすべてのGM̲Solidの表面
積の累計とする。
GM̲MultiSolid::area : Area
6.6
Geometric complexパッケージ
6.6.1
意味 幾何複体(GM̲Complex)は,共通の座標系において,その内部に交差のないプリミティブ
な幾何オブジェクトの集合とする。さらに,プリミティブが幾何複体に含まれる場合,その複体にはプリ
ミティブの集合が存在し,点としての和集合がこのプリミティブの境界となる。
複体の部分複体は,その複体のプリミティブの部分集合で,それ自身がまた幾何複体となるものとする。
ある複体の上位複体は,プリミティブの上位集合で,それ自身がまた複体となるものとする。これらの定
義は,本質的には部分集合及び上位集合の定義に複体とならなければならない制限を付加する。複体がよ
80
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
り大きな複体の部分複体とならない場合,その複体は,極大とする。
幾何複体に含まれる幾何オブジェクトの境界は,その複体の部分複体となる。最も単純な複体は,単独
の点とする。最も単純な一次元複体は,曲線とその二つの端点である。最も単純な二次元複体は,曲面と
その境界曲線並びにその曲線の始点及び終点である。
複体の根底にある幾何は,通常,“多様体”に属する。例えば複数の“図面”をまとめて構成した“地図
帳”が世界地図となるように,複体の構造として構成したプリミティブ要素が多様体の幾何となる。
プリミティブの集合から複体を生成する一つの方法(もちろん,唯一の方法ではない)として,それら
のプリミティブをもとに次の操作を実行する方法がある。
a) 二つのプリミティブが重複する場合,それらを分割し,重複がなくなるまで重複部分を取り除く。
b) 同様に,プリミティブが単純でない場合,その交差する個所で分割し,重複がなくなるまで重複部分
を取り除く。
c) プリミティブが点でない場合,生成した集合中の既存のプリミティブを可能な限り使用して,その境
界を他のプリミティブの集まりとして求め,その複体に追加する。
d) “a”〜“c”を新しいプリミティブを必要としなくなるまで繰り返す。
多くのシステムが二次元に対する全域フェイス又は三次元に対する全域位相立体の概念をもつ。これは
複体の根底にある空間が非有界なユークリッド空間である場合にだけ有効である。この場合,二次元にお
いて全域フェイスはGM̲Complex内の内側境界輪だけをもつ(その外側境界は,無限遠点にある)曲面と
する。同様に,三次元において全域位相立体は,内部境界殻だけをもつものとする。球面のような有界多
様体では無限遠点は存在せず,すべてのプリミティブは有界である。ジョルダンの分割定理を除いてすべ
ての境界は,基本的に内部境界である。双曲線面のようなその他の非有界多様体では非有界なプリミティ
ブが一つ以上存在してもよい。この規格はこの種の非有界多様体には直接言及しないので,この規格を地
理情報以外のそのような多様体に用いる場合には,幾つかの要素の基数について柔軟に扱う必要があるか
もしれない。この規格は,全域フェイス又は全域位相立体のいずれも特別扱いせず,それらとその境界と
の間の関係は,その他の境界関係と同じ方法で扱う。
備考 極大複体は,応用システムの内部的な意味によっては,そのプリミティブの強集成とみなすこ
とが合理的である場合もある。このため,GM̲ComplexがGM̲Primitiveを含む方法は,規定し
ない。極大複体に強集成を用いる場合,部分複体の包含関連にはその中のプリミティブを参照
する際の名前空間として極大複体を使用することとしてもよい。いずれの場合でも,複体に含
まれるGM̲Primitive又は極大なGM̲Complexの部分複体となるGM̲Complexのいずれの場合
でも,その境界取得操作はそれを表現するGM̲Objectを生成する必要はない。なぜなら,複体
の定義から,含まれるオブジェクトの境界を表すのに必要なオブジェクトは既に存在し,
GM̲Object::boundary操作にとってはこれらのオブジェクトへの参照だけが必要となるからで
ある。GM̲Complex同士の包含関係は,部分集合と上位集合との関係であり,一方GM̲Complex
の中のGM̲Primitiveの包含関係は,要素と集合との関係であることに注意すること。
6.6.2
GM̲Complex
6.6.2.1
意味 GM̲Complex(幾何複体)(図25参照)は,幾何的に交差のない単純なGM̲Primitiveの集
合とする。GM̲Point以外のGM̲PrimitiveがあるGM̲Complexに含まれている場合,そのGM̲Complexの
中にそのプリミティブの境界を形成するより低い次元のプリミティブの集合が存在する。
備考 幾何複体は,集合として二つの異なる観点から考えることができる。第一に,その要素メンバ
を代理するオブジェクトの有限集合であり,第二に幾何オブジェクトの下位型の点の値の無限
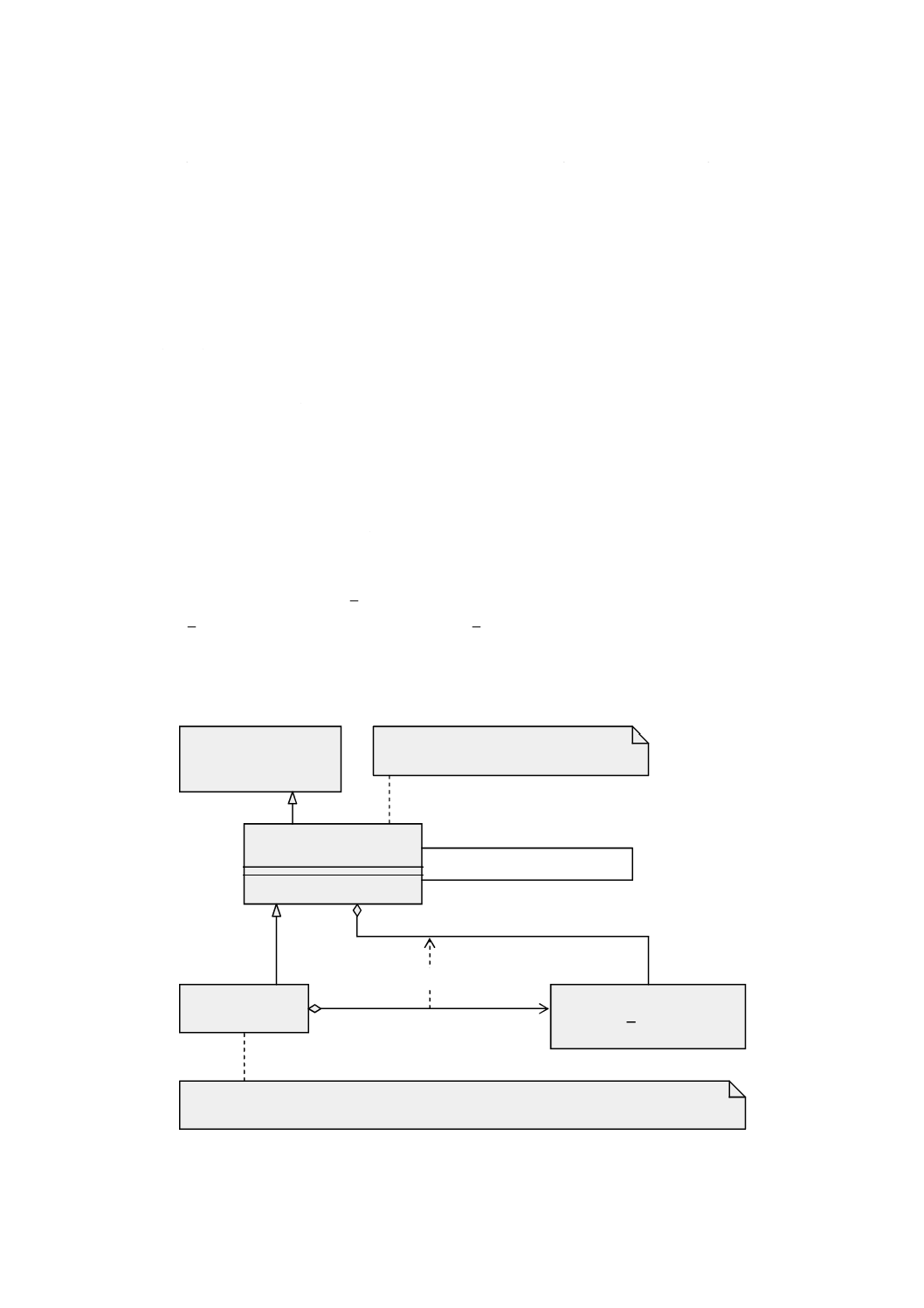
81
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
集合である。代理と型派生とを併用するには,集合インタフェースの二つの型を区別しなけれ
ばならない。GM̲Primitive PがGM̲Complex Cの要素であるか否かを判定するためには,
C.element().contains(P) を呼び出す。
“element”属性は,GM̲Complexが,GM̲Objectを通じてTransfiniteSet<DirectPosition>から継承した振
る舞いと混同せずに,Set<GM̲Primitive>の同じ振る舞いを継承できるようにする。
計算位相幾何を使用する場合のように幾何の共有が重要な場合には,応用スキーマに複体を使用しなけ
ればならない。複体においては,プリミティブは,地物の属性に使用する合成体に多対多で集成してよい。
この例を附属書Dのスキーマに示す。
6.6.2.2
isMaximal ブール値を返す“isMaximal”(極大判定)操作は,GM̲Complexが極大である場合に
だけTRUEを返す。
GM̲Complex::isMaximal() : Boolean
6.6.2.3
Contains関連 “Contains”(包含)関連は,Set<GM̲Primitive>のcontains操作を関連としてイン
スタンス化する。
GM̲Complex::subComplex [0..n] : GM̲Complex
GM̲Complex::superComplex [0..n] : GM̲Complex
6.6.2.4
Complex関連 “Complex”(複体)関連は,TransfiniteSet<DirectPosition>から継承したGM̲Object
の“contains”操作によって定義する。
GM̲Complex::element [1..n] : GM̲Primitive
複体がGM̲Primitiveを含む場合,複体は,そのGM̲Primitiveの境界の要素も含まなければならない。
GM̲Complex:
// 境界取得操作について閉じている。
self->forAll(self->includesAll(boundary()))
«Type»
GM̲Object
(from Geometry root)
«Type»
GM̲Complex
+ isMaximal() : Boolean
«Type»
GM̲Composite
«Type»
GM̲Primitive
(from Geometric primitive)
+ composite
0..n
+ generator
1..n
Composition
subset
Complex
0..n
+ complex
1..n + element
0..n
+ subComplex
0..n
+ superComplex
Contains
-- 複体は境界演算に対して閉じている
{subComplex includes boundary()}
-- generatorのすべてのプリミティブはこの複体に(プリミティブの集合として)含まれる
{Set::element->includesAll(generator)}
図 25 GM̲Complex
82
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.6.3
GM̲Composite
6.6.3.1
意味 幾何合成体型であるGM̲Composite(図26)は,基本幾何形状がプリミティブと同形とな
る幾何複体とする。よって,合成曲線は,(かなり複雑な曲線かもしれないが)単一の曲線によってその幾
何インタフェースを満たすことができる曲線の集まりとする。合成体は,通常はその位相的性質を明示す
るために,基本幾何形状を分解してデータ集合の属性値として使用することを意図している。
6.6.3.2
generator Composition::generator(生成子)関連役割は,その和集合がその合成体の基本幾何形
状となるような,種類が同一のGM̲Primitiveの集合とする。複体は,generatorのすべてのプリミティブを
含み,さらにそれらのプリミティブの境界となるすべてのプリミティブを含み,次々とGM̲Pointまで含
む。よって,GM̲CompositeのComposition::generator関連役割は,GM̲ComplexのComplex::element関連
役割の部分集合となる。
GM̲Composite::generator[1..n] : GM̲Primitive
generatorの幾何の型は,合成体オブジェクトの次元によって完全に決まる。構成要素となる曲線及び曲
面は,合成体として組み立てることができるよう,適切に構成した方法に従って向き付けされる。
GM̲CompositePoint:
generator.type = GM̲Point
GM̲CompositeCurve:
generator.type = GM̲OrientableCurve
GM̲CompositeSurface:
generator.type = GM̲OrientableSurface
GM̲CompositeSolid:
generator.type = GM̲Solid
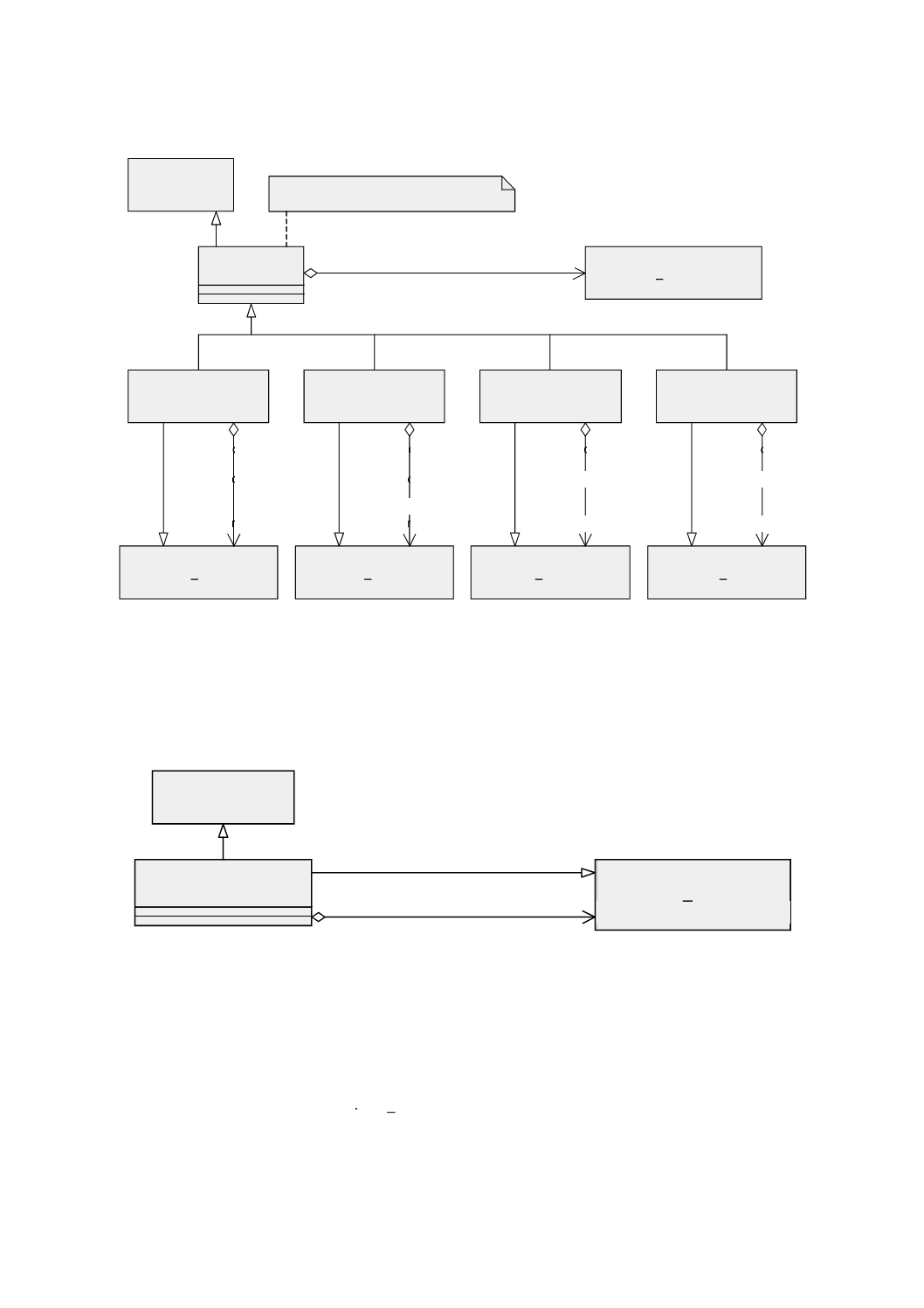
83
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
GM̲Complex
«Type»
GM̲Composite
«Type»
GM̲Primitive
(from Geometric primitive)
«Type»
GM̲CompositePoint
«Type»
GM̲CompositeCurve
«Type»
GM̲CompositeSurface
«Type»
GM̲CompositeSolid
«Type»
GM̲Point
(from Geometric primitive)
«Type»
GM̲Curve
(from Geometric primitive)
«Type»
GM̲Surface
(from Geometric primitive)
«Type»
GM̲Solid
(from Geometric primitive)
0..n
+ composite
+ generator
1
Composition
0..n
+ composite
+ generator
1..n
Composition
0..n
+ composite
+ generator
1..n
Composition
0..n
+ composite
+ generator
1..n
Composition
{sequence}
+ composite
0..n
+ generator
0..n
Composition
{dimension() = generator.dimension()}
図 26 GM̲Composite
6.6.4
GM̲CompositePoint
6.6.4.1
意味 合成点のための独立したクラスGM̲CompositePoint(合成点)(図27)は,完全性のため
に存在する。これは,ただ一つのGM̲Pointだけを含むGM̲Complexとする。
«Type»
GM̲Composite
«Type»
GM̲CompositePoint
«Type»
GM̲Point
(from Geometric primitive)
0..n
+ composite
1
+ generator
Composition
図 27 GM̲CompositePoint
6.6.4.2
generator Composition::generator(生成子)関連役割は,このGM̲CompositePointをこの複体の
唯一のプリミティブに関連付ける。
GM̲CompositePoint::generator [1] : GM̲Point
6.6.5
GM̲CompositeCurve
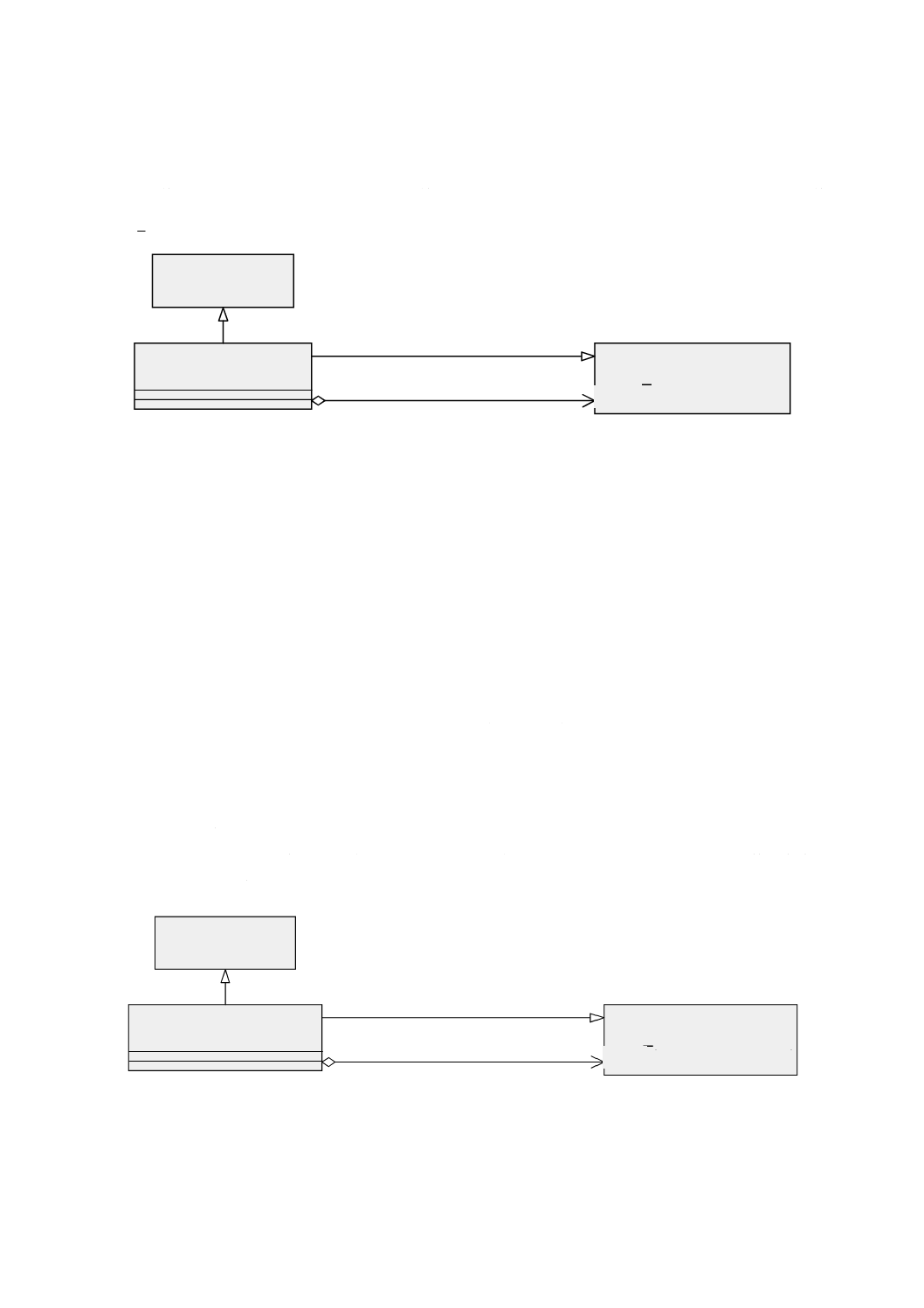
84
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.6.5.1
意味 合成曲線型であるGM̲CompositeCurve(図28)は,曲線のすべての幾何的特性をもつ
GM̲Compositeとする。これらの特性は“曲線”の操作としてインスタンス化される。本質的に合成曲線
は,各曲線(最初のものを除く。)が直前の曲線の終端から始まるという方法で方向が揃った,有向曲線
(GM̲OrientableCurve)のリストである。
«Type»
GM̲Composite
«Type»
GM̲CompositeCurve
«Type»
GM̲OrientableCurve
(from Geometric primitive)
0..n
+ composite
1..n
+ generator
{sequence}
Composition
図 28 GM̲CompositeCurve
6.6.5.2
generator Composition::generator(生成子)関連役割は,GM̲CompositeCurveを,この複体の核
を形成する曲線とし,このgeneratorの集合であるGM̲Curveプリミティブ及びGM̲OrientableCurveプリ
ミティブに関連付ける。
GM̲CompositeCurve::generator : Sequence<GM̲OrientableCurve>
// generatorの各有向曲線の始点は,直前の曲線の終点とする。
GM̲CompositeCurve:
forAll (1 < j < generator.count - 1) -> generator[j].endPoint =
generator[j+1].startPoint;
備考 GM̲Complexの要素を完全に表現するためには,GM̲Curveのgeneratorの集合の境界上の
GM̲Pointをgeneratorのリストの曲線に追加する。
6.6.6
GM̲CompositeSurface
6.6.6.1
意味 合成曲面型であるGM̲CompositeSurface(図29)は,曲面のすべての幾何的特性をもつ
GM̲Complexとし,よって有向曲面(GM̲OrientableSurface)の型とみなすこともできる。本質的に合成曲
面は,共通の境界曲線の対で結合した有向曲面の集合であり,全体として一つの曲面を形成する。
«Type»
GM̲Composite
«Type»
GM̲CompositeSurface
«Type»
GM̲OrientableSurface
(from Geometric primitive)
0..n
+ composite
1..n
+ generator
Composition
図 29 GM̲CompositeSurface
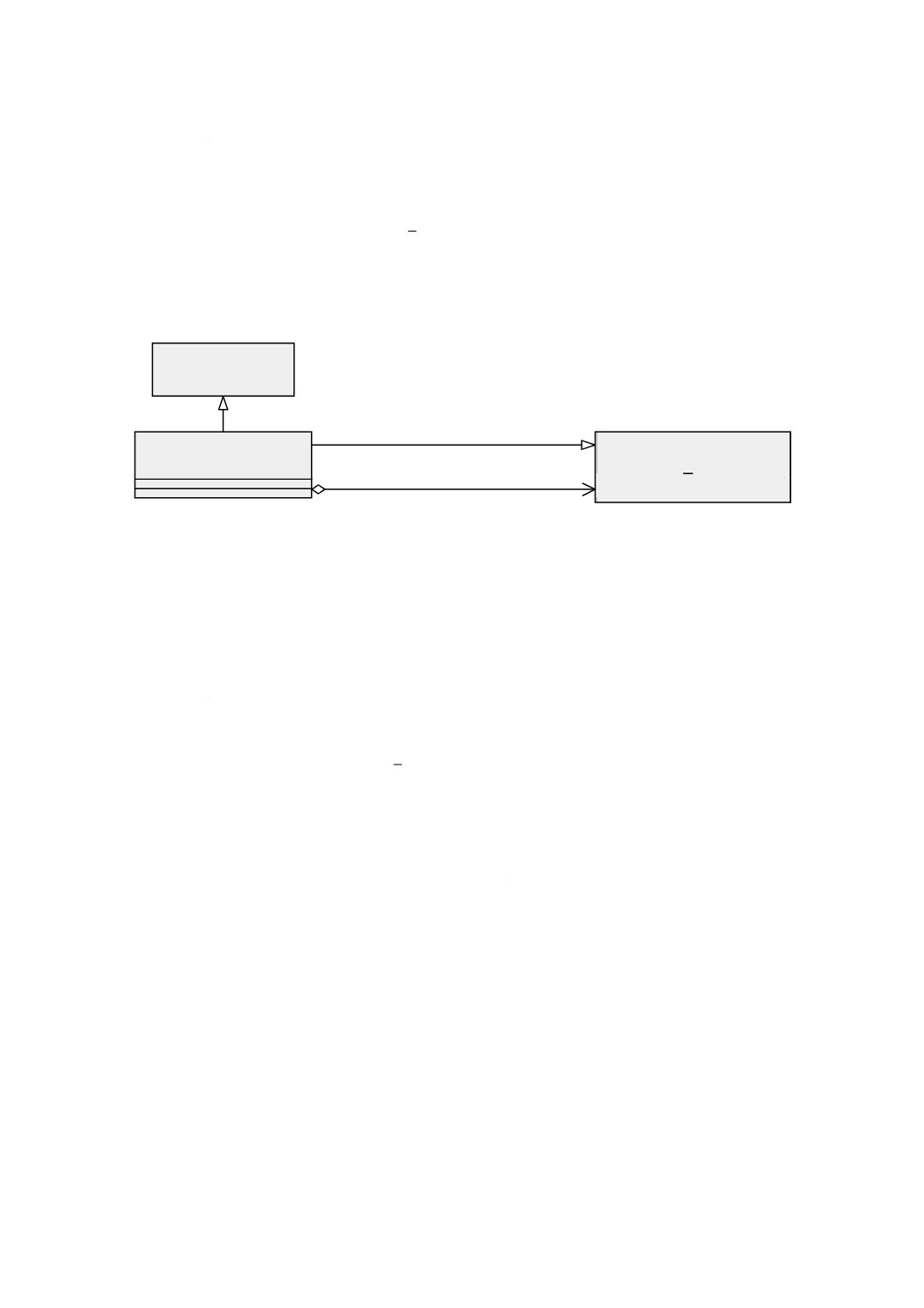
85
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.6.6.2
generator Composition::generator(生成子)関連役割は,GM̲CompositeSurfaceを,この複体の
核を形成するGM̲Surfaceのリストであり,このgeneratorの集合であるGM̲Surfaceプリミティブ及び
GM̲OrientableSurfaceプリミティブに関連付ける。
GM̲CompositeSurface::generator : Set<GM̲OrientableSurface>
備考 GM̲Complexの要素を完全に表現するためには,GM̲Surfaceのgeneratorの集合の境界上の
GM̲Curve及びGM̲Pointをgeneratorのリストの曲線に追加する。
6.6.7
GM̲CompositeSolid
«Type»
GM̲Composite
«Type»
GM̲CompositeSolid
«Type»
GM̲Solid
(from Geometric primitive)
0..n
+ composite
1..n
+ generator
Composition
図 30 GM̲CompositeSolid
6.6.7.1
意味 GM̲CompositeSolid(合成立体)(図30)は,立体のすべての幾何的特性をもつGM̲Complex
とする。本質的に合成立体は,一つの立体を形成するよう共通の境界曲面の対を結合した立体の集合であ
る。
6.6.7.2
generator Composition::generator(生成子)関連役割は,GM̲CompositeSolidを,この複体の核
を形成する立体であり,このgeneratorの集合であるGM̲Solidプリミティブに関連付ける。
GM̲CompositeSolid::generator : Set<GM̲Solid>
備考 GM̲Complexの要素を完全に表現するためには,GM̲Solidのgeneratorの集合の境界上の
GM̲Surface,GM̲Curve及びGM̲Pointをgeneratorのリスト中に追加する。
7. Topologyパッケージ
7.1
意味 位相(topology)の最も生産的な使用法は,計算幾何の処理の高速化である。これを機能させ
る方法は,地物インスタンスと幾何オブジェクトとを,それらの暗黙の幾何的関係から一貫して派生した
法則で明確に関連付けることである(附属書DのD.3参照)。場合によっては,これらの関連は,地物イ
ンスタンスの表現と合致しない概念的な幾何から派生することがある。このような目的には,6.で示した
幾何パッケージに対応する位相パッケージを定義する必要がある。図31は,これらのパッケージ及びその
相互依存性を示している。
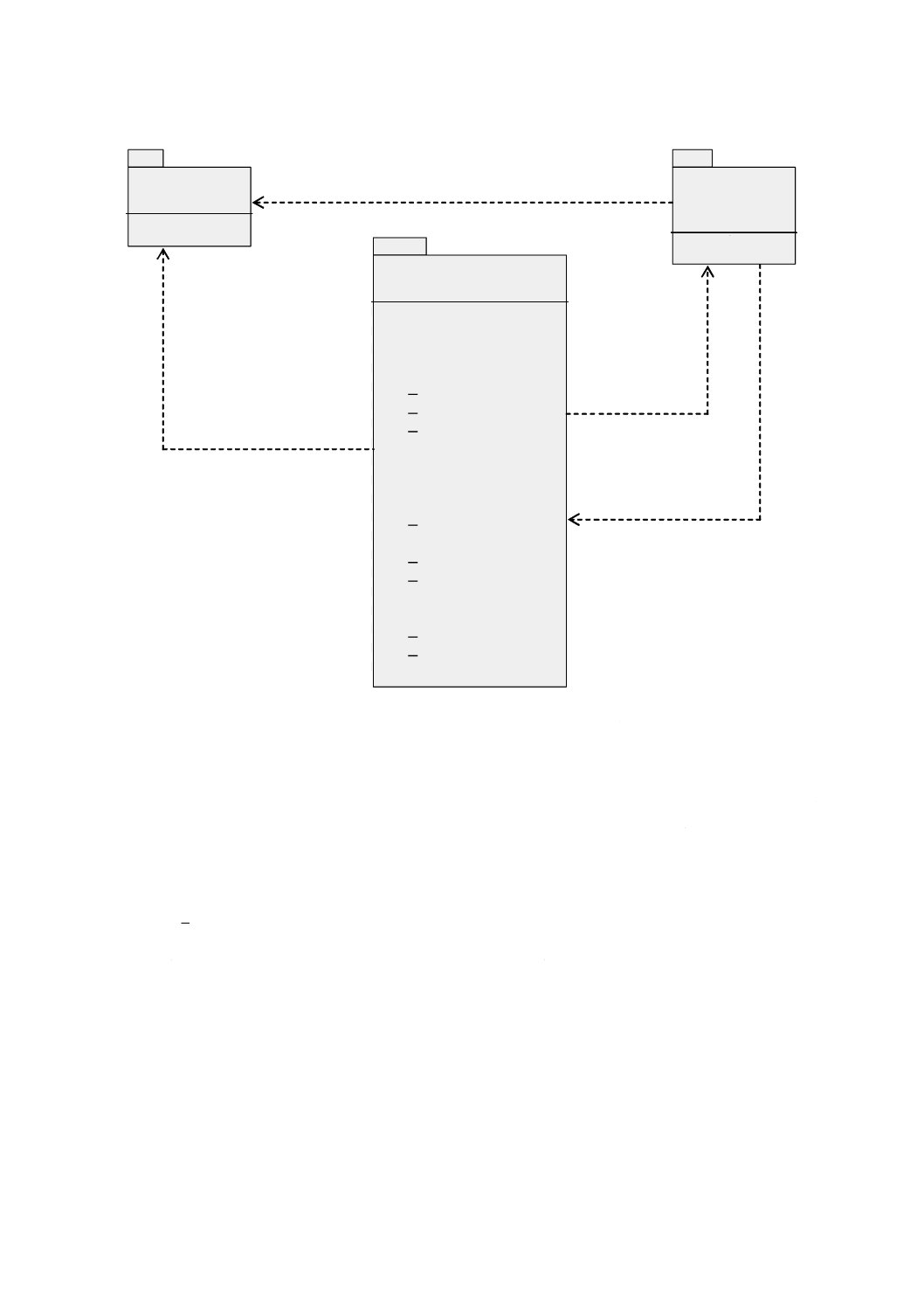
86
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Leaf»
Topology root
+ TP̲Object
«Leaf»
Topological
Complex
+ TP̲Complex
«Leaf»
Topological primitive
+ TP̲Boundary
+ TP̲ComplexBoundary
+ TP̲DirectedTopo
+ TP̲DirectedEdge
+ TP̲DirectedFace
+ TP̲DirectedNode
+ TP̲DirectedSolid
+ TP̲Edge
+ TP̲EdgeBoundary
+ TP̲Expression
+ TP̲ExpressionTerm
+ TP̲Face
+ TP̲FaceBoundary
+ TP̲Node
+ TP̲Primitive
+ TP̲PrimitiveBoundary
+ TP̲Ring
+ TP̲Shell
+ TP̲Solid
+ TP̲SolidBoundary
図 31 Topology(位相)パッケージ群,クラス内容及び内部依存性
図32は,基本的な位相パッケージ群のクラス構造の概要を示す。この図の基底クラスは,TP̲Objectで
ある。その下にTP̲Primitive及びTP̲Complexがあり,これらは,GM̲PrimitiveとGM̲Complexとの関係
と同じように,TP̲ComplexがTP̲Primitiveを組織する構造として関係する。主要な違いは,GM̲Primitive
は,GM̲Complexにより緩く連結しており単独で存在できるが,TP̲Primitiveは,最低一つのTP̲Complex
に属さなければならないことである。TP̲DirectedTopoのインスタンスは,6.3.13のGM̲OrientablePrimitive
と同様にTP̲Primitiveの参照及び向き付けパラメタを含む。次元に関係なく二つの向きだけが可能なので,
各プリミティブは,GM̲OrientableCurveとGM̲Curveとの間の関係のように二つの有向位相実体に関連付
ける。オブジェクトの数を圧縮し,正の向きをもつプリミティブの識別ができるよう,それぞれの次元の
それぞれのプリミティブは,有向位相オブジェクトに合致するように下位クラスを設ける。これについて
は,7.3.11.2において定める。
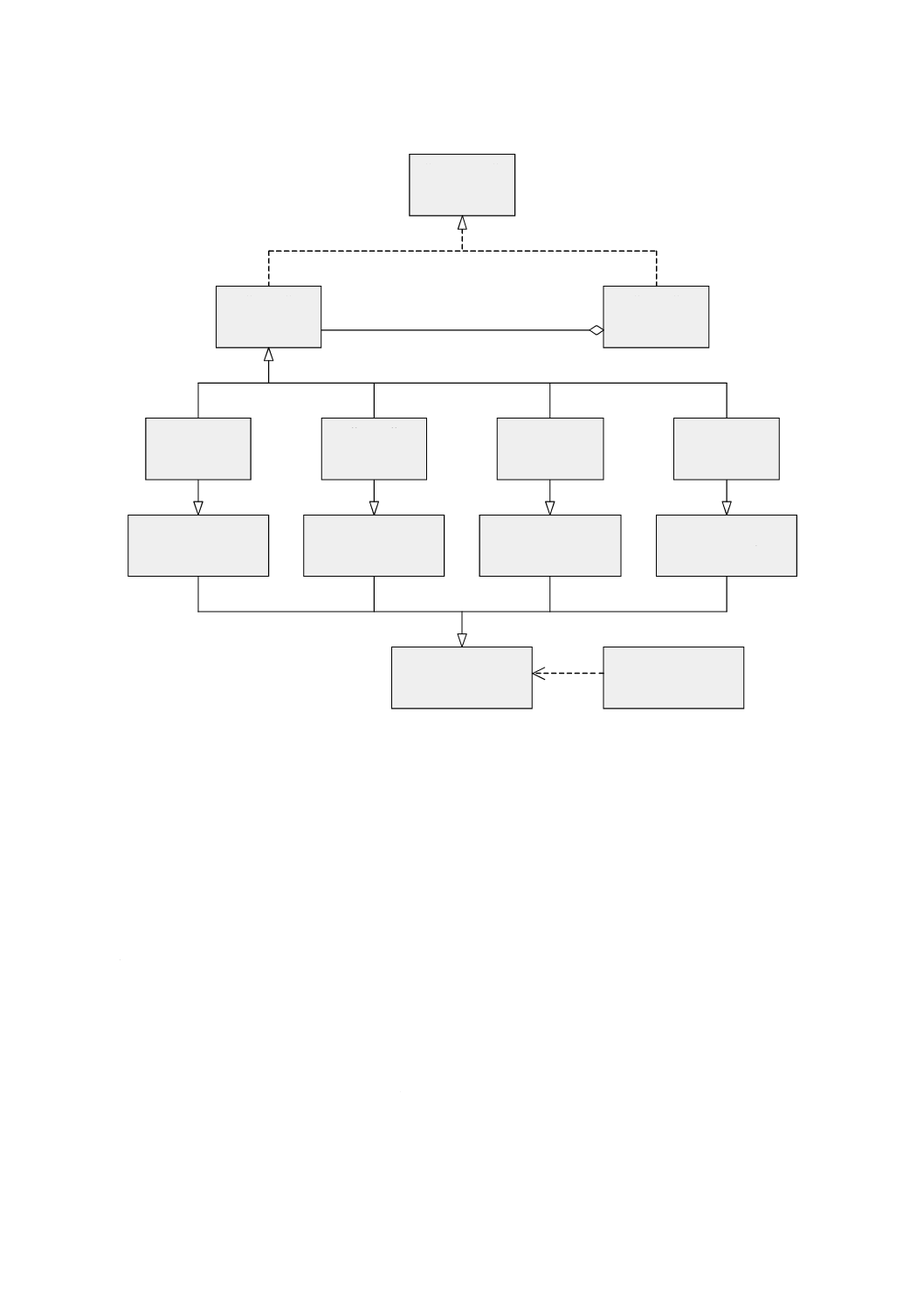
87
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Interface»
TP̲Object
«Type»
TP̲Primitive
«Type»
TP̲Complex
Complex
+element
1..n
+complex
1..n
«Type»
TP̲Node
«Type»
TP̲DirectedNode
«Type»
TP̲DirectedEdge
«Type»
TP̲DirectedFace
«Type»
TP̲DirectedSolid
«Type»
TP̲Edge
«Type»
TP̲Face
«Type»
TP̲Solid
«Type»
TP̲DirectedTopo
«DataType»
TP̲Expression
図 32 位相クラス図
7.2
Topology rootパッケージ
7.2.1
意味 ポリゴン内の点の包含,隣接,境界,ネットワーク追跡などのような幾何的計算は,計算処
理が集中する。そのため,位相複体として知られる組合せ構造は,計算幾何アルゴリズムを組合せアルゴ
リズムに変えたものとして構築する。他の目的としては,地理情報の領域において,地物インスタンス同
士をその幾何とは独立に関係させることがある。最初の目的を達成するため,この箇条では,位相に関す
る定義を6.の幾何に関する定義と対応させている。二つ目の目的を達成するため,これらのパッケージ群
に含まれるクラスについて,それらをその幾何とは独立に使用することができるよう規定する。
位相複体は,その次元以下のすべての種類の位相プリミティブの集まりからなる。そのため,二次元複
体はフェイス,エッジ及びノードを含まなければならず,一方,一次元複体又はグラフは,エッジ及びノ
ードだけを含む。
備考 位相プリミティブは,幾何プリミティブの下位クラスではなく対等である。これは,計算幾何
の処理を最適化するために位相複体を組合せアルゴリズムを使用して構成するという目的に反
しない。このことは,同時に幾何複体によって実現されない位相複体を使用して幾何的な制約
を無視した構造を生成することもできる。
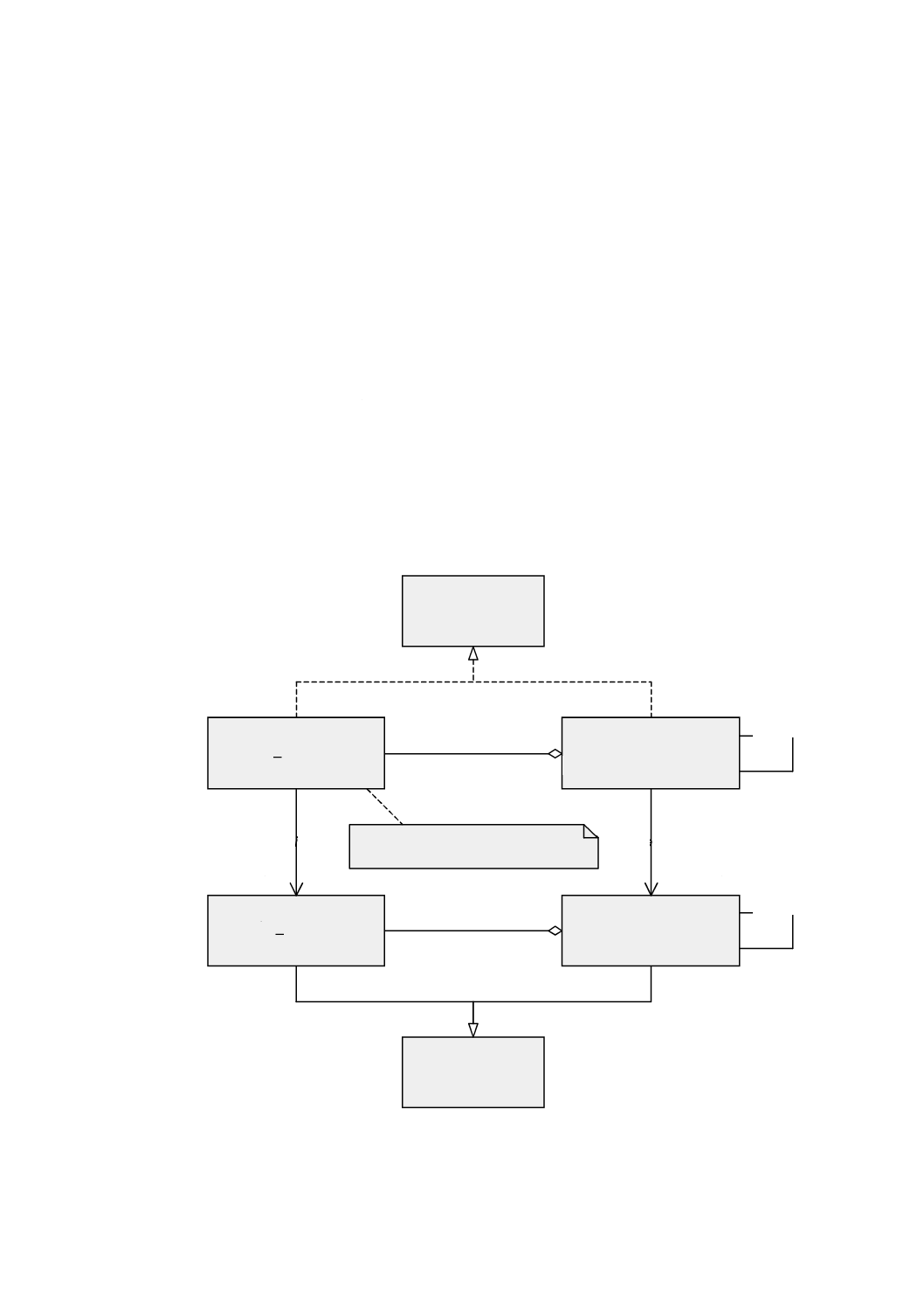
88
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
計算位相幾何の利用を理解するためには双方のシステムで関係する処理をみるとよい。図33に示すとお
り,プリミティブと複体とは,二つのクラス系列の中にあって相互に関係するその方式が非常に類似して
いる。
位相システムは,多変量多項式の代数的な操作を基礎としている。位相パッケージ中の処理,関数及び
操作は,幾何の領域における幾何的な問題を位相の領域における代数的な問題に置き換えて,そこで解い
た解を再び幾何の領域に置き換えられるものとして定義する。この代数における位相表現は,変数が位相
プリミティブに一致した多変量一次多項式とする。
図33は,位相と幾何との関係を要約して示す。このOCL制約は,この図において,TP̲Primitive::complex
役割にTP̲Complex.geometryを続けてたどったものが,TP̲Primitive::geometry役割にGM̲Primitive::complex
を続けてたどったものと等しいことを意味している。
備考 一つのGM̲Primitiveは,複数の独立したGM̲Complexと関係することができ,それらはそれ
ぞれ異なるTP̲Complexの実現となる可能性がある。そのためGM̲Primitiveは,TP̲Primitive
が一つの極大TP̲Complex(7.3.10.2参照)にしか含まれないことから,複数の異なるTP̲Primitive
に対する実現となってよい。インスタンス化可能なクラスはTP̲Primitive及びTP̲Complex又
はGM̲Primitive及びGM̲Complexの両方を実装することがあるので,TP̲Primitiveの特定のイ
ンスタンスをGM̲Compositeによって実現してもよい(附属書DのD.3参照)。
+ subComplex
1..n
1..n
+superComplex
«Interface»
TP̲Object
(from Topology root)
«Type»
TP̲Primitive
(from Topological primitive)
«Type»
GM̲Primitive
(from Geometric primitive)
«Type»
TP̲Complex
(from Topological Complex)
«Type»
GM̲Complex
(from Geometric complex)
{geometry.complex->includesAll(
complex.geometry)}
+ topology
0..n
+ geometry
0..1
Realization
0..1
+ topology
0..1
+ geometry
Realization
/Contains
+ subComplex
0..n
0..n
+superComplex
Contains
Complex
1..n
+element
1..n
+complex
Complex
+element
1..n
«Type»
GM̲Object
(from Geometry root)
0..n
+complex
図 33 幾何と位相との間の関係
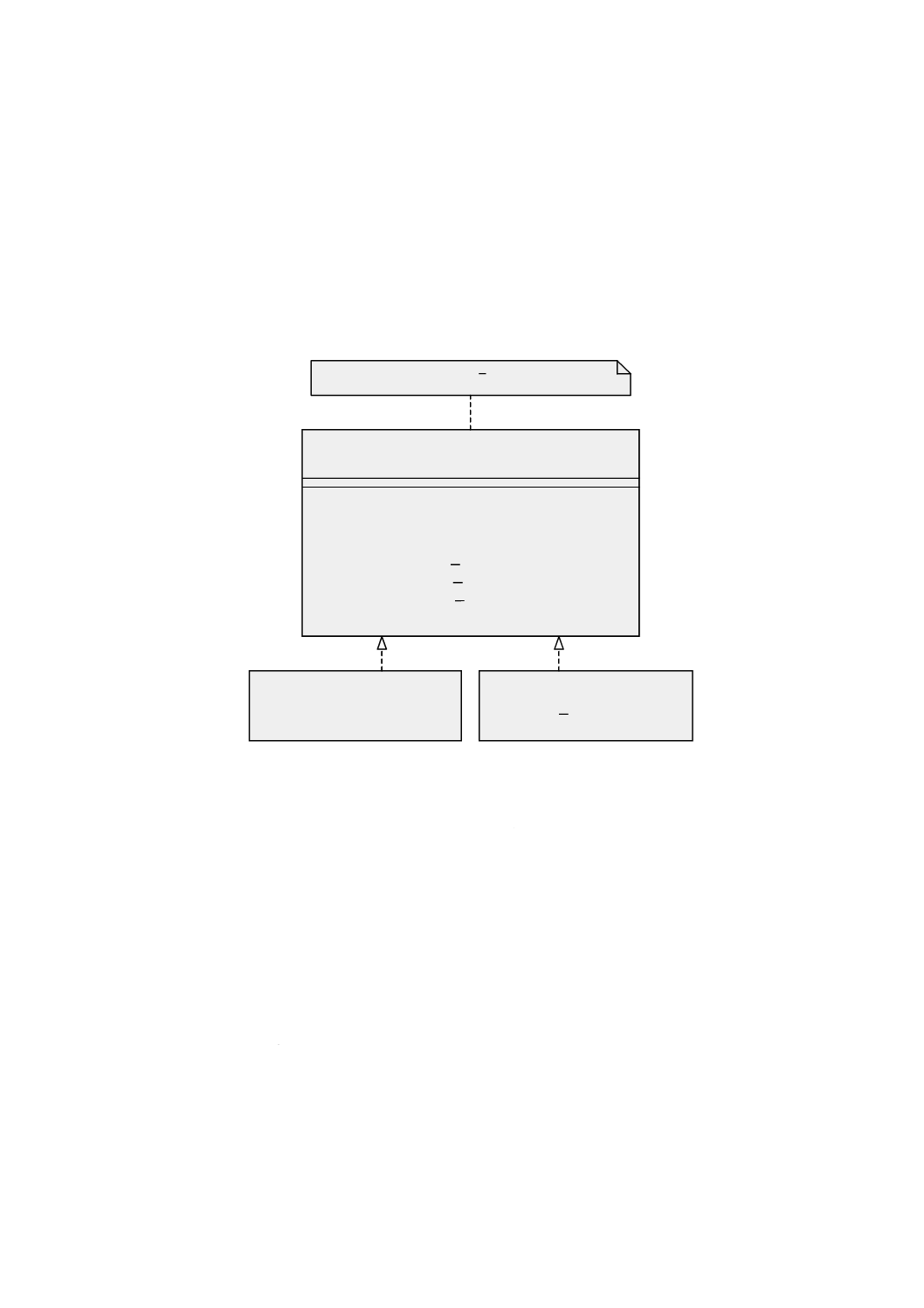
89
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.2.2
TP̲Object
7.2.2.1
意味 位相オブジェクト型であるTP̲Object(図34参照)は,抽象クラスであり,位相複体及び
位相プリミティブの基底型を供給する。
論理的及び構造的に,位相オブジェクトと幾何オブジェクトとは,同じ下位クラス構造を共有できる。
しかし,境界取得操作を維持した状態での位相から幾何への完全な準同形が存在するため,この手法は,
位相オブジェクトの境界とそれに対応する幾何オブジェクトの境界との間で混乱を生じさせることがある。
二つの仕組みは,準同形の示す多くの計算上の特徴を共有するが,それらは異なる操作であり明確に分け
て考える必要がある。
«Interface»
TP̲Object
+ dimension() : Integer
+ boundary() : TP̲Boundary
+ coBoundary() : Set<TP̲DirectedTopo>
+ interior() : Set<TP̲Primitive>
+ closure() : Set<TP̲Primitive>
+ exterior() : Set<TP̲Primitive>
+ maximalComplex() : TP̲Complex
«Type»
TP̲Primitive
(from Topological primitive)
«Type»
TP̲Complex
(from Topological Complex)
{boundary().dimension() = dimension() - 1}
図 34 TP̲Object
7.2.2.2
dimension “dimension”(次元取得)操作が返す整数は,このTP̲Objectの位相次元とする。そ
の値は,オブジェクトをインスタンス化したクラスに完全に依存し,そのオブジェクトのクラスを変更せ
ずにそのオブジェクトの次元を変更することはできない。例えばノードの次元の値は0,エッジは1,フェ
イスは2,位相立体は3とする。このTP̲Objectに関連したGM̲Objectは,すべてこれと同じ位相次元を
もつ。
TP̲Object::dimension() : Integer
7.2.2.3
boundary “boundary”(境界取得)操作はTP̲DirectedTopoの集合をTP̲Objectの境界を表現す
るTP̲Boundaryとして構造化し,それを返す。
TP̲Object::boundary() : TP̲Boundary
このTP̲ObjectがGM̲Objectと関連している場合,その境界は,幾何パッケージの中で記述される
GM̲Objectと向きが一致する。
制約条件として,境界の次元は,元のオブジェクトの次元より常に一次元低くなければならない。その
ため,空集合の次元は“-1”とみなす。
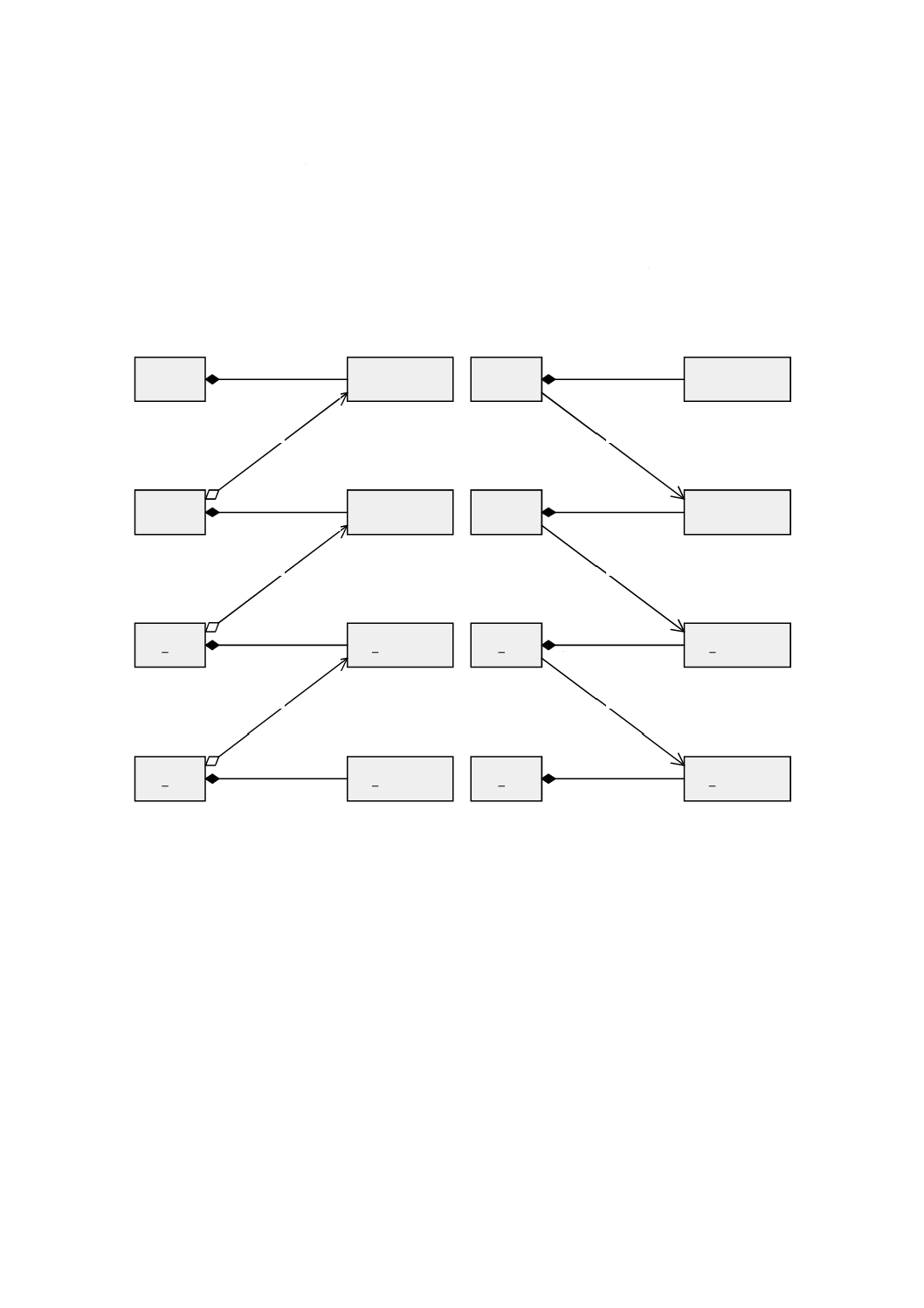
90
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲Object:
boundary.dimension() = dimension() ‒ 1
図35は,境界取得操作が,それぞれの次元のオブジェクトから一つ低い次元のオブジェクトへの関連と
しての表現を示す。
多くの場合,戻り値はTP̲Expression(7.3.20参照)の妥当な値となる。返される境界は,項を最も単純
にしなければならないという要件のため,妥当なTP̲Expressionとならない場合がある。フェイスのぶら
下がりエッジ(一方のノードをフェイス境界に,もう一方のノードをフェイス内にもつエッジ)又は孤立
エッジ(同じフェイス内に両側のノードをもつエッジ)は位相式へ変換する際に消去する。
«Type»
TP̲Node
«Type»
TP̲DirectedNode
+ proxy
2
1
+ topo
Center
«Type»
TP̲Edge
«Type»
TP̲DirectedEdge
+ proxy
2
1
+ topo
Center
«Type»
TP̲Face
«Type»
TP̲DirectedFace
+ proxy
2
1
+ topo
Center
«Type»
TP̲Solid
«Type»
TP̲DirectedSolid
+ proxy
2
1
+ topo
Center
+ boundary
2
«Type»
TP̲Node
«Type»
TP̲DirectedNode
2
+ proxy
+ topo
1
Center
«Type»
TP̲Edge
«Type»
TP̲DirectedEdge
2
+ proxy
+ topo
1
Center
«Type»
TP̲Face
«Type»
TP̲DirectedFace
2
+ proxy
+ topo
1
Center
«Type»
TP̲Solid
«Type»
TP̲DirectedSolid
2
+ proxy
+ topo
1
Center
1
+ hub
0..n
+ primitive
Boundary
+ boundary
1..n
0..n
+ primitive
Boundary
+ boundary
1..n
0..2
+ primitive
Boundary
CoBoundary
0..n
+ spoke
1..n
+ hub
CoBoundary
0..n
+ spoke
{CircularSequence}
1..n
+ hub
CoBoundary
0..2
+ spoke
図 35 関連として表される境界及び双対境界操作
7.2.2.4
coBoundary “coBoundary”(双対境界取得)操作は,このTP̲Objectを境界上にもつすべての
TP̲Objectを表現する,TP̲DirectedTopoの集合を返す。
多くの場合,戻り値は,TP̲Expression(7.3.20参照)の妥当な値になる。この例外として,対応する
GM̲Objectが始点及び終点が同じ点となる曲線のような閉じたオブジェクトの境界上にある場合がある。
そのようなGM̲Objectに対応するTP̲Objectは,互いに反対向きの二つのTP̲DirectedTopoの集合となり,
そのためcoBoundaryをTP̲DirectedTopoの集合からTP̲Expressionに変換する時に相殺される。
TP̲Object::coBoundary() : Set<TP̲DirectedTopo>
図35の右側の図は,この操作をTP̲Primitiveの次元レベル間の関係として表現している。その関係は,
boundary操作と類似してはいるが,次元の向きが逆であり,減少ではなく次元が増加する方向に向かって
いる。
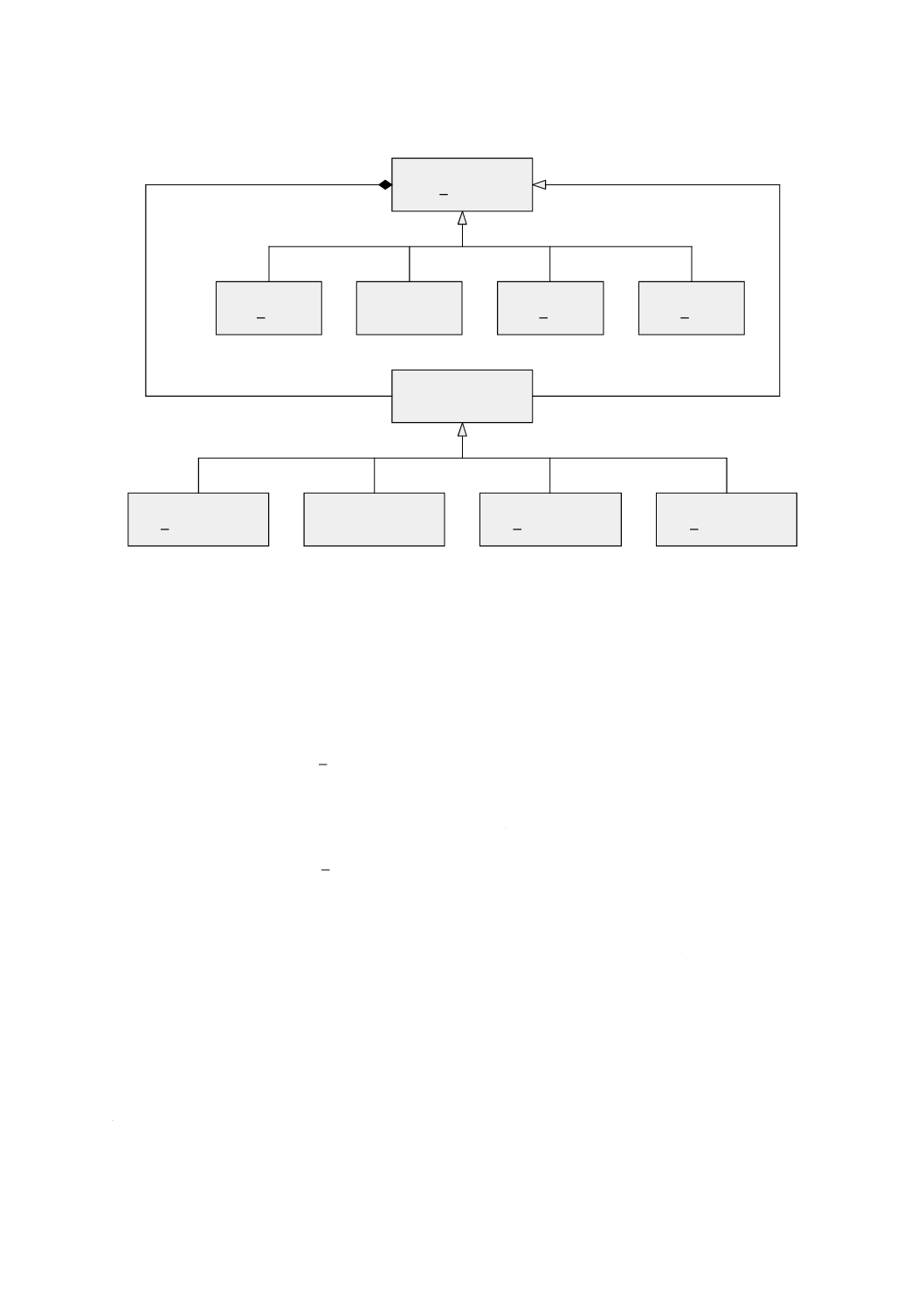
91
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
TP̲DirectedNode
«Type»
TP̲DirectedEdge
«Type»
TP̲DirectedFace
«Type»
TP̲DirectedSolid
«Type»
TP̲DirectedTopo
«Type»
TP̲Node
«Type»
TP̲Edge
«Type»
TP̲Face
«Type»
TP̲Solid
«Type»
TP̲Primitive
1
+ topo
2
+ proxy
Center
図 36 位相における重要なクラス
7.2.2.5
interior “interior”(内部取得)操作は,このオブジェクトの極大複体中の,このオブジェクト
の内部からなるTP̲Primitiveの有限集合を返す。TP̲Primitiveの場合,これは自己参照になる。TP̲Complex
の場合,これは,TP̲Complexの境界上のものを除いたTP̲ComplexのすべてのTP̲Primitive要素である。
これは,このTP̲Objectの幾何実現の内部と準同形である。
TP̲Object::interior() : Set<TP̲Primitive>
7.2.2.6
exterior “exterior”(外部取得)操作は,このオブジェクトの極大複体中の,このオブジェクト
の外部からなるTP̲Primitiveの有限集合を返す。これは,この複体に対する極大TP̲Complex中のすべて
のTP̲Primitiveのうち,このTP̲Objectの内部及び境界を除いたものからなる。
TP̲Object::exterior() : Set<TP̲Primitive>
7.2.2.7
closure “closure”(閉包取得)操作は,多くの場合で実用的である。これは,オブジェクトの
内部及び境界の和集合として定義され,それゆえ基本的な実装には必要としない。
TP̲Object::closure() = interior().union(boundary())
7.2.2.8
maximalComplex “maximalComplex”(極大複体)操作は,このTP̲Objectを含む極大TP̲Complex
を返す。
TP̲Object::maximalComplex() : TP̲Complex
TP̲Objectは,ただ一つの極大TP̲Complexに含まれなければならない。
備考 複体は,より大きい複体に含まれない場合極大である。この操作が暗示する多重度に対する制
約は,どのTP̲Objectも常にただ一つの極大複体の中にあることを意味する。
7.3
Topological primitiveパッケージ
92
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.1
意味 Topological primitive(位相プリミティブ)パッケージは,各次元のすべてのプリミティブを
含み,その構造上の関係を表現するためのクラスに対応する。
7.3.2
TP̲Boundary この位相境界データ型クラスは,位相パッケージで使用するすべての境界データ型
の基底クラスとする。これはTP̲Expressionであり,輪体となることを除き,他の詳細な要件はない。
TP̲Boundary:
isCycle();
7.3.3
TP̲ComplexBoundary この位相複体境界データ型クラスは,位相複体に対して位相パッケージで
使用するすべての境界データ型の基本クラスとする。これは,TP̲Expressionであることを除き,他の詳細
な要件はない。
7.3.4
TP̲PrimitiveBoundary 位相プリミティブは,その境界を返すことができる。TP̲PrimtiveBoundary
(位相プリミティブ境界)(図37参照)の下位のデータ型は,便利な方法でこれらの境界を構築するのに
使用する。TP̲Nodeは空の境界をもつので,その境界には特別なデータ型は定義しない。
すべての幾何オブジェクトの境界は,(境界をもたない)輪体であることは自明の事実である。曲面の境
界要素は,各々が閉じた環状合成曲線の集合である。位相と幾何との間の一貫性のため,このことは
TP̲Boundaryのすべての下位クラスにも必す(須)となる。TP̲Complexが幾何複体の位相を表す場合,幾
何実現は,この制約を強制する。
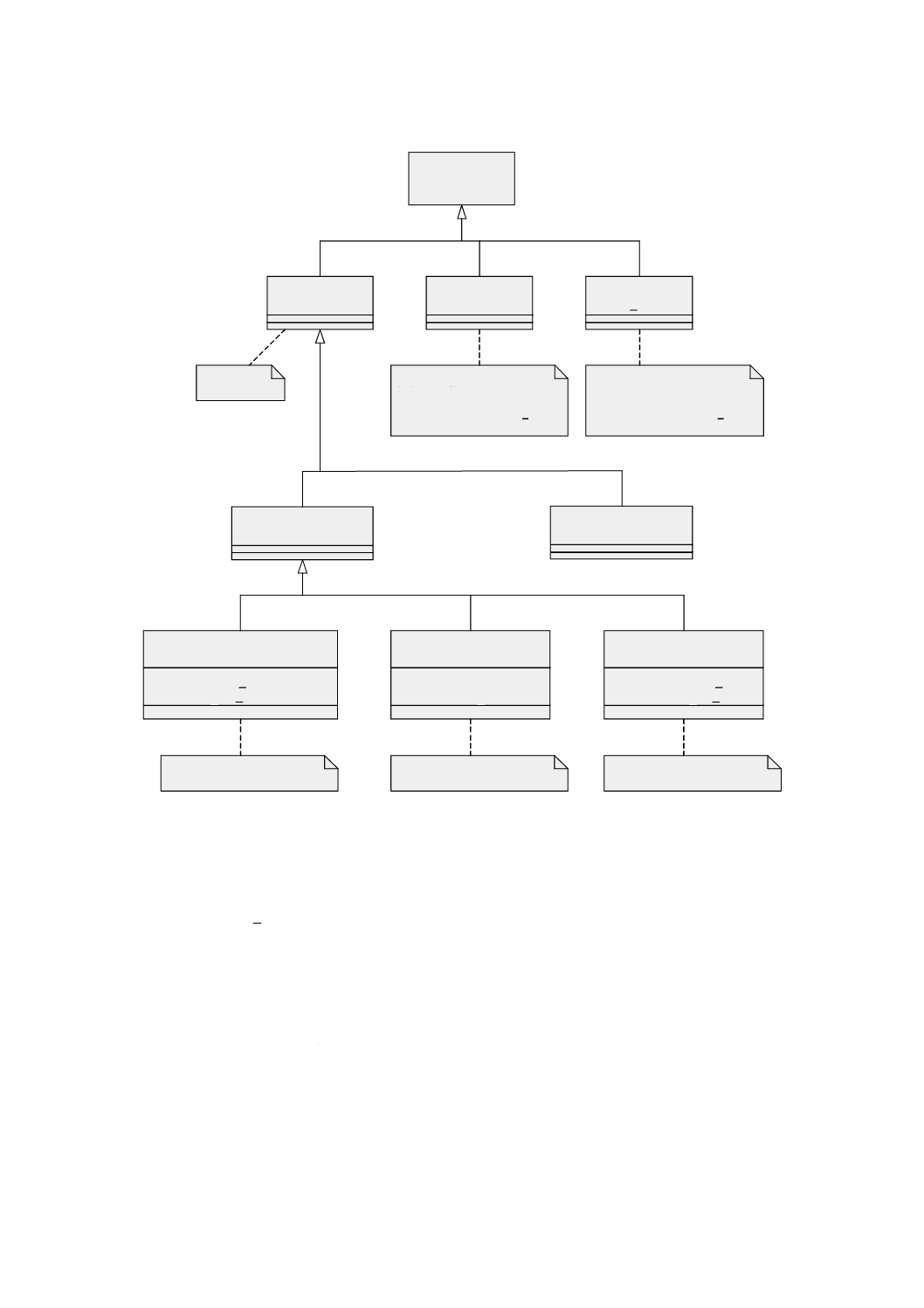
93
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«DataType»
TP̲Expression
«DataType»
TP̲Ring
«DataType»
TP̲Boundary
«DataType»
TP̲PrimitiveBoundary
«DataType»
TP̲Shell
«DataType»
TP̲ComplexBoundary
«DataType»
TP̲EdgeBoundary
+ startNode : TP̲DirectedNode
+ endNode : TP̲DirectedNode
«DataType»
TP̲FaceBoundary
+ exterior[0..1] : TP̲Ring
+ interior[0..n] : TP̲Ring
«DataType»
TP̲SolidBoundary
+ exterior[0..1] : TP̲Shell
+ interior[0..n] : TP̲Shell
{isCycle()}
{isCycle()}
{isSimple()}
{isConnected()}
{support().dimension() = 2}
{isCycle()}
{isSimple()}
{isConnected()}
{support().dimension() = 1}
{support().dimension() = 0}
{support().dimension() = 1}
{support().dimension() = 2}
図 37 境界関係データ型
7.3.5
TP̲EdgeBoundary TP̲EdgeBoundary(エッジ境界)(図37参照)は,TP̲DirectedNodeインスタ
ンスとして二つのTP̲Node参照を含む。startNodeは正の方向をもち,endNodeは負の方向をもつ。
TP̲Expressionとして,TP̲EdgeBoundaryは次のように表される。
Edge.boundary() = +endNode-startNode
TP̲EdgeBoundaryの属性は,次のとおりとする。
TP̲EdgeBoundary::startNode : TP̲DirectedNode;
TP̲EdgeBoundary::endNode : TP̲DirectedNode;
7.3.6
TP̲FaceBoundary TP̲FaceBoundary(フェイス境界)は,その境界の様々な要素に対応する幾つ
かのTP̲Ringからなる。通常の二次元では,これらの輪の内の一つは,外部境界として区別する。一般的
な多様体では,これは常に当てはまるとは限らず,その場合,すべての境界が内部境界として示され,外
部境界は空となる。
94
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲FaceBoundary::exterior[0,1] : TP̲Ring;
TP̲FaceBoundary::interior[0..n] : TP̲Ring;
各輪は,フェイスが輪の左側となるように向き付けられることを使用して,フェイスの境界を次の表現
で得る。
Boundary(face) = b : TP̲FaceBoundary = b.exterior + b.interior
7.3.7
TP̲SolidBoundary TP̲SolidBoundary(位相立体境界)は,TP̲FaceBoundaryと同様とする。通常
のユークリッド空間では,一つの位相殻は,外部として区別される。より一般的な場合,これは常に当て
はまるとは限らない。
TP̲SolidBoundary::exterior[0,1] : TP̲Shell;
TP̲SolidBoundary::interior[0..n] : TP̲Shell;
各殻は,位相立体が位相殻の下方となるように向き付けられることを用いて,位相立体の境界を次の表
現で得る。
Boundary(solid) = b : TP̲SolidBoundary = b.exterior + b.interior
7.3.8
TP̲Ring TP̲Ring(位相輪)は,TP̲FaceBoundaryの一つの接続した要素を表すのに使用する。
それは輪体(境界が空となるオブジェクト)内の接続した幾つかのTP̲DierctedEdgeからなる。TP̲Ring
は,列の各TP̲DirectedEdgeのendNodeが列の次のTP̲DirectedEdgeのstartNodeとなる点で構造上
GM̲CompositeCurveと類似している。列は環状列となるので,この規則には例外はない。
TP̲Expressionとして,TP̲Ringは有向なエッジの列とみなす。正の方向で用いる各エッジ“e”は“+e”
として表現され,負の方向を示す各エッジ“d”は“-d”として表現される。TP̲RingはTP̲FaceBoundary
オブジェクトの中で使用されるため,位相輪はすべての幾何実現においてフェイスがその左側になるよう
に方向付けられる。
7.3.9
TP̲Shell TP̲Shell(位相殻)は,TP̲SolidBoundaryの一つの接続した要素を表すのに用いる。こ
れは位相輪体(境界は空となるオブジェクト)内の接続した幾つかのTP̲Faceからなる。TP̲Ringとは異
なり,TP̲Shellは,自然な並べ替え順序をもたない。
TP̲Expressionとして,TP̲Shellは有向フェイスの集合とみなす。正の方向で用いる各フェイス“f”は
“+f”という表現で表し,負の方向を表す各フェイス“g”は“-g”という表現で表す。TP̲Shellは
TP̲SolidBoundaryオブジェクトで使用されるため,位相殻は,upNormalが立体から離れる方向を指すよう
に方向付けられる。
7.3.10 TP̲Primitive
7.3.10.1 意味 位相プリミティブTP̲Primitive(図38参照)は,位相複体の分解不可能な要素とする。そ
のため,これらは通常は幾何複体の要素である同次元の幾何プリミティブに対応する。幾何複体が位相複
体の実現となる場合,そのプリミティブ同士は,それぞれ次元を保ちつつ一対一対応しなければならない。
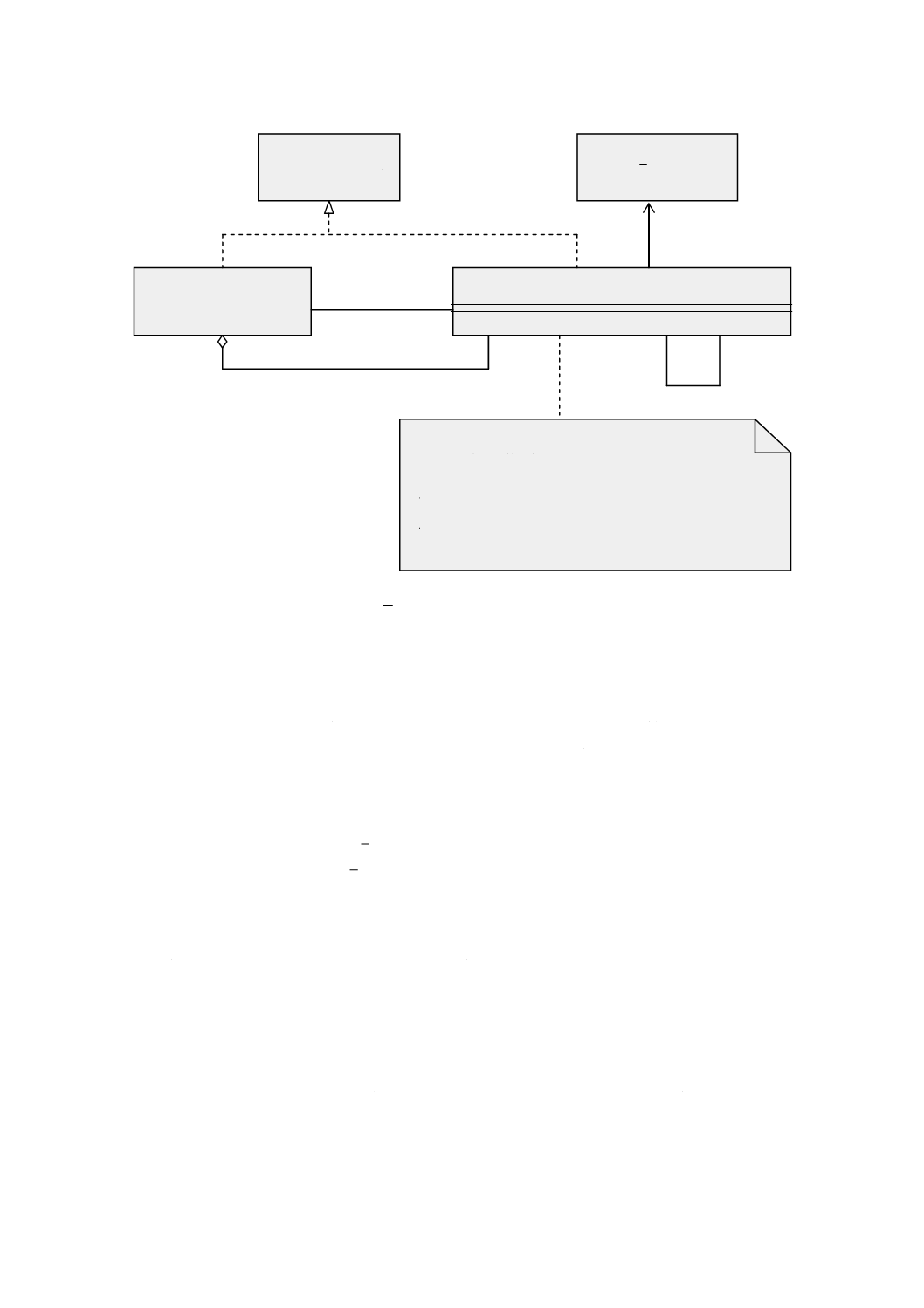
95
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Interface»
TP̲Object
(from Topology root)
«Type»
GM̲Primitive
(from Geometric primitive)
-- 位相次元は幾何次元に一致する
{geometry->forAll(geometry.dimension() = dimension())}
-- 基本的な幾何演算は保たれる
{complex.geometry->forAll(element->includes(geometry))}
{boundary().asTP̲Primitive().geometry = geometry.boundary()}
-- 孤立した位相プリミティブは次元が2以上小さい
{coincidentSubelement.dimension() < dimension() -1}
-- プリミティブはそれ自身の正のTP̲DirectedTopoとなる
{asTP̲DirectedTopo(+) = self}
«Type»
TP̲Primitive
+ asTP̲DirectedTopo(orientation : Sign) : TP̲DirectedTopo
«Type»
TP̲Complex
(from Topological Complex)
0..1
+ geometry
0..n
+ topology
Realization
+ maximalComplex
1
+ complex
1..n
+ element
1..n
0..1
+ container
0..n
+ isolated
IsolatedIn
図 38 TP̲Primitive (位相プリミティブ)
7.3.10.2 Realization “Realization”(実現)関連は,このTP̲Primitiveをその極大複体の中でこれを表現
するGM̲Primitiveに関連させる。このTP̲PrimitiveをGM̲Complexによって実現できない論理的位相構造
を記述するために使用する場合,この関係は,このTP̲Primitiveの極大TP̲Complexに含まれるすべての
TP̲Primitiveに対して空となる。各GM̲Primitiveは,各TP̲Complexに対して最大で一つのTP̲Primitive
と関連してよい。このTP̲Primitiveが,実現をもつTP̲Complexに含まれる場合,これは,必ず一つの
GM̲Primitiveと関連しなければならない。GM̲Primitiveは,異なるTP̲Complexの中の異なるTP̲Primitive
に関連してよい。
TP̲Primitive::geometry [0,1] : GM̲Primitive
GM̲Primitive::topology [0..n] : TP̲Primitive
備考 GM̲Compositeは,対応するプリミティブの下位型であるため,TP̲Primitiveの実現が同じ次元
のGM̲Compositeとなるようなスキーマを定義できる。このため,TP̲Edgeは,
GM̲CompositeCurveとして実現できる(附属書DのD.3参照)。
位相オブジェクト及びその境界取得操作と幾何オブジェクト及びその境界取得操作との間での準同形を
維持するために,この関連によって定義される写像は,次元を保たなければならず,二つの領域で要素と
複体との間の関連が保たれなければならない。
TP̲Primitive:
dimension() = geometry.dimension();
7.3.10.3 Complex関連 “Complex”(複体)関連は,このTP̲Primitiveを,それを含むTP̲Complexの有
限集合に関連させる。いずれのTP̲Primitiveも,そのTP̲Primitiveを含む一意な極大TP̲Complexの部分
複体となる,幾つかのTP̲Complexに含まれる。
96
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲Primitive::complex [1..n] : TP̲Complex
TP̲Complex::element [1..n] : TP̲Primitive
7.3.10.4 Isolated In関連 次元の差が1又は0のプリミティブ間の位相での隣接関係はすべて,境界取得
操作及び双対境界取得操作によって扱われる。これらの操作は,一つ高い次元の他のプリミティブの境界
上にある一つのプリミティブのインスタンス又は共通の境界要素を共有する同じ次元のインスタンスだけ
を扱う。これは両側に同じフェイスをもつ“ぶら下がり”エッジ又は両側に同じ位相立体をもつ“ぶら下
がり”フェイスのインスタンスを含む。この例外は,一つのプリミティブが中間的なプリミティブなしに
二つ以上高い次元をもつプリミティブによって完全に囲まれている場合である。これらは,真に孤立
(isolated)している。フェイスでは,そのフェイスの境界上の中間的なエッジと接続しないノードはこれ
に含まれる。三次元空間では孤立ノードは,フェイスを実現する曲面に直交する曲線によって実現される
エッジの場合のように,当該曲面の境界上にない他のエッジと結合することができる。位相立体では,こ
の位相立体の境界上の曲面に属さないノード又はエッジを含むことができる。
TP̲Primitive::isolated [0..n] : TP̲Primitive
TP̲Primitive::container [0,1] : TP̲Primitive
TP̲Primitive:
isolated.dimension() < self.dimension() ‒ 1;
container.count = 0 implies TP̲Primitive->exists(boundary().topo->includes(self))
7.3.10.5 boundary TP̲Primitiveの境界取得操作は,TP̲DirectedTopoの集合に構造を追加することによっ
てTP̲Objectで定義された境界を置き換える。
TP̲Primitive::boundary() : TP̲PrimitiveBoundary
TP̲Primitiveは抽象型であるため,追加構造はその下位型に対してそれぞれ定義する。
7.3.11 TP̲DirectedTopo
7.3.11.1 意味 計算上の観点から見ると,TP̲DirectedTopo(有向位相)(図39及び図40参照)の要素は,
geometryパッケージの様々な有向幾何オブジェクト(GM̲OrientableObject)に相当(GM̲OrientableCurve
及びGM̲OrientableSurface)する。TP̲DirectedNode及びTP̲DirectedSolidは,それに相当する個別の幾何
オブジェクトをもたない。
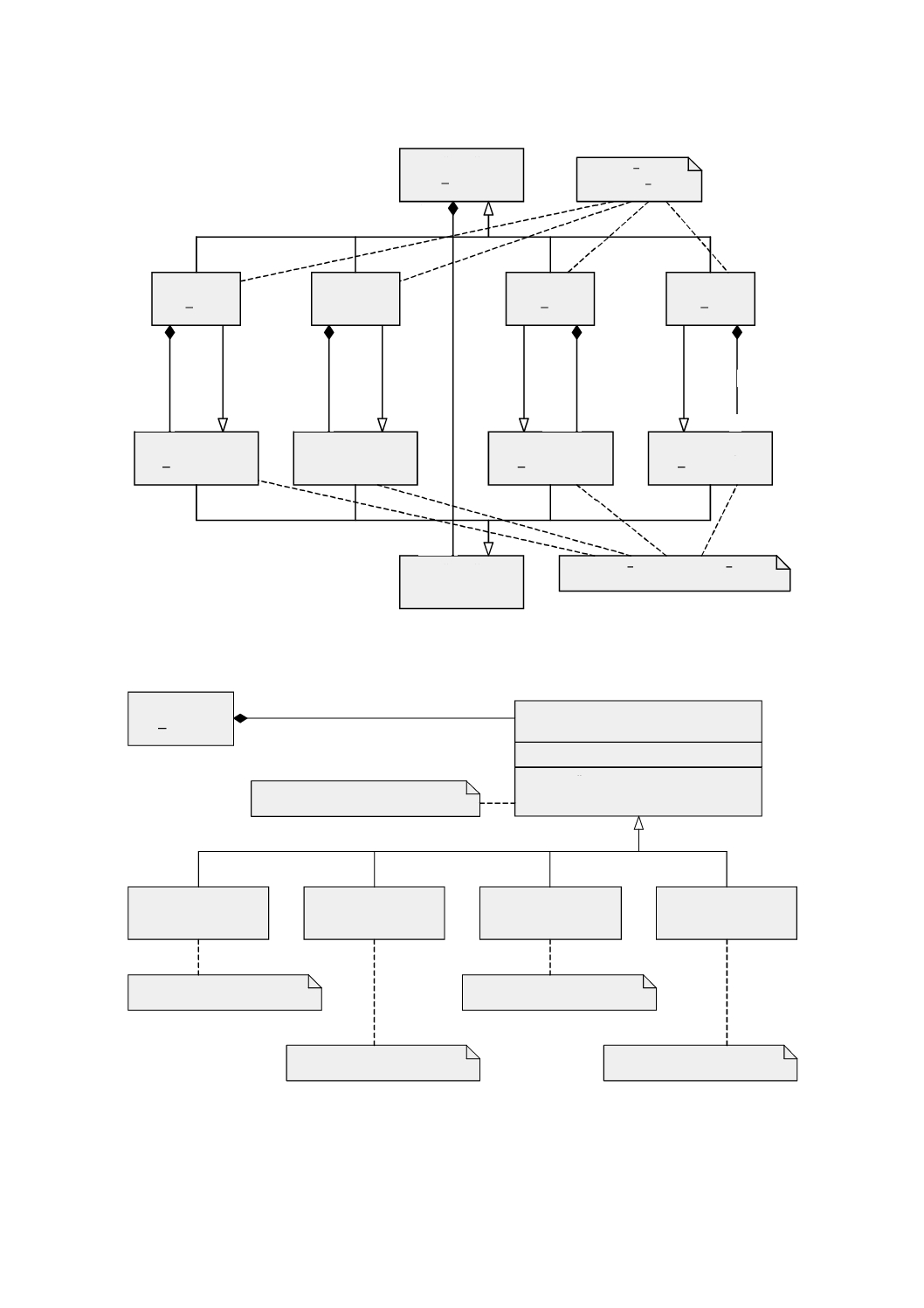
97
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
«Type»
TP̲DirectedNode
«Type»
TP̲DirectedEdge
«Type»
TP̲DirectedFace
«Type»
TP̲DirectedSolid
«Type»
TP̲DirectedTopo
«Type»
TP̲Node
«Type»
TP̲Edge
«Type»
TP̲Face
«Type»
TP̲Solid
«Type»
TP̲Primitive
{primitive = self}
{orientation = "+"}
{orientation = "+" implies topo = self}
+ topo
1
+ topo
1
+ topo
1
+ topo
1
+ proxy 2
+ proxy 2
+ proxy 2
2 + proxy
+ topo
1
+ proxy 2
Center
Center
Center
Center
Center
図 39 TP̲DirectedTopoの下位クラス
«Type»
TP̲Primitive
«Type»
TP̲DirectedTopo
+ orientation : Sign = "+"
+ negate() : TP̲DirectedTopo
+ asTP̲Expression() : TP̲Expression
«Type»
TP̲DirectedNode
«Type»
TP̲DirectedEdge
«Type»
TP̲DirectedFace
«Type»
TP̲DirectedSolid
{topo.isKindOf(TP̲Node)}
{topo.isKindOf(TP̲Edge)}
{topo.isKindOf(TP̲Face)}
{topo.isKindOf(TP̲Solid)}
{(orientation = "+") = (topo = self)}
+ topo
1
+ proxy
2
Center
図 40 TP̲DirectedTopo
98
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
幾何の場合と同様に,各位相プリミティブは,その対応する有向位相プリミティブを継承するが,より
多くの制約をみたす。これは,TP̲Nodeが正のTP̲DirectedNodeと等価であり,TP̲Edgeが正の
TP̲DirectedEdgeと等価であるなどを意味する。
備考 他の型階層の選択肢として,TP̲PrimitiveとTP̲DirectedTopoとを分離するものを考えると,各
プリミティブにプリミティブ自身,それと等価な正の有向位相プリミティブ及びその逆(負の
有向位相プリミティブ)の三つのオブジェクトを必要とする。この選択肢は,このモデルの抽
象型の有効な実装ではあるが,位相プリミティブとその正の有向位相プリミティブとの論理的
な等価性は強調されない。代数的な観点から,正の有向プリミティブでプリミティブを識別す
る下位クラス化及びOCL制約は,これを“x = + x”となる代数の単項“+”(プラス)の標準的
な解釈と等価にする。位相オブジェクトの最も有効な利用は,その記号操作にあるので,代数
による比ゆ(喩)を扱うことは適切である。
隣接次元の有向位相オブジェクト間には,暗黙の関係がある。境界及び双対境界における操作と関係と
は,同じ方向性の意味を保持している。そのため,正の有向エッジがフェイスの境界上にある場合,正の
有向フェイスは関連付けられたエッジの双対境界となる。正の有向ノードがエッジの境界上にある場合,
対応する正の有向エッジは,関連付けられたノードの双対境界となる。
7.3.11.2 orientation “orientation”(方向性取得)属性は,この有向位相オブジェクトがその元になる
TP̲Primitiveに対する向きとする。
TP̲DirectedTopo::orientation : Sign = “+”
7.3.11.3 negate “negate”(反転取得)操作は,このプリミティブの逆向きを返す。
TP̲DirectedTopo::negate() : TP̲DirectedTopo
7.3.11.4 asTP̲Expression “asTP̲Expression”(位相式変換)操作はTP̲DirectedTopoからTP̲Expression
を生成し,方向性の向き及び符号を保つ。この操作は,TP̲Expressionクラスのコンストラクタとする。
TP̲DirectedTopo::asTP̲Expression() : TP̲Expression
7.3.11.5 Center関連 “Center”(中心)関連の“topo”(位相)役割は,関連付けられたTP̲Primitiveを
識別する。反対の“proxy”(代理)役割は,TP̲Primitiveに関連付けられた二つのTP̲DirectedTopoインス
タンスを識別する。
TP̲DirectedTopo::topo [1] : TP̲Primitive
TP̲Primitive::proxy [2] : TP̲DirectedTopo
7.3.11.6 制約 有向位相オブジェクトの意味上の体系に従うため,有向位相オブジェクトに関連付けられ
る位相は,適切な型をもたなければならない。
TP̲DirectedNode:
topo.isKindOf(TP̲Node);
TP̲DirectedEdge:
topo.isKindOf(TP̲Edge);
TP̲DirectedFace:
topo.isKindOf(TP̲Face);
TP̲DirectedSolid:
topo.isKindOf(TP̲Solid);
備考 これらの制約は,位相プリミティブに対応する有向位相プリミティブのクラスがこの対応する
位相プリミティブの型を実現しなければならないことを示すのに,OCL演算子の“isKindOf”
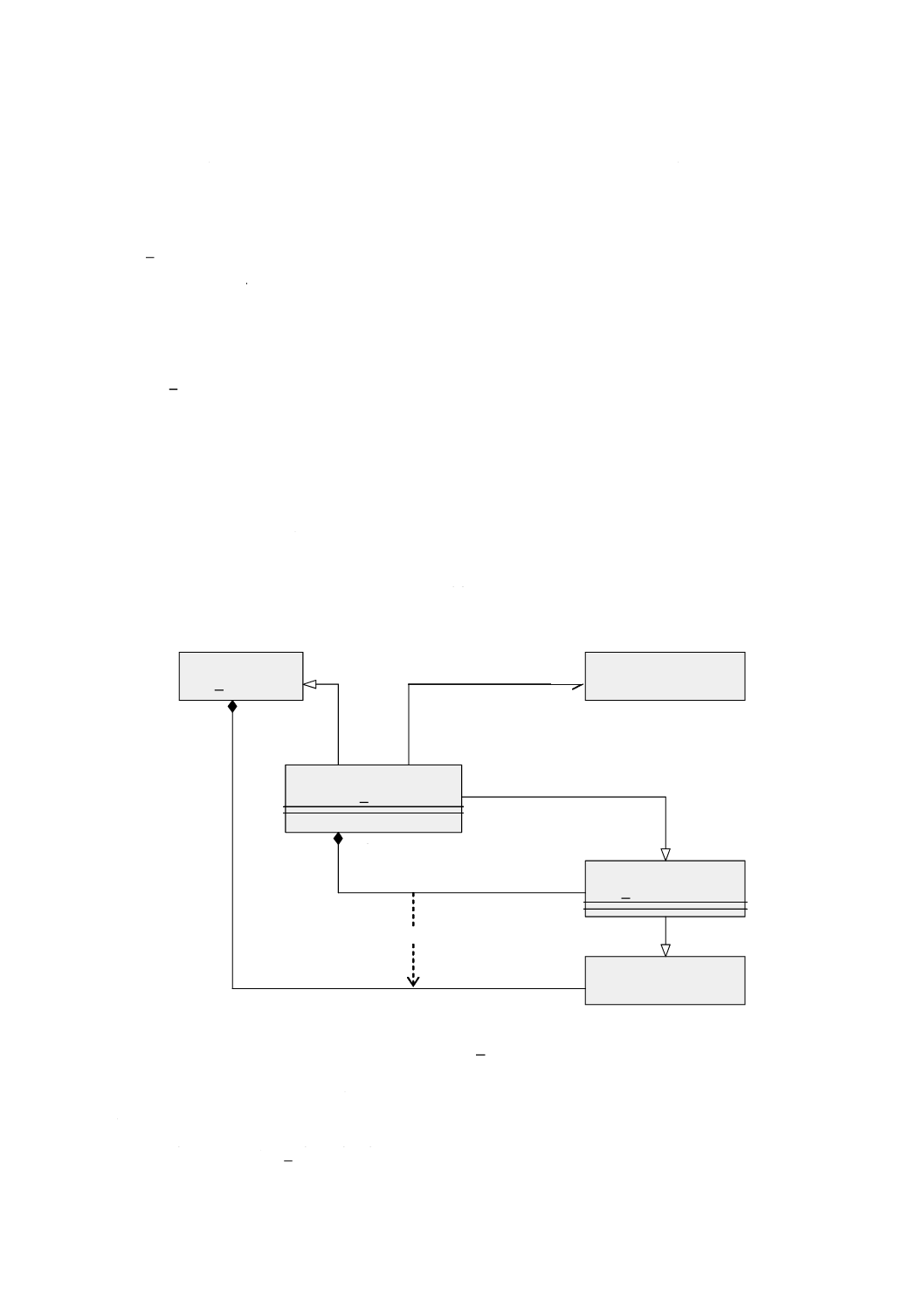
99
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を使用している。
“Center”関連は,“boundary”及び“coBoundary”操作の代数の重要な部分を形成する。
TP̲DirectedTopo:
[boundary() = (orientation)*topo.boundary()]
TP̲Primitive:
[boundary() = (proxy.orientation)*proxy.boundary()]
TP̲DirectedTopo:
negate.topo = topo;
negate.orientation <> orientation;
7.3.12 TP̲Node
7.3.12.1 意味 TP̲Node(ノード)(図41参照)は,そのすべてのインタフェースをTP̲Primitiveから境
界及び双対境界の構造を多少同化しながら継承する。
TP̲Nodeの場合,TP̲Objectで定義した“coBoundary”操作は,常に,そのノードに入るエッジ(正の
TP̲DirectedEdge)と出るエッジ(負のTP̲DirectedEdge)とを示す,TP̲DirectedEdgeへの参照の集合を返
す。この操作は,TP̲Objectから継承したものを置き換える。同じ情報を関連として表現してよい。
備考 このTP̲Nodeを含む二次元の極大TP̲Complexでは,coBoundaryは,その極大TP̲Complexの
幾何実現において時計回りの環状列として並べてもよい。三次元複体では,順序は不定である。
TP̲Node::coBoundary() : Set<TP̲DirectedEdge> {size = [0..n]}
TP̲Node::CoBoundary.spoke : Set<TP̲DirectedEdge> {size = [0..n]}
«Type»
TP̲Primitive
«Type»
TP̲Node
«Type»
TP̲DirectedEdge
«Type»
TP̲DirectedTopo
«Type»
TP̲DirectedNode
1
+ topo
0..n
+ spoke
CoBoundary
+ hub
1
1
+ topo
+ proxy
2
+ proxy
2
subset
Center
Center
+boundary() : NULL
図 41 TP̲Node
7.3.12.2 Center関連 TP̲Nodeを含む各TP̲Primitiveは,二つのTP̲DiectedTopoインスタンスに関連付
けられる。
TP̲Node::proxy [2] : TP̲DirectedNode
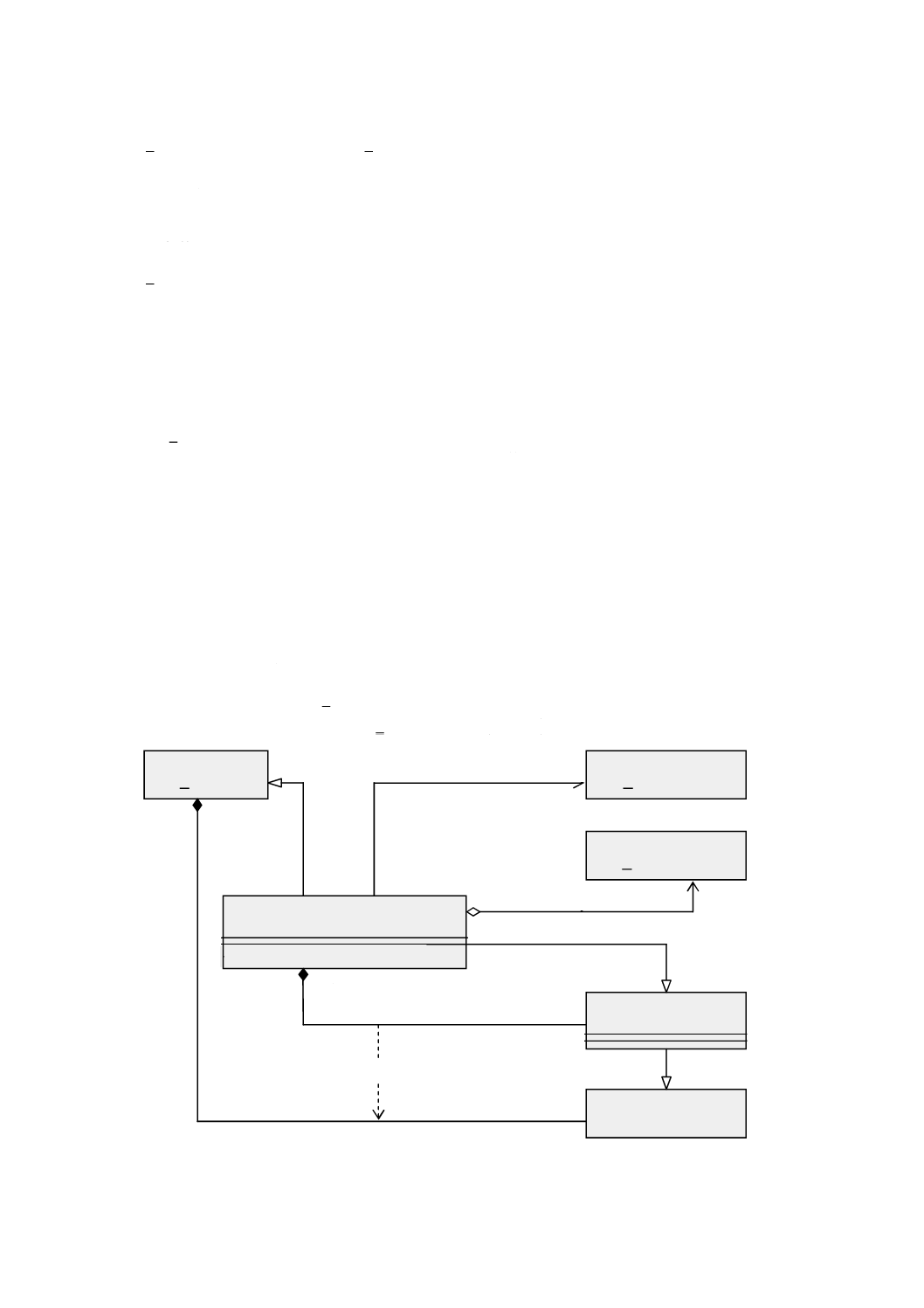
100
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲DirectedNode [1] : Reference<TP̲Node>
7.3.12.3 boundary TP̲Nodeの境界取得操作は,空集合を指定することによって,TP̲Objectで定義され
た境界を置き換える。
TP̲Primitive::boundary() : NULL
7.3.12.4 制約 TP̲Nodeの次元は0でなければならず,その境界は空(NULL)とする。
TP̲Node:
TP̲Object::dimension = 0;
TP̲Object::boundary() = NULL;
備考 ノードは,エッジがそれを含むフェイスの境界上にない限り,フェイスの中で孤立しながらも
エッジの端点となってよい。この幾何実現には,空間にぶら下がった曲線が曲面と交差する場
合がある。
7.3.13 TP̲DirectedNode
7.3.13.1 意味 TP̲DirectedNode(有向ノード)クラスは,計算位相幾何クラスのTP̲Expressionにおいて,
TP̲Nodeに対応する。TP̲Nodeの場合,TP̲Objectで定義した“boundary”操作は,常に空となる幾何に
対応した0値式を返す。この操作は,TP̲Objectから継承したものを置き換える。
TP̲Node::boundary() : NULL
7.3.14 TP̲Edge
7.3.14.1 意味 TP̲Edge(エッジ)プリミティブ(図42参照)は,位相のための一次元プリミティブとす
る。TP̲Edgeの場合,TP̲Objectで定義した“boundary”操作は,一方がエッジの始点(負のTP̲DirectedNode)
に,もう一方がエッジの終点(正のTP̲DirectedNode)となるノードの対を返す。この操作は,TP̲Object
から継承したものを置き換える。同じ情報を関連として表現してよい。
TP̲Edge::boundary() : Set<TP̲DirectedNode> {size = 2}
TP̲Edge::Boundary.boundary : Set<TP̲DirectedNode> {size = 2}
図 42 TP̲Edge
«Type»
TP̲Primitive
«Type»
TP̲Edge
«Type»
TP̲DirectedFace
«Type»
TP̲DirectedTopo
«Type»
TP̲DirectedEdge
1
+ topo
+ spoke
0..n
CoBoundary
+ hub
1..n
1
+ topo
+ proxy
2
+ proxy
2
subset
Center
Center
«Type»
TP̲DirectedNode
Boundary
0..n
+ primitive
+ boundary
2
+boundary() : TP̲EdgeBoundary
{CircularSequence}
101
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.14.2 coBoundary TP̲Edgeの場合,TP̲Objectで定義した“coBoundary”(双対境界取得)操作は,こ
のエッジ(正のTP̲DirectedFaceの場合)又はその逆向きの代替表現(負のTP̲DiretedFaceの場合)をそ
の境界として使用しているフェイスを示す,有向フェイスの環状列を返す。環状列は,このTP̲Edgeを含
む極大TP̲Complexの幾何実現において,これらのフェイスを関連付けられた曲線の端点から見て時計回
りに列挙して表現しなければならない。この操作は,TP̲Objectから継承したものを置き換える。同じ情
報を関連として実装してよい。
TP̲Edge::coBoundary() : CircularSequence<TP̲DirectedFace> {size = [0..n]}
TP̲Edge::coBoundary.spoke : CircularSequence<TP̲DirectedFace> {size = [0..n]}
備考 二次元平面の場合,双対境界は,最大でも二つのフェイスとなる。完全位相の場合,ちょうど
二つが存在し,一方の有向フェイスは正である“+”の向きをもって関連付けられたフェイス
がエッジの左側に位置して,もう一方は負である“-”の向きをもって関連付けられたフェイス
がエッジの右側に位置する。
7.3.14.3 boundary TP̲Edgeのboundary操作は,始点ノード及び終点ノードからなるTP̲EdgeBoundary
を指定することによって,TP̲Objectからの継承として置き換える。
TP̲Edge::boundary() : TP̲EdgeBoundary
TP̲Edgeは,Boundary関連及びboundary関連役割も格納しなければならない。boundary関連役割は,こ
れと同じ情報を,終点ノードに対して正の方向を向き,始点ノードに対して負の方向を向く二つの有向エ
ッジとして規定する。
TP̲Edge::boundary [2] : TP̲DirectedNode
7.3.14.4 Center関連 TP̲Edgeを含む各TP̲Primitiveは,二つのTP̲DirectedTopoインスタンスに関連付
けられる。
TP̲Edge::proxy [2] : TP̲DirectedEdge
TP̲DirectedEdge::topo [1] : Reference<TP̲Edge>
備考 二次元平面では,各有向エッジは,最大でも一つのフェイスの境界となり,完全平面位相では,
ちょうど一つのフェイスの境界となる。三次元又は非平面二次元複体では,有向エッジは,幾
つかのフェイスの境界となることができる。
7.3.14.5 制約 TP̲Edgeの次元は,1でなければならない。
TP̲Edge:
TP̲Object::dimension() = 1
7.3.15 TP̲DirectedEdge TP̲DirectedEdge(有向エッジ)クラスは計算位相幾何クラスのTP̲Expression
においてTP̲Edgeに対応する。これは,元となる曲線・エッジが必要なときにその代替として機能すると
いう点で,GM̲OrientableCurveの概念に類似する。
7.3.16 TP̲Face
7.3.16.1 意味 TP̲Face(フェイス)クラス(図43参照)は,GM̲Surfaceに対応する位相プリミティブ
を提供する。
7.3.16.2 boundary TP̲Faceの場合,TP̲Objectで定義した“boundary”(境界取得)操作は,適切な方向
性をもつ有向エッジの集合を返す。この操作は,TP̲Objectから継承したものを置き換える。同じ情報を
関連として表現してよい。
TP̲Face::boundary() : TP̲FaceBoundary
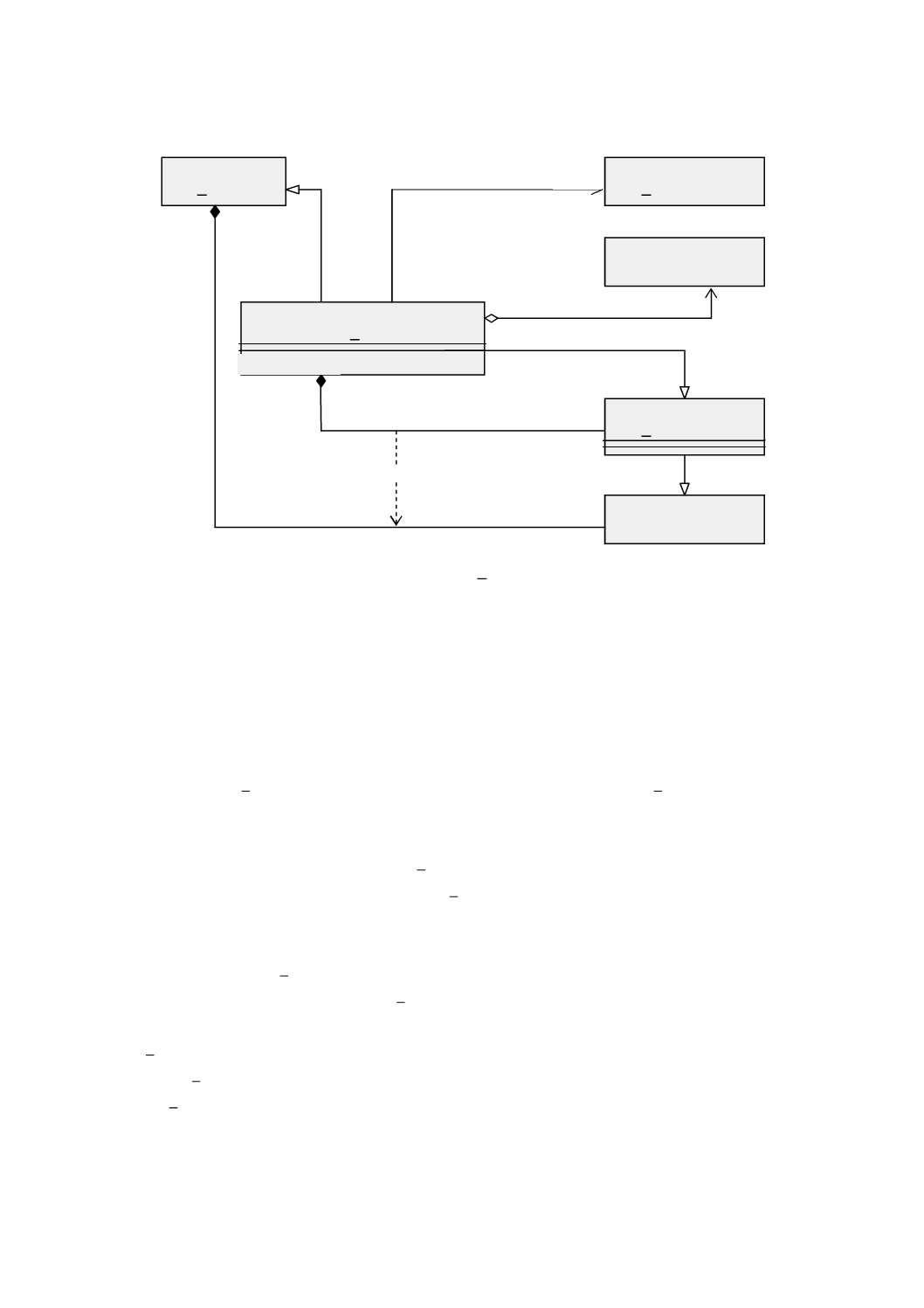
102
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 exteriorの意味について,幾何と同一の制約を位相にも適用する。
«Type»
TP̲Primitive
«Type»
TP̲Face
«Type»
TP̲DirectedSolid
«Type»
TP̲DirectedTopo
«Type»
TP̲DirectedFace
1
+ topo
+ spoke
0..2
CoBoundary
+ hub
1..n
1
+ topo
+ proxy
2
+ proxy
2
subset
Center
Center
«Type»
TP̲DirectedEdge
Boundary
0..n
+ primitive
+ boundary
1..n
+boundary() : TP̲FaceBoundary
図 43 TP̲Face
TP̲Faceは,Boundary関連及びboundary関連役割も格納しなければならない。boundary関連
役割は,これと同じ情報を,エッジの左側に対して正の方向を向き,エッジの右側に対して負
の方向を向く有向エッジとして規定する。
TP̲Face::boundary [1..*] : TP̲DirectedEdge
境界取得操作は,TP̲FaceBoundaryを構成する輪及び外部となる輪の指定を付加情報として
返す。
7.3.16.3 coBoundary TP̲Faceの場合,TP̲Objectで定義した“coBoundary”(双対境界取得)操作は,こ
のフェイス(正のTP̲DirectedSolidの場合)又はその逆向きの代替表現(負のTP̲DirectedSolidの場合)を
その境界に用いる位相立体を示す,有向位相立体への参照の集合を返す。この操作は,TP̲Objectから継
承したものを置き換える。同じ情報を関連として実装してよい。
TP̲Face::coBoundary() [0..2] : Reference<TP̲DirectedSolid>
TP̲Face::CoBoundary.spoke [0..2] : Reference<TP̲DirectedSolid>
7.3.16.4 Center関連 TP̲Faceを含む各TP̲Primitiveは,二つのTP̲DirectedTopoインスタンスに関連付
けられる。
TP̲Face::proxy [2] : TP̲DirectedFace
TP̲DirectedFace::topo [1] : Reference<TP̲Face>
7.3.16.5 制約 TP̲Faceの次元は,2でなければならない。
TP̲Face:
TP̲Face: TP̲Object::dimension = 2
7.3.17 TP̲DirectedFace TP̲DirectedFace(有向フェイス)は,TP̲Solidの境界の定義に用いる。これは,
元となる曲面・フェイスが必要なときに,その代替として機能するという点で,GM̲OrientableSurfaceの
概念に類似している。
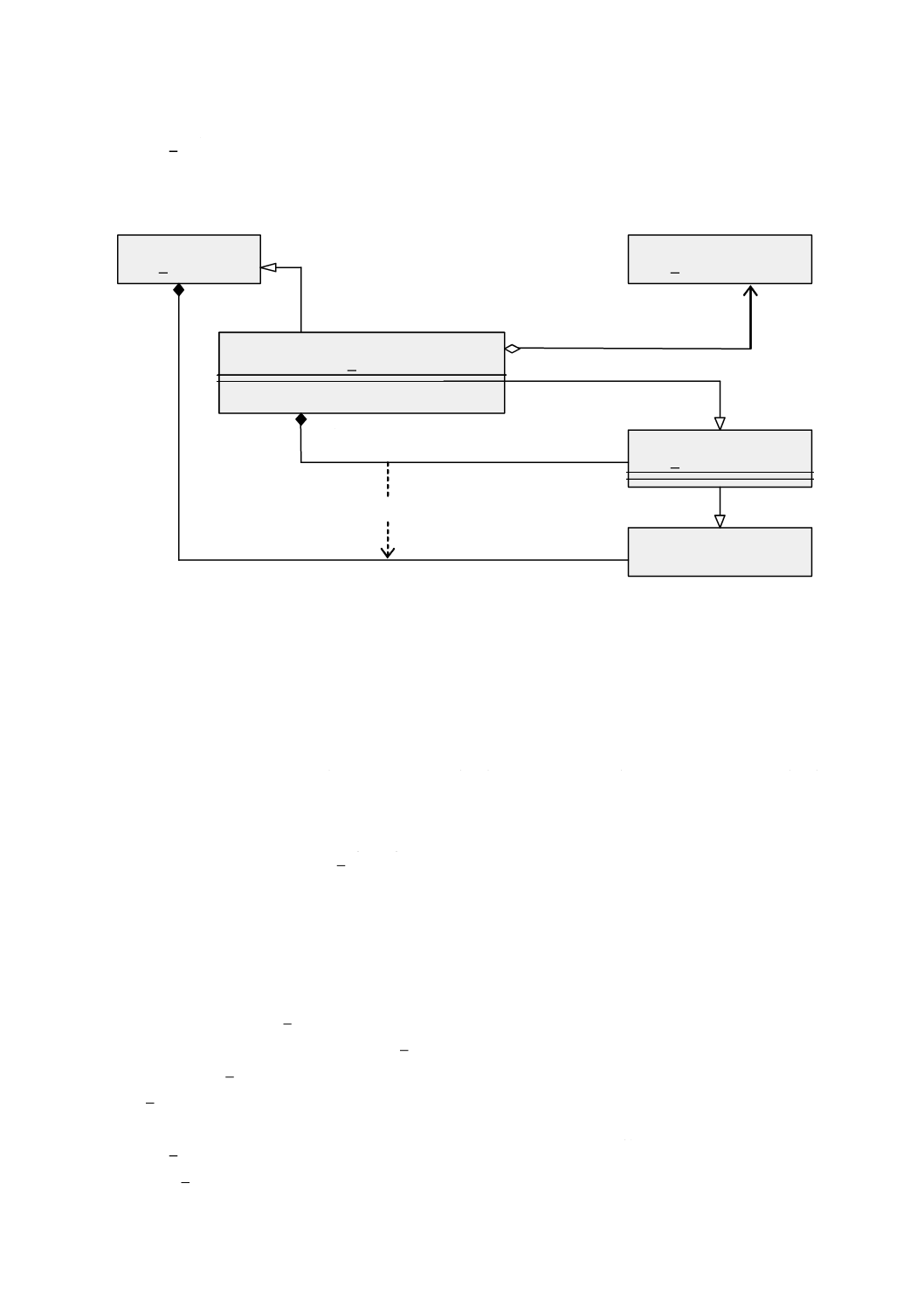
103
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.18 TP̲Solid
7.3.18.1 意味 TP̲Solid”(位相立体)クラス(図44参照)は,GM̲Solidに対応する位相プリミティブを
提供する。
«Type»
TP̲Primitive
«Type»
TP̲Solid
«Type»
TP̲DirectedTopo
«Type»
TP̲DirectedSolid
1
+ topo
1
+ topo
+ proxy
2
+ proxy
2
subset
Center
Center
«Type»
TP̲DirectedFace
Boundary
+ primitive
0..2
+ boundary
1..n
+boundary (): TP̲SolidBoundary
図 44 TP̲Solid
7.3.18.2 boundary TP̲Solidの場合,TP̲Objectで定義した“boundary”(境界取得)操作は,フェイス又
はその負の代替表現の集合を返す。この操作は,TP̲Objectから継承したものを置き換える。同じ情報を
関連として表現してよい。
TP̲Solid::boundary() : TP̲SolidBoundary
TP̲Solidは,Boundary関連及びboundary関連役割も格納しなければならない。boundary関連役割
は,これと同じ情報を,フェイスの下方に対して正の方向を向き,フェイスの上方に対して負の方向
を向く有向エッジとして規定する。
TP̲Solid::boundary [1..*] : TP̲DirectedFace
境界取得操作は,TP̲FaceBoundaryを構成する殻及び外部となる殻の指定を付加情報として返す。
7.3.18.3 coBoundary TP̲Solidの場合,“coBoundary”(双対境界取得)操作は,NULLを返す。
TP̲Solid::coBoundary() : NULL
7.3.18.4 Center関連 TP̲Solidを含む各TP̲Primitiveは,二つのTP̲DirectedTopoインスタンスと関連付
けられる。
TP̲Solid::proxy [2] : TP̲DirectedSolid
TP̲DirectedSolid::topo [1] : Reference<TP̲Solid>
7.3.18.5 制約 TP̲Solidの次元は3でなければならない。
TP̲Solid:
TP̲Object::dimension = 3
7.3.19 TP̲DirectedSolid “TP̲DirectedSolid”(有向位相立体)クラスは,計算幾何クラスのTP̲Expression
においてTP̲Solidに対応する。
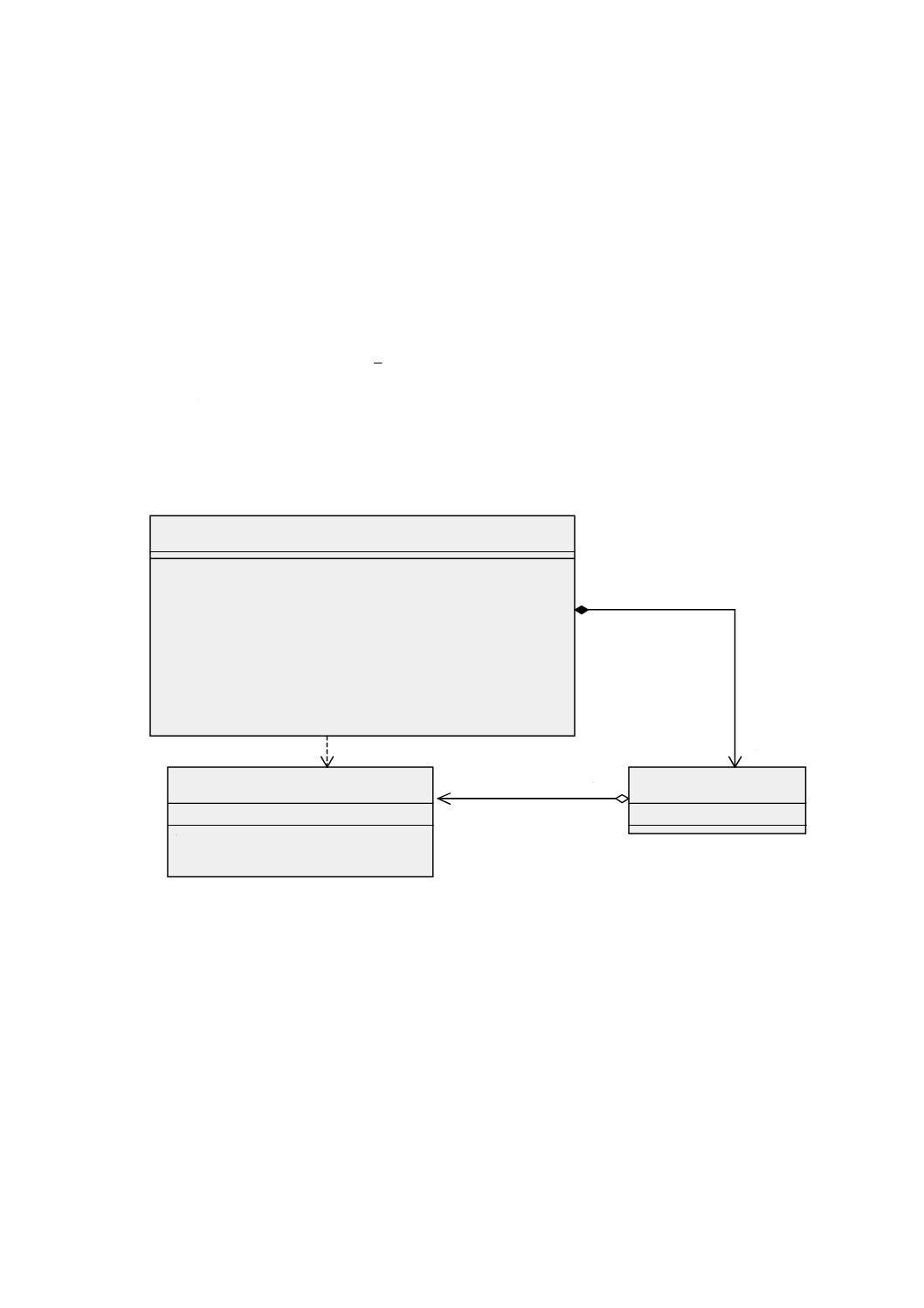
104
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.20 TP̲Expression
7.3.20.1 意味 代数位相幾何及び計算位相幾何は,TP̲Primitiveに対応する変数となる多変数一次多項式
の演算として考えると簡単になる。TP̲DirectedTopoクラスは,この代数における項を表す。TP̲Expression
(位相式データ)クラス(図45参照)は多項式を表す。
多項式の項の順序は,その値に影響しないので,TP̲ExpressionクラスはSet<TP̲DirectedTopo>の下位ク
ラスとして表す。TP̲Expressionクラスの演算は,これらの多項式の生成,操作及び試験に必要な演算とす
る。
計算位相幾何の特徴は,位相の各要素を代数的又は組合せ的な手法で取り扱うことができる点にある。
この代数で扱うプリミティブは,TP̲Primitiveである。単項式(単一変数で単一項の多項式)は
TP̲ExpressionTermとしてインスタンス化した整数係数をもつTP̲Primitiveのインスタンスである。
多変数一次多項式代数の満たす制約は,TP̲Expressionに対しても次のとおり有効でなければならない。
TP̲DirectedTopo:
negate().asTP̲Expression() = asTP̲Expression().negate()
asTP̲Expression.negate().plus(asTP̲Expression).isZero()
«DataType»
TP̲Expression
+ TP̲Expression(dt : TP̲DirectedTopo) : TP̲Expression
+ TP̲Expression(sdt : Set<TP̲DirectedTopo>) : TP̲Expression
+ plus(s : TP̲Expression) : TP̲Expression
+ minus(s : TP̲Expression) : TP̲Expression
+ negate() : TP̲Expression
+ isZero() : Boolean
+ isCycle() : Boolean
+ boundary() : TP̲Expression
+ coBoundary() : TP̲Expression
+ equals(s : TP̲Expression) : Boolean
+ support() : TP̲Complex
«Type»
TP̲DirectedTopo
+ orientation : Sign = "+"
+ negate() : TP̲DirectedTopo
+ asTP̲Expression() : TP̲Expression
«DataType»
TP̲ExpressionTerm
+ coefficient : Integer = 1
Variable
+ variable
1
+ term
0..n
Terms
+ expression
1
+ term
0..n
図 45 TP̲Expression
7.3.20.2 TP̲ExpressionTerm TP̲Expressionは,多項式のように変数及び係数からなる項の集合で構成さ
れる。
TP̲ExpressionTerm = < coefficient : Integer = 1,
variable : Reference<TP̲DirectedTopo>>
計算は,通常の多項式操作と一致する。
7.3.20.3 TP̲Expression(コンストラクタ) “TP̲Expression”コンストラクタは,TP̲DirectedTopoから
TP̲Expressionを生成する。この操作は,他のTP̲Objectのようなクラスが位相式を生成するのに使用され
る。
105
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲Expression( dt : TP̲DirectedTopo) : TP̲Expression = { <1, dt> }
TP̲Expression(sdt : Set<TP̲DirectedTopo>) : TP̲Expression =
{ <1,dt> | sdt.contains(dt)}
7.3.20.4 plus “plus”(加法)操作は,TP̲Expressionの多項式加算として機能する。これは,元となる
TP̲Primitiveのインスタンスが共通なTP̲DirectedTopo要素同士を,その“方向性”係数を加えることによ
って結合したものとする。係数が0になった項は,削除する。
TP̲Expression::plus(s : TP̲Expression) : TP̲Expression
7.3.20.5 minus “minus”(減法)操作は,TP̲Expressionの多項式減算として機能する。これは,元とな
るTP̲Primitiveのインスタンスが共通なTP̲DirectedTopo要素同士を,その“方向性”係数を引くことに
よって結合したものとする。係数が0になった項は,削除する。
TP̲Expression::minus(s : TP̲Expression) : TP̲Expression
7.3.20.6 negate “negate”(反転取得)操作は,TP̲Expressionの各項の符号を反転させる。これは,多項
式の単項減法演算子である。
TP̲Expression::negate() : TP̲Expression
7.3.20.7 isZero “isZero”(0値判定)操作は,多項式の項数が0になったときTRUEを返す。これは,
“Set.isEmpty”操作に等しい。
TP̲Expression::isZero() : Boolean
7.3.20.8 isCycle “isCycle”(輪体判定)操作は,[TP̲Expression::boundary()で定義される]境界が0とな
る多項式に対してTRUEを返す。TP̲Expressionは,多角形の境界のように閉じた幾何オブジェクトを表現
している場合,サイクルになる。GISの大多数では,“isCycle”がTRUEを返すことは,元の幾何オブジェ
クトが別の幾何オブジェクトの境界となることを暗示している。これは“isZero(boundary())”に等しい。
TP̲Expression::isCycle() : Boolean
備考 境界取得操作の像は,いずれも輪体となる。これは boundary().boundary().isZero() = TRUE を意
味する。
7.3.20.9 boundary “boundary”(境界取得)操作は,このTP̲Expressionの各TP̲DirectedTopoの各
TP̲Primitiveをその境界で置き換え,結果として得られる式を可能な限り単純にする。境界は,常に一つ
低い次元のTP̲Primitiveからなる。このTP̲ExpressionのすべてのTP̲Primitiveの次元が0(TP̲Primitive
がすべてノード)の場合,境界取得操作は,項数が0のTP̲Expressionを返す。
TP̲Expression::boundary() : TP̲Expression
7.3.20.10 coBoundary “coBoundary”(双対境界取得)操作はこのTP̲Expressionの各TP̲DirectedTopoの
各TP̲Primitiveをその双対境界で置き換え,結果として得られる式を可能な限り単純にする。双対境界は
常に一つ高い次元のTP̲Primitiveからなる。このTP̲ExpressionのすべてのTP̲Primitiveの次元が対応する
極大TP̲Complexの次元と等しい場合は,双対境界操作は項数が0のTP̲Expressionを返す。
TP̲Expression::coBoundary() : TP̲Expression
7.3.20.11 equals “equals”(等値判定)操作は多項式が等値の場合TRUEを返す。要素(項)の順序は意
味をもたない。
TP̲Expression::equals(s : TP̲Expression) : Boolean
7.3.20.12 support “support”(対応変換)操作は,このTP̲Expressionを幾何演算子の計算に使用する
TP̲Primitiveの集合に変換する。この操作は,本質的に“asSet”操作の後にTP̲DirectedTopo及びTP̲Primitive
の間の“Center”関連をたどることに相当する。
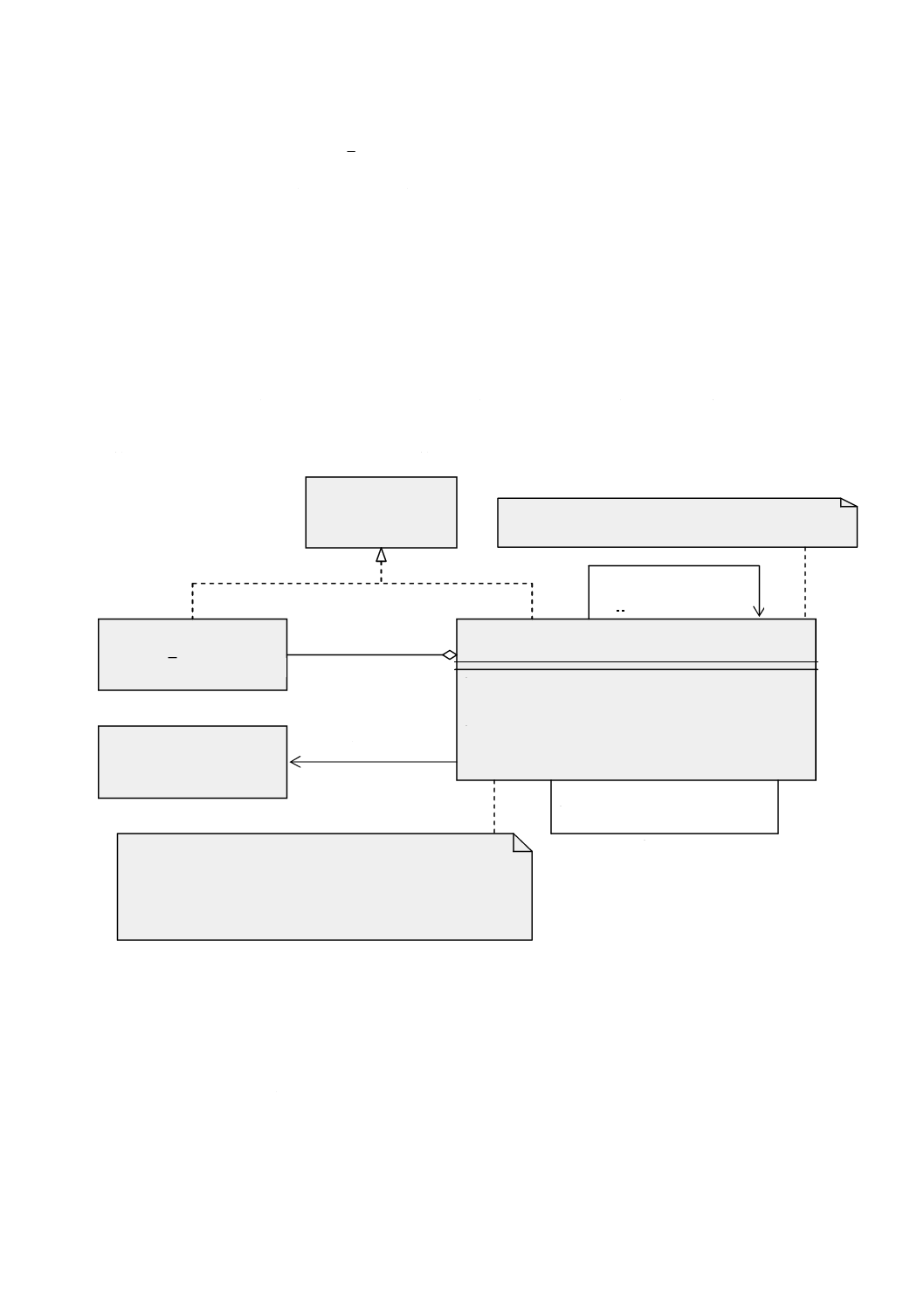
106
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲Expression::support() : Set<TP̲Primitive>
7.3.20.13 asSet “asSet”(集合変換)操作は,このTP̲Expressionを幾何演算子の計算に使用する
TP̲DirectedTopoの集合に変換する。この変換は,TP̲DirectedNodeにたどり着くまでに集合へ追加したす
べての境界要素を含む。別の言い方をすれば,TP̲Expressionに対応するのは有効なTP̲Complexでなけれ
ばならない。
TP̲Expression::asSet() : Set<TP̲DirectedTopo>
7.4
Topological complexパッケージ
7.4.1
意味 “Topology complex”(位相複体)パッケージは,TP̲Complexの生成を行う追加のクラスを
提供する。
7.4.2
TP̲Complex
7.4.2.1
意味 この箇条は,6.6で既に導入された幾何複体に対応する位相複体の定義を含む。TP̲Complex
(位相複体)(図46)は,元となる幾何実現(GM̲Complex)の幾何のelementが表す直接位置集合に集合
演算を行うために,そのelementに同じ集合演算を使用してよい。
+superComplex + subComplex
1..n
1..n
«Interface»
TP̲Object
(from Topology root)
«Type»
TP̲Primitive
(from Topological primitive)
«Type»
TP̲Complex
+ isMaximal() : Boolean
+ isConnected() : Boolean
+ boundary() : TP̲ComplexBoundary
+ TP̲Complex(GC : GM̲Complex) : TP̲Complex
«Type»
GM̲Complex
(from Geometric complex)
- maximalComplex
1
Realization
Contains
Complex
+ element
1..n
+ complex
1..n
+ geometry
0..1
+ topology
0..1
-- maximalComplexが示す複体は,この複体を含む
{superComplex->contains(maximalComplex)}
-- 極大複体はそれ自身にのみ”包含(Contains)”される
{(self = maximalComplex) implies (superComplex = {self})}
{isMaximal() implies (self = maximalComplex)}
-- maximalComplexは,7.4.2.3 の記述では非公開
となっているため,それに合わせている
図 46 TP̲Complex
7.4.2.2
TP̲Complex(コンストラクタ) 既定の位相複体の構築は,幾何複体からその位相複体を生成
する。構築の後,幾何複体は,位相複体の幾何実現となる。幾何プリミティブが互いに交差しない幾何複
体だけが誤りのない位相複体を生成する。
TP̲Complex::TP̲Complex(GC : GM̲Complex) : TP̲Complex
それぞれの幾何複体に対する既定の位相複体を定義する既定のコンストラクタを使用することは,
107
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TP̲Complexの表現する位相がGM̲Complexの表現する幾何形状の位相となることを保証する。
“Realization”関連は,TP̲Complexの各部分をGM̲Complexの適切な部分までたどる。これによって,位
相複体(TP̲Complex)の位相演算が幾何複体(GM̲Complex)から直接発生したものとみなすことができ
る。
7.4.2.3
maximalComplex 非公開の“maximalComplex”(極大複体)属性は,このTP̲Complexが属する
一意の極大位相複体への参照を含む。これは,符号化でデータ集合の出力の限界を判断するのに必要とな
る。
- TP̲Complex::maximalComplex : Reference<TP̲Complex>
7.4.2.4
isMaximal ブール値を返す“isMaximal”(極大判定)操作は,このTP̲Complexがより大きな
TP̲Complexに含まれていない場合,TRUEを返す。
TP̲Complex::isMaximal() : Boolean
7.4.2.5
isConnected ブール値を返す“isConnected”(連結判定)操作は,このTP̲Complexが位相連結
の場合TRUEを返す。
TP̲Complex::isConnected() : Boolean
備考 TP̲Complexが連結の場合,その幾何実現もまた連結である。このことは,合成体はプリミテ
ィブと位相同形であるという強い制約を満たさなければならないため,その複体が(幾何的に
も位相的にも)合成体であることを示すものではない。幾何実現を参照しない位相複体が連結
か否かを検証するためには,boundary,coBoundary及びIsolatedIn関連の推移的な閉包を計算する
必要がある。複体のすべてのプリミティブが,その複体の中間的な各プリミティブとなる関連役割
の列によって,その複体の他のいずれのプリミティブともつながる場合,複体は連結となる。
7.4.2.6
Contains関連 “Contains”(包含)派生関連はこのTP̲ComplexにTP̲Primitiveの集合として含
まれている他のTP̲Complexを記述する。“superComplex”役割は二つの複体のうち大きいほうを表し,
“subComplex”役割は小さいほうを表す。この関係はSet<TP̲Primitive>から継承した“contains”操作と一致する。
TP̲Complex::subComplex [1..n] : Reference<TP̲Complex>
TP̲Complex::superComplex [1..n] : Reference<TP̲Complex>
7.4.2.7
Complex関連 “Complex”(複体)関連はこのTP̲ComplexにTP̲Primitive要素を関係付ける。
この関連はTP̲ComplexをSet<TP̲Primitive>に変換する。“Contains”が暗示する集合演算は,プリミティ
ブの集合としてのこのTP̲Complexの定義と一致しなければならない。
TP̲Complex::element [1..n] : Reference<TP̲Primitive>
TP̲Primitive::complex [[1..n] : Reference<TP̲Complex>
7.4.2.8
Realization関連 “Realization”(実現)関連は,このTP̲Complexと対応するGM̲Complexが存
在すれば,関連付ける。
TP̲Complex::geometry [0,1] : GM̲Complex
GM̲Complex::topology [0,1] : TP̲Complex
8. 派生位相関係

108
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.1
一般 この箇条では,位相関係を問合せで用いる演算子として特徴付けるための仕組みについて規
定する。これらの問合せ演算子は,GM̲Object及びその下位型上で定義される集合論の演算子及び
TP̲Expression上で定義される代数演算子とを使って計算可能である。これら二つの仕組みは,対応する位
相複体の実現である幾何複体に対して等価となる。この箇条で定義する演算子は,主に問合せ評価を目的
としたものであり,等価な情報内容をもつデータ集合に対して等価な結果を保証するような各種の実装を
容認する。
この規格は,特定の空間演算子に規定の名前を定めない。応用スキーマは,応用システム固有の演算子
を規定するのに次の3分類の手法の幾つか又はすべてを使用することを前提とする。次の場合,分類法は,
TP̲Objectに基づく。これは,また,前に定義したGM̲Objectの集合からTP̲Complexを生成するための
制約が満たすような同じ演算をGM̲Objectに定義する。これに従うのは,点,曲線,曲面及び立体オブジ
ェクトとして妥当なものだけである。次元が一定でない集成オブジェクトのための理論は,いまだに標準
規格の基礎とするほど十分なものではない。
問合せシステムがこの規格のこの部分に適合するためには,対応する位相問合せ演算子を後続の箇条の
いずれかに規定している特性に従って定義できること,及びこの箇条で定義されているすべての演算子を,
直接,又は対応する演算子の十分に理解された組合せを通じて利用可能にできることが必要となる。この
箇条に適合するためには,最小限,次が満たされなければならない。
a) ブール値問合せ演算は,ここに含まれる箇条に一致して定義される。
b) 8.1,8.2又は8.3のうちの一つ以上の内容で定義可能なすべての妥当なブール値演算子が使用できる。
完全な適合には,この箇条全体の内容で定義可能な有効なブール値演算子のすべてに対応することが求
められる。
8.2
ブール値演算子及び集合演算子
8.2.1
ブール値演算子の形式 集合論の演算子は,しばしばブール値演算子として参照される。このよう
な演算子は,集合の内部と境界との間を区別しないため,閉包取得操作は,それらを組み合わせて使用す
る。
GM̲Object::closure() :== interior().union(boundary())
二つのオブジェクトA及びBに対して,次の四つの交差演算が可能である。
intersection(closure(A), closure(B))
intersection(closure(A), exterior (B))
intersection(exterior (A), closure (B)) intersection(exterior (A), exterior (B))
この演算を要素とする行列は,各集合について空か否かを試験するので,AとBとの関係を24すなわち
16のクラスに分類する。
演算子は,二つのオブジェクト間の特定の空間関係を試験することによって得られた交差演算行列に適
用されるテンプレートとして定義してよい。このテンプレートは,表8で説明する拡張ブール値を四つ用
いた行列であり,34すなわち81の演算子テンプレートが有効となる。
表 8 交差演算行列におけるブール値の意味
記号
空でないか
意味
T
TRUE
行列のこの位置の交差は,空でない。
F
FALSE
行列のこの位置の交差は,空である。
N
NULL
この演算子は,この位置の交差を試験しない。
備考 TRUEの値は,集合が空でないことを意味する(見出しを参照)。
二つのオブジェクトが特定の演算子テンプレートを満たす関係にあるか否かを試験するため,行列の形
109
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
態に応じてNULLに関連付けられていない交差は,計算され,空でないか試験される。一致する場合,こ
の二つのオブジェクトの演算子の値はTRUEとなり,そうでなければ値はFALSEとなる。
8.2.2
ブール値関係 “bRelate”(ブール値関係)演算子は,これらのオブジェクトが,二つの幾何オブ
ジェクトの閉包及び外部の間の交差の試験によって,“intersectionPatternMatrix”(交差演算行列)の値によ
って指示されたとおりに空間的に関係する場合,TRUEを返す。
Boolean bRelate(GM̲Object, GM̲Object, intersectionPatternMatrix)
Boolean bRelate(TP̲Object, TP̲Object, intersectionPatternMatrix)
intersectionPatternMatrixは,行優先形式,すなわち,最初の行の二つの値の後に行列の第二行の二つが続
く形式で与えられる,T,F又はNで構成される四文字の文字列として指定される。
8.2.3
集合操作との関係 このブール値関係は6.2.2.18で定義されるGM̲Objectの“contains”操作,
“intersects”操作及び“equals”操作を実装するために使用することができる。
例 C : GM̲Composite, G : GM̲Object;
C.contains(G) = bRelate(C, G, “TNFT” );
8.3
エーゲンホーファ演算子
8.3.1
エーゲンホーファ演算子の形式 二つのオブジェクトA及びBに対して九つの交差演算が可能と
なる(参考文献[8]及び[9]を参照)。
Intersection[
boundary(A),
boundary(B)
]
Intersection[
boundary(A),
interior(B)
]
Intersection[
boundary(A),
exterior(B)
]
Intersection[
interior(A),
boundary(B)
]
Intersection[
interior(A),
interior(B)
]
Intersection[
interior(A),
exterior(B)
]
Intersection[
exterior(A),
boundary(B)
]
Intersection[
exterior(A),
interior(B)
]
Intersection[
exterior(A),
exterior(B)
]
この演算を要素とする行列(“九行列”と呼ぶ。)について,それぞれが空か否かを調べる試験をしてよ
い。これは,AとBとの関係を29,すなわち,512のクラスに分類する。実際には,512のすべてが幾何
的に有効ではないが,どれだけが満たされるべきかは重要ではない。
演算子は,二つのオブジェクト間の特定の空間関係を試験する交差行列に適用されるテンプレートとし
て定義してよい。このテンプレートは,前の表と同じ内容の表9で説明する拡張ブール値を九つ用いた行
列であり,39,すなわち19,683の演算子テンプレートが可能である。
表 9 エーゲンホーファ交差演算行列の意味
記号 空でないか
意味
T
TRUE
行列のこの位置の交差は空でない。
F
FALSE
行列のこの位置の交差は空である。
N
NULL
この演算子は行列のこの位置の交差を試験しない。
二つのオブジェクトが特定の演算子を満たす関係にあるか否かを試験するため,行列の形態に応じて
NULLに関連付けられていない交差は計算され空でないか試験される。一致する場合,この二つのオブジ
ェクトの演算子の値はTRUEとなり,そうでなければ値はFALSEとなる。

110
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.3.2
エーゲンホーファ関係 “eRelate”演算子は,これらのオブジェクトが,二つの幾何オブジェク
トの内部,境界及び外部の間の交差の試験によって,intersectionPatternMatrix(交差演算行列)の値によっ
て指示されたとおりに空間的に関係する場合,TRUEを返す。
Boolean eRelate(GM̲Object, GM̲Object, intersectionPatternMatrix)
Boolean eRelate(TP̲Object, TP̲Object, intersectionPatternMatrix)
intersectionPatternMatrixは,行優先形式で与えられる,T,F又はNで構成される9文字の文字列として
指定される。
8.3.3
集合操作との関係 “エーゲンホーファ”関係は,6.6.2.18で定義されるGM̲Objectの“contains”
操作,“intersects”操作及び“equals”操作を実装するために使用することができる。
例 C : GM̲Primitive, G : GM̲Primitive;
C.contains(G) = eRelate(C, G, “NFNNTNNFT” );
C : GM̲Primitive, G : GM̲Composite;
C.contains(G) = eRelate(C, G, “FFNTTNFFT” );
8.4
完全位相演算子
8.4.1
完全位相演算子の形式 完全位相演算子は,次元の違いを扱い[この拡張のより詳しい分析につい
ては,参考文献4)及び5)を参照],エーゲンホーファ演算子と同様な方法で実行されるが,とり得る値が
より細かく区別される。
表 10 完全位相交差形態行列の意味
記号 空でないか
意味
0
TRUE
行列のこの位置の交差は,点だけを含む。
1
TRUE
行列のこの位置の交差は,点及び曲線だけを含む。
2
TRUE
行列のこの位置の交差は,点,曲線及び曲面だけを含む。
3
TRUE
行列のこの位置の交差は,点,曲線,曲面及び立体を含む。
F
FALSE
行列のこの位置の交差は,空である。
N
NULL
この演算子は,行列のこの位置の交差を試験しない。
二つのオブジェクトが,可能性のある69 = 10,077,696の演算子テンプレートの内の一つを満たす関係に
あるか否かを試験するため,NULLに関連付けられていない交差について,上の行列に基づいて,次元及
び空でないかを計算し試験する。一致する場合,この二つのオブジェクトの演算子の値はTRUEとなり,
一致しない場合,値はFALSEとなる。
8.4.2
完全位相関係 “cRelate”演算子は,これらのオブジェクトが,二つの幾何オブジェクトの内部,
境界及び外部の間の交差の試験によって,intersectionPatternMatrix(交差演算行列)の値によって指示され
たとおりに空間的に関係する場合,TRUEを返す。
Boolean cRelate(GM̲Object, GM̲Object, intersectionPatternMatrix)
Boolean cRelate(TP̲Object, TP̲Object, intersectionPatternMatrix)
intersectionPatternMatrixは,行優先形式で与えられる,0,1,2,3,F又はNで構成される9文字の文字
列として指定される。
8.5
組合せ 演算は,8.2〜8.4の箇条で示した一つ以上のプリミティブな演算子による組合せブール値と
して定義してよい。
111
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定)抽象試験項目群
A.1 幾何プリミティブ
A.1.1 幾何プリミティブのデータ型
A.1.1.1 零次元幾何のデータ型
a) 試験目的 応用スキーマ又はプロファイルがposition属性及びGM̲Objectから継承した
CoordinateReferenceSystem関連をもつGM̲Pointをインスタンス化することを検証する。応用スキーマ
又はプロファイルがGM̲MultiPointもインスタンス化する場合,それがposition属性及びelementへの
関連を含むことを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の6.1,6.2.1,6.2.2.17,6.3.10.1,6.3.11.1,6.3.11.2,6.4.1,6.5.1,6.5.2.1,6.5.2.2,6.5.3及
び6.5.4
d) 試験種類 機能
A.1.1.2 一次元幾何のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.1のすべての要件を満たすと同時に,orientation
属性及びSegmentation関連をもつGM̲Curve並びにすべての属性をもつGM̲CurveSegmentのインス
タンス化可能な一つ以上の下位型をインスタンス化することを検証する。応用スキーマ又はプロファ
イルがGM̲MultiCurveもインスタンス化する場合,それがelement属性及びlength属性を含むことを
検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.1並びに本体の6.3.5,6.3.13,6.3.14.1,6.3.16,6.4.1,6.4.6,6.4.8〜6.4.31及び6.5.5
d) 試験種類 機能
A.1.1.3 二次元幾何のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.2のすべての要件を満たし,orientation属性,
InteriorTo関連及びSegmentation関連をもつGM̲Surface並びにすべての属性をもつGM̲SurfacePatch
の一つ以上の下位型をインスタンス化することを検証する。応用スキーマ又はプロファイルが,
GM̲MultiSurfaceもインスタンス化する場合,それがelement属性,area属性及びperimeter属性を含
むことを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.2並びに本体の6.3.6,6.3.7,6.3.10.4,6.3.15,6.3.17.1,6.3.17.3,6.4.6,6.4.32〜6.4.48及
び6.5.6
d) 試験種類 機能
A.1.1.4 三次元幾何のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.3のすべての要件を満たすと同時に,InteriorTo
関連をもつGM̲Solidをインスタンス化することを検証する。応用スキーマ又はプロファイルが
GM̲MultiSolidもインスタンス化する場合,それがelement属性,area属性及びvolume属性を含むこ
とを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
112
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
c) 参照 A.1.1.3並びに本体の6.3.8,6.3.9,6.3.10.4,6.3.18.1及び6.5.7
d) 試験種類 機能
A.1.2 幾何プリミティブの単純操作
A.1.2.1 零次元幾何の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.1のすべての要件を満たすと同時に,GM̲Point
をインスタンス化したものが,boundary操作,mbRegin操作及びrepresentativePoint操作を含むことを
検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.1並びに本体の6.2.2.2,6.2.2.3,6.2.2.4,6.3.10.2及び6.3.11.3
d) 試験種類 機能
A.1.2.2 一次元幾何の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.2及びA.1.2.1のすべての要件を満たすと同時に,
GM̲Curveをインスタンス化したものが,boundary操作,mbRegin操作及びrepresentativePoint操作を
含むことを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.2及びA.1.2.1並びに本体の6.2.2.2,6.2.2.3,6.2.2.4,6.3.10.2及び6.3.16.2
d) 試験種類 機能
A.1.2.3 二次元幾何の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.3及びA.1.2.2のすべての要件を満たすと同時に,
GM̲Surfaceをインスタンス化したものが,boundary操作,mbRegin操作及びrepresentativePoint操作
を含むことを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.3及びA.1.2.2並びに本体の6.2.2.2,6.2.2.3,6.2.2.4,6.3.10.2及び6.3.17.2
d) 試験種類 機能
A.1.2.4 三次元幾何の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.4及びA.1.2.3のすべての要件を満たすと同時に,
GM̲Solidをインスタンス化したものが,boundary操作,mbRegin操作及びrepresentativePoint操作を
含むことを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.4及びA.1.2.3並びに本体の6.2.2.2,6.2.2.3,6.2.2.4,6.3.10.2及び6.3.18.2
d) 試験種類 機能
A.1.3 幾何プリミティブの完全操作
A.1.3.1 零次元幾何の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,GM̲Point及びGM̲MultiPointを,それがGM̲Object
及びGM̲Primitiveから継承した属性,操作及び関連並びに各クラスに固有に定義された属性,操作及
び関連のうち,Complex関連及びmaximalComplex操作を除くすべてをもつようにインスタンス化す
ることを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の6.1,6.2,6.3.10,6.3.11,6.3.12,6.4.1〜6.4.5及び6.5.1〜6.5.4
d) 試験種類 機能
113
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.1.3.2 一次元幾何の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.3.1のすべての要件を満たすと同時に,GM̲Curve,
GM̲CurveSegment及びGM̲MultiCurveを,直接又は非抽象下位型を通じてインスタンス化すること
を検証する。インスタンス化されたこれらのものが,GM̲Object,GM̲GenericCurve及びGM̲Primitive
から継承した属性,操作及び関連並びに各クラスに固有に定義された属性,操作及び関連のうち,
Complex関連及びmaximalComplex操作を除くすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.3.1並びに本体の6.3.1,6.3.2,6.3.4,6.3.5,6.3.13,6.3.14,6.3.16,6.4.6〜6.4.31及び6.5.5
d) 試験種類 機能
A.1.3.3 二次元幾何の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.3.2のすべての要件を満たすと同時に,GM̲Surface,
GM̲SurfacePatch及びGM̲MultiSurfaceを,直接又は非抽象下位型を通じてインスタンス化すること
を検証する。インスタンス化されたこれらのものが,GM̲Object,GM̲GenericSurface及びGM̲Primitive
から継承した属性,操作及び関連並びに各クラスに固有に定義された属性,操作及び関連のうち,
Complex関連及びmaximalComplex操作を除くすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.3.2並びに本体の6.3.6,6.3.7,6.3.15,6.3.17,6.4.32〜6.4.48及び6.5.6
d) 試験種類 機能
A.1.3.4 三次元幾何の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.3.3のすべての要件を満たすと同時に,GM̲Solid
及びGM̲MultiSolidを,直接又は非抽象下位型を通じてインスタンス化することを検証する。インス
タンス化されたこれらのものが,GM̲Object,GM̲GenericSolid及びGM̲Primitiveから継承した属性,
操作及び関連並びに各クラスに固有に定義された属性,操作及び関連のうち,Complex関連及び
maximalComplex操作を除くすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.3.3並びに本体の6.3.8,6.3.18及び6.5.7
d) 試験種類 機能
A.2 幾何複体
A.2.1 幾何複体のデータ型
A.2.1.1 一次元幾何複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.2のすべての要件を満たすと同時に,GM̲Complex,
GM̲CompositePoint及びGM̲CompositeCurveをインスタンス化することを検証する。それが,
Set<GM̲Primitive>とGM̲Complexとの間のContains関連,GM̲Primitive(GM̲Point及びGM̲Curve)
とGM̲Complexとの間のComplex関連,並びにGM̲PointとGM̲CompositePointとの間及びGM̲Curve
とGM̲CompositeCurveとの間のComposition関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.2並びに本体の6.6.3,6.6.1,6.6.2.1,6.6.2.3,6.6.2.4及び6.6.3〜6.6.5
a) 試験種類 機能
A.2.1.2 二次元幾何複体のデータ型
114
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.3及びA.2.1.1のすべての要件を満たすと同時に,
GM̲SurfaceとGM̲Complexとの間のComplex関連及びGM̲SurfaceとGM̲CompositeSurfaceとの間
のComposition関連をもつGM̲CompositeSurfaceをインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.3,A.2.1.1及び本体の6.6.6
d) 試験種類 機能
A.2.1.3 三次元幾何複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.4及びA.2.1.2のすべての要件を満たすと同時に,
GM̲SolidとGM̲Complexとの間のComplex関連,及びGM̲SolidとGM̲CompositeSolidとの間の
Composition関連をもつGM̲CompositeSolidをインスタンス化することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.4,A.2.1.2及び本体の6.6.7
d) 試験種類 機能
A.2.2 幾何複体の単純操作
A.2.2.1 一次元幾何複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.2.2及びA.2.1.1のすべての要件を満たすことを検
証する。GM̲Complex,GM̲CompositePoint及びGM̲CompositeCurveをインスタンス化したものが,
それぞれboundary操作,envelope操作,representativePoint操作及びisMaximal操作に対応することを
検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.2.2,A.2.1.1及び本体の6.6.2.2
d) 試験種類 機能
A.2.2.2 二次元幾何複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.2.3,A.2.1.2及びA.2.2.1のすべての要件を満たす
ことを検証する。GM̲CompositeSurfaceをインスタンス化したものが,boundary操作,envelope操作,
representativePoint操作及びisMaximal操作に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.2.3,A.2.1.2及びA.2.2.1
d) 試験種類 機能
A.2.2.3 三次元幾何複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.2.4,A.2.1.3及びA.2.2.2のすべての要件を満たす
ことを検証する。GM̲CompositeSolidをインスタンス化したものが,boundary操作,envelope操作,
representativePoint操作及びisMaximal操作に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.2.4,A.2.1.3及びA.2.2.2
d) 試験種類 機能
A.2.3 幾何複体の完全操作
A.2.3.1 一次元幾何複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.3.2及びA.2.2.1のすべての要件を満たすことを検
証する。GM̲CompositePoint,GM̲CompositeCurve及びGM̲Complexをインスタンス化したものが,
115
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
それぞれ,GM̲Object,GM̲Complex及びGM̲Compositeから継承した属性,操作及び関連並びに各
クラスに固有に定義された属性,操作及び関連のすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.3.2及びA.2.2.1
d) 試験種類 機能
A.2.3.2 二次元幾何複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.3.3及びA.2.2.2のすべての要件を満たすことを検
証する。GM̲CompositeSurfaceをインスタンス化したものが,GM̲Object,GM̲Complex及び
GM̲Compositeから継承した属性,操作及び関連並びにこのクラスに固有に定義された属性,操作及
び関連のすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.3.3及びA.2.2.2
d) 試験種類 機能
A.2.3.3 三次元幾何複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.3.4及びA.2.2.3のすべての要件を満たすことを検
証する。GM̲CompositeSolidをインスタンス化したものが,GM̲Object,GM̲Complex及び
GM̲Compositeから継承した属性,操作及び関連並びにこのクラスに固有に定義された属性,操作及
び関連のすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.3.4及びA.2.2.3
d) 試験種類 機能
A.3 位相複体
A.3.1 位相複体のデータ型
A.3.1.1 一次元位相複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,TP̲Complex,TP̲Node,TP̲DirectedNode,TP̲Edge
及びTP̲DirectedEdgeをインスタンス化することを検証する。TP̲DirectedNode及びTP̲DirectedEgde
をインスタンス化したものが共にorientation属性に対応することを検証する。応用スキーマ又はプロ
ファイルが,TP̲ComplexとそれぞれのTP̲Primitive(TP̲Node及びTP̲Edge)との間のComplex関連
に対応することを検証する。それが,TP̲NodeとTP̲DirectedNodeとの間及びTP̲Edgeと
TP̲DirectedEdgeとの間のCenter関連に対応することを検証する。これが,TP̲DirectedNodeとTP̲Edge
との間のBoundary派生関連及びTP̲NodeとTP̲DirectedEdgeとの間のCoBoundary派生関連に対応す
ることを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の7.1,7.2.1,7.3.1,7.3.2,7.3.3,7.3.8.1,7.3.8.3,7.3.9.1,7.3.9.2,7.3.9.5,7.3.9.6,7.3.10,
7.3.11,7.3.12.1,7.3.12.3,7.3.12.4,7.3.13,7.4.1,7.4.2.1,7.4.2.3,7.4.2.6及び7.4.2.7
d) 試験種類 機能
A.3.1.2 二次元位相複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.3.1.1のすべての要件を満たすと同時に,TP̲Face及
びTP̲DirectedEdgeをインスタンス化することを検証する。TP̲DirectedFaceをインスタンス化したも
116
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
のが,orientation属性に対応することを検証する。応用スキーマ又はプロファイルが,TP̲Primitiveの
間のIsolatedIn関連,TP̲ComplexとTP̲Faceとの間のComplex関連及びTP̲FaceとTP̲DirectedFace
との間のCenter関連に対応することを検証する。これが,TP̲DirectedEdgeとTP̲Faceとの間の
Boundary関連,及びTP̲EdgeとTP̲DirectedFaceとの間のCoBoundary派生関連に対応することを検
証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.1.1並びに本体の7.3.4,7.3.6,7.3.8.4,7.3.14.1,7.3.14.4及び7.3.14.5
d) 試験種類 機能
A.3.1.3 三次元位相複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.3.1.2のすべての要件を満たすと同時に,TP̲Solid及
びTP̲DirectedSolidをインスタンス化することを検証する。TP̲DirectedSolidをインスタンス化したも
のが,orientation属性に対応することを検証する。応用スキーマ又はプロファイルが,TP̲Complexと
TP̲Solidとの間のComplex関連及びTP̲SolidとTP̲DirectedSolidとの間のCenter関連に対応すること
を検証する。これが,TP̲DirectedFaceとTP̲Solidとの間のBoundary関連及びTP̲Faceと
TP̲DirectedSolidとの間のCoBoundary派生関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.1.2並びに本体の7.3.5,7.3.7,7.3.16.1,7.3.16.4及び7.3.16.5
d) 試験種類 機能
A.3.2 位相複体の単純操作
A.3.2.1 一次元位相複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.3.1.1のすべての要件を満たし,TP̲Complex,TP̲Node
及びTP̲Edgeをインスタンス化したものが,それぞれboundary操作,coBoundary操作及び
maximalComplex操作に対応することを検証する。GM̲Complexをインスタンス化したものが,
isMaximal操作に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.1.1並びに本体の7.2.2.3,7.2.2.4,7.2.2.8,7.3.12.2及び7.4.2.4
d) 試験種類 機能
A.3.2.2 二次元位相複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.3.1.2及びA.3.2.1のすべての要件を満たし,TP̲Face
をインスタンス化したものが,それぞれboundary操作,coBoundary操作及びmaximalComplex操作に
対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.1.2,A.3.2.1,7.3.14.2及び7.4.14.3
d) 試験種類 機能
A.3.2.3 三次元位相複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.3.1.3及びA.3.2.2のすべての要件を満たし,TP̲Solid
をインスタンス化したものが,それぞれboundary操作,coBoundary操作及びmaximalComplex操作に
対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.1.3及びA.3.2.2並びに本体の7.3.16.2及び7.3.16.3
117
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 試験種類 機能
A.3.3 位相複体の完全操作
A.3.3.1 一次元位相複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,TP̲Complex,TP̲Expression,TP̲ExpressionTerm,
TP̲Node,TP̲DirectedNode,TP̲Edge及びTP̲DirectedEdgeをインスタンス化することを検証する。
これらのインスタンス化したものがそれぞれ,TP̲Object,TP̲Primitive及びTP̲DirectedTopoから継
承した属性,操作及び関連並びに各クラスに固有に定義された属性,操作及び関連のうち,Realization
関連を除くすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の7.1,7.2,7.3.1,7.3.2,7.3.3,7.3.6,7.3.8.1,7.3.8.3,7.3.8.4,7.3.9〜7.3.13,7.3.18,7.4.1
及び7.4.2.1〜7.4.2.7
d) 試験種類 機能
A.3.3.2 二次元位相複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.3.3.1のすべての要件を満たすと同時に,それが
TP̲Face及びTP̲DirectedFaceをインスタンス化することを検証する。TP̲Face及びTP̲DirectedFace
をインスタンス化したものがそれぞれ,TP̲Object,TP̲Primitive及びTP̲DirectedTopoから継承した
属性,操作及び関連並びに各クラスに固有に定義された属性,操作及び関連のうち,Realization関連
を除くすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.3.1並びに本体の7.3.4,7.3.14及び7.3.15
d) 試験種類 機能
A.3.3.3 三次元位相複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.3.3.2のすべての要件を満たすと同時に,それが
TP̲Solid及びTP̲DirectedSolidをインスタンス化することを検証する。TP̲Solid及びTP̲DirectedSolid
をインスタンス化したものがそれぞれ,TP̲Object,TP̲Primitive及びTP̲DirectedTopoから継承した
属性,操作及び関連並びに各クラスに固有に定義された属性,操作及び関連のうち,Realization関連
を除くすべてに対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.3.3.2並びに本体の7.3.5,7.3.16及び7.3.17
d) 試験種類 機能
A.4 幾何実現を伴う位相複体
A.4.1 幾何実現を伴う位相複体のデータ型
A.4.1.1 幾何実現を伴う一次元位相複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.2及びA.3.1.1のすべての要件を満たすことを検
証する。それがまた,TP̲Primitive(TP̲Node及びTP̲Edge)とGM̲Primitive(GM̲Point及びGM̲Curve)
とをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complexとをそれぞれインスタ
ンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.2及びA.3.1.1並びに本体の7.3.8.2及び7.4.2.8
118
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 試験種類 機能
A.4.1.2 幾何実現を伴う二次元位相複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.3及びA.3.1.2のすべての要件を満たすと同時に,
TP̲FaceとGM̲Surfaceとをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complex
とをそれぞれインスタンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.3及びA.3.1.2並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.1.3 幾何実現を伴う三次元位相複体のデータ型
a) 試験目的 応用スキーマ又はプロファイルが,A.1.1.4及びA.3.1.3のすべての要件を満たすと同時に,
TP̲SolidとGM̲Solidとをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complex
とをそれぞれインスタンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.1.4及びA.3.1.3並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.2 幾何実現を伴う位相複体の単純操作
A.4.2.1 幾何実現を伴う一次元位相複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.2.2及びA.3.2.1のすべての要件を満たすと同時に,
TP̲Primitive(TP̲Node及びTP̲Edge)とGM̲Primitive(GM̲Point及びGM̲Curve)とをそれぞれイ
ンスタンス化したものの間,及びTP̲ComplexとGM̲Complexとをそれぞれインスタンス化したもの
の間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.2.2及びA.3.2.1並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.2.2 幾何実現を伴う二次元位相複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.2.3及びA.3.2.2のすべての要件を満たすと同時に,
TP̲FaceとGM̲Surfaceとをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complex
とをそれぞれインスタンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.2.3及びA.3.2.2並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.2.3 幾何実現を伴う三次元位相複体の単純操作
a) 試験目的 応用スキーマ又はプロファイルが,A.1.2.4及びA.3.2.3のすべての要件を満たすと同時に,
TP̲SolidとGM̲Solidとをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complex
とをそれぞれインスタンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.1.2.4及びA.3.2.3並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.3 幾何実現を伴う位相複体の完全操作
A.4.3.1 幾何実現を伴う一次元位相複体の完全操作
119
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 試験目的 応用スキーマ又はプロファイルが,A.2.3.1及びA.3.3.1のすべての要件を満たすことを検
証する。それがまた,TP̲Primitive(TP̲Node及びTP̲Edge)とGM̲Primitive(GM̲Point及びGM̲Curve)
とをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complexとをそれぞれインスタ
ンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.2.3.1及びA.3.3.1並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.3.2 幾何実現を伴う二次元位相複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.2.3.2及びA.3.3.2のすべての要件を満たすと同時に,
TP̲FaceとGM̲Surfaceとをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complex
とをそれぞれインスタンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.2.3.2及びA.3.3.2並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.4.3.3 幾何実現を伴う三次元位相複体の完全操作
a) 試験目的 応用スキーマ又はプロファイルが,A.2.3.3及びA.3.3.3のすべての要件を満たすと同時に,
TP̲SolidとGM̲Solidとをそれぞれインスタンス化したものの間,及びTP̲ComplexとGM̲Complex
とをそれぞれインスタンス化したものの間のRealization関連に対応することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.2.3.3及びA.3.3.3並びに本体の7.3.8.2及び7.4.2.8
d) 試験種類 機能
A.5 ブール値演算子
A.5.1 集合演算子
a) 試験目的 応用スキーマ又はプロファイルが8.2で規定したすべての集合演算子をその箇条に従って
定義することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の8.2
d) 試験種類 機能
A.5.2 エーゲンホーファ演算子
a) 試験目的 応用スキーマ又はプロファイルが8.3で規定したすべてのエーゲンホーファ演算子をその
箇条に従って定義することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の8.3
d) 試験種類 機能
A.5.3 完全位相演算子
a) 試験目的 応用スキーマ又はプロファイルが8.4で規定したすべての集合演算子をその箇条に従って
定義することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 本体の8.4
120
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 試験種類 機能
A.5.4 すべての位相演算子
a) 試験目的 応用スキーマ又はプロファイルが8.で規定したすべての集合演算子をその箇条に従って定
義することを検証する。
b) 試験方法 応用スキーマ又はプロファイルの文書を検査する。
c) 参照 A.5.1,A.5.2及びA.5.3
d) 試験種類 機能
121
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考)用語とその定義の概念による編成
序文 この附属書は,B.1に示す目的のために記述するものであり,規定の一部ではない。
B.1 目的 この附属書は,本体4.の用語及びその定義をその概念関係に基づき整理して示す。
B.2 全般的な用語
応用(application)(本体4.1) 利用者の要求に応えるために行われるデータの操作及び処理(ISO 19101)。
応用スキーマ(application schema)(本体4.2) 一つ以上の応用システムによって要求されるデータのた
めの概念スキーマ(ISO 19101)。
境界(boundary)(本体4.4) 実体の広がりの限界を示す集合。
備考 境界が最もよく使用されるのは,集合が点の集まり又はこれらの点を表すオブジェクトの集ま
りであるような幾何に関する記述においてである。他の分野では,この用語を,実体とその論
議領域での余事象との遷移領域を比ゆ(喩)的に記述するために使用する。
地物(feature)(本体4.39) 実世界の現象の抽象概念(ISO 19101)。
備考 地物は,型又はインスタンスとして現れる。型又はインスタンスの一方だけを意味するときに
は,地物型又は地物インスタンスという用語を使うことが望ましい。
地物属性(feature attribute)(本体4.40) 地物の特性(ISO 19101)。
備考 地物属性は,それに関連付けられた名前,データ型及び値の定義域をもつ。地物インスタンスの
地物属性は,加えてその定義域から選ばれた属性値をもつ(ISO 19109)。
地理情報(geographic information)(本体4.42) 地球に関係した場所と暗示的又は明示的に関連付けら
れた現象に関する情報(ISO 19101)。
空間オブジェクト(spatial object)(本体4.69) 地物の空間特性を表現するために用いるオブジェクト。
空間演算子(spatial operator)(本体4.70) その定義域又は値域に最低一つの空間パラメタをもつ関数又
は手続。
備考 空間オブジェクトに対するすべてのUML操作は,この規格の8.の問合せ演算子もそうである
ように,空間演算子として分類することができる。
B.3 コレクション型とその関連用語
集合(set)(本体4.65) 繰返しを許さない,関連する項目(オブジェクト又は値)の,有限で順序をも
たない集まり。
列(sequence)(本体4.64) 繰返しを許した,関連する項目(オブジェクト又は値)の,有限で順序をも
つ集まり。
備考 論理的には,列は <項目,相対位置> の対の集合である。この規格では,括弧で列を区切り,
列の要素をコンマで分けるLISP構文を用いる。
多重集合(bag)(本体4.3) 繰返しのある,関連する項目(オブジェクト又は値)の,有限非順序な集
まり。
備考 論理的には,多重集合は, <項目,項数> の対の集合である。
122
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
環状列(circular sequence)(本体4.6) 論理的な開始点をもたないために,それ自身のどのような循環的
なシフトとも同一になり,結果として最後の項目が順列の最初の項目に先行するとみなされる列。
レコード(record)(本体4.62) 有限の,名前をもつ,相互に関連性のある項目(オブジェクト又は値)
の集まり。
備考 論理的に,レコードは, <名称,項目> の対の集合となる。
領域(domain)(本体4.32) 明確に定義された集合(ISO TS 19103)。
備考 領域は,演算子及び関数の定義域と値域とを定義するのに用いる。
関数(function)(本体4.41) ある領域[この関数の定義域(source, domain)]の各要素を,別の領域[こ
の関数の値域(target, co-domain, range)]の一意な要素に関連付ける規則。
B.4 モデル化の用語
クラス(class)(本体4.7) 同じ属性,操作,メソッド,関係及び意味を共有するオブジェクトの集合の
記述(ISO TS 19103)。
備考 クラスは,その環境に提供する操作の集まりを規定するために,インタフェースの集合を使用
してもよい。この用語は,最初にオブジェクト指向プログラミングの一般的な理論の中でこの
用法で使用され,後にUMLにおいても同じ意味で使用するものとして採用された。
オブジェクト(object)(本体4.59) 状態と振る舞いとをカプセル化し,明確に定義された境界及び識別
をもつ実体[UML Semantics 19]。
備考 この用語は,最初にオブジェクト指向プログラミングの一般理論の中でこの用法で使用され,
後にUMLの中で同じ意味で使用するものとして採用された。オブジェクトはクラスのインス
タンスである。属性と関係とが状態を表す。操作,メソッド及び状態機構は,振る舞いを表す。
インスタンス(instance)(本体4.53) クラスを実現するオブジェクト。
強代替性(strong substitutability)(本体4.73) あるクラス,型又はインタフェースを継承又は実現した
下位クラスの任意のインスタンスを,その原型のインスタンスの代わりとして任意の状況において用いる
ことのできる能力。
備考 代替性の弱い形式は,暗黙の代替を行う状況に様々な制限を設ける。
B.5 位置の用語
直接位置(direct position)(本体4.26) 座標参照系の中で一組の座標によって記述された位置。
座標(coordinate)(本体4.19) n次元空間内の点の位置を示すn個の数値の列(JIS X 7111)。
備考 座標参照系では,それらの数値には単位を付与しなければならない。
座標参照系(coordinate reference system)(本体4.21) 原子(datum)によって地球に関連付けられた座標
系(JIS X 7111)。
座標系(coordinate system)(本体4.22) 点にどのように座標を割り当てるかを規定するための数学的規
則の集合(JIS X 7111)。
座標次元(coordinate dimension)(本体4.20) ある座標系における位置を記述するために必要な計測値
又は座標軸の数。
B.6 幾何の用語
B.6.1 幾何概念全般
123
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ベクトル幾何(vector geometry)(本体4.86) 構成的な幾何プリミティブの使用による幾何の表現。
計算幾何(computational geometry)(本体4.13) 幾何演算を実装するための,幾何表現に関する操作及
び計算。
例 計算幾何演算は,幾何包含若しくは交差の試験,凸包若しくはバッファ領域の計算又は幾何オブ
ジェクト間の最短経路探索を含む。
幾何集合(geometric set)(本体4.50) 直接位置の集合。
備考 この集合は,ほとんどの場合無限集合である。
凸集合(convex set)(本体4.18) 自分自身が含む任意の二つの直接位置について,それらを結ぶ直線分
上の任意の直接位置をも含むような幾何集合[Dictionary of Computing (7)]。
備考 凸集合は,“単連結”である。すなわち,内部に穴をもたない。通常は,適切な次元のユークリ
ッド球と位相同形とみなしてよい。また,球の表面は,測地的には測地線を直線とみなせば凸
と考えることができる。
凸包(convex hull)(本体4.17) 与えられた幾何オブジェクトを含む最小の凸集合 [Dictionary of
Computing (7)]。
備考 “最小”とは,集合論的に最小のことであり,計量的な意味をもつものではない。この定義は,
“その幾何オブジェクトを含むすべての凸集合の積集合”と言いかえることもできる。
近傍(neighbourhood)(本体4.57) 指定された直接位置を内部に含み,その直接位置から指定された距
離以内のすべての直接位置を含む幾何集合。
幾何次元(geometric dimension)(本体4.46) 幾何集合の中のどの直接位置も,その直接位置を内部に含
みn次元ユークリッド空間Rnと相似(同形)な部分集合と関連付けることができるような数nの最大値。
備考 曲線は,実数直線の一部の連続写像であるので,1の幾何次元をもつ。曲面は,その全体をR2
に写像することはできないが,各点位置の周りには微小な近傍があってそれがR2の単位円の内
部に(連続関数によって)写像されることがわかることから,二次元である。この規格では,
主要な曲面分(GM̲SurfacePatchのインスタンス)のほとんどは,それを定義する内挿の方法
によってR2の一部に写像される。
B.6.2 幾何オブジェクト
B.6.2.1 全般的な概念
幾何オブジェクト(geometric object)(本体4.47) 幾何集合を表す空間オブジェクト。
備考 幾何オブジェクトは,幾何プリミティブ,幾何プリミティブの集まり又は単一の実体として扱
われる幾何複体からなる。幾何オブジェクトは,地物又は地物の重要な部分の空間表現に用い
てよい。
幾何境界(geometric boundary)(本体4.44) 幾何オブジェクトの範囲を限定する,より低い幾何次元の
幾何プリミティブの集合によって表現される境界。
輪体(cycle)(本体4.25) 境界をもたない空間オブジェクト。
備考 輪体は境界の構成要素[殻(shell)及び輪(ring)を参照]を記述するために使用する。輪体は,そ
れ自身の上で閉じているため,境界をもたないが,有界である(すなわち,範囲は無限ではな
い。)。例えば,円周又は球面は境界をもたないが有界である。
内部(interior)(本体4.54) 幾何オブジェクト上にありその境界上にはないすべての直接位置の集合。
備考 位相オブジェクトの内部は,その任意の幾何実現の内部の準同形の像である。これは,位相幾
何学の定理から導かれるので,ここでの定義には含めない。
124
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
外部(exterior)(本体4.37) 全体集合とある集合の閉包との差集合。
備考 外部の概念は,位相複体及び幾何複体の両方に適用できる。
閉包(closure)(本体4.8) 位相オブジェクト又は幾何オブジェクトの内部と境界との和集合。
単純(simple)(本体4.67) 内部が等方的(すべての点が同形な近傍をもつ。)で,したがって,至ると
ころ適切な次元のユークリッド座標空間の開部分集合に局所的に同形である,という幾何オブジェクトの
特性。
備考 これは,内部の直接位置がいかなる種類の自己交差にも関与しないことを意味する。
連結(connected)(本体4.15) オブジェクト上の任意の二つの直接位置がそのオブジェクト内に完全に
含まれる曲線上に配置できることを意味する幾何オブジェクトの性質。
備考 位相オブジェクトは,幾何実現が連結である場合にだけ,連結である。これは,位相幾何学の
定理から導かれるので,定義には含まれない。
バッファ(buffer)(本体4.5) 指定された幾何オブジェクトから与えられた距離以内のすべての直接位
置を含む幾何オブジェクト。
幾何集成(geometric aggregate)(本体4.43) 内部構造をもたない幾何オブジェクトの集まり。
幾何境界(geometric boundary)(本体4.44) 幾何オブジェクトの範囲を限定する,より低い幾何次元の
幾何プリミティブの集合によって表現される境界。
B.6.2.2 幾何プリミティブとその関連用語
幾何プリミティブ(geometric primitive)(本体4.48) 単一の連結で均質な空間の要素を表す幾何オブジ
ェクト。
備考 幾何プリミティブは,幾何構成についての情報を表す不可分なオブジェクトである。点,曲線,
曲面及び立体は幾何プリミティブである。
点(point)(本体4.61) 位置を表現する零次元の幾何プリミティブ。
備考 点の境界は,空集合である。
曲線(curve)(本体4.23) 直線の連続な像を表現する一次元の幾何プリミティブ。
備考 曲線の境界は,その両端の点の集合である。曲線が閉路の場合,二つの端は同一であり,その
曲線は(位相的に閉じている場合には),境界をもたないとみなす。最初の点を始点,最後のも
のを終点と呼ぶ。“直線の連続的な像”という定義文の語句によって,曲線の連結性が保証され
る。位相幾何学の定理は,連結している集合の連続的な像は連結であることを規定している。
始点(start point)(本体4.72) 曲線の最初の点。
終点(end point)(本体4.36) 曲線の最後の点。
曲線分(curve segment)(本体4.24) 一定の内挿及び定義の方法を用いて曲線の連続した部分を表現す
るために用いる一次元の幾何オブジェクト。
備考 単一の曲線分によって表現される幾何集合は,一つの曲線と等しい。
輪(ring)(本体4.63) 輪体である単純曲線。
備考 輪は二次元及び三次元座標系における曲面の境界の要素を記述するために使用する。
曲面(surface)(本体4.75) 局所的に平面領域の連続な像を表す二次元の幾何プリミティブ。
備考 曲面の境界は,曲面の限界の輪郭を描く向きをもつ閉曲線である。球面又はn次元トーラス(n
次元“把”をもつ位相球面)と同形である曲面は,境界をもたない。このような曲面を輪体と
呼ぶ。
曲面分(surface patch)(本体4.76) 一定の内挿及び定義方法を用いて曲面の連続した部分を表す二次元
125
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の連結な幾何オブジェクト。
殻(shell)(本体4.66) 輪体である単純曲面。
備考 殻は三次元座標系における立体の境界の要素を記述するために用いる。
立体(solid)(本体4.68) 三次元ユークリッド空間のある領域の連続な像を表す三次元の幾何プリミテ
ィブ。
備考 立体は,直接位置の三つのパラメタをもつ集合によって局所的に実現することができる。立体
の境界は,その立体の限界を包含する,向きをもつ閉曲面の集合である。
B.6.2.3 幾何複体
幾何複体(geometric complex)(本体4.45) 互いに素な幾何プリミティブの集合で,各幾何プリミティ
ブの境界を,その集合の中の,より低い次元の幾何プリミティブの和集合として表すことのできる集合。
備考 集合の幾何プリミティブは,複数の幾何プリミティブの内部に存在するような直接位置はない
という意味で互いに素である。集合は,境界演算で閉じているが,これは,幾何複体の各要素
について,その要素の境界を表す幾何プリミティブの集まり(これも幾何複体となる。)が存在
することを意味する。既に述べたように,点(幾何の唯一の零次元プリミティブオブジェクト
型)の境界は,空集合である。したがって,最も高い次元の幾何プリミティブが立体(三次元)
の場合,この定義の境界演算を次々と適用していくと,高々3ステップ後には終結する。また,
任意のオブジェクトの境界は輪体となる。
部分複体(subcomplex)(本体4.74) すべての要素が,より大きな複体の一部でもあるような複体。
備考 幾何複体及び位相複体の定義が要求するのは,境界演算について閉じることだけであることか
ら,特定の次元又はそれ以下の任意のプリミティブの集合は,常に元のより大きな複体の部分
複体になる。したがって,任意の完全平面位相複体は,部分複体であるエッジノードグラフを
含む。
合成曲線(composite curve)(本体4.10) 列の各曲線が(最初のものを除き)直前の曲線の終点から開始
するような曲線の列。
備考 合成曲線は,直接位置の集合として,曲線のすべての性質をもつ。
合成立体(composite solid)(本体4.11) 共有された境界曲面に沿って互いに隣接する立体の連結な集合。
備考 合成立体は,直接位置の集合として,立体のすべての性質をもつ。
合成曲面(composite surface)(本体4.12) 共有された境界曲線に沿って互いに隣接する曲面の連結な集
合。
備考 合成曲面は,直接位置の集合として,曲面のすべての性質をもつ。
B.7 位相の用語
B.7.1 位相の概念
計算位相幾何(computational topology)(本体4.14) 通常,計算幾何において実行される,位相オブジ
ェクトの演算の支援,拡張又は定義を行う位相的な概念,構造及び代数。
B.7.2 位相オブジェクト
B.7.2.1 一般的な概念
位相境界(topological boundary)(本体4.77) 位相オブジェクトの範囲を制限する,より低い位相次元
の向きをもった位相プリミティブの集合で表される境界。
備考 位相複体の境界は,この位相複体の幾何実現の境界と整合する。
126
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
位相複体(topological complex)(本体4.78) 境界演算について閉じている位相プリミティブの集まり。
備考 境界演算について閉じているとは,位相プリミティブが位相複体に含まれる場合には,その境
界オブジェクトもまたこの位相複体に含まれることを意味する。
位相オブジェクト(topological object)(本体4.81) 連続した変換のもとでも変わらない空間特性を表す
空間オブジェクト。
備考 位相オブジェクトは,位相プリミティブ,位相プリミティブの集まり又は位相複体である。
双対境界(coboundary)(本体4.9) ある位相オブジェクトに対応して,その位相オブジェクトを境界と
してもつ,より高い位相次元の位相プリミティブの集合。
備考 ノードがエッジの境界に存在する場合,このエッジは,そのノードの双対境界上にある。この
二つの関係のいずれか一つに関連付けられた任意の方向パラメタは,もう一方の関係に対して
も関連付けられる。これは,ノードがエッジの終点ノードである(正の有向エッジの終端とし
て定義される)場合,そのノードの正の方向(正の有向ノードとして定義される)が双対境界
上にエッジをもつようにするためである(図35参照)。
位相次元(topological dimension)(本体4.79) 幾何オブジェクト内の直接位置を他の位置と区別するの
に必要な自由変数の最小の数。
備考 上の自由変数は,多くの場合局地座標系として考えることができる。三次元座標空間において,
uとvとを実数,Aを平面上の任意の点,X及びYを平面の二つの接ベクトルとすると,平面は
P(u,v) = A + u X + v Yと書き表すことができる。この平面の位置はuとvとによって(ここで
は至る所を)識別できるので,平面は二次元であり,(u,v)はこの平面上の点の座標となる。
一般の曲面では,通常は,至る所を普遍的に識別するのは不可能である。曲面上の点を曲面の
接平面上へ射影すると,接点の微小近傍の局所同形を通常得ることができる。曲面に対するこ
の“局所座標”系は,曲面が二次元位相オブジェクトであるための要件を満たす。
この規格は空間座標だけを取り扱うので,任意の三次元オブジェクトは座標がその位相次元を
定めることに依存することができる。四次元モデル(時空間)では,接空間は三次元までのオ
ブジェクトの位相次元を定めるという重要な役割も果たす。
B.7.2.2 位相プリミティブ及びその関連用語
位相プリミティブ(topological primitive)(本体4.82) 単独の不可分な要素を表す位相オブジェクト。
備考 位相プリミティブは幾何実現の同じ次元の幾何プリミティブの内部に相当する。
ノード(node)(本体4.58) 零次元の位相プリミティブ。
備考 ノードの境界は,空集合である。
連結ノード(connected node)(本体4.16) 一つ以上のエッジが開始又は終了するノード。
孤立ノード(isolated node)(本体4.55) どのエッジとも関係しないノード。
始点ノード(start node)(本体4.71) エッジを含む位相複体の有効な幾何実現において,そのエッジを
実現する曲線の始点に対応する,このエッジの境界のノード。
終点ノード(end node)(本体4.35) エッジを含む位相複体の有効な幾何実現において,そのエッジを実
現する曲線の終点に対応する,このエッジの境界のノード。
エッジ(edge)(本体4.33) 一次元の位相プリミティブ。
備考 エッジの幾何実現は曲線である。エッジの境界は,位相複体中でこのエッジと関連付けられた
一つ又は二つのノードの集合である。
フェイス(face)(本体4.38) 二次元の位相プリミティブ。
127
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 フェイスの幾何実現は曲面である。フェイスの境界は,境界関係をとおしてフェイスに関連付
けられる同じ位相複体における有向エッジの集合である。これらは,輪の形に揃えることがで
きる。
位相立体(topological solid)(本体4.83) 三次元の位相プリミティブ。
備考 位相立体の境界は有向フェイスの集合からなる。
B.7.2.3 位相複体とその関連用語
位相複体(topological complex)(本体4.78) 境界演算について閉じている位相プリミティブの集まり。
備考 境界演算について閉じているとは,位相プリミティブが位相複体に含まれる場合には,その境
界オブジェクトもまたこの位相複体に含まれることを意味する。
全域フェイス(universal face)(本体4.84) 二次元複体中の非有界フェイス。
備考 全域フェイスは,通常どのような地物の一部でもなく,データ集合の非有界の部分を表すため
に用いる。通常,この内部境界(それは外部境界をもたない。)をデータ集合によって表された
地図の外部境界とみなす。この規格は,全域フェイスを特別扱いしないが,応用スキーマでは
そうすることが有効な場合もある。
全域位相立体(universal solid)(本体4.85) 三次元複体中の非有界位相立体。
備考 全域位相立体は,三次元において全域フェイスに相当するものであり,通常はどのような地物
の一部でもない。
位相式(topological expression)(本体4.80) 多変量多項式のように演算される,向きをもつ位相プリミ
ティブの集まり
備考 位相式は,計算位相幾何の多くの計算で使用する。
有向位相オブジェクト(directed topological object)(本体4.31) 位相プリミティブとその方向の一つと
の間の論理的な関連を表す位相オブジェクト。
有向ノード(directed node)(本体4.29) ノードとその方向の一つとの間の関連を表す有向位相オブジェ
クト。
備考 有向ノードは,双対境界関係においてエッジとノードとの間の空間的な関連を保持するために
用いる。一つのエッジに関するノードの向きは,そのエッジの終点ノードでは“+”,始点ノー
ドは“-”になる。これは,“ベクトル=終点−始点”というベクトルの概念と整合している。
有向エッジ(directed edge)(本体4.27) エッジとその向きの一つとの間の関連を表す有向位相オブジェ
クト。
備考 有向エッジは,そのエッジと向きが一致しているものは + という向きを,そうでなければ ‒
という向きをもつとする。有向エッジは,位相幾何においては同一のエッジの右側(-)と左側
(+)とを区別する場合,同一のエッジの始点ノード(-)と終点ノード(+)とを区別するため
に,そして計算位相幾何においてはこれらの概念を表現するために用いる。
有向フェイス(directed face)(本体4.28) フェイスとその向きの一つとの間の関連を表す関連を表す有
向位相オブジェクト。
備考 有向フェイスの外部境界を構成する有向エッジは,その有向フェイスの正の側からみて,正の
向きが決まる。位相立体の境界を示す有向フェイスの向きは,この位相立体から離れる方向を
指す。隣接する位相立体では,それらが共有する境界には異なる向きを付けることになるが,
これは,隣接するフェイスとそれらが共有するエッジとの間は同種の関連で整合している。有
向フェイスは,双対境界関係においてフェイスとエッジとの間の空間的な関係を保持するため
128
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に用いる。
有向位相立体(directed solid)(本体4.30) 位相立体とその向きの一つとの間の関連を表す有向位相オブ
ジェクト。
備考 有向位相立体は,双対境界関係においてフェイスと位相立体との間の空間的な関係を保持する
ために用いる。一つのフェイスに関する位相立体の向きは,そのフェイスの上方法線が位相立
体の外側へ向く場合は“+”,内側に向く場合は“-”である。これは,立体の境界となる曲面に
対して“上方=外側”という概念と整合する。
B.7.2.4 位相複体の型
グラフ(graph)(本体4.51) 一部がエッジによって結合されているノードの集合。
備考 地理情報システムでは,グラフは,二つのノードに結合するエッジを複数もつことができ,同
じノードを両端にもつエッジをもつこともできる。
エッジノードグラフ(edge-node graph)(本体4.34) ある位相複体内に埋め込まれているグラフで,そ
の複体内のすべてのエッジとそれに連結したノードからなるもの。
備考 エッジノードグラフは,それが埋め込まれている複体の部分複体である。
平面位相複体(planar topological complex)(本体4.60) 二次元ユークリッド空間に埋め込むことができ
る幾何実現をもつ位相複体。
B.8 幾何及び位相複体の関係性
準同形(homomorphism)(本体4.52) 一方から他方への構造を保存する関数をもつ二つの領域(二つの
複体のような)の間の関係。
備考 準同形は逆関数を必要としない点で同形と異なる。同形には,本質的には互いに逆関数の関係
にあたる二つの準同形がある。連続関数は,“位相的な特性”を保存するので位相準同形である。
位相複体の幾何実現への写像は,境界の概念を保存する。したがって,一つの準同形である。
ある言語から他への自動翻訳は,記述の意味を維持できるため,通常準同形である。それらは,
慣用的な違い及び不規則性,並びに文化に特有な意味伝達への比ゆ(喩)使用のため,対象の
文をその元の資料に常に写像することができないので,同形であることはほとんどない。例え
単純な場合であっても,イギリス英語及びアメリカ英語のように,語い(彙)及び文法が本質
的に同一となるような場合は,特定の行から推論することは妥当でないという意味のアメリカ
の慣用句“that dog won't hunt”のような,主として文化に由来する慣用表現に依存する。
同形(isomorphism)(本体4.56) 二つの領域の一方から他方への一対一で構造を保存する関数が存在し
て,それら二つの関数をどの順序で合成しても恒等関数に一致するような,二つの領域(二つの複体のよ
うな)の間の関係。
備考 要素が一対一対応し,その対応で次元及び境界が保存される場合,幾何複体は,位相複体に同
形である。
幾何実現(geometric realization)(本体4.49) 位相複体の位相プリミティブに一対一対応した幾何プリ
ミティブをもつ幾何複体。その二つの複体の境界関係は一致する。
備考 この実現では,位相プリミティブは,対応する幾何プリミティブの内部を表現するものとみな
す。合成したものは閉じている。
129
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考)空間スキーマ概念の事例
序文 この附属書は,空間スキーマ概念を適用した事例を記述するものであり,規定の一部ではない。
C.1 幾何
C.1.1 意味 ここに示した例では,この規格で規定した型の名称を,あたかもインスタンス化可能なクラ
スであるものとして使用している。UMLの通常の意味での型ではないが,この記法は,幾つかの解釈のも
とで妥当と認められる。第一に,適合性の箇条では,この規格での型が応用スキーマに含まれることを必
要としないが,応用スキーマの各クラスが,これらの型を実現することを必要としている。この論理的な
要求では,インスタンス化されたクラスが,標準の型及びインタフェースと異なった名前をもつことを要
求するものではない。第二に,強力な名前空間規約を用いるデザインシステムを仮定すると,異なる名前
空間の項目は,同じ局所名をもつことができる。言い換えれば,局所名は,広域的には一意ではない。第
三に,これらの例は,型の識別を実現するものであればいかなる実装クラスに対しても有効である。いず
れの実装(応用スキーマ)も,これらの型について,それを実現する実装クラスに関連させるようなスキ
ーマ写像をもつ必要がある。記法上妥当な写像であればそれは適切であるといえる。
一般に,“比ゆ(喩)的に言えば同一”だが,技術的には異なる実体に対して,共通の名前を用いること
は有効である。この規格のUMLモデルは抽象型を定義し,応用スキーマは概念クラスを定義し,様々な
ソフトウェアシステムは実装クラス及びデータ構造を定義し,符号化規格によるXMLはエンティティタ
グを定義する。これらすべては,同一の情報内容を参照している。実装されたデジタルの実体によって深
い水準で著しい技術的差異があっても,同じ情報内容の表現に同じ名前を用いることを可能にするのは困
難ではない。このことから,UMLモデル中で定義した型を,応用スキーマで直接用いることが“可能”で
あるといえる。
C.1.2 二次元座標参照系の幾何オブジェクト この例は,単純な復号処理の場面に基づいている。これは,
実効的な位相エディタの生成についての詳細な検討の必要を除去しており,編集の対極となる用途向けの
ものである。次の仮定は,ISO 19109(1) に従って定義した応用スキーマに対するものである。
注(1) 未発行
a) この幾何及び位相のスキーマはこの文書の定義する空間スキーマに適合し,この規格の規定が定義す
る主要な幾何及び位相の型のインスタンス化できる下位クラスを含む。可読性を高めるため,この規
格の規定で使用した型の名前をそのインスタンス化できる下位型タイプ名の代わりに使用する。
b) このスキーマは二次元完全位相を使用する必要がある。
c) このスキーマは二次元座標参照系を含む。
d) この地物スキーマは,附属書DのMiniTopoの解説で示される主題,地物及び地物要素と同等のもの
を含む。
e) 永続的なオブジェクトは,その生成後に“Datastore”と呼ばれるデータ保持領域に挿入される。
図C.1は,平面多様体に基づくGM̲Complexの幾何を示す。この複体を構築するため,次の例では,オ
ブジェクトを図式の示す組合せに基づいたコンストラクタで生成するような機能的段階構文を使用する。
いったん生成されたオブジェクトは,その後の表記にいつでも使用することができる。この規定の箇条で
正式なコンストラクタが示されていないオブジェクトの場合,単純にオブジェクトの状態のレコード表現
130
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
をとり,それをデータ型と同様のコンストラクタに対する引数として使用するような,既定のコンストラ
クタを仮定する。これは,SQL99で行われる方法と非常によく一致する。SQLは,挿入の意味での要件に
基づき,任意のUDT(利用者定義型)に対して自動的に既定のコンストラクタを生成する。“< >”がレコ
ード又は順序集合(リスト)を記述し,“{ }”が非順序集合又は多重集合を記述することに注意する必要
がある。
構築は,点の生成から開始できる。ここでは,GM̲Pointは,型であるためインスタンス化できないこと
による小さな問題がある。応用スキーマを適合させるため,GM̲Pointの下位型となるインスタンス化可能
なクラスを含まなければならず,そして,そのクラスは,次の生成段階構文で使用するGM̲Pointをそれ
ぞれ置き換えなければならない。まず,{P1, ,,, P7} として識別する黒点で示した七つのGM̲Point
を生成する。
P1 = GM̲Point < position = < 1.00, 5.00 > >
P2 = GM̲Point < position = < 3.00, 5.00 > >
P3 = GM̲Point < position = < 3.00, 2.00 > >
P4 = GM̲Point < position = < 1.75, 2.75 > >
P5 = GM̲Point < position = < 1.50, 4.50 > >
P6 = GM̲Point < position = < 2.00, 3.25 > >
P7 = GM̲Point < position = < 5.00, 4.00 > >
Insert P1,P2,P3,P4,P5,P6,P7 into Datastore
x
x
x
x
P1
P2
P3
P7
P4
C6
C4
C3
C2
C1
x
x
S1
S2
S3
(1.00, 5.00)
(3.00, 5.00)
(1.75, 2.75)
(1.00, 2.00)
(3.00, 2.00)
(4.25, 4.00)
(5.00, 4.00)
(4.25, 3.25)
(5.00, 3.25)
(6.00, 2.00)
(6.00, 5.00)
x
P5
C5
(1.50, 4.50)
(1.90, 4.25)
(2.00, 4.00)
P6(2.00, 3.25)
x
図 C.1 複数のGM̲Primitiveからなるデータ集合
これらの点が存在することによって,{CS1,CS2,CS3,CS4,CS5,CS6,CS7} として識別する七つ
のGM̲CurveSegmentの段階構文を継続して構築することができ,それらをその後の曲線の構築に使用す
ることができる。GM̲CurveSegmentの下位型は,データ型であり,永続的な識別値を保持できないことに
131
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注意が必要である。すなわち,次の曲線分の定義に使用する変数は“ヒープ”又は局所変数であって,構
築の段階では定義されるが,オブジェクト型(この場合,後で定義する曲線)のメンバとして含まれるま
で永続的に保持されるものではない。ここで定義する曲線分は,折れ線又は円弧のいずれかとする。
CS1 = GM̲CurveSegment <controlPoint = <P1, P2>, interpolation = “linear”>
CS2 = GM̲CurveSegment <controlPoint = <P2, P3>, interpolation = “linear”>
CS3 = GM̲CurveSegment <controlPoint = <P2, (6, 5), (6, 2), P3>,
interpolation = “linear” >
CS4 = GM̲CurveSegment <controlPoint = <P1, (1, 2), P3>, interpolation = “linear”>
CS5 = GM̲CurveSegment <controlPoint = <P5, (1.9, 4.25), (2, 4)>,
interpolation = “arc”>
CS6 = GM̲CurveSegment <controlPoint = <(2, 4), P6>, interpolation = “linear”>
CS7 = GM̲CurveSegment <controlPoint = <P7, (4.25, 4), (4.25, 3.25), (5, 3.25), P7>,
interpolation =“linear”>
ここでは,既にデータ保持領域に記録されたP1のような永続的変数は,局所実体と永続実体との同期
を保持しつつ操作できるものと暗黙的に仮定する。したがって,GM̲Positionデータ型に基づいたGM̲Point
を使用して,曲線分を(後の曲線のメンバとして)挿入することができる。SQL言語応用プログラムイン
タフェース(API)だけを使用するオブジェクトリレーショナルデータベースの場合,応用システムは変
数への参照をたどって,続く挿入文でそれらを使用する。同様に同じデータ保持領域へのオブジェクトイ
ンタフェースを使用する場合,データベースAPIは,この参照をたどる操作をプログラマに対して透過な
ものにする。
このようにして曲線分は,{C1, ... C6} として識別する六つのGM̲Curveの永続オブジェクトを構築す
るのに使用することができる。インスタンス化可能な型についての同じ解説が適用され,そのため局所応
用スキーマは,GM̲Curveの代わりに,必要とするGM̲Curveの下位型を使用しなければならない。
C1 = GM̲Curve segments = <CS1>
C2 = GM̲Curve segments = <CS2>
C3 = GM̲Curve segments = <CS3>
C4 = GM̲Curve segments = <CS4>
C5 = GM̲Curve segments = <CS5, CS6>
C6 = GM̲Curve segments = <CS7>
Insert C1,C2,C3,C4,C5,C6 into Datastore
さらに,曲線は曲面の構築に使用することができる。この場合,この座標空間は二次元なので,平面多
角形のコンストラクタを使用することができる。その曲面のupNormal(上方法線)は,曲面に対する標準
のupNormal(しばしばkとして表記する。)にほかならないため,指定する必要はない。完全位相複体を
定義することが目的であるため,座標面の範囲を曲面で完全に覆う必要がある。全域フェイスはしばしば
“フェイス0”として参照されるため,ここではそのフェイスの幾何実現をS0として定義する。そこで,
{S0, S1, S2, S3} として識別される四つのGM̲Surfaceを定義する。
S0 = GM̲Surface patch = <GM̲Polygon interior = << C1, C3, -C4 >> >
-- この全域フェイスは完全平面グラフをもつ位相複体の構築にだけ必要である。
S1 = GM̲Surface patch = <GM̲Polygon exterior = < C4, -C2, -C1 >,interior = << C5, -C5 >> >
S2 = GM̲Surface patch = <GM̲Polygon exterior = < -C3, C2 >,interior = << -C6 >> >
132
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
S3 = GM̲Surface patch = <GM̲Polygon exterior = < C6 > >
Insert S0,S1,S2,S3 into Datastore
GM̲Objectの集まりの型であるGM̲Complexの生成のために必要な幾何要素がすべて定義できたので,
あとは必要なオブジェクトの完全なリストを与えさえすればよい。これは,TP̲Complexの生成に直接的
につなげることができる。
GComplex = GM̲Complex <
surfaces = {S0, S1, S2, S3},
curves = {C1, C2, C3, C4, C5, C6}
points = {P1, P2, P3, P4, P5, P6, P7} >
TComplex = TP̲Complex < realization = GComplex >
Insert GComplex,TComplex into Datastore
これで,この箇条の最初の図式にある幾何データを幾何及び位相の記述によって構築する作業が完了し
た。この規格の対象からは外れるが,地物の構築(図C.2)の事例を次のようにまとめる。
Lake = AreaFeature featureType=“Hydrography::WaterBody”, extent = S3
RoadCenterline = LineFeature featureType = “Transportation::Road”,
centerline = C2
RoadArea
= RoadCenterLine.centerline.buffer < distance = 10m >
RoadExtent = AreaFeature featureType = “LandCover::Road”, extent = RoadArea
RoadInstance = ComplexFeature featureType = “LandUse::Road”, featureComponents = {RoadCenterline,
RoadArea }
Trail = LineFeature featureType = “CulturalFacilities::HikingTrail”, centerline = C5
School = PointFeature featureType = “CulturalFacilities::School”, Location = P4
Insert Lake, RoadCenterline, RoadExtent, RoadInstance, Trail, School into Datastore
School
図 C.2 サンプルデータの単純な地図表現
133
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.1.3 幾何オブジェクトの三次元座標参照系 図C.3は,平面で構成された三次元立体である。それは直
方体で,そこに直方体のくぼみを切り取っており,さらにそのくぼみが1単位だけ沈んだ状態がさかさま
になったものである。
P1 = GM̲Point position = <2.00, 5.00, 4.00>
P2 = GM̲Point position = <5.00, 5.00, 4.00>
P3 = GM̲Point position = <5.00, 3.00, 4.00>
P4 = GM̲Point position = <2.00, 3.00, 4.00>
P5 = GM̲Point position = <2.00, 5.00, 2.00>
P6 = GM̲Point position = <5.00, 5.00, 2.00>
P7 = GM̲Point position = <5.00, 3.00, 2.00>
P8 = GM̲Point position = <2.00, 3.00, 2.00>
P9 = GM̲Point position = <1.00, 5.00, 1.00>
P10 = GM̲Point position = <9.00, 5.00, 1.00>
P11 = GM̲Point position = <9.00, 1.00, 1.00>
P12 = GM̲Point position = <1.00, 1.00, 1.00>
P13 = GM̲Point position = <1.00, 5.00, 7.00>
P14 = GM̲Point position = <9.00, 5.00, 7.00>
P15 = GM̲Point position = <9.00, 1.00, 7.00>
P16 = GM̲Point position = <1.00, 1.00, 7.00>
(1,1,1)
(9,1,1)
(9,5,1)
(1,5,1)
(1,1,7)
(1,5,7)
(9,1,7)
(9,5,7)
(2,3,2)
(2,5,2)
(5,5,2)
(5,3,2)
(2,3,4)
(2,5,4)
(5,5,4)
(5,3,4)
図 C.3 座標表記をもつ三次元幾何オブジェクト
この曲面は(自身を包み込んで位相円柱を形成する)GM̲GriddedSurface及び(位相円柱の両端の蓋と
して振る舞う)二つのGM̲Polygonとして表現され,すべて平面による内挿である。
S1 = GM̲Surface patch =

134
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
< <GM̲BilinearGrid rows = 4, columns = 5,
controlPoint = <
<P1, P2, P3, P4, P1>,
<P5, P6, P7, P8, P5>
<P9, P10,P11,P12,P9>,
<P13,P14,P15,P16,P13> >,
GM̲Polygon exteriorVertices = <P1, P2, P3, P4, P1 >,
GM̲Polygon exteriorVertices = <P16,P15,P14,P13,P16> >
図C.4の例はGM̲Point [P1],GM̲Curve [C1]及びGM̲Surface [S1]からなる。GM̲SurfaceのSegmentation
関連は九つのGM̲SurfacePatchを指している。一つ目のGM̲SurfacePatchは破線の左側の範囲を表す。他
の八つのGM̲SurfacePatchはすべてGM̲Triangleであり,破線の右側の範囲を表す。
(4,2,0)
(8,2,0)
(14,2,0)
(14,6,0)
(14,12,0)
(8,12,0)
(4,12,0)
(12,4,2)
(11,10,1)
(8,7,0)
P1
C1
X
X
X
X
X
X
X
X
S1
図 C.4 曲面の例
P1 = GM̲Point (4,12,0)
C1 = GM̲Curve segment = <Segment 1>
Segment 1 = GM̲CurveSegment controlPoint = <(4,12,0), (4,2,0), (14,2,0), (14,12,0),
(4,12,0)>
Patch1 = GM̲Polygon exterior = <P1, (4,2,0), (8,2,0), (8,12,0), P1>
Post1 = GM̲Position (8,12,0)
Post2 = GM̲Position (14,12,0)
Post3 = GM̲Position (11,10,1)
Post4 = GM̲Position (8,7,0)
Post5 = GM̲Position (14,6,0)
Post6 = GM̲Position (12,4,2)
Post7 = GM̲Position (8,2,0)
Post8 = GM̲Position (14,2,0)
T1 = GM̲Triangle exterior = <Post1, Post2, Post3, Post1>
T2 = GM̲Triangle exterior = <Post1, Post3, Post4, Post1>
T3 = GM̲Triangle exterior = <Post3, Post5, Post4, Post3>
T4 = GM̲Triangle exterior = <Post2, Post5, Post3, Post2>
T5 = GM̲Triangle exterior = <Post4, Post5, Post6, Post4>
135
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
T6 = GM̲Triangle exterior = <Post4, Post6, Post7, Post4>
T7 = GM̲Triangle exterior = <Post5, Post8, Post6, Post5>
T8 = GM̲Triangle exterior = <Post7, Post6, Post8, Post7>
S1 = GM̲Surface patch = <Patch1, T1, T2, T3, T4, T5, T6, T7, T8>
同じ例を,片方を一つのGM̲SurfacePatch P1からなるGM̲Surface,もう一方を八つのGM̲Triangleか
らなるGM̲TriangulatedSurfaceとして,二つのGM̲Surfaceの集合として記述できることに注意すべきであ
る。さらに,これら二つのGM̲Surfaceは,前記のGM̲Surfaceと等価な,GM̲CompositeSurfaceとして結
合することができる。
136
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(参考)応用スキーマの例
序文 この附属書は,D.1に示す目的のために記述するものであり,規定の一部ではない。
D.1 背景 ISO 19109 を使用して構築した応用スキーマは,この規格で定義するパッケージを,このパッ
ケージのクラス及びインタフェースについて,ここで規定した要素規約(属性,操作又は両方)の拡張に
基づいて下位クラスを定義して使用してよい。
この仕組みは,構造的な多態性を通じてこの規格内のパッケージの必要なインタフェースに対応するよ
うなインスタンス化可能なクラスを定義する。
この附属書は,幾何に関してこの仕組みを用いて作成された骨格的な応用スキーマを含む。
D.2 単純位相
D.2.1 単純位相のパッケージ 具象位相クラスの構築は,位相及び幾何の二重オブジェクトとしての多重
継承を用いる方法を選ぶことを除いて,幾何クラスの構築に類似している。このことが,スキーマの多重
継承のために実装の多重継承で生じるような種類の問題を引き起こすことは通常はないが,オブジェクト
の幾何境界(GM̲Object::boundary)と位相境界(TP̲Object::boundary)とを区別する際には注意を払わな
ければならない。
図 D.1 単純位相のパッケージ及びクラス
Geometric
primitive
<<Leaf>>
(from Geometry)
Simple Topology
+ TS̲CurveComponent
+ TS̲DirectedEdge
+ TS̲DirectedFace
+ TS̲DirectedNode
+ TS̲DirectedTopo
+ TS̲Edge
+ TS̲Face
+ TS̲Feature
+ TS̲Node
+ TS̲PointComponent
+ TS̲Root
+ TS̲Solid
+ TS̲SurfaceComponent
+ TS̲Theme
<<Leaf>>
Topological
primitive
<<Leaf>>
(from Topology)
Features
(from JIS X 7109 Rules for App Schema)
<<Leaf>>
(from Topology Simple)
+ FE̲FeatureCollection
+ FE̲FeatureAttribute
+ FE̲Feature
+ FE̲ContainerFeatureCollection
137
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.2.2 単純位相のクラス
D.2.2.1 意味 このパッケージで定義する型(図D.1,図D.2)は,一つはTP̲Primitiveの様々な型から,
もう一つはGM̲Primitiveの様々な型から,すべて二重に境界演算を継承する。これまで,二つの継承経路
に異なる意味をもたせるような多重継承を用いてきたが,ここでの場合はそれには当てはまらない。本質
的に,二つの境界演算子が異なる継承木から発生しているにも関わらず,この単純位相ではそれらは一致
する。
D.2.2.2 TS̲Root TS̲Rootは,基底クラスとして振る舞うので,このパッケージで使用されるすべての幾
何クラス及び位相クラスに対して制約を定めたスキーマとすることができる。TS̲Rootオブジェクトの境
界は,他のTS̲Rootオブジェクトだけを含む。
TS̲Root:
TP̲Primitive::boudary->isTypeOf(TS̲Root);
TP̲Primitive::boundary = GM̲Primitive::boundary;
備考 TS̲Rootは,TP̲Primitive及びGM̲Primitiveの下位型である。これは,境界演算子が二重に定
義されていることを意味する。二番目の制約は,それにもかかわらず境界演算子が一致するこ
とを示す。これは,境界演算子に関しての制約を,結果として解決するのではなく,整形式の
制約として記述する。TP̲Primitive及びGM̲Primitiveの境界演算子は同形であり,この場合に
は全く一致するので,この制約は,どちらのプリミティブから継承された境界演算に対しても
簡単に適用できる。
D.2.2.3 TS̲Node TS̲Node(TSノード)は,位相及び幾何の両方のデータ及び機能に対応できるよう,
TP̲Node及びGM̲Pointを多重継承する。
D.2.2.4 TS̲Edge TS̲Edge(TSエッジ)は,位相及び幾何の両方データ及び機能に対応できるよう,
TP̲Edge及びGM̲Curveを多重継承する。
D.2.2.5 TS̲DirectedEdge TS̲DirectedEdge(TS有向エッジ)は,位相及び幾何の両方のデータ及び機能
に対応できるよう,TP̲DirectedEdge及びGM̲OrientableCurveを多重継承する。
D.2.2.6 TS̲Face TS̲Face(TSフェイス)は,位相及び幾何の両方のデータ及び機能に対応できるよう,
TP̲Face及びGM̲OrientableSurfaceを多重継承する。
D.2.2.7 TS̲Theme TS̲Theme(TS主題)(図D.3)は,類似の幾何オブジェクト,この場合は交通網,行
政界などの互いに関係した種類の様々な地物及び地物要素を一つに集めることによって,GM̲Complexに
よく似た振る舞いをする。TS̲Themeは,GM̲Complexを継承する。これは,Feature Attributeを保持でき
るようFeatureの下位クラスでもある。
D.2.2.8 TS̲Feature TS̲Feature(TS地物)は,このパッケージの地物クラスの基底クラスとして振る舞
う。これは,このパッケージのすべての地物オブジェクトが任意の適切な種類の属性をとれるよう,ISO
19109 で規定する一般地物モデルからFeatureクラスを継承する。
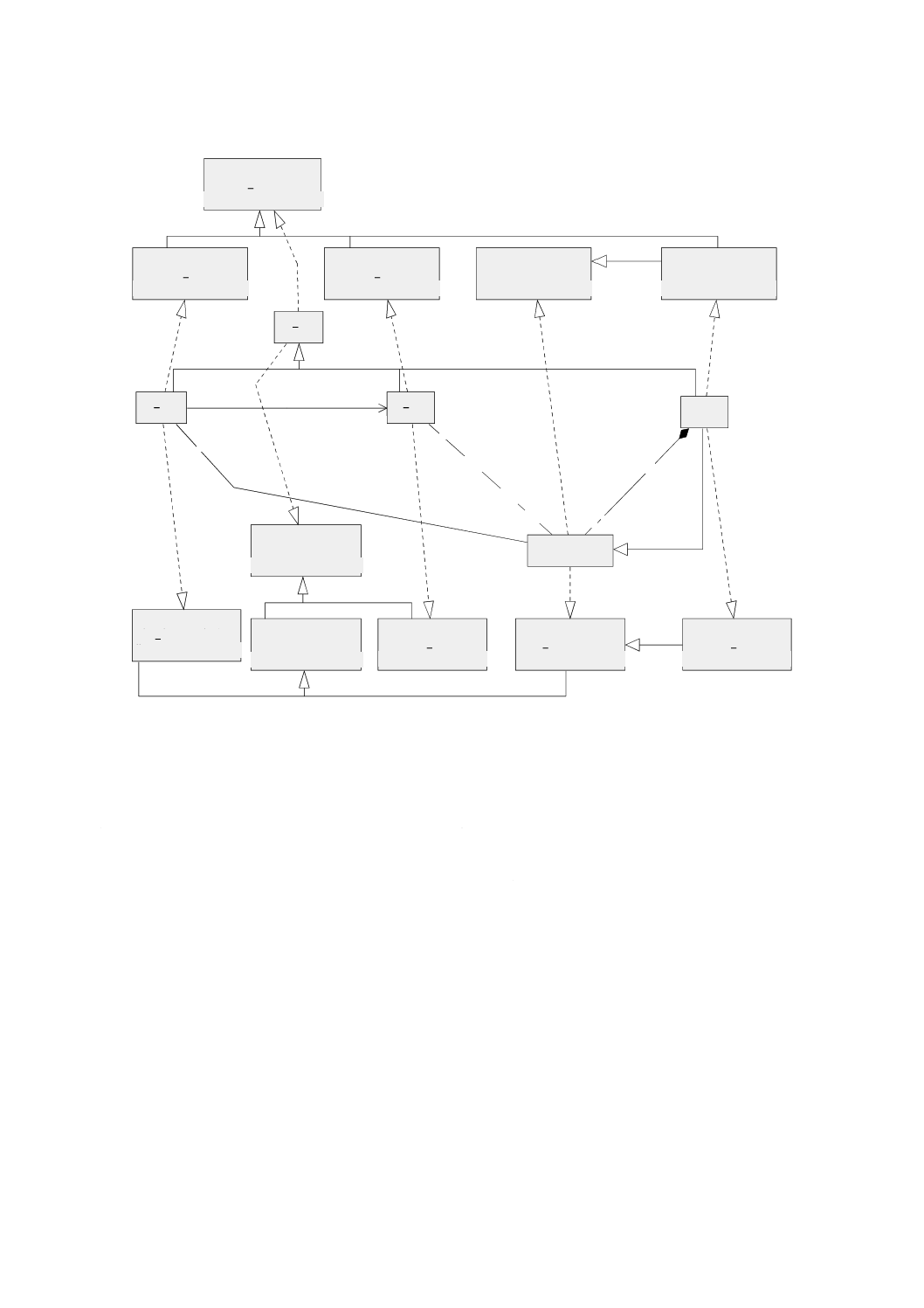
138
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
TS̲Root
GM̲Point
(from Geometric primitive)
<<Type>>
GM̲OrientableCurve
(from Geometric primitive)
<<Type>>
GM̲OrientableSurface
(from Geometric primitive)
<<Type>>
GM̲Curve
(from Geometric primitive)
<<Type>>
TS̲Edge
TS̲Node
TS̲Face
0..1
0..n
+theFace
0..1
+isolatedNode
0..n
Within
TS̲DirectedEdge
2
1
+proxy
2
+side
1
Center
0..n
1
+spoke
0..n
+hub
CoBoundary
{circular list}
1
1..n
+primitive
1
+boundary
Boundary
GM̲OrientablePrimitive
(from Geometric primitive)
<<Type>>
GM̲Primitive
(from Geometric primitive)
<<Type>>
TP̲Primitive
(from Topological primitive)
<<Type>>
TP̲Edge
(from Topological primitive)
<<Type>>
TP̲Node
(from Topological primitive)
<<Type>>
TP̲Face
(from Topological primitive)
<<Type>>
TP̲DirectedEdge
(from Topological primitive)
<<Type>>
図 D.2 単純位相における位相及び幾何クラス
D.2.2.9 TS̲PointComponent TS̲PointComponent(点要素クラス)は,独立した幾何及び地物として振る
舞えるよう,TS̲Feature及びGM̲CompositePointを多重継承する。
D.2.2.10 TS̲CurveComponent TS̲CurveComponent(曲線要素クラス)は,独立した幾何及び地物とし
て振る舞えるよう,TS̲Feature及びGM̲CompositeCurveを多重継承する。
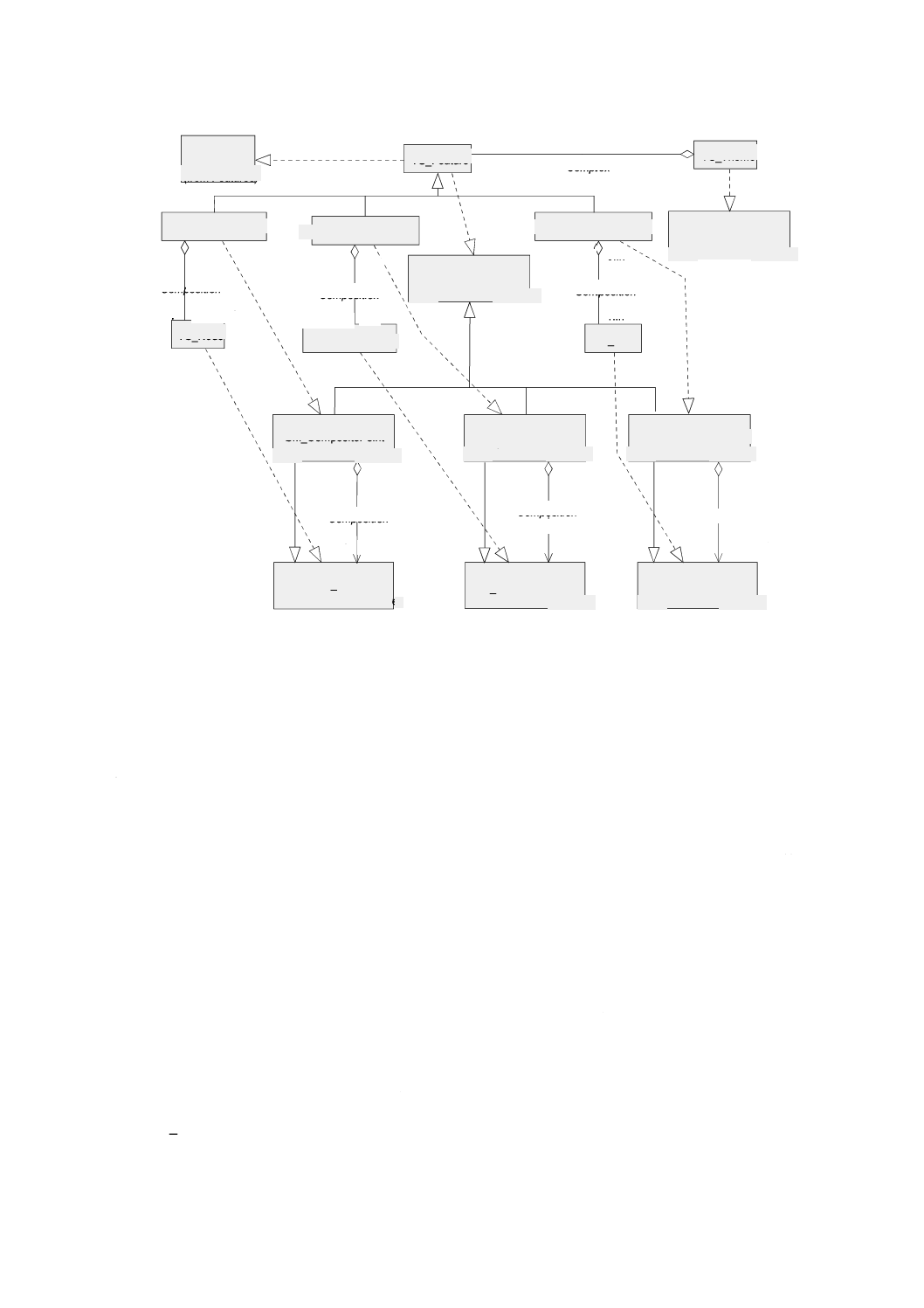
139
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 D.3 単純位相における地物要素
D.2.2.11 TS̲SurfaceComponent TS̲SurfaceComponent(曲面要素クラス)は,独立した幾何及び地物と
して振る舞えるよう,TS̲Feature及びGM̲CompositeSurfaceを多重継承する。
D.3 地物位相
D.3.1 意味 このパッケージの背景にある基本的な概念は,ここで地物要素として定義した合成幾何オブ
ジェクトが,その空間属性の位相構造から独立した(しかし,一貫した)位相構造を構成できるようにす
ることである。したがって,TP̲Complex及びGM̲Complexの下位クラスである主題の中で,基本的なは
ん(汎)主題(すべての主題を意味する)幾何オブジェクトによって構成されたものと同一の位相構造に
基づいて,地物要素どうしが互いに関係をもつことを可能にする。ここでは,地物要素がその主題の中で
他の地物オブジェクトと交差することによって切断されることを前提としている。
D.3.2 主題水準における地物位相のクラス
D.3.2.1 FT̲Complex FT̲Complex(複体クラス)(図D.4)は,位相及び幾何の両方の情報を集成(aggregate)
できるよう,TP̲Complex及びGM̲Complexを(TS̲Themeを通じて)多重継承する。このように構造化
した方法をとることによって,データ集合のそれぞれの主題が,その固有の位相情報を保持できるように
する。各地物要素が常に唯一の主題であるという単純化した仮定は,位相オブジェクト及び幾何オブジェ
クトに二分する方法を維持するというやや複雑な構造に改める。
D.3.2.2 FT̲Primitive FT̲Primitive(プリミティブクラス)は,TP̲Primitiveと同じ機能を有し,FT̲Complex
の中でインスタンス化されるTP̲Complexの基本的な部品となる。
GM̲CompositeCurve
(from Geometric complex)
<<Type>>
GM̲OrientableCurve
(from Geometric primitive)
<<Type>>
+composite
0..n
+generator
1..n
Composition
GM̲Composite
(from Geometric complex)
GM̲OrientableSurface
(from Geometric primitive)
<<Type>>
GM̲CompositeSurface
(from Geometric complex)
<<Type>>
+generator
1..n
+composite
0..n
Composition
FE̲Feature
(from Features)
<<Type>>
GM̲CompositePoint
(from Geometric complex)
<<Type>>
(from Geometric primitive)
<<Type>>
TS̲Node
TS̲PointComponent
1
0..n
+generator
1
+composite
0..n
Composition
TS̲DirectedEdge
0..n
+composite
0..n
Composition
TS̲Face
TS̲SurfaceComponent
+generator
+composite
Composition
TS̲Feature
TS̲Theme
+element
+theme
GM̲Complex
(from Geometric complex)
<<Type>>
+composite
0..n
Composition
+generator
1
GM̲Point
Complex
<<Type>>
{sequence}
TS̲CurveComponent
0..n
1..n
1..n
+generator
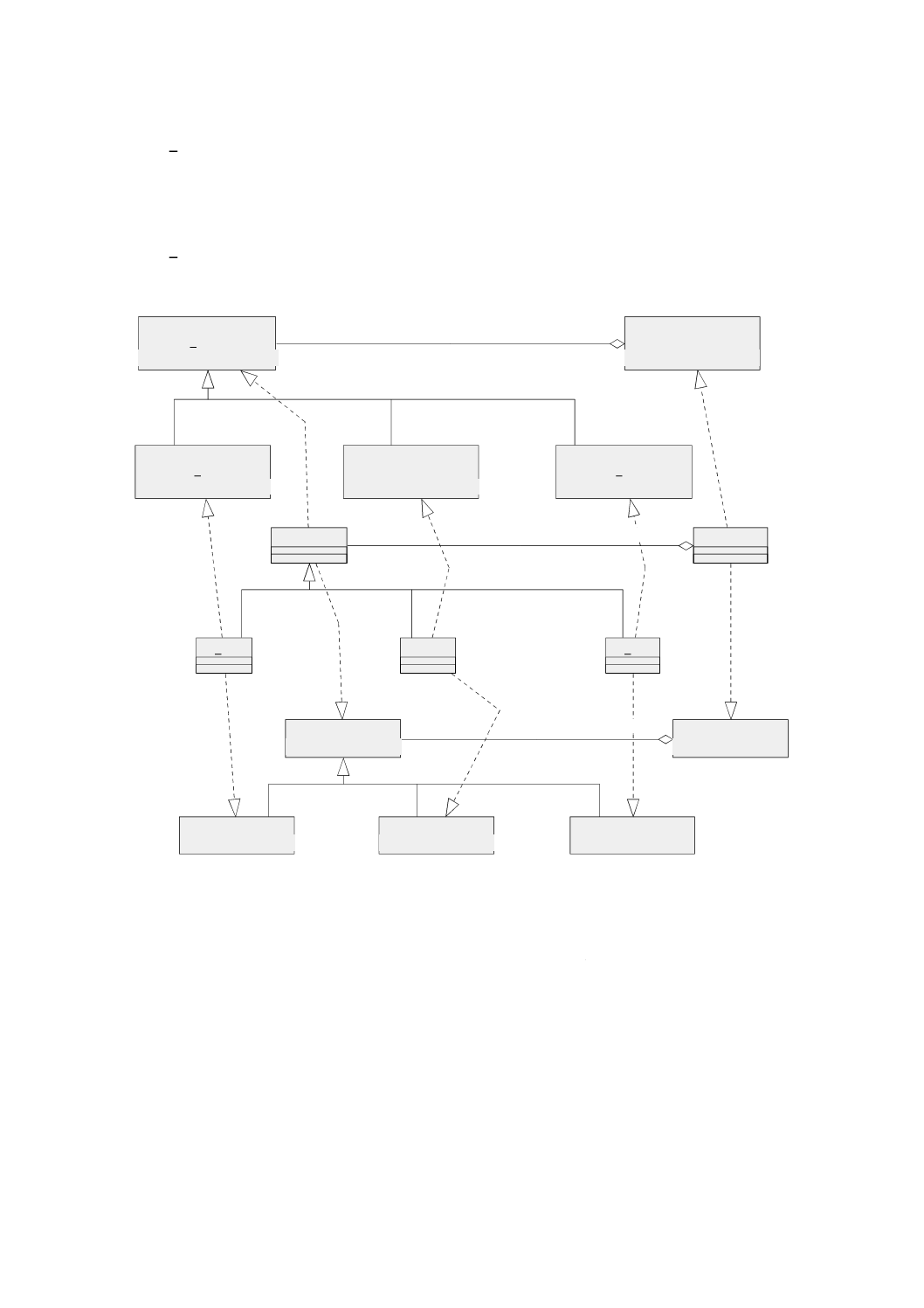
140
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.3.2.3 FT̲Node FT̲Node(ノードクラス)は,TP̲Node及びTS̲PointComponentのいずれでもある。そ
のため,必要な場合,主題の中の点地物要素は,地物位相複体の中でノードの役割を果たす。
D.3.2.4 FT̲Edge FT̲Edge(エッジクラス)は,TP̲Edge及びTS̲CurveComponentのいずれでもある。そ
のため,必要な場合,主題の中の曲線地物要素は,地物位相複体の中でエッジの役割を果たす。
D.3.2.5 FT̲Face FT̲Face(フェイスクラス)は,TP̲Face及びTS̲SurfaceComponentのいずれでもある。
そのため,必要な場合,主題の中の面地物要素は,地物位相複体の中でフェイスの役割を果たす。
TP̲Node
(from Topological primitive)
<<Type>>
TP̲Edge
(from Topological primitive)
<<Type>>
TP̲Face
(from Topological primitive)
<<Type>>
TS̲PointComponent
(from Simple Topology)
FT̲Node
TS̲CurveComponent
(from Simple Topology)
FT̲Edge
TS̲SurfaceComponent
(from Simple Topology)
FT̲Face
TP̲Primitive
(from Topological primitive)
<<Type>>
TP̲Complex
(from Topological Complex)
<<Type>>
1..n
1..n
+element
1..n
+complex
1..n
Complex
FT̲Complex
FT̲Primitive
+complex
+element
Complex
TS̲Theme
(from Simple Topology)
TS̲Feature
(from Simple Topology)
+theme
+element
Complex
図 D.4 主題に基づく地物位相
D.4 MiniTopo(最小位相プロファイル) MiniTopoプロファイルは,新しいクラスを定義せずに,単純に
既存のクラスの使用に制約を加える。すなわち,“Isolated In”関連を,フェイス中で孤立したノードだけ
を示す“Within”に特化させている。
MC&G又はMiniTopoと呼ばれた初期のモデルから導出されたDIGESTの基礎的位相モデルでは,図D.5
のように,位相的に隣接しているという情報の大部分はフェイスに関連する有向エッジ(DE)の対によっ
て保持されている。このスキーマ(図D.6)において,それに対応する情報は,境界及び双対境界の操作
並びに関係を構造化することによって保持する。表D.1は,各MiniTopoポインタを現在のモデルにおいて
対応する情報に関係付けたものである。
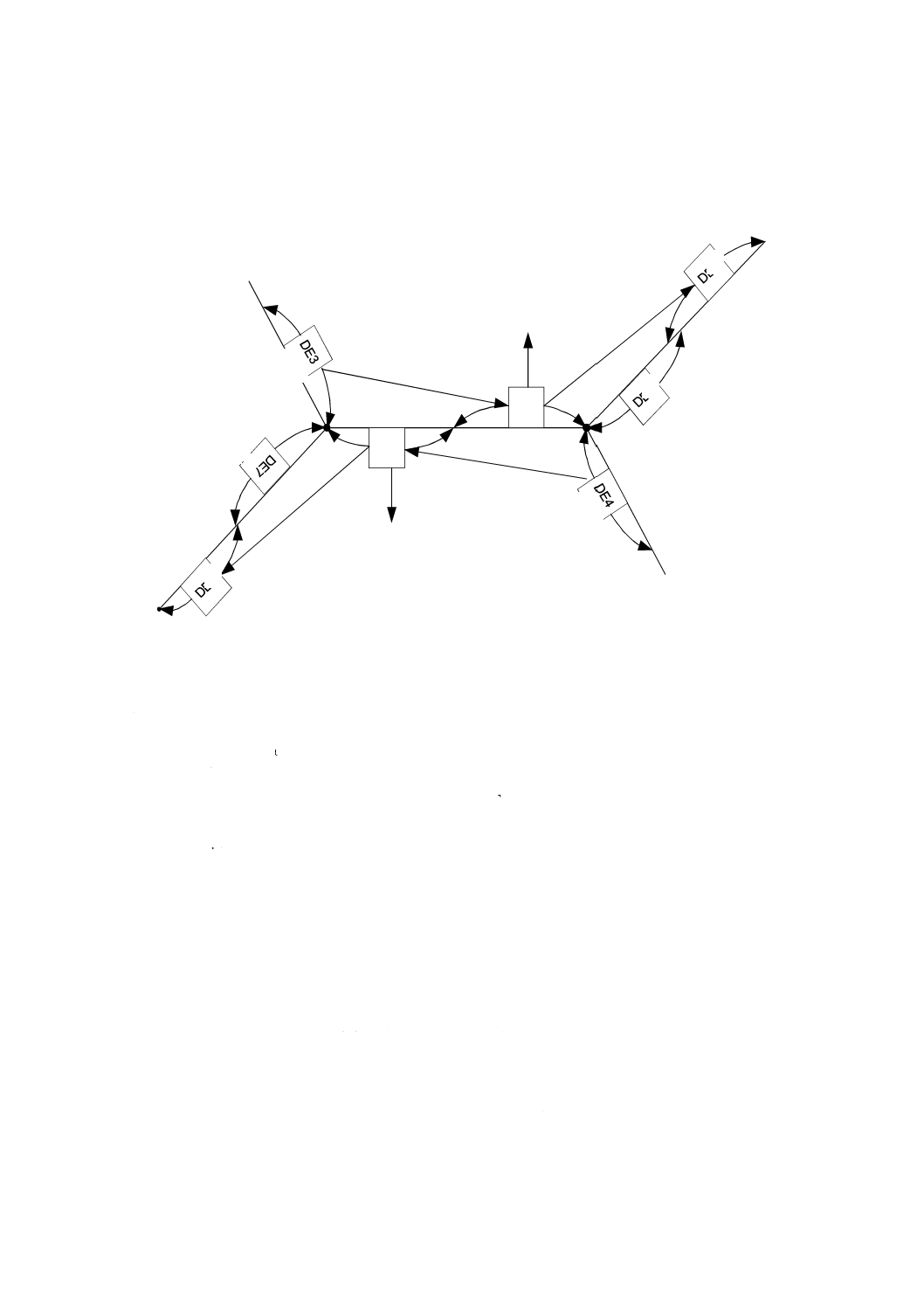
141
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
MiniTopoのレコード構造は,地物について四つ,幾何及び位相について四つ,並びに通常レコード番号
として実装されるこれらの型への参照を表すための補助概念について一つの,合わせて九つのレコード基
本型をもっていた。MiniTopo位相−幾何レコード型は,ノード,エッジ,有向エッジ及びフェイスから構
成された。
DE2
D
E4
D
E3
DE1
Face 1
Face 2
DE7
DE5
DE6
DE8
図 D.5 MiniTopo位相構造の幾何の例
幾何及び位相のためのレコード型は,次のように(SQL99類似の構文を用いて)定義された構造をもっ
ていた。
Create Node record as {
nodeID : RecordIdentifier NOT NULL PrimaryKey,
containingFace : RecordIdentifer ForeignKey to Face,
-- エッジに接続するノードでは,NULLとなる。
position : CoordinatePoint NOT NULL }
Create Edge record as {
edgeID : RecordIdentifier NOT NULL Primary Key,
positiveDE : RecordIdentifer NOT NULL Foreign Key to DirectedEdge,
negativeDE : RecordIdentifer NOT NULL Foreign Key to DirectedEdge,
coordinatList : Variable Array Of CoordinatePoint NOT NULL }
Create DirectedEdge record as {
directedEdgeID : RecordIdentifier NOT NULL Primary Key,
nodeID : RecordIdentifer NOT NULL Foreign Key to Node,
nextDE : RecordIdentifer NOT NULL Foreign Key to DirectedEdge,
face : RecordIdentifer NOT NULL Foreign Key to Face }
Create Face record as {
faceID : RecordIdentifier NOT NULL Primary Key
}
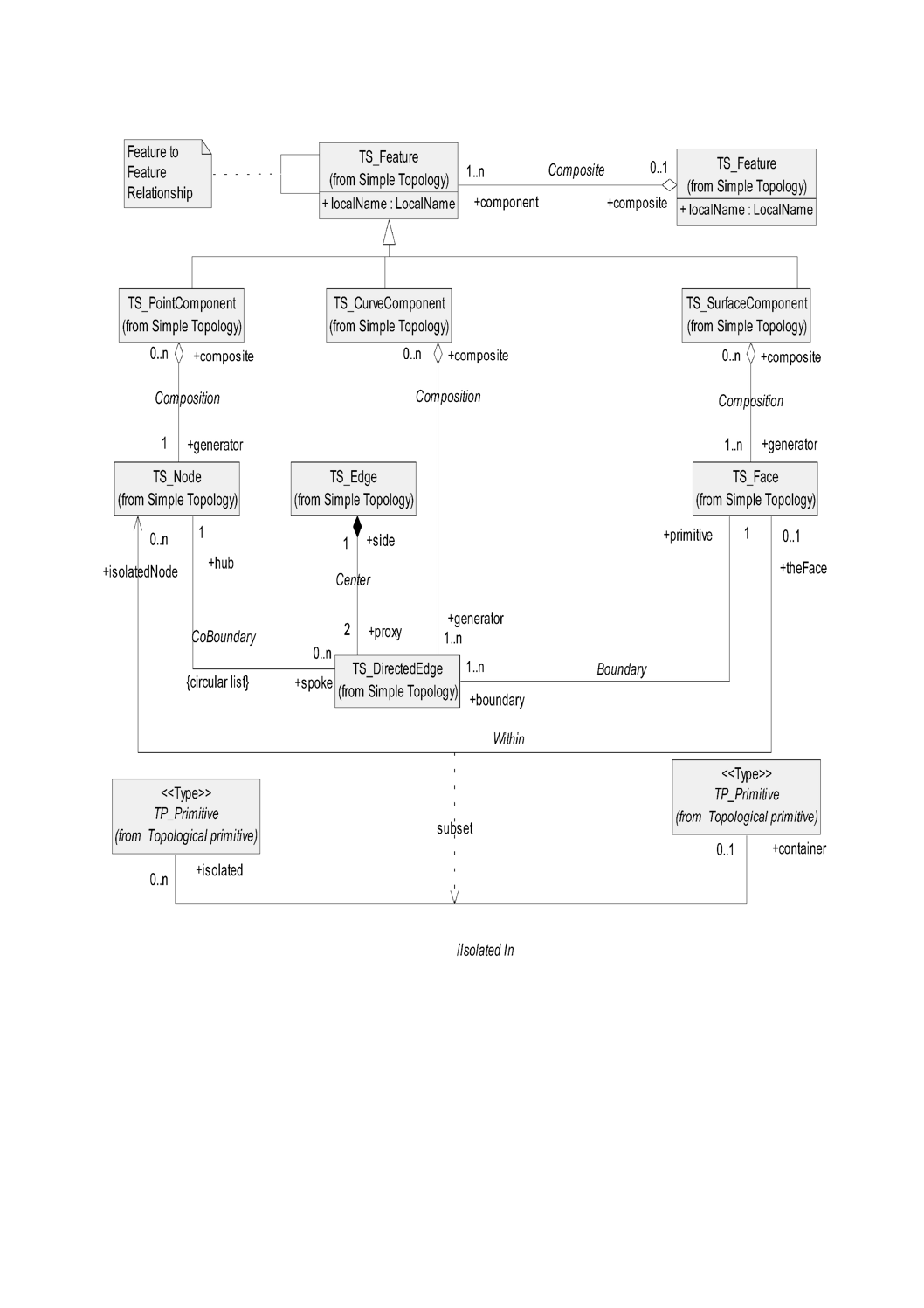
142
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 D.6 MiniTopo
この構造の基本的な利点の一つは,各レコードが固定長であることと,高い水準で正規化されているこ
とであった。この構造は,含まれる冗長性を最小とするよう配慮されており,そのため最小冗長位相とい
う意味でこの名が付けられた。
エッジの座標値を図形レコードへの参照としたことによって,各MiniTopoオブジェクトは,それぞれ固
定長となった。これには,様々な関係に対して逆方向キーを与えるか否かに応じて,異なった構造が存在
143
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
しえた。しかし,元の単階層ファイルによる交換構造においては,可変長レコードを伴う必要があること
から,このような逆方向キーは保持されなかった。また,通常,edgeID,+edgeID 及び -edgeIDと記述し,
意味上は主キーとなる三つの情報をもった一つのレコードとなるような,エッジ及び有向エッジを組合せ
たもう一つの構造も存在しえた。
幾何及び位相のレコードに加えて,四つの地物レコードの型があった。
Create PointFeature as { -- 本質的には多点
featureID : RecordIdentifier NOT NULL Primary Key,
nodeID : Variable Array Of RecordIdentifier NOT NULL Foreign Key to Node,
attribute : Variable Array of <Name : CharacterString, Value : CharacterString> }
Create LineFeature as { -- 本質的には合成曲線
featureID : RecordIdentifier NOT NULL Primary Key,
directedEdgeID : Variable Array Of RecordIdentifier NOT NULL Foreign Key to DirectedEdge,
attribute : Variable Array of <Name : CharacterString, Value : CharacterString> }
Create AreaFeature as { -- 本質的には合成曲面
featureID : RecordIdentifier NOT NULL Primary Key,
faceID : Variable Array Of RecordIdentifier NOT NULL Foreign Key to Face,
attribute : Variable Array of <Name : CharacterString, Value : CharacterString> }
Create ComplexFeature as { -- 本質的には集成(aggregate)地物
featureID : RecordIdentifier NOT NULL Primary Key,
pointComponentID : Variable Array Of RecordIdentifier Foreign Key to PointFeature,
lineComponentID : Variable Array Of RecordIdentifier Foreign Key to LineFeature,
areaComponentID : Variable Array Of RecordIdentifier Foreign Key to AreaFeature,
subfeatureID : Variable Array Of RecordIdentifier Foreign Key to ComplexFeature,
attribute : Variable Array of <Name : CharacterString, Value : CharacterString> }
これらの各種レコードは,他のいずれの地物にも含まれない複合地物の型である主題(theme)レコード
の概念と,各地物及び各位相のレコード情報が他動的にメンバとして所属した主題を示す主題マスク属性
の概念を含んでいた。
Create Theme as { -- 本質的には複合地物の一種
featureID : RecordIdentifier NOT NULL Primary Key,
pointComponentID : Variable Array Of RecordIdentifier Foreign Key to PointFeature,
lineComponentID : Variable Array Of RecordIdentifier Foreign Key to LineFeature,
areaComponentID : Variable Array Of RecordIdentifier Foreign Key to AreaFeature,
subfeatureID : Variable Array Of RecordIdentifier Foreign Key to ComplexFeature,
-- 主題(theme)自体は,複合地物ではないので,他のいずれのComplexFeature
-- 又はThemeにも保持されない(各ポインタは明確に示されている)。
attribute : Variable Array of <Name : CharacterString, Value : CharacterString>
ThemeMask : Integer -- ComplexFeatureと地物要素の各型にそれぞれ付加した
-- ビットマスクとして用いられる。
-- 主題マスクの大きさによって主題の数は通常32までに限定される。}
次の図D.7は,標準的なレコードの例を示す。
144
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
現行のモデルとMiniTopoモデルとの主な違いは,その起源による。MiniTopoは,もともと交換構造と
して設計され,順次構造の単階層ファイル構造のもつ制約によって,多様なオブジェクトモデルをもたな
かった。MiniTopo構造の背景にある概念水準でのモデルは,エッジとフェイス及びエッジとノードとの間
にある境界構造に関して現行のモデルと正確に一致したものであった。容量を節約し,交換構造から計算
可能な構造への変換を迅速化するために,MiniTopo(最小位相)が導入された。図D.5で示したように,
MiniTopoには,現行のモデルでは明示的に表現されている境界及び双対境界の構造の内部構造を表現する
ために,有向エッジを用いた離散リンクリスト構造が使用された。現行のモデルで用いているUMLの,
より多様なオブジェクト・モデル化能力によって,MiniTopoの本来の概念モデルは,明示的なオブジェク
ト構造として,より厳密に表現できる。
これは,多様なオブジェクト・モデル化環境の大きな利点の一つである“意味とのかい(乖)離”の狭
小化を示すものである。“意味とのかい(乖)離”は概念モデルと実装モデルとの間の違いを記述する便宜
上の用語である。“かい(乖)離”の多くは,概念構造をプログラム言語の構造体で再表現しなければなら
ない場合に起こる。多様なオブジェクトのモデルは言語構造により強力な語い(彙)を与えるので,“かい
(乖)離”を少なくすることができる。これはアルゴリズムの複雑さと,データ構造の複雑さ及びサイズ
との間の費用のトレードオフをもたらす。1984年にMiniTopoが設計されたとき,費用のトレードオフで
は,小さくより簡潔なデータ構造が好まれ,より強力な概念モデルに対して,メモリ消費における費用の
観点から,オブジェクト構造を再構成することとなった。MiniTopo構造の開発を取り巻く制限のため,そ
の原作者による完全な文書化が行われたことはなく,これまで公開文書として刊行されたのはトレードオ
フの適切な説明のない交換構造についてだけであった。今日,このトレードオフは大きく変わり,計算モ
デル及び永続記憶モデルのいずれでも概念構造の保持が好まれている。その費用には,より冗長で拡張的
な永続記憶モデル,及び計算モデルの複雑さの増加を含んでいる。その利点は,“意味とのかい(乖)離”
を狭小化して他との一貫性を保ったモデルであること,及び論理的に一貫し多様な意味を表現できる概念
モデルにさらに近づいた計算環境であることである。実際に,このモデルは,MiniTopoの本来の概念モデ
ルと矛盾するものではなく,それを文書化して,より現代的なオブジェクト環境における実装に更新する
ものである。
145
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Theme
Complex Feature
Point Feature
Line Feature
Area Feature
Node
Directed Edge
Face
Edge
図 D.7 古典的なMiniTopoのレコードの様子

146
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 D.1 本来のMiniTopoのポインタと現行モデルとの対応関係
MiniTopoの
ポインタ
現行のモデル
解説
Edgeから
正のDEへ
TP̲Edgeを継承した,TS̲Edgeから自身への関連
Center::side : TP̲DirectedEdge
各エッジは,その正の有向エッジと
なる。
Edgeから
負のDEへ
TP̲Edgeを継承した,TS̲Edgeから負の方向をもつ
TS̲DirectedEdgeへの関連
Center::side : TP̲DirectedEdge
各エッジは,負の方向をもつ有向エ
ッジの一つと関連する。
正のDEから
終点Nodeへ
TP̲Edgeの境界演算子を派生して継承した,TS̲Edge
から正の方向をもつTS̲DirectedNodeへの関連
/boundary::boundary : TP̲DirectedNode
エッジは,一つは正の方向とし,も
う一つは負の方向とする,二つの有
向ノードからなる境界をもつ。正の
有向ノードは終点ノードに,負の有
向ノードは始点ノードに対応する。
負のDEから
始点Nodeへ
TP̲Edgeの境界演算子を派生して継承した,TS̲Edge
から負の方向をもつTS̲DirectedNodeへの関連
/boundary::boundary : TP̲DirectedNode
正のDEから
左側Faceへ
TP̲Edgeの双対境界演算子を派生して継承した,
TS̲Edgeから正の方向をもつTS̲DirectedFaceへの関連
/coBoundary::spoke : TP̲DirectedFace
エッジは,一つは正の方向とし,も
う一つは負の方向とする,二つの有
向フェイスからなる双対境界をも
つ。正の有向フェイスは左側のフェ
イスに,負の有向フェイスは右側の
フェイスに対応する。
負のDEから
右側Faceへ
TP̲Edgeの双対境界演算子を派生して継承した,
TS̲Edgeから負の方向をもつTS̲DirectedFaceへの関連
/coBoundary::spoke : TP̲DirectedFace
DEから(Face
の周囲に沿っ
た)次のDEへ
TP̲Faceの境界演算子を派生して継承した関連におけ
る,TS̲FaceからTS̲DirectedEdgeへの“境界”役割の
構造
/boundary::boundary : Set<TP̲Ring>
フェイスの境界は,輪の集合であ
る。各輪は,有向エッジの環状列で
ある。この列で隣接するエッジは,
本来のMiniTopoモデルにおけるDE
→(次のDE)の対である。
147
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E(参考)参考文献
備考 幾つかの定義及び追加の情報は次に示した出典から採用し,この規格の内容に合わせて幾分か
の明確化や簡約化を加えている。
1) Abadi, Martín, and Luca Cardelli, A Theory of Objects, Springer-Verlag, New York, 1996.
2) Bartels, Richard H., John C. Beatty, Brian A. Barsky, An Introduction to Splines for Use in Computer
Graphics & Geometric Modeling, Morgan Kaufmann Publishers, Inc., 1987
3) Clapham, Christopher, Concise Dictionary of Mathematics, Second Edition, Oxford University Press,
1996.
4) Clementini E. and Di Felice P., A Comparison of Methods for Representing Topological Relationships,
Information Sciences 80, 1-34, 1994.
5) Clementini, Eliseo, Di Felice, P., A Model for Representing Topological Relationships Between Complex
Geometric Features in Spatial Databases, Information Sciences 90 (1-4):121-136 , 1996.
6) Daintith, John, and R. D. Nelson, Dictionary of Mathematics, Penguin Books, London, 1989.
7) Dictionary of Computing, Fourth Edition, Oxford University Press, 1996.
8) Egenhofer, M.F. and Franzosa, Point Set Topological Spatial Relations,
International Journal of Geographical Information Systems, vol 5, no 2, 161-174, 1991.
9) Egenhofer, M.J., Clementini, E. and Di Felice, P., Topological relations between regions with holes,
International Journal of Geographical Information Systems, vol 8, no 2, pp 129-142, 1994.
10) Farin, Gerald, Curves and Surfaces for Computer Aided Geometric Design, A Practical Guide, Second
Edition, Academic Press, Inc., Boston, 1990.
11) Farin, Gerald, NURB Curves and Surfaces, From Projective Geometry to Practical Use, A. K. Peters,
Wellesley, Massachusetts, 1995.
12) Faux, I. D., and M. J. Pratt, Computational Geometry for Design and Manufacture, Ellis Norwood
Publishers, reprinted with corrections, 1981.
13) ISO/IEC 13249-3:1999, Information technology - Database languages - SQL Multimedia and Application
Packages - Part 3: Spatial, ISO/IEC JTC1 SC 32, 1999
14) Kostov, Vladimir, and Elena Degtiariova-Kostova, Some properties of clothoids, INRIA, Nice ‒ Sophia
Antipolis, Research Report N0 2752, December 1995.
15) OMG/UML
,
Object
Constraint
Language
Specification
,
version
1.3
,
ed.
http://www.rational.com/uml/resources/documentation/formats.jsp, 1997.
16) OMG/UML
,
UML
Notation
Guide
,
version
1.3
,
http://www.rational.com/uml/resources/documentation/formats.jsp, 1997.
17) OMG/UML,UML Semantics,version 1.3,http://www.rational.com/uml/resources/documentation/formats.jsp,
1997.
18) Prenter, P. M., Splines and Variational Methods, John Wiley & Sons, New York, 1975, republished
in Wiley Classics Edition, 1989.
148
X 7107:2005 (ISO 19107:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
19) Rogers, David F., J. Alan Adams, Mathematical Elements for Computer Graphics, Second Edition,
McGraw Hill Publishing Company, 1990.
20) The OpenGIS Abstract Specification, Volumes 1-14, OpenGIS™ Consortium, 1997.