Q 0035:2008 (ISO Guide 35:2006)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲 ························································································································· 2
2 引用規格 ························································································································· 3
3 用語及び定義 ··················································································································· 3
4 記号······························································································································· 5
5 認証プロジェクトの設計 ···································································································· 6
5.1 概説 ···························································································································· 6
5.2 プロジェクトの明確化 ···································································································· 6
5.3 輸送の問題点 ················································································································ 6
5.4 原料物質の収集 ············································································································· 6
5.5 フィージビリティスタディ······························································································· 7
5.6 要求される寿命及び保管期限···························································································· 7
5.7 試料の調製 ··················································································································· 7
5.8 均質性試験 ··················································································································· 9
5.9 安定性試験 ··················································································································· 9
5.10 測定方法の選択 ··········································································································· 11
5.11 認証 ·························································································································· 11
5.12 プロジェクト設計の要約 ······························································································· 11
6 測定の不確かさの評価 ······································································································ 12
6.1 (C)RMの特性値の不確かさを評価するための基礎 ······························································· 12
6.2 バッチの値付けのための基本モデル ·················································································· 13
6.3 不確かさの要因 ············································································································ 14
6.4 分布関数にかかわる問題点······························································································ 14
6.5 比率の使用 ·················································································································· 15
6.6 包含係数の選択 ············································································································ 15
6.7 再認証 ························································································································ 15
7 均質性試験 ····················································································································· 16
7.1 序文 ··························································································································· 16
7.2 物質 ··························································································································· 16
7.3 均質性の概念 ··············································································································· 17
7.4 実務 ··························································································································· 17
7.5 測定 ··························································································································· 17
7.6 統計的に有効なサンプリングスキーム及び傾向分析 ····························································· 18
7.7 均質性試験の評価 ········································································································· 18
7.8 瓶間均質性試験 ············································································································ 19
Q 0035:2008 (ISO Guide 35:2006) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
7.9 測定方法の併行精度が不十分な場合 ·················································································· 20
7.10 瓶内均質性 ················································································································· 20
8 安定性試験 ····················································································································· 21
8.1 (不)安定性のタイプ ··································································································· 21
8.2 実験計画 ····················································································································· 22
8.3 結果の評価 ·················································································································· 23
8.4 安定性のモニタリング ··································································································· 26
8.5 長期安定性からの保管期限の決定····················································································· 28
9 特性値の決定 ·················································································································· 28
9.1 概説 ··························································································································· 28
9.2 トレーサビリティの確立及び実証····················································································· 29
9.3 実務的方法 ·················································································································· 31
9.4 測定の設計 ·················································································································· 31
9.5 特性に関連した考察 ······································································································ 35
10 データ及び不確かさの評価 ······························································································ 38
10.1 モデル ······················································································································· 38
10.2 データフォーマット ····································································································· 39
10.3 分布 ·························································································································· 41
10.4 データのスクリーニング ······························································································· 42
10.5 データの評価 ·············································································································· 42
10.6 不確かさの評価 ··········································································································· 44
10.7 不確かさに基づく評価 ·································································································· 44
10.8 特定の問題点 ·············································································································· 46
11 認証 ···························································································································· 47
附属書A(参考)統計的方法 ································································································· 48
附属書B(参考)事例 ·········································································································· 53
参考文献 ···························································································································· 61
Q 0035:2008 (ISO Guide 35:2006)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づき,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本
工業規格である。これによって,JIS Q 0035:1997は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
Q 0035:2008 (ISO Guide 35:2006) 目次
(4)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
白 紙
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Q 0035:2008
(ISO Guide 35:2006)
標準物質−認証のための一般的及び統計的な原則
Reference materials−General and statistical principles for certification
序文
この規格は,2006年に第3版として発行されたISO Guide 35を基に,技術的内容及び対応国際規格の
構成を変更することなく作成した日本工業規格である。
標準物質(reference material: RM)の生産,キャラクタリゼーション(characterization)及び認証は,世界中で
整合性のとれた測定系を改善及び維持するときに中心となる活動である。JIS Q 0032及びJIS Q 0033に詳
細な規定があるように,認証標準物質(certified reference material: CRM)は,校正,品質管理及び方法の妥当
性確認の目的,並びにそれによってCRMにすることもできる他の物質への値の付与のために用いる。さ
らに,CRMは,オクタン価,硬さ目盛及びpHのような従来の目盛に対するトレーサビリティを維持し,
又は確立するために使用される。最後に,同じくらい重要なこととして,ある種の純物質も,国際温度目
盛を維持するため使用される場合のあることを付記しておく。
CRMの生産者に対しては,3種類の日本工業規格(JIS)があり,それらはRMの生産及び認証を行い,ま
た,こうして生産したCRMの品質がエンドユーザーの要求事項を確実に満たすための施設作りを支援す
る。JIS Q 0034は,CRM生産者が能力を実証するために満たすべき要求事項の概要を規定しており,こう
した要求事項を満たす方法について手助けをする。この規格は,かなり包括的なレベルで,均質性試験,
安定性試験及び候補CRMのキャラクタリゼーションについてモデルを提示している。JIS Q 0031はCRM
の認証書の様式と内容について規定している。
場合によっては,この規格は,CRMの生産の特性に関してみると,測定における不確かさの表現のガイ
ド(Guide to the Expression of Uncertainty in Measurement: GUM)の応用とみることができる。GUMでは,測
定から得た値の測定不確かさの評価方法を詳細に説明しているので,この規格は,可能な場合,GUMを
参照している。この規格は,(依然として存在する)バッチの不均質性及びCRMの不安定性による不確か
さを特性値の不確かさに含めること,及びこれら不確かさの寄与分の決定に追加的な指針を規定している
という点で,GUMを補完している。
この規格は,RMの生産及びキャラクタリゼーションを最善で行えるよう支援するために作成されたも
のであるが,特定の部分が個別のCRMに適用できるかどうかを十分配慮せずに使用すると,特性値(及
びその不確かさ)が間違った,又は欠陥のある根拠に基づいて決まる結果になることがある。この種の文
書の使用者は,この文書が“批判的な思考,知的誠実さ及び専門技能”(GUM:1993,3.4.8)に代わるもの
ではないことを考慮することが望ましい。“製品”CRMの品質は,適正な手順及び方法をとることと同じ
くらいこうした側面に左右される。
通常の認証プロジェクトにおいて,実験データを正しく処理し,かつ,解釈するためには,物質及びそ
の特性を知ること,並びに物質の均質性試験,安定性試験及びキャラクタリゼーションのときに使用する
測定方法について知識をもつことが,統計的方法についての完全な知識とともに必要となる。これら必要
2
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
な技能が複合しているために,RMの生産及び認証が大変複雑になっているのである。これらのプロジェ
クトで最大の課題となるのは,プロジェクト計画の円滑な実施を可能にするために,これらの技能を組み
合わせることである。
この規格の内容のほとんどは,RMの生産に適用することができる。特性値のトレーサビリティのよう
な要求事項,特に,測定の不確かさ評価を徹底する必要性は,例えば,RMを校正物質として使用するた
め,ある方法の性能特性を確認する手段として使用するため,又は,別の物質に値を付与するために,ほ
とんどの種類のRMに適用できる。
薬局方の標準(standards)及び物質(substances)は,薬局方監督機関がこの規格の一般原則に従って確定し,
配布している。これらの種類のRMの生産に関しては,特別な指針が存在する。
なお,分析及び有効期限の証明書によって使用者に情報を与えるために薬局方監督機関がとる方法は,
異なるので注意することが望ましい。また,付与された値の不確かさは,関係する要領にあるこれらのRM
を規定どおりに使っても,不確かさを容認するわけではないので,規定していない。
1
適用範囲
この規格は,付随する不確かさの評価を含め,標準物質の特性に値を付与し,これら値の計量学的トレ
ーサビリティを確立するための妥当な方法を理解し,開発することを支援する目的で,標準物質認証のた
めの一般的及び統計学的な原則を規定する。この規格に規定するすべてのステップを経た標準物質(RM)
には,通常,認証書が付いており,そのRMは認証標準物質(CRM)と呼ばれる。この規格は,国家又は国
際的規模での測定結果の同等性(comparability),精確さ(accuracy)及び両立性(compatibility)を確保する手助け
として,CRMにその可能性を十分もたせたい場合に有用である。
国境を越えて,また長期にわたって比較可能にするために,測定が,該当し,かつ,規定された標準(stated
references)にトレーサブルであることが必要である。CRMは,物質及び/又は試料を取り扱う科学の中で
も,特に化学,生物学及び物理学の測定結果において,トレーサビリティという概念を具体化する上で重
要な役割を果たす。試験所は,測定結果の国際規格へのトレーサビリティを確立するために,容易にアク
セス可能な測定標準(measurement standards)としてこれらのCRMを使用する。CRMによって決められる特
性値は,生産過程で,SI単位又はその他の国際的合意を得ている単位に対してトレーサブルであるとする
ことができる。この規格は,該当する規定の標準までトレーサブルであり,かつ,十分に確立された特性
値を導く方法をどのようにしたら開発できるかを記載したものであり,混合ガスから生物材料にいたる非
常に広範囲の物質(マトリックス),並びに化学組成から物理的及び免疫測定法(immunoassay)によって求
められる特性にいたる非常に広範囲の特性を対象としている。
この規格で示す方法は,RMの生産及び付随する不確かさを含めた特性値の確定について,すべての点
を網羅しようとするものではない。この規格に規定する方法は,大きなグループのRMの生産及び値の付
与のための主流の方法とみなし得るが,特殊なケースについては,適切な修正が必要である。この規格で
規定する統計的方法は,方法の概略を例示するものであり,例えば,正規分布したデータを念頭において
いる。特に,データが明らかに正規分布をしていない場合は,妥当な特性値及び付随する不確かさを得る
ために別の統計的方法を採用してもよい。この規格では,CRMの生産プロジェクトの設計について,一般
的な要項を規定する。
なお,この規格で点線の下線を施している参考事項は,対応国際規格にはない事項である。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO Guide 35:2006,Reference materials−General and statistical principles for certification (IDT)
3
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
なお,対応の程度を表す記号(IDT)は,ISO/IEC Guide 21に基づき,一致していることを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Q 0030 標準物質に関連して用いられる用語及び定義
注記 対応国際規格:ISO Guide 30,Terms and definitions used in connection with reference materials
(IDT)
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: Probability and general
statistical terms (MOD)
Guide to the expression of uncertainty in measurement, issued by BIPM, IEC, IFCC, ISO, IUPAC, IUPAP and
OIML (GUM)
International vocabulary of basic and general terms in metrology, issued by BIPM, IEC, IFCC, ISO, IUPAC,
IUPAP and OIML (VIM)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS Z 8101-1,JIS Q 0030及びVIMによるほか,次による。使
用する記号を,箇条4に示す。
3.1
標準物質 (reference material: RM)
一つ以上の規定特性について,十分均質,かつ,安定であり,測定プロセスでの使用目的に適するよう
に作製された物質。
注記1 RMとは,総称的な用語である。
注記2 特性には,定量的なもの又は定性的なもの[例えば,物質(substances)又は種の同定]がある。
注記3 使用目的には,測定系の校正,測定手順の評価,他の物質(materials)への値の付与,及び精度
管理(quality control)を含んでいる。
注記4 RMは,ある測定における単一の目的にだけ使用することができる。
3.2
認証標準物質 (certified reference material: CRM)
一つ以上の規定特性について,計量学的に妥当な手順によって値付けされ,規定特性の値及びその不確
かさ,並びに計量学的トレーサビリティを記載した認証書が付いている標準物質。
注記1 値の概念は,同定又は序列(sequence)のような定性的な属性(attributes)を含んでいる。このよ
うな属性に対する不確かさは確率で表してよい。
注記2 標準物質の生産及び認証のための計量学的に妥当な手順は,特にJIS Q 0034及びこの規格に
記載がある。
注記3 JIS Q 0031は,認証書の内容に関する指針を規定している。
3.3
(標準物質の)特性値 [property value (of a reference material)]
(認証)標準物質の物理学的,化学的又は生物学的特性を代表する量に帰せられる値。
4
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.4
(標準物質の)キャラクタリゼーション,値付け [characterization (of a reference material)]
認証プロセスの一環として,標準物質の特性値を決定するプロセス。
注記1 値付けのプロセスによって,定量化対象の特性に値を与える。
注記2 バッチ認証では,値付けとはバッチの特性値を指す。
3.5
瓶間均質性 (between-bottle homogeneity)
標準物質の特性の瓶間変動。
注記 “瓶間均質性”という用語は,別のタイプのパッケージ(例えば,バイアル)及び別の物理的
形状並びに試験片にも適用される。
3.6
瓶内均質性 (within-bottle homogeneity)
1本の瓶内での,標準物質の特性の変動。
3.7
配合 (blending)
特定の特性をもつ物質を得るために,2種類以上のマトリックス物質を混ぜ合わせること。
3.8
マトリックス物質 (matrix material)
自然界,工業生産現場又はそれ以外から採取した物質。
例 土壌,飲料水,空気
3.9
スパイク (spiking)
マトリックス物質に既知量の化合物又は元素を加えること。
3.10
短期安定性 (short-term stability)
特定の輸送条件下で輸送している間の,標準物質の特性の安定性。
3.11
長期安定性 (long-term stability)
CRM生産者の下で規定された保存条件下にある,標準物質の特性の安定性。
3.12
(標準物質の)寿命 [life time (of a reference material)]
標準物質の特性の安定性を持続できる期間。
3.13
(RM及びCRMの)保管期限 [shelf life (of an RM/CRM)]
CRMの生産者がその安定性を保証する期間。
注記 保管期限は,JIS Q 0031で説明するように,認証書の有効期間に等しい。
5
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
記号
Ai
バイアス項 (ANOVA)
a
グループ数 (ANOVA)
Bi
バイアス項 (ANOVA)
b
サブグループ数 (ANOVA)
ε
誤差項 (ANOVA)1)
注1) この規格では,誤差という用語は厳密に統計的意味で使用しており,観測値とその数学的
予測値との間の差のことである。
k
包含係数
MS
平均平方 (ANOVA)
n
観測数
n0
(サブ)グループメンバーの(有効)数 (ANOVA)
p
共同実験における試験所の数
sbb
瓶間(不)均質性の標準偏差
slor
併行精度の不足による標準偏差
slts
長期(不)安定性の標準偏差
sr
併行標準偏差
sstab
(不)安定性による標準偏差
ssts
短期(不)安定性の標準偏差
swb
瓶内標準偏差
SS
平方和 (ANOVA)
ubb
瓶間(不)均質性による標準不確かさ
uchar
値付けによる標準不確かさ
uCRM 特性値の標準不確かさ
ults
長期(不)安定性による標準不確かさ
usts
短期(不)安定性による標準不確かさ
UCRM 特性値の拡張不確かさ
xchar
値付けから得た特性値
xCRM CRMの特性値
δ xbb 瓶間(不)均質性を示す誤差項
δ xlts 長期(不)安定性を示す誤差項
δ xsts 短期(不)安定性を示す誤差項
xij
実験における単一測定の結果 (ANOVA)
μ
母集団平均(期待値)
注記1 箇条によっては,認証プロジェクトにおける統計的問題点の解決のための代表的方法を示す
ため記号を使っている。これらの記号は本文の中で説明する。
注記2 記号のMS及びSSは文献から採用したものであって,記号の使い方に関してJISに規定する
規則に従っているわけではない。しかしながら,分かりやすさのためには,科学文献におけ
る慣習が広まることが望ましい。
6
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
認証プロジェクトの設計
5.1
概説
CRMの生産には,プロジェクトで実際に何らかの活動にとりかかる前に多くの計画策定が必要になる。
計画策定のかなりの部分で,物質の必要量並びに均質性試験,安定性試験及び値付け試験についての設計
を取り扱う。同様に,その設計は,これらの試験のための適切な測定方法の選択も含む。生産する試料数
は,計画策定のプロセスにおいて非常に重要な変数となる。試料数及び原料物質の量は,これらすべての
要因によって左右される。均質性試験についての箇条7,安定性試験の箇条8,並びに値付けの箇条9及び
箇条10では,認証プロジェクトの一環として,こうしたプロセスをどのように計画し,実施するかについ
ての指針を示す。フィージビリティスタディも,プロジェクト計画の一部となることがある。
5.2
プロジェクトの明確化
プロジェクトの計画策定は,どのようなCRMを生産するかについて明確にすることから始まる。こう
した明確化の代表的例を,次に示す。
“一連の微量元素を,環境分析化学に適した含有量レベルで含む土壌のCRMを,認証値に伴う不確か
さx %以下で調製すること”
この記載は,プロジェクトをかなりよく表している。環境化学に適するということは,事例ごとに異な
る場合があるが,物質の範囲を十分絞り込む。同様に,“土壌”もマトリックスに対する選択肢の数を絞り
込む。あらゆる場合において,生産すべきものを規定することが重要である。プロジェクトの設計段階に
おいて,明確化すべき内容をより詳細に規定することができる。最後に,規定された目標不確かさによっ
て,その物質が意図された用途に適するものとなる。例えば,校正標準の値の不確かさは,微量環境分析
法の妥当性確認のための物質の値の不確かさに比べて,相当程度小さいことが望ましい。
特性値のトレーサビリティが確立されている“規定された標準”を正しく選択することは,プロジェク
トの設計にかかわる大きな問題である。これは,どんな標準が利用できるか,測定を日常的に実施する試
験所で特定のCRMが役に立つためには何が必要か,また,何が技術的に可能か,によって大きく左右さ
れる。CRMは,主として,その後の測定をトレーサブルにするために使用するので,適切な標準の選択は,
生産するCRMの値に対し,計量学的,かつ,商業的に決定的な因子である。
同様に,CRMを用いる範囲も明記することが望ましい。ほとんどの場合,使用範囲はプロジェクトの定
義によって示されるが,更に詳細に示す必要がある場合もある。こうした使用範囲は,他の用途を必ずし
も排除するものではないが,こうした用途を(必ずしも)認証書又は提供される文書が対象として含むと
は限らないので注意することが望ましい。RMを使用すべき範囲は,法規及び/又は国際協定に基づくこ
とがある。
5.3
輸送の問題点
実際の作業を開始する前に,CRMが準備できた後に,既存の規制に従って出荷できるかどうかを考慮す
ることが重要である。人がその物質に直接さらされると,健康又は安全に対してリスクを被るCRMが多
い。適正な包装及び適切なラベリングは,(害のある可能性のあるものも含め)有害物を輸送する場合の規
制を満たすための主要な要件となる。ある特性をもつ物質(例えば,ウイルス,病原菌)の輸送が,法律
又は規制によって禁止されることがあり,このことは,CRMが全く販売できないことを意味することがあ
る。実際の認証プロジェクトを開始する前に,輸送及び包装のあらゆる側面を見直すことが望ましい。
5.4
原料物質の収集
認証プロジェクトの最初の業務は,必要とする特性をもつ原料物質(starting material)を十分量入手するこ
とである。マトリックス物質の場合,物質の特性に関して制限があることに注意することが望ましい。物
7
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
質と特性との組合せにはまれ(稀)な場合があり,他の特性との組合せにおいてまれ(稀)なものがある
場合もある。多くの場合,妥協点を見つけなければならない。配合及び/又はスパイク技術によって,こ
の問題が解決できる場合もある。
物質の必要量は,次によって決まる。
− (C)RMの必要な試料数
− フィージビリティスタディの必要性
− 均質性試験に必要な試料数
− 安定性試験に必要な試料数
− 候補CRMの値付けに必要な試料数
− 1回の測定に必要な物質の量
候補CRMが必要とする所要試料数は,商業上の問題であり,前もって注意深く計画することが望まし
い。重要な変数は,CRMの寿命期間中に供給される可能性のある試料数である。寿命は物質固有の安定性
と相関するので,この変数も必要な原料物質の量に影響を与える。例えば,多くの微生物標準物質は,固
有の安定性が限られており,したがって,その寿命は,例えば,微量元素について認証された乾燥底質よ
り短くなることが予想される。年間当たり発送される試料数が同じとすると,微生物標準物質に必要な試
料数は,乾燥底質の場合より少なくなる。他方,微生物CRMについては,最初の何年か又は物質の寿命
期間全体を通じて,安定性試験に必要な試料数ははるかに多い場合がある。
5.5
フィージビリティスタディ
十分に均質で安定したCRMを生産し,値付けすることに懸念がある場合は,フィージビリティスタデ
ィを検討してもよい(参考文献[11]参照)。例えば,試料を調製する最良の方法,物質の安定性又は目的に
対する適合性について問題があれば,プロジェクトにフィージビリティスタディを含めてもよい(参考文
献の[11]及び[12]参照)。場合によっては,フィージビリティスタディを組織化して,値付けに参加する可
能性のある試験所が,自分の機器及び手順を微調整することができるようにする。値付けを目的とするフ
ィージビリティスタディの場合,候補CRMに使用する物質及び若干異なる物質のバッチを用意すること
が望ましい。
5.6
要求される寿命及び保管期限
標準物質の予想寿命は,認証プロジェクトの計画策定に当たり重要な変数となる。安定性にかかわるも
う一つの関連パラメータが,CRMの保管期限である。物質の安定性に影響するメカニズムの性質に応じて,
保管期限及び/又は寿命を改善するために様々な措置をとってもよい。過剰な乾燥又は大量の水分含有量
が物質を不安定にする可能性があるので,水分活性の調整が最初に考慮すべき選択肢の一つとなる。多く
の場合,水分は,マトリックス及び/又はパラメータの不安定性を引き起こすメカニズムにおいて主要な
役割を果たす。他の場合には,微生物の活性を止めるために,殺菌又は滅菌を考慮することもある場合が
ある。しかしながら,これらの措置が安定性に負の作用を及ぼすこともある。安定性及び保存条件につい
ての関連情報は文献で見つけるか,又は同種の物質の使用者(業界など)から入手することができる。溶
液を調製する場合,添加剤が保管期限及び/又は寿命を延ばす場合がある。物質の保管期限は,保存条件
及び安定性試験の品質と相関している。安定性試験の品質は,その検討結果をどの程度まで外挿できるか
を決めることになる(8.5参照)。
5.7
試料の調製
5.7.1
序文
標準物質の調製について一般的な指針を示すことは難しい。この細分箇条では,網羅的になることなく,
8
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
特定な側面の一部について指針を与える。単に,認証プロジェクトの成否にかかわることが多く,細心の
配慮を必要とする幾つかの側面を集めている。
5.7.2
調製物質
純物質,溶液及び混合ガスのような調製標準物質(synthetic reference material)は,大部分のマトリックス
標準物質とは全く異なった方法で調製する。純物質を調製する場合,不純物の総量を減らすために精製技
術が必要になることがある。こうした技術の選択は当該主要成分に依存しており,また,蒸留及び/又は
再結晶化のような技術を含む場合がある。(バッチCRMを調製する場合の)小分けプロセスの後,バッチ
を5.7〜5.9の規定に従って処理することが望ましい。
溶液又は混合ガスは,十分に確定した不確かさバジェット表(明細)を入手できる重量法(質量比法)
によって調製する。原料物質の純度(又は組成)は,その不確かさと同様に,候補CRMの組成を計算す
るモデルに組み込む。物質のバッチの調製に当たっては,容量法も広く利用されている。通常,容量法の
取扱いは幾分容易ではあるが,重量法で調製する場合よりも大きな不確かさを伴う。
5.7.3
物質の配合
特定の特性値が高すぎる又は低すぎると判断した場合は,二つ以上のマトリックスの配合を考慮しても
よい。このプロセスは,同種類のマトリックスを用いると最もうまくいくが,“同種類”と考えられるもの
が大幅に異なることがある。適切な配合を行うためには,物質を,粒子の凝集を抑えることができる状態
にすることが望ましい。通常,物質の水分含有量が支配的要因となる。物質が空気乾燥(air-dry)の場合は,
通常(ただし,必ずそうであるとは限らない。),十分な混合プロセスの間に凝集物は消滅する。このこと
は,スラリーと同様の挙動をする物質の場合も同様である。混合中に凝集物が消滅しないという潜在的な
問題がある。粒子がある程度凝集することは避けられない場合がある。例えば,水分が2 %未満の大豆粉
はまだ粘着性をもっている。
さらに,異なるマトリックスを適切に配合するための要求事項として,配合対象物質の密度及び粒径分
布が十分に類似し,分布については十分に範囲が狭いことが挙げられる。これによって,偏析の危険性が
大幅に低減する。粒径低減の適切な技術及び実施並びに配合技術を用いれば,通常は,均質性及び安定性
に関して,十分な特性をもつ物質バッチを得ることができる。
疑いがある場合は,配合した物質を簡易な均質性試験にかけ,配合した物質の幾つかの部分について認
証特性の均質性を調査する。こうした検討は,少数ではあっても,均質性についてある程度理解するのに
十分な数の部分について行うとよい。通常,10個分について試験を行うことによって,配合物質が,その
後の処理に適しているかどうか判断する上で,有意な結果が得られると考えられる。
5.7.4
スパイク
標準物質生産のための適切な方法として,スパイクすることが望ましいと考えられる場合がある。こう
した例としては,固体状物質から抽出物を調製するケースがある。別の例としては,豚肉の脂身中のPCB
測定用CRMが3種類存在し,高い温度領域においてCRMは液体となっているものがある。要求するCRM
特性を得るためにスパイクするとよい別の例は,液体,金属及び合金,オイル並びに作業環境である。
スパイクの大きな課題は,候補標準物質について十分な均質性及び安定性を達成することである。適切
なスパイク方法を用いると,固体状の物質でさえも,均質性及び安定性の面での要求事項を満たす物質を
調製することができる。例えば,固体に適したスパイク方法としては,スパイク対象の成分を,固体表面
を完全に湿潤化させるのに十分な,適量の溶剤に溶解させる“含浸法 (incipient wetness)”がある。溶剤は,
その蒸発速度を制御できるように選択することが望ましい。蒸発速度が大きすぎると,スパイクが孔から
再度出てきて塊になる場合がある。この場合,スパイクは十分に表面に付着せず,物質の安定性に影響を
9
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
与える。蒸発速度が小さすぎると,マトリックス中の他の成分が移動するか,失われることになる。
しかしながら,組成CRMの一部のグループの場合,スパイクが,認証対象の特性にとって望ましい値
をもつ物質を得る方法として,明らかに不適切なことがあるが,これはスパイクによって,CRMが通常の
日常試料と全く異なった挙動をすることがあるからである。一般に,自然界に存在した分析種と,スパイ
クをした分析種との間には結合に大きな違いのあることが想定され,その結果,例えば,抽出物の挙動に
差が生じる場合がある。したがって,自然の(汚染された)物質に対するスパイクをした物質の等価性を
確認して,物質が実際の試料を代表するものとなるようにすることが望ましい。
5.7.5
均質化及び小分け
試料とした物質は,標準物質になる前に幾つかの準備段階を経るのが普通である。このプロセスで必要
な段階は,乾燥,粒径の低減,ふるい分け,安定化,及び小分け,すなわち容器詰めを含む。プロジェク
トの設計段階では,試料の調製をどの程度まで拡大するかを確定することが望ましい。例えば,試料とし
た物質を抽出物として直接測定できるように調製することは可能である。しかしながら,多くの場合は,
試料の調製は試料の物質がその本来の状態をとどめるようにする。ただし,試料調製プロセスの結果,不
均質性が減少し,安定性は大きくなることが望ましい。
RMの特性値について要求される不確かさ及び必要な寿命が,試料調製技術を選ぶときの要求事項とな
る。候補標準物質を調製する方法が,物質の用途に影響を与えることがあるので注意することが望ましい。
例えば,抽出物を送付すると,顧客の試験所における抽出段階の精確さを確認することが不可能になる。
したがって,CRMを調製する目的を考慮して,CRMの利用範囲に照らしながら,原料を認証に適した物
質にする方法を決定することが望ましい。
5.8
均質性試験
バッチ認証プロジェクトにおいて,均質性試験は瓶(単位)のバッチが十分均質であることを実証する
ために必要になる。品質保証という面から見ても,CRMの特性値の不確かさ推定値に含まれる不確かさ成
分である,残存するバッチの瓶間変動を決定することと同じくらい重要である。溶液のように,物質が均
質と予想される場合にも,瓶間不均質性の評価が必要になる。スラリー,スラッジなどを含む,固体状態
の標準を扱う場合,瓶内均質性の検討を見越して,試料最小はかりとり量を決定することが望ましい。通
常,こうした均質性試験は,当該特性値の不確かさを増大するものではない。必要とされる余剰試料数は,
主として,瓶間均質性試験によって左右される。任意に選択した最小瓶数は10〜30であり,一般的に10
未満は避けたほうがよい。
均質性試験に最適な試料数は,統計的な根拠のある設計技術によって決定することができる。通常,こ
のような方法は,例えば,測定の不確かさがあるために不均質性を検出できないことを考慮に入れている。
さらに,瓶数はバッチサイズに依存するので,バッチから取り出した試料数がバッチ全体を“代表する”
ものと考えてもよい。要求事項として,(併行条件において)測定の併行標準偏差及び反復測定数の関数で
ある測定の不確かさと釣り合いをとることが望ましい。上記の統計学的技術は,瓶数と反復測定数とのバ
ランスをとる上で役立つため,最もよい方法といえる。
5.9
安定性試験
安定性試験は,調製後の候補RMの残存する不安定度を決定するか,又は物質の安定性を確認すること
を目的としている。“安定した”物質であっても,一つ又は複数の特性値に対して不安定性を示すことがあ
る。次のような規定条件の下での不安定性について区別する。
− 保存条件(長期安定性),及び
− 輸送条件
10
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
均質性試験の場合と同様に,品質保証という観点は,不安定性の影響による不確かさのバジェット表を
決定することと同様に重要である。長期安定性は,規定された保存条件におけるCRMの特性値に残存す
る不安定性に関連する。したがって,これらの条件を規定し,また,同一条件の下で物質の安定性を検討
することが重要になる。標準的な温度は,物質がこの温度において安定であることが実際に確実になるよ
うに選択することが望ましい。バイオ及び環境標準物質の多くは,最適保存条件を定義又は決定するため
の努力を行っても,ある程度の不安定性を示す。理想的には,輸送条件は,輸送中の物質の不安定性が生
産者の保管庫における物質の不安定性を超えることがないように選択することが望ましい。したがって,
CRMの安定性が保存条件を超えて規定の輸送条件(例えば,生産者から使用者まで)による影響を受ける
場合,短期安定性だけが不確かさ成分となる。
短期安定性試験は,通常,異なった温度が物質の特性に与える影響を検討するために,異なった温度で
実施する。試料の温度は,包装のタイプ及び輸送手段によって,輸送中に,−50 ℃〜+70 ℃の間で変化
することがある。観察された影響に基づき輸送条件を定義し,また,包装についての指示事項を作成して,
望ましくない副作用を効果的に排除してもよい。短期安定性試験には通常1〜2か月を要するが,最適保存
条件を同時に決定する場合は,更に延長してもよい。
安定性試験には,相当数の瓶(単位)が必要になる。各時点において,二つ以上の瓶を利用できること
が望ましい。ほとんどの長期安定性試験が24〜36か月続き,通常,5〜6の時点をとるので,各温度当た
り少なくとも10〜12個の瓶が必要になる。長期安定性試験の設計で複数の温度を想定する場合,瓶数をこ
れに応じて増やすことが望ましい。短期安定性試験においては,通常,2週間にわたり3〜5の時点をとる。
長期安定性試験の場合と同じ理由から,短期安定性試験では各温度当たり6〜10個の瓶数が望ましい。物
質の不均質性も安定性試験に必要な単位数に影響を与える。物質が不均質な場合は,2,3個の(a few)瓶に
ついて反復測定するよりは,数個の(several)瓶について1回の測定をするほうがよい。
バッチ認証において安定性試験を行うに当たって望ましい方法は,併行条件下で検討作業をすることで
ある。そうでないと,不安定性による不確かさ推定値が,安定性の試験中に得られた結果の再現精度の影
響によって,必要以上に大きくなってしまう。併行条件下での作業は,同時期測定型設計(isochronous design)
を用いると可能になる(参考文献[13]参照)。試料はすべて,不安定性が全く予想されない標準的な温度(必
ずしも,予測された保存温度とは限らない。)で維持する。試料は,安定性試験を行う温度にさらし,また,
すべての試料の測定が完了するまでこの温度を維持する。測定の時点は,試験対象の温度に設定した瞬間
から測定が行われた瞬間までの経過時間によって決定する。
8.2に規定する方法を用いるときは,十分な再現精度特性をもつ測定方法を選択することが望ましい。測
定方法の再現精度を良好なレベルに維持することは,1回の実験中に良好な併行精度を維持するよりも,
かなり困難であることから,従来の設計より同時期測定型設計が有利となる。この点を除くと,従来の設
計を使っての評価における不確かさは,同時期測定型を使った場合よりいずれの場合も大きくなり,同時
期測定型安定性試験から得る(不確かさを一定とする)ことのできる保管期限は,従来の手法を使った安
定性試験の場合より長くなる。こうした利点は,特に,併行精度及び再現精度が(比較的)劣る方法の場
合,安定性試験の期間中データがないという不利を十分補償する。中間データが必要な場合,これらの測
定値を,同時期測定型による安定性試験とは独立に求めることが望ましい。単一の人工物(artefact)を認証
する場合は,従来の手法以外に選択の余地はない。
安定性試験に関する実験の設計は,最適な時点数及び使用試料数の決定を含め,例えば,測定方法が全
く不安定性を検出できないことを考慮した上で,統計的実験計画に基づくようにしてもよい。さらに,一
般的な安定性試験の場合と同様に経験的モデルを使用する。したがって,時点数は,モデルの妥当性確認
11
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を正しく評価するだけの十分な数であることが望ましい。すなわち,例えば,パラメータを二つ(切片及
びこう配)もつ線形モデルの場合,時点数は少なくとも3又は4必要になるが,しばしば,より精確な評
価を行うために更に多くを必要とすることもある。さらに,パラメータが多いモデルの場合は,安定性試
験における(時間)点の数はそれに応じて増やすことが望ましい。
5.10 測定方法の選択
均質性試験で使用する測定方法は,非常に良い併行精度及び選択性をもっていることが望ましい。日を
変えて試料を測定する安定性試験の場合,測定方法の選択性及び再現精度が重要となる。したがって,均
質性及び安定性試験に関する方法は,必ずしも同じである必要はない。均質性試験及び安定性試験並びに
値付けの結果が共通の標準までトレースできるようになっていれば,このことは問題とならない。このよ
うな標準は,各種校正を評価するのに適した物質であってもよいし,異なる測定方法からの結果であって
もよい。認証プロジェクトにおいて,すべての測定方法についてトレーサビリティを確保することが重要
な要求事項となる(例えば,JIS Q 0034及び参考文献[14]参照)。
候補標準物質の値付け,特に,組成標準物質の場合,複数の方法,時には,複数の試験所を使用するこ
とが非常に望ましい。試験所の方法及びパフォーマンスは,最新のものであることが望ましく,また,そ
の測定をプロジェクトの設計で規定する標準までトレーサブルにすることが望ましい。
候補標準物質の値付けは,異なる方法で実施してもよい。主要な方法として次の二つがある。
a) 単一の方法による値付け,及び
b) 複数の方法及び/又は複数の試験所による値付け
方法b)は,共同実験又は共同試験と呼ばれる実験的構成を含む。両者の名前が示すように,標準物質へ
の値付けを行うためのコーディネータ及び参加者の共同活動が必要である。すべての場合において,値付
けで使用する測定手順は,“規定された標準”,できれば,SI単位までトレーサブルであることが望ましい。
測定結果のトレーサビリティという側面は,実際の測定範囲を大幅に超えるものであり,また,試料の前
処理(transformation)も含む。試料の前処理とは,物質(又は,人工物)をある(物理的,化学的)状態か
ら別の状態にもっていくことである。試料の分解(destruction),及び分析種の抽出は,こうした試料の前処
理の例である。
最後に,物質の均質性試験,安定性試験,及び値付けに関連する測定を組み合わせて,特性値とその標
準不確かさについて正しい推定値を得ることが望ましい。データに対する要求事項は,これらデータが同
一の“目盛”を参照していること,すなわち,すべての測定が正しく校正された機器で実施されているこ
と,及びこれらの校正結果を相互に比較できることである。特に,多くの試験所がかかわる場合,校正間
の一致の度合いを検証するために,ある種の標準となる物質,混合物又は溶液を用いてもよい。この点が,
適切な標準を定義するという,すなわち,計量学的なトレーサビリティを確立するということであり,プ
ロジェクトの様々な段階で得た結果の妥当性及び同等性を実証できるようにするということでもある。
5.11 認証
CRMの認証については,箇条11で規定する。
5.12 プロジェクト設計の要約
要約すると,標準物質の調製には,次のステップを含む。
a) 標準物質の明確化,すなわち,マトリックス,認証対象となる特性及びその要求レベル,並びに要求
する不確かさのレベル
b) 試料採取手順の設計
c) 試料調製手順の設計
12
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 均質性及び安定性試験に適した測定方法の選択
e) 標準物質の値付けの設計
f)
試料採取
g) 試料調製
h) 値付けに適した方法の選択
i)
均質性試験
j)
安定性試験
k) 標準物質の値付け
l)
測定の不確かさの完全な評価を含む,均質性試験,安定性試験及び値付けの結果の合成
m) 認証書及び,該当する場合は,認証報告書の設計
6
測定の不確かさの評価
6.1
(C)RMの特性値の不確かさを評価するための基礎
GUMは,測定の不確かさを評価する基礎となる。CRMを得るためのプロジェクトは,ほとんどが,GUM
の箇条8の方法によって評価することができる。CRMの場合,この手順の概要は次のとおりである。
a) 認証対象の特性値と,数理的な特性値のすべての入力量との間の関係を明らかにする。この関係は測
定モデルと呼ばれるもので,特性値の不確かさに大きく関与するすべての量を含むことが望ましい。
b) 一連のデータの統計的解析又はその他の手段による統計的解析に基づく,すべての入力量の値を決定
する。
c) データの統計的解析から得た量についてはAタイプ評価法を,また,その他のすべての量については
Bタイプ評価法を用いて,すべての入力量の標準不確かさを評価する。
d) 入力量の間の共分散を評価する。
e) 特性値(x),すなわち,認証対象となる特性の値を計算する。
f)
GUMの箇条5に掲げた伝ぱ(播)公式を使い,入力量に伴う数々の標準不確かさ及び共分散から,
特性値に付随する合成標準不確かさを決定する。
g) 拡張不確かさ(U)を求めるため,包含係数(k)を決定する。すなわち,ここで,間隔(x−U,x+U)には,
大部分の値の分布が含まれ,認証対象の特性に当然帰属すると考えてよい。包含係数は,規定の信頼
水準(95 %とすることが多い),yの確率密度関数及び(該当する場合は)自由度数に基づき選択す
ることが望ましい。
h) JIS Q 0031の規定に従い,特性値は,拡張不確かさ(U)及び包含係数(k)とともに報告することが望まし
い。
ほとんどの場合,上記の方法に従うことができる。しかし,GUMで取り上げているように,他の方法
を選んだほうがよいという状況も存在する。そのような状況には,次の場合がある。
− 特性値と入力量との関係を説明するモデルに当てはまる数学式がない場合,及び
− 不確かさを合成及び伝ぱ(播)させる式を適用して得られる線形近似が,明らかに無効である場合
これらの場合は,モンテカルロ又はブートストラップ法を含む他の統計的手法を使って,CRMの特性値
に付随する不確かさを決定してもよい。この規格では,上記の方法を適用することとする。その他のケー
スは,GUMに合わせて処理することが望ましい。
不確かさの単一成分の評価方法の詳細はGUMに記載している。多くの場合,妥当性の検討結果のよう
な既存データを有利に活用して,不確かさの成分を集合して定義することもできる(参考文献[15]の第7
13
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
章参照)。
評価について特定の指針を必要とする不確かさの成分には,バッチ不均質性,長期安定性及び短期安定
性による不確かさがある。これら不確かさ成分の評価は,この規格の箇条7(均質性試験)及び箇条8(安
定性試験)で規定する。箇条9及び箇条10では,バッチに対する特性値を決定するときの測定の不確かさ
の評価を規定する。
単一校正に基づき認証されている単一人工物CRMから得た特性値の不確かさは,GUMに規定するよう
な通常手順を使って評価してもよい。しかし,この種のCRMの不確かさバジェットには,長期安定性の
影響も含めることを注意することが望ましい。
6.2
バッチの値付けのための基本モデル
不確かさを評価するための値付けプロセスのモデル化は,所定の作業でも,また厳密に数学的な作業で
もない。特定の候補CRMの特性値に対し,適切なモデルを確立することは複雑な作業であり,関連する
すべての物質の生産及び認証手順を考慮するよう最大限の注意を払うことが望ましい。CRMの特性値に付
随する不確かさに大きく関与する要因をすべて含めることは,モデルの基本要求事項の一つである。した
がって,完全を期すには,標準物質の合成標準不確かさについては,均質性並びに長期及び短期安定性も,
バッチの値付けに関する不確かさに加えて,重要な役割を果たすことを認識しておくことが望ましい。し
たがって,標準物質の不確かさは,次のように表すことができる。
a) バッチについて得た認証値の不確かさ(値付け)
b) 単一のパッケージへの移替え(均質性)
c) 顧客に引き渡されるとき(短期安定性)
d) 販売時(長期安定性)
CRMの特性値に付随する不確かさについての上の記載には,次のような要素を考慮に入れている。
e) 物質の(完全な)値付けには,不確かさが付随する。
f)
使用者は(通例)1回に1試料だけを用いる。
g) 物質は生産者及び販売者が長期間保管する。
h) 使用者へ物質を輸送しなければならない。
これらの要因は,CRMの測定対象に付与される値(すなわち,認証を受ける値)に付随する不確かさに
すべて大きくかかわっている。これら影響要因を正しく評価することは,通常の作業の範囲内で行うこと
である。不確かさの評価は,CRMについての事故,過失,不適切な使用,不適切な輸送などを考慮するこ
とは意図しておらず,また,そのような使用をしてはならない。この方法は,GUMの3.4.8に規定してい
るのと同じである。
モデルは,式(1)のように表現することができる。
sts
lts
bb
char
CRM
x
x
x
x
x
δ
δ
δ
+
+
+
=
······················································· (1)
ここに,
xCRM: 特性値
xchar: バッチの値付けから得た特性値,又は単一の人工物
に値付けする場合,この人工物について得た特性値
δ xbb: 瓶間変動による誤差項
δ xlts及びδ xsts: 長期及び短期不安定性による誤差項
通常,均質性及び安定性試験は,これらの誤差項がゼロになるような方法で設計するが,その不確かさ
はゼロにならない。
変数が互いに独立であると仮定すると,CRMの特性値に付随する不確かさは,式(2)で表すことができ
14
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
2
sts
2
lts
2
bb
2
char
CRM
u
u
u
u
u
+
+
+
=
·························································· (2)
式(2)では,GUMのE.8の伝ぱ(播)式を用いている。不確かさの成分ubb(瓶間の標準不確かさ),長
期安定性の標準不確かさ(ults)及び短期安定性の標準不確かさ(usts)は,モデルの誤差項に相当する。CRMの
特性値に付随する合成標準不確かさは,その物質の保管期限に関連することがある(箇条8参照)。
時には,放射性同位元素について認証される標準物質のように,長期安定性の項が時間の関数となるこ
とがある。したがって,この種のCRMの特性値に付随する不確かさの評価に使用するモデルは,認証値
の時間依存性を考慮することが望ましい。
測定のモデル化については,GUM及び幾つかの補足的文書,例えば,Eurachem/Citacのガイドがある(参
考文献[15]参照)。モデル化及びデータ評価については,標準物質の認証における主要なモデル化ステップ
について,箇条7,箇条8,箇条9及び箇条10に具体的な指針を規定する。
状況によっては,上記基本モデルから逸脱することができる。このような状況としては,試料の輸送を
しない場合,又は認証書の不確かさには試料の輸送を考慮していないことが明記してある場合が挙げられ
る。こうした不確かさ成分の推定は,箇条7,箇条8,箇条9及び箇条10に規定する。
例えば,高温の影響を受けやすい試料が,その輸送に最高でも1週間程度と予想したが,生産者から顧
客のところまで6週間かかったとすれば,CRMの特性は大きな変化をしている場合がある。したがって,
生産者がその認証書,又はより適切と判断した場合に追加文書で規定することを前提として,生産者はこ
れら規定に応じて短期安定性試験の期間を限定してもよい。
6.3
不確かさの要因
既述の不確かさの要因のほかに,測定手順において共通的に見られる不確かさの要因も,モデルに含め
ることが望ましい。GUM及び参考文献[15]がこれらの不確かさの要因をリストにしている。モデルを作成
する場合,関連するすべての不確かさ成分を網羅する手間を軽減するため,このような総合的リストを利
用することが望ましい。測定方法は,既に測定の不確かさによって評価済みであり,このような方法で利
用できるモデルが,CRMの特性値の不確かさの評価にも適用できることは多い。当該測定手順を変更した
場合には,不確かさモデルの見直しをすることが望ましい。
しばしば,測定方法の不確かさモデルが,集合した成分,すなわち,幾つか他の成分に依存する不確か
さの成分を含んでいることがある。これらの集合成分は,当該測定方法を日常測定に使用したときに発生
しない場合であっても,共分散を引き起こすことがある(6.1参照)。共分散及び相関の評価は,CRMの特
性値に付随する合成標準不確かさを正しく評価するためには重要な意味をもつ。共分散を検出するプロセ
スを容易にするには,どの不確かさの成分が集合不確かさ成分に含まれているか文書化することが望まし
い。この文書化によって,共分散及び相関の要因として考え得るものを比較的短時間に特定できる。GUM
の附属書Fには,結果として生じる共分散の評価方法について,上記より詳しい指針が規定されている。
6.4
分布関数にかかわる問題点
一般的に統計的手法では,検討対象の変数の確率密度関数について幾つか仮定することが,暗示的に又
は明示的に必要とされる。評価プロセスのどこかの段階で,確率密度関数を決定又は仮定しているので,
GUMによる方法も例外ではない。標準物質の認証で使用するモデルも,基本統計理論に基づいているた
めに,この規則の例外ではない。このような仮定は,明示的に仮定するよりは,暗示的に(例えば,特定
の統計的推定・Bタイプの評価手法を使って)仮定することが多い。統計的方法は,例えば,正規分布の
データを仮定するものが多い。この仮定は,この規格で規定するほとんどの統計の基礎である。組成測定
15
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
から得られるデータでは,一般的にこの近似化が正しいが,一方,小さな数をカウントするような他の測
定の場合,この仮定は無効になることがある。
回帰分析及び分散分析は,データが正規分布に従うことを仮定している。いずれにせよ,これらの統計
的ツールは,ひと山型の分布関数のデータではうまくいくが,その関数を分散の推定のために使用する場
合にだけ適用できる(例えば,箇条7及び箇条8並びに参考文献[21]を参照)。
値付けデータの実験的分布が複数の最大値を示す場合,よく知られている問題が発生する。最悪の場合,
試験所からの結果及び/又は測定方法からの結果が一致しないために,物質の認証ができなくなる。単一
の特性値を付与することは,方法間及び/又は試験所間で結果が一致する場合にだけ有効である。わずか
な違いは,この作用を考慮した不確かさの成分を追加することで解決できることもある。特定の方法を使
用することによって試験所間の結果が一致する場合,方法に依存した認証を考えてもよいが,結果として,
特性値は方法に依存したものとなる。試験所間で結果が一致せず,また方法によってグループ分けしても
問題が解決しない場合,値付けデータは特性値の確定に適さないことになる。
6.5
比率の使用
例えば,安定性試験(参考文献[16]参照)の場合などのように,比率の使用には潜在的な問題がある。
二つの正規分布変数の比も,必ずしも正規分布にならないことに注意することが望ましい(参考文献[17]
参照)。二つの変数の比の実際の分布は,当該二つの変数の分布及びこれら分布関数のパラメータの実際の
値に依存する。例えば,ある種の色の測定の場合のように,特性値がゼロになり得る場合は特に,比の値
を用いると問題が生じることがあるが,これは,比の値がコーシー分布に従うからである(参考文献[17]
参照)。この分布はモーメントをもたず,これは例えば,分散が定義されていないということを意味してい
る。この結果,付与された確率分布に基づいて測定の不確かさを評価することはできない。
測定による偶然誤差成分の影響は,不確かさの伝ぱ(播)の法則の適切な適用,すなわち,比を形成す
る二つの変数の間に必要な共分散の項を挿入することで,最小限に抑えることができる。こうした“不確
かさの低減”には,比率の使用が効果的であることが多い(参考文献[16]参照)。観測データについて不確
かさの伝ぱ(播)則を使うことは,人工物の場合,比率の分布関数では安全という利点があり,また,同
時に,“偶然誤差成分の抑制”という望ましい効果も得られることになる(参考文献[18]参照)。
6.6
包含係数の選択
6.1に規定する方法のステップg)で使用される包含係数は,特性値(正規分布のことが多い)に対して
推定した分布関数及び信頼水準(95 %とすることが多い)に基づいて決定する。この結果,こうした基本
(正規分布,95 %の信頼水準)に基づいて,包含係数をk=2とすることが多い。自由度(有効)数が低
いと考えられる場合は,包含係数の代わりにスチューデントのt-分布を用いてもよい。
特性値に付与された分布が非対称的と考えられる場合,例えば,ポアソン分布によるカウントの結果の
場合では,拡張不確かさ及び包含係数の代わりに,信頼区間を明記することが望ましい。
6.7
再認証
CRMの実際の特性値は,時間の経過とともに認証値から外れることがある。CRMの実際の特性値がそ
の認証書に示されている範囲から外れている場合,問題対処の方法として二つの基本的な方法がある。
− CRM又はRMの撤回
− 物質の再認証
これら二つの選択肢は,経済的及び技術的要因に基づいている。撤回のための技術的要因に含まれるも
のは,例えば,マトリックス又はその一つ若しくは複数の成分の劣化など,安定性試験又は安定性モニタ
リングから導いた結論であることもある(8.4参照)。残りの品目バッチを再認証するのにはあまりにも小
16
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
さすぎる場合は,CRMを市場から引き上げるとよい。
再認証とは,標準物質の均質性試験,安定性試験及び/又は値付け(の関連部分)を再度実施すること
を意味する。また,個々の分野の測定能力の改善を,(経済的に可能であれば)再認証の理由としてもよい。
生産した物質が十分に良質な状態であっても,CRMの使用者が再び使用できるように,特性値の確定方法
を改善して不確かさを減らすことが望ましい。
別のタイプの再認証として実際に見られるものは,物質の特性が徐々に変化することが原因になる場合
である。例えば,石炭が可能な限り最良の条件で保管されている場合でも,経時的に変化するという石炭
発熱価の事例が該当する。
7
均質性試験
7.1
序文
大部分のRMは,品目(例えば,瓶,バイアル又は試験片)のバッチとして調製する。多くのRMの調
製における最終段階が,利用可能な品目への小分けである。品目バッチのサブセット,通常,10〜30個を
サンプリングスキームによって選択して均質性試験をする。バッチからサブセットを選択する方法には,
例えば,単純ランダムサンプリング,層別サンプリング又は系統サンプリングのような方法がある。一般
的に,単純ランダムサンプリング法又は層別サンプリング法を用いることができ,その結果,通常,バッ
チ全体を代表するとみなしてもよいサブセットを与える。バッチ内での不均質性が検出されないことが確
かな場合には,系統サンプリング法を用いてもよい。
瓶間均質性試験の結果2)は,認証モデルの不確かさ成分の一つの評価を提供する(箇条6参照)。この不
確かさ成分の度合いは,主としてRMの性質によって,大きく変動することがある。このタイプの均質性
試験は,品目の一つのバッチに対して有効な認証書が発行される場合にだけ適用される。
二番目に重要なタイプの不均質性は,瓶内均質性であり,その影響は,使用における適正な指示によっ
てかなり低減できる。これらの指示には,試料の再混合及び粒状物質の場合は,最小試料はかりとり量を
含めてもよい。これは,はかりとりが正しければ,認証された不確かさの範囲内でそのRMを代表すると
考えてよい最小の試験部分である。
注2) “瓶間均質性”という場合,同じことが他の物理的形状のRM,例えば,バイアル又は試験片
に適用できる。
7.2
物質
溶液又は純粋化合物(不純物ではなく,純度について認証する場合)として調製したRMは,物理的(熱
力学的)根拠から高度に均質であると予想される。しかし,これらの物質は,例えば,密度こう配又は吸
蔵ガスを含む金属に起因する異質性を示すことがある。これら物質の均質性に関する試験の目的は,主と
して,調製中に検出できなかった問題に起因する不純物,干渉又は不ぞろいなものを検出することである。
これらの場合,無視できるほどではないが非常に小さい不確かさの寄与が,瓶間均質性試験から予想され
る。完全な均質性が推定されるこれらの場合でも,このような推定は均質性試験で実験的に検証すること
が望ましい。
混合粉末,鉱石,合金などの物質は,本来組成が不均質である。したがって,このような物質から調製
したRMは,不均質性の程度を評価する試験を行うことが望ましい。瓶間不均質性に起因する不確かさ成
分の大きさは,例えば,安定性試験又は値付けに伴う不確かさに比べると,小さいか又は無視できること
さえある。しかし,特性値の決定(値付け)からの不確かさ成分と同じ大きさになることが避けられない
場合もある。バッチの不均質性を低減するための調製において利用する選択肢によって大きく変わってく
17
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
7.3
均質性の概念
理論的には,一つの部分(品目)の特性値が他の部分のものと異ならない場合,物質はある特定の特性
について完全に均質である。しかし,実際には,一つの部分(品目)の特性の値と他の部分の値との間の
差が,例えば,値付けからの不確かさ成分と比べて無視できる場合に,物質は特定の特性について均質で
あるとして受け入れられる。
バッチの不均質性(ubb)の検出には,実験上の限界がある。例えば,測定方法に由来する限界に起因する,
この不確かさ成分を過小評価しないように注意することが望ましい。特に,併行精度が低い方法だけしか
利用できない場合,そのような過小評価のリスクが存在する。さらに,可能な限り,測定のために採取し
た十分な大きさの小分け試料を用いることでこのような小分けが測定の併行精度の不確かさに大きく影響
しないようにすることが望ましい(7.10も参照)。
この細分箇条では,主に,大部分の標準物質について最も関連がある不均質性のタイプである,バルク
不均質性を取り扱う。しかし,重要な例外がある。例えば,表面分析の場合,標準物質がウェハ又はホイ
ルのことがある。もちろん,関連する不均質性は,表面を横切る不均質性であり,表面に対し垂直の方向
ではない。この箇条での大部分の考慮事項は他のタイプの不均質性にも有効であるが,提供される指針は
関連する測定方法を規定した規格を含む,より専門的な文献と比較することが望ましい。
7.4
実務
理想的には,関係する特性ごとに,不均質性の程度に関してRMに値付けすることが望ましい。認証す
べき特性が比較的多いRMの場合,すべての特性について不均質性の程度を評価することは,経済的にも,
物理的にも負担が大きく,場合によっては実行不可能である。しかし,生産したRMの品質が(何にもま
して)バッチ不均質性の正しい評価に依存することを理解することが望ましい。
実際には,望ましい方法が実行不可能な場合,そのようなRMの均質性の程度を,選択した特性だけで
(ある条件の下で)評価してもよい。これら特性を,確定された化学的又は物理的相関に基づいて適正に
選択することが必すである。例えば,RMの鉱物相における元素間随伴性(inter-element concomitance)によ
って,選択されていない元素についてもRMは同程度の均質性をもつと仮定することも妥当である。均質
性試験に含む特性を減らすことができる他の例に,無煙炭及び褐炭があり,この場合,不均質性は,灰分
及び/又は硫黄分が正しく反映している。他の特性については,通常,バッチ均質性はこれらの特性より
も高い。
すべての場合,均質性試験によって実験的にカバーできない特質の均質性について,追加の証拠を得る
ことが望ましい。そのような証拠は,例えば,文献,安定性試験又は物質のキャラクタリゼーションから
得ることができる。こうして得た証拠によって,不均質性の程度を過小評価していないという十分な証拠
をもとに,観測された一つの特性から他の特性へと,不均質性の大きさを定量的に移動できるようにする
ことが望ましい。
7.5
測定
均質性試験における測定は,併行条件の下で実施することが望ましい(併行条件の定義については,JIS
Z 8402-1参照)。さらに,測定方法の併行精度標準偏差は,小さいことが望ましい。可能な場合,単一瓶の
定量に伴う不確かさ(
n
/
sr
)は,特性値の定量からの(予想される)合成標準不確かさよりかなり小さい
状況を作り上げることが望ましい。場合によっては,これは実行不可能であり,7.9で規定した方法に代わ
る方法が必要になるが,一般的には不確かさの推定値は高くなる(参考文献[19]参照)。
測定は,測定時の傾向(ドリフト)が試料バッチの傾向から分離できるような方法で実施することが望
18
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ましい。これは,均質性試験で用いる試料の複製をランダム化した順序で測定することで実現できる。又
は,次に示す例のように,試料測定の順序を複製の間で入れ替えてもよい。
例 均質性試験のために,10個の試料を用いて3回の反復を行うとすると,測定を行う適切なスキー
ムは次のようになる。
複製No.1: 1−3−5−7− 9−2−4−6−8−10
複製No.2:10−9−8−7− 6−5−4−3−2− 1
複製No.3: 2−4−6−8−10−1−3−5−7− 9
測定時のドリフトによる傾向は,正確な測定順序に従って,結果についての傾向分析を行うことによっ
て検出することができる。試料調製における傾向は,瓶平均値をそのシーケンス番号の関数として解析す
ることによって検出することができる。したがって,試料バッチのシーケンス番号は,試料調製プロセス,
特に小分けプロセスと論理的に関連していることが重要である。
7.6
統計的に有効なサンプリングスキーム及び傾向分析
均質性試験のために,瓶(品目)を選定するサンプリング法は,単純ランダムサンプリング法,層別サ
ンプリング法,又は,場合によっては,系統サンプリング法を用いてよい。サンプリング法は,試料調製
方法の潜在的欠点を考慮し,調製したバッチの厳密な検査ができるようにすることが望ましい。層別サン
プリング法は,均質性試験のために選択した瓶がバッチ全体に均等に分布していることを保証するために,
多くの状況で推奨される。系統サンプリング法は,事実上,バッチ内の系統的影響又は傾向を見逃すリス
クがない場合に適用してもよい。
試料に存在する傾向が,測定自体に存在すると考えられる傾向に干渉しないような方法で,測定を実施
することが望ましい。測定スキームでは,例えば,瓶の順番のランダム化と試料の測定順序の変更とを組
み合わせることによって実現することができる。
瓶間均質性標準不確かさの大きさを定量する前に,得られた実験データに傾向があるかどうかを検査す
ることが望ましい。8.3.1に規定する,安定性試験で傾向分析の基本的レシピを規定する。これは,瓶数の
関数として均質性試験データを適用できる方法論でもある。瓶に有意な傾向がある場合,通常は,調製し
たバッチはバッチ認証には不適である。測定結果の傾向は,統計的に有意であるかどうかにかかわらず補
正すべきものである。傾向分析の方法,及び必要ならば機器ドリフトの補正を行う方法は,機器で直接測
定することができる精度管理試料を用いることである。バッチに傾向がある場合,こうした傾向を効果的
に除くため,小分け手順の再設計が必要になることがある。
7.7
均質性試験の評価
i=1…a瓶及びj=1…ni測定から構成される均質性試験の基本モデルは,式(3)のように表すことができ
る(例えば,参考文献の[20]〜[22]参照)。
ij
i
ij
A
x
ε
μ
+
+
=
·········································································· (3)
ここで,xijは,均質性実験における単一の測定結果である。μ は,xijの(数学的)期待値で,無限に測
定を繰り返した場合にとる総平均(平均値の平均)の値である。測定にかたよりがなければ,μ は真値に
等しくなる。Ai及びε ijは,それぞれ,瓶間均質性及びランダム測定誤差に関する誤差項である。これらの
項の分散は,それぞれ,瓶間分散及び併行精度分散である。通常,Ai及びε ijは相互に独立であると推定す
ることができる。すなわち,瓶間不均質性は測定の併行精度に影響を与えないし,逆もまた同様である。
さらに,変数Aiは,平均値ゼロ及び分散(σA2)の正規分布であると仮定できることが多い。同様に,ラ
ンダム測定誤差ε ijは,平均値ゼロで分散がσ 2の正規分布変数と仮定できることが多い(参考文献[21]参照)。
様々な実験計画を,瓶間均質性試験について作ることができる。B.2に,完全枝分かれ一元配置分散分
19
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
析の例が記載されている。
7.8
瓶間均質性試験
瓶間均質性試験は,単位間の変動を測定することを目的としている。ここで,7.7で扱った“グループ”
は,瓶(単位)を表す。瓶間均質性試験に関する二つの代表的な実験配置を,図1及び図2に示す。
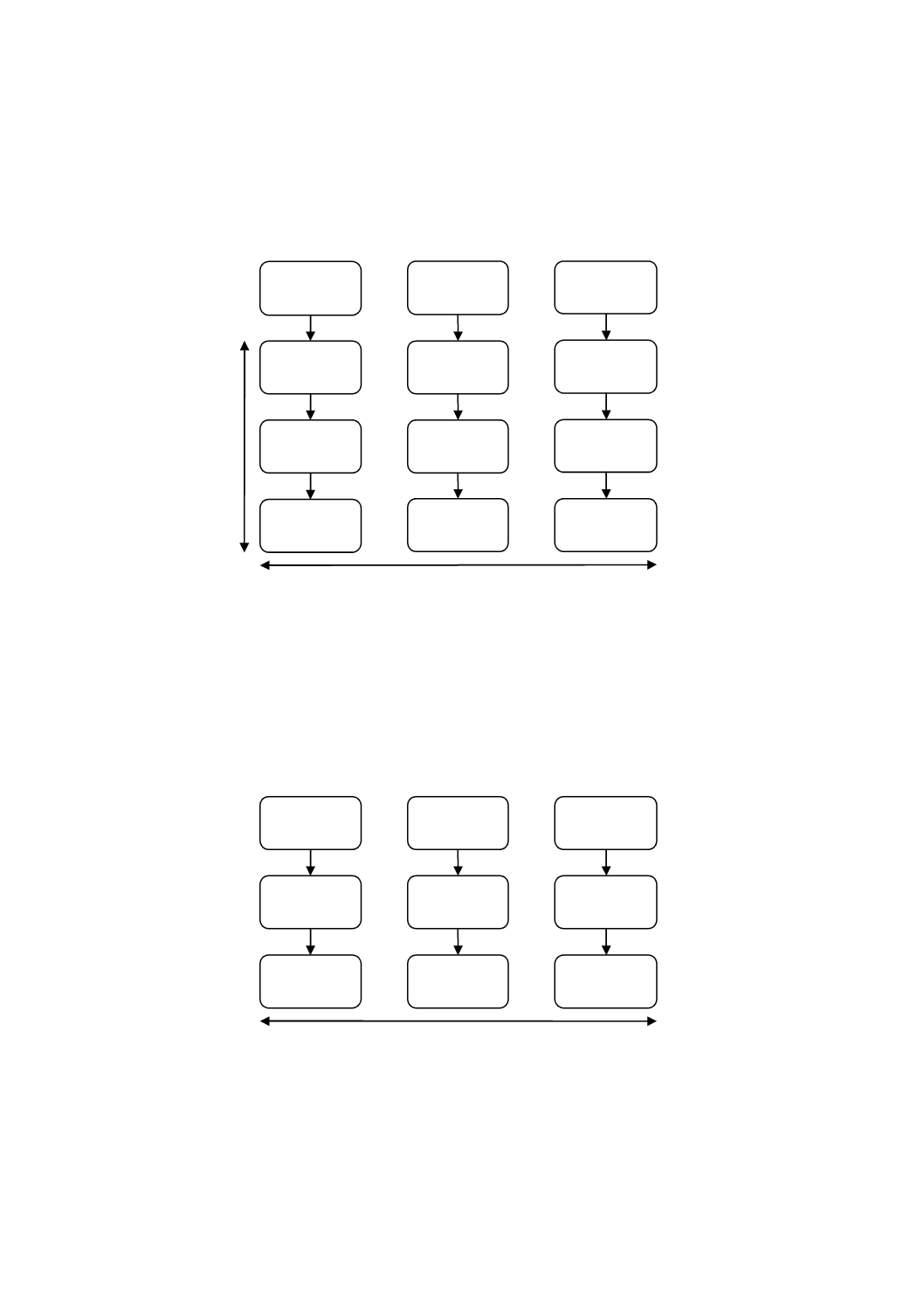
図1−瓶間均質性試験のレイアウト(参考文献[22]参照)
図1に,品目の小分けサンプリングが可能で,これまでに実施されてきた理想的な事例を示す。この設
計では,バッチの各試料から複数の試験部分を採取して個別に前処理しているため,“瓶間”変動は瓶間の
異質性だけを含む。一方,“瓶内”変動は,測定,前処理及び小分けに起因する不確かさを含んでいる。物
質の異質性についてかたよりのない推定をするという観点から,これが理想的な状況である。
図2−瓶間均質性試験の代替レイアウト(参考文献[22]参照)
図2に,品目の小分けが不可能な場合,又は例えば経済的理由などで単に実施されない場合の設計を示
す。この設計では,瓶間均質性の影響は,試料の前処理から生じるすべての影響と同様に,“グループ間”
グループ間
グ
ル
ー
プ
内
瓶No.1
前処理
n
測定
n
測定
前処理
瓶No.2
n
測定
前処理
瓶No.k
グループ間
瓶No.1
n
小分け試料
n
前処理
n
測定
n
測定
n
前処理
n
小分け試料
瓶No.2
n
測定
n
前処理
n
小分け試料
瓶No.k
グ
ル
ー
プ
内
20
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
分散に含まれている。“グループ内”分散は,測定の併行精度だけを包含する。1回だけの試験しかできな
い試験片や“single-shot”試料の,反復数nは1に等しくなる。これらの場合,考慮すべき瓶内均質性の効
果はない。試料を,前処理後に複数回の測定をすることが可能な場合,nは一般的に大きくなる。n>1の
場合,データは分散分析によって処理することができる(A.1及びB.2参照)。
一元配置分散分析を使用する場合,瓶間均質性標準偏差(sbb)は,両方のケースについて式(4)によって計
算することができる。
0
within
among
2
2
bb
n
MS
MS
s
s
A
−
=
=
·························································· (4)
これらの場合,瓶間変動(
2
bb
s)は
2
bb
uと同一である。
7.9
測定方法の併行精度が不十分な場合
均質性試験が,十分な併行精度をもつ測定方法によって,常に実施することができるとは限らない。そ
のような場合は,最大の影響を推定しようとする代替方法が必要になることがある。ubbが,認証用モデル
において含めるべきバッチ不均質性に起因する不確かさ成分を表す場合には,式(5)に留意することが望ま
しい。
0
2
2
bb
2
bb
within
among
n
s
s
u
n
MS
MS
r
+
−
≦
≦
·················································· (5)
併行精度分散は個別に導くことができ,MSwithinに等しいと設定することもできる。式(5)の右辺は,一つ
の瓶の結果についての平方標準不確かさを表す。左辺は,分散分析から推定される,瓶間不均質性による
“純粋な”影響を表す。
式(4)の結果以外に,測定方法の併行精度の不十分さを考慮した不確かさ推定値を得るための様々な方法
がある(参考文献[19]参照)。併行精度標準偏差のsbbへの影響は,式(6)で説明できる。
4
within
bb
within
2
MS
n
MS
u
ν
=
······························································ (6)
ここでいうMSwithinは,瓶間均質性試験で使用した測定値の併行精度分散に等しく,ν MSWithinはその自由
度である。
式(6)は,sbbについて信頼区間が求められること及び95 %信頼区間の半値幅が,標準不確かさに変換し
て,sbbの推定値に与える方法の併行精度の影響の尺度とすることができるという考えに基づいている。式
(6)は,不均質性を推定できないことを説明するための例である。代わりの式を作成してもよいが,式(5)
に示す規準を満たすことが望ましい。
7.10 瓶内均質性
瓶内均質性は,候補RMの瓶(単位)が小分けできる場合にだけ生じる問題である。多くの場合,瓶内
異質性による分散を正しく推定することは不可能である。試験方法の併行精度は,ある程度常に,瓶内均
質性の推定値に含まれる。これは瓶内標準偏差swbの推定値を常に“安全なもの”とし,実際の不確かさ
より大きな値とすることである。図3に,瓶内均質性試験のレイアウトを示す。
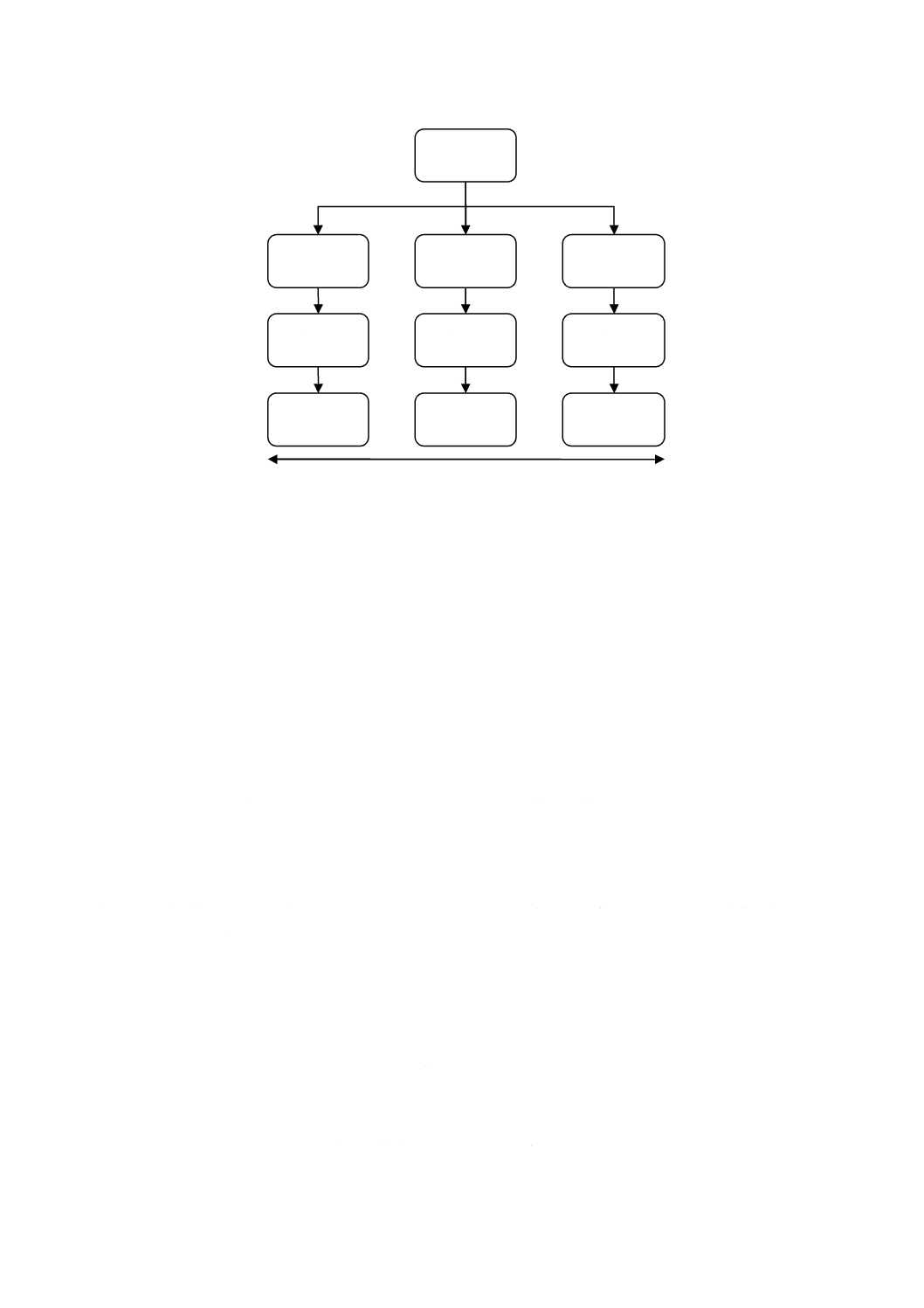
21
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3−瓶内均質性試験のためのレイアウト(参考文献[22]参照)
一つの試料から複数の試験部分を採取し,通常1度だけ前処理をすることができる(図3参照)。同一試
験部分について複数回の測定が可能な蛍光X線分析法を使用する例のような,顕著な例外もある。これら
の場合,瓶間均質性の場合とちょうど同様に,一元配置分散分析手法を考えてもよい(A.1参照)。グルー
プが小分け試料を表すとき,関連する標準偏差はグループ間標準偏差である。
最小試料はかりとり量は,異なる試験部分について瓶内均質性試験を行うことによって決定される。瓶
内均質性の標準偏差は,ある特性をもつ粒子の数に依存しているので,最小粒子数(又は最小試験部分)
を決めることが可能である。この最小値は,試験部分の標準偏差が測定方法の併行標準偏差と等しくなる
場合に,最小試料はかりとり量となる。
最小試料はかりとり量は,実験によって又は外挿によって求めてもよい。異なる小分け試料量から求め
た瓶内標準偏差の外挿は,その特定のパラメータのために測定併行精度に影響しない最小小分け試料量を
求めるために用いてもよい。瓶内均質性の標準偏差が通常過大評価されているため,最小試料はかりとり
量も通常過大に評価されている。
この問題に対する別の方法は,特定の試料はかりとり量に対して,試験部分の標準偏差が測定方法の併
行標準偏差と等しいことを実証することである。このような評価は,分散をカイ二乗(χ 2)検定を行うこと
で可能になる(詳細については,JIS Q 0033を参照。)。このような実験で使用した試料はかりとり量を,
最小試料はかりとり量としてもよい。
8
安定性試験
8.1
(不)安定性のタイプ
標準物質の認証で,2種類の(不)安定性を考慮する必要がある。
− 長期安定性(例えば,保管期限),及び
− 短期安定性(例えば,“輸送条件”下での物質の安定性)
標準物質の長期安定性は,生産者の保管庫におけるRMの変化に対応するものである。短期安定性は,
小分け試料
No.1
前処理
n
測定
前処理
小分け試料
No. 2
n
測定
前処理
小分け試料
No.a
n
測定
グ
ル
ー
プ
間
瓶
グループ内
22
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試料の輸送条件によって起こる追加的な影響に関係する。輸送中に,RMの安定性を維持するための適切
な条件を得ることができない場合は,特性値に更に不確かさを追加することが望ましい。
CRMの認証書で明記する不確かさの妥当性に関して,長期及び短期の安定性による影響を推定すること
は,そのバッチの不均質性を評価することと同じくらい重要なことである(箇条7参照)。CRMの使用期
限までの間,認証書の不確かさの妥当性を実証し,CRMが安定性に関する要求事項を満たすことができる
ようにすることが望ましい。
適切な輸送条件を維持できない場合,試料に起こり得ることを知ることも,しばしば,同じように重要
である。多くの場合,初めて使用する前にCRMを簡単に検証すれば,認証書の妥当性を十分に再確認で
きるが,一方でCRMが使えないことが明らかになる場合もある。こうした知識をもつことで,生産者は
使用者に対してより優れた助言を与えることができる。また,使用者の視点からは製品がより優れたもの
となる。したがって,安定性についての検討は,物質の安定性に伴う測定の不確かさの評価をするだけで
なく,適切な保存及び輸送条件を規定するためのものでもある(5.9も参照)。
8.2
実験計画
安定性の検討については,二つの基本的実験手法がある(参考文献の[13]及び[23]参照)。
− 従来型安定性試験,及び
− 同時期測定型安定性試験
従来型の安定性の検討は,同時に(すなわち,バッチとして)調製した個々の試料を,同一の条件下で,
時間が経過したあとで測定する。この場合,作業は,(試験所内の)再現性条件の下で実施するが,この場
合,その試験所の測定システムの不安定性も含まれるため,不確かさは比較的大きくなる。
同時期測定型安定性試験は,安定性試験のすべての測定を併行条件下で行うために導入される方法であ
り(参考文献[13]参照),この方法では,1回の校正で一連の測定をすべて行う。“同時期”(isochronous)
という言葉は,従来の方法のように,安定性試験期間の各区切りでばらばらに測定を行うのではなく,す
べての測定を同時期に行うという意味で使用している。
この同時期測定型安定性試験の方法を用いることによって,経時的に異なった時点で測定をすることに
よって発生するばらつきを減らし,それによって安定性試験の“分解能”を高めることができる。この結
果,同時期測定型安定性試験による不確かさは,測定の併行精度が(試験所内)再現精度より小さい分だ
け,従来の方法に比べて小さくなる。この手法を実施するための前提としては,標準物質の劣化が起こら
ないか,又は,少なくとも,保存のための条件とは異なった速度で劣化が起こる条件を設定できることが
必要である。同時期測定型安定性試験の手法は,試料が多数存在するバッチ型標準物質の認証のためにだ
け設計されるものであり,単品の認証には適用できない。
両方の実験手法は,長期・短期安定性の検討に適用できる。短期安定性試験については,(少なくとも)
推奨(規定)された包装及び輸送条件の下で標準物質の挙動とその特性値の変化を調べる。輸送の条件が
細かく決められていれば,それだけ短期安定性の検討は少なくてもよい。標準物質の不安定性が,長期安
定性より大きくならないような輸送の条件を決めることが望ましい。このような条件を用いることによっ
て,短期(不)安定性に対する不確かさを認証値に含める必要がなくなる。ある種の標準物質(例えば,
臨床的,生物学的及び環境分析用標準物質)の場合,標準物質に与える影響が無視できるような輸送条件
に維持できているかどうかが,常に明らかであるとは限らない。そのマトリックスと特性との組合せにつ
いてそれ以前に経験がない場合は,短期安定性試験を異なった温度で実施して,適切な保存条件及び輸送
中注意しなければならない事項について情報を得るようにしておくのがよい。
このような試験は,通常,約2か月が必要であるが,長期安定性について追加情報を得るために6〜12
23
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
か月まで延長することが必要になる。2か月経過した後の試験は,保存条件だけに関するものであるため,
必要な場合,こうした条件における温度範囲は適宜狭くしてもよい。CRMの輸送は,輸送に必要な時間が
可能な限り短くなるように手配することができる,また,そのようにすることが望ましい。経験上,2週
間が妥当とされるが,例外があることもある。いずれにせよ,短期安定性は,少なくともCRMに許され
たのと同じ期間にわたり,輸送中に発生する温度(例えば,70 ℃以下,−50 ℃以上)を含むことが望ま
しい。輸送期間が,例えば,3週間と限られる場合,短期安定性の試験には3〜4週間で十分である。
8.3
結果の評価
8.3.1
傾向(トレンド)の解析
安定性試験のデータを評価する最初のステップは,データに何らかの傾向が見られるかどうかを確認す
ることである。基礎となる動的メカニズムが分かっていない場合で,不安定性が小さい場合については,
線形近似モデルが適用できる。不安定性のメカニズムが十分に分かっている場合は,(経験的な)線形モデ
ルよりも,こうした線形近似モデルを適用するのが望ましい。直線以外のモデルに比べて数学的に若干複
雑になるが,F検定によって傾向の有意性を確認する評価も同様に行うことができる。
メカニズムが十分に分かっていない場合,安定性の検討のための基本モデルは,式(7)のように表現でき
る(参考文献[24]参照)。
ε
β
β
+
+
=
X
Y
1
0
········································································ (7)
ここに, β 0及びβ 1: 回帰係数
ε: 偶然誤差成分
例 放射性同位元素を含むRMは,放射線崩壊という明確なメカニズムをもつパラメータの一例であ
る。
偶然誤差成分(ε )は,偶然誤差だけで構成されることもあるが,一つ又は複数の系統要素を含む場合もあ
る。安定性試験の式で,Xは時間を,Yは候補CRMの特性値を表す。安定した標準物質の場合,β1はゼロ
と予想される。パラメータβ0及びβ1を推定するための式を展開するには,異なった種類の分散を計算する
ときと同様に,参考文献[20]で示す分散分析の式を展開する場合と同じ手順をとる。
Y及びXのn対の観測値が与えられているとすると,各Yiに対して,式(8)を展開できる。
i
i
i
X
Y
ε
β
β
+
+
=
1
0
······································································· (8)
測定の繰返し,測定の時点において瓶を一つ以上用いていることなどによって,各Xiについて,複数の
Yi値が得られることが多い。これらの側面を,個々の安定性試験のモデルに含めることが望ましい。ただ
し,傾向分析の場合は,Xi時におけるすべての瓶の平均値を用いることができる。これから先は,この箇
条及び参考文献[20]に基づき,極めて簡単に展開できる。
回帰パラメータは以下の式から計算できる。こう配の係数の推定は,式(9)を用いることができる。
(
)(
)
(
)2
1
1
1
∑
∑
=
=
−
−
−
=
n
i
i
i
n
i
i
X
X
Y
Y
X
X
b
······························································· (9)
切片の推定値は,式(10)を用いることができる。
X
b
Y
b
1
0
−
=
··········································································· (10)
誤差の解析から,b1及びb0における標準偏差を計算することができる。b1の推定された標準偏差は,式
(11)で与えられる。
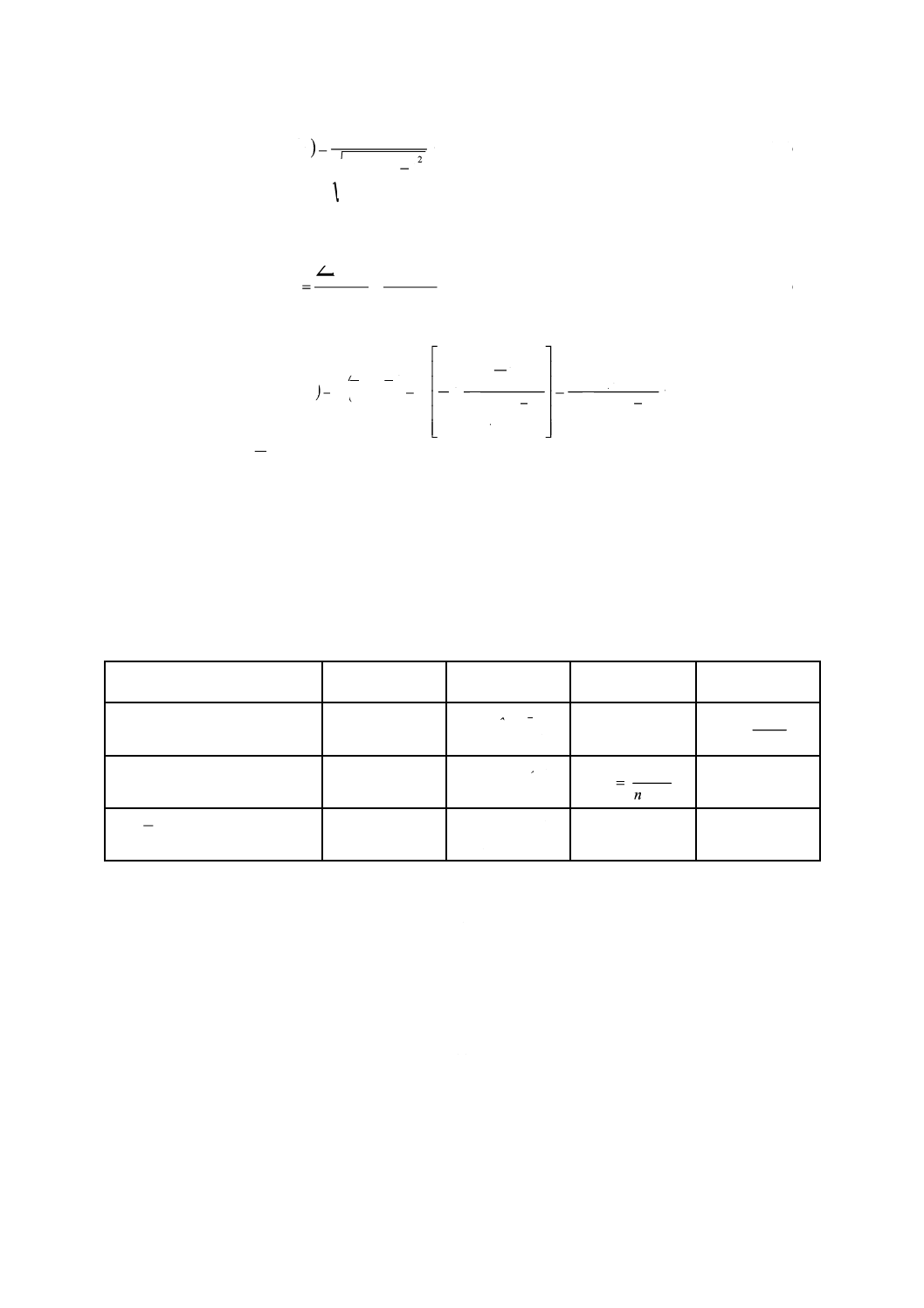
24
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
(
)2
1
1
∑
=
−
=
n
i
i
X
X
s
b
s
································································(11)
ここで,
(
)
2
1
2
1
0
2
−
−
−
=∑
=
n
X
b
b
Y
s
n
i
i
i
····························································· (12)
b0の推定分散は,
()(
)
(
)
(
)
∑
∑
∑
=
=
=
−
=
−
+
=
−
=
n
i
i
n
i
i
n
i
i
X
X
n
X
s
X
X
X
n
s
X
b
Y
V
b
V
1
2
1
2
2
1
2
2
2
1
0
1
··················· (13)
から与えられる。b1とYとの間には相関がないことに注意するほうがよい(参考文献[24]参照)。
b1の標準偏差に基づいて,判断をすることができる。式(11)及び該当するt係数(関連する自由度はn−
2に等しい)を用いて,b1の有意性について検定をすることができる。この方法はあまり複雑ではないが,
通常のソフトウェアでは計算されないパラメータであるs(b1)を計算する必要がある。しかし,一般的なソ
フトウェアでは,F表を計算することができるようになっており,これを回帰の有意性を評価するために
使用することもできる(表1参照)。
表1−線形回帰のための分散分析表
変動の要因
自由度
平方和
SS
平均平方
MS
F
回帰による変動
1
(
)
∑
=
−
n
i
i
Y
Yˆ
1
2
MSreg
2
reg
s
MS
F=
回帰(残差)まわりの変動
n−2
(
)
∑
=
−
n
i
i
i
Yˆ
Y
1
2
2
2
−
=nSS
s
平均Yについて補正された合計
n−1
(
)
∑
=
−
n
i
i
Y
Y
1
2
回帰による平均平方は,SS(b1|b0)と表され,“b0について余裕をとった後のb1の平方和”と呼ぶ。回帰線
を中心とする平方和(s2)は,σ 2Y,Xで表される特性の推定値であり,回帰まわりの分散と呼ぶ。
比率MSreg:s2の有意性は,F表を使って検定する。表1は,自由度に関する必要な情報を提示している。
t検定の代わりにこのF表を使用する利点は二つある。
− F表が,ほとんどのソフトウェアシステムにおいて,デフォルトで作成されること,及び
− F表を他の回帰モデルにも容易に拡張でき,適用範囲が広いこと
どのような試験を採用するかに関係なく,測定の併行標準偏差が,可能ならば瓶間均質性とともに,十
分に小さい場合にだけ,その試験の結果が意味をもつ。併行標準偏差が,標準物質の均質性試験及びキャ
ラクタリゼーション(例えば,特性値の決定)の場合と同程度であれば,測定の併行精度についての要求
事項は満たされているといえる。瓶間に不均質性がある場合は,各時点で複数の瓶について測定すること
によってその影響を低減することができる。こうした方法は,sbbが測定の併行精度と同等又はそれ以上の
25
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とき必要になる。特性値にある傾向が見られる場合は,通常,この標準物質を認証することはできない。
こうした決定をするための基準は,標準物質の特性値に付随する(予想される)不確かさ,(望まれる)保
管期限及びこの期間における傾向に基づくことが望ましい。この傾向が(望ましい)保管期限の間,RM
の特性値に付随する不確かさに関して有意であるとすると,標準物質は安定性が欠如しているために,認
証を受けることができないか,又はその保管期限を短くすることが望ましい。
8.3.2
傾向がない場合の不確かさの評価
安定性試験には,次の不確かさの成分を含む。
− 測定の併行精度
− 標準物質の不安定性
− 測定システムの不安定性(従来型安定性試験の場合)
− 校正を含む再現性(例えば,測定者,機器)(従来型安定性試験の場合)
− 瓶間均質性(バッチ標準物質認証の場合)
このリストから明らかなように,検討すべき成分数が少ないため,従来型の方式よりも,できるだけ同
時期測定型安定性試験を優先して行うことが望ましい。代表的な同時期測定型安定性試験では,3種類の
不確かさの成分だけが残る。これらは,完全に枝分かれした,二方向分散分析によって分けることができ
る(参考文献の[20]及び[23]参照)。こうした実験での単一測定の不確かさは,式(14)のように表す。
()
2
2
bb
2
stab
2
r
ijk
s
s
s
y
u
+
+
=
································································ (14)
ここに, sstab: 不安定性による標準偏差
sbb: 瓶間均質性の標準偏差
sr: 併行標準偏差
i: すべての時点にわたる指標
j: すべての瓶にわたる指標
k: すべての繰返し測定にわたる指標
均質性試験の場合と同様に,推定の指標(sstab)の質は,sbb(及びsr)に依存する。すなわち,瓶間均質性
が不安定性に関する推定の指標の質を決める。これは,分散分析の性質上やむを得ないことである(参考
文献の[20]及び[30]参照)。結果の処理は,A.2の事例に示した二方向ANOVAで実施することができる。(少
なくとも,一般的には)安定性試験からsbbを推定することは可能である(参考文献[23]参照)。安定性試
験で複数の温度がある場合,基準温度について求めたsbb推定値が最も良いものであろう。この温度では,
標準物質が安定していると考えられるからである。標準物質が明らかに安定していない温度では,標準物
質の変化が推定値sbbに影響を与えることがあり得る。
これまで物質の均質性と安定性とは独立しているという想定をしてきた。そういう場合が多いが,例外
はあり得る。瓶間不均質性が大きい場合,標準物質の安定性が,瓶間で異なるものと予想される。標準物
質の安定性が,(何にもまして)物質の組成に依存しているからである。安定性を乱すような成分があり,
バッチ全体を通じて相当の不均質性がある場合は,均質性と安定性との間に相関関係が出てくることもあ
る。
従来の安定性試験では,複数測定した場合の不確かさは,式(15)のように表す。
()
2
2
bb
2
lor
2
stab
2
r
ijk
s
s
s
s
y
u
+
+
+
=
························································· (15)
ここでは,項目を一つ追加している。それは,併行精度の欠如3)による分散,slor2である。この項は,測
26
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定システムの安定性を表すものである。従来型の安定性試験では,測定を(試験所内)再現性条件の下で
実施しており,その結果,測定システムの安定性と候補標準物質の安定性とを区別できないという問題が
生じる。この結果,不安定性に対する不確かさは,同時期測定型の手法より従来型の手法のほうが必ず大
きくなる。
もう一つの選択肢は,こう配がゼロの回帰曲線に関連させた不確かさを通じて,安定性の不確かさを推
定する方法である(参考文献[16]参照)。この方法では,標準物質の潜在的劣化について“安全な”推定値
を与えることになる。
各種割当値(sstab,sbb,sr)は,それぞれの平均平方(M)から求めることができる。二元配置ANOVAをA.2
に示す。完全に分岐したANOVA設計の詳細については,参考文献の[20]及び[21]を参照。
注3) “併行精度の欠如”とは,時点間で,測定の併行精度に加えて再現精度が影響することを意味
する。
8.4
安定性のモニタリング
8.4.1
実験によるモニタリング
CRMの保存期間中,モニタリングを計画しておくことが望ましい。安定性試験がもつ基本的問題点は,
理論的には,これらが過去のことを説明するだけで,現在又は将来については何も説明しないことにある。
一部の劣化又はその他の不安定性の問題は,進行が非常に遅く,かつ,漸進的であるが,多くの場合,あ
る程度急激な特性変化がある時期に発生して,実質的にCRMの寿命を終わらせてしまうことにある。こ
うしたメカニズムは全く予測不可能であるため,安定性のモニタリングが必要になる。
モニタリングは,従来型の手法を使って行う。これは,同時期測定型手法が安定性試験の終了時点での
データを提供するのに対して,モニタリングの場合重要なのは,CRMの保存期間中(寿命のある間)にデ
ータが得られるからである。これは,他の2種類の安定性試験と異なって,CRMの特性値に付随する不確
かさについては何の影響も与えない。なぜなら,モニタリングとは,認証書における不確かさがまだ有効
であることを実証するためだけのものだからである。CRMの検証中は,当然,あまり多くの不確かさが加
わらないように,モニタリングを十分注意を払って実施することが望ましい。しかし,CRMの特性値に付
随する合成標準不確かさに生じた結果まで,説明する必要はない。
従来型のモニタリング方法の重要な代替法が,半連続的安定性試験において同時期測定型実験手法を適
用する方法である。この種の安定性モニタリングの例を,図4に示す。
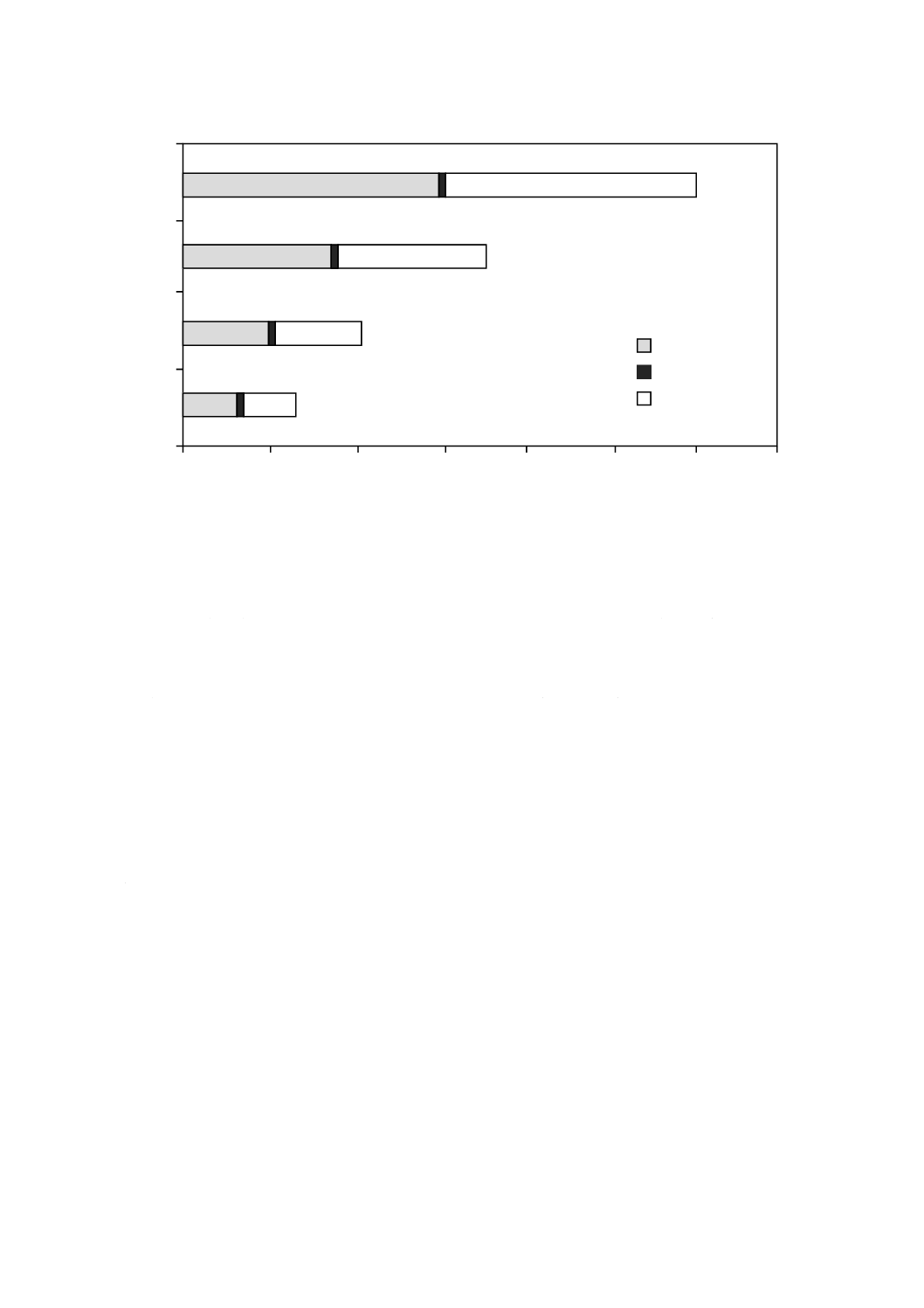
27
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4−半連続的安定性試験(参考文献[23]参照)
ロジスティックスの期間では,選定した適切な温度で試料を保管する。この期間の後,すべての試料を
(理想的には)併行条件で測定する。測定に1日以上かかることがあり,厳密な併行精度の下で作業する
ことが可能ではない場合もある。保管期限を,この測定データから求める(8.5参照)。その次の試験での
測定は,決められた保管期限の終了前に行うことが重要である。この手法を適用することによって,保管
期限の推定値の改良は少しだけであるため,他の安定性試験の結果を組み合わせる必要はほとんどない。
このタイプの安定性試験が連続的になり得ない理由は,同時期に測定を行うという方法を採用している
ことによる。すなわち,こうした測定は,安定性試験期間の後1回で実施するために安定性試験を中断す
ることが必要になる。そうした中断後に,これら新しい安定性試験データは,不安定性による不確かさの
推定値を更新するために使用されるので,CRMの特性値に付随する不確かさを再検討することもできる。
基本的に,この“中断”は,それぞれの同時期測定型安定性試験を1回だけの校正によって行うために必
要である。こうした校正は,新しい試験を行うたびに必要となる。他方,従来型の手法では,通常すべて
のデータポイントで新しい校正が必要であり,“併行精度の欠如”という問題が発生する。
8.4.2
不確かさの評価
安定性モニタリングにおける不確かさの評価は,長短期的な安定性試験とは全く異なるものである。第
一に,安定性のモニタリングは,認証書に示す標準物質の不確かさ(uCRM)に影響を与えないことに留意す
ることが望ましい。これは,実証されるように,標準物質の保管管理の面からは不可能であり,また不必
要である。理想的には,測定値に付随する不確かさ(umeas)がuCRMより大幅に小さいことが望ましいが,こ
れは必ずしも実現可能ではない。さらに,測定方法の妥当性確認を,当該CRMを用いて実証するような
ことをしてはならない。二つのことを,1回の実験で同時に確認することはできない。CRMの妥当性を確
認する必要があるが,測定が信頼できるものであることを実証可能な場合にだけ妥当である。
式(16)の条件を満たすと,標準物質は十分に安定していると判断され,また,安定性が実証されている
と考える(ただし,測定方法にバイアスがないことが条件である。)。
A
B
C
D
0
20
40
60
80
100
120
140
時間(か月)
試
験
ロジスティックス
測定
保管期限
28
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
meas
CRM
meas
CRM
u
u
k
x
x
+
−
≦
······················································ (16)
ここに, xCRM: CRMの特性値
xmeas: 測定中の観測値
k: 信頼水準95 %に該当する包含係数
これらの実験条件を満たしたとき,特性値及びその拡張不確かさを再確認できたことになる。測定によ
る不確かさが別途考慮すべきものであるため,当該条件下ではuCRMを大きくする必要がない。このことは,
CRMのモニタリング及び通常使用にも該当する。しかし,モニタリング測定を妥当性のあるものにするた
めに,umeasはできるだけ小さくし,自分の測定を検証するため同じような方法をとるCRMの通常使用者
のumeasを超えることは当然望ましくない。
モニタリング又は継続的同時期測定型安定性試験から,特性値がその不確かさの範囲内ではもはや有効
ではないことが分かった場合には,次の二つの選択肢がある(6.7も参照)。
− (認証)標準物質の撤回,又は
− 再認証
8.5
長期安定性からの保管期限の決定
保管期限は長期安定性による標準不確かさに対して,式(17)のように関連付けることができる。安定性
データに有意な傾向がないことが基本である。
(
)
(
)
X
b
Y
X
b
b
Y
′
+
=
′
1
,
,
0
0
······························································ (17)
ここで,特性値Yが,時間(X)の関数として一定な相対劣化速度(b′)で,初期値(Y0)から直線的に減少する
と仮定する。CRMの特性値に付随する不確かさは,従属変数の不確かさu(Y0),u(X)及びu(b′)を独立変数
Y0,X及びb′に伝ぱ(播)させることで推定できる。
()
()
()
()
b
u
b
Y
X
u
X
Y
Y
u
Y
Y
Y
u
′
×
′
∂
∂
+
×
∂∂
+
×
∂∂
=
2
2
2
2
0
2
2
0
2
····················· (18)
最後の項は,長期安定性による標準不確かさを保管期限に関連付けるための基準とすることができる(参
考文献[25]参照)。偏微分係数が,認証後の経過時間であるXに等しくなることに留意することが望ましい。
一次の方法(first-order approach)を用いると,時間Xにおいて式(19)が成り立つ。
b
Xu
Y
u
0
lts=
············································································ (19)
式(19)は,保管期限(X)を一定としたときに有意の劣化がない場合,試料の長期的不安定性による不確か
さに対し余裕をとる基礎となる。
9
特性値の決定
9.1
概説
特性値の付与には,幾つかの技術的に有効な方法がある。これらの方法には,1か所又は数箇所の試験
所で行われる一つ又は複数の方法による測定が含まれる。標準物質のタイプ,最終用途における要求事項,
関係試験所の資格認定,方法の品質,及び特性に付随する不確かさを正しく推定する能力に応じて,一つ
の適切な方法を選択することができる。
箇条9及び箇条10は,単一の特性値を決定する事例に限定する。幾つかの分野では,CRMの特性がス
ペクトルのような他の形態をとることがある。通常,箇条9及び箇条10の内容は,これらの事例にも当て
はまるが,数学的手法は特性値の場合よりも更に複雑である。この規格で規定する概念を適用するために
29
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は,統計的モデル化手法について十分な知識をもつことが必要である。瓶間均質性,長期安定性,及び可
能であれば短期安定性も,スペクトル又は曲線のような特性がかかわる事例に適用することができる。
9.2
トレーサビリティの確立及び実証
測定標準としての役割を果たすとき,CRMの特性値は,適切な単位及び/又は標準までトレーサブルで
あることが必要である。このための方法が幾つかあり,CRMの意図する用途に基づき適正な選択をするこ
とが望ましい。次のモデルがある。
a) 可能な場合,特性値はSI単位にトレーサブルであり,対応する単位で表現することが望ましい。
b) 多くのRMは,標準的方法で定義された一つの単位の(正確な)現示を形成している。これらRMは,
この規格の方法及び/又はその方法に基づき作成された標準操作手順に,厳密に従って得られた結果
に対してトレーサブルであることが望ましい。
c) RMは,CRM及びRMを含む,他の測定標準又は人工物までトレーサブルにすることができる。
また,取決めによる目盛もあり,これらは,例えば,pHの目盛及びガソリンのオクタン価を含め,少な
くともその一部は,標準物質によって維持されている。pH測定の場合,国際的に公認された一次標準の現
示は,Harnedセルによるものである(参考文献[26]参照)。常にではないが,多くの場合,取決めによる目
盛は,こうした目盛を確定するための定められたRM調製方法(調製レシピ)に従って維持される。利用
できる場合は,こうしたレシピに厳密に従うことが望ましい。
多くの組成標準物質の場合,状況は更に複雑である。特性値の決定自体は,例えば,使用する測定機器
の校正を通じて,該当する単位にまでトレーサブルにすることはできるが,試料を一つの物理的(化学的)
状態から別の状態への変換するようなステップは,トレーサブルにすることはできない。こうした変換は,
(存在する場合はその)標準との比較又は変換自体の間での比較しかできない場合がある。変換によって
は,標準物質が既に定義されており,こうした変換に伴う不確かさを評価することが,認証プロジェクト
において使用されることがある。また,同一方法を用いている様々な試験所間での比較しかできない場合
もある。この場合,認証は,独立した測定結果の間が一致するかどうかに基づいて行われる(箇条10参照)。
測定結果のトレーサビリティは,通常,該当する標準を基準とする校正によって保証される。認証プロ
ジェクトで使用するのに適した多くの測定システムでは,測定標準を用いた機器の校正によって行うこと
ができる場合もある。これら測定標準は,他のCRM又はRMを含むことがあり,その場合,CRMのトレ
ーサビリティが明示されているので,他のRMに優先してこれらのCRMを使用することは注意すること
が望ましい。機器の適切な校正及び結果のトレーサビリティを確認するための尺度が適切かどうかは,例
えば,特別に設計され,かつ,調製された対照試料(校正に使用することもある試料のようなもの)によ
って検証できる。この特別な目的のためには,これらの試料は値(及び不確かさ)を付けずに用意され,
これによって,校正手順の評価が可能となる。CRMは,共同実験活動において一つの測定から得られた結
果の妥当性を実証するために用いてもよい。
試料の一つの物理的(化学的,生物学的)状態からの変換が,測定方法の重要な一部分となっているこ
とが多い。場合によっては,測定チェーンの中でこれらのステップを検証する選択肢がないことがある。
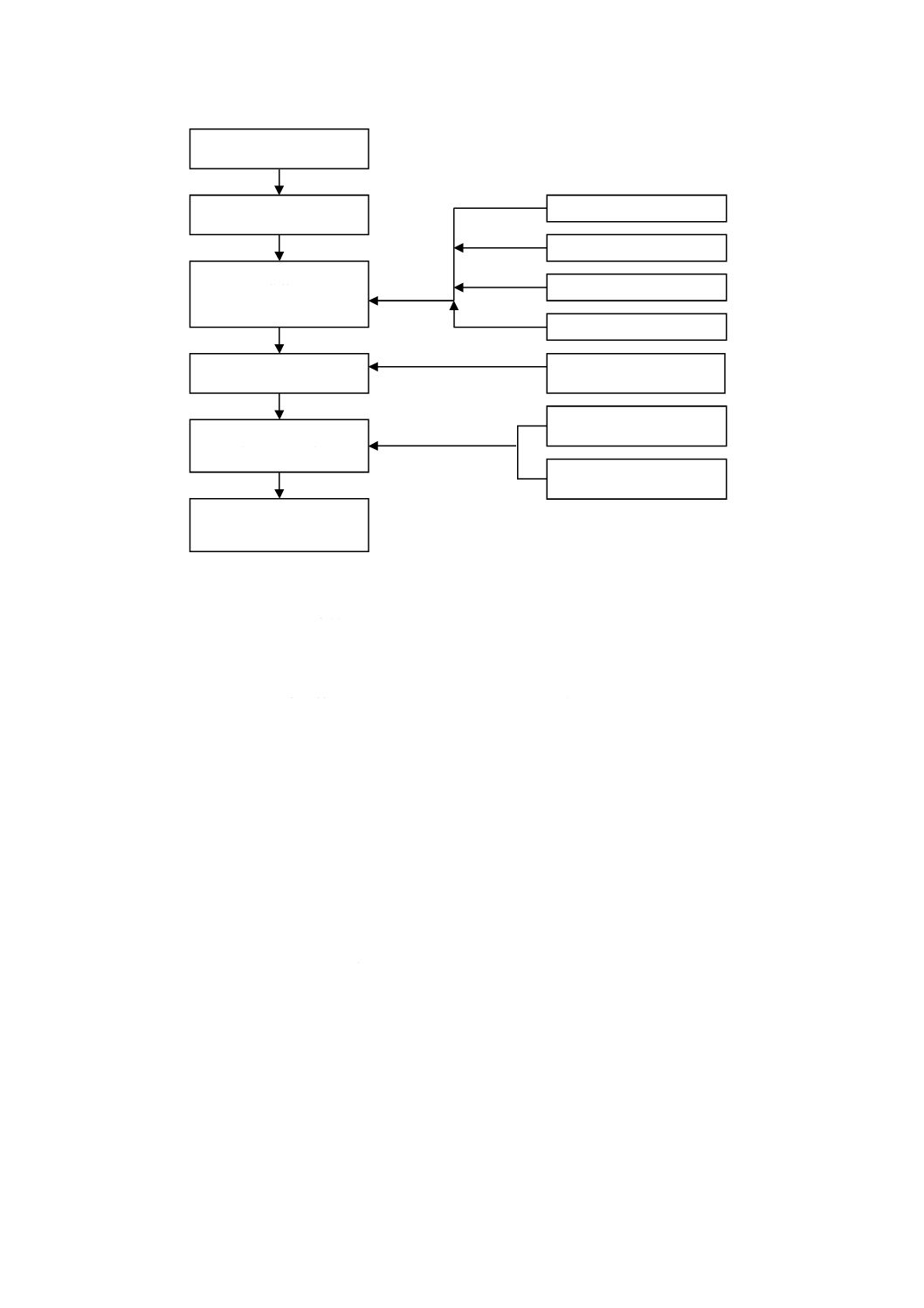
図5に,測定結果のトレーサビリティを確立及び/又は検証するための代表的な選択肢の概要を示す(参
考文献の[27]及び[28]参照)。
30
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図5−測定チェーンの各部分
組成CRM,組成RM及び精度管理用(QC)物質は,未知試料の値付けと並行して測定された測定結果の
妥当性を実証するために使用する場合がある。これらの物質の使用は,結果のトレーサビリティを裏打ち
するものであるが,トレーサビリティを直接実証すると考えることはできない。これらの物質の使用は,
測定全般にわたってある程度の管理を行っていること(例えば,詳細については,JIS Q 0033参照)を示
しており,このことは,候補標準物質の認証で使う結果のトレーサビリティを確保するための前提条件で
ある。
ブランク組成物質,ブランク抽出物などは,値付けされるべき対象が存在しない場合に,その測定方法
がゼロからそれほど異ならない結果を与えることを実証するため(組成測定時によく行われる),又は補正
若しくは補正係数(及び不確かさ)を確立するために使用される。
校正は,該当する標準にトレーサブルな測定標準を基準として行うことが望ましい。CRMは,この目的
に沿ったものである限り,この目的に用いてもよい。校正は,正確な測定に十分なもので,したがって,
不必要な余分の不確かさを導入しないことが望ましい。選択する標準は,SI単位(例えば,組成測定及び
多くの物理量の場合)か,又は取決めによる目盛(例えば,方法で定義した特性の場合)であってよい。
スパイクした物質,スパイクしたブランクなどは,測定チェーンの各部の検証又は物質に値を付与する
プロセスを支援するために用いてもよい。このステップがトレーサビリティの確立又は実証を行う程度は,
これらのスパイクをした試料がどのようにして調製されたか,及びそれらの値がどのようにして付与され
たかによって決まる。
測定結果のトレーサビリティを確立及び/又は実証するために管理する必要がある項目としては,次の
ものがある。
− 試料のはかり量
− 試薬,溶剤,“純粋物質”の純度
試料
小分け試料
分解,抽出
誘導体化
分離
測定
結果の計算
(+不確かさ)
結果の報告
(+不確かさ)
標準物質による校正
組成CRM/QC物質
ブランク物質
スパイクをした試料/抽出物
ブランク抽出物
補正
ブランク値
31
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 一般的な試験所機器及びガラス器具の校正状態
− 測定信号での干渉
− 計算をするための適切で,妥当性を確認された統計的,すなわち数学的技術(例えば,校正曲線,補
間),及び
− 測定プロセス中の汚染,損失,きず
これらは,方法の妥当性確認を行うことで適切に管理できる事項である。認証プロジェクトで用いる方
法はすべて適切に妥当性を確認し,また,この測定方法で得られた結果は,すべて方法の妥当性確認によ
って確定された仕様を満たすことが立証できることが望ましい。試験所間比較は,方法の妥当性確認の一
部分としてもよい。取決めによる方法(すなわち,方法に依存している特性)では,その方法の試験所間
での妥当性確認が必すである。他の方法についても,試験所間の妥当性確認を実施することが非常に望ま
しい。
9.3
実務的方法
候補CRMは,技術的に可能ならば,通常,正確さを基準に値付けされる。したがって,認証値は,現
実的な最良の“真の値”の推定値である。場合によっては,測定しても“真の値”という意味では理解で
きないことがあるが,その場合には,ある規定された方法で付与された特性値を採用する。ここでは,RM
の認証には,共同実験活動をする必要がなく,付与された値及びそのCRMを校正(値付け)に用いる関
連測定技術について記載するだけでよい。
認証値は,記載されている測定の不確かさを超えて“真の”値から逸脱しないことが期待される。特性
値に対して記載される不確かさには,測定プロセスに内在するすべての系統的及び偶然誤差,並びに試料
間(均質性)と時間経過(安定性)との間における物質の変動性を考慮することが望ましい。
JIS Q 0034では値付けに対する基本的方法を,次の四つに区分する。これらの方法は,RMの生産者ご
と及び認証機関ごとに様々であり,次のように実施されている。
a) 1試験所で単一の(一次)標準測定法を用いて行う測定
b) 1試験所で二つ以上の参照分析法を用いて行う測定
c) 実証可能な精確さをもつ一つ又は複数の方法によって,試験所ネットワークで行う測定
d) 試験所ネットワークによって,特定された方法だけで評価された特性値を与える方法固有の方法
認証方法を選択する場合考慮すべき最も重要な点は,不確かさの各種成分がどの程度まで特性値に付随
する不確かさに寄与するかである。さらに,付与された特性値及びその不確かさが,実証可能であること
も重要である。認証のための方法a)は,人工物(artefact)の校正を行うという事例に限られる。化学組成の
認証については,方法a)が有効であることを実証した代表例がある(9.5.2参照)。ほとんどの組成CRMで
は,方法a)は,マトリックス効果及び/又は干渉を見落とすというリスクが伴う。こうしたCRMの場合,
これらのリスクを最小限に抑えるために,異なったグループが実施した,独立の(一次)標準測定法によ
って,二つの独立した結果を得るようにすることが望ましい。RMの値付けに最も良い方法の選択は,利
用可能な方法及びRMのマトリックスに影響される。
9.4
測定の設計
9.4.1
1試験所で,一つ又は複数の(参照)分析法による測定
特に方法a)の場合,同様に方法b)でも用いることのできる重要な測定方法は,一次標準測定法である。
化学測定の分野では,一次標準測定法を物質量諮問委員会(CCQM)(以下,CCQMという。)が定義して
いる(参考文献[29]参照)。
“一次標準測定法とは,最高の計量学的な特性をもち,その操作を完全に記載及び理解でき,完全な不
32
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
確かさの記載がSI単位に基づいて記載できる方法である。
一次標準直接法は,同じ量の標準を参照することなく未知の値を測定する。
一次標準比率法は,同じ量の標準に対する未知のものの比の値を測定する。その操作は,測定方程式に
よって完全に記載されなければならない。”
この定義から,RMに値を付与する方法の一つが,一次標準測定法を用いることであることが分かる(参
考文献[30]参照)。しかし,一次標準測定法がすべての量について存在するわけではないので,必ず用いる
ことができるというわけではない。多くのRMでは,対象の量の測定が非常に複雑であるため,SI単位に
基づいて完全な不確かさの記載を確立するために必要な程度まで記載することはできない。
CCQMは,一次標準測定法となり得る幾つかの方法を特定している(参考文献[31]参照)。
− 同位体希釈質量分析法 (IDMS)
− 電量分析法
− 重量法
− 滴定法
− 凝固点降下法
注記 このリストは,将来拡張されると考えられる。
重量法(質量比法)は,混合ガス(参考文献[32]参照)及び溶液の調製技術として広く利用されている。
凝固点降下法は,(物質分率の量として)物質の純度を直接決定する方法として用いてもよい(参考文献
[33]参照)。同位体希釈質量分析法(IDMS)は,物質への値の付与及び他の目的に使われる高品質測定の
ための方法として幅広く用いられる。
9.4.2
複数の試験所が参加する方法
9.4.2.1
概念
複数の方法間及び/又は試験所間での一致に基づきRMの特性値を決定するという概念は,少なくとも
二つの仮定の上に成り立っている。
a) RMの特性について,許容できる精確さをもつ結果を出す同等の能力をもつ方法・試験所の母集団が
ある。
b) (暗に)方法内・試験所内及びこれらの間で,個々の結果に出た差は,原因(すなわち,測定手順,
要員,機器などの差異)に関係なく,事実上統計的である。
各方法各試験所の平均は,物質の特性値のかたよりのない推定値であることが前提である。通常,方法・
試験所の平均値の平均は,この特性の最良の推定値であると想定している。さらに,共同実験で得た各結
果は,9.2で規定するトレーサビリティに関する要求事項を満たさなければならない。共同実験活動の結果
の分布が,例えば,微量元素の分析の例で見られるように非常に不規則な場合は,メジアン又は切捨て平
均値のような,よりロバスト統計量を使うほうが,特性値の推定に適している。
実際に,このようなプログラムで利用できる方法・試験所の母集団の数は限定される。したがって,ほ
とんどの場合,ランダム設計モデルを完全には実施できない。さらに,各方法・各試験所のすべての結果
が同じ母集団に所属するという仮定は,注意して扱うことが望ましい。“最新技術”レベルであっても,単
一母集団という仮定を無効にする場合がある分析方法の性能特性の違い及び試験所の不確かさの差が存在
し得る。
さらに,この種の方法が有効であるためには,すべての方法及び/又は試験所のすべての結果が,該当
する規定の標準にまでトレーサブルになっている(9.2参照)と仮定しなければならない。特性値を得るた
めに共同実験を設計する場合,これらの標準は注意して選択する。
33
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
一つの値を得るために必要な,一連の作業の特定部分にかかわる誤差をランダム化するために,このよ
うな共同実験に複数の試験所が関与することが必要である。このステップには,一般に,試料の前処理操
作(例えば,抽出,試料の分解),前処理された試料の更なる処理(例えば,クリーンアップ),異なった
測定方法の影響も含まれることがある。これらの場合で,単一の方法によって(かつ,単一の試験所内で)
得た結果の測定の不確かさを完全に評価することができないときは,箇条9で説明する方法を,箇条10
に規定した方法に優先して行う必要がある。
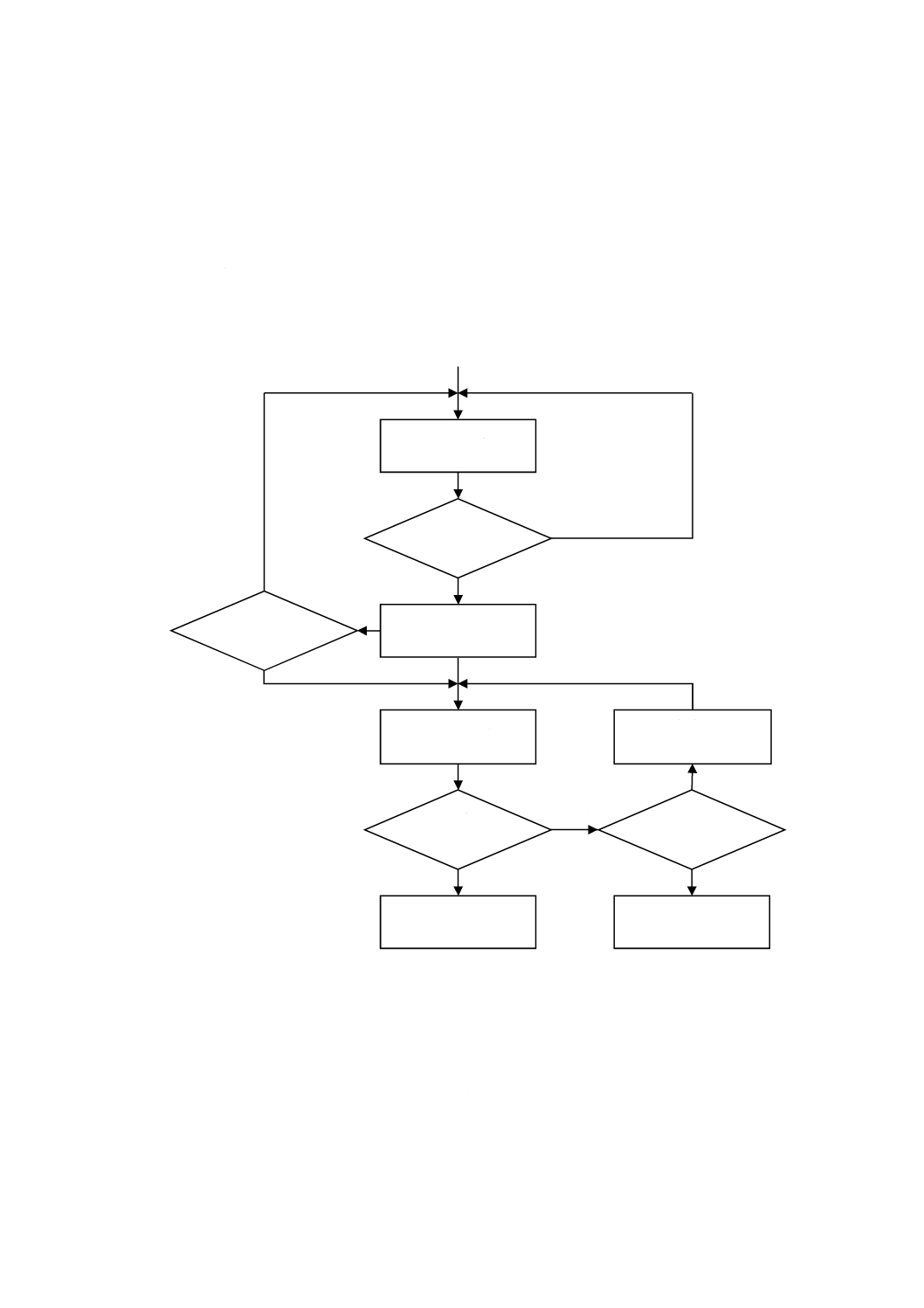
共同実験による候補CRMの値付けのための一般的手順を,図6に示す。各段階は区別され,また,判
断基準があり,次の段階に進む前にこの判断基準を満たさなければならない。
図6−共同実験のレイアウト
9.4.2.2
マネジメント及びスケジュール
共同実験のマネジメントは,主として,認証に責任をもつ組織が一義的な責任をもつ。作業が円滑に進
むように,関係者すべてに十分な指針を提供することが望ましい。成果を得るためには,共同実験は十分
明確化された目的をもち,参加している試験所及び/又は測定者が容易に従うことができる明確,かつ,
簡潔なガイドラインを用意して,効果的に企画し組織化しなければならない。測定者として又は試験所と
して,こうしたプログラムに参加することは,これらガイドラインを順守することに同意したことを意味
いいえ
共同実験活動
安定性及び
均質性の試験
物質の調製
均質性は確認
されたか?
共同実験活動の
継続
物質は認証不可能
改善は可能か?
特性値の計算
物質は認証可能
目的に適って
いるか?
はい
いいえ
いいえ
いいえ
はい
はい
はい
34
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
する。これらのガイドラインは,目標期限,試料数,試料当たりの反復測定回数,測定方法,該当する場
合は,試料量などで構成する。
作成するガイドラインでは,9.2及び9.3に規定する事項を説明するとともに,すべての関係者が測定結
果の品質及びトレーサビリティについての要求事項を認識するように,これら事項を明確に説明指導する
ことが望ましい。ガイドラインは,データ及びその品質に関する推定を検証するメカニズムを含んでいる
ことが望ましい。
主催者は,タイムスケジュール(すなわち,試料を配布する日付,発送方法)を定め,また,試料の保
存及び取扱い方について,発送者及び受領者に明確な指示を与えなければならない。主催者は,測定結果
の報告時期も示すことが望ましい。このスケジュールについては,主催者と,関係担当者・試験所との間
で合意しなければならない。
9.4.2.3
技術的要求事項
9.4.2.3.1
必要な結果の数
しばしば,特定の特性値を決定するための測定方法の数が非常に限られていることがある。可能ならば,
様々な方法からの結果を点検して,これらがそれぞれの不確かさの範囲内で一致するか確認することが望
ましい。この場合は,方法間での一致に基づいて平均値を求めてもよい。
RMの測定の不確かさの評価が,共同実験活動の期間にできるだけ多くの要因をランダム化することに
よって確定される場合は,多数の試験所による方法を優先する。これら“試験所”は,一つの団体内の異
なった部署又はグループであってもよい。RMの値付けをするための共同実験活動に参加する試験所の最
小数は,必要な測定手順の複雑さに応じて変化する。手順が複雑になれば,試験所間のばらつきが大きく
なるものと予想され,それによって,満足できる不確かさをもつ特性値を得るために参加試験所の数を増
やす必要がある。残念ながら,実際には,手順が複雑化すればするほど,これを実行する能力をもつグル
ープ・試験所が少なくなる。極端な場合,ある特殊なRM候補については,認証機関が試験所間共同実験
プログラムを全く行わないで済まさざるを得ないことがある。
目的物質の特性について,十分に確立された測定方法がある場合は,値付けにかかわる試験所・グルー
プの数は2又は3程度でよい。その代表例は,組成RMの測定に一次標準測定法を使う場合である。統計
的及び計量学的な管理が劣るが,すべての技術的に有効な結果を(一般的に)受け入れるのに十分な場合
は,関係試験所の最小数は,通常,6〜8になる。最後に,統計的,技術的には無効な結果を得る可能性が,
無視できないほどある場合(すなわち,統計的管理に限りがある場合),試験所の数は,少なくとも10,
望ましくは15である。この最小試験所数では,外れ値の処理技術の助けを借りてデータを吟味することが
可能になり,また,こうして確立された特性値に対する,適切なレベルの不確かさを得ることが可能にな
る。
これ以外の考慮すべき変数は,利用可能な分析方法の数であり,共同実験にこれらの方法をバランスよ
く含むとよい。一次標準測定法を利用できない場合,理想的には,6か所の有能な試験所又はグループが3
種類の分析方法(可能ならば)を用いて行うことが望ましい。
9.4.2.3.2
試料数及び反復測定数
通常は,2試料(units)で十分であり,約6回の反復測定を2日間(以上)にわたって実施する。すべての
反復測定は,独立して検量線(calibrations)を描いて行うことが望ましい。しかしながら,共同実験の結果を,
RMの均質性の最終確認として使用する場合は,瓶間標準偏差の推定をするのに十分な数の自由度を確保
するために,最低3又は4試料のRMの特性値をそれぞれの参加試験所が決定する。
9.4.2.3.3
測定方法
35
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
共同実験の主催者は,十分に確立された“標準”測定手順が利用できる場合は,参加試験所に対して単
一の方法を使用するよう規定してもよい。この方法は,特定の方法(例えば,浸出特性)によって定義で
きる特性にも有効である。その他の場合は,主催者は,各参加試験所に,独自に選択した方法を提案する
ことを認めることが望ましいが,こうした方法の妥当性には根拠がなければならない。主催者は,個別の
特性を決定するのに適した主要な方法を十分説明し,また,関係当事者全員の間で,各試験所又は各グル
ープがその方法を採用することについて意見の合意に達するよう努力することが望ましい。
さらに,主催者は,共同実験活動に用いるすべての方法が正しく妥当性確認をされていること,すなわ
ち,共同実験の各測定の結果を,前もって定めておいたパフォーマンス判断基準に基づいて検証できるこ
とを要求することが望ましい。方法の妥当性確認の重要な部分は,特定のタイプの測定にかかわる範囲内
で国際的に認められた標準にまでトレーサビリティのあることを検証することである。新しい測定分野で
は,利用可能な方法は,JIS Z 8402の規格群(参考文献の[1]〜[6]参照)で規定する試験所間の共同実験に
よって妥当性確認を行うことが多く,これは測定方法で定義した特性には十分であろう。
最後に,(試料の配布及び測定の実施前に)関係する試験所・グループと会合をもつことによって,すべ
ての関係当事者が共同実験中に実施する手順をそろえることができるようになり,また,潜在的問題点及
び/又は落とし穴を話し合えるようになる。
9.4.2.3.4
結果の報告
結果不確かさを各試験所が報告するかどうかに応じて,2種類の報告方法が適用できる。
参加グループ・試験所がその測定の不確かさを記載することを要求されている場合は,通常,測定結果,
その拡張不確かさ及び包含係数を報告することで十分である。しかしながら,できれば,各試験所がすべ
ての不確かさの明細を付けた完全な不確かさモデルを報告すれば,結果の間の共分散(参考文献の[34]及
び[38]参照)の評価がしやすくなる。
不確かさについての情報が必要ない場合,参加グループ・試験所は,個々の結果(平均値ではなく)を
報告することが望ましい。報告する有効けた数は,プログラムのガイドラインに適合することが望ましい。
いずれの場合も,採用した測定手順の概要を,測定プロセスのすべての前処理段階(例えば,化学分析
における,試料の分解及び目的成分の分離)の理解ができるように,十分詳細に報告することが望ましい。
文献を参照した場合は,そのことを記載する。
9.5
特性に関連した考察
9.5.1
物理的特性のためのRM
従来,基本単位,それらの最も共通する倍数及びその約数についての最も正確な測定は,国立計量研究
所(NMI)が実施している。この場合,誤差及び不確かさのすべての原因はかなり詳細に調査されている。
測定方法,ときには校正方法は長年にわたって改良を加えられて,推定不確かさを低減してきた。これら
測定の正確さは,十分に確立されているのが普通であり,特に,基幹比較(key comparison)の対象となって
いる場合はそうである。試験所が内部で妥当性確認をした方法を採用している場合のように,基幹比較が
ない場合は測定について留保しておくことが望ましい。別の試験所と比較してある方法の性能特性を実証
することは,試験所の指定にかかわらず,測定結果の品質及びトレーサビリティを保証する土台となる。
したがって,新たに設置された試験所は,自分の推定値及びその不確かさが同等であり,かつ,不確かさ
に関与するような重要な要因を見逃していないことを確認するために,多くの比較を行う必要がある。
校正レジメ(calibration regime)に基づき決定できないような物理的特性には,特別の注意を払うことが望
ましい。通常,幾つかの方法によって得られた結果及び認証調査で得られた試験結果の不確かさの評価は,
校正レジメに基づき決定された場合ほど十分に確定されたものではない。熱伝導率,耐衝撃じん性,クリ
36
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ープ,圧縮強度などの特性について,物質の特性値を決定する場合,この点を考慮することが望ましい。
これらの場合,共同実験(箇条10参照)は,特性値を決定するために,より適正な方法となる場合がある。
更に複雑なのは,これらの試験の多くでは,(基幹)比較が行われていない点である。これらの点では,物
理的特性の認証と,例えば,化学的組成の認証との間で基本的違いはない。
基幹比較及びその他のタイプの試験所間比較は,計量試験所が個々に算出した不確かさに対する信頼感
を増大させる。理想的には,これらの比較結果を用いて,不確かさモデル並びに/若しくはその変数及び
/又は不確かさを改善することが望ましい。これらの改善が必要ないとしても,これらの比較に参加する
ことは(計量)試験所の測定能力を実証する重要な手段となる。比較によって,適切に考慮されなかった
誤差が検出でき,測定に影響する要因を十分に管理及び/又は推定していない状況を検出できるようにな
る。
あらゆる努力を払った場合でも,単一の(計量)試験所の結果に基づく標準物質の特性値の決定は,見
逃すことのできないリスクを含む。物理的特性又は物質量の認証をする場合,主要な計量試験所の間で(基
幹)比較をし,その後,すべての参加者が加わった徹底的な討議をして,潜在的不一致を解決することが
重要である。国立計量研究所(NMI)が測定にかかわらない場合は,個々の国家試験所への参加試験所の完
全なトレーサビリティを確保してから開始することが望ましい。
二つ以上の方法が可能であり,また,これらの方法が同等の妥当性をもつように見える場合は,それら
の比較をすることが重要である。ただし,これらは同じ精確さであることが望ましく,そうでない場合は,
候補標準物質の認証のために,より精確な方法を優先すべきである。
限られたケースでは,単一の試験所が,その方法を考え得るあらゆる他の方法と比較をし,また,ほと
んどの誤差要因を除去した後,偶発的な誤差発生源を避けるよう相当な注意を払いつつ,不確かさを減少
させてその方法を改善することができる。
9.5.2
化学的組成に対するRM
9.5.2.1
CRMの純度
純粋物質は,化学における多くのトレーサビリティチェーンの基礎を形成している。“純粋”という形容
詞は,非現実的な状態であり,100 %純粋という物質はなく,必ず少量の不純物がある。純度について物
質の認証をすることは,化学的測定のトレーサビリティの重要な土台となる。CRMは,試験所が校正用標
準を調製するため,又は他のCRM,例えば,溶液若しくは混合ガスの認証若しくは調製をするために使用
される。スパイクを行う場合(5.7.4参照)は,使用する物質が,純度について徹底的に値付け(characterize)
されていることが重要である。さらに,質量分率から物質量分率に変換できるように,不純物及びその質
量分率を記載した完全な表を作成することが望ましい。
例えば,熱量測定(凝固点降下)によって直接的方法をとる場合は別として,純度は,次のような分析
化学的手法を用いた差数法によって決定することが多い。
− 物質の生産で使用した製造プロセスに基づき,存在する可能性のある不純物のリストを作成する。
− 認証を受ける物質において,存在する可能性のある不純物を個別に定量する。
− 純度を差数法によって計算する。
ほとんどの不純物は検出限界及び/又は定量限界に近いことから,不純物を決定するために必要な測定
は困難なことが多い。不純物の測定には,9.4.2に規定する方法のように,複数の方法・試験所が関係する。
この結果,これら不純物の物質量分率に対する相対不確かさが大きくなる。また,数学的限界近くである
ため(物質量分率及び質量分率は,0と1との間でだけ定義可能である。),不確かさの評価によって,こ
うした分率に対する負の推定値を含めて,更に問題が起こる場合がある(例えば,参考文献[15]の附属書F
37
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参照)。
物質量分率(xi)をもつk不純物の関数としての,主成分yの物質量分率のモデルは,式(20)で表される。
∑
=
−
=
k
i
ix
y
1
1
············································································ (20)
不純物の物質量分率が相互に独立していると想定すると(実際にこういうことが多いが),主成分の物質
量分率に付随する合成標準不確かさは,式(21)で表される。
()
()
∑
=
=
k
i
ix
u
y
u
1
2
2
······································································ (21)
これは,GUMからの不確かさ伝ぱ(播)公式をモデルへ適用して直接得たものである4)。これら不純物
が含まれていないか又はその存在レベルが測定方法の検出限界を下回っているために,物質量分率xiがゼ
ロということは往々にしてある。検出限界を,不純物に対する値を決めるために用いている場合は,この
検出限界が検出不可能なある不純物の最高レベルを決めていることを考慮すると,この検出限界を標準不
確かさの確定に用いてもよい。
注4) この式は,モデルが線形でありxi値が独立していると仮定しているので,正確である。
9.5.2.2
調製RM及び混合ガス
溶液及び混合ガスのような調製標準物質(synthetic reference material)を,校正のために用いる。これら
CRMは,主として重量法(質量比法)によって作られることが多い。重量法を用いて,後で試料の小分け
及び瓶詰め手順に供するバルク溶液を調製する場合,バッチは次のようにして認証する。
− ステップ1:重量法による組成を認証のための基礎とする。
− ステップ2:重量法による組成を適切な分析方法によって検証する。
− ステップ3:瓶間の変動を求めるために均質性試験をする。
− ステップ4:長期的安定性を求めるために安定性試験をする。
ステップ2及びステップ3が測定の不確かさに対して与える影響は,小さいと考えられる(これらステ
ップの詳細については,箇条7及び箇条8を参照。)が,これらを含めることが望ましい。これらが,無視
できるほど小さい場合,これらの影響の大きさは,CRMの特性値に付随する標準不確かさに影響を与える
ほどではない。検証の不確かさは,(組成を検証する能力に応じた範囲内で,)重量法の不確かさとともに
モデルに含める。CRMの特性値に付随する合成標準不確かさは,式(22)のようになる。
2
lts
2
bb
2
ver
2
grav
CRM
u
u
u
u
u
+
+
+
=
······················································ (22)
例えば,混合ガスの場合,モデルは重量法を用いる調製のために定めたものであり,ある程度までは,
この分野以外でも適用されることがある。ISO 6142では,混合ガスの重量法による調製のための調製方法
及び値の付与について規定している(参考文献[35]参照)。しかし,ガスシリンダのバッチの場合は,他の
技術も用いることが多い(参考文献[36]参照)。これらバッチは,重量法で調製した混合ガスを校正RMと
して利用して認証される。ISO 6142に規定する方法に基づく詳細な不確かさモデルがある(参考文献[32]
参照)。混合ガスの重量法による調製に基づき,混合物の組成を親ガスの成分の物質量分率として表現する
ことができる。これらの親ガスは,それ自体が混合物又は純ガスであり,混合物の調製に使用される(9.5.2.1
参照)。
ISO 6142のモデルは,親ガスの不純物を考慮したもので,これは,SI単位,この場合はモルにまでトレ
ーサブルにするための混合ガスを調製するための重要な必要条件である。モデルに取り込まれない影響も
あり,例えば,シリンダに入る組成が必ずしもシリンダから出るものと同じとは限らない。これは着脱・
38
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
脱着作用の影響によるものである。さらに,調製中の間違いの有無を品質管理によって確認することも必
要である。このために,通常,重量での物質量分率を測定(“検証”)した物質量分率と比較し,調製から
算出された組成が,分析して検証したものと異ならないものと仮定する(参考文献の[35]及び[37]参照)。
9.5.2.3
スパイクブランク及びブランクマトリックス
調製CRMを調製するための方法は,ブランク及び/又はブランクマトリックスのスパイクにも使用で
きる。スパイクする物質が本当に“ブランク”であるか,又はスパイクする少量の物質が存在することを
実証するための検証作業が唯一複雑である。この場合,これらの量を特性値のモデルで考慮し,その結果
として,不確かさモデルでも考慮することが望ましい。
認証のための方法は,9.5.2.1に規定するものと同様であるが,試料の前処理(9.2参照)で問題がある場
合,又はこのステップの不確かさを判断するときに問題がある場合は,方法の一つを採用してもよい。実
際の選択は,9.2及び9.3に規定する事項に依存するところが非常に大きい。
9.5.3
取決めによる特性の値付け
化学,生化学及びその他の分野での測定では,多くの特性を一つの方法,一つの試験手順又は個別の機
器だけで定義している。例えば,物質の機械的特性,酵素の活性などである。これらの測定又は試験の結
果は,大きな経済的負担を伴う非常に大きな変動を受けることがある。
他の測定の場合と同様に,結果は,手順をどのように適用するかに依存する。しかし,文書化された規
格にすべての必要な詳細にわたった手順を規定しているとは限らず,また,測定者が手順の解釈及び適用
についての方法を検証する手段がない場合がある。このため標準物質が必要になる。
同様に,試験が個別の機械又は機器の使用に依存している場合,機器がすべての仕様を満足しているこ
とを検証することはできるが,非常に時間及びコストがかかる。この検査を簡単に回避する方法は,既知
の特性をもつ試料の測定又は試験である。結果が満足すべきものであれば,機器が良好な状態にあり,し
たがって,その結果が関連する文書化された規格で規定した測定スケールにまでトレーサブルであると考
えてもよい。
いうまでもないが,こうした特性又は測定スケールについてCRMを確立するための値付けの作業では,
これまでに説明したのと同じ原則を適用する必要がある。質量,体積,長さ,温度などのパラメータの測
定は,それ自体が正確で,かつ,トレーサブルでなければならず,したがって,徹底的な校正が必要にな
ることがある。手順及び機器の各種パラメータが測定結果に与える影響を調査するためには,相当の努力
を必要とする。十分に一致しているように見える画一的な予断,及び正確であるという錯覚を避けるため
には,検証及び校正を,2〜3の試験所で独立して実施しなければならない。
10 データ及び不確かさの評価
10.1 モデル
最も経験的なデータ評価でさえも,単一又は幾つかの規則によって行われており,その規則は(数学的)
方程式で公式化できるとは限らない。ここで考慮している技術上の目的のためには,規則及び関係を数学
的方程式の形で表現できるものをモデルと呼ぶ。モデルは,二つの基本形に対応しなければならない。
a) 第一に,測定手順の影響変数と決定しようとする特性値との間の確立された(しばしば物理的な)関
係を記載する理論的モデル。式は厳密なものと考えられ,数値決定に用いられる。第二段階では,同
じ測定モデルを用いて,影響変数に起因する不確かさの伝ぱ(播)を推定する。
b) 第二に,潜在的(想定された)分布のランダム変数と特定のパラメータとの間に想定される関係を記
載する経験的モデル。これらのモデルは,関係するランダム変数について,合理的な統計的パラメー
39
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
タの推定値を決定する手順を作成するために用いる。
二つの基本形を結びつけた形式のモデルも幾つかあり,しばしば半経験的モデルと呼ばれる。厳密に経
験的なモデルの例は,この規格の附属書Aに示されており,様々な影響係数でのANOVA手順が記載され
ている。理論的及び半経験的モデル,並びに不確かさ推定におけるこれらの利用についてはGUMに規定
する(参考文献[15]も参照)。
10.2 データフォーマット
データフォーマットが,一つの方法の単一又は複数の測定結果及び目的に適した不確かさの記載(次を
参照)からなる9.3に規定する方法a)の場合を除き,報告されるデータは,各参加試験所について,次の
ものを含むデータのマトリックスというフォーマットをとることができる。
1) 決定しようとする特性値に対する適正な推定値(平均又は相加平均)及び不確かさの記載,又は
2) 対象となる特性値の幾つかの単一測定結果(反復測定)
フォーマット1)は,参加試験所が適切な測定モデルをもつと想定して,不確かさに基づく評価(10.7参
照)を可能にし,また,より“伝統的な”フォーマットである2)は,基本となる分布関数を仮定して行う
統計的評価を必要とする。
参加試験所が提出する結果は,図7に示す手順によって評価されることが望ましい。
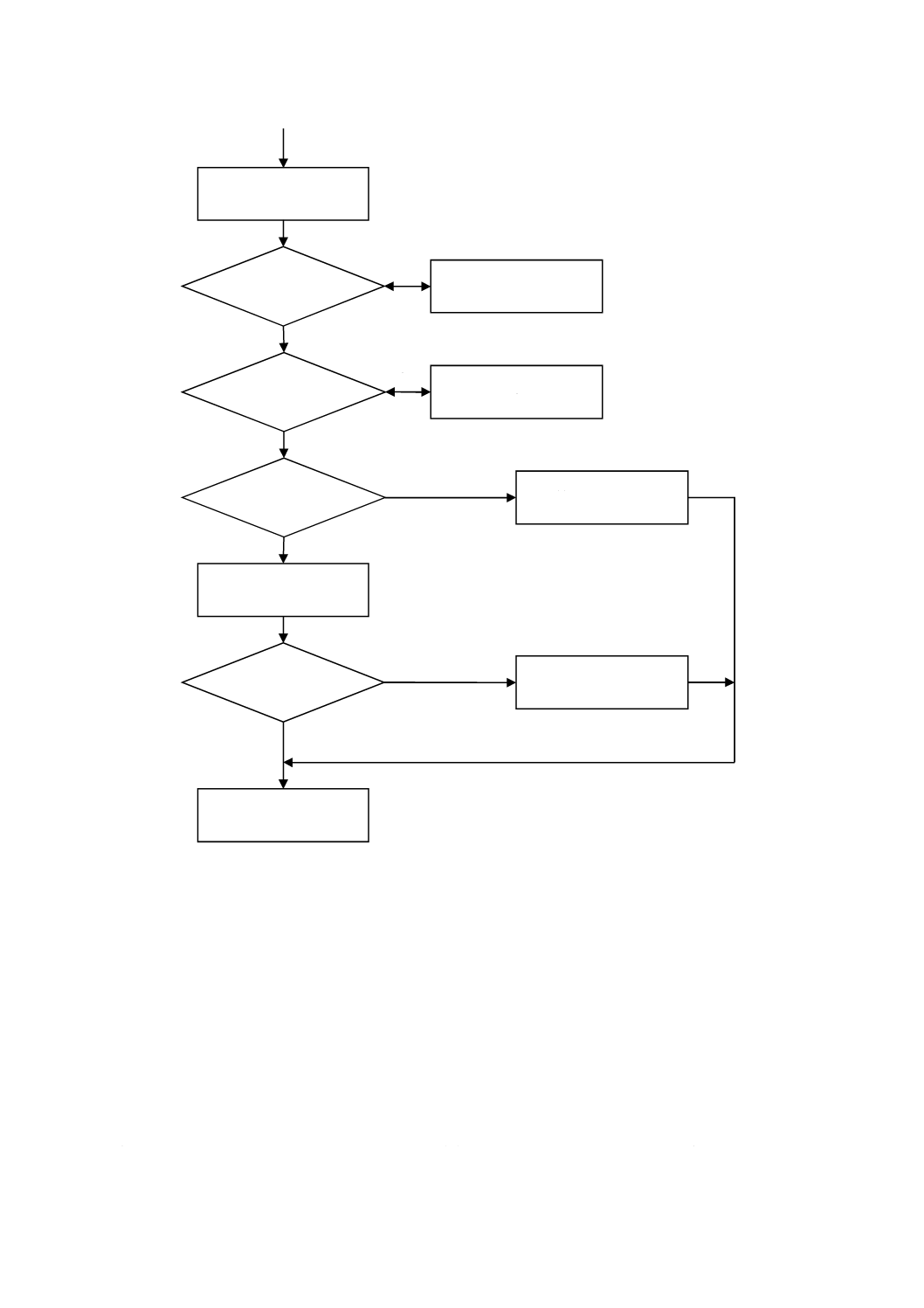
40
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図7−データの処理
データ処理の都合上,また,将来参照できるように,このタイプの共同実験から得られた結果を特性に
基づいてグループ分けして,系統的に表にまとめることが望ましい。この表は,グループ・試験所の識別
及び方法,個別的結果,並びに試験所平均値及びこれに対応する標準偏差を含むことが望ましい。しかし,
参加試験所が,二つ以上のRM試料(unit)について特性値を決定している場合,試料内(within-unit)及び全体
の平均値並びにこれに対応する標準偏差を,表の中の個別の結果とは別のところに表示することが望まし
い。参加試験所が,異なった測定方法で得られる特性値について二つ以上の一連の結果を提出した場合,
各一連の結果を独立したものとして,すなわち,それぞれ別の試験所から提出されたものと同じように扱
うことが望ましい。
結果はグラフの形式で提示することが望ましい。
結果の不確かさを各試験所から報告する必要の有無に応じて,2種類の報告方法が適用される。
共同実験活動
データの破棄又は
置換え
データの破棄又は
置換え
物質は認証できない
物質は認証できない
報告
技術的に無効な
結果
統計的に無効な
データ
十分な均一性/
安定性
認証の基準
特性値と不確かさの計算
はい
いいえ
はい
はい
はい
いいえ
いいえ
いいえ
41
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参加グループ・試験所が,自分の測定の不確かさを報告することを要求される場合は,通常,測定結果,
その拡張不確かさ及び包含係数で十分である。しかしながら,結果間の共分散の評価(参考文献の[34]及
び[38]参照)に役立つため,各試験所は,すべての不確かさの明細を付けた完全な不確かさモデルを報告
することが望ましい。
不確かさについての情報が要求されない場合,参加グループ・試験所は,(平均値でなく)個々の結果を
報告することが望ましい。報告される有効けた数は,当該プログラムに対するガイドラインに適合するこ
とが望ましい。
いずれの場合も,測定プロセスにおけるすべての前処理段階(例えば,化学分析では,試料の分解及び
目的成分の分離)を理解できるだけの十分な詳細さで,使用した測定手順の概要を報告することが望まし
い。文献の引用(該当する場合)を明記することが望ましい。
10.3 分布
確率変数の期待値を推定するための適切な推定量を求めることは,一般的に,確率密度関数として表現
される基本的な分布(想定されたもの又は決定されたもの)に深くかかわっている。多くの場合,分布は
ヒストグラムを作成して図式的に観察することができる。想定をしていない場合,一定数の測定値のデー
タ評価は,全面的に次のものに基づいて行うことができる。
− 適切な推定手順[例えば,カーネル(Kernel)推定]を用いた測定値分布の調査,又は
− JIS Z 8101-1(モーメントの計算)に規定する原則による関連推定値の計算
ただし,統計的に妥当な数の測定値を利用できることが条件となる。不確かさの影響を定量化するため
に一般に使用されている他の分布としては,例えば,一様又は三角形のような対称な分布もある(GUM
も参照)。
10.5及び10.6に規定する方法は,必ず正規分布したデータについて述べている(Bタイプの不確かさ影
響評価に関する場合を除く。)。このような理由から,選択した方法の妥当性を確認するために,利用可能
な一連のデータの正規性に関する試験が必要になることがある。
ほとんどの結果が,二つ以上の集団(cluster)を形成している場合は,方法・試験所間の調和がとれていな
いと推定する。次の可能性を考慮に入れることが望ましい。
a) これらの集団が測定方法手順と相関している場合,及びこれら集団の平均値間の差が,統計的及び物
理的に有意な場合,単一の特性値がないことになる。この場合,測定方法手順の改善をして,問題解
決を図る必要がある。
b) これらの集団が測定方法手順と何ら相関関係がない場合,及びこれら集団の間の差が,統計的及び物
理的に有意な場合,比較的質の良くない測定方法をカバーするためにより多量のデータを集めること
が必要な場合がある。
異なる方法からの結果の間で若干の矛盾がある場合,この点を説明する不確かさ成分を追加導入するこ
とで解決できることがある。このような方法が有用かどうかは,この不確かさ成分の寄与度を決定し,ま
た,このようにして得た特性値に付随する合成標準不確かさを,認証用の一連の基準に照らして検証した
後で初めて判断できる。この推定の問題については幾つかの方法がある。参考文献[43]で有益な討議をし
ている。
ほとんどの結果が単一集団になっている場合,その分布は,ひと山の形になっていると推測できる。測
定対象の特性値の推定方法として最も明らかな選択は,結果の平均をとることである。
分布がひと山型の場合,正規分布の仮定の妥当性を判断することが望ましい。この決定は,ヒストグラ
ムを目視で観察して下してもよいし,正規性の検定又はこの決定事項の性質に関する過去の経験に基づい
42
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
てもよい。
場合によっては,結果を変換して,正規分布に近似する必要がある。通常採用される変換方式として,
対数,平方根及び指数関数方式がある。
特性値及びその不確かさの評価をする場合,分布関数の仮定は,外れ値検定ほど重要ではなくなる。し
かし,ほとんどの統計学が正規分布に基づいているので,データの分布が正規分布に十分一致するか,又
は正規分布データを仮定した統計的手法が使えるように変換することが可能かどうかを確認することが望
ましい。
10.4 データのスクリーニング
フォーマットに関係なく,一連のデータは,10.5又は10.6に規定する手順を適用する前に,目視的及び
図式的に検査することが望ましい。何らかの異常が観測されたときは,考えられるさ(些)細な理由(送
信エラー,ミスプリントなど)及び,さ(些)細でない理由(ドロップアウト,機器故障など)の有無を
調査することが望ましい。エラー又は故障が確認された場合は,これに対応する結果を棄却することが望
ましい。
さらに,結果については,技術的な根拠の有無を確認しなければならない。技術的な根拠のない結果は,
測定報告を綿密に調べることによって発見できる。技術的な根拠のない結果は,必ずしも統計的にも無効
な結果ということではない。疑わしい結果が有効な結果の範囲内に入ることもあるが,この結果を求めた
条件が正常でないことは明らかである。技術的な根拠のない結果は,一連のデータから除外することが望
ましい。
10.5 データの評価
10.5.1 方法A:1か所の試験所において単一の方法を使用
不確かさの記載が付随する(一次)標準測定法から単一の値を得ることができる場合は,不確かさの付
随するこの値が値付けの結果となる。一連の値がある場合は,これら一連の値の平均値が値付けの結果と
なる。この場合,不確かさは,通常,値が与えられている測定方法の不確かさの評価に基づいており,ま
た一連の値の標準偏差と比較することが望ましい。平均値の標準偏差と測定方法について求めた完全な不
確かさのバジェット表とが,一致することが望ましい。
10.5.2 方法C:方法及び/又は試験所のネットワーク
データフォーマットは,次のどちらでもよい。
− それぞれが不確かさの記載を伴った一連の値,又は
− 各試験所における一連の観測事項
最初のケースでは,データのスクリーニングの一部として,不確かさの記載は,例えば,測定方法の説
明を基準とする確認・検査によって妥当性の確認を行うことが望ましい。その後のデータの取扱いは10.7
の規定による。
一連の観測事項しかない場合,データは,附属書Aの記載によって取り扱うことができる(参考文献の
[11]及び[12]も参照)。手順は,次に示す事項を含むことができる。
a) 単一値の平均又は試験所の平均値の平均の,どちらを選択することが望ましいかを決定するための基
礎として,試験所の平均値間の有意な差を求める試験
b) a)に基づく決定によって選択した一連のデータの正規性及びその外れ値を調べる試験。外れ値の取扱
いは10.5.5による。
c) 全データセットの中で外れ値を出した試験所の変動を調べる試験(必要な場合,すなわち異常な変動
がある場合)
43
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
一連のデータがほぼ正規分布を示す場合は,a)に基づいて選択した平均値が初期の選択した値付け値と
なる。認証すべき特性値を平均値の平均とする場合,すなわち,
∑
=
=
p
i
iY
p
Y
1
1
············································································ (23)
このとき,平均値の平均に付随する合成標準不確かさの基礎となるのは,式(24)によって得られる標準
偏差である。
(
)
∑
=
−
−
=
p
i
iY
Y
p
s
1
2
2
1
1
································································ (24)
この場合,合成標準不確かさは,式(25)に等しくなる。
p
s
u
=
char
·············································································· (25)
これらの式において,pは試験所の数を表す。この式の妥当性は,Yi値の独立性によって大きく左右さ
れる。したがって,方法・試験所に対する結果の独立性についての仮定がどの程度妥当かを検証すること
が望ましい。特に,pの値が大きい場合,この検証作業は重要である(10.6.2も参照)。
10.5.3 方法B:1か所の試験所において複数の方法を使用
この場合も,二つのデータフォーマットがある。
− それぞれ不確かさの記載をもつ一連の値,又は
− 各試験所の一連の観測事項
最初のケースでは,各値及び付随する不確かさの記載を,値付けにかかわる各方法について10.5.1に規
定するように調査を行う。その結果,10.7に規定する方法が適用できる。
10.5.2に規定する方法は,2番目のケースについて用いることができる。少なくとも一つの方法について
は,推定した不確かさを検証でき,かつ,測定バイアスを評価できるように,すべての不確かさのバジェ
ット表を利用することが望ましい(この規定によって,関係するすべての方法は,9.2に規定するトレーサ
ビリティ要求事項を満たすべきである,というような要求事項が追加されることはない。)。
10.5.4 方法D:方法で定義されたパラメータ
方法で定義されたパラメータは,10.5.2に規定する方法で取り扱ってよい。
10.5.5 外れ値の取扱い
一連の結果の中で,又は他の一連のデータにおいて他のデータからの,正確さ又は精度の点での偏差が,
規定の頻度分布に関する統計的変動で許容される以上に大きくなっている場合,単一の結果又は結果全体
は,統計的に無効な結果(外れ値)である可能性がある。したがって,外れ値検出の有効性は,頻度分布
の仮定の妥当性に依存する。十分な数の観測値及び背景の情報が利用でき,外れ値に関して正しく判断で
きるようにしておくことが同様に重要である。外れ値に対する検定は,外れ値検定に関する有効な方法の
選択及び解析の実施という点で,統計学者の特権であることが望ましい。
外れ値は,あらゆるレベルの共同実験で発生し得る。すなわち,単一観測,観測事項のサブグループ(例
えば,試料瓶別のグループ化),又は完全な方法・試験所の結果を外れ値と見ることができる。外れ値は破
棄するか,又はまれ(稀)ではあるが例えば,計算エラーの場合などには,是正したデータに置き換える
ことが望ましい。可能な場合にはいつでも,外れ値は2回以上の外れ値検定の結果に基づいてだけ取り除
くことが望ましい。分散における外れ値は,極端な場合,すなわち一連のデータと矛盾する場合にだけ排
除することが望ましい。追加測定は通常は認められないが,これはデータを得た条件がすべての結果に対
して同一ではなくなっているからである。
44
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最後に,5 %外れ値(stragglers)と,1 %外れ値(outliers)とは,区別することが多いので注意することが望
ましい(例えば,JIS Z 8402-2参照)。通常,1 %外れ値は取り除いても,5 %外れ値は一連のデータ中に
残すことが望ましい。ほとんどの場合,これによって,不確かさの推定が過小評価にならないで済むこと
になる。
注記 JIS Z 8402-2では,stragglerは5 %外れ値を,outlierは1 %外れ値を指す。
10.6 不確かさの評価
10.6.1 方法A:1か所の試験所での単一の方法
10.5.1で規定した不確かさは,値付けによる不確かさ(uchar)である。
10.6.2 方法C:複数の方法及び/又は複数の試験所のネットワーク
各試験所から報告された値に不確かさの記載が付随している場合は,10.7に規定した方法を用いて,計
算した不確かさが値付けによる不確かさ(uchar)になる。
各試験所が一連の値だけを報告している場合,平均についての標準偏差は,少なくとも,通常は値付け
による不確かさ(uchar)になる。不確かさ及び/又はかたよりに共通の発生源がある場合,平均についての標
準偏差を,これらの不確かさの発生源に対する推定値で補足する必要がある。
10.6.3 方法B:1か所の試験所での複数の方法
各試験所から報告された値に不確かさの記載が付随している場合は,10.7に規定した方法を使用し,計
算した不確かさは値付けによる不確かさ(uchar)になる。
その他の状況では,平均についての標準偏差は,少なくとも,通常は値付けによる不確かさ(uchar)になる。
使用した方法のうちの一つの方法の結果に付随する不確かさとの両立性について確認・検査した結果,差
異があることが示される場合は,不確かさバジェット表にこのような不一致に対する許容幅を設けること
が望ましい。
10.6.4 方法D:測定方法で定義されたパラメータ
測定方法で定義されたパラメータについての不確かさの評価は,10.6.2に規定する方法と同様な方法で
取り扱ってよい。
10.7 不確かさに基づく評価
10.7.1 基本
不確かさについての情報が得られる場合,異なった方法・試験所からの結果の評価を行う統計学者がま
ず行うべきことは,その不確かさを含める結果を組み合わせて,単一の値(特性値)及び合成標準不確か
さを得ることである。不確かさを決定したら,その共同実験活動の一部である測定に対する不確かさモデ
ルが利用できるようになる。可能な限り良い結果を得るためには,これらの不確かさのモデルをデータ評
価の一部として収集することが非常に望ましい。
特性値はある種の平均値として定義されるのが普通であり,必要な場合は,この平均に,前もって定め
た重み付けスキームによって重みを付ける。不確かさモデルが利用できる場合は,特性値に付随する合成
標準不確かさに対する式を,試験所間での結果の有意なばらつき(scattering)を説明する不確かさの付加的
要因を追加してから,標準的な不確かさの伝ぱ(播)公式(参考文献[5]の5章を参照)を用いることによ
って直接得ることができる。これが最も直接的な方法であるが,いつもこのように進められるとは限らな
い。
考え得る代替案がある(参考文献の[34]及び[38]参照)。特性値に付随する合成標準不確かさは,式(26)
によって定義できる。
45
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
2
2
char
Ⅳ
Ⅲ
Ⅱ
Ⅰ
u
u
u
u
u
+
+
+
=
···························································· (26)
ここでは,次の四つのタイプの不確かさを考慮している。
− タイプⅠ:試験所固有の不確かさ
− タイプⅡ:すべての試験所に共通する不確かさ
− タイプⅢ:試験所のグループ間に共通する不確かさ
− タイプⅣ:参加試験所からの値の間の不一致
この不確かさの評価を手作業で実施することは手間がかかり,間違いを起こしやすい。測定モデルに基
づき,共同実験の一環として収集された情報がモデル内の相関性のある変数を特定できる場合には,これ
を手作業で行う必要はない。すべての不確かさ成分を正しくデータベースに登録すると,このデータベー
スをすべての異なったタイプの不確かさを作成するために利用できる。これは,異なった方法,すなわち,
各項に対する必要な式を直接求めるか(参考文献[34]参照),又は,例えば,χ 2-フィッティング5)などによ
って行うことができる(参考文献の[38]及び[39]参照)。
注5) 文献では,これは“最小二乗”又は“最小二乗フィッティング ”としても知られている。χ 2-
フィッティングは,通常は,倍率が“最小二乗フィッティング”と異なるだけで,フィッティ
ング手順の後に統計量χ 2の評価ができる。
10.7.2 χ 2-フィッティング
χ 2-フィッティング方法は,次のように実行する。式(27)のマトリックス式を展開することができる。
a
x
x
x
y
y
y
p
p
2
1
2
1
=
Λ
Λ
········································································· (27)
ここに,
a: 特性値
yi: 共同実験で得た測定結果
x: 設計ベクトル
この個別の事例では,xi値は,フィッティングの問題が定義されればすぐに分かる。この状況では,x1
=x2=…xp=1となる。結果のyには不確かさが付いている。これらは,分散−共分散マトリックスで説明
でき,式(28)のように定義される。
()
()
(
)
(
)
(
)
()
(
)
(
)
(
)
()
,
,
,
,
,
,
2
2
1
2
2
2
1
2
1
2
1
1
2
=
p
p
p
p
p
y
u
y
y
u
y
y
u
y
y
u
y
u
y
y
u
y
y
u
y
y
u
y
u
y
V
Λ
Λ
Λ
Λ
Λ
Λ
Λ
································ (28)
このマトリックスは,次元がp×pとなっており,また,対称(すなわち,上の三角形が下の三角形と同
じ要素を含んでいる。)となっていることに注意することが望ましい。各試験所ペアの間の共分散は,結果
の計算にかかわるすべての変数を探すこと,及び各試験所で共有されている変数を特定することで値が決
まる。この探索では,これらの成分が,調査中の2か所だけで共有されているか,又はそれ以上の試験所
で共有されているかどうかは関心事でない。共分散の存在をペアごとに調査するプロセスは,このプロセ
スの間,タイプⅡ及びタイプⅢの不確かさを区別していないことを意味する(10.7.1参照)。
共分散マトリックスV(y)を確定した後,フィッティングの問題は式(29)のように定義してもよい。
46
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()(
)
(
)a
X
y
V
a
X
y
a
T
ˆ
ˆ
ˆ
1
−
−
=
−
ϕ
························································ (29)
特性値は,式(30)のように表現できる。
y
V
CX
x
a
T
1
char
ˆ
−
=
=
··································································· (30)
ここで,
(
)1
1
C
−
−
=
X
V
XT
········································································ (31)
また,その分散は,式(32)から求まる。
()
2
char
u
C
a
V
=
=
········································································ (32)
式(29)に示すようなフィッティングの問題を解決する安定アルゴリズムは無数にある。さらに,マトリ
ックスVについて何らかの説明がなされることが望ましい。このマトリックスは,比較にかかわるすべて
の不確かさ成分を含んでいる場合は,V(y)と等しい。そうでない場合は,追加の分散−共分散マトリック
スをV(y)に追加する。こうしたマトリックスの構造は,V(y)と同じであり,したがって対角線上の要素だ
けが入ることが多い。
ここに示すのは,枠組みをそのまま説明どおりに実施する方法である。これは決して唯一の方法ではな
い(参考文献の[40]及び[41]参照)。外れ値の問題は,このレシピの使用前に処理しておくことが望ましい
(10.5.5も参照)。同様に,不確かさの記載について,その信頼性を厳しく検討し,また,必要な場合は,
それに応じて重み付けスキームを調整する(参考文献[42]参照)(10.5.1も参照)。よく知られているように,
χ 2-フィッティングは,外れ結果及び重み付けにかかわる問題の影響を受けやすい。
10.8 特定の問題点
10.8.1 分散分析を用いたデータ評価
方法C及びDの場合,また方法Bの一部としての場合,分散分析(ANOVA)は,データを処理するため
のツールとして用いてもよい。分散分析の使用は,瓶間均質性(例えば,10.8.2及びA.2参照)又は試験
所間標準偏差(A.3参照)のような不確かさ成分を評価する場合に特に有用になることがある。その他の
場合,これらの不確かさの方法に関して平均値の平均を代わりに計算してもよい。
10.8.2 共同実験の一環としての均質性確認
共同実験の結果は,RMの均質性を最終確認するものとなることがある。このために,二元配置枝分か
れ実験計画を行うが,この場合,pqユニットを使用し,またp試験所及び/又は方法を採用して,それぞ
れがqユニットの特性値を,ユニットごとにn回反復測定を行い決定する(均質性試験についての詳細は,
箇条7を参照)。分散分析に関する要求事項を満たし,かつ,その基礎となる仮定に合わせるためには,こ
の実験計画に厳密に従うことが重要である(参考文献[20]参照)。A.2に,関連する分散を計算するために
必要な統計手法を示す。
10.8.3 特性値の合成標準不確かさ
一連の測定に基づいて特性値を確立するために,他の広範囲のスキームを開発してもよい。このような
特性値は,通常ある種の平均であるか,又はロバスト平均のときもある(参考文献[42]参照)。この細分箇
条では,分散分析に基づく方法から得た平均を含めて,平均に対する式を特性値の不確かさ(uchar)に変換す
る方法を規定する。
共同実験の平均は,式(33)による。
∑
=
i
ix
w
x
············································································· (33)
ここに,
xi: 結果
47
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
wi: 重み
重み付けの性質については仮定はしておらず,重み付けは,観測数,試験所の結果に付随する不確かさ,
又はその他のスキームに基づくことができる。ただし,この式では,重み付けスキームがその和を1に等
しくなると仮定する。
すべてのxiから不確かさの記載を得ることができる場合,特性値に付随する不確かさは,式(34)を用い
て表現できる。
()
()
∑
=
=
i
i
x
u
w
u
x
u
2
2
2
char
2
···························································· (34)
ただし,すべての値xiが相互に独立していることが条件となる。この基本的方法は,10.4に規定する方
法にも適用してもよい。不確かさの記載を使用する場合は,不確かさの記述の信ぴょう性を確認すること
が望ましい(10.6.1も参照)。不確かさのデータが利用できない場合は,平均値の平均を計算する(10.5.2
及び10.6.2参照)ことも不確かさの評価の方法の一つとして用いてもよい。
11 認証
CRMという概念は,特殊なRMの一つとして導入されたものである。JIS Q 0030に規定するRMの特
性に加えて,CRMには,JIS Q 0031に規定されている認証書が添付され,特に次の情報が与えられる。
− 対象となる諸特性
− 特性の値
− 特性の不確かさ
− 特性値の計量学的トレーサビリティに関する記載
市場には,上記のCRMに関する情報を含む文書が添付されたRMが出回っているが,この文書は,法
規上の理由又はその他(技術面に関係ない)の理由から“認証書”とは呼ばない。これらのRMは,CRM
と同一の要求事項を満たさなければならず,CRMと同じ目的に使用できるため,同様にこの規格に含めた。
これらのRMは,“CRM”という用語の中に含まれる。この規格は,RMが認証を受けるために,又は少
なくとも上記の情報を含む一組の文書を備えたRMとして市場に出荷するために,候補RMの調製プロセ
スを規定する。
さらに,JIS Q 0031によると,CRMに付随している認証書は,物質の選定,その適切性の評価,そして
認証対象となる諸特性の測定を含む作業など,広範な計画を要約したものである。CRMの使用者の多くは,
認証書に含まれているこれらの情報以上のものを更に要求することはないであろうが,(CRMと一緒に提
供される,又は要請によって入手できる)認証報告書の形式で入手できるか,又は生産者へ申し込むこと
で提供される状況にしておくべきである。認証書の内容に責任を負う者として,認証部門の代表者の名前
を認証書に含めることは重要である。認証書に署名をするか否かについては,認証機関の裁量にゆだねて
よい。
48
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
統計的方法
A.1 一元配置分散分析 (ANOVA)
a個のグループがあり,それぞれがni個のメンバーをもつ場合を考察する。理想的には各グループにお
けるメンバー数が等しいとよいが,実際には必ずしもそうならない。データによっては“欠測”になるこ
ともあり,これらの欠測データを考慮する式が開発されている(参考文献の[20]及び[21]参照)。また,不
完全な一連のデータを取り扱う場合(グループ内のメンバー数が不ぞろいな場合),他の方法よりもこれら
の式を優先することが推奨される。一連のデータが不完全になれば,推定値の品質はそれだけ悪くなるこ
とに注意が必要である。
データのばらつき(scattering)は,“平方和”ともいわれる差の平方和によって表される。これら平方和は,
分散分析における各(階層)レベルにおけるばらつきを表している(参考文献[20]参照)。表計算プログラ
ムから得られるようないわゆる平均平方は,式(A.1)及び式(A.2)によって分散に変換できる。
within
2
within
MS
s
=
······································································· (A.1)
0
within
among
2
n
MS
MS
sA
−
=
······························································ (A.2)
ここで,
−
−
=
∑
∑
∑
=
=
=
a
i
i
a
i
a
i
i
n
n
n
a
n
i
1
1
2
1
0
1
1
·························································· (A.3)
欠測データがない場合,n0はnに等しくなる。ここに示したメカニズムによって,測定値のばらつきは
物質及び測定プロセスに影響する各種の不確かさ成分に原因を求めることができる。グループ間効果が全
くない場合,sA2はゼロになる(又はゼロに近づく)。sA2に対してわずかな程度の負の値が,実験上の理由
から,得られる場合は,この値をゼロに設定する。
例 瓶間均質性試験において,sAは瓶間均質性の標準偏差sbbと同じになる。それぞれの瓶が一つのグ
ループとなる。
A.2 データ解析における枝分かれランダム効果:3段枝分かれ分散分析
このモデルは,共同実験活動の結果が,物質の均質性の確認及びその値付けに使用される場合に用いて
もよい。実験スキームを,試験所間共同実験という個別の場合について,図A.1に示す。共同実験活動が
異なった方法からなる場合,共同実験活動の配置は本質的に同じになる。
この結果は,式(A.4)を用いて表現できる。
ijk
ij
i
ijk
B
A
x
ε
μ
+
+
+
=
······························································· (A.4)
ここに,
xijk: 方法・試験所iから報告された試料単位jのk番目の結果
Ai: 方法・試験所iによる誤差
Bij: 方法・試験所iの内部でのj番目の試料単位による誤差
ε ijk: 測定誤差
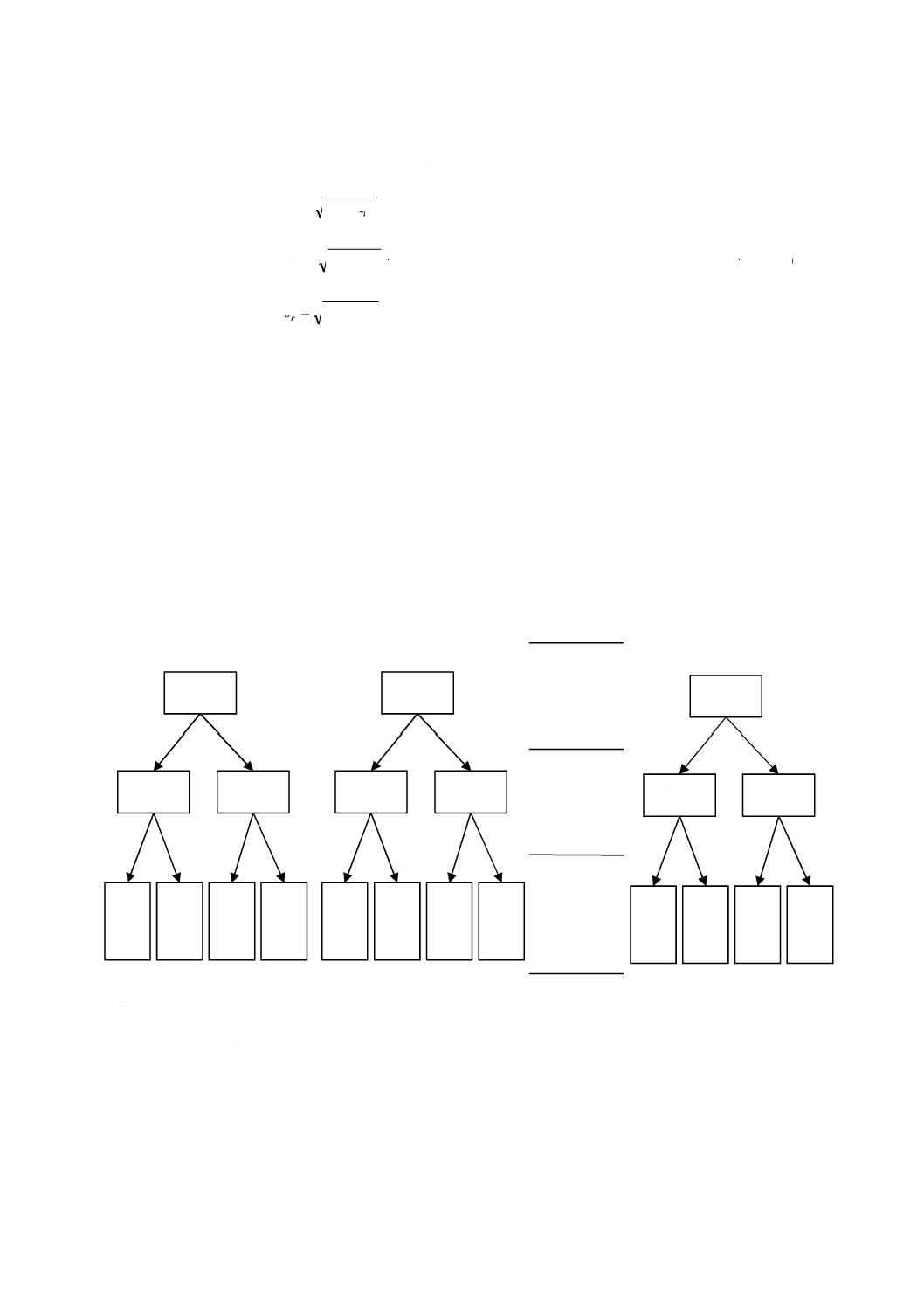
49
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
推定すべきパラメータは,総平均,試験所間標準偏差sL,瓶間均質性の標準偏差sbb及び併行標準偏差
srである。これらは誤差項と式(A.5)のように関連付けられる。
)
Var(
L
iA
s=
)
Var(
bb
ij
B
s=
······································································· (A.5)
)
Var(ijk
rs
ε
=
瓶間均質性標準偏差(sbb)については,本体の7.9に規定した均質性試験自体に関するバッチの不均質性を
検出できないことについての考慮事項を適用する。
これらパラメータはすべて,技術的又は統計的に無効な結果を排除した後でも十分な数の,同数の反復
測定結果(各単位からの同数の反復測定及び方法・試験所当たり同数の単位)がある場合,分散分析
(ANOVA)方法(参考資料[20]参照)によって同時に推定することができる。この分散分析の要求事項を,
結果が無効及び/又は欠測しているために満たせない場合は,瓶間分散の有意性を他の手段によって判断
することが望ましい(箇条7参照)。
バランス形の分散分析及びアンバランス形の分散分析に関する理論的な詳細及び追加的方法は,標準的
な参考文献に記載がある(参考文献の[44]及び[45]参照)。標準物質の認証の文脈内での分散分析の検討は,
文献に挙げてある(参考文献の[18],[20],[22]及び[23]参照)。
図A.1−バッチの均質性試験を組み合わせた共同実験の概要
[RMの値付け(3段枝分かれ配置)]
キー
A 試験所間の変動
B 瓶間の変動
W 測定の併行精度
Lab No.1
瓶No.1
瓶No.2
Ms.
No.1
Ms.
No.1
Ms.
No.2
Ms.
No.2
Lab No.2
瓶No.1
瓶No.2
Ms.
No.1
Ms.
No.1
Ms.
No.2
Ms.
No.2
Lab No.p
瓶No.1
瓶No.2
Ms.
No.1
Ms.
No.1
Ms.
No.2
Ms.
No.2
A
B
W
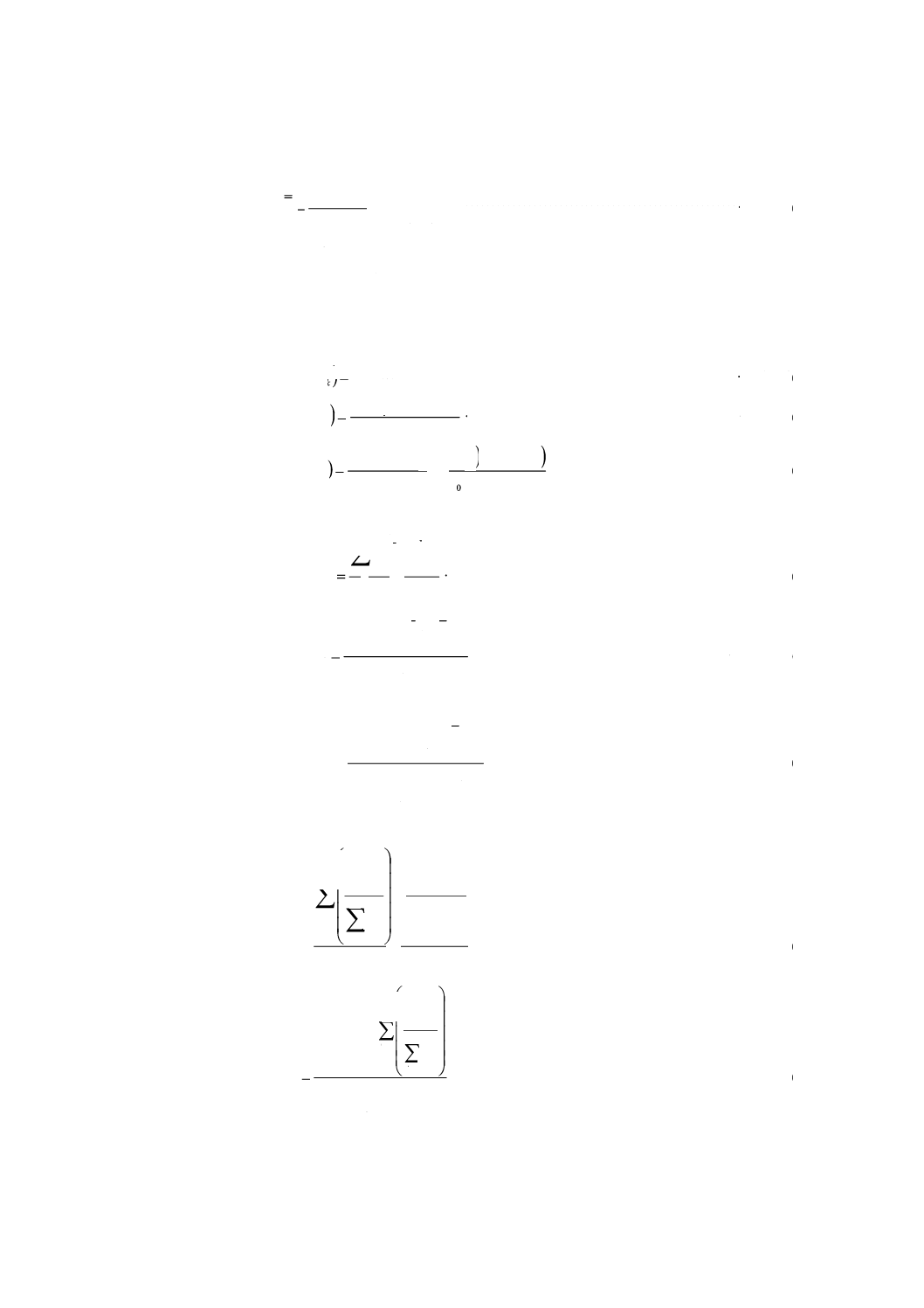
50
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これまで説明した推定値を計算する公式は,次のようになる(参考文献の[20]及び[21]参照)。総平均は,
式(A.6)を用いて計算する。
∑∑∑
∑∑
=
=
=
=
=
=
p
i
b
j
n
k
ijk
p
i
b
j
ij
i
ij
i
x
n
x
1
1
1
1
1
1
························································ (A.6)
ここに,
p: 試験所数
bi: 方法・試験所iで使用する瓶数
nij: 瓶ijについての反復測定回数
このときの分散は,式(A.7)〜式(A.9)を用いて計算する。
()
within
Var
MS
ijk=
ε
··································································· (A.7)
()
0
within
Var
n
MS
MS
B
A
B
ij
−
=
⊂
························································ (A.8)
()
()
()
()0
0
among
Var
Var
Var
nb
B
n
MS
A
ijk
ij
i
ε
−
′
−
=
······································· (A.9)
ここで,
(
)
1
1
2
among
−
−
=∑
=
p
x
x
n
MS
p
i
A
i
···························································(A.10)
(
)
p
b
x
x
n
MS
p
i
i
p
i
b
j
A
B
ij
A
B
i
−
−
=
∑
∑∑
=
=
=
⊂
1
1
1
2
····················································· (A.11)
(
)
∑
∑
∑
∑∑∑
=
=
=
=
=
=
−
−
=
p
i
p
i
i
b
j
ij
p
i
b
j
n
k
B
ijk
b
n
x
x
MS
i
i
ij
1
1
1
1
1
1
2
within
··················································(A.12)
及び
1
1
1
1
1
2
1
1
1
2
0
−
−
=
′
∑∑
∑∑
∑∑∑
=
=
=
=
=
=
=
p
n
n
n
n
n
p
i
b
j
ij
p
i
b
j
ij
p
i
b
j
ij
b
j
ij
i
i
i
i
·····················································(A.13)
p
b
n
n
n
n
p
i
i
p
i
p
i
b
j
ij
b
j
ij
b
j
ij
i
i
i
−
−
=
∑
∑
∑∑∑
∑
=
=
=
=
=
=
1
1
1
1
1
2
1
0
·························································(A.14)
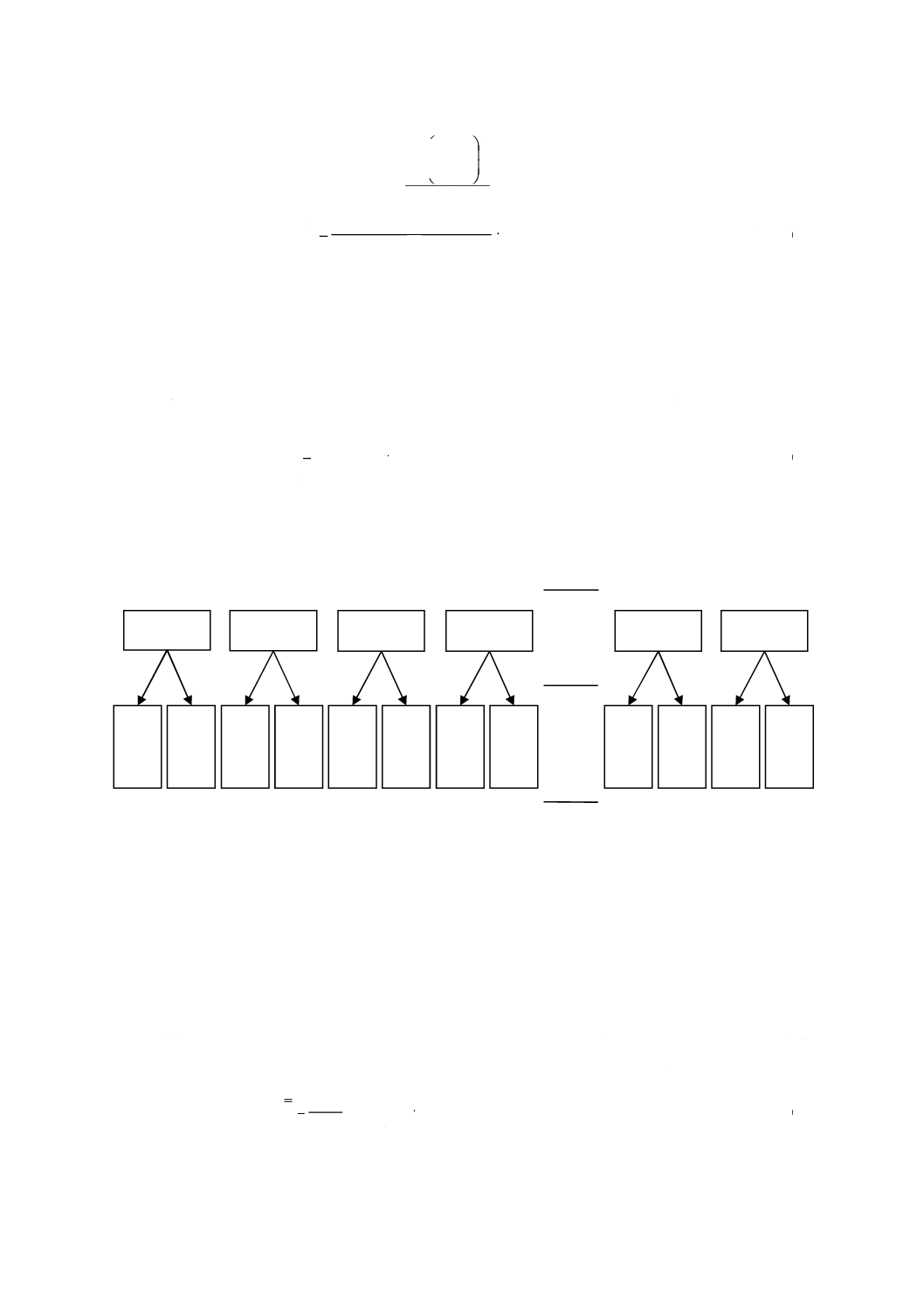
51
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
1
1
1
1
1
2
1
1
0
−
−
=
∑
∑∑
∑∑
∑
=
=
=
=
=
=
p
n
n
n
nb
p
i
p
i
b
j
ij
p
i
b
j
ij
b
j
ij
i
i
i
·················································(A.15)
平均平方(MS)は,通常の表計算プログラム又は統計的ソフトウェアパッケージを用いても求められる。
ここに示す式を用いることによって,欠測及び/又は削除した(無効な)データへの対処も可能である。
完全な一連のデータについては,JIS Z 8402-3に規定するより簡潔な公式を用いてもよい。
A.3 データ解析における枝分かれランダム効果:一元配置分散分析
このモデルは,瓶間の均質性が他の手段で既に検証されている場合に用いる(箇条7参照)。実験スキー
ムは,図A.2に示す。この場合の結果は,式(A.16)のように簡易化することができる。
ij
i
ij
A
x
ε
μ
+
+
=
······································································(A.16)
ここに,
xij: 方法・試験所iで報告されたj番目の結果
Ai: 方法・試験所iによる誤差
ε ij: 測定誤差
図A.2−一元配置分散分析:共同実験活動の配置
[RMの値付け(一元配置)]
記号の意味は,二元配置(A.2参照)と共通である。推定するパラメータは,総平均,試験所間標準偏差
(sL),及び併行標準偏差(sr)である。これらは,A.2で説明する誤差項に関連している。パラメータの推定値
は,次の式から得られる(参考文献[20]及び[21])。総平均は,式(A.17)を用いて計算することができる。
∑∑
∑
=
=
=
=
p
i
n
j
ij
p
i
i
i
x
n
x
1
1
1
1
·································································(A.17)
キー
A
試験所間の変動
W 測定の併行精度
Lab No.1
Ms.
No.1
Ms.
No.2
A
Lab No.2
Ms.
No.1
Ms.
No.2
Lab No.3
Ms.
No.1
Ms.
No.2
Lab No.4
Ms.
No.1
Ms.
No.2
Lab No.p-1
Ms.
No.1
Ms.
No.2
Lab No.p
Ms.
No.1
Ms.
No.2
W
52
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
within
2
MS
sr=
··········································································(A.18)
0
within
among
2
n
MS
MS
sL
−
=
·····························································(A.19)
ここに示した記号の意味は,A.1と共通である。
53
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
事例
B.1
概説
この附属書に示す事例は,箇条7〜箇条10で示した統計的方法をどのように利用するか,実際に例示す
ることを主な目的としている。したがって,ほとんどの事例は,その背景を記載しない。これらの事例に
ついて実際に生じた結果を示し,また,これらデータをこの規格に従って処理する方法を示している。こ
の規格の統計的レシピは本質的に基本的なものであり,必ずしも個別の問題に対する最適な解決策を示す
とは限らない。データの評価には,付加的な問題点(例えば,データの妥当性,外れ値の検出,不確かさ
の記載の信頼性に関する評価,及びソフトウェアアルゴリズムの数値安定性)が多くあるが,これらはこ
の規格の範囲を超えている。しかし,これらは,“正しい”統計的方法を選択することと同じくらい重要で
ある。
標準物質は,物理校正によって又はこれら標準物質を調製するときのデータを使って認証することがあ
る。このような校正の例は,公開文献に示されており,したがって,この附属書には記載しない。これら
プロジェクトの問題点の多くは,RMの生産に固有なものではなく,GUMの適用に関するものである。
認証プロジェクト全体についての例示をすることは,この規格の文脈では不可能である。このような例
は,RM生産者グループの一部にだけ関連するものである。公開文献としての認証に関する報告書は,こ
の規格で規定した指針とともに,認証プロジェクトの設計における適切な根拠となる。
この附属書では,重要なキーとなる統計的レシピを示すため認証プロジェクトの一部を選んで記載した。
事例の関連性については,この箇条の最初に示した記載を考慮して理解することが望ましい。対象とする
特性及びマトリックスは示されているが,どの場合についても,例えば,パラメータの影響を受ける均質
性試験などからのデータを評価するためにレシピが選ばれたわけではない。これら事例は,データが多少
ともガウス分布をしていることを唯一の規準として選択されている。
B.2
値付けモデル
CRM IRMM IFCC 452(γ -グルタミル転移酵素)の拡張不確かさ(参考文献[46]参照)は,特性値に
付随する全体としての不確かさに対する値付け,均質性及び安定性の寄与を合成することで推定する。
2
sts
2
lts
2
bb
2
char
CRM
u
u
u
u
k
U
+
+
+
=
包含係数はk=2を使用した。輸送条件は,輸送による(不)安定性についての不確かさを追加して考慮
に入れる必要がないように選択した。この結果,usts=0となった。
これ以外のすべての不確かさは,値付けによる特性値(xchar)6)への相対値として示した。この製造バッチ
の場合,値付けの結果の不確かさucharは,0.61 %と推定された。ubb及びultsは,それぞれ相対値で0.29 %
及び0.78 %と推定された。したがって,拡張不確かさUCRMは,次の式のようになると推定される7)。
IU/L
36
2
ˆ
07
2
78
0
29
0
61
0
2
2
2
2
CRM
.
.
.
.
.
U
=
=
+
+
=
%
この不確かさは,保管期限を6年としている。物質の安定性に関して更に裏付けが得られれば,保管期
限を延長してもよい(参考文献の[46]及び[47]参照)。
54
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注6) すべての不確かさが同じ値に対する相対値で示されるときだけ,相対不確かさを合成すること
ができる。疑義がある場合は,絶対単位で表現した標準不確かさを複合する方法をとることが
望ましい。
7) 単位IU/L(リットル当たりの国際単位)は,酵素活性の単位である。
B.3
均質性試験
瓶間均質性試験は,土壌中のクロムに対するCRMを調製するためのプロジェクトで実施した。表B.1
に,均質性試験データを示した。
表B.1−土壌中のクロムについての瓶間均質性試験の測定データ
単位 mg/kg
瓶番号
結果No.1
結果No.2
結果No.3
1
121.30
128.74
119.91
2
120.87
121.32
119.24
3
122.44
122.96
123.45
4
117.60
119.66
118.96
5
110.65
112.34
110.29
6
117.29
120.79
121.42
7
115.27
121.45
117.48
8
118.96
123.78
123.29
9
118.67
116.67
114.58
10
126.24
123.51
126.20
11
128.65
122.02
121.93
12
126.84
124.72
123.14
13
122.61
128.48
126.20
14
118.95
123.82
118.11
15
118.74
118.23
117.38
16
119.74
121.78
121.01
17
121.21
123.28
116.38
18
129.30
124.10
122.02
19
136.81
129.80
128.47
20
127.81
117.66
122.90
これらのデータは,各グループの平均,標準偏差及び測定数として示すこともできる。表B.2は,表B.1
の各瓶について,平均,標準偏差及び測定数を求めたものである。
注記 “測定数”については,原文はmembers in each groupであるが,前後の文脈からnumbers of
observation又はcountを意味している。
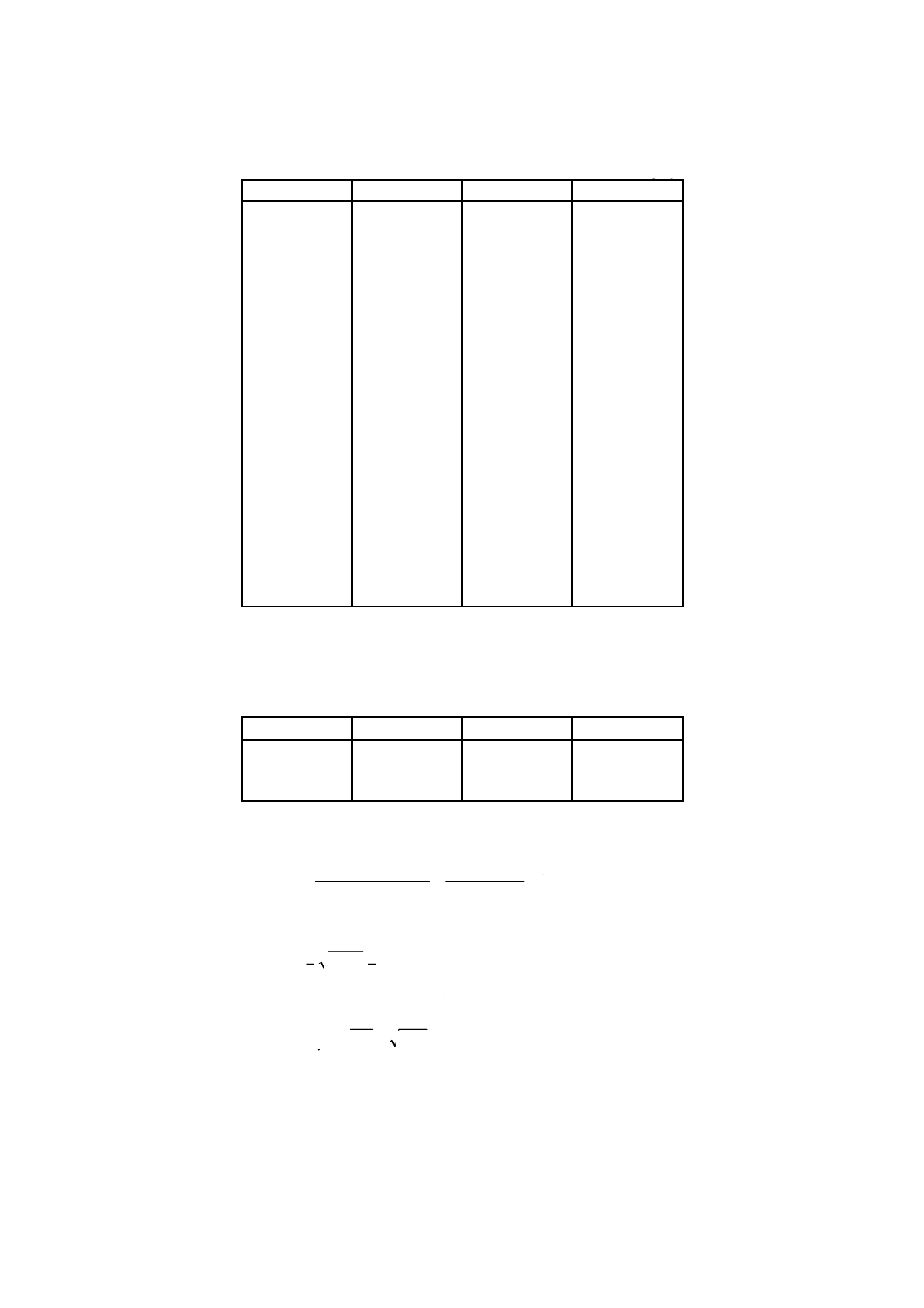
55
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.2−瓶当たりの平均,分散及び繰返し数
単位 mg/kg
瓶番号
平均
分散
繰返し数
1
123.32
22.54
3
2
120.48
1.20
3
3
122.95
0.26
3
4
118.74
1.10
3
5
111.09
1.20
3
6
119.83
4.95
3
7
118.07
9.81
3
8
122.01
7.04
3
9
116.64
4.18
3
10
125.32
2.45
3
11
124.20
14.85
3
12
124.90
3.45
3
13
125.76
8.76
3
14
120.29
9.50
3
15
118.12
0.47
3
16
120.84
1.06
3
17
120.29
12.54
3
18
125.14
14.06
3
19
131.69
20.08
3
20
122.79
25.76
3
表B.3に示す分散分析は,例えば,表計算ソフトウェアを使って計算することができる。
表B.3−土壌中のクロムについての瓶間均質性試験のための分散分析表
変動の要因
SS
自由度
MS
瓶間
1 037.1
19
54.59
瓶内
330.5
40
8.26
合計
1 367.6
59
瓶間の分散は,次の式を用いて推定する。
44
.
15
3
26
.8
59
.
54
0
within
among
2
=
−
=
−
=
n
MS
MS
sA
瓶間均質性の標準偏差は,この分散の平方根である。
mg/kg
93
.3
44
.
15
bb
=
=
s
併行標準偏差は,MSwithinから次の式を用いて計算できる。
mg/kg
87
.2
26
.8
within
=
=
=MS
sr
B.4
試験方法の併行精度に限度があることを考慮した場合の瓶間均質性
7.9に規定する方法は,次のように説明できる。事例は,参考文献[46]からとってきている。
豚の腎臓組織を,塩化ナトリウムで希釈して,均質化した。沈殿を繰り返した後,生成物についてDEAE
56
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Trisacrylカラムを用いたクロマトグラフィによる精製を行い,次に,ハイドロキシルアパタイトカラムで
のクロマトグラフィによる精製を行った。質量濃度60 g/Lのウシ血清アルブミンをマトリックスとして選
択した。この物質を添加しても,部分的に精製した酵素の触媒特性が変わらないからである。注入手順は,
規則的に間隔をおいてとった101本のアンプルの質量を測定して確認した。注入をしている間,何の傾向
も見られなかった。最後に,この物質を凍結乾燥した。
この物質の,汚染酵素の有無,純度,水分及び残留酸素濃度を調べ,その結果,CRMとして適している
ことが分かった。
試料の質量が充てん手順から変動しても,不均質が生じることを意味しない。単位体間変動を定量化す
るため,均質性評価のためのデータを,以前の認証実施時のものからとった。20本のアンプルをそれぞれ
2日間かけて3回分析した。2日間の結果をまとめ,アンプルごとにグループ化したデータについて分散分
析を実施した。単位体内標準偏差(swb),単位間標準偏差(sbb)及び分析の変動が単位体間標準偏差に与える
影響(u*bb)を計算した。分散分析の結果を,各種レベルでの分散の推定値を含めて,表B.4に示す。
表B.4−豚の腎臓細胞についての結果
平均
67.78 IU/L
Mamong
1.76 IU2/L2
Mwithin
1.63 IU2/L2
sr
1.88 %
sbb
0.22 %
u′bb
0.29 %
瓶間標準偏差は,次の式を用いて計算する。
7
021
.0
6
63
.1
76
.1
0
within
among
2
bb
=
−
=
−
=
n
MS
MS
s
ここから,sbbに対する推定値は0.147 IU/L,相対値0.22 %になる。
なお,各グループは3回一組の測定を2回実施した。すなわち,n=n0=6となる。併行標準偏差は,Mwithin
から計算できる。
IU/L
28
.1
63
.1
within
=
=
=MS
sr
7.9に規定する式を使い,併行標準偏差としては比較的大きい値を示す瓶間標準偏差の推定値を得ること
ができる。
IU/L
196
.0
100
2
6
63
.1
2
4
within
within
bb
=
×
=
×
=
MS
n
MS
u
v
瓶間変動(sbb)の推定値は,0.196 IU/Iと推定された併行標準偏差(sr)がsbbに与える影響より小さいことが
分かり,これ以降この値を瓶間変動の上限として用いた。
B.5
安定性試験及び保管期限
土壌中のクロムに対する候補標準物質について,安定性の検討をした。実験データを表B.5に示す。

57
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.5−土壌中クロムの安定性データ
時間
(月)
Cr含有量
(mg/kg)
0
97.76
12
101.23
24
102.14
36
97.72
この候補標準物質の劣化メカニズムを現実的に説明するような物理的・化学的モデルがないので,経験
モデルとして直線を用いた。事実,このマトリックス(土壌)におけるこの特性値(クロム含有率)の場
合,切片が,値付けから求めた値に(不確かさの範囲内で)等しくなり,他方,こう配はゼロから有意に
異ならないと予想した。
こう配は,次の式を用いて計算できる。
(
)(
)
(
)
583
006
.0
720
74
.4
1
2
1
1
=
=
−
−
−
=∑
∑
=
=
n
i
i
n
i
i
i
X
X
Y
Y
X
X
b
ここで,次の式に注意する。
18
5
712
.
99
=
=
X
Y
及び
切片は,次の式を用いて計算できる。
(
)
594
.
99
18
583
006
.0
5
712
.
99
1
0
=
×
−
=
−
=
X
b
Y
b
直線に沿った幾つかの点の標準偏差は,次の式を用いて計算できる。
(
)
973
.7
2
947
.
15
2
1
2
1
0
2
=
=
−
−
−
=∑
=
n
X
b
b
Y
s
n
i
i
i
平方根をとるとs=2.823 7 mg/kgとなり,こう配にかかわる不確かさは,次の式を用いて計算できる。
()
(
)
233
105
.0
720
7
823
.2
1
2
1
=
=
−
=
∑
=
n
i
i
X
X
s
b
s
自由度がn−2で,p=0.95 (95 %信頼水準)におけるスチューデントのt係数は,4.30に等しくなる。
b1 <t0.95,n−2×s (b1)
であることから,こう配は有意ではない。この結果,不安定性は見られなかった。
この代わりに,回帰から分散分析表を評価することもできる。表B.6はこの結果を示したものである。
表B.6−土壌中クロムの安定性データの線形回帰に対する分散分析表
自由度
SS
MS
F
p
回帰
1
0.031 205
0.031 205
0.003 914
0.956
残差
2
15.947
7.973 3
合計
3
15.978
p値は,回帰が有意でないことを示す(例えば,p<0.05に対応する信頼水準95 %の場合は,有意とな
58
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。)。
8.5に規定する方法を用いると,長期的安定性による不確かさの寄与は,保管期限がt=36か月の場合,
次のようになる。
mg/kg
78
.3
36
233
105
.0
b
lts
=
×
=
×
=
t
s
u
この例の制限因子は,相対的に安定性の悪いデータである。土壌中のクロムがもつ不安定性の影響その
ものは,実質的にこれより小さいものと予想できる。
B.6
分散分析を用いた値付け
次の例は,γ -グルタミル転移酵素(以下,GGTという。)に対する,測定温度37 ℃における国際臨床化
学会(IFCC)の規定したIFCC参照方法に基づく標準物質の値付け事例からとったものである。認証は,異
なった試験所で得た結果の一致に基づいて行った。これら試験所は,それぞれが,37 ℃での触媒濃度を測
定するために同じ標準操作手順書(以下,SOPという。)を用いていた。各参加試験所は,凍結乾燥した
GGT物質入りのバイアル7個を,内部精度管理用試料,SOP,再構成手順並びに結果報告及び要請された
情報のためのデータシートとともに,受け取った。3個のバイアルは,2日間のそれぞれの日に再構成され,
各バイアルについて,GGTの触媒濃度の測定を1回,再構成の日に実施した。市販の校正用物質を入れた
バイアルを,独立な品質評価の手段として,CRMとともに配布した。
重量法,容量法及び熱分析のトレーサビリティを実証し,文書化した。分光光度法のトレーサビリティ
は,認証を受けている重クロム酸カリウム溶液を用いることによって確保した。
試験所内の相対標準偏差が2.5 %を超えることは,認証測定では認められないと,あらかじめ決定して
あった。1か所の試験所がこの限度を超えた。この試験所からの精度管理物質についての結果もかたよっ
ていたので,これらデータを使用しないことにした。個々の結果と,受け入れた12か所の試験所からの6
回の試験の試験所平均値,標準偏差及びRSD(相対標準偏差)を表B.7に示す(結果は,四捨五入して,
小数部のけたをそろえた。)。
表B.7−GGTに対する試験所間共同実験からの値付けデータ
試験所
実験結果
IU/L
平均
IU/L
標準偏差
IU/L
相対標準偏差
%
lab 01
118.1
118.9
119.0
118.1
118.1
119.2
118.6
0.5
0.4
lab 04
112.6
112.6
110.6
114.0
114.0
114.0
113.0
1.3
1.2
lab 05
111.9
113.7
110.3
112.4
113.0
110.9
112.0
1.3
1.1
lab 07
111.1
111.4
115.1
109.3
111.0
109.7
111.3
2.1
1.8
lab 08
113.0
115.0
112.6
112.6
113.7
113.1
113.3
0.9
0.8
lab 09
113.3
112.4
113.8
110.2
112.5
114.4
112.8
1.5
1.3
lab 10
114.0
115.3
114.9
113.7
114.3
112.8
114.2
0.9
0.8
lab 11
116.8
116.9
117.4
116.7
117.0
116.6
116.9
0.3
0.2
lab 13
112.6
113.0
113.7
111.7
113.6
111.0
112.6
1.1
1.0
lab 14
114.9
115.5
114.5
115.7
115.5
115.4
115.3
0.5
0.4
lab 15
117.1
118.6
117.9
116.4
117.7
118.4
117.7
0.8
0.7
lab 16
113.9
112.5
111.0
111.1
110.8
112.4
112.0
1.2
1.1
一元配置分散分析を用いて,表B.8の結果を求めた。

59
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.8−表B.7のデータから得た一元配置分散分析結果
変動要因
SS
自由度
MS
グループ間
388.64
11
35.33
グループ内
76.45
60
1.27
合計
465.09
71
総平均は,次の式を用いて求める。
IU/L
12
.
114
72
9.
216
8
9.
216
8
6
12
1
1
1
1
1
=
=
×
×
=
=
∑∑
∑
=
=
=
p
i
n
j
ij
p
i
i
i
x
n
x
一連のデータが完全なため(各グループがn=6の結果を含む),総平均も平均値の平均として求めた。
IU/L
12
.
114
5.
369
1
12
1
12
1
1
=
×
=
=∑
=
p
i
ix
x
総平均に伴う不確かさは,次の式に等しくなる。
()
IU/L
70
.0
49
.0
72
27
.1
12
68
.5
2
2
=
=
+
=
×
+
=
p
n
s
p
s
x
u
r
L
ただし,
27
.1
within
2
=
=MS
sr
及び
68
.5
6
27
.1
33
.
35
0
within
among
2
=
−
=
−
=
n
MS
MS
sL
が与えられているものとする。
B.7
重み付き平均を用いた値付け
CRMの値付けにかかわった試験所には,それぞれの結果に伴う測定の不確かさを評価するように求めた。
結果のトレーサビリティは,(1)既知量のクロムを含む溶液,及び(2)例えば,試料の前処理のパフォーマン
スを確認・検査するため十分に値付けした対照試料によって検証した。これらツールを用いて,RM生産
者は,まず,関係する試験所がそれぞれの方法に対して十分な管理を実施しているか評価した。値付けの
結果を表B.9にまとめる。個々の結果を,表B.9の第2欄(xi)に,また,それに伴う標準不確かさ(ui)を第3
欄に示す。対照試料のデータの評価から,不確かさの記載が信頼性をもつものと想定(また,評価)され
た。不確かさの記載に信頼がもてない場合,ここで説明した方法に基づくデータの重み付けをしないこと
が一般に望ましい。
60
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.9−土壌中クロムの値付けデータ
単位 mg/kg(乾燥状態)
試験所
xi
ui
重みw'i
最終重みwi
1
135
12
0.006 94
0.037 5
2
122
8
0.015 63
0.084 5
3
123
9
0.012 35
0.066 7
4
117
8
0.015 63
0.084 5
5
102
8
0.015 63
0.084 5
6
120
10
0.010 00
0.054 1
7
121
8
0.015 63
0.084 5
8
124
12
0.006 94
0.037 5
9
114
8
0.015 63
0.084 5
10
133
8
0.015 63
0.084 5
11
124
12
0.006 94
0.037 5
12
131
8
0.015 63
0.084 5
13
131
11
0.008 26
0.044 7
14
123
13
0.005 92
0.032 0
15
121
11
0.008 26
0.044 7
16
123
10
0.010 00
0.054 1
w′欄は,次の式を用いて計算する。
2
1
u
w'=
重み付けが合計して1になるという条件を満たすために,それぞれの重みw′をその和で除して,最終重
みを得る。
∑
=
′
′
=
p
i
iw
w
w
1
これらの重みは,表B.9の最終欄に記載する。平均は,次の式を用いて計算する。
∑
=
=
mg/kg
9.
121
i
ix
w
x
関連する標準不確かさは,次の式を用いて計算する。
()
()
mg/kg
3.2
2
2
char
=
=
=
∑
i
i
x
u
w
u
x
u
61
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] JIS Z 8402-1:1999 測定方法及び測定結果の精確さ(真度及び精度)−第1部:一般的な原理及び定義
注記 対応国際規格:ISO 5725-1:1994,Accuracy (trueness and precision) of measurement methods and
results−Part 1: General principles and definitions (IDT)
[2] JIS Z 8402-2:1999 測定方法及び測定結果の精確さ(真度及び精度)−第2部:標準測定方法の併行精
度及び再現精度を求めるための基本的方法
注記 対応国際規格:ISO 5725-2:1994,Accuracy (trueness and precision) of measurement methods and
results−Part 2: Basic method for the determination of repeatability and reproducibility of a
standard measurement method (IDT)
[3] JIS Z 8402-3:1999 測定方法及び測定結果の精確さ(真度及び精度)−第3部:標準測定方法の中間精
度
注記 対応国際規格:ISO 5725-3:1994,Accuracy (trueness and precision) of measurement methods and
results−Part 3: Intermediate measures of the precision of a standard measurement method (IDT)
[4] JIS Z 8402-4:1999 測定方法及び測定結果の精確さ(真度及び精度)−第4部:標準測定方法の真度を
求めるための基本的方法
注記 対応国際規格:ISO 5725-4:1994,Accuracy (trueness and precision) of measurement methods and
results−Part 4: Basic methods for the determination of the trueness of a standard measurement
method (IDT)
[5] JIS Z 8402-5:2002 測定方法及び測定結果の精確さ(真度及び精度)−第5部:標準測定方法の精度
を求めるための代替法
注記 対応国際規格:ISO 5725-5:1998,Accuracy (trueness and precision) of measurement methods and
results−Part 5: Alternative methods for the determination of the precision of a standard
measurement method (IDT)
[6] JIS Z 8402-6:1999 測定方法及び測定結果の精確さ(真度及び精度)−第6部:精確さに関する値の
実用的な使い方
注記 対応国際規格:ISO 5725-6:1994,Accuracy (trueness and precision) of measurement methods and
results−Part 6: Use in practice of accuracy values (IDT)
[7] JIS Q 0031:2002 標準物質−認証書及びラベルの内容
注記 対応国際規格:ISO Guide 31:2000,Reference materials−Contents of certificates and labels
(IDT)
[8] JIS Q 0032:1998 化学分析における校正及び認証標準物質の使い方
注記 対応国際規格:ISO Guide 32:1997,Calibration in analytical chemistry and use of certified
reference materials (IDT)
[9] JIS Q 0033:2002 認証標準物質の使い方
注記 対応国際規格:ISO Guide 33:2000,Uses of certified reference materials (IDT)
[10] JIS Q 0034:2001 標準物質生産者の能力に関する一般要求事項
注記 対応国際規格:ISO Guide 34:2000,General requirements for the competence of reference
material producers (IDT)
[11] European Commission, Guidelines for the production and certification of BCR reference materials−Part A:
62
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Guide to proposers of reference materials projects”, Doc. BCR/01/97, Brussels (B), 1 September 1997
[12] European Commission, “Guidelines for the production and certification of BCR reference materials”, Doc.
BCR/48/93, Brussels (B), 15 December 1994
[13] LAMBERTY, A., SCHIMMEL, H., PAUWELS, J., “The study of the stability of reference materials by
isochronous measurements”, Fresenius J. Anal. Chemistry, 360 (1997), pp.359-361
[14] International Laboratory Accreditation Cooperation, “ILAC G12 Guidelines for the Requirements for the
Competence of Reference Materials Producers”, ILAC, 2000
[15] ELLISON, S.L.R, ROSSLEIN, M., WILLIAMS, A. (eds.),“Eurachem/Citac Guide−Quantifying uncertainty
in analytical measurement”, LGC, London 2000
[16] GRIEPINK, B., MAIER, E., MUNTAU, H., WELLS, D.E., “The certification of the contents of six
chlorobipbenyls (Nos 28, 52, 101, 118, 153 and 180) in dried sludge. CRM 392”, EUR 12823 EN, Luxemburg
1990
[17] RICE, J.A., “Mathematical statistics and data analysis”, 2nd edition, Duxbury Press, Belmont CA, 1995,
chapters 3 and 4
[18] VAN DER VEEN, A.M.H., LINSINGER, T.P.J, LAMBERTY, A., PAUWELS, J., “Uncertainty calculations in
the certification of reference materials. 4. Characterization and certification”, Accreditation and Quality
Assurance, 6 (2001), pp.290-294
[19] LINSINGER, T.P.J., PAUWELS, J., VAN DER VEEN, A.M.H., SCHIMMEL, H., LAMBERTY, A.,
“Homogeneity and Stability of Reference Materials”, Accreditation and Quality Assurance, 6 (2001), pp.20-25
[20] VAN DER VEEN, A.M.H., PAUWELS, J., “Uncertainty calculations in the certification of reference materials.
1. Principles of analysis of variance”, Accreditation and Quality Assurance, 5 (2000), pp.464-469
[21] SOKAL, R.R., ROHLF, F.J., “Biometry”, 3rd edition, Freeman, New York 1995
[22] VAN DER VEEN, A.M.H., LINSINGER, T.P.J, PAUWELS, J., “Uncertainty calculations in the certification
of reference materials. 2. Homogeneity study”, Accreditation and Quality Assurance, 6 (2001), pp.26-30
[23] VAN DER VEEN, A.M.H., LINSINGER, T.P.J., LAMBERTY, A., PAUWELS, J., “Uncertainty calculations
in the certification of reference materials. 3. Stability study”, Accreditation and Quality Assurance, 6 (2001),
pp.257-263
[24] DRAPER, N.R., SMITH, H., “Applied regression analysis”, 2nd edition, J. Wiley and Sons, New York, 1981,
chapter 1
[25] LINSINGER, T.P.J., PAUWELS, J., LAMBERTY, A., SCHIMMEL, H., VAN DER VEEN, A.M.H.,
SIEKMANN, L., “Estimating the uncertainty of stability for matrix CRMs”, Fresenius J. Anal. Chem., 370
(2001), pp.183-188
[26] BUCK, R.P., RONDINI, S., COVINGTON, A.K., BAUCKE, F.G.K., BRETT, C.M.A., CAMÕES M.F.,
MILTON, M.J.T., MUSSINI, T., NAUMANN, R., PRATT, K.W., SPITZER, P., WILSON, G.S.,
“Measurement of pH. Definition, standards and procedures”, IUPAC Recommendations 2002, Pure Appl.
Chem., 74 (2002), pp.2169-2200
[27] KING, B., “Metrology and analytical chemistry: bridging the cultural gap”, Metrologia, 34 (1997), pp.41-47
[28] SCHILLER, S.B., “Statistical aspects of the certification of chemical batch SRMs”, NIST Special Publication
260-125, Gaithersburg MD, July 1996
[29] Minutes from the fifth meeting (February 1998) of the Consultative Committee on the Quantity of Material
63
Q 0035:2008 (ISO Guide 35:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(CCQM) of the Bureau International des Poids et Mesures (BIPM), Sèvres, France (1988)
[30] MAY, W., PARRIS, R., BECK, C., FASSETT, J., GREENBERG, R., GUENTHER, F., KRAMER, G., WISE,
S., GILLS, T., COLBERT, J., GETTINGS, R., MACDONALD, B., “Definition and terms and modes used at
NIST for value-assignment of reference materials for chemical measurements”, NIST Special Publication
260-136, Gaithersburg MD, January 2000
[31] KAARLS, R., QUINN, T.J., “The Comité Consultatif pour la Quantité de Matière: a brief review of its origin
and present activities”, Metrologia, 34 (1997), pp.1-5
[32] ALINK, A., VAN DER VEEN, A.M.H., “Uncertainty calculations for the preparation of primary gas mixtures.
1. Gravimetry”, Metrologia, 37 (2000), pp.641-650
[33] BLAINE, R.L., SCHOFF, C.K. (eds.), “Purity Determinations by Thermal Methods”, ASTM STP 838, ASTM,
Philadelphia, 1984
[34] PAUWELS, J., LAMBERTY, A., SCHIMMEL, H., “The determination of the uncertainty of reference
materials certified by laboratory intercomparison”, Accreditation and Quality Assurance, 3 (1998) pp.180-184
[35] ISO 6142:2001,Gas analysis−Preparation of calibration gas mixtures−Gravimetric method
[36] GUENTHER, F.R., DORKO, W.D., MILLER, W.R., RHODERICK, G.C., “The NIST Traceable Reference
Material Program for gas standards”, NIST Special Publication 260-126, Gaithersburg MD, July 1996
[37] ISO 6143:2001,Gas analysis−Comparison methods for determining and checking the composition of
calibration gas mixtures
[38] VAN DER VEEN, A.M.H., “Determination of the certified value of a reference material appreciating the
uncertainty statements obtained in the collaborative study”, in Ciarlini P., Cox M.G., Filipe E., Pavese F.,
Richter D., “Advanced Mathematical and Computational Tools in Metrology, V”, World Scientific, Singapore,
2000, pp.326-340
[39] NIELSEN, L., “Evaluation of measurement intercomparisons by the method of least squares”, Technical
Report CCEM WGKC 00-13, CCEM Working Group on Key Comparisons, 2000
[40] COX, M.G., FORBES, A.B., HARRIS, P.M., “SSfM Best Practice Guide 4−Discrete modelling”, Centre for
Mathematics and Scientific Computing, NPL, Teddington (UK), Version 1.1, March 2002
[41] COX, M.G., DAINTON, M.P., HARRIS, P.M., “SSfM Best Practice Guide 6−Uncertainty and statistical
modelling”, Centre for Mathematics and Scientific Computing, NPL, Teddington (UK), March 2001
[42] COX, M.G., “A discussion of approaches for determining a reference value in the analysis of key-comparison
data”, CISE 42/99, Centre for Mathematics and Scientific Computing, NPL, Teddington (UK), October 1999
[43] LEVENSON, M. S., BANKS, D. L., EBERHARDT, K. R., GILL, L. M., GUTHRIE, W. F., LIU, H. K.,
VANGEL, M. G., YEN, J. H., ZHANG, N. F., “An approach to combining results from multiple methods
motivated by the ISO GUM”, J. Res. Natl. Inst. Stand. Technol., 105 (2000), pp.571-579
[44] JOHN, P.W.M., “Statistical design and analysis of experiments”, New York, NY, Macmillan, 1971, p.76
[45] SEARLE, S.R., “Linear models”, New York, NY, John Wiley, 1971
[46] LINSINGER, T, KRISTIANSEN, N, SCHIMMEL, H, PAUWELS, J et al. (2000). Catalytic Concentration of
γ-Glutamyltransferase (GGT) determined by the IFCC-Method at 37 ℃. IRMM/IFCC-452, EUR19577EN
[47] SCHIELE, F., SIEST, G., MOSS, D.W., COLINET, E. The certification of the catalytic concentration of
gamma-glutamyltransferase in a reconstituted lyophilized material (CRM 319), 1986; CEC Report EUR
10628 EN
















