M 8010:2020
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 記号······························································································································· 6
5 計量に用いる流量計 ········································································································· 10
6 表示の方法 ····················································································································· 10
7 計量に関する一般事項 ······································································································ 10
8 オリフィス流量計を用いる計量 ·························································································· 14
9 容積流量計を用いる計量 ··································································································· 30
10 渦流量計を用いる計量 ···································································································· 33
11 超音波流量計を用いる計量 ······························································································ 36
12 物性値 ························································································································· 40
13 計量値の不確かさの概算 ································································································· 45
附属書A(規定)オリフィス板の前後に必要な直管長(整流装置を用いない場合) ·························· 48
附属書B(規定)オリフィス板の前後に必要な直管長
[19管束管状式整流装置(1998)を用いる場合] ································································ 53
附属書C(規定)オリフィス板前後に必要となる直管長(ザンカ式整流板を用いる場合) ················· 59
附属書D(参考)オリフィス流量計の流出係数 ········································································· 62
附属書E(参考)オリフィス流量計の膨張補正係数 ···································································· 73
附属書F(規定)体積分率からモル分率への換算 ······································································· 74
附属書G(規定)微量成分の割当 ··························································································· 75
附属書H(規定)Z数表(2015) ··························································································· 76
附属書I(規定)Z数表(1993)····························································································· 87
附属書J(規定)完全気体とみなしたアイゼントロピック指数 ····················································· 99
附属書K(規定)オリフィス板表面及びオリフィス配管内壁面の表面粗さ条件······························· 101
附属書L(規定)空気の相対密度の概算値··············································································· 103
M 8010:2020
(2)
まえがき
この規格は,産業標準化法第16条において準用する同法第12条第1項の規定に基づき,天然ガス鉱業
会(JGA)及び一般財団法人日本規格協会(JSA)から,産業標準原案を添えて日本産業規格を改正すべき
との申出があり,日本産業標準調査会の審議を経て,経済産業大臣が改正した日本産業規格である。これ
によって,JIS M 8010:1993は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本産業規格 JIS
M 8010:2020
天然ガス計量方法
Measuring methods of quantity of natural gas
序文
この規格は1963年に制定され,その後に4回の改正を経て今日に至っている。前回の改正は1993年に
行われたが,各流量計及び物性値算出方法の最新技術に対応するために改正した。
なお,対応国際規格は現時点で制定されていない。
1
適用範囲
この規格は,オリフィス流量計,容積流量計,渦流量計又は超音波流量計を用い,天然に産するメタン
を主成分とする可燃性天然ガス及びLNG気化ガスの燃料ガス(以下,ガスという。)を計量する方法につ
いて規定する。
この規格は,ガスが熱的・成分的に安定で均質であり,計量を行う管路において,管路内を気相だけが
充満して定常的に流れる場合に適用できる。
警告 この規格の使用者は,一般的な試験操作に精通していることが望ましい。この規格は,安全に
関する全ての問題に対する処理を網羅していない。したがって,安全及び健康に関する適切な
基準の遵守,並びに全ての法規制に従うことは,この規格の使用者の責務である。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS K 2301 燃料ガス及び天然ガス−分析・試験方法
JIS Z 8762-1:2007 円形管路の絞り機構による流量測定方法−第1部:一般原理及び要求事項
JIS Z 8762-2:2007 円形管路の絞り機構による流量測定方法−第2部:オリフィス板
ISO/IEC Guide 98-3:2008,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1
標準状態(normal condition)
温度0 ℃,絶対圧101.325 kPa,相対湿度0 %としたガスの状態。変数に添え字Nを用いることによっ
て,標準状態での値であることを表す。
2
M 8010:2020
3.2
基準状態(standard condition)
温度15.6 ℃,絶対圧101.325 kPa,相対湿度100 %としたガスの状態。変数に添え字Sを用いることに
よって,基準状態での値であることを表す。
基準状態における計量値は,次の式(1)又は式(2)を用い,標準状態における値を変換して求める。
qvS=1.075 9qvN ·········································································· (1)
VS=1.075 9VN ··········································································· (2)
ここに,
qvS: 基準状態における体積流量[m3/h (Standard),m3/d (Standard)]
qvN: 標準状態における体積流量[m3/h (Normal),m3/d (Normal)]
VS: 基準状態における通過体積[m3 (Standard)]
VN: 標準状態における通過体積[m3 (Normal)]
3.3
測定状態(metering condition)
計量中における流量計の位置でのガスの状態。変数に添え字Mを用いることによって,測定状態での値
であることを表す。
3.4
オリフィス流量計(orifice flowmeter)
ガスが流れる配管にオリフィス板を取り付け,オリフィス板前後の圧力差を測定して流量を求める流量
計。
3.5
容積流量計(positive displacement flowmeter, PD flowmeter)
ガスが流れる配管に運動子をもつ計量室を取り付け,計量室を通過するガスが運動子を駆動することに
よって運動子に回転又は往復運動が発生し,その運動周期に依存して出力されるパルス信号の数を計数し
て流量を求める流量計。
3.6
渦流量計(vortex flowmeter)
ガスが流れる配管に渦発生体をもつ測定管を取り付け,測定管内を通過するガスの流れによって発生す
る渦の周波数又は周期を測定して流量を求める流量計。
3.7
超音波流量計(ultrasonic flowmeter)
ガスが流れる配管に超音波の送受信機をもつ測定管を取り付け,送信機から放射された超音波信号が受
信機に到達するまでの伝ぱ(播)時間を測定し,伝ぱ(播)時間がガスの流速に依存することを利用して
流量を求める流量計。
3.8
Kファクタ,KF(K-factor)
流量計がこれを通過するガスの流量に比例したパルスを出力する場合に用いる流量計に固有な定数。1 L
のガスが通過したときに流量計が発するパルス数として,次の式(3)で定義される。
M
n
F
V
I
K=
················································································· (3)
ここに,
KF: Kファクタ(pulses/L)
In: 積算パルス数(pulses)
3
M 8010:2020
VM: 流量計を通過したガスの測定状態での通過体積(L)
3.9
オリフィス板(orifice plate)
オリフィス流量計の要素であり,オリフィス孔をもつ薄い平板。オリフィス孔を通ってガスが流れると
き,オリフィス板の前後に流量に依存した差圧が発生する。
3.10
オリフィス孔(orifice)
オリフィス板の中心にあけた流量を測定するための円形の孔。
3.11
オリフィス配管(measuring pipe of the orifice)
オリフィス板を取り付ける配管(直管)。
3.12
オリフィス配管径,D(internal diameter of the measuring pipe upstream of the orifice)
計量中におけるオリフィス配管の直径(内径)。計量中におけるオリフィス配管の温度を用い,オリフィ
ス配管径の測定値D0を温度補正した値とするが,温度補正が必要ない場合には測定値D0で代用する。
注記 ここに定義する“オリフィス配管径”は,JIS Z 8762-1:2007及びJIS Z 8762-2:2007において“管
内径”として用いるDに等しい。オリフィス配管径Dは流量の計算に用いるため,配管の呼び
内径ではないことに注意する。
3.13
オリフィス配管径の測定値,D0(measured value of the internal diameter of the measuring pipe upstream of the
orifice)
オリフィス配管内でオリフィス板の上流側の指定範囲におけるオリフィス配管直径の測定値(内径)。
8.2.4.2に従って測定し,直径測定中のオリフィス配管の温度TD0とともに用いる。
3.14
オリフィス孔径,d(diameter of the orifice)
計量中におけるオリフィス孔の直径。計量中におけるオリフィス板の温度を用い,オリフィス孔径の測
定値d0を温度補正した値とするが,温度補正が必要ない場合には測定値d0で代用する。
注記 ここに定義する“オリフィス孔径”は,JIS Z 8762-1:2007及びJIS Z 8762-2:2007において“絞
り孔径”として用いるdに等しい。
3.15
オリフィス孔径の測定値,d0(measured value of the diameter of the orifice)
オリフィス孔直径の測定値。直径測定中のオリフィス板の温度Td0とともに用いる。
3.16
オリフィス直径比,β(diameter ratio of the orifice)
オリフィス配管径に対するオリフィス孔径の比。次の式(4)で定義される。
D
d
β=
····················································································· (4)
ここに,
β: オリフィス直径比
d: 計量中におけるオリフィス孔径(m)
D: 計量中におけるオリフィス配管の直径(内径)(m)
4
M 8010:2020
注記 ここに定義する“オリフィス直径比”は,JIS Z 8762-1:2007及びJIS Z 8762-2:2007において“絞
り直径比”として用いるβに等しい。
3.17
レイノルズ数,Re(Reynolds number)
ガスの流れの慣性力と粘性力との比を表す無次元数。次の式(5)で定義される。
μ
ρ
L
v
R=
e
················································································ (5)
ここに,
Re: レイノルズ数
v: 流速(m/s)
L: 代表寸法(m)
ρ: ガスの密度(kg/m3)
μ: ガスの粘度(Pa・s)
注記1 流量を計測する場合,一般に,流量計を取り付ける配管の直径(内径)を代表寸法Lとし,
流速v,密度ρ,及び粘度μは,その位置における値とする。
注記2 オリフィス流量計及び渦流量計では,通常,レイノルズ数を一致させることによって,温度,
圧力などが異なる状態又は異なる気体若しくは液体を用いて補正係数(流出係数,Kファク
タなど)を実測することができる。超音波流量計では,通常,レイノルズ数を一致させるこ
とによって,温度,圧力などが異なる状態又は異なる気体を用いて補正係数(流量補正係数,
Kファクタなど)を実測することができる。
3.18
オリフィス配管径に基づくレイノルズ数,ReD(pipe Reynolds number)
オリフィス流量計で用いるレイノルズ数。上流側の圧力取出断面における流れの慣性力と粘性力との比
を表す。式(5)において上流側の圧力取出断面における値を用いるが,質量流量,上流側圧力取出断面にお
ける粘度,及びオリフィス配管径の測定値を用いた,次の式(6)で近似する。
1
0
m
eD
4
μ
D
π
q
R=
············································································ (6)
ここに, ReD: オリフィス配管径に基づくレイノルズ数
D0: オリフィス配管径の測定値(m)
μ1: オリフィス流量計の上流側圧力取出断面における粘度(Pa・s)
qm: オリフィス流量計を流れる質量流量(kg/s)
注記 式(6)で用いるオリフィス配管径の値は,正確には計量中の値Dとしなければならないが,流出
係数のレイノルズ数依存性に対する感度は大きくないため,オリフィス配管径の測定値D0を用
いた近似で十分である。
3.19
直管(straight pipe)
配管軸に沿って配管断面積が一定であり,その全長にわたって配管軸が直線から0.4 %以上の偏差をも
たない配管。
3.20
圧力取出口(pipe-wall pressure tapping)
配管内を流れるガスの静圧を測定するために配管壁面に設けた孔で,7.7に従って製作する。
3.21
圧力取出軸(centerline of the pipe-wall pressure tapping)
5
M 8010:2020
配管壁面内にある圧力取出口の導圧孔の,流れに接する円筒部の中心軸。
3.22
圧力取出直径,dp(diameter of the pipe-wall pressure tapping)
配管壁面内にある圧力取出口の導圧孔の,流れに接する円筒部分の断面直径。
3.23
配管軸(centerline of the pipe)
配管の流れ方向の中心軸。
3.24
配管断面(cross section of the pipe)
配管軸に垂直な配管の断面(流路断面)。
3.25
圧力取出断面(cross section of the pipe at the pipe-wall pressure tapping)
圧力取出軸を含む配管断面。
3.26
継手(fitting)
流路を構成する配管及び流量計以外の要素の総称であり,配管を接続するフランジのほかに,ベンド,
ティー,収縮管,拡大管,バルブ,温度センサ用ポケット・ウェルなどの要素も含む。
3.27
圧力損失係数,K(pressure loss coefficient)
動圧に対する圧力損失の比。次の式(7)で定義される。
2
Δ
2
ρv
K =
················································································ (7)
ここに,
K: 圧力損失係数
Δ: 圧力損失(Pa)
v: 流速(m/s)
ρ: ガスの密度(kg/m3)
3.28
ガスの圧力,p(pressure of the gas)
絶対圧力で表したガスの圧力。
3.29
ガスの温度,T(temperature of the gas)
摂氏温度(℃)又は絶対温度(K)で表したガスの温度。
注記 摂氏温度(℃)を絶対温度(K)に変換するためには,摂氏温度値に273.15を加える。摂氏温
度を用いる式もあるため注意する。
3.30
モル質量,N(molar mass)
ガスの単位モル当たりの質量。
3.31
水蒸気モル分率,xwv(mole fraction of water vapor)
単位モル当たりのガスに含まれる水蒸気のモル数。

6
M 8010:2020
3.32
乾燥したガス(dry gas)
水蒸気モル分率が0.000 3未満であるガス。
3.33
Z数表(2015)(Z table 2015)
AGA8-92DC法で計算した圧縮係数の値を数表化したもの。ガスの温度,圧力及び含有成分のモル分率
の関数をパラメータとし,数表の値を内挿して圧縮係数を求める。
3.34
Z数表(1993)(Z table 1993)
スタンディング・アンド・カッツ(Standing & Katz)の線図の近似数式解による圧縮係数の値を数表化
したもの。ガスの温度,圧力及び含有成分のモル分率の関数をパラメータとし,数表の値を内挿して圧縮
係数を求める。
3.35
旋回がないとみなせる流れ(flow approximates to be swirl-free)
配管断面上の全ての位置における旋回角が2°未満となる流れ。
3.36
流速分布が完全に発達しているとみなせる流れ(flow approximates to be fully developed)
配管断面上の全ての位置において,流速の配管軸方向成分uとその配管断面上でのその最大値umaxとの
比(u/umax)が,同じ直径の直管内を旋回のない流れが配管直径の100倍以上の距離を流れた後に発生する
分布における値(u/umax)と比較して,配管断面上の同じ位置同士で5 %以内で一致する流れ。
4
記号
記号は,表1による。
表1−記号
記号
記号の意味
a
オリフィス流量計の単孔の孔径又は環状室リングのスリット幅
ai,bi
Z数表で使用するi番目の成分に関する定数
aZA0,aZA1,
bZA0,bZA1,bZA2,
cZA0,cZA1,cZA2
空気の圧縮係数を求めるための定数
aμ0〜aμ3,bμ1〜bμ3
大気圧における粘度を求めるための定数
b
オリフィス流量計の環状室リングの内径
c
オリフィス流量計の環状室の上流側のリング厚さ
c'
オリフィス流量計の環状室の下流側のリング厚さ
0p,i
c
i番目の成分の完全気体とみなした定圧比熱
cs
ガス中の音速
d
計量中におけるオリフィス孔径
dt
19管束管状式整流装置(1998)の小管の外径
dp
圧力取出口直径
d0
オリフィス孔径の測定値
e
オリフィス孔のエッジの厚さ
ecl
オリフィス板取付けにおける同心の確認に用いるパラメータ(平行方向)

7
M 8010:2020
表1−記号(続き)
記号
記号の意味
ecn
オリフィス板取付けにおける同心の確認に用いるパラメータ(垂直方向)
fr
オリフィス流量計の環状室のスリット厚さ
f
流量計が出力するパルス信号の周波数
g
オリフィス流量計の環状室の幅
h
オリフィス流量計の環状室の高さ
j
オリフィス流量計の環状室を導圧管に接続するための接続口のリング内への出口直径
lp
圧力取出口の導圧孔の流れに接する円筒部分の長さ
lpath
パス長
l1
D・D/2タップオリフィス流量計及びフランジタップオリフィス流量計の上流側圧力取出口
の位置を指定する間隔
l2
D・D/2タップオリフィス流量計の下流側圧力取出口の位置を指定する間隔
l'2
フランジタップオリフィス流量計の下流側圧力取出口の位置を指定する距離
p
ガスの圧力
pdp
露点温度測定時のガスの圧力
pswv(T)
温度Tにおける水蒸気の飽和蒸気圧
pM
計量中における流量計の位置でのガスの圧力(測定状態の圧力)
pN
標準状態におけるガスの圧力=101 325 Pa
p1
オリフィス流量計の上流側圧力取出断面におけるガスの圧力
p2
オリフィス流量計の下流側圧力取出断面におけるガスの圧力
qm
オリフィス流量計を流れる質量流量
qtheo
オリフィス流量計を流れる質量流量の理論値
qvM
測定状態における体積流量(流量計が計量する体積流量)
qvN
標準状態における体積流量
qvS
基準状態における体積流量
s
段差までの距離
u
流速の配管軸方向成分
umax
配管断面上でのuの最大値
v
流速
v
超音波パス上の平均流速
xi
i番目の成分のモル分率
xwv
水蒸気モル分率
xV,i
i番目の成分の体積分率
A
オリフィス流量計の流出係数に用いるパラメータ
AD
測定管の断面積
AZ
Z数表の横軸の値
Aκ,Bκ
完全気体とみなしたアイゼントロピック指数を計算するパラメータ
Aμ〜Hμ
粘度の圧力補正を行うパラメータ
Aμ0,Aμ1,Aμ2
〜
Hμ0,Hμ1,Hμ2
粘度の圧力補正パラメータに用いる定数
BZ
Z数表の縦軸の値
B0〜B2
アイゼントロピック指数の圧力補正を行うパラメータ
BJ,i〜JJ,i
完全気体とみなした定圧比熱を求めるためのi番目のガス成分の定数
Cd
オリフィス流量計の流出係数
D
計量中におけるオリフィス配管の直径(内径)
Df
19管束管状式整流装置(1998)の小管束の最大外径
D0
オリフィス配管径の測定値

8
M 8010:2020
表1−記号(続き)
記号
記号の意味
Dn
配管の呼び径
EA
アナログ信号の比例係数に乗じる補正係数
EO
オリフィス板の厚さ
EK
KF0に乗じるKファクタの補正係数
Fwv
湿度補正係数
GA
アナログ出力の比例係数
In
積算パルス数(pulses)
K
圧力損失係数
Kc
超音波流量計で用いる流量補正係数
KF
Kファクタ
KF0
Kファクタの代表値
KFx
流量計の使用可能範囲におけるKファクタの最大値
KFn
流量計の使用可能範囲におけるKファクタの最小値
L
代表寸法[流量計を取り付けた配管の直径(内径)]
Lf
オリフィス板に最も近い上流側継手の下流端とオリフィス板との間隔
Lt
19管束管状式整流装置(1998)の小管の長さ
Ls
オリフィス板とザンカ式整流板の下流面との間隔
L1
オリフィス流量計の流出係数に用いるパラメータ
L'2
M'2を求めるためのパラメータ
M'2
オリフィス流量計の流出係数に用いるパラメータ
N
ガスのモル質量
Ni
i番目の成分のモル質量
Nrel
モル質量パラメータ
NN
標準状態におけるガスのモル質量
R
普遍気体定数
Ra
オリフィス配管の内壁面の表面粗さ
Re
レイノルズ数
ReD
オリフィス配管径に基づくレイノルズ数
ReD0
使用範囲におけるオリフィス配管径に基づくレイノルズ数の最小値
S
2個のベンド管の距離
T
ガスの温度
Td
計量中におけるオリフィス板の温度
Td0
オリフィス孔径を測定したときのオリフィス板の温度
Tdp
露点温度
Tran
温度パラメータ(ランキン温度)
TB
計量中における渦発生体の温度
TB0
Kファクタを決定したときの渦発生体の温度
TD
計量中におけるオリフィス配管又は測定管の温度
TD0
オリフィス配管径を測定したときのオリフィス配管の温度又はKファクタを決定したとき
の測定管の温度
TM
計量中における流量計の位置でのガスの温度(測定状態の温度)
TN
標準状態におけるガスの温度=273.15 K
T1
オリフィス流量計を流れるガスの温度
Ud
オリフィス孔径測定値の相対不確かさ
Uf
周波数の測定値の相対不確かさ
Up1
オリフィス流量計の上流側圧力取出断面における圧力測定値の相対不確かさ
UqN
標準状態における体積流量計量値の相対不確かさ

9
M 8010:2020
表1−記号(続き)
記号
記号の意味
Ux,i
モル分率測定値の相対不確かさ
UCd
オリフィス流量計の流出係数の相対不確かさ
UD
オリフィス配管径測定値の相対不確かさ
UK0
Kファクタの相対不確かさ
UPM
圧力測定値(測定状態の圧力の測定値)の相対不確かさ
UT1
オリフィス流量計の上流側圧力取出断面における温度測定値の相対不確かさ
UTM
温度測定値(測定状態の温度の測定値)の相対不確かさ
UV
標準状態における体積計量値の相対不確かさ
UZM
測定状態における圧縮係数の相対不確かさ
UZN
標準状態における圧縮係数の相対不確かさ
UZ1
オリフィス流量計の上流側圧力取出断面における圧縮係数の相対不確かさ
UΔp
オリフィス流量計の差圧測定値の相対不確かさ
Uε
オリフィス流量計の膨張補正係数の相対不確かさ
VM
測定状態における通過体積(流量計を通過したガスの状態での通過体積,流量計が測定する
通過体積)
VN
標準状態における通過体積
VS
基準状態における通過体積
X
アナログ信号出力電圧
X0
アナログ信号のゼロ点出力電圧
Z
ガスの圧縮係数
Zi
表F.1に示すi番目の成分のZの値
ZA
空気の圧縮係数
ZM
測定状態における圧縮係数
ZN
標準状態におけるガスの圧縮係数
Z1
オリフィス流量計の上流側圧力取出断面におけるガスの圧縮係数
α
オリフィス板の逃げ角
αd
オリフィス板の線膨張率
αB
渦発生体の線膨張率
αD
オリフィス配管又は測定管の線膨張率
β
オリフィス直径比
ε
オリフィス流量計の膨張補正係数
κ
ガスのアイゼントロピック指数
κ0
完全気体を仮定したアイゼントロピック指数
κ01
オリフィス流量計の上流側圧力取出断面における完全気体を仮定したアイゼントロピック
指数
κ1
オリフィス流量計の上流側圧力取出断面におけるアイゼントロピック指数
μ
ガスの粘度
μ0
大気圧におけるガスの粘度
μ01
オリフィス流量計の上流側圧力取出断面における温度で大気圧におけるガスの粘度
μ1
オリフィス流量計の上流側圧力取出断面におけるガスの粘度
Δd%
温度補正をしないことによるdの差
ΔD
配管の接続面における段差の大きさ
ΔD%
温度補正をしないことによるDの差
ΔUCd1
D0に依存するオリフィス流量計の流出係数の不確かさの追加項(%)
ΔUCd2
β及びReDに依存するオリフィス流量計の流出係数の相対不確かさの追加項(%)
Δp
差圧
Δμp
粘度の圧力補正項

10
M 8010:2020
表1−記号(続き)
記号
記号の意味
Δμp1
オリフィス流量計の上流側圧力取出断面における粘度の圧力補正項
Δ
圧力損失
ρ
ガスの密度
ρ1
オリフィス流量計の上流側圧力取出断面における密度
ρcc
密度パラメータ
ρr
相対密度
ρM
計量中における流量計の位置でのガスの密度
ρN
標準状態におけるガスの密度
5
計量に用いる流量計
ガスの計量に用いる流量計は,オリフィス流量計,容積流量計,渦流量計又は超音波流量計とする。
6
表示の方法
体積流量値及び通過体積値の表示は,次による。
a) 体積流量値の表示 体積流量を計量する場合,次のいずれかの方法で表示する。
1) 標準状態における体積流量値は,m3/h又はm3/dで表し,単位表記は,通常,それぞれm3/h (Normal)
又はm3/d (Normal)とする。括弧内はSI単位と重複しない範囲で短縮して表記してもよい。
2) 基準状態における体積流量値は,m3/h又はm3/dで表し,単位表記は,通常,それぞれm3/h (Standard)
又はm3/d (Standard)とする。括弧内はSI単位と重複しない範囲で短縮して表記してもよい。
b) 通過体積値の表示 通過体積を計量する場合,次のいずれかの方法で表示する。
1) 標準状態における通過体積値は,m3で表し,通常,m3 (Normal)と表記する。括弧内はSI単位と重
複しない範囲で短縮して表記してもよい。
2) 基準状態における通過体積値は,m3で表し,通常,m3 (Standard)と表記する。括弧内はSI単位と重
複しない範囲で短縮して表記してもよい。
注記 短縮した表記には,m3/h (Nor),m3/d (Nor),m3 (Nor),m3/h (Std),m3/d (Std),m3 (Std)などがあ
る。
7
計量に関する一般事項
7.1
流量計
流量計は,ガス,その他の代替流体において,十分な使用実績又は校正実績があるもの,又は性能が同
等ならばそれらと同型のものとする。オリフィス流量計以外の流量計では,使用する流量範囲において,
パルス出力の場合には7.13に従ってKファクタが定数として扱えるものとし,アナログ出力の場合には,
アナログ信号及び流量の比例係数が定数として扱えるものとする。オリフィス板の流出係数のレイノルズ
数依存性は,式(8)を満たさなければならない。ただし,箇条8に従うオリフィス流量計は式(8)を満たすた
め,確認の必要はない。
eD0
eD
d
0.02
eD0
R
R
C
R
<
∂
∂
········································································ (8)
11
M 8010:2020
ここに,
Cd: オリフィス流量計の流出係数
ReD: オリフィス配管径に基づくレイノルズ数
ReD0: 使用範囲におけるオリフィス配管径に基づくレイノルズ数
の最小値
7.2
ガスの性状
流量を計測する範囲では,ガスは物理的及び熱的に均質であり,単一の相(気相)で流れていなければ
ならない。
注記 流量計内部などに流路断面積が減少する箇所がある場合,断面積の減少に伴って流速が増加し
ガスの温度及び圧力が低下するため,これによって凝縮が起こらないように注意する。特に,
露点温度の高い成分が含まれている場合に注意する。
7.3
流量変動の排除
ガスの流れは,流量が一定か,又は時間的に僅かに,かつ,ゆっくり変化するものとし,脈動流であっ
てはならない[JIS Z 8762-1:2007の6.3(流れの状態)参照]。
7.4
漏れの排除
ガスの流量を計測する領域においては,漏れがあってはならない。ドレンホールがある場合には,計量
中にはこれを閉じる。
7.5
計量範囲
ガスの流量,温度,圧力,ガス種などの条件は,流量計の使用可能範囲内になければならない。
7.6
温度測定
温度測定は,ガスの温度が流量計を通過するときの温度と同じとなる位置で行う。流量計に温度センサ
挿入部が設けられていない場合には,この条件を満たす範囲内で,なるべく流量計から離して設置するこ
とが望ましい。
計量するガスの温度と環境温度とが大きく異なるときには,流量計と温度センサとを含む十分広い範囲
で配管を保温する。
流れの中に突出する温度センサ,これを取り付けるポケット,及びウェルは可能な限り小さくし,流量
計位置に発生する流速分布の乱れを最小とする。
温度センサ及び圧力取出口の双方を流量計の上流側又は下流側の一方に設置する場合,圧力取出軸の配
管軸から見た配管断面上での方向と,温度センサの配管軸から見た配管断面上の方向とを一致させず,か
つ,温度センサを,ガスの温度が流量計位置での温度と同じに保たれる範囲で可能な限り流量計から離し,
温度センサがもたらす乱れが圧力測定に与える影響を最小とする。
流速分布のひずみに対する特性変化の感度は流量計によって異なるため,温度センサなど配管内に突出
する要素の取付方法に関しては,製造業者に問い合わせる。
7.7
圧力取出口
圧力取出口は,圧力取出断面における流れの静圧を圧力センサに正しく伝える必要があり,その形状は
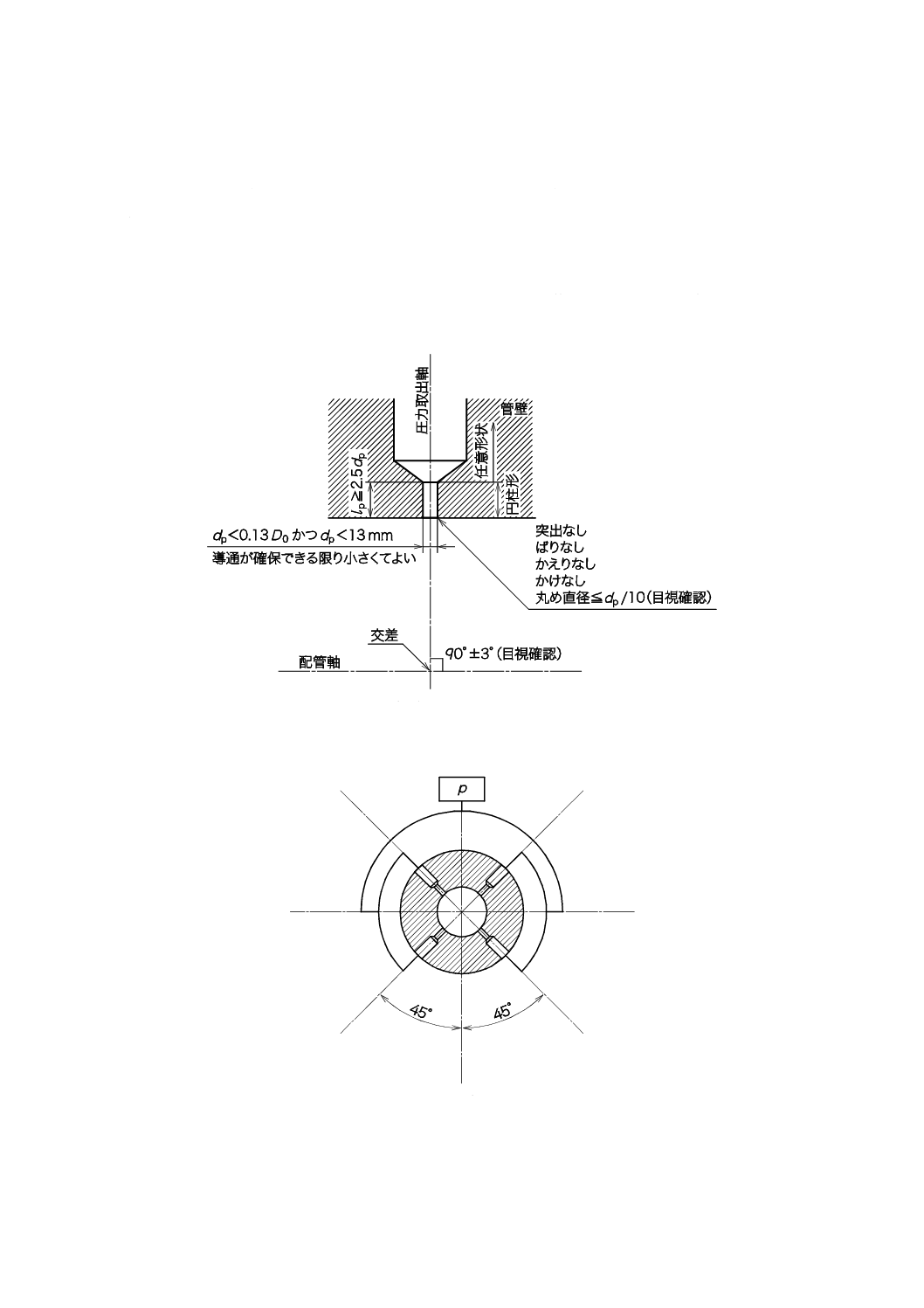
次による。推奨する圧力取出口の形状は図1を参照する。
a) 圧力取出口の流れに接する開口の縁は,配管の内壁面に一致させ,突出,ばり,かえり及びかけのな
いものとする。
b) 圧力取出口の流れに接する開口の縁を丸める場合には,丸め直径を圧力取出口直径dpの1/10以下とす
る。
c) 配管壁内における圧力取出口の導圧部分の形状は,ガスに接する側では円筒形とし,圧力取出口直径
12
M 8010:2020
dpを0.13D0未満,かつ,13 mm未満とし,円筒部分の長さlpを2.5dp以上とする。
d) 配管壁内における圧力取出口の形状は,配管内壁面から2.5dp以上離れた位置では任意でよい。
e) 圧力取出軸は,配管軸に対して90°±3°の範囲内の角度で配管軸と交差させる。その確認は目視でよ
い。
f)
圧力取出口の側壁,縁及び管壁には,圧力取出口を塞ぐ凸凹があってならない。その確認は目視でよ
い。
g) 圧力取出口直径dpは,不確かさに影響を与えない範囲で圧力導通が確保できる場合は,小さくしても
よい。このとき,堆積物,凝縮などによって詰まりが起こらないよう注意する。
図1−推奨する圧力取出口の形状
静圧測定断面に4か所の圧力取出口を設ける場合,図2に示すトリプルT接続とすることが望ましい。
図2−トリプルT接続
7.8
ガスの圧力による形状変化
過大なガスの圧力によって生じる,配管及び流量計の流路断面積の変化,流量計構造物の寸法変化,運
13
M 8010:2020
動子のしゅう(摺)動特性の変化などによって発生する計量誤差を避けるため,各要素の使用可能圧力範
囲内で使用する。
7.9
配管及び流量計の温度変化による形状変化
流量計が使用可能な温度範囲を守り,温度補正方法が確立されている場合にはそれを適用する。
7.10 レイノルズ数を求めるための準備
測定値の補正にレイノルズ数を用いる場合に必要となる,ガスの密度及び粘度の値は,箇条12に従って
求める。
7.11 流量計を取り付ける配管
流量計を取り付ける配管内は清潔に保つ。配管内に簡単に取り除くことのできる堆積物,付着物,金属
の剝がれなどがある場合にはこれらを取り除く。
7.12 外乱影響に対する配慮
流量計を設置するときの外乱影響に対する配慮は,次による。
a) 圧力検出,温度検出,渦検出,超音波検出,及び機械動作に影響を与える配管振動がある場所には,
流量計を設置しない。
b) 検出回路に支障をもたらす電気ノイズがある場所には,流量計を設置しない。
c) 超音波流量計では,超音波検出に影響をもたらす音響ノイズがある場所には設置しない。
d) 流量計の材質は,ガスに対してその長期安定性を損なう腐食・壊食がないものとする。硫化水素,メ
ルカプタン,硫黄などの濃度が320 μmol/mol以上の場合は,流量計に腐食しない材質が用いられてい
ることを確認する。
e) ガスへの固液混入,ガスからの塩類析出などを避け,長期暴露によっても流量計の特性が変化しない
ようにする。
f)
流速分布の乱れ,配管内ガス温度の偏り,脈動などによる特性変化が無視できない流量計は,十分な
上流直管長がない場所,十分に保温されていない場所,脈動がある場所などには設置しない。
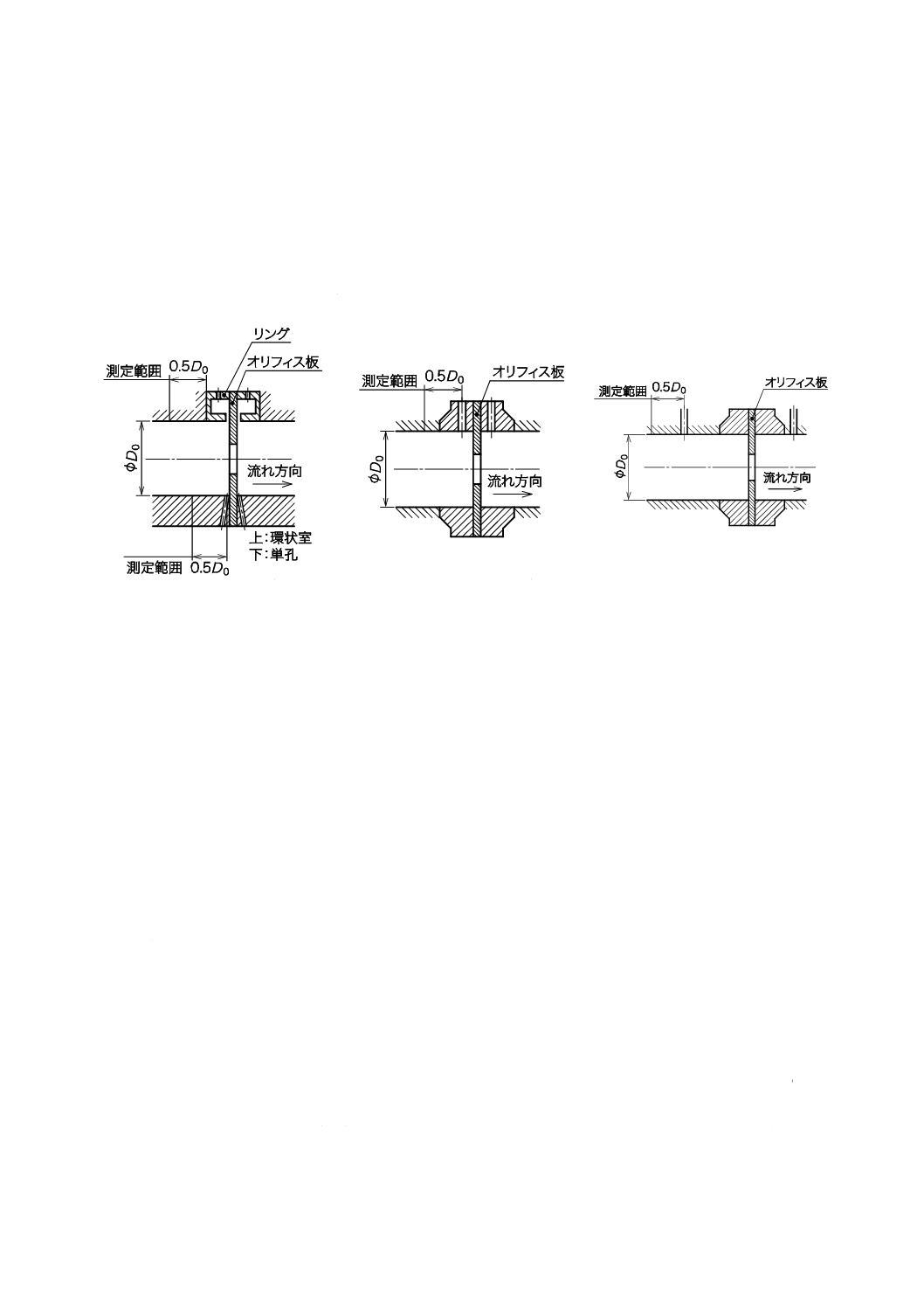
7.13 状態依存性をもつKファクタの代表値の決定
流量,圧力,レイノルズ数などのパラメータの大きさによってKファクタに変化が認められる流量計で
は,図3に示すとおりに求めた平均KファクタをKファクタの代表値KF0とする。
図3−状態依存性をもつKファクタの代表値KF0の決定
14
M 8010:2020
8
オリフィス流量計を用いる計量
8.1
概要
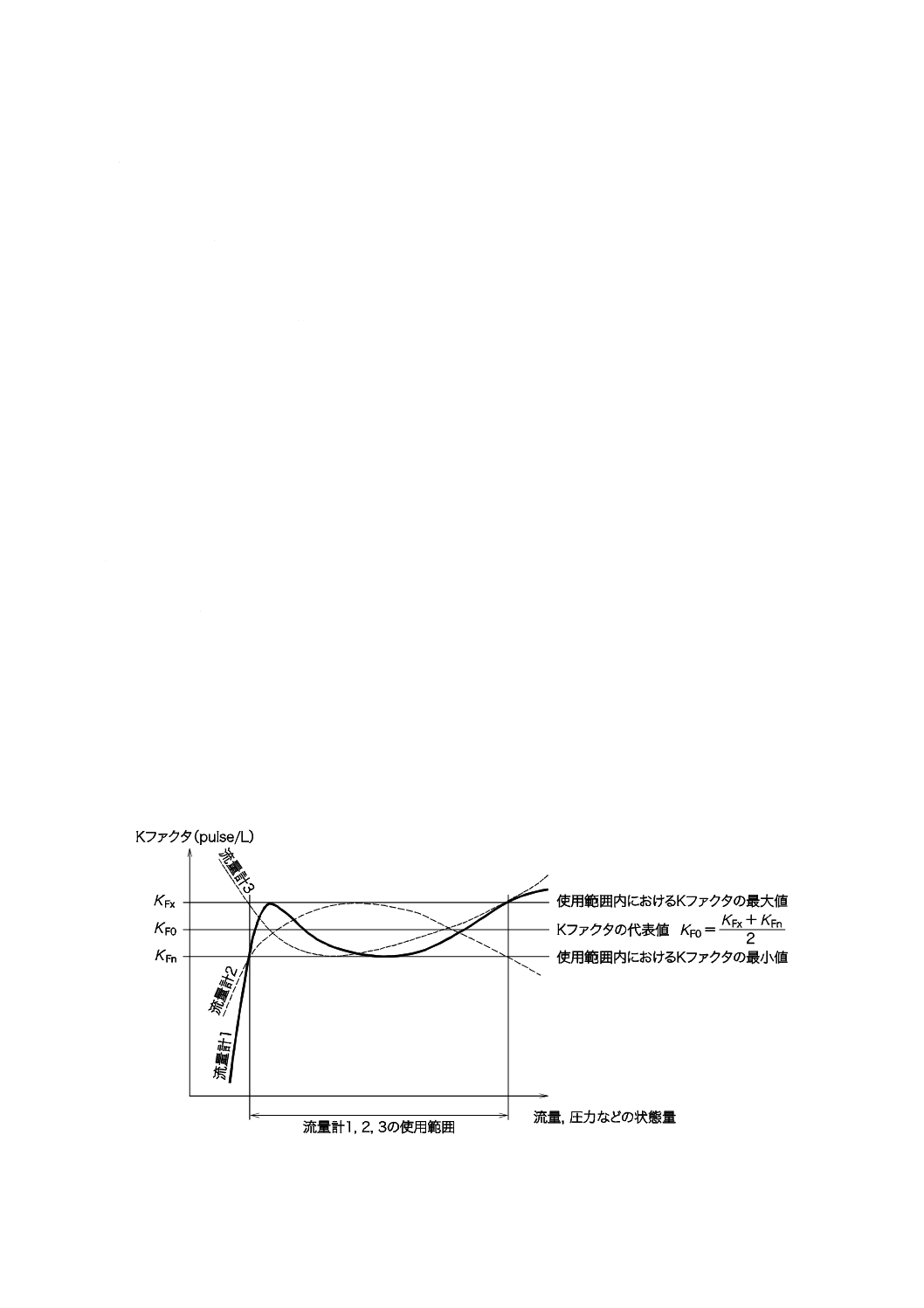
オリフィス流量計は,ガスが流れる管路にオリフィス板を取り付け(図4参照),このオリフィス板の前
後に発生する圧力差の測定値,オリフィス板の使用条件,及びガスの性質からこの管路を流れるガスの流
量を求める。オリフィス板は校正したものと相似形であり,その校正におけるレイノルズ数範囲内で用い
ることを前提とする。差圧の取出方法には様々なものがあるが,この規格では,コーナタップ,フランジ
タップ,又はD・D/2タップだけを扱う。
a) コーナタップ
b) フランジタップ
c) D・D/2タップ
図4−圧力取出方法及びオリフィス配管径D0の測定範囲
8.2
計量に必要な事項
8.2.1
使用する流出係数
オリフィス流量計の流出係数は,8.2.2以降に従う場合には8.3に従って求めるか,JIS Z 8762-1:2007及
びJIS Z 8762-2:2007に従って求めるか,又は実ガス若しくは代替流体を用いてレイノルズ数を一致させた
校正によって実測する。ただし,液体を用いた校正ではオリフィス板における圧力降下によってキャビテ
ーションが発生しない範囲,気体を用いた校正では膨張補正係数が有効な範囲にとどめる。
8.2.2
オリフィス板に流入する流れの条件
8.4.1に従って流出係数の不確かさを求める場合には,オリフィス板のすぐ上流側で,ガスの流れが次を
満たすことを確認しなければならない。ただし,8.2.4に従ってオリフィス板を取り付けた場合にはこれら
を実測して確認する必要はない。
a) 旋回がないとみなせる流れとなっている(3.35参照)。
b) 流速分布が完全に発達しているとみなせる流れとなっている(3.36参照)。
8.2.3
オリフィス板の使用条件及び寸法範囲
下流側圧力取出断面におけるガスの圧力p2は,上流側圧力取出断面におけるガスの圧力p1の0.75倍以
上とする。オリフィス板の寸法は,次のいずれかによる。
a) コーナタップ及びD・D/2タップの場合は,式(9)〜式(13)を満たすものとする。
d0≧12.5 mm·············································································· (9)
50 mm≦D0≦1 000 mm ······························································ (10)
0.10≦β≦0.75 ···········································································(11)
0.10≦β≦0.56のときReD≧5 000 ················································· (12)
15
M 8010:2020
0.56<β≦0.75のときReD≧16 000 β2かつReD≧170 β2 D0 ··················· (13)
ここに,
d0: オリフィス孔径の測定値(mm)
D0: オリフィス配管径の測定値(mm)
β: オリフィス直径比
ReD: オリフィス配管径に基づくレイノルズ数
b) フランジタップの場合は,式(14)〜式(17)を満たすものとする。
d0≧12.5 mm············································································ (14)
50 mm≦D0≦1 000 mm ······························································ (15)
0.10≦β≦0.75 ·········································································· (16)
ReD≧5 000,かつ,ReD≧170 β2 D0 ··············································· (17)
ここに,
d0: オリフィス孔径の測定値(mm)
D0: オリフィス配管径の測定値(mm)
β: オリフィス直径比
ReD: オリフィス配管径に基づくレイノルズ数
8.2.4
オリフィス板を取り付ける配管
8.2.4.1
形状
オリフィス板の上流側及び下流側配管は,直径が一定の円断面をもつ直管(3.19参照)とする。
8.2.4.2
オリフィス配管径の測定
オリフィス配管径の測定値D0は,次に従って決定する(図4参照)。
a) 上流側圧力取出断面からその上流側0.5Dnまでの範囲内で行った配管内径測定結果の算術平均値をオ
リフィス配管径の測定値D0とする。
b) 算術平均するための直径は,a)に指定する範囲内で配管軸方向に最低3か所の配管断面上で測定する。
c) 直径測定を行う配管断面の位置は,a)に指定する範囲内で等間隔に位置させ,その内の2断面は,上
流側圧力取出断面から0.0Dn及び0.5Dn上流側の位置とする。
d) 直径測定を行う各配管断面上では,一定の角度間隔で最低4方向の直径を測定する。
e) ウェルドネック構造の場合には,直径測定を行う1断面を溶接面と一致させる。
f)
コーナタップで環状室リングを用いる場合(図9参照)には,直径を測定する0.5Dnの範囲は,環状
室リングの上流端からはかる。
g) 以上の測定を行ったときの配管温度TD0を記録する。
8.2.4.3
オリフィス板を取り付ける直管(オリフィス配管)
オリフィス配管をフランジ接続によって組み立てる場合には,直線からの偏差が0.4 %を超えないよう
に接続する。偏差の大きさの検査は目視でよい。
オリフィス配管の配管断面が円形であることは,配管内壁又は外壁の目視検査で十分とする。ただし,
オリフィス板から上流側の2D0の範囲は,8.2.4.6に従う。
フルボアバルブを用いるとき,次の条件を満たせばこれを直管の一部として扱う。
a) フルボアバルブの呼び径が前後直管の呼び径と同じ。
b) 全開にしたときの段差が,8.2.4.7及び8.2.4.8に規定する直管の許容段差以下。
c) 全開状態にある。
オリフィス板前後で直管が必要となる範囲において,直管をフランジ接続によって組み立てる場合
(8.2.4.7及び8.2.4.8参照)には,配管の相対位置を固定するために,合いくぎ(シベル)又は芯合わせを
容易にするガスケット面座(溝形,はめ込み形など)を用いることが望ましい。
16
M 8010:2020
8.2.4.4
必要直管長
8.4.1によって流出係数の不確かさを求めるが,オリフィス板に流入する流れが8.2.2のa)及びb)を満た
すことを実測で確認しない場合には,次のいずれかによる。
a) 整流装置を用いない場合,附属書Aに従う。
b) 19管束管状式整流装置(1998)を用いる場合,附属書Bに従う。
c) ザンカ式整流板を用いる場合,附属書Cに従う。
d) b)及びc)以外のJIS Z 8762-1:2007の適合試験に合格した整流装置を用いる場合,JIS Z 8762-2:2007の
6.3.1に従う。
注記 JIS Z 8762-1:2007の適合試験に合格した整流装置に関しては,JIS Z 8762-1:2007の附属書C及
びJIS Z 8762-2:2007の附属書B参照。
ヘッダの下流には強い偏流,旋回流などが発生するため,配管断面積が例えば1.5倍以上となるヘッダ
などの下流側には整流装置を取り付けた後に,必要直管長を確保することが強く望まれる。流量制御を行
う場合には,制御バルブをオリフィス板の下流側に取り付けることが望ましい。
8.2.4.5
シーム管の使用
オリフィス板を取り付ける直管をシーム管とする場合,必要な直管長の全域にわたり,管内の溶接ビー
ドを管軸に平行とし,かつ,溶接ビードの高さがいかなる位置においても8.2.4.7及び8.2.4.8で規定する
段差を超えてはならない。
差圧測定に環状室を用いる場合,配管断面上で配管軸から見た溶接ビードの方向は任意でよい。環状室
以外を用いる場合,配管断面上で配管軸から見た溶接ビードの方向は,全ての圧力取出口に関し,配管断
面上で配管軸から見た圧力取出軸の方向の±30°にあってはならない。
スパイラル状の巻き管を用いる場合には,内面が円断面になるように切削する。
8.2.4.6
オリフィス板から2D0上流側までの直管の配管断面直径
オリフィス板の上流面又は環状室リング(図9参照)がある場合にはその上流面を起点として,上流側
に0D0から2D0までの範囲では,オリフィス配管の配管断面の直径は,全ての位置においてD0±0.3 %の
範囲内とする。
8.2.4.7
オリフィス板から2D0以上10D0以下の上流側における直管の接続
オリフィス板の上流面又はリングがある場合にはその上流面を起点とし,上流側に2D0以上で10D0以下
の範囲では,次を満たせば,複数の直管を接続したものであっても,それら全体を一つの直管とみなす。
この範囲にボールバルブを取り付ける場合は,ボールバルブは直管と同じ呼び径をもつフルボアとし,全
開位置でボールを止めるための回止めを備えていなければならない。この範囲でフランジ接続するときに
は,合いくぎ(シベル)又は芯合わせを容易にするガスケット面座(溝形,はめ込み形など)を用い,配
管の相対位置を固定することが望ましい。次を満たさない段差がある場合には,8.2.4.10に従う。
a) 配管(ボールバルブを含む。)の接続面における内径差が0.003D0以下。
b) 配管(ボールバルブを含む。)の接続面において配管軸のずれ及び内径差がもたらす段差が内周上のい
かなる位置においても0.003D0以下。
8.2.4.8
オリフィス板から10D0以上上流側における直管の接続
オリフィス板の上流面又はリングがある場合にはその上流面を起点とし,上流側に10D0以上離れた範囲
では,次を満たせば,複数の直管を接続したものであってもそれら全体を一つの直管とみなす。この範囲
にボールバルブを取り付ける場合,ボールバルブは直管と同じ呼び径をもつフルボアとし,全開位置でボ
ールを止めるための回止めを備えていなければならない。この範囲では,ガスケットの厚さは3.2 mm未
17
M 8010:2020
満とし,かつ,管路内にはみ出さないようにすることが望ましい。次を満たさない段差がある場合には,
8.2.4.10に従う。全開したボールバルブにこれらの条件を満たさない段差がある場合には,附属書A又は
附属書Bに従う。
a) 配管の接続面における内径差が0.02D0以下。
b) 配管の接続面において配管軸のずれ及び内径差がもたらす段差が内周上のいかなる位置においても
0.02D0以下。ただし,上流側の配管内径が下流側の配管内径より大きい場合には,0.06D0まで許され
る。段差の前後で,配管の内径は0.98D0以上かつ1.06D0以下でなければならない。
8.2.4.9
オリフィス板から10D0以上上流側で表A.1に従って設置した拡大管の上流条件
オリフィス板の上流面又はリングがある場合にはその上流面を起点とし,上流側に10D0を超える範囲に
表A.1の第10欄A列に従って取り付けた拡大管がある場合,オリフィス板から見て最初の拡大管の上流
側の全ての配管の接続面における段差の大きさが次の条件を満たせば,流出係数に付加不確かさは生じな
い。次を満たさない段差がある場合には,8.2.4.10に従う。
a) 配管の内径差が0.06D0未満。
b) 配管軸のずれ及び内径差がもたらす段差が,内周上のいかなる位置においても0.06D0以下。
c) 上流側及び下流側の配管の内径が,0.94D0以上でかつ1.06D0以下。
8.2.4.10 配管の接続面の段差によって付加される不確かさ
いずれか二つの配管の間に8.2.4.7〜8.2.4.9で許容される以上の段差∆Dが一つだけある場合で,式(18)
を満たす場合は,流出係数の不確かさは,8.4.1に従って求めた値に0.2 %を単純加算したものとする。
+
+
4
0
0
3.2
1.0
4.0
002
.0
Δ
β
D
s
D
D<
かつ
05
.0
Δ
0
<
D
D
·································· (18)
ここに, ΔD: 配管の接続面における段差の大きさ(mm)
D0: オリフィス配管径の測定値(mm)
s: 上流側の圧力取出断面から段差までの距離又はリングを使う
場合には,リングが形成するへこみの上流端から段差までの
距離(mm)
β: オリフィス直径比
式(18)を満足しない段差がある場合,及び8.2.4.7〜8.2.4.9を満足しない段差が二つ以上ある場合には,
付加不確かさを求めることはできない。
8.2.4.11 オリフィス板の下流側の直管
オリフィス板の上流面を起点として下流側へ2D0までの範囲における下流側の直管は,この範囲内で少
なくとも1断面上の1方向で内径を測定し,D0に対して0.03D0を超える差がないことを確認する。設置に
は,合いくぎ(シベル)又は芯合わせを容易にするガスケット面座(溝形,はめ込み形など)を用い,配
管の相対位置を固定することが望ましい。
8.2.4.12 オリフィス板の前後直管の粗さ
8.4.1に従って求めた不確かさを用いるためには,附属書Kに従い配管内面の粗さが許容範囲内である
ことを確認する。管内粗さは経年変化するため,必要に応じ,定期的に洗浄又は再評価する。
8.2.4.13 ドレンホール及びベントホール
配管には,固形物,混入粒子などを排出するために,ドレンホール又はベントホールを設けることがで
きるが,計量中にはこれらのホールを完全に閉じ,ガスが流出しないようにする。
18
M 8010:2020
これらのドレンホール又はベントホールは,オリフィス板から十分離れたところに設けることが望まし
いが,これができない場合には,次の全ての条件を満たすものとする。
a) ドレンホール又はベントホールの直径が0.08D0未満。
b) ドレンホール又はベントホールと同じ側にある圧力取出断面との距離が0.5D0以上。
c) 配管断面上で配管軸から見た圧力取出口及びドレンホール又はベントホールの方向が,互いに30°以
上離れている。
8.2.5
オリフィス板
オリフィス板は,計量を行うレイノルズ数範囲の全域において校正を行い流出係数の実測値が与えられ
ているものか,JIS Z 8762-1:2007及びJIS Z 8762-2:2007に従って製作されたものか,又は次による。
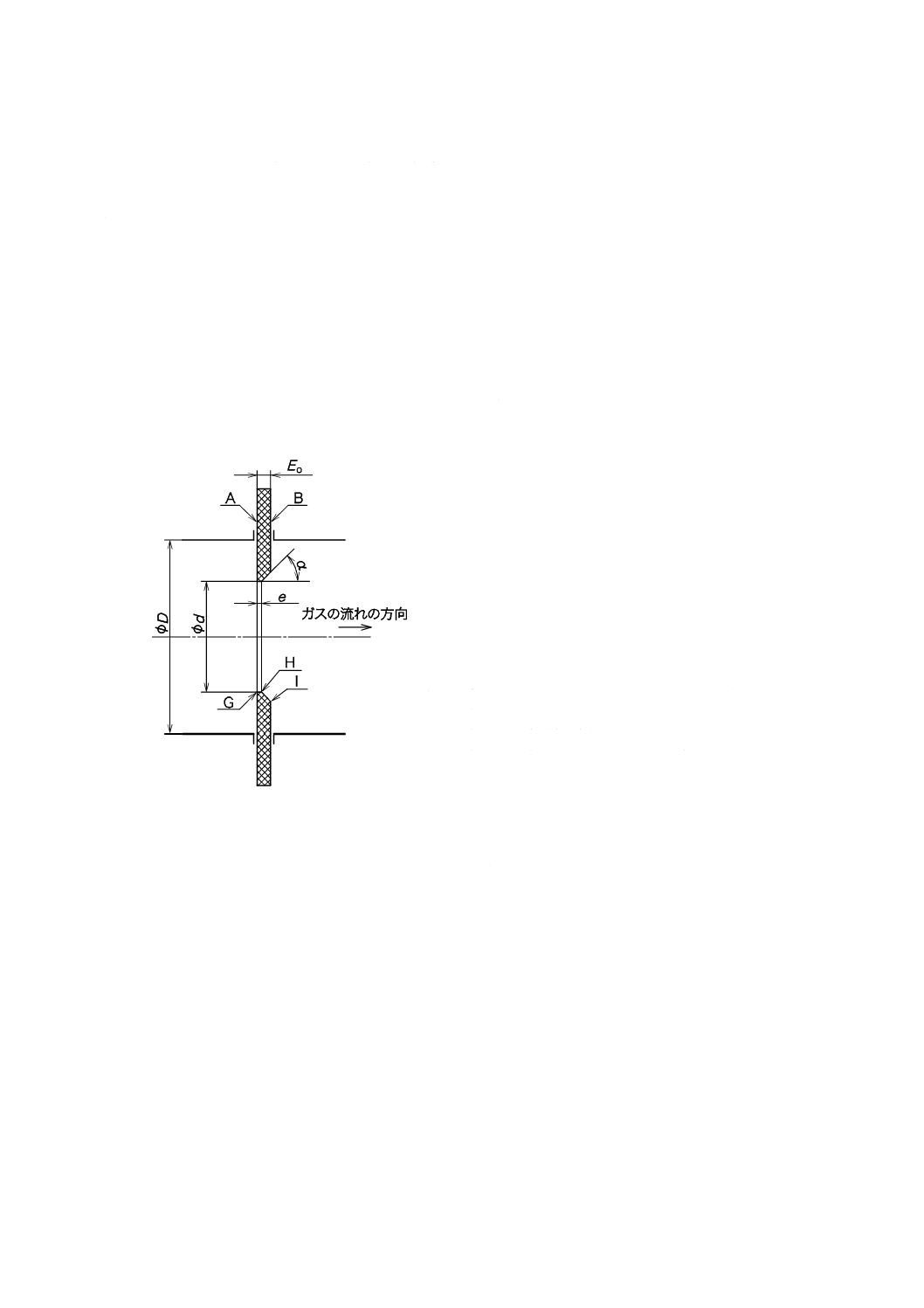
a) 形状 オリフィス板の表面は平面で厚さは一定とし,図5の形状に基づき各寸法を指定したものとす
る。オリフィス板は,エッジのある面を上流側,逃げ角をもって広がる方向を下流側として正しく取
り付ける。そのために,上流面と下流面とを区別する目印を付けておくことが望ましい。
記号
A 上流面
B 下流面
I
下流側エッジ(絞り部)
G 上流側エッジ
H 下流側エッジ(絞り部)
d
オリフィス孔径
D オリフィス配管径
EO オリフィス板の厚さ
e
エッジの厚さ
α
逃げ角
図5−オリフィス板の形状
b) オリフィス板の材質 オリフィス板の材質は,線形膨張係数が既知のものとする。
c) オリフィス板の平面度 オリフィス板の表面は,配管に取り付けた状態で,差圧がないときに平面と
する。ゆがみを発生させずに配管への取付けができる場合には,オリフィス板の平面度を配管から取
り外した状態で確認してもよい。オリフィス板の上流面の平面度は,オリフィス板の上流面において,
平面からの偏差(直線定規とオリフィスエッジとの間隔)を測定し(図6参照),この偏差がいかなる
方向においても0.05(D0−d0)/2未満のとき,そのオリフィス板の表面を平面とみなす。この間隔測定
は,隙間ゲージで測定する。
注記 この許される最大偏差は,表面の傾きが0.5 %未満であることに相当する。
オリフィス板の下流面は上流面と平行とし,下流面の平面度及び上流面との平行度は目視検査で十
分である。

19
M 8010:2020
図6−オリフィス板の平面度測定
d) 塑性座屈及び弾性変形 計量中におけるオリフィス板の平面からの偏差(図6参照)は,1 %以下と
する。
注記 ガスが流れることによってオリフィス板に力がかかり,オリフィス板が弾性変形又は塑性座
屈することがある。
e) オリフィス板の表面粗さ オリフィス板の上流面の表面粗さは,オリフィス孔のエッジ測定に支障を
来さない大きさとする。配管内に露出する部分の表面粗さの算術平均値Raは,表K.1を用いて評価す
るか又は実測によって0.000 1 d0未満であることを確認する。これが満たされない場合には,配管内に
露出する部分の表面を清掃するか,又は再度磨く。
下流面の表面粗さが十分に小さいことは,目視検査とする。
f)
厚さEO及びe エッジ厚さeは,0.005D0≦e≦0.02D0とする。eの値には,いかなる位置においても
0.001D0を超える差があってはならない。オリフィス板の厚さEOは,e≦EO≦0.05D0とする。ただし,
50 mm≦D0≦64 mmの配管では,EOは3.2 mmまで大きくしてもよい。また,c)の条件も満たさなけれ
ばならない。
オリフィス板の厚さEOは,いかなる位置においても,式(19)又は式(20)の値を超える差があっては
ならない。
D0≧200 mmのとき0.001D0 ······················································· (19)
D0<200 mmのとき0.2 mm ························································ (20)
ここに,
D0: オリフィス配管径の測定値(mm)
g) 逃げ角α オリフィス板の厚さEOがエッジ厚さeより厚い場合には,エッジの下流側に45°±15°の
逃げ角を付ける。
h) エッジG,H及びI(図5参照) 上流側エッジGの角度(上流側エッジGと下流側エッジHとを結
ぶ絞り部の面と上流面とがなす角度)は,90°±0.3°とする。エッジは,ばり,かえりなどの欠陥が
ないものとし,上流側エッジGは鋭いものとする。
エッジの丸め半径が0.000 4 d0未満のとき,エッジは鋭いとする。このことは,d0≧25 mmの場合に
は,エッジに光線を当てて裸眼で反射面が見つからないことで確認する。d0<25 mmの場合には,目
視検査では不十分なため,エッジの丸め半径を測定する。
注記 下流側エッジH及び下流側エッジIは,剝離領域のため,上流側エッジGのような厳しい制
限はない。
i)
オリフィス孔径 オリフィス孔径の測定値d0は,ほぼ等間隔で角度を変えた最低4方向の測定値の平
均値とする。これらの測定を行ったときのオリフィス板の温度Td0を測定しておく。どの方向に測定
20
M 8010:2020
した直径も,平均値から0.05 %以上の差があってはならない。使用可能なd0の範囲は8.2.3による。
j)
正逆両方向用オリフィス板 正逆両方向用オリフィス板は,逃げ角をもたずに上流側及び下流側の双
方に鋭いエッジをもつ。その仕様はJIS Z 8762-2:2007の5.1.9に従う。
8.2.6
オリフィス板の設置
8.2.6.1
オリフィス板の取付け
オリフィス板のオリフィス配管への取付けは,次による。
a) オリフィス孔の中心軸を配管軸に一致させる。
b) オリフィス板の方向を正しく取り付ける[8.2.5 a)参照]。
c) オリフィス板の表面の角度を,配管軸に対して90°±1°とする。
d) 一旦,オリフィス板を適切な位置に取り付けた後,オリフィス板の再固定,締付けなどを行う場合に
は,元の状態が再現されるようにする。
e) 二つのフランジ間にオリフィス板を保持する場合,オリフィス板が自由に熱膨張できるようにし,か
つ,座屈及びゆがみが生じないようにする。
f)
ガスケット又はシールリングを用いる場合,適切に製作したものを適切に取り付け,いずれの箇所に
おいても,ガスケット又はシールリングが配管内壁面から飛び出したり,圧力取出口を覆ったり,コ
ーナタップではスロットを覆ったりすることがないようにする。また,オリフィス板と配管との相対
位置が変わらないようにするために,ガスケット又はシールリングは可能な限り薄くする。ガスケッ
トをオリフィス板と環状室リングとの間に用いる場合,ガスケットは環状室に突き出てはならない。
8.2.6.2
オリフィス板及び配管の同心の確認
オリフィス板が正しく取り付けられていることは,次に従って判断する。これらの判断は,上流側及び
下流側の全ての圧力取出口について行う。
a) 図7を参照し,圧力取出断面とオリフィス孔との中心軸が交差する位置を,圧力取出軸に平行な成分
(ecl)及び垂直な成分(ecn)として測定する。
b) 上流側及び下流側において,
4
0
cl
3.2
1.0
5
002
.0
β
D
e
+
≦
及び
4
0
cn
3.2
1.0
005
.0
β
D
e
+
≦
の場合には,オリフィス板は正常
に取り付けられており,流出係数の不確かさは,8.4.1に従って求めた値とする。
c)
4
0
cl
4
0
3.2
1.0
005
.0
3.2
1.0
5
002
.0
β
D
e
β
D
+
+
≦
<
となる圧力取出口が一つでもあるときは,流出係数の不確かさは,8.4.1
に従って求めた値に0.3 %を加算(単純加算)する。
注記 複数の圧力取出口でこの式が成立しても,付加不確かさは0.3 %のままである。
d)
4
0
cl
3.2
1.0
005
.0
β
D
e
+
>
又は
4
0
cn
3.2
1.0
005
.0
β
D
e
+
>
となる圧力取出口がある場合,不確かさは評価できない。
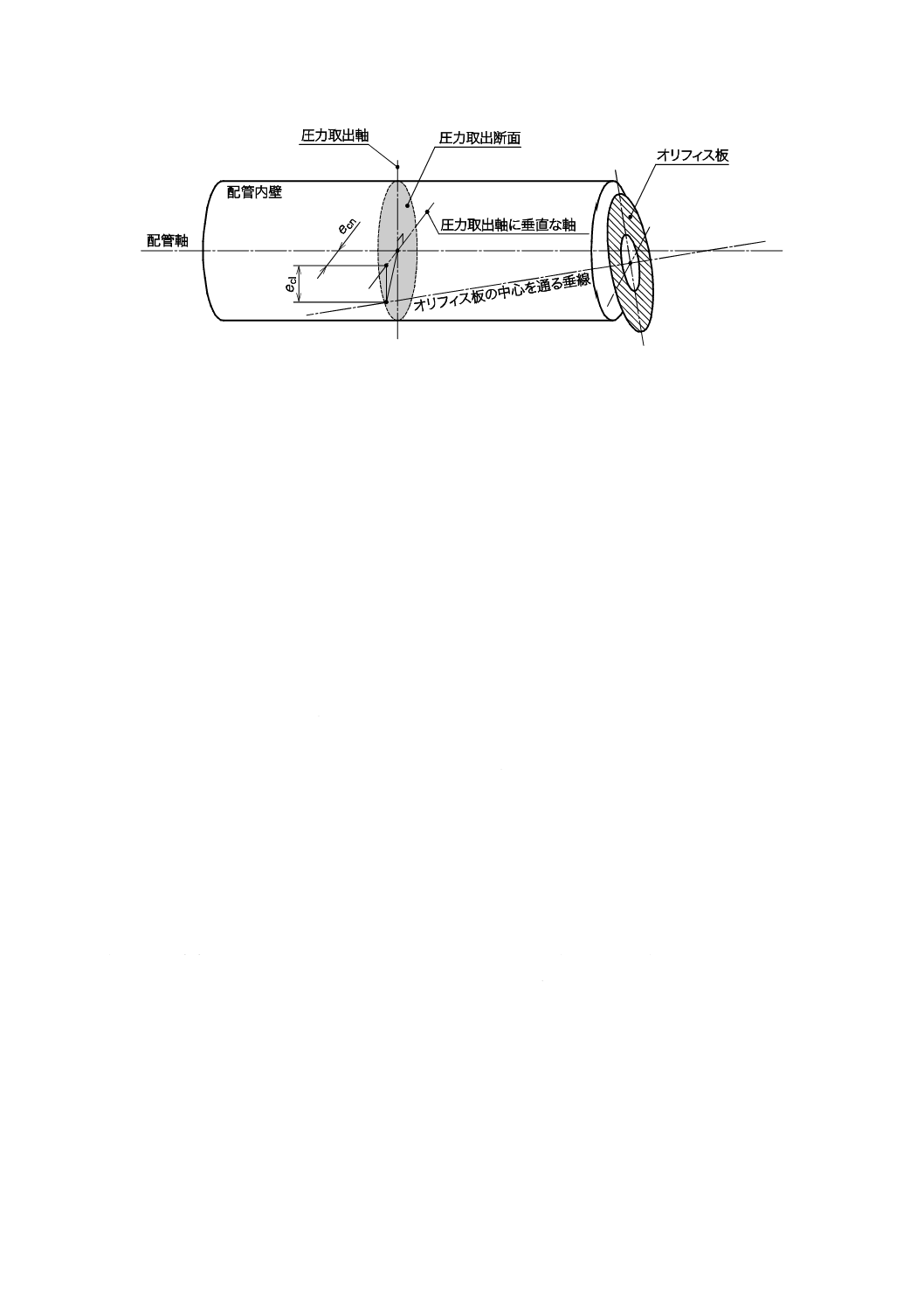
21
M 8010:2020
図7−オリフィス板の取付け
8.2.7
密度及び圧力測定
上流側又は下流側の圧力取出断面におけるガスの圧力又は密度の測定では,差圧測定に影響を与えない
ことが確認できた場合には,差圧測定用の上流側又は下流側圧力取出口(環状室を含む。)を併用するか,
又は同一断面上に設けた別の静圧孔を用いて測定する。このとき,8.2.9.2にも従う。
8.2.8
温度測定
温度の測定位置は,オリフィス板の位置から下流側に5D0以上で15D0以下とすることが望ましいが,温
度が同じであることが確認され,流量測定に支障を来す流速分布の乱れを与えない位置の場合は,その範
囲外にあってもよい。
8.2.9
圧力取出方法
8.2.9.1
差圧の取出方法
差圧の取出方法は,フランジタップ,コーナタップ,又はD・D/2タップとし(図4参照),上流側及び
下流側の圧力取出方法は同じにする。それぞれの圧力取出方法において,オリフィス板の上流側及び下流
側のそれぞれに,少なくとも1個の圧力取出口又はスリットを設ける。
8.2.9.2
同一断面上にある複数個の圧力取出口
上流側及び下流側のそれぞれの圧力取出断面において,複数個の圧力取出口を設けてもよい。その場合,
圧力取出断面上で配管軸から見た各取出口の方向を互いに30°以上離し,同一断面上の圧力取出口の間の
干渉を避ける。同一断面において4か所の圧力取出口を設ける場合,トリプルT接続(図2参照)とする
ことが望ましい。
8.2.9.3
D・D/2タップ及びフランジタップ
8.2.9.3.1
一般事項
D・D/2タップ又はフランジタップを用いる場合,上流側及び下流側のそれぞれの圧力取出断面に,同一
形状で同一寸法の圧力取出口を設ける。それぞれの圧力取出口の形状は7.7に従う。
圧力取出断面の位置は,図8に示す間隔l1及びl2又はl'2で指定する。これらの間隔は,オリフィス板の
上流面又は下流面(圧力取出方法によって変わる)から圧力取出断面までの距離であり,ガスケット,シ
ール材などの厚さも含める。
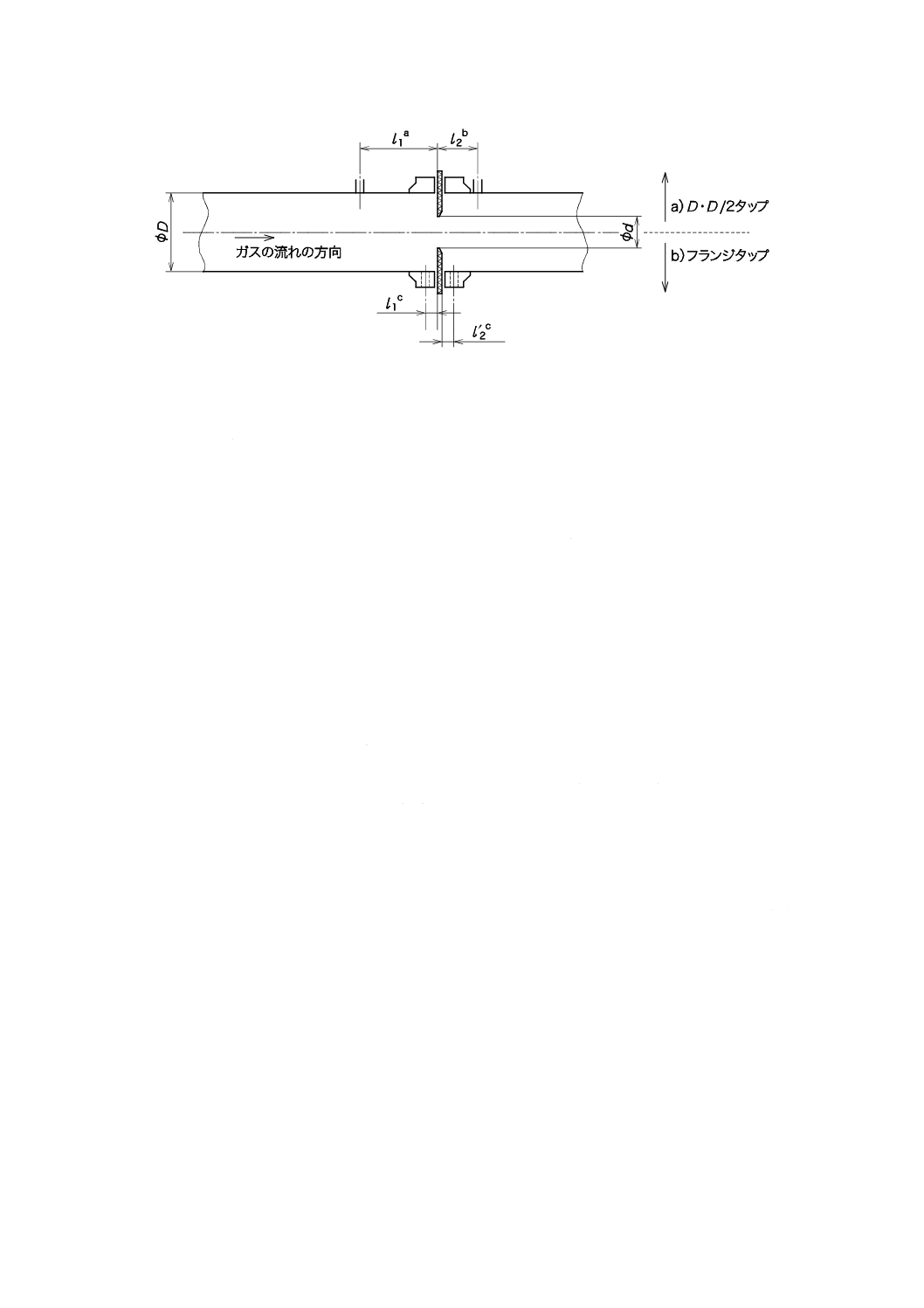
22
M 8010:2020
記号
d
オリフィス孔径
D オリフィス配管径
a
l1=(1±0.1)D0
b
l2=(0.5±0.02)D0 β≦0.6の場合
(0.5±0.01)D0 β>0.6の場合
c
l1=l'2=(25.4±1) mm
β≦0.6の場合
(25.4±1) mm
β>0.6で,かつ,150 mm≦D0≦1 000 mmの場合
(25.4±0.5) mm β>0.6で,かつ,D0<150 mmの場合
図8−D・D/2タップ及びフランジタップの圧力取出口
8.2.9.3.2 D・D/2タップの圧力取出断面の位置(l1及びl2)
D・D/2タップでは,l1及びl2は,共にオリフィス板の上流面を起点としてはかる。
0.9D0<l1<1.1D0とするが,l1=D0とすることが望ましい。l2は,式(21)又は式(22)の範囲とする。
β≦0.6のとき,(0.50±0.02)D0 ···················································· (21)
β>0.6のとき,(0.50±0.01)D0 ···················································· (22)
ここに,
β: オリフィス直径比
D0: オリフィス配管径の測定値(mm)
l2: D・D/2タップオリフィス流量計の下流側圧力取出口の位置を
指定する間隔(mm)
8.2.9.3.3
フランジタップの圧力取出断面の位置(l1及びl'2)
フランジタップでは,l1及びl'2は,それぞれオリフィス板の上流面及び下流面を起点としてはかる。
l1及びl'2は,式(23),式(24),又は式(25)の範囲内とする。
β≦0.6のとき,25.4 mm±1 mm ·················································· (23)
β>0.6かつD0<150 mmのとき,25.4 mm±0.5 mm ························· (24)
β>0.6かつ150 mm≦D0<1 000 mmのとき,25.4 mm±1 mm ············ (25)
ここに,
β: オリフィス直径比
D0: オリフィス配管径の測定値(mm)
8.2.9.3.4
圧力取出軸の方向
フランジタップでは,圧力取出軸は配管軸と交差し,かつ,それらの成す角度が90°±3°にあることを
確認する。その検査は目視検査とする。
配管断面上で配管軸から見た上流側及び下流側の圧力取出軸の方向は,上流側と下流側とで同じである
ことが望ましいが,異なっていてもよい。
23
M 8010:2020
8.2.9.4
コーナタップ
8.2.9.4.1
一般事項
コーナタップは次のa)又はb)による。
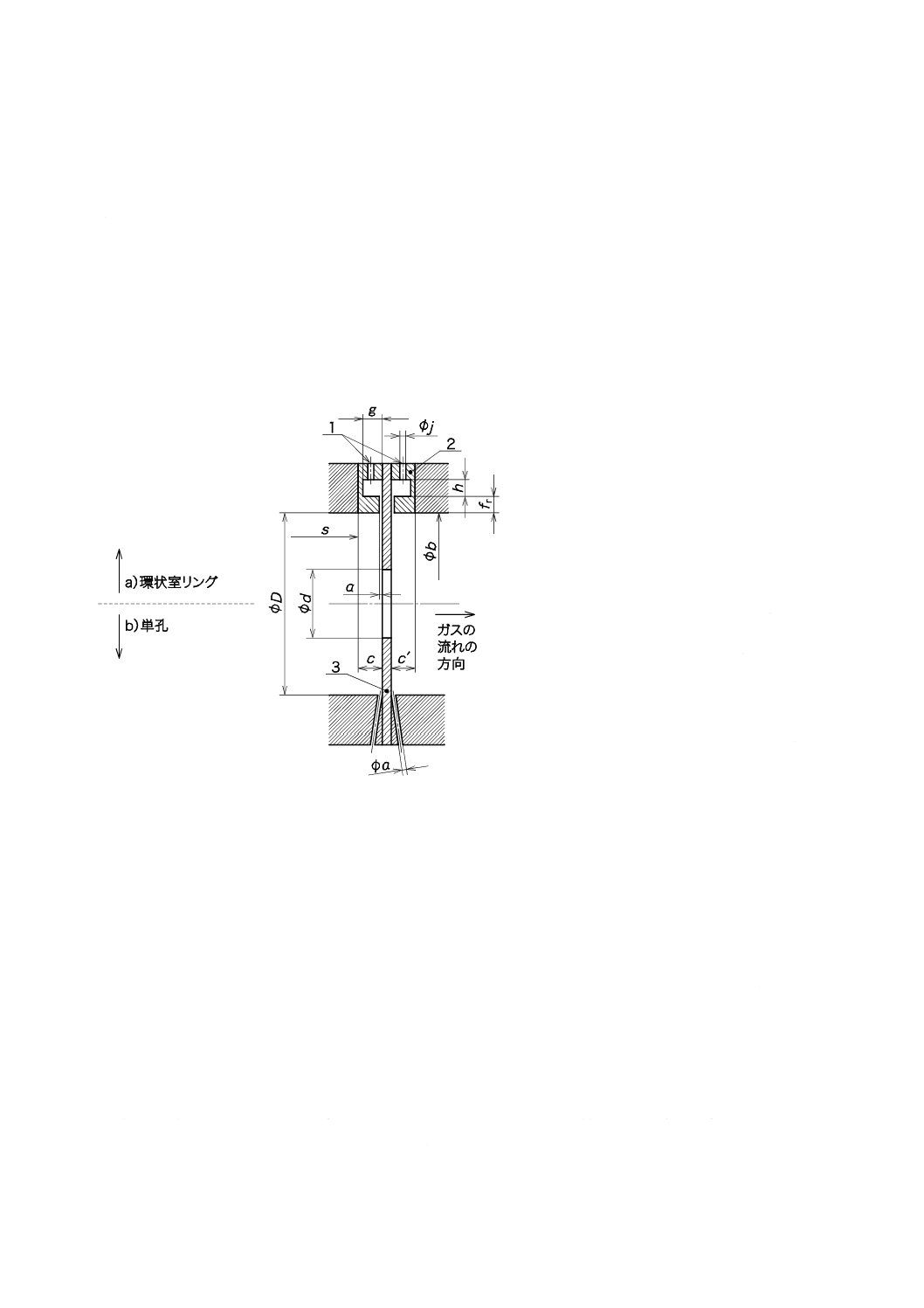
a) 環状室を用いる方法 上流側と下流側とに環状室をもつリングを配管に挿入して[図9 a)参照]差圧
を測定する。環状室は,環状室内と配管内とを導通させるために,配管内壁を貫通する環状のスリッ
トをもつ。
b) 単孔を用いる方法 上流側及び下流側のそれぞれの配管又はフランジに圧力取出口を設けて[図9 b)
参照]差圧を測定する。上流側及び下流側の単孔は,同一形状で同一寸法とする。一つの断面で複数
個の単孔を設ける場合には,8.2.9.2に従い,かつ,配管軸から見た各単孔の方向を等間隔とし,さら
に,それぞれの圧力取出軸の角度を同一断面上で同一とする。
記号
1
圧力取出口
2
リング
3
オリフィス板
fr
スリットの厚さ
c
上流側リングの厚さ
c' 下流側リングの厚さ
b
リング内径
a
単孔の孔径又は環状室
用スリットの幅
s
環状室から上流側段差
までの距離
g, h 環状室の寸法
j
導圧管接続孔径(環状
室の場合)
D オリフィス配管径
d
オリフィス孔径
図9−コーナタップの圧力取出口
8.2.9.4.2
単孔の位置
配管の内壁面上にある単孔の開口の中心は,オリフィス板の上流面及び下流面からa/2(aは単孔の直径)
だけ離れた位置とする[図9 b)参照]。
8.2.9.4.3
単孔の形状
7.7に従う。
8.2.9.4.4
単孔の中心軸の方向
単孔の中心軸は配管軸と交差させ,それらが成す角度を可能な限り90°に近づける[図9 b)参照]。
8.2.9.4.5
環状室のスリットの位置
環状室のスリットの一方の内面は,オリフィス板の表面に一致させ,他方の内面は,オリフィス板の表
面からa(スリット幅)だけ離れた位置とする[図9 a)参照]。
8.2.9.4.6
単孔の孔径a及び環状室リングのスリット幅a
単孔の孔径a及び環状室リングのスリット幅aは,次による。aの最小値は,静圧が変動したときにそ
の値を正しく伝えることができること及び導圧管の詰まりによる測定誤差が発生しないようにすることを
24
M 8010:2020
考慮し,使用現場に即した値とする。
a) LNG気化ガスで単孔を用いる場合 aは,D0及びβの大きさに依存して式(26)又は式(27)の範囲内と
するが,βの大きさにかかわらず式(28)の範囲に制限する。
1) β≦0.65のとき,
0.005D0≦a≦0.03D0 ·································································· (26)
2) β>0.65のとき,
0.01D0≦a≦0.02D0 ··································································· (27)
4 mm≦a≦10 mm ····································································· (28)
ここに,
β: オリフィス直径比
D0: オリフィス配管径の測定値(mm)
a: オリフィス流量計の単孔の孔径又は環状室リングのスリット
幅(mm)
b) a)以外の場合 aは,D0及びβの大きさに依存して式(29)又は式(30)の範囲内とするが,βの大きさに
かかわらず式(31)の範囲に制限する。ただし,D0<100 mmの場合には,βの大きさにかかわらずaの
最小値を2 mmとしてもよい。
1) β≦0.65のとき,
0.005D0≦a≦0.03D0 ·································································· (29)
2) β>0.65のとき,
0.01D0≦a≦0.02D0 ··································································· (30)
1 mm≦a≦10 mm ····································································· (31)
ここに,
β: オリフィス直径比
D0: オリフィス配管径の測定値(mm)
a: オリフィス流量計の単孔の孔径又は環状室リングのスリット
幅(mm)
8.2.9.4.7
環状室のスリットの形状
環状室のスリットは,単一スリットとして配管内壁全周にわたるリング状の開口とするか,又は等間隔
に配置させた4個以上のスリットの集合体とする。スリットを分割する場合には,それぞれのスリットの
開口面積は12 mm2以上とする。
スリット厚さfr[図9 a)参照]は,fr≧2aとする。
8.2.9.4.8
環状室の断面積
環状室の断面積g×h[図9 a)参照]は,流れに接するスリットの開口面積(複数のスリットを用いる場
合には開口面積の総和)の1/2以上とする。
8.2.9.4.9
環状室のリングの形状
リング内径b[図9 a)参照]は,D0≦b≦1.04D0とし,式(32)を満たすものとする。
4
0
0
0
3.2
1.0
1.0
100
β
D
c
D
D
b
+
×
×
−
<
···················································· (32)
ここに,
β: オリフィス直径比
D0: オリフィス配管径の測定値(mm)
b: オリフィス流量計の環状室リングの内径(mm)
c: オリフィス流量計の上流側の環状室リングの厚さ(mm)
リング厚さc及びc'[図9 a)参照]は,c<0.5D0,c'<0.5D0とする。
流体と接触するリングの面は清浄で滑らかなものとし,8.4.1に従って流出係数の不確かさを求めるため
25
M 8010:2020
には,その表面の仕上げを,附属書Kの管内内壁面の条件を満たすものとする。
上流側及び下流側のリングは,必ずしも互いに対称な形状でなくてもよい。
環状室のリングはオリフィス板の一部とみなし,オリフィス配管径D0の測定範囲,及び,オリフィス板
の上流にある段差の位置は,リングの上流側端面を起点としてはかる[図9 a)のs参照]。
8.2.9.4.10 環状室と導圧管との接続口
環状室を導圧管に接続するための接続口は,リング内への出口面の断面[図9 a)参照]を直径jの円形
として4 mm≦j≦10 mmとし,その縁をリングの内壁面に一致させてばり及びかえりをなくし,丸みはj/10
以内とする。
8.3
流量及び流出係数
8.3.1
標準状態における体積流量
測定状態における質量流量は式(33),及び標準状態における体積流量は式(34)で求める。密度,湿度補正
係数,圧縮係数及びモル質量は,箇条12に従って求める。
1
2
4
d
m
Δ
2
4
π
1
pρ
d
ε
β
C
q
−
=
························································ (33)
1
1
N
1
wv
N
4
d
2
vN
Δ
1
082
.
31
T
Z
N
p
p
F
Z
ε
β
C
d
q
−
=
············································ (34)
ここに,
qm: オリフィス流量計を流れる質量流量(kg/s)
qvN: 標準状態における体積流量[m3/h (Normal)]
Cd: オリフィス流量計の流出係数
β: オリフィス直径比
ε: オリフィス流量計の膨張補正係数
d: 計量中におけるオリフィス孔径(m)
Δp: 差圧(Pa)
Fwv: 湿度補正係数
ZN: 標準状態におけるガスの圧縮係数
T1: オリフィス流量計を流れるガスの温度(K)
p1: オリフィス流量計の上流側圧力取出断面におけるガスの圧力
(Pa)
Z1: オリフィス流量計の上流側圧力取出断面におけるガスの圧縮
係数
ρ1: オリフィス流量計の上流側圧力取出断面におけるガスの密度
(kg/m3)
NN: 標準状態におけるガスのモル質量(kg/mol)
注記 質量流量qmは,流出係数の再帰計算を行うときに用いる(8.3.4参照)。
8.3.2
流出係数Cd
8.2に従うオリフィス流量計の流出係数Cdは,D0≧71.12 mmの場合には式(35),D0<71.12 mmの場合に
は式(36)で求める。
a) D0≧71.12 mmの場合
26
M 8010:2020
3.1
1.12
2
4
4
7
10
3.0
eD
6
5.3
7.0
eD
6
8
2
d
)
8.0
(
031
.0
1)
11
.0
1
)(
e
123
.0
e
080
.0
043
.0(
10
)
3
006
.0
8
018
.0(
10
521
000
.0
216
.0
1
026
.0
1
596
.0
1
1
β
M'
M'
β
β
A
R
β
A
R
β
β
β
C
L
L
−
−
−
−
−
+
+
+
+
+
−
+
=
−
−
······················ (35)
ここに,
Cd: オリフィス流量計の流出係数
β: オリフィス直径比
ReD: オリフィス配管径に基づくレイノルズ数
L1: 式(39)〜式(41)で定義するパラメータ
A: 式(37)で定義するオリフィス流量計の流出係数に用いるパラ
メータ
M'2: 式(38)で定義するパラメータ
b) D0<71.12 mmの場合
−
−
+
−
−
−
−
−
+
+
+
+
+
−
+
=
−
−
4.
25
8.2
)
75
.0(
011
.0
)
8.0
(
031
.0
1)
11
.0
1
)(
e
123
.0
e
080
.0
043
.0(
10
)
3
006
.0
8
018
.0(
10
521
000
.0
216
.0
1
026
.0
1
596
.0
0
3.1
1.12
2
4
4
7
10
3.0
eD
6
5.3
7.0
eD
6
8
2
d
1
1
D
β
β
M'
M'
β
β
A
R
β
A
R
β
β
β
C
L
L
······················ (36)
ここに,
Cd: オリフィス流量計の流出係数
β: オリフィス直径比
ReD: オリフィス配管径に基づくレイノルズ数
L1: 式(39)〜式(41)で定義するパラメータ
A: 式(37)で定義するオリフィス流量計の流出係数に用いるパラ
メータ
M'2: 式(38)で定義するパラメータ
D0: オリフィス配管径の測定値(mm)
式(35)及び式(36)で使用するパラメータA及びパラメータM'2の値は,それぞれ式(37)及び式(38)で求め
る。
8.0
eD
000
19
=
R
β
A
····································································· (37)
ここに,
A: 式(35)及び式(36)で使用するオリフィス流量計の流出係数に用
いるパラメータ
β: オリフィス直径比
ReD: オリフィス配管径に基づくレイノルズ数
β
L'
M'
−
=12
2
2
············································································ (38)
27
M 8010:2020
ここに, M'2: 式(35)及び式(36)で使用するパラメータ
β: オリフィス直径比
L'2: 式(39)〜式(41)で定義するパラメータ
式(35)及び式(36)で使用するパラメータL1並びに式(38)で使用するパラメータL'2は,圧力取出方式で場
合分けをし,式(39),式(40)又は式(41)で求める。
L1=L'2=0(コーナタップ) ······················································ (39)
L1=1,L'2=0.47(D・D/2タップ) ·············································· (40)
0
2
1
4.
25
D
L'
L
=
=
(フランジタップ) ············································· (41)
ここに,
L1: 式(35)及び式(36)で使用するパラメータ
L'2: 式(38)で使用するパラメータ
D0: オリフィス配管径の測定値(mm)
注記 Cdの参考値を,附属書Dに示す。
8.3.3
膨張補正係数ε
膨張補正係数εは,測定状態における上流側圧力取出断面でのガスのアイゼントロピック指数κ1を用い,
式(42)で求める。アイゼントロピック指数は,箇条12に従って求める。
−
+
+
−
=
1
1
1
2
8
4
1
)
93
.0
256
.0
351
.0(
1
κ
p
p
β
β
ε
·································· (42)
ここに,
ε: オリフィス流量計の膨張補正係数
β: オリフィス直径比
p2: オリフィス流量計の下流側圧力取出断面におけるガスの圧力
(Pa)
p1: オリフィス流量計の上流側圧力取出断面におけるガスの圧力
(Pa)
κ1: オリフィス流量計の上流側圧力取出断面におけるアイゼント
ロピック指数
注記 εの参考値を,附属書Eに示す。
8.3.4
流出係数の再帰計算
オリフィス流量計の流量と流出係数とは相互に依存するため,必要とする不確かさの大きさによっては,
再帰計算が必要となる場合がある。再帰計算は,次による。
a) 流出係数Cdの値として代表的な値(例えば,0.6)を設定する。
b) 設定したCdの値を用いて質量流量qmを計算する。
c) b)で得られたqmの値を用いてオリフィス配管径に基づくレイノルズ数ReDを計算する。
d) c)で得られたReDの値を用いてCdを計算する。
e) d)で得られたCdの値を用いて質量流量qmを計算する。
f)
e)で得られたqmの値を用いてReDを計算する。
g) f)で得られたReDの値を用いてCdを計算する。
h) g)で得られたCdの値とb)で設定したCdの値との差が,必要不確かさより大きければ,g)で得られた
Cdの値を設定値としてb)から計算を繰り返す。差が十分に小さければ,g)で得られたCdを式(33)及び
式(34)で用いる流出係数の値とする。
注記 一般的な条件では,初期値を適切に選ぶことによって,2回目に得られたCdで十分に収束した
値が得られる場合が多い。
28
M 8010:2020
8.3.5
形状寸法の補正
配管形状が圧力に依存して変形するとd及びDが変化して誤差が発生する場合があるため,十分に強度
のある配管を用いるか,又は管壁の変形による内径偏差を実測若しくは推定する。
測定状態におけるオリフィス板及びオリフィス配管の温度が,オリフィス板及びオリフィス配管の形状
測定時又は校正時における温度と異なる場合には,流量の計算に用いるオリフィス孔径及びオリフィス配
管径の値には,式(43)及び式(44)で求めたd及びDの値を用いる。ただし,計量において予想される最大
及び最小温度を用いて求めたd及びDの値と,d0及びD0の値との差が十分に小さければ,d及びDの代
わりにそれぞれd0及びD0を用いてもよい。
d=d0[1+αd(Td−Td0)] ································································ (43)
D=D0[1+αD(TD−TD0)] ······························································ (44)
ここに,
d: 計量中におけるオリフィス孔径(m)
D: 計量中におけるオリフィス配管の直径(m)
Td: 計量中におけるオリフィス板の温度(℃)
TD: 計量中におけるオリフィス配管の温度(℃)
d0: オリフィス孔径の測定値(m)
D0: オリフィス配管径の測定値(m)
αd: オリフィス板の線膨張率(1/℃)
αD: オリフィス配管の線膨張率(1/℃)
Td0: オリフィス孔径を測定したときのオリフィス板の温度(℃)
TD0: オリフィス配管径を測定したときのオリフィス配管の温度
(℃)
8.4
不確かさ及び圧力損失
8.4.1
流出係数の不確かさ
流出係数の不確かさの求め方は,次による。
a) 8.2及び8.3に従うオリフィス板の流出係数の相対不確かさは,β,D0,ReD及びRa/D0の不確かさを除
き,式(45),式(46)又は式(47)で求める。
1) 0.1≦β<0.2のとき
UCd=0.7−β+ΔUCd1+ΔUCd2 ······················································· (45)
2) 0.2≦β≦0.6のとき
UCd=0.5 ················································································ (46)
3) 0.6<β≦0.75のとき
UCd=1.667β−0.5 ····································································· (47)
ここに,
UCd: オリフィス流量計の流出係数の相対不確かさ(%)
β: オリフィス直径比
ΔUCd1: D0に依存するオリフィス流量計の流出係数の不確かさの追
加項(%)
ΔUCd2: β及びReDに依存するオリフィス流量計の流出係数の相対不
確かさの追加項(%)
b) 追加項ΔUCd1は,式(48)又は式(49)で求める。
1) D0<71.12 mmのとき
(
)
−
−
=
4.
25
8.2
75
.0
9.0
Δ
0
Cd1
D
β
U
················································ (48)
2) D0≧71.12 mmのとき
ΔUCd1=0 ················································································ (49)
29
M 8010:2020
ここに, ΔUCd1: D0に依存するオリフィス流量計の流出係数の不確かさの追
加項(%)
β: オリフィス直径比
D0: オリフィス配管径の測定値(mm)
c) 追加項ΔUCd2は,式(50)又は式(51)で求める。
1) β>0.5かつReD<10 000のとき
ΔUCd2=0.5·············································································· (50)
2) 1) 以外のとき
ΔUCd2=0 ················································································ (51)
ここに, ΔUCd2: β及びReDに依存するオリフィス流量計の流出係数の相対不
確かさの追加項(%)
β: オリフィス直径比
ReD: オリフィス配管径に基づくレイノルズ数
8.4.2
膨張補正係数の不確かさ
膨張補正係数の不確かさは,β,Δp/p1及びκ1の不確かさを除き,式(52)で求める。
1
1
Δ
5.3
p
κ
p
Uε=
·········································································· (52)
ここに,
Uε: オリフィス流量計の膨張補正係数の相対不確かさ(%)
Δp: 上流側及び下流側圧力取出断面の間の差圧(Pa)
p1: オリフィス流量計の上流側圧力取出断面におけるガスの圧
力(Pa)
κ1: オリフィス流量計の上流側圧力取出断面におけるアイゼン
トロピック指数
8.4.3
圧力損失
8.2及び8.3に従うオリフィス板の圧力損失Δ は,式(53)で求める。
(
)
(
)
p
β
C
β
C
C
β
C
β
Δ
1
1
1
1
Δ
2
d
2
d
2d
4
2d
4
+
−
−
−
−
−
=
·················································· (53)
ここに,
Δ: 圧力損失(Pa)
Δp: 上流側及び下流側圧力取出断面の間の差圧(Pa)
β: オリフィス直径比
Cd: オリフィス流量計の流出係数
注記 式(53)は,オリフィス板付近の近寄衝撃圧力が無視できる上流側位置(オリフィス板からおよ
そ1D0上流)における静圧と,噴流が拡大して静圧が完全に回復したとみなされる下流側位置
(オリフィス板からおよそ6D0下流)における静圧との差である。
式(53)の代わりに式(54)で近似してもよい。
p
β
Δ
)
1(
Δ
9.1
−
=
····································································· (54)
ここに, Δ: 圧力損失(Pa)
Δp: 上流側及び下流側圧力取出断面の間の差圧(Pa)
β: オリフィス直径比
オリフィス板の圧力損失係数Kは,式(55)で求める。
(
)
2
2
d
2d
4
1
1
1
−
−
−
=
β
C
C
β
K
·························································· (55)
30
M 8010:2020
ここに,
K: 圧力損失係数
β: オリフィス直径比
Cd: オリフィス流量計の流出係数
8.5
性能の維持
オリフィス流量計の特性は,オリフィス孔のエッジ形状に敏感であり,使用状況に応じて目視検査を行
い,堆積物,付着物,だれ,変形,破損などの形状変化がないことを確認する。差圧,異物の衝突などに
よってオリフィス板が曲がることがあるため注意する。異常があった場合には,新しいオリフィス板に交
換するか,又は流量校正設備を用いて再校正を行う。
9
容積流量計を用いる計量
9.1
概要
容積流量計は,計量室内の運動子がガスの流れによる力で運動するときの運動周期に基づいて流量を求
める。運動子のしゅう(摺)動部分の特性を維持するために,容積流量計を指定の姿勢で設置し,計量室
が変形するストレスを与えないように接続する必要がある。また,運動機構が損傷を受けるような大きな
衝撃,振動,急激な流量変動などは与えてはならない。
容積流量計は,これに流入する流れの分布の影響を受けにくいとされ,必要直管長に関する一般的な規
定はないが,極端な偏流などによって運動子に偏った力がかからないよう注意する。
容積流量計の出力はガスの体積によって直接決まるため,ガス種に対する依存性は低いとされ,空気な
どの一般的な気体を用いて校正した結果をその他のガスで用いてもよい。
周期運動をする運動子には機械的な共振周波数があり,さらに,これに付随するギヤの歯数などによっ
て高い周波数での共振もあり得る。流入する流れに周期的な変動がある場合には,その周波数が容積流量
計の共振周波数から十分に離れている必要がある。
容積流量計では,運動子の運動によって下流側の流れが乱されるため,通常,圧力の測定は容積流量計
の上流側で行う。
容積流量計の特性は,しゅう(摺)動部分の特性に大きく支配され,これに異常があると圧力損失が明
確に変化するため,容積流量計の圧力損失を監視することによって容積流量計の状態が把握できる。
代表的な容積流量計として,ルーツ式,オーバルギヤ式,膜式などがある。使用する容積流量計は,ガ
ス又はその代替流体を用いた使用実績又は校正実績があるものとする。
9.2
計量に必要な事項
9.2.1
容積流量計の設置
設置することのできる配管構造,位置,前後配管の接続面に許される段差の大きさ,パッキンの取付位
置などについては,容積流量計の製造業者に確認する。
9.2.2
異物の除去
異物の流入を避けるため,容積流量計の上流側にストレーナを設置する。ストレーナと容積流量計との
間の配管は,腐食などが発生しないものとし,内部を十分に清掃する。
9.2.3
姿勢の管理
容積流量計は,運動子の特性を維持するために,製造業者が指定するとおりの姿勢で設置する。
9.2.4
配管ストレスの回避
容積流量計の測定室のケースをひずませる配管ストレスを与えない。
31
M 8010:2020
9.2.5
脈動の排除
コンプレッサ,調圧弁,ヘッダなどによって大きな脈動が発生する可能性のある位置では,運動子の運
動がその影響を受けないように十分に注意する。
9.2.6
温度測定
容積流量計に温度センサの取付口が用意されている場合には,その取付口を用いて温度センサを取り付
けることが望ましい。温度センサ取付口を配管に設ける場合には,製造業者による特別な指定がない限り,
7.6に従う。
9.2.7
圧力取出口
容積流量計に圧力取出口が用意されている場合には,その取出口を用いて圧力を測定することが望まし
い。圧力取出口を配管に取り付ける場合には,製造業者による特別な指定がない限り,7.7に従い,容積流
量計の上流側に取り付ける。
9.2.8
慣らし運転
急激にガスの温度が変化するとき,冷間からの起動直後などでは,運動子が規定の特性で運動するまで
に慣らし運転が必要な場合がある。慣らし運転に必要な条件及び時間は,容積流量計の製造業者に確認す
る。
9.2.9
使用温度条件
運動子が適切に運動するためには,容積流量計の使用可能な温度範囲に注意する。許容される温度条件
は,容積流量計の製造業者に確認する。
9.3
通過体積及び体積流量の計算
9.3.1
流量に比例した周波数のパルス列が出力される場合
9.3.1.1
Kファクタの用意
容積流量計には,7.13に従って求めたKファクタの代表値KF0及び必要に応じてその不確かさが校正実
績に基づいて与えられているものとする。Kファクタの補正係数EKを使用する場合には,製造業者が校正
実績に基づいて指定した値を用いるか,又は実測する。
9.3.1.2
標準状態における通過体積及び体積流量の計算
標準状態における通過体積及び体積流量の計算は,次による。
なお,それぞれの計算に用いる湿度補正係数は12.1に,圧縮係数は12.3に従って求める。
a) 標準状態における通過体積VN 式(56)によって求める。
wv
F0
K
n
M
N
M
M
N
950
370
1
F
K
E
I
Z
Z
T
p
V=
················································· (56)
ここに,
VN: 標準状態における通過体積[m3 (Normal)]
KF0: Kファクタの代表値(pulses/L)
EK: KF0に乗じるKファクタの補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
In: 積算パルス数(pulses)
Fwv: 湿度補正係数
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
b) 標準状態における体積流量qvN 式(57)によって求める。
wv
F0
K
M
N
M
M
vN
042
.
103
1
F
K
E
f
Z
Z
T
p
q
=
················································ (57)
32
M 8010:2020
ここに, qvN: 標準状態における体積流量[m3/h (Normal)]
KF0: Kファクタの代表値(pulses/L)
EK: KF0に乗じるKファクタの補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
f: 容積流量計が出力するパルス信号の周波数(Hz)
Fwv: 湿度補正係数
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
9.3.2
流量に比例したアナログ信号が出力される場合
9.3.2.1
比例係数の用意
使用範囲となる温度,圧力及び流量の全域において有効な出力と流量との比例係数GVを,容積流量計
の製造業者が校正実績に基づいて提供するか,又は容積流量計を校正して決定する。Kファクタが与えら
れている容積流量計に周波数を変換する回路を取り付ける場合は,その周波数変換回路の出力と周波数と
の比例係数をGfとするとき,Gf/KFを,容積流量計のアナログ出力から流量を得るための係数として用い
る。比例係数の補正係数Eを使用する場合には,製造業者が校正実績に基づいて指定した値を用いるか,
又は実測する。
9.3.2.2
標準状態における体積流量の計算
標準状態における体積流量は,アナログ信号出力電圧X及び流量がゼロのときのアナログ信号のゼロ点
出力電圧X0を用い,式(58)によって求める。
なお,計算に用いる湿度補正係数は12.1に,圧縮係数は12.3に従って求める。
(
)wv
0
A
A
M
N
M
M
vN
042
.
103
1
F
X
X
G
E
Z
Z
T
p
q
−
=
······································· (58)
ここに, qvN: 標準状態における体積流量[m3/h (Normal)]
GA: アナログ出力の比例係数[L/(s・V)]
EA: アナログ信号の比例係数に乗じる補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
X: アナログ信号出力電圧(V)
X0: アナログ信号のゼロ点出力電圧(V)
Fwv: 湿度補正係数
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
注記 アナログ信号出力電圧及び比例係数の単位は,アナログ信号の形態によって変わる場合がある。
9.3.3
容積流量計の出力が通信などの場合
KFなどの係数,その他の必要な入力値が正しく入力されていることを確認し,通信,電文などで受信し
た値をそのまま用いる。
9.4
性能の維持
9.4.1
容積流量計圧力損失の監視
必要に応じ,容積流量計の圧力損失を監視し,これが正常な範囲内にあることを確認する。圧力損失測
定の最適位置及び正常な圧力損失値の範囲は,容積流量計の使用実績から判断して製造業者が指定した範
囲か,又は校正中に実測する。圧力損失が許容範囲を超えた場合には,適切な保守が必要であり,再校正
が必要となる場合がある。
33
M 8010:2020
9.4.2
流量範囲の厳守
運動子の破損を避けるため,容積流量計に許される流量上限を厳守する。
9.4.3
急激な流量変化の禁止
流量が急激に変化すると,運動子に過大な差圧がかかったり運動子が振動して破損することがあるため,
容積流量計には急激な流量変化を与えてはならない。容積流量計に許容される最大流量変化率は,製造業
者の指示に従う。
10 渦流量計を用いる計量
10.1 概要
渦流量計は,流れに対して垂直方向に長く細い渦発生体を測定管路内に取り付け,流体がこれを通過す
るときに発生する渦(カルマン渦)の周波数が流速にほぼ比例することを利用して流量を測定する。
渦流量計の特性を表すKファクタは,渦流量計がカルマン渦の発生を検出して発したパルス数と,その
パルスを発する間に通過した流体の体積との比(パルス数/体積)として定義される。Kファクタの値は,
通常,実流校正によって決定するが,流れが非圧縮として扱える範囲のときは,レイノルズ数を合わせる
ことによって,温度及び/又は圧力が異なる状態での校正,又は空気若しくは水の代替流体を用いた校正
によって決定することもできる。
Kファクタは,渦発生体の形状及びその配管壁面への取付部の形状に敏感であるため,流れの中の異物,
ミスト,配管壁面上への堆積物などに注意する。また,渦の発生は流れが渦発生体を通過するときの流速
分布に敏感であるため,上流側及び下流側に十分な長さの直管が必要となる。温度センサの挿入によって
流速分布が変わることがあるため,温度取出口は,通常,渦流量計の下流側に設置する。
流れの中にカルマン渦の発生周波数に近い周波数の乱れがあると,渦発生の引込み現象が起こり,大き
な誤差が発生することがあるため,流量,圧力などの周期的な変動に十分に注意する。
十分な長さの上流直管長が確保できない場合には,整流装置を用いることで使用可能となる場合がある
が,整流装置の有無によってKファクタが変わることがあるため注意する。使用する渦流量計は,ガス又
はその代替流体を用いた使用実績又は校正実績があるものとする。
10.2 計量に必要な事項
10.2.1 異物などの排除
渦発生体を変形させる異物,付着物,ミストなどが流れに混入しないようにする。配管内面は清浄にし,
配管内部の溶接ビードは除去する。
10.2.2 流れの乱れの周波数に対する注意
コンプレッサ,調圧弁,ヘッダなどの近傍で,圧力,流量などの脈動が大きい所への設置は避けること
が望ましい。
10.2.3 上流側及び下流側直管の用意
渦流量計の上流側及び下流側に必要となる直管長に関しては,渦流量計の製造業者の指示に従う。
渦流量計に接続する配管の内径は,渦流量計の内径に一致させ,段差がないように接続することが望ま
しい。接続面において,接続する配管の内壁が渦流量計の内壁よりも管内側に突出すること及びガスケッ
トが管内側にはみ出すことは避ける。
10.2.4 整流装置に関する注意
整流装置を使用する場合には,渦流量計の製造業者の指示に従うか,又は整流装置を取り付けた状態で
校正する。
34
M 8010:2020
10.2.5 材質
渦発生体及びこれを取り付ける測定管は,線膨張係数が既知の材質で製作する。
10.2.6 測定範囲に関する注意
流量が小さすぎる場合には,渦の欠損及び精度低下が起こり,流量が大きすぎる場合には,渦検出部の
レンジオーバー及び圧縮性の影響で誤差が大きくなることがあるため,製造業者が指定する流量範囲を厳
守する。
10.2.7 温度測定
温度センサは,7.6に従って渦流量計の下流側に取り付ける。圧力取出口も渦流量計の下流側に取り付け
るため(10.2.8参照),流れの中に挿入する温度センサが圧力測定に影響を及ぼさないように注意する。
10.2.8 圧力測定
圧力取出口は,渦流量計の下流側端面から下流側の2Dn〜7Dnの間に,7.7に従って取り付ける。
10.3 通過体積及び体積流量の計算
10.3.1 流量に比例した周波数のパルス列が出力される場合
10.3.1.1 Kファクタの用意
渦流量計には,7.13に従って求めたKファクタの代表値KF0及び必要に応じてその不確かさが校正実績
に基づいて与えられているものとする。Kファクタの補正係数EKを使用する場合には,製造業者が校正実
績に基づいて提供するか,又は実測する。
10.3.1.2 標準状態における通過体積及び体積流量の計算
標準状態における通過体積及び体積流量の計算は,次による。
なお,それぞれの計算に用いる湿度補正係数は12.1に,圧縮係数は12.3に従って求める。
a) 標準状態における通過体積VN 式(59)によって求める。
(
)
(
)
wv
F0
n
K
0
D
D
D
0
B
B
B
M
N
M
M
N
2
1
950
370
1
F
K
I
E
T
T
α
T
T
α
Z
Z
T
p
V
−
+
−
+
=
············· (59)
ここに,
VN: 標準状態における通過体積[m3 (Normal)]
KF0: Kファクタの代表値(pulses/L)
EK: KF0に乗じるKファクタの補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
In: 積算パルス数(pulses)
Fwv: 湿度補正係数
αB: 渦発生体の線膨張率(1/℃)
αD: 測定管の線膨張率(1/℃)
TB: 計量中における渦発生体の温度(℃)
TB0: Kファクタを決定したときの渦発生体の温度(℃)
TD: 計量中における測定管の温度(℃)
TD0: Kファクタを決定したときの測定管の温度(℃)
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
b) 標準状態における体積流量qvN 式(60)によって求める。
(
)
(
)
wv
F0
K
0
D
D
D
0
B
B
B
M
N
M
M
vN
2
1
042
.
103
1
F
K
f
E
T
T
α
T
T
α
Z
Z
T
p
q
−
+
−
+
=
·············· (60)
ここに, qvN: 標準状態における体積流量[m3/h (Normal)]
KF0: Kファクタの代表値(pulses/L)
EK: KF0に乗じるKファクタの補正係数
35
M 8010:2020
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
f: 渦流量計が出力するパルス信号の周波数(Hz)
Fwv: 湿度補正係数
αB: 渦発生体の線膨張率(1/℃)
αD: 測定管の線膨張率(1/℃)
TB: 計量中における渦発生体の温度(℃)
TB0: Kファクタを決定したときの渦発生体の温度(℃)
TD: 計量中における測定管の温度(℃)
TD0: Kファクタを決定したときの測定管の温度(℃)
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
10.3.2 流量に比例したアナログ信号が出力される場合
10.3.2.1 比例係数の用意
使用範囲となる温度圧力流量の全域において有効な出力と流量との比例係数GVを,渦流量計の製造業
者が校正実績に基づいて提供するか,又は渦流量計を校正して決定する。Kファクタが与えられている渦
流量計に周波数を変換する回路を取り付ける場合は,その周波数変換回路の出力と周波数との比例係数を
Gfとするとき,Gf/KFを,渦流量計のアナログ出力から流量を得るための係数として用いる。比例係数の
補正係数Eを使用する場合には,製造業者が校正実績に基づいて指定した値を用いるか,又は実測する。
10.3.2.2 標準状態における体積流量の計算
標準状態における体積流量は,アナログ信号出力電圧X及び流量がゼロのときのアナログ信号のゼロ点
出力電圧X0を用い,式(61)によって求める。
なお,計算に用いる湿度補正係数は12.1に,圧縮係数は12.3に従って求める。
(
)
(
)
[
](
)wv
0
A
0
D
D
D
0
B
B
B
A
M
N
M
M
vN
2
1
042
.
103
1
F
X
X
G
T
T
α
T
T
α
E
Z
Z
T
p
q
−
−
+
−
+
=
·· (61)
ここに, qvN: 標準状態における体積流量[m3/h (Normal)]
GA: アナログ出力の比例係数[L/(s・V)]
EA: アナログ信号の比例係数に乗じる補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
X: アナログ信号出力電圧(V)
X0: アナログ信号のゼロ点出力電圧(V)
Fwv: 湿度補正係数
αB: 渦発生体の線膨張率(1/℃)
αD: 測定管の線膨張率(1/℃)
TB: 計量中における渦発生体の温度(℃)
TB0: Kファクタを決定したときの渦発生体の温度(℃)
TD: 計量中における測定管の温度(℃)
TD0: Kファクタを決定したときの測定管の温度(℃)
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
注記 アナログ信号出力電圧及び比例係数の単位は,アナログ信号の形態によって変わる場合がある。
10.3.3 渦流量計の出力が通信などの場合
KFなどの係数,その他の必要な入力値が正しく入力されていることを確認し,通信,電文などで受信し
た値をそのまま用いる。
36
M 8010:2020
10.4 性能の維持
渦流量計の内部を適宜目視点検し,測定管,渦発生体などに,異物の堆積,付着などがないこと,及び
変形がないことを確認する。特に,渦発生体のエッジのだれ,かけ及び変形に注意して点検を行う。
点検の結果,必要に応じて清掃,渦流量計全体の交換,又は渦発生体の交換を行う。渦発生体の交換を
行ったときの再校正の必要性については,製造業者の指示に従う。
渦流量計の上流側及び下流側の直管部に関しても,同様な目視点検,清掃及び交換を行う。
内部の点検周期については,流れるガスの状況に大きく依存するため,使用状況に応じて決定する。
11 超音波流量計を用いる計量
11.1 概要
超音波流量計では,流体が流れる管内に超音波を発してこれを流れに重畳させ,その超音波を流れ方向
に離れた位置で受信して送信波と受信波との時間差を測定し,その時間遅れから超音波パス上の平均流速
vを計算し,これに測定管の断面積ADを乗じて体積流量とする。この場合,流路断面上での流速が一定の
ときは,ガスの圧力,温度,組成などに関係なく正しい体積流量となるが,実際の流れには流速分布があ
るために偏差が発生する。超音波流量計では,この偏差を減らすために,一般的な流速分布を仮定して求
めた流量補正係数Kcを乗じ,式(62)で求めた値を体積流量qvMとして出力する。
v
A
K
q
D
c
vM=
·········································································· (62)
ここに, qvM: 測定状態における体積流量(m3/h)
Kc: 超音波流量計で用いる流量補正係数
AD: 測定管の断面積(m2)
v: 超音波パス上の平均流速(m/s)
超音波流量計の圧力損失は,通常は直管とほぼ同じ程度で非常に小さく,上流側で発生した乱れがほと
んど減衰せずにそのまま通過するため,上流側の配管条件に十分に注意する必要がある。その影響を減ら
すために,複数のパスを用いて様々な演算を行うマルチパス方式が開発されているが,パスのレイアウト,
演算方式などは多岐にわたり,流速分布,ガス種などに対する依存性はそれぞれの超音波流量計に固有の
ものとなるため,配管条件に適したものを選択するためには製造業者に問い合わせる。
超音波流量計には高速で信号処理を行う高度な処理能力のSPU(signal processing unit)が搭載されてい
るため,これを利用し,同時に様々な補正,演算なども行うものがある。そのため,超音波流量計の仕様
を十分に確認し,重複した補正,補正不足などを避けなければならない。
超音波流量計は,SPUを利用し,様々な形態で測定結果の出力ができるものが多く,流量に比例したパ
ルス信号を出力する場合には,Kファクタに相当するものを用いて容積流量計及び渦流量計と同様に扱う
ことができる。このとき,KファクタKFと式(62)で使用する流量補正係数Kcとを混同しないように十分に
注意する。
注記 流量補正係数Kcは,パルスを出力する前に超音波流量計内部で用いられるものであり,Kファ
クタKFは,パルスが出力された後に,通常は超音波流量計外部で用いられる。
超音波の送受信を行うトランスデューサは,測定対象とする流体とのマッチングが取られており,対象
とする流体の種類,含有成分の比率などが異なる場合に測定できなくなることがあるため,超音波流量計
の仕様を十分に確認する。
流量補正係数Kcはレイノルズ数によってほぼ決まるため,レイノルズ数を一致させることによって異な
る気体又は状態で校正することができる。異なる気体を用いて校正する場合には,その気体でも超音波の
37
M 8010:2020
送受信が可能であることを確認しなければならない。
使用する超音波流量計は,ガス又はその代替流体を用いた使用実績又は校正実績があるものとする。
11.2 計量に必要な事項
11.2.1 前後に必要な直管
必要直管長は,パスの構成,演算の方法などに依存して大きく変わるため,取付配管の構成に関しては,
超音波流量計の製造業者の指示に従う。
超音波流量計に接続する前後配管の内径は,超音波流量計の内径に一致させ,段差がないように接続す
ることが望ましい。超音波流量計と配管との接続面に段差が発生することが避けられない場合には,超音
波流量計の内径よりも前後配管の内径を大きくすることが望ましく,このときの許容段差は,超音波流量
計の製造業者の指定に従う。パッキン,ガスケットなどが配管内壁面から突出することは避ける。
11.2.2 整流装置の使用
整流装置を使用する場合には,最適な配管構成に関して超音波流量計の製造業者の指示に従うか,又は
使用する配管構成で校正する。
11.2.3 音響ノイズへの注意
バルブ,絞り,コンプレッサなどの音響ノイズ源から十分に離れた位置に設置するか,又はノイズ発生
源と超音波流量計との間に消音機構を取り付ける。ノイズ発生源の近くに設置せざるを得ない場合には,
超音波流量計をノイズ発生源の上流側に取り付けることが望ましい。ノイズ除去に関しては,様々な手法
が開発されているため,最新の技術を参照する。
11.2.4 異物の除去
ガスの流れに異物が含まれないようにする。トランスデューサ,測定管路などに異物が堆積している場
合には,必要に応じ清掃する。
11.2.5 適正なトランスデューサの使用
対象とするガスが測定可能なものであることを確認する。特に,CO2濃度が3 %以上,又は超音波流量
計の呼び径が300 mm以上の場合は,十分な信号強度が得られることを確認する。
11.2.6 温度測定
製造業者の特別な指定がない限り,7.6に従い,温度センサは超音波流量計の下流側に取り付ける。上流
側に取り付けることが避けられない場合には,校正,使用実績などを参照して最適位置を決めるか,又は
必要な場合は温度センサを取り付けたまま校正を行う。
11.2.7 圧力取出口
超音波流量計に圧力取出口がある場合には,その圧力取出口を用いる。流量計を設置する配管に圧力取
出口を設ける場合には,7.7に従い,流量計の下流側端面から下流側の2Dn〜5Dnの間に取り付けることが
望ましい。超音波流量計の内径がその前後配管の内径と異なる場合には,圧力ポートをもつ超音波流量計
を用いる。
11.2.8 補正機能の確認
超音波流量計には,流量補正係数Kcを定数としてSPUに設定するもの,流量補正係数Kcを流れの状態
の関数として温度圧力の入力を必要とするもの,流量補正係数Kcを1として補正を行わないものなど様々
な形態のものがあるため,超音波流量計の仕様を確認し,必要な補正を重複なく有効に機能させる。
11.2.9 出力周波数パルス波形の確認
パルス受信機も含めて出力パルスが欠損なく測定可能であることを確認する。集中的なパルス発信を行
う超音波流量計では,パルス受信機の帯域に注意する。
38
M 8010:2020
11.2.10 正流逆流の双方向測定における注意
双方向測定が可能な超音波流量計を用いる場合,温度センサの取付位置は,超音波流量計製造業者の指
示に従う。
11.3 通過体積及び体積流量の計算
11.3.1 流量に比例した数のパルスが出力される場合
11.3.1.1 流量補正係数Kcの登録及びKファクタKF0の用意
超音波流量計のSPUに流量補正係数Kcが登録されており(Kc=1とする場合を含む。),超音波流量計が
測定した通過体積に比例した数のパルスが出力されるように設定されていることを確認する。このパルス
の数を流量に変換するための定数は,次においてKファクタKF(pulses/L)として扱い,超音波流量計に
は,7.13に従って求めたKファクタの代表値KF0及び必要に応じてその不確かさが校正実績に基づいて与
えられているものとする。Kファクタの補正係数EKを使用する場合には,製造業者が校正実績に基づいて
提供するか,又は実測する。
注記 流量補正係数KcとKファクタKFとを混同しないように注意する。
11.3.1.2 標準状態における通過体積及び体積流量の計算
標準状態における通過体積及び体積流量の計算は,次による。
なお,それぞれの計算に用いる湿度補正係数は12.1に,圧縮係数は12.3に従って求める。
a) 標準状態における通過体積VN 式(63)によって求める。
(
)
wv
F0
n
K
0
D
D
D
M
N
M
M
N
3
1
950
370
1
F
K
I
E
T
T
α
Z
Z
T
p
V
−
+
=
······························· (63)
ここに,
VN: 標準状態における通過体積[m3 (Normal)]
KF0: Kファクタの代表値(pulses/L)
EK: KF0に乗じるKファクタの補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
In: 積算パルス数(pulses)
Fwv: 湿度補正係数
αD: 測定管の線膨張率(1/℃)
TD: 計量中における測定管の温度(℃)
TD0: Kファクタを決定したときの測定管の温度(℃)
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
b) 標準状態における体積流量qvN 式(64)によって求める。
(
)
wv
F0
K
0
D
D
D
M
N
M
M
vN
3
1
042
.
103
1
F
K
f
E
T
T
α
Z
Z
T
p
q
−
+
=
······························ (64)
ここに, qvN: 標準状態における体積流量[m3/h (Normal)]
KF0: Kファクタの代表値(pulses/L)
EK: KF0に乗じるKファクタの補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
f: 超音波流量計が出力するパルス信号の周波数(Hz)
Fwv: 湿度補正係数
αD: 測定管の線膨張率(1/℃)
TD: 計量中における測定管の温度(℃)
TD0: Kファクタを決定したときの測定管の温度(℃)
ZN: 標準状態におけるガスの圧縮係数
39
M 8010:2020
ZM: 測定状態における圧縮係数
11.3.2 流量に比例したアナログ信号が出力される場合
11.3.2.1 流量補正係数Kcの登録と比例係数GAの用意
超音波流量計のSPUに流量補正係数Kcが登録されていることを確認する(Kc=1とする場合を含む。)。
使用範囲となる温度圧力流量の全域において有効な出力と流量との比例係数GVを,超音波流量計の製造
業者が校正実績に基づいて提供するか,又は超音波流量計を校正して決定する。Kファクタが与えられて
いる流量計に周波数を変換する回路を取り付ける場合は,その周波数変換回路の出力と周波数との比例係
数をGfとするとき,Gf/KFを,超音波流量計のアナログ出力から流量を得るための係数として用いる。必
要に応じ,比例係数の補正係数Eを,製造業者が校正実績に基づいて指定した値を用いるか,又は実測す
る。
11.3.2.2 標準状態における体積流量の計算
標準状態における体積流量は,アナログ信号出力電圧X及び流量がゼロのときのアナログ信号のゼロ点
出力電圧X0を用い,式(65)によって求める。
なお,計算に用いる湿度補正係数は12.1に,圧縮係数は12.3に従って求める。
(
)
[
](
)wv
0
A
0
D
D
D
A
M
N
M
M
vN
3
1
042
.
103
1
F
X
X
G
T
T
α
E
Z
Z
T
p
q
−
−
+
=
················· (65)
ここに, qvN: 標準状態における体積流量[m3/h (Normal)]
GA: アナログ出力の比例係数[L/(s・V)]
EA: アナログ信号の比例係数に乗じる補正係数
pM: 計量中における流量計の位置でのガスの圧力(Pa)
TM: 計量中における流量計の位置でのガスの温度(K)
X: アナログ信号出力電圧(V)
X0: アナログ信号のゼロ点出力電圧(V)
Fwv: 湿度補正係数
αD: 測定管の線膨張率(1/℃)
TD: 計量中における測定管の温度(℃)
TD0: Kファクタを決定したときの測定管の温度(℃)
ZN: 標準状態におけるガスの圧縮係数
ZM: 測定状態における圧縮係数
注記 アナログ信号出力電圧及び比例係数の単位は,アナログ信号の形態によって変わる場合がある。
11.3.3 超音波流量計の出力が通信などの場合
超音波流量計のSPUに流量補正係数Kcが登録されていること(Kc=1とする場合を含む。),その他の必
要な入力値が正しく入力されていることを確認し,通信,電文などで受信した値をそのまま用いる。
11.4 性能の維持
11.4.1 一般事項
超音波流量計の内部及び回路機能の点検は,専門知識をもつ超音波流量計製造業者の点検技術者が実施
することが望ましい。超音波流量計内部及びSPU回路の定期的な点検が困難な場合は,超音波流量計の自
己診断機能による指示に従う。
11.4.2 内部の点検
超音波流量計の内部を目視点検し,管内及びトランスデューサ表面に異物の堆積,付着などがないこと
を確認し,必要に応じて清掃,保守などを行う。
11.4.3 回路機能の点検
超音波流量計とその上位システムとのループチェック,SPUの機能が正常であることなどを確認し,必
40
M 8010:2020
要に応じて保守及び交換を行う。
11.4.4 音速を利用した測定値の確認
トランスデューサの交換及び超音波流量計の特性の再確認が必要となった場合には,超音波流量計が測
定する音速と,ガスの温度圧力及び成分比を用いて必要な精度でアイゼントロピック指数,圧縮係数,及
びモル質量を求め,式(66)で求めた音速の値とを比較する。測定結果に影響をもたらす大きさの差が認め
られた場合には,製造業者に問い合わせる。
p
ρ
N
κZRT
c
κ
=
=
s
································································· (66)
ここに,
cs: ガス中の音速(m/s)
κ: ガスのアイゼントロピック指数
Z: ガスの圧縮係数
R: 普遍気体定数(8.314 46)[J/(K・mol)]
N: ガスのモル質量(kg/mol)
T: ガスの温度(K)
ρ: ガスの密度(kg/m3)
p: ガスの圧力(Pa)
12 物性値
12.1 湿度補正係数Fwv
12.1.1 乾燥条件(Fwv=1としても良い条件)
ガスが式(67)を満たす場合,ガスは乾燥しているものとしてFwv=1とする。それ以外の場合には,湿度
補正係数の値を12.1.4に従って求める。水蒸気のモル分率は,12.1.2に従って求める。
なお,LNG気化ガスの場合には,ガスは乾燥しているとしてもよい。
xwv<0.000 3 ············································································ (67)
ここに,
xwv: 水蒸気モル分率
この乾燥条件は,露点温度の測定結果を用い,式(68)で判断してもよい。
pdp≦0.000 9Tdp4+0.095Tdp3+4.818 3Tdp2+146.16Tdp+2 029 ················ (68)
ここに,
pdp: 露点温度測定時のガスの圧力(kPa)
Tdp: 露点温度(℃)
12.1.2 ガスが含有する水蒸気のモル分率
ガスが含有する水蒸気のモル分率は,露点温度を用い,式(69)で求める。飽和蒸気圧は,12.1.3に従って
求める。
dp
dp
swv
wv
)
(
p
T
p
x
=
······································································· (69)
ここに,
xwv: 水蒸気モル分率
Tdp: 露点温度(℃)
pdp: 露点温度測定時のガスの圧力(kPa)
pswv(T): 温度T(℃)における水蒸気の飽和蒸気圧(kPa)
12.1.3 水蒸気の飽和蒸気圧
温度T(℃)における水蒸気の飽和蒸気圧は,式(70)で求める。
()
+
=
T
T
T
p
12
.
243
62
.
17
exp
2
611
.0
swv
················································ (70)
ここに, pswv(T): 温度T(℃)における水蒸気の飽和蒸気圧(kPa)
T: ガスの温度(℃)
41
M 8010:2020
12.1.4 湿度補正係数
湿度補正係数は,式(71)で求める。
Fwv=1−xwv ············································································ (71)
ここに, Fwv: 湿度補正係数
xwv: 水蒸気モル分率
12.2 標準状態におけるガスのモル質量
標準状態におけるガスのモル質量は,乾燥させたガスの成分分析をJIS K 2301に従って行い,式(72)で
求める。各成分のモル質量は,表2の値を用いる。測定状態におけるモル質量も,式(72)で求めた値とす
る。各成分の分析結果が体積分率で与えられる場合,附属書Fに従ってモル分率に変換する。
∑
=
i
i
iN
x
NN
········································································· (72)
ここに,
NN: 標準状態におけるガスのモル質量(kg/mol)
Ni: i番目の成分のモル質量(kg/mol)
xi: i番目の成分のモル分率
表2−各成分のモル質量
成分
モル質量(kg/mol)
CO2
0.044 009 5
N2
0.028 013 4
H2
0.002 015 9
CO
0.028 010 1
O2
0.031 998 8
CH4
0.016 042 5
C2H6
0.030 069 0
C3H8
0.044 095 6
iC4H10
0.058 122 2
nC4H10
0.058 122 2
iC5H12
0.072 148 8
nC5H12
0.072 148 8
C6H14
0.086 175 4
C7H16
0.100 201 9
C8H18
0.114 228 5
ガスの成分分析においては,次の条件に従う。
a) C5以上のアルカン異性体は,モル質量で加算して通常のアルカンとして扱ってもよい。
b) 表2に示されない微量成分のモル分率は,附属書Gに従って適切な成分に割り当てる。
c) C7以上のモル分率は,C6+として一括して扱ってもよい。
式(72)で用いるxiは規格化されたものとし,全てのiについてxiを加えた値が1.000 0になることを確認
する。
12.3 圧縮係数
12.3.1 ガスの圧力が1 MPaを超える場合
圧縮係数は,附属書Hに示すZ数表(2015)又はAGA8-92DC法による直接計算によって求める。直接
計算による場合には,表3に示す全てのサンプルガス(Gas 1〜Gas 6)について圧縮係数を計算し,その
全ての値が表3の圧縮係数サンプル値に対して0.02 %以下の偏差でなければならない。
注記 AGA8-92DC法は,AGA Report No.8(2nd ed., 1992)のほかに,ISO 12213-1,ISO 12213-2及
42
M 8010:2020
びISO 20765-1にも計算方法が示されているため,直接計算ではこれらを参照することができ
る。
12.3.2 ガスの圧力が1 MPa以下の場合
附属書Hに示すZ数表(2015),附属書Iに示すZ数表(1993),又はAGA8-92DC法による直接計算に
よって圧縮係数を求める。直接計算による場合には,表3に示す全てのサンプルガス(Gas 1〜Gas 6)に
ついて全ての温度及び圧力における圧縮係数を計算し,その全ての値が表3の圧縮係数サンプル値に対し
て0.02 %以下の偏差でなければならない。
表3−圧縮係数の計算値を検証するためのサンプルガスの成分及び圧縮係数
モ
ル
分
率
成分
Gas 1
Gas 2
Gas 3
Gas 4
Gas 5
Gas 6
xCO2
0.006
0.005
0.015
0.016
0.076
0.011
xN2
0.003
0.031
0.010
0.100
0.057
0.117
xH2
0.00
0.00
0.00
0.095
0.00
0.00
xCO
0.00
0.00
0.00
0.01
0.00
0.00
xCH4
0.965
0.907
0.859
0.735
0.812
0.826
xC2H6
0.018
0.045 0
0.085
0.033
0.043
0.035
xC3H8
0.004 5
0.008 4
0.023
0.007 4
0.009
0.007 5
xiC4H10
0.001 0
0.001 0
0.003 5
0.001 2
0.001 5
0.001 2
xnC4H10
0.001 0
0.001 5
0.003 5
0.001 2
0.001 5
0.001 2
xiC5H12
0.000 5
0.000 3
0.000 5
0.000 4
0.00
0.000 4
xnC5H12
0.000 3
0.000 4
0.000 5
0.000 4
0.00
0.000 4
xC6H14
0.000 7
0.000 4
0.00
0.000 2
0.00
0.000 2
xC7H16
0.00
0.00
0.00
0.000 1
0.00
0.000 1
xC8H18
0.00
0.00
0.00
0.000 1
0.00
0.00
圧
縮
係
数
サ
ン
プ
ル
値
圧力
(MPa)
温度
(℃)
Gas 1
Gas 2
Gas 3
Gas 4
Gas 5
Gas 6
6
−3.15
0.840 53
0.833 48
0.793 80
0.885 50
0.826 09
0.853 80
6
6.85
0.861 99
0.855 96
0.822 06
0.901 44
0.849 69
0.873 70
6
16.85
0.880 06
0.874 84
0.845 44
0.915 01
0.869 44
0.890 52
6
36.85
0.908 67
0.904 66
0.881 83
0.936 74
0.900 52
0.917 23
6
56.85
0.930 11
0.926 96
0.908 68
0.953 18
0.923 68
0.937 30
12
−3.15
0.721 33
0.710 44
0.641 45
0.810 24
0.695 40
0.750 74
12
6.85
0.760 25
0.750 66
0.689 71
0.837 82
0.737 80
0.785 86
12
16.85
0.793 17
0.784 75
0.731 23
0.861 37
0.773 69
0.815 69
12
36.85
0.845 15
0.838 63
0.796 97
0.899 13
0.830 22
0.863 11
12
56.85
0.883 83
0.878 70
0.845 53
0.927 66
0.872 11
0.898 62
12.4 密度
ガスの密度は実測するか,又はガスの圧力p及び温度Tの測定値,12.2に従って求めたモル質量,並び
に12.3に従って求めた圧縮係数の値を用い,式(73)で求める。
T
p
Z
N
ρ
51
314
.8
=
······································································ (73)
ここに,
ρ: ガスの密度(kg/m3)
p: ガスの圧力(Pa)
T: ガスの温度(K)
N: ガスのモル質量(kg/mol)
Z: ガスの圧縮係数
43
M 8010:2020
注記 式(73)に含まれる定数8.314 51は普遍気体定数の値であり,CODATAによる調整で若干変更さ
れることがあるが,その変更は天然ガスの計量には影響を与えない大きさである。箇条12に示
す圧縮係数,アイゼントロピック指数などは,1986年のCODATA調整値である8.314 51を用
いて求めたものである。
なお,CODATAとは,科学技術データ委員会(Committee on Data for Science and Technology)
の略語である。
12.5 アイゼントロピック指数
12.5.1 一般事項
ガスのアイゼントロピック指数の値は,許容される不確かさの大きさに依存して,12.5.2によって適合
曲線を用いて求めるか,12.5.3によって直接計算若しくは実測値を用いるか,又は12.5.4によって求めた
定数を用いる。
12.5.2 適合曲線を用いる場合
12.3に従って求めた圧縮係数Z及び表H.1に示す定数ai及びbiを用い,式(74)〜式(80)で求める。式(74)
で用いるκ0の値は,式(75)によるか,又は附属書Jによって求める。
2
2
1
0
0
Z
B
Z
B
B
κ
κ
+
+
+
=
······························································· (74)
75
.0
κ
κ
0
950
.0
42
000
.0
1.647
−
−
−
=
B
A
T
κ
········································ (75)
3
2
0
722
0.009
85
0.175
3
0.971
1.468
p
p
p
B
+
−
+
−
=
···························· (76)
3
2
1
504
0.018
55
0.335
4
1.908
3.117
p
p
p
B
−
+
−
=
······························· (77)
3
2
2
1
873
0.008
769
0.160
79
0.948
1.654
p
p
p
B
+
−
+
−
=
······················· (78)
∑
=
i
i
ix
a
Aκ
··········································································· (79)
∑
=
i
i
ix
b
Bκ
··········································································· (80)
ここに,
κ: ガスのアイゼントロピック指数
κ0: 完全気体を仮定したアイゼントロピック指数
p: ガスの圧力(MPa)
T: ガスの温度(℃)
ai: Z数表で使用するi番目の成分に関する定数(表H.1参
照)(K)
bi: Z数表で使用するi番目の成分に関する定数(表H.1参
照)(kPa)
xi: i番目の成分のモル分率
Z: ガスの圧縮係数
Aκ,Bκ: 完全気体とみなしたアイゼントロピック指数を計算す
るパラメータ
B0,B1,B2: アイゼントロピック指数の圧力補正を行うパラメータ
注記 Z数表(2015)が十分小さい誤差で使用可能となるガスの場合,式(75)によるκ0の値を用いて
式(74)で計算したアイゼントロピック指数の値は,ISO 20765-1などの熱力学的計算方法で計算
44
M 8010:2020
したアイゼントロピック指数の値に対し,1 MPaで最大で約±1 %,6 MPaで最大で約±2 %,
10 MPaで最大で約±4 %の差となる。κ0の計算に式(75)の代わりに式(J.2)を用いれば,低圧側に
おいて,この差を約1 %小さくすることができる。
12.5.3 直接計算又は実測値によって求める場合
測定状態におけるガスのアイゼントロピック指数を直接計算で求める方法又は公開されている実測値,
若しくは実測した値を用いる。
12.5.4 定数とする場合
定数1.3又は式(75)若しくは附属書Jに従って求めたκ0の値をアイゼントロピック指数の定数として用
いる場合,12.5.2又は12.5.3に従って求めたアイゼントロピック指数で計算した膨張補正係数と,アイゼ
ントロピック指数を1.3として求めた膨張補正係数との差が0.1 %以下となることを確認する。
12.6 粘度
ガスの粘度は,式(81)〜式(87)を用いて求める。これらに使用する定数を,表4に示す。
p
0
Δμ
μ
μ
+
=
··········································································· (81)
+
+
+
+
+
+
=
ran
rel
3
μ
ran
2
μ
rel
1
μ
ran
rel
3
μ
ran
2
μ
rel
1
μ
0
μ
0
ln
ln
ln
ln
1
ln
ln
ln
ln
exp
000
1
T
N
b
T
b
N
b
T
N
a
T
a
N
a
a
μ
··············· (82)
3
cc
μ
2
cc
μ
cc
μ
μ
3
cc
μ
2
cc
μ
cc
μ
μ
p
000
1
Δ
ρ
H
ρ
G
ρ
F
E
ρ
D
ρ
C
ρ
B
A
μ
+
+
+
+
+
+
=
········································ (83)
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
2
ran
2
μ
ran
1
μ
0
μ
μ
T
H
T
H
H
H
T
G
T
G
G
G
T
F
T
F
F
F
T
E
T
E
E
E
T
D
T
D
D
D
T
C
T
C
C
C
T
B
T
B
B
B
T
A
T
A
A
A
+
+
=
+
+
=
+
+
=
+
+
=
+
+
=
+
+
=
+
+
=
+
+
=
····················································· (84)
67
.
491
5
9
ran
+
=T
T
··································································· (85)
000
1
cc
ρ
ρ=
············································································· (86)
962
.
28
rel
N
N=
·········································································· (87)
ここに,
μ: ガスの粘度(μPa・s)
μ0: 大気圧におけるガスの粘度(μPa・s)
Δμp: 粘度の圧力補正項(μPa・s)
aμ0〜aμ3,bμ1〜bμ3: 大気圧における粘度を求めるための定数(表4参照)
Aμ〜Hμ: 粘度の圧力補正を行うパラメータ
Aμ0,Aμ1,Aμ2〜Hμ0,Hμ1,Hμ2: 粘度の圧力補正パラメータに用いる定数(表4参照)

45
M 8010:2020
Tran: 温度パラメータ
T: ガスの温度(℃)
ρcc: 密度パラメータ
ρ: ガスの密度(kg/m3)
Nrel: モル質量パラメータ
N: ガスのモル質量(g/mol)
注記 Nの単位がg/molであることに注意する。
表4−粘度の計算に用いる定数
aμ0
−6.398 210E+00
Aμ0
9.533 630E-01
aμ1
−6.045 922E-01
Aμ1
−1.073 840E+00
aμ2
7.497 680E-01
Aμ2
1.317 290E-03
aμ3
1.261 051E-01
Bμ0
−9.710 280E-01
bμ1
6.971 800E-02
Bμ1
1.120 770E+01
bμ2
−1.013 889E-01
Bμ2
9.013 000E-02
bμ3
−2.152 940E-02
Cμ0
1.018 030E+00
Cμ1
4.989 860E+00
Cμ2
3.027 370E-01
Dμ0
−9.905 310E-01
Dμ1
4.175 850E+00
Dμ2
−6.366 200E-01
Eμ0
1.000 000E+00
Eμ1
−3.196 460E+00
Eμ2
3.909 610E+00
Fμ0
−1.003 640E+00
Fμ1
−1.816 330E-01
Fμ2
−7.790 890E+00
Gμ0
9.980 800E-01
Gμ1
−1.621 080E+00
Gμ2
6.348 360E-04
Hμ0
−1.001 030E+00
Hμ1
6.768 750E-01
Hμ2
4.624 810E+00
13 計量値の不確かさの概算
13.1 一般事項
一般的な状況における計量値の不確かさの概算値は,表5に示す代表的な要因について,13.2〜13.4に
従って求める。極端な条件の不確かさ評価を行う場合,及び厳格な不確かさ評価を行う場合は,ISO/IEC
Guide 98-3:2008などの必要な手順に従う。
各流量計に固有の不確かさ要因は,可能なものは表5の不確かさ要因に割り当てる。割り当てができな
い特殊な要因がある場合には,ISO/IEC Guide 98-3:2008などの必要な手順に従う。
46
M 8010:2020
表5−主要な不確かさ要因及び代表的な評価法
対象流量計
不確かさ要因
相対不確かさ
の記号
不確かさ評価法の代表例
オリフィス流量計
流出係数
UCd
8.4.1による。
膨張補正係数
Uε
8.4.2による。
オリフィス孔径
Ud
測定の不確かさを用いる。
オリフィス配管径
UD
差圧
UΔp
上流側圧力取出断面における温度
UT1
上流側圧力取出断面における圧力
Up1
オリフィス流量計
以外
測定状態の温度
UTM
測定状態の圧力
UPM
周波数
Uf
Kファクタ
UK0
流量計とともに提供されたKファクタの
不確かさ又は校正の不確かさを用いる。
オリフィス流量計
上流側圧力取出断面における圧縮
係数
UZ1
AGA8-92DC法を用いる場合にはISO
12213-2を参照する。Z数表(2015)を用
いる場合には,附属書Hを参考にして推定
する。
全流量計
標準状態における圧縮係数
UZN
測定状態における圧縮係数
UZM
モル分率
Ux,i
モル分率測定又は体積分率測定の不確か
さを用いる。
注記 成分のモル分率xiを係数とする各項をiに関して加算する不確かさ要因では,各項の不確かさの最大値の半
分程度のものまでを考慮する。
13.2 オリフィス流量計による計量値(標準状態における体積流量)の不確かさ
オリフィス流量計で計量した標準状態における体積流量の相対不確かさの概算値は,式(88)で求める。
各要素の不確かさは,表5を参照して評価する。
(
)(
)
2
ZN
2
ε
2
Cd
2
x,
N
2
Δp
2
T1
2
p1
2
Z1
2
D
8
2
d
2
4
qN
4
1
1
4
U
U
U
U
N
N
x
U
U
U
U
U
β
U
β
U
i
i
i
i
+
+
+
+
+
+
+
+
+
−
≈
∑
····· (88)
ここに, UqN: 標準状態における体積流量計量値の相対不確かさ(%)
UCd: オリフィス流量計の流出係数の相対不確かさ(%)
Ud: オリフィス孔径測定値の相対不確かさ(%)
UD: オリフィス配管径測定値の相対不確かさ(%)
Uε: オリフィス流量計の膨張補正係数の相対不確かさ(%)
UZN: 標準状態における圧縮係数の相対不確かさ(%)
UΔp: オリフィス流量計の差圧測定値の相対不確かさ(%)
UZ1: オリフィス流量計の上流側圧力取出断面における圧縮係数の
相対不確かさ(%)
Ux,i: モル分率測定値の相対不確かさ(%)
UT1: オリフィス流量計の上流側圧力取出断面における温度測定値
の相対不確かさ(%)
Up1: オリフィス流量計の上流側圧力取出断面における圧力測定値
の相対不確かさ(%)
xi: i番目の成分のモル分率
47
M 8010:2020
Ni: i番目の成分のモル質量(kg/mol)
NN: 標準状態におけるガスのモル質量(kg/mol)
β: オリフィス直径比
13.3 オリフィス流量計以外による計量値(標準状態における体積)の不確かさ
オリフィス流量計以外の流量計を用い,パルスを測定して計量した標準状態における体積の相対不確か
さの概算値は,式(89)で求める。各要素の不確かさは,表5を参考にして求める。
2
n
2
K0
2
ZM
2
ZN
2
TM
2
PM
V
000
10
I
U
U
U
U
U
U
+
+
+
+
+
≈
························· (89)
ここに,
In: 積算パルス数(pulses)
UV: 標準状態における体積計量値の相対不確かさ(%)
UPM: 圧力測定値の相対不確かさ(%)
UTM: 温度測定値の相対不確かさ(%)
UZN: 標準状態における圧縮係数の相対不確かさ(%)
UZM: 測定状態における圧縮係数の相対不確かさ(%)
UK0: Kファクタの相対不確かさ(%)
13.4 オリフィス流量計以外による計量値(標準状態における体積流量)の不確かさ
オリフィス流量計以外の流量計を用い,パルスを測定して計量した標準状態における体積流量の相対不
確かさの概算値は,式(90)で求める。各要素の不確かさは,表5を参考にして求める。
2
f
2
K0
2
ZM
2
ZN
2
TM
2
PM
qN
U
U
U
U
U
U
U
+
+
+
+
+
≈
···························· (90)
ここに, UqN: 標準状態における体積流量計量値の相対不確かさ(%)
UPM: 圧力測定値の相対不確かさ(%)
UTM: 温度測定値の相対不確かさ(%)
Uf: 周波数測定値の相対不確かさ(%)
UZN: 標準状態における圧縮係数の相対不確かさ(%)
UZM: 測定状態における圧縮係数の相対不確かさ(%)
UK0: Kファクタの相対不確かさ(%)
48
M 8010:2020
附属書A
(規定)
オリフィス板の前後に必要な直管長
(整流装置を用いない場合)
A.1 概要
表A.1に規定する継手をオリフィス板の上流側に取り付け,流出係数の不確かさを求めるためには,A.2
又はA.3による直管長の直管をオリフィス板の前後に取り付ける。表A.1に規定するバルブは,呼び径が
これを取り付ける直管と同じで,全開したときの段差が8.2.4.7及び8.2.4.8で許容する大きさを超えるも
のである。
注記 フランジを用いた配管接続に関しては8.2.4.7〜8.2.4.11を,全開したバルブの段差が8.2.4.7及
び8.2.4.8で規定する許容段差以下の場合には 8.2.4.3を参照。
A.2 継手が1個だけの場合
表A.1に規定する継手の1個だけをオリフィス板の上流側に取り付ける場合には,次のa)〜d)による。
ただし,この継手に流入する流れは,8.2.2の条件を満足しなければならない。また,表A.1に規定する2
個のベンドの組合せは1個の継手として扱い,2個の単体ベンドとして扱うことはできない。
注記 この継手の上流側条件は,通常,継手の上流側に十分に長い直管があることを前提とする。
a) 必要直管長 オリフィス板の上流側及び下流側の直管を,表A.1のA列又はB列の値にD0を乗じた
長さ以上とする。A列又はB列のいずれかを使用するかによって,不確かさが異なる[b)〜d)及び図
A.1参照]。
ここに規定する直管長は必要となる最小値であり,校正など不確かさを最小とする必要がある場合
には,規定の必要直管長の2倍以上の長さをもつ直管を用いることが望ましい。
49
M 8010:2020
表A.1−オリフィス板の上流側に継手が1個だけある場合のオリフィス板前後に必要となる最小の必要直管長
単位 D0
−
上流側
下流側
90°ベンド
・90°ティー
単体
・マイタ
90°ベン
ド
45°ベンド
同心収縮管
同心拡大管
全開した
バルブi)
段差
温度計ポケット
又はウェルc)
・第2欄〜第
11欄の継
手
・密度計ポケ
ット
・単体
・任意平面上
で接続し
た2個でS
>30D0の
ものa)
同一平面上で接続した
2個(S字形)
互いに垂直な平面上で接続
した2個
・単体
・同一平面上
で接続し
た2個(S
字形)でS
≧2D0の
ものa)
・長さが
1.5D0
〜
3D0で配
管直径が
2D0から
D0に収縮
するもの
・長さが1D0
〜2D0で
配管直径
が0.5D0か
らD0に拡
大するも
の
・フルボアボ
ールバル
ブ
・仕切弁
・軸対称で配
管断面積
の減少
・直径が
0.03D0以
下のもの
d)
・30D0≧S>
10D0のも
のa)
・S≦10D0の
ものa)
・30D0≧S≧
5D0のも
のa)
・S<5D0の
ものa),b)
第1欄
第2欄
第3欄
第4欄
第5欄
第6欄
第7欄
第8欄
第9欄
第10欄
第11欄
第12欄
第13欄
第14欄
オリフィス
直径比β
A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f) A列e) B列f)
β≦0.20
6
3
10
g)
10
g)
19
18
34
17
3
g)
7
g)
5
g)
6
g)
12
6
30
15
5
3
4
2
0.20<β≦
0.40
16
3
10
g)
10
g)
44
18
50
25
9
3
30
g)
5
g)
12
8
12
6
30
15
5
3
6
3
0.40<β≦
0.50
22
9
18
10
22
10
44
18
75
34
19
9
30
18
8
5
20
9
12
6
30
15
5
3
6
3
0.50<β≦
0.60
42
13
30
18
42
18
44
18
65h)
25
29
18
30
18
9
5
26
11
14
7
30
15
5
3
7
3.5
0.60<β≦
0.67
44
20
44
18
44
20
44
20
60
18
36
18
44
18
12
6
28
14
18
9
30
15
5
3
7
3.5
0.67<β≦
0.75
44
20
44
18
44
22
44
20
75
18
44
18
44
18
13
8
36
18
24
12
30
15
5
3
8
4
注記1 表による直管長は,オリフィス板の上流側又は下流側に取り付けられた各継手とオリフィス板との間に必要な直管長(D0に対する直径比で表す)の最小値である。
注記2 ベンドの必要直管長は,ほとんどの場合において,曲率半径が1.5D0のベンドを用いて決定されたことに注意する。
注a)
ベンド間隔Sは,上流側ベンドの湾曲部の最下流端から下流側ベンドの湾曲部の最上流端までの距離である。
b)
この取付方法はあまり推奨されず,可能であれば整流装置を使用する。
c)
温度ポケット及び温度センサの取付けは,他の継手の上流側の必要直管長に影響しない。
d)
温度ポケット及び温度センサの外径が0.03D0より大きく0.13D0 以下の場合,A列及びB列の数値をそれぞれ20及び10にする。しかしながら,そのような取付けは望ましくない。
e)
A列は,“ゼロ付加不確かさ”値に対応した長さである[A.2 b) 参照]。
f)
B列は,“0.5 %付加不確かさ”値に対応した長さである[A.2 c) 参照]。
g)
B列の数値はない。
h)
S<2D0でReD>2×106のとき,95とする。
i)
全開したバルブの段差が8.2.4.7及び8.2.4.8で規定する許容段差以下の場合,これを継手として附属書Aでは扱わず,8.2.4.7及び8.2.4.8による。
11
M
8
0
1
0
:
2
0
2
0
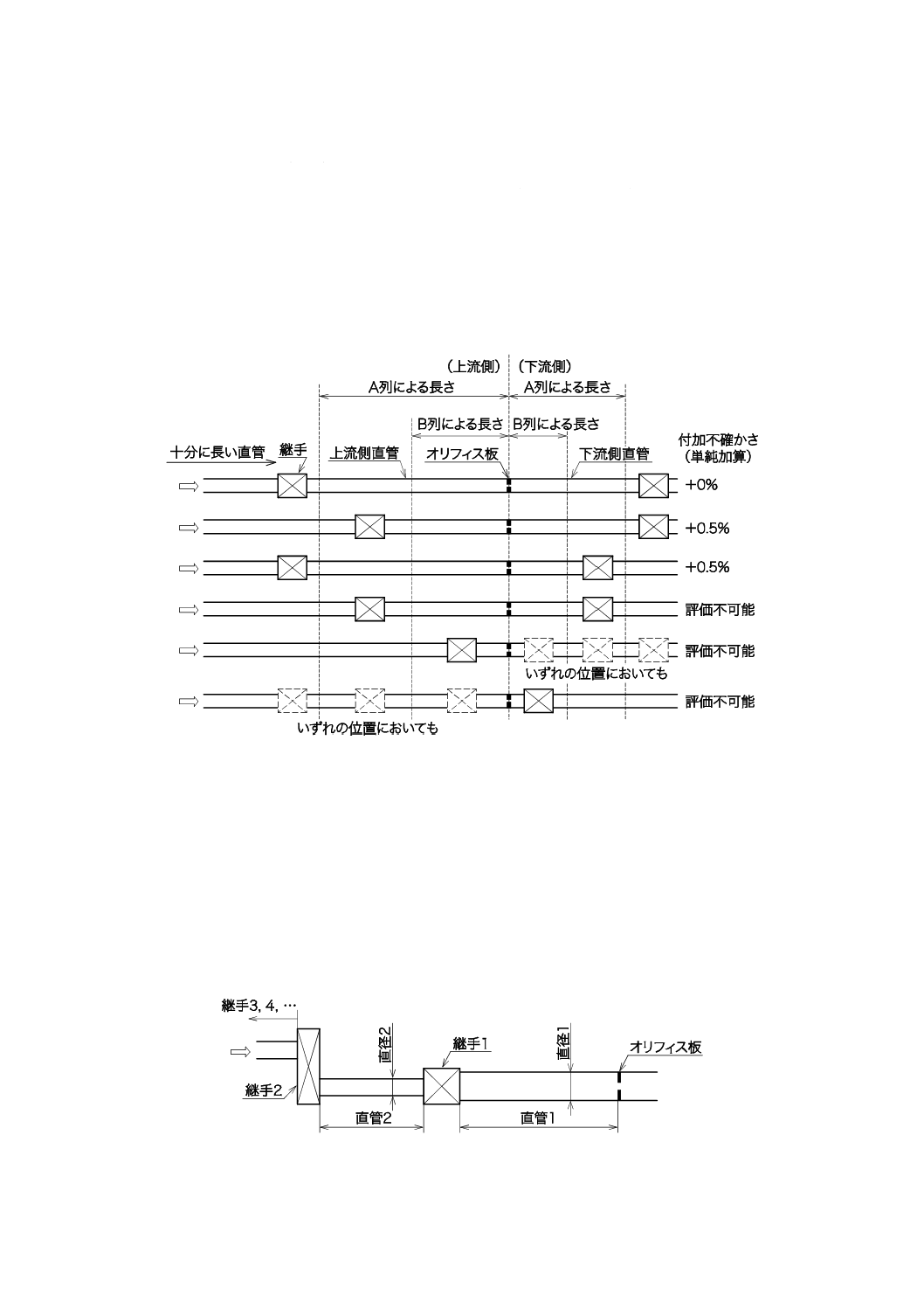
50
M 8010:2020
b) 付加不確かさのない設置方法 オリフィス板の上流側直管及び下流側直管の双方を,共に表A.1のA
列の長さ以上とした場合,流出係数の不確かさは8.4.1による。
c) 付加不確かさがある設置方法 オリフィス板の上流側直管又は下流側直管の一方が表A.1のA列の長
さ未満で,かつ,B列の長さ以上であり,他方がA列の長さ以上の場合,流出係数の不確かさは,8.4.1
で求めた値に0.5 %を単純加算したものとする。
d) 不確かさが評価できない設置方法 オリフィス板の上流側及び下流側直管の一方が表A.1のB列の長
さ未満の場合,及び両方の直管が共にA列の長さ未満の場合には,8.4.1によって流出係数の不確かさ
を求めることはできない。
注記 継手は表A.1に含まれるものだけである。
図A.1−表A.1による直管長の組合せの付加不確かさ
A.3 複数個の継手を用いる場合
表A.1に規定する継手の2個以上を直列に接続してオリフィス板の上流側に取り付ける場合,次のa)〜
h)による。このとき,表A.1に規定する第8欄(45°ベンド)以外の2個のベンドの組合せは1個の継手
として扱い,2個の単体ベンドとして扱うことはできない。
オリフィス板に最も近い継手を継手1,その次に近いものを継手2,オリフィス板と継手1とを接続する
直管を直管1,継手1と継手2とを接続する直管を直管2とする(図A.2参照)。
図A.2−複数の継手の直列接続
51
M 8010:2020
a) 直管1の長さ 直径1の直管に継手1を1個だけ取り付ける場合で,使用するオリフィス板のオリフ
ィス直径比において必要となる直管長を表A.1によって求め,直管1はそれ以上の長さとする。
b) 直管2の長さ 直径2の直管に継手2を1個だけ取り付ける場合で,0.67のオリフィス直径比におい
て必要となる直管長を表A.1によって求め,直管2はその半分以上の長さとする。
注記 オリフィス板の実際のオリフィス直径比にかかわらず,オリフィス直径比を0.67として求め
ることに注意する。
c) 個々の継手とオリフィス板との距離 継手が複数個ある場合の個々の継手に関し,直管1にそれらを
1個だけ取り付ける場合で,使用するオリフィス板のオリフィス直径比において必要となる直管長を
表A.1によって求め,それぞれの継手の下流端とオリフィス板との間隔を,それぞれに関して求めた
必要直管長以上とする。このとき,個々の継手の下流端とオリフィス板との間隔は,配管の中心軸に
沿ってはかる。
d) 付加不確かさ a)及びb)において,直管1及び直管2の直管長を共に表A.1のA列によって求めた場
合,付加不確かさをゼロとし,流出係数の不確かさは8.4.1による。a)及びb)において,直管1及び直
管2の直管長の一方をA列,他方をB列によって求めた場合,流出係数の不確かさは,8.4.1で求め
た値に0.5 %を単純加算したものとする。c)において,表A.1のB列の範囲に入る継手が1個でもある
場合,流出係数の不確かさは,8.4.1で求めた値に0.5 %を単純加算したものとする。ただし,複数個
の継手がB列の範囲に入っても単純加算は1回だけとし,また,a)及びb)の条件で0.5 %の付加不確
かさが発生する場合には,c)の条件による付加不確かさはゼロとする。
注記 これらのいかなる場合においても,付加不確かさの総計は,0 %又は0.5 %のいずれかである。
e) 継手1がフルボアボールバルブの場合 a)〜c)による直管において継手2とオリフィス板との間隔を
維持したまま,フルボアボールバルブを継手2の出口面の直下に移動してもよい[図A.3 b)参照]。
f)
継手2がベンドの組合せであるときのSの条件 継手2がベンドの組合せである場合(表A.1の第3
欄〜第6欄及び第8欄),ベンド間隔Sの条件は,D0ではなくベンド自身の直径を用いて判断する。
g) 継手2の上流条件 継手2の上流側には任意の継手を任意の位置に取り付けてよい。
h) 下流側直管 オリフィス板の下流側直管の長さは,表A.1の第14欄による。
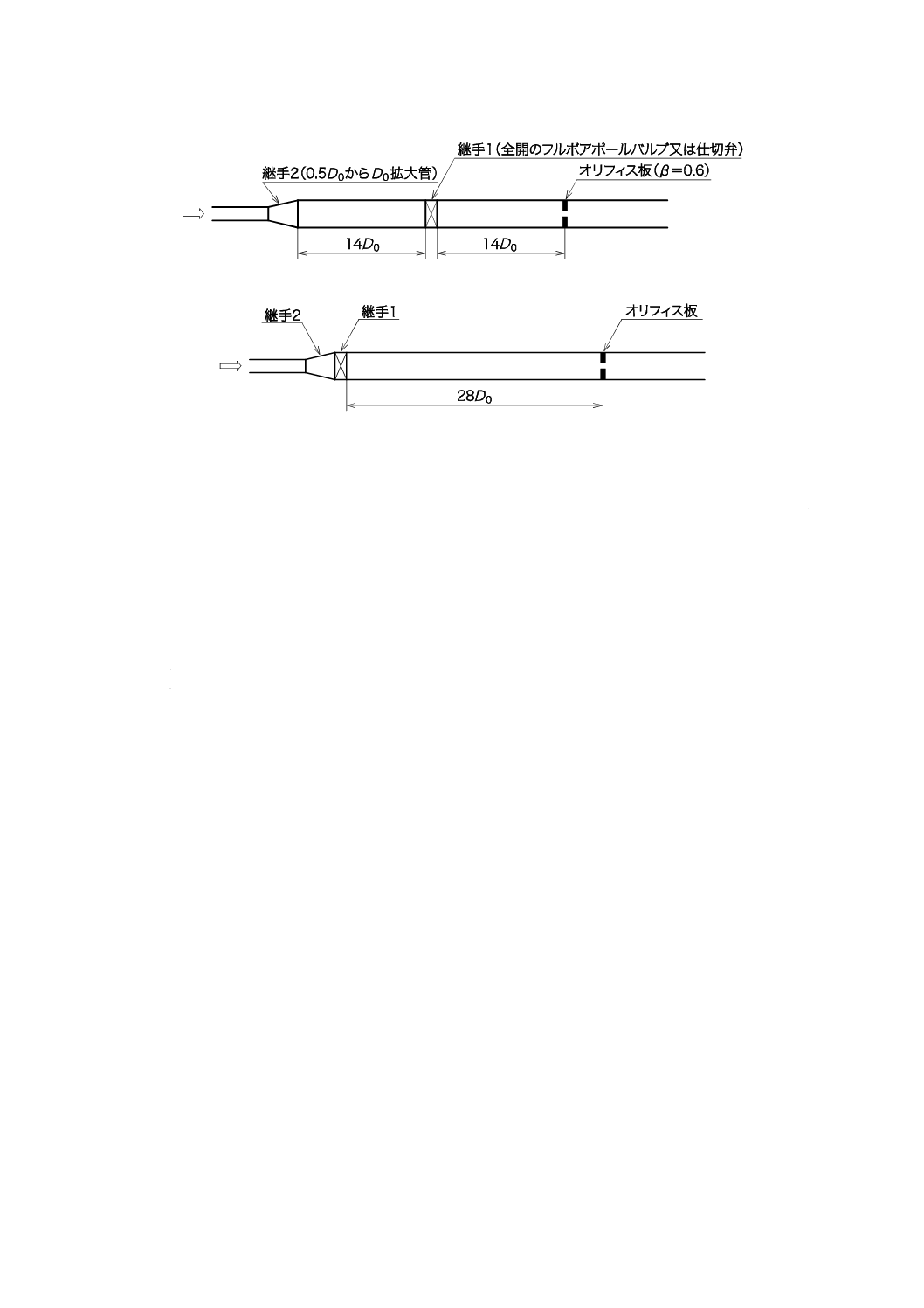
52
M 8010:2020
a) フルボアボールバルブを表A.1に従って設置する場合
b) フルボアボールバルブを継手2の直下に移動する場合
注記1 図A.3 a)の配置は,次のとおりに導かれる。
− 表A.1において,“フルボアボールバルブ(第11欄)”では,β=0.60でのA列の値が14のため,
A.3 a)によって,フルボアボールバルブとオリフィス板との間隔は14D0となる。
− 表A.1において,“0.5D0からD0拡大管(第10欄)”では,β=0.67でのA列の値が28のため,A.3 b)
によって,拡大管とフルボアボールバルブとの間隔は14D0となる。
− これらは,同時にA.3 c)も満たしている。このとき,全ての直管長がA列の範囲内となるため,A.3
d)によって,付加不確かさは発生しない。
なお,フルボアボールバルブが8.2.4.8の条件を満たす場合には,これを直管の一部とみなすため,図
A.3の配置に従う必要はない[表A.1の注i)参照]。
注記2 図A.3 b)は,A.3 e)によって,拡大管とオリフィス板との間隔を維持したまま,フルボアボールバルブを
拡大管出口に直接に取り付けたものである。
注記3 A.3 g)によって,拡大管に流入する流れには条件がないため,拡大管の上流側には何を取り付けても問題
ない。
図A.3−継手2が0.5D0からD0拡大管で継手1をフルボアボールバルブとする配置(β=0.6の場合)
53
M 8010:2020
附属書B
(規定)
オリフィス板の前後に必要な直管長
[19管束管状式整流装置(1998)を用いる場合]
B.1
概要
フランジ以外の継手をオリフィス板の上流側に取り付け,B.2による19管束管状式整流装置(1998)を
用いて整流する場合,流出係数の不確かさを求めるために必要となる直管長は,任意の継手に有効な設置
法,単一継手の詳細設置法,又は複数継手の詳細設置法によって求める。19管束管状式整流装置(1998)
の圧力損失係数Kは,およそ0.75である。
注記1 19管束管状式整流装置(1998)は,JIS Z 8762-2:2007において管状式整流装置と呼ばれるも
のと同一である。
注記2 任意の継手に有効な設置法はβ≦0.67の場合に適用できるが,詳細設置法は,β>0.67であっ
ても適用でき,任意の継手に有効な設置法によるよりも必要直管長を短くできる。
注記3 フランジを用いた配管接続に関しては8.2.4.7〜8.2.4.11を,全開したバルブの段差が8.2.4.7
及び8.2.4.8で規定する許容段差以下の場合には 8.2.4.3を参照。
B.2
構造
19管束管状式整流装置(1998)の構造は,次に従う(図B.1参照)。
a) 呼び径をオリフィス配管に一致させる。
b) 19本の円筒小管束を互いに平行に束ね,配管に堅ろう(牢)に固定する。
c) 小管束と管壁との間で発生する旋回流を抑えるため,小管束の最大外径Dfを0.95D0≦Df≦D0とする。
d) 小管の長さLtは2D0≦Lt≦3D0とするが,2D0に近い方が望ましい。
e) 19管束管状式整流装置(1998)で使用する全ての小管は,肉厚を0.025D0未満としてなるべく薄くし,
それぞれの表面粗さ,外径及び肉厚は同じとする。
f)
全ての小管の両端面は,内側を面取りする。
g) 各小管は,少なくとも両端の接触点で互いに溶接し,小管束を頑丈にする。
h) 各小管は互いに平行とし,かつ,取り付ける配管の配管軸に対しても平行とする。
i)
小管束を配管と同軸に取り付けるために,配管軸に平行な小さい突出部又は小さい棒としたセンタリ
ングスペーサを数箇所に設けてもよい。
j)
小管束を配管内の指定場所に堅ろう(牢)に固定するとき,各小管を変形させないようにする。
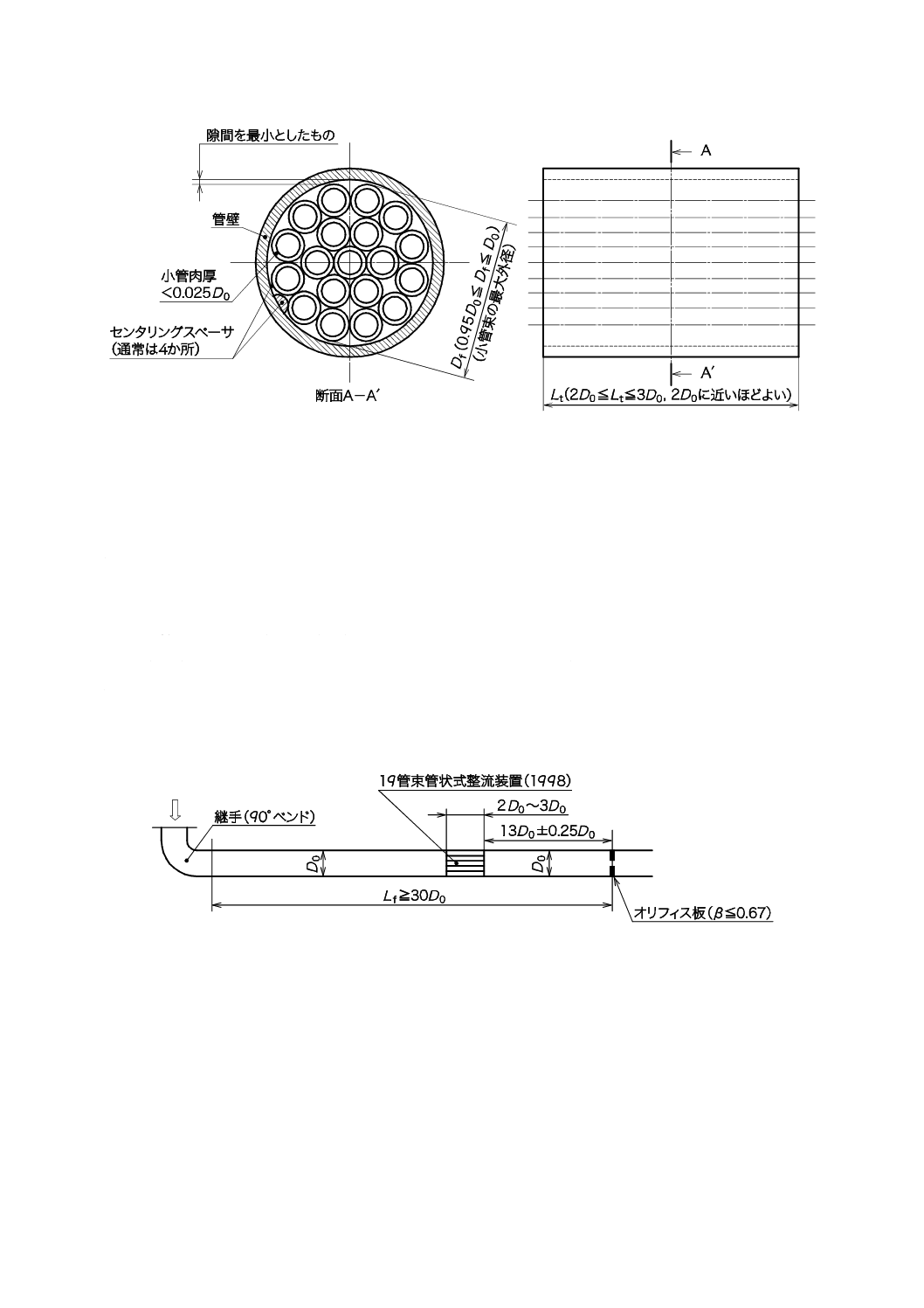
54
M 8010:2020
図B.1−19管束管状式整流装置(1998)の構造
B.3
設置法
B.3.1 任意の継手に有効な設置法
任意の継手に有効な設置法(図B.2参照)は,次による。
a) β≦0.67とする。
b) 使用する直管は,オリフィス配管と同じ呼び径のものとする。
c) 継手の下流端とオリフィス板との間隔Lfを30D0以上とし,継手と19管束管状式整流装置(1998)と
を直管で接続する(図B.2参照)。
d) 19管束管状式整流装置(1998)とオリフィス板とを接続する直管の長さを,13D0±0.25D0とする。
e) 流出係数の不確かさは,8.4.1に従って求めた値とする。
f)
継手の上流側には何を取り付けてもよい。
注記 B.3.2によれば,更に広い範囲に整流装置を取り付けることができる場合がある。
図B.2−継手を90°ベンドとした場合の19管束管状式整流装置(1998)の設置例
B.3.2 単一継手の詳細設置法
B.3.2.1 一般
継手の下流端とオリフィス板との間隔Lfを式(B.1)及び式(B.2)の二つの範囲に分け,表B.1のA列又はB
列の値にD0を乗じた長さを,オリフィス板と19管束管状式整流装置(1998)との間の直管に必要な長さ
の範囲とする。使用する直管の呼び径はオリフィス配管と一致させる。表B.1に規定する2個のベンドの
組合せは1個の継手として扱い,2個の単体ベンドとして扱うことはできない。オリフィス板の下流側の
直管に必要となる長さは,表A.1の第14欄による。
注記 表B.1が規定する必要直管長は,最小長さではなく,許される長さの範囲であることに注意す
55
M 8010:2020
る。
30D0>Lf≧18D0 ······································································ (B.1)
Lf≧30D0 ··············································································· (B.2)
ここに,
D0: オリフィス配管径の測定値(mm)
Lf: 継手とオリフィス板との間隔(mm)
B.3.2.2 “任意の継手”の欄を用いる単一継手の詳細設置法
“任意の継手”の欄を用いる単一継手の詳細設置法は,次による。
a) いかなる継手にも適用できる。
b) 継手に流入する流れに条件はない。
c) 表B.1の“任意の継手”の欄を用いて直管長を決定する。
d) 使用する直管の呼び径はオリフィス配管と一致させる。
e) 流出係数の不確かさは,A列を用いた場合には8.4.1で求めた値とし,B列を用いた場合には8.4.1で
求めた値に0.5 %を単純加算したものとする。
B.3.2.3 “任意の継手”の欄以外を用いる単一継手の詳細設置法
“任意の継手”の欄以外を用いる単一継手の詳細設置法は,次による。
a) 表B.1の“任意の継手”の欄以外の欄に規定する継手に適用できる。
b) 継手に流入する流れは,8.2.2の条件を満たしていなければならない。
注記 この継手の上流側条件は,通常,継手の上流側に十分に長い直管があることを前提とする。
c) 表B.1を用いて直管長を決定する。
d) 使用する直管の呼び径はオリフィス配管と一致させる。
e) 表B.1のA列を用いる場合には,流出係数の不確かさは8.4.1で求めた値とするが,B列を用いる場
合には,付加不確かさが発生するか,又は不確かさが評価できない(B.3.2.3.1〜B.3.2.3.3参照)。
f)
継手の下流端とオリフィス板との間隔Lfは,ベンド又はティーの湾曲部の最下流端,収縮管又は拡大
管の円すい部又は湾曲部の最下流端から測定する。
注記 表B.1で空欄になっている条件では,19管束管状式整流装置(1998)を使用しないほうがよ
い。その条件ではLfを増やす必要があり,かつ,βを小さくしなければならない場合がある。

56
M 8010:2020
表B.1−19管束管状式整流装置(1998)の下流端とオリフィス板との間に必要な直管長の範囲
単位 D0
−
単体の90°ベンドb)
任意平面上で接続した2個の
90°ベンドb)(2D0≧S)a)
単体の90°ティー
任意の継手(フランジを除く)
30>Lf≧18
Lf≧30
30>Lf≧18
Lf≧30
30>Lf≧18
Lf≧30
30>Lf≧18
Lf≧30
第1欄
第2欄
第3欄
第4欄
第5欄
第6欄
第7欄
第8欄
第9欄
オリフィス
直径比β
A列c)
B列d)
A列c)
B列d)
A列c)
B列d)
A列c)
B列d)
A列c)
B列d)
A列c)
B列d)
A列c)
B列d)
A列c)
B列d)
β≦0.2
5〜14.5
1〜n e)
5〜25
1〜n e)
5〜14.5
1〜n e)
5〜25
1〜n e)
5〜14.5
1〜n e)
1〜25
1〜n e)
5〜11
1〜n e)
5〜13
1〜n e)
0.2<β≦0.4
5〜14.5
1〜n e)
5〜25
1〜n e)
5〜14.5
1〜n e)
5〜25
1〜n e)
5〜14.5
1〜n e)
1〜25
1〜n e)
5〜11
1〜n e)
5〜13
1〜n e)
0.4<β≦0.5
11.5〜14.5
3〜n e)
11.5〜25
3〜n e)
9.5〜14.5
1〜n e)
9〜25
1〜n e)
11〜13
1〜n e)
9〜23
1〜n e)
f), g)
3〜n e)
11.5〜14.5
3〜n e)
0.5<β≦0.6
12〜13
5〜n e)
12〜25
5〜n e)
13.5〜14.5
6〜n e)
9〜25
1〜n e)
f), h)
7〜n e)
11〜16
1〜n e)
f)
7〜n e)
12〜16
6〜n e)
0.6<β≦0.67
13
7〜n e)
13〜16.5
7〜n e)
13〜14.5
7〜n e)
10〜16
5〜n e)
f)
8〜n e)
11〜13
6〜n e)
f)
8〜n e)
13
7〜n−
1.5 e)
0.67<β≦0.75
14
8〜n e)
14〜16.5
8〜n e)
f)
9.5〜n e)
12〜12.5
8〜n e)
f)
9〜n e)
12〜14
7〜n e)
f)
9.5
f)
8〜22
推奨i)
13
β≦0.67
13
β≦0.75
14〜16.5
β≦0.75
14〜16.5
β≦0.75
13.5〜14.5
β≦0.67
13.5〜14.5
β≦0.75
12〜12.5
β≦0.75
12〜12.5
β≦0.75
13
β≦0.54
13
β≦0.75
12〜13
β≦0.75
12〜13
β≦0.75
9.5
β≦0.46
9.5
β≦0.75
13
β≦0.67
13
β≦0.75
注記 表による直管長は,個々の継手がオリフィス板から指定位置(オリフィス板から上流側にLfの位置)に設置された場合,整流装置の下流端とオリフィス板との間に必要となる直管長さの範囲であり,最小長
さではないことに注意する。
注a) ベンド間隔Sは,上流側ベンドの湾曲部の最下流端から下流側ベンド湾曲部の最上流端までの距離である。
b) ベンドの曲率半径は1.5D0であることが望ましい。
c)
A列は,“ゼロ付加不確かさ”値に対応した長さである(B.3.2.3.1参照)。
d) B列は,“0.5 %付加不確かさ”値に対応した長さである(B.3.2.3.2参照)。
e) nは,整流装置に最も近い継手の湾曲部又は円すい部の下流端と整流装置の上流端との間の直管長を1D0としたときの整流装置の下流端とオリフィス板との間の直管長(単位D0とした値)であり,上限がn
の場合には整流装置の上流直管長を1D0まで短くすることができる。ただし,整流装置の下流端とオリフィス板との間の直管長が規定を満足するのであれば,整流装置の上流直管長は2.5D0以上とすること
が望ましい。
f)
このLfの範囲では,整流装置を用いることはできない。
g) β=0.46の場合には9.5としてもよい。
h) β=0.54の場合には13としてもよい。
i)
“推奨”に示す値は,指定のβの範囲で使用可能である。
11
M
8
0
1
0
:
2
0
2
0
57
M 8010:2020
B.3.2.3.1 付加不確かさのない直管長
オリフィス板と19管束管状式整流装置(1998)とを接続する直管の長さを表B.1のA列の範囲内とし,
かつ,オリフィス板の下流側の直管の長さを表A.1の第14欄A列の長さ以上のとき,付加不確かさは生
じない。このとき,流出係数の不確かさは8.4.1による値とする。
B.3.2.3.2 付加不確かさがある直管長
オリフィス板と19管束管状式整流装置(1998)とを接続する直管の長さが,次のいずれの場合でも,付
加不確かさが生じる。流出係数の不確かさは,いずれの場合でも,8.4.1による値に0.5 %を単純加算した
ものとする。
a) 表B.1のA列の範囲外でB列の範囲内にあり,かつ,オリフィス板の下流側の直管長が表A.1の第
14欄A列の長さ以上の場合。
b) 表B.1のA列の範囲内にあり,かつ,オリフィス板の下流側の直管長が表A.1の第14欄A列の長さ
未満であって第14欄B列の長さ以上の場合。
B.3.2.3.3 不確かさが評価できない直管長
次のいずれの場合でも,流出係数の不確かさを求めることができない。
a) オリフィス板と19管束管状式整流装置(1998)とを接続する直管の長さが,表B.1のB列の最小長
さより短い場合。
b) オリフィス板の下流側の直管の長さが,表A.1の第14欄B列の長さより短い場合。
c) オリフィス板と19管束管状式整流装置(1998)とを接続する直管の長さが,表B.1のA列の範囲外
であり,かつ,オリフィス板の下流側の直管の長さが,表A.1の第14欄A列の長さより短い場合。
B.3.3 複数継手の詳細設置法
複数継手の詳細設置法は,次による(図B.3参照)。
a) 表B.1の“任意の継手”の欄以外の欄に規定する継手に適用する。
b) 使用する直管の呼び径はオリフィス配管と一致させる。
c) オリフィス板に最も近い継手を継手1,その次に近い継手を継手2とし,B.3.2に従って継手1を設置
する。
d) 継手2を継手1の15D0以上上流側に設置する。
e) 継手2に流入する流れに条件はない。
f)
流出係数の不確かさは,B.3.2.3.1〜B.3.2.3.3に従って求める。
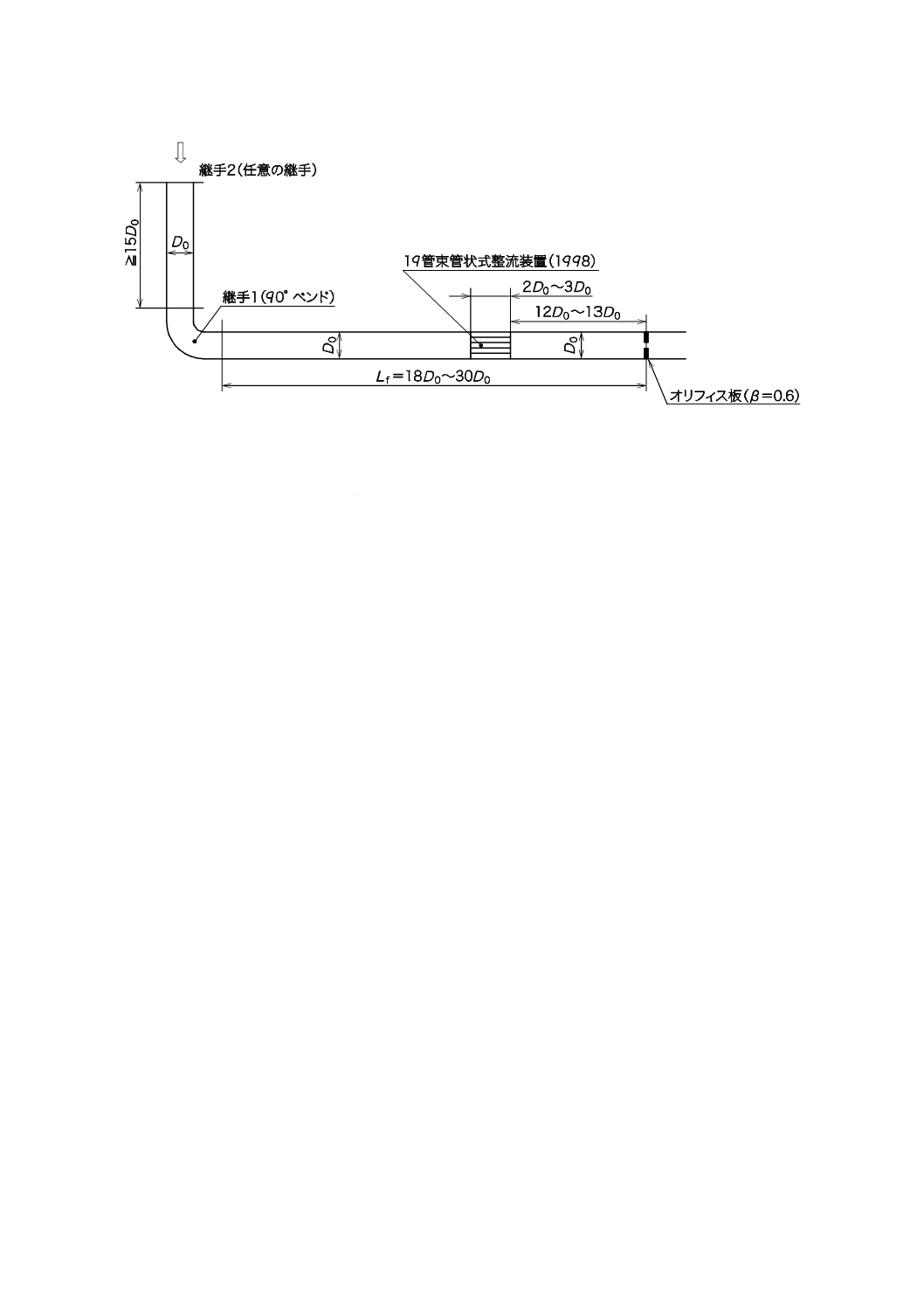
58
M 8010:2020
注記 継手1を90°ベンドとした場合の複数継手と19管束管状式整粒装置(1998)の配置は,次のとおりに導かれる。
− 表B.1で単体の90°ベンドのLf=18D0〜30D0(第2欄)におけるβ=0.6でのA列の値が12〜13であるた
め,B.3.3 c)によって,19管束管状式整流装置(1998)の位置はオリフィス板から12D0〜13D0の範囲となる。
− B.3.3 d)によって,継手2は継手1から直管で15D0以上離れた位置となる。
− B.3.3 e)によって,継手2の上流側には何を接続しても問題ない。
− B.3.3 f)によって,付加不確かさは,表B.1のA列を使用したため,ゼロとなる。
図B.3−継手1を90°ベンドとした場合の複数継手と19管束管状式整流装置(1998)の設置
(β=0.6,Lf=18D0〜30D0,付加不確かさゼロの場合)
59
M 8010:2020
附属書C
(規定)
オリフィス板前後に必要となる直管長
(ザンカ式整流板を用いる場合)
C.1 概要
フランジ以外の継手をオリフィス板の上流側に取り付け,C.2によるザンカ式整流板を用いて整流する
場合,流出係数の不確かさを求めるために必要となる直管長を,C.3によって求める。継手に流入する流
れに条件はなく,いかなる継手であっても流出係数の不確かさは8.4.1によって求めた値となる。圧力損
失係数Kは,およそ3である。ザンカ式整流板は,ザンカ式整流装置から派生した整流装置であるが,両
者は異なる構造をもつため,区別しなければならない。
注記1 ザンカ式整流装置は,ザンカ式整流板と同じ前面構造をもつが,前面板が薄く,その後方に
格子状のハニカムがある(JIS Z 8762-1:2007の附属書C,及びJIS Z 8762-2:2007の6.3.3.2を
参照)。
注記2 フランジを用いた配管接続に関しては8.2.4.7〜8.2.4.11を,全開したバルブの段差が8.2.4.7
及び8.2.4.8で規定する許容段差以下の場合には8.2.4.3を参照。
C.2 構造
ザンカ式整流板は,図C.1に規定する32個の孔をもち,板厚をD0/8とした1枚の板とする。
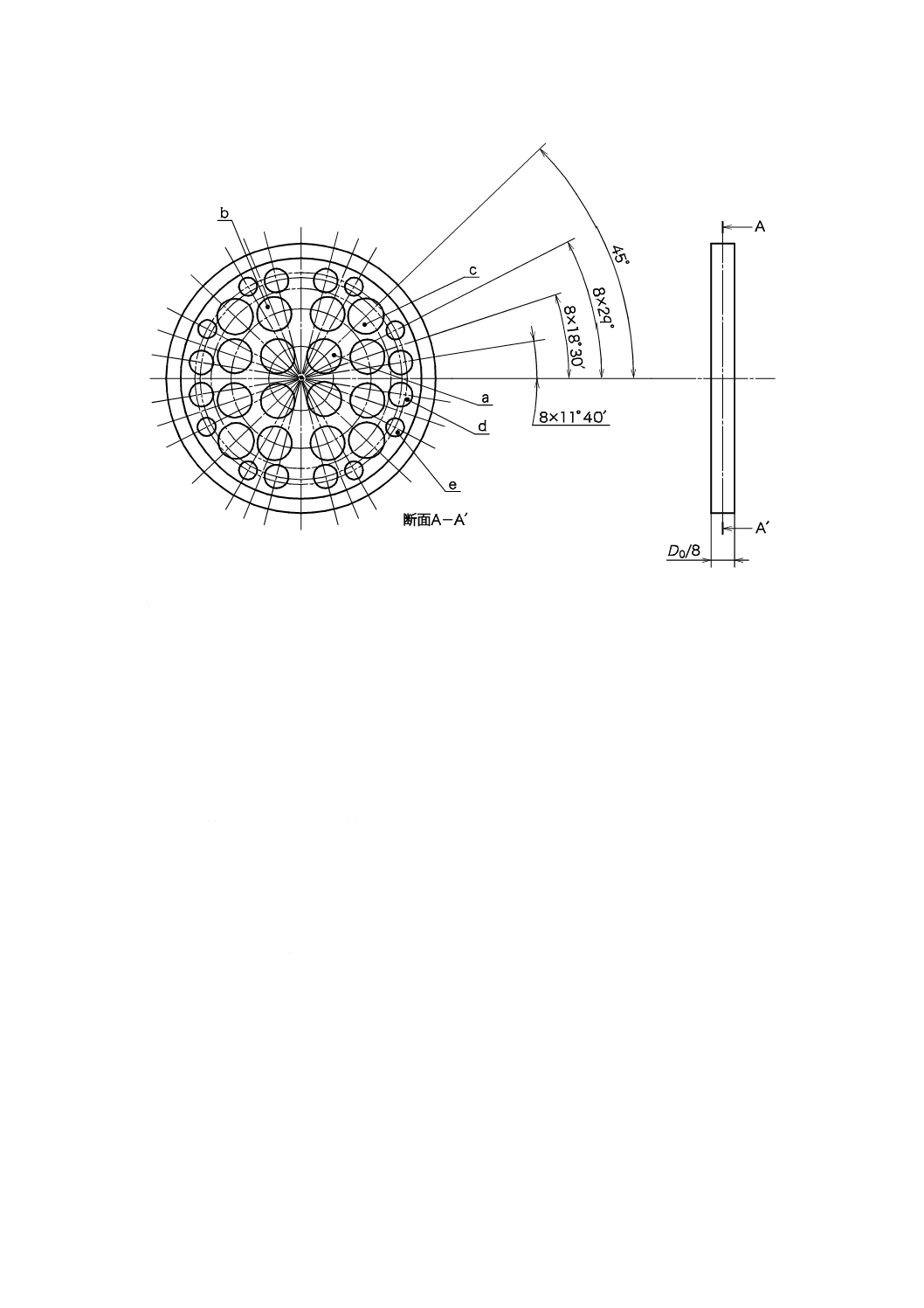
60
M 8010:2020
記号
a
4個の孔の孔径は0.141D0で,ピッチ円の直径は0.25D0
b
8個の孔の孔径は0.139D0で,ピッチ円の直径は0.56D0
c
4個の孔の孔径は0.136 5D0で,ピッチ円の直径は0.75D0
d
8個の孔の孔径は0.11D0で,ピッチ円の直径は0.85D0
e
8個の孔の孔径は0.077D0で,ピッチ円の直径は0.90D0
図C.1−ザンカ式整流板
C.3 設置
a) β≦0.67とする。
b) 使用する直管は,オリフィス配管と同じ呼び径のものとする。
c) Lf≧17D0とする(図C.2参照)。Lfは,継手がベンド若しくはベンドの組合せ又はティーである場合に
は,継手の湾曲部の下流端までの間隔とし,収縮管又は拡大管の場合には,収縮管又は拡大管の湾曲
部又は円すい部の下流端までの間隔とする。
d) オリフィス板とザンカ式整流板とを接続する直管の長さをLsとし,7.5D0≦Ls≦Lf−8.5D0とする。
e) 継手に流入する流れに条件はない。
f)
いかなる継手であっても付加不確かさは発生しない。
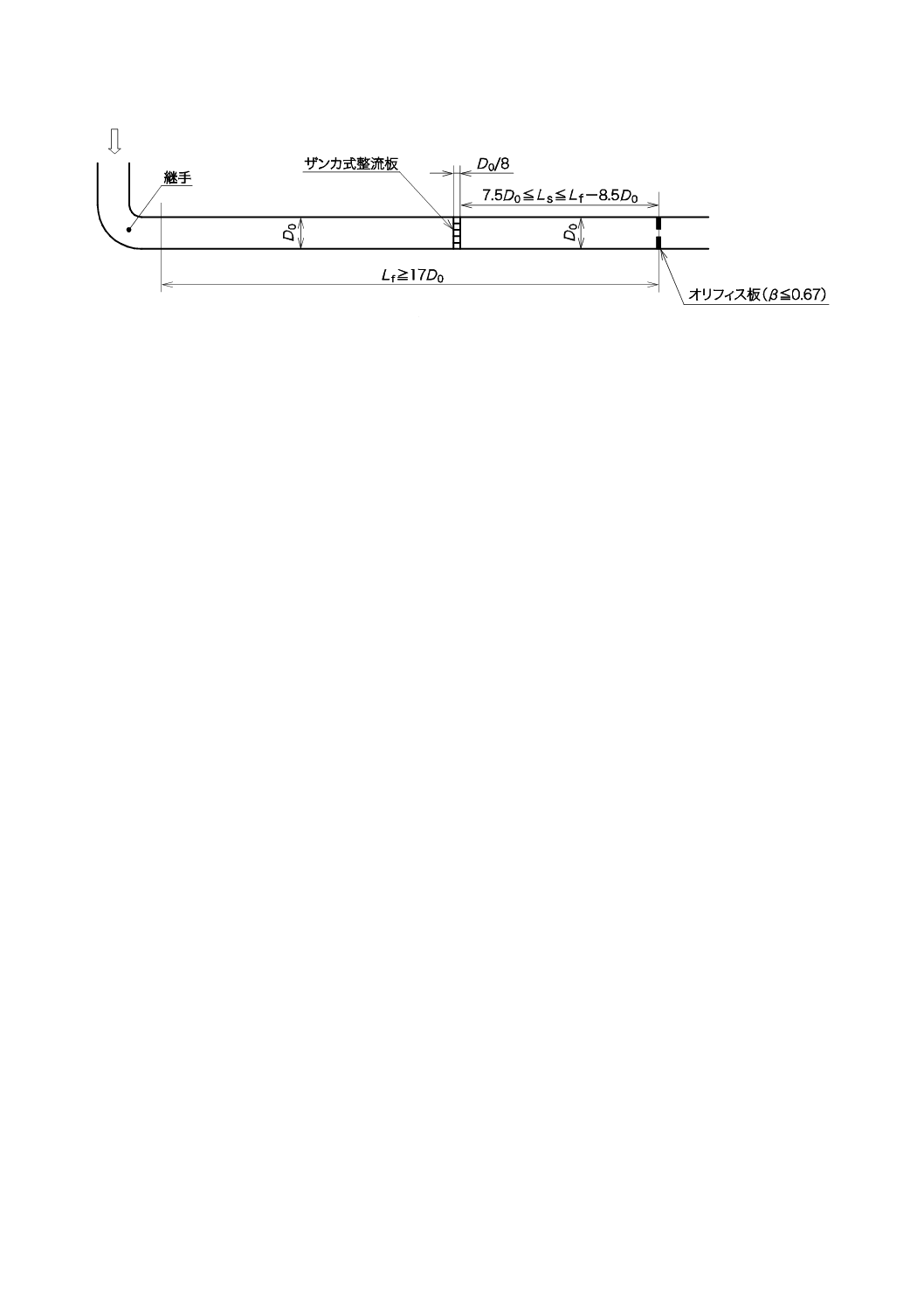
61
M 8010:2020
図C.2−ザンカ式整流板の取付け
62
M 8010:2020
附属書D
(参考)
オリフィス流量計の流出係数
D.1 コーナタップ
表D.1−コーナタップオリフィス流量計の流出係数Cd(D0≧71.12 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 6
0.599 0
0.598 0
0.597 6
0.597 2
0.597 0
0.596 9
0.596 6
0.596 5
0.596 4
0.596 4
0.596 4
0.12
0.601 4
0.599 5
0.598 3
0.597 9
0.597 5
0.597 3
0.597 1
0.596 8
0.596 6
0.596 5
0.596 5
0.596 5
0.14
0.602 1
0.600 0
0.598 7
0.598 2
0.597 7
0.597 5
0.597 3
0.596 9
0.596 8
0.596 6
0.596 6
0.596 6
0.16
0.602 8
0.600 5
0.599 1
0.598 5
0.598 0
0.597 8
0.597 6
0.597 1
0.596 9
0.596 8
0.596 8
0.596 8
0.18
0.603 6
0.601 1
0.599 5
0.598 9
0.598 3
0.598 1
0.597 8
0.597 4
0.597 1
0.597 0
0.597 0
0.596 9
0.20
0.604 5
0.601 7
0.600 0
0.599 3
0.598 7
0.598 4
0.598 1
0.597 6
0.597 4
0.597 2
0.597 2
0.597 1
0.22
0.605 3
0.602 3
0.600 5
0.599 8
0.599 1
0.598 7
0.598 5
0.597 9
0.597 6
0.597 4
0.597 4
0.597 4
0.24
0.606 2
0.603 0
0.601 0
0.600 2
0.599 5
0.599 1
0.598 8
0.598 2
0.597 9
0.597 7
0.597 6
0.597 6
0.26
0.607 2
0.603 8
0.601 6
0.600 7
0.599 9
0.599 6
0.599 2
0.598 6
0.598 2
0.598 0
0.597 9
0.597 9
0.28
0.608 3
0.604 6
0.602 2
0.601 3
0.600 4
0.600 0
0.599 7
0.599 0
0.598 6
0.598 3
0.598 2
0.598 1
0.30
0.609 5
0.605 4
0.602 9
0.601 9
0.601 0
0.600 5
0.600 1
0.599 4
0.598 9
0.598 6
0.598 5
0.598 4
0.32
0.610 7
0.606 3
0.603 6
0.602 6
0.601 6
0.601 1
0.600 6
0.599 8
0.599 3
0.599 0
0.598 8
0.598 7
0.34
0.612 0
0.607 3
0.604 4
0.603 3
0.602 2
0.601 7
0.601 2
0.600 3
0.599 8
0.599 3
0.599 2
0.599 1
0.36
0.613 5
0.608 4
0.605 3
0.604 0
0.602 9
0.602 3
0.601 8
0.600 8
0.600 2
0.599 7
0.599 6
0.599 4
0.38
0.615 1
0.609 6
0.606 2
0.604 9
0.603 6
0.603 0
0.602 4
0.601 3
0.600 7
0.600 1
0.599 9
0.599 8
0.40
0.616 8
0.610 9
0.607 2
0.605 8
0.604 4
0.603 7
0.603 1
0.601 9
0.601 2
0.600 6
0.600 3
0.600 1
0.42
0.618 7
0.612 2
0.608 3
0.606 7
0.605 2
0.604 4
0.603 8
0.602 5
0.601 7
0.601 0
0.600 7
0.600 5
0.44
0.620 7
0.613 7
0.609 4
0.607 7
0.606 1
0.605 2
0.604 5
0.603 1
0.602 2
0.601 4
0.601 1
0.600 8
0.46
0.622 8
0.615 2
0.610 6
0.608 7
0.607 0
0.606 1
0.605 3
0.603 7
0.602 7
0.601 9
0.601 5
0.601 2
0.48
0.625 1
0.616 9
0.611 8
0.609 8
0.607 9
0.606 9
0.606 1
0.604 3
0.603 3
0.602 3
0.601 9
0.601 5
0.50
0.627 6
0.618 6
0.613 1
0.610 9
0.608 8
0.607 8
0.606 9
0.605 0
0.603 8
0.602 7
0.602 2
0.601 8
0.51
0.628 9
0.619 5
0.613 8
0.611 5
0.609 3
0.608 2
0.607 3
0.605 3
0.604 0
0.602 9
0.602 4
0.601 9
0.52
0.630 2
0.620 4
0.614 4
0.612 1
0.609 8
0.608 7
0.607 7
0.605 6
0.604 3
0.603 0
0.602 5
0.602 0
0.53
0.631 6
0.621 3
0.615 1
0.612 6
0.610 3
0.609 1
0.608 0
0.605 9
0.604 5
0.603 2
0.602 6
0.602 1
0.54
0.633 0
0.622 3
0.615 8
0.613 2
0.610 8
0.609 5
0.608 4
0.606 1
0.604 7
0.603 3
0.602 7
0.602 1
0.55
0.634 4
0.623 2
0.616 5
0.613 8
0.611 2
0.609 9
0.608 8
0.606 4
0.604 9
0.603 4
0.602 8
0.602 2
0.56
−
0.624 2
0.617 2
0.614 3
0.611 7
0.610 3
0.609 1
0.606 6
0.605 0
0.603 5
0.602 8
0.602 2
0.57
−
0.625 2
0.617 9
0.614 9
0.612 1
0.610 7
0.609 5
0.606 9
0.605 2
0.603 6
0.602 8
0.602 2
0.58
−
0.626 2
0.618 5
0.615 5
0.612 6
0.611 1
0.609 8
0.607 0
0.605 3
0.603 6
0.602 8
0.602 1
0.59
−
0.627 2
0.619 2
0.616 0
0.613 0
0.611 4
0.610 1
0.607 2
0.605 4
0.603 6
0.602 8
0.602 0
0.60
−
0.628 2
0.619 8
0.616 5
0.613 4
0.611 7
0.610 3
0.607 3
0.605 4
0.603 5
0.602 7
0.601 9
0.61
−
0.629 2
0.620 5
0.617 0
0.613 7
0.612 0
0.610 6
0.607 4
0.605 4
0.603 4
0.602 5
0.601 7
0.62
−
0.630 2
0.621 1
0.617 5
0.614 0
0.612 3
0.610 8
0.607 5
0.605 4
0.603 3
0.602 3
0.601 4
0.63
−
0.631 2
0.621 7
0.617 9
0.614 3
0.612 5
0.610 9
0.607 5
0.605 2
0.603 0
0.602 1
0.601 1
0.64
−
0.632 1
0.622 2
0.618 3
0.614 5
0.612 6
0.611 0
0.607 4
0.605 1
0.602 8
0.601 7
0.600 7
0.65
−
0.633 1
0.622 7
0.618 6
0.614 7
0.612 7
0.611 0
0.607 3
0.604 8
0.602 4
0.601 3
0.600 2
0.66
−
0.634 0
0.623 2
0.618 9
0.614 8
0.612 8
0.611 0
0.607 1
0.604 5
0.602 0
0.600 8
0.599 7
0.67
−
0.634 8
0.623 6
0.619 1
0.614 9
0.612 7
0.610 8
0.606 8
0.604 1
0.601 4
0.600 2
0.599 0
0.68
−
0.635 7
0.623 9
0.619 3
0.614 9
0.612 6
0.610 6
0.606 4
0.603 6
0.600 8
0.599 5
0.598 3
0.69
−
0.636 4
0.624 2
0.619 3
0.614 7
0.612 4
0.610 4
0.605 9
0.603 0
0.600 1
0.598 7
0.597 4
0.70
−
0.637 2
0.624 4
0.619 3
0.614 5
0.612 1
0.610 0
0.605 3
0.602 3
0.599 2
0.597 8
0.596 4
0.71
−
0.637 8
0.624 5
0.619 2
0.614 2
0.611 7
0.609 4
0.604 6
0.601 4
0.598 2
0.596 7
0.595 3
0.72
−
0.638 3
0.624 4
0.618 9
0.613 8
0.611 1
0.608 8
0.603 8
0.600 5
0.597 1
0.595 5
0.594 0
0.73
−
0.638 8
0.624 3
0.618 6
0.613 2
0.610 4
0.608 0
0.602 8
0.599 3
0.595 8
0.594 2
0.592 6
0.74
−
0.639 1
0.624 0
0.618 1
0.612 5
0.609 6
0.607 1
0.601 6
0.598 0
0.594 3
0.592 6
0.591 0
0.75
−
0.639 4
0.623 6
0.617 4
0.611 6
0.608 6
0.606 0
0.600 3
0.596 5
0.592 7
0.590 9
0.589 2
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
63
M 8010:2020
D.2 D・D/2タップ
表D.2−D・D/2タップオリフィス流量計の流出係数Cd(D0≧71.12 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 3
0.598 7
0.597 7
0.597 3
0.596 9
0.596 7
0.596 6
0.596 3
0.596 2
0.596 1
0.596 1
0.596 0
0.12
0.601 0
0.599 1
0.597 9
0.597 5
0.597 1
0.596 9
0.596 7
0.596 4
0.596 2
0.596 1
0.596 1
0.596 1
0.14
0.601 6
0.599 5
0.598 2
0.597 7
0.597 2
0.597 0
0.596 8
0.596 5
0.596 3
0.596 2
0.596 1
0.596 1
0.16
0.602 3
0.600 0
0.598 5
0.598 0
0.597 4
0.597 2
0.597 0
0.596 6
0.596 4
0.596 2
0.596 2
0.596 2
0.18
0.602 9
0.600 4
0.598 9
0.598 2
0.597 7
0.597 4
0.597 1
0.596 7
0.596 5
0.596 3
0.596 3
0.596 3
0.20
0.603 7
0.600 9
0.599 2
0.598 5
0.597 9
0.597 6
0.597 4
0.596 9
0.596 6
0.596 4
0.596 4
0.596 4
0.22
0.604 4
0.601 5
0.599 6
0.598 9
0.598 2
0.597 9
0.597 6
0.597 1
0.596 8
0.596 6
0.596 5
0.596 5
0.24
0.605 3
0.602 1
0.600 1
0.599 3
0.598 5
0.598 2
0.597 9
0.597 3
0.597 0
0.596 7
0.596 7
0.596 6
0.26
0.606 2
0.602 7
0.600 6
0.599 7
0.598 9
0.598 5
0.598 2
0.597 5
0.597 2
0.596 9
0.596 9
0.596 8
0.28
0.607 2
0.603 4
0.601 1
0.600 2
0.599 3
0.598 9
0.598 5
0.597 8
0.597 5
0.597 2
0.597 1
0.597 0
0.30
0.608 2
0.604 2
0.601 7
0.600 7
0.599 8
0.599 3
0.598 9
0.598 2
0.597 8
0.597 4
0.597 3
0.597 3
0.32
0.609 4
0.605 1
0.602 4
0.601 3
0.600 3
0.599 8
0.599 4
0.598 6
0.598 1
0.597 7
0.597 6
0.597 5
0.34
0.610 7
0.606 0
0.603 1
0.602 0
0.600 9
0.600 4
0.599 9
0.599 0
0.598 5
0.598 1
0.597 9
0.597 8
0.36
0.612 1
0.607 1
0.604 0
0.602 7
0.601 6
0.601 0
0.600 5
0.599 5
0.598 9
0.598 4
0.598 3
0.598 1
0.38
0.613 7
0.608 2
0.604 9
0.603 5
0.602 3
0.601 6
0.601 1
0.600 0
0.599 4
0.598 8
0.598 6
0.598 5
0.40
0.615 3
0.609 5
0.605 9
0.604 4
0.603 1
0.602 4
0.601 8
0.600 6
0.599 9
0.599 3
0.599 1
0.598 9
0.42
0.617 2
0.610 9
0.607 0
0.605 4
0.603 9
0.603 2
0.602 5
0.601 2
0.600 5
0.599 8
0.599 5
0.599 3
0.44
0.619 2
0.612 4
0.608 2
0.606 5
0.604 9
0.604 1
0.603 4
0.601 9
0.601 1
0.600 3
0.600 0
0.599 7
0.46
0.621 4
0.614 0
0.609 4
0.607 6
0.605 9
0.605 0
0.604 2
0.602 7
0.601 7
0.600 8
0.600 5
0.600 2
0.48
0.623 8
0.615 7
0.610 8
0.608 8
0.607 0
0.606 0
0.605 2
0.603 5
0.602 4
0.601 4
0.601 0
0.600 6
0.50
0.626 4
0.617 6
0.612 3
0.610 1
0.608 1
0.607 1
0.606 2
0.604 3
0.603 1
0.602 0
0.601 6
0.601 1
0.51
0.627 8
0.618 6
0.613 1
0.610 8
0.608 7
0.607 6
0.606 7
0.604 7
0.603 5
0.602 3
0.601 9
0.601 4
0.52
0.629 2
0.619 7
0.613 9
0.611 5
0.609 3
0.608 2
0.607 2
0.605 2
0.603 9
0.602 7
0.602 1
0.601 6
0.53
0.630 7
0.620 7
0.614 7
0.612 3
0.610 0
0.608 8
0.607 8
0.605 6
0.604 3
0.603 0
0.602 4
0.601 9
0.54
0.632 2
0.621 8
0.615 5
0.613 0
0.610 6
0.609 4
0.608 3
0.606 1
0.604 7
0.603 3
0.602 7
0.602 1
0.55
0.633 7
0.622 9
0.616 4
0.613 8
0.611 3
0.610 0
0.608 9
0.606 5
0.605 0
0.603 6
0.603 0
0.602 4
0.56
−
0.624 1
0.617 3
0.614 5
0.611 9
0.610 6
0.609 5
0.607 0
0.605 4
0.603 9
0.603 2
0.602 6
0.57
−
0.625 3
0.618 2
0.615 3
0.612 6
0.611 2
0.610 0
0.607 5
0.605 8
0.604 2
0.603 5
0.602 8
0.58
−
0.626 5
0.619 1
0.616 1
0.613 3
0.611 9
0.610 6
0.607 9
0.606 2
0.604 5
0.603 8
0.603 0
0.59
−
0.627 7
0.620 0
0.616 9
0.614 0
0.612 5
0.611 2
0.608 4
0.606 6
0.604 8
0.604 0
0.603 2
0.60
−
0.629 0
0.621 0
0.617 7
0.614 7
0.613 1
0.611 8
0.608 8
0.607 0
0.605 1
0.604 2
0.603 4
0.61
−
0.630 3
0.621 9
0.618 6
0.615 4
0.613 8
0.612 4
0.609 3
0.607 3
0.605 3
0.604 4
0.603 6
0.62
−
0.631 6
0.622 9
0.619 4
0.616 1
0.614 4
0.612 9
0.609 7
0.607 7
0.605 6
0.604 6
0.603 7
0.63
−
0.632 9
0.623 8
0.620 2
0.616 8
0.615 0
0.613 5
0.610 2
0.608 0
0.605 8
0.604 8
0.603 9
0.64
−
0.634 3
0.624 8
0.621 0
0.617 5
0.615 6
0.614 0
0.610 6
0.608 3
0.606 0
0.605 0
0.603 9
0.65
−
0.635 6
0.625 8
0.621 9
0.618 2
0.616 2
0.614 6
0.610 9
0.608 6
0.606 2
0.605 1
0.604 0
0.66
−
0.637 0
0.626 8
0.622 7
0.618 8
0.616 8
0.615 1
0.611 3
0.608 8
0.606 3
0.605 1
0.604 0
0.67
−
0.638 4
0.627 7
0.623 5
0.619 5
0.617 4
0.615 6
0.611 6
0.609 0
0.606 4
0.605 2
0.604 0
0.68
−
0.639 8
0.628 7
0.624 3
0.620 1
0.617 9
0.616 1
0.612 0
0.609 2
0.606 5
0.605 2
0.603 9
0.69
−
0.641 1
0.629 6
0.625 0
0.620 7
0.618 5
0.616 5
0.612 2
0.609 4
0.606 5
0.605 1
0.603 8
0.70
−
0.642 5
0.630 5
0.625 8
0.621 3
0.618 9
0.616 9
0.612 5
0.609 5
0.606 5
0.605 1
0.603 7
0.71
−
0.643 9
0.631 5
0.626 5
0.621 8
0.619 4
0.617 3
0.612 7
0.609 6
0.606 4
0.604 9
0.603 5
0.72
−
0.645 3
0.632 3
0.627 2
0.622 3
0.619 8
0.617 6
0.612 8
0.609 6
0.606 3
0.604 7
0.603 2
0.73
−
0.646 7
0.633 2
0.627 9
0.622 8
0.620 2
0.617 9
0.612 9
0.609 6
0.606 1
0.604 5
0.602 9
0.74
−
0.648 0
0.634 0
0.628 5
0.623 3
0.620 6
0.618 2
0.613 0
0.609 5
0.605 9
0.604 2
0.602 5
0.75
−
0.649 4
0.634 9
0.629 1
0.623 7
0.620 9
0.618 4
0.613 0
0.609 4
0.605 6
0.603 8
0.602 1
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
64
M 8010:2020
D.3 フランジタップ
表D.3−フランジタップオリフィス流量計の流出係数Cd(D0=50 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.25
0.610 2
0.606 9
0.604 8
0.604 0
0.603 2
0.602 9
0.602 5
0.601 9
0.601 6
0.601 4
0.601 3
0.601 2
0.26
0.610 6
0.607 1
0.605 0
0.604 1
0.603 3
0.602 9
0.602 6
0.602 0
0.601 6
0.601 4
0.601 3
0.601 2
0.28
0.611 4
0.607 6
0.605 3
0.604 4
0.603 5
0.603 1
0.602 8
0.602 1
0.601 7
0.601 4
0.601 3
0.601 2
0.30
0.612 3
0.608 2
0.605 7
0.604 7
0.603 8
0.603 4
0.603 0
0.602 2
0.601 8
0.601 5
0.601 4
0.601 3
0.32
0.613 2
0.608 9
0.606 2
0.605 2
0.604 2
0.603 7
0.603 2
0.602 4
0.601 9
0.601 6
0.601 4
0.601 3
0.34
0.614 3
0.609 7
0.606 8
0.605 6
0.604 5
0.604 0
0.603 5
0.602 6
0.602 1
0.601 7
0.601 6
0.601 4
0.36
0.615 5
0.610 5
0.607 4
0.606 2
0.605 0
0.604 4
0.603 9
0.602 9
0.602 3
0.601 9
0.601 7
0.601 6
0.38
0.616 9
0.611 5
0.608 1
0.606 8
0.605 5
0.604 9
0.604 3
0.603 2
0.602 6
0.602 1
0.601 9
0.601 7
0.40
0.618 4
0.612 5
0.608 9
0.607 5
0.606 1
0.605 4
0.604 8
0.603 6
0.602 9
0.602 3
0.602 1
0.601 9
0.42
0.620 0
0.613 7
0.609 8
0.608 2
0.606 8
0.606 0
0.605 4
0.604 1
0.603 3
0.602 6
0.602 3
0.602 1
0.44
0.621 9
0.615 0
0.610 8
0.609 1
0.607 5
0.606 7
0.606 0
0.604 5
0.603 7
0.602 9
0.602 6
0.602 3
0.46
0.623 9
0.616 4
0.611 9
0.610 0
0.608 3
0.607 4
0.606 7
0.605 1
0.604 1
0.603 3
0.602 9
0.602 6
0.48
0.626 0
0.618 0
0.613 0
0.611 0
0.609 2
0.608 2
0.607 4
0.605 7
0.604 6
0.603 6
0.603 2
0.602 8
0.50
0.628 4
0.619 6
0.614 3
0.612 1
0.610 1
0.609 1
0.608 2
0.606 3
0.605 1
0.604 0
0.603 6
0.603 1
0.51
0.629 7
0.620 5
0.614 9
0.612 7
0.610 6
0.609 5
0.608 6
0.606 6
0.605 4
0.604 2
0.603 7
0.603 3
0.52
0.631 0
0.621 4
0.615 6
0.613 3
0.611 1
0.610 0
0.609 0
0.606 9
0.605 6
0.604 4
0.603 9
0.603 4
0.53
0.632 4
0.622 4
0.616 3
0.613 9
0.611 6
0.610 5
0.609 4
0.607 3
0.605 9
0.604 6
0.604 1
0.603 5
0.54
0.633 8
0.623 4
0.617 1
0.614 5
0.612 2
0.610 9
0.609 9
0.607 6
0.606 2
0.604 8
0.604 2
0.603 7
0.55
0.635 2
0.624 4
0.617 8
0.615 2
0.612 7
0.611 4
0.610 3
0.608 0
0.606 5
0.605 0
0.604 4
0.603 8
0.56
0.636 7
0.625 4
0.618 6
0.615 9
0.613 3
0.611 9
0.610 8
0.608 3
0.606 7
0.605 2
0.604 5
0.603 9
0.57
0.638 3
0.626 5
0.619 4
0.616 5
0.613 8
0.612 4
0.611 2
0.608 7
0.607 0
0.605 4
0.604 7
0.604 0
0.58
0.639 9
0.627 6
0.620 2
0.617 2
0.614 4
0.613 0
0.611 7
0.609 0
0.607 3
0.605 6
0.604 8
0.604 1
0.59
0.641 6
0.628 7
0.621 0
0.617 9
0.615 0
0.613 5
0.612 2
0.609 3
0.607 5
0.605 8
0.605 0
0.604 2
0.60
0.643 3
0.629 9
0.621 8
0.618 6
0.615 5
0.614 0
0.612 6
0.609 7
0.607 8
0.605 9
0.605 1
0.604 3
0.61
0.645 0
0.631 0
0.622 7
0.619 3
0.616 1
0.614 5
0.613 1
0.610 0
0.608 0
0.606 0
0.605 1
0.604 3
0.62
0.646 8
0.632 2
0.623 5
0.620 0
0.616 7
0.615 0
0.613 5
0.610 3
0.608 2
0.606 2
0.605 2
0.604 3
0.63
0.648 6
0.633 4
0.624 3
0.620 7
0.617 3
0.615 5
0.613 9
0.610 6
0.608 4
0.606 2
0.605 3
0.604 3
0.64
0.650 5
0.634 7
0.625 2
0.621 4
0.617 8
0.616 0
0.614 4
0.610 9
0.608 6
0.606 3
0.605 3
0.604 3
0.65
0.652 4
0.635 9
0.626 0
0.622 1
0.618 4
0.616 4
0.614 8
0.611 1
0.608 8
0.606 4
0.605 3
0.604 2
0.66
0.654 4
0.637 1
0.626 9
0.622 8
0.618 9
0.616 9
0.615 2
0.611 4
0.608 9
0.606 4
0.605 2
0.604 1
0.67
0.656 4
0.638 4
0.627 7
0.623 4
0.619 4
0.617 3
0.615 5
0.611 6
0.609 0
0.606 3
0.605 1
0.603 9
0.68
0.658 4
0.639 6
0.628 5
0.624 1
0.619 9
0.617 7
0.615 8
0.611 7
0.609 0
0.606 2
0.605 0
0.603 7
0.69
0.660 4
0.640 9
0.629 3
0.624 7
0.620 4
0.618 1
0.616 1
0.611 9
0.609 0
0.606 1
0.604 8
0.603 5
0.70
0.662 5
0.642 1
0.630 1
0.625 3
0.620 8
0.618 5
0.616 4
0.612 0
0.609 0
0.606 0
0.604 5
0.603 2
0.71
0.664 6
0.643 4
0.630 9
0.625 9
0.621 2
0.618 8
0.616 6
0.612 0
0.608 9
0.605 7
0.604 3
0.602 8
0.72
0.666 7
0.644 6
0.631 6
0.626 5
0.621 6
0.619 0
0.616 8
0.612 0
0.608 8
0.605 5
0.603 9
0.602 4
0.73
0.668 9
0.645 9
0.632 3
0.627 0
0.621 9
0.619 3
0.617 0
0.612 0
0.608 6
0.605 1
0.603 5
0.601 9
0.74
0.671 0
0.647 1
0.633 0
0.627 5
0.622 2
0.619 5
0.617 1
0.611 9
0.608 4
0.604 7
0.603 0
0.601 4
0.75
0.673 2
0.648 3
0.633 7
0.627 9
0.622 4
0.619 6
0.617 1
0.611 7
0.608 1
0.604 3
0.602 5
0.600 8
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
65
M 8010:2020
表D.4−フランジタップオリフィス流量計の流出係数Cd(D0=75 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.17
0.602 7
0.600 3
0.598 8
0.598 2
0.597 7
0.597 4
0.597 2
0.596 7
0.596 5
0.596 4
0.596 4
0.596 3
0.18
0.603 1
0.600 5
0.599 0
0.598 4
0.597 8
0.597 5
0.597 3
0.596 8
0.596 6
0.596 4
0.596 4
0.596 4
0.20
0.603 8
0.601 1
0.599 4
0.598 7
0.598 1
0.597 7
0.597 5
0.597 0
0.596 7
0.596 6
0.596 5
0.596 5
0.22
0.604 6
0.601 6
0.599 8
0.599 0
0.598 4
0.598 0
0.597 7
0.597 2
0.596 9
0.596 7
0.596 7
0.596 6
0.24
0.605 4
0.602 2
0.600 2
0.599 4
0.598 7
0.598 3
0.598 0
0.597 4
0.597 1
0.596 9
0.596 9
0.596 8
0.26
0.606 4
0.602 9
0.600 7
0.599 9
0.599 1
0.598 7
0.598 4
0.597 7
0.597 4
0.597 1
0.597 0
0.597 0
0.28
0.607 4
0.603 6
0.601 3
0.600 4
0.599 5
0.599 1
0.598 7
0.598 0
0.597 6
0.597 4
0.597 3
0.597 2
0.30
0.608 4
0.604 4
0.601 9
0.600 9
0.600 0
0.599 5
0.599 1
0.598 4
0.597 9
0.597 6
0.597 5
0.597 4
0.32
0.609 6
0.605 3
0.602 6
0.601 5
0.600 5
0.600 0
0.599 6
0.598 8
0.598 3
0.597 9
0.597 8
0.597 7
0.34
0.610 9
0.606 2
0.603 3
0.602 2
0.601 1
0.600 6
0.600 1
0.599 2
0.598 7
0.598 3
0.598 1
0.598 0
0.36
0.612 3
0.607 3
0.604 2
0.602 9
0.601 7
0.601 2
0.600 7
0.599 7
0.599 1
0.598 6
0.598 4
0.598 3
0.38
0.613 9
0.608 4
0.605 1
0.603 7
0.602 5
0.601 8
0.601 3
0.600 2
0.599 5
0.599 0
0.598 8
0.598 6
0.40
0.615 5
0.609 7
0.606 0
0.604 6
0.603 2
0.602 5
0.602 0
0.600 8
0.600 0
0.599 4
0.599 2
0.599 0
0.42
0.617 4
0.611 0
0.607 1
0.605 5
0.604 1
0.603 3
0.602 7
0.601 4
0.600 6
0.599 9
0.599 6
0.599 4
0.44
0.619 4
0.612 5
0.608 3
0.606 6
0.605 0
0.604 2
0.603 5
0.602 0
0.601 2
0.600 4
0.600 1
0.599 8
0.46
0.621 6
0.614 1
0.609 5
0.607 7
0.605 9
0.605 1
0.604 3
0.602 7
0.601 8
0.600 9
0.600 5
0.600 2
0.48
0.623 9
0.615 8
0.610 8
0.608 9
0.607 0
0.606 0
0.605 2
0.603 5
0.602 4
0.601 4
0.601 0
0.600 6
0.50
0.626 4
0.617 6
0.612 3
0.610 1
0.608 1
0.607 0
0.606 1
0.604 2
0.603 1
0.602 0
0.601 5
0.601 1
0.51
0.627 8
0.618 6
0.613 0
0.610 7
0.608 6
0.607 5
0.606 6
0.604 6
0.603 4
0.602 2
0.601 7
0.601 3
0.52
0.629 2
0.619 6
0.613 8
0.611 4
0.609 2
0.608 1
0.607 1
0.605 0
0.603 7
0.602 5
0.602 0
0.601 5
0.53
0.630 6
0.620 6
0.614 5
0.612 1
0.609 8
0.608 6
0.607 6
0.605 4
0.604 1
0.602 8
0.602 2
0.601 7
0.54
0.632 1
0.621 6
0.615 3
0.612 8
0.610 4
0.609 2
0.608 1
0.605 8
0.604 4
0.603 0
0.602 4
0.601 9
0.55
0.633 6
0.622 7
0.616 1
0.613 5
0.611 0
0.609 7
0.608 6
0.606 2
0.604 7
0.603 3
0.602 7
0.602 1
0.56
0.635 2
0.623 8
0.617 0
0.614 2
0.611 6
0.610 3
0.609 1
0.606 6
0.605 1
0.603 5
0.602 9
0.602 2
0.57
0.636 8
0.624 9
0.617 8
0.614 9
0.612 2
0.610 8
0.609 6
0.607 0
0.605 4
0.603 8
0.603 1
0.602 4
0.58
0.638 5
0.626 1
0.618 6
0.615 6
0.612 8
0.611 4
0.610 1
0.607 4
0.605 7
0.604 0
0.603 2
0.602 5
0.59
0.640 2
0.627 3
0.619 5
0.616 4
0.613 4
0.611 9
0.610 6
0.607 8
0.606 0
0.604 2
0.603 4
0.602 6
0.60
0.641 9
0.628 4
0.620 3
0.617 1
0.614 0
0.612 5
0.611 1
0.608 2
0.606 3
0.604 4
0.603 5
0.602 7
0.61
0.643 7
0.629 6
0.621 2
0.617 8
0.614 6
0.613 0
0.611 6
0.608 5
0.606 5
0.604 5
0.603 6
0.602 8
0.62
0.645 5
0.630 9
0.622 1
0.618 6
0.615 2
0.613 5
0.612 0
0.608 8
0.606 7
0.604 7
0.603 7
0.602 8
0.63
−
0.632 1
0.622 9
0.619 3
0.615 8
0.614 0
0.612 5
0.609 1
0.606 9
0.604 8
0.603 8
0.602 8
0.64
−
0.633 3
0.623 8
0.620 0
0.616 4
0.614 5
0.612 9
0.609 4
0.607 1
0.604 8
0.603 8
0.602 8
0.65
−
0.634 6
0.624 6
0.620 7
0.616 9
0.615 0
0.613 3
0.609 7
0.607 3
0.604 9
0.603 8
0.602 7
0.66
−
0.635 8
0.625 5
0.621 3
0.617 4
0.615 4
0.613 7
0.609 9
0.607 4
0.604 8
0.603 7
0.602 6
0.67
−
0.637 0
0.626 3
0.622 0
0.617 9
0.615 8
0.614 0
0.610 0
0.607 4
0.604 8
0.603 6
0.602 4
0.68
−
0.638 2
0.627 0
0.622 6
0.618 4
0.616 2
0.614 3
0.610 2
0.607 4
0.604 6
0.603 4
0.602 1
0.69
−
0.639 5
0.627 8
0.623 2
0.618 8
0.616 5
0.614 5
0.610 2
0.607 4
0.604 5
0.603 1
0.601 8
0.70
−
0.640 7
0.628 5
0.623 7
0.619 1
0.616 8
0.614 7
0.610 2
0.607 3
0.604 2
0.602 8
0.601 4
0.71
−
0.641 8
0.629 2
0.624 2
0.619 4
0.617 0
0.614 8
0.610 2
0.607 1
0.603 9
0.602 4
0.601 0
0.72
−
0.643 0
0.629 8
0.624 6
0.619 7
0.617 1
0.614 9
0.610 1
0.606 8
0.603 5
0.601 9
0.600 4
0.73
−
0.644 1
0.630 4
0.625 0
0.619 9
0.617 2
0.614 9
0.609 9
0.606 5
0.603 0
0.601 4
0.599 8
0.74
−
0.645 1
0.631 0
0.625 3
0.620 0
0.617 3
0.614 9
0.609 6
0.606 1
0.602 5
0.600 8
0.599 1
0.75
−
0.646 2
0.631 4
0.625 6
0.620 1
0.617 2
0.614 7
0.609 3
0.605 6
0.601 8
0.600 0
0.598 3
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
66
M 8010:2020
表D.5−フランジタップオリフィス流量計の流出係数Cd(D0=100 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.13
0.601 4
0.599 4
0.598 2
0.597 7
0.597 3
0.597 1
0.596 9
0.596 6
0.596 4
0.596 3
0.596 2
0.596 2
0.14
0.601 8
0.599 7
0.598 4
0.597 9
0.597 4
0.597 2
0.597 0
0.596 6
0.596 4
0.596 3
0.596 3
0.596 3
0.16
0.602 5
0.600 1
0.598 7
0.598 1
0.597 6
0.597 4
0.597 2
0.596 8
0.596 5
0.596 4
0.596 4
0.596 4
0.18
0.603 2
0.600 6
0.599 1
0.598 5
0.597 9
0.597 6
0.597 4
0.596 9
0.596 7
0.596 5
0.596 5
0.596 5
0.20
0.603 9
0.601 2
0.599 5
0.598 8
0.598 2
0.597 9
0.597 6
0.597 1
0.596 9
0.596 7
0.596 6
0.596 6
0.22
0.604 7
0.601 7
0.599 9
0.599 2
0.598 5
0.598 1
0.597 9
0.597 3
0.597 0
0.596 9
0.596 8
0.596 8
0.24
0.605 6
0.602 4
0.600 4
0.599 6
0.598 8
0.598 5
0.598 2
0.597 6
0.597 3
0.597 0
0.597 0
0.596 9
0.26
0.606 5
0.603 0
0.600 9
0.600 0
0.599 2
0.598 8
0.598 5
0.597 9
0.597 5
0.597 3
0.597 2
0.597 1
0.28
0.607 5
0.603 8
0.601 4
0.600 5
0.599 7
0.599 2
0.598 9
0.598 2
0.597 8
0.597 5
0.597 4
0.597 4
0.30
0.608 6
0.604 6
0.602 1
0.601 1
0.600 2
0.599 7
0.599 3
0.598 5
0.598 1
0.597 8
0.597 7
0.597 6
0.32
0.609 8
0.605 4
0.602 8
0.601 7
0.600 7
0.600 2
0.599 8
0.598 9
0.598 5
0.598 1
0.598 0
0.597 9
0.34
0.611 1
0.606 4
0.603 5
0.602 4
0.601 3
0.600 7
0.600 3
0.599 4
0.598 8
0.598 4
0.598 3
0.598 2
0.36
0.612 5
0.607 5
0.604 3
0.603 1
0.601 9
0.601 3
0.600 8
0.599 8
0.599 3
0.598 8
0.598 6
0.598 5
0.38
0.614 1
0.608 6
0.605 2
0.603 9
0.602 6
0.602 0
0.601 5
0.600 4
0.599 7
0.599 2
0.599 0
0.598 8
0.40
0.615 7
0.609 9
0.606 2
0.604 8
0.603 4
0.602 7
0.602 1
0.600 9
0.600 2
0.599 6
0.599 4
0.599 2
0.42
0.617 6
0.611 2
0.607 3
0.605 7
0.604 2
0.603 5
0.602 9
0.601 5
0.600 8
0.600 1
0.599 8
0.599 6
0.44
0.619 6
0.612 7
0.608 4
0.606 7
0.605 1
0.604 3
0.603 6
0.602 2
0.601 3
0.600 5
0.600 2
0.600 0
0.46
0.621 7
0.614 2
0.609 7
0.607 8
0.606 1
0.605 2
0.604 4
0.602 9
0.601 9
0.601 0
0.600 7
0.600 3
0.48
0.624 1
0.615 9
0.611 0
0.609 0
0.607 1
0.606 1
0.605 3
0.603 6
0.602 5
0.601 5
0.601 1
0.600 7
0.50
0.626 6
0.617 7
0.612 4
0.610 2
0.608 1
0.607 1
0.606 2
0.604 3
0.603 1
0.602 0
0.601 6
0.601 1
0.51
0.627 9
0.618 7
0.613 1
0.610 8
0.608 7
0.607 6
0.606 7
0.604 7
0.603 4
0.602 3
0.601 8
0.601 3
0.52
0.629 3
0.619 7
0.613 8
0.611 5
0.609 2
0.608 1
0.607 1
0.605 1
0.603 8
0.602 5
0.602 0
0.601 5
0.53
0.630 7
0.620 7
0.614 6
0.612 1
0.609 8
0.608 6
0.607 6
0.605 4
0.604 1
0.602 8
0.602 2
0.601 7
0.54
0.632 2
0.621 7
0.615 3
0.612 8
0.610 4
0.609 1
0.608 1
0.605 8
0.604 4
0.603 0
0.602 4
0.601 8
0.55
−
0.622 7
0.616 1
0.613 5
0.610 9
0.609 7
0.608 5
0.606 2
0.604 7
0.603 2
0.602 6
0.602 0
0.56
−
0.623 8
0.616 9
0.614 1
0.611 5
0.610 2
0.609 0
0.606 5
0.605 0
0.603 4
0.602 8
0.602 1
0.57
−
0.624 9
0.617 7
0.614 8
0.612 1
0.610 7
0.609 5
0.606 9
0.605 2
0.603 6
0.602 9
0.602 2
0.58
−
0.626 0
0.618 5
0.615 5
0.612 7
0.611 2
0.610 0
0.607 2
0.605 5
0.603 8
0.603 1
0.602 3
0.59
−
0.627 1
0.619 3
0.616 2
0.613 2
0.611 7
0.610 4
0.607 6
0.605 8
0.604 0
0.603 2
0.602 4
0.60
−
0.628 3
0.620 1
0.616 9
0.613 8
0.612 2
0.610 8
0.607 9
0.606 0
0.604 1
0.603 3
0.602 5
0.61
−
0.629 4
0.620 9
0.617 6
0.614 3
0.612 7
0.611 3
0.608 2
0.606 2
0.604 2
0.603 3
0.602 5
0.62
−
0.630 6
0.621 8
0.618 2
0.614 9
0.613 2
0.611 7
0.608 5
0.606 4
0.604 3
0.603 3
0.602 4
0.63
−
0.631 8
0.622 6
0.618 9
0.615 4
0.613 6
0.612 0
0.608 7
0.606 5
0.604 3
0.603 3
0.602 4
0.64
−
0.632 9
0.623 3
0.619 5
0.615 9
0.614 0
0.612 4
0.608 9
0.606 6
0.604 3
0.603 3
0.602 2
0.65
−
0.634 1
0.624 1
0.620 1
0.616 3
0.614 4
0.612 7
0.609 1
0.606 7
0.604 2
0.603 1
0.602 1
0.66
−
0.635 3
0.624 9
0.620 7
0.616 8
0.614 8
0.613 0
0.609 2
0.606 7
0.604 1
0.603 0
0.601 9
0.67
−
0.636 4
0.625 6
0.621 2
0.617 2
0.615 1
0.613 2
0.609 2
0.606 6
0.604 0
0.602 8
0.601 6
0.68
−
0.637 5
0.626 3
0.621 8
0.617 5
0.615 3
0.613 4
0.609 3
0.606 5
0.603 7
0.602 5
0.601 2
0.69
−
0.638 7
0.626 9
0.622 2
0.617 8
0.615 5
0.613 5
0.609 2
0.606 3
0.603 4
0.602 1
0.600 8
0.70
−
0.639 7
0.627 5
0.622 6
0.618 0
0.615 7
0.613 6
0.609 1
0.606 1
0.603 1
0.601 6
0.600 3
0.71
−
0.640 8
0.628 0
0.623 0
0.618 2
0.615 7
0.613 6
0.608 9
0.605 8
0.602 6
0.601 1
0.599 7
0.72
−
0.641 8
0.628 5
0.623 3
0.618 3
0.615 7
0.613 5
0.608 6
0.605 4
0.602 0
0.600 5
0.599 0
0.73
−
0.642 8
0.629 0
0.623 5
0.618 3
0.615 7
0.613 3
0.608 3
0.604 9
0.601 4
0.599 8
0.598 2
0.74
−
0.643 7
0.629 3
0.623 6
0.618 3
0.615 5
0.613 1
0.607 8
0.604 3
0.600 6
0.598 9
0.597 3
0.75
−
0.644 5
0.629 6
0.623 7
0.618 1
0.615 3
0.612 7
0.607 2
0.603 6
0.599 8
0.598 0
0.596 2
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
67
M 8010:2020
表D.6−フランジタップオリフィス流量計の流出係数Cd(D0=150 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 5
0.598 8
0.597 8
0.597 4
0.597 1
0.596 9
0.596 7
0.596 5
0.596 3
0.596 2
0.596 2
0.596 2
0.12
0.601 2
0.599 3
0.598 1
0.597 7
0.597 3
0.597 1
0.596 9
0.596 6
0.596 4
0.596 3
0.596 3
0.596 3
0.14
0.601 8
0.599 8
0.598 5
0.598 0
0.597 5
0.597 3
0.597 1
0.596 7
0.596 5
0.596 4
0.596 4
0.596 4
0.16
0.602 5
0.600 2
0.598 8
0.598 2
0.597 7
0.597 5
0.597 3
0.596 9
0.596 6
0.596 5
0.596 5
0.596 5
0.18
0.603 3
0.600 7
0.599 2
0.598 6
0.598 0
0.597 7
0.597 5
0.597 0
0.596 8
0.596 7
0.596 6
0.596 6
0.20
0.604 1
0.601 3
0.599 6
0.598 9
0.598 3
0.598 0
0.597 7
0.597 2
0.597 0
0.596 8
0.596 8
0.596 7
0.22
0.604 9
0.601 9
0.600 0
0.599 3
0.598 6
0.598 3
0.598 0
0.597 5
0.597 2
0.597 0
0.596 9
0.596 9
0.24
0.605 7
0.602 5
0.600 5
0.599 7
0.599 0
0.598 6
0.598 3
0.597 7
0.597 4
0.597 2
0.597 1
0.597 1
0.26
0.606 7
0.603 2
0.601 1
0.600 2
0.599 4
0.599 0
0.598 7
0.598 0
0.597 7
0.597 4
0.597 4
0.597 3
0.28
0.607 7
0.603 9
0.601 6
0.600 7
0.599 8
0.599 4
0.599 1
0.598 4
0.598 0
0.597 7
0.597 6
0.597 5
0.30
0.608 8
0.604 8
0.602 3
0.601 3
0.600 3
0.599 9
0.599 5
0.598 7
0.598 3
0.598 0
0.597 9
0.597 8
0.32
0.610 0
0.605 6
0.603 0
0.601 9
0.600 9
0.600 4
0.600 0
0.599 1
0.598 7
0.598 3
0.598 2
0.598 1
0.34
0.611 3
0.606 6
0.603 7
0.602 6
0.601 5
0.600 9
0.600 5
0.599 6
0.599 0
0.598 6
0.598 5
0.598 4
0.36
0.612 7
0.607 7
0.604 5
0.603 3
0.602 1
0.601 5
0.601 0
0.600 0
0.599 5
0.599 0
0.598 8
0.598 7
0.38
0.614 3
0.608 8
0.605 4
0.604 1
0.602 8
0.602 2
0.601 7
0.600 6
0.599 9
0.599 4
0.599 2
0.599 0
0.40
0.616 0
0.610 1
0.606 4
0.605 0
0.603 6
0.602 9
0.602 3
0.601 1
0.600 4
0.599 8
0.599 6
0.599 4
0.42
0.617 8
0.611 4
0.607 5
0.605 9
0.604 4
0.603 7
0.603 0
0.601 7
0.600 9
0.600 2
0.600 0
0.599 7
0.44
0.619 8
0.612 8
0.608 6
0.606 9
0.605 3
0.604 5
0.603 8
0.602 3
0.601 5
0.600 7
0.600 4
0.600 1
0.46
−
0.614 4
0.609 8
0.607 9
0.606 2
0.605 3
0.604 6
0.603 0
0.602 0
0.601 1
0.600 8
0.600 5
0.48
−
0.616 0
0.611 1
0.609 1
0.607 2
0.606 2
0.605 4
0.603 6
0.602 6
0.601 6
0.601 2
0.600 8
0.50
−
0.617 8
0.612 4
0.610 2
0.608 2
0.607 1
0.606 2
0.604 3
0.603 1
0.602 1
0.601 6
0.601 2
0.51
−
0.618 7
0.613 1
0.610 8
0.608 7
0.607 6
0.606 7
0.604 7
0.603 4
0.602 3
0.601 8
0.601 3
0.52
−
0.619 7
0.613 8
0.611 4
0.609 2
0.608 1
0.607 1
0.605 0
0.603 7
0.602 5
0.602 0
0.601 5
0.53
−
0.620 6
0.614 5
0.612 1
0.609 7
0.608 6
0.607 5
0.605 4
0.604 0
0.602 7
0.602 1
0.601 6
0.54
−
0.621 6
0.615 3
0.612 7
0.610 3
0.609 0
0.608 0
0.605 7
0.604 2
0.602 9
0.602 3
0.601 7
0.55
−
0.622 6
0.616 0
0.613 3
0.610 8
0.609 5
0.608 4
0.606 0
0.604 5
0.603 1
0.602 4
0.601 8
0.56
−
0.623 7
0.616 7
0.614 0
0.611 3
0.610 0
0.608 8
0.606 3
0.604 7
0.603 2
0.602 5
0.601 9
0.57
−
0.624 7
0.617 5
0.614 6
0.611 9
0.610 5
0.609 2
0.606 6
0.605 0
0.603 4
0.602 6
0.602 0
0.58
−
0.625 8
0.618 2
0.615 2
0.612 4
0.610 9
0.609 6
0.606 9
0.605 2
0.603 5
0.602 7
0.602 0
0.59
−
0.626 9
0.619 0
0.615 9
0.612 9
0.611 4
0.610 0
0.607 2
0.605 4
0.603 6
0.602 8
0.602 0
0.60
−
0.628 0
0.619 8
0.616 5
0.613 4
0.611 8
0.610 4
0.607 4
0.605 5
0.603 6
0.602 8
0.602 0
0.61
−
0.629 0
0.620 5
0.617 1
0.613 8
0.612 2
0.610 7
0.607 6
0.605 6
0.603 7
0.602 8
0.601 9
0.62
−
0.630 1
0.621 2
0.617 7
0.614 3
0.612 6
0.611 1
0.607 8
0.605 7
0.603 6
0.602 7
0.601 8
0.63
−
−
0.621 9
0.618 2
0.614 7
0.612 9
0.611 4
0.608 0
0.605 8
0.603 6
0.602 6
0.601 6
0.64
−
−
0.622 6
0.618 8
0.615 1
0.613 2
0.611 6
0.608 1
0.605 8
0.603 5
0.602 4
0.601 4
0.65
−
−
0.623 3
0.619 3
0.615 5
0.613 5
0.611 8
0.608 1
0.605 7
0.603 3
0.602 2
0.601 1
0.66
−
−
0.623 9
0.619 7
0.615 8
0.613 8
0.612 0
0.608 1
0.605 6
0.603 1
0.601 9
0.600 8
0.67
−
−
0.624 5
0.620 2
0.616 0
0.613 9
0.612 1
0.608 1
0.605 4
0.602 8
0.601 6
0.600 4
0.68
−
−
0.625 1
0.620 5
0.616 2
0.614 0
0.612 1
0.607 9
0.605 2
0.602 4
0.601 1
0.599 9
0.69
−
−
0.625 6
0.620 9
0.616 4
0.614 1
0.612 1
0.607 7
0.604 9
0.601 9
0.600 6
0.599 3
0.70
−
−
0.626 0
0.621 1
0.616 5
0.614 1
0.612 0
0.607 4
0.604 4
0.601 4
0.600 0
0.598 6
0.71
−
−
0.626 4
0.621 3
0.616 5
0.614 0
0.611 8
0.607 1
0.603 9
0.600 7
0.599 3
0.597 8
0.72
−
−
0.626 7
0.621 4
0.616 4
0.613 8
0.611 5
0.606 6
0.603 3
0.600 0
0.598 4
0.596 9
0.73
−
−
0.626 9
0.621 4
0.616 2
0.613 5
0.611 1
0.606 0
0.602 6
0.599 1
0.597 5
0.595 9
0.74
−
−
0.627 1
0.621 3
0.615 9
0.613 1
0.610 6
0.605 3
0.601 7
0.598 1
0.596 4
0.594 7
0.75
−
−
0.627 1
0.621 1
0.615 4
0.612 5
0.610 0
0.604 4
0.600 7
0.596 9
0.595 1
0.593 4
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
68
M 8010:2020
表D.7−フランジタップオリフィス流量計の流出係数Cd(D0=200 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 5
0.598 9
0.597 9
0.597 5
0.597 1
0.596 9
0.596 8
0.596 5
0.596 3
0.596 3
0.596 2
0.596 2
0.12
0.601 2
0.599 3
0.598 2
0.597 7
0.597 3
0.597 1
0.596 9
0.596 6
0.596 4
0.596 3
0.596 3
0.596 3
0.14
0.601 9
0.599 8
0.598 5
0.598 0
0.597 5
0.597 3
0.597 1
0.596 7
0.596 6
0.596 4
0.596 4
0.596 4
0.16
0.602 6
0.600 3
0.598 9
0.598 3
0.597 8
0.597 5
0.597 3
0.596 9
0.596 7
0.596 6
0.596 5
0.596 5
0.18
0.603 3
0.600 8
0.599 3
0.598 6
0.598 1
0.597 8
0.597 5
0.597 1
0.596 9
0.596 7
0.596 7
0.596 7
0.20
0.604 1
0.601 4
0.599 7
0.599 0
0.598 4
0.598 1
0.597 8
0.597 3
0.597 1
0.596 9
0.596 8
0.596 8
0.22
0.605 0
0.602 0
0.600 1
0.599 4
0.598 7
0.598 4
0.598 1
0.597 6
0.597 3
0.597 1
0.597 0
0.597 0
0.24
0.605 8
0.602 6
0.600 6
0.599 8
0.599 1
0.598 7
0.598 4
0.597 8
0.597 5
0.597 3
0.597 2
0.597 2
0.26
0.606 8
0.603 3
0.601 1
0.600 3
0.599 5
0.599 1
0.598 8
0.598 1
0.597 8
0.597 5
0.597 5
0.597 4
0.28
0.607 8
0.604 1
0.601 7
0.600 8
0.600 0
0.599 5
0.599 2
0.598 5
0.598 1
0.597 8
0.597 7
0.597 6
0.30
0.608 9
0.604 9
0.602 4
0.601 4
0.600 5
0.600 0
0.599 6
0.598 8
0.598 4
0.598 1
0.598 0
0.597 9
0.32
0.610 1
0.605 8
0.603 1
0.602 0
0.601 0
0.600 5
0.600 1
0.599 2
0.598 8
0.598 4
0.598 3
0.598 2
0.34
0.611 4
0.606 7
0.603 8
0.602 7
0.601 6
0.601 1
0.600 6
0.599 7
0.599 2
0.598 7
0.598 6
0.598 5
0.36
0.612 8
0.607 8
0.604 7
0.603 4
0.602 2
0.601 7
0.601 2
0.600 2
0.599 6
0.599 1
0.598 9
0.598 8
0.38
0.614 4
0.608 9
0.605 6
0.604 2
0.602 9
0.602 3
0.601 8
0.600 7
0.600 0
0.599 5
0.599 3
0.599 1
0.40
−
0.610 2
0.606 5
0.605 1
0.603 7
0.603 0
0.602 4
0.601 2
0.600 5
0.599 9
0.599 7
0.599 5
0.42
−
0.611 5
0.607 6
0.606 0
0.604 5
0.603 8
0.603 1
0.601 8
0.601 0
0.600 3
0.600 1
0.599 8
0.44
−
0.612 9
0.608 7
0.607 0
0.605 4
0.604 5
0.603 8
0.602 4
0.601 5
0.600 8
0.600 4
0.600 2
0.46
−
0.614 5
0.609 9
0.608 0
0.606 3
0.605 4
0.604 6
0.603 0
0.602 1
0.601 2
0.600 8
0.600 5
0.48
−
0.616 1
0.611 1
0.609 1
0.607 2
0.606 2
0.605 4
0.603 7
0.602 6
0.601 6
0.601 2
0.600 9
0.50
−
0.617 9
0.612 4
0.610 2
0.608 2
0.607 1
0.606 2
0.604 3
0.603 2
0.602 1
0.601 6
0.601 2
0.51
−
0.618 8
0.613 1
0.610 8
0.608 7
0.607 6
0.606 7
0.604 7
0.603 4
0.602 3
0.601 8
0.601 3
0.52
−
0.619 7
0.613 8
0.611 4
0.609 2
0.608 1
0.607 1
0.605 0
0.603 7
0.602 5
0.601 9
0.601 4
0.53
−
0.620 6
0.614 5
0.612 0
0.609 7
0.608 5
0.607 5
0.605 3
0.603 9
0.602 6
0.602 1
0.601 5
0.54
−
0.621 6
0.615 2
0.612 6
0.610 2
0.609 0
0.607 9
0.605 6
0.604 2
0.602 8
0.602 2
0.601 6
0.55
−
−
0.615 9
0.613 2
0.610 7
0.609 4
0.608 3
0.605 9
0.604 4
0.603 0
0.602 3
0.601 7
0.56
−
−
0.616 6
0.613 8
0.611 2
0.609 9
0.608 7
0.606 2
0.604 6
0.603 1
0.602 4
0.601 8
0.57
−
−
0.617 4
0.614 5
0.611 7
0.610 3
0.609 1
0.606 5
0.604 8
0.603 2
0.602 5
0.601 8
0.58
−
−
0.618 1
0.615 1
0.612 2
0.610 7
0.609 4
0.606 7
0.605 0
0.603 3
0.602 5
0.601 8
0.59
−
−
0.618 8
0.615 6
0.612 7
0.611 1
0.609 8
0.607 0
0.605 1
0.603 3
0.602 5
0.601 8
0.60
−
−
0.619 5
0.616 2
0.613 1
0.611 5
0.610 1
0.607 2
0.605 2
0.603 4
0.602 5
0.601 7
0.61
−
−
0.620 2
0.616 8
0.613 5
0.611 9
0.610 4
0.607 3
0.605 3
0.603 3
0.602 4
0.601 6
0.62
−
−
0.620 9
0.617 3
0.613 9
0.612 2
0.610 7
0.607 5
0.605 3
0.603 3
0.602 3
0.601 4
0.63
−
−
0.621 6
0.617 8
0.614 3
0.612 5
0.610 9
0.607 6
0.605 3
0.603 2
0.602 2
0.601 2
0.64
−
−
0.622 2
0.618 3
0.614 7
0.612 8
0.611 1
0.607 6
0.605 3
0.603 0
0.601 9
0.600 9
0.65
−
−
0.622 8
0.618 8
0.615 0
0.613 0
0.611 3
0.607 6
0.605 2
0.602 8
0.601 6
0.600 6
0.66
−
−
0.623 4
0.619 2
0.615 2
0.613 2
0.611 4
0.607 5
0.605 0
0.602 5
0.601 3
0.600 2
0.67
−
−
0.623 9
0.619 5
0.615 4
0.613 3
0.611 4
0.607 4
0.604 7
0.602 1
0.600 9
0.599 7
0.68
−
−
0.624 4
0.619 8
0.615 5
0.613 3
0.611 4
0.607 2
0.604 4
0.601 6
0.600 3
0.599 1
0.69
−
−
0.624 8
0.620 1
0.615 6
0.613 3
0.611 2
0.606 9
0.604 0
0.601 1
0.599 7
0.598 4
0.70
−
−
0.625 2
0.620 2
0.615 5
0.613 1
0.611 0
0.606 5
0.603 5
0.600 4
0.599 0
0.597 6
0.71
−
−
0.625 5
0.620 3
0.615 4
0.612 9
0.610 7
0.606 0
0.602 8
0.599 6
0.598 2
0.596 7
0.72
−
−
0.625 7
0.620 3
0.615 2
0.612 6
0.610 3
0.605 4
0.602 1
0.598 8
0.597 2
0.595 7
0.73
−
−
0.625 8
0.620 2
0.614 9
0.612 2
0.609 8
0.604 7
0.601 2
0.597 7
0.596 1
0.594 5
0.74
−
−
0.625 8
0.619 9
0.614 5
0.611 6
0.609 2
0.603 8
0.600 2
0.596 6
0.594 9
0.593 2
0.75
−
−
0.625 6
0.619 6
0.613 9
0.611 0
0.608 4
0.602 8
0.599 1
0.595 3
0.593 5
0.591 7
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
69
M 8010:2020
表D.8−フランジタップオリフィス流量計の流出係数Cd(D0=250 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 5
0.598 9
0.597 9
0.597 5
0.597 1
0.596 9
0.596 8
0.596 5
0.596 4
0.596 3
0.596 3
0.596 3
0.12
0.601 2
0.599 4
0.598 2
0.597 7
0.597 3
0.597 1
0.597 0
0.596 6
0.596 5
0.596 4
0.596 3
0.596 3
0.14
0.601 9
0.599 8
0.598 5
0.598 0
0.597 6
0.597 3
0.597 1
0.596 8
0.596 6
0.596 5
0.596 5
0.596 4
0.16
0.602 6
0.600 3
0.598 9
0.598 3
0.597 8
0.597 6
0.597 4
0.596 9
0.596 7
0.596 6
0.596 6
0.596 6
0.18
0.603 4
0.600 9
0.599 3
0.598 7
0.598 1
0.597 8
0.597 6
0.597 1
0.596 9
0.596 8
0.596 7
0.596 7
0.20
0.604 2
0.601 4
0.599 7
0.599 0
0.598 4
0.598 1
0.597 9
0.597 4
0.597 1
0.596 9
0.596 9
0.596 9
0.22
0.605 0
0.602 0
0.600 2
0.599 4
0.598 8
0.598 4
0.598 1
0.597 6
0.597 3
0.597 1
0.597 1
0.597 1
0.24
0.605 9
0.602 7
0.600 7
0.599 9
0.599 1
0.598 8
0.598 5
0.597 9
0.597 6
0.597 4
0.597 3
0.597 3
0.26
0.606 8
0.603 4
0.601 2
0.600 4
0.599 6
0.599 2
0.598 8
0.598 2
0.597 8
0.597 6
0.597 5
0.597 5
0.28
0.607 9
0.604 1
0.601 8
0.600 9
0.600 0
0.599 6
0.599 2
0.598 5
0.598 1
0.597 9
0.597 8
0.597 7
0.30
0.609 0
0.604 9
0.602 5
0.601 5
0.600 5
0.600 1
0.599 7
0.598 9
0.598 5
0.598 2
0.598 1
0.598 0
0.32
0.610 2
0.605 8
0.603 2
0.602 1
0.601 1
0.600 6
0.600 2
0.599 3
0.598 8
0.598 5
0.598 4
0.598 3
0.34
0.611 5
0.606 8
0.603 9
0.602 8
0.601 7
0.601 1
0.600 7
0.599 8
0.599 2
0.598 8
0.598 7
0.598 6
0.36
−
0.607 9
0.604 7
0.603 5
0.602 3
0.601 7
0.601 2
0.600 2
0.599 7
0.599 2
0.599 0
0.598 9
0.38
−
0.609 0
0.605 6
0.604 3
0.603 0
0.602 4
0.601 8
0.600 7
0.600 1
0.599 6
0.599 4
0.599 2
0.40
−
0.610 2
0.606 6
0.605 1
0.603 8
0.603 1
0.602 5
0.601 3
0.600 6
0.600 0
0.599 7
0.599 5
0.42
−
0.611 6
0.607 6
0.606 1
0.604 6
0.603 8
0.603 2
0.601 9
0.601 1
0.600 4
0.600 1
0.599 9
0.44
−
0.613 0
0.608 7
0.607 0
0.605 4
0.604 6
0.603 9
0.602 5
0.601 6
0.600 8
0.600 5
0.600 2
0.46
−
0.614 5
0.609 9
0.608 1
0.606 3
0.605 4
0.604 7
0.603 1
0.602 1
0.601 2
0.600 9
0.600 6
0.48
−
0.616 2
0.611 2
0.609 1
0.607 2
0.606 3
0.605 5
0.603 7
0.602 6
0.601 7
0.601 3
0.600 9
0.50
−
−
0.612 5
0.610 3
0.608 2
0.607 2
0.606 3
0.604 4
0.603 2
0.602 1
0.601 6
0.601 2
0.51
−
−
0.613 1
0.610 8
0.608 7
0.607 6
0.606 7
0.604 7
0.603 4
0.602 3
0.601 8
0.601 3
0.52
−
−
0.613 8
0.611 4
0.609 2
0.608 1
0.607 1
0.605 0
0.603 7
0.602 4
0.601 9
0.601 4
0.53
−
−
0.614 5
0.612 0
0.609 7
0.608 5
0.607 5
0.605 3
0.603 9
0.602 6
0.602 1
0.601 5
0.54
−
−
0.615 2
0.612 6
0.610 2
0.608 9
0.607 9
0.605 6
0.604 1
0.602 8
0.602 2
0.601 6
0.55
−
−
0.615 9
0.613 2
0.610 7
0.609 4
0.608 3
0.605 9
0.604 4
0.602 9
0.602 3
0.601 7
0.56
−
−
0.616 6
0.613 8
0.611 2
0.609 8
0.608 6
0.606 1
0.604 5
0.603 0
0.602 3
0.601 7
0.57
−
−
0.617 3
0.614 4
0.611 6
0.610 2
0.609 0
0.606 4
0.604 7
0.603 1
0.602 4
0.601 7
0.58
−
−
0.618 0
0.615 0
0.612 1
0.610 6
0.609 3
0.606 6
0.604 9
0.603 2
0.602 4
0.601 7
0.59
−
−
0.618 7
0.615 5
0.612 5
0.611 0
0.609 7
0.606 8
0.605 0
0.603 2
0.602 4
0.601 6
0.60
−
−
0.619 4
0.616 1
0.613 0
0.611 4
0.610 0
0.607 0
0.605 1
0.603 2
0.602 3
0.601 5
0.61
−
−
0.620 1
0.616 6
0.613 4
0.611 7
0.610 3
0.607 1
0.605 1
0.603 1
0.602 3
0.601 4
0.62
−
−
0.620 7
0.617 1
0.613 8
0.612 0
0.610 5
0.607 2
0.605 1
0.603 1
0.602 1
0.601 2
0.63
−
−
0.621 4
0.617 6
0.614 1
0.612 3
0.610 7
0.607 3
0.605 1
0.602 9
0.601 9
0.601 0
0.64
−
−
0.622 0
0.618 1
0.614 4
0.612 5
0.610 9
0.607 3
0.605 0
0.602 7
0.601 7
0.600 6
0.65
−
−
0.622 6
0.618 5
0.614 7
0.612 7
0.611 0
0.607 3
0.604 8
0.602 4
0.601 3
0.600 3
0.66
−
−
0.623 1
0.618 9
0.614 9
0.612 8
0.611 0
0.607 2
0.604 6
0.602 1
0.600 9
0.599 8
0.67
−
−
0.623 6
0.619 2
0.615 0
0.612 9
0.611 0
0.607 0
0.604 3
0.601 7
0.600 4
0.599 3
0.68
−
−
0.624 0
0.619 4
0.615 1
0.612 9
0.610 9
0.606 7
0.603 9
0.601 2
0.599 9
0.598 6
0.69
−
−
−
0.619 6
0.615 1
0.612 8
0.610 7
0.606 4
0.603 5
0.600 5
0.599 2
0.597 9
0.70
−
−
−
0.619 7
0.615 0
0.612 6
0.610 5
0.605 9
0.602 9
0.599 8
0.598 4
0.597 0
0.71
−
−
−
0.619 7
0.614 8
0.612 3
0.610 1
0.605 4
0.602 2
0.599 0
0.597 5
0.596 1
0.72
−
−
−
0.619 6
0.614 5
0.611 9
0.609 6
0.604 7
0.601 4
0.598 0
0.596 5
0.595 0
0.73
−
−
−
0.619 4
0.614 1
0.611 4
0.609 0
0.603 9
0.600 4
0.596 9
0.595 3
0.593 7
0.74
−
−
−
0.619 1
0.613 6
0.610 8
0.608 3
0.602 9
0.599 4
0.595 7
0.594 0
0.592 3
0.75
−
−
−
0.618 7
0.613 0
0.610 0
0.607 4
0.601 8
0.598 1
0.594 3
0.592 5
0.590 8
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
70
M 8010:2020
表D.9−フランジタップオリフィス流量計の流出係数Cd(D0=375 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 6
0.598 9
0.597 9
0.597 5
0.597 1
0.597 0
0.596 8
0.596 5
0.596 4
0.596 3
0.596 3
0.596 3
0.12
0.601 3
0.599 4
0.598 2
0.597 8
0.597 4
0.597 2
0.597 0
0.596 7
0.596 5
0.596 4
0.596 4
0.596 4
0.14
0.602 0
0.599 9
0.598 6
0.598 1
0.597 6
0.597 4
0.597 2
0.596 8
0.596 6
0.596 5
0.596 5
0.596 5
0.16
0.602 7
0.600 4
0.599 0
0.598 4
0.597 9
0.597 6
0.597 4
0.597 0
0.596 8
0.596 7
0.596 6
0.596 6
0.18
0.603 5
0.600 9
0.599 4
0.598 7
0.598 2
0.597 9
0.597 7
0.597 2
0.597 0
0.596 8
0.596 8
0.596 8
0.20
0.604 2
0.601 5
0.599 8
0.599 1
0.598 5
0.598 2
0.597 9
0.597 4
0.597 2
0.597 0
0.597 0
0.596 9
0.22
0.605 1
0.602 1
0.600 3
0.599 5
0.598 8
0.598 5
0.598 2
0.597 7
0.597 4
0.597 2
0.597 2
0.597 1
0.24
0.606 0
0.602 8
0.600 8
0.600 0
0.599 2
0.598 9
0.598 6
0.598 0
0.597 7
0.597 4
0.597 4
0.597 3
0.26
0.606 9
0.603 5
0.601 3
0.600 5
0.599 7
0.599 3
0.598 9
0.598 3
0.597 9
0.597 7
0.597 6
0.597 6
0.28
0.608 0
0.604 2
0.601 9
0.601 0
0.600 1
0.599 7
0.599 3
0.598 6
0.598 3
0.598 0
0.597 9
0.597 8
0.30
−
0.605 1
0.602 6
0.601 6
0.600 6
0.600 2
0.599 8
0.599 0
0.598 6
0.598 3
0.598 2
0.598 1
0.32
−
0.606 0
0.603 3
0.602 2
0.601 2
0.600 7
0.600 3
0.599 4
0.599 0
0.598 6
0.598 5
0.598 4
0.34
−
0.606 9
0.604 0
0.602 9
0.601 8
0.601 3
0.600 8
0.599 9
0.599 4
0.598 9
0.598 8
0.598 7
0.36
−
0.608 0
0.604 9
0.603 6
0.602 4
0.601 9
0.601 4
0.600 4
0.599 8
0.599 3
0.599 1
0.599 0
0.38
−
0.609 1
0.605 8
0.604 4
0.603 1
0.602 5
0.602 0
0.600 9
0.600 2
0.599 7
0.599 5
0.599 3
0.40
−
−
0.606 7
0.605 3
0.603 9
0.603 2
0.602 6
0.601 4
0.600 7
0.600 1
0.599 9
0.599 7
0.42
−
−
0.607 8
0.606 2
0.604 7
0.603 9
0.603 3
0.602 0
0.601 2
0.600 5
0.600 2
0.600 0
0.44
−
−
0.608 9
0.607 1
0.605 5
0.604 7
0.604 0
0.602 6
0.601 7
0.600 9
0.600 6
0.600 3
0.46
−
−
0.610 0
0.608 2
0.606 4
0.605 5
0.604 8
0.603 2
0.602 2
0.601 3
0.601 0
0.600 7
0.48
−
−
0.611 3
0.609 2
0.607 3
0.606 4
0.605 5
0.603 8
0.602 7
0.601 8
0.601 3
0.601 0
0.50
−
−
0.612 5
0.610 3
0.608 3
0.607 2
0.606 3
0.604 4
0.603 2
0.602 1
0.601 7
0.601 2
0.51
−
−
0.613 2
0.610 9
0.608 8
0.607 7
0.606 7
0.604 7
0.603 5
0.602 3
0.601 8
0.601 4
0.52
−
−
0.613 9
0.611 5
0.609 2
0.608 1
0.607 1
0.605 0
0.603 7
0.602 5
0.601 9
0.601 5
0.53
−
−
0.614 5
0.612 1
0.609 7
0.608 5
0.607 5
0.605 3
0.603 9
0.602 6
0.602 1
0.601 5
0.54
−
−
0.615 2
0.612 6
0.610 2
0.609 0
0.607 9
0.605 6
0.604 1
0.602 8
0.602 2
0.601 6
0.55
−
−
0.615 9
0.613 2
0.610 7
0.609 4
0.608 2
0.605 8
0.604 3
0.602 9
0.602 2
0.601 7
0.56
−
−
0.616 6
0.613 8
0.611 1
0.609 8
0.608 6
0.606 1
0.604 5
0.603 0
0.602 3
0.601 7
0.57
−
−
−
0.614 4
0.611 6
0.610 2
0.608 9
0.606 3
0.604 7
0.603 0
0.602 3
0.601 7
0.58
−
−
−
0.614 9
0.612 0
0.610 6
0.609 3
0.606 5
0.604 8
0.603 1
0.602 3
0.601 6
0.59
−
−
−
0.615 5
0.612 4
0.610 9
0.609 6
0.606 7
0.604 9
0.603 1
0.602 3
0.601 5
0.60
−
−
−
0.616 0
0.612 8
0.611 2
0.609 8
0.606 9
0.604 9
0.603 0
0.602 2
0.601 4
0.61
−
−
−
0.616 5
0.613 2
0.611 6
0.610 1
0.607 0
0.605 0
0.603 0
0.602 1
0.601 2
0.62
−
−
−
0.617 0
0.613 6
0.611 8
0.610 3
0.607 0
0.604 9
0.602 8
0.601 9
0.601 0
0.63
−
−
−
0.617 4
0.613 9
0.612 1
0.610 5
0.607 1
0.604 8
0.602 6
0.601 7
0.600 7
0.64
−
−
−
0.617 8
0.614 1
0.612 2
0.610 6
0.607 0
0.604 7
0.602 4
0.601 4
0.600 3
0.65
−
−
−
0.618 2
0.614 3
0.612 4
0.610 6
0.606 9
0.604 5
0.602 1
0.601 0
0.599 9
0.66
−
−
−
0.618 5
0.614 5
0.612 4
0.610 6
0.606 8
0.604 2
0.601 7
0.600 5
0.599 4
0.67
−
−
−
0.618 8
0.614 6
0.612 4
0.610 6
0.606 5
0.603 9
0.601 2
0.600 0
0.598 8
0.68
−
−
−
0.619 0
0.614 6
0.612 4
0.610 4
0.606 2
0.603 4
0.600 6
0.599 3
0.598 1
0.69
−
−
−
−
0.614 5
0.612 2
0.610 2
0.605 8
0.602 9
0.600 0
0.598 6
0.597 3
0.70
−
−
−
−
0.614 4
0.612 0
0.609 8
0.605 3
0.602 2
0.599 2
0.597 7
0.596 4
0.71
−
−
−
−
0.614 1
0.611 6
0.609 4
0.604 6
0.601 5
0.598 2
0.596 8
0.595 3
0.72
−
−
−
−
0.613 8
0.611 1
0.608 8
0.603 9
0.600 6
0.597 2
0.595 6
0.594 1
0.73
−
−
−
−
0.613 3
0.610 5
0.608 1
0.602 9
0.599 5
0.596 0
0.594 4
0.592 8
0.74
−
−
−
−
0.612 6
0.609 8
0.607 3
0.601 9
0.598 3
0.594 6
0.592 9
0.591 3
0.75
−
−
−
−
0.611 9
0.608 9
0.606 3
0.600 7
0.596 9
0.593 1
0.591 3
0.589 6
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
71
M 8010:2020
表D.10−フランジタップオリフィス流量計の流出係数Cd(D0=760 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 6
0.599 0
0.597 9
0.597 5
0.597 2
0.597 0
0.596 9
0.596 6
0.596 4
0.596 3
0.596 3
0.596 3
0.12
0.601 3
0.599 4
0.598 3
0.597 8
0.597 4
0.597 2
0.597 0
0.596 7
0.596 5
0.596 4
0.596 4
0.596 4
0.14
0.602 0
0.599 9
0.598 6
0.598 1
0.597 7
0.597 4
0.597 2
0.596 9
0.596 7
0.596 6
0.596 6
0.596 5
0.16
0.602 8
0.600 5
0.599 0
0.598 5
0.597 9
0.597 7
0.597 5
0.597 1
0.596 9
0.596 7
0.596 7
0.596 7
0.18
0.603 5
0.601 0
0.599 4
0.598 8
0.598 2
0.598 0
0.597 7
0.597 3
0.597 0
0.596 9
0.596 9
0.596 8
0.20
−
0.601 6
0.599 9
0.599 2
0.598 6
0.598 3
0.598 0
0.597 5
0.597 3
0.597 1
0.597 1
0.597 0
0.22
−
0.602 2
0.600 4
0.599 6
0.598 9
0.598 6
0.598 3
0.597 8
0.597 5
0.597 3
0.597 3
0.597 2
0.24
−
0.602 9
0.600 9
0.600 1
0.599 3
0.599 0
0.598 7
0.598 1
0.597 8
0.597 6
0.597 5
0.597 5
0.26
−
0.603 6
0.601 4
0.600 6
0.599 8
0.599 4
0.599 1
0.598 4
0.598 1
0.597 8
0.597 7
0.597 7
0.28
−
−
0.602 0
0.601 1
0.600 3
0.599 8
0.599 5
0.598 8
0.598 4
0.598 1
0.598 0
0.598 0
0.30
−
−
0.602 7
0.601 7
0.600 8
0.600 3
0.599 9
0.599 2
0.598 7
0.598 4
0.598 3
0.598 2
0.32
−
−
0.603 4
0.602 3
0.601 3
0.600 8
0.600 4
0.599 6
0.599 1
0.598 7
0.598 6
0.598 5
0.34
−
−
0.604 2
0.603 0
0.602 0
0.601 4
0.601 0
0.600 0
0.599 5
0.599 1
0.599 0
0.598 8
0.36
−
−
0.605 0
0.603 8
0.602 6
0.602 0
0.601 5
0.600 5
0.599 9
0.599 5
0.599 3
0.599 2
0.38
−
−
0.605 9
0.604 6
0.603 3
0.602 7
0.602 1
0.601 0
0.600 4
0.599 9
0.599 7
0.599 5
0.40
−
−
−
0.605 4
0.604 1
0.603 4
0.602 8
0.601 6
0.600 9
0.600 3
0.600 0
0.599 8
0.42
−
−
−
0.606 4
0.604 9
0.604 1
0.603 5
0.602 2
0.601 4
0.600 7
0.600 4
0.600 2
0.44
−
−
−
0.607 3
0.605 7
0.604 9
0.604 2
0.602 7
0.601 9
0.601 1
0.600 8
0.600 5
0.46
−
−
−
0.608 4
0.606 6
0.605 7
0.604 9
0.603 4
0.602 4
0.601 5
0.601 2
0.600 8
0.48
−
−
−
0.609 4
0.607 5
0.606 5
0.605 7
0.604 0
0.602 9
0.601 9
0.601 5
0.601 1
0.50
−
−
−
−
0.608 4
0.607 4
0.606 5
0.604 6
0.603 4
0.602 3
0.601 8
0.601 4
0.51
−
−
−
−
0.608 9
0.607 8
0.606 9
0.604 9
0.603 6
0.602 5
0.602 0
0.601 5
0.52
−
−
−
−
0.609 4
0.608 2
0.607 3
0.605 2
0.603 9
0.602 6
0.602 1
0.601 6
0.53
−
−
−
−
0.609 9
0.608 7
0.607 6
0.605 4
0.604 1
0.602 8
0.602 2
0.601 7
0.54
−
−
−
−
0.610 3
0.609 1
0.608 0
0.605 7
0.604 3
0.602 9
0.602 3
0.601 7
0.55
−
−
−
−
0.610 8
0.609 5
0.608 4
0.606 0
0.604 4
0.603 0
0.602 4
0.601 8
0.56
−
−
−
−
0.611 2
0.609 9
0.608 7
0.606 2
0.604 6
0.603 1
0.602 4
0.601 8
0.57
−
−
−
−
0.611 7
0.610 3
0.609 0
0.606 4
0.604 7
0.603 1
0.602 4
0.601 7
0.58
−
−
−
−
0.612 1
0.610 6
0.609 3
0.606 6
0.604 8
0.603 1
0.602 4
0.601 7
0.59
−
−
−
−
0.612 5
0.611 0
0.609 6
0.606 8
0.604 9
0.603 1
0.602 3
0.601 6
0.60
−
−
−
−
0.612 9
0.611 3
0.609 9
0.606 9
0.605 0
0.603 1
0.602 2
0.601 4
0.61
−
−
−
−
0.613 2
0.611 6
0.610 1
0.607 0
0.605 0
0.603 0
0.602 1
0.601 2
0.62
−
−
−
−
0.613 6
0.611 8
0.610 3
0.607 0
0.604 9
0.602 8
0.601 9
0.601 0
0.63
−
−
−
−
−
0.612 0
0.610 4
0.607 0
0.604 8
0.602 6
0.601 6
0.600 6
0.64
−
−
−
−
−
0.612 2
0.610 5
0.606 9
0.604 6
0.602 3
0.601 3
0.600 3
0.65
−
−
−
−
−
0.612 3
0.610 5
0.606 8
0.604 4
0.602 0
0.600 9
0.599 8
0.66
−
−
−
−
−
0.612 3
0.610 5
0.606 6
0.604 1
0.601 5
0.600 4
0.599 2
0.67
−
−
−
−
−
0.612 3
0.610 4
0.606 3
0.603 7
0.601 0
0.599 8
0.598 6
0.68
−
−
−
−
−
0.612 2
0.610 2
0.606 0
0.603 2
0.600 4
0.599 1
0.597 9
0.69
−
−
−
−
−
0.611 9
0.609 9
0.605 5
0.602 6
0.599 6
0.598 3
0.597 0
0.70
−
−
−
−
−
0.611 6
0.609 5
0.604 9
0.601 9
0.598 8
0.597 4
0.596 0
0.71
−
−
−
−
−
0.611 2
0.609 0
0.604 2
0.601 0
0.597 8
0.596 3
0.594 9
0.72
−
−
−
−
−
0.610 7
0.608 4
0.603 4
0.600 1
0.596 7
0.595 1
0.593 6
0.73
−
−
−
−
−
0.610 0
0.607 6
0.602 4
0.598 9
0.595 4
0.593 8
0.592 2
0.74
−
−
−
−
−
−
0.606 7
0.601 2
0.597 6
0.594 0
0.592 3
0.590 6
0.75
−
−
−
−
−
−
0.605 6
0.599 9
0.596 2
0.592 3
0.590 6
0.588 8
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
72
M 8010:2020
表D.11−フランジタップオリフィス流量計の流出係数Cd(D0=1 000 mmの場合)
オリフィス
直径比β
オリフィス配管径に基づくレイノルズ数 ReD
5×103
1×104
2×104
3×104
5×104
7×104
1×105
3×105
1×106
1×107
1×108
∞
0.10
0.600 6
0.599 0
0.598 0
0.597 6
0.597 2
0.597 0
0.596 9
0.596 6
0.596 4
0.596 3
0.596 3
0.596 3
0.12
0.601 3
0.599 4
0.598 3
0.597 8
0.597 4
0.597 2
0.597 0
0.596 7
0.596 6
0.596 5
0.596 4
0.596 4
0.14
0.602 0
0.599 9
0.598 7
0.598 1
0.597 7
0.597 4
0.597 3
0.596 9
0.596 7
0.596 6
0.596 6
0.596 6
0.16
0.602 8
0.600 5
0.599 0
0.598 5
0.598 0
0.597 7
0.597 5
0.597 1
0.596 9
0.596 7
0.596 7
0.596 7
0.18
−
0.601 0
0.599 5
0.598 8
0.598 3
0.598 0
0.597 7
0.597 3
0.597 1
0.596 9
0.596 9
0.596 9
0.20
−
0.601 6
0.599 9
0.599 2
0.598 6
0.598 3
0.598 0
0.597 5
0.597 3
0.597 1
0.597 1
0.597 1
0.22
−
0.602 2
0.600 4
0.599 6
0.599 0
0.598 6
0.598 4
0.597 8
0.597 5
0.597 3
0.597 3
0.597 3
0.24
−
0.602 9
0.600 9
0.600 1
0.599 4
0.599 0
0.598 7
0.598 1
0.597 8
0.597 6
0.597 5
0.597 5
0.26
−
−
0.601 5
0.600 6
0.599 8
0.599 4
0.599 1
0.598 4
0.598 1
0.597 9
0.597 8
0.597 7
0.28
−
−
0.602 1
0.601 2
0.600 3
0.599 9
0.599 5
0.598 8
0.598 4
0.598 1
0.598 1
0.598 0
0.30
−
−
0.602 7
0.601 7
0.600 8
0.600 4
0.600 0
0.599 2
0.598 8
0.598 5
0.598 3
0.598 3
0.32
−
−
0.603 5
0.602 4
0.601 4
0.600 9
0.600 5
0.599 6
0.599 2
0.598 8
0.598 7
0.598 6
0.34
−
−
0.604 3
0.603 1
0.602 0
0.601 5
0.601 0
0.600 1
0.599 6
0.599 1
0.599 0
0.598 9
0.36
−
−
−
0.603 8
0.602 7
0.602 1
0.601 6
0.600 6
0.600 0
0.599 5
0.599 4
0.599 2
0.38
−
−
−
0.604 6
0.603 4
0.602 7
0.602 2
0.601 1
0.600 5
0.599 9
0.599 7
0.599 5
0.40
−
−
−
0.605 5
0.604 1
0.603 4
0.602 8
0.601 6
0.600 9
0.600 3
0.600 1
0.599 9
0.42
−
−
−
0.606 4
0.604 9
0.604 2
0.603 5
0.602 2
0.601 4
0.600 7
0.600 5
0.600 2
0.44
−
−
−
−
0.605 8
0.605 0
0.604 3
0.602 8
0.601 9
0.601 2
0.600 9
0.600 6
0.46
−
−
−
−
0.606 7
0.605 8
0.605 0
0.603 4
0.602 4
0.601 6
0.601 2
0.600 9
0.48
−
−
−
−
0.607 6
0.606 6
0.605 8
0.604 0
0.603 0
0.602 0
0.601 6
0.601 2
0.50
−
−
−
−
0.608 5
0.607 5
0.606 5
0.604 6
0.603 5
0.602 4
0.601 9
0.601 5
0.51
−
−
−
−
0.609 0
0.607 9
0.606 9
0.604 9
0.603 7
0.602 5
0.602 0
0.601 6
0.52
−
−
−
−
0.609 5
0.608 3
0.607 3
0.605 2
0.603 9
0.602 7
0.602 2
0.601 7
0.53
−
−
−
−
0.609 9
0.608 7
0.607 7
0.605 5
0.604 1
0.602 8
0.602 3
0.601 7
0.54
−
−
−
−
0.610 4
0.609 1
0.608 1
0.605 8
0.604 3
0.603 0
0.602 4
0.601 8
0.55
−
−
−
−
−
0.609 6
0.608 4
0.606 0
0.604 5
0.603 1
0.602 4
0.601 8
0.56
−
−
−
−
−
0.609 9
0.608 8
0.606 3
0.604 7
0.603 1
0.602 5
0.601 8
0.57
−
−
−
−
−
0.610 3
0.609 1
0.606 5
0.604 8
0.603 2
0.602 5
0.601 8
0.58
−
−
−
−
−
0.610 7
0.609 4
0.606 7
0.604 9
0.603 2
0.602 4
0.601 7
0.59
−
−
−
−
−
0.611 0
0.609 7
0.606 8
0.605 0
0.603 2
0.602 4
0.601 6
0.60
−
−
−
−
−
0.611 3
0.609 9
0.606 9
0.605 0
0.603 1
0.602 3
0.601 5
0.61
−
−
−
−
−
0.611 6
0.610 2
0.607 0
0.605 0
0.603 0
0.602 1
0.601 3
0.62
−
−
−
−
−
0.611 9
0.610 3
0.607 1
0.604 9
0.602 9
0.601 9
0.601 0
0.63
−
−
−
−
−
0.612 1
0.610 5
0.607 0
0.604 8
0.602 6
0.601 6
0.600 7
0.64
−
−
−
−
−
0.612 2
0.610 6
0.607 0
0.604 7
0.602 3
0.601 3
0.600 3
0.65
−
−
−
−
−
−
0.610 6
0.606 8
0.604 4
0.602 0
0.600 9
0.599 8
0.66
−
−
−
−
−
−
0.610 5
0.606 6
0.604 1
0.601 6
0.600 4
0.599 3
0.67
−
−
−
−
−
−
0.610 4
0.606 3
0.603 7
0.601 0
0.599 8
0.598 6
0.68
−
−
−
−
−
−
0.610 2
0.606 0
0.603 2
0.600 4
0.599 1
0.597 9
0.69
−
−
−
−
−
−
0.609 9
0.605 5
0.602 6
0.599 7
0.598 3
0.597 0
0.70
−
−
−
−
−
−
0.609 5
0.604 9
0.601 9
0.598 8
0.597 4
0.596 0
0.71
−
−
−
−
−
−
0.609 0
0.604 2
0.601 0
0.597 8
0.596 3
0.594 9
0.72
−
−
−
−
−
−
0.608 4
0.603 3
0.600 0
0.596 7
0.595 1
0.593 6
0.73
−
−
−
−
−
−
0.607 6
0.602 4
0.598 9
0.595 4
0.593 8
0.592 2
0.74
−
−
−
−
−
−
0.606 6
0.601 2
0.597 6
0.593 9
0.592 2
0.590 6
0.75
−
−
−
−
−
−
0.605 5
0.599 9
0.596 1
0.592 3
0.590 5
0.588 7
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。

73
M 8010:2020
附属書E
(参考)
オリフィス流量計の膨張補正係数
表E.1−オリフィス流量計の膨張補正係数ε
オリフィス直径比
p2/p1
β
β4
0.98
0.96
0.94
0.92
0.90
0.85
0.80
0.75
κ=1.2
0.100 0
0.000 1
0.994 1
0.988 3
0.982 4
0.976 4
0.970 5
0.955 5
0.940 4
0.925 2
0.562 3
0.100 0
0.993 6
0.987 1
0.980 6
0.974 1
0.967 6
0.951 1
0.934 5
0.917 7
0.668 7
0.200 0
0.992 7
0.985 3
0.977 9
0.970 5
0.963 1
0.944 3
0.925 4
0.906 3
0.740 1
0.300 0
0.991 5
0.982 9
0.974 3
0.965 7
0.957 0
0.935 2
0.913 2
0.891 0
0.750 0
0.316 4
0.991 2
0.982 4
0.973 6
0.964 8
0.955 9
0.933 5
0.910 9
0.888 1
κ=1.3
0.100 0
0.000 1
0.994 6
0.989 1
0.983 7
0.978 2
0.972 7
0.958 7
0.944 6
0.930 3
0.562 3
0.100 0
0.994 0
0.988 1
0.982 1
0.976 0
0.970 0
0.954 7
0.939 1
0.923 4
0.668 7
0.200 0
0.993 2
0.986 4
0.979 6
0.972 7
0.965 8
0.948 4
0.930 7
0.912 8
0.740 1
0.300 0
0.992 1
0.984 2
0.976 2
0.968 2
0.960 2
0.939 9
0.919 3
0.898 5
0.750 0
0.316 4
0.991 9
0.983 8
0.975 6
0.967 4
0.959 1
0.938 3
0.917 2
0.895 8
κ=1.4
0.100 0
0.000 1
0.995 0
0.989 9
0.984 8
0.979 7
0.974 6
0.961 5
0.948 3
0.934 8
0.562 3
0.100 0
0.994 5
0.988 9
0.983 3
0.977 7
0.972 0
0.957 7
0.943 1
0.928 3
0.668 7
0.200 0
0.993 7
0.987 4
0.981 0
0.974 6
0.968 1
0.951 8
0.935 3
0.918 4
0.740 1
0.300 0
0.992 7
0.985 3
0.977 9
0.970 4
0.962 9
0.943 9
0.924 6
0.905 0
0.750 0
0.316 4
0.992 5
0.984 9
0.977 3
0.969 6
0.961 9
0.942 4
0.922 6
0.902 5
κ=1.66
0.100 0
0.000 1
0.995 8
0.991 5
0.987 2
0.982 8
0.978 4
0.967 3
0.955 8
0.944 1
0.562 3
0.100 0
0.995 3
0.990 6
0.985 9
0.981 1
0.976 3
0.964 0
0.951 5
0.938 6
0.668 7
0.200 0
0.994 7
0.989 3
0.983 9
0.978 5
0.973 0
0.959 0
0.944 7
0.930 1
0.740 1
0.300 0
0.993 8
0.987 6
0.981 3
0.974 9
0.968 5
0.952 3
0.935 7
0.918 6
0.750 0
0.316 4
0.993 6
0.987 2
0.980 8
0.974 3
0.967 7
0.951 0
0.934 0
0.916 4
注記 この表は,便宜上のものであるため,補間した値及び補外は高精度の測定には適していない。
74
M 8010:2020
附属書F
(規定)
体積分率からモル分率への換算
成分分析結果が体積分率で与えられる場合には,式(F.1)を用いてモル分率に換算する。
∑
=
i
i
i
i
i
i
Z
x
Z
x
x
,
V
,
V
··········································································· (F.1)
ここに,
xi: i番目の成分のモル分率
xV,i: i番目の成分の体積分率
Zi: 表F.1に規定するi番目の成分の圧縮係数
表F.1−モル分率の計算に使用するZiの値
成分
Zi
CO2
0.993 3
N2
0.999 5
H2
1.000 6
CO
0.999 3
O2
0.999 0
CH4
0.997 6
C2H6
0.990 0
C3H8
0.978 9
iC4H10
0.958 0
nC4H10
0.957 2
iC5H12
0.937 0
nC5H12
0.918 0
C6H14
0.892 0
75
M 8010:2020
附属書G
(規定)
微量成分の割当
ガスが表2にない微量成分を含有し,それらが表G.1にある場合,その微量成分のモル分率を表G.1が
示す割当先に加算したものをモル分率として用いる。
表G.1−微量成分の割当
微量成分
化学式
割当先
2,2-ジメチルプロパン,2,2-Dimethylpropane (Neo-pentan)
C5H12
nC5H12
2-メチルペンタン,2-Methylpentane
C6H14
C6H14
3-メチルペンタン,3-Methylpentane
C6H14
C6H14
2,2-ジメチルブタン,2,2-Dimethylbutane
C6H14
C6H14
2,3-ジメチルブタン,2,3-Dimethylbutane
C6H14
C6H14
エチレン,Ethylene
C2H4
C2H6
プロピレン(プロペン),Propylene (Propene)
C3H6
C3H8
1-ブテン,1-Butene
C4H8
nC4H10
シス-2-ブテン,cis-2-Butene
C4H8
nC4H10
トランス-2-ブテン,trans-2-Butene
C4H8
nC4H10
2-メチルプロペン,2-Methyl-propene
C4H8
nC4H10
1-ペンテン,1-Pentene
C5H10
nC5H12
プロパジエン,Propadiene
C3H4
C3H8
1,2-ブタジエン,1,2-Butadiene
C4H6
nC4H10
1,3-ブタジエン,1,3-Butadiene
C4H6
nC4H10
アセチレン(エチン),Acetylene (Ethyne)
C2H2
C2H6
シクロペンタン,Cyclopentane
C5H10
nC5H12
メチルシクロペンタン,Methylcyclopentane
C6H12
C6H14
エチルシクロペンタン,Ethylcyclopentane
C7H14
C7H16
シクロヘキサン,Cyclohexane
C6H12
C6H14
メチルシクロヘキサン,Methylcyclohexane
C7H14
C7H16
エチルシクロヘキサン,Ethylcyclohexane
C8H16
C8H18
ベンゼン,Benzene
C6H6
nC5H12
トルエン(メチルベンゼン),Toluene (Methylbenzene)
C7H8
C6H14
エチルベンゼン,Ethylbenzene
C8H10
C7H16
o-キシレン,o-Xylene
C8H10
C7H16
その他のC6,all other C6 hydrocarbons
C6
C6H14
その他のC7,all other C7 hydrocarbons
C7
C7H16
その他のC8,all other C8 hydrocarbons
C8
C8H18
その他のC9,all other C9 hydrocarbons
C9
C9H20
その他のC10,all other C10 hydrocarbons
C10
C10H22
C11以上,all higher hydrocarbons
C10
C10H22
メタノール(メチルアルコール),Methanol (Methyl alcohol)
CH4O
C2H6
メタンチオール(メチルメルカプタン),Methanethiol (Methyl mercaptan)
CH4S
C3H8
アンモニア,Ammonia
NH3
CH4
青酸(シアン化水素),Hydrogen cyanide
HCN
C2H6
カルボニルスルフィド(炭素オキシスルフィド),Carbonyl sulfide (Carbon oxysulfide)
COS
nC4H10
二硫化炭素,Carbon disulfide
CS2
nC5H12
二酸化硫黄,Sulfur dioxide
SO2
nC4H10
酸化二窒素,Nitrous oxide
N2O
CO2
76
M 8010:2020
附属書H
(規定)
Z数表(2015)
H.1 Z数表(2015)を用いた圧縮係数の計算
Z数表(2015)を用いた圧縮係数の計算は,次の手順に従う。
a) ガスの温度,圧力,成分のモル分率並びに表H.1に規定する定数ai及び定数biを用い,式(H.1)及び式
(H.2)でパラメータAZ及びBZを計算する。ガスが表H.1に含まれない成分を含有する場合,附属書G
が適用できる場合には,Z数表(2015)を使用することができる。
∑
=
i
i
ix
a
T
AZ
········································································· (H.1)
∑
=
i
i
ix
b
p
BZ
·········································································· (H.2)
ここに,
AZ: Z数表の横軸の値
BZ: Z数表の縦軸の値
ai: 表H.1に規定するi番目の成分の定数(K)
bi: 表H.1に規定するi番目の成分の定数(kPa)
xi: i番目の成分のモル分率
T: ガスの温度(K)
p: ガスの圧力(kPa)
注記 Z数表(2015)で使用するai及びbiは,Z数表の誤差を最小化するための定数であり,臨界定
数などの物理的意味をもつものではないことに注意する。
表H.1−Z数表(2015)の使用に必要となる定数ai及びbi
成分
ai(K)
bi(kPa)
CO2
295.889 3
6854.100 0
N2
124.742 8
3292.538 9
H2
55.175 5
3157.200 0
CO
136.937 5
3498.750 0
O2
154.770 0
5080.020 0
CH4
209.387 5
5104.748 0
C2H6
333.832 8
5372.235 0
C3H8
429.821 5
4256.660 0
iC4H10
546.848 6
4741.906 0
nC4H10
529.372 8
4555.944 0
iC5H12
616.933 3
2666.872 0
nC5H12
629.264 0
3712.632 0
C6H14
682.107 0
909.486 0
C7H16
432.126 4
2052.585 0
C8H18
454.878 4
1747.634 0
b) 表H.4の1行目からAZの値を挟む二つの列,1列目からBZの値を挟む二つの行を抜き出し,これら
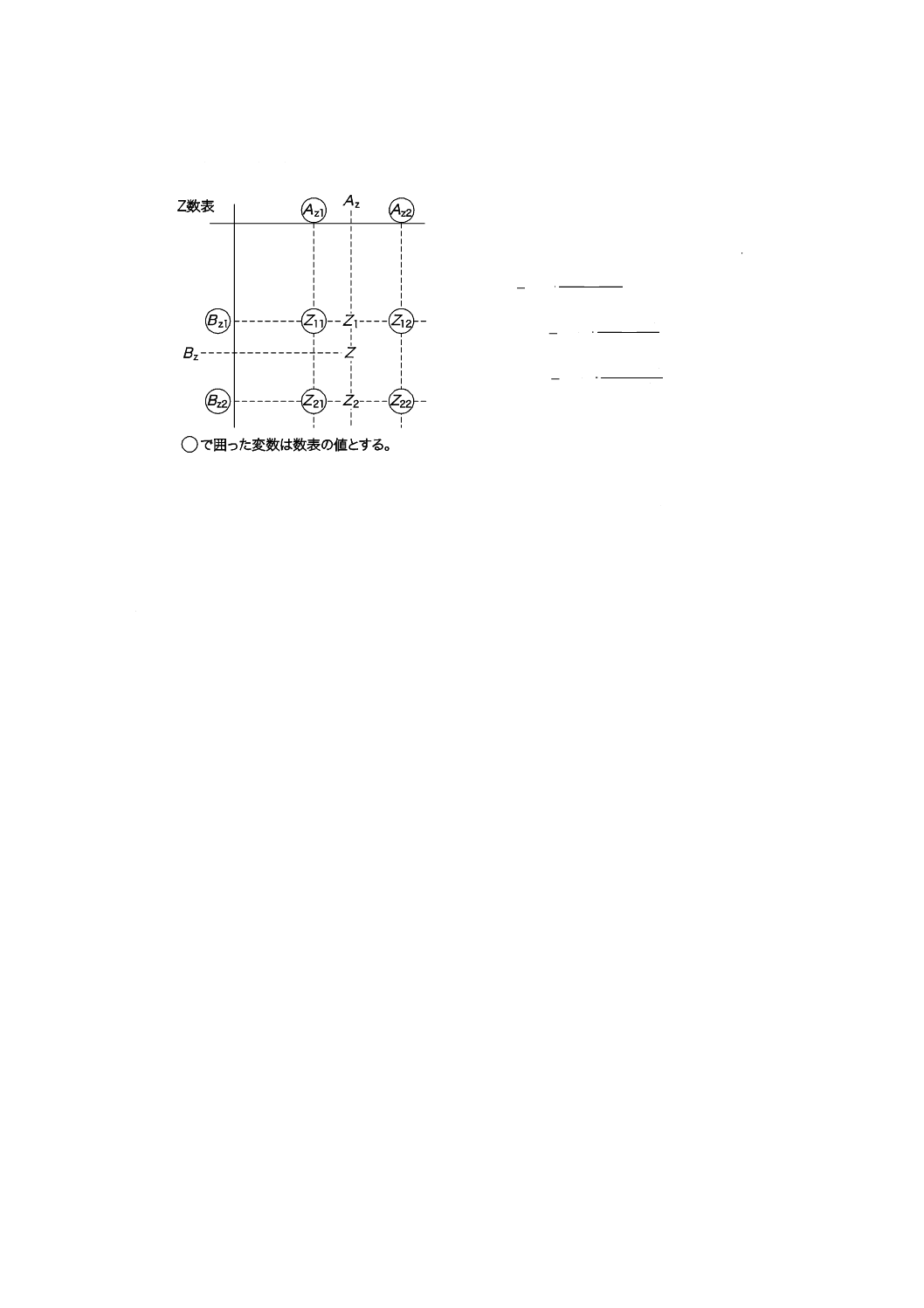
77
M 8010:2020
の行及び列の交差する位置における表H.4の値をAZ及びBZの値で内挿し,得られた値を圧縮係数の
値とする(図H.1参照)。
パラメータが(AZ, BZ)となったときの圧縮係数Z
)
(
1
Z
Z
1
Z
2
Z
1
2
1
B
B
B
B
Z
Z
Z
Z
−
−
−
+
=
)
(
1
Z
Z
1
Z
2
Z
11
12
11
1
A
A
A
A
Z
Z
Z
Z
−
−
−
+
=
)
(
1
Z
Z
1
Z
2
Z
21
22
21
2
A
A
A
A
Z
Z
Z
Z
−
−
−
+
=
図H.1−Z数表内挿の一例
Z数表(2015)を内挿して求めた圧縮係数の値は,AGA8-92DC法を用いて計算した値に対して誤差を
もち,その大きさは,含有成分比,温度及び圧力に依存する。表H.2に規定する最小含有比と最大含有比
との各組合せの範囲内にあるガスについて,Z数表(2015)を用いて求めた圧縮係数のAGA8-92DC法を
用いた結果からの差の目安を表H.3に示す。
注記 この誤差の目安は,成分範囲内でまんべんなく分布する多数の仮想ガスを用いて統計的に求め
たものであり,ほとんどのガスでは誤差は目安の値以下となるが,極端な成分分布をもつガス
では,これを超える誤差が発生することがあるため,AGA8-92DC法による直接計算を行うこ
とが望ましい。
表H.3を用いて誤差の目安を推定するためには,対象となるガスの相対密度を附属書L,総発熱量をJIS
K 2301に従って求め,それらの値が表H.2に規定する範囲内になければならない。AGA8-92DC法で計算
した値自体にも誤差があるため,Z数表を用いて得た圧縮係数の誤差は,Z数表自体がもつ誤差のほかに,
AGA8-92DC法の不確かさを付加する必要がある。
注記 AGA8-92DC法の不確かさは多くの場合で0.1 %となるが,極端な成分分布をもつ条件ではこれ
より大きくなる。その条件で不確かさを求める場合はISO 12213-2:2006[2]を参照する。
78
M 8010:2020
表H.2−Z数表(2015)の不確かさの評価範囲
成分
最小モル分率
最大モル分率
min1
min2
max1
max2
max3
CO2
0
0
0.2
0.043
0.07
N2
0
0
0.2
0.025
0.04
H2
0
0
0.1
0.000 5
0
CO
0
0
0.03
0.001
0
O2
0
0
0.000 2
0.000 5
0.001
CH4
0.7
0.55
1
1
0.95
C2H6
0
0
0.1
0.116
0.16
C3H8
0
0
0.035
0.063
0.15
iC4H10
0
0
0.015
0.012
0.03
nC4H10
0
0
0.015
0.018
0.03
iC5H12
0
0
0.005
0.006
0.01
nC5H12
0
0
0.005
0.006
0.01
C6H14
0
0
0.001
0.009
0.005
C7H16
0
0
0.000 5
0.000 5
0.001
C8H18
0
0
0.000 5
0.000 5
0.001
総発熱量範囲:30 MJ/m3〜48 MJ/m3
相対密度範囲:0.55〜0.90
表H.3−表H.2のガス種に関するZ数表(2015)内挿値の
AGA8-92DC法で求めた値からの差(%)の目安
MPa
−20 ℃〜0 ℃
0 ℃〜80 ℃
min1
min2
min1
min2
max1
max2
max3
max1
max2
max3
max1
max2
max3
max1
max2
max3
1
0.05
0.05
0.05
0.15
0.15
0.15
0.05
0.10
0.10
0.10
0.10
0.10
2
0.10
0.10
0.10
0.25
0.30
0.30
0.10
0.20
0.20
0.15
0.20
0.20
4
0.25
0.30
0.25
0.35
0.50
0.50
0.15
0.40
0.35
0.25
0.40
0.25
6
0.35
0.40
0.50
0.35
0.50
0.50
9.25
0.50
0.55
0.30
0.45
0.40
8
0.45
0.60
0.70
0.40
0.60
0.70
0.30
0.45
0.65
0.30
0.50
0.55
10
0.45
1.35
0.95
0.65
1.35
1.00
0.30
0.50
0.65
0.40
0.50
0.65

79
M 8010:2020
表H.4−Z数表(2015)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
0.01
0.996 67
0.997 14
0.997 54
0.997 87
0.998 15
0.998 39
0.998 60
0.998 78
0.998 93
0.999 06
0.999 18
0.999 28
0.999 36
0.999 44
0.999 51
0.999 57
0.999 63
0.999 68
0.999 72
0.999 76
0.999 79
0.02
0.993 32
0.994 27
0.995 07
0.995 74
0.996 31
0.996 79
0.997 20
0.997 55
0.997 86
0.998 12
0.998 35
0.998 55
0.998 73
0.998 89
0.999 02
0.999 15
0.999 26
0.999 35
0.999 44
0.999 52
0.999 59
0.03
0.989 95
0.991 39
0.992 59
0.993 60
0.994 45
0.995 18
0.995 80
0.996 33
0.996 79
0.997 18
0.997 53
0.997 83
0.998 10
0.998 33
0.998 54
0.998 72
0.998 88
0.999 03
0.999 16
0.999 28
0.999 38
0.04
0.986 58
0.988 50
0.990 11
0.991 46
0.992 60
0.993 57
0.994 40
0.995 10
0.995 71
0.996 24
0.996 70
0.997 11
0.997 46
0.997 77
0.998 05
0.998 30
0.998 51
0.998 71
0.998 88
0.999 04
0.999 18
0.05
0.983 19
0.985 60
0.987 62
0.989 31
0.990 75
0.991 96
0.992 99
0.993 88
0.994 64
0.995 31
0.995 88
0.996 39
0.996 83
0.997 22
0.997 56
0.997 87
0.998 14
0.998 39
0.998 61
0.998 80
0.998 98
0.06
0.979 78
0.982 69
0.985 12
0.987 17
0.988 89
0.990 35
0.991 59
0.992 65
0.993 57
0.994 37
0.995 06
0.995 67
0.996 20
0.996 67
0.997 08
0.997 45
0.997 78
0.998 07
0.998 33
0.998 56
0.998 77
0.07
0.976 36
0.979 77
0.982 62
0.985 01
0.987 03
0.988 73
0.990 18
0.991 43
0.992 50
0.993 43
0.994 24
0.994 95
0.995 57
0.996 11
0.996 60
0.997 03
0.997 41
0.997 75
0.998 05
0.998 33
0.998 57
0.08
0.972 93
0.976 84
0.980 11
0.982 86
0.985 16
0.987 12
0.988 78
0.990 20
0.991 43
0.992 49
0.993 42
0.994 23
0.994 94
0.995 56
0.996 11
0.996 60
0.997 04
0.997 43
0.997 78
0.998 09
0.998 37
0.09
0.969 48
0.973 90
0.977 60
0.980 69
0.983 30
0.985 50
0.987 37
0.988 98
0.990 36
0.991 56
0.992 60
0.993 51
0.994 31
0.995 01
0.995 63
0.996 18
0.996 67
0.997 11
0.997 50
0.997 86
0.998 17
0.10
0.966 01
0.970 95
0.975 08
0.978 53
0.981 43
0.983 88
0.985 97
0.987 75
0.989 29
0.990 62
0.991 78
0.992 79
0.993 68
0.994 46
0.995 15
0.995 76
0.996 31
0.996 80
0.997 23
0.997 62
0.997 97
0.11
0.962 53
0.967 99
0.972 55
0.976 36
0.979 56
0.982 26
0.984 56
0.986 53
0.988 22
0.989 69
0.990 96
0.992 07
0.993 05
0.993 91
0.994 67
0.995 34
0.995 94
0.996 48
0.996 96
0.997 39
0.997 77
0.12
0.959 03
0.965 03
0.970 02
0.974 19
0.977 68
0.980 64
0.983 15
0.985 30
0.987 15
0.988 75
0.990 14
0.991 36
0.992 42
0.993 36
0.994 19
0.994 93
0.995 58
0.996 16
0.996 69
0.997 15
0.997 58
0.13
0.955 52
0.962 05
0.967 48
0.972 01
0.975 81
0.979 02
0.981 75
0.984 08
0.986 08
0.987 82
0.989 32
0.990 64
0.991 80
0.992 81
0.993 71
0.994 51
0.995 22
0.995 85
0.996 42
0.996 92
0.997 38
0.14
0.951 99
0.959 06
0.964 93
0.969 83
0.973 93
0.977 39
0.980 34
0.982 85
0.985 01
0.986 88
0.988 51
0.989 93
0.991 17
0.992 27
0.993 23
0.994 09
0.994 86
0.995 54
0.996 15
0.996 69
0.997 18
0.15
0.948 44
0.956 06
0.962 38
0.967 64
0.972 05
0.975 77
0.978 93
0.981 63
0.983 95
0.985 95
0.987 69
0.989 21
0.990 55
0.991 72
0.992 76
0.993 68
0.994 50
0.995 22
0.995 88
0.996 46
0.996 99
0.16
0.944 88
0.953 04
0.959 81
0.965 45
0.970 17
0.974 14
0.977 52
0.980 40
0.982 88
0.985 02
0.986 88
0.988 50
0.989 92
0.991 18
0.992 28
0.993 26
0.994 13
0.994 91
0.995 61
0.996 23
0.996 79
0.17
0.941 30
0.950 02
0.957 25
0.963 25
0.968 28
0.972 52
0.976 11
0.979 17
0.981 81
0.984 09
0.986 06
0.987 79
0.989 30
0.990 63
0.991 81
0.992 85
0.993 78
0.994 60
0.995 34
0.996 00
0.996 60
0.18
0.937 70
0.946 99
0.954 67
0.961 06
0.966 39
0.970 89
0.974 70
0.977 95
0.980 74
0.983 15
0.985 25
0.987 08
0.988 68
0.990 09
0.991 33
0.992 44
0.993 42
0.994 29
0.995 07
0.995 77
0.996 40
0.19
0.934 09
0.943 94
0.952 09
0.958 85
0.964 50
0.969 26
0.973 29
0.976 72
0.979 67
0.982 22
0.984 44
0.986 37
0.988 06
0.989 55
0.990 86
0.992 02
0.993 06
0.993 98
0.994 81
0.995 55
0.996 21
0.20
0.930 45
0.940 89
0.949 50
0.956 65
0.962 61
0.967 63
0.971 87
0.975 50
0.978 61
0.981 29
0.983 62
0.985 66
0.987 44
0.989 00
0.990 39
0.991 61
0.992 70
0.993 67
0.994 54
0.995 32
0.996 02
0.21
0.926 80
0.937 82
0.946 91
0.954 43
0.960 71
0.965 99
0.970 46
0.974 27
0.977 54
0.980 36
0.982 81
0.984 95
0.986 82
0.988 46
0.989 92
0.991 20
0.992 35
0.993 37
0.994 28
0.995 09
0.995 83
0.22
0.923 12
0.934 74
0.944 30
0.952 22
0.958 82
0.964 36
0.969 05
0.973 05
0.976 48
0.979 43
0.982 00
0.984 24
0.986 20
0.987 92
0.989 45
0.990 79
0.991 99
0.993 06
0.994 01
0.994 87
0.995 64
0.23
0.919 43
0.931 65
0.941 69
0.950 00
0.956 92
0.962 72
0.967 64
0.971 82
0.975 41
0.978 51
0.981 19
0.983 53
0.985 58
0.987 39
0.988 98
0.990 39
0.991 64
0.992 75
0.993 75
0.994 65
0.995 45
0.24
0.915 72
0.928 55
0.939 08
0.947 77
0.955 01
0.961 09
0.966 22
0.970 60
0.974 35
0.977 58
0.980 38
0.982 83
0.984 97
0.986 85
0.988 51
0.989 98
0.991 29
0.992 45
0.993 49
0.994 42
0.995 26
0.25
0.911 99
0.925 43
0.936 45
0.945 54
0.953 11
0.959 45
0.964 81
0.969 37
0.973 28
0.976 65
0.979 57
0.982 12
0.984 35
0.986 31
0.988 04
0.989 57
0.990 93
0.992 15
0.993 23
0.994 20
0.995 07
0.26
0.908 24
0.922 30
0.933 82
0.943 31
0.951 20
0.957 81
0.963 39
0.968 15
0.972 22
0.975 73
0.978 77
0.981 42
0.983 74
0.985 78
0.987 57
0.989 17
0.990 58
0.991 84
0.992 97
0.993 98
0.994 88
0.27
0.904 46
0.919 16
0.931 18
0.941 07
0.949 29
0.956 17
0.961 98
0.966 92
0.971 15
0.974 80
0.977 96
0.980 71
0.983 12
0.985 24
0.987 11
0.988 76
0.990 23
0.991 54
0.992 71
0.993 76
0.994 70
0.28
0.900 67
0.916 01
0.928 53
0.938 83
0.947 38
0.954 53
0.960 56
0.965 70
0.970 09
0.973 87
0.977 15
0.980 01
0.982 51
0.984 71
0.986 64
0.988 36
0.989 88
0.991 24
0.992 45
0.993 54
0.994 51
0.29
0.896 85
0.912 84
0.925 88
0.936 58
0.945 46
0.952 88
0.959 15
0.964 47
0.969 03
0.972 95
0.976 35
0.979 31
0.981 90
0.984 17
0.986 18
0.987 96
0.989 53
0.990 94
0.992 19
0.993 32
0.994 33
0.30
0.893 01
0.909 67
0.923 21
0.934 33
0.943 54
0.951 24
0.957 73
0.963 25
0.967 96
0.972 03
0.975 55
0.978 61
0.981 29
0.983 64
0.985 72
0.987 55
0.989 19
0.990 64
0.991 94
0.993 10
0.994 14
0.31
0.889 15
0.906 47
0.920 54
0.932 08
0.941 62
0.949 60
0.956 31
0.962 02
0.966 90
0.971 10
0.974 74
0.977 91
0.980 68
0.983 11
0.985 26
0.987 15
0.988 84
0.990 34
0.991 68
0.992 88
0.993 96
0.32
0.885 27
0.903 27
0.917 86
0.929 82
0.939 70
0.947 95
0.954 90
0.960 80
0.965 84
0.970 18
0.973 94
0.977 21
0.980 07
0.982 58
0.984 79
0.986 75
0.988 49
0.990 04
0.991 43
0.992 67
0.993 78
0.33
0.881 36
0.900 05
0.915 18
0.927 55
0.937 77
0.946 30
0.953 48
0.959 57
0.964 78
0.969 26
0.973 14
0.976 51
0.979 46
0.982 05
0.984 33
0.986 36
0.988 15
0.989 75
0.991 17
0.992 45
0.993 60
0.34
0.877 43
0.896 81
0.912 48
0.925 28
0.935 85
0.944 65
0.952 06
0.958 35
0.963 72
0.968 34
0.972 34
0.975 81
0.978 85
0.981 52
0.983 88
0.985 96
0.987 81
0.989 45
0.990 92
0.992 23
0.993 42
0.35
0.873 47
0.893 57
0.909 78
0.923 01
0.933 92
0.943 00
0.950 65
0.957 13
0.962 66
0.967 42
0.971 54
0.975 12
0.978 25
0.981 00
0.983 42
0.985 56
0.987 46
0.989 16
0.990 67
0.992 02
0.993 23
0.36
0.869 48
0.890 31
0.907 07
0.920 73
0.931 98
0.941 35
0.949 23
0.955 90
0.961 60
0.966 50
0.970 74
0.974 42
0.977 64
0.980 47
0.982 96
0.985 16
0.987 12
0.988 86
0.990 42
0.991 81
0.993 06
0.37
0.865 48
0.887 03
0.904 35
0.918 45
0.930 05
0.939 70
0.947 81
0.954 68
0.960 54
0.965 58
0.969 94
0.973 73
0.977 04
0.979 95
0.982 51
0.984 77
0.986 78
0.988 57
0.990 17
0.991 59
0.992 88
0.38
0.861 44
0.883 74
0.901 62
0.916 16
0.928 11
0.938 05
0.946 39
0.953 46
0.959 49
0.964 67
0.969 14
0.973 04
0.976 44
0.979 42
0.982 05
0.984 38
0.986 44
0.988 28
0.989 92
0.991 38
0.992 70
0.39
0.857 38
0.880 43
0.898 89
0.913 87
0.926 17
0.936 39
0.944 97
0.952 23
0.958 43
0.963 75
0.968 35
0.972 34
0.975 84
0.978 90
0.981 60
0.983 98
0.986 10
0.987 98
0.989 67
0.991 17
0.992 52
0.40
0.853 29
0.877 11
0.896 15
0.911 57
0.924 23
0.934 74
0.943 55
0.951 01
0.957 37
0.962 83
0.967 55
0.971 65
0.975 23
0.978 38
0.981 14
0.983 59
0.985 76
0.987 69
0.989 42
0.990 96
0.992 35
0.41
0.849 17
0.873 78
0.893 39
0.909 27
0.922 28
0.933 08
0.942 13
0.949 79
0.956 32
0.961 92
0.966 76
0.970 96
0.974 64
0.977 86
0.980 69
0.983 20
0.985 42
0.987 40
0.989 17
0.990 75
0.992 17
0.42
0.845 02
0.870 43
0.890 63
0.906 96
0.920 34
0.931 43
0.940 72
0.948 57
0.955 26
0.961 00
0.965 97
0.970 27
0.974 04
0.977 34
0.980 24
0.982 81
0.985 09
0.987 12
0.988 93
0.990 54
0.992 00
0.43
0.840 85
0.867 06
0.887 86
0.904 65
0.918 39
0.929 77
0.939 30
0.947 35
0.954 21
0.960 09
0.965 17
0.969 59
0.973 44
0.976 82
0.979 79
0.982 42
0.984 75
0.986 83
0.988 68
0.990 34
0.991 82
0.44
0.836 64
0.863 68
0.885 08
0.902 33
0.916 44
0.928 11
0.937 88
0.946 13
0.953 15
0.959 18
0.964 38
0.968 90
0.972 84
0.976 30
0.979 34
0.982 03
0.984 42
0.986 54
0.988 44
0.990 13
0.991 65
11
M
8
0
1
0
:
2
0
2
0

80
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
0.45
0.832 40
0.860 28
0.882 30
0.900 01
0.914 48
0.926 45
0.936 46
0.944 91
0.952 10
0.958 27
0.963 59
0.968 21
0.972 25
0.975 78
0.978 90
0.981 65
0.984 09
0.986 26
0.988 19
0.989 92
0.991 48
0.46
0.828 13
0.856 86
0.879 50
0.897 69
0.912 52
0.924 79
0.935 04
0.943 69
0.951 05
0.957 36
0.962 80
0.967 53
0.971 65
0.975 27
0.978 45
0.981 26
0.983 75
0.985 97
0.987 95
0.989 72
0.991 31
0.47
0.823 83
0.853 43
0.876 70
0.895 36
0.910 57
0.923 13
0.933 62
0.942 47
0.950 00
0.956 45
0.962 01
0.966 85
0.971 06
0.974 75
0.978 00
0.980 88
0.983 42
0.985 69
0.987 71
0.989 51
0.991 14
0.48
0.819 49
0.849 98
0.873 88
0.893 02
0.908 60
0.921 46
0.932 20
0.941 25
0.948 94
0.955 54
0.961 23
0.966 16
0.970 47
0.974 24
0.977 56
0.980 49
0.983 09
0.985 40
0.987 47
0.989 31
0.990 97
0.49
0.815 12
0.846 51
0.871 06
0.890 68
0.906 64
0.919 80
0.930 78
0.940 03
0.947 90
0.954 63
0.960 44
0.965 48
0.969 88
0.973 73
0.977 12
0.980 11
0.982 76
0.985 12
0.987 23
0.989 11
0.990 80
0.50
0.810 71
0.843 03
0.868 23
0.888 34
0.904 68
0.918 13
0.929 36
0.938 81
0.946 85
0.953 73
0.959 66
0.964 80
0.969 29
0.973 22
0.976 67
0.979 73
0.982 43
0.984 84
0.986 99
0.988 91
0.990 63
0.51
0.806 27
0.839 52
0.865 39
0.885 99
0.902 71
0.916 47
0.927 94
0.937 59
0.945 80
0.952 82
0.958 87
0.964 12
0.968 70
0.972 71
0.976 23
0.979 35
0.982 11
0.984 56
0.986 75
0.988 71
0.990 46
0.52
0.801 79
0.836 00
0.862 53
0.883 64
0.900 74
0.914 80
0.926 52
0.936 38
0.944 75
0.951 92
0.958 09
0.963 44
0.968 11
0.972 20
0.975 79
0.978 97
0.981 78
0.984 28
0.986 51
0.988 51
0.990 29
0.53
0.797 27
0.832 46
0.859 67
0.881 28
0.898 76
0.913 14
0.925 10
0.935 16
0.943 70
0.951 01
0.957 31
0.962 77
0.967 52
0.971 69
0.975 35
0.978 59
0.981 45
0.984 00
0.986 28
0.988 31
0.990 13
0.54
0.792 71
0.828 90
0.856 80
0.878 91
0.896 79
0.911 47
0.923 68
0.933 95
0.942 66
0.950 11
0.956 53
0.962 09
0.966 94
0.971 18
0.974 91
0.978 21
0.981 13
0.983 73
0.986 04
0.988 11
0.989 96
0.55
0.788 11
0.825 33
0.853 92
0.876 55
0.894 81
0.909 80
0.922 26
0.932 73
0.941 61
0.949 21
0.955 75
0.961 42
0.966 35
0.970 68
0.974 48
0.977 83
0.980 81
0.983 45
0.985 81
0.987 91
0.989 80
0.56
0.783 47
0.821 73
0.851 04
0.874 17
0.892 83
0.908 13
0.920 84
0.931 52
0.940 57
0.948 31
0.954 97
0.960 74
0.965 77
0.970 17
0.974 04
0.977 46
0.980 48
0.983 17
0.985 57
0.987 72
0.989 64
0.57
0.778 79
0.818 11
0.848 14
0.871 80
0.890 85
0.906 46
0.919 42
0.930 30
0.939 53
0.947 41
0.954 19
0.960 07
0.965 19
0.969 67
0.973 61
0.977 08
0.980 16
0.982 90
0.985 34
0.987 52
0.989 47
0.58
0.774 06
0.814 48
0.845 23
0.869 41
0.888 87
0.904 79
0.918 00
0.929 09
0.938 48
0.946 51
0.953 42
0.959 40
0.964 61
0.969 17
0.973 17
0.976 71
0.979 84
0.982 63
0.985 11
0.987 32
0.989 31
0.59
0.769 29
0.810 82
0.842 31
0.867 03
0.886 88
0.903 12
0.916 58
0.927 88
0.937 44
0.945 61
0.952 64
0.958 73
0.964 03
0.968 67
0.972 74
0.976 34
0.979 52
0.982 35
0.984 88
0.987 13
0.989 15
0.60
0.764 47
0.807 14
0.839 38
0.864 63
0.884 89
0.901 45
0.915 16
0.926 66
0.936 40
0.944 72
0.951 87
0.958 06
0.963 45
0.968 17
0.972 31
0.975 97
0.979 20
0.982 08
0.984 65
0.986 94
0.988 99
0.61
0.759 60
0.803 44
0.836 44
0.862 24
0.882 90
0.899 77
0.913 75
0.925 45
0.935 36
0.943 82
0.951 10
0.957 39
0.962 87
0.967 67
0.971 88
0.975 60
0.978 89
0.981 81
0.984 42
0.986 75
0.988 83
0.62
0.754 68
0.799 72
0.833 49
0.859 83
0.880 91
0.898 10
0.912 33
0.924 24
0.934 33
0.942 93
0.950 33
0.956 73
0.962 30
0.967 17
0.971 45
0.975 23
0.978 57
0.981 54
0.984 19
0.986 55
0.988 67
0.63
0.749 71
0.795 98
0.830 53
0.857 43
0.878 92
0.896 43
0.910 91
0.923 03
0.933 29
0.942 04
0.949 56
0.956 06
0.961 72
0.966 67
0.971 02
0.974 86
0.978 25
0.981 27
0.983 96
0.986 36
0.988 52
0.64
0.744 69
0.792 22
0.827 57
0.855 02
0.876 92
0.894 75
0.909 49
0.921 82
0.932 25
0.941 15
0.948 79
0.955 40
0.961 15
0.966 18
0.970 59
0.974 49
0.977 94
0.981 00
0.983 73
0.986 17
0.988 36
0.65
0.739 61
0.788 43
0.824 59
0.852 60
0.874 92
0.893 08
0.908 07
0.920 62
0.931 22
0.940 26
0.948 02
0.954 74
0.960 58
0.965 68
0.970 17
0.974 12
0.977 63
0.980 74
0.983 51
0.985 99
0.988 20
0.66
0.734 48
0.784 62
0.821 60
0.850 18
0.872 92
0.891 40
0.906 66
0.919 41
0.930 18
0.939 37
0.947 25
0.954 07
0.960 01
0.965 19
0.969 74
0.973 76
0.977 31
0.980 47
0.983 28
0.985 80
0.988 05
0.67
0.729 28
0.780 79
0.818 60
0.847 75
0.870 92
0.889 73
0.905 24
0.918 20
0.929 15
0.938 48
0.946 49
0.953 41
0.959 44
0.964 70
0.969 32
0.973 40
0.977 00
0.980 21
0.983 06
0.985 61
0.987 89
0.68
0.724 03
0.776 94
0.815 58
0.845 32
0.868 92
0.888 05
0.903 83
0.917 00
0.928 12
0.937 59
0.945 73
0.952 76
0.958 87
0.964 21
0.968 90
0.973 03
0.976 69
0.979 94
0.982 84
0.985 43
0.987 74
0.69
0.718 71
0.773 06
0.812 56
0.842 89
0.866 91
0.886 38
0.902 41
0.915 79
0.927 09
0.936 71
0.944 96
0.952 10
0.958 30
0.963 72
0.968 48
0.972 67
0.976 38
0.979 68
0.982 62
0.985 24
0.987 59
0.70
0.713 33
0.769 15
0.809 53
0.840 45
0.864 91
0.884 70
0.901 00
0.914 59
0.926 06
0.935 82
0.944 20
0.951 44
0.957 73
0.963 23
0.968 06
0.972 31
0.976 08
0.979 42
0.982 40
0.985 06
0.987 44
0.71
0.707 88
0.765 22
0.806 49
0.838 00
0.862 90
0.883 02
0.899 58
0.913 39
0.925 03
0.934 94
0.943 44
0.950 79
0.957 17
0.962 74
0.967 64
0.971 95
0.975 77
0.979 16
0.982 18
0.984 87
0.987 29
0.72
0.702 36
0.761 27
0.803 43
0.835 55
0.860 88
0.881 35
0.898 17
0.912 19
0.924 00
0.934 06
0.942 68
0.950 13
0.956 61
0.962 26
0.967 22
0.971 59
0.975 46
0.978 90
0.981 96
0.984 69
0.987 14
0.73
0.696 77
0.757 29
0.800 37
0.833 10
0.858 87
0.879 67
0.896 75
0.910 99
0.922 98
0.933 18
0.941 93
0.949 48
0.956 04
0.961 78
0.966 80
0.971 24
0.975 16
0.978 64
0.981 74
0.984 51
0.986 99
0.74
0.691 10
0.753 29
0.797 29
0.830 64
0.856 86
0.877 99
0.895 34
0.909 79
0.921 95
0.932 30
0.941 17
0.948 83
0.955 48
0.961 29
0.966 39
0.970 88
0.974 86
0.978 38
0.981 52
0.984 33
0.986 84
0.75
0.685 35
0.749 25
0.794 21
0.828 17
0.854 84
0.876 31
0.893 93
0.908 59
0.920 93
0.931 42
0.940 42
0.948 18
0.954 92
0.960 81
0.965 98
0.970 53
0.974 55
0.978 13
0.981 31
0.984 15
0.986 69
0.76
0.679 53
0.745 20
0.791 11
0.825 71
0.852 82
0.874 64
0.892 52
0.907 39
0.919 91
0.930 55
0.939 67
0.947 53
0.954 37
0.960 33
0.965 56
0.970 17
0.974 25
0.977 87
0.981 09
0.983 97
0.986 54
0.77
0.673 61
0.741 11
0.788 00
0.823 23
0.850 80
0.872 96
0.891 11
0.906 19
0.918 89
0.929 67
0.938 91
0.946 89
0.953 81
0.959 85
0.965 15
0.969 82
0.973 95
0.977 62
0.980 88
0.983 79
0.986 40
0.78
0.667 61
0.737 00
0.784 88
0.820 76
0.848 78
0.871 28
0.889 70
0.905 00
0.917 87
0.928 80
0.938 16
0.946 24
0.953 25
0.959 37
0.964 74
0.969 47
0.973 65
0.977 36
0.980 66
0.983 61
0.986 25
0.79
0.661 51
0.732 86
0.781 75
0.818 27
0.846 76
0.869 60
0.888 29
0.903 81
0.916 85
0.927 93
0.937 42
0.945 60
0.952 70
0.958 90
0.964 33
0.969 12
0.973 35
0.977 11
0.980 45
0.983 44
0.986 11
0.80
0.655 32
0.728 69
0.778 61
0.815 79
0.844 74
0.867 93
0.886 88
0.902 61
0.915 84
0.927 06
0.936 67
0.944 96
0.952 15
0.958 42
0.963 92
0.968 77
0.973 06
0.976 86
0.980 24
0.983 26
0.985 97
0.81
0.649 03
0.724 49
0.775 46
0.813 30
0.842 71
0.866 25
0.885 47
0.901 42
0.914 82
0.926 19
0.935 92
0.944 31
0.951 59
0.957 95
0.963 52
0.968 42
0.972 76
0.976 61
0.980 03
0.983 09
0.985 82
0.82
0.642 63
0.720 26
0.772 29
0.810 80
0.840 68
0.864 57
0.884 07
0.900 23
0.913 81
0.925 32
0.935 18
0.943 67
0.951 04
0.957 47
0.963 11
0.968 08
0.972 46
0.976 36
0.979 82
0.982 91
0.985 68
0.83
0.636 12
0.716 01
0.769 12
0.808 30
0.838 66
0.862 89
0.882 66
0.899 04
0.912 79
0.924 46
0.934 44
0.943 04
0.950 50
0.957 00
0.962 71
0.967 73
0.972 17
0.976 11
0.979 61
0.982 74
0.985 54
0.84
0.629 49
0.711 72
0.765 93
0.805 80
0.836 63
0.861 22
0.881 26
0.897 86
0.911 78
0.923 59
0.933 69
0.942 40
0.949 95
0.956 53
0.962 30
0.967 39
0.971 88
0.975 86
0.979 41
0.982 57
0.985 40
0.85
0.622 75
0.707 40
0.762 73
0.803 29
0.834 60
0.859 54
0.879 85
0.896 67
0.910 77
0.922 73
0.932 96
0.941 76
0.949 40
0.956 06
0.961 90
0.967 04
0.971 59
0.975 61
0.979 20
0.982 40
0.985 26
0.86
0.615 87
0.703 05
0.759 52
0.800 78
0.832 56
0.857 86
0.878 45
0.895 48
0.909 77
0.921 87
0.932 22
0.941 13
0.948 86
0.955 60
0.961 50
0.966 70
0.971 29
0.975 37
0.978 99
0.982 23
0.985 12
0.87
0.608 87
0.698 67
0.756 30
0.798 26
0.830 53
0.856 19
0.877 05
0.894 30
0.908 76
0.921 01
0.931 48
0.940 50
0.948 32
0.955 13
0.961 10
0.966 36
0.971 01
0.975 12
0.978 79
0.982 06
0.984 99
0.88
0.601 72
0.694 26
0.753 07
0.795 74
0.828 50
0.854 51
0.875 65
0.893 12
0.907 76
0.920 15
0.930 75
0.939 87
0.947 77
0.954 67
0.960 71
0.966 02
0.970 72
0.974 88
0.978 59
0.981 89
0.984 85
11
M
8
0
1
0
:
2
0
2
0

81
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
0.89
0.594 43
0.689 82
0.749 83
0.793 22
0.826 46
0.852 84
0.874 25
0.891 94
0.906 75
0.919 30
0.930 01
0.939 24
0.947 23
0.954 20
0.960 31
0.965 68
0.970 43
0.974 64
0.978 38
0.981 73
0.984 72
0.90
0.586 98
0.685 35
0.746 58
0.790 69
0.824 43
0.851 16
0.872 85
0.890 76
0.905 75
0.918 44
0.929 28
0.938 61
0.946 70
0.953 74
0.959 91
0.965 34
0.970 14
0.974 40
0.978 18
0.981 56
0.984 58
0.91
0.579 37
0.680 84
0.743 31
0.788 16
0.822 39
0.849 49
0.871 45
0.889 58
0.904 75
0.917 59
0.928 55
0.937 98
0.946 16
0.953 28
0.959 52
0.965 01
0.969 86
0.974 16
0.977 98
0.981 39
0.984 45
0.92
0.571 59
0.676 30
0.740 04
0.785 62
0.820 36
0.847 81
0.870 06
0.888 41
0.903 75
0.916 74
0.927 82
0.937 36
0.945 62
0.952 82
0.959 13
0.964 67
0.969 57
0.973 92
0.977 78
0.981 23
0.984 31
0.93
0.563 64
0.671 73
0.736 75
0.783 08
0.818 32
0.846 14
0.868 66
0.887 23
0.902 76
0.915 89
0.927 09
0.936 74
0.945 09
0.952 36
0.958 74
0.964 34
0.969 29
0.973 68
0.977 58
0.981 07
0.984 18
0.94
0.555 50
0.667 12
0.733 46
0.780 54
0.816 28
0.844 47
0.867 27
0.886 06
0.901 76
0.915 04
0.926 37
0.936 12
0.944 56
0.951 91
0.958 35
0.964 01
0.969 01
0.973 44
0.977 39
0.980 90
0.984 05
0.95
0.547 17
0.662 48
0.730 15
0.777 99
0.814 24
0.842 80
0.865 88
0.884 89
0.900 77
0.914 19
0.925 65
0.935 50
0.944 02
0.951 45
0.957 96
0.963 68
0.968 73
0.973 21
0.977 19
0.980 74
0.983 92
0.96
0.538 64
0.657 81
0.726 83
0.775 44
0.812 20
0.841 13
0.864 49
0.883 72
0.899 78
0.913 35
0.924 92
0.934 88
0.943 49
0.951 00
0.957 57
0.963 35
0.968 45
0.972 97
0.976 99
0.980 58
0.983 79
0.97
0.529 91
0.653 11
0.723 51
0.772 89
0.810 16
0.839 46
0.863 10
0.882 55
0.898 79
0.912 51
0.924 20
0.934 26
0.942 97
0.950 55
0.957 18
0.963 02
0.968 17
0.972 74
0.976 80
0.980 42
0.983 66
0.98
0.520 98
0.648 38
0.720 17
0.770 33
0.808 12
0.837 79
0.861 71
0.881 38
0.897 80
0.911 66
0.923 49
0.933 65
0.942 44
0.950 10
0.956 80
0.962 69
0.967 89
0.972 51
0.976 61
0.980 26
0.983 53
0.99
0.511 85
0.643 61
0.716 82
0.767 78
0.806 08
0.836 12
0.860 33
0.880 22
0.896 82
0.910 83
0.922 77
0.933 03
0.941 91
0.949 65
0.956 41
0.962 36
0.967 62
0.972 27
0.976 41
0.980 11
0.983 41
1.00
0.502 54
0.638 81
0.713 46
0.765 21
0.804 04
0.834 46
0.858 94
0.879 06
0.895 83
0.909 99
0.922 05
0.932 42
0.941 39
0.949 20
0.956 03
0.962 04
0.967 34
0.972 04
0.976 22
0.979 95
0.983 28
1.01
0.493 07
0.633 97
0.710 10
0.762 65
0.802 00
0.832 79
0.857 56
0.877 90
0.894 85
0.909 15
0.921 34
0.931 81
0.940 87
0.948 75
0.955 65
0.961 72
0.967 07
0.971 81
0.976 03
0.979 79
0.983 16
1.02
0.483 47
0.629 11
0.706 72
0.760 08
0.799 96
0.831 13
0.856 18
0.876 74
0.893 87
0.908 32
0.920 63
0.931 20
0.940 35
0.948 31
0.955 27
0.961 39
0.966 80
0.971 59
0.975 84
0.979 64
0.983 03
1.03
0.473 81
0.624 22
0.703 34
0.757 51
0.797 93
0.829 46
0.854 80
0.875 58
0.892 89
0.907 49
0.919 92
0.930 59
0.939 83
0.947 86
0.954 89
0.961 07
0.966 53
0.971 36
0.975 65
0.979 48
0.982 91
1.04
0.464 13
0.619 29
0.699 94
0.754 94
0.795 89
0.827 80
0.853 42
0.874 43
0.891 91
0.906 66
0.919 21
0.929 99
0.939 31
0.947 42
0.954 52
0.960 75
0.966 26
0.971 13
0.975 47
0.979 33
0.982 79
1.05
0.454 52
0.614 34
0.696 54
0.752 37
0.793 85
0.826 14
0.852 05
0.873 27
0.890 94
0.905 83
0.918 50
0.929 39
0.938 79
0.946 98
0.954 14
0.960 43
0.965 99
0.970 91
0.975 28
0.979 18
0.982 66
1.06
0.445 06
0.609 36
0.693 13
0.749 79
0.791 81
0.824 48
0.850 68
0.872 12
0.889 97
0.905 00
0.917 80
0.928 78
0.938 28
0.946 54
0.953 77
0.960 12
0.965 72
0.970 68
0.975 09
0.979 03
0.982 54
1.07
0.435 83
0.604 36
0.689 71
0.747 22
0.789 77
0.822 83
0.849 31
0.870 97
0.889 00
0.904 18
0.917 10
0.928 18
0.937 77
0.946 10
0.953 39
0.959 80
0.965 45
0.970 46
0.974 91
0.978 88
0.982 42
1.08
0.426 90
0.599 33
0.686 29
0.744 64
0.787 73
0.821 17
0.847 94
0.869 83
0.888 03
0.903 36
0.916 40
0.927 58
0.937 26
0.945 67
0.953 02
0.959 49
0.965 19
0.970 24
0.974 73
0.978 73
0.982 30
1.09
0.418 34
0.594 27
0.682 86
0.742 06
0.785 70
0.819 52
0.846 57
0.868 68
0.887 06
0.902 54
0.915 70
0.926 99
0.936 75
0.945 23
0.952 65
0.959 17
0.964 92
0.970 02
0.974 54
0.978 58
0.982 19
1.10
0.410 22
0.589 20
0.679 42
0.739 48
0.783 66
0.817 87
0.845 20
0.867 54
0.886 10
0.901 72
0.915 00
0.926 39
0.936 24
0.944 80
0.952 28
0.958 86
0.964 66
0.969 80
0.974 36
0.978 43
0.982 07
1.11
0.402 59
0.584 11
0.675 97
0.736 90
0.781 63
0.816 22
0.843 84
0.866 40
0.885 14
0.900 90
0.914 30
0.925 80
0.935 73
0.944 37
0.951 92
0.958 55
0.964 40
0.969 58
0.974 18
0.978 29
0.981 95
1.12
0.395 47
0.579 01
0.672 52
0.734 31
0.779 60
0.814 57
0.842 48
0.865 26
0.884 18
0.900 09
0.913 61
0.925 21
0.935 23
0.943 94
0.951 55
0.958 24
0.964 14
0.969 36
0.974 00
0.978 14
0.981 84
1.13
0.388 89
0.573 89
0.669 07
0.731 73
0.777 56
0.812 92
0.841 12
0.864 13
0.883 22
0.899 28
0.912 92
0.924 62
0.934 72
0.943 51
0.951 19
0.957 93
0.963 88
0.969 14
0.973 82
0.978 00
0.981 72
1.14
0.382 85
0.568 77
0.665 61
0.729 15
0.775 53
0.811 28
0.839 77
0.862 99
0.882 26
0.898 46
0.912 23
0.924 03
0.934 22
0.943 08
0.950 82
0.957 62
0.963 62
0.968 93
0.973 65
0.977 85
0.981 61
1.15
0.377 34
0.563 64
0.662 15
0.726 57
0.773 51
0.809 64
0.838 41
0.861 86
0.881 31
0.897 66
0.911 54
0.923 45
0.933 72
0.942 66
0.950 46
0.957 32
0.963 36
0.968 72
0.973 47
0.977 71
0.981 50
1.16
0.372 33
0.558 51
0.658 69
0.723 98
0.771 48
0.808 00
0.837 06
0.860 73
0.880 36
0.896 85
0.910 86
0.922 86
0.933 23
0.942 23
0.950 10
0.957 01
0.963 11
0.968 50
0.973 30
0.977 57
0.981 38
1.17
0.367 80
0.553 38
0.655 22
0.721 40
0.769 46
0.806 36
0.835 71
0.859 61
0.879 41
0.896 05
0.910 17
0.922 28
0.932 73
0.941 81
0.949 74
0.956 71
0.962 85
0.968 29
0.973 12
0.977 43
0.981 27
1.18
0.363 70
0.548 26
0.651 76
0.718 82
0.767 43
0.804 73
0.834 36
0.858 48
0.878 47
0.895 25
0.909 49
0.921 70
0.932 23
0.941 39
0.949 39
0.956 41
0.962 60
0.968 08
0.972 95
0.977 29
0.981 16
1.19
0.360 00
0.543 16
0.648 29
0.716 24
0.765 41
0.803 10
0.833 02
0.857 36
0.877 52
0.894 45
0.908 81
0.921 12
0.931 74
0.940 97
0.949 03
0.956 11
0.962 35
0.967 87
0.972 78
0.977 15
0.981 05
1.20
0.356 66
0.538 08
0.644 82
0.713 66
0.763 39
0.801 47
0.831 68
0.856 24
0.876 58
0.893 65
0.908 14
0.920 54
0.931 25
0.940 55
0.948 68
0.955 81
0.962 10
0.967 66
0.972 60
0.977 01
0.980 95
1.21
0.353 64
0.533 02
0.641 36
0.711 09
0.761 38
0.799 84
0.830 34
0.855 13
0.875 64
0.892 85
0.907 46
0.919 97
0.930 76
0.940 13
0.948 32
0.955 51
0.961 85
0.967 45
0.972 43
0.976 87
0.980 84
1.22
0.350 92
0.528 00
0.637 90
0.708 51
0.759 37
0.798 22
0.829 01
0.854 02
0.874 70
0.892 06
0.906 79
0.919 39
0.930 27
0.939 72
0.947 97
0.955 21
0.961 60
0.967 25
0.972 27
0.976 74
0.980 73
1.23
0.348 46
0.523 01
0.634 44
0.705 94
0.757 36
0.796 60
0.827 67
0.852 90
0.873 77
0.891 27
0.906 12
0.918 82
0.929 79
0.939 31
0.947 62
0.954 92
0.961 35
0.967 04
0.972 10
0.976 60
0.980 63
1.24
0.346 24
0.518 07
0.630 99
0.703 38
0.755 35
0.794 98
0.826 34
0.851 80
0.872 84
0.890 48
0.905 45
0.918 25
0.929 30
0.938 89
0.947 27
0.954 62
0.961 10
0.966 84
0.971 93
0.976 47
0.980 52
1.25
0.344 23
0.513 19
0.627 54
0.700 81
0.753 34
0.793 37
0.825 02
0.850 69
0.871 91
0.889 70
0.904 78
0.917 69
0.928 82
0.938 48
0.946 92
0.954 33
0.960 86
0.966 64
0.971 77
0.976 33
0.980 42
1.26
0.342 41
0.508 37
0.624 10
0.698 25
0.751 34
0.791 76
0.823 69
0.849 59
0.870 98
0.888 91
0.904 11
0.917 12
0.928 34
0.938 08
0.946 58
0.954 04
0.960 62
0.966 43
0.971 60
0.976 20
0.980 31
1.27
0.340 77
0.503 61
0.620 67
0.695 69
0.749 35
0.790 15
0.822 37
0.848 49
0.870 06
0.888 13
0.903 45
0.916 56
0.927 86
0.937 67
0.946 23
0.953 75
0.960 37
0.966 23
0.971 44
0.976 07
0.980 21
1.28
0.339 28
0.498 93
0.617 24
0.693 14
0.747 35
0.788 54
0.821 05
0.847 39
0.869 14
0.887 35
0.902 79
0.916 00
0.927 38
0.937 26
0.945 89
0.953 46
0.960 13
0.966 03
0.971 27
0.975 94
0.980 11
1.29
0.337 94
0.494 33
0.613 83
0.690 59
0.745 36
0.786 94
0.819 74
0.846 30
0.868 22
0.886 58
0.902 13
0.915 44
0.926 91
0.936 86
0.945 55
0.953 17
0.959 89
0.965 84
0.971 11
0.975 81
0.980 01
1.30
0.336 72
0.489 82
0.610 43
0.688 05
0.743 38
0.785 34
0.818 43
0.845 21
0.867 30
0.885 80
0.901 48
0.914 88
0.926 43
0.936 46
0.945 21
0.952 89
0.959 65
0.965 64
0.970 95
0.975 68
0.979 91
1.31
0.335 63
0.485 40
0.607 05
0.685 51
0.741 40
0.783 75
0.817 12
0.844 12
0.866 39
0.885 03
0.900 82
0.914 32
0.925 96
0.936 06
0.944 87
0.952 60
0.959 42
0.965 44
0.970 79
0.975 56
0.979 81
1.32
0.334 64
0.481 09
0.603 68
0.682 98
0.739 42
0.782 16
0.815 82
0.843 03
0.865 48
0.884 26
0.900 17
0.913 77
0.925 49
0.935 66
0.944 54
0.952 32
0.959 18
0.965 25
0.970 63
0.975 43
0.979 72
11
M
8
0
1
0
:
2
0
2
0

82
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
1.33
0.333 75
0.476 88
0.600 32
0.680 46
0.737 45
0.780 58
0.814 51
0.841 95
0.864 57
0.883 50
0.899 52
0.913 22
0.925 02
0.935 26
0.944 20
0.952 04
0.958 94
0.965 05
0.970 48
0.975 31
0.979 62
1.34
0.332 96
0.472 79
0.596 99
0.677 94
0.735 48
0.778 99
0.813 22
0.840 87
0.863 67
0.882 73
0.898 87
0.912 67
0.924 56
0.934 87
0.943 87
0.951 76
0.958 71
0.964 86
0.970 32
0.975 18
0.979 52
1.35
0.332 25
0.468 81
0.593 68
0.675 43
0.733 52
0.777 42
0.811 92
0.839 80
0.862 76
0.881 97
0.898 23
0.912 12
0.924 09
0.934 47
0.943 53
0.951 48
0.958 48
0.964 67
0.970 16
0.975 06
0.979 43
1.36
0.331 62
0.464 96
0.590 38
0.672 93
0.731 56
0.775 84
0.810 63
0.838 73
0.861 86
0.881 21
0.897 59
0.911 58
0.923 63
0.934 08
0.943 20
0.951 20
0.958 25
0.964 48
0.970 01
0.974 94
0.979 33
1.37
0.331 06
0.461 22
0.587 11
0.670 44
0.729 61
0.774 27
0.809 35
0.837 66
0.860 97
0.880 46
0.896 94
0.911 03
0.923 17
0.933 69
0.942 87
0.950 93
0.958 02
0.964 29
0.969 86
0.974 81
0.979 24
1.38
0.330 57
0.457 62
0.583 87
0.667 96
0.727 67
0.772 71
0.808 06
0.836 59
0.860 07
0.879 70
0.896 31
0.910 49
0.922 71
0.933 30
0.942 55
0.950 65
0.957 79
0.964 10
0.969 71
0.974 69
0.979 15
1.39
0.330 14
0.454 14
0.580 65
0.665 48
0.725 73
0.771 15
0.806 79
0.835 53
0.859 18
0.878 95
0.895 67
0.909 95
0.922 25
0.932 92
0.942 22
0.950 38
0.957 56
0.963 92
0.969 55
0.974 58
0.979 06
1.40
0.329 77
0.450 79
0.577 46
0.663 02
0.723 80
0.769 59
0.805 51
0.834 47
0.858 30
0.878 20
0.895 04
0.909 42
0.921 80
0.932 53
0.941 90
0.950 11
0.957 34
0.963 73
0.969 40
0.974 46
0.978 97
1.41
0.329 46
0.447 58
0.574 30
0.660 57
0.721 87
0.768 04
0.804 24
0.833 41
0.857 41
0.877 46
0.894 41
0.908 88
0.921 34
0.932 15
0.941 57
0.949 83
0.957 11
0.963 55
0.969 26
0.974 34
0.978 88
1.42
0.329 20
0.444 49
0.571 17
0.658 13
0.719 95
0.766 50
0.802 97
0.832 36
0.856 53
0.876 71
0.893 78
0.908 35
0.920 89
0.931 77
0.941 25
0.949 57
0.956 89
0.963 36
0.969 11
0.974 22
0.978 79
1.43
0.328 99
0.441 54
0.568 08
0.655 70
0.718 04
0.764 96
0.801 71
0.831 31
0.855 65
0.875 97
0.893 15
0.907 82
0.920 44
0.931 39
0.940 93
0.949 30
0.956 67
0.963 18
0.968 96
0.974 11
0.978 70
1.44
0.328 83
0.438 71
0.565 02
0.653 28
0.716 13
0.763 42
0.800 45
0.830 27
0.854 77
0.875 23
0.892 53
0.907 29
0.919 99
0.931 01
0.940 61
0.949 03
0.956 45
0.963 00
0.968 82
0.973 99
0.978 62
1.45
0.328 72
0.436 01
0.562 00
0.650 88
0.714 23
0.761 89
0.799 20
0.829 23
0.853 90
0.874 50
0.891 90
0.906 76
0.919 55
0.930 63
0.940 30
0.948 77
0.956 23
0.962 82
0.968 67
0.973 88
0.978 53
1.46
0.328 64
0.433 44
0.559 02
0.648 49
0.712 34
0.760 37
0.797 95
0.828 19
0.853 03
0.873 77
0.891 28
0.906 24
0.919 10
0.930 26
0.939 98
0.948 50
0.956 01
0.962 64
0.968 53
0.973 77
0.978 45
1.47
0.328 61
0.430 99
0.556 08
0.646 12
0.710 46
0.758 85
0.796 70
0.827 15
0.852 17
0.873 04
0.890 67
0.905 71
0.918 66
0.929 88
0.939 67
0.948 24
0.955 79
0.962 46
0.968 39
0.973 66
0.978 36
1.48
0.328 63
0.428 67
0.553 17
0.643 76
0.708 58
0.757 34
0.795 46
0.826 12
0.851 30
0.872 31
0.890 05
0.905 19
0.918 22
0.929 51
0.939 35
0.947 98
0.955 57
0.962 29
0.968 24
0.973 55
0.978 28
1.49
0.328 68
0.426 46
0.550 32
0.641 41
0.706 72
0.755 83
0.794 22
0.825 10
0.850 44
0.871 59
0.889 44
0.904 68
0.917 78
0.929 14
0.939 04
0.947 72
0.955 36
0.962 11
0.968 10
0.973 44
0.978 20
1.50
0.328 76
0.424 37
0.547 50
0.639 08
0.704 86
0.754 33
0.792 99
0.824 07
0.849 59
0.870 86
0.888 83
0.904 16
0.917 35
0.928 78
0.938 74
0.947 46
0.955 15
0.961 94
0.967 97
0.973 33
0.978 12
1.51
0.328 89
0.422 39
0.544 74
0.636 77
0.703 01
0.752 83
0.791 77
0.823 06
0.848 73
0.870 15
0.888 23
0.903 65
0.916 91
0.928 41
0.938 43
0.947 21
0.954 94
0.961 77
0.967 83
0.973 22
0.978 04
1.52
0.329 05
0.420 52
0.542 02
0.634 48
0.701 17
0.751 34
0.790 54
0.822 04
0.847 88
0.869 43
0.887 62
0.903 14
0.916 48
0.928 04
0.938 12
0.946 95
0.954 73
0.961 60
0.967 69
0.973 11
0.977 96
1.53
0.329 25
0.418 76
0.539 35
0.632 20
0.699 34
0.749 86
0.789 33
0.821 03
0.847 04
0.868 72
0.887 02
0.902 63
0.916 05
0.927 68
0.937 82
0.946 70
0.954 52
0.961 43
0.967 56
0.973 01
0.977 88
1.54
0.329 48
0.417 10
0.536 72
0.629 94
0.697 52
0.748 39
0.788 11
0.820 02
0.846 19
0.868 01
0.886 42
0.902 12
0.915 62
0.927 32
0.937 52
0.946 45
0.954 31
0.961 26
0.967 42
0.972 91
0.977 80
1.55
0.329 75
0.415 54
0.534 15
0.627 70
0.695 71
0.746 92
0.786 91
0.819 02
0.845 35
0.867 30
0.885 82
0.901 62
0.915 20
0.926 96
0.937 21
0.946 20
0.954 10
0.961 09
0.967 29
0.972 80
0.977 72
1.56
0.330 05
0.414 07
0.531 64
0.625 49
0.693 91
0.745 45
0.785 70
0.818 02
0.844 52
0.866 60
0.885 23
0.901 11
0.914 77
0.926 61
0.936 92
0.945 95
0.953 90
0.960 92
0.967 15
0.972 70
0.977 65
1.57
0.330 39
0.412 70
0.529 17
0.623 29
0.692 12
0.744 00
0.784 51
0.817 03
0.843 69
0.865 90
0.884 64
0.900 61
0.914 35
0.926 25
0.936 62
0.945 70
0.953 69
0.960 76
0.967 02
0.972 60
0.977 57
1.58
0.330 76
0.411 42
0.526 76
0.621 11
0.690 34
0.742 55
0.783 31
0.816 04
0.842 86
0.865 20
0.884 05
0.900 12
0.913 93
0.925 90
0.936 32
0.945 45
0.953 49
0.960 59
0.966 89
0.972 50
0.977 50
1.59
0.331 16
0.410 22
0.524 40
0.618 96
0.688 57
0.741 11
0.782 13
0.815 05
0.842 03
0.864 50
0.883 46
0.899 62
0.913 51
0.925 55
0.936 03
0.945 21
0.953 29
0.960 43
0.966 76
0.972 40
0.977 43
1.60
0.331 59
0.409 11
0.522 10
0.616 82
0.686 82
0.739 67
0.780 95
0.814 07
0.841 21
0.863 81
0.882 88
0.899 13
0.913 10
0.925 20
0.935 73
0.944 97
0.953 09
0.960 27
0.966 64
0.972 30
0.977 36
1.61
0.332 05
0.408 08
0.519 85
0.614 71
0.685 07
0.738 25
0.779 77
0.813 09
0.840 39
0.863 12
0.882 30
0.898 64
0.912 68
0.924 85
0.935 44
0.944 72
0.952 89
0.960 11
0.966 51
0.972 20
0.977 29
1.62
0.332 55
0.407 12
0.517 66
0.612 63
0.683 34
0.736 83
0.778 60
0.812 12
0.839 58
0.862 44
0.881 72
0.898 15
0.912 27
0.924 50
0.935 15
0.944 48
0.952 69
0.959 95
0.966 38
0.972 11
0.977 22
1.63
0.333 07
0.406 24
0.515 53
0.610 56
0.681 62
0.735 42
0.777 44
0.811 15
0.838 76
0.861 76
0.881 14
0.897 66
0.911 86
0.924 16
0.934 87
0.944 25
0.952 50
0.959 79
0.966 26
0.972 01
0.977 15
1.64
0.333 62
0.405 43
0.513 45
0.608 53
0.679 91
0.734 01
0.776 28
0.810 19
0.837 96
0.861 08
0.880 57
0.897 18
0.911 46
0.923 81
0.934 58
0.944 01
0.952 30
0.959 63
0.966 13
0.971 92
0.977 08
1.65
0.334 20
0.404 68
0.511 43
0.606 51
0.678 21
0.732 62
0.775 13
0.809 23
0.837 15
0.860 40
0.880 00
0.896 70
0.911 05
0.923 47
0.934 30
0.943 77
0.952 11
0.959 48
0.966 01
0.971 83
0.977 01
1.66
0.334 81
0.404 00
0.509 46
0.604 53
0.676 53
0.731 23
0.773 98
0.808 27
0.836 35
0.859 73
0.879 43
0.896 22
0.910 65
0.923 13
0.934 01
0.943 54
0.951 92
0.959 32
0.965 89
0.971 73
0.976 95
1.67
0.335 44
0.403 39
0.507 56
0.602 56
0.674 86
0.729 85
0.772 84
0.807 32
0.835 56
0.859 06
0.878 87
0.895 74
0.910 25
0.922 80
0.933 73
0.943 31
0.951 73
0.959 17
0.965 77
0.971 64
0.976 88
1.68
0.336 10
0.402 83
0.505 71
0.600 63
0.673 21
0.728 48
0.771 70
0.806 37
0.834 77
0.858 39
0.878 30
0.895 27
0.909 85
0.922 46
0.933 45
0.943 07
0.951 54
0.959 02
0.965 65
0.971 55
0.976 82
1.69
0.336 78
0.402 33
0.503 91
0.598 72
0.671 56
0.727 12
0.770 57
0.805 43
0.833 98
0.857 73
0.877 75
0.894 80
0.909 45
0.922 13
0.933 17
0.942 84
0.951 35
0.958 87
0.965 53
0.971 46
0.976 75
1.70
0.337 49
0.401 89
0.502 17
0.596 84
0.669 94
0.725 76
0.769 45
0.804 50
0.833 19
0.857 07
0.877 19
0.894 33
0.909 05
0.921 80
0.932 90
0.942 62
0.951 17
0.958 72
0.965 42
0.971 38
0.976 69
1.71
0.338 22
0.401 50
0.500 49
0.594 99
0.668 32
0.724 42
0.768 33
0.803 57
0.832 41
0.856 41
0.876 64
0.893 86
0.908 66
0.921 47
0.932 62
0.942 39
0.950 98
0.958 57
0.965 30
0.971 29
0.976 63
1.72
0.338 96
0.401 16
0.498 87
0.593 17
0.666 72
0.723 08
0.767 22
0.802 64
0.831 63
0.855 76
0.876 08
0.893 40
0.908 27
0.921 14
0.932 35
0.942 16
0.950 80
0.958 42
0.965 19
0.971 20
0.976 57
1.73
0.339 73
0.400 87
0.497 30
0.591 37
0.665 14
0.721 75
0.766 12
0.801 72
0.830 86
0.855 11
0.875 54
0.892 94
0.907 88
0.920 82
0.932 08
0.941 94
0.950 62
0.958 28
0.965 07
0.971 12
0.976 51
1.74
0.340 52
0.400 63
0.495 78
0.589 60
0.663 57
0.720 44
0.765 02
0.800 80
0.830 09
0.854 46
0.874 99
0.892 48
0.907 50
0.920 49
0.931 81
0.941 72
0.950 44
0.958 13
0.964 96
0.971 03
0.976 45
1.75
0.341 33
0.400 43
0.494 32
0.587 87
0.662 01
0.719 13
0.763 93
0.799 89
0.829 33
0.853 82
0.874 45
0.892 02
0.907 11
0.920 17
0.931 54
0.941 50
0.950 26
0.957 99
0.964 85
0.970 95
0.976 39
1.76
0.342 15
0.400 28
0.492 92
0.586 16
0.660 48
0.717 83
0.762 85
0.798 98
0.828 57
0.853 18
0.873 91
0.891 56
0.906 73
0.919 85
0.931 28
0.941 28
0.950 08
0.957 85
0.964 74
0.970 87
0.976 34
11
M
8
0
1
0
:
2
0
2
0

83
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
1.77
0.342 99
0.400 17
0.491 56
0.584 48
0.658 95
0.716 54
0.761 77
0.798 08
0.827 81
0.852 54
0.873 37
0.891 11
0.906 35
0.919 53
0.931 01
0.941 06
0.949 90
0.957 71
0.964 63
0.970 79
0.976 28
1.78
0.343 85
0.400 10
0.490 26
0.582 84
0.657 45
0.715 26
0.760 70
0.797 19
0.827 06
0.851 91
0.872 84
0.890 66
0.905 97
0.919 22
0.930 75
0.940 85
0.949 73
0.957 57
0.964 52
0.970 71
0.976 23
1.79
0.344 72
0.400 07
0.489 02
0.581 22
0.655 96
0.713 99
0.759 63
0.796 30
0.826 31
0.851 28
0.872 31
0.890 22
0.905 60
0.918 90
0.930 49
0.940 63
0.949 55
0.957 43
0.964 42
0.970 63
0.976 17
1.80
0.345 60
0.400 08
0.487 82
0.579 63
0.654 48
0.712 73
0.758 58
0.795 41
0.825 57
0.850 65
0.871 78
0.889 77
0.905 22
0.918 59
0.930 23
0.940 42
0.949 38
0.957 29
0.964 31
0.970 55
0.976 12
1.81
0.346 50
0.400 12
0.486 67
0.578 08
0.653 02
0.711 48
0.757 53
0.794 53
0.824 83
0.850 03
0.871 26
0.889 33
0.904 85
0.918 28
0.929 97
0.940 21
0.949 21
0.957 16
0.964 21
0.970 48
0.976 07
1.82
0.347 41
0.400 20
0.485 58
0.576 56
0.651 58
0.710 24
0.756 48
0.793 65
0.824 09
0.849 41
0.870 73
0.888 89
0.904 48
0.917 97
0.929 72
0.940 00
0.949 04
0.957 02
0.964 10
0.970 40
0.976 02
1.83
0.348 34
0.400 31
0.484 53
0.575 06
0.650 16
0.709 02
0.755 45
0.792 78
0.823 36
0.848 79
0.870 21
0.888 45
0.904 12
0.917 67
0.929 46
0.939 79
0.948 87
0.956 89
0.964 00
0.970 33
0.975 97
1.84
0.349 27
0.400 46
0.483 53
0.573 60
0.648 76
0.707 80
0.754 42
0.791 92
0.822 63
0.848 18
0.869 70
0.888 02
0.903 75
0.917 36
0.929 21
0.939 58
0.948 70
0.956 76
0.963 90
0.970 25
0.975 92
1.85
0.350 22
0.400 64
0.482 58
0.572 17
0.647 37
0.706 59
0.753 40
0.791 06
0.821 91
0.847 57
0.869 19
0.887 59
0.903 39
0.917 06
0.928 96
0.939 38
0.948 54
0.956 63
0.963 80
0.970 18
0.975 87
1.86
0.351 18
0.400 84
0.481 68
0.570 78
0.646 00
0.705 39
0.752 39
0.790 21
0.821 19
0.846 96
0.868 68
0.887 16
0.903 03
0.916 76
0.928 71
0.939 17
0.948 37
0.956 50
0.963 70
0.970 11
0.975 82
1.87
0.352 15
0.401 08
0.480 82
0.569 41
0.644 64
0.704 21
0.751 38
0.789 36
0.820 48
0.846 36
0.868 17
0.886 73
0.902 67
0.916 46
0.928 46
0.938 97
0.948 21
0.956 37
0.963 60
0.970 04
0.975 78
1.88
0.353 13
0.401 34
0.480 01
0.568 08
0.643 31
0.703 03
0.750 38
0.788 52
0.819 77
0.845 76
0.867 67
0.886 31
0.902 32
0.916 16
0.928 22
0.938 77
0.948 05
0.956 24
0.963 51
0.969 97
0.975 73
1.89
0.354 12
0.401 64
0.479 24
0.566 77
0.641 99
0.701 87
0.749 39
0.787 68
0.819 06
0.845 17
0.867 16
0.885 89
0.901 96
0.915 87
0.927 98
0.938 57
0.947 89
0.956 12
0.963 41
0.969 90
0.975 69
1.90
0.355 12
0.401 95
0.478 52
0.565 50
0.640 70
0.700 72
0.748 41
0.786 85
0.818 36
0.844 58
0.866 67
0.885 47
0.901 61
0.915 58
0.927 73
0.938 37
0.947 73
0.955 99
0.963 32
0.969 83
0.975 64
1.91
0.356 13
0.402 30
0.477 83
0.564 26
0.639 42
0.699 58
0.747 43
0.786 02
0.817 67
0.843 99
0.866 17
0.885 05
0.901 26
0.915 29
0.927 49
0.938 18
0.947 57
0.955 87
0.963 23
0.969 77
0.975 60
1.92
0.357 15
0.402 67
0.477 19
0.563 05
0.638 16
0.698 45
0.746 46
0.785 20
0.816 97
0.843 41
0.865 68
0.884 64
0.900 92
0.915 00
0.927 26
0.937 98
0.947 42
0.955 75
0.963 13
0.969 70
0.975 56
1.93
0.358 18
0.403 06
0.476 59
0.561 88
0.636 91
0.697 33
0.745 50
0.784 39
0.816 29
0.842 83
0.865 19
0.884 23
0.900 57
0.914 71
0.927 02
0.937 79
0.947 26
0.955 63
0.963 04
0.969 64
0.975 52
1.94
0.359 21
0.403 47
0.476 03
0.560 73
0.635 69
0.696 22
0.744 55
0.783 58
0.815 60
0.842 25
0.864 71
0.883 82
0.900 23
0.914 43
0.926 79
0.937 60
0.947 11
0.955 51
0.962 95
0.969 57
0.975 48
1.95
0.360 26
0.403 91
0.475 51
0.559 62
0.634 49
0.695 13
0.743 61
0.782 78
0.814 93
0.841 68
0.864 22
0.883 41
0.899 89
0.914 15
0.926 55
0.937 41
0.946 96
0.955 39
0.962 87
0.969 51
0.975 44
1.96
0.361 31
0.404 37
0.475 03
0.558 53
0.633 30
0.694 05
0.742 67
0.781 99
0.814 25
0.841 11
0.863 74
0.883 01
0.899 55
0.913 87
0.926 32
0.937 22
0.946 81
0.955 28
0.962 78
0.969 45
0.975 40
1.97
0.362 37
0.404 85
0.474 59
0.557 48
0.632 14
0.692 98
0.741 74
0.781 20
0.813 58
0.840 55
0.863 27
0.882 61
0.899 22
0.913 59
0.926 09
0.937 04
0.946 66
0.955 16
0.962 69
0.969 39
0.975 37
1.98
0.363 43
0.405 35
0.474 18
0.556 46
0.630 99
0.691 92
0.740 82
0.780 41
0.812 92
0.839 99
0.862 80
0.882 21
0.898 89
0.913 31
0.925 86
0.936 85
0.946 51
0.955 05
0.962 61
0.969 33
0.975 33
1.99
0.364 51
0.405 87
0.473 81
0.555 47
0.629 87
0.690 87
0.739 91
0.779 63
0.812 26
0.839 43
0.862 33
0.881 82
0.898 56
0.913 04
0.925 64
0.936 67
0.946 37
0.954 93
0.962 52
0.969 28
0.975 30
2.00
0.365 59
0.406 41
0.473 47
0.554 51
0.628 76
0.689 84
0.739 01
0.778 86
0.811 61
0.838 88
0.861 86
0.881 43
0.898 23
0.912 76
0.925 42
0.936 49
0.946 22
0.954 82
0.962 44
0.969 22
0.975 26
2.01
0.366 68
0.406 97
0.473 17
0.553 58
0.627 67
0.688 82
0.738 11
0.778 10
0.810 96
0.838 33
0.861 40
0.881 04
0.897 90
0.912 49
0.925 19
0.936 31
0.946 08
0.954 71
0.962 36
0.969 16
0.975 23
2.02
0.367 77
0.407 54
0.472 90
0.552 68
0.626 61
0.687 81
0.737 23
0.777 34
0.810 31
0.837 78
0.860 94
0.880 65
0.897 58
0.912 23
0.924 97
0.936 13
0.945 94
0.954 60
0.962 28
0.969 11
0.975 20
2.03
0.368 87
0.408 14
0.472 66
0.551 81
0.625 56
0.686 81
0.736 35
0.776 58
0.809 67
0.837 24
0.860 48
0.880 27
0.897 26
0.911 96
0.924 75
0.935 95
0.945 80
0.954 50
0.962 20
0.969 06
0.975 17
2.04
0.369 98
0.408 74
0.472 46
0.550 97
0.624 53
0.685 83
0.735 48
0.775 84
0.809 04
0.836 70
0.860 03
0.879 89
0.896 94
0.911 70
0.924 54
0.935 78
0.945 66
0.954 39
0.962 12
0.969 00
0.975 14
2.05
0.371 09
0.409 37
0.472 28
0.550 16
0.623 52
0.684 86
0.734 62
0.775 10
0.808 41
0.836 17
0.859 58
0.879 51
0.896 63
0.911 43
0.924 32
0.935 60
0.945 52
0.954 28
0.962 05
0.968 95
0.975 11
2.06
0.372 21
0.410 01
0.472 14
0.549 38
0.622 53
0.683 90
0.733 77
0.774 36
0.807 78
0.835 64
0.859 13
0.879 13
0.896 31
0.911 17
0.924 11
0.935 43
0.945 39
0.954 18
0.961 97
0.968 90
0.975 08
2.07
0.373 34
0.410 67
0.472 02
0.548 63
0.621 57
0.682 95
0.732 92
0.773 63
0.807 16
0.835 11
0.858 69
0.878 76
0.896 00
0.910 92
0.923 90
0.935 26
0.945 25
0.954 08
0.961 90
0.968 85
0.975 05
2.08
0.374 47
0.411 34
0.471 94
0.547 90
0.620 62
0.682 02
0.732 09
0.772 91
0.806 54
0.834 59
0.858 25
0.878 39
0.895 69
0.910 66
0.923 69
0.935 09
0.945 12
0.953 98
0.961 82
0.968 80
0.975 03
2.09
0.375 60
0.412 02
0.471 88
0.547 20
0.619 69
0.681 10
0.731 26
0.772 20
0.805 93
0.834 07
0.857 81
0.878 02
0.895 39
0.910 41
0.923 48
0.934 93
0.944 99
0.953 88
0.961 75
0.968 76
0.975 00
2.10
0.376 75
0.412 72
0.471 85
0.546 54
0.618 78
0.680 20
0.730 45
0.771 49
0.805 33
0.833 56
0.857 37
0.877 66
0.895 08
0.910 16
0.923 28
0.934 76
0.944 86
0.953 78
0.961 68
0.968 71
0.974 98
2.11
0.377 89
0.413 43
0.471 85
0.545 89
0.617 89
0.679 30
0.729 64
0.770 79
0.804 73
0.833 05
0.856 94
0.877 30
0.894 78
0.909 91
0.923 07
0.934 60
0.944 73
0.953 68
0.961 61
0.968 67
0.974 96
2.12
0.379 04
0.414 16
0.471 87
0.545 28
0.617 03
0.678 42
0.728 84
0.770 09
0.804 13
0.832 54
0.856 52
0.876 94
0.894 48
0.909 66
0.922 87
0.934 44
0.944 60
0.953 58
0.961 54
0.968 62
0.974 93
2.13
0.380 20
0.414 89
0.471 92
0.544 69
0.616 18
0.677 56
0.728 05
0.769 40
0.803 54
0.832 04
0.856 09
0.876 58
0.894 18
0.909 41
0.922 67
0.934 27
0.944 48
0.953 49
0.961 48
0.968 58
0.974 91
2.14
0.381 36
0.415 64
0.471 99
0.544 13
0.615 35
0.676 70
0.727 27
0.768 72
0.802 96
0.831 54
0.855 67
0.876 23
0.893 89
0.909 17
0.922 47
0.934 12
0.944 36
0.953 40
0.961 41
0.968 54
0.974 89
2.15
0.382 53
0.416 41
0.472 09
0.543 60
0.614 54
0.675 86
0.726 50
0.768 04
0.802 38
0.831 05
0.855 26
0.875 88
0.893 60
0.908 93
0.922 28
0.933 96
0.944 23
0.953 30
0.961 35
0.968 50
0.974 87
2.16
0.383 69
0.417 18
0.472 21
0.543 09
0.613 75
0.675 04
0.725 74
0.767 37
0.801 80
0.830 56
0.854 84
0.875 53
0.893 31
0.908 69
0.922 08
0.933 80
0.944 11
0.953 21
0.961 28
0.968 46
0.974 85
2.17
0.384 87
0.417 96
0.472 36
0.542 61
0.612 98
0.674 22
0.724 98
0.766 71
0.801 23
0.830 08
0.854 43
0.875 19
0.893 02
0.908 45
0.921 89
0.933 65
0.943 99
0.953 12
0.961 22
0.968 42
0.974 84
2.18
0.386 05
0.418 76
0.472 52
0.542 15
0.612 23
0.673 42
0.724 24
0.766 06
0.800 67
0.829 59
0.854 02
0.874 85
0.892 74
0.908 22
0.921 70
0.933 50
0.943 87
0.953 04
0.961 16
0.968 38
0.974 82
2.19
0.387 23
0.419 56
0.472 71
0.541 72
0.611 50
0.672 63
0.723 51
0.765 41
0.800 11
0.829 12
0.853 62
0.874 51
0.892 45
0.907 99
0.921 51
0.933 35
0.943 76
0.952 95
0.961 10
0.968 34
0.974 80
2.20
0.388 41
0.420 38
0.472 92
0.541 32
0.610 79
0.671 86
0.722 78
0.764 77
0.799 55
0.828 64
0.853 22
0.874 17
0.892 17
0.907 76
0.921 32
0.933 20
0.943 64
0.952 86
0.961 04
0.968 31
0.974 79
11
M
8
0
1
0
:
2
0
2
0

84
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
2.21
0.389 60
0.421 20
0.473 15
0.540 93
0.610 10
0.671 10
0.722 07
0.764 13
0.799 00
0.828 18
0.852 82
0.873 84
0.891 90
0.907 53
0.921 14
0.933 05
0.943 53
0.952 78
0.960 98
0.968 27
0.974 78
2.22
0.390 79
0.422 04
0.473 40
0.540 58
0.609 42
0.670 35
0.721 36
0.763 50
0.798 46
0.827 71
0.852 43
0.873 51
0.891 62
0.907 30
0.920 95
0.932 90
0.943 41
0.952 70
0.960 92
0.968 24
0.974 76
2.23
0.391 99
0.422 88
0.473 67
0.540 24
0.608 77
0.669 62
0.720 66
0.762 88
0.797 92
0.827 25
0.852 04
0.873 18
0.891 35
0.907 08
0.920 77
0.932 76
0.943 30
0.952 62
0.960 87
0.968 21
0.974 75
2.24
0.393 19
0.423 73
0.473 96
0.539 93
0.608 14
0.668 90
0.719 97
0.762 27
0.797 39
0.826 79
0.851 65
0.872 86
0.891 08
0.906 86
0.920 59
0.932 62
0.943 19
0.952 54
0.960 81
0.968 18
0.974 74
2.25
0.394 39
0.424 59
0.474 27
0.539 64
0.607 52
0.668 20
0.719 30
0.761 66
0.796 86
0.826 34
0.851 27
0.872 53
0.890 81
0.906 64
0.920 41
0.932 48
0.943 09
0.952 46
0.960 76
0.968 15
0.974 73
2.26
0.395 59
0.425 46
0.474 59
0.539 38
0.606 92
0.667 50
0.718 63
0.761 06
0.796 33
0.825 89
0.850 89
0.872 22
0.890 55
0.906 42
0.920 24
0.932 34
0.942 98
0.952 38
0.960 71
0.968 12
0.974 72
2.27
0.396 80
0.426 34
0.474 94
0.539 14
0.606 35
0.666 83
0.717 97
0.760 46
0.795 82
0.825 45
0.850 52
0.871 90
0.890 29
0.906 20
0.920 06
0.932 20
0.942 87
0.952 30
0.960 66
0.968 09
0.974 72
2.28
0.398 01
0.427 23
0.475 30
0.538 91
0.605 79
0.666 16
0.717 32
0.759 88
0.795 30
0.825 01
0.850 14
0.871 59
0.890 03
0.905 99
0.919 89
0.932 06
0.942 77
0.952 23
0.960 61
0.968 06
0.974 71
2.29
0.399 22
0.428 12
0.475 67
0.538 72
0.605 25
0.665 51
0.716 68
0.759 30
0.794 80
0.824 58
0.849 77
0.871 28
0.889 77
0.905 78
0.919 72
0.931 93
0.942 67
0.952 15
0.960 56
0.968 04
0.974 70
2.30
0.400 43
0.429 02
0.476 07
0.538 54
0.604 73
0.664 87
0.716 05
0.758 72
0.794 30
0.824 15
0.849 41
0.870 97
0.889 51
0.905 57
0.919 55
0.931 80
0.942 57
0.952 08
0.960 51
0.968 01
0.974 70
2.31
0.401 65
0.429 93
0.476 48
0.538 38
0.604 22
0.664 25
0.715 43
0.758 16
0.793 80
0.823 72
0.849 05
0.870 67
0.889 26
0.905 36
0.919 39
0.931 67
0.942 47
0.952 01
0.960 47
0.967 99
0.974 70
2.32
0.402 87
0.430 85
0.476 90
0.538 25
0.603 74
0.663 64
0.714 82
0.757 60
0.793 31
0.823 30
0.848 69
0.870 37
0.889 01
0.905 16
0.919 22
0.931 54
0.942 37
0.951 94
0.960 42
0.967 97
0.974 69
2.33
0.404 09
0.431 77
0.477 34
0.538 13
0.603 27
0.663 04
0.714 22
0.757 05
0.792 82
0.822 88
0.848 33
0.870 07
0.888 76
0.904 95
0.919 06
0.931 41
0.942 28
0.951 87
0.960 38
0.967 94
0.974 69
2.34
0.405 31
0.432 70
0.477 80
0.538 03
0.602 82
0.662 45
0.713 63
0.756 51
0.792 34
0.822 47
0.847 98
0.869 77
0.888 52
0.904 75
0.918 90
0.931 28
0.942 18
0.951 81
0.960 34
0.967 92
0.974 69
2.35
0.406 53
0.433 64
0.478 27
0.537 96
0.602 39
0.661 88
0.713 04
0.755 97
0.791 87
0.822 06
0.847 63
0.869 48
0.888 28
0.904 56
0.918 74
0.931 16
0.942 09
0.951 74
0.960 30
0.967 90
0.974 69
2.36
0.407 76
0.434 58
0.478 75
0.537 90
0.601 97
0.661 33
0.712 47
0.755 44
0.791 40
0.821 65
0.847 29
0.869 19
0.888 04
0.904 36
0.918 58
0.931 04
0.942 00
0.951 68
0.960 26
0.967 89
0.974 69
2.37
0.408 98
0.435 53
0.479 24
0.537 87
0.601 58
0.660 78
0.711 91
0.754 92
0.790 94
0.821 25
0.846 95
0.868 90
0.887 80
0.904 17
0.918 43
0.930 92
0.941 91
0.951 61
0.960 22
0.967 87
0.974 69
2.38
0.410 21
0.436 48
0.479 75
0.537 85
0.601 20
0.660 25
0.711 36
0.754 40
0.790 48
0.820 86
0.846 61
0.868 62
0.887 56
0.903 98
0.918 27
0.930 80
0.941 82
0.951 55
0.960 18
0.967 85
0.974 70
2.39
0.411 44
0.437 44
0.480 28
0.537 85
0.600 84
0.659 73
0.710 81
0.753 89
0.790 03
0.820 46
0.846 28
0.868 34
0.887 33
0.903 79
0.918 12
0.930 68
0.941 73
0.951 49
0.960 14
0.967 84
0.974 70
2.40
0.412 68
0.438 41
0.480 81
0.537 87
0.600 49
0.659 23
0.710 28
0.753 39
0.789 58
0.820 08
0.845 95
0.868 06
0.887 10
0.903 60
0.917 97
0.930 57
0.941 64
0.951 43
0.960 11
0.967 82
0.974 71
2.41
0.413 91
0.439 38
0.481 36
0.537 90
0.600 16
0.658 74
0.709 76
0.752 90
0.789 14
0.819 69
0.845 62
0.867 79
0.886 88
0.903 41
0.917 83
0.930 45
0.941 56
0.951 37
0.960 07
0.967 81
0.974 71
2.42
0.415 15
0.440 35
0.481 92
0.537 95
0.599 85
0.658 26
0.709 24
0.752 41
0.788 70
0.819 32
0.845 30
0.867 52
0.886 65
0.903 23
0.917 68
0.930 34
0.941 48
0.951 32
0.960 04
0.967 80
0.974 72
2.43
0.416 38
0.441 33
0.482 49
0.538 03
0.599 56
0.657 80
0.708 74
0.751 93
0.788 27
0.818 94
0.844 98
0.867 25
0.886 43
0.903 05
0.917 54
0.930 23
0.941 40
0.951 26
0.960 01
0.967 79
0.974 73
2.44
0.417 62
0.442 32
0.483 07
0.538 11
0.599 28
0.657 34
0.708 25
0.751 46
0.787 85
0.818 57
0.844 67
0.866 99
0.886 21
0.902 87
0.917 40
0.930 12
0.941 32
0.951 21
0.959 98
0.967 78
0.974 74
2.45
0.418 86
0.443 31
0.483 67
0.538 22
0.599 01
0.656 91
0.707 76
0.750 99
0.787 43
0.818 21
0.844 35
0.866 72
0.885 99
0.902 70
0.917 26
0.930 01
0.941 24
0.951 16
0.959 95
0.967 77
0.974 75
2.46
0.420 10
0.444 31
0.484 27
0.538 34
0.598 77
0.656 48
0.707 29
0.750 54
0.787 02
0.817 85
0.844 04
0.866 46
0.885 78
0.902 52
0.917 12
0.929 91
0.941 16
0.951 10
0.959 92
0.967 76
0.974 76
2.47
0.421 34
0.445 31
0.484 89
0.538 48
0.598 54
0.656 07
0.706 82
0.750 09
0.786 61
0.817 49
0.843 74
0.866 21
0.885 57
0.902 35
0.916 98
0.929 80
0.941 09
0.951 05
0.959 89
0.967 76
0.974 77
2.48
0.422 58
0.446 31
0.485 51
0.538 63
0.598 32
0.655 67
0.706 37
0.749 64
0.786 21
0.817 14
0.843 44
0.865 95
0.885 36
0.902 18
0.916 85
0.929 70
0.941 01
0.951 01
0.959 87
0.967 75
0.974 78
2.49
0.423 83
0.447 32
0.486 15
0.538 80
0.598 12
0.655 28
0.705 92
0.749 21
0.785 81
0.816 79
0.843 14
0.865 70
0.885 15
0.902 01
0.916 72
0.929 60
0.940 94
0.950 96
0.959 84
0.967 75
0.974 80
2.50
0.425 07
0.448 34
0.486 79
0.538 98
0.597 94
0.654 91
0.705 48
0.748 78
0.785 42
0.816 45
0.842 85
0.865 46
0.884 95
0.901 85
0.916 59
0.929 50
0.940 87
0.950 91
0.959 82
0.967 74
0.974 81
2.51
0.426 32
0.449 35
0.487 45
0.539 18
0.597 77
0.654 55
0.705 06
0.748 36
0.785 04
0.816 11
0.842 56
0.865 21
0.884 75
0.901 68
0.916 46
0.929 40
0.940 80
0.950 87
0.959 80
0.967 74
0.974 83
2.52
0.427 57
0.450 38
0.488 11
0.539 39
0.597 62
0.654 20
0.704 64
0.747 94
0.784 66
0.815 77
0.842 27
0.864 97
0.884 55
0.901 52
0.916 33
0.929 31
0.940 73
0.950 83
0.959 78
0.967 74
0.974 84
2.53
0.428 81
0.451 40
0.488 79
0.539 62
0.597 48
0.653 86
0.704 23
0.747 54
0.784 28
0.815 45
0.841 99
0.864 73
0.884 35
0.901 37
0.916 21
0.929 21
0.940 67
0.950 78
0.959 76
0.967 74
0.974 86
2.54
0.430 06
0.452 43
0.489 47
0.539 86
0.597 36
0.653 54
0.703 84
0.747 14
0.783 91
0.815 12
0.841 71
0.864 50
0.884 16
0.901 21
0.916 08
0.929 12
0.940 60
0.950 74
0.959 74
0.967 74
0.974 88
2.55
0.431 31
0.453 46
0.490 16
0.540 11
0.597 25
0.653 22
0.703 45
0.746 75
0.783 55
0.814 80
0.841 43
0.864 27
0.883 97
0.901 06
0.915 96
0.929 03
0.940 54
0.950 70
0.959 72
0.967 74
0.974 90
2.56
0.432 56
0.454 50
0.490 86
0.540 38
0.597 15
0.652 93
0.703 07
0.746 36
0.783 20
0.814 48
0.841 16
0.864 04
0.883 78
0.900 90
0.915 85
0.928 94
0.940 48
0.950 67
0.959 71
0.967 75
0.974 92
2.57
0.433 81
0.455 54
0.491 56
0.540 67
0.597 07
0.652 64
0.702 70
0.745 98
0.782 84
0.814 17
0.840 89
0.863 81
0.883 59
0.900 75
0.915 73
0.928 86
0.940 42
0.950 63
0.959 69
0.967 75
0.974 94
2.58
0.435 06
0.456 58
0.492 28
0.540 96
0.597 01
0.652 36
0.702 34
0.745 61
0.782 50
0.813 87
0.840 63
0.863 59
0.883 41
0.900 61
0.915 61
0.928 77
0.940 36
0.950 60
0.959 68
0.967 76
0.974 97
2.59
0.436 32
0.457 63
0.493 00
0.541 27
0.596 95
0.652 10
0.701 99
0.745 25
0.782 16
0.813 56
0.840 37
0.863 37
0.883 23
0.900 46
0.915 50
0.928 69
0.940 30
0.950 56
0.959 67
0.967 76
0.974 99
2.60
0.437 57
0.458 68
0.493 73
0.541 59
0.596 91
0.651 85
0.701 65
0.744 90
0.781 82
0.813 27
0.840 11
0.863 16
0.883 05
0.900 32
0.915 39
0.928 61
0.940 24
0.950 53
0.959 65
0.967 77
0.975 01
2.61
0.438 82
0.459 73
0.494 47
0.541 92
0.596 89
0.651 61
0.701 32
0.744 55
0.781 50
0.812 97
0.839 86
0.862 94
0.882 87
0.900 18
0.915 28
0.928 53
0.940 19
0.950 50
0.959 64
0.967 78
0.975 04
2.62
0.440 08
0.460 79
0.495 22
0.542 27
0.596 88
0.651 38
0.701 00
0.744 21
0.781 17
0.812 68
0.839 61
0.862 73
0.882 70
0.900 04
0.915 17
0.928 45
0.940 14
0.950 47
0.959 63
0.967 79
0.975 07
2.63
0.441 33
0.461 85
0.495 97
0.542 63
0.596 88
0.651 17
0.700 69
0.743 88
0.780 86
0.812 40
0.839 36
0.862 52
0.882 53
0.899 90
0.915 07
0.928 37
0.940 08
0.950 44
0.959 63
0.967 80
0.975 09
2.64
0.442 59
0.462 91
0.496 73
0.543 00
0.596 90
0.650 97
0.700 39
0.743 55
0.780 55
0.812 12
0.839 12
0.862 32
0.882 36
0.899 77
0.914 97
0.928 30
0.940 04
0.950 41
0.959 62
0.967 81
0.975 12
11
M
8
0
1
0
:
2
0
2
0

85
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
2.65
0.443 85
0.463 98
0.497 50
0.543 38
0.596 92
0.650 77
0.700 10
0.743 23
0.780 24
0.811 84
0.838 88
0.862 12
0.882 20
0.899 64
0.914 87
0.928 22
0.939 99
0.950 39
0.959 62
0.967 83
0.975 15
2.66
0.445 10
0.465 05
0.498 27
0.543 77
0.596 96
0.650 59
0.699 81
0.742 92
0.779 94
0.811 57
0.838 65
0.861 92
0.882 03
0.899 51
0.914 77
0.928 15
0.939 94
0.950 36
0.959 61
0.967 84
0.975 18
2.67
0.446 36
0.466 12
0.499 05
0.544 17
0.597 02
0.650 43
0.699 54
0.742 61
0.779 65
0.811 31
0.838 42
0.861 73
0.881 87
0.899 38
0.914 67
0.928 08
0.939 90
0.950 34
0.959 61
0.967 86
0.975 21
2.68
0.447 62
0.467 19
0.499 84
0.544 59
0.597 08
0.650 27
0.699 27
0.742 32
0.779 36
0.811 05
0.838 19
0.861 53
0.881 72
0.899 26
0.914 57
0.928 01
0.939 85
0.950 32
0.959 61
0.967 87
0.975 25
2.69
0.448 88
0.468 26
0.500 63
0.545 01
0.597 16
0.650 12
0.699 02
0.742 03
0.779 07
0.810 79
0.837 96
0.861 35
0.881 56
0.899 13
0.914 48
0.927 95
0.939 81
0.950 30
0.959 61
0.967 89
0.975 28
2.70
0.450 14
0.469 34
0.501 43
0.545 45
0.597 25
0.649 99
0.698 77
0.741 75
0.778 80
0.810 54
0.837 75
0.861 16
0.881 41
0.899 01
0.914 39
0.927 88
0.939 77
0.950 28
0.959 61
0.967 91
0.975 31
2.71
0.451 39
0.470 42
0.502 23
0.545 89
0.597 36
0.649 86
0.698 54
0.741 47
0.778 53
0.810 29
0.837 53
0.860 98
0.881 26
0.898 90
0.914 30
0.927 82
0.939 73
0.950 26
0.959 61
0.967 93
0.975 35
2.72
0.452 65
0.471 51
0.503 04
0.546 35
0.597 47
0.649 75
0.698 31
0.741 20
0.778 26
0.810 04
0.837 32
0.860 80
0.881 11
0.898 78
0.914 21
0.927 76
0.939 69
0.950 25
0.959 61
0.967 95
0.975 39
2.73
0.453 91
0.472 59
0.503 86
0.546 81
0.597 60
0.649 65
0.698 09
0.740 94
0.778 00
0.809 81
0.837 11
0.860 62
0.880 97
0.898 67
0.914 13
0.927 70
0.939 66
0.950 23
0.959 62
0.967 97
0.975 42
2.74
0.455 18
0.473 68
0.504 68
0.547 29
0.597 73
0.649 56
0.697 88
0.740 69
0.777 75
0.809 57
0.836 90
0.860 45
0.880 83
0.898 55
0.914 04
0.927 64
0.939 62
0.950 22
0.959 62
0.967 99
0.975 46
2.75
0.456 44
0.474 77
0.505 51
0.547 77
0.597 88
0.649 48
0.697 68
0.740 44
0.777 50
0.809 34
0.836 70
0.860 28
0.880 69
0.898 45
0.913 96
0.927 58
0.939 59
0.950 21
0.959 63
0.968 02
0.975 50
2.76
0.457 70
0.475 86
0.506 34
0.548 26
0.598 04
0.649 41
0.697 48
0.740 20
0.777 25
0.809 12
0.836 50
0.860 11
0.880 55
0.898 34
0.913 88
0.927 53
0.939 56
0.950 20
0.959 64
0.968 04
0.975 54
2.77
0.458 96
0.476 95
0.507 18
0.548 77
0.598 22
0.649 35
0.697 30
0.739 97
0.777 02
0.808 90
0.836 31
0.859 95
0.880 42
0.898 23
0.913 81
0.927 48
0.939 53
0.950 19
0.959 65
0.968 07
0.975 58
2.78
0.460 22
0.478 05
0.508 02
0.549 28
0.598 40
0.649 30
0.697 13
0.739 75
0.776 78
0.808 68
0.836 12
0.859 79
0.880 29
0.898 13
0.913 73
0.927 43
0.939 50
0.950 18
0.959 66
0.968 09
0.975 63
2.79
0.461 48
0.479 14
0.508 86
0.549 80
0.598 59
0.649 26
0.696 96
0.739 53
0.776 56
0.808 47
0.835 93
0.859 63
0.880 16
0.898 03
0.913 66
0.927 38
0.939 47
0.950 17
0.959 67
0.968 12
0.975 67
2.80
0.462 75
0.480 24
0.509 72
0.550 33
0.598 80
0.649 23
0.696 80
0.739 32
0.776 34
0.808 26
0.835 75
0.859 48
0.880 04
0.897 93
0.913 58
0.927 33
0.939 44
0.950 17
0.959 68
0.968 15
0.975 71
2.81
0.464 01
0.481 35
0.510 57
0.550 87
0.599 01
0.649 21
0.696 66
0.739 11
0.776 12
0.808 06
0.835 57
0.859 32
0.879 91
0.897 84
0.913 51
0.927 28
0.939 42
0.950 16
0.959 70
0.968 18
0.975 76
2.82
0.465 27
0.482 45
0.511 44
0.551 41
0.599 24
0.649 21
0.696 52
0.738 92
0.775 91
0.807 86
0.835 40
0.859 18
0.879 79
0.897 74
0.913 45
0.927 24
0.939 40
0.950 16
0.959 71
0.968 21
0.975 80
2.83
0.466 53
0.483 55
0.512 30
0.551 97
0.599 47
0.649 21
0.696 39
0.738 73
0.775 71
0.807 67
0.835 22
0.859 03
0.879 67
0.897 65
0.913 38
0.927 20
0.939 38
0.950 16
0.959 73
0.968 25
0.975 85
2.84
0.467 80
0.484 66
0.513 17
0.552 53
0.599 72
0.649 22
0.696 26
0.738 54
0.775 51
0.807 48
0.835 06
0.858 89
0.879 56
0.897 56
0.913 32
0.927 15
0.939 36
0.950 16
0.959 74
0.968 28
0.975 90
2.85
0.469 06
0.485 77
0.514 05
0.553 10
0.599 97
0.649 24
0.696 15
0.738 37
0.775 32
0.807 30
0.834 89
0.858 75
0.879 45
0.897 48
0.913 25
0.927 12
0.939 34
0.950 16
0.959 76
0.968 31
0.975 95
2.86
0.470 32
0.486 88
0.514 93
0.553 67
0.600 24
0.649 28
0.696 04
0.738 20
0.775 13
0.807 12
0.834 73
0.858 61
0.879 34
0.897 39
0.913 19
0.927 08
0.939 32
0.950 16
0.959 78
0.968 35
0.976 00
2.87
0.471 59
0.487 99
0.515 81
0.554 26
0.600 51
0.649 32
0.695 95
0.738 04
0.774 95
0.806 94
0.834 58
0.858 48
0.879 23
0.897 31
0.913 14
0.927 04
0.939 31
0.950 16
0.959 80
0.968 39
0.976 05
2.88
0.472 85
0.489 10
0.516 70
0.554 85
0.600 80
0.649 37
0.695 86
0.737 88
0.774 78
0.806 77
0.834 42
0.858 35
0.879 12
0.897 23
0.913 08
0.927 01
0.939 30
0.950 17
0.959 83
0.968 43
0.976 10
2.89
0.474 12
0.490 22
0.517 59
0.555 45
0.601 09
0.649 43
0.695 78
0.737 73
0.774 61
0.806 61
0.834 27
0.858 22
0.879 02
0.897 15
0.913 03
0.926 98
0.939 28
0.950 18
0.959 85
0.968 46
0.976 16
2.90
0.475 38
0.491 33
0.518 48
0.556 06
0.601 40
0.649 50
0.695 71
0.737 59
0.774 44
0.806 44
0.834 13
0.858 10
0.878 92
0.897 08
0.912 97
0.926 95
0.939 27
0.950 18
0.959 88
0.968 50
0.976 21
2.91
0.476 65
0.492 45
0.519 38
0.556 67
0.601 71
0.649 58
0.695 64
0.737 46
0.774 28
0.806 29
0.833 99
0.857 98
0.878 83
0.897 01
0.912 92
0.926 92
0.939 26
0.950 19
0.959 90
0.968 55
0.976 26
2.92
0.477 91
0.493 57
0.520 28
0.557 29
0.602 03
0.649 67
0.695 59
0.737 33
0.774 13
0.806 13
0.833 85
0.857 86
0.878 73
0.896 94
0.912 88
0.926 89
0.939 26
0.950 20
0.959 93
0.968 59
0.976 32
2.93
0.479 18
0.494 69
0.521 19
0.557 92
0.602 36
0.649 76
0.695 54
0.737 21
0.773 98
0.805 99
0.833 71
0.857 75
0.878 64
0.896 87
0.912 83
0.926 87
0.939 25
0.950 22
0.959 96
0.968 63
0.976 38
2.94
0.480 44
0.495 81
0.522 10
0.558 55
0.602 70
0.649 87
0.695 50
0.737 10
0.773 84
0.805 84
0.833 58
0.857 64
0.878 55
0.896 80
0.912 79
0.926 84
0.939 25
0.950 23
0.959 99
0.968 68
0.976 44
2.95
0.481 71
0.496 93
0.523 01
0.559 19
0.603 05
0.649 99
0.695 47
0.736 99
0.773 70
0.805 70
0.833 46
0.857 53
0.878 47
0.896 74
0.912 74
0.926 82
0.939 24
0.950 25
0.960 02
0.968 72
0.976 49
2.96
0.482 97
0.498 06
0.523 93
0.559 84
0.603 41
0.650 11
0.695 45
0.736 89
0.773 57
0.805 57
0.833 33
0.857 43
0.878 38
0.896 67
0.912 70
0.926 80
0.939 24
0.950 26
0.960 05
0.968 77
0.976 55
2.97
0.484 24
0.499 18
0.524 85
0.560 49
0.603 77
0.650 24
0.695 43
0.736 80
0.773 45
0.805 44
0.833 21
0.857 32
0.878 30
0.896 62
0.912 66
0.926 78
0.939 24
0.950 28
0.960 08
0.968 82
0.976 62
2.98
0.485 50
0.500 31
0.525 77
0.561 15
0.604 15
0.650 38
0.695 43
0.736 71
0.773 33
0.805 31
0.833 10
0.857 23
0.878 22
0.896 56
0.912 63
0.926 76
0.939 24
0.950 30
0.960 12
0.968 86
0.976 68
2.99
0.486 77
0.501 44
0.526 70
0.561 82
0.604 53
0.650 53
0.695 43
0.736 63
0.773 21
0.805 19
0.832 99
0.857 13
0.878 15
0.896 50
0.912 59
0.926 75
0.939 25
0.950 32
0.960 15
0.968 91
0.976 74
3.00
0.488 03
0.502 57
0.527 63
0.562 49
0.604 92
0.650 69
0.695 43
0.736 55
0.773 10
0.805 08
0.832 88
0.857 04
0.878 07
0.896 45
0.912 56
0.926 74
0.939 25
0.950 34
0.960 19
0.968 97
0.976 80
3.01
0.489 30
0.503 70
0.528 56
0.563 17
0.605 32
0.650 86
0.695 45
0.736 49
0.773 00
0.804 96
0.832 77
0.856 95
0.878 00
0.896 40
0.912 53
0.926 72
0.939 26
0.950 36
0.960 23
0.969 02
0.976 87
3.02
0.490 56
0.504 83
0.529 50
0.563 85
0.605 72
0.651 04
0.695 47
0.736 43
0.772 90
0.804 86
0.832 67
0.856 86
0.877 94
0.896 35
0.912 50
0.926 71
0.939 27
0.950 39
0.960 27
0.969 07
0.976 93
3.03
0.491 83
0.505 96
0.530 44
0.564 54
0.606 14
0.651 22
0.695 51
0.736 37
0.772 81
0.804 75
0.832 58
0.856 78
0.877 87
0.896 31
0.912 47
0.926 71
0.939 28
0.950 41
0.960 31
0.969 12
0.977 00
3.04
0.493 09
0.507 09
0.531 38
0.565 23
0.606 56
0.651 41
0.695 54
0.736 32
0.772 72
0.804 66
0.832 48
0.856 70
0.877 81
0.896 26
0.912 45
0.926 70
0.939 29
0.950 44
0.960 35
0.969 18
0.977 07
3.05
0.494 36
0.508 23
0.532 32
0.565 93
0.606 99
0.651 61
0.695 59
0.736 28
0.772 64
0.804 56
0.832 39
0.856 62
0.877 75
0.896 22
0.912 43
0.926 70
0.939 30
0.950 47
0.960 39
0.969 24
0.977 14
3.06
0.495 63
0.509 36
0.533 27
0.566 63
0.607 42
0.651 82
0.695 64
0.736 25
0.772 56
0.804 47
0.832 31
0.856 55
0.877 69
0.896 18
0.912 41
0.926 69
0.939 31
0.950 50
0.960 44
0.969 29
0.977 21
3.07
0.496 89
0.510 50
0.534 22
0.567 34
0.607 86
0.652 04
0.695 70
0.736 22
0.772 49
0.804 39
0.832 22
0.856 48
0.877 64
0.896 14
0.912 39
0.926 69
0.939 33
0.950 53
0.960 48
0.969 35
0.977 28
3.08
0.498 16
0.511 64
0.535 17
0.568 06
0.608 32
0.652 26
0.695 77
0.736 20
0.772 42
0.804 30
0.832 14
0.856 41
0.877 58
0.896 11
0.912 37
0.926 69
0.939 34
0.950 56
0.960 53
0.969 41
0.977 35
11
M
8
0
1
0
:
2
0
2
0
86
M 8010:2020
表H.4−Z数表(2015)(続き)
Bz
Az
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
3.09
0.499 42
0.512 78
0.536 13
0.568 78
0.608 77
0.652 49
0.695 85
0.736 18
0.772 36
0.804 23
0.832 07
0.856 34
0.877 53
0.896 08
0.912 36
0.926 69
0.939 36
0.950 59
0.960 57
0.969 47
0.977 42
3.10
0.500 69
0.513 92
0.537 09
0.569 50
0.609 24
0.652 73
0.695 93
0.736 17
0.772 31
0.804 16
0.832 00
0.856 28
0.877 49
0.896 05
0.912 34
0.926 70
0.939 38
0.950 63
0.960 62
0.969 53
0.977 49
3.11
0.501 95
0.515 06
0.538 05
0.570 23
0.609 71
0.652 98
0.696 02
0.736 17
0.772 26
0.804 09
0.831 93
0.856 22
0.877 44
0.896 02
0.912 33
0.926 70
0.939 40
0.950 66
0.960 67
0.969 60
0.977 57
3.12
0.503 22
0.516 20
0.539 01
0.570 96
0.610 19
0.653 23
0.696 12
0.736 17
0.772 21
0.804 02
0.831 86
0.856 17
0.877 40
0.895 99
0.912 32
0.926 71
0.939 43
0.950 70
0.960 72
0.969 66
0.977 64
3.13
0.504 48
0.517 34
0.539 97
0.571 70
0.610 67
0.653 49
0.696 22
0.736 18
0.772 17
0.803 96
0.831 80
0.856 12
0.877 36
0.895 97
0.912 32
0.926 72
0.939 45
0.950 74
0.960 78
0.969 73
0.977 72
3.14
0.505 75
0.518 48
0.540 94
0.572 44
0.611 16
0.653 76
0.696 33
0.736 19
0.772 14
0.803 91
0.831 75
0.856 07
0.877 33
0.895 95
0.912 31
0.926 73
0.939 48
0.950 78
0.960 83
0.969 79
0.977 80
3.15
0.507 02
0.519 62
0.541 91
0.573 19
0.611 66
0.654 04
0.696 45
0.736 22
0.772 11
0.803 86
0.831 69
0.856 02
0.877 29
0.895 93
0.912 31
0.926 74
0.939 50
0.950 82
0.960 89
0.969 86
0.977 88
3.16
0.508 28
0.520 77
0.542 89
0.573 94
0.612 17
0.654 32
0.696 58
0.736 24
0.772 08
0.803 81
0.831 64
0.855 98
0.877 26
0.895 91
0.912 31
0.926 76
0.939 53
0.950 86
0.960 94
0.969 93
0.977 96
3.17
0.509 55
0.521 91
0.543 86
0.574 70
0.612 68
0.654 61
0.696 71
0.736 28
0.772 06
0.803 77
0.831 60
0.855 94
0.877 23
0.895 90
0.912 31
0.926 77
0.939 56
0.950 91
0.961 00
0.970 00
0.978 04
3.18
0.510 81
0.523 06
0.544 84
0.575 46
0.613 20
0.654 91
0.696 85
0.736 32
0.772 05
0.803 73
0.831 56
0.855 90
0.877 21
0.895 89
0.912 31
0.926 79
0.939 59
0.950 95
0.961 06
0.970 07
0.978 12
3.19
0.512 08
0.524 20
0.545 82
0.576 23
0.613 72
0.655 22
0.696 99
0.736 36
0.772 04
0.803 70
0.831 52
0.855 87
0.877 18
0.895 88
0.912 31
0.926 81
0.939 63
0.951 00
0.961 12
0.970 14
0.978 20
3.20
0.513 34
0.525 35
0.546 80
0.576 99
0.614 25
0.655 53
0.697 14
0.736 41
0.772 04
0.803 67
0.831 48
0.855 84
0.877 16
0.895 87
0.912 32
0.926 83
0.939 66
0.951 05
0.961 18
0.970 21
0.978 28
3.21
0.514 61
0.526 50
0.547 78
0.577 77
0.614 78
0.655 85
0.697 30
0.736 47
0.772 04
0.803 65
0.831 45
0.855 81
0.877 14
0.895 86
0.912 33
0.926 85
0.939 70
0.951 10
0.961 24
0.970 28
0.978 37
3.22
0.515 87
0.527 65
0.548 76
0.578 54
0.615 32
0.656 17
0.697 47
0.736 53
0.772 04
0.803 63
0.831 42
0.855 78
0.877 13
0.895 86
0.912 34
0.926 88
0.939 74
0.951 15
0.961 30
0.970 36
0.978 45
3.23
0.517 14
0.528 80
0.549 75
0.579 32
0.615 87
0.656 50
0.697 64
0.736 60
0.772 05
0.803 61
0.831 40
0.855 76
0.877 11
0.895 86
0.912 35
0.926 90
0.939 78
0.951 20
0.961 37
0.970 43
0.978 54
3.24
0.518 40
0.529 94
0.550 74
0.580 11
0.616 42
0.656 84
0.697 82
0.736 68
0.772 07
0.803 60
0.831 38
0.855 74
0.877 10
0.895 86
0.912 36
0.926 93
0.939 82
0.951 26
0.961 43
0.970 51
0.978 62
3.25
0.519 67
0.531 09
0.551 73
0.580 90
0.616 98
0.657 19
0.698 00
0.736 76
0.772 09
0.803 59
0.831 36
0.855 73
0.877 10
0.895 86
0.912 38
0.926 96
0.939 86
0.951 31
0.961 50
0.970 59
0.978 71
3.26
0.520 93
0.532 25
0.552 72
0.581 69
0.617 54
0.657 54
0.698 19
0.736 84
0.772 12
0.803 59
0.831 34
0.855 71
0.877 09
0.895 87
0.912 40
0.926 99
0.939 90
0.951 37
0.961 57
0.970 67
0.978 80
3.27
0.522 19
0.533 40
0.553 72
0.582 48
0.618 11
0.657 90
0.698 39
0.736 94
0.772 15
0.803 59
0.831 33
0.855 70
0.877 09
0.895 88
0.912 42
0.927 02
0.939 95
0.951 42
0.961 64
0.970 75
0.978 89
3.28
0.523 46
0.534 55
0.554 72
0.583 28
0.618 69
0.658 26
0.698 59
0.737 03
0.772 19
0.803 59
0.831 33
0.855 70
0.877 09
0.895 89
0.912 44
0.927 06
0.940 00
0.951 48
0.961 71
0.970 83
0.978 98
3.29
0.524 72
0.535 70
0.555 71
0.584 08
0.619 27
0.658 63
0.698 80
0.737 14
0.772 23
0.803 60
0.831 32
0.855 69
0.877 09
0.895 90
0.912 46
0.927 09
0.940 04
0.951 54
0.961 78
0.970 91
0.979 07
3.30
0.525 99
0.536 85
0.556 71
0.584 89
0.619 85
0.659 01
0.699 02
0.737 25
0.772 27
0.803 62
0.831 32
0.855 69
0.877 10
0.895 91
0.912 49
0.927 13
0.940 09
0.951 60
0.961 85
0.970 99
0.979 17
11
M
8
0
1
0
:
2
0
2
0

87
M 8010:2020
附属書I
(規定)
Z数表(1993)
I.1
Z数表(1993)を用いた圧縮係数の計算
Z数表(1993)を用いた圧縮係数の計算は,次の手順による。
a) ガスの温度,圧力,成分のモル分率,並びに表I.1に規定する定数ai及びbiを用い,式(I.1)及び式(I.2)
でパラメータAZ及びBZを計算する。ガスが表I.1に含まれない成分を含有する場合で,附属書Gが
適用できる場合には,Z数表(1993)を使用することができる。
∑
=
i
i
ix
a
T
AZ
·········································································· (I.1)
∑
=
i
i
ix
b
p
BZ
··········································································· (I.2)
ここに,
AZ: Z数表の横軸の値
BZ: Z数表の縦軸の値
ai: 表I.1に規定するi番目の成分の定数(K)
bi: 表I.1に規定するi番目の成分の定数(kPa)
xi: i番目の成分のモル分率
T: ガスの温度(K)
p: ガスの圧力(kPa)
注記 Z数表(1993)で使用するai及びbiは,それぞれ,各成分の臨界温度及び臨界圧力である。
b) 表I.2の1行目からAZの値を挟む二つの列,1列目からBZの値を挟む二つの行を抜き出し,これらの
行及び列が交差する位置における表の値をAZ及びBZの値で内挿し,得られた値を圧縮係数の値とす
る(図H.1参照)。
表I.1−Z数表(1993)の使用に必要となる定数ai及びbi(臨界定数)
成分
ai(K)
bi(kPa)
CO2
304.128 2
7386
N2
126.192
3390
H2
33.19
1297
CO
132.86
3494
O2
154.595
5043
CH4
190.564
4598.8
C2H6
305.322
4880
C3H8
369.825
4250
iC4H10
407.817
3648
nC4H10
425.125
3784
iC5H12
460.35
3381
nC5H12
469.7
3364
C6H14
507.82
3030
C7H16
540.13
2740
C8H18
569.32
2490
88
M 8010:2020
表I.2−Z数表(1993)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
0.01
0.998 0 0.998 2 0.998 4 0.998 6 0.998 8 0.998 9 0.999 0 0.999 2 0.999 3 0.999 5 0.999 6 0.999 7 0.999 8 0.999 9 0.999 9 1.000 0 1.000 0
0.02
0.996 0 0.996 5 0.996 9 0.997 2 0.997 5 0.997 8 0.998 0 0.998 4 0.998 7 0.998 9 0.999 1 0.999 3 0.999 6 0.999 7 0.999 9 0.999 9 1.000 0
0.03
0.994 0 0.994 7 0.995 3 0.995 8 0.996 3 0.996 7 0.997 0 0.997 5 0.998 0 0.998 4 0.998 7 0.999 0 0.999 3 0.999 6 0.999 8 0.999 9 1.000 0
0.04
0.991 9 0.992 9 0.993 7 0.994 4 0.995 0 0.995 6 0.996 0 0.996 7 0.997 4 0.997 9 0.998 3 0.998 6 0.999 1 0.999 5 0.999 7 0.999 9 1.000 0
0.05
0.989 9 0.991 1 0.992 2 0.993 0 0.993 8 0.994 4 0.995 0 0.995 9 0.996 7 0.997 4 0.997 9 0.998 3 0.998 9 0.999 3 0.999 6 0.999 8 1.000 0
0.06
0.987 9 0.989 3 0.990 6 0.991 6 0.992 5 0.993 3 0.994 0 0.995 1 0.996 1 0.996 8 0.997 5 0.998 0 0.998 7 0.999 2 0.999 6 0.999 8 1.000 0
0.07
0.985 9 0.987 6 0.989 0 0.990 2 0.991 3 0.992 2 0.993 0 0.994 3 0.995 4 0.996 3 0.997 0 0.997 6 0.998 5 0.999 1 0.999 5 0.999 8 1.000 0
0.08
0.983 8 0.985 8 0.987 4 0.988 8 0.990 1 0.991 1 0.992 0 0.993 5 0.994 8 0.995 8 0.996 6 0.997 3 0.998 3 0.998 9 0.999 4 0.999 8 1.000 0
0.09
0.981 8 0.984 0 0.985 9 0.987 4 0.988 8 0.990 0 0.991 0 0.992 7 0.994 1 0.995 3 0.996 2 0.996 9 0.998 1 0.998 8 0.999 4 0.999 7 1.000 0
0.10
0.979 7 0.982 2 0.984 3 0.986 0 0.987 6 0.988 9 0.990 0 0.991 9 0.993 5 0.994 7 0.995 8 0.996 6 0.997 8 0.998 7 0.999 3 0.999 7 1.000 0
0.11
0.977 7 0.980 4 0.982 7 0.984 6 0.986 3 0.987 8 0.989 0 0.991 0 0.992 8 0.994 2 0.995 4 0.996 3 0.997 6 0.998 6 0.999 2 0.999 7 1.000 0
0.12
0.975 6 0.978 6 0.981 1 0.983 2 0.985 1 0.986 7 0.988 0 0.990 2 0.992 2 0.993 7 0.994 9 0.995 9 0.997 4 0.998 4 0.999 1 0.999 7 1.000 0
0.13
0.973 6 0.976 8 0.979 5 0.981 8 0.983 8 0.985 6 0.987 1 0.989 4 0.991 5 0.993 2 0.994 5 0.995 6 0.997 2 0.998 3 0.999 1 0.999 6 1.000 0
0.14
0.971 5 0.975 0 0.977 9 0.980 4 0.982 6 0.984 4 0.986 1 0.988 6 0.990 9 0.992 7 0.994 1 0.995 3 0.997 0 0.998 2 0.999 0 0.999 6 1.000 0
0.15
0.969 5 0.973 2 0.976 3 0.979 0 0.981 3 0.983 3 0.985 1 0.987 8 0.990 2 0.992 2 0.993 7 0.994 9 0.996 8 0.998 1 0.998 9 0.999 6 1.000 0
0.16
0.967 4 0.971 4 0.974 8 0.977 6 0.980 1 0.982 2 0.984 1 0.987 0 0.989 6 0.991 6 0.993 3 0.994 6 0.996 6 0.997 9 0.998 9 0.999 5 1.000 0
0.17
0.965 3 0.969 6 0.973 2 0.976 2 0.978 8 0.981 1 0.983 1 0.986 2 0.988 9 0.991 1 0.992 9 0.994 3 0.996 4 0.997 8 0.998 8 0.999 5 1.000 0
0.18
0.963 2 0.967 8 0.971 6 0.974 8 0.977 6 0.980 0 0.982 1 0.985 4 0.988 3 0.990 6 0.992 5 0.993 9 0.996 2 0.997 7 0.998 7 0.999 5 1.000 0
0.19
0.961 2 0.965 9 0.970 0 0.973 4 0.976 3 0.978 9 0.981 1 0.984 6 0.987 7 0.990 1 0.992 0 0.993 6 0.996 0 0.997 6 0.998 7 0.999 5 1.000 1
0.20
0.959 1 0.964 1 0.968 4 0.972 0 0.975 1 0.977 8 0.980 1 0.983 8 0.987 0 0.989 6 0.991 6 0.993 3 0.995 8 0.997 4 0.998 6 0.999 5 1.000 1
0.21
0.957 0 0.962 3 0.966 8 0.970 6 0.973 8 0.976 7 0.979 1 0.983 0 0.986 4 0.989 1 0.991 2 0.993 0 0.995 6 0.997 3 0.998 6 0.999 4 1.000 1
0.22
0.954 9 0.960 5 0.965 2 0.969 2 0.972 6 0.975 5 0.978 1 0.982 2 0.985 7 0.988 6 0.990 8 0.992 6 0.995 3 0.997 2 0.998 5 0.999 4 1.000 1
0.23
0.952 8 0.958 7 0.963 6 0.967 8 0.971 3 0.974 4 0.977 1 0.981 4 0.985 1 0.988 1 0.990 4 0.992 3 0.995 1 0.997 1 0.998 4 0.999 4 1.000 1
0.24
0.950 7 0.956 8 0.962 0 0.966 3 0.970 1 0.973 3 0.976 1 0.980 6 0.984 5 0.987 5 0.990 0 0.992 0 0.994 9 0.997 0 0.998 4 0.999 4 1.000 1
0.25
0.948 6 0.955 0 0.960 4 0.964 9 0.968 8 0.972 2 0.975 1 0.979 8 0.983 8 0.987 0 0.989 6 0.991 7 0.994 7 0.996 8 0.998 3 0.999 3 1.000 1
0.26
0.946 5 0.953 2 0.958 8 0.963 5 0.967 6 0.971 1 0.974 1 0.979 0 0.983 2 0.986 5 0.989 2 0.991 3 0.994 5 0.996 7 0.998 2 0.999 3 1.000 1
0.27
0.944 4 0.951 3 0.957 2 0.962 1 0.966 3 0.970 0 0.973 2 0.978 2 0.982 6 0.986 0 0.988 8 0.991 0 0.994 3 0.996 6 0.998 2 0.999 3 1.000 1
0.28
0.942 2 0.949 5 0.955 5 0.960 7 0.965 1 0.968 9 0.972 2 0.977 4 0.981 9 0.985 5 0.988 4 0.990 7 0.994 1 0.996 5 0.998 1 0.999 3 1.000 1
0.29
0.940 1 0.947 6 0.953 9 0.959 3 0.963 8 0.967 8 0.971 2 0.976 6 0.981 3 0.985 0 0.988 0 0.990 4 0.993 9 0.996 4 0.998 1 0.999 3 1.000 1
0.30
0.938 0 0.945 8 0.952 3 0.957 9 0.962 6 0.966 7 0.970 2 0.975 8 0.980 7 0.984 5 0.987 6 0.990 1 0.993 7 0.996 2 0.998 0 0.999 2 1.000 1
11
M
8
0
1
0
:
2
0
2
0
89
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
0.31
0.935 9 0.943 9 0.950 7 0.956 4 0.961 3 0.965 5 0.969 2 0.975 0 0.980 0 0.984 0 0.987 2 0.989 7 0.993 5 0.996 1 0.997 9 0.999 2 1.000 2
0.32
0.933 7 0.942 1 0.949 1 0.955 0 0.960 1 0.964 4 0.968 2 0.974 2 0.979 4 0.983 5 0.986 8 0.989 4 0.993 3 0.996 0 0.997 9 0.999 2 1.000 2
0.33
0.931 6 0.940 2 0.947 5 0.953 6 0.958 8 0.963 3 0.967 2 0.973 4 0.978 8 0.983 0 0.986 4 0.989 1 0.993 1 0.995 9 0.997 8 0.999 2 1.000 2
0.34
0.929 4 0.938 4 0.945 8 0.952 2 0.957 6 0.962 2 0.966 2 0.972 6 0.978 2 0.982 5 0.986 0 0.988 8 0.992 9 0.995 8 0.997 8 0.999 2 1.000 2
0.35
0.927 3 0.936 5 0.944 2 0.950 8 0.956 3 0.961 1 0.965 2 0.971 9 0.977 5 0.982 0 0.985 6 0.988 5 0.992 7 0.995 7 0.997 7 0.999 1 1.000 2
0.36
0.925 1 0.934 6 0.942 6 0.949 3 0.955 1 0.960 0 0.964 3 0.971 1 0.976 9 0.981 5 0.985 2 0.988 2 0.992 5 0.995 5 0.997 6 0.999 1 1.000 2
0.37
0.923 0 0.932 8 0.941 0 0.947 9 0.953 8 0.958 9 0.963 3 0.970 3 0.976 3 0.981 0 0.984 8 0.987 8 0.992 4 0.995 4 0.997 6 0.999 1 1.000 2
0.38
0.920 8 0.930 9 0.939 4 0.946 5 0.952 6 0.957 8 0.962 3 0.969 5 0.975 7 0.980 5 0.984 4 0.987 5 0.992 2 0.995 3 0.997 5 0.999 1 1.000 2
0.39
0.918 6 0.929 0 0.937 7 0.945 1 0.951 3 0.956 7 0.961 3 0.968 7 0.975 0 0.980 0 0.984 0 0.987 2 0.992 0 0.995 2 0.997 5 0.999 1 1.000 3
0.40
0.916 5 0.927 2 0.936 1 0.943 6 0.950 0 0.955 6 0.960 3 0.967 9 0.974 4 0.979 5 0.983 6 0.986 9 0.991 8 0.995 1 0.997 4 0.999 1 1.000 3
0.41
0.914 3 0.925 3 0.934 5 0.942 2 0.948 8 0.954 4 0.959 3 0.967 1 0.973 8 0.979 0 0.983 2 0.986 6 0.991 6 0.995 0 0.997 4 0.999 1 1.000 3
0.42
0.912 1 0.923 4 0.932 8 0.940 8 0.947 5 0.953 3 0.958 3 0.966 4 0.973 2 0.978 5 0.982 8 0.986 3 0.991 4 0.994 9 0.997 3 0.999 0 1.000 3
0.43
0.909 9 0.921 5 0.931 2 0.939 4 0.946 3 0.952 2 0.957 4 0.965 6 0.972 6 0.978 0 0.982 4 0.986 0 0.991 2 0.994 8 0.997 3 0.999 0 1.000 3
0.44
0.907 7 0.919 6 0.929 6 0.937 9 0.945 0 0.951 1 0.956 4 0.964 8 0.971 9 0.977 6 0.982 0 0.985 7 0.991 0 0.994 7 0.997 2 0.999 0 1.000 3
0.45
0.905 5 0.917 8 0.927 9 0.936 5 0.943 8 0.950 0 0.955 4 0.964 0 0.971 3 0.977 1 0.981 7 0.985 4 0.990 8 0.994 5 0.997 1 0.999 0 1.000 3
0.46
0.903 3 0.915 9 0.926 3 0.935 1 0.942 5 0.948 9 0.954 4 0.963 2 0.970 7 0.976 6 0.981 3 0.985 0 0.990 6 0.994 4 0.997 1 0.999 0 1.000 4
0.47
0.901 1 0.914 0 0.924 7 0.933 6 0.941 3 0.947 8 0.953 4 0.962 5 0.970 1 0.976 1 0.980 9 0.984 7 0.990 4 0.994 3 0.997 0 0.999 0 1.000 4
0.48
0.898 9 0.912 1 0.923 0 0.932 2 0.940 0 0.946 7 0.952 4 0.961 7 0.969 5 0.975 6 0.980 5 0.984 4 0.990 3 0.994 2 0.997 0 0.999 0 1.000 4
0.49
0.896 7 0.910 2 0.921 4 0.930 8 0.938 8 0.945 6 0.951 5 0.960 9 0.968 9 0.975 1 0.980 1 0.984 1 0.990 1 0.994 1 0.996 9 0.999 0 1.000 4
0.50
0.894 5 0.908 3 0.919 7 0.929 3 0.937 5 0.944 5 0.950 5 0.960 1 0.968 3 0.974 6 0.979 7 0.983 8 0.989 9 0.994 0 0.996 9 0.998 9 1.000 4
0.51
0.892 2 0.906 4 0.918 1 0.927 9 0.936 2 0.943 4 0.949 5 0.959 4 0.967 6 0.974 2 0.979 3 0.983 5 0.989 7 0.993 9 0.996 8 0.998 9 1.000 4
0.52
0.890 0 0.904 5 0.916 4 0.926 5 0.935 0 0.942 3 0.948 5 0.958 6 0.967 0 0.973 7 0.979 0 0.983 2 0.989 5 0.993 8 0.996 8 0.998 9 1.000 5
0.53
0.887 8 0.902 5 0.914 8 0.925 0 0.933 7 0.941 2 0.947 6 0.957 8 0.966 4 0.973 2 0.978 6 0.982 9 0.989 3 0.993 7 0.996 7 0.998 9 1.000 5
0.54
0.885 5 0.900 6 0.913 1 0.923 6 0.932 5 0.940 1 0.946 6 0.957 1 0.965 8 0.972 7 0.978 2 0.982 6 0.989 1 0.993 6 0.996 7 0.998 9 1.000 5
0.55
0.883 3 0.898 7 0.911 5
0.922 2 0.931 2 0.938 9 0.945 6 0.956 3 0.965 2 0.972 2 0.977 8 0.982 3 0.989 0 0.993 5 0.996 6 0.998 9 1.000 5
0.56
0.881 0 0.896 8 0.909 8 0.920 7 0.930 0 0.937 8 0.944 6 0.955 5 0.964 6 0.971 8 0.977 4 0.982 0 0.988 8 0.993 4 0.996 6 0.998 9 1.000 5
0.57
0.878 8 0.894 9 0.908 2 0.919 3 0.928 7 0.936 7 0.943 7 0.954 8 0.964 0 0.971 3 0.977 1 0.981 7 0.988 6 0.993 3 0.996 6 0.998 9 1.000 6
0.58
0.876 5 0.893 0 0.906 5 0.917 9 0.927 5 0.935 6 0.942 7 0.954 0 0.963 4 0.970 8 0.976 7 0.981 4 0.988 4 0.993 2 0.996 5 0.998 9 1.000 6
0.59
0.874 3 0.891 0 0.904 9 0.916 4 0.926 2 0.934 5 0.941 7 0.953 2 0.962 8 0.970 3 0.976 3 0.981 1 0.988 2 0.993 1 0.996 5 0.998 9 1.000 6
0.60
0.872 0 0.889 1 0.903 2 0.915 0 0.924 9 0.933 4 0.940 7 0.952 5 0.962 2 0.969 9 0.975 9 0.980 8 0.988 1 0.993 0 0.996 4 0.998 9 1.000 6
11
M
8
0
1
0
:
2
0
2
0
90
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
0.61
0.869 7 0.887 2 0.901 5 0.913 5 0.923 7 0.932 3 0.939 8 0.951 7 0.961 6 0.969 4 0.975 6 0.980 5 0.987 9 0.992 9 0.996 4 0.998 9 1.000 6
0.62
0.867 4 0.885 2 0.899 9 0.912 1 0.922 4 0.931 2 0.938 8 0.950 9 0.961 0 0.968 9 0.975 2 0.980 2 0.987 7 0.992 8 0.996 3 0.998 8 1.000 7
0.63
0.865 1 0.883 3 0.898 2 0.910 7 0.921 2 0.930 1 0.937 8 0.950 2 0.960 4 0.968 4 0.974 8 0.980 0 0.987 5 0.992 7 0.996 3 0.998 8 1.000 7
0.64
0.862 9 0.881 3 0.896 6 0.909 2 0.919 9 0.929 0 0.936 8 0.949 4 0.959 8 0.968 0 0.974 4 0.979 7 0.987 4 0.992 6 0.996 2 0.998 8 1.000 7
0.65
0.860 6 0.879 4 0.894 9 0.907 8 0.918 1 0.927 9 0.935 9 0.948 7 0.959 2 0.967 5 0.974 1 0.979 4 0.987 2 0.992 5 0.996 2 0.998 8 1.000 7
0.66
0.858 3 0.877 5 0.893 2 0.906 4 0.917 4 0.926 8 0.934 9 0.947 9 0.958 6 0.967 0 0.974 7 0.979 1 0.987 0 0.992 4 0.996 2 0.998 8 1.000 8
0.67
0.856 0 0.875 5 0.891 6 0.904 9 0.916 2 0.925 7 0.933 9 0.947 2 0.958 0 0.966 6 0.973 3 0.978 8 0.986 8 0.992 3 0.996 1 0.998 8 1.000 8
0.68
0.853 6 0.873 6 0.889 9 0.903 5 0.914 9 0.924 6 0.933 0 0.946 4 0.957 4 0.966 1 0.973 0 0.978 5 0.986 7 0.992 2 0.996 1 0.998 8 1.000 8
0.69
0.851 3 0.871 6 0.888 2 0.902 0 0.913 7 0.923 5 0.932 0 0.945 7 0.956 9 0.965 6 0.972 6 0.978 2 0.986 5 0.992 1 0.996 0 0.998 8 1.000 8
0.70
0.849 0 0.869 6 0.886 5 0.900 6 0.912 4 0.922 4 0.931 0 0.944 9 0.956 3 0.965 2 0.972 2 0.977 9 0.986 3 0.992 0 0.996 0 0.998 8 1.000 9
0.71
0.846 7 0.867 7 0.884 9 0.899 1 0.911 1 0.921 3 0.930 1 0.944 2 0.955 7 0.964 7 0.971 9 0.977 6 0.986 1 0.991 9 0.995 9 0.998 8 1.000 9
0.72
0.844 3 0.865 7 0.883 2 0.897 7 0.909 9 0.920 3 0.929 1 0.943 4 0.955 1 0.964 2 0.971 5 0.977 4 0.986 0 0.991 8 0.995 9 0.998 8 1.000 9
0.73
0.842 0 0.863 8 0.881 5 0.896 3 0.908 6 0.919 2 0.928 2 0.942 7 0.954 5 0.963 8 0.971 2 0.977 1 0.985 8 0.991 7 0.995 9 0.998 8 1.000 9
0.74
0.839 7 0.861 8 0.879 9 0.894 8 0.907 4 0.918 1 0.927 2 0.941 9 0.953 9 0.963 3 0.970 8 0.976 8 0.985 6 0.991 6 0.995 8 0.998 8 1.001 0
0.75
0.837 3 0.859 8 0.878 2 0.893 4 0.906 1 0.917 0 0.926 2 0.941 2 0.953 3 0.962 9 0.970 4 0.976 5 0.985 5 0.991 5 0.995 8 0.998 8 1.001 0
0.76
0.835 0 0.857 9 0.876 5 0.891 9 0.904 9 0.915 9 0.925 3 0.940 4 0.952 8 0.962 4 0.970 1 0.976 2 0.985 3 0.991 5 0.995 8 0.998 8 1.001 0
0.77
0.832 6 0.855 9 0.874 8 0.890 5 0.903 6 0.914 8 0.924 3 0.939 7 0.952 2 0.962 0 0.969 7 0.975 9 0.985 1 0.991 4 0.995 7 0.998 8 1.001 1
0.78
0.830 2 0.853 9 0.873 1 0.889 1 0.902 4 0.913 7 0.923 4 0.938 9 0.951 6 0.961 5 0.969 4 0.975 7 0.985 0 0.991 3 0.995 7 0.998 8 1.001 1
0.79
0.827 9 0.851 9 0.871 5 0.887 6 0.901 1 0.912 6 0.922 4 0.938 2 0.951 0 0.961 0 0.969 0 0.975 4 0.984 8 0.991 2 0.995 6 0.998 8 1.001 1
0.80
0.825 5 0.849 9 0.869 8 0.886 2 0.899 9 0.911 5
0.921 5 0.937 5 0.950 4 0.960 6 0.968 6 0.975 1 0.984 6 0.991 1 0.995 6 0.998 8 1.001 1
0.81
0.823 1 0.848 0 0.868 1 0.884 7 0.898 6 0.910 4 0.920 5 0.936 7 0.949 9 0.960 1 0.968 3 0.974 8 0.984 5 0.991 0 0.995 6 0.998 8 1.001 2
0.82
0.820 7 0.846 0 0.866 4 0.883 3 0.897 4 0.909 3 0.919 5 0.936 0 0.949 3 0.959 7 0.967 9 0.974 6 0.984 3 0.990 9 0.995 5 0.998 8 1.001 2
0.83
0.818 4 0.844 0 0.864 7 0.881 8 0.896 2 0.908 3 0.918 6 0.935 3 0.948 7 0.959 2 0.967 6 0.974 3 0.984 1 0.990 8 0.995 5 0.998 8 1.001 2
0.84
0.816 0 0.842 0 0.863 0 0.880 4 0.894 9 0.907 2 0.917 6 0.934 5 0.948 2 0.958 8 0.967 2 0.974 0 0.984 0 0.990 8 0.995 5 0.998 8 1.001 3
0.85
0.813 6 0.840 0 0.861 4 0.879 0 0.893 7 0.906 1 0.916 7 0.933 8 0.947 6 0.958 3 0.966 9 0.973 7 0.983 8 0.990 7 0.995 4 0.998 8 1.001 3
0.86
0.811 2 0.838 0 0.859 7 0.877 5 0.892 4 0.905 0 0.915 8 0.933 1 0.947 0 0.957 9 0.966 5 0.973 5 0.983 7 0.990 7 0.995 4 0.998 8 1.001 3
0.87
0.808 7 0.836 0 0.858 0 0.876 1 0.891 2 0.903 9 0.914 8 0.932 3 0.946 4 0.957 5 0.966 2 0.973 2 0.983 5 0.990 5 0.995 4 0.998 8 1.001 4
0.88
0.806 3 0.834 0 0.856 3 0.874 6 0.889 9 0.902 8 0.913 9 0.931 6 0.945 9 0.957 0 0.965 8 0.972 9 0.983 3 0.990 4 0.995 3 0.998 9 1.001 4
0.89
0.803 9 0.832 0 0.854 6 0.873 2 0.888 7 0.901 8 0.912 9 0.930 9 0.945 3 0.956 6 0.965 5 0.972 6 0.983 2 0.990 3 0.995 3 0.998 9 1.001 4
0.90
0.801 5 0.830 0 0.852 9 0.871 7 0.887 4 0.900 7 0.912 0 0.930 2 0.944 7 0.956 1 0.965 1 0.972 4 0.983 0 0.990 2 0.995 3 0.998 9 1.001 5
11
M
8
0
1
0
:
2
0
2
0
91
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
0.91
0.799 1 0.828 0 0.851 2 0.870 3 0.886 2 0.899 6
0.911 0 0.929 4 0.944 2 0.955 7 0.964 8 0.972 1 0.982 9 0.990 2 0.995 3 0.998 9 1.001 5
0.92
0.796 6 0.826 0 0.849 5 0.868 9 0.885 0 0.898 5 0.910 1 0.928 7 0.943 6 0.955 3 0.964 5 0.971 8 0.982 7 0.990 1 0.995 2 0.998 9 1.001 5
0.93
0.794 2 0.824 0 0.847 9 0.867 1 0.883 7 0.897 5 0.909 1 0.928 0 0.943 1 0.954 8 0.964 1 0.971 6 0.982 6 0.990 0 0.995 2 0.998 9 1.001 6
0.94
0.791 7 0.821 9 0.846 2 0.866 0 0.882 5 0.896 4 0.908 2 0.927 3 0.942 5 0.954 4 0.963 8 0.971 3 0.982 4 0.989 9 0.995 2 0.998 9 1.001 6
0.95
0.789 3 0.819 9 0.844 5 0.864 5 0.881 2 0.895 3 0.907 3 0.926 6 0.941 9 0.953 9 0.963 4 0.971 0 0.982 2 0.989 8 0.995 1 0.998 9 1.001 6
0.96
0.786 8 0.817 9 0.842 8 0.863 1 0.880 0 0.894 2 0.906 3 0.925 8 0.941 4 0.953 5 0.963 1 0.970 8 0.982 1 0.989 8 0.995 1 0.998 9 1.001 7
0.97
0.784 4 0.815 9 0.841 1 0.861 7 0.878 8 0.893 2 0.905 4 0.925 1 0.940 8 0.953 1 0.962 8 0.970 5 0.981 9 0.989 7 0.995 1 0.998 9 1.001 7
0.98
0.781 9 0.813 9 0.839 4 0.860 2 0.877 5 0.892 1 0.904 5 0.924 4 0.940 3 0.952 6 0.962 4 0.970 3 0.981 8 0.989 6 0.995 1 0.998 9 1.001 7
0.99
0.779 5 0.811 9 0.837 7 0.858 8 0.876 3 0.891 0 0.903 5 0.923 7 0.939 7 0.952 2 0.962 1 0.970 0 0.981 6 0.989 5 0.995 0 0.998 9 1.001 8
1.00
0.777 0 0.809 8 0.836 0 0.857 4 0.875 1 0.890 0 0.902 6 0.923 0 0.939 2 0.951 8 0.961 7 0.969 7 0.981 5 0.989 5 0.995 0 0.999 0 1.001 8
1.01
0.774 5 0.807 8 0.834 3 0.855 9 0.873 8 0.888 9 0.901 7 0.922 3 0.938 6 0.951 4 0.961 4 0.969 5 0.981 3 0.989 4 0.995 0 0.999 0 1.001 8
1.02
0.772 0 0.805 8 0.832 6 0.854 5 0.872 6 0.887 8 0.900 8 0.921 6 0.938 1 0.950 9 0.961 1 0.969 2 0.981 2 0.989 3 0.995 0 0.999 0 1.001 9
1.03
0.769 5 0.803 7 0.830 9 0.853 0 0.871 4 0.886 8 0.899 8 0.920 9 0.937 5 0.950 5 0.960 8 0.969 0 0.981 0 0.989 2 0.994 9 0.999 0 1.001 9
1.04
0.767 0 0.801 7 0.829 2 0.851 6 0.870 1 0.885 7 0.898 9 0.920 2 0.937 0 0.950 1 0.960 4 0.968 7 0.980 9 0.989 2 0.994 9 0.999 0 1.002 0
1.05
0.764 6 0.799 7 0.827 5 0.850 2 0.868 9 0.884 6 0.898 0 0.919 5 0.936 4 0.949 6 0.960 1 0.968 5 0.980 8 0.989 1 0.994 9 0.999 0 1.002 0
1.06
0.762 1 0.797 7 0.825 9 0.848 7 0.867 7 0.883 6 0.897 1 0.918 8 0.935 9 0.949 2 0.959 8 0.968 2 0.980 6 0.989 0 0.994 9 0.999 0 1.002 0
1.07
0.759 6 0.795 6 0.824 2 0.847 3 0.866 5 0.882 5 0.896 1 0.918 1 0.935 4 0.948 8 0.959 4 0.967 9 0.980 5 0.988 9 0.994 9 0.999 0 1.002 1
1.08
0.757 0 0.793 6 0.822 5 0.845 9 0.865 2 0.881 5 0.895 2 0.917 4 0.934 8 0.948 4 0.959 1 0.967 7 0.980 3 0.988 9 0.994 8 0.999 1 1.002 1
1.09
0.754 5 0.791 6 0.820 8 0.844 5 0.864 0 0.880 4 0.894 3 0.916 7 0.934 3 0.948 0 0.958 8 0.967 4 0.980 2 0.988 8 0.994 8 0.999 1 1.002 2
1.10
0.752 0 0.789 8 0.819 1 0.843 0 0.862 8 0.879 4 0.893 4 0.916 0 0.933 7 0.947 6 0.958 5 0.967 2 0.980 0 0.988 7 0.994 8 0.999 1 1.002 2
1.11
0.749 5 0.787 5 0.817 4 0.841 6 0.861 6 0.878 3 0.892 5 0.915 3 0.933 2 0.947 1 0.958 1 0.966 9 0.979 9 0.988 7 0.994 8 0.999 1 1.002 2
1.12
0.747 0 0.785 4 0.815 7 0.840 2 0.860 4 0.877 3 0.891 6 0.914 6 0.932 7 0.946 7 0.957 8 0.966 7 0.979 7 0.988 6 0.994 8 0.999 1 1.002 1
1.13
0.744 5 0.783 4 0.814 0 0.838 7 0.859 1 0.876 2 0.890 7 0.913 9 0.932 1 0.946 3 0.957 5 0.966 4 0.979 6 0.988 5 0.994 7 0.999 1 1.002 3
1.14
0.741 9 0.781 4 0.812 3 0.837 3 0.857 9 0.875 2 0.889 7 0.913 2 0.931 6 0.945 9 0.957 2 0.966 2 0.979 5 0.988 5 0.994 7 0.999 2 1.002 4
1.15
0.739 4 0.779 3 0.810 6 0.835 9 0.856 7 0.874 1 0.888 8 0.912 5 0.931 1 0.945 5 0.956 9 0.966 0 0.979 3 0.988 4 0.994 7 0.999 2 1.002 4
1.16
0.736 9 0.777 3 0.808 9 0.834 5 0.855 5 0.873 1 0.887 9 0.911 9 0.930 5 0.945 1 0.956 5 0.965 7 0.979 2 0.988 3 0.994 7 0.999 2 1.002 5
1.17
0.734 3 0.775 2 0.807 3 0.833 1 0.854 3 0.872 0 0.887 0 0.911 2 0.930 0 0.944 7 0.956 2 0.965 5 0.979 1 0.988 3 0.994 7 0.999 2 1.002 5
1.18
0.731 8 0.773 2 0.805 6 0.831 6 0.853 1 0.871 0 0.886 1 0.910 5 0.929 5 0.944 3 0.955 9 0.965 2 0.978 9 0.988 2 0.994 7 0.999 2 1.002 5
1.19
0.729 3 0.771 2 0.803 9 0.830 2 0.851 9 0.869 9 0.885 2 0.909 8 0.929 0 0.943 8 0.955 6 0.965 0 0.978 8 0.988 1 0.994 6 0.999 3 1.002 6
1.20
0.726 7 0.769 1 0.802 2 0.828 8 0.850 7 0.868 9 0.884 3 0.909 1 0.928 4 0.943 4 0.955 3 0.964 7 0.978 7 0.988 1 0.994 6 0.999 3 1.002 6
11
M
8
0
1
0
:
2
0
2
0
92
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
1.21
0.724 2 0.767 1 0.800 5 0.827 4 0.849 5 0.867 9 0.883 4 0.908 5 0.927 9 0.943 0 0.955 0 0.964 5 0.978 5 0.988 0 0.994 6 0.999 3 1.002 7
1.22
0.721 6 0.765 0 0.798 8 0.826 0 0.848 3 0.866 8 0.882 5 0.907 8 0.927 4 0.942 6 0.954 7 0.964 3 0.978 4 0.987 9 0.994 6 0.999 3 1.002 7
1.23
0.719 1 0.763 0 0.797 2 0.824 6 0.847 1 0.865 8 0.881 6 0.907 1 0.926 9 0.942 2 0.954 3 0.964 0 0.978 3 0.987 9 0.994 6 0.999 3 1.002 8
1.24
0.716 5 0.761 0 0.795 5 0.823 2 0.845 9 0.864 8 0.880 8 0.906 4 0.926 4 0.941 8 0.954 0 0.963 8 0.978 1 0.987 8 0.994 6 0.999 4 1.002 8
1.25
0.714 0 0.758 9 0.793 8 0.821 8 0.844 7 0.863 8 0.879 9 0.905 8 0.925 9 0.941 4 0.953 7 0.963 6 0.978 0 0.987 8 0.994 6 0.999 4 1.002 9
1.26
0.711 4 0.756 9 0.792 1 0.820 4 0.843 5 0.862 7 0.879 0 0.905 1 0.925 3 0.941 0 0.953 4 0.963 3 0.977 9 0.987 7 0.994 5 0.999 4 1.002 9
1.27
0.708 9 0.754 8 0.790 5 0.819 0 0.842 3 0.861 7 0.878 1 0.904 4 0.924 8 0.940 6 0.953 1 0.963 1 0.977 7 0.987 6 0.994 5 0.999 4 1.003 0
1.28
0.706 3 0.752 8 0.788 8 0.817 5 0.841 1 0.860 7 0.877 2 0.903 8 0.924 3 0.940 3 0.952 8 0.962 9 0.977 6 0.987 6 0.994 5 0.999 5 1.003 0
1.29
0.703 8 0.750 8 0.787 1 0.816 2 0.839 9 0.859 7 0.876 3 0.903 1 0.923 8 0.939 9 0.952 5 0.962 6 0.977 5 0.987 5 0.994 5 0.999 5 1.003 1
1.30
0.701 2 0.748 7 0.785 4 0.814 8 0.838 7 0.858 7 0.875 5 0.902 5 0.923 3 0.939 5 0.952 2 0.962 4 0.977 3 0.987 5 0.994 5 0.999 5 1.003 1
1.31
0.698 7 0.746 7 0.783 8 0.813 4 0.837 5 0.857 6 0.874 6 0.901 8 0.922 8 0.939 1 0.951 9 0.962 2 0.977 2 0.987 4 0.994 5 0.999 5 1.003 2
1.32
0.696 1 0.744 7 0.782 1 0.812 0 0.836 4 0.856 6 0.873 7 0.901 1 0.922 3 0.938 7 0.951 6 0.961 9 0.977 1 0.987 4 0.994 5 0.999 6 1.003 2
1.33
0.693 6 0.742 6 0.780 4 0.810 6 0.835 2 0.855 6 0.872 8 0.900 5 0.921 8 0.938 3 0.951 3 0.961 7 0.977 0 0.987 3 0.994 5 0.999 6 1.003 3
1.34
0.691 0 0.740 6 0.778 8 0.809 2 0.834 0 0.854 6 0.872 0 0.899 8 0.921 3 0.937 9 0.951 0 0.961 5 0.976 8 0.987 2 0.994 5 0.999 6 1.003 3
1.35
0.688 5 0.738 6 0.777 1 0.807 8 0.832 8 0.853 6 0.871 1 0.899 2 0.920 8 0.937 5 0.950 7 0.961 3 0.976 7 0.987 2 0.994 5 0.999 6 1.003 4
1.36
0.685 9 0.736 6 0.775 5 0.806 4 0.831 7 0.852 6 0.870 2 0.898 5 0.920 3 0.937 1 0.950 4 0.961 0 0.976 6 0.987 1 0.994 5 0.999 7 1.003 4
1.37
0.683 4 0.734 6 0.773 8 0.805 0 0.830 5 0.851 6 0.869 4 0.897 9 0.919 8 0.936 8 0.950 1 0.960 8 0.976 5 0.987 1 0.994 5 0.999 7 1.003 5
1.38
0.680 8 0.732 5 0.772 2 0.803 7 0.829 3 0.850 6 0.868 5 0.897 2 0.919 3 0.936 4 0.949 8 0.960 6 0.976 4 0.987 0 0.994 5 0.999 7 1.003 5
1.39
0.678 3 0.730 5 0.770 5 0.802 3 0.828 2 0.849 6 0.867 7 0.896 6 0.918 8 0.936 0 0.949 5 0.960 4 0.976 2 0.987 0 0.994 4 0.999 8 1.003 6
1.40
0.675 8 0.728 5 0.768 9 0.800 9 0.827 0 0.848 6 0.866 8 0.896 0 0.918 3 0.935 6 0.949 3 0.960 1 0.976 1 0.986 9 0.994 4 0.999 8 1.003 6
1.41
0.673 2 0.726 5 0.767 2 0.799 5 0.825 8 0.847 6 0.865 9 0.895 3 0.917 8 0.935 2 0.949 0 0.959 9 0.976 0 0.986 9 0.994 4 0.999 8 1.003 7
1.42
0.670 7 0.724 5 0.765 6 0.798 2 0.824 7 0.846 6 0.865 1 0.894 7 0.917 3 0.934 9 0.948 7 0.959 7 0.975 9 0.986 8 0.994 4 0.999 8 1.003 7
1.43
0.668 2 0.722 5 0.764 0 0.796 8 0.823 5 0.845 7 0.864 2 0.894 0 0.916 8 0.934 5 0.948 4 0.959 5 0.975 8 0.986 8 0.994 4 0.999 9 1.003 8
1.44
0.665 7 0.720 5 0.762 3 0.795 5 0.822 4 0.844 7 0.863 4 0.893 4 0.916 4 0.934 1 0.948 1 0.959 3 0.975 7 0.986 7 0.994 4 0.999 9 1.003 8
1.45
0.663 2 0.718 5 0.760 7 0.794 1 0.821 2 0.843 7 0.862 6 0.892 8 0.915 9 0.933 8 0.947 8 0.959 1 0.975 5 0.986 7 0.994 4 0.999 9 1.003 9
1.46
0.660 7 0.716 5 0.759 1 0.792 7 0.820 1 0.842 7 0.861 7 0.892 2 0.915 4 0.933 4 0.947 5 0.958 8 0.975 4 0.986 6 0.994 4 1.000 0 1.004 0
1.47
0.658 2 0.714 6 0.757 5 0.791 4 0.818 9 0.841 7 0.860 9 0.891 8 0.914 9 0.933 0 0.947 3 0.958 6 0.975 3 0.986 6 0.994 4 1.000 0 1.004 0
1.48
0.655 7 0.712 6 0.755 8 0.790 1 0.817 8 0.840 8 0.860 0 0.890 9 0.914 4 0.932 6 0.947 0 0.958 4 0.975 2 0.986 6 0.994 4 1.000 0 1.004 1
1.49
0.653 2 0.710 6 0.754 2 0.788 7 0.816 7 0.839 8 0.859 2 0.890 3 0.914 0 0.932 3 0.946 7 0.958 2 0.975 1 0.986 5 0.994 4 1.000 1 1.004 1
1.50
0.650 7 0.708 6 0.752 6 0.787 4 0.815 5 0.838 8 0.858 4 0.889 7 0.913 5 0.931 9 0.946 4 0.958 0 0.975 0 0.986 5 0.994 4 1.000 1 1.004 2
11
M
8
0
1
0
:
2
0
2
0
93
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
1.51
0.648 3 0.706 7 0.751 0 0.786 0 0.814 4 0.837 9 0.857 5 0.889 0 0.913 0 0.931 6 0.946 1 0.957 8 0.974 9 0.986 4 0.994 4 1.000 1 1.004 2
1.52
0.645 8 0.704 7 0.749 4 0.784 7 0.813 3 0.836 9 0.856 7 0.888 4 0.912 5 0.931 2 0.945 9 0.957 6 0.974 8 0.986 4 0.994 4 1.000 2 1.004 3
1.53
0.643 4 0.702 8 0.747 8 0.783 4 0.812 2 0.835 9 0.855 9 0.887 8 0.912 1 0.930 8 0.945 6 0.957 4 0.974 7 0.986 3 0.994 4 1.000 2 1.004 4
1.54
0.640 9 0.700 8 0.746 2 0.782 0 0.811 0 0.835 0 0.855 1 0.887 2 0.911 6 0.930 5 0.945 3 0.957 2 0.974 5 0.986 3 0.994 5 1.000 2 1.004 4
1.55
0.638 5 0.698 9 0.744 7 0.780 7 0.809 9 0.834 0 0.854 3 0.886 6 0.911 1 0.930 1 0.945 0 0.957 0 0.974 4 0.986 3 0.994 5 1.000 3 1.004 5
1.56
0.636 1 0.697 0 0.743 1 0.779 4 0.808 8 0.833 1 0.853 4 0.886 0 0.910 7 0.929 8 0.944 8 0.956 8 0.974 3 0.986 2 0.994 5 1.000 3 1.004 5
1.57
0.633 7 0.695 0 0.741 5 0.778 1 0.807 7 0.832 1 0.852 6 0.885 4 0.910 2 0.929 4 0.944 5 0.956 6 0.974 2 0.986 2 0.994 5 1.000 4 1.004 6
1.58
0.631 1 0.693 1 0.739 9 0.776 8 0.806 6 0.831 2 0.851 8 0.884 8 0.909 7 0.929 1 0.944 2 0.956 4 0.974 1 0.986 1 0.994 5 1.000 4 1.004 7
1.59
0.628 9 0.691 2 0.738 4 0.775 5 0.805 5 0.830 3 0.851 0 0.884 2 0.909 3 0.928 7 0.944 0 0.956 2 0.974 0 0.986 1 0.994 5 1.000 4 1.004 7
1.60
0.626 6 0.689 3 0.736 8 0.774 2 0.804 4 0.829 3 0.850 2 0.883 6 0.908 8 0.928 4 0.943 7 0.956 0 0.973 9 0.986 1 0.994 5 1.000 5 1.004 8
1.61
0.624 2 0.687 4 0.735 3 0.772 9 0.803 3 0.828 4 0.849 4 0.883 0 0.908 4 0.928 0 0.943 4 0.955 8 0.973 8 0.986 0 0.994 5 1.000 5 1.004 8
1.62
0.621 9 0.685 6 0.733 7 0.771 6 0.802 2 0.827 5 0.848 6 0.882 4 0.907 9 0.927 7 0.943 2 0.955 6 0.973 7 0.986 0 0.994 5 1.000 5 1.004 9
1.63
0.619 6 0.683 7 0.732 2 0.770 3 0.801 1 0.826 5 0.847 8 0.881 8 0.907 5 0.927 3 0.942 9 0.955 4 0.973 6 0.985 9 0.994 5 1.000 6 1.005 0
1.64
0.617 3 0.681 8 0.730 6 0.769 0 0.800 0 0.825 6 0.847 0 0.881 2 0.907 0 0.927 0 0.942 7 0.955 2 0.973 5 0.985 9 0.994 5 1.000 6 1.005 0
1.65
0.615 0 0.680 0 0.729 1 0.767 8 0.799 0 0.824 7 0.846 2 0.880 6 0.906 6 0.926 6 0.942 4 0.955 0 0.973 4 0.985 9 0.994 5 1.000 7 1.005 1
1.66
0.612 8 0.678 1 0.727 6 0.766 5 0.797 9 0.823 8 0.845 4 0.880 0 0.906 1 0.926 3 0.942 1 0.954 8 0.973 3 0.985 8 0.994 5 1.000 7 1.005 1
1.67
0.610 5 0.676 3 0.726 1 0.765 2 0.796 8 0.822 9 0.844 7 0.879 4 0.905 7 0.925 9 0.941 9 0.954 6 0.973 2 0.985 8 0.994 6 1.000 8 1.005 2
1.68
0.608 3 0.674 5 0.724 6 0.764 0 0.795 8 0.822 0 0.843 9 0.878 8 0.905 2 0.925 6 0.941 6 0.954 4 0.973 1 0.985 8 0.994 6 1.000 8 1.005 3
1.69
0.606 1 0.672 6 0.723 1 0.762 7 0.794 7 0.821 1 0.843 1 0.878 3 0.904 8 0.925 3 0.941 4 0.954 2 0.973 0 0.985 8 0.994 6 1.000 8 1.005 3
1.70
0.603 9 0.670 8 0.721 6 0.761 5 0.793 6 0.820 1 0.842 3 0.877 7 0.904 3 0.924 9 0.941 1 0.954 0 0.972 9 0.985 7 0.994 6 1.000 9 1.005 4
1.71
0.601 8 0.669 1 0.720 1 0.760 2 0.792 6 0.819 3 0.841 5 0.877 1 0.903 9 0.924 6 0.940 9 0.953 8 0.972 9 0.985 7 0.994 6 1.000 9 1.005 5
1.72
0.599 6 0.667 3 0.718 6 0.759 0 0.791 5 0.818 4 0.840 8 0.876 5 0.903 5 0.924 3 0.940 6 0.953 7 0.972 8 0.985 7 0.994 6 1.001 0 1.005 5
1.73
0.597 5 0.665 5 0.717 1 0.757 7 0.790 5 0.817 5 0.840 0 0.876 0 0.903 0 0.923 9 0.940 4 0.953 5 0.972 7 0.985 6 0.994 6 1.001 0 1.005 6
1.74
0.595 4 0.663 7 0.715 7 0.756 5 0.789 5 0.816 6 0.839 3 0.875 4 0.902 6 0.923 6 0.940 1 0.953 3 0.972 6 0.985 6 0.994 6 1.001 1 1.005 7
1.75
0.593 3 0.662 0 0.714 2 0.755 3 0.788 4 0.815 7 0.838 5 0.874 8 0.902 2 0.923 3 0.939 9 0.953 1 0.972 5 0.985 6 0.994 7 1.001 1 1.005 7
1.76
0.591 3 0.660 3 0.712 8 0.754 1 0.787 4 0.814 8 0.837 7 0.874 3 0.901 7 0.923 0 0.939 6 0.952 9 0.972 4 0.985 5 0.994 7 1.001 1 1.005 8
1.77
0.589 3 0.658 5 0.711 3
0.752 9 0.786 4 0.813 9 0.837 0 0.873 7 0.901 3 0.922 6 0.939 4 0.952 7 0.972 3 0.985 5 0.994 7 1.001 2 1.005 9
1.78
0.587 3 0.656 8 0.709 9 0.751 7 0.785 3 0.813 1 0.836 2 0.873 1 0.900 9 0.922 3 0.939 1 0.952 6 0.972 2 0.985 5 0.994 7 1.001 2 1.005 9
1.79
0.585 3 0.655 2 0.708 5 0.750 5 0.784 3 0.812 2 0.835 5 0.872 6 0.900 5 0.922 0 0.938 9 0.952 4 0.972 1 0.985 5 0.994 7 1.001 3 1.006 0
1.80
0.583 3 0.653 5 0.707 1 0.749 3 0.783 3 0.811 3
0.834 8 0.872 0 0.900 0 0.921 7 0.938 7 0.952 2 0.972 1 0.985 4 0.994 7 1.001 3 1.006 1
11
M
8
0
1
0
:
2
0
2
0
94
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
1.81
0.581 4 0.651 8 0.705 7 0.748 1 0.782 3 0.810 5 0.834 0 0.871 5 0.899 6 0.921 4 0.938 4 0.952 0 0.972 0 0.985 4 0.994 8 1.001 4 1.006 2
1.82
0.579 5 0.650 2 0.704 3 0.746 9 0.781 3 0.809 6 0.833 3 0.870 9 0.899 2 0.921 0 0.938 2 0.951 9 0.971 9 0.985 4 0.994 8 1.001 4 1.006 2
1.83
0.577 7 0.648 5 0.702 9 0.745 7 0.780 3 0.808 8 0.832 5 0.870 4 0.898 8 0.920 7 0.937 9 0.951 7 0.971 8 0.985 4 0.994 8 1.001 5 1.006 3
1.84
0.575 8 0.646 9 0.701 5 0.744 6 0.779 3 0.807 9 0.831 8 0.869 8 0.898 4 0.920 4 0.937 7 0.951 5 0.971 7 0.985 4 0.994 8 1.001 5 1.006 4
1.85
0.574 0 0.645 3 0.700 1 0.743 4 0.778 3 0.807 1 0.831 1 0.869 3 0.898 0 0.920 1 0.937 5 0.951 3 0.971 6 0.985 3 0.994 8 1.001 6 1.006 4
1.86
0.572 2 0.643 7 0.698 8 0.742 2 0.777 3 0.806 2 0.830 4 0.868 7 0.897 6 0.919 8 0.937 2 0.951 2 0.971 6 0.985 3 0.994 9 1.001 6 1.006 5
1.87
0.570 5 0.642 1 0.697 4 0.741 1 0.776 4 0.805 4 0.829 7 0.868 2 0.897 1 0.919 5 0.937 0 0.951 0 0.971 5 0.985 3 0.994 9 1.001 7 1.006 6
1.88
0.568 7 0.640 6 0.696 1 0.740 0 0.775 4 0.804 6 0.828 9 0.867 7 0.896 7 0.919 2 0.936 8 0.950 8 0.971 4 0.985 3 0.994 9 1.001 7 1.006 6
1.89
0.567 0 0.639 0 0.694 8 0.738 8 0.774 4 0.803 7 0.828 2 0.867 1 0.896 3 0.918 9 0.936 6 0.950 7 0.971 3 0.985 3 0.994 9 1.001 8 1.006 7
1.90
0.565 4 0.637 5 0.693 4 0.737 7 0.773 5 0.802 9 0.827 5 0.866 6 0.895 9 0.918 6 0.936 3 0.950 5 0.971 2 0.985 2 0.995 0 1.001 8 1.006 8
1.91
0.563 7 0.636 0 0.692 1 0.736 6 0.772 5 0.802 1 0.826 8 0.866 1 0.895 5 0.918 3 0.936 1 0.950 3 0.971 2 0.985 2 0.995 0 1.001 9 1.006 9
1.92
0.562 1 0.634 5 0.690 8 0.735 5 0.771 6 0.801 3 0.826 1 0.865 6 0.895 1 0.918 0 0.935 9 0.950 2 0.971 1 0.985 2 0.995 0 1.002 0 1.006 9
1.93
0.560 6 0.633 0 0.689 5 0.734 4 0.770 6 0.800 5 0.825 4 0.865 0 0.894 7 0.917 7 0.935 7 0.950 0 0.971 0 0.985 2 0.995 0 1.002 0 1.007 0
1.94
0.559 0 0.631 6 0.688 3 0.733 3 0.769 7 0.799 7 0.824 7 0.864 5 0.894 3 0.917 4 0.935 4 0.949 8 0.970 9 0.985 2 0.995 1 1.002 1 1.007 1
1.95
0.557 5 0.630 1 0.687 0 0.732 2 0.768 8 0.798 9 0.824 0 0.864 0 0.894 0 0.917 1 0.935 2 0.949 7 0.970 9 0.985 2 0.995 1 1.002 1 1.007 2
1.96
0.556 0 0.628 7 0.685 8 0.731 1 0.767 8 0.798 1 0.823 4 0.863 5 0.893 6 0.916 8 0.935 0 0.949 5 0.970 8 0.985 2 0.995 1 1.002 2 1.007 2
1.97
0.554 5 0.627 3 0.684 5 0.730 0 0.766 9 0.797 3 0.822 7 0.863 0 0.893 2 0.916 5 0.934 8 0.949 4 0.970 7 0.985 1 0.995 1 1.002 2 1.007 3
1.98
0.553 1 0.625 9 0.683 3 0.729 0 0.766 0 0.796 5 0.822 0 0.862 5 0.892 8 0.916 2 0.934 6 0.949 2 0.970 7 0.985 1 0.995 2 1.002 3 1.007 4
1.99
0.551 7 0.624 5 0.682 1 0.727 9 0.765 1 0.795 7 0.821 3 0.861 9 0.892 4 0.915 9 0.934 3 0.949 1 0.970 6 0.985 1 0.995 2 1.002 3 1.007 5
2.00
0.550 3 0.623 2 0.680 8 0.726 9 0.764 2 0.794 9 0.820 7 0.861 4 0.892 0 0.915 6 0.934 1 0.948 9 0.970 5 0.985 1 0.995 2 1.002 4 1.007 5
2.01
0.549 0 0.621 8 0.679 6 0.725 8 0.763 3 0.794 2 0.820 0 0.860 9 0.891 6 0.915 3 0.933 9 0.948 7 0.970 5 0.985 1 0.995 3 1.002 5 1.007 6
2.02
0.547 7 0.620 5 0.678 5 0.724 8 0.762 4 0.793 4 0.819 3 0.860 4 0.891 3 0.915 0 0.933 7 0.948 6 0.970 4 0.985 1 0.995 3 1.002 5 1.007 7
2.03
0.546 4 0.619 2 0.677 3 0.723 8 0.761 5 0.792 6 0.818 7 0.859 9 0.890 9 0.914 8 0.933 5 0.948 4 0.970 3 0.985 1 0.995 3 1.002 6 1.007 8
2.04
0.545 2 0.617 9 0.676 1 0.722 7 0.760 6 0.791 9 0.818 0 0.859 5 0.890 5 0.914 5 0.933 3 0.948 3 0.970 3 0.985 1 0.995 4 1.002 6 1.007 9
2.05
0.544 0 0.616 7 0.675 0 0.721 7 0.759 8 0.791 1 0.817 4 0.859 0 0.890 1 0.914 2 0.933 1 0.948 1 0.970 2 0.985 1 0.995 4 1.002 7 1.007 9
2.06
0.542 8 0.615 4 0.673 8 0.720 7 0.758 9 0.790 4 0.816 7 0.858 5 0.889 8 0.913 9 0.932 9 0.948 0 0.970 1 0.985 1 0.995 4 1.002 8 1.008 0
2.07
0.541 6 0.614 2 0.672 7 0.719 8 0.758 0 0.789 6 0.816 1 0.858 0 0.889 4 0.913 6 0.932 7 0.947 9 0.970 1 0.985 1 0.995 5 1.002 8 1.008 1
2.08
0.540 5 0.613 0 0.671 6 0.718 8 0.757 2 0.788 9 0.815 5 0.857 5 0.889 0 0.913 4 0.932 5 0.947 7 0.970 0 0.985 1 0.995 5 1.002 9 1.008 2
2.09
0.539 4 0.611 8 0.670 5 0.717 8 0.756 3 0.788 2 0.814 8 0.857 0 0.888 7 0.913 1 0.932 3 0.947 6 0.969 9 0.985 0 0.995 5 1.002 9 1.008 3
2.10
0.538 3 0.610 7 0.669 4 0.716 8 0.755 5 0.787 5 0.814 2 0.856 5 0.888 3 0.912 8 0.932 1 0.947 4 0.969 9 0.985 0 0.995 6 1.003 0 1.008 3
11
M
8
0
1
0
:
2
0
2
0
95
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
2.11
0.537 3 0.609 5 0.668 3 0.715 9 0.754 7 0.786 7 0.813 6 0.856 1 0.888 0 0.912 6 0.931 9 0.947 3 0.969 8 0.985 0 0.995 6 1.003 1 1.008 4
2.12
0.536 3 0.608 4 0.667 3 0.714 9 0.753 8 0.786 0 0.813 0 0.855 6 0.887 6 0.912 3 0.931 7 0.947 1 0.969 8 0.985 0 0.995 6 1.003 1 1.008 5
2.13
0.535 3 0.607 3 0.666 2 0.714 0 0.753 0 0.785 3 0.812 3 0.855 1 0.887 2 0.912 0 0.931 5 0.947 0 0.969 7 0.985 0 0.995 7 1.003 2 1.008 6
2.14
0.534 4 0.606 2 0.665 2 0.713 1 0.752 2 0.784 6
0.811 7 0.854 7 0.886 9 0.911 8
0.931 3 0.946 9 0.969 7 0.985 0 0.995 7 1.003 2 1.008 7
2.15
0.533 4 0.605 1 0.664 2 0.712 1 0.751 4 0.783 9
0.811 1 0.854 2 0.886 5 0.911 5
0.931 1 0.946 7 0.969 6 0.985 0 0.995 7 1.003 3 1.008 7
2.16
0.532 5 0.604 1 0.663 2
0.711 2 0.750 6 0.783 2 0.810 5 0.853 7 0.886 2 0.911 2
0.930 9 0.946 6 0.969 6 0.985 0 0.995 8 1.003 4 1.008 8
2.17
0.531 7 0.603 1 0.662 2 0.710 3 0.749 8 0.782 5 0.809 9 0.853 3 0.885 8 0.911 0
0.930 7 0.946 5 0.969 5 0.985 0 0.995 8 1.003 4 1.008 9
2.18
0.530 8 0.602 0 0.661 2 0.709 4 0.749 0 0.781 8 0.809 3 0.852 8 0.885 5 0.910 7 0.930 5 0.946 3 0.969 4 0.985 0 0.995 9 1.003 5 1.009 0
2.19
0.530 0 0.601 1 0.660 2 0.708 5 0.748 2 0.781 1 0.808 7 0.852 4 0.885 2 0.910 5 0.930 3 0.946 2 0.969 4 0.985 0 0.995 9 1.003 6 1.009 1
2.20
0.529 2 0.600 1 0.659 2 0.707 7 0.747 5 0.780 5 0.808 1 0.851 9 0.884 8 0.910 2 0.930 2 0.946 1 0.969 3 0.985 0 0.995 9 1.003 6 1.009 2
2.21
0.528 5 0.599 1 0.658 3 0.706 8 0.746 7 0.779 8 0.807 6 0.851 5 0.884 5 0.910 0 0.930 0 0.945 9 0.969 3 0.985 1 0.996 0 1.003 7 1.009 3
2.22
0.527 7 0.598 2 0.657 4 0.706 0 0.745 9 0.779 1 0.807 0 0.851 0 0.884 1 0.909 7 0.929 8 0.945 8 0.969 2 0.985 1 0.996 0 1.003 8 1.009 3
2.23
0.527 0 0.597 3 0.656 4 0.705 1 0.745 2 0.778 5 0.806 4 0.850 6 0.883 8 0.909 5 0.929 6 0.945 7 0.969 2 0.985 1 0.996 1 1.003 8 1.009 4
2.24
0.526 4 0.596 4 0.655 5 0.704 3 0.744 4 0.777 9 0.805 8 0.850 1 0.883 5 0.909 2 0.929 4 0.945 5 0.969 1 0.985 1 0.996 1 1.003 9 1.009 5
2.25
0.525 7 0.595 5 0.654 6 0.703 4 0.743 7 0.777 2 0.805 3 0.849 7 0.883 1 0.909 0 0.929 2 0.945 4 0.969 1 0.985 1 0.996 1 1.004 0 1.009 6
2.26
0.525 1 0.594 7 0.653 8 0.702 6 0.743 0 0.776 5 0.804 7 0.849 3 0.882 8 0.908 7 0.929 1 0.945 3 0.969 1 0.985 1 0.996 2 1.004 0 1.009 7
2.27
0.524 5 0.593 8 0.652 9 0.701 8 0.742 2 0.775 9 0.804 2 0.848 8 0.882 5 0.908 5 0.928 9 0.945 2 0.969 0 0.985 1 0.996 2 1.004 1 1.009 8
2.28
0.523 9 0.593 0 0.652 1 0.701 0 0.741 5 0.775 3 0.803 6 0.848 4 0.882 2 0.908 2 0.928 7 0.945 1 0.969 0 0.985 1 0.996 3 1.004 2 1.009 9
2.29
0.523 4 0.592 2 0.651 2 0.700 2 0.740 8 0.774 6 0.803 1 0.848 0 0.881 9 0.908 0 0.928 5 0.944 9 0.968 9 0.985 1 0.996 3 1.004 3 1.010 0
2.30
0.522 8 0.591 4 0.650 4 0.699 5 0.740 1 0.774 0 0.802 5 0.847 6 0.881 5 0.907 8 0.928 4 0.944 8 0.968 9 0.985 1 0.996 4 1.004 3 1.010 0
2.31
0.522 3 0.590 7 0.649 6 0.698 7 0.739 4 0.773 4 0.802 0 0.847 1 0.881 2 0.907 5 0.928 2 0.944 7 0.968 8 0.985 1 0.996 4 1.004 4 1.010 1
2.32
0.521 8 0.589 9 0.648 8 0.697 9 0.738 7 0.772 8 0.801 5 0.846 7 0.880 9 0.907 3 0.928 0 0.944 6 0.968 8 0.985 1 0.996 5 1.004 5 1.010 2
2.33
0.521 4 0.589 2 0.648 0 0.697 2 0.738 1 0.772 2 0.800 9 0.846 3 0.880 6 0.907 1 0.927 9 0.944 5 0.968 8 0.985 2 0.996 5 1.004 5 1.010 3
2.34
0.520 9 0.588 5 0.647 2 0.696 4 0.737 4 0.771 6 0.800 4 0.845 9 0.880 3 0.906 8 0.927 7 0.944 4 0.968 7 0.985 2 0.996 6 1.004 6 1.010 4
2.35
0.520 5 0.587 8 0.646 5 0.695 7 0.736 7 0.771 0 0.799 9 0.845 5 0.880 0 0.906 6 0.927 5 0.944 2 0.968 7 0.985 2 0.996 6 1.004 7 1.010 5
2.36
0.520 1 0.587 2 0.645 7 0.695 0 0.736 1 0.770 4 0.799 4 0.845 1 0.879 7 0.906 4 0.927 4 0.944 1 0.968 7 0.985 2 0.996 7 1.004 8 1.010 6
2.37
0.519 8 0.586 5 0.645 0 0.694 3 0.735 4 0.769 8 0.798 9 0.844 7 0.879 4 0.906 2 0.927 2 0.944 0 0.968 6 0.985 2 0.996 7 1.004 8 1.010 7
2.38
0.519 4 0.585 9 0.644 3 0.693 6 0.734 8 0.769 3 0.798 4 0.844 3 0.879 1 0.905 9 0.927 1 0.943 9 0.968 6 0.985 2 0.996 8 1.004 9 1.010 8
2.39
0.519 1 0.585 3 0.643 6 0.692 9 0.734 1 0.768 7 0.797 9 0.843 9 0.878 8 0.905 7 0.926 9 0.943 8 0.968 6 0.985 2 0.996 8 1.005 0 1.010 9
2.40
0.518 8 0.584 7 0.642 9 0.692 2 0.733 5 0.768 1 0.797 4 0.843 5 0.878 5 0.905 5 0.926 7 0.943 7 0.968 5 0.985 3 0.996 9 1.005 1 1.011 0
11
M
8
0
1
0
:
2
0
2
0
96
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
2.41
0.518 5 0.584 1 0.642 2 0.691 5 0.732 9 0.767 6 0.796 9 0.843 1 0.878 2 0.905 3 0.926 6 0.943 6 0.968 5 0.985 3 0.996 9 1.005 1 1.011 0
2.42
0.518 3 0.583 5 0.641 6 0.690 9 0.732 3 0.767 0 0.796 4 0.842 7 0.877 9 0.905 1 0.926 4 0.943 5 0.968 5 0.985 3 0.997 0 1.005 2 1.011 1
2.43
0.518 0 0.583 0 0.640 9 0.690 2 0.731 7 0.766 5 0.795 9 0.842 4 0.877 6 0.904 9 0.926 3 0.943 4 0.968 4 0.985 3 0.997 0 1.005 3 1.011 2
2.44
0.517 8 0.582 5 0.640 3 0.689 6 0.731 1 0.765 9 0.795 4 0.842 0 0.877 3 0.904 6 0.926 1 0.943 3 0.968 4 0.985 3 0.997 1 1.005 4 1.011 3
2.45
0.517 6 0.582 0 0.639 7 0.689 0 0.730 5 0.765 4 0.795 0 0.841 6 0.877 0 0.904 4 0.926 0 0.943 2 0.968 4 0.985 4 0.997 1 1.005 5 1.011 4
2.46
0.517 4 0.581 5 0.639 0 0.688 3 0.729 9 0.764 9 0.794 5 0.841 2 0.876 7 0.904 2 0.925 8 0.943 1 0.968 3 0.985 4 0.997 2 1.005 9 1.011 5
2.47
0.517 2 0.581 0 0.638 4 0.687 7 0.729 3 0.764 4 0.794 0 0.840 8 0.876 5 0.904 0 0.925 7 0.943 0 0.968 3 0.985 4 0.997 2 1.005 6 1.011 6
2.48
0.517 1 0.580 5 0.637 9 0.687 1 0.728 7 0.763 8 0.793 6 0.840 5 0.876 2 0.903 8 0.925 5 0.942 9 0.968 3 0.985 4 0.997 3 1.005 7 1.011 7
2.49
0.517 0 0.580 1 0.637 3 0.686 5 0.728 2 0.763 3 0.793 1 0.840 1 0.875 9 0.903 6 0.925 4 0.942 8 0.968 3 0.985 4 0.997 4 1.005 8 1.011 8
2.50
0.516 9 0.579 7 0.636 7 0.685 9 0.727 6 0.762 8 0.792 7 0.839 8 0.875 6 0.903 4 0.925 3 0.942 7 0.968 2 0.985 5 0.997 4 1.005 9 1.011 9
2.51
0.516 8 0.579 3 0.636 2 0.685 4 0.727 1 0.762 3 0.792 2 0.839 4 0.875 4 0.903 2 0.925 1 0.942 6 0.968 2 0.985 5 0.997 5 1.005 9 1.012 0
2.52
0.516 7 0.578 9 0.635 7 0.684 8 0.726 5 0.761 8 0.791 8 0.839 0 0.875 1 0.903 0 0.925 0 0.942 5 0.968 2 0.985 5 0.997 5 1.006 0 1.012 1
2.53
0.516 7 0.578 5 0.635 1 0.684 3 0.726 0 0.761 4 0.791 4 0.838 7 0.874 8 0.902 8 0.924 8 0.942 4 0.968 2 0.985 6 0.997 6 1.006 1 1.012 2
2.54
0.516 6 0.578 1 0.634 6 0.683 8 0.725 5 0.760 9 0.790 9 0.838 3 0.874 6 0.902 6 0.924 7 0.942 3 0.968 2 0.985 6 0.997 7 1.006 2 1.012 3
2.55
0.516 6 0.577 8 0.634 2 0.683 2 0.725 0 0.760 4 0.790 5 0.838 0 0.874 3 0.902 4 0.924 6 0.942 2 0.968 1 0.985 6 0.997 7 1.006 3 1.012 4
2.56
0.516 6 0.577 5 0.633 7 0.682 7 0.724 5 0.759 9 0.790 1 0.837 6 0.874 1 0.902 2 0.924 4 0.942 2 0.968 1 0.985 6 0.997 8 1.006 3 1.012 5
2.57
0.516 6 0.577 2 0.633 2 0.682 2 0.724 0 0.759 5 0.789 7 0.837 3 0.873 8 0.902 1 0.924 3 0.942 1 0.968 1 0.985 7 0.997 8 1.006 4 1.012 6
2.58
0.516 6 0.576 9 0.632 8 0.681 7 0.723 5 0.759 0 0.789 3 0.837 0 0.873 5 0.901 9 0.924 2 0.942 0 0.968 1 0.985 7 0.997 9 1.006 5 1.012 7
2.59
0.516 7 0.576 6 0.632 3 0.681 2 0.723 0 0.758 6 0.788 9 0.836 6 0.873 3 0.901 7 0.924 0 0.941 9 0.968 1 0.985 7 0.998 0 1.006 6 1.012 8
2.60
0.516 7 0.576 3 0.631 9 0.680 7 0.722 5 0.758 1 0.788 5 0.836 3 0.873 0 0.901 5 0.923 9 0.941 8 0.968 1 0.985 8 0.998 0 1.006 7 1.012 9
2.61
0.516 8 0.576 1 0.631 5 0.680 2 0.722 0 0.757 7 0.788 1 0.836 0 0.872 8 0.901 3 0.923 8 0.941 7 0.968 0 0.985 8 0.998 1 1.006 8 1.013 0
2.62
0.516 9 0.575 8 0.631 1 0.679 7 0.721 6 0.757 3 0.787 7 0.835 7 0.872 5 0.901 1 0.923 7 0.941 7 0.968 0 0.985 8 0.998 1 1.006 9 1.013 1
2.63
0.517 0 0.575 6 0.630 7 0.679 3 0.721 1 0.756 8 0.787 3 0.835 3 0.872 3 0.901 0 0.923 5 0.941 6 0.968 0 0.985 9 0.998 2 1.006 9 1.013 2
2.64
0.517 1 0.575 4 0.630 3 0.678 9 0.720 7 0.756 4 0.786 9 0.835 0 0.872 1 0.900 8 0.923 4 0.941 5 0.968 0 0.985 9 0.998 3 1.007 0 1.013 3
2.65
0.517 3 0.575 2 0.629 9 0.678 4 0.720 2 0.756 0 0.786 5 0.834 7 0.871 8 0.900 6 0.923 3 0.941 4 0.968 0 0.985 9 0.998 3 1.007 1 1.013 4
2.66
0.517 4 0.575 0 0.629 6 0.678 0 0.719 8 0.755 6 0.786 2 0.834 4 0.871 6 0.900 4 0.923 2 0.941 4 0.968 0 0.986 0 0.998 4 1.007 2 1.013 5
2.67
0.517 6 0.574 8 0.629 2 0.677 6 0.719 4 0.755 2 0.785 8 0.834 1 0.871 4 0.900 3 0.923 1 0.941 3 0.968 0 0.986 0 0.998 5 1.007 3 1.013 6
2.68
0.517 7 0.574 7 0.628 9 0.677 2 0.719 0 0.754 8 0.785 4 0.833 8 0.871 1 0.900 1 0.923 0 0.941 2 0.968 0 0.986 0 0.998 5 1.007 4 1.013 7
2.69
0.517 9 0.574 5 0.628 6 0.676 8 0.718 6 0.754 4 0.785 1 0.833 5 0.870 9 0.899 9 0.922 8 0.941 1 0.968 0 0.986 1 0.998 6 1.007 5 1.013 8
2.70
0.518 1 0.574 4 0.628 3 0.676 4 0.718 2 0.754 0 0.784 7 0.833 2 0.870 7 0.899 8 0.922 7 0.941 1 0.968 0 0.986 1 0.998 7 1.007 6 1.013 9
11
M
8
0
1
0
:
2
0
2
0
97
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
2.71
0.518 3 0.574 3 0.628 0 0.676 0 0.717 8 0.753 6 0.784 4 0.832 9 0.870 5 0.899 6 0.922 6 0.941 0 0.968 0 0.986 1 0.998 8 1.007 7 1.014 0
2.72
0.518 6 0.574 2 0.627 7 0.675 7 0.717 4 0.753 3 0.784 0 0.832 6 0.870 2 0.899 5 0.922 5 0.940 9 0.967 9 0.986 2 0.998 8 1.007 7 1.014 1
2.73
0.518 8 0.574 1 0.627 4 0.675 3 0.717 0 0.752 9 0.783 7 0.832 3 0.870 0 0.899 3 0.922 4 0.940 9 0.967 9 0.986 2 0.998 9 1.007 8 1.014 2
2.74
0.519 1 0.574 0 0.627 1 0.674 9 0.716 6 0.752 5 0.783 4 0.832 0 0.869 8 0.899 1 0.922 3 0.940 8 0.967 9 0.986 3 0.999 0 1.007 9 1.014 3
2.75
0.519 3 0.574 0 0.626 9 0.674 6 0.716 3 0.752 2 0.783 1 0.831 7 0.869 6 0.899 0 0.922 2 0.940 7 0.967 9 0.986 3 0.999 0 1.008 0 1.014 4
2.76
0.519 6 0.573 9 0.626 6 0.674 3 0.715 9 0.751 8 0.782 7 0.831 5 0.869 4 0.898 8 0.922 1 0.940 7 0.967 9 0.986 4 0.999 1 1.008 1 1.014 5
2.77
0.519 9 0.573 9 0.626 4 0.674 0 0.715 6 0.751 5 0.782 4 0.831 2 0.869 2 0.898 7 0.922 0 0.940 6 0.967 9 0.986 4 0.999 2 1.008 2 1.014 7
2.78
0.520 2 0.573 9 0.626 2 0.673 6 0.715 2 0.751 2 0.782 1 0.830 9 0.869 0 0.898 5 0.921 9 0.940 6 0.967 9 0.986 4 0.999 2 1.008 3 1.014 8
2.79
0.520 5 0.573 8 0.626 0 0.673 3 0.714 9 0.750 8 0.781 8 0.830 6 0.868 8 0.898 4 0.921 8 0.940 5 0.967 9 0.986 5 0.999 3 1.008 4 1.014 9
2.80
0.520 8 0.573 8 0.625 8 0.673 0 0.714 6 0.750 5 0.781 5 0.830 4 0.868 5 0.898 2 0.921 7 0.940 4 0.968 0 0.986 5 0.999 4 1.008 5 1.015 0
2.81
0.521 2 0.573 9 0.625 6 0.672 8 0.714 3 0.750 2 0.781 2 0.830 1 0.868 4 0.898 1 0.921 6 0.940 4 0.968 0 0.986 6 0.999 5 1.008 6 1.015 1
2.82
0.521 5 0.573 9 0.625 4 0.672 5 0.713 9 0.749 9 0.780 9 0.829 8 0.868 2 0.898 0 0.921 5 0.940 3 0.968 0 0.986 6 0.999 5 1.008 7 1.015 2
2.83
0.521 8 0.573 9 0.625 3 0.672 2 0.713 6 0.749 6 0.780 6 0.829 6 0.868 0 0.897 8 0.921 4 0.940 3 0.968 0 0.986 7 0.999 6 1.008 8 1.015 3
2.84
0.522 2 0.574 0 0.625 1 0.672 0 0.713 3 0.749 3 0.780 3 0.829 3 0.867 8 0.897 7 0.921 3 0.940 2 0.968 0 0.986 7 0.999 7 1.008 9 1.015 4
2.85
0.522 6 0.574 0 0.625 0 0.671 7 0.713 1 0.749 0 0.780 1 0.829 1 0.867 6 0.897 6 0.921 2 0.940 2 0.968 0 0.986 8 0.999 8 1.009 0 1.015 5
2.86
0.523 0 0.574 1 0.624 8 0.671 5 0.712 8 0.748 7 0.779 8 0.828 8 0.867 4 0.897 4 0.921 1 0.940 1 0.968 0 0.986 8 0.999 9 1.009 1 1.015 6
2.87
0.523 4 0.574 2 0.624 7 0.671 2 0.712 5 0.748 4 0.779 5 0.828 6 0.867 2 0.897 3 0.921 1 0.940 1 0.968 0 0.986 9 0.999 9 1.009 2 1.015 7
2.88
0.523 8 0.574 2 0.624 6 0.671 0 0.712 2 0.748 2 0.779 3 0.828 4 0.867 0 0.897 2 0.921 0 0.940 0 0.968 0 0.986 9 1.000 0 1.009 3 1.015 9
2.89
0.524 2 0.574 3 0.624 5 0.670 8 0.712 0 0.747 9 0.779 0 0.828 1 0.866 8 0.897 0 0.920 9 0.940 0 0.968 0 0.987 0 1.000 1 1.009 4 1.016 0
2.90
0.524 6 0.574 4 0.624 4 0.670 6 0.711 7 0.747 6 0.778 8 0.827 9 0.866 7 0.896 9 0.920 8 0.939 9 0.968 0 0.987 0 1.000 2 1.009 4 1.016 1
2.91
0.525 1 0.574 6 0.624 3 0.670 4 0.711 5 0.747 4 0.778 5 0.827 7 0.866 5 0.896 8 0.920 7 0.939 9 0.968 1 0.987 1 1.000 3 1.009 5 1.016 2
2.92
0.525 5 0.574 7 0.624 2 0.670 2 0.711 2 0.747 1 0.778 3 0.827 4 0.866 3 0.896 7 0.920 7 0.939 9 0.968 1 0.987 1 1.000 3 1.009 6 1.016 3
2.93
0.525 9 0.574 8 0.624 2 0.670 0 0.711 0 0.746 9 0.778 0 0.827 2 0.866 2 0.896 5 0.920 6 0.939 8 0.968 1 0.987 2 1.000 4 1.009 7 1.016 4
2.94
0.526 4 0.575 0 0.624 1 0.669 9 0.710 8 0.746 6 0.777 8 0.827 0 0.866 0 0.896 4 0.920 5 0.939 8 0.968 1 0.987 2 1.000 5 1.009 8 1.016 5
2.95
0.526 8 0.575 1 0.624 1 0.669 7 0.710 6 0.746 4 0.777 6 0.826 8 0.865 8 0.896 3 0.920 4 0.939 7 0.968 1 0.987 3 1.000 6 1.010 0 1.016 6
2.96
0.527 3 0.575 3 0.624 0 0.669 6 0.710 3 0.746 2 0.777 3 0.826 6 0.865 7 0.896 2 0.920 4 0.939 7 0.968 1 0.987 3 1.000 7 1.010 1 1.016 3
2.97
0.527 8 0.575 5 0.624 0 0.669 4 0.710 1 0.745 9 0.777 1 0.826 3 0.865 5 0.896 1 0.920 3 0.939 7 0.968 2 0.987 4 1.000 7 1.010 2 1.016 9
2.98
0.528 3 0.575 7 0.624 0 0.669 3 0.709 9 0.745 7 0.776 9 0.826 1 0.865 3 0.896 0 0.920 2 0.939 6 0.968 2 0.987 5 1.000 8 1.010 3 1.017 0
2.99
0.528 8 0.575 9 0.624 0 0.669 1 0.709 8 0.745 5 0.776 7 0.825 9 0.865 2 0.895 9 0.920 1 0.939 6 0.968 2 0.987 5 1.000 9 1.010 4 1.017 1
3.00
0.529 3 0.576 1 0.624 0 0.669 0 0.709 6 0.745 3 0.776 5 0.825 7 0.865 0 0.895 8 0.920 1 0.939 6 0.968 2 0.987 6 1.001 0 1.010 5 1.017 2
11
M
8
0
1
0
:
2
0
2
0
98
M 8010:2020
表I.2−Z数表(1993)(続き)
BZ
AZ
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.60
2.80
3.00
3.01
0.529 8 0.576 3 0.624 0 0.668 9 0.709 4 0.745 1 0.776 3 0.825 5 0.864 9 0.895 7 0.920 0 0.939 5 0.968 2 0.987 6 1.001 1 1.010 6 1.017 3
3.02
0.530 3 0.576 5 0.624 0 0.668 8 0.709 2 0.744 9 0.776 1 0.825 3 0.864 7 0.895 5 0.920 0 0.939 5 0.968 3 0.987 7 1.001 2 1.010 7 1.017 5
3.03
0.530 9 0.576 8 0.624 1 0.668 7 0.709 1 0.744 7 0.775 9 0.825 2 0.864 6 0.895 4 0.919 9 0.939 5 0.968 3 0.987 8 1.001 3 1.010 8 1.017 6
3.04
0.531 4 0.577 0 0.624 1 0.668 6 0.708 9 0.744 5 0.775 7 0.825 0 0.864 4 0.895 3 0.919 8 0.939 5 0.968 3 0.987 8 1.001 3 1.010 9 1.017 7
3.05
0.531 9 0.577 3 0.624 1 0.668 5 0.708 8 0.744 4 0.775 5 0.824 8 0.864 3 0.895 3 0.919 8 0.939 4 0.968 3 0.987 9 1.001 4 1.011 0 1.017 8
3.06
0.532 5 0.577 5 0.624 2 0.668 5 0.708 6 0.744 2 0.775 4 0.824 6 0.864 2 0.895 2 0.919 7 0.939 4 0.968 4 0.988 0 1.001 5 1.011 1 1.017 9
3.07
0.533 0 0.577 8 0.624 3 0.668 4 0.708 5 0.744 0 0.775 2 0.824 4 0.864 0 0.895 1 0.919 7 0.939 4 0.968 4 0.988 0 1.001 6 1.011 2 1.018 0
3.08
0.533 6 0.578 1 0.624 3 0.668 3 0.708 3 0.743 9 0.775 0 0.824 2 0.863 9 0.895 0 0.919 6 0.939 4 0.968 4 0.988 1 1.001 7 1.011 3 1.018 2
3.09
0.534 2 0.578 4 0.624 4 0.668 3 0.708 2 0.743 7 0.774 9 0.824 1 0.863 8 0.894 9 0.919 6 0.939 3 0.968 5 0.988 1 1.001 8 1.011 4 1.018 3
3.10
0.534 8 0.578 1 0.624 5 0.668 2 0.708 1 0.743 6 0.774 7 0.823 9 0.863 6 0.894 8 0.919 5 0.939 3 0.968 5 0.988 2 1.001 9 1.011 5 1.018 4
3.11
0.535 3 0.579 0 0.624 6 0.668 2 0.708 0 0.743 4 0.774 6 0.823 7 0.863 5 0.894 7 0.919 5 0.939 3 0.968 5 0.988 3 1.002 0 1.011 6 1.018 5
3.12
0.535 9 0.579 3 0.624 7 0.668 2 0.707 9 0.743 3 0.774 4 0.823 6 0.863 4 0.894 6 0.919 4 0.939 3 0.968 6 0.988 3 1.002 1 1.011 7 1.018 6
3.13
0.536 5 0.579 6 0.624 8 0.668 2 0.707 8 0.743 1 0.774 3 0.823 4 0.863 3 0.894 5 0.919 4 0.939 3 0.968 6 0.988 4 1.002 2 1.011 8 1.018 8
3.14
0.537 1 0.579 9 0.624 9 0.668 1 0.707 7 0.743 0 0.774 1 0.823 3 0.863 2 0.894 5 0.919 3 0.939 3 0.968 6 0.988 5 1.002 2 1.012 0 1.018 9
3.15
0.537 7 0.580 2 0.625 0 0.668 1 0.707 6 0.742 9 0.774 0 0.823 1 0.863 0 0.894 4 0.919 3 0.939 3 0.968 7 0.988 6 1.002 3 1.012 1 1.019 0
3.16
0.538 3 0.580 6 0.625 2 0.668 1 0.707 5 0.742 8 0.773 9 0.823 0 0.862 9 0.894 3 0.919 2 0.939 2 0.968 7 0.988 6 1.002 4 1.012 2 1.019 1
3.17
0.539 0 0.580 9 0.625 3 0.668 1 0.707 5 0.742 7 0.773 7 0.822 8 0.862 8 0.894 2 0.919 2 0.939 2 0.968 7 0.988 7 1.002 5 1.012 3 1.019 2
3.18
0.539 6 0.581 3 0.625 5 0.668 2 0.707 4 0.742 6 0.773 6 0.822 7 0.862 7 0.894 2 0.919 2 0.939 2 0.968 8 0.988 8 1.002 6 1.012 4 1.019 4
3.19
0.540 2 0.581 7 0.625 6 0.668 2 0.707 4 0.742 5 0.773 5 0.822 6 0.862 6 0.894 1 0.919 1 0.939 2 0.968 8 0.988 8 1.002 7 1.012 5 1.019 5
3.20
0.540 9 0.582 0 0.625 8 0.668 2 0.707 3 0.742 4 0.773 4 0.822 4 0.862 5 0.894 0 0.919 1 0.939 2 0.968 9 0.988 9 1.002 8 1.012 6 1.019 6
3.21
0.541 5 0.582 4 0.626 0 0.668 2 0.707 3 0.742 3 0.773 3 0.822 3 0.862 4 0.894 0 0.919 1 0.939 2 0.968 9 0.989 0 1.002 9 1.012 7 1.019 7
3.22
0.542 1 0.582 8 0.626 1 0.668 3 0.707 2 0.742 2 0.773 2 0.822 2 0.862 3 0.893 9 0.919 0 0.939 2 0.968 9 0.989 1 1.003 0 1.012 8 1.019 9
3.23
0.542 8 0.583 2 0.626 3 0.668 3 0.707 2 0.742 1 0.773 1 0.822 0 0.862 2 0.893 8 0.919 0 0.939 2 0.969 0 0.989 1 1.003 1 1.013 0 1.020 0
3.24
0.543 5 0.583 6 0.626 5 0.668 4 0.707 1 0.742 0 0.773 0 0.821 9 0.862 1 0.893 8 0.919 0 0.939 2 0.969 0 0.989 2 1.003 2 1.013 1 1.020 1
3.25
0.544 1 0.584 0 0.626 7 0.668 5 0.707 1 0.742 0 0.772 9 0.821 8 0.862 0 0.893 7 0.918 9 0.939 2 0.969 1 0.989 3 1.003 3 1.013 2 1.020 2
3.26
0.544 8 0.584 4 0.626 9 0.668 5 0.707 1 0.741 9 0.772 8 0.821 7 0.861 9 0.893 7 0.918 9 0.939 2 0.969 1 0.989 4 1.003 4 1.013 3 1.020 3
3.27
0.545 5 0.584 8 0.627 2 0.668 6 0.707 1 0.741 9 0.772 8 0.821 6 0.861 9 0.893 6 0.918 9 0.939 2 0.969 2 0.989 4 1.003 5 1.013 4 1.020 5
3.28
0.546 1 0.585 2 0.627 4 0.668 7 0.707 1 0.741 8 0.772 7 0.821 5 0.861 8 0.893 6 0.918 9 0.939 2 0.969 2 0.989 5 1.003 6 1.013 5 1.020 6
3.29
0.546 8 0.585 7 0.627 6 0.668 8 0.707 1 0.741 8 0.772 6 0.821 4 0.861 7 0.893 5 0.918 8 0.939 2 0.969 3 0.989 6 1.003 7 1.013 7 1.020 7
3.30
0.547 5 0.586 1 0.627 8 0.668 9 0.707 1 0.741 7 0.772 5 0.821 3 0.861 6 0.893 5 0.918 8 0.939 2 0.969 3 0.989 7 1.003 8 1.013 8 1.020 9
11
M
8
0
1
0
:
2
0
2
0

99
M 8010:2020
附属書J
(規定)
完全気体とみなしたアイゼントロピック指数
J.1
完全気体とみなしたアイゼントロピック指数の計算
ガスを完全気体とみなしたアイゼントロピック指数の計算は,次の手順a)及びb)に従う。
a) 表J.1に規定する定数を用い,ガスが含有する各成分の個々について,完全気体とみなした定圧比熱
0p,i
cを式(J.1)で求める。
+
+
+
+
=
2
J,
J,
J,
2
J,
J,
J,
2
J,
J,
J,
2
J,
J,
J,
J,
0p,
cosh
sinh
cosh
sinh
51
314
.8
T
J
T
J
I
T
H
T
H
G
T
F
T
F
E
T
D
T
D
C
B
c
i
i
i
i
i
i
i
i
i
i
i
i
i
i
····· (J.1)
ここに,
0p,i
c: i番目の成分の完全気体とみなした定圧比熱
[J/(K・mol)]
BJ,i,CJ,i,EJ,i,GJ,i,IJ,i: 表J.1に規定する定数
DJ,i,FJ,i,HJ,i,JJ,i: 表J.1に規定する定数(K)
T: ガスの温度(K)
b) ガスを全気体とみなしたアイゼントロピック指数κ0を式(J.2)で求める。
51
314
.8
0p,
0p,
0
−
=∑
i
i
i
ic
c
x
κ
···························································· (J.2)
ここに,
κ0: 完全気体とみなしたガスのアイゼントロピック指数
xi: i番目の成分のモル分率
0p,i
c: i番目の成分の完全気体とみなした定圧比熱[J/(K・mol)]
100
M 8010:2020
表J.1−完全気体とみなした定圧比熱を求めるための定数
成分
BJ,i
CJ,i
DJ,i
EJ,i
FJ,i
GJ,i
HJ,i
IJ,i
JJ,i
CO2
3.500 02
2.044 52
919.306 −1.060 4
−865.07
2.033 66
483.55
0.013 93
341.109
N2
3.500 31
0.137 32
662.738 −0.146 6
−680.562
0.900 66 1740.06
0
0
H2
2.479 06
0.958 06
228.734
0.454 44
326.843
1.560 39 1651.71 −1.375 60
1671.69
CO
3.500 55
1.028 65 1550.450
0.004 93
704.525
0
0
0
0
O2
3.501 46
1.075 58 2235.710
1.013 34
1116.69
0
0
0
0
H2O
4.003 92
0.010 59
268.795
0.987 63
1141.41
3.069 04 2507.37
0
0
H2S
4
3.119 42 1833.630
1.002 43
847.181
0
0
0
0
He
2.5
0
0
0
0
0
0
0
0
Ar
2.5
0
0
0
0
0
0
0
0
CH4
4.000 88
0.763 15
820.659
0.004 60
178.410
8.744 32 1062.82 −4.469 21
1090.53
C2H6
4.002 63
4.339 39
559.314
1.237 22
223.284
13.197 4
1031.38 −6.019 89
1071.29
C3H8
4.029 39
6.605 69
479.856
3.197 00
200.893
19.192 1
955.312 −8.372 67
1027.29
iC4H10
4.067 14
8.975 75
438.270
5.251 56
198.018
25.142 3
1905.02
16.138 8
893.765
nC4H10
4.339 44
9.448 93
468.270
6.894 06
183.636
24.461 8
1914.10
14.782 4
903.185
iC5H12
4
11.761 8
292.503
20.110 1
910.237
33.168 8
1919.37
0
0
nC5H12
4
8.950 43
178.670
21.836
840.538
33.403 2
1774.25
0
0
C6H14
4
11.697 7
182.326
26.814 2
859.207
38.616 4
1826.59
0
0
C7H16
4
13.726 6
169.789
30.470 7
836.195
43.556 1
1760.46
0
0
C8H18
4
15.686 5
158.922
33.802 9
815.064
48.173 1
1693.07
0
0
C9H20
4
18.024 1
156.854
38.123 5
814.882
53.341 5
1693.79
0
0
C10H22
4
21.006 9
164.947
43.493 1
836.264
58.365 7
1750.24
0
0
101
M 8010:2020
附属書K
(規定)
オリフィス板表面及びオリフィス配管内壁面の表面粗さ条件
オリフィス板表面及びオリフィス配管内壁面の表面粗さは,表K.1に従って決定するか,又はJIS Z
8762-1:2007に従って測定する。
表K.1−管内の表面平均粗さRa目安
単位 mm
材料
管内壁の状態
Ra
黄銅,銅,アルミニウム,
プラスチック,ガラス
付着物がなく滑らか
<0.01
鋼
新しいステンレス
<0.01
新しい継目なしの冷間引抜き
<0.01
新しい継目なしの熱間引抜き
≦0.03
新しい継目なしの圧延
新しい継目なしの溶接
新しいスパイラル溶接
0.03
僅かなさび
0.03〜0.06
さび
0.06〜0.10
あか
0.15〜0.6
甚だしいあか
>0.6
れき青質塗料(新しいもの)
0.01〜0.015
れき青質塗料
0.03〜0.06
亜鉛めっき
0.04
鋳鉄
新しいもの
0.08
さび
0.3〜0.5
あか
>0.5
れき青質(新しいもの)
0.01〜0.015
アスベストセメント
絶縁性及び非絶縁性塗料(新しいもの)
≦0.01
非絶縁性塗料
0.015
オリフィス板の位置から上流側に10D0までの配管内壁のRaを評価し,Raが次の条件を満たす場合には,
8.4.1に従って求めた値をオリフィス流量計の流出係数の不確かさとすることができる。
− Ra<0.000 1d0
− 104 Ra/D0の値が,表K.2の値より小さい。
− 104 Ra/D0の値が,表K.3の値より大きい。
注記 D≧150 mmの場合には,これらの三つの条件は,次のようになる。
− β≦0.6かつReD≦5×107のときに1 μm≦Ra≦6 μm
− β>0.6かつReD≦1.5×107のときに1.5 μm≦Ra≦6 μm

102
M 8010:2020
表K.2−104 Ra/D0の最大値
β
ReD
≦104
3×104
105
3×105
106
3×106
107
3×107
108
≦0.20
15
15
15
15
15
15
15
15
15
0.30
15
15
15
15
15
15
15
14
13
0.40
15
15
10
7.2
5.2
4.1
3.5
3.1
27
0.50
11
7.7
4.9
3.3
2.2
1.6
1.3
1.1
0.9
0.60
5.6
4
2.5
1.6
1.0
0.7
0.6
0.5
0.4
≧0.65
4.2
3
1.9
1.2
0.8
0.6
0.4
0.3
0.3
表K.3−104 Ra/D0の最小値
β
ReD
≦3×106
107
3×107
108
≦0.50
0.0
0.0
0.0
0.0
0.60
0.0
0.0
0.003
0.004
≧0.65
0.0
0.013
0.016
0.012
103
M 8010:2020
附属書L
(規定)
空気の相対密度の概算値
L.1
空気の相対密度の概算値
Z数表(2015)の使用において相対密度の有効範囲を確認するためには,相対密度を式(L.1)で求める。
Z
Z
N
ρ
A
r
97
.
28
=
········································································ (L.1)
ここに,
ρr: 相対密度
ZA: 空気の圧縮係数
Z: ガスの圧縮係数
N: ガスのモル質量(kg/kmol)
式(L.1)に使用する空気の圧縮係数は,表L.1に規定する定数を用い,式(L.2)で求める。
ZA=aZA0+aZA1T+(bZA0+bZA1T+bZA2T2)p+(cZA0+cZA1T+cZA2T2)p2 ······ (L.2)
ここに,
ZA: 空気の圧縮係数
T: 空気の温度(℃)
p: 空気の圧力(MPa)
aZA0〜cZA2: 表L.1に示す定数
表L.1−空気の圧縮係数を求めるために使用する定数の値
定数
値
aZA0
1.000 5
aZA1
−4.72×10−6
bZA0
−0.006 7
bZA1
0.000 138
bZA2
−5.46×10−7
cZA0
0.000 338
cZA1
−3.817×10−6
cZA2
1.523×10−8
注記 式(L.2)による空気の圧縮係数の値は,Z数表(2015)の条件判断には十分な精度をもつが,高
精度の計算では使用しないことが望ましい。
参考文献
[1] ISO 12213-1:2006,Natural gas−Calculation of compression factor−Part 1: Introduction and guidelines
[2] ISO 12213-2:2006,Natural gas−Calculation of compression factor−Part 2: Calculation using
molar-composition analysis
[3] ISO 20765-1,Natural gas−Calculation of thermodynamic properties−Part 1: Gas phase properties for
transmission and distribution applications
[4] JIS Q 17025 試験所及び校正機関の能力に関する一般要求事項