K 7252-2:2016 (ISO 16014-2:2012)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 2
4 ユニバーサルキャリブレーション法の原理 ············································································ 3
5 試薬······························································································································· 5
6 装置······························································································································· 5
7 操作······························································································································· 5
8 データ収集及び解析 ·········································································································· 5
9 結果の表示 ······················································································································ 5
9.1 ユニバーサルキャリブレーション曲線の作成 ······································································· 5
9.2 平均分子量の計算 ·········································································································· 5
9.3 微分分子量分布曲線 ······································································································· 7
9.4 積分分子量分布曲線 ······································································································· 7
10 精度 ····························································································································· 8
11 試験報告書 ···················································································································· 8
11.1 一般 ··························································································································· 8
11.2 装置及び測定条件 ········································································································· 8
11.3 装置の校正 ·················································································································· 8
11.4 校正曲線 ····················································································································· 8
11.5 結果 ··························································································································· 8
附属書A(参考)ユニバーサルキャリブレーション法の補足························································· 9
附属書B(参考)マーク・ホーウィンク・桜田式におけるK及びaの値 ········································ 11
K 7252-2:2016 (ISO 16014-2:2012)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,日本プラスチック
工業連盟(JPIF)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を改
正すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格であ
る。
これによって,JIS K 7252-2:2008は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS K 7252の規格群には,次に示す部編成がある。
JIS K 7252-1 第1部:通則
JIS K 7252-2 第2部:ユニバーサルキャリブレーション法
JIS K 7252-3 第3部:常温付近での方法
JIS K 7252-4 第4部:高温での方法
JIS K 7252-5 第5部:光散乱検出による方法
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 7252-2:2016
(ISO 16014-2:2012)
プラスチック−
サイズ排除クロマトグラフィーによる
高分子の平均分子量及び分子量分布の求め方−
第2部:ユニバーサルキャリブレーション法
Plastics-Determination of average molecular mass and molecular mass
distribution of polymers using size-exclusion chromatography-
Part 2: Universal calibration method
序文
この規格は,2012年に第2版として発行されたISO 16014-2を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,サイズ排除クロマトグラフィー(以下,SECという。)によって,標準校正曲線の代わり
にユニバーサルキャリブレーション曲線を用いた高分子の平均分子量及び分子量分布の求め方(ユニバー
サルキャリブレーション法)について規定する(附属書A参照)。
注記1 この方法は,相対法に分類される(JIS K 7252-1の附属書A参照)。
注記2 ユニバーサルキャリブレーション法は,SECにおける溶出時間が,高分子の大きさ(流体力
学的体積)又は固有粘度[η]と分子量Mとの積と相関があることに基づいている。実験的に,
化学構造,分岐度,組成又は立体規則性にかかわらず,多くのランダムコイル形高分子で,
この相関が確認されている。ユニバーサルキャリブレーション曲線は,狭い分子量分布をも
つポリスチレンのような分子量標準高分子物質を用いて,溶出時間t又は溶出体積Vに対し
て[η]Mの対数をプロットすることによって作成する。未知の高分子試料の分子量Miは,作
成したユニバーサルキャリブレーション曲線の各溶出時間における[η]Mの値及びマーク・ホ
ーウィンク・桜田(Mark-Houwink-Sakurada)式([]
[]
1
+
=
→
=
a
a
KM
M
KM
η
η
)における[η],
又はK及びaの値から求めることができる。ここに,K及びaは,実験条件に依存した定数
及び指数である。したがって,この方法は,JIS K 7252-1に規定する相対法として分類され
るが,絶対法によって求めた値に等しいか又はほぼ等しい平均分子量及び分子量分布を求め
ることができる。
注記3 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 16014-2:2012,Plastics−Determination of average molecular mass and molecular mass
2
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
distribution of polymers using size-exclusion chromatography−Part 2: Universal calibration
method(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS K 7252-1 プラスチック−サイズ排除クロマトグラフィーによる高分子の平均分子量及び分子量
分布の求め方−第1部:通則
注記 対応国際規格:ISO 16014-1,Plastics−Determination of average molecular mass and molecular
mass distribution of polymers using size-exclusion chromatography−Part 1: General principles
(IDT)
JIS K 7252-3 プラスチック−サイズ排除クロマトグラフィーによる高分子の平均分子量及び分子量
分布の求め方−第3部:常温付近での方法
注記 対応国際規格:ISO 16014-3,Plastics−Determination of average molecular mass and molecular
mass distribution of polymers using size-exclusion chromatography−Part 3: Low-temperature
method(IDT)
JIS K 7252-4 プラスチック−サイズ排除クロマトグラフィーによる高分子の平均分子量及び分子量
分布の求め方−第4部:高温での方法
注記 対応国際規格:ISO 16014-4,Plastics−Determination of average molecular mass and molecular
mass distribution of polymers using size-exclusion chromatography−Part 4: High-temperature
method(IDT)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS K 7252-1による。JIS K 7252-1で規定した種々の平均分子
量の定義を,利用者の利便性から次に示す。
なお,4種の平均分子量は,式(1)〜式(4)によって定義する1)。式中,Niは,分子量Miの成分の分子数で
あり,aは,マーク・ホーウィンク・桜田式の指数である。
注1) 定義は,JIS K 7252-1と同一であるが,式中のMi値は,箇条4に記載するユニバーサルキャリ
ブレーション曲線によって求められる。
3.1
数平均分子量,Mn(number-average molecular mass)
次の式(1)によって求める,平均分子量。
(
)
∑
∑
∞
=
∞
=
×
=
1
1
n
i
i
i
i
i
N
M
N
M
····································································· (1)
ここに,
Mn: 数平均分子量
Ni: 各溶出時間の成分の分子数
3
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Mi: 各溶出時間の成分の分子量
3.2
質量平均分子量,Mw(mass-average molecular mass)
次の式(2)によって求める,平均分子量。
(
)
(
)
∑
∑
∞
=
∞
=
×
×
=
1
1
2
w
i
i
i
i
i
i
M
N
M
N
M
···································································· (2)
ここに, Mw: 質量平均分子量
Ni: 各溶出時間の成分の分子数
Mi: 各溶出時間の成分の分子量
3.3
Z平均分子量,Mz(z-average molecular mass)
次の式(3)によって求める,平均分子量。
(
)
(
)
∑
∑
∞
=
∞
=
×
×
=
1
2
1
3
z
i
i
i
i
i
i
M
N
M
N
M
····································································· (3)
ここに,
Mz: Z平均分子量
Ni: 各溶出時間の成分の分子数
Mi: 各溶出時間の成分の分子量
3.4
粘度平均分子量,Mv(viscosity-average molecular mass)
次の式(4)によって求める,平均分子量。
(
)
(
)
a
i
i
i
i
a
i
i
M
N
M
N
M
1
1
1
1
v
×
×
=∑∑∞=
∞
=
+
····························································· (4)
ここに,
Mv: 粘度平均分子量
Ni: 各溶出時間の成分の分子数
Mi: 各溶出時間の成分の分子量
a: マーク・ホーウィンク・桜田式の指数
4
ユニバーサルキャリブレーション法の原理
SEC測定は,JIS K 7252-1,JIS K 7252-3及びJIS K 7252-4と同様に行うが,各溶出時間の分子量Miは,
ユニバーサルキャリブレーション法によって求める。理論的には,この方法は,絶対法による値に等しい
か又はほとんど等しい平均分子量及び分子量分布値を与える。
式(5)に示すように,溶液中の高分子の大きさ,すなわち,流体力学的体積Vhは,固有粘度[η]と分子量
Mとの積に比例する。
[]
[]
h
h
V
M
M
V
∝
→
∝
η
η
······························································ (5)
ここに,
[η]: 固有粘度
Vh: 流体力学的体積
M: 分子量
4
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SECの場合,多くのランダムコイル形高分子は,化学構造,分岐度,組成又は立体規則性とは無関係に,
特定のカラム,溶媒及び温度の条件下で,溶出時間は,[η]とMとの積の対数におよそ反比例する。[η]M
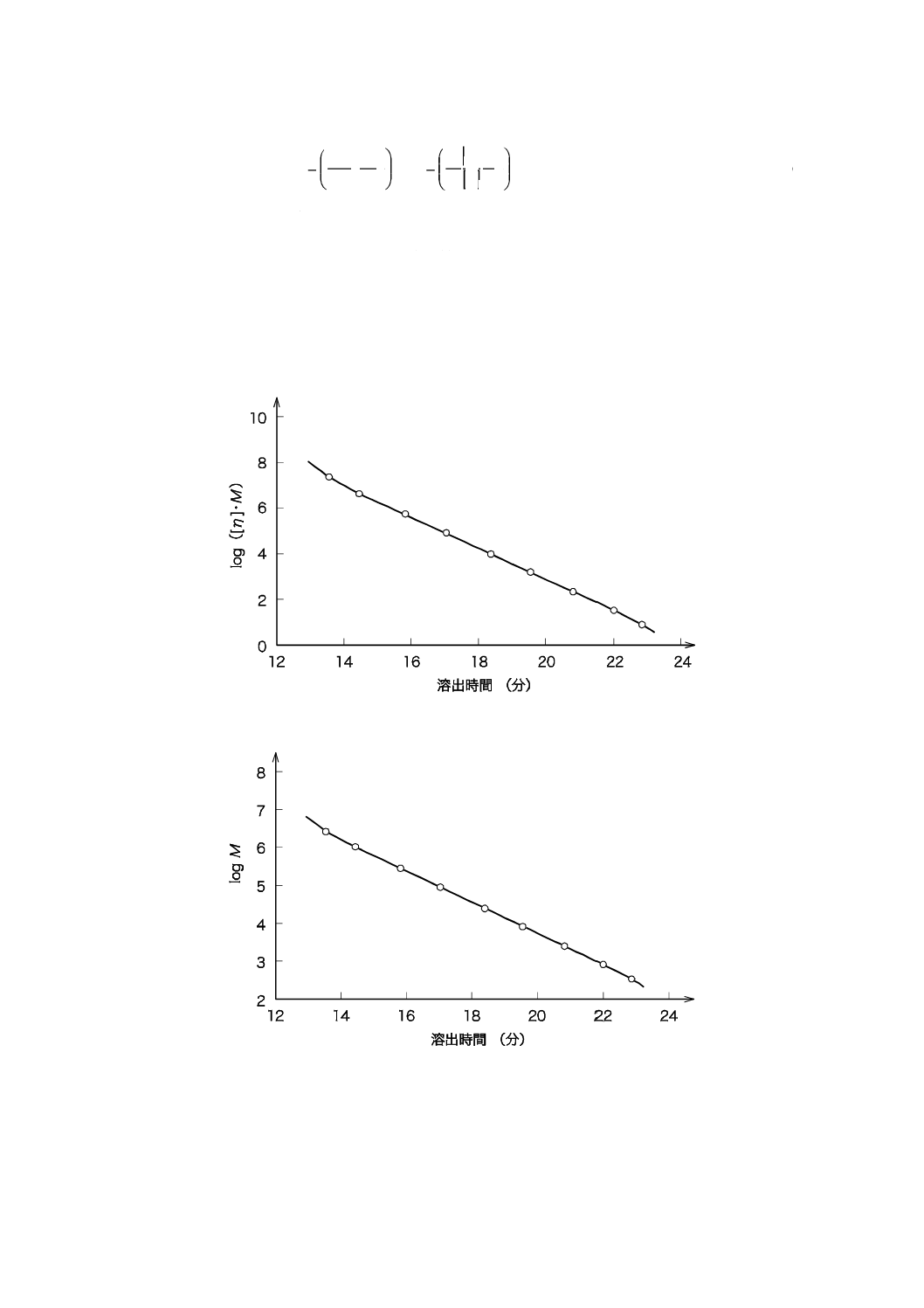
の対数と溶出時間との関係は,“ユニバーサルキャリブレーション曲線”(図1参照)と呼ばれ,この校正
曲線を用いて平均分子量及び分子量分布を求める方法は,“ユニバーサルキャリブレーション法”と呼ばれ
る。
初めに,分子量分布が狭い複数の分子量標準物質(分子量Ms)を用いて,それぞれの溶出時間tsを求め
る。次に,K及びaが既知の場合,式(6)のマーク・ホーウィンク・桜田式によってそれぞれの[η]sを求め
る。
なお,K及びaが未知の場合,当該実験条件で各標準物質の[η]sを,直接測定して求め(9.1参照),マー
ク・ホーウィンク・桜田式を基に対数プロットしたグラフによってK及びaを求める。
[]
s
s
s
s
a
M
K
=
η
············································································· (6)
ここに,
[η]: 固有粘度
K: マーク・ホーウィンク・桜田式の定数
M: 分子量
a: マーク・ホーウィンク・桜田式の指数
添字s: 分子量標準物質
次に,分子量標準物質を用いて溶出時間tsに対する[η]sMsの対数をプロットし,ユニバーサルキャリブ
レーション曲線を作成する。
次に,高分子試料のSECを測定する。各ピークの溶出時間tiにおける[η]iMiを,分子量標準物質を用い
て作成したユニバーサルキャリブレーション曲線から求める。求めた[η]iMiを用いてマーク・ホーウィン
ク・桜田式(7)から誘導される式(8)によってMiを求める。
[]
a
KM
=
η
················································································ (7)
ここに,
[η]: 固有粘度
K: マーク・ホーウィンク・桜田式の定数
M: 分子量
a: マーク・ホーウィンク・桜田式の指数
[]
[]
1
,s
,s
+
=
=
a
i
i
i
i
i
KM
M
M
η
η
···························································· (8)
ここに,
[η]: 固有粘度
K: マーク・ホーウィンク・桜田式の定数
M: 分子量
a: マーク・ホーウィンク・桜田式の指数
添字i: 各溶出時間の成分
添字s: 分子量標準物質
最後に,9.2,9.3及び9.4に示す式を用いて,各溶出時間における分子量Mi及びシグナル強度Hiから平
均分子量及び分子量分布を求める。
ユニバーサルキャリブレーション曲線に関するその他の情報,及びユニバーサルキャリブレーション理
論に基づく高分子試料校正曲線の使用方法については,9.1及びA.2.1を参照する。
固有粘度[η]に関するその他の情報については,A.2.2を参照する。
幾つかの高分子について,マーク・ホーウィンク・桜田式におけるK及びaの値は,附属書Bを参照す
る。
5
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
試薬
JIS K 7252-1の箇条5(試薬)による。
6
装置
JIS K 7252-1の箇条6(装置)による。
7
操作
JIS K 7252-1の箇条7(操作)による。
8
データ収集及び解析
JIS K 7252-1の箇条8(データ収集及び解析)による。
9
結果の表示
9.1
ユニバーサルキャリブレーション曲線の作成
幾つかの分子量標準物質について,溶出時間に対して[η]sMsの対数をプロットし,ユニバーサルキャリ
ブレーション曲線を作成する。特定の溶離条件下における分子量標準物質の[η]s値は,マーク・ホーウィ
ンク・桜田式から求めても,直接測定して求めてもよい。
注記 直接,固有粘度[η]を求めるには,SEC装置に粘度検出器を連結して分子量既知の単分散高分子
を測定する方法と,毛細管粘度計を用いてバッチ式に分子量既知の単分散高分子を測定する方
法とがある。
市販されている分子量標準物質の分子量については,JIS K 7252-1の附属書Bを参照。
ユニバーサルキャリブレーション曲線には,溶出時間tの一次式(9)か,又は三次の多項式(10)が広く用
いられる。校正曲線の近似をよくするために,より高次の式を用いてもよい。
[]
(
)
t
A
A
M
×
+
=
1
0
s
s
logη
······························································· (9)
[]
(
)
3
3
2
2
1
0
s
s
log
t
A
t
A
t
A
A
M
×
+
×
+
×
+
=
η
········································ (10)
ここに,
[η]s: 溶出時間tにおける分子量標準物質の固有粘度
Ms: 溶出時間tにおける分子量標準物質の分子量
A0,A1,A2,A3: 係数
t: 溶出時間
図1にユニバーサルキャリブレーション曲線の例を示す。溶出時間tを,溶出体積Ve(Ve=t×Q,ここ
に,Qは,流量)に置き換えることもできる。
ユニバーサルキャリブレーション法に基づく高分子試料校正曲線の作成については,A.2.1及び図2を参
照。
9.2
平均分子量の計算
各溶出時間tiにおける高分子試料の分子量Miは,式(13)によって,式(12)に示す[η]s,iMs,iとマーク・ホー
ウィンク・桜田式(11)のK及びaとから求めるか,又は粘度検出器を用いて得られた[η]iから求める。
[]
a
KM
=
η
(高分子試料) ··························································(11)
[]
[]
1
,s
,s
+
=
=
a
i
i
i
i
i
KM
M
M
η
η
·························································· (12)
6
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[]
[][]
=
=
+
i
i
i
a
i
i
i
M
K
M
M
η
η
η
,s
,s
)1
/(
1
,s
,s
··············································· (13)
ここに,
[η]: 固有粘度
K: マーク・ホーウィンク・桜田式の定数
M: 分子量
a: マーク・ホーウィンク・桜田式の指数
添字i: 各溶出時間の成分
添字s: 分子量標準物質
各溶出時間tiにおけるシグナル強度Hiは,JIS K 7252-1の8.3.1(ベースラインの決定)及び8.3.2(計算
範囲の決定)によって補正した高分子試料クロマトグラムのベースラインと計算区間とから計算する。
図1−ユニバーサルキャリブレーション曲線の例
図2−高分子試料校正曲線の例
式(14)〜式(18)によって,Mi及びHiから平均分子量及び多分散度を計算する。
7
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
∑
=
=
=
n
i
i
i
n
i
i
M
H
H
M
1
1
n
)
/
(
··································································· (14)
∑
∑
=
=
×
=
n
i
i
n
i
i
i
H
M
H
M
1
1
w
)
(
··································································· (15)
∑
∑
=
=
×
×
=
n
i
i
i
n
i
i
i
M
H
M
H
M
1
1
2
z
)
(
)
(
·································································· (16)
a
n
i
i
n
i
a
i
i
H
M
H
M
1
1
1
v
)
(
×
=
∑
∑
=
=
····························································· (17)
多分散度 =
n
w
M
M
···································································· (18)
ここに, Mn,Mw,Mz,Mv: 数,質量,Z及び粘度平均分子量
Hi: 各溶出時間におけるシグナル強度
Mi: 各溶出時間における分子量
a: マーク・ホーウィンク・桜田式の指数
9.3
微分分子量分布曲線
微分分子量分布曲線は,log Miに対してdWi/d(logMi)をプロットすることによって作成する。Wiは,次の
式(19)〜式(21)によって求める。
∑
=
=
n
i
i
i
i
H
H
W
1
Δ
·········································································· (19)
I
W
w
i
i
1
Δ
×
=
··········································································· (20)
(
)
(
)
i
i
i
i
i
M
t
w
M
W
log
d
d
log
d
d
×
−
=
························································ (21)
ここに,
I: データ収集間隔(分)
試料が分子量1 000未満の成分を含有している場合,M1 000に相当する位置に垂線を引く。
9.4
積分分子量分布曲線
積分分子量分布曲線は,log Miに対して質量分率Ciをプロットすることによって作成する。Ciは,次の
式(22)によって求める。
(
)
∑
=
−+
=
i
j
j
j
i
W
W
C
1
1
2
Δ
Δ
···························································· (22)
8
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
10 精度
高分子試料と分子量標準物質の校正曲線とがほとんど等しい場合,試験法の精度は,JIS K 7252-3及び
JIS K 7252-4の箇条10(精度)による。
11 試験報告書
11.1 一般
JIS K 7252-1の11.1(一般)による。
11.2 装置及び測定条件
JIS K 7252-1の11.2(装置及び測定条件)による。
11.3 装置の校正
JIS K 7252-3又はJIS K 7252-4で行われた方法を報告する。
11.4 校正曲線
JIS K 7252-1の11.4(校正曲線)による。ユニバーサルキャリブレーション曲線のグラフ又はユニバー
サルキャリブレーション曲線から求めた高分子試料校正曲線のグラフを報告する。
11.5 結果
JIS K 7252-1の11.5(結果)による。
9
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
ユニバーサルキャリブレーション法の補足
A.1 方法の適用性(箇条1参照)
ユニバーサルキャリブレーション法は,1967年ブノワ(Benoit)ら[1]によってSECに導入された。この
方法は,ユニバーサルキャリブレーションで用いる[η]Mが,流体力学的体積に関連しているという概念に
基づいている。SECにおいて,溶出時間t又は溶出体積Vに対して各ポリマーのlog([η]M)をプロットする
とき,多くのランダムコイル形ポリマーの結果が,同一の曲線,すなわち,ユニバーサルキャリブレーシ
ョン曲線に合致する。それゆえに,狭い分子量分布をもつ分子量標準物質,例えば,ポリスチレン,ポリ
メタクリル酸メチルなどを用いてユニバーサルキャリブレーション曲線を作成すれば,マーク・ホーウィ
ンク・桜田式を用いて高分子試料の絶対等価分子量及び分子量分布を求めることができる。
この方法は,高分子試料とカラム充塡剤との間に相互作用がある場合には,正しい結果は,得られない。
また,長鎖分岐がある場合又は分析対象とする分子量域においてK及びaの値が一定でない場合にも,再
現性はよいが,信頼できる結果は得られない。粘度若しくは光散乱の測定を同時に行うSECを用いて直接
分子量を求めるか,又はSECによって分画して固有粘度を測定して間接的に分子量を求めるか,いずれの
方法を用いるかは,使用者の判断である。
SECが適用できない場合の説明は,JIS K 7252-1のA.1(試験方法の適用範囲)を参照する。
A.2 ユニバーサルキャリブレーション法の原理(箇条4参照)
A.2.1 校正曲線
ユニバーサルキャリブレーション法では,tに対してlog([η]sMs)をプロットすることによってユニバーサ
ルキャリブレーション曲線を作成し,分子量を求める。ここにt,[η]s及びMsは,それぞれ溶出時間,固
有粘度及び分子量である。
ユニバーサルキャリブレーション曲線を用いる代わりに,tに対してlog Mをプロットすることによって
分子量校正曲線を作成して,分子量を求めることもできる。この場合Mは,式(A.1)〜式(A.4)を用いて計
算する。固有粘度と分子量との関係は,マーク・ホーウィンク・桜田式(A.1及びA.2)で示される。
分子量標準物質:
S
s
s
s]
[
a
M
K
=
η
················································· (A.1)
高分子試料 :
a
KM
=
]
[η
····················································· (A.2)
同一の溶出時間では式(A.3)の関係が成り立つ。
M
M
]
[
]
[
s
s
η
η
=
······································································· (A.3)
それゆえに,Mは次の式(A.4)で示される。
s
s
s
log
1
1
log
1
1
log
M
a
a
K
K
a
M
+
+
+
+
=
············································ (A.4)
ここに,
Ms,M: 分子量標準物質及び高分子試料の分子量
[η]s,[η]: 分子量標準物質及び高分子試料の固有粘度
Ks,K: 分子量標準物質及び高分子試料のマーク・ホーウィン
ク・桜田式の定数
as,a: 式(A.1)及び式(A.2)の指数
さらに,より正確な校正曲線を作成するためには,高分子試料と溶媒との相互作用による固有粘度[η]に
10
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
対する影響を補正した式(A.5)及び式(A.6)によって計算する[2]。
)
(
]
[
)
(
]
[
s
s
s
ε
η
ε
η
f
M
f
M
=
······································································ (A.5)
ここに,
2
s
s
s
86
.2
63
.2
1
)
(
ε
ε
ε
+
−
=
f
3/)1
2(
s
s
−
=
a
ε
as: 式(A.1)の指数
2
86
.2
63
.2
1
)
(
ε
ε
ε
+
−
=
f
3/)1
2( −
=
a
ε
a: 式(A.2)の指数
それゆえに,Mは次の式(A.6)で示される。
s
s
s
s
log
1
1
)
(
)
(
log
1
1
log
M
a
a
Kf
f
K
a
M
+
+
+
+
=
ε
ε
······································· (A.6)
A.2.2 固有粘度
箇条4で記載した分子量Miと固有粘度[η]との関係は,ユニバーサルキャリブレーション法の基本であ
る。固有粘度[η]は,高分子溶液粘度を溶液濃度の関数で表したときの微分係数として定義される。実験的
には,数点の濃度の溶液粘度の測定を行い,ηsp又はηrelの対数を濃度で除したデータを求め,濃度に対し
てプロットを行い,式(A.7)及び式(A.8)に示すように,濃度ゼロに外挿して[η]を求める。
[]
(
)
c
c
/
lim
sp
0
η
η
→
=
······································································· (A.7)
又は
[]
(
)
c
c
/
ln
lim
rel
0
η
η
→
=
···································································· (A.8)
ここに,
ηrel: (溶液粘度)/(溶媒粘度)で定義する相対粘度
ηsp: ηrel−1で定義する相対粘度増分
c: 高分子溶液の濃度
A.3 ユニバーサルキャリブレーション曲線の作成(9.1参照)
9.1に規定するユニバーサルキャリブレーション曲線の代わりに,ユニバーサルキャリブレーション法に
基づく高分子試料校正曲線を作成してもよい。この場合,高分子試料の分子量は,式(A.4)又は式(A.6)によ
って求める。
ユニバーサルキャリブレーション法に基づく高分子試料校正曲線は,溶出時間tに対して分子量の対数
(log M)をプロットし,その相関を近似式(A.9)又は近似式(A.10)を用い,計算して作成する。標準的には,
溶出時間tの三次の多項式が広く用いられる。高分子試料校正曲線の近似をよくするために,より高次の
式を用いてもよい。
t
A
A
M
1
0
log
+
=
······································································ (A.9)
3
3
2
2
1
0
log
t
A
t
A
t
A
A
M
+
+
+
=
·····················································(A.10)
ここに,
M: 時間tに溶出する高分子試料の分子量
A0,A1,A2,A3: 係数
t: 溶出時間
ユニバーサルキャリブレーション法に基づく高分子試料校正曲線の例は,図2を参照。
11
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
マーク・ホーウィンク・桜田式におけるK及びaの値
多くの高分子のマーク・ホーウィンク・桜田式におけるK及びaの値は,参考文献[3],参考文献[4]など
を参照する。
K及びaの幾つかの例を,表B.1に示す。
表B.1−マーク・ホーウィンク・桜田式におけるK及びaの例
高分子
溶媒
温度
℃
K×102
cm3/g
a
参考文献
ポリスチレン
テトラヒドロフラン
25
1.4
0.70
[5]
ポリスチレン
クロロホルム
30
0.49
0.796
[6]
ポリスチレン
o-ジクロロベンゼン
135
1.38
0.70
[7]
ポリスチレン
1,2,4-トリクロロベンゼン
135
1.21
0.707
[8]
ポリメタクリル酸メチル
テトラヒドロフラン
25
1.28
0.69
[9]
ポリメタクリル酸メチル
テトラヒドロフラン
23
0.93
0.69
[10]
ポリエチレン
o-ジクロロベンゼン
135
4.77
0.70
[11]
ポリエチレン
1,2,4-トリクロロベンゼン
135
4.06
0.725
[12]
ポリプロピレン
1,2,4-トリクロロベンゼン
135
1.37
0.75
[8]
ポリプロピレン
o-ジクロロベンゼン
135
1.30
0.78
[13]
ポリ塩化ビニル
テトラヒドロフラン
25
1.63
0.766
[14]
ポリ酢酸ビニル
テトラヒドロフラン
25
3.5
0.63
[15]
ポリカーボネート
テトラヒドロフラン
25
4.9
0.67
[16]
ポリイソプレン
テトラヒドロフラン
25
1.77
0.735
[17]
ポリジメチルシロキサン
クロロホルム
30
0.54
0.77
[6]
注記 参考文献[3]では,粘度式のKの値として“K×103 (mL/g)”で表記されている。
12
K 7252-2:2016 (ISO 16014-2:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献 [1] GRUBISIC, Z., REMPP, P., BENOIT, H., Polymer Letters, p.753 (1967)
[2] PTITSYN, O. B., EIZNER, Y. E., Sov. Phys. Tech. Phys., 4, p.1020 (1960)
[3] Polymer Handbook, Fourth edition, Volume 2, edited by J. Brandrup, E. H. Immergut and E. A.
Grulke, John Wiley & Sons (1999)
[4] MORI, S., BARTH, H. G., Size Exclusion Chromatography, Springer (1999)
[5] STRAZIELLE, C., BENOIT, H., VOGL, O., Eur. Polym. J., 14, p.331 (1978)
[6] DAWKINS, J. V., J., Macromol. Sci. Phys., B2, p.623 (1968)
[7] DAWKINS, J. V., MADDOCK, J. W. D., COUP, J., J. Polym. Sci., Part A-2, 8, p.1803 (1970)
[8] COLL, H., GILDING, D. K., J. Polym. Sci., Part A-2, 8, p.89 (1970)
[9] RUDIN, A., HOEGY, H. L. W., J. Polym. Sci., Part A-1, 10, p.217 (1972)
[10] GRUBISIC, Z., REMPP, P., BENOIT, H., J. Polym. Sci., Part B-5, p.753 (1967)
[11] TROTH, H. G., 5th International Seminar for GPC (1968)
[12] SCHOLTE, Th. G., MEIJERINK, N. L. J., SCHOFFELEERS, H.M., BRANDS, A. M. G., J. Appl.
Polym. Sci., 29, pp.3763-3782 (1984)
[13] YAU, W. W., KIRKLAND, J. J., BLY, D. D., Modern Size Exclusion Liquid Chromatography, John
Wiley & Sons, p.252 (1979)
[14] PROVDER, T., ROSEN, E. M., Separ. Sci., 5, p.437 (1970)
[15] GOEDHAR, D., OPSHOOR, A., J. Polym. Sci., Part A-2, 8, p.1227 (1970)
[16] MOORE, W. R., UDDIN, M., Eur. Polym. J., 5, p.185 (1969)
[17] KRAUS, C., STACY, C. J., J. Polym. Sci., Part A-2, 10, 657 (1972)