K 7244-1 : 1998 (ISO 6721-1 : 1994)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。
JIS K 7244-1には,次に示す附属書がある。
附属書A(参考) 共振曲線
附属書B(参考) 線形挙動からのずれ
附属書C(参考) 参考文献
JIS K 7244は,規格名称を“プラスチック−動的機械特性の試験方法”とし,次の各部によって構成さ
れる。
第1部:通則 (Part 1 : General principles)
第2部:ねじり振子法 (Part 2 : Torsion-pendulum method)
第3部:曲げ振動−共振曲線法 (Part 3 : Flexural vibration−Resonance-curve method)
第4部:引張振動−非共振法 (Part 4 : Tensile vibration−Non-resonance method)
第5部:曲げ振動−非共振法 (Part 5 : Flexural vibration−Non-resonance method)
第6部:せん断振動−非共振法 (Part 6 : Shear vibration−Non-resonance method)
第7部:ねじり振動−非共振法 (Part 7 : Torsional vibration−Non-resonance method)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 7244-1 : 1998
(ISO 6721-1 : 1994)
プラスチック−動的機械特性の
試験方法−第1部:通則
Plastics−Determination of dynamic mechanical properties
−Part 1 : General principles
序文 この規格は,ISO 6721-1 : 1994, Plastics−Determination of dynamic mechanical properties−Part 1 :
General principlesを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業規格であ
る。
なお,この規格で点線の下線を施してある箇所は,原国際規格にはない事項である。
1. 適用範囲
この規格の各部では,線形粘弾性挙動を示す範囲での硬質プラスチックの動的機械特性試験方法を規定
する。第1部は導入部分であり,用語の定義及び後続の部における個々の試験方法に共通する事項につい
て記述する。
異なる変形モードで測定した場合,必ずしも一致しない結果が得られる場合がある。例えば,引張振動
試験では試料の厚み方向で一様の応力が得られるのに対して,曲げ試験では表面領域における試験片の特
性の影響を強く受ける。
ひずみの値が応力と比例関係にある範囲で,かつ,試験片が均一な場合にだけ,曲げ試験結果の値は引
張試験結果と一致する。
2. 引用規格
次の規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この規格の発行
の時点では,引用規格はここに示す発行年の版の規格が有効であるが,すべての規格は改正されることが
あるので,この規格の使用者は,引用規格の最新版を適用できるかどうか検討することが望ましい。
ISO 291 : 1977 Plastics−Standard atomospheres for conditioning and testing
ISO 293 : 1986 Plastics−Compression moulding test specimens of thermoplastic materials
参考 JIS K 7151(プラスチック−熱可塑性プラスチック材料の圧縮成形試験片)が,この国際規
格と一致している。
ISO 294 : − Plastics−Injection moulding of test specimens of thermoplastic materials
参考 JIS K 7152(プラスチック−熱可塑性プラスチック材料の射出成形試験片)が,この国際規
格と一致している。
ISO 295 : 1991 Plastics−Compression moulding of test specimens of thermosetting materials
2
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ISO 1268 : 1974 Plastics−Preparation of glass fibre reinforced, resin bonded, low-pressure laminated plates
or panels for test purposes
ISO 2818 : 1994 Plastics−Preparation of test specimens by machining
参考 JIS K 7144(プラスチック−機械加工による試験片の調製)が,この国際規格と一致してい
る。
ISO 4593 : 1993 Plastics−Film and sheeting−Determination of thickness by mechanical scanning
ISO 6721-2 : 1994 Plastics−Determination of dynamic mechanical properties−Part 2 : Torsion-pendulum
method
参考 JIS K 7244-2(プラスチック−動的機械特性の試験方法−第2部:ねじり振子法)が,この
国際規格に一致している。
ISO 6721-3 : 1994 Plastics−Determination of dynamic mechanical properties−Part 3 : Flexural vibration−
Resonance-curve method
3. 定義
この規格の各部において,次に示す定義を適用する。
備考1. ここで定義する用語の多くは,JIS K 6900-1994(ISO 472: 1988, Plastics−Vocabulary)におい
ても定義されている。ここでの定義はISO 472 : 1988と厳密に同一ではないが,同等のもので
ある。
3.1
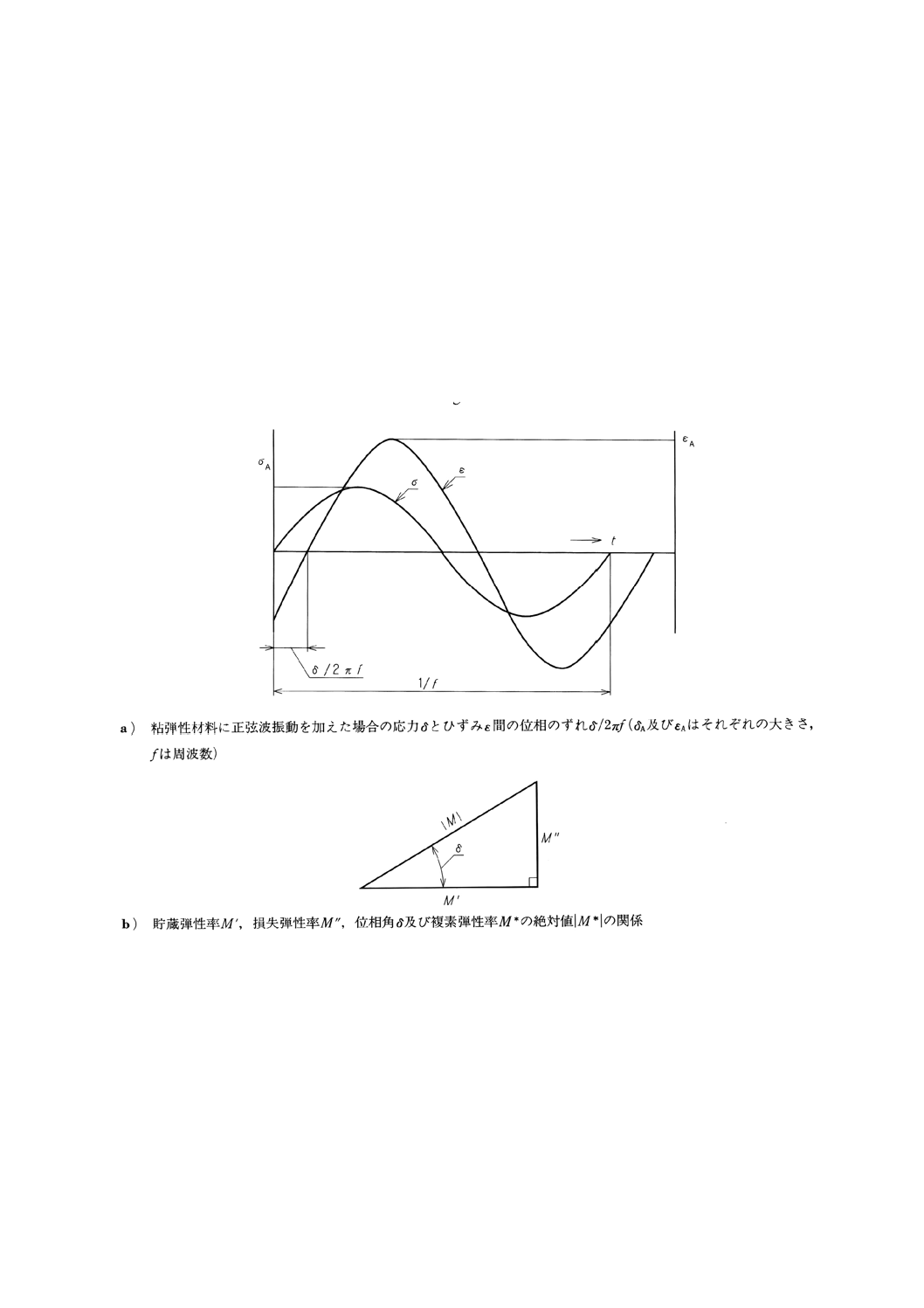
複素弾性率 (complex modulus),M*:粘弾性材料に正弦波振動を加えた場合の動的応力 σ (t) {=
σAexp (i2πft)} と動的ひずみε (t) {=εAexp [i (2πft-δ)]} の比。ここに,σAとεAは,それぞれ応力の振幅及び
ひずみの振幅,fは周波数,δは応力とひずみとの間の位相角(3.5及び図1参照)であり,tは時間である。
単位はパスカル (Pa) である。
変形のモードによって,複素弾性率には,E*,G*,K*又はL*などの種類がある(表3参照)。
M*=M´+iM´´(3.2及び3.3参照) ··············································· (1)
ここに,
i= (−1) 1/2=
1
−
異なる種類の弾性率の間の関係は,表1を参照。
備考2. 等方性の粘弾性体においては,弾性パラメータG*,E*,K*,L*及びμ*のうち二つだけが独
立である(μ*は複素ポアソン比であり,μ*=μ´+μ´´で表す。)。
3. ポアソン比μを含む最も重要な項は“体積項”1−2μであり,これはμが0.5〜0.3の範囲のと
き0〜0.4の間の値をとる。“体積項”を含む表1の関係は,この値が十分な精度で分かって
いる場合にだけ使用することができる。表1から,“体積項”1−2μは体積弾性率K又は一軸
ひずみ弾性率L及びE又はGのいずれかとの組合せにおいて,これらの精度をもってのみ推
定できることが分かる。これは,K及びLの測定には体積ひずみ成分の比較的大きい変形を
伴うためである。
4. これまでのところ,動的体積弾性率Kの測定は行われておらず,K (t) の緩和実験に関する
少数の結果が文献に記載されている。
5. 一軸ひずみ弾性率Lは高い静水圧応力成分の荷重に基づくものである。したがって,Kの替
わりにLの値を使い,(G,L)及び(E,L)の弾性率の組合せから十分な精度で“体積項”1
−2μを算出することができる。Gは静水圧成分に基づかないことから,弾性率の組合せとし
ては(G,L)が好適である。
3
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6. 表1の弾性率間の関係は,複素弾性率についても妥当なものである。
7. この規格の他の部(パート)に示されている弾性率の算出のための関係は,ある程度近似的
なものである。すなわち,例えば,試験片のクランプによって生じる“末端効果”を考慮せ
ず,また他の単純化を施すことがある。したがって,表1に示した関係を使用する際,付加
的な補正が必要となることがある。これらの方法は文献に記載されている[例えば,参考文
献(1),(2)を参照]。
8. 線形粘弾性挙動に対しては,複素コンプライアンスC*は複素弾性率M*の逆数となる。すな
わち,
M*=(C*)−1 ·············································································· (2)
したがって,
M´+iM´´=(C´−iC´´ ) / {(C´)2+(C´´)2} ············································· (3)
図1 位相角と複素弾性率
4
K
7
2
4
4
-1
:
1
9
9
8
(I
S
O
6
7
2
1
-1
:
1
9
9
4
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
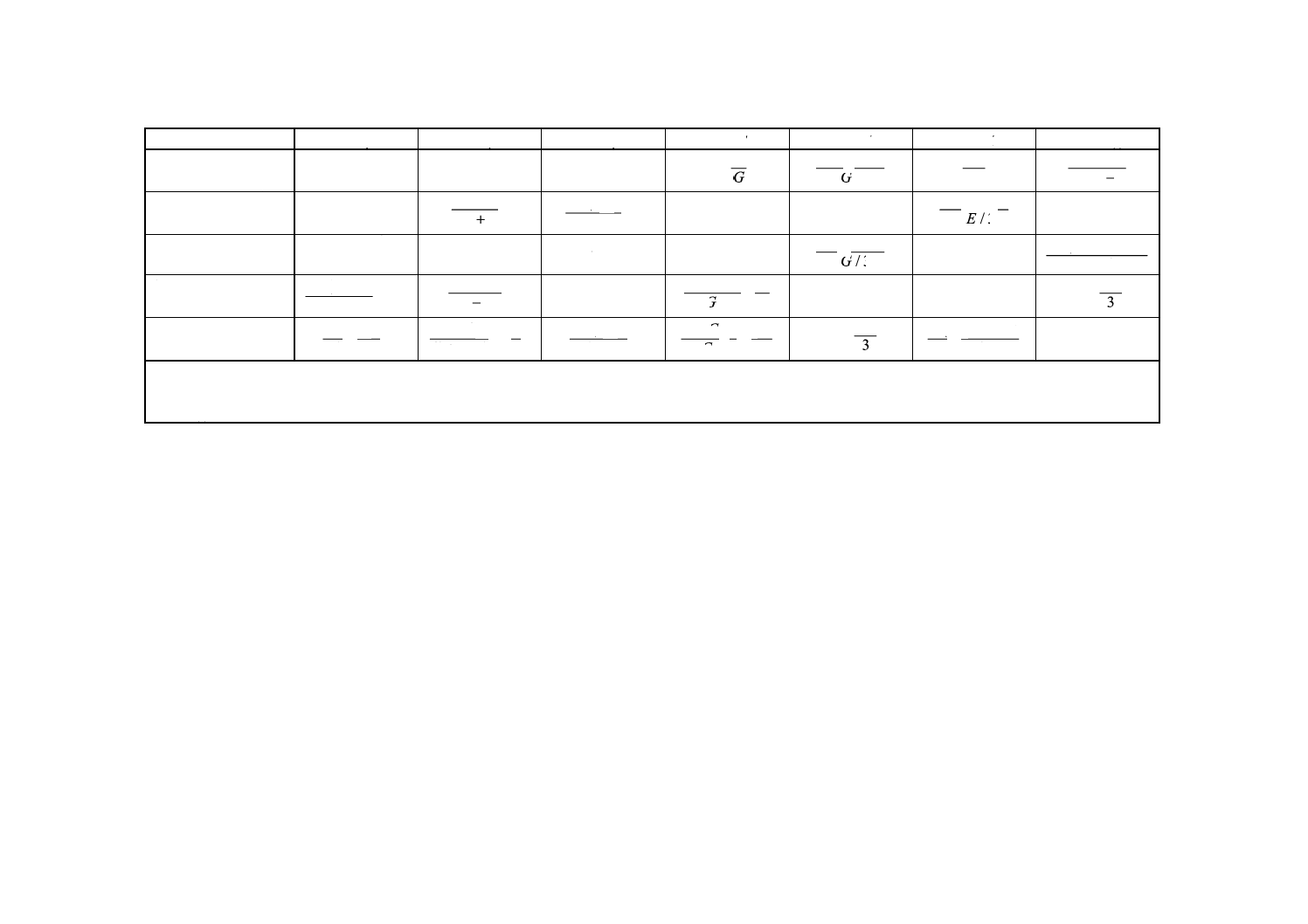
表1 均一等方材料における各種弾性率の関係
Gとμ
Eとμ
Kとμ
GとE
GとK
EとK
GとL(1)
ポアソン比,μ
1−2μ (2)
GE
−
3
K
GK
G
3/
1
/
+
K
E
3
1
/1−
G
L
せん断弾性率,G
)
1(2
μ
+E
)
1(2
)
2
1(
3
μ
μ
+
−
K
K
EE3/
3−
引張弾性率,E
(
)
μ
+
1
2G
)
2
1(
3
μ
−
K
K
GG3/
1
3
+
L
G
L
G
G
/
1
)
3
/
4
1(
3
−
−
体積弾性率,K(3)
)
2
1(3
)
1(
2
μ
μ
−
+
G
)
2
1(3
μ
−E
)1
/
3(3
−
E
GG
34G
L−
一軸ひずみ弾性率又
は縦波弾性率,L
μ
μ
2
1
)
1(
2
−
−
G
)
2
1
)(
1(
)
1(
μ
μ
μ
−
+
−
E
μ
μ
+
−
1
)
1(
3K
1
/
3
)1
/
4(
−
−
E
G
E
G
G
34G
K+
K
E
K
E
K
9
/
1
)
3
/
1(
−
−
注(1) 備考5.参照
(2) 備考3.参照
(3) 備考4.参照
5
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.2
貯蔵弾性率 (storage modulus),M´:複素弾性率M*の実数部分[図1b)参照]。
貯蔵弾性率は,パスカル (Pa) で表示される。
貯蔵弾性率は荷重サイクルを通じて蓄積される最大エネルギーに比例し,粘弾性材料の剛性を表す。
変形モードの違いに基づく貯蔵弾性率の種類は,引張貯蔵弾性率E´f,曲げ貯蔵弾性率E´t,せん断貯蔵
弾性率G´s,ねじり貯蔵弾性率G´to,体積貯蔵弾性率K´,一軸ひずみ貯蔵弾性率L´c及び縦波貯蔵弾性率
L'Wである。
3.3
損失弾性率 (loss modulus),M´´:複素弾性率の虚数部分である[図1b)参照]。
損失弾性率は,パスカル (Pa) で表す。
損失弾性率は1回の荷重サイクルで散逸(消失)したエネルギーに比例する。貯蔵弾性率(3.2参照)と
同様,変形のモードを表3に示した。例えば,E´´tは引張損失弾性率を表す。
3.4
複素弾性率の絶対値 (magnitude of the complex modulus),|M*|:貯蔵弾性率及び損失弾性率の二乗平
均値の平方根であり,次の式で表す。
|M*|2=(M´)2+(M´´)2=(бA/εA)2 ······················································ (4)
ここに,бA及びεAは,それぞれ応力の振幅及びひずみの振幅である。
複素弾性率は,パスカル (Pa) で表される。
複素弾性率における貯蔵弾性率M´,損失弾性率M´´,位相角δ及び絶対値|M*|の関係は図1b)に示されて
いる。貯蔵弾性率と同様,変形のモードは表3に示されている。例えば,|E*t|は引張複素弾性率の大きさ
を表す。
3.5
位相角 (phase angle),δ:粘弾性材料に正弦波振動を加えたときの動的応力と動的ひずみとの位相の
差である(図1参照)。
位相角は,ラジアン (rad) で表す。
貯蔵弾性率(3.2参照)と同様,変形のモードは表3に示してある。例えば,δtは引張位相角を表す。
3.6
損失係数 (loss factor),tanδ:損失弾性率と貯蔵弾性率の比であり,次の式で表される。
tanδ=M´´/M´ ············································································· (5)
ここに, δは応力とひずみの位相角である(3.5参照)。
損失係数は,無次元数として表す。
損失係数tanδは粘弾性系における減衰の尺度としてよく使用される。貯蔵弾性率(3.2参照)と同様,
変形のモードは,表3に示してある。例えば,tanδtは引張損失係数を表す。
3.7
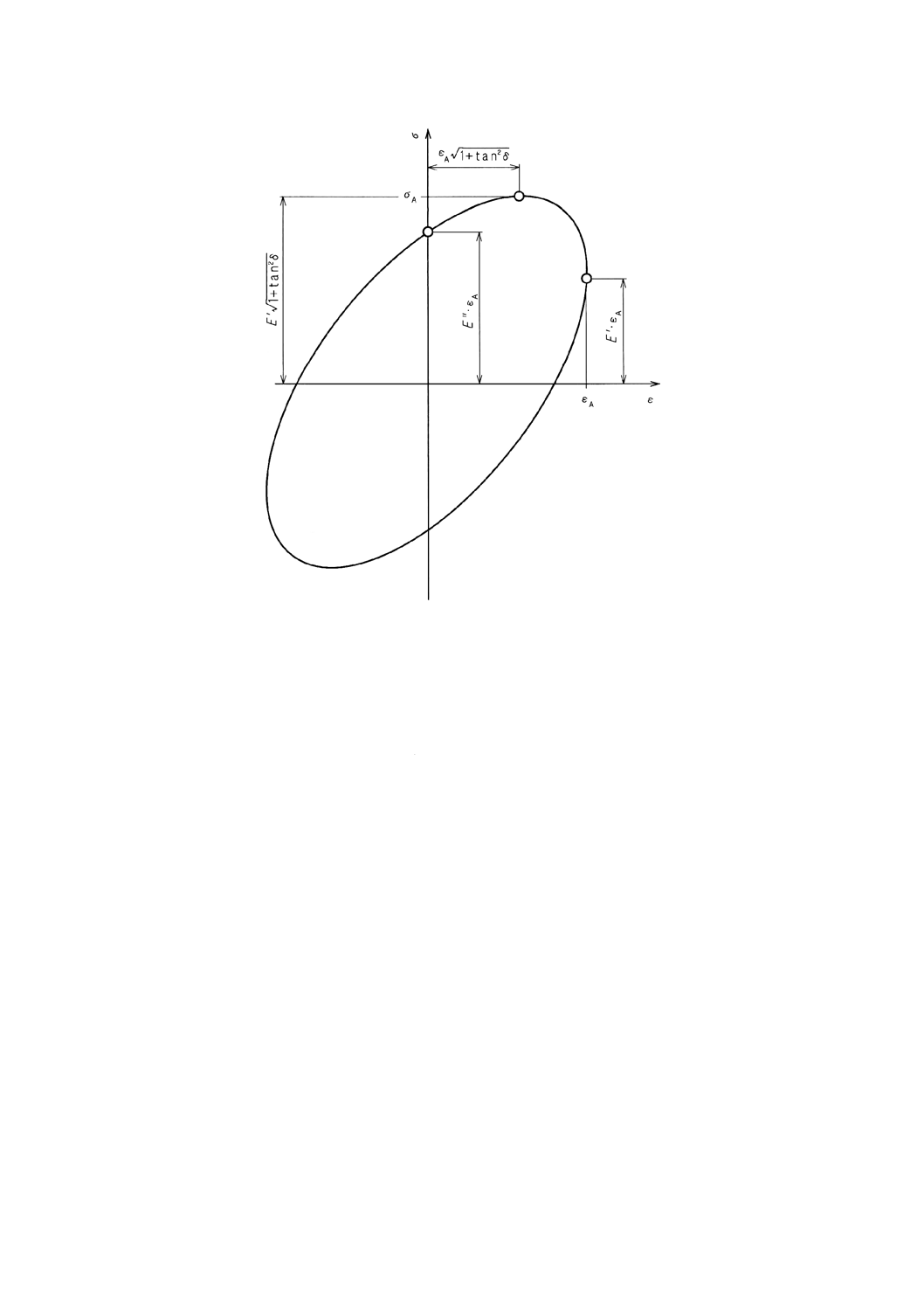
応力−ひずみ履歴曲線 (stress-strain hysteresis loop):粘弾性材料に正弦波振動を加えたときの応力を
ひずみの関数として表示したものである。粘弾性的性質が線形であれば,この曲線は,だ円形となる(図
2参照)。
6
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2 線形粘弾性材料に正弦波引張振動を加えた場合の動的応力−ひずみ曲線
3.8
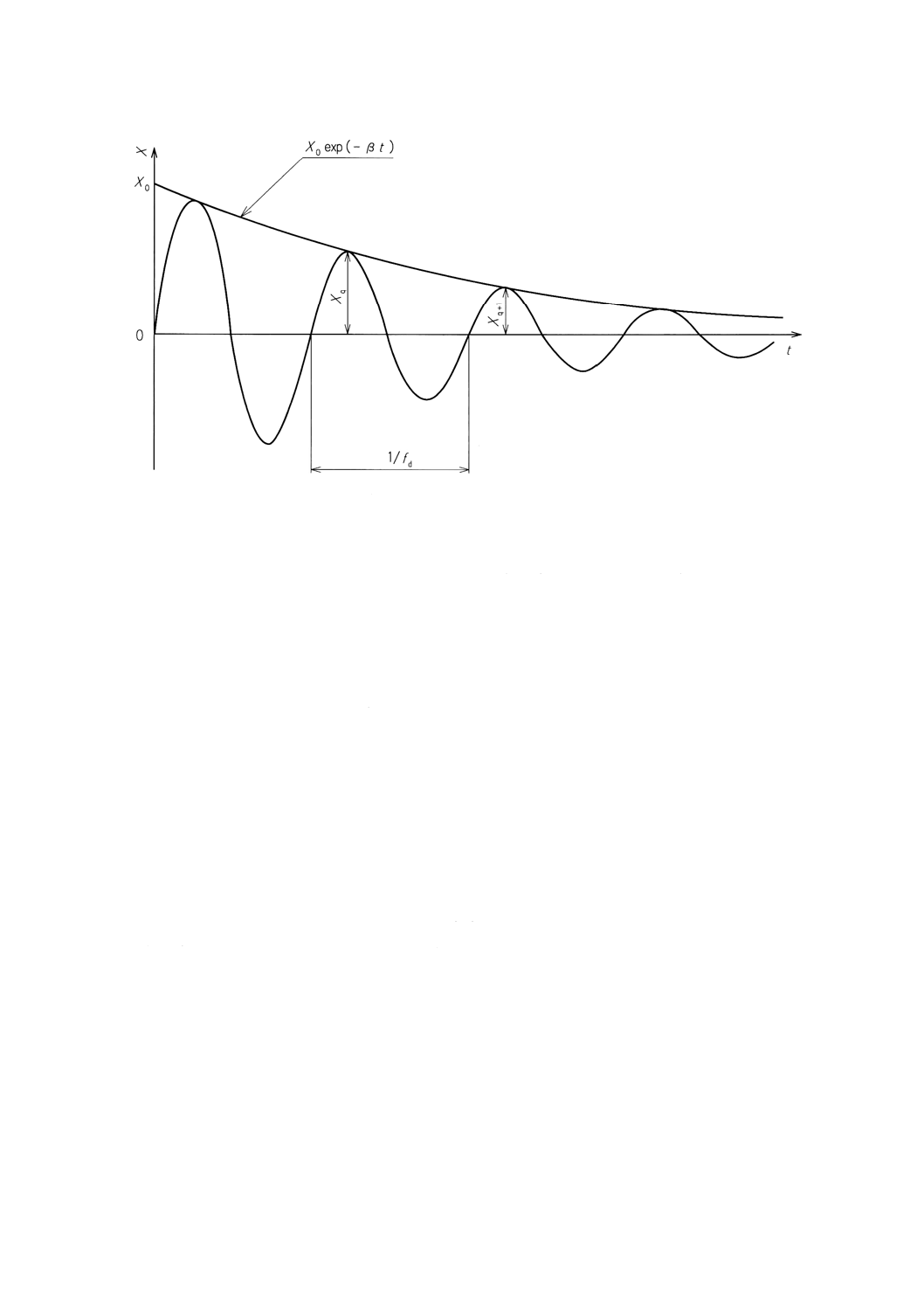
減衰振動 (dampedvibration):粘弾性系が自由減衰振動しているときの時間依存性をもつ変形又は変
形速度X (t) であり(図3参照),次の式で表す。
X (t)=X0exp(−βt)×sin2πfdt ·························································· (6)
ここに,
X0: 時間0における振幅(包絡線)の大きさ
fd: 減衰系の周波数
β: 減衰定数(3.9参照)
3.9
減衰定数 (decay constant),β:自由減衰振動の時間依存性を決める係数,すなわち,変形又は変形速
度におけるXqの時間依存性[図3及び式(6)参照]。
減衰定数は時間の逆数で表す(単位:s−1)。
7
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3 粘弾性体が自由減衰振動しているときの減衰振動曲線
[Xは時間依存性の変形又は変形速度,Xqはq番目サイクルの振幅であり,X0及びβは振幅の指数関数
的に減衰する包絡線を決定する−式(6)を参照]
3.10 対数減衰率 (logarithmic decrement),Λ:粘弾性系の自由減衰振動において,連続した二つの,同一
方向の振幅の比の自然対数をとったものであり(図3参照),次の式で表す。
Λ=ln (Xq/Xq+1) ·········································································· (7)
ここで,Xq及びXq+1は,二つの連続した同一方向の変形又は変形速度の振幅である。
対数減衰率は,無次元数として表す。
対数減衰率は,粘弾性系の減衰の尺度として使用する。
減衰定数βと周波数fdを使用して,対数減衰率は,次の式で表される。
Λ=β/fd ···················································································· (8)
損失係数tanδは,対数減衰率と近似的に,次の式のように表される。
tanδ≒Λ/π ················································································· (9)
備考9. 自由減衰振動は試験を行っている材料の減衰様式(すなわち,粘弾性挙動が線形か非線形か)
及び装置の可動部分と固定部分の摩擦を解析するために,特に適切な方法である(附属書B
参照)。
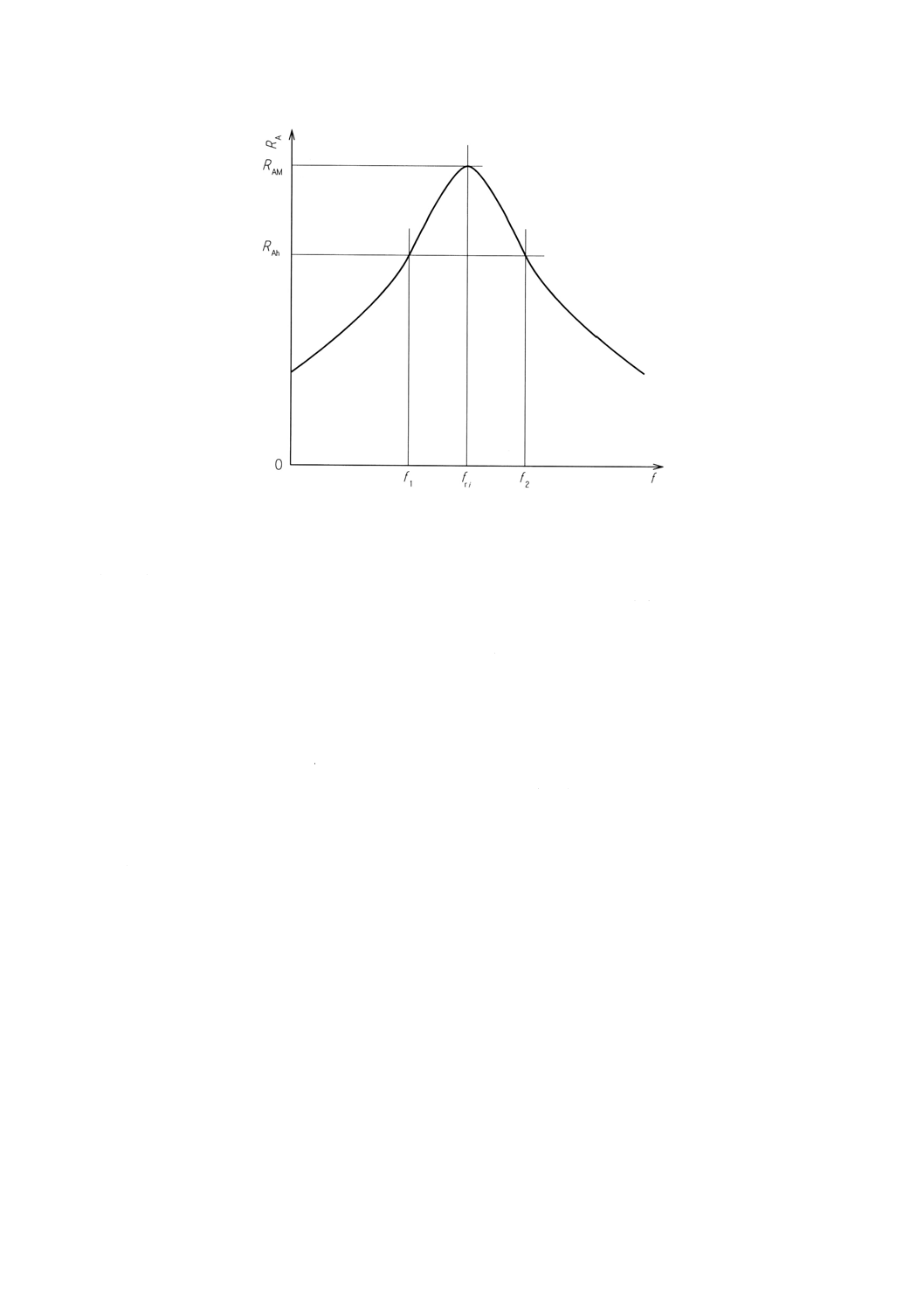
3.11 共振曲線 (resonance curve):一定の荷重振幅 (LA) で,共振点を含む近傍周波数の強制振動を受ける
粘弾性体の変形振幅 (DA),又は変形速度振幅 (RA) の周波数依存性を示す曲線(図4及び附属書A参照)。
8
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4 強制振動を受ける粘弾性体の共振曲線
(一定荷重振幅における変形−速度振幅RAと周波数fの関係,周波数は対数目盛)
3.12 共振周波数 (resonance frequencies) fri:共振曲線のピーク頂上の周波数。iは共振振動の次数を示す(単
位:Hz)。
備考10. 変位振幅の測定から得られる粘弾性材料の共振周波数は,変位速度の測定から得られるもの
とわずかに異なる。材料内の損失が大きいほど,この差異が大きくなる(附属書A参照)。
貯蔵弾性率と損失弾性率は,変位−速度曲線から得られる共振周波数と厳密に関係付けられ
る。変位測定に基づいた共振周波数を使用すると誤差は小さくなるが,試験片が大きな損失
を示す場合には,この誤差が大きくなる。このような条件のときには,共振試験は不適当で
ある。
3.13 共振ピークの幅 (width of a resonance peak) ⊿fi:i番目の共振ピークの周波数f1とf2の差。ここで,
f1とf2における共振曲線の高さ (RAh) はi番目のピークの高さ (RAMi) と次の式の関係がある。
RAh=2−1/2RAM=0.707RAM ··························································· (10)
(図4参照)(単位:Hz)
⊿fiは損失係数(tanδ)と式(11)の関係がある。
tanδ=⊿fi/fri ············································································· (11)
共振曲線が変位−速度振幅に基づき,かつ,⊿fiの周波数範囲内で損失係数があまり変化しないときに,
式(11)は厳密に成り立つ(附属書A参照)。
4. 原理
あらかじめ形状が分かっている試験片に,特定の振動モードと変形モードの機械的振動を加える。振動
モードは,非共振,共振又は共振点近傍かの違いによって,四つのモードI〜IVに分けられる。これらを
表2に示す。
弾性率の種類は変形モードによって異なる(表3参照)。
表4には種々の弾性率の測定法を示す。表5には,この規格(パート)で規定する方法の要約を示す。
9
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
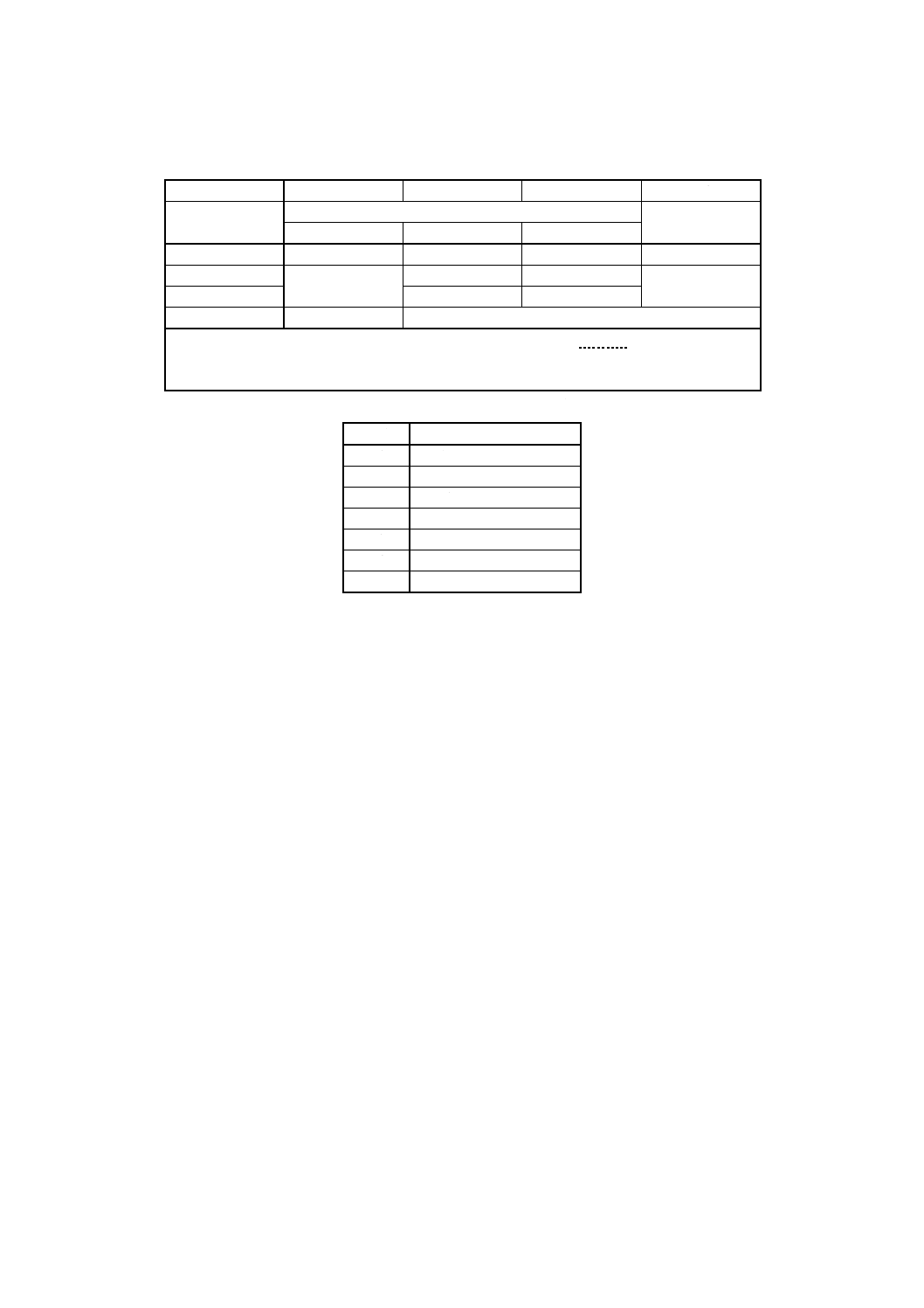
表2 振動モード
(太字が振動モードを示し,細字は付加的な情報を示す。)
振動モード
I
II
III
IV(1)
強制振動
自由減衰の振幅
一定周波数
共振周波数
共振曲線
周波数
非共振
共振
掃引,共振点近傍 おおむね共振点
荷重振幅
一方は定数
他方を測定
定数(2)
定数
励振パルス
変形振幅
測定
測定
慣性質量
なし
周波数範囲によって試験片及び/又は付加質量
注(1) 使用したねじり振子の種類は添字A又はBで示す[JIS K 7244-2 (ISO 6721-2) の図1
及び図2を参照]。
(2) 荷重は変形速度と同位相でなければならない。
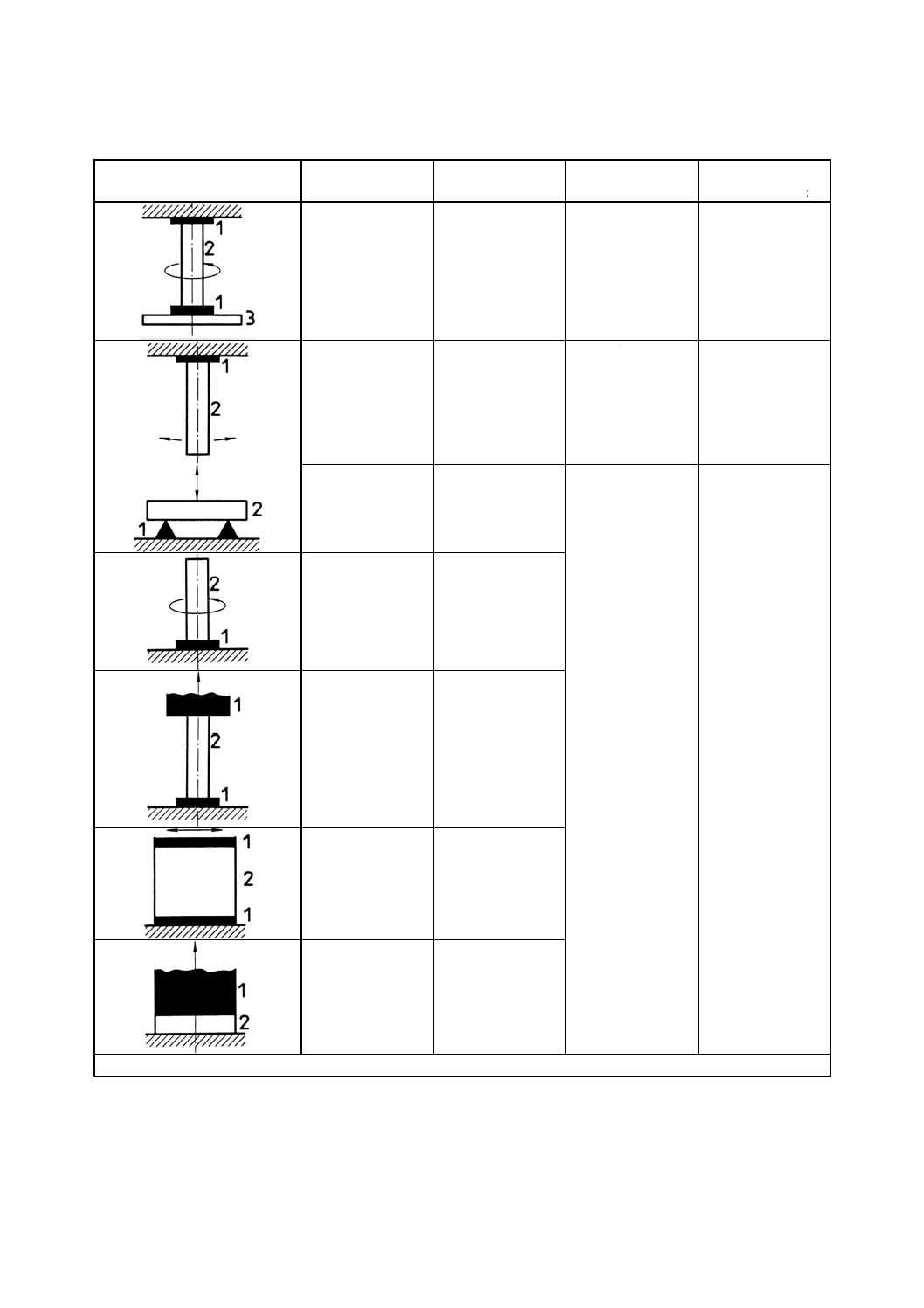
表3 弾性率の種類(変形モード)
記号
弾性率の種類
Et*
引張り
Ef*
曲げ
GS*
せん断
Gto*
ねじり
K*
体積圧縮
Lc*
(薄いシートの)1軸圧縮
Lw*
縦弾性波
10
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
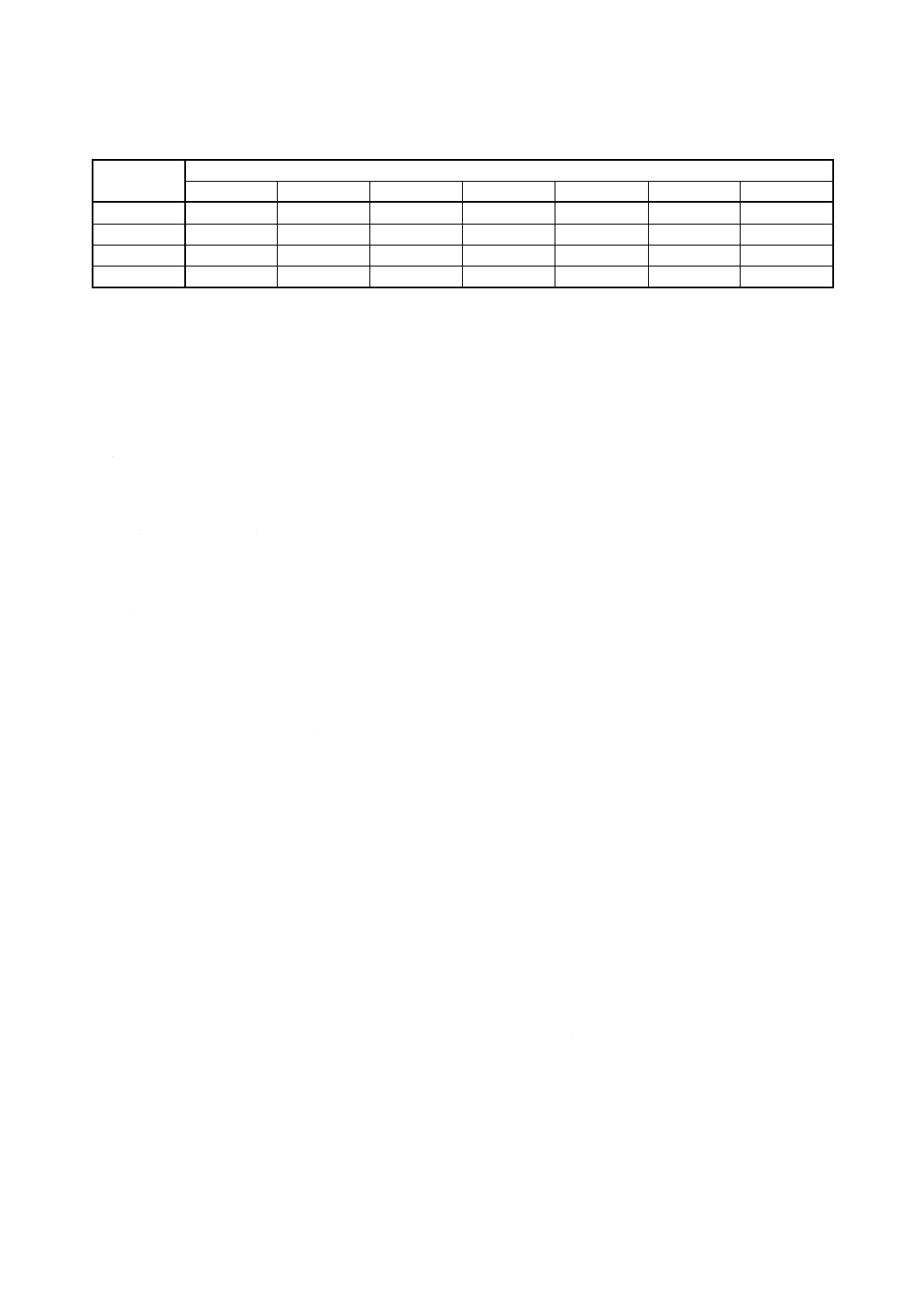
表4 一般的に使われる試験装置
試験装置の模式図
弾性率の種類
と振動モード
適用するJIS K
7244のパート
慣性質量
周波数範囲の
目安 Hz
Gto* IV
パート2
慣性体
0.1〜10
Ef* III
パート3
試験片
10〜1 000
Ef* I
パート5
なし
10−3〜100
Gto* I
パート7
Et* I
パート4
GS* I
パート6
Lc* I
将来は可能
図中 1−つかみ具,支点,支持具;2−試験片;3−慣性体
11
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5 この規格(パート)に規定する方法
振動モード
(表2参照)
弾性率の種類(表3参照)
Et*
Ef*
Gs*
Gto*
K*
Lc*
Lw*
I
パート4
パート5
パート6
パート7
将来は可能
将来は可能
II
III
パート3
IV
パート2
5. 試験装置
5.1
形式
装置は,適用する規格(パート)に詳細に規定されている(序文及び4.参照)。
5.2
機械,電気及び記録装置
適用する規格(パート)による。
5.3
恒温槽
試験片とクランプ又は支持具は,空気又は適切な不活性ガスで満たされた恒温槽内に取り付ける。
恒温槽は試験に十分な温度範囲が得られるものを使用する(例えば,−100℃〜300℃)。恒温槽は,温度
プログラム機能を備え付けたものが望ましい。
槽内の温度は,試験片長さに沿って±1℃以内で均一でなければならない。一定温度の試験の場合(9.5
参照)には,試験中に±1℃以内で安定させる。定速昇温(又は降温)の場合には,温度変化速度は120℃
/hを超えてはいけない。
また,1回の測定(例えば,開始信号後の一連の自由振動又は共振曲線の測定)の中で,±0.5℃以上の
変動があってはならない。
5.4
ガス供給装置
空気又は適切な不活性ガスを,槽内置換のために供給する。
5.5
温度計
試験片の雰囲気温度を測定する温度計は,±0.5℃以内の精度が必要である。応答速度が早い温度計が望
ましい。
5.6
試験片の寸法測定装置
この規格(パート)で弾性率の計算に使用する試験片寸法は室温で測定する。弾性率の温度依存性を測
定する場合にも,熱膨脹の影響は考慮しない。
試験片の長さ,幅,厚さは,±0.5%以内の精度の測定装置を使用して測定する(ISO 4593による。)。
6. 試験片
粘弾性は,試験片寸法の不均一さ及び物理的状態(例えば,結晶化度,配向,又は内部応力)によって,
変化する。
個々の材料について,試験片の寸法と許容差,作製法又は状態調節法を決定する際には,これらの因子
を考慮する必要がある。
均質材料,積層材料いずれでも,試験片のひけ及び反りは,測定温度範囲内で無視できる程度でなけれ
ばならない。
6.1
形状及び寸法
12
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
適用する規格(パート)による。
6.2
試験片の作製
試験片は,原材料,最終製品を問わず,その材料に適用される規格(パート)に従って作製する。圧縮
成形板[JIS K 7151-1995 (ISO 293),ISO 295及びISO 1268による。],又は最終製品から切削加工[JIS K
7144 (ISO 2818) による。]してもよいし,射出成形[JIS K 7152-1995 (ISO 294) による。]してもよい。
7. 試験片の数
単一の温度と周波数で測定する場合には,最低3個の試験片を用いる。品質管理のために,温度及び/
又は周波数を変化させる場合には,1個の試験片でよい。それ以外の場合には,最低2個の試験片を用い
る。
8. 状態調節
試験片は,試験される材料の規格に規定する方法によって状態調節を行う。この規定がなく,受渡当事
者間の協定もない場合は,ISO 291の中の最も適した条件を選んで行う。
9. 手順
9.1
試験雰囲気
試験温度(又は温度の変化速度),雰囲気(空気又は不活性ガス),及び相対湿度は試験法と試験の目的
に従って,選択する。
9.2
試験片断面積の測定
試験前に,各試験片の厚さと幅を長さ方向に沿った5か所で±0.5%の精度で測定する。肉眼で分かる欠
陥,例えば,凹みがある試験片や厚さ又は幅の変動が平均値の3%より大きい試験片は使用しない。厚さ
が不均一な試験片,例えば,末端の切り落とし部分は,損失係数の測定だけに使用できる。
これ以外の形状の試験片の寸法測定方法は,受渡当事者間の合意による。
9.3
試験片の取付け
適用する規格(パート)による。
9.4
温度依存性の測定
試験片温度は,測定中に低温から高温に変化させるのがよい。振動周波数は一定のまま(振動モードI),
温度上昇とともに低下する(振動モードIIとIV),又は変化させる(振動モードIII)(表2参照)。
温度依存性の試験では,試験片全体が各温度で平衡状態になるように,階段状の昇温か,又は十分に遅
い定速昇温を行う。平衡状態に達する時間は試験片の大きさと使用する装置によって変化する。1℃/min
〜2℃/minの定速昇温,又は2℃〜5℃のステップで3分〜5分安定させる階段状昇温が適切である。振動
モードIIIではステップ間隔10分が望ましい。
高分子材料の動的弾性率は,一般に測定時の試験片の物理的エージング状態によって変化する。エージ
ング状態は,試験片の熱履歴に依存し,α−緩和の中心温度θα以下の温度では時間とともに変化する。α
−緩和は最も高温の力学緩和機構であり,非晶性高分子ではガラス状態からゴム状態への転移に対応する。
物理的エージング状態の変化は分子運動性に影響し,さらに動的な荷重や変形に対する応答に影響を与え
る。
昇温過程で測定する場合に,温度がθαに近づくと物理的エージング状態の変化が試験中でも起こる。試
験後に試験片を冷却し再測定しても,一般に試験前とは異なった物理的状態になるので,初期の値とは異
13
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
なる値になる。測定精度向上のためには,試験片の熱履歴及び昇温測定の場合には昇温速度を記録するこ
とが必要である。
9.5
周波数依存性の測定
周波数依存性の測定の場合には,試験温度は一定にする。試験片の振動周波数は,粘弾性測定の合間に
変化させる。
10. 結果の表示
表3の変形モードと表2の振動モードを組み合わせて弾性率を表示する。例えば,
E´´f (III)−共振曲線を用いて測定した曲げ損失弾性率
貯蔵弾性率と損失弾性率のそれぞれの平均値と,必要なときには標準偏差を報告する。
また,複数の周波数で測定した貯蔵弾性率と損失弾性率の温度依存性のグラフ及び複数の温度で測定し
た貯蔵弾性率と損失弾性率の周波数依存性のグラフを用意する。このとき,弾性率と周波数は対数表示す
る。
詳細は,適用する各部(パート)による。
11. 精度
ISO 6721の各部(パート)のうち,関連する規格(パート)による。
12. 報告
試験報告は,次の事項を含むこと。
a) 規格番号:ISO 6721の各部(パート)。
b) 試験材料の特定に必要なすべての事項:形式,出所,製造番号及び履歴を含む。
c) 試験片がシートの場合,次の事項:シートの厚み及びシートの主軸に対する試験片の方向。
d) 測定日。
e) 試験片の形及び寸法。
f)
試験片の作製方法。
g) 試験片の状態調節の詳細。
h) 試験片の数。
i)
試験雰囲気が空気以外の場合,その試験雰囲気の詳細。
j)
試験機に関する記述。
k) 試験の温度プログラムについての次のような事項:開始温度,終了温度及び昇温速度,又は昇温ステ
ップの型と持続時間。
l)
10. 結果の表示の項に記したように作製したデータの表。
m) 10. 結果の表示の項に記したように作製した弾性率対温度又は弾性率対周波数のプロット。
14
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(参考) 共振曲線
A.1 力学的に不動な粘弾性体が一定振幅で異なる周波数の振動力を受けると,単一共振又は多重共振挙動
を示す。この挙動は変形の振幅DA又は変形速度の振幅RAで表す。
A.2 振動試験で,共振の挙動は変形振幅DA対周波数fのプロットで表される。この種の共振DA (f) の特
徴は,A.2.1〜A.2.4に示される。
A.2.1 単一の振動次数に対して,低周波数においては,DAは限界となる“静的”振幅DAO (f=0) になり,
高周波数では,両軸を同じ対数目盛を使ってプロットすると,限界となる傾き−2 (−40dB/decade) になる。
A.2.2 ピーク振幅DAMでの共振周波数fRDは,固有周波数fn(同じ系で減衰のない場合)と異なる。しかし
ながら,最後のパラメータは複素弾性率の貯蔵成分M´を決定する。したがって,M´は,DA (f) 曲線から
近似的に計算することができる。
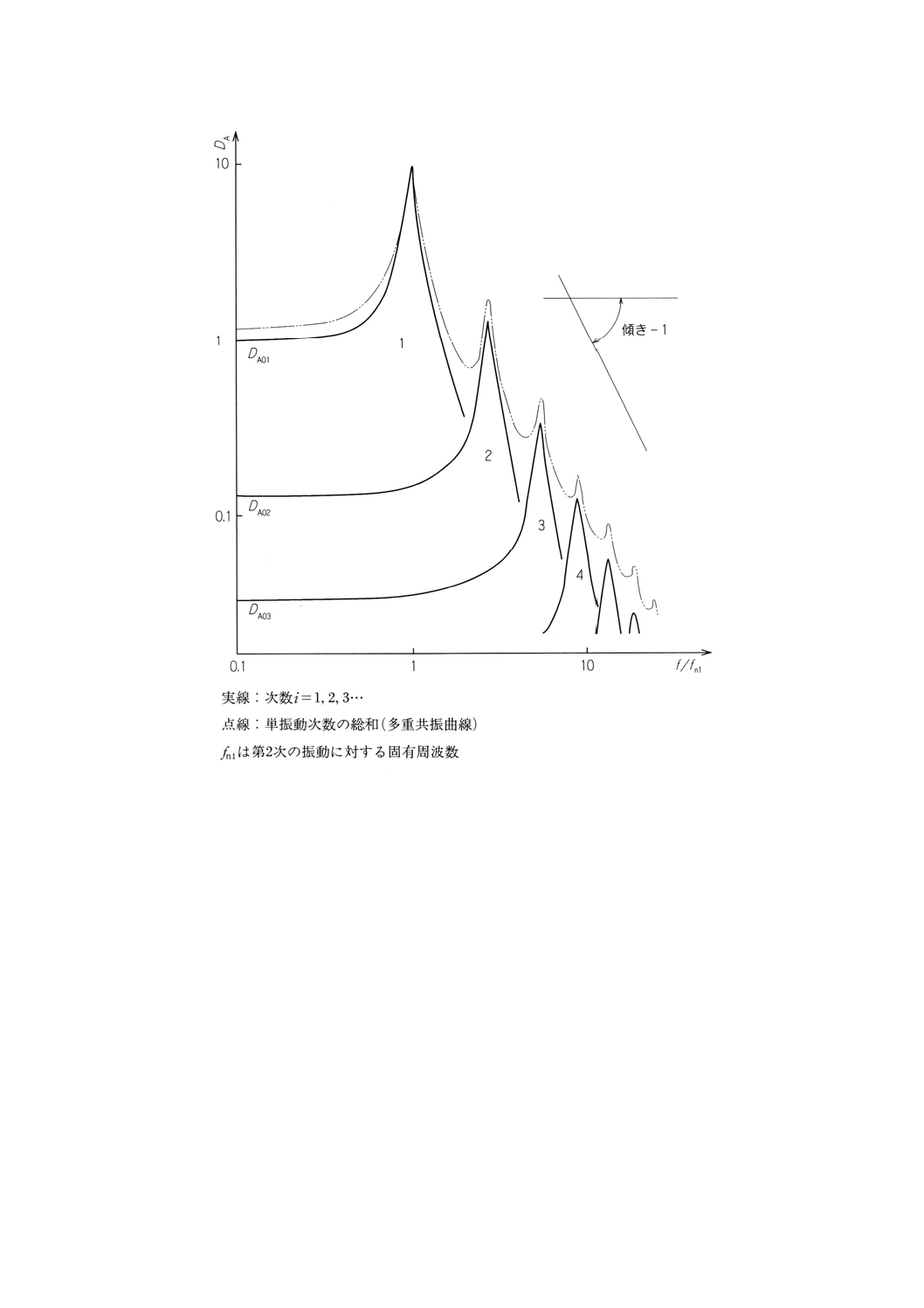
A.2.3 一連の振動次数iで共振振幅DAMiは,ほぼ (fRi)−2に比例して著しく減少する(図A.2参照)。
A.2.4 DA (f) 共振曲線の周波数幅⊿f(3.13参照)に対して複雑な式が存在し,損失係数tanδがおおよそ算
出できる(表A.1参照)。
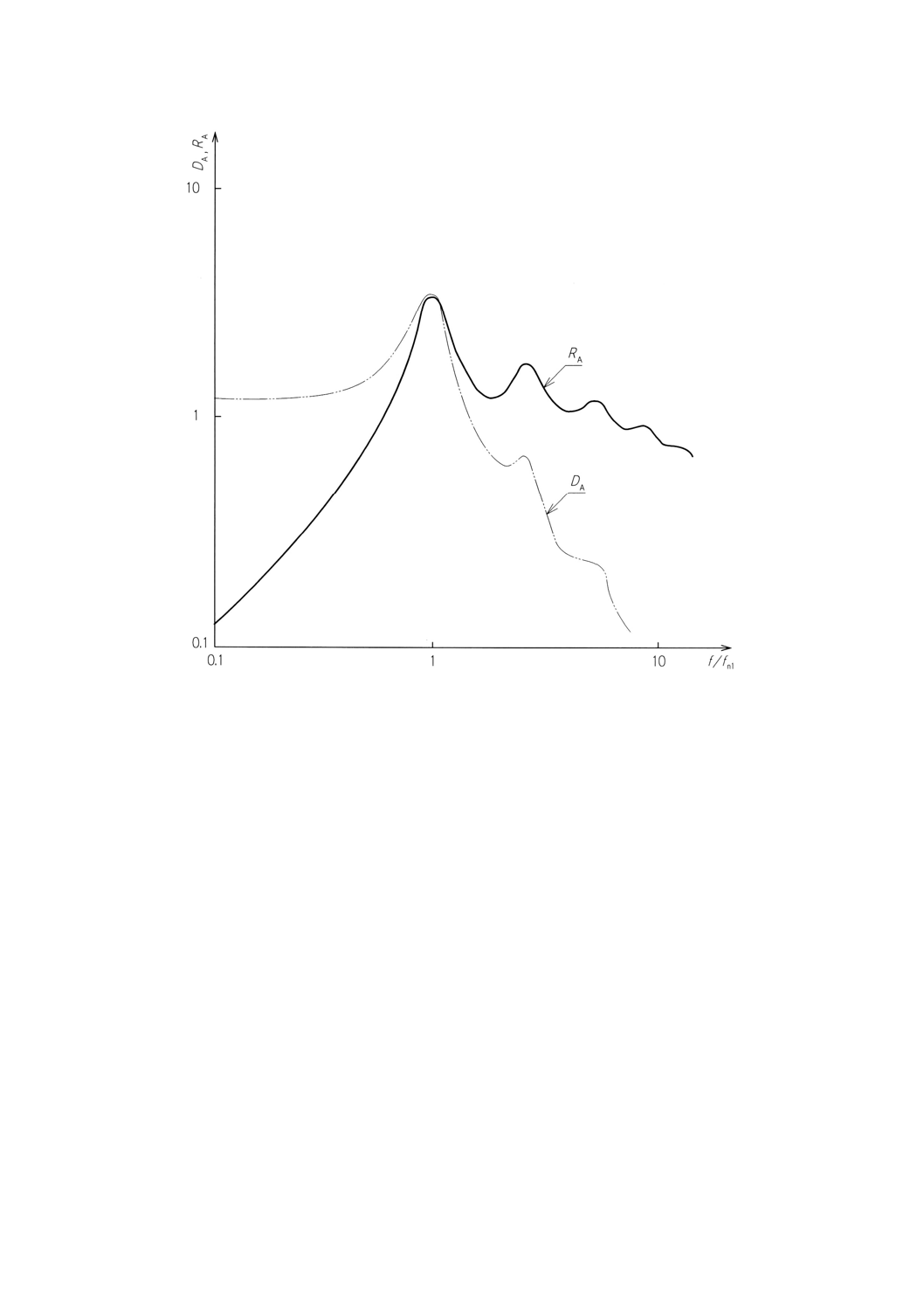
A.3 共振曲線は,変形速度振幅RA (f) のプロットとしても表される。前述したDA (f) のプロットと比較す
ると,A.3.1〜A.3.4に示すように,この形のプロットは多くの長所をもつ。
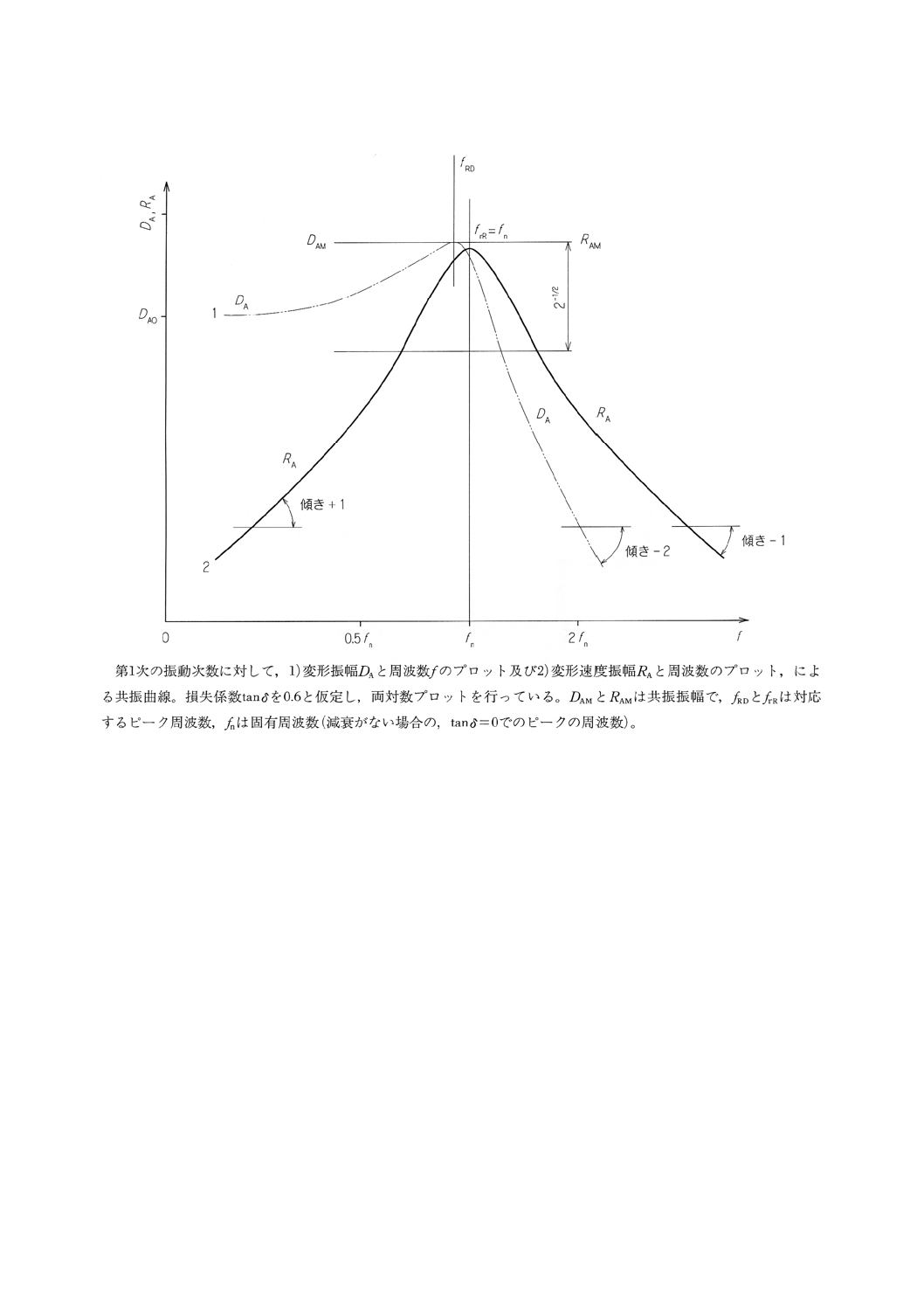
A.3.1 単一共振に対しては,RA (f) 共振曲線を同じ対数目盛でプロットすると,対称形の曲線となり低周
波数で傾き+1の直線,高周波数で−1の傾きの直線 (±20dB/decade) に漸近する(3.13及び図A.1参照)。
A.3.2 ピーク振幅RAMでの共振周波数frRは固有振動数fnと一致する。これは複素弾性率の貯蔵成分M´に
対する正確な方程式を与える(備考10.参照)。
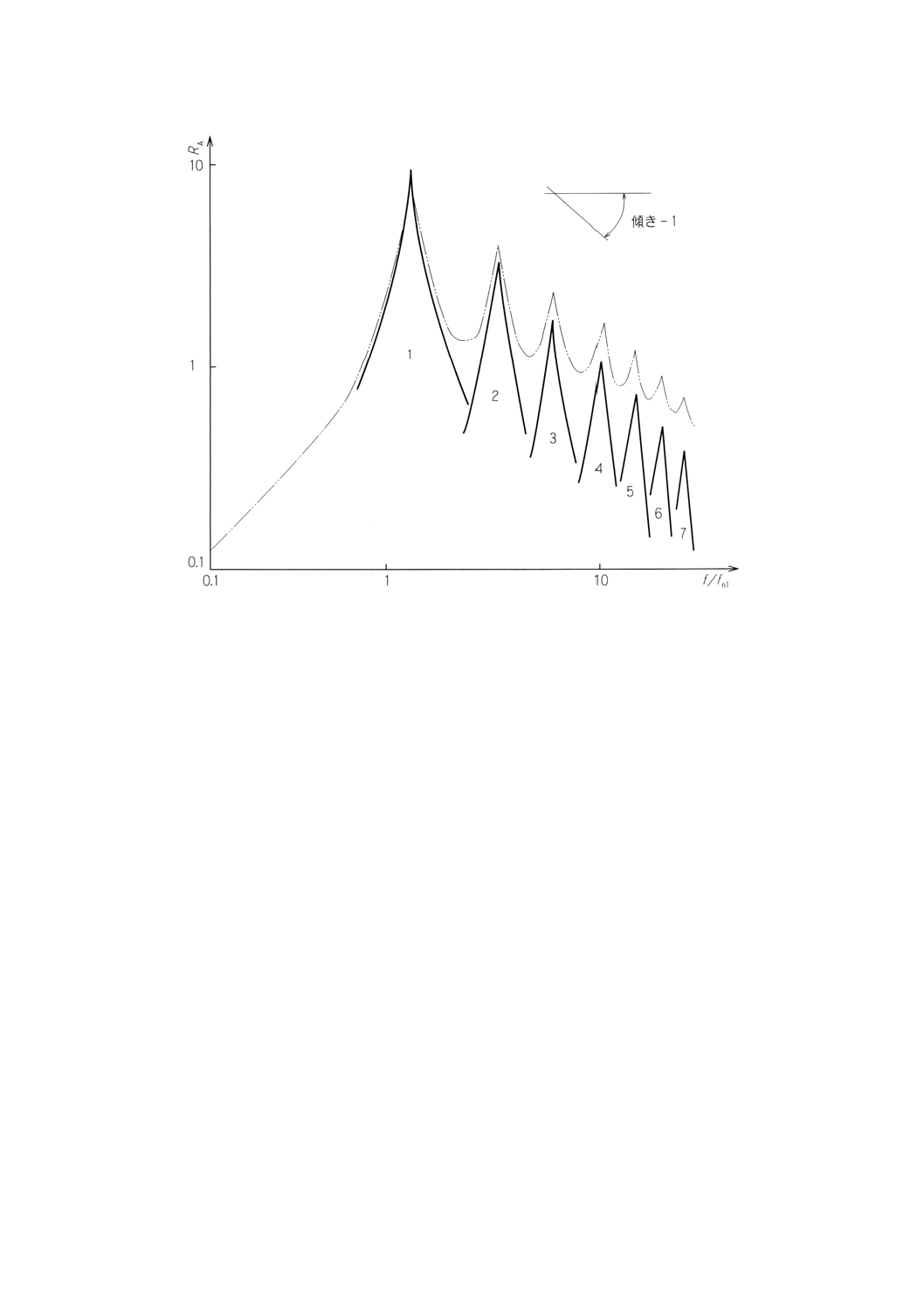
A.3.3 一連の共振次数で,共振振幅RAMiは,(fni)−1にだけ比例して減少する。高減衰材料に対しては,かな
り広い範囲の振動次数(図A.3参照)があり,高次 (i>1) でよい分解能を示す(図A.4参照)。
A.3.4 周波数幅⊿fと損失係数の間の簡単な関係がある(表A.1及び3.13参照)。
A.4 ほとんどの型式の測定装置で,誘導タイプの振動検出器が使われているので,変形速度の振幅が記録
される(搬送周波数系では,変形振幅が測定される。)。
A.5 表A.1に示した方程式から分かるように,変形タイプの共振曲線に対する関係と,変形速度タイプの
共振曲線に対する関係との間の差は,損失係数≦0.1では無視できる。
1
5
K
7
2
4
4
-1
:
1
9
9
8
(I
S
O
6
7
2
1
-1
:
1
9
9
4
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
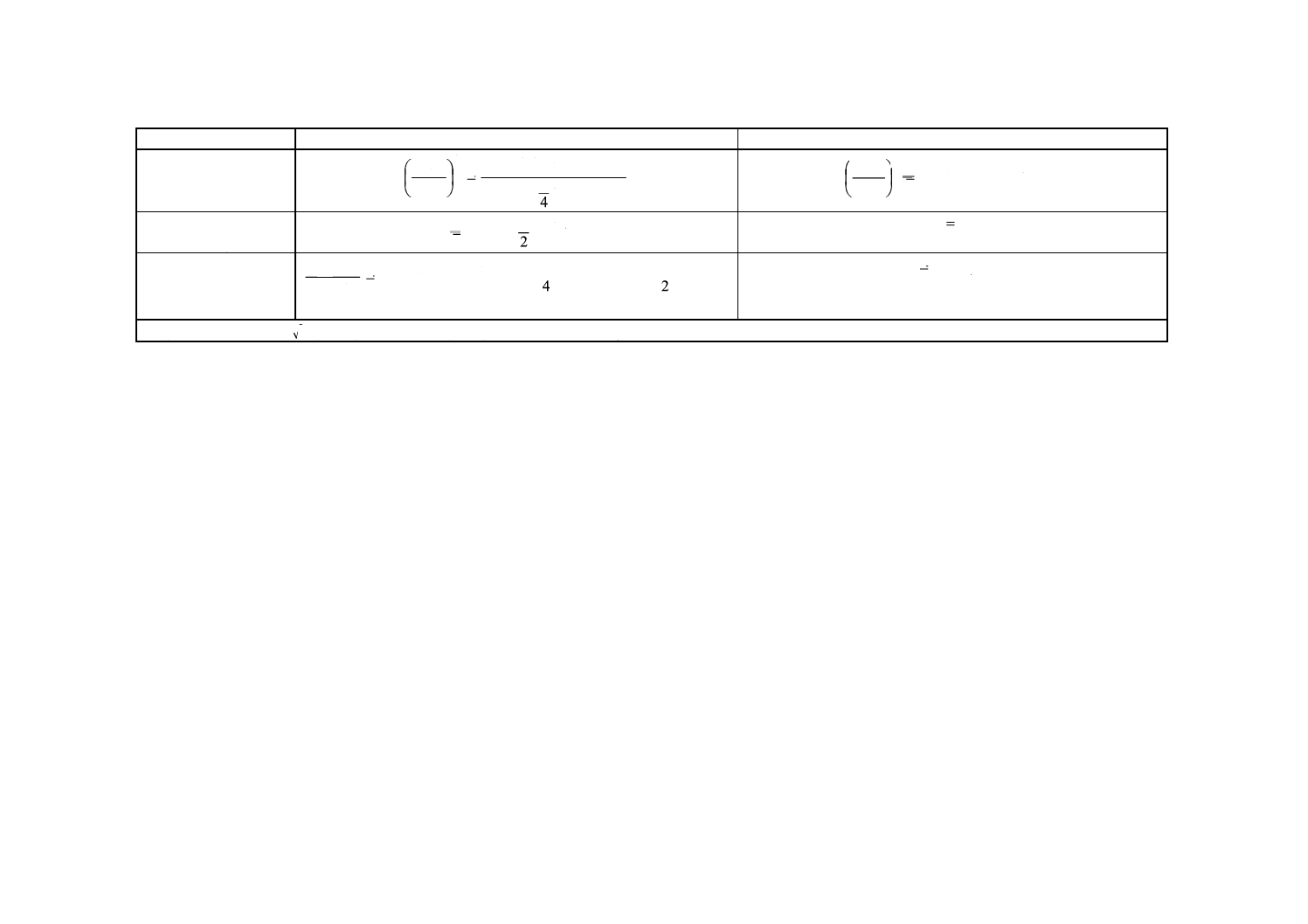
表A.1 変形共振DA (f) と変形速度共振RA (f) を含む方程式(単一振動次数)
変形振幅DA
変形速度振幅RA
共振曲線の方程式
ここで,x=f/fn
δ
δ
2
2
2
2
2
2
tan
41
1
tan
/
)
1(
−
+
−
=
x
x
D
D
A
AM
δ
2
2
1
2
tan
/
)
(
1
−
+
+
=
x
x
R
R
A
AM
固有周波数
ここで,M'∝fn2
(
)
2
/
1
2
tan
21
1
−
−
=
δ
RD
n
f
f
rR
n
f
f=
幅⊿fと⊿f2
ここで,aは振幅の相
対的な減少(減衰)(1)
(
)
(
)
2
/
1
2
2
/
1
2
2
/
1
2
2
2
tan
21
1
tan
41
1
)1
(
tan
)
(2
δ
δ
δ
−
×
+
×
−
×
=
∆
a
f
f
RD
2
/1
2
)1
(
tan
/
−
=
∆
a
f
f
n
δ
注(1) aの推奨する値は (〜3dB),すなわち,(a2−1)1/2=1。この場合,⊿fは普通,半値幅と呼ばれる。
2
16
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.1 共振曲線
17
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.2 tanδ=0.1で,両端自由の曲げ振動試料について,振動次数i=1,2,3の変形振幅DAを
プロットした共振曲線
18
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.3 変形速度振幅RAの関数としてプロットした図A.2と同様な共振曲線
19
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.4 tanδ=0.6での図2,図3と同様な多重共振曲線
20
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考) 線形挙動からのずれ
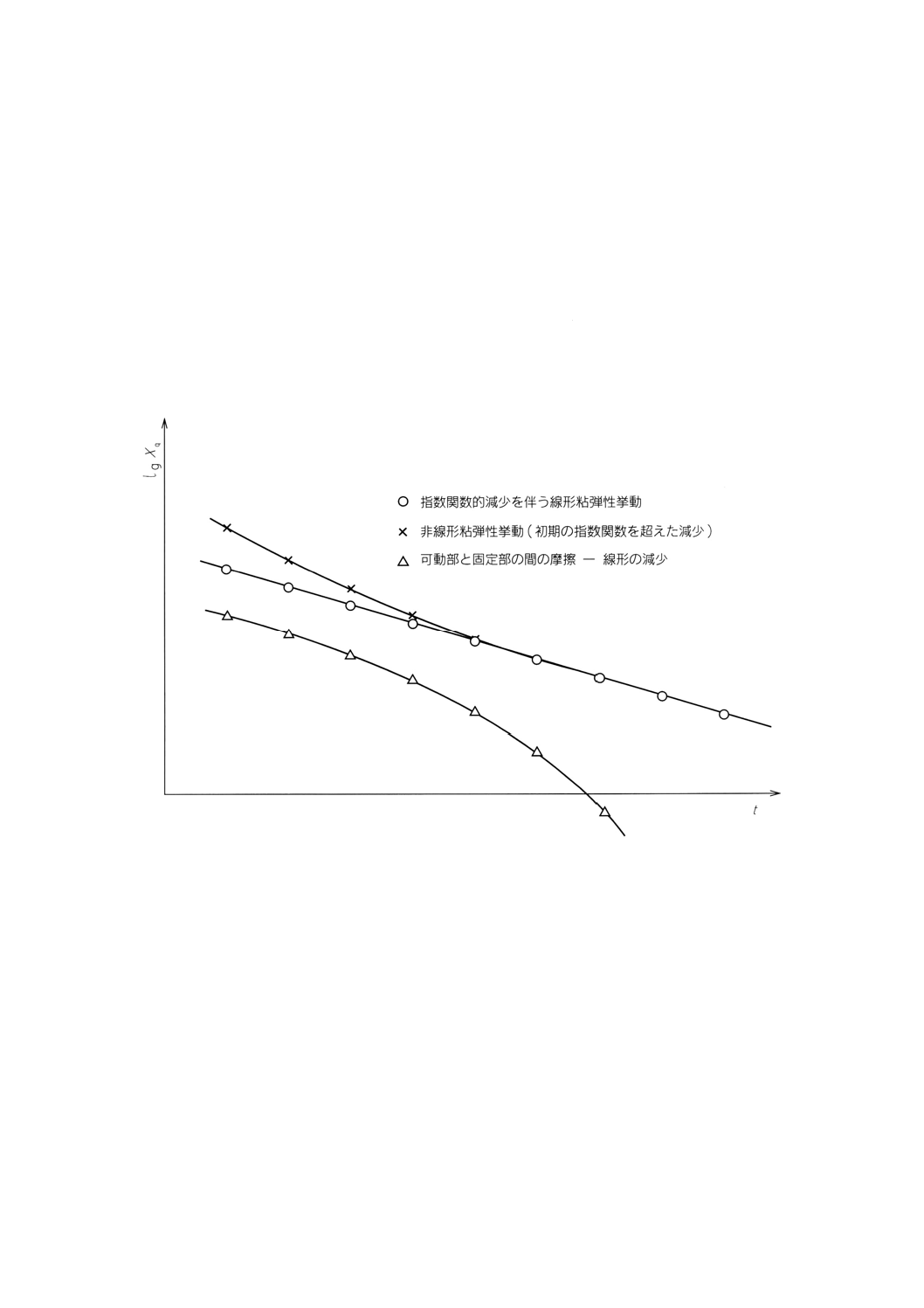
図B.1は,自由減衰振幅Xqと時間t(丸で示された点)の関係の片対数プロットを示している。この種
のプロットは減衰特性の線形性についての良いテストとなる。テストで,材料の線形挙動の範囲を超えて
いる初期振幅は,一般に指数関数を超えた減衰(図B.1でのx)を示す。もし,試料の減衰が極端に低く,
周囲を取り巻く空気による振動系の減衰が重要となるならば,同様な挙動が観察される。しかしながら,
三角形で示した点は指数関数的なプロットの代わりに振幅と時間の線形のプロットに対して逆の曲率をも
つ曲線を与える。この種のプロットは装置の可動部と固定部の間の摩擦を示す。両タイプの線形粘弾性挙
動からのずれは自由減衰振動の測定によってだけ検知される。強制振動では,ただ極端に弱い非調和性の
変形が生じる。
図B.1 自由減衰振幅Xqの対数と時間tとの関係
21
K 7244-1 : 1998 (ISO 6721-1 : 1994)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 参考文献
(1) NEDERVEEN, C. J., and VAN DER WAL, C. W. Rheol. Acta, 6 (4), p.316 (1967).
(2) READ, B.E., and DEAN, G.D.“The Determination of Dynamic Properties of Polymers and Composites”,
Adam Hilger, Bristol, 1978.
JIS原案作成委員会 構成表
氏名
所属
本委員会
分科会
(委員長)
中 山 和 郎
物質工学工業技術研究所
○
○
宮 入 裕 夫
東京医科歯科大学医用器材研究所
○
○
宗 宮 詮
慶応義塾大学理工学部
○
増 田 優
通商産業省基礎産業局
○
岡 林 哲 夫
工業技術院標準部
○
橋 本 繁 晴
財団法人日本規格協会
○
小 林 政治郎
小林技術事務所
○
松 島 哲 也
松島塑材研究所
○
小 牧 和 夫
大阪工業技術研究所材料物理部
○
阿 部 聰
東京都立工業技術センター有機化学部
○
馬 場 文 明
三菱電機株式会社材料デバイス研究所
○
我 妻 誠
日本電信電話株式会社NTTグル−プ
事業推進本部
○
○
三 原 観 治
株式会社東洋精機製作所第一技術部
○
増 瀬 英 雄
株式会社島津製作所試験計測事業部
○
斉 藤 英 隆
株式会社エー・アンド・ディ開発技術
センター
○
○
川 村 好 宏
三菱樹脂株式会社平塚研究所
○
○
横 山 昭
三井石油化学工業株式会社サン分析
センター材料物性研究所
○
○
田 辺 久 光
三菱化学株式会社四日市総合研究所物性
分析研究所
○
塚 原 浩
旭化成工業株式会社樹脂技術センター
○
田 中 耕 三
三井東圧化学株式会社総合研究所技術
研究所
○
金 沢 宏 之
住友化学工業株式会社メタアクリル・光学
製品事業部
○
高 野 忠 夫
財団法人高分子素材センター試験・検査
事業部
○
石 田 勝 己
株式会社東洋精機製作所第一技術部
○
市 村 裕
セイコー電子工業株式会社科学機器事業部
○
野 村 亨
レオメトリックス・サイエンティフィク・
エフ・イ−株式会社
○
平 山 泰 生
株式会社リガク新事業開発室
○
桑 田 広 治
株式会社島津製作所試験計測事業部
○
(事務局)
濱 島 俊 行
日本プラスチック工業連盟
○
○
樋 口 秀 臣
財団法人高分子素材センター
○
○
解説文責 中山 和郎













