2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 7131-1994
プラスチックフィルムの
熱刺激電流試験方法
Testing method for thermally stimulated current of plastic films
1. 適用範囲 この規格は,プラスチックフィルムの熱刺激電流(以下,TSCという。)試験方法につい
て規定する。
備考 この規格の引用規格を,次に示す。
JIS B 7503 ダイヤルゲージ
JIS B 7507 ノギス
JIS K 6900 プラスチック−用語
JIS K 7100 プラスチックの状態調節及び試験場所の標準状態
2. 用語の定義 この規格で用いる主な用語の定義は,JIS K 6900によるほか,次のとおりとする。
(1) 熱刺激電流 (TSC) プラスチックのような誘電体や絶縁体の試験片に低温で凍結された誘電分極や
トラップされた電荷が,昇温によって解放されて熱平衡に移行するときに,試験片を挟む外部回路に
流れる電流(図1参照)。
(2) ポーリング電界 誘電分極やトラップへの電荷蓄積を起こさせるため,試験片に印加する直流電界。
(3) 緩和時間 緩和に要する時間の目安となる特性的な時間定数。次の式によって示す。
=
kT
H
exp
0τ
τ
ここに,
τ: 双極子分極の緩和時間 (s)
τ0: 双極子の振動角周波数に関する定数 (s)
k: ボルツマン定数 [1.380 7×10-23 (J/K)]
H: 双極子の配向分極の活性化エネルギー (J)
T: 絶対温度 (K)
(4) 双極子分極 有極性分子の双極子モーメントの配向に基づく分極。次の式によって示す。
P
P
kT
E
N
P
3
2
0
μ
=
ここに,
P0: 飽和分極量 (C/m2)
N: 双極子の密度 (m-3)
μ: 双極子能率 (C・m)
Ep: ポーリング電界 (V/m)
Tp: ポーリング温度 (K)
(5) 誘電率 電束密度Dと電界Eとの関係をD=εEと表すときの比例定数ε。
(6) 比誘電率 誘電率と真空誘電率との比εr。次の式によって示す。
2
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0ε
ε
ε=
r
ここに,
εr: 比誘電率
ε: 誘電率 (F/m)
ε0: 真空誘電率 [8.854×10-12 (F/m)]
(7) 比誘電損率 誘電体に交流電界を掛けるとき,電束密度の変化に位相的遅れがある場合,比誘電率は
複素数となり,次の式によって示される虚数部。
εr=ε'r−iε''r
ここに,
εr: 比誘電率
ε'r: 複素比誘電率の実数部
ε''r: 複素比誘電率の虚数部
(8) ポーリング温度 ポーリング電界を掛けているときの温度。
3. 測定の原理 有極性分子を含むプラスチックフィルムの両面に電極を付着させポーリング電界を印加
すると,双極子分極が発生する。この状態で試験片を冷却して,双極子分極を凍結してから,ポーリング
電界を除いて両電極を電流計を通して接続する。次いで,試験片の温度を上昇させていくと双極子分極の
凍結が消滅していくので,分極電荷によって両電極に誘起されていた正負の電荷が電流計を通して流れ,
TSCが測定される(図1参照)。
4. 試験片の状態調節及び試験室の温度・湿度
4.1
試験片の状態調節 試験片は,原則として試験前にJIS K 7100の標準温度状態2級及び標準湿度状
態2級[温度23±2℃及び相対湿度 (50±5) %]において,48時間以上状態調節を行う。
4.2
試験室の温度・湿度 試験は,原則として4.1に規定する温度及び湿度の室内で行う。
5. 試験装置及び器具
5.1
試験装置 TSCの測定に用いる試験装置は,試験片の温度を一定温度に保持,急冷及び一定の速度
で昇温できる温度制御装置付き試験片容器,試験片を分極するための直流電源,TSCを測定するための直
流微小電流計,温度及び電流を同時に記録する装置などで構成される。
また,TSCは試験環境に依存するため,試験片を一定の雰囲気に保つことができる装置を備えていなけ
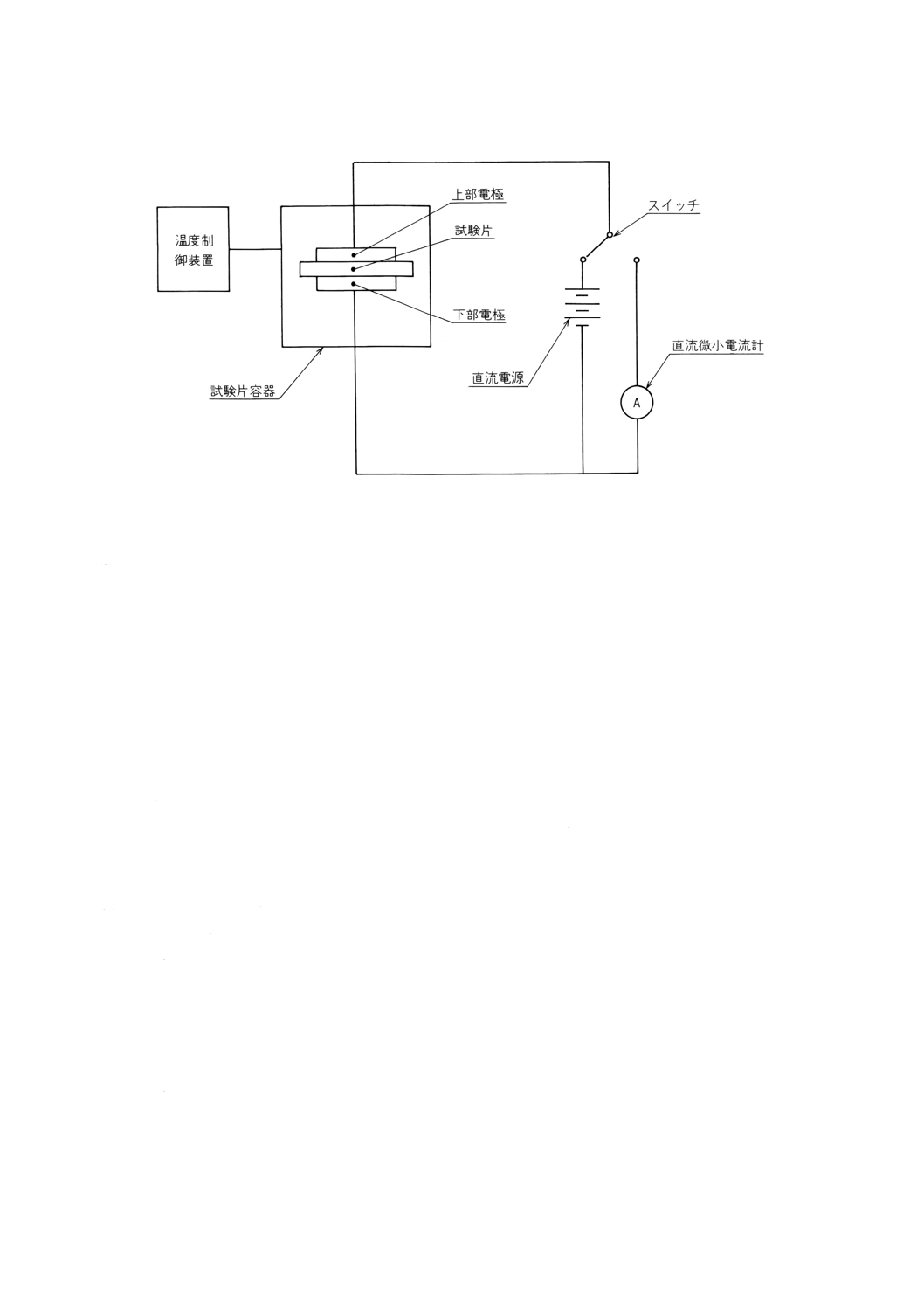
ればならない。試験装置の構成の一例を,図1に示す。
3
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1 試験装置の構成の一例
(1) 試験片容器 試験片容器は,温度制御装置によって所定の温度雰囲気に設定でき,試験片にポーリン
グ電圧を印加し,TSCを測定するための上部電極と下部電極が,それぞれの仮想中心線が一致するよ
う備え付けられているものとする。
(2) 温度制御装置 温度制御装置は,試験片容器中の試験片の温度を一定に保つことができ,かつ,一定
の速度で昇温できるものとする。
また,ポーリング温度から急冷することができる装置(例えば,強制空冷,水冷又は液体窒素冷却)
を備えていなければならない。
(3) 直流微小電流計 直流微小電流計は,TSCを測定するためのもので,0.1pA〜10μAの範囲の直流電流
が測定できるものとする。
5.2
寸法測定器具
(1) 厚さ測定器具 厚さ測定器具は,試験片の厚さを測定するためのもので,JIS B 7503に規定する目盛
0.001mmのダイヤルゲージ又はこれと同等以上の精度のものとする。
(2) ノギス ノギスは,試験片の幅及び長さを測定するためのもので,JIS B 7507に規定する最大測定長
300mm,最小読取値0.05mmのノギス又はこれと同等以上の精度のものとする。
6. 試験片
6.1
試験片の形状及び寸法 試験片の形状は,厚さが均一なフィルム状のもので,大きさは,1〜100cm2
とする。厚さは数100μm以下が望ましい。
6.2
試験片の材質 試験片の材質は,試験時において温度が上昇する間,試験片内部の温度が一様に保
ちうるものでなければならない。
6.3
試験片の数 試験片の数は,5個以上とする。
7. 操作
7.1
試験の準備 試験の準備は,次による。
(1) 寸法測定 試験片の厚さ,幅及び長さを測定する。厚さは,試験片の中心を含む数箇所で0.001mmま
で測定し,平均値を求めておく。
4
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(2) 上部電極及び下部電極に接触する試験片上下面の前処理 上部電極及び下部電極に接触する試験片
の上下面には,同じ面積だけ金属蒸着を行ったり,導電性塗料を塗布するなどして,上部電極及び下
部電極との接触が十分に行われるようにする。
また,試験前に試験片に金属蒸着を行ったり導電性塗料を塗布した有効面積を測定しておかなけれ
ばならない。
7.2
TSCの測定 TSCの測定は,次による。
(1) 試験片容器内の下部電極上に試験片を載せ,試験片の両面に対向するように上部電極を接触させる。
(2) 所定のポーリング温度に保持する。
(3) 試験片にポーリング電界を所定のポーリング時間印加する。
備考 ポーリング電界は,−108〜108V/m程度であり,ポーリング電界の印加時間は数十秒から数十
分である。
(4) 所定のポーリング時間を経過後,試験片の温度を所定の低温まで急冷する。
(5) 温度が所定の低温に安定した後,ポーリング電界を取り去る。
(6) 試験片の表面に付いている不要の電荷を取り去るため,両電極を短絡させた後,所定の速度で昇温す
る。
参考 所定の昇温速度は,毎分1〜10℃程度である。
なお,昇温の最高温度は,試験片の形状が変化を起こさない程度とする。
(7) 昇温中のTSCを読み取り記録する。
備考 記録方法は,試験装置によって異なるが,温度に対するTSC値の変化の曲線をX−Y記録計な
どで作図するとよい。
(8) 繰り返し試験を行う場合は,以下の操作[(9)及び(10)]を行う。
(9) TSCを測定後,次の電界を印加する温度まで冷却する。
(10) 次いで(1)から(7)までの操作を繰り返す。この場合,ポーリング温度,ポーリング電界,ポーリング時
間,昇温速度などを順次変化させて測定する。
8. 試験結果の表し方 試験結果の表し方は,附属書の3.(計算及び試験結果の表し方)による。
9. 報告 報告には必要に応じて次の事項を記録する。
(1) 試験した材料の種類,等級及び製造業者名
(2) 試料の作製方法
(3) 試験片の形状及び寸法
(4) 試験した試験片の数
(5) 試験片の状態調節の温度,湿度及び時間
(6) 試験装置の型式
(7) 試験片に金属蒸着又は塗布した導電性塗料の種類及び有効面積 (cm2)
(8) ポーリング電圧 (V) , ポーリング温度 (℃) 及びポーリング時間 (min)
(9) 試験条件
(a) 昇温開始温度 (℃)
(b) 最高温度 (℃)
(c) 昇温速度 (℃/min)
5
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(10) TSC曲線図
(11) 試験年月日
(12) その他特記すべき事項
6
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書 熱刺激電流測定の原理及び試験結果の表し方
1. 適用範囲 この附属書は,熱刺激電流(以下,TSCという。)の測定の原理及び試験結果の表し方に
ついて規定する。
2. 測定の原理 両面に電極を接触させた厚さのフィルム状試験片において,次の式(1)で求められる緩和
時間をもつ双極子分極をもっているとすれば,温度Tpでポーリング電界
d
V
E
P
P
:
厚さ
電圧
の印加によって次
の式(2)の双極子分極の飽和分極量P0が形成される。
=
kT
H
exp
0τ
τ
········································································ (1)
ここに,
τ: 双極子分極の緩和時間 (s)
τ0: 双極子の振動角周波数に関する定数 (s)
H: 活性化エネルギー (J)
k: ボルツマン定数 [1.380 7×10−23 (J/K)]
T: 絶対温度 (K)
P
P
kT
E
N
P
3
2
0
μ
=
··········································································· (2)
ここに,
P0: 飽和分極量 (C/m2)
N: 双極子の密度 (m−3)
μ: 双極子能率 (C・m)
この場合,電界印加時間tpが,温度Tpにおける双極子分極の緩和時間τより十分長くない場合には,次
の式(3)に従って双極子分極Piが形成される。
−
−
=
τ
P
i
t
P
P
exp
1
0
································································ (3)
ここに,
τ: 温度Tpにおける双極子分極の緩和時間 (s)
tp: 温度Tpにおける電界印加時間 (s)
この場合,tpがτより十分長ければPi=P0となる。
このように双極子分極Piが形成された状態で,急速に試験片を冷却すれば,双極子分極は変化せず,凍
結されたことになる。ここで電界を取り去り,短絡回路で試験片を一定の速度βで昇温すれば,昇温中に
双極子の脱分極によって次の式(4)で求められる電流Iが温度Tの関数として観測され,これがTSCと呼ば
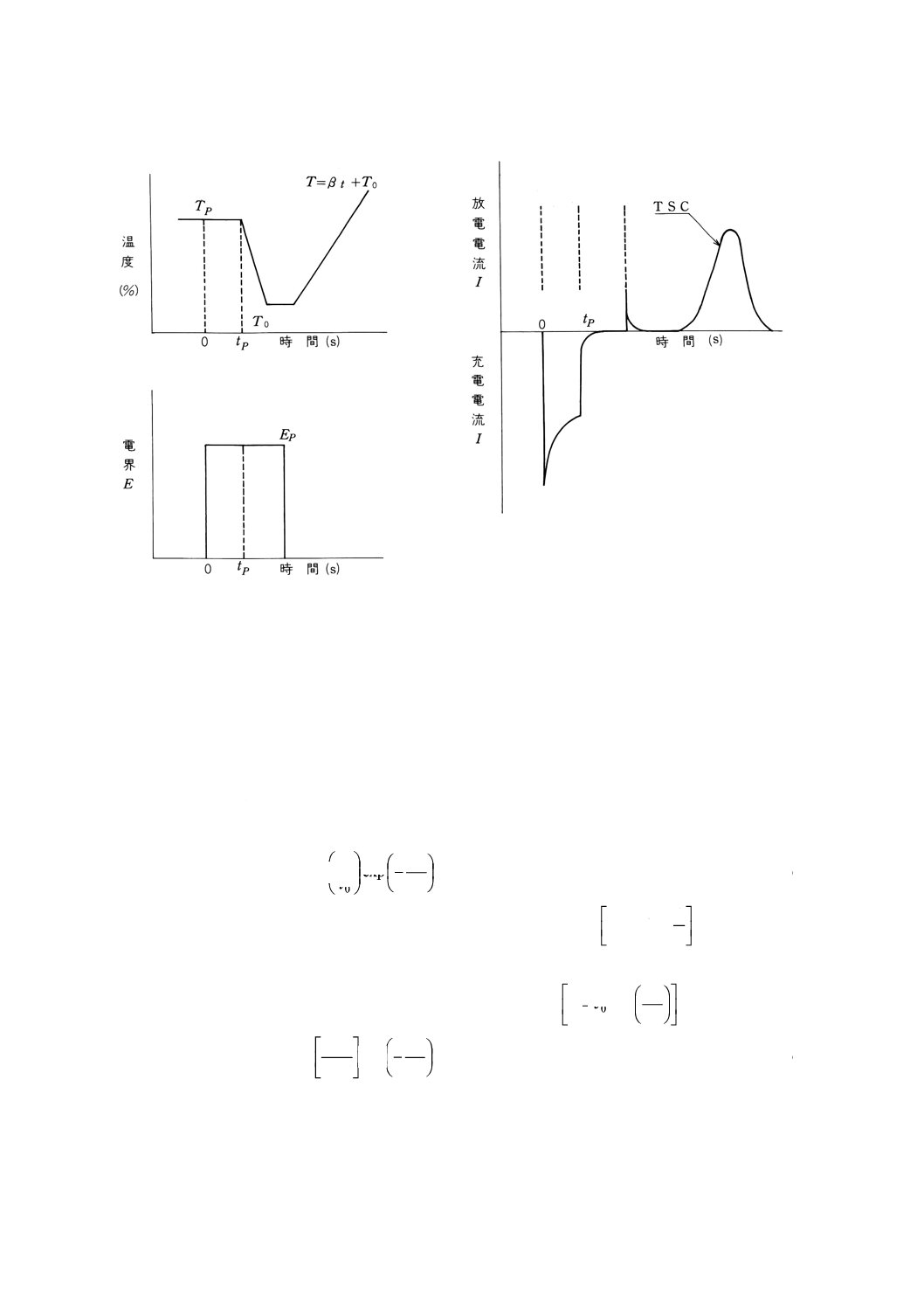
れる。TSC測定の温度,電界及び電流の時間特性を附属書図1に示す。
−
=
kT
H
P
T
I
iexp
)
(
0τ
−
−
∫
−
T
T
dT
kT
H
0
exp
)
(
exp
1
0
βτ
················································· (4)
ここに,
T0: 昇温開始温度 (℃)
β: 昇温速度 (℃/s)
式(4)で求められる電流IがTSCであり,電流ピークが観測され,その時間積分である電荷量はPiとな
る。式(4)のTSCからPi,τ0及びHが求められる。これらを用いて式(1)及び式(3)からP0が計算される。更
に,その双極子分極に起因した誘電率の周波数特性が得られる。
7
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図1 TSCの測定手順
3. 計算及び試験結果の表し方
3.1
双極子分極の決定 双極子分極では,TSCの電界依存性を測定すれば,式(4)の電流値又はその積分
であるTSC電荷量Piが電界Epに比例する。
また,電界の正負で対称的となる。
TSC電荷量Piは,
∫∞
=
0
)
(
dt
T
I
Pi
で表される。
参考 電界範囲は,−108〜+108V/m程度である。
3.2
活性化エネルギー及び緩和時間の求め方
3.2.1
TSCの初期立ち上がり法 TSCの初期立ち上がりにおいて,式(4)は次の式(5)のように近似できる。
−
kT
H
P
T
I
iexp
)
(
0τ
≒
······························································ (5)
したがって,TSCの立ち上がり部分の電流の対数と温度の逆数の関係
T
T
I
1
〜
)
(
ln
をプロットするこ
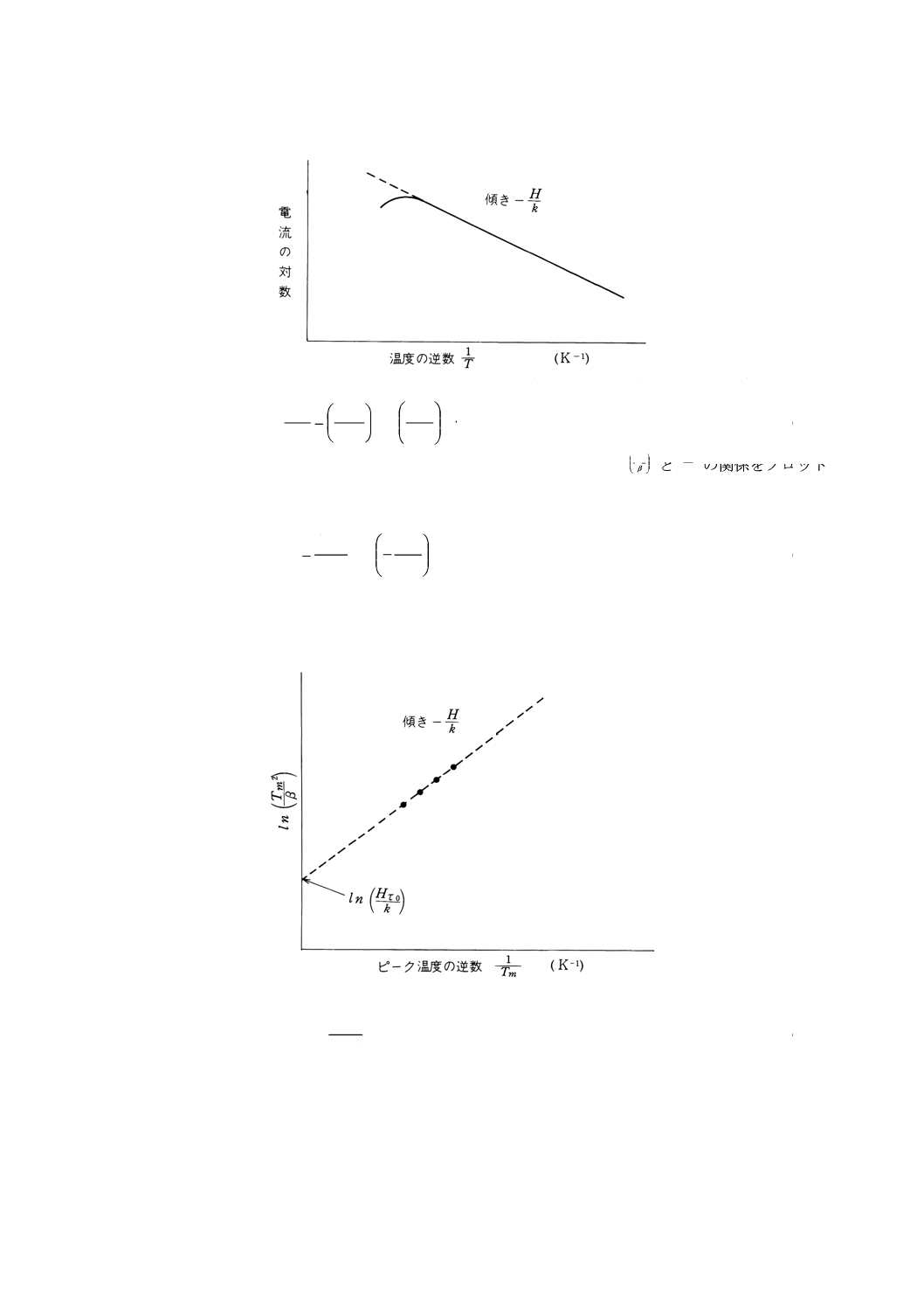
とで傾きから,活性化エネルギーが求められる。この関係を附属書図2に示す。このとき,3.1のTSC電
荷量Piが得られていれば,次の式(6)からτ0が決定され,緩和時間
=
kT
H
exp
0τ
τ
が求められる。
−
kT
H
T
I
i
exp
)
(
P
0≒
τ
······························································· (6)
8
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図2 TSCの初期立ち上がり法
3.2.2
ピーク温度法 式(4)を微分し,TSCがピークとなる温度をTmとすれば,次の式(7)が成立する。
=
m
m
kT
H
k
H
T
exp
0
2
τ
β
····························································· (7)
βを変えてTSCを幾つか測定すれば,βによってTmが変化する。そこで,
β2
ln
m
T と
m
T
1 の関係をプロット
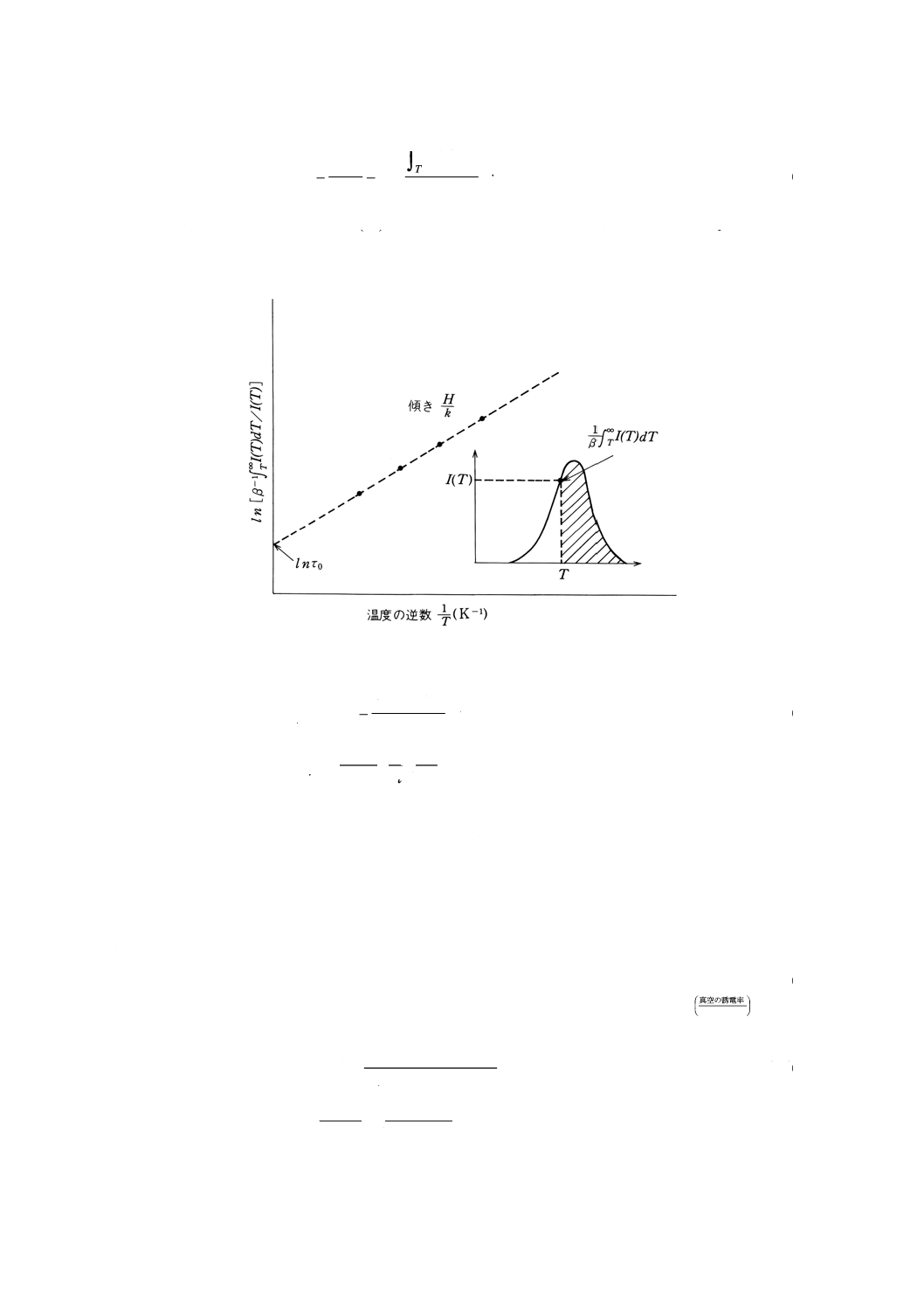
すれば傾きからHが得られ,次の式(8)を用いることでτ0,更にτが求められる。この方法を附属書図3に
示す。
−
=
m
m
kT
H
H
kT
exp
2
0
β
τ
······························································· (8)
一つのTSCを測定してTm,βを得て,3.2.1の初期立ち上がり法を用いてHを求めて,式(8)にTm,H,
及びβを代入すればτ0が求められ,τが計算できる。
附属書図3 TSCのピーク温度法
3.2.3
積分法(Bucci法) 式(4)は,次の式(9)のように書き直すことができる。
)
(
)
(
)
(
T
T
P
T
I
τ
=
············································································ (9)
ここに,
P (T): 温度Tにおける残留分極量
そこで,次の式(10)が導かれる。
9
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)
(
)
(
)
(
)
(
)
(
1
T
I
dT
T
I
T
I
T
P
T
T∫∞
−
=
=
β
τ
···················································· (10)
したがって,附属書図4のように式(10)の分母及び分子を実験から求め,その対数及び T1 の関係をプロ
ットすれば,その直線の傾きが kH となりτ0及びHが求められる。
附属書図4 積分法
3.3
誘電率の周波数特性の求め方 双極子分極のτが得られると,デバイの式から次の式(11)の誘電率の
周波数特性が求められる。
2
2
1
)
(
)
(
τ
ω
ε
ε
ε
εγ
+
∞
−
=
∞
−
′
r
rS
r
·························································· (11)
[
]
)
1(
)
(
2
2τ
ω
ωτ
ε
ε
εγ
+
∞
−
=
′′
r
rS
ここに,
ε'r: 複素比誘電率の実数部
ε''r: 複素比誘電率の虚数部
εrS: 比静誘電率
εr (∞): 双極子の緩和が起こらないような十分高い周波数に
おける比誘電率
ω: 角周波数
この様子を附属書図5に示す。式(11)の [εrS−εr (∞)] と式(2)の飽和分極量P0との間には,次の式(12)の
関係がある。
[
]
d
E
C
P
P
r
rS
0
0
0
)
(
ε
ε
ε
∞
−
=
························································ (12)
ここに, C0: 単位面積当たりの試験片の幾何学的容量
厚さ
真空の誘電率
したがって,式(11)は,次の式(13)のように書き表される。
]
)
1
[(
)
(
'
0
0
2
2
0
d
E
C
P
P
r
r
ε
τ
ω
ε
ε
+
=
∞
−
················································ (13)
]
)
1
[(
"
0
0
2
2
0
d
E
C
P
P
r
ε
τ
ω
ωτ
ε
+
=
このようにTSCから計算されたτ及びP0を用いて,式(13)の誘電率の周波数特性を求めることができる。
10
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
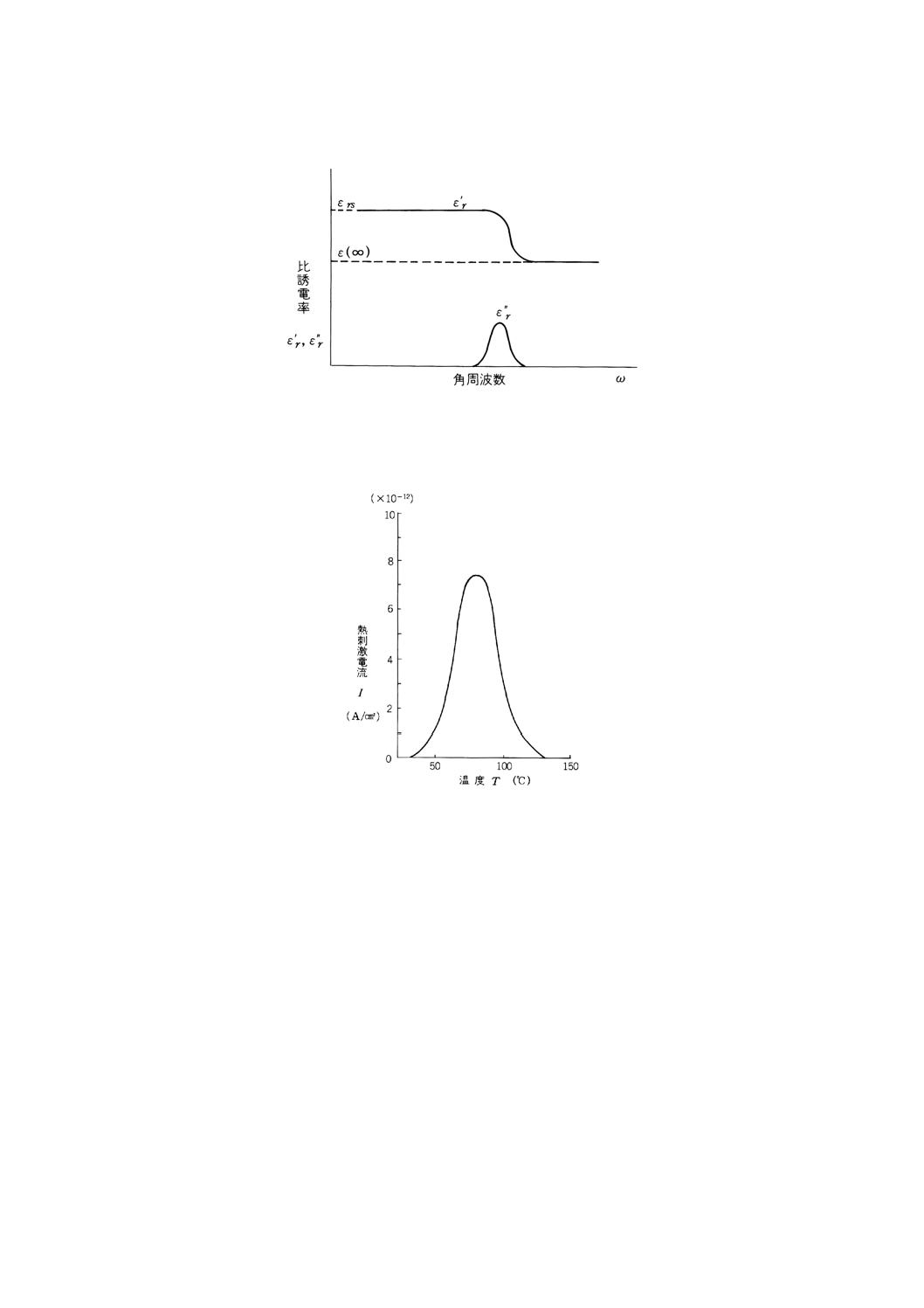
附属書図5 誘電率の周波数特性
3.4
TSC値の温度依存性の表し方 TSC値の温度依存性の表し方は,記録用紙の横軸に温度を,縦軸に
TSC (A/cm2) を用い,温度に対するTSC値をプロットする(附属書図6を参照)。
附属書図6 TSC値の温度依存曲線の表し方の一例
11
K 7131-1994
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
高機能性高分子材料本委員会 構成表
氏名
所属
(委員長)
相 坂 登
工業技術院繊維高分子材料研究所
(委員)
中 島 邦 雄
通商産業省基礎産業局
鷲 見 良 彦
通商産業省基礎産業局
地 崎 修
工業技術院標準部
日 野 太 郎
神奈川大学
北 野 武
工業技術院繊維高分子材料研究所
河 野 嗣 男
東京都立科学技術大学
山 下 正 人
労働省職業訓練大学校
金 子 剛
財団法人日本電気用品試験所
中 村 孔三郎
日本電信電話株式会社
中 山 和 郎
工業技術院繊維高分子材料研究所
冠 木 公 明
株式会社東芝
高 堀 恭 雄
株式会社本田技術研究所
山 田 三郎衛
旭化成工業株式会社
金 井 日出夫
三菱化成株式会社
土 井 浩
積水化学工業株式会社
永 井 聰
工業技術院計量研究所
(事務局)
鹿 毛 紀久雄
財団法人高分子素材センター
新 鍋 秀 文
財団法人高分子素材センター
熱刺激電流試験方法分科会 構成表
氏名
所属
(分科会長)
日 野 太 郎
神奈川大学
水 谷 照 吉
名古星大学
金 子 双 男
新潟大学
金 子 剛
財団法人日本電気用品試験所
山 下 建
日本板硝子株式会社
池 田 勝 則
株式会社東洋精機製作所
佐 藤 俊 昭
株式会社東洋精機製作所
石 野 巌
三菱油化株式会社
小 林 勝
工業技術院標準部
角 田 悦 啓
工業技術院標準部
(事務局)
鹿 毛 紀久雄
財団法人高分子素材センター
新 鍋 秀 文
財団法人高分子素材センター




