K6225 : 1998
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。
今回の制定は,国際規格に整合させるために,ISO 4661-2 : 1987, Rubber, vulcanized−Preparation of samples
and test pieces−Part 2:Chemical testsを基礎として用いた。
JIS K 6225 : 1998には,次に示す附属書がある。
附属書(参考) ゴム−化学試験測定値の正確さ及びかたよりの決定
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K6225 : 1998
加硫ゴム−試料及びテストピースの
調製方法−化学試験
Rubber, vulcanized−Preparation of samples and test pieces−Chemical
tests
序文 この規格は,1987年に発行されたISO 4661-2, Rubber vulcanized−Preparation of samples and test pieces
−Part 2:Chemical testsを翻訳し,技術的内容を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある箇所は,原国際規格にはない事項である。
1. 適用範囲 この規格は,化学試験に用いる加硫ゴムからの試料の調製方法について規定する。
備考 この規格の対応国際規格はISO 4661-2 : 1987, Rubber, vulcanized−Preparation of samples and test
pieces−Part 2:Chemical testsである。
2. 試料の採り方 化学試験を行う加硫ゴムの試料調製を行う際,測定しようとする特性や組成に関して
どの試験部位も試料を代表するものであるように注意を払う。
配合組成を推定する際には表面ブルーム物も試料に含め,一方,最終的なバルク組成を調べる場合には
ブルーム物は機械的な手段によって除去する。
製品から採取した試験片を用いて試験を行う場合には,製品の構成部分,例えば加硫ゴムを覆っている
金属,糸,テープ,繊維及びコーティング又はベニヤ板などから加硫ゴムをまず分離する必要がある。こ
の分離にはできる限り機械的な手段,例えば,刃物,研磨器又はやすりを用いて行い熱の発生を避けるよ
うにする。
3. 試料の作り方
3.1
試料は,別に規定がない場合,はさみ,やすり,グラインダー又は凍結粉砕によって約1.7mmのふ
るい目を通過する大きさにするか,若しくは,実験室用ミルの冷えたロールによって薄通しを行い,0.5mm
以下の厚さのシートとする。
使用するグラインダー又はミルは,試料が汚染されたり過度な発熱がないものであれば形式は問わない。
3.2
エボナイト 試料は粉末状に削って,約400μmのふるい目を通過する大きさとし,混入した鉄粉を
磁石で除去する。
3.3
ゴム引き複合材 ゴムを機械的に分離できない場合,次の操作によって分離する。
適切な溶媒蒸気に暴露してゴムを分離する。NR,SBR,BRをベースとした複合材に対してはジクロロ
メタン又は1,1,1−トリクロロエタンが適切な溶媒である。ただし,溶媒暴露はゴム試料から可塑剤が
抽出されるのを避けるために極力短時間で行う。
2
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
その後,膨潤したゴムは分離後室温において溶媒を除去し,3.1に従い処理する。
ゴムが基材と化学結合している場合,基材と結合している領域のゴム組成は,バルク組成とは異なって
いることに注意する。
全般的に,たとえ基材とゴムがきれいにはがせても,はがしたゴムが複数の構成成分から成り立ってい
る場合に,3.1の操作を行うとゴム試料が混ざってしまい,元の構成を再現しない分析対象試料となってし
まう。複数の構成成分が積層されていることは,材料の構成断面を顕微鏡で観察することによって確認で
きる。
複合積層体の場合,注意深く研磨又は切断することによって各構成成分の分析のためのゴム試料を作製
することが可能である。
ゴムが基材から分離できない場合,試料を2mmのふるい目を通過する小さい立方体に切断し,全体を
分析する。
この場合,複合材中のゴムの質量比は高沸点溶媒中で加熱してゴムを除去し,処理の前後で質量を測定
することによって求められる。複合材中の有機材料(例えば布)が一部溶解する可能性があり,測定結果
は注意して解釈する。
試料が採取できれば,複合材中にゴムを含まない部分も同様に分析する。
分析結果を報告する際には,用いた分離方法を明記する。分離が不可能な場合には,分析試料はゴムと
基材との混合物であり,材料の不十分な分離によって分析結果に誤りの可能性があることを示す必要があ
る。
上記手法によって分離が困難であったり,その後の分析に支障をきたす場合,その分離方法については
受渡当事者間の協議によって定める。
3
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書(参考)
ゴム−化学試験測定値の正確さ及びかたよりの決定
この附属書(参考)は,化学試験測定値の正確さ及びかたよりの決定について記述するもので,規定の
一部ではない。
序文 この附属書は1993年に発行されたISO/TR 9474, Rubber and rubber products−Determination of
accuracy and bias of chemical test methodsを翻訳し,内容を変更することなく作成した附属書である。
このISO/TRは化学製品の試験方法の対応国際規格の調査中に見い出したもので,何件かのゴム試験方法
に引用されていたため,整合化の際に引用等で利用される可能性が高いと判断し,共通的な“JIS K 6225
(加硫ゴム−試料及びテストピースの調製方法−化学試験)”に附属書(参考)として掲載することとした。
1. 適用範囲 この附属書では,ISO/TC 45が定める試験方法に基づく結果の正確さ及びかたよりを評価
するための指針を示す。この指針は,ISO 5725及びISO/TR 9272に示す指針に追加されるものであり,正
確さ及びかたよりを表示する形式を提示する。
この附属書では試験方法の正確さの評価について扱い,適用範囲を次の標準試験方法に限定する。
− 試験結果が量的連続変数で表される標準試験方法
− 試験結果が定数項で定量化できる標準試験方法
試験室間の試験によって決定された正確さ及びかたよりを表示することによって次の事項の評価が可能
となる。
a) 試験室間の試験に供される試験方法の妥当性。ここでいう妥当性とは,試験方法の正確さ,並びに低
値の固定かたよりBF及び相対かたよりBRを指す。
b) 実験者に起因するかたより
c) 試料に起因するかたより
2. 引用規格
ISO 5725 Precision of test methods−Determination of repeatability and reproducibility by interlaboratory
tests
ISO/TR 9272 Rubber and rubber products−Determination of precision for test method standards
ISO Standards Handbook3:1989, Statistical methods(このハンドブックには次のISO規格が収録され
ている。ISO 2602, ISO 2854, ISO 2859-1, ISO 2859-2, ISO 3207, ISO 3301, ISO 3494, ISO 3534, ISO
3534-3, ISO 3951, ISO 5725)
3. 定義 この附属書では,次の定義を適用する。
備考1
繰返し精度及び再現精度の定義はISO 5275に,解説は,ISO/TR 9272に収録されている。精
度はISO 3534で定義される。精度とは,互いに一致する試験結果を生ずる能力を表す試験又
は測定上の概念の一つである。通常,一致の種類は標準偏差によって逆に表され,精度が高
ければ標準偏差は小さくなる。精度が高い場合で,かたよりが大きかったり,正確さが低い
4
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ことがある。
3.1
真の値(ISO 3534 : 1977,2.82参照) ある特性について承認された標準値又は理想値。測定誤差の
原因がすべて排除される場合だけ実験的に求めることができる。
備考2
実際には標準試料を用いることが多い。特定の化合物又は元素を全く含まないか,又は含有
量が正確にわかっているゴムは入手できることが多いし,また,調製することもできる。
3.2
正確さ (A) 試験に関係する材料又は現象について,測定値の平均と,真の値すなわち承認された
標準値若しくは規格値との一致の程度を表す概念。
備考3
標準値は,理論的に決まる場合もあり,承認規格への参照,別の試験方法への参照,又は既
知試料の調製によって求められる場合もある。
3.3
かたより (B) 実験的に求めた測定結果の平均値と,真の値,すなわち承認された標準値との差。
かたよりには“固定”と“相対”があり,両者が同時に存在する場合もある。
備考4
正確さが高いということは,かたよりが小さい,又は無視できるという意味である。かたよ
りがあるときには,試験回数を増やしても正確さは向上せず,精度が増すにすぎない。各種
のかたよりを7.1に図解する。今,正確さ100%=完全,すなわち,試験誤差なしという正確
さAを考えるならば,
(
)
100
1
×
−
−
=
T
R
T
V
T
V
A
ここに,VT:真の値,TR:試験結果であり, (VT−VR) は絶対値を表す。結果が100に近
いほど正確さが高い。かたよりには複数の要因が関係すると考えられるが,化学分析の場合,
一般に,試料中に他の妨害物質が存在することに起因する。このような妨害物質はそれ自体
が分析中に反応することがあり,その場合には,固定かたよりを生ずる。また,目的の化学
物質の反応を抑制したり,促進させたりする可変かたよりとして作用することもある。通常,
かたよりの程度は妨害物質の濃度によって異なる。
3.3.1 固定かたより (BF) かたよりの値が,測定しようとする特性の水準又は平均値に依存しないとき,
かたよりは“固定”されている。
3.3.2
相対かたより (BR) かたよりの値が,測定しようとする特性の水準又は平均値によって変化する
とき,かたよりは“相対的”である。
3.3.3
複合かたより (BC) 複合かたよりは試験結果に依存し,“試験結果のある特定の水準における複
合かたよりBC”と表記される。
4. かたよりの決定
4.1
かたよりがない場合には,あるパラメーターの測定値の平均Yと真の値VTは1対1に対応する。す
なわち,
Y=VT±ε ················································································ (1)
ここに,εは確率変数成分であり,十分に長い時間をとったときには平均が0となる。固定かたよりがある
場合には,測定値の式は次のようになる。
Y'=VT+BF ·············································································· (2)
相対かたよりがある場合には,測定値の式は次のようになる。
Y''=aVT ·················································································· (3)
ここに,aは一般式y=axで表される直線の傾きであり, (a−1) がかたよりである。固定かたよりと相対
5
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
かたよりが同時に存在する場合には,方程式は次のようになる。
Y'''=aVT+BF ··········································································· (4)
測定誤差又は“複合かたより”は,次の式で表される。
Y'''−VT= (a−1) VT+BF=BC ······················································ (5)
備考5
この技術報告書では,“測定値”と“真の値”の関係が一次式で表される場合だけを考える。
4.2
かたよりを決定するには,“測定値”及び1個以上の“真の値”の両方を知る必要がある。“真の値”
が正確に分かっている試料が市販されていることもあるが,そのような試料を調製することもできる。“真
の値”を知ることは絶対に不可能であるが,不確かさの許容範囲(平均偏差)について“真の値”を問題
にすることは,測定技術の精度について“真の値”を問題にする頻度に比べるとかなり少ない(10分の1
程度)のが普通である。これは特に化学分析についていえることであり,“技術的な”物理的性質について
いうことはまれ(稀)である。
4.3
一般に,かたよりの評価には,次の方法を用いる。
a) 1個の標準試料を用いる方法
b) 複数個の標準試料を用いる方法
これらの方法について,5.に述べる。
5. かたよりの決定方法
5.1
一般事項 この箇条で説明する方法は,誤差の分布が正規分布に従うという仮定に基づいている。
この仮定は適当な統計的手法を用いて検証することが望ましい。
備考6
誤差の分布が正規分布に従わない測定方法は多い。したがって,この箇条で提案する方法で
は,系に存在する真のかたよりの近似値が得られるにすぎない。標準試料は目的の化学物質
を既知の濃度で含有し,それ以外の重要な点がすべて測定用試料と同じでなければならない。
5.2
1個の標準試料を用いる方法
5.2.1
標準試料が1試料だけの場合には,観察されたかたよりを“固定”要素と“相対”要素に分けるこ
とはできない。“複合”かたよりBCだけを評価することができる。
5.2.2
複合かたよりは,次の式で表される。
BC=Y−VT ·············································································· (6)
ここに,Yはn回の測定の平均値であり,VTは“真の値”である。
5.2.3
複合かたよりの統計的処理の基礎となるのは,かたよりがスチューデントのt分布に従う確率変数
であるという考え方である。tの値t (calc) は次の式を用いて評価する。
(
)
()2/1
)
(
n
S
V
Y
calc
t
T
−
=
········································································ (7)
ここに,t (calc) の自由度は (n−1) であり,Yはn個の独立した測定値の平均,Sはn個の測定値の標準
偏差である。Sを計算するための一般式を式(8)に示す。ただし,Σはi=1からi=nまでの和である。
(
)(
)
2/1
2
1
1
1
−
Σ
×
−
=
Y
Y
n
S
···························································· (8)
6
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2.4
次に,t (calc) の有意性について述べる。すなわち,Yの計算に用いた測定値の変動に比較して,
かたより,すなわち (Y−VT) の大きさが0(ゼロ)に比べて有意に異なるかどうかという点である。この
ためには,ある選ばれた確率水準又は有意水準においてt (calc) の値をtの臨界値t (crit) と比較しなけれ
ばならない。確率値は0.05とするのが普通であり,これは95%の信頼水準に等しい。すなわち,t (calc) の
値が0より十分に大きいというとき,この記述が真である確率は95%であり,逆にいえば,誤りである確
率は5% (0.05) である。より高い有意性が要求されるときには,それぞれ98%有意,99%有意に相当する
0.02,0.01などの確率水準又は有意水準を用いてもよい。要求される自由度におけるtの臨界値は,出版
されている統計表から求めてもよい(例えば,Physical Testing of Rubber,R. P. Brown編,Elseivier Applied
Science刊など)。
5.2.5
式(9)が成り立つならば,帰無仮説は棄却される。ここに,|t (calc) |は絶対値を表す。
|t (calc)|>t (crit) ··········································································· (9)
5.2.6
複合かたより (Y−VT) に対する信頼区間CIは,次の式で表される。
CI=±(
)
()2
/1
n
S
calc
t
······································································· (10)
5.2.7
5.2.4で定める選定有意水準において,ある許容範囲,すなわち±δの範囲内にある複合かたよりを
求めるのに適した標本数(測定回数n)は,次の式から求められる。
n=(
)
2
δ
S
crit
t
········································································· (11)
5.3
複数個の標準試料を用いる方法
5.3.1
複数個の標準試料には線形回帰法を用いる。その例を7.2に示す。
5.3.2
一組の標準試料を選ぶか,又は調製する。これらいずれについても,分析試料中の目的成分は異な
る既知の値,すなわち,真の値 (Xt) をもつ。 (Xt) の値は,試験方法に見合う正常範囲に広がっているこ
とが望ましい。これらの各標準試料について,目的成分を1回以上測定する。測定値の平均をYiで表す。
Yi=aXi+b ············································································· (12)
(単純化するため,Xの添字tは省略した。)
5.3.3
XYグラフ上にXi及びYiの値をプロットする。最小二乗法を用いて回帰直線の傾きa及びY切片
の値bを求める。計算には,電子計算機又は7.3に示す“手作業”法を用いることができる。
5.3.4
固定かたよりBFの不偏値はbに等しく,相対かたよりBRは (a−1) に等しい。あるXの値(必ず
しも測定値である必要はない)に対する複合かたよりBCは,次の式で表される。
BC= (a−1) X+b ····································································· (13)
5.3.5
次の式によって傾きの標準誤差S (a) を求める。
S (a) =(
)2
/1
XX
R
S
S
····································································· (14)
ここに,SRは“推定値の標準誤差”(回帰直線近傍の点変動)であり,次の式で表される。
SR=
2/1
2
2
−
−
n
S
S
S
XX
XY
YY
································································ (15)
また,
SXY=Σ (Yi−Y) 2(i=1からi=nまでの和) ································· (16)
7
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SXX及びSXY2の定義は7.3を参照のこと。
次の式によって,Y切片bの標準誤差S (b) を求める。
S (b) =
2/1
2
1
+
XX
R
S
X
n
S
···························································· (17)
備考7
SRの値は,相関係数rXY(XとYの間の)を用いると次のように表せる。
SR=
(
)
[
]
2/1
2
1
2
−
−
XY
YY
r
n
S
························································· (18)
5.3.6
5.2.4に示す自由度 (n−2) における信頼(有意)確率に対応する相対系統誤差 (a−1) の信頼区間
は,次の式で表される。
(a−1)−t (crit) S (a) ; (a−1) +t (crit) S (a) ······································ (19)
また,5.2.4に示す自由度 (n−2) における信頼(有意)確率に対応する固定かたよりbの信頼区間は,次
の式で表される。
b−t (crit) S (b) ; b+t (crit) S (b) ···················································· (20)
5.3.7
自由度が (n−2) である信頼(有意)水準について,選んだ許容範囲±Lに対する相対かたより (a
−1) を求めるのに適した標本数(X,Yデータの組数)nRは,次の式で表される。
nR=2+(
)
[
]
(
)
[
]
(
)2
2
2
2
XX
XY
XX
YY
S
L
S
S
S
crit
t
−
················································ (21)
5.3.8
自由度が (n−2) である信頼(有意)水準について,選んだ許容範囲±Mの中に対する固定かたよ
りbを計算するために必要な標本数nFは,次の式で表される。
nF=(
)
[
]
(
)
XX
i
R
S
X
S
M
crit
t
2
2
2
2
Σ
×
×
························································· (22)
ここに,Σはi=1からi=nまでの和である。
備考8
5.3.7及び5.3.8では,要求される許容範囲,すなわち,正確さの範囲に含まれるパラメーター
値 (a−1) 及びbを推定するために行う追加作業又は試験に必要な標本数nR及びnFを,標本
(最初の試験プログラム用に選ばれた)数nでの試験結果を用いて求めている。
5.3.9
5.3に述べた方法は,nが5を超える場合にだけ用いることができる。
6. 試験結果の表現
6.1
試験方法の評価
6.1.1
試験方法の予備評価の際に,試験プログラムに1個以上の標準値又は標準試料を加えることによっ
てかたよりの評価が可能となる。数個の標準試料を用いれば(4又は5個),3種類のかたより要素,すな
わちBF,BR,BCを求めることができる。
6.1.2
この後に試験プログラムを変更すると,かたよりの値が変化する場合がある。
6.2
試験室での作業の評価
6.2.1 ある試験室での結果において,他の試験室での結果と比較して著しく大きなかたよりが生じた場合,
その試験室における試験方法又は装置を注意深く調査する必要がある。
6.2.2 ある試験者による結果において,他の試験者の結果と比較して著しく大きなかたよりが生じた場合,
適当な手段を用いてかたよりの原因を調べる必要がある。
8
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3
かたよりの報告
6.3.1
一般に,かたよりの大きさは,試験方法に加えて,試料中に存在する目的以外の(本質的でない)
物質の種類にも依存する。このため,試験方法に特有のかたよりを試験全体のかたよりとして示すことは
できない。
6.3.2
かたよりのあることが明らかになったら,化学的な面又は操作面から試験方法を変更し,かたより
を排除することが望ましい。これが実用的でない場合には,試験方法の適当な箇所に,かたよりのある不
正確な結果を生じやすい条件を明示した警告を挿入しなければならない。
7. かたよりの種類と計算
7.1
かたよりの種類 この項には,各種のかたよりを簡単なグラフを用いて示してある。いずれの図も,
グラフは理想的な場合のものである。
7.1.1
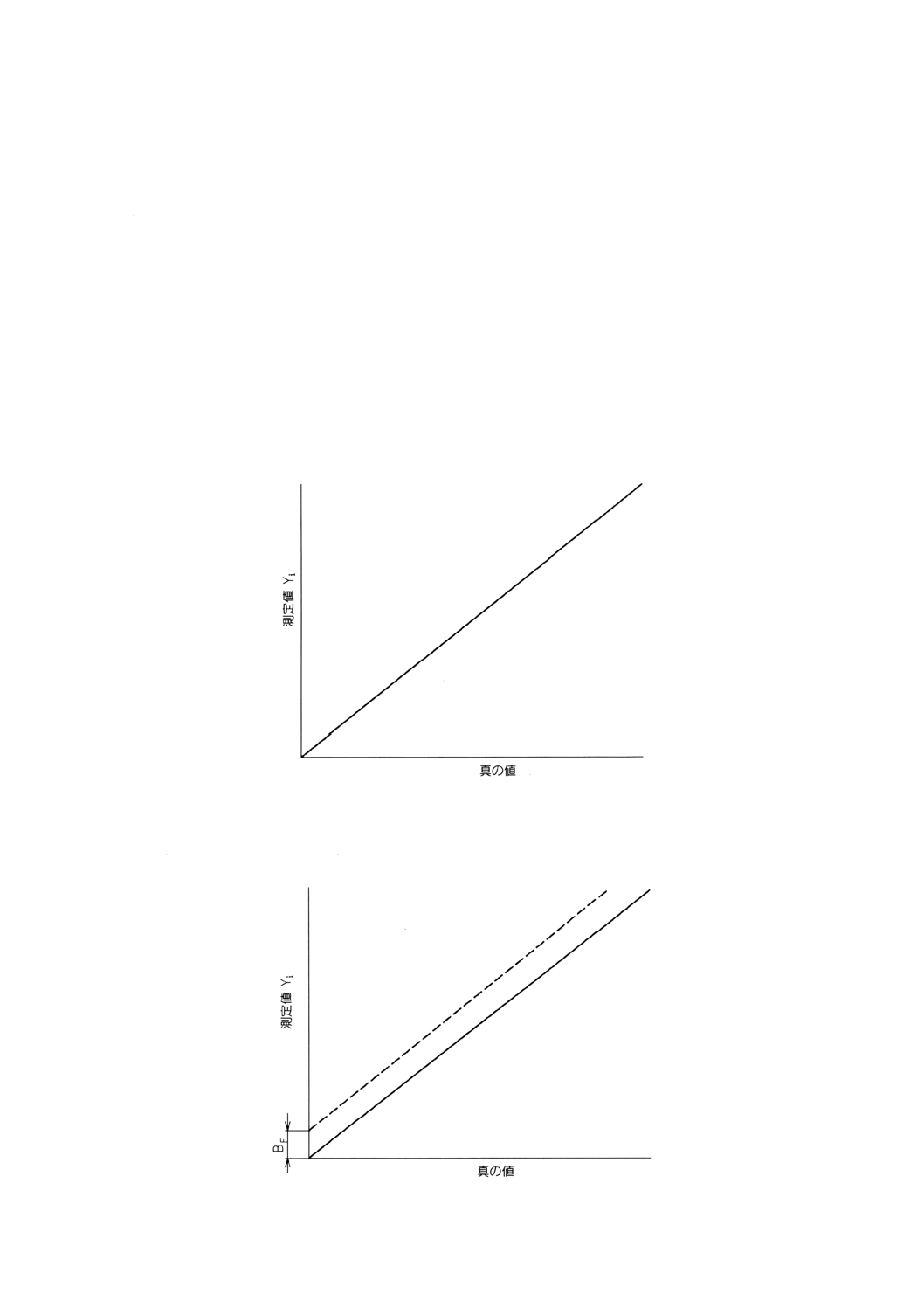
かたよりなし 校正曲線は原点を通り,測定値と真の値の間には1対1の対応(傾き1の直線関係)
がある。
図1 かたよりがない場合
7.1.2
固定かたより 校正曲線は傾き1の直線(実線)に平行である。実線と校正曲線の間のy軸方向の
距離は一定であり,この距離が固定かたよりBFである。
9
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2 固定かたよりの例
7.1.3
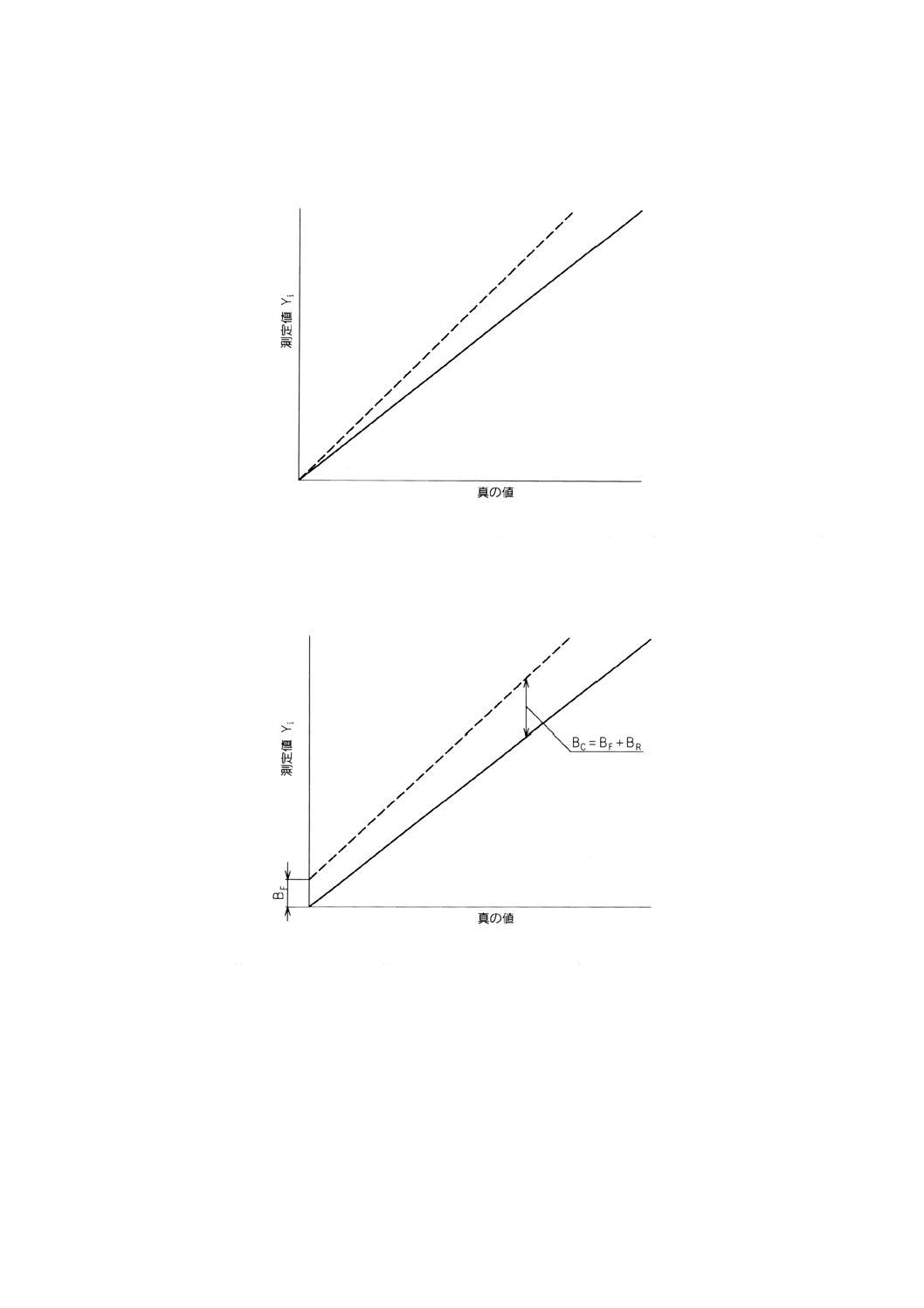
相対かたより この場合,校正曲線は傾き1の直線(実線)に対してある角度をなしているが,固
定かたよりはない。
図3 相対かたよりの例
7.1.4
固定かたよりと相対かたより この場合,校正曲線は傾き1の直線(実線)より上方にあり,実線
に対してある角度をなしている。y軸の切片BFは,固定かたよりとなる。校正曲線の傾きは1より大きい
ため,真の値が大きくなるほど相対かたよりが大きくなる。傾き1の直線上の任意の点,すなわち任意の
真の値における複合かたよりは,BC=BF+BRで表される。
図4 複合(固定+相対)かたよりの例
7.2
かたよりの計算例 5.3に示した計算式を用いて,一組の分析データからかたよりを求める方法の1
例を次に示す。表1は,一組の試料に含まれる銅の定量分析から得られたデータである。
表1 銅の分析試験で得られたデータ
真の値,X
測定(分析)値,Y
3.0
5.0
6.0
8.3
9.0
12.1
12.0
15.1
15.0
19.0
10
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
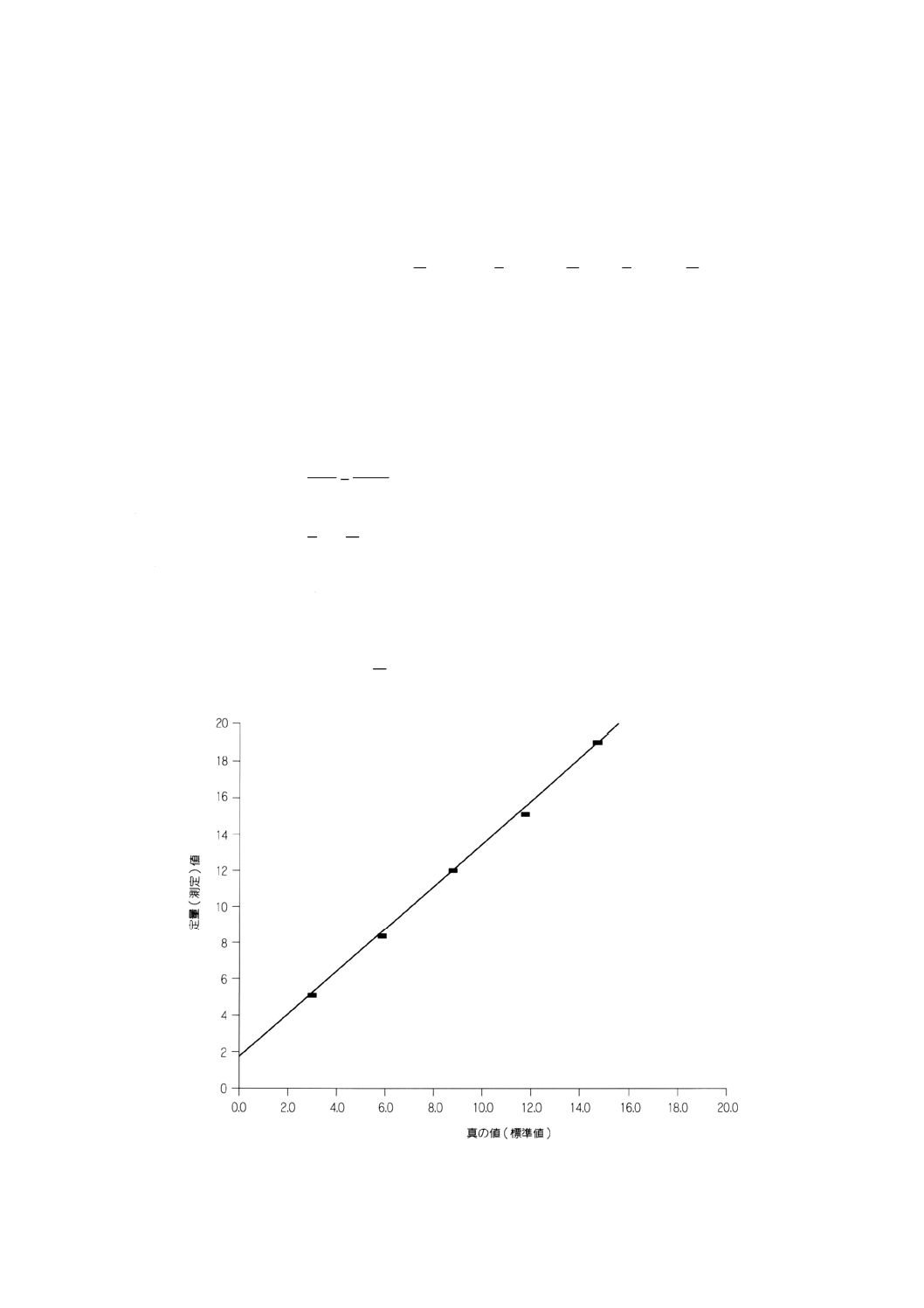
適当なリニアスケールのグラフ用紙にプロットすると,各点は1本の直線のまわりにわずかに分散して
いる。この直線は原点を通らず,傾き1の直線にも平行でないことから,固定かたよりと相対かたよりが
あることを示している(図5を参照のこと)。表2は,定量(測定)値及び真の値をもとに作成したもので
ある。これを用いて段階を追って計算を進める。
表2 かたよりのパラメータの計算
真の値,X 測定値,Y
(X−X)
(Y−Y)
(X−X) (Y−Y) (X−X) 2
3.0
5.0
−6
−6.9
41.4
36
6.0
8.3
−3
−3.6
10.8
9
9.0
12.1
0
0.2
0
0
12.0
15.1
3
3.2
9.6
9
15.0
19.0
6
7.1
42.6
36
和=45
和=59.5
SXY=104.4
SXX=90
平均=9
平均=11.9
表2から,
a=
90
4.
104
=
XX
XY
S
S
=1.16
固定かたよりbは
b=Y−aX=11.9−1.16×9=1.46
したがって
BF=b=1.46
BR= (a−1) =0.16
真の値が9.0ならば,(この銅含有量における)複合かたよりBCは
BC= (a−1) X+b=0.16×9+1.46=2.9
となる。
図5 銅含有量の定量における複合かたよりの例
11
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3
回帰線パラメータの計算式 回帰線パラメータの計算式を次に示す。線形項の値,すなわち,傾きa
は,次の式によって算出する。
a=
XX
XY
S
S
ここに, SXY=Σ (Xi−X) (Yi−Y)
Σはi=1からi=nまでの和
SXX=Σ (Xi−X) 2
Σはi=1からi=nまでの和
回帰線の固定かたよりbの値は
b=Y−aX
平均値X,Yは,通常の方法で計算する。
12
K6225 : 1998
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ゴム製品分析方法原案作成委員会・分科会 構成表
氏名
所属
委員会
分科会
(委員長)
本 間 輝 武
神奈川工科大学応用化学科
◎
(委員)
西 本 右 子
神奈川大学理学部
○
◎
増 田 優
通商産業省基礎産業局化学製品課
○
大 嶋 清 治
工業技術院標準部材料規格課
○
中 室 輝 夫
工業技術院標準部材料規格課
○
橋 本 繁 晴
財団法人日本規格協会
○
○
鈴 木 守
社団法人日本ゴム協会
○
神 代 啓
社団法人日本化学工業協会
○
秋 山 節 夫
株式会社ブリヂストン研究部
○
○
永 武 寿 宏
横浜ゴム株式会社
○
○
浅 田 美佐子
株式会社ゼオン分析センター
○
○
伊 藤 政 幸
日本原子力研究所
○
○
小 野 茂 之
NOK株式会社筑波技術研究所
○
○
鹿 庭 正 昭
国立衛生研究所療品部
○
○
塩 沢 功
鬼怒川ゴム工業株式会社
○
○
岩 田 知 晴
株式会社明治ゴム化成
○
○
福 岡 清
ニチアス株式会社鶴見研究所
○
○
橋 本 和 信
東海ゴム工業株式会社
○
○
中 村 修 蔵
株式会社社興国ゴム技術研究所
○
○
栗 田 光 造
古河電気工業株式会社平塚研究所
○
○
中 村 博 雄
日本合成ゴム株式会社四日市工場
○
○
鈴 木 裕 次
財団法人化学品検査協会
○
○
(事務局)
三 須 武
社団法人日本化学工業協会
○
○
濱 島 俊 行
社団法人日本化学工業協会
○
○
伊 藤 茂 樹
財団法人化学品検査協会
○
○
◎委員長,分科会主査を示す


