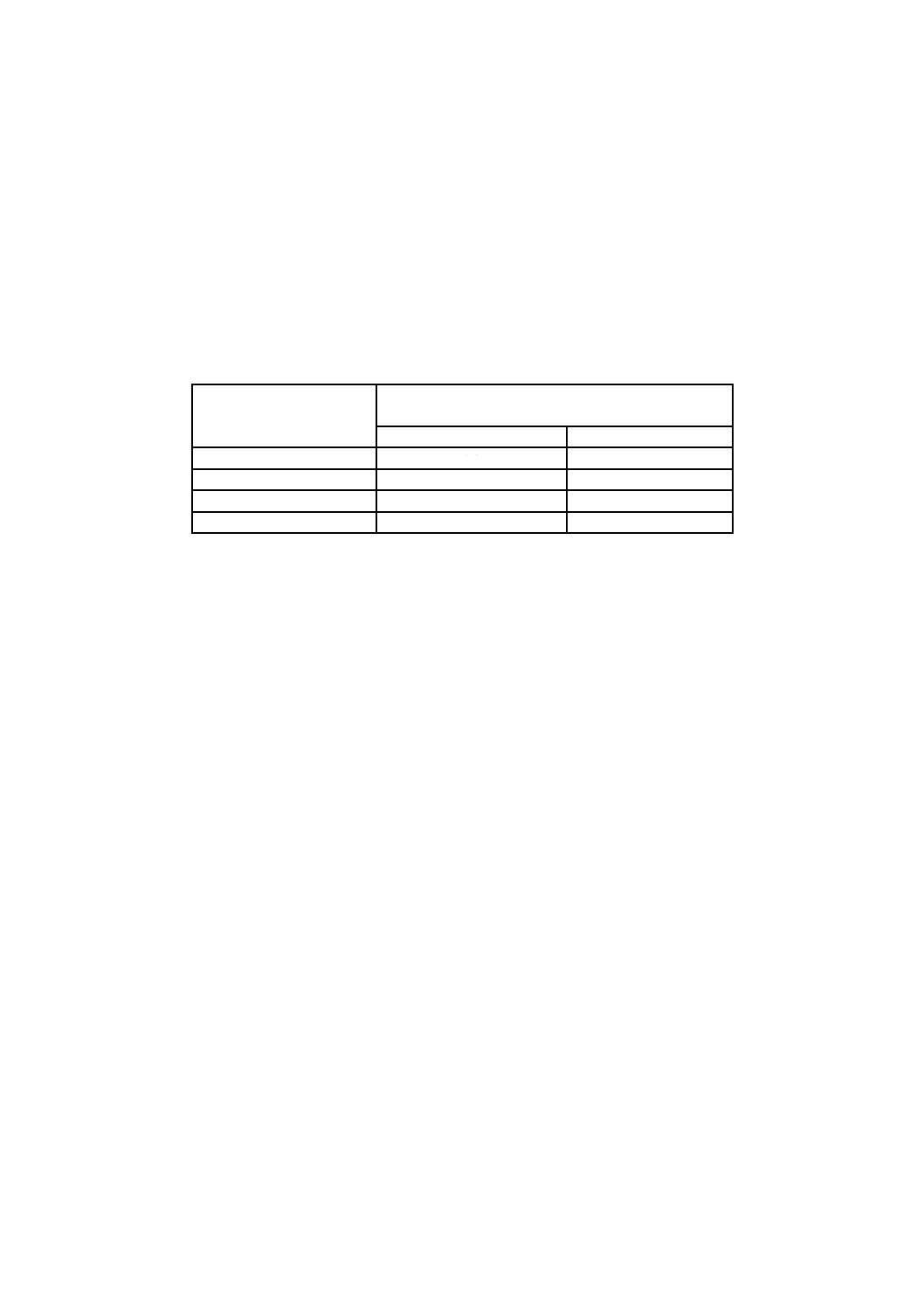K 0156:2018 (ISO 23812:2009)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 2
4 記号及び略語 ··················································································································· 2
5 デルタ多層標準物質に対する要求事項 ·················································································· 3
6 測定手順························································································································· 4
7 校正手順························································································································· 4
7.1 校正の原理 ··················································································································· 4
7.2 標準物質によるスパッタリング率の決定方法 ······································································· 5
7.3 分析試料の深さ軸校正 ···································································································· 7
7.4 校正深さの標準不確かさ ································································································· 8
8 結果の表現 ······················································································································ 9
8.1 標準物質で用いたスパッタリング条件での校正 ···································································· 9
8.2 標準物質で用いたスパッタリング率と異なる条件での校正 ····················································· 9
8.3 濃度校正 ······················································································································ 9
9 分析結果の報告 ················································································································ 9
附属書A(参考)シリコン中における酸素イオンの投影飛程························································ 10
附属書B(参考)アトミックミキシングによるピークシフトの見積り ············································ 11
附属書C(参考)ピークの重なりに起因するピークシフトの見積り··············································· 14
附属書D(参考)不確かさの導出方法 ····················································································· 16
K 0156:2018 (ISO 23812:2009)
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,表面化学分析技術国際標準化委員会(JSCA)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本工業規格 JIS
K 0156:2018
(ISO 23812:2009)
表面化学分析−二次イオン質量分析法−
デルタ多層標準物質を用いたシリコンの深さ校正方法
Surface chemical analysis-Secondary-ion mass spectrometry-Method for
depth calibration for silicon using multiple delta-layer reference materials
序文
この規格は,2009年に第1版として発行されたISO 23812を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
二次イオン質量分析法(SIMS)は,シリコン中のドーパントに対する深さ方向分布測定の有力な手段で
ある。しかしながら,表面近傍の領域(50 nm未満)では,二次イオン収率及びスパッタリング率の遷移
的な挙動が深さ方向分布の形状に著しく影響する[1]。このため,真の深さ方向分布を得ることが困難であ
る。これは,一次イオン種である酸素イオン又はセシウムイオンが試料表面に注入されて蓄積することに
よって生じるものであり,ここで一次イオン種の蓄積は二次イオン収率を増加させるためには不可欠であ
る。初期表面では,一次イオン種の濃度が低い状態で試料物質のスパッタリングが起こるのに対し,スパ
ッタリングの進行とともに,一次イオン種は表面に取り込まれて試料物質とともにスパッタされるので,
スパッタリング率が変化する。この非定常領域でのスパッタリング率の変化の結果,均一なスパッタリン
グ率を用いて深さ校正を行うと,浅いSIMS深さ方向分布に著しいシフトが生じる。
このような浅い領域での深さの校正には,上記の深さ方向分布のシフト量を正確に評価することが不可
欠である。この規格は,非定常領域を超えた表面近傍の領域における深さスケールの標準物質としてデル
タ多層を用い,深さスケールを校正するための手順を規定している。
この規格は,JIS K 0169とは適用範囲が異なる。JIS K 0169は,デルタ多層標準物質を用いてSIMS深
さ方向分布分析における深さ方向分解能パラメータを推定する方法を規定しているのに対し,この規格は
浅い領域での深さスケールの校正方法を規定している。
1
適用範囲
1.1
この規格は,デルタ多層標準物質を用いた,50 nm未満の浅い領域でのシリコンのSIMS深さ方向分
布分析における深さスケールの校正方法について規定する。
1.2
この規格は,スパッタリング率が定常状態に達しない表面の遷移領域には適用できない。
1.3
この規格は,単結晶シリコン,多結晶シリコン及び非晶質シリコンに適用できる。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 23812:2009,Surface chemical analysis−Secondary-ion mass spectrometry−Method for depth
calibration for silicon using multiple delta-layer reference materials(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
2
K 0156:2018 (ISO 23812:2009)
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS K 0147-1 表面化学分析−用語−第1部:一般用語及び分光法に関する用語
注記 対応国際規格:ISO 18115-1:2013,Surface chemical analysis−Vocabulary−Part 1: General terms
and terms used in spectroscopy(IDT)
JIS K 0169 表面化学分析−二次イオン質量分析法−デルタ多層標準物質を用いた深さ分解能パラメ
ータ評価方法
注記 対応国際規格:ISO 20341,Surface chemical analysis−Secondary-ion mass spectrometry−Method
for estimating depth resolution parameters with multiple delta-layer reference materials(IDT)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS K 0147-1による。
4
記号及び略語
この規格で用いる主な記号及び略語は,次による。
a
回帰直線の切片
b
回帰直線の傾き
()z
I
深さzにおけるイオン強度
k
一次イオン電流密度に対する補正係数
l
回帰分析に使用したデルタ層の数
SL
深さ軸のシフト距離
()p
LS
デルタ層のピーク位置の定義に依存するシフト距離(7.2.1参照)
m
定常状態のスパッタリング率決定に用いた最深部におけるデルタ層番号
n
スパッタリング率が定常状態に達する最浅部におけるデルタ層番号
r
スパッタリング率
ir
i番目のシリコン層における平均スパッタリング率
Sr
定常状態におけるスパッタリング率
0s
RM
s
及びksを除いた,深さの推定値に対する標準不確かさ
1s
RM
s
を含む,深さの標準不確かさ
2s
RM
s
及びksを含む,深さの標準不確かさ
bs
bの標準不確かさ
ks
kの標準不確かさ
RM
s
標準物質における層の深さの標準不確かさ
ts
スパッタリング時間tの標準不確かさ
ts
tの標準不確かさ
(
)
α
,1
−
−n
m
T
自由度(
)1
−
−n
m
,有意水準
α
100 %でのスチューデントのt分布表から得られる棄却限
界値
3
K 0156:2018 (ISO 23812:2009)
t
スパッタリング時間
t
デルタ層間の平均スパッタリング時間
ft
クレータを形成するのに必要なスパッタリング時間
it
スパッタリング時間に対するイオン強度分布におけるi番目のデルタ層に達するまでのスパッタ
リング時間の測定値
itˆ
i番目のデルタ層までの時間の推定値
z
スパッタ深さ
z
デルタ層の平均深さ
zˆ
深さの推定値
ai
z
( )1
−
i
番目とi番目のデルタ層との間で強度が最小となる位置
bi
z
i番目と(
)1
+
i
番目のデルタ層との間で強度が最小となる位置
cz
重心位置
dz
本来のデルタ層の位置
fz
クレータ深さ
iz
i番目のデルタ層の深さ
>
<
iz
i番目のデルタ層の深さ分布の重心位置
LM
z
極大位置
PC
z
ピーク中心位置
it
∆
i番目のデルタ層のスパッタリング時間
iz
∆
i番目のデルタ層の厚さ
SIMS 二次イオン質量分析法
5
デルタ多層標準物質に対する要求事項
5.1
5.2〜5.8の規定は,標準物質として使用するデルタ層に対して適用する。
5.2
SIMSの深さ方向分布測定中に,SIMSのマトリックス効果又はデルタ層でのスパッタリング率の変
化によって,デルタ層を含むマトリックス(シリコン)の信号は変化してはならない。
5.3
デルタ層の深さの試料面内における一様性は,要求される深さ校正精度と同等か,又はそれより良
好でなければならない。
5.4
厚さの僅かなばらつきが分布形状に影響しないように,ドープされたデルタ層のそれぞれの厚さは
一次イオンの投影飛程(O2+イオンの例については附属書A参照)よりも十分小さくなければならない。
5.5
深さ方向分布において,隣り合うデルタ層の深さ方向分布のピークと谷との二次イオン強度比が10
以上となるように,隣り合うデルタ層の間隔を十分に大きくしなければならない。
5.6
デルタドープ領域においてスパッタリング率が定常状態に達していることを確認するために,標準
物質は少なくとも三つのデルタ層を含まなければならない。
5.7
デルタ層の厚さ,位置及び界面の粗さは,断面透過電子顕微鏡法,低角X線反射率測定法,中速イ
オン散乱分光法又は他の適切な手法で決定しなければならない。
5.8
表面酸化膜の厚さは,結晶シリコン表面上の自然酸化膜の厚さ(典型的には1〜2 nm)と同等なもの
でなければならない。酸化膜の厚さは,適切な測定方法で決定しなければならない。
4
K 0156:2018 (ISO 23812:2009)
6
測定手順
6.1
深さ軸の正確な校正を行うために,分析試料及びデルタ多層標準物質を同じエネルギー及び入射角
の一次イオンを用いて測定しなければならない。イオン照射条件(エネルギー,入射角,イオン電流及び
走査領域)の設定に対して,スパッタリング率,深さ補正係数及び深さ軸のシフト距離(7.2.3参照)を一
旦決定しておけば,あらかじめ決定した値を深さ軸の決定に用いることができる。スパッタリング率の再
現性の限界によって,深さ軸にはばらつきがあることに注意することが望ましい(6.5参照)。
6.2
二次イオン質量分析計の調節及び最適化に関して,イオンエネルギー,イオン種,イオン電流,二
次イオン極性,一次イオン走査領域,分析領域,一次イオン電流の安定性,試料導入,検出二次イオンな
どの分析条件は,装置に添付されている取扱説明書又は各機関で文書化された手順書に従って設定するの
がよい。
6.3
デルタ多層標準物質のSIMS深さ方向分布は,表面から多層膜と基板との界面近くまで,又は標準
物質に添付される説明書に記載された深さまで測定しなければならない。ただし,イオン照射によって発
生する表面荒れによって上記深さに達する前に二次イオン強度の変化が生じる場合には,表面荒れが生じ
る前に深さ方向分布測定を終えなければならない。
6.4
各デルタ層に対して測定点数が20を超えるように,一次イオン強度,走査領域などの測定条件を決
めなければならない。
6.5
再現性を確かめる測定では,デルタ多層標準物質のSIMS深さ方向分布を3回測定し,分布の繰返
し性を確認しなければならない。各デルタ層に達する時間は分析に要求される正確さで再現しなければな
らない。デルタ多層標準物質のSIMS分布を再現しない場合には,一次イオン電流の変動,走査の均一性
などの項目に対して装置の性能を確認しなければならない。
6.6
分析試料のSIMS深さ方向分布は,デルタ多層標準物質と同じ条件で測定しなければならない。
なお,必要に応じて一次イオン電流及び/又は一次イオン走査領域を変化させることによって,一次イ
オン電流密度を変えてもよい。
7
校正手順
7.1
校正の原理
7.1.1
この規格は,スパッタリングの初期の非定常領域におけるスパッタリング率変化を補正することで
深さ軸の校正をするための式を示す。
7.1.2
スパッタ深さ方向分析によって得られるデルタ層の分布(例を,図1に示す。)は,本来のデルタ
層の層構造とは異なり,スパッタリング率が定常状態に達した後であってもデルタ層のピーク位置シフト
が生じる。アトミックミキシング及びピークの重なりによるピーク位置シフトの見積りを,附属書B及び
附属書Cに記載する。
5
K 0156:2018 (ISO 23812:2009)
X 深さ(nm)
Y イオン強度(counts・s−1)
図1−シリコン中のボロンデルタ層のSIMS深さ分布[2]
7.2
標準物質によるスパッタリング率の決定方法
7.2.1
標準物質のスパッタ深さ方向分布(スパッタリング時間に対するイオン強度)によって,標準物質
のデルタ層の位置を決定する。ピーク位置を決定する方法には四つあり,これらの中から一つを採用し,
ピーク位置として決定することができる。
なお,採用する方法ごとに得られるピーク位置は異なり,その結果シフト距離も異なる。このシフト距
離を与える次に示す四つの方法のうち,分析試料の測定データに最も適した方法を選ぶ。
a) デルタ層位置を,デルタ層分布の極大値となる位置とする。
b) デルタ層位置を,デルタ層分布それぞれの半値全幅の中心となる位置とする。
c) デルタ層位置を,式(1)に示すi番目のデルタ層の重心位置(iz)とする。
()
()
∑
∑
=
bi
ai
bi
ai
z
z
z
z
i
z
I
z
zI
z
·········································································· (1)
ここに,
ai
z: (
)1
−
i
番目とi番目のデルタ層との間で強度が最小となる位置
bi
z: i番目と(
)1
+
i
番目のデルタ層との間で強度が最小となる位置
()z
I
: 深さzにおけるイオン強度
d) デルタ層位置を,JIS K 0169に規定する手順に基づく式(C.1)の
0zとする。
a) 及びb) の場合,統計変動を考慮した適切な平滑化処理を実施することが望ましい。
注記1 これらのデルタ層位置は,アトミックミキシングによって本来のデルタ層の位置からシフト
しているかもしれない。また,シフトの方向はマトリックス元素及び分析元素の相対的なノ
ックオン現象に依存する。シフト量は,一次イオンエネルギー及び入射角に依存する。この
シフトを軽減するには,適切な一次イオンエネルギー及び入射角を選ばなければならない。
アトミックミキシング効果がマトリックス元素と分析元素で同じであると仮定すれば,アト
ミックミキシングによるピークシフトは,附属書Bに示したように見積もることができる。
6
K 0156:2018 (ISO 23812:2009)
シリコン中のほう素は,この単純な事例とみなすことができる。附属書Bによれば,一次イ
オンエネルギー1 keV以下の場合において,この差異は1 nm未満に収まっている。
注記2 デルタ層のピークは,重心位置に比べて2倍かそれ以上に及ぶエネルギーに非線形に依存し
た顕著なシフトを示すことが報告されている。隣り合ったピークの重なりが無視できて(7.2.3
の注記1参照),アトミックミキシング効果がマトリックス元素と分析元素で同じである場合,
重心位置は本来のデルタ位置をほぼ示す。
7.2.2
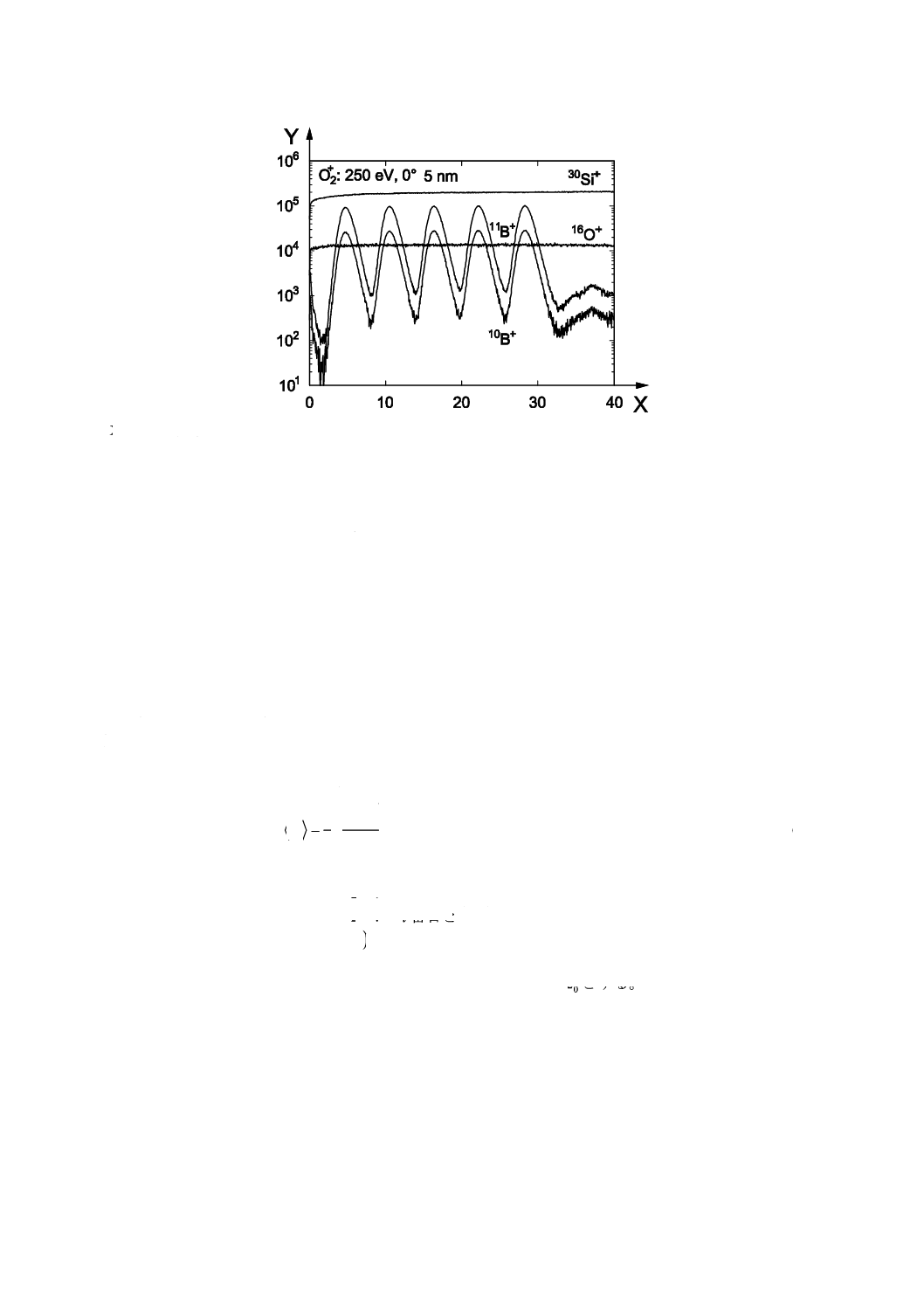
表面からi番目のデルタ層位置へ達するまでのスパッタリング時間をitと定義する(図2参照)。隣
り合うデルタ層位置のスパッタリング時間差
(
)
1
Δ
−
−
=
i
i
i
t
t
t
は,表面からi番目のシリコン層をスパッタする
のに必要な時間を意味する(ここで,
0
0=
t
とする)。i番目の深さを
izとし,i番目のシリコン層の厚さ
を
(
)
1
−
−
=
∆
i
i
i
z
z
z
とする。このとき,i番目の層の平均スパッタリング率を式(2)に示す。
i
i
i
t
z
r
∆
∆
=
··················································································· (2)
SIMS分析では,測定初期においてイオン収率が変化する。このイオン収率の遷移的な振舞いによって,
最初のデルタ層又は最初の二つのデルタ層の位置は決められない場合がある。このような場合,位置を決
められるデルタ層を使って深さ校正を行うこととする。最初に検出できるデルタ層よりも浅い領域では,
スパッタ深さは表面から最初に検出できるデルタ層までの平均スパッタリング率を使って概算する。
X スパッタリング時間
Y スパッタ深さ
図2−浅い領域におけるスパッタ深さとスパッタリング時間との関係を示す模式図
7.2.3
それぞれのデルタ層の平均スパッタリング率を決定する。一般に,平均スパッタリング率は表面近
傍では大きいが,数ナノメートルをスパッタした後,定常値(定常状態におけるスパッタリング率
Sr)に
達する。n番目の層及びそれよりも深い領域において,irをSrとみなすことができた場合,スパッタリン
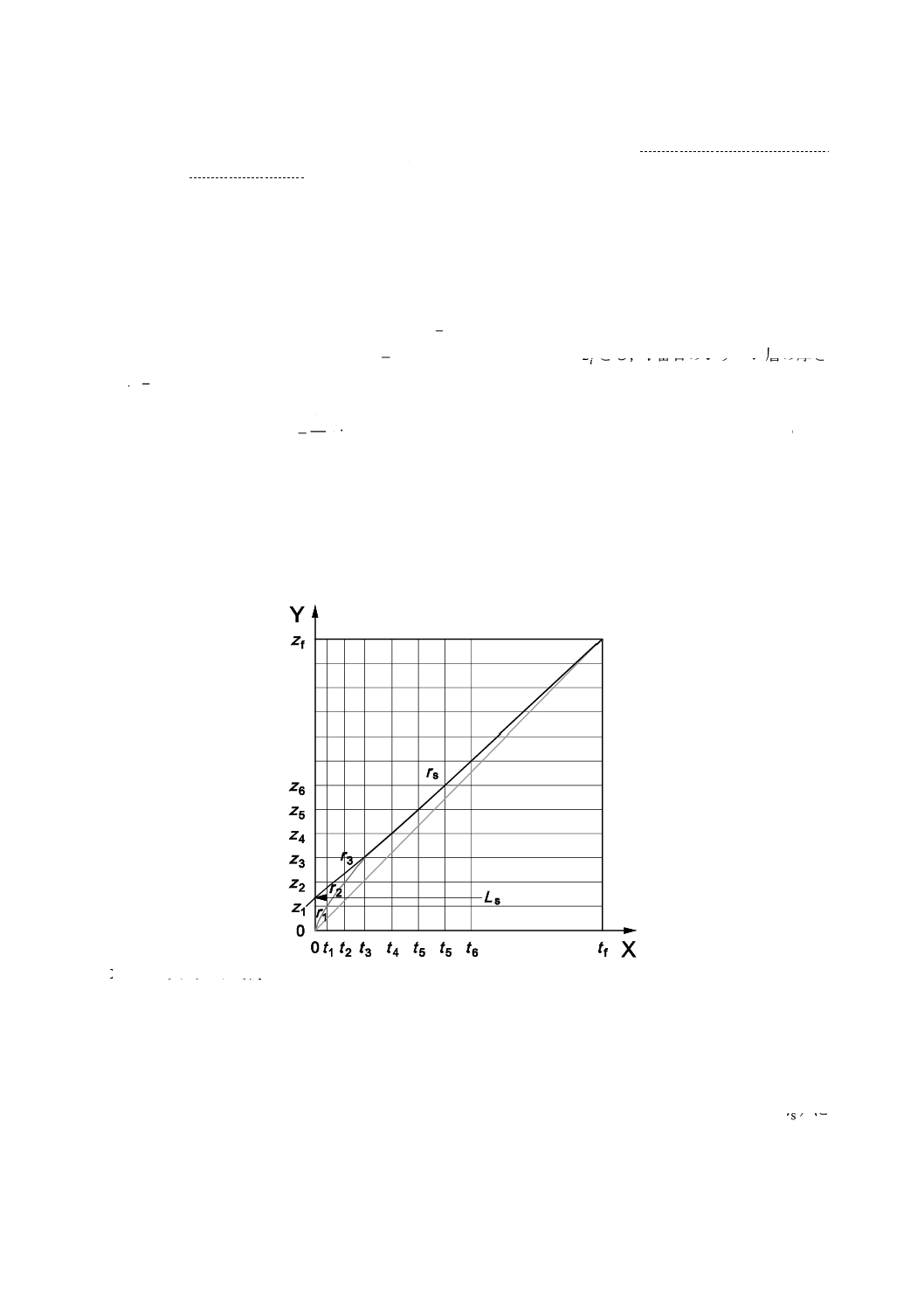
グ時間tにおけるスパッタ深さzを式(3)に示す。

7
K 0156:2018 (ISO 23812:2009)
(
)
(
)
∑
−
=
−
−
−
+
−
=
1
1
1
S
1
n
i
n
i
i
i
t
t
r
t
t
r
z
(
)
∑
−
=
−
−
+
−
−
=
1
1
S
1
S
1
n
i
n
i
i
i
t
r
t
r
t
t
r
(
)
nz
z≧
t
r
L
S
S+
=
················································································ (3)
ここに,
(
)
∑
−
=
−
−−
−
=
1
1
1
S
1
S
n
i
n
i
i
i
t
r
t
t
r
L
∑
−
=
−
∆
=
1
1
S
1
n
i
i
i
r
r
z
····························································· (4)
SLは深さ軸のシフト距離であり,一次イオン電流密度には依存しない。
注記1 短周期の多層デルタ層試料では,測定されたデルタ層分布がお互いに重なることによって,
5.5の条件を満たさないかもしれない。分布の重なりが顕著な場合には測定されたデルタ位置
はその重なりに影響される。しかしながら,重なりの影響を受けたピークシフトは深いデル
タ層では定常値に達する。このため,デルタ層間距離
iz
∆は深さ校正に使うことができる。
隣り合ったデルタ層分布のピーク谷比が2よりも大きい場合,深さ校正に3番目又はそれよ
り深いデルタを使うことができる。ピーク谷比が10以上の場合,それぞれの層は独立してい
るとみなすことができる。この場合,最初のデルタ層に達する前にスパッタリングが定常状
態に達していれば,最初のデルタ層も使うことができる。デルタ層分布の重なりによるピー
クシフトの見積りを附属書Cに記載している。
注記2
SL値は7.2.1に規定の手順a),b),c) 及びd) に依存し得る。
7.2.4
n番目〜m番目のデルタ層を使う場合,
nz
z≧
におけるデルタ層の認証された深さを参照すること
で,
SL及びSrは線形回帰を使って決定しなければならない。
(
)∑
∑
∑∑∑∑
=
=
=
=
=
=
−
+
−
−
=
m
n
i
m
n
i
i
i
m
n
i
m
n
i
m
n
i
m
n
i
i
i
i
i
i
i
t
n
m
z
t
t
z
t
L
2
2
2
S
1
······················································· (5)
(
)
(
)∑
∑
∑
∑∑
=
=
=
=
=
−
+
−
−
+
−
=
m
n
i
m
n
i
i
i
m
n
i
m
n
i
m
n
i
i
i
i
i
t
t
n
m
z
t
z
t
n
m
r
2
2
S
1
1
····················································· (6)
アトミックミキシングによるシフトに起因する
SLの不確かさを,深さ校正の際に考慮しなければならな
い。
7.3
分析試料の深さ軸校正
7.3.1
標準物質で用いたスパッタリング条件での深さ校正
デルタ多層標準物質から決められたスパッタリング率を使って,
nz
z≧
でのスパッタ深さを校正する場
合,式(7)を用いて行う。この場合,分析試料のスパッタリング条件は標準物質と同じにしなければならな
い。

8
K 0156:2018 (ISO 23812:2009)
t
r
L
z
S
S+
=
··············································································· (7)
7.3.2
標準物質で用いたスパッタリング率と異なる条件での深さ校正
一次イオン電流密度がk倍だけ標準物質で使われた条件と異なる場合,ほかのスパッタリング条件は変
化しないとしてスパッタ深さを式(8)に示す。
−
+
−
=
−
−
=
−
∑
k
t
t
kr
k
t
k
t
kr
z
n
n
i
i
i
i
1
S
1
1
1
(
)
∑
−
=
−
−
+
−
−
=
1
1
S
1
S
1
n
i
n
i
i
i
t
kr
t
r
t
t
r
(
)
nz
z≧
t
kr
L
S
S+
=
·············································································· (8)
nz
z≧
でのスパッタ深さは,標準物質から決められた
SLとSrとを用いて,式(8)によって決定する。
注記 式(8)は,同じ一次イオン電流密度において分析試料のスパッタリング率が標準物質のスパッタ
リング率とk倍異なる場合にも使うことができる。この現象はシリコンの密度が分析試料と標
準物質とで異なる場合に生じる。
7.4
校正深さの標準不確かさ
7.4.1
デルタ層の位置のシフトは,7.2.1に規定するピーク位置の決定方法に依存する。したがって,SLは
用いた方法に依存して異なる。各種ピーク位置の決定方法及び一次イオン条件によるシフト距離の見積り
を,附属書Bに示す。ただし,実際のシフトは,イオン照射条件だけでなくデルタ層の元素にも依存し,
一般的な式は使用できない。ここでは,定義に依存するシフト距離を,()p
LS
と表現する。
7.4.2
n番目の層〜m番目の層のデルタ層を使ってrSを決定するとき,式(7)を使って校正した深さの
)
2
1(
100
α
−
×
%信頼区間を,式(9)に示す。
()
(
)
1
S
S
,1
s
n
m
T
t
r
p
L
×
−
−
±
+
α
························································· (9)
ここに,(
)
α
,1
−
−n
m
T
は,自由度(
)1
−
−n
m
,有意水準
α
100 %でのスチューデントのt分布表から得ら
れる棄却限界値である。また,1sは標準物質における層の深さの標準不確かさ
RM
s
を用いて,式(10)から
計算する。
()
2
1
S
2
RM
2
S
S
S
2
1
2
2
2
S
S
1
1
1
1
1
1
1
1
1
1
1
+
−
+
−
−
×
+
−
−
+
−
−
+
+
−
+
×
=
∑
∑
∑
∑
=
=
=
=
m
n
i
i
i
m
n
i
m
n
i
i
i
m
n
i
i
r
s
z
r
r
p
L
t
n
m
z
n
m
z
t
n
m
t
r
n
m
r
s
········ (10)
式(8)に対しては,校正した深さに対する
(
)
α
2
1
100
−
×
%信頼区間を,式(11)に示す。
()
(
)
2
S
S
,1
s
n
m
T
t
kr
p
L
×
−
−
±
+
α
·······················································(11)
ここに,
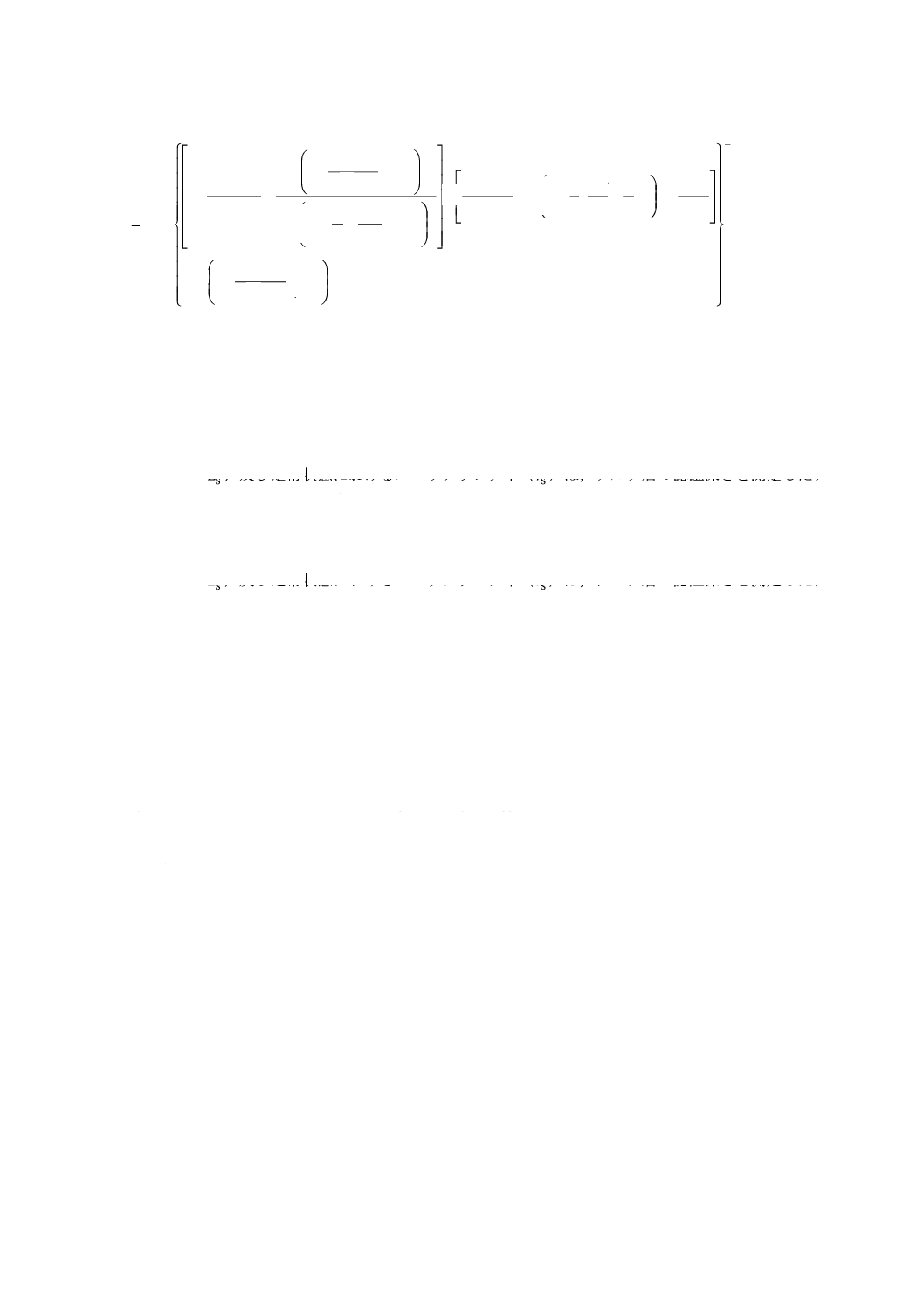
9
K 0156:2018 (ISO 23812:2009)
()
2
1
2
2
2
S
2
RM
2
S
S
S
2
2
2
S
S
2
1
1
1
1
1
1
1
1
1
1
1
1
+
−
−
+
+
−
+
−
−
×
+
−
−
+
−
−
+
+
−
+
×
=
∑
∑
∑
∑
∑
=
=
=
=
=
k
m
n
i
i
m
n
i
i
i
m
n
i
m
n
i
i
i
m
n
i
i
s
t
n
m
t
k
r
s
z
r
r
p
L
t
n
m
z
n
m
z
t
n
m
t
r
n
m
kr
s
····· (12)
及びskは,kの標準不確かさである。
これらの式の導出方法を,附属書Dに示す。
8
結果の表現
8.1
標準物質で用いたスパッタリング条件での校正
シフト距離(
SL)及び定常状態におけるスパッタリング率(Sr)は,デルタ層の認証深さと測定したデ
ルタ層のスパッタリング時間とを線形回帰することによって決定する。スパッタリング時間は,式(7)を用
いてスパッタリング深さに変換する。
8.2
標準物質で用いたスパッタリング率と異なる条件での校正
シフト距離(
SL)及び定常状態におけるスパッタリング率(Sr)は,デルタ層の認証深さと測定したデ
ルタ層のスパッタリング時間とを線形回帰することによって決定する。スパッタリング時間は,式(8)を用
いてスパッタリング深さに変換する。
8.3
濃度校正
必要に応じて,別のJIS若しくは国際規格又はその他の文書化された手順に従って,イオン強度を原子
濃度に変換しなければならない。
9
分析結果の報告
分析結果の報告は,次の情報を含む。
a) 試料,装置,研究機関及び分析日を特定できる全ての情報
b) 使用したデルタ多層標準物質
c) 分析条件
d) 分析中に気付いた通常とは異なる事項
e) 結果に影響を及ぼす特別な作業など,この規格によらない作業
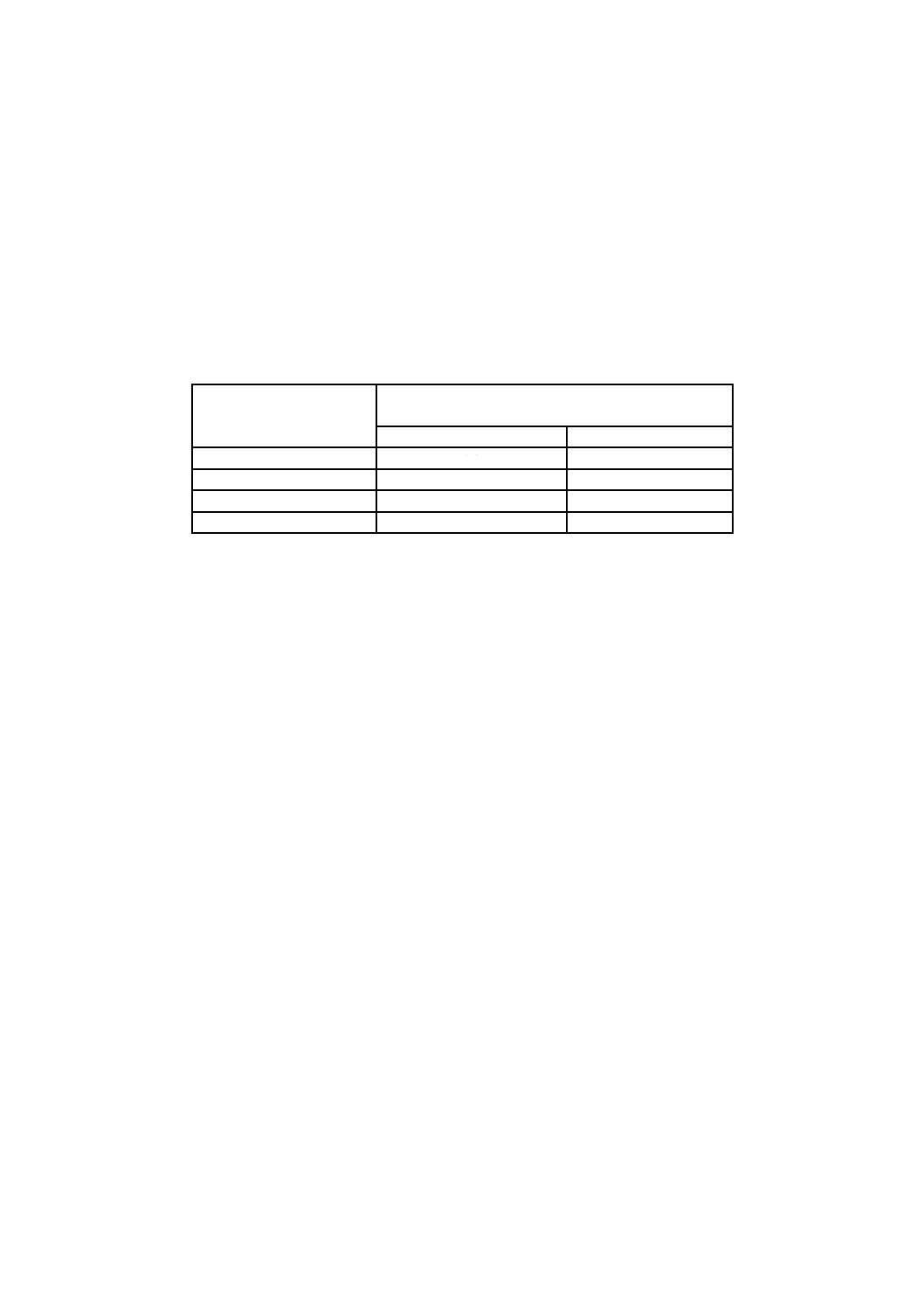
10
K 0156:2018 (ISO 23812:2009)
附属書A
(参考)
シリコン中における酸素イオンの投影飛程
この附属書は,SRIM(http://www.srim.org/参照)を用いて計算したシリコン中O2+一次イオンの飛程を
示す。
自然酸化膜の影響は,計算に含まれていない。
表A.1−シリコン中でのO2+の投影飛程
一次イオンエネルギー
eV
投影飛程
nm
0°入射
45°入射
250
1.3
1.1
500
2.0
1.7
1 000
3.0
2.4
2 000
4.7
3.7
11
K 0156:2018 (ISO 23812:2009)
附属書B
(参考)
アトミックミキシングによるピークシフトの見積り
B.1
一般
この附属書は,SIMSによる浅い深さ方向分布のイオンスパッタリング条件の基準を与えるために,ア
トミックミキシングに起因するデルタ層分布のピークシフトについて示す。シリコン中のボロンの深さ方
向分布の測定から得られたそれぞれのデルタ層の重心位置,極大位置及び半値全幅の中心位置と,理論モ
デルから見積もられるデルタ層の位置とを比較した。理論モデルはマトリックスと分析元素のアトミック
ミキシングとが同じであると仮定していることに注意する。シリコン中のボロンは単純なモデルで扱われ
ているが,測定試料の原子番号がマトリックスの原子番号と大きく異なる場合又は照射誘起偏析が生じる
場合には,実測ピーク位置は異なった振舞いをし得る。
B.2
手順
シリコン中のBNデルタ多層標準物質のSIMS深さ方向分布は,アトミックミキシング,表面荒れ及び
情報深さ(MRI)モデル[4]を基に解析した。SIMSにおいて情報深さはゼロと考えられる[5]ことから,本
解析ではアトミックミキシングと表面荒れとの二つのパラメータだけを,測定データをフィッティングす
るために用いた。デルタ層の物質に偏析が生じなければ,MRIモデルによって,測定された深さ方向分布
から正確な本来のデルタ層の位置を決定することができる。重心位置,極大位置及び半値全幅の中心位置
は,各デルタ層の分布から導出する。MRIモデルの仮定となるミキシングが均質に進行する場合,重心位
置は本来のデルタ位置と一致する。そのため,ピーク位置のシフト量を,重心位置からの差として決定し
た。用いた試料は,BNデルタ層が十分に分離された試料である[2]。シリコンスペーサー層(デルタ層間)
の厚さは,18.5 nmである。計算では,同じパラメータをデルタ層とマトリックス原子とに適用した。
B.3
結果
一次イオンO2+の種々のイオンエネルギー及び入射角に対する,本来のデルタ層の位置(dz)との重心
位置(
cz)の差を,図B.1に示す。czは,3 keVを除き,ほとんど変化しないと考えられる。極大位置(
LM
z
)
と半値全幅のピーク中心位置(
PC
z)とは,重心位置と比較して,表面側へと大きくシフトしている。重
心位置に対するこれらの位置のシフト(
c
LMz
z
−
及び
c
PC
z
z−
)をそれぞれ図B.2及び図B.3に示す。シフ
ト量は,主にイオンエネルギーに依存し,半値全幅の中心位置よりも極大位置の方が大きい。極大位置の
シフトの値は,半値全幅の中心位置の値の約2倍大きい。イオンエネルギーが1 keV又はそれ以下では,
極大位置のシフトは1 nm未満である。
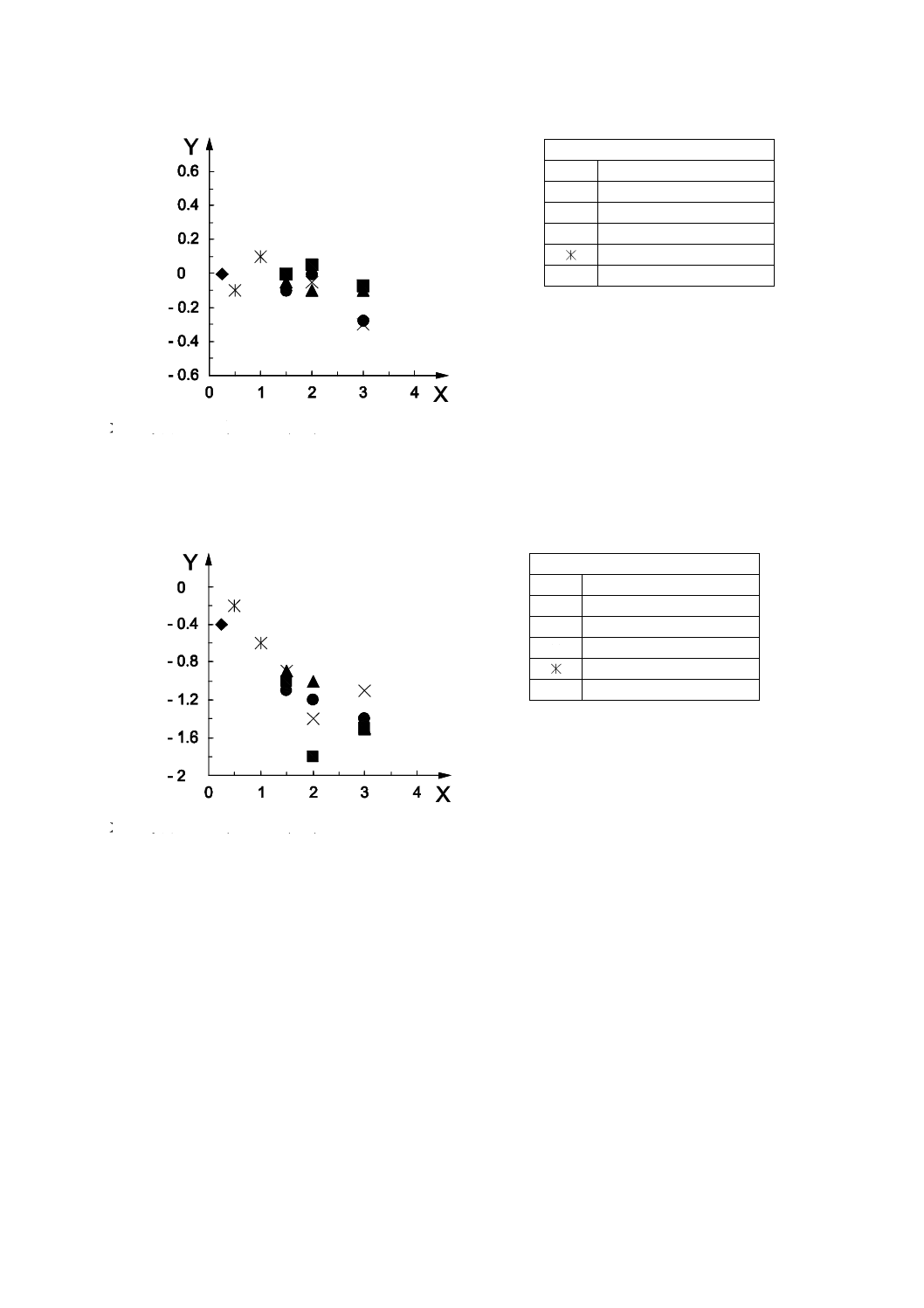
12
K 0156:2018 (ISO 23812:2009)
X 一次イオンエネルギー(keV)
Y
d
c
z
z−
(nm)
図B.1−デルタ層とマトリックス原子とで同じ値を用いてMRIモデルで計算された本来のデルタ層の位置
に対する重心位置のシフト
X 一次イオンエネルギー(keV)
Y
c
LM
z
z
−
(nm)
図B.2−デルタ層の重心位置に対する極大位置のシフト
入射角
入射角
◆
0°
■
9°
▲
27°
×
45°
45°(酸素吹付け)
●
63°
入射角
◆
0°
■
9°
▲
27°
×
45°
45°(酸素吹付け)
●
63°
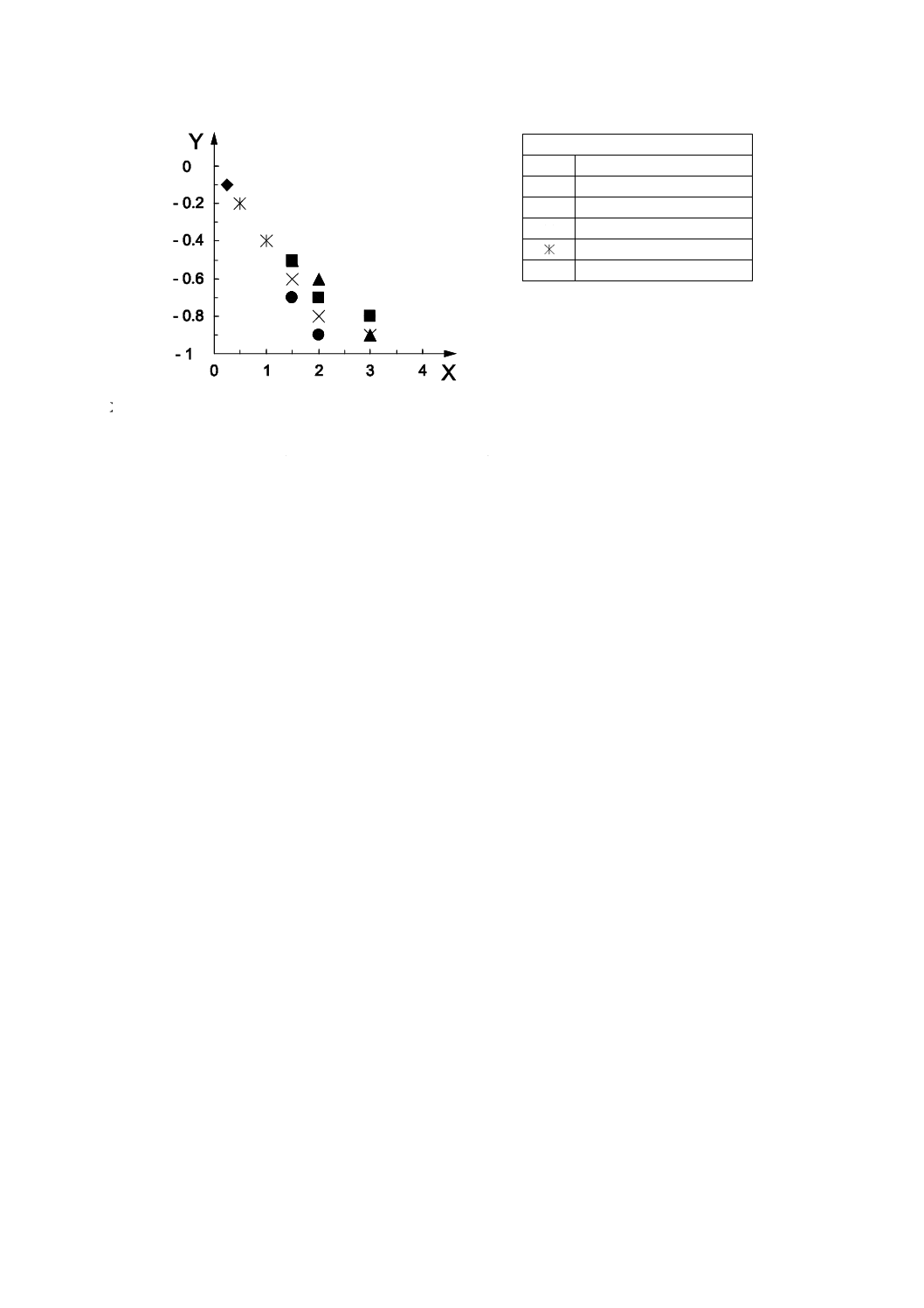
13
K 0156:2018 (ISO 23812:2009)
X 一次イオンエネルギー(keV)
Y
c
PC
z
z −
(nm)
図B.3−デルタ層の重心位置に対するピーク半値全幅中心位置のシフト
入射角
◆
0°
■
9°
▲
27°
×
45°
45°(酸素吹付け)
●
63°
14
K 0156:2018 (ISO 23812:2009)
附属書C
(参考)
ピークの重なりに起因するピークシフトの見積り
C.1 一般
この附属書は,SIMSによる浅い深さ分布のための参照物質としてデルタ多層の基準を与えるため,ピ
ークの重なりに起因したデルタ多層分布の見掛け上のピークシフトを示す。深さ分布の定常状態における
デルタ層の重心位置,極大位置及び半値全幅の中心位置は,短周期デルタ多層膜のシミュレーション分布
から見積もられた。
C.2 手順
デルタ多層膜のSIMS深さ分布は,デルタ層のモデル分布関数[6]を用いて,数値的に合成された式(C.1)
で表される。
()
(
)
(
)
+
−
−
+
+
+
−
+
+
=
2
T
T
0
2
2
L
L
0
1
T
L
5.0
exp
erf
1
5.0
exp
erf
1
1
λ
σ
λ
ξ
λ
σ
λ
ξ
λ
λ
z
z
z
z
z
I
··········· (C.1)
ここに,
−
−
−
=
L
0
1
2
1
λ
σ
σ
ξ
z
z
·············································································· (C.2)
−
−
=
T
0
2
2
1
λ
σ
σ
ξ
z
z
················································································· (C.3)
ここに,
z0: 見掛け上のピーク深さ
λL: 上昇端ディケイ長さ
λT: 下降端ディケイ長さ
σ: ガウス型応答関数における標準偏差(JIS K 0169参照)
隣接するデルタ層間の間隔が小さくなると,デルタピークは互いに重なり始める。このピークに対する
重なりを評価するため,重なったピークのピーク谷比を用いた。重心位置,極大位置及び半値全幅の中心
位置の見掛け上の深さを,重なりの定常状態において導出した(例えば,重なりが定常状態になる前での
最初の二つ又は三つのデルタピークを除いた。)。シミュレーションに用いたパラメータは,
1.0
L=
λ
nm,
7.0
T=
λ
nm及び
4.0
=
σ
nm,並びに
3.0
L=
λ
nm,
2
T=
λ
nm及び
5.0
=
σ
nmである。これらの値は,
O2+ビームエネルギー250 eV及び2 keVの条件で測定したシリコン中のBNデルタ多層のフィッティング
によって得られた二つの条件に相当する。デルタ層のスペースに関しては,前者の場合2 nm,3 nm,4 nm,
5 nm及び6 nmに設定し,後者の場合3.5nm,5 nm,7 nm,11 nm及び14 nmに設定した。
C.3 結果
重なりの程度に依存する見掛け上のピークシフトを図解するため,O2+ビームエネルギー250 eV及び2
keVに対するピーク谷比に対する重心位置,極大位置及び半値全幅の中心位置の見掛け上の深さをそれぞ
れ図C.1及び図C.2に示す。これらのシフトは,重なっていない重心位置との差である。重心位置は,重
なりに最も敏感であり,特に,ピーク谷比の低いところで顕著である。一方,極大位置は重なりにほとん
ど影響されない。ピーク半値全幅の中心位置の振舞いは,中間である。しかしながら,重心位置でさえ,
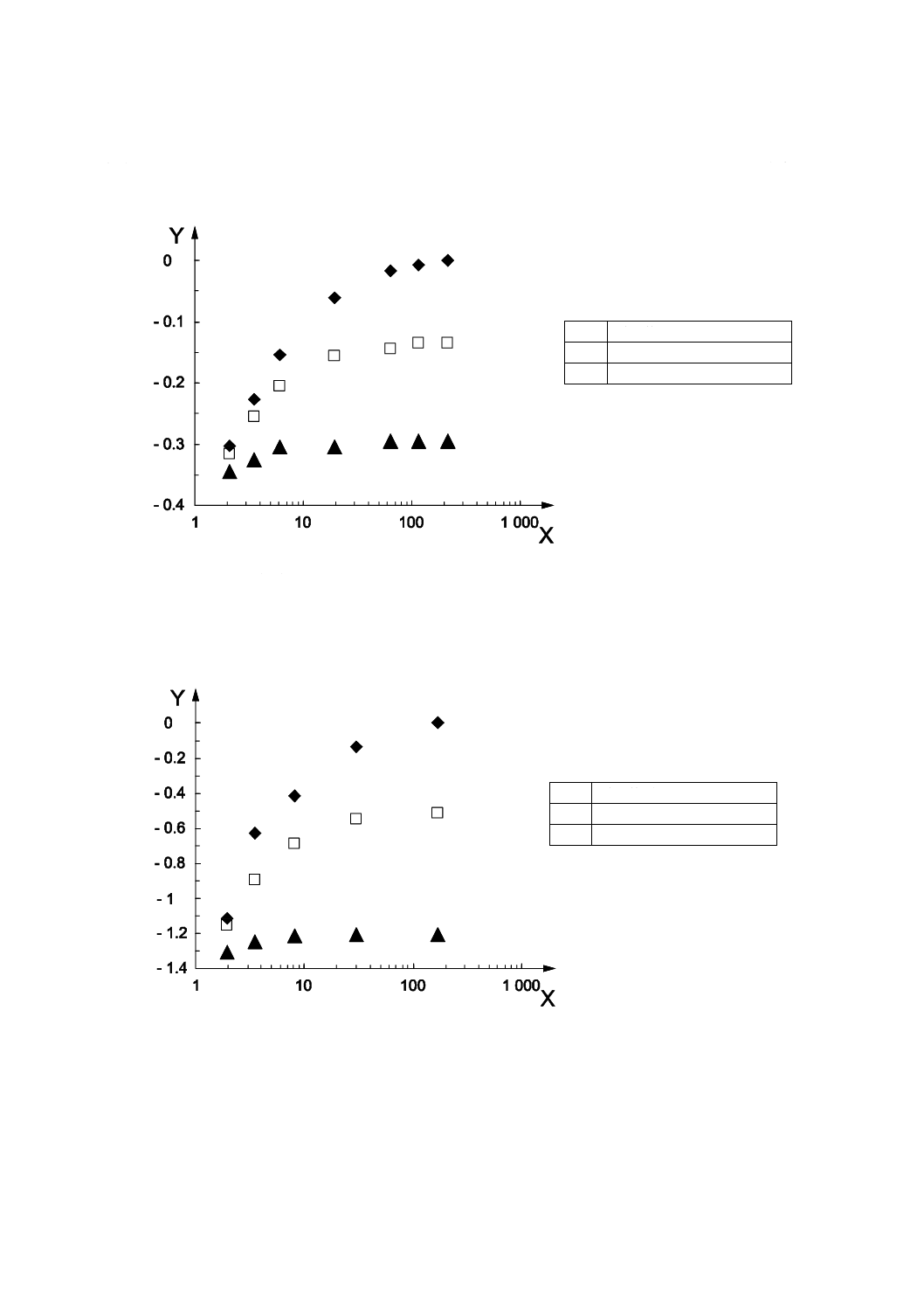
15
K 0156:2018 (ISO 23812:2009)
ピーク谷比が10以上であれば,シフト量は小さい。そのような状況下では,250 eVではシフトは0.1 nm
以下,2 keV以上では0.4 nm未満である。このため,ピーク谷比が10以上では,重なりの影響を無視でき
る。
X ピーク谷比
Y 見掛け上のシフト(nm)
図C.1−一次イオンO2+,250 eVでの独立したデルタ層の重心位置に対する重なりに起因したピーク位置
の見掛けのシフト(λL=0.1 nm,λT=0.7 nm及びσ=0.4 nm)
X ピーク谷比
Y 見掛け上のシフト(nm)
図C.2−一次イオンO2+,2 keVでの独立したデルタ層の重心位置に対する重なりに起因したピーク位置
の見掛けのシフト(λL=0.3 nm,λT=2nm及びσ=0.5 nm)
◆
重心位置
□
半値全幅の中心位置
▲
極大位置
◆
重心位置
□
半値全幅の中心位置
▲
極大位置

16
K 0156:2018 (ISO 23812:2009)
附属書D
(参考)
不確かさの導出方法
標準物質のn番目〜m番目のl個(
)1
+
−
=
n
m
のデルタ層が用いられた場合,スパッタリング時間(t)に
対するスパッタ深さ()zの回帰直線は,式(D.1)で表される。
(
)
(
)
z
z
b
t
bz
z
b
t
bz
a
t
−
+
=
+
−
=
+
=
·············································· (D.1)
分析試料の時間(t)においてスパッタ深さの推定値は,式(D.2)で表される。
b
t
t
z
z
−
+
=
ˆ
··········································································· (D.2)
深さの推定値の分散は,標準不確かさ()sを用いて式(D.3)で表される。
2
2
2
2
2
2
2
0
ˆ
ˆ
ˆ
b
t
t
s
b
z
s
t
z
s
t
z
s
∂∂
+
∂∂
+
∂∂
≅
2
2
2
2
2
2
2
1
1
b
t
t
s
b
t
t
s
b
s
b
−
−
+
−
+
=
(
)
(
)
−
×
−
+
×
+
=
∑
i
i
t
t
t
z
z
s
b
t
t
l
s
b
b
s
2
2
4
2
2
2
2
2
1
(
)
(
)
2
2
2
2
2
1
1
b
s
z
z
b
t
t
l
t
i
i
×
−
−
+
+
=
∑
·················································· (D.3)
ここで,スパッタリング時間の標準不確かさは,式(D.4)で与えられる。
(
)
[
]
(
)
2
1
2
2
1
2
1
2
ˆ
2
−
−
=
−
+
−
=
∑
∑
l
t
t
l
bz
a
t
s
i
i
i
i
t
······································· (D.4)
したがって,深さの標準不確かさは,式(D.5)で与えられる。
(
)
(
)
(
)
2
1
2
2
1
2
2
2
0
2
ˆ
1
1
1
−
−
×
−
−
+
+
=
∑
∑
l
t
t
z
z
b
t
t
l
b
s
i
i
i
i
i
································· (D.5)
(
)
α
2
1
100
−
×
%の信頼区間は,式(D.6)で与えられる。
(
)
0
,2
ˆ
s
l
T
z
×
−
±
α
····································································· (D.6)
17
K 0156:2018 (ISO 23812:2009)
ここに,(
)
α
,2
−
l
T
は,自由度(
)2
−
l
でのスチューデントのt分布の
α
100 %における棄却限界値である。
標準物質の不確かさが
RM
s
の場合,ts及び
RM
s
の二乗平均(
)2
/1
2
RM
2
bs
st+
が,式(D.3)のtsとして代用される。
したがって,深さの推定値の不確かさは式(D.7)で与えられる。
(
)
(
)
(
)
(
)
2
1
2
RM
2
2
1
2
2
2
1
2
ˆ
1
1
1
+
−
−
×
−
−
+
+
×
=
∑
∑
bs
l
t
t
z
z
b
t
t
l
b
s
i
i
i
i
······················ (D.7)
この規格では,
t
r
L
z
S
S+
=
及び
z
r
r
L
t
S
S
S
1
+
−
=
である。
式(D.7)のitˆの代わりに
i
bz
a+
を,aの代わりに
S
S
r
L
−
を,bの代わりに
S
1
rを,及びlの代わりに
1
+
−n
m
を
置くことによって,式(10)が得られる。
異なるスパッタリング率(k倍)を用いた場合の校正には,式(D.8)〜式(D.11)が用いられる。
(
)
z
k
b
z
b
t
z
k
b
a
t
1
1
+
−
=
+
=
························································ (D.8)
k
b
z
b
t
t
z
1
ˆ
+
−
=
·········································································· (D.9)
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
k
b
t
t
s
k
b
t
t
s
k
b
t
t
s
k
b
s
k
b
s
−
−
+
−
−
+
−
+
=
(
)
(
)
(
)
2
2
4
2
2
2
4
2
2
2
2
2
2
2
k
i
i
t
t
t
s
b
k
t
t
z
z
s
b
k
t
t
l
s
b
k
s
b
k
−
+
−
×
−
+
×
+
=
∑
········(D.10)
(
)
(
)
(
)
(
)
2
1
2
2
2
2
SR
2
2
2
2
2
2
ˆ
1
1
−
+
+
−
−
×
−
−
+
+
=
∑
∑
k
i
i
i
i
i
s
k
t
t
bs
l
t
t
z
z
b
t
t
l
b
k
s
·· (D.11)
式(D.11)のitˆの代わりに
i
bz
a+
を,aの代わりに
S
S
r
L
−
を,bの代わりに
S
1
rを,及びlの代わりに
1
+
−n
m
を置くことによって,式(12)が得られる。
18
K 0156:2018 (ISO 23812:2009)
参考文献
[1] WITTMAACK, K. Sputtering yield changes, surface movement and apparent profile shifts in SIMS depth
analyses of silicon using oxygen primary ions, Surf. Interface Anal., 1996, 24, pp. 389-398
[2] HOMMA, Y., TAKENAKA H., TOUJOU, F., TAKANO, A., HAYASHI, S., and SHIMIZU, R. Evaluation of the
sputtering rate variation in SIMS ultra-shallow depth profiling using multiple short-period delta layers, Surf.
Interface Anal., 2003, 35, pp. 544-547
[3] WITTMAACK, K., HAMMERL, E., EISELE, I., and PATEL, S.B. Peak or centroid−Which parameter is
better suited for quantifying apparent marker locations in low-energy sputter depth profiling with reactive
primary ion beams? Surf. Interface Anal., 2001, 31, pp. 893-896
[4] HOFMANN, S. Atomic mixing, surface roughness and information depth in high-resolution AES depth
profiling of a GaAs/AlAs superlattice structure, Surf. Interface Anal., 1994, 21, pp. 673-678
[5] TAKANO, A., HOMMA, Y., HIGASHI, Y., TAKENAKA, H., HAYASHI, S., GOTO, K., INOUE, M., and
SHIMIZU,
R.
Evaluation
of
SIMS
depth
resolution
using
delta-doped
multilayers
and
mixing-roughness-information depth model, Appl. Surf. Sci., 2003, 203-204, pp. 294-297
[6] DOWSETT, M.G., ROWLANDS, G., ALLEN, P.N., and BARLOW, R.D. An analytic form for the SIMS
response function measured from ultra-thin impurity layers, Surf. Interface Anal., 1994, 21, pp. 310-315