C 61280-4-4:2015 (IEC 61280-4-4:2006)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 記号及び略語 ··················································································································· 2
4 背景:PMD特性 ·············································································································· 3
5 測定方法························································································································· 5
5.1 PMD測定方法 ··············································································································· 5
5.2 基準測定方法 ················································································································ 7
6 装置······························································································································· 7
6.1 光源及び偏光器 ············································································································· 8
6.2 光入力部品 ··················································································································· 8
6.3 クラッドモードストリッパ ······························································································ 8
6.4 高次モード・フィルタ ···································································································· 8
6.5 出力接続 ······················································································································ 8
6.6 光出力部品 ··················································································································· 8
6.7 光検出器 ······················································································································ 9
6.8 コンピュータ ················································································································ 9
6.9 ASEの影響を弱める手段 ································································································· 9
7 サンプリング及び被測定対象 ······························································································ 9
8 手順······························································································································· 9
9 計算又は結果の解釈 ·········································································································· 9
10 書類 ····························································································································· 9
10.1 各測定に必要な情報 ······································································································ 9
10.2 利用可能な情報 ··········································································································· 10
11 仕様情報 ······················································································································ 10
附属書A(規定)固定アナライザ法 ························································································ 11
附属書B(規定)ストークスパラメータ解析法 ·········································································· 17
附属書C(規定)干渉法 ······································································································· 22
附属書D(規定)戻り光を用いたストークスパラメータ解析法····················································· 31
附属書E(規定)変調位相シフト法 ························································································ 33
附属書F(規定)偏波位相シフト法 ························································································· 41
附属書G(参考)方法CによるPMDの決定 ············································································ 47
参考文献 ···························································································································· 50
C 61280-4-4:2015 (IEC 61280-4-4:2006)
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人光産業技術振興協会(OITDA)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
また,令和2年6月22日,産業標準化法第17条又は第18条の規定に基づく確認公示に際し,産業標準
化法の用語に合わせ,規格中“日本工業規格”を“日本産業規格”に改めた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS C 61280の規格群には,次に示す部編成がある。
JIS C 61280-1-3 中心波長及びスペクトル幅測定
JIS C 61280-2-1 受信感度及びオーバロード測定
JIS C 61280-2-2 光アイパターン,光波形及び消光比測定
JIS C 61280-2-3 第2-3部:ジッタ及びワンダ測定
JIS C 61280-2-8 Q値測定を用いた低ビット誤り率の決定法
JIS C 61280-2-9 高密度波長分割多重システムの光信号対雑音比測定
JIS C 61280-2-10 第2-10部:レーザ送信器の時間分解チャープ及びアルファファクタ測定
JIS C 61280-2-11 光信号品質評価のための強度ヒストグラム評価を用いた平均化Q値測定
JIS C 61280-4-4 第4-4部:ケーブル設備及びリンク−既設リンクの偏波モード分散測定
日本産業規格 JIS
C 61280-4-4:2015
(IEC 61280-4-4:2006)
光ファイバ通信サブシステム試験方法−
第4-4部:ケーブル設備及びリンク−
既設リンクの偏波モード分散測定
Fiber optic communication subsystem test procedures-
Part 4-4: Cable plants and links-
Polarization mode dispersion measurement for installed links
序文
この規格は,2006年に第1版として発行されたIEC 61280-4-4を基に,技術的内容及び構成を変更する
ことなく作成した日本産業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,既設のシングルモード光ファイバからなるリンクの偏波モード分散(PMD)を測定する均
一な方法について規定する。既設リンクとは送信機と受信機との間の光の経路,又はその一部を指す。こ
れらの測定方法は,対象となるリンクが高ビットレートの伝送用途に適しているかどうかを判断するため
に,又は伝送に関する様々な部品の相関関係を洞察するために用いることができる。この規格の原理は,
製造時の測定に焦点が置かれた光ファイバ及び光ファイバケーブルの試験方法JIS C 6842(参考文献参照)
に沿ったものである。この規格は,製造時の測定の代わりに,既設されていてもよい長距離のリンクのた
めの測定方法及び測定用件に焦点を当てている。この場合のリンクには,増幅器,高密度波長分割多重用
部品,合波器などのその他の光部品が含まれていてもよい。
PMDは統計的なパラメータである。測定の再現性は,個々の方法に依存するが,リンクのPMDの度合
いによっても制限を受ける。Gisinは,この測定再現性の理論限界を,無限の測定波長域及び理想的な測定
条件を仮定することによって導き出した[3]1)。
注記1 製造時の光ファイバ及び光ファイバケーブルの試験方法については,JIS C 6842に記載して
いる。
注記2 光増幅器の試験方法については,JIS C 6122-11-1及びIEC 61290-11-2に記載している。
注記3 受動部品の試験方法については,JIS C 61300-3-32に記載している。
注記4 分散補償器又は光増幅器のような部品を含むリンクでのPMDの計算のガイドラインについ
ては,IEC/TR 61282-3に記載している。
注1) 角括弧内の数字は,参照する参考文献の番号を示す。
方法Dを除くこの規格の全ての方法で,光増幅器を含むリンクの利得帯域におけるPMDを測定できる。
増幅器を含むリンクを試験するとき,増幅された自然放出光(ASE)雑音は,測定波長付近で無偏光状態
2
C 61280-4-4:2015 (IEC 61280-4-4:2006)
のスペクトルエネルギーを生成する。一般的に,ASEは測定精度を落とす。方法A,B,C,E及びFにつ
いては,この結果は受信端で光学又は電気的フィルタを用いることで緩和できる。ただし,光学フィルタ
は,信号スペクトル部のASEを取り除くことができない。広帯域光源のスペクトルをフィルタのスペクト
ル幅によって十分に減らせない場合,精度はより低い偏光度(DOP)によって制限される。より低いDOP
で有用なデータとするには,より長くデータを取り込む必要がある。そうしなければ,結果は多くの雑音
成分を含み,解釈を誤ることとなる。
いずれの方法も,偏波依存損失(PDL)が10 dB以上あるリンクの偏波モード分散を測ることはできな
い。PDLの値が1 dB未満のリンクは,合理的な精度で測定できる。1 dBを超えるPDLがあると測定精度
が落ちる場合がある。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 61280-4-4:2006,Fibre optic communication subsystem test procedures−Part 4-4: Cable plants and
links−Polarization mode dispersion measurement for installed links(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この引用
規格は,その最新版(追補を含む。)を適用する。
IEC 60793-1-44,Optical fibres−Part 1-44: Measurement methods and test procedures−Cut-off wavelength
3
記号及び略語
この規格で用いる主な記号及び略語は,次による。
c
真空中の光速(299 792 458 m/s)
(velocity of light in vacuum)
h
結合長
(coupling length)
L
リンク長
(length of the link)
tc
光源のコヒーレンス時間(方法C)
[optical source coherence time (method C)]
δλ
波長間隔(ステップ幅)
[wavelength increment (step size)]
δν
光周波数間隔(ステップ幅)
[optical frequency increment (step size)]
Δλ
光源スペクトル幅又は線幅
(記載のない場合,半値全幅)
[optical source spectral width or linewidth (FWHM
unless noted otherwise)]
Δθ
ポアンカレ球上の回転角度
(rotation angle on Poincaré sphere)
δτ
異種偏波成分の差動到達時間
(differential arrival times of different polarization
components)
δτmin
測定可能な最小δτ
(minimum δτ value that can be measured)
Δτ
群遅延時間差の値
(differential group delay value)
<Δτ>
群遅延時間差の波長域での平均,
PMDAVG
(average DGD over a wavelength range or PMDAVG
value)
<Δτ2>1/2
群遅延時間差の波長域での二乗平均
平方根(RMS),PMDRMS
測定可能な最大δτ値
(root mean-square (RMS) of DGD over a wavelength
range or PMDRMS value)
Δτmax
(maximum Δτ value that can be measured)
3
C 61280-4-4:2015 (IEC 61280-4-4:2006)
Δω
方法Bにおける角周波数変動
(angular frequency variation in method B)
λ
PMD測定に用いられる試験波長
(test wavelength used to measure PMD)
λ0
光源の中心波長
(central wavelength of the light source)
v
光周波数
(optical light frequency)
σR
フーリエ変換データの
二次モーメントの平方根
(square root of second moment of Fourier transform
data)
σ0
二乗自己相関包絡線の
二乗平均平方根(RMS)幅
(RMS width of the squared autocorrelation envelope)
σx
二乗相互相関包絡線の
二乗平均平方根(RMS)幅
(RMS width of the squared cross-correlation envelope)
σε
インターフェログラムのRMS幅
(RMS width of interferogram)
ω
光角周波数
(angular optical frequency)
ASE
増幅された自然放出光
(amplified spontaneous emission)
DGD
群遅延時間差
(differential group delay)
DOP
偏光度
(degree of polarization)
DUT
被試験物
(device under test)
FA
固定アナライザ法
(fixed analyzer)
FET
電界効果トランジスタ
(field effect transistor)
FWHM
半値全幅
(full-width half-maximum)
GINTY
一般的な干渉法
(general interferometric analysis)
I/O
入出力
(input-output)
JME
ジョーンズ行列固有値解析法
(Jones matrix eigenanalysis)
LED
発光ダイオード
(light emitting diode)
MPS
変調位相シフト
(modulation phase shift)
PDL
偏波依存損失
(polarization dependent loss)
PIN (diode) pin(ダイオード)
[positive insulated negative (diode)]
PMD
偏波モード分散
(polarization mode dispersion)
PPS
偏波位相シフト
(polarization phase shift)
PSA
ポアンカレ球解析法
(Poincaré sphere analysis)
PSP
主SOP
(principal SOP)
RBW
分解能帯域幅
(resolution bandwidth)
RMS
二乗平均平方根
(root mean-square)
SOP
偏波状態
(state of polarization)
SPE
ストークスパラメータ解析法
(Stokes parameter evaluation)
TINTY
慣例的な干渉法
(traditional interferometric analysis)
4
背景:PMD特性
PMDは時間領域での光パルスの広がりを引き起こす。この分散は通信システムの性能を低下させる。こ
の影響は,信号の異なる偏波成分ごとの位相差並びに群速度及び対応する到達時間δτに関係する。十分に
狭帯域の光源では,この効果は,その波長で対となる直交偏波の主偏波状態(PSP)の群遅延時間差(DGD)
4
C 61280-4-4:2015 (IEC 61280-4-4:2006)
の値Δτに相当する。広帯域伝送の場合には,この遅延は分離し時間領域で広がりをもつ出力パルスとな
る。この場合,パルス広がりはDGD値の二乗平均に関係する。
DGDは光ファイバ長に沿った複屈折の詳細な特性に依存するため,長距離の光ファイバ間では時間領域
及び波長領域でランダムに変化する。また,光ファイバの時間に依存する温度及び機械的な変動にも敏感
である。このため,長い光ファイバでのPMDを評価する方法としては,期待値<Δτ>又はDGDの波長域で
の平均値を用いることが有用である。原理上,対象とする光ファイバにおいて,期待値<Δτ>は,δτ又はΔτ
のようなパラメータとは異なり,時間又は光源によって大きな変化をしない。さらに,<Δτ>は伝送特性の
有効な指標である。
PMDは二つの偏波モードが異なる群速度をもつ(一方は速い群速度及び短い到達時間をもち,他方は遅
い群速度及び長い到達時間をもち,それらの到達時間の差がDGDである)ことを示す一般的な意味と,
期待値<Δτ>を表す特別な意味との二つがある。後者は,この規格の目的にそった厳密なPMDの定義を示
す。このDGD値Δτ又はパルス幅δτは,波長,周波数,時間又は温度で平均化でき,<Δτ>λ,<Δτ>ν,<Δτ>t
又は<Δτ>Tのように表される。<Δτ>取得に関して,ほとんどの目的において,このような様々な条件を区
別する必要はない。<Δτ>を用いて式(1a)のようにPMDAVGを定義する。
τ
∆
=
AVG
PMD
········································································ (1a)
式(1a)の表現はしばしばDGD値の線形平均と呼ばれる。光ファイバケーブル及び多くのその他の部品を
規定する目的で報告される。もう一つの量としてDGD値のRMSも,特に方法Cに基づくような,ある種
の測定器において報告される。この量を,式(1b)のように定義する。
2/1
2
RMS
τ
∆
=
PMD
··································································· (1b)
多くのリンクにおいて,DGD値はマクスウェル分布に近い形でランダムに分布する。マクスウェル分布
と完全に一致するとの仮定のもとでは,DGDの線形平均値<Δτ>及びRMS値<Δτ2>1/2の二つの量の関係は,
式(1c)で与えられる。
2/1
2
2/1
3
8
τ
τ
∆
π
=
∆
······························································· (1c)
注記 DGDの値の分布がマクスウェル分布の場合に,式(1c)を適用する。残りのリンクに比べて相対
的に高い複屈折の要素がある場合には,この仮定は妥当ではない可能性がある。ITU-Tに整合
したリンクに規定されるDGDの最大値を決めるため,リンク所有者が許容可能な確率限界に
基づき3〜3.7の乗数(IEC/TR 61282-3参照)がPMDAVGに掛けられる。乗数はマクスウェルの
仮定に基づき,分布の非常に長い裾を反映している。リンクが高い複屈折要素を含んでいる場
合,PMDAVG及びPMDRMSの計量は両方とも実際のDGDの分布の実際の裾に対して増加し(小
さな乗数が使用可能なことを示唆している。),ただし,DGD分布が3自由度をもつ非心カイ二
乗分布の平方根に基づく分布に近づくため,式(1c)は成り立たないことがある。このような場
合,PMDRMSは一般に式(1c)によって示されるPMDAVGに対して大きくなる。この条件は,方法
Cのような時間領域の測定において干渉しま(縞)の包絡線が“フラットトップ”となること,
及び,方法Bのような周波数領域の測定において双峰性のDGD分布となることによって示さ
れる。
式(1c)の期待値演算子は全波長にわたる長期の期待値を表す。実際には,ある時点及び条件での有限な
波長範囲が抽出され,ある種のデータ平均が計算される。時間,波長及び条件に関するエルゴード性を仮
定する場合このように見積られた平均の期待値は長期の期待値に等しい。この仮定が妥当でない場合,抽
5
C 61280-4-4:2015 (IEC 61280-4-4:2006)
出される波長に強く依存して変化する結果となる。エルゴード性2)の条件によっては,測定再現性は波長
域やPMDの水準によって変化する可能性がある[3]。
注2) エルゴード性:あらゆるシーケンス又は相当量のサンプルが,等しく全体の代表値となるプロ
セス,又は,類するもの。
5
測定方法
5.1
PMD測定方法
PMDの測定には六つの基本的な測定方法がある。各方法の詳細については附属書に記載する。各方法に
ついて記載順に次に列挙する。幾つかの試験法については,測定結果の解析に複数の手段がある。
− 方法A 固定アナライザ法(FA)
− フーリエ変換法(FT)
− 方法B ストークスパラメータ解析法(SPE)
− ジョーンズ行列固有値解析法(JME)
− ポアンカレ球解析法(PSA)
− 方法C 干渉法(INTY)
− 慣例的な干渉法(TINTY)
− 一般的な干渉法(GINTY)
− 方法D 戻り光を用いたストークスパラメータ解析法
− ジョーンズ行列固有値解析法(JME)
− ポアンカレ球解析法(PSA)
− 方法E 変調位相シフト法
− 全掃引法
− ミューラー分析法
− 方法F 偏波位相シフト法(PPS)
各方法には,例えば,次のようなメリット及びデメリットがある。
架空ケーブルで見られるように,リンクが振動すると,個々のDGD値を計算するためのデータを測定
中に,光ファイバの特性が変化してしまう。このような場合,方法A,B,D,E及びFでは,測定に乱れ
が生じることがある。この効果を低減するため,幾つかの商用フィールド試験システムでは高速測定が行
われている。方法Cは,広帯域光源及び干渉計を用いて,時間領域で測定した干渉波形の相互相関の包絡
線からPMDを求めるため,光ファイバが振動する場合でも使用できる。
方法B,E及びFは,測定の時に,光源と受信装置との間に,通信リンク及び調整が必要である。すな
わち,別の通信チャネルが必要である。リンク自体をこのチャネルのために使用してもよい。方法Dを用
いる場合,試験中のリンクの片端に全ての測定器を配置できる。ただし,適切な反射特性を得るには,遠
端に注意が必要である。場合によって,遠端に反射終端器を取り付ける必要がある。方法A及びCを用い
る場合,光源及び受信装置をリンクの両端に配置する。だだし,測定の間に光源及び受信装置の設定を調
整する必要はない。
全ての方法の中で,方法Eは最も狭い帯域におけるDGDを測定できるが,リンクのDGD値が約0.5 ps
以上である必要がある。方法B,D及びFの場合は,近接する2波長で得られた出力データを数値微分す
るため,方法Eよりも帯域を広くする必要がある。ただし,方法B,D及びFは,最も小さいDGDを測
6
C 61280-4-4:2015 (IEC 61280-4-4:2006)
定できる。方法Cは,個々のDGD値を測定せず,光源スペクトル波長全体におけるDGDのRMS(PMDRMS)
を測定する。
方法Eでミューラー行列を用いて測定する場合,方法Fは方法Eと同様である。ただし,方法Fは,方
法B及び方法Dと同様に,一つのDGD値を得るために近接する2波長での測定が必要である。
いずれの方法も,一つ以上の既知で明瞭に偏波状態が制御された光源を必要とする。スペクトル領域(例
えば,1 300 nm帯,1 550 nm帯など)の特性を示すPMD値を得るために,いずれの方法もスペクトル領
域全体に光を注入する必要がある。
これらの方法には次の点で違いがある。
− 光源のスペクトル特性
− 検知部の帯域
− 実際に測定される物理的特性
− 解析方法
方法Aは,実施形態にもよるが,広帯域光源又は波長可変光源からのSOP入力を一つだけ必要とする。
固定の検光子を用いて,波長の関数であるストークスベクトルの1要素の相対パワー変化を追跡する。フ
ーリエ変換をこのデータに適用すると,結果は仮想的な半干渉波形となり,方法C(TINTY)と同様な手
順で評価される。
方法Bは波長帯域にわたって狭帯域光を変化させ,偏光の変化を測定することによってPMDAVGを測定
する。各波長について,例えば,(ポアンカレ球上で順に直交関係にある)0°,45°及び90°の直線偏光
状態といった既知の異なる三つのSOPを用いて,リンク中を伝送した出力ストークスベクトルを測定する。
光角周波数(波長)ω及び入力SOPの変化に伴うストークスベクトルの変化量から,式(2)及び式(3)の
定義に基づく関係を用いて波長の関数のDGDを求める。
()
()()
ω
ω
ω
ω
s
Ω
s
)
)
)
×
=
d
d
···································································· (2)
()
()
ω
ω
τ
Ω)
=
∆
··········································································· (3)
ここに,
s): 光角周波数ωにおける出力ストークスベクトル
Ω): PSPベクトル,又は光角周波数ωにおける偏波分散ベクトル
(PDV)
Δτ: 光角周波数ωにおけるDGD値
JMEは,出力ストークスベクトルをジョーンズ行列に変換することによって行われる[2]。隣接する波長
における適切な行列の組を求め,計算した固有値計算に偏角式を適用することによって,基底周波数の
DGD値を得る。
PSAは,隣接波長において循環複屈折と関連のある出力ストークスベクトルを推察するために,規格化
されたストークスベクトルを行列計算し,アークサインの公式用いて基底周波数のDGDを得る。
JMEとPSAとは,いずれもある波長域でのDGDの平均値からその領域におけるPMDを計算する。JME
とPSAとは数学的には等価である。狭帯域光源を使う場合には,コヒーレント干渉効果を引き起こし得る
光学反射を最小にするなどの通常の配慮がなされるのが望ましい。
さらに,(掃引システムとは対極の)スタート・ストップ測定系では狭帯域光源のステップ間隔は,期待
されるDGDスペクトル(DGD変化は波長の関数)を考慮して慎重に選択するのがよい。ステップ間隔の
7
C 61280-4-4:2015 (IEC 61280-4-4:2006)
選択についての詳細はB.2に記載している。狭帯域光源の線幅はナイキスト基準に一致して選択するステ
ップ間隔に調整することが望ましい。
方法Cは,一つ以上の既知の偏光状態に偏光させた広帯域光源を用いる測定方法である。出力光の干渉
パターンによって,電磁界分布の相互相関が決定する。TINTYの場合は,干渉波形の相互相関の包絡線の
RMS幅を計算することによって,干渉パターンを評価する。また,GINTYの場合は,干渉波形の相互相
関及び自己相関の両方の包絡線の二乗したRMS幅を計算することによって,干渉パターンを評価する。
これらのRMS幅によって,光源スペクトル(光源帯域)に対応した波長範囲におけるPMD値を得る。増
幅器を含むリンクでは光源帯域が制限されるため,方法Cの測定精度は低下する。方法Cでは,PMDRMS
値だけを測定する。
方法Dは,原理的には方法Bと同じであるが,リンクの終端で反射されて光源側に戻ってくる出力スト
ークスベクトルを測定することによってDGD値を得る。反射を考慮して変形した式によって,要求する
帯域におけるPMD値を計算する。この方法では反射が必要なため,光アイソレータ(光増幅器内でしば
しば見られる)を含むリンクには適していない。また,狭帯域光源が用いられる場合においても,誤った
DGDとして現れるコヒーレント干渉効果及びファブリペロー形エタロン効果を避けるために注意が必要
である。これらの効果は,遅延として記録される。反射光強度を強めるために装置終端に反射器が用いら
れる場合を除いて,方法Dは40 km程度の距離に制限される。
方法Eは,変調された狭帯域光源を用いて,二つ以上の入力偏光状態間の位相差を測定する。全掃引法
では,特定の位相シフトを得るために,一対の直交する入力偏光状態を入射する必要がある。この対の偏
光軸をポアンカレ球全体にわたって変化させて,位相シフト差の最大値を得る。得られた最大の位相シフ
ト差を用いて,光源スペクトルの中心波長におけるDGD値を求める。ミューラーセット法[1]では,波長
(光源スペクトル)ごとに,ミューラーセットを表す四つの偏光状態を入射する必要がある。これらの偏
光状態に対応した位相シフトを解析することによって,その波長におけるDGD値が得られる。ある波長
範囲内の複数の波長に対して測定が行われる場合は,DGD値の平均値がその波長範囲のPMD期待値とな
る。
方法Fは,方法Eと同様に,直交する直線偏光状態のような既知の偏光状態間の位相差を測定する。た
だし,必要な直交入力偏光状態が二つだけである点で方法Eとは異なる。このため,方法Fは一つのDGD
値を計算するために2波長での測定が必要となる。
全ての方法に共通の情報は,箇条1〜箇条8に規定する。六つの方法各々に付随する要求事項は附属書
A〜附属書Fにそれぞれ記載する。
5.2
基準測定方法
各方法には,それぞれ独自に最適な適用先があるため,基準測定方法はない。
6
装置
次に示す装置は全ての測定方法に共通である。附属書A〜附属書Fは,六つの方法各々について,配置
図,設備に必要な条件などを含んでいる。
装置の中で,送信に関わる全ての要素は測定するMDに何らかの影響を及ぼす。PMD測定における同
一スペクトル範囲内で,最も低い最大DGD値とPDLを得るためにこれらの要素を選ばなくてはならない。
短尺(2 m)で低いPMDをもつ光ファイバを用いた測定によって,これらの要素の全面的な寄与の評価が
必要となる。これらの要素のPMD寄与が顕著な場合,測定するリンクPMD値の二乗から測定システムの
PMD値の二乗を差し引いて平方根を取ることによって最終値を求めることもできる。
8
C 61280-4-4:2015 (IEC 61280-4-4:2006)
6.1
光源及び偏光器
光源のスペクトル特性の詳細条件は,附属書A〜附属書Fを参照する。光源は要求する波長で放射し,
光強度は測定を行う間十分安定したものでなければならない。要求するPMDが測定できる波長範囲に対
応していることが望ましい。
全ての方法について,光源は被測定光ファイバに挿入される前に,一つ以上の既知のSOPで偏光されて
いる必要がある。偏光子,波長板を用いた偏光調整器,液晶遅延プレート,機械式の複屈折の光ファイバ
ループ又は電気光学結晶素子を,試験光ファイバの入力端の光源のSOPの固定及び被測定光ファイバの出
力端のアナライザの偏光軸の固定に用いてもよい。偏光調整機能の性能は三つの直線偏光の既知SOPにお
ける出力を測定することによって評価することができる。出力が互いに3 dB以内にある場合,調整機能は
適切である。
方法A,B,D[狭帯域波長可変光源(TLS)を用いて行う場合],E及びFについては,全ての測定条
件のもとで,測定される全DGD値について,光ファイバから得られる光の偏光が保たれるように,光源
の実効スペクトル幅Δλ[ガウス形スペクトル,半値全幅(FWHM)]は,十分に狭い必要がある。90 %又
はそれ以上のDOPが望ましく,25 %以下で行う場合には精度が下がる。DOPとスペクトル幅Δλ,中心波
長λ0及びDGD値Δτとの関係は,式(4)のとおりである。
()
∆
∆
π
−
×
=
2
2
0
2
ln
4
1
exp
100
λ
λ
τ
c
DOP
(%) ···································· (4)
6.2
光入力部品
リンクに光を送り出すために接続用試験コードを用いる。その他の光入力部品もこの試験コードに接続
する。接続は測定中に安定している必要がある。
方法Dについては,測定システム試験コード及び反射制御へのリンクのインタフェース上に特別の必要
条件がある(附属書D参照)。
6.3
クラッドモードストリッパ
リンクの光ファイバからクラッドモードを除去する装置を用いる。ほとんどの状況下では,光ファイバ・
コーティングはクラッドモードを除去する役割をする。
6.4
高次モード・フィルタ
リンクの遮断波長(IEC 60793-1-44)以上の個別に規定する波長域における高次伝達モードを除去する
手段を用いる。例えば,光ファイバを曲げ半径=30 mmで1周巻けば,一般に十分である。
6.5
出力接続
リンクを光出力部品に接続するために接続用光ファイバピッグテールを用いてもよい。この接続は測定
中に安定していなければならない。
方法Dについては,リンクの遠端(光源に対して)から反射される光は,反射を最大限にする特別の終
端処理を必要とする。この方法については,接続の出力は入力接続と同一である。
6.6
光出力部品
適切な附属書(附属書A〜附属書Fのいずれか)を参照する。
幾つかのリンク測定では,アナライザの検出器に適した光強度を保つために,光増幅器と可変減衰器と
を組み合わせて試験系に用いる。この場合,出力調整装置は,一般的に検出器直前に設置する。
方法Dについては,光出力部品は光入力部品と同じ場所に設置する。
9
C 61280-4-4:2015 (IEC 61280-4-4:2006)
6.7
光検出器
信号検知については,光検出器は,測定を行う上で直面する強度幅,波長帯域及び測定回数にわたって
線形で安定しているものを用いる。典型的なシステムは,チョッパー/ロックインアンプ,光強度測定器,
光スペクトラムアナライザ,干渉計又はポラリメータによる同期検波を含むこともある。光源の全スペク
トル域を用いるために,光検知装置は,光源によって生み出される波長を含む波長域をもつものとする。
更なる詳細については,適切な附属書(附属書A〜附属書Fのいずれか)を参照する。
6.8
コンピュータ
装置制御,強度測定及び最終結果を得るためのデータ処理などを作業を行うためにコンピュータを用い
る。
6.9
ASEの影響を弱める手段
ASEは受信光の無偏光化をもたらす。実装及び方法によって,次の選択肢を使用してもよい。
− 検知回路内の電気フィルタと組み合わせた信号光変調
− 光ファイバ・リンクの出力端に置かれ信号光波長に固定された可変光フィルタ
7
サンプリング及び被測定対象
被測定対象は,長尺のシングルモード光ファイバのリンクである。方法Cを除いて,リンクは,振動又
は温度変化が測定期間内で最小となるときに測定することが望ましい。リンクが光増幅器を含む場合,光
増幅器を使用しながら測定することが望ましい。
8
手順
手順は,次による。
a) 必要なコネクタを接続し,リンクの終端を準備する。
注記 方法Dにおいては,入力終端からの反射を最小化するために,斜め研磨の光ファイバ終端が
必要である。
b) 光入出力部品の終端処理を行う。
注記 方法Dについては,光入出力部品は同一である。これらが付いているリンクの終端は入力終
端と呼ばれる。入力端への適切な反射を確保するために,リンクの出力端には,特別な配慮
が必要となる場合がある。
c) コンピュータを用いて,六つの測定方法に関する附属書A〜附属書Fのいずれかに記された掃引及び
測定を完了する。
d) 測定報告書を完成する。
9
計算又は結果の解釈
附属書A〜附属書Fは,測定データをDGD値又はPMD値に変換するための計算を提供する。IEC/TR
61282-3は,光ファイバ及び成分値の統計に基づいたリンクPMDの計算についての情報を提供する。
10 書類
10.1 各測定に必要な情報
各測定に必要な情報は次による。
− リンク
10
C 61280-4-4:2015 (IEC 61280-4-4:2006)
− 識別情報
− 詳細説明(例えば,光増幅器,その他のコンポーネントの有無)
− 距離(km)
− 光ファイバ及びケーブルの種類
− 試験日
− 試験結果
− PMDAVG又はPMDRMSとしてのPMD値
− 試験系光源のスペクトル及び線幅
− 方法B,D,E及びFの場合,波長及び/又は周波数の関数としてのDGD値
− 方法Cの場合,干渉波形
− 方法Aの場合,波長又は周波数の関数としての強度及びフーリエ変換
− 測定を行う波長又は周波数範囲
10.2 利用可能な情報
次の情報は,用いる装置の製造番号,モデル番号,シリアル番号及び関連するモジュール詳細を記録す
ることによって,通常,追跡可能である。
− 試験系
− 測定方法
− 計算手引き(分析)
− 設備の記載
− 光源の詳細特性
− アナライザの詳細特性
− 使用した場合,その他附属品
− 校正
− 最新の校正期日
− 校正方法
− 不確かさの分析
− 方法B,D及びE:抽出波長数
− 方法C:干渉しま(縞)の検出技術の種類
11 仕様情報
仕様情報は次による。
− 波長帯
− この規格に記載する手順との差異
11
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書A
(規定)
固定アナライザ法
この附属書は,固定アナライザ法(FA)に特有の要求事項について規定する。
A.1 装置
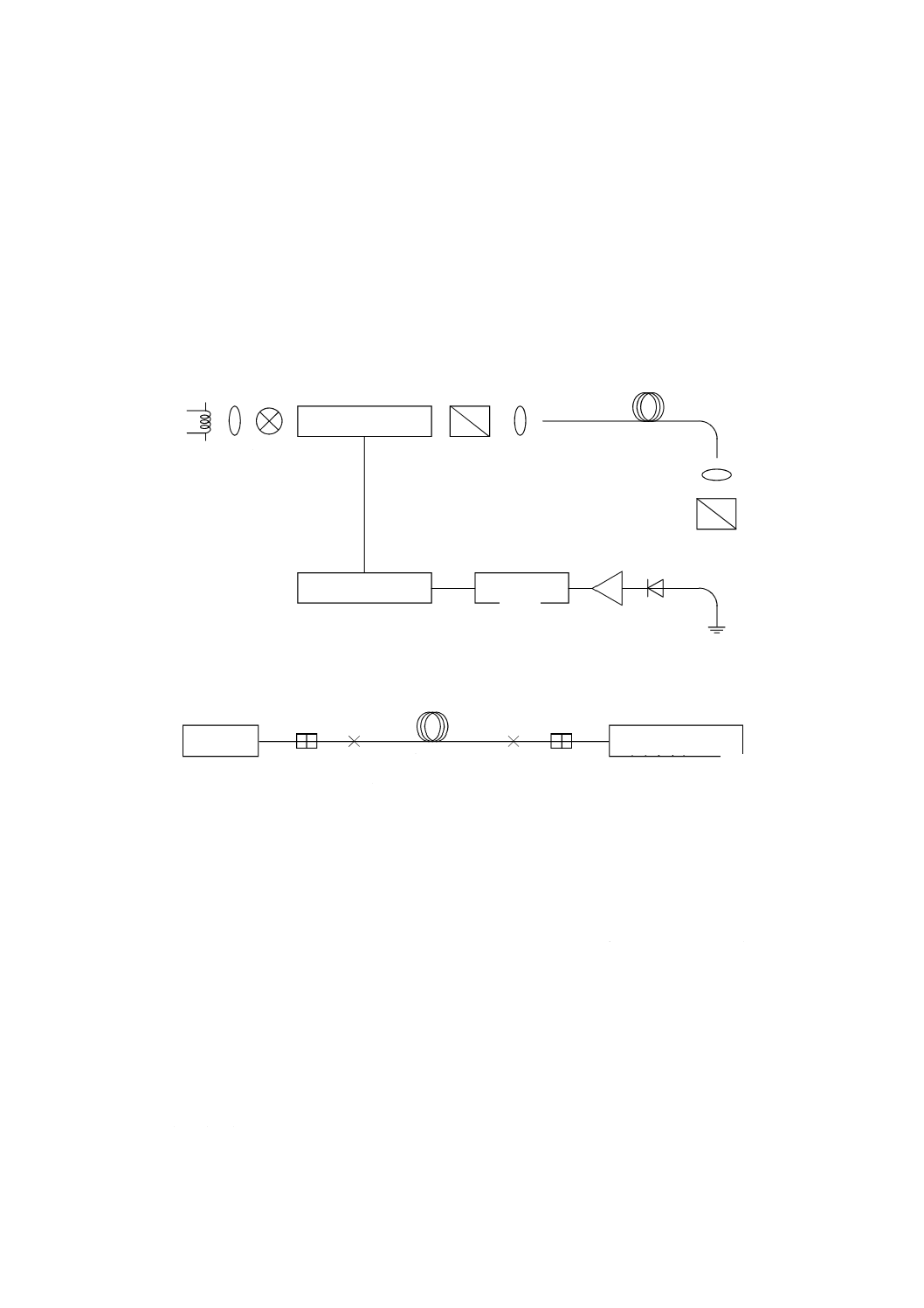
図A.1は測定系のブロック図の一例である。
光源
モノクロメータ
偏光子
被測定ファイバ
偏波アナライザ
検出器
コンピュータ
チョッパー
ロックイン
アンプ
a) ランプとモノクロメータとを組み合わせた狭帯域光源を用いた測定系
広帯域光源
光スペクトラム
アナライザ
偏光器
検光子
スプライス
スプライス
被試験ファイバ
IEC 002/06
b) 広帯域光源を用いた測定系
図A.1−固定アナライザ法のブロック図
A.1.1 光源
全ての測定系において受光部の種類に応じて2種類の光源を使用できる。図A.1 a) に示すように,広帯
域光源とモノクロメータとの組合せのような狭帯域光源を偏波アナライザとともに用いることができる。
図A.1 b) に示すように,広帯域光源の場合は,光スペクトラムアナライザ,又はフーリエ変換スペクトラ
ムアナライザである干渉計のような狭帯域フィルタアナライザを検光子の前に置いて,共に用いることが
できる。広帯域光源を用いる場合,透過フィルタの幅は,計算の目的に合ったスペクトル幅とする。
広帯域光源,狭帯域光源のいずれの場合も,スペクトル幅は,要求される偏光度(5.1参照)を満たすよ
うに十分に小さくなければならない。また,逆に,不必要なコヒーレント干渉効果及びスプリアス雑音を
回避するために,決定した測定間隔に対して小さすぎないようにしなければならない。いずれの光源の場
合も波長範囲は,決められた波長範囲において十分正確なPMDを測定するために十分に広くしなければ
ならない(A.3参照)。
光スペクトルに関する全ての特性を適切に決定するためには,光源のスペクトル幅は式(A.1)を満たして
12
C 61280-4-4:2015 (IEC 61280-4-4:2006)
いなければならない。
(
)1
max
0
8
/
−
∆
<
∆
τ
λ
λ
ν
································································· (A.1)
ここに,
v=c/λ: 光周波数
Δλ: スペクトル幅
Δτmax: 予測される最大のDGD値
波長1 550 nm近傍では,式(A.1)は,Δλ(nm)はΔτ(ps)の逆数より小さいという条件に緩和される。
A.1.2 検光子
検光子の角度方向の設定は重要ではないが,測定中は固定されていなければならない。
モード結合を無視できるとき及びPMDの値が小さいときは,図A.2に示した振幅強度を最大にするた
めに検光子を調整することが有効である。これは光ファイバのスプライス又は光コネクタの部分を回転す
ることでも可能である。
注記 検光子はポラリメータに置き換えることも可能である。
A.2 測定方法
A.2.1 波長範囲及び測定間隔
光路に検光子を入れた場合,及び入れない場合について,ある波長範囲内で決められた波長ステップで,
波長(又は光周波数)の関数として光パワーを測定する。波長範囲は測定結果の精度に影響を与える(A.3
参照)。波長測定間隔は,式(A.1)においてΔλを測定間隔に置き換えて式(A.1)を満足するように決定しなけ
ればならない。
フーリエ変換法を用いる場合は,測定間隔は理想的には光周波数上で均一,かつ,ステップ数は2の累
乗でなければならない。モノクロメータの光周波数ステップδνは,測定するDGDの最大値に対応する振
動周波数の二分の一よりも小さくなければならない。強くモード結合した光ファイバの場合は,二次モー
メントの外側に多くのパワーが存在するため,ナイキスト条件によって,周波数ステップは予想される
DGDの最大値に対応するRMS幅(二次モーメントの平方根)周波数の三分の一よりも小さくなければな
らない。すなわち,式(A.2)を満足しなければならない。
max
6
1
τ
ν∆
>
δ
·········································································· (A.2)
注記1 フーリエ変換において大半のエネルギーがΔτmax近傍に存在することが明らかな場合,測定間
隔を小さくして測定を繰り返すことが望ましい。
注記2 一般的に光源のスペクトル幅は最小の測定波長間隔以下である。例えば,Δτmaxが0.67 psの
場合,1 550 nmにおけるモノクロメータのスペクトル幅は2 nm(δν=249 GHz)が一般的で
ある。
A.2.2 掃引実行
検光子を光路に入れて掃引を実行する。受光パワーをPA(λ)として記録する。
検光子を光路から取り除いて掃引を繰り返す。トータル受光パワーをPtot(λ)として記録する。
パワー比R(λ)を式(A.3)によって計算する。
()
()()
λ
λ
λ
tot
A
P
P
R
=
········································································· (A.3)
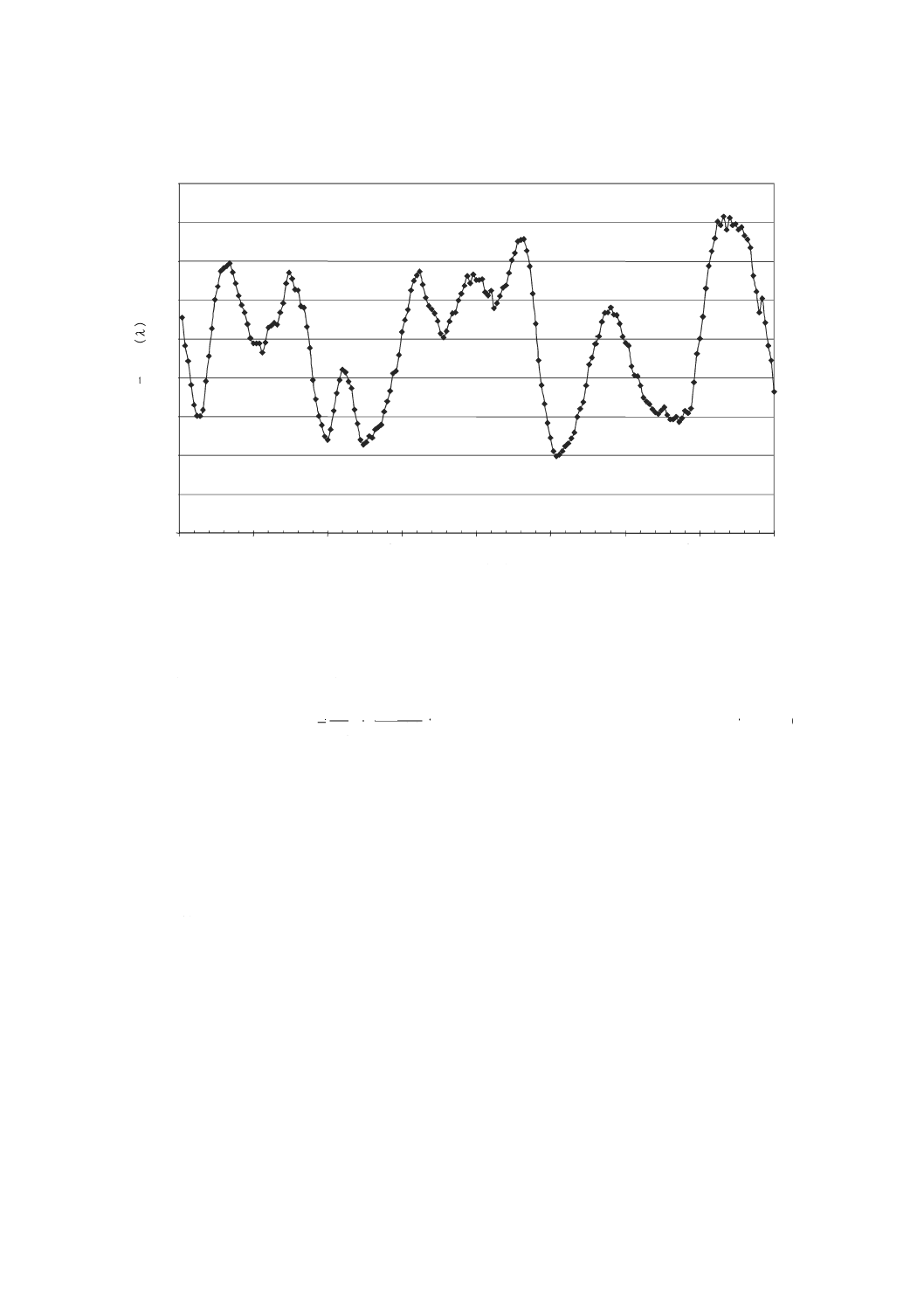
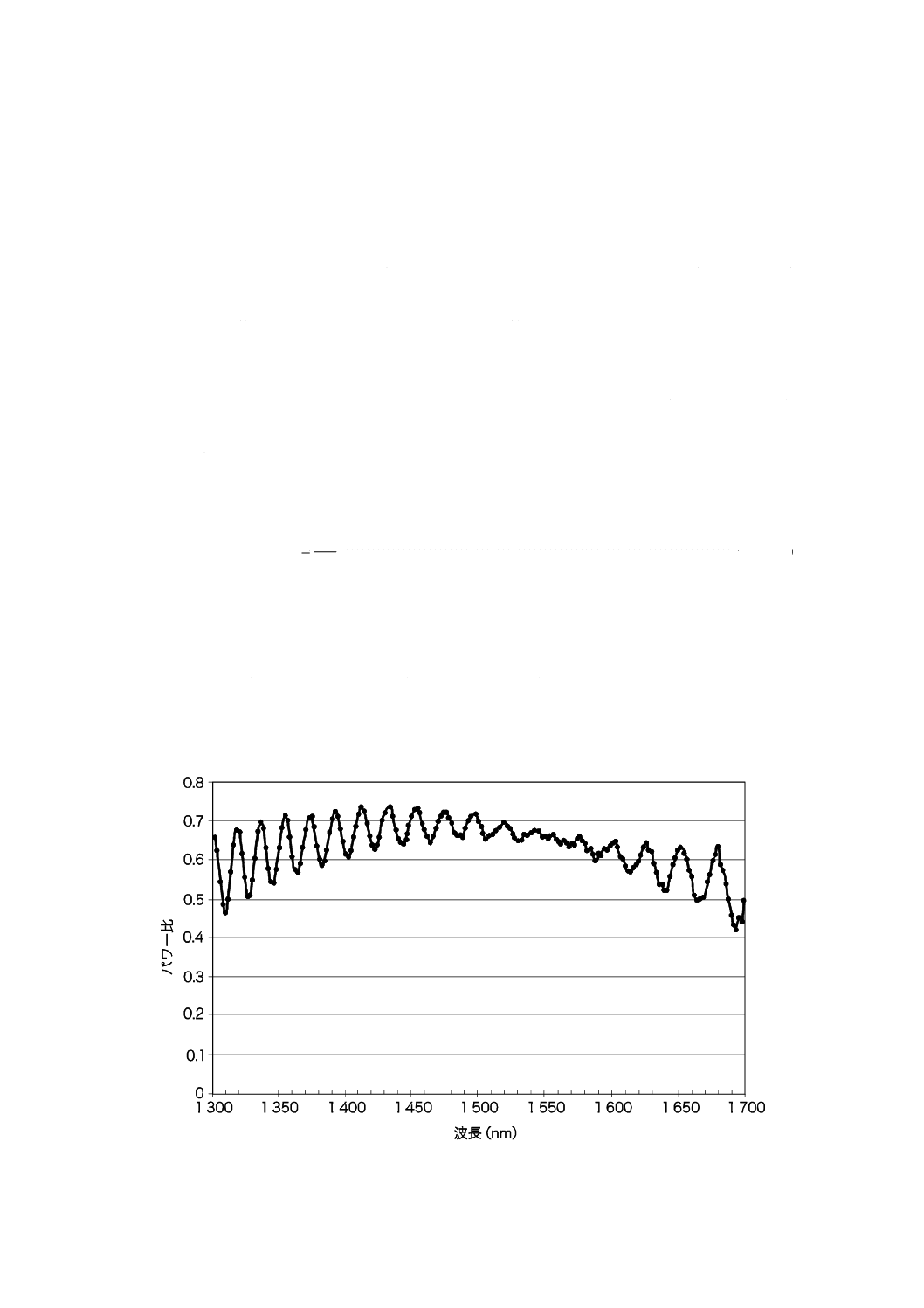
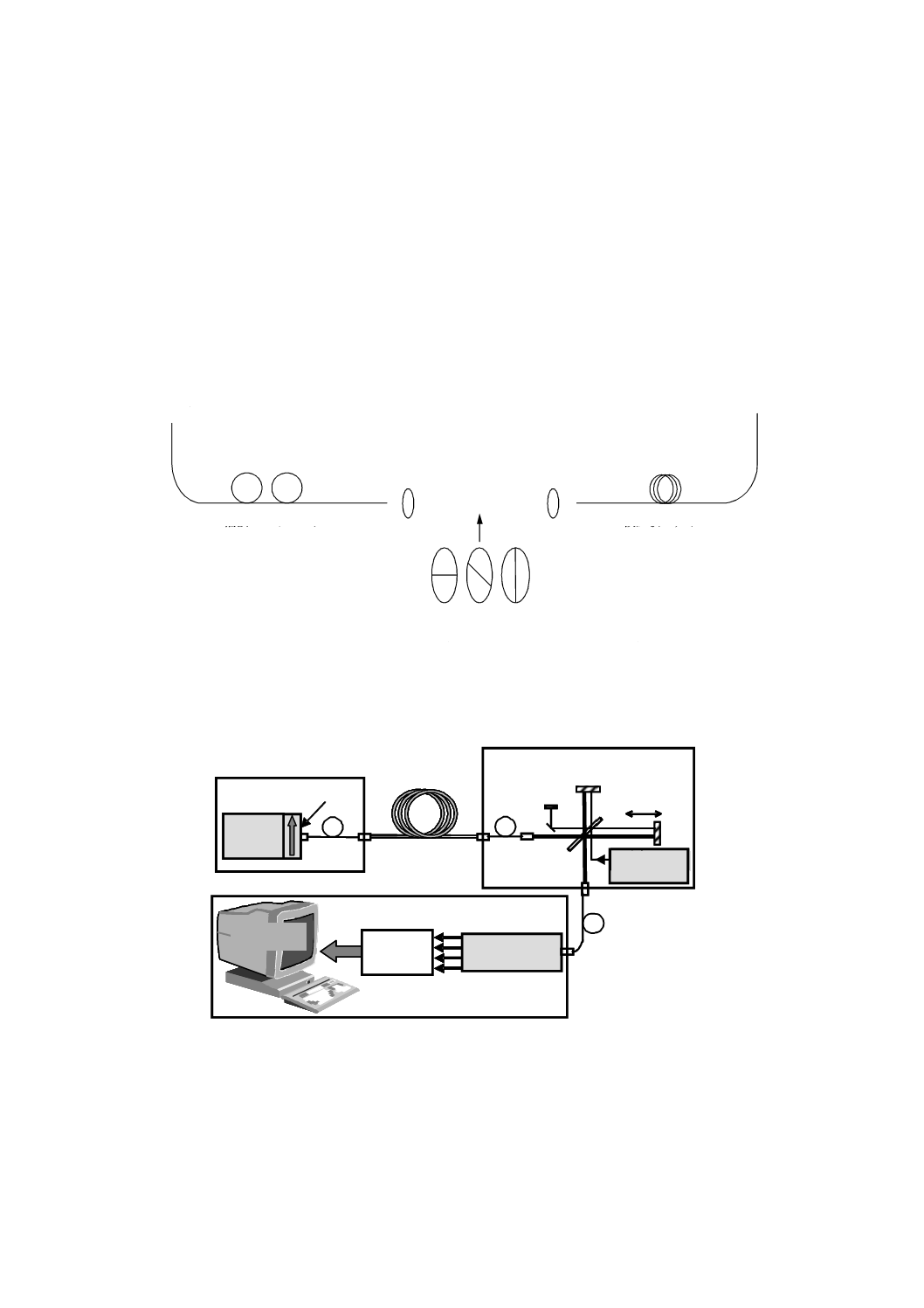
図A.2はリンクシステムにおいてランダムにモード結合した場合の結果を示した例である。
13
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図A.2−固定アナライザ法でのパワー比R(λ)の例
代替測定方法として2回目の掃引のとき,検光子を置いたまま90°偏波面を回転させPB(λ)を記録する。
パワー比計算は式(A.4)によって計算する。
()
()
()
()
λ
λ
λ
λ
B
A
A
P
P
P
R
+
=
······························································· (A.4)
注記1 差分PB−PAを合計で割ったコサインフーリエ変換は相互相関関数である。
注記2 受光素子としてポラリメータを用いる場合は,正規化されたストークスパラメータを波長ご
とに測定する。三つのスペクトル関数(ベクトル成分ごとに一つ)は受光パワーに対して独
立で,同じ方法で解析する直交検光子間の三つの独立した差分関数に相当する。
A.3 計算−フーリエ変換
PMDの計算には,通常,光周波数νの領域で表現されるパワー比R(λ)のフーリエ解析を用いる。フーリ
エ変換はこの光周波数領域のデータを時間領域へ変換する。フーリエ変換は,光が到達する時間δτの分布
に関する直接的な情報を与える。このデータを後述するように処理して,被試験光ファイバのPMD期待
値<Δτ>を計算する。この方法は一般的にランダムなモード結合をもつリンクに適用できる。この方法はモ
ード結合が無視できる場合にも適用できる。
A.3.1 データ前処理及びフーリエ変換
この方法を用いるためには,フーリエ変換は通常光周波数において等間隔での処理を必要とする。等間
隔とすることによって,λの値にてR(λ)のデータを光周波数領域において等間隔で収集することができる,
又は,(例えば,三次のスプライン関数を用いて)等しい波長(λ)間隔で取得したデータをフィットさせ
て補間するか,若しくは,より高等なスペクトル推定技術を使用して求めてもよい。いずれの場合におい
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1 300
1 350
1 400
1 450
1 500
1 550
1 600
1 650
1 700
波長 λ (nm)
パ
ワー
比R(λ)
IEC 003/06
R
14
C 61280-4-4:2015 (IEC 61280-4-4:2006)
ても,用いる各波長における比率R(λ)を式(A.3)又は式(A.4)を用いて適切に計算する。
R(λ)に対してゼロ点付加,データ補間及び直流成分除去を行ってもよい。フーリエ変換の前の事前調整
手段として,データに窓関数を与えてもよい。フーリエ変換を行うことで,δτの各値に対して強度データ
分布P(δτ)を求めることができる。
A.3.2 変換データフィット
R(λ)の直流成分は部分的には検光子の挿入損失という可能性があるため,注意深く除去しない場合,δτ
がゼロにおけるフーリエ変換のデータは意味がない。直流レベルが除去できない場合,通常,2点のデー
タまではその後の計算において無視する(使用しない)。計算に含めるδτがゼロよりも大きい“最初の有
効データ点”がj=0になるように,変数jを定義することができる。
その後の計算からの測定雑音を除去するために,P(δτ)をしきい値T1と比較する。しきい値T1は一般的
に受信系のRMS雑音レベルの200 %に設定する。この時点で,光ファイバのランダムモード結合が無視で
きるかどうかを決定しておく必要がある。
P(δτ)の有効データの最初のX点が全てT1未満である場合は,P(δτ)がモード結合を無視できる光ファイ
バの離散的なスパイク状の特性であることを示している。フーリエ解析前にゼロ点付加をしない場合,X
の値は3となる。この場合,Xの値は式(A.5)で決定できる。
L
N
X
3
=
··············································································· (A.5)
ここに,
N: 測定データ点数
L: ゼロ点付加後の配列の全長
モード結合が無視できる光ファイバにおいては式(A.6)を用いてPMDを計算する。ランダムモード結合
する光ファイバにおいてはPMDは式(A.7a)及び式(A.7b)を用いて計算する。
A.3.2.1 モード結合が無視できる光ファイバにおけるPMD計算
校正に用いる光ファイバなどの,モード結合が無視できる光ファイバ(例えば,高複屈折光ファイバ)
又は複屈折コンポーネントにおいては,R(λ)はチャープした正弦波になる(図A.2A)。
図A.2A−ランダムにモード結合を無視できる場合
15
C 61280-4-4:2015 (IEC 61280-4-4:2006)
注記 対応国際規格には図A.2Aの記載がないが,誤りであるため追記した。
相対的なパルス到着時間δτに相当する位置に離散的スパイクをもつP(δτ)出力をフーリエ変換によって
求める。この重心がPMD期待値<Δτ>である。
スパイクの重心のPMD期待値<Δτ>を定義するために,式(A.6)において,前もって定義する第2のしき
い値T2を超えるデータ点を計算に用いる。T2は一般的に受信系の雑音レベルのRMSの200 %に設定する。
()
[
]
()
∑
∑
′
=
′
=
=
∆
M
e
e
M
e
e
e
δ
P
δ
δ
P
0
0
τ
τ
τ
τ
···························································· (A.6)
ここに,
M'+1: スパイクの中でT2を超えるPのデータ点の数
式(A.6)において,<Δτ>は通常ピコ秒で表記する。一つもスパイクが検出されない(すなわちM'+1=0)
場合,PMDはゼロである。スパイクのRMS幅,スパイクのピーク値などのその他のパラメータも必要に
応じて記録する。
被試験デバイスが一つ以上の複屈折要素をもっている場合,二つ以上のスパイクが発生する。n本の連
結した光ファイバ・デバイスについては,最大2(n-1)個のスパイクが得られる。
A.3.2.2 ランダムなモード結合のある光ファイバのPMD計算
ランダムなモード結合のある場合は,R(λ)は図A.2のような複雑な波形となる。正確な特性は光ファイ
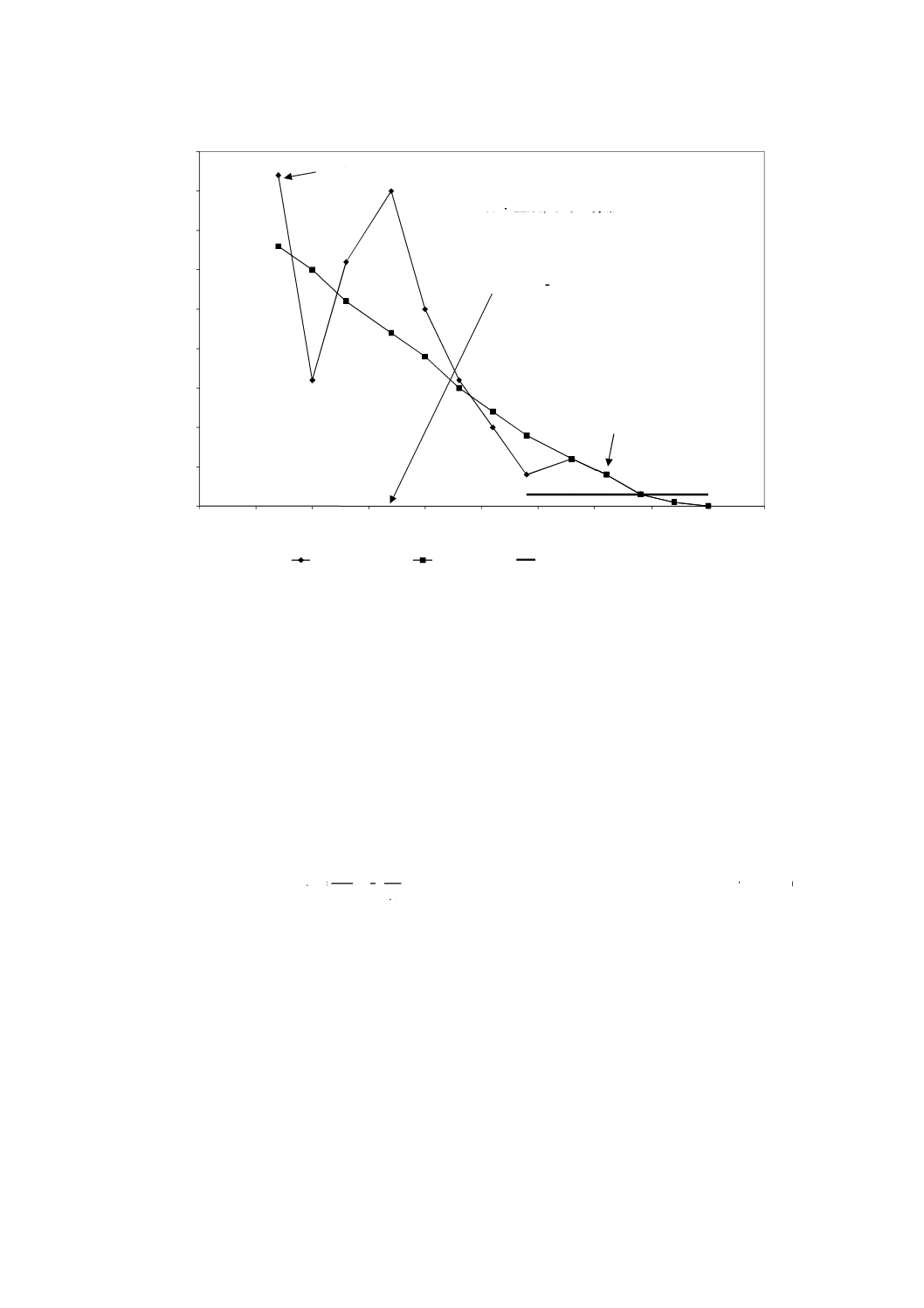
バ/ケーブル内の結合過程の実際の統計に基づく。そして,フーリエ変換されたデータはP(δτ)の分布にな
る。この分布は,光ファイバ内の光パルス到達時間δτの確率分布の自己相関を示す(図A.3参照)。
T1を超えるPの最初のポイントとしてj=0から数え始め,X個以上のT1以下となるデータ点が続く点
までとする。この点は,ランダムモード結合をもつ光ファイバにおける分布P(δτ)の最後の重要な点(すな
わち“終わり”)を表している。その点は実質的に測定雑音の影響を受けない。この点のδτ値をδτlastと表
し,δτlastでのjの値をM"と表す。
光ファイバのPMDRMSである<Δτ2>1/2を,この分布の二次モーメントの平方根σRとして定義し,式(A.7a)
によって計算する。
2
1
0
0
2
2/1
2
])
(
[
)
(
=
=
∆
∑
∑
=
=
''
''
M
j
j
M
j
j
j
R
δ
P
δ
δ
P
τ
τ
τ
σ
τ
]
[
·········································· (A.7a)
ここで,DGDがマクスウェル分布に従うと仮定する場合,式(A.7b)がDGDのRMSで定義される
PMD<Δτ2>1/2と,DGDの平均によって定義されるPMD<τ>との関係を与える。
2/1
2
2/1
3
8
τ
τ
∆
π
=
∆
····························································(A.7b)
A.3.2.3 混合結合する光ファイバシステムにおけるPMD計算
モード結合を無視できる光ファイバ/コンポーネント及びランダムなモード結合の光ファイバの両方が
連結してリンクを形成する場合もある。この場合,重心決定[式(A.6)]及び二次モーメント計算[式(A.7)]
の両方が必要となる。
なお,P(δτ)内のスパイクは,計算したδτlastに関係なく決定されることに注意する。
16
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図A.3−フーリエ解析によるPMD
A.3.3 スペクトル領域
ランダム結合のある光ファイバにおいて,十分な精度とともにスペクトルのアンサンブルを形成するた
めには十分なスペクトル領域を使用しなければならない。可能な限り広範囲のスペクトル領域(例えば,
200 nm以上)を用いることによって,統計的な不確かさを最小にできる。測定の前に,要求する精度,す
なわちスペクトル領域を規定しなければならない。
さらに,非常に低いδτ値はR(λ)において非常に長い周期に相当し,可能な場合,λ1からλ2までのスペク
トル領域は二つ以上の完全な“周期”に及ぶことが望ましい。このスペクトル領域はδτの最小値δτminを
定義する。この最小値は,式(A.8)のように受光パワーP(δτ)において得ることができる。
0
1
2
2
1
min
)
(
2
c
τ
δ
λ
λ
λ
λ
−
=
··································································· (A.8)
ここで,A.2に記載した受光パワーPにおいて一般的にゼロ又はゼロ付近の二つのデータポイントを無
視することに対応して,係数2を導入している。例えば,波長λ1=1 270 nm及び波長λ2=1 700 nmにおい
て,δτmin=0.033 psとなる。
図A.2Aのように,パワー比R(λ)のランダムモード結合が無視できる高PMD光ファイバの場合は,試験
する波長におけるPMDの変化を許容するために,上記のスペクトル平均化への要求条件を緩和して,ス
ペクトル領域を狭く[例えば,(λ2−λ1)は約30 nm]設定してもよい。
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0,045
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
相対パルス到達時間 ps
確
率
(
a
.u
.)
FFT 強度
ガウシアン
近似
閾値 = 0.001 5
X 2 = 22.61,ガウス分布
PMD = 0.167 ps(二次モーメント)
PMD 係数 = 0.033 4 ps/km1/2
j = 0
j = M'' = 9
しきい値 = 0.001 5
17
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書B
(規定)
ストークスパラメータ解析法
この附属書は,ストークスパラメータ解析法に特有の要求事項について規定する。
B.1
装置
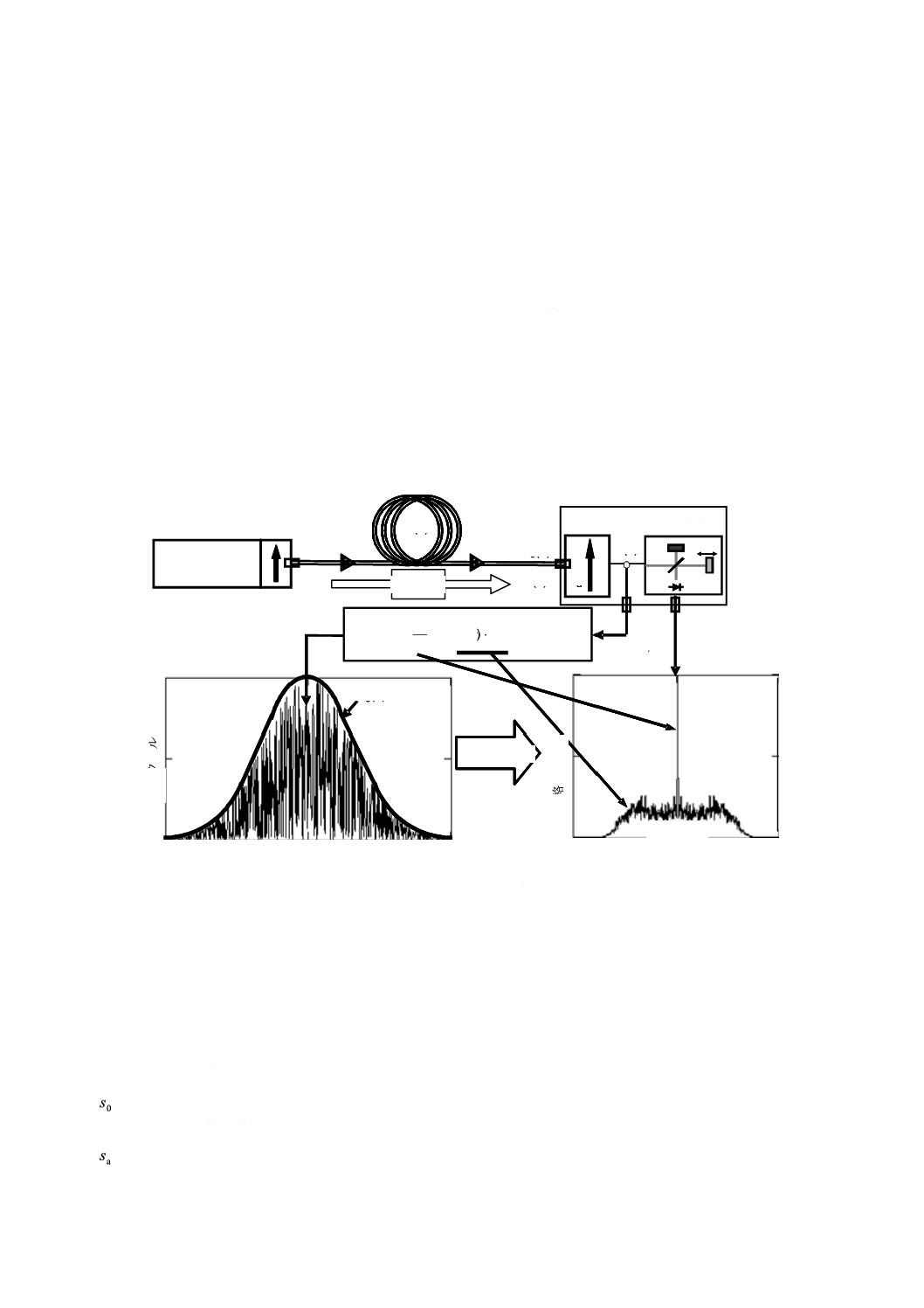
図B.1に,通常JMEとともに用いる方法Bの実現可能なブロック図を示す。
図B.1−狭帯域(波長可変レーザ)光源を用いた方法Bのブロック図
図B.2に,通常,PSAとともに用いる方法Bの他の実現可能なブロック図を示す。
図B.2−広帯域(ASE)光源を用いた方法Bのブロック図
B.1.1 光源
全ての場合において,ポラリメータの種類によって,2種類の光源を使用できる。図B.1に示す波長可
変レーザのような狭帯域の光源は,偏波アナライザとともに使用できる。光増幅器を用いたリンクでは,
波長可変
レーザ
偏波コントローラ
0°
45°
90°
ポラリメータ
被試験ファイバ
IEC 005/06
ストークス
ベクトル
マイケルソン
干渉計
HeNeLaser
リンク
Analysis
ASE
Source
主偏波状態生成機
アナライザ
ヘリウム
ネオンレーザ
Analysis
解析
ASE
光源
ポラリメータ
IEC 006/06
18
C 61280-4-4:2015 (IEC 61280-4-4:2006)
光増幅器によるASEの悪影響を避けるため,狭帯域光源の偏光度は,該当する波長範囲にわたり,ある制
限値以上となるように保たれなければならない。また,図B.2に示す高出力の広帯域光源は,光スペクト
ラムアナライザ又は干渉計のような狭帯域透過ポラリメータとともに用いる。この干渉計は,ポラリメー
タの前又は被測定リンクの前若しくは後に設置するフーリエ変換スペクトラムアナライザとして用いる。
また,広帯域光源を用いる場合,透過フィルタの幅は,計算の目的に合ったスペクトル幅とする。光増幅
器を含むリンクは,リンクのASEが高く評価対象となる全波長範囲でスペクトルが平たんである場合を除
き,広帯域光源は狭帯域光源と同等の偏光度が不要となるように十分な波長数を常に含む必要がある。
いずれの場合も,必要とされる偏光度(5.1参照)を保つように十分に小さくする。不要なコヒーレント
干渉効果及びその他のスプリアスノイズを避けるため,スペクトル幅は選択したステップ幅に比べ極端に
小さくならないようにしなければならない。いずれの場合も,波長範囲は,十分な精度で有効なPMD測
定ができるように十分に広くしなければならない(B.3参照)。
偏波コントローラは三つ以上の,既知で,かつ,異なる偏波状態の範囲で可変でなければならない。異
なるSOPは,通常,直線偏光で0°,45°及び90°[各測定波長に対しては式(E.4)参照]である。
B.1.2 ポラリメータ
選択した各入力偏波状態及び波長に対して,出力ストークスベクトルを測定するため,ポラリメータを
用いる。
B.2
手順
リンクの出力は,ポラリメータを含むアナライザに接続する。要求する波長領域に適切な範囲で,望ま
しい精度(B.3参照)の波長間隔δλで波長を掃引する。狭帯域光源に関しては,推定DGDの最大値Δτmax,
測定領域の中心波長λ0,真空での光速c(299 792 458 m/s)として,波長間隔δλは式(B.1)で求める。
max
2
0
2τ
λ
λ
∆
c
δ≦
········································································ (B.1)
例えば,DGDの最大値と波長間隔の幅との積は,波長1 550 nmでΔτmaxが4 ps·nm以下,波長1 300 nm
でΔτmaxが2.8 ps·nm以下となるように保たれなければならない。これによって,一つの波長条件から次の
波長条件まで,出力偏波状態はポアンカレ球の基本状態軸に対して180°以内でしか回転しない。Δτmaxの
概算ができない場合,一連のサンプル測定をその波長範囲にわたり行う。各測定には,スペクトル幅及び
光源の最小可変波長間隔に適合した近接する波長の組を用いる。この方法で測定されるDGDの最大値に
安全係数3を乗じた値を式(B.1)のΔτmaxに代入することで,実測定で使われるδλの値が求められる。測定
に用いる波長間隔が大きすぎる懸念がある場合,少ない波長間隔で測定を繰り返してもよい。波長に対す
るDGDの曲線の形及びDGDの平均値が基本的に変化しない場合,初期の波長間隔は適切である。
広帯域光源に関しては,アナライザの分解能帯域幅は式(B.2)の関係を満たさなければならない。
max
2
0
5
τ
λ
λ
∆
c
RBW≦
···································································· (B.2)
各波長でデータ測定を行う。各波長について,用いる偏波状態[式(E.4)参照]に応じて入力偏波状態を
回転し,対応する出力ストークスベクトル,Hˆ,Vˆ及びQˆを記録する。出力ストークスベクトルは,単位
長さ当たりに規格化する。B.3.1に規定するJMEの計算に当たっては,計算を終える前に,規格化ストー
クスベクトルを,式(E.4)(0<θ<πの範囲を仮定)を用い規格化ジョーンズベクトルに変換しなければな
らない。B.3.2に規定するPSAに関しては,規格化出力ストークスベクトルは規格化ジョーンズベクトル
に変換せずに用いる。
19
C 61280-4-4:2015 (IEC 61280-4-4:2006)
B.3
計算
これらの計算手法は,一つの光角周波数ωにおけるベクトルと次のω+Δωにおけるベクトルとの差分
の評価を必要とする(光角周波数はω=2πc/λで与えられる)。
JME及びPSAとも,波長に応じた一連のDGD値を計算する。図E.4にその例を示す。また,DGD値は
図E.5のようにヒストグラム形式で表示してもよい。
これらのDGD値の波長域での平均はPMD期待値となる。
注記 JME及びPSAの計算は,一次のPMD期待値の推定で,PDLを無視できる条件下では,数学的
に等価である。
B.3.1 ジョーンズ行列固有値解析法(JME)
JMEに関して,応答ジョーンズ行列はストークスパラメータから各波長に対し計算される。各波長間隔
に関し,高い光周波数のジョーンズ行列T(ω+Δω)と低い光周波数の逆ジョーンズ行列T −1(ω)との積を計
算する。特定の波長間隔に対するDGD値Δτは,式(B.3)に示す偏角式から求められる。
ω
ρ
ρ
τ
∆
=
∆
2
1
Arg
······································································ (B.3)
ここに,
ρ1及びρ2: T(ω+Δω)T −1(ω)の複素固有値
Arg: 偏角関数。すなわち,Arg(ηeiθ)=θ[ηは,複素絶対値
(実数)]。
T(ω+Δω)及びT(ω)は,B.3.1.1の測定及び計算から導かれる。
データ解析の目的上は,各DGD値Δτは低い周波数側でのDGD値である。波長範囲にわたる一連の波
長間隔から得られた一連のDGD値が,一つのリンクのPMD測定結果である。
B.3.1.1 ジョーンズ行列固有値解析法(JME)DGD計算
R. C. Jonesは,未知の線形かつ時間不変な光リンクの前方伝達ジョーンズ行列を実験的に決定するため
の明確なアルゴリズムを示した[2]。線形性の制限によって,新たな光周波数を生み出す光リンクは考慮し
ない。時間不変の制限は,リンクで発生する偏波変換に対してだけ適用され,絶対的な光学位相遅延は含
まない。このため,DGD測定装置が位相遅延変化による影響を受けない場合,光ファイバ内で位相遅延が
測定中に変化したとしても,この手法は光ファイバ網の特性評価に用いることができる。
ジョーンズ行列の測定は,リンクに対する直線偏光のような,三つの既知で,かつ,異なる偏波状態を
用いる必要がある。次に説明するプロセスでは,ジョーンズによって説明され,また,図E.3にも図示さ
れているとおり,0°,45°及び90°で生じる直線偏光状態を用いる。その他の入力偏波状態を考慮して
も,この計算は一般化できる。
いかなるジョーンズベクトルVも,強度,絶対位相,及びポアンカレ球上の偏波状態を定める単位ベク
トルによって完全に規定できる。リンクのジョーンズ行列を測定するために,x軸(0°)に平行な直線偏
光状態の励振光場がはじめに生成され,その応答単位ジョーンズベクトルhˆが,リンクの出力において測
定され計算される。同様に,y軸(90°)に平行,かつ正方向のx軸及びy軸間(45°)の二等分線に平
行な直線偏光状態の励振光場は,各々,応答単位ジョーンズベクトルvˆ及びqˆとなる。
三つの励振場の強度に依存しない三つの複素比率は,hˆ,vˆ及びqˆのx成分及びy成分から式(B.4)のよ
うになる。
y
xh
h
k=
1
y
x
k
ν
ν
=
2
y
xq
q
k=
3
···································· (B.4)
20
C 61280-4-4:2015 (IEC 61280-4-4:2006)
そして,4番目の比率k4=(k3−k2)/(k1−k3)が求まる。複素定数βの範囲内で,伝達ジョーンズ行列は式(B.5)
で表される。
=
1
4
2
4
1kk
k
k
T
········································································· (B.5)
B.3.1.2 群遅延時間差(DGD)測定
主偏波状態の定義によって,一般的なリンクは二つの入力主偏波状態() ω
xˆ
に関連付けられる。入力偏波
状態が一定で光角周波数ωが少ししか変化しない場合,() ω
xˆ
は出力側で単位ベクトルがωに一次近似的
には依存しない二つの主偏波状態となる。一般伝達ジョーンズ行列T(ω)に関し,出力主偏波状態は強度
σ(ω)及び絶対位相φ(ω)を用いて,単位ベクトル() ω
yˆ
との積を式(B.6)のように表すことができる。単位ベク
トルは,出力主偏波の偏波状態を規定する。
()
()()
()
ω
σ
ω
ω
ω
ω
φy
e
ω
x
T
y
i
ˆ
)
(
=
ˆ
=
)
(
················································· (B.6)
σ(ω)及びφ(ω)は,ωに応じて変化する場合があるが() ω
yˆ
は,出力主偏波状態の定義によって,一次近似
では周波数に依存しない。ωでの微分を示すプライムを使うことで,式(B.6)の微分y′は式(B.7)のようにな
る。
y
e
y
i
x
T
y
i′
+
′
+
′
′
′
ˆ
=
ˆ
=
φ
σ
φ
σ
σ
······················································ (B.7)
絶対位相の一次微分φ'は,ネットワークにわたる群遅延τgである。ネットワークが不完全に偏光してい
る場合,その伝達ジョーンズ行列Tは正則で,その入力は出力を用いて
y
T
x
1
ˆ
−
=
と表される。y′ˆを明示的
に0に設定することによって,式(B.8)に示す固有値方程式を得る。
0
ˆ
g
1
=
+
−
=
−
y
I
i
'
y
T'T
'y
ei
τ
σ
σ
σφ
·············································· (B.8)
ここに, I: 単位行列。対角の値が1で,それ以外の値が0である正方行列
伝達ジョーンズ行列の積の固有値の虚部は,主偏波状態に関連する群遅延である。PMDを導くDGD値
Δτは,二つの固有値の虚部の差である。出力主偏波状態自体は,T'T −1の固有ベクトルである。この固有
値はPDLを含むネットワークではユニタリ行列とならない場合もあるが,この場合,出力主偏波状態は必
ずしも直交している必要はない。
絶対位相の測定を含むT'及びTの測定によって,二つの群遅延及びΔτを直接計算できるが,実際には,
上記のとおりジョーンズ行列測定方法によって二つの制限がある。直接T'を測定しない代わりに,有限の
Δωに関し,T'〜[T(ω+Δω)−T(ω)]/Δωと近似しなければならない。周波数間隔Δωが十分に小さく各出力
主偏波状態がωとω+Δωとでほぼ同じ減衰量となる場合,σ'Δω/σは0となり,式(B.8)は式(B.9)に書き換
えることができる。
(
)()(
)
[
]
0
1
1
=
∆
+
−
∆
+
−
y
I
i
T
T
gω
τ
ω
ω
ω
············································ (B.9)
二番目の制限要因は,二つの群遅延が個別に決まることを避けるため,T(ω+Δω)T −1(ω)並びにその関連
する固有値ρ1及びρ2は,複素定数の範囲でしか決まらないことである。被測定リンクの減衰量が偏波に依
存しない場合,T(ω+Δω)T −1(ω)の固有値は,βρ1及びβρ2となる。ここで,βは複素定数であり,ρkは
ρk=exp(iτg,kΔω)と表される。ゆえに,DGD値Δτは式(B.10)となる。
Δτ = |τg,1 ‒ τg,2| = |Arg(ρ1 /ρ2) / Δω| ················································· (B.10)
ここに,
ρ1及びρ2: T(ω+Δω)T −1 (ω)の固有値
Arg: 偏角関数,すなわちArg (αeiθ)=θ
21
C 61280-4-4:2015 (IEC 61280-4-4:2006)
PDLが存在する場合であっても,固有値は式(B.11)のように近似できる。
ρk = 1 + iτg,kΔω ≡ exp(iτg,kΔω) ····················································· (B.11)
実際には,Δτの測定時にPDLが与える影響は,十分に小さい光角周波数間隔Δωを用いることで低減で
きる。多値性をもつ偏角関数の曖昧さを避けるため,全ての場合でΔτΔω<πという条件を満たさなければ
ならない。
B.3.2 ポアンカレ球解析法(PSA)DGD計算
[4]に示された解析は,JMEの偏角関数の代替手法で,それはアークサイン関数に基づくものである。
測定される規格化ストークスベクトル,Hˆ,Vˆ及びQˆから,hˆ,vˆ及びqˆは,式(B.12)のように計算さ
れる。
H
h
ˆ
ˆ=
,
H
Q
H
Q
H
q
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
×
×
×
=
,
q
V
q
V
q
v
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
×
×
×
=
····························· (B.12)
この計算処理によって,この解析法では入力偏波状態に依存しなくなり,結果として,その入力偏波状
態を知る必要がなくなる。
そのストークスベクトルから,hˆ,vˆ及びqˆは,各波長での
q
h
c
ˆ
ˆ
ˆ
×
=
及び
v
q
c
ˆ
ˆ
ˆ
×
=
′
というベクトル積を構
成する。各波長間隔に関し,有限差分を計算する。
)
(ˆ
)
(ˆ
ˆ
ω
ω
ω
h
h
h
−
∆
+
=
∆
)
(ˆ
)
(ˆ
ˆ
ω
ω
ω
q
q
q
−
∆
+
=
∆
)
(ˆ
)
(ˆ
ˆ
ω
ω
ω
v
v
v
−
∆
+
=
∆
)
(ˆ
)
(ˆ
ˆ
ω
ω
ω
c
c
c
−
∆
+
=
∆
)
(ˆ
)
(ˆ
ˆ
ω
ω
ω
c
c
c
′
−
∆
+
′
=
′
∆
·························· (B.13)
式(B.14)によって,特定波長の増分に対するDGD値τ
∆が求まる。
(
)
(
)
′
∆
+
∆
+
∆
+
∆
+
∆
+
∆
∆
=
∆
2
2
2
2
2
2
ˆ
ˆ
ˆ
2
1
2
1
arcsin
ˆ
ˆ
ˆ
2
1
2
1
arcsin
1
c
v
q
c
q
h
ω
τ
····· (B.14)
注記
h
h
h
ˆ
ˆ
ˆ2
∆
×
∆
=
∆
各DGD値は,相当する波長間隔の中点におけるDGD値を表す。
22
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書C
(規定)
干渉法
この附属書は,干渉法(INTY)を用いたPMD測定方法(方法C)の詳細な要求事項について規定する。
この方法では通常,PMDRMS[DGDのRMS,式(1b)参照]を測定し,DGD分布がマクスウェル分布に完全
に一致するという仮定の下で,式(1c)を用いてPMDAVG(DGDの線形平均)に変換する。
方法Cには,次の2種類の測定方法がある。
− 基本的な測定系を用いる,慣例的な干渉法(TINTY)[9-11]
− TINTYを一部変更した測定系を用いる,一般的な干渉法(GINTY)[12]
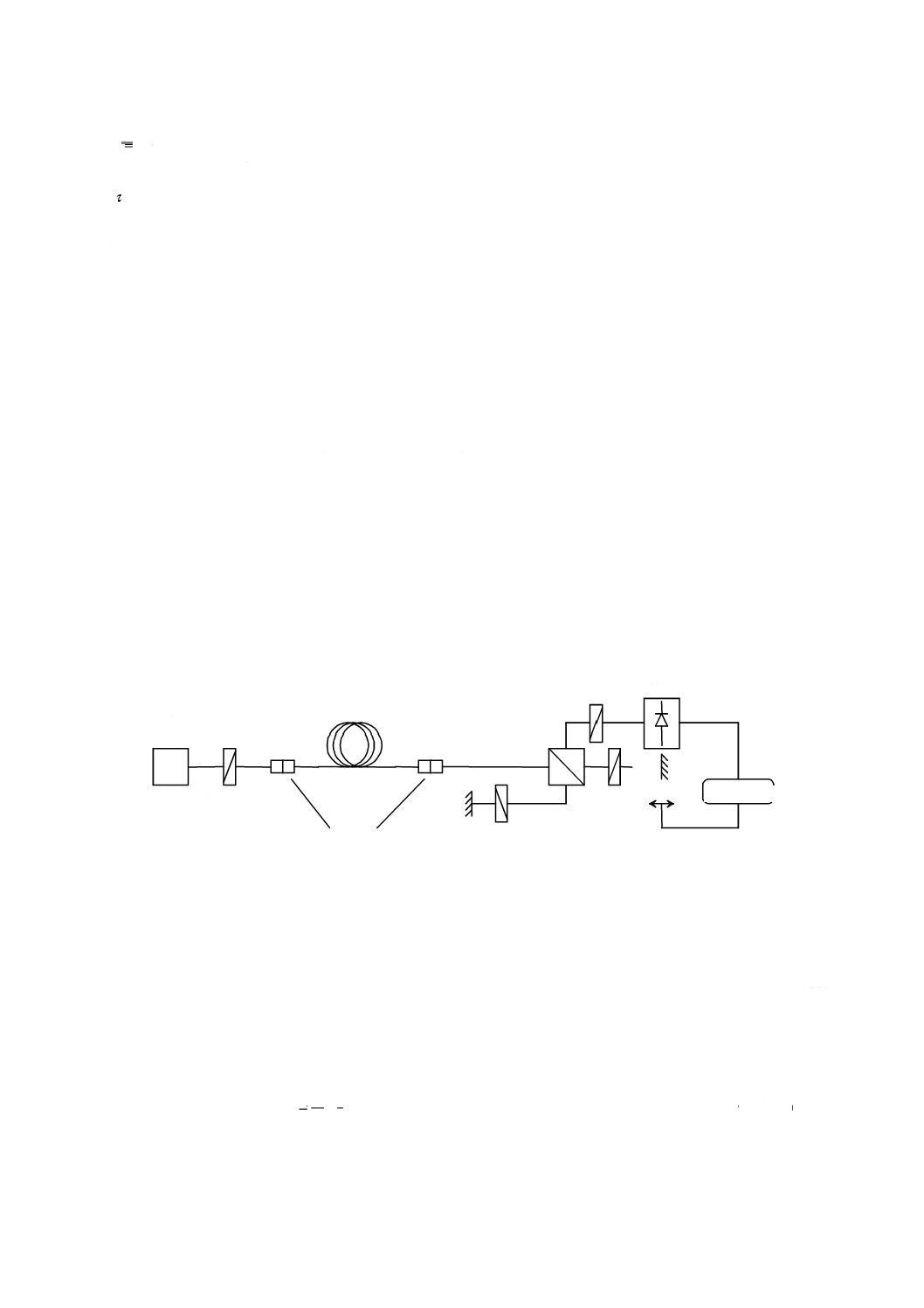
図C.1が,方法C(INTY)の一般的な測定系の試験構成である。この測定系を変更した図C.2,図C.3
の測定系を用いることもある。
干渉計
被測定リンク
S(ν)
検光子
フーリエ変換
遅延 (τ)
相互相関
correlation
SOP
So(ν)
広帯域
光源
偏光子
自己相関
フリンジ
包絡
線
E
(τ
)
SOP
偏波状態
S(ν) = {1 + [ŝ(ν) ŝa ]} So(ν)
1
2
Ss(ν)
ŝo
ŝ(ν)
J(ν)
ŝa
P(τ)
~
So(ν)
ス
ペク
トル
S
(ν
)
IEC 007/06
図C.1−INTY(方法C)の一般的な測定系
図C.1及びこの附属書で用いるパラメータを,次のように定める。
ν
光周波数(λν=c)
τ
干渉計の二つの光路間の往復遅延時間差
Ss(ν)
被測定リンク入力における光スペクトル
So(ν)
被測定リンク出力(検光子入力)における光スペクトル
S(ν)
検光子出力(干渉計入力)における光スペクトル
0ˆs
被測定リンク入力における入力SOP(単位ストークスベクトル)
)
(ˆν
s
被測定リンク出力における出力SOP
aˆs
検光子透過軸
23
C 61280-4-4:2015 (IEC 61280-4-4:2006)
x(ν)
)
(ˆ
ˆa
ν
s
s
≡
)
(ˆν
s
の検光子透過軸に対する射影成分。このパラメータx(ν)がPMDの情報を含んでいる。
)
(τ
P
遅延時間τの関数とした,干渉計の出力光パワー
)
(~τ
P
P(τ)のτに依存した成分(交流成分)
P0
P(τ)の一定部分(直流部分)
E(τ)
干渉しま(縞)の包絡線
Ex(τ)
相互相関包絡線
E0(τ)
自己相関包絡線
干渉計の出力光パワーP(τ)は,交流成分と直流成分との和に等しい。両成分はτ=0で等しいので,交流
成分を計算することができる。理想的な干渉計では交流成分は偶関数であり,その右半分が検光子から出
力される光スペクトルS(ν)のコサインフーリエ変換に等しい。理想的でない干渉計では,測定の詳細によ
って何らかの補正を行ってもよい。
TINTYでは,干渉波形の包絡線E(τ)が交流成分の絶対値となる。GINTYにおける相互相関及び自己相関
の包絡線を得るための付加的な計算は,C.2.1.3に記載する。これらの計算には,互いに直交する二つの
SOPに検光子をそれぞれ設定して測定した,二つの干渉波形を用いる。
C.1 慣例的な干渉法(TINTY)
C.1.1 装置
図C.2は,方法CのうちTINTYを用いたリンク測定のブロック図である。
図C.2−TINTY(TINTY方法C)の概略図
C.1.1.1 光源
測定する波長帯で発光する,偏光した広帯域光源を用いる。例えば,LED,スーパーフローレッセント
光源(superfluorescent source)などを偏光子とともに用いればよい。中心波長λ0は,1 310 nm帯,1 550 nm
帯又はその他の測定波長帯内にあるものとする。スペクトル形状はほぼガウス形である必要があり,出力
光の自己相関関数に影響を与えるリップルがあってはならない。式(C.1)で定めるコヒーレンス時間tcを計
算するため,光源線幅(LEDの分野ではスペクトル幅とも呼ばれる)Δλは,既知でなければならない。
c
t
2
0
c
λ
λ
∆
=
·············································································· (C.1)
ここに,
λ0: 光源の中心波長
Δλ: 光源の線幅
コントローラ
被測定リンク
コネクタ
偏光子
ミラー
可動ミラー
フリンジ包絡線
検出
光源
IEC 008/06
24
C 61280-4-4:2015 (IEC 61280-4-4:2006)
c: 真空中の光速
C.1.1.2 ビームスプリッタ
ビームスプリッタは,偏光した入射光を干渉計の各光路を伝搬する二つの成分に分岐するために用いる。
これは,光ファイバカプラ又はコーナーキューブビームスプリッタでもよい。
C.1.1.3 干渉計
空間形又は光ファイバ形のいずれかのマイケルソン干渉計を被測定リンクの検出端に設置する。干渉計
の自己相関ピーク応答を除去するためには,例えば,四分の一波長板を用いることができる。ただし,LED
の帯域の全波長において四分の一波長と等しく,自己相関ピークを効果的かつ完全に除去できるような四
分の一波長板を見つけることは極めて難しい。
C.1.2 手順
C.1.2.1 校正
既知のPMDをもつ高複屈折光ファイバを測定することで,装置の校正を行う。代わりに,既知のPMD
をもった高複屈折光ファイバの接続物を測定してもよい。
C.1.2.2 定常操作
被測定リンクの片端を光源の偏光出力に接続し,他端を干渉計の入力に接続する。これは,標準的な光
ファイバコネクタ,スプライス又はファイバ調芯系を用いて行うことができる。ファイバ調芯系を用いる
場合には,接続部の反射を避けるために屈折率整合オイルを用いる。
光源の出力光パワーを,用いる検出系特有の基準値となるように調整する。十分なコントラストの干渉
しま(縞)を得るため,干渉計の両光路の光パワーがほぼ等しくなるように設定する。
まず初めに,干渉計アームの一方のミラーを動かして二つのアームの光路長差を変更しながら,光強度
を記録する。一つの入力SOPに対して得られた干渉しま(縞)パターンから,C.1.3に記載する方法でPMD
の遅延を計算する。ランダムな偏波モード結合がある場合の干渉しま(縞)パターンの典型例を,図C.3
に示す。干渉しま(縞)パターンは,理想的なランダムモード結合を表わすスムーズなガウス形スペクト
ルである必要がある。
モード結合が不十分な場合,又は,PMDが低い場合は,異なる入力SOPに対して繰り返し測定をする
か,又は,全ての入力SOPに対する平均を得るために,測定中に偏光状態を変調することが望ましい。
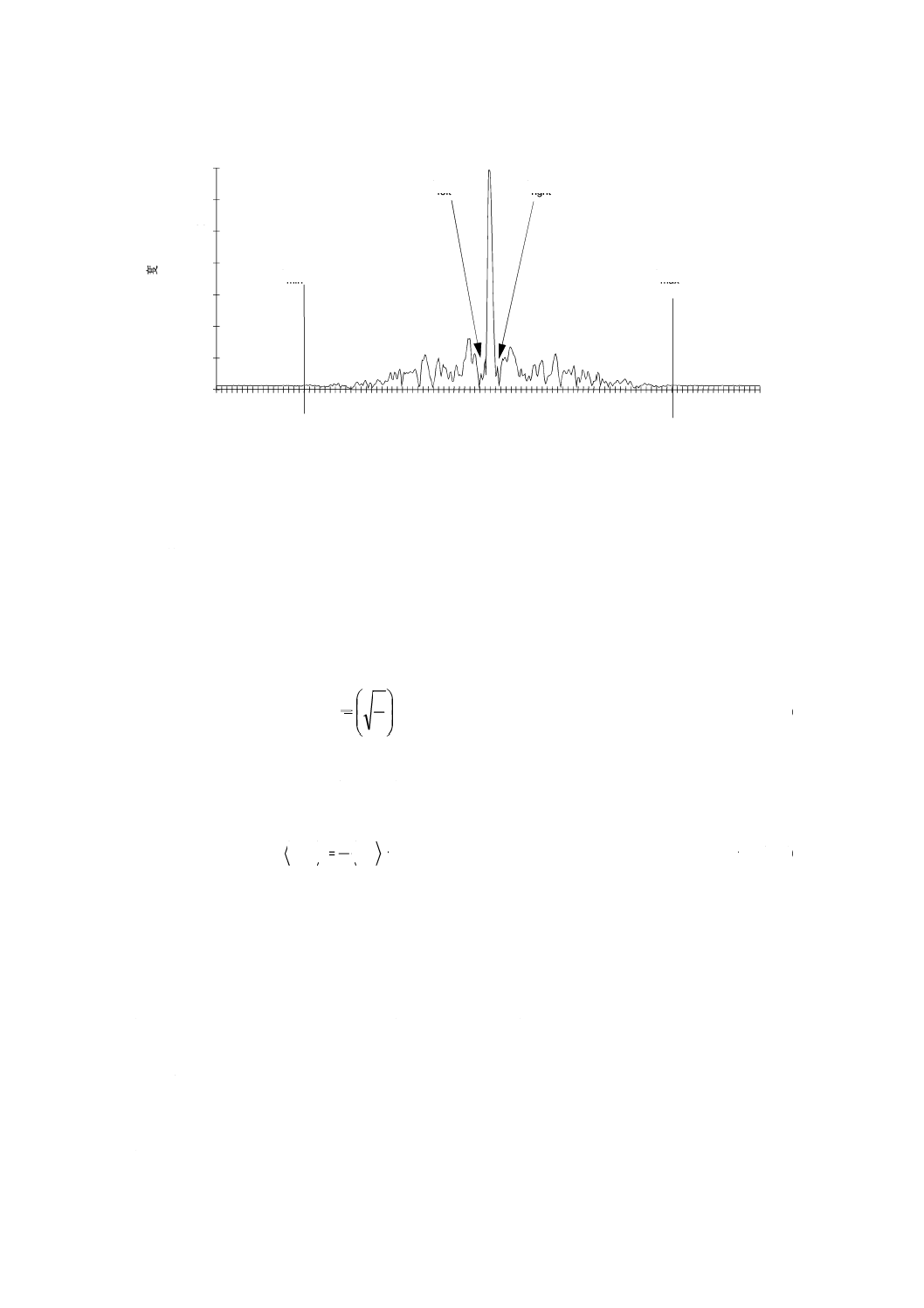
25
C 61280-4-4:2015 (IEC 61280-4-4:2006)
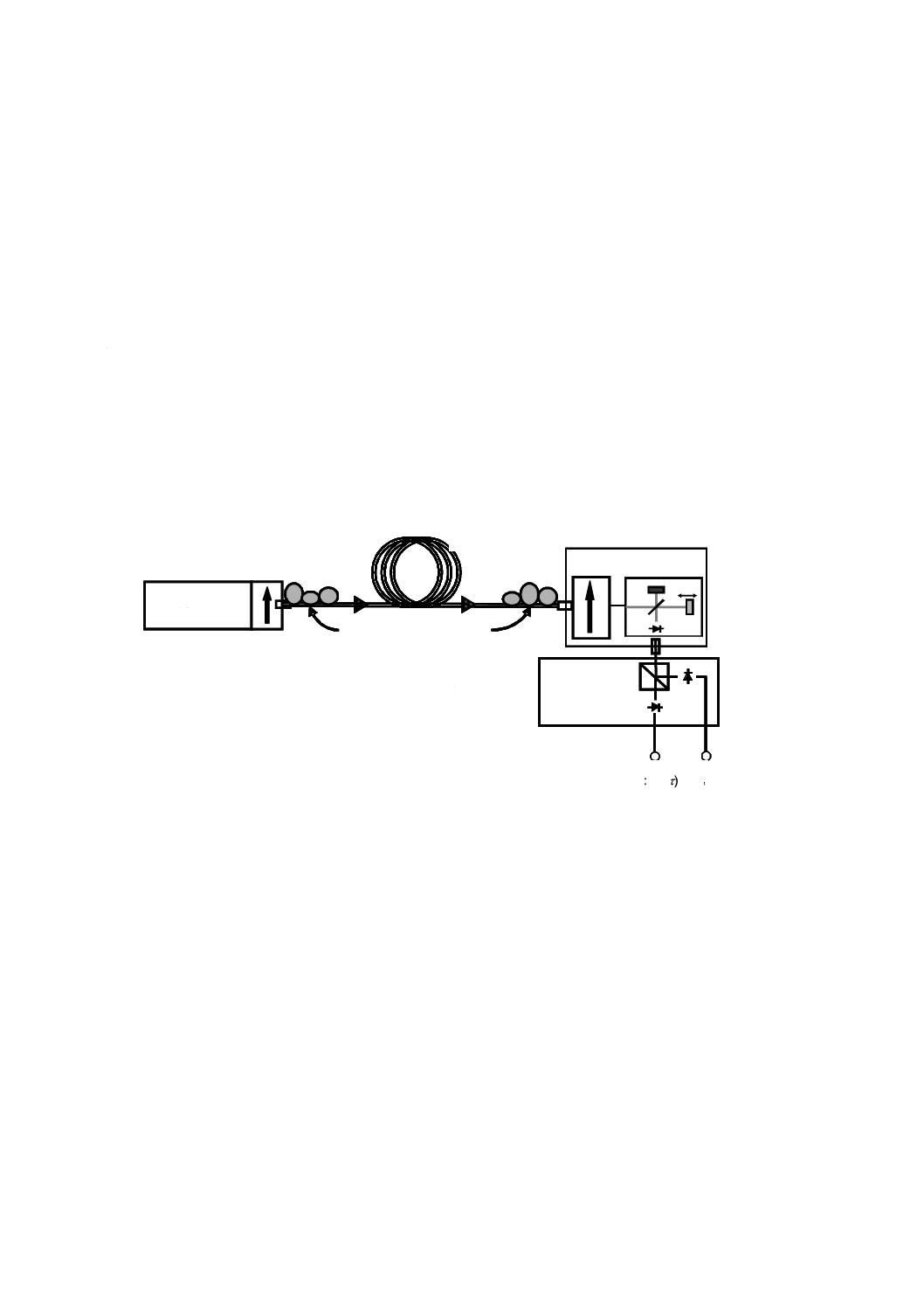
図C.3−TINTY(方法C)によって得られる典型的なデータ
C.1.3 計算
次の計算は,リンクのモード結合が強い場合,又はランダムな場合に適している。中央部分のピークを
無視して,干渉波形の広がりを評価する。
検出信号(干渉波形)の相互相関関数の二次モーメントの平方根(RMS幅)から,PMDRMS値を式(C.2)
によって決定する。
ε
PMD
σ
=
4
3
RMS
·································································· (C.2)
ここに,
σε: 相互相関包絡線のRMS幅
測定した干渉しま(縞)の包絡線から計算するアルゴリズムの詳細は,G.1に記載する。
幾つかの仮定に基づくと,理論上[9-11],式(C.2)は式(C.3)で式(1b)と関係付けることができる。
2
2
4
3
ε
σ
τ=
∆
······································································· (C.3)
式(C.3)に用いた仮定は,次のとおりである。
− 理想的なランダムモード結合
注記1 理想的なランダムモード結合とは,L/h → ∞であり,かつ,複屈折率軸が均一に分布している
ことを意味する。ここで,Lはリンクの長さ,hは偏波結合長である。長さhの複屈折率部
分がN個つながっているリンクの場合は,軸が均一に分布し,N → ∞であることに相当する
注記2 モード結合がない場合,又は無視できる場合の解析も可能である。
− リップルのない,純粋なガウス形スペクトルをもつ光源
− PMD >> σ0
ここで,σ0は自己相関包絡線のRMS幅である。
− エルゴード性
注記3 光源がガウス形スペクトルをもつ場合,測定結果はDGD値の加重平均となる。この加重は
PMD 遅延 ps
0
500
1 000
1 500
2 000
2 500
3 000
3 500
tj min
tj left
tj right
tj max
‒5
‒4
‒3
‒2
‒1
0
1
2
3,01
4,01
5,01
強度
IEC 009/06
26
C 61280-4-4:2015 (IEC 61280-4-4:2006)
GINTYでは規定しているが,TINTYでは規定がない。この理由から,方法CのうちTINTY
では,同じ波長範囲及び時間に対して,方形加重を用いた方法とは異なる結果になると予想
される。エルゴード性の仮定によって,予想できる値の関係性が有効になるが,実際には,
その他の方法の異なる測定では波長範囲もまた異なるため,測定結果もまた異なることを意
味している。
C.2 一般的な干渉法(GINTY)
GINTYは,TINTYにおいて式(C.3)で必要だった仮定のうち,幾つかを次のように取り除くことができ
る。
− 理想的なランダムモード結合の仮定を必要としない。
− ガウス形光源の仮定を必要としない。
− PMDが自己相関関数のRMS幅に比べて大きいという仮定を必要としない。
C.2.1 装置
図C.2に示した測定系に加えて,図C.4には方法C(GINTY)を用いたリンク測定のブロック図を示す。
広帯域
光源
偏光子
被測定リンク
SOP スクランブラ
偏波ビーム
スプリッタ
干渉計
偏波
ダイバーシティ
検出器
フリンジ: P (τ) P (τ)
検光子
~
~
IEC 010/06
x
y
図C.4−方法C(GINTY)の概略図
図C.4の測定系を用いてGINTY(方法C)を行い,二つの干渉波形Px及びPyを得る。これら二つの干
渉波形は,図C.1の測定系において,検光子を直交する二つの方向に配置を変えて測定した場合に対応す
る。偏波スクランブラによって,入力SOP及び二つの検光子の実効的な透過軸をランダムに変更する。図
C.4の“干渉しま(縞)”が,理想的な干渉波形の交流成分に相当し,図C.1においては,ある一つの入力
SOP及び検光子透過軸の組合せに対して得られたものである。これら二つの干渉しま(縞)の和及び差を
二乗することで,自己相関関数及び相互相関関数の二乗包絡線を得る。
C.2.1.1 光源
測定する波長帯で発光する,LED,スーパーフローレッセント光源などの広帯域光源を用いる。中心波
長は,1 310 nm帯,1 550 nm帯又はその他の測定波長帯内にあるものとする。これ以外に,光源スペクト
ルに対する特別な要求事項はない。
27
C 61280-4-4:2015 (IEC 61280-4-4:2006)
C.2.1.2 偏光子,スクランブラ
偏光状態のスクランブルは,物理的には被測定リンクの入出力端それぞれに一つずつ可変偏光子を挿入
することで行い,1回の干渉計掃引に対して異なる入力偏光状態及び検光子軸を設定する。複数の入出力
偏光状態を選択することで,一つの入出力偏光状態で測定する場合よりも,更に詳細な干渉波形包絡線及
び平均二乗包絡線を得ることができる。単一偏光状態での測定は,スクランブラを必要としない選択肢の
一つではあるが,複数の偏光状態を用いることによって,PMD測定精度を方法Bと同程度にまで改善す
ることができる。また,複数のアナライザ設定を用いることもある(C.2.1.3参照)。概念的には,スクラ
ンブルの手順は次による。
− 入力偏光子及びその後に続くスクランブラは,ポアンカレ球上の任意の点に軸が設定された等価な偏
光子単体として働き,入力偏光状態を決定する。
− スクランブラ及びその後に続く検光子は,ポアンカレ球上の任意の点に軸が設定された等価なアナラ
イザとして働き,出力偏光状態を決定する。
一組の入力偏光状態と検光子軸との組合せは,一つの入出力偏光状態として認識される。その目的は,
均一に分布した入出力偏光状態において平均化した二乗平均包絡線を得ることにある。この目的を達成す
るためには,実際には次に示す幾つかの方法が可能である。
C.2.1.2.1 9-偏光状態のミューラーセット
九つの特定の入出力偏光状態においてそれぞれ観測された二乗包絡線の合計は,均一にスクランブルさ
れた二乗平均包絡線と厳密に等しい。これら九つの入出力偏光状態とは,直角三面体を形成する三つの入
力偏光状態,及びそれぞれの偏光状態に対してまた直角三面体を形成する三つの検光子軸のことである。
C.2.1.2.2 ランダムスクランブル
− 掃引ごとのスクランブル:それぞれの掃引において,スクランブラを自動又は手動にて設定する。
− 連続スクランブル:二乗包絡線を合計する場合,掃引中にスクランブルが実行される。自動スクラン
ブラは,ポアンカレ球を網羅するよう,時間に応じて連続的に設定される。
− 高速・単一掃引スクランブル:スクランブラが十分に速い場合は,一度の掃引で十分にスクランブル
された二乗包絡線を観測することができる。しかし,そのためには干渉波形の交流部分と直流部分と
の間のクロストークを避けるための特別な対策が必要である。
C.2.1.3 偏波ビームスプリッタ
偏波ビームスプリッタ(PBS)は,同じ入出力SOPの組合せに対して直交する(ポアンカレ球の反対側
にある)出力SOPから干渉波形を得るために用いる。これら二つの干渉波形から,自己相関及び相互相関
を別々の関数として計算することができる。PBSは,検出系とともに偏波ダイバーシティ検出系を構成す
る。直交する出力SOPからこれらの干渉波形を得るには,PBS以外の手段を用いることもできる。
互いに直交する二つの検光子軸(ポアンカレ球の反対側)において観測される二つの干渉しま(縞)パ
ターンを用いて,自己相関及び相互相関の包絡線を次のように計算することができる。
− 単一の入出力SOPに対する自己相関包絡線
)
(
~
)
(
~
)
(
y
x
0
τ
τ
τ
P
P
E
+
=
······························································ (C.4a)
− 単一の入出力SOPに対する相互相関包絡線
)
(
~
)
(
~
)
(
y
x
x
τ
τ
τ
P
P
E
−
=
······························································ (C.4b)
28
C 61280-4-4:2015 (IEC 61280-4-4:2006)
C.2.1.4 干渉計
空間形又は光ファイバ形のいずれかのマイケルソン干渉計を被測定リンクの検出端に設置する。
C.2.2 手順
C.2.2.1 校正
C.1.2.1にしたがって,装置を校正する。
C.2.2.2 定常操作
図C.2の測定系を用いる場合は,リンクの片端を偏光源の偏光出力に接続し,他端を干渉計の入力に接
続する。図C.4の測定系を用いる場合は,リンクの片端をスクランブラと偏光子との組合せの出力に接続
し,他端をスクランブラと干渉計との組合せの入力に接続する。
光源の光出力パワーを,用いる検出系特有の基準値となるように調整する。十分なコントラストの干渉
しま(縞)を得るため,干渉計の両光路の光パワーがほぼ等しくなるように設定する。
まず初めに,干渉計アームのミラーを動かし,光強度を記録する。一組の入出力SOPに対して得られた
干渉しま(縞)パターン,又は,スクランブルによるN組の入出力SOPに対して各々得られた干渉しま(縞)
パターンから,C.2.3に記載する方法でPMDの遅延を計算する。代表的なリンクにおいて,ランダム及び
混合偏波モード結合がある場合に測定される平均二乗相互相関包絡線の例を,図C.5及び図C.6にそれぞ
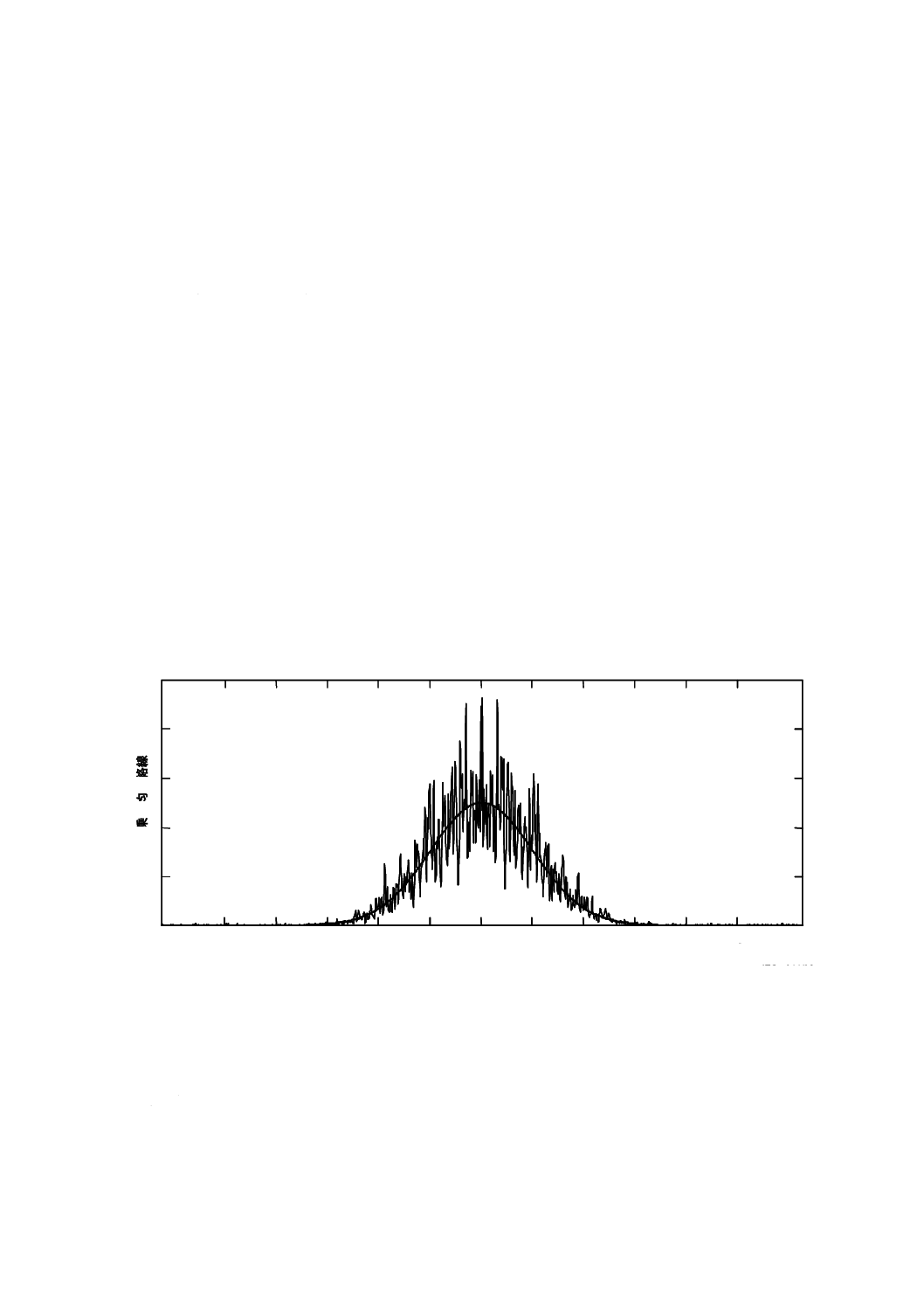
れ示す。
− 図C.5は,ランダムモード結合の場合を示しており,L/h=100,PMD=4.94 ps,σA=50 fs,PMD/σA〜
100である。
注記 図C.5のスムージングは,図を見やすくための目安である。解析には,平滑化処理も曲線回
帰も用いない。
‒16
‒12
‒8
‒4
0
4
8
12
16
‒20
20
遅延 ps
二乗
平均
包絡線
IEC 011/06
図C.5−GINTY(方法C)で得られる典型的なランダムモード結合データ
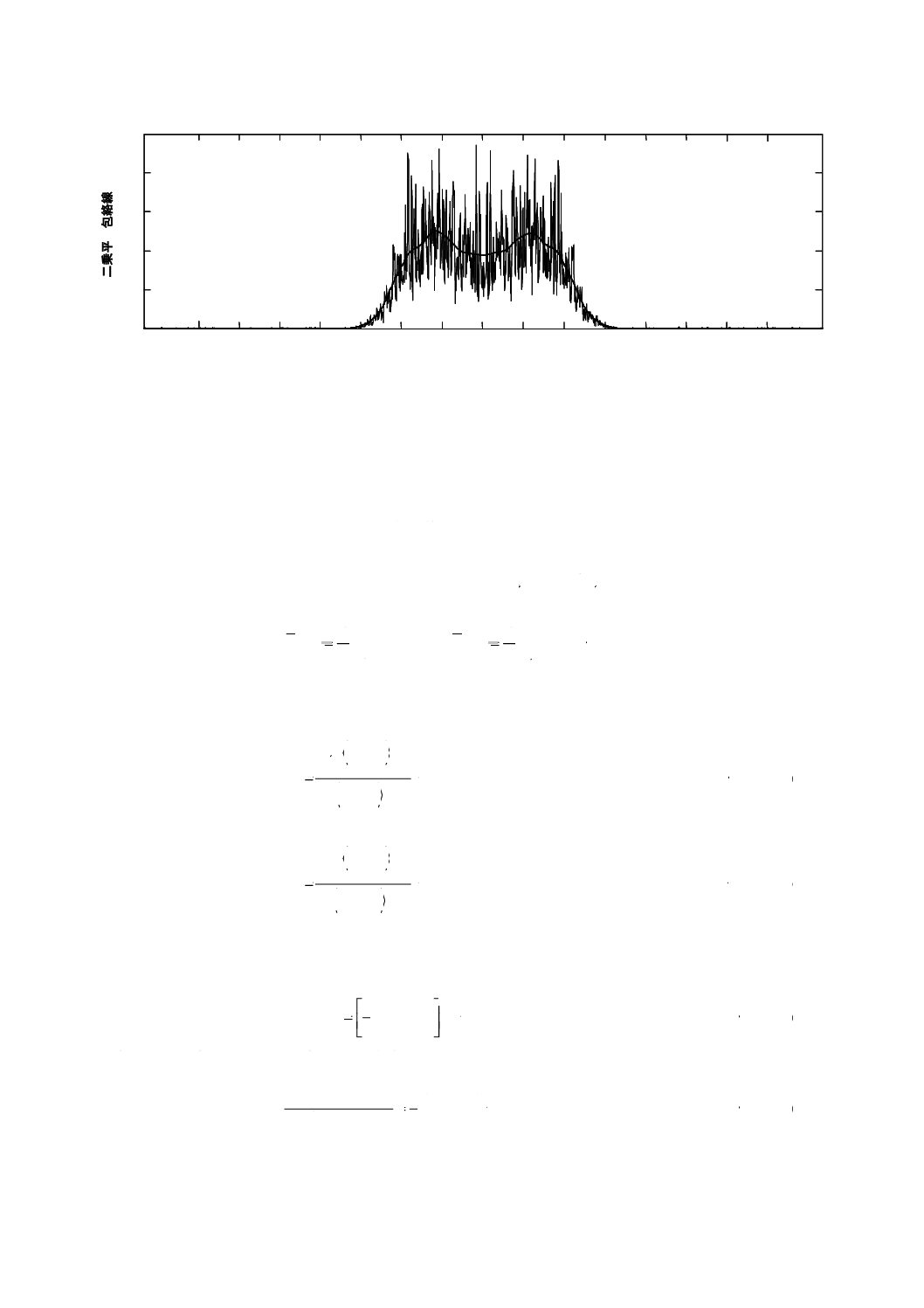
− 図C.6は,混合モード結合の場合を示しており,ほぼ平たんな包絡線をもつ。L/hの定義は重要な意
味をもたなくなる。被測定リンクは,L/h=10のランダムモード結合部分と,DGD=PMDRandom/4,PMD
=9.97 ps,σA=50 fsのモード結合を無視できる部分とから構成される。
注記 図C.6のスムージングは,図を見やすくための目安である。解析には,平滑化処理も曲線回
帰も用いない。
29
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図C.6−GINTY(方法C)で得られる典型的な混合モード結合データ
C.2.3 計算
リンクのいかなるモード結合に対しても,次の計算を適用することができる。
相互相関及び自己相関の干渉波形の二乗包絡線に基づいてPMDを決定する。
まず最初に,N組の入出力SOPの組合せ(番号i)に対して,それぞれ干渉波形を測定し,式(C.4)によ
って包絡線E0i(τ)及びExi(τ)を求める。次に,二乗包絡線
)
(
2
0τ
i
E
及び
)
(
2τ
xi
E
を求め,式(C.5)によって二乗平
均包絡線を計算する。
()
()
∑
=
i
i
E
N
E
τ
τ
2
0
2
0
1
()
()
∑
=
i
xi
x
E
N
E
τ
τ
2
2
1
································· (C.5)
そして,得られた二つの二乗平均包絡線のRMS幅σ0及びσxをそれぞれ計算する。この計算アルゴリズ
ムはG.2に記載する。これらRMS幅の理想的な定義は式(C.6a)及び(C.6b)のとおりである。
∫
∫
=
τ
τ
E
E
τ
τ
τ
τ
τ
σ
d
)
(
d
)
(
2
0
2
0
2
2
0
································································ (C.6a)
∫
∫
=
τ
x
τ
x
E
E
τ
τ
τ
τ
τ
σ
d
)
)(
d
)
(
2
2
2
2
x
································································ (C.6b)
式(C.6a)及び式(C.6b)の期待値演算子は,入出力SOPの均一でランダムな抽出に関するものである。
式(C.7)からPMDRMSを計算することができる。
(
)
2/1
2
0
2
RMS
2
3
−
=
σ
σx
PMD
························································· (C.7)
式(C.7)は,式(C.8)を用いて式(1b)と関係付けることができる[12]。
()()
()
(
)
2
0
2
2
0
2
0
2
2
3
d
d
σ
σ
ν
ν
ν
ν
ν
τ
−
=
∆
∫
∫
x
S
S
···················································· (C.8)
式(C.6a)及び式(C.6b)のRMS幅の理想的な定義を用いると,式(C.8)は,いかなる測定時のDGD曲線,又
0
6
12
18
24
30
0,4
0,8
1,2
1,6
36
42
遅延 ps
二
乗
平
均
包
絡
線
‒6
‒12
‒18
‒24
‒30
‒36
‒42
IEC 012/06
30
C 61280-4-4:2015 (IEC 61280-4-4:2006)
はいかなる光源スペクトル特性に対しても厳密に正しい。式(C.8)の左辺は,スペクトル上で(二乗するこ
とによって)加重のかかったRMS計算となる。
エルゴード性を仮定すると,式(C.9)の関係を得ることができる。
()()
()
∫
∫∆
=
∆
ν
ν
ν
ν
ν
τ
τ
d
d
2
0
2
0
2
2
S
S
······················································ (C.9)
31
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書D
(規定)
戻り光を用いたストークスパラメータ解析法
この附属書は,戻り光を用いたストークスパラメータ解析法によるPMD測定(方法D)のときに必要
となる詳細な要求事項について記載する。この方法によって,光増幅器を含まない最大40 kmのリンクに
対して有効な結果を得ることができる。
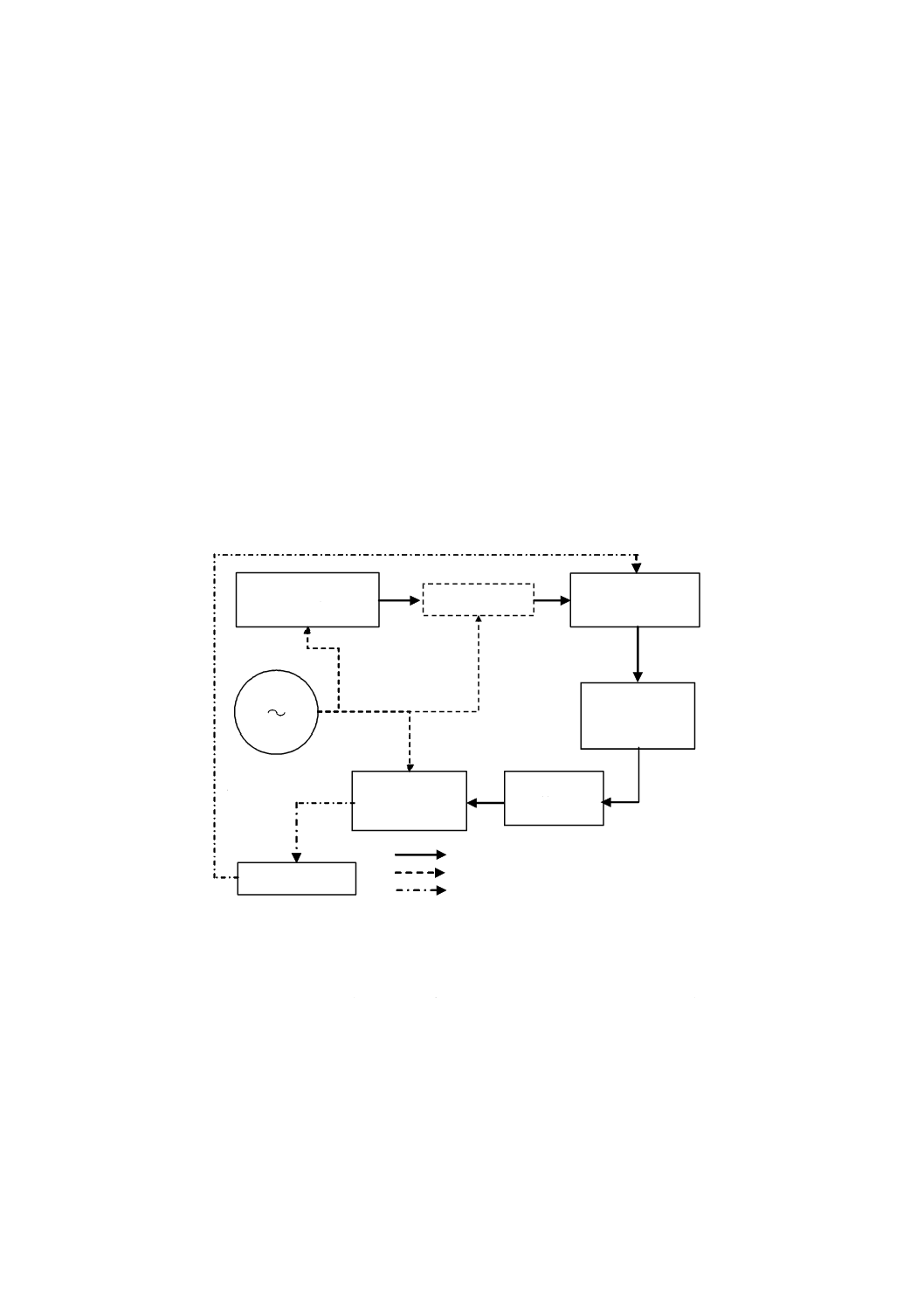
D.1 装置
図D.1に装置の配置を示す。
外部共振器
レーザ
偏波
コントローラ
方向性
結合器
斜め研磨
コネクタ
被測定
ファイバ
接続選択
偏波アナライザ
制御信号
A
1
2
3
IEC 013/06
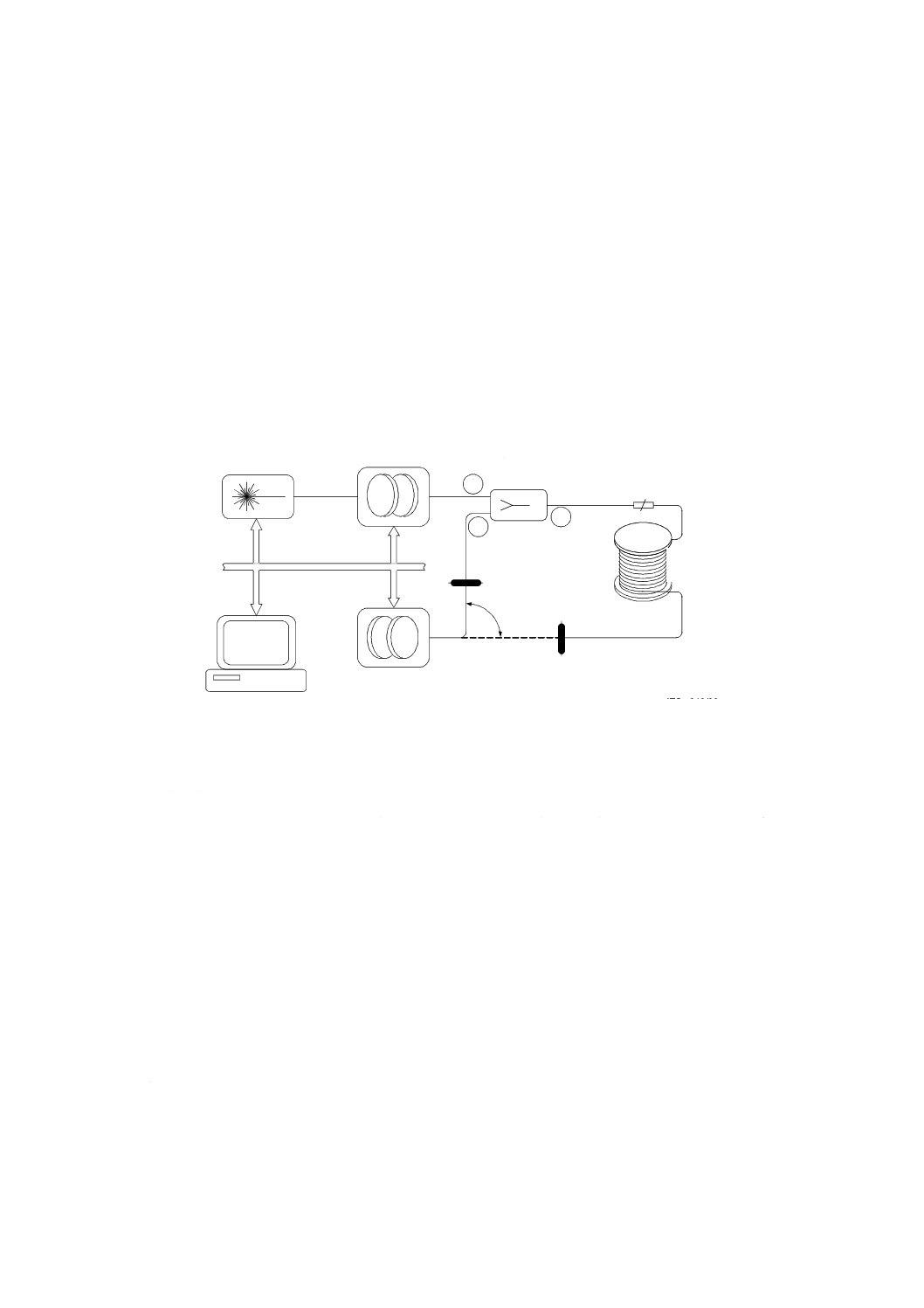
図D.1−方法Dによる配置
装置の多くのものは方法Bで用いるものと同じである。異なる要素について次に記載する。
D.1.1 方向性結合器
方向性結合器は,光源からリンクへ入射する光と,リンクの遠端で反射されて偏波アナライザに入力す
る光とを結合する。この結合器は低PMD(0.1 ps),低PDL(0.1 dB),かつ,低反射ロス(50 dB以上)で
なければならない。また,結合器は測定時に安定させることが望ましい。
D.1.2 斜め研磨コネクタ
このコネクタは,偏波アナライザでの混合信号を避けるため,反射ロス(50 dB以上)でなければなら
ない。方向性結合器と角度付きコネクタとの間のパッチコードは,測定時に安定させることが望ましい。
D.1.3 遠端終端
リンクの遠端は,出力偏光状態を検出するポラリメータに対して十分な光を反射しなければならない。
光ファイバの軸に対して垂直で滑らかな端面切断が必要となる場合もある。
D.2 手順
方法Dの手順は,リンクの入力部が測定器の入出力に相当する点を除き,方法Bと同じである。ただし,
リンクの入力部の角度付きコネクタ,及びリンクの出力部の反射端は,特別に準備する必要がある。
32
C 61280-4-4:2015 (IEC 61280-4-4:2006)
D.3 計算及び結果の解釈
所与の波長でのDGDの計算は,方法Bと同様である。方法Bとの相違点は,これらのDGDの平均値
がリンクのPMDとはならない点である。<ΔτB>は,後方反射DGD測定の平均として定義する。測定した
波長領域でのリンクのPMD(ps)は,式(D.1)となる。
B
PMD
τ
∆
π
=2
······································································ (D.1)
33
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書E
(規定)
変調位相シフト法
この附属書は,変調位相シフト法に特有の要求事項について記載する。
E.1
装置
主に次の二つの方法を用いる。
− 入力偏光状態を全掃引する方法
− 入力偏光状態のミューラーセットに関連する出力偏光状態の測定に基づく方法
全掃引法は,単純に一つの偏波コントローラ,又は偏波コントローラを偏波変調器と併せて用いること
で,実現できる。図E.1に,単純な制御構成を,位相の基準となる経路を制御するための代替の接続と併
せて示す。図E.2に,偏波変調の場合の構成を示す。図E.1の中の装置でミューラーセット法を行うこと
ができる。
図E.1−基本装置
E.1.1 光源
各特定波長のDGDの測定には,複数のレーザダイオード,波長可変光源,又は単色光分光器若しくは
別のフィルタによってフィルタされた発光ダイオードを用いる。スタートストップ方式の波長試験システ
ムにおいて,試験装置の選定における主要な問題は,評価対象のスペクトルによって必要とされる測定ス
テップ幅をまず決定し,そして,そのステップ幅に基づくナイキスト制限から光源の線幅を選定すること
である。
E.1.1.1 レーザダイオード
中心波長及び変調された出力位相を含むレーザ光源のスペクトルは,バイアス電流,変調周波数,及び
光源
(狭帯域)
偏波
コントローラ
被測定
リンク
光検出器
位相測定回路
高周波発振器
変調信号
コンピュータ
基準信号
強度変調器
f = 0,01 GHz -10 GHz
IEC 014/06
光信号
変調信号
制御信号及び出力信号
34
C 61280-4-4:2015 (IEC 61280-4-4:2006)
ダイオードの温度について,測定中,安定していなくてはならない。
温度制御及び出力安定制御(例えば,PINダイオードによる帰還制御)された単一縦モード発振レーザ
ダイオードは,シングルモード光ファイバとともに用いるのに適している。
E.1.1.2 フィルタリングされた発光ダイオード
一つ以上の発光ダイオードを用いる。中心波長及び変調された出力位相を含む発光ダイオードのスペク
トルは,バイアス電流,変調周波数,及び発光ダイオードの温度について,測定中安定していなくてはな
らない。
FWHM線幅が1 nm〜5 nmに範囲に入るように発光ダイオードの光スペクトルをフィルタする。モノク
ロメータは,フィルタリング又は波長選択のために用いる。
E.1.1.3 波長可変レーザ
一つ以上の波長可変レーザを用いる。中心波長及び使用各波長における各レーザの変調位相を含むレー
ザスペクトルは,バイアス電流,変調周波数,及びダイオード温度について,測定中安定していなくては
ならない。通常,温度制御を内蔵した外部共振器レーザユニットを用いる。
E.1.2 変調
単一の主フーリエ成分を含む波形を作るため,光源の強度変調を行う。変調周波数は適切な測定精度を
保つため十分に高く,また十分に安定していなくてはならない。
変調は,レーザダイオード又は発光ダイオードへの直接(内部)電流注入によって行う。その他の(外
部の)変調手段も使用できる。例えば,光をリンクに入れる前に変調するために,レーザの後に電気光学
変調器デバイスを配置する(図E.1参照)。変調器は,適切な測定精度を保つように十分に安定していなく
てはならない。
正弦波,台形又は,く形波変調を用いることができる。0.01 ppmの周波数安定性があれば,通常,十分
である。
位相シフトの測定時に2πnラジアン(nは整数)の多義性を避けることが重要である。これは,大きな
PMD係数をもつ場合には変調器周波数を減らすなどによって実現できる。
例えば,変調周波数を2πの差動位相シフトに相当する周波数よりも低い周波数を用いなければならない。
この限界周波数は式(E.1)で見積もることができる。
max
3
max
10
DGD
f
=
(GHz) ·························································· (E.1)
ここに,
DGDmax: 予測される最大の典型的なDGD値(ps)
実際,典型的なDGD値が100 ps未満の場合,fmaxが10 GHzより大きくなり,fmaxが,次に示すデバイ
スの帯域制限に因る通常の使用範囲(10 MHz〜10 GHz)の最大値を一般的に超えてしまう。
周波数fでの変調は,光源の中心波長から±f離れた側波帯を生み出し,非常に狭帯域のリンクでは,こ
れは制限となる。正確な位相測定を行うため,変調側帯波及び光源の線幅を含む全占有帯域はリンクの帯
域以下でなければならない。周波数fは,デバイス帯域による制限の中で,位相検波回路に都合のよい領
域が通常用いられる。fは,通常10 MHz〜10 GHzの範囲である。
DGDminは,DGD測定値のRMS再現性によって決定し,さらに,用いる最小変調周波数fminを決定する。
fminは,位相検出器の位相分解能δφを用いて(E.2)式で計算される。
min
3
min
π
2
10
DGD
δ
f
×
×
=
φ
(GHz) ······················································ (E.2)
ここに,
DGDmin: DGD再現性のRMS値(ps)
35
C 61280-4-4:2015 (IEC 61280-4-4:2006)
δφ: 位相検出器の位相分解能のRMS値
E.1.3 偏波制御
被測定リンクへの入力偏光状態は,偏波コントローラを用いて制御する。偏光状態は,コンピュータか
ら制御信号によって制御する。コンピュータは,直交する偏光状態のように,適切,既知,かつ独立な偏
光状態を用いることで,偏光状態間の遅延時間差を測定できる。
偏波コントローラは,被測定リンクの入力部において,複数の偏光状態をもつ偏光を作り出すために用
いる。光源の出力光が無偏光状態の場合,偏波コントローラは入力部に偏光子を含まなければならない。
この偏光状態は,偏光子の後に置かれる可変複屈折素子によって制御する。偏波コントローラの例として
は,液晶遅延板,機械的に動作する複屈折光ファイバループ,電気光学結晶部品がある。
E.1.4 入出力部の光学部品
測定中,各光源の物理的及び光学的な経路長が一定となるように,光源出力とリンク入力部とを接続し,
またリンク出力と検出システムの入力部とを接続する(これは,偏光状態間の位相差が各経路長の違いに
よって変化しないようにするためである)。接続部品としては,複数チャネルのシングルモード光スイッチ
又は着脱可能な光コネクタが適切であるが,最も一般的には,融着が用いられる。これらのデバイスは,
測定する波長範囲において,固有の最大DGD,PDL及び群遅延が十分に小さくなるよう,選ばなければ
ならない。
注記 校正用光ファイバ測定では,リンクの代わりに,校正用光ファイバを用いる。
偏波コントローラ以降の光経路にある全ての光ファイバコード,ピグテール,及びその他の光学部品は,
測定波長域において,固有最大DGD,PDL及び群遅延が最小となるようにしなければならない。これら
の要素は,リンクのDGDを決める際の不確かさとなる場合がある。
偏光状態の選択は,一般的にコンピュータ制御によって行う。測定結果が光ファイバコードによる遅延
の熱的なドリフトに影響されないようにするため,その偏光状態における位相差の測定は十分に速く行わ
なければならない。
送信時の偏光状態を掃引することによって,DGD値を最大位相差によって決定する。位相検出回路及び
コンピュータから構成されるシステムは,幾つかの方法で実現できる。二つの例を次に記載する。
第1の例は,図E.1に記載のとおり,位相測定回路及びコンピュータによって,最初の偏光状態で位相
を記録する。そして,偏波コントローラは,別の偏光状態に設定し,この偏光状態で位相を記録する。選
択された波長におけるDGDは,2回の位相読出値の最大の差分によって求めることができる。
第2の例を図E.2に示す。偏波切換器偏波コントローラへの入力部における光の偏光状態を変調するた
めに用いる。偏波切換装置は,回転複屈折素子及び変調器(電気光学形又は光弾性形)で構成される。さ
らに,その他の素子を用いてもよい。位相測定回路からの真の位相差出力をロックイン検出できるように,
偏波は,例えば数十Hzの周波数Fで直交する二つの完全に独立な偏光状態の間で交互に入れ替える(E.1.5
参照)。この“偏波変調”は,熱的なドリフトの効果を取り除くことができる。位相検出器は,二つの偏光
状態間の位相差に比例した振幅をもち,偏光状態変調に同期したAC信号を生成する。この後,信号は,
位相差を示すDC信号を得るため,ロックインアンプによって復調される。選定波長におけるDGDは,
出力偏光状態をポアンカレ球上にわたって掃引した際の最大位相差から決定する。
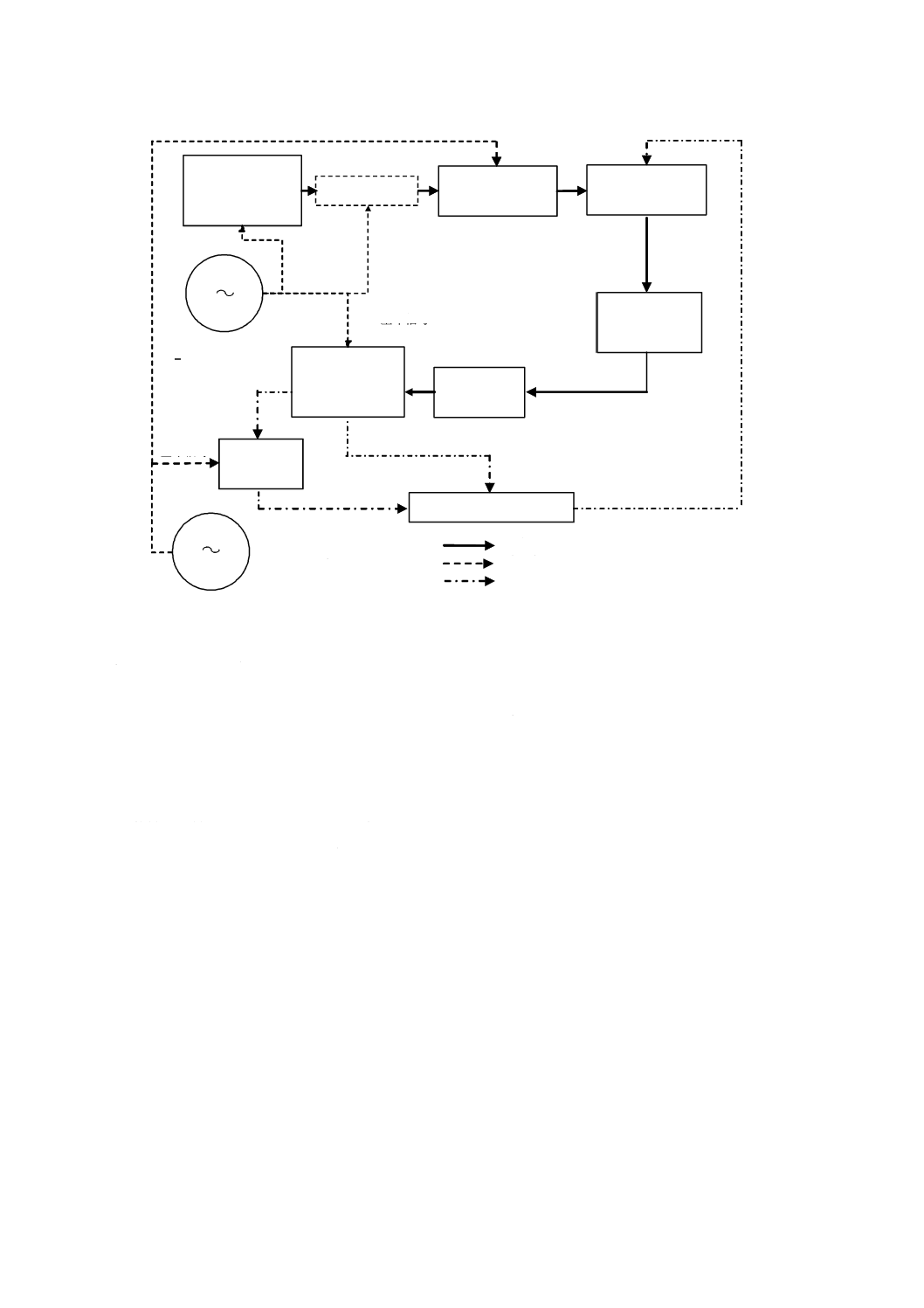
36
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図E.2−偏波変調用の装置配置
E.1.5 光検出器及び位相測定回路
位相測定回路と併せて,測定波長範囲で敏感な光検出器を用いる。増幅器を検出システム感度を上げる
ために用いてもよい。一般的なシステムでは,PINフォトダイオード,FET増幅器,及び,位相検波器又
はベクトル電圧計を含む。
可変光減衰器,光ファイバ増幅器などの光学部品は,受光パワーを制御するために用いる。これらのデ
バイスは光検出器の直前に配置する。これらのデバイスは測定波長範囲にわたり,固有最大DGD,PDL
及び群遅延が最も小さくなるように注意して選ぶ必要がある。
光検出器,増幅器,位相検出を含むシステムは,変調信号の主フーリエ成分にだけ反応しなければなら
ない。また,検出光パワーの範囲にわたって信号位相シフトが一定でなければならない。
位相測定回路及びコンピュータは,各偏光状態で生成される位相を記録するとともに,二つの偏光状態
間の位相差を出力する。
E.1.6 基準信号
位相測定回路に変調信号と同様の基本フーリエ成分をもつ基準信号を与え,それに対する信号光源の位
相差信号を測定する。基準信号は,変調信号に同期していなければならない。
なお,基準信号は,変調信号から生成してもよい。
基準信号の例を次に示す。
− 校正中のように信号光源と光検出器とが同じ場所にある場合,信号生成器と位相測定回路の基準信号
入力部との間に,電気的な結合を用いる。
− 試験標本の前に挿入された,光検出器とともに用いる光スプリッタを,同じ場所に設置した装置に用
いる。光検出器の出力は増幅され,この信号は位相測定回路への基準信号として用いられる。
光源
(例 レーザ)
偏波コントローラ
被測定
リンク
光検出器
位相測定回路
高周波発振器
f = 0.01 GHz -10 GHz
変調信号
ロックイン
アンプ
基準信号
変調器
偏波切換器
コンピュータ
低周波発振器
F = 1 Hz - 1 000 Hz
IEC 015/06
基準信号
光信号
変調信号
制御信号及び出力信号
F=1 Hz〜1 000 Hz
37
C 61280-4-4:2015 (IEC 61280-4-4:2006)
− 入力部の変調器は,電気変調器が位相測定回路と同じ場所に配置されているような別のチャネルによ
って出力端から制御してもよい。
E.2
手順
E.2.1 変調周波数
予想されるDGDmax及びDGDminの値(E.1参照)を考慮して変調周波数を設定する。
E.2.2 波長掃引及びDGDの測定
次に示す手法について,特定の波長におけるDGD値を得る方法がある。光源を要求する波長域で掃引
し,各波長について次の手順でDGD値を測定する。
波長掃引の完了後,リンクのPMD期待値はDGD値の平均として計算する。
E.2.2.1 全掃引手順
直交する入力SOPのいずれの組合せについても,与えられた波長について,位相シフト差がある。この
測定の前提としては,その波長におけるDGD値は,あらゆる組合せの直交する入力SOPの最大位相シフ
トから導かれるものとする。この最大値が生じる組合せのSOPはPSPとして知られている。
一般に,リンクのPSPの方向と,テスト装置のアナライザにおける偏波軸との関係は,最初は未知であ
る。また,リンクのPSPは時間及び波長によって変化する。これらの軸を見つけることに伴う不確定さの
ほかにも,不確定さの主な要因としては装置に含まれるファイバコードにある。SP自体が,上記のように
任意である場合には,PSPの間の正確なDGD値を決定するには幾つかの方法がある。SOP探索法におい
て,不確実性の要因として,入力SOPを真のPSPに調整する際のエラーがある。例えば,5度の調整エラ
ーは0.4 %のDGD値の不確定性を引き起こす場合がある。確実に偏波探索調整エラーを抑制するようにす
る。
望ましい実施の例としては次のような例を挙げることができる。
− 偏波コントローラを“探索及び測定”モードで各試験波長に対し用いる。測定速度を最適化するため
に,様々な探索アルゴリズムが適用できる。与えられた波長において,着目したSOPを掃引するため
に偏波コントローラを用い,各々のSOPの位相シフトを記録する。様々なSOPを含んだ条件下で測
定を行うことで,記録された位相シフトの最大値及び最小値が,リンクのPSPに入力された光に相当
する。現在の波長のDGD値は最大位相シフトと最小位相シフトとの差に比例する(計算については
E.3を参照)。この差は,差分位相シフトと呼ばれる。リンク自体への総入力SOPが二つのPSP又は
基本軸に調整されたかのように,主複屈折はSOPに作用する。最大及び最小の位相が検知されると,
この波長の真のDGD値は,この二つのSOP間の遅延差である。
− 偏波変調の場合には(図E.2),“探索及び測定”法が適用できる。すなわち,偏波コントローラが掃
引されると,差分位相シフトは直接検知される。この方法は,E.3の関係によってDGD値に比例関係
にある最大差分位相シフトを見つける探索作業を単純化する。
測定波長における最大差分位相シフトは式(E.3)のように表すことができる。
()
()
()
λ
φ
λ
φ
λ
φ
i
i
′
∆
−
∆
=
∆
max
max
··················································· (E.3)
ここに,
i: 様々な入力SOPを表す指数
Δφ,Δφʼ: 入力SOPの位相シフト
E.2.2.2 ミューラーセット解析
入力SOPのミューラーセットは,最も簡単には図E.3にあるようなポアンカレ球によって表す。
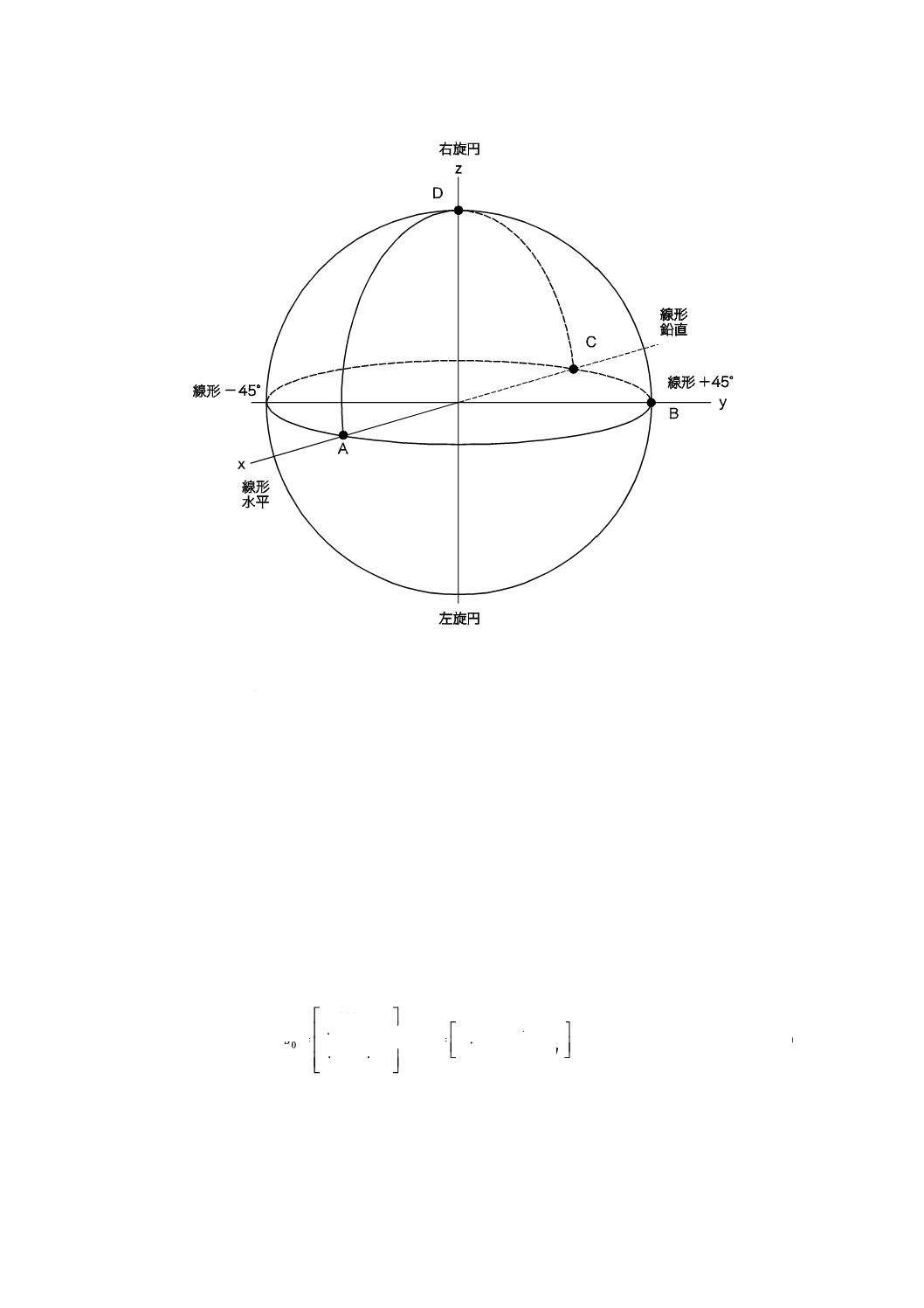
38
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図E.3−ミューラー状態及びポアンカレ球
注記 対応国際規格では,ポアンカレ球上にミューラー行列の基準となる四つの偏光状態をA,B,C
及びDとして示しているが,式(E.4)におけるジョーンズベクトルのパラメータも記載している。
このパラメータを,ポアンカレ球の球座標と誤解する可能性があるため,図E.3の4点のパラ
メータの記載を削除した。
直交するSOPはポアンカレ球上では,180°離れている。図E.3に描かれているように三つのSOPは球
の大円上にあり,相互に90°離れている。“北極点”に関して右手の法則を用いて,大円上の任意の点,A
からはじめると,B,Cは90°を加えたところに位置する。位置Dはその他の点に直行しており,右手の
法則を用いた上方を向いている。式(E.4)は規格化入力ストークスベクトル,s0を表し,ストークスベクト
ルは,“赤道”の大円上にあるミューラーセットの例を規定するのに用いられる。パラメータθは関連した
規格化ジョーンズベクトルj0の線形方位である。パラメータμはベクトルのx成分とy成分との位相差で
ある。
=
μ
θ
μ
θ
θ
sin
2
sin
cos
2
sin
2
cos
0s
,
(
)
(
)
−
=
2/
exp
sin
2/
exp
cos
0
μ
θ
μ
θ
i
i
j
··································· (E.4)
表E.1にミューラーセットの例を示す。
39
C 61280-4-4:2015 (IEC 61280-4-4:2006)
表E.1−ミューラーセットの例
位置
θ
μ
説明
A
0
0
0°の直線偏光(水平)
B
π/4
0
45°直線偏光(45°)
C
π/2
0
90°直線偏光(垂直)
D
π/4
π/2
円偏光(球状)
各々の波長について,偏波コントローラを位置A,B,C及びDの順に回転する。各々の位置について,
位相シフト(ラジアン)を測定して,それぞれΔφA(λ),ΔφB(λ),ΔφC(λ)及びΔφD(λ)と定める。これらの測定
値を用いた計算法はE.3に記載している。
E.2.3 校正
定期的に(例えば,日ごと,週ごと),測定装置を特定の場所にセットして,位相校正用光ファイバ,す
なわち長さ2 mの低PMDシングルモード光ファイバを装置に挿入し,参照信号を確認する。必要な各々
の試験波長について,測定手順を繰り返す。平均差分位相が無視できることが分かった場合,光ファイバ
コード及び光ファイバピッグテールの寄与もまた無視できる。
E.3
計算
E.3.1 DGD計算
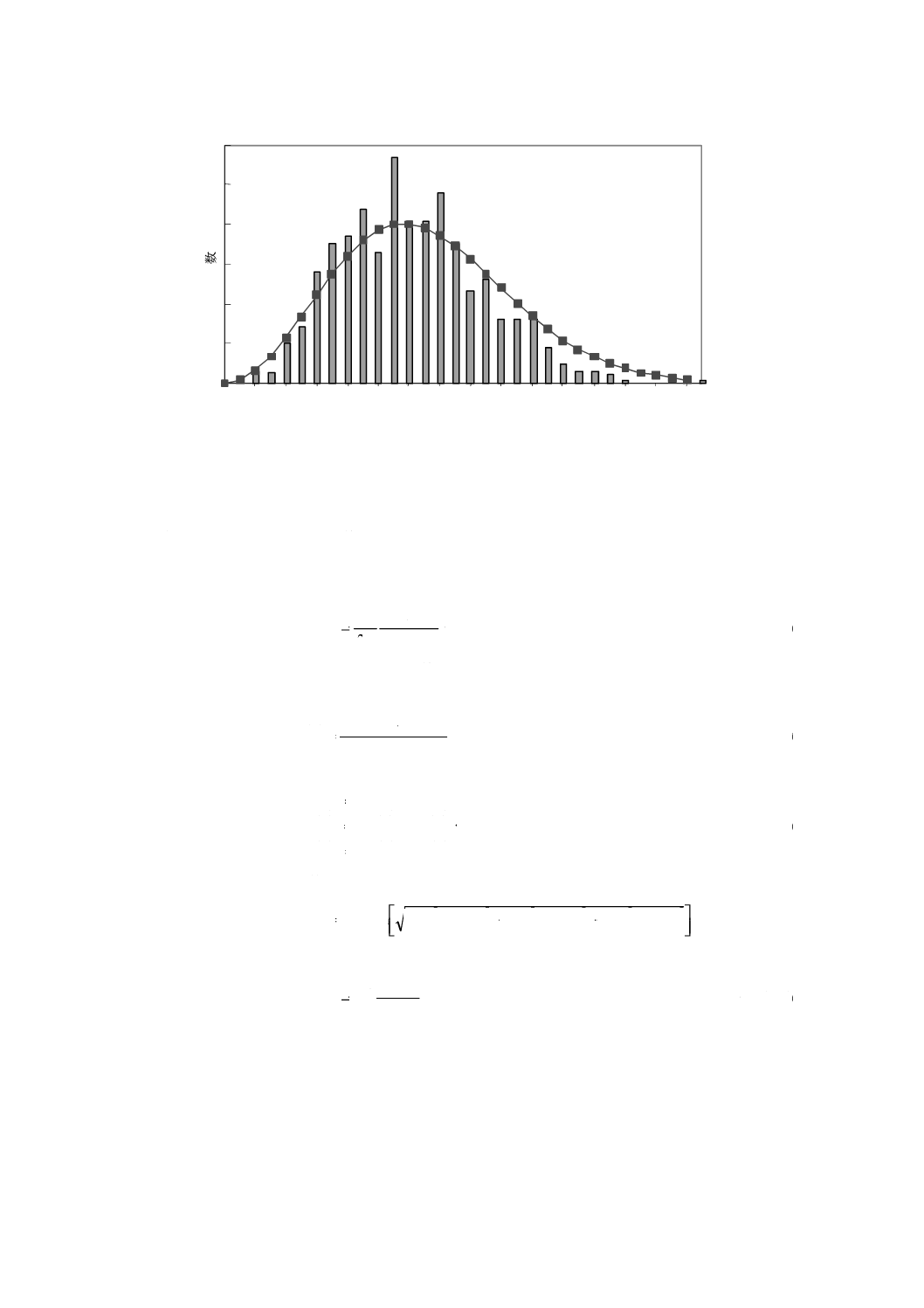
いずれのDGD計算手法も波長に対する一連のDGD値を与えることができる。図E.4にこのような関数
の例を示す。他にも,DGD値は図E.5のようにヒストグラム形式で表してもよい。
図E.4−DGDの波長依存性
0
50
100
150
200
250
300
350
1 520
1 540
1 560
1 580
1 600
1 620
波長 nm
D
G
D
p
s
IEC 017/06
40
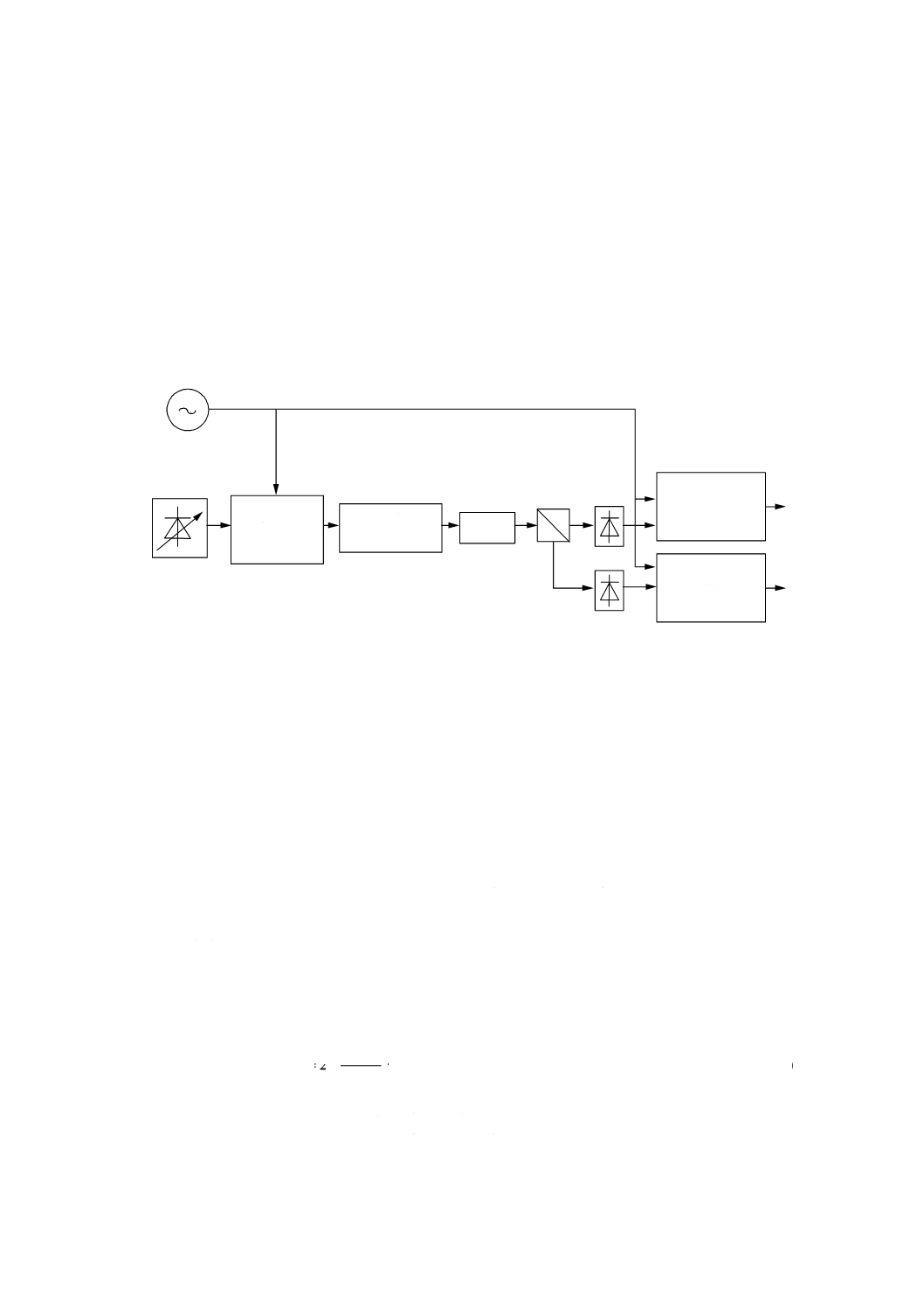
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図E.5−ヒストグラム形式で表したDGD
E.3.1.1 全掃引法を用いたDGD計算
最大位相差分ΔφMax(λ)(rad)(E.2.2.1参照)及び変調周波数f(GHz)から,各波長λ(nm)におけるDGD
値(ps)を次のように計算する。
()
()
f
DGD
λ
φ
λ
Max
3
2
10∆
π
=
···························································· (E.5)
E.3.1.2 ミューラーセット法を用いたDGD計算
E.2.2.2によって,二つのPSPの平均位相φRF(λ)を式(E.6)のように計算する。
()
()
()
2
C
A
RF
λ
φ
λ
φ
λ
φ
∆
+
∆
=
·························································· (E.6)
測定される位相を平均位相で次のように調整する。
()
()
()
()
()
()
()
()
()
λ
φ
λ
φ
λ
φ
λ
φ
λ
φ
λ
φ
λ
φ
λ
φ
λ
φ
RF
D
D
RF,
RF
B
B
RF,
RF
A
A
RF,
−
∆
=
−
∆
=
−
∆
=
·························································· (E.7)
位相差δRF(λ)を次のように計算する。
()
()
[
]
()
[
]
()
[
]
+
+
=
λ
φ
λ
φ
λ
φ
λ
δ
D
RF,
2
B
RF,
2
A
RF,
2
RF
tan
tan
tan
arctan
2
············ (E.8)
δRF(λ)(radian)及び変調周波数f(GHz)を用いて,DGD値(ps)は次のように計算する。
()
()
f
DGD
π
=
2
10
RF
3
λ
δ
λ
······························································· (E.9)
E.3.2 PMD計算
ある波長域におけるPMD期待値(ps)はその波長域でのDGD値の平均である。
0
20
40
60
80
100120140160180200220240260280300
DGD ps
周
波数
IEC 018/06
41
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書F
(規定)
偏波位相シフト法
この附属書は,偏波位相シフト法に特有の要求事項について記載する([5],[6],[7]及び[8]参照)。
F.1
装置
図F.1に,偏波位相シフト法のブロック図を示す。
波長可変
レーザ
S
P
RF 信号源
偏波
分岐器
光強度
変調器
受光器
変調
振幅及び位相
比較器
偏波
コントローラ
DUT
振幅及び位相比較用参照信号
振幅及び位相
比較器
図F.1−方法Fのブロック図
F.1.1
光源
光源として波長可変レーザを用いる。レーザの波長可変範囲は,必要とするPMD測定に十分な範囲で
なければならない。一般的に,完全に自己完結形の温度制御及び電流制御された外部共振器レーザを用い
る。
F.1.2
変調
F.1.2.1
RF信号源
RF信号源は光強度変調器用の変調信号を供給する。変調信号の一部を振幅及び位相比較器へ参照信号と
して送る。RF信号源は,一般的に50 MHz〜3 GHzの周波数範囲で正弦変調信号を供給する必要があるた
め,広帯域特性を必要とする。変調周波数を選択する場合には,変調サイドバンドの不要な干渉及びDGD
測定分解能を考慮しなくてはいけない。
サイドバンドは光信号の両側に,変調周波数に相当する周波数差fで発生する。このことは光スペクト
ル拡散を表す。効果的な波長分解能Δλ(nm)はサイドバンドによって制限され,一般的に式(F.1)で与えら
れる。
c
f
×
×
=
∆
2
2λ
λ
········································································ (F.1)
ここに,
λ: 波長(nm)
f: 変調周波数(GHz)
c: 真空中の光速(m/s)
42
C 61280-4-4:2015 (IEC 61280-4-4:2006)
さらに,DGD測定分解能ΔDGD(ps)も変調周波数fで制限され,一般的に式(F.2)で与えられる。
f
DGD
×
×
∆
=
∆
360
103
φ
···································································· (F.2)
ここに,
Δφ: 位相比較器の位相分解能(degree)
f: 変調周波数(GHz)
RF信号源の周波数安定性を含む全位相精度は,十分な測定精度を確保するために±0.3°以下でなけれ
ばならない。
F.1.2.2
光強度変調器
光強度変調器はRF信号源から変調信号を受けて,波長可変レーザの出力光の強度を変調する。一般的
にLiNbO3変調器を用いる。
F.1.3
偏波制御
DUTに特有のSOPの偏波を供給するために偏波コントローラを用いる。偏波コントローラは,偏光子,
四分の一波長板,及び二分の一波長板の三つのコンポーネントから構成される。二つの位相差板の一式を
回転することで任意のSOPを発生することができる。偏波コントローラは,期待する測定精度を提供する
ために,優れた特性を必要とする。角度調整分解能として±0.1°が要求される。偏光消光比として,一般
的に期待している波長範囲において30 dB以上が要求される。
注記 一般的に四分の一波長板及び二分の一波長板の波長特性が平たんではないことが,この方法の
一つの制約となっている。
F.1.4
出力用光部品
DUTからの出力を,受光器の前に偏波分岐器に結合する。偏波分岐器はDUTからの出力を二つの偏光
された波,すなわち,P偏光及びS偏光に分離する。偏波分岐器はカルサイトプリズムのような非等方結
晶で構成され,一般的に高い偏光消光比並びに非常に低いDGD,群遅延及び偏波依存損失特性をもってい
る。これらの特性が可能となる波長範囲は一般的に非常に広い。
F.1.5
受光器
受光器はDUTからの変調光信号を電気信号に変換する。一般的に,線形性のよいPINフォトダイオー
ドを用いる。PINフォトダイオードは,RF信号源の変調周波数に応用するために,十分なバンドパス特性
をもたなければならない。さらに,高い信号対雑音比を確保するために,広帯域の増幅器を受光器の後段
に用いることが望ましい。
F.1.6
振幅及び位相比較器
振幅及び位相比較器は,RF信号源からの参照変調信号を用いてそれぞれの偏光成分の信号を比較するこ
とによって,振幅及び位相を測定する。群遅延τ(ps)は位相を用いて式(F.3)によって計算される。
f
τ
×
×
=360103
φ
············································································· (F.3)
ここに,
φ: 位相(°)
f: 変調周波数(GHz)
F.1.7
参照信号
RF信号源から出力された変調信号の一部である参照信号は,振幅及び位相比較器へ供給される。参照信
号は変調信号と同期していなければならない。
43
C 61280-4-4:2015 (IEC 61280-4-4:2006)
F.2
手順
F.2.1
変調周波数
測定結果に求められる波長分解能Δλ及びDGD測定分解能ΔDGDに基づいて変調周波数を選択する。
詳細な情報についてはF.1.2.1を参照する。
F.2.2
波長間隔
DGDの計算では,波長間隔における波長差δλを用いるため,DGD値を求めるには二つの波長が必要で
ある。この波長の間隔δλを波長間隔(ステップ幅)と呼ぶ。このδλの決定の手順について説明する。波
長可変レーザの波長をδλ,δλ=(λ+δλ)−λに変更した場合には,DUTからの出力のSOPの偏光角度変化が
45°より小さくする。このδλは通常次のように表す。
max
3
2
4
10
τ
λ
λ
∆
×
×
≤
c
δ
······································································ (F.4)
ここに,
λ: 測定範囲の波長(nm)
c: 真空中の光速(m/s)
Δτmax: DUTの予想される最大のDGD値(ps)
例えば,最大DGD値Δτmaxと波長間隔λとの積は1 550 nmにおいて2 ps·nmより小さい。
F.2.3
波長掃引及びDGD測定
要求される波長範囲において波長ごとの測定を実行するために,波長可変レーザ光源を用い,各波長に
おいてDGD値を計算する。さらに,測定波長範囲において先に得られたDGD値に基づいて平均のDGD
値を計算した後に,DUTのPMD期待値を計算することができる。
この方法は,一対の直交した偏波(0°及び90°の直線偏光)を用いる。0°及び90°の直線偏波をDUT
に入射して,出力を偏光分岐器によって二つの偏波に分岐する。
その後,特定の測定波長において各偏波(P偏光及びS偏光)の振幅及び群遅延を測定する。始めに,0°
直線偏光においてP偏光及びS偏光の振幅(それぞれ,|T11|2mea及び|T21|2mea)及び群遅延(それぞれ,
dφ11/dωmea及びdφ21/dωmea)を測定する。次に,90°直線偏光においてP偏光及びS偏光の振幅(それぞれ,
|T12|2mea及び|T22|2mea)及び群遅延(それぞれ,dφ12/dωmea及びdφ22/dωmea)を測定する。
F.2.4
校正
DUT測定の前に,長さ1 m以下の低PMDのシングルモード光ファイバにおいて校正を行う。最初に,
偏光分岐器のP偏光に一致する0°直線偏光を発生するために四分の一波長板及び二分の一波長板の調整
を行う。次に,偏光分岐器のS偏光に一致する90°直線偏光を発生する。
その後,0°及び90°の直線偏波を交互に入射している間に,特定の測定波長において,偏光分岐器に
よって分岐した二つの偏波(P偏光及びS偏光)に対して振幅及び群遅延特性を測定する。始めに,0°直
線偏波に対してP偏光及びS偏光の振幅(それぞれ,|T11|2cal及び|T21|2cal)及び群遅延(それぞれ,
dφ11/dωcal及びdφ21/dωcal)を測定する。次に,90°直線偏波に対してP偏波及びS偏波の振幅(それぞれ,
|T12|2cal及び|T22|2cal)及び群遅延(それぞれ,dφ12/dωcal及びdφ22/dωcal)を測定する。F.3.1に記載の式
を用いて測定値からDGD値を計算する。
F.3
計算
F.3.1
DGD決定理論
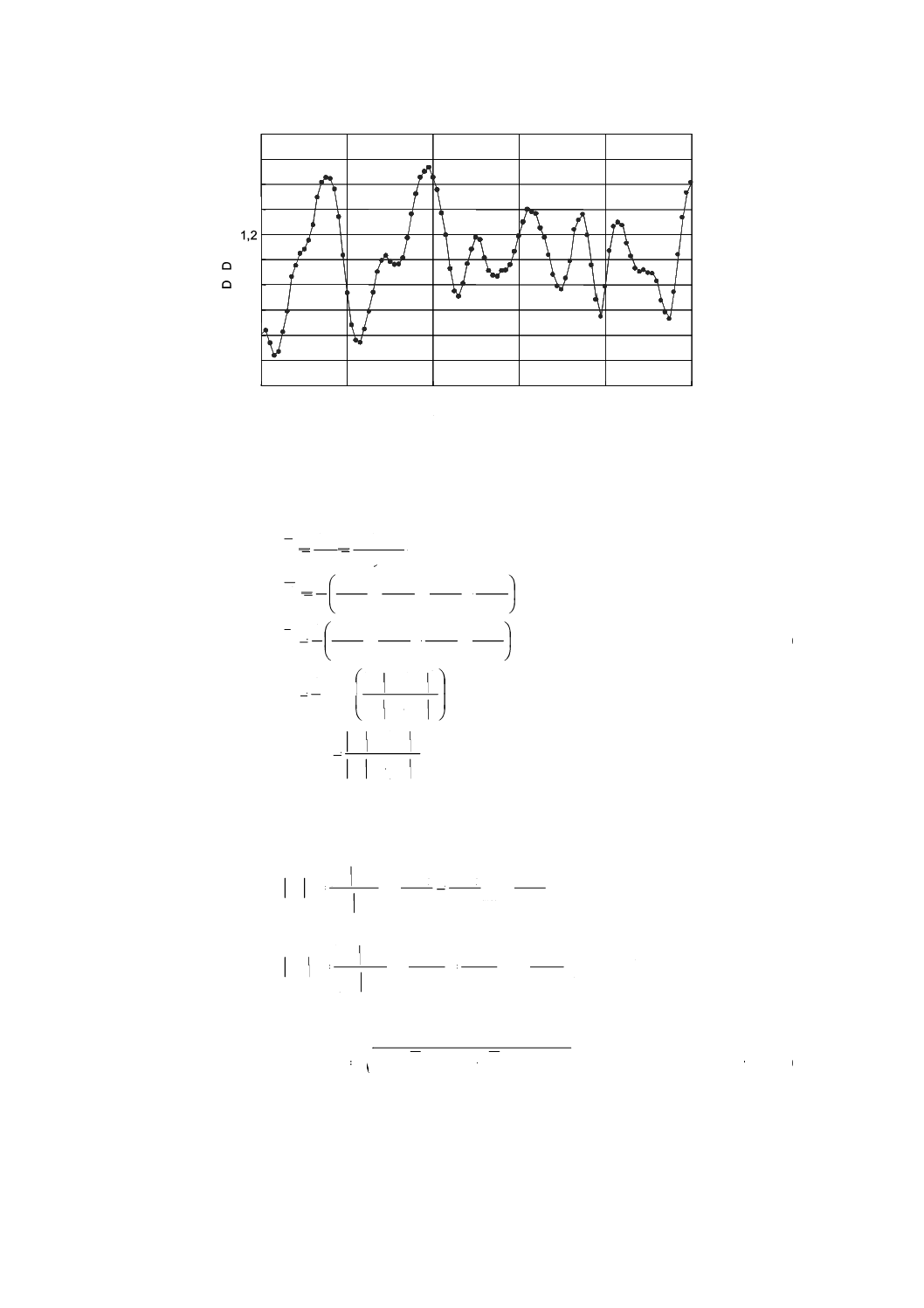
この計算方法を用いることによって,連続するDGDと波長との関係を得ることができる。図F.2は実際
のリンクを模擬した特性例である。
44
C 61280-4-4:2015 (IEC 61280-4-4:2006)
図F.2−ランダムにモード結合した被測定リンクのDGDと波長との関係
式(F.5)のパラメータはF.2.3及びF.2.4における測定値を用いて計算する。
2
21
2
11
2
21
2
11
0
2
21
2
11
2
21
2
11
1
12
21
22
11
1
12
21
22
11
1
f
i
1
cos2
cos
2
1
d
d
d
d
d
d
d
d
4
1
d
d
d
d
d
d
d
d
4
1
π
2
T
T
T
T
Θ
T
T
T
T
Θ
Φ
Φ
Φ
Φ
γ
Φ
Φ
Φ
Φ
δ
c
Θ
Θ
α
+
−
=
+
−
=
−
+
−
=
+
−
−
=
∆
=
∆
∆
=
−
ω
ω
ω
ω
ω
ω
ω
ω
β
λ
λ
λ
ω
············································· (F.5)
ここに, λi及びλf: 波長間隔δλでの最短波長及び最長波長
ΔΘ: λiにおけるΘとλfにおけるΘとの差分
Δτmax: DUTの予想される最大のDGD値(ps)
cal
2
11
mea
2
2
T
T
T
kl
kl
=
cal
11
mea
d
d
d
d
d
d
ω
ω
ω
Φ
Φ
Φ
kl
kl
−
=
kl=11 and 12
cal
2
22
mea
2
2
T
T
T
mn
mn
=
cal
22
mea
d
d
d
d
d
d
ω
ω
ω
Φ
Φ
Φ
mn
mn
−
=
mn=21 and 22
各波長におけるDGD値をα1,β1,γ1及びΘ0を用い,式(F.6)によって計算する。
0
1
1
2
1
2
1
2
1
2
cos
2
2
)
(
Θ
DGD
γ
β
γ
β
α
λ
+
+
+
=
··································· (F.6)
F.3.2
DGDの決定
この測定方法に関するDGDの計算ついて述べる。光伝達関数行列は式(F.7)のように表せる。
1 550
1 570
1 590
1 610
0,4
0,8
1,6
D
G
D
p
s 1,2
波長 nm
IEC 020/06
45
C 61280-4-4:2015 (IEC 61280-4-4:2006)
(
)
jΦ
j
j
Θ
j
j
Θ
j
j
Θ
j
j
Θ
jΦ
T
jΦ
T
jΦ
T
jΦ
T
T
−
×
+
+
−
+
+
−
−
−
−
=
−
−
−
−
=
exp
)
exp(
cos
)
exp(
sin
)
exp(
sin
)
exp(
cos
)
exp(
)
exp(
)
exp(
)
exp(
)
(
22
22
21
21
12
12
11
11
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ω
·········· (F.7)
ここに, λi及びλf: 波長間隔δλでの最短波長及び最長波長
ΔΘ: λiにおけるΘとλfにおけるΘとの差分
Δτmax: DUTの予想される最大のDGD値(ps)
Θは偏光角度,φはT11とT21との位相差,ψはT11とT12との位相差,Φは偏波無依存位相シフトである。
出力偏光ベクトル,Eout(ω)はT(ω)を用いて式(F.8)で表せる。
)
(
)
(
)
(
in
out
ω
ω
ω
E
T
E
=
································································ (F.8)
ここに,
Ein(ω): 光入力信号のフーリエ変換
Eout(ω)は光中心周波数ω0におけるテイラー展開によって式(F.9)で表せる。
2
2
out
2
out
0
out
out
0
0
d
d
!2
1
d
d
)
(
)
(
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
δ
E
δ
E
E
E
=
=
+
+
=
·························· (F.9)
ここに,
δω: ω−ω0
伝達関数微分演算子と呼ばれる一次PMD演算子D(ω)は式(F.10)で表せる。
1
)
(
d
)
(
d
)
(
−
=
ω
ω
ω
ω
T
T
D
······························································ (F.10)
したがって,式(F.10)を式(F.9)に代入することで式(F.11)を得る。
)
(
d
d
2
1
exp
)
(
d
d
2
1
2
1
1
)
(
0
out
2
0
out
2
2
2
out
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
E
δ
D
δ
D
E
δ
D
δ
D
δ
D
E
+
≅
+
+
+
=
·························· (F.11)
ここで,高次の項は無視できる。D(ω)は一次のPMD演算子であり,dD(ω)/dωは二次のPMD演算子で
ある。それらは互いに可換ではない。
D(ω)を単一演算子Xを用いて対角化することによって,式(F.12)を得る。
)
(
)
exp(
0
0
)
exp(
)
(
)
exp(
)
(
0
out
1
0
out
1
1
out
1
ω
ω
ω
ω
ω
ω
E
X
δ
jΓ
δ
jΓ
E
XX
Dδ
X
E
X
−
−
+
−
−
−
−
−
=
=
····················· (F.12)
ここに,
−jΓ+/−: D(ω)の固有値
Γ+及びΓ−: それぞれ,最大群遅延及び最小群遅延。すなわち,D(ω)
の固有値の虚数部の間の差,Γ+−Γ−がDGD
式(F.7)で記載した四つの独立したパラメータΘ,φ,ψ及びΦは,テイラー展開を用いて式(F.13)で表せ
る。
2
2
1
0
2
2
1
0
2
2
1
0
2
2
1
0
2
1
2
1
2
1
2
1
ω
β
ω
β
ω
γ
ω
γ
ψ
ψ
ω
β
ω
β
φ
φ
ω
α
ω
α
δ
δ
Φ
Φ
δ
δ
δ
δ
δ
δ
Θ
Θ
+
+
=
+
+
=
+
+
=
+
+
=
·························································· (F.13)
46
C 61280-4-4:2015 (IEC 61280-4-4:2006)
ここに,
δω: ω−ω0
Θ0,φ0,ψ0及びΦ0: ω−ω0におけるΘ,φ,ψ及びΦの値
α1,β1,γ1及びβ1: Θ,φ,ψ及びΦのテイラー展開の一次係数
α2,β2,γ2及びβ2: Θ,φ,ψ及びΦのテイラー展開の二次係数
一次のPMD演算子D(ω)は式(F.13)を用いて式(F.14)で表せる。
−
−
+
+
+
−
+
−
−
=
+
−
Θ
Θ
j
Θ
j
Θ
j
j
D
j
j
2
cos
e)
2
sin
(
e)
2
sin
(
2
cos
1
00
1
)
(
1
1
2
1
1
2
1
1
1
1
1
γ
β
γ
α
γ
α
γ
β
β
ω
φ
φ
(F.14)
したがって,D(ω)の固有値は式(F.15)となる。
Θ
j
j
jΓ
2
cos
2
1
1
2
1
2
1
2
1
1
γ
β
γ
β
α
β
+
+
+
±
−
=
±
································· (F.15)
ここに,
β1: 偏波無依存群遅延
DGD値Δτは,式(F.16)のように二つの固有値の虚数部の間の差で表せる。
Θ
Γ
Γ
2
cos
2
2
1
1
2
1
2
1
2
1
γ
β
γ
β
α
τ
+
+
+
=
−
=
∆
−
+
····························· (F.16)
F.3.3
PMD計算
測定波長範囲内のPMD期待値は,測定波長範囲全体におけるDGD平均値(PMDAVG)によって得られ
る。
47
C 61280-4-4:2015 (IEC 61280-4-4:2006)
附属書G
(参考)
方法CによるPMDの決定
この附属書は,方法Cを用いて測定される干渉データのRMS幅を決定するアルゴリズムを提供する。
このような干渉の例を附属書Cに示す。このアルゴリズムの主な目的はノイズの影響を除去することにあ
る。
G.1
慣例的解析
次のアルゴリズムは,附属書Cに示されている仮定を前提として,方法CのうちTINTYにだけ適用可
能である。
I~jは位置tj(ps)をj=1からNまで増加したときの干渉波形の測定強度とする。
− 手順1:零強度
0
~I及びノイズ振幅Naの計算
定義:Ns=round(5N/100)はNの約5 %となる整数である。
(
)
s
1
0
2
~
~
~
s
s
N
I
I
I
N
j
j
N
j
∑
=
−
+
=
·································································· (G.1)
(
)
s
1
2
2
2
2
~
~
s
s
N
I
I
X
N
j
j
N
j
∑
=
−
+
=
································································· (G.2)
(
)
2
0
2
~I
X
Na
−
=
····································································· (G.3)
− 手順2:シフト強度Ijの定義
0
~
~
I
I
I
j
j
−
=
(
)
Na
I
Ij
4
~
~
0>
−
の場合 ··········································· (G.4)
0
=
jI
(
)
Na
I
Ij
4
~
~
0≦
−
の場合 ················································ (G.5)
− 手順3:干渉波形の中心Cの計算
∑
∑
=
=
=
s
s
1
1
N
j
j
N
j
j
j
I
I
t
C
··········································································· (G.6)
− 手順4:自己相関ピークの除去
定義:
jl:C ‒ tj > tcとなる最大指標j ···················································· (G.7)
jr:tj ‒ C > tcとなる最小指標j ···················································· (G.8)
ここに,
tc: 光源のコヒーレンス時間
注記 相互相関の干渉波形については,式(G.9)を適用している。
jr = jl + 1 ················································································ (G.9)
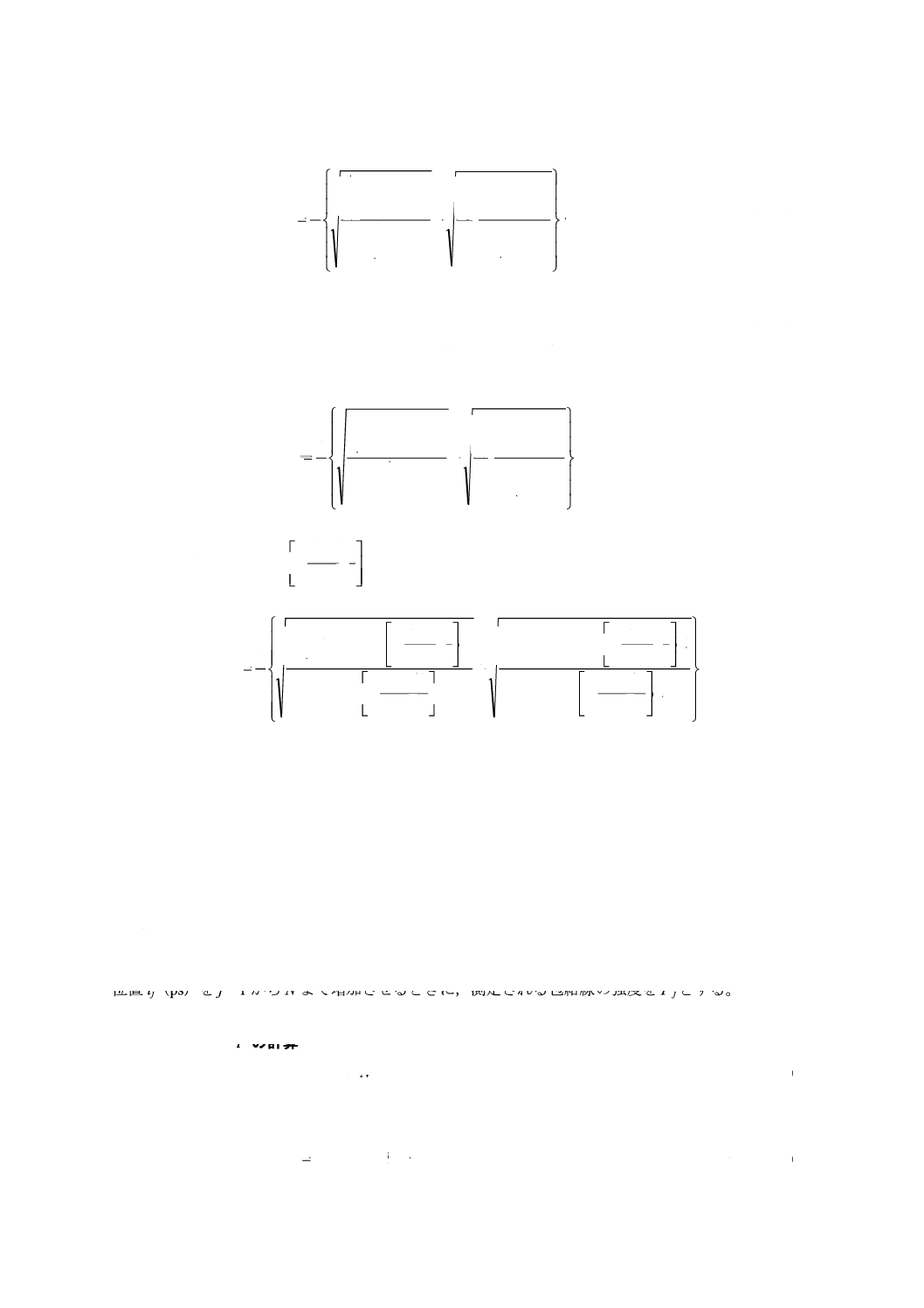
48
C 61280-4-4:2015 (IEC 61280-4-4:2006)
− 手順5:干渉波形の二次モーメントSの計算
−
+
−
=
Σ
Σ
Σ
Σ
=
=
=
=
j
N
j
j
j
j
N
j
j
j
j
j
j
j
j
j
I
I
C
t
I
I
C
t
S
r
r
l
l
2
1
2
1
)
(
)
(
2
1
···································· (G.10)
− 手順6:干渉波形の切捨て
jminをC ‒ tj >2Sとなる最大指標jに設定····································· (G.11)
jmaxをtj ‒ C >2Sとなる最小指標jに設定 ···································· (G.12)
− 手順7:干渉波形の二次モーメントの平方根
ε
σの計算
−
+
−
=
Σ
Σ
Σ
Σ
=
=
=
=
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
ε
I
I
C
t
I
I
C
t
max
r
max
r
l
l
min
2
1
2
)
(
)
(
2
1
σ
································· (G.13)
− 手順8:ガウス関数
(
)
−
−
2
2
2
exp
ε
C
t
σ
のσεの計算
(
)
(
)
(
)
(
)
(
)
(
)
−
−
−
−
−
+
−
−
−
−
−
=
∫
∫
∫
∫
t
C
t
t
C
t
C
t
t
C
t
t
C
t
C
t
j
j
j
j
j
j
j
j
t
t
ε
t
t
ε
t
t
ε
t
t
ε
d
2
exp
d
2
exp
d
2
exp
d
2
exp
2
1
max
max
r
1
min
1
min
2
2
2
2
2
2
2
2
2
2
r
σ
σ
σ
σ
σε
········· (G.14)
ε
σは式(G.14)から反復計算される。
G.2
一般的解析
次のアルゴリズムは,方法CのうちGINTYを用いて,合成二乗相互相関又は自己相関包絡線について,
信頼性の高いRMS幅を与える。
これは反復アルゴリズムである。ある反復において,全データ列は二つの組に分けられ,信号を含む中
心部の組M,及びノイズを含むテール部の組Tからなる。反復結果のたびに,これらの組は再度定義され
る。計算されたRMS幅が変化しなくなるか,組の定義が変化しなくなるところで,収束した結果を得る。
一度の反復について,各々の組のデータ点数を,NM及びNTとする。
位置tj(ps)をj=1からNまで増加させるときに,測定される包絡線の強度をI~jとする。
組Tの初期定義は,全データ列の最初及び最後の5 %とする。
− 手順1:零強度
0
~Iの計算
∑
∈
=
T
j
T
jN
I
I
/
~
~
0
······································································ (G.15)
− 手順2:シフトされた強度Ijの定義
0
~
~
I
I
I
j
j
−
=
all N ···································································· (G.16)
49
C 61280-4-4:2015 (IEC 61280-4-4:2006)
− 手順3:干渉波形の中心Cの計算
∑
∑
∈
∈
=
M
j
j
M
j
j
j
I
I
t
C
·········································································· (G.17)
− 手順4:二乗包絡線のRMS幅σの計算
(
)
∑
∑
∈
∈
−
=
M
j
j
M
j
j
j
I
I
C
t
2
2
σ
································································ (G.18)
− 手順5:組の再定義
MをC−4σ≦tj≦C+4σを満たす点の組とする。
Tを残りのデータ点の組とする。
− 手順6:結果が収束するまで手順1〜手順5の繰返し
50
C 61280-4-4:2015 (IEC 61280-4-4:2006)
参考文献
[1] WILLIAMS, PA. Modulation phase-shift measurement of PMD using only four launched polarization states: a
new algorithm. Electronics Letters Online No. 19991068, July, 1999.
[2] JONES, RC. A new calculus for the treatment of optical systems. VI. Experimental determination of the matrix.
J. Optical Soc. Am., 1947, 37, pp. 110-112.
[3] GISIN, N., GISIN, B., VON DER WEID, J.P. and PASSY, R. How accurately can one measure a statistical
quantity like polarization-mode dispersion. Photonics Technology Letters, Dec 1996, Vol. 8, No. 12.
[4] CYR, N., SCHINN, G.W. and GIRARD, A. Stokes parameter analysis method, the consolidated test method for
PMD measurements. The National Fiber Optic Engineers Conference (NFOEC), ʼ99 Session A6, Polarization
effects in systems, Sept. 26-30, 1999.
[5] SANO, K., KUDOU, T. and OZEKI, T. Simultaneous Measurement of Group Delay Time Dispersion and
Polarization Mode Dispersion. ECOC ʼ96, TuP-09, pp.253-256.
[6] SANO, K., KUDOU, T. and OZEKI, T. A New Measurement Method of Polarization Mode Dispersion.
OECC ʼ96, Oslo.
[7] OZEKI, T. Mathematical Analysis on Definition, and Statistics of Polarization Mode Dispersion. SB-8-1, IEICE
Spring Conference in Hiroshima 2000.
[8] YAMASHITA, T.and IMAMURA, M. Simultaneous and High Resolution Measurement of Polarization Mode
Dispersion, Group Delay, Chromatic Dispersion and Amplitude for Ultra-High Speed Optical Components.
NFOECʼ01, vol.3, pp.1348-1352, 2001.
[9] GISIN, N., VON DER WEID, J.P. and PELLAUX, J.P. Polarization mode-dispersion of short and long
single-mode fibers. J. Lightwave Technol., 1991, Vol. 9, 821-827.
[10] GISIN, N., PASSY, R. and VON DER WEID, J.P. Definitions and measurements of polarization mode
dispersion: Interferometric versus fixed anaylser methods. Photon. Technol. Let.., Vol. 6, 730-732, 1994.
[11] GISIN, N. Solutions of the dynamical equation for polarization dispersion. Opt. Commun., 1991,Vol. 86,
371-373.
[12] CYR, N. Polarization-mode dispersion measurement: generalization of the interferometric method to any
coupling regime. J. Lightwave Technol., March 2004, Vol. 22, No. 3, 794- 805.
JIS C 6122-11-1 光増幅器−測定方法−第11-1部:偏波モード分散パラメータ−ジョーンズマトリクス固
有値解析(JME)法
注記 対応国際規格:IEC 61290-11-1,Optical amplifiers−Test methods−Part 11-1: Polarization mode
dispersion parameter−Jones matrix eigenanalysis (JME)
JIS C 6842 光ファイバ偏波モード分散試験方法
注記 対応国際規格:IEC 60793-1-48,Optical fibres−Part 1-48: Measurement methods and test
procedures−Polarization mode dispersion
JIS C 61300-3-32 光ファイバ接続デバイス及び光受動部品−基本試験及び測定手順−第3-32部:光受動
部品の偏波モード分散測定
注記 対応国際規格:IEC 61300-3-32,Fibre optic interconnecting devices and passive components−Basic
51
C 61280-4-4:2015 (IEC 61280-4-4:2006)
test and measurement procedures−Part 3-32: Examinations and measurements−Polarization mode
dispersion measurement for passive optical components
IEC/TR 61282-3,Fibre optic communication system design guides−Part 3: Calculation of link polarization mode
dispersion
IEC 61290-11-2,Optical amplifiers−Test methods−Part 11-2: Polarization mode dispersion parameter−Poincaré
sphere analysis method (PSA)



















