C 61280-2-8:2010 (IEC 61280-2-8:2003)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 用語及び定義並びに略語 ···································································································· 1
2.1 用語及び定義 ················································································································ 1
2.2 略語 ···························································································································· 1
3 低ビット誤り率の測定 ······································································································· 2
3.1 一般的な考察 ················································································································ 2
3.2 Q値の背景 ··················································································································· 3
4 可変識別しきい値法 ·········································································································· 5
4.1 概要 ···························································································································· 5
4.2 試験装置 ······················································································································ 8
4.3 被測定物 ······················································································································ 8
4.4 試験手順 ······················································································································ 8
4.5 計算及び結果の解釈 ······································································································ 10
4.6 測定の記録 ·················································································································· 13
4.7 具体的な情報 ··············································································································· 14
5 可変光しきい値法 ············································································································ 14
5.1 概要 ··························································································································· 14
5.2 試験装置 ····················································································································· 14
5.3 被測定物 ····················································································································· 15
5.4 基本的な光ファイバリンクの試験手順··············································································· 15
5.5 自己完結型システムの試験手順 ······················································································· 15
5.6 結果の評価 ·················································································································· 16
附属書A(規定)Q値における最大誤差の計算 ········································································· 18
附属書B(参考)正弦波干渉法 ······························································································ 20
C 61280-2-8:2010 (IEC 61280-2-8:2003)
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人光産業技術振興協会(OITDA)及
び財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,
日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
また,令和2年6月22日,産業標準化法第17条又は第18条の規定に基づく確認公示に際し,産業標準
化法の用語に合わせ,規格中“日本工業規格”を“日本産業規格”に改めた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権及び出願公開後の実用新案登録出願にかかわる確認について,責
任はもたない。
JIS C 61280の規格群には,次に示す部編成がある。
JIS C 61280-1-3 中心波長及びスペクトル幅測定
JIS C 61280-2-1 受信感度及びオーバロード測定
JIS C 61280-2-2 光アイパターン,光波形及び消光比測定
JIS C 61280-2-8 Q値測定を用いた低ビット誤り率の決定法
JIS C 61280-2-9 高密度波長分割多重システムの光信号対雑音比測定
JIS C 61280-2-11 光信号品質評価のための強度ヒストグラム評価を用いた平均化Q値測定
日本産業規格
JIS
C 61280-2-8:2010
(IEC 61280-2-8:2003)
光ファイバ通信サブシステム試験方法−
Q値測定を用いた低ビット誤り率の決定法
Fiber optic communication subsystem test procedures-
Determination of low BER using Q-factor measurements
序文
この規格は,2003年に第1版として発行されたIEC 61280-2-8を基に,技術的内容及び対応国際規格の
構成を変更することなく作成した日本産業規格である。
1
適用範囲
この規格は,低ビット誤り率の決定のために加速して測定する,可変識別しきい値法(箇条4参照)及
び可変光しきい値法(箇条5参照)について規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 61280-2-8:2003,Fibre optic communication subsystem test procedures−Digital systems−Part
2-8: Determination of low BER using Q-factor measurements(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
用語及び定義並びに略語
2.1
用語及び定義
この規格で用いる主な用語及び定義は,次による。
2.1.1
ビット誤り率,BER(bit error rate)
誤りビット数の総ビット数に対する比。
2.1.2
符号間干渉,ISI(intersymbol interference)
データストリームにおける符号間の相互干渉。通常,伝送経路の非線形の効果と帯域幅制限とで引き起
こされる。
2.1.3
Q値(Q-factor)
1レベルの平均電圧と0レベルの平均電圧との差のそれらの標準偏差の和に対する比。
2.2
略語
ASE 増幅された自然放出光
(amplified spontaneous emission)
CW 連続波
(continuous wave)
2
C 61280-2-8:2010 (IEC 61280-2-8:2003)
DC 直流電流
(direct current)
DSO デジタルサンプリングオシロスコープ
(digital sampling oscilloscope)
DUT 被測定物
(device under test)
PRBS 擬似ランダムビットパターン
(pseudo random bit sequence)
3
低ビット誤り率の測定
3.1
一般的な考察
光ファイバ通信システム及びサブシステムは,非常に高いビットレートにおいても非常に高い誤り性能
を提供できる。システムの性質によるが,平均ビット誤り率は,通常,10−12〜10−20となる。この種の性
能はデジタル信号に対する実用的な性能要求より高く,それによって誤り訂正技術を使わずに多くのリン
クを長距離にわたって接続できる。
そのような低ビット誤り率の測定には,統計的に有意な結果を得るために十分多くの誤りを測定しなけ
ればならず,時間を要するという問題がある。15個の誤りの測定に必要な平均時間を,表1に示す。この
誤りの数は50 %のばらつき及び75 %の信頼度で,統計的に有意であるとみなせる。
表1−ビットレート及びビット誤り率と15個の誤りを累積するための平均時間との関係
ビットレート
(Bit/s)
BER
10−6
10−7
10−8
10−9
10−10
10−11
10−12
10−13
10−14
10−15
1.0 M
1.5 s
15 s
2.5 min
25 min
4.2 h
1.7 d
17 d
170 d
4.7年
47年
2.0 M
750 ms
7.5 s
75 s
750 s
2.1 h
21 h
8.8 d
88 d
2.4年
24年
10 M
150 ms
1.5 s
15 s
2.5 min
25 min
4.2 h
1.7 d
17 d
170 d
4.7年
50 M
30 ms
300 ms
3.0 s
30 s
5.0 min
50 min
8.3 h
3.5 d
35 d
350 d
100 M
15 ms
150 ms
1.5 s
15 s
2.5 min
25 min
4.2 h
1.7 d
17 d
170 d
500 M
3 ms
30 ms
300 ms
3.0 s
30 s
5.0 min
50 min
8.3 h
3.5 d
35 d
1.0 G
1.5 ms
15 ms
150 ms
1.5 s
15 s
2.5 min
25 min
4.2 h
1.7 d
17 d
10 G
150 μs
1.5 ms
15 ms
150 ms
1.5 s
15 s
2.5 min
25 min
4.2 h
1.7 d
40 G
38 μs
380 μs
3.8 ms
38 ms
380 ms
3.8 s
38 s
6.3 min
63 min
10.4 h
100 G
15 μs
150 μs
1.5 ms
15 ms
150 ms
1.5 s
15 s
2.5 min
25 min
4.2 h
注記 網掛け部は,測定時間が非現実的に長い領域を示す。
表1に示す時間は,ビットレートの低い場合,設置又は保守作業の間に光ファイバ通信システムで予想
されるビット誤り率を測定することは現実的でないことを示す。この課題を克服する一つの方法は,受信
器において制御された方法で人工的に信号対雑音比を損ない,ビット誤り率を増加させることである。こ
れによって,測定時間を減少できる。この方法では,誤り性能を様々な劣化のレベルに対して測定する。
次に,結果を劣化のないレベルまで外挿する。このとき,理論的又は実証的な回帰アルゴリズムに基づき,
計算又は図表による方法を用いる。
誤り性能の決定のためのいかなる回帰技法を使用しても,理論上のビット誤り率が補誤差関数(erfc)
を介して劣化のレベルに関連するという課題がある。これは,非常に小さい劣化の変化が非常に大きいビ
ット誤り率の変化となることである。例えば,10−15のビット誤り率では,劣化のレベルにおいておよそ1
dBの変化が,ビット誤り率において3けたの変化をもたらす。さらに,外挿に基づく方法では,測定され
た最も低いビット誤り率よりも約3けた下方の値を正しく見積もることができないという課題もある。ま
た,デジタル再生部の場合,得られる結果は,試験する受信器を含む再生部にだけ適用することに注意し
3
C 61280-2-8:2010 (IEC 61280-2-8:2003)
なければならない。上流の再生部で生成された誤りによってエラーフロアを生じ得るが,このことを試験
対象の再生部の誤り性能評価において考慮しなければならない。
低ビット誤り率の決定のために加速して測定を行う,可変識別しきい値法(箇条4参照)及び可変光し
きい値法(箇条5参照)について示す。また,参考として,もう一つの方法である正弦波干渉法について
附属書Bに示す。
これらの方法は,振幅ベースの劣化に関する誤り性能の決定に適用する。ジッタもシステムの誤り性能
に影響することがあるが,その検証は他の方法による。誤り性能においてジッタによる劣化が支配的な場
合,通常,この規格で示す振幅ベースの方法は,実測値より低いビット誤り率となる。
可変識別しきい値法は,光学系の未知又は予測できない雑音統計量に対し最も正確にQ値及びビット誤
り率を測定できる方法である。ただし,可変識別しきい値法を使用してQ値及びビット誤り率を測定する
には,識別しきい値を操作するために受信器を電気的に操作する手段が必要である。そのような操作がで
きないシステムでは,代替の可変光しきい値法を利用するのがよい。測定及び計算の点で両方の方法は,
自動化することができる。
3.2
Q値の背景
Q値は識別回路での信号対雑音比(SNR)であり,通常,式(1)で表す[3]。
0
1
0
1σ
σ
μ
μ
Q
+
−
=
·············································································· (1)
ここに,
Q: Q値
μ1: 1レベルの平均電圧(V)
μ0: 0レベルの平均電圧(V)
σ1: 1レベルの雑音の標準偏差(V)
σ0: 0レベルの雑音の標準偏差(V)
正確なシステムの伝送性能又はQ値の評価には,原理的な劣化要因及び現実的な不完全性による劣化要
因を考慮しなければならない。二つの重要な要因とは,増幅された自然放出光(ASE)雑音及び符号間干
渉(ISI)である。付加的な雑音は主として光増幅器のASEによって生じる。ISIは,波長分散,光ファイ
バ非線形,マルチパスの干渉,偏波モード分散,電気的な帯域制限の使用などのように,多くの要因によ
って起こる。また,他の要因が存在する可能性がある。例えば,不十分なインピーダンス整合は波形のリ
ンギング及び/又は長い下降時間(慣用的には,“立ち下がり時間”ともいう。)などの劣化を引き起こす
場合もある。
Q値を測定する方法の一つに,電圧ヒストグラム法がある。デジタルサンプリングオシロスコープで波
形のQ値を測定するために2値のアイパターンの時間軸の中心で電圧ヒストグラムを測定する[4]。この方
法では,パターン発生器を信号源として使用し,オシロスコープを受信アイパターンの開口と電圧レベル
の雑音標準偏差とを測定するのに使用する。目安としては,オシロスコープ上に見られる雑音分布の端の
ポイントが,ガウス分布における標準偏差の3倍のポイントに相当する。オシロスコープを使用してアイ
パターンを測定する利点は,実際の伝送路において最小設備で即座に測定ができることである。
オシロスコープを使用するQ値の測定法には,幾つかの短所がある。高速データ(数Gbit/sのオーダ)
のアイパターンの測定に使用すると,オシロスコープのデジタルサンプリング限界(通常数百kHzのオー
ダ)によって,高速データストリームのわずかな部分だけしかQ値測定に使用できない。ただし,観測時
間を長くすることによって,遅いサンプリングの影響を減らすことができる。より基本的な短所は,アイ
パターンの中心の電圧ヒストグラムから得られたQ値の見積りがしばしば不正確なことである。様々なパ
ターン効果とオシロスコープの電気フロントエンドからとの雑音付加はしばしば本当の雑音分散をあいま
4
C 61280-2-8:2010 (IEC 61280-2-8:2003)
いにすることがある。
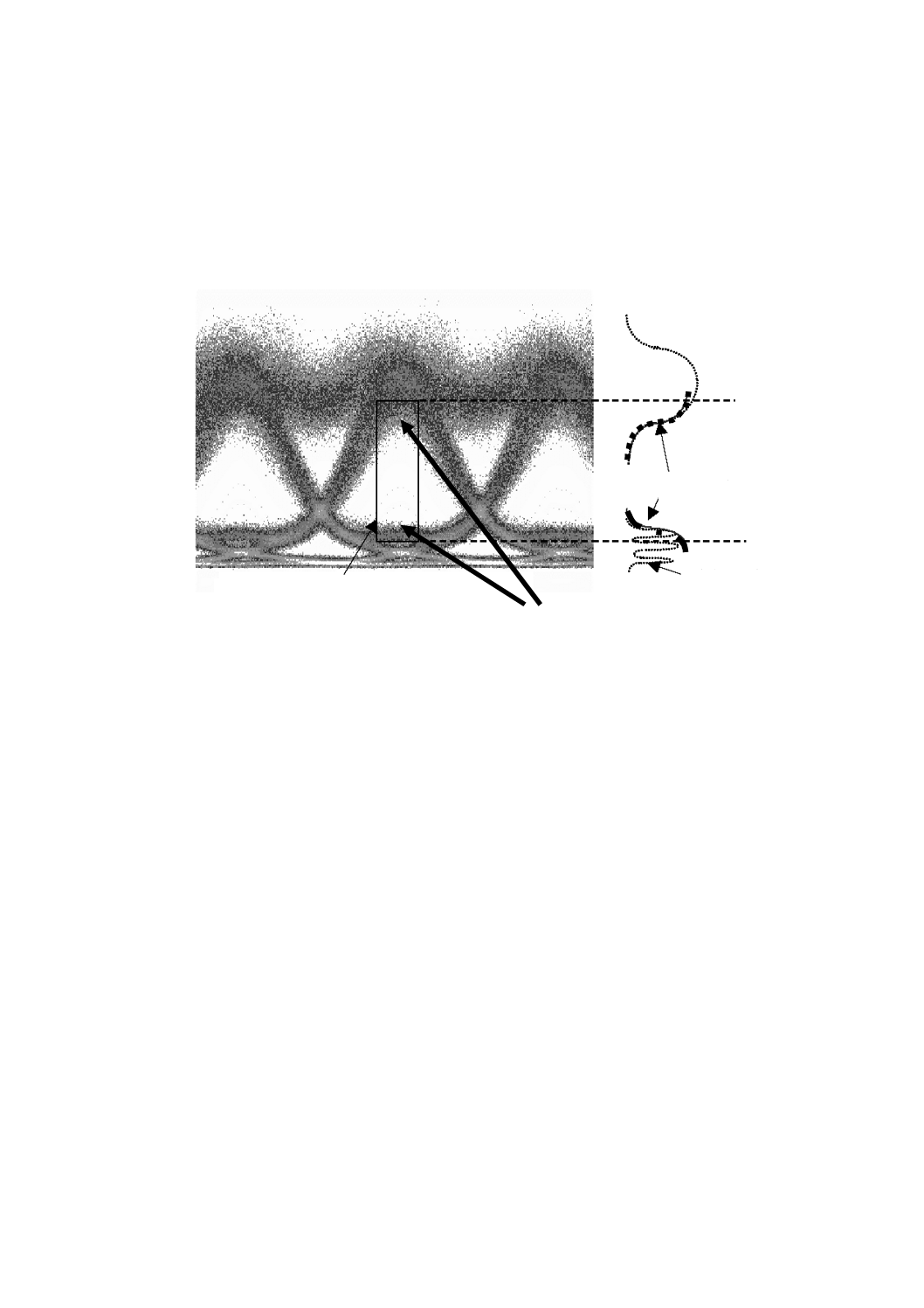
動作中システムでのアイパターンの例を,図1に示す。図1では,アイパターンの中心を通る垂直なヒ
ストグラムでパターン効果を見ることができる(オシロスコープの電気フロントエンドで加わった雑音に
よって,不鮮明になっている。)。このように測定したQ値と試験装置で測定した実際のビット誤り率との
関係を予測することは難しい。
ガウス分布のすそからQ値測定のためのデータを取得する。
図1−パターン効果が見られるアイパターンの例
オシロスコープを使ってQ値を測定する別の方法を,図2に示す。この方法では,アイパターンの開口
を見積もるのにアイパターンの中心を使い,雑音を見積もるのにアイパターンとアイパターンとの間を用
いる。これによってパターン効果のヒストグラムへの影響を小さくする。この方法の欠点は,受信器が実
際には使用しないアイパターンの一部分の測定に依存することである。
識別回路はこの範囲で動作する。
実際の分布
ガウス近似
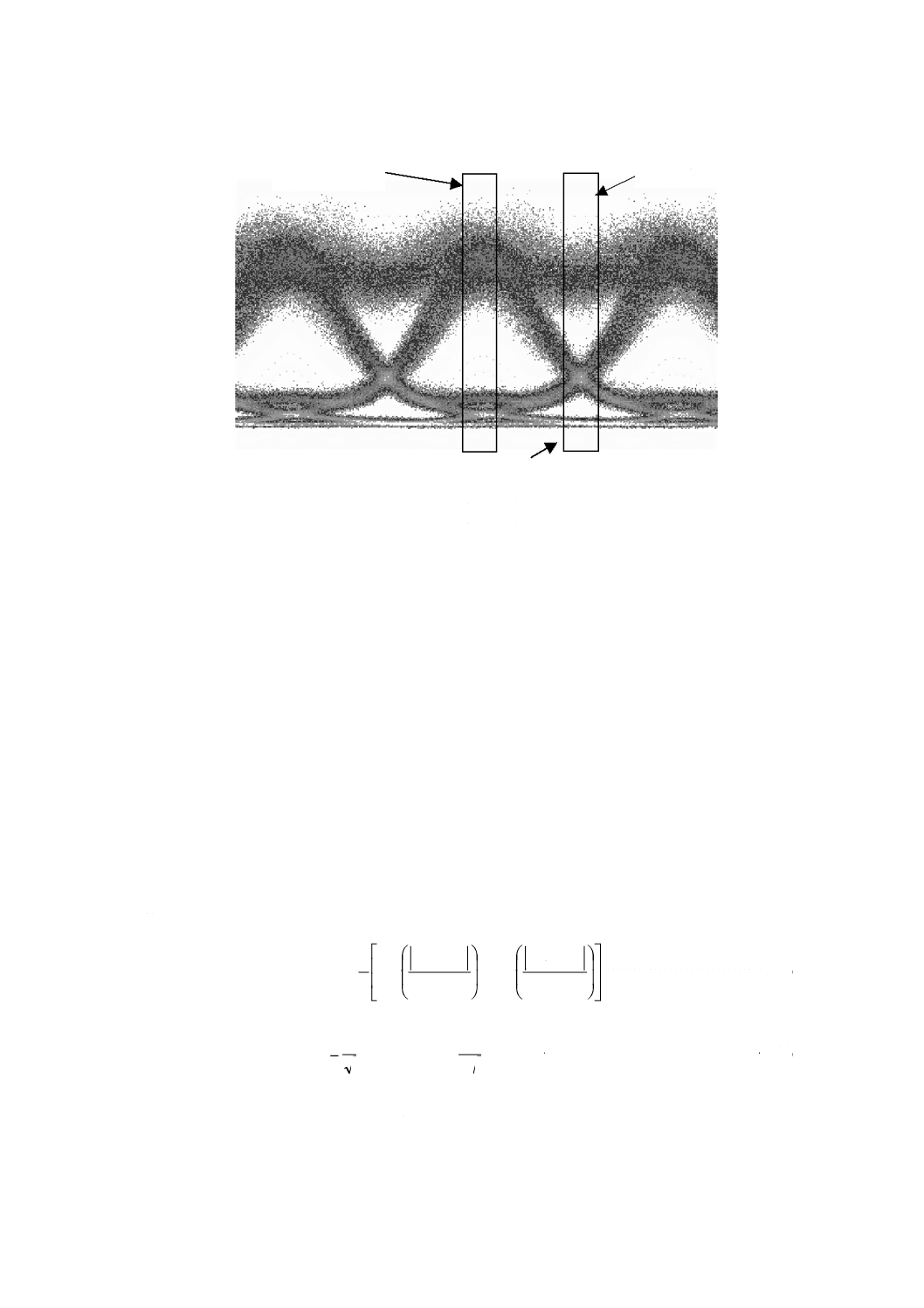
5
C 61280-2-8:2010 (IEC 61280-2-8:2003)
μ1:
μ0:
σ1:
σ0:
1レベルの平均電圧(V)
0レベルの平均電圧(V)
1レベルの雑音の標準偏差(V)
0レベルの雑音の標準偏差(V)
図2−DSOを使用してアイパターンの間の雑音統計を抽出するより正確な測定技術
これらのオシロスコープを用いた方法では,σ1及びσ0が過大に評価される傾向があるが,測定するQ値
が常に真のQ値より低い値になるとは限らない。例えば,アイパターンの開口の平均値が過大に評価され
るような方法でヒストグラムの分布がゆがめられ,Q値が高く評価されることもある。オシロスコープの
提供するQ値測定値とビット誤り率性能との関係は,容易に関連付けられない。
4
可変識別しきい値法
4.1
概要
可変識別しきい値法は,可変識別しきい値がある受信器に適用する。システムのビット誤り率を測定す
る幾つかの手段を必要とする。通常,誤り試験系ではPRBSを使用して測定するが,実際の伝送路で使う
ことのできる代替の手法もある。この測定は,ガウス分布に基づくデータのBERを,式(2)によって解析
的に計算できることを利用する。
−
+
−
=
0
0
th
1
1
th
th
2
1
)
(
σ
μ
σ
μ
V
erfc
V
erfc
V
BER
································ (2)
∫
∞
−
−
≈
=
x
x
e
x
d
e
x
erfc
2/
2/
2
2
2
1
2
1
)
(
π
β
π
β
············································ (3)
ここに,
BER: ビット誤り率
erfc: 補誤差関数
Vth: 識別しきい値(V)
μ1: 1レベルの平均電圧(V)
ここでアイパターンの開口を測定する。
ここで雑音を測定する。
雑音は,ここで独立した“1”を除いて見積もる。
σ1+σ0
μ1−μ0
6
C 61280-2-8:2010 (IEC 61280-2-8:2003)
μ0: 0レベルの平均電圧(V)
σ1: 1レベルの雑音の標準偏差(V)
σ0: 0レベルの雑音の標準偏差(V)
注記 x>3で,近似はほぼ正確になる。
式(2)に示すビット誤り率は,二つの項の平均である。最初の項は“1”が送信されたときに“0”が受信
されたと識別する確率で,2番目の項は“0”が送信されたときに“1”が受信されたと識別する確率であ
る。
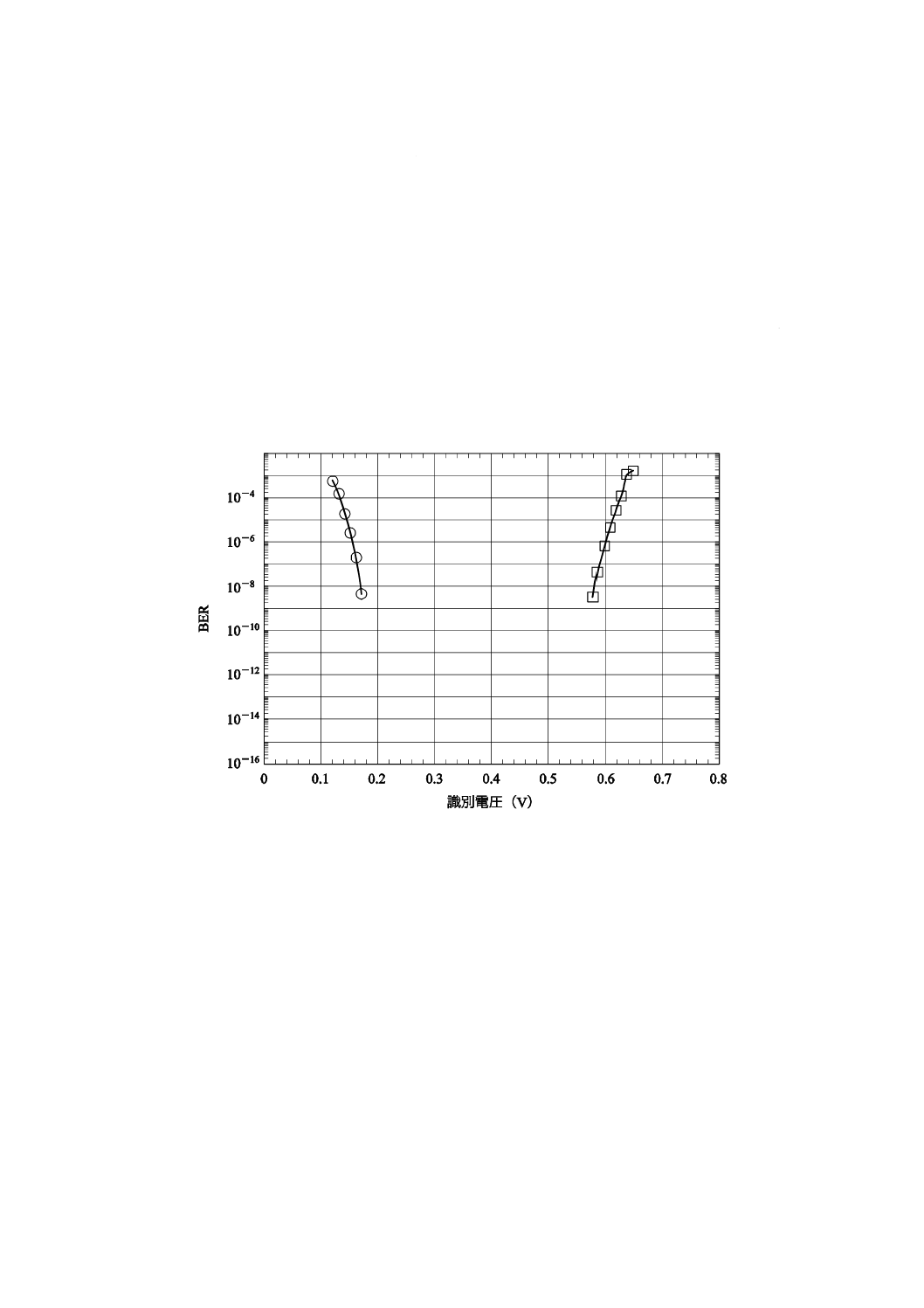
識別しきい値電圧を変えながらビット誤り率を測定する(図3参照)。次に,式(4)を使って,データを
Q値対しきい値のプロットに変換する。このとき,Q値は式(2)のいずれかの項の補誤差関数の引数となる。
変換においては,ビット誤り率は,しきい値がアイパターンの1レベル又は0レベルの近い方が,式(2)で
支配的になるという近似を使う。
図3−識別しきい値対ビット誤り率の測定例
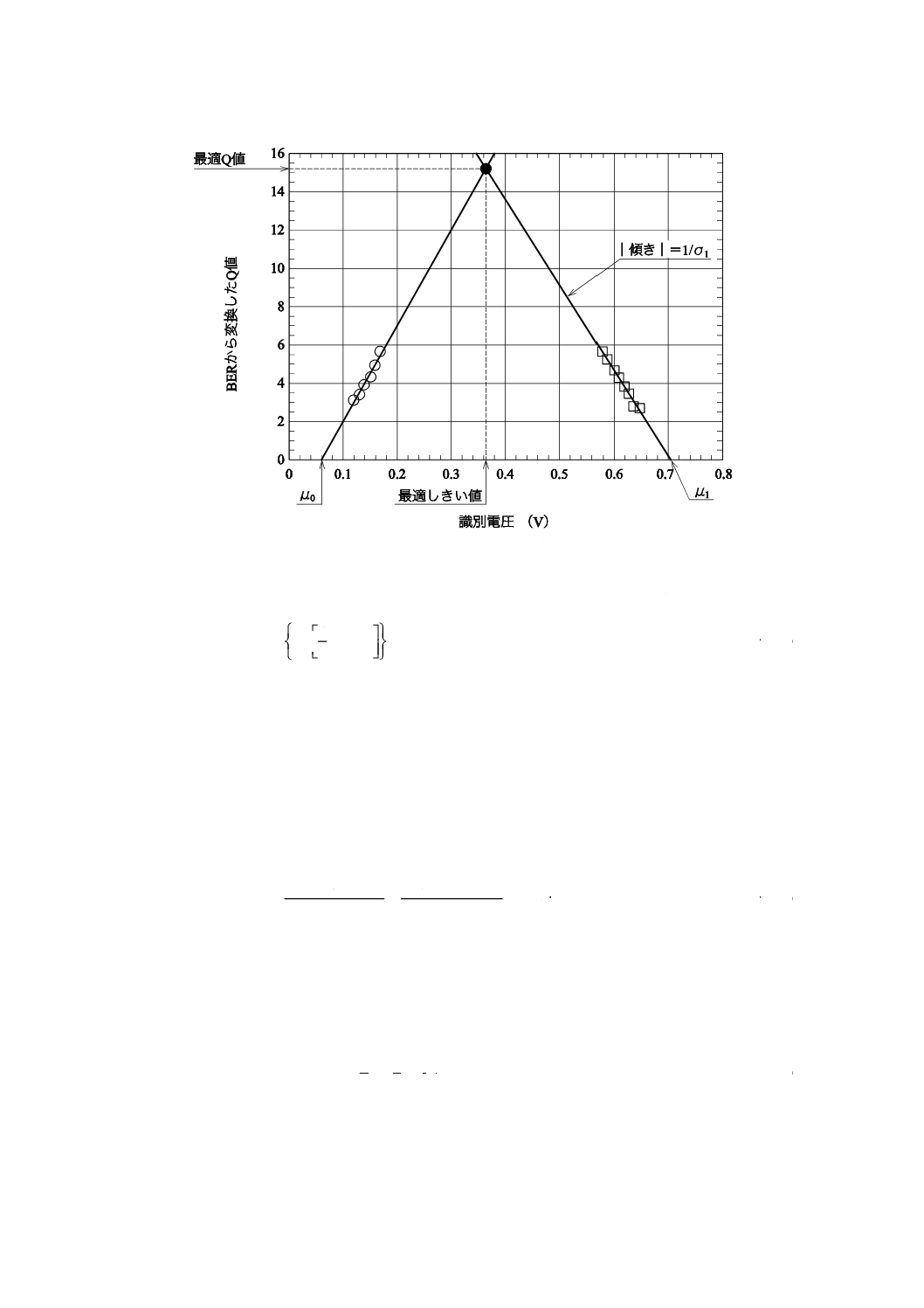
図3のデータをQ値対しきい値のプロットに変換した結果を,図4に示す。最適なQ値及びそれを実現
するための最適しきい値は,アイパターンの1レベルの近似直線と0レベルの近似直線との交点から求め
る[2]。
7
C 61280-2-8:2010 (IEC 61280-2-8:2003)
図4−しきい値電圧対Q値
最適しきい値及び最適Q値は,逆誤差関数に近似を行うことによって,解析的に算出できる[式(4)参照]。
2
1
2
016
.0
1
668
.0
192
.1
)
(
2
1
log
x
x
x
erfc
−
−
≈
−
·································· (4)
ここに,
x: log(BER)で,記号{ }-1は,xに関する逆関数を意味する。
式(4)は,ビット誤り率が10−5〜10−10で,±0.2 %の精度である。
逆誤差関数を見積もった後に,データを識別しきい値に対してプロットする。図4に示すとおり,線形
回帰によって各々のデータ群を直線で近似する。Q値計算のための等価的な標準偏差及び平均値は,各々
グラフの傾き及び切片から求める。
式(2)の二つの項の引数が等しくなるとき,しきい値は最適値となり,ビット誤り率は最小となる[式(5)
参照]。
opt
0
0
optimal
th
1
optimal
th
1
)
(
)
(
Q
V
V
=
−
=
−
−
−
σ
μ
σ
μ
··········································· (5)
ここに,
Vth−optimal: 最適しきい値(V)
Qopt: 最適Q値
式(5)を変換し,最適しきい値は,0レベル及び1レベルの平均電圧及び雑音の標準偏差を使って表せる
[式(6)参照]。
1
0
0
1
1
0
optimal
th
σ
σ
μ
σ
μ
σ
+
+
=
−
V
······························································· (6)
最適Q値を,式(1)によって求める。最適しきい値におけるビット誤り率は式(2)によって求められるが,
近似的には式(7)によって算出できる。
8
C 61280-2-8:2010 (IEC 61280-2-8:2003)
π
2
opt
)2/
(
optimal
2opt
Q
e
BER
Q
−
≈
·································································· (7)
ここに, BERoptimal: 最適しきい値におけるビット誤り率
この近似は,Qopt>3でほぼ正確である。
可変識別しきい値法は,ガウス分布を利用しているものの,雑音の統計がガウス分布に従わないシステ
ム,例えば典型的な光増幅システム[5][6]においても正確な結果を与える。これは図1に示すように,光受
信器の識別回路は,アイパターンの内側だけで動作する。すなわち,光受信器が識別に用いるのは,垂直
方向のヒストグラムにおいてアイパターンの内側に伸びた“すそ”だけである。可変識別しきい値法は,
アイパターン中心部における実際の分布のすそを,ガウス分布で近似する。この部分の分布が,光受信器
の動作に直接影響する。図1の例が示すとおり,ガウス近似は実際のヒストグラムとは全く一致はしない
が,Q値の見積りでは一致する必要はない。
可変識別しきい値法の技法は,実際のアイパターンをガウス分布をもつ架空のアイパターンで置き換え
たものと考えることもできる。 ビット誤り率と識別しきい値との関係は,これら二つのアイパターンの間
で同一である。したがって,アイパターンの細部は異なっても,両者は等価的に同一のQ値をもつとみな
せる。ただし,“すそ”をガウス分布で近似できない雑音源が支配的なシステムでは,このような分析を行
えない。例えば,クロストーク又はモード雑音が支配的なシステムがこれに当たる。測定において,Q値
としきい値との関係を直線で近似できないことが,このような雑音源の存在を示すよい目安となる。
可変識別しきい値法で測定したQ値と実際に測定したビット誤り率との間に,統計的に正しいレベルで
相関関係があることが実験的に示されている。
4.2
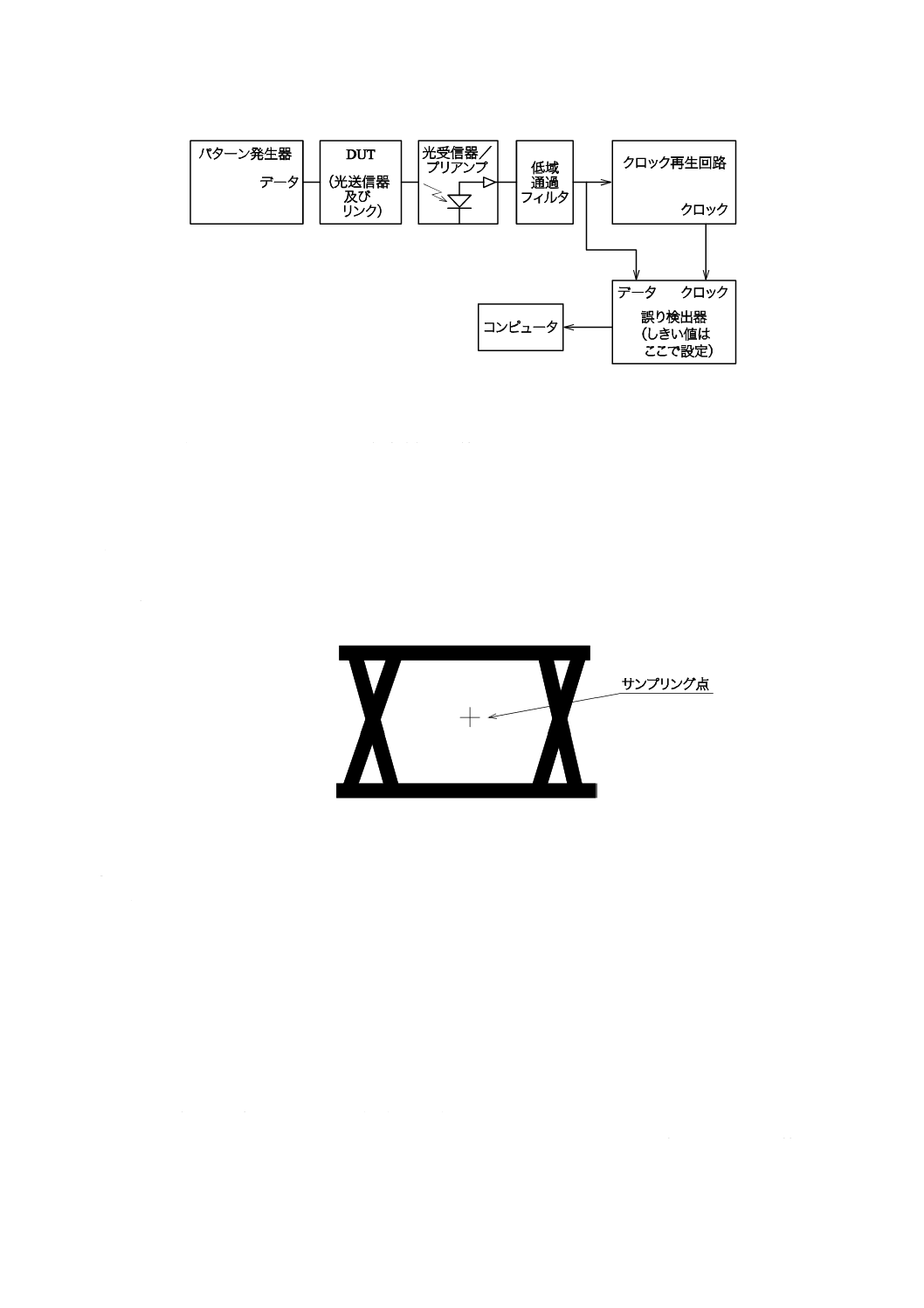
試験装置
ビット誤り率試験装置は,パターン発生器,光受信器,低域通過フィルタ,クロック再生回路,誤り検
出器及びコンピュータで構成する。
4.3
被測定物
被測定物(DUT)は,デジタル光ファイバ通信システムであり,一方に電気/光変換を伴う光送信器を,
もう一方に光/電気変換を伴う光受信器をもつ。光送信器と光受信器との間には,光ファイバによる光ネ
ットワークがあってもよい(例えば,DWDMネットワーク)。
4.4
試験手順
アイパターンの“1”付近及び“0”付近の識別しきい値に対して,ビット誤り率を10−5〜10−10で測定
し,Q値の見積りに必要なデータを次の手順で収集する。
9
C 61280-2-8:2010 (IEC 61280-2-8:2003)
図5−可変識別しきい値法のビット誤り率試験装置接続方法
a) 図5に従って,DUTをビット誤り率試験装置に接続する。
b) クロック発生回路の周波数を所望の周波数に設定する。
c) パターン発生器のパターン,データ振幅,クロック振幅,オフセット,極性及び終端を所望の測定条
件に設定する。
d) 誤り検出器のパターン,データ極性及び終端を所定どおりに設定する。
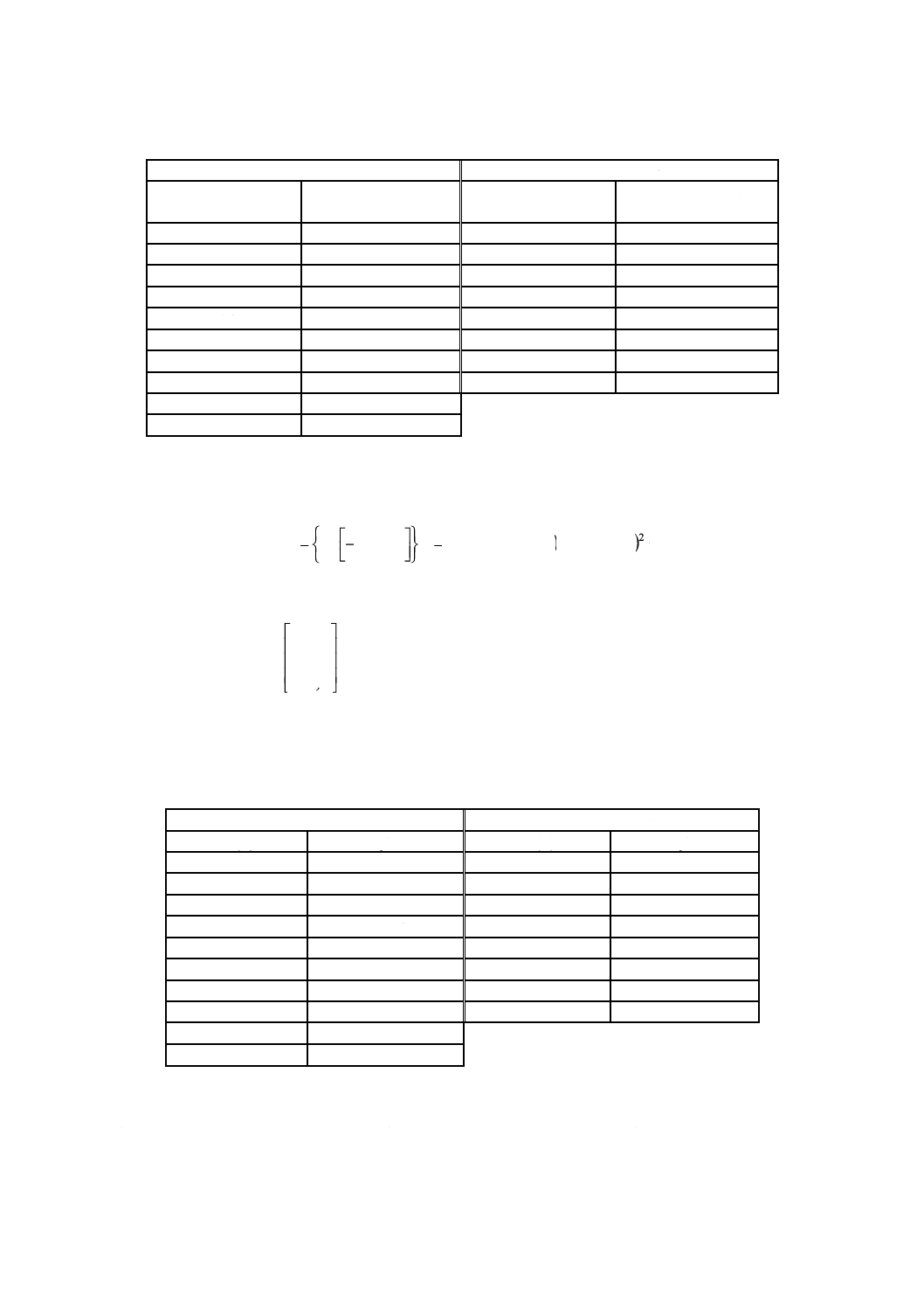
e) 図6に示すように,サンプリング点がアイパターンのほぼ中心になるように,識別しきい値電圧及び
データ入力遅延時間を設定する。これが最初のサンプリング点となる。
図6−識別しきい値の初期設定(アイパターンのほぼ中央)
f)
誤り検出器のゲート機能を有効にして,誤り数によるゲートがかかるように設定する。誤り数の最小
値は10,100又は1 000とする。
g) 誤り検出器の識別しきい値電圧を正の方向に調整し,ビット誤り率の測定値が1×10−10以上になるよ
うにする。このときの識別しきい値電圧(Vb1)及びビット誤り率を記録する。
h) 識別しきい値電圧を増加させ,ビット誤り率が10−5以上になるようにして,識別しきい値電圧(Va1)
及びビット誤り率を記録する。
i)
二つの識別しきい値電圧(Va1及びVb1)の差を記録し,両者の間に十分な数(5以上)の測定点が得
られるようにステップ値(Vstep1)を選択する。識別しきい値電圧Va1から開始し,ステップ値Vstep1で
識別しきい値電圧を減少させる。各ステップにおいて誤り検出器でゲート測定を行う。測定したビッ
ト誤り率及び対応する識別しきい値電圧を記録する。
j)
誤り検出器のゲート測定では,f)で設定した誤り数の最小値に達するまで,データ及び誤りの情報を
蓄積する。誤り数の最小値を大きな値にすると,統計的により正確なビット誤り率を得ることができ
10
C 61280-2-8:2010 (IEC 61280-2-8:2003)
る。ただし,特に低いビット誤り率の値を測定する場合に測定時間は長くなる。統計的に有意な結果
を得るには,カウントする誤り数を15未満にしないほうがよい。
k) ビット誤り率が10−10以下になるまで測定を続ける。この識別しきい値電圧に対するビット誤り率の
データ群は,“1”レベルに対応する。
l)
識別しきい値電圧を初期のサンプリング点まで戻し,ビット誤り率の測定値が10−10以上になるよう
に識別しきい値電圧を負の方向に調整する。このときの識別しきい値電圧(Vb0)及びビット誤り率を
記録する。
m) 識別しきい値電圧を減少させ,ビット誤り率が10−5以上の値になるようにして,識別しきい値電圧
(Va0)及びビット誤り率を記録する。
n) 二つの識別しきい値電圧(Va0及びVb0)の差を記録し,両者の間に十分な数(5以上)の測定点が得
られるようにステップ値(Vstep0)を選択する。識別しきい値電圧Va0から開始し,ステップ値Vstep0で
識別しきい値電圧を増加させる。各ステップにおいて誤り検出器でゲート測定を行う。測定したビッ
ト誤り率及び対応する識別定しきい値電圧を記録する。
o) ビット誤り率が10−10以下になるまで測定を続ける。この識別しきい値電圧に対するビット誤り率の
データ群は,“0”レベルに対応する。
4.5
計算及び結果の解釈
得られたデータにガウス分布を仮定したフィッティングをすることによって,“1”と“0”とに対する等
価的な平均値(μ)及び標準偏差(σ)を決定する。その後,式(1)を使ってQ値を計算する。
4.5.1
データ群
4.4に示す試験手順によって,次の形式をもった2組のデータ群(“0”レベル及び“1”レベルに対応)
を得る。
n
nBER
D
BER
D
BER
D
,
,
,
2
2
1
1
Μ
ここに,
Di: i番目の測定における識別しきい値電圧(i=1, 2..., n)
BERi: i番目の測定におけるビット誤り率(i=1, 2..., n)
n: データの数
注記 “0”レベル及び“1”レベルに対するデータの数が等しい必要はない。
取得した識別しきい値電圧及びビット誤り率の例を,表2に示す。
11
C 61280-2-8:2010 (IEC 61280-2-8:2003)
表2−識別しきい値電圧とBERとの関係
“1”レベル
“0”レベル
識別しきい値電圧
V
ビット誤り率
識別しきい値電圧
V
ビット誤り率
−1.75
5.18×10−5
−4.37
8.76×10−5
−1.80
2.09×10−5
−4.34
1.90×10−5
−1.85
7.33×10−6
−4.31
5.18×10−6
−1.90
2.77×10−6
−4.28
1.06×10−6
−1.95
9.61×10−7
−4.25
2.12×10−7
−2.00
1.96×10−7
−4.22
3.45×10−8
−2.05
6.30×10−8
−4.19
3.52×10−9
−2.10
1.95×10−8
−4.16
2.77×10−10
−2.15
3.45×10−9
−2.20
1.39×10−9
4.5.2
逆誤差関数を使ったビット誤り率の変換
次に,式(4)の近似を使って,各々のビット誤り率の値を式(8)によって変換する。
()
()2
1
2
016
.0
1
668
.0
192
.1
)
(
2
1
log
i
i
i
i
x
x
x
erfc
f
−
−
=
=
−
························ (8)
ここに,
xi: log10(BERi)
この変換によって,次の形式をもつ2組のデータ群(“1”レベル及び“0”レベルに対応)を生成する。
n
nf
D
f
D
f
D
,
,
,
2
2
1
1
Μ
これらのデータは,ほぼ直線でフィッティングできる。
表2の値を変換すると,表3のデータを得る。
表3−Diとfiとの関係
“1”レベル
“0”レベル
Di (V)
fi
Di (V)
fi
−1.75
3.757 8
−4.37
3.636 0
−1.80
3.963 8
−4.34
3.984 7
−1.85
4.195 6
−4.31
4.270 6
−1.90
4.404 3
−4.28
4.605 2
−1.95
4.625 7
−4.25
4.929 3
−2.00
4.944 9
−4.22
5.275 7
−2.05
5.162 9
−4.19
5.682 3
−2.10
5.379 9
−4.16
6.097 5
−2.15
5.685 8
−2.20
5.839 0
4.5.3
線形回帰
線形回帰法を用いて,具体的に各々のデータ群を順番に,次の式に示す直線にフィッティングさせる。
12
C 61280-2-8:2010 (IEC 61280-2-8:2003)
BX
A
Y
+
=
ここで,Y及びXには,次の関係がある。
(
)
1
2
1
−
=
BER
erfc
Y
(ビット誤り率の逆誤差関数)
ただし,記号[ ]-1は,BERに関する逆関数を意味する。
D
X=
(しきい値電圧)
“1”レベル及び“0”レベルに対応するデータ群に対し,次の計算を行う[7]。
n
X
X
n
Y
X
XY
B
∑
∑
∑∑
∑
−
−
=
2
2
)
(
)
)(
(
−
−
−
=
∑
∑
∑
∑
∑
∑∑
n
Y
Y
n
X
X
n
Y
X
XY
R
2
2
2
2
2
2
)
(
)
(
)
)(
(
n
X
B
n
Y
A
∑
∑
−
=
ここに,
A: フィッティングした直線の切片
B: フィッティングした直線の傾き
n: データ群に属するデータ数
R2: 決定係数(データが直線にどのくらいよくフィットす
るかを示す指標)
Σ: 1からnまでの和
表3の値から表4の値を得る。
表4−線形回帰で得られる値
“1”レベル
“0”レベル
A
B
R
A
B
R
−4.612 5
−4.763 8
0.998 9
53.989
11.530 7
0.998 4
4.5.4
標準偏差と平均
“1”又は“0”の雑音領域の標準偏差及び平均を,次の式によって求める。
B
1
−
=
σ
B
A
−
=
μ
ここに,
μ1又はμ0: “1”又は“0”の雑音領域の標準偏差
σ1又はσ0: “1”又は“0”の雑音領域の平均
表4の例から表5の値を得る。
13
C 61280-2-8:2010 (IEC 61280-2-8:2003)
表5−平均及び標準偏差
“1”レベル
“0”レベル
μ1
σ1
μ0
σ0
−0.968 2
0.209 9
−4.682 2
0.086 724 9
4.5.5
最適識別しきい値
最適Q値Qoptを,次の式によって求める。
0
1
0
1
opt
σ
σ
μ
μ
+
−
=
Q
最適識別しきい値を,次の式によって求める。
1
0
0
1
1
0
optimal
th
σ
σ
μ
σ
μ
σ
+
+
=
−
V
表5の例の場合,Qoptは12.52となり,最適識別しきい値は−3.596 Vとなる。
4.5.6
最適識別しきい値におけるビット誤り率
最適しきい値におけるビット誤り率は,次の式によって求める。
π
2
opt
2
2
Q
e
BER
Q
−
=
4.5.5の例によってQoptの値を12.52とすると,ビット誤り率は1×10−18未満となる。
4.5.7
最適識別しきい値ではない場合のビット誤り率
最適識別しきい値ではない場合のビット誤り率は,次の式によって求める。
−
+
−
=
−
−
−
−
π
σ
μ
π
σ
μ
σ
μ
σ
μ
2
2
2
1
)
(
0
0
2
1
1
2
2
0
0
2
1
1
D
e
D
e
D
BER
D
D
4.5.8
誤差の上限
得られた最適Q値の誤差の上限は,式(A.5)によって求めることができる。
4.5.7の例においては,Q値の誤差の上限は±0.5である。
4.6
測定の記録
各々の試験において,次に示す情報を記録する。
a) 試験の日付
b) この規格の番号
c) サンプル(すなわち試験した光伝送システム)の識別情報
d) 2組のデータ群(最適しきい値より上のデータ及び下のデータ)
e) 各々のデータ群は,しきい値に対するビット誤り率(10−5から10−10までの範囲にわたるもの)の測
定値を5個以上含める。
f)
最適Q値及び最適識別しきい値
g) Q値に対する誤差範囲
14
C 61280-2-8:2010 (IEC 61280-2-8:2003)
4.7
具体的な情報
次に示す情報を記録する。
a) この規格の番号
b) 試験に対する特別な要求事項
c) 合否判定の基準
5
可変光しきい値法
5.1
概要
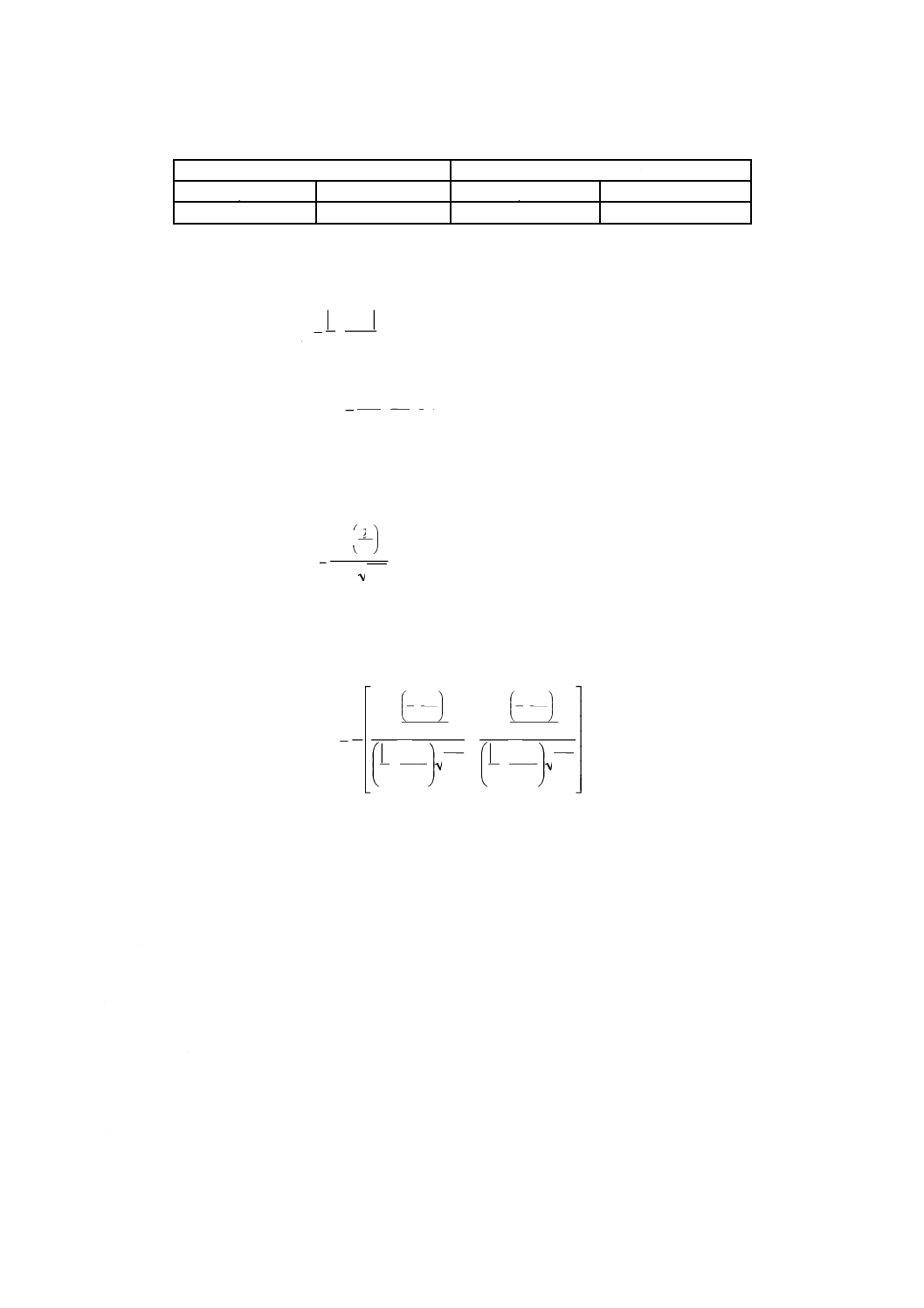
可変光しきい値法では,ビット誤り率の測定値を増加させるために,あらかじめ調節したバイアス光を,
受信した光信号に合波する。バイアス光のパワーを変えて幾つかの測定を行い,それらの結果をバイアス
が零の点に外挿して,通常運用時のビット誤り率の値を見積もる。この方法は,DC結合された光受信器
に対してだけ適用できる。バイアス光を合波することの効果を,図7に示す。
図7−バイアス光の効果
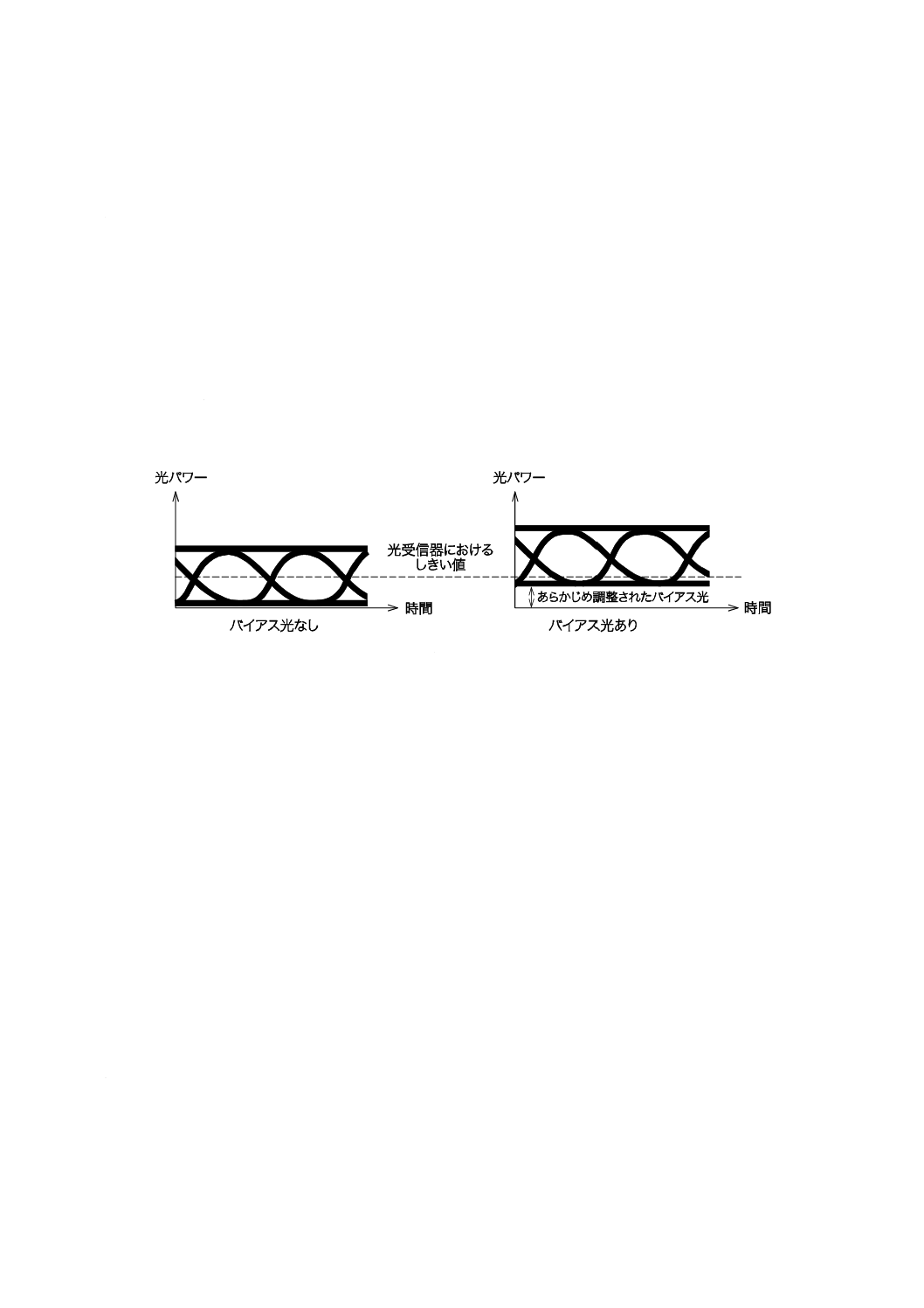
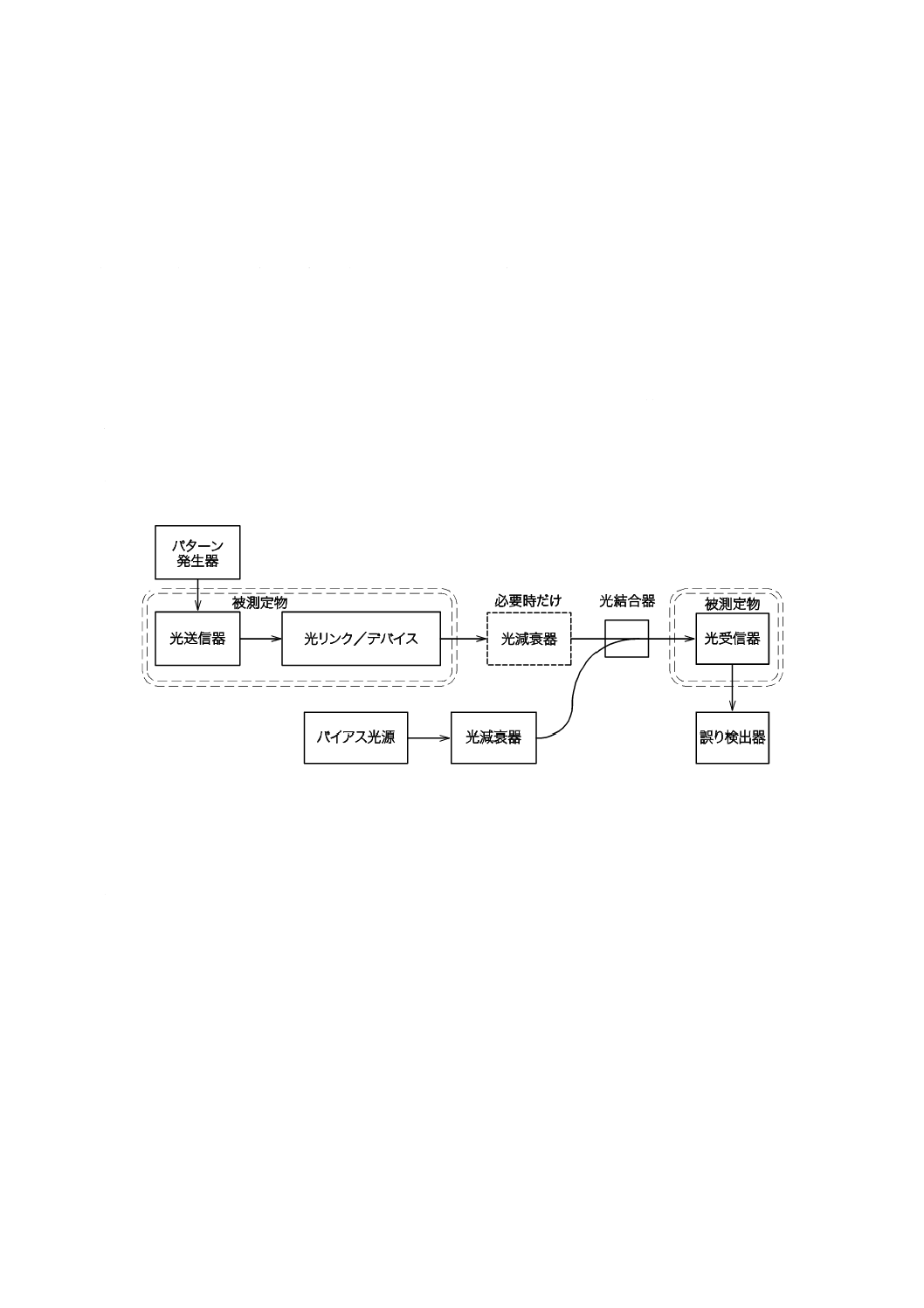
この方法によって,図8に示すような光リンク又は光能動部品の誤り特性を評価できる。また,図9に
示すような試験系を用いて,システム全体の誤り特性を評価することもできる。この方法の利点は,装置
の内部へのアクセスが不要なこと,及び被測定システムが内部にもつ誤り監視装置を利用できることであ
る。誤り監視機能がなければ,システムのデータ入出力端子に一般的なビット誤り率試験装置を接続して
もよい。
5.2
試験装置
試験装置は,次のa)〜d)で構成する。
a) 通常の誤り測定装置:パターン発生器及び遠隔操作に適した誤り検出器から構成する装置。この規格
に記載するすべての方式に共通して使用できる。ただし,誤り監視装置を備えたシステムの評価には
必要ない。
b) あらかじめ調節した光源:被試験システムに近い波長に調節し,光出力の変動が1時間当たり0.1 dB
以内に安定している装置。
c) 光減衰器:1時間当たり0.1 dB以内に安定している装置。1対の送信器と受信器とを試験するときな
ど,受信器で高い光信号レベルを受ける場合には,同じ安定度をもつ光減衰器がもう1台必要である。
d) 光分岐器/結合器:分岐比が通常50:50と10:90の間にあり,システム及びバイアス光源と光ファ
イバとが適合する装置。
15
C 61280-2-8:2010 (IEC 61280-2-8:2003)
5.3
被測定物
試験対象は,デジタル送信器及びDC結合したデジタル受信器から構成する光ファイバデジタルシステ
ムである。光ファイバ/光ケーブル及び光受動/能動部品から構成する光ファイバリンクによって,両者
を接続する。1対の送信器/受信器だけを試験する場合,それらに固定/可変の光減衰器を接続しなけれ
ばならない。また,光再生器又は光増幅器のような能動部品から構成する光ファイバリンクで接続した送
信端及び受信端をもつ自己完結型の伝送システムも試験対象になる。そのようなシステムは誤り監視装置
を備えている可能性があるが,備えている場合にはその装置によって誤り率を測定してもよい。
5.4
基本的な光ファイバリンクの試験手順
基本的な光ファイバリンクの試験手順を,次に示す(図8参照)。
a) 送信器及び受信器を動作させ,光受信器の光入力パワーを監視しながら,光減衰器を調整する。
b) ビット誤り率が適切な高い値(10−4など)に達するまで,バイアス光を調節する。
c) バイアスを1回に1ステップずつ減少し,1ステップごとに誤り検出器によって測定したビット誤り
率を記録する。各ビット誤り率を有効数字2けたまで測定する。
d) 5組以上のデータを取得するまで,c)を繰り返す。
図8−基本的な光ファイバリンクのセットアップ
5.5
自己完結型システムの試験手順
自己完結型システムの試験手順を,次に示す(図9参照)。
a) 被測定システムを設置する。光結合器を含まない場合,受信器の入力端子に光結合器を挿入する。シ
ステムに誤り監視装置がない場合,パターン発生器を送信端子のデータ入力に,対応する誤り検出器
を適切なデータ出力端子にそれぞれ接続する。
b) ビット誤り率が適切な高い値(10−4など)に達するまで,バイアス光のパワーを調節する。
c) バイアスを1回に1ステップずつ減少し,1ステップごとに誤り検出器によって測定したビット誤り
率を記録する。各ビット誤り率を有効数字2けたまで測定する。
d) 5組以上のデータを取得するまで,c)を繰り返す。
16
C 61280-2-8:2010 (IEC 61280-2-8:2003)
図9−自己完結型システムのセットアップ
5.6
結果の評価
光バイアス信号を注入することは,検出しきい値を変化させることと同じである。したがって,結果を
評価するための数学的モデルは,可変識別しきい値法に使用するモデルと実質的に同じである。一次近似
として,光バイアス信号の振幅とビット誤り率の結果値との関係は,次の式によって表現できる。
BX
A
Y
+
=
ここに,
Y: ビット誤り率の対数値
X: バイアスの振幅
A: フィッティングした直線の切片
B: フィッティングした直線の傾き
試験結果の例を,表6に示す。
表6−可変光しきい値法の結果
バイアス
µW
ビット誤り率
log(BER)
6.00
1.0×10−4
−4.00
5.75
2.7×10−5
−4.57
5.50
7.0×10−5
−5.15
5.25
1.4×10−6
−5.85
5.00
3.0×10−7
−6.52
4.75
5.0×10−8
−7.30
4.50
1.0×10−8
−8.00
ビット誤り率に有効数字2けたの精度を得るため,100個程度の十分なエラーを蓄積しなければならな
い。ただし,振幅がわずかに変化しても後の外挿処理に大きな影響を与えるため,エラー測定に時間をか
けることによって,光バイアスの振幅の安定性を損ねてはならない。
表6の結果に4.5.3に示した線形回帰法を適用すると,ビット誤り率の基本値は,図10に示すように外
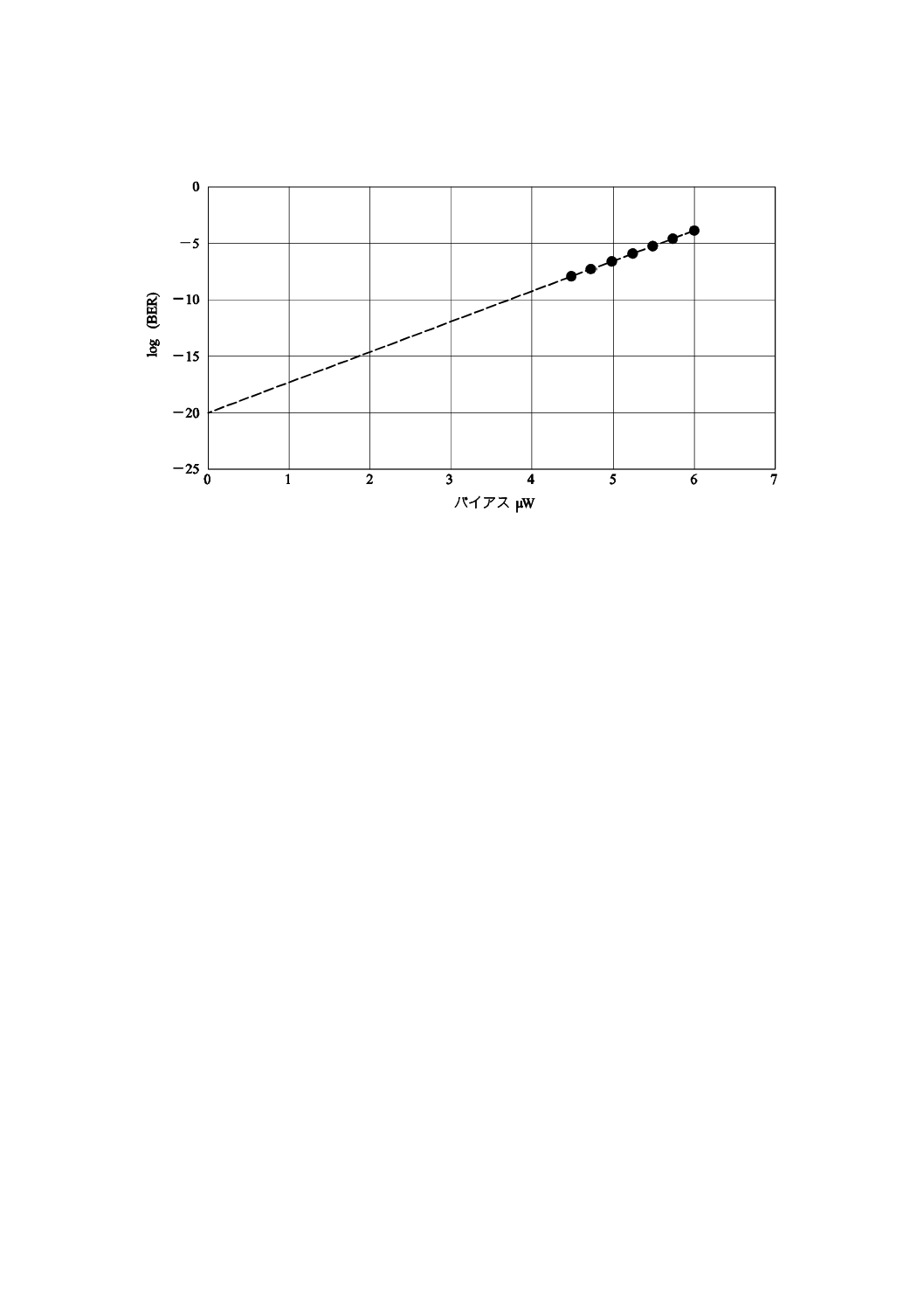
17
C 61280-2-8:2010 (IEC 61280-2-8:2003)
挿によって決まる。
図10−バイアスの関数としてのlog(BER)の外挿
表6の結果の場合,図10から,ビット誤り率は10−20と推定できる。
18
C 61280-2-8:2010 (IEC 61280-2-8:2003)
附属書A
(規定)
Q値における最大誤差の計算
Q値における誤差の上限の計算を,次に示すように求める。
線形回帰フィット(Y=A+BX式)によって,次のように“0”及び“1”のレベルに2個の直線フィッ
トが発生すると仮定する。
X
B
A
Y
0
0
0
+
=
(“0”レベル)
X
B
A
Y
1
1
1
+
=
(“1”レベル) ·················································· (A.1)
図4に示すように,2直線は最適識別しきい値で交差するので,Y0とY1とが等しく,次の関係にある。
optimal
1
1
optimal
0
0
X
B
A
X
B
A
+
=
+
ここに,
Xoptimal: 最適識別しきい値
A0: “0”レベルに対してフィッティングした直線の切片
B0: “0”レベルに対してフィッティングした直線の傾き
A1: “1”レベルに対してフィッティングした直線の切片
B1: “1”レベルに対してフィッティングした直線の傾き
すなわち,
1
0
0
1
optimal
B
B
A
A
X
−
−
=
···································································· (A.2)
最適識別しきい値でのYの値がQ値であり,式(A.3)となる。
optimal
1
1
X
B
A
Q
+
=
1
0
1
0
0
1
B
B
B
A
B
A
−
−
=
······································································ (A.3)
ここに,
Q: Q値
変数A0,A1,B0及びB1のそれぞれに対するQの導関数は,式(A.4)となる。
β
α
=
∂
∂
=
∂
∂
1
0
,AQ
A
Q
βγ
αγ
−
=
∂
∂
−
=
∂
∂
1
0
,BQ
B
Q
······························································ (A.4)
ここに,
α:
1
0
1B
B
B
−
−
β:
1
0
0B
B
B
−
γ:
1
0
1
0B
B
A
A
−
−
Qにおける最大誤差は,式(A.5)によって求める。
19
C 61280-2-8:2010 (IEC 61280-2-8:2003)
2B
2
1
2B
2
0
2A
2
1
2A
2
0
2max
1
0
1
0
σ
σ
σ
σ
∂∂
+
∂∂
+
∂∂
+
∂∂
=
∆
B
Q
B
Q
A
Q
A
Q
Q
(
)
(
)
2A
2B
2
2
2A
2B
2
2
1
1
0
0
σ
α
γ
β
σ
σ
γ
α
+
+
+
=
··································· (A.5)
ここに,
∆Qmax: Qにおける最大誤差
2A
0
σ
: “0”レベルのY-切片における不確定性
2A
1
σ
: “1”レベルのY-切片における不確定性
2B
0
σ
: “0”レベルのスロープにおける不確定性
2B
1
σ
: “1”レベルのスロープにおける不確定性
A0,A1,B0及びB1の要素は無相関であると仮定する。式(A.5)によってQ値における絶対最大誤差が得
られる。これらの分散は式(A.6)で得られる[8]。
∆
≈∑
2
2
2A
X
S
σ
∆×
≈
2
2B
S
N
σ
·········································································· (A.6)
ここに,
A
2
σ: Y-切片における不確定性
B
2
σ: スロープにおける不確定性
N: データポイントの数
Δ:
∑
∑
−
=
∆
2
2
)
(
X
X
N
S2:
∑
−
−
−
2)
(
2
1
BX
A
Y
N
20
C 61280-2-8:2010 (IEC 61280-2-8:2003)
附属書B
(参考)
正弦波干渉法
B.1
概要
正弦波干渉法では,測定するビット誤り率を増加させるために,受信器識別回路の前段でデジタル信号
に光学的及び電気的に干渉正弦波信号を加える。正弦波の振幅を毎回減少しながら数回測定した値を零振
幅まで外挿し,システムのビット誤り率を得る。
正弦波信号は,光データ入力に加えることによって,受信器に光学的に注入できる。識別回路へのアク
セスは,通常,運用装置内ではできないため,光注入による方式はシステム及びリンクレベルでの試験に
利用できる唯一の手順である。正弦波信号を電気的に加えるためには,受信器の識別回路に電気的なアク
セスが必要であり,この方式は部品及びサブシステムレベルでの試験により適している。
光正弦波干渉法及び電気正弦波干渉法とも干渉がなくなる点までの外挿を行うため,同様の結果が得ら
れる。
光学方式は,AC結合受信器に適用できる。一方,電気方式はAC結合受信器及びDC結合受信器に適用
できる。
B.2
試験装置
通常の誤り測定装置であるパターン発生器及び誤り検出器は,すべての方式に共通して使用できる。そ
の他の試験装置は,次による。
a) 正弦波発生器:被試験システムの通過帯域内で周波数を発生し,3けた以上の振幅分解能で1 mVと1
Vとの間で安定した出力レベルを生成することができる装置。典型的な周波数シンセサイザであれば
適用できる。
b) アナログレーザ送信器:調節可能なCW出力パワー,0.1 dB/h以上の安定性及び被試験システムに近
い波長をもち,被試験受信器の通過帯域内で十分に対応できる周波数で変調可能な装置。これは“干
渉レーザ”として動作する。
c) 光学分岐器/結合器:分岐比が通常50:50と10:90との間にあり,システム及び干渉レーザと光フ
ァイバとの適合性がある装置。
d) アナログ光受信器:被試験システムの通過帯域内で周波数を検出することができ,干渉レーザの正確
な動作を確認できる装置。
B.3
被測定物
試験対象は,デジタル送信器及びデジタル受信器から構成する光ファイバデジタルシステムである。送
信器と受信器との間に,光ファイバ/ケーブル及び受動/能動部品(運用リンクを試験する場合)で構成
する光ファイバリンクを,又は可変光減衰器(一対の送信器/受信器だけを試験する場合)を接続する。
B.4
試験手順
B.4.1 光正弦波干渉法
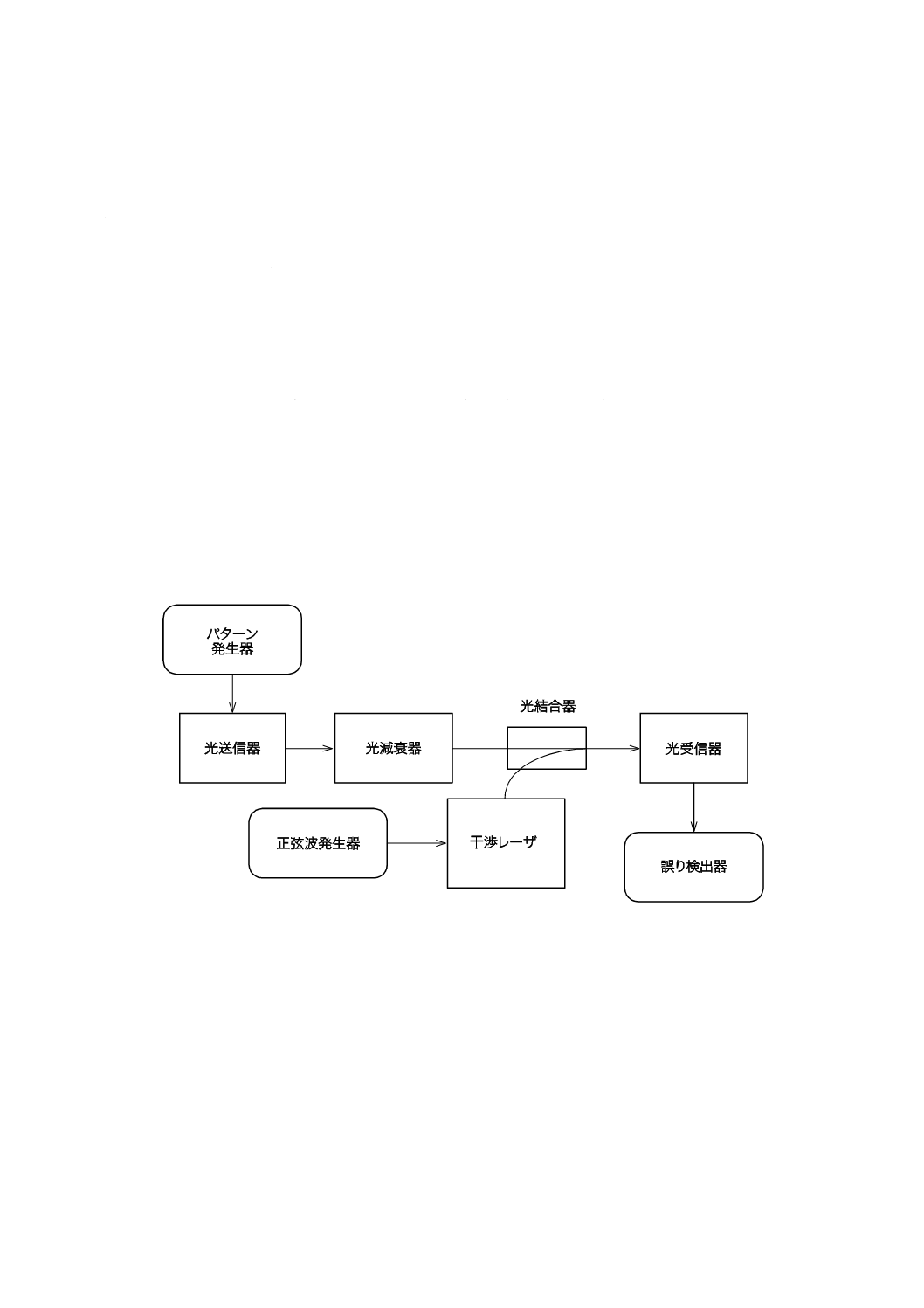
光正弦波干渉法の試験手順を,次に示す(図B.1参照)。
21
C 61280-2-8:2010 (IEC 61280-2-8:2003)
a) 光結合器の一方の入力ポートを光ファイバリンク又は光減衰器のいずれかに,他方の入力ポートを干
渉レーザにそれぞれ接続する。出力ポートを受信器に接続する。干渉レーザは正弦波発生器によって
変調される。光受信器を誤り検出器に接続する。
b) 光送信器及びアナログ光受信器を所望の条件に設定する。データパターン及び減衰器を使用する場合
は受信パワーを調節する。受信入力パワーレベルは測定作業の間,一定に保持する。
c) 正弦波発生器を,受信器の通過帯域内で十分に対応でき,かつ,ビットレートに調和的に関連しない
周波数に調節する。この周波数は,低速ビート現象が発生しないように,ビットレートと十分に異な
る値にする(例えば,1 Mbit/sなど)。
d) 干渉レーザを起動し,光結合器の出力側で見えるレーザのパワーが,被試験データリンクのレーザ送
信器からのパワーとほぼ等しくなるように,干渉レーザの出力レベルを調節する。干渉レーザを変調
し,ビット誤り率がほぼ10−4に達するまで変調度を調節する(前提条件として,ビット誤り率は干渉
信号を加える前は測定不能なほど低くなければならない。)。干渉レーザ出力に,アナログ光受信器で
モニタリングしてひずみがないことを確認する。これらの要件を満たすためには,分岐比の異なる別
の結合器の選択,又は干渉レーザの信号レベルの調節が必要となることがある。
e) 正弦波発生器の出力レベルを調節することによって,干渉レーザの変調度を1回に1ステップずつ低
減する。1ステップごとに誤り検出器で測定したビット誤り率を記録する。
f)
ビット誤り率を有効数字2けたまで測定し,5組以上のデータを得る。
図B.1−光注入による正弦波干渉法のセットアップ
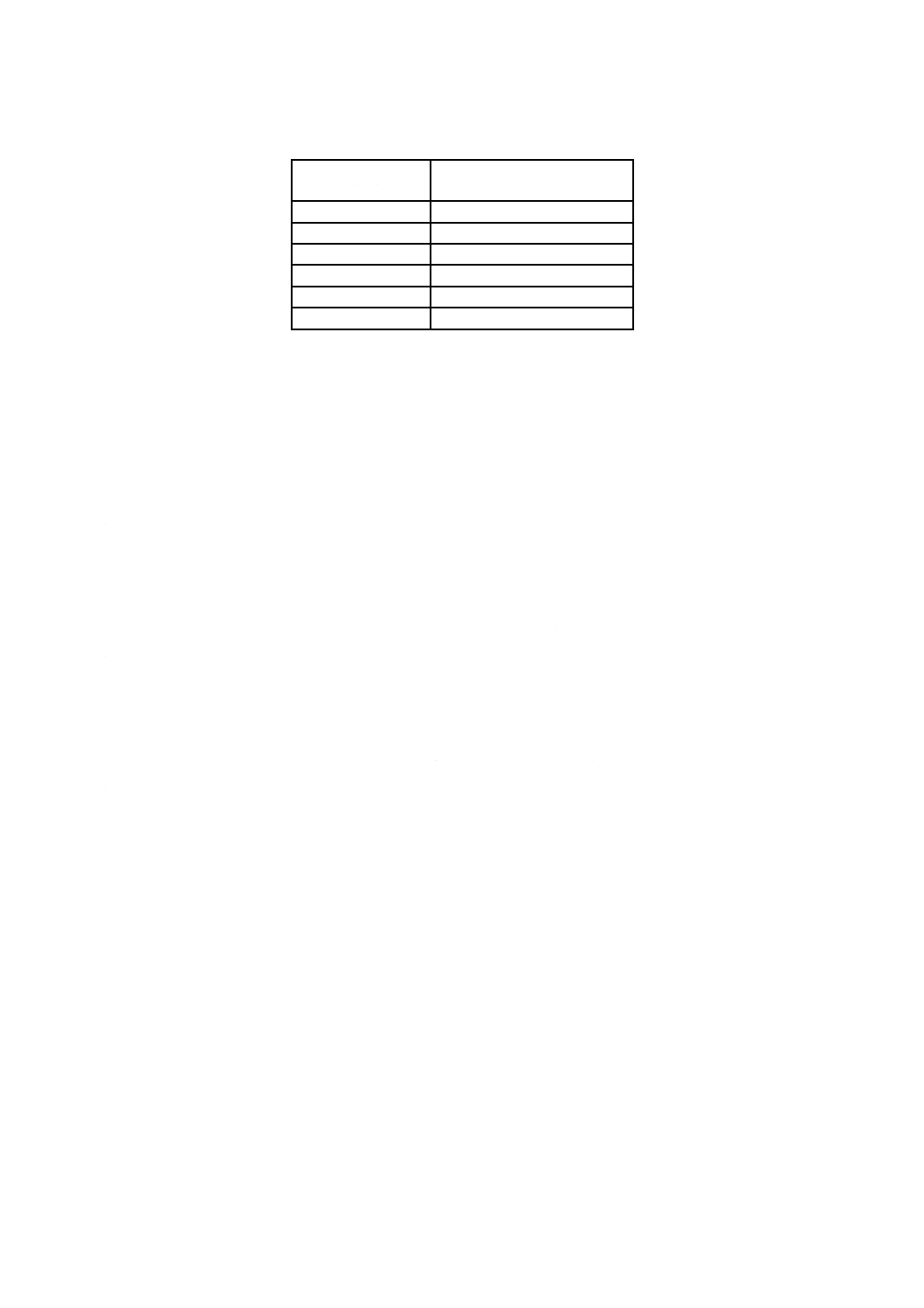
表B.1に測定結果の例を示す。
22
C 61280-2-8:2010 (IEC 61280-2-8:2003)
表B.1−正弦波注入の測定結果
正弦波振幅
A(mV)
ビット誤り率
100
5.0×10−5
95
1.1×10−5
90
6.3×10−6
85
9.8×10−7
80
2.3×10−7
75
4.8×10−8
ビット誤り率に有効数字2けたの精度を得るため, 100個程度の十分なエラーを蓄積しなければならな
い。ただし,干渉信号の振幅がわずかに変化しても後の外挿処理に大きな影響を与えるため,エラー測定
に時間をかけることによって,干渉信号の振幅の安定性を損ねてはならない。
B.4.2 電気正弦波干渉法
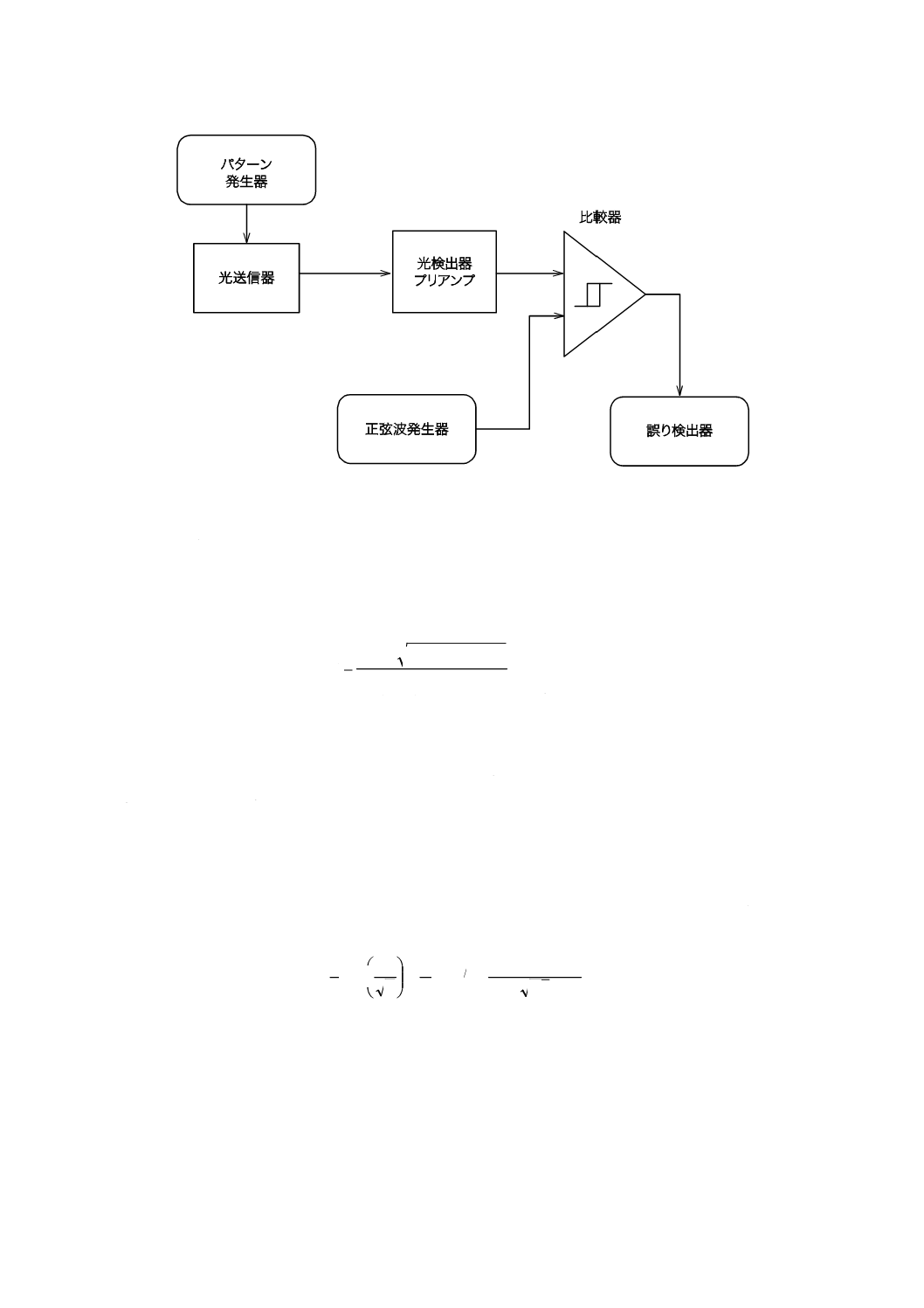
電気正弦波干渉法の試験手順を,次に示す(図B.2参照)。
a) 被試験受信器内の比較器の識別しきい値入力に,正弦波発生器を交流結合する。比較器に差動データ
入力端子がある場合,大きな直列抵抗を使用することによって比較器のデータ信号を正弦波発生器か
ら隔離できる。隔離が困難な場合,箇条4に示す可変識別しきい値法による。
b) 光送信器及びアナログ光受信器を所望の条件に設定する。データパターン及び減衰器を使用している
場合は,受信パワーを測定作業の間一定に保持するように調節する。
c) 正弦波発生器の周波数には,アナログ光受信器の通過帯域内で十分に対応でき,かつ,ビットレート
に調和的に関連しない周波数に調節する。この周波数は,低速のビート現象が発生しないように,ビ
ットレートと十分に異なる値にする(例えば,1 Mbit/sなど)。また,周波数は,アナログ光受信器内
のAGC又はしきい値トラッキングのループ応答よりも十分に上回らなければならない。
d) 正弦波発生器の振幅を,ビット誤り率がほぼ10−4に達するまで調節する。
e) 正弦波発生器の出力を低減することによって,干渉の振幅を1回に1ステップずつ低減する。1ステ
ップごとに誤り検出器でビット誤り率を記録する。結果のデータは4.5.1のデータと類似していなけれ
ばならない。
23
C 61280-2-8:2010 (IEC 61280-2-8:2003)
図B.2−電気的注入による正弦波干渉法のセットアップ
B.5
計算及び結果の外挿
B.5.1 数学的分析
次に示す計算は,B.4.1及びB.4.2に適用する。表B.1のデータを(Ai,BERi)として表す。ビット誤り
率を,次の式によって求める。
1
3
1
22
2
2
)
(
4
)
(
c
x
c
c
c
c
BER
i
i
+
−
+
−
=
Ψ
ここに,
Ψ(BERi): i番目の正弦波振幅のビット誤り率
xi: ln(2×BERi)
c1: 0.492 6
c2: 0.294 8
c3: 0.792 1
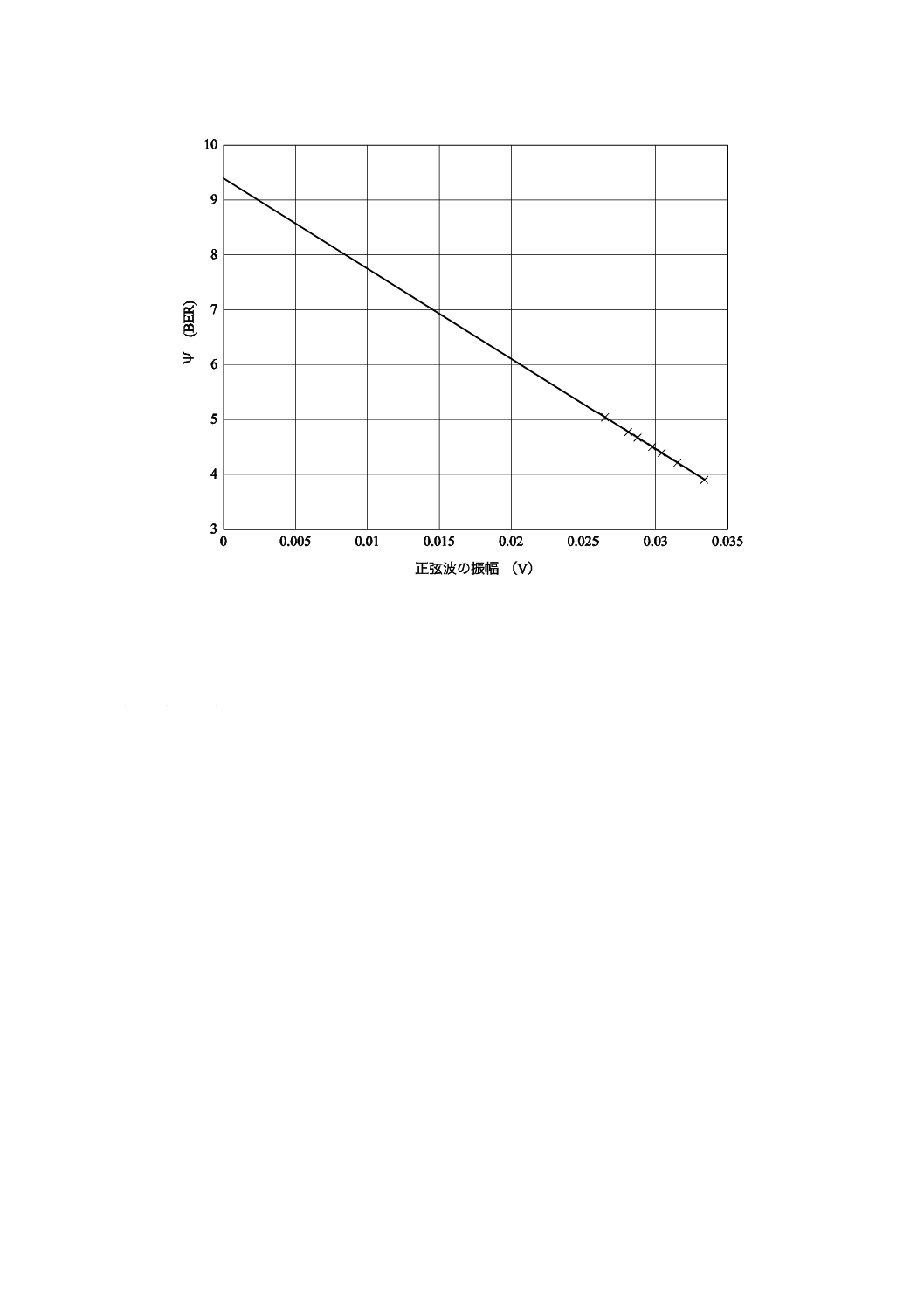
B.5.2 外挿法によるビット誤り率の計算
Ψ(BERi)対Aiのグラフを作成し,直線でフィッティングする。その直線をA0=0の縦座標に外挿し,
Ψ(BER0)=Qの値を得る(図B.3参照)。
被試験システムが動作しているときのビット誤り率の推定値を,次の式によって求める。ただし,erfc
近似を使用するので高いビット誤り率には適用できないため,10−4より高いビット誤り率のデータを使用
してはならない。
π
2
3
1
1
2
2
1
4
2
2
2
−
−
−
+
−
×
≈
=
Q
Q
e
Q
Q
erfc
BER
Q
ここに,
BER: ビット誤り率
erfc: 補誤差関数
Q: Q値
24
C 61280-2-8:2010 (IEC 61280-2-8:2003)
図B.3−正弦波干渉法に基づくビット誤り率の結果(データポイント及び外挿直線)
B.5.3 外挿法による結果の例
50 Mbit/sシングルモードデータリンクのビット誤り率を次の三つの方式によって測定し,B.5.2に示す
外挿法で求めた結果の例を,図B.4に示す。
− 10−10までの通常のビット誤り率測定
− B.4.1の光正弦波干渉法による外挿
− B.4.2の電気正弦波干渉法による外挿
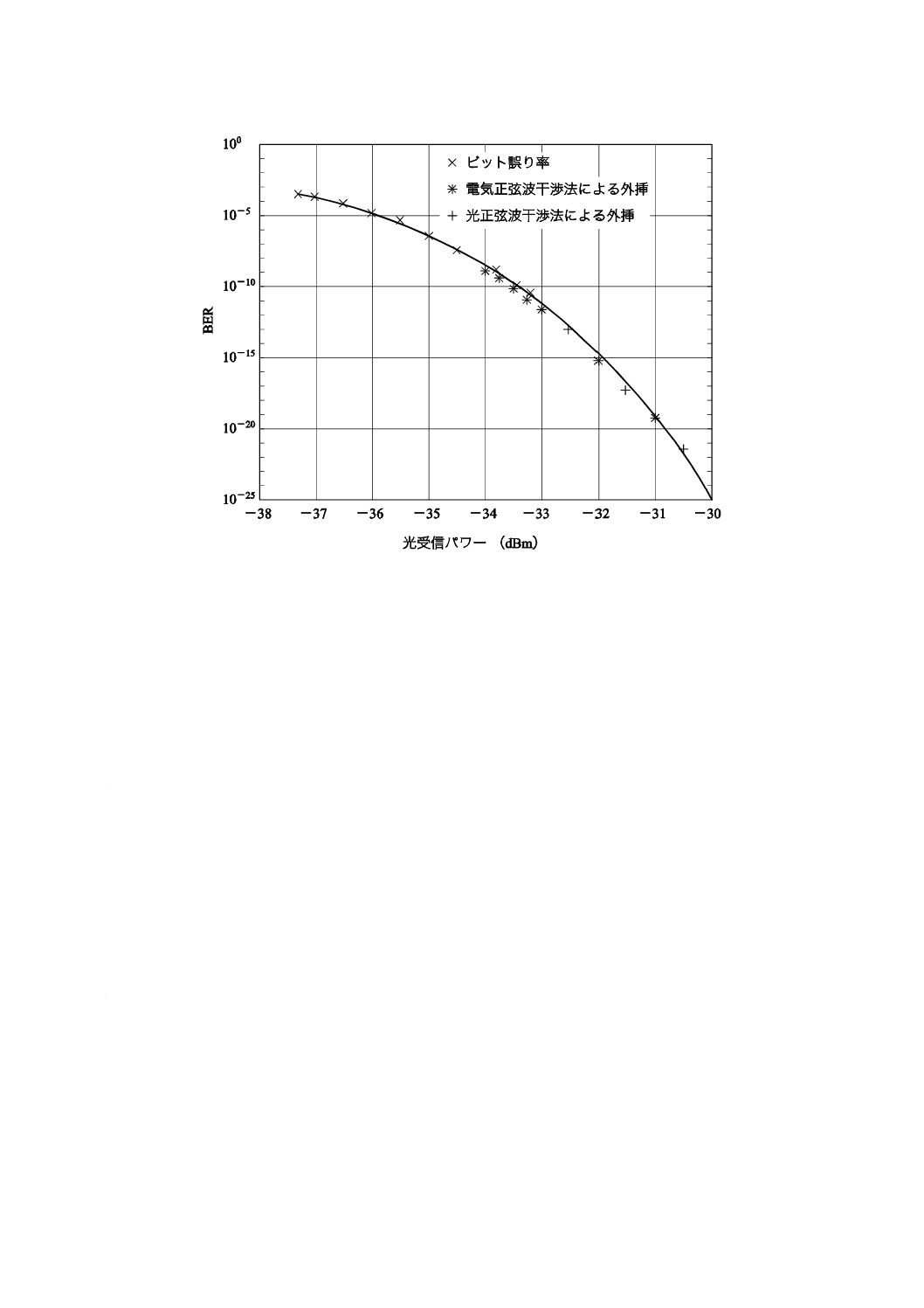
25
C 61280-2-8:2010 (IEC 61280-2-8:2003)
図B.4−三つの方式のビット誤り率対光パワー
実線は,光受信器及び光送信器の雑音に最良推定値を適用して測定データに誤差関数をフィットさせた
ものである。光受信器の雑音は受信パワーに依存せず,光送信器からの雑音は受信パワーに比例する。
B.6
測定の記録
各々の試験において,次に示す情報を記録する。
a) 試験の日付
b) この規格の番号
c) サンプルの識別情報
d) 光送信器の種別
e) 光受信器の種別
B.7
具体的な情報
次に示す情報を記録する。
a) この規格の番号
b) 試験に対する特別な要求事項
c) 合否判定の基準
26
C 61280-2-8:2010 (IEC 61280-2-8:2003)
参考文献
[1] TIA/EIA-526-4A,OFSTP-4 Optical Eye Pattern Measurement Procedure
[2] TIA/EIA-526-8,OFSTP-8 Accelerated Measurement of Low BER in Digital Fibre Optic Systems
[3] TIA/EIA-526-9,OFSTP-9 Accelerated Measurement Procedure for Determining BER and Q-Factor in Optical
Transmission Systems Using the Variable Threshold Method
[4] PALACHARLA, P. et al. Techniques for Accelerated Measurement of Low Bit Error Rates in Computer Data
Links. International Conference on Computers and Communications, Phoenix, March 1995
[5] BERGANO, NS., KERFOOT, FW. and DAVIDSON, CR. Margin Measurements in Optical Amplifier Systems.
IEEE Photonics Technology Letters, March 1993, Vol. 5, No. 3, p.304-306
[6] HUMBLET, PA. and AZIZOGLU, M. On the bit error rate of lightwave systems with optical amplifiers. IEEE
/OSA J. Lightwave Technol., 1991, vol. LT-9, p.1576-1582
[7] HP E4543A:Q Factor and Eye Contour Application Software
[8] BEVINGTON, Philip R. Data Reduction and Error Analysis for the Physical Sciences. McGraw Hill, 1969,
p.92

















