C 6842:2012
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 光ファイバの種類 ············································································································· 2
5 試験状態························································································································· 3
6 概要······························································································································· 3
6.1 偏波モード分散 ············································································································· 3
6.2 偏波モード分散試験方法 ································································································· 3
6.3 基準試験方法 ················································································································ 6
6.4 注意事項 ······················································································································ 6
7 装置······························································································································· 7
7.1 一般事項 ······················································································································ 7
7.2 光源及び偏光子 ············································································································· 7
7.3 入射光学系 ··················································································································· 7
7.4 入射位置決め装置 ·········································································································· 7
7.5 クラッドモード除去器 ···································································································· 7
7.6 高次モードフィルタ ······································································································· 7
7.7 出射位置決め装置 ·········································································································· 7
7.8 出射光学系 ··················································································································· 7
7.9 光検出器 ······················································································································ 8
7.10 コンピュータ ··············································································································· 8
8 サンプリング及び試料 ······································································································· 8
8.1 一般事項 ······················································································································ 8
8.2 試料の長さ ··················································································································· 8
8.3 設置 ···························································································································· 9
9 手順······························································································································· 9
10 計算又は結果の解釈 ········································································································ 9
11 結果 ····························································································································· 9
11.1 測定ごとに報告する情報 ································································································ 9
11.2 要求に応じて提供する情報 ···························································································· 10
12 仕様情報 ······················································································································ 10
附属書A(規定)偏波モード分散試験方法A−固定アナライザ法(FA) ········································ 11
附属書B(規定)偏波モード分散試験方法B−ストークスパラメータ解析法(SPE) ························ 21
附属書C(規定)偏波モード分散試験方法C−干渉法(INTY) ··················································· 26
C 6842:2012 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
附属書D(参考)フリンジ包絡線からのRMS幅の決定 ······························································ 36
附属書E(参考)記号及び用語 ······························································································ 40
附属書JA(参考)JISと対応国際規格との対比表 ······································································ 43
C 6842:2012
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人光産業技術振興協会(OITDA)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
C 6842:2012
光ファイバ偏波モード分散試験方法
Measurement methods and test procedures―Polarization mode dispersion
of optical fibers
序文
この規格は,2008年に第3版として発行されたIEC 60793-1-1及び2007年に第2版として発行された
IEC 60793-1-48を基に,対応する部分については対応国際規格を基とし作成した日本工業規格であるが,
対応国際規格には規定されていない規定項目(光ファイバの種類及び試験状態)を追加している。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JAに示す。
1
適用範囲
この規格は,シングルモード光ファイバ及びケーブルの偏波モード分散の実用的試験方法について規定
する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 60793-1-1:2008,Optical fibres−Part 1-1: Measurement methods and test procedures−General
and guidance
IEC 60793-1-48:2007,Optical fibres−Part 1-48: Measurement methods and test procedures−
Polarization mode dispersion(全体評価:MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS C 6122-11-1 光増幅器−測定方法−第11-1部:偏波モード分散パラメータ−ジョーンズマトリク
ス固有値解析(JME)法
注記 対応国際規格:IEC 61290-11-1:2008,Optical amplifiers−Test methods−Part 11-1: Polarization
mode dispersion parameter−Jones matrix eigenanalysis (JME)(IDT)
JIS C 6820 光ファイバ通則
注記 対応国際規格:IEC 60793-1-1,Optical fibres−Part 1-1: Measurement methods and test procedures
−General and guidance(MOD)
JIS C 6825 光ファイバ構造パラメータ試験方法−光学的特性
注記 対応国際規格:IEC 60793-1-44,Optical fibres−Part 1-44: Measurement methods and test
2
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
procedures−Cut-off wavelength(MOD)
JIS C 6835 石英系シングルモード光ファイバ素線
注記 対応国際規格:IEC 60793-2-50,Optical fibres−Part 2-50: Product specifications−Sectional
specification for class B single-mode fibres(MOD)
JIS C 6870-3 光ファイバケーブル−第3部:屋外ケーブル−品種別通則
注記 対応国際規格:IEC 60794-3,Optical fibre cables−Part 3: Sectional specification−Outdoor cables
(MOD)
JIS C 60068-1 環境試験方法−電気・電子−通則
IEC 61280-4-4,Fibre optic communication subsystem test procedures−Part 4-4: Cable plants and links−
Polarization mode dispersion measurement for installed links
IEC/TR 61282-3,Fibre optic communication system design guides−Part 3: Calculation of link polarization
mode dispersion
IEC/TR 61282-9,Fibre optic communication system design guides−Part 9: Guidance on polarization mode
dispersion measurements and theory
IEC 61290-11-2,Optical amplifiers−Test methods−Part 11-2: Polarization mode dispersion parameter−
Poincaré sphere analysis method
IEC/TR 61292-5,Optical amplifiers−Part 5: Polarization mode dispersion parameter−General information
IEC 61300-3-32,Fibre optic interconnecting devices and passive components−Basic test and measurement
procedures−Part 3-32: Examinations and measurements−Polarization mode dispersion measurement for
passive optical components
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS C 6820による。
注記 参考として,記号及び用語の一覧を,附属書Eに記載している。
4
光ファイバの種類
光ファイバの偏波モード分散試験方法において規定する光ファイバは,JIS C 6820によって表1のよう
に分類する。
表1−光ファイバの種類
光ファイバの種類
JIS記号
対応国際規格IEC記号
シングルモード1 310 nmゼロ分散形光ファイバ
SMA
B1.1
シングルモード1 550 nmカットオフシフト形光ファイバ
SMA・T
B1.2
シングルモード1 310 nmゼロ分散・低OH形光ファイバ
SMA・U
B1.3
シングルモード1 550 nm分散シフト形光ファイバ
SMB
B2
シングルモードノンゼロ分散シフト形光ファイバ
SMD
B4
シングルモード広波長域ノンゼロ分散シフト形光ファイバ
SME
B5
シングルモード低OH・曲げ損失低減形光ファイバ
SMF・A
B6̲a
シングルモード曲げ損失低減形光ファイバ
SMF・B
B6̲b
3
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
試験状態
試験状態は,JIS C 60068-1の5.3[測定及び試験のための標準大気条件(標準状態)]に規定する大気条
件の標準範囲(温度15〜35 ℃,相対湿度25〜75 %,気圧86〜106 kPa)とする。ただし,標準大気状態
で試験することが困難な場合は,判定に疑義が生じない場合,標準大気状態以外で試験を行ってもよい。
その場合は,試験状態を記録する。
6
概要
6.1
偏波モード分散
偏波モード分散(PMD)は,時間領域でパルス幅を広げる。この分散は伝送システムの性能を劣化させ
る。この影響は群速度差及び位相差に関係し,信号の異なる偏光成分の到達時間差δτに相当する。十分に
スペクトル線幅の狭い光源に対しては,その影響は群遅延差(DGD)に相当し,光源の波長での直交する
主偏光状態(PSP)の間での差Δτとなる。広帯域伝送に対しては,遅延は二つに分かれ,時間領域で広が
った出力パルスとなる。この場合,パルス広がりはDGDの平均値に相当する。
長距離伝送では,DGDは,光ファイバ長全体に沿った複屈折の状態に依存するため,距離及び波長に対
してランダムである。光ファイバの時間に依存した温度変化及び機械的な変動にも影響される。このよう
な理由から,長距離の光ファイバのPMD特性を定めるには,期待値<Δτ>,すなわち波長に対する平均DGD
で表すことが有効である。一般に期待値<Δτ>は,δτ又はΔτのパラメータと違い,日々の変化又は光源の
違いによる変化に対して大きな変動は起こらない。加えて<Δτ>は光伝送システム性能の有効な指標となる。
“PMD”という用語は,異なる群速度をもつ二つの偏波モード間のDGDという一般的な意味又は期待値
<Δτ>という規定した意味で用いる。DGD値Δτ又はパルス広がりδτは波長,時間又は温度に対して平均化
することで,それぞれ<Δτ>λ,<Δτ>t及び<Δτ>Tを求めることができる。多くの場合,<Δτ>を求めるこれら
の様々な条件を区別する必要はない。
結合長lcは,二つの偏光状態の間ではっきりとしたモード結合が起こる光ファイバ又はケーブルの長さ
である。光ファイバ長Lが,L<<lcの条件を満たす場合は,モード結合は無視することができ,<Δτ>は光
ファイバ長に比例する。この場合の“短距離”の偏波モード分散係数PMDSは,次のようになる。
L
PMD
τ
∆
=
S
実際のシステムでは,光ファイバはほとんどL>>lcの条件であり,モード結合はランダムである。モー
ド結合がランダムである場合,<Δτ>は光ファイバ長の平方根に比例する。この場合の“長距離”の偏波モ
ード分散係数PMDLは,次のようになる。
L
PMD
τ
∆
=
L
6.2
偏波モード分散試験方法
この規格は,三つのPMD試験方法を規定する(詳細は,附属書A,附属書B及び附属書C参照)。次
に試験方法を示す。方法によって,複数の測定結果解析方法がある。
− 方法A:固定アナライザ法(FA)
・極値カウント法(EC)
・フーリエ変換法(FT)
・コサインフーリエ変換法(CFT)
4
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 方法B:ストークスパラメータ解析法(SPE)
・ジョーンズ行列解析法(JME)
・ポアンカレ球解析法(PSA)
・偏光状態法(SOP)
− 方法C:干渉法(INTY)
・慣例的解析法(TINTY)
・一般的解析法(GINTY)
PMDの値は,DGD値Δτと定義し,通常,波長によってランダムに変化するため,次の二つの統計的な
量のうちのいずれかで表す。式(1)は線形な平均値を表し,光ファイバケーブルの特性に用いる。式(2)は二
乗平均平方根(RMS)の値を表し,幾つかの方法によって求めることができる。DGDがランダムなマク
スウェル分布に従っていると推定できるとき,式(3)を用いて,一つの値をもう一方の値に変換することが
できる。
τ
∆
=
AVG
PMD
········································································· (1)
2/1
2
RMS
τ
∆
=
PMD
····································································· (2)
2
/1
2
2
/1
3
8
τ
π
τ
∆
=
∆
································································ (3)
注記 式(3)は,DGDの分布がマクスウェル分布である場合にだけ適用する。例えば,光ファイバの
モード結合がランダムである場合である。式(3)の一般的な使用方法は統計的解析法によって検
証できる。光ファイバ中にその他の部分に比べて複屈折が大きくなる箇所がある場合は,マク
スウェル分布とならないことがある。例えば,強い曲げ又は張力がかかった状態で連続的に曲
げ半径が小さくなる配置状態のようなモード結合を減少させる箇所が存在する場合である。こ
れらの場合は,DGD分布は三つの自由度をもった非心カイ二乗分布の平方根に近くなっていく。
このような場合,PMDRMSの値は,式(3)で表すPMDAVGの値に比べて大きくなる。PMDRMSを基
にした方法C及び方法Aのコサインフーリエ解析といった時間領域の解析方法では,PMDAVG
に変換するために式(3)を用いることができる。モード結合が少ない場合には,これらの方法で
得たPMDの値は,方法Bのような周波数領域での測定方法で求めたPMDAVGよりも大きくな
る場合がある。
偏波モード分散係数は,PMD値を光ファイバの距離で規格化した値である。ランダムなモード結合が起
こりDGDがマクスウェル分布に従う通常の伝送用光ファイバに対しては,PMDの値を光ファイバ長の平
方根で除して,偏波モード分散係数は
km
ps
の単位で表す。偏波面保存光ファイバのように,モード結
合が無視できる光ファイバの場合には,PMDの値を光ファイバ長で除して,偏波モード分散係数はps/km
の単位で表す。
全ての方法は,製造時の光ファイバ又は光ファイバケーブルの測定に適している。全ての方法において,
測定品の配置を変えることによって,測定結果が変化する。動いたり振動が加わる敷設した光ファイバケ
ーブルに対しては,方法C又は方法B(ミリ秒単位の測定時間で完了する。)を用いるのが適切である。
全ての方法に対して,一つ以上の偏光状態に制御した光源が必要である。全ての方法に対して,測定波
5
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
長帯域(例えば,1 300 nm又は1 550 nm)でのPMD特性値を得るために,広い波長領域(例えば,50 nm
から200 nmまでの幅)にわたるスペクトル領域をもつ入射光が必要である。各試験方法は,次の点で異
なる。
a) 光源の波長特性
b) 実際に測定する物理的特性
c) 解析方法
方法Aにおいて,PMDは,スペクトル幅の狭い光を利用して,測定波長領域での変化を測定すること
によって求めることができる。光源から発生する光は,一つ以上の直線偏光状態をもつ。それぞれの偏光
状態に対して,固定の検光子を通過する光パワーの波長に対する変化を,検光子がない場合の光パワーと
比較して測定する。測定した結果は,次の三つの方法のうちのいずれかを用いて解析する。
− 曲線のピーク及び谷の数を数え(極値カウント),DGDを算出する[1]。DGDがマクスウェル分布であ
る場合には,DGDの平均値に一致する。この解析法は,周波数領域測定である。
− 測定した結果にフーリエ変換を行う。このフーリエ変換は,方法Cの広帯域伝送によって得られるパ
ルス広がりと等価である。DGDがマクスウェル分布である場合には,フーリエ変換関数の広がり特性
はDGDの平均値に一致する。
− 互いに垂直な二つの検光子の設定によって得た規格化スペクトルの差をコサインフーリエ変換し,二
乗包絡線のRMSを計算することで,PMDRMSの値を得ることができる。この方法は,干渉法で得た相
互相関関数のフリンジパターンの計算と等価である。
方法Bにおいて,PMDは,スペクトル幅の狭い光を利用して,測定波長領域での変化を測定すること
によって求めることができる。光源から発生する光は,一つ以上の直線偏光状態をもつ。各波長に対する
出力光のストークスベクトルを測定する。波長に対するDGDは,これらのストークスベクトルの光角周
波数ω及び入力偏光状態に対する変化から,次に示す式(4)及び式(5)の関係を用いて求める。
()
()()
ω
ω
ω
ω
s
d
ds
×
Ω
=
····································································· (4)
()
()
ω
ω
τ
Ω
=
∆
·········································································· (5)
ここに,
s: 規格化出力ストークスベクトル
Ω: PSPの方向をもつ偏波分散ベクトル(PDV)
Δτ: DGD
JME法及びPSA法はいずれも,通常,0°,45°及び90°(ポアンカレ球上において直交する)の三つ
の直線偏光状態の光を各波長で入射させる。
JME法は,各波長において,出力ストークスベクトルをジョーンズ行列に変換[2]し,隣接する波長の適
切な行列の組を求め,計算した固有値に偏角公式を適用することによって,DGDの計算を行う。
PSA法は,隣接する二つの波長のポアンカレ球上の出力ストークスベクトルの回転を推定するために,
規格化出力ストークスベクトルを行列計算し,アークサイン公式の応用を用いてDGDを求める。JME法
及びPSA法は,共通の仮定において数学的に等価である(IEC/TR 61282-9参照)。
SOP法は,規格化した測定ストークスベクトルを用いた式(4)の区分的な評価を基にしている。SOP法は,
出力ストークスベクトルの変化が規則的(モード結合を無視することができる。)な場合,正確な結果を得
6
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ることができるが,出力ベクトルが急激に又は不規則に変化したときは不正確な結果になる(IEC/TR
61282-9参照)。JME法及びPSA法で用いる三つの入力偏光状態で測定することによって,より正確に測
定できる。
方法Cは,直線偏光状態の広帯域光源を用いる。出力する電磁場の相互相関を,出力光の干渉パターン,
すなわち干渉スペクトルによって決定する。光源の波長スペクトル領域に対するPMD遅延を,干渉スペ
クトルのフリンジパターンの包絡線から決定する。PMD遅延を求めるために,次の二つの解析方法を用い
ることができ(IEC/TR 61282-9参照),その両方でPMDRMSの値を算出できる。
− TINTYは,適切な測定結果を得るための特定の測定条件において,基本設定を用いる。
− GINTYは,測定条件に制限はなく,TINTYと同様な基本設定以外に,異なる設定も用いることがで
きる。
GINTYは,TINTYよりも複雑である。PMDの再現性は,PMD値及び測定波長範囲に依存している[3]。
広い測定波長範囲及び高いPMD値に対して,相対的により良い再現性が達成できる。低PMD値の測定と
比較した場合,高PMD,例えば,0.5 psの測定においては,解析方法の違いは重要ではない。
三つの試験方法に共通する事項を,箇条6から箇条12に示す。また,各試験方法に関する事項は,それ
ぞれ附属書A,附属書B及び附属書Cに規定する。全ての方法に対する数式は,IEC/TR 61282-9による。
6.3
基準試験方法
基準試験方法は,方法B ストークスパラメータ解析法(JME法及びPSA法だけ)である。
6.4
注意事項
光ファイバのPMDは,統計的に扱う値であり,PMDQ又はリンク設計値と呼ばれる値は,光ファイバケ
ーブルのサンプル測定及びそれらを連結した線路に対する計算に基づく(PMDの統計的な規定は,JIS C
6870-3による)。光ファイバケーブルのPMDは,ケーブルの構造及び製造工程の影響のため,ケーブル化
していない光ファイバの値から変化する場合があるが,ケーブル化した光ファイバのPMDQの限界値を得
るためには,ケーブル化していない光ファイバのPMDQの限界値が必要である。一般的な慎重論では,ケ
ーブル化していない光ファイバのPMDQは,ケーブル化した光ファイバのPMDQの半分以下とみなしてい
る。特別な構造及び安定なケーブル化工程によって,別の限界値も定めてもよい。
光ファイバ又はケーブル配置は,外部要因によるモード結合が最小になるように設定する。そのような
外部要因として,次の項目を挙げることができる。
a) 過大な張力
b) 次の要因による過大な曲げ
・出荷用ボビン上の光ファイバの重なり
・小さすぎるスプールにケーブルを巻いたときの縮み
・小さすぎる曲げ半径
c) 過大なねじり
光ファイバを変動することによって,全てのモード結合の組合せを起こして,測定の再現性を評価する。
これは,例えば,温度を僅かに変化させたり,配置状態を少し変えたりすることで実現できる。測定にお
ける再現性の基本的な限界に関して,PMDが大きくなるにつれ,又は光源のスペクトル線幅が広がるにつ
れ,繰り返し測定のばらつきが改善する[3]。PMD測定が光ファイバケーブルの統計的特性の評価を兼ねて
7
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
いる場合(JIS C 6870-3参照),この変化特性によって,リンク設計値の測定値が実際の値よりも大きくな
る場合がある。
分散補償器,光増幅器などの他の光部品を含んだシステムに対するPMD計算の指針は,IEC/TR 61282-3
による。光増幅器に対する試験方法は,JIS C 6122-11-1及びIEC 61290-11-2により,また他の設計指針は
IEC/TR 61292-5による。増幅された箇所を含むテストリンクに対する試験方法は,IEC 61280-4-4による。
光部品に対する試験方法は,IEC 61300-3-32による。PMDに対する一般的な情報,試験方法の適用に関連
する数式,及び異なる光源又は検出器の使用に関するサンプリング理論に対する検討は,IEC/TR 61282-9
による。
7
装置
7.1
一般事項
次に示す装置は,三つの全ての測定方法に共通である。附属書A,附属書B及び附属書Cに,構成図及
び三つの各測定に必要な装置を示す。
7.2
光源及び偏光子
光源のスペクトル特性に関する詳細な条件は,附属書A,附属書B及び附属書Cによる。光源は,目的
とする波長で十分な強度が必要であり,測定中安定なものとする。入射光源の偏光状態(SOP),偏光度
(DOP),及び偏光子又は偏光コントローラを用いることに関する指針は,IEC/TR 61282-9による。
7.3
入射光学系
試料を励振するために,光学レンズ系又は光ファイバピグテールを設置する。試料に入射する光パワー
は,試料の入射端面の位置に相対的に影響を受けないことが望ましい。この状態は,入射光が入射端面を
空間的,角度的に十分覆うことで達成される。
突合せ接続を用いる場合は,干渉効果を避けるため,光ファイバピグテールと試料との間に屈折率整合
剤を使用する。入射結合状態は,測定中安定に維持する。
7.4
入射位置決め装置
試料の入射端を光源に合わせる装置を準備する。例えば,x-y-z微調位置合わせ装置,又はコネクタ,真
空結合,3-ロッド結合などの機械的結合装置である。光ファイバの位置は,測定中安定に維持する。
7.5
クラッドモード除去器
クラッドモードを除去する装置を用いる。ある条件下では,光ファイバ被覆がこの機能を果たす。
7.6
高次モードフィルタ
試料のカットオフ波長(JIS C 6825参照)以上の波長領域の高次伝搬モードを取り除くための手段を用
いる。例えば,一般的には,曲げ半径30 mmの1周回のループを光ファイバに与えることで十分である。
7.7
出射位置決め装置
光ファイバの出射端面を出射光学系に合わせるための適切な手段を用いる。そのための結合方法として,
レンズを用いるか,又は検出器ピグテールに対して機械的コネクタを用いる。
光ファイバを出射光学系から一定の距離に設置するために,側面観察顕微鏡,十字線を備えたカメラな
どの手段を用意する。真空チャックなどの装置によって光ファイバの側面を固定している場合には,軸方
向調整だけで十分である。
7.8
出射光学系
附属書A,附属書B及び附属書Cによる。
8
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.9
光検出器
光検出器は,測定強度範囲にわたり線形で,測定中安定な計器を用いる。典型的なシステムは,チョッ
パ/ロックイン増幅器による同期検出器,光パワー検出器,光スペクトラムアナライザ又は偏光解析器を
含む。光源のスペクトル範囲全体を用いるために,検出システムは,光源からの発生波長を含む波長領域
で動作する必要がある。個別な詳細に対しては,附属書A,附属書B及び附属書Cによる。
7.10 コンピュータ
装置を制御し,強度測定を行い,最終的な結果を得るためのデータ解析を行うために,コンピュータを
用いる。
8
サンプリング及び試料
8.1
一般事項
試料は,既知の長さのケーブル化しているか又はしていないシングルモード光ファイバ(JIS C 6835)
とする。試料及びピグテールは,測定中は通常一定温度の場所に固定する。個別規格に規定がない場合,
標準大気状態で行う。敷設した光ファイバ及びケーブルの場合は,一般的な設置状態を用いる。
試験装置の機械的及び温度安定性は,次の手順によって観測する。方法Aでは,一定の波長での光ファ
イバからの出力パワーを適切な出力解析器によって測定する。標準的な測定時間内での光源の出力パワー
変化を,波長依存性による変化に比べて小さくする。方法Bでは,ポアンカレ球上における試料の出力偏
光状態(SOP)を観察する。隣接するジョーンズ行列対を測定する時間内での出力偏光状態の変化を,波
長依存性による変化に比べて小さくする。方法Cは,僅かな温度変動又は光ファイバの動きに対して影響
を受けにくい。
試料の入射及び出射端面は,装置及び手順に合わせて適切に準備する。全ての反射を避けるように注意
する。
8.2
試料の長さ
試料の長さは,次の三つの条件を用いて規定する。
a) 最小要求PMD係数
b) モード結合状態
c) 信号雑音比
各試験方法は,測定可能な最小PMD(ps)に制限を受ける。多くの場合,この最小値は理論的に決定で
きる。また,測定ばらつきを調べることによって,実験的に決定することもできる。ランダムなモード結
合法則に従う光ファイバに対しては,最小PMD係数は,PMDを光ファイバ長の平方根で除して求める。
モード結合を無視できる場合は,光ファイバ長で除して求める。よって,試料の長さ及び測定可能な最小
PMDで,測定可能な最小PMD係数を決定できる。この最小値より長い光ファイバ又はケーブルを選択す
るか,又は条件を満足する長さになるように試料を切断する。測定可能な最小PMD値を記録し,個々の
試料の長さを記録する。
注記 長さは,設置方法(8.3参照)又は装置のダイナミックレンジによって制限を受ける場合もある。
JIS C 6870-3及びIEC/TR 61282-3で規定する値は,
km
ps
の単位のPMD係数で表現しており,実質
的にこの規格では,測定長がランダムモード結合状態を満足する長さであることを仮定している。光ファ
イバの種類又はケーブル構造が既知の場合には,試料をカットバックし,幾つかの長さ条件に対してPMD
値を測定するカットバック測定を行うことによって,モード結合状態を確認することができる。PMDが条
9
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
長の平方根に比例している場合,その長さの光ファイバでは,ランダムなモード結合状態であるとみなす。
試験方法,光源のパワー,及び長さに依存する試料全体の損失は,ダイナミックレンジを制限する。こ
の制限は,一般的に測定手段に依存する装置構成によって決まる。
8.3
設置
光ファイバ及びケーブルの設置状態は結果に影響を与える。仕様適合評価に用いる通常の測定に対して
は,次の条件を適用する。
8.3.1
ケーブル化していない光ファイバ
ケーブル化していない光ファイバの測定では,設置によるモード結合の発生を最小にすることが重要で
あり,ケーブル化した光ファイバのPMDQを測定する第一要件を満たすことで達成できる。光ファイバは
大きなボビン(通常,最低150 mmの巻き半径をもつボビン)に巻き,光ファイバにかかる張力をできる
だけ小さくし(例えば,5 g以下),光ファイバの重なりには張力がかからないようにする。この設置要求
事項は,ボビン径にもよるが,測定可能な光ファイバ条長を制限し,測定が不可能となる場合がある。多
層巻きは可能であるが,短い光ファイバ条長での1層巻きとの比較によって,問題がないことを確認する。
ケーブル化していない光ファイバを出荷ボビンに巻いた状態で測定することは望ましくない。この状態
でのPMD測定結果は,高PMD光ファイバに対してはケーブル状態で得られる値よりも小さく,また低
PMD光ファイバに対してはケーブル状態で得る値よりも大きな値が観察される場合がある。
8.3.2
光ファイバケーブル
出荷用ドラムに巻いたケーブルのPMDは,敷設設置した光ファイバケーブルのPMDとは必ずしも一致
しない。したがって,製造時の測定においては,敷設を模擬した状態又はドラムに巻いた状態のPMDと
巻いていない状態のPMDとを関連付けるマッピング関数を用いてもよい。厳密な設置状態は,供給者と
使用者との間の同意による。
9
手順
9.1
光ファイバ又はケーブルを配置し,末端を準備する。
9.2
末端に,入射及び出射光学系を接続する。
9.3
三つの測定方法に対して,附属書A,附属書B及び附属書Cに規定する掃引又は測定を実行するた
めに,コンピュータを用いる。
9.4
データ記録を完了する。
10 計算又は結果の解釈
附属書A,附属書B及び附属書Cに,測定データをPMDに変換する計算例を示す。PMD係数の計算は,
ランダムモード結合か又はモード結合を無視できる状態かに従って行う。JIS C 6835に規定する光ファイ
バに対しては,PMDは,光ファイバ長の平方根で規格化した値(単位:
km
ps
)である。
11 結果
11.1 測定ごとに報告する情報
測定ごとに次の情報を報告する。
a) 試料の識別
b) 測定実施期日
c) 試料の長さ
10
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 用いた波長領域(例えば,1 550 nm)
e) ps単位のPMD,及びPMDAVG又はPMDRMSのうちいずれかの測定か
f)
PMD係数及びその単位(
km
ps
又はps/km)
11.2 要求に応じて提供する情報
次の情報は,要求がある場合,提供する。
a) 用いた測定方法
b) 用いた計算方法
c) 設置方法の詳細(光ファイバを固定する装置を含む。)
d) 用いた波長範囲
e) 方法A及び方法Bで,狭帯域光源を波長ステップモードで用いた場合は,波長ステップ数
f)
方法Cを用いた場合は,フリンジ検出方法の種類
g) 試験装置構成
h) 測定装置の最新の校正日時
i)
モード結合状態(PMD係数の単位で示す。)の根拠
j)
方法Bで狭帯域光源を波長ステップモードで用いた場合は,波長領域の分解能
k) 方法Bで広帯域光源(BBS)を用いた場合は,3dB線幅及び3dB線幅測定時の中心波長
12 仕様情報
詳細な仕様は,次の情報を明示する。
a) 光ファイバ又はケーブルの種類
b) 合否判定基準
c) 使用波長領域
d) 適用する手順との差異
11
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
偏波モード分散試験方法A−固定アナライザ法(FA)
A.1 装置
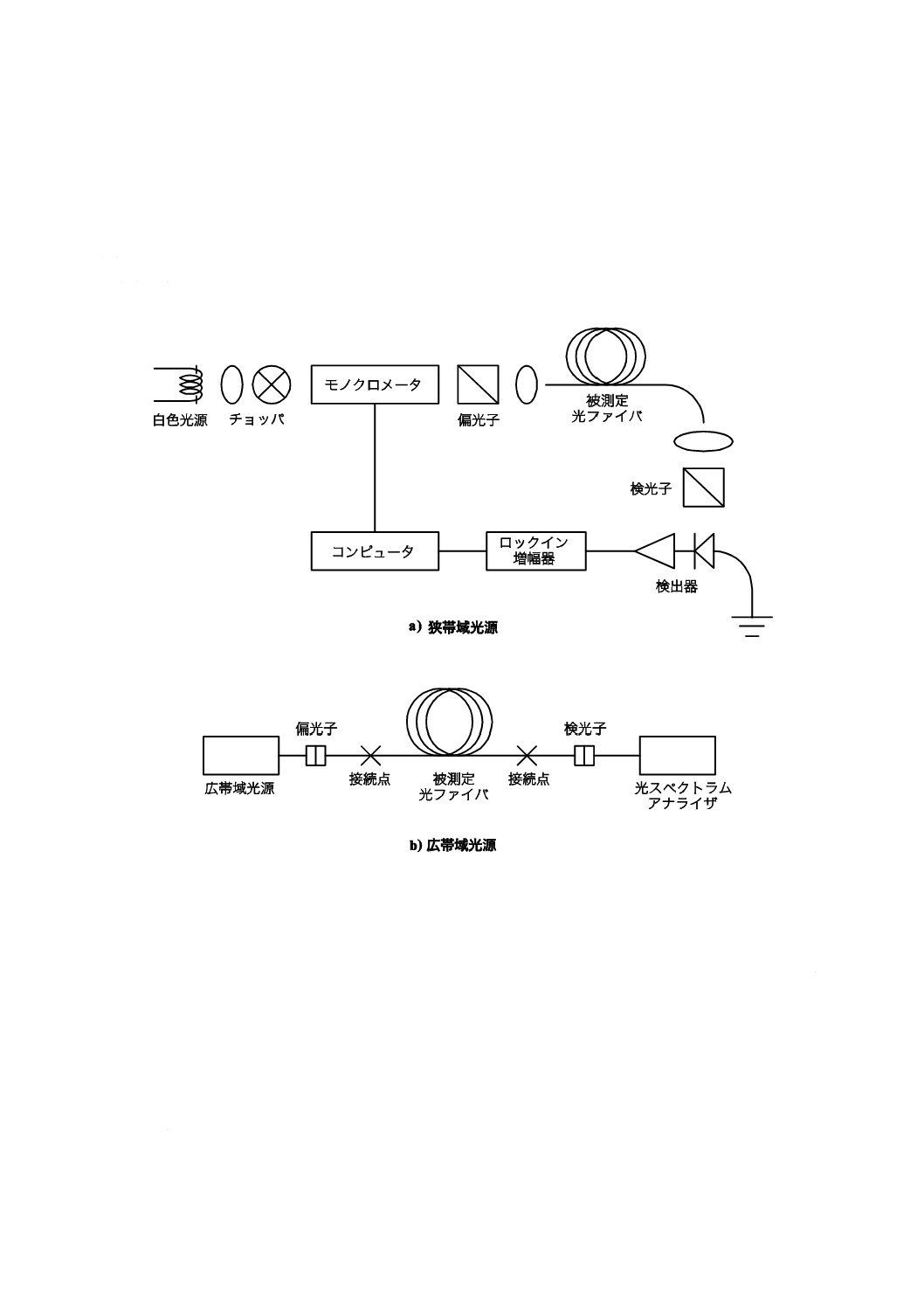
試験構成を,図A.1に示す。
図A.1−方法Aの試験構成
A.1.1 光源
解析装置の種類に応じ,二種類の光源のうち適切な一つを選択して用いる。例えば,図A.1 a) に示す白
色光源とモノクロメータとの組合せなどによる狭帯域光源は,偏光解析装置とともに用いる。図A.1 b) に
示す広帯域光源は,光スペクトラムアナライザ,又は検光子の前にフーリエ変換スペクトル解析装置を用
いた干渉計のような狭帯域透過解析装置と共に用いる。広帯域光源の場合,フィルタの幅を計算に必要な
スペクトル幅とする。
いずれの光源を用いる場合でも,スペクトル幅は,必要とする偏光度(7.2参照)を維持するために,十
分に小さくする。また,波長範囲は,規定した波長領域で十分正確なPMD測定が行うことができるよう
に,十分広くする(A.3参照)。
光スペクトルにおいて全ての特性を適切に決定するために,スペクトル幅が次の式(A.1)の関係を満足す
12
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
るようにする。
(
)1
max
0
8
−
∆
<
∆
τ
λ
λ
v
····································································· (A.1)
ここに,
ν=c/λ: 光周波数
Δλ: スペクトル幅
Δτmax: 予想最大DGD
A.1.2 検光子
検光子の角度方向は,重要ではないが,測定中一定に維持する。モード結合が無視できる場合又は低PMD
値の場合,検光子の調整によって,図A.2に示す変動強度を最大にできることもある。これは,接合部及
びコネクタ部における光ファイバを回転することによって達成できる。CFT法に対しては,検光子は,最
初の設定に対して垂直な設定にするために軸を回転できるようにする。
注記 検光子はポラリメータに変えることもできる。
A.2 手順
A.2.1 波長範囲及び測定間隔
測定範囲内で規定した波長又は光周波数の間隔で,光路に検光子を挿入した場合及び挿入しない場合に
対して,又は光路に検光子を挿入した場合及び検光子を最初の設定に対して垂直に変えた場合に対して,
波長(又は光周波数)の関数としてパワーを測定する。波長範囲は,測定結果の精度に影響を与える(A.3
参照)。測定波長の間隔は,式(A.1)において,Δλを測定波長間隔δλで置き換えた次の式(A.1A)を満足する
ように,設定する。
(
)1
max
0
8
−
∆
<
τ
λ
δλ
v
···································································· (A.1A)
FT法又はCFT法を用いる場合は,光周波数のステップ幅を理想的には均一とし,ステップ数は2の乗
数とする。モノクロメータ使用時のステップ幅(δν;光周波数)は,測定最大DGDに相当する振動周波
数の二分の一よりも小さくする。ランダムなモード結合をもつ光ファイバに対しては,二次モーメント以
外の多くの量のパワーのために,ナイキスト条件は少なくとも予測される最大DGDの二次モーメント周
波数の三倍とする。すなわち,光周波数δνは,次の式(A.2)を満足するように設定する。
max
6
1
τ
δ
∆
>
v
··········································································· (A.2)
注記1 FTによって,Δτmax近傍に多くのエネルギーが存在していることが明らかになった場合には,
測定間隔を狭めて再び測定する。
注記2 光源のスペクトル幅は,一般的に測定波長間隔以下である。例えば,Δτmax=0.67 psに対して
は,1 550 nmにおけるモノクロメータのスペクトル幅の典型値は2 nmである。
A.2.2 掃引の完了
光路中に設置した検光子を用いて掃引を完了する。受光パワーをPA(λ)として記録する。
光路から検光子を取り外し,掃引を繰り返す。受光パワーをPTot(λ)として記録する。
出力パワー比R(λ)を次の式(A.3)によって算出する。モード結合を無視できる場合及びランダムなモード
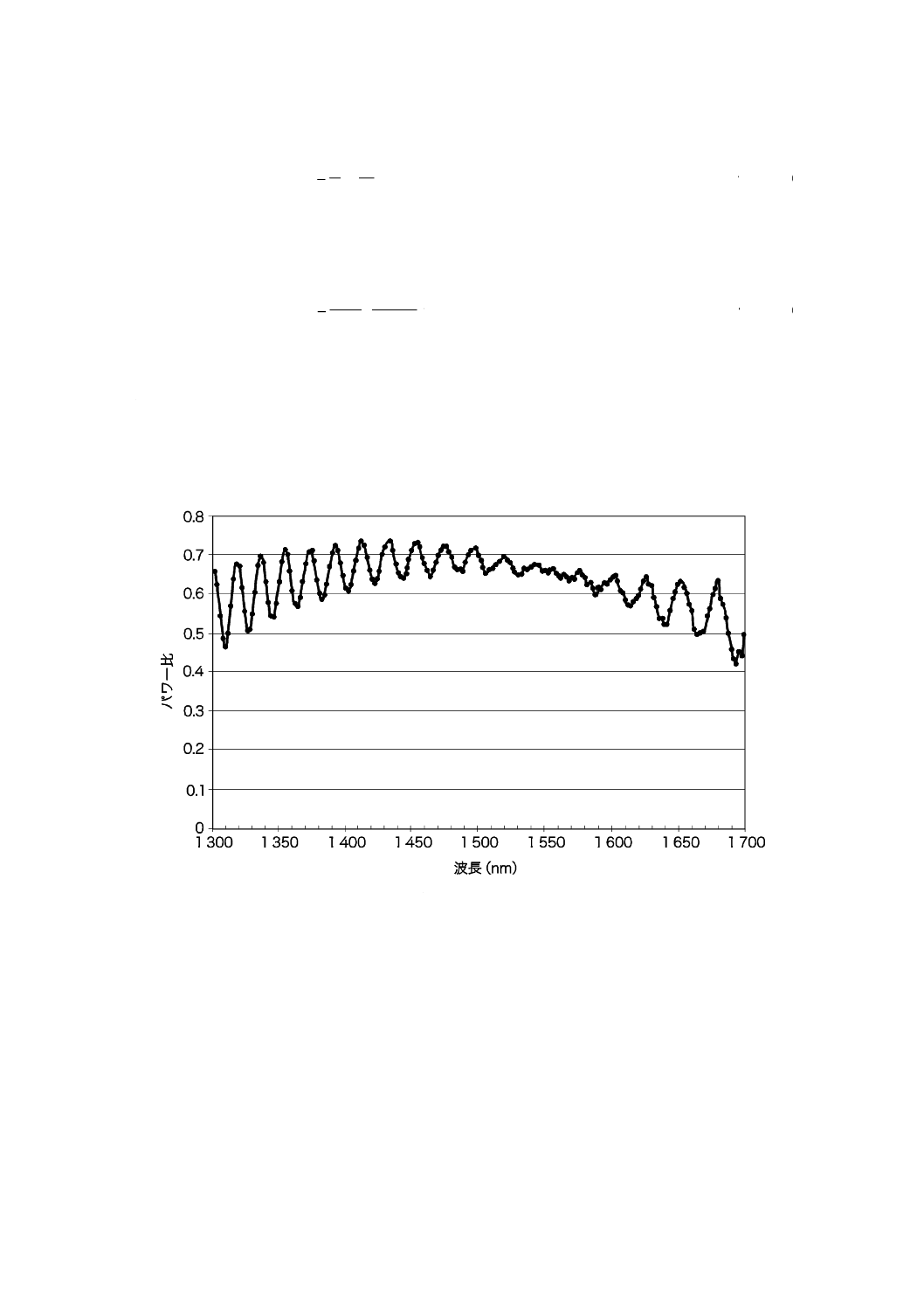
13
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
結合の場合の例を,図A.2に示す。
()
()()
λ
λ
λ
Tot
A
P
P
R
=
········································································ (A.3)
代替的な手順は,検光子を置いたまま角度を90度回転して2回目の掃引を行う方法である。パワーを
PB(λ)として記録する。パワー比は,次の関係式(A.4)によって算出する。
()
()
()
()
λ
λ
λ
λ
B
A
A
P
P
P
R
+
=
································································ (A.4)
注記1 極値カウント法を適用する場合にも,パワー比PA/PBを用いることができる。
注記2 検出装置としてポラリメータを用いる場合は,波長に対する規格化ストークスパラメータを
測定する。三つのスペクトル関数(ベクトル要素に対する)は受光パワーに対して独立で,
同じ方法で解析する三つの独立したパワー比関数に相当する。
a) モード結合を無視できる場合
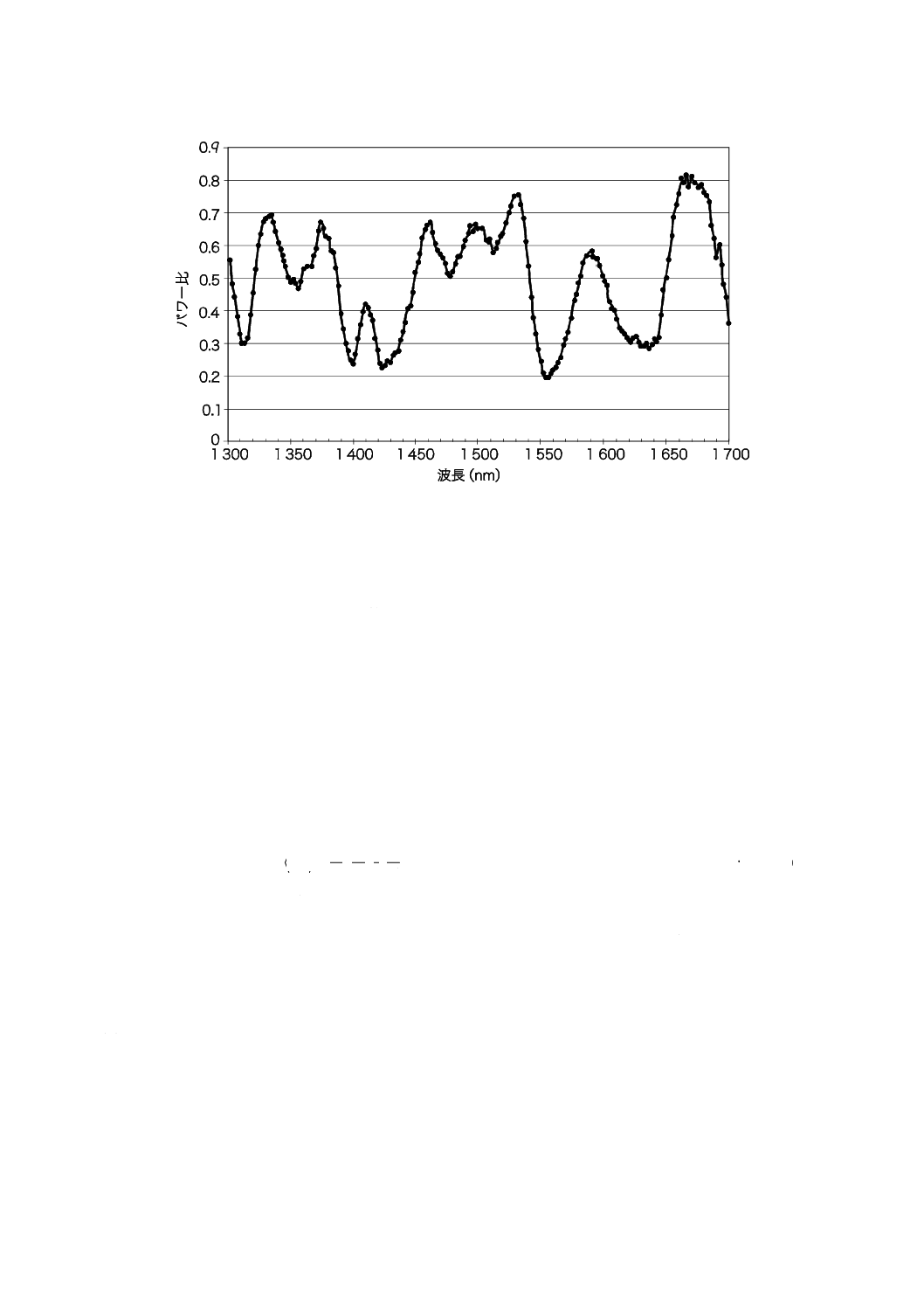
図A.2−方法Aによる典型的な測定結果
14
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) ランダムなモード結合の場合
図A.2−方法Aによる典型的な測定結果(続き)
A.3 計算
PMDを測定したパワー比関数から計算するためには,次の3通りの方法がある。
− 極値カウント法(EC)
− フーリエ変換法(FT)
− コサインフーリエ変換法(CFT)
A.3.1 極値カウント法(EC)
関数R(λ)は,最短波長λ1から最長波長λ2までの間で等しい波長間隔で求める。Eは波長範囲内の極値(極
大値及び極小値)の数である。また,λ1及びλ2が極値に当たるように波長範囲を定義し直すこともでき,
その場合には,Eは極値(λ1及びλ2を含む)の数から1を引いた値である。PMD値は,次の式(A.5)によ
って求める。
(
)
1
2
2
1
2
λ
λ
λ
λ
τ
−
=
∆
c
kE
··································································· (A.5)
ここに,
c: 真空中の光速度
k: モード結合係数 ランダムなモード結合
がない場合には1.0,完全にランダムなモ
ード結合がある場合には0.82である。
検出装置としてポラリメータを用いる場合は,三つの規格化ストークスパラメータによって導く値の平
均値をPMDとする。
雑音がある場合,極値を定めることが難しい。一つの解決方法は,極値評価のために,各データ点にお
いて,データを多項式でフィットさせることである。八つの波長点による三次多項式がよく用いられる。
A.3.2 フーリエ変換法(FT)
この方法において,R(λ)は通常,光周波数領域νの関数で表し,そのフーリエ解析はPMDを導出するた
めに用いる。フーリエ変換は光周波数領域データを時間領域データに変換し,直接,光の到達時間δτの分
15
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
布情報を与える。このデータを後で示すように処理して,被測定光ファイバのPMD期待値<Δτ>を導く。
この方法はモード結合が無視できるか又はランダムな場合に適用できる。
A.3.2.1 データの前処理及びフーリエ変換
フーリエ変換では,通常,光波長に対して得られたR(λ)のデータが,光周波数領域で等間隔となる必要
がある。代わりに,光周波数領域で等間隔の点を求めるために,等しい波長(λ)間隔で測定したデータをフ
ィット(例えば,三次スプライン関数を用いて)させて補間するか,又はより高等なスペクトル推定技術
を用いて求めてもよい。いずれの場合でも,各波長での比率R(λ)は,式(A.3)又は式(A.4)を用いて適切に計
算できる。
R(λ)に対して,ゼロ点付加,データ補間及び直流成分除去を行ってもよい。フーリエ変換前の事前調整
手段として,データにウインドウ関数を与えてもよい。フーリエ変換を行うことで,各値δτに対する強度
データ分布P(δτ)を求めることができる。
A.3.2.2 変換データフィット
R(λ)の直流成分は,部分的には検光子の挿入損失という可能性があるため,注意深く取り除かない場合
は,δτがゼロでのフーリエ変換データは意味をもたない。直流成分を取り除かない場合,その後の計算に
おいては,通常,2点のデータまでは無視する(用いない)。計算に含めるδτ=0よりも大きい最初の有効
データ点がj=0となるように,変数jを定義することができる。
その後の計算から測定雑音を取り除くため,典型的には検出システムのRMS雑音レベルの200 %に設定
するしきい値レベルT1とP(δτ)とを比較する。この時点で,光ファイバがモード結合を無視できるかラン
ダムであるかを決定しておく必要がある。
P(δτ)の有効データの最初のX点が全てT1よりも小さい場合は,P(δτ)がモード結合を無視できる光ファ
イバの離散的なスパイク状の特性であることを示している。フーリエ変換前にゼロ挿入をしない場合,X
の値は3である。ゼロ挿入を行った場合のXの値は,元のデータのポイント数を3倍して,ゼロ挿入後の
配列の全長で除した値とする。
モード結合を無視できる光ファイバに対して,PMDは式(A.6)によって算出する。また,ランダムなモ
ード結合の光ファイバに対して,PMDは式(A.7)によって算出する。
A.3.2.2.1 モード結合を無視できる光ファイバのPMD計算
モード結合を無視できる光ファイバ(例えば,高複屈折光ファイバ)又は複屈折部品に対しては,R(λ)
はチャープした正弦波形になる[図A.2 a)]。相対パルス到達時間δτに相当する位置に離散的スパイクを
もつP(δτ)出力をフーリエ変換によって求め,その重心がPMD値<Δτ>であり,その重心の決定は,式(A.6)
によって算出する。
スパイクの重心を決定するために,典型的には検出システムのRMS雑音レベルの200 %に設定するしき
い値レベルT2を事前に定め,P(δτ)がしきい値レベルT2を超えるデータ点を計算に用いる。
()
[
]
()
∑
∑
′
=
′
=
=
∆
M
e
e
M
e
e
e
P
P
0
0
/
δτ
δτ
δτ
τ
············································· (A.6)
ここに,
<Δτ>: PMD値。一般に,単位は,ピコ秒である。
M'+1: T2を超えるスパイク内のPのデータ点数
スパイクが検出されない場合(M'+1=0)は,PMDはゼロである。スパイクのRMS幅,ピーク値など
の他のパラメータも必要に応じて記録する。
被測定物が二つ以上の複屈折要素を含んでいる場合には,二つ以上のスパイクが発生する。n個を接続
16
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
した光ファイバ又は部品に対して,2(n−1)個までのスパイクが観測される。
A.3.2.2.2 ランダムなモード結合のある光ファイバのPMD計算
ランダムなモード結合がある場合は,R(λ)は図A.2 b) のような複雑な波形となり,これは実際の光ファ
イバ/ケーブル中での結合過程の統計に基づく正確な特性である。フーリエ変換データは,光ファイバ中
での光パルス到達時間δτの自己相関関数と相互相関関数との組合せを表す分布P(δτ)となる(図A.3参照)。
T1を超えたデータ点をPの最初のデータ点としてj=0から数え始め,少なくともX個のT1以下になる
データ点が後ろに続く点までとする。ランダムなモード結合の光ファイバに対しては,この点は分布P(δτ)
における最後の有意な(すなわち,終わりの)点を表しており,測定雑音にほとんど影響されない。この
点に対するδτの値をδτlastで示し,δτlastでのjの値をM"で示す。
光ファイバのPMD<Δτ>を,この分布の二次モーメントの平方根σRとして定義し,次の式(A.7)によって
算出する。
()
[
]
()
[
]
{
}21
0
0
2
R
/
∑
∑
′′
=
′′
=
=
=
∆
M
j
M
j
j
j
j
P
P
δτ
δτ
δτ
σ
τ
······························ (A.7)
A.3.2.2.3 複数のモード結合状態を接続した光ファイバシステムのPMD計算
被測定システムが,モード結合を無視できる光ファイバ/光部品とランダムなモード結合の光ファイバ
とを接続して構成している場合,重心の決定[式(A.6)]及び二次モーメントの導出[式(A.7)]の両方が必
要である。P(δτ)のスパイクは,計算したδτlastとは関係なく決定されることに注意する。
図A.3−フーリエ解析によるPMD
17
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.3.3 コサインフーリエ変換法(CFT)
この解析法は,検光子から出射する光のスペクトルのコサインフーリエ変換が,方法Cで得た干渉フリ
ンジパターンであるという見解に基づいている。互いに垂直な二つの検光子の角度設定によって得られる
フリンジパターン間の差は相互相関関数となる。検光子に無限のスペクトルを入射すると自己相関関数の
幅はゼロになるが,実際には,光源スペクトルが光周波数領域で有限なため,ウインドウ関数として作用
し,時間領域において自己相関関数の幅はゼロでない有限の値となる。
方法Cで用いる相互相関関数及び自己相関関数の二乗解析であるGINTY解析[4]では,これらの関数の
二乗RMS幅の差は,DGD値の(強度を二乗した)スペクトル加重RMSの二乗に比例している[式(C.9)
参照]。
解析結果はスペクトル形状に依存せず,これはウインドウ関数の条件を十分に考慮できていることを意
味する。モード結合の程度にも依存しておらず,異なるモード結合条件を取り扱うときにも解析手段を変
更する必要がない。
また,解析結果は,測定するスペクトル幅及び光周波数間隔に制限される。PMDが増加するに従い,光
周波数間隔は小さくする必要があるが,ある条件において,方法C(GINTY)よりも実用的な場合がある。
PMDRMSの量は,解析によって求める。ランダムなモード結合が存在する場合は,結果は式(3)を用いて
PMDAVGに変換できる。
A.3.3.1 概要
互いに垂直な二つの検光子の角度設定条件で出射するパワーの測定が必要である。式(A.4)の比率Rを,
式(A.8)に書き直す。
()
()
()
()
()
v
P
v
P
v
P
v
P
v
R
B
A
B
A
+
−
=
································································· (A.8)
ここに,
ν=c / λ: 光周波数(THz)
ポラリメータを用いる場合には,三つの規格化出力ストークスベクトル要素のそれぞれが,式(A.8)で表
す値に相当する三つの独立した規格化比率となる。各ストークスベクトル要素は,互いに垂直な二つの検
光子の角度設定条件における出射パワーの差に相当する。三つの要素間での相違は,検光子の角度基準が
ストークスベクトル空間において互いに垂直である点である。
データに,両端で滑らかにゼロとなるウインドウ関数W(ν)を乗じる。R(ν)W(ν)及びW(ν)を,測定してい
ない低い光周波数に対してゼロ点付加を行った配列に代入する。各配列に高速コサインフーリエ変換
(FCFT)を適用して,時間領域のフリンジ包絡線r(t)w(t)及びw(t)を得る。相互相関及び自己相関の包絡線
の二乗,Ex2及びE02は,これらを二乗して求める。入射及び出射偏光状態をスクランブルしている例など
において,入射偏光子に対する検光子の角度基準設定が異なる複数の条件(又は異なるストークス出射ベ
クトル要素)があり,複数(N個)の比関数を用いることができる場合,二乗平均包絡線は,式(A.9)及び
式(A.10)となる。
∑
=
i
i
E
N
E
2
x
2
x
1
······································································· (A.9)
∑
=
i
i
E
N
E
2
0
2
0
1
······································································(A.10)
これら二つの関数のRMS幅,σx及びσ0は,D.2のRMS計算方法を用いて計算する。PMDRMSは,式(A.11)
18
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
によって算出する。
(
)
2
/1
2
0
2
x
RMS
2
3
−
=
σ
σ
PMD
························································ (A.11)
この値は,式(A.12)に示すDGDの(ウインドウ値の二乗による)スペクトル加重RMSと関連している。
()()
()
2/1
2
2
2
RMS
∆
=
∫
∫
dv
v
W
dv
v
W
v
PMD
τ
···············································(A.12)
期待値の演算子は,ランダムな入射及び出射偏光状態に関連している。
A.3.3.2 詳細
この細分箇条では,測定する周波数範囲,周波数間隔Δν,周波数シフト及びFCFTの解析結果[5]に関す
る詳細を説明する。
データの周波数間隔は均一とし,付加したゼロ点を含むデータ点の総数は,1+2k(k:整数)とする。
nmで測定したデータの周波数間隔が均一でない場合,スプライン関数などの多項式にフィットさせ,
データを補間する。nmで測定したデータ数-3個の均一な周波数間隔要素をもつ三次元スプライン関数[6]
によって,全てのデータを完全にフィットさせ,補間を行うことができる。
測定データの両端がνminM及びνmaxMであり,最小光周波数が最大光周波数の半分よりも大きい場合,処
理する配列の大きさを小さくするために周波数シフトを適用できる。測定データ配列の計算で用いる周波
数の両端を,任意のnを選んで,式(A.13)のように設定することができる。
M
v
v
n
n
v
min
min
max
1
≦
=
−
,
M
v
v
max
max=
·········································(A.13)
ここに,
n: 正の整数
測定周波数範囲よりも小さい周波数での値はゼロとする。
FCFTを行った場合,データ配列は,時間がゼロからtmax=Δt2kの時間領域フリンジパターンを含み,時
間間隔Δtは,式(A.14)で算出できる。
(
)
min
max
max
2
1
2
v
v
v
n
t
−
=
=
∆
························································(A.14)
干渉計から得たフリンジパターンを正の時間から負の時間に拡張する。負の時間での値は,正の時間で
の値と等しい。関数は偶関数であり,原点に対して対称である。
RMS幅の計算には,測定可能な最小PMDRMSよりも小さい時間領域の値も必要となるため,周波数シフ
トの選択は,この点に気を付けて行う。
周波数間隔Δνは,測定ポイント数,周波数シフト及び測定できる最大PMDRMSにも関連している。Δν
は,式(A.15)の制約を満足する必要がある。
max
RMS
min
max
24
1
2
−
−
=
∆
PMD
v
v
v
k
≦
···············································(A.15)
19
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
フィルタ後の光源のスペクトル幅は,この値の半分とする。実際の掃引を均一な波長間隔で行った場合,
測定範囲の低波長端での波長間隔が式(A.15)の制約を満たす必要がある。
ウインドウ関数W(ν)は,二次元関数など,理論的にはどんな関数でもよいが,σ0の値を最小にするもの
が望ましい。関数は,両端で滑らかにゼロになり,一次微分も両端でゼロになるものが望ましく,これに
よってσ0が増加する波形振動を最小にできる。
A.3.3.3 例
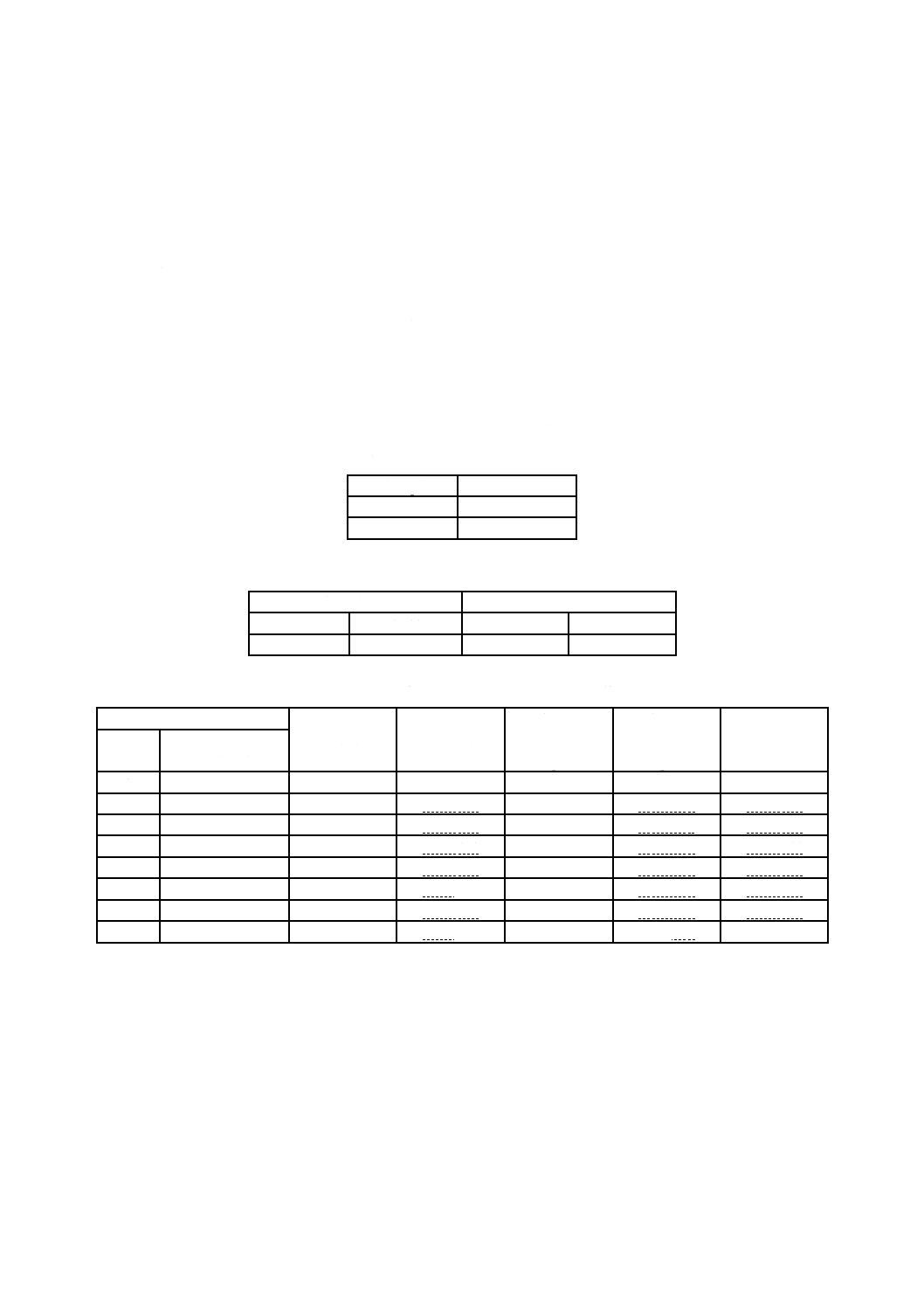
計算例のシートを,表A.1に示す。測定波長範囲及びkを記載している。幾つかの周波数シフトのn値
それぞれに対して,その他のパラメータを計算している。PMDRMSの最小値を3Δtとし,低波長限界での
波長間隔も示している。明らかにトレードオフがあり,測定されるPMDRMSの範囲に依存している。一般
に,波長範囲が広く,周波数間隔が小さいことが望ましい。
表A.1−コサイン変換計算
a) 計算に使用したパラメータ
c(nm/ps)
299 792.5
k
11
測定データ数
2 048
b) 測定データの波長及び周波数範囲
波長(nm)
周波数(THz)
最大波長
1 700
176.348 5
最小νminM
最小波長
1 300
230.609 6
最大νmaxM
c) 周波数シフトの各n値に対するパラメータの計算結果
周波数シフト
時間間隔
Δt(ps)
周波数間隔
Δν(THz)
測定可能な
最小PMDRMS
(ps)
測定可能な
最大PMDRMS
(ps)
波長間隔
δλ(nm)
n
計算最小周波数
νmin(THz)
1
0
0.002 168
0.112 602
0.006 504
0.370 034
0.635 076
2
115.304 807 7
0.004 336
0.056 301
0.013 009
0.740 067
0.317 460
3
153.739 743 6
0.006 504
0.037 534
0.019 513
1.110 101
0.211 623
4
172.957 211 5
0.008 673
0.028 151
0.026 018
1.480 135
0.158 711
5
184.487 692 3
0.010 841
0.022 520
0.032 522
1.850 169
0.126 966
6
192.174 679 5
0.013 009
0.018 767
0.039 027
2.220 202
0.105 803
7
197.665 384 6
0.015 177
0.016 086
0.045 531
2.590 236
0.090 687
8
201.783 413 5
0.017 345
0.014 075
0.052 036
2.960 270
0.079 351
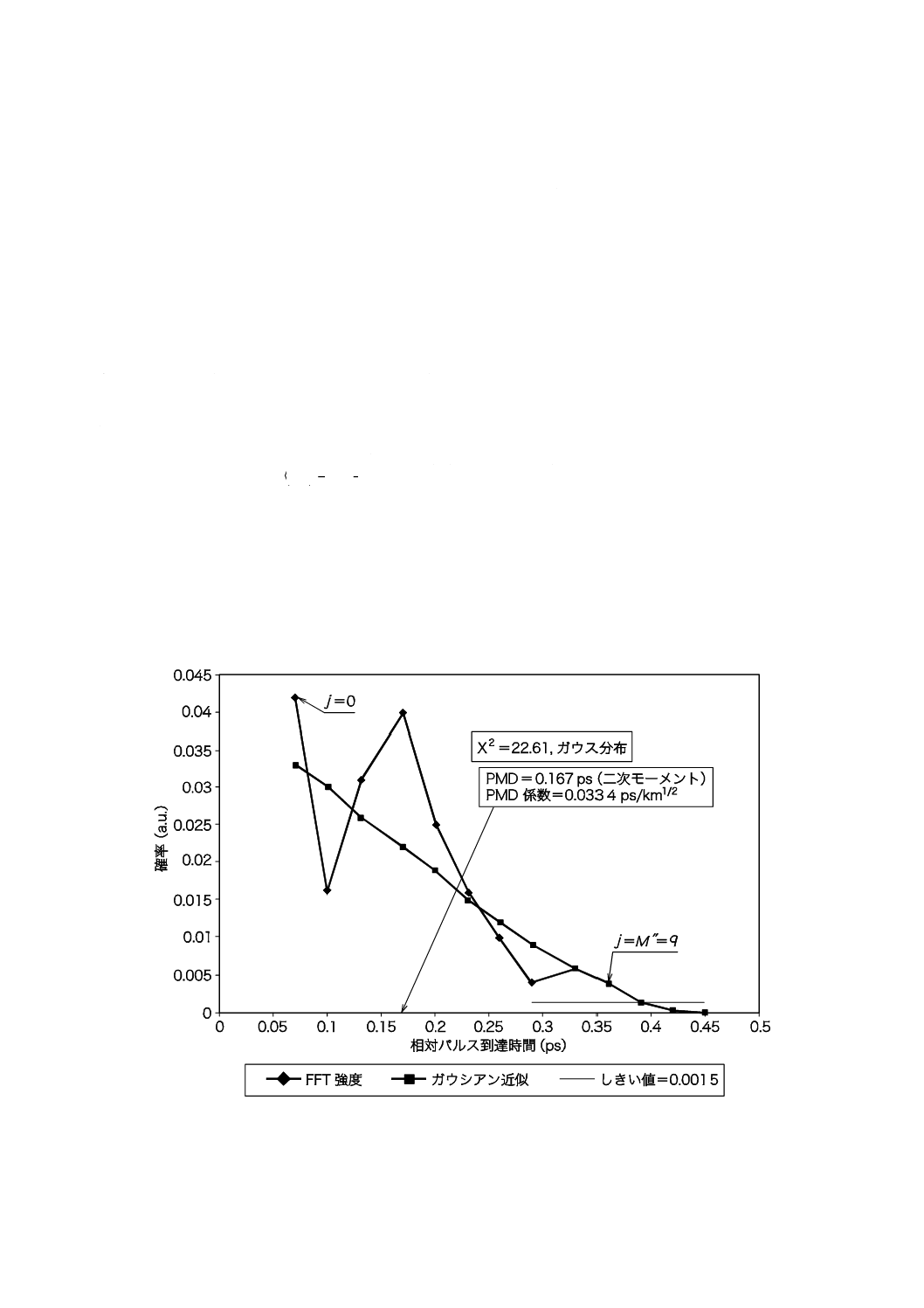
図A.4は,PMDRMS=0.2 psの光ファイバから得た結果を示している。標準偏差23 nmのガウス分布をウ
インドウ関数として用い,一回掃引による相互相関平均及び自己相関平均を表している。理想的なランダ
ムモード結合をもつ光ファイバとして,シミュレーションから得られた結果である。このシミュレーショ
ン結果に対する解析結果は0.185 psであった。
20
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.4−相互相関関数及び自己相関関数
21
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(規定)
偏波モード分散試験方法B−ストークスパラメータ解析法(SPE)
B.1 装置
方法Bの試験構成を,図B.1に示す。
図B.1−方法Bの試験構成
B.1.1 光源
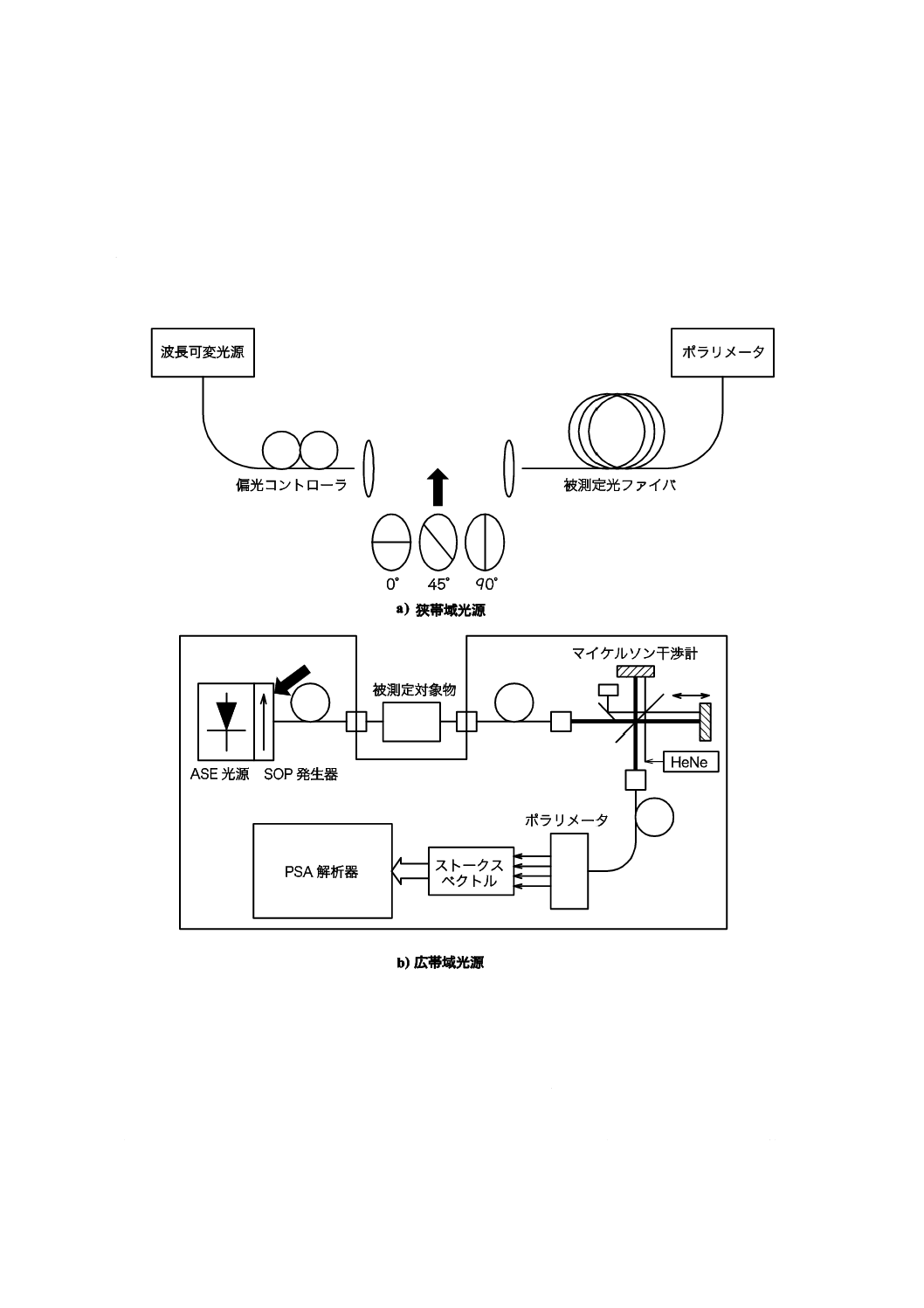
ポラリメータの種類に応じて二種類の光源を用いることができる。図B.1 a) に示す波長可変光源のよう
な狭帯域光源を,偏光解析装置とともに用いる。又は,図B.1 b) に示す広帯域光源を,ポラリメータの前
に光スペクトラムアナライザ又はフーリエ変換スペクトラム解析器としての干渉計を設置したような狭帯
域透過ポラリメータとともに用いる。また,広帯域光源を用いる場合,透過フィルタの幅は,計算の目的
に合ったスペクトル幅とする。
22
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
いずれの場合も,必要な偏光度を維持できるように,スペクトル幅は十分に小さくする(7.2参照)。さ
らに,規定する波長領域内において十分な精度でPMD測定が行えるように,測定波長範囲を十分に広く
する(B.3参照)。
JME法及びPSA法において,偏光子は,各測定波長において三つの互いに直交する直線偏光状態(0°,
45°及び90°)に切り替えることを可能とする。
B.1.2 ポラリメータ
各入力偏光状態及び波長に対する出力ストークスベクトルを測定するためにポラリメータを用いる。
B.2 手順
光ファイバの出力をポラリメータに接続する。測定波長域において適切で,かつ,要求する精度(B.3
参照)を満足する波長増分δλを設定して,波長掃引を行う。狭帯域光源の場合,波長増分は,予想する最
大DGD値Δτmaxと,測定波長λ0及び真空中の光速度cとの関係式(B.1)で求める。
max
2
0
2τ
λ
δλ
∆
c
≦
········································································ (B.1)
例えば,最大DGDと波長増分との積を,1 550 nmにおいて4 ps・nmよりも小さく,1 300 nmにおいて
は2.8 ps・nmよりも小さくする。この条件は,ある測定波長から隣の測定波長までの,ポアンカレ球上の
主偏光軸を回転軸とした出力偏光状態の回転角が,180°より小さいことを保証する。Δτmaxの大まかな見
積りができない場合は,スペクトル幅及び光源の最小調整刻みに相当する小さい波長間隔を設定して,測
定波長全域の測定を行う。実際の測定で用いるδλの値は,このようにして測定したDGDの最大値に安全
係数3を乗じ,この値を式(B.1)のΔτmaxに置き換えて,計算できる。測定に用いた波長間隔が大きすぎる
懸念がある場合には,より小さい波長間隔で再測定を行う。DGDの波長依存性曲線の形状及び平均DGD
が本質的に変わらない場合,もとの波長間隔は要求条件を満足している。
広帯域光源の場合は,解析器の分解帯域幅(RBW)が式(B.2)の関係を満足する必要がある。
max
2
0
5τ
λ
∆
c
RBW≦
····································································· (B.2)
各波長に対して測定データを取得する。JME法及びPSA法では,各波長に対して三つの入力偏光状態を
0°,45°及び90°と変え,そのときの出力ベクトルを測定する。出力ベクトルは単位長さ当たりに規格
化し,三つの入力偏光状態に対応して,それぞれ,Hˆ,Qˆ及びVˆとして記録する。SOP法では,各波長
に対する規格化出力ストークスベクトルを,sˆとして記録する。
B.3 計算
三つの全ての計算手法において,各々の光角周波数ω0及びその隣の周波数ω0+Δωにおける偏光状態の
差の評価を行い,(光角周波数はω=2πc/λである。)波長に対して連続したDGDを求める。モード結合を
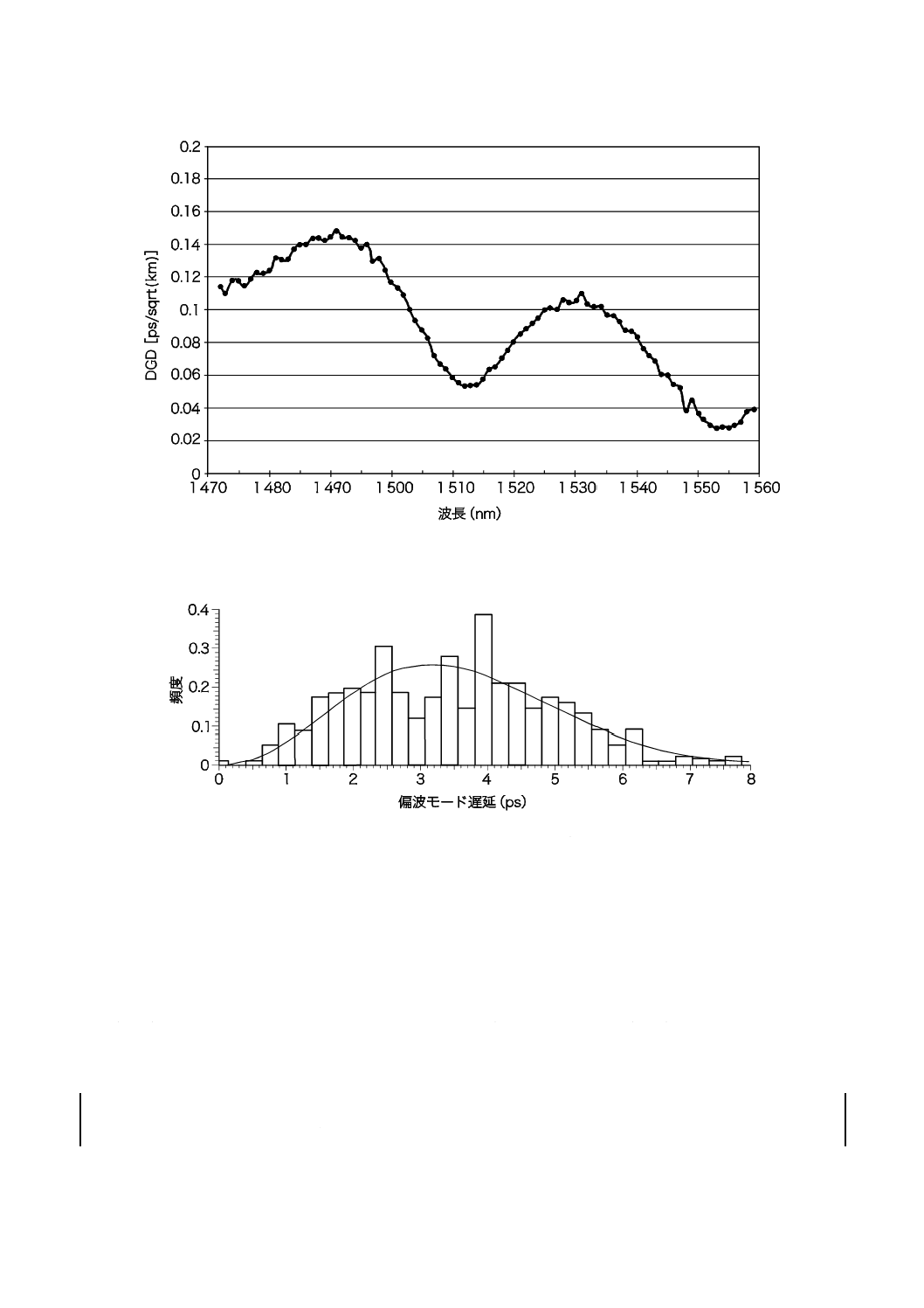
無視できる場合には,DGDは典型的に波長に対して一定である。ランダムなモード結合のある場合は,
DGDは典型的に図B.2に示すように波長に対して変化する。また,DGDは図B.3のようなヒストグラム
を示すこともある。測定したDGDの平均値が,連結係数として用いるPMDの値である。
方法Bの三つの手法に関連する詳細な数式及び計算方法は,JME法とPSA法との間の理論的関係とと
もに,IEC/TR 61282-9に規定している。SOP法における計算にも言及しているが,確定していない。
23
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.2−典型的なランダムなモード結合のある場合の方法Bによる結果
図B.3−DGD値の典型的なヒストグラム
注記 ヒストグラムにマクスウェル曲線を重ねている。
JME法及びPSA法の解析手法は,偏光依存性損失がない一次近似に対して数学的に等価である。
B.3.1 ジョーンズ行列解析法(JME)
各周波数に対するT行列は,ω0及びω0+Δωで表す周波数の対に対して,各周波数に対する三つの出力
ストークスベクトルをジョーンズベクトルに変換し,求めたジョーンズベクトルの要素の比率を用いて計
算する。
周波数ω0及びω0+Δωで表す各周波数対に対して,各周波数において測定した三つの出力ストークスベ
クトルを,式(B.3A)によって変換する。
24
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
H
h
ˆ
ˆ=
H
Q
H
Q
H
q
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
×
×
×
=
q
V
q
V
q
v
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
×
×
×
=
························· (B.3A)
一般にsˆで示される規格化出力ストークスベクトルを,jˆで示すジョーンズベクトルに変換するために,
式(B.3)の関係を用いる。
=
μ
θ
μ
θθ
sin
2
sin
cos
2
sin
2
cos
ˆs
⇔
(
)
(
)
−
=
2/
exp
sin
2/
exp
cos
ˆ
μ
θ
μ
θ
i
i
j
······························ (B.3)
ここに,
θ: 直線偏光変数
μ: 回転偏光変数
μはジョーンズベクトルのx及びy成分の位相差でもある。この計算において,θは0とπとの間の値と
仮定することができる。
各周波数における各ジョーンズベクトルのx及びy成分を,hx,hy,qx,qy,vx及びvyと表す。比率は,
式(B.4)を用いて計算する。
y
xh
h
k
/
1=
y
xv
v
k
/
2=
y
xq
q
k
/
3=
3
1
2
3
4
k
k
k
k
k
−
−
=
························· (B.4)
各周波数に対するジョーンズ変換行列Tは,式(B.5)のように計算する。
=
1
4
2
4
1k
k
k
k
T
······································································· (B.5)
周波数変換行列Jは,周波数対の各T行列を用いて,式(B.6)のように計算する。
(
)
()
0
1
0
ω
ω
ω
−
∆
+
=
T
T
J
······························································ (B.6)
Jの固有値を計算し,ρ1及びρ2とする。DGD値Δτは式(B.7)のように計算する。
ω
ρ
ρ
τ
∆
=
∆
2
1
Arg
······································································ (B.7)
Argは偏角関数であり,m≧0かつ
π
θ<
に対して
(
)θ
θ=
i
me
Arg
である。
JME法の数式及び詳細な計算方法は,IEC/TR 61282-9による。
B.3.2 ポアンカレ球解析法(PSA)
PSA法において,周波数による出力ストークスベクトルの回転は,規格化出力ストークスベクトルを用
いて行列計算を行って求める。
周波数ω0及びω0+Δωで表す各周波数対に対して,各周波数において測定した三つの出力ストークスベ
25
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
クトルを,式(B.8)によって変換する。
H
h
ˆ
ˆ=
H
Q
H
Q
H
q
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
×
×
×
=
q
V
q
V
q
v
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
×
×
×
=
··························· (B.8)
各周波数に対するベクトル積
q
h
c
ˆ
ˆ
ˆ
×
=
及び
v
q
c
ˆ
ˆ
ˆ
×
=
′
をストークスベクトルhˆ,vˆ及びqˆから求め,各周波
数対における有限差分を式(B.9)によって求める。
(
)
()
0
0
ˆ
ˆ
ˆ
ω
ω
ω
h
h
h
−
∆
+
=
∆
(
)
()
0
0
ˆ
ˆ
ˆ
ω
ω
ω
q
q
q
−
∆
+
=
∆
(
)
()
0
0
ˆ
ˆ
ˆ
ω
ω
ω
v
v
v
−
∆
+
=
∆
(
)
()
0
0
ˆ
ˆ
ˆ
ω
ω
ω
c
c
c
−
∆
+
=
∆
(
)
()
0
0
ˆ
ˆ
ˆ
ω
ω
ω
c
c
c
′
−
∆
+
′
=
′
∆
······················································· (B.9)
DGD値Δτは,周波数増分を用いて,式(B.10)によって算出する。
(
)
(
)
′
∆
+
∆
+
∆
+
∆
+
∆
+
∆
∆
=
∆
2
2
2
2
2
2
ˆ
ˆ
ˆ
2
1
2
1
arcsin
ˆ
ˆ
ˆ
2
1
2
1
arcsin
1
c
v
q
c
q
h
ω
τ
······················ (B.10)
ここに
h
h
h
ˆ
ˆ
ˆ2
∆
•
∆
=
∆
PSAの数式及び詳細な計算方法は,IEC/TR 61282-9による。
B.3.3 偏光状態法(SOP)
SOP解析において,波長に対する偏光状態の変化を示すポアンカレ球上の軌跡は,測定した規格化出力
ストークスベクトルから計算する。主偏光状態が明確に存在し,かつ,不変であると仮定できる波長区分
(二つ以上の波長測定点を含む。)を考慮し,その区分ごとに軌跡を解析する。各区分内におけるポアンカ
レ球上の主偏光軸及び区分内の波長変化量δλに対応する回転角Δθは,幾何学的な考察によって決定でき
る。
測定点を3点ずつ考慮し,二つの測定点対によって特定する円弧の軸の交点を見付けることで,ポアン
カレ球上の軌跡の解析を行うことができる。Δθの値は,この点から三角法の関係によって計算することが
できる。
DGD値Δτは,式(B.11)によって算出する。
f
i
2
λ
λ
δλ
π
θ
ω
θ
τ
∆
=
∆
∆
=
∆
c
······························································· (B.11)
ここに,λi及びλfはそれぞれδλの最初及び最後の波長である。
SOPの数式及び詳細な計算方法は,IEC/TR 61282-9による。
注記 ある周波数において,出力ストークスベクトルが主偏光状態に一致する場合には,その周波数
で算出したDGD値 Δτは,実際の値よりもかなり小さくなる可能性がある。
26
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(規定)
偏波モード分散試験方法C−干渉法(INTY)
C.1 装置
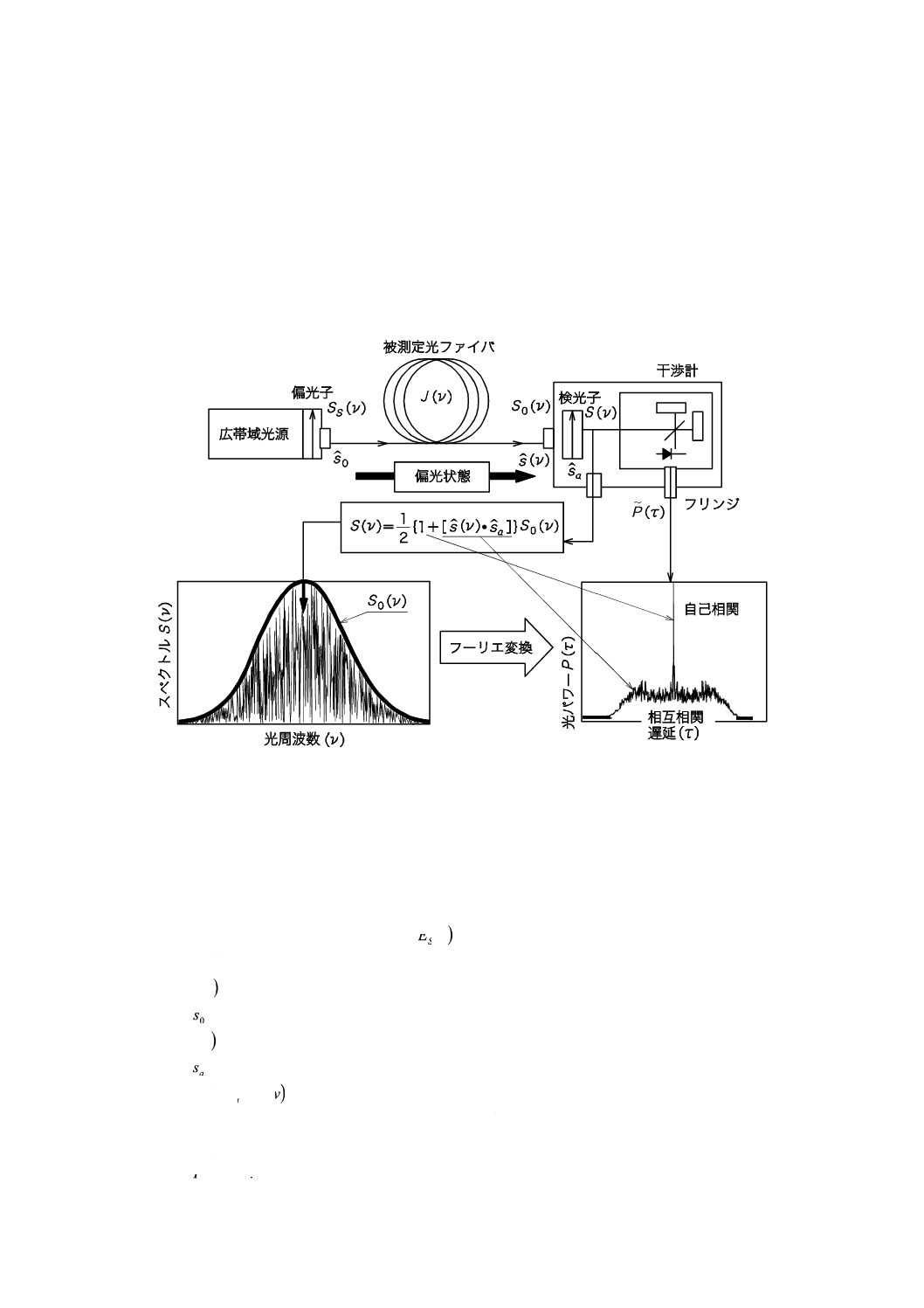
方法Cの一般的な測定の試験構成を,図C.1に示す。
図C.1−方法Cの試験構成(一般的な測定)
図C.1内及び後の説明に用いる変数を,次のように定める。
ν
:光周波数(λν=c)
τ
:干渉計の二つの光路間の往復遅延時間差
()
v
SS
:被測定光ファイバ入力における光スペクトル
光源の電界スペクトル
()v
ESρ
のスペクトル密度と等しい。
()
v
S0
:被測定光ファイバ出力(検光子入力)における光スペクトル
()v
S
:検光子出力(干渉計入力)における光スペクトル
0ˆs
:入力偏光状態(被測定光ファイバ入力;単位ストークスベクトル)
()v
sˆ
:出力偏光状態(被測定光ファイバ出力)
asˆ
:検光子透過軸
()
as
v
s
ˆ
ˆ
•
:()vsˆ を検光子透過軸へ投影して得られるストークスパラメータ
このパラメータがPMDの情報を含んでいる。
()
τ
P
:遅延時間τの関数として,干渉計の出力光パワー
()
τ
P~
:()
τ
P
のτに依存した成分(交流成分)
27
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0P
:() τ
P
の一定成分(直流成分)
()
τ
E
:干渉フリンジ包絡線
()
τ
x
E
:相互相関包絡線
()
τ
0
E
:自己相関包絡線
干渉計の出力光パワー() τ
P
は交流成分と直流成分との和に等しい。両成分はτ=0で等しいので,交流成
分を計算することができる。理想的な干渉計では交流成分が偶関数であり,その正領域側は検光子から出
力する光スペクトル()v
S
のコサインフーリエ変換に等しい。理想的でない干渉計では,測定の詳細によっ
て何らかの補正を適用する。
TINTYにおいては,干渉スペクトルの包絡線() τ
E
が交流成分の絶対値である。GINTYにおける相互相
関及び自己相関包絡線を得るための付加的な計算は,C.2.2.2及びC.3.2に規定する。これらの計算には,
検光子を互いに垂直な二つの偏光状態に設定して測定した二つの干渉スペクトルを用いる。
三つの具体的な測定のための試験構成を,図C.2に示す。
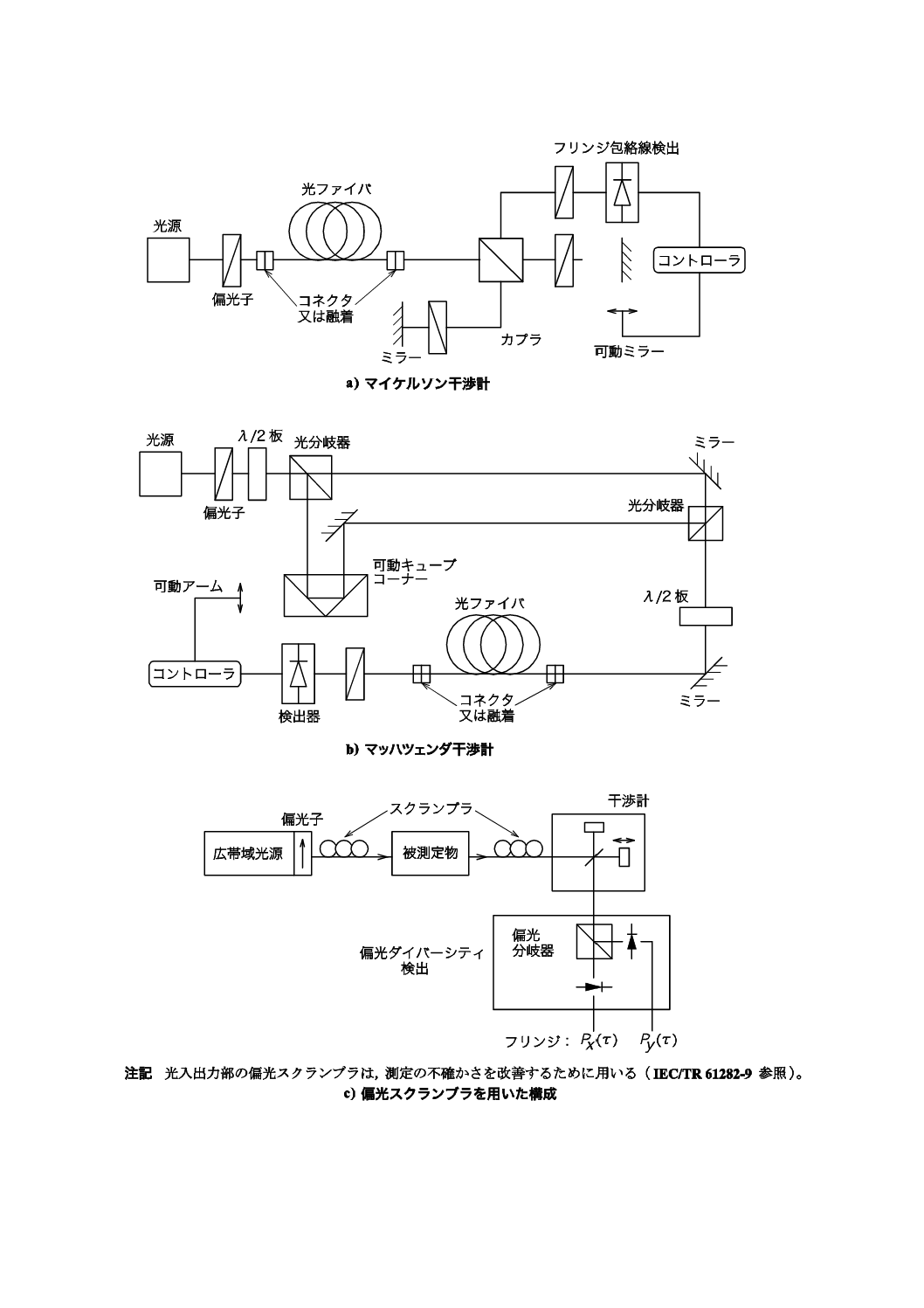
28
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図C.2−方法Cのその他の試験構成
29
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.1.1 光源
測定する波長帯で発光するLED,ASE光源,スーパーフロレッセント光源などの広帯域光源を用いる。
図C.1に示すように,光が偏光しており,中心波長λ0が,1 310 nm帯,1 550 nm帯又は他の測定する波
長帯内にある光源を用いる。TINTYによる測定系では,広帯域光源のスペクトル形状はほぼガウス曲線で
ある必要があり,また,発生する光の自己相関関数に影響を与えるリップルがあってはならない。GINTY
による測定系ではそのような光源特性への要求はなく,いかなるスペクトル形状の光源でも用いることが
できる。式(C.1)で定めるコヒーレンス時間tcを計算するために,光源のスペクトル線幅(3 dB幅)Δλが
既知である必要がある。
c
t
∆
=λλ20
c
············································································· (C.1)
C.1.2 光分岐器
偏光された入射光を干渉計の二つの光路に伝搬する二成分に分けるために光分岐器を用いる。分岐器と
して,光ファイバカプラ又はキューブビームスプリッタを用いることができる。
C.1.3 検光子
図C.1に示す検光子は,干渉計の中に設置する。TINTY法において,検光子は,最初の偏光軸設定に対
して垂直な二つ目の偏光軸設定に回転できる必要がある。
C.1.4 干渉計
干渉計には,空間形又は光ファイバ形の計器を用いることができる。干渉計は,マイケルソン形又はマ
ッハツェンダ形であり,光源側又は被測定光ファイバ終端の検出器側に設置する。いずれの場合において
も,干渉計は互いに直交する偏光状態どうしが干渉するように構成する。これを実現する多数の方法があ
る。
第一の方法は,図C.1に示すように干渉計の入力部に検光子を設置する方法である。入力部に偏光子を
設置しないで,干渉計の両方の光路において偏光状態が影響を受けない場合,PMDを示す相互相関スペク
トルは観測できない。干渉計の入力部に偏光子を設置しない場合は,その他の方法を考える。
第二の方法は,空間形干渉計の片方の光路に波長板を挿入する方法である。一般的に,全ての二光路形
干渉計における二光路の往復伝搬はジョーンズ行列T1及びT2で表すことができる。これは片方の光路だ
けにジョーンズ行列T=T1T2+の波長板を挿入した場合と等価である。光ファイバ形干渉計の場合,ルフェ
ーブルループ(偏光状態制御器)を片方の光路に挿入し,必要な効果(与えた相互相関−自己相関の比)
を得ることができるT=T1T2+の状態になるように調整する。
もう一つの特別な場合として,マイケルソン干渉計の片方の光路に1/4波長板(又はマッハツェンダ干
渉計の片方の光路に1/2波長板)を挿入する方法がある。この構成では相互相関スペクトルだけが観測で
きる。
C.1.5 偏光スクランブラ
図C.2 c) の偏光スクランブラによって,被測定光ファイバの入出力に対し任意の偏光状態を選ぶことが
できる。偏光分岐器によって,二つの垂直な検光子設定において検出する2信号の同時検出が可能となる。
入力における様々な偏光状態及び出力における様々な検光子の設定を選択できる偏光スクランブラの機能
性は,その他の手段によっても達成できる。
C.1.6 偏光分岐器
偏光分岐器(PBS)を,図C.2 c) において,同じ入出力偏光状態の組合せに対して,互いに垂直な(ポ
30
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
アンカレ球上で反対側にある。)出力偏光状態間の干渉スペクトルを求めるために用いる。自己相関及び相
互相関は,これらの二つの干渉スペクトルによって,別の関数として計算することができる。PBSは,検
出システムと組み合わせて,偏光ダイバーシティ検出系を構成している。互いに垂直な出力偏光状態間の
干渉スペクトルを得るのに,PBS以外の手段を用いてもよい。
C.2 手順
C.2.1 校正
既知のPMD遅延をもつ複屈折光ファイバを用いて遅延線の機構を確認することによって,装置を校正
する。代わりに,既知の特性をもった複数の複屈折光ファイバの接続物を用いてもよい。測定中の環境及
び入射条件は一定とする。
C.2.2 定常操作
被測定光ファイバの片端を偏光光源の偏光出力に接続する。他方の端は干渉計の入力に接続する。接続
は,標準的な光ファイバコネクタ,融着又は光ファイバ接続光学系によって行う。光ファイバ接続光学系
の場合には,接続点の反射を防ぐために屈折率整合オイルを用いる。
光源の出力光パワーを用いる検出系に合ったパワーに調整する。十分なコントラストの干渉フリンジを
得るために,両光路の光パワーをほぼ等しくなるように設定する。
C.2.2.1 TINTYの手順
まず初めに,干渉計アームのミラーを動かし,光の強度を記録する。干渉フリンジパターン() τ
P~
は,干
渉スペクトルから直流成分を差し引くことによって計算する。すなわち()
()
0
~
P
P
P
−
=
τ
τ
である。一般的な
フリンジ包絡線はフリンジパターンの絶対値である。偏波モード結合が無視できる場合及びランダムな偏
波モード結合がある場合のフリンジ包絡線の典型例を,図C.3に示す。
偏波モード結合があまり起きない場合,又はPMDが小さい場合,異なる偏光状態で測定を繰り返すか,
又は全偏光状態に対する平均を得るために測定中に偏光状態を変調することが望ましい。
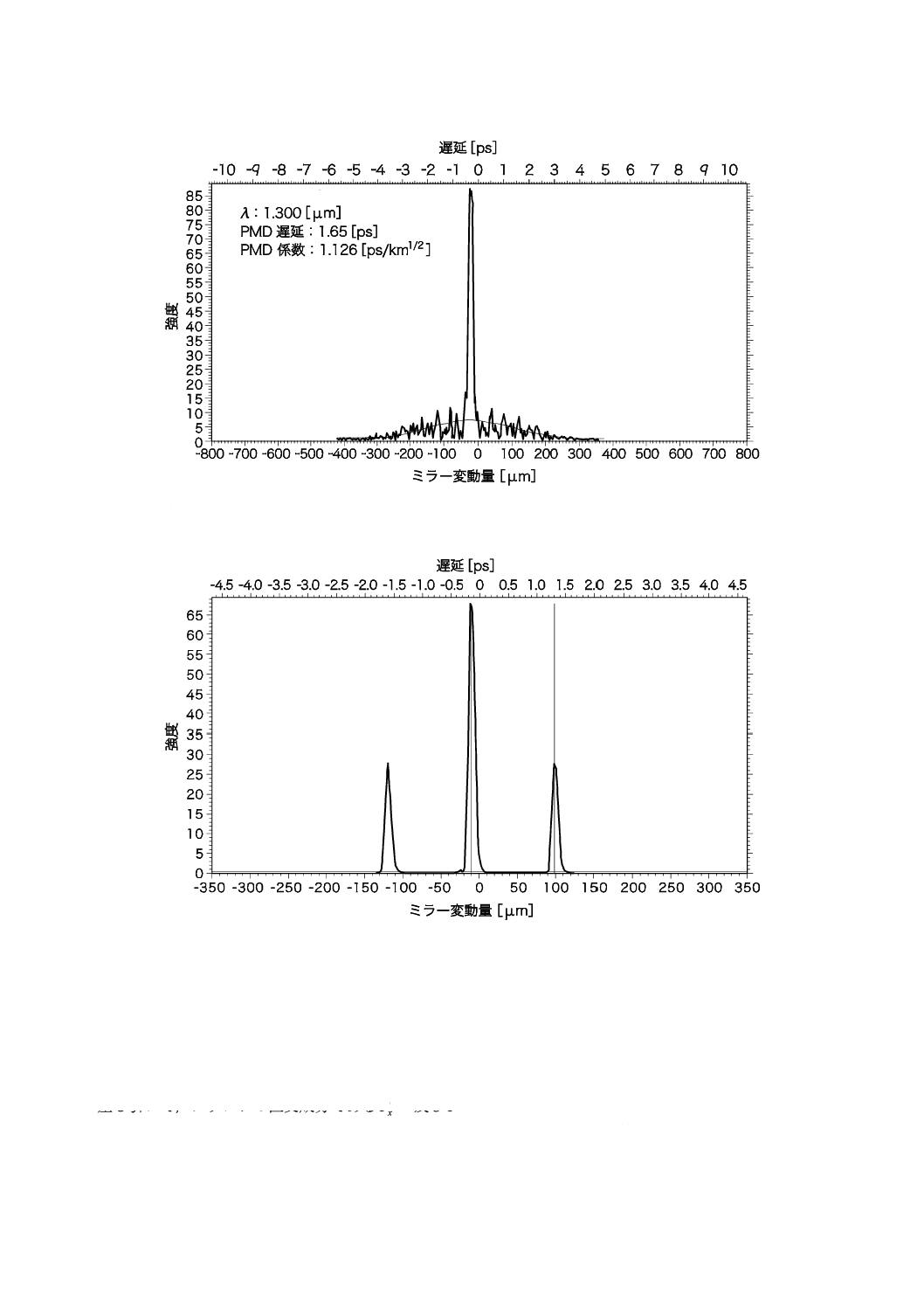
31
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 一つの入出力偏光状態でのTINTYによる測定系を用いたランダムなモード結合がある場合
b) 一つの入出力偏光状態でTINTYによる測定系を用いたモード結合が無視できる場合
図C.3−偏波モード結合が無視できる場合及びランダムな偏波モード結合がある場合のフリンジ包絡線
C.2.2.2 GINTYの手順
特定の入射部偏光子の設定と検光子の互いに垂直な二つの設定との組合せを,I/O偏光状態という。二
つの互いに垂直な検光子設定に対して,二つの干渉スペクトルを求める掃引を行い,それぞれ直流成分を
差し引いて,フリンジの直交成分である() τ
xP~
及び() τ
y
P~
を得る。
相互相関フリンジEx(τ)及び自己相関フリンジE0(τ)は,式(C.2)によって計算する。
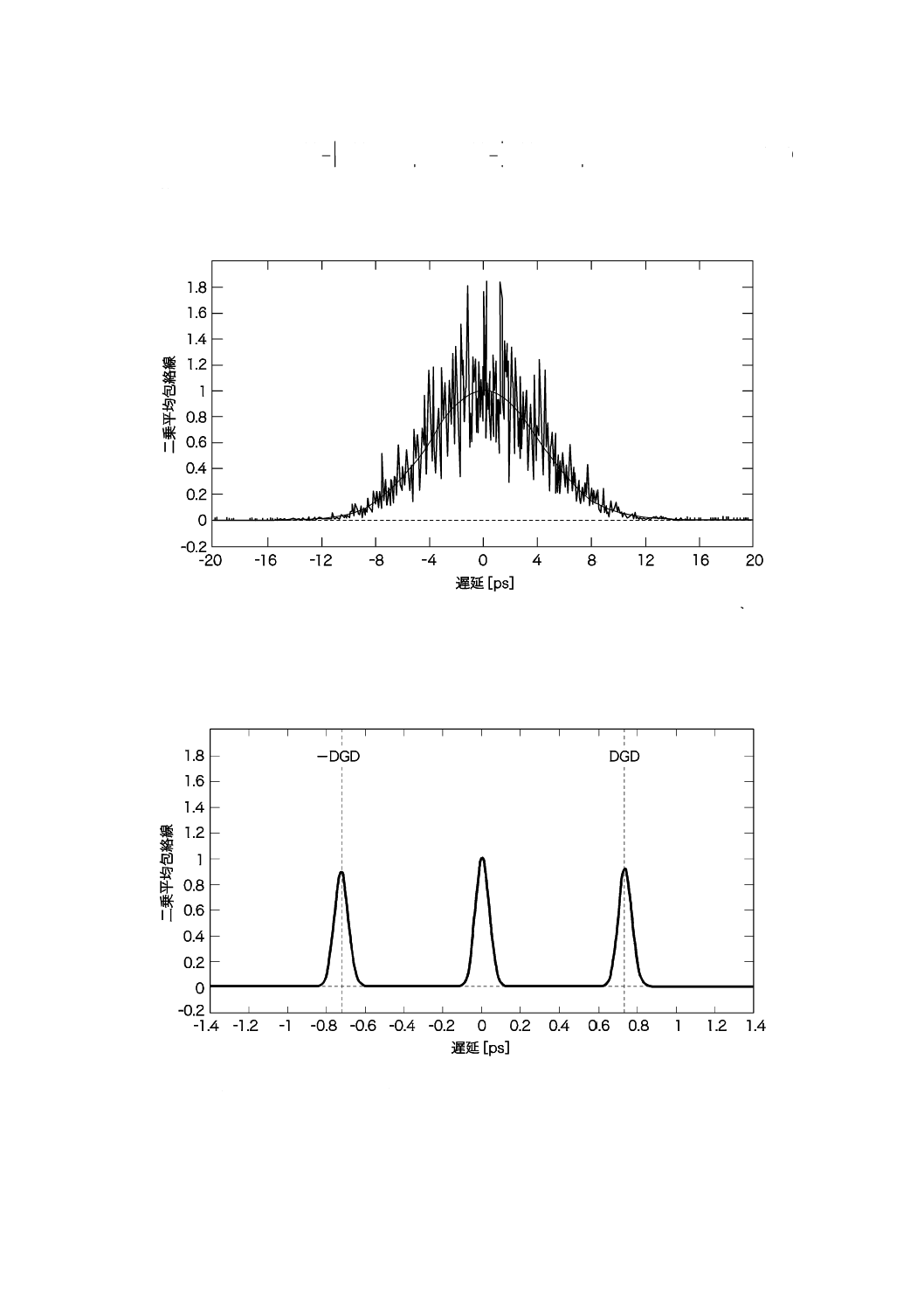
32
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
()
()
τ
τ
τ
y
x
x
P
P
E
~
~
−
=
()
()
()
τ
τ
τ
y
x
P
P
E
~
~
0
+
=
································ (C.2)
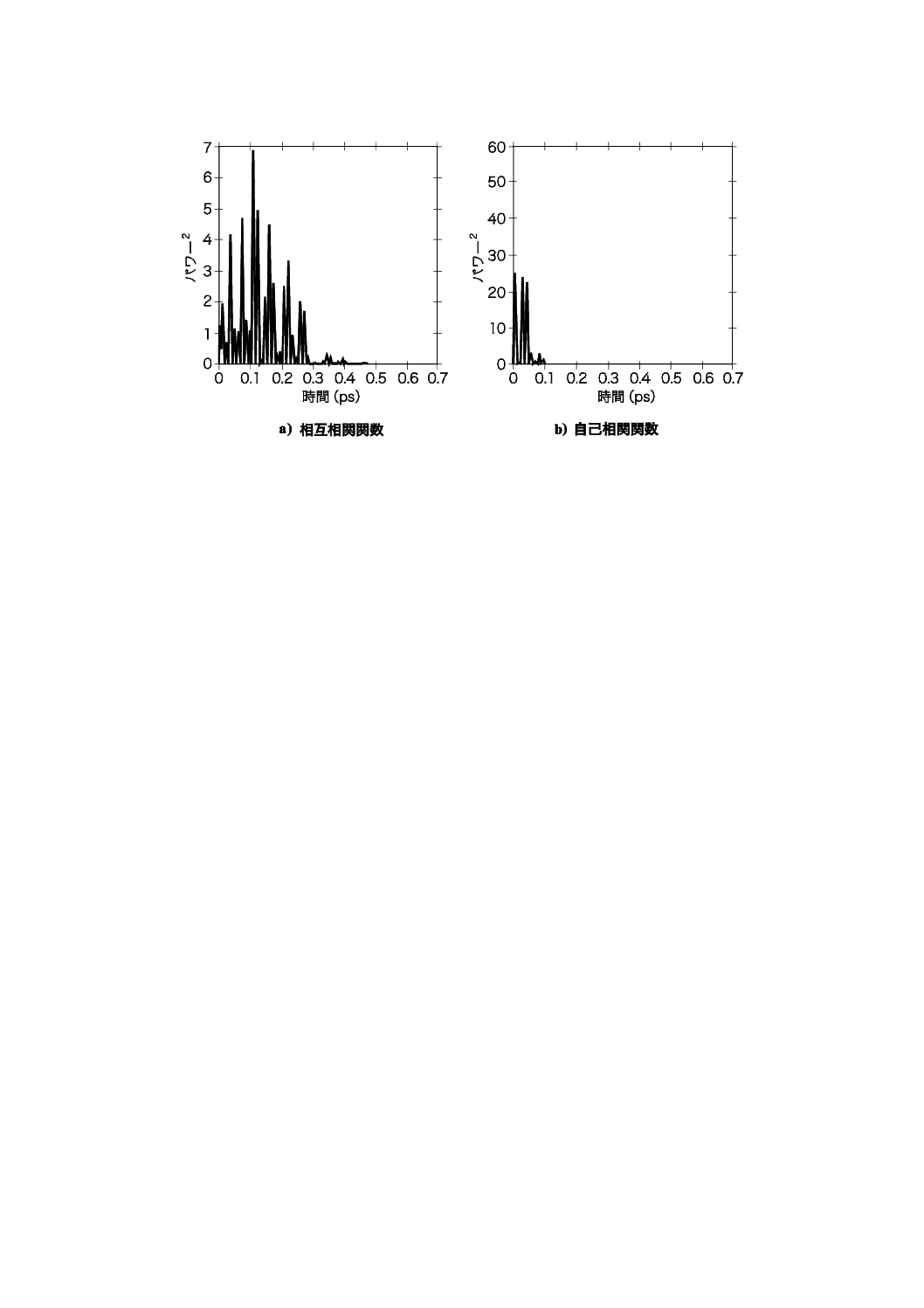
後の計算及び表示のために,これらの関数を二乗する。二乗相互相関の結果を図C.4に示す。TINTYで
見られた自己相関ピークが存在しないことが分かる。
注記1 L/lc=100,PMD/σA〜100(σA=自己相関包絡線のRMS幅);PMD=4.94 ps,σA=50 fs;
図中の黒線はガウシアン曲線近似包絡線である。この曲線は見やすくするための目安
であり,解析に近似曲線は用いない。
a) I/O偏光状態スクランブルでのGINTYによる測定システムを用いたランダム
なモード結合がある場合の干渉スペクトル
注記2 L/lc<<1,DGD=0.732 ps,σA=50 fs,DGD/σA〜14.7
b) I/O偏光状態スクランブルでのGINTYによる測定システムを用いたモード
結合が無視できる場合の干渉スペクトル
図C.4−偏波モード結合が無視できる場合及びランダムな偏波モード結合がある
場合のフリンジ包絡線(GINTY法)
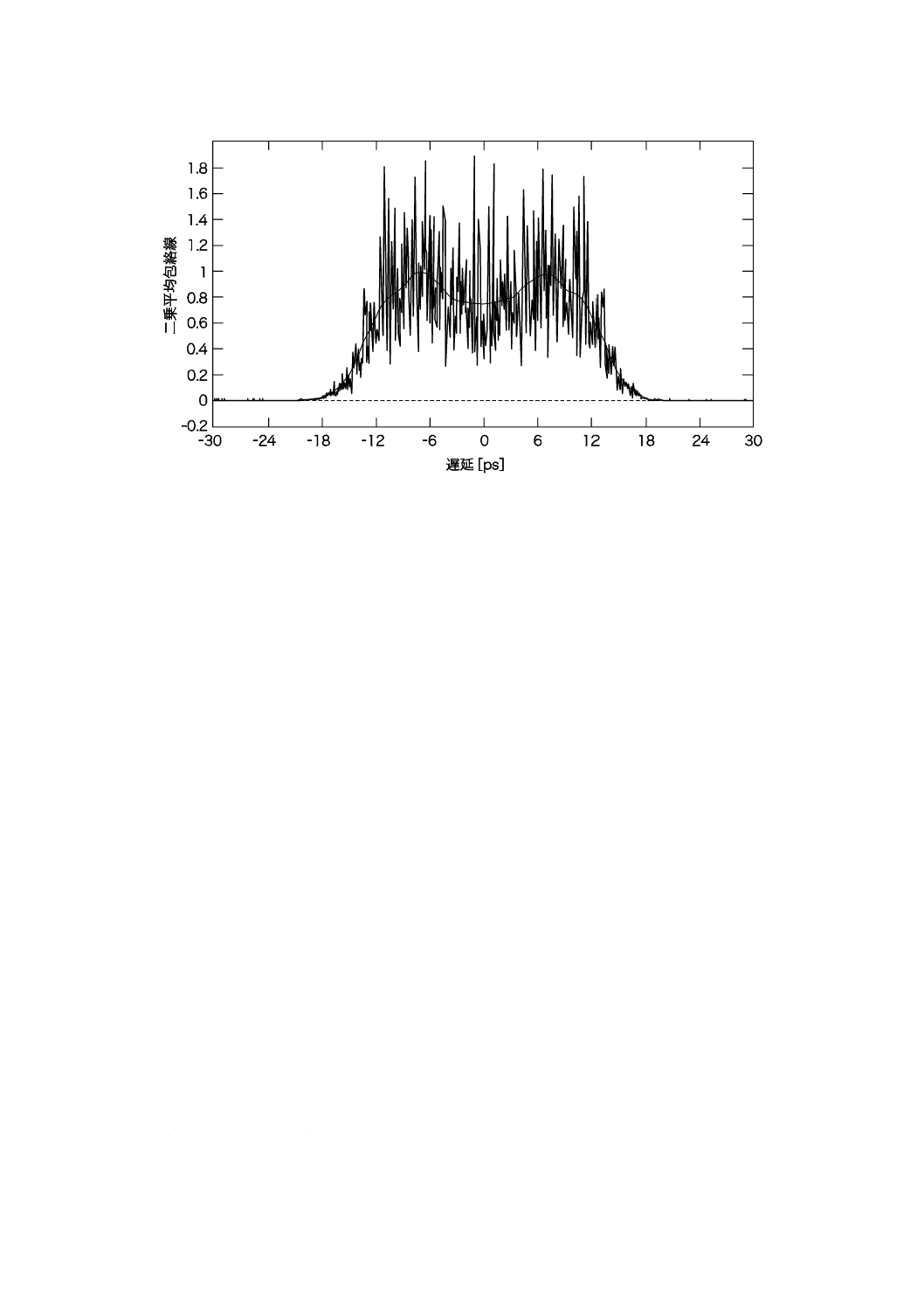
33
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記3 L/lc=10のランダムモード結合部分+DGD=PMDRandom/4のモード結合を無視できる部
分;PMD=9.97 ps,σA=50 fsで,ほぼ平たんな包絡線をもつ。
c) I/O偏光状態スクランブルでのGINTYによる測定システムを用いた複数の
モード結合状態が接続されている場合の干渉スペクトル
図C.4−偏波モード結合が無視できる場合及びランダムな偏波モード結合がある
場合のフリンジ包絡線(GINTY法)(続き)
偏光スクランブルの選択肢を次に示す。複数のI/O偏光状態で測定し,後の計算のために指数iを付け
る。
C.2.2.2.1 9状態のミューラ設定
九つの特定のI/O偏光状態で測定した二乗包絡線の和は,均一にスクランブルした平均二乗包絡線と厳
密に等しい。これらの九つのI/O偏光状態は,直角によって三面体を形成する三つの検光子の軸それぞれ
に対して,同じように直角によって三面体を形成する三つの入射偏光状態を組み合わせたものである。
C.2.2.2.2 ランダムスクランブル
掃引間でのスクランブル:各掃引において自動又は手動でスクランブラを設定する。
連続スクランブル:二乗包絡線の和をとるために,掃引中にスクランブルする。時間の関数として連続
的にポアンカレ球を覆うように,自動のスクランブラを設定する。
単一掃引高速スクランブル:スクランブラが十分に高速である場合,単一の掃引において十分にスクラ
ンブルされた二乗包絡線が観測できる。ただし,この方法では,干渉スペクトルの交流成分と直流成分と
の間のクロストークを避けるための特別な前準備が必要である。
C.3 計算
PMDRMSは,C.3.1及びC.3.2に規定する二つの計算方法で求める。理想的なランダムモード結合があり,
干渉スペクトルが理想的なガウス曲線の場合,式(3)を用いてPMDAVGに変換できる。
C.3.1 TINTY計算
モード結合が無視できる場合,PMD遅延は,C.3.1に規定するTINTY法及びC.3.2に規定するGINTY
法の両測定系において同じ手法で決定する。PMD遅延は,図C.3 b) 及び図C.4 b) に示す,被測定光ファ
34
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
イバのDGDによって中心から各々遅延した二つのコヒーレンスピークの分離距離から,式(C.3)によって
算出する。この場合,DGD値は,PMD遅延値と等しい。
0
2
c
L
∆
=
∆τ
··········································································· (C.3)
ΔLは両側の二つのコヒーレントピーク間の光遅延線の移動距離,c0は空間での光速度である。モード結
合が無視できる場合のPMD係数は<Δτ>/Lで与えられ,Lはkm単位の光ファイバ条長である。
式(C.4)の計算は,長距離光ファイバ/ケーブル又はリンクのようなランダムモード結合領域に対して適
している。フリンジ包絡線(中心ピークは無視する。)の広がりが特性を表す。
PMDRMS値は,検出信号(フリンジ包絡線)の相互相関関数の二次モーメント(RMS幅)から式(C.4)に
よって決定する。
ε
RMS
4
3σ
=
PMD
·································································· (C.4)
ここに,
σε: 相互相関包絡線のRMS幅
測定したフリンジ包絡線からσεを計算する詳細な手順は,D.1による。
以下の仮定において,式(C.4)と式(2)とは,式(C.5)の関係にあり,
2
ε
2
4
3σ
τ=
∆
······································································· (C.5)
式(C.5)は,次の仮定における理論から得ることができる。
− 理想的なランダムモード結合
注記1 理想的なランダムモード結合とは,L/h→∞であり,かつ,複屈折軸が均一に分布している
ことを意味する。Lは対象物の長さであり,hは偏光結合長である。長さhの複屈折部分
がN個つながっている対象物に対しては,軸が均一に分布し,N→∞であることに相当す
る。
注記2 モード結合がないか又は無視できる場合にも解析できる。
− リップルがなくきれいなガウシアン光源
− PMD>>σ0 σ0:自己相関包絡線のRMS幅
− エルゴード性
注記3 光源がガウシアンの場合,測定結果はDGDの加重平均の形になる。この加重はTINTYで
は規定がなく,GINTYでは規定している。この理由によって,この方法は方形加重を用い
る方法(例えば,RTMのような方法)とは,測定波長領域及び時間に対して異なる結果に
なると予想される。エルゴード性の仮定によって,予想できる値の関係性が有効になるが,
実際には,別の手法の異なる測定では測定波長領域もまた異なるため,同じように異なっ
た結果が得られることを意味している。
C.3.2 GINTY計算
GINTYは,TINTYにおける式(C.5)で必要な幾つかの仮定を取り除くことができる[4]。
35
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 理想的なランダムモード結合の仮定は必要ない。
− ガウシアン光源の仮定は必要ない。
− 自己相関関数の幅に比較してPMDが大きいという仮定は必要ない。
相互相関包絡線及び自己相関包絡線の二乗平均
()
τ
2
x
E
及び
()
τ
2
0
E
は式(C.6)となる。
()
()
∑
=
i
xi
x
E
N
E
τ
τ
2
2
1
()
()
∑
=
i
i
E
N
E
τ
τ
2
0
2
0
1
································· (C.6)
ここに,
N: I/O偏光状態の数
二つの二乗平均包絡線のRMS幅σ0及びσxを計算する。この計算のアルゴリズムの例はD.2による。こ
れらの幅の数学的な定義は,式(C.7)である。
()
()
()
∫
∫
=
τ
τ
τ
τ
τ
τ
τ
τ
σ
d
E
d
E
x
x
x
2
2
2
2
()
()
()
∫
∫
=
τ
τ
τ
τ
τ
τ
τ
τ
σ
d
E
d
E
2
0
2
0
2
2
0
··························· (C.7)
上式の期待値演算子は,均一でランダムなI/O偏光状態での測定に関連している。
PMDRMSの値は,式(C.8)によって算出する。
(
)
2
/1
2
0
2
RMS
2
3
−
=
σ
σx
PMD
························································· (C.8)
式(C.8)と式(2)とは,式(C.9)の関係にある[4]。
()()
()
(
)
2
0
2
2
0
2
0
2
2
3
σ
σ
τ
−
=
∆
∫
∫
x
dv
v
S
dv
v
S
v
····················································· (C.9)
式(C.7)のRMS幅の理想的な定義を用いると,式(C.9)は,測定時の全てのDGD曲線及び全ての光源スペ
クトル特性に対して正確である。式(C.9)の左辺は,スペクトル(二乗パワー)によって加重のかかったRMS
計算である。
エルゴード性を仮定すると,式(C.10)の関係がある。
()()
()
∫
∫∆
=
∆
dv
v
S
dv
v
S
v
2
0
2
0
2
2
τ
τ
······················································ (C.10)
36
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
フリンジ包絡線からのRMS幅の決定
序文
この附属書は,フリンジ包絡線からRMS幅を決定する二つの方法を記載する。主に干渉法によるPMD
測定で,これらの方法を用いる。D.1は自己相関ピークがある包絡線に対するもので,TINTY解析に適用
する。D.2はこのピークがない場合に対するもので,GINTY解析に適用する。
D.1 TINTYに対するRMS計算
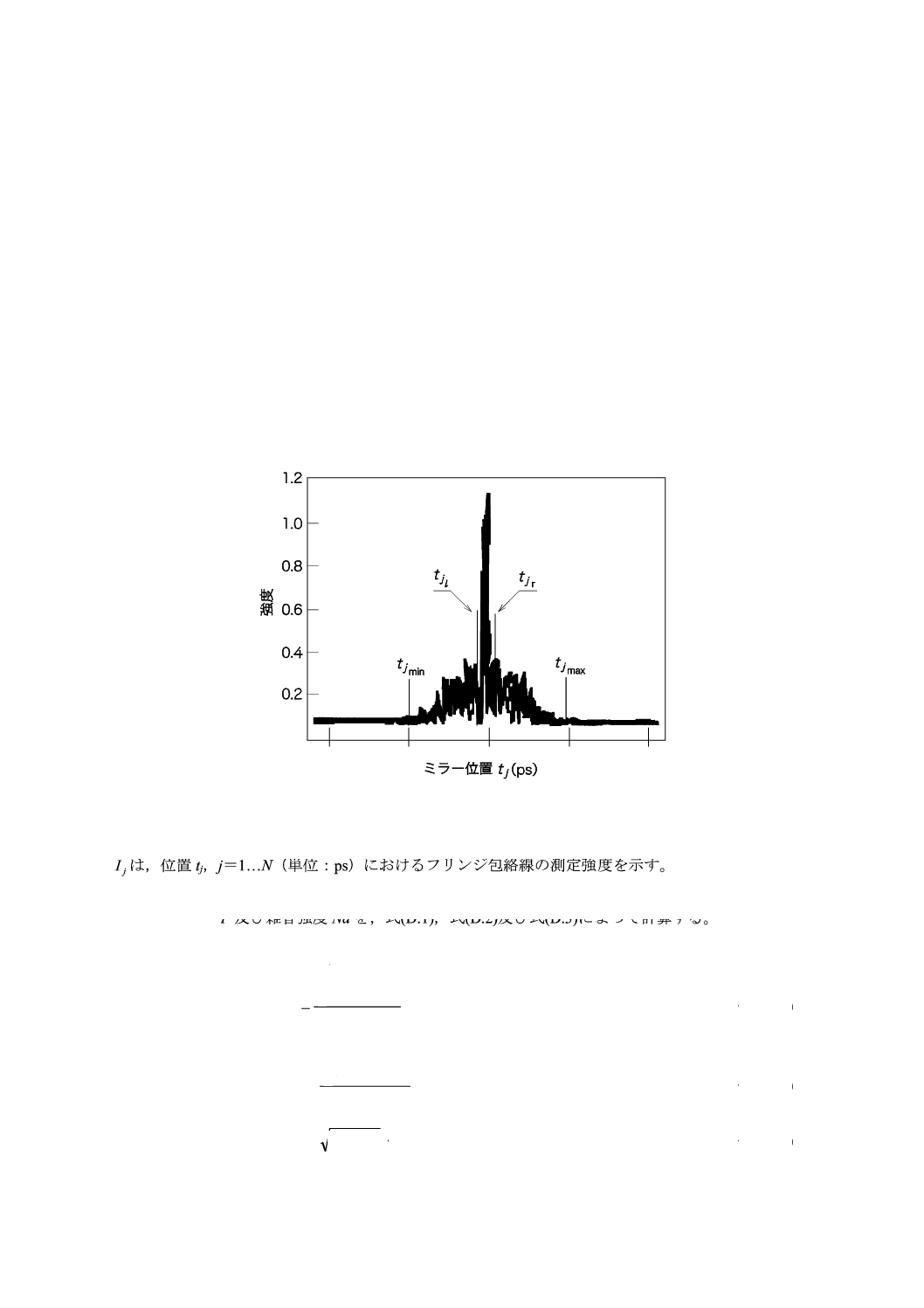
中心に自己相関ピークが存在するフリンジ包絡線を,図D.1に示す。
図D.1−干渉スペクトル解析のための変数
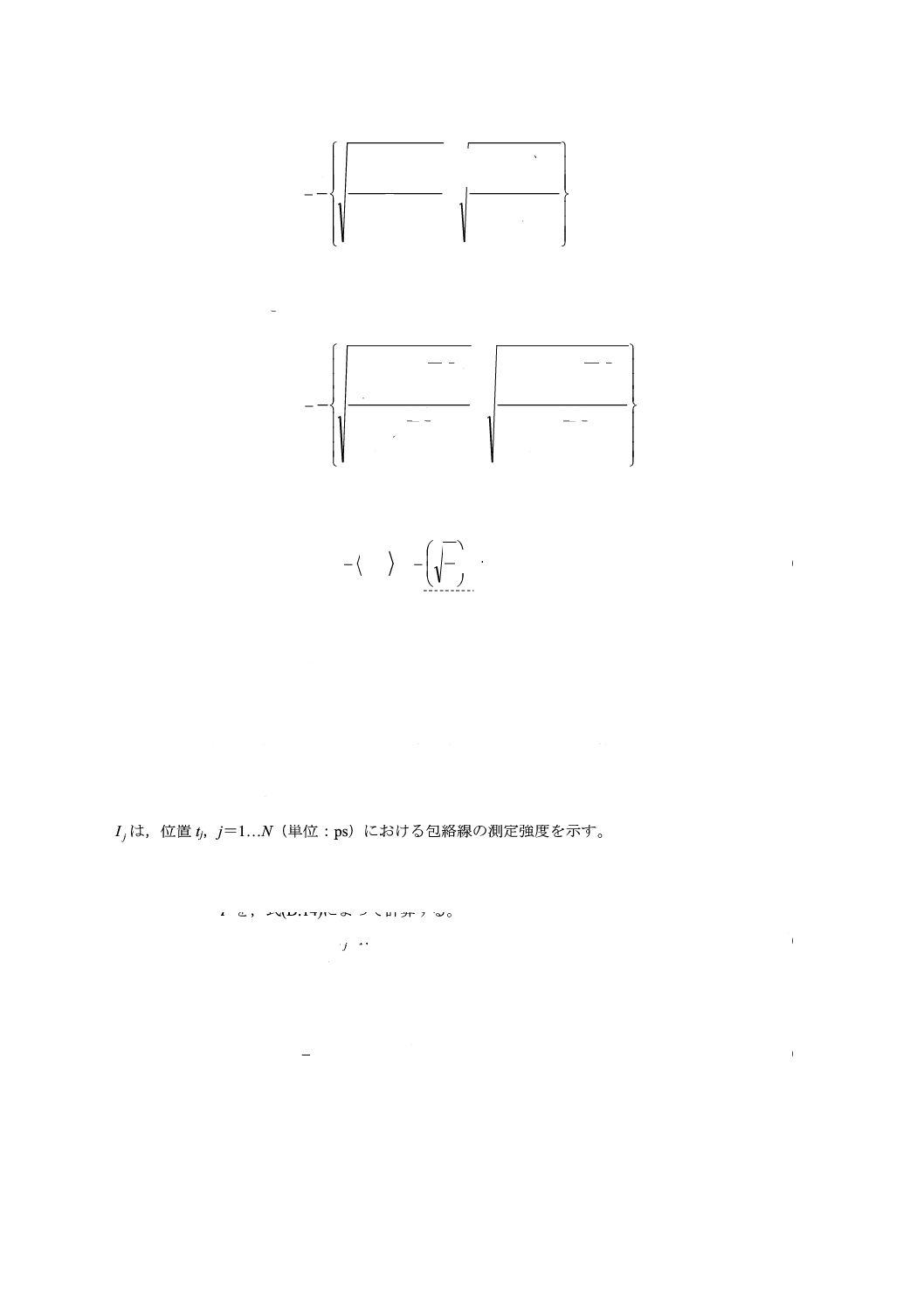
jI~は,位置tj,j=1…N(単位:ps)におけるフリンジ包絡線の測定強度を示す。
手順1−ゼロ強度
0
~I及び雑音強度Naを,式(D.1),式(D.2)及び式(D.3)によって計算する。
定義:N5=round(5N/100) round:小数点以下四捨五入
(
)
5
1
0
2
~
~
~
5
N
I
I
I
N
j
j
N
j
∑
=
−
+
=
··································································· (D.1)
(
)
5
1
2
2
2
2
~
~
5
N
I
I
X
N
j
j
N
j
∑
=
−
+
=
································································· (D.2)
2
0
2
I
X
Na
−
=
······································································· (D.3)
37
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順2−シフト強度Ijを,式(D.4),又は式(D.5)によって計算する。
0
~
~
:
I
I
I
j
j
−
=
(
Na
I
Ij
4
~
~
0>
−
のとき) ····································· (D.4)
0
:=
jI
(
Na
I
Ij
4
~
~
0≦
−
のとき) ····································· (D.5)
手順3−干渉スペクトルの中心Cを,式(D.6)によって計算する。
∑
∑
=
=
=
N
j
j
N
j
j
j
I
I
t
C
1
1
··········································································· (D.6)
手順4−中心の自己相関ピークを取り除くための指数を,式(D.7A)及び式(D.7B)によって決定する。
式(D.7A)である,jの最大指数をjlと定める。
ct
t
C
j>
−
············································································ (D.7A)
式(D.7B)である,jの最小指数をjrと定める。
ct
C
tj
>
−
············································································ (D.7B)
ここに,
tc: 光源のコヒーレンス時間
注記 相互相関干渉スペクトルに対しては,式(D.7)の定義を適用する。
1
:
+
=
l
r
j
j
············································································· (D.7)
手順5−干渉スペクトルの二次モーメントSを式(D.8)によって計算する。
(
)
(
)
−
+
−
=
∑
∑
∑
∑
=
=
=
=
N
j
j
j
N
j
j
j
j
j
j
j
j
j
j
j
r
r
l
l
I
I
C
t
I
I
C
t
S
2
1
1
2
2
1
····································· (D.8)
手順6−干渉スペクトルを切り取るための指数を,式(D.9)及び式(D.10)によって決定する。
式(D.9)である,jの最大指数をjminと定める。
S
t
C
j
2
>
−
············································································ (D.9)
式(D.10)である,jの最小指数をjmaxと定める。
S
C
tj
2
>
−
···········································································(D.10)
手順7−切り出した干渉スペクトルの二次モーメントσεを,式(D.11)によって計算する
38
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
(
)
−
+
−
=
∑
∑
∑
∑
=
=
=
=
max
max
min
min
2
2
ε
2
1
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
r
r
l
l
I
I
C
t
I
I
C
t
σ
·································· (D.11)
手順8−ガウス曲線
(
)
2
2
2σ
C
t
e
−
−
のσを,式(D.12)によって計算する。
(
)
(
)
(
)
(
)
(
)
(
)
−
+
−
=
∫
∫
∫
∫
−
−
−
−
−
−
−
−
max
2
2
max
2
2
min
2
2
min
2
2
2
2
2
2
2
2
ε
2
1
j
rj
j
rj
lj
j
lj
j
t
t
C
t
t
t
C
t
t
t
C
t
t
t
C
t
dt
e
dt
e
C
t
dt
e
dt
e
C
t
σ
σ
σ
σ
σ
·····················(D.12)
手順9−PMDRMS<Δτ2>1/2を,式(D.13)によって決定する。
σ
τ
=
∆
=
4
3
2/1
2
RMS
PMD
····················································(D.13)
D.2 GINTYに対するRMS計算
方法C(GINTY)における複合した二乗相互相関又は自己相関に対する明確なRMS幅は,次のアルゴ
リズムによって求める。
アルゴリズムは反復計算である。反復計算において,全てのデータ配列は二つの組に分けることができ
る。中央部Mは信号を含み,裾の部分Tは雑音を含んでいる。各反復計算は,これらの組に対して異なる
定義となる。計算されたRMS幅が変化しなくなるか又は組の定義が安定である場合に,結果は収束する。
反復において,各組のデータ点数をNM及びNTで示す。
jI~は,位置tj,j=1…N(単位:ps)における包絡線の測定強度を示す。
Tの最初の定義は全体の配列の最初及び最後の5 %である。
手順1−ゼロ強度
0
~Iを,式(D.14)によって計算する。
∑
∈
=
T
j
jN
I
I
T
0
/
~
~
······································································(D.14)
手順2−シフト強度Ijを,式(D.15)によって定義する。
0
~
~
I
I
I
j
j
−
=
N全てにおいて ················································(D.15)
手順3−干渉スペクトルの中心Cを,式(D.16)によって計算する。
39
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
∑
∈
∈
=
M
j
j
M
j
j
j
I
I
t
C
··········································································(D.16)
手順4−二乗包絡線のRMS幅σを,式(D.17)によって計算する。
(
)
∑
∑
∈
∈
−
=
M
j
j
M
j
j
j
I
I
C
t
2
2
σ
·································································(D.17)
手順5−組を再定義する。
MをC−4σ≦tj≦C+4σに対する点の組と定義する。
Tを残りの点の組と定義する。
手順6−結果が収束するまで手順1から手順5を繰り返す。
40
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(参考)
記号及び用語
記号
用語
Arg
偏角関数
ASE
増幅された自然放出光
BBS
広帯域光源
c/c0
真空/空間での光速度
DGD
群遅延差
DGDmax
最大DGD値
DOP
偏光度
E
R(λ)の極値の数(方法A)
EC
極値カウント法
f(Δτ)
マクスウェル確率分布
FA
固定アナライザ法(方法A)
FT
フーリエ変換法
GINTY
方法Cに対する一般的解析法
INTY
干渉法(方法C)
I/O
入出力
JME
ジョーンズ行列解析法(方法B)
k
モード結合係数
lc
結合長
L
被測定光ファイバ条長又は光ファイバケーブル条長
LED
発光ダイオード
N
測定回数又はモード結合光ファイバの集まり又は波長間隔の総数
PA(λ)
検光子を最初の設置状態で記録した光パワー(方法A)
PF
DGDmaxを超える確率
PB(λ)
検光子を90°に回転した状態で記録した光パワー(方法A)
PTot(λ)
検光子を取り外した状態で記録した光パワー(方法A)
Px(τ)/Py(τ)
方法Cでのフリンジに相当する二つの直交偏光状態の軸の受光パワー
PBS
偏光分岐器
PDL
偏光依存性損失
PDV
偏波分散ベクトル
PMD
偏波モード分散
PMDQ
リンク設計でのPMD値
PSA
ポアンカレ球解析法(方法B)
R(λ)
PMD測定系からの出力パワー比(方法A)
RBW
分解帯域幅
41
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
RTM
基準試験方法
s
規格化出力ストークスベクトル
SOP
偏光状態法(方法B)
SPE
ストークスパラメータ解析法(方法B)
T
ジョーンズ行列
T−1
ジョーンズ行列の逆行列
tc
光源のコヒーレンス時間(方法C)
TINTY
方法Cに対する慣例的解析法
α
マクスウェル分布を規定する単一パラメータ
Χ2
カイ二乗変数
c
q
v
h
ˆ
/ˆ
/ˆ
/ˆ
∆
∆
∆
∆
ストークスベクトルから計算する有限の差
δλ
波長刻み幅
Δλ
光源のスペクトル幅(その他の規定がない場合,半値全幅FWHM)
δν
光周波数の刻み幅
Δθ
ポアンカレ球上の回転角度
δτ
信号の異なる偏光成分の到達時間又はパルス広がり
δτmax
測定したδτの最大値
δτmin
測定したδτの最小値
Δτ
DGD値
Δτmax
最大DGD
<Δτ>
波長掃引範囲での平均DGD又はPMD値
<Δτ2>1/2
波長掃引範囲でのDGDの二乗平均又はPMD値(方法C)
<Δτ>0
モード結合光ファイバの集まりにおいて各光ファイバで起こり得る最大PMD特性
<Δτ>t
時間に対する平均DGD
<Δτ>T
温度に対する平均DGD
<Δτ>λ
波長に対する平均DGD
Δω
方法Bにおける角周波数変化
λ
PMD測定で用いる測定波長
λ0
光源の中心波長
λ1/λ2
測定波長の最初及び最後の波長[又は方法AにおけるR(λ)の最初/最後の極大値又は
極小値の位置]
ν
光周波数
ρ1/ρ2
T(ω+Δω)T−1(ω) の複素固有値
σ
標準偏差の不確定性
σ0
自己相関干渉スペクトルの二乗包絡線の二乗平均幅(方法CのGINTY)
σA
自己相関包絡線の二乗平均幅(方法C)
σR
フーリエ変換データの二次モーメント(方法A)
σx
相互相関干渉スペクトルの二乗包絡線の二乗平均幅(方法CのTINTY)
σε
相互相関包絡線の二乗平均幅(方法CのTINTY)
ω
光角周波数
42
C 6842:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Ω
PDV
参考文献
[1] C.D.Poole and D.L.Favin, “Polarization-mode dispersion measurements based on transmission spectra
through an analyzer,” JLT, vol. 12, No. 6, p. 917, June, 1994.
[2] R.C.Jones, “A new calculus for the treatment of optical systems. VI. Experimental determination of the
matrix,” J. Optical Soc. Am., 37, pp. 110-112, 1947.
[3] N.Gisin, B.Gisin, J.P.Von der Weid, and R.Passy, “How accurately one can measure a statistical quantity like
polarisation-mode dispersion?,” IEEE Photonics Technology Letters, Vol. 8, No. 12, pp. 1671-1673, Dec.,
1996.
[4] N.Cyr, “Polarization-mode dispersion measurement: generalization of the interferometric method to any
coupling regime,” J. Lightwave Technol., Vol. 22, No. 3, pp. 794-805, March 2004.
[5] W. Press, W.Vettering, S. Teukolsky, and B.Flannery, “Numerical Recipes in C,” Cambridge University Press,
p. 518, 1992.
[6] L. Lawson and R.Hanson, “Solving Least Squares Problems,” Prentiss-Hall, pp. 222-225, 1972.
附属書JA
(参考)
JISと対応国際規格との対比表
JIS C 6842:2012 光ファイバ偏波モード分散試験方法
IEC 60793-1-1:2008 Optical fibres−Part 1-1: Measurement methods and test
procedures−General and guidance
IEC 60793-1-48:2007 Optical fibres−Part 1-48: Measurement methods and test
procedures−Polarization mode dispersion
(I)JISの規定
(II)
国際規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
1 適用範
囲
IEC
60793-1-48
1
JISに同じ
一致
2 引用規
格
3 用語及
び定義
3
JISに同じ
一致
4 光ファ
イバの種
類
IEC
60793-1-1
8
JISとほぼ同じ
変更
JIS体系に従った形名を用い
た。
参考としてIEC記号を追加し
た。
JISでは従来からの整合性を整え
るため,日本において普及した名
称を用いている。
5 試験状
態
5
JISとほぼ同じ
変更
JIS C 60068-1を引用し,標準
大気条件を変更した。
現場測定の条件を考慮している。
実質的な差異はない。
6 概要
6.1
6.2〜6.4
偏波モード分散及
び試験方法の概要
IEC
60793-1-48
Introduction
4
JISとほぼ同じ
一致
変更
IEC規格の式(3)を変更した。
IEC規格の誤表記による修正で
あり,実質的な差異はない。
7 装置
7.1
7.2〜7.10
5
5.1〜5.9
JISとほぼ同じ
変更
細分箇条番号を追加した。
細分箇条番号を振り直した。
実質的な差異はない。
2
C
6
8
4
2
:
2
0
1
2
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
8 サンプ
リング及
び試料
8.1
8.2〜8.3
IEC
60793-1-48
6
6.1〜6.2
JISとほぼ同じ
変更
細分箇条番号を追加した。
細分箇条番号を振り直した。
実質的な差異はない。
9 手順
7
JISに同じ
一致
10 計算
又は結果
の解釈
8
JISに同じ
一致
11 結果
9
JISに同じ
一致
12 仕様
情報
10
JISに同じ
一致
附属書A
(規定)
A.3.3.3
コサインフーリエ
変換法の解析例
Annex A
(normative)
A.3.3.3
JISとほぼ同じ
変更
IEC規格Table A.1内のΔν,最
大PMDRMS,及び波長間隔の数
値を変更した。
式(A.15)によって算出するΔν,最
大PMDRMS,及びΔνから求める
波長間隔の値について修正した。
IEC規格の計算値が誤って記載
されているための修正であり,測
定方法に実質的な差異はない。
附属書B
(規定)
B.3.1
ジョーンズ行列解
析法を規定
Annex B
(normative)
B.3.1
JISとほぼ同じ
追加
式(B.3A)を追加した。
JME法では,PSA法の式(B.8)に
対応する手順の記載がないため,
計算手法をより明確にするため
に式(B.3A)を追加した。実質的な
差異はない。
附属書C
(規定)
Annex B
(normative)
JISに同じ
一致
2
C
6
8
4
2
:
2
0
1
2
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
附属書D
(参考)
D.1
D.2
フリンジ包絡線か
らのRMS幅の決定
方法
IEC
60793-1-48
Annex D
(informative)
D.1
D.2
JISとほぼ同じ
変更
IEC規格(I-7)及び(I-8)の式番
号を(D.7A)及び(D.7B)に変更。
また,式(D.13)を変更。
nmをNMに変更。
前後の式番号との整合性のため,
式番号を変更した。また,(D.13)
及びNMについてはIEC規格の誤
表記による修正である。いずれも
実質的な差異はない。
附属書E
(参考)
JISと国際規格との対応の程度の全体評価:IEC 60793-1-1:2008,IEC 60793-1-48:2007 : MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 一致……………… 技術的差異がない。
− 追加……………… 国際規格にない規定項目又は規定内容を追加している。
− 変更……………… 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD…………… 国際規格を修正している。
2
C
6
8
4
2
:
2
0
1
2
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。