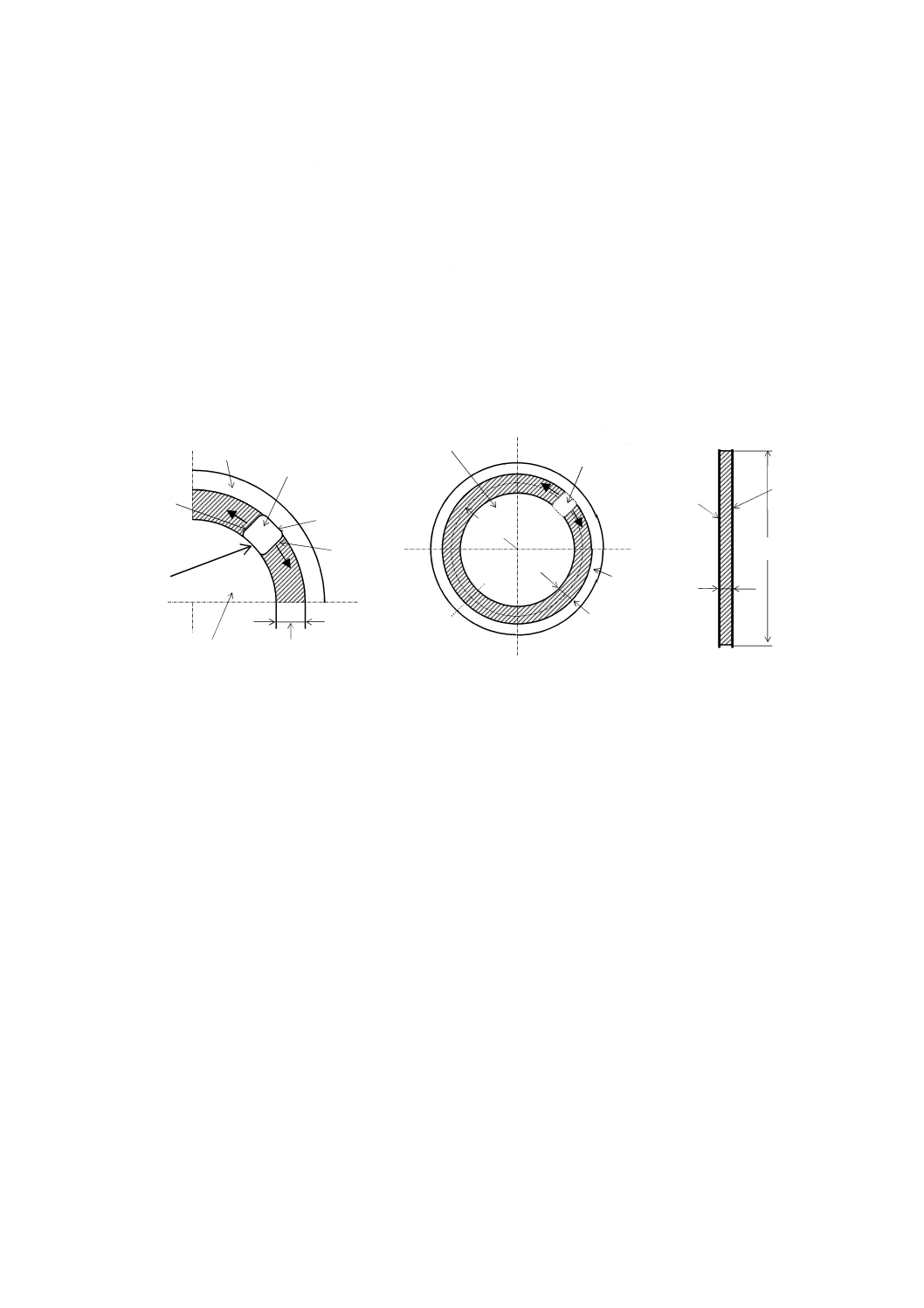C 2139-1:2019
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
3.1 一般的用語及び定義 ······································································································· 1
3.2 電気抵抗特性に関する用語及び定義··················································································· 3
3.3 誘電特性に関する用語及び定義 ························································································ 4
3.4 測定回路及び測定装置に関する用語及び定義 ······································································· 6
4 電気絶縁材料の性質に影響を及ぼす因子 ··············································································· 9
4.1 一般的事項 ··················································································································· 9
4.2 電気抵抗特性及び誘電特性に影響を及ぼす因子 ···································································· 9
5 測定方法及び測定装置 ······································································································ 11
5.1 一般的事項 ·················································································································· 11
5.2 抵抗特性の測定方法 ······································································································ 11
5.3 誘電特性の測定方法 ······································································································ 12
5.4 測定装置 ····················································································································· 12
6 試験手順························································································································ 13
附属書JA(参考)電気分極,脱分極,緩和時間及び吸収電流 ······················································ 14
附属書JB(参考)体積抵抗率及び表面抵抗率−概念及び測定方法 ················································ 18
附属書JC(参考)表面抵抗測定−2端子測定の問題点及び3端子測定の利点 ·································· 22
附属書JD(参考)比誘電率測定−縁端静電容量の補正について ··················································· 24
附属書JE(参考)測定回路−ブリッジ回路及び共振回路 ···························································· 27
附属書JF(参考)ガード及びガード回路 ················································································· 33
参考文献 ···························································································································· 39
附属書JG(参考)JISと対応国際規格との対比表 ······································································ 40
C 2139-1:2019
(2)
まえがき
この規格は,産業標準化法第12条第1項の規定に基づき,一般社団法人電気学会(IEEJ)及び一般財団
法人日本規格協会(JSA)から,産業標準原案を添えて日本産業規格を制定すべきとの申出があり,日本
産業標準調査会の審議を経て,経済産業大臣が制定した日本産業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS C 2139の規格群には,次に示す部編成がある。
JIS C 2139-1 第1部:基本事項
JIS C 2139-3-1 第3-1部:直流電圧印加による抵抗特性の測定−体積抵抗及び体積抵抗率
JIS C 2139-3-2 第3-2部:直流電圧印加による抵抗特性の測定−表面抵抗及び表面抵抗率
JIS C 2139-3-3 第3-3部:直流電圧印加による抵抗特性の測定−絶縁抵抗
日本産業規格 JIS
C 2139-1:2019
固体電気絶縁材料の誘電特性及び抵抗特性−
第1部:基本事項
Dielectric and resistive properties of solid insulating materials-
Part 1: General
序文
この規格は,2011年に第1版として発行されたIEC 62631-1を基とし,技術的内容及び構成を変更して
作成した日本産業規格である。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JGに示す。また,附属書JA〜附属書JFは対応国際規格に
はない事項である。
1
適用範囲
この規格は,固体絶縁材料の誘電特性及び電気抵抗特性を測定するための基本的かつ普遍的な指針につ
いて規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 62631-1:2011,Dielectric and resistive properties of solid insulating materials−Part 1: General
(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS C 2142 固体電気絶縁材料−試験前及び試験時における標準状態
JIS C 2139-3(規格群) 固体電気絶縁材料の誘電特性及び抵抗特性
IEC 60050-212,International Electrotechnical Vocabulary−Part 212: Electrical insulating solids, liquids, and
gases
3
用語及び定義
この規格で用いる主な用語及び定義は,IEC 60050-212によるほか,次による。
3.1
一般的用語及び定義
3.1.1
電気絶縁材料(electrical insulating material)
2
C 2139-1:2019
電気伝導度が無視できる程度に小さく,異なった電位をもつ導電性部品を分離するために用いる固体材
料。
3.1.2
伝導電流(conduction current)
直流電圧を印加したとき,過渡電流が認められなくなった後に測定される時間的に変化しない電流[1]。
3.1.3
充電電流(charging current)
試験片を誘電体とするキャパシタを充電する間に流れる電流のうちの過渡電流成分。
注記 静電容量素子として,キャパシタ及びコンデンサの呼称が混用されている。しかし,コンデン
サはまれに冷凍設備の凝縮器又は熱機関の復水器と混同されることがあるため,この規格では
キャパシタで統一した。
3.1.4
電界の強さ,E(electric field strength)
空間のある点に単位電荷を静止させて置いたとき,その電荷に作用する電気的な力のベクトル量。
注記 電荷量Qをもつ静止している荷電粒子に力Fが働いているとき,電荷量Qとの積がFとなる
ようなベクトル量Eをいう。
E
Q
F
×
=
················································································ (1)
3.1.5
電気分極,P(electric polarization)
電界の作用によって,物質全体が電界方向に電気双極子モーメントを生じる現象。単に分極又は誘電分
極ということもある。無限に小さいとみなすことのできる体積vのある微小領域内の一点における分極の
大きさを表す量Pは,その微小領域内に含まれる物質の電気双極子モーメントpを体積vで除した値に等
しいベクトル量である。
v
p
P=
····················································································· (2)
注記 分極は,荷電粒子の変位又は双極子の配向の結果として生じる。分極は,電気絶縁材料内部の
界面及び電極界面にも生じる。全ての分極は,時間及び周波数に強く依存し,温度にも同様に
依存する。そのため,分極は,誘電特性及び電気抵抗特性の両方に大きな影響を与える。また,
直流電圧印加に伴って電気絶縁材料が分極を完了するまでの時間変化の過程は,通常,電気絶
縁材料の電気抵抗特性を測定する際に観測される分極現象として理解されている。
3.1.6
電束密度,D(electric flux density)
電荷が存在することによって生じるベクトル量。電界Eと真空誘電率ε0との積に分極Pを加えて,空間
のある一点で得られるベクトル量[1]。
D=ε0E+P ················································································ (3)
3.1.7
脱分極(depolarization)
電気絶縁材料から電気分極を取り除く過程及び処理[4](附属書JA参照)。
注記 一般に脱分極処理は,電気絶縁材料の電気抵抗特性を測定する前に,測定誤差を避けるために
行う。
3
C 2139-1:2019
3.1.8
分極電流(polarization current)
電圧印加に伴って流れる過渡電流成分(附属書JA参照)。
注記 分極電流は,前もって両電極を十分に長い時間短絡して,短絡電流が無視できるようになって
から測定する。
3.1.9
脱分極電流(depolarization current)
ある時点で直流電圧を印加した後,絶縁体に接触した二つの電極間を短絡したときに流れる電流(附属
書JA参照)。
注記 通常,脱分極電流は,直流電圧印加後,分極電流が無視できる程度に小さくなってから測定す
る。
3.1.10
緩和時間,τ(relaxation time)
電気絶縁材料に電圧を印加したとき,分極が平衡状態に達するまでに要する時間,又は静電界中で分極
した電気絶縁材料から電圧を取り去ったとき,脱分極が終わるまでに要する時間(附属書JA参照)。
注記 現象及び/又は状態が非平衡から平衡に向かって変化するとき,変化に要する時間の指標とな
る数値。ここで平衡とは,対象としている任意の量が時間とともに一定となる定常状態を指す。
3.2
電気抵抗特性に関する用語及び定義
3.2.1
一般的事項
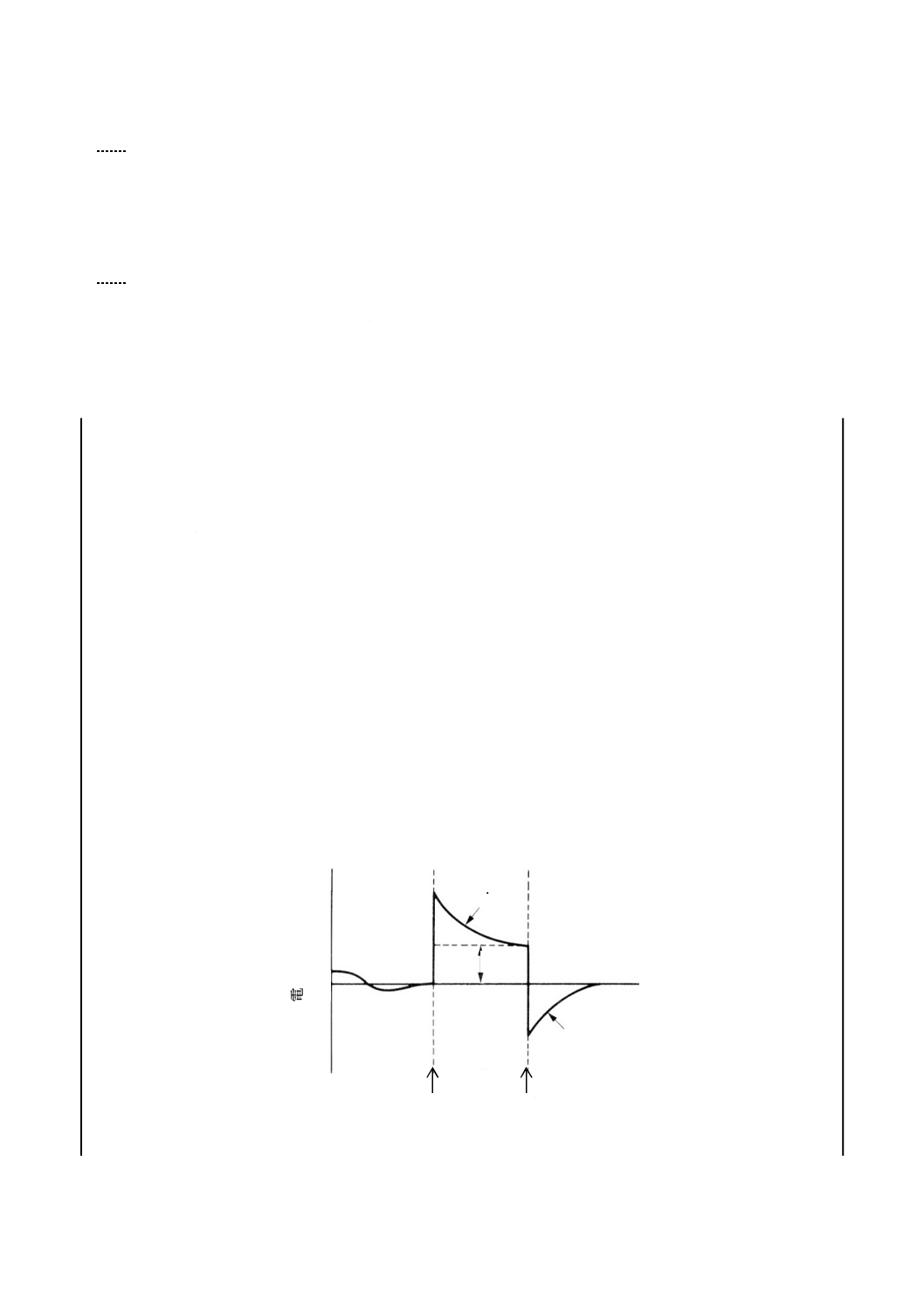
一定の時間領域において,直流によって測定される3.2.2〜3.2.6に規定する包括的な材料の性質を定義す
る。
注記 試験片を流れる電流は,図1に示すような複雑な変化を示すことがある。図中のAの領域は,
直流電圧の印加前に電極間を短絡した場合で,残留電荷の消滅に伴う電流の時間変化の一例で
ある。Bの領域は,電圧印加後に電流が時間的に変化する様子を示す。電流は,充電電流成分
iaと伝導電流成分i0との和となり,電流iaは時間とともに減少する。電流iaを吸収電流という
ことがある。Cの領域は,電圧を取り除き,電極間を短絡した後の脱分極電流ia' であり,電流
ia' の極性は反転し,その大きさは時間とともに減少する[6](附属書JA参照)。
図1−試験片を流れる電流の時間変化[6]
電圧印加
電圧除去
時間
電
流
0
ia'
i0
ia
A
B
C
4
C 2139-1:2019
3.2.2
絶縁抵抗(insulation resistance)
規定された条件の下で,絶縁材料によって隔てられた二つの導体間の電気抵抗。
注記 絶縁抵抗は,規定された幾何学形状の試験片における体積抵抗及び表面抵抗の二つの成分を含
む。
3.2.3
体積抵抗(volume resistance)
絶縁体に接触する二つの電極間の直流電圧を,電圧印加から一定時間経過後に絶縁体を通って流れる電
流で除した値(附属書JB参照)。
注記 この定義に関する限り,絶縁体の表面を流れる電流は除外され,かつ,絶縁体と二つの電極と
の界面にそれぞれ生じる可能性のある分極現象は無視する。
3.2.4
体積抵抗率,ρ(volume resistivity)
電圧印加から一定時間経過後における絶縁体内部の電界の強さを電流密度で除した値。実際には,試験
片を単位体積の立方体に換算した体積抵抗である(附属書JB参照)。
注記 体積抵抗率の単位は,オーム・メートル(Ω・m)である。オーム・センチメートル(Ω・cm)
(CGS単位系)もしばしば用いられる。1(Ω・m)=100(Ω・cm)である。
3.2.5
表面抵抗(surface resistance)
表面に沿った電気伝導による絶縁抵抗の成分(附属書JB及び附属書JC参照)。
注記 表面電流は,一般的に電圧印加後の経過時間に強く依存し,しばしば不規則に変化する。
3.2.6
表面抵抗率,σ(surface resistivity)
絶縁材料の表面層における直流電界の強さを,電極の単位長さ当たりの電流で除した値。実際には,試
験片表面上の正方形の面に換算した表面抵抗である(附属書JB及び附属書JC参照)。
注記 表面抵抗率の単位は,オーム[Ω]である。Ω/□又はΩ/sqの表記も用いられている。
3.3
誘電特性に関する用語及び定義
3.3.1
誘電体(dielectric)
誘電分極を示す物質。
注記 電気絶縁材料は,誘電体の性質をもつ[4]。
3.3.2
静電容量,C(capacitance)
二つの導体と誘電体との配置において,導体の間に電位差がある場合に,電荷の蓄積の許容量を表す特
性値。
注記 静電容量Cは,電位差Uに対する電荷量qの比である。静電容量の値は,常に正である。電荷
量の単位をクーロン(C),電位差の単位をボルト(V)とすれば,静電容量の単位はファラッ
ド(F)である。
U
q
C=
···················································································· (4)
5
C 2139-1:2019
3.3.3
誘電率,ε(absolute permittivity)
電界中に置かれた誘電体に電気分極が生じる程度を表す定数で,電束密度Dを電界Eで除した値。すな
わち,次の式である。
D=εE ····················································································· (5)
注記 誘電率は,ファラッド/メータ(F/m)で表す。
3.3.4
比誘電率,εr(relative permittivity)
真空誘電率ε0に対する供試誘電体の誘電率εの比。したがって,次の式となる。
ε=ε0・εr ···················································································· (6)
注記1 真空誘電率ε0は,次の値である。
ε0=8.854×10−12 [F/m] ································································ (7)
注記2 定常電界及び超低周波交流電界の場合,等方性又は準等方性誘電体の比誘電率は,電極間隙
及び電極周囲を,その誘電体だけで完全に満たしたキャパシタの,同じ電極配置を真空中に
置いたキャパシタの静電容量に対する比に等しい。
注記3 誘電率という用語は,通常,比誘電率を指して用いる。
注記4 絶縁材料の比誘電率εrは,二つの電極を供試誘電体媒質の中に置いたキャパシタの静電容量
Cxを,真空中に置いた同じ電極配置の静電容量C0で除した値である。
0
x
r
C
C
ε=
··················································································· (8)
しかし,実際にはCxの代わりに二つの電極間隙だけを供試誘電体で満たし,周囲の媒質は
普通空気の状態でキャパシタの静電容量Cx'を測定する。したがって,特に誘電率を正しく測
定するためには,一般に縁端静電容量Ceの補正を行う(附属書JD参照)。ここに,Ce=Cx
−Cx'である。
二酸化炭素を含まない乾燥空気の比誘電率εrは,常圧では1.00 053である。そこで実用上
は,電極間を真空に置換した静電容量(真空静電容量)C0の代わりに,通常は空気中の所定
の電極配置における静電容量Caを用いて,十分な精度で比誘電率εrを測定することができる。
3.3.5
複素比誘電率,ε*r(relative complex permittivity)
一定の正弦波電界下における次の式で表される複素数表示の比誘電率。
ε*r=ε'r−jε''r=εr・e−jδ ··································································· (9)
ここで,ε'r及びε''rは正の値,δは損失角である。
注記1 複素比誘電率ε*rは,通常ε'r及びε''r又はε'r及びtan δで表される。ε'r≫ε''rならばεr≈ε'rであ
り,共に比誘電率と呼ぶ。
注記2 ε''rは,誘電損率(loss index)と呼ぶ。
3.3.6
誘電正接,tan δ[dielectric dissipation factor,(dielectric) loss tangent,tan δ]
複素比誘電率の虚数部の実数部に対する比の値。
tan δ=ε''r/ε'r ············································································ (10)
注記 したがって,絶縁材料の誘電正接は,供試固体絶縁材料だけが試験キャパシタの誘電体として
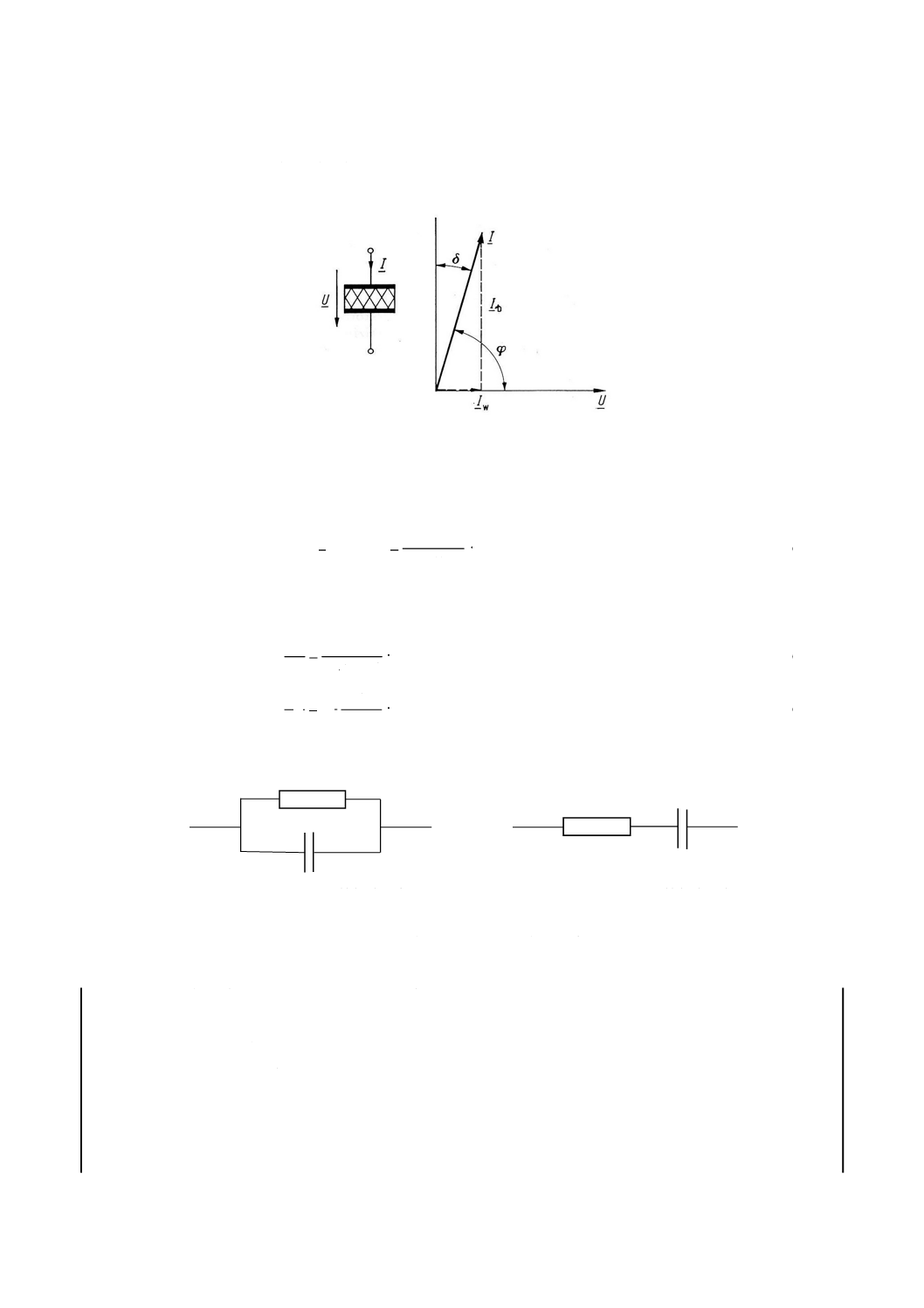
6
C 2139-1:2019
用いられている場合に,印加電圧とそれによって生じる電流の位相差φのπ/2[rad]との差δ
の正接である(図2参照)。
図2−誘電正接
誘電正接は,理想キャパシタとそれに直列又は並列に接続された抵抗の等価回路とによっても表すこと
ができる(図3参照)。
p
p
s
s
1
tan
R
ωC
R
ωC
δ
×
=
×
=
·························································(11)
ここに,周波数をfとすれば,
πf
ω2
=
で,角周波数と呼ばれる。図3に示すCp,Cs,Rp,Rs及びtan δ
との間には,次の関係がある。
δ
C
C
2
s
p
tan
1
1
+
=
········································································ (12)
δ
R
R
2
s
p
tan
1
1+
=
········································································ (13)
Rp:等価並列抵抗 Cp:等価並列容量
Rs:等価直列抵抗 Cs:等価直列容量
a) 等価並列回路
b) 等価直列回路
図3−誘電体キャパシタの等価回路
3.4
測定回路及び測定装置に関する用語及び定義
3.4.1
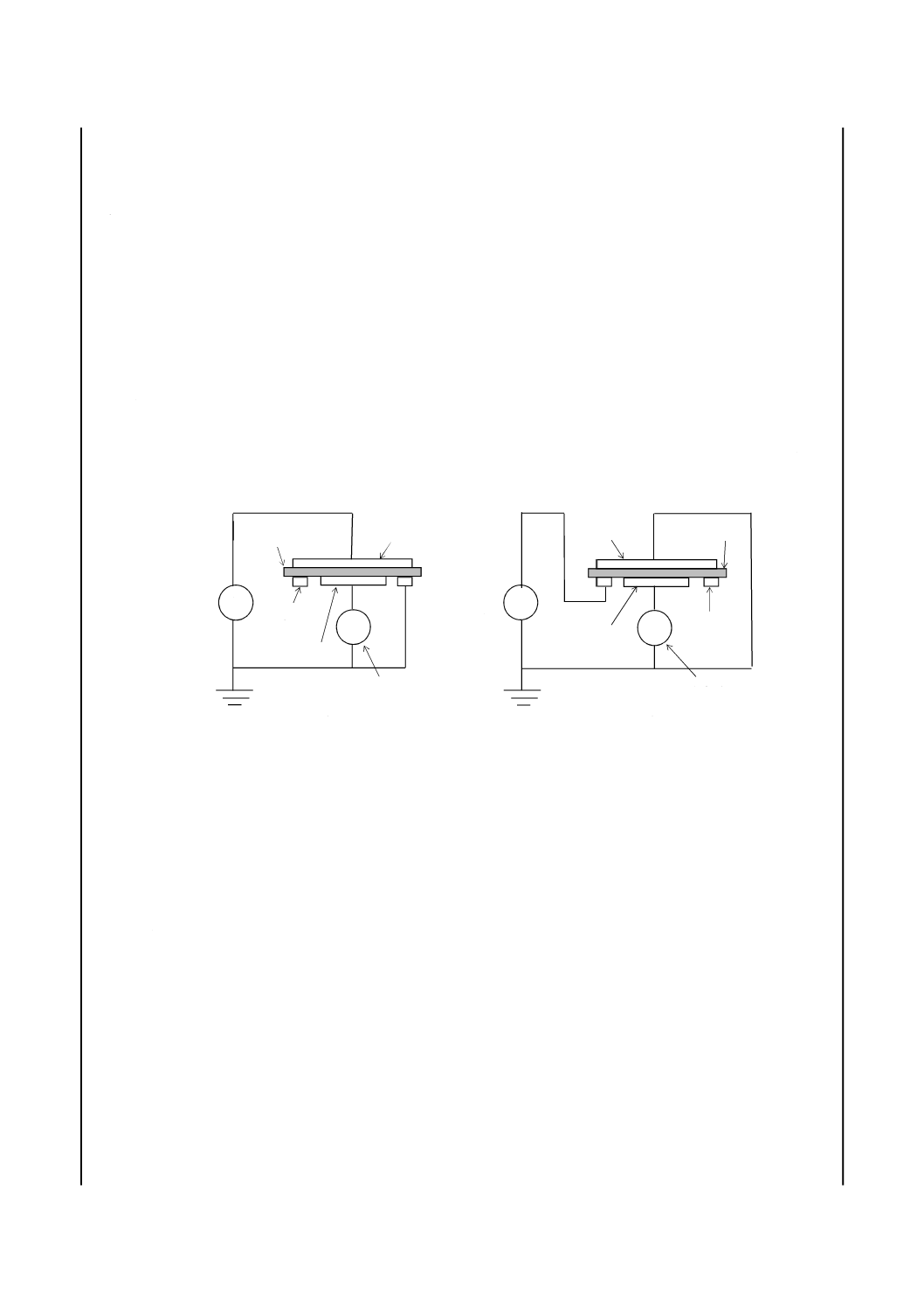
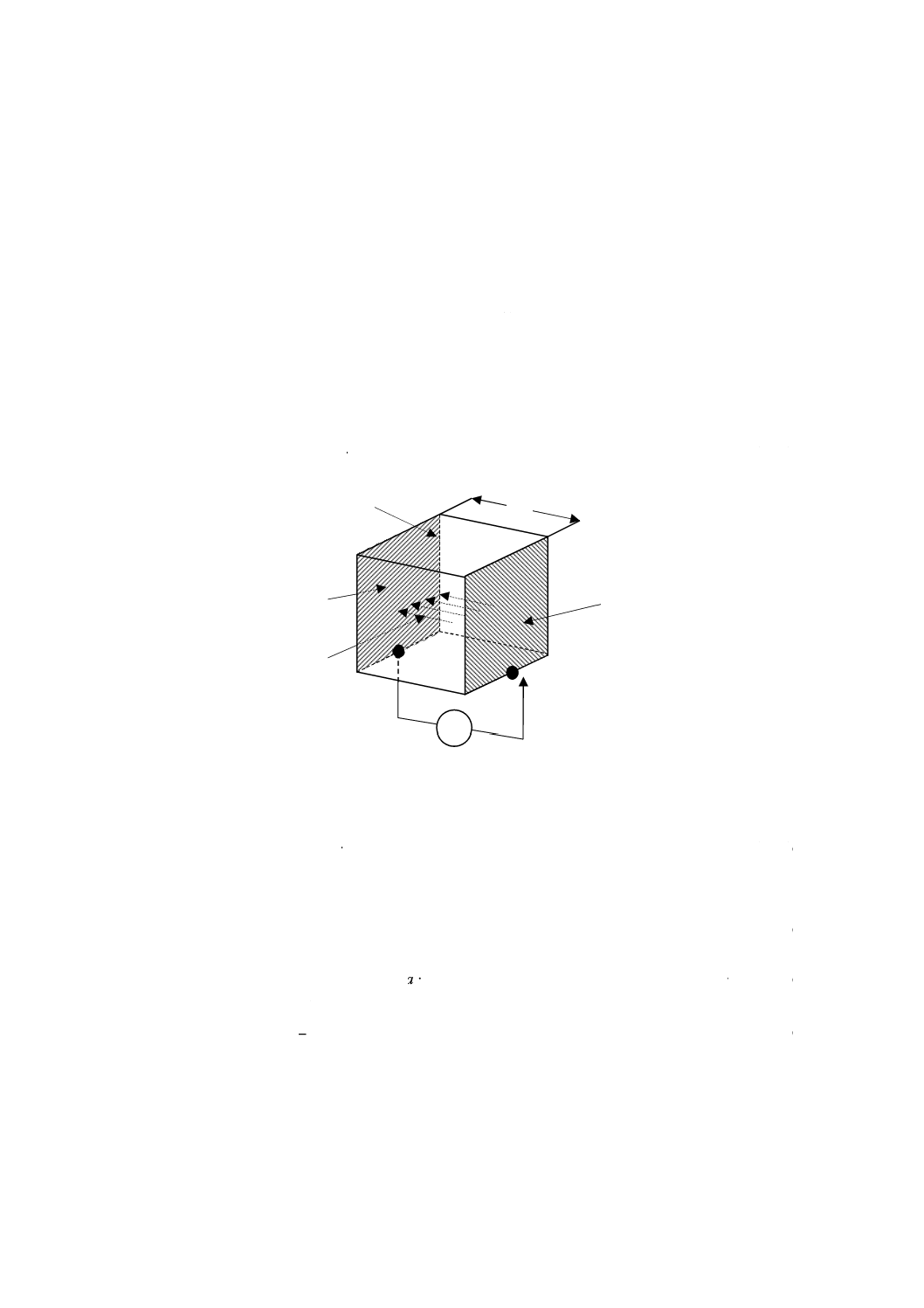
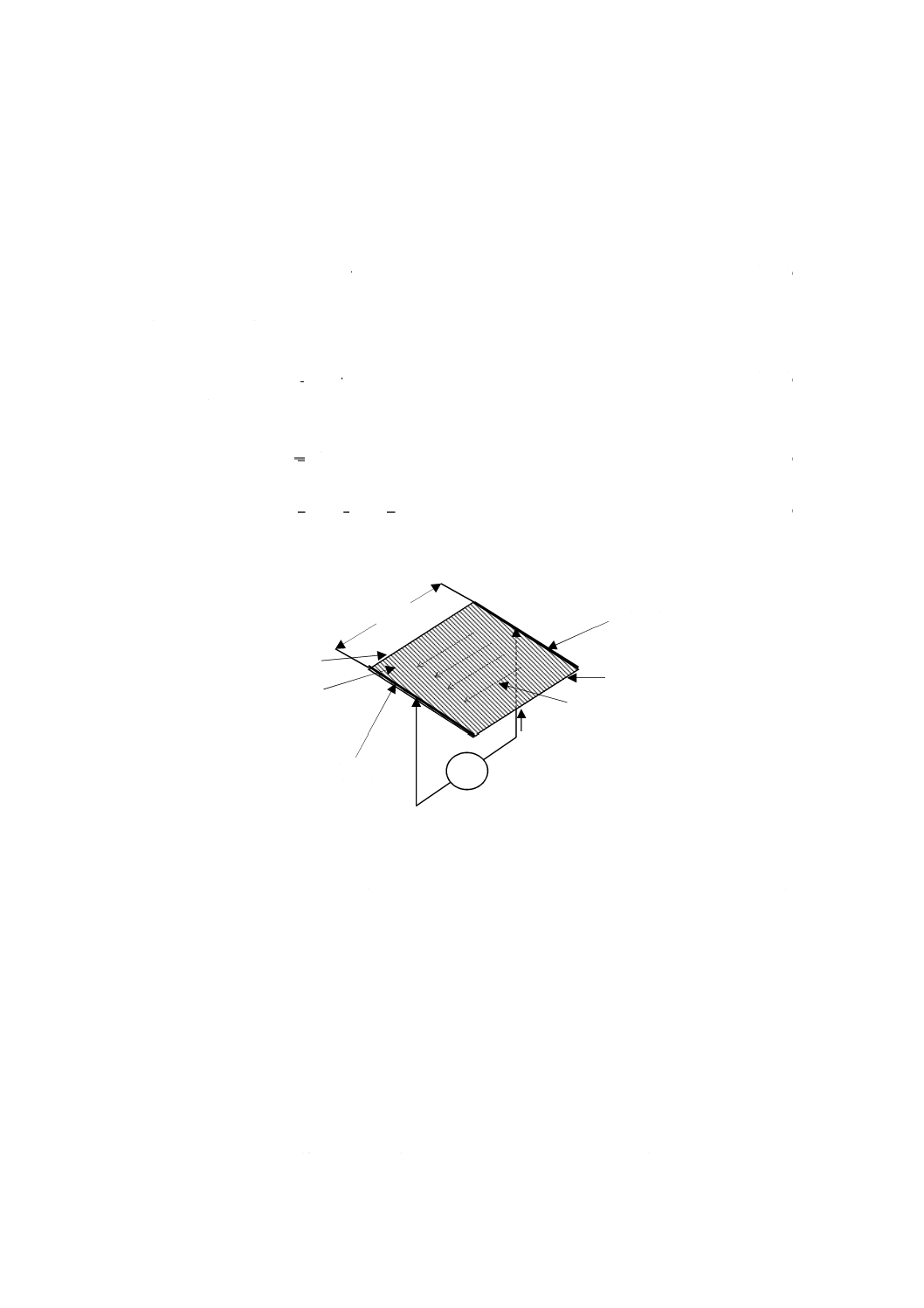
主電極(main electrode)
誘電率,誘電正接又は絶縁抵抗試験において,試験片に設けられた電極のうち,測定電流だけを流す側
の電極(図4及び附属書JB参照)。
3.4.2
対電極(counter electrode)
Cp
Rs
Cs
Rp
7
C 2139-1:2019
誘電率,誘電正接又は絶縁抵抗試験において,試験片に設けた電極のうち,試験片を挟んで主電極と対
向し,測定電流に漏れ電流を加えた全電流を流す電極(図4及び附属書JB参照)。
3.4.3
ガード電極(guard electrode)
誘電率,誘電正接又は絶縁抵抗試験において,測定誤差をなくすために設けた漏れ電流を流す電極(図
4及び附属書JB参照)。
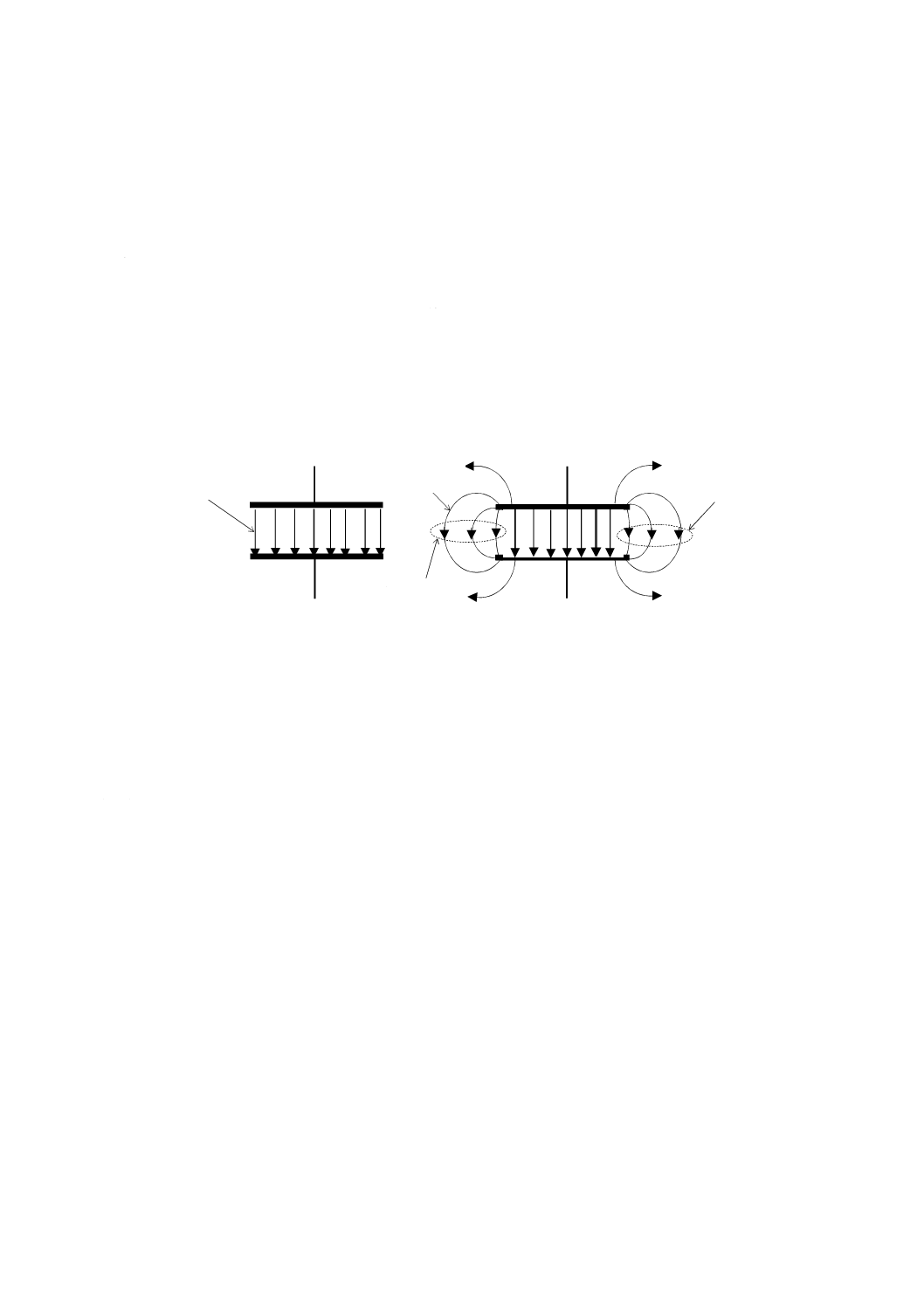
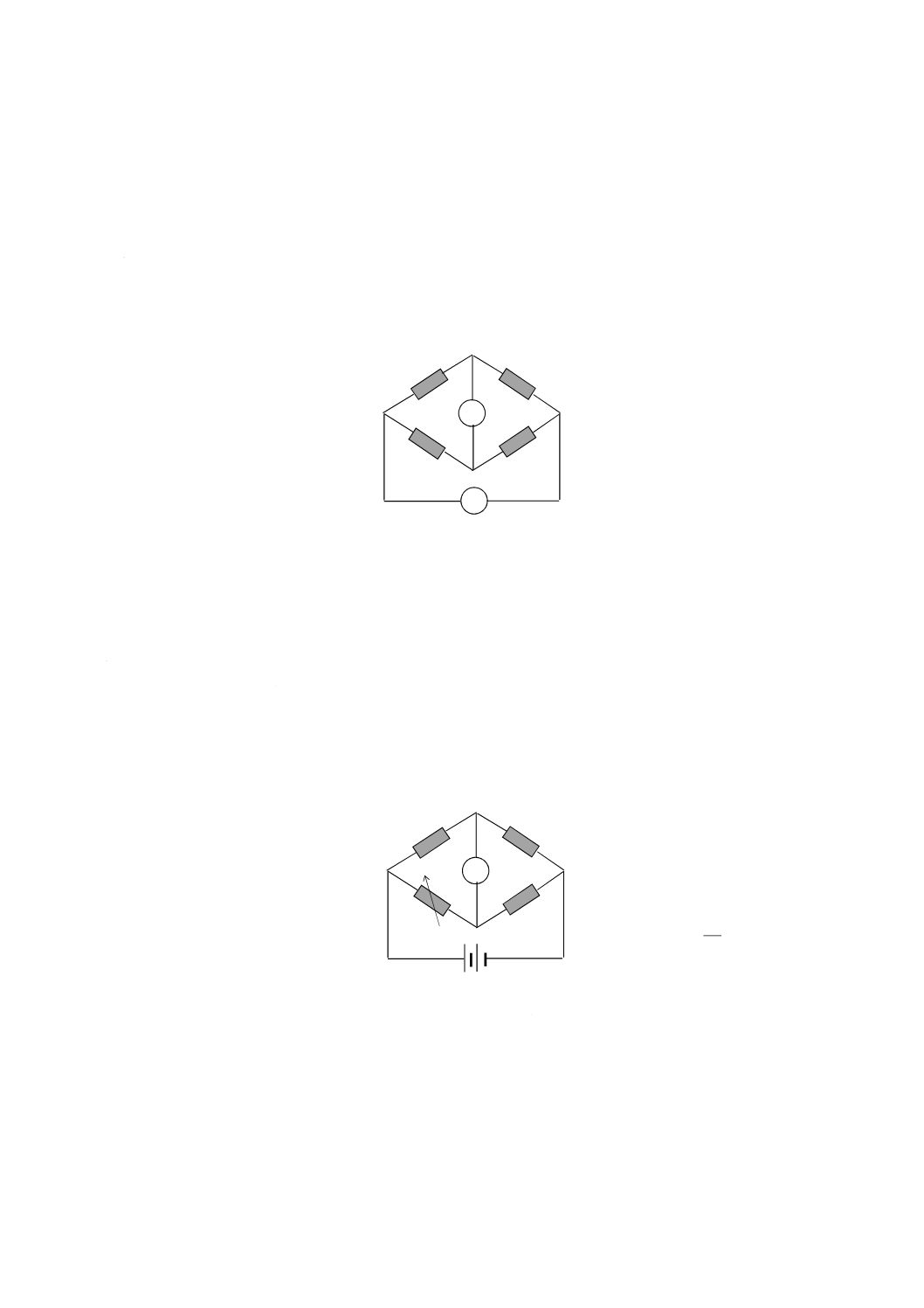
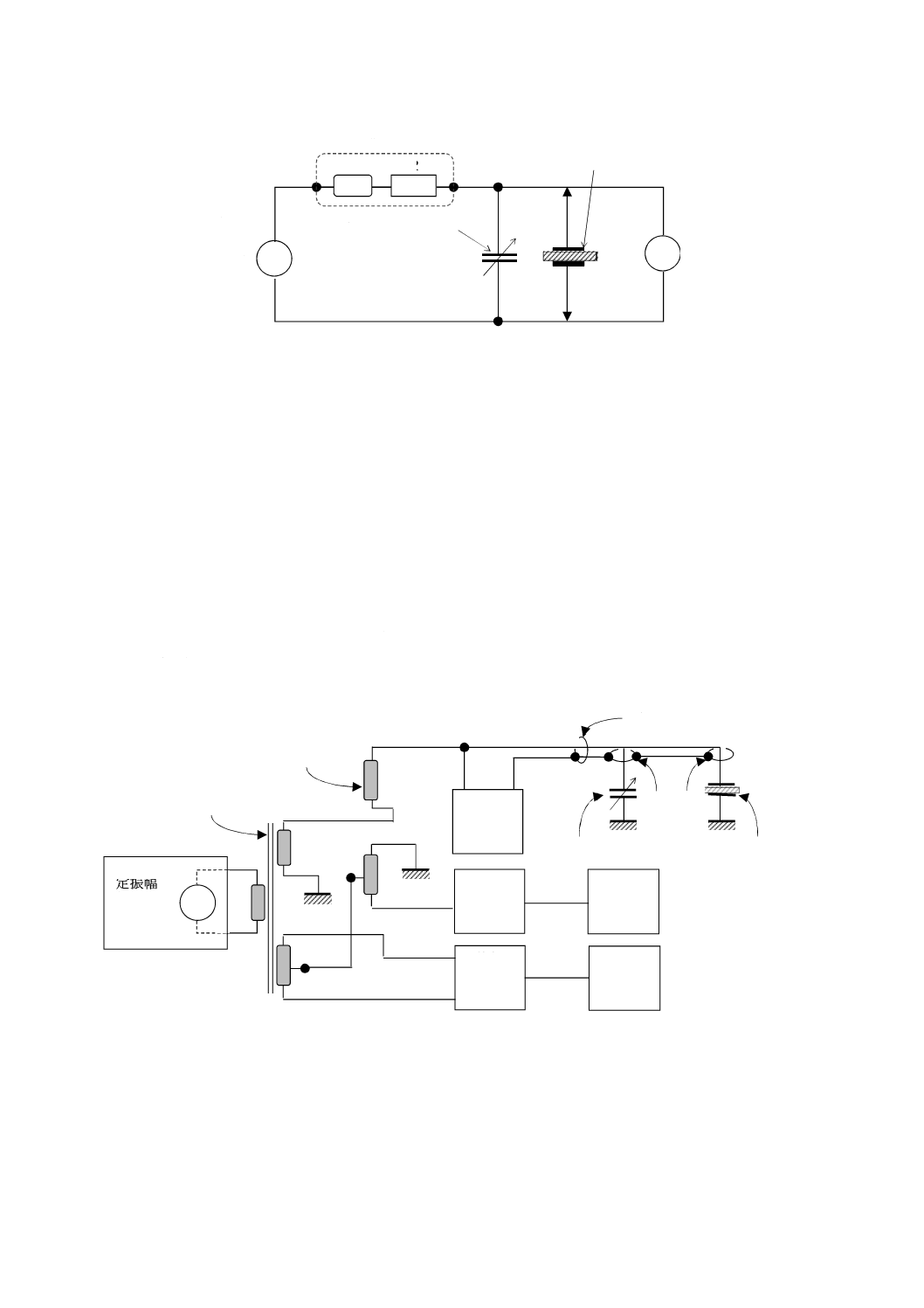
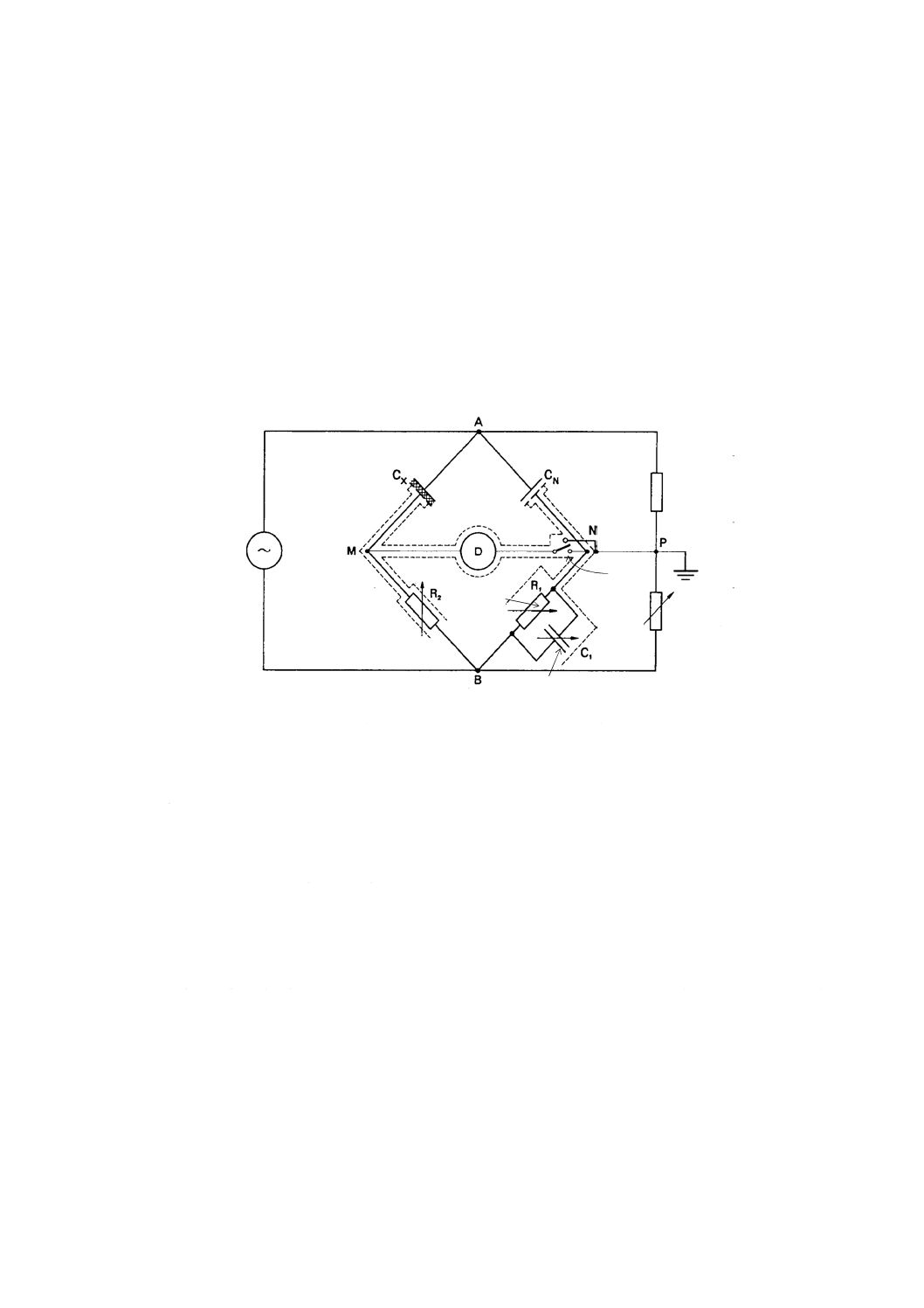
注記1 主電極,対電極及びガード電極の三つから成る電極構成を3端子電極と呼ぶことがある。
注記2 実際の測定回路では,高い電圧を測定装置に印加することを避けるために,図4に示すよう
に主電極と接地との間に電流計などの測定装置を接続する。したがって,主電極が低電圧側
で,対電極が高電圧側となる(図4参照)。
注記3 体積抵抗及び体積抵抗率の測定回路並びに表面抵抗及び表面抵抗率の測定回路では,図4に
示すように,対電極とガード電極とが入れ代わる。
注記4 図4 a)に示す回路のガード電極は,その形状から,“ガードリング”と呼ばれることが多い。
a) 体積抵抗及び体積抵抗率
b) 表面抵抗及び表面抵抗率
図4−体積抵抗及び体積抵抗率測定並びに表面抵抗及び表面抵抗率測定の基本回路
3.4.4
ブリッジ回路(bridge circuit)
四つの素子を互いに直列接続及び並列接続して構成する回路(附属書JE参照)。
注記 4辺ブリッジともいう。抵抗及びインピーダンスの測定に用いる。
3.4.5
共振回路(resonance circuit)
コイルとキャパシタとによる共振現象を利用してインピーダンス値を得る回路。Qメータが代表的な装
置である。Qメータは回路素子用のインピーダンス測定器であるが,適切な電極装置を用いることによっ
て,高周波誘電特性の測定器としても使用できる(附属書JE参照)。
3.4.6
受動ブリッジ回路(passive bridge circuit)
4辺が全て受動素子(抵抗,キャパシタ及びコイル)で構成するブリッジ回路(附属書JE参照)。
注記1 4辺が全て抵抗のブリッジをホイートストンブリッジという。抵抗の精密測定に広く用いら
れてきたが,現在は抵抗変化形のセンサ出力の検出回路として重要である。
A
↑
A
↑
直
流
電
源
直
流
電
源
対電極
対電極
主電極
主電極
ガード
電極
ガード
電極
電流計
電流計
試験片
試験片

8
C 2139-1:2019
注記2 4辺のうち,2辺はそれぞれ未知の静電容量及び標準容量で,残る2辺はそれぞれ無誘導抵抗
から成るシェーリングブリッジは,誘電率及び誘電正接の測定装置として最も古くから用い
られている。
注記3 変成器の等価な二つの二次巻線を4辺ブリッジの2辺として用いるブリッジを変成器ブリッ
ジという。誘電特性の測定に広く用いられている。
3.4.7
能動ブリッジ回路(active bridge circuit)
演算増幅器などの能動素子を用いるブリッジ。広い周波数範囲にわたり,高精度のインピーダンス測定
が可能で,多くのインピーダンスメータに用いられている(附属書JE参照)。
3.4.8
ガード(guard)
直流又は交流を問わず,測定対象以外の不要な漏れ電流成分を除くための回路及び装置。これらをまと
めてガード系と呼ぶことがある(附属書JF参照)。
3.4.9
受動ガード(passive guard)
測定対象以外の不要な漏れ電流成分を,測定器を通さずに大地又は電源の低圧側に流して捨てるための
回路及び装置(附属書JF参照)。
注記1 3.4.3に記載の体積抵抗及び体積抵抗率の測定用電極が備える円環状のガード電極(ガードリ
ング)は,受動ガード装置の代表例である[図4 a)及びJIS C 2139-3-1参照]。
注記2 シェーリングブリッジ,変成器ブリッジなど,種々のブリッジ回路に設けられている自動平
衡形接地回路(ワグナー接地回路)は,受動ガード回路の代表例である。
3.4.10
能動ガード
利得が1で出力抵抗が十分に低い演算増幅器による自動電位平衡器の出力を,ガード系に接続して駆動
することによって,信号線とガード系との電位差を常に0に保ち,漏れ電流が発生しないようにする(附
属書JF参照)。
3.4.11
漏れ電流(leakage current)
測定対象以外の不要な電流。交流又は直流を問わない。
3.4.12
残留インピーダンス(residual impedance)
測定回路を構成する端子,リード線などに残存する抵抗,静電容量及びインダンクタンスによる予測困
難なインピーダンス。交流電圧印加の測定の際に,特に高周波領域で大きな誤差の原因となる。
3.4.13
漂遊容量(stray capacity)
電気・電子回路における回路の設計者及び電気・電子計測の分野における計測者が意図しない,電気・
電子部品の物理的構造(配線,端子,その他の導体構造物)に起因する静電容量。残留インピーダンスの
主要原因の一つとなる。
9
C 2139-1:2019
4
電気絶縁材料の性質に影響を及ぼす因子
4.1
一般的事項
電気絶縁材料は,具体的な用途に応じて必要とされる電気抵抗特性及び誘電特性に加えて,適切な機械
的,化学的,熱的及びその他の必要な特性を備えなければならない。
絶縁抵抗は,二つの成分,すなわち,表面抵抗及び体積抵抗からなる。両者共に多くの要因,例えば,
湿度,温度,電界の強さ,試験片の形状,表面の状態,電極などによって影響を受ける。温度,化学的及
び周囲の気体の状況,湿度並びに電界の強さによる電気抵抗の変化は大きい場合があり,動作条件の設計
を行う際にはよく調べなければならない。
誘電率及び誘電正接は,同様に多くの要因によって影響を受けるが,その程度は絶縁抵抗に比較して大
きくはない。ただし,温度の影響以外は,周波数による影響が大きい。
4.2
電気抵抗特性及び誘電特性に影響を及ぼす因子
4.2.1
一般的事項
電気絶縁材料の誘電特性及び電気抵抗特性には,次の諸要因が影響を与えるため,試験の報告にそれぞ
れ記載しなければならない。
4.2.2
時間
3.1.5に概説したように,電気分極現象には時間依存性がある。分極の種類によって,緩和時間は大きく
異なる。この緩和時間の大小によって,測定値(例えば,電気抵抗特性)は,電圧印加時間に依存して変
わる。
ある種の材料では緩和時間は極めて長い(数か月以上に及ぶ場合もある。)。したがって,適切な試験結
果を得るため,非常に長時間の測定を行う必要がある。しかし,実用上の理由から,この1分値と電気絶
縁材料の実際の挙動との間の差異を許容して,電気抵抗特性の測定は,電圧印加の1分後に行う。
4.2.3
周波数
誘電率及び誘電正接は,広い周波数範囲にわたって一定ではないため,誘電材料が実際に用いられる周
波数領域において誘電正接及び誘電率を測定する必要がある。
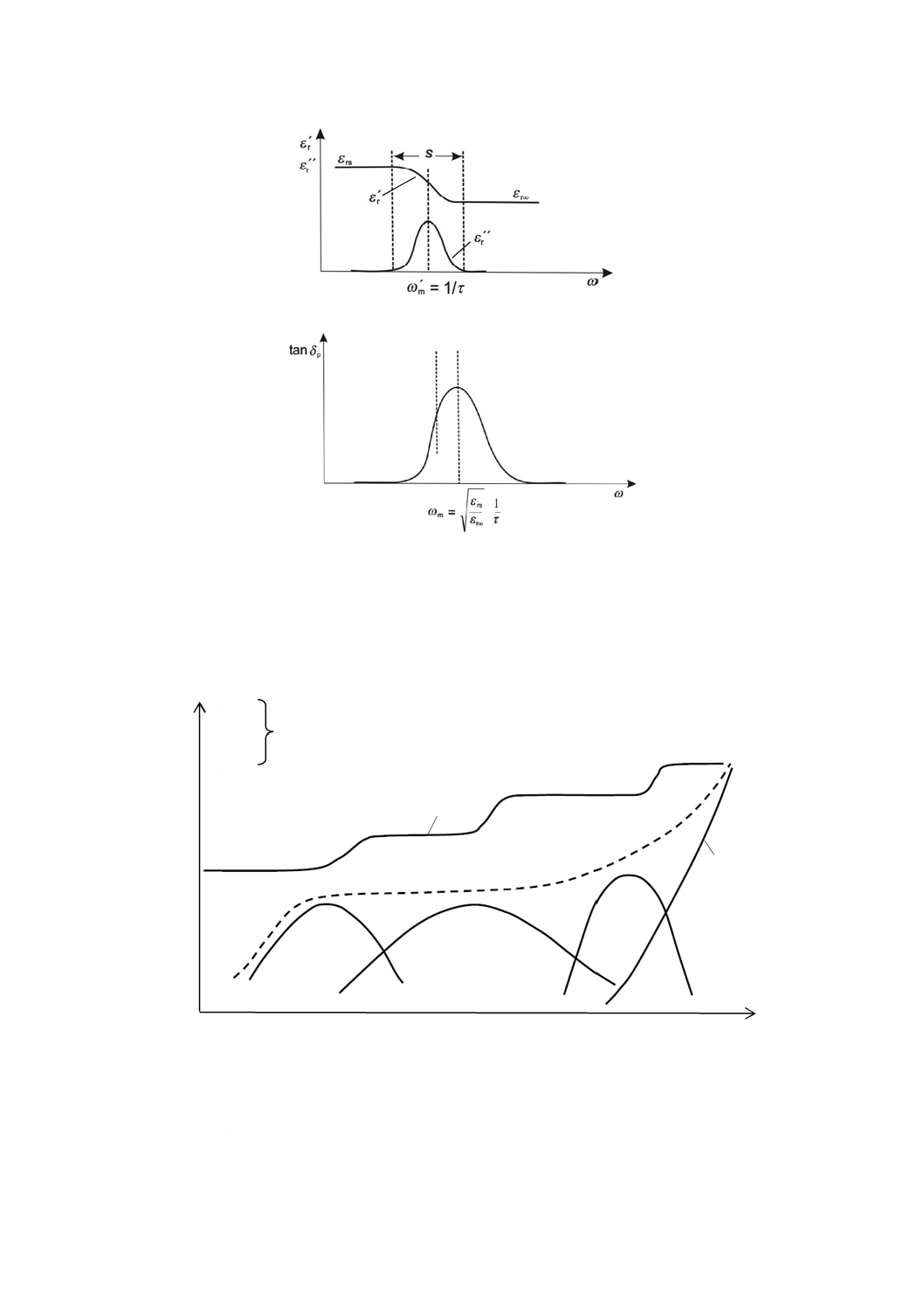
ある周波数で,誘電損率ε''rが緩和過程の遷移領域で極大となる様子を図5に模式図として示す。この緩
和過程領域内では,誘電率ε'rは高い値εrs(静誘電率)から低い値εr∞(周波数無限大)に変化する。この
ような挙動の理由は,緩和時間で表す分極の時間依存性にある。
τ
ω'
1
m=
················································································ (14)
しかし,分極過程との関連によって,実際には複数の緩和過程の遷移が表れる(附属書JA参照)。
誘電正接にも周波数依存性がある。3.3.6に規定した定義及び周波数が高くなるほどε'rが小さくなること
から,誘電損率ε''rに比べてtan δの極大は,次の式に従って,より高い周波数側に移動する。
m
r
rs
m
ω'
ε
ε
ω =
∞
······································································· (15)
注記 時間依存性と周波数依存性とには互いに密接な関係があり,デバイの理論によって説明される。
10
C 2139-1:2019
図5−誘電率及び誘電正接の周波数依存性の模式図
4.2.4
温度
温度は分極に影響を与え,温度の上昇とともに緩和時間が短くなるため,温度が高くなるに従って,誘
電正接は一つ以上の極大を示す(図6参照)。その結果として,比誘電率は温度とともに階段状に増大す
る。
図6−誘電率εr及び誘電正接tan δに及ぼす温度の影響(例)
さらに,高い温度では電荷(イオン,電子)がより自由に運動しやすくなり,導電率の増大に寄与する。
同じ理由から,絶縁抵抗,表面抵抗率又は体積抵抗率の値は,温度に強く依存する場合がある。
注記1 熱による老化も供試材料の誘電正接及び電気抵抗特性に影響する場合がある。IEC 60216-1
℃
tan δP1
tan δP2
tan δP3
tan δ
εr
tan δP1
tan δP2
tan δP3
異なる双極子分極又は
界面分極によるtan δ
tan δ L
tan δL:導電率の増加によるtan δ
比誘電率εr
tan δ(累積曲線)
×
11
C 2139-1:2019
及びIEC 60505による電気絶縁材料及び絶縁システムの性能評価において,誘電的挙動又は
電気抵抗の挙動を調べることは有用である。
注記2 特に高い温度では,材料の電気抵抗特性の結果として生じる伝導電流が,誘電正接の増大に
著しく関与する場合がある。
4.2.5
湿度
誘電率,誘電正接,体積抵抗率,表面抵抗率など全ての誘電特性及び絶縁抵抗特性は,湿度によって影
響を受ける。したがって,試験片の状態調節は,試験前及び試験時の両方において,水分含有量の管理と
同様に極めて重要である。
4.2.6
電界の強さ
界面分極以外のあらゆる種類の誘電分極現象は,電子放出又は関連効果が生じない限り,印加した電界
の強さにほぼ比例して振る舞う。界面分極が存在する場合には,自由イオンの数が電界の強さとともに増
大し,誘電正接の極大値の大きさ及び位置が変化する。イオン化の効果が生じない限り,誘電率及び誘電
正接は,電界の強さに対してほんの僅かな依存性しか示さない。
4.2.7
電圧
測定電圧又は電界の強さを増すにつれて,それぞれ非線形の効果が現れる場合がある。時間とともに変
化する充電電流にも電圧依存性がある。
4.2.8
状態調節
ほとんどの固体絶縁材料の電気抵抗特性及び誘電特性は,4.2.2〜4.2.7の各項目に示した要因によって影
響を受ける。したがって,試験前及び試験時の両方において,JIS C 2142に規定する試験片の状態調節手
順の方式及び処理時間を明示することが必要である。
試験前及び試験時に推奨する状態調節の雰囲気は,温度23 ℃±2 K及び相対湿度(50±5) %である。
材料の挙動は,表面状態によって影響を受ける。クリーニングの状態が試験結果に影響することもあり,
場合によっては,状態調節を行う前に試験片表面をクリーニングする必要がある。
4.2.9
試験片
試験片の形状及び寸法は,測定値に影響する場合がある。試験片の推奨寸法は,JIS C 2139-3規格群の
試験手順に用いられるものとする。ただし,試験片の形状及び寸法は,絶縁材料の種類及び用途によって
大きく変わるため,その形状については,場合に応じて個々の適切な製品規格によって規定する必要があ
る。
4.2.10 電極材料
適切な電極材料の選定は,確かな試験結果を得るためには極めて重要であり,電極については5.4.2で取
り扱う。
5
測定方法及び測定装置
5.1
一般的事項
この規格が対象とする電気絶縁材料の抵抗特性及び誘電特性は,基本的には二つの電極間の試験片にそ
れぞれ直流又は交流の電圧を印加して測定する。
5.2
抵抗特性の測定方法
抵抗特性の測定では,二つの電極間の試験片に直流電圧を印加し,試験片に流れる電流を測定して電気
抵抗の値を求める。電極と試験片とは密着していなければならない。電極保持のための絶縁材料,測定器
の端子の絶縁材料など,試験片以外を流れる漏れ電流は大きな誤差要因となる。漏れ電流を抑制するため

12
C 2139-1:2019
には,適切なガード系を設けることが必要である(附属書JF参照)。
体積抵抗及び体積抵抗率の測定には,試験片の表面を流れる電流成分を取り除くためのガードを設ける。
また,表面抵抗及び表面抵抗率の測定には,試験片の内部を流れる体積電流成分を取り除くためのガー
ドを設ける(附属書JB参照)。
5.3
誘電特性の測定方法
誘電特性測定の場合には,二つの電極間に挟んだ試験片を誘電体とするキャパシタの静電容量から比誘
電率を求める。また,このキャパシタの等価並列抵抗又は等価直列抵抗の値から誘電正接を求める(3.3.6
及び図2参照)。測定方式によっては,試験片と電極との間に空隙を設けて測定する場合がある。
誘電正接の測定では,漏れ電流は大きな誤差要因となるので,適切なガード系を設ける必要がある。
2端子電極で比誘電率を測定するときは,縁端静電容量による誤差に注意し,必要に応じて縁端静電容
量の補正を行う(附属書JD参照)。比誘電率測定の精度を確保するためには,ガード電極(ガードリング)
を設けて3端子電極とし,縁端静電容量の影響を減らすことが有効である。しかし,高い周波数(通常,
数10 MHz以上)では,ガード導体に起因する残留インピーダンス(3.4.12参照)の影響が大きくなるた
め,ガードの使用は不適切である(附属書JF参照)。
5.4
測定装置
5.4.1
一般的事項
抵抗特性及び誘電特性の測定には,適切な電極及び/又は電極装置が必要である。
抵抗特性の測定には,微小電流の測定が必要であり,通常,エレクトロメータを用いる。
100 MHzまでの比較的低い周波数の誘電特性の測定には,従来は4辺ブリッジの2辺を変成器の二次巻
線に置き換えた変成器ブリッジなどの各種インピーダンス測定用ブリッジ回路及び共振回路(Qメータ)
が用いられてきた。測定可能な周波数範囲は,おおよそブリッジ回路が0.1 Hz〜数10 MHz,共振回路が
10 kHz〜100 MHzである。しかし,近年は,これらに代わって演算増幅器を用いたインピーダンスメータ
が広く用いられている。
5.4.2
電極及び電極装置
絶縁材料の抵抗特性を試験するための電極は,試験片表面に容易に装着又は密着でき,かつ,電極の電
気抵抗又は試験片の汚損によって明らかな誤差を生じることがあってはならない。
誘電特性の測定においては,十分に表面導電率が低い試験片に対して,非接触電極装置を用いて試験片
と電極との間に空隙を設けて測定する場合がある。
測定値から誘電特性及び導電特性を導き出す場合には,深刻な誤差の発生を避けるためにも,試験片の
厚さと同時に電極の形状も慎重に決めなければならない。それぞれの測定に対する適切な電極装置の詳細
な情報は,それぞれに対応する試験手順の項目に記載がある。
5.4.3
抵抗特性の測定装置
ほとんどの場合,直流電圧,直流電流及び電気抵抗の測定は,デジタルマルチメータ(以下,DMMと
いう。)が用いられている。DMMは,演算増幅器(OPアンプともいう。)を用いた測定器であり,汎用の
DMMは,電圧及び電流の値がそれぞれ1 μV(10−6 V)及び1 μA(10−6 A)以上,かつ,抵抗値が1 GΩ
(109 Ω)以下の測定には十分な性能をもっている。しかし,電気絶縁材料の抵抗特性の測定には,多くの
場合,上記の測定範囲では不十分であり,エレクトロメータを用いる。これは,より高度の機能をもつDMM
で,100 pA(10−10 A)よりも小さく,最小で1 fA(フェムトアンペア:10−15 A)の電流,又は1 GΩ(109
Ω)を超えて,10 PΩ(ペタオーム:1015 Ω)までの抵抗値を測定することができる。

13
C 2139-1:2019
5.4.4
誘電特性の測定装置
5.4.1に記載するように,電気絶縁材料の誘電特性の測定には,変成器ブリッジが広く用いられてきた。
しかし,近年は,変成器の二つの二次巻線を演算増幅器に置き換えた能動ブリッジ(アクティブ・ブリッ
ジ)が用いられている。これは,変成器ブリッジは巻線間の残留インピーダンスのため高い周波数では使
用できないが,能動ブリッジは直流から100 MHz程度の高い周波数まで使用できるためである(附属書
JE参照)。
5.4.5
ガード
電気絶縁材料の抵抗特性及び誘電特性の測定において,有効なガード回路の使用は不可欠である。不要
な漏れ電流を側路を通して大地に流すための受動ガードは古くから使用されていたが,高い周波数領域で
はガード導体によって漂遊容量が増大することから,使用は困難であった。
しかし,近年,演算増幅器の普及に伴って,利得が1の演算増幅器でガード導体を駆動し,測定電流又
は電圧信号が流れる信号線とガード導体との間の電位差を常に0に保つ能動ガードが容易に使用できるよ
うになった。能動ガードは,漏れ電流の発生ばかりでなく,ガード導体に起因する漂遊容量もほとんど0
にすることができるため,計測に要する応答時間(セットリング時間)を大幅に短縮することができる。
この時間短縮によって,計測の自動化が著しく容易になった(附属書JF参照)。
6
試験手順
試験の手順は,JIS C 2139-3規格群に記載されている。
所定の試験方法に従って,抵抗特性及び誘電特性を測定するために,入手可能な任意の試験装置又は器
具類を用いてもよい。ただし,試験機器類の精度は常に明示されており,かつ,それは供試材料の要求を
満たすために適切なものでなければならない。
14
C 2139-1:2019
附属書JA
(参考)
電気分極,脱分極,緩和時間及び吸収電流
JA.1 一般的事項
この附属書では,この規格で用いる用語である電気分極(3.1.5),脱分極(3.1.7)及び緩和時間(3.1.10)
について,詳しく説明する。また,電気分極及び脱分極の現象に伴って,それぞれ観測される分極電流(3.1.8)
及び脱分極電流(3.1.9)について説明するときにしばしば用いられる“吸収電流”も併せて説明する。
JA.2 電気分極(electric polarization)[5]
誘電体試験片を直流電界中に置くと,図JA.1に示すように,誘電体を構成する原子又は分子の中の正電
荷は電界(E)の方向に,負電荷は電界と反対の方向に変位し,無数の電気双極子を誘起する。この状態
を,原子又は分子が“分極”したという。また,このとき誘電体の表面には,電極と反対符号の電荷が現
われる。この状態を,誘電体が“分極”したという。静電界が作用してから分極が平衡状態に達するまで
には,一定の時間が必要である。
図JA.1−電気分極
均質な誘電体の分極現象を,電子,原子又は分子の挙動によって大別すると,電子分極,原子分極(イ
オン分極)及び双極子分極(配向分極)の三つに分類することができる。このほか,電極と試験片との界
面,又は試験片内部の物質の不連続境界面にイオンなどの空間電荷が蓄積することによって生じる分極(界
面分極又は空間電荷分極)がある(図JA.2参照)。これらのうち,電子分極及び原子分極の場合は, 双極
子分極及び界面分極と比較すると,ほとんど瞬間的に分極が形成される。双極子分極の場合には,双極子
が電界方向に向きを変えようとする配向運動に対して,周囲の分子から配向を妨げようとする作用が生じ
る。すなわち,配向運動に対して粘性抵抗を受けるため,分子が電界方向に整列して分極が平衡状態に達
するまでに,電子分極及び原子分極よりも長い時間を要する。界面分極の場合も,イオンが移動して蓄積
するために時間を要する。
○
● ○
● ○
● ○
●
○
● ○
● ○
● ○
●
○
● ○
● ○
● ○
●
○
● ○
● ○
● ○
●
○
● ○
● ○
● ○
●
E
○ ○ ○ ○
○ ○ ○ ○
○ ○ ○ ○
○ ○ ○ ○
○ ○ ○ ○
●:正電荷
〇:負電荷
(a) E
=
a) E=0
b) E=E
+
−

15
C 2139-1:2019
a) 電子分極
b) 原子分極(イオン分極)
c) 双極子分極(配向分極)
d) 界面分極
図JA.2−電気分極の種類
図JA.3は,物質の誘電率の周波数依存性を示す模式図である。瞬間的に配向する電子分極及び原子分極
は,光の周波数領域(1010 Hz以上)に現れるのに対して,双極子分極は電磁波周波数領域(104 Hz〜108 Hz)
及びそれ以下に対応している。また,界面分極は,より低い周波数領域に対応していることが分かる。
図JA.3−分極の周波数依存性
JA.3 脱分極(depolarization)
静電界中で誘電体の分極が平衡状態にあるとき,静電界を取り去ると,分極は一定の時間をかけて消滅
する。この過程及び状態を脱分極という。分極するときと同様に,電子分極及び原子分極は瞬間的に脱分
極が完了するが,双極子分極及び界面分極の脱分極には,一定の時間が必要である。
双極子分極(配向分極)
原子分極(イオン分極)
電子分極
界面分極(空間電荷分極)
誘
電
率
周波数(Hz)
赤
外
線
領
域
紫
外
線
領
域
〇:正イオン ●:負イオン
電界E
無電界
電界E
無電界
永久双極子モーメント
○ ● ○ ● 〇
● 〇 ● 〇 ●
○ ● ○ ● 〇
● 〇 ● 〇 ●
〇 ● 〇 ● 〇
● 〇 ● 〇 ●
〇 ● 〇 ● 〇
● 〇 ● 〇 ●
電界E
無電界
イオン結晶
〇:正イオン ●:負イオン
−
+
電界E
−
+
無電界
原子核
電子雲

16
C 2139-1:2019
JA.4 分極電流(polarization current)
JA.2に記載した電気分極現象によって生じる時間変化を伴う電流で,図JA.4のia(充電電流)である。
JA.5 脱分極電流(depolarization current)
JA.3に記載した脱分極現象によって生じる時間変化を伴う電流で,図JA.4のia'(放電電流)である。
JA.6 緩和時間(relaxation time)[5]
“緩和”という言葉は,この規格では電気的な現象に対して用いているが,物理的,化学的又は機械的
な何らかの系が,温度,圧力,電界などの外部要因によって変化するとき,その変化が徐々に進行して平
衡状態に達するまでの過程をいう。緩和の過程が経過時間tとともに指数関数的に,すなわち,exp(−t/τ)
の形で変化するとき,τを緩和時間という。
電気分極及び脱分極が平衡状態に達するまでには,共に一定の時間が必要である(JA.2及びJA.3参照)。
緩和時間は,この時間の指標として用いられる。
図JA.4 a)は,時刻t1で電圧を印加し,時刻t2で電圧を除去したときの双極子分極の緩和に伴う充・放電
時の分極Pd(3.1.5参照)の時間に伴う変化を示している。
充電時のPdの変化は,t1=0とした場合,次の式である。
()
(
)τ
t
t
P
/
exp
1
d
−
−
∝
······························································· (JA.1)
放電時のPdの変化は,t2=0とした場合,次の式である。
()
(
)τ
t
t
P
/
exp
d
−
−
∝
································································· (JA.2)
図JA.4 b)は,充・放電時に観測される電流の時間変化である。時刻t1に電圧を印加すると,電子分極及
び原子分極[JA.2,図JA.2 a)及びb)参照]による瞬時充電電流が流れ,その後,双極子分極による充電電
流が流れて指数関数的に減少する。この電流は,図1の充電電流iaである。双極子分極が平衡に達した後
の時刻t2に印加電圧を取り除くと,電子分極及び原子分極の脱分極による瞬時放電電流が流れ,その後,
双極子分極の脱分極による充電電流とは逆極性の放電電流が流れ,指数関数的に減少する。この電流は,
図1の脱分極電流ia'である。
a) 分極Pd及び電荷量Qdの時間変化
b) 充・放電電流の時間変化
図JA.4−双極子分極の充・放電過程
様々な緩和過程に伴う図JA.4に示すような観測値の時間変化は,極めて一般的である。
式(JA.1)及び式(JA.2)を一般化してそれぞれ次の式となる。
Pd
放電
t
t
t1
t2
瞬時充電電流
瞬時放電電流
充電電流
(ia)
放電電流
(ia')
t1
t2
時刻t1:電圧印加
時刻t2:電圧除去
時刻t1:電圧印加
時刻t2:電圧除去
I
充電
17
C 2139-1:2019
)
/
exp(
1
1
τ
t
I
−
−
=
··································································· (JA.3)
)
/
exp(
2
τ
t
I
−
=
······································································· (JA.4)
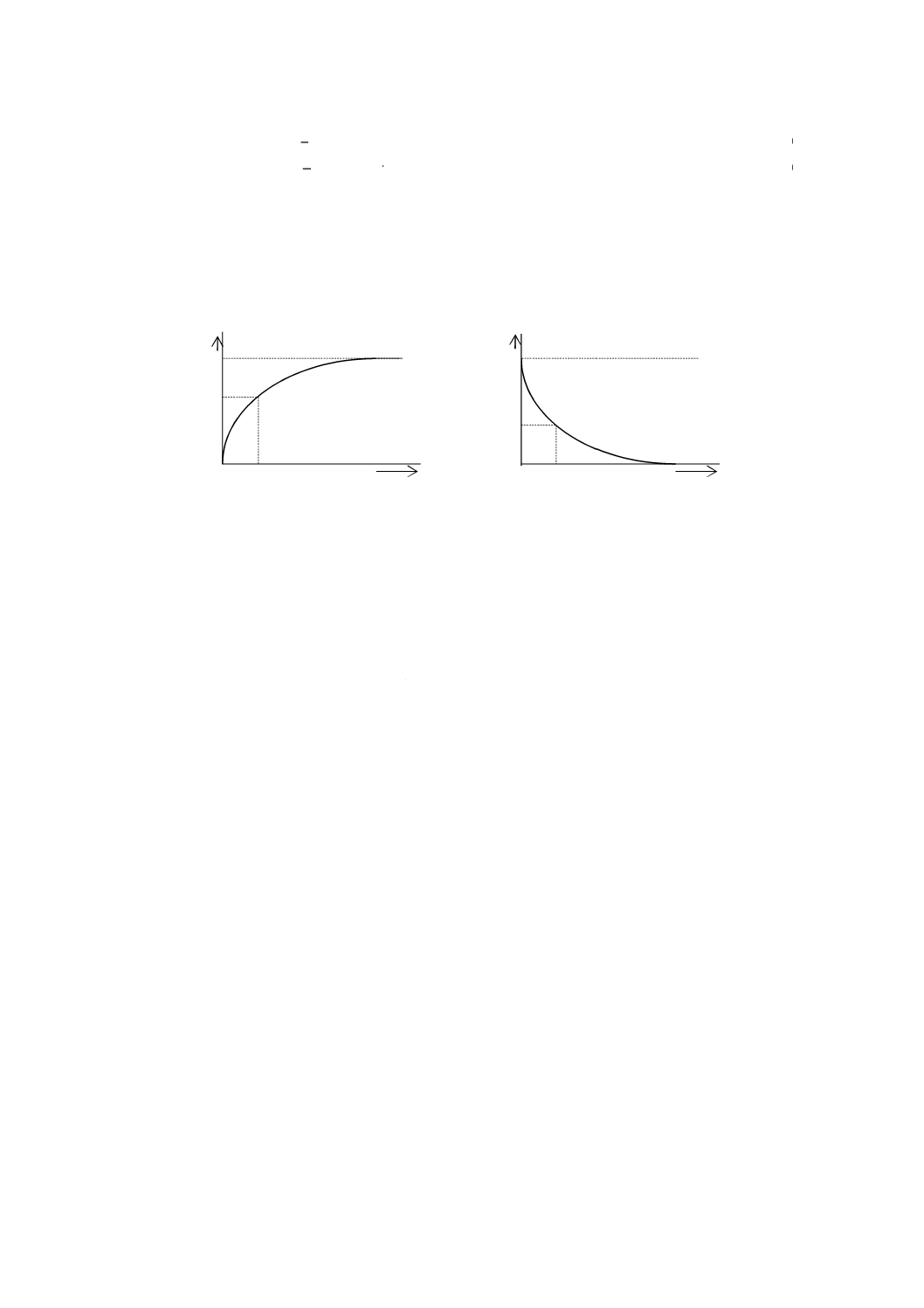
式(JA.3)及び式(JA.4)は,それぞれ図JA.5 a)及びb)のように図示できる。
t=τのとき,式(JA.3)及び式(JA.4)から,それぞれI1=1−(1/e)及びI2=1/e[e=2.718 28…:自然対数の底
(ネイピア数)]となり,縦軸の値I1≒0.63及びI2≒0.37によって横軸(時間)の値を読み取れば,緩和時
間τを求めることができる。
a) 充電電流
b) 放電電流
図JA.5−緩和時間τ
JA.7 吸収電流(absorption current)
誘電体試験片に直流電圧を印加したときに流れる電流のうち,誘電分極による電流成分に対して吸収電
流という呼称をしばしば用いる。分極電流ia及び脱分極電流ia'が吸収電流で,それぞれ充電吸収電流及び
放電吸収電流と呼ぶことがある。この電流には,電圧印加直後に瞬間的に幾何静電容量を充電する電流及
び3.1.2に定義した伝導電流(図1のi0)は含まない[4]。
注記 幾何静電容量とは,電極間を空にしたときの電極寸法(電極面積及び電極間隔)だけで決まる
静電容量である。
I1
1
1
I2=exp(−t/τ)
I2
I1=1−exp(−t/τ)
0.63
0.37
τ
τ
t
t
18
C 2139-1:2019
附属書JB
(参考)
体積抵抗率及び表面抵抗率−概念及び測定方法
JB.1 体積抵抗率及び表面抵抗率の概念
JB.1.1 体積抵抗率
体積抵抗率は,供試材料を1辺が単位長さの立方体に換算した体積抵抗の値を用いる。試験片の材料が
無限に広がった媒質があると仮定し,その中に図JB.1に示すように1辺の長さがaの立方体を考える。向
かい合った二つの面SA及びSBにそれぞれ電極があるとして,その間に印加する電圧をVとする。この二
つの電極間の試験片内部を流れる伝導電流として,電流Iを測定して,次の式から抵抗RVを求める(オー
ムの法則)。ただし,電極面に挟まれた四つの面の内側だけに流れる伝導電流を,Iとする。
RV=V / I ·············································································· (JB.1)
図JB.1−体積抵抗率の概念図
二つの対向面電極間の電界の強さをEとすれば,電極間隔はaであるから,次の式となる。
a
V
E
/
=
··············································································· (JB.2)
また,電流密度J,すなわち,電極面SA及びSBに平行な断面の単位面積当たりを通過する電流は,電
極面積をS(=a2)とすれば,次の式となる。
2
/
/
a
I
S
I
J
=
=
····································································· (JB.3)
体積抵抗率(ρ)の定義(3.2.4)によって式(JB.2)及び式(JB.3)を用いて,式(JB.4)を得る。
(
)a
I
V
J
E
ρ
×
=
=
/
/
································································ (JB.4)
したがって,式(JB.4)から,体積抵抗率は式(JB.5)となる。
a
R
ρ
×
=
V
··········································································· (JB.5)
ここで,aが単位長さ(a=1)の場合,ρ=Rである。
実際の立方体試験片では,電極面SA及びSBに挟まれた四つの面を流れる電流(表面電流)が必ず存在
し,体積電流に加算されて測定されるので,上記の状態の実現は不可能である。したがって,体積抵抗の
説明にしばしば用いられる図JB.1の立方体は,あくまで仮想的なものであることに注意する。
a
電極面SA
(面積S)
電極面SB
(面積S)
立方体試験片
↑
印加電圧V
伝導電流
電流I
○
−
○
+
19
C 2139-1:2019
JB.1.2 表面抵抗率
表面抵抗率は,任意の寸法の正方形に換算した表面抵抗の値である。平たん(坦)で,かつ,無限に広
い試験片の表裏いずれかの面上に,図JB.2に示すように1辺の長さaの正方形を考える。向かい合った二
つの辺A及び辺Bにそれぞれ線電極LA及び線電極LBがあるとして,その間に印加する直流電圧をVとし
たとき,表面を流れる電流Iから求めた抵抗をRSとした場合,
I
V
R
/
S=
············································································· (JB.6)
である(オームの法則)。ただし,正方形は厚さのない2次元面であり,したがって,体積電流は存在せず,
また,線電極LA及び線電極LBに挟まれた二つの辺の内側だけに流れている電流をIとする。
二つの対向辺電極間の電界の強さEは,電極間隔はaであるから,次の式である。
a
V
E
/
=
··············································································· (JB.7)
また,電流密度J,すなわち,正方形表面上の辺A及び辺Bに平行な単位長さ当たりを通過する電流は,
次の式となる。
a
I
J
/
=
··············································································· (JB.8)
表面抵抗率(σ)の定義(3.2.6)によって,式(JB.6),式(JB.7)及び式(JB.8)から,次の式となる。
S
/
/
R
I
V
J
E
σ
=
=
=
······························································· (JB.9)
すなわち,表面抵抗率(σ)は,電極間隔a及び正方形の寸法に依存せず,RSに等しい。
図JB.2−表面抵抗率の概念図
実際の試験片には厚さがあり,表,裏及び両側面の表面を流れる電流並びに試験片内部を流れる体積電
流成分がある。また,試験片表面に正方形の領域を設け,相対する二つの辺に線電極を形成した場合には,
正方形の領域の外側に漏れ出す電流成分がある。したがって,表面抵抗率の説明にしばしば用いられる図
JB.2のような正方形は,体積抵抗率における図JB.1の立方体と同様に,仮想的なものであることに注意
する。
JB.2 体積抵抗率及び表面抵抗率の測定方法
JB.2.1 一般的事項
電極を試験片に取り付けて電圧を印加し,絶縁材料の抵抗を測定するとき,電極が二つ(2端子電極)
の場合には,測定電流は試験片内部及び試験片表面を流れる電流のほか,電極を保持するための構造絶縁
物,測定器の端子又はリード線に使われる絶縁物などに流れる漏れ電流も全て含むことになる。このよう
a
↑
印加電圧V
表面電流
電流I
正方形表面
(2次元面,
厚さ0,
表裏なし)
線電極LB
(辺B)
線電極LA
(辺A)
(辺C)
(辺D)
○
−
○
+
20
C 2139-1:2019
な測定電流から得られる抵抗値は,単に絶縁抵抗と呼ばれている。
体積抵抗及び体積抵抗率を測定するためには,試験片内部を流れる電流(体積電流)だけを測定する必
要があり,それ以外の漏れ電流,特に試験片表面を流れる表面電流成分を取り除く必要がある。また,表
面抵抗及び表面抵抗率の測定には,体積電流成分を取り除き,表面電流だけを測定する必要がある。
JB.2.2 電極構成
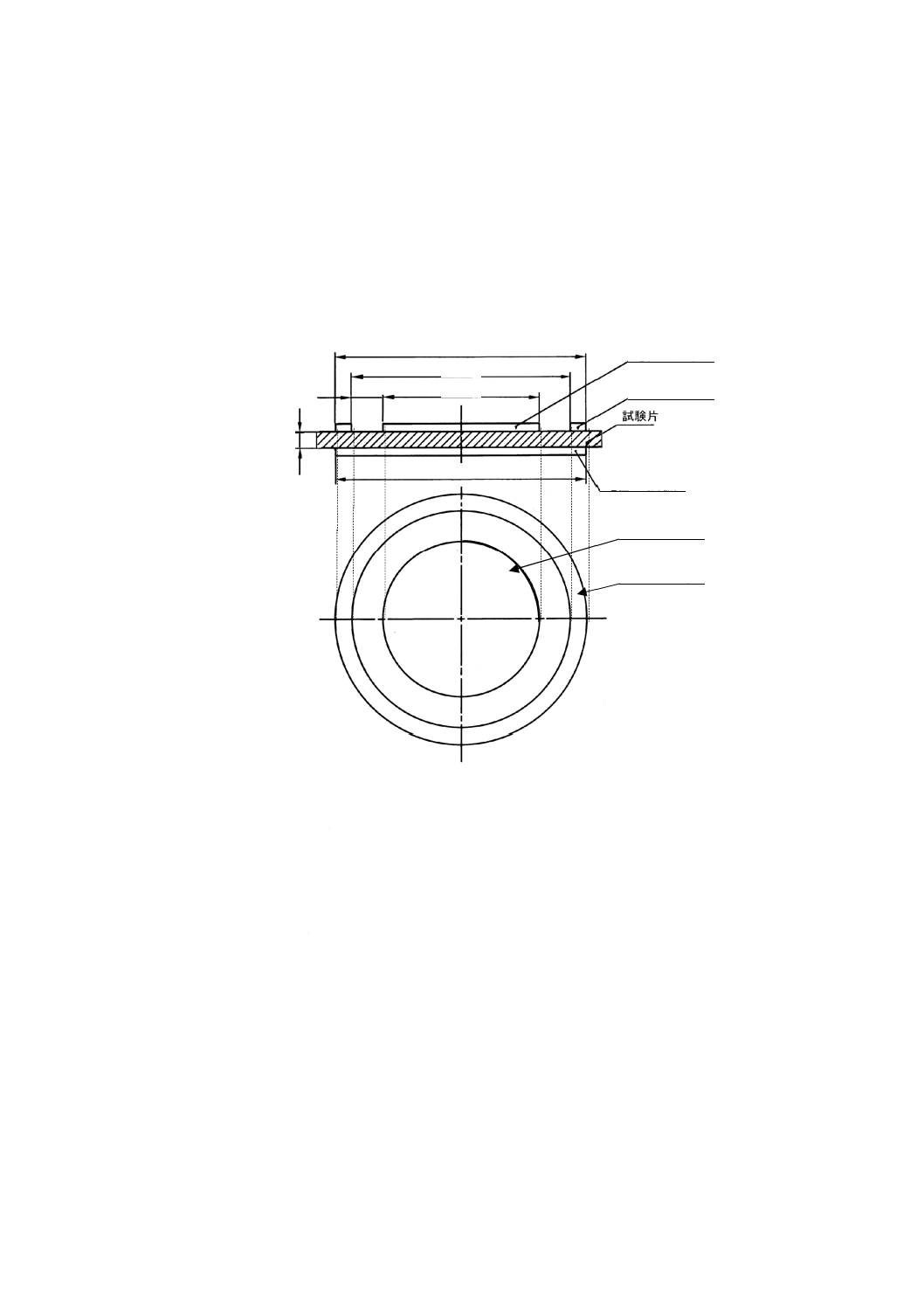
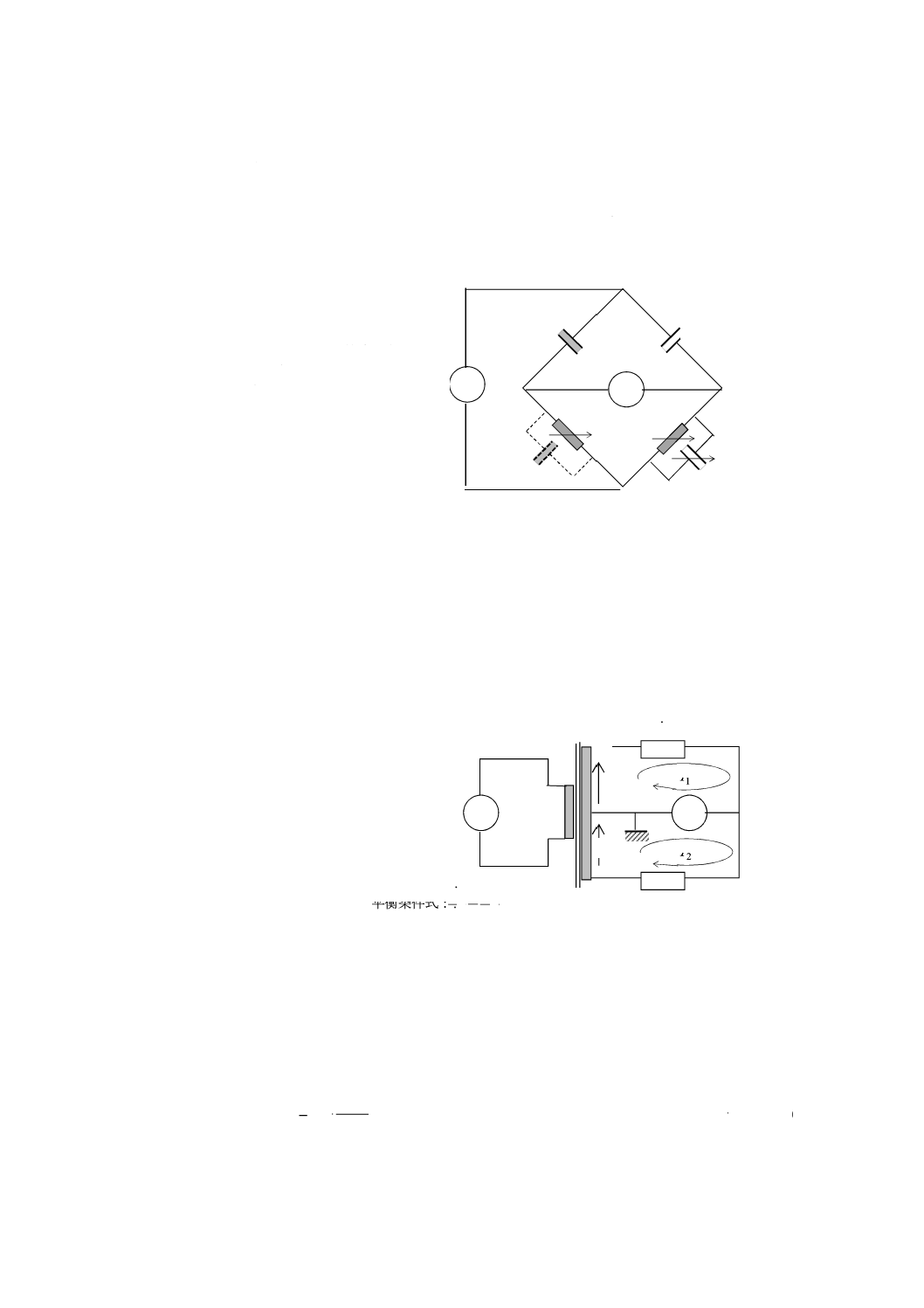
体積抵抗及び体積抵抗率,並びに表面抵抗及び表面抵抗率を測定するために,古くから図JB.3に示すよ
うな円板状の電極1及び電極3,並びに円環状の電極2から成る3端子電極が用いられている。
図JB.3−3端子電極
JB.2.2.1 電極配置−体積抵抗及び体積抵抗率測定
体積抵抗及び体積抵抗率の測定を行う場合の電極配置は,図JB.3の電極1及び電極3がそれぞれ主電極
及び対電極となり,対電極(電極3)に高電圧を印加する。主電極は,試験片の絶縁抵抗に比べて十分に
内部抵抗の低い電流測定機器を介して接地する。電極2は,表面電流を取り除くためのガード電極で,接
地して主電極(電極1)とほぼ同電位にする。このとき,電流は試験片内を図JB.4 a)に矢印で示したよう
に流れる。主電極(電極1)とガード電極(電極2)とは同電位であり,両電極間の環状の空隙表面には電
流は流れない。また,主電極の直下から外側の試験片の内部及び表面に沿って,対電極(電極3)から主
電極に向かって流れる漏れ電流は,ガード電極が吸収して大地に流れ,主電極には到達しない。したがっ
て,主電極直下の試験片内部を流れる電流だけを測定することができる。
JB.2.2.2 電極配置−表面抵抗及び表面抵抗率測定
表面抵抗及び表面抵抗率の測定を行う場合の電極配置は,電極1及び電極2がそれぞれ主電極及び対電
極となり,電極3が体積電流を取り除くためのガード電極の役割を果たす。対電極(電極2)に高電圧を
印加し,主電極を低圧側とするのはJB.2.2.1と同様である。電流は,試験片内を図JB.4 b)に示した矢印の
電極2(円環)
d2
d1
d3
d4
試験片の厚さh
電極1(円板)
電極2(円環)
電極1(円板)
電極3(円板)
g

21
C 2139-1:2019
ように流れる。対電極から円環状の試験片表面を主電極に向かって流れる表面電流が,測定電流となる。
このとき,体積電流は円環状の対電極の直下から試験片内を流れ,ガード電極から大地に流れる。試験片
の外縁に沿って流れる表面電流も,同様にガード電極に達して大地に流れ,測定電流に影響を与えない。
試験片の主電極とガード電極とに挟まれた試験片中央の領域は,これら二つの電極がほぼ同電位(接地電
位)のため,無電界の状態であり,電流も存在しない。したがって,対電極と主電極とに挟まれた円環状
の試験片表面を流れる電流だけを測定することができる。
“円環状の試験片表面を流れる電流”と記載したが,実際には円環状表面の直下を流れる体積電流(表
面層電流)も存在する。図JB.4 b)からも分かるように,表面電流測定時のガード電極の機能は,図JB.4 a)
の体積電流測定の場合ほど有効ではないが,体積電流成分を表面近くに押し上げる効果がある。この効果
は,試験片の厚さが増すほど減少する。いずれにせよ,ここで測定される電流とは,表面電流に“表面層
電流”を加えた値となる。
一般に試験片を置く雰囲気,環境条件などが,表面抵抗の測定に大きく影響する。また,体積抵抗率が
高く,表面抵抗成分が絶縁抵抗にとって支配的な場合には,表面層電流,すなわち,体積抵抗成分は無視
できる。
真の表面電流の測定には,様々な難しい点があるが,適切なガードを施して体積電流成分を極力最小に
とどめることは極めて重要である。
a) 体積電流測定時の電流経路
b) 表面電流測定時の電流経路
図JB.4−3端子電極の電流経路
○
+
(対電極)
○
+
○
+
○
−
(ガード
電極)
○
−
(ガード電極)
○
−
測定電流(表面電流)
(主電極)
(対電極)
(対電極)
(ガード電極)
○
−
(主電極)
○
−
無電界領域
(体積電流なし)
漏
れ
電
流
(
表
面
電
流
)
漏
れ
電
流
(
表
面
電
流
)
漏
れ
電
流
(
表
面
電
流
)
測定電流
(体積電流)
漏れ電流
(体積電流)
漏れ電流
(体積電流)
22
C 2139-1:2019
附属書JC
(参考)
表面抵抗測定−2端子測定の問題点及び3端子測定の利点
JC.1 一般的事項
表面抵抗率は,学術的には体積抵抗率と同様に一つの材料に一つの値が決まる物性値と考えられている。
しかし,物質表面の状態は試験片の置かれた環境,雰囲気などによって大きく影響を受けるため,真の表
面抵抗率の値を得ることは非常に難しい。また,JB.2.2.2に記載した測定上の問題点もあり,体積抵抗率
に比べれば物性値としては軽視されている。さらに,絶縁抵抗の値は,体積電流,表面電流,その他の漏
れ電流の総和から求められるが,材料の使用条件によっては,しばしば表面電流が支配的となる。このよ
うな場合には,ガードを用いない2端子測定による絶縁抵抗の値を表面抵抗とする場合があり,また,体
積抵抗率に,必要に応じた係数を乗じて表面抵抗率とすることも行われている。しかし,これら2端子測
定による表面抵抗及び表面抵抗率の値は,材料の物性値としての意味をもたない。
JC.2 2端子測定の問題点
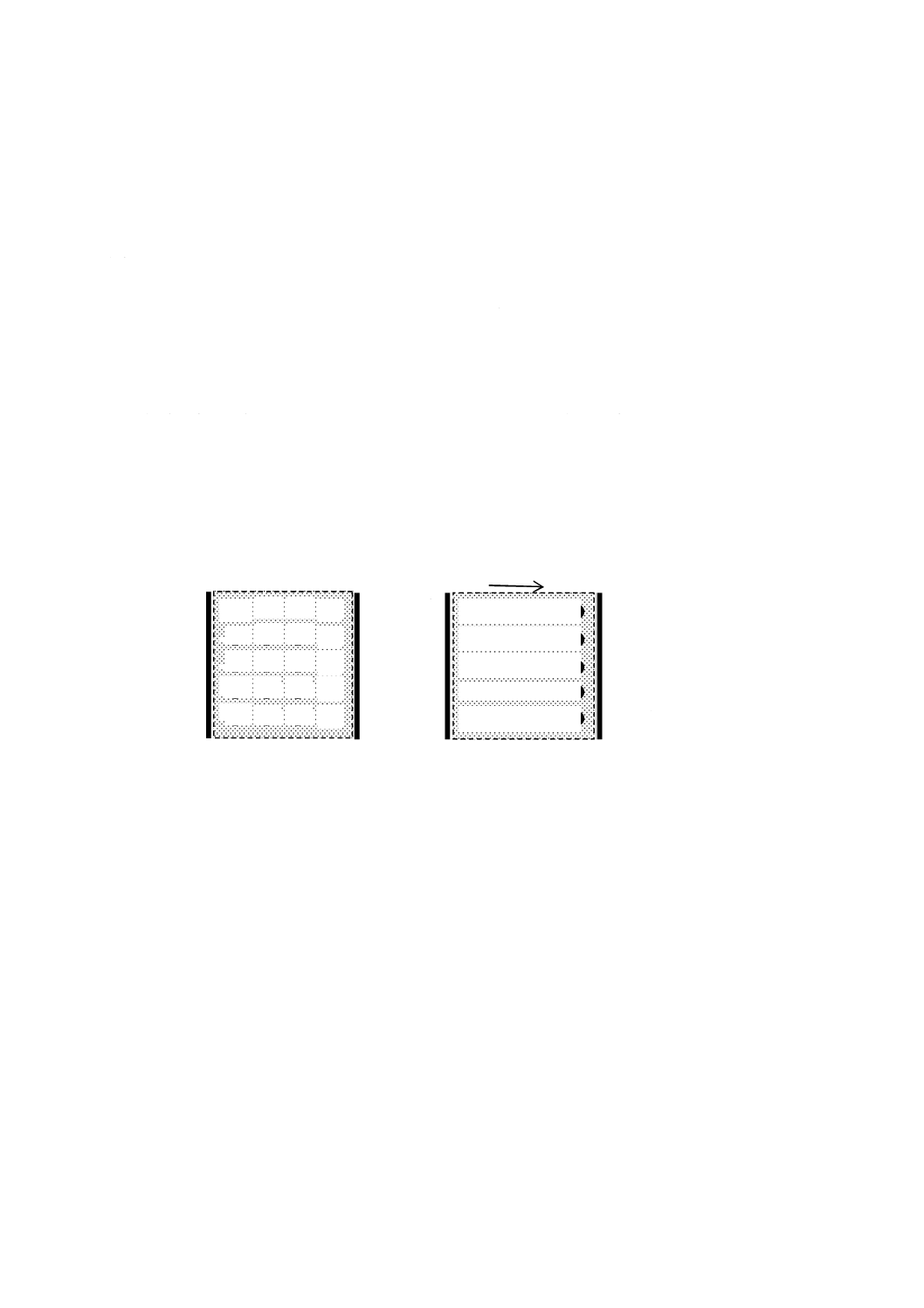
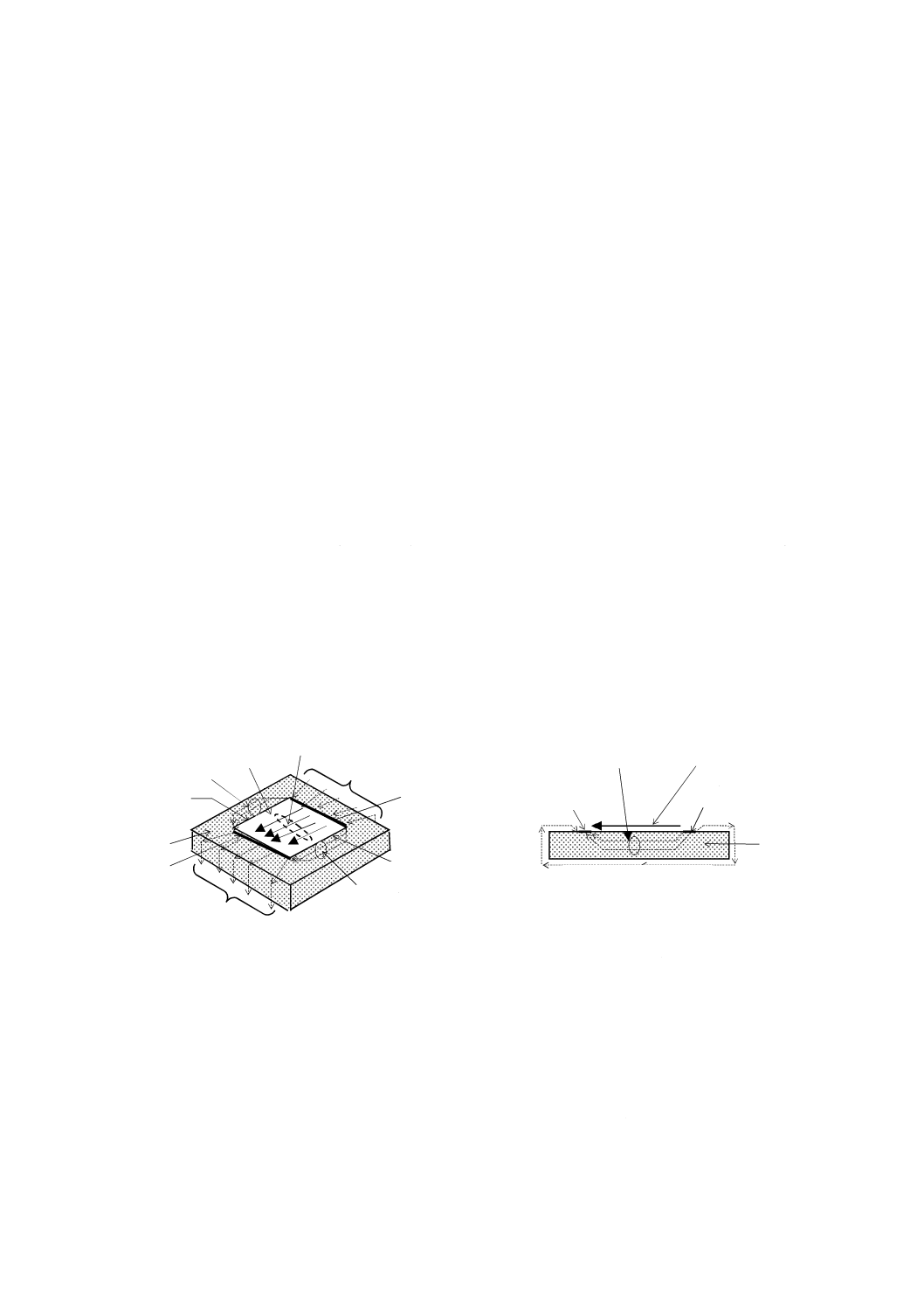
板状試験片の片面に,“ライン電極”と呼ばれ,図JC.1 a)の辺A及び辺B上にそれぞれ設けた電極○+及
び電極○−に示すように導電性塗料によって2本の電極を設け,その間の抵抗値を測定して“表面抵抗率”
と称している例がある。辺A,辺B,辺C及び辺Dに囲まれた表面の領域が,図JB.2の辺A,辺B,辺C
及び辺Dに対応する。しかし,図JC.1 a)に示した測定対象領域の外を流れる漏れ電流のほか,図JB.4 b)
と異なりガード電極がないため,図JC.1 b)に示すように,試験片の外側の表面,体積電流成分,その他全
ての漏れ電流が測定電流に含まれ,絶縁抵抗を測定しているに過ぎない。
a) 2端子測定及び電流経路
(表面電流)
b) 2端子測定及び電流経路
(表面電流及び体積電流)
図JC.1−2端子測定
JC.3 3端子測定の利点
2端子測定[図JC.1 a)参照]の測定対象領域を,図JC.2 a)に示すように3端子測定の電極間隙の一部に
置き換えてみる。辺B及び辺Aの“ライン電極”は,それぞれ主電極及び対電極に対応し,辺C及び辺D
の外側を流れる漏れ電流は依然として存在する。次に,図JC.2 b)に示すように,辺C及び辺Dをそれぞ
れ円周に沿って矢印のように移動し,測定領域を拡張して二つの辺C及び辺Dが線EFで一致したとする。
(辺A)
電極 ○
+
(辺B)
電極 ○
−
(辺C)
(辺D)
漏れ電流
漏れ電流
表面電流(測定対象)
漏れ電流
測定対象領域
試験片
漏れ電流(表面電流)
(辺A)
電極 ○
+
漏れ電流
(表面層電流)
(辺B)
電極 ○
−
表面電流(測定対象)
試験片
漏れ電流
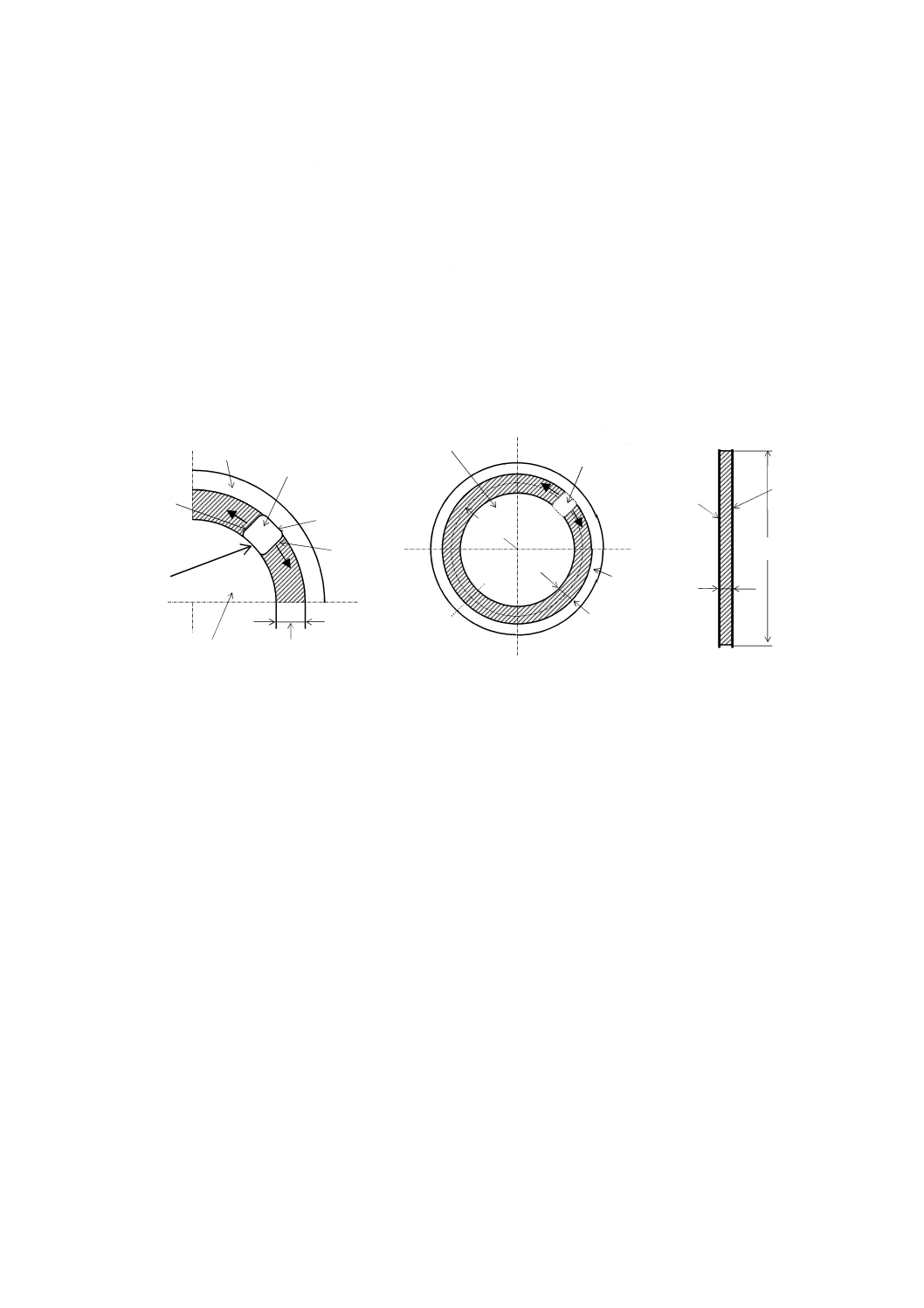
23
C 2139-1:2019
このとき,電極間隙の円環全体が測定対象領域となり,辺C及び辺Dは消滅する。したがって,辺C及
び辺Dの外側を流れる漏れ電流も消滅する。また,図JC.1 b)に示す試験片の裏面を流れる漏れ電流は,
裏面に設けたガード電極に吸収されて測定電流に影響を与えない[図JB.4 b)参照]。図JC.2 b)の円環状の
測定領域の外周と内周との間隙をgとし,一点鎖線で示した間隙の中心の円の半径をrgとすれば,この円
の円周長は2πrgであるから,この測定領域は,図JC.2 c)に示す長さ及び幅がそれぞれ2πrg及びgの長方
形に近似する。この長方形の測定領域は,図JB.3の概念図に極めて近い状態を実現している。このように,
3端子電極で測定された表面電流を,1辺が2πrgの正方形に換算,すなわち,測定電流にg/2πrgを乗じた
電流値から誤差の少ない表面抵抗の値を求めることができる。誤差の要因としては,図JC.1 b)に示した表
面層電流だけを考慮すればよいが,体積抵抗率の高い絶縁材料ほど,表面層電流は小さく,測定誤差も少
ない。
a) 測定領域の置換
b) 測定領域の拡張
c) 測定領域のく(矩)形近似
図JC.2−3端子電極による表面抵抗測定の利点
正方形
(近似領域)
(辺A)
(辺B)
(辺C)
(辺D)
主電極 ○
−
対電極 ○
+
電極間隙g
rg
g
g
2πrg
対電極
○
+
主電極
○
−
F
E
主電極
○
−
対電極
○
+
正方形
(近似領域)
24
C 2139-1:2019
附属書JD
(参考)
比誘電率測定−縁端静電容量の補正について
JD.1 一般的事項
誘電特性の測定は,通常,平行平板キャパシタを構成して行う。JA.7に記載した幾何静電容量の値は,
図JD.1 a)に示すように,二つの電極間の電気力線がキャパシタの外に漏れ出さないと仮定して,電極面積
及び電極間隔から計算する。しかし,実際には図JD.1 b)に示すように,電気力線がキャパシタの外に漏れ
出す。この現象を縁端効果という。縁端効果のために静電容量の測定値は幾何容量の値よりも大きくなり,
その差を縁端静電容量又は縁端容量という。縁端静電容量は,特に比誘電率の測定では大きな誤差要因と
なる。
a) 仮定の電気力線(幾何静電容量)
b) 実際の電気力線
図JD.1−縁端効果及び縁端静電容量
縁端効果による比誘電率の測定誤差の発生を避けるために,電極系にはガード電極を備えることが望ま
しい。この場合,ガード電極の幅は,試験片の厚さの2倍以上が必要であり,ガード電極と主電極との間
の間隙は,試験片の厚さよりも狭くする必要がある。実際の測定には,円板電極を用いることが多く,そ
の場合のガード電極は円環(リング)となるので,しばしば“ガードリング”と呼ばれる(3.4.3の注記4
参照)。
ガードリングを使用できない場合には,縁端静電容量に対する補正が必要である。補正のための近似式
を,表JD.1に示す。これらの式は経験式であり,試験片の形状の限定された範囲でだけ成り立つ。
縁端静電容量は,これらの補正式を用いる代わりに,ガードリングのある場合とない場合との測定値の
差から求めてもよい。このようにして求めた縁端静電容量は,異なる周波数及び温度における補正に用い
ても十分な精度が得られる。
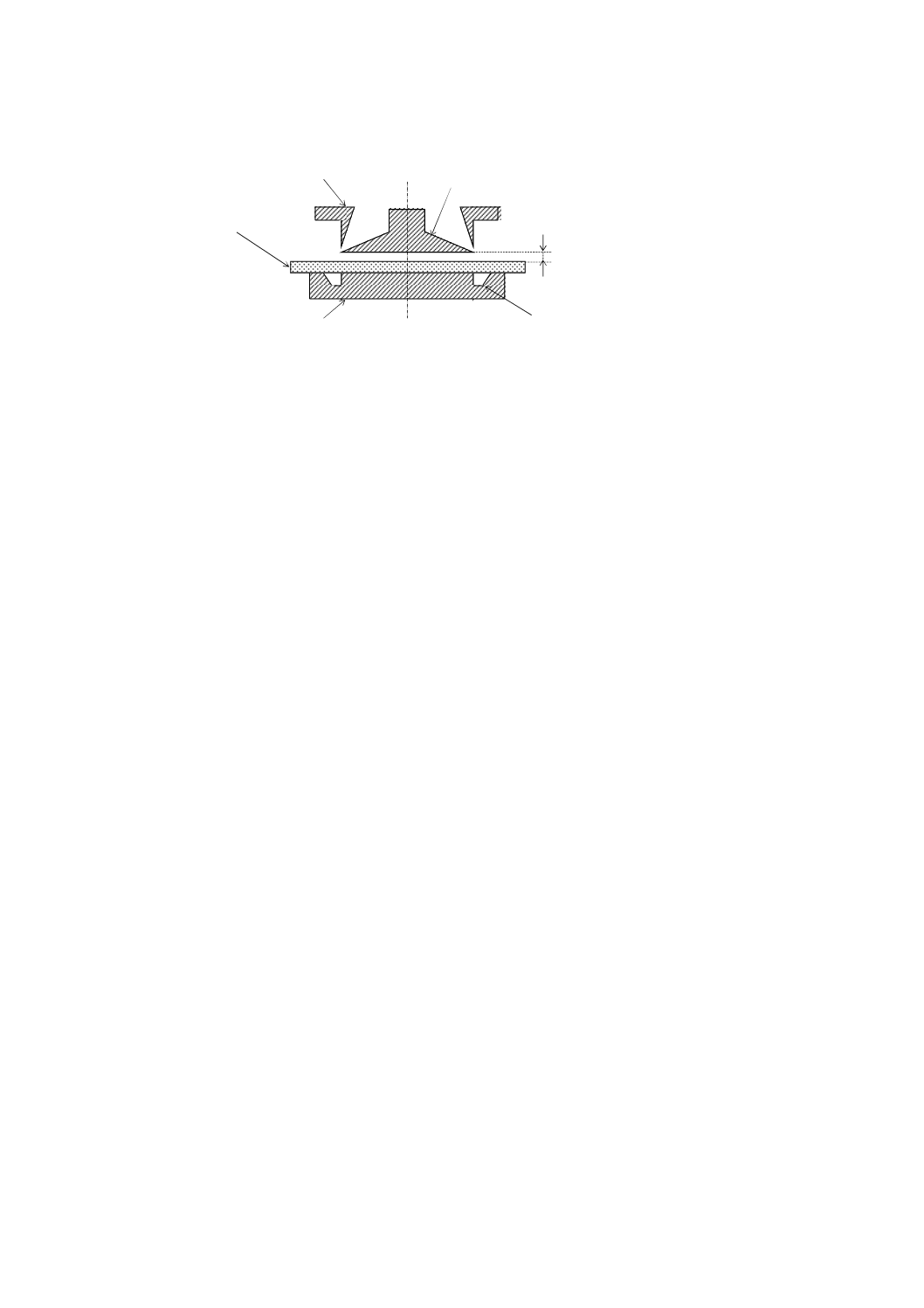
JD.2 シールドリングの形状及び縁端効果 [9], [10]
図JE.10(精密マイクロメータ電極)に採用されている3端子電極では,電極縁端における電気力線分
布の精密な実験的検討によって決定した主電極を囲む円環電極及び対電極の形状によって,500 kHz〜200
MHzの高周波数領域においても縁端静電容量による誤差が1 %以下の極めて優れた結果を得ている。ここ
で,一般にガード電極は主電極と同電位であるが,円環電極は対電極と同電位の接地電位となっているた
め,シールドリングと呼んでいる。その電極形状(断面図)を図JD.2に示す。この電極装置では,試験片
と電極との間に空隙を設けて測定する。
○
+
○
+
○
−
○
−
電気力線
電気力線
縁端効果
縁端効果
25
C 2139-1:2019
図JD.2−縁端効果の少ない誘電特性測定用3端子電極(例)
主電極(非接地)
シールドリング(接地電位)
対電極(接地電位)
試験片
(この電極装置では,試験片
と電極との間に空隙を設け
て測定する。)
空隙
環状の溝
26
C 2139-1:2019
表JD.1−真空静電容量及び縁端静電容量補正の計算
電極及び試験片の形状・寸法
寸法の単位:cm
電極間真空静電容量の計算式
静電容量の単位:pF
寸法の単位:cm
縁端静電容量の補正計算式
静電容量の単位:pF
寸法の単位:cm
1. ガードリング付きの円板電極
h
A
h
A
C
54
088
.0
0
0
=
×
=ε
(
)2
1
4
g
d
A
+
=π
Ce=0
2. ガードリングなしの円板電極
a) 電極の直径=試験片の直径
h
d
π
ε
C
2
1
0
0
4×
×
=
h
d2
1
54
069
.0
=
a≪hのとき
h
P
C
log
058
.0
029
.0
e
−
=
1d
Pπ
=
b) 試験片よりも小さく直径が同一の電
極
a≪hのとき
010
.0
log
058
.0
019
.0
1
e
+
−
=
h
ε
P
C
1d
Pπ
=
ここに,ε1:試験片の誘電率の近似値
c) 直径が異なる電極
a≪hのとき
045
.0
log
077
.0
041
.0
1
e
+
−
=
h
ε
P
C
1d
Pπ
=
ここに,ε1:試験片の誘電率の近似値
3. ガードリング付きの円筒電極
(
)
(
)
1
2
1
0
0
/
ln
2
d
d
g
l
ε
C
+
×
=
π
(
)
(
)
1
2
1
/
log
6
241
.0
d
d
g
l+
=
Ce=0
4. ガードリングなしの円筒電極
(
)
1
2
1
0
0
/
ln
2
d
d
l
ε
C
π
×
=
(
)
1
2
1
/
ln
6
241
.0
d
d
l
=
1d
h
h
+
<101の場合,
010
.0
log
058
.0
019
.0
1
e
+
−
=
h
ε
P
C
(
)
h
d
P
+
=
1
π
ここに,ε1:試験片の誘電率の近似値
試験片の比誘電率:
0
e
x
r
C
C
C−
′
=
ε
ここに, C'x :電極間の静電容量の測定値
ln :自然対数
log :常用対数
27
C 2139-1:2019
附属書JE
(参考)
測定回路−ブリッジ回路及び共振回路
JE.1 一般的事項
ブリッジ回路とは,基本的には3.4.4に規定したように,四つの素子を互いに直列接続及び並列接続して
構成する回路である。その基本回路を図JE.1に示す。
図JE.1−ブリッジ回路(4辺ブリッジ)
JE.2 受動ブリッジ回路(passive bridge circuit)
JE.2.1 一般的事項
受動ブリッジとは,4辺を全て受動素子(抵抗,キャパシタ及びコイル)で構成したブリッジ回路であ
る。
JE.2.2 ホイートストンブリッジ
電源が直流で,4辺が全て抵抗のブリッジをホイートストンブリッジという。その基本回路を,図JE.2
に示す。抵抗測定に広く用いられてきたが,現在では抵抗変化形のセンサ出力の検出回路としての用途が
重要である。
図JE.2−ホイートストンブリッジ
JE.2.3 シェーリングブリッジ
電源が交流で,4辺にそれぞれインピーダンス素子を用いた交流ブリッジは,目的に応じて数多くの回
路が考案され,インピーダンス測定又は場合によっては周波数測定器としても用いられている。
それらの中で,シェーリングブリッジは,最も古くから誘電率及び誘電正接の測定装置として用いられ
S
A
B
X
R
R
R
R=
平衡条件式:
D
RS
RX
RB
RA
RA,RB:既知抵抗
RS:既知抵抗(可変)
RX:未知抵抗
D:平衡点検出器(検流計)
直流電源
D
S
Z1
Z2
Z3
Z4
Z1,Z2,Z3,Z4:
4辺のインピーダンス
D:平衡点検出器(検流計)
S:電源(直流又は交流)
平衡条件:Z1 Z3=Z2 Z4
28
C 2139-1:2019
ている。その基本回路を,図JE.3に示す。このブリッジは,商用周波数(50 Hz又は60 Hz)を含む約100
kHzまでを上限とし,静電容量が50 pF〜1 000 pF(試験片キャパシタ又は測定対象機器の通常の静電容量)
の範囲で使用する。また,通常,ワグナー接地回路と呼ばれるガード系(JF.2参照)を備える。
シェーリングブリッジは,誘電正接を指標として商用周波数(50 Hz又は60 Hz)で用いる高電圧ケーブ
ル,高電圧機器などの絶縁診断を行う場合に,現在も広く用いられている。
CX:試験片キャパシタ
CN:標準キャパシタ(無損失)
R1,R2:可変抵抗
C1:可変キャパシタ
(C2):バイパス・キャパシタ
D:平衡点検出器(検流計)
S:交流信号源
図JE.3−シェーリングブリッジの基本回路
JE.2.4 変成器ブリッジ
絶縁材料の誘電特性測定に広く用いられてきたもう一つのブリッジに,変成器ブリッジがある。このブ
リッジは,変成器の等価な二つの二次巻線を4辺ブリッジの2辺として用いる。基本回路を,図JE.4に示
す。変成器ブリッジは,シェーリングブリッジよりも高い数10 MHzの周波数領域まで用いることができ
る。変成器ブリッジにも,ほとんどの場合,ワグナー接地回路(JF.2参照)を備える。
図JE.4−変成器ブリッジの基本回路
注記1 図JE.4〜図JE.7における電気量(電圧E,電流I,インピーダンスZなど)の記号の上にあ
る“・”(ドット)は,これらの量がベクトル量(力,速度,電界,電流などの大きさ及び向
きをもつ量)であり,複素数で表されることを示す。一例を挙げれば,キャパシタのインピ
ーダンスは,次の式のように記載する。
C
jω
R
Z
1
+
=
&
········································································ (JE.1)
ここに,
R: 抵抗値
C: 静電容量
Ż1,Ż2:未知及び既知インピーダンス
İ1,İ2:回路電流
Ė1,Ė2:二次巻線の電圧
N1,N2:二次巻線の巻数
D:平衡点検出器(検流計)
S:交流信号源
〜
S
N2
D
Ė2
Ż2
Ż1
Ė1
N1
2
1
2
1
N
N
Z
Z=
平衡条件式:&&
1I&
2I&
D
〜
S
C1
R1
CX
CN
(C2)
R2
29
C 2139-1:2019
ω: 角周波数(=2πf,f:周波数)
j: 虚数単位(=
1
−)
注記2 電気工学の分野では,虚数単位として通常使われる“i”は,電流と混同される場合があるた
め,“j”を用いる。大きさだけをもつ量(質量,長さ,エネルギー,電位,電荷量など)を
スカラー量といい,“・”(ドット)は付けない。
JE.3 能動ブリッジ回路(active bridge circuit)
JE.3.1 一般的事項
能動ブリッジとは,演算増幅器などの能動素子を用いるブリッジである。広い周波数範囲で高精度のイ
ンピーダンス測定が可能であり,多くのインピーダンスメータに用いられている。
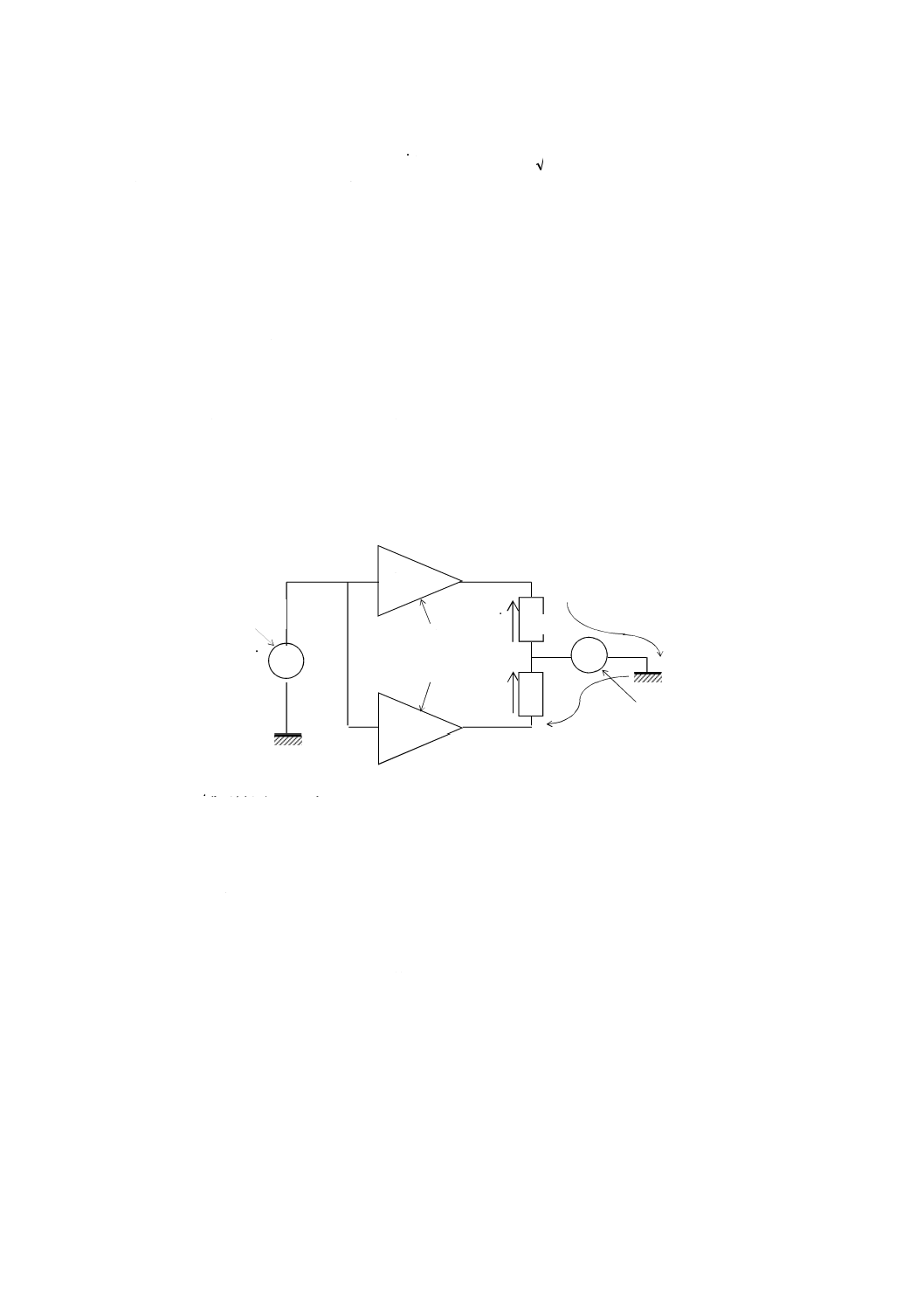
能動ブリッジの基本回路を図JE.5に示す。この回路は,変成器ブリッジの等価な二つの二次巻線を利得
が1の非反転演算増幅器及び−1の反転演算増幅器に置き換えたものとみなすことができる。しかし,変
成器の二次巻線には,必然的に生じる巻線のインダクタンス,巻線間の静電容量など残留インピーダンス
が大きいため,高い周波数では使用できない。一方,演算増幅器には,残留インピーダンスの影響がはる
かに少ないため,高い周波数(100 MHz程度)まで使用できる。
Żx:未知インピーダンス
Żs:既知インピーダンス
図JE.5−能動ブリッジの基本回路
JE.3.2 静電容量ブリッジ
静電容量ブリッジの基本回路を図JE.6に示す。この回路では,能動ブリッジ(図JE.5)の未知インピ
ーダンスŻx及び既知インピーダンスŻsをそれぞれ未知容量Cx及び既知容量Csに置き換え,反転増幅器の
前段に入力信号の振幅を制御するための演算増幅器を挿入している。この増幅器の利得がAのときにブリ
ッジが平衡した場合,平衡条件Cx=ACsから未知容量Cxを求めることができる。
1
−1
D
Ė
Ė
Ė
〜
Żx
Żs
İs
İx
平衡条件式:Żx=Żs
交流信号源
非反転演算増幅器
反転演算増幅器
平衡点検出器
(検流計)
30
C 2139-1:2019
図JE.6−静電容量ブリッジの基本回路
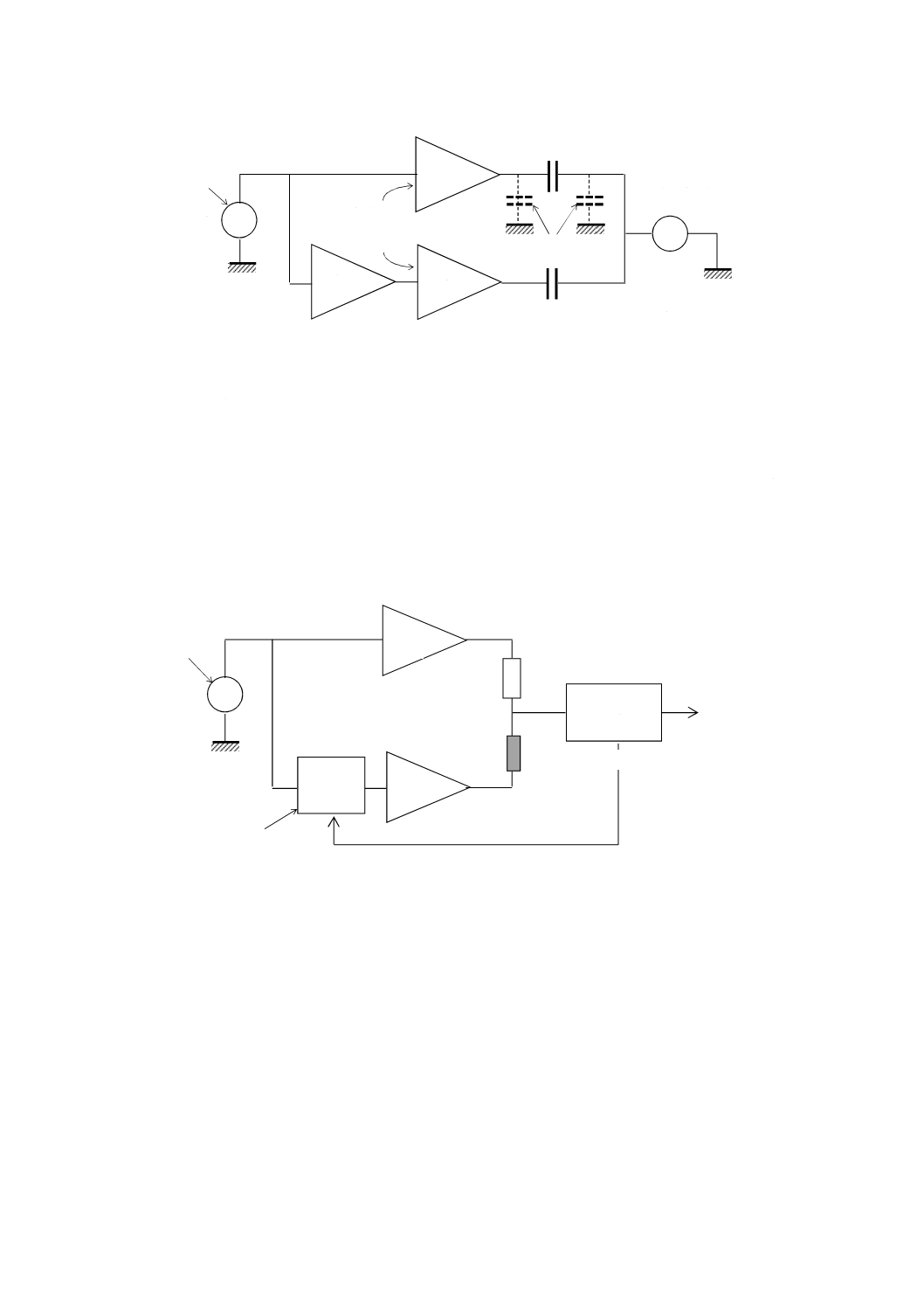
JE.3.3 インピーダンスメータ
図JE.7は,任意の未知インピーダンスを測定するための回路で,インピーダンスメータと呼ばれる。
この回路では,既知インピーダンスとして純抵抗(RS)を用い,反転増幅器の前段に入力信号の振幅(A)
及び位相(φ)の制御回路を設ける。この振幅と位相とは,検出器の出力信号が0となるように自動的に
調節され,未知の複素インピーダンス(Żx)の実部及び虚部,又は実部及び位相角がデジタル表示される。
この回路の未知インピーダンスとして,電気絶縁材料の試験片キャパシタを接続し,静電容量及び位相
角を求めることによって,試験片の誘電特性を測定することができる。
図JE.7−能動ブリッジによるインピーダンスメータ
JE.4 共振回路(resonant circuit)
JE.4.1 Qメータ
キャパシタ及びコイルによって構成する共振回路を用いた測定回路(Qメータ)は,本来は電子回路素
子の定数(インダクタンス,静電容量など)の測定用装置であるが,ブリッジ回路とともに,50 kHz〜100
MHzの比較的高い周波数領域の誘電特性の測定に古くから用いられてきた。図JE.8にその基本回路を示
す。
1
−1
平衡点検出
制御
非反転増幅器
利得A
位相φ
〜
振幅・位相制御回路
Ė
RS(既知抵抗)
交流信号源
Żx(未知インピーダンス)
測定値表示
1
−1
D
非反転増幅器
反転増幅器
(漂遊容量)
平衡点検出器
(検流計)
未知容量Cx
既知容量Cs
A
〜
増幅器(利得:A)
平衡条件式:Cx=ACs
交流信号源
Ė
31
C 2139-1:2019
図JE.8−Qメータの基本回路
Qメータによる誘電特性測定手順の詳しい説明は省略するが,ある周波数で共振状態にあるQメータに
可変標準キャパシタCSに並列に試験片キャパシタCxを接続し,可変標準キャパシタを調整して,増加し
たCx分を補償し,再度共振状態とする。このときの共振電圧は,試験片キャパシタCxの接続前よりも減
少するが,その減少分が試験片キャパシタの誘電正接に対応する。この測定方法にはガードは使用できな
い。Qメータには,通常附属品としてマイクロメータ電極と呼ばれる誘電特性測定用の電極が用意されて
いる。
JE.4.2 広帯域誘電特性測定器 [11]
Qメータを改良して,1 kHzの低周波から100 MHzの高周波までの広い周波数領域にわたる高精度測定
を可能にした測定器がある。回路の概略を図JE.9に示す。
この測定器は,全周波数領域にわたり有効なガードを備えている。また,位相指示器の付加によって,
共振点を簡単かつ正確に知ることができるなど,従来のQメータにはない数々の特長を備えている。
図JE.9−広帯域インピーダンスメータのブロックダイアグラム
この測定器に,ガード電極を備えた精密なマイクロメータ電極を組み合わせることによって,高い精度
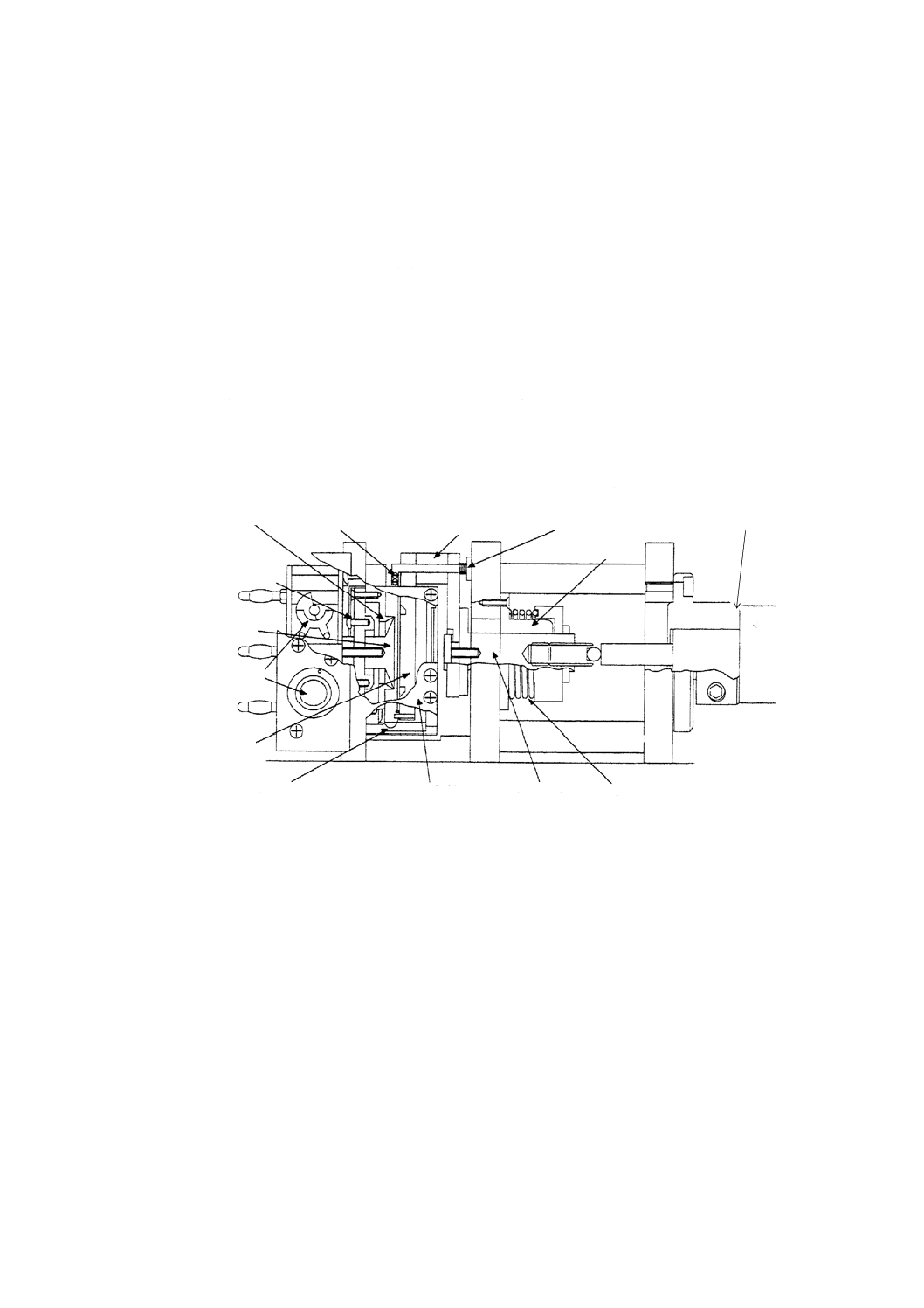
で誘電特性の測定を行うことができる。そのために開発されたマイクロメータ電極の一例を図JE.10に示
す。
この電極装置は,液浸間隙変化法と呼ばれる誘電特性の高精度測定のために開発された。電極と試験片
振幅
検波器
(LD)
振幅
指示器
(LM)
ガード
増幅器
(GA)
位相
検波器
(PD)
位相
指示器
(PM)
定振幅
信号源
(OSC)
共振コイル(L)
結合トランス(T)
精密マイクロ
メータ電極
(EA)
(図JE.10参照)
標準可変キャパシタ
〜
ガード
ガード
Ė
交流信号源
〜
標準コイル
L R
CS
可変標準キャパシタ
Cx
試験片キャパシタ
V
高周波
電圧計
32
C 2139-1:2019
とは密着せず,一定の間隙を設けて測定する。特に,比誘電率の測定において,従来非常に大きな誤差要
因となっていた試験片の厚さの測定を必要とせず,むしろ測定結果から試験片の平均厚さを求めることが
できる。
図JE.10中に断面図で示されている“非接地側電極”及び“接地側電極”が,それぞれ主電極及び対電
極である。詳しい説明は省略するが,“シールドリング”は,ガードリングとは役割が異なる(JD.2参照)。
また,本来のガードの機能をもつ“ガード導体”を備えている。それぞれの電極の独特な断面形状は,綿
密な電界の分析から割り出されたもので,縁端静電容量に起因する誘電率の測定誤差を1 %以内にとどめ
ている(参考文献[10],[11]参照)。
また,これら電極の主要部分はセル(電極容器)に納められ,誘電率が既知の液体誘電体,例えば,粘
度が1 cSt(センチストークス)程度の低粘度シリコーン油を満たして測定する。
近年測定需要の多いフィルム及び薄いシート材料を測定対象としているため,主電極と対電極との間隔
は最大で3 mmまでとなっている。
図JE.10−精密マイクロメータ電極(例)
シールドリング
試験片圧着ジグ
セラミック
絶縁ブロック
試験片圧着用
スプリング
軸受
精密マイクロメータヘッド
ガード導体
主電極(非接地)
補助可変キャパシタ
対電極(接地)
銅はく
電極容器
電極駆動軸
電極駆動用スプリング
33
C 2139-1:2019
附属書JF
(参考)
ガード及びガード回路
JF.1 一般的事項
直流電圧印加による絶縁抵抗特性の測定では,高い抵抗値を測定対象としなければならない。したがっ
て,測定電極の機械的構造を保持するための部品,測定器の端子,ケーブルなど,測定対象以外の各部に
用いられる絶縁材料の漏れ電流の影響は無視できない。その対策を怠れば,しばしば大きな測定誤差を生
じるため,適切なガードを設けることが必要である。
また,絶縁抵抗の体積抵抗成分を表面抵抗成分と区別して測定するためには,測定電流から表面電流成
分を効果的に取り除くためのガードが必要である。同様に,表面抵抗成分を測定したい場合には,体積電
流を極力取り除くためのガードが必要である。
交流電圧印加による誘電特性の測定の場合には,電極間に試験片を挿入又は挟んで試験片を誘電体とす
るキャパシタを構成して測定する。この場合,低い周波数ではキャパシタのインピーダンスが高いため,
上記の直流電圧印加による絶縁抵抗特性測定の場合と同様に,漏れ電流を取り除くためのガードが必要で
ある。高い周波数では,キャパシタのインピーダンスが相対的に低くなるため,漏れ電流の影響は小さく
なるが,その一方で,周波数が高くなるほどケーブルのインダクタンス,電極,その他の金属構成部品と
周囲の導体間との漂遊容量などによる残留インピーダンスの影響が大きくなり,ガードの使用は困難とな
る。
このように,高周波測定においては制約があるが,直流及び低周波測定では,測定対象以外の不要な電
流を取り除くために,ガード電極,ガード回路などからなるガード系の使用が必要である。
JF.2 受動ガード
受動ガードは,漏れ電流を測定対象の電流から分離し,ガード導体による側路を設けて大地(アース)
に流れるように構成する。
図JF.1 a)に,ガードのない2端子接続の測定系を示す。この測定系では,図JF.1 b)の等価回路で示すよ
うに,試験片の抵抗RSと支持絶縁物A及びBの漏れ抵抗RA及びRBとの和が並列接続の状態となる。ま
た,試験台Cが絶縁物の場合には,その漏れ抵抗RCも加わる。これらの漏れ抵抗の影響は非常に大きく,
測定誤差の最大の要因となる。例えば,抵抗RSの値が1012 Ωの試験片を測定しようとするとき,支持絶
縁物のRA,RB及びRCのオーダーが1010 Ω程度の場合には,電圧を印加したとき,流れる電流は試験片よ
りも漏れ抵抗の方がはるかに大きく,RSを求めることはできない。
a) 2端子接続
b) 等価回路
図JF.1−ガードのない2端子測定系
試験片(抵抗 RS)
支持絶縁物 A
(漏れ抵抗 RA)
支持絶縁物 B
(漏れ抵抗 RB)
試験台 C
(漏れ抵抗 RC)
RS
RA+RB(+RC)
測定端子 X
測定端子 Y
X
Y
測定電流IS
漏れ電流IL
34
C 2139-1:2019
このような漏れ電流の影響は,図JF.2 a)に示すように,同じ測定系にガードを設けることによって避け
ることができる。図JF.2 b)は,その等価回路である。測定端子のX及びYをそれぞれ高圧側及び低圧側
とし,支持絶縁物A及びBの漏れ抵抗をそれぞれRA及びRBとした場合,漏れ抵抗RAの片方の端子は高
圧側測定端子Xに接続しているため,漏れ抵抗RAの両端には高電圧が印加され,流れる漏れ電流iLAは大
きい。一方,低圧側測定端子Yは電流計を介して接地されるが,一般的に電流計の内部抵抗の値は試験片
の抵抗RSよりもはるかに小さいため,低圧側測定端子Yと接地Eとの間の電位差は極めて小さい。した
がって,漏れ抵抗RBを通って接地Eに分流する漏れ電流iLBは,漏れ電流iLAに比べて無視できる。この
ように,漏れ電流は,ガード導体を介して接地Eに流れるため,測定誤差は大幅に低減される。
また,ガード導体は,外部からの雑音によって測定電流の流れる信号線に雑音電流が誘起されるのを防
ぐ遮蔽(シールド)の役割も果たす。
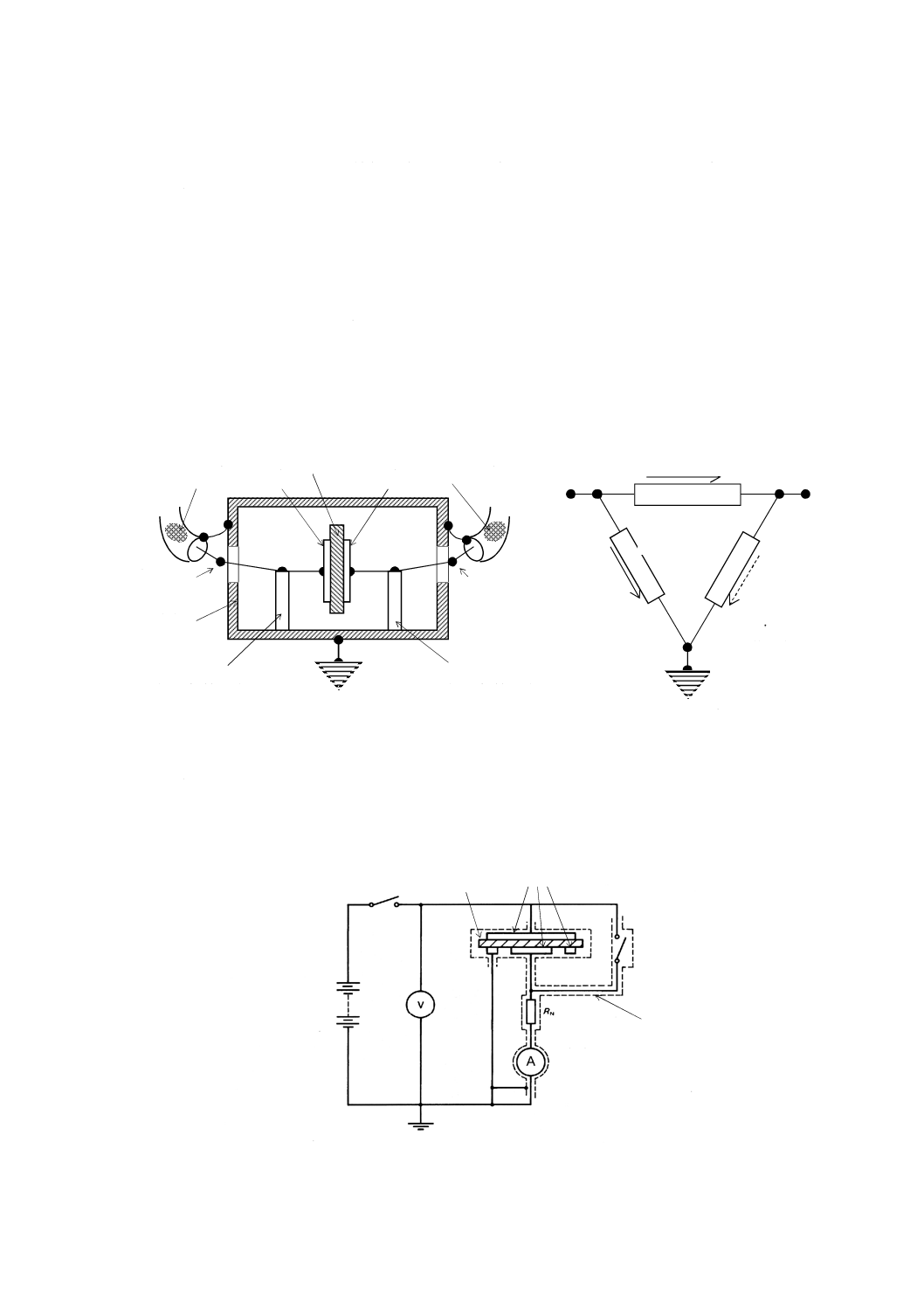
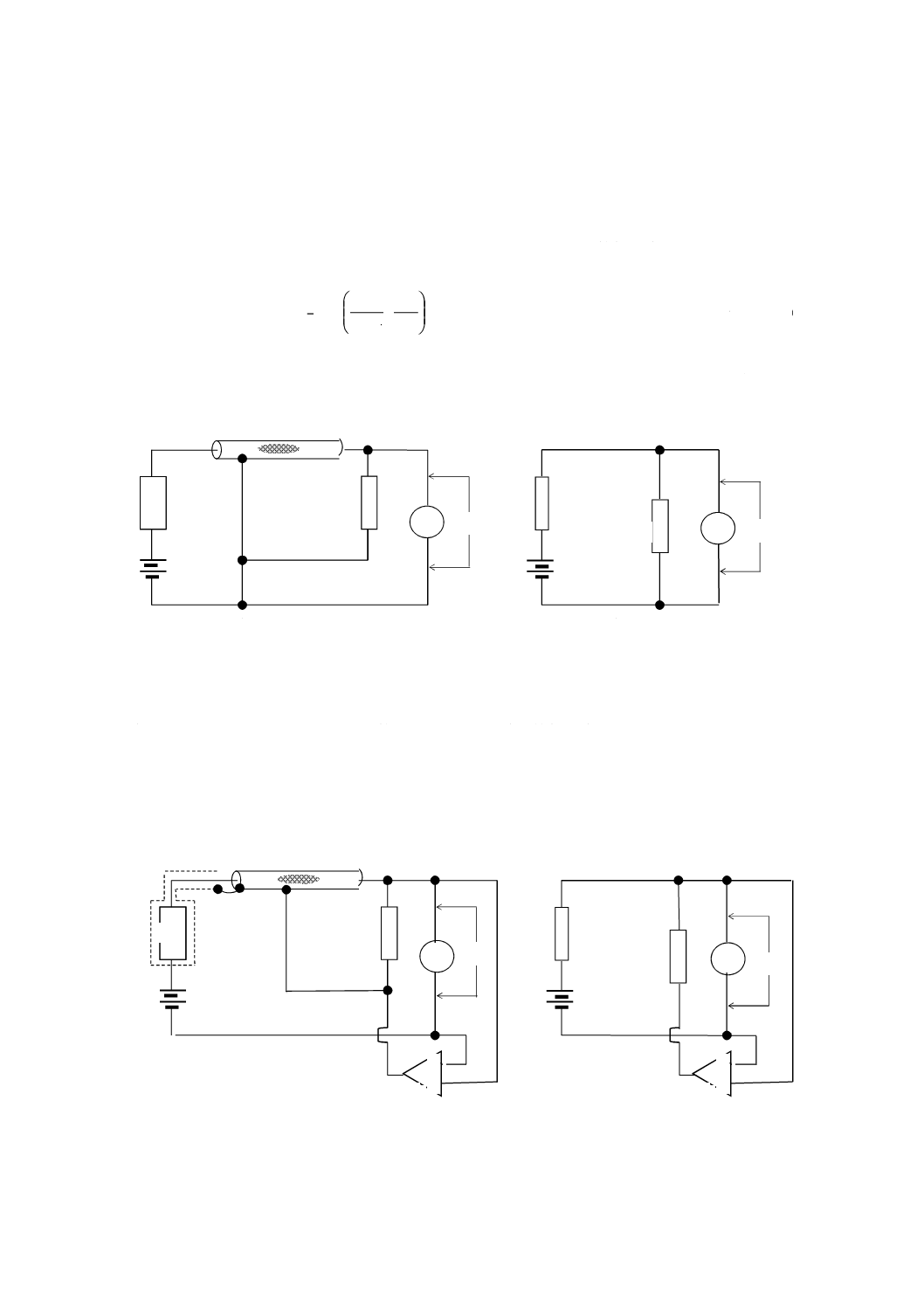
図JB.3に示す3端子電極による測定は,上記の受動ガードの原理に基づいている。
a) 3端子接続
b) 等価回路
図JF.2−ガード付き3端子測定系
図4は,絶縁抵抗測定のための3端子電極を用いた基本回路である。実際には,この回路にもガードを
施すのが一般的であり,図JF.3に体積抵抗測定に用いられる電流計法と呼ばれる回路図を示す。ガード導
体は,破線で示されている。
図JF.3−ガード系を備えた体積抵抗測定回路(例)
直流電源S
直流
電圧計
直流
電流計
3端子電極
試験片
試験片短絡
スイッチ
ガード導体
支持絶縁物 B
(漏れ抵抗 RB)
支持絶縁物 A
(漏れ抵抗 RA)
ガード導体
(接地電位)
接地(E)
同軸ケーブル
同軸ケーブル
試験片(抵抗 RS)
電極
高圧側
測定端子X
低圧側
測定端子Y
Y
X
RA
RB
RS
接地(E)
電極
高
圧
側
低
圧
側
iLA
(大)
iLB
(微小)
漏
れ
電
流
漏
れ
電
流
測定電流IS+漏れ電流iLB
35
C 2139-1:2019
比較的低い周波数領域の誘電特性測定回路にも,受動ガードは用いられている。その一例として,シェ
ーリングブリッジを図JF.4に示す。ガード導体は,図JF.3と同様に破線で示されている。外部比例辺イ
ンピーダンスのZA及びZBを付加し(ワグナー接地回路と呼ばれる。),その中間点Pをガード導体に接続
して接地する。切替スイッチNによって,二組のブリッジ,すなわち,主ブリッジAMNB及び副ブリッ
ジAMPB(又はANPB)を同時に平衡状態にすることによって,ガード導体を設けたことによる漂遊容量
による残留インピーダンスの影響を低減する。測定操作としては,切換スイッチNを何度も切り換えなが
ら,可変のR1,R2,C1及びZBの調整を繰り返すことが煩雑であり,多少の熟練を要する。この回路では,
交流信号源Sの両端子共に非接地としなければならないことに注意する。非接地できない場合には,より
複雑な回路構成(二重遮蔽ブリッジと呼ばれる。)が必要になる。
図JF.4−ワグナー接地回路付きシェーリングブリッジ
JF.3 能動ガード
JF.3.1 一般的事項
漏れ抵抗に起因する測定誤差は,絶縁抵抗特性測定においては,受動ガードによって大きく低減される。
この効果は,低周波数領域における誘電特性測定においても同様である。一方,高周波数領域では,交流
信号が流れる主電極,リード線(信号線)を含む全ての部品とガード導体との間の漂遊静電容量,及びリ
ード線のインダクタンスによる残留インピーダンスの影響が増大するため,ガードの使用は困難である。
また,JF.2でワグナー接地回路に関して記載したように,測定操作が煩雑であるため,自動平衡回路と
呼ばれる操作を自動化するための電子回路装置が用いられている。
図JF.5に自動平衡回路の概略図を示す。詳細な説明は省略するが,図JF.5 a)の回路では,高利得差動増
幅器を利得A=1の低出力インピーダンス増幅器として用い,ガード導体を常に検出器Dと同電位に保つ。
図JF.5 b)の回路では,高利得差動増幅器の負帰還回路にブリッジ回路を組み込み,平衡点検出器Dの一端
Nを常にガード導体と同電位に保つ。
図JF.5の回路は,いずれも増幅器の位相偏移を無視できる低周波数領域で用いる。
このように,古くから電子回路による能動ガードの試みは行われていたが,高利得かつ安定な差動増幅
器の作製は,過去の電子回路技術では必ずしも容易ではなかった。
交流信号源S
試験片キャパシタ
標準キャパシタ
(ガードリング
付き3端子)
(ガード付
き3端子)
付加比例辺イン
ピーダンスZA
付加比例辺イン
ピーダンスZB
(可変)
平衡点
検出器
可変抵抗器
可変
抵抗器
可変キャパシタ
切
換
ス
イ
ッ
チ
36
C 2139-1:2019
a) ボルテージフォロワ(A=1)
を用いた自動平衡回路
b) 高利得差動増幅器(A=∞)
を用いた自動平衡回路
図JF.5−自動平衡回路を備えたブリッジ
JF.3.2 演算増幅器による能動ガード回路
近年,高利得,高入力インピーダンス,低出力インピーダンスなど優れた性能を備えた演算増幅器が容
易に使用できるようになり,演算増幅器を用いた利得が1の増幅器(ボルテージフォロワ又はユニティゲ
インアンプと呼ぶ。)を用いてガード導体を駆動し,常に交流信号が流れる主電極,リード線などとガード
導体との間を同電位に保つ能動ガード(又はアクティブガード)が広く用いられる。この能動ガードによ
って,測定系を構成する絶縁体内部には電界は発生せず,漏れ電流を常にほぼ0にすることができる。演
算増幅器による能動ガードは,100 MHz程度の高周波数領域まで使用できる。
注記1 演算増幅器はOPアンプとも呼ばれ,半導体デバイスによる作動増幅器を組み込んだ集積回
路素子である。演算増幅器は,通常,反転入力端子(−)及び非反転入力端子(+)の二つ
の入力端子並びに一つの出力端子をもち,極性の異なる正負の電源で動作する。その典型的
な特性値(オーダー)は,裸利得:105,入力インピーダンス:106 Ω(トランジスタ入力)
又は109 Ω(FET入力),出力インピーダンス:102 Ω,などである。回路記号を図JF.6 a)に示
す。
注記2 利得が1の増幅器は,図JF.6 b)に示すように,演算増幅器の反転入力端子を出力端子に接続
した回路である。入力と出力とは同位相である。入力インピーダンスは非常に高く,インピ
ーダンス変換器としても広く用いられている。
a) 回路記号
b) ボルテージフォロワ
図JF.6−演算増幅器(OPアンプ)
+
A
−
非反転入力端子
反転入力端子
V OUT
V IN
正電源V S+
E(接地端子)
+
A
−
V IN
V OUT
非反転入力端子
反転入力端子
出力端子
出力端子
負電源V S−
〜
D
ガード導体に接続
〜
−
+
−
+
S
S
D
ガード導体に接続
A=1
A=∞
37
C 2139-1:2019
JF.3.3 測定誤差の低減
能動ガードの概念を明瞭にするために,まず,図JF.7 a)に示すようなガードが施されていない回路を考
える。この図において,RXは試料の抵抗値,VRXは流れた電流によって試料抵抗器の両端に現れる電圧,
VMは電圧計によって実際に測定された電圧,及びRLKGはケーブルの絶縁物の漏れ抵抗に電圧計の入力抵
抗を併せて考慮した等価並列抵抗の値である。図JF.7 b)は,図JF.7 a)の等価回路である。この図から明ら
かなように,試料抵抗器の両端に現れる電圧はRXとRLKGとによって分圧され,測定電圧VMは,
+
=
LKG
X
X
RX
M
R
R
R
V
V
······························································ (JF.1)
となり,VRXよりも小さくなる。この式から,RX及びRLKGが共に109 Ωの場合,誤差は50 %となることが
分かる。また,RLKGが1桁大きく1010 Ωの場合にも,VM=0.909VRXとなって,9 %以上の誤差を生じる。
a) 測定回路
b) 等価回路
図JF.7−ガードなし測定回路
このような難点は,JF.3.2に記載した演算増幅器(利得A=1)を用い,図JF.8 a)に示すような能動ガー
ド回路を設けることによって,大きく改善される。この回路の等価回路を,図JF.8 b)に示す。図JF.7 a)
では,RLKGの一端はケーブルの外部導体と一緒に接地されていたが,図JF.8 a)では,RLKGの一端及びケー
ブルの外部導体は共に演算増幅器の出力に接続され,演算増幅器によって駆動される。この増幅器の利得
は1であるから,RLKGの両端の電位は常に等しく保たれるため,RLKGを通る漏れ電流は発生しない。
a) 測定回路
b) 等価回路
図JF.8−ガード付き測定回路
RX
RLKG
VRX
ガード導体
ケーブル外被
VRX
RLKG
RX
V
−
+
−
+
V
演算増幅器(利得A=1)
演算増幅器(利得A=1)
VM
VM
RX
V
RLKG
VRX
ケーブル外被
V
VRX
VM
VM
RLKG
RX
38
C 2139-1:2019
また,演算増幅器の出力インピーダンスは非常に低いため,出力端子に使われている絶縁体を通る漏れ
電流は測定にほとんど影響を与えない。このような能動ガード回路の働きによって,VRXと電圧計Vによ
る測定電圧VMとの値はほとんど一致し,測定誤差は極めて小さくなる。
JF.3.4 計測に要する応答時間(セットリング時間)の短縮
能動ガードを用いると,信号線とガード導体との間に電界が発生しないので,漏れ抵抗による誤差を低
減する働きばかりでなく,信号線とガード導体との間の静電容量をほぼ0にすることができる。実際に測
定を行う場合,試料抵抗器と測定器とを接続するリード線として比較的低容量のケーブルを使った場合で
も,試料抵抗値とケーブル容量との積で与えられる時定数が問題となる。この時定数が大きいほど,計測
に要する応答時間(以下,セットリング時間という。)が長くなる。例えば,1013 Ωの抵抗値を1 m当たり
100 pFの容量をもつケーブルを用いて測定する場合,その時定数(R×Cの値)は,単純計算で1 000秒(約
17分)となり,非常に長い。特に自動計測の場合には,セットリング時間(例えば,最終到達値の±0.001 %
までの到達時間)を考慮しなければならず,その値は時定数の5倍〜10倍とされている。すなわち,測定
時間は5 000秒〜10 000秒となり,このままの状態では自動計測は事実上不可能である。
しかし,測定回路のガード導体を,入力インピーダンスが非常に高く,かつ,出力インピーダンスが極
めて低い,利得が1のボルテージフォロワで駆動することによって,上記の測定時間を2桁以上短縮する
ことができる。また,同時に,漏れ抵抗による電流も原理的には0とすることができる。さらに,ケーブ
ルの信号線と外部導体との間の電位差も常に0に保たれているため,両者の間に電気力線は発生せず,ケ
ーブル容量は等価的にほとんど0となる。したがって,試験片及び試験回路を構成する絶縁材料部品の漏
れ抵抗の値と,ガード導体の漂遊容量及びケーブルの分布容量の和との積で与えられる時定数は極めて小
さくなり,測定時間は短縮され,自動計測が十分に可能となる。
用いる同軸ケーブルの長さによって,信号線とガード系の導体との間の静電容量は,数100 pF以上の大
きな値となることがある。このような大きな容量性負荷を駆動するための専用のボルテージフォロワ用素
子も多数市販されている。
今日の高抵抗測定においては,能動ガードは必須と考えられており,市販されている微小電流計及びエ
レクトロメータの多くは,能動ガード回路を内蔵し,その出力をガード端子として備えるなど,容易に能
動ガード回路を構成することができる。
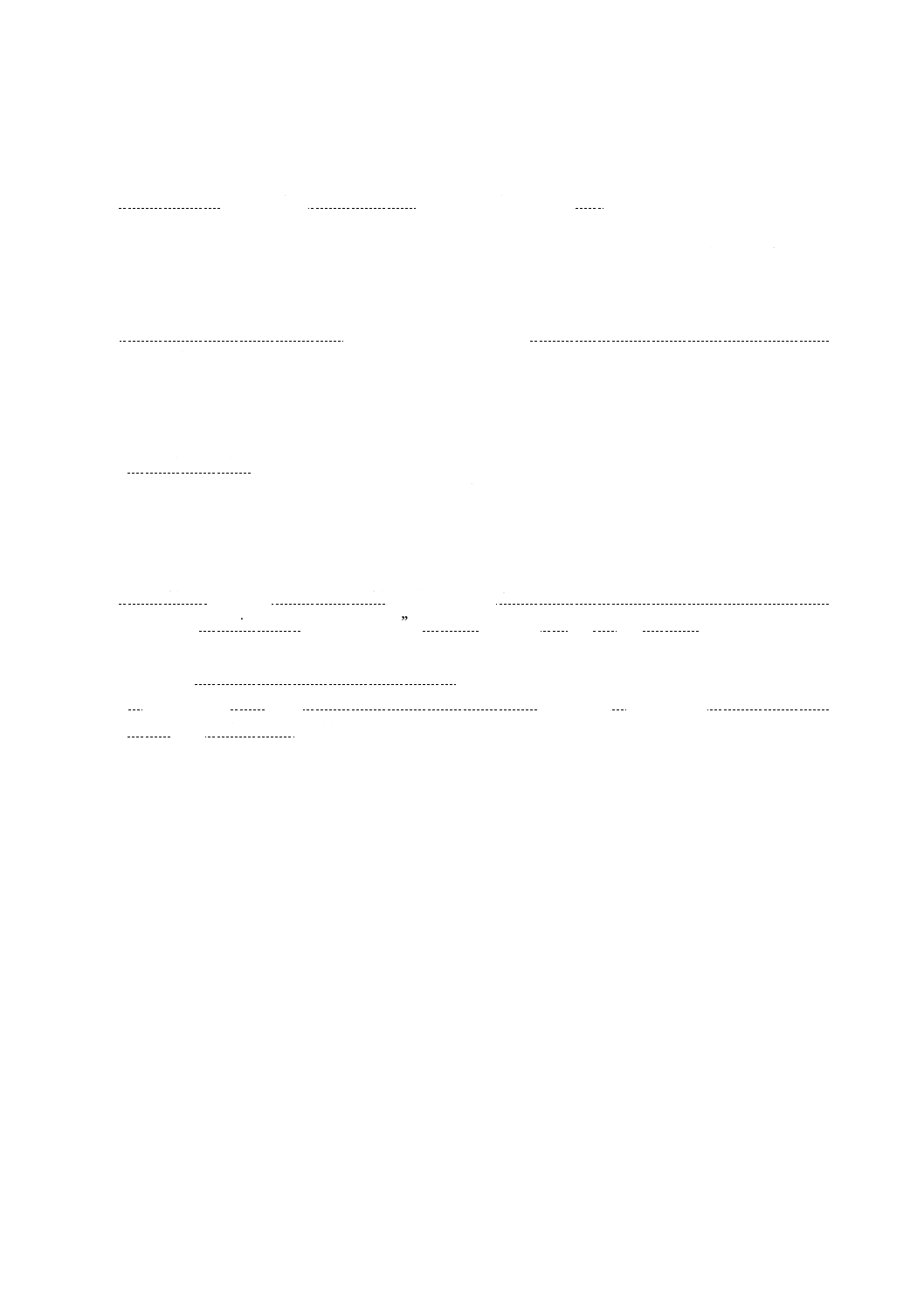
39
C 2139-1:2019
参考文献
[1] IEC 60050-121, International Electrotechnical Vocabulary (IEV)−Part 121: Electromagnetism
注記 IEC 60050は,http://www.electropedia.org/から無料でアクセスできる。
[2] IEC 60216-1,Electrical insulating materials−Thermal endurance properties−Part 1: Ageing procedures and
evaluation of test results
[3] IEC 60505,Evaluation and qualification of electrical insulation systems
[4] 電気学会 電気専門用語集 No. 16“絶縁材料”,電気学会 電気用語標準特別委員会・絶縁材料用語
小委員会[コロナ社,昭和58年(1983年)]
[5] 電気学会大学講座“誘電体現象論”,鳳誠三郎,犬石嘉雄,中島達治,川辺和夫,家田正之,[電気学
会,昭和48年(1973年)]
[6] 電気学会 電気規格調査会規格JEC-6148“電気絶縁材料の絶縁抵抗試験方法通則”[電気書院,平成
14年(2002年)]
[7] 電気学会 電気規格調査会規格JEC-6150“電気絶縁材料の誘電率および誘電正接試験方法通則”[電
気書院,平成12年(2000年)]
[8] 電気・電子・情報工学基礎講座5“新版電気・電子計測”,新妻弘明,中鉢憲賢[朝倉書店,平成15
年(2003年)]
[9] A. Kakimoto, I. Ogawa & T. Matsushita, “Improvements on the measurements of dielectric constant and
dissipation factor in a wide frequency range”, Rev. Sci. Instrum., Vol. 48, No. 12, 1977-12
[10] 小川一三,柿元章:縁端効果の少ない誘電体測定用電極とその特性試験法,電機学会論文誌A,99巻
9号,pp. 441-448[1979年(昭和54年)9月]
[11] A. Kakimoto, A. Etoh, et.al. “Precise measurement of dielectric properties at frequencies from 1 kHz to 100
MHz”, Rev. Sci. Instrum., 58(2), 1987-2
40
C 2139-1:2019
附属書JG
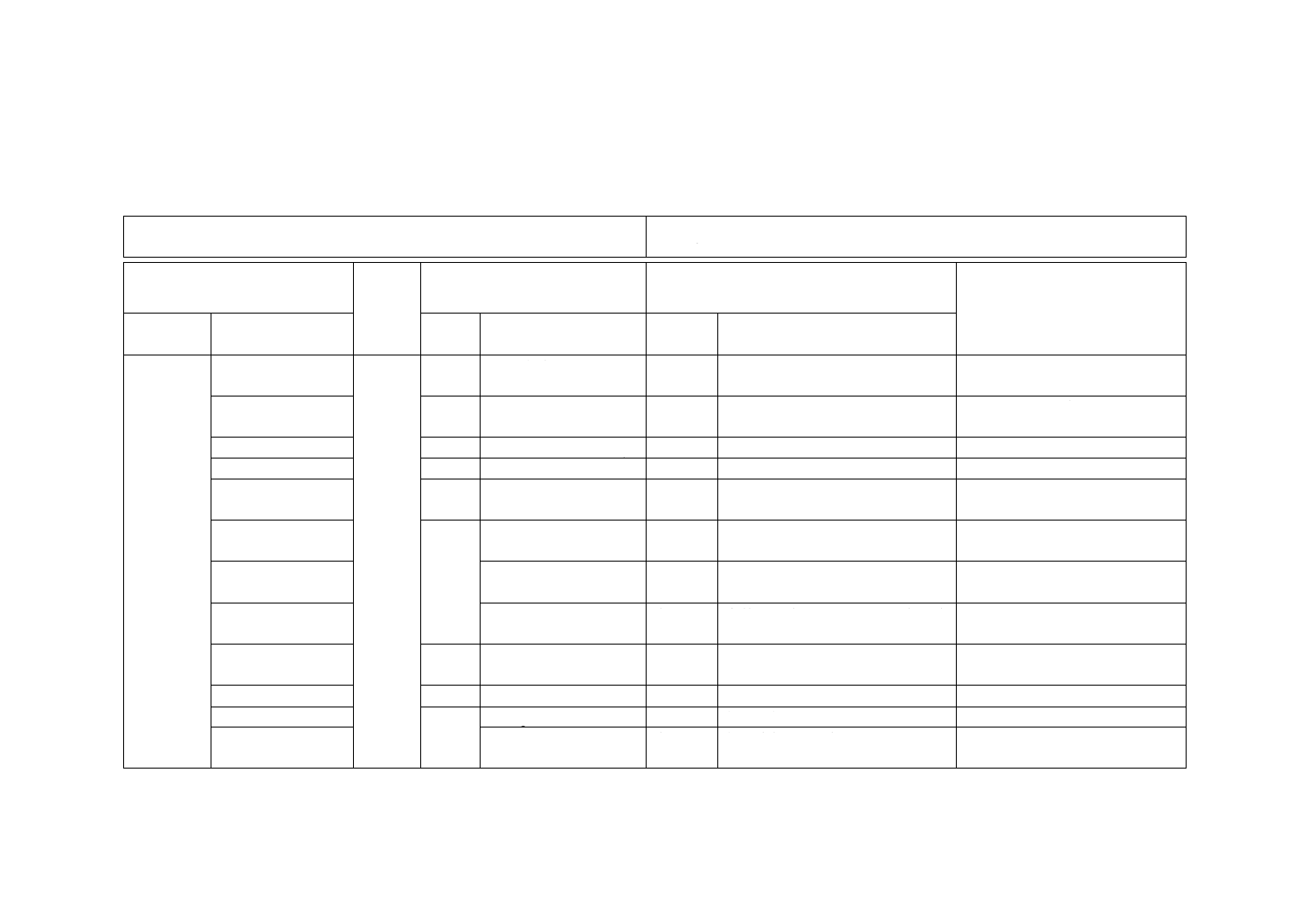
(参考)
JISと対応国際規格との対比表
JIS C 2139-1:2019 固体電気絶縁材料の誘電特性及び抵抗特性−第1部:基本事
項
IEC 62631-1:2011,Dielectric and resistive properties of solid insulating materials−Part 1:
General
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごと
の評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
3 用語及び
定義
3.1.1〜3.1.9
3
3.1.1及び3.7〜3.14にそ
れぞれ対応。
変更
細分箇条番号を変更。
IECに修正提案を予定。
3.1.3 充電電流,
注記
−
−
追加
注記を追加。
IECに追加を提案の予定。
3.1.6 電束密度
3
3.10 electric flux density
追加
電束密度の原理を追加で記載。
IECに追加を提案の予定。
3.1.10 緩和時間
−
−
追加
多く使用される用語の追加。
IECに追加を提案の予定。
3.2.1 一般的事項
−
−
追加
細分箇条番号を追加し,一般的事項
及び図1を記載。
IECに追加を提案の予定。
3.2.2〜3.2.6
3
3.2.1〜3.2.5にそれぞれ
対応。
変更
細分箇条番号を変更。
IECに修正提案を予定。
3.2.4 体積抵抗率
3.2.3 volume resistivity,
NOTE 1
削除
記載内容が不適切と判断し,削除。 IECに削除を提案の予定。
3.2.6 表面抵抗率
3.2.5 surface resistivity
変更
定義が不適切と判断し,記載を変
更。
IECに修正提案を予定。
3.3 誘電特性に関す
る用語及び定義
−
−
追加
細分箇条を追加。
IECに修正提案を予定。
3.3.1 誘電体
−
−
追加
細分箇条を追加。
IECに追加を提案の予定。
3.3.2 静電容量
3
3.4 capacitance
変更
細分箇条番号を変更。
IECに修正提案を予定。
3.3.3〜3.3.6
3.3.1〜3.3.4にそれぞれ
対応。
変更
細分箇条番号を変更。
IECに修正提案を予定。
4
0
C
2
1
3
9
-1
:
2
0
1
9
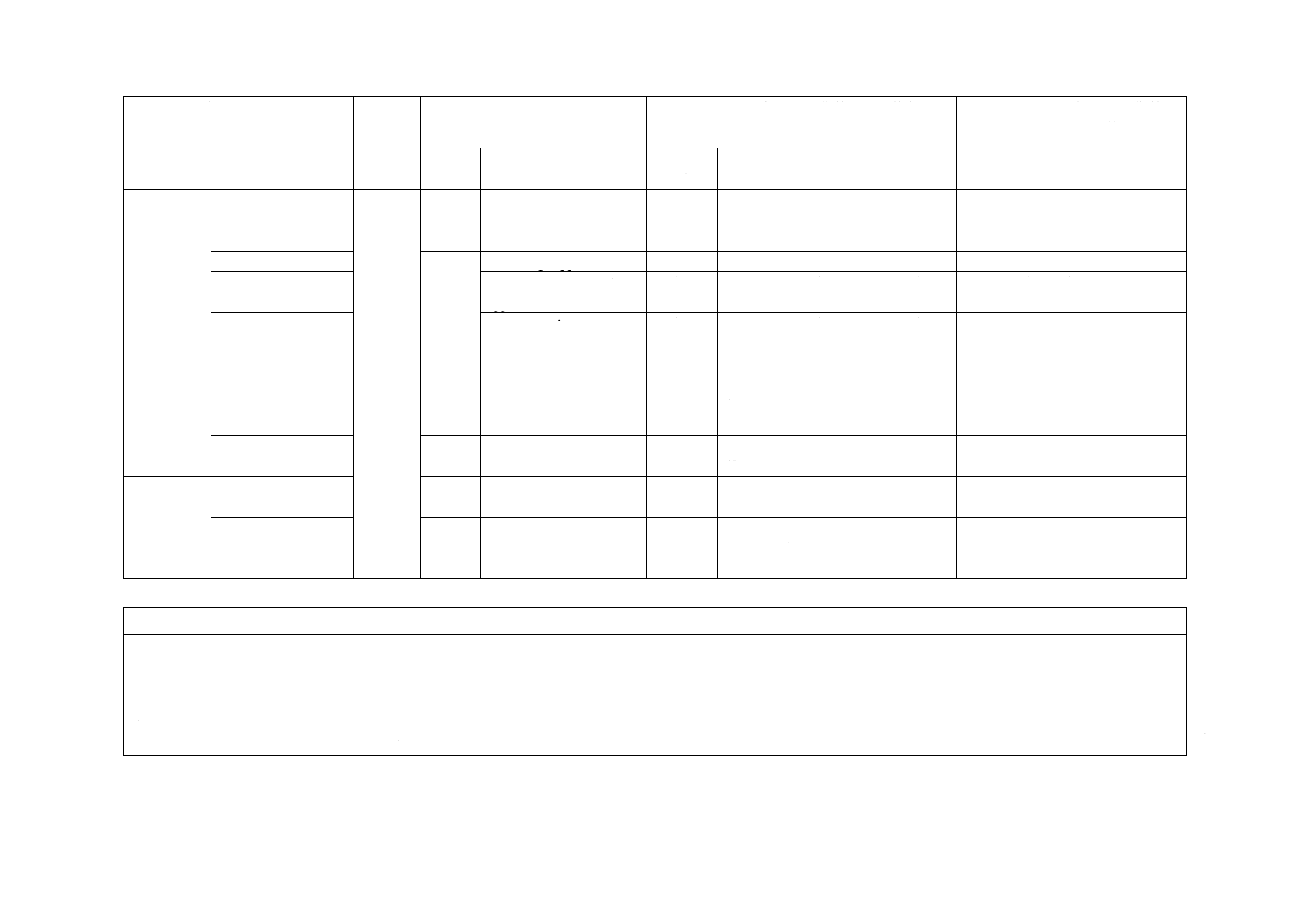
41
C 2139-1:2019
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごと
の評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
3 用語及び
定義(続き)
3.4 測定回路及び測
定装置に関する用
語及び定義
−
−
追加
3.4.1〜3.4.13の細分箇条を追加。
IECに追加を提案の予定。
−
3
3.5 voltage application
削除
用語として不適切と判断し削除。
IECに削除を提案の予定。
−
3.6 current after voltage
application
削除
用語として不適切と判断し削除。
IECに削除を提案の予定。
−
3.15 measuring electrodes 削除
用語として不適切と判断し削除。
IECに削除を提案の予定。
4 電気絶縁
材料の性質
に影響を及
ぼす因子
4.2.8 状態調節
4.2.8
JISとほぼ同じ
変更
JISでは電気固体絶縁物に関する状
態調節の規定はJIS C 2142に従う。
引用規格をISO 291及びISO 558か
らJIS C 2142(対応国際規格IEC
60212)に変更。
IECに修正提案を予定。
4.2.10 電極材料
4.2.10
Electrode material
変更
電極に関する記載として5.4.2に記
載。
IECに修正提案を予定。
5 測定方法
及び測定装
置
測定方法及び装置
に関する規定
−
−
追加
抵抗特性及び誘電特性の測定方法
及び装置について追加。
IECに修正提案を予定。
5.4.2 電極及び電極
装置
5
Electrode systems
変更
対応国際規格の箇条5の内容をこ
の細分箇条に記載。記載内容は変更
なく採用。
IECに修正提案を予定。
JISと国際規格との対応の程度の全体評価:IEC 62631-1:2011,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 削除 ················ 国際規格の規定項目又は規定内容を削除している。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
4
1
C
2
1
3
9
-1
:
2
0
1
9