3
B 7072-2:2020
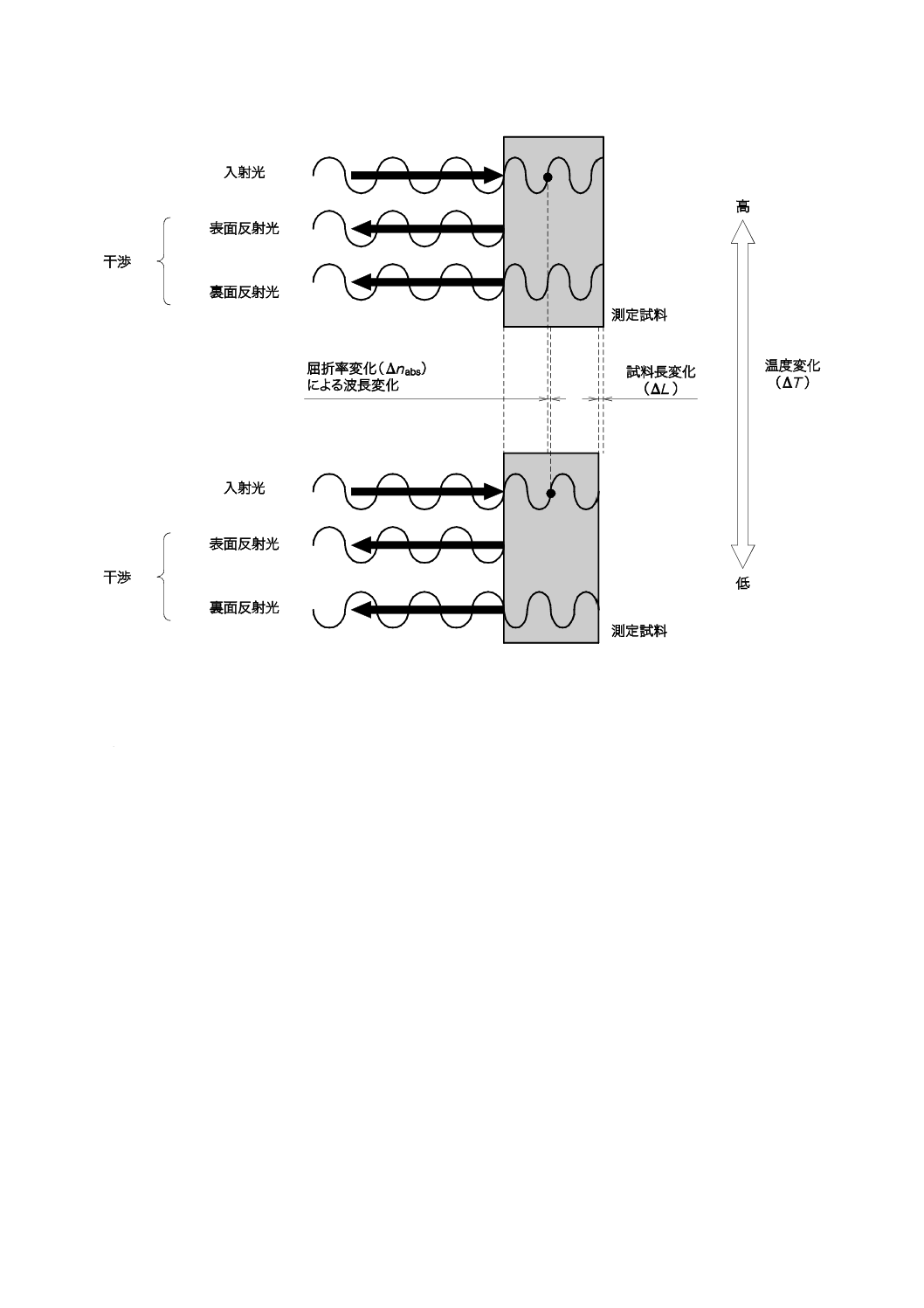
図1−温度変化に伴う測定試料内の光路長変化及び反射光の干渉の概念図
5
測定装置
5.1
一般
測定装置は,干渉じま(縞)の明暗変化の周期数の読取りが1/10周期以下の分解能で,測定試料そのも
のが干渉空間を構成するフィゾー干渉式の測定装置を用いる。測定装置の概略図の一例を図2に示す。
B 7072-2:2020
(1)
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 測定原理························································································································· 1
5 測定装置························································································································· 3
5.1 一般 ···························································································································· 3
5.2 光源 ···························································································································· 4
5.3 温度可変容器 ················································································································ 5
5.4 平面板 ························································································································· 5
5.5 検出器 ························································································································· 7
5.6 温度計 ························································································································· 7
5.7 気圧計 ························································································································· 7
6 測定試料························································································································· 7
7 測定手順························································································································· 7
8 計算方法························································································································· 8
8.1 絶対屈折率の温度係数 ···································································································· 8
8.2 測定試料の線膨張係数 ···································································································· 8
8.3 相対屈折率の温度係数 ···································································································· 9
9 屈折率の温度係数の表し方 ································································································ 10
10 測定報告書 ··················································································································· 10
附属書A(規定)屈折率の温度係数を用いた任意の温度における測定試料の絶対屈折率の計算 ··········· 12
附属書B(規定)空気の屈折率の計算式及び空気の屈折率の温度係数の計算式 ································ 15
B 7072-2:2020
(2)
まえがき
この規格は,産業標準化法第12条第1項の規定に基づき,一般社団法人日本光学硝子工業会(JOGMA)
及び一般財団法人日本規格協会(JSA)から,一般社団法人日本光学硝子工業会の団体規格(JOGIS 18)
を基に作成した産業標準原案を添えて日本産業規格を制定すべきとの申出があり,日本産業標準調査会の
審議を経て,経済産業大臣が制定した日本産業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 7072の規格群には,次に示す部編成がある。
JIS B 7072-1 第1部:最小偏角法
JIS B 7072-2 第2部:干渉法
日本産業規格 JIS
B 7072-2:2020
光学ガラスにおける屈折率の温度係数の測定方法−
第2部:干渉法
Measuring method for temperature coefficient of refractive index of optical
glass-Part 2: Interferometry
1
適用範囲
この規格は,干渉法を用いて光学ガラスの温度変化に伴う光路長の変化を干渉じま(縞)の明暗変化の
周期数で読み取り,その光路長の変化から屈折率の温度係数を算出する測定方法について規定する。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 7072-1 光学ガラスにおける屈折率の温度係数の測定方法−第1部:最小偏角法
JIS Z 8120 光学用語
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 7072-1及びJIS Z 8120による。
4
測定原理
測定試料長L及び絶対屈折率nabsである平行平面に研磨された光学ガラス試料表面に,垂直に光源から
の光が入射すると,その表面及び裏面の反射光の干渉作用によって干渉じま(縞)が生じる。この測定試
料に連続的に温度変化を与えたとき,測定試料の測定試料長変化(ΔL)及び屈折率変化(Δnabs)によって,
測定試料内光路往復における光路長の変化(2×Δs)が生じる。この光路長の変化を,干渉じま(縞)の
明暗変化の周期の数[p(以下,周期数という。)]として読み取る。同時に測定試料の温度変化(ΔT)も
読み取り,光路長変化の温度係数を算出する。この光路長変化の温度係数は,屈折率の温度係数起因の光
路長変化の温度係数[(Δnabs/ΔT)×L]と線膨張起因の光路長変化の温度係数[(ΔL/ΔT)×nabs]との和で表さ
れる[式(1)参照]。屈折率の温度係数は,光路長変化の温度係数(Δs/ΔT)と(1/L)の積から,所定温度
範囲の線膨張係数[ΔL/(L×ΔT)]と屈折率との積を減じることによって求められる[式(2)及び式(3)参照]。
abs
abs
n
T
L
L
T
n
T
s
×
∆
∆
+
×
∆
∆
=
∆
∆
···························································· (1)
abs
abs
1
1
n
T
L
L
T
s
L
T
n
×
∆
∆
×
−
∆
∆
×
=
∆
∆
······················································· (2)
また,線膨張係数をαとして,式(3)のように表すことも可能である。
2
B 7072-2:2020
abs
abs
1
n
T
s
L
T
n
×
−
∆
∆
×
=
∆
∆
α
······························································ (3)
干渉法での光路長変化は,フィゾー干渉法の往復光路による係数(1/2),干渉じま(縞)の明暗変化の
周期数(p)及び入射光の波長(λ)を用いて,式(4)によって算出する。
λ
×
×
=
∆
p
s
2
1
············································································ (4)
式(4)を式(3)に代入すると,式(5)となって絶対屈折率の温度係数が得られる。
abs
abs
2
1
n
T
L
p
T
n
×
−
∆
×
×
×
=
∆
∆
α
λ
·························································· (5)
線膨張起因の光路長変化を取り除く項(−α×nabs)の測定試料の屈折率は,式(5)では絶対屈折率(nabs)
であるが,相対屈折率(nrel)を計算に用いてもその差は微小であり,一般の光学ガラスの屈折率の温度係
数で最大6×10−9 K−1程度の差にとどまる。したがって,データ取扱いの簡便性を考慮し,絶対屈折率の
温度係数は,相対屈折率を用いた式(6)を用いて算出してもよい。
rel
abs
2
1
n
T
L
p
T
n
×
−
∆
×
×
×
=
∆
∆
α
λ
··························································· (6)
相対屈折率の温度係数は,ここで求めた絶対屈折率の温度係数によって8.3の式(10)で算出する。そこで
必要な,ΔTの温度幅の上下境界温度における絶対屈折率は,基準温度T0で測定した相対屈折率nrel(T0) を
用いて,附属書Aに示す計算式から算出する。
測定原理の概念図を図1に示す。この図は,測定試料の温度が変化したときに屈折率及び測定試料長の
変化が生じることによって光路長が変化し,測定試料の裏面反射光の位相がずれることが原因で,裏面反
射光と表面反射光との干渉光の強度に変化が生じることを示している。

3
B 7072-2:2020
図1−温度変化に伴う測定試料内の光路長変化及び反射光の干渉の概念図
5
測定装置
5.1
一般
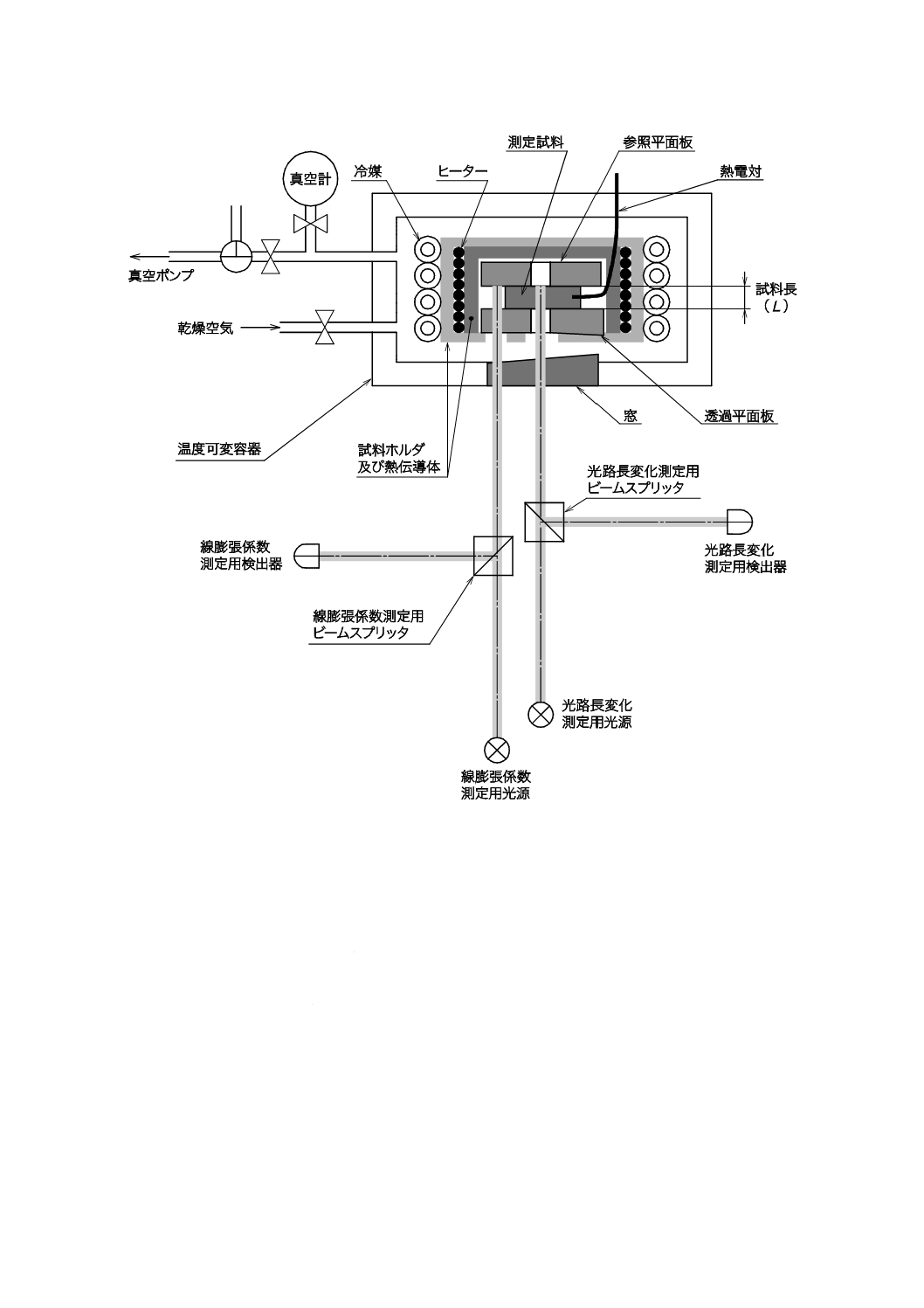
測定装置は,干渉じま(縞)の明暗変化の周期数の読取りが1/10周期以下の分解能で,測定試料そのも
のが干渉空間を構成するフィゾー干渉式の測定装置を用いる。測定装置の概略図の一例を図2に示す。
4
B 7072-2:2020
図2−干渉式測定装置の概略図の一例(フィゾー干渉式)
5.2
光源
光源は,光路長変化測定用及び線膨張係数測定用ともに,算出する波長及び精度で干渉じま(縞)を得
るために十分な光強度,単色性及び可干渉性をもつものを用いる。
光路長変化測定用光源の波長λと線膨張係数測定用光源の波長λαとは,同じである必要はない。
注記 光源の例としては,JIS B 7090[1]の表1(基準波長と可視光線領域及び紫外線領域における推奨
波長),表2(赤外線領域における推奨波長)及び表3(レーザーの推奨波長)がある。
5
B 7072-2:2020
5.3
温度可変容器
温度可変容器は,次による。
a) 測定試料に温度変化を与えながら,測定試料の光路長変化及び測定試料長変化を測定する能力をもつ。
b) 測定試料の温度を−50 ℃〜70 ℃まで変える能力をもつ。
c) 昇降温中の測定試料内の温度分布を1.0 K以内の範囲に保持することができる構造及び温度変化速度
を実現する能力をもつ。
d) 内部は,結露防止の目的のために相対湿度0 %の乾燥空気を満たすか,又は10 Pa以下の真空とする
ことができる。温度可変容器内を乾燥空気で満たす場合は,温度可変容器内の気圧が容器周囲の大気
圧と同じ圧力になるような構造とする。
e) 温度可変容器外殻の窓は対向平面に6分(0.1°)程度のくさび(楔)角を付けて両面を研磨した石英
ガラスを用いる。
注記 石英ガラスを用いるのは,高い透過率をもつ波長範囲が広く,かつ,温度変化に対して高い
耐久性があり,割れにくいためである。
5.4
平面板
平面板は,測定試料の線膨張係数を干渉作用によって光路長変化と同時に測定する目的で,一対で使用
する透過平面板及び参照平面板であり,次による。
a) 透過平面板及び参照平面板は,それぞれに6分(0.1°)程度のくさび(楔)角を付けて両面を研磨し
た石英ガラス,又は極低膨張ガラスセラミックス材を用いる。
b) 干渉作用に用いる面の平面度は,λ/2(線膨張係数測定波長の1/2)以下とする。
c) 透過平面板には,測定試料の光路長変化測定の光路確保のため,中央に孔を設ける。
d) 参照平面板の干渉に関与しない裏面は,研磨せずに擦りガラス面としてもよい。この場合は,参照平
面板のくさび(楔)角は必要ない。
e) 参照平面板の測定試料側平面の光路長測定に用いる光が当たる範囲は,反射を防止する加工を行う。
例として,砂面加工及び該当位置に孔をあけてドーナツ形とする加工がある。
なお,参照平面板の測定試料側平面の光路長測定光が当たる範囲は,干渉作用に用いない。この部
分の反射光は正確な測定を阻害するため,反射を防止する。
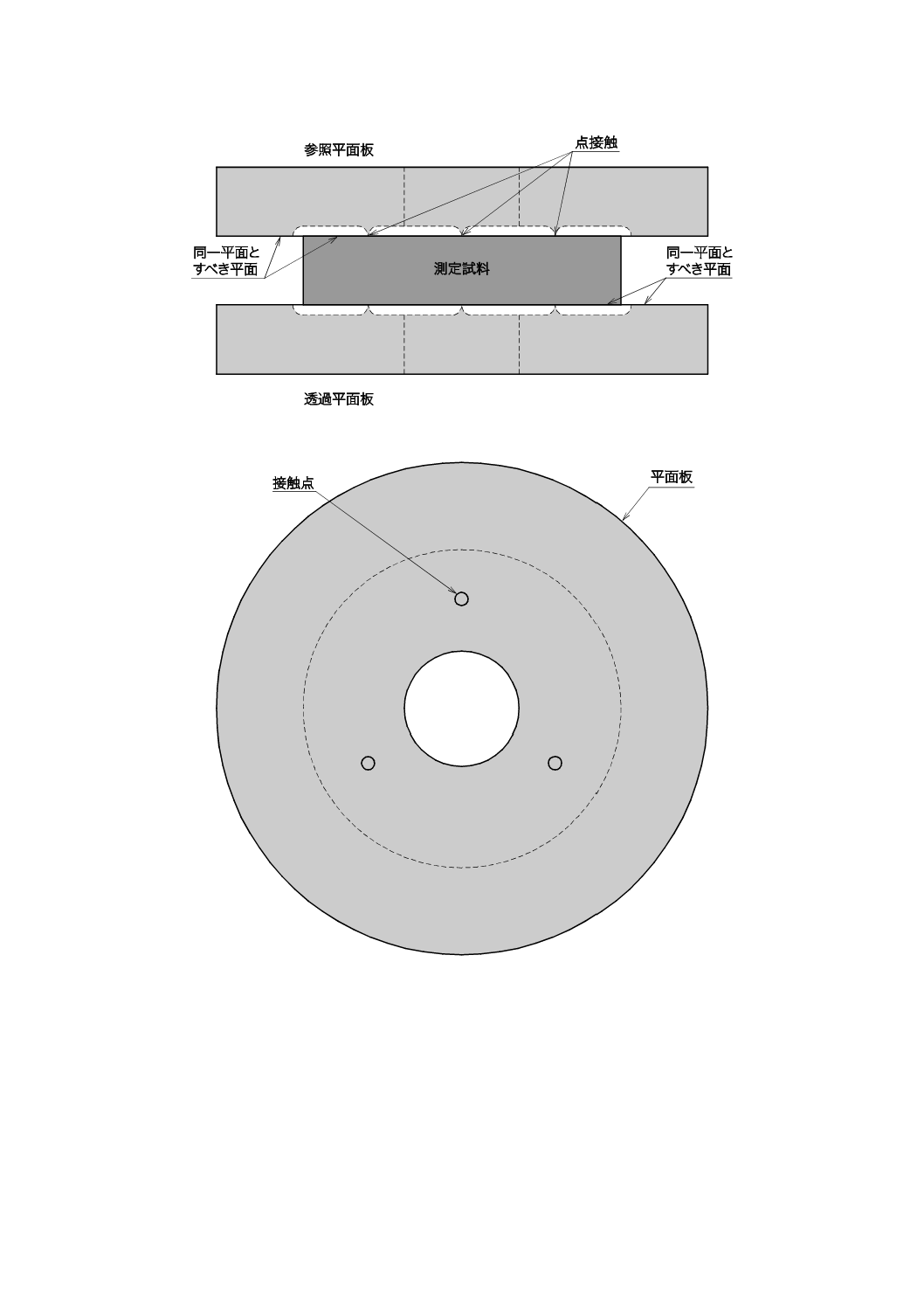
f)
2枚の平面板を,それぞれの干渉に関わる平面が測定試料と同一平面となるように,温度可変容器内
で測定試料を挟むように組み付ける。例として,点接触,線接触,面接触などがある。点接触の例を
図3に示す。
6
B 7072-2:2020
図3−測定試料と2枚の平面板との点接触の例
7
B 7072-2:2020
5.5
検出器
検出器は,測定試料からの反射光の干渉作用による明暗変化及び2枚の平面板からの反射光の干渉作用
による明暗変化を検出できるものを用いる。
5.6
温度計
測定試料の温度を測定するために使用する温度計は,測定精度0.2 K以下とする。
温度可変容器内を乾燥空気で満たした場合,平面板で挟まれた空間の温度を測定するための温度計も必
要となる。これも測定精度0.2 K以下とする。平面板で挟まれた空間の温度と測定試料の温度との間に差
がないことが分かっている場合は,平面板で挟まれた空間の温度は測定試料の温度で代用してもよい。
5.7
気圧計
気圧計は,温度可変容器内の乾燥空気を満たした場合に使用する。測定精度は0.05 kPa以下とする。
6
測定試料
測定試料は,次による。
a) 測定試料は,複屈折による位相差が1 cm当たり5 nm以下になるようにアニールが十分に施されたも
のであって,脈理,泡及び異物のいずれも目視で確認できない材料を用いる。
b) 寸法・形状は,測定する光路長変化量,測定試料内温度分布及び測定光の可干渉性を考慮し,直径20
mm〜25 mm,試料長5 mm前後の平行平板を用いることが望ましい。
c) 対向平面の平行度は10秒(約0.003°)以下とし,平面度はλ/2(測定波長の1/2)以下とする。
d) 基準温度T0における絶対屈折率nabs(T0) 又は相対屈折率nrel(T0) が既知である。T0は23 ℃±2 ℃とする。
注記 例えば,測定試料に近接したガラス材料の部位からプリズムを製作し,JIS B 7071-1[2]に従っ
て基準温度T0における相対屈折率nrel(T0) を測定することができる。
7
測定手順
測定手順は,次による。
a) 測定試料を干渉式測定装置に設置する(図2参照)。
b) 温度可変容器内を相対湿度0 %の乾燥空気で満たすか,又は10 Pa以下の真空とする。
c) 測定試料温度を−50 ℃以下に下げ,そこから測定試料内の温度分布が1.0 K以内になる速度で70 ℃以
上まで昇温しながら,又は測定試料温度を70 ℃以上に上げ,そこから−50 ℃以下まで降温しながら,
いずれか一方向の温度変化における測定試料温度及び干渉じま(縞)の明暗変化の周期数(p)を連続
して記録する。このとき干渉じま(縞)の明暗変化の読取り分解能は10分の1周期以下とする。
d) c) と同時に2枚の平面板間の干渉空間の干渉じま(縞)の明暗変化の周期数(pα)を連続して測定す
る。このとき,干渉じま(縞)の明暗変化の読取り分解能は10分の1周期以下とする。
e) 温度可変容器内を相対湿度0 %の乾燥空気で満たす場合は,d) と同時に平面板で挟まれた空間の乾燥
空気の温度を連続して記録する。
f)
温度可変容器内を相対湿度0 %の乾燥空気で満たす場合は,d) と同時に温度可変容器内の気圧の測定
及び記録を行う。温度可変容器内の気圧と容器周囲の大気圧とが同じになる構造の場合は,大気圧の
測定で代用してもよい。

8
B 7072-2:2020
8
計算方法
8.1
絶対屈折率の温度係数
絶対屈折率の温度係数の計算は,式(5)を用いて式(7)による。ここで,測定試料の温度変化ΔTは20 K
とし,−40 ℃〜−20 ℃,−20 ℃〜0 ℃,0 ℃〜20 ℃,20 ℃〜40 ℃及び40 ℃〜60 ℃の五つの温度領域で
の絶対屈折率の温度係数を算出する。
()
0
abs
6
abs
10
2
1
T
n
T
p
L
T
n
×
−
∆
×
×
×
=
∆
∆
−
α
λ
·············································· (7)
ここに,
T
n
∆
∆abs: 測定試料の絶対屈折率の温度係数(K−1)
2
1: フィゾー干渉法の往復光路による係数
λ: 屈折率の温度係数測定光波長(nm)
L: 測定試料長さ(mm)
p: ΔTに対応する測定試料の光路長変化に伴う干渉じま
(縞)の明暗変化周期数
ΔT: 試料の温度差(K)
nabs(T0): 大気中の温度T0 ℃のときの測定試料の絶対屈折率
T0: 測定試料の屈折率を測定する基準温度。23 ℃±2 ℃
α: 測定試料の線膨張係数(K−1)
10−6: 測定波長と測定試料長さとの桁をそろえるための変換
係数
なお,箇条4で説明したように,絶対屈折率のnabs(T0) の代わりに相対屈折率のnrel(T0) を使用してもよ
い。
8.2
測定試料の線膨張係数
測定試料の線膨張係数の計算は,次による。
a) 温度可変容器内が真空の場合は,式(8)によって算出する。
T
L
p
∆
×
×
×
×
=
−
α
αλ
α
6
10
2
1
································································· (8)
b) 温度可変容器内が相対湿度0 %の乾燥空気で満たされている場合は,式(9)によって算出する。
任意の温度T及び任意の気圧Pにおける空気の屈折率の計算式及び空気の屈折率の温度係数の計算
式は,附属書Bによる。
(
)
()
(
)
P
T
n
T
P
n
P
T
n
T
L
p
,
1
,
10
2
1
air
air
air
6
×
∆
∆
−
×
∆
×
×
×
×
=
−
α
α
αλ
α
································· (9)
ここに,
α: 測定試料の線膨張係数(K−1)
2
1: フィゾー干渉法の往復光路による係数
pα: ΔTαに対応する2枚の平面板に挟まれた干渉空間の干渉
じま(縞)の明暗変化周期数
λα: 線膨張係数測定波長(nm)
L: 測定試料長さ(mm)
ΔTα: 2枚の平面板に挟まれた干渉空間の空気の温度変化量
(K)
nair(T, P): 2枚の平面板に挟まれた干渉空間の空気の温度T及び気
圧Pにおける空気の屈折率
T: 屈折率の温度係数計算温度範囲の中央値(℃)

9
B 7072-2:2020
P: 屈折率の温度係数計算温度範囲の測定中におけ
る温度可変容器内の平均気圧(Pa)
()
T
P
n
∆
∆air
: 屈折率の温度係数計算温度範囲の気圧Pにおける空気の
屈折率の温度係数(K−1)
10−6: 測定波長と測定試料長さとの桁をそろえるための変換
係数
8.3
相対屈折率の温度係数
相対屈折率の温度係数は,8.1で求めた絶対屈折率の温度係数の値を用いて,式(10)によって算出する。
ここで,測定試料の温度変化ΔTは20 Kとし,−40 ℃〜−20 ℃,−20 ℃〜0 ℃,0 ℃〜20 ℃,20 ℃〜40 ℃
及び40 ℃〜60 ℃の五つの温度領域での相対屈折率の温度係数を算出する。空気の屈折率の温度係数は,
スペクトル線の波長ごとに表1による。それ以外の波長の場合は,附属書Bの式(B.1)から算出できる。T1
及びT2における測定試料の絶対屈折率の算出は,附属書Aによる。
()
()
T
n
T
n
T
n
T
n
T
n
∆
∆
×
+
−
∆
∆
=
∆
∆
air
2
abs
1
abs
abs
rel
2
··········································· (10)
ここに,
T
n
∆
∆rel: 測定試料の相対屈折率の温度係数(K−1)
T
n
∆
∆abs: 測定試料の絶対屈折率の温度係数(K−1)
nabs(T1): 温度T1における測定試料の絶対屈折率
nabs(T2): 温度T2における測定試料の絶対屈折率
T1: 該当
∆
∆
T
nrel
の温度幅の低温側境界の温度(℃)
T2: 該当
∆
∆
T
nrel
の温度幅の高温側境界の温度(℃)
T
n
∆
∆air: 空気の屈折率の温度係数(K−1)
10
B 7072-2:2020
表1−空気の屈折率の温度係数(気圧1.013 25×105 Pa,相対湿度0 %)
単位 10−6 K−1
スペクトル線
波長(nm)
温度範囲
−40 ℃〜−20 ℃
−20 ℃〜0 ℃
0 ℃〜20 ℃
20 ℃〜40 ℃
40 ℃〜60 ℃
i
365.01
−1.40
−1.19
−1.03
−0.90
−0.79
h
404.66
−1.38
−1.18
−1.02
−0.89
−0.78
g
435.83
−1.38
−1.17
−1.01
−0.89
−0.78
F'
479.99
−1.37
−1.17
−1.01
−0.88
−0.77
F
486.13
−1.37
−1.17
−1.01
−0.88
−0.77
e
546.07
−1.36
−1.16
−1.00
−0.88
−0.77
d
587.56
−1.36
−1.16
−1.00
−0.87
−0.77
He-Ne
632.8
−1.35
−1.16
−1.00
−0.87
−0.77
C'
643.85
−1.35
−1.16
−1.00
−0.87
−0.77
C
656.27
−1.35
−1.15
−1.00
−0.87
−0.77
r
706.52
−1.35
−1.15
−1.00
−0.87
−0.76
t
1 013.98
−1.34
−1.15
−0.99
−0.86
−0.76
9
屈折率の温度係数の表し方
絶対屈折率の温度係数及び相対屈折率の温度係数の表示は,8.1及び8.3で算出したそれぞれ五つの値を
1×10−8の桁で四捨五入し,10−6 K−1の指数表示とする。例を表2に示す。
表2−屈折率の温度係数の表し方の例
単位 10−6 K−1
スペクトル線
波長(nm)
温度範囲
−40 ℃〜−20 ℃
−20 ℃〜0 ℃
0 ℃〜20 ℃
20 ℃〜40 ℃
40 ℃〜60 ℃
d
587.56
3.8
3.8
3.9
4.0
4.1
10
測定報告書
測定報告書には,次の事項を記載する。
a) 規格番号
b) 測定年月日
c) 測定試料を識別する詳細
d) 光源の種類及びその波長
11
B 7072-2:2020
e) 測定条件
f)
計算によって得られた屈折率の温度係数
なお,記載した温度係数が,絶対屈折率のものか相対屈折率のものかを明記する。

12
B 7072-2:2020
附属書A
(規定)
屈折率の温度係数を用いた任意の温度における
測定試料の絶対屈折率の計算
A.1 屈折率の計算式
任意の温度Tにおける測定試料の絶対屈折率nabs(T) は,測定試料の基準温度(T0)における既知の屈折
率が絶対屈折率nabs(T0) か相対屈折率nrel(T0) かによって,式(A.1)又は式(A.2)から算出する。式(A.2)を用い
る場合,基準温度T0における空気の屈折率nair(T0) は,附属書Bの式(B.1)から算出できる。
()
()
abs
0
abs
abs
n
T
n
T
n
∆
+
=
····························································· (A.1)
()
()
()
abs
0
air
0
rel
abs
n
T
n
T
n
T
n
∆
+
×
=
··················································· (A.2)
ここに,
nabs(T): 温度Tにおける測定試料の絶対屈折率
nabs(T0): 基準温度T0における測定試料の絶対屈折率
nrel(T0): 基準温度T0における測定試料の相対屈折率
nair(T0): 基準温度T0における空気の屈折率
Δnabs: 絶対屈折率の温度係数及び温度変化量から求めた屈折
率変化量
屈折率温度係数は温度範囲によって異なるので,Tの値によって,式(A.3)〜式(A.7)のいずれかを用いて
式(A.1)又は式(A.2)でのΔnabsを算出する。
なお,この規格において基準温度T0は,23 ℃±2 ℃である。
A.2 任意の温度(T)における屈折率変化量計算式
A.2.1 −40 ℃≦T<−20 ℃の場合の計算式
(
)
(
)
20
,
40
abs
0,
20
abs
20
,0
abs
40
,
20
abs
0
abs
20
20
20
20
−
−
−
∆
∆
×
+
+
∆
∆
×
−
∆
∆
×
−
∆
∆
×
−
=
∆
T
n
T
T
n
T
n
T
n
T
n
····························· (A.3)
ここに,
Δnabs: 絶対屈折率の温度係数及び温度変化量から求めた屈
折率変化量
T0: 基準温度(23 ℃±2 ℃)
40
,
20
abs
∆∆T
n
: 20 ℃〜40 ℃での絶対屈折率の温度係数
20
,0
abs
∆∆T
n
: 0 ℃〜20 ℃での絶対屈折率の温度係数
0,
20
abs
−
∆∆T
n
: −20 ℃〜0 ℃での絶対屈折率の温度係数
20
,
40
abs
−
−
∆∆T
n
: −40 ℃〜−20 ℃での絶対屈折率の温度係数
T: 任意温度(℃)
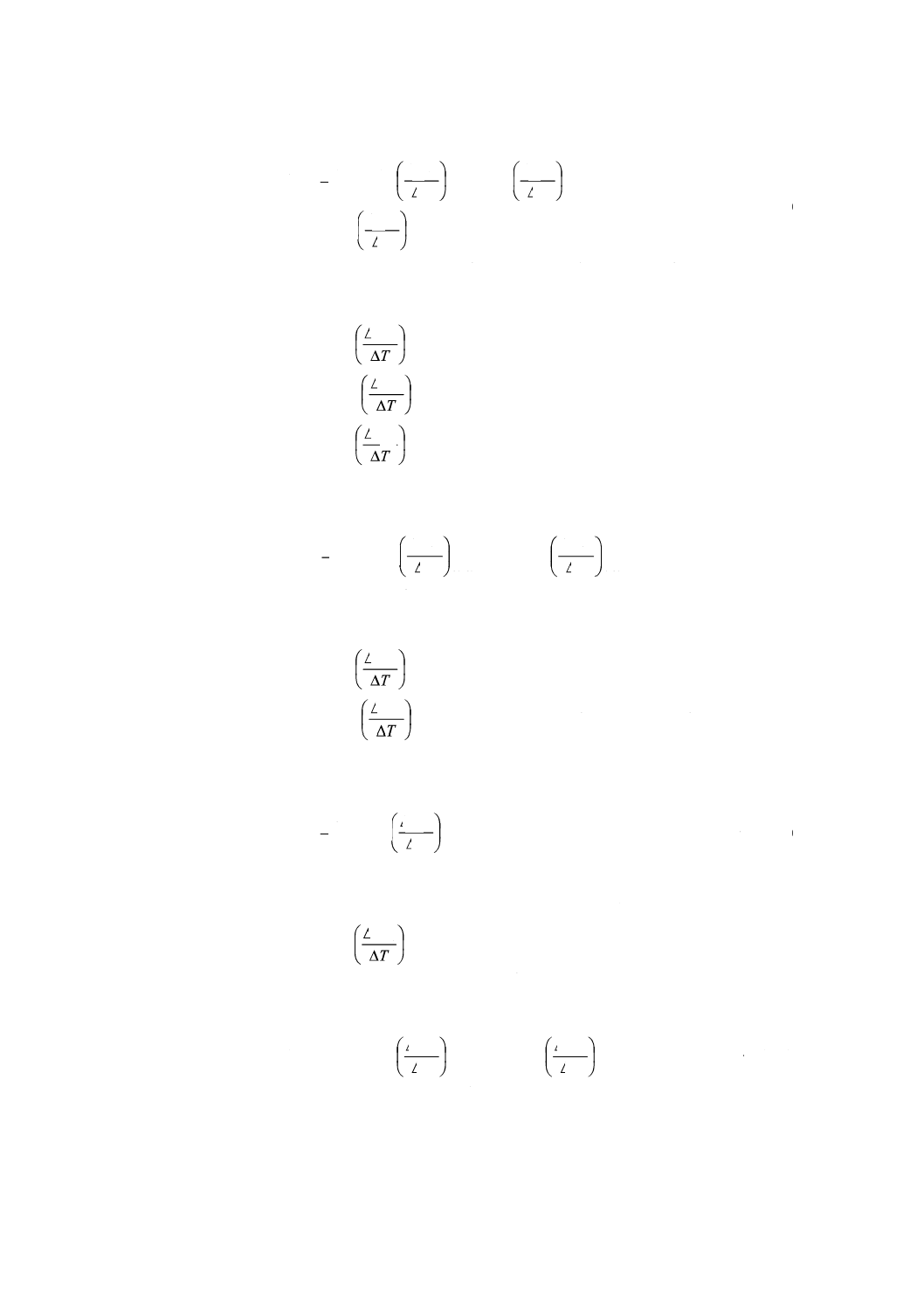
13
B 7072-2:2020
A.2.2 −20 ℃≦T<0 ℃の場合の計算式
(
)
0,
20
abs
20
,0
abs
40
,
20
abs
0
abs
20
20
−
∆
∆
×
+
∆
∆
×
−
∆
∆
×
−
=
∆
T
n
T
T
n
T
n
T
n
································ (A.4)
ここに,
Δnabs: 絶対屈折率の温度係数及び温度変化量から求めた屈
折率変化量
T0: 基準温度(23 ℃±2 ℃)
40
,
20
abs
∆∆T
n
: 20 ℃〜40 ℃での絶対屈折率の温度係数
20
,0
abs
∆∆T
n
: 0 ℃〜20 ℃での絶対屈折率の温度係数
0,
20
abs
−
∆∆T
n
: −20 ℃〜0 ℃での絶対屈折率の温度係数
T: 任意温度(℃)
A.2.3 0 ℃≦T<20 ℃の場合の計算式
(
)
(
)
20
,0
abs
40
,
20
abs
0
abs
20
20
∆
∆
×
−
+
∆
∆
×
−
=
∆
T
n
T
T
n
T
n
························· (A.5)
ここに,
Δnabs: 絶対屈折率の温度係数及び温度変化量から求めた屈
折率変化量
T0: 基準温度(23 ℃±2 ℃)
40
,
20
abs
∆∆T
n
: 20 ℃〜40 ℃での絶対屈折率の温度係数
20
,0
abs
∆∆T
n
: 0 ℃〜20 ℃での絶対屈折率の温度係数
T: 任意温度(℃)
A.2.4 20 ℃≦T<40 ℃の場合の計算式
(
)
40
,
20
abs
0
abs
∆∆
×
−
=
∆
T
n
T
T
n
······················································· (A.6)
ここに,
Δnabs: 絶対屈折率の温度係数及び温度変化量から求めた屈
折率変化量
T0: 基準温度(23 ℃±2 ℃)
40
,
20
abs
∆∆T
n
: 20 ℃〜40 ℃での絶対屈折率の温度係数
T: 任意温度(℃)
A.2.5 40 ℃≦T<60 ℃の場合の計算式
(
)
(
)
60
,
40
abs
40
,
20
abs
0
abs
40
40
∆∆
×
−
+
∆∆
×
−
=
∆
T
n
T
T
n
T
n
························· (A.7)
ここに,
Δnabs: 絶対屈折率の温度係数及び温度変化量から求めた屈
折率変化量
T0: 基準温度(23 ℃±2 ℃)
14
B 7072-2:2020
40
,
20
abs
∆∆T
n
: 20 ℃〜40 ℃での絶対屈折率の温度係数
60
,
40
abs
∆∆T
n
: 40 ℃〜60 ℃での絶対屈折率の温度係数
T: 任意温度(℃)
15
B 7072-2:2020
附属書B
(規定)
空気の屈折率の計算式及び空気の屈折率の温度係数の計算式
B.1
屈折率の計算式
空気の屈折率は,参考文献[3]に示されている式を元にした式(B.1)〜式(B.4)[4]から求めることが可能であ
る。この式を用いることで,波長300 nm〜1 700 nm,温度−40 ℃〜100 ℃,気圧10 kPa〜140 kPa及び相
対湿度0 %〜100 %の範囲で空気の屈折率をこの規格で必要な精度で算出することが可能である。
注記1 参考文献[3]に示されている式は,エドレン(Edlén)の式と呼ばれる。
注記2 参考文献[3]に示されている式は,相対湿度に関する項が温度に依存しない形式で書かれてい
る。式(B.1)〜式(B.4)は,広い温度範囲で計算精度が向上するように,参考文献[3]に示されて
いる式の相対湿度に関する項を修正したものである。
(
)
(
)
V
10
air
1
040
.0
5
734
.3
15
.
273
75
.
292
10
,
P
S
T
P
T
n
n
×
×
−
×
+
×
−
=
−
················ (B.1)
(
)
(
)
D
X
n
P
P
T
n
1
1
,
s−
+
=
····························································· (B.2)
−
+
−
+
+
=
−
S
C
S
B
A
n
9.
38
130
10
1
8
s
············································· (B.3)
(
)
T
G
P
T
F
E
X
×
+
×
−
+
=
−
1
10
1
8
···························································· (B.4)
ここに,
nair: 温度T,気圧P及び相対湿度(PV/PSV)%の空気の屈折
率
PV: 水蒸気分圧(Pa)
PSV: 温度Tの空気の飽和水蒸気圧(Pa)
n(T, P): 温度T,気圧P及び相対湿度0 %の空気の屈折率
T: 温度(℃)
P: 気圧(Pa)
S: 1/λ2(μm−2)
λ: 真空中の光の波長(μm)
A=8 342.54
B=2 406 147
C=15 998
D=96 095.43
E=0.601
F=0.009 72
G=0.003 661
これらの式に実際の数値を入れて計算した代表的なスペクトル線の空気の屈折率の値を,表B.1に示す。

16
B 7072-2:2020
表B.1−空気の屈折率(気圧1.013 25×105 Pa,相対湿度0 %)
スペクトル線
波長(nm)
温度
−40 ℃
−20 ℃
0 ℃
20 ℃
40 ℃
60 ℃
i
365.01
1.000 352 35
1.000 324 45
1.000 300 63
1.000 280 07
1.000 262 13
1.000 246 34
h
404.66
1.000 349 34
1.000 321 68
1.000 298 07
1.000 277 68
1.000 259 89
1.000 244 24
g
435.83
1.000 347 57
1.000 320 05
1.000 296 55
1.000 276 27
1.000 258 57
1.000 243 00
F'
479.99
1.000 345 66
1.000 318 29
1.000 294 92
1.000 274 75
1.000 257 15
1.000 241 67
F
486.13
1.000 345 44
1.000 318 08
1.000 294 73
1.000 274 57
1.000 256 98
1.000 241 51
e
546.07
1.000 343 66
1.000 316 44
1.000 293 22
1.000 273 16
1.000 255 66
1.000 240 27
d
587.56
1.000 342 74
1.000 315 60
1.000 292 43
1.000 272 43
1.000 254 98
1.000 239 63
He-Ne
632.8
1.000 341 95
1.000 314 87
1.000 291 76
1.000 271 80
1.000 254 39
1.000 239 07
C'
643.85
1.000 341 78
1.000 314 72
1.000 291 61
1.000 271 67
1.000 254 27
1.000 238 95
C
656.27
1.000 341 60
1.000 314 55
1.000 291 46
1.000 271 52
1.000 254 13
1.000 238 83
r
706.52
1.000 340 98
1.000 313 97
1.000 290 93
1.000 271 03
1.000 253 67
1.000 238 39
t
1 013.98
1.000 338 97
1.000 312 13
1.000 289 22
1.000 269 44
1.000 252 18
1.000 236 99
B.2
任意の気圧における空気の屈折率の温度係数の計算式
任意の気圧における空気の屈折率の温度係数は,式(B.1)の計算によって求められた20 K幅ごとの空気
の屈折率の差を式(B.5)によって温度幅20 Kで除して算出する。
()
(
)
(
)
20
,
,
1
air
2
air
air
P
T
n
P
T
n
T
P
n
−
=
∆
∆
·················································· (B.5)
ここに,
()
T
P
n
∆
∆air
: 気圧Pにおける空気の屈折率の温度係数
P: 任意の気圧(Pa)
nair(T1, P): 温度T1,気圧Pにおける空気の屈折率
nair(T2, P): 温度T2,気圧Pにおける空気の屈折率
T1: 該当
()
∆
∆
T
P
nair
の温度幅の低温側境界の温度(℃)
T2: 該当
()
∆
∆
T
P
nair
の温度幅の高温側境界の温度(℃)
17
B 7072-2:2020
参考文献
[1] JIS B 7090 光学及び光学機器−基準波長
[2] JIS B 7071-1 光学ガラスの屈折率測定方法−第1部:最小偏角法
[3] K. P. Birch and M.J. Downs, "Correction to the updated Edlén equation for the refractive index of air",
Metrologia 31, 315-316 (1994).
[4] ENGINEERING METROLOGY TOOLBOX [online]. National Institute of Standards and Technology (NIST),
2004, updated October 2017 [cited 12 February 2019]. Available from World Wide Web:
<https://emtoolbox.nist.gov/Wavelength/Documentation.asp>