B 6327-1985  

(1) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

目次 

ページ 

1. 適用範囲 ························································································································ 1 

1.1 規格の適用 ··················································································································· 1 

1.2 規格の準拠性 ················································································································ 1 

2. 用語の意味 ····················································································································· 1 

3. 言語の規定方法 ··············································································································· 1 

4. 座標系 ··························································································································· 2 

5. 文字，文及びパートプログラム ·························································································· 2 

5.1 英字 ···························································································································· 2 

5.1.1 意味 ·························································································································· 2 

5.1.2 構文 ·························································································································· 2 

5.2 数字 ···························································································································· 2 

5.2.1 意味 ·························································································································· 2 

5.2.2 構文 ·························································································································· 2 

5.3 特殊文字 ······················································································································ 2 

5.3.1 意味 ·························································································································· 2 

5.3.2 構文 ·························································································································· 2 

5.4 文字 ···························································································································· 3 

5.4.1 意味 ·························································································································· 3 

5.4.2 構文 ·························································································································· 3 

5.5 文字列 ························································································································· 3 

5.5.1 意味 ·························································································································· 3 

5.5.2 構文 ·························································································································· 3 

5.6 符号のない数 ················································································································ 3 

5.6.1 意味 ·························································································································· 3 

5.6.2 構文 ·························································································································· 3 

5.7 予約語 ························································································································· 3 

5.7.1 意味 ·························································································································· 3 

5.8 単純名前 ······················································································································ 3 

5.8.1 意味 ·························································································································· 3 

5.8.2 構文 ·························································································································· 3 

5.9 名前 ···························································································································· 3 

5.9.1 意味 ·························································································································· 4 

5.9.2 構文 ·························································································································· 4 

5.10 名札 ··························································································································· 4 

5.10.1 意味 ························································································································· 4 

B 6327-1985 目次 

(2) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

5.10.2 構文 ························································································································· 4 

5.11 文 ······························································································································ 4 

5.11.1 意味 ························································································································· 4 

5.11.2 構文 ························································································································· 4 

5.12 入れ子 ························································································································ 4 

5.12.1 意味 ························································································································· 4 

5.13 パートプログラム ········································································································· 4 

5.13.1 意味 ························································································································· 5 

5.13.2 構文 ························································································································· 5 

6. 算術文 ··························································································································· 5 

6.1 意味と構文 ··················································································································· 5 

6.1.1 意味 ·························································································································· 5 

6.1.2 構文 ·························································································································· 5 

6.2 演算子 ························································································································· 6 

6.2.1 意味 ·························································································································· 6 

6.3 スカラー関数 ················································································································ 6 

6.3.1 代数関数 ···················································································································· 6 

6.3.2 三角関数 ···················································································································· 6 

6.3.3 指数関数 ···················································································································· 7 

6.3.4 ベクトル関数 ·············································································································· 7 

6.3.5 雑関数 ······················································································································· 8 

7. プログラム定義文 ············································································································ 9 

7.1 意味と構文 ··················································································································· 9 

7.1.1 意味 ·························································································································· 9 

7.1.2 構文 ·························································································································· 9 

7.2 同義語宣言文 ················································································································ 9 

7.2.1 意味 ·························································································································· 9 

7.2.2 構文 ························································································································· 10 

7.3 確保宣言文 ·················································································································· 10 

7.3.1 意味 ························································································································· 10 

7.3.2 構文 ························································································································· 10 

7.4 マクロ定義文及びマクロ終了文 ························································································ 10 

7.4.1 意味 ························································································································· 10 

7.4.2 構文 ························································································································· 11 

8. パートプログラムの実行制御 ···························································································· 11 

8.1 パートプログラムの開始と終了 ························································································ 11 

8.1.1 パートプログラム識別文 ······························································································ 11 

8.1.2 パートプログラム終了文 ······························································································ 11 

8.2 プログラム制御文 ········································································································· 12 

8.2.1 意味と構文 ················································································································ 12 

B 6327-1985 目次  

  

(3) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

8.2.2 ポストプロセッサ呼出し文 ··························································································· 12 

8.2.3 ポストプロセッサ呼出し禁止文 ····················································································· 12 

8.2.4 印字文 ······················································································································ 12 

8.2.5 せん孔文 ··················································································································· 13 

8.2.6 読込み文 ··················································································································· 14 

8.2.7 工具経路印字文 ·········································································································· 14 

8.2.8 標題印字文 ················································································································ 14 

8.2.9 繰返し開始文及び繰返し終了文 ····················································································· 15 

8.2.10 無条件飛起し文 ········································································································· 15 

8.2.13 コピー文及びインデックス文 ······················································································· 16 

8.2.14 マクロ実行文 ············································································································ 18 

8.2.15 注釈文 ····················································································································· 18 

9. 図形定義文 ···················································································································· 19 

9.1 意味と構文 ·················································································································· 19 

9.1.1 意味 ························································································································· 19 

9.1.2 構文 ························································································································· 20 

9.2 局所座標系 ·················································································································· 21 

9.2.1 意味と構文 ················································································································ 21 

9.2.2 局所座標系の宣言 ······································································································· 21 

9.2.3 局所座標系の終了 ······································································································· 21 

9.3 Z面の宣言 ··················································································································· 21 

9.3.1 意味と構文 ················································································································ 21 

9.3.2 XY平面からの高さによるZ面の宣言 ············································································· 21 

9.3.3 平面によるZ面の宣言 ································································································· 22 

9.3.4 円柱によるZ面の宣言 ································································································· 22 

9.3.5 球によるZ面の宣言 ···································································································· 23 

9.3.6 円すいによるZ面の宣言 ······························································································ 23 

9.3.7 二次曲面によるZ面の宣言 ··························································································· 24 

9.4 点定義文 ····················································································································· 25 

9.4.1 意味と構文 ················································································································ 25 

9.4.2 座標による点の定義 ···································································································· 26 

9.4.3 2直線の交点による点の定義 ························································································· 26 

9.4.4 直線と円の交点による点の定義 ····················································································· 27 

9.4.6 極座標による点の定義 ································································································· 28 

9.4.7 円とX軸からの角度による点の定義 ··············································································· 29 

9.4.8 パターン内の点の定義 ································································································· 29 

94.8.1 意味 ························································································································ 29 

9.4.9 円の中心による点の定義 ······························································································ 30 

9.4.10 直線と円すい曲線との交点による点の定義 ····································································· 30 

B 6327-1985 目次 

(4) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.4.11 直線とタブシルの交点による点の定義 ··········································································· 31 

9.4.13 指定した点からの増分量による点の定義 ········································································ 32 

9.4.14 指定した点からの距離と角度による点の定義 ·································································· 32 

9.4.15 直線上の指定のX座標又はY座標をもつ点の定義 ··························································· 33 

9.4.16 タブシル上の点からタブシルに沿って指定した距離だけ離れた点の定義 ······························ 33 

9.5 パターン定義文 ············································································································ 34 

9.5.1 意味と構文 ················································································································ 34 

9.5.2 始点，終点及びパターン内の点の総数によるパターンの定義 ··············································· 35 

9.5.3 始点，ベクトル及びパターン内の点の総数によるパターンの定義 ········································· 35 

9.5.4 始点，ベクトル及び間隔の総数とジ増分によるパターンの定義 ············································ 36 

9.5.5 始点，角度及び間隔の総数と増分の組によるパターンの定義 ··············································· 36 

9.5.6 円，始点の角度，終点の角度，向き及び点の総数による円弧パターンの定義 ·························· 37 

9.5.7 円，角度向き及び円周を等分割する点の総数による円弧パターンの定義 ································ 38 

9.5.8 円，角度，向き及び間隔の総数と角度の増分の組による円弧パターンの定義 ·························· 38 

9.5.9 二つのパターンによる格子パターンの定義 ······································································ 39 

9.5.10 パターン，ベクトル及び総数による格子パターンの定義 ··················································· 40 

9.5.11 パターン，ベクトル及び間隔の総数と増分の組による格子パターンの定義 ··························· 41 

9.5.12 二つのパターンによる格子パターンの定義 ····································································· 42 

9.5.13 二つのパターンによるパターンの定義 ··········································································· 43 

9.5.14 点，パターンによるパターンの定義 ·············································································· 44 

9.5.15 直線に対称なパターンの定義 ······················································································· 45 

9.6 直線定義文 ·················································································································· 46 

9.6.1 意味と構文 ················································································································ 46 

9.6.2 2点を通る直線の定義 ·································································································· 47 

9.6.3 座標軸の一つとしての直線の定義 ·················································································· 47 

9.6.4 点を通り直線に平行な直線の定義 ·················································································· 47 

9.6.5 点を通り直線に垂直な直線の定義 ·················································································· 48 

9.6.6 直線に平行でその直線と指定した距離をもつ直線の定義 ····················································· 48 

9.6.7 点を通り直線とある角度をなす直線の定義 ······································································ 49 

9.6.8 点を通り直線とあるこう配をもつ直線の定義···································································· 49 

9.6.9 X軸からの角度と切片による直線の定義·········································································· 50 

9.6.10 X軸に関するこう配と切片による直線の定義 ·································································· 50 

9.6.11 点を通り円に接する直線の定義 ···················································································· 51 

9.6.122 円に接する直線の定義 ······························································································ 51 

9.6.13 直線とある角度をなし円に接する直線の定義 ·································································· 52 

9.6.15 点を通り円すい曲線に接する直線の定義 ········································································ 53 

9.6.16 円すい曲線上の点とこの点で円すい曲線に垂直な直線の定義 ············································· 53 

9.6.17 点を通り円すい曲線に垂直な直線の定義 ········································································ 54 

9.6.18 点を通りタブシルに接する直線の定義 ··········································································· 54 

9.6.19 点を通りタブシルに垂直な直線の定義 ··········································································· 55 

B 6327-1985 目次  

  

(5) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.7 平面定義文 ·················································································································· 55 

9.7.1 意味と構文 ················································································································ 55 

9.7.2 平面の方程式の係数による平面の定義 ············································································ 56 

9.7.3 3点を通る平面の定義 ·································································································· 56 

9.7.4 点を通り平面に平行な平面の定義 ·················································································· 57 

9.7.5 平面に平行で指定した距離をもつ平面の定義···································································· 57 

9.7.6 点を通りベクトルに垂直な平面の定義 ············································································ 58 

9.7.7 2点を通り平面に垂直な平面の定義 ················································································ 59 

9.7.8 点を通り2平面に垂直な平面の定義 ··············································································· 59 

9.7.9 点を通り円柱に接する平面の定義 ·················································································· 60 

9.8 ベクトル定義文 ············································································································ 61 

9.8.1 意味と構文 ················································································································ 61 

9.8.2 成分によるベクトルの定義 ··························································································· 61 

9.8.3 2点によるベクトルの定義 ···························································································· 62 

9.8.4 平面に垂直な単位ベクトルの定義 ·················································································· 62 

9.8.5 他のベクトルのスカラー倍によるベクトルの定義······························································ 63 

9.8.6 二つのベクトルの外積としてのベクトルの定義································································· 63 

9.8.7 ベクトルの正規化による単位ベクトルの定義···································································· 64 

9.8.8 大きさと角度によるベクトルの定義 ··············································································· 64 

9.8.9 2平面の交線による単位ベクトルの定義 ·········································································· 65 

9.8.10 ベクトルの和又は差としてのベクトルの定義 ·································································· 66 

9.8.11 XY平面で直線とある角度をなす単位ベクトルの定義 ······················································· 66 

9.9 円定義文 ····················································································································· 67 

9.9.1 意味と構文 ················································································································ 67 

9.9.2 中心の座標と半径による円の定義 ·················································································· 68 

9.9.3 中心と半径による円の定義 ··························································································· 69 

9.9.4 中心と接線による円の定義 ··························································································· 69 

9.9.5 中心と円周上の点による円の定義 ·················································································· 70 

9.9.6 円周上の3点による円の定義 ························································································ 70 

9.9.7 中心と接円による円の定義 ··························································································· 71 

9.9.8 二つの接線と半径による円の定義 ·················································································· 72 

9.9.9 接線，円周上の点及び半径による円の定義 ······································································ 72 

9.9.10 二つの接円と半径による円の定義 ················································································· 73 

9.9.11 接線，接円及び半径による円の定義 ·············································································· 73 

99.11.1 意味 ······················································································································ 73 

9.9.12 接線，接するタブシル及び半径による円の定義 ······························································· 74 

9.9.13. 3接線による円の定義 ································································································ 75 

9.9.14 円周上の2点と半径による円の定義 ·············································································· 75 

9.9.15 円周上の点，接円及び半径による円の定義 ····································································· 76 

B 6327-1985 目次 

(6) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.9.16 接線，接する円すい曲線及び半径による円の定義 ···························································· 77 

9.9.17 二つの接するタブシルと半径による円の定義 ·································································· 77 

9.9.18 円，接するタブシル及び半径による円の定義 ·································································· 78 

9.9.19 円周上の点，接するタブシル及び半径による円の定義 ······················································ 79 

9.9.20 中心を通る直線，接するタブシル及び半径による円の定義 ················································ 79 

9.9.21 中心座標，円柱の軸の方向余弦及び半径による円の定義 ··················································· 80 

9.10 円柱定義文 ················································································································· 81 

9.10.1 意味と構文 ··············································································································· 81 

9.10.2 点，ベクトル及び半径による円柱の定義 ········································································ 81 

9.10.3 二つの接平面と半径による円柱の定義 ··········································································· 82 

9.10.4 接平面，接する円柱及び半径による円柱の定義 ······························································· 83 

9.10.5 接する2円柱と半径による円柱の定義 ··········································································· 84 

9.11 球定義文 ···················································································································· 85 

9.11.1 意味と構文 ··············································································································· 85 

9.11.2 中心座標と半径による球の定義 ···················································································· 85 

9.11.3 中心と半径による球の定義 ·························································································· 86 

9.11.4 中心と球面上の点による球の定義 ················································································· 86 

9.11.5 中心と接平面による球の定義 ······················································································· 87 

9.11.6 球面上の4点による球の定義 ······················································································· 87 

9.12 円すい定義文 ·············································································································· 88 

9.12.1 意味と構文 ··············································································································· 88 

9.12.2 頂点，ベクトル及び半頂角による円すいの定義 ······························································· 88 

9.12.3 頂点の座標，ベクトル成分及び半頂角の余弦による円すいの定義 ······································· 89 

9.13 だ円定義文 ················································································································· 89 

9.13.1 意味と構文 ··············································································································· 89 

9.13.2 中心，長軸半径，短軸半径及び角度によるだ円の定義 ······················································ 90 

9.14 双曲線定義文 ·············································································································· 90 

9.14.1 意味と構文 ··············································································································· 90 

9.14.2 中心，交軸半長，共役軸半長及び角度による双曲線の定義 ················································ 90 

9.15 ロフトコニック定義文 ·································································································· 91 

9.15.1 意味と構文 ··············································································································· 91 

9.15.2 5点による円すい曲線の定義 ························································································ 91 

9.15.3 4点とこう配による円すい曲線の定義 ············································································ 92 

9.15.4 3点と二つのこう配による円すい曲線の定義 ··································································· 92 

9.16 ゼネラルコニック定義文 ······························································································· 93 

9.16.1 意味と構文 ··············································································································· 93 

9.16.2 陰関数表現の円すい曲線方程式による円すい曲線の定義 ··················································· 93 

9.16.3 Xの陽関数表現の円すい曲線方程式による円すい曲線の定義 ············································· 94 

9.16.4 Yの陽関数表現の円すい曲線方程式による円すい曲線の定義 ············································· 94 

9.17 二次曲面定義文 ··········································································································· 95 

B 6327-1985 目次  

  

(7) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.17.1 意味と構文 ··············································································································· 95 

9.17.2 二次曲面方程式による二次曲面の定義 ··········································································· 95 

9.18 タブシル定義文 ··········································································································· 98 

9.18.1 意味と構文 ··············································································································· 98 

9.18.2 点列によるタブシルの定義 ·························································································· 99 

9.18.3 極座標点列によるタブシルの定義 ················································································ 100 

9.18.4 点列とベクトルによるタブシルの定義 ·········································································· 101 

9.18.5 指定したタブシルから箏距離にあるタブシルの定義 ························································ 101 

9.19 マトリックス定義文 ···································································································· 102 

9.19.1 意味と構文 ·············································································································· 102 

9.19.212 個の係数によるマトリックスの定義 ·········································································· 103 

9.19.3 平行移動をするマトリックスの定義 ············································································· 103 

9.19.4 回転をするマトリックスの定義 ··················································································· 104 

9.19.5 尺度の変換をするマトリックスの定義 ·········································································· 104 

9.19.6 直線対称又は平面対称を求めるマトリックスの定義 ························································ 105 

9.19.7 座標平面対称を求めるマトリックスの定義 ···································································· 105 

9.19.8 3平面によるマトリックスの定義 ················································································· 106 

9.19.9 1点と2ベクトルによるマトリックスの定義 ·································································· 107 

9.19.10 二つのマトリックスの組合せによるマトリックスの定義 ················································· 107 

9.19.11 逆マトリックスとしてのマトリックスの定義 ································································ 108 

9.20 ルールドサーフェス定義文 ··························································································· 108 

9.20.1 意味と構文 ·············································································································· 108 

9.20.2 2曲面と，3点又は2点と1ベクトルが定める2平面によるルールドサーフェスの定義 ·········· 108 

9.20.3 曲面と，3点又は2点と1ベクトルが定める平面及び点によるルールドサーフェスの定義 ······ 109 

10. 幾何学的実行文 ··········································································································· 110 

10.1 意味と構文 ················································································································ 110 

10.1.1 意味 ······················································································································· 110 

10.1.2 構文 ······················································································································· 110 

10.2 運動文 ······················································································································ 110 

10.2.1 意味と構文 ·············································································································· 110 

10.2.2 工具初期位置設定文 ·································································································· 111 

10.2.3 絶対位置決め文及び多点位置決め文 ············································································· 111 

10.2.4 相対位置決め文 ········································································································ 113 

10.2.5 連続運動始動文 ········································································································ 114 

10.2.6 特殊連続運動始動文 ·································································································· 115 

10.2.7 連続運動中間文と連続運動終了文 ················································································ 116 

10.3 工具経路制御文 ·········································································································· 117 

10.3.1 意味と構文 ·············································································································· 117 

10.3.2 工具とドライブサーフェスの関係文 ············································································· 117 

B 6327-1985 目次 

(8) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

10.3.3 工具とパートサーフェスの関係文 ················································································ 118 

10.3.4 切残し量文 ·············································································································· 119 

10.3.5 許容誤差文 ·············································································································· 119 

10.3.6 工具文 ···················································································································· 120 

10.3.7 パートサーフェス文 ·································································································· 120 

10.4 始動方向制御文 ·········································································································· 121 

10.4.1 意味と構文 ·············································································································· 121 

10.4.2 点による始動方向制御文 ···························································································· 121 

10.4.3 ベクトルによる始動方向制御文 ··················································································· 122 

10.4.4 面のベクトルによる始動方向制御文 ············································································· 122 

10.5 工具経路変換文 ·········································································································· 123 

10.5.1 意味 ······················································································································· 123 

10.5.2 構文 ······················································································································· 124 

10.6 工具経路出力制御文 ···································································································· 124 

10.6.1 意味 ······················································································································· 124 

10.6.2 構文 ······················································································································· 125 

附属書1 連続運動の詳細な意味 ··························································································· 126 

1. 連続運動文の種類 ·········································································································· 126 

2. 連続運動始動文 ············································································································· 126 

2.1 意味 ·························································································································· 126 

2.2 パートサーフェスの指定のある一面始動 ··········································································· 126 

2.3 パートサーフェスの指定がない一面始動 ··········································································· 127 

2.4 パートサーフェスに無関係な一面始動 ·············································································· 127 

2.5 パートサーフェスの指定と始動の向きのある一面始動 ························································· 128 

2.6 パートサーフェスに無関係で始動の向きのある一面始動 ······················································ 128 

2.7 二面始動 ···················································································································· 129 

2.8 指定の向きのある二面始動····························································································· 129 

2.9 三面始動 ···················································································································· 130 

2.10 指定の向きのある三面始動 ··························································································· 130 

3. 連続運動中間文と連線連動終了文 3.1 意味 ······································································· 131 

3.1 意味 TC ····················································································································· 131 

3.2 許容誤差 ···················································································································· 131 

3.3 連動の向き ················································································································· 133 

3.4 チェックサーフェスの省略····························································································· 133 

3.5 多重交差 ···················································································································· 134 

3.6 多重チェックサーフェス································································································ 135 

附属書2 数値制御パートプログラム用言語の 媒体上での記述規則 ············································· 136 

1. 文の記述 ······················································································································ 136 

2. 行の継続 ······················································································································ 136 

3. 文の多重記述 ················································································································ 136 

B 6327-1985 B 6327-1985目次  

  

(9) 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

4. 注釈 ···························································································································· 136 

5. 空白 ···························································································································· 136 

附属書3 数値制御パートプログラム用言語の 一般形の記述規則 ················································ 137 

1. 一般形 ························································································································· 137 

2. 予約語 ························································································································· 137 

3. 規制詞 ························································································································· 137 

4. 変数 ···························································································································· 137 

5. 面規制詞 ······················································································································ 137 

6. 波括弧 ························································································································· 137 

7. 角括弧 ························································································································· 137 

8. 要素の省略 ··················································································································· 137 

9. 繰返し ························································································································· 137 

10. 円記号 ······················································································································· 137 

11. 線号の左辺の省略 ········································································································· 137 

附属書4 数値制御パートプログラム用言語の 構文の記述規則 ··················································· 138 

1. 記法 ···························································································································· 138 

2. 超言語記号 ··················································································································· 138 

3. 超言語変数の名前 ·········································································································· 138 

4. 空白 ···························································································································· 138 

5. 言語記号 ······················································································································ 138 

6. 作成規則 ······················································································································ 138 

7. 構成を省略している超言語変数 ························································································ 138 

附属書5 予約語一覧表 ······································································································· 139 

附属書6 推奨同義語表 ······································································································· 145 

附属書7 推奨する標準形 ···································································································· 146 

1. 標準形 ························································································································· 146 

2. 図形 ···························································································································· 146 

  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

日本工業規格          JIS 

B 6327-1985 

数値制御パートプログラム用言語 

NC Processor Input−Basic Part Program Reference Language 

1. 適用範囲 

1.1 

規格の適用 この規格は，数値制御プロセッサの入力であるパートプログラムを記述するための言

語について規定する。数値制御プロセッサは，パートプログラムを処理して，特定の数値制御装置に依存

しない標準的な形態の工具経路情報や機械の諸機能に対する指令情報などを含むCLDATAを作成し，この

CLDATAから特定の数値制御装置に依存する数値制御用の情報を出力する。 

1.2 

規格の準拠性 パートプログラムが，ここに規定されている言語を用いて書かれ，ここに規定され

ている解釈をもつものであれば，この規格に準拠しているという。数値制御プロセッサは，ここに規定さ

れる解釈を満たす処理を実行してCLDATAを作成するならば，規格に準拠しているという。数値制御プロ

セッサが，この規格にあるすべての言語を処理し得るものであることを，要求してはいない。すなわち，

この規格にある言語の一部を処理し得るものであっても，その数値制御プロセッサは規格に準拠している

という。 

また，ここに規定されている言語の形式及び解釈と矛盾がなければ，形式及び解釈の拡張を含んでいて

も，又はこの規格にない言語を処理するようなものであっても，その数値制御プロセッサは規格に準拠し

ているという。 

引用規格： 

JIS B 0181 数値制御工作機械用語 

JIS B 6310 数値制御工作機械の座標軸と運動の記号 

JIS B 6325 数値制御プロセッサの出力−CLDATA 

JIS B 6326 数値制御プロセッサの出力−2000タイプレコードのマイナ要素 

JIS C 6230 情報処理用語 

対応国際規格： 

ISO/DIS 4342 Numerical control of machines−NC processor input−Basic part program reference 

language 

2. 用語の意味 この規格で用いる主な用語の意味 は，JIS B 0181（数値制御工作機械用語），JIS C 6230

（情報処理用語），JIS B 6325（数値制御プロセッサの出力−CLDATA），JIS B 6326（数値制御プロセッサ

の出力−2000タイプレコードのマイナ要素）及びJIS B 6310（数値制御工作機械の座標軸と運動の記号）

による。 

3. 言語の規定方法 この言語は，言語の意味，パートプログラムに使用する形で記述した一般形（附属

書3参照）及び超言語形式による構文（附属書4参照）を用いて規定する。 

2 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

4. 座標系 この言語で用いる座標系は，次による。 

(1) 座標系は，基準座標系及び局所座標系とする。 

(2) 基準座標系は，工作物に固定された右手直交座標系とする。 

(3) 基準軸は，基準座標系の各座標軸の正の向きとし，それぞれ基準軸X，基準軸Y及び基準軸Zと呼ぶ。 

(4) 局所座標系は，9.2に定義する。 

(5) これら二つの座標系の上で，ここに規定する言語を使用して工作物の形状及び工作物に対する工具の

運動をプログラムする。 

5. 文字，文及びパートプログラム 

5.1 

英字 

5.1.1 

意味 英字は，固有の意味をもたず，予約語，単純名前，文字列，名札などを構成する要素とする。 

5.1.2 

構文 構文は，次による。 

＜英字＞ :: ＝A｜B｜C｜D｜E｜F｜G｜H｜I｜J｜K｜L｜M｜N｜O｜P｜Q｜R｜S｜T｜U｜V｜

W｜X｜Y｜Z 

5.2 

数字 

5.2.1 

意味 数字は，固有の意味をもたず，単純名前，符号のない数，文字列，名札などを構成する要素

とする。 

5.2.2 

構文 構文は，次による。 

＜数字＞ :: ＝0｜1｜2｜3｜4｜5｜6｜7｜8｜9 

5.3 

特殊文字 

5.3.1 

意味 特殊文字は，次のものとする。 

＋ 正符号 

− 負符号 

＊ アステリスク 

／ 斜線 

） 右小括弧 

（ 左小括弧 

． ピリオド 

＝ 等号 

， コンマ 

¥ 

円記号 

$ 

ドル記号 

空白 

ʼ 

アポストロフィ 

： コロン 

； セミコロン 

5.3.2 

構文 構文は，次による。 

＜特殊文字＞ :: ＝＋｜−｜＊｜／｜）｜（｜．｜＝｜，｜¥｜$｜△｜ʼ｜：｜； 

備考 △の記号は，特殊文字の空白を表す。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

5.4 

文字 

5.4.1 

意味 文字は，英字，数字及び特殊文字からなる。 

5.4.2 

構文 構文は，次による。 

＜文字＞ :: ＝＜英字＞｜＜数字＞｜＜特殊文字＞ 

5.5 

文字列 

5.5.1 

意味 文字列は，標題印字文及び注釈文（8.2.8及び8.2.15参照）において標題及び注釈を記述し

た文字の並びとする。 

備考1. アポストロフィʼを文字列の前と後に付け，文字列の区切りに用いる。 

2. 文字列の中の空白は，一つの文字として意味をもつ。 

5.5.2 

構文 構文は，次による。 

＜文字列＞ :: ＝＜文字列の区切り記号＞k0［＜文字＞］＜文字列の区切り記号＞ 

＜文字列の区切り記号＞ :: ＝ʼ 

5.6 

符号のない数 

5.6.1 

意味 符号のない数は，正負の符号をもたない10進の実数とする。小数点が含まれていない数は，

最下位けたの数字の右側に小数点があるとみなす。 

備考 数は内部処理では実数形式とし，整数と実数を区別しない。 

例： 符号のない数の例 

47711 

58. 

3.14 

5.6.2 

構文 構文は，次による。 

＜符号のない数＞ :: ＝k0［＜数字＞］10［. ］｜ 

k0［＜数字＞］．n1［＜数字＞］ 

5.7 

予約語 

5.7.1 

意味 予約語は，メイジャワードとマイナワードとし，それらは固有の意味をもつ語とする。メイ

ジャワードは，文の主要な意味を表す語とする。文の意味がメイジャワードだけでは不十分なときは，メ

イジャワードに斜線／を続け，その後に付加情報としてマイナパートを付加する。マイナワードは，マイ

ナパートの中にあって動作，条件，状態の表示などの意味を表す語とする。予約語は附属書5及びJIS B 6326

の附属書3に示す。予約語は，あらかじめ定義した同義語によって置き換えることができる（7.2及び附

属書6参照）。 

5.8 

単純名前 

5.8.1 

意味 単純名前は，固有の意味 をもたず，規制詞［9.1.1(3)参照］，名札，変数名（6.1.1参照）及

びマクロ名（7.4.1参照）に用いる。 

例： 単純名前の例 

P 

L1 

BOBBY 

5.8.2 

構文 構文は，次による。 

＜単純名前＞ :: ＝＜英字＞50［＜英字＞｜＜数字＞］ 

5.9 

名前 

4 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

5.9.1 

意味 名前は，単純名前又は単純名前に添字を伴ったもので，固有の意味をもたない。添字付き名

前は，規制詞及び変数名に用いる。 

備考 単純名前に添字を伴ったものを添字付き名前という。 

例： 名前の例 

P1 

P2 (5) 

5.9.2 

構文 構文は，次による。 

＜名前＞ :: ＝＜単純名前＞10［（＜算術式＞）］ 

5.10 名札 

5.10.1 意味 名札は，文の前に付け，文の識別のために用いる。名札は，条件付き飛越し文，無条件飛越

し文又は幾何学的飛越し文によって参照される。 

備考 名札は，常に右小括弧又はコロンを伴う名札と組にして用いる（5.11.2参照）。 

例： 名札の例 

TRANTO/A1 

・・・ 

・・・ 

A1) GOTO/P1 

5.10.2 構文 構文は，次による。 

＜名札＞ :: ＝61［＜数字＞］｜＜単純名前＞ 

5.11 文 

5.11.1 意味 文は，一つの完全な命令又は情報単位とする。文は，算術文，プログラム定義文，プログラ

ム制御文，図形定義文，幾何学的実行文及びポストプロセッサ文の6種類とする。文には，名札を付ける

ことができる。 

備考 ポストプロセッサ文は，JIS B 6326による。 

例： 文の例 

A＝ABS (Y) 

FINI 

P1＝POINT/INTOF, L1, L2 

5.11.2 構文 構文は，次による。 

＜文＞ :: ＝10［＜名札＞11 [ ）｜:] ］＜名札のない文＞ 

＜名札のない文＞ :: ＝＜算術文＞｜＜プログラム定義文＞｜＜プログラム制御文＞｜ 

＜図形定義文＞｜＜幾何学的実行文＞｜＜ポストプロセッサ文＞ 

5.12 入れ子 

5.12.1 意味 入れ子は，図形定義文のうち局所座標系の宣言及びZ面の宣言を除いた図形定義文又はそ

の等号の右辺を，左小括弧と右小括弧の間に書いたものとする（9.1.2参照）。入れ子の図形定義文は，そ

れ以降その名前によって引用することができる。 

例： 入れ子の例 

L2＝LINE/ (PT4＝POINT/3, 6), PT1 

L3＝LINE/PT4, (POINT/5, 5) 

5.13 パートプログラム 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

5.13.1 意味 パートプログラムは，パートプログラム識別文で始まり，論理的に順序立った一連の文が続

き，パートプログラム終了文で終わる（8.1参照）。 

5.13.2 構文 構文は，次による。 

＜パートプログラム＞ :: ＝＜パートプログラム識別文＞k0［＜文＞］＜パートプログラム終了文＞ 

6. 算術文 

6.1 

意味と構文 

6.1.1 

意味 算術文は，名前，等号及びそれに続く算術式で構成され，算術式の値を名前に代入する。こ

の名前を変数名と呼ぶ。算術式における算術演算は，加減演算，乗除演算及び指数演算とする。 

(1) 演算子 演算子は，算術式の構成要素間の演算の種類を示す。演算を表す記号は，加法演算子には＋，

減法演算子には−，乗法演算子には＊，除法演算子には／及び指数演算子には＊＊を用いる。 

(2) 演算の優先順位 演算の優先順位は，次による。 

優先順位 

演算子 

1 

（ ） 

2 

＊＊ 

3 

＊，／ 

4 

＋，− 

例えば，A＝2＋3＊4という算術文においては，演算子＊が演算子＋に優先しAの値は14となる 

し，またA＝ (2＋3) ＊4という算術文においては，括弧内にある演算が優先しAの値が20となる。 

(3) 値の代入 等号は，その左辺の名前にその右辺の算術式の値を代入するという意味をもつ。したがっ

て，A＝A＋1は，Aに1を加えた値が新しいAの値となる。 

(4) スカラー関数 算術式に使用される関数は，代数関数，三角関数，指数関数，ベクトル関数及び雑関

数とする。これらをスカラー関数という。 

(5) スカラー量の引用 変数名によって算術文のスカラー量を引用することができる。その変数名は算術

文の等号の左辺の名前である。 

6.1.2 

構文 構文は，次による。 

＜加減演算子＞ :: ＝＋｜− 

＜乗除演算子＞ :: ＝＊｜／ 

＜指数演算子＞ :: ＝＊＊ 

＜一次子＞ :: ＝＜符号のない数＞｜＜名前＞｜＜スカラー関数＞｜（＜算術式＞） 

＜因子＞ :: ＝＜一次子＞10［＜指数演算子＞＜一次子＞］ 

＜項＞ :: ＝10［＜項＞＜乗除演算子＞］＜因子＞ 

＜算術式＞ :: ＝10［＜加減演算子＞］＜項＞｜ 

＜算術式＞＜加減演算子＞＜項＞ 

＜スカラー＞ :: ＝10［＜加減演算子＞］＜一次子＞｜ 

（＜名前＞＝＜算術式＞） 

＜算術文＞ :: ＝＜名前＞＝＜算術式＞ 

＜代数関数＞ :: ＝11 [ABS｜SQRT] （＜算術式＞） 

＜三角関数＞ :: ＝11 [SIN｜COS｜TAN｜ASINI｜ACOS｜ATAN] （＜算術式＞） 

6 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

＜指数関数＞ :: ＝11 [EXP｜LOG] （＜算術式＞） 

＜ベクトル関数＞ :: ＝LNTH（＜ベクトル規制詞＞）｜ 

DOT（＜ベクトル規制詞＞，＜ベクトル規制詞＞） 

＜雑関数＞ :: ＝ANGL（＜円規制詞＞，＜点規制詞＞）｜ 

DIST（＜点規制詞＞，＜点規制詞＞）｜ 

NUM（＜パターン規制詞＞） 

＜スカラー関数＞ :: ＝＜代数関数＞｜＜三角関数＞｜＜指数関数＞｜＜ベクトル関数＞｜＜雑

関数＞ 

6.2 

演算子 

6.2.1 

意味 演算子の意味は，次による。 

(1) 加減演算子 加減演算子は，単項演算子と2項演算子とする。 

(a) 単項演算子 演算子の後には項を置く。 

＋ 次の項の符号を変えない。 

− 次の項の符号を変える。 

(b) 2項演算子 演算子の前には算術式を置き，後には項を置く。 

＋ 算術式に項を加える。 

− 算術式から項を減ずる。 

(2) 乗除演算子 乗除演算子の前には項を置き，後には因子を置く。 

＊ 項に因子を乗ずる。 

／ 項を因子で除する。 

備考1. A＝5 (3＋2) は，A＝5＊ (3＋2) と書かなければならない。 

2. 

4

3

2

1

+

+

=

A

は，A＝ (1＋2＋3) /4と書かなければならない。 

(3) 指数演算子 指数演算子の前には一次子を置き，後にも一次子を置く。 

＊＊ 前の一次子を後の一次子でべき乗する。 

例： 決算子の例 

A＝B＋C 

A＝B＊C 

A＝B＊＊C 

A＝ (B＋C) /D 

A＝ (B−C) ＊D 

6.3 

スカラー関数 

6.3.1 

代数関数 

6.3.1.1 

意味 代数関数は，これに続く括弧で囲まれた算術式に対して実行する処理の種類を表示する。 

ABS 

算術式の絶対値を求める処理 

SQRT 

算術式の非負の平方根を求める処理 

備考 算術式の値は，非負の実数でなければならない。 

例： 代数関数の例 

A＝ABS (−2) 

A＝SQRT (9) 

6.3.2 

三角関数 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

6.3.2.1 

意味 三角関数は，これに続く括弧で囲まれた算術式に対して実行する三角法の処理の種類を表

示する。 

SIN 

算術式の正弦を求める処理 

COS 

算術式の余弦を求める処理 

TAN 

算術式の正接を求める処理 

ASIN 

算術式で与える正弦に対する角度を求める処理 

ACOS 

算術式で与える余弦に対する角度を求める処理 

ATAN 算術式で与える正接に対する角度を求める処理 

備考 正関数SIN，COS及びTANが処理する算術式の値は，度単位の角度とする。逆関数ASIN，ACOS

及びATANが処理する算術式の値は，それぞれ〔−1, 1〕，〔−1, 1〕及び〔−∞，∞〕とし，処

理結果として求められる値は，それぞれ〔−90, 90〕，〔0, 180〕及び〔−90, 90〕の範囲にある度

単位の角度とする。 

例： 三角関数の例 

A＝SIN (30) 

A＝COS (30) 

A＝TAN (45) 

A＝ASIN (0.5) 

A＝ASIN (−0.5) 

A＝ACOS (0.866) 

A＝ACOS (−0.866) 

A＝ATAN (1) 

A＝ATAN (−1) 

6.3.3 

指数関数 

6.3.3.1 

意味 指数関数は，これに続く括弧で囲まれた算術式に対して実行する指数演算の処理の種類を

表示する。 

EXP 

自然対数の底eを算術式でべき乗した値を求める処理 

LOG 

算術式の自然対数を求める処理 

備考 LOGの対象となる算術式の値は，正の実数でなければならない。 

例： 指数関数の例 

A＝EXP (2) 

A＝LOG (2) 

6.3.4 

ベクトル関数 

6.3.4.1 

意味 ベクトル関数は，これに続く括弧で囲まれたベクトルに対して実行するベクトル処理の種

類を表示する。 

LNTH 

括弧で囲まれたベクトルの長さを求める処理 

DOT 

括弧で囲まれた二つのベクトルの内積を求める処理 

8 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

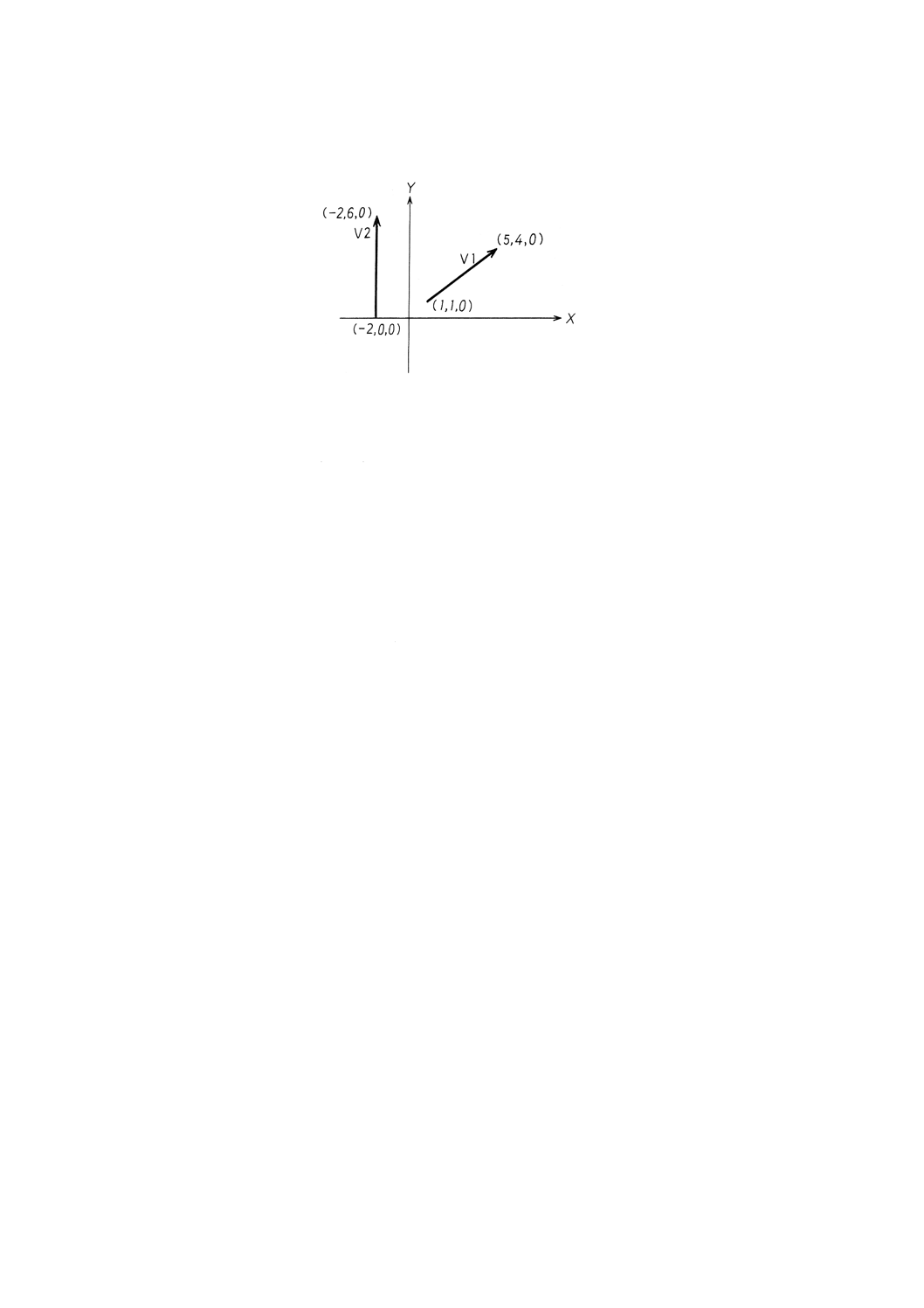
例： ベクトル関数の例 

V1＝VECTOR/1, 1, 0, 5, 4, 0 
V2＝VECTOR/−2, 0, 0, −2, 6, 0 
A1＝LNTH (V1) 
A2＝LNTH (V2) 
A3＝DOT (V1, V2) 

6.3.5 

雑関数 

6.3.5.1 

意味 雑関数は，これに続く括弧で囲まれた円，点又はパターンなどに対して実行する処理の種

類を表示する。 

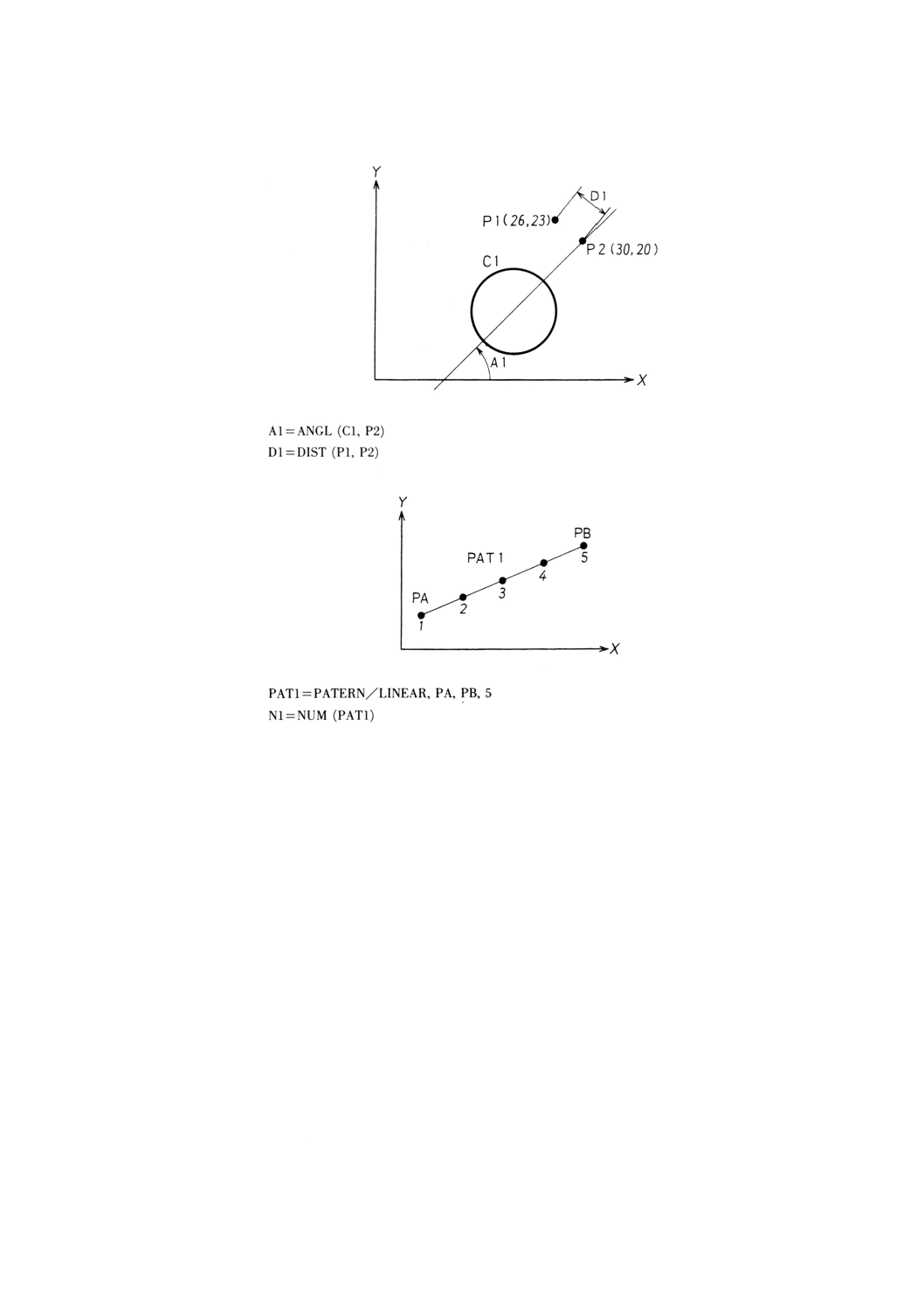
ANGL 正の向きをもつ基準軸Xから反時計回りに指定の点と指定の円の中心とを結ぶ直線に向か

って測った度単位の角度を求める処理 

DIST 

指定の2点間の距離を求める処理 

NUM 

指定のパターンの中の点の個数を求める処理 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 雑関数の例 

7. プログラム定義文 

7.1 

意味と構文 

7.1.1 

意味 プログラム定義文は，予約語の同義語，データの格納領域及び繰返し使用する一連の文をあ

らかじめ定義する。 

7.1.2 

構文 構文は，次による。 

＜プログラム定義文＞ :: ＝＜同義語宣言文＞｜＜確保宣言文＞｜＜マクロ領域＞ 

7.2 

同義語宣言文 

7.2.1 

意味 同義語宣言文は，予約語に対してそれと同一の意味を与える別の名前を同義語として定義す

る。一般形は，次のとおりとする。 

SYN／同義語1，予約語1，同義語2，予約語2，…，同義語n，予約語n 

備考1. 同義語は，単純名前とする。 

2. 同義語1，…，同義語nは，それぞれ予約語1，…，予約語nと同義のものとする。 

3. 予約語は，附属書5及びJIS B 6326の附属書3に示す。 

4. 予約語の中で特定の予約語は，附属書6に示す同義語を推奨する。 

5. 同義語宣言文以降は，同義語は予約語と同じ扱いを受ける。 

6. 一度同義語として宣言した単純名前は，他のいかなる文においても再定義することはできな

10 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

い。 

例： 同義語宣言文の例 

SYN/P, POINT, C, CIRCLE, TT, TANTO, L, LINE 

この宣言によって次の文を書くことができる。 

L1＝L/RIGHT, TT, C1, RIGHT, TT, C2 

この文は，次の文と同じとなる。 

L1＝LINE/RIGHT, TANTO, C1, RIGHT, TANTO, C2 

しかし，同義語として一たん宣言されたPは，次の文のように名前として使用することはできな

い。 

P＝POINT/0, 1, 2 

7.2.2 

構文 構文は，次による。 

＜同義語のパラメータの並び＞ :: ＝＜単純名前＞，＜予約語＞k0［，＜単純名前＞，＜予約語＞］ 

＜同義語宣言文＞ :: ＝SYN／＜同義語のパラメータの並び＞ 

7.3 

確保宣言文 

7.3.1 

意味 確保宣言文は，適当な大きさをもつデータ領域を，名前と添字の最大数によって確保する。

一般形は，次のとおりとする。 

RESERV／単純名前1，最大値1，単純名前2，最大値2，…，単純名前n，最大値n 

備考1. 単純名前1，単純名前2，…，単純名前nは，添字を付けたい名前とする。 

2. 最大値1，最大値2，…，最大値nは，添字の最大数とする。 

3. 確保宣言文は，添字付きの名前を使用する前に指定しなければならない（5.9.1参照）。 

例： 確保宣言文の例 

RESERV/P1, 10, P2, 7, PAT1, 12 

この文により，単純名前P1，P2，PAT1は添字付きの名前となり，添字の最大数はそれぞれ10，

7及び12となる。したがって， 

P1 (8) ＝POINT/INTOF, L1, L2 

は許されるが， 

P2 (8) ＝POINT/INTOF, L1, L2 

は許されない。 

7.3.2 

構文 構文は，次による。 

＜確保のパラメータの並び＞ :: ＝＜単純名前＞，＜符号のない数＞k0［,＜単純名前＞， 

＜符号のない数＞］ 

＜確保宣言文＞ :: ＝RESERV／＜確保のパラメータの並び＞ 

7.4 

マクロ定義文及びマクロ終了文 

7.4.1 

意味 マクロ定義文及びマクロ終了文は，一連の文の集まりをパートプログラム中で複数回使用す

るために，その一連の文の集まりをマクロ領域とすることを指令する。 

一般形は，次のとおりとする。 

(1) マクロ名＝MACRO［／パラメータ1［＝標準値1］，パラメータ2［＝標準値2］，…，¥ 

パラメータn［＝標準値n］］ 

(2) TERMAC 

備考1. マクロ領域の開始は，一般形(1)のMACRO文とする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2. マクロ領域の終了は，一般形(2)のTERMACとする。 

3. マクロ名は，マクロに対して付けられる名前とする。 

4. パラメータ1，パラメータ2，…，パラメータnは，単純名前とする。 

5. 標準値1，標準値2，…，標準値nは，パラメータにあらかじめ与える値とする。 

6. 標準値が与えられていないパラメータは，マクロ実行文でマクロ定義を呼び出すときに実効

値を与える（8.2.14参照）。 

7. マクロ領域内にPARTNO，FINI，繰返し開始文，繰返し終了文及び他のマクロ定義を書いて

はならない。 

例： マクロ定義文及びマクロ終了文の例 

MAC1＝MACRO 

GOTO/P1 

GODLTA/0.5 

TERMAC 

MAC3＝MACRO/A, B＝−15 

GOTO/A 

GODLTA/B 

GODLTA/−B 

TERMAC 

7.4.2 

構文 構文は，次による。 

＜標準マクロ項目＞ :: ＝＜予約語＞｜＜単純名前＞｜＜符号のない数＞｜（＜算術式＞） 

＜マクロ項目の並び＞ :: ＝＜単純名前＞｜ 

＜単純名前＞＝＜標準マクロ項目＞｜ 

＜マクロ項目の並び＞，＜単純名前＞｜ 

＜マクロ項目の並び＞，＜単純名前＞＝＜標準マクロ項目＞ 

＜マクロ定義文＞ :: ＝＜単純名前＞＝MACRO10［／＜マクロ項目の並び＞］ 

＜マクロ終了文＞ :: ＝TERMAC 

＜マクロ領域＞ :: ＝＜マクロ定義文＞k0［＜文＞］＜マクロ終了文＞ 

8. パートプログラムの実行制御 

8.1 

パートプログラムの開始と終了 

8.1.1 

パートプログラム識別文 

8.1.1.1 

意味 パートプログラム識別文は，パートプログラムの識別のための文字列を与え，パートプロ

グラムの始まりを指示する。 

一般形は，次のとおりとする。 

PARTNO／ʼ文字列ʼ 

例： パートプログラム識別文の例 

PARTNO/ʼVALVE HOUSING, DRAWING NO72445ʼ 

8.1.1.2 

構文 構文は，次による。 

＜パートプログラム識別文＞ :: ＝PARTNO／＜文字列＞ 

8.1.2 

パートプログラム終了文 

12 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

8.1.2.1 

意味 パートプログラム終了文は，パートプログラムの終了を指示する。 

一般形は，次のとおりとする。 

FINI 

8.1.2.2 

構文 構文は，次による。 

＜パートプログラム終了文＞ :: ＝FINI 

8.2 

プログラム制御文 

8.2.1 

意味と構文 

8.2.1.1 

意味 プログラム制御文は，データの入出力及びプログラムの流れを制御する。 

8.2.1.2 

構文 構文は，次による。 

＜プログラム制御文＞ :: ＝＜ポストプロセッサ呼出し文＞｜＜ポストプロセッサ呼出し禁止文＞｜ 

＜印字文＞｜＜せん孔文＞｜＜読込み文＞｜＜工具経路印字文＞｜＜標題印字文＞｜ 

＜繰返し開始文＞｜＜繰返し終了文＞｜＜無条件飛越し文＞｜＜条件付き飛越し文＞｜ 

＜幾何学的飛越し文＞｜＜コピー文＞｜＜インデックス文＞｜＜マクロ実行文＞｜ 

＜注釈文＞ 

8.2.2 

ポストプロセッサ呼出し文 

8.2.2.1 

意味 ポストプロセッサ呼出し文は，ポストプロセッサを呼び出す。 

一般形は，次のとおりとする。 

MACHIN／名前［，数］

   

数

予約語

，

，

   

数

予約語

，

n

n

1

1

備考1. 予約語は，附属書5及びJIS B 6326の附属書3に示す。 

2. ポストプロセッサ呼出し禁止文があるときは，ポストプロセッサ呼出し文があっても呼び出

されない。 

3. ポストプロセッサ呼出し文は，必要とするポストプロセッサをパートプログラム中で呼び出

すために幾つでも書ける。 

例： ポストプロセッサ呼出し文の例 

MACHIN/EXPOST, 0 

8.2.2.2 

構文 構文は，次による。 

＜ポストプロセッサ呼出し文＞ :: ＝MACHIN／＜ポストプロセッサのパラメータの並び＞ 

＜ポストプロセッサのパラメータの並び＞ :: ＝＜単純名前＞10［，＜符号のない数＞］ 

k0［，＜予約語＞｜，＜スカラー＞］ 

8.2.3 

ポストプロセッサ呼出し禁止文 

8.2.3.1 

意味 ポストプロセッサ呼出し禁止文は，ポストプロセッサの呼出しを禁止する。たとえポスト

プロセッサ呼出し文が指定されても，呼出しは無視される。 

一般形は，次のとおりとする。 

NOPOST 

8.2.3.2 

構文 構文は，次による。 

＜ポストプロセッサ呼出し禁止文＞ :: ＝NOPOST 

8.2.4 

印字文 

8.2.4.1 

意味 印字文は，図形定義文の図形の標準形［9.1.1(2)参照］及び算術文の変数の値の印字を指令

する。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

一般形は，次のとおりとする。 

(1) PRINT／

OFF

ON

(2) PRINT/

PAGE

0

(3) PRINT/

n

1

NONAME

n

1

2

，名前

，

，名前

，名前

，

，名前

(4) PRINT/

n

1

n

1

3

，名前

，

名前

，名前

，

，名前

(5) PRINT/

ALLALL

3，

備考1. ONは，この文以後，図形定義文の直後にその標準形の印字及び算術文の直後にその変数の

値の印字を開始する。 

2. OFFは，以後の印字を停止する。 

3. 0及びPAGEは，改ページする。 

4. 2，名前1，…，名前n及びNONAME，名前1，…，名前nは，指定された名前の図形の標

準形及び変数の値を名前なしで印字する。 

5. 3，名前1，…，名前n及び名前1，…，名前nは，指定された名前の図形の標準形及び変数

の値を名前付きで印字する。 

6. 3，ALL及びALLは，すべての図形の標準形及び変数の値を名前付きで印字する。 

例： 印字文の例 

PRINT/3, L1, C2, ANGL4, PT2 

8.2.4.2 

構文 構文は，次による。 

＜印字文＞ :: ＝PRINT／＜印字のパラメータの並び＞ 
＜印字のパラメータの並び＞ :: ＝11 [ON｜OFF] ｜ 

11 [0｜PAGE] ｜ 

10 [NONAME｜2｜3]，＜名前＞k0［，＜名前＞］｜ 

10 [3, ] ALL 

8.2.5 

せん孔文 

8.2.5.1 

意味 せん孔文は，図形定義文の図形の標準形及び算術文の変数の値のせん孔を指令する。 

一般形は，次のとおりとする。 

(1) PUNCH/

OFF

ON

(2) PUNCH/

n

1

n

1

1

，名前

，

名前

，名前

，

，名前

(3) PUNCH/

ALLALL

1，

備考1. ONは，この文以後，図形定義文の直後にその標準形のせん孔及び算術文の直後にその変数

の値のせん孔を開始する。 

2. OFFは，以後のせん孔を停止する。 

14 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3. 1，名前1，…，名前n及び名前1，…，名前nは，指定された名前の図形の標準形及び変数

の値をせん孔する。 

4. 1，ALL及びALLは，すべての図形の標準形及び変数の値をせん孔する。 

例： せん孔文の例 

PUNCH/1, A, B, C 

8.2.5.2 

構文 構文は，次による。 

＜せん孔文＞ :: ＝PUNCH／＜せん孔のパラメータの並び＞ 

＜せん孔のパラメータの並び＞ :: ＝11 [ON｜OOF] ｜ 

10 [1, ] ＜名前＞k0［，＜名前＞］｜ 

10 [1, ] ALL 

8.2.6 

読込み文 

8.2.6.1 

意味 読込み文は，せん孔した図形定義文の図形の標準形及び算術文の変数の値の読込みを指令

する。 

一般形は，次のとおりとする。 

(1) READ/

ALL

1

(2) READ/ 1，名前1，…，名前n 

備考1. 1は，読込みを指令する。 

2. ALLは，せん孔したすべての図形の標準形及び変数の値を，名前とともに読み込む。 

3. 1，名前1，…，名前nは，せん孔したすべての図形の標準形及び変数の値に新しい名前を割

り当てて読み込む。 

8.2.6.2 

構文 構文は，次による。 

＜読込み文＞ :: ＝READ／＜読込みのパラメータの並び＞ 

＜読込みのパラメータの並び＞ :: ＝11 [1｜ALL] ｜ 

1，＜名前＞k0［，＜名前＞］ 

8.2.7 

工具経路印字文 

8.2.7.1 

意味 工具経路印字文は，CLDATAの印字を指令する。 

一般形は，次のとおりとする。 

CLPRNT

n

OMIT,

OFF

ON

／

備考1. 省略は，すべてのCLDATAを印字する。 

2. ONは，CLDATAの印字を開始する。 

3. OFFは，CLDATAの印字を停止する。 

4. CLPRNT/OMIT, nは，最初の点，n＋1番目，2n＋1番目，3n＋1番目，…及び最後の点を印

字する。 

8.2.7.2 

構文 構文は，次による。 

＜工具経路印字文＞ :: ＝CLPRNT10［／＜工具経路印字のパラメータの並び＞］ 

＜工具経路印字のパラメータの並び＞ :: ＝11［ON｜OFF｜OMIT，＜スカラー＞］ 

8.2.8 

標題印字文 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

8.2.8.1 

意味 標題印字文は，印字する出力に標題を付けることを指令する。 

一般形は，次のとおりとする。 

TITLES／ʼ文字列ʼ 

この文を実行すると，すぐに文字列を印字する。 

例： 標題印字文の例 

PRINT/PAGE 

TITLES/ʼ…ʼ 

PRINT/3, S1, S2, S3, S4 

8.2.8.2 

構文 構文は，次による。 

＜標題印字文＞ :: ＝TITLES／＜文字列＞ 

8.2.9 

繰返し開始文及び繰返し終了文 

8.2.9.1 意味 繰返し開始文及び繰返し終了文は，一連の文の集まりを繰返し領域とすることを指令する。 

一般形は，次のとおりとする。 

(1) LOOPST 

(2) LOOPND 

繰返し領域の中では，飛越し文によってパートプログラムの実行順序を変更できる。 

例： 繰返し開始文及び繰返し終了文の例 

J＝1 

LOOPST 

A) … 

… 

IF(J−100)B, C, C 

B) J＝J＋1 

JUMPTO/A 

C) LOOPND 

8.2.9.2 

構文 構文は，次による。 

＜繰返し開始文＞ :: ＝LOOPST 

＜繰返し終了文＞ :: ＝LOOPND 

8.2.10 無条件飛起し文 

8.2.10.1 意味 無条件飛越し文は，パートプログラムの逐次的な実行を中断し，指定する名札をもつ文に

制御を移すことを指令する。 

一般形は，次のとおりとする。 

JUMPTO／名札 

16 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 幾何学的飛越し文の例 

8.2.12.2 構文 構文は，次による。 

＜幾何学的飛越し文＞ :: ＝TRANTO／＜名札＞ 

8.2.13 コピー文及びインデックス文 

8.2.13.1 意味 コピー文及びインデックス文は，一連の工具経路に対応する文の集まりをコピー領域とし，

工具経路を指定回数複写することを指令する。 

一般形は，次のとおりとする。 

(1) INDEX/ii [, NOMORE] 

(2) COPY/i, 

マトリックス

角度

MODIFY,

,

ZXROT

YZROT

XYROT

c

b,

a,

TRANSL,

SAME

, n 

コピー領域とする一連の文の先頭には，INDEX/iの文を置き，コピー領域の終わりには，COPY/i, …の

文を置く。工具経路を複写する場合には，工具経路を変換することが可能で，変換はCOPY/i, …に書かれ

た情報によって指定する。工具経路をn回複写する場合は，まず変換前の工具経路を出力し，直前の工具

経路を指定の変換によりn回出力する。したがって，n回目の工具経路の変換は，n−1回目の工具経路に

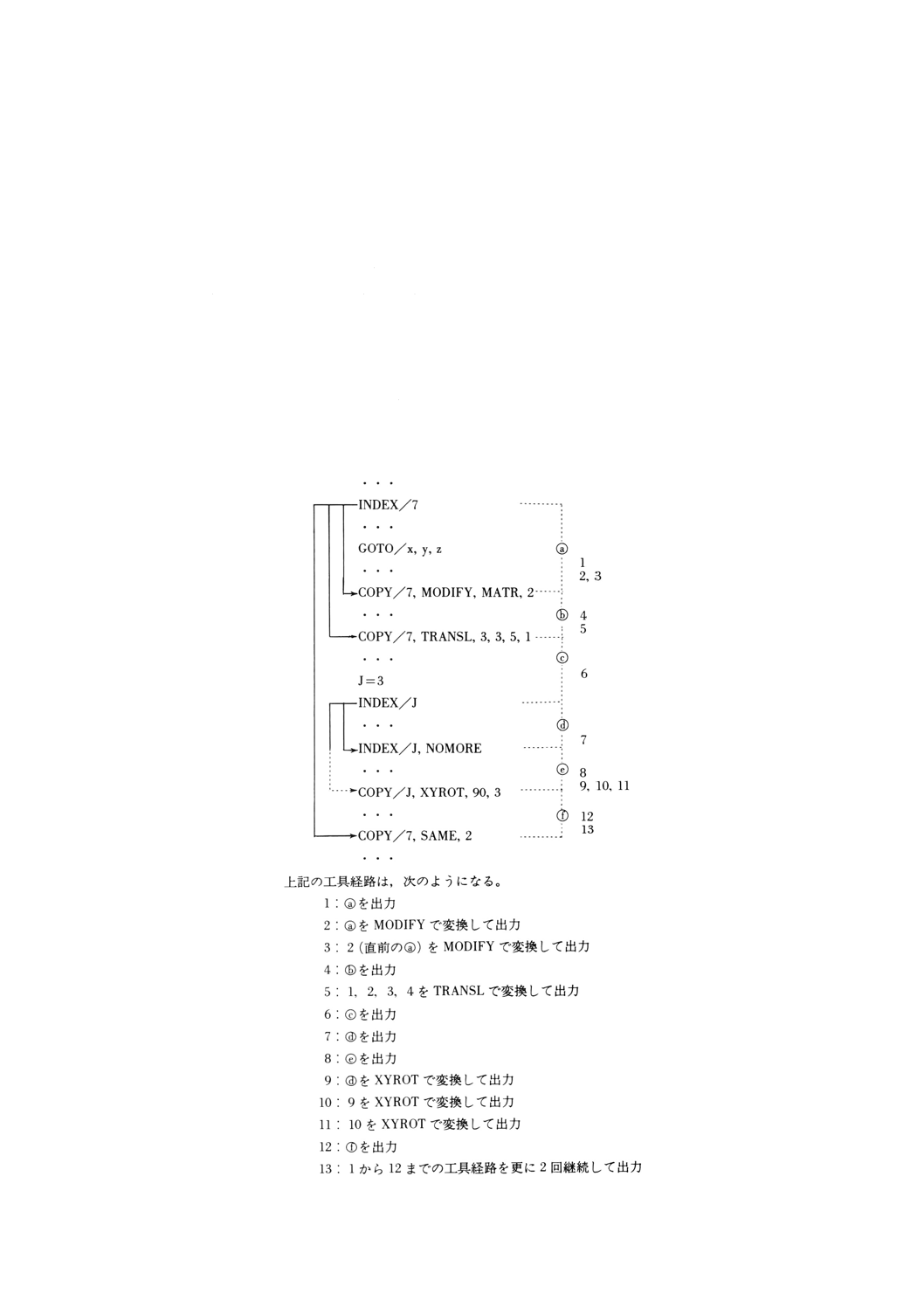
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

対して行う。INDEX/i, NOMOREは，INDEX/iとCOPY/i, …の間に置く。INDEX/iからINDEX/i, NOMORE

の範囲の工具経路だけを変換して出力する。 

備考1. iは，コピー領域を識別するスカラーとする。 

2. nは，複写の回数とする。 

3. SAMEは，変換なしとする。 

4. a，b，cは，それぞれ座標軸X，Y，Zの平行移動の値とする。 

5. 角度は，座標平面上の回転の角度とする［9.1.1(5)参照］。 

6. MODIFY，マトリックスは，座標変換マトリックスとする（9.19参照）。 

7. コピー領域は，工具経路変換文（10.5参照）が指定する範囲内にあってもよく，また工具経

路変換文が指定する範囲内にコピー領域があってもよい。 

8. コピー領域内にコピー領域を含んでもよい。 

9. 複数個のコピー領域がある場合，識別用のスカラーとして同じものは使用できない。 

例： コピー文及びインデックス文の例 

18 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

8.2.13.2 構文 構文は，次による。 

＜インデックス文＞ :: ＝INDEX／＜スカラー＞10 [, NOMORE]  

＜コピー文＞ :: ＝COPY／＜コピーのパラメータの並び＞ 

＜コピーのパラメータの並び＞ :: ＝＜スカラー＞，11［SAME｜TRANSL33［，＜スカラー＞］｜ 

11[XYROT｜YZROT｜ZXROT]，＜スカラー＞｜ 

MODIFY，＜マトリックス規制詞＞］，＜スカラー＞ 

8.2.14 マクロ実行文 

8.2.14.1 意味 マクロ実行文は，パートプログラム中のマクロ定義文の実行を指令する。 

一般形は，次のとおりとする。 

CALL／マクロ名［［，パラメータ1＝実効値1］，…［，パラメータn＝実効値n］］ 

備考1. 実効値が指定された場合はパラメータはそれに置き換わり，実効値が指定されない場合はパ

ラメータはマクロ定義文中の標準値をとる。 

2. マクロ名は，パートプログラム中に定義されたマクロの名前でなければならない。 

3. 一つのマクロ実行文で与えるパラメータの実効値は，その実行においてだけ適用される。 

4. マクロ実行文は，パートプログラムのどこに置いてもよい。繰返し領域内やマクロ領域内に

置いてもよい。 

5. マクロ実行文を別のマクロ領域内に置くとき，マクロ実行文中のパラメータは，マクロ領域

内のパラメータと一致してはならない。 

例： マクロ実行文の例 

… 

MACNAM＝MACRO/A, A, B＝10, PL, H, P 

… 

CALL/POCKET, D＝10, E＝3 

… 

TERMAC 

… 

PL5＝PLANE/… 

… 

CALL/MACNAM, A＝S, PL＝PL5, H＝H5, P＝POINT 

8.2.14.2 構文 構文は，次による。 

＜マクロ実行文＞ :: ＝CALL／＜単純名前＞10［＜仮マクロ項目代入の並び＞］ 

＜仮マクロ項目代入の並び＞ :: ＝k1［，＜仮マクロ項目＞］ 

＜仮マクロ項目＞ :: ＝＜単純名前＞＝＜標準マクロ項目＞ 

8.2.15 注釈文 

8.2.15.1 意味 注釈文は，パートプログラムの印字中に注釈を表示することを指令する。 

一般形は，次のとおりとする。 

REMARK／ʼ文字列ʼ 

例： 注釈文の例 

REMARK/ʼGEOMETRICAL DEFINITIONS FOLLOWʼ 

8.2.15.2 構文 構文は，次による。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

＜注釈文＞ :: ＝REMARK／＜文字列＞ 

9. 図形定義文 

9.1 

意味と構文 

9.1.1 

意味 図形定義文は，工作物の形状などを記述するために必要な図形の定義，ベクトルやマトリッ

クスの定義及び局所座標系の定義を行う。 

図形定義文においては，構文的に正しい文であっても，幾何学的に制限される場合がある。例えば，半

径が負の円を定義することはできないし，また交点をもたない円の交点を定義することもできない。 

(1) 座標系 図形は，基準座標系（4.参照）又は局所座標系（9.2参照）のいずれかの座標系のもとで定義

する。 

(2) 標準形 点，直線などの図形は，数値制御プロセッサの処理を容易にするため，プロセッサの内部で

は，それぞれの図形のデータの表現形式を定めている。この図形のデータの表現形式を標準形と呼ぶ

（附属書7参照）。 

(3) 規制詞 規制詞は，定義する図形を示すための言葉とする。入れ子にされた図形の定義文も含まれる。 

例えば，座標 (2, 5) をもつ点の定義文P1＝POINT/2, 5においては，名前P1が点規制詞である。中

心の座標 (3, 8) で半径rをもつ円の定義文C1＝CIRCLE/CENTER, (POINT/3, 8), RADIUS, rにおいては， 

(POINT/3, 8) が点規制詞であり，名前C1が円規制詞である。 

規制詞は，次の種類に分ける。 

点規制詞 

パターン規制詞 

直線規制詞 

平面規制詞 

ベクトル規制詞 

円規制詞 

円柱規制詞 

球規制詞 

円すい規制詞 

だ円規制詞 

双曲線規制詞 

ロフトコニック規制詞 

ゼネラルコニック規制詞 

二次曲面規制詞 

タブシル規制詞 

マトリックス規制詞 

ルールドサーフェス規制詞 

面規制詞 

円すい曲線規制詞 

図形定義文の一般形の中で述べる点，パターン，直線，平面，ベクトル，円，円柱，球円すい，だ

円，双曲線，ロフトコニック，ゼネラルコニック，二次曲面，タブシル，マトリックス，ルールドサ

ーフェス，面及び円すい曲線は，各々の規制詞のこととする。 

なお，点1，点2，…，点nの例のように数字又は英字を伴う場合も，各々の規制詞を意味する。 

(4) 図形を明示的に定義するための修飾語 修飾語は，図形の定義に候補となる幾つかの図形から一つの

図形を選択するために用いる。修飾語は，次のものとする。 

NEGX 

IN 

XLARGE 

RIGHT 

LARGE 

CLW 

POSX 

OUT 

XSMALL 

LEFT 

SMALL 

CCLW 

NEGY 

YLARGE 

POSY 

YSMALL 

NEGZ 

ZLARGE 

POSZ 

ZSMALL 

ここで， 

(a) NEGX，…，POSZ：各修飾語の最後に指定する座標軸に関してそれぞれ負又は正の向きを示し，ベ

クトルの定義において希望のベクトルの向きを選択するために用いる。 

20 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

(b) IN，OUT：定義する円又は円柱と指定の図形の包含関係を示し，INは内接関係，OUTは外接関係

を示す。円又は円柱の定義において，図形定義文中にあらかじめ指定された図形に対する包含関係

から，希望の円又は円柱を選択するために用いる。 

(c) XLARGE，…，ZSMALL：各修飾語の最初に指定する座標軸に関してそれぞれ座標の大小関係を示

し，図形の定義において希望の図形を選択するために用いる。その用い方を，表9.1.1に示す。例え

ば，XLARGEはX軸に関して座標の大きい側の図形を選択することを指示する。 

表9.1.1 XLARGE，…，ZSMALLの使い方 

図形の種類 

選択の方法 

Z面 

指定の座標軸と二つの候補のZ面との交点の座標の大小による。 

点 

二つの候補点を指定の座標軸上に投影したときの座標の大小による。 

直線 

指定の座標軸と二つの候補の直線との交点の座標の大小による。 

平面 

指定の座標軸と二つの候補の平面との交点の座標の大小による。 

円 

(1) 指定の座標軸に関し指定の図形が分ける二つの候補領域の座標の大小による。 
(2) 指定の座標軸に投影した二つの候補の円の中心の座標の大小による。 

円柱 

(1) 指定の座標軸に関し平面が分ける二つの候補領域の座標の大小による。 
(2) 指定の座標軸に関し二つの候補の円柱の中心軸の座標の大小による。 

(d) RIGHTＣLEFT：はじめに指定した図形から2番目に指定した図形を見て，右又は左のいずれかに

より希望の図形を選択する。 

(e) LARGE，SMALL：候補の円のうちそれぞれ半径の大きい円又は半径の小さい円を選択する。 

(f) CLW，CCLW：それぞれ時計回り又は反時計回りの向きの図形を選択する。 

(5) 角度 角度の単位は度とする。角度は，指定された座標平面上で基準軸から反時計回りの向きに測る。

基準軸は，各座標軸において正の向きをもつ軸とする。座標平面と基準軸の関係を，表9.1.2に示す。

例えば，XYPLAN又はXYROTを用いる場合は，XY平面上で基準軸Xから反時計回りの向きの角度

を正とする。 

表9.1.2 座標平面と基準軸 

座標平面 

基準軸 

座標平面を指定する予約語 

XY 

X 

XYPLAN 

XYROT 

YZ 

Y 

YZPLAN 

YZROT 

ZX 

Z 

ZXPLAN 

ZXROT 

9.1.2 

構文 構文は，次による。 

＜図形定義文＞ :: ＝＜局所座標系の宣言＞｜＜Z面の宣言＞｜＜点定義文＞｜＜パターン定義文

＞｜ 

＜直線定義文＞｜＜平面定義文＞｜＜ベクトル定義文＞｜＜円定義文＞｜＜円柱定義

文＞｜ 

＜球定義文＞｜＜円すい定義文＞｜＜だ円定義文＞｜＜双曲線定義文＞｜ 

＜ロフトコニック定義文＞｜＜ゼネラルコニック定義文＞｜＜二次曲面定義文＞｜ 

＜タブシル定義文＞｜＜マトリックス定義文＞｜＜ルールドサーフェス定義文＞ 

＜面規制詞＞ :: ＝＜直線規制詞＞｜＜平面規制詞＞｜＜円規制詞＞｜＜円柱規制詞＞｜＜球規制

詞＞｜ 

＜円すい規制詞＞｜＜円すい曲線規制詞＞｜＜二次曲面規制詞＞｜＜タブシル規制詞

＞｜ 

＜ルールドサーフェス規制詞＞ 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

＜円すい曲線規制詞＞ :: ＝＜だ円規制詞＞｜＜双曲線規制詞＞｜＜ロフトコニック規制詞＞｜ 

＜ゼネラルコニック規制詞＞ 

9.2 

局所座標系 

9.2.1 

意味と構文 

9.2.1.1 

意味 局所座標系は，基準座標系に関して回転移動や平行移動した座標系とする。パートプログ

ラムにおいて，局所座標系を用いて図形を定義してもよい。局所座標系は，局所座標系の宣言によって示

し，局所座標系の終了までの図形定義に対して効力を及ぼす。局所座標系内の図形は，数値制御プロセッ

サにより処理され，基準座標系における図形に変換される。 

9.2.1.2 

構文 構文は，次による。 

＜局所座標系の宣言＞ :: ＝REFSYS／＜局所座標系のパラメータの並び＞ 

＜局所座標系のパラメータの並び＞ :: ＝＜マトリックス規制詞＞｜NOMORE 

9.2.2 

局所座標系の宣言 

9.2.2.1 

意味 局所座標系の開始を示す。 

一般形は，次のとおりとする。 

REFSYS／マトリックス 

備考 マトリックスは，局所座標系上の図形を基準座標系に変換するためのマトリックスとする。 

9.2.3 

局所座標系の終了 

9.2.3.1 

意味 局所座標系の終了を示す。 

一般形は，次のとおりとする。 

REFSYS/NOMORE 

9.3 

Z面の宣言 

9.3.1 

意味と構文 

9.3.1.1 

意味 Z面を宣言すると，この宣言以後に定義される点及びパターンの中の点が明示的なZ座標

をもたない場合に，それらの点にこの面のZ座標が割り当てられる。Z面の宣言がない場合は，これらの

点のZ座標の値は0とする。 

9.3.1.2 

構文 構文は，次による。 

＜Z面の宣言＞ :: ＝ZSURF／＜Z面のパラメータの並び＞ 

＜Z面のパラメータの並び＞ :: ＝＜スカラー＞｜ 

＜平面規制詞＞｜ 

＜円柱規制詞＞10[, ZLARGE｜, ZSMALL] ｜ 

＜球規制詞＞10[, ZLARGE｜, ZSMALL] ｜ 

＜円すい規制詞＞10[, ZLARGE｜, ZSMALL] ｜ 

＜二次曲面規制詞＞10[, ZLARGE｜, ZSMALL] 

9.3.2 

XY平面からの高さによるZ面の宣言 

9.3.2.1 

意味 XY平面からの高さによりZ面を宣言する。 

一般形は，次のとおりとする。 

ZSURF／高さ 

備考 高さは，XY平面からの高さとする。 

22 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： XY平面からの高さによるZ面の宣言の例 

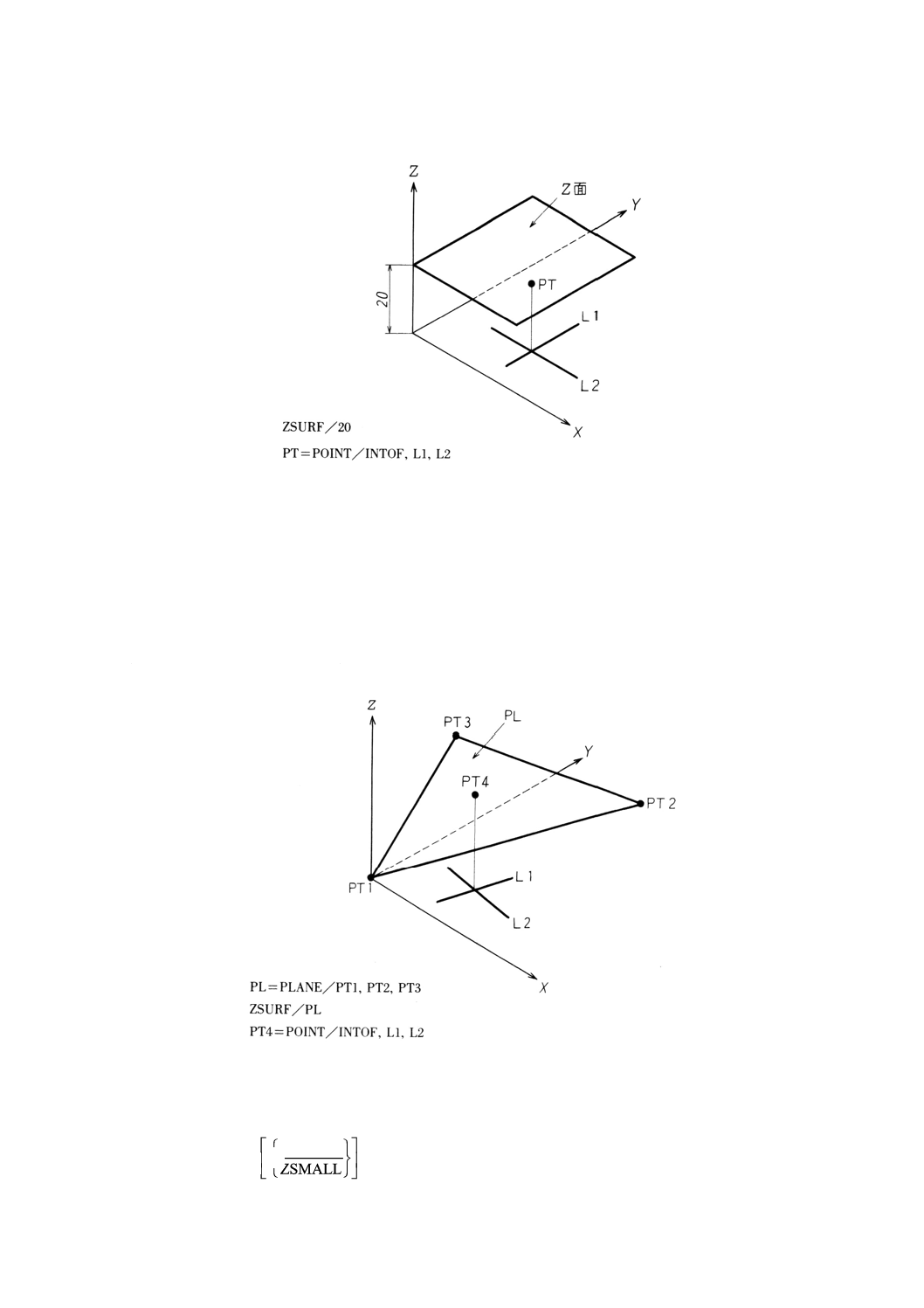
9.3.3 

平面によるZ面の宣言 

9.3.3.1 

意味 平面によりZ面を宣言する。 

一般形は，次のとおりとする。 

ZSURF／平面 

備考1. 平面がXY平面に平行ならば，Z座標はXY平面からの高さとする。もし，平面がXY平面

に平行でないならば，X座標及びY座標によって点のZ座標は変化する。 

2. 平面は，XY平面に垂直であってはならない。 

例： 平面によるZ面の宣言の例 

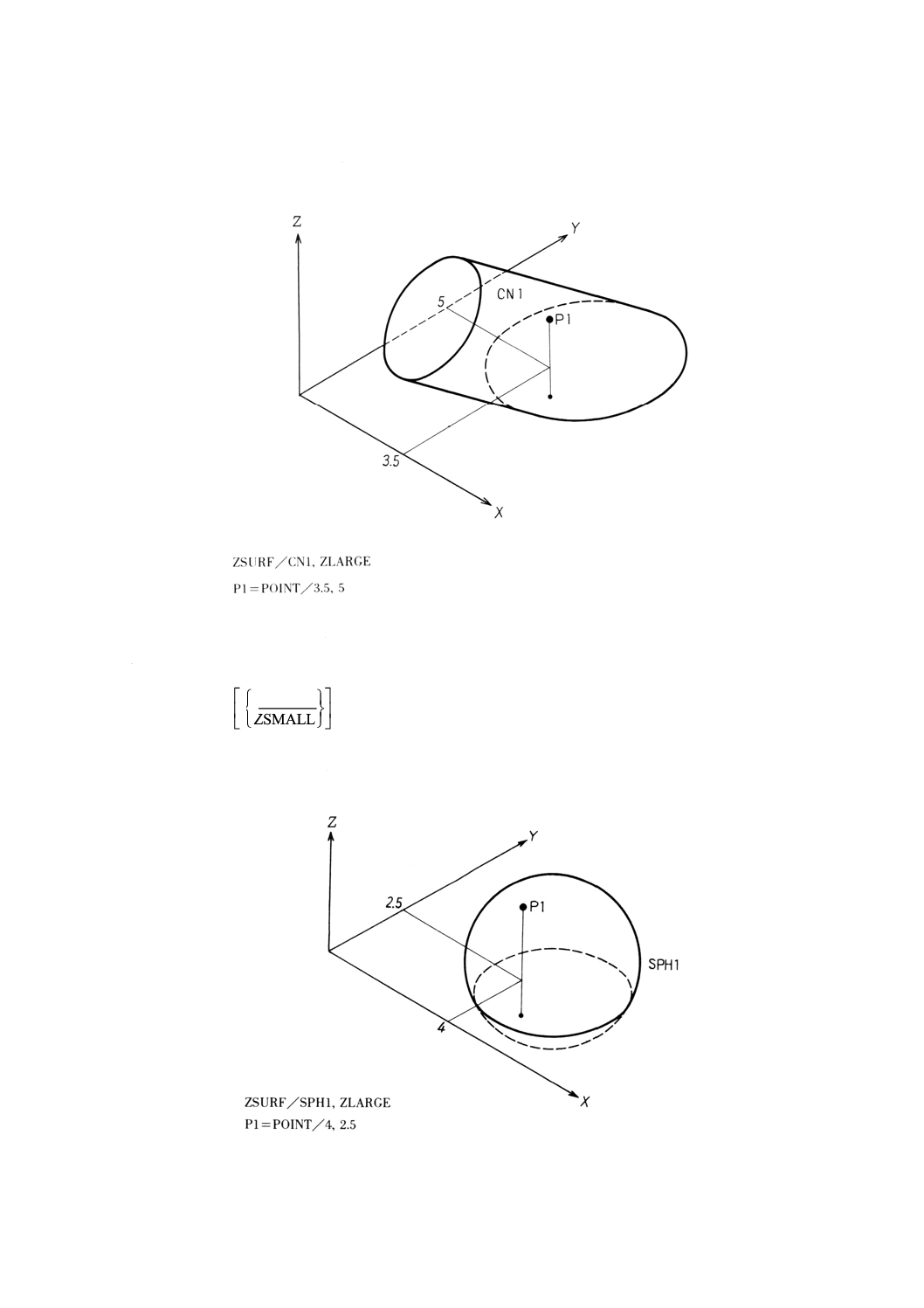
9.3.4 

円柱によるZ面の宣言 

9.3.4.1 

意味 円柱によりZ面を宣言する。 

一般形は，次のとおりとする。 

ZSURF／円柱

ZSMALL

ZLARGE

，

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

備考 このZ面の宣言後，定義する点又はパターンの各点を通りZ軸に平行な直線は，円柱と交わる

か又は接していなければならない。 

例： 円柱によるZ面の宣言の例 

9.3.5 

球によるZ面の宣言 

9.3.5.1 

意味 球によりZ面を宣言する。 

一般形は，次のとおりとする。 

ZSURF／球

ZSMALL

ZLARGE

，

備考 このZ面の宣言後，定義する点又はパターンの各点を通りZ軸に平行な直線は，球と交わるか

又は接していなければならない。 

例： 球によるZ面の宣言の例 

9.3.6 

円すいによるZ面の宣言 

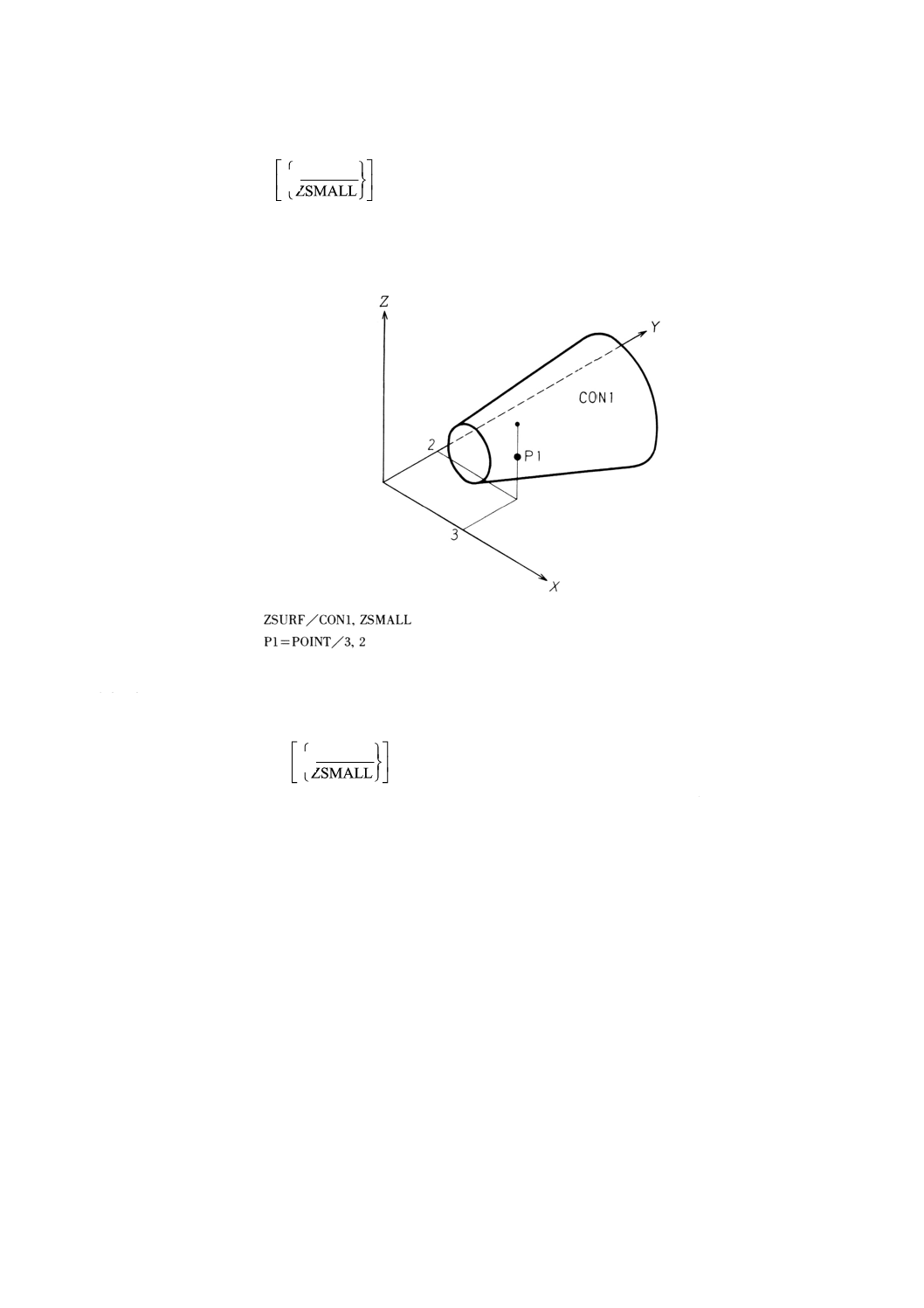
9.3.6.1 

意味 円すいによりZ面を宣言する。 

24 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

一般形は，次のとおりとする。 

ZSURF／円すい

ZSMALL

ZLARGE

，

備考 このZ面の宣言後，定義する点又はパターンの各点を通りZ軸に平行な直線は，円すいと交わ

るか又は接していなければならない。 

例： 円すいによるZ面の宣言の例 

9.3.7 

二次曲面によるZ面の宣言 

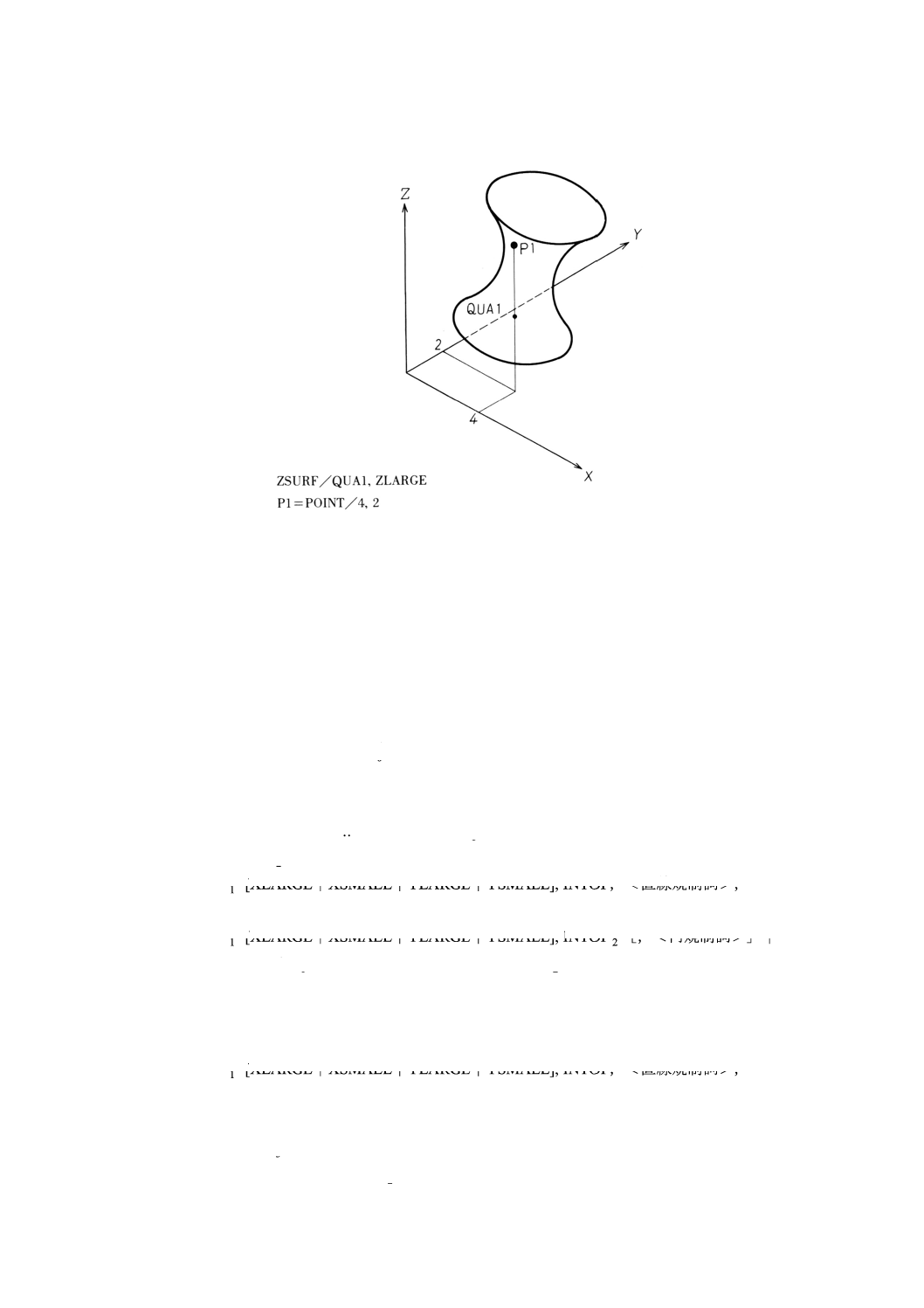
9.3.7.1 

意味 二次曲面によりZ面を宣言する。 

一般形は，次のとおりとする。 

ZSURF／二次曲面

ZSMALL

ZLARGE

，

備考 このZ面の宣言後，定義する点又はパターンの各点を通りZ軸に平行な直線は，二次曲面と交

わるか又は接していなければならない。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 二次曲面によるZ面の宣言の例 

9.4 

点定義文 

9.4.1 

意味と構文 

9.4.1.1 

意味 点定義文は，点を定義する。点は3個の座標をもつ。Z座標が明示されていない点のZ座

標は，Z面が与えられた場合はそのZ面からその座標を求め，Z面が与えられていない場合は0とする（9.3

参照）。3個の座標により点を定義する場合，又は3平面の交点として点を定義する場合は，Z面を無視す

る。 

9.4.1.2 

構文 構文は，次による。 

＜点定義文＞ :: ＝＜名前＞＝POINT／＜点のパラメータの並び＞ 

＜点規制詞＞ :: ＝＜名前＞｜（10［＜名前＞＝］POINT／＜点のパラメータの並び＞） 

＜拡張点規制詞＞ :: ＝＜点規制詞＞｜ 

＜スカラー＞，＜スカラー＞ 

＜点のパラメータの並び＞ :: ＝＜スカラー＞21［，＜スカラー＞］｜ 

INTOF22［，＜直線規制詞＞］｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL], INTOF，＜直線規制詞＞， 

＜円規制詞＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL], INTOF22［，＜円規制詞＞］｜ 

RTHETA, 11 [XYPLAN｜YZPLAN｜ZXPLAN] 22［，＜スカラー＞］｜ 

＜円規制詞＞，ATANGL，＜スカラー＞｜ 

＜パターン規制詞＞，＜スカラー＞｜ 

CENTER，＜円規制詞＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL], INTOF，＜直線規制詞＞， 

＜円すい曲線規制詞＞｜ 

INTOF，＜直線規制詞＞，＜タブシル規制詞＞，＜点規制詞＞｜ 

INTOF33［，＜平面規制詞＞］｜ 

＜点規制詞＞，DELTA22［，＜スカラー＞］｜ 

26 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

＜点規制詞＞，11 [THETAR｜RTHETA] 22［，＜スカラー＞］｜ 

＜直線規制詞＞，11 [XCOORD｜YCOORD]，＜スカラー＞｜ 

＜点規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜タブシル規制詞＞， 

＜スカラー＞ 

9.4.2 

座標による点の定義 

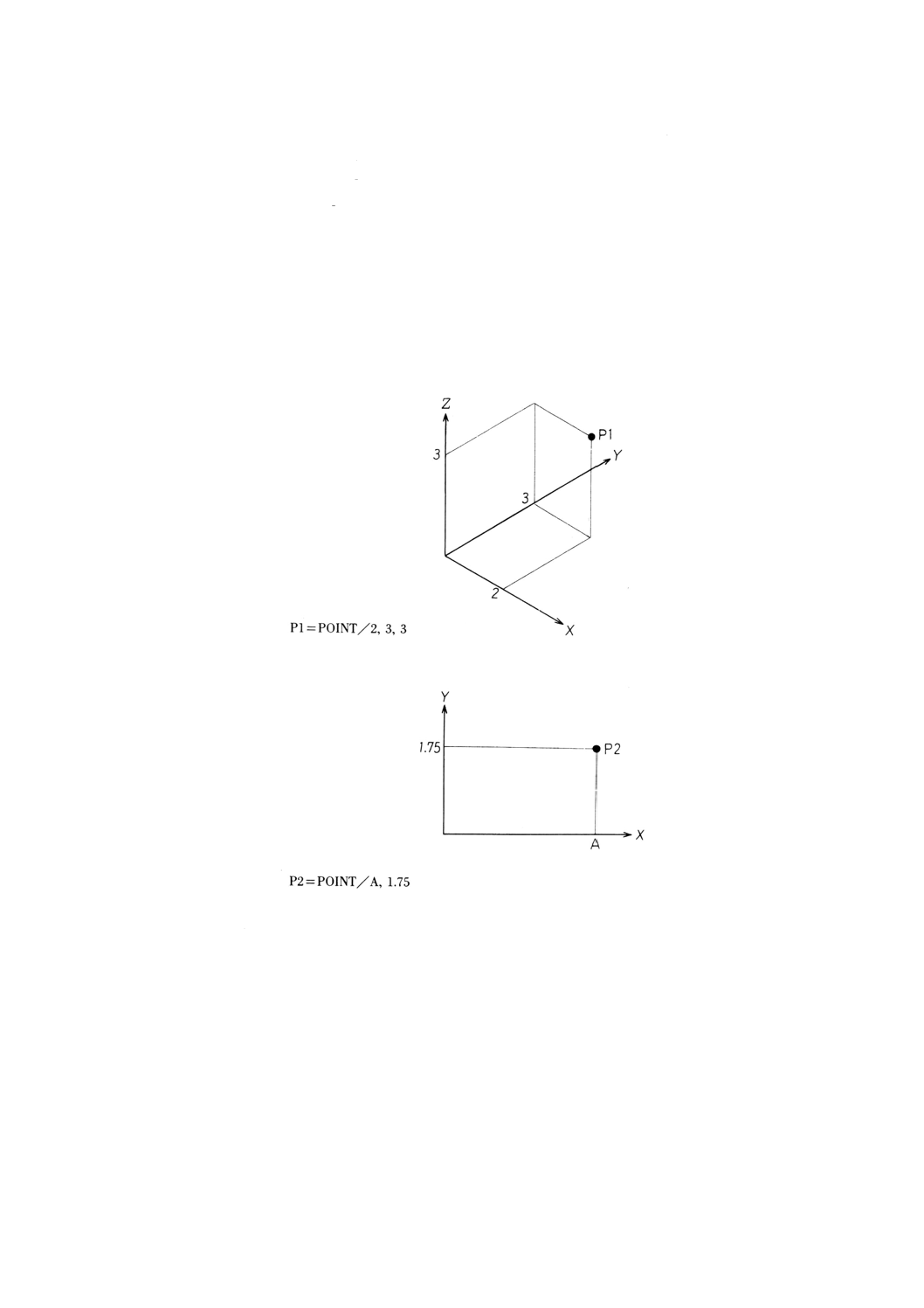
9.4.2.1 

意味 直交座標により点を定義する。 

一般形は，次のとおりとする。 

POINT/x, y [, z] 

備考 (x, y, z) は，点の座標とする。 

例： 座標による点の定義の例 

9.4.3 

2直線の交点による点の定義 

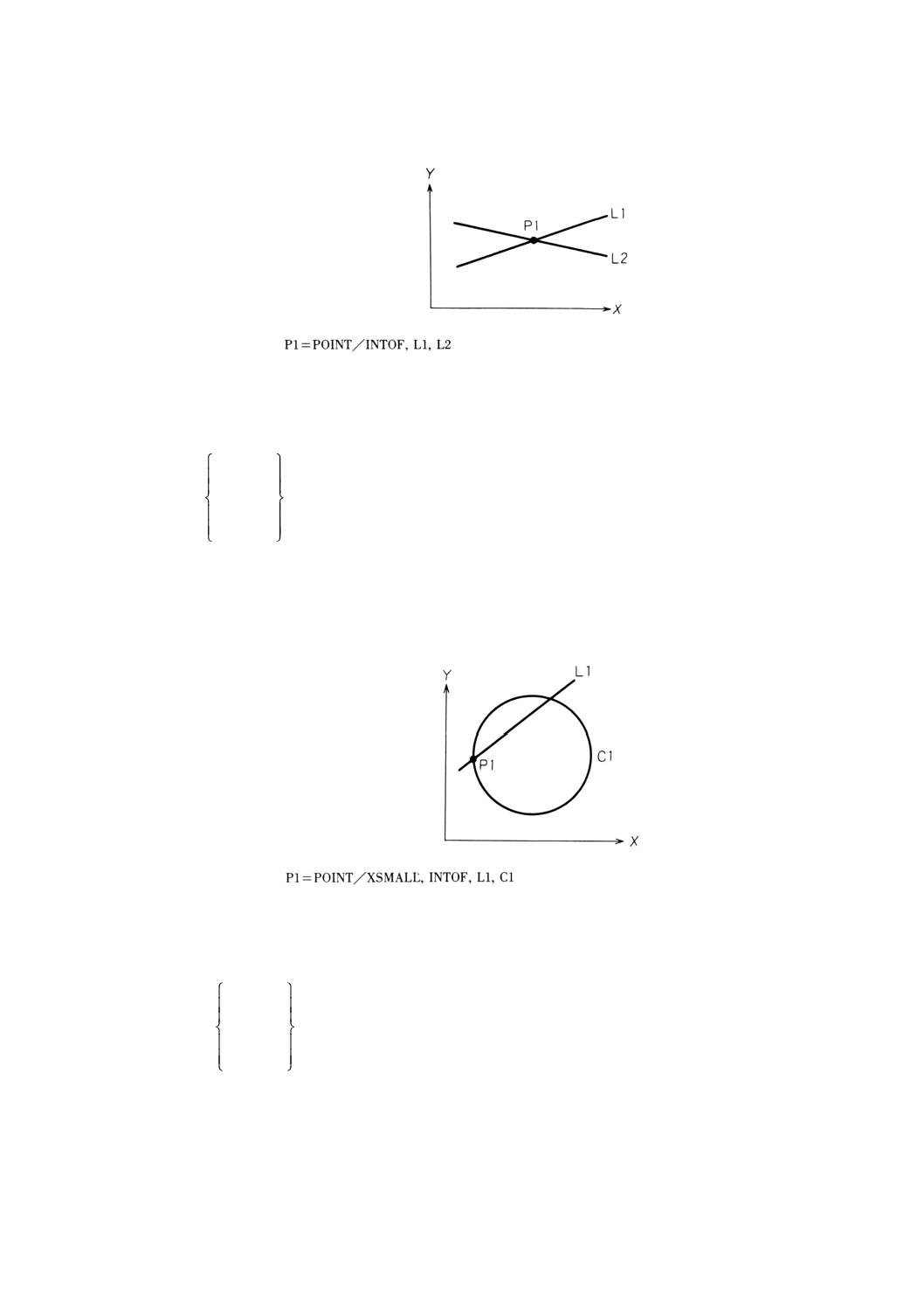
9.4.3.1 

意味 2直線の交点により点を定義する。 

一般形は，次のとおりとする。 

POINT/INTOF，直線1，直線2 

備考 直線1，直線2は，異なる直線とし，かつ互いに平行であってはならない。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 2直線の交点による点の定義の例 

9.4.4 

直線と円の交点による点の定義 

9.4.4.1 

意味 直線と円の交点により点を定義する。 

一般形は，次のとおりとする。 

POINT/

YSMALL

YLARGE

XSMALL

XLARGE

，INTOF，直線，円 

備考1. 直線と円は，交わるか又は接していなければならない。 

2. 直線が座標軸に平行な場合，その軸に関する修飾語だけが使用できる。例えば，直線がX軸

に平行な場合，XLARGE又はXSMALLだけが使用できる。 

例： 直線と円の交点による点の定義の例 

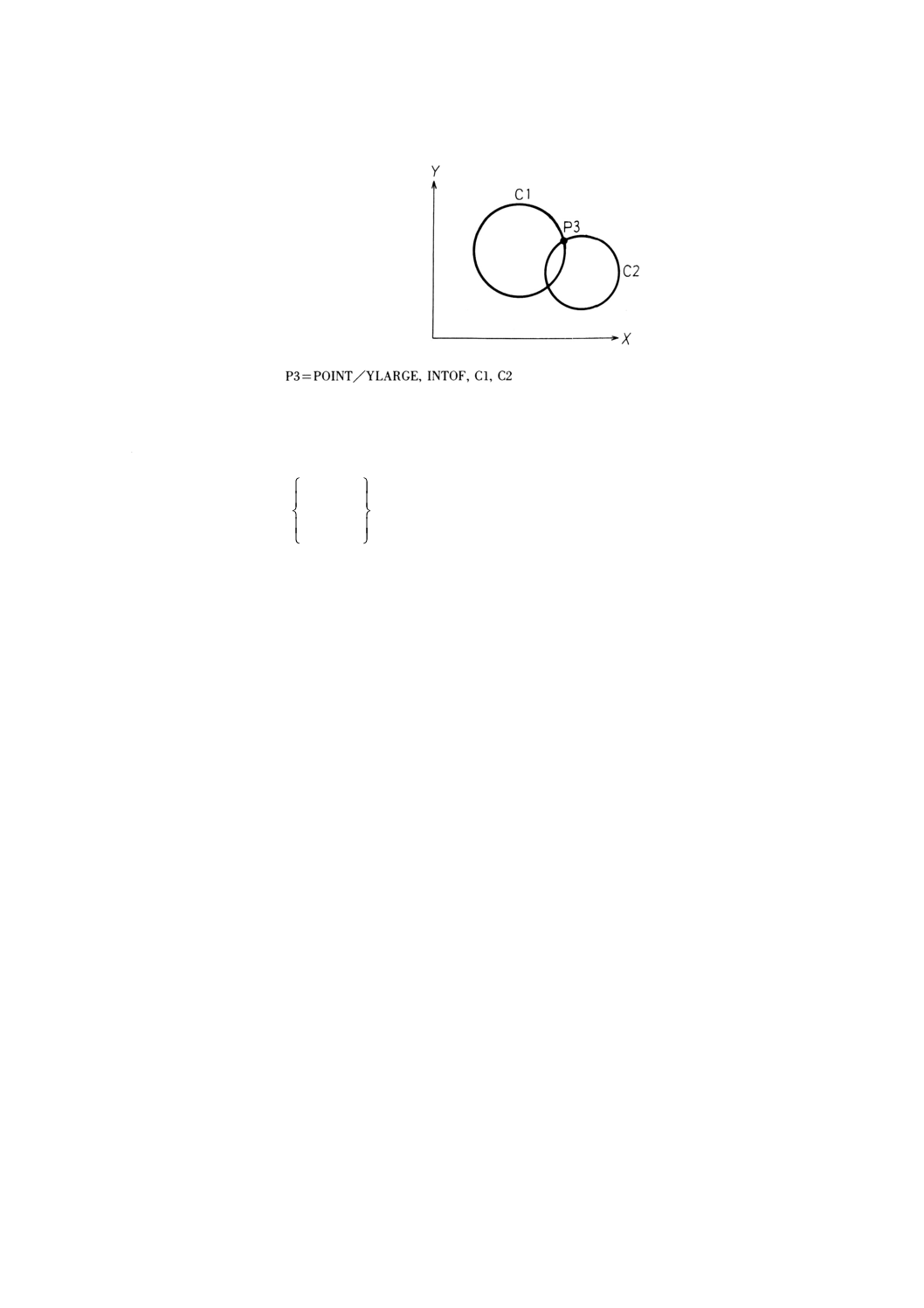
9.4.5.2 

円の交点による点の定義 

9.4.5.1 

意味 2円の交点により点を定義する。 

一般形は，次のとおりとする。 

POINT/

YSMALL

YLARGE

XSMALL

XLARGE

，INTOF，円1，円2 

備考1. 円1，円2は，交わるか又は接していなければならない。 

2. 円1，円2の中心を結ぶ直線が座標軸に平行な場合，一方の座標軸に関する修飾語だけが使

用できる。例えば，円1，円2の中心のX座標が等しい場合，YLARGE又はYSMALLだけ

が使用できる。 

28 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 2円の交点による点の定義の例 

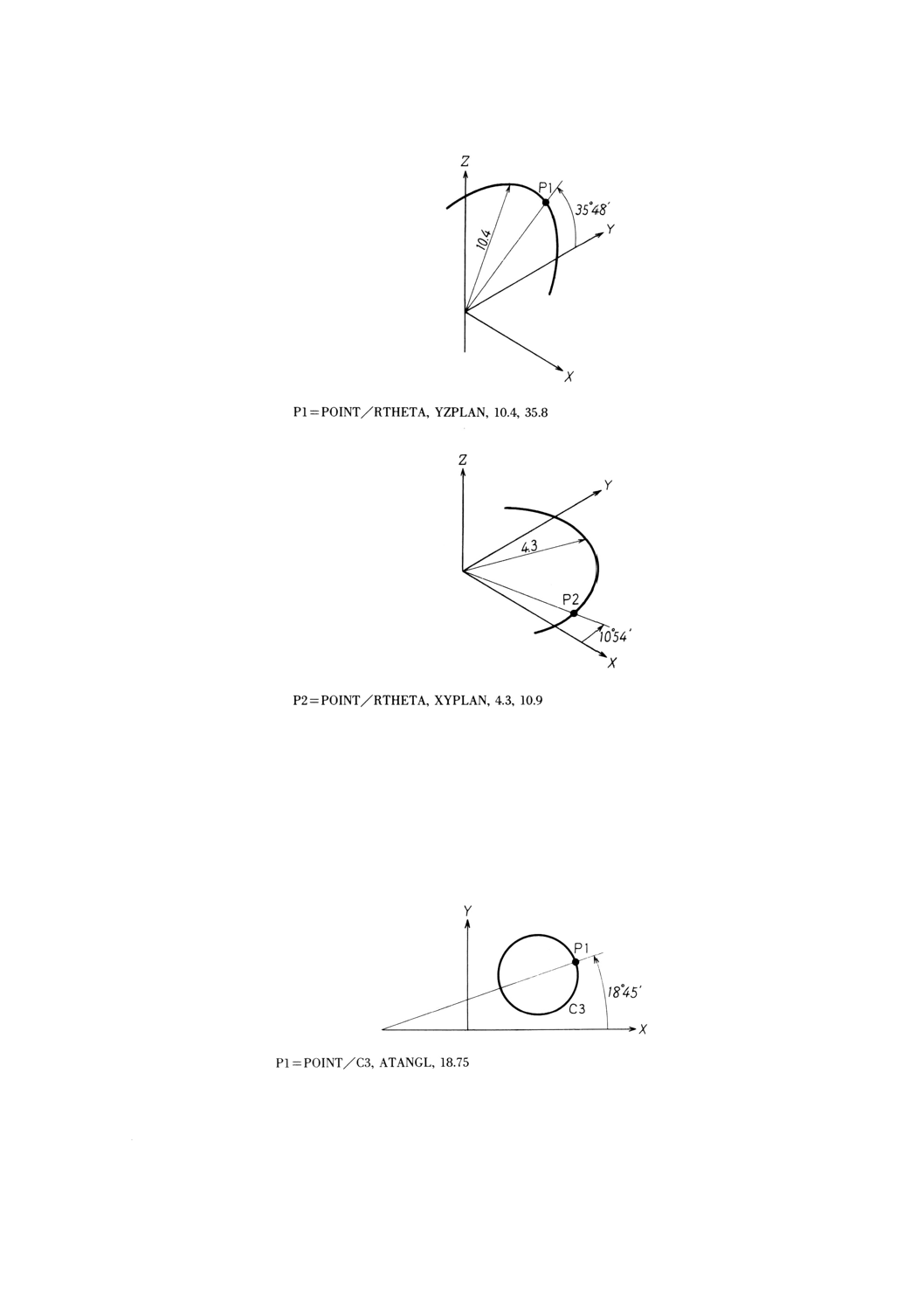
9.4.6 

極座標による点の定義 

9.4.6.1 

意味 指定座標平面上での極座標により点を定義する。 

一般形は，次のとおりとする。 

POINT/RTHETA，

ZXPLAN

YZPLAN

XYPLAN

，動径，角度 

備考1. 動径は，座標系の原点からの距離とする。 

2. 角度は，座標系の原点から定義する点に向け結んだ直線とのなす角度とし，反時計回りの向

きに測った角度を正とする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 極座標による点の定義の例 

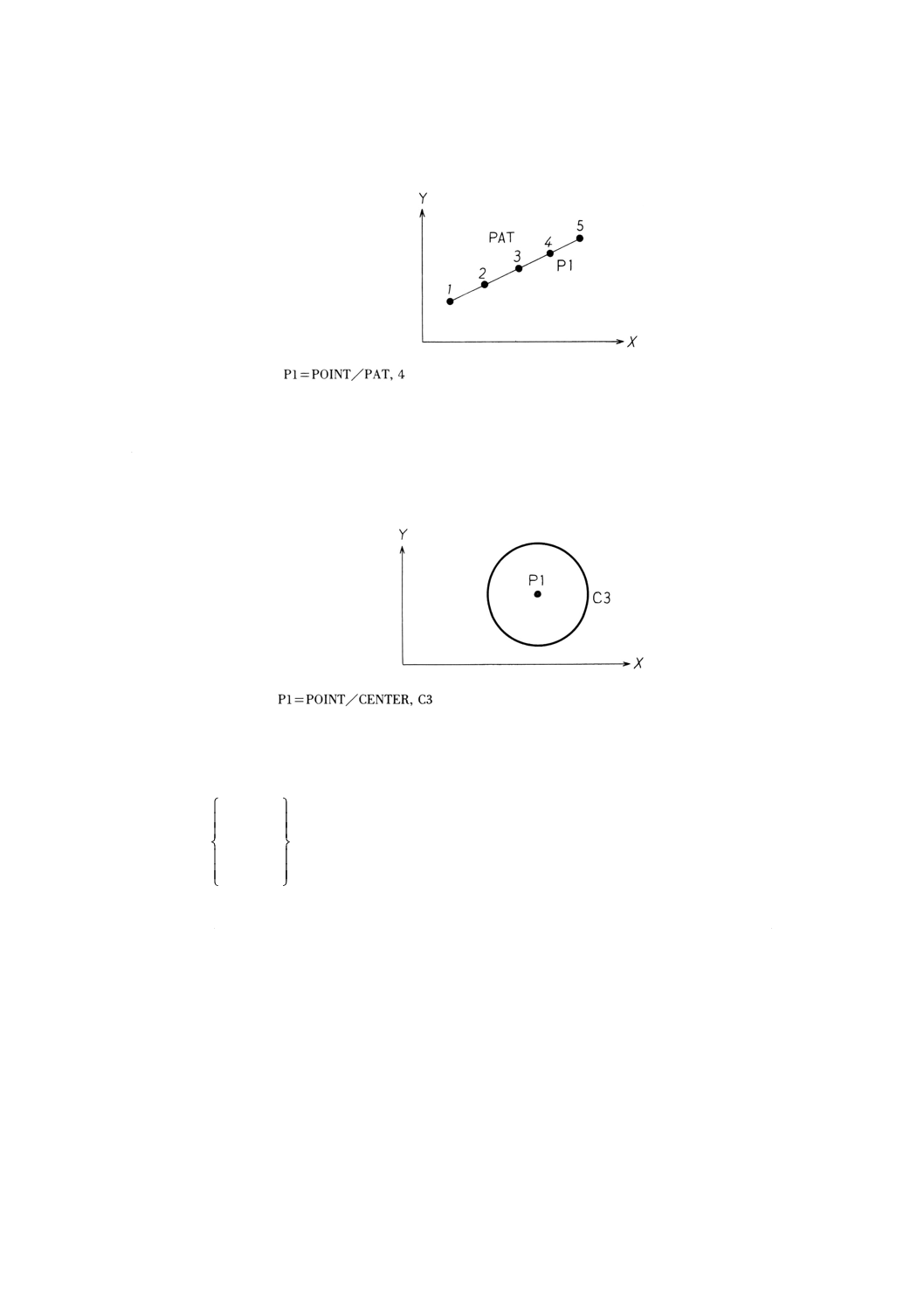
9.4.7 

円とX軸からの角度による点の定義 

9.4.7.1. 意味 円とX軸からの角度により円弧上の点を定義する。 

一般形は，次のとおりとする。 

POINT／円，ATANGL，角度 

備考 角度は，基準軸Xと，円の中心から円弧上の定義する点に向け結んだ直線とのなす角度とし，

反時計回りの向きに測った角度を正とする。 

例： 円とX軸からの角度による点の定義の例 

9.4.8 

パターン内の点の定義 

94.8.1 意味 ターン内のn番目の点を点として定義する。 

一般形は，次のとおりとする。 

POINT／パターン，点番号 

30 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

備考 点番号は，パターン内での点の順番号とする。 

例： パターン内の点の定義の例 

9.4.9 

円の中心による点の定義 

9.4.9.1 

意味 円の中心を点として定義する。 

一般形は，次のとおりとする。 

POINT/CENTER，円 

例： 円の中心による点の定義の例 

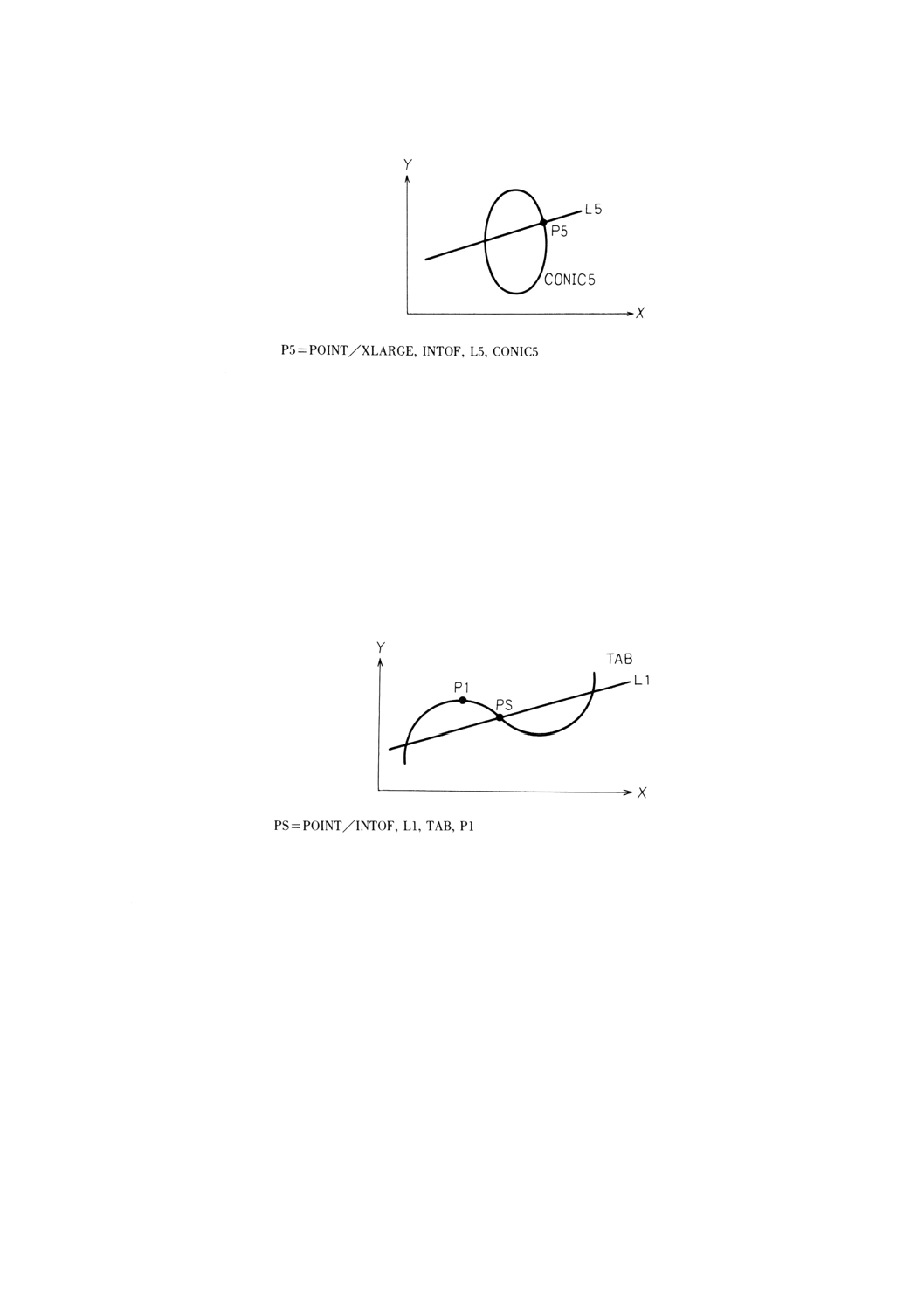
9.4.10 直線と円すい曲線との交点による点の定義 

9.4.10.1 意味 直線と円すい曲線との交点により点を定義する。 

一般形は，次のとおりとする。 

POINT/

YSMALL

YLARGE

XSMALL

XLARGE

，INTOF ，直線，円すい曲線 

備考1. 直線と円すい曲線は，交わるか又は接していなければならない。 

2. 直線が座標軸に平行な場合，その軸に関する修飾語だけが使用できる。例えば，直線がX軸

に平行な場合，XLARGE又はXSMALLだけが使用できる。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 直線と円すい曲線との交点による点の定義 

9.4.11 直線とタブシルの交点による点の定義 

9.4.11.1 意味 直線とタブシルの交点により点を定義する。 

一般形は，次のとおりとする。 

POINT/INTOF，直線，タブシル，点 

備考1. タブシルは，XY平面に垂直なタブシルとする。 

2. 点は，直線とタブシルとが多重交差することもあるので，その交点のどれを定義する点とし

て選択するかを決めるために，その交点の近傍にあってタブシルの定義に用いた点を指定す

る。したがって，指定した点の近傍にあるタブシルと直線とが多重交差してはならない。 

3. 直線とタブシルは，交わるか又は接していなければならない。 

例： 直線とタブシルの交点による点の定義の例 

9.4.12 

3平面の交点による点の定義 

9.4.12.1 意味 3平面の交点により点を定義する。 

一般形は，次のとおりとする。 

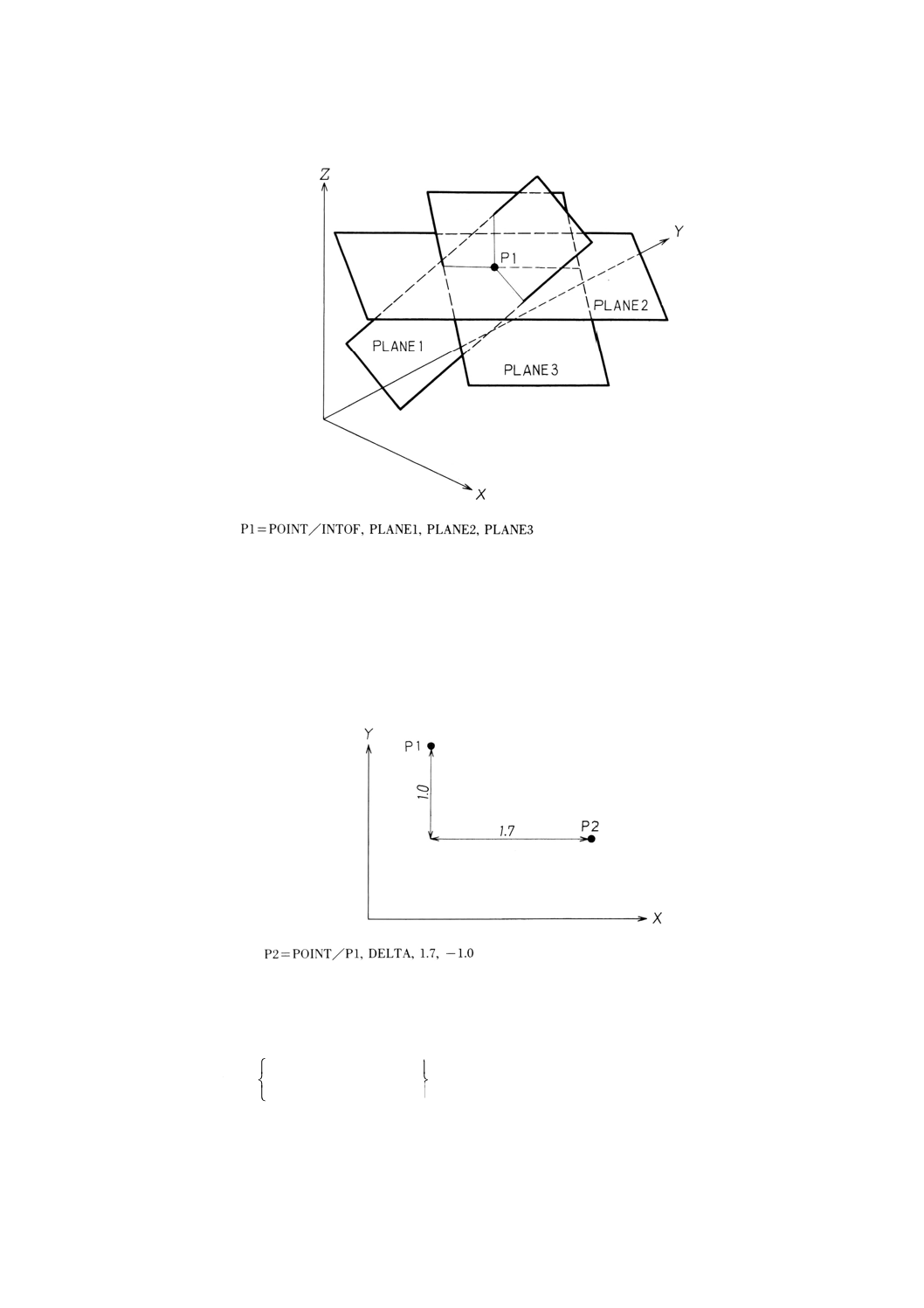
POINT/INTOF，平面1，平面2，平面3 

備考 平面1，平面2，平面3は，互いに同一であっても平行であってもならない。 

32 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 3平面の交点による点の定義の例 

9.4.13 指定した点からの増分量による点の定義 

9.4.13.1 意味 指定した点からの増分量により点を定義する。 

一般形は，次のとおりとする。 

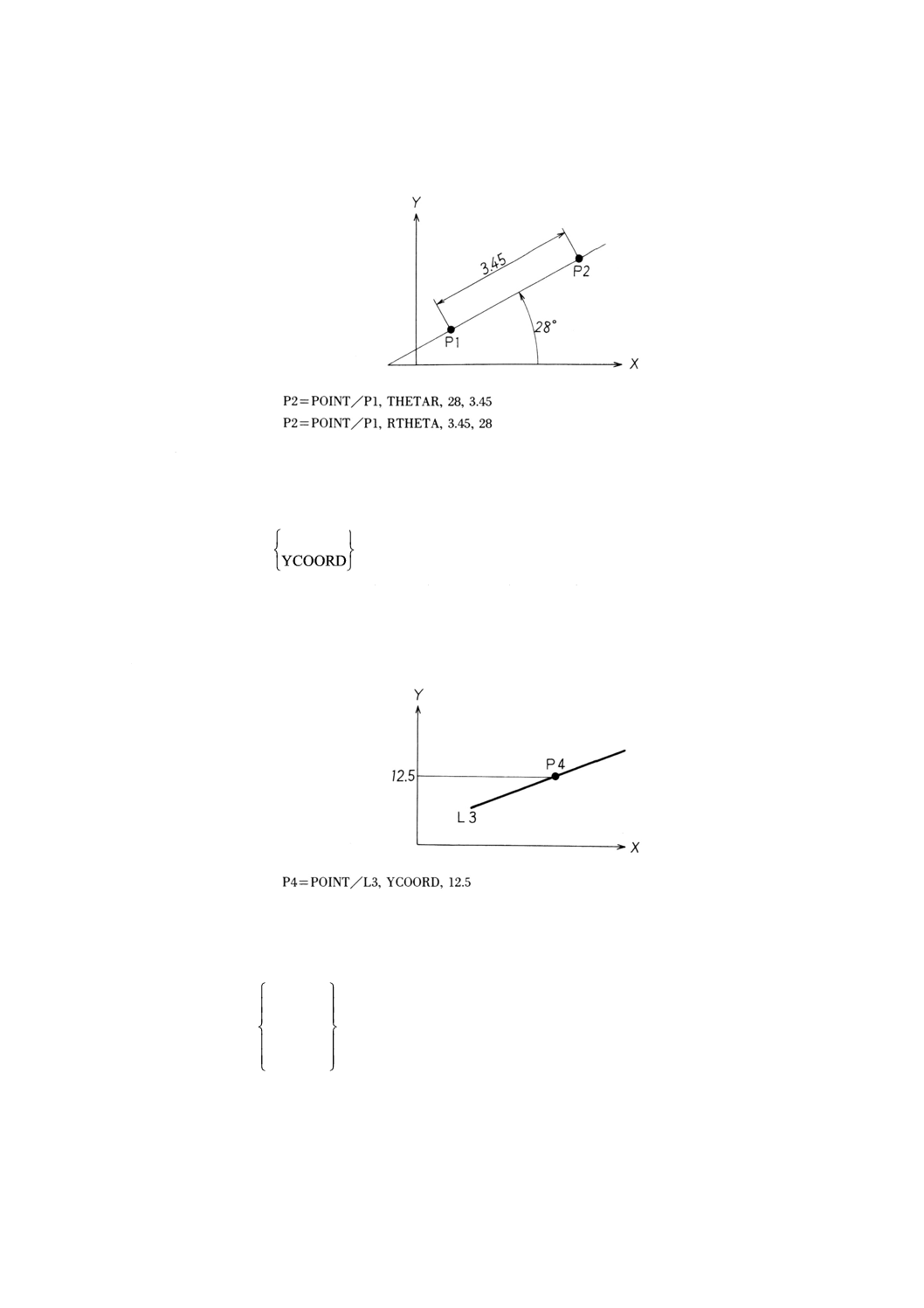
POINT／点，DELTA，増分1，増分2 

備考 増分1，増分2は，それぞれX方向及びY方向の増分とする。 

例： 指定した点からの増分量による点の定義の例 

9.4.14 指定した点からの距離と角度による点の定義 

9.4.14.1 意味 指定した点からの距離と角度により点を定義する。 

一般形は，次のとおりとする。 

POINT／点，

，距離，角度

，角度，距離

RTHETA

THETAR

備考1. 角度は，基準軸Xと，指定した点から定義する点に向け結んだ直線とのなす角度とし，反時

計回りの向きに測った角度を正とする。 

2. 距離は，指定した点から定義する点までの距離とする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3. 距離は，正でなければならない。 

例： 指定した点からの距離と角度による点の定義の例 

9.4.15 直線上の指定のX座標又はY座標をもつ点の定義 

9.4.15.1 意味 直線上の指定のX座標又はY座標をもつ点を定義する。 

一般形は，次のとおりとする。 

POINT／直線，

YCOORD

XCOORD

，数 

備考1. XCOORD，YCOORDは，数がX座標又はY座標のいずれであるかを示す。 

2. 直線は，XCOORDが選択されるときY軸に平行であってはならず，YCOORDが選択される

ときX軸に平行であってはならない。 

例： 直線上の指定のX座標又はY座標をもつ点の定義の例 

9.4.16 タブシル上の点からタブシルに沿って指定した距離だけ離れた点の定義 

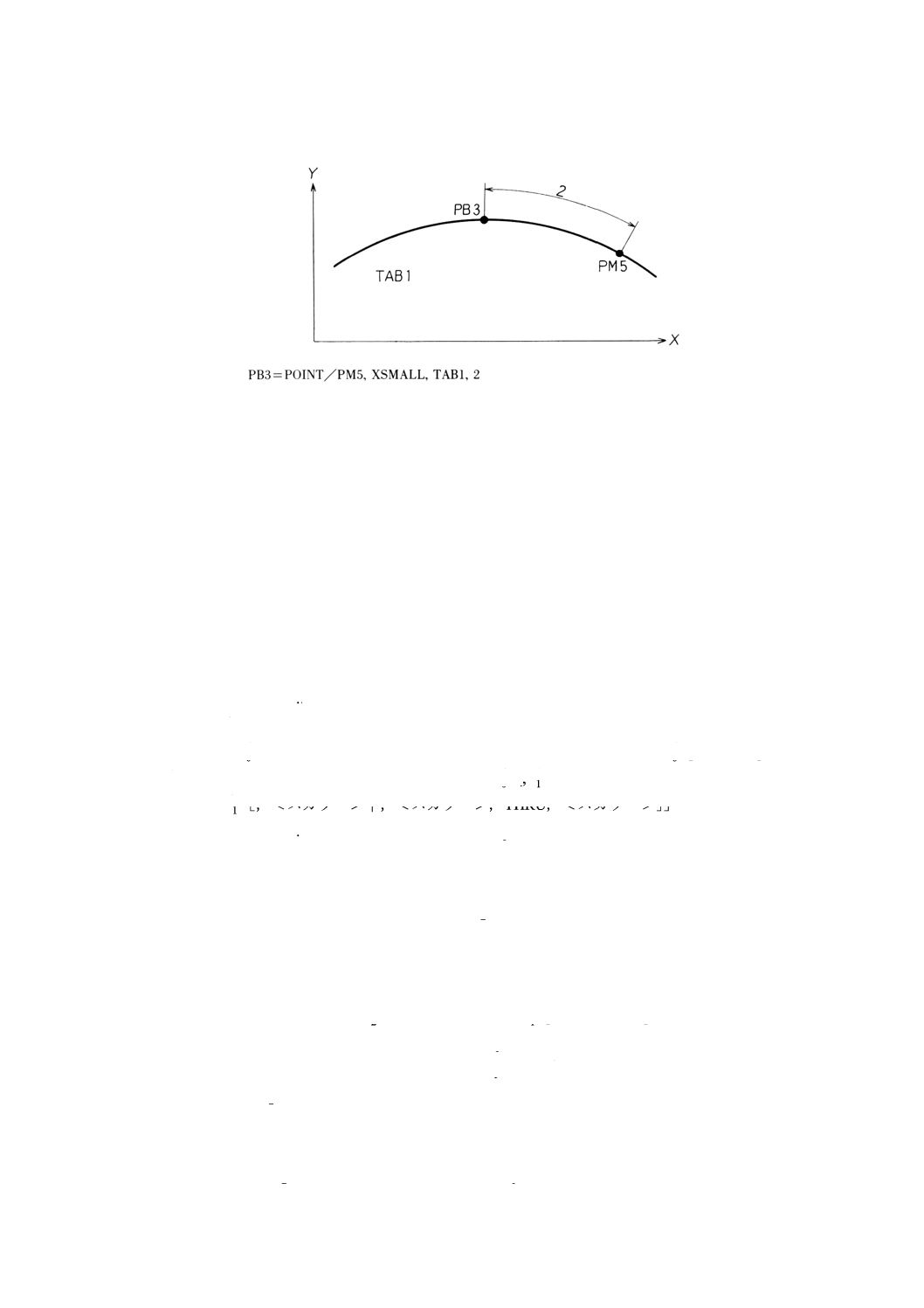
9.4.16.1 意味 タブシル上の点からタブシルに沿い指定した距離だけ離れた点を定義する（9.18参照）。 

一般形は，次のとおりとする。 

POINT／点，

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル，距離 

備考1. タブシルは，XY平面に垂直とする。 

2. 距離は，指定したタブシル上に指定した点と定義する点とのタブシル上で測った距離とする。 

3. 距離は，正でなければならない。 

34 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： タブシル上の点からタブシルに沿って指定した距離だけ離れた点の定義の例 

9.5 

パターン定義文 

9.5.1 

意味と構文 

9.5.1.1 

意味 パターン定義文は，XY平面上の一群の点を定義する。この一群の点をパターンと呼ぶ。

パターンのうち特に，点を直線上，円弧上及び格子上に配列したものをそれぞれ線形パターン，円弧パタ

ーン及び格子パターンと呼ぶ。パターンの各点のZ座標は，Z面が与えられた場合はZ面のZ座標とし，

Z面が与えられていない場合は0とする。パターンは，定義の方法で定められた順番号をもつ。順番号を

逆転するには修飾語INVERSを使う。あるパターンからある順番号をもつ点を省略するには修飾語OMIT

を，ある順番号をもつ点だけを保持するには修飾語RETAINを使う。削除したり選択したりする点の順番

号の並びは，コンマで区切り，順番号が連続しているときは，最初の順番号と最後の順番号の間にTHRU

を入れて示す。 

9.5.1.2 

構文 構文は，次による。 

＜パターン定義文＞ :: ＝＜名前＞＝PATERN／＜パターンのパラメータの並び＞10 [, INVERS] 

＜パターン規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］PATERN／＜パターンのパラメータの並び＞10 [, INVERS] ） 

＜修飾されたパターン＞ :: ＝＜パターン規制詞＞10 [, 11 [OMIT｜RETAIN] 

k1［，＜スカラー＞｜，＜スカラー＞，THRU，＜スカラー＞］］ 

＜パターンデータ＞ :: ＝＜パターンデータ項目＞k0[，＜パターンデータ項目＞］ 

＜パターンデータ項目＞ :: ＝＜スカラー＞｜ 

＜スカラー＞，AT，＜スカラー＞ 

＜パターンのパラメータの並び＞ :: ＝LINEAR22［，＜点規制詞＞］，＜スカラー＞｜ 

LINEAR，＜点規制詞＞，＜ベクトル規制詞＞，＜スカラー＞｜ 

LINEAR，＜点規制詞＞，＜ベクトル規制詞＞，INCR，＜パターンデータ＞｜ 

LINEAR，＜点規制詞＞，ATANGL，＜スカラー＞，INCR，＜パターンデータ＞｜ 

ARC，＜円規制詞＞22［，＜スカラー＞］，11 [CLW｜CCLW]，＜スカラー＞｜ 

ARC，＜円規制詞＞，＜スカラー＞，11 [CLW｜CCLW]，＜スカラー＞｜ 

ARC，＜円規制詞＞，＜スカラー＞，11 [CLW｜CCLW], INCR，＜パターンデータ＞｜ 

GRID22［，＜修飾されたパターン＞］｜ 

GRID，＜修飾されたパターン＞，＜ベクトル規制詞＞，＜スカラー＞｜ 

GRID，＜修飾されたパターン＞，＜ベクトル規制詞＞，INCR，＜パターンデータ＞｜ 

TRAFO22［，＜修飾されたパターン＞］10［, XYROT，＜スカラー＞］｜ 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

CIRCUL22［，＜修飾されたパターン＞］｜ 

RANDOM，11［＜点規制詞＞｜＜修飾されたパターン＞］k0［，＜点規制詞＞｜ 

，＜修飾されたパターン＞］｜ 

MIRROR，＜直線規制詞＞，＜修飾されたパターン＞ 

9.5.2 

始点，終点及びパターン内の点の総数によるパターンの定義 

9.5.2.1 意味 始点，終点及びパターン内の点の総数により点が等間隔に並んだ線形パターンを定義する。 

一般形は，次のとおりとする。 

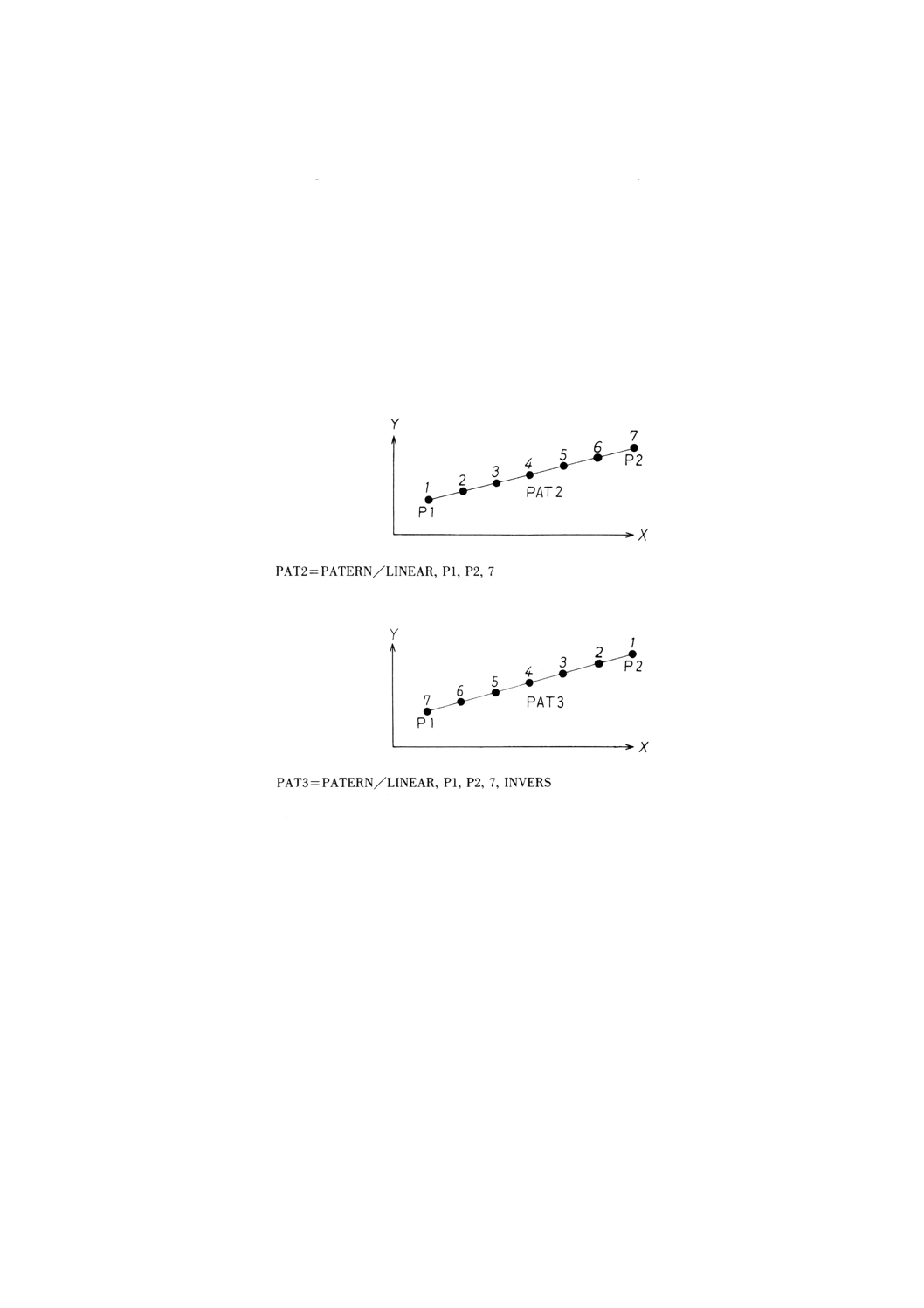
PATERN/LINEAR，点1，点2，数 [, INVERS] 

備考1. 点1，点2は，それぞれ始点及び終点とする。 

2. 数は，始点及び終点を含む点の総数とする。 

例： 始点，終点及びパターン内の点の総数によるパターンの定義の例 

備考 PAT3では，P1の順番号が7でP2の順番号が1となる。 

9.5.3 

始点，ベクトル及びパターン内の点の総数によるパターンの定義 

9.5.3.1 

意味 始点，ベクトル及びパターン内の点の総数により線形パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/LINEAR，点，ベクトル，数 [, INVERS] 

備考1. 点は，始点とする。 

2. ベクトルは，線形パターンの向きと点間隔とする。 

3. 数は，始点を含む点の総数とする。 

36 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

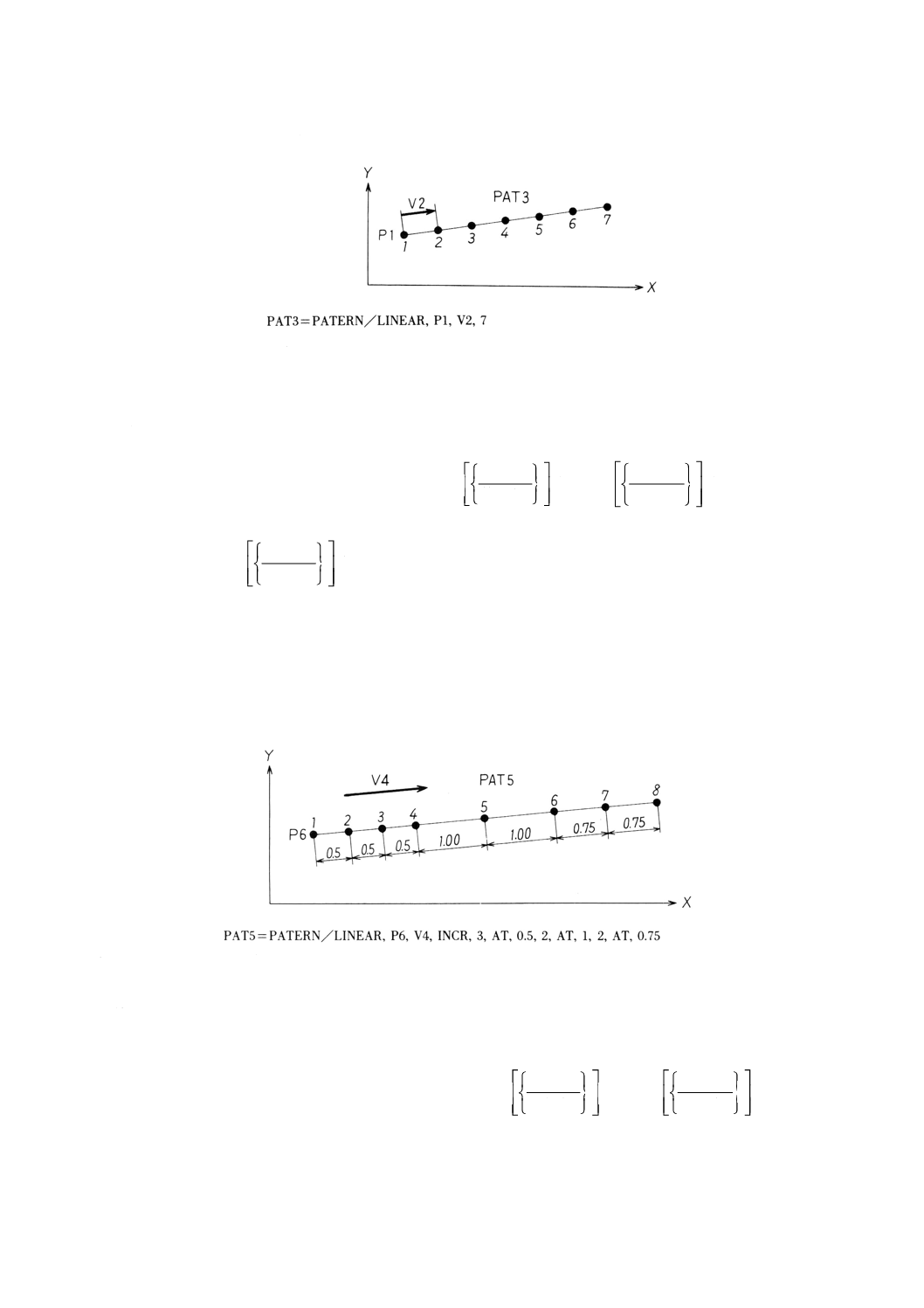
例： 始点，ベクトル及びパターン内の点の総数によるパターンの定義の例 

9.5.4 

始点，ベクトル及び間隔の総数とジ増分によるパターンの定義 

9.5.4.1 

意味 始点からベクトルの向きに等間隔に点を置くための間隔の総数と増分の組により線形パ

ターンを定義する。 

一般形は，次のとおりとする。 

PATERN/LINEAR，点，ベクトル，INCR，

,

AT

1,

AT

,1

数

増分1，

,

AT

2,

AT

,1

数

増分2，¥ 

…

,

AT

n,

AT

,1

数

増分n］[, INVERS] 

備考1. 点は，始点とする。 

2. ベクトルは，線形パターンの向きとする。 

3. 数1，数2，…，数nは，それぞれ増分1，増分2，…，増分nを用いる回数とする。 

4. 数の値が1のときは，数，ATを省略することができる。 

例： 始点，ベクトル及び間隔の総数と増分によるパターンの定義の例 

9.5.5 

始点，角度及び間隔の総数と増分の組によるパターンの定義 

9.5.5.1 

意味 始点，向きを示す角度及びその向きに等間隔に点を置くための間隔の総数と増分の組によ

り線形パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/LINEAR，点，ATANGL，角度，INCR，

,

AT

1,

AT

,1

数

増分1，

,

AT

2,

AT

,1

数

¥ 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

増分2，…，

,

AT

n,

AT

,1

数

増分n］[, INVERS] 

備考1. 点は，始点とする。 

2. 角度は，基準軸Xと，始点から定義する点に向け結んだ直線とのなす角度とし，反時計回り

の向きに測った角度を正とする。 

3. 数1，数2，…，数nは，それぞれ増分1，増分2，…，増分nを用いる回数とする。 

4. 数の値が1のときは，数，ATを省略することができる。 

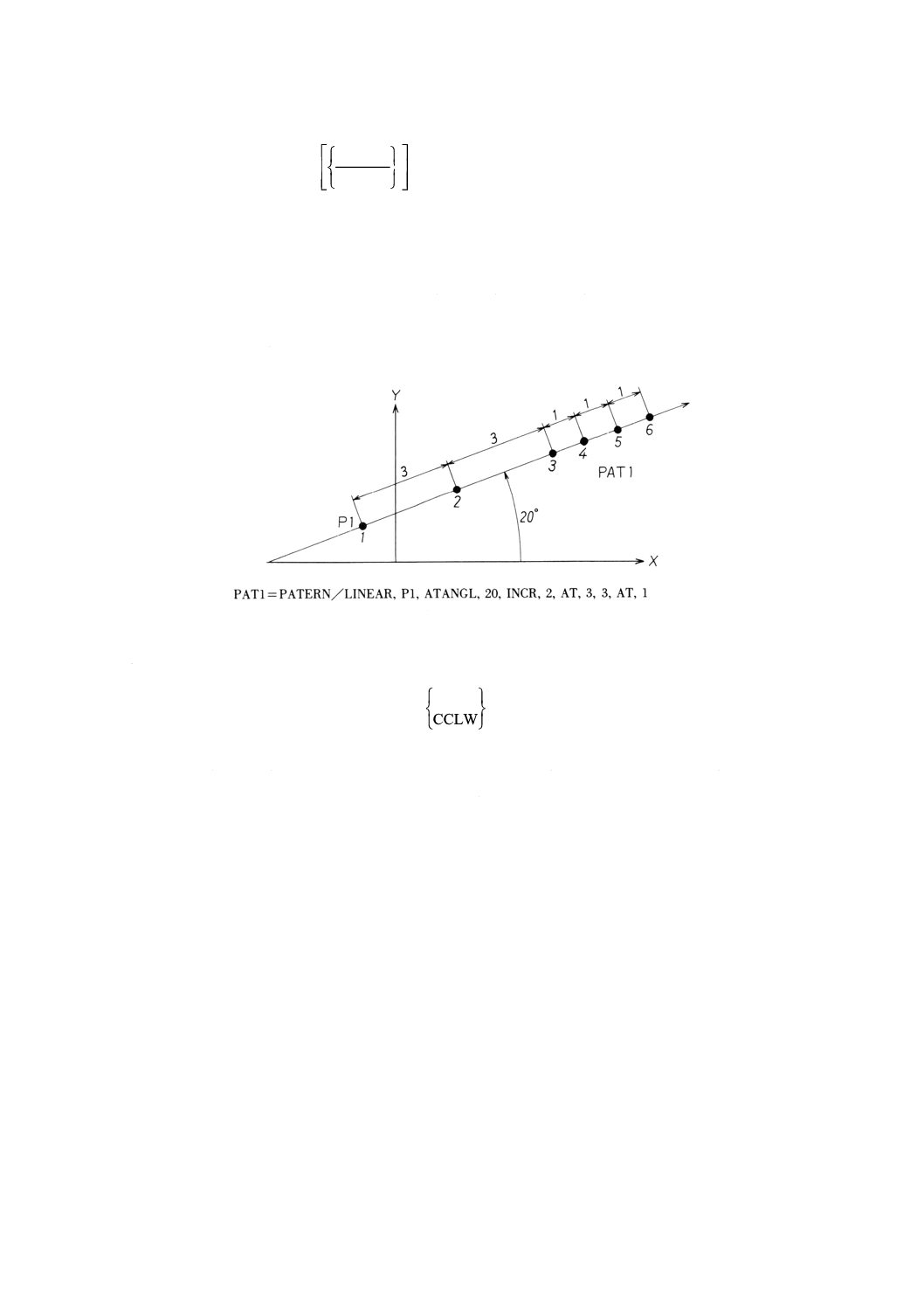
例： 始点，角度及び間隔の総数と増分の組によるパターンの定義の例 

9.5.6 

円，始点の角度，終点の角度，向き及び点の総数による円弧パターンの定義 

9.5.6.1 

意味 円，始点の角度，終点の角度，向き及び点の総数により円弧パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/ARC，円，角度1，角度2，

CCLW

CLW

，数 [, INVERS] 

備考1. 円弧パターンは，円周上のパターンとする。 

2. 角度1，角度2は，それぞれ始点と終点を決める角度とする。いずれも基準軸Xと，円の中

心から始点又は終点に向かって結んだ直線とのなす角度とし，反時計回りの向きに測った角

度を正とする。 

3. 数は，始点及び終点を含む点の総数とする。 

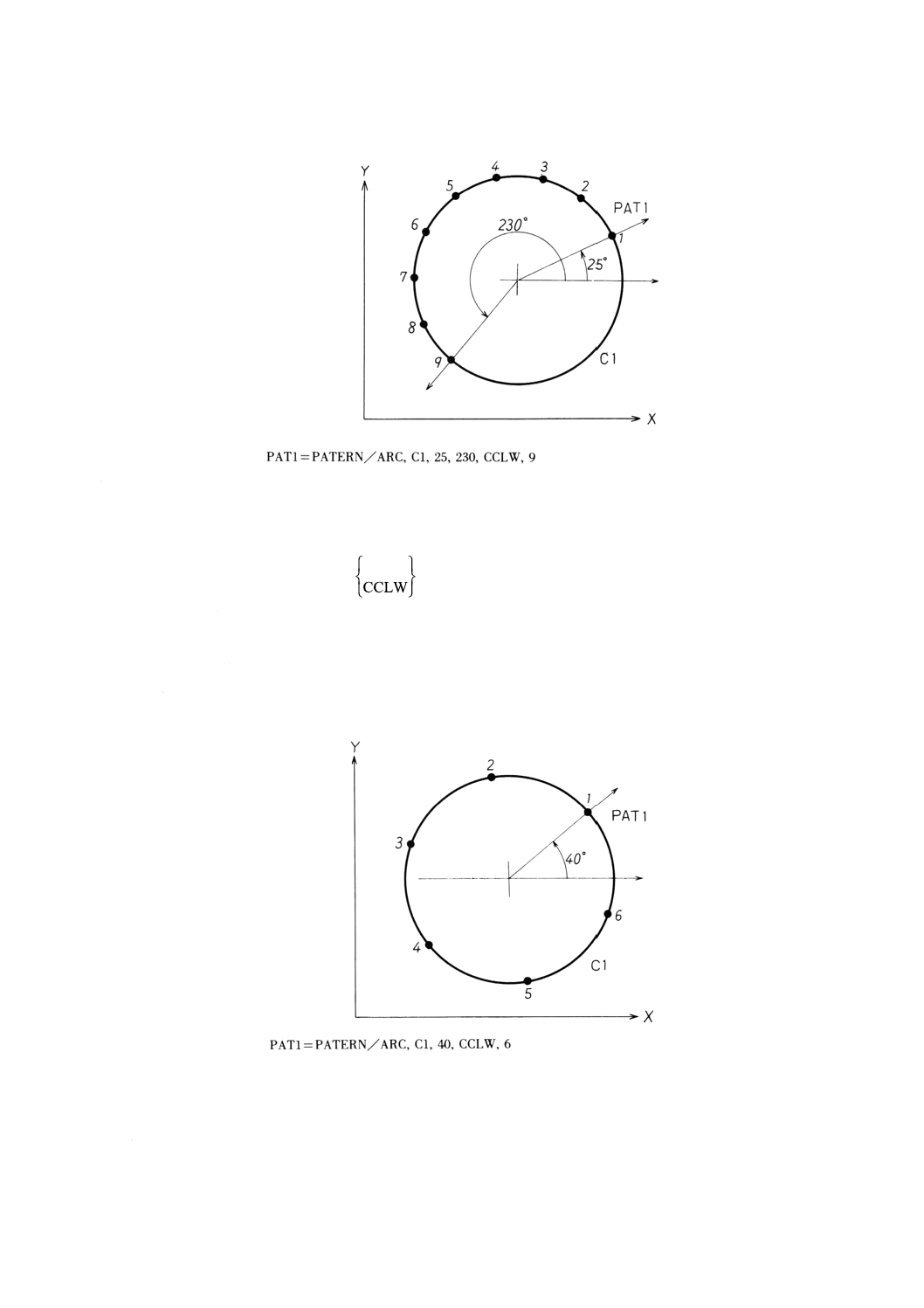
38 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 円，始点及び終点の角度，向き並びに点の総数による円弧パターンの定義の例 

9.5.7 

円，角度向き及び円周を等分割する点の総数による円弧パターンの定義 

9.5.7.1 

意味 円，始点の角度，向き及び円周を等分割する点の総数により円弧パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/ARC，円，角度，

CCLW

CLW

，数 [, INVERS] 

備考1. 円弧パターンは，円周上のパターンとする。 

2. 角度は，始点を決める角度とする。いずれも基準軸Xと，円の中心から始点に向かって結ん

だ直線とのなす角度とし，反時計回りの向きに測った角度を正とする。 

3. 数は，点の総数とする。 

例： 円，角度，向き及び円周を等分割する点の総数による円弧パターンの定義の例 

9.5.8 

円，角度，向き及び間隔の総数と角度の増分の組による円弧パターンの定義 

9.5.8.1 

意味 円，始点の角度及び指定する向きに等間隔に点を置くための間隔の総数と増分の角度の組

により円弧パターンを定義する。 

一般形は，次のとおりとする。 

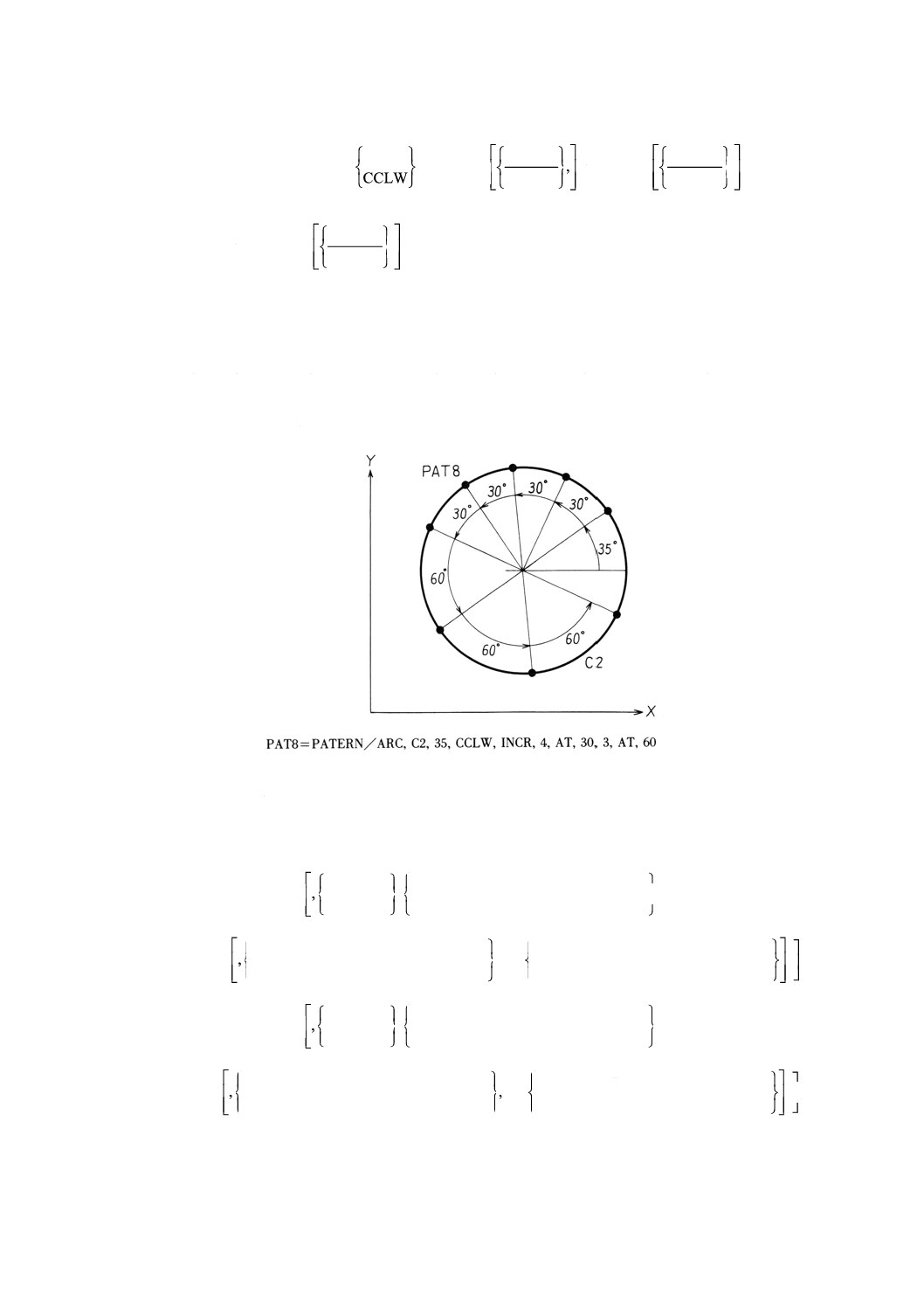
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

PATERN/ARC，円，角度，

CCLW

CLW

，INCR，

,

AT

1,

AT

1,

数

増分1［, 

,

AT

2,

AT

1,

数

¥ 

増分2, …, 

,

AT

n,

AT

1,

数

増分n］ [, INVERS] 

備考1. 円弧パターンは，円周上のパターンとする。 

2. 角度は，始点を決める角度とする。いずれも基準軸Xと，円の中心から始点に向かって結ん

だ直線とのなす角度とし，反時計回りの向きに測った角度を正とする。 

3. 数1，数2，…，数nは，それぞれ増分1，増分2，…，増分nを用いる回数とする。 

4. 数の値が1のときは，数，ATを省略することができる。 

例： 円，角度，向き及び間隔の総数と角度の増分の組による円弧パターンの定義の例 

9.5.9 

二つのパターンによる格子パターンの定義 

9.5.9.1 

意味 二つの線形パターンにより格子パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/GRID, ¥ 

パターン1

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

m

,

,

6

THRU

5

4

,

パターン2

￥

，点の順番号

，

点の順番号

点の順番号

9

THRU

8

7

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

s

THRU

r

n

,

,

12

THRU

11

10

,

[, INVERS]  

備考1. パターン1の個々の点からパターン2が始まるように格子パターンを作成する。 

40 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2. 格子パターンの点の順番号は，パターン1の順番号から始め，以後各列（又は行）ごとに折

り返して逆の順番とする。 

3. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

例： 二つのパターンによる格子パターンの定義の例 

9.5.10 パターン，ベクトル及び総数による格子パターンの定義 

9.5.10.1 意味 線形パターン，ベクトル及び線形パターンの総数により格子パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/GRID,¥ 

パターン

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

n

,

,

6

THRU

5

4

,

ベクトル，数 [, INVERS]  

備考1. ベクトルは，指定した線形パターンの移動の向きと移動間隔を示す。 

2. 数は，格子パターンを作成するのに使われる線形パターンの総数とする。 

3. 格子パターンの点の順番号は，線形パターンの順番号から始め，以後各列（又は行）ごとに

折り返して逆の順番とする。 

4. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

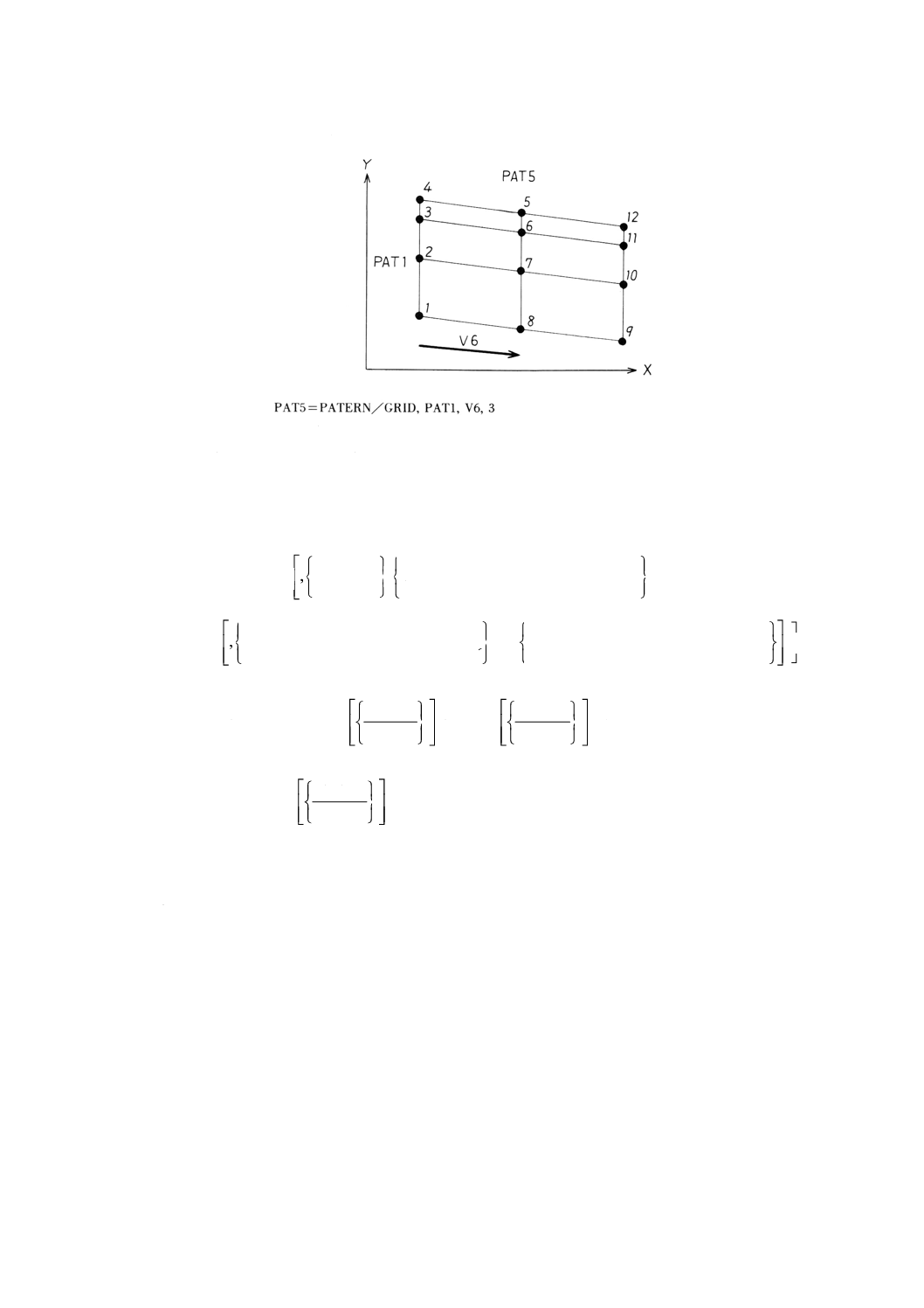
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： パターン，ベクトル及び総数による格子パターンの定義の例 

9.5.11 パターン，ベクトル及び間隔の総数と増分の組による格子パターンの定義 

9.5.11.1 意味 線形パターン，その線形パターンの移動の向きを指定するベクトル及び等間隔に移動する

ための間隔の総数と増分の組により格子パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/GRID, ¥ 

パターン

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

n

,

,

6

THRU

5

4

,

ベクトル，INCR, 

,

AT

1,

AT

1,

数

増分1[, 

,

AT

,2

AT

1,

数

 増分2，…，￥ 

,

AT

n,

AT

1,

数

 増分n］[, INVERS]  

備考1. ベクトルは，指定した線形パターンの移動の向きを示す。 

2. 数1，数2，…，数nは，それぞれ増分1，増分2，…，増分nを用いる回数とする。 

3. 格子パターンの点の順番号は，線形パターンの順番号から始め，以後各列（又は行）ごとに

折り返して逆の順番とする。 

4. 数の値が1のときは，数，ATを省略することができる。 

5. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

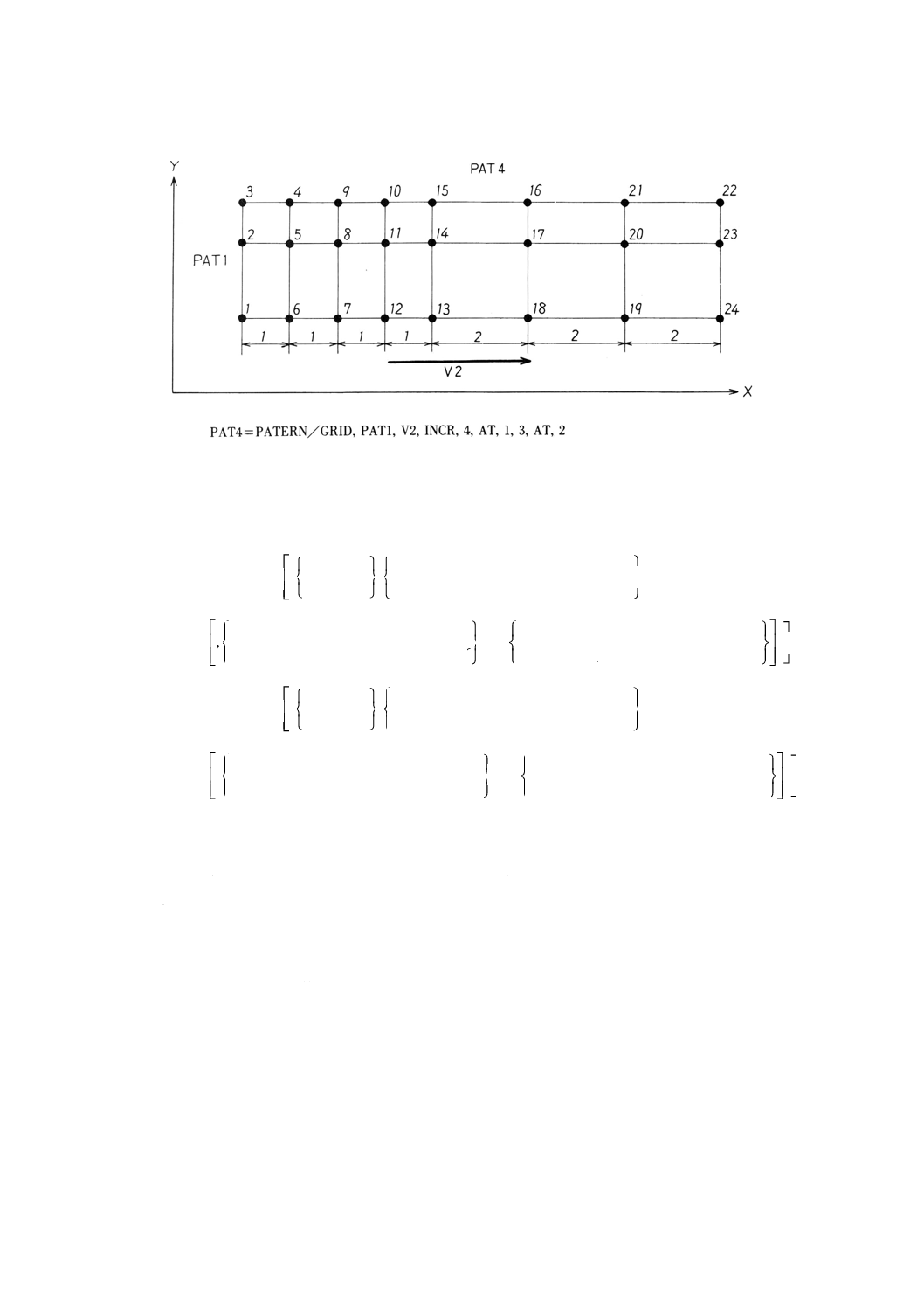
42 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： パターン，ベクトル及び間隔の総数と増分の組による格子パターンの定義の例 

9.5.12 二つのパターンによる格子パターンの定義 

9.5.12.1 意味 二つの線形パターンにより格子パターンを定義する。 

一般形は，次のとおりとする。 

PATERN/TRAFO, ¥ 

パターン1

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

m

,

,

6

THRU

5

4

,

パターン2

￥

，点の順番号

，

点の順番号

点の順番号

9

THRU

8

7

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

s

THRU

r

n

,

,

12

THRU

11

10

,

［，XYROT,角度］[, INVERS] 

備考1. ［，XYROT,角度］を書かないときは，回転を指定しない。 

2. 角度は，パターン2のXY平面内での回転角度とし，反時計回りの向きの回転を正とする。 

3. パターン2を指定した角度で回転して，その始点をパターン1の個々の点に移動してパター

ンを作成する。 

4. この格子パターンの点の順番号は，パターン2の順番号から始まり，以後各列（又は行）ご

とに折り返して逆の順番とする。 

5. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 二つのパターンによる格子パターンの定義の例 

9.5.13 二つのパターンによるパターンの定義 

9.5.13.1 意味 二つのパターンによりパターンを定義する。 

一般形は，次のとおりとする。 

PATERN/CIRCUL, ¥ 

パターン1

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

m

,

,

6

THRU

5

4

,

パターン2

￥

，点の順番号

，

点の順番号

点の順番号

9

THRU

8

7

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

s

THRU

r

n

,

,

12

THRU

11

10

,

[, INVERS] 

備考1. パターン1は線形パターンとし，パターン2は円弧パターンとする。 

2. パターン2の中心をパターン1の各点に，順番号に従って移動してパターンを作成する。た

だし，作成されたパターンは，パターン1及びパターン2を含まない。 

3. パターンの点の順番号は，パターン1の順番号に従って，パターン2の点の順番号の向きに

順次番号付けする。 

4. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

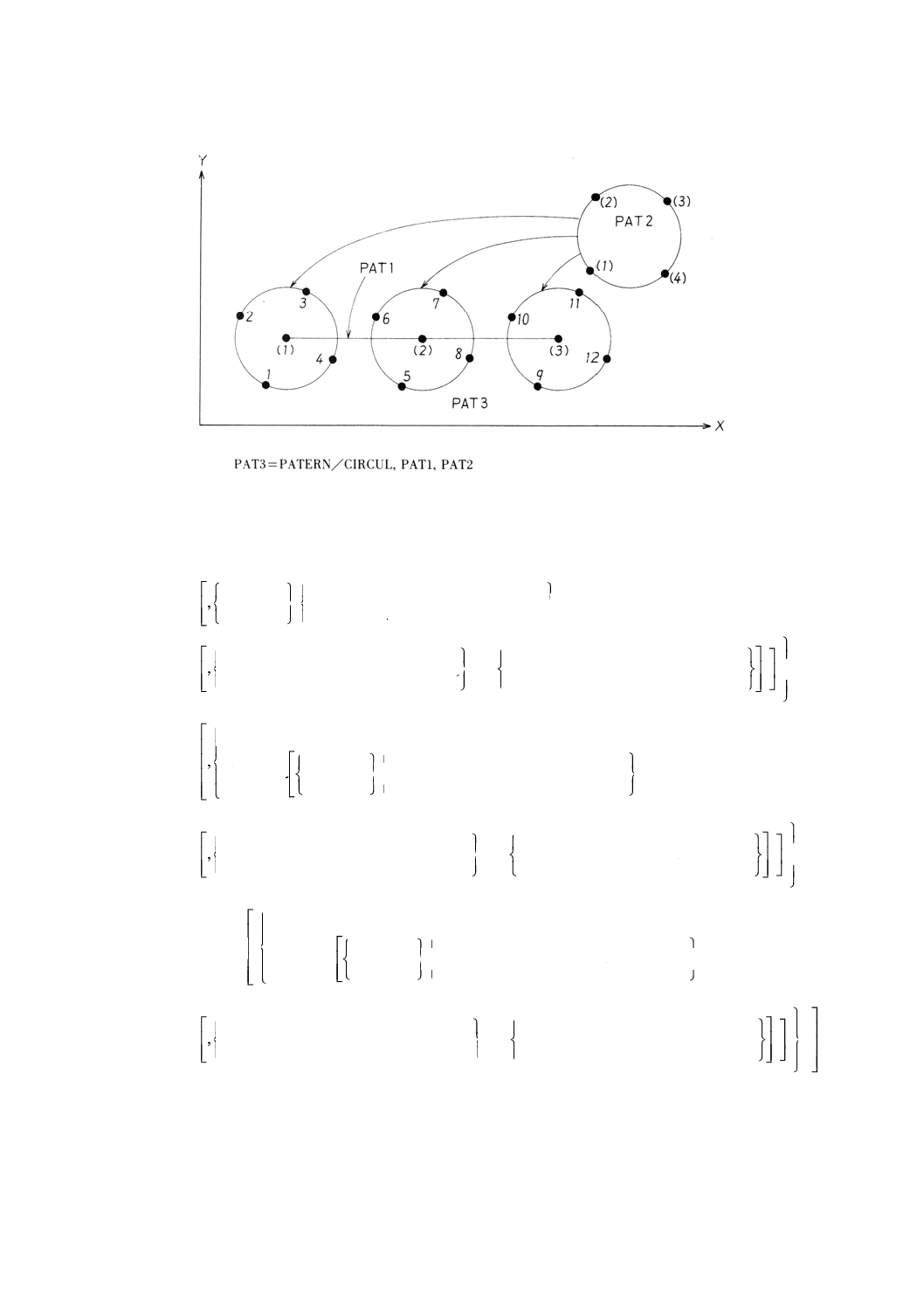
44 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 二つのパターンによるパターンの定義の例 

9.5.14 点，パターンによるパターンの定義 

9.5.14.1 意味 点，パターンによりパターンを定義する。 

一般形は，次のとおりとする。 

PATERN/RANDOM, ¥ 

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

k

,

,

6

THRU

5

4

,

￥

，点の順番号

，

点の順番号

点の順番号

，

パターン

点

9

THRU

8

7

RETRAIN

OMIT

2

2

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

s

THRU

r

m

,

,

12

THRU

11

10

,

，…，

￥

，点の順番号

，

点の順番号

点の順番号

，

パターン

点

15

THRU

14

13

RETRAIN

OMIT

n

n

,

￥

，

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

u

THRU

r

n

,

,

18

THRU

17

16

,

[, INVERS]  

備考1. パターンの点の順番号は，定義文に記述した点やパターンの順序に従う。 

2. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点，パターンによるパターンの定義の例 

9.5.15 直線に対称なパターンの定義 

9.5.15.1 意味 直線に対称なパターンを定義する。 

一般形は，次のとおりとする。 

PATERN/MIRROR, ¥ 

直線，パターン

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETRAIN

OMIT

,

，￥

，点の順場号

，

点の順場号

点の順場号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

m

,

,

6

THRU

5

4

,

[，INVERS] 

備考1. パターンは，指定した直線に対称に移動するパターンとする。 

2. 移動して作成されたパターンの点の順番号は，指定したパターンの順番号に対応する。 

3. 点の順番号1，点の順番号2，…，点の順番号nは，省略又は保持する点の順番号とする。 

例： 直線に対称なパターンの定義の例 

46 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.6 

直線定義文 

9.6.1 

意味と構文 

9.6.1.1 

意味 直線定義文は，直線を定義する。直線は，この直線を含むXY平面に垂直な平面として扱

う。したがって，直線は，XY平面に垂直であってはならない。 

9.6.1.2 

構文 構文は，次による。 

＜直線定義文＞ :: ＝＜名前＞＝LINE／＜直線のパラメータの並び＞ 

＜直線規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］LINE／＜直線のパラメータの並び＞） 

＜直線のパラメータの並び＞ :: ＝＜点規制詞＞，＜点規制詞＞｜ 

＜スカラー＞33[，＜スカラー＞］｜ 

＜スカラー＞55[，＜スカラー＞］｜ 

XAXIS｜ 

YAXIS｜ 

＜点規制詞＞，PARLEL，＜直線規制詞＞｜ 

＜点規制詞＞，PERPTO，＜直線規制詞＞｜ 

PARLEL，＜直線規制詞＞,11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]， 

＜スカラー＞｜ 

＜点規制詞＞，ATANGL，＜スカラー＞10［, XAXIS｜, YAXIS｜，＜直線規制詞＞］｜ 

＜点規制詞＞，SLOPE，＜スカラー＞10［, XAXIS｜, YAXIS｜，＜直線規制詞＞］｜ 

ATANGL，＜スカラー＞，｜NTERC10 [, XAXIS｜, YAXIS]，＜スカラー＞｜ 

SLOPE，＜スカラー＞，｜NTERC10 [, XAXIS｜, YAXIS]，＜スカラー＞｜ 

＜点規制詞＞，11 [R｜GHT｜LEFT] , TANTO，＜円規制詞＞｜ 

11[RIGHT｜LEFT] , TANTO，＜円規制詞＞，11 [RIGHT｜LEFT]，TANTO，＜円規制詞＞

｜ 
ATANGL, ＜スカラー＞, ＜直線規制詞＞，11［XLARGE｜XSMALL｜YLARGE｜ 

YSMALL］，TANTO, ＜円規制詞＞｜ 

INTOF22［，＜平面規制詞＞］｜ 

＜点規制詞＞，11 [RIGHT｜LEFT], TANTO, ＜円すい曲線規制詞＞｜ 

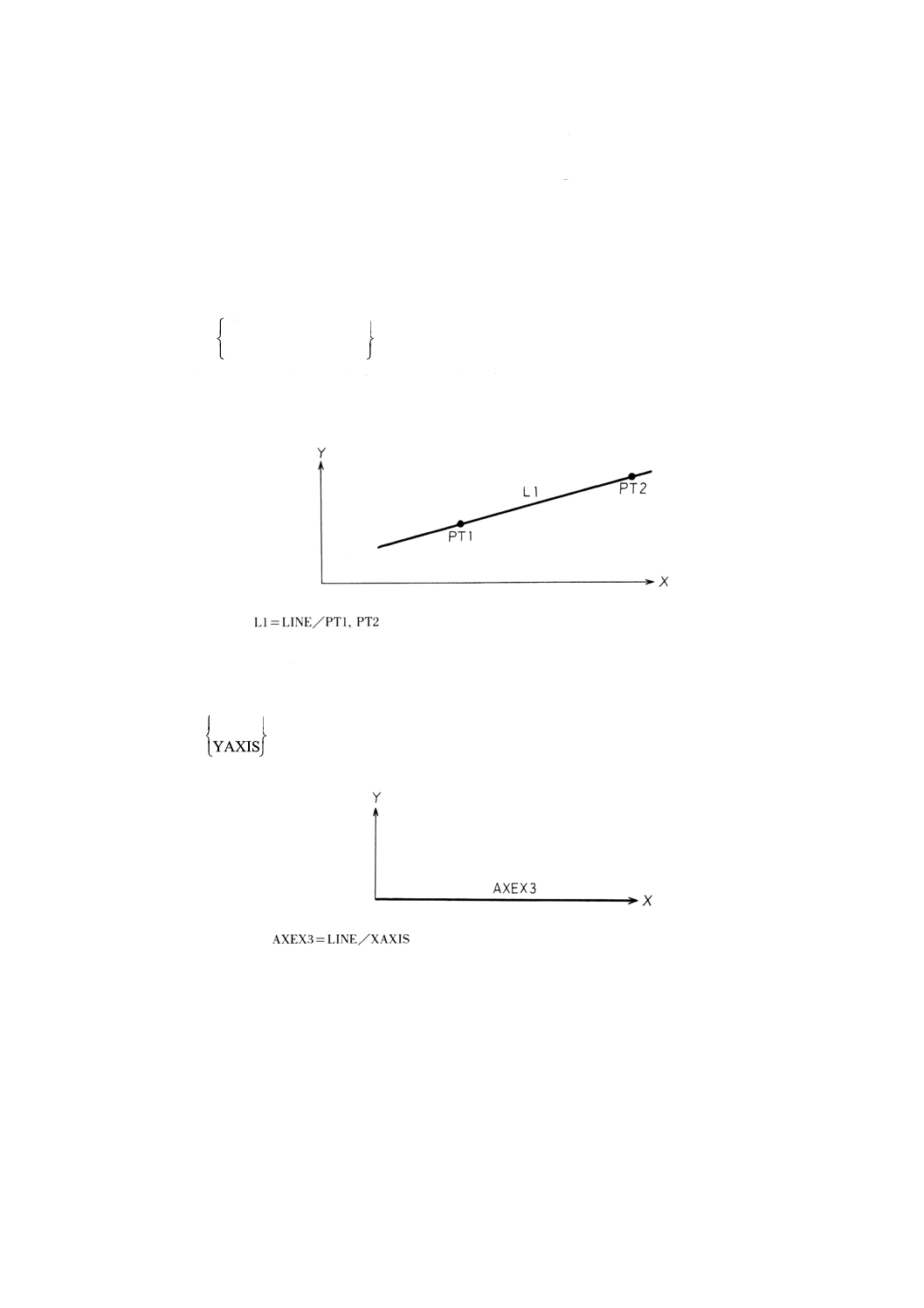
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

＜点規制詞＞，PERPTO，＜円すい曲線規制詞＞｜ 

＜点規制詞＞，PERPTO，＜円すい曲線規制詞＞22［，＜点規制詞＞］｜ 

＜点規制詞＞，TANTO，＜タブシル規制詞＞，＜点規制詞＞｜ 

＜点規制詞＞，PERPTO，＜タブシル規制詞＞，＜点規制詞＞ 

9.6.2 

2点を通る直線の定義 

9.6.2.1 

意味 2点により直線を定義する。 

一般形は，次のとおりとする。 

LINE／

2

1

z2]

y2[,

x2,

z1],

y1[,

x1,

点

，

点

備考1. (x1, y1, z1)， (x2, y2, z2) は，それぞれ点の座標とする。 

2. 点1，点2は，異なる二つの点である。 

例： 2点を通る直線の定義の例 

9.6.3 

座標軸の一つとしての直線の定義 

9.6.3.1 

意味 座標軸を直線として定義する。 

一般形は，次のとおりとする。 

LINE/

YAXIS

XAXIS

例： 

座標軸の一つとしての直線の定義の例 

9.6.4 

点を通り直線に平行な直線の定義 

9.6.4.1 

意味 1点を通り一つの直線に平行な直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，PARLEL，直線 

備考1. 点1は，定義する直線上の点とする。 

2. 直線は，定義する直線と平行な直線とする。 

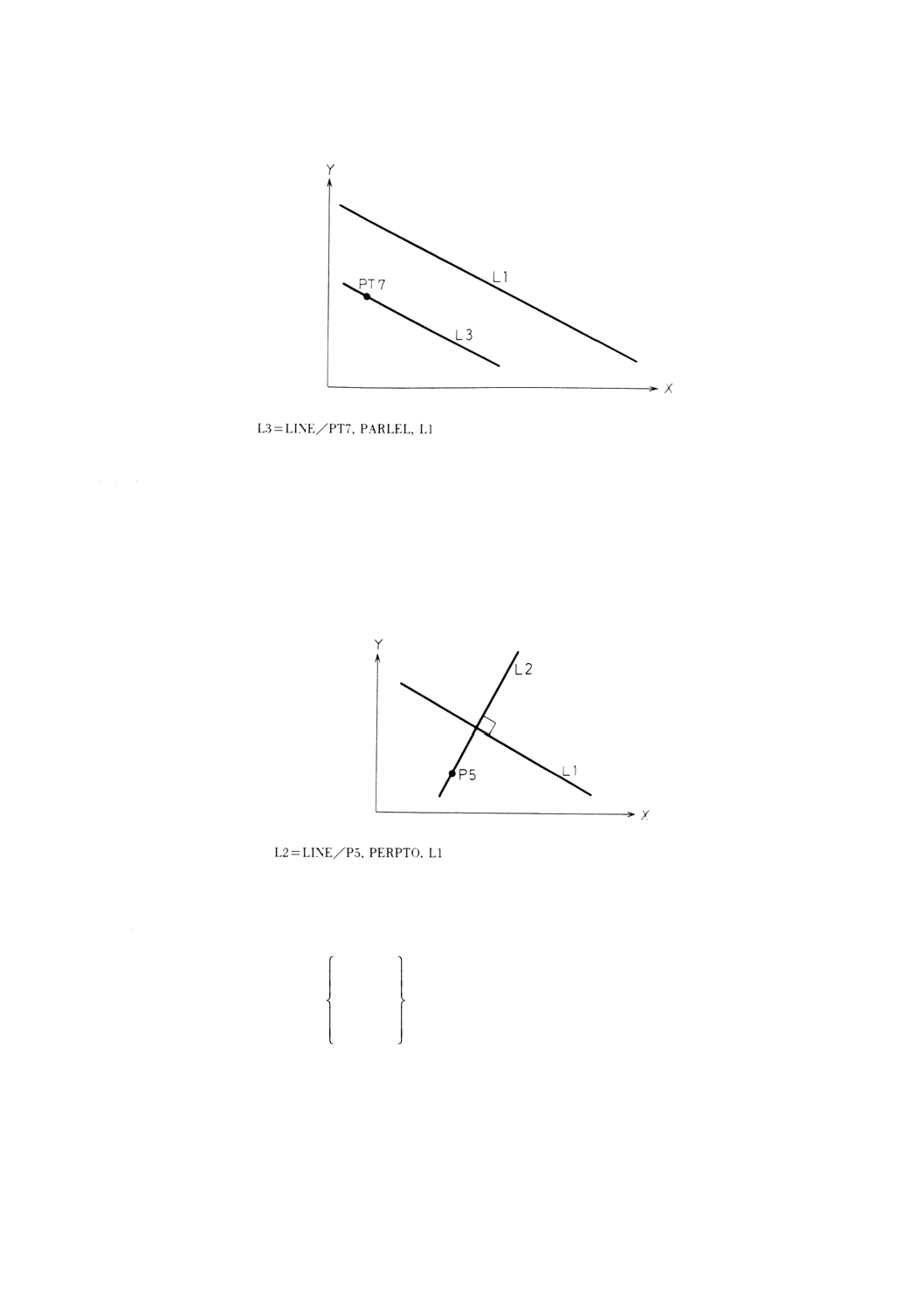
48 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点を通り直線に平行な直線の定義の例 

9.6.5 

点を通り直線に垂直な直線の定義 

9.6.5.1 

意味 1点を通り一つの直線に垂直な直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，PERPTO，直線 

備考1. 点は，定義する直線上の点とする。 

2. 直線は，定義する直線と直交する直線とする。 

例： 点を通り直線に垂直な直線の定義の例 

9.6.6 

直線に平行でその直線と指定した距離をもつ直線の定義 

9.6.6.1 

意味 一つの直線に平行でその直線と指定した距離をもつ直線を定義する。 

一般形は，次のとおりとする。 

LINE/PARLEL，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，距離 

備考1. 直線は，定義する直線と平行な直線とする。 

2. 距離は，2直線間の距離とする。 

3. 指定した直線が一方の座標軸に垂直な場合，その座標軸に関する修飾語だけが使用てきる。

例えば，Y軸に垂直な場合．YLARGE又はYSMALLだけが使用できる。 

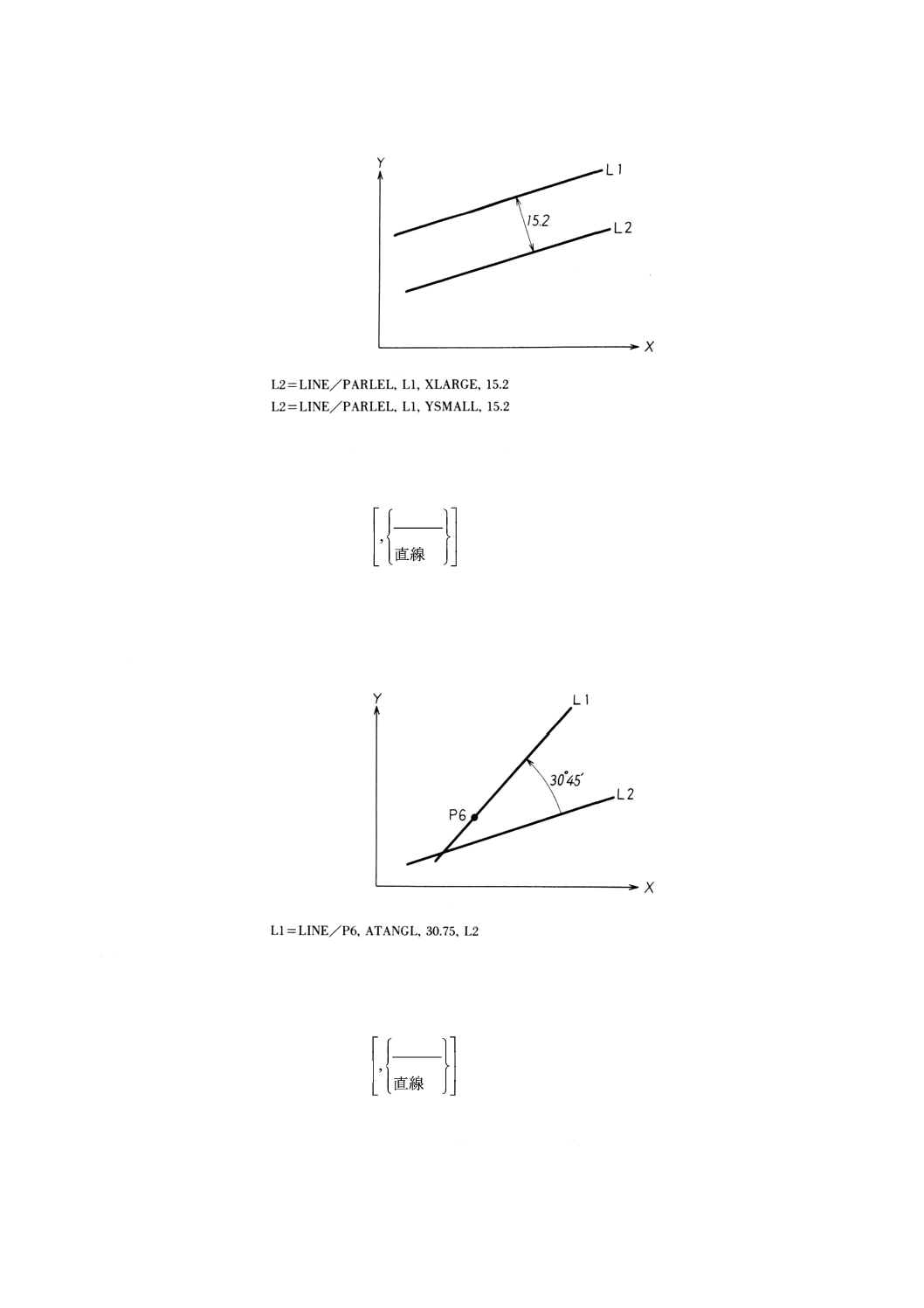
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 直線に平行でその直線と指定した距離をもつ直線の定義の例 

9.6.7 

点を通り直線とある角度をなす直線の定義 

9.6.7.1 

意味 1点を通り一つの直線とある角度をなす直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，ATANGL，角度，

直線

YAXIS

XAXIS

,

備考1. 点は，定義する直線上の点とする。 

2. 角度は，基準軸X，基準軸Y又は直線と定義する直線とのなす角度とし，反時計回りの向き

に測った角度を正とする。 

例： 点を通り直線とある角度をなす直線の定義の例 

9.6.8 

点を通り直線とあるこう配をもつ直線の定義 

9.6.8.1 

意味 1点を通り一つの直線とあるこう配をもつ直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，SLOPE，こう配，

直線

YAXIS

XAXIS

,

備考1. 点は，定義する直線上の点とする。 

2. こう配は，基準軸X，基準軸Y又は直線と定義する直線とのなす角度の正接とし，基準軸か

ら反時計回りの向きに測った角度を正とする。 

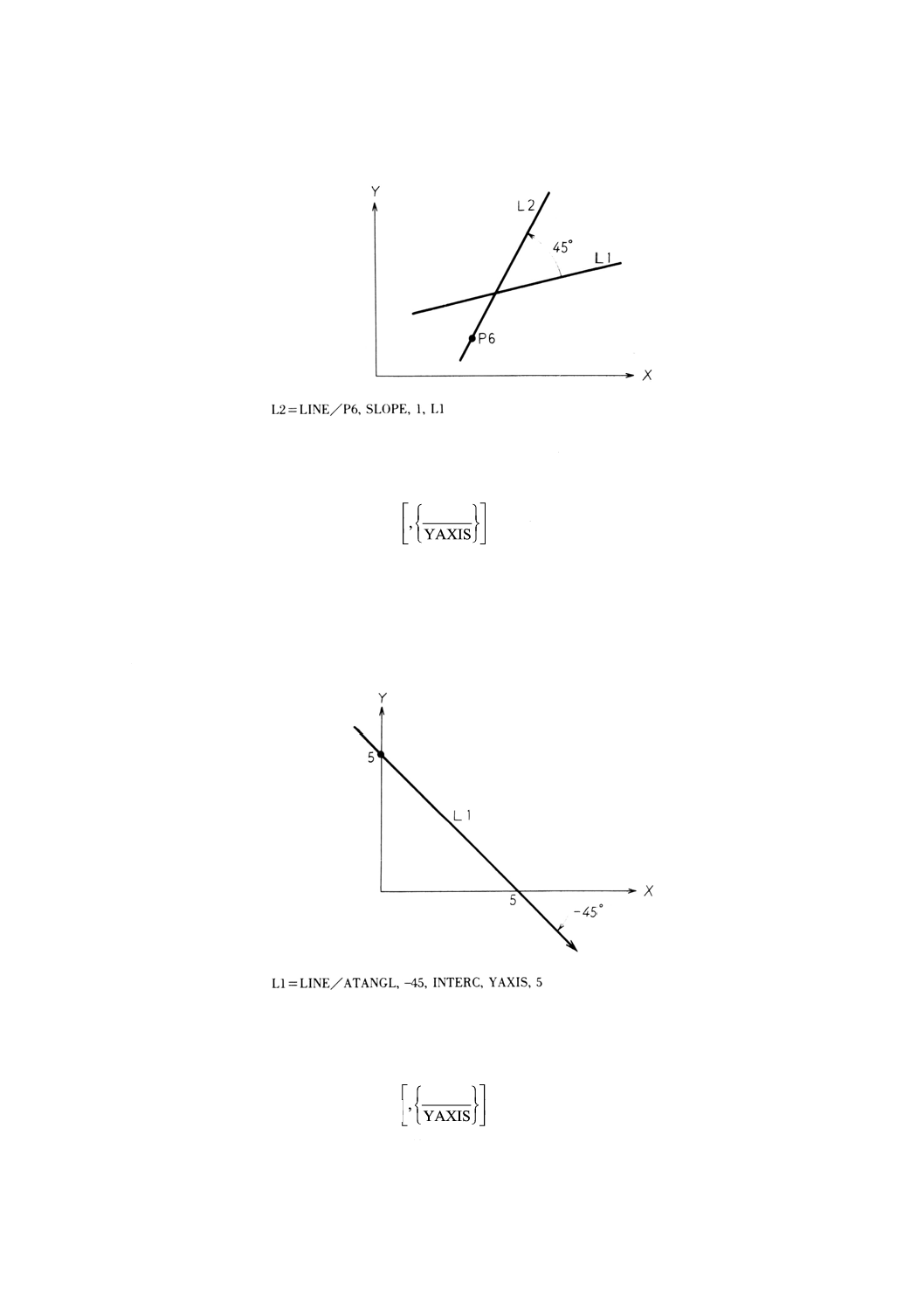
50 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3. 基準軸又は指定した直線に垂直な直線は，この方法では定義することはできない。 

例： 点を通り直線とあるこう配をもつ直線の定義の例 

9.6.9 

X軸からの角度と切片による直線の定義 

9.6.9.1 

意味 X軸からの角度と指定した座標軸の切片により直線を定義する。 

一般形は，次のとおりとする。 

LINE/ATANGL，角度，INTERC，

YAXIS

XAXIS

,

，切片 

備考1. 角度は，基準軸Xと定義される直線とのなす角度とし，基準軸から反時計回りの向きに測っ

た角度を正とする。 

2. 切片は，指定した座標軸の切片とする。基準軸の指定がないときは，基準軸Y軸が指定され

たものとする。 

例： X軸からの角度と切片による直線の定義の例 

9.6.10 X軸に関するこう配と切片による直線の定義 

9.6.10.1 意味 X軸に関するこう配と指定した座標軸の切片により直線を定義する。 

一般形は，次のとおりとする。 

LINE/SLOPE，こう配，INTERC，

YAXIS

XAXIS

,

，切片 

備考1. こう配は基準軸Xと定義する直線とのなす角度の正接とし，基準軸から反時計回りの向きに

測った角度を正とする。 

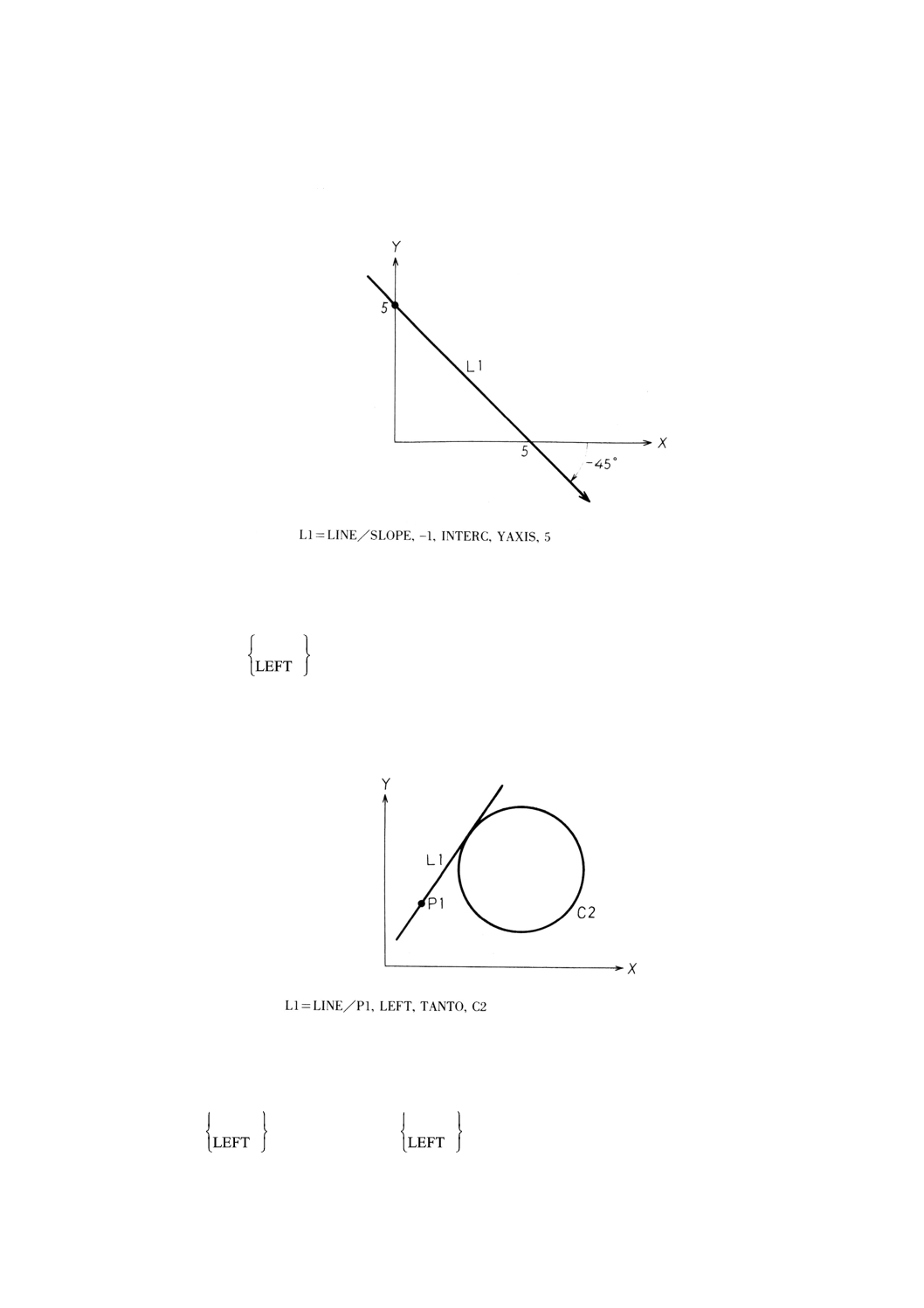
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2. 切片は，指定した座標軸の切片とする。基準軸の指定がないときは，基準軸Yが指定された

ものとする。 

3. 基準軸に垂直な直線は，この方法では定義できない。 

例： X軸に関するこう配と切片による直線の定義の例 

9.6.11 点を通り円に接する直線の定義 

9.6.11.1 意味 1点を通り円に接する直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，

LEFT

RIGHT

，TANTO，円 

備考1. 点は，円周上又は円外の点とする。 

2. 円は，定義する直線に接する円とする。 

例： 点を通り円に接する直線の定義の例 

9.6.122 円に接する直線の定義 

9.6.12.1 意味 2円に接する直線を定義する。 

一般形は，次のとおりとする。 

LINE/

LEFT

RIGHT

，TANTO，円1，

LEFT

RIGHT

，TANTO，円2 

備考1. 円1と円2は異なる円とし，いずれか一方の円が他の円の中に含まれてはならない。 

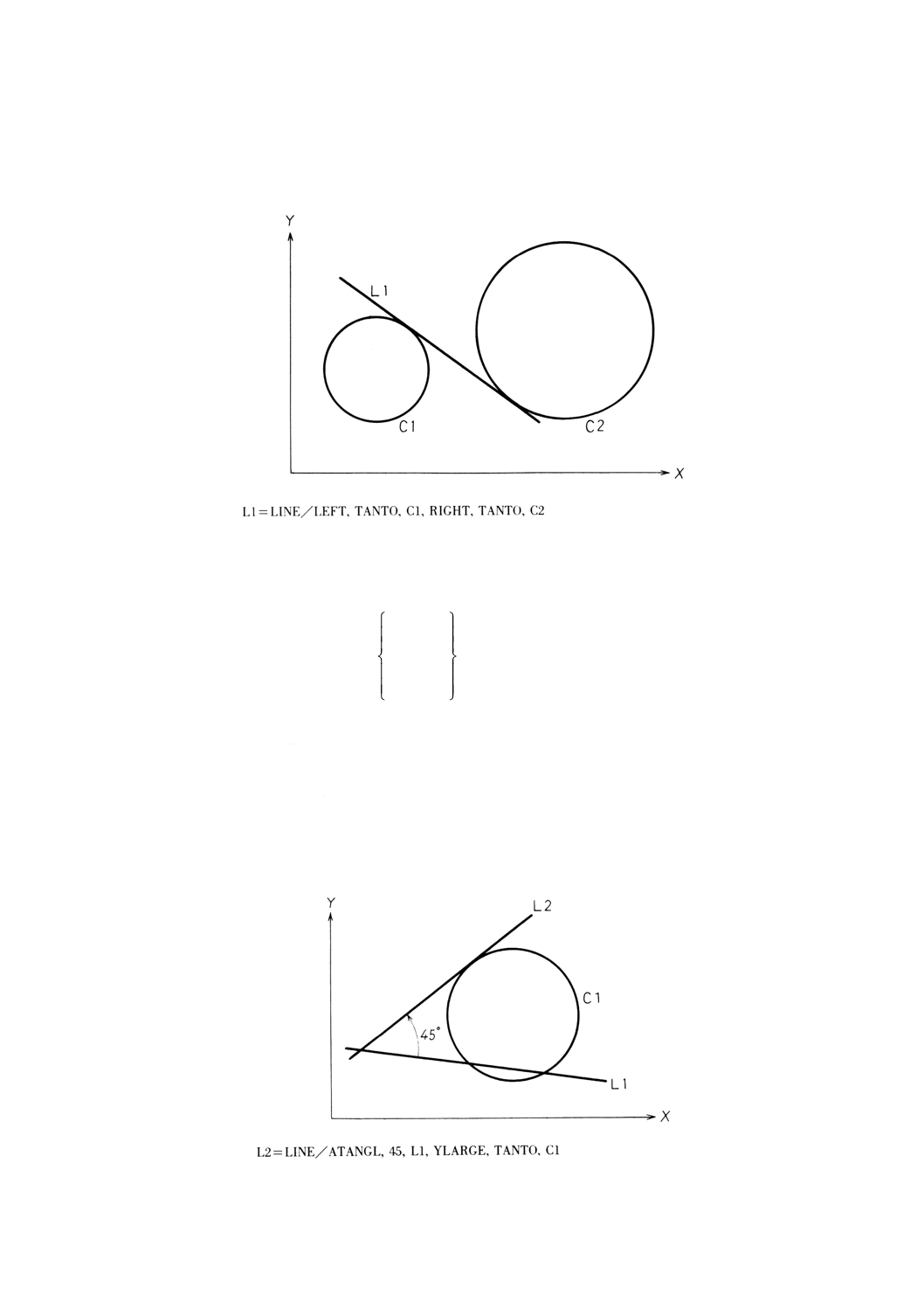
52 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2. 円1と円2とが接している場合，円1についてRIGHTを選択したなら，円2についてはLEFT

を選択し，円1についてLEFTを選択したなら，円2についてはRIGHTを選択する。 

例： 2円に接する直線の定義の例 

9.6.13 直線とある角度をなし円に接する直線の定義 

9.6.13.1 意味 一つの直線とある角度をなし円に接する直線を定義する。 

一般形は，次のとおりとする。 

LINE/ATANGL，角度，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，TANTO，円 

備考1. 角度は，指定する直線と定義する直線とのなす角度とし，指定する直線から反時計回りの向

きに測った角度を正とする。 

2. 直線は，直線に対し定義する直線が指定の角度をもつ直線とする。 

3. 円は，定義する直線が接する円とする。 

4. 定義する直線が座標軸に垂直な場合，その軸に関する修飾語だけが使用できる。例えば，Y

軸に垂直な場合，YLARGE又はYSMALLだけが使用できる。 

例： 直線とある角度をなし円に接する直線の定義の例 

9.6.14 

2平面の交線としての直線の定義 

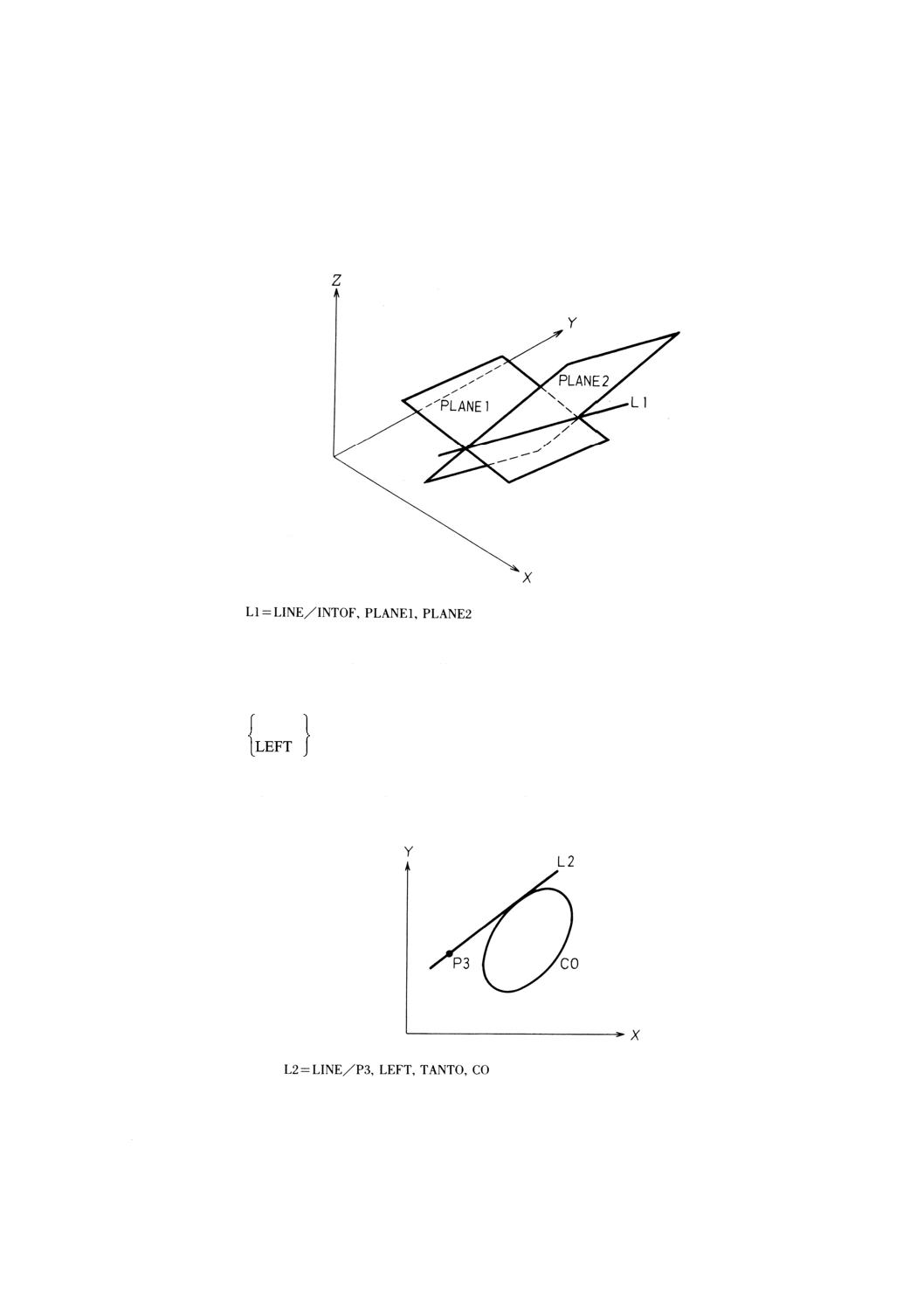
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.6.14.1 意味 2平面の交線を直線として定義する。 

一般形は，次のとおりとする。 

LINE/INTOF，平面1，平面2 

備考 平面1と平面2とは異なる平面とし，互いに平行でない平面とする。 

例： 2平面の交線としての直線の定義の例 

9.6.15 点を通り円すい曲線に接する直線の定義 

9.6.15.1 意味 1点を通り円すい曲線に接する直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，

LEFT

RIGHT

，TANTO，円すい曲線 

備考1. 点は，円すい曲線上又は円すい曲線外の点とする。 

2. 円すい曲線は，定義する直線に接する円すい曲線とする。 

例： 点を通り円すい曲線に接する直線の定義の例 

9.6.16 円すい曲線上の点とこの点で円すい曲線に垂直な直線の定義 

9.6.16.1 意味 円すい曲線上の1点とこの点で円すい曲線に垂直な直線を定義する。 

一般形は，次のとおりとする。 

LINE／点，PERPTO，円すい曲線 

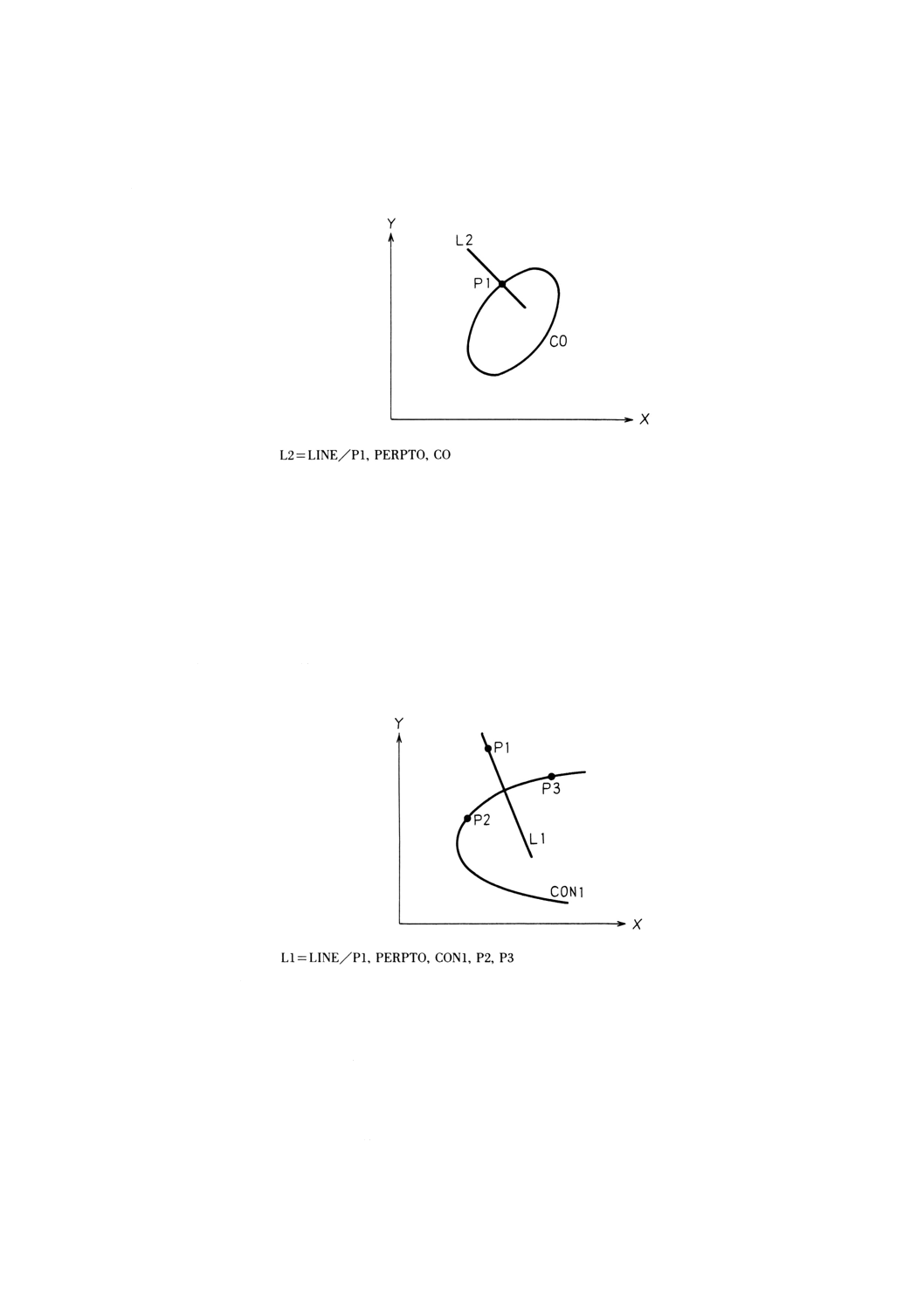
54 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

備考1. 点は，円すい曲線上の点とする。 

2. 円すい曲線は，定義する直線と垂直の円すい曲線とする。 

例： 円すい曲線上の点とこの点で円すい曲線に垂直な直線の定義の例 

9.6.17 点を通り円すい曲線に垂直な直線の定義 

9.6.17.1 意味 1点を通り円すい曲線に垂直な直線を定義する。 

一般形は，次のとおりとする。 

LINE／点1，PERPTO，円すい曲線，点2，点3 

備考1. 点1は，定義する直線が通る点とする。 

2. 円すい曲線は，定義する直線と垂直な円すい曲線とする。 

3. 定義する直線は，点2と点3の区間の円すい曲線について垂直とする。 

4. 複数の垂直な直線が引ける可能性があるときは，定義できない。 

例： 点を通り円すい曲線に垂直な直線の定義の例 

9.6.18 点を通りタブシルに接する直線の定義 

9.6.18.1 意味 1点を通り指定した点の近傍でタブシルに接する直線を定義する。 

一般形は，次のとおりとする。 

LINE／点1，TANTO，タブシル，点2 

備考1. 点1は，直線が通る点とする。 

2. 点2は，タブシルと定義する直線との接点の近傍にあってタブシルの定義に用いた点とする。 

3. タブシルは，定義する直線に接するタブシルとし，XY平面に垂直とする。 

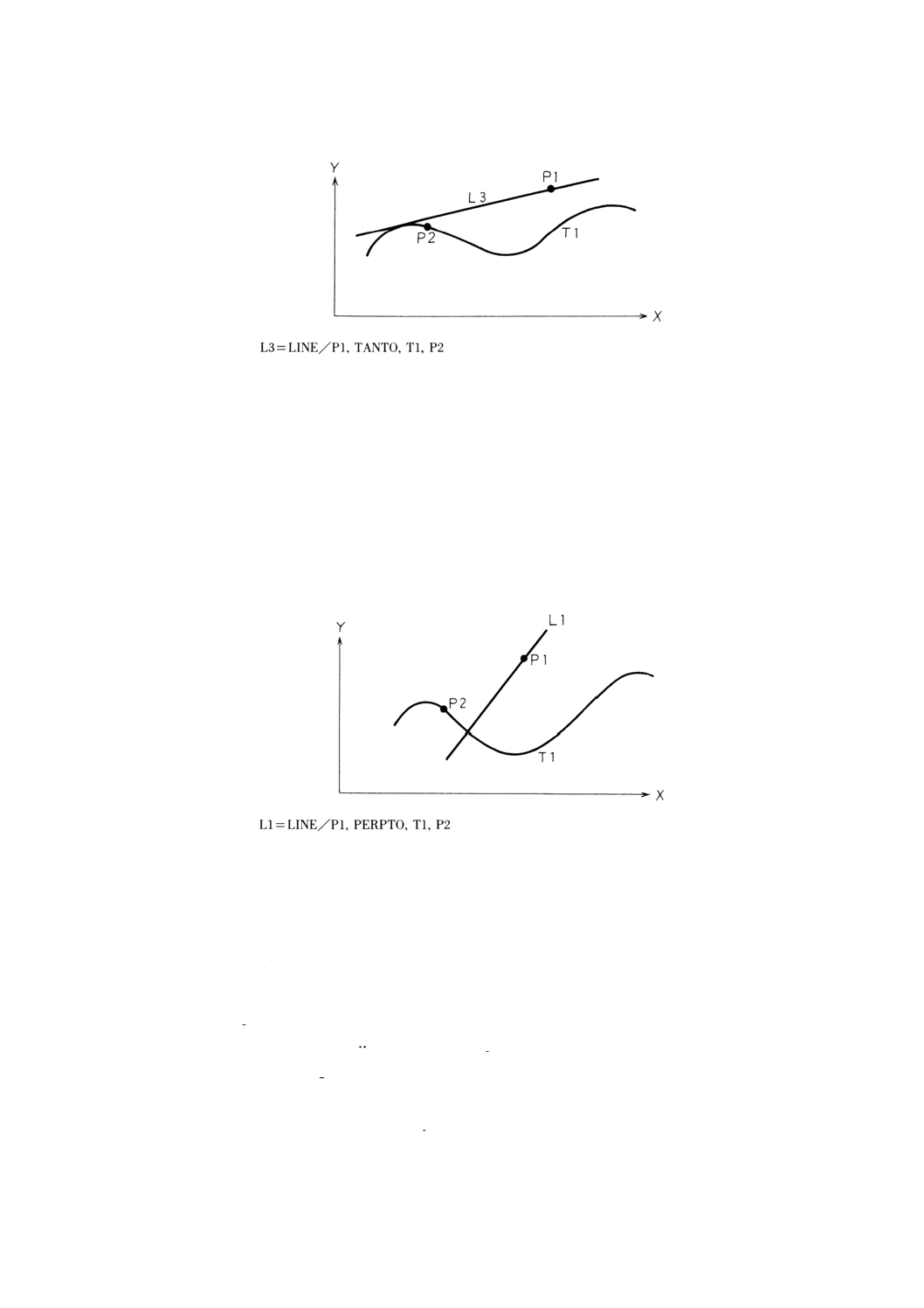
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点を通りタブシルに接する直線の定義の例 

9.6.19 点を通りタブシルに垂直な直線の定義 

9.6.19.1 意味 1点を通り指定した点の近傍でタブシルに垂直な直線を定義する。 

一般形は，次のとおりとする。 

LINE／点1，PERPTO，タブシル，点2 

備考1. 点1は，直線が通る点とする。 

2. タブシルは，定義する直線と垂直なタブシルとし，XY平面に垂直とする。 

3. 点2は，定義する直線とタブシルが垂直に交わる交点の近傍にあってタブシルの定義に用い

た点とする。 

例： 点を通りタブシルに垂直な直線の定義の例 

9.7 

平面定義文 

9.7.1 

意味と構文 

9.7.1.1 

意味 平面定義文は，平面を定義する。 

9.7.1.2 

構文 構文は，次による。 

＜平面定義文＞ :: ＝＜名前＞＝PLANE／＜平面のパラメータの並び＞ 

＜平面規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］PLANE／＜平面のパラメータの並び＞） 

＜平面のパラメータの並び＞ :: ＝＜スカラー＞33［，＜スカラー＞］｜ 

＜点規制詞＞22［，＜点規制詞＞］｜ 

＜点規制詞＞，PARLEL，＜平面規制詞＞｜ 

PARLEL，＜平面規制詞＞，11[XLARGE｜XSMALL｜YLARGE｜YSMALL｜ZLARGE｜ 

ZSMALL]，＜スカラー＞｜ 

＜点規制詞＞，PERPTO，＜ベクトル規制詞＞｜ 

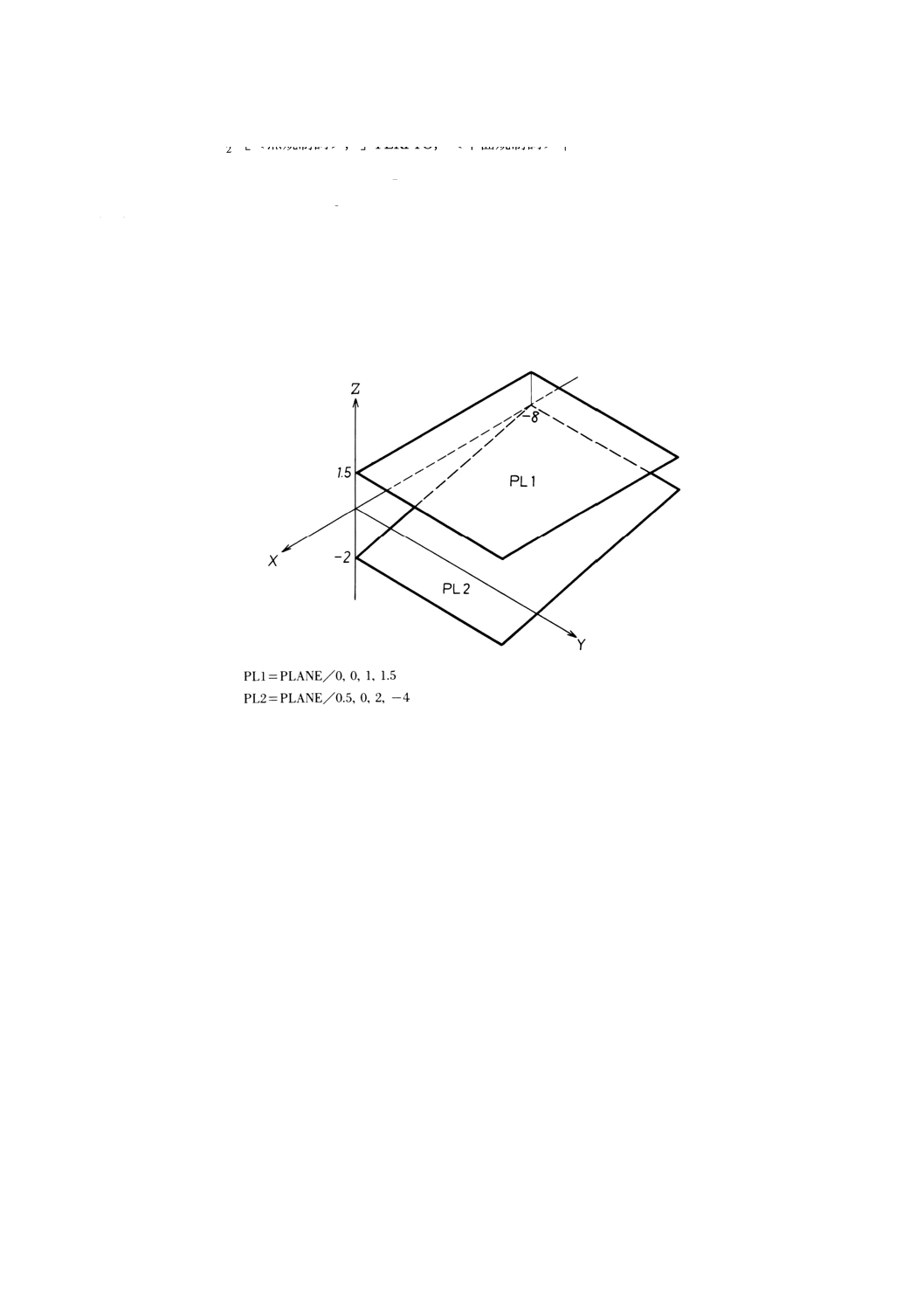
56 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

22［＜点規制詞＞，］PERPTO，＜平面規制詞＞｜ 

＜点規制詞＞，PERPTO22［，＜平面規制詞＞］｜ 

＜点規制詞＞，11 [RIGHT｜LEFT], TANTO，＜円柱規制詞＞ 

9.7.2 

平面の方程式の係数による平面の定義 

9.7.2.1 

意味 平面の方程式の係数により平面を定義する。 

一般形は，次のとおりとする。 

PLANE/a, b, c, d 

備考 a，b，c，dは，ax＋by＋cz＝dにおける係数とする。 

例： 平面の方程式の係数による平面の定義の例 

9.7.3 

3点を通る平面の定義 

9.7.3.1 

意味 3点により平面を定義する。 

一般形は，次のとおりとする。 

PLANE／点1，点2，点3 

備考 点1，点2，点3は，定義する平面上にある点とする。 

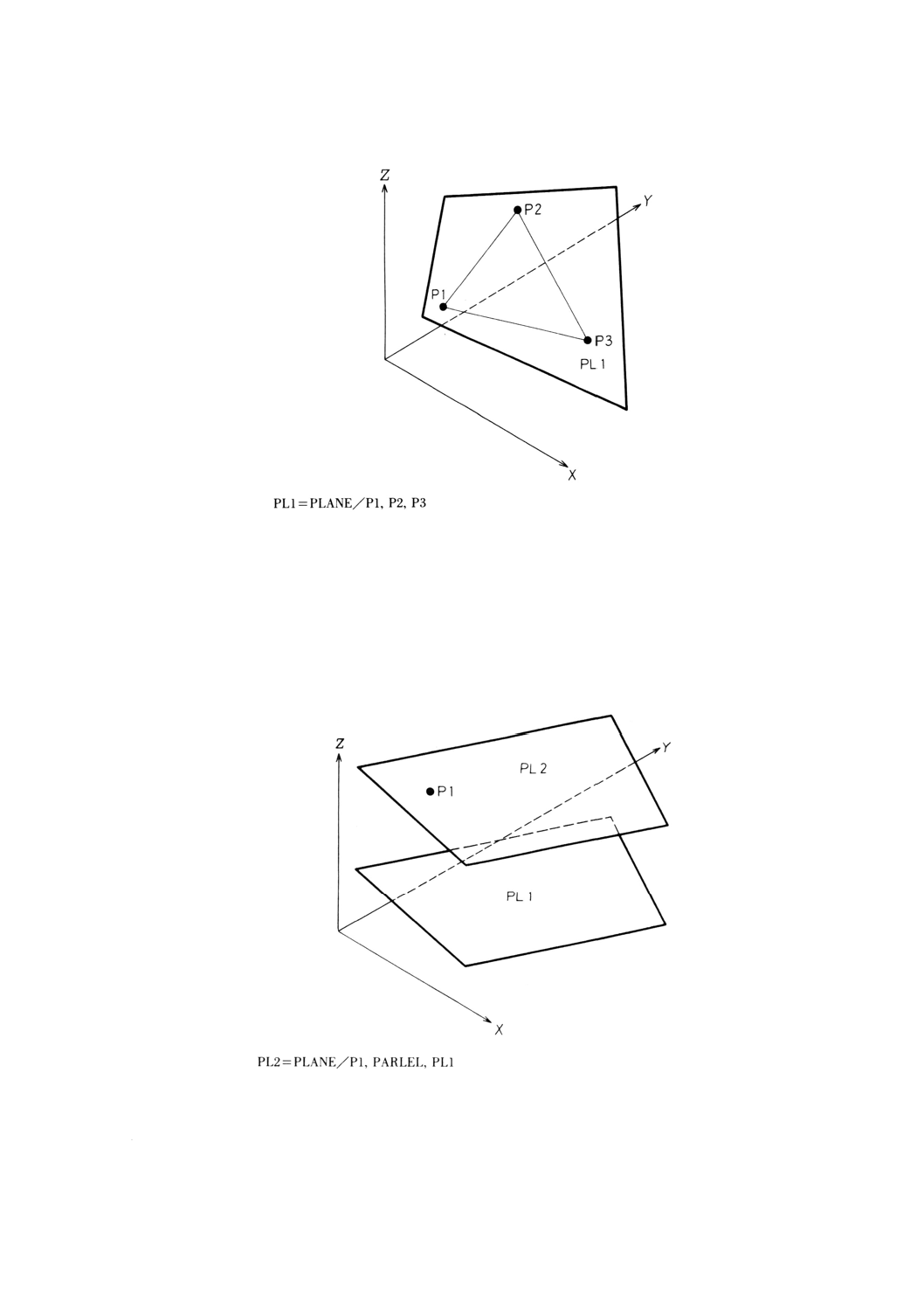
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 3点を通る平面の定義の例 

9.7.4 

点を通り平面に平行な平面の定義 

9.7.4.1 

意味 1点を通り平面に平行な平面を定義する。 

一般形は，次のとおりとする。 

PLANE／点，PARLEL,平面 

備考1. 点は，定義する平面上の点とする。 

2. 平面は，定義する平面と平行な平面とする。 

例： 点を通り平面に平行な平面の定義の例 

9.7.5 

平面に平行で指定した距離をもつ平面の定義 

9.7.5.1 

意味 一つの平面に平行で，その平面と指定した距離をもつ平面を定義する。 

一般形は，次のとおりとする。 

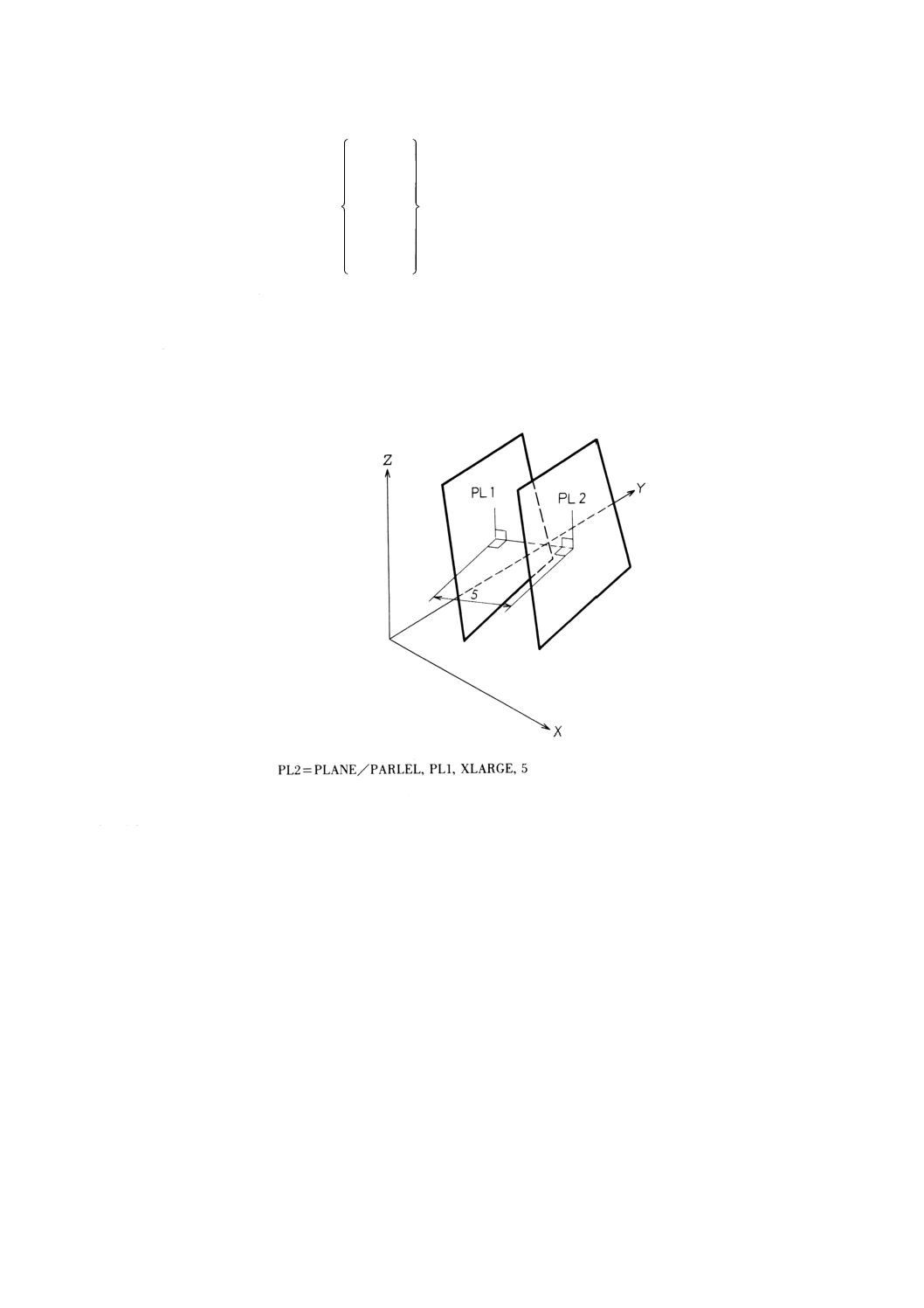
58 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

PLANE/PARLEL，平面，

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，距離 

備考1. 平面は，定義する平面と平行な平面とする。 

2. 距離は，2平面間の距離とする。 

3. 指定した平面が座標軸に平行な場合，その軸に関する修飾語は使用できない。例えば，Y軸

に平行な場合，YLARGE又はYSMALLを使用することはできない。 

例： 平面に平行で指定した距離をもつ平面の定義の例 

9.7.6 

点を通りベクトルに垂直な平面の定義 

9.7.6.1 

意味 1点を通り指定したベクトルに垂直な平面を定義する。 

一般形は，次のとおりとする。 

PLANE／点，PERPTO，ベクトル 

備考1. 点は，定義する平面上の点とする。 

2. ベクトルは，定義する平面に垂直なベクトルとする。 

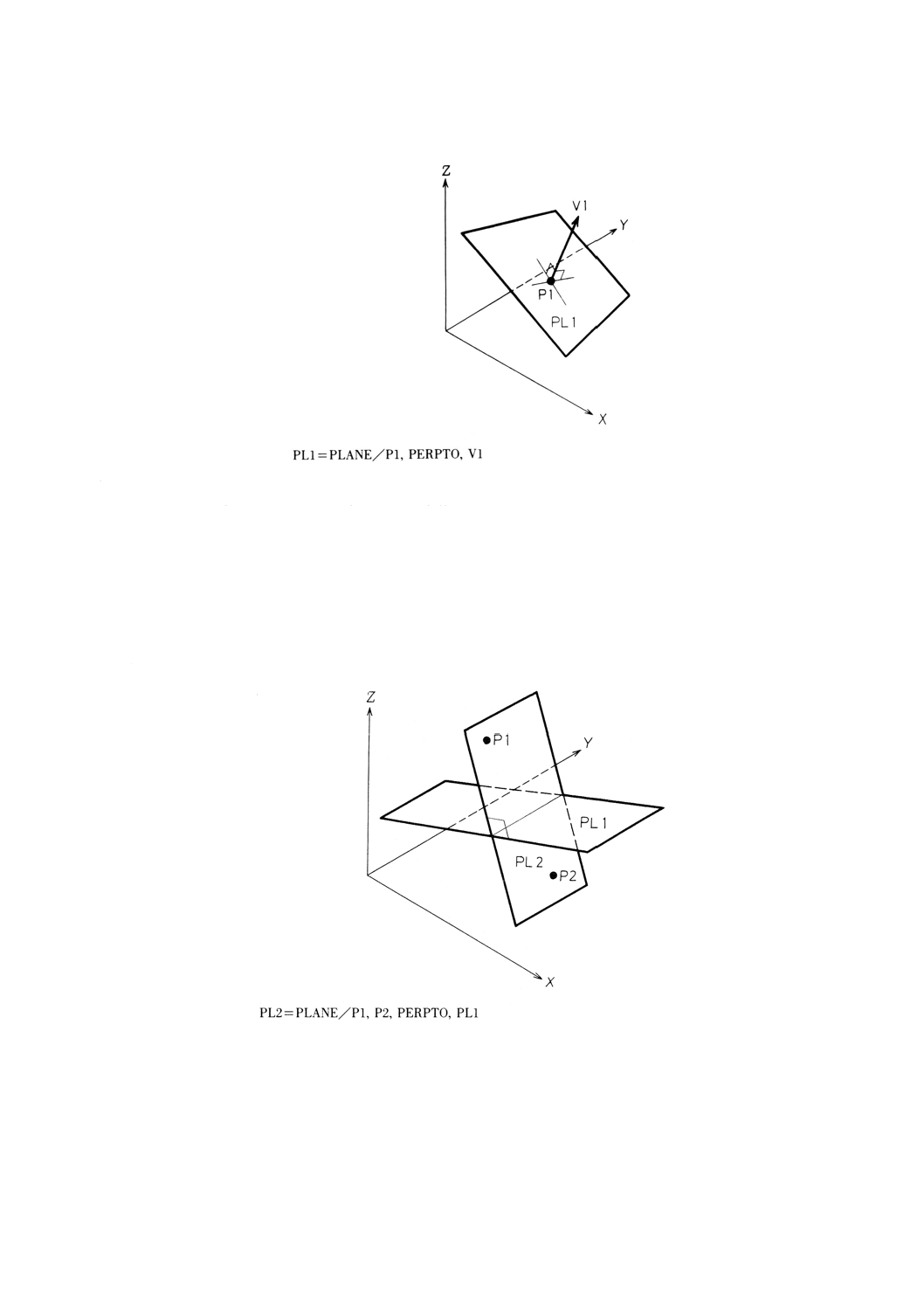
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点を通りベクトルに垂直な平面の定義の例 

9.7.7 

2点を通り平面に垂直な平面の定義 

9.7.7.1 

意味 2点を通り平面に垂直な平面を定義する。 

一般形は，次のとおりとする。 

PLANE／点1，点2，PERPTO，平面 

備考1. 点1，点2は，定義する平面上の点とする。 

2. 平面は，定義する平面と垂直な平面とする。 

3. 点1と点2を結ぶ直線は，平面に直角であってはならない。 

例： 2点を通り平面に垂直な平面の定義の例 

9.7.8 

点を通り2平面に垂直な平面の定義 

9.7.8.1 

意味 1点を通り2平面に垂直な平面を定義する。 

一般形は，次のとおりとする。 

PLANE／点，PERPTO，平面1，平面2 

備考1. 点は，定義する平面上の点とする。 

2. 平面1，平面2は，それぞれ定義する平面に垂直とする。 

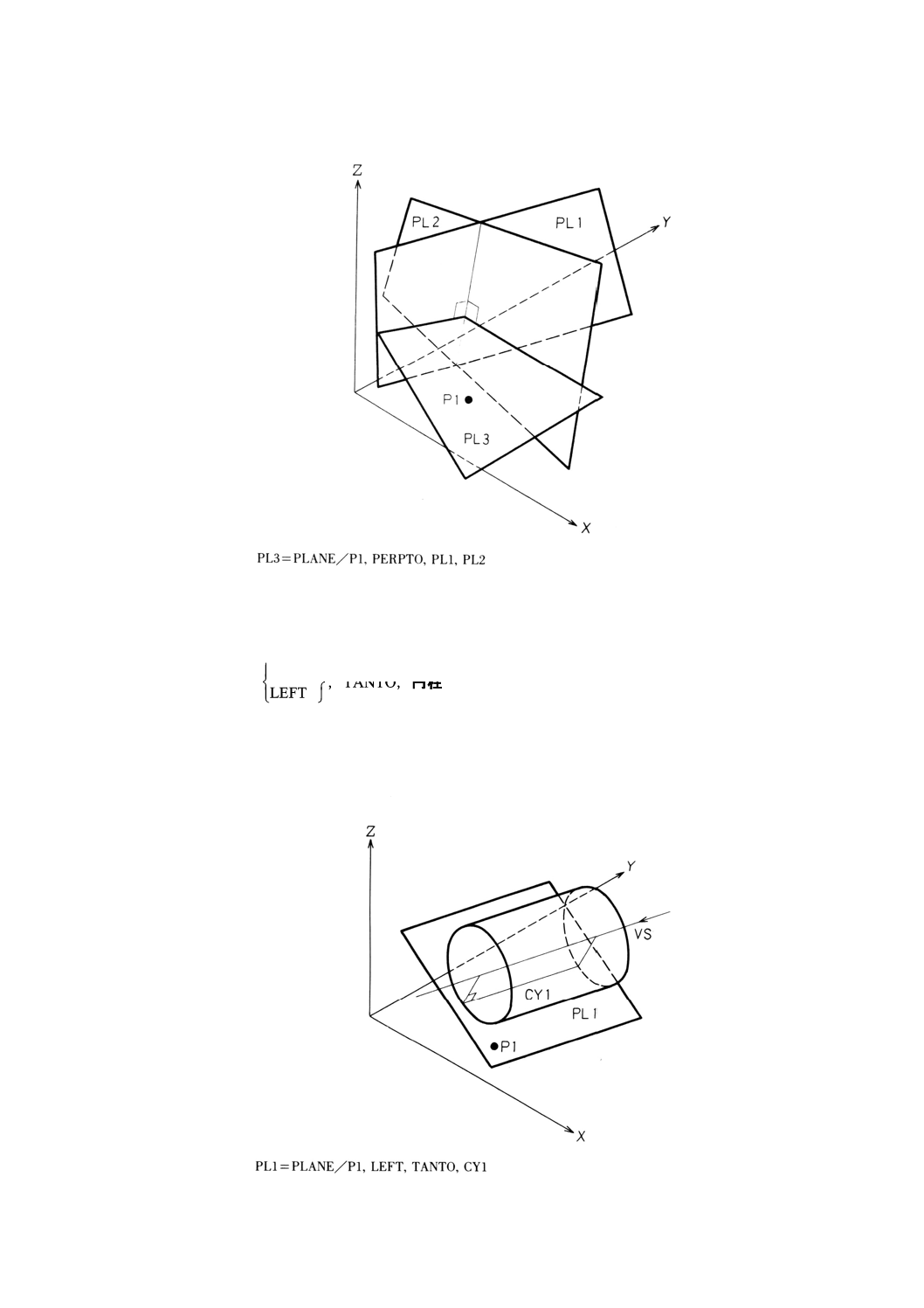
60 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点を通り2平面に垂直な平面の定義の例 

9.7.9 

点を通り円柱に接する平面の定義 

9.7.9.1 

意味 1点を通り円柱に接する平面を定義する。 

一般形は，次のとおりとする。 

PLANE／点，

LEFT

RIGHT，TANTO，円柱 

備考1. 点が円柱上にあるときは，RIGHT又はLEFTのいずれでもよい。 

2. 円柱の中心軸のベクトルと平行の向きに点の位置に立つとして，RIGHT又はLEFTの選択を

行う。 

例： 点を通り円柱に接する平面の定義の例 

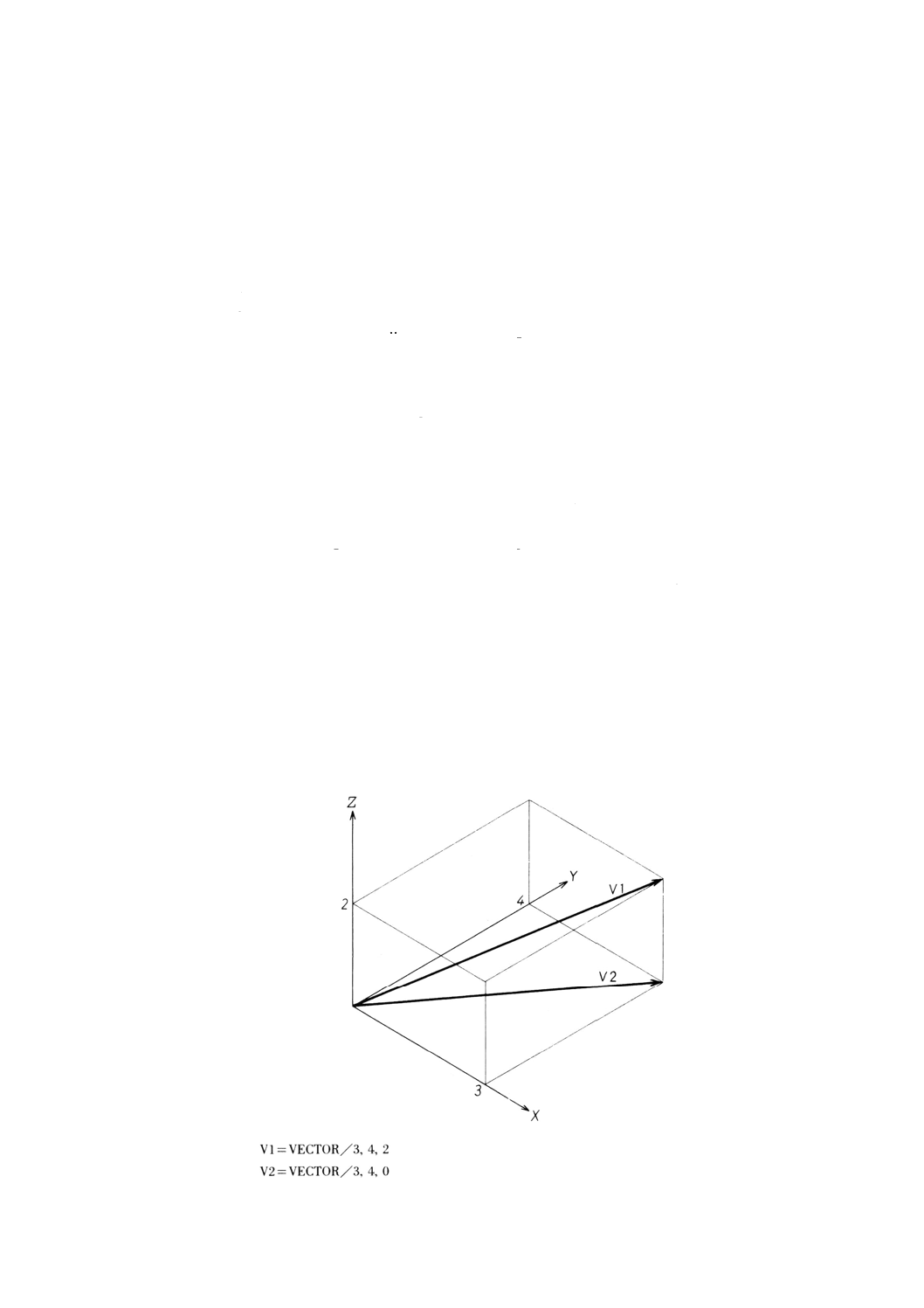
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.8 

ベクトル定義文 

9.8.1 

意味と構文 

9.8.1.1 

意味 ベクトル定義文は，ベクトルを定義する。 

9.8.1.2 

構文 構文は，次による。 

＜ベクトル定義文＞ :: ＝＜名前＞＝VECTOR／＜ベクトルのパラメータの並び＞ 

＜ベクトル規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］VECTOR／＜ベクトルのパラメータの並び＞） 

＜ベクトルのパラメータの並び＞ :: ＝＜スカラー＞22［，＜スカラー＞］｜ 

＜スカラー＞55［，＜スカラー＞］｜ 

＜点規制詞＞，＜点規制詞＞｜ 

PERPTO，＜平面規制詞＞，11 [POSX｜POSY｜POSZ｜NEGX｜NEGY｜NEGZ] ｜ 

＜スカラー＞，TIMES，＜ベクトル規制詞＞｜ 

＜ベクトル規制詞＞，CROSS，＜ベクトル規制詞＞｜ 

UNIT, 11［＜スカラー＞22［，＜スカラー＞］｜＜ベクトル規制詞＞］｜ 

LENGTH，＜スカラー＞，ATANGL，＜スカラー＞，11 [XYPLAN｜YZPLAN｜ZXPLAN] ｜ 

PARLEL, INTOF22［，＜平面規制詞＞］，11[POSX｜POSY｜POSZ｜NEGX｜NEGY｜ 

NEGZ]｜ 

＜ベクトル規制詞＞，11 [PLUS｜MINUS] ，＜ベクトル規制詞＞｜ 

ATANGL，＜スカラー＞，＜直線規制詞＞，11 [POSX｜POSY｜NEGX｜NEGY] 

9.8.2 

成分によるベクトルの定義 

9.8.2.1 

意味 座標系の基準軸の成分によりベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR/a, b, c 

備考 (a, b, c) は，それぞれ定義するベクトルの座標軸X，Y及びZの成分とする。 

例： 成分によるベクトルの定義の例 

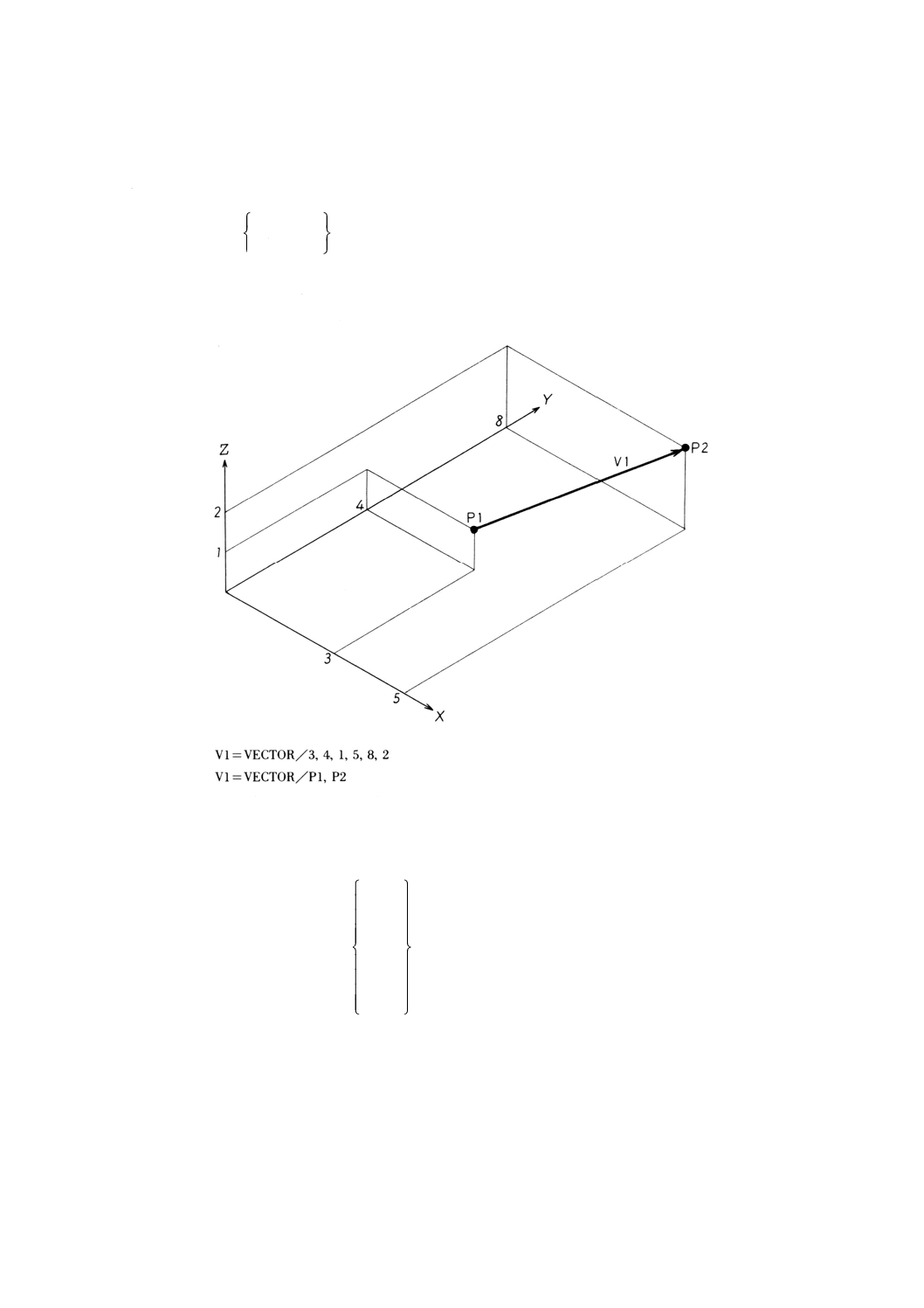
62 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.8.3 

2点によるベクトルの定義 

9.8.3.1 

意味 2点によりベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR／

2

1,

f

e,

d,

c,

b,

a,

点

点

備考1. (a, b, c)，(d, e, f) は，定義するベクトルの始点及び終点の座標とする。 

2. 点1，点2は，定義するベクトルの始点と終点の点規制詞とする。 

例： 2点によるベクトルの定義の例 

9.8.4 

平面に垂直な単位ベクトルの定義 

9.8.4.1 

意味 平面に垂直な単位ベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR/PERPTO，平面，

NEGZ

NEGY

NEGX

POSZ

POSY

POSX

備考1. 平面は，定義するベクトルに垂直な平面とする。 

2. 指定した平面が座標軸に垂直な場合，その軸に関する修飾語だけが使用できる。例えば，X

軸に垂直な平面の場合，POSX又はNEGXだけが使用できる。 

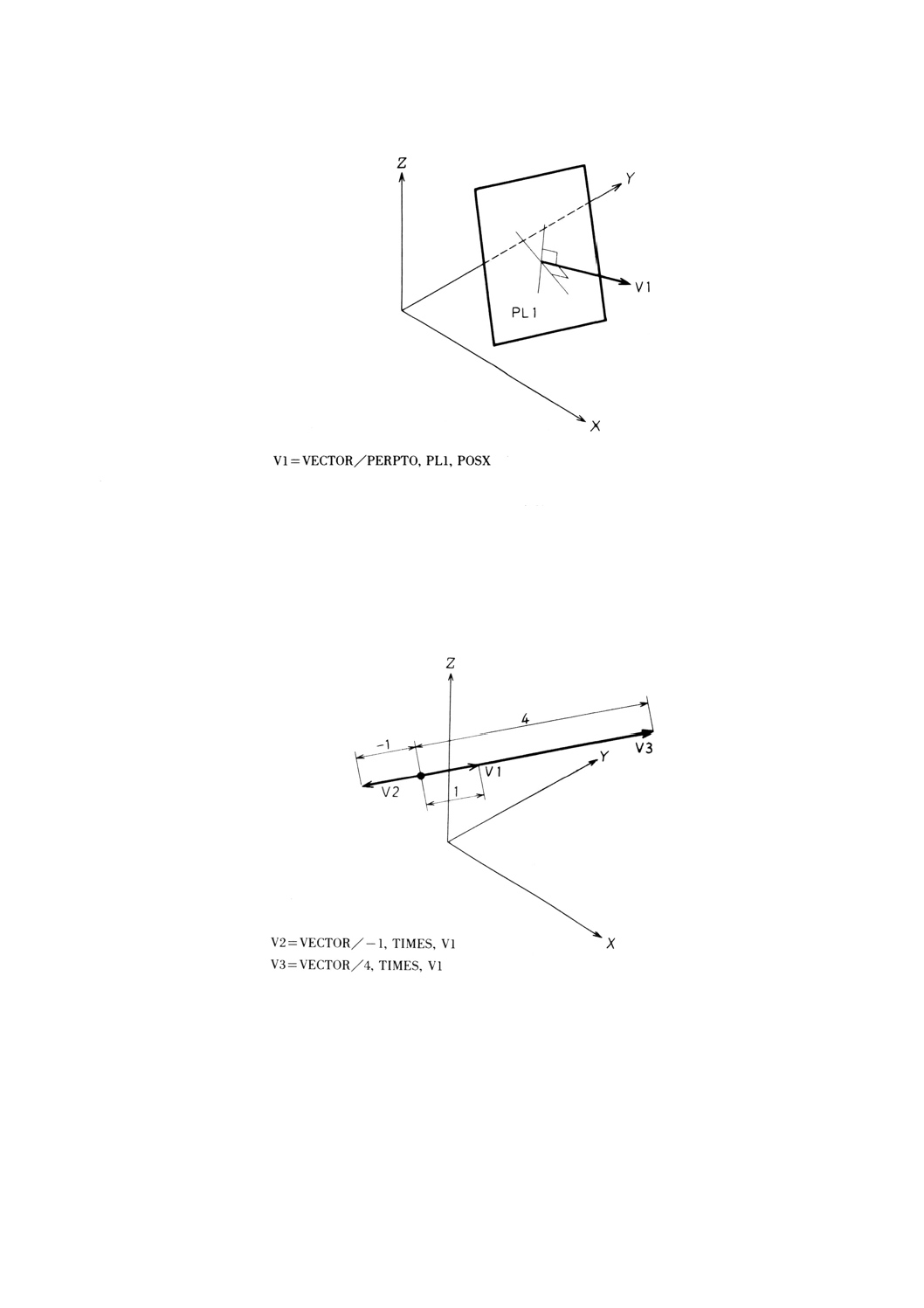
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 平面に垂直な単位ベクトルの定義の例 

9.8.5 

他のベクトルのスカラー倍によるベクトルの定義 

9.8.5.1 

意味 他のベクトルのスカラー倍によりベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR/a，TIMES，ベクトル 

備考 aは，指定するベクトルに乗ずるスカラーとする。aの符号が正のときは，定義するベクトルの

向きは指定したベクトルの向きとし，負のときは逆の向きとする。 

例： 他のベクトルのスカラー倍によるベクトルの定義の例 

9.8.6 

二つのベクトルの外積としてのベクトルの定義 

9.8.6.1 

意味 二つのベクトルの外積により得られるベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR／ベクトル1，CROSS，ベクトル2 

備考 ベクトル1とベクトル2は，その外積が定義するベクトルとなる二つのベクトルとする。 

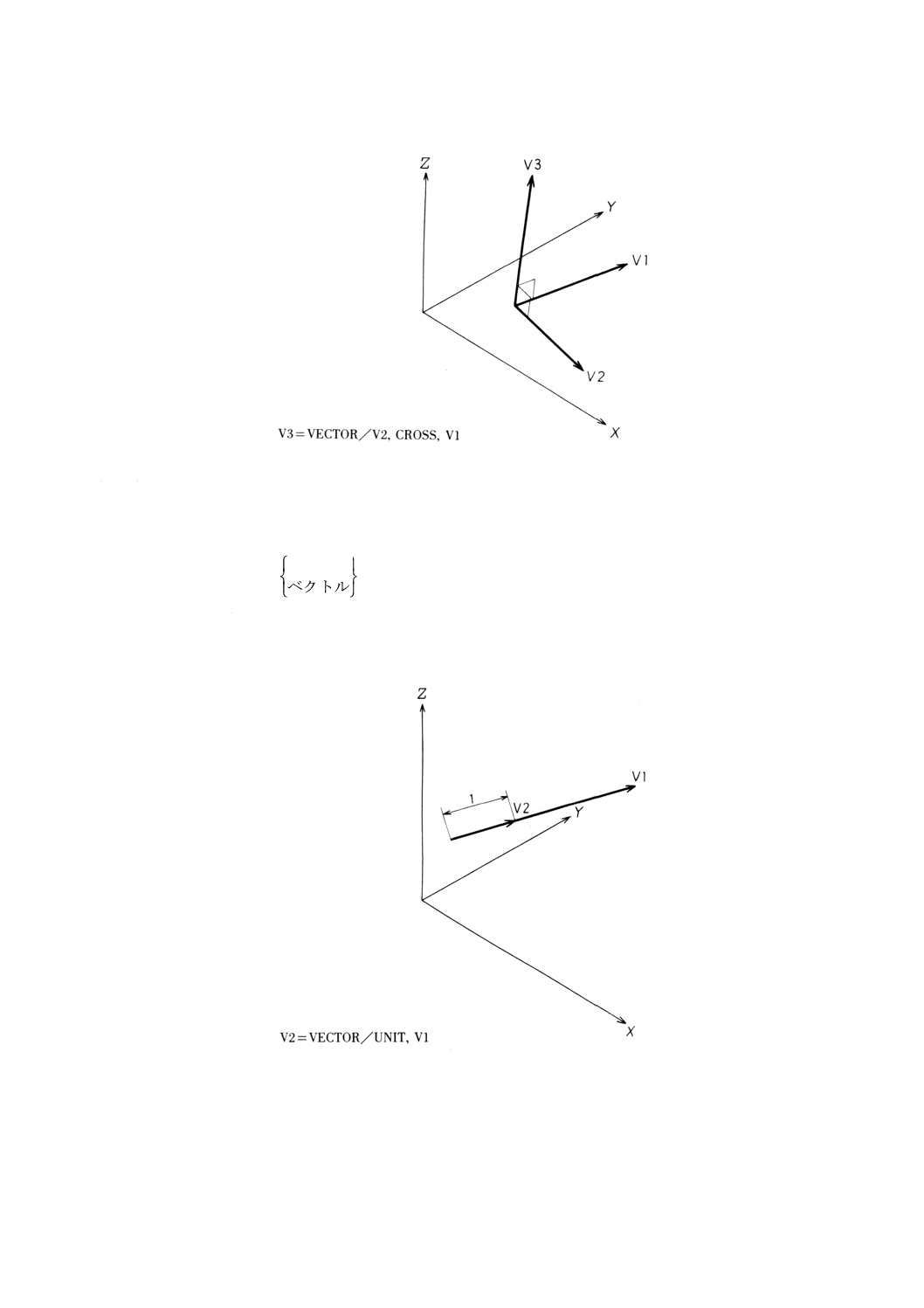
64 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 二つのベクトルの外積としてのベクトルの定義の例 

9.8.7 

ベクトルの正規化による単位ベクトルの定義 

9.8.7.1 

意味 ベクトルの正規化により単位ベクトルを定義する。定義するベクトルは，指定したベクト

ルと同じ向きをもつ単位ベクトルとする。 

一般形は，次のとおりとする。 

VECTOR/UNIT，

ベクトル

c

b,

a,

備考1. (a, b, c) は，定義するベクトルの座標軸X，Y，Z軸の成分とする。 

2. ベクトルは，正規化するベクトルとする。 

例： ベクトルの正規化による単位ベクトルの定義の例 

9.8.8 

大きさと角度によるベクトルの定義 

9.8.8.1 

意味 大きさと角度によりベクトルを定義する。 

一般形は，次のとおりとする。 

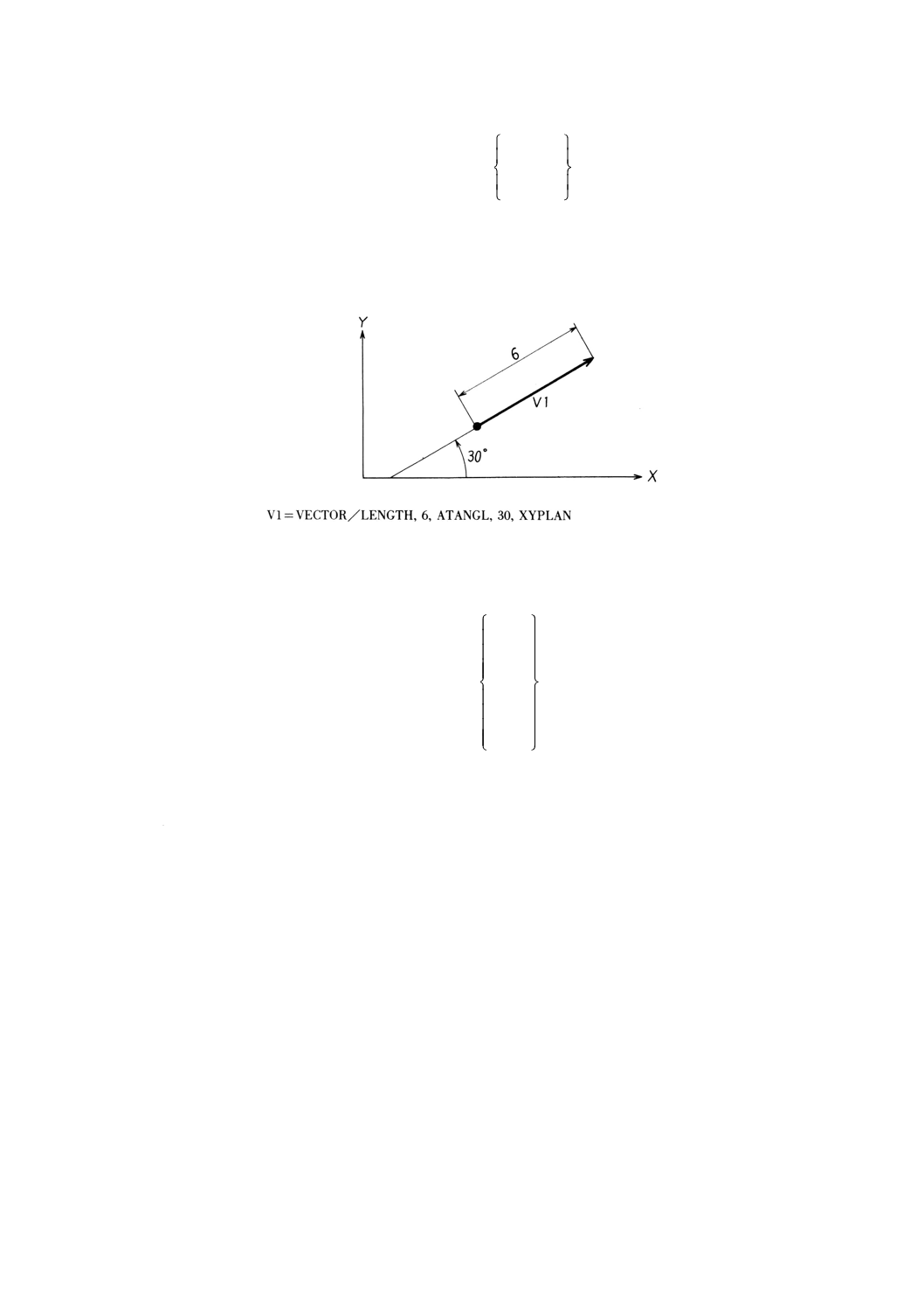
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

VECTOR/LENGTH，大きさ，ATANGL，角度，

ZXPLAN

YZPLAN

XYPLAN

備考1. 大きさは，ベクトルの大きさとする。 

2. 角度は，指定した座標平面の基準軸と定義するベクトルとのなす角度とし，基準軸から反時

計回りの向きに測った角度を正とする。 

例： 大きさと角度によるベクトルの定義の例 

9.8.9 

2平面の交線による単位ベクトルの定義 

9.8.9.1 

意味 2平面の交線により単位ベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR/PARLEL，INTOF，平面1，平面2，

NEGZ

NEGY

NEGX

POSZ

POSY

POSX

備考1. 平面1，平面2は，交わる平面とする。 

2. 定義するベクトルの向きは，修飾語の選択によって指定する。 

3. 交線が座標軸に平行な場合，その軸に関する修飾語だけが使用できる。 

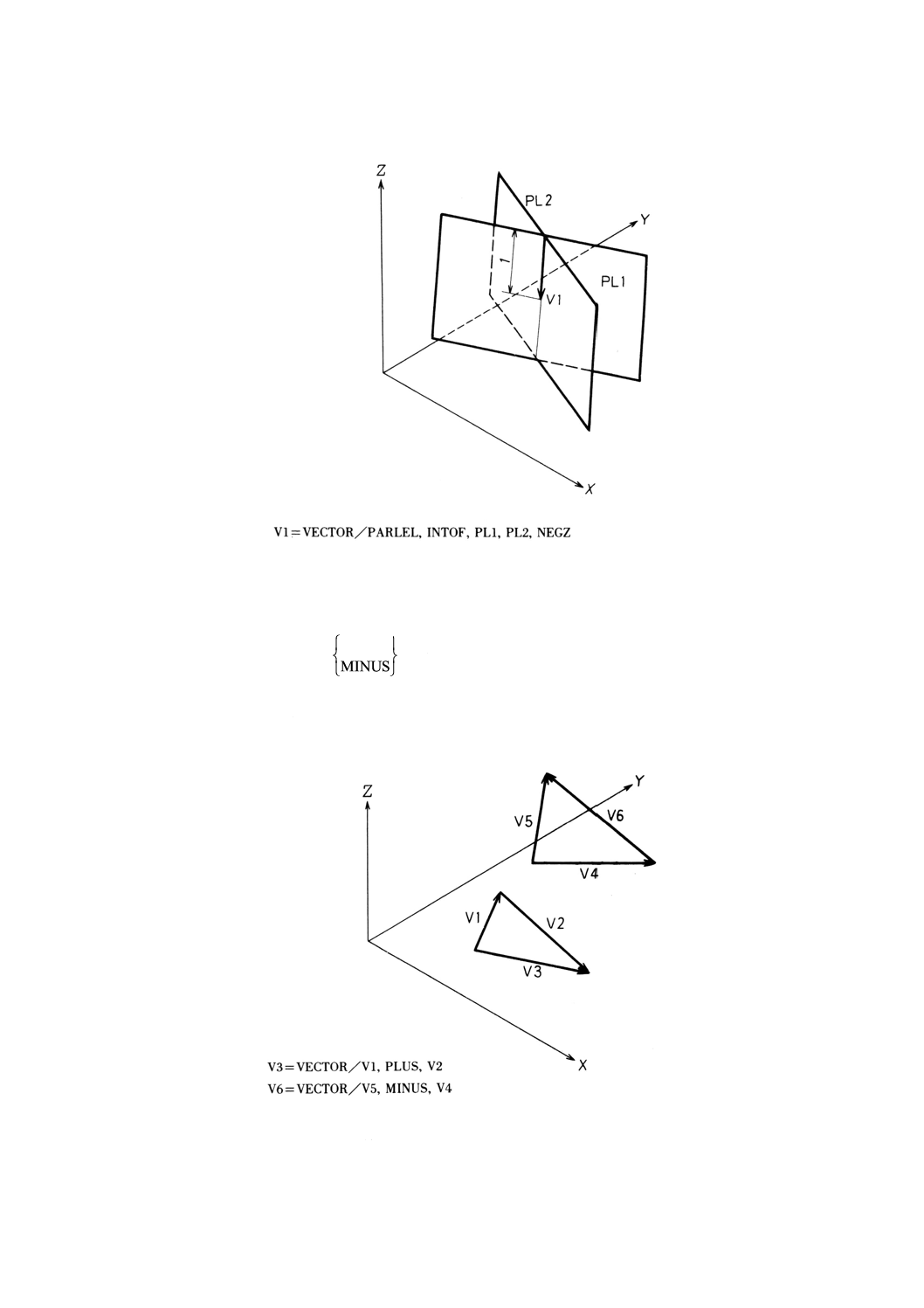
66 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 2平面の交線による単位ベクトルの定義の例 

9.8.10 ベクトルの和又は差としてのベクトルの定義 

9.8.10.1 意味 ベクトルの和又は差としてのベクトルを定義する。 

一般形は，次のとおりとする。 

VECTOR／ベクトル1，

MINUS

PLUS

，ベクトル2 

備考 ベクトル1にベクトル2を加えたものを，又はベクトル1からベクトル2を減じたものを，ベ

クトルの和又は差とする。 

例： ベクトルの和又は差としてのベクトルの定義の例 

9.8.11 XY平面で直線とある角度をなす単位ベクトルの定義 

9.8.11.1 書味XY平面上で指定した直線とある角度をなす単位ベクトルを定義する。 

一般形は，次のとおりとする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

VECTOR/ATANGL，角度，直線，

NEGY

NEGX

POSY

POSX

備考 角度は，指定した直線と定義するベクトルとのなす角度とし，指定した直線から反時計回りの

向きに測った角度を正とする。 

例： XY平面で直線とある角度をなす単位ベクトルの定義の例 

9.9 

円定義文 

9.9.1 

意味と構文 

9.9.1.1 

意味 円定義文は，円を定義する。円は，XY平面に垂直な円柱として扱う。 

9.9.1.2 

構文 構文は，次による。 

＜円定義文＞ :: ＝＜名前＞＝CIRCLE／＜円のパラメータの並び＞ 

＜円規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］CIRCLE／＜円のパラメータの並び＞） 

＜円のパラメータの並び＞ :: ＝＜スカラー＞33［，＜スカラー＞］｜ 

＜スカラー＞22［，＜スカラー＞］｜ 

CENTER，＜点規制詞＞，RADIUS，＜スカラー＞｜ 

CENTER，＜点規制詞＞，TANTO，＜直線規制詞＞｜ 

CENTER22［, ＜点規制詞＞］｜ 

＜点規制詞＞22［, ＜点規制詞＞］｜ 

CENTER，＜点規制詞＞，11 [LARGE｜SMALL], TANTO, ＜円規制詞＞｜ 

22［11［XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜直線規制詞＞，］RADIUS, 

＜スカラー＞｜ 

TANTO，＜直線規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]， 

＜点規制詞＞，RADIUS，＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL], 22 [11 [IN｜OUT]，＜円規制詞＞,］ 

RADIUS，＜スカラー＞｜ 

68 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜直線規制詞＞， 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL], 11 [IN｜OUT]， 

＜円規制詞＞，RADIUS，＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜直線規制詞＞， 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜タブシル規制詞＞， 

＜点規制詞＞，RAD｜US，＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜直線規制詞＞ 

22 [，11［XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜直線規制詞＞］｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL] 22［，＜点規制詞＞］， 

RADIUS，＜スカラー＞｜ 

＜点規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL], 11 [IN｜OUT]， 

＜円規制詞＞, RAD｜US, ＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜直線規制詞＞, 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，11 [IN｜OUT]， 

＜円すい曲線規制詞＞，＜点規制詞＞，RADIUS，＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]，＜タブシル規制詞＞, 

＜点規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]， 

＜タブシル規制詞＞, ＜点規制詞＞，RADIUS，＜スカラー＞｜ 

11 [IN｜OUT]，＜円規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]， 

＜タブシル規制詞＞，＜点規制詞＞，RADIUS，＜スカラー＞｜ 

＜点規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]， 

＜タブシル規制詞＞，＜点規制詞＞，RADIUS，＜スカラー＞｜ 

ON，＜直線規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL]， 

＜タブシル規制詞＞，＜点規制詞＞，RADIUS，＜スカラー＞｜ 

＜スカラー＞66［，＜スカラー＞］ 

9.9.2 

中心の座標と半径による円の定義 

9.9.2.1 

意味 中心の座標と半径により円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/a, b [, c], r 

備考1. (a, b, c) は，定義する円の中心座標とする。 

2. rは，定義する円の半径とする。 

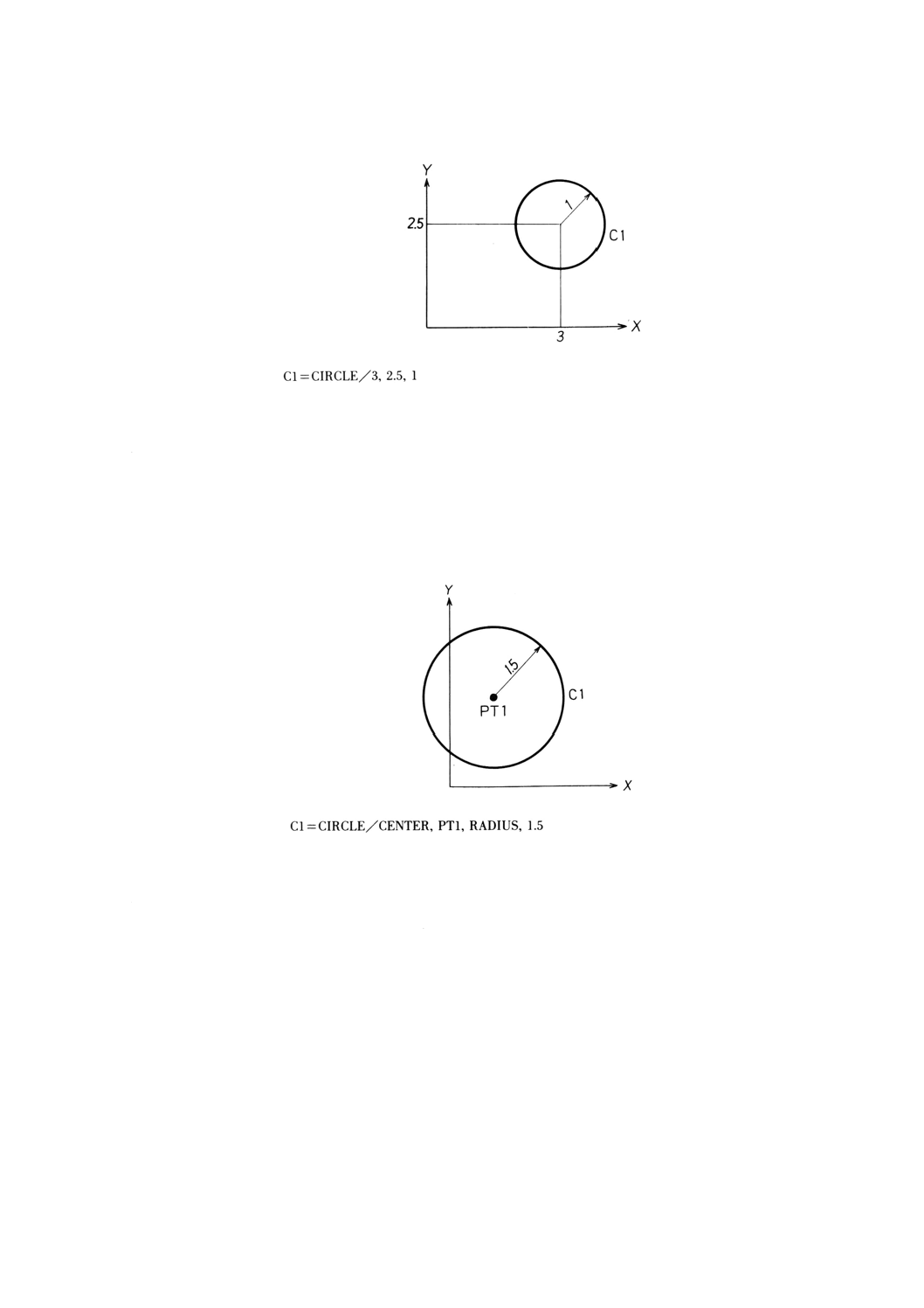
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 中心の座標と半径による円の定義の例 

9.9.3 

中心と半径による円の定義 

9.9.3.1 

意味 中心と半径により円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/CENTER，点，RADIUS，r 

備考1. 点は，定義する円の中心とする。 

2. rは，定義する円の半径とする。 

例： 中心と半径による円の定義の例 

9.9.4 

中心と接線による円の定義 

9.9.4.1 

意味 直線に接し，指定の点を中心とする円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/CENTER，点，TANTO，直線 

備考1. 点は，定義する円の中心とし，直線上にあってはならない。 

2. 直線は，定義する円に接する直線とする。 

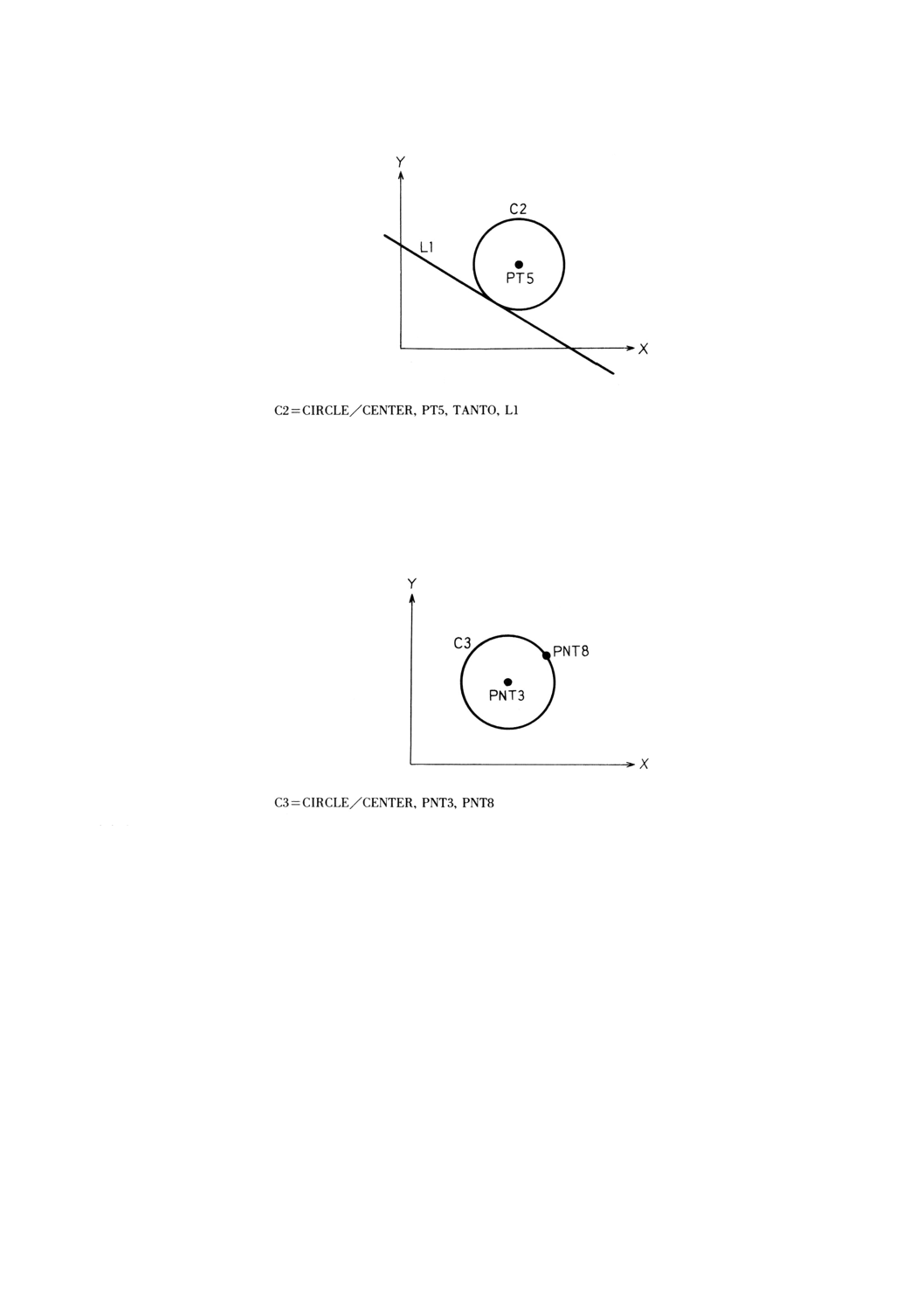
70 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 中心と接線による円の定義の例 

9.9.5 

中心と円周上の点による円の定義 

9.9.5.1 

意味 指定の点を中心とし，もう一つの指定の点を通る円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/CENTER，点1，点2 

備考 点1，点2は，それぞれ定義する円の中心及び円周上の点とする。 

例： 中心と円周上の点による円の定義の例 

9.9.6 

円周上の3点による円の定義 

9.9.6.1 

意味 指定の3点を通る円を定義する。 

一般形は，次のとおりとする。 

CIRCLE／点1，点2，点3 

備考1. 点1，点2，点3は，定義する円の円周上の点とする。 

2. 点1，点2，点3は，一直線上にあってはならない。 

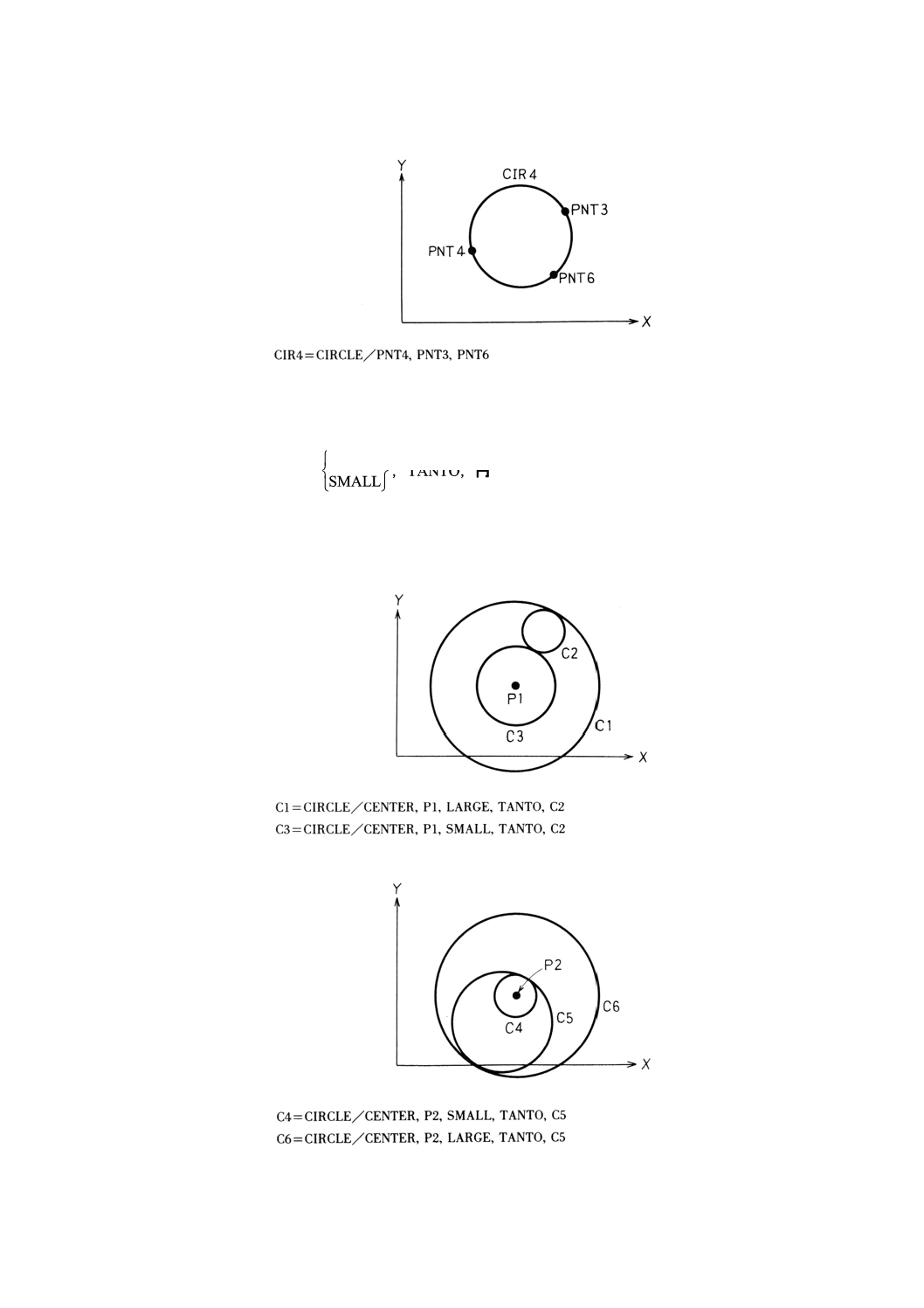
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 円周上の3点による円の定義の例 

9.9.7 

中心と接円による円の定義 

9.9.7.1 

意味 指定の点を中心とし，指定の円に接する円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/CENTER，点，

SMALL

LARGE，TANTO，円 

備考1. 点は，定義する円の中心とする。 

2. 円は，定義する円に接する円とする。 

例： 中心と接円による円の定義の例 

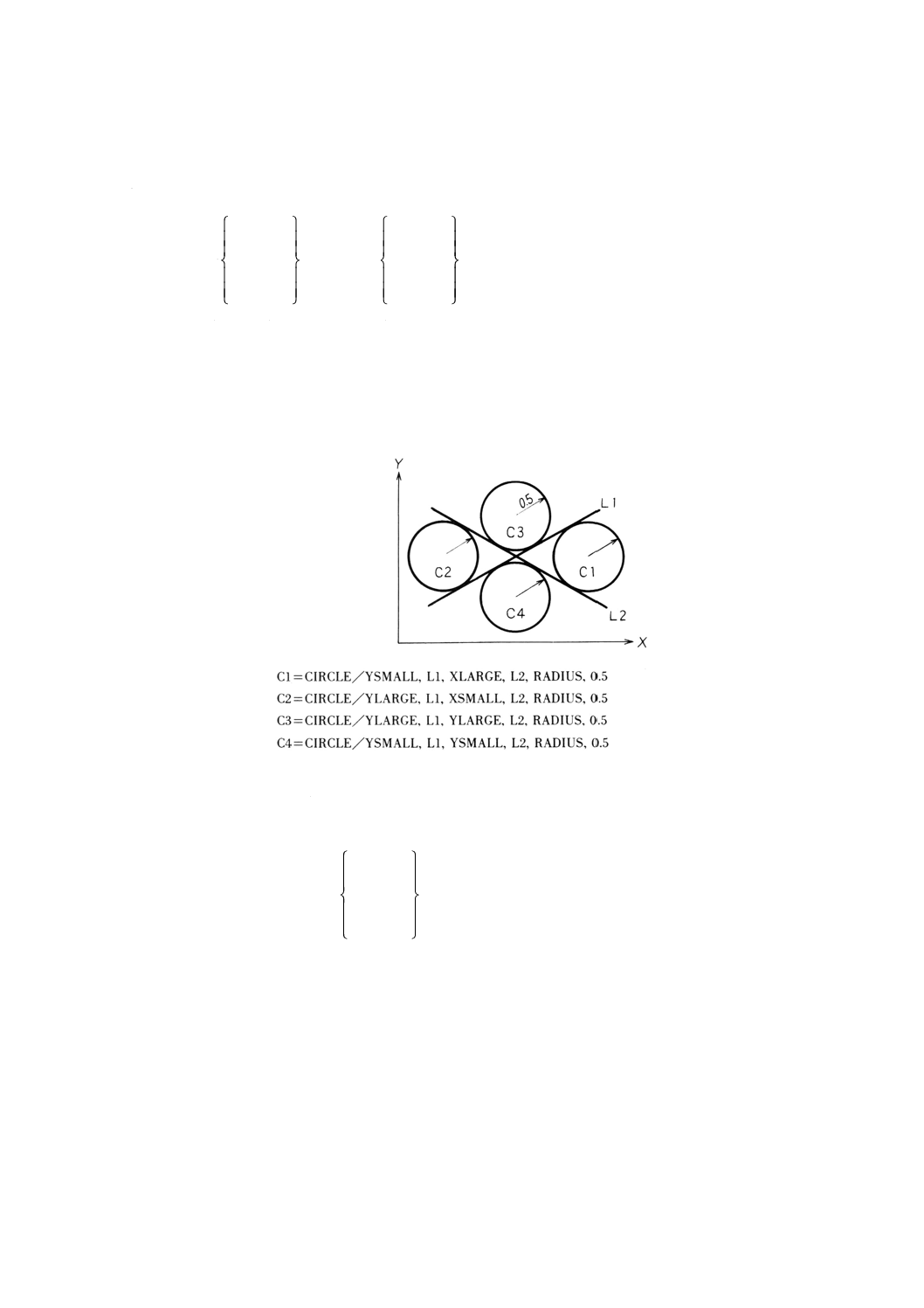
72 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.9.8 

二つの接線と半径による円の定義 

9.9.8.1 

意味 二つの直線に接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，直線1，

YSMALL

YLARGE

XSMALL

XLARGE

，直線2，RADIUS，r 

備考1. 直線1，直線2は，交わる直線とする。 

2. rは，定義する円の半径とする。 

3. 接線となる直線が座標軸に平行な場合，その軸に関する修飾語をその直線に対して用いては

ならない。例えば，X軸に平行な直線に対しては，XLARGE及びXSMALLは使用できない。 

例： 二つの接線と半径による円の定義の例 

9.9.9 

接線，円周上の点及び半径による円の定義 

9.9.9.1 

意味 点を通り，直線に接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/TANTO，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，点，RADIUS，r 

備考1. 直線は，定義する円に接する直線とする。 

2. 点は，定義する円の円周上にある点とする。 

3. rは，定義する円の半径とする。 

4. 接線となる直線が座標軸に平行な場合，点が接線上になければその軸に関する修飾語を用い

なければならず，また点が接線上にあればその軸に関する修飾語を用いてはならない。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 接線，円周上の点及び半径による円の定義の例 

9.9.10 二つの接円と半径による円の定義 

9.9.10.1 意味 二つの円に接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，

OUT

IN

,円1，

OUT

IN

，円2，RADIUS, r 

備考1. 円1，円2は，交わる二つの円で定義する円に接する。 

2. rは，定義する円の半径とする。 

3. 指定した二つの円の中心を結ぶ直線が座標軸に平行な場合，その軸に関する修飾語を用いて

はならない。 

例： 二つの接円と半径による円の定義の例 

9.9.11 接線，接円及び半径による円の定義 

99.11.1 意味 直線と円に接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

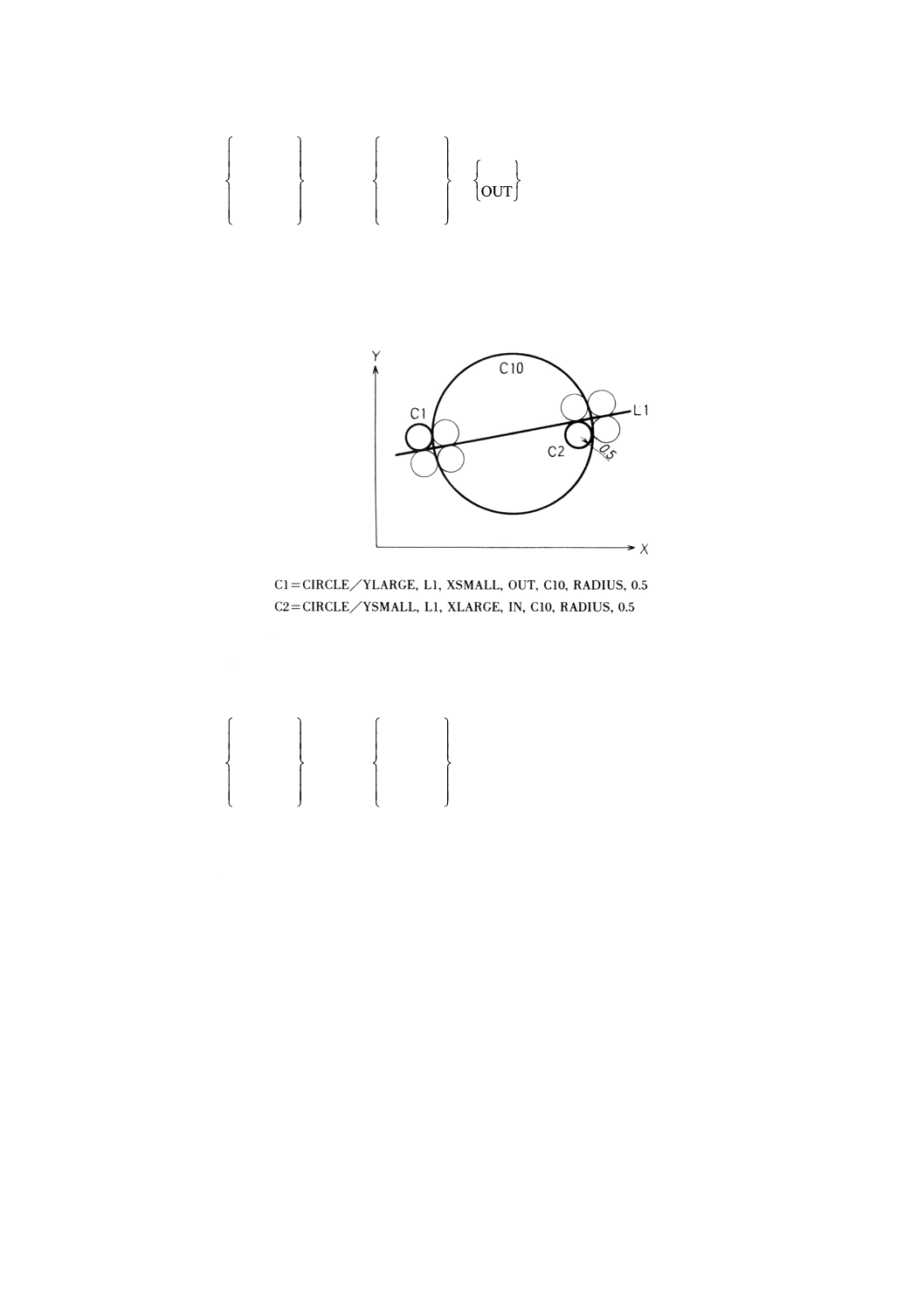
74 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，

OUT

IN

，円，RADIUS，r 

備考1. 直線は，定義する円に接する直線とする。 

2. 円は，定義する円に接する円とする。 

3. rは，定義する円の半径とする。 

例： 接線，接円及び半径による円の定義の例 

9.9.12 接線，接するタブシル及び半径による円の定義 

9.9.12.1 意味 直線とタブシルとに接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル，点，RADIUS，r 

備考1. 直線は，定義する円に接する直線とする。 

2. 点は，定義する円とタブシルとが接する近傍にあってタブシルの定義に用いた点とする。 

3. タブシルは，XY平面に垂直とし，定義する円に接する。 

4. rは，定義する円の半径とする。 

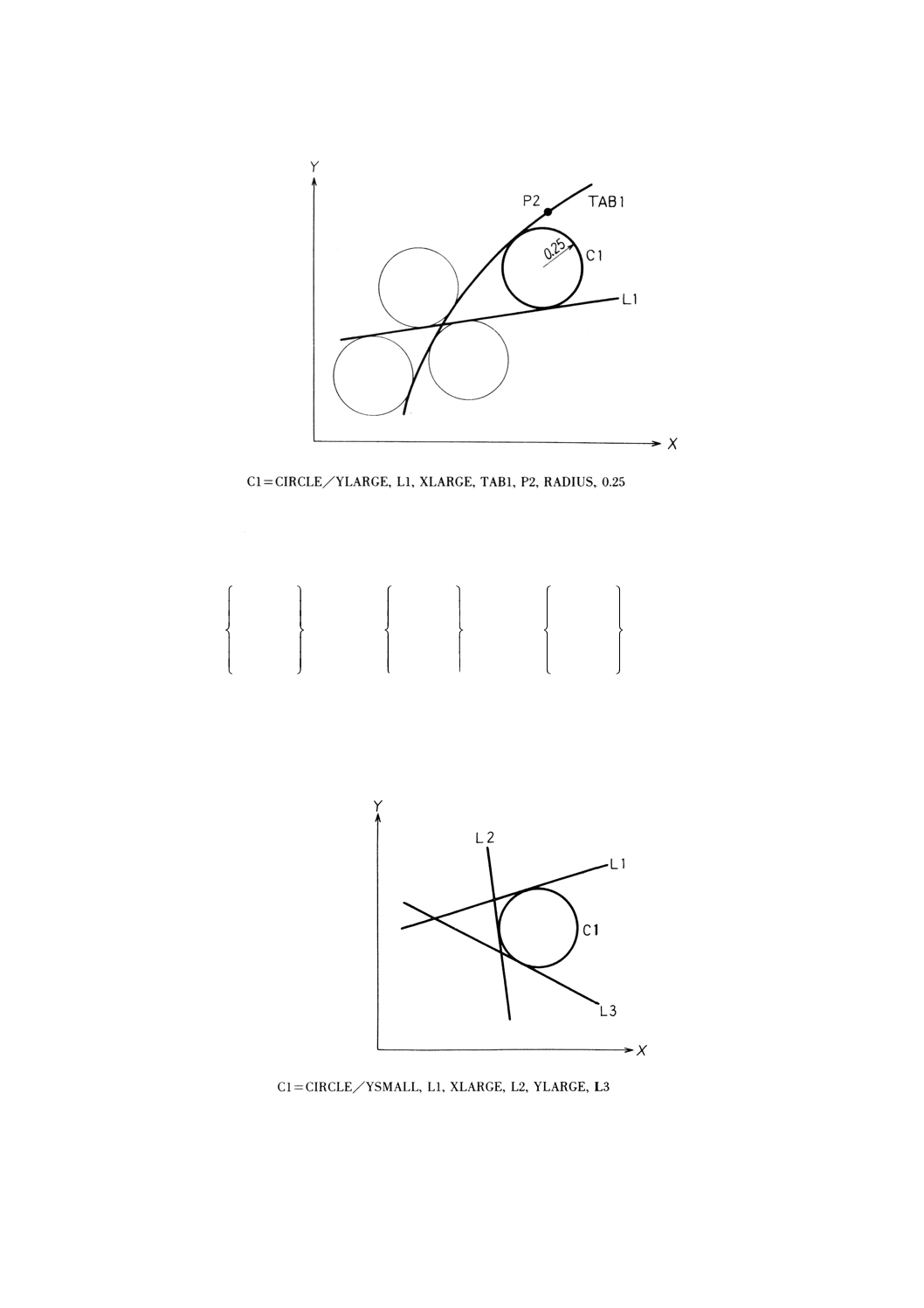
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 接線，接するタブシル及び半径による円の定義の例 

9.9.13. 3接線による円の定義 

9.9.13.1 意味 3直線に接する円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，直線1，

YSMALL

YLARGE

XSMALL

XLARGE

，直線2，

YSMALL

YLARGE

XSMALL

XLARGE

，直線3 

備考1. 直線1，直線2，直線3は，それぞれ定義する円に接する直線とする。 

2. 接線となる直線が座標軸に平行な場合，その軸に関する修飾語をその直線に対して用いては

ならない。例えば，X軸に平行な直線に対しては，XLARGE及びXSMALLは使用できない。 

例： 3接線による円の定義の例 

9.9.14 円周上の2点と半径による円の定義 

9.9.14.1 意味 二つの点を通り，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

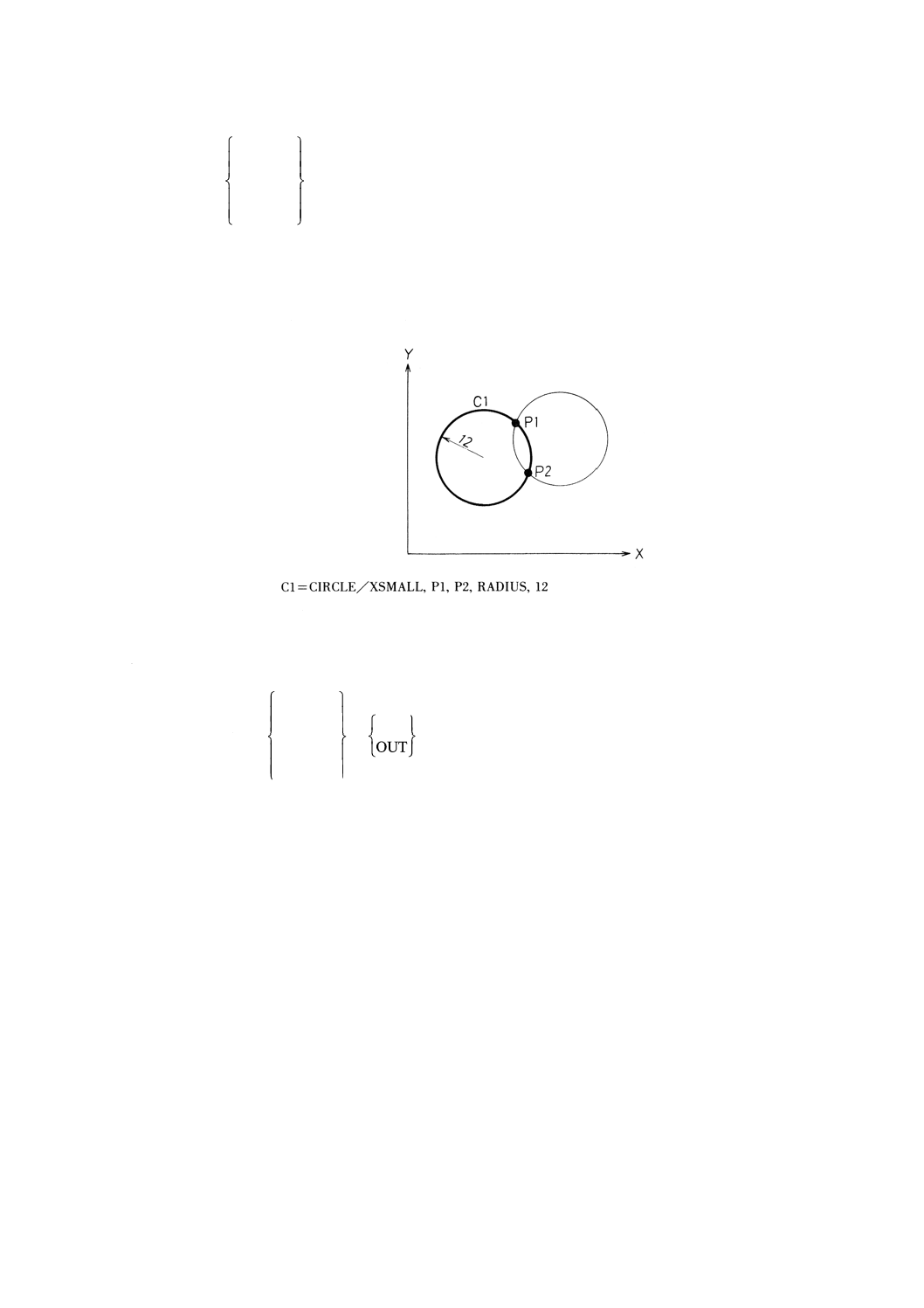
76 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，点1，点2，RADIUS，r 

備考1. 点1，点2は，定義する円の円周上の点とする。 

2. rは，定義する円の半径とする。 

3. 2点を結ぶ直線が座標軸に平行な場合，その座標軸に関する修飾語を用いてはならない。 

例： 円周上の2点と半径による円の定義の例 

9.9.15 円周上の点，接円及び半径による円の定義 

9.9.15.1 意味 点を通り，円に接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE／点，

YSMALL

YLARGE

XSMALL

XLARGE

，

OUT

IN

，円，RADIUS，r 

備考1. 点は，定義する円の円周上の点とする。 

2. 円は，定義する円に接する円とする。 

3. rは，定義する円の半径とする。 

4. 点と円の中心を結ぶ直線が座標軸に平行な場合，その座標軸に関する修飾語を用いてはなら

ない。 

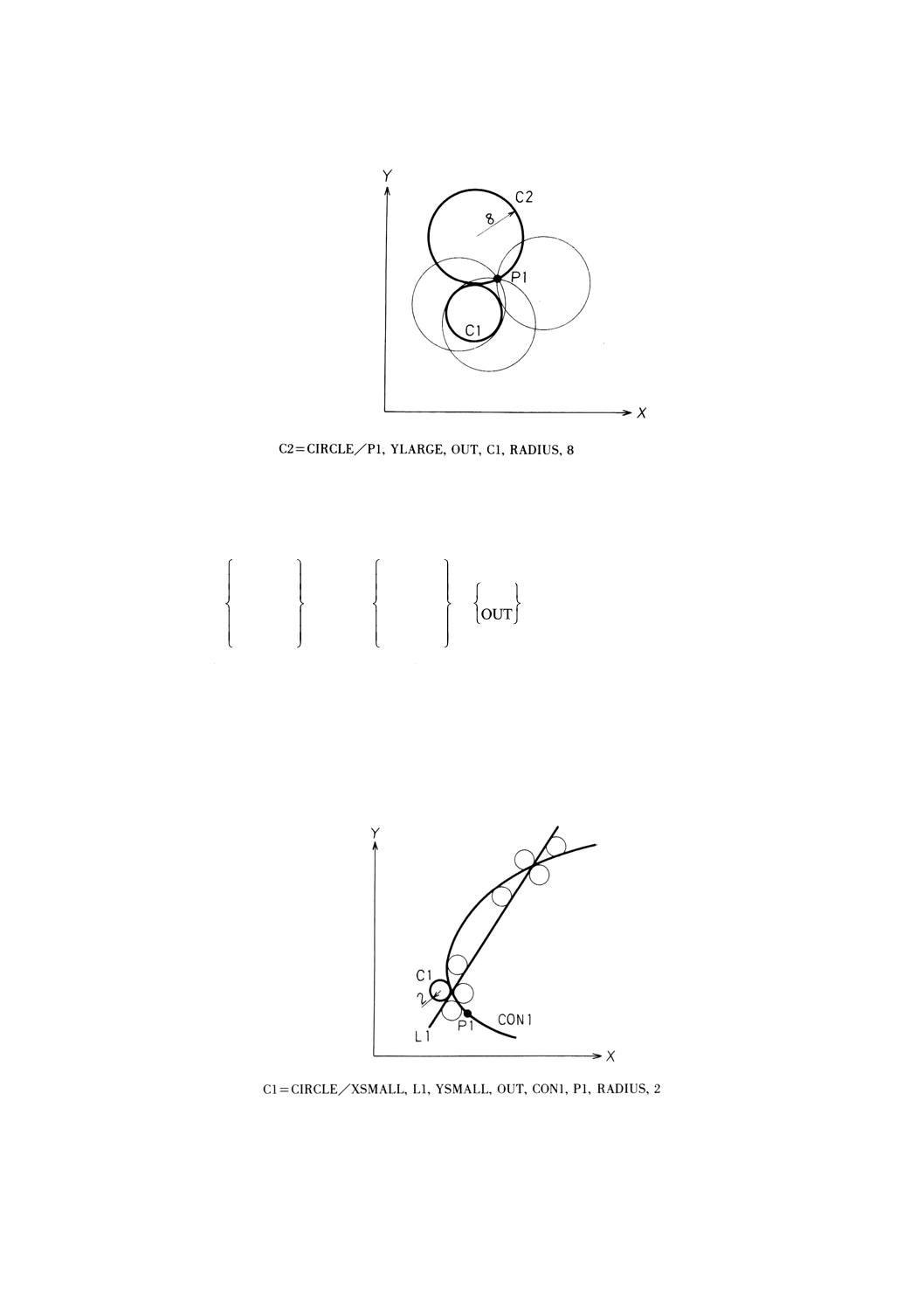
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 円周上の点，接円及び半径による円の定義の例 

9.9.16 接線，接する円すい曲線及び半径による円の定義 

9.9.16.1 意味 直線と円すい曲線とに接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，

OUT

IN

，円すい曲線，点，RADIUS，r 

備考1. 直線は，定義する円に接する直線とする。 

2. 円すい曲線は，定義する円に接する円すい曲線とする。 

3. 点は，定義する円と円すい曲線とが接する近傍にあって円すい曲線上の点とする。 

4. rは，定義する円の半径とする。 

5. 直線が座標軸と平行な場合，その座標軸に関する修飾語を用いてはならない。 

例： 接線，接する円すい曲線及び半径による円の定義の例 

9.9.17 二つの接するタブシルと半径による円の定義 

9.9.17.1 意味 二つのタブシルに接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

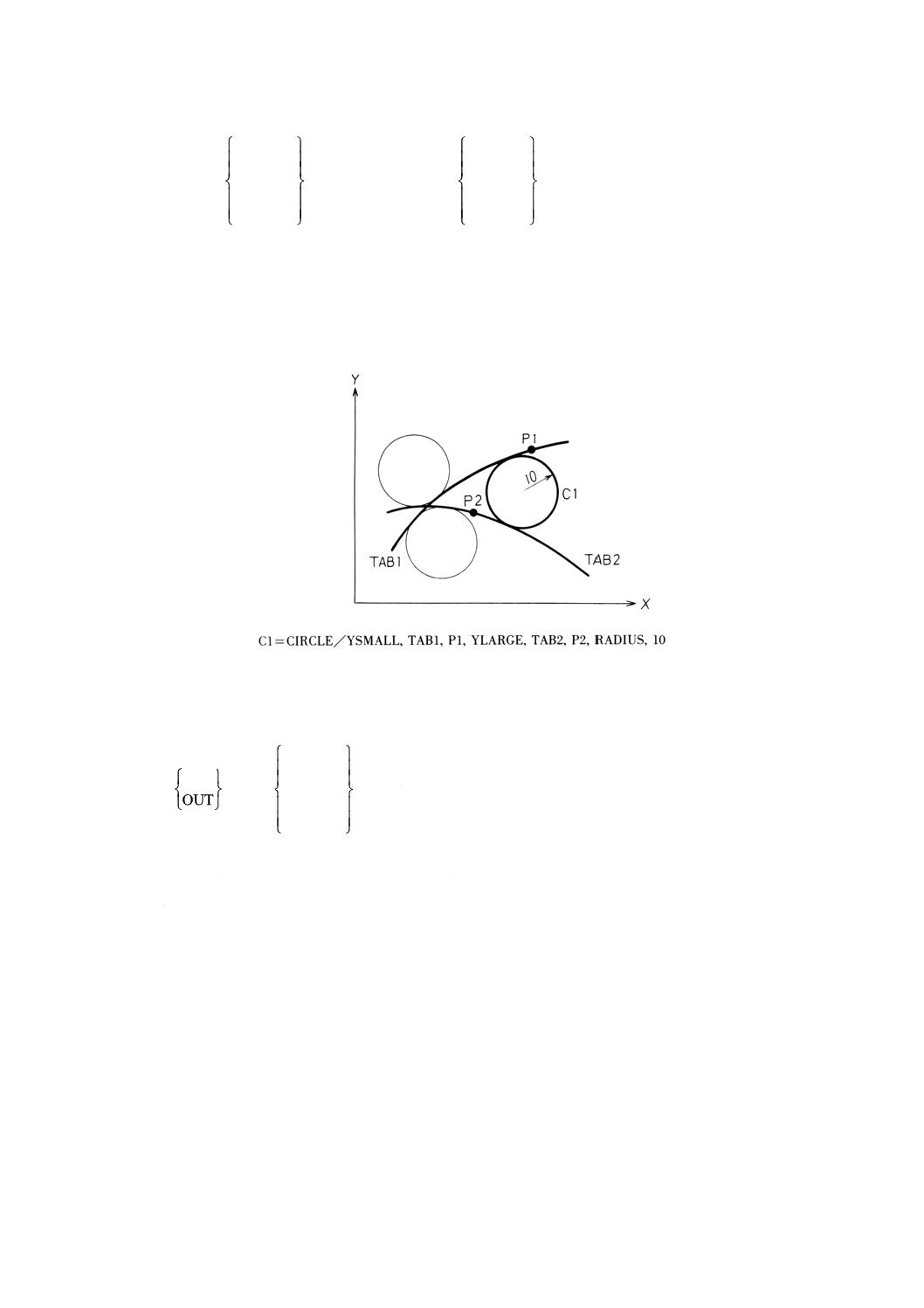
78 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

CIRCLE/

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル1，点1，

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル2，点2，RADIUS，r 

備考1. タブシル1，タブシル2は，定義する円に接するタブシルとし，XY平面に垂直とする。 

2. 点1，点2は，求める円とタブシル1及びタブシル2とがそれぞれ接する近傍にあってタブ

シルの定義に用いた点とする。 

3. rは，定義する円の半径とする。 

例： 二つの接するタブシルと半径による円の定義の例 

9.9.18 円，接するタブシル及び半径による円の定義 

9.9.18.1 意味 円とタブシルとに接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/

OUT

IN

，円，

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル，点，RADIUS，r 

備考1. 円は，定義する円に接する円とする。 

2. タブシルは，定義する円に接するタブシルとし，XY平面に垂直とする。 

3. 点は，求める円とタブシルとが接する近傍にあってタブシルの定義に用いた点とする。 

4. rは，定義する円の半径とする。 

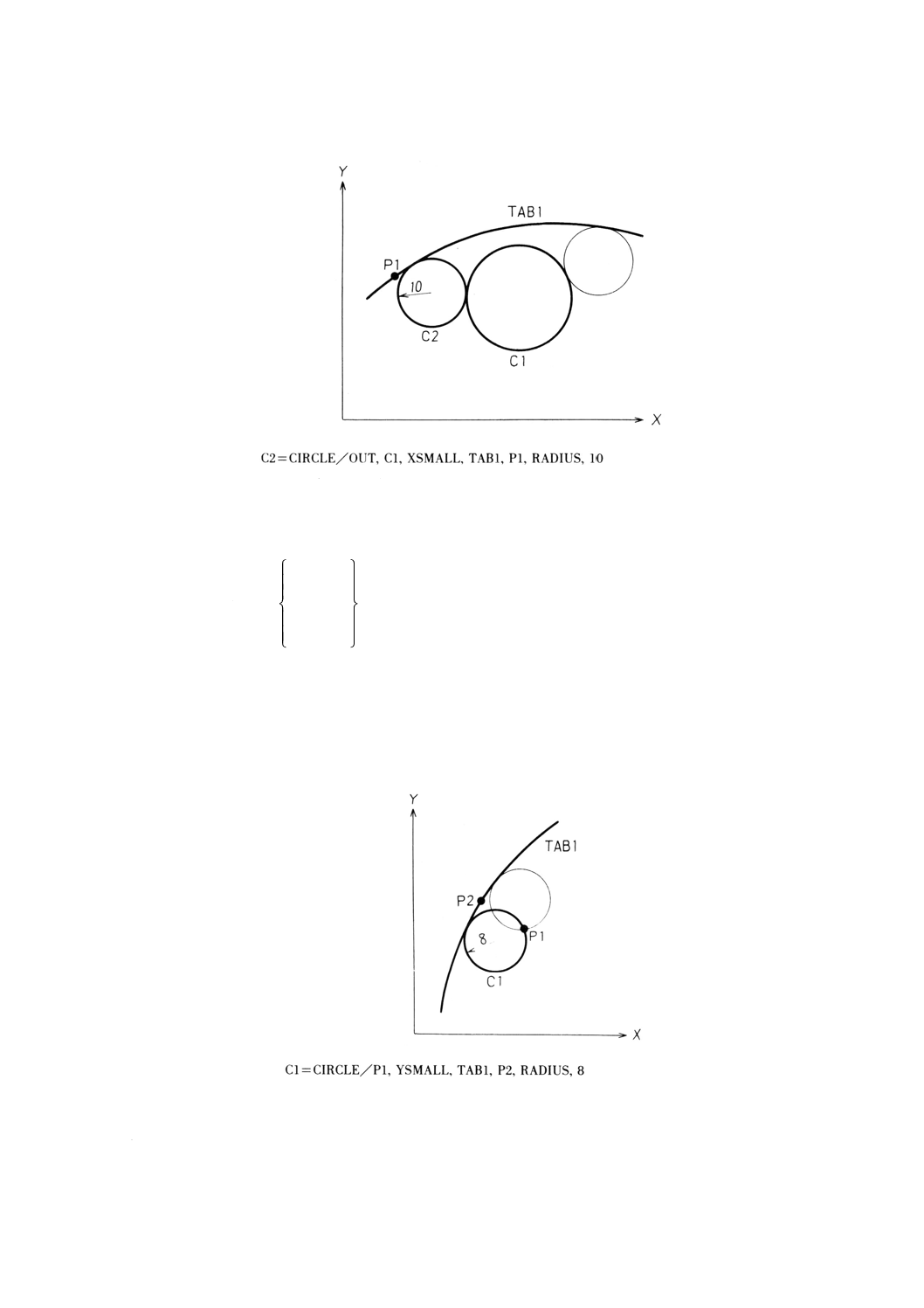
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 円，接するタブシル及び半径による円の定義の例 

9.9.19 円周上の点，接するタブシル及び半径による円の定義 

9.9.19.1 意味 点を通り，タブシルに接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

CIRCLE／点1，

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル，点2，RADIUS，r 

備考1. 点1は，定義する円の円周上の点とする。 

2. タブシルは，定義する円に接するタブシルとし，XY平面に垂直とする。 

3. 点2は，定義する円とタブシルとが接する近傍にあってタブシルの定義に用いた点とする。 

4. rは，定義する円の半径とする。 

例： 円周上の点，接するタブシル及び半径による円の定義の例 

9.9.20 中心を通る直線，接するタブシル及び半径による円の定義 

9.9.20.1 意味 直線上に中心があり，タブシルに接し，指定の半径をもつ円を定義する。 

一般形は，次のとおりとする。 

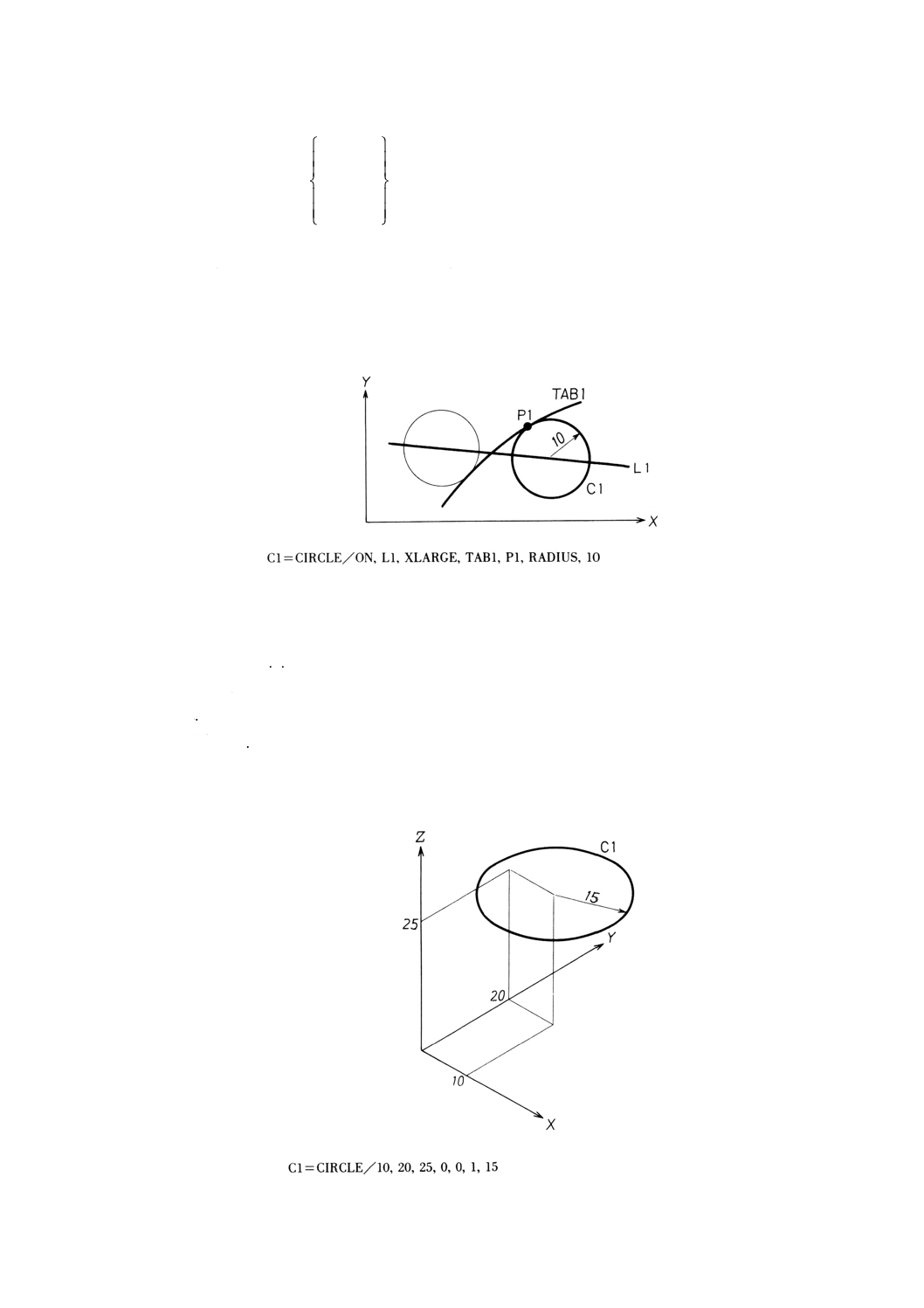
80 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

CIRCLE/ON，直線，

YSMALL

YLARGE

XSMALL

XLARGE

，タブシル，点，RADIUS，r 

備考1. 直線は，定義する円の中心を通る直線とする。 

2. タブシルは，定義する円に接するタブシルとし，XY平面に垂直とする。 

3. 点は，定義する円とタブシルとが接する近傍にあってタブシルの定義に用いた点とする。 

4. rは，定義する円の半径とする。 

例： 中心を通る直線，接するタブシル及び半径による円の定義の例 

9.9.21 中心座標，円柱の軸の方向余弦及び半径による円の定義 

9.9.21.1 意味 中心座標，円柱の軸の方向余弦及び半径により円を定義する。 

一般形は，次のとおりとする。 

CIRCLE/x, y, z, i, j, k, r 

備考1. (x, y, z) は，定義する円の中心座標とする。 

2. (i, j, k) は，定義する円を断面にもつXY平面に垂直な円柱の軸の方向余弦とする。したがっ

て， (i, j, k) は， (0, 0, 1) でなければならない。 

3. rは，定義する円の半径とする。 

例： 中心座標，円柱の軸の方向余弦と半径による円の定義の例 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.10 円柱定義文 

9.10.1 意味と構文 

9.10.1.1 意味 円柱定義文は，円柱を定義する。 

9.10.1.2 構文 構文は，次による。 

＜円柱定義文＞ :: ＝＜名前＞＝CYLNDR／＜円柱のパラメータの並び＞ 

＜円柱規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］CYLNDR／＜円柱のパラメータの並び＞） 

＜円柱のパラメータの並び＞ :: ＝11［＜スカラー＞22［，＜スカラー＞］｜＜点規制詞＞］ 

11［33［，＜スカラー＞］｜，＜ベクトル規制詞＞］，＜スカラー＞｜ 

22［11 [［XLARGE｜XSMALL｜YLARGE｜YSMALL｜ZLARGE｜ZSMALL],  

＜平面規制詞＞，］RADIUS，＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL｜ZLARGE｜ZSMALL], 

＜平面規制詞＞，11 [XLARGE｜XSMALL｜YLARGE｜YSMALL｜ZLARGE｜ 

ZSMALL], 11 [IN｜OUT]，＜円柱規制詞＞，RADIUS，＜スカラー＞｜ 

11 [XLARGE｜XSMALL｜YLARGE｜YSMALL｜ZLARGE｜ZSMALL]  

22［，11 ［IN｜OUT]，＜円柱規制詞＞］，RADIUS，＜スカラー＞ 

9.10.2 点，ベクトル及び半径による円柱の定義 

9.10.2.1 意味 点，ベクトル及び半径により円柱を定義する。 

一般形は，次のとおりとする。 

CYLNDR／

点z

y,

x,

，

ベクトル

c

b,

a,

，r 

備考1. (x, y, z) は，円柱の軸上の点の座標とする。 

2. 点は，円柱の軸上の点とする。 

3. (a, b, c) は，円柱の軸と平行なベクトルの座標軸X，Y及びZの成分とする。 

4. ベクトルは，円柱の軸の方向を示すベクトルとする。 

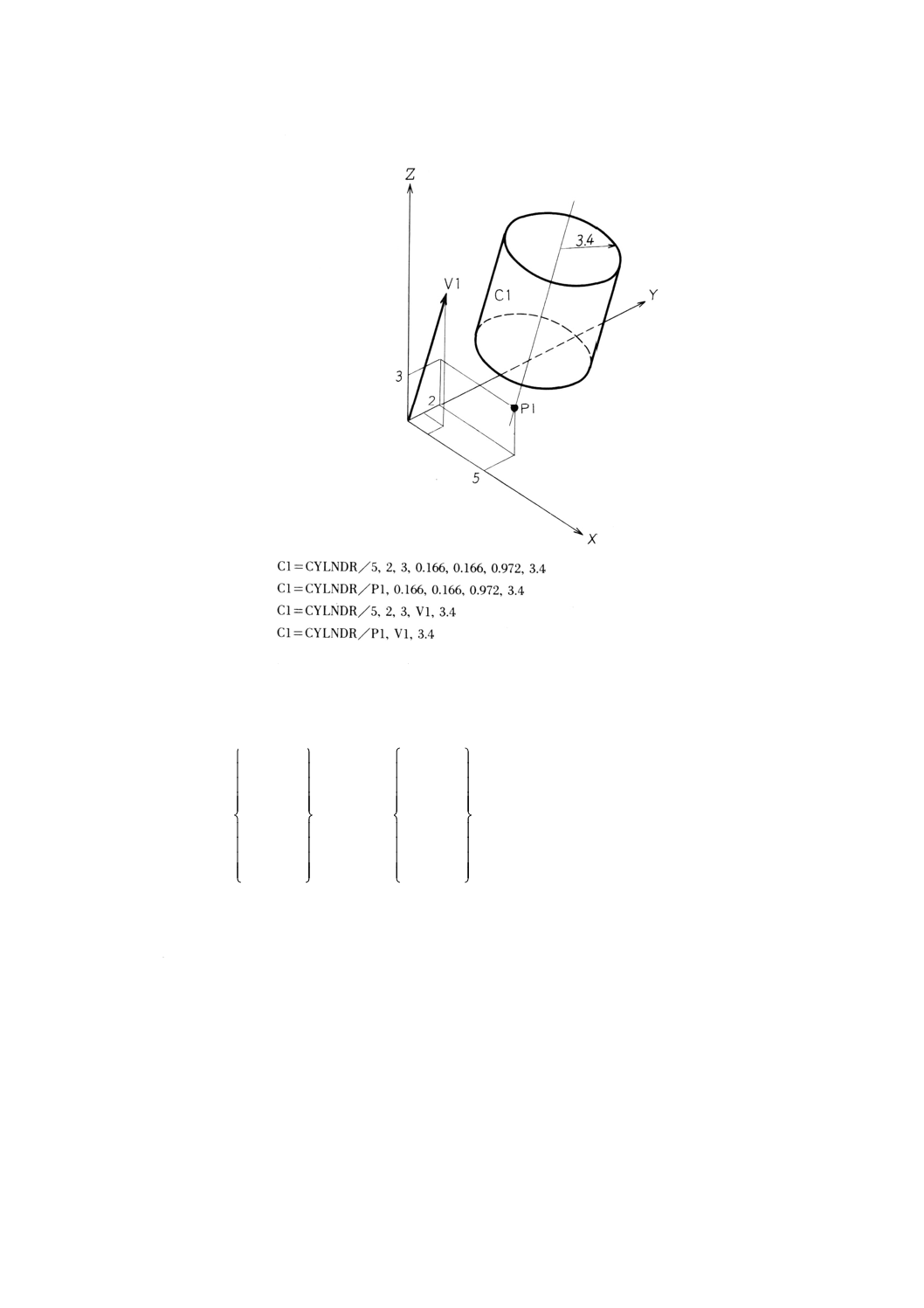
82 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点，ベクトル及び半径による円柱の定義の例 

9.10.3 二つの接平面と半径による円柱の定義 

9.10.3.1 意味 二つの平面に接し，指定の半径をもつ円柱を定義する。 

一般形は，次のとおりとする。 

CYLNDR/

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，平面1，

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，平面2，RADIUS，r 

備考1. 平面1，平面2は，定義する円柱に接する平面とする。 

2. rは，定義する円柱の半径とする。 

3. 平面が座標平面に平行な場合，その座標平面と垂直な座標軸に関する修飾語を用いてはなら

ない。 

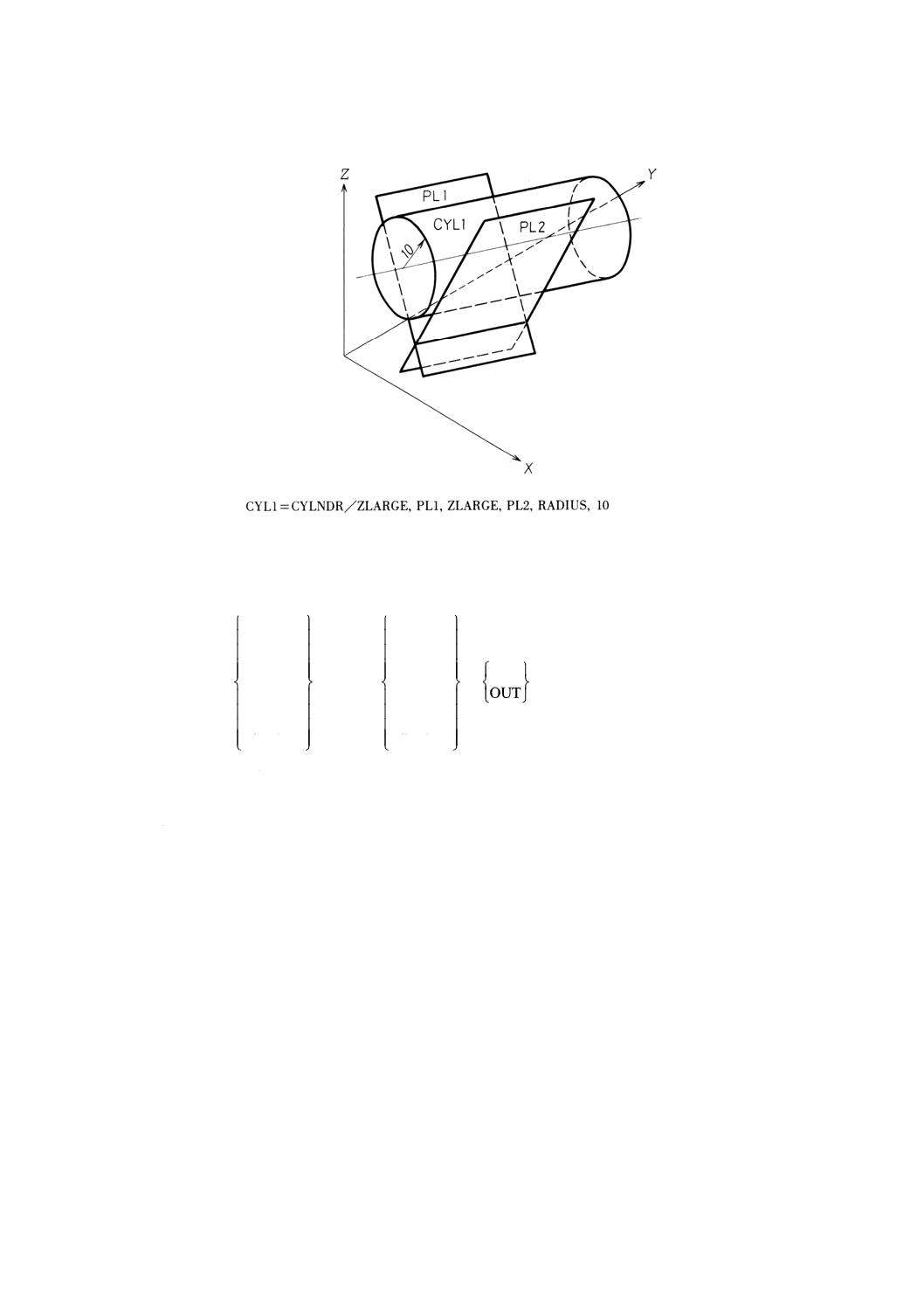
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 二つの接平面と半径による円柱の定義の例 

9.10.4 接平面，接する円柱及び半径による円柱の定義 

9.10.4.1 意味 平面と円柱とに接し，指定の半径をもつ円柱を定義する。 

一般形は，次のとおりとする。 

CYLNDR/

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，平面，

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，

OUT

IN

，円柱，RADIUS，r 

備考1. 平面は，定義する円柱に接する平面とする。 

2. 円柱は，定義する円柱に接する円柱とする。 

3. rは，定義する円柱の半径とする。 

4. 指定した円柱の軸と指定した平面は，平行でなければならない。 

5. 平面が座標平面に平行な場合，その座標平面と垂直な座標軸に関する修飾語を用いてはなら

ない。 

6. 円柱の軸が座標軸と平行な場合，その座標軸に関する修飾語を用いてはならない。 

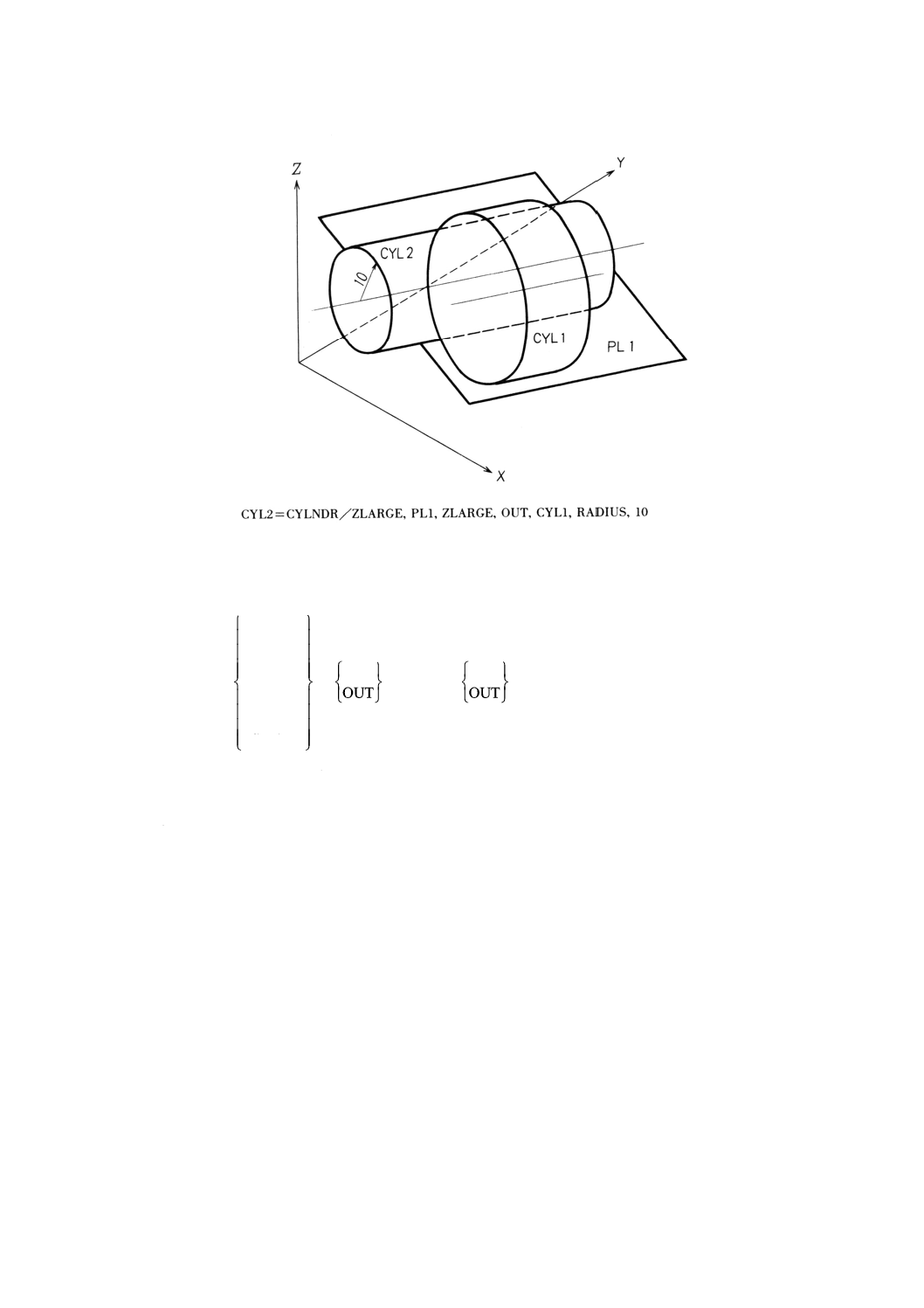
84 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 接平面，接する円柱及び半径による円柱の定義の例 

9.10.5 接する2円柱と半径による円柱の定義 

9.10.5.1 意味 二つの円柱に接し，指定の半径をもつ円柱を定義する。 

一般形は，次のとおりとする。 

CYLNDR/

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，

OUT

IN

，円柱1，

OUT

IN

，円柱2，RADIUS，r 

備考1. 円柱1，円柱2は，定義する円柱に接する円柱とする。 

2. rは，定義する円柱の半径とする。 

3. 指定した二つの円柱の軸は，平行でなければならない。 

4. 円柱の軸が座標軸と平行な場合，その座標軸に関する修飾語を用いてはならない。 

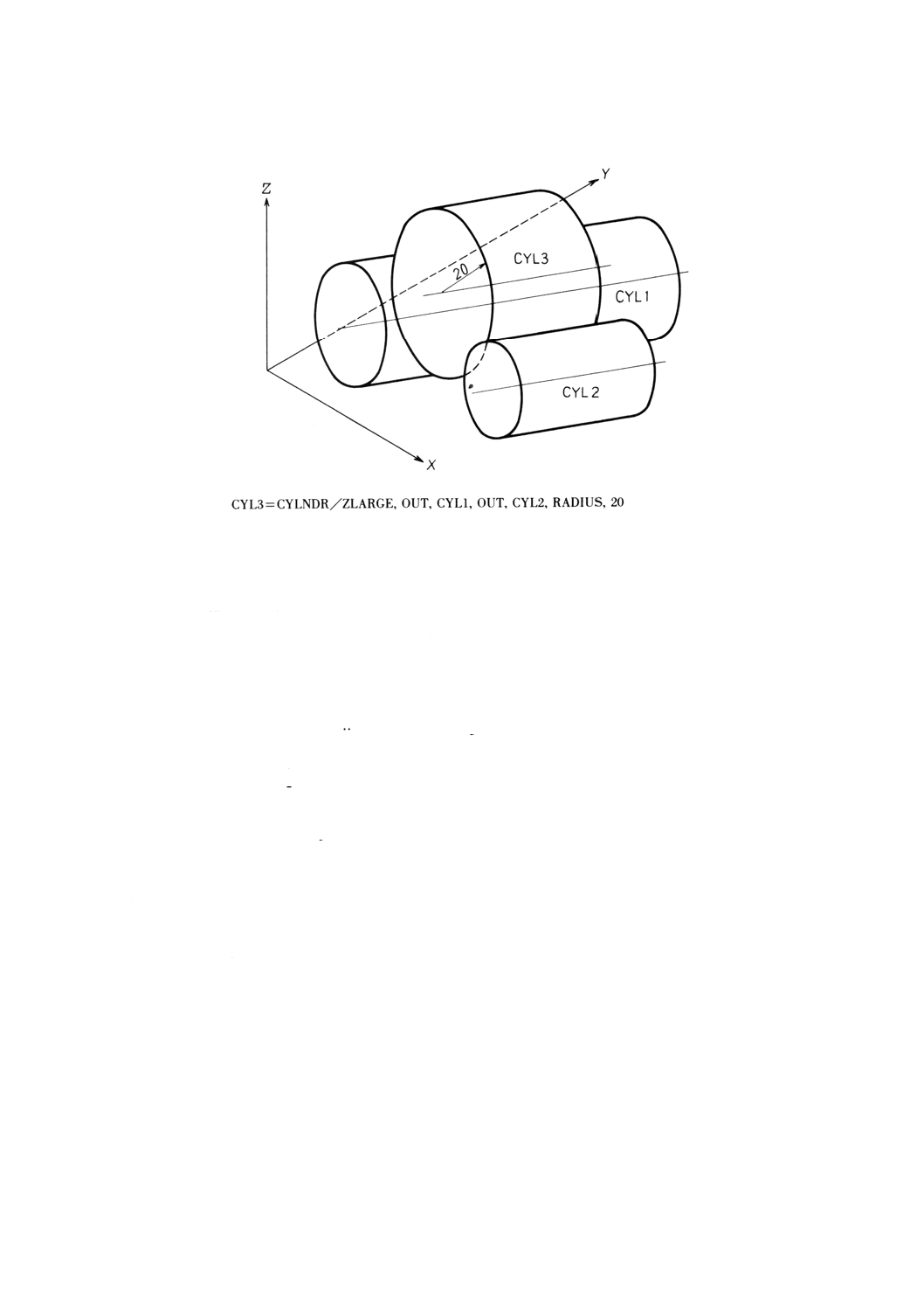
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 接する2円柱と半径による円柱の定義の例 

9.11 球定義文 

9.11.1 意味と構文 

9.11.1.1 意味 球定義文は，球を定義する。 

9.11.1.2 構文 構文は，次による。 

＜球定義文＞ :: ＝＜名前＞＝SPHERE／＜球のパラメータの並び＞ 

＜球規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］SPHERE／＜球のパラメータの並び＞） 

＜球のパラメータの並び＞ :: ＝＜スカラー＞33[，＜スカラー＞］｜ 

CENTER，＜点規制詞＞，RADIUS，＜スカラー＞｜ 
CENTER22［，＜点規制詞＞］｜ 

CENTER，＜点規制詞＞，TANTO，＜平面規制詞＞｜ 

＜点規制詞＞33［，＜点規制詞＞］ 

9.11.2 中心座標と半径による球の定義 

9.11.2.1 意味 中心座標と半径により球を定義する。 

一般形は，次のとおりとする。 

SPHERE/x, y, z, r 

備考1. (x, y, z) は，定義する球の中心座標とする。 

2. rは，定義する球の半径とする。 

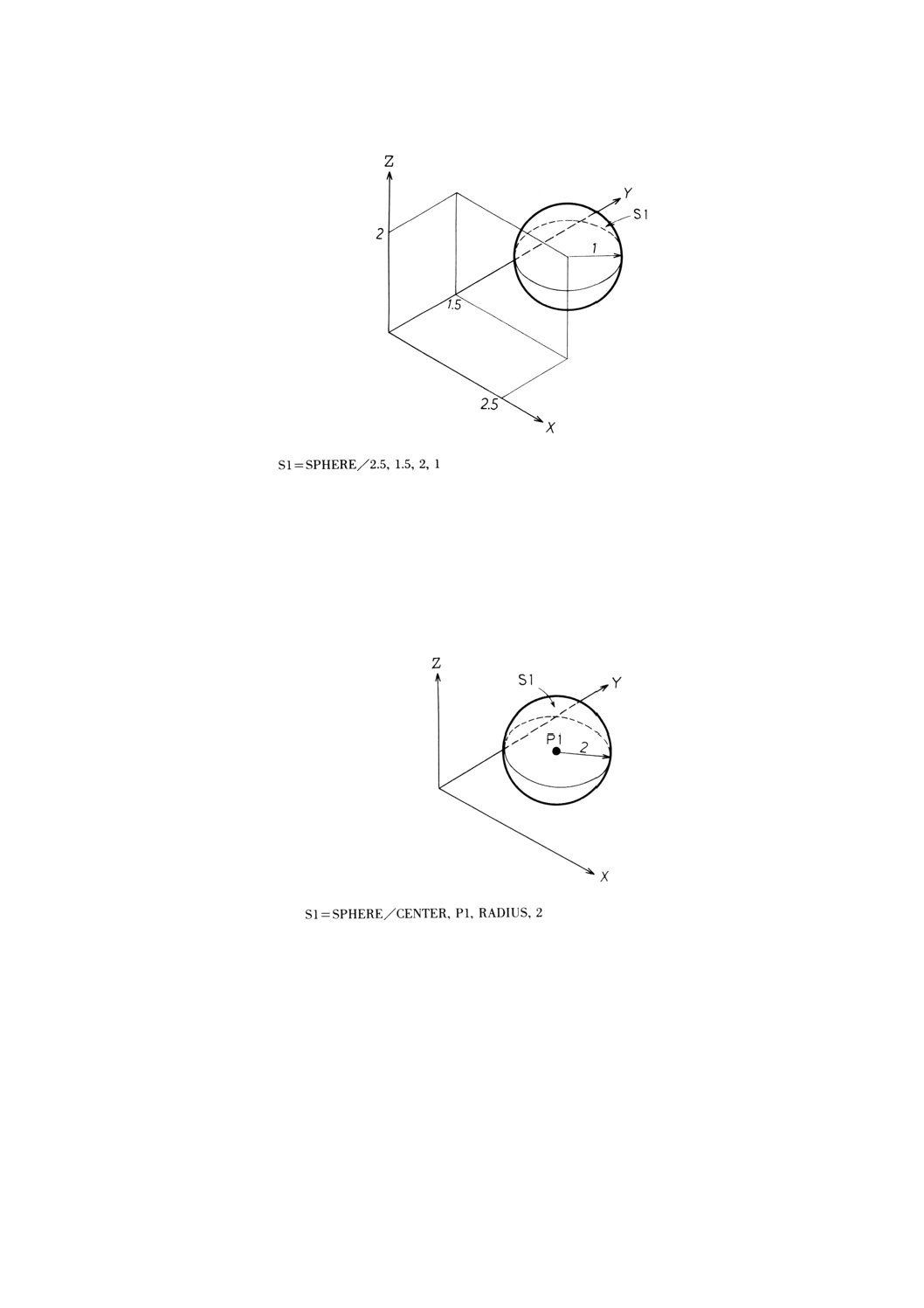
86 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 中心座標と半径による球の定義の例 

9.11.3 中心と半径による球の定義 

9.11.3.1 意味 中心と半径により球を定義する。 

一般形は，次のとおりとする。 

SPHERE/CENTER，点，RADIUS，r 

備考1. 点は，定義する球の中心とする。 

2. rは，定義する球の半径とする。 

例： 中心と半径による球の定義の例 

9.11.4 中心と球面上の点による球の定義 

9.11.4.1 意味 中心と球面上の点により球を定義する。 

一般形は，次のとおりとする。 

SPHERE/CENTER，点1，点2 

備考 点1，点2は，それぞれ定義する球の中心及び球面上の点とする。 

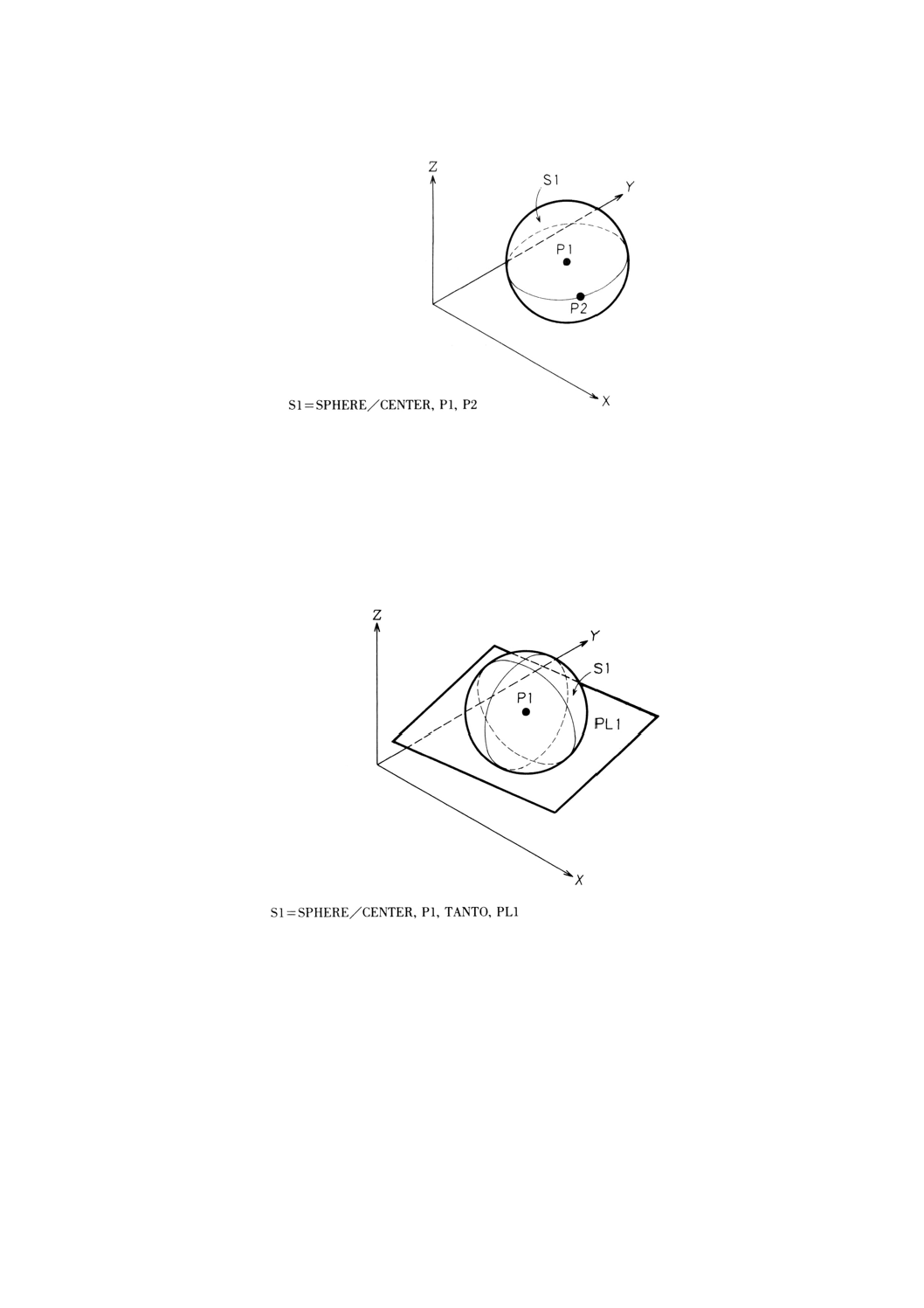
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 中心と球面上の点による球の定義の例 

9.11.5 中心と接平面による球の定義 

9.11.5.1 意味 指定の点を中心とし，平面に接する球を定義する。 

一般形は，次のとおりとする。 

SPHERE/CENTER，点，TANTO，平面 

備考1. 点は，定義する球の中心とする。 

2. 平面は，定義する球に接する平面とする。 

例： 中心と接平面による球の定義の例 

9.11.6 球面上の4点による球の定義 

9.11.6.1 意味 球面上の4点により球を定義する。 

一般形は，次のとおりとする。 

SPHERE／点1，点2，点3，点4 

備考 点1，点2，点3，点4は，定義する球の球面上の点とする。 

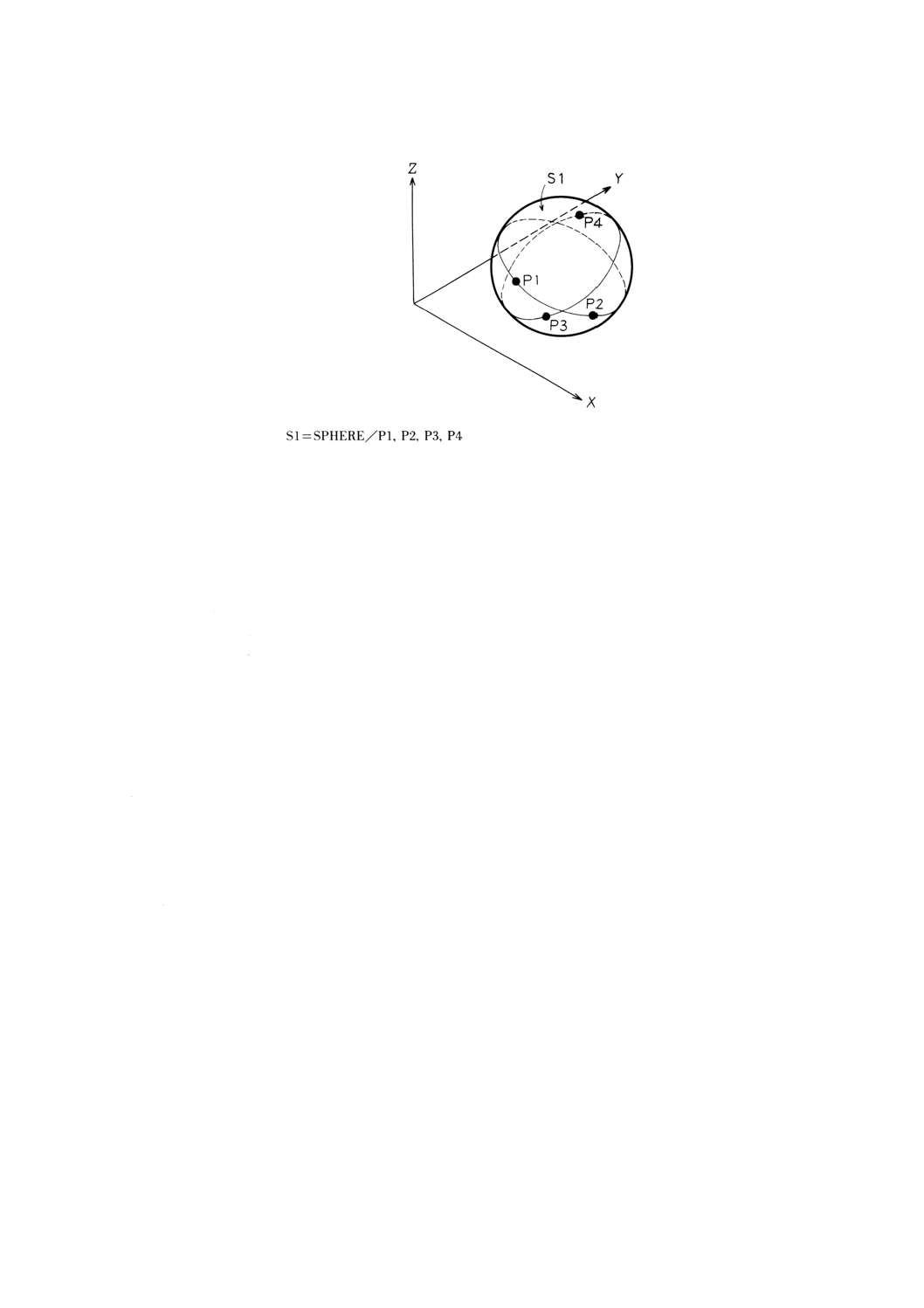
88 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 球面上の4点による球の定義の例 

9.12 円すい定義文 

9.12.1 意味と構文 

9.12.1.1 意味 円すい定義文は，円すいを定義する。定義する円すいは一葉だけとする。 

備考 半頂角は，正でなければならない。 

9.12.1.2 構文 構文は，次による。 

＜円すい定義文＞ :: ＝＜名前＞＝CONE／＜円すいのパラメータの並び＞ 

＜円すい規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］CONE／＜円すいのパラメータの並び＞） 

＜円すいのパラメータの並び＞ :: ＝＜点規制詞＞，＜ベクトル規制詞＞，＜スカラー＞｜ 

＜スカラー＞66［，＜スカラー＞］ 

9.12.2 頂点，ベクトル及び半頂角による円すいの定義 

9.12.2.1 意味 指定の点を頂点とし，指定の角度の半頂角をもち，指定のベクトルの向きの軸をもち，そ

の向きに広がる円すいを定義する。 

一般形は，次のとおりとする。 

CONE／点，ベクトル，角度 

備考1. 点は，定義する円すいの頂点とする。 

2. ベクトルは，定義する円すいの軸の向きを示すベクトルとする。 

3. 角度は，半頂角の角度とし，0度を超え90度未満の値とする。 

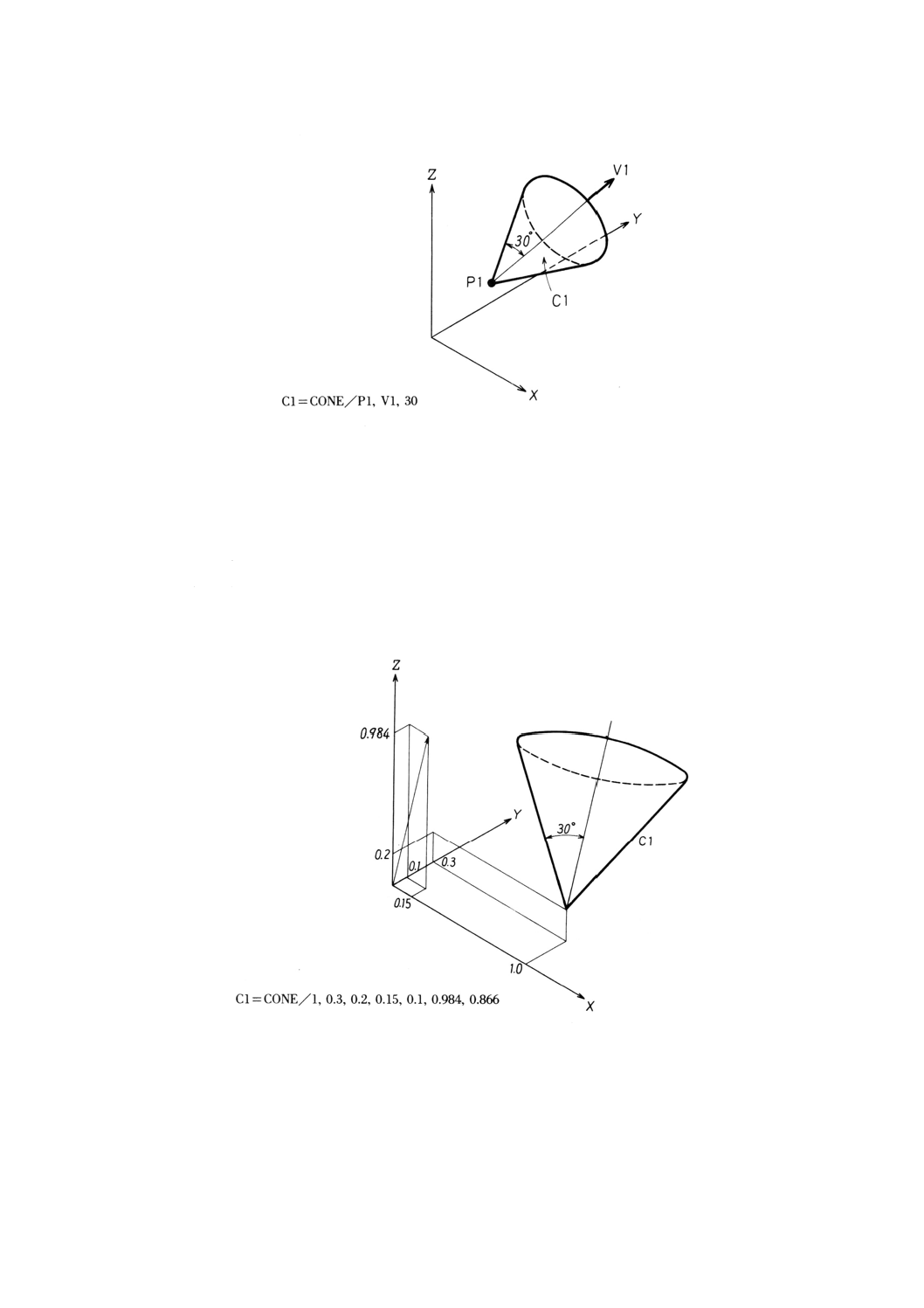
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 頂点，ベクトル及び半直角による円すいの定義の例 

9.12.3 頂点の座標，ベクトル成分及び半頂角の余弦による円すいの定義 

9.12.3.1 意味 指定の点を頂点とし，指定の余弦の半頂角をもち，指定のベクトル成分をもつベクトルの

向きを軸とする円すいを定義する。 

一般形は，次のとおりとする。 

CONE/x, y, z, a, b, c, d 

備考1. (x, y, z) は，定義する円すいの頂点の座標とする。 

2. (a, b, c) は，円すいの軸の向きを示すベクトルの座標軸X，Y及びZの成分とする。 

3. dは，0度を超え90度未満の半頂角の余弦の値とする。 

例： 頂点の座標，ベクトル成分及び半頂角の余弦による円すいの定義の例 

9.13 だ円定義文 

9.13.1 意味と構文 

9.13.1.1 意味 だ円定義文は，だ円を定義する。だ円は，XY平面に垂直なだ円柱として扱う。 

9.13.1.2 構文 構文は，次による。 

＜だ円定義文＞ :: ＝＜名前＞＝ELLIPS／＜だ円のパラメータの並び＞ 

＜だ円規制詞＞ :: ＝＜名前＞｜ 

90 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

（10［＜名前＞＝］ELLIPS／＜だ円のパラメータの並び＞） 

＜だ円のパラメータの並び＞ :: ＝CENTER，＜点規制詞＞33［，＜スカラー＞］ 

9.13.2 中心，長軸半径，短軸半径及び角度によるだ円の定義 

9.13.2.1 意味 中心，長軸半径，短軸半径及びX軸と長軸のなす角度によりだ円を定義する。 

一般形は，次のとおりとする。 

ELLIPS/CENTER，点，a，b，角度 

備考1. 点は，定義するだ円の中心とする。 

2. aは，長軸半径（長軸の長さの半分）とする。 

3. bは，短軸半径（短軸の長さの半分）とする。 

4. 角度は，基準軸Xと長軸のなす角度とし，基準軸から反時計回りの向きに測った角度を正と

する。 

例： 中心，長軸半径，短軸半径及び角度によるだ円の定義の例 

9.14 双曲線定義文 

9.14.1 意味と構文 

9.14.1.1 意味 双曲線定義文は，双曲線を定義する。双曲線の2葉とも定義される。双曲線は，XY平面

に垂直な双曲柱として扱う。 

9.14.1.2 構文 構文は，次による。 

＜双曲線定義文＞ :: ＝＜名前＞＝HYPERB／＜双曲線のパラメータの並び＞ 

＜双曲線規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］HYPERB／＜双曲線のパラメータの並び＞） 

＜双曲線のパラメータの並び＞ :: ＝CENTER，＜点規制詞＞33［，＜スカラー＞］ 

9.14.2 中心，交軸半長，共役軸半長及び角度による双曲線の定義 

9.14.2.1 意味 中心，交軸半長，共役軸半長及びX軸と交軸のなす角度により双曲線を定義する。 

一般形は，次のとおりとする。 

HYPERB/CENTER，点，a，b，角度 

備考1. 点は，定義する双曲線の中心とする。 

2. aは，定義する双曲線の交軸半長（長軸の長さの半分）とする。 

3. bは，定義する双曲線の共役軸半長（短軸の長さの半分）とする。 

4. 角度は，基準軸Xと定義する双曲線の交軸のなす角度とし，基準軸から反時計回りの向きに

測った角度を正とする。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 中心，交軸半長，共役軸半長及び角度による双曲線の定義の例 

9.15 ロフトコニック定義文 

9.15.1 意味と構文 

9.15.1.1 意味 ロフトコニック定義文は，円すい曲線を定義する。円すい曲線は，XY平面に垂直な円す

い曲線柱として扱う。 

9.15.1.2 構文 構文は，次による。 

＜ロフトコニック定義文＞ :: ＝＜名前＞＝LCONIC／＜ロフトコニックのパラメータの並び＞ 

＜ロフトコニック規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］LCONIC／＜ロフトコニックのパラメータの並び＞） 

＜ロフトコニツクのパラメータの並び＞ :: ＝＜拡張点規制詞＞44［，＜拡張点規制詞＞］｜ 

＜拡張点規制詞＞，SLOPE，＜スカラー＞33［，＜拡張点規制詞＞］｜ 

＜拡張点規制詞＞22［，SLOPE，＜スカラー＞，＜拡張点規制詞＞］ 

9.15.2 5点による円すい曲線の定義 

9.15.2.1 意味 指定した5点を通る円すい曲線を定義する。 

一般形は，次のとおりとする。 

LCONIC／

1y1

x1,

点

，

2y2

x2,

点

，

3y3

x3,

点

，

4y4

x4,

点

，

5y5

x5,

点

備考1. (x1, y1)， (x2, y2)， (x3, y3)， (x4, y4)， (x5, y5) は，定義する円すい曲線上の点の座標とす

る。 

2. 点1，点2，点3，点4，点5は，定義する円すい曲線上の点とする。 

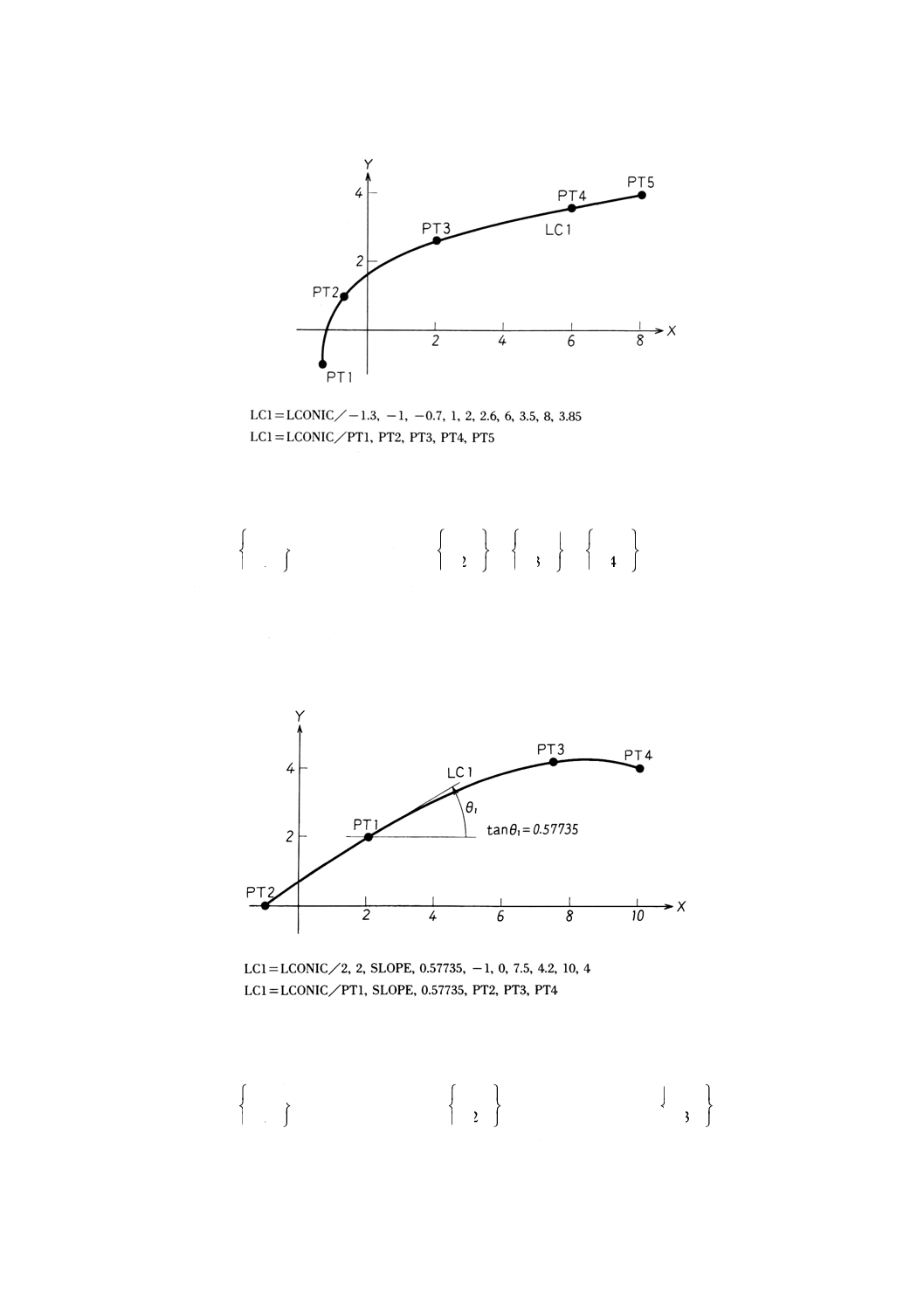
92 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 5点による円すい曲線の定義の例 

9.15.3 4点とこう配による円すい曲線の定義 

9.15.3.1 意味 指定した4点を通り，第1の点で指定したこう配をもつ円すい曲線を定義する。 

一般形は，次のとおりとする。 

LCONIC／

1y1

x1,

点

，SLOPE，こう配，

2y2

x2,

点

，

3y3

x3,

点

，

4y4

x4,

点

備考1. (x1, y1)， (x2, y2)， (x3, y3)， (x4, y4) は，定義する円すい曲線上の点の座標とする。 

2. 点1，点2，点3，点4は，定義する円すい曲線上の点とする。 

3. こう配は，点 (x1, y1) 又は点1における円すい曲線の接線と基準軸Xとのなす角度の正接と

し，基準軸から反時計回りの向きに測った角度を正とする。 

例： 4点とこう記による円すい曲線の定義の例 

9.15.4 3点と二つのこう配による円すい曲線の定義 

9.15.4.1 意味 指定した3点を通り，第1の点，第2の点で指定したこう配をもつ円すい曲線を定義する。 

一般形は，次のとおりとする。 

LCONIC／

1y1

x1,

点

，SLOPE，こう配1，

2y2

x2,

点

，SLOPE，こう配2，

3y3

x3,

点

備考1. (x1, y1)，(x2, y2)，(x3, y3) は，定義する円すい曲線上の点の座標とする。 

2. 点1，点2，点3は，定義する円すい曲線上の点とする。 

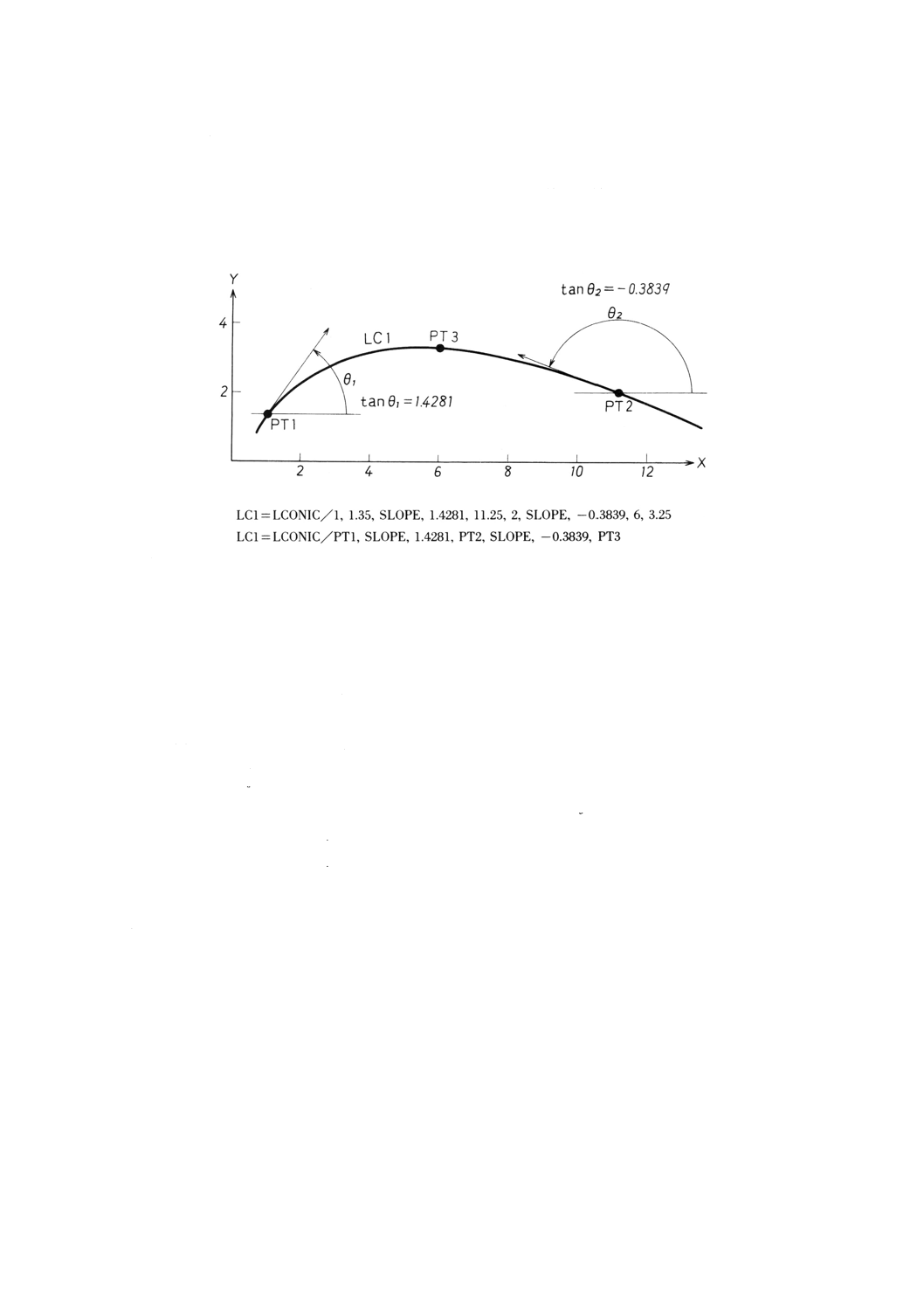
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3. こう配1は，点 (x1, y1) 又は点1における円すい曲線の接線と基準軸Xとのなす角度の正接

とし，基準軸から反時計回りの向きに測った角度を正とする。 

4. こう配2は，点 (x2, y2) 又は点2における円すい曲線の接線と基準軸Xとのなす角度の正接

とし，基準軸から反時計回りの向きに測った角度を正とする。 

例： 3点と二つのこう配による円すい曲線の定義の例 

9.16 ゼネラルコニック定義文 

9.16.1 意味と構文 

9.16.1.1 意味 ゼネラルコニック定義文は，円すい曲線を定義する。円すい曲線は，XY平面に垂直な円

すい曲線柱として扱う。 

9.16.1.2 構文 構文は，次による。 

＜ゼネラルコニック定義文＞ :: ＝＜名前＞＝GCONIC／ 

＜ゼネラルコニックのパラメータの並び＞ 

＜ゼネラルコニック規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］GCONIC／＜ゼネラルコニックのパラメータの並び＞） 

＜ゼネラルコニックのパラメータの並び＞ :: ＝＜スカラー＞55［，＜スカラー＞］｜ 

＜スカラー＞44［，＜スカラー＞］｜ 

＜スカラー＞44［，＜スカラー＞］，FUNOFY 

9.16.2 陰関数表現の円すい曲線方程式による円すい曲線の定義 

9.16.2.1 意味 陰関数表現の円すい曲線方程式の係数により円すい曲線を定義する。 

一般形は，次のとおりとする。 

GCONIC/a, b, c, d, e, f 

備考 a，b，c，d，e，fは，円すい曲線の方程式ax2＋bxy＋cy2＋dx＋ey＋f＝0の係数とする。 

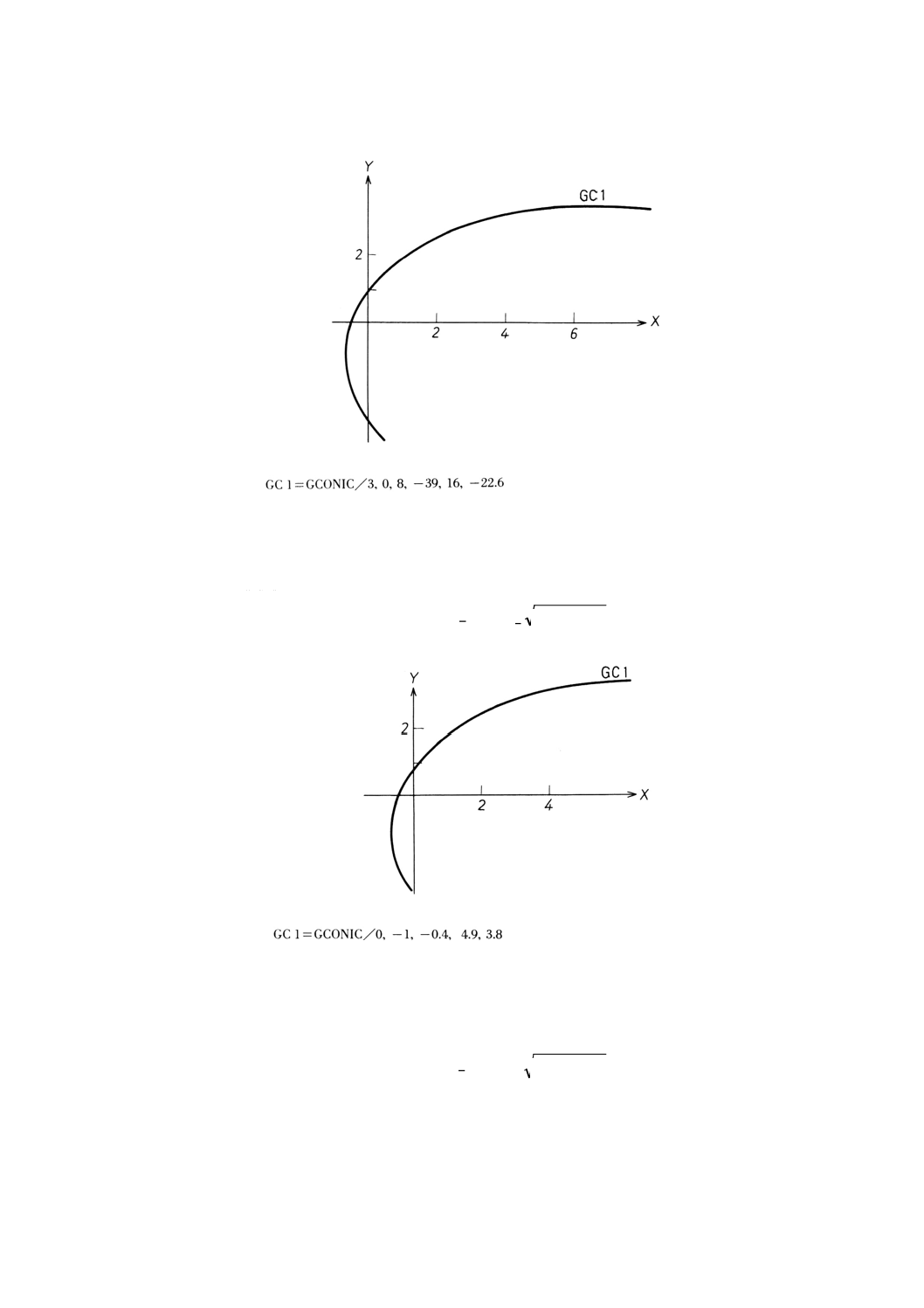
94 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 陰関数表現の円すい曲線方程式による円すい曲線の定義の例 

9.16.3 Xの陽関数表現の円すい曲線方程式による円すい曲線の定義 

9.16.3.1 意味 Xの陽関数表現の円すい曲線方程式の係数により円すい曲線を定義する。 

一般形は，次のとおりとする。 

GCONIC/p, q, r, s, t 

備考 p，q，r，s，tは，円すい曲線の方程式

t

sx

rx

q

px

y

+

+

±

+

=

2

の係数とする。 

例： Xの陽関数表現の円すい曲線方程式による円すい曲線の定義の例 

9.16.4 Yの陽関数表現の円すい曲線方程式による円すい曲線の定義 

9.16.4.1 意味 Yの陽関数表現の円すい曲線方程式の係数により円すい曲線を定義する。 

一般形は，次のとおりとする。 

GCONIC/p, q, r, s, t, FUNOFY 

備考 p，q，r，s，tは，円すい曲線の方程式

t

sy

ry

q

py

x

+

+

±

+

=

2

の係数とする。 

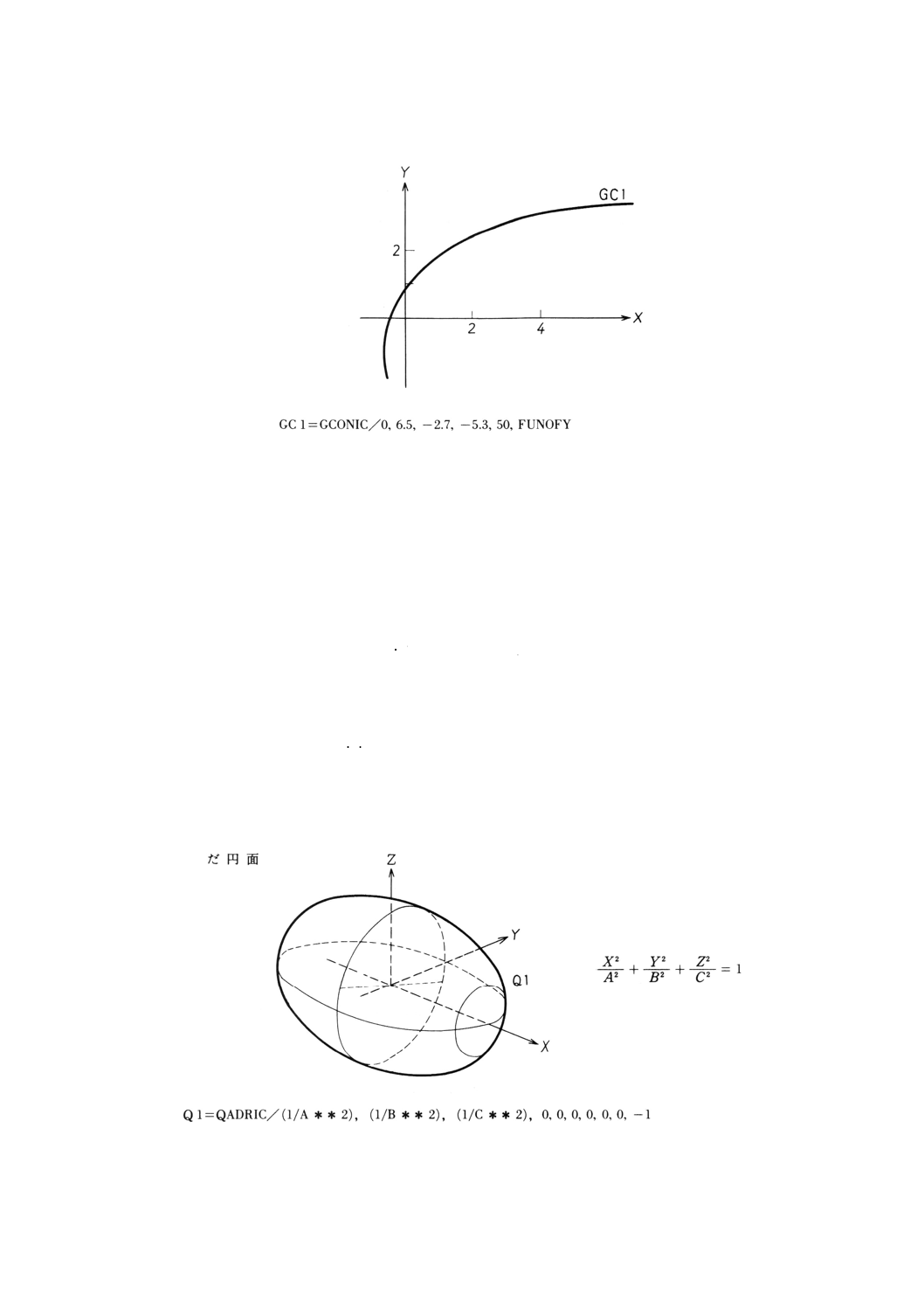
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： Yの陽関数表現の円すい曲線方程式による円すい曲線の定義の例 

9.17 二次曲面定義文 

9.17.1 意味と構文 

9.17.1.1 意味 二次曲面定義文は，二次曲面を定義する。 

9.17.1.2 構文 構文は，次による。 

＜二次曲面定義文＞ :: ＝＜名前＞＝QADRIC／＜二次曲面のパラメータの並び＞ 

＜二次曲面規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］QADRIC／＜二次曲面のパラメータの並び＞） 

＜二次曲面のパラメータの並び＞ :: ＝＜スカラー＞99［，＜スカラー＞］ 

9.17.2 二次曲面方程式による二次曲面の定義 

9.17.2.1 意味 10個の二次曲面方程式の係数により二次曲面を定義する。 

一般形は，次のとおりとする。 

QADRIC/a, b, c, d, e, f, g, h, i, j 

備考 a，b，c，d，e，f，g，h，i，jは，二次曲面の方程式 

ax2＋by2＋cz2＋dyz＋ezx＋fxy＋gx＋hy＋iz＋j＝0の係数とする。 

例： 二次曲面方程式による二次曲面の定義の例 

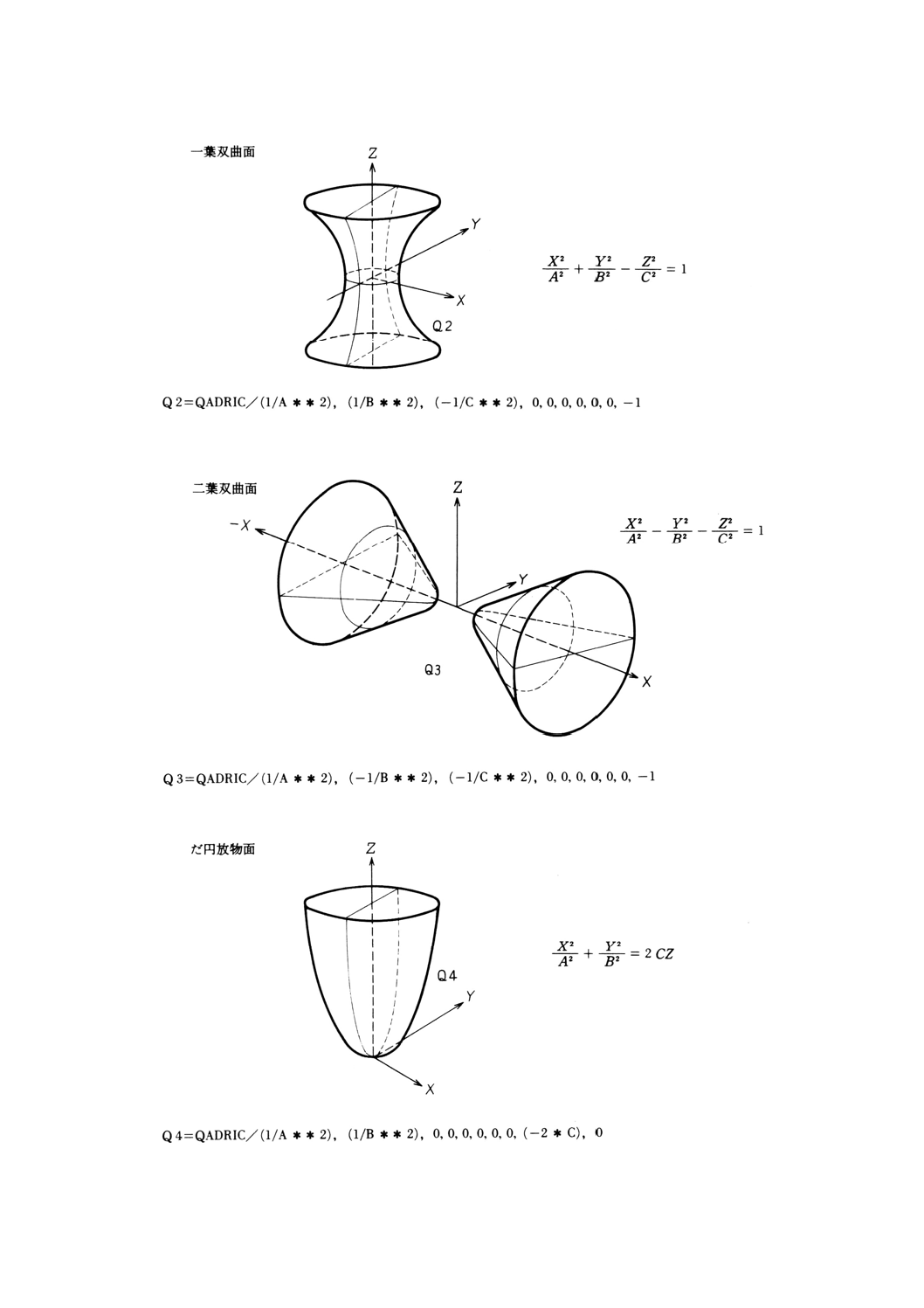
96 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

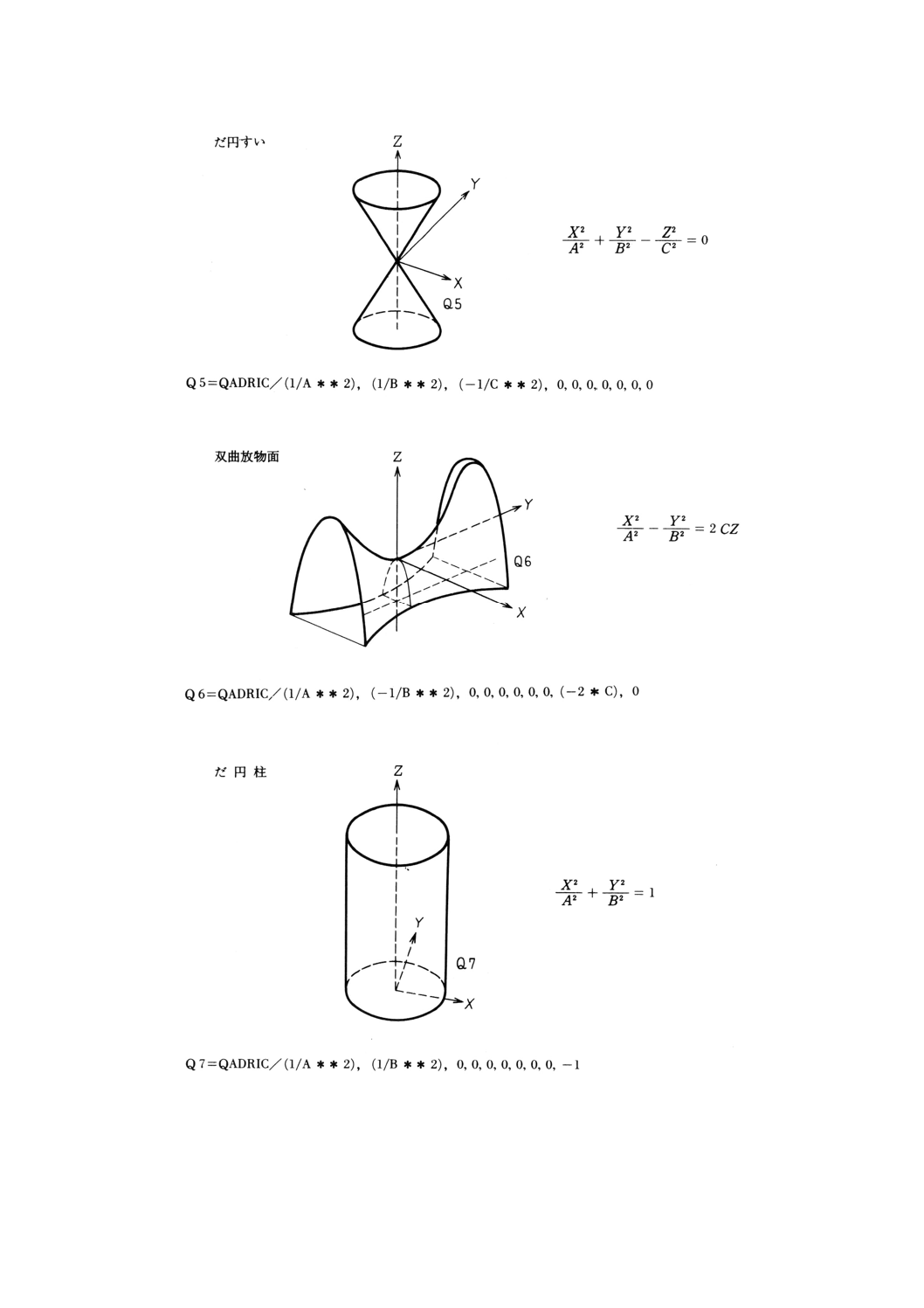
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

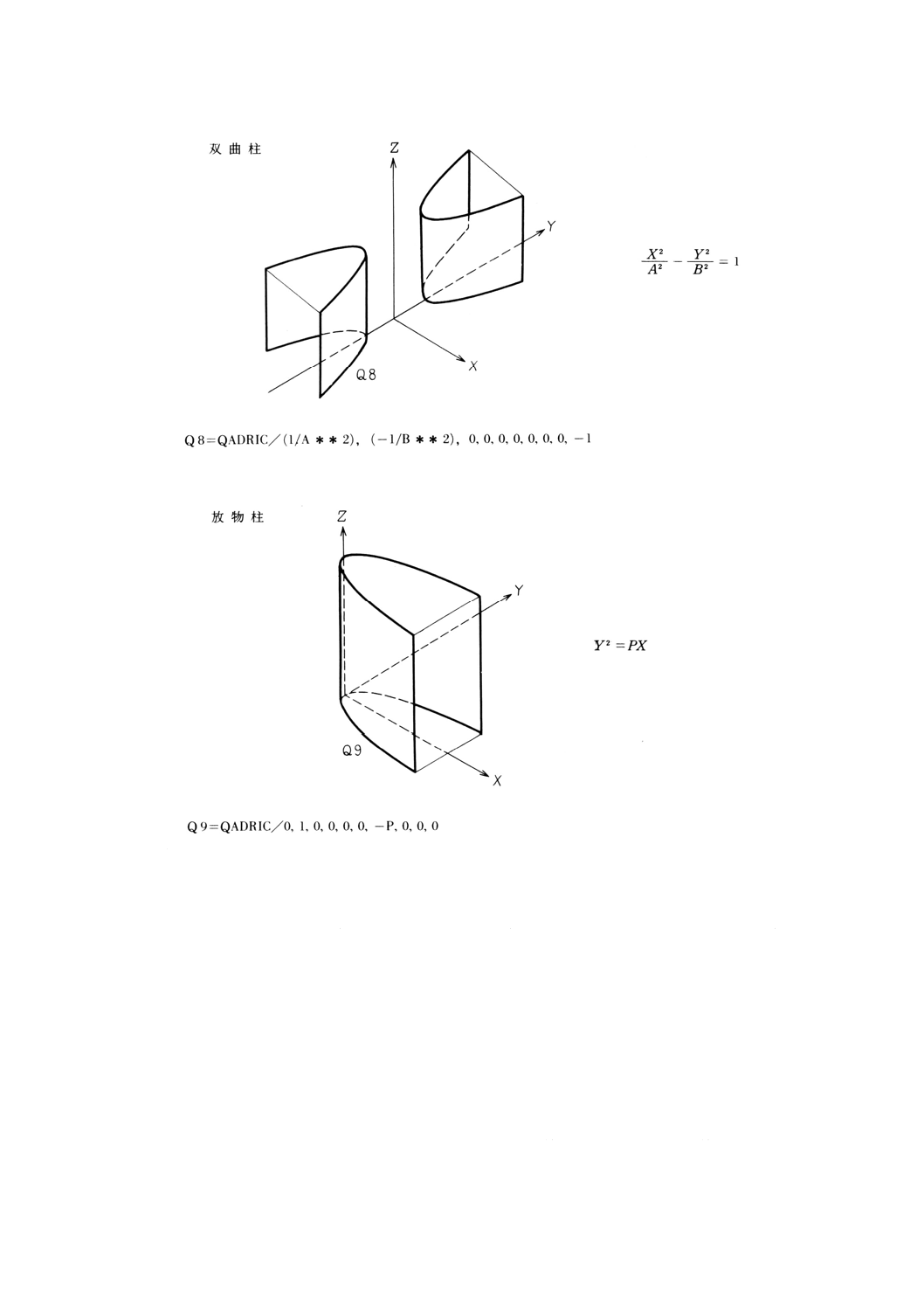
98 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.18 タブシル定義文 

9.18.1 意味と構文 

9.18.1.1 意味 タブシル定義文は，タビュレイテッドシリンダを定義する。タビュレイテッドシリンダを

タブシルと呼ぶ。タブシルは，準線に沿って平行に動く母線によって構成される柱面とする。準線は，点

の列を滑らかに接続する補間によって創成された曲線と，最初と最後の点において接線方向に有限長の線

分を延長付加した直線とで構成される曲線とする。タブシルの向きは，準線上の最初の点から最後の点に

向かう向きとする。点列を結ぶ準線は，準線上の各点の接線と曲率が連続な曲線とする。TRFORMに続く

マトリックスは，タブシルの定義における入力データを変換するためのものとする。ただし，9.18.4の定

義においては母線に対する座標変換をする。 

備考1. タブシルの定義は，次のいずれかを指定しなければならない。 

(1) 4点以上の点列 

(2) 3点以上の点列と，点列の一つの端点における法線，こう配若しくは接線 

(3) 2点以上の点列と，点列の両端点における法線，こう配若しくは接線 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

2. タブシルの定義の例に示す図では，最初と最後の点に延長付加させる線分は図示しない。 

9.18.1.2 構文 構文は，次による。 

＜タブシル定義文＞ :: ＝＜名前＞＝TABCYL／＜タブシルのパラメータの並び＞ 

＜タブシル規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］TABCYL／＜タブシルのパラメータの並び＞） 

＜タブシルのパラメータの並び＞ :: ＝11 [NOX｜NOY｜NOZ], SPLINE 

10［，TRFORM，＜マトリックス規制詞＞］，＜拡張点規制詞＞10［，TANTO， 

＜直線規制詞＞｜，SLOPE, ＜スカラー＞｜，NORMAL，＜スカラー＞］ 

1371［，＜拡張点規制詞＞］10［，TANTO，＜直線規制詞＞｜，SLOPE，＜スカラー

＞｜，NORMAL，＜スカラー＞］｜ 

11 [RTHETA｜THETAR]，SPLINE10［，TRFORM，＜マトリックス規制詞＞］ 

22［，＜スカラー＞］10［，TANTO，＜直線規制詞＞｜，SLOPE，＜スカラー＞｜ 

，NORMAL, ＜スカラー＞］1371［22[，＜スカラー＞］］10［，TANTO， 

＜直線規制詞＞｜，SLOPE，＜スカラー＞｜，NORMAL，＜スカラー＞］｜ 

XYZ, SPLINE10［，TRFORM，＜マトリックス規制詞＞］，＜ベクトル規制詞＞ 

1381［，＜点規制詞＞｜33［，＜スカラー＞］］｜ 

PARLEL，＜タブシル規制詞＞10［，＜点規制詞＞］，11 [XLARGE｜XSMALL｜ 

YLARGE｜YSMALLIZLARGE｜ZSMALL], ＜スカラー＞ 

9.18.2 点列によるタブシルの定義 

9.18.2.1 意味 点又は任意の二つの座標軸の座標で表現された点の列，必要ならば端点における法線，こ

う配又は接線によりタブシルを定義する。二つの座標軸は，NOX，NOY又はNOZで選択する。例えば，

NOZを指定した場合は，X軸が第1座標軸，Y軸が第2座標軸として選択され，タブシルの母線は，Z軸

に平行となる。 

一般形は，次のとおりとする。 

TABCYL/

NOZ

NOY

NOX

，SPLINE［，TRFORM，マトリックス］，

b1

a1,

1

点

¥ 

2

TANTO,

2

SLOPE,

2

NORMAL,

bn

an,

b2

a2,

2

1

TANTO,

1

SLOPE,

1

NORMAL,

,

直線

こう配

角度

，

点ｎ

，･･･，

点

，

直線

こう配

角度

備考1. マトリックスは，タブシルの定義における入力データを変換するマトリックスとする。 

2. 点1，点2，…，点nは，定義するタブシル上の点とし，NOX，NOY又はNOZによって選

択された座標面上の点とする。 

3. (a1, b1)，…， (an, bn) は，定義するタブシル上の点の座標とし，NOX，NOY又はNOZによ

って選択された座標平面上の第1座標軸と第2座標軸の座標とする。 

4. 角度1，角度2は，第1座標軸の基準軸からそれぞれ最初の点，最後の点における法線に向

かって測った角度とし，基準軸から反時計回りの向きに測った角度を正とする。 

5. こう配1，こう配2は，第1座標軸の基準軸からそれぞれ最初の点，最後の点における接線

に向かって測った角度の正接とし，角度の測り方は備考4.と同様とする。 

6. 直線1，直線2は，それぞれ最初の点，最後の点における接線とする。ただし接線の指定は，

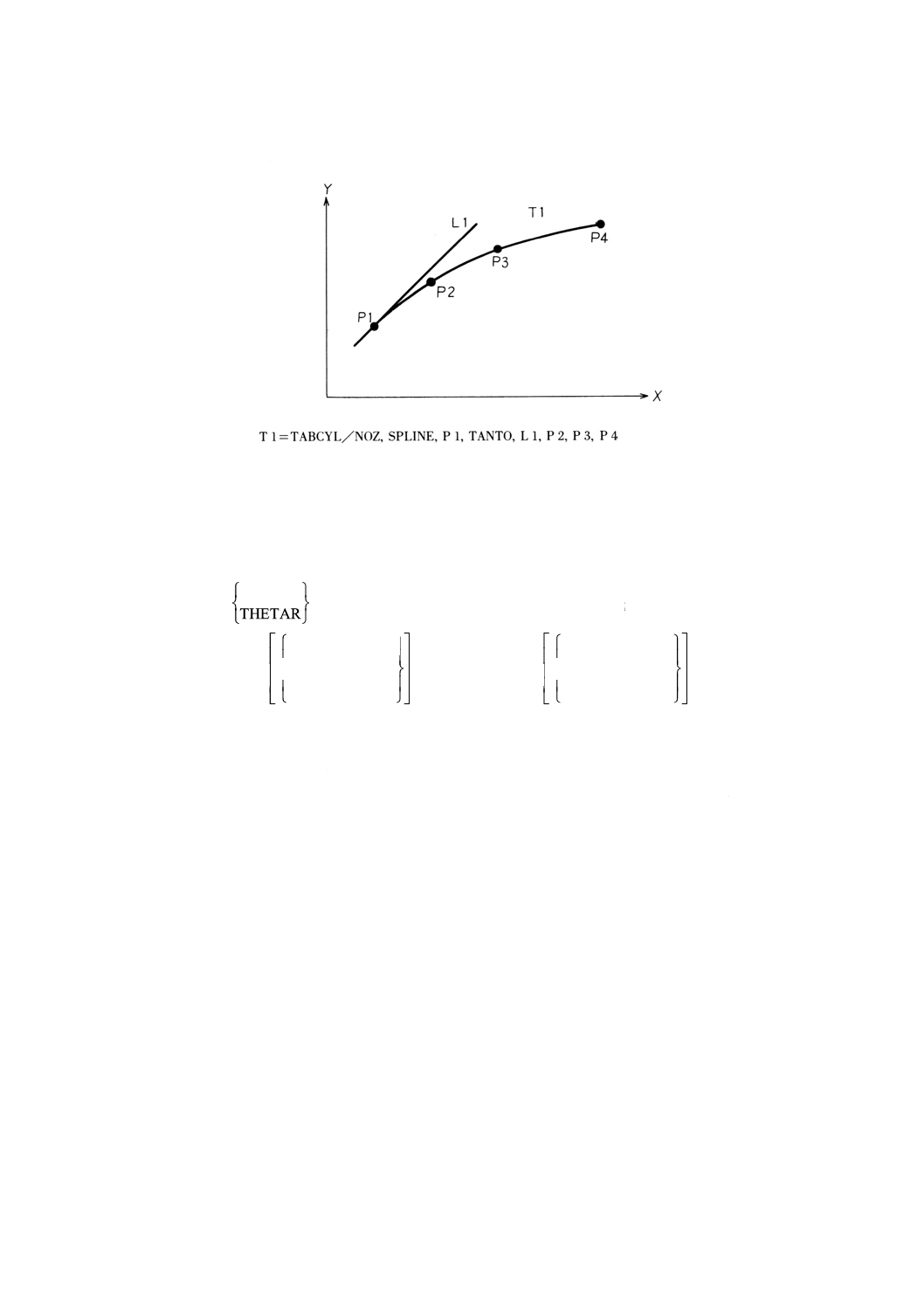
100 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

NOZのときだけ使用できる。 

例： 点列によるタブシルの定義の例 

9.18.3 極座標点列によるタブシルの定義 

9.18.3.1 意味 XY平面上の極座標による点の列，必要ならば端点における法線，こう配又は接線により

タブシルを定義する。タブシルの座標を変換する必要があるとき，変換マトリックスを指定することがで

きる。母線は，Z軸に平行となる。 

一般形は，次のとおりとする。 

TABCYL/

THETAR

RTHETA

，SPLINE［，TRFORM，マトリックス］，¥ 

a1, b1

1

TANTO,

1

SLOPE,

1

NORMAL,

直線

こう配

角度

，

，a2, b2,…，an, bn

2

TANTO,

2

SLOPE,

2

NORMAL,

直線

こう配

角度

，

備考1. マトリックスは，タブシルの定義における入力データを変換するマトリックスとする。 

2. (a1, b1)，…， (an, bn) は，それぞれRTHETAのときは，a1〜anが動径，b1〜bnが角度とし，

THETARのときは逆とする。 

3. 角度1，角度2は，基準軸X軸からそれぞれ最初の点，最後の点における法線に向かって測

った角度とし，基準軸から反時計回りの向きに測った角度を正とする。 

4. こう配1，こう配2は，基準軸X軸からそれぞれ最初の点，最後の点における接線に向かっ

て測った角度の正接とし，角度の測り方は備考3.と同様とする。 

5. 直線1，直線2は，それぞれ最初の点，最後の点における接線とする。 

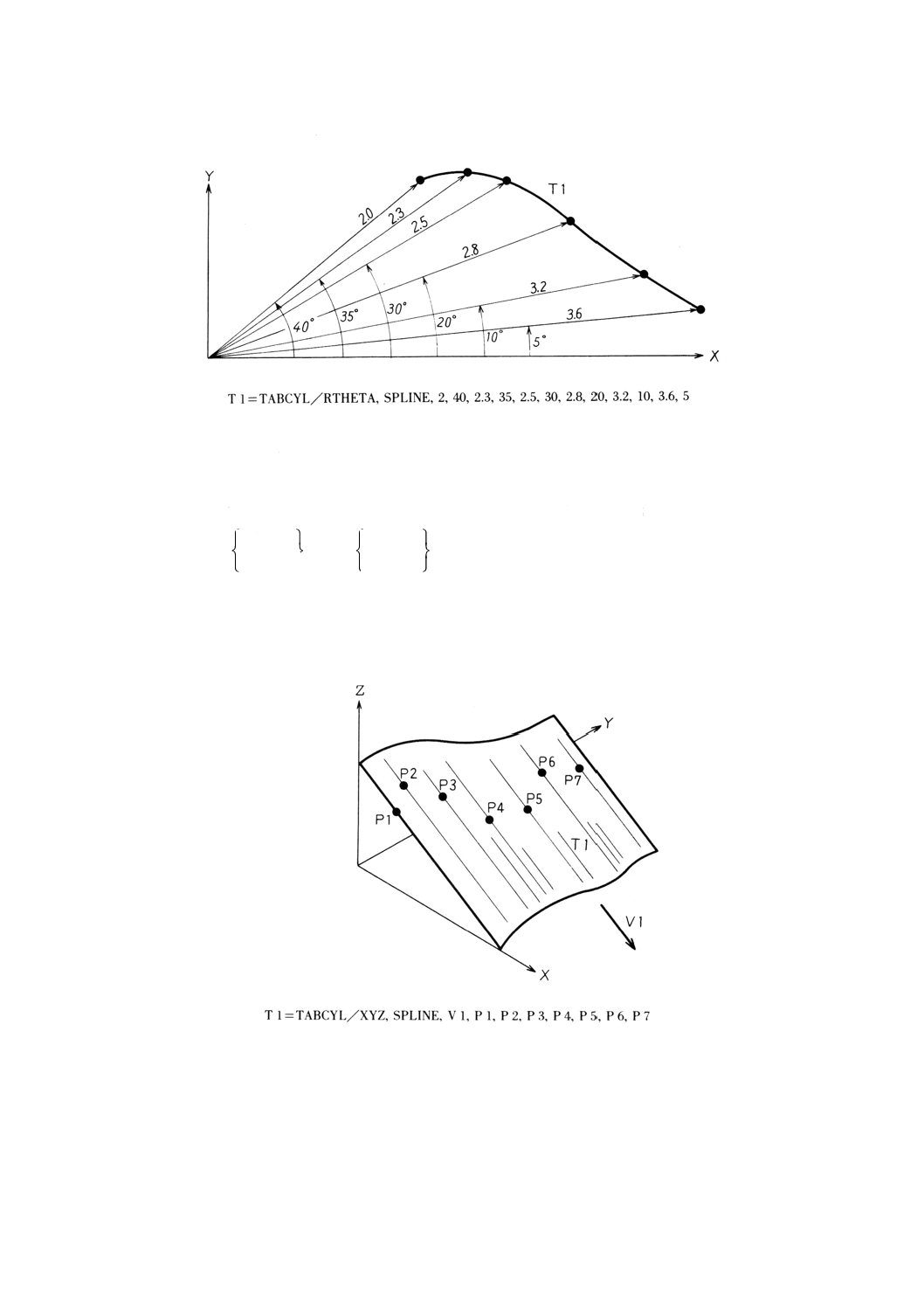
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 極座標点列によるタブシルの定義の例 

9.18.4 点列とベクトルによるタブシルの定義 

9.18.4.1 意味 点列と母線に平行なベクトルとによりタブシルを定義する。 

一般形は，次のとおりとする。 

TABCYL/XYZ, SPLINE［，TRFORM，マトリックス］，ベクトル，¥ 

z1

y1,

x1,

1

点

，…，

zn

yn,

xn,

2

点

備考1. マトリックスは，定義するタブシルの母線に対する座標変換をするマトリックスとする。 

2. ベクトルは，定義するタブシルの母線に平行なベクトルとする。 

3. 点1，点2，…，点nは，定義するタブシル上の点とする。 

4. (x1, y1, z1)， (x2, y2, z2)，…， (xn, yn, zn) は，定義するタブシル上の点の座標とする。 

9.18.5 指定したタブシルから箏距離にあるタブシルの定義 

9.18.5.1 意味 指定したタブシルと指定した距離にあるタブシルを定義する。 

一般形は，次のとおりとする。 

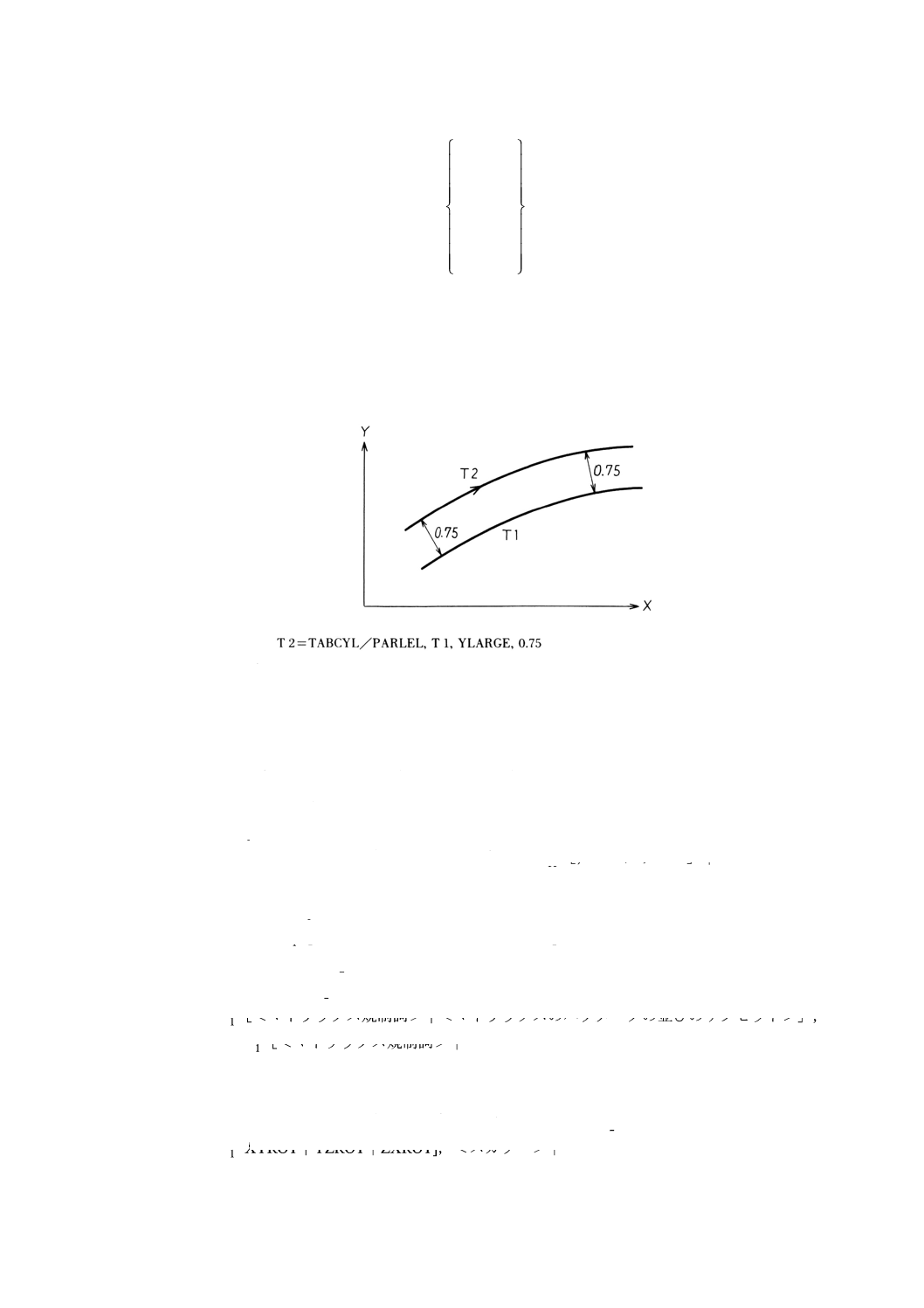
102 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

TABCYL/PARLEL，タブシル［，点］，

ZSMALL

ZLARGE

YSMALL

YLARGE

XSMALL

XLARGE

，距離 

備考1. タブシルは，定義するタブシルに平行とする。 

2. 点は，指定したタブシルから，指定した距離にある二つのタブシルのいずれかを選択するた

めの修飾語の判定を行う点とする。 

3. 距離は，指定したタブシルとそれに平行な定義するタブシルとの隔たりとする。 

例： 指定したタブシルから等距離にあるタブシルの定義の例 

9.19 マトリックス定義文 

9.19.1 意味と構文 

9.19.1.1 意味 マトリックス定義文は，座標系の変換を行うマトリックスを定義する。 

9.19.1.2 構文 構文は，次による。 

＜マトリックス定義文＞ :: ＝＜名前＞＝MATRIX／＜マトリックスのパラメータの並び＞ 

＜マトリックス規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］MATRIX／＜マトリックスのパラメータの並び＞） 

＜マトリックスのパラメータの並び＞ :: ＝＜スカラー＞11

11［，＜スカラー＞］｜ 

＜マトリックスのパラメータの並びのサブセット＞｜ 

MIRROR，11［＜直線規制詞＞｜＜平面規制詞＞］｜ 

MIRROR31 [, XYPLAN｜, YZPLAN｜, ZXPLAN] ｜ 

＜平面規制詞＞22［，＜平面規制詞＞］｜ 

＜点規制詞＞22［，＜ベクトル規制詞＞］｜ 

11［＜マトリックス規制詞＞｜＜マトリックスのパラメータの並びのサブセット＞］， 

11［＜マトリックス規制詞＞｜ 

＜マトリックスのパラメータの並びのサブセット＞］｜ 

INVERS，＜マトリックス規制詞＞ 

＜マトリックスのパラメータの並びのサブセット＞ :: ＝TRANSL32［，＜スカラー＞］｜ 

11 XYROT｜YZROT｜ZXROT]，＜スカラー＞｜ 

SCALE，＜スカラー＞ 

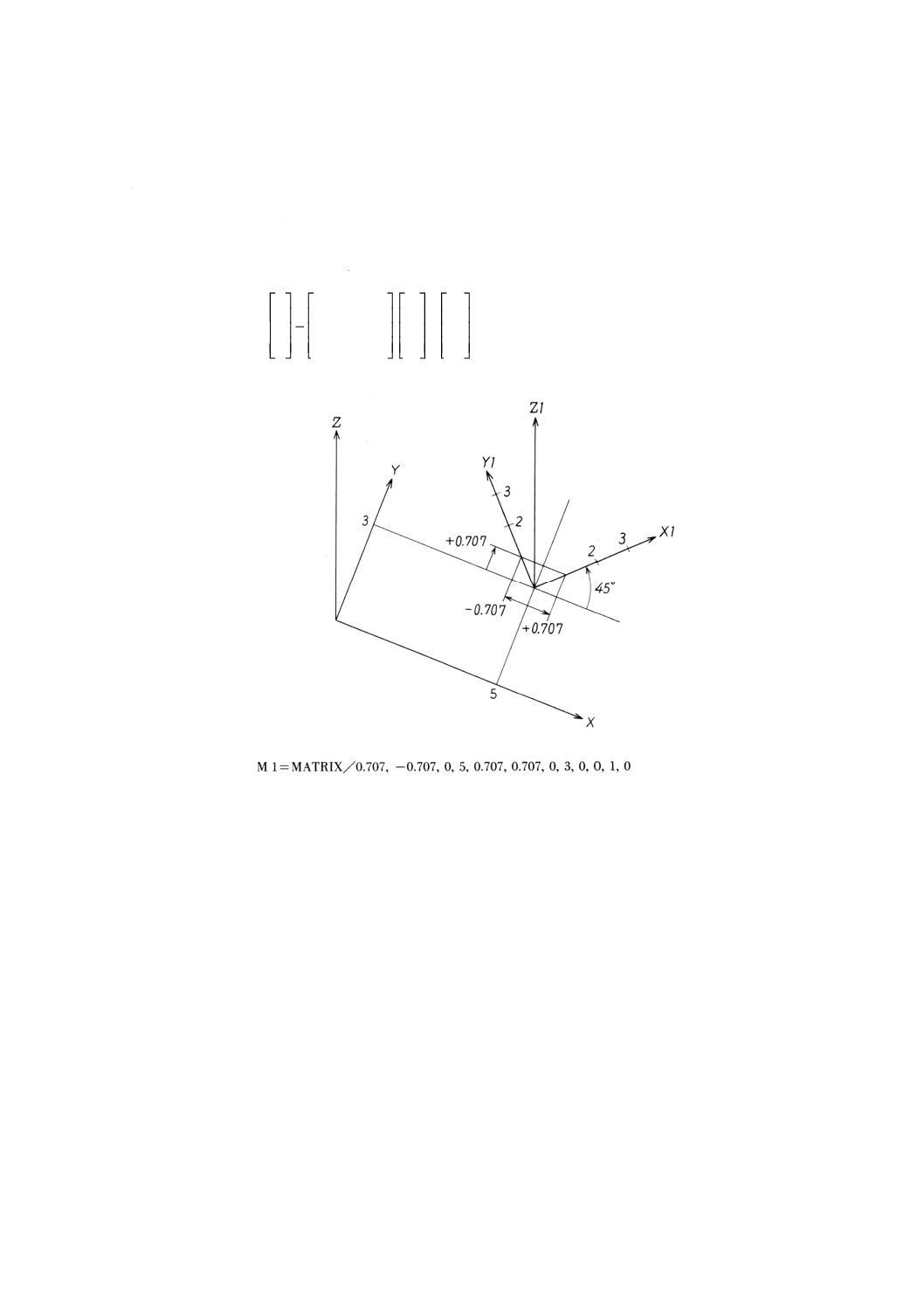
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.19.212 個の係数によるマトリックスの定義 

9.19.2.1 意味 12個の係数によりマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3 

備考 a1，b1，c1，d1，a2，b2，c2，d2，a3，b3，c3，d3は，新座標系と旧座標系の関係を示す変換

式の係数とする。 (x, y, z) (x1, y1, z1) をそれぞれ旧座標系，新座標系の座標とする。 

すなわち，

+

=

3

2

1

1

1

1

3

3

3

2

2

2

1

1

1

d

d

d

z

y

x

c

b

a

c

b

a

c

b

a

z

y

x

例： 12個の係数によるマトリックスの定義の例 

備考 この例では，新座標系のX1軸，Y1軸及びZ1軸は，それぞれ旧座標系のX軸，Y軸

及びZ軸に関して (0.707, 0.707, 0)， (−0.707, 0.707, 0) 及び (0, 0, 1) の方向余弦をも
つ。新座標系の原点は，旧座標系上の座標において (5, 3, 0) である。 

9.19.3 平行移動をするマトリックスの定義 

9.19.3.1 意味 座標系の平行移動をするマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/TRANSL, a, b [, c] 

備考 a，b，cは，新座標系の原点の旧座標系での座標とする。cが省略されたときは，cは0とみな

す。 

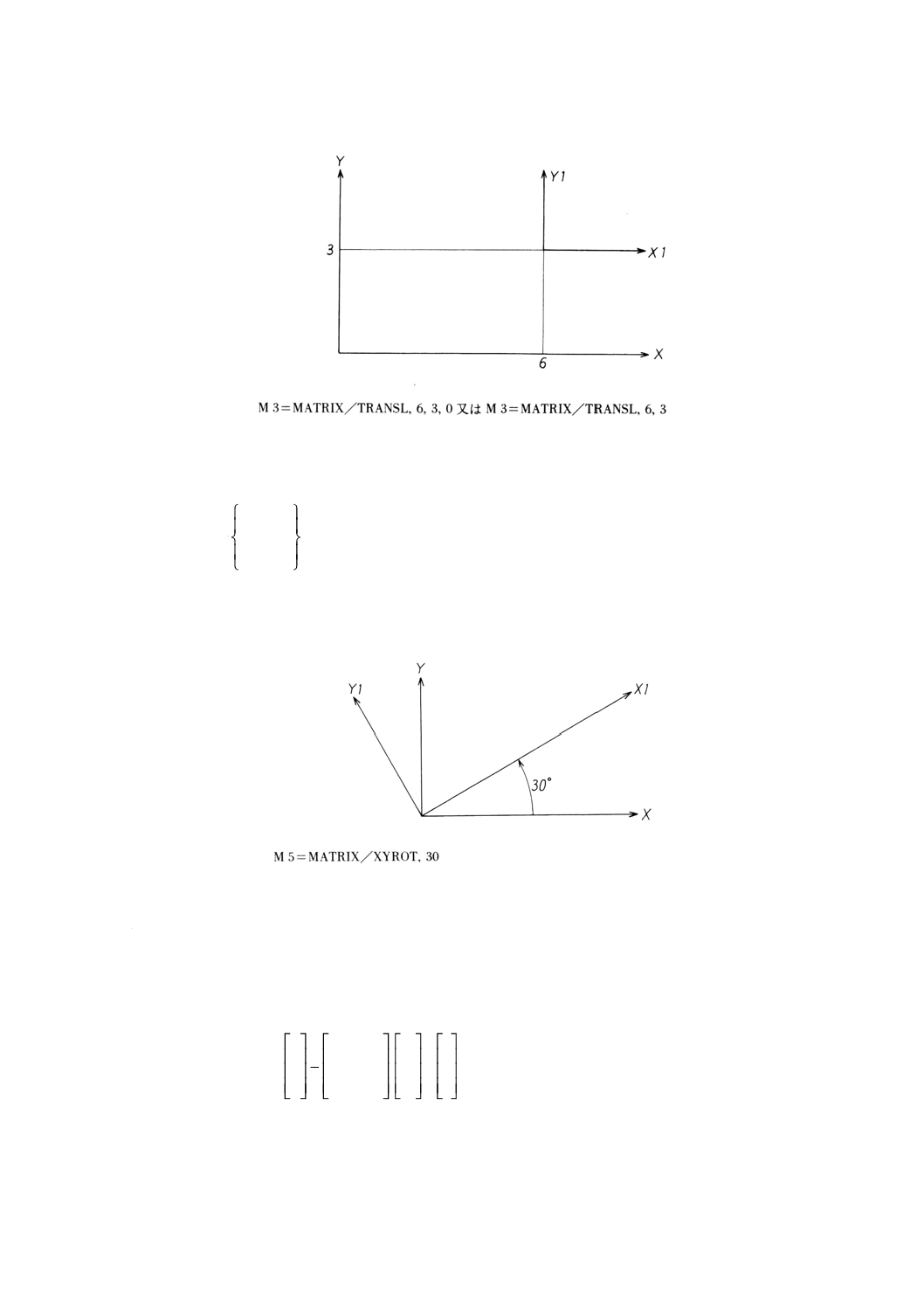
104 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 平行移動をするマトリックスの定義の例 

9.19.4 回転をするマトリックスの定義 

9.19.4.1 意味 座標系の座標平面内における回転をするマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/

ZXROT

YZROT

XYROT

，角度 

備考1. XYROT，YZROT，ZXROTは，回転させる座標平面を指定する。 

2. 角度は，基準軸からの回転角度とし，基準軸から反時計回りの向きに測った角度を正とする。 

例： 回転をするマトリックスの定義の例 

9.19.5 尺度の変換をするマトリックスの定義 

9.19.5.1 意味 座標軸の尺度変換をするマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/SCALE，尺度 

備考 尺度は，旧座標系の単位ベクトルに対する新座標系の単位ベクトルの大きさの比とする。 

尺度がnの変換式は，次式とする。 

+

=

0

0

0

0

0

0

0

0

0

1

1

1

z

y

x

n

n

n

z

y

x

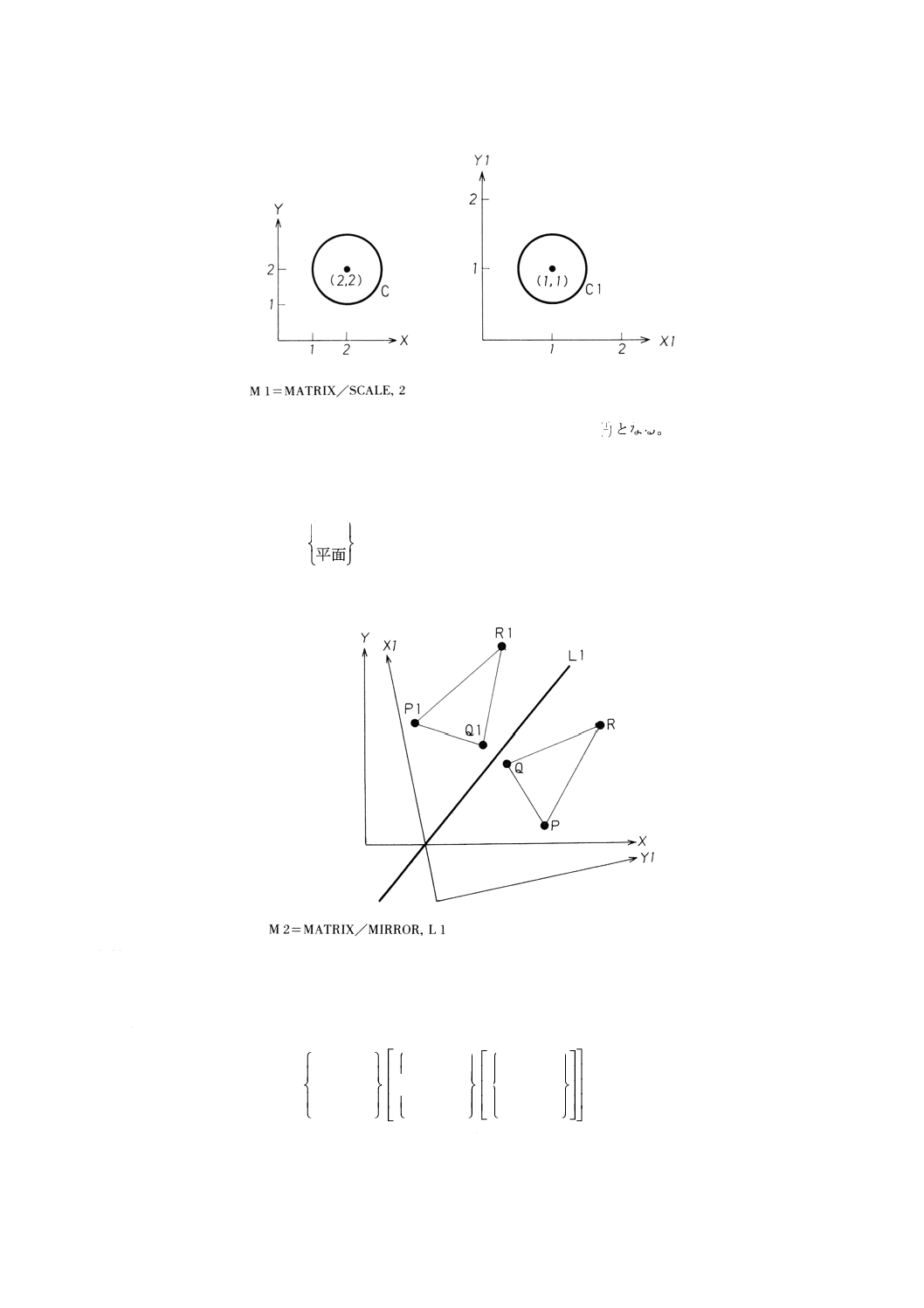
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 尺度の変換をするマトリックスの定義の例 

備考 この例では，旧座標系上の円 C : (x−2) 2＋ (y−2) 2＝12は， 

     新座標系上の円 C1 : (x1−1) 2＋ (y1−1) 2＝

2

2

1

となる。 

9.19.6 直線対称又は平面対称を求めるマトリックスの定義 

9.19.6.1 意味 直線対称又は平面対称を求めるマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/MIRROR，

平面

直線

備考 直線，平面は，それぞれ旧座標系と新座標系との対称関係を示す直線及び平面とする。 

例： 直線対称又は平面対称を求めるマトリックスの定義の例 

9.19.7 座標平面対称を求めるマトリックスの定義 

9.19.7.1 意味 一つの座標平面，二つの座標平面の交線又は三つの座標平面の交点に対する対称を求める

マトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/MIRROR, 

ZXPLAN

YZPLAN

XYPLAN

ZXPLAN

YZPLAN

XYPLAN

ZXPLAN

YZPLAN

XYPLAN

，

，

備考 対称を求めるための平面は，同一のものを複数個指定してはならない。 

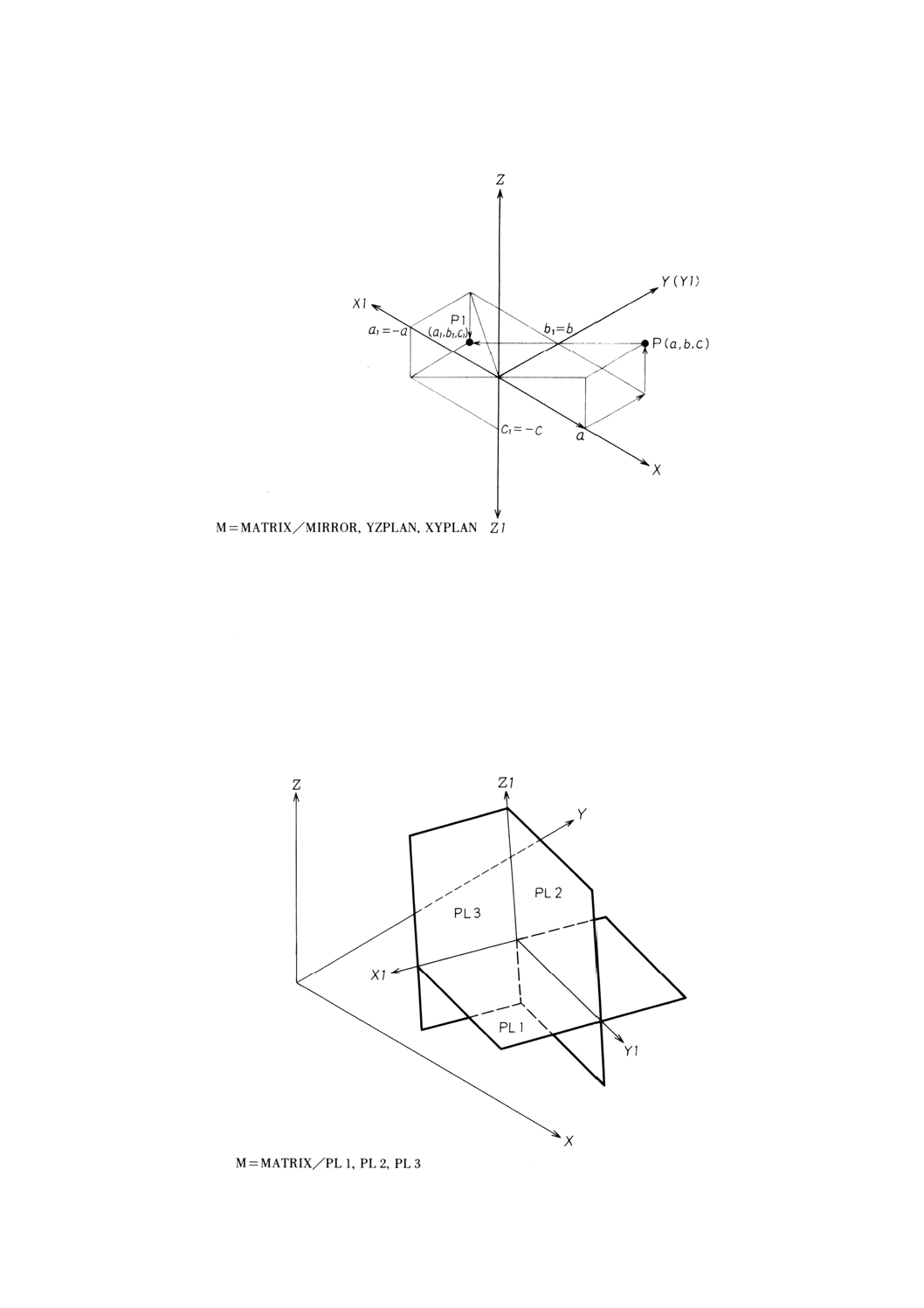
106 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 座標平面対称を求めるマトリックスの定義の例 

9.19.8 3平面によるマトリックスの定義 

9.19.8.1 意味 三つの直交平面の交線が新座標系となるようなマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX／平面1，平面2，平面3 

備考1. 平面1，平面2，平面3は，それぞれ新座標系のXY，YZ，ZXの平面とする。 

2. X軸の正の向きはYZ平面の面ベクトルの向き，Y軸の正の向きはZX平面の面ベクトルの

向き，Z軸の正の向きはXY平面の面ベクトルの向きとする。 

例： 3平面によるマトリックスの定義の例 

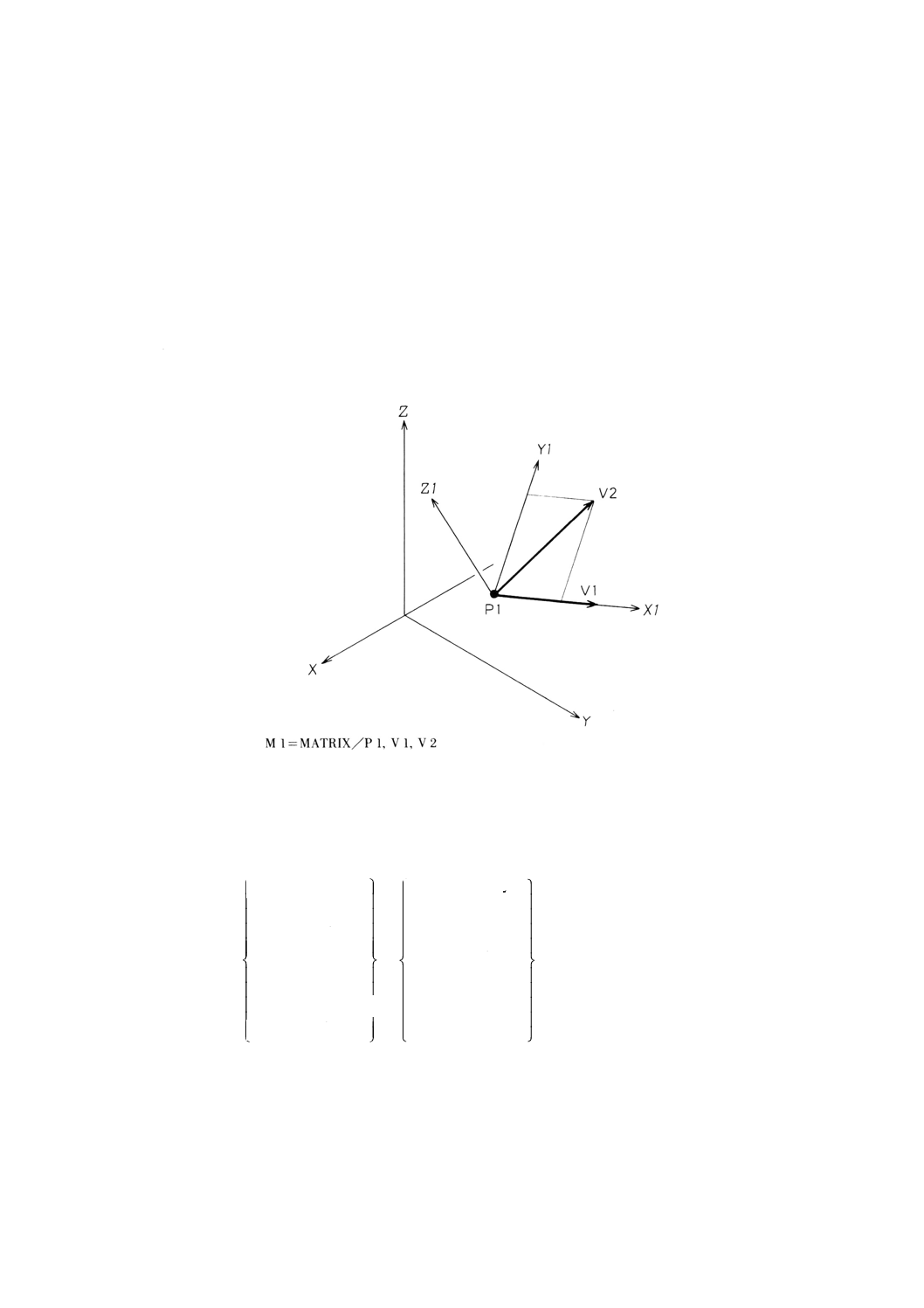
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

9.19.9 1点と2ベクトルによるマトリックスの定義 

9.19.9.1 意味 原点を示す点，X軸を示すベクトル及びこのベクトルともう一つのベクトルにより決まる

平面をXY平面とする新座標系を作るマトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX／点，ベクトル1，ベクトル2 

備考1. 点は，新座標系の原点とする。 

2. ベクトル1，ベクトル2は，新座標系のXY平面上のベクトルとし，ベクトル1は，新座標

系のX軸とする。 

3. 二つのベクトルは，平行であってはならない。 

例： 1点と2ベクトルによるマトリックスの定義の例 

9.19.10 二つのマトリックスの組合せによるマトリックスの定義 

9.19.10.1 意味 第1のマトリックスを適用し，第2のマトリックスを次に適用するマトリックスとして定

義する。 

一般形は，次のとおりとする。 

MATRIX／

1

SCALE,

c1

b1,

a1,

TRANSL,

b1

a1,

TRANSL,

1

ZXROT,

1

YZROT,

1

XYROT,

1

尺度

角度

角度

角度

マトリックス

，

2

SCALE,

c2

b2,

a2,

TRANSL,

b2

a2,

TRANSL,

2

ZXROT,

2

YZROT,

2

XYROT,

2

尺度

角度

角度

角度

マトリックス

備考1. マトリックス1は，第1に適用するマトリックスとし，マトリックス2は，第2に適用するマト

リックスとする。 

2. 角度1は，第1に適用する回転の角度とし，角度2は，第2に適用する回転の角度とする。 

3. 角度1，角度2は，第1基準軸からの回転角度とし，反時計回りの向きに測った角度を正と

する。 

108 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

4. (a1, b1)， (a1, b1, c1) は，第1に適用する平行移動量とし，(a2, b2)，(a2, b2, c2) は，第2に

適用する平行移動量とする。 

5. 尺度1は，第1に適用する尺度の変換とし，尺度2は，第2に適用する尺度の変換とする。 

9.19.11 逆マトリックスとしてのマトリックスの定義 

9.19.11.1 意味 指定したマトリックスの逆マトリックスを定義する。 

一般形は，次のとおりとする。 

MATRIX/INVERS，マトリックス 

備考 マトリックスは，このマトリックスの逆マトリックスを定義するマトリックスとする。 

9.20 ルールドサーフェス定義文 

9.20.1 意味と構文 

9.20.1.1 意味 ルールドサーフェス定義文は，2本の空間曲線を結ぶ直線で作られる面（ルールドサーフ

ェス）を定義する。 

9.20.1.2 構文 構文は，次による。 

＜ルールドサーフェス定義文＞ :: ＝＜名前＞＝RLDSRF／ 

＜ルールドサーフェスのパラメータの並び＞ 

＜ルールドサーフェス規制詞＞ :: ＝＜名前＞｜ 

（10［＜名前＞＝］RLDSRF／＜ルールドサーフェスのパラメータの並び＞） 

＜ルールドサーフェスのパラメータの並び＞ :: ＝＜面規制詞＞22［，＜点規制詞＞］， 

11［＜点規制詞＞｜＜ベクトル規制詞＞］，＜面規制詞＞22［，＜点規制詞＞］， 

11［＜点規制詞＞｜＜ベクトル規制詞＞］｜ 

＜面規制詞＞22［，＜点規制詞＞］，11［＜点規制詞＞｜＜ベクトル規制詞＞］， 

＜点規制詞＞ 

9.20.2 2曲面と，3点又は2点と1ベクトルが定める2平面によるルールドサーフェスの定義 

9.20.2.1 意味 二つの曲面と二つの平面とが交わる二つの空間曲線の対応点を結ぶ直線群によってルー

ルドサーフェスを定義する。二つの平面は，三つの点又は二つの点と一つのベクトルにより定まる平面で，

各平面上の二つの点は，それぞれ対応点となる。 

一般形は，次のとおりとする。 

RLDSRF／曲面1，点1，点2，

1

3

ベクトル

点

，曲面2，点4，点5，

2

6

ベクトル

点

備考1. 曲面1，曲面2は，定義するルールドサーフェスの空間曲線を含む曲面とする。 

2. 点1，点2，点3は，一つの平面上の点とする。 

3. 点4，点5，点6は，もう一つの平面上の点とする。 

4. 点1，点2，ベクトル1は，一つの平面上の点及びベクトルとする。 

5. 点4，点5，ベクトル2は，もう一つの平面上の点及びベクトルとする。 

6. 点1，点2は，それぞれ定義するルールドサーフェスの空間曲線の始点及び終点とする。 

7. 点4，点5は，それぞれ定義するルールドサーフェスの空間曲線の始点及び終点とする。 

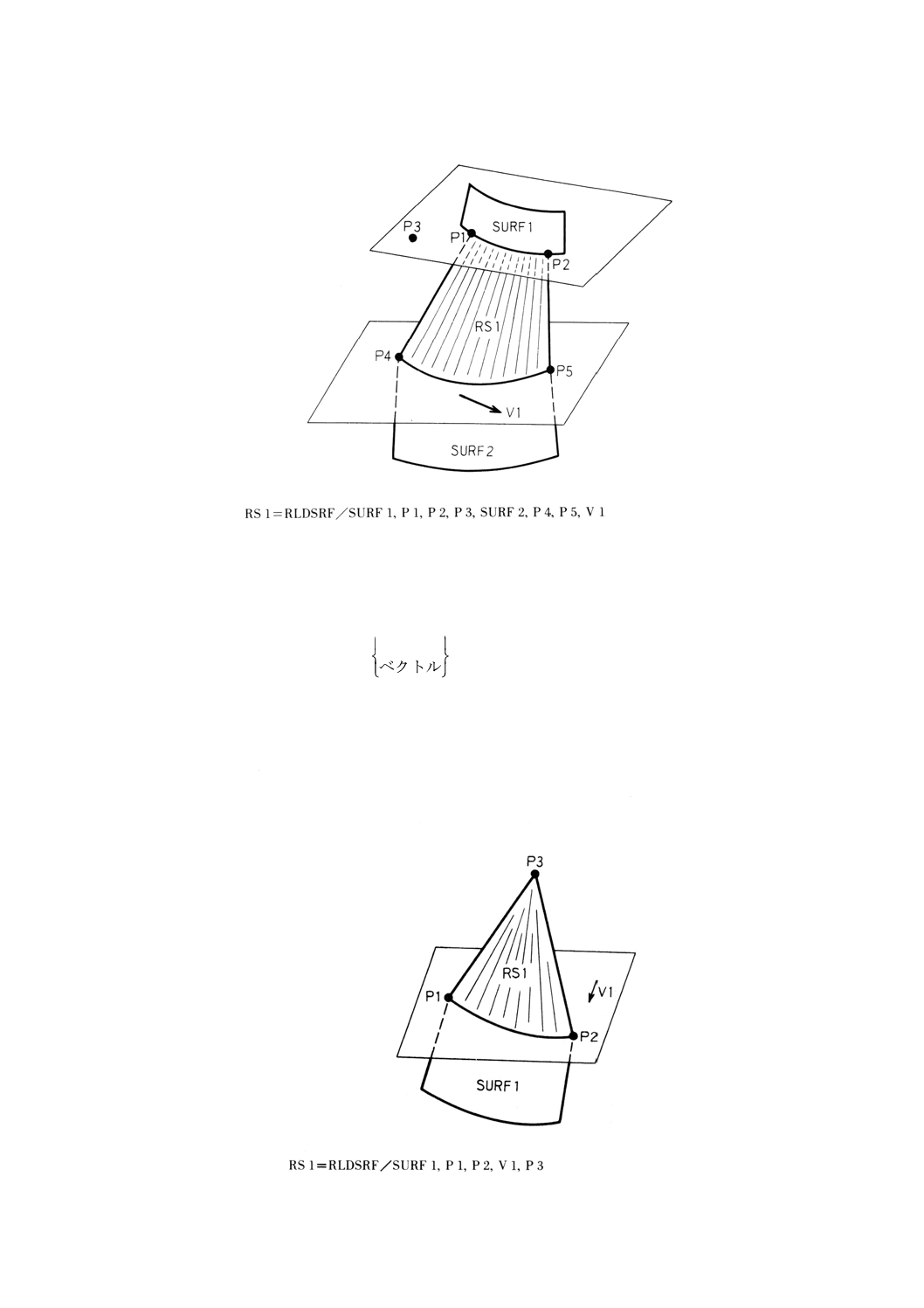
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 2曲面と，3点又は2点と1ベクトルが定める2平面によるルールドサーフェスの定義の例 

9.20.3 曲面と，3点又は2点と1ベクトルが定める平面及び点によるルールドサーフェスの定義 

9.20.3.1 意味 曲面と，3点が定める平面又は2点と1ベクトルが定める平面とが交わる空間曲線上の点

と，指定した点を結ぶ直線群によってルールドサーフェスを定義する。 

一般形は，次のとおりとする。 

RLDSRF／曲面，点1，点2，

ベクトル

点3

，点4 

備考1. 曲面は，定義するルールドサーフェスの空間曲線を含む曲面とする。 

2. 点1，点2，点3は，一つの平面上の点とする。 

3. 点1，点2，ベクトルは，一つの平面上の点及びベクトルとする。 

4. 点4は，定義するルールドサーフェス上の点とする。 

5. 点1，点2は，それぞれ定義するルールドサーフェスの空間曲線の始点及び終点とする。 

例： 曲面と，3点又は2点と1ベクトルが定める平面及び点によるルールドサーフェスの定義の例 

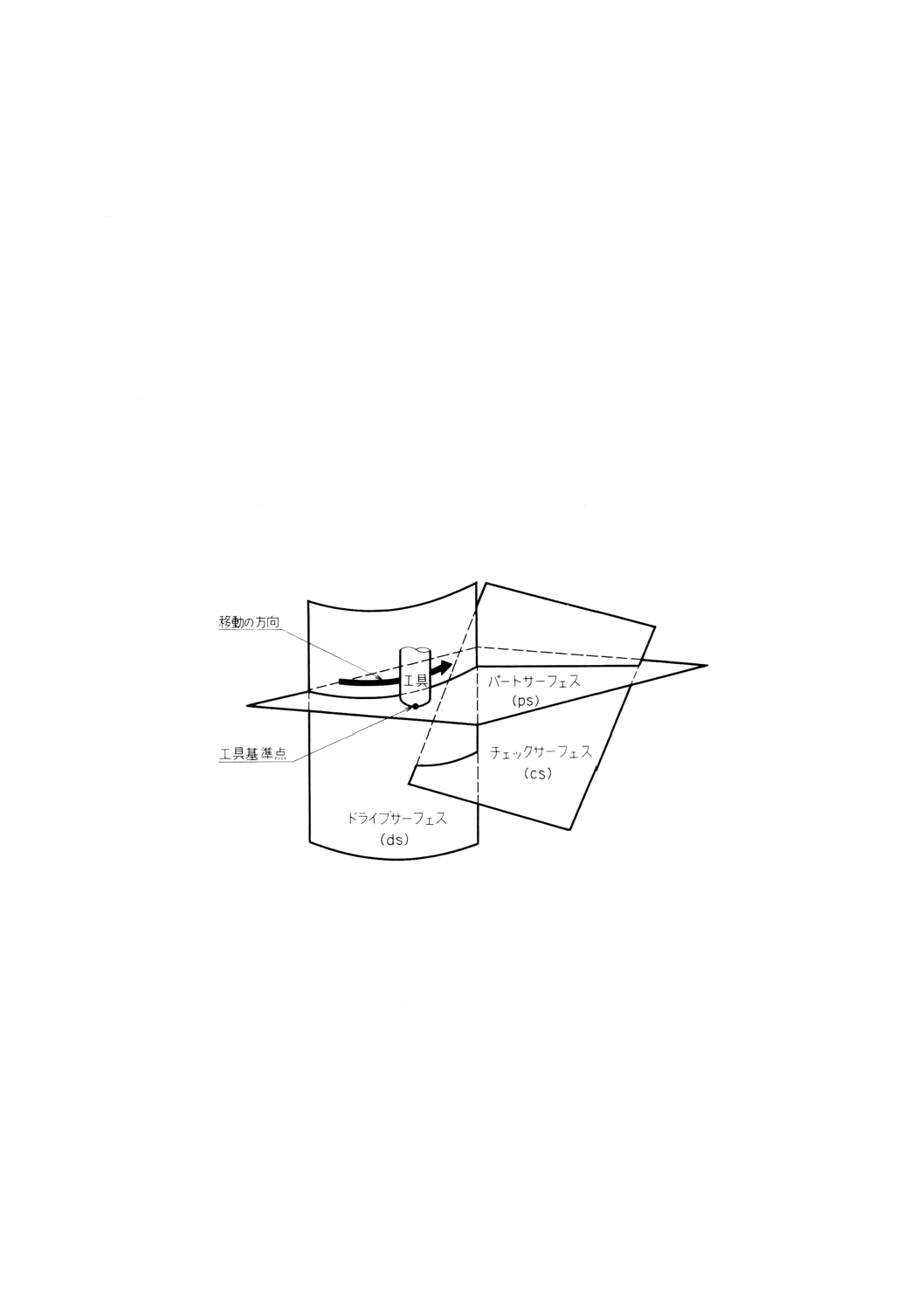
110 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

10. 幾何学的実行文 

10.1 意味と構文 

10.1.1 意味 幾何学的実行文は，形状が既に定義されている工作物を加工するための工具の動きを制御す

る。 

(1) 座標系 幾何学的実行文の中の座標は，基準座標系の座標とする。 

(2) 規制詞 幾何学的実行文の一般形の中で示されている点，パターン，直線，平面，ベクトル，円，円

柱，球，円すい，だ円，双曲線，ロフトコニック，ゼネラルコニック，二次曲面，タブシル，マトリ

ックス，ルールドサーフェス，面及び円すい曲線は，各々の規制詞のこととする。 

なお，点1，点2，…，点nのように数字又は英字を伴う場合も各々の規制詞を意味する。 

(3) 運動の制御面 連続運動において工具は，常に二つの面に沿って運動する。これら二つの面をドライ

ブサーフェス及びパートサーフェスという。パートサーフェスは，連続運動始動文又はパートサーフ

ェス文によって定まり，連続運動中間文及び連続連動終了文における工具は，常にこのパートサーフ

ェスに沿って動く。ドライブサーフェスは連続運動始動文，連続運動中間文及び連続運動終了文にお

いてその都度指定する。チェックサーフェスはドライブサーフェス及びパートサーフェスに沿って運

動してきた工具が停止すべき位置を決める面である。これらの制御面は面規制詞であり，一般形にお

いてドライブサーフェスをds，パートサーフェスをps，チェックサーフェスをcsと記述する。 

例： ドライブサーフェス，パートサーフェス及びチェックサーフェスの例 

10.1.2 構文 構文は，次による。 

＜幾何学的実行文＞ :: ＝＜運動文＞｜＜工具経路制御文＞｜＜始動方向制御文＞｜ 

＜工具経路変換文＞｜＜工具経路出力制御文＞ 

10.2 運動文 

10.2.1 意味と構文 

10.2.1.1 意味 運動文は，工具の動きを指令する。運動文は，次のとおり分類する。 

なお，連続運動文は前後関係や機能が複雑であるため，附属書1にその詳細を示す。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

10.2.1.2 構文 構文は，次による。 

＜運動文＞ :: ＝＜工具初期位置設定文＞｜＜絶対位置決め文＞｜＜多点位置決め文＞｜ 

＜相対位置決め文＞｜＜連続運動始動文＞｜＜特殊連続運動始動文＞｜ 

＜連続運動中間文＞｜＜連続運動終了文＞ 

10.2.2 工具初期位置設定文 

10.2.2.1 意味 工具初期位置設定文は，工具の運動の出発点を与え，その点に工具の基準点（10.3.6参照）

を位置付ける。 

一般形は，次のとおりとする。 

FROM／

z]

[,

y

x,

点

備考1. 点は，工具の運動の出発点とする。 

2. x，y，zは，工具の運動の出発点の座標とする。 

3. zが与えられていないとき，Z面が指定されていればその値とし，Z面が指定されていなけれ

ば0とする。 

10.2.2.2 構文 構文は，次による。 

＜工具初期位置設定文＞ :: ＝FROM／11［＜点規制詞＞｜＜スカラー＞21［，＜スカラー＞］］ 

例： 工具初期位置設定文の例 

STPT＝POINT/1, 2, 0 

FROM/STPT 

又は 

FROM/1, 2, 0 

10.2.3 絶対位置決め文及び多点位置決め文 

10.2.3.1 意味 絶対位置決め文は直前の運動の終わりから指定の点への，また多点位置決め文はパターン

の点への，工具の基準点（10.3.6参照）の運動を指令する。 

112 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

一般形は，次のとおりとする。 

(1) GOTO／

z]

[,

y

x,

点

(2) GOTO／パターン

￥

，点の順番号

，

点の順番号

点の順番号

3

THRU

2

1

,

RETAIN

OMIT

,

￥

，点の順番号

，

点の順番号

点の順番号

，点の順番号

，

点の順番号

点の順番号

…

q

THRU

p

m

,

,

6

THRU

5

4

,

￥

，点の順番号

，

点の順番号

点の順番号

9

THRU

8

7

d,

AVOID,

,

￥

，点の順番号

，

点の順番号

点の順番号

，点の順番号

，

点の順番号

点の順番号

…

s

THRU

r

n

,

,

12

THRU

11

10

,

[, ZIGZAG] [, INVERS] 

備考1. 点は，工具の基準点を位置付ける点とする。 

2. x，y，zは，工具の基準点を位置付ける点の座標とする。zが与えられていないとき，Z面が

指定されていればその値とし，Z面が指定されていなければ0とする。 

3. パターンは，工具の基準点を位置付ける点のパターンとする。 

4. OMIT又はRETAINに続く点の順番号1，…，点の順番号mは，省略又は保持する点の順番

号とする。 

5. AVOID，d，に続く点の順番号7，…，点の順番号nは，指定した点に対してdだけ退避動作

を行う。 

dは，工具の軸方向におけるXY平面又はZ面から工具基準点への距離とする。 

6. ZIGZAGは，工具を格子パターンの点群において，パターンの点群を順番号どおりではなく，

各列とも第1列（又は第1行）の順番号の大きくなる向きに工具を進ませる。 

7. INVERSは，パターンの点群を順番号の逆の順序に工具を進ませる。 

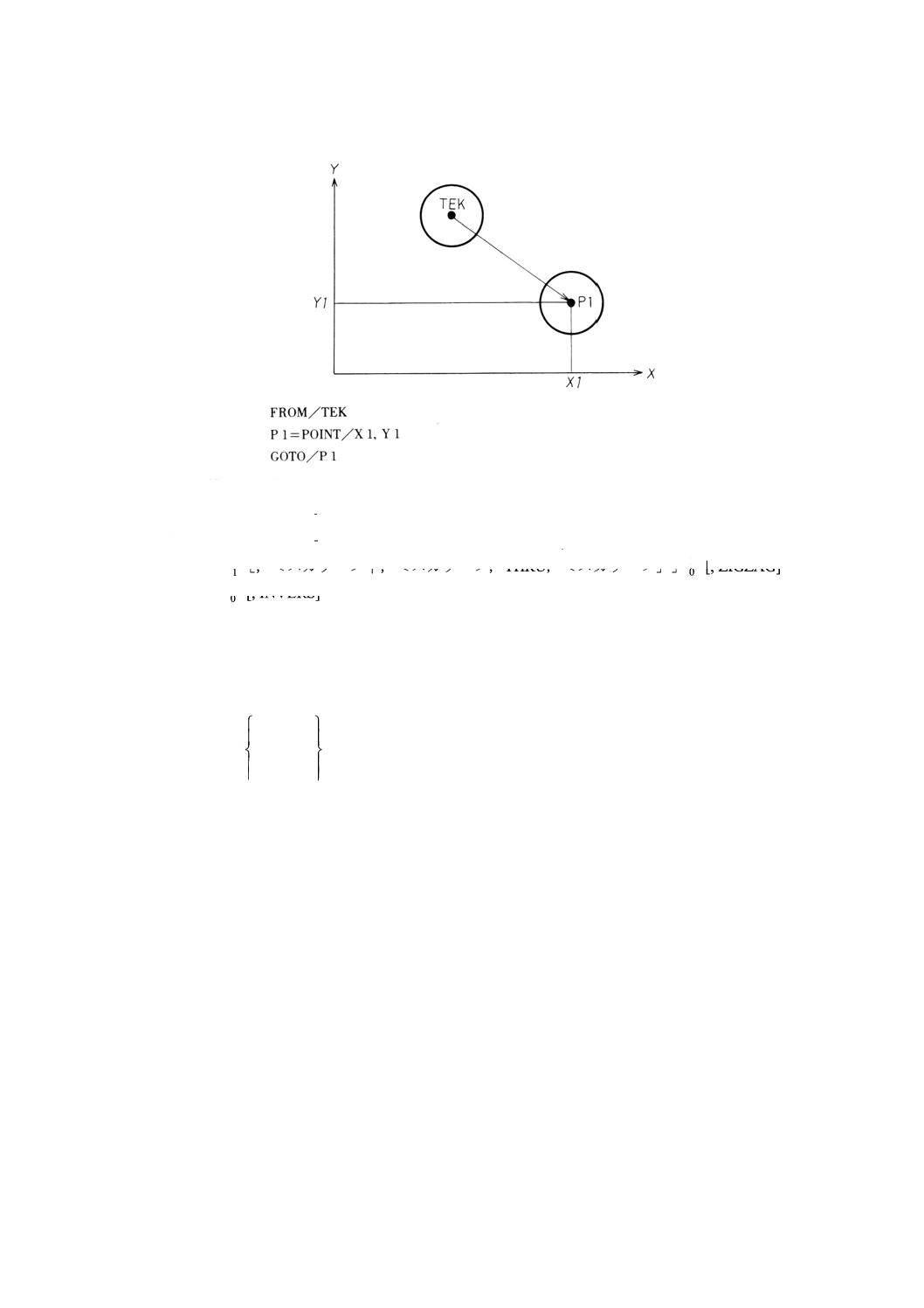
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 絶対位置決め文の例 

10.2.3.2 構文 構文は，次による。 

＜絶対位置決め文＞ :: ＝GOTO／11［＜点規制詞＞｜＜スカラー＞21［，＜スカラー＞］］ 

＜多点位置決め文＞ :: ＝GOTO／＜修飾されたパターン＞10［，AVOID，＜スカラー＞ 

k1［，＜スカラー＞｜，＜スカラー＞，THRU，＜スカラー＞］］10 [, ZIGZAG] 

10 [, INVERS] 

10.2.4 相対位置決め文 

10.2.4.1 意味 相対位置決め文は，直前の工具の運動の終わりから指定の増分だけ工具の基準点（10.3.6

参照）を移動する。 

一般形は，次のとおりとする。 

GODLTA／

ベクトル

d

c

b,

a,

備考1. a，b，cは，それぞれX軸方向，Y軸方向及びZ軸方向における工具の基準点を移動する増

分とする。 

2. dは，Z軸方向における工具の基準点を移動する増分とする。 

3. ベクトルは，工具の基準点の増分を示すベクトルとする。 

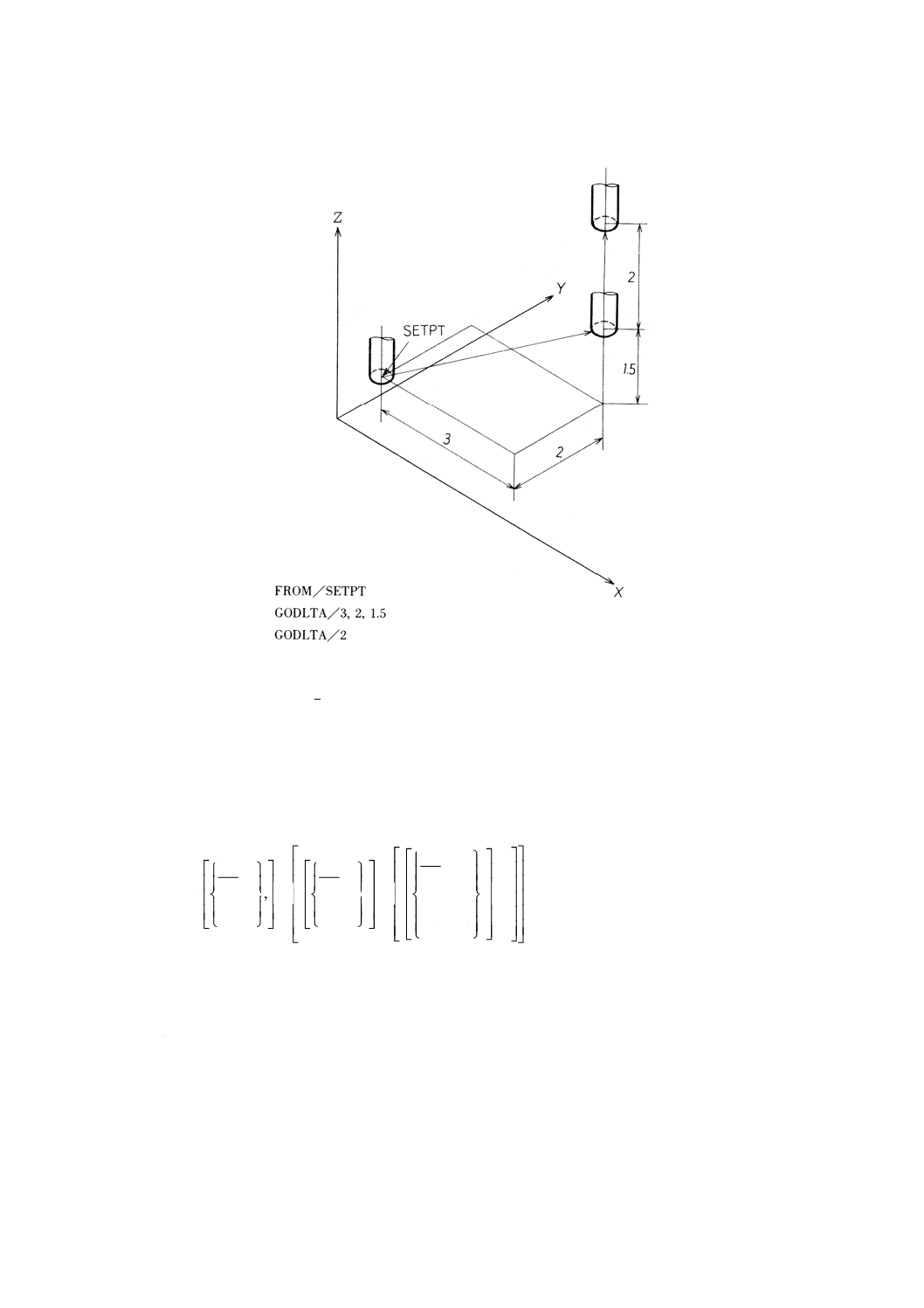
114 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 相対位置決め文の例 

10.2.4.2 構文 構文は，次による。 

＜相対位置決め文＞ :: ＝GODLTA／11［＜スカラー＞10［，＜スカラー＞，＜スカラー＞］｜ 

＜ベクトル規制詞＞］ 

10.2.5 連続運動始動文 

10.2.5.1 意味 連続運動始動文は，一連の連続運動を開始するとき，所定の位置に工具を位置付けする。 

動作の詳細は，他の文との関係が深いので附属書1に示す。 

一般形は，次のとおりとする。 

GO／

cs

,

TANTO

PAST

ON

TO

,

ps

,

PAST

ON

TO

,

ds

,

PAST

ON

TO

備考1. TOは，工具を制御面の手前から制御面に接する状態で停止させる修飾語とする。 

2. ONは，工具を制御面の手前から工具の基準点が制御面上にある状態で停止させる修飾語と

する。 

3. PASTは，工具を制御面の手前から制御面を通り過ぎて制御面に接する状態で停止させる修

飾語とする。 

4. TANTOは，ドライブサーフェスとチェックサーフェスとが接しているとき，工具をその接点

で接する状態で停止させる修飾語とする。 

5. 修飾語TOは，略すことができる。 

6. ds，ps及びcsについては，10.1.1(3)参照のこと。 

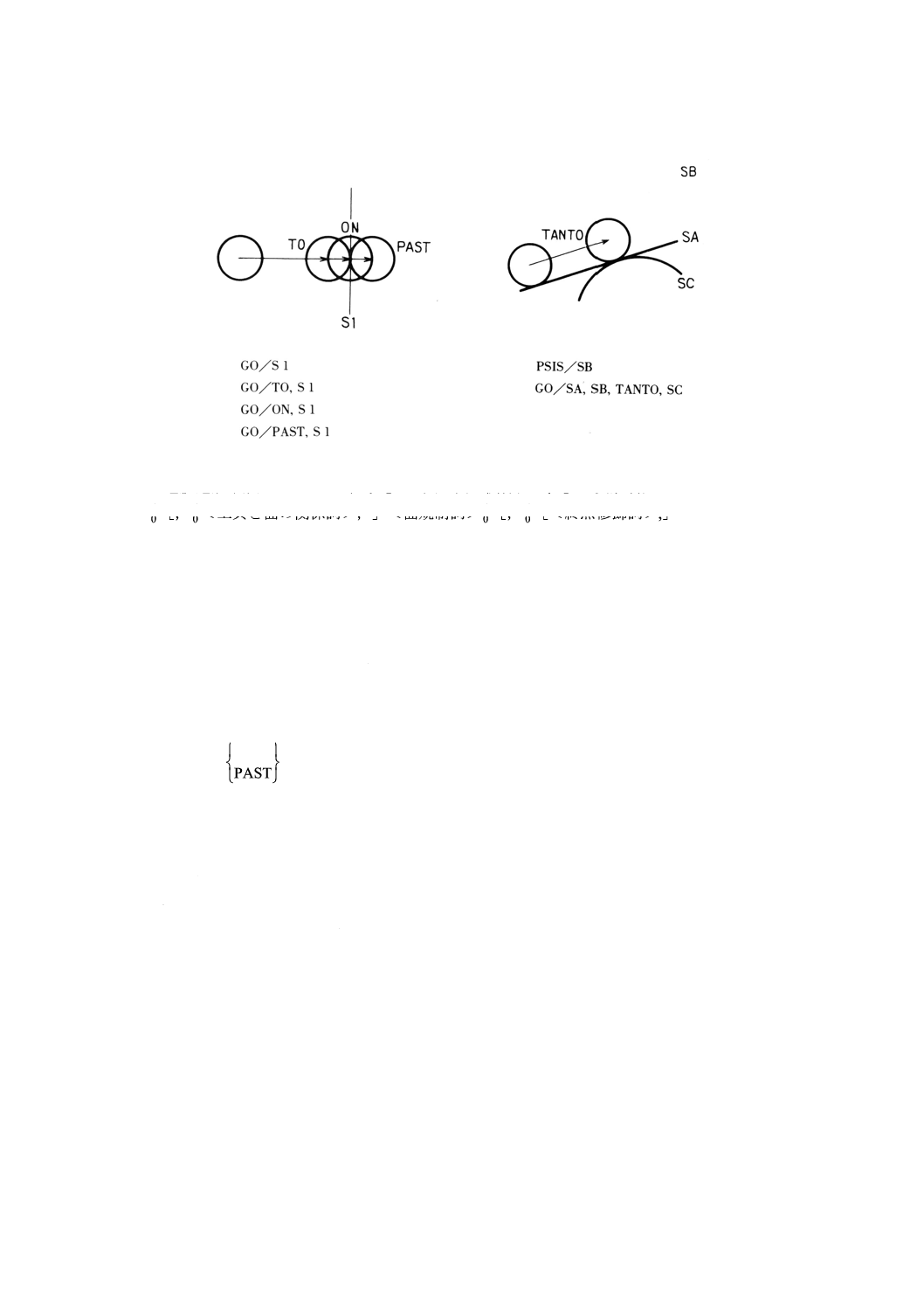
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 連続運動始動文の例 

10.2.5.2 構文 構文は，次による。 

＜連続運動始動文＞ :: ＝GO／10［＜工具と面の関係詞＞，］＜面規制詞＞ 

10［，10＜工具と面の関係詞＞，］＜面規制詞＞10［，10［＜終点修飾詞＞,］ 

＜面規制詞＞］］ 

＜工具と面の関係詞＞ :: ＝TO｜ON｜PAST 

＜終点修飾詞＞ :: ＝＜工具と面の関係詞＞｜TANTO 

10.2.6 特殊連続運動始動文 

10.2.6.1 意味 特殊連続運動始動文は，これに続く一連の連続運動の開始時に，チェックサーフェスに対

して工具を所定の位置に置くことを指令する。この文の前の工具の始動の向きを指定する始動方向制御文

によって，チェックサーフェスに対する工具の停止位置を明示的に指定する。 

一般形は，次のとおりとする。 

OFFSET/

PAST

TO

，cs 

備考1. 修飾語TO又はPASTは10,2.5を参照のこと。 

2. 始動方向制御文としてINDIRP文があるときは，工具の現在位置からそれが指定する点まで

を結ぶ直線とチェックサーフェスcsとの交点において，工具がチェックサーフェスに対して

修飾詞TO又はPASTが指定する位置関係を保つ。 

3. 始動方向制御文としてINDIRV文があるときは，工具の現在位置を通りそれが指定するベク

トルに対し平行な直線とチェックサーフェスcsとの交点において，工具がチェックサーフェ

スに対して，修飾詞TO又はPASTが指定する位置関係を保つ。 

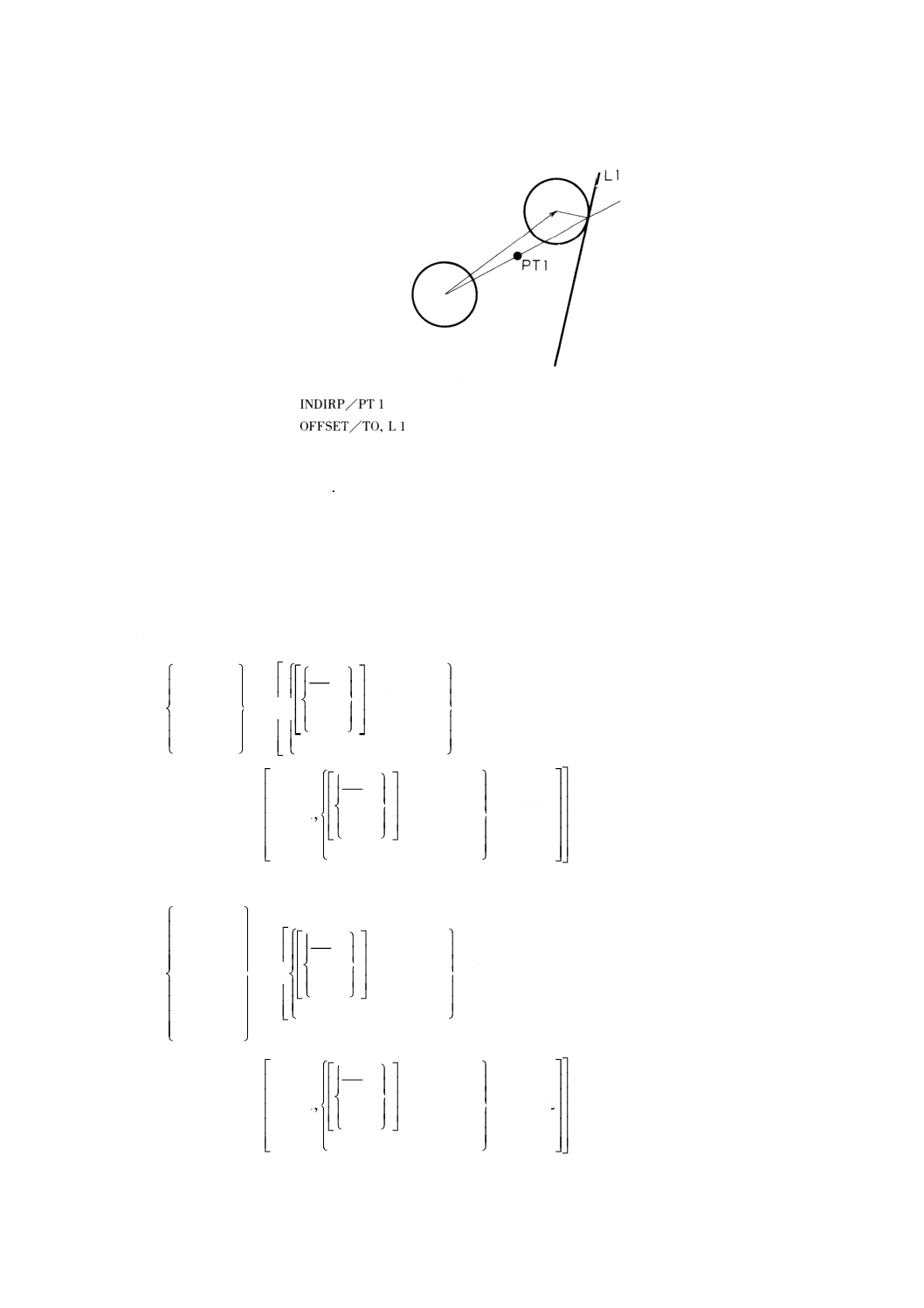
116 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 特殊連続運動始動文の例 

10.2.6.2 構文 構文は，次による。 

＜特殊連続運動始動文＞ :: ＝OFFSET／11［TO｜PAST］，＜面規制詞＞ 

10.2.7 連続運動中間文と連続運動終了文 

10.2.7.1 意味 連続運動中間文と連続運動終了文は，直前の運動の終わりの位置からドライブサーフェス

とパートサーフェスに沿ってチェックサーフェスまで工具を移動させる。動作の詳細は，他の文との関係

が深いので附属書1に示す。 

一般形は，次のとおりとする。 

(1) 連続運動中間文の一般形 

[

]

￥

，

／

cs1

TANTO,

INTOF,

n1,

,

PAST

ON

TO

ds

GORGT

GOLFT

GOBACK

GOFWD

[

]

2

cs2,

TANTO,

INTOF,

n2,

,

PAST

ON

TO

1,

,

名札

名札

(2) 連続運動終了文の一般形 

[

]

￥

／

cs1

TANTO,

INTOF,

n1,

,

PAST

ON

TO

ds

GODOWN

GOUP

GORGT

GOLFT

GOBACK

GOFWD

[

]

2

cs2,

TANTO,

INTOF,

n2,

,

PAST

ON

TO

1,

,

名札

名札

備考1. n1，n2は，ドライブサーフェスdsに沿って移動している工具を，チェックサーフェスcs1に

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

対してはn1回目の交差において，修飾詞が指定する位置に位置付け，チェックサーフェスcs2

に対してはn2回目の交差において，修飾詞が指定する位置に位置付ける（附属書1の3.5参照）。 

2. 名札1は，工具がcs1をチェックサーフェスとしたとき名札1をもつ文に制御を移し，名札

2は，工具がcs2をチェックサーフェスとしたとき名札2をもつ文に制御を移す。 

10.2.7.2 構文 構文は，次による。 

＜連続運動中間文＞ :: ＝＜運動方向文＞／＜面規制詞＞10［10［，＜終点修飾詞＞｜ 

，＜工具と面の関係詞＞10［，＜スカラー＞，INTOF］］，＜面規制詞＞ 

10［，＜名札＞10［，＜終点修飾詞＞｜，＜工具と面の関係詞＞ 

10［，＜スカラー＞, INTOF］］，＜面規制詞＞，＜名札＞］］ 

＜連続運動終了文＞ :: ＝＜終点運動方向文＞／＜面規制詞＞10［，＜終点修飾詞＞｜ 

，＜工具と面の関係詞＞［，＜スカラー＞，INTOF］］，＜面規制詞＞ 

［，＜名札＞［，＜終点修飾詞＞｜，＜工具と面の関係詞＞ 

［，＜スカラー＞，INTOF］］，＜面規制詞＞, ＜名札＞］ 

＜終点運動方向文＞ :: ＝＜運動方向文＞｜GOUP｜GODOWN 

＜運動方向文＞ :: ＝GOFWD｜GOBACK｜GORGT｜GOLFT 

10.3 工具経路制御文 

10.3.1 意味と構文 

10.3.1.1 意味 工具経路制御文は，制御面と工具との関係，切残し量，許容誤差，工具形状及びパートサ

ーフェスを指定する。 

10.3.1.2 構文 構文は，次による。 

＜工具経路制御文＞ :: ＝＜工具とドライブサーフェスの関係文＞｜ 

＜工具とパートサーフェスの関係文＞｜＜切残し量文＞｜＜許容誤差文＞｜ 

＜工具文＞｜＜パートサーフェス文＞ 

10.3.2 工具とドライブサーフェスの関係文 

10.3.2.1 意味 工具とドライブサーフェスの関係文は，工具の運動の向きに見て工具がドライブサーフェ

スのどちら側を運動するかを指令する。連続運動文としの関係は，附属書1の3.4を参照のこと。 

一般形は，次のとおりとする。 

(1) TLLFT 

(2) TLRGT 

(3) TLON 

TLLFTは工具の運動の向きに見て工具がドライブサーフェスの左側，TLRGTは右側にあり，TLONは

工具の基準点（10.3.6参照）がドライブサーフェス上にあることを指令する。 

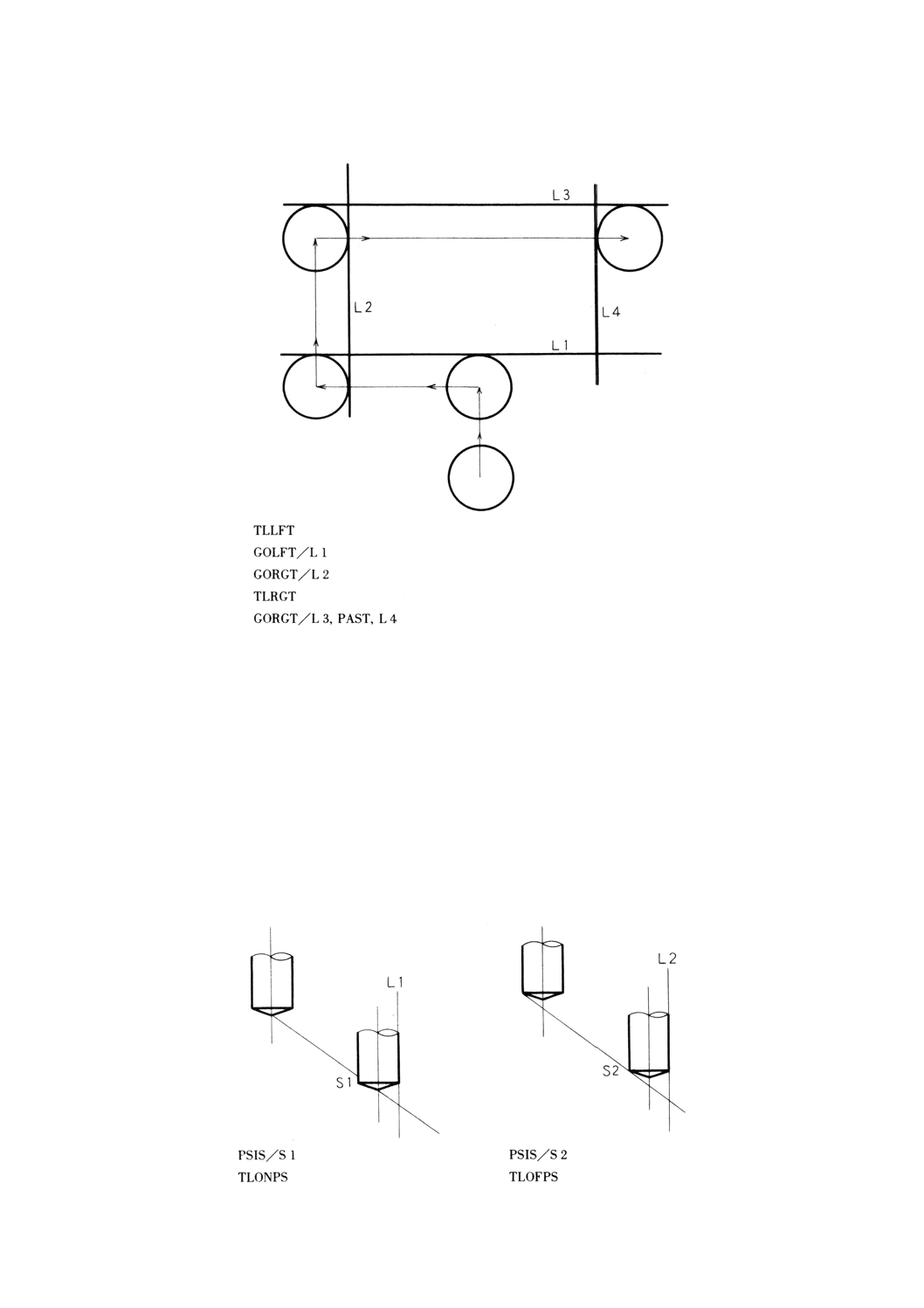
118 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 工具とドライブサーフェスの関係文の例 

10.3.2.2 構文 構文は，次による。 

＜工具とドライブサーフェスの関係文＞ :: ＝TLLFT｜TLRGT｜TLON 

10.3.3 工具とパートサーフェスの関係文 

10.3.3.1 意味 工具とパートサーフェスの関係文は，工具とパートサーフェスの位置関係を指令する。 

一般形は，次のとおりとする。 

(1) TLONPS 

(2) TLOFPS 

TLONPSは，工具の基準点（10.3.6参照）がパートサーフェスの上にあることを指令し，TLOFPSは工

具がパートサーフェスと接していることを指令する。TLONPSが記述されないうちは，TLOFPSが指示さ

れているものとみなす。 

例： 工具とパートサーフェスの関係文の例 

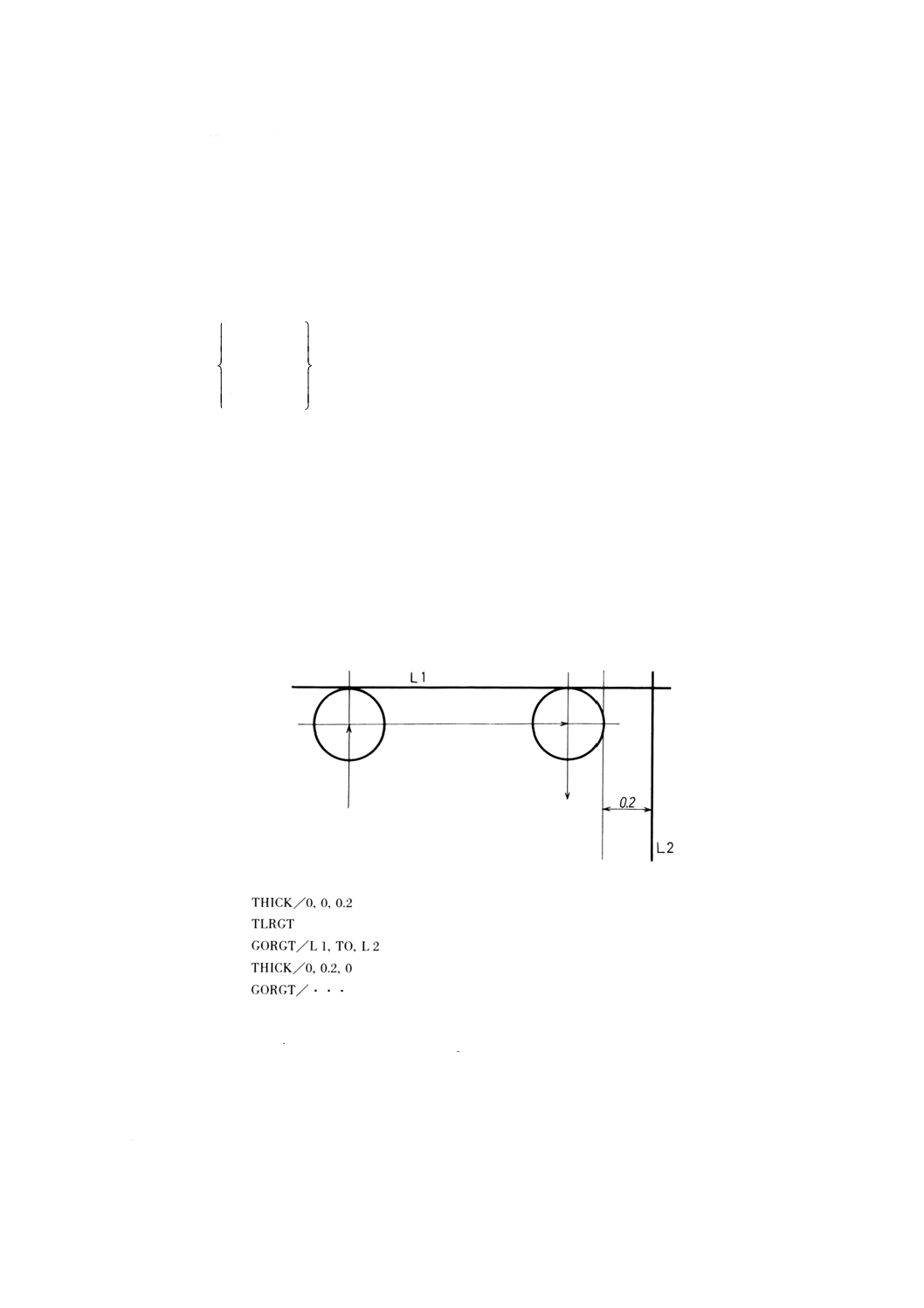
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

10.3.3.2 構文 構文は，次による。 

＜工具とパートサーフェスの関係文＞ :: ＝TLONPS｜TLOFPS 

10.3.4 切残し量文 

10.3.4.1 意味 切残し量文は，実際にプログラムした面から指定した距離にある面を加工することを指令

する。切残し量として正の値を指定したときは切り残した状態に，負の値を指定したときは切り込んだ状

態になる。 

一般形は，次のとおりとする。 

THICK/

d6

d5,

d4,

d2,

d5

d4,

d2,

d3

d2,

d1

備考1. d1は，パートサーフェス，ドライブサーフェス及びチェックサーフェスに適用される切残し

量とする。 

2. d2は，パートサーフェスに適用される切残し量とする。 

3. d3は，ドライブサーフェス及びチェックサーフェスに適用される切残し量とする。 

4. d4は，ドライブサーフェスに適用される切残し量とする。 

5. d5は，チェックサーフェスに適用される切残し量とする。 

6. d6は，第2のチェックサーフェスに適用される切残し量とする（附属書1の3.6参照）。 

例： 切残し量文の例 

10.3.4.2 構文 構文は，次による。 

＜切残し量文＞ :: ＝THICK／＜スカラー＞30［，＜スカラー＞］ 

10.3.5 許容誤差文 

10.3.5.1 意味 許容誤差文は，連続運動文による工具経路の計算に用いる許容誤差を指定する。許容誤差

の指定は，直線以外の形状に対して有効とする（附属書1の3.2参照）。 

一般形は，次のとおりとする。 

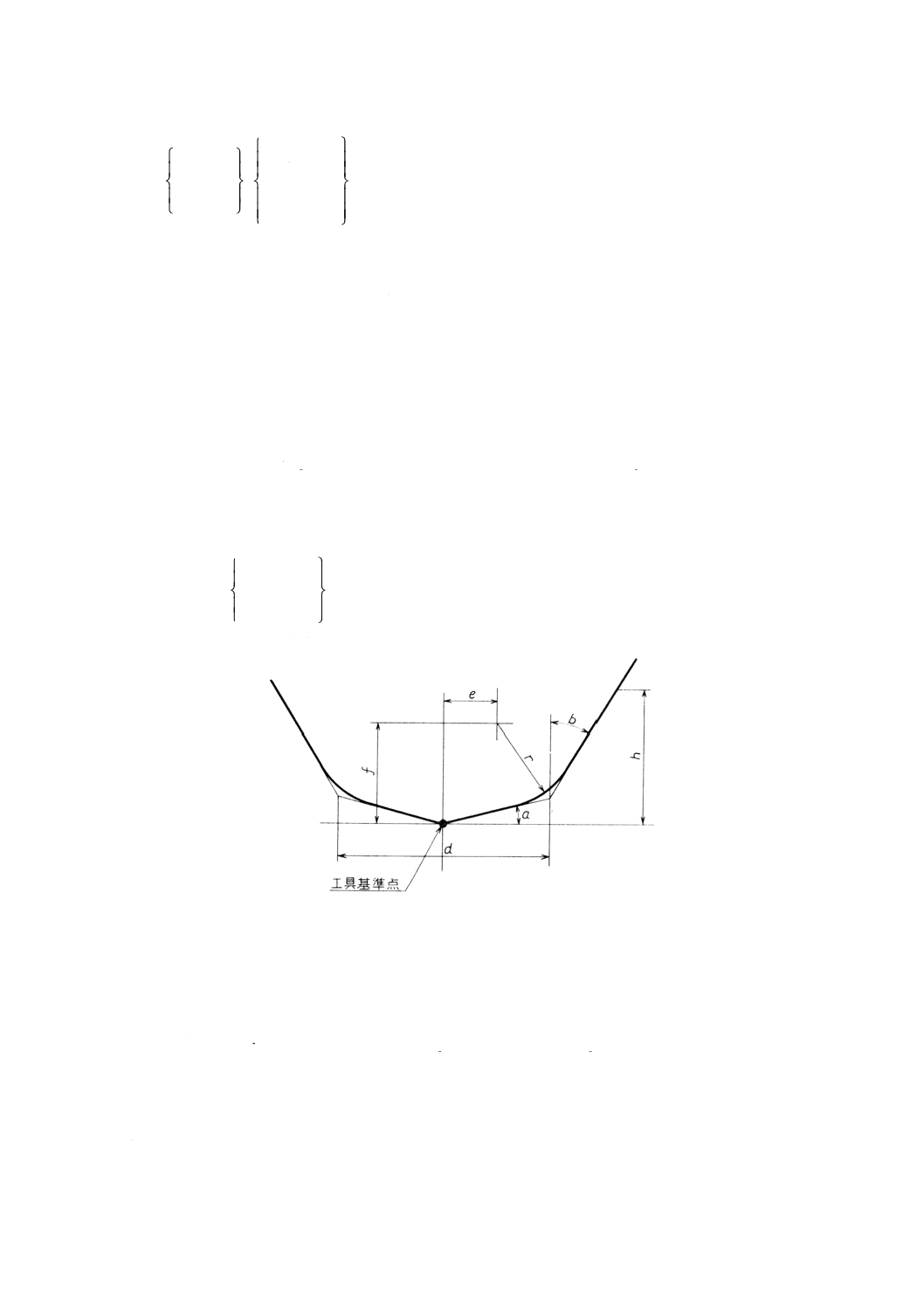
120 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

OUTTOL

INTOL

TOLER

/

d6

d5,

d4,

d2,

d5

d4,

d2,

d3

d2,

d1

備考1. d1は，パートサーフェス，ドライブサーフェス及びチェックサーフェスに適用される許容誤

差とする。 

2. d2は，パートサーフェスに適用される許容誤差とする。 

3. d3は，ドライブサーフェス及びチェックサーフェスに適用される許容誤差とする。 

4. d4は，ドライブサーフェスに適用される許容誤差とする。 

5. d5は，チェックサーフェスに適用される許容誤差とする。 

6. d6は，第2のチェックサーフェスに適用される許容誤差とする（附属書1の3.6参照）。 

10.3.5.2 構文 構文は，次による。 

＜許容誤差文＞ :: ＝11 [TOLER｜INTOL｜OUTTOL] ／＜スカラー＞30［，＜スカラー＞］ 

10.3.6 工具文 

10.3.6.1 意味 工具文は，工具位置を計算するために用いる工具の形状と工具の基準点を定義する。 

一般形は，次のとおりとする。 

CUTTER/

h

b,

a,

f,

e,

r,

d,

r

d,

d

備考1. パラメータの意味は，下図による。 

一般形の第2形式の場合は，e＝2d−r，f＝r，a＝0，b＝0，h＝固定値とする。第3形式の

場合は，r＝0，e＝2d，f＝0，a＝0，b＝0，h＝固定値とする。 

2. d，r，f，a及びhは，負ではいけない。 

3. 工具の基準点は，工具軸上の工具の先端とする。 

10.3.6.2 構文 構文は，次による。 

＜工具文＞ :: ＝CUTTER／＜スカラー＞10［，＜スカラー＞｜66［，＜スカラー＞］］ 

10.3.7 パートサーフェス文 

10.3.7.1 意味 パートサーフェス文は，パートサーフェスを定義したり，パートサーフェスの一時的な無

視を指令したりする。連続運動始動文との詳細な関係は，附属書1に示す。 

一般形は，次のとおりとする。 

(1) PSIS／面 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

(2) NOPS 

(3) AUTOPS 

備考1. PSISは，この定義以降の連続運動における新しいパートサーフェスを指定するときに用いる。 

2. NOPSは，この定義以降の連続運動始動文において，パートサーフェスの一時的な無視を指

令する。ただし，連続運動始動文は，一面始動（附属書1参照）のものでなければならない。 

3. AUTOPSは，現在の工具の基準点を通るXY平面に平行な平面を，この定義以降の連続運動

におけるパートサーフェスとする。 

4. パートサーフェスが定義されていないときは，XY平面をパートサーフェスとみなす。 

10.3.7.2 構文 構文は，次による。 

＜パートサーフェス文＞ :: ＝PSIS／＜面規制詞＞｜ 

NOPS｜ 

AUTOPS 

10.4 始動方向制御文 

10.4.1 意味と構文 

10.4.1.1 意味 始動方向制御文は，これに続く連続運動始動文に始動の向きを与える。始動するに先立ち，

工具が現在の位置からチェックサーフェス，パートサーフェス又はドライブサーフェスに対して，それぞ

れ所定の関係を保って停止するように明示的に始動の向きを与える。連続運動始動文との詳細な関係は，

附属書1に示す。 

10.4.1.2 構文 構文は，次による。 

＜始動方向制御文＞ :: ＝INDIRP/11［＜点規制詞＞20［，＜点規制詞＞］｜＜スカラー＞ 

       22［，＜スカラー＞］20［33［，＜スカラー＞］］］｜ 

     11 [INDIRVlSRFVCT]/11［＜ベクトル規制詞＞20［，＜ベクトル規制詞＞］｜ 

       ＜スカラー＞22［，＜スカラー＞］20［33,＜スカラー＞］］］ 

10.4.2 点による始動方向制御文 

10.4.2.1 意味 点による始動方向制御文は，工具の現在の位置から指定した点への向きを始動の向きとし

て与える。 

一般形は，次のとおりとする。 

INDIRP／

z3

y3,

x3,

3

,

z2

y2,

x2,

2

,

z1

y1,

x1,

1

点

点

点

備考1. 点1又は座標が (x1, y1, z1) の点は，ドライブサーフェスに対する始動の向きとする。 

2. 点2又は座標が (x2, y2, z2) の点は，パートサーフェスに対する始動の向きとする。 

3. 点3又は座標が (x3, y3, z3) の点は，チェックサーフェスに対する始動の向きとする。 

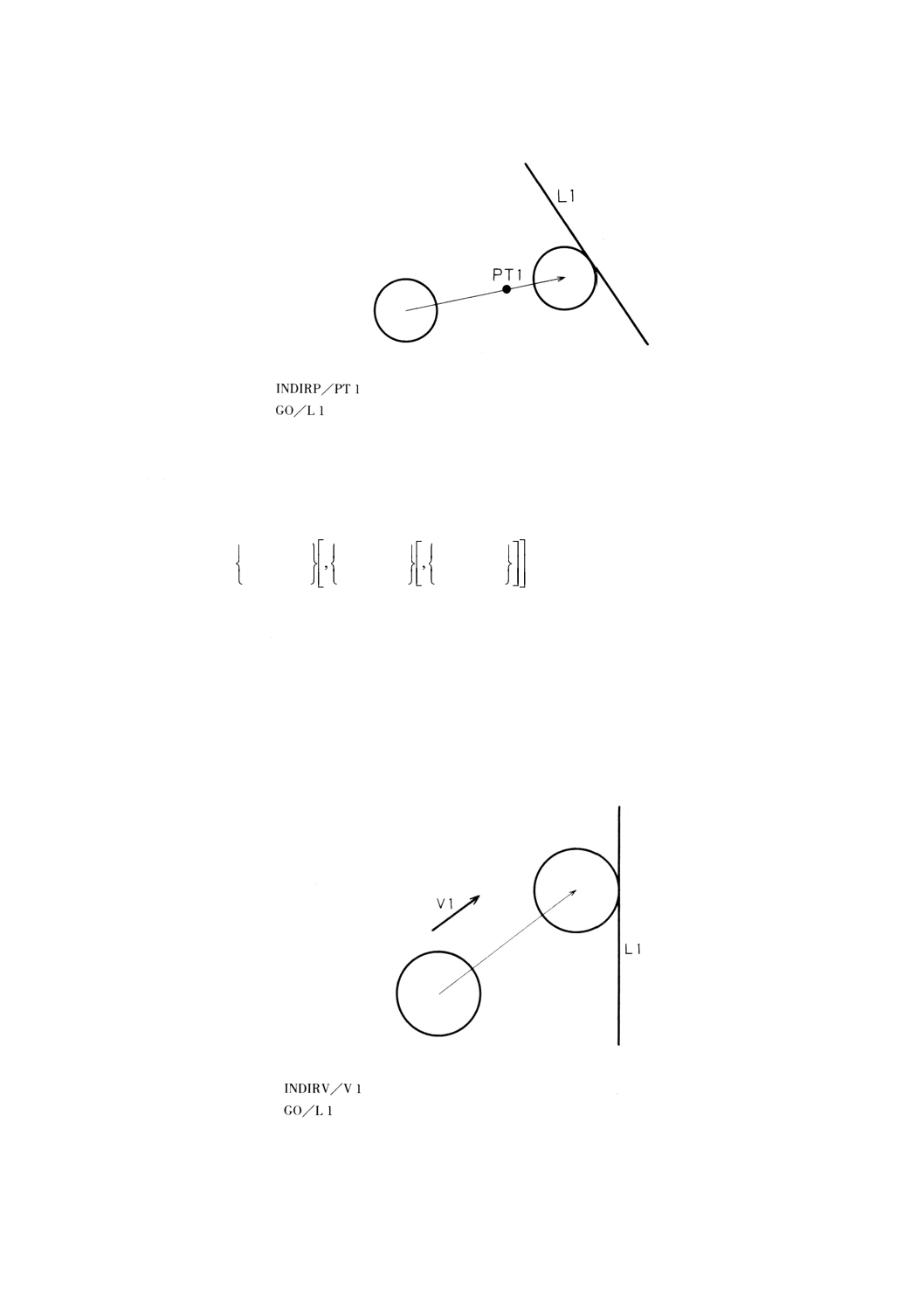
122 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 点による始動方向制御文の例 

10.4.3 ベクトルによる始動方向制御文 

10.4.3.1 意味 ベクトルによる始動方向制御文は，工具の位置から指定したベクトルの向きを始動の向き

として与える。 

一般形は，次のとおりとする。 

INDIRV／

c3

b3,

a3,

3

,

c2

b2,

a2,

2

,

c1

b1,

a1,

1

ベクトル

ベクトル

ベクトル

備考1. ベクトル1又はX軸，Y軸及びZ軸の各成分が (a1, b1, c1) のベクトルは，ドライブサーフェ

スに対する始動の向きとする。 

2. ベクトル2又はX軸，Y軸及びZ軸の各成分が (a2, b2, c2) のベクトルは，パートサーフェ

スに対する始動の向きとする。 

3. ベクトル3又はX軸，Y軸及びZ軸の各成分が (a3, b3, c3) のベクトルは，チェックサーフ

ェスに対する始動の向きとする。 

例： ベクトルによる始動方向制御文の例 

10.4.4 面のベクトルによる始動方向制御文 

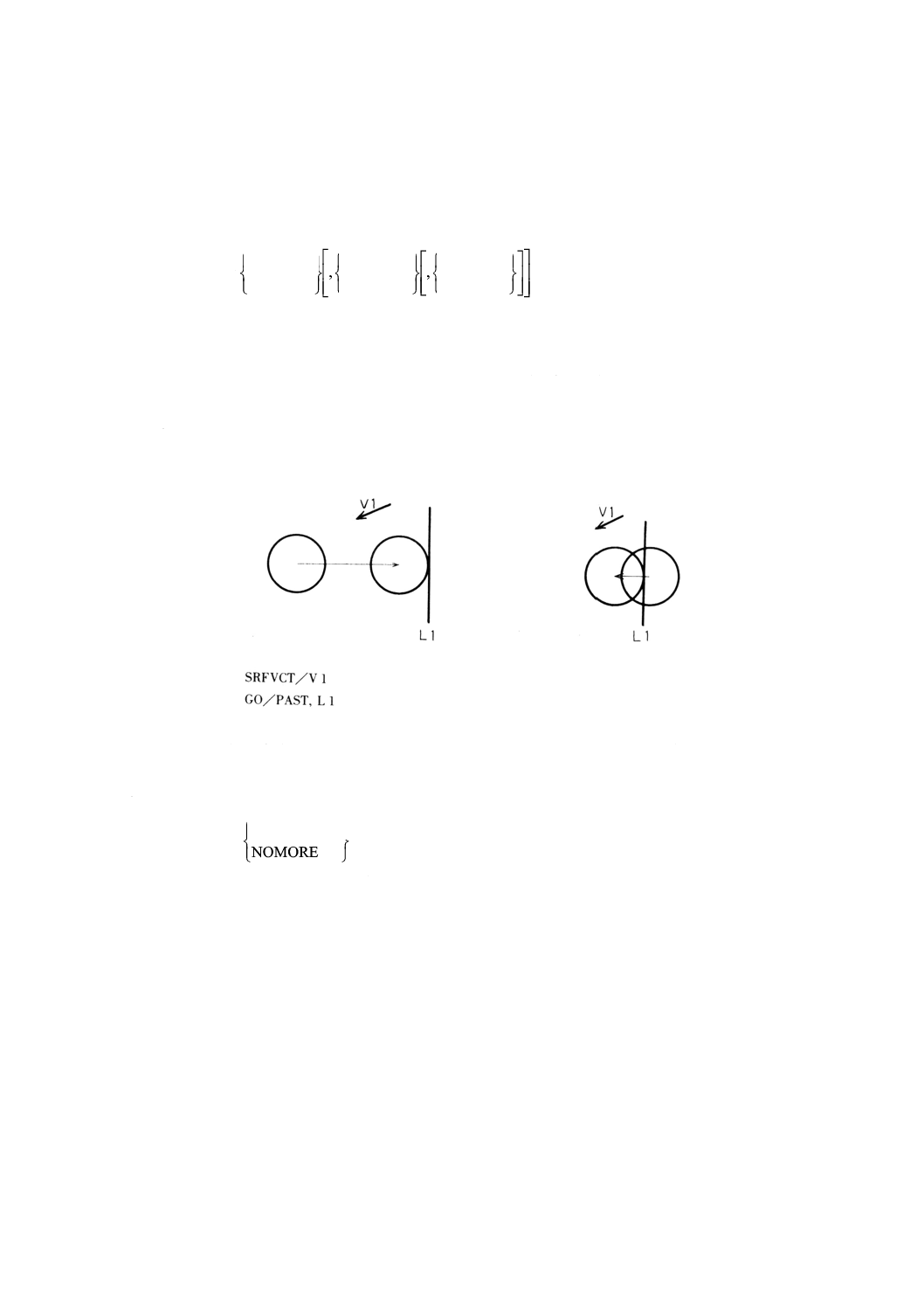
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

10.4.4.1 意味 面のベクトルによる始動方向制御文は，工具が制御面に関して停止する位置関係を示す面

のベクトルを与える。そのベクトルにより制御面への停止の位置を与える。そのベクトルの向きで制御面

に関して，手前側をTO，向こう側をPASTと定める。 

一般形は，次のとおりとする。 

SRFVCT／

c3

b3,

a3,

3

,

c2

b2,

a2,

2

,

c1

b1,

a1,

1

ベクトル

ベクトル

ベクトル

備考1. ベクトル1又はX軸，Y軸及びZ軸の各成分が (a1, b1, c1) のベクトルは，ドライブサーフェ

スの面ベクトルとする。 

2. ベクトル2又はX軸，Y軸及びZ軸の各成分が (a2, b2、c2) のベクトルは，パートサーフェ

スの面ベクトルとする。 

3. ベクトル3又はX軸，Y軸及びZ軸の各成分が (a3, b3, c3) のベクトルは，チェックサーフ

ェスの面ベクトルとする。 

例： 面のベクトルによる始動方向制御文の例 

10.5 工具経路変換文 

10.5.1 意味 工具経路変換文は，これに続く工具の運動文によって求められた工具経路の値を指定のマト

リックスで座標変換したり，この座標変換を終了したりする。 

一般形は，次のとおりとする。 

TRACUT／

NOMORE

マトリックス

備考1. マトリックスは，座標変換のマトリックスとする。 

2. NOMOREは，座標変換の終了を示す。 

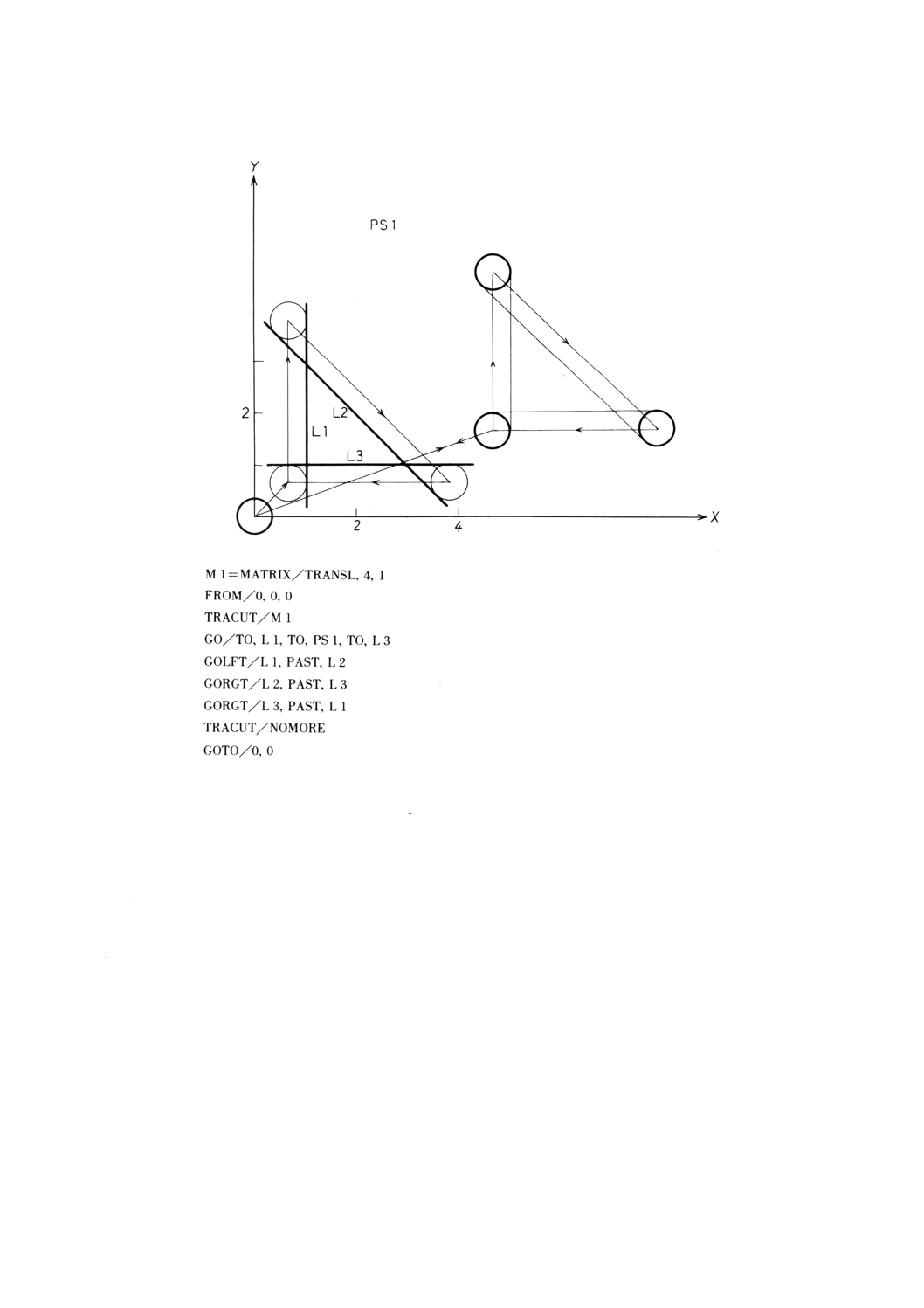
124 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

例： 工具経路変換文の例 

10.5.2 構文 構文は，次による。 

＜工具経路変換文＞ :: ＝TRACUT／11［＜マトリックス規制詞＞｜NOMORE］ 

10.6 工具経路出力制御文 

10.6.1 意味 工具経路出力制御文は，計算した工具経路をポストプロセッサに送ったり，送らなかったり

する。 

一般形は，次のとおりとする。 

(1) DNTCUT 

(2) CUT 

パートプログラムされている一部の工具経路を削除する（ポストプロセッサに送ることを中止する）

には，削除したい運動文の直前にDNTCUTを置き，削除の終了する文の直後にCUTを置く。削除し

た部分の工具経路は，DNTCUTを挿入したその直前の位置からCUTを挿入する直前の位置まで直線

で移動する。 

例： 工具経路出力制御文の例 

図においてS1とS2が接しているとき， 

GOLFT/S1, TANTO, S2 

GOFWD/S2 

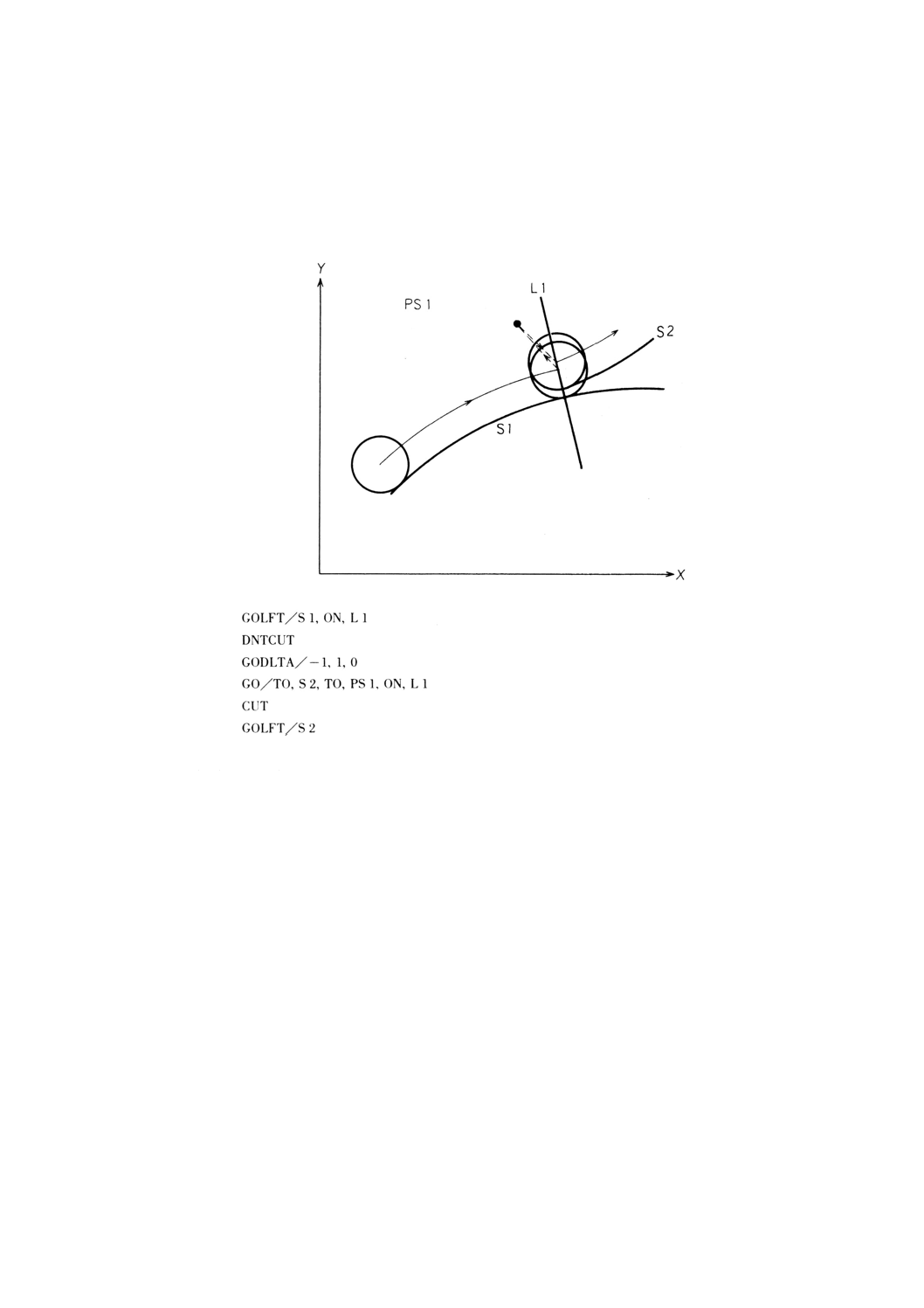
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

… 

とプログラムすれば，工具経路はS1からS2に沿って求められる。しかし，S1やS2が複雑な形

状の場合にはS1とS2が接している保証がないため，プログラムがエラーとして処理され工具経

路が求められないことがある。このとき，図に示すようにL1という仮のチェックサーフェスを

用いて，次のようなプログラムを作成すれば，正しい工具経路が求められる。 

10.6.2 構文 構文は，次による。 

＜工具経路出力制御文＞ :: ＝DNTCUT｜CUT 

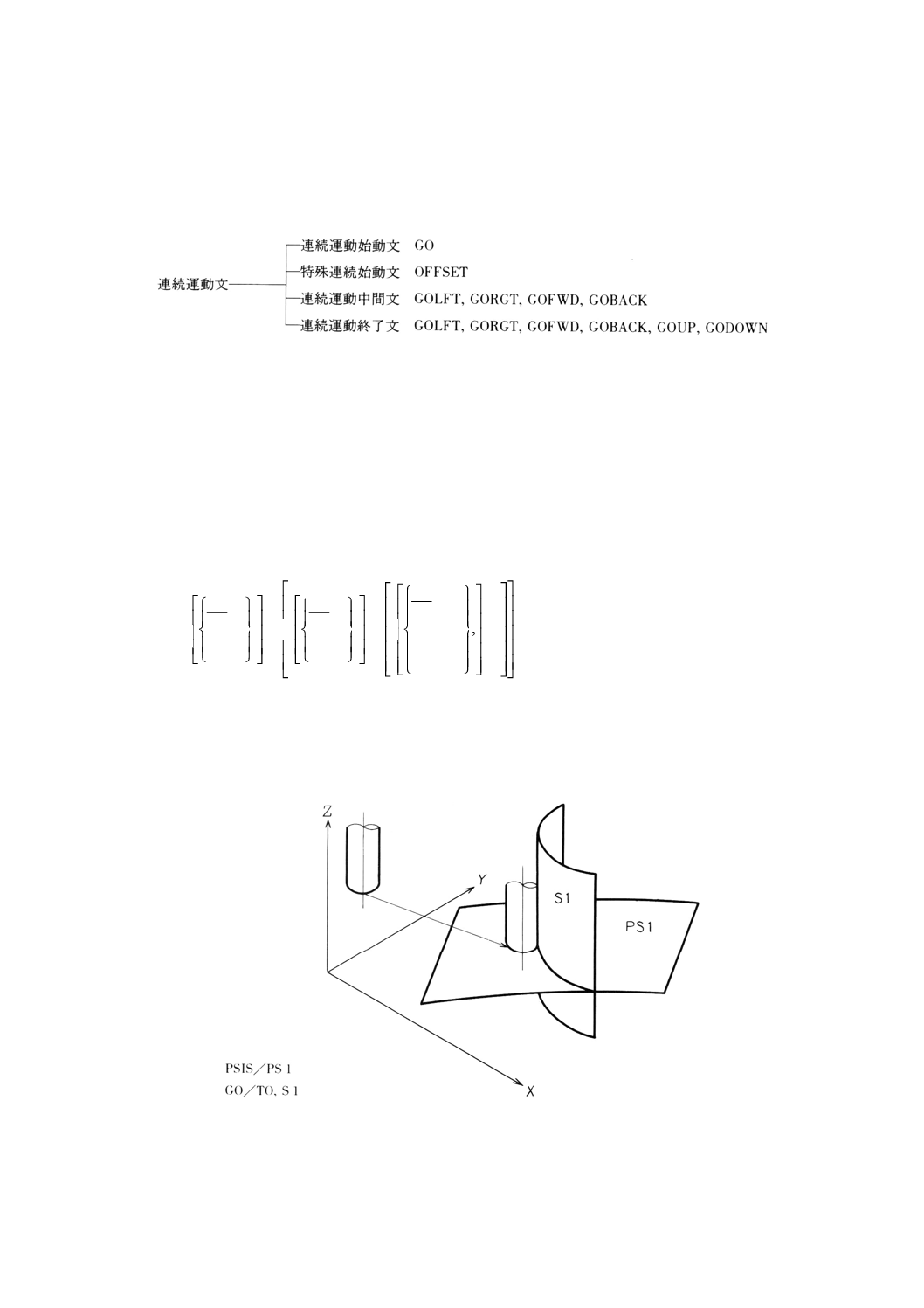
126 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 連続運動の詳細な意味 

1. 連続運動文の種類 運動文の中の連続運動文を次の通り分類する。 

連続運動文は，概念が非常に複雑である。更に，工具経路制御文及び始動方向制御文が効果を及ぼすた

め，より複雑となる。次に，それらの関係の詳細を規定する。 

2. 連続運動始動文 

2.1 

意味 連続運動始動文は，一連の連続運動を開始するとき，工作物に対し所定の位置に工具を位置

決めすることを指令する。この文は，工具を現在の位置から始動する。そして，工具の制御面に対する位

置関係を指定する修飾語を考慮しながら一つ，二つ又は三つの制御面に対して許容誤差内に停止する。こ

れらをそれぞれ一面始動，二面始動又は三面始動という。 

一般形は，次のとおりとする（10.2.5.1参照）。 

GO/

cs

,

TANTO

PAST

ON

TO

,

ps

,

PAST

ON

TO

,

ds

,

PAST

ON

TO

2.2 

パートサーフェスの指定のある一面始動 工具は，あらかじめ指定されているパートサーフェス及

び指定の面に対し最短距離で動く。パートサーフェスの指定は，PSIS又はAUTOPSを用いる。工具の動

きを附属書1図1及び附属書1図2に示す。 

附属書1 図1 

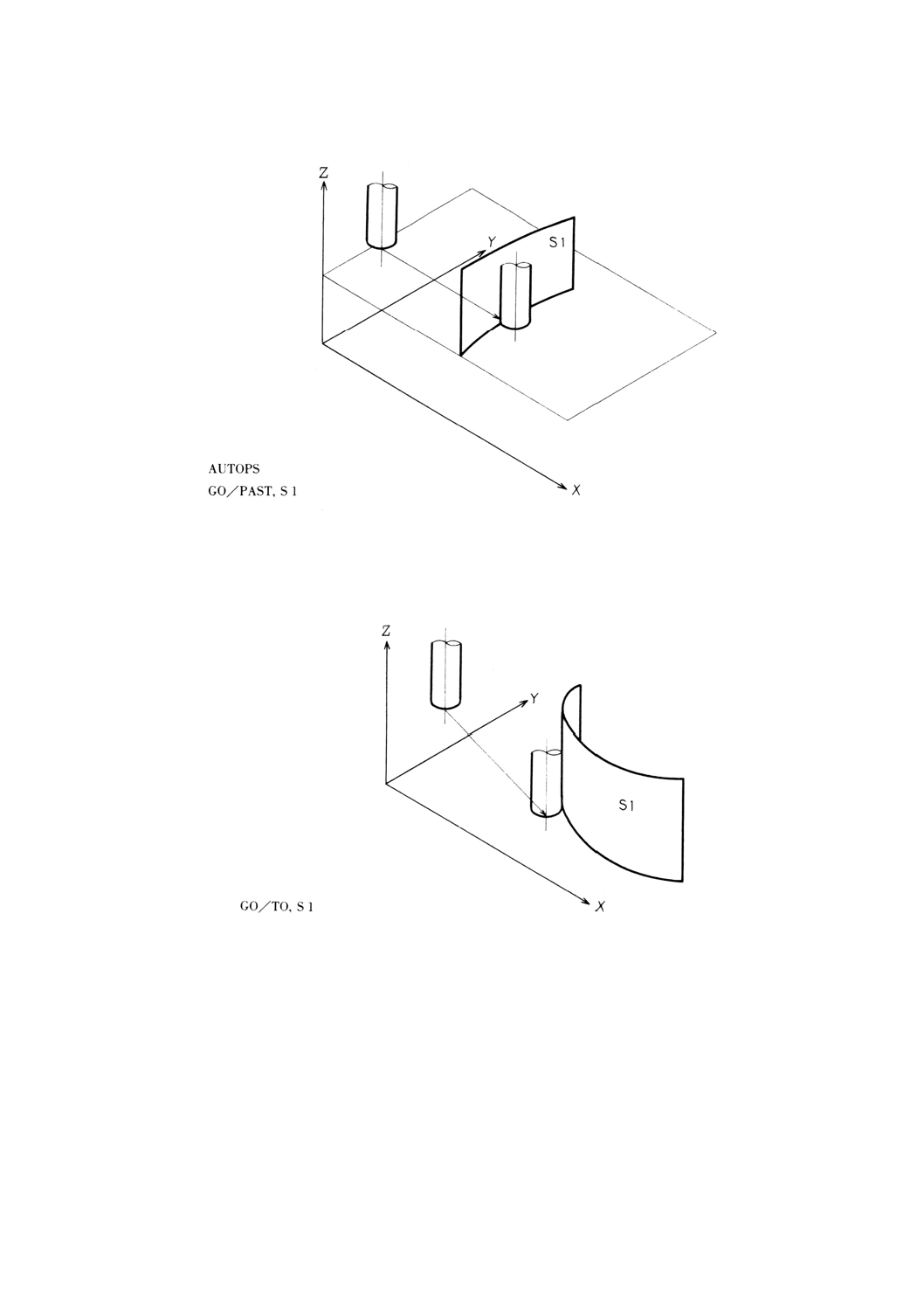
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 図2 

2.3 

パートサーフェスの指定がない一面始動 パートサーフェスの指定がない一面始動は，XY平面をパ

ートサーフェスとみなす。工具は，XY平面と指定の面に対し共に許容誤差内に停止するように最短距離

で動く。工具の動きを附属書1図3に示す。 

附属書1 図3 

2.4 

パートサーフェスに無関係な一面始動 一面始動の直前のNOPSにより，工具はパートサーフェス

に無関係に，指定の面に対し許容誤差内で停止するように最短距離で動く。NOPSは，直後の連続運動始

動文に対してだけ有効とする。工具の動きを附属書1図4に示す。 

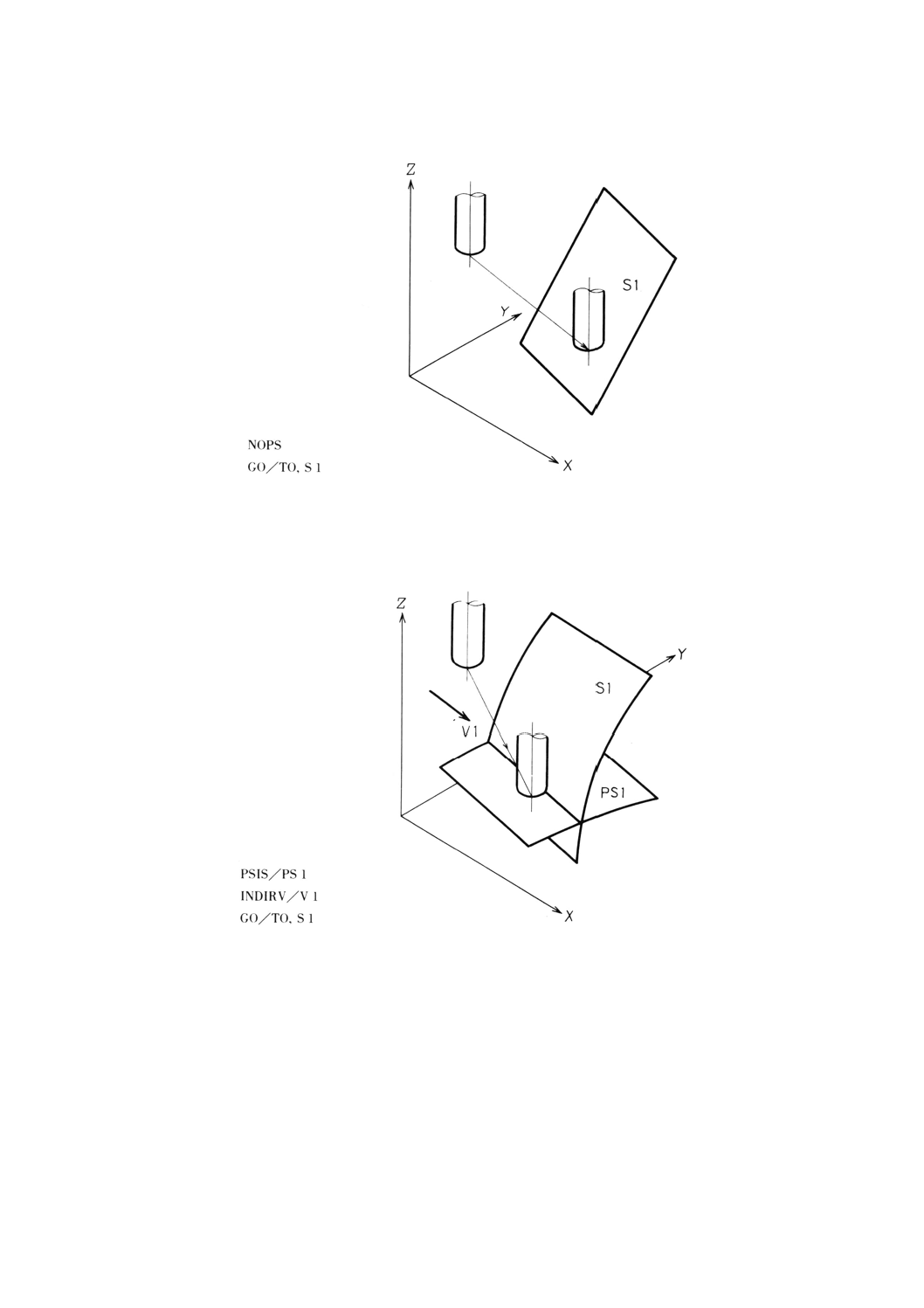
128 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 図4 

2.5 

パートサーフェスの指定と始動の向きのある一面始動 工具は，INDIRV文又はINDIRP文が指定す

る始動の向きで，パートサーフェスと指定の面に対し指定の位置関係で許容誤差内で停止するように動く。

工具の動きを附属書1図5に示す。 

附属書1 図5 

2.6 

パートサーフェスに無関係で始動の向きのある一面始動 工具は，INDIRV文又はINDIRP文が指定

する始動の向きで，パートサーフェスに無関係に指定の面に対し指定の位置関係で許容誤差内で停止する

ように動く。工具の動きを附属書1図6に示す。 

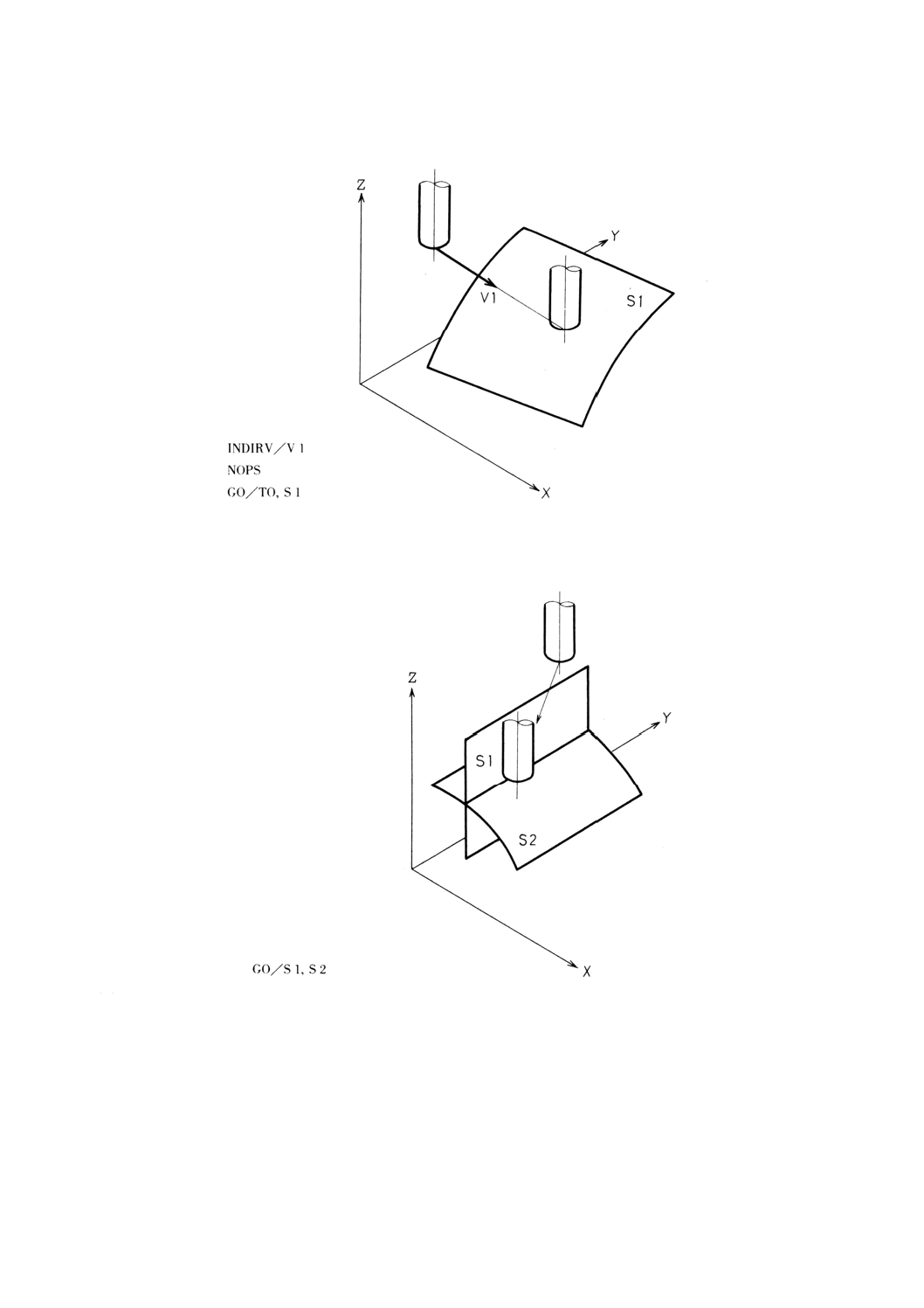
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 図6 

2.7 

二面始動 工具は，指定の面に対して最短距離の位置へ動く。最初の面は以後の運動文のドライブ

サーフェスとなり，第2の面はパートサーフェスとなる。工具の動きを附属書1図7に示す。 

附属書1 図7 

2.8 

指定の向きのある二面始動 工具は，INDIRV文又はINDIRP文が指定する始動の向きで，それぞれ

二つの面に対して最短距離で指定する位置関係で許容誤差内で停止するように動く。ただし，SRFVCT文

によって面のベクトルが与えられたときは，工具が停止する位置関係はこの面のベクトルによって規制さ

れる。SRFVCT文は，面のTO側及びPAST側を決定するために用いる。工具の動きを附属書1図8に示

す。 

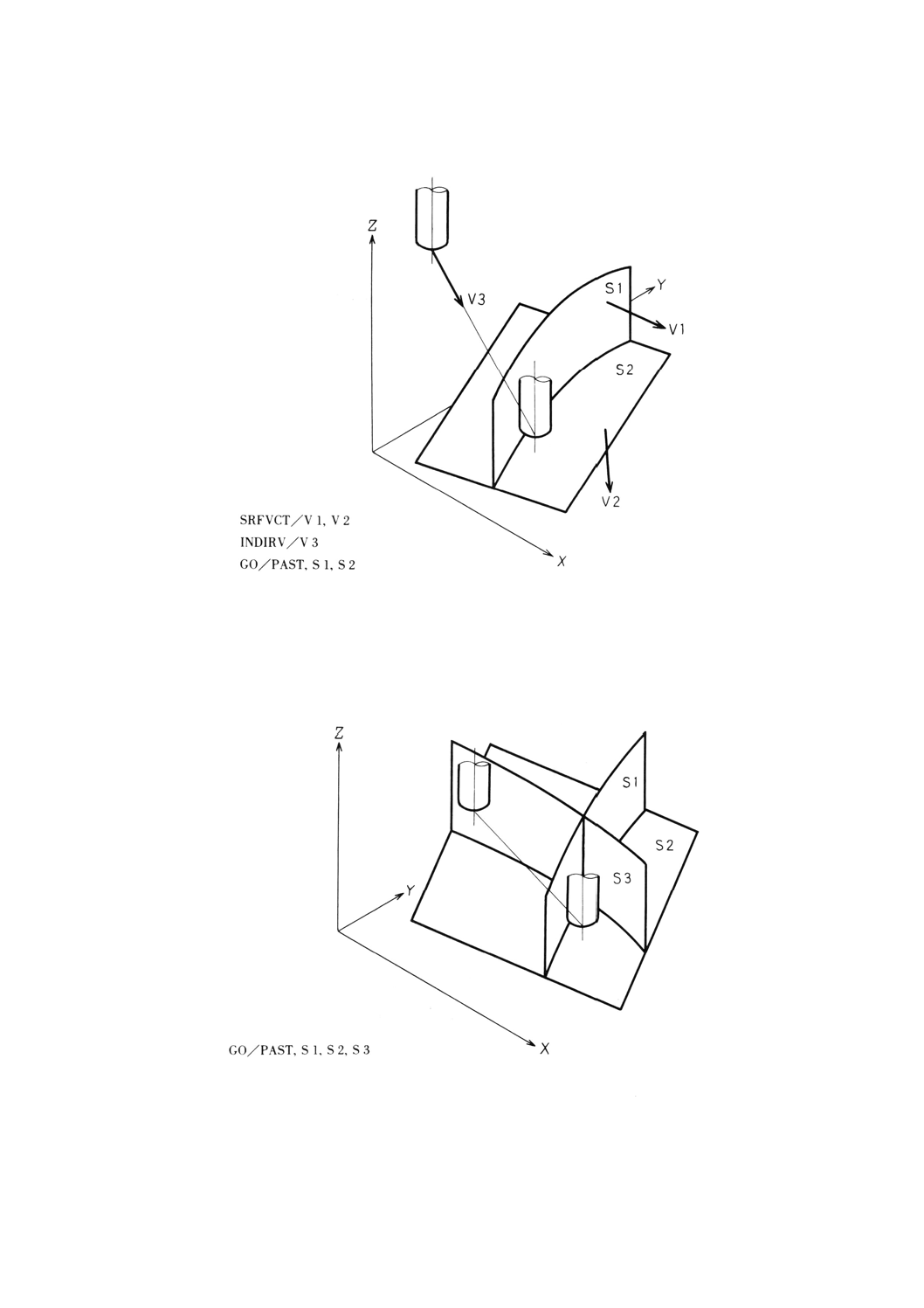
130 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 図8 

2.9 

三面始動 最初の面は，以後の運動文のドライブサーフェスとなり，第2の面はパートサーフェス

となり，第3の面は始動におけるチェックサーフェスとなる。工具は，与えられた関係を満足する位置へ

動く。修飾語TANTOは，第3の面にだけ用いることができ，第2の面と第3の面が指定された工具位置

で接していることを示す。工具の動きを附属書1図9に示す。 

附属書1 図9 

2.10 指定の向きのある三面始動 指定の向きのある二面始動と同様に，INDIRV文，INDIRP文及び

SRFVCT文は，単に始動の方向と指定の面のTO側又はPAST側を決定する補助的な役割として用いる。

したがって，実際の工具の動きを決めるものではない。工具は，与えられた関係を満足する位置へ動く。 

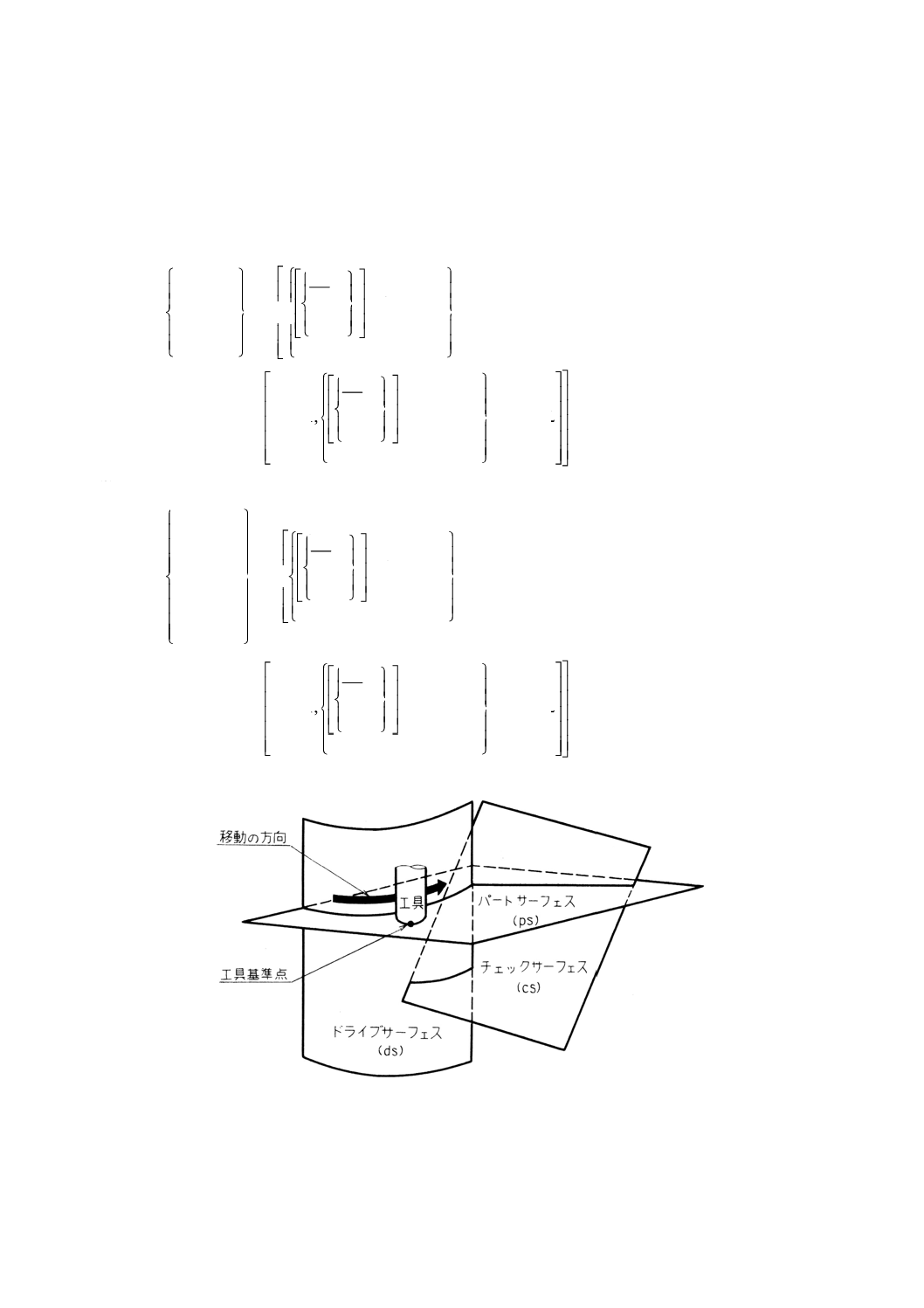
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3. 連続運動中間文と連線連動終了文 

3.1意味 連続運動中間文と連続運動終了文は，直前の運動の終わりの位置からドライブサーフェスとパー

トサーフェスに沿ってチェックサーフェスまで工具を移動させる。 

一般形は，次のとおりとする（附属書1図10参照）。 

(1) 連続運動中間文の一般形 

[

]

￥

，

／

cs1

TANTO,

INTOF,

n1,

,

PAST

ON

TO

ds

GORGT

GOLFT

GOBACK

GOFWD

[

]

2

cs2,

TANTO,

INTOF,

n2,

,

PAST

ON

TO

1,

,

名札

名札

(2) 連続運動終了文の一般形 

[

]

￥

／

cs1

TANTO,

INTOF,

n1,

,

PAST

ON

TO

ds

GODOWN

GOUP

GORGT

GOLFT

GOBACK

GOFWD

[

]

2

cs2,

TANTO,

INTOF,

n2,

,

PAST

ON

TO

1,

,

名札

名札

附属書1 図10 

3.2 

許容誤差 許容誤差は，指定の面を一様に覆った指定の厚さの層で与えられる。層の厚さによって

工具経路と幾何学的に定義された面との間の寸法差を限定する（附属書1図11参照）。 

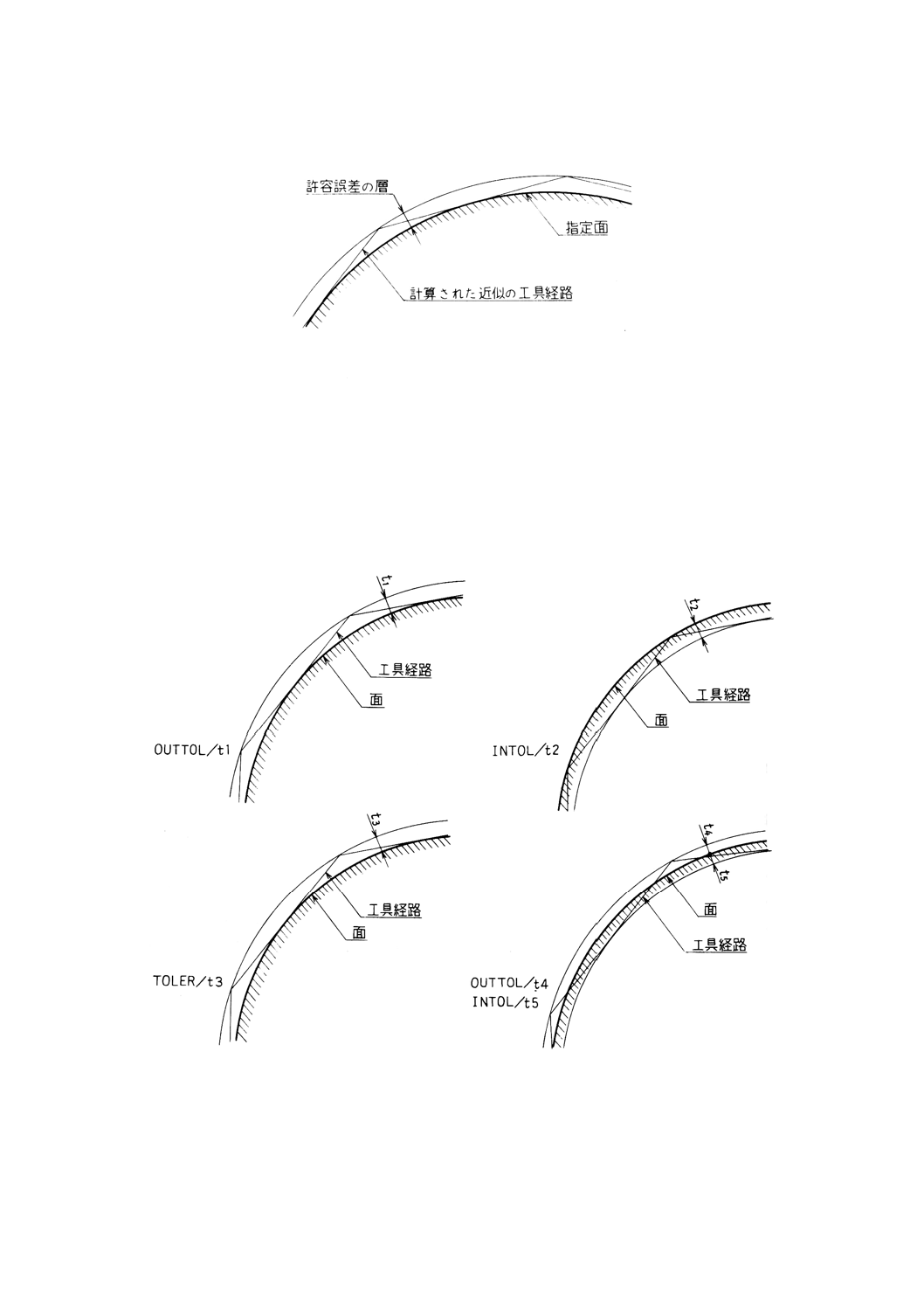
132 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 図11 

許容誤差は，TOLER，OUTTOL及びINTOLによって指定する。OUTTOLは，許容誤差の層を指定の面

の外側に作る。したがって，工具の縁が接触するすべての点は面の外側とする。INTOLは，許容誤差の層

を面の内側に作る。したがって，工具の縁が接触するすべての点は面の内側とする。TOLERは，以前の

INTOL及びOUTTOLの指定を取り消すと同時に，新たに許容誤差の層を面の外側に作る。もし，INTOL

とOUTTOLを一緒に指定すると，その効果が組み合わされる。 

なお，いずれの文も，三つの制御面に対してそれぞれ別の許容誤差を与えることができる。指定の例を

附属書1図12に示す。 

附属書1 図12 

工具の制御面に対する修飾語としてONを指定した場合は，工具の基準点が作る工具経路は指定の許容

誤差の層の内側に，TO又はPASTを指定した場合は，工具の外円が作る面は指定の許容誤差の層の内側に

なければならない。 

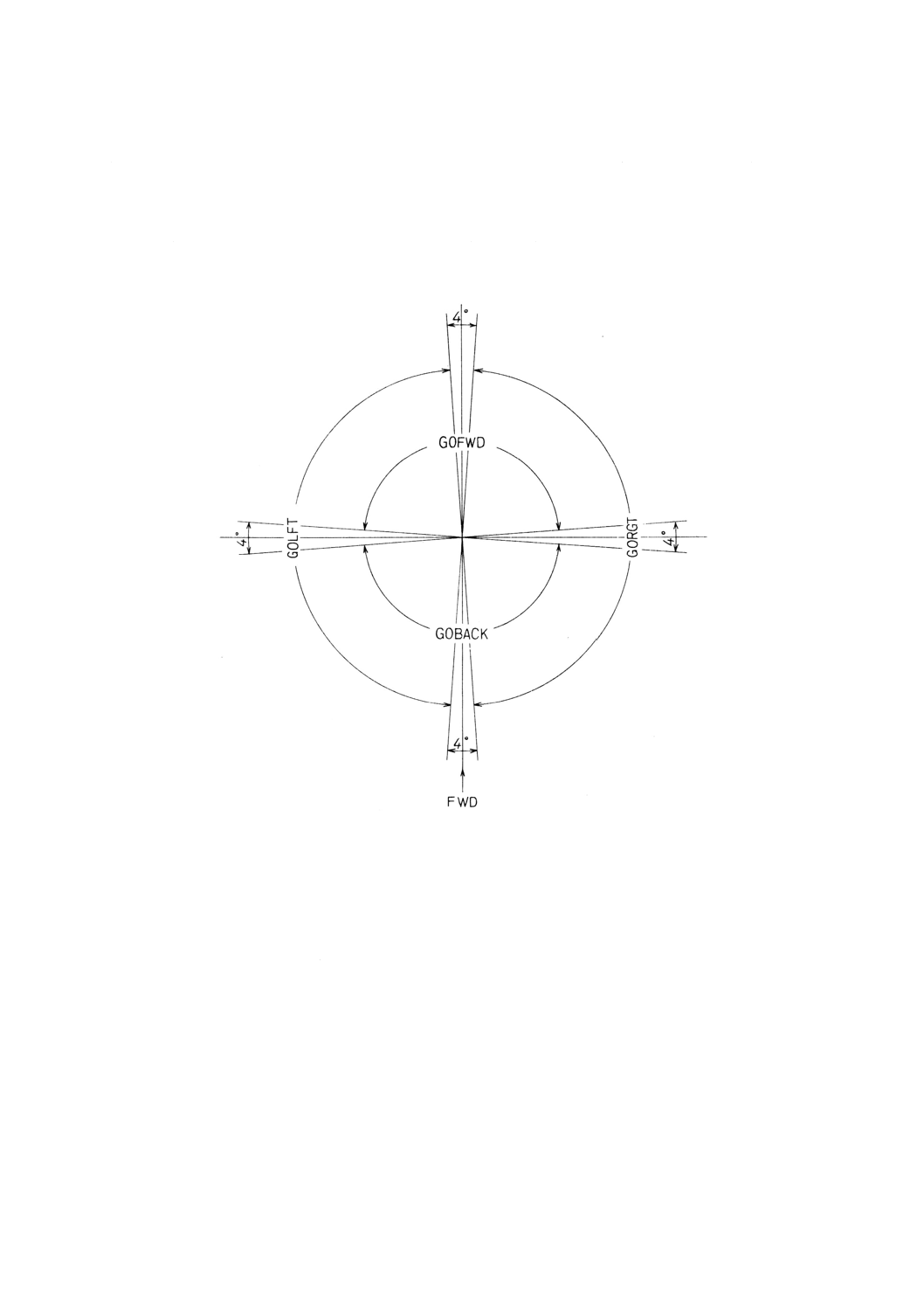
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3.3 

連動の向き 直前の工具運動文による工具運動に続いて，連続運動中間文や連続運動終了文

（GOFWD，GOBACK，GORGT，GOLFT，GOUP又はGODOWNをメイジャワードにもつ文）による工

具運動を続けるとき，工作物の形状によって決まる工具の運動の向きに応じて，メイジャワードを正しく

選択しなければならない。附属書1図13に，工具が工作物の形状に沿い運動すべき向きと選択するメイジ

ャワード（GOFWD，GOBACK，GORGT又はGOLFT）との関係を示す。 

附属書1 図13 

GOUP及びGODOWNは，それぞれ工具端から工具の根本の向きへの工具の運動及びその逆向きの工具

の運動を指令する。GOUP又はGODOWNに続く連続運動中間文のメイジャワード（GOFWD，GOBACK，

GORGT又はGOLFT）を選択するときは，GOUP又はGODOWNによる工具運動の方向に，工具軸以外の

動きがあればその最終の向きに対して選択し，工具軸以外の動きがなければGOUP及びGODOWNの直前

の運動の向きに対して選択する。 

3.4 

チェックサーフェスの省略 連続運動中間文及び連続運動終了文が連続してプログラムされている

場合，ある文でチェックサーフェスを省略すると，それより前の文で指定されているチェックサーフェス

を想定する。これを暗黙のチェックサーフェスと呼ぶ。このとき暗黙のチェックサーフェスの修飾語は，

想定可能でなければならない。このため，工具のドライブサーフェスに対する関係文（TLLFT，TLRGT

又はTLON）を暗黙のチェックサーフェスを使用する連続運動中間文及び連続運動終了文の前に宣言しな

ければならない。附属書1表1に，工具とドライブサーフェスに対する関係文，後続する次の連続運動文

及び暗黙のチェックサーフェスに対する面の修飾語の関係を示す。 

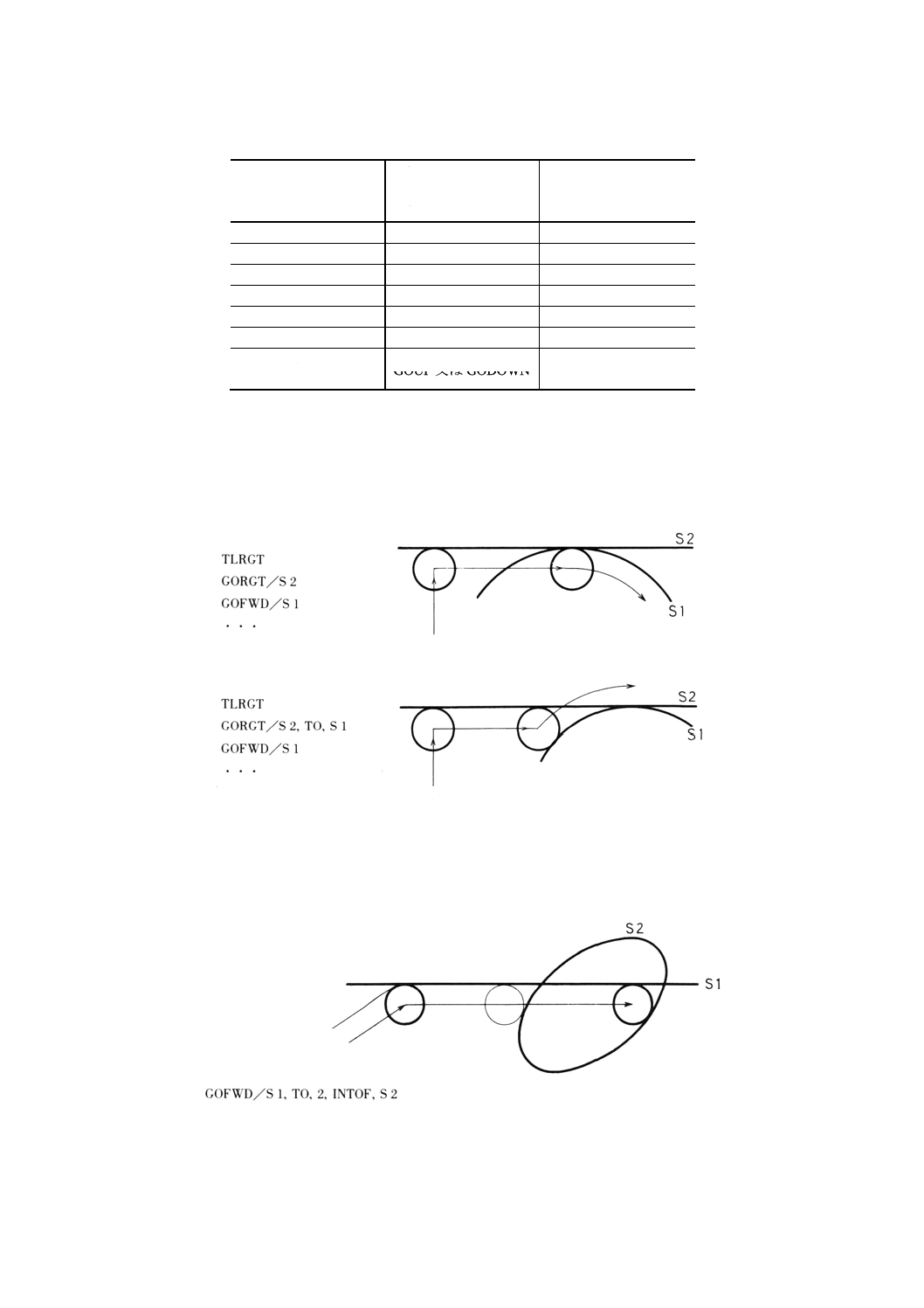
134 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書1 表1 

工具とドライブサーフ
ェスの関係文 

(n＋1) 番目の連続運動
中間文又は連続運動終
了文 

n番目の連続運動中間

文の暗黙のチェックサ
ーフェスの修飾語 

TLLFT 

GOLFT 

TO 

TLRGT 

GORGT 

TO 

TLLFT 

GORGT 

PAST 

TLRGT 

GOLFT 

PAST 

TLON 

GOLFT又はGORGT 

ON 

任意 

GOFWD又はGOBACK 

TANTO 

任意 

GOUP又はGODOWN 暗黙のチェックサーフ

ェス不可 

GOUP文及びGODOWN文は，暗黙のチェックサーフェスを使用できない。 

またGOUP文及びGODOWN文の前の連続運動中間文は，暗黙のチェックサーフェスを使用してはなら

ない。GOBACK文及びGOFWD文は，暗黙のチェックサーフェスを使用した連続運動中間文のつながり

の中でだけ，前の文の暗黙のチェックサーフェスに対してTANTOを想定する（附属書1図14参照）。 

附属書1 図14 

3.5 

多重交差 チェックサーフェスがドライブサーフェスと多重交差をもつとき，その文による工具の

移動の終点は，チェックサーフェスに対する修飾語の後に交点の番号とINTOFを指定して示す（附属書1

図15参照）。 

附属書1 図15 

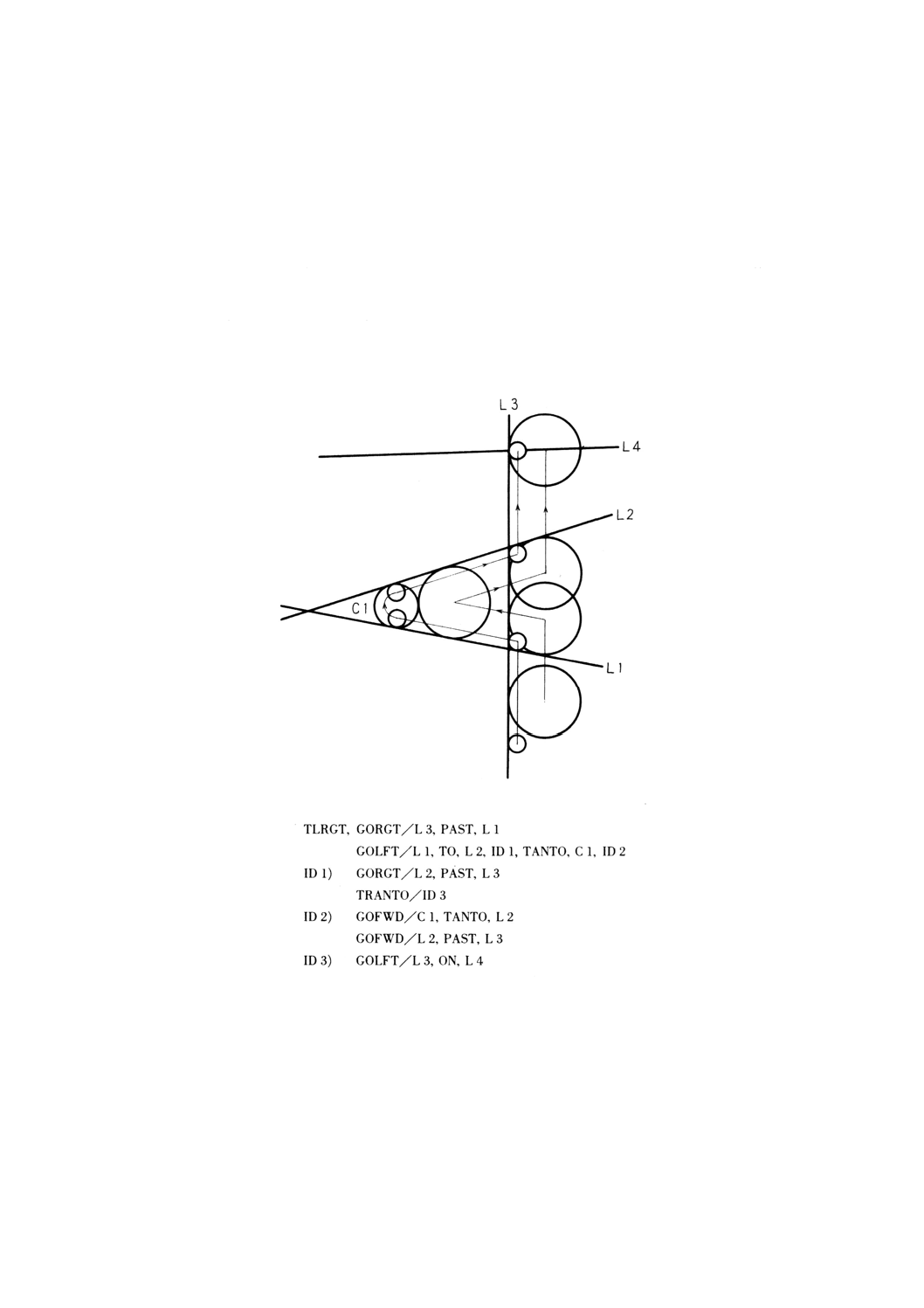
2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

3.6 

多重チェックサーフェス 工具が運動しているとき，工具が二つの面のどちらに接触するかを決定

することが困難な場合がある。この場合，チェックサーフェスを二つ指定することができる。計算された

工具経路は，二つのチェックサーフェスのどちらに先に到達するかによって変わる。それぞれのチェック

サーフェスには，名札を指定することができる。この名札は，それぞれのチェックサーフェスに工具が到

達したときに進むべき文に付けられ，この名札が付いている文は，多重チェックサーフェスを含む文より

後に現れなければならない。多重チェックサーフェス使用の例として，異なる大きさの工具で荒削りと仕

上げ削りを行うことを一つのプログラムで実現する場合がある。例えば，附属書1図16のような工作物を

切削する場合，直線L1，円C1及び直線L2が作る切込み部分の円C1の半径より大きな半径の工具で荒削

りをし，次に円C1の半径より小さな半径の工具で仕上げ削りを行うことができる。 

附属書1 図16 

136 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書2 数値制御パートプログラム用言語の 

媒体上での記述規則 

1. 文の記述 パートプログラムの文は，文を記録する媒体の行方向に完全に自由形式で記述できる。行

は，第1文字で始まり，第72文字で終わる。 

例： 

2. 行の継続 一つの文は，複数行にまたがって記述することができる。一つの行の途中に円記号又はド

ル記号を一つ記述することにより，その行を終了させ，次の行に継続させることができる。この方法は，

一つの文が1行に入らない場合や複数行にまたがって記述したほうが見やすい場合に用いる。 

例： 

3. 文の多重記述 複数の文を，一つの行に記述することができる。各文は，記号；により分離する。 

例： 

4. 注釈 パートプログラムを媒体上に記述しているとき，注釈文によらずに注釈を記述することができ

る。注釈行は，行の先頭に¥¥又は$$を記述した形とする。この¥¥又は$$の後には，第72文字まで任意の文

字の列が記述でき，注釈となる。 

また，文の記述が完結した後に¥¥又は$$を書いて，第72文字までに任意の文字の列を記述すれば，注釈

となる。更に，一つの文を次の行に継続するために記述した¥又は$の後も，第72文字までが注釈のために

利用できる。 

例： 

5. 空白 空白は，文字列を除いて意味をもたない。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書3 数値制御パートプログラム用言語の 

一般形の記述規則 

1. 一般形 一般形は，プログラマが構文とその意味を理解しやすくするために，プログラミングに使用

する形で記述する。 

2. 予約語 一般形の記述における予約語又はその推奨同義語は，英大文字の列とする（附属書5及び附

属書6参照）。 

3. 規制詞 一般形の記述における規制詞及びマクロ名は，ゴシック体の単語とする。例えば，円規制詞

は円及び円2などのように，点規制詞は点及び点2などのように書く。規制詞の種類については，本体の

9.1.1(3)及び10.1.1(2)を参照のこと。 

4. 変数 一般形の記述における変数の種類は，理解しやすい日本語又は英小文字で書く。ただし，同種

類の変数が複数個あるときは，自然数の1〜n又は英小文字を付ける。 

5. 面規制詞 一般形の記述におけるドライブサーフェス，パートサーフェス及びチェックサーフェスは，

面規制詞であり，それぞれds，ps及びcsと書く［10.1.1(3)参照］。 

6. 波括弧 一般形の記述における｛ ｝は，その中に縦に並べられた複数個の要素の中から一つの要素

を選択することを指示する。 

7. 角括弧 一般形の記述における［ ］は，その中の要素を使わない場合は，省略してもよいことを意

味する。 

8. 要素の省略 一般形の記述におけるアンダーラインのある要素は，その要素を選択した場合，省略し

てもよい。 

なお，その場合は，その要素を囲む波括弧のすぐ外側にある波括弧又は角括弧の中のコンマも合わせて

省略する。 

9. 繰返し 一般形の記述における…は，同種類のものを繰り返すことを意味する。 

10. 円記号 一般形の記述における円記号¥は，一般形が1行で書ききれないで複数行にまたがる場合に用

いる。 

11. 線号の左辺の省略 一般形の記述においては，記述の簡素化を図るため，名前＝の部分を省いてある。 

138 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書4 数値制御パートプログラム用言語の 

構文の記述規則 

1. 記法 この言語の構文は，拡張したバッカス記法を用いた超言語式により記述する。 

2. 超言語記号 超言語記号は，次による。 

(1) ：：＝ “記号の左辺は，記号の右辺とする”ことを示す。 

(2) ｜   “又は”を示す。 

(3) ＜ ＞ 超言語変数を示す。 

(4) 

ki[ ] 左大括弧と右大括弧の間の全体を，少なくともi回から多くともk回まで繰り返すことを示す。 

例：＜数字＞ :: ＝0｜1｜2｜3｜4｜5｜6｜7｜8｜9 

52[＜a＞]  少なくとも2回，多くても5回超言語変数＜a＞を繰り返すことを示す。 

22[＜a＞]  必ず2回繰り返すことを示す。 

10[＜a＞]  超言語変数＜a＞が一つあるか何もないことを示す。 

3. 超言語変数の名前 超言語変数の名前は，括弧＜と＞で囲んで他のものと区別する。 

例： ＜パートプログラム＞ 

4. 空白 文字列の中の空白は意味をもつが，それ以外の空白は意味をもたない。 

5. 言語記号 言語記号の要素は，予約語，超言語変数，数字，英字及び特殊文字のうちの次のものとす

る。すなわち，＋，−，＊，／，ピリオド．，左括弧（，右括弧），等号＝，及びコンマ，とする。 

6. 作成規則 超言語式の左辺は：：＝によって右辺と分離する。左辺は超言語変数であり，右辺は超言

語変数，超言語記号及び言語記号から構成する。左辺の超言語変数は，右辺の超言語の“又は”を示す｜

で分けられる幾つかの構成のそれぞれに対応する。 

7. 構成を省略している超言語変数 超言語変数＜予約語＞及び＜ポストプロセッサ文＞の構成は超言語

式では示していない。＜予約語＞は，附属書5及びJIS B 6326の附属書3による。また，＜ポストプロセ

ッサ文＞は，JIS B 6326による。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書5 予約語一覧表 

予約語 

意味 

左の予約語をマイナ

ワードとして使える

メイジャワード 

参照する構文

の掲出の箇条

番号 

ABS 

絶対値関数 (absolute value function) の記号 

6.1.2 

ACOS 

逆余弦関数 (arc cosine function) の記号 

6.1.2 

ALL 

すべて (all) の記号 

PRINT 

8.2.4 

PUNCH 

8.2.5 

READ 

8.2.6 

ANGL 

角度関数 (angle function) の記号 

6.1.2 

ARC 

弧 (arc) の記号 

PATERN 

9.5.1 

ASIN 

逆正弦関数 (arc sine function) の記号 

6.1.2 

AT 

で (at) の記号 

PATERN 

9.5.1 

ATAN 

逆正接関数 (arc tangent function) の記号 

6.1.2 

ATANGL 

角度で (at angle) の記号 

POINT 

9.4.1 

PATERN 

9.5.1 

LINE 

9.6.1 

VECTOR 

9.8.1 

AUTOPS 

現在の工具高さ（Z値）の自動パートサーフェス(（automatic partsurface) 

の記号 

10.3.7 

AVOID 

避ける (avoid) の記号 

GOTO 

10.2.3 

CALL 

マクロコール (macro call) の記号 

8.2.14 

CCLW 

反時計回り (counter-clockwise) の記号 

PATERN 

9.5.1 

CENTER 

中心 (center) の記号 

POINT 

9.4.1 

CIRCLE 

9.9.1 

SPHERE 

9.11.1 

ELLIPS 

9.13.1 

HYPERB 

9.14.1 

CIRCLE 

円定義 (circle definition) の記号 

9.9.1 

CIRCUL 

円形 (circular) の記号 

PATERN 

9.5.1 

CLPRNT 

工具位置印字 (cutter1ocation print) の記号 

8.2.7 

CLW 

時計回り (clockwise) の記号 

PATERN 

9.5.1 

CONE 

円すい定義 (cone definition) の記号 

9.12.1 

COPY 

コピー文 (copy) の記号 

8.2.13 

COS 

余弦関数 (cosine function) の記号 

6.1.2 

CROSS 

ベクトルの外積 (cross product) の記号 

VECTOR 

9.8.1 

CUT 

工具経路の出力の削除の終了 (cut) の記号 

10.6.2 

CUTTER 

工具定義 (cutter definition) の記号 

10.3.6 

CYLNDR 

円柱定義 (cylinder definition) の記号 

9.10.1 

DELTA 

増分 (delta) の記号 

POINT 

9.4.1 

DIST 

距離 (distance) の記号 

6.1.2 

DNTCUT 

工具経路の出力の削除の開始 (do not cut) の記号 

10.6.2 

DOT 

ベクトルの内積 (dot product) の記号 

6.1.2 

ELLIPS 

だ円定義 (ellipse definition) の記号 

9.13.1 

EXP 

指数関数 (exponential function) の記号 

6.1.2 

FINI 

パートプログラムの終了 (finish of part program) の記号 

8.1.2 

140 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

予約語 

意味 

左の予約語をマイナ

ワードとして使える

メイジャワード 

参照する構文

の掲出の箇条

番号 

FROM 

から (from) の記号 

10.2.2 

FUNOFY 

Yの関数 (function of Y) の記号 

GCONIC 

9.16.1 

GCONIC 

ゼネラルコニック定義 (general conic definition) の記号 

9.16.1 

GO 

進む (go) の記号 

10.2.5 

GOBACK 

戻る (go back) の記号 

10.2.7 

GODLTA 

増分だけ進む (go delta) の記号 

10.2.4 

GODOWN 

下降する (go down) の記号 

10.2.7 

GOFWD 

前進する (go forward) の記号 

10. 2.7 

GOLFT 

左折する (go left) の記号 

10.2.7 

GORGT 

右折する (go right) の記号 

10.2.7 

GOTO 

ある位置に行く (go to) の記号 

10.2.3 

GOUP 

上昇する (go up) の記号 

10.2.7 

GRID 

格子 (grid) の記号 

PATERN 

9.5.1 

HYPERB 

双曲線関数 (hyperbolic function) の記号 

9.14.1 

IF 

もし…ならば (if) の記号 

8.2.11 

IN 

内接 (in) の記号 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

INCR 

増分 (increment) の記号 

PATERN 

9.5.1 

INDEX 

インデックス (index) の記号 

8.2.13 

INDIRP 

点の向きに (in direction of point) の記号 

10.4.1 

INDIRV 

ベクトルの向きに (in direction of vector) の記号 

10.4.1 

INTERC 

切片 (intercept) の記号 

LINE 

9.6.1 

INTOF 

の交差 (intersection of) の記号 

POINT 

9.4.1 

LINE 

9.6.1 

VECTOR 

9.8.1 

GOFWD 

10.2.7 

GOBACK 

10.2.7 

GOLFT 

10.2.7 

GORGT 

10.2.7 

GOUP 

10.2.7 

GODOWN 

10.2.7 

INTOL 

内側許容誤差 (inner tolerance) の記号 

10.3.5 

INVERS 

逆向き (inverse) の記号 

PATERN 

9.5.1 

MATRIX 

9.19.1 

GOTO 

10.2.3 

JUMPTO 

へ飛ぶ (jump to) の記号 

8.2.10 

LARGE 

大きい (large) の記号 

CIRCLE 

9.9.1 

LCONIC 

ロフトコニック定義 (loftconic definition) の記号 

9.15.1 

LEFT 

左側 (left) の記号 

LINE 

9.6.1 

PLANE 

9.7.1 

LENGTH 

長さ (length) の記号 

VECTOR 

9.8.1 

LINE 

直線定義 (line definition) の記号 

9.6.1 

LINEAR 

直線 (linear) の記号 

PATERN 

9.5.1 

LNTH 

ベクトル長定義 (vector length definition) の記号 

6.1.2 

LOG 

自然対数関数 (natural logarithm function) の記号 

6.1.2 

LOOPND 

繰返し終了 (loop end) の記号 

8.2.9 

LOOPST 

繰返し開始 (loop start) の記号 

8.2.9 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

予約語 

意味 

左の予約語をマイナ

ワードとして使える

メイジャワード 

参照する構文

の掲出の箇条

番号 

MACHIN 

機械 (machine) の記号 

8.2.2 

MACRO 

マクロ定義 (macro definition) の記号 

7.4.2 

MATRIX 

マトリックス定義 (matrix definition) の記号 

9.19.1 

MINUS 

ベクトル減算 (vector subtruction) の記号 

VECTOR 

9.8.1 

MIRROR 

直線又は平面についての鏡像定義 (mirror image definition) の記号 

PATERN 

9.5.1 

MATRIX 

9.19.1 

MODIFY 

修正する (modify) の記号 

COPY 

8.2.13 

NEGX 

X軸の負の向き (negative X) の記号 

VECTOR 

9.8.1 

NEGY 

Y軸の負の向き (negative Y) の記号 

VECTOR 

9.8.1 

NEGZ 

Z軸の負の向き (negative Z) の記号 

VECTOR 

9.8.1 

NOMORE 

モーダルな指令の終了 (no more) の記号 

INDEX 

8.2.13 

REFSYS 

9.2.1 

TRACUT 

10.5.2 

NONAME 

名前なしの出力 (no name) の記号 

PRINT 

8.2.4 

NOPOST 

ポストプロセッサ呼出し禁止 (no post-processor) の記号 

8.2.3 

NOPS 

一時的にパートサーフェスの無視 (no part surface) の記号 

10.3.7 

NORMAL 

法線 (norma1) の記号 

TABCYL 

9.18.1 

NOX 

X座標のない (no X coordinates) の記号 

TABCYL 

9.18.1 

NOY 

Y座標のない (no Y coordinates) の記号 

TABCYL 

9.18.1 

NOZ 

Z座標のない (no Z coordinates) の記号 

TABCYL 

9.18.1 

NUM 

番号 (number) の記号 

6.1.2 

OFF 

オフにする (off) の記号 

PRINT 

8.2.4 

PUNCH 

8.2.5 

CLPRNT 

8.2.7 

OFFSET 

オフセットする (offset) の記号 

10.2.6 

OMIT 

省略 (omit) の記号 

CLPRNT 

8.2.7 

PATERN 

9.5.1 

GOTO 

10.2.3 

ON 

オンにする，又は上に (on) の記号 

PRINT 

8.2.4 

PUNCH 

8.2.5 

CLPRNT 

8.2.7 

CIRCLE 

9.9.1 

GO 

10.2.5 

OUT 

外接 (out) の記号 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

OUTTOL 

外側許容誤差 (outer tolerance) の記号 

10.3.5 

PAGE 

ページ (page) の記号 

PRlNT 

8.2.4 

PARLEL 

平行 (parallel) の記号 

LINE 

9.6.1 

PLANE 

9.7.1 

VECTOR 

9.8.1 

TABCYL 

9.18.1 

PARTNO 

部品番号 (part number) の記号 

8.1.1.  

PAST 

過ぎて (past) の記号 

GO 

10.2.5 

OFFSET 

10.2.6 

PATERN 

パターン定義 (pattern definition) の記号 

9.5.1 

PERPTO 

垂直 (perpendicular to) の記号 

LINE 

9.6.1 

PLANE 

9.7.1 

142 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

予約語 

意味 

左の予約語をマイナ

ワードとして使える

メイジャワード 

参照する構文

の掲出の箇条

番号 

VECTOR 

9.8.1 

PLANE 

平面定義 (plane definition) の記号 

9.7.1 

PLUS 

ベクトル加算 (vector addition) の記号 

VECTOR 

9.8.1 

POINT 

点定義 (point definition) の記号 

9.4.1 

POSX 

X軸の正の向き (positive X) の記号 

VECTOR 

9.8.1 

POSY 

Y軸の正の向き (positive Y) の記号 

VECTOR 

9.8.1 

POSZ 

Z軸の正の向き (positive Z) の記号 

VECTOR 

9.8.1 

PRINT 

印字する (print) の記号 

8.2.4 

PSIS 

パートサーフェス定義 (part surface definition) の記号 

10.3.7 

PUNCH 

せん孔する (Punch) の記号 

8.2.5 

QADRIC 

二次曲面定義 (quadric definition) の記号 

9.17.1 

RADIUS 

半径 (radius) の記号 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

SPHERE 

9.11.1 

RANDOM 

ランダム (random) の記号 

PATERN 

9.5.1 

READ 

読む (read) の記号 

8.2.6 

REFSYS 

局所座標系 (reference system) の記号 

9.2.1 

REMARK 

注釈 (remark) の記号 

8.2.15 

RESERV 

確保 (reserve) の記号 

7.3.2 

RETAIN 

保持する (retain) の記号 

PATERN 

9.5.1 

GOTO 

10.2.3 

RIGHT 

右側 (right) の記号 

LINE 

9.6.1 

PLANE 

9.7.1 

RLDSRF 

ルールドサーフェス定義 (ruled surface definition) の記号 

9.20.1  

RTHETA 

R,θ座標 (R,θ coordinates) の記号 

POINT 

9.4.1 

TABCYL 

9.18.1 

SAME 

同じ (same) の記号 

COPY 

8.2.13 

SCALE 

尺度 (scale) の記号 

MATRIX 

9.19.1 

SIN 

正弦関数 (sine function) の記号 

6.1.2 

SLOPE 

こう配 (slope) の記号 

LINE 

9.6.1 

LCONIC 

9.15.1 

TABCYL 

9.18.1 

SMALL 

小さい (small) の記号 

CIRCLE 

9.9.1 

SPHERE 

球定義 (sphere definition) の記号 

9.11.1 

SPLINE 

スプライン (spline) の記号 

TABCYL 

9.18.1 

SQRT 

平方根関数 (square root function) の記号 

6.1.2 

SRFVCT 

面ベクトル (Surface vector) の記号 

10.4.1 

SYN 

同義語 (synonym) の記号 

7.2.2 

TABCYL 

タビュレーテッドシリンダ定義 (tabulated cylinder definition) の記号 

9.18.1 

TAN 

正接関数 (tangent function) の記号 

6.1.2 

TANTO 

に接する (tangent to) の記号 

LINE 

9.6.1 

PLANE 

9.7.1 

CIRCLE 

9.9.1 

SPHERE 

9.11.1 

TABCYL 

9.18.1 

GO 

10.2.5 

TERMAC 

マクロ定義の終了 (terminate macro definition) の記号 

7.4.2 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

予約語 

意味 

左の予約語をマイナ

ワードとして使える

メイジャワード 

参照する構文

の掲出の箇条

番号 

THETAR 

θ，R座標 (θ, R coordinates) の記号 

P0INT 

9.4.1 

TABCYL 

9.18.1 

THICK 

厚さ (thick) の記号 

10.3.4 

THRU 

初めから終わりまで (through) の記号 

PATERN 

9.5.1 

GOTO 

10.2.3 

TIMES 

倍 (times) の記号 

VECTOR 

9.8.1 

TITLES 

タイトル (titles) の記号 

8.2.8 

TLLFT 

ドライブサーフェスの左側に工具を (tool left) の記号 

10.3.2 

TLOFPS 

パートサーフェスに接して工具を (tool offset part surface) の記号 

10.3.3 

TLON 

ドライブサーフェスの上に工具を (tool on) の記号 

10.3.2 

TLONPS 

パートサーフェスの上に工具を (tool on part surface) の記号 

10.3.3 

TLRGT 

ドライブサーフェスの右側に工具を (tool right) の記号 

10.3.2 

TO 

チェックサーフェスまで (to) の記号 

GO 

10.2.5 

OFFSET 

10.2.6 

TOLER 

許容誤差 (tolerance) の記号 

10.3.5 

TRACUT 

工具位置データの変換 (transform cutter location data) の記号 

10.5.2 

TRAFO 

二つのパターンを格子パターンに変換する (transform) の記号 

PATERN 

9.5.1 

TRANSL 

平行移動 (translation) の記号 

COPY 

8.2.13 

MATRIX 

9.19.1 

TRANTO 

に移す (transfer to) の記号 

8.2.12 

TRFORM 

マトリックスによる入カデータの変換 (transform) の記号 

TABCYL 

9.18.1 

UNIT 

単位 (unit) の記号 

VECTOR 

9.8.1 

VECTOR 

ベクトル定義 (vector definition) の記号 

9.8.1 

XAXIS 

X軸 (X axis) の記号 

LINE 

9.6.1 

XCOORD 

X座標 (X coordinate) の記号 

POINT 

9.4.1 

XLARGE 

X座標の大きい (X large) の記号 

POINT 

9.4.1 

LINE 

9.6.1 

PLANE 

9.7.1 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

TABCYL 

9.18.1 

XSMALL 

X座標の小さい (X small) の記号 

POINT 

9.4.1 

LINE 

9.6.1 

PLANE 

9.7.1 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

TABCYL 

9.18.1 

XYPLAN 

XY平面 (XY plane) の記号 

POINT 

9.4.1 

VECTOR 

9.8.1 

MATRlX 

9.19.1 

XYROT 

XY平面上の回転 (rotation in XY plane) の記号 

COPY 

8.2.13 

PATERN 

9.5.1 

MATRIX 

9.19.1 

XYZ 

X, Y, Z座標 (X, Y, Z coordinate) の記号 

TABCYL 

9.18.1 

YAXIS 

Y軸 (Y axis) の記号 

LINE 

9.6.1 

YCOORD 

Y座標 (Y coordinate) の記号 

POINT 

9.4.1 

YLARGE 

Y座標の大きい (Y large) の記号 

POINT 

9.4.1 

144 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

予約語 

意味 

左の予約語をマイナ

ワードとして使える

メイジャワード 

参照する構文

の掲出の箇条

番号 

LINE 

9.6.1 

PLANE 

9.7.1 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

TABCYL 

9.18.1 

YSMALL 

Y座標の小さい (Y small) の記号 

POINT 

9.4.1 

LINE 

9.6.1 

PLANE 

9.7.1 

CIRCLE 

9.9.1 

CYLNDR 

9.10.1 

TABCYL 

9.18.1 

YZPLAN 

YZ平面 (YZ plane) の記号 

POINT 

9.4.1 

VECTOR 

9.8.1 

MATRIX 

9.19.1 

YZROT 

YZ平面上の回転 (rotation in YZ plane) の記号 

COPY 

8.2.13 

MATRIX 

9.19.1 

ZIGZAG 

ジグザグ (zigzag) の記号 

GOTO 

10.2.3 

ZLARGE 

Z座標の大きい (Z large) の記号 

ZSURF 

9.3.1 

PLANE 

9.7.1 

CYLNDR 

9.10.1 

TABCYL 

9.18.1 

ZSMALL 

Z座標の小さい (Z small) の記号 

ZSURF 

9.3.1 

PLANE 

9.7.1 

CYLNDR 

9.10.1 

TABCYL 

9.18.1 

ZSURF 

Z座標を決める面 (Z coordinate surface) の記号 

9.3.1 

ZXPLAN 

ZX平面 (ZX plane) の記号 

POINT 

9.4.1 

VECTOR 

9.8.1 

MATRIX 

9.19.1 

ZXROT 

ZX平面上の回転 (rotation in ZX plane) の記号 

COPY 

8.2.13 

MATRIX 

9.19.1 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書6 推奨同義語表 

推奨する予約語の同義語を示す。 

同義語 

予約語 

同義語 

予約語 

ANG 

ATANGL 

P 

POINT 

C 

CIRCLE 

PAR 

PARLEL 

CE 

CENTER 

PAT 

PATERN 

CL 

CALL 

PER 

PERPTO 

DE 

DELTA 

PL 

PLANE 

DP 

INDIRP 

PT 

PAST 

DV 

INDIRV 

RAD 

RADIUS 

FM 

FROM 

RT 

RIGHT 

GB 

GOBACK 

SM 

SMALL 

GD 

GODLTA 

T 

TABCYL 

GF 

GOFWD 

TC 

TRACUT 

GL 

GOLFT 

TR 

THETAR 

GR 

GORGT 

TT 

TANTO 

GT 

GOTO 

V 

VECTOR 

INT 

INTOF 

X 

XCOORD 

L 

LINE 

XL 

XLARGE 

LG 

LARGE 

XS 

XSMALL 

LT 

LEFT 

Y 

YCOORD 

M 

MACRO 

YL 

YLARGE 

MAT 

MATRIX 

YS 

YSMALL 

146 

B 6327-1985  

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

附属書7 推奨する標準形 

1. 標準形 数値制御プロセッサの処理を容易にするために，プロセッサ内部での図形データの表現形式

の標準形を定める。 

2. 図形 図形を表すデータの標準形として，次のものを推奨する。 

(1) 点の標準形は，点のX座標，Y座標，z座標 (a, b, c) のスカラー量の並びa，b，cとする。 

(2) 直線の標準形は，直線の方程式ax＋by＋cz＝dの係数であるスカラー量の並びa，b，0，dとする。 

(3) 円の標準形は，中心の座標 (a, b, c)，中心軸のベクトルの座標軸X，Y，Zの成分 (0, 0, 1) 及び半径r

のスカラー量の並びa，b，c，0，0，1，rとする。円の方程式は， (x−a) 2＋ (y−b) 2＝r2である。 

(4) 平面の標準形は，平面の方程式ax＋by＋cz＝dの係数であるスカラー量の並びa，b，c，dとする。こ

こで，a2＋b2＋c2＝1とする。 

(5) 円柱の標準形は，円柱の軸上の点の座標 (a, b, c)，軸のベクトルに平行なベクトルの座標軸X，Y，Z

の成分 (f, g, h) 及び半径rのスカラー量の並びa，b，c，f，g，h，rとする。 

(6) 球の標準形は，球の方程式 (x−a) 2＋ (y−b) 2＋ (z−c) 2＝r2の係数であるスカラー量の並びa，b，c，

rとする。 

(7) 二次曲面の標準形は，二次曲面の方程式ax2＋by2＋cz2＋2dyz＋2ezx＋2fxy＋2gx＋2hy＋2iz＋j＝0の係数

であるスカラー量の並びa，b，c，j，d，e，j，g，h，iとする。 

(8) だ円，双曲線，ロフトコニック及びゼネラルコニックの標準形は，二次曲面の方程式においてz＝0と

したときの係数であるスカラー量の並びa，b，0，j，0，0，f，g，h，0とする。 

(9) 円すいの標準形は，頂点の座標 (a, b, c)，軸のベクトルに平行なベクトルの座標軸X，Y，Zの成分 (f，

g, h) 及び半頂角の余弦の値dのスカラー量の並びa，b，c，f，g，h，dとする。 

(10) マトリックスの標準形は，

+

=

3

2

1

1

1

1

3

3

3

2

2

2

1

1

1

2

2

2

d

d

d

z

y

x

c

b

a

c

b

a

c

b

a

z

y

x

におけるスカラー量の並びa1，b1，c1，d1，

a2，b2，c2，d2，a3，b3，c3，d3とする。 

(11) ベクトルの標準形は，ベクトルの座標軸X，Y，Zの成分 (a, b, c) のスカラー量の並びa，b，cとす

る。 

2019年7月1日の法改正により名称が変わりました。まえがきを除き，本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。 

原案作成委員会 構成表 

（主査） 

研 野 和 人 

株式会社小松製作所 

井 上 久仁子 

工業技術院機械技術研究所 

井 上 高 志 

日本建鉄株式会社 

大 高 義 穂 

社団法人日本工作機械工業会 

神 谷 勝 義 

三菱重工業株式会社 

坂 井 喜 毅 

通商産業省工業技術院 

白 髭 昌 雄 

石川島播磨重工業株式会社 

関 口 久 夫 

東芝機械株式会社 

田 中 久仁夫 

ファナック株式会社 

武 田 智 雄 

日本アイ・ビー・エム株式会社 

長 見   茂 

株式会社ファンテック 

桧 木 武 久 

社団法人日本電子工業振興協会 

花 田 洋 一 

株式会社日立製作所 

松 村   豊 

日立精機株式会社 

三 好 長 則 

沖電気工業株式会社 

矢 部 其 一 

日本電気株式会社 

原案作成作業委員会 構成表 

（主査） 

研 野 和 人 

株式会社小松製作所 

井 上 久仁子 

工業技術院機械技術研究所 

井 上 高 志 

日本建鉄株式会社 

関 口 久 夫 

東芝機械株式会社 

田 中 久仁夫 

ファナック株式会社 

三 好 長 則 

沖電気工業株式会社