B 6190-7:2019 (ISO 230-7:2015)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 2
3.1 一般用語 ······················································································································ 2
3.2 誤差運動に関する用語 ···································································································· 7
3.3 回転軸誤差運動の感度方向に関する用語············································································· 8
3.4 回転軸誤差運動の方向に関する用語··················································································· 9
3.5 回転周波数に基づく回転軸誤差運動に関する用語 ································································ 11
3.6 回転軸誤差運動線図に関する用語····················································································· 11
3.7 回転軸誤差運動線図中心に関する用語··············································································· 13
3.8 回転軸誤差運動値に関する用語 ······················································································· 14
3.9 構造誤差運動に関する用語 ····························································································· 16
3.10 軸ずれに関する用語 ····································································································· 16
4 一般事項························································································································ 17
4.1 測定単位 ····················································································································· 17
4.2 JIS B 6190-1の参照 ······································································································· 17
4.3 推奨する測定器 ············································································································ 17
4.4 環境 ··························································································································· 17
4.5 試験する回転部品 ········································································································· 17
4.6 回転部品の暖機運転 ······································································································ 18
4.7 構造誤差運動試験 ········································································································· 18
5 主軸ユニットの誤差運動試験方法 ······················································································· 18
5.1 一般 ··························································································································· 18
5.2 試験条件及びその詳細 ··································································································· 18
5.3 主軸回転軸の試験−回転感度方向····················································································· 19
5.4 主軸回転軸の試験−固定感度方向····················································································· 23
6 回転テーブル及び旋回主軸頭の回転軸誤差運動試験方法 ························································· 27
6.1 一般 ··························································································································· 27
6.2 軸方向誤差運動 ············································································································ 27
6.3 半径方向誤差運動 ········································································································· 28
6.4 傾斜方向誤差運動 ········································································································· 29
附属書A(参考)回転軸に関する共通概念 ··············································································· 31
附属書B(参考)基準球の真円度誤差除去方法 ·········································································· 49
附属書C(参考)回転軸のコンプライアンス特性に関する用語及び定義 ········································· 53
B 6190-7:2019 (ISO 230-7:2015) 目次
(2)
ページ
附属書D(参考)主軸,回転テーブル及び旋回主軸頭に発生する熱的誤差に関する用語及び定義 ········ 54
附属書E(参考)静的誤差運動試験方法··················································································· 55
附属書F(参考)回転軸の試験における測定不確かさの推定 ························································ 56
附属書G(参考)索引(50音順) ·························································································· 60
附属書H(参考)変位計の周波数帯域及び軸の回転速度 ····························································· 62
参考文献 ···························································································································· 65
B 6190-7:2019 (ISO 230-7:2015)
(3)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
工作機械工業会(JMTBA)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業
規格を改正すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業
規格である。
これによって,JIS B 6190-7:2008は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 6190の規格群には,次に示す部編成がある。
JIS B 6190-1 第1部:幾何精度試験
JIS B 6190-2 第2部:数値制御による位置決め精度試験
JIS B 6190-3 第3部:熱変形試験
JIS B 6190-4 第4部:数値制御による円運動精度試験
JIS B 6190-5 第5部:騒音放射試験(予定)
JIS B 6190-6 第6部:対角位置決め精度試験(予定)
JIS B 6190-7 第7部:回転軸の幾何精度試験
TR B 6190-8 第8部:振動試験(予定)
TR B 6190-9 第9部:JIS B 6190の規格群に規定する試験における測定の不確かさの推定(予定)
JIS B 6190-10 第10部:プロービングシステムの測定性能評価方法
TR B 6190-11 第11部:測定器及び幾何精度試験への応用(予定)
日本工業規格 JIS
B 6190-7:2019
(ISO 230-7:2015)
工作機械試験方法通則−
第7部:回転軸の幾何精度試験
Test code for machine tools-
Part 7: Geometric accuracy of axes of rotation
序文
この規格は,2015年に第2版として発行されたISO 230-7を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
この規格は,回転軸の誤差運動が回転テーブルに及ぼす影響,並びに複数の感度方向が決定的に重要に
なるフライス削り及び穴あけについて産業界及び学界から寄せられた意見に基づき改正した。この改正で
は,用語及び定義を更新し,かつ,半径方向誤差運動の第一次高調波が方向によって異なる特別な場合に
ついて対応するようにした。さらに,一般概念及びその適用について,より明確にするために用語の構成
を変更した。複数の感度方向がある場合だけでなく,回転軸の誤差運動が部品の半径方向位置に影響を及
ぼす場合(二次元の感度方向)についても記載した。
1
適用範囲
この規格は,工作機械で用いられる回転軸の幾何精度試験方法について規定する。工作機械の主軸,旋
回主軸頭及び傾斜回転テーブルは,全て回転軸をもっている。これらの軸は全て複数の誤差が原因となっ
て空間内で意図しない運動を発生する。
この規格は,次の回転軸の特性を含む。
− 回転軸の誤差運動
− 速度に起因する軸ずれ
熱が原因で発生する軸ずれ,環境温度変動が原因で発生する軸ずれのような回転軸の特性については,
JIS B 6190-3による。
この規格は,次の回転軸の特性については含まない。
− 角度位置決め精度(JIS B 6190-1及びJIS B 6190-2参照)
− 表面及び部品の振れ(JIS B 6190-1参照)
− 工具保持具インタフェースの仕様
− 振動測定(ISO/TR 230-8参照)
− 騒音測定(JIS B 6195参照)
− 回転速度範囲及び精度(JIS B 6331-5及びJIS B 6336-6参照)
− 釣合い測定又は方法(ISO 1940-1及びISO 6103参照)
− アイドル運転損失(動力損失)
2
B 6190-7:2019 (ISO 230-7:2015)
− 熱影響(JIS B 6190-3参照)
なお,附属書Aは,主軸だけでなく,回転テーブル,旋回主軸頭などの全ての回転軸に共通する概念に
ついて記載している。また,附属書Bは,基準球の真円度誤差除去方法について記載している。附属書C
は,回転軸のコンプライアンス特性に関する用語及びその定義を,附属書Dは,主軸,回転テーブル及び
旋回主軸頭に発生する熱的誤差に関する用語及びその定義を記載している。附属書Eは,静的誤差運動試
験方法について,附属書Fは,回転軸の試験における測定不確かさの推定方法についてそれぞれ記載して
いる。附属書Gは,この規格で用いる用語について,対応英語とともに索引として示す。さらに,附属書
Hは,適切な周波数帯域をもった変位計を選択する場合の情報及び指針について記載している。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 230-7:2015,Test code for machine tools−Part 7: Geometric accuracy of axes of rotation(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この引用
規格は,その最新版(追補を含む。)を適用する。
JIS B 6190-1 工作機械試験方法通則−第1部:幾何精度試験
注記 対応国際規格:ISO 230-1,Test code for machine tools−Part 1: Geometric accuracy of machines
operating under no-load or quasi-static conditions(IDT)
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
注記 五十音順に並べた索引は,附属書Gに示す。
3.1
一般用語
3.1.1
主軸ユニット(spindle unit)
工具又は工作物を保持し,回転軸の回りにその工具又は工作物を回転させる機能を提供する工作機械の
装置。
注記 工作機械は,一つ以上の主軸ユニットをもっている。
3.1.2
回転テーブル(rotary table,swivelling table)
工作物を搬送し,その工作物の角度位置を回転軸の回りに変える機能を提供する工作機械の装置。
注記 マシニングセンタの回転テーブルが旋削に使用できる場合,回転テーブルは,旋削用主軸とみ
なすことができる。
3.1.3
旋回主軸頭(swivelling head,rotary head)
工具を保持する主軸ユニットを備え,その主軸ユニットの角度位置を回転軸の回りに変える機能を提供
する工作機械の装置。
注記 一つの機械のユニットの中に複数の回転軸が組み込まれているものもある。
3
B 6190-7:2019 (ISO 230-7:2015)
3.1.4
主軸,ロータ(spindle,rotor)
主軸ユニット(又は回転テーブル若しくは旋回主軸頭)のうちの回転する要素。
3.1.5
主軸ハウジング,ステータ(spindle housing,stator)
主軸ユニット(又は回転テーブル若しくは旋回主軸頭)のうちの静止している要素。
3.1.6
軸受(bearing)
ロータを支持し,ロータとステータとの間で回転を可能にするための主軸ユニット(又は回転テーブル
若しくは旋回主軸頭)の要素。
3.1.7
回転軸(axis of rotation)
回転の中心線となる線分。
(出典:JIS B 6190-1の3.5.2)
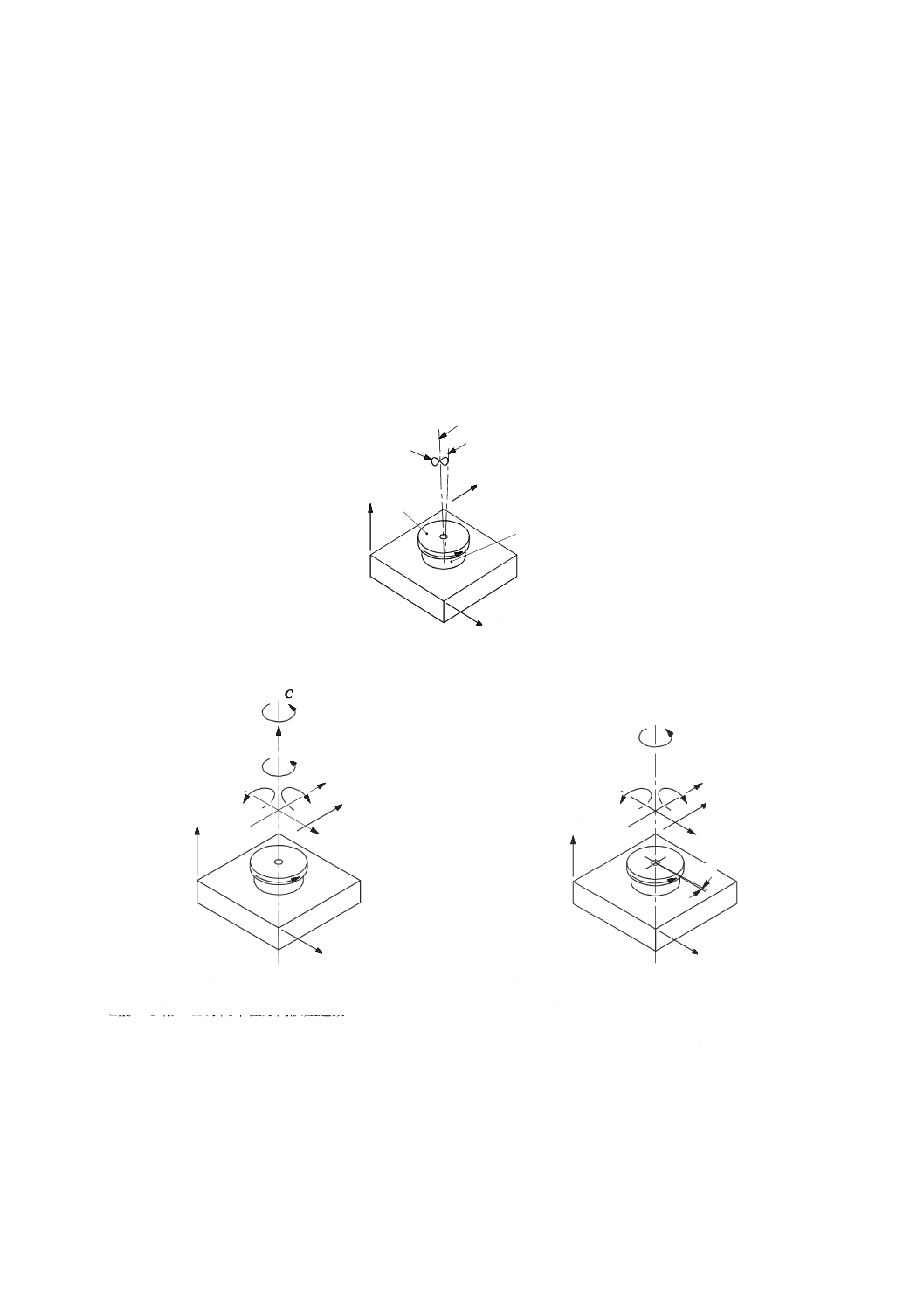
注記1 図1 a) 参照。
注記2 一般に,回転中,この線分は,図1のa) 及びb) に示すように,軸受及び軸受座面,構造運
動又は軸ずれにおける不精確さによって,(軸及び半径方向に)平行移動し,基準座標系内で
傾く。
3.1.8
正の方向(positive direction)
工作物の寸法が増加する運動の向き。
注記 JIS B 6310参照。
3.1.9
完全回転軸,完全主軸(perfect axis of rotation,perfect spindle)
(軸平均線に対して)誤差運動が全くない回転軸(又は主軸)。
3.1.10
完全工作物(perfect workpiece)
中心線回りに完全な回転面をもつ剛体。
3.1.11
機能点(functional point)
切削工具の先端点又は材料除去を行うために切削工具が工作物に接触する工作機械の部品と関連する点。
(出典:JIS B 6190-1の3.4.2)
3.1.12
軸平均線(axis average line)
基準座標系に対して配置した,回転軸の平均位置及び向きを表す直線の線分。
注記1 図1 a) 参照。
注記2 軸平均線は,負荷,温度又は速度変化に対応して回転軸の位置及び向きの変化を記載する有
用な用語である。
注記3 軸平均線の位置及び向きは,軸方向に離れた二つの位置で測定した半径方向誤差運動のデー
タから算出した最小二乗中心を結び決定するのが望ましい(3.4参照)。
4
B 6190-7:2019 (ISO 230-7:2015)
注記4 JIS B 6310は,“Z軸は,機械の主軸に平行にとる。”と定義している。これは,機械のZ軸
が主軸の軸平均線に平行であることを意味する。ただし,軸平均線の定義を他の軸及び回転
軸にも適用するので,一般に全ての回転軸が機械のZ軸に平行であるというわけではない。
軸平均線は,工作機械の主軸と関連する場合だけに機械のZ軸に平行にとるのが望ましい。
3.1.13
軸ずれ(axis shift)
状態変化による軸平均線の,工具と工作物との間の準静的な相対角度及び変位。
注記1 図1 c) 参照。
注記2 軸ずれは,熱影響,負荷変化,速度変化,方向変化などが原因で生じる。回転軸誤差運動の
測定は,軸ずれを回避できる時間(回転数)及び条件で行う。
5
a)
a)
a)
2
3
4
1
X
Z
Y
1 主軸(ロータ)
2 回転軸誤差運動の軌跡
3 軸平均線
4 回転軸(所定の回転角度位置での)
5 主軸ハウジング(ステータ)
a) 基準座標軸,軸平均線及び回転軸の誤差運動
EAC
EXC
a)
a)
a)
EBC
EZC
ECC
EYC
X
Z
Y
EB(0X)C
EA(0Y)C
EY0C
EX0C
a)
a)
a)
X
Z
Y
C
EC0C
b) 回転軸の誤差運動
c) 軸平均線の位置及び角度誤差(軸ずれ)
EXC C軸のX方向半径方向誤差運動
EYC C軸のY方向半径方向誤差運動
EZC C軸の軸方向誤差運動
EAC C軸のX軸回り角度誤差運動
EBC C軸のY軸回り角度誤差運動
ECC C軸の角度位置決め誤差運動
EX0C
C軸のX方向位置誤差
EY0C
C軸のY方向位置誤差
EA(0Y)C Y軸に対するC軸の直角度誤差
EB(0X)C X軸に対するC軸の直角度誤差
EC0C
C軸のゼロ点の角度位置誤差
注a) 基準軸
図1−主軸又は回転軸をC軸とするときの基準座標軸,軸平均線及び回転軸の誤差運動
5
B 6190-7:2019 (ISO 230-7:2015)
3.1.14
構造ループ(structural loop)
2個の指定した対象物(すなわち,工作物と工具と)の間の相対位置及び向きを維持する要素の集合。
注記 指定した対象物の代表的な組合せは,工作機械,例えば,旋盤上の切削工具と工作物との組合
せである。この場合,構造ループは,チャック,主軸,主軸軸受・主軸ハウジング,主軸台,
ベッド,案内面,往復台,刃物台及び工具保持具を含む。
3.1.15
所定の点における回転軸の半径振れ(radial throw of a rotary axis at a given point)
回転軸に接続された部品(又は基準器)の幾何学的な軸線と軸平均線とが一致しないときの,二つの軸
線間の距離。
(出典:JIS B 6190-1の3.5.10)
3.1.16
所定の断面における機能面の振れ(run-out of a functional surface at a given section)
運動している面を検出する変位計又は固定した表面を動いて検出する変位計によって測定された全変位。
注記1 用語“TIR”(total indicator reading)及び“FIM”(full indicator movement)は,振れと同等で
ある。
注記2 測定された回転面の振れは,面の輪郭(形状)誤差,回転軸の半径振れ,回転軸の誤差運動,
回転軸に対する(工作物の動的な励振による)面の動き,及び構造誤差運動を含む。
(出典:JIS B 6190-1の3.9.7)
3.1.17
静止点の振れ(stationary point run-out)
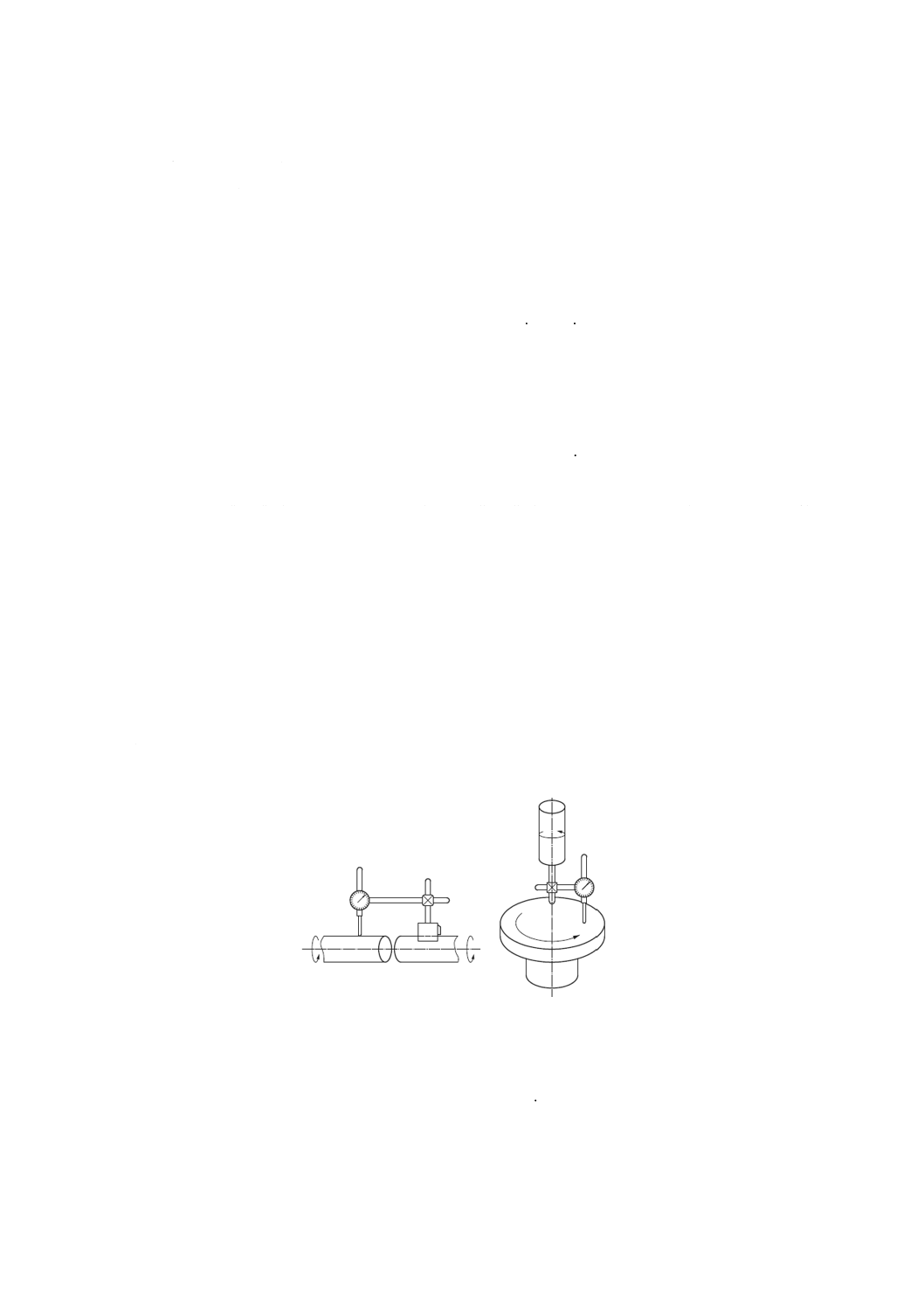
変位計と測定面とが一緒に回転し,変位計に対する横方向の運動を無視できる場合に,回転している面
上の点について検出する変位計によって測定された全変位。
注記 図2及びJIS B 6190-1の10.2.2参照。
図2−静止点の振れの測定方法例(半径方向振れ及び端面方向振れ試験)
3.1.18
二つの軸平均線間の直角度誤差(squareness error between two axis average lines)
機械の回転部品の軸平均線と機械のそれ以外の回転部品の軸平均線との90°からの角度偏差。
(出典:JIS B 6190-1の3.6.9)
6
B 6190-7:2019 (ISO 230-7:2015)
3.1.19
直進軸の運動と軸平均線との直角度誤差(squareness error between a linear axis of motion and an axis average
line)
直進運動する部品上の点の基準直線と機械の回転部品の軸平均線との90°からの角度偏差。
注記 回転軸の正の方向は,JIS B 6310に規定する右手座標系に基づき,各直進運動の正の方向に右
ねじが進む方向にとる。
(出典:JIS B 6190-1の3.6.8)
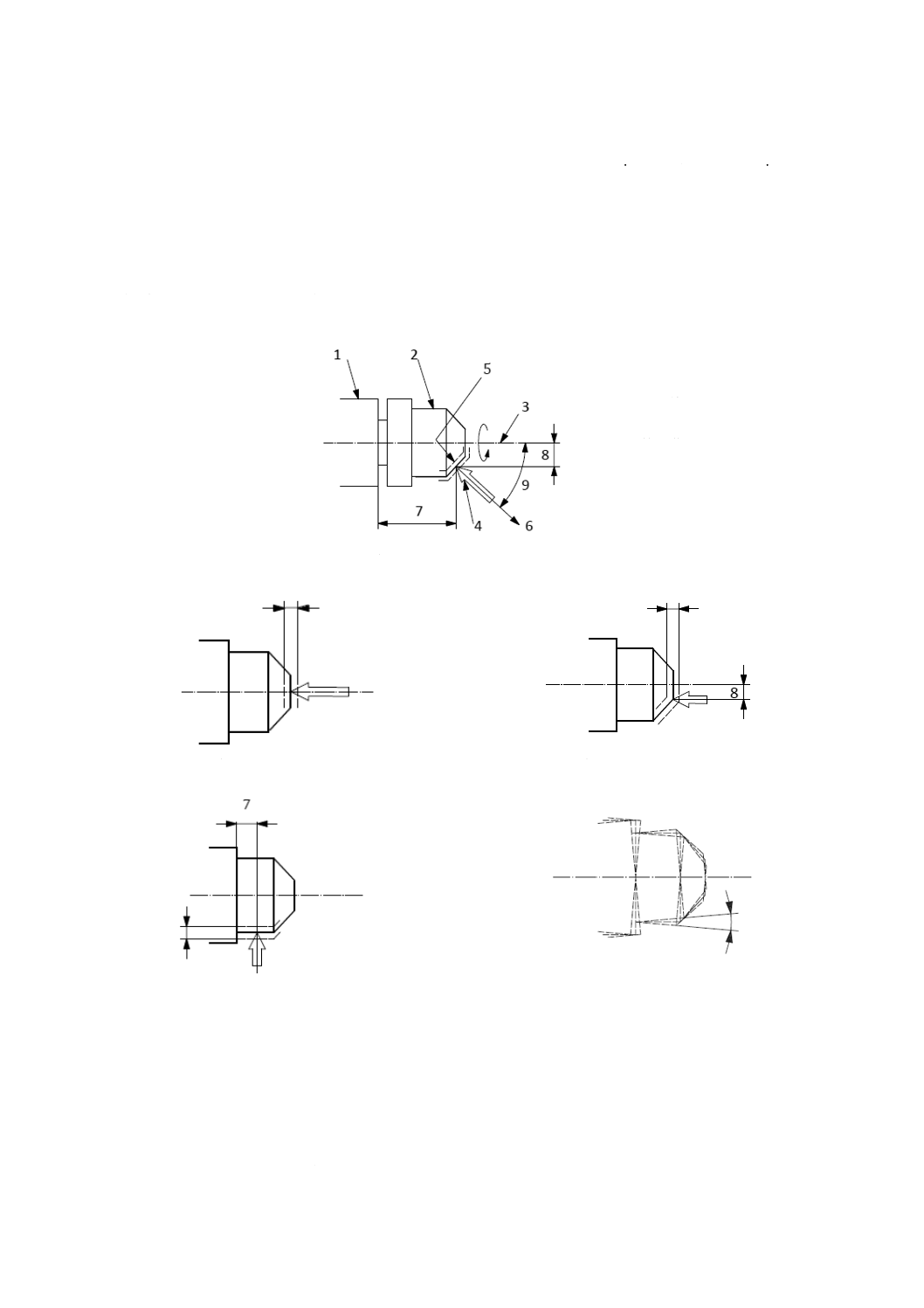
1 主軸
2 工作物
3 軸平均線
4 変位計
5 誤差運動
6 感度方向
7 軸方向位置
8 半径方向位置
9 感度方向角度
a) 回転軸誤差運動の一般例
b) 軸方向誤差運動
c) 端面方向誤差運動
d) 半径方向誤差運動
e) 傾斜方向誤差運動
図3−回転軸誤差運動の一般例,固定感度方向における軸方向,端面方向,半径方向
及び傾斜方向の誤差運動
3.1.20
遊び(play)
一つの構造ループ内の要素間に存在する隙間によって,限られた範囲で剛性がゼロで変位する状態。
(出典:JIS B 6190-1の3.3.3)
7
B 6190-7:2019 (ISO 230-7:2015)
3.1.21
ヒステリシス(hysteresis)
力(又はモーメント)を連続的に負荷し,その後に反対方向に除荷したときに生じる二つの物体間の変
位(又は角度)。
注記 ヒステリシスは,駆動機構の隙間,案内面の隙間,機械的な変形,摩擦,緩んだ結合部などで
発生する。
(出典:JIS B 6190-1の3.3.4)
3.1.21.1
試験装置のヒステリシス(setup hysteresis)
通常,機械的な結合部の緩みが原因で発生する試験装置の様々な部品のヒステリシス。
(出典:JIS B 6190-1の3.3.5)
3.1.21.2
機械ヒステリシス(machine hysteresis)
特定の負荷を受けたときに発生する機械構造のヒステリシス。
(出典:JIS B 6190-1の3.3.6)
3.2
誤差運動に関する用語
3.2.1
回転軸誤差運動(axis of rotation error motion)
回転部品の回転角度位置の関数として軸平均線に対する回転軸の位置及び向きにおける望ましくない変
化。
(出典:JIS B 6190-1の3.5.4)
注記1 図3参照。
注記2 この誤差運動は,回転軸と同軸の中心線をもった基準円筒又は基準球の面の運動として測定
してもよい。
注記3 誤差運動は,図3 a) に示すように,位置及び方向で指定する。ただし,温度,負荷又は回転
速度の変化に伴う軸ずれによる運動を含まない。
3.2.2
構造誤差運動(structural error motion)
内部又は外部からの加振によって引き起こされ,かつ,構造ループ内のばね,質量,ダンパの影響を受
ける誤差運動。
注記1 3.9参照。
注記2 構造誤差運動は,測定に影響を及ぼす主軸,回転テーブル又は旋回主軸頭の回転によって引
き起こされることがある。
3.2.3
軸受誤差運動(bearing error motion)
静止している部品と回転部品との間で発生する不完全な軸受による誤差運動。
注記 附属書A参照。
3.2.4
静的誤差運動(static error motion)
主軸(又は回転テーブル若しくは旋回主軸頭)を一連の離散的な回転角度位置で静止させて測定した誤
8
B 6190-7:2019 (ISO 230-7:2015)
差運動の特別な場合。
注記 これは,動的な影響を排除して誤差運動を測定するために用いる。
3.3
回転軸誤差運動の感度方向に関する用語
注記 回転軸誤差運動の測定は,回転軸の用途を考慮する。3.2.1に定義するように,回転軸誤差運動
は,軸平均線に対する回転軸の三次元空間における全誤差運動を示す。工作物の精度に及ぼす
誤差運動の影響は,加工方法によって変わる。例えば,バイトによる旋削及び中ぐりのような
最も簡単な加工の場合には,任意の時点における切削工具の向きの誤差運動の成分だけが重要
になる。ただし,多刃工具によるフライス加工の場合は,誤差運動の複数の方向の成分が重要
になる可能性がある。同様に回転テーブル上に取り付けた工作物にドリルで円周上に穴をあけ
る場合は,軸平均線に垂直な平面内において穴間隔に対応する回転テーブルの回転軸誤差運動
を知る必要がある。さらに,非円形面の旋削では,回転軸誤差運動と加工した部品の輪郭との
関係は,切削工具の向きの誤差運動だけでは決まらない。次の定義は,回転軸がどのような加
工に使われるかを考慮に入れ,この誤差運動を測定及び解析する方法の基礎を提供する。
3.3.1
感度方向(sensitive direction)
機能点における工作物表面に垂直な方向。
注記1 図3参照。
注記2 多くの加工及び測定では,関心ある感度方向は,たった一つであるが,多数ある場合もある。
ただし,試験の目的のためには,一つの感度方向を考慮すれば,特に指定しない限り十分で
ある。
3.3.2
非感度方向(non-sensitive direction)
感度方向に垂直な方向。
3.3.3
固定感度方向(fixed sensitive direction)
機械座標系における機能点が回転部品の回転角度位置と一緒に変わることのない感度方向。
注記1 図4参照。
注記2 固定感度方向については,工具と工作物との間の相対変位の測定の結果が工作物の加工面の
形状誤差に対応する。
注記3 バイトによる旋削加工は,固定感度方向になる。ただし,非円形面を旋削する場合は,固定
感度方向にはならない。
注記4 回転テーブルには,複数の感度方向がある場合がある。例えば,X方向又はY方向において
バイトによる旋削を行う回転テーブルは,二つの固定感度方向があることになる。
図4−端面削り,外丸削り及び面取りにおける固定感度方向の例
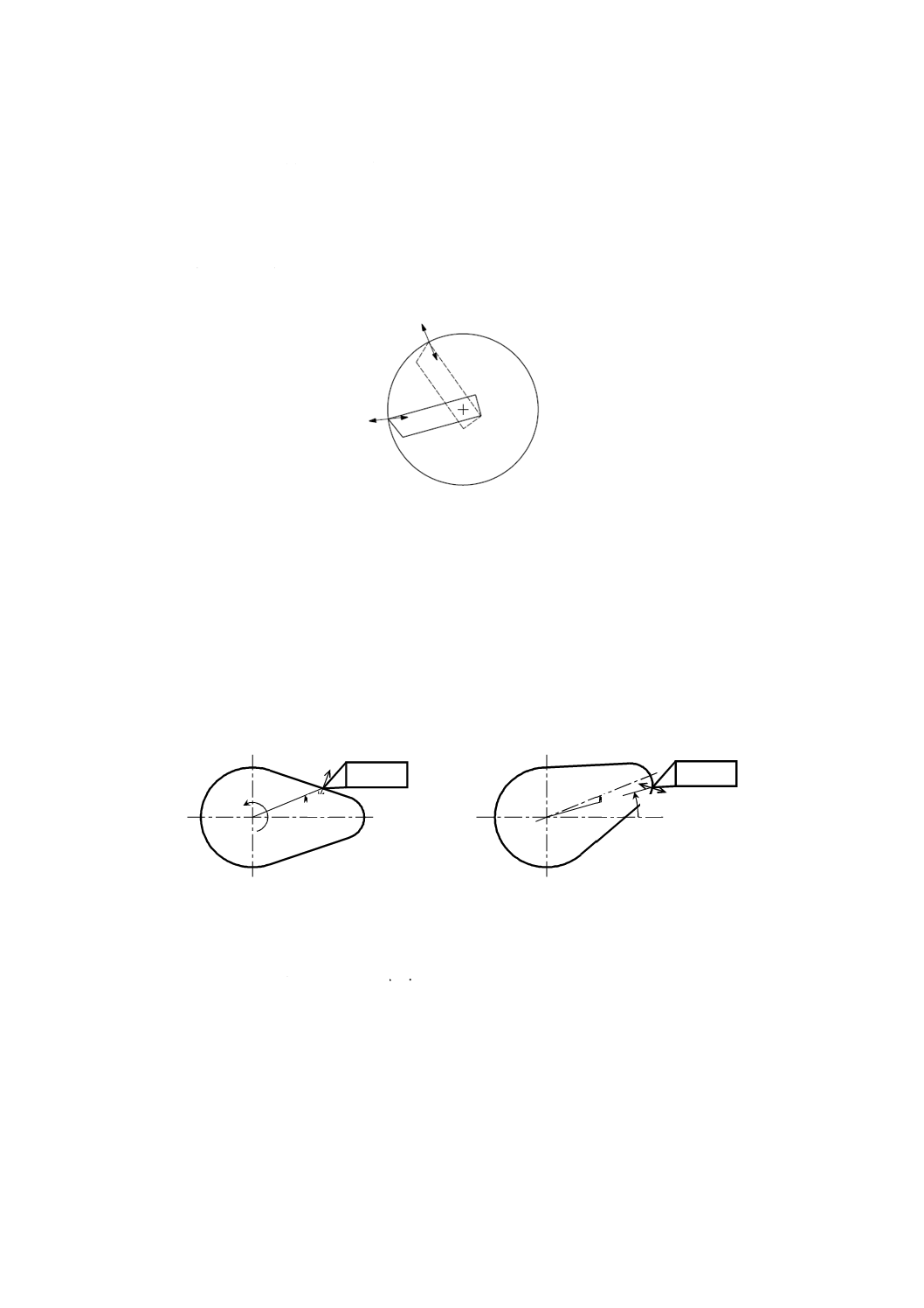
9
B 6190-7:2019 (ISO 230-7:2015)
3.3.4
回転感度方向(rotating sensitive direction)
回転部品の回転角度位置と共に同期して回転する感度方向。
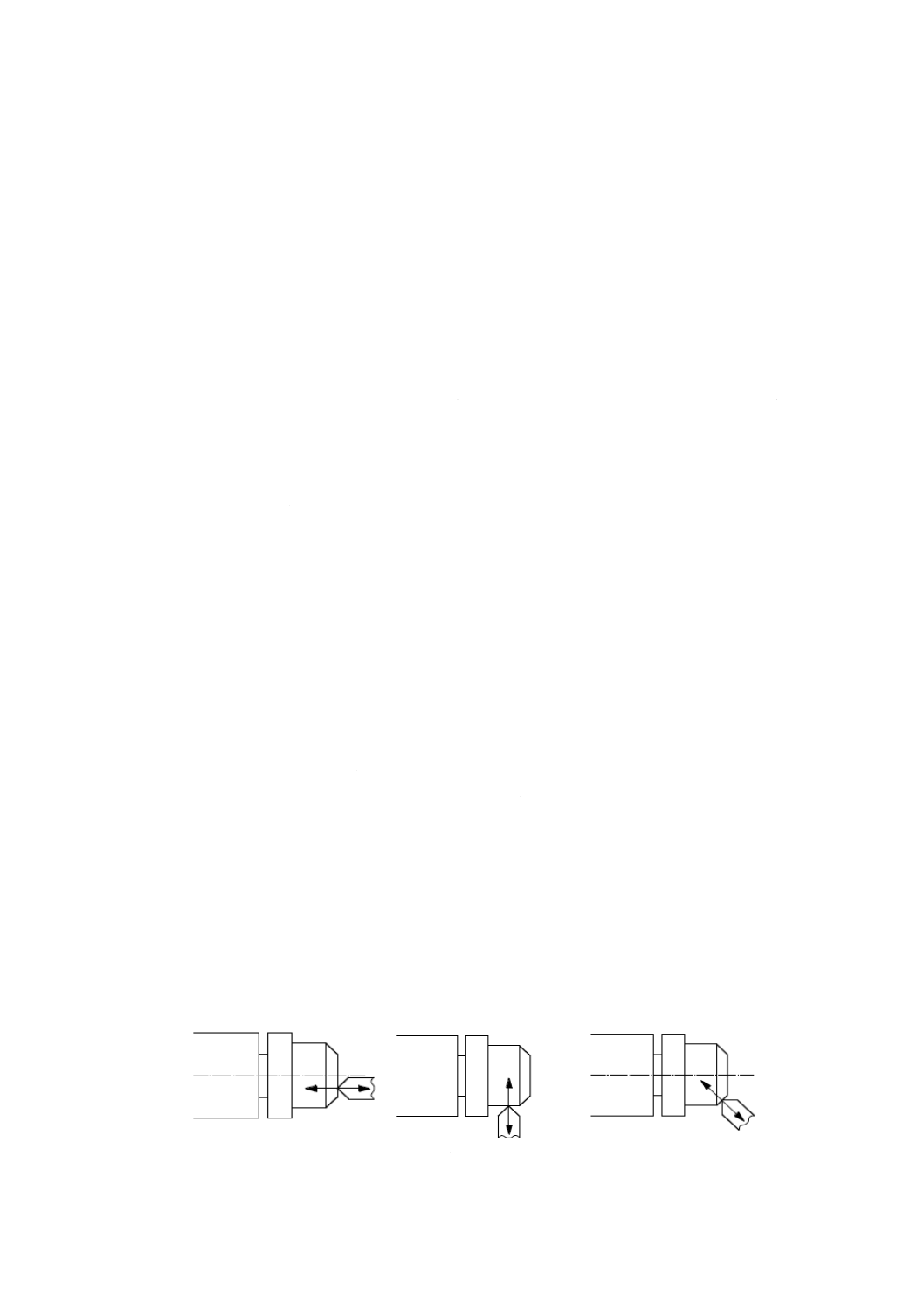
注記1 図5参照。
注記2 ジグ中ぐり盤は,回転感度方向をもっている。多刃工具を取り付けたフライス主軸の回転感
度方向は,多数ある。
図5−穴をジグ中ぐりしているときの,ある二つの瞬間における回転感度方向の例
3.3.5
変動感度方向(varying sensitive direction)
回転部品の回転角度位置の関数として変化する感度方向(工作物表面の形状によって垂直な表面が変化
する結果として)。
注記1 図6参照。
注記2 例えば,非円形工作物のバイトによる旋削,旋盤上でのポリゴンの加工,又はカム研削。
q
q1
q2
q1
図6−カム旋削のときの変動感度方向
3.3.6
回転軸誤差運動の二次元影響(2D effect of axis of rotation error motion)
軸平均線に垂直な平面内における機能点の位置に与える回転軸誤差運動の影響。
注記 回転テーブル上に取り付けた工作物にドリルで円周上に複数の穴をあけるとき,回転軸誤差運
動は,穴の位置に誤差を発生させる。
3.4
回転軸誤差運動の方向に関する用語
注記 直進軸の誤差運動と同様に,回転軸誤差運動を三つの直交軸に平行な方向に分解する。感度方
向に平行な回転軸誤差運動の成分は,加工された部品の形状に影響することから,三次元空間
における誤差運動は,感度方向に平行に測定し解析する。次の定義で,誤差運動の方向による
10
B 6190-7:2019 (ISO 230-7:2015)
分類を示す。
3.4.1
半径方向誤差運動(radial error motion)
指定した軸方向の位置における軸平均線と垂直な方向の誤差運動。
注記1 図3 d) 参照。
注記2 この誤差運動は,回転軸と一致している中心線をもった,完全な基準円筒又は基準球の表面
の半径方向の運動として測定してもよい。
注記3 用語“半径振れ”は,心合わせによる誤差及び基準器の真円度誤差を含んでいることから,
半径方向誤差運動と同じではない。
3.4.2
純粋半径方向誤差運動(pure radial error motion)
回転軸が軸平均線に平行で,かつ,感度方向において軸平均線と垂直に運動する誤差運動。
注記 純粋半径方向誤差運動とは,傾斜方向誤差運動のない理想的な半径方向誤差運動のことである。
それを測定しようとしないのが望ましい。
3.4.3
傾斜方向誤差運動(tilt error motion)
軸平均線に対してある角度をもった方向の誤差運動。
注記1 図3 e) 参照。
注記2 この運動は,軸平均線に沿ったある距離だけ離れた二つの断面における半径方向の誤差運動
を同時に測定し,その断面間の距離で除すことによって評価できる。
注記3 英語表記の“coning”,“wobble”,“swash”,“tumbling”及び“towering”誤差は,傾斜方向誤
差運動を表す用語としては不適切である。
注記4 “角運動(angular motion)”よりもむしろ“傾斜方向誤差運動”という用語を選んだ理由は,
その軸の周りの回転又は回転テーブルのような装置の角度位置決め誤差(angular positioning
error)との混乱を避けるためである。
3.4.4
軸方向誤差運動(axial error motion)
軸平均線と同軸の誤差運動。
注記1 図3 b) 参照。
注記2 この運動は,軸平均線に平行な軸方向において,回転軸と一致した中心線をもつ完全に平ら
な円盤又は完全な球面の運動として測定してもよい。
注記3 軸方向の滑り(axial slip),カミング(end-camming),往復運動(pistoning)及び酔歩(drunkenness)
は,軸方向の誤差運動の用語として好ましくない。
3.4.5
端面方向誤差運動(face error motion)
指定された半径方向位置における軸平均線に平行な誤差運動。
注記1 図3 c) 参照。
注記2 端面方向誤差運動は,軸方向誤差運動と傾斜方向誤差運動とが合成されたものである。“面振
れ”は,“半径振れ”と類似した用語として受け入れられているが,端面方向誤差運動とは同
じではない。
11
B 6190-7:2019 (ISO 230-7:2015)
3.5
回転周波数に基づく回転軸誤差運動に関する用語
3.5.1
全誤差運動(total error motion)
何回も回転させて記録した,回転軸及び構造の誤差運動の同期・非同期成分からなる誤差運動。
3.5.2
同期誤差運動(synchronous error motion)
回転周波数の整数倍で起こる全誤差運動の成分。
注記 何回も回転させて平均化した全誤差運動の極座標線図の輪郭である。
3.5.3
基本誤差運動(fundamental error motion)
回転周波数で発生する全誤差運動の正弦波成分。
注記1 A.7.6参照。
注記2 通常,基本半径方向誤差運動は,無視できる。その理由は,固定感度方向又は回転感度方向
が一つの場合に,半径方向の誤差運動は,回転周波数で加工した工作物に形状誤差を発生さ
せない。
注記3 ほとんどの場合,測定した(見掛けの)基本半径方向誤差運動は,基準器の半径振れである。
注記4 基本半径方向誤差運動がX方向とY方向とで異なる場合は,変動感度方向の場合及び/又は
機能点の位置での二次元影響を決める場合には無視できない。
3.5.4
剰余同期誤差運動(residual synchronous error motion)
基本回転周波数以外の周波数の整数倍で発生する同期誤差運動の成分。
3.5.5
非同期誤差運動(asynchronous error motion)
回転周波数の整数倍以外の周波数で発生する全誤差運動の成分。
注記1 非同期誤差運動は,全誤差運動と同期誤差運動との差である。
注記2 非同期誤差運動は,次の誤差運動成分を含む。
a) 周期的でない成分
b) 回転周波数及びその整数倍以外の周波数で発生する周期的成分
c) 回転周波数の分数調波である周波数での周期的成分
3.6
回転軸誤差運動線図に関する用語
3.6.1
誤差運動線図(error motion polar plot)
主軸(又は回転テーブル若しくは旋回主軸頭)の回転角度に対して変位を描いて作成した回転軸誤差運
動の極座標線図。
注記 図7参照。
3.6.2
全誤差運動線図(total error motion polar plot)
記録されたままの全ての誤差運動の極座標線図。
注記 図7 a) 参照。
12
B 6190-7:2019 (ISO 230-7:2015)
3.6.3
同期誤差運動線図(synchronous error motion polar plot)
回転周波数の整数倍の周波数をもつ誤差運動要素の極座標線図。
注記1 3.5.2及び図7 b) 参照。
注記2 全誤差運動線図の平均をとることによって同期誤差運動線図を求めることができる。
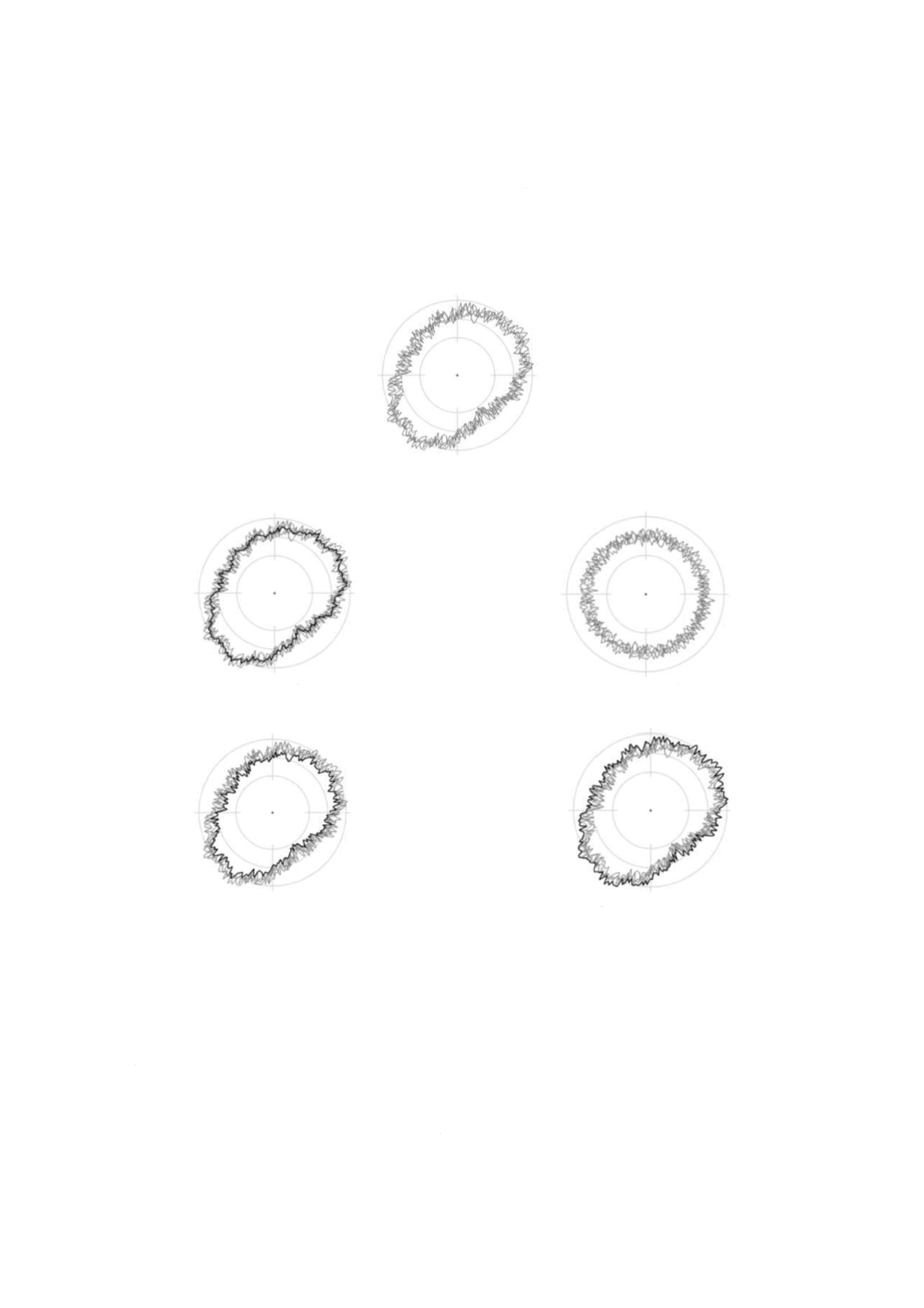
a) 全誤差運動
b) 同期誤差運動
c) 非同期誤差運動
d) 内側誤差運動
e) 外側誤差運動
図7−誤差運動の極座標線図
3.6.4
非同期誤差運動線図(asynchronous error motion polar plot)
非同期誤差運動を極座標で表示した線図。
注記 図7 c) 参照。
3.6.5
基本誤差運動線図(fundamental error motion polar plot)
指定された極座標線図中心回りに描いた,軸方向又は端面方向同期誤差運動の極座標線図の最適合円。

13
B 6190-7:2019 (ISO 230-7:2015)
3.6.6
剰余同期誤差運動線図(residual synchronous error motion polar plot)
剰余同期誤差運動を極座標で表示した線図。
3.6.7
内側誤差運動線図(inner error motion polar plot)
全誤差運動線図の内側境界の輪郭だけを表示した極座標線図。
注記 図7 d) 参照。
3.6.8
外側誤差運動線図(outer error motion polar plot)
全誤差運動線図の外側境界の輪郭だけを表示した極座標線図。
注記 図7 e) 参照。
3.7
回転軸誤差運動線図中心に関する用語
注記 回転軸誤差運動は,極座標線図として可視化しているが,誤差運動値の評価は,この線図の中
心の求め方と関係する。この箇条では,誤差運動値を評価するための中心について定義する。
表1は,誤差運動の種類ごとの望ましい極座標線図の中心を記載する。
表1−誤差運動の種類に対する望ましい中心
誤差運動の種類
望ましい中心
半径方向誤差運動
LSC中心
傾斜方向誤差運動
LSC中心
軸方向誤差運動
PC中心
端面方向誤差運動
PC中心
3.7.1
誤差運動極座標中心(error motion polar plot centre)
誤差運動の極座標表示の評価をするために定義した中心。
注記 図8参照。
3.7.2
極座標線図中心,PC中心(polar chart centre,PC centre)
極座標線図の中心。
注記 図8参照。
3.7.3
極座標輪郭中心(polar profile centre)
数学的又は図解的な方法によって極座標線図の輪郭から導いた中心。
3.7.4
最小二乗円中心,LSC中心(least-squares circle centre,LSC centre)
測定された誤差運動線図の半径偏差を一定間隔で十分な数に区切ったとき,その中心からの半径偏差の
二乗の和を最小にする円の中心。
注記 図8参照。

14
B 6190-7:2019 (ISO 230-7:2015)
1 誤差運動線図
2 LSC中心に対する誤差運動値
図8−誤差運動線図,PC(極座標)中心及びLSC(最小二乗円)中心
並びにLSC中心に対する誤差運動値
3.7.5
最小半径間隔中心,MRS中心(minimum radial separation centre,MRS centre)
誤差運動線図を挟む二つの同心円の半径差を最小にする中心。
3.7.6
最大内接円中心,MIC中心(maximum inscribed circle centre,MIC centre)
誤差運動線図の中で,内接できる最大円の中心。
3.7.7
最小外接円中心,MCC中心(minimum circumscribed circle centre,MCC centre)
誤差運動線図を含む最小円の中心。
注記1 極座標線図の輪郭中心は,同期誤差運動線図を使用して求めることができる。
注記2 極座標中心が,選んだ極座標線図の輪郭中心と一致しているときは,工作物は心出し誤差ゼ
ロで中心に位置する。
3.8
回転軸誤差運動値に関する用語
注記 多くの場合,誤差運動値は,対応する誤差運動線図を包含する,二つの同心円の半径の差に等
しい。また,得られたこの値は,これらの二つの円の共通する中心位置に依存する。3.8.1〜3.8.8
に規定する用語及びその定義は,現象及び計算を理解するときの一助となる。数学的な解析を
用いれば,極座標線図を用いることなく誤差運動値を計算できる。
3.8.1
誤差運動値(error motion value)
指定された回転数における誤差運動成分の評価値。
3.8.2
全誤差運動値(total error motion value)
全誤差運動線図を包含するのに十分な,指定された誤差運動中心を中心とする二つの同心円の半径の差。
注記 四つの全誤差運動,すなわち,全半径方向誤差運動,全傾斜方向誤差運動,全軸方向誤差運動
及び全端面方向誤差運動が決まる。
3.8.3
同期誤差運動値(synchronous error motion value)
同期誤差運動線図を包含するのに十分な,指定された誤差運動中心を中心とする二つの同心円の半径の

15
B 6190-7:2019 (ISO 230-7:2015)
差。
注記 図9参照。
1 非同期誤差運動値
2 同期誤差運動値
3 同期誤差運動線図
図9−同期誤差運動線図,非同期誤差運動値及び同期誤差運動値
3.8.4
非同期誤差運動値(asynchronous error motion value)
指定された極座標輪郭中心を通る半径方向の線に沿って評価した非同期誤差運動線図の最大の幅。
注記1 図9参照。
注記2 非同期誤差運動値は,“雲バンド”(cloud band)の最大半径の幅として円周方向の任意の角度
における全誤差運動の極座標線図から見付ける。それは,同心円を使わない唯一の測定であ
る。なぜならば,円周全体の半径変化ではなく,特定の角度での半径変化を表す値だからで
ある。厳密には,非同期誤差運動値は,直感的には正しく思えなくても,極座標輪郭中心よ
りもむしろ極座標図中心(PC)から半径方向に測定するのが望ましい(図9参照)。
3.8.5
基本軸方向誤差運動値(fundamental axial error motion value)
同期誤差運動線図の指定された極座標輪郭中心とPC中心との間の距離の2倍。
注記1 この値は,回転周波数成分の振幅で代替できる。
注記2 基本半径方向誤差運動値は,固定感度方向又は回転感度方向が一つの場合には,無視できる
(3.5.3参照)。
3.8.6
剰余同期誤差運動値(residual synchronous error motion value)
剰余同期誤差運動線図を包含するのに十分な,指定された誤差運動中心からの二つの同心円の半径の差。
3.8.7
内側誤差運動値(inner error motion value)
内側誤差運動線図を包含するのに十分な,指定された誤差運動中心からの二つの同心円の半径の差。
3.8.8
外側誤差運動値(outer error motion value)
外側誤差運動線図を包含するのに十分な,指定された誤差運動中心からの二つの同心円の半径の差。
16
B 6190-7:2019 (ISO 230-7:2015)
3.9
構造誤差運動に関する用語
3.9.1
主軸(又は回転テーブル若しくは旋回主軸頭)の回転中の構造誤差運動[structural error motion with rotating
spindle (or rotary table/swivelling head)]
主軸(又は回転テーブル若しくは旋回主軸頭)が回転している間に測定された構造ループのある要素の
他の要素に対する相対的な運動。
注記 機械によっては,回転軸の駆動方式が構造に大きなたわみを起こすことがある。
3.9.2
主軸(又は回転テーブル若しくは旋回主軸頭)の非回転中の構造誤差運動[structural error motion with
non-rotating spindle (or rotary table/swivelling head)]
主軸(又は回転テーブル若しくは旋回主軸頭)が回転していないときに測定された,回転軸に対する構
造ループの一つ以上の要素の運動。
注記 多くの場合には,外部振動源,すなわち,冷却油剤ポンプ若しくは油圧ポンプ又は床の振動に
よって引き起こされる加振に対して構造運動源を隔離することが重要になる。
3.9.3
構造誤差運動線図(structural error motion plot)
構造誤差運動を記録するために,横軸を時間軸として記録した変位線図又は極座標線図。
注記 全構造誤差運動の成分のうち,どの成分が主軸回転と同期するのかを知るために,極座標線図
が必要になることがある。
3.9.4
構造誤差運動値(structural error motion value)
決められた時間にわたって,指定された運転条件で測定された変位の範囲(最大−最小)。
3.10
軸ずれに関する用語
3.10.1
半径方向ずれ(radial shift)
軸平均線に垂直な方向への軸ずれ。
3.10.2
傾斜方向ずれ(tilt shift)
軸平均線に対してある角度の方向への軸ずれ。
3.10.3
軸方向ずれ(axial shift)
軸平均線に平行な方向への軸ずれ。
(例えば,EZ0,TABLE,EZ0,SPINDLENOSE)
3.10.4
端面方向ずれ(face shift)
指定された半径位置で測定された,回転軸の軸方向ずれと傾斜方向ずれとの組合せ。
注記 図3 c) 参照。
3.10.5
速度誘起形軸ずれの表示(speed-induced axis shift plot)
回転速度が変化したときに起こる回転軸のずれの直交座標表示。
17
B 6190-7:2019 (ISO 230-7:2015)
3.10.6
速度誘起形軸ずれの値(speed-induced axis shift value)
指定された様々な速度において1個の変位計(又は傾斜及び端面測定用の変位計との組合せ)で測定し
た回転軸の最大変位と最小変位との差。
4
一般事項
4.1
測定単位
この規格では,全ての長さ寸法,偏差及び対応する許容値はミリメートル(mm)で表す。角度寸法は
度(°)で表し,角度偏差及び対応する許容値は比で表すが,場合によってはマイクロラジアン又は秒で
表す。これらの間には,次の式が成り立つ。
0.010/1 000=10 μrad≒2”
4.2
JIS B 6190-1の参照
この規格を適用する場合は,特に,試験前の機械の据付け,主軸及び他の運動部品の暖機,測定方法の
記載及び測定器の推奨不確かさについては,JIS B 6190-1を参照しなければならない。
4.3
推奨する測定器
この規格で推奨する次の測定器は,単なる例示である。同じ量を測定することができ,同等又はそれよ
り小さい測定不確かさをもつ他の測定器を用いてもよい。
a) 主軸の測定については,適切な測定範囲,分解能,熱的安定性,精度及び周波数帯域を備え,試験用
基準器の材料の違いに鈍感な非接触変位計。必要な周波数帯域は,測定したい1回転当たりの山数(こ
れは,周波数解析するのが望ましい。)及び主軸の速度範囲による。ほとんどの工作機械については,
周波数帯域10 kHzは,6 000 min−1以下の回転速度で許容できる。そのような変位計は,この回転速
度で1回転当たり50山まで検出できる。通常,工作機械主軸の回転による山数は,そのように多くは
ない。したがって,より速い主軸速度に対しても,通常は周波数帯域10 kHzの変位計を使用してもよ
い。一般に,より速い主軸速度及びより多い山数(表H.1参照)に対しては,速度に比例した高い周
波数帯域が必要になる。回転テーブル及び旋回主軸頭の測定では,接触式の変位計も使用することが
できる。
b) 後で行う解析のために,変位データを収集し,格納するためのコンピュータを使ったシステムのよう
なデータ収集装置。
c) 機種別の性能試験規格に規定されているか,又は受渡当事者間の協定に基づくテストバー。JIS B
6190-1のA.3(回転軸の基準直線)参照。
d) 変位計を取り付けるための取付具。
測定器の長期間にわたる精度は,例えば,変換器のドリフト試験によって確かめられなければならない。
試験を開始する前には,測定器は熱的に安定していなければならない。
4.4
環境
機械,及び関連している場合には測定器も,試験を開始する前に熱的に安定した状態に達するように十
分長く試験環境に(望ましくは,夜通し)置いておかなければならない。それらは,日光,暖房機器など
のような外部の熱放射及び隙間風から保護されなければならない。
4.5
試験する回転部品
回転部品は,完全に組み立てられ,かつ,完全な操作ができるものでなければならない。回転軸の試験
18
B 6190-7:2019 (ISO 230-7:2015)
は,無負荷状態で行わなければならない。
注記 この試験は,主軸ユニット(又は回転テーブル若しくは旋回主軸頭)の形式検査ではない。異
なる機械で同じ主軸ユニット又は回転テーブル若しくは旋回主軸頭の試験をすると,据付け,
熱影響及び振動状態によって異なる結果になる場合がある。
4.6
回転部品の暖機運転
試験に先立って,製造業者の指定した手順,及び/又は受渡当事者間で協定した適切な手順で暖機運転
を行わなければならない。ほかに条件が指定されていない場合には,予備的な運動は,旋回主軸頭及び傾
斜回転テーブルについては測定器を取り付けるために必要な運動だけに制限しなければならない。主軸は,
最低10分間,最高速度の半分の速度で暖機運転をした後に試験するのが望ましい。
4.7
構造誤差運動試験
4.7.1
一般
この試験は,機械構造及び環境によって引き起こされる,主軸と工作物との間での相対運動を測定する
ことを意図している。
4.7.2
試験方法
まず,機械及び附属装置の電源を入れた状態で機械の駆動をオフにし,すなわち,非常停止状態で構造
運動を測定する。
次に,機械の電源及び油圧装置のような附属装置の電源を入れ,機械の駆動をオンにし,すなわち,機
械をフィードホールドモードにして構造運動を測定する。
4.7.3
結果の分析
構造誤差運動値は,(例えば,1秒などのように)比較的短い期間にわたって観察した変位の最大値(又
は最大範囲)とする。
5
主軸ユニットの誤差運動試験方法
5.1
一般
単一の感度方向における主軸ユニットの誤差運動は,工作物を切削したときに1対1で形状誤差及び仕
上げ誤差を発生させ,工作機械の性能を特徴付ける最も重要な特性をもつ。非感度方向の誤差運動は,評
価しない。ただし,微小径の旋削部品のような場合は,2次のオーダの影響がある可能性がある。
5.2
試験条件及びその詳細
実施する各測定に対して,次の条件を記録するのが望ましい。
a) 測定を行った半径方向,軸方向又は端面方向の位置
b) 使用した全ての基準器,目標物及び取付具
c) 測定装置の位置
d) 試験中の装置に接続する直進又は回転位置決め台の位置
e) 感度方向の向き。例えば,軸方向,半径方向,又は適切な中間的な角度
f)
測定結果の表示。例えば,誤差運動値,極座標線図,横軸を時間軸としたグラフ,横軸を周波数軸と
したグラフ
g) 主軸の回転速度(静的誤差運動については,ゼロ)
h) 主軸の回転時間(秒)又は回転数
i)
適切な暖機運転又は慣らし運転の手順
j)
測定器の周波数応答。ヘルツ(Hz)又は1回転当たりのサイクル数で与えられる。電子フィルタのロ
19
B 6190-7:2019 (ISO 230-7:2015)
ールオフ特性,デジタル測定器の場合には,変位計の分解能及びサンプリングレートを含む。
k) 構造ループ。誤差運動を報告する変位計の主軸ハウジングに対する変位計の位置及び向き,主軸軸線
及び基準座標軸の位置及び向きの基準となる対象物,並びにこの対象物を接続する要素を含む。
l)
測定を実施した日時
m) 試験に使用した全ての測定器の種類及び校正の状況
n) 周囲温度のような,測定に影響を及ぼし得るその他の運転条件
5.3
主軸回転軸の試験−回転感度方向
5.3.1
一般
この試験は,回転工具を使った加工,例えば,中ぐり,フライス削り,穴あけ及び輪郭研削に適用でき
る。
5.3.2
半径方向誤差運動
5.3.2.1
試験装置
図10は,試験装置の概略図を示す。このような装置では,精密な基準球又は基準円筒のような他の適切
な基準器を機械の主軸に取り付けて測定する。二つの変位計は,直交させて機械のテーブル(又は工作物
取付部品)上に取り付ける。基準球は,(半径振れを最小にするために)回転軸に心合わせする。主軸の回
転角度位置は,主軸に取り付けたロータリエンコーダのような角度検出器を用いて測定する。
ロータリエンコーダの代わりに,基準球を僅かに偏心させて取り付けて主軸の回転角度位置を求めるこ
ともできる。すなわち,基準球を偏心させると,1回転ごとに90°位相のずれた正弦波信号が得られる。
この正弦波信号に変位計の出力に重畳させる。そうすることによって,回転角度位置は,極座標表示に必
要な正弦波信号を使って計算できる。ただし,測定した誤差の1回転当たり1山の成分は,データ解析に
先立って除去しなければならない。
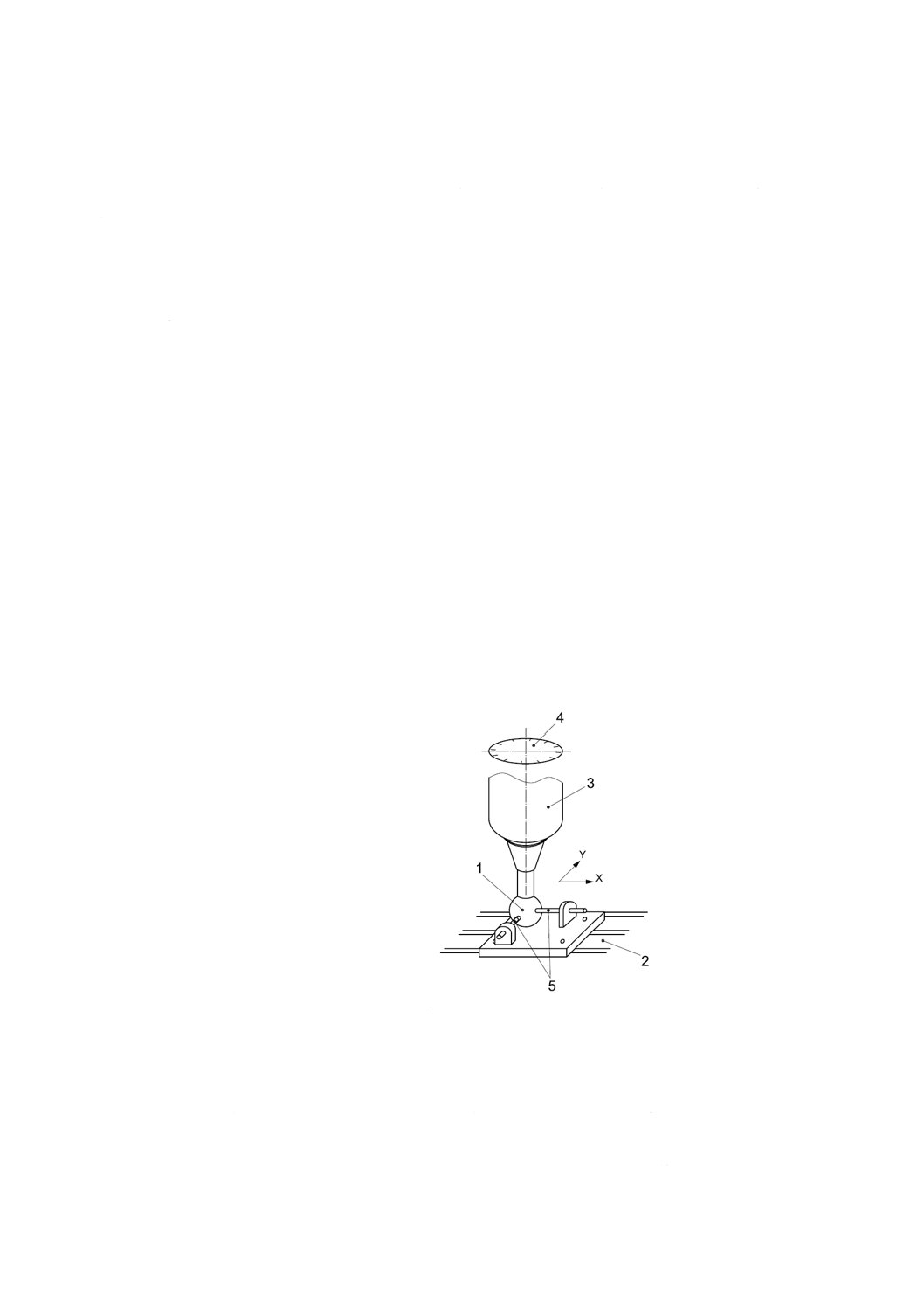
1 基準球
2 テーブル
3 主軸
4 角度検出器
5 変位計
図10−回転感度方向をもつ主軸に取り付けた角度測定装置と,心合わせした基準器(球)とを用いた
半径方向誤差運動の測定方法(Vanherck/Petersの方法)
回転感度方向の半径方向誤差運動の測定は,Tlusty(参考文献[13])の方法に基づき,オシロスコープを
利用すると最も簡単に行うことができる。図11は,1個の基準球の半径方向の変位を検出するために,二
つの変位計を水平及び垂直方向に配置した様子を示す。二つの変位計からの信号は,増幅されてそれぞれ
オシロスコープの水平及び垂直軸に入力される。ワッブル板を用いれば,軸平均線に対して基準球を偏心
20
B 6190-7:2019 (ISO 230-7:2015)
させることができる。完全主軸の場合,主軸が回転したときの結果は,完全な円になる。不完全な主軸の
場合,基準球の偏心の方向における半径方向誤差運動がオシロスコープに表示される波形を変えてしまう。
基準球の偏心に対して直角な方向の運動は,基礎円の接線方向にオシロスコープの光点を移動させるので,
その波形に及ぼす影響は無視できる。このような変位計の配置は,回転感度方向に平行な半径方向誤差運
動を測定していることになる。この回転感度方向は,軸平均線と偏心させた基準球の幾何学的中心とを結
んだ線に平行になる。切削工具又は変位計の軸に対する向きが一定の場合,基準球は,その向きにおいて
偏心していなければならない。その向きが任意の場合,軸は,少なくとも二つの方向に90°ずらして偏心
させた基準球を使って試験をするのが望ましい。
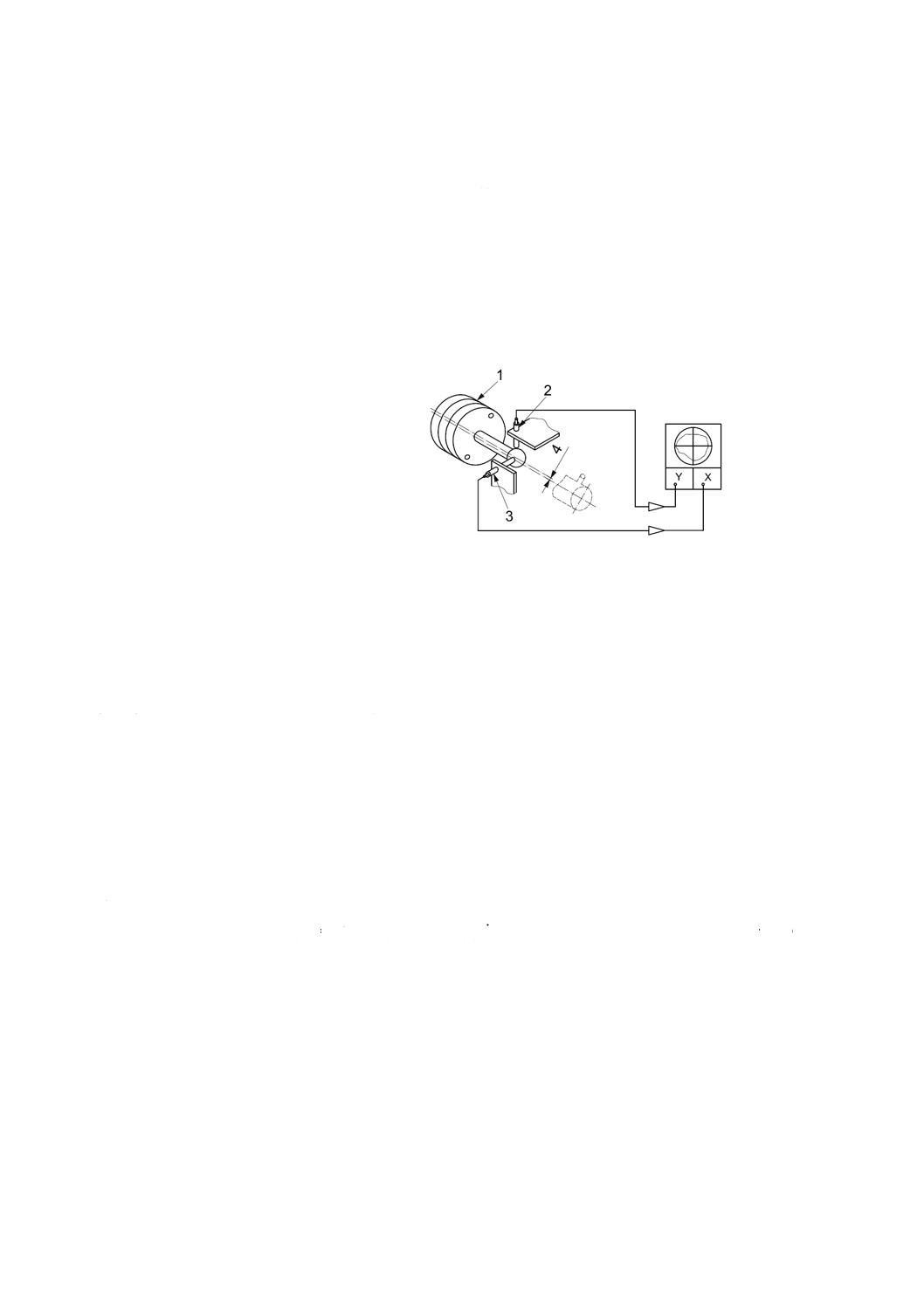
1 ワッブル板
2 垂直方向変位計
3 水平方向変位計
4 工具方向にオフセットした基準球
図11−回転感度方向及び主軸に偏心させて取り付けた基準球を用いた半径方向誤差運動の測定方法
(Tlustyの方法)
5.3.2.2
試験方法
半径方向誤差運動測定は,3段階の主軸速度1) で実施しなければならない。この3段階の主軸速度は,
機械の仕様上の最高速度の百分率で指定しなければならない。変位計の読みは,各速度において主軸の回
転角度位置の関数として記録しなければならない。
注1) 工作機械の使用者は,工作機械の全速度範囲にわたってゆっくりと主軸速度を変えながら測定
システムの出力を観察することを推奨する。構造誤差運動によって過剰な誤差運動が起こった
速度を観察する。そのような速度は,機械加工を行うときに避けるのが望ましい。
5.3.2.3
データ解析
半径方向誤差運動は,互いに直交するように配置された二つの変位計によって,静止基準に対する主軸
(ロータ)半径方向変位を主軸の回転角度位置の関数として記録し,次の式(1)によって求めることができ
る。
()
()
()
q
q
q
q
q
sin
cos
0
ΔY
ΔX
r
r
+
+
=
················································· (1)
ここに,
θ: 主軸の回転角度位置
r(θ)−r0: 回転角度位置θにおける半径方向誤差運動
ΔX(θ): X軸方向の変位計の出力
ΔY(θ): Y軸方向の変位計の出力
r0: 見やすくするために極座標線図を調整するための値
式(1)は,θが回転感度方向と一致していると仮定している。そのようなアライメントは,この試験中は
可能でない場合がある。したがって,回転感度方向に対するθのゼロ位置を報告しなければならない。各
速度における主軸の回転軸誤差運動線図の表示は,十分な回転数2) について行う。一つの主軸速度に対す
る代表的な曲線を図7 a) に示す。この規格では,半径方向誤差運動の同期成分及び非同期成分の値の二つ

21
B 6190-7:2019 (ISO 230-7:2015)
の誤差運動値だけを,誤差運動表示(LSC中心を用いて)から計算する[図7 b),図7 c) 及び図9参照]。
半径方向誤差運動値は,測定値を求めた軸方向の位置と共に報告しなければならない。同期・非同期の半
径方向誤差運動値は,3段階の主軸速度に対応させてそれぞれ報告しなければならない。
非対称(非円)形状部品の旋削に用いる主軸については,変動感度方向rn(θ)(部品が主軸と共に回転す
るとき,部品の表面に垂直な方向)に沿った半径方向誤差運動の影響は,式(2)を使って計算できる。
()
()
()
n
n
n
ΔY
ΔX
r
r
q
q
q
q
q
sin
cos
0
+
+
=
·············································· (2)
ここに,θnは,回転軸の所定の回転角度位置θで工作物に垂直な面の角度で,θの関数とする。
多刃工具を取り付ける主軸については,それぞれの方向に沿った半径方向誤差運動の影響を式(2)を使っ
て計算する。そのような場合には,角度θnは,360°を刃数で除した値になる。
注2) 主軸については,最少で20回転させる。
5.3.3
傾斜方向誤差運動
5.3.3.1
試験装置
傾斜方向誤差運動の測定では,図12に示すような空間的に離れた2点での半径方向誤差運動の測定が必
要となる。2個の基準球をある距離だけ離して取り付けた基準器又は円筒テストバーを主軸に取り付け,
主軸回転軸に心合わせをする。主軸の前側軸受内径に対する,二つの基準球間又は変位計間の推奨最小距
離を表2に示す。
傾斜方向誤差運動の測定には,二つの方法がある。すなわち,方法1は,二つの変位計を用いる方法で
あり,方法2は,傾斜を測定するために四つの変位計を用いる方法である。両方の方法とも使用できる。
ただし,二つの異なる時間周期で求めた二組のデータ間の同期を取ることが難しいことから,二つの方法
によって得られた結果は,同じにならない可能性がある。
表2−傾斜方向誤差運動の測定に用いる二つの基準球間又は変位計間の推奨最小距離
主軸の前側軸受内径
(mm)
変位計間の最小距離
を超え
以下
(mm)
10
25
10
18
32
18
30
40
30
50
50
50
80
63
80
120
80
120
180
100
180
250
125
250
150
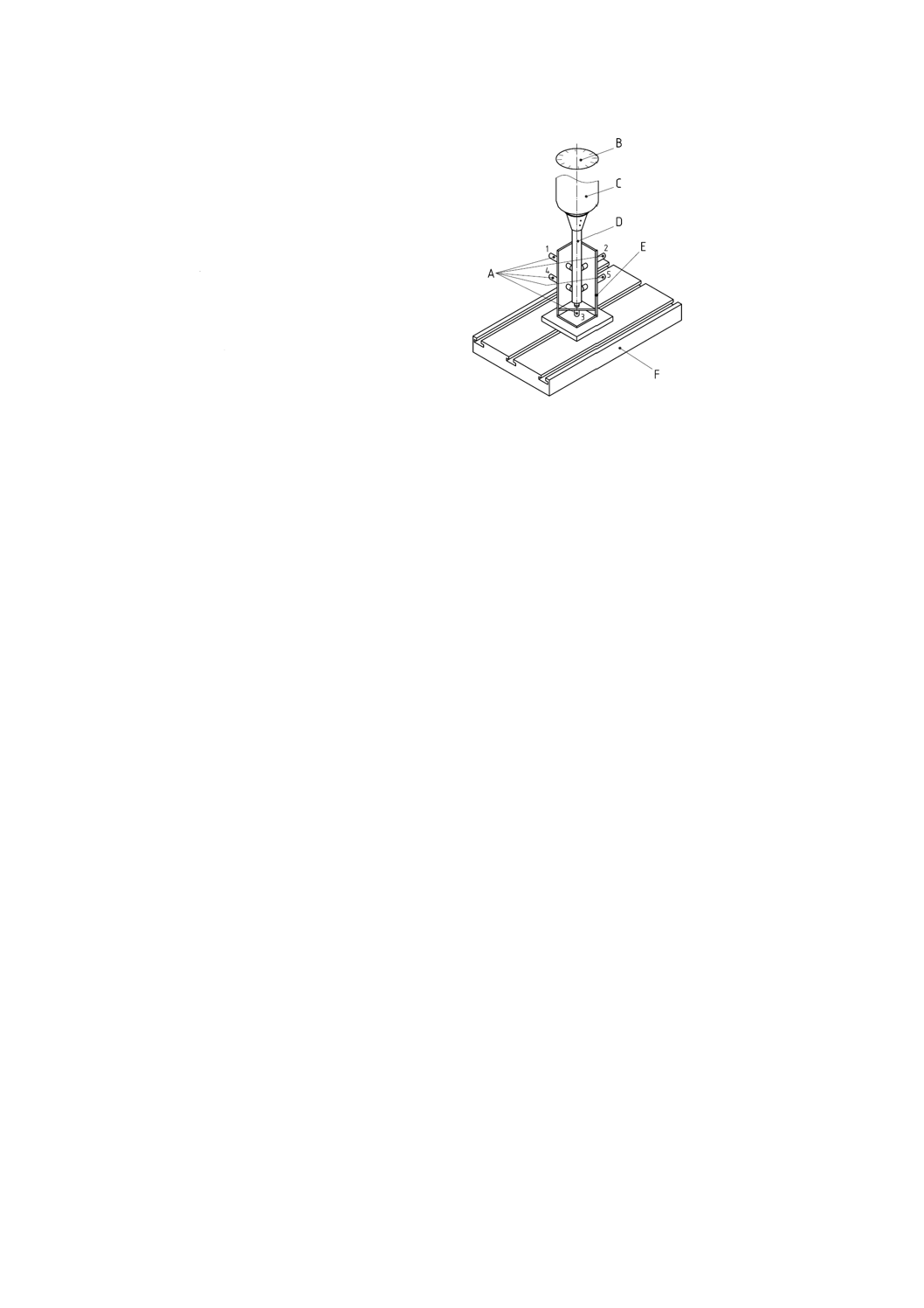
22
B 6190-7:2019 (ISO 230-7:2015)
A 変位計(1〜5)
B 回転角度位置検出器
C 主軸
D テストバー
E 変位計取付具
F テーブル
図12−主軸誤差運動の回転感度方向の測定に用いる五つの変位計を用いた測定システム
(傾斜方向誤差運動を測定する方法2)
5.3.3.2
試験方法−方法1
まず,基準球又はその他の基準器及び変位計は,5.3.2.1に従って取り付け,3段階の主軸速度3) で半径
方向誤差運動の測定を行う。この3段階の主軸速度は,機械の仕様における最高速度の百分率で指定しな
ければならない。各回転速度における変位計の読みは,主軸の回転角度位置の関数として記録しなければ
ならない。
次に,この基準球又は基準器を,先に測定を行った位置から,軸方向の推奨最小距離(表2参照)の位
置に取り付け直し,二組目の測定値を3段階の主軸速度で記録する。
注3) 機械の使用者は,全速度範囲にわたってゆっくり主軸速度を変えていく間に,誤差表示システ
ムの出力を観察することを推奨する。速度を変えていくと,異常な誤差運動が構造誤差運動に
よって発生することを観察できる場合がある。機械加工するとき,そのような速度を避けるの
が望ましい。
5.3.3.3
データ解析−方法1
二つの軸方向の位置で5.3.2.3に従ってそれぞれの主軸速度に対応する同期半径方向誤差運動及び非同期
半径方向誤差運動を決定しなければならない。同期半径方向誤差運動の測定値の差を二つの変位計間の距
離(表2参照)で除した値を同期傾斜運動誤差と定義する。非同期半径方向誤差運動の測定値の差をその
距離で除した値を非同期傾斜運動誤差と定義する。これらの単位は,いずれもラジアンとする。
5.3.3.4
試験方法−方法2
基準器及び変位計は,5.3.3.1に従って取り付け,3段階の主軸速度で測定する。この3段階の主軸速度
は,機械の仕様における最高速度の百分率で指定しなければならない。各回転速度における変位計の読み
は,主軸の回転角度位置の関数として記録しなければならない。
5.3.3.5
データ解析−方法2
二つの軸方向の位置におけるそれぞれの主軸速度に対応する同期半径方向誤差運動及び非同期半径方向
誤差運動は,5.3.2.3に従って求める。変位計1と4との出力差及び変位計2と5との出力差は,式(1)に与
えた半径方向誤差方程式のΔX及びΔYとして使用し,r0は,ゼロに合わせてセットする(図12に示す変
位計3は必要ないことに注意する。)。
同期傾斜運動は,同期誤差を変位計間の距離で除すことによって得られる。極座標表示は,5.3.2.3に記
23
B 6190-7:2019 (ISO 230-7:2015)
載するように行い,解析する。非同期誤差運動は,非同期誤差を変位計間の距離で除して得られる。いず
れも単位はラジアンとする。
5.3.4
軸方向誤差運動
5.3.4.1
試験装置
図13は,軸方向誤差運動測定用の試験装置の概略図を示す。この図に示すように,基準球は主軸に取り
付け,変位計は,基準球に向けて軸方向に平行にテーブルに取り付ける。基準球は,同心誤差を最小にす
るために回転軸上で心合わせをする。主軸の回転角度位置は,主軸に取り付けたロータリエンコーダのよ
うな角度検出器を用いて測定する。
5.3.4.2
試験方法
変位計は,図13に示すように軸方向に向けて取り付け,3段階の主軸速度4) で軸方向誤差運動を測定
する。この3段階の主軸速度は,機械の仕様における最高速度の百分率で指定しなければならない。各速
度における変位計の読みは,主軸の回転角度位置の関数として記録しなければならない。
注4) 機械の使用者は,全速度範囲にわたってゆっくり主軸速度を変えていく間に,誤差表示システ
ムの出力を観察することを推奨する。速度を変えていくと,異常な誤差運動が構造誤差運動に
よって発生することを観察できる場合がある。機械加工するとき,そのような速度を避けるの
が望ましい。
5.3.4.3
データ解析
軸方向誤差運動に対する誤差運動の極座標線図の解析は,基本誤差運動を解析的に除去しないほうがよ
いこと以外は,半径方向誤差運動の解析と概念的に同じである。軸方向誤差運動は,誤差運動と主軸の回
転角度位置との関係を直交座標上に表示してもよい。非同期軸方向誤差運動値は,主軸を十分な回数5) だ
け回転させときの変位の最大範囲になる。同期軸方向誤差運動値は,主軸の回転角度位置に対応する軸方
向偏差の平均値の範囲になる。
注5) 主軸については,最少で20回転させる。
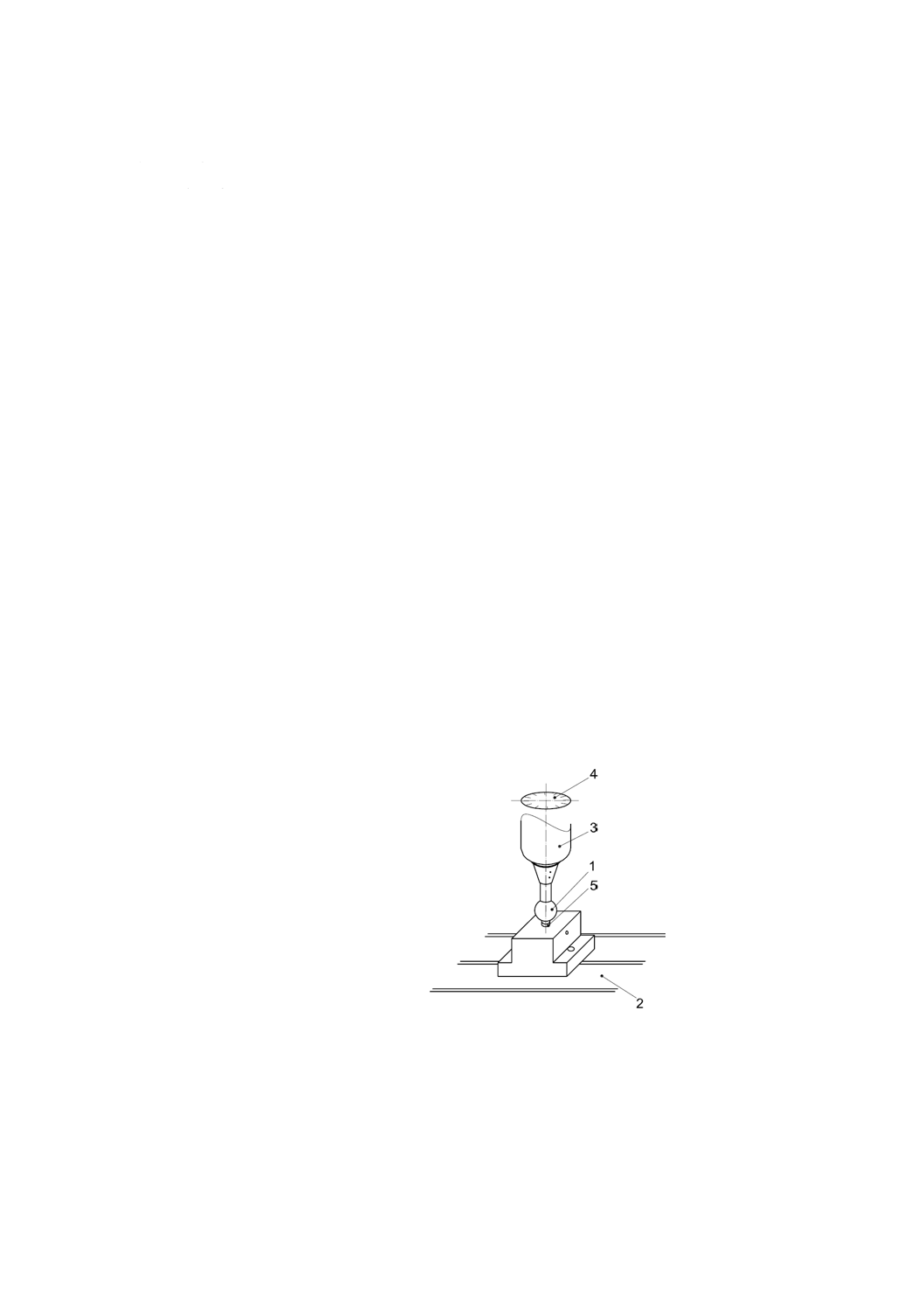
1 基準球
2 テーブル
3 主軸
4 回転角度位置検出器
5 変位計
図13−回転感度方向に対する軸方向誤差運動測定装置
5.4
主軸回転軸の試験−固定感度方向
5.4.1
一般
この試験は,固定感度方向をもつ機械加工,例えば,旋削及び円筒研削に適用できる。
5.4.2
試験装置
24
B 6190-7:2019 (ISO 230-7:2015)
図14は,固定感度方向,すなわち,工作主軸の誤差運動の測定に適した試験装置の概略図を示す。この
試験では,主軸の角度位置に比例した信号を発生できることから,主軸角度の関数として誤差運動の極座
標線図を生成できると仮定している。基準球又は他の適切な基準器は,主軸に取り付け,変位計は,刃物
台又は刃物台に取り付けた固定具にしっかりと取り付ける。その基準球又は基準器は,半径振れを最小に
するように心出しするのが望ましい。半径振れは,基本軸方向誤差運動と間違いやすいので注意が必要と
なる。
5.4.3
半径方向誤差運動
5.4.3.1
試験方法
半径方向誤差運動は,図14のように変位計を半径方向に向けて位置決めし,測定しなければならない。
半径方向の変位計は,所定の感度方向に取り付けなければならない。5.3.2.1(図10及び図11)のように
二つの変位計を直交させるのではなく,それぞれZ方向に並べて取り付ける。それは,試験の目的がこの
感度方向における半径方向誤差運動を測定することだからである。
半径方向誤差運動の測定は,3段階の主軸速度6) で行わなければならない。この3段階の主軸速度は,
機械の仕様における最高速度の百分率で指定しなければならない。各速度における変位計の読みは,主軸
の回転角度位置の関数として記録しなければならない。
固定感度方向の半径方向誤差運動測定にオシロスコープを用いる場合は,基礎円を生成するための手段
が別途必要になる。図15にBryanら(参考文献[14])の方法を示す。比較的低い感度の変位計を用いて直
角方向に0.1 mm偏心させた二つの円形カムの変位を検出して基礎円生成用の正弦波及び余弦波信号を生
成している。カムが1個でも90°離して取り付けた二つの変位計を使って同じことができる。半径方向誤
差運動は,軸平均線を中心とする(軸平均線にできるだけ近づけた)基準球に対する三つ目の高感度の変
位計を使って検出する。正弦波及び余弦波信号にそれぞれ半径方向誤差運動を重畳した信号をオシロスコ
ープの二つの軸に入力する。固定した半径方向誤差運動の変位計からの信号を基礎円上に展開すると,回
転軸の角度位置に対する半径方向誤差運動の極座標線図になる。偏心カム及び低感度変位計は,回転軸に
物理的に取り付けることができる市販の小形角度検出器と置き換えることができる(参考文献[15])。
上記の方法による回転角度位置の求め方は,回転感度方向の測定にも使うことができる。
注6) 主軸については,最少で20回転させる。
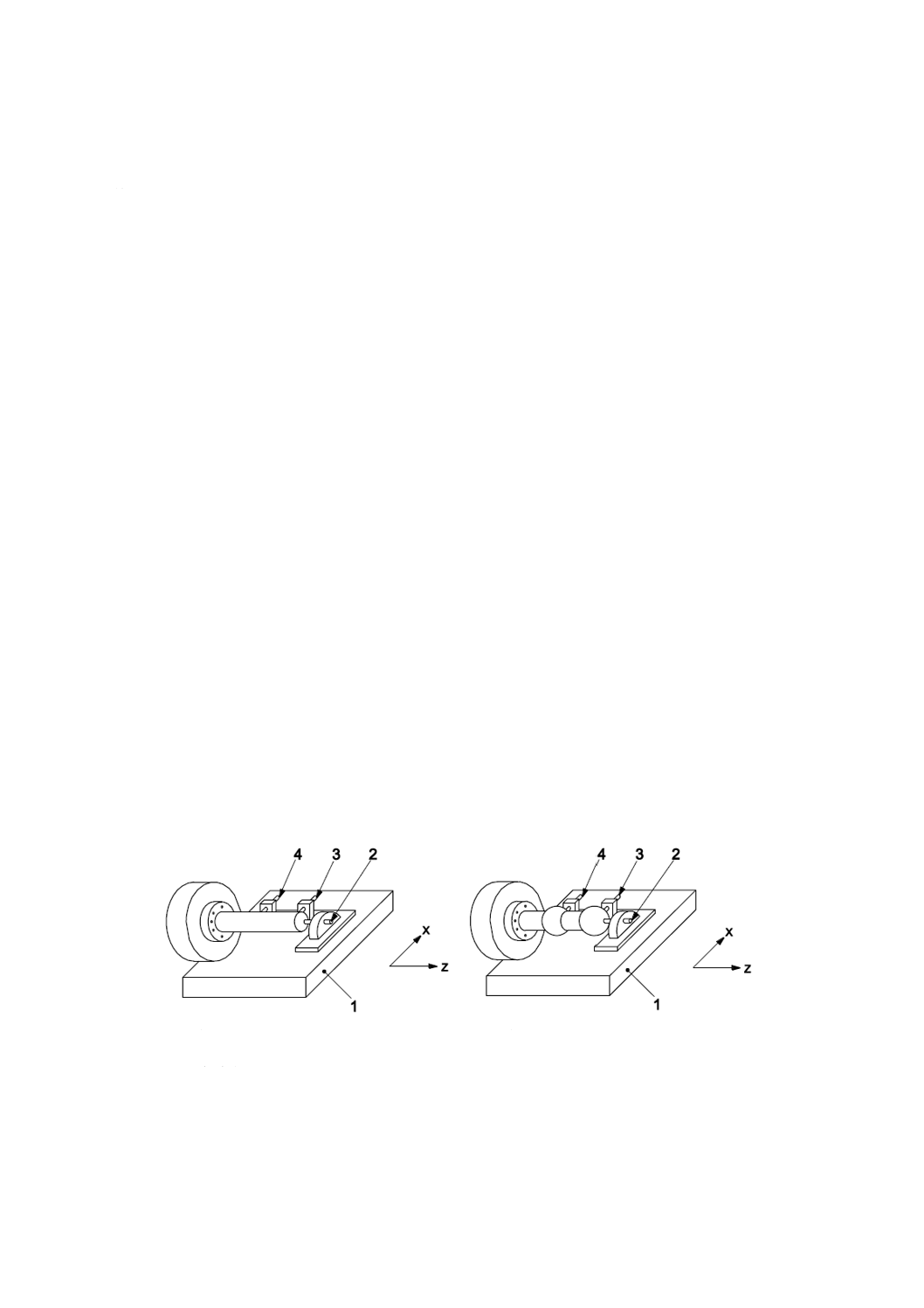
a) テストバーを用いる場合
b) 2個の基準球を用いる場合
1 クロススライド
3 半径方向変位計2
2 軸方向変位計
4 半径方向変位計1
図14−主軸の固定感度方向誤差運動の測定に使用する試験装置
25
B 6190-7:2019 (ISO 230-7:2015)
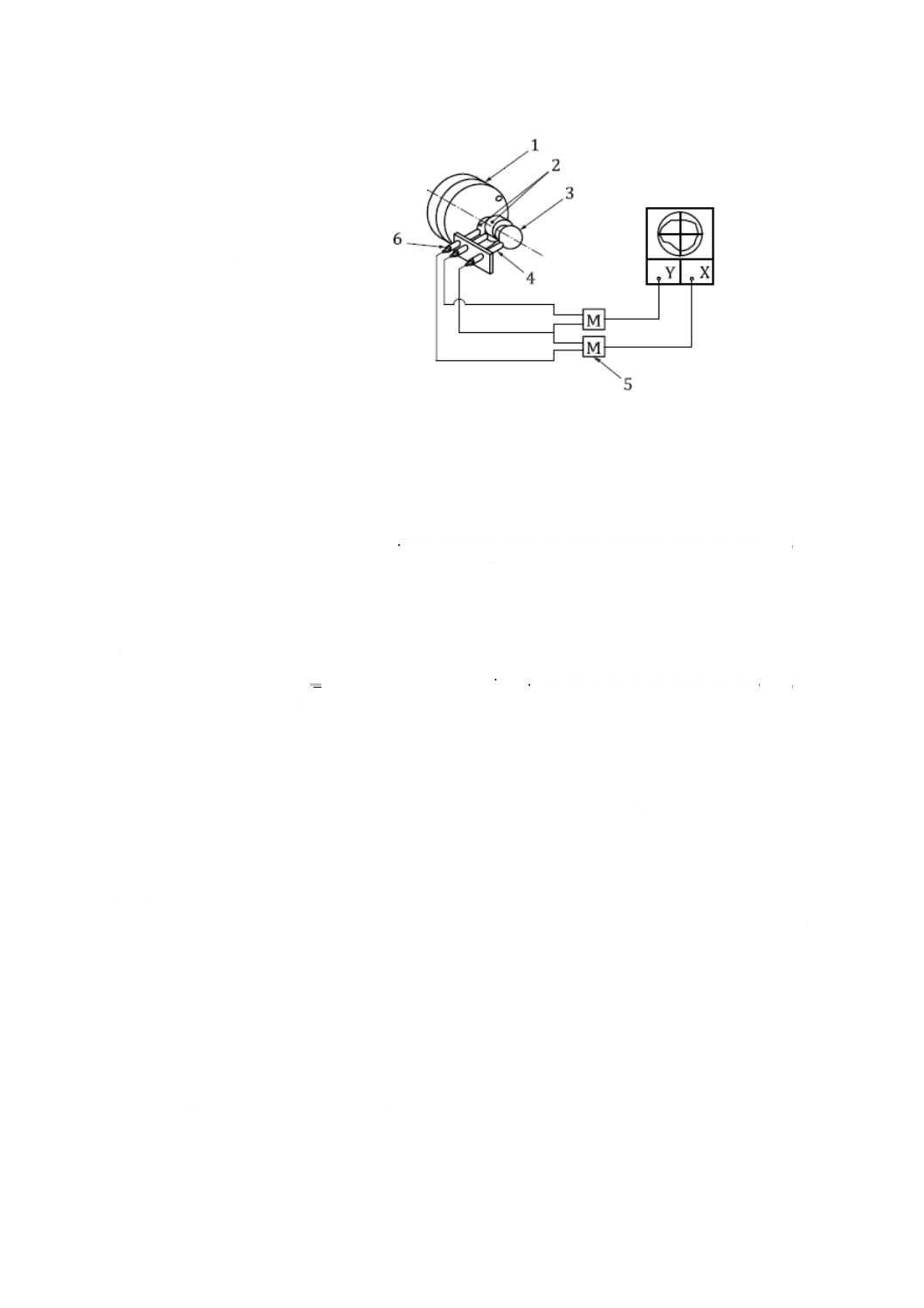
1 ワッブル板
2 基礎円生成カム
3 基準球
4 変位計
5 乗算器
6 低感度の変位計
図15−固定感度方向をもつ半径方向誤差運動の試験方法(Bryanの方法)
5.4.3.2
データ解析
変位計を固定感度方向に取り付ける場合は,半径方向誤差運動[r(θ)−r0]を求めるために,式(1)を次の
ように変形する。
()
()
q
q
ΔX
r
r
+
=0
········································································ (3)
ここに,
ΔX(θ): 固定感度方向に向けた変位計の出力
ただし,固定感度方向がX軸に対してある角度θfをもっている場合には,変位計は感度方向に平行に取
り付けて式(1)を用いるか,又は二つ目の変位計をそれと直角な方向(Y軸方向)に取り付けて行う。この
場合には,式(1)は次のようになる。
()
()
()
f
f
ΔY
ΔX
r
r
q
q
q
q
q
sin
cos
0
+
+
=
··············································· (4)
ここに,
θ: 主軸の回転角度位置
r(θ)−r0: 回転角度位置θにおける半径方向誤差運動
θf: 固定感度方向とX軸とのなす角度
ΔX(θ): X軸方向の変位計の出力
ΔY(θ): Y軸方向の変位計の出力
r0: 見やすくするために極座標線図を調整するための値
各回転速度における主軸誤差運動の極座標線図を描くためには,主軸を十分な回数,回転7) させなけれ
ばならない。一つの主軸速度に対する代表的な極座標線図を図7 a) に示す。この表示は,固定感度方向と
回転感度方向とが同じように見えるが,実際には別のものを表示している。この規格の目的のために,誤
差運動表示から二つの誤差運動値だけを求める。非同期誤差運動値は,図9に示したように,極座標線図
の中心を通る放射状の線に沿って測定した(平均する前の)全誤差運動の極座標線図の最大幅でなければ
ならない。同期誤差運動の極座標線図は,全回転数に対する全誤差運動の極座標線図の平均をとることに
よって計算しなければならない。典型的な同期誤差運動の極座標線図を,図7 b) 及び図9に太線で示す。
図9に示すように,同期半径方向誤差運動値は,同期誤差運動の極座標線図を十分に含む,LSC中心を中
心とする二つの同心円の半径差となる。同期半径方向誤差運動値は,測定を行った軸方向の位置と一緒に
指定しなければならない。
注7) 主軸については,最少で20回転させる。
5.4.4
軸方向誤差運動
5.4.4.1
試験方法
26
B 6190-7:2019 (ISO 230-7:2015)
軸方向誤差運動は,図13に示すように,変位計を軸方向に向けて取り付け,測定しなければならない。
軸方向誤差運動が,5.3.4.2に示した回転感度方向の軸方向誤差運動の試験方法と同じ方法で,かつ,同じ
主軸速度で測定しなければならない。
5.4.4.2
データ解析
基本誤差運動(同心誤差)を解析的に除去しないほうがよいこと以外は,軸方向誤差運動の誤差運動極
座標線図の解析も半径方向誤差運動の解析と概念的に同じになる。軸方向誤差運動は,主軸の回転角度位
置と誤差運動とを直交座標で表示してもよい。非同期軸方向運動値は,主軸を十分な回数,回転8) させた
ときの変位の最大範囲になる。軸方向の同期誤差運動値は,主軸の回転角度位置に対応する平均軸方向偏
差の範囲としなければならない。
注8) 主軸については,最少で20回転させる。
5.4.5
傾斜方向誤差運動
5.4.5.1
測定装置
固定感度方向における傾斜方向誤差運動を測定するには,図14に示すように半径方向の変位計1と2
とを用いて空間的に離れた2点で半径方向誤差運動の測定を行う必要がある。ある距離(表2参照)だけ
離れた2個の球をもった基準器又はテストバーを主軸に取り付け,半径振れを最小にするために主軸の回
転軸に精密に心合わせをする。
傾斜方向誤差運動の測定方法には,方法1及び方法2の二つの方法がある。方法1は,一つの変位計を
使用する方法であり,方法2は,傾斜を測定するために二つの変位計を使用する方法である。これら二つ
の方法とも測定に利用することができる。ただし,一つの変位計で別々に得られた二つのデータを同期さ
せることは難しいために,これら二つの方法によって得られた結果は,同じ結果にならない可能性がある。
5.4.5.2
試験方法−方法1
基準球又はテストバー,及び変位計を5.4.3.1に従って(感度方向に一つの変位計を)取り付け,3段階
の主軸速度で半径方向誤差運動を測定する。この3段階の主軸速度は,機械の仕様における最高速度の百
分率として指定しなければならない。各速度における変位計の読みは,主軸の回転角度位置の関数として
記録しなければならない。
次に,基準球又はテストバーと変位計とは,先に行った測定位置からの50 mm〜100 mm離れた位置に
取り付け直し,同じ回転速度で,この位置における測定値を主軸の回転角度位置の関数として記録する。
5.4.5.3
データ解析−方法1
軸方向の2か所の位置における各主軸速度に対応する半径方向の同期誤差運動及び非同期誤差運動値は,
5.4.3.2に従って求める。二つの変位計間の距離で除した半径方向誤差運動の測定値の差を同期傾斜運動誤
差の値と定義する。その距離で除した半径方向の非同期誤差運動値の差を傾斜方向の非同期運動誤差の値
と定義する。単位は,ラジアンとする。
5.4.5.4
試験方法−方法2
次の解析は,二つの変位計が距離Ld離れて,基準球の赤道上又はテストバーに平行に取り付いていると
仮定して行う。二つの変位計の感度(出力電圧/変位)が同じになるように調整して何らかの主軸運動誤
差解析システムに入力する前にそれらの出力の差を取るか,又はソフトウェアでそれらの感度を校正し,
差を取る。
主軸は,5.4.5.2に規定したように,選んだ3段階の主軸速度で十分な回数,回転9) させて,二つの読み
の差(変位計1及び変位計2)を極座標線図として描く。
注9) 主軸については,最少で20回転させる。
27
B 6190-7:2019 (ISO 230-7:2015)
5.4.5.5
データ解析−方法2
傾斜方向非同期誤差運動値は,極座標中心を通る半径線に平行に測定され,二つの変位計間の距離Ld
で除した2個の変位計の読みの差から得られた全誤差運動の極座標線図の非同期成分を表す。すなわち,
()
()
()
{
}
d
1
2
L
r
r
q
q
q
β
−
=
···································································· (5)
ここに,
β(θ): 傾斜誤差運動値(ラジアン)
r2(θ): 変位計2での半径方向誤差運動値
r1(θ): 変位計1での半径方向誤差運動値
Ld: 2個の変位計の中心間の距離
θ: 主軸(極座標線図上での角度)の回転角度位置
傾斜方向同期誤差運動値は,二つの位置に対応させて,二つの変位計間の距離で二つの同期誤差運動値
の差を除すことによって得られる。
変位計が固定感度方向に並んでいない場合には,式(5)は,5.4.3.2と同様に修正することができる。
6
回転テーブル及び旋回主軸頭の回転軸誤差運動試験方法
6.1
一般
回転テーブル及び旋回主軸頭の回転軸誤差運動の特性は,主軸と同様とする。ただし,回転速度は,主
軸よりもかなり低く,回転範囲も多くの場合に360°未満となる。したがって,試験方法及びその考え方
が似ていても,試験条件は異なる。
回転テーブル及びトラニオンのような低速度で回転する回転軸については,固定感度方向及び回転感度
方向の場合,その回転軸に機械的又は電気的に同期して回転する機構をもった極座標記録計を使って対応
することができる。回転感度方向については,基準球は,構造本体に取り付け,変位計は,回転軸に取り
付ける。回転軸を1回転又は数回転させる場合は,変位計のケーブルが測定結果に影響を及ぼさない方法
で回転軸の回りに巻き付ける。連続回転させる場合は,スリップリング,無線式データ送信又は同等の方
法が必要になる。
回転テーブル及び旋回主軸頭は,直進軸と同様に工具及び工作物の位置決めに使用する。したがって,
半径方向,軸方向及び傾斜方向の誤差運動を測定するための試験条件は,JIS B 6190-1に記載されている
方法と同様になる。
場合によっては,特に傾斜回転テーブルの中には,回転軸上に基準器(例えば,小さな精密球)を定置
することができないものがある。その場合には,特殊な基準器が必要になる(例えば,大きな直径の球又
は円筒の一部)。基準球の位置を測定する三つの変位計を組み込んだ測定器(R-test)は,そのような場合
に使用できる[JIS B 6190-1の11.3.5.3(三つの変位計と基準球とによる方法)参照]。ただし,この場合,
測定に関係する直進軸の誤差運動によって測定不確かさが増加することに留意するのが望ましい。
6.2
軸方向誤差運動
6.2.1
試験装置
精密な基準球又は他の適切な基準器は,回転軸上に配置するために適切な取付具を用いて機械の回転部
品に取り付け,変位計は,その測定値が工具と工作物との間の相対運動を表すように軸方向に向けて非回
転部品上に取り付ける。基準球又は基準器は,回転軸と心合わせするのが望ましい(半径振れを最小化す
る)(図16参照)。
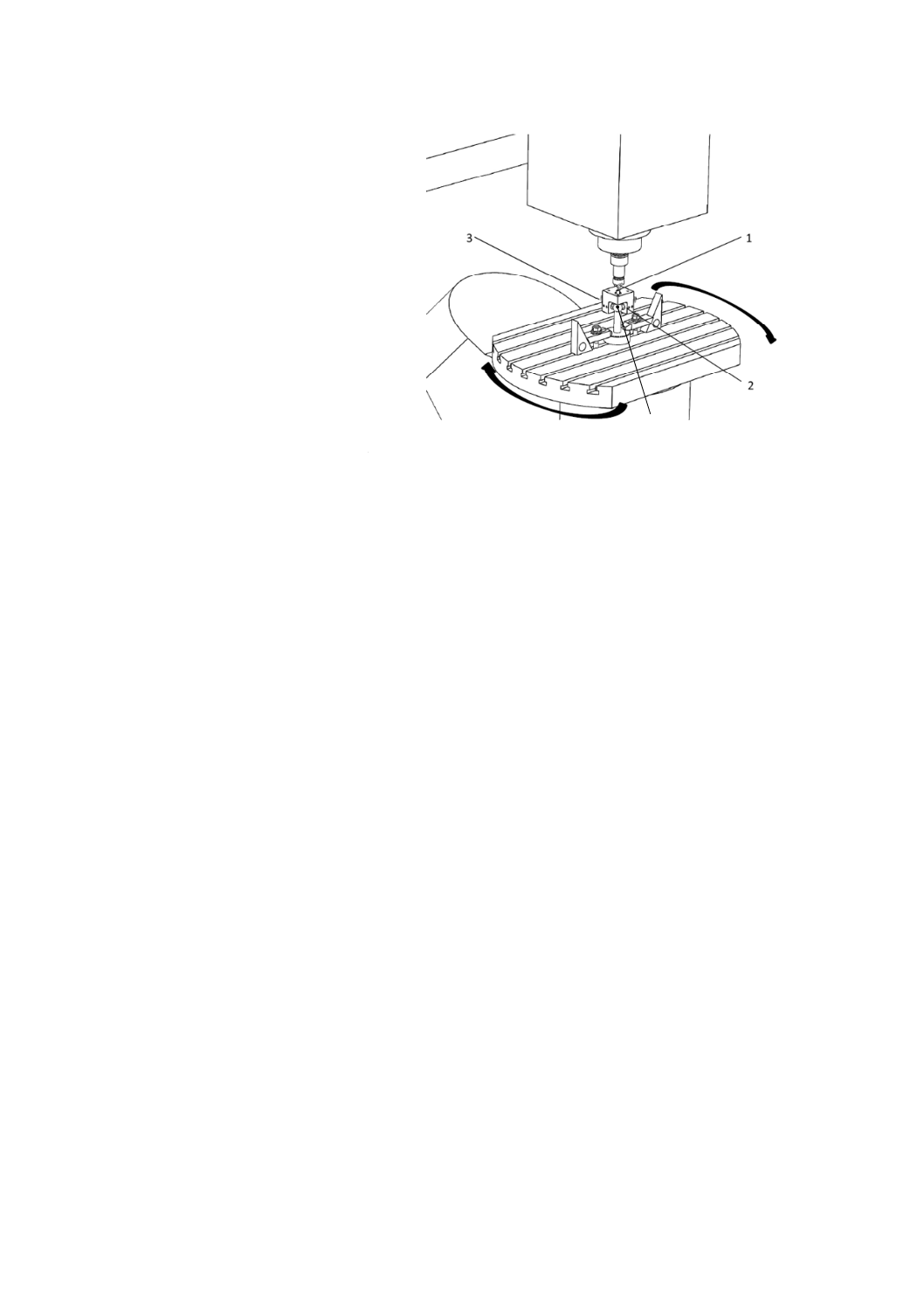
28
B 6190-7:2019 (ISO 230-7:2015)
1 軸方向変位計
2 X方向に平行な半径方向変位計
3 Y方向に平行な半径方向変位計
4 基準球
4
図16−回転テーブルの軸方向及び半径方向誤差運動の測定装置
6.2.2
試験方法
試験する回転部品(テーブル又は主軸頭)は,関心のある回転範囲について設定した一連の目標位置ま
で回転させなければならない。測定間隔は,回転範囲が90°以下の軸については回転範囲の1/10を超え
てはならない。連続回転のできる回転軸については,その間隔は,30°を超えてはならない。一つの目標
位置で測定データを記録するために,機械は十分に長く停止しなければならない。測定は,使用する測定
器及び工作機械の使用目的に応じて連続運転して行ってよい。
回転テーブルについては,最少で時計回りに5回転,反時計回りに5回転それぞれ回転させる。旋回主
軸頭及び傾斜回転テーブルについては,最少で時計回りに5回,反時計回りに5回,全移動範囲にわたっ
て回転させる。
回転速度は,使用する測定器・試験装置,及び/又は工作機械の使用目的に合わせなければならない。
6.2.3
データ解析
軸方向誤差運動は,回転軸の回転角度位置に対して誤差運動を極座標又は直交座標に表示するのが望ま
しい。非同期軸方向誤差運動値は,回転部品を何回も回転させたときの変位の最大範囲としなければなら
ない。同期軸方向誤差運動値は,回転テーブル又は主軸頭の回転角度位置に対応する平均軸方向偏差の範
囲としなければならない。
6.3
半径方向誤差運動
6.3.1
試験装置
基準球又はテストバーのような他の適切な基準器を回転軸上に配置するために適切な取付具を用いて機
械の回転部品に取り付ける。変位計は,工具と工作物との間の相対運動が観察できるように直交させて機
械の非回転部品上に取り付ける。基準球は,回転軸と心合わせする(半径振れを最小化する。)(図16参
照)。
6.3.2
試験方法
試験する回転部品(テーブル又は主軸頭)は,関心のある回転範囲について設定した一連の目標位置ま
で回転させなければならない。測定間隔は,回転範囲が90°以下の軸については回転範囲の1/10を超え
てはならない。連続回転(360°)のできる回転軸については,その間隔は,30°を超えてはならない。一
つの目標位置で測定データを記録するために,機械は十分に長く停止しなければならない。測定は,使用
29
B 6190-7:2019 (ISO 230-7:2015)
する測定器及び工作機械の使用目的に応じて連続運転して行ってよい。
回転テーブルについては,最少で時計回りに4回,反時計回りに4回それぞれ回転させる。旋回主軸頭
及び傾斜回転テーブルについては,最少で時計回りに2回,反時計回りに2回それぞれ回転させる。
回転速度は,使用する測定器・試験装置及び/又は工作機械の使用目的に合わせなければならない。
6.3.3
回転感度方向のデータ解析
半径方向誤差運動は,互いに直交するように配置された二つの変位計で測定した回転角度位置の関数と
して回転部品の半径方向変位を記録し,次の式(6)に従って誤差運動を計算し,極座標線図として表示する
ことによって求めることができる。
()
()
()
q
q
q
q
q
sin
cos
0
ΔY
ΔX
r
r
+
+
=
················································· (6)
ここに,
θ: 機械の回転部品の回転角度位置
r(θ)−r0: 回転角度位置θでの半径方向誤差運動
ΔX(θ): X軸方向の変位
ΔY(θ): Y軸方向の変位
r0: 見やすくするために極座標線図に加える値
半径方向誤差運動を極座標で表した代表的な曲線を図7 a) に示す。この規格の目的のために,二つの誤
差運動値は,誤差運動線図(LSC中心を用いて)から計算する。非同期半径方向誤差運動及び同期半径方
向誤差運動値は,図7 b),図7 c) 及び図9参照。半径方向誤差運動値は,測定値を求める軸方向の位置を
使って指定しなければならない。同期・非同期半径方向誤差運動値は,報告しなければならない。
工作物を載せる回転テーブルについては,半径方向誤差運動が軸平均線に垂直な面内で配置された工作
物の位置に及ぼす影響(回転軸誤差運動の二次元影響)は,[ΔX(θ),ΔY(θ)]によって表される。
6.3.4
固定感度方向のデータ解析
半径方向誤差運動は,回転角度位置の関数として一つの変位計で測定した回転部品の半径方向変位を記
録する。半径方向誤差運動を極座標で表した代表的な曲線を図7 a) に示す。この規格の目的のために,二
つの誤差運動値は,誤差運動線図(LSC中心を用いて)から計算する。非同期半径方向誤差運動及び同期
半径方向誤差運動値は,図7 b),図7 c) 及び図9参照。半径方向誤差運動値は,測定値を求める軸方向の
位置を使って指定しなければならない。同期・非同期半径方向誤差運動値は,報告しなければならない。
非同期誤差運動値は,図9に示したように,極座標中心を通る放射状の線に沿って測定した(平均する
前の)全誤差運動の極座標線図の最大幅でなければならない。同期誤差運動の極座標線図は,全回転回数
に対する全誤差運動の極座標線図を平均することによって計算しなければならない。典型的な同期誤差運
動の極座標線図は,図7 b) 及び図9に太線で示す。同期半径方向誤差運動値は,同期誤差運動の極座標線
図を含むのに十分なLSC中心で中心を合わせた二つの同心円の半径の差となる。半径方向誤差運動値は,
測定を行った軸方向の位置と共に指定しなければならない。
6.4
傾斜方向誤差運動
6.4.1
試験装置
傾斜方向誤差運動の測定では,空間的に離れた2点での半径方向誤差運動の測定が必要となる。2個の
基準球をある距離だけ離して取り付けた基準器又は円筒テストバーを主軸に取り付け,回転部品の回転軸
に心合わせをする。
5.3.3及び5.4.5に規定する二つの方法を適用できる。
6.4.2
試験方法
試験する回転部品(テーブル又は主軸頭)は,関心のある移動範囲について設定した一連の目標位置ま
30
B 6190-7:2019 (ISO 230-7:2015)
で回転させなければならない。測定間隔は,回転範囲が90°以下の軸については回転範囲の1/10を超え
てはならない。連続回転のできる回転軸については,その間隔は,30°を超えてはならない。一つの目標
位置で,機械は,測定データを記録するために十分に長く停止しなければならない。測定は,使用する測
定器及び工作機械の使用目的に応じて連続運転して行ってよい。
回転テーブルについては,最少で時計回りに4回,反時計回りに4回それぞれ回転させる。旋回主軸頭
及び傾斜回転テーブルについては,最少で時計回りに2回,反時計回りに2回それぞれ回転させる。
回転速度は,使用する測定器・試験装置及び/又は工作機械の使用目的に合わせなければならない。
1個の基準球を用いた試験装置を使用する場合には,その基準球は,軸方向の異なる位置に再配置し,
試験方法は,同様に行わなければならない。
6.4.3
回転感度方向のデータ解析
二つの軸方向の位置での同期半径方向誤差運動値及び非同期半径方向誤差運動値は,5.3.2.3に従って求
めなければならない。二つの位置間の距離で同期半径方向誤差運動の測定値の差を除した値を,同期傾斜
運動誤差の値と定義する。その距離で非同期誤差運動値の差を除した値を,非同期傾斜運動誤差の値とし
て定義する。いずれの値とも単位は,ラジアンとする。
2個の基準球を用いた試験装置を使用する場合は,同じ方向(X又はY)に配置した二つの変位計の出
力の差を同期・非同期半径方向誤差運動値の計算に用いる。これらの値を2個の基準球間の距離で除した
値が,傾斜方向の同期・非同期誤差運動値になる。
6.4.4
固定感度方向のデータ解析
二つの軸方向の位置での同期半径方向誤差運動値及び非同期半径方向誤差運動値は,5.4.3.2に従って求
めなければならない。二つの位置間の距離で同期半径方向誤差運動の測定値の差を除した値を,同期傾斜
運動誤差の値と定義する。その距離で非同期誤差運動値の差を除した値を,非同期傾斜運動誤差の値とし
て定義する。いずれの値とも単位は,ラジアンとする。
2個の基準球を用いた試験装置を使用する場合は,同じ方向(X又はY)に配置した二つの変位計の出
力の差を同期・非同期半径方向誤差運動値の計算に用いる。これらの値を2個の基準球間の距離で除した
値が,傾斜方向の同期・非同期誤差運動値になる。
31
B 6190-7:2019 (ISO 230-7:2015)
附属書A
(参考)
回転軸に関する共通概念
A.1 概要
この附属書は,工作機械の回転軸の品質の仕様及び測定に関する共通概念について記載する。この附属
書は,回転軸に関する参考文献[12]を基礎にして作成している。
この附属書は,理解を容易にするために例として旋盤主軸を用いる。ただし,この附属書に記載してい
る共通概念は,工作機械の部品,例えば,回転テーブル,傾斜回転テーブル,回転センタなどの全ての回
転軸に適用できる。
A.2 完全回転軸
A.2.1 一般
まず,完全回転軸に適合する要件について考えることから始める。完全回転軸とは,“空間に固定された
線の周りを純粋に回転する工作物の軸”のように表現してもよい場合があるが,この表現では十分でなく,
幾つかの点に留意する必要がある。
A.2.2 相対運動
海上で横揺れしている船上に固定されている旋盤を想定すると,この旋盤の主軸の回転軸は,“空間”で
明らかに大きく動いているが,工作物の精度に影響を及ぼすことはない。重要なことは工作物と工具との
相対運動である。相対運動は,工作物と工具との相対的な位置を維持するために必要な構成要素のつなが
りを表す構造ループ(3.1.14参照)と関係している。旋盤の場合の構造ループは,チャック−主軸−主軸
軸受・主軸ハウジング−主軸台−ベッド−案内面−往復台−刃物台及び工具保持具になる。
A.2.3 感度方向
旋盤で端面削りを行う場合を考える。主軸軸受が不完全なために切削点で工作物が工具に対して軸方向
に僅かに動くと仮定すると,誤差は,1回転ごとに工作物に刻まれる。この場合に軸方向の動きは感度方
向にあるという。これとは逆に面に接する方向の小さな動きは,切削誤差を生じさせない。したがって,
この動きは非感度方向にあるという。その例については,図4参照。一般に,感度方向は,加工点を通り,
創成される回転面の法線に平行な方向であり,感度方向に垂直な,どの線も非感度方向となる。
A.2.4 回転感度方向
中ぐり加工では,工作物を固定し工具を回転させて切削する。この場合の感度方向は,切削点を通る線
に常に平行で工具と共に回転することになる(図5参照)。機械のベッドを基準として,機械の感度方向
が固定であるか,又は回転であるかによって異なった試験方法を適用する。同様に,フライス加工では,
多数(切れ刃の数又はインサートの数に基づく)の回転感度方向が存在する。
A.2.5 変動感度方向
旋盤でカムを旋削する場合を考える。カムの旋削を行うためには,主軸の回転と縦送り台の運動とを同
期させることになる。カムの形状が回転対称でないことから,カムに垂直な面の方向は,主軸の回転角度
位置に対して変化する。したがって,感度方向は主軸の回転角の関数として変化する(図6参照)。
A.2.6 複数の感度方向がある場合
回転軸の用途に応じて複数の感度方向があり得る。例えば,多数の切れ刃をもつフライス工具は,複数
32
B 6190-7:2019 (ISO 230-7:2015)
の回転感度方向をもっている。同様に,(二つの異なる軸方向の位置で)2直交方向からのバイトによる工
作物の旋削に使用する回転テーブルは,二つの感度方向をもっている。
A.2.7 変位計及び工具
上記の例は,全て工具を基準として記載している。ここで用いる“工具”とは,幅広く,研削といしの
ようなものまで含む。さらに,上記の全ての記載は,切削工具に代えて変位計を取り付ければ測定機にも
適用できる。
上記の議論に基づけば,工作機械の完全回転軸の必要条件について,より詳細に記載することができる。
“完全回転軸は,感度方向において工具に対して動かない線の回りに工作物を回転させることができる
軸(又は,固定工作物及び回転工具の場合についても同様)である。”
厳密には,この表現は,図A.1に示す円筒のような曲面を扱う場合に非感度方向における運動が何らか
の誤差を生じさせる可能性があることから,非感度方向における相対運動を制限していないところに問題
がある。ただし,非感度方向における回転軸の誤差運動を測定しない場合,測定にかける労力を大幅に減
らすことができる。一方で,回転テーブル上に取り付けた工作物にドリル穴をあけるような場合には,非
感度方向の誤差運動は,1対1で穴の位置に誤差を発生させる可能性がある。そのような場合には,軸平
均線に垂直な面内で回転軸の位置の変化を測定する必要がある(これを,“回転軸誤差運動の二次元影響”
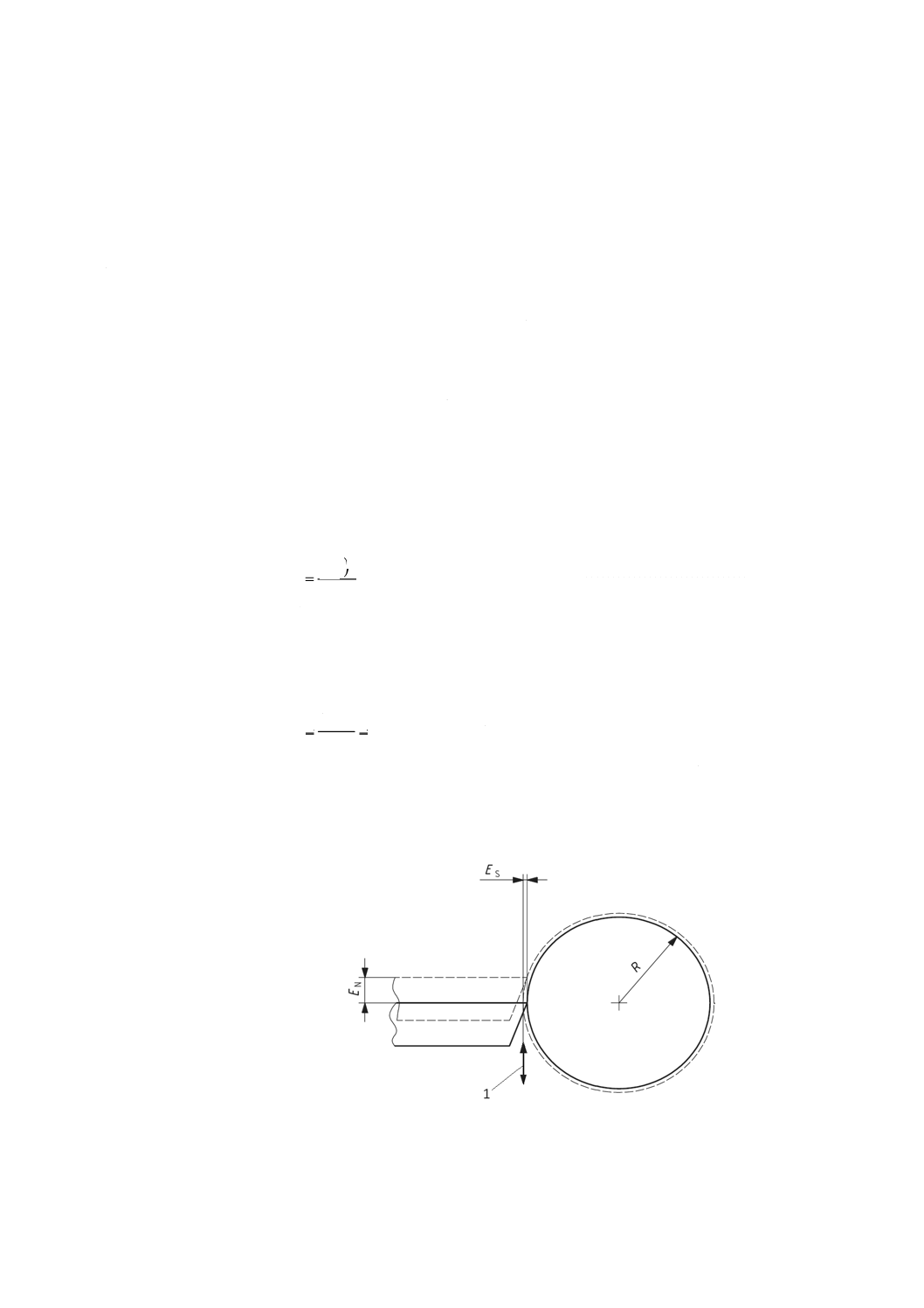
という。3.3.6参照)。次の式は,非感度方向の運動に起因する誤差の推定に役立つ。
()
R
E
E
2
2
N
S=
(RよりもENが小さい場合) ···································· (A.1)
ここに,
EN: 非感度方向の運動
ES: ENによる感度方向の誤差
R: 工作物半径
例えば,EN=0.02 mm及びR=10 mmとすると,
5
2
S
10
2
10
2
02
.0
−
×
=
×
=
E
mm=0.02 μm
半径10 mmの円の場合,非感度方向に20 μmの誤差運動が発生すると,その円の接線方向の誤差運動に
よる誤差は0.02 μmとなる。これは,2次のオーダの誤差を表す。したがって,感度方向の誤差運動と非
感度方向の誤差運動とがほとんど同じ場合は,非感度方向の誤差運動は無視しても差し支えない。
1 非感度方向
図A.1−曲面に沿った非感度方向の相対運動による2次のオーダの誤差
33
B 6190-7:2019 (ISO 230-7:2015)
A.3 不完全回転軸−誤差運動
実際の回転軸に対して,工具と工作物との間の感度方向における相対変位を説明するために,用語“誤
差運動”を用いる。誤差運動の物理的要因として,軸受の非真円成分による軸受誤差運動,並びに内部又
は外部加振源と関係している構造ループにある有限の質量,ばね及び減衰による構造誤差運動の二つの要
因を考えることができる。A.7.5に記載するように,極座標線図に同期させてデータを記録することは,こ
の点で有益ではある。ただし,誤差運動試験データをこれらの二つの要因に分離できない場合もある。
A.4 構造誤差運動
構造ループの振動であること及び相対運動であることを強調するために,用語“振動”よりも“構造誤
差運動”を用いることが多い。例えば,旋盤の刃物台に加速度計を取り付けて,その出力を2回積分して
構造誤差運動を求める方法は,刃物台と工作物との相対変位を測定しているのではなく,絶対運動を検出
しているために不正確になる。構造ループの剛性が十分に高いとき,構造ループ全体が同じように振動す
るが,構造誤差運動は無視できる程度に小さくなる。
相対運動だけが重要であることから,マイクロメータのC形フレームに取り付けられたアンビルとスピ
ンドルとの関係が重要であるのと同様に,回転軸の機能のために構造ループは重要になる。転がり軸受に
よる構造誤差運動を含めて駆動歯車若しくはモータからの構造誤差運動を除くこと,及び主軸の共振だけ
を含めて刃物台の共振を除くことは,いずれも現実的ではない。この規格に採用している方法は,あらゆ
る要因による構造誤差運動を含めるが,使用者の目的に合わせて最も適切な構造ループを選択してもよい。
したがって,この規格は,定盤上に定置した主軸ユニット又は完成機に組み込まれた製品として行う主軸
試験に適用できる。誤差運動の測定又は仕様に関係する構造ループについては,曖昧なところがないほう
がよい。
A.5 熱影響
工具と工作物との間に相対運動が生じる要因の一つに,構造ループ内の温度分布変化がある。熱膨張又
は熱収縮によって感度方向に生じる相対運動を,“熱影響”と呼ぶ。この熱影響は,通常,誤差運動よりも
応答時間が長いので,誤差運動とは分けて扱う。熱影響については,JIS B 6190-3参照。
A.6 誤差運動の幾何学
A.6.1 一般
この箇条は,工作物を剛体として扱い,かつ,工作物が回転すると仮定して,幾つかの基本誤差運動の
測定から,どのようなサイズ及び形状の工作物に対しても,誤差運動を予測できるように幾何学的な関係
について記載する。
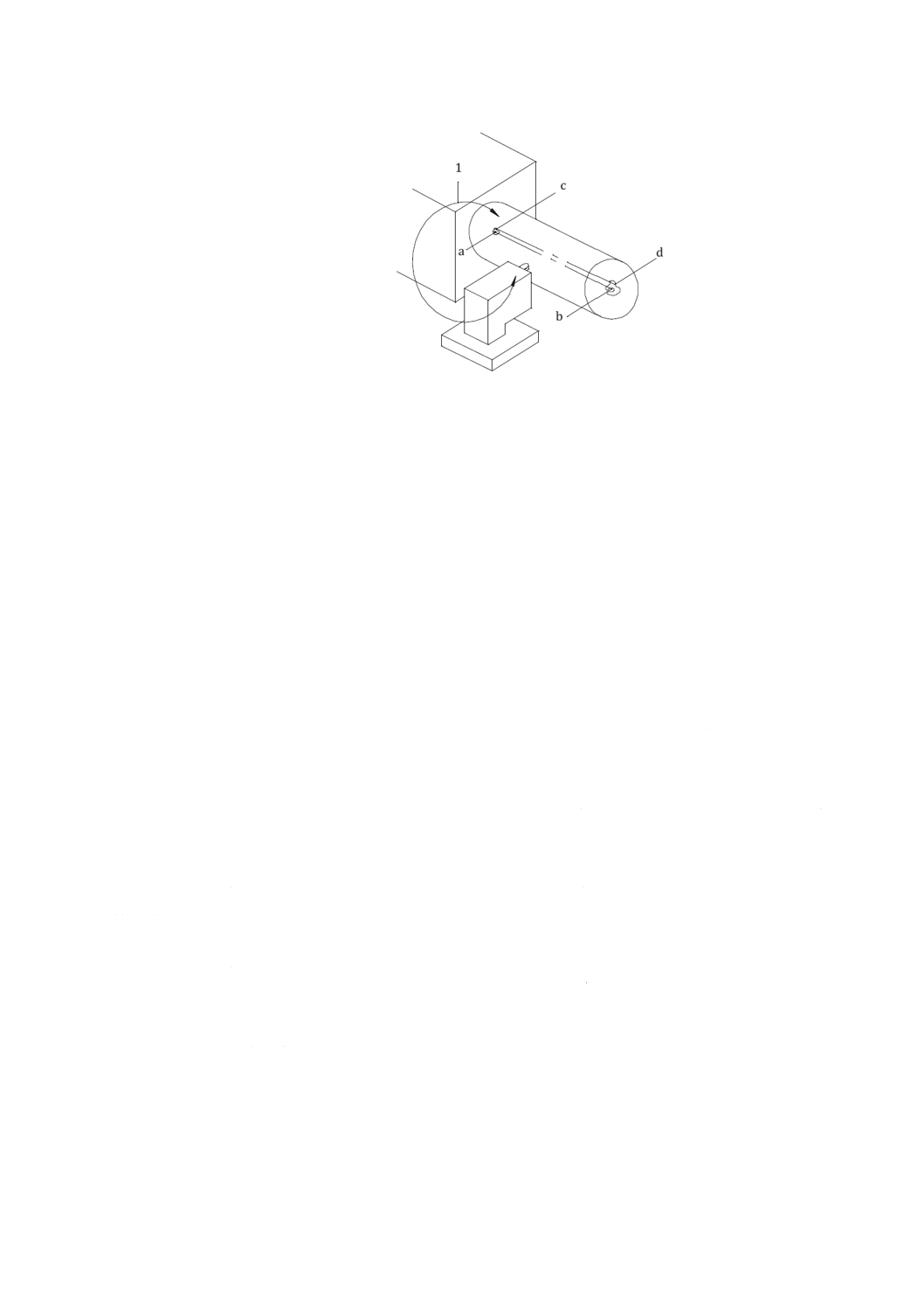
図A.2に示すように,二つの線分の相対運動という観点で工具と工作物との相対運動を扱うと都合がよ
い。この線分の一つである回転軸は,工作物に埋め込まれ,工作物と共に運動する。もう一つの線分は,
回転軸の平均位置で工具に対して固定される。この線分は軸平均線と呼ばれる。完全回転軸の場合は,こ
れら二つの線分は同じになる。
34
B 6190-7:2019 (ISO 230-7:2015)
1
構造ループ
ab 軸平均線
cd 時刻tにおける回転軸
図A.2−回転軸の例,abは工具に対して固定され,cdは工作物の中にある。
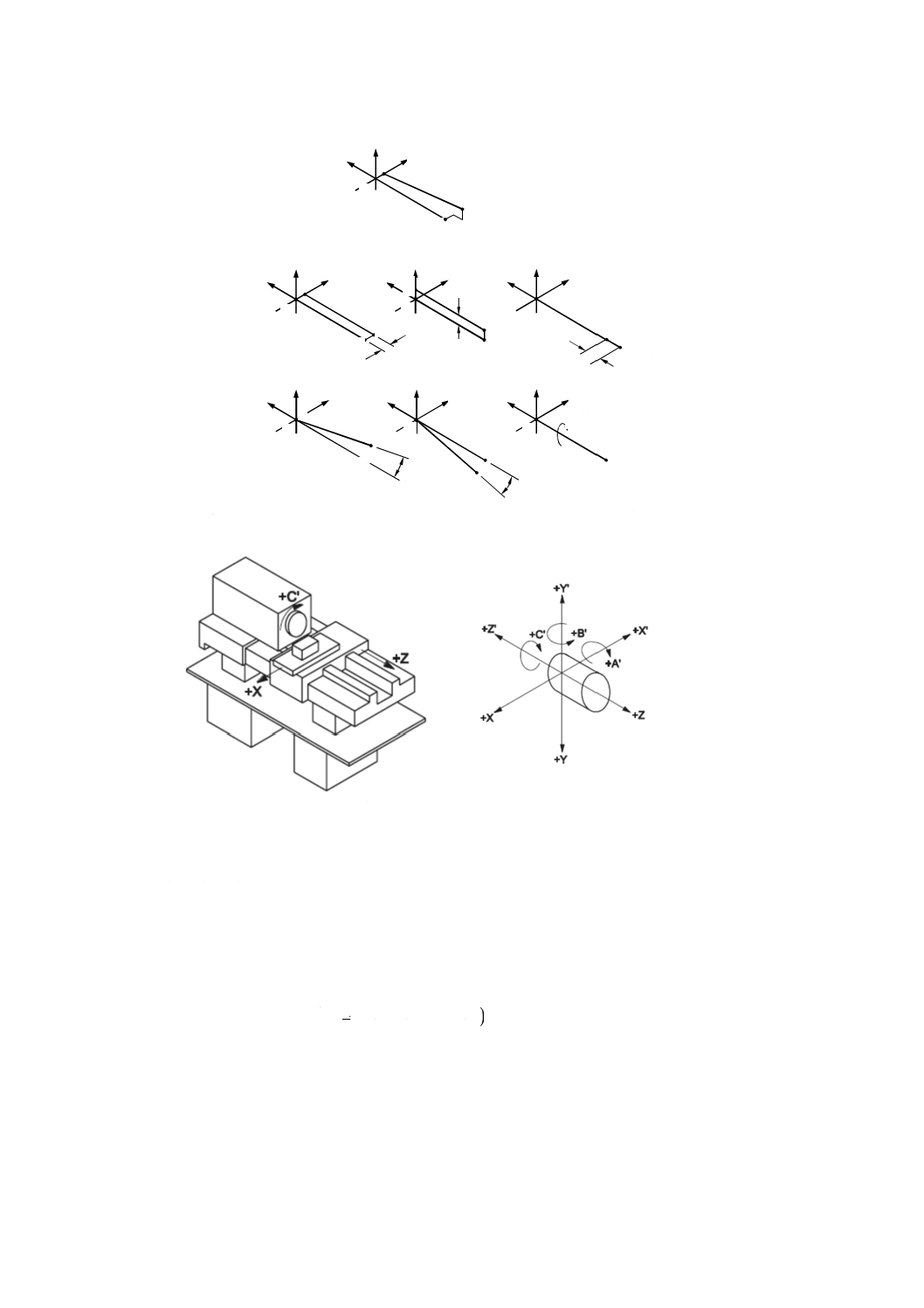
一般に工作物は,図A.3に示すように,時刻tにおける3直進運動と3回転運動とからなる6自由度を
もっている。この6自由度のうち,軸平均線回りの回転運動Cは,回転軸としての機能をもつ。残りの5
自由度のどれが誤差運動に大きく影響するかは,感度方向,並びに加工点の軸方向位置及び半径方向位置
によって変わる。旋盤作業については,感度方向は常に案内面に平行な平面内にある。
注記 例えば,Y軸運動を使って旋削工具を接近させる場合の感度方向はYZ面内にあることになる。
工作物が回転する他の工作機械の試験は,ほとんど全ての場合,感度方向が一平面に限られている。こ
れを便宜上X'Z'面と呼び,回転軸をC軸と呼ぶと,運動EYC(t) 及びEAC(t) は,ほとんどの場合(複数の
感度方向がある場合を除いて)非感度方向にあり,無視することができる。言い換えれば,関係する誤差
運動は,X'Z'投影平面に現れる運動EXC(t),EZC(t) 及びEBC(t) だけになる。この三つの誤差運動については,
A.6.2〜A.6.4に示す用語を用いる10)。
注10) 図A.3に示す旋盤の座標系は,JIS B 6310による。JIS B 6310によると“構成要素の運動の正
の方向は,工作物の寸法が増える向きである”[図A.3 b) 参照]。図A.3 a) の概略図では,工具
の運動を表す場合は,プライム( ')なしの文字を用い,工作物の運動を表す場合は,プライム
付きの文字を用いて表している。工作物の運動の正の方向は,対応するプライムなしの文字の
運動とは逆となる。JIS B 6310は,X',Y'及びZ'周りの回転運動をA',B'及びC'で表すと規定
している。ただし,この規格では,読みやすくするためにプライムを付けない。
A.6.2 純粋半径方向誤差運動(pure radial error motion)
回転軸が軸平均線と平行を保ったままで,感度方向において軸平均線に垂直に運動する図A.3 a) に示す
誤差運動EXC(t)。
A.6.3 軸方向誤差運動(axial error motion)
回転軸が軸平均線と同軸を保ったままで,軸方向に運動する図A.3 a) に示す誤差運動EZC(t)。
A.6.4 傾斜方向誤差運動(tilt error motion)
軸方向誤差運動と純粋半径方向誤差運動とが起こる平面内で,回転軸の向きが軸平均線に対して変化す
る図A.3 a) に示す誤差運動EBC(t)。
35
B 6190-7:2019 (ISO 230-7:2015)
X
Y
Z
X
Y
Z
X
Y
Z
X
Y
Z
X
Y
Z
X
Y
Z
X
Y
Z
a
b
c
d
a
b
c
d
a
b
c
d
a
b
c
d
a
b
d
a
b
c
d
a
b
EAC(t)
d
EXC(t)
EYC(t)
EBC(t)
C(t)
EZC(t)
c
a) 時刻tにおける軸平均線と回転軸との間の一般的な相対運動及び6基本自由度
b) JIS B 6310に規定する座標系
図A.3−旋盤の回転軸誤差運動の記号
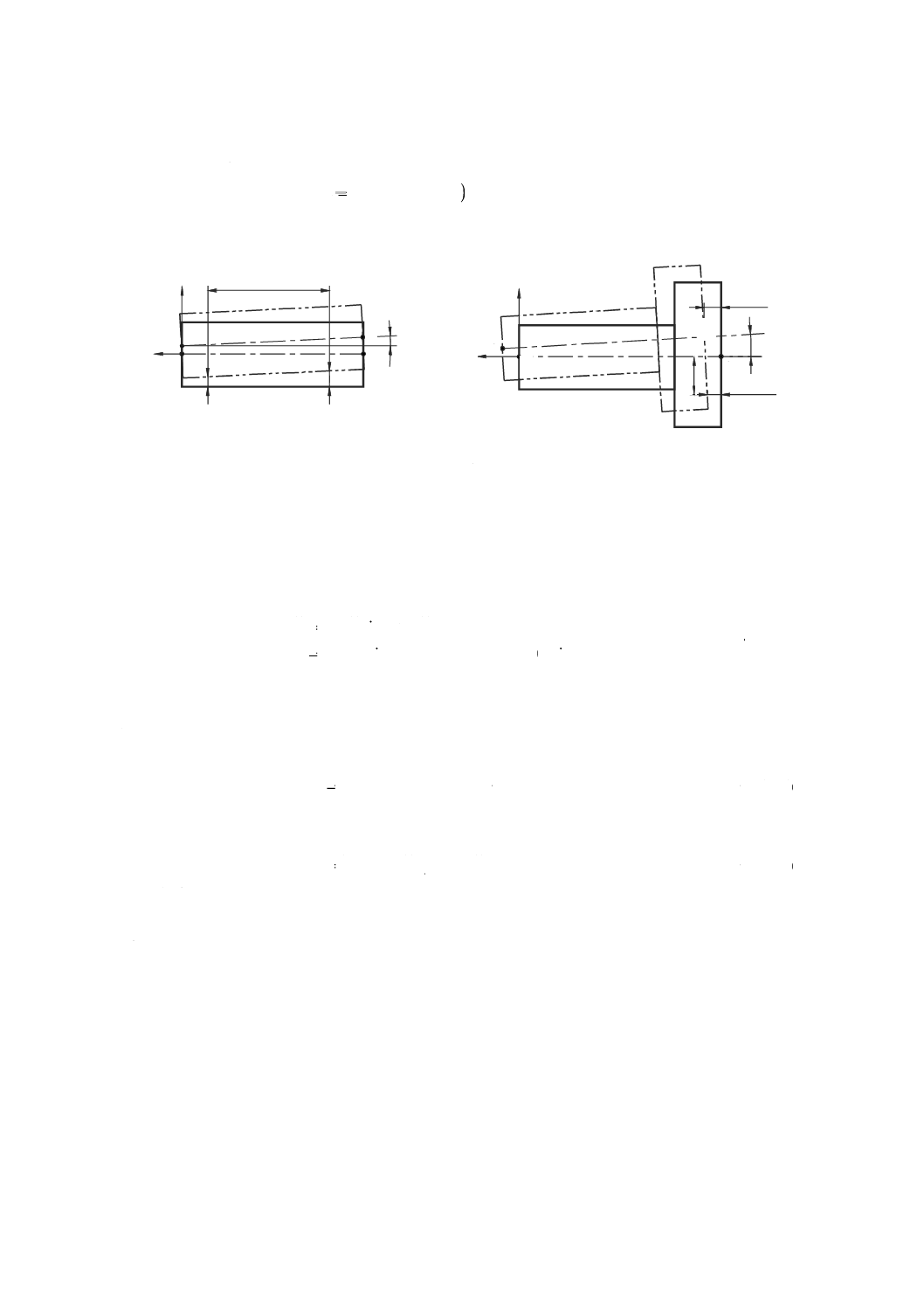
A.6.5 半径方向誤差運動(radial error motion)
一般に,傾斜方向誤差運動と純粋半径方向誤差運動とは同時に起こり,任意の軸方向位置での合計が半
径方向誤差運動になる。軸上の一つ位置(z1)での半径方向誤差運動EXC(t)|z1と傾斜方向誤差運動EBC(t) と
が分かれば,図A.4 a) に示すようにその位置以外の軸方向位置(z2)での半径方向誤差運動EXC(t)|z2を求
めることができる。
()
()
()t
E
L
t
E
t
E
BC
1z
XC
2
z
XC
|
|
×
+
=
[EXC(t)≪Lとする。] ······················ (A.2)
ここに,Lは二つの位置の距離とする。
半径方向誤差運動は,軸の位置によって変化するので半径方向誤差運動測定の軸の位置は,指定する必
要がある。
A.6.6 端面方向運動(face motion)
もう一つの特別な用語は,端面方向運動である。これは,図A.4 b) に示すように軸平均線から指定した
36
B 6190-7:2019 (ISO 230-7:2015)
距離Rの位置における軸方向の誤差運動である。端面方向運動EZC(t)|Rは,軸方向誤差運動と傾斜方向誤
差運動とから次の式で表せる。 ()
()
()t
E
R
t
E
t
E
BC
ZC
R
ZC
|
×
−
=
[EBC(t)|R≪Rとする。] ························ (A.3)
端面方向運動は半径位置と共に変化するので,端面方向運動の測定半径は指定する必要がある。
b
d
a
c
R
c
a
d
b
EBC(t)
Zʼ
Xʼ
EXC(t)|z1
EXC(t)|z2
EBC(t)
EZC(t)
EZC(t)|R
Zʼ
Xʼ
L
a) 軸方向位置と共に変化する半径方向誤差運動
b) 半径位置と共に変化する端面方向誤差運動
図A.4−半径方向誤差運動及び端面方向誤差運動の模式図
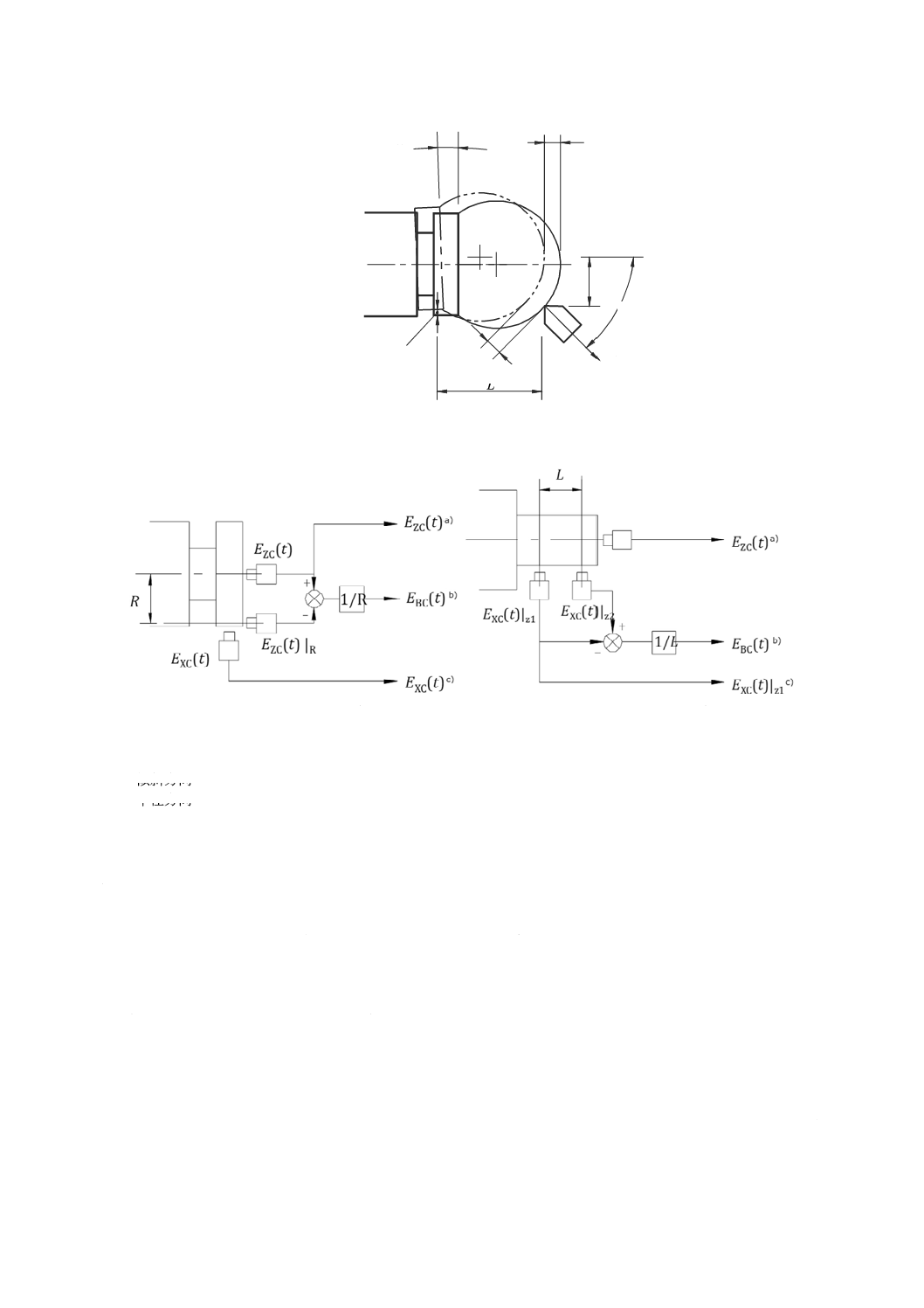
A.6.7 誤差運動−一般的な場合
誤差運動の最も一般的な場合は,図A.5に示す球面の場合のように,軸平均線に対して感度方向のなす
角度θの関数として与えられる。誤差運動は,軸方向及び半径方向の位置に依存し,その位置は,θで指
定する。半径方向,軸方向及び傾斜方向の誤差運動から感度方向の誤差運動軸e(t) は,次の式で表せる。
()
()
()
()
()
()(
)
q
q
q
q
q
q
cos
sin
cos
sin
cos
sin
BC
ZC
C
0
X
XC
R
L
t
E
t
E
t
E
t
F
t
E
t
e
−
+
+
=
+
=
···················· (A.4)
式(A.2)〜式(A.4)から,一般的な場合又は特別な場合の誤差運動は,軸方向誤差運動EZC(t),傾斜方向誤
差運動EBC(t) 及び既知の軸方向の位置(z1)での半径方向誤差運動EXC(t)|z1から求めることができること
が分かる。
傾斜方向誤差運動は,式(A.3)を用いて端面方向誤差運動から導くことができる。
()(
)
()
()
[
]
R
ZC
ZC
BC
|
1
t
E
t
E
R
t
E
−
=
··················································· (A.5)
式(A.2)から傾斜方向誤差運動を求めるためには,二つの位置(z1及びz2)における半径方向誤差運動
の測定値を用いる。
()(
)
()
()
[
]
1z
XC
2
z
XC
BC
|
|
1
t
E
t
E
L
t
E
−
=
··············································· (A.6)
純粋半径方向誤差運動EXC(t) は,上のどの式にも現れないことに注意を要する。この運動は,誤差運動
を理解するための概念として有用であるが,回転軸の挙動を決定するために測定しなければならない事項
ではない。
固定感度方向を用いた半径方向,軸方向及び傾斜方向運動の測定方法の例を,図A.6に示す。
37
B 6190-7:2019 (ISO 230-7:2015)
注a) 感度方向
EBC(t)
EZC(t)
R
EXC(t)|z1
Le(t)
a)
q
図A.5−誤差運動の一般的な場合
a) 半径方向,端面方向及び軸方向
b) 軸方向に一つの変位計及び半径方向に
それぞれに変位計を配置した測定方法
二つの変位計を配置した測定方法
注a) 軸方向
b) 傾斜方向
c) 半径方向
図A.6−固定感度方向を用いた半径方向,軸方向及び傾斜方向運動の測定方法
A.7 誤差運動の極座標線図
A.7.1 一般
回転軸の誤差運動測定値の有益な表示方法は,軸の回転角度位置C(t) に対して誤差運動を極座標線図で
表示することである[図A.3 a) 参照]。この方法には,次の利点がある。
a) 部品の真円度及び表面粗さの予測
b) 軸受誤差運動及び構造誤差運動の診断
c) 基準球の心出しに要求される精度の軽減
d) 誤差運動値の評価
A.7.2 具体例−半径方向誤差運動の極座標線図
具体例の説明の基礎として,固定感度方向における誤差運動の極座標線図を用いる。図A.7 a) は,半径
方向誤差運動の測定における基準球(真球で,かつ,完全に回転軸と同軸であるとする。)及び感度方向11)
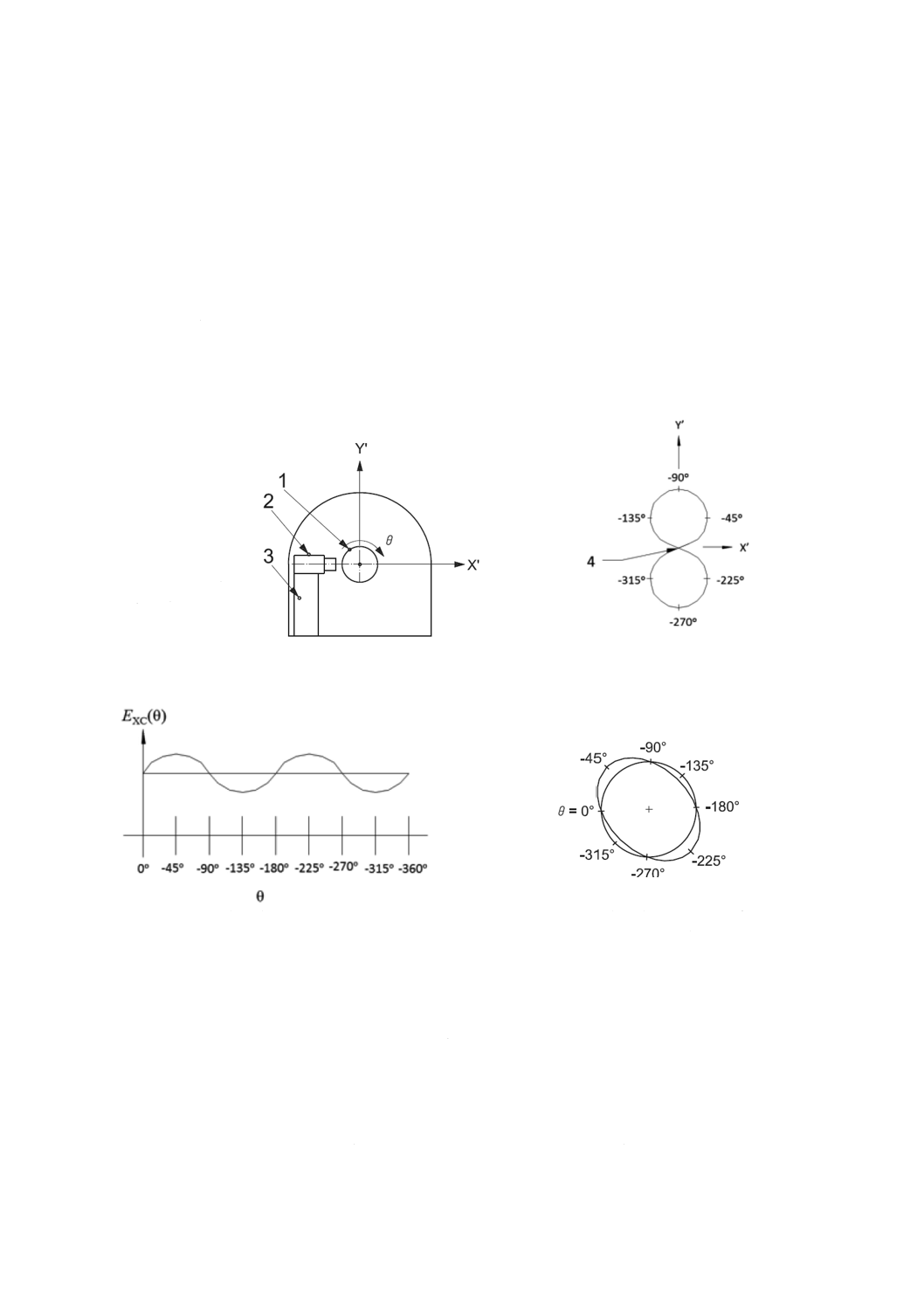
38
B 6190-7:2019 (ISO 230-7:2015)
に配置した変位計を示す。図A.7 b) は,変位計に対してX'Y'平面内での回転軸の仮想経路を拡大した図を
示す。この図では,仮想経路に回転角の値を添えて示してあるが,繰返し性のある8の字パターンを描い
ている。図A.7 c) は,基準球の運動が8の字パターンを描いたときの結果を,回転角を横軸にとり,縦軸
に変位計で測定した半径方向誤差運動をとって表示した図を表す。変位計から離れる方向の基準球の運動
は,正の誤差運動(正負の表示は,JIS B 6310による。)になることに注意する必要がある。図A.7 d) は,
図A.7 c) と同じデータを用いて描いた半径方向誤差運動の極座標線図を表す。この図は,任意の一定半径
の円に対して描いてある。図示したように,8の字パターンは,長軸が傾いただ円形をした半径方向誤差
運動の極座標線図になる。もちろん,非感度方向にほかの運動が生じても半径方向誤差運動は変わらない
ので,だ円を描くのに8の字パターンが必要というわけではない。
注11) 旋盤の場合は,主軸の正回転はθの負の方向であることに注意する必要がある。
1 基準球
2 変位計
3 刃物台
4 X,Z基準軸
θ 回転角
a) 心押し台側から見た半径方向誤差運動試験
b) 心押し台側から見たX'-Y'平面内における
回転軸の経路の拡大図
c) 半径方向誤差運動の直交座標表示
[回転角度位置に対する図b) のX'成分]
d) 半径方向誤差運動の極座標線図
[図c) の極座標線図]
図A.7−半径方向誤差運動の測定及び表示の例
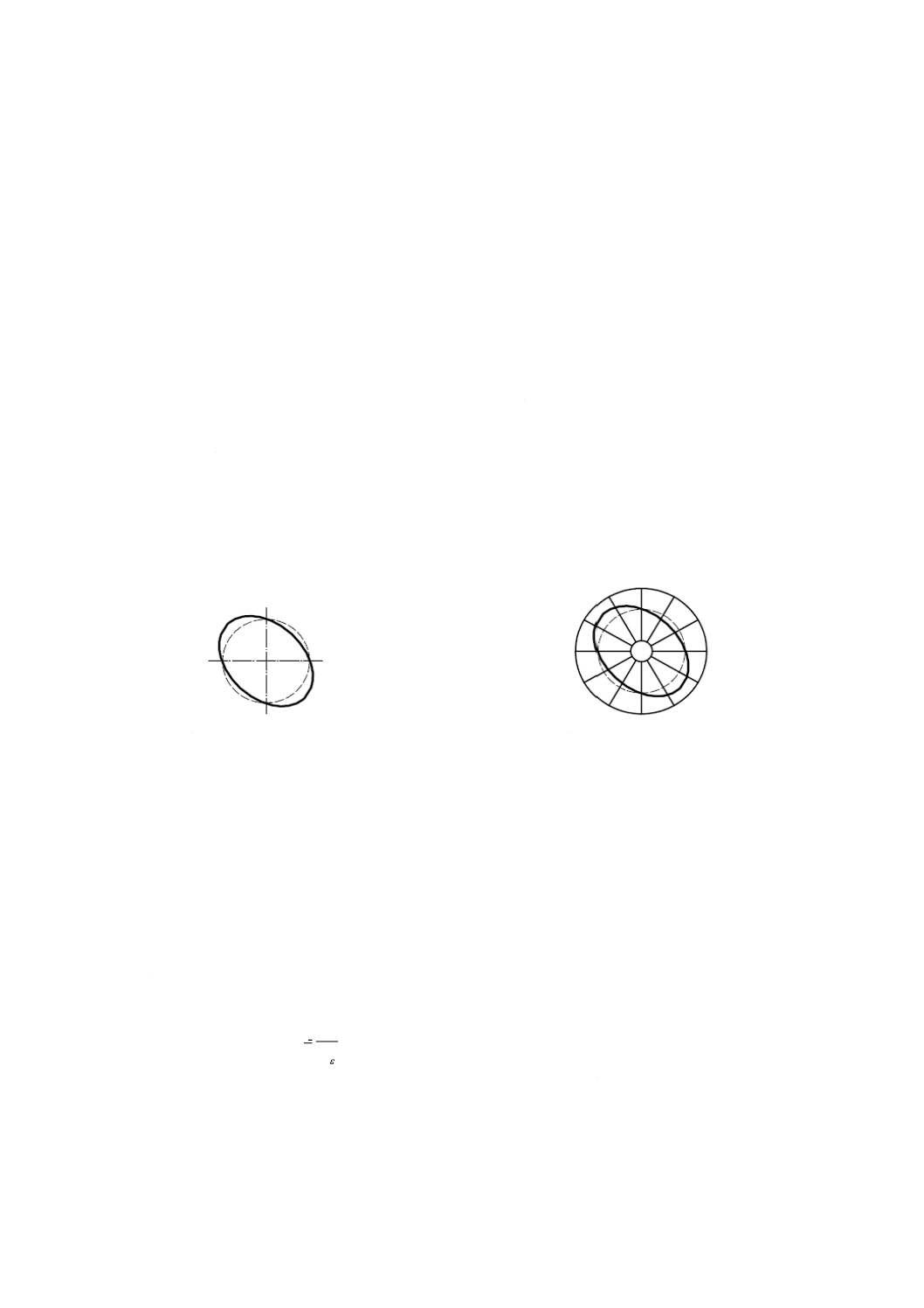
A.7.3 平均半径方向誤差運動及び工作物の真円度
図A.7 a) の変位計を理想の切削工具(たわみ,摩耗などがなく,位置と正確に一致させて切削できる工
具)と置き換えると,工作物は,8の字パターンの運動によって非円形になることは明らかである。感度
方向にある軸の運動だけが工作物の半径に影響する。したがって,正の半径方向誤差運動(刃物台からの)
は工作物直径を大きくし,負の半径方向誤差運動は直径を小さくする。その工作物を取り外し,真円度測
定器に載せて測定すると,真円度曲線は図A.8に示すように図A.7 d) の曲線と同じになる。すなわち,二
39
B 6190-7:2019 (ISO 230-7:2015)
つの図の真円度は同じになる。したがって,回転軸の半径方向誤差運動の極座標線図は,理想切削状態で
仕上げることができる最良の工作物真円度を与えることになる。理想的でない実際の切削では,構成刃先,
工具摩耗,工具のたわみなどのほか,送りマーク,チャッキングによる変形,熱変形,残留応力の解放な
どのような他の要因があってこの真円度を実現することはできない。
理想的な切削が行われ,半径方向誤差運動に繰返し性がある場合に,工作物を切削後に外すことなくそ
のままチャックした状態で,変位計を刃物台上に取り付けて測定すると,工作物表面の半径方向の振れは
ゼロになる。半径方向誤差運動と工作物真円度誤差とは,大きさは等しいが符号が異なるために打ち消さ
れる。これは,半径方向誤差運動及び半径方向の振れの測定値の違いの例を表す(A.8参照)。
この例では,回転軸の誤差運動が1回転ごとに正確に繰り返されると仮定し理想化している。実際には
図7に示すように繰返し性のない運動になる。図7 a) は,繰返し性のない誤差運動の典型的な例であり,
全誤差運動線図を表す。図7 b) は,図7 a) に示す各回転角度位置で記録した回転数分の半径方向誤差運
動を平均化した同期誤差運動線図を表す。図7 c) は,全誤差運動線図と同期誤差運動線図との差をとった
非同期誤差運動線図を表す。
旋削作業については同期誤差運動線図は,工作物の形状誤差の指標であるといえる場合もある(半径方
向誤差運動が工作物の真円度の指標となるように)。これは,1回転ごとの全誤差運動の極座標線図の形が
同期誤差運動線図の形に似ているときに成り立つ。
a) 半径方向誤差運動線図
b) 工作物の真円度曲線
図A.8−工作物の真円度と半径方向誤差運動との関係(図A.7の例)
A.7.4 非同期誤差運動及び表面粗さ
非同期誤差運動線図は,理想的な切削条件下で得られる表面粗さの予測に利用することができる。通常,
旋削仕上げ面の表面粗さは,回転方向にできる送りマークに対して直角な方向(すなわち,円筒の軸に平
行な方向,端面の場合は放射方向)に測定することを考えると,この表面粗さ測定は,全誤差運動線図に
おける一つの回転角度位置で連続的に求めた軌跡の,ある回転数分の断面を取り出して行っていることと
一致している。非同期誤差運動がゼロの場合,よく知られている“理論上の仕上げ”になり,表面粗さは,
図A.9 a) に示すように工具刃先半径に関連した“筋状のマーク”だけになる。理論上の仕上げ面の山の最
大高さRtは,刃先半径をrε及び1回転当たりの送り量をsとすると,次式で近似できる。
εr
s
R
8
2
t=
(sがrεと比べて小さい場合) ······································ (A.7)
Rtの値は,簡単に小さくすることができる。例えば,s=0.02 mm/rev及びrε=5 mmのとき,Rt=0.01 μm
になる。
しかし,非同期運動が存在すると,連続回転させたとき表面は,図A.9 b) に示すように1回転ごとに山
の高さが変化しながら切削されることになる。表面粗さのカットオフ値(通常,送り量が0.02 mm/revの

40
B 6190-7:2019 (ISO 230-7:2015)
とき0.8 mm)が1回転当たりの送り量よりも数倍大きい場合には,非同期誤差運動の大きさがそれと等し
い表面粗さの最大高さ粗さに変換される。非同期誤差運動の大きさと式(A.7)から求めたRtとの和が理想的
な切削条件下での機械のもつ潜在的な表面粗さの最大高さになり,この値の約1/4がRa(算術平均粗さ)
になる。この潜在的な表面粗さは,非鉄金属材料を鋭い刃先をもつダイヤモンドバイトで切削したときに
得られる。しかし,ほとんどの切削条件ではバイトにできる構成刃先によって表面粗さの値が大きくなる。
幾つかの条件,例えば,平先バイトによる外丸削り,といし車による円筒研削,又はどの工具でも送り速
度がゼロになるドウエルのような工具が何回転も工作物上の同じ点と接触を繰り返すような場合は,工具
に対する工作物の最大の変位位置まで材料が除去されるといえる。したがって,(図A.9の符号の定義を用
いて)図7 e) に示す全誤差運動線図の内側を包絡する輪郭線である内側誤差運動線図から部品の潜在的な
真円度を予測することができる。円筒穴内面を研削する場合は,外側誤差運動線図が同様の意味をもつ[図
7 d) 参照]。切削条件が理想的でない場合と同様に,連続して測定した極座標線図の繰返し性が低いとこ
のような予測の信頼性は制限を受ける。
s
R
t
a)
a) 非同期運動がゼロのときの理想的な
b) 理想的な切削による最大高さ粗さに及ぼす
切削による理論上の仕上げ
非同期運動の影響
注a) 非同期誤差運動
図A.9−表面粗さと非同期誤差運動との関係
A.7.5 軸受及び構造誤差運動
極座標線図は,回転軸の性能予測に有効なことに加えて,観察された誤差運動の物理的な要因の診断に
も利用できる。この意味で,完全に繰り返す同期誤差運動線図に非同期誤差運動線図を重畳した全誤差運
動を表示することは有益である。同期誤差運動線図の輪郭に,軸の回転周波数に等しいか又は整数倍の周
波数の成分だけが含まれることを数学的に示すことができる。したがって,主軸(又は回転テーブル若し
くは旋回主軸頭)の軸受及びその駆動系が同期誤差運動の要因になる可能性が高い。特に,流体軸受(動
圧,静圧及び空気圧)は,繰返し性の高いパターンを示す。
用語,“非同期誤差運動”は,その物理的要因が統計的な意味でランダムである必要はなく,何回か回転
させた後の全誤差運動線図を単に指している。実際には,非同期誤差運動は,軸の回転周波数の整数倍で
ない周波数で運転されるモータ又はポンプのようなランダムでない要因によって発生することがよくある。
このような考察は,同期誤差運動が軸受誤差運動と同じであり,かつ,非同期誤差運動は構造誤差運動
と同じであることを示唆している。しかし,これでは,通常,単純化をし過ぎていることになる。非同期
誤差運動は,空気軸受では低レベルの空気ハンマによる不安定性,また,転がり軸受では転動体(球,こ
ろ)又は転動面の不完全さによって発生する。玉軸受及びころ軸受は,軸の回転速度の約1/2の速度で回
転する転動体の公転周期が原因で,2回転に1回の周期のパターンを示すことがある12)。滑り軸受は,回
転速度の1/2弱の周波数で振動するオイルホワールと呼ばれる動圧作用によって振動を発生することがあ
る。この場合には,1回転ごとの全誤差運動線図の違いが軸受の誤差運動に起因する非同期誤差運動を表
41
B 6190-7:2019 (ISO 230-7:2015)
す。同期誤差運動は,軸の回転周波数の整数倍で駆動する軸の構成部品,又は軸の回転周波数と偶然に同
期することがある回転軸に関係しない部品のような軸受以外の要因によって起こり得る。
誤差運動の原因を特定する有効な方法は,スイッチを入れたり切ったりするか,又は速度を変えたりし
たときの変化に注目することである。もう一つの方法は,回転軸の速度を変化させることである。軸の速
度がゼロのとき,残っている“雲バンド(cloud band)”の厚さは,軸受及び駆動系以外の要因による非同
期誤差運動を表す。また,軸を静止させ,回転角度位置を少しずつ変えて測定した静的誤差運動線図から,
軸の速度ゼロにおける同期誤差運動線図を求めることができる。この回転角度位置の間隔を密にしないで
あけてしまうと,平均誤差運動線図から高周波成分(1回転当たりのサイクル数を単位として)も取り除
かれてしまうことに注意するとよい。同期誤差運動線図に高周波成分が存在する可能性があり,ローパス
フィルタを使用すると同期誤差運動の一部が取り除かれる可能性があるので,非同期誤差運動を除去する
ためのローパスフィルタの使用は避ける。FFTのような周波数解析は,誤差運動の同期・非同期成分を分
離するために使用できる。
この附属書は,回転軸の評価に誤差運動のどの原因を含めるかについて指定しているわけではない。例
えば,機械が高いレベルの建物振動の影響を受ける場合には,通常は,機械が環境の犠牲になっていると
見ることができる。ただし,誤差運動の発生原因として建物振動を含むことを意図している場合には,機
械をそのような環境で使用することを意図して,特別に設計した機能の付いた機械を購入することがある。
そのような場合には,意図的に建物振動を誤差原因として含んだ誤差運動試験を行うことが望ましい。
注12) 軸受の転動体と関係する繰返しパターンの正確な回転数xは,軸受の内径Ri,転動体中心半径
Rbによって決まる。すなわち,x=2Rb/Ri。
A.7.6 基本及び剰余誤差運動
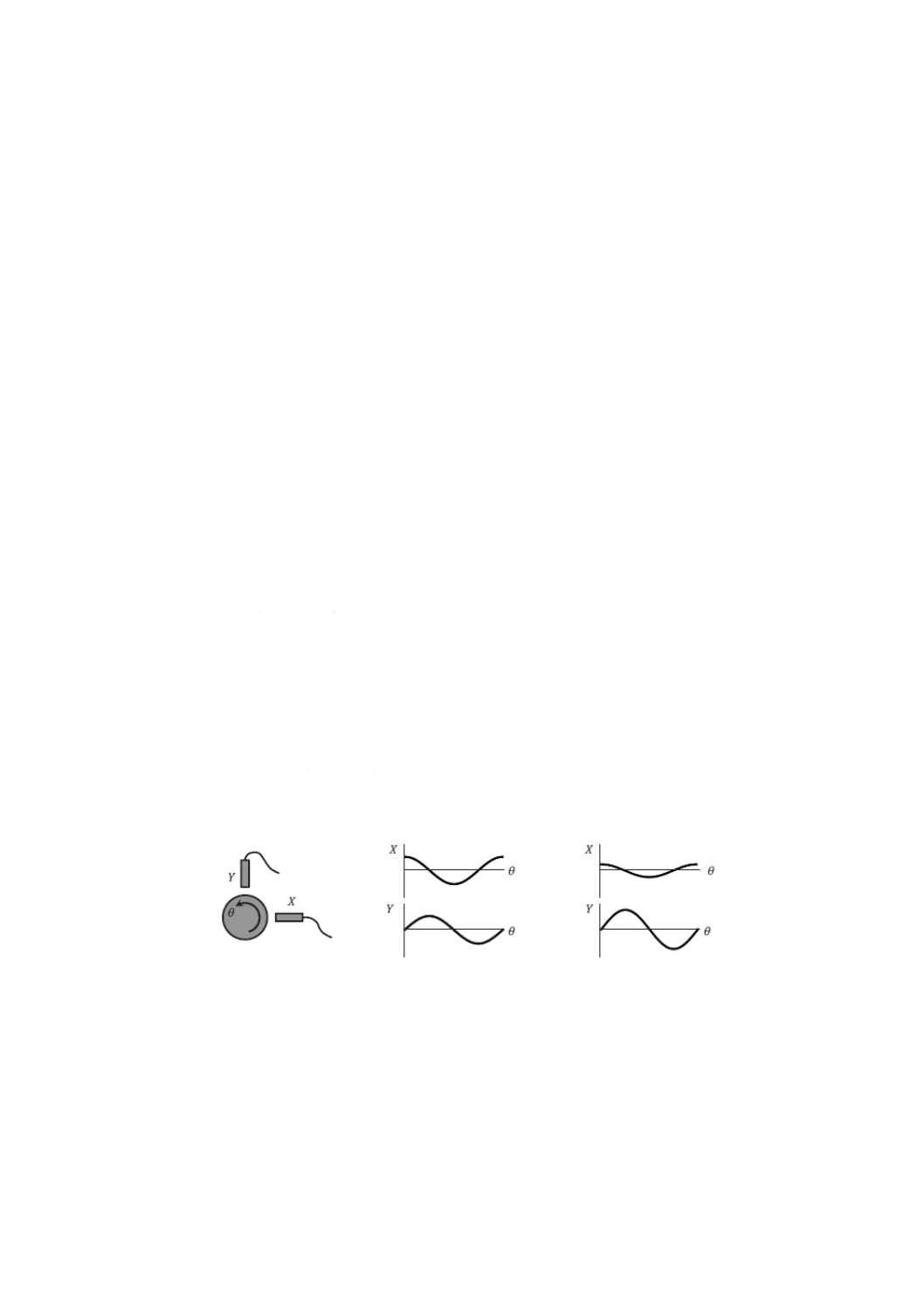
用語,“基本誤差運動”は,1回転に一度の周期で現れる正弦波状の誤差運動(1次の調和振動成分)の
意味で用いる。直交2方向に配置した変位計で検出される基本誤差運動は,回転部品の構造剛性が方向に
よって変化するなどの様々な要因によって発生する。X方向とY方向との間に構造上の差異がない場合,
観察される基本誤差運動は,図A.10 b) に示すように90°位相がずれている点を除いて同じとなる。ただ
し,構造が非対称になるとX方向とY方向との基本誤差運動は,図A.10 c) に示すように振幅と位相とに
差が現れることがある。
a) 変位計及び回転軸
b) 構造上対称な誤差運動
c) 構造上非対称な誤差運動
図A.10−構造対称及び非対称による回転軸の誤差運動
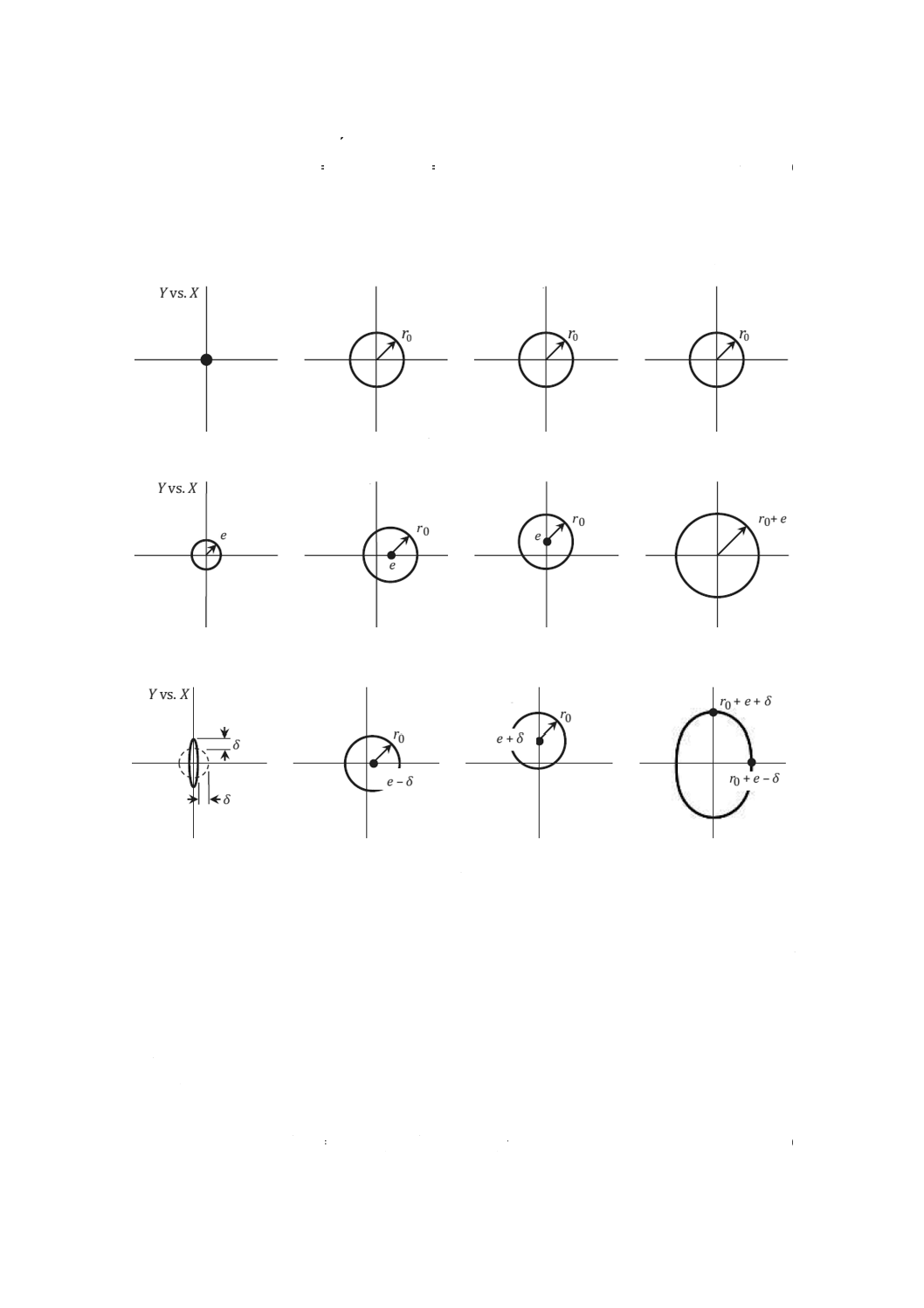
例えば,図A.11は,回転軸の誤差運動の測定値が構造の対称・非対称によってどのように影響されるか
を示している。完全主軸(ΔX=ΔY=0)については,測定値は,図A.11 a) に示すように,回転感度方向
(RSD)の極座標線図と同様に固定感度方向(FSD)において完全円を描いている。半径r0は,線図を描
くために用いた基礎円の半径を表す。
構造対称による基本誤差運動eをもった主軸[図A.11 b) 参照]については,変位計で検出される運動
42
B 6190-7:2019 (ISO 230-7:2015)
は,次の式(A.8)で表すことができる。 ()
q
cos
e
ΔXe=
,
()
q
sin
e
ΔYe=
··················································· (A.8)
ここに,eは,方向によって変化しないコンプライアンスをもった構造の弾性変形によって生じる,1
回転当たり一定の誤差運動成分を表す。
運動
FSD X方向
FSD Y方向
RSD 極座標線図
a) 完全主軸
b) 構造対称による基本誤差運動eをもった主軸
c) 構造対称による基本誤差運動e及び構造非対称による基本誤差運動δをもった主軸
図A.11−回転軸誤差運動に及ぼす構造の対称及び非対称の影響
図A.11 b) は,誤差運動を表す固定感度方向及び回転感度方向の極座標線図を示す。これらの線図から
結果として得られる運動は,旋削作業(固定感度方向)においては旋削した部品の形状に影響を及ぼすこ
とはない。同様に中ぐり作業(回転感度方向)においては穴の輪郭が円形であり形状誤差はない。一方,
そのような運動は,工作物の寸法に影響を与えるが,加工中に使用する工具オフセットによって調整でき
る。したがって,この種の基本誤差運動の影響は,基準球を回転軸に心合わせすることによって測定値か
ら取り除くことができる。
構造非対象による基本誤差運動δ[図A.11 c) 参照]をもつ回転軸について,変位計で観察できる誤差運
動は,式(A.9)及び式(A.10)で表すことができる。
()
q
δ
δ
cos
−
=
ΔX
,
()
q
δ
δ
sin
=
ΔY
················································ (A.9)
ここに,δは,方向依存性のあるコンプライアンス(構造非対称)をもつ弾性構造による1回転当たり
43
B 6190-7:2019 (ISO 230-7:2015)
の誤差運動成分を表す。
剛性の非対称が原因になる場合には,δの値は,回転周波数,不釣合い質量,並びに回転軸のX及びY
方向の剛性の関数となる[14]。
図A.11 c) に示すように,構造の対称・非対称の成分が組み合わさると,完全回転軸は,円軌跡ではな
くだ円軌跡上を運動する。この場合に変位計で観察する運動は,次の式(A.10)で表すことができる。
(
)
q
δcos
−
=e
ΔX
,
(
)
q
δsin
+
=e
ΔY
··········································(A.10)
だ円になることは,図A.10 c) に示すようにX方向及びY方向の基本誤差運動の振幅が異なることを意
味している。その結果,回転感度方向(RSD)の極座標線図は円ではなく,構造の非対称による誤差運動
δをもつだ円形になる。式(A.10)から,X方向の剛性が無限でY方向に弾性変形する特殊な場合には,X
軸がr0及びY軸がr0+2δのだ円となる。したがって,構造非対称による基本誤差運動は,無視できない
形状誤差を発生する可能性がある。
要約すると,基本誤差運動には二つの要素がある。すなわち,回転の向き(θ)と共に変化し1回転に一
度の正弦波状の誤差運動と関係する正の基本成分,及び回転の向きとは反対の向き(−θ)に変化する1
回転に一度の正弦波状の誤差運動と関係する負の基本成分からなる。特に,図A.11 c) のX,Yのデータ
は,二つの対に分解することができる。すなわち,一つの対は,図A.11 b) に似ていて,X,Yデータ間
に90°の位相遅れが存在する振幅eの正弦波の対に,もう一つの対は,90°の位相進みが存在する振幅δ
の正弦波の対に分解できる。この基本誤差成分の対の“正”又は“負”の性質は,XY空間で見ることが
できる。すなわち,ベクトル(X,Y)は,構造の対称による第1の対に対してθ(正の向き)と共に回転
し,一方,そのベクトル(X,Y)は,構造非対称による第2の対に対して−θ(負の向き)と共に回転す
る。
同様に,構造対称(軸平均線の方向として)による傾斜方向誤差運動の基本成分の影響は,直進軸の運
動によって補正することができる。したがって,基本傾斜方向誤差運動は,回転軸の試験では考慮しない。
これは,不完全回転軸上に取り付けた完全円筒を考えることによって理解することができる。円筒の両端
で心合わせ誤差がないように調整して取り付ければ,1回転に一度の傾斜方向誤差運動は現れない。よく
知られている用語“coning”,“wobble”及び“swash”は,1回転に一度現れる成分を想起させるが,傾斜
方向誤差運動の用語としては適切でない。
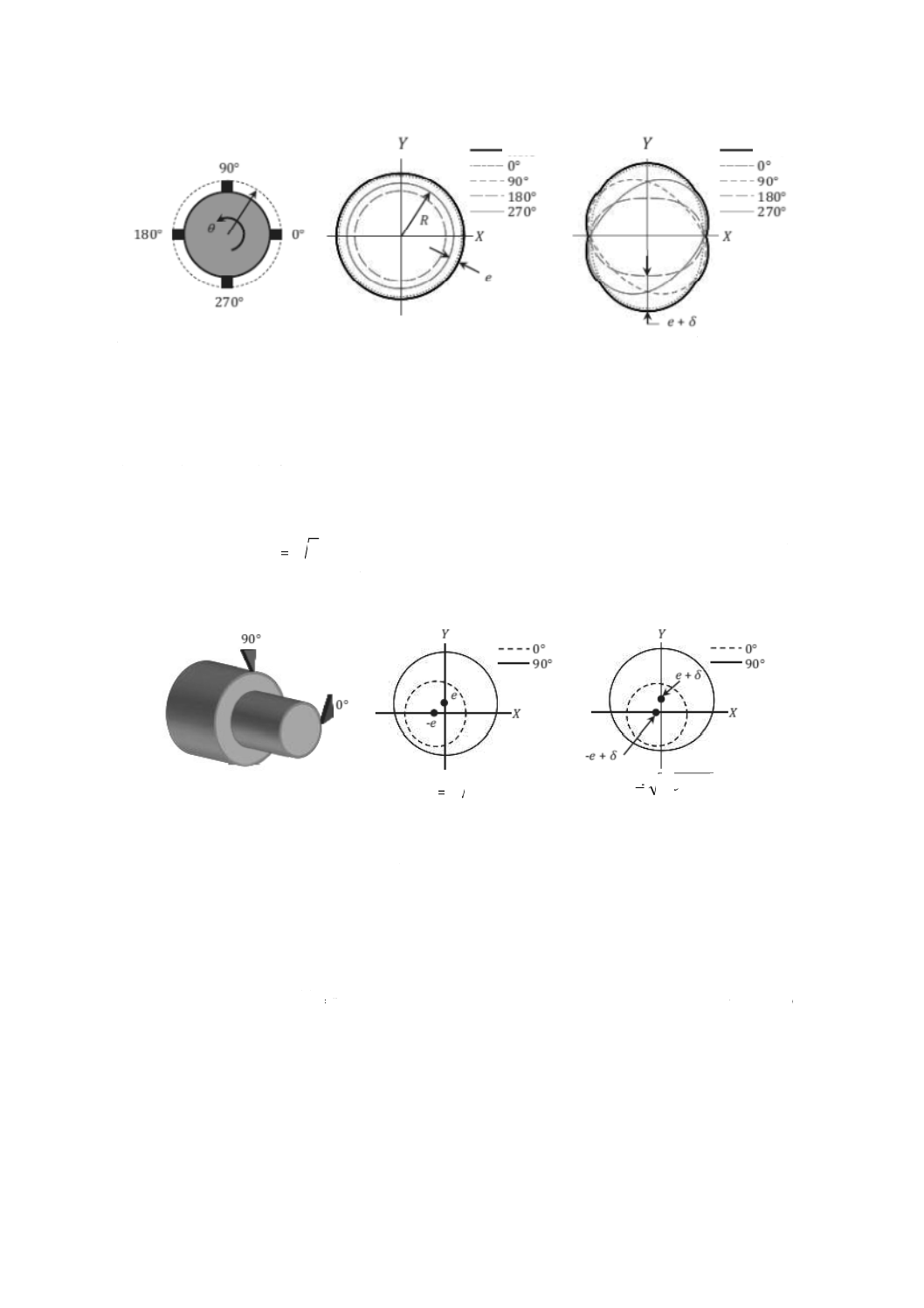
構造非対称は,複数の回転感度方向を伴う場合には,無視できない形状誤差を発生させる可能性がある。
例えば,図A.12 a) は,直径回りに均等に配列された4枚の切れ刃をもつ中ぐり棒を示すが,中ぐり加工
中に切れ刃が接触していれば,それぞれの切れ刃は,回転感度方向の式(1)に従って穴の輪郭を創成する。
純粋に構造対称だけが式(A.8)に従って存在する場合,中ぐり穴の断面形状は,図A.12 b) に示すように設
定した半径Rよりも僅かに大きな円形になる。ただし,式(A.8)及び式(A.9)に従う構造対称・非対称が存在
すると,穴は図A.12 c) に示すように構造非対称δに依存してその形状が大きくなり,かつ,非円形にな
る。
44
B 6190-7:2019 (ISO 230-7:2015)
穴
穴
a) 90°間隔に配列された4枚の
b) 構造の対称だけによる
c) 構造の対称及び非対称の両方に
切れ刃をもつ中ぐり棒
中ぐりされた穴の断面
よる中ぐりされた穴の断面
図A.12−構造の対称及び非対称の両方による中ぐりされた穴の断面
構造の対称・非対称は,二つ以上の固定感度方向に関係する場合に無視できない大きさの位置及び角度
誤差を発生させる。例えば,図A.13 a) に示すように,互いに直交する向きから二つのバイトで2段にな
った軸を旋削する場合を考える。それぞれのバイトは,図A.11 a) に示す軸の輪郭を創成する。式(A.8)に
従う構造の対称だけ存在する場合には,旋削した軸は,見掛けは円筒になるが,図A.13 b) に示すように
二つの円筒の中心は,
2
O
e
C=
だけオフセットする。同様に式(A.9)に従う構造の非対称だけが存在する
場合には,旋削した軸は,図A.13 c) に示すように,さらに,δだけオフセットした円筒になる。
a) 直交して配置した二つの
b) 構造の対称だけによる
c) 構造の対称及び非対称の両方に
バイトによる旋削
軸の断面
よる中ぐりされた軸の断面
図A.13−構造の対称と非対称とが存在するときに複数の向きから旋削された軸の断面
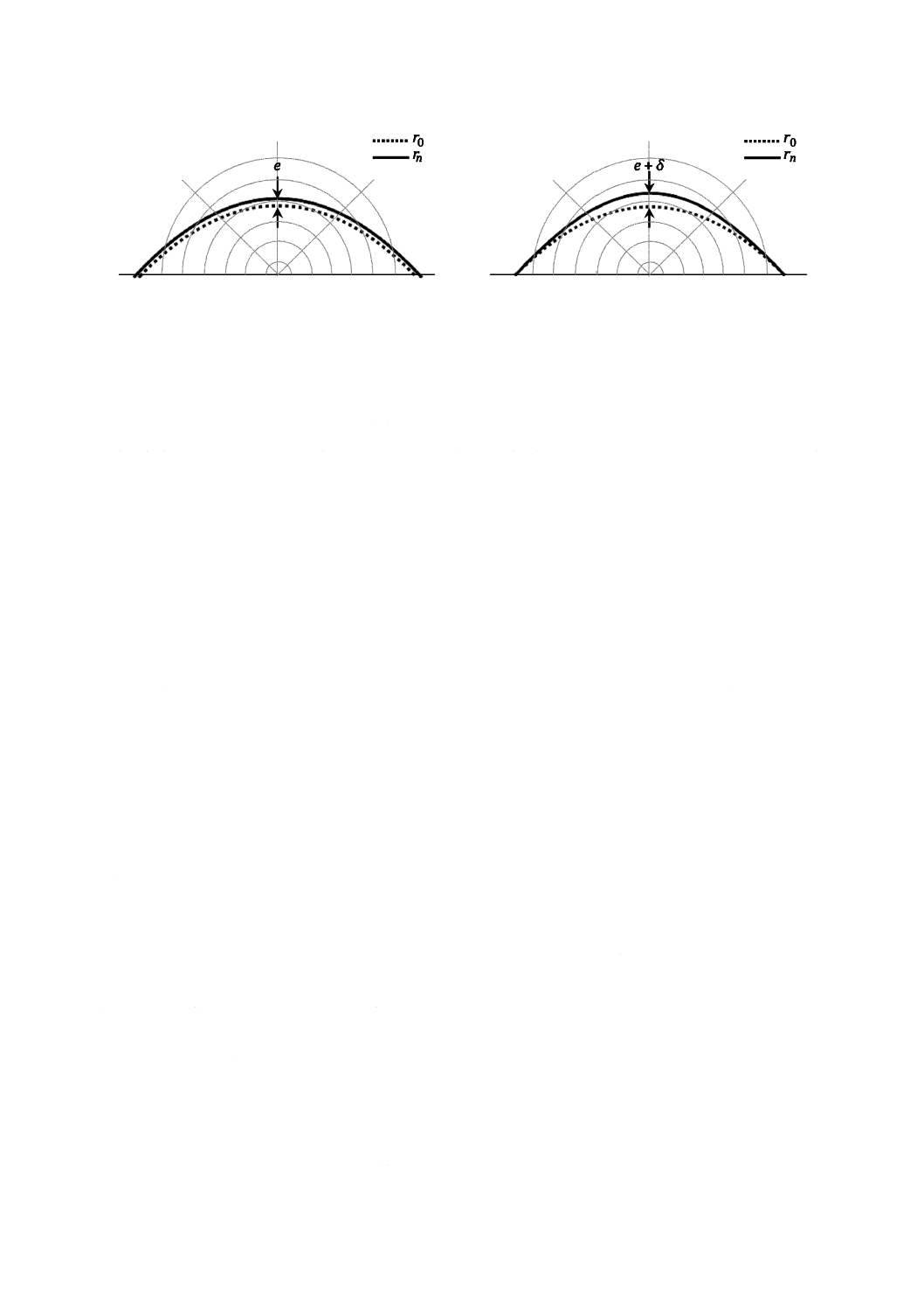
変動感度方向の場合も,無視できない形状,位置及び向きの誤差が発生することがあるので,注意する
のが望ましい。構造の対称・非対称の成分e及びδに起因する基本誤差運動について,変動感度方向に沿
った半径方向誤差運動の影響は,式(1)及び式(A.10)を使って次のように導くことができる。
()
(
)
(
)
q
q
δ
q
q
q
+
−
−
+
=
n
n
n
e
r
r
cos
cos
············································ (A.11)
ここに,θnは,θの関数として感度方向の角度を表す。
例として,図A.14は,構造の対称・非対称による基本誤差運動がもたらした放物線形状からの偏差を示
す。
(
)
2
2
O
2
δ
+
=
e
C
2
O
e
C=
45
B 6190-7:2019 (ISO 230-7:2015)
図A.14−構造の対称と非対称とによる基本誤差運動の変動感度方向に及ぼす影響
逆に,軸方向誤差運動の基本成分は,加工された部品の形状誤差に1対1の影響を与える。これは,軸
平均線に平行な回転軸の1回転に一度の軸方向の滑り運動によるもので,例えば,軸平均線と直角でない
スラスト軸受から発生している可能性がある。したがって,これは,通常,回転軸の試験で評価する。
式(A.3)は,基本端面方向誤差運動が存在し,基本軸方向誤差運動に等しいことを示している。これは,
完全回転軸に取り付けられた完全に平らな円板を想像すれば理解することができる。取付誤差は,1回転
に一度の正弦波の端面方向運動(半径に正比例して増加する。)になるが,円板が回転軸と完全に直角の場
合,その端面方向運動は発生しない。そこで,円板が回転軸と完全に直角であるとし,完全回転軸から基
本軸方向誤差運動の生じている軸まで変化するとすれば,同じ基本誤差運動が全ての半径方向で起こるこ
とになる。したがって,基本端面方向運動が全ての半径方向で同じの場合,完全に平らな円板は,不完全
な回転軸と直角になる。回転軸に直角でなく円板を取り付けると基本端面方向運動を打ち消すことが可能
になるが,この打消しは一つの半径でだけ可能になる。基本端面運動を打ち消すのに必要な円盤の傾きは,
半径が小さければ小さいほど大きくなり,半径ゼロでは打消しは不可能になる。
基本端面方向誤差運動が存在する場合,端面を加工し測定すると面白い結果が現れる。基本軸方向誤差
運動が存在することを除いて完全な軸上で円盤の面削りを行うと,仕上げられた端面は,多数の面削りさ
れた薄いリングから構成されているように見える。しかも,それぞれのリングには,回転軸との直角度に
僅かに狂いがある。その量は,半径の減少と共に大きくなる。そのような部品は,端面全体を見ると平面
ではない。ただし,その部品を軸方向変位の検出ができる変位計を備えた真円度測定器に載せて部品の中
心と同心の円経路上をその変位計でなぞるようにして測定したとき,部品を傾ければ平面度誤差が検出さ
れないようにすることができる。そのような部品は,円形の平面度をもつといわれている。そうでない場
合,端面全体の領域で見ると平面ではないので,円経路上での平面度測定は適切に理解されず誤解される
可能性がある。
剰余誤差運動は,同期誤差運動と基本誤差運動との差を表す。剰余誤差運動の結果は,同期半径方向誤
差運動の結果と似ている。例えば,加工中の剰余端面方向運動は,同期半径方向誤差運動が真円度の誤差
につながるのと同様に,円経路上で測定した平面度の狂いになる。軸平均線からの任意の感度方向角度ϕ
における一般的な誤差運動の場合に,基本誤差運動は,基本軸方向誤差運動のcosϕ倍に比例する[式(A.4)
参照]。例えば,45°テーパは基本端面方向誤差運動の70.7 %が関係していることになる。
A.8 不釣合いの影響
回転部品の不釣合いは,主軸速度の二乗に比例した正弦波状に変化し,回転感度方向に作用する力が最
大値となる。完全回転軸に不釣合いがあると,その結果は,ある速度では完全に丸い部品を加工できるが,
それと異なる速度では心出し誤差が現れることを示している。一つの円筒部品の2か所を別々の速度で加
工すると,その2か所の円筒断面の中心線は同軸にならない。その回転体に対する回転軸のずれが,半径
46
B 6190-7:2019 (ISO 230-7:2015)
方向成分と同様に,傾きに関係する場合には,これら二つの円筒の中心線は平行にはならない。また,傾
斜方向における軸ずれは,機械の案内面に対する回転軸の平行度又は直角度を変えるので,円筒がテーパ
状に加工されたり端面が円すい状に加工されたりする。
この議論は,最初に心出し済みの基準球が不釣合いによって円形の軌道を通ると仮定している。構造ル
ープが非線形ばね定数及び/又は非対称ばね定数をもっている場合の不釣合いは,円筒部の真円度及び端
面の平面度の狂いにつながる高次の調和運動を起こす可能性がある。回転要素の釣合いを調整することは,
この理由から重要となる。
旋削による表面仕上げを行う場合に,その表面仕上げは,不釣合いと全く関係しない。鏡面仕上げを実
現するためには,滑らかで,静粛で,かつ,振動のない機械が必要とされるのが明らかなように,このこ
とを信じられないと思っている人がいる。それは,事実,円筒研削盤の場合には絶対的に基本的なことだ
からである。それではなぜそれが旋盤に必要でないかを理解するには,同期振動と非同期振動との差を考
える必要がある。不釣合いは,次のような同期運動を引き起こす。すなわち,旋削における同期運動は,
工具と回転軸との相対位置が1回転ごとに同じであるので仕上げに影響しない。不釣合いが大きくても,
それ以外が完全な旋盤の場合,理論上の仕上げを達成できる[図A.9 a) 参照]。
非同期誤差運動は,主軸回転周波数の整数倍以外の周波数で生じる主軸に対する工具の運動を表す。そ
れは,1回転ごとの回転軸に対する工具の位置に影響し,その結果,表面仕上げに影響する[図A.9 b) 参
照]。円筒研削盤による表面仕上げは,不釣合いの影響を受ける。それは,といし軸と工作主軸との回転速
度が違っていて,といし軸の同期誤差運動が自動的に工作主軸に対する非同期誤差運動になるからである。
A.9 基準球の誤差
これまで,幾何学的に完全な基準球又は同等の基準器が様々な誤差運動測定の例で使用できると仮定し
てきた。1個の基準球に幾何学的な誤差があると誤った誤差運動測定を行っていることになることは明白
であり,常にその基準球が無視し得る程度の誤差しかないと仮定できるわけではない。附属書Bに,回転
軸の同期誤差運動成分から基準の誤差を分離する方法を示す。
A.10 誤差運動と振れ又はTIRとの違い
誤差運動の測定は,振れ又はTIR(読みの最大差)の測定と幾つかの点で異なっていることに注意した
ほうがよい。過去,回転軸の精度評価に振れ試験が広く採用されてきた。したがって,振れ試験との違い
を理解しておくことは重要となる。振れは,“運動する表面に対して測定器で測定された全変位,又は固定
した表面に対して運動した全変位”と定義されている。この定義では,半径方向の振れの測定は,変位計
が検出する表面の真円度誤差及び心出し誤差の両方を含むことになる。したがって,半径方向の振れは,
これら真円度誤差及び心出し誤差の両方がゼロの場合にだけ半径方向誤差運動と同じになる。既に記載し
たように,これらをゼロにすることは容易ではない。心出し誤差は,誤差運動よりも大きな振れを発生さ
せることは避けられないが,真円度誤差は,誤差運動よりも振れを大きくしたり,小さくしたりすること
ができる。変位計で検出する表面を同じ主軸の軸受を使って加工する場合には,A.7.3で議論したように,
真円度誤差は,誤差運動よりも小さくなる。同様の議論は,端面方向運動と端面の振れとの関係にも適用
できる。端面の振れの測定は,円板の直角度の誤差及び平面度誤差の両方を含んでいる(A.7.6も参照)。
A.11 固定感度方向の測定に二つの変位計を使用する場合の課題
Bryan(図15)の示した測定方法では特別な装置が必要なことから,固定感度方向をもつ半径方向誤差
47
B 6190-7:2019 (ISO 230-7:2015)
運動の測定にTlusty(図11)の提案した二つの変位計を使用する方法に代えることを考えるのは自然であ
る。この方法を採用すると,半径方向誤差運動線図は,A.7.3で議論したように潜在的な部品の真円度の狂
いを表さなくなる。θ=0°が固定感度方向の場合,極座標線図にはθ=0°及びθ=180°の近傍においてだ
けこの方向の半径方向誤差運動が現れる。さらに,θ=0°では回転軸に与えられた運動が極座標線図の山
として現れ,θ=180°で起こる同様の運動は,符号が反転して谷として現れる。θ=90°とθ=270°とで
はこの運動は極座標線図に現れない。
このようなことを考察しても,まだ,固定感度方向と回転感度方向とで,たとえ極座標線図の詳細が異
なっていても,半径方向誤差運動値は,おおむね同じであると直観的には見える。この見方は,非同期半
径方向誤差運動については妥当である。ただし,同期半径方向誤差運動の場合は,固定感度方向で試験し
たとき,だ円のパターンを示す軸は,回転感度方向で試験したとき半径方向誤差運動を示さない場合があ
る。この場合には,次の誤差運動が発生する。
()
q
q
2
cos
A
ΔX
=
····································································(A.12)
()
q
q
2
sin
A
ΔY
=
····································································(A.13)
ここに,座標系は図A.7 a) に示すものと同じになる。X軸に平行な固定感度方向における半径方向誤差
運動線図は,次の式で表すことができる。
()
q
q
2
cos
0
A
r
r
+
=
··································································(A.14)
ここに,r0は基礎円の半径を表す。式(A.14)は,θ=0°及びθ=180°で値r0−Aを,θ=90°及びθ=270°
で値r0+Aをもつだ円を表す。いずれの極座標輪郭中心に基づく半径方向誤差運動値も2Aとなる。感度方
向が角度θと共に回転すれば,半径方向誤差運動は,次式で与えられる。
()
()
()
q
q
q
q
q
sin
cos
0
ΔY
ΔX
r
r
+
+
=
·············································(A.15)
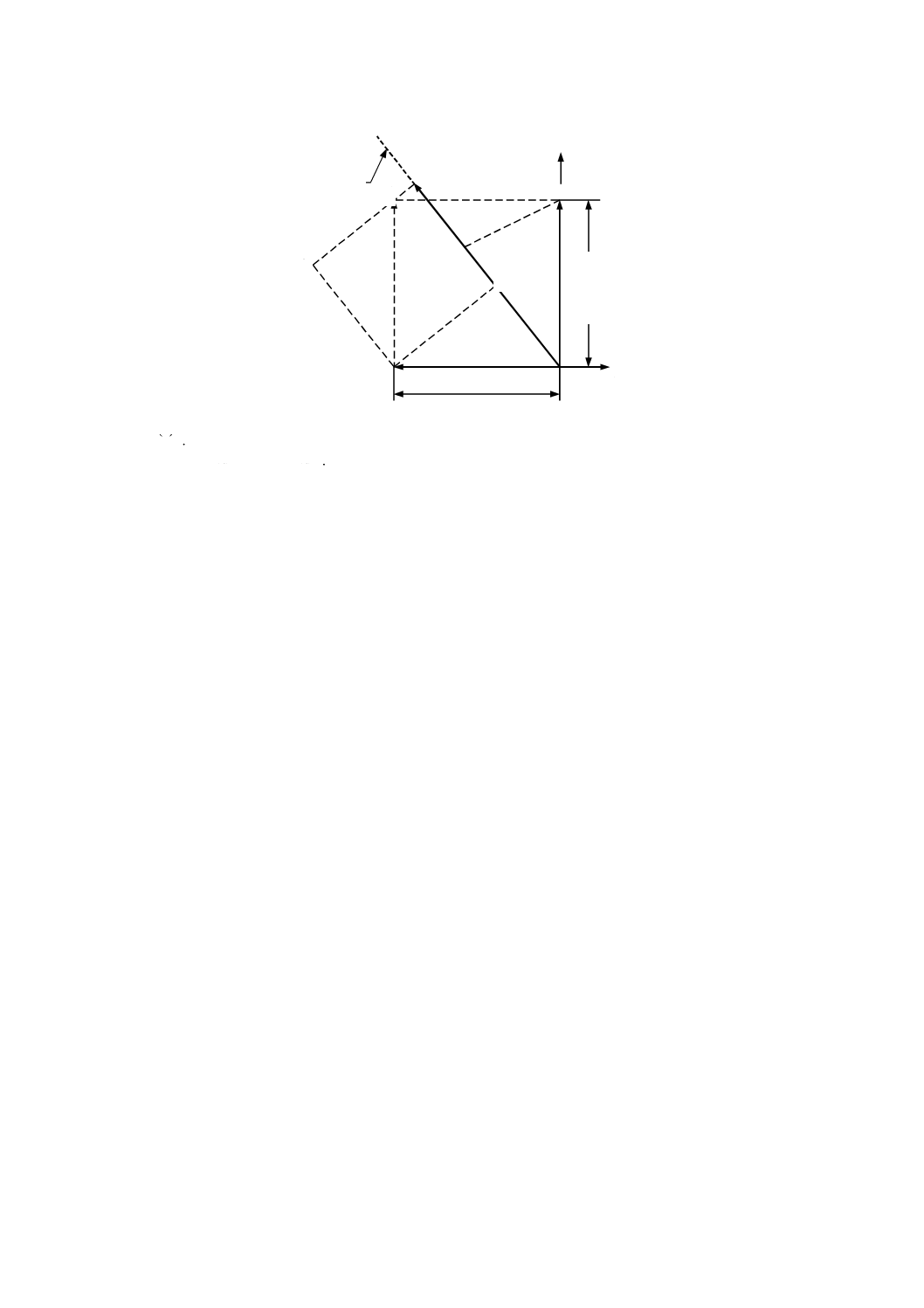
図A.15は,式(A.15)を導くために回転感度方向に平行な成分ΔX(θ) 及びΔY(θ) を示す。式(A.12)及び式
(A.13)を式(A.15)と合成するために,三角関数の定理を用いる。
[
])
cos(
)
cos(
2
1
cos
cos
β
α
β
α
β
α
+
+
−
=
········································(A.16)
[
])
cos(
)
cos(
2
1
sin
sin
β
α
β
α
β
α
+
−
−
=
·········································(A.17)
その結果,式(A.15)は,次のようになる。
[
]
[
]
q
q
q
q
q
q
cos
3
cos
cos
2
3
cos
cos
2
)
(
0
0
A
r
A
A
r
r
+
=
−
+
+
+
=
···············(A.18)
式(A.18)は,原点から距離Aだけオフセットした円の方程式を表す。したがって,二つの変位計で測定
すると,軸は,完全な軸になる。
上記の考察に関して次の二つの考察を追加する。まず,オフセットした円を極座標(PC)中心からの同
心円を用いて評価すると,固定感度方向で値2Aが得られるように思う場合がある。しかし,基礎円は,
図10の試験方法を用いて極座標線図と独立して発生させることはできないので,PC中心位置を合わせる
ために最初に電子的にゼロにする方法がない。もう一つは,上記の例は実際に起こりそうにない,“数学的
に奇異な状態である”と思われる場合がある。しかし,半径方向誤差運動線図は,一般的にだ円パターン
を示す。また,X及びY方向の変位に式(A.12)及び式(A.13)の成分が含まれていても半径方向誤差運動値に
は全く影響しないことに注意を要する。
48
B 6190-7:2019 (ISO 230-7:2015)
a)
f
e′
d′
a′
d
e
a
DX(q )
D
Y
(
q
)
X′
Y′
b
ab=ΔX (θ) cos θ
ad=ΔY (θ) sin θ=a'd'
af=ab+a'd'=ΔX (θ) cos θ+ΔY (θ) sin θ
注a) 感度方向
図A.15−回転感度方向のベクトル図
49
B 6190-7:2019 (ISO 230-7:2015)
附属書B
(参考)
基準球の真円度誤差除去方法
B.1
概要
半径方向誤差運動の測定は,変位計が直接検出対象とする基準球又は基準円盤の真円度誤差に影響され
る。この附属書は,Donaldsonの論文(参考文献[16])に基づいて回転軸の半径方向誤差運動から基準球の
真円度誤差を除去する方法について示す。
基準球の真円度は,P(C)[記号Pは部品(part)を意味する。]で表し,半径方向誤差運動は,S(C)[記
号Sは,回転軸(spindle)を意味する。]で表す。
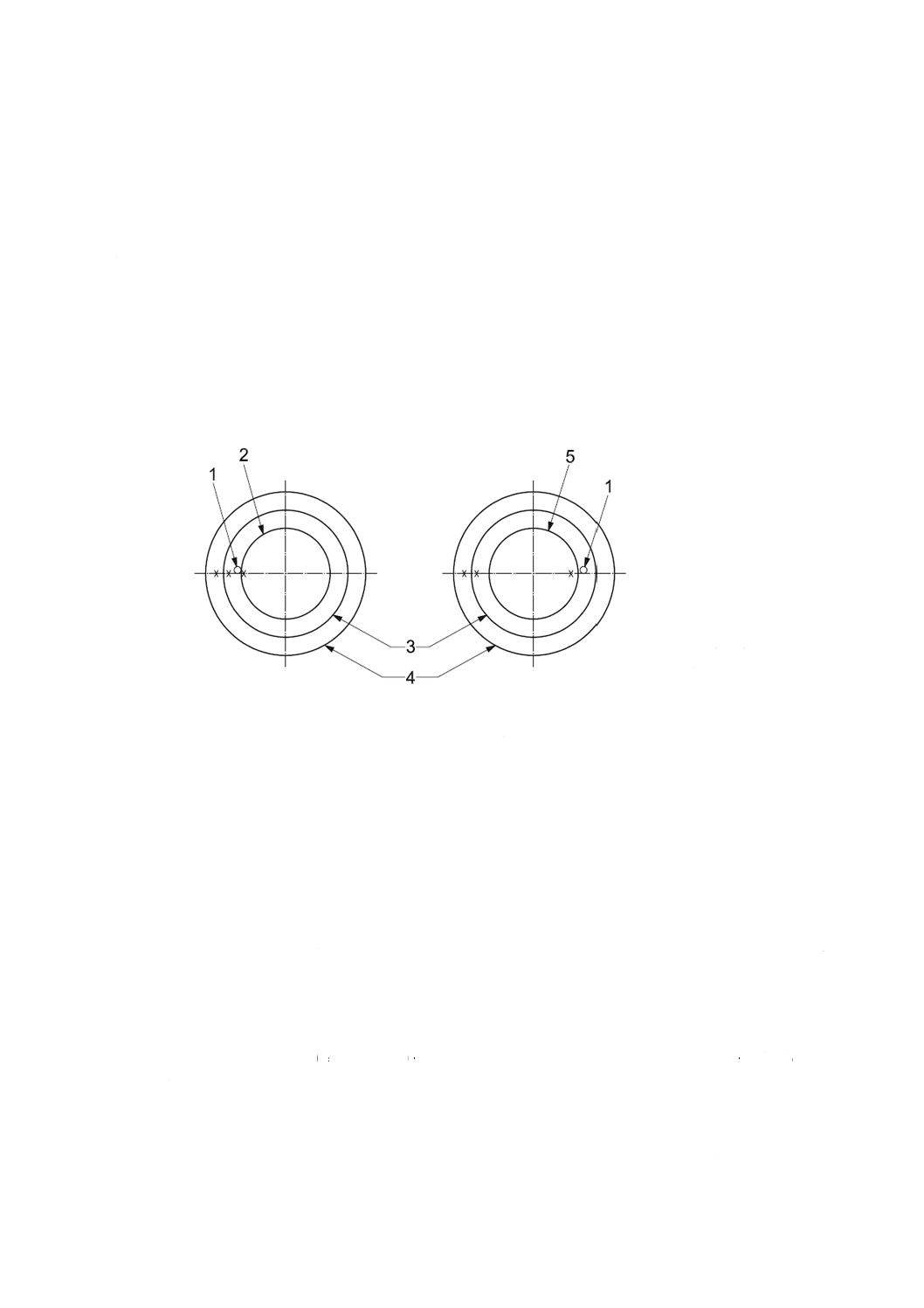
1 変位計
2 基準球
3 回転軸
4 ハウジング
5 反転した基準球
a) T1(C)[式(B.1)参照]
b) T2P(C)[式(B.2)参照]及びT2S(C)[式(B.4)参照]
図B.1−測定用の基準球及び変位計の配置図
B.2
曲線加算平均法
B.2.1 一般
この箇条では,回転軸には非同期半径方向誤差運動がないものと仮定する。非同期誤差運動の取扱いに
ついては,B.4に示す。消去する方法は,二つの方法,すなわち,基準球の真円度誤差を求める方法Pと
半径方向誤差運動を求める方法Sとがある。
B.2.2 方法P
方法Pは,まず初期の極座標線図を記録することから始める。基礎円からの偏差をT1(C) とする。図B.1 a)
は,基準球及び変位計の配置図を示す。この図に示すように,測定装置は,変位計,回転軸及びそのハウ
ジングから構成されている。初期位置は,基準球上に×印を付けた位置をC=0°とする。記録したT1(C) は,
基準球の真円度曲線P(C) と半径方向誤差運動S(C) との和になる。
()
()
()
C
S
C
P
C
T
+
=
1
·································································· (B.1)
極座標線図の山と谷とが基準球の山と谷とに対応するように,真円度測定に慣用的に用いている符号の
付け方を採用する。方法Pの第2ステップは,回転軸とハウジングとに付けた印がC=0°で一致している
図B.1 b) の配置を利用して,二つ目の極座標線図T2P(C) を得るために行う。ただし,ここでは基準球と変
位計との位置とが逆になる(回転軸の回りに基準球を180°回転させる。)。T1(C) と同じ符号を用いる。図
50
B 6190-7:2019 (ISO 230-7:2015)
B.1 a) と図B.1 b) とは,変位計と基準球との相対的な位置を変えずに基準球の真円度を同じ方法で記録し
たものを表す。ただし,半径方向誤差運動は,図B.1 b) にあるように符号を逆にして記録したものを表す。
それは,図B.1 a) に示す変位計に対する回転軸の運動が図B.1 b) に示す変位計から遠ざかる方向の動き
になるためである。式として表すと,
()
()
()
C
S
C
P
C
T
−
=
P
2
································································ (B.2)
式(B.1)と式(B.2)との和をとってP(C) を求めると,
()
()
()
2
2
1
C
T
C
T
C
P
P
+
=
······························································· (B.3)
式(B.3)は,基準球の真円度曲線P(C) が第1と第2との極座標線図の平均になることを示している。T1(C)
とT2P(C) とを同じ極座標上に記録すると,図B.2 a) に示すように最初の二つの極座標線図の中間に3番目
の曲線を描くことによって,P(C) を求めることができる。
B.2.3 方法S
方法Sは,方法Pと同様に第1の線図T1(C) を記録することから始める。符号の使い方を逆にしなけれ
ばならない点を除いて,方法Sの第2ステップも方法Pの第2ステップと同じになる。二つ目の極座標線
図をT2S(C) とすると,次の式で表される。
()
()
()
()
C
S
C
P
C
T
C
T
+
−
=
−
=
P
2
S
2
·················································· (B.4)
式(B.1)と式(B.4)との和とってS(C) を求めると,
()
()
()
2
2
1
C
T
C
T
C
S
S
+
=
································································ (B.5)
式(B.5)は,T1(C) とT2S(C) との中間に描かれた第3の極座標線図が半径方向誤差運動の極座標線図S(C)
になることを示す。
上記の二つの方法をまとめると,次のようになる。
方法
記録2で反転させるもの
平均
P
基準球,変位計
基準球,真円度
S
基準球,変位計,符号
半径方向誤差運動
基準球又は変位計のいずれが回転したかは述べていない。したがって,上記の方法は,固定感度方向又
は回転感度方向のいずれでも同じように適用できる。
B.3
曲線差分法
場合によっては,極座標線図T2P(C) 及びT2S(C) のうちの一つだけを求めるのが合理的になる。P(C) か
S(C) のいずれかを平均することによって求められれば,もう一方は,式(B.1)に示すようにT1(C) から既知
の曲線との差分を取ることによって求めることができる。図を使って,元の図から移された十分な数の半
径差を新しい基礎円に対して表示することによって新しい極座標線図を図示する必要がある。図B.3 a) 及
び図B.3 b) は,それぞれ図B.2 a) 及び図B.2 b) の曲線を使用してこの手順を説明している。より難しく
て,誤差を生じやすいので,曲線加算平均法を使用できる場合には,曲線差分法を使用することは推奨で
きない。
51
B 6190-7:2019 (ISO 230-7:2015)
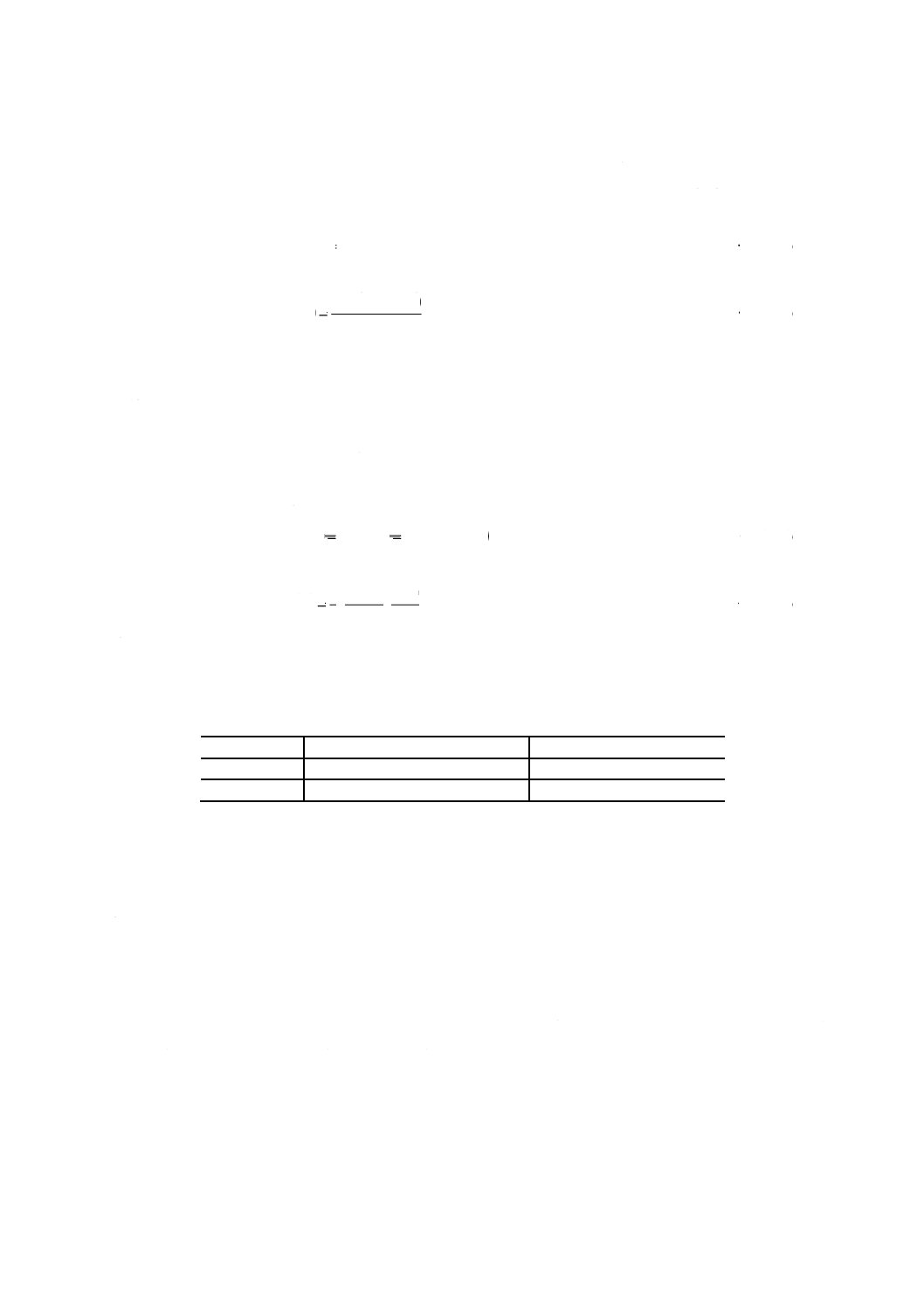
T1(C)
T2P(C)
P (C)
T1(C)
T2S(C)
S (C)
a) 基準球の真円度P(C)
b) 半径方向誤差運動S(C)
図B.2−球の真円度P(C) と半径方向誤差運動S(C) の誤差との分離のために輪郭を平均化
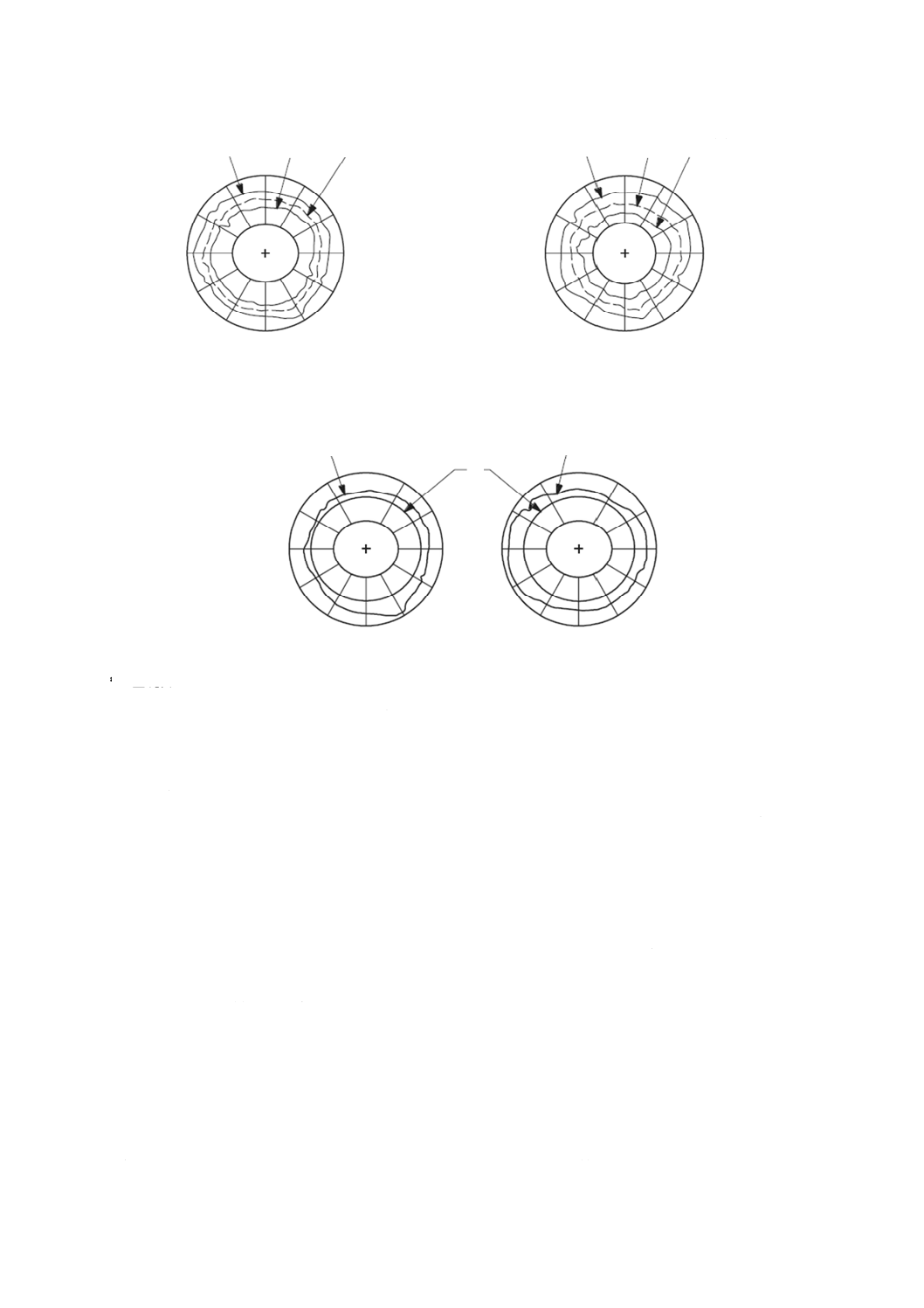
S(C) = T1(C) −P (C)
P (C)= T1(C) −S (C)
a)
b)
a)
a) 基礎円
図B.3−図B.2のデータを用いた曲線差分法による誤差分離
B.4
実用上の考察
正確な結果を得るためには幾つか実用上の課題がある。上記の式における重要な点は,P(C) とS(C) と
の両方が1回目及び2回目の測定で再現されると仮定していることにある。基準球の真円度曲線の再現性
については,変位計で測定する二つの軌道が軸方向にずれたり又は傾斜したりすることがないように,細
心の注意を払って基準球及び変位計の両方を180°逆に回すことも関係する。最初の測定で,軌道を意図
的に僅かにずらして,T1(C) の再現性を見れば,軌道の位置に対して測定結果がどの程度影響されるかを試
験できる。
非同期半径方向誤差運動があると,S(C) は,同期半径方向誤差運動の極座標線図として解釈しなければ
ならない。得られた精度は,二つの測定で再現性のある平均半径方向誤差運動が得られるかどうかに依存
している。これは,最初の測定でT1(C) を連続記録することによって試験することができる。1回転以上の
再現性は,特に転がり軸受を使っているとき同じ出発点まで軸を逆回転して戻すことによって改良される
ときもある。
主軸の回転角度位置と誤差運動の読みとを同期させると,基準球の真円度誤差の除去が容易になる。主
軸の後端部にロータリエンコーダを付けることで同期をとることができる。このようにして同期したデー
タを取得し,1回転中の誤差運動の読取りは,常に同じ回転角度位置から始める。そうすると,数回転分
のデータだけを平均化するだけで,非同期誤差運動が除去できる。計算で基本周期成分を取り除くことに
52
B 6190-7:2019 (ISO 230-7:2015)
よって極座標線図の中心に合わせることができる。その信号に基本周波数を追加すれば,基準円が作成で
きる。二つの信号の和又は差は,容易に計算できる。
53
B 6190-7:2019 (ISO 230-7:2015)
附属書C
(参考)
回転軸のコンプライアンス特性に関する用語及び定義
C.1
コンプライアンス(compliance)
構造ループ内の2点間の単位力当たりの変位。
力の作用位置及び向き,並びに変位の測定位置及び向きは規定する。
C.2
剛性(stiffness)
コンプライアンスの逆数。
C.3
半径方向コンプライアンス(radial compliance)
力及び変位の方向がZ基準軸に垂直なときのコンプライアンス。
C.4
傾斜方向コンプライアンス(tilt compliance)
Z基準軸を含む平面内におけるモーメント及び傾き変位に適用できるコンプライアンス。
C.5
軸方向コンプライアンス(axial compliance)
力及び変位の方向がZ基準軸と同軸であるときのコンプライアンス。
C.6
端面方向コンプライアンス(face compliance)
力及び変位の方向がZ基準軸と同軸,かつ,平行であり,指定した半径方向位置で適用できるコンプラ
イアンス。
C.7
コンプライアンス線図(compliance plot)
力と変位との関係を表す直交座標線図。
C.8
コンプライアンス値(compliance value)
指定された変位又は力に対するコンプライアンス線図の勾配。
54
B 6190-7:2019 (ISO 230-7:2015)
附属書D
(参考)
主軸,回転テーブル及び旋回主軸頭に発生する
熱的誤差に関する用語及び定義
D.1
半径方向の熱的誤差(thermally-induced radial error)
Z基準軸に垂直に測定された軸の半径方向ずれ。
D.2
傾斜方向の熱的誤差(thermally-induced tilt error)
熱影響によって生じるZ基準軸に対する軸の傾斜方向ずれ。
D.3
軸方向の熱的誤差(thermally-induced axial error)
Z基準軸と同軸又は平行な軸方向ずれ。
D.4
端面方向の熱的誤差(thermally-induced face error)
指定した半径方向位置で測定された軸方向及び傾斜方向の軸ずれの組合せ。
D.5
熱的誤差線図(thermal error plot)
時間に対して記録した熱的誤差の線図。
D.6
熱的誤差の値(thermal error value)
指定された一つ(又は複数)の速度で測定された温度変化の,指定された時間にわたる最大値と最小値
との差。
55
B 6190-7:2019 (ISO 230-7:2015)
附属書E
(参考)
静的誤差運動試験方法
E.1
一般
静的誤差運動試験は,主軸駆動システムの動的な影響によって引き起こされる主軸誤差運動から主軸軸
受誤差を分離することを目的に行う。主軸軸受によって引き起こされる誤差を分離することは重要である。
主軸駆動系に問題が生じたとき,それが原因であると非難されることが多いからである。
E.2
試験方法
試験装置は,5.3及び5.4に規定したものと同様のものを使用する。
主軸は,ニュートラル位置に置く。主軸がベルト駆動の場合には,ベルトに張力をかけないのが望まし
い。できれば,主軸は全ての外力から解放する。
主軸は,1回転当たり最少8点の位置で止めて測定する。主軸は,少なくとも手で2回転させる。
手の力を全て解放して各点で読みを取り,平均化する。各点での読みを平均化することによって主軸が
停止しているときの構造誤差運動の影響を排除できる。
E.3
データ解析
データは,5.3及び5.4に規定した方法を用いて,半径方向,傾斜方向及び軸方向の誤差運動を解析する。
56
B 6190-7:2019 (ISO 230-7:2015)
附属書F
(参考)
回転軸の試験における測定不確かさの推定
F.1
測定不確かさの推定
測定不確かさの推定は,ISO/TR 230-9に記載する手順及び式に従って行う。測定不確かさUは,包含係
数をk=2として計算する。
測定不確かさは,長さ測定値(すなわち,半径及び軸方向運動)についてはマイクロメートル(μm),
及び角度測定値(すなわち,傾斜方向運動)についてはマイクロメートル/メートル(μm/m)で表すのが
望ましい。
半径及び軸方向運動の測定不確かさは,異なる可能性がある。測定不確かさは,周波数範囲が違うと異
なる,すなわち,主軸速度範囲が違うと異なる可能性がある。
F.2
測定不確かさに及ぼす要因
F.2.1
一般
一般に,回転軸の試験における測定不確かさに及ぼす主な要因は,測定器及び環境変動誤差(EVE)であ
る。
次の仮定をする。
− 測定器は,測定器の製造業者の指針に従って正しく使用する。
− 全ての必要な心出し及び調整の手順は,正しく実行する。
− 適用できる場合には,長さ測定器も,触ることのできる表面に直角に置く。
− 測定器は,静的及び動的に強固に,かつ,少しのバックラッシもなく取り付ける。
− 測定器を保持する機械の部品は,剛体として振る舞う。
− 測定器は,試験報告書に記載されている位置からの差が10 mm以内になるように工作機械上に定置す
る。
− 測定器は,その製造業者の指定した許容周波数範囲内で使用する。
− ソフトウェア評価の不確かさは,測定器の測定不確かさに含める。
これらの仮定が満たされない場合には,測定不確かさに新たな要因を追加することを考えるのが望まし
い。
F.2.2
測定器による不確かさ,UDEVICE
校正された測定器を使用することを推奨する。校正証明書に,長さ測定値についてはμmで,角度測定
値についてはμm/mで不確かさが記載されている場合には,式(F.1)を適用する。
N
CALIBRATIO
DEVICE
U
U
=
································································ (F.1)
ここに,
UDEVICE: 長さ測定値をμmで,角度測定値をμm/mで表した測
定器の不確かさ
UCALIBRATION: 包含係数をk=2として,長さ測定値をμm,角度測定
値をμm/mで表した校正証明書に従った校正の不確
かさ
校正証明書は利用できないが,製造業者が長さ測定値をμm及び角度測定値をμm/mで測定値の誤差範
囲を記載している場合は,式(F.2)を用いる。一般に,測定器の分解能の影響は無視でき,ISO/TR 230-9:2005
57
B 6190-7:2019 (ISO 230-7:2015)
の式(C.3)に従って確かめることができる。
DEVICE
DEVICE
6.0R
U
=
·································································· (F.2)
ここに,
UDEVICE: 包含係数をk=2とし,長さ測定値をμm,角度測定値を
μm/mで表した測定器の不確かさ
RDEVICE: 長さ測定値をμm,角度測定値をμm/mで表した測定器
の製造業者が与えた誤差範囲
測定器が,異なった部品から構成されている場合には,少なくとも次の要因をその測定器の測定不確か
さの推定に用いるのが望ましい。
− 基準器の真円度及び表面仕上げ
− 関係する場合には,試験中の主軸上の基準器の心出し
− 変位計の測定不確かさ
− 変位計の分解能
− 傾斜方向運動の測定不確かさを評価するための半径方向又は端面方向の測定点間の距離
− 基準器の表面への変位計の位置決め
− 読み取った測定値の評価(平均値,中心の決定などのパラメータ)
F.2.1に記載した他の全ての仮定を満足するのが望ましい。測定器の測定不確かさの推定は,ISO/TR
230-9:2005の式(1)〜式(7)を用いることができ,包含係数をk=2とするのが望ましい。この推定は,試験
している軸の速度範囲が違えば異なる。
F.2.3
環境変動誤差(EVE,又は温度ドリフト)による不確かさ,UEVE
ほとんどの場合,測定中に工作機械及び測定器に影響する温度変化及び振動が観察される。これらの影
響,特にドリフトは最小限に抑える必要がある。
その影響は,単純な試験,すなわち,ドリフト試験で確かめることができる。
この規格に従った測定を始める前に,試験中の回転軸は停止させる。回転軸の測定に必要な時間の間,
測定器の読みを記録する。読取りの範囲(EVE)は,ISO/TR 230-9の式(C.9)に基づいた式(F.3)に従って対
応する不確かさを推定するために用いる残留環境変動誤差である。
VE
VE
6.0E
UE
=
········································································· (F.3)
ここに,
UEVE: 包含係数をk=2とし,長さ測定値をμm,角度測定値を
μm/mで表した環境変動による測定器の不確かさ
EVE: 長さ測定値をμm,角度測定値をμm/mで表したドリフ
ト試験からの範囲
F.3
誤差運動線図及び誤差運動値の不確かさの推定
F.3.1
一般
非同期誤差運動,内側誤差運動及び外側誤差運動[図7のd) 及びe) 参照]は,1回の測定値の最大値
又は最小値に基づき,同期誤差運動[図7 b) 参照)]は,数回の誤差運動線図の平均値に基づいている。
誤差運動値については,図9に示すように誤差運動線図の二つの極端な値を用いる。
次の仮定をする。
− 誤差運動中心の評価は,正しく行われる。
− 正しい誤差運動中心は,誤差運動値の評価に用いる。
− 測定不確かさの主な要因は,測定器及び環境変動誤差である。
− 環境変動誤差は,異なった線図及び異なった角度に対して相関がない。
58
B 6190-7:2019 (ISO 230-7:2015)
− 試験中の軸を360°以上回転したときの測定値がある。
これらの仮定が満たされる場合には,誤差運動線図及び誤差運動値の不確かさを推定するために
ISO/TR 230-9:2005の式(1),式(3)及び式(A.7)を適用することができる。
F.3.2
全誤差運動線図,非同期誤差運動線図,内側誤差運動線図,外側誤差運動線図の不確かさの推定,
U(single plot)
同期誤差運動線図を除く全ての線図は,幾つかの単一の線図の最大線図に基づいている。したがって,
二つの主な要因の不確かさは,相関関係にないと仮定できるが,ISO/TR 230-9:2005の式(1)に従って推定
する。
2
V
2
DEVICE
)
plot
single
(
E
E
U
U
U
+
=
························································ (F.4)
ここに, U(single plot): 包含係数をk=2として,長さ測定値をμm,角度測定値
をμm/mで表した全誤差運動線図,非同期誤差運動線図,
内側誤差運動線図,外側誤差運動線図の不確かさ
UDEVICE: 長さ測定値をμm,角度測定値をμm/mで表した測定器
による不確かさ
UEVE: 長さ測定値をμm,角度測定値をはμm/mで表した環境
変動による測定不確かさ
F.3.3
同期誤差運動線図の不確かさの推定,U(synchronous plot)
同期誤差運動線図については,幾つかの線図を用いて平均線図を計算する。ここで,環境変動誤差の影
響は,ISO/TR 230-9:2005の式(A.7)及び式(1)に基づいて減らすことができ,この不確かさは,式(F.5)で表
すことができる。
n
U
U
U
E
2
VE
2
DEVICE
)
plot
s
synchronou
(
+
=
·················································· (F.5)
ここに, U(synchronous plot): 包含係数をk=2として,長さ測定値をμm,角度測
定値をμm/mで表した同期誤差運動線図の不確かさ
UDEVICE: 長さ測定値をμm,角度測定値をμm/mで表した測定
器の不確かさ
UEVE: 長さ測定値をμm,角度測定値をμm/mで表した環境
変動による測定不確かさ
n: 同期誤差運動線図を計算するための極座標線図の数
同期誤差運動線図を計算するために多くの線図が必要になる場合は,環境変動誤差は少なくともその線
図の取得時間と同じ時間のドリフト試験から取得するのが望ましい。
F.3.4
全誤差運動値,非同期誤差運動値,内側誤差運動値,外側誤差運動値の不確かさの推定,
U(single plot value)
誤差運動値は,誤差運動線図の半径方向の最大偏差と最小偏差との差に基づいている。一般に最大値と
最小値とは,現れる回転軸の角度位置が異なるので,不確かさの要因は相関がないとみなされる。この不
確かさは,ISO/TR 230-9の式(1)を使って式(F.6)で表せる。
)
plot
single
(
)
value
plot
single
(
4.1U
U
=
·························································· (F.6)
ここに,
U(single plot value): 包含係数をk=2として,長さ測定値をμm,角度測
定値をμm/mで表した全誤差運動値,非同期誤差運
動値,内側誤差運動値,外側誤差運動値の不確かさ
59
B 6190-7:2019 (ISO 230-7:2015)
U(single plot): 全誤差運動線図,非同期誤差運動線図,内側誤差運
動線図,外側誤差運動線図の不確かさ
F.3.5
同期誤差運動値の不確かさ,U(synchronous plot value)
同期誤差運動値は,同期誤差運動線図の半径方向の最大偏差と最小偏差との差に基づいている。一般に
最大値と最小値とは,現れる回転軸の角度位置が異なるので,不確かさの要因は相関がないとみなされる。
この不確かさは,ISO/TR 230-9の式(1)を使って式(F.7)で表せる。
)
plot
s
synchronou
(
)
value
plot
s
synchronou
(
4.1U
U
=
················································ (F.7)
ここに,
U(synchronous plot value): 包含係数k=2として,長さ測定値をμm,角度
測定値をμm/mで表した同期誤差運動値の不確
かさ
U(synchronous plot): 同期誤差運動線図の不確かさ
60
B 6190-7:2019 (ISO 230-7:2015)
附属書G
(参考)
索引(50音順)
用語
対応英語
箇条
遊び
play
3.1.20
内側誤差運動線図
inner error motion polar plot
3.6.7
内側誤差運動値
inner error motion value
3.8.7
回転感度方向
rotating sensitive direction
3.3.4
回転軸
axis of rotation
3.1.7
回転軸誤差運動
axis of rotation error motion
3.2.1
回転軸誤差運動の二次元影響
2D effect of axis of rotation error motion
3.3.6
回転軸の半径振れ(所定の点での)
radial throw of a rotary axis at a given point
3.1.15
回転テーブル
rotary (or swivelling) table
3.1.2
完全回転軸
perfect axis of rotation
3.1.9
完全工作物
perfect workpiece
3.1.10
感度方向
sensitive direction
3.3.1
機能点
functional point
3.1.11
機能面の振れ(所定の断面での)
run-out of a functional surface at a given section
3.1.16
基本誤差運動
fundamental error motion
3.5.3
基本誤差運動線図
fundamental error motion polar plot
3.6.5
基本軸方向誤差運動値
fundamental axial error motion value
3.8.5
極座標線図(PC)中心
polar chart (PC) centre
3.7.2
極座標輪郭中心
polar profile centre
3.7.3
傾斜方向誤差運動
tilt error motion
3.4.3
傾斜方向ずれ
tilt shift
3.10.2
構造誤差運動
structural error motion
3.2.2
構造誤差運動(主軸の回転中の)
structural error motion with rotating spindle
3.9.1
構造誤差運動(主軸の非回転中の)
structural error motion with non-rotating spindle
3.9.2
構造誤差運動線図
structural error motion plot
3.9.3
構造誤差運動値
structural error motion value
3.9.4
構造ループ
structural loop
3.1.14
誤差運動線図
error motion polar plot
3.6.1
誤差運動値
error motion value
3.8.1
誤差運動極座標中心
error motion polar plot centre
3.7.1
固定感度方向
fixed sensitive direction
3.3.3
最小外接円(MCC)中心
minimum circumscribed circle (MCC) centre
3.7.7
最小二乗円(LSC)中心
least-squares circle (LSC) centre
3.7.4
最小半径間隔(MRS)中心
minimum radial separation (MRS) centre
3.7.5
最大内接円(MIC)中心
maximum inscribed circle (MIC) centre
3.7.6
軸受
bearing
3.1.6
軸受誤差運動
bearing error motion
3.2.3

61
B 6190-7:2019 (ISO 230-7:2015)
用語
対応英語
箇条
軸ずれ
axis shift
3.1.13
軸平均線
axis average line
3.1.12
軸方向誤差運動
axial error motion
3.4.4
軸方向ずれ
axial shift
3.10.3
主軸
spindle
3.1.4
主軸ハウジング
spindle housing
3.1.5
主軸ユニット
spindle unit
3.1.1
純粋半径方向誤差運動
pure radial error motion
3.4.2
剰余同期誤差運動
residual synchronous error motion
3.5.4
剰余同期誤差運動線図
residual synchronous error motion polar plot
3.6.6
剰余同期誤差運動値
residual synchronous error motion value
3.8.6
静止点の振れ
stationary point run-out
3.1.17
静的誤差運動
static error motion
3.2.4
正の方向
positive direction
3.1.8
旋回主軸頭
rotary (or swivelling) head
3.1.3
全誤差運動
total error motion
3.5.1
全誤差運動線図
total error motion polar plot
3.6.2
全誤差運動値
total error motion value
3.8.2
速度誘起形軸ずれの値
speed-induced axis shift value
3.10.6
速度誘起形軸ずれの表示
speed-induced axis shift plot
3.10.5
外側誤差運動線図
outer error motion polar plot
3.6.8
外側誤差運動値
outer error motion value
3.8.8
端面方向誤差運動
face error motion
3.4.5
端面方向ずれ
face shift
3.10.4
直角度誤差(直進軸の運動と軸平均線との) squareness error between a linear axis of motion
and an axis average line
3.1.19
直角度誤差(二つの軸平均線間の)
squareness error between two axis average lines
3.1.18
同期誤差運動
synchronous error motion
3.5.2
同期誤差運動線図
synchronous error motion polar plot
3.6.3
同期誤差運動値
synchronous error motion value
3.8.3
半径方向誤差運動
radial error motion
3.4.1
半径方向ずれ
radial shift
3.10.1
非感度方向
non-sensitive direction
3.3.2
ヒステリシス
hysteresis
3.1.21
非同期誤差運動
asynchronous error motion
3.5.5
非同期誤差運動線図
asynchronous error motion polar plot
3.6.4
非同期誤差運動値
asynchronous error motion value
3.8.4
変動感度方向
varying sensitive direction
3.3.5
62
B 6190-7:2019 (ISO 230-7:2015)
附属書H
(参考)
変位計の周波数帯域及び軸の回転速度
H.1 一般
工作機械主軸の回転軸誤差運動の測定は,静電容量式又は渦電流式のような非接触変位計を用いて行う。
この種の変位計は,目標物が回転して変位計に近づいたり遠ざかったりするとき,回転する目標物の一方
向変位を測定する。測定システムの周波数帯域は,目標物の回転周波数に適合するのが望ましい。この附
属書は,適切な周波数帯域をもった変位計を選択する場合の情報及び指針を提供する。
H.2 変位計の周波数帯域
一般に変位計は,動きの量に比例して出力電圧を変化させ,目標物の位置の変化に応答する。ただし,
目標物の動きの周波数が高くなると,ある周波数を超えたとき変位計の応答が減少し始める。図H.1にそ
の例を示す。この例では,変位計の出力は,10 kHzまで“フラット”とみなすことができる。どんな変位
計でも,その仕様上の周波数帯域は,出力電圧が低い周波数(又はDC)での出力レベルの70.7 %(−3 dB)
まで下がる周波数までであるとしている。図H.1の例では,変位計の周波数帯域は15 kHzである。これは,
10 µm変位している目標物が15 kHzでは7 μmの変位として測定されることを意味している。
10
5
00
10k15k
-3 dB
100%
70.7%
周波数
Hz
電
圧
V8
図H.1−10 kHzまでフラットな応答をする,周波数帯域15 kHzの変位計の周波数応答の例
H.3 目標物の振動周波数に対する考察
H.3.1 基本周波数
半径振れがあると,回転している目標物は,1回転を1周期とする誤差運動を示す。これを,“基本周波
数”という。10 kHzまでフラットな応答の変位計は,600 000 r/minまでの速度で目標物の基本誤差運動を
精度よく測定することができる。15 kHzの周波数帯域をもった変位計は,900 000 r/minの回転速度の場合,
実際の変位振幅の70 %を測定することができる。
H.3.2 基本周波数以外の振動周波数
基本周波数以外の振動周波数も主軸の誤差運動に存在する。軸受部品,主軸の組付け,モータ,構造振
動などは,それぞれの固有の振動周波数成分をもっている。これらの原因による誤差運動は,基本周波数
の整数倍とそれ以外の周波数とで発生する。
H.3.3 モータのロータ及びステータによる誤差
63
B 6190-7:2019 (ISO 230-7:2015)
モータのロータ及びステータは,完全には丸くない。これが原因で,通常,基本周波数に同期する主軸
誤差運動とは別の振動周波数を発生させる。まゆ形の2山成分及びお結び形の3山成分をもった形状は,
一般的な真円度誤差である。このような成分をもった形状誤差は,基本周波数の2倍及び3倍の誤差運動
周波数を発生させる。それ以上の成分をもった形状の測定を精度よく行うためには,より高い周波数帯域
をもった変位計が必要になる。例えば,3山成分をもった誤差運動を精度よく測定するために10 kHzのフ
ラットな応答をもつ変位計を使えば,200 000 r/minまでの主軸速度を測定できる。
H.3.4 組付け方が誘起する誤差
主軸の組付け方によって,僅かな変形が軸受内に起こり応力が発生する。この応力は,基本的にステー
タ及びロータ形状による誤差と同様に同期誤差運動を発生させる。理論的には,組立に用いる固定具の締
付け状態によって同期誤差運動に新たな成分が追加されることがある。
H.3.5 モータ磁極の転写
モータの磁極は,モータのロータに極上と極間とで異なる力を発生させる。この力の変化は,回転ごと
に繰り返す。極間で発生する力は,モータのロータに発生する。主軸軸受の剛性に依存するが,この力の
変化は,主軸の誤差運動となって現れる。この誤差運動は,基本周波数と同期する。
駆動モータの極数は,転写誤差の形を決定する。例えば,8極のモータは,8山のパターンを生成し,10
kHzまでフラットな応答の変位計を使った場合は,75 000 r/minまでの回転速度で精度よく測定できる。代
表的な駆動モータは,4極,6極又は8極である。大形のモータは,そのサイズが大きいことから更に極数
を多くすることができるが,かなり低速で回転するため誤差運動の周波数を比較的小さく保てる。
H.3.6 構造振動
工作機械構造自体が主軸誤差運動となって現れる固有振動数をもっている。機械構造の大きさ及び質量
から,その固有振動数は,通常は低く(10 Hz〜30 Hz),基本周波数と同期したり,しなかったりする。
H.3.7 転がり軸受
転がり軸受は,転動体(玉又はころ),内輪,外輪及び保持器の四つの基本要素から構成されている。軸
受が回転するとき,これらの基本要素は互いに機械的に作用する。軸受に特有の損傷があると,軸受にか
かる力及び回転軸の偏差が発生し,主軸誤差運動になる。
軸受の各要素には,主軸に誤差運動を発生させる固有の形状誤差がある。軸受に発生する振動周波数は,
軸受のピッチ円直径と転動体直径との比,転動体の接触角,軸の回転周波数(基本周波数)と関係する。
主軸の共振を防ぐために,この周波数と主軸モータの回転子とが同期しないようにして軸受を選択するの
が望ましい。そのため,軸受に発生する振動は,基本周波数以外の周波数で発生する。
H.3.8 転がり軸受の振動周波数
転がり軸受の振動周波数には,保持器回転周波数,内輪玉通過周波数,外輪玉通過周波数,玉自転振動
数及びこれらの調和振動周波数がある。これらの振動周波数は,基本周波数の定数倍として現れる。表
H.1は,代表的な軸受の振動周波数の例を基本周波数の定数倍として示す。この表に示す最も高い周波数
は,基本周波数の8.32倍である。誤差運動を精度よく測定するには,10 kHzまでのフラットな応答をもつ
変位計を用いて70 000 r/minまでの主軸速度で行うことである。

64
B 6190-7:2019 (ISO 230-7:2015)
表H.1−代表的な転がり軸受の振動周波数の例
玉数
玉径
(mm)
ピッチ円直
径
(mm)
外輪玉通過周波数
(基本周波数の定数
倍)
内輪玉通過周波数
(基本周波数の定数
倍)
保持器回転周波数
(基本周波数の定数
倍)
玉自転周波数
(基本周波数の
定数倍)
15
8
72.5
6.68
8.32
0.45
4.48
注記 この表の値の計算では,接触角α=10°としている。
65
B 6190-7:2019 (ISO 230-7:2015)
参考文献
[1] JIS B 6190-2:2016 工作機械試験方法通則−第2部:数値制御による位置決め精度試験
注記 対応国際規格:ISO 230-2:2014,Test code for machine tools−Part 2: Determination of accuracy and
repeatability of positioning of numerically controlled axes及びAmendment 1:2016(IDT)
[2] JIS B 6190-3:2014 工作機械試験方法通則−第3部:熱変形試験
注記 対応国際規格:ISO 230-3:2007,Test code for machine tools−Part 3: Determination of thermal
effects(IDT)
[3] JIS B 6195:2003 工作機械−騒音放射試験方法通則
注記 対応国際規格:ISO 230-5:2000,Test code for machine tools−Part 5: Determination of the noise
emission(IDT)
[4] JIS B 6310:2003 産業オートメーションシステム−機械及び装置の制御−座標系及び運動の記号
注記 対応国際規格:ISO 841:2001,Industrial automation systems and integration−Numerical control of
machines−Coordinate system and motion nomenclature(IDT)
[5] JIS B 6331-5 数値制御旋盤及びターニングセンタ−検査条件−第5部:送り速度,主軸速度及び補間
運動の精度
注記 対応国際規格:ISO 13041-5,Test conditions for numerically controlled turning machines and
turning centres−Part 5: Accuracy of speeds and interpolations(IDT)
[6] JIS B 6336-6:2018 マシニングセンタ−試験条件−第6部:速度及び補間運動の精度
注記 対応国際規格:ISO 10791-6:2014,Test conditions for machining centres−Part 6: Accuracy of
speeds and interpolations(IDT)
[7] ISO/TR 230-8,Test code for machine tools−Part 8: Vibrations
[8] ISO/TR 230-9:2005,Test code for machine tools−Part 9: Estimation of measurement uncertainty for machine
tool tests according to series ISO 230, basic equations
[9] ISO 1940-1:2003,Mechanical vibration−Balance quality requirements for rotors in a constant (rigid) state−
Part 1: Specification and verification of balance tolerances
[10] ISO/TR 230-11,Test code for machine tools−Part 11: Measuring instruments suitable for machine tool
geometry tests
[11] ISO 6103,Bonded abrasive products−Permissible unbalances of grinding wheels as delivered−Static testing
[12] Unification Document Axes of Rotation, ME Annals of the CIRP, 2/1976
[13] Tlusty J. System and Methods of Testing Machine Tools. Microtechnic. 1959, 13 p. 162
[14] Bryan J., Clouser R., Holland E. Spindle Accuracy, American Machinist, Spec. Rpt. No.612, Dec 4, 1967
[15] Peters J, & Vanherck P An Axis of Rotation Analyser, Proceedings of the 14th International MTDR Conference,
Manchester 1973
[16] Donaldson R. A Simple Method for Separating Spindle Error from Test Ball Roundness Error. CIRP Ann. 1972,
21 (1) p. 125
[17] Lu X., & Jamalian A. A new method for characterizing axis of rotation radial error motion: Part 1.
Two-dimensional radial error motion theory. Precis. Eng. 2011, v35




































