B 2704-1:2018
(1)
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 材料······························································································································· 1
5 設計計算························································································································· 2
5.1 一般 ···························································································································· 2
5.2 記号 ···························································································································· 3
5.3 ばねの設計に用いる基本式 ······························································································ 4
5.4 ばねを設計するときに考慮する事項··················································································· 9
6 ばね特性························································································································ 15
6.1 圧縮ばね ····················································································································· 15
6.2 引張ばね ····················································································································· 15
6.3 ねじりばね ·················································································································· 16
7 設計応力························································································································ 16
7.1 一般 ··························································································································· 16
7.2 静的な力(荷重)を受けるばね ······················································································· 16
7.3 繰返し力(荷重)を受けるばね ······················································································· 18
B 2704-1:2018
(2)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
ばね工業会(JSMA)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を
改正すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格で
ある。これによって,JIS B 2704-1:2009は改正され,この規格に置き換えられ,また,JIS B 2709-1:2009
は廃止され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 2704の規格群には,次に示す部編成がある。
JIS B 2704-1 第1部:基本計算方法
JIS B 2704-2 第2部:仕様の表し方
日本工業規格
JIS
B 2704-1:2018
コイルばね−第1部:基本計算方法
Coil springs-Part 1: Basic calculation methods
1
適用範囲
この規格は,一般に使用するばねのうち,円形断面の金属材料を用いた,圧縮コイルばね,引張コイル
ばね及びねじりコイルばね(以下,ばねという。)の基本計算方法について規定する。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0103 ばね用語
JIS B 0156 ばね記号
JIS B 2711 ばねのショットピーニング
JIS G 3521 硬鋼線
JIS G 3522 ピアノ線
JIS G 3560 ばね用オイルテンパー線
JIS G 3561 弁ばね用オイルテンパー線
JIS G 4314 ばね用ステンレス鋼線
JIS G 4801 ばね鋼鋼材
JIS H 3260 銅及び銅合金の線
JIS H 3270 ベリリウム銅,りん青銅及び洋白の棒並びに線
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 0103による。
4
材料
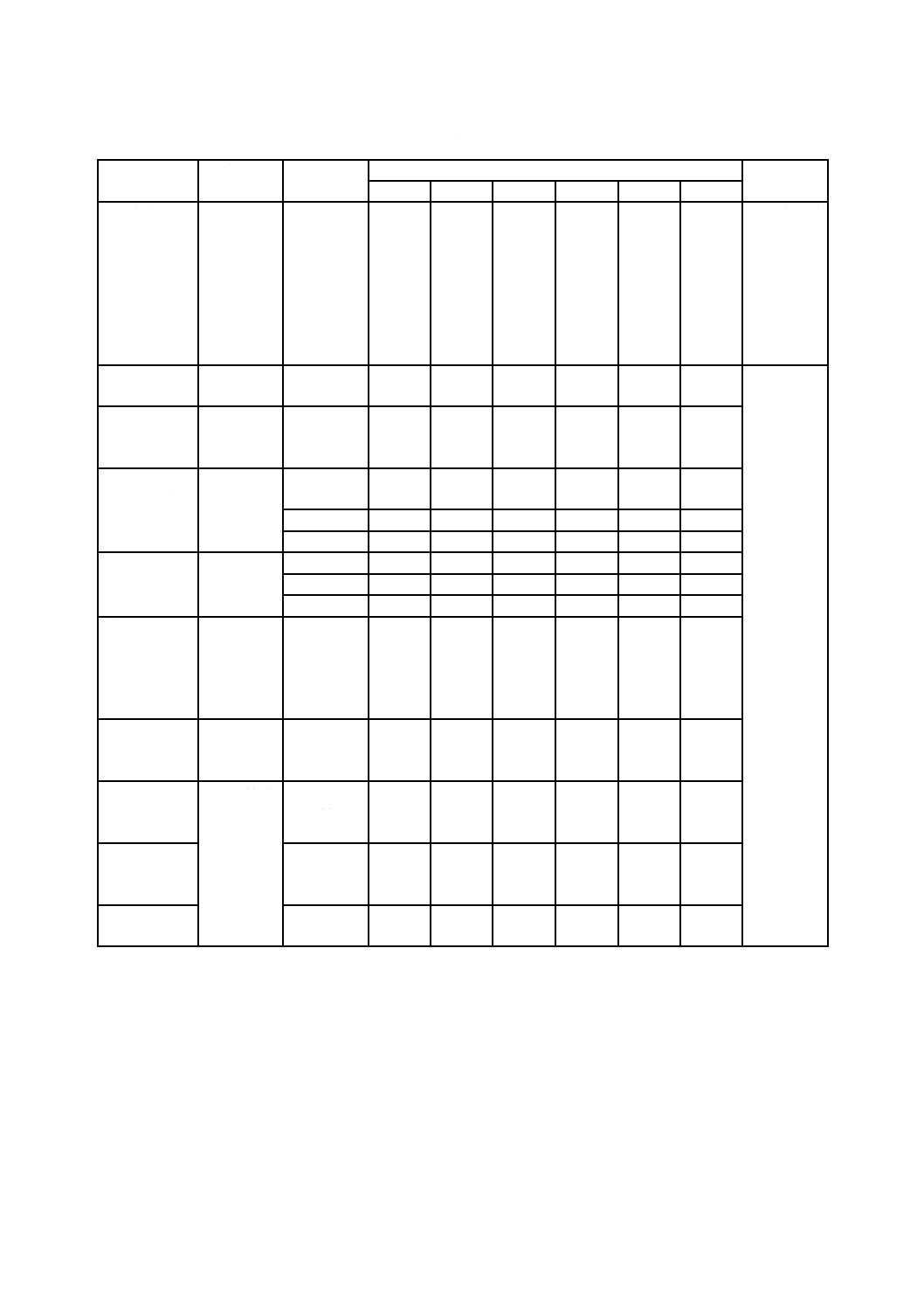
ばねに用いる材料は,表1による。表1に示す○印は,用途ごとの推奨材料を示す。表1以外の材料及
び他の用途に使用する場合は,受渡当事者間の協定による。
2
B 2704-1:2018
表1−ばねの材料
種類
規格番号
記号
用途(参考)
注記
汎用
導電
非磁
耐熱
耐食
耐疲労
ばね鋼鋼材
JIS G 4801
SUP6
SUP7
SUP9
SUP9A
SUP10
SUP11A
SUP12
SUP13
○
○
熱間成形ば
ねに用いる
硬鋼線
JIS G 3521
SW-B
SW-C
○
冷間成形ば
ねに用いる
ピアノ線
JIS G 3522
SWP-A
SWP-B
SWP-V
○
○
ばね用オイル
テンパー線
JIS G 3560
SWO-A
SWO-B
○
SWOSC-B
○
○
SWOSM
○
弁ばね用オイ
ルテンパー線
JIS G 3561
SWO-V
○
SWOCV-V
○
○
SWOSC-V
○
○
ばね用ステン
レス鋼線
JIS G 4314
SUS302
SUS304
SUS304N1
SUS316
SUS631J1
○
○
○
黄銅線
JIS H 3260
C 2600 W
C 2700 W
C 2800 W
○
○
○
洋白線
JIS H 3270
C 7521 W
C 7541 W
C 7701 W
○
○
○
りん青銅線
C 5102 W
C 5191 W
C 5212 W
○
○
○
ベリリウム銅
線
C 1720 W
○
○
○
5
設計計算
5.1
一般
ばねの設計は,要求ばね特性に従い行う。そのばね特性が,“ばねのたわみ又は長さと力(荷重)との関
係”が圧縮方向である場合には,圧縮コイルばね(以下,圧縮ばねという。)を選び,引張方向である場合
には,引張コイルばね(以下,引張ばねという。)を選ぶ。また,“ばねのねじれ角とモーメント又は力(荷
重)との関係”の場合には,ねじりコイルばね(以下,ねじりばねという。)を選ぶ。
次に,そのばね特性を満足するように線径,コイル内外径,巻数,自由長さなどの寸法を決めることが
多い。しかし,これらのばねの寸法及び形状は,ばねの組付けスペース,相手部品形状,加工限界,設計
3
B 2704-1:2018
上考慮すべき事項などによって制約を受ける場合がある。
さらに,寸法及び形状によって,成形方法及び材料を選定する。特に材料については,耐疲労性,耐熱
性,耐食性,導電性,非磁性などの特別な要求を伴うこともあるので,ばねの用途によって,適切に選定
する。
設計の手順としては,ばね特性の要求に対して線径,コイル内外径及び巻数の概略値を設定してばね特
性の計算を行い,寸法及び形状に対する制約,その他特別な要求を満足するように設定した概略値を相互
の関連性を考慮して見直し,最終的なばねの寸法,形状,材料などの諸元を決めるのがよい。
5.2
記号
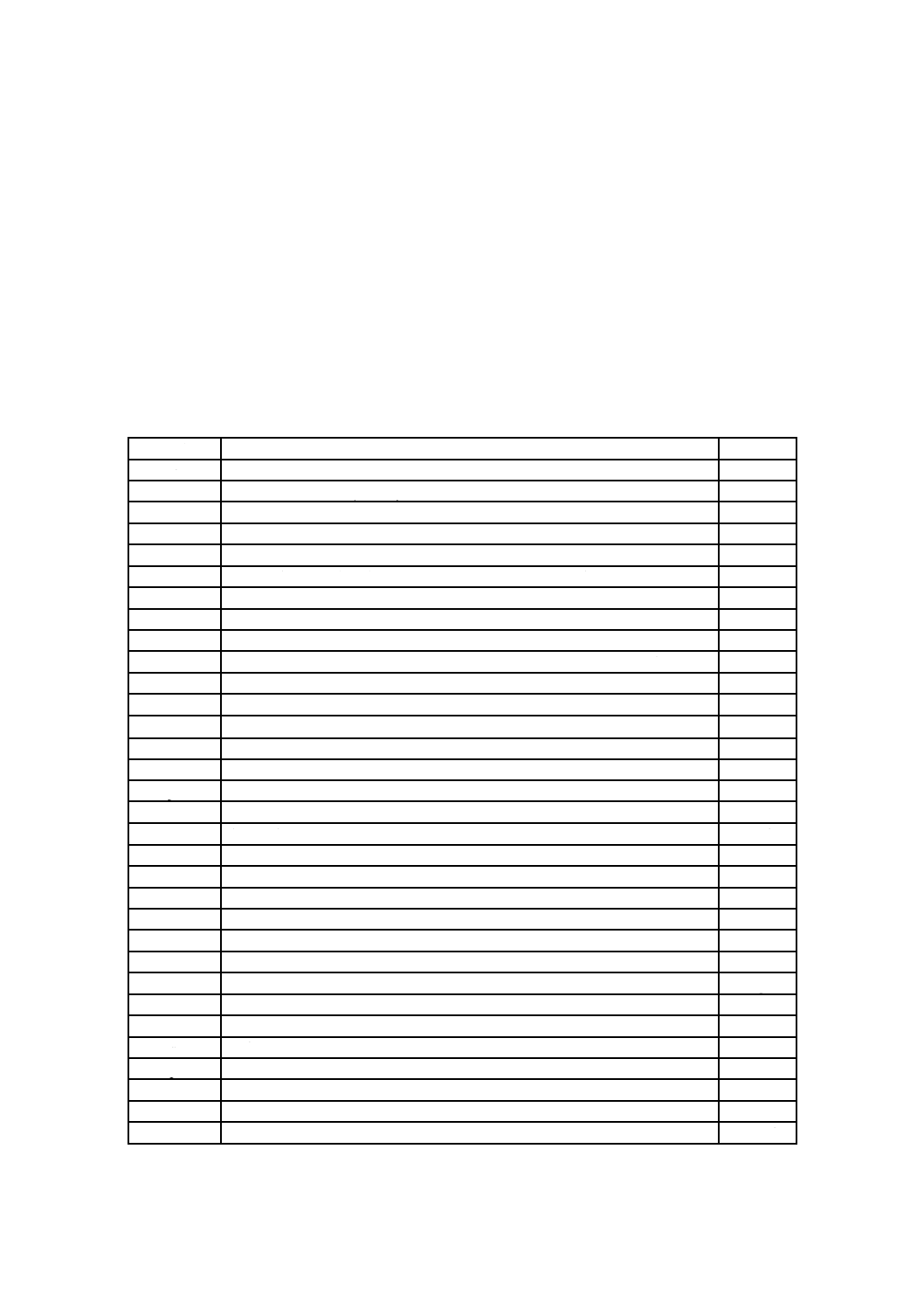
この規格に用いる記号は,表2による(JIS B 0156参照)。
なお,JIS B 2704-2に用いる記号も含む。
表2−記号
記号
記号の意味
単位
c
ばね指数 c=D/d
−
D
コイル平均径 D=(Di+De)/2
mm
De
コイル外径
mm
Di
コイル内径
mm
Dd
案内棒の径
mm
ΔD
ねじりばねに力(荷重)を与えたときのコイル平均径の変化量
mm
d
線径(計算に用いる線径又は製品の材料の直径)
mm
dmax
線径の最大値
mm
E
縦弾性係数
N/mm2
e1
圧縮ばねのコイル外側面の傾き又は圧縮ばねのコイル外側面の直角度
mm
F
ばね力又はばねに作用する力(荷重)
N
FA,FB
ねじりばねの腕部A,Bにおけるばね力
N
Fi
引張ばねの初張力
N
F1,F2,…
圧縮ばね及び引張ばねの指定ばね長さL1,L2,… における指定ばね力
N
Fmax
最大試験力
N
fe
固有振動数
Hz
G
横弾性係数
N/mm2
I
断面二次モーメント
mm4
Lc
圧縮ばねの密着長さ
mm
L0
圧縮ばねの自由長さ又は引張ばねの自由長さ
mm
L1,L2,…
圧縮ばね及び引張ばねの指定ばね力F1,F2,… における指定ばね長さ
mm
ld
ねじりばねの有効部展開長さ
mm
lw,A,lw,B
ねじりばねの腕部A,Bの有効作用長さ(ねじりモーメントの考慮を含む。)
mm
M
ねじりモーメント又はトルク
N・mm
ms
ばねの運動部分の質量
kg
M1,M2,… ねじりばねの指定ばね力F1,F2,… におけるねじりモーメント
N・mm
n
圧縮ばねの有効巻数又は引張ばね及びねじりばねの巻数
−
nt
総巻数
−
p
ばねのピッチ
mm
R
圧縮ばね及び引張ばねのばね定数
N/mm
RM
ねじりばねのばね定数
N・mm/rad
RMd
ねじりばねのばね定数
N・mm/°
4
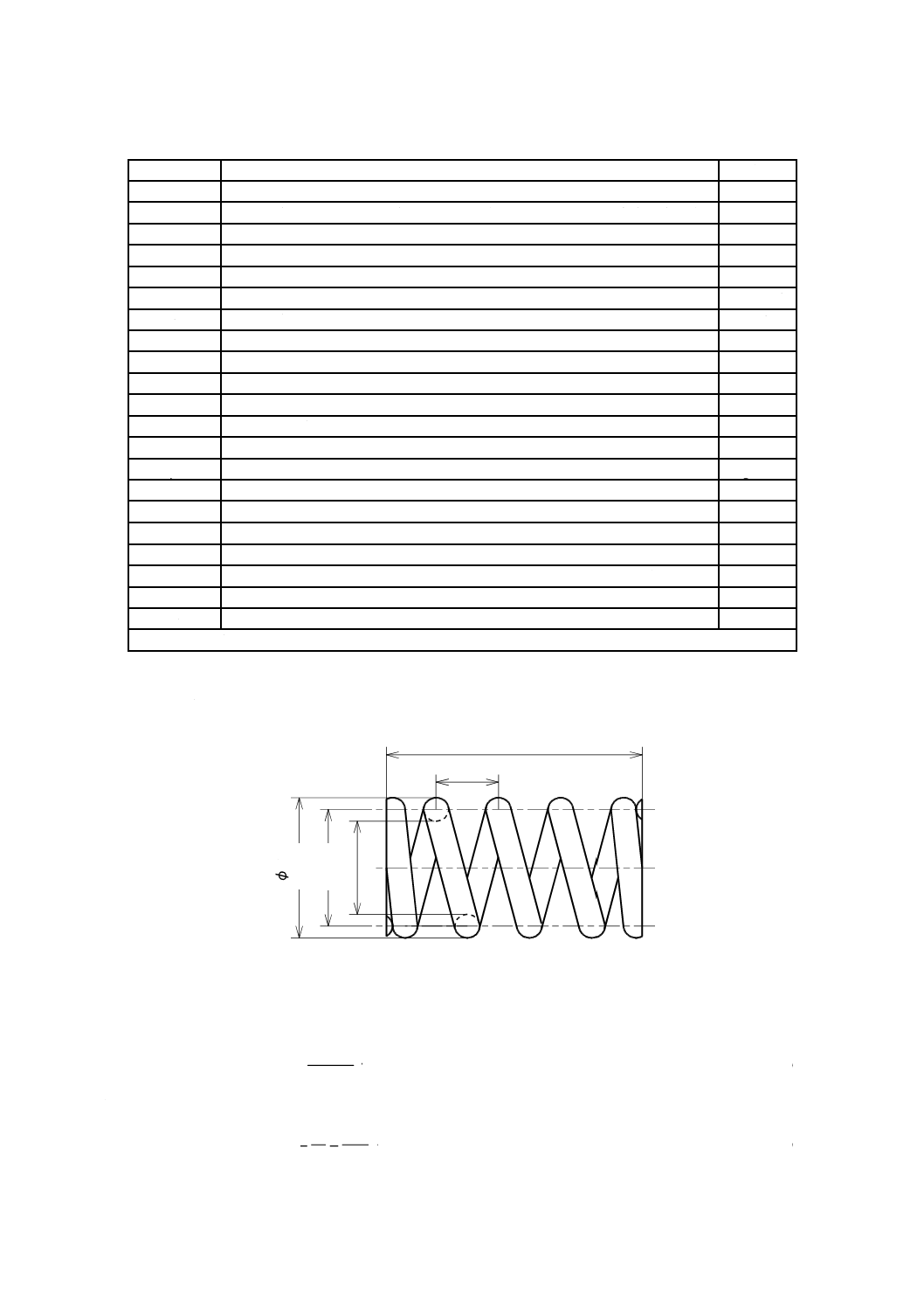
B 2704-1:2018
表2−記号(続き)
記号
記号の意味
単位
rw
ねじりばねの腕部の有効作用半径(ねじりモーメントの考慮を含む。)
mm
rw,A,rw,B
ねじりばねの腕部A,Bの有効作用半径(ねじりモーメントの考慮を含む。)
mm
s
圧縮ばね及び引張ばねのたわみ
mm
U
ばねに蓄えられるエネルギー
J
Z
断面係数
mm3
α0
ねじりばねの自由角度
rad又は°
α
ねじりばねのねじれ角
rad
αd
ねじりばねのねじれ角
°
α1,α2,…
ねじりばねの指定ねじりモーメントM1,M2,… におけるねじれ角
rad又は°
αC
ねじりばねのコイル部のねじれ角
rad
αA,αB
ねじりばねの各腕部のたわみ角
rad
κ
せん断応力修正係数
−
κb
曲げ応力修正係数
−
ρ
材料の単位体積当たり質量(密度)
kg/mm3
σ
曲げ応力
N/mm2
σB
材料の引張強さ
N/mm2
σ1,σ2,…
ねじりばねの指定ねじりモーメントM1,M2,… における曲げ応力
N/mm2
τκ
せん断修正応力
N/mm2
τκ,1,τκ,2,… 圧縮ばね及び引張ばねの指定ばね荷重F1,F2,… におけるせん断修正応力
N/mm2
τ0,i
引張ばねの初せん断未修正応力
N/mm2
τ 0
圧縮ばね又は引張ばねのせん断未修正応力
N/mm2
注記 1 N/mm2=1 MPa
5.3
ばねの設計に用いる基本式
5.3.1
圧縮ばねの場合
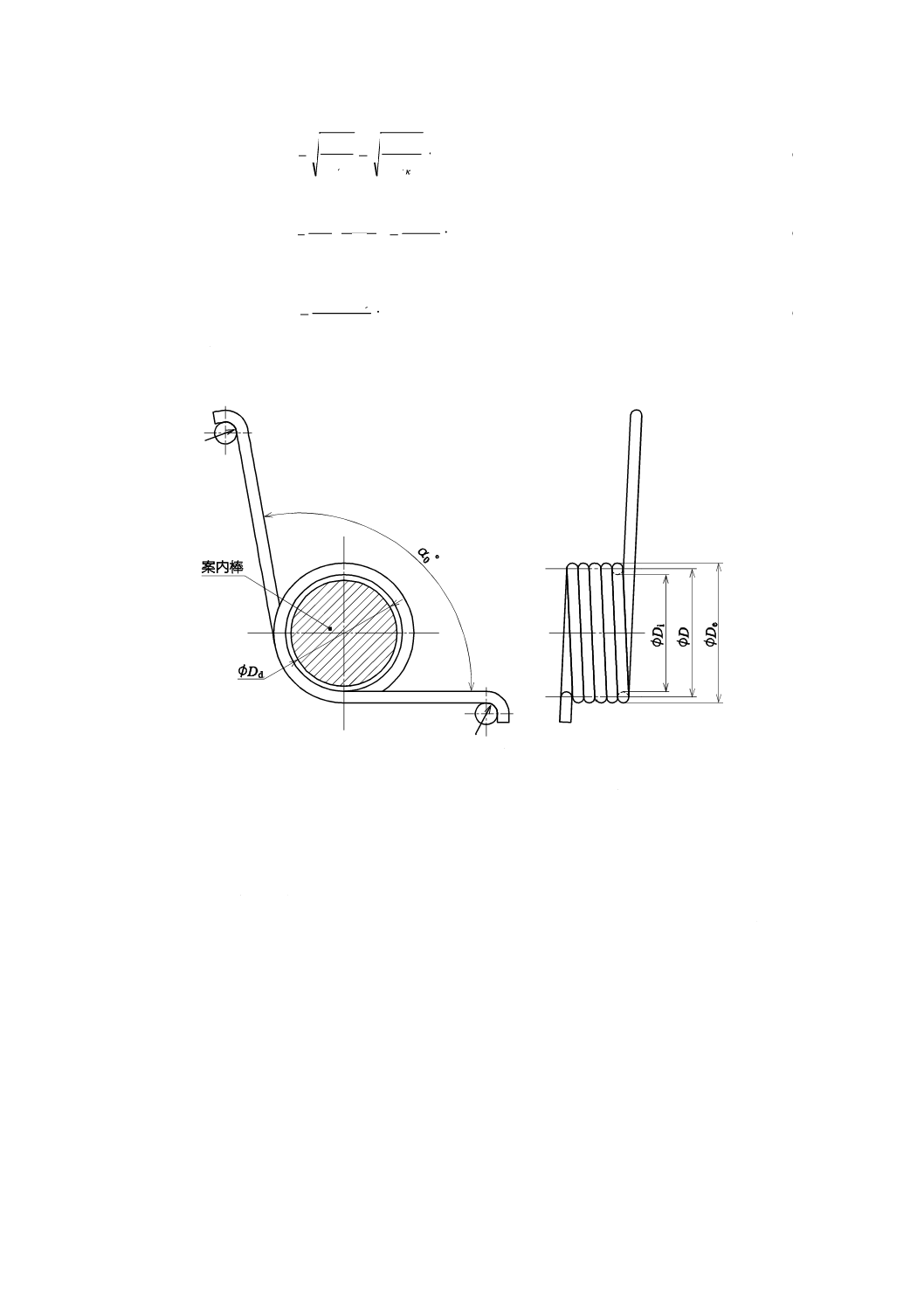
図1−圧縮ばね
図1のような圧縮ばねの設計に用いる基本式は,次による。
a) 圧縮ばねのたわみsは,式(1)による。
4
3
8
Gd
F
nD
s=
··············································································· (1)
b) ばね定数Rは,式(2)による。
3
4
8nD
Gd
s
F
R
=
=
·········································································· (2)
L0
p
φ
D
i
φ
D
e
φ
D
5
B 2704-1:2018
c) せん断未修正応力τ0は,式(3)による。
2
3
0
π
π
8
D
n
Gds
d
DF
τ
=
=
······································································ (3)
d) せん断修正応力τκは,せん断応力修正係数をκとして式(4)による。
0
κτ
τκ=
··················································································· (4)
e) 線径dは,式(5)による。
3
3
0
π
8
π
8
κτ
κDF
τ
DF
d
=
=
·································································· (5)
f)
有効巻数nは,式(6)による。
R
D
Gd
F
D
s
Gd
n
3
4
3
4
8
8
=
=
······································································ (6)
g) ばねに蓄えられるエネルギーUは,式(7)による。
2
2
2
Rs
Fs
U
=
=
··········································································· (7)
5.3.2
引張ばねの場合(ただし,F>Fi)
図2−引張ばね
図2のような初張力がある引張ばねの設計に用いる基本式は,次による。
なお,初張力がない場合は,Fi=τ0,i=0とおけばよい。
a) 引張ばねのたわみsは,式(8)による。
(
)
4
i
3
8
Gd
F
F
nD
s
−
=
········································································ (8)
b) ばね定数Rは,式(9)による。
3
4
i
8nD
Gd
s
F
F
R
=
−
=
····································································· (9)
c) せん断未修正応力τ0は,式(10)による。
i
0,
2
3
0
π
π
8
τ
nD
Gds
d
DF
τ
+
=
=
······························································ (10)
d) せん断修正応力τκは,せん断応力修正係数をκとして,式(4)による。
0
κτ
τκ=
··················································································· (4)
e) 線径dは,式(5)による。
L0
φ
D
i
φ
D
e
φ
D
6
B 2704-1:2018
3
3
0
π
8
π
8
κτ
κDF
τ
DF
d
=
=
·································································· (5)
f)
巻数nは,式(11)による。
(
)
R
D
Gd
F
F
D
s
Gd
n
3
4
i
3
4
8
8
=
−
=
······························································(11)
g) 引張ばねに蓄えられるエネルギーUは,式(12)による。
(
)
2
is
F
F
U
+
=
·········································································· (12)
5.3.3
ねじりばねの場合
5.3.3.1
一般
図3−ねじりばね
ねじりばねの設計に用いる基本式は,図3〜図6などのように,ばねを巻き込む方向にモーメント又は
力(荷重)が作用する場合でコイル軸の周りに一様なねじりモーメント(トルク)だけを受け,コイル外
側の材料の表面が曲げ応力の引張面となる場合に用いる。また,ねじりばねを巻き込む方向にモーメント
又は力(荷重)が作用する場合でも,ばね指数が小さい又は巻数が少ないねじりばねは,ばねを巻き込む
につれてコイル部の傾き,ずれなどが発生し,コイル外側の材料の表面に発生する応力が一様にならない。
したがって,ねじりばねの設計に用いる基本式は,ばね指数3以上及び巻数3以上のときを対象とする。
5.3.3.2
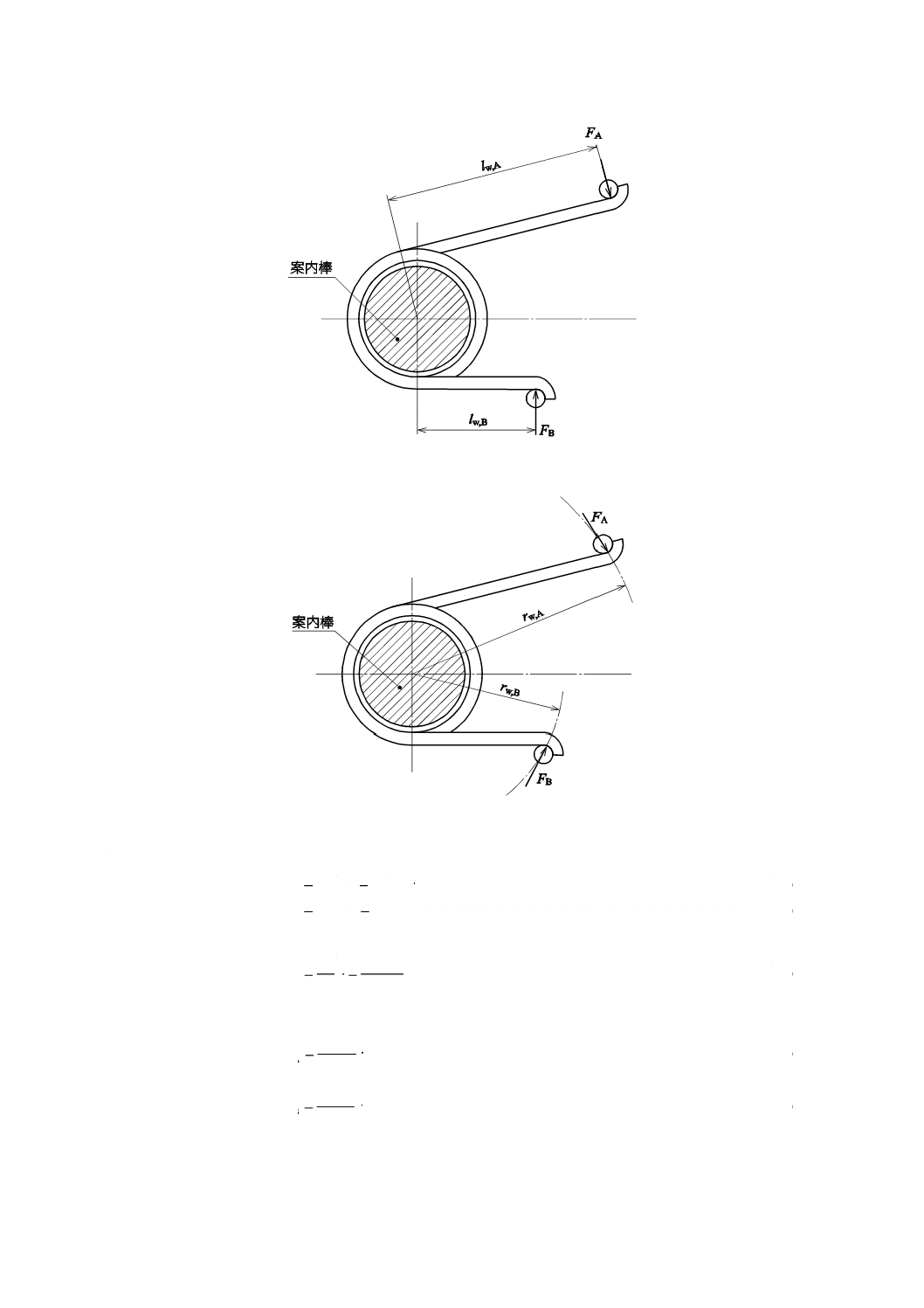
腕の長さを考慮しなくてもよい場合
図4のような腕の長さを考慮しなくてもよいねじりばねの設計に用いる基本式は,次による。
7
B 2704-1:2018
図4−腕の長さを考慮しなくてもよい場合
a) ねじりばねに作用するねじりモーメントMは,式(13)による。
w
Fr
M=
················································································ (13)
b) ねじりばねの有効部展開長さldは,式(14)による。
Dn
l
π
d=
················································································ (14)
c) ねじりばねのねじれ角αは,式(15)による。
4
d
64
π
Ed
MDn
EI
Dn
M
EI
Ml
α
=
=
=
························································ (15)
d) ばね定数R Mは,式(16)による。
Dn
Ed
M
R
64
4
M
=
=α
······································································ (16)
e) 曲げ応力σは,式(17)による。
Dn
Edα
d
M
Z
M
σ
π
2
π
32
3=
=
=
······························································ (17)
また,式(15)〜式(17)を角度(°)で示す場合は,式(18)〜式(20)による。
4
4
d
667
3
π
180
64
Ed
MDn
Ed
MDn
α
≒
=
··················································· (18)
Dn
Ed
Dn
Ed
R
667
3
180
π
64
4
4
Md
≒
=
······················································ (19)
Dn
Edα
σ
360
d
=
············································································· (20)
5.3.3.3
腕の長さを考慮する必要がある場合[(lw,A+lw,B)≧0.09πDn]
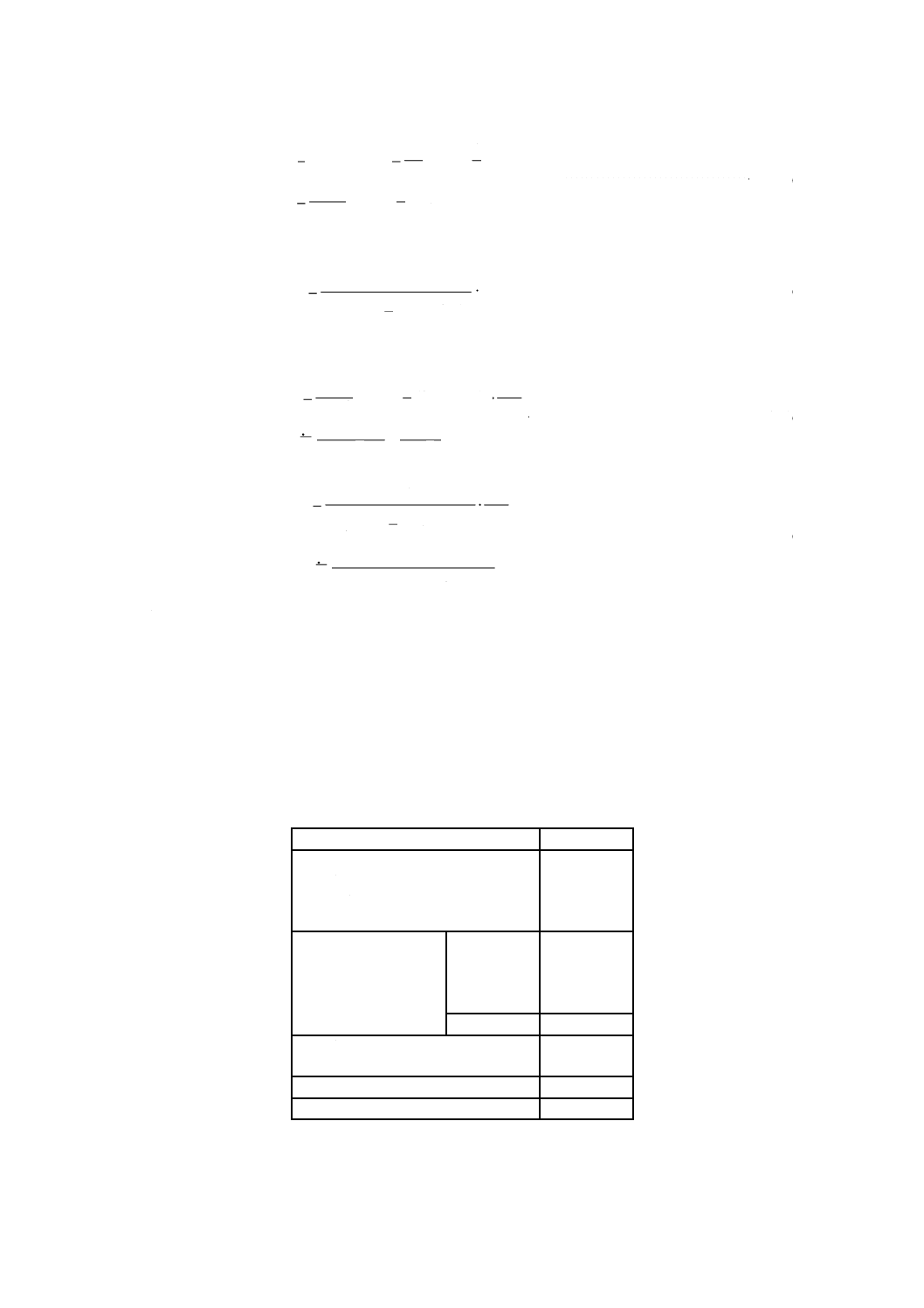
図5及び図6のような腕の長さを考慮する必要があるねじりばねの設計に用いる基本式は,次による。
8
B 2704-1:2018
図5−腕の長さを考慮する必要がある場合(1)(腕部計算時)
図6−腕の長さを考慮する必要がある場合(2)(コイル部計算時)
a) ねじりばねに作用するねじりモーメントMは,式(21)及び式(22)による。
B
w,
B
A
w,
A
l
F
l
F
M
=
=
··································································· (21)
B
w,
B
A
w,
A
r
F
r
F
M
=
=
·································································· (22)
b) ねじりばねのコイル部のねじれ角αCは,式(23)による。
EI
Dn
M
EI
Ml
α
π
d
C
=
=
··································································· (23)
c) ねじりばねの腕部lw,A,lw,Bのたわみ角αA,αBは,式(24)及び式(25)による。
EI
Ml
α
3
A
w,
A=
············································································· (24)
EI
Ml
α
3
B
w,
B=
············································································· (25)
d) ねじりばね全体のねじれ角αは,式(26)による。
9
B 2704-1:2018
)]
(
3
1
π[
π
64
)]
(
3
1
[π
B
w,
A
w,
4
B
w,
A
w,
B
A
C
l
l
Dn
d
E
M
l
l
Dn
EI
M
α
α
α
α
+
+
=
+
+
=
+
+
=
······································ (26)
e) ばね定数RMは,式(27)による。
)]
(
3
1
π[
64
π
B
w,
A
w,
4
M
l
l
Dn
d
E
R
+
+
=
······················································· (27)
また,式(26)及び式(27)を角度(°)で示す場合は,式(28)及び式(29)による。
)
(
389
667
3
π
180
)]
(
3
1
π[
π
64
B
w,
A
w,
4
4
B
w,
4
d
l
l
Ed
M
Ed
MDn
l
l
Dn
d
E
M
α
+
+
+
+
=
≒
A
w,
············································· (28)
)
(
389
667
3
180
π
)]
(
3
1
π[
64
π
B
w,
A
w,
4
B
w,
A
w,
4
Md
l
l
Dn
Ed
l
l
Dn
d
E
R
+
+
+
+
=
≒
··············································· (29)
5.4
ばねを設計するときに考慮する事項
5.4.1
弾性係数
5.4.1.1
横弾性係数
圧縮ばね及び引張ばねの設計に用いる横弾性係数(G)は,材料によって適切な値を用いなければなら
ない。
主な材料の横弾性係数(G)は,表3による。
表3−横弾性係数(G)
単位 N/mm2
材料
Gの値
ばね鋼鋼材
硬鋼線
ピアノ線
オイルテンパー線
7.85×104
ばね用ステンレス鋼線 SUS302
SUS304
SUS304N1
SUS316
6.85×104
SUS631J1
7.35×104
黄銅線
洋白線
3.90×104
りん青銅線
4.20×104
ベリリウム銅線
4.40×104
10
B 2704-1:2018
5.4.1.2
縦弾性係数
ねじりばねの設計に用いる縦弾性係数(E)は,材料によって適切な値を用いなければならない。
主な材料の縦弾性係数(E)は,表4による。
表4−縦弾性係数(E)
単位 N/mm2
材料
Eの値
ばね鋼鋼材
硬鋼線
ピアノ線
オイルテンパー線
2.06×105
ばね用ステンレス鋼線 SUS302
SUS304
SUS304N1
SUS316
1.86×105
SUS631J1
1.96×105
黄銅線
0.98×105
洋白線
1.08×105
りん青銅線
0.98×105
ベリリウム銅線
1.27×105
5.4.2
有効巻数
ばねの設計に用いる有効巻数は,次による。また,有効巻数は,3未満にするとばね特性が不安定にな
るので,3以上とすることが望ましい。
a) 圧縮ばねの場合 圧縮ばねの場合は,次による。また,圧縮ばねの有効巻数nは,式(30)による。
n=nt−(X1+X2)········································································ (30)
ここに, X1,X2: コイル両端部のそれぞれの座巻数
1) コイル端部が,次のコイルに接している端部形状で,座巻数が両端部とも1巻の場合
X1=X2=1
したがって,n=nt−2
2) コイル端部が,次のコイルに接していない端部形状で,座巻数が両端部とも0.75巻の場合
X1=X2=0.75
したがって,n=nt−1.5
b) 引張ばねの場合 引張ばねの巻数nは,次による。ただし,フック部を除く。
n=nt
c) ねじりばねの場合 ねじりばねの巻数nは,次による。ただし,腕部を除く。
n=nt
5.4.3
応力修正係数
5.4.3.1
圧縮ばね及び引張ばねのせん断応力修正係数
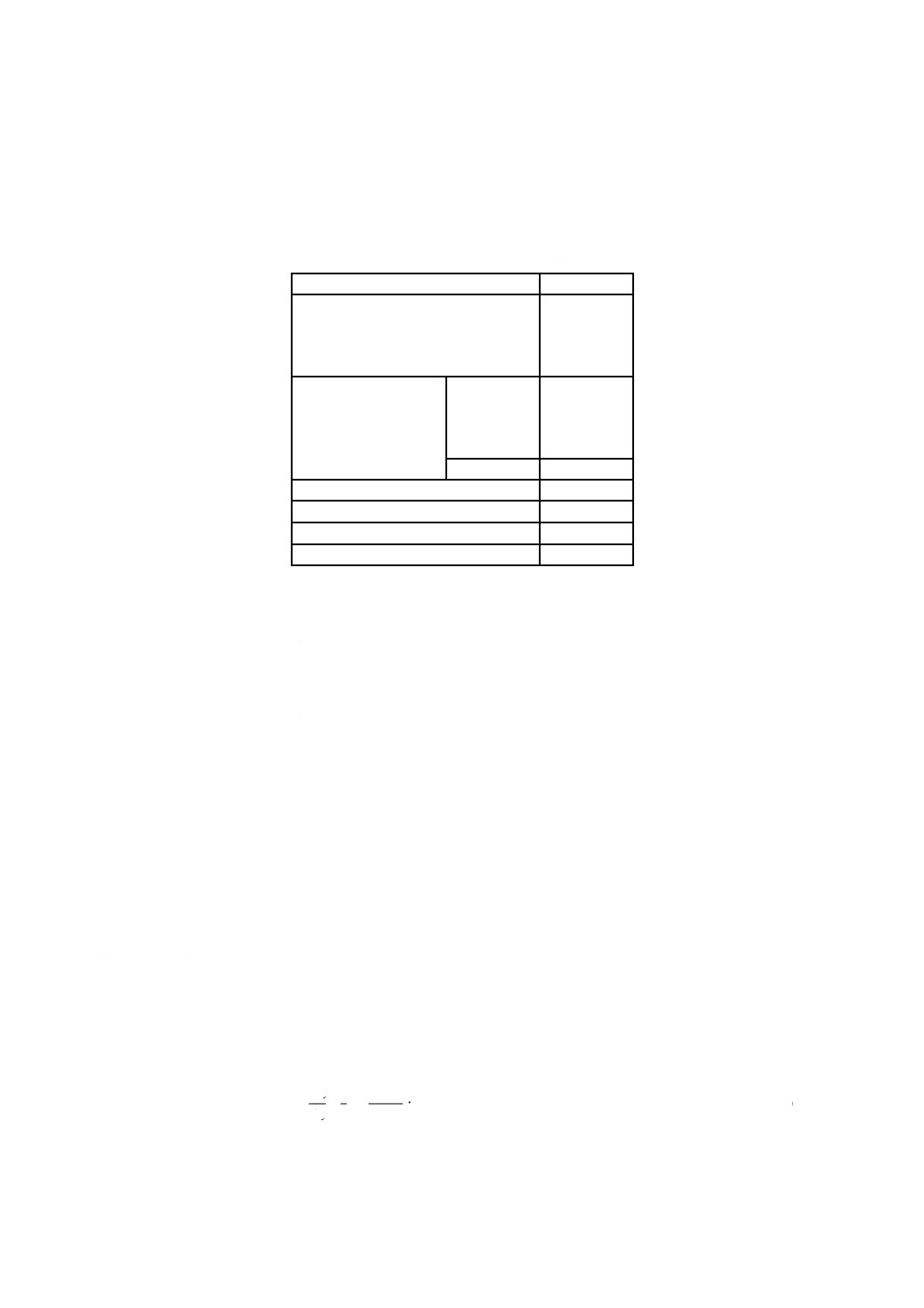
ばね指数cの値に対するせん断応力修正係数κは,式(31)又は図7による。
c
c
c
κ
615
.0
4
4
1
4
+
−
−
=
···································································· (31)
ばね指数cの値に対するせん断応力修正係数κは,式(31)以外に,式(32)などがあるが,式(31)以外の式 1)
を用いる場合は,受渡当事者間の協定による。
11
B 2704-1:2018
75
.0
5.0
−
+
=cc
κ
············································································ (32)
注1) せん断応力修正係数の式としては,ワール(A.M.Wahl)の式[式(31)],ベルグストラッサー
(M.Bergsträsser)の式[式(32)],ゲーナー(Göhner)の式などが用いられており,ほかにも幾
つかの式が知られているが,この規格では,最も広く使用されている式(31)[ワール(A.M.Wahl)
の式]を採用している。
せ
ん
断
応
力
修
正
係
数
κ
1.0
1.1
1.2
1.3
1.4
1.5
1.6
3
4
5
6
7
8
910111213141516171819202122
ばね指数
d
D
c=
図7−せん断応力修正係数(κ)
5.4.3.2
ねじりばねの曲げ応力修正係数
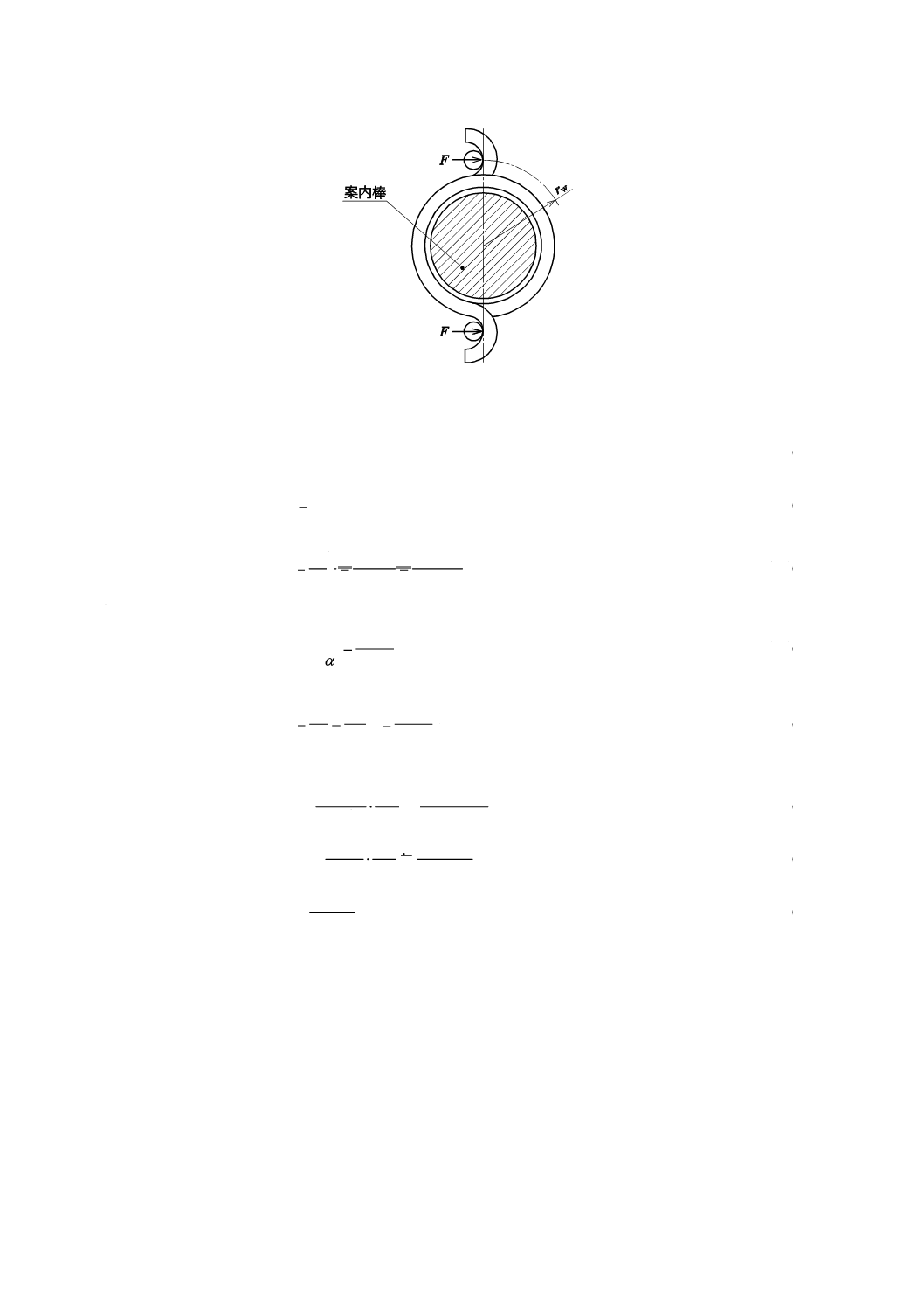
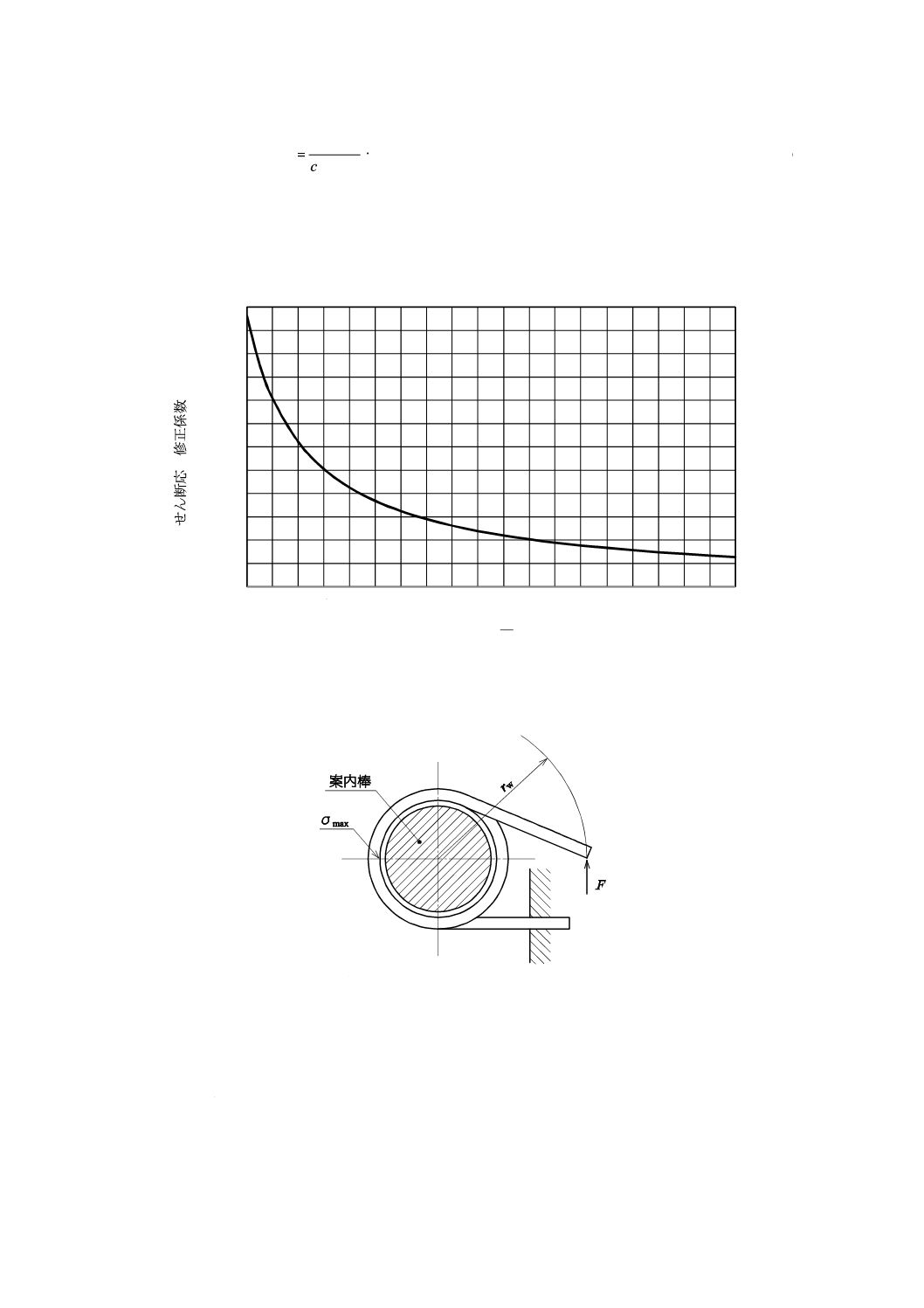
図8−ねじりばねを巻き戻す方向に力(荷重)が作用する場合
図8のように,ねじりばねを巻き戻す方向に力(荷重)が作用する場合は,コイル内側の材料の表面に
最大の曲げ応力σが生じる。また,このコイル内側の応力の計算では,コイル部の湾曲の影響を考慮し,
ばね指数に応じた曲げ応力修正係数を用いる。
なお,この曲げ応力の最大値σmaxは,力の作用点から最も離れたコイル内側の材料の表面に生じ,式(33)
による。
12
B 2704-1:2018
3
b
w
max
π
)2
/
(
32
d
Fκ
D
r
σ
+
=
····························································· (33)
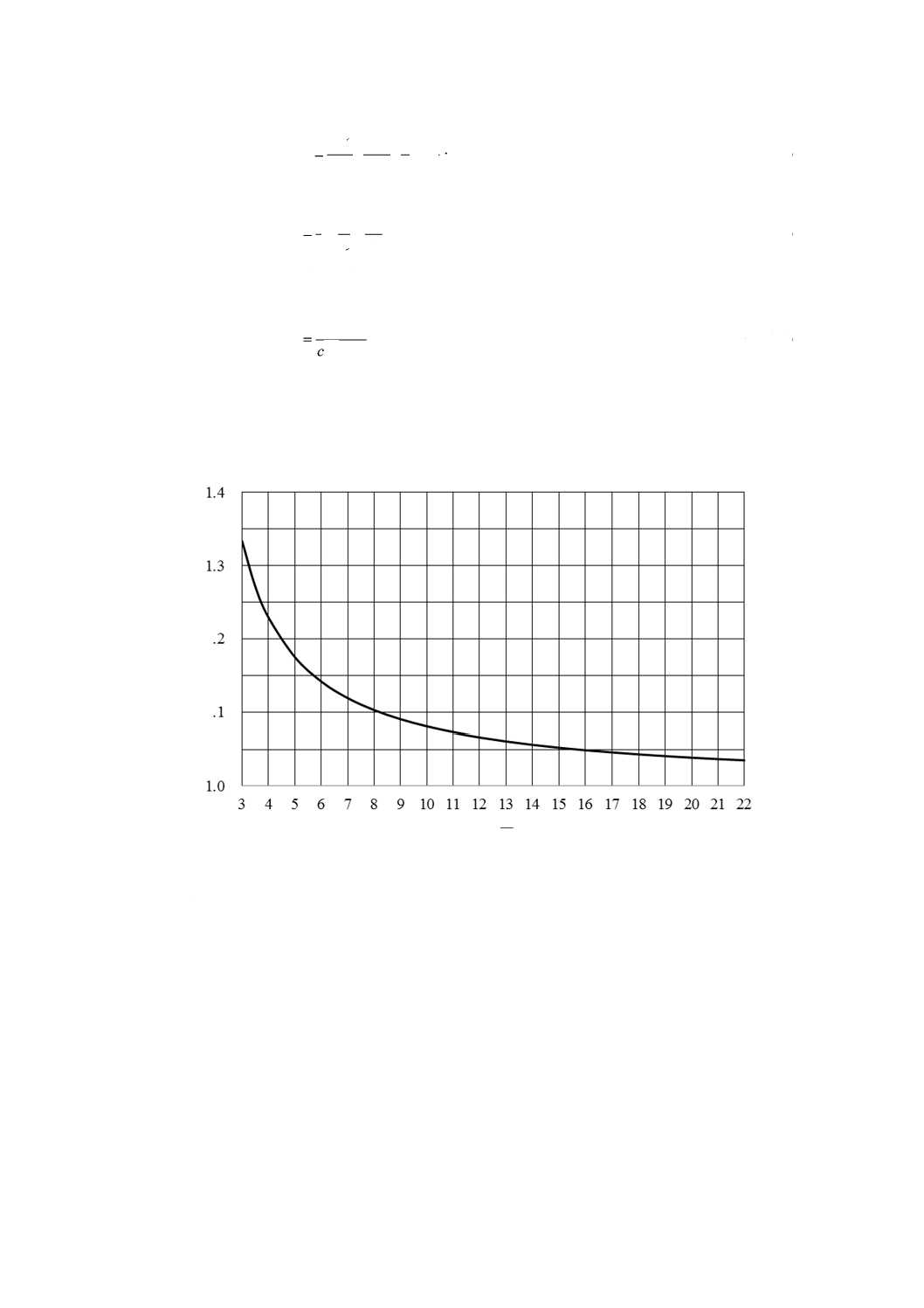
ばね指数cの値に対する曲げ応力修正係数κbは,式(34)又は図9による。
)1
(
4
1
42
b
−
−
−
=
c
c
c
c
κ
······································································· (34)
ばね指数cの値に対する曲げ応力修正係数κbは,式(34)以外に,式(35)などがあるが,式(34)以外の式 2) を
用いる場合は,受渡当事者間の協定による。
75
.0
5.0
b
−
+
=cc
κ
··········································································· (35)
注2) 曲げ応力修正係数の式としては,ワール(A.M.Wahl)の式[式(34)],ベルグストラッサー
(M.Bergsträsser)の式[式(35)],ゲーナー(Göhner)の式などが用いられており,ほかにも幾
つかの式が知られているが,この規格では,最も広く使用されている式(34)[ワール(A.M.Wahl)
の式]を採用している。
曲
げ
応
力
修
正
係
数
κ
b
ばね指数
d
D
c=
図9−曲げ応力修正係数(κb)
5.4.4
圧縮ばねの密着長さ
圧縮ばねの密着長さLcは,一般に略算式(36)による。ただし,圧縮ばねの密着長さは,参考とする。
Lc=(nt−1)d+(t1+t2)································································· (36)
ここに,
(t1+t2): コイル両端部のそれぞれの厚さの和
なお,両端部が研削又はテーパ加工を行った圧縮ばねで,特に密着長さの指定を必要とするときは,式
(37)で求めた値を密着長さLcの最大値として指定するが,ばねの形状によっては,この値より大きくなる
ことがあるので注意する。
Lc=nt×dmax ············································································ (37)
5.4.5
引張ばねの初張力
密着巻の引張ばねには,初張力Fiが生じる。この場合の初張力は,式(38)による。
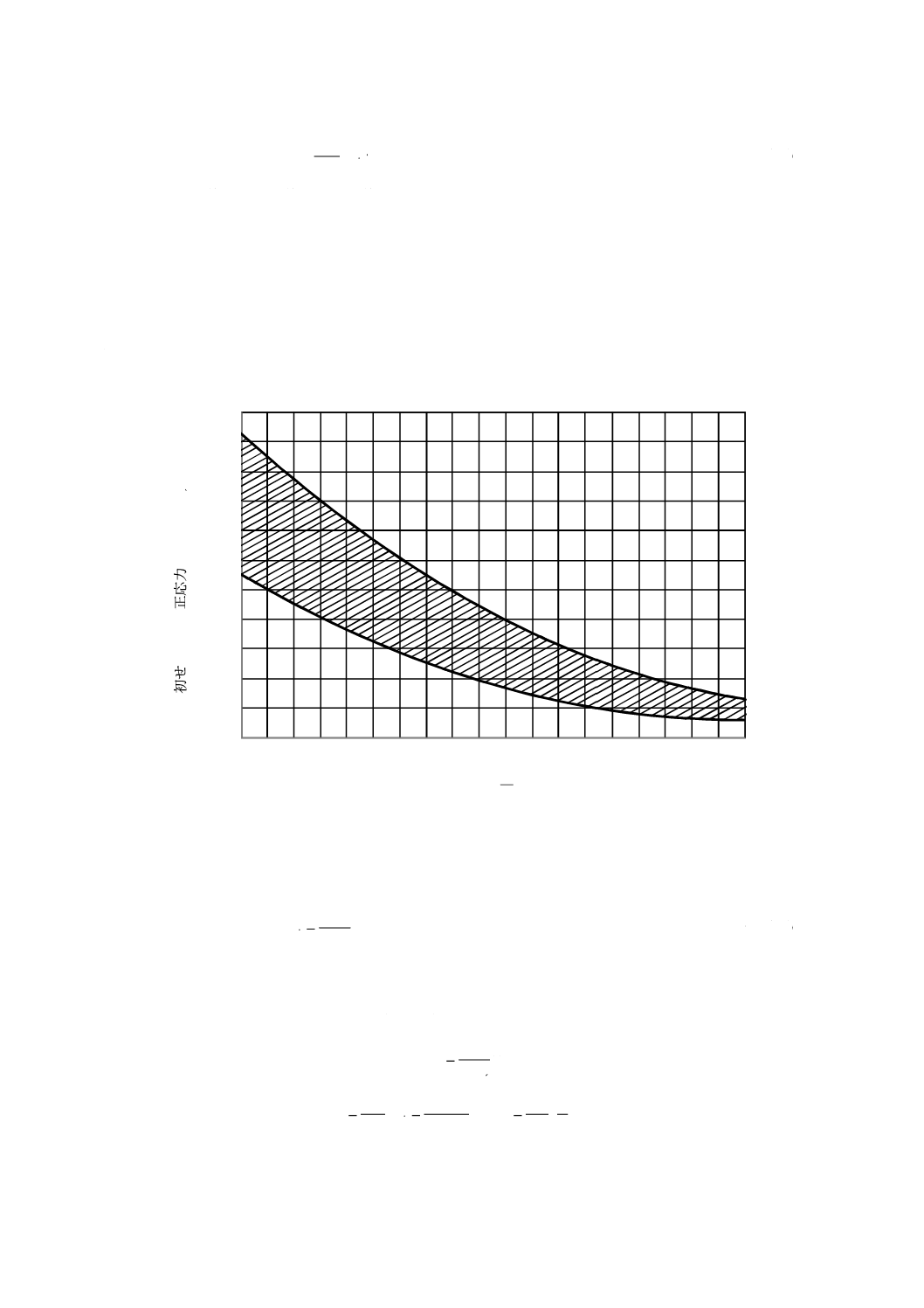
13
B 2704-1:2018
i0,
3
i
8
π
τ
D
d
F=
············································································ (38)
なお,ピアノ線及び硬鋼線などの鋼線で密着巻に成形し,低温焼なましを行っていない場合の初せん断
未修正応力τ0,iは,図10の斜線の範囲内とする。ただし,鋼線以外の材料を使用する場合及び低温焼なま
しを実施する場合は,図10の斜線の範囲内から読み取った初せん断未修正応力の値を,次によって修正
する。
a) ばね用ステンレス鋼線の場合は,鋼線の初せん断未修正応力の15 %減とする。
b) りん青銅線,黄銅線,洋白線などの場合は,鋼線の初せん断未修正応力の50 %減とする。
c) 成形後に低温焼なましを実施する場合は,上記で求めた値に対し,ピアノ線及び硬鋼線などの鋼線で
は20〜35 %減とし,ばね用ステンレス鋼線では15〜25 %減とする。
初
せ
ん
断
未
修
正
応
力
τ
0
,i
(
N
/m
m
2)
ばね指数
d
D
c=
図10−初せん断未修正応力(τ0,i)鋼線で成形された低温焼なまし前の値
低温焼なまし前の初せん断未修正応力τ0,iの値を図10から読み取る代わりに,経験式(39)によってもよ
い。
c
G
τ
100
i
0,=
·············································································· (39)
なお,経験式(39)を用いて初張力Fiを算出する計算例を,次に示す。
例1 ピアノ線及び硬鋼線の場合
G=7.85×104(N/mm2)
初せん断未修正応力
75
.0
100
i
0,
×
=
c
G
τ
(0.75は,低温焼なまし実施による25 %減)
初張力
2
4
2
4
i0,
3
i
231
75
.0
255
8
D
d
D
Gd
τ
D
πd
F
=
×
=
=
例2 ばね用ステンレス鋼線の場合
0
20
40
60
80
100
120
140
160
180
200
220
3
4
5
6
7
8
910111213141516171819202122
14
B 2704-1:2018
G=6.85×104(N/mm2)
初せん断未修正応力
8.0
100
i
0,
×
=
c
G
τ
(0.8は,低温焼なまし実施による20 %減)
初張力
2
4
2
4
i
0,
3
i
215
8.0
255
8
D
d
D
Gd
τ
D
πd
F
=
×
=
=
5.4.6
ねじりばねの案内棒の径
ねじりばねを巻き込む方向にねじるとコイル内径が減少するので,ねじりばねの案内棒の径Ddは,ねじ
りばねが最も巻き込まれた最大使用のときのコイル内径(Di−ΔD)の約90 %にとることが望ましい。
a) 負荷状態におけるコイル内径の減少は,コイル平均径の変化量∆Dと同じで,式(40)及び式(41)による。
πn
D
α
ΔD
2
max
=
··········································································· (40)
n
D
α
360
dmax
=
·········································································· (41)
ここに, αmax: 最大ねじれ角(角度表示がradの場合)
αdmax: 最大ねじれ角(角度表示が°の場合)
b) ねじりばねの案内棒の径Ddは,最大使用のときのコイル内径(Di−ΔD)の約90 %とし,式(42)によ
る。
Dd=0.9(Di−ΔD) ······································································ (42)
5.4.7
圧縮ばね及び引張ばねのサージング
サージングを避けるために,圧縮ばね及び引張ばねの固有振動数は,圧縮ばね及び引張ばねに作用する
加振源の全ての振動と共振するのを避けるように選ばなければならない。
なお,圧縮ばね及び引張ばねの固有振動数feは,式(43)による。
ρ
G
πnD
d
a
m
R
a
f
2
s
3
e
36
.
22
10
=
=
························································ (43)
ここに,
2
i
a=
: 両端自由又は固定の場合
4
1
2−
=i
a
: 一端固定で他端自由の場合
i=1,2,3 …
G=7.85×104(N/mm2),ρ=7.85×10−6(kg/mm3)の材料(例えば,ピアノ線)で製作された圧縮ばね及
び引張ばねの支持条件を両端自由又は固定とした場合,ばねの1次の固有振動数fe,1は,式(44)による。
2
5
1,e
10
56
.3
nD
d
f
×
=
·································································· (44)
5.4.8
設計計算でのその他考慮する事項
ばねの設計計算では,次の事項についても考慮しなければならない。
a) ばね指数 ばね指数が小さくなると局部応力が過大となり,また,ばね指数が大きい場合及び小さい
場合は,加工性が問題となる。したがって,ばね指数は,熱間で成形する場合には4〜15,冷間で成
形する場合には3〜22の範囲とすることが望ましい。
b) 縦横比 圧縮ばねの縦横比(自由長さとコイル平均径との比)が大きくなると比較的低い力(荷重)
で圧縮ばねが座屈を起こす。座屈が起こる限界は,圧縮ばねの支持方法によって異なるが,設計上で
座屈が避けられない寸法になった場合は,圧縮ばねの内側に案内棒を入れるか,圧縮ばねを筒状の案
15
B 2704-1:2018
内に入れて使用する。ただし,案内の方法(寸法,形状,材料など)は,圧縮ばねと案内との摩擦の
影響などに注意を要する。また,縦横比が小さいと有効巻数が少なくなり,有効巻数の増減の影響に
よってばね特性及び応力値が計算と合致しなくなり,実用上で問題となる。したがって,圧縮ばねの
縦横比は,座屈を考慮して4以下とし,更に有効巻数の確保のために0.8以上とすることが望ましい。
c) ピッチ 圧縮ばねのたわみ及びせん断応力を計算する基本式は,ピッチ角が小さいことを前提に力(荷
重)Fによって材料がねじりモーメントを受けたとして導いたものである。ピッチが0.5Dを超えると,
一般的に,力(荷重)の増加に伴いコイル径が変化するため,基本式から求めたたわみ及びせん断応
力の修正が必要となるので,0.5D以下とする。
なお,一般にピッチpの推定は,略算式(45)による。
d
n
L
L
p
+
−
c
0
=
······································································· (45)
6
ばね特性
6.1
圧縮ばね
圧縮ばねのばね特性は,圧縮ばねのたわみ又は長さと力(荷重)との関係を表すもので,熱間成形の場
合は,次のa) 又はb) を,冷間成形の場合は,b) を指定する。
なお,ばね定数を指定する必要がある場合は,c) による。
a) 指定力のときの長さ 指定力のときの長さは,そのときのたわみが全たわみ3)の20〜80 %になるよう
に定める。ただし,指定力は,最大試験力4)の80 %以下とする。
なお,最大試験力については,7.2.1による。
注3) 全たわみとは,計算上の自由長さから密着長さを減じた計画たわみをいう。
4) 最大試験力とは,許容せん断応力(図11参照)と等しいせん断未修正応力が発生するときの
力(荷重)をいう。
b) 指定長さのときの力(荷重) 指定長さのときの力(荷重)は,最大試験力の80 %以下とする。指定
長さは,全たわみの20〜80 %になるように定める。
c) ばね定数 ばね定数は,全たわみの30〜70 %にある二つの力(荷重)点における力(荷重)の差及び
たわみの差によって定める。ただし,二つの力(荷重)点はいずれも最大試験力の80 %以下とする。
6.2
引張ばね
引張ばねのばね特性は,引張ばねのたわみ又は長さと力(荷重)との関係を表すもので,熱間成形の場
合は,次のa) 又はb) を,冷間成形の場合は,b) を指定する。
なお,ばね定数を指定する必要がある場合は,c) による。
a) 指定力のときの長さ 指定力のときの長さは,そのときのたわみが最大試験力5)のときのたわみの20
〜80 %になるように定める。
なお,最大試験力については,7.2.3による。
注5) 最大試験力とは,コイル部に,次の許容せん断応力と等しいせん断未修正応力が発生すると
きの力(荷重)をいう。引張ばねの許容せん断応力は,熱間成形の場合は,図11に示す値の
67 %,冷間成形の場合は,図11に示す値の80 %とする。
b) 指定長さのときの力(荷重) 指定長さのときの力(荷重)は,最大試験力の80 %以下とする。指定
長さは,最大試験力のときのたわみの20〜80 %になるように定める。
c) ばね定数 ばね定数は,最大試験力のときのたわみの30〜70 %にある二つの力(荷重)点における力
16
B 2704-1:2018
(荷重)の差及びたわみの差によって定める。
6.3
ねじりばね
ねじりばねのばね特性は,ねじりばねのねじれ角とモーメント又は力(荷重)との関係を表すもので,
必要がある場合に指定ねじれ角のときのモーメントとして指定する。ただし,ねじりばね特性は,ねじり
ばねの端末形状,ねじりばねと案内棒との摩擦及び作動のときのばねの姿勢などの影響で同じ設計値でも
異なる場合があるため,ばね特性の指定条件及び測定方法については受渡当事者間の協定による。
7
設計応力
7.1
一般
7.1.1
圧縮ばね及び引張ばね
設計応力とは,圧縮ばね及び引張ばねの使用状態によって圧縮ばね及び引張ばねに生じる計算上のせん
断応力で,材料の全周に一様な値のせん断応力が生じると仮定した式(3)及び式(10)を用いてせん断未修正
応力を計算する。ただし,実際の圧縮ばね及び引張ばねでは,コイル部の湾曲の影響によって,コイル内
側の材料表面の応力が外側の材料表面の応力より大きくなる。この現象及び直接せん断力の影響を考慮し
たものがせん断応力修正係数で,式(3)及び式(10)にせん断応力修正係数を乗じたものが,せん断修正応力
の式(4)である。静的な力(荷重)を取り扱う場合は,平均的な応力を問題にしなければならないので,せ
ん断未修正応力を用いる。また,繰返し力(荷重)による疲労を問題にする場合は,最大応力値が重要で
あるので,せん断修正応力を用いる。
引張ばねのフック部の応力は,フック形状又はコイル本体からフックに立ち上がる部分での応力集中な
どの影響で,コイル部の応力より大きくなる。したがって,フックの立ち上がる部分の曲げ半径は,線径
より大きくして応力集中を避ける設計が必要である。
引張ばねのフック部の応力は,形状によって解析が複雑となり,一般式として規定することが難しいた
め,この規格では,引張ばねのコイル部の許容せん断応力を圧縮ばねの80 %とし,フック部の応力が高く
なることを考慮している。
7.1.2
ねじりばね
設計応力とは,ねじりばねの使用状態によってねじりばねに生じる計算上の曲げ応力である。ねじりば
ねコイル部の曲げ応力は,モーメント又は力(荷重)がねじりばねを巻き込む方向に作用する場合,式(17)
を用いて計算する。また,モーメント又は力(荷重)がねじりばねを巻き戻す方向に作用する場合には,
式(33)を用い計算する。
なお,ねじりばねの腕部に生じる応力は,腕がコイル本体から立ち上がる部分で応力集中などの影響も
あり大きくなる。したがって,端末の腕はできるだけ単純な形状とし,腕部の曲げ半径は,線径より大き
くして応力集中を避ける設計が必要である。
7.2
静的な力(荷重)を受けるばね
7.2.1
一般
静的な力(荷重)を受けるばねとは,ばねの使用状態で力(荷重)変動のほとんどないもの,又は力(荷
重)変動が,ばねの使用期間を通じて繰返し回数約1 000回以下のものを指す。
静的な力(荷重)を受けるばねの設計応力は,ばね使用のときの温度,へたりに対する要求レベルなど
を考慮して許容せん断応力及び許容曲げ応力に対して適切な値を選ばなければならない。
7.2.2
圧縮ばね
圧縮ばねの許容せん断応力は,図11による。圧縮ばねの密着せん断未修正応力は,許容せん断応力を超
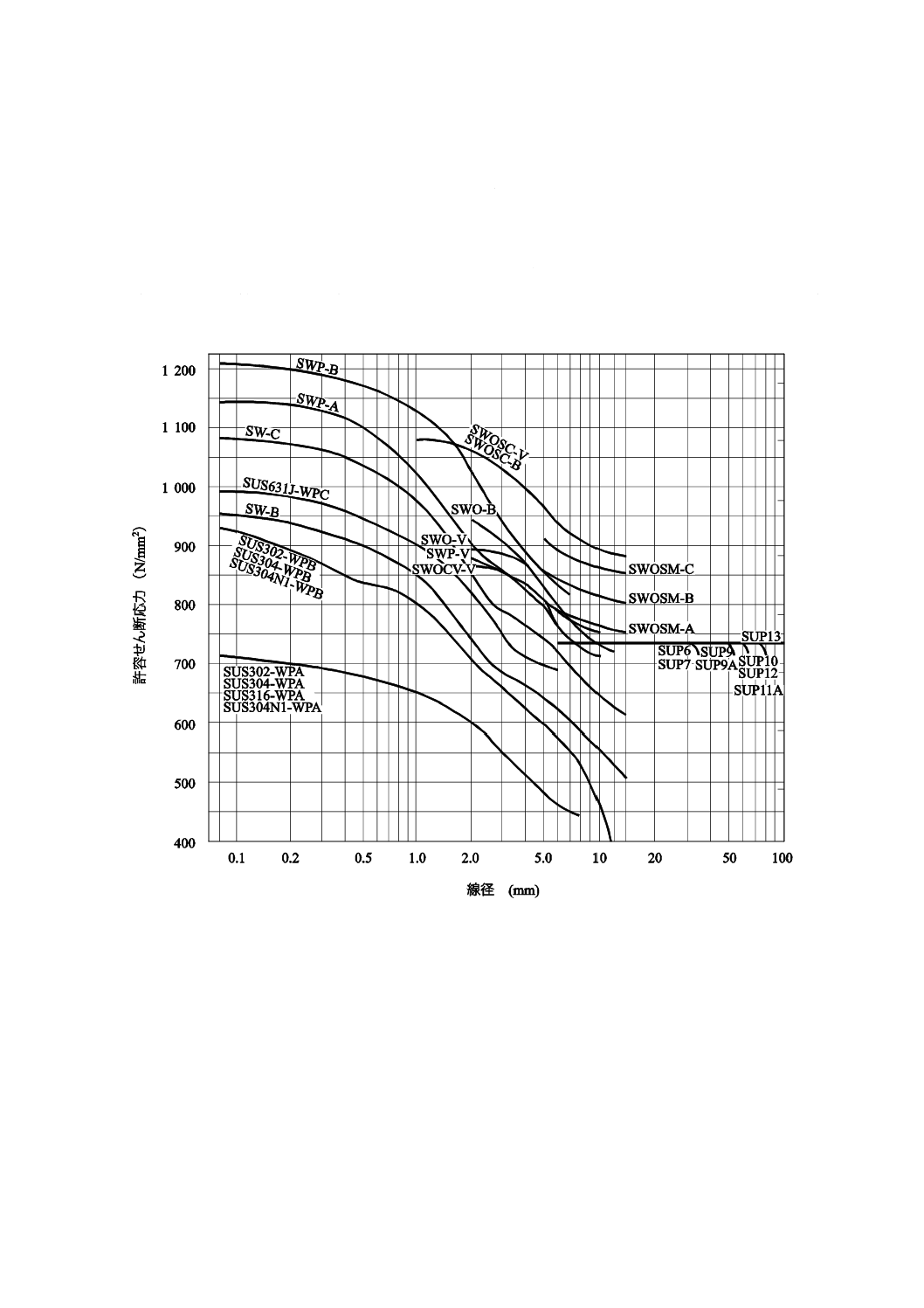
17
B 2704-1:2018
えないことが望ましく,圧縮ばねの最大試験力のときのせん断未修正応力は,許容せん断応力とする。ま
た,圧縮ばねの使用上の最大せん断未修正応力は,許容せん断応力の80 %以下とする。ただし,図11に
記載していない材料を使用する場合は,受渡当事者間の協定による。
7.2.3
引張ばね
引張ばねの許容せん断応力は,熱間成形の場合は,図11に示す値の67 %,冷間成形の場合は,図11に
示す値の80 %とし,引張ばねの最大試験力のときのせん断未修正応力は,許容せん断応力とする。また,
引張ばねの使用上の最大せん断未修正応力は,許容せん断応力の80 %以下とする。ただし,図11に記載
していない材料を使用する場合は,受渡当事者間の協定による。
図11−圧縮ばね及び引張ばねの許容せん断応力
7.2.4
ねじりばね
ねじりばねの許容曲げ応力は,図12による。ねじりばねの設計応力は,許容曲げ応力を超えないことが
望ましい。ただし,図12に記載していない材料を使用する場合は,受渡当事者間の協定による。
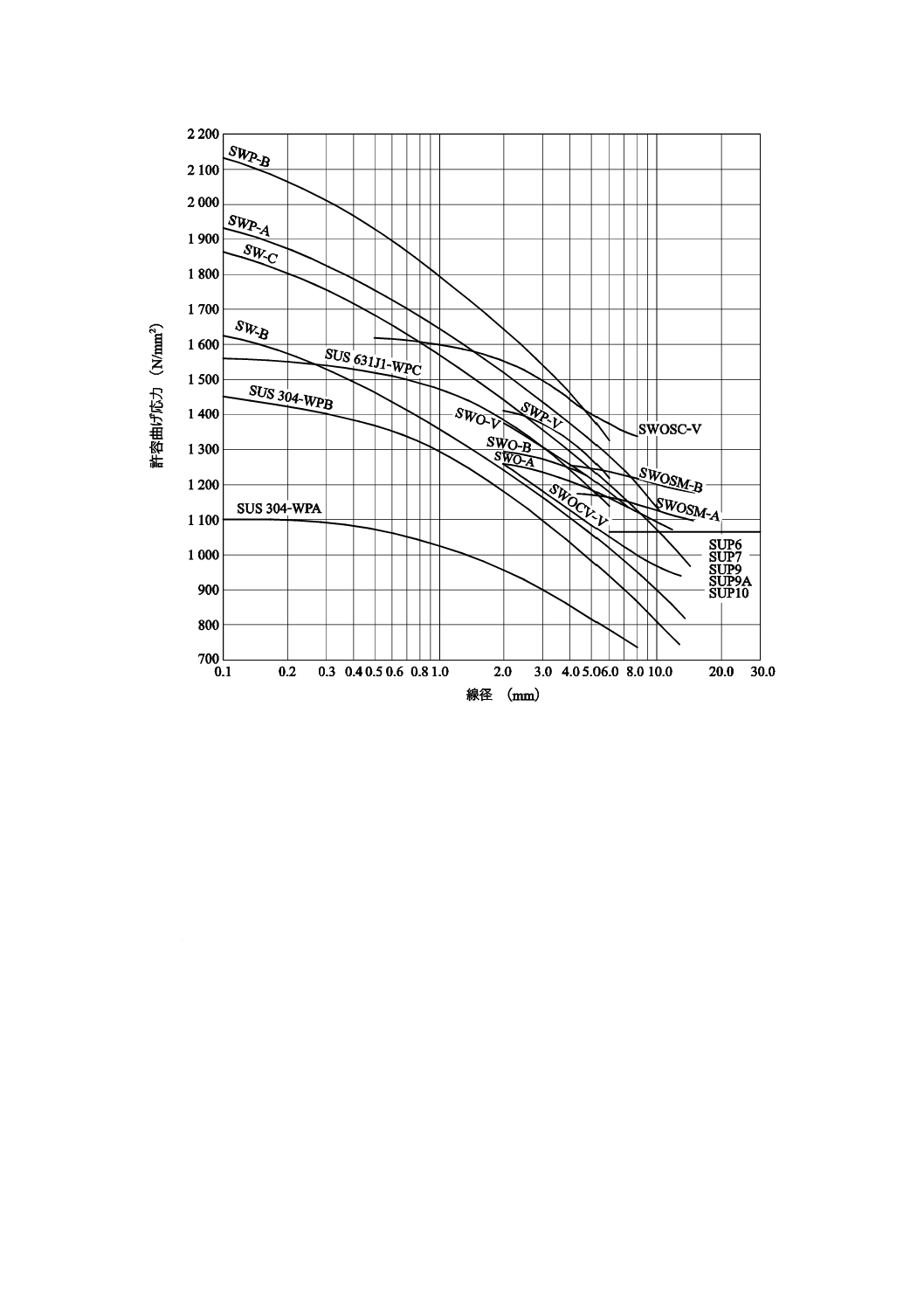
18
B 2704-1:2018
図12−ねじりばねの許容曲げ応力
7.3
繰返し力(荷重)を受けるばね
7.3.1
圧縮ばね及び引張ばね
7.3.1.1
一般
繰返し力(荷重)を受ける圧縮ばね及び引張ばねのせん断修正応力は,式(4)による。設計応力は,圧縮
ばね及び引張ばねの使用範囲(下限応力と上限応力との関係),繰返し回数,線の表面状態,使用環境,製
造方法など疲労強度に及ぼす諸因子を考慮して寿命を推定し,適切な値を選ばなければならない。
7.3.1.2
適用例
ばねの寿命を推定する方法の一例を,次に示す。
なお,この推定方法は,冷間成形による圧縮ばね及び引張ばねに限る。
ピアノ線及び弁ばね用オイルテンパー線など耐疲労性の優れた線を用いた圧縮ばね及び引張ばねでショ
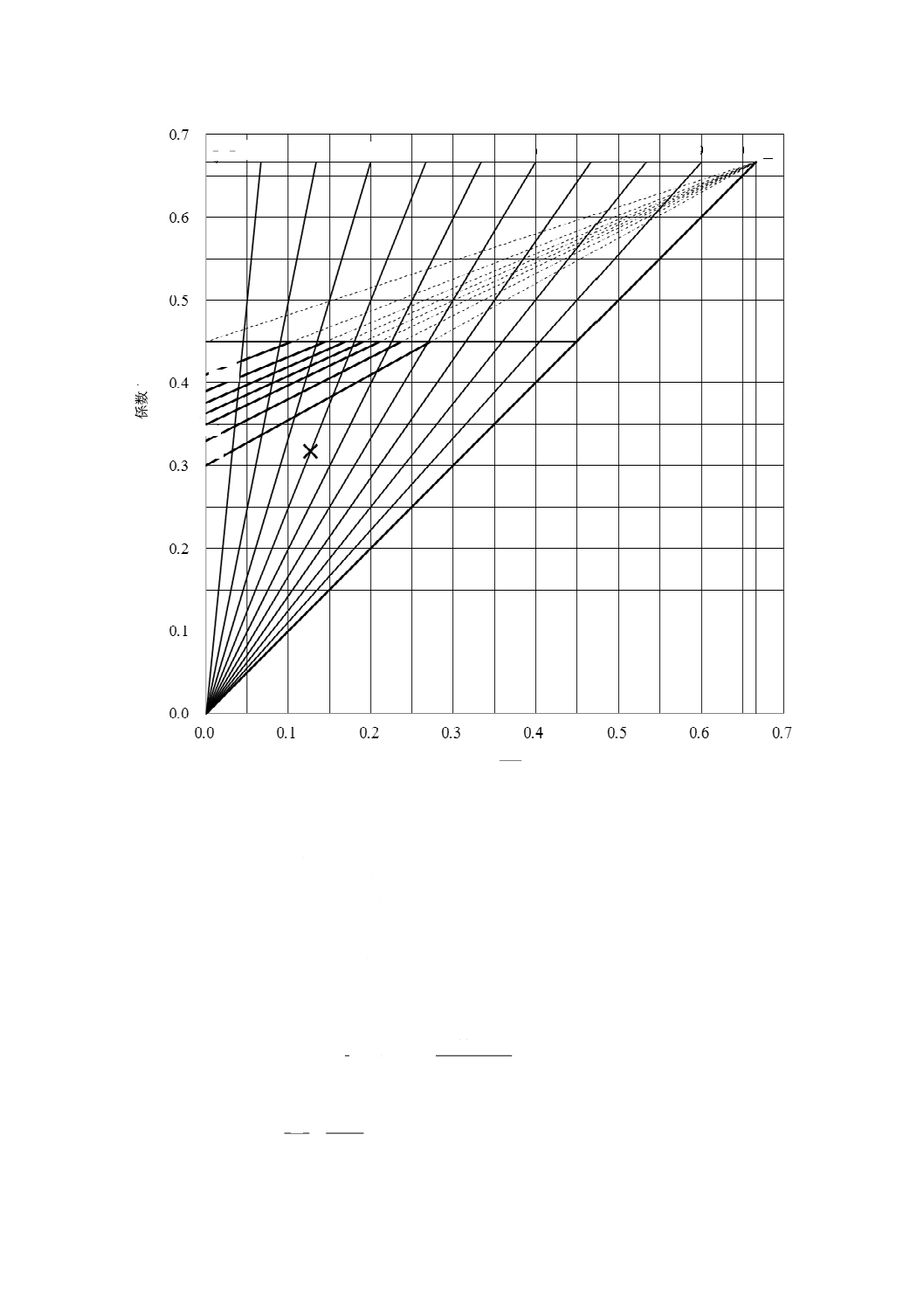
ットピーニングを施さない場合には,図13の疲労強度線図を用いて,通常の雰囲気における繰返し力(荷
重)を受ける際の寿命を推定することができる。
一般的に,設計の当初において,使用範囲の力(荷重)は分かっていることが多い。取付けのときの力
(荷重)をF1,最大使用のときの力(荷重)をF2とし,図13に,その比を斜線で記載した。その比は,
最大使用のときの力(荷重)F2に対する取付けのときの力(荷重)F1比,又は最大使用のときの応力τκ,2
に対する取付けのときの応力τκ,1の比であり,式(46)による。

19
B 2704-1:2018
2
1
2
κ
1
κ
F
F
τ
τ
=
,
,
··············································································· (46)
ただし,式(46)では,τκ,1,τκ,2は,サージングなどによる付加応力がない場合で,この影響があるときは,
付加応力を考慮したτκ,1,τκ,2によって線図を用いる必要がある。
また,図13中の上限応力係数0.45の太い横線は,圧縮ばね及び引張ばねのへたりの許容度によって上
下に移動するもので,僅かなへたりを許容する場合は,係数τκ,2/σBのτκ,2を図11に示す許容せん断応力ま
でとって,太い横線を上方に移動してもよい。
なお,図13の左端の下限応力係数0の縦軸上の係数を材料の引張強さに乗じた値は,片振り疲労強度と
なる。
また,この引張強さに対する片振り疲労強度の係数は,JIS B 2711によるショットピーニングを施すこ
とによって有効な圧縮残留応力があるときは,20 %程度上昇させて表5のようにしてもよい。
表5−上限応力係数の例
繰返し回数
片振り疲労強度
107回
σB×0.36
106回
σB×0.40
105回
σB×0.42
104回
σB×0.50
20
B 2704-1:2018
上
限
応
力
係
数
下限応力係数
B
,
σ
τ1
κ
図13−せん断応力の疲労強度線図の例
図13において,次のばねとする。
材料: ピアノ線B種SWP-B
d= 1.0(mm)
D= 10.0(mm)
n= 8
nt= 10
L0= 32(mm)
このばねの使用範囲がL1=24(mm),F1=9.8(N)からL2=12(mm),F2=24.5(N)で毎分800回の
正弦波状の繰返し力(荷重)を受ける場合の寿命回数を推定する。
717
0.1
π
5.
24
10
8
15
.1
π
8
3
3
,
=
×
×
×
×
=
×
=
d
DF
κ
τ
2
2
κ
(N/mm2)
上限応力係数は,
317
.0
260
2
717
B
,
=
=
σ
τ2
κ
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
3
2
107
106
105
6×104
4×104
3×104
2×104
104
=
2
κ
1
κ
τ
τ
,
,
σ
B
τ
κ,
2
21
B 2704-1:2018
この場合のσBの値は,材料の引張強さの規格値の最小値とする。
なお,主な材料の引張強さ規格値の最小値は,表6及び表7による。ただし,C 5102 W及びC 5212 W
(りん青銅線)並びにC 7541 W(洋白線)については,JIS H 3270に規定する引張強さの最小値を参考と
する。
4.0
5.
24
8.9
=
=
2
1
F
F
下限応力係数は,
127
.0
317
.0
4
0
B
,
B
,
=
×
=
×
=
.
σ
τ
F
F
σ
τ
2
κ
2
1
1
κ
以上の結果によって,図13に示す×印の点を得る。この点は,図から明らかなように107回以上の寿命
と推定することができる。
7.3.2
ねじりばね
7.3.2.1
一般
繰返しモーメント又は力(荷重)を受けるねじりばねの設計応力は,ばねの使用範囲(下限応力と上限
応力との関係),繰返し回数,線の表面状態,使用環境及び製造方法など疲労強度に及ぼす諸因子を考慮し
て寿命を推定し,適切な値を選ばなければならない。
7.3.2.2
適用例
ばねの寿命を推定する方法の一例を,次に示す。
なお,この推定方法は,冷間成形によるねじりばねに限る。
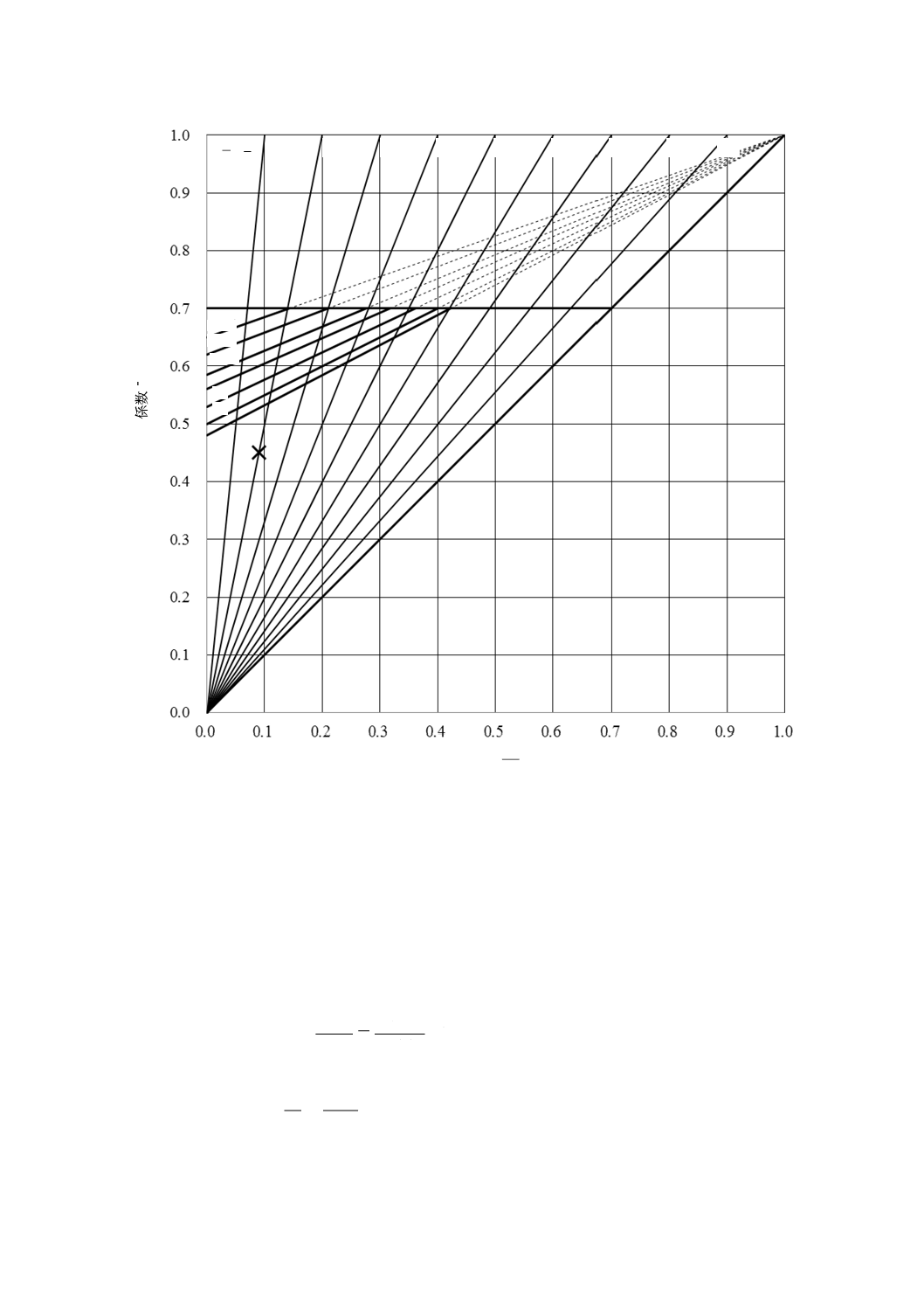
ピアノ線,弁ばね用オイルテンパー線など耐疲労性の優れた線を用いたねじりばねの場合,図14の疲労
強度線図を用いて,通常の雰囲気におけるモーメント又は力(荷重)を受ける際の寿命を推定することが
できる。
一般的に,設計の当初において,使用範囲のモーメント又はねじれ角が分かっていることが多い。取付
けのときのモーメントをM1,ねじれ角をα1,最大使用のときのモーメントをM2,ねじれ角をα2として,
図14に,その比を斜線で記載した。その比は,最大使用のときのモーメントM2に対する取付けのときの
モーメントM1の比,最大使用のときの応力σ2に対する取付けのときの応力σ1の比,又は最大使用のとき
のねじれ角α2に対する取付けのときのねじれ角α1の比であり,式(47)による。
2
1
2
1
2
1
α
α
M
M
σ
σ
=
=
········································································ (47)
なお,図14中の上限応力係数0.7の太い横線は,ねじりばねのへたりの許容度によって上下に移動する
もので,僅かなへたりを許容する場合は,係数σ2 /σBのσ2を図12に示す許容曲げ応力までとって太い横線
を上方に移動してもよい。また,図14の左端の下限応力係数0の縦軸上の係数を材料の引張強さに乗じ
た値は,片振り疲労強度となる。
22
B 2704-1:2018
上
限
応
力
係
数
下限応力係数
B
σ
σ1
図14−曲げ応力の疲労強度線図の例
図14において,次のばねとする。
材料: ピアノ線B種SWP-B
d= 1.0(mm)
D= 9.0(mm)
n= 4
端末の形状: ショートフック
このねじりばねにM2=100 N・mm,M1=20 N・mmが,ねじりばねを巻き込む方向に作用する場合の寿命
回数を推定する。
019
1
0.1
π
100
32
π
32
3
3
=
×
×
=
=
d
M
σ
2
2
(N/mm2)
上限応力係数は,
45
.0
260
2
019
1
B
=
=
σ
σ2
この場合のσBの値は,材料の引張強さ規格値の最小値とする。
107
106
105
5×104
4×104
3×104
2×104
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
=
2
1
σ
σ
σ
B
σ
2
23
B 2704-1:2018
なお,主な材料の引張強さ規格値の最小値は,表6及び表7による。ただし,C 5102 W及びC 5212 W
(りん青銅線)並びにC 7541 W(洋白線)については,JIS H 3270に規定する引張強さの最小値を参考と
する。
2.0
100
20=
=
2
1
M
M
下限応力係数は,
09
.0
45
.0
2.0
B
B
=
×
=
×
=
σ
σ
M
M
σ
σ
2
2
1
1
以上の結果によって,図14に示す×印の点を得る。この点は,図から明らかなように107回以上の寿命
と推定することができる。
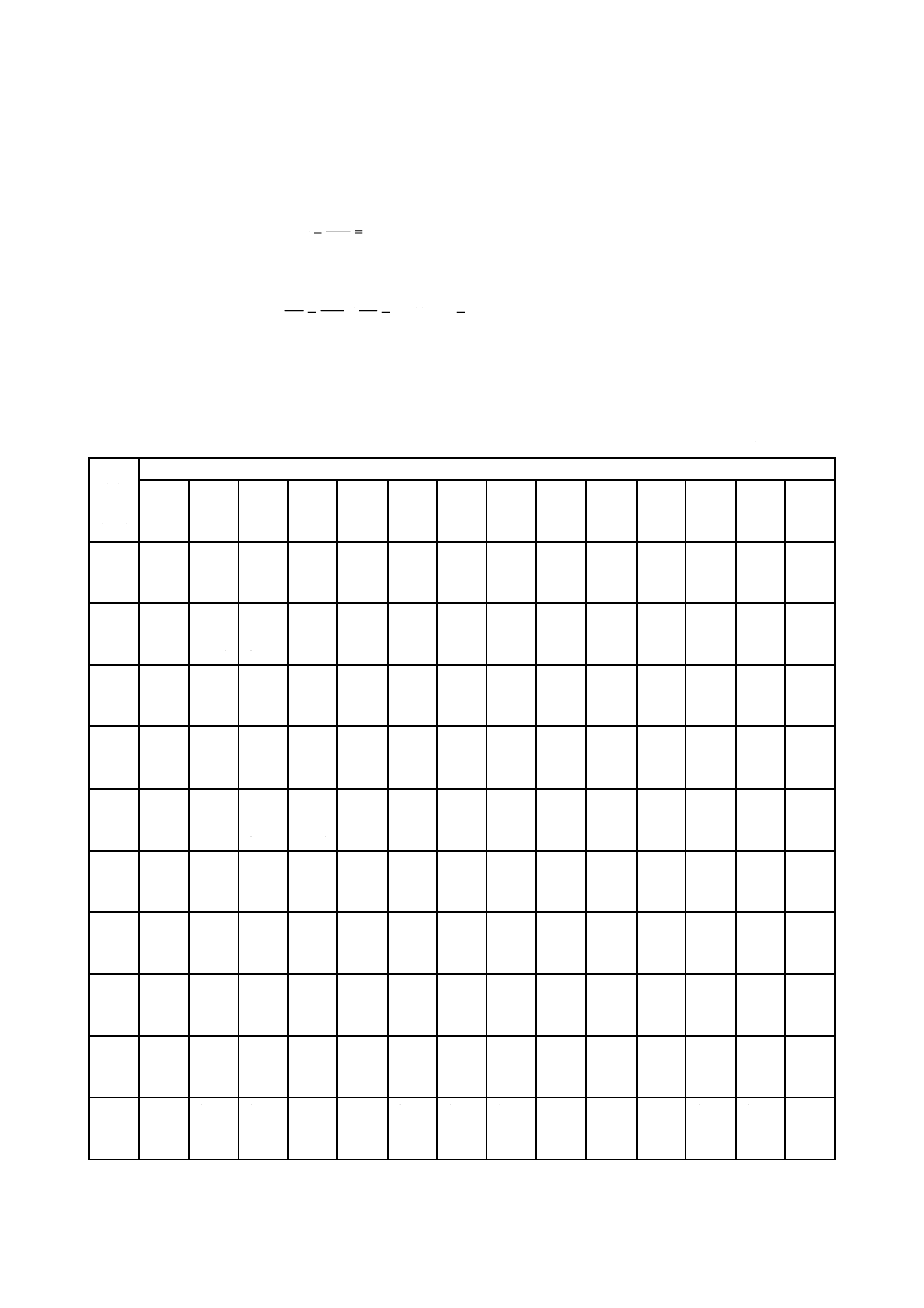
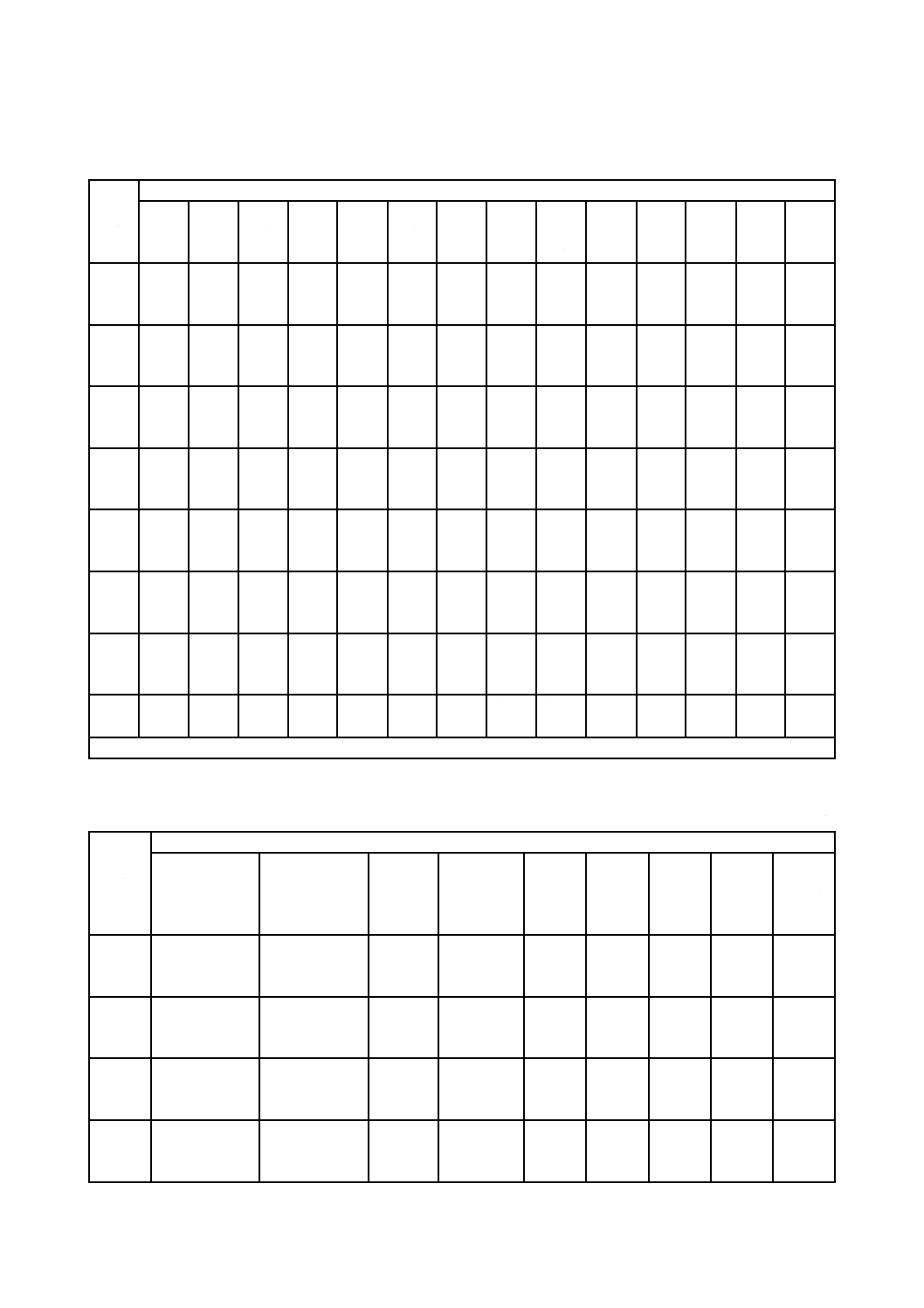
表6−材料の引張強さ規格値の最小値
単位 N/mm2
材料の
直径
d
(mm)
材料
SW-B SW-C
SWP
-A
SWP
-B
SWP
-V
SWO
-A
SWO
-B
SW
OSC
-B
SW
OSM
-A
SW
OSM
-B
SW
OSM
-C
SWO
-V
SW
OCV
-V
SW
OSC
-V
0.08 2 450
2 790
2 890
3 190
−
−
−
−
−
−
−
−
−
−
0.09 2 400
2 750
2 840
3 140
−
−
−
−
−
−
−
−
−
−
0.10 2 350
2 700
2 790
3 090
−
−
−
−
−
−
−
−
−
−
0.12 2 300
2 650
2 750
3 040
−
−
−
−
−
−
−
−
−
−
0.14 2 260
2 600
2 700
2 990
−
−
−
−
−
−
−
−
−
−
0.16 2 210
2 550
2 650
2 940
−
−
−
−
−
−
−
−
−
−
0.18 2 210
2 500
2 600
2 890
−
−
−
−
−
−
−
−
−
−
0.20 2 210
2 500
2 600
2 840
−
−
−
−
−
−
−
−
−
−
0.23 2 160
2 450
2 550
2 790
−
−
−
−
−
−
−
−
−
−
0.26 2 110
2 400
2 500
2 750
−
−
−
−
−
−
−
−
−
−
0.29 2 060
2 350
2 450
2 700
−
−
−
−
−
−
−
−
−
−
0.32 2 010
2 300
2 400
2 650
−
−
−
−
−
−
−
−
−
−
0.35 2 010
2 300
2 400
2 650
−
−
−
−
−
−
−
−
−
−
0.40 1 960
2 260
2 350
2 600
−
−
−
−
−
−
−
−
−
−
0.45 1 910
2 210
2 300
2 550
−
−
−
−
−
−
−
−
−
−
0.50 1 910
2 210
2 300
2 550
−
−
−
−
−
−
−
−
−
2 010
0.55 1 860
2 160
2 260
2 500
−
−
−
−
−
−
−
−
−
−
0.60 1 810
2 110
2 210
2 450
−
−
−
−
−
−
−
−
−
2 010
0.65 1 810
2 110
2 210
2 450
−
−
−
−
−
−
−
−
−
−
0.70 1 770
2 060
2 160
2 400
−
−
−
−
−
−
−
−
−
2 010
0.80 1 770
2 010
2 110
2 350
−
−
−
−
−
−
−
−
−
2 010
0.90 1 770
2 010
2 110
2 300
−
−
−
−
−
−
−
−
−
2 010
1.00 1 720
1 960
2 060
2 260
2 010
−
−
1 960
−
−
−
−
−
2 010
1.20 1 670
1 910
2 010
2 210
1 960
−
−
1 960
−
−
−
−
−
2 010
1.40 1 620
1 860
1 960
2 160
1 910
−
−
1 960
−
−
−
−
−
1 960
1.60 1 570
1 810
1 910
2 110
1 860
−
−
1 960
−
−
−
−
−
1 960
1.80 1 520
1 770
1 860
2 060
1 810
−
−
1 960
−
−
−
−
−
1 960
2.00 1 470
1 720
1 810
2 010
1 770
1 570
1 720
1 910
−
−
−
1 620
1 570
1 910
2.30 1 420
1 670
1 770
1 960
1 720
1 570
1 720
1 910
−
−
−
1 620
1 570
1 910
2.60 1 420
1 670
1 770
1 960
1 720
1 570
1 720
1 910
−
−
−
1 620
1 570
1 910
24
B 2704-1:2018
表6−材料の引張強さ規格値の最小値(続き)
単位 N/mm2
材料の
直径
d
(mm)
材料
SW-B SW-C
SWP
-A
SWP
-B
SWP
-V
SWO
-A
SWO
-B
SW
OSC
-B
SW
OSM
-A
SW
OSM
-B
SW
OSM
-C
SWO
-V
SW
OCV
-V
SW
OSC
-V
2.90 1 370
1 620
1 720
1 910
1 720
1 520
1 670
1 910
−
−
−
1 620
1 570
1 910
3.20 1 370
1 570
1 670
1 860
1 670
1 470
1 620
1 860
−
−
−
1 570
1 570
1 860
3.50 1 370
1 570
1 670
1 810
1 670
1 470
1 620
1 860
−
−
−
1 570
1 570
1 860
4.00 1 370
1 570
1 670
1 810
1 670
1 420
1 570
1 810
1 470
1 570
1 670
1 570
1 520
1 810
4.50 1 320
1 520
1 620
1 770
1 620
1 370
1 520
1 810
1 470
1 570
1 670
1 520
1 520
1 810
5.00 1 320
1 520
1 620
1 770
1 620
1 370
1 520
1 760
1 470
1 570
1 670
1 520
1 470
1 760
5.50 1 270
1 470
1 570
1 710
1 570
1 320
1 470
1 760
1 470
1 570
1 670
1 470
1 470
1 760
6.00 1 230
1 420
1 520
1 670
1 520
1 320
1 470
1 710
1 470
1 570
1 670
1 470
1 470
1 710
6.50 1 230
1 420
1 520
1 670
−
1 320
1 470
1 710
1 470
1 570
1 670
−
1 420
1 710
7.00 1 180
1 370
1 470
1 620
−
1 230
1 370
1 660
1 420
1 520
1 620
−
1 420
1 660
7.50
−
−
−
−
−
1 230
1 370
1 660
1 420
1 520
1 620
−
1 370
1 660
8.00 1 180
1 370
1 470
1 620
−
1 230
1 370
1 660
1 420
1 520
1 620
−
1 370
1 660
8.50
−
−
−
−
−
1 230
1 370
1 660
1 420
1 520
1 620
−
1 370
−
9.00 1 130
1 320
1 420
−
−
1 230
1 370
1 660
1 420
1 520
1 620
−
1 370
−
9.50
−
−
−
−
−
1 180
1 320
1 660
1 370
1 470
1 570
−
1 370
−
10.0
1 130
1 320
1 420
−
−
1 180
1 320
1 660
1 370
1 470
1 570
−
1 370
−
10.5
−
−
−
−
−
1 180
1 320
1 660
1 370
1 470
1 570
−
−
−
11.0
1 080
1 270
−
−
−
1 180
1 320
1 660
1 370
1 470
1 570
−
−
−
11.5
−
−
−
−
−
1 180
1 320
1 660
1 370
1 470
1 570
−
−
−
12.0
1 080
1 270
−
−
−
1 180
1 320
1 610
1 370
1 470
1 570
−
−
−
13.0
1 030
1 230
−
−
−
−
−
1 610
1 370
1 470
−
−
−
−
14.0
−
−
−
−
−
−
−
1 610
1 370
1 470
−
−
−
−
15.0
−
−
−
−
−
−
−
1 610
−
−
−
−
−
−
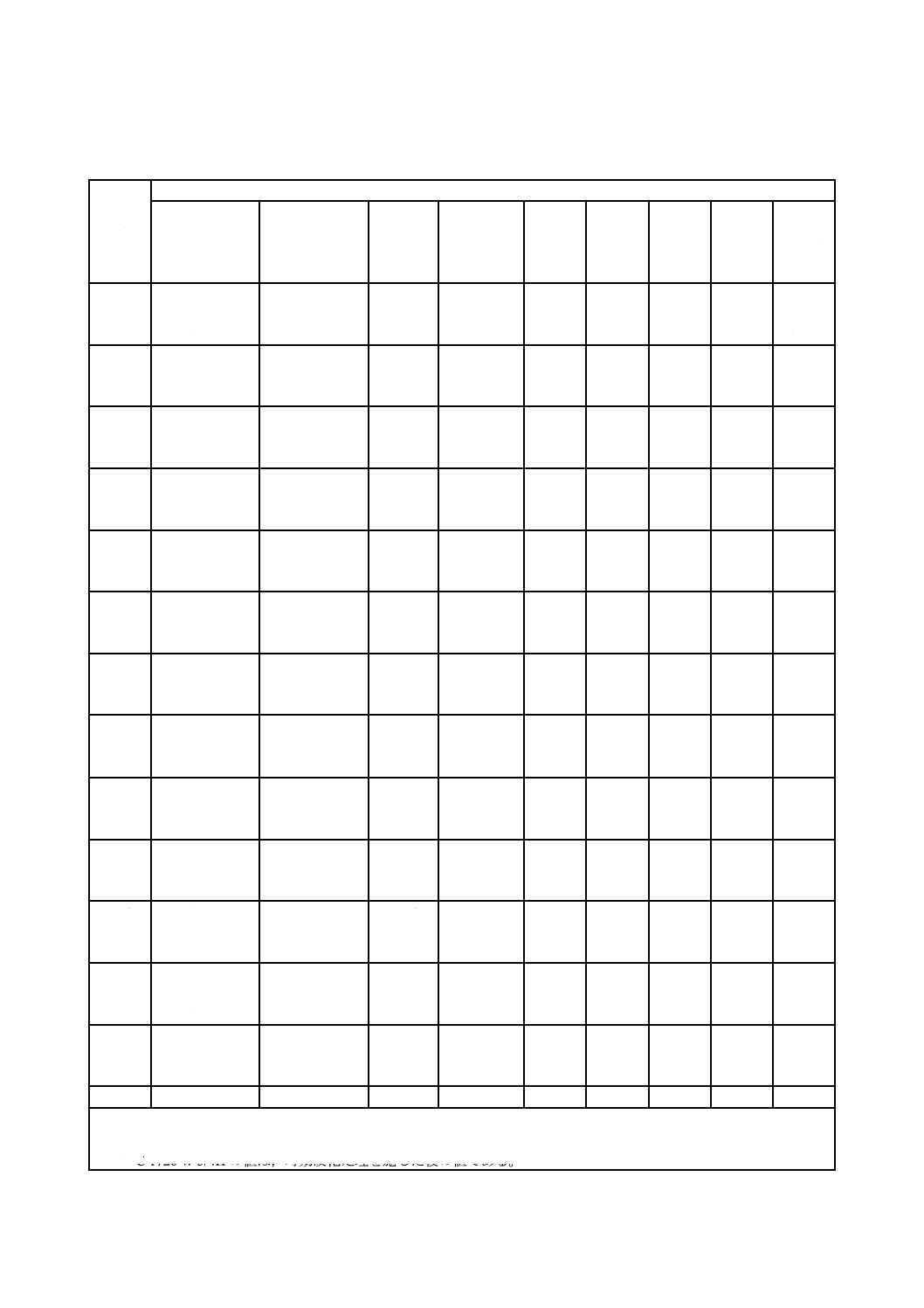
注記 この表は,それぞれの材料(表1参照)の日本工業規格で規定している引張強さの最小値によるものである。
表7−材料の引張強さ規格値の最小値
単位 N/mm2
材料の
直径
d
(mm)
材料
SUS302-WPA
SUS304-WPA
SUS304N1-WPA
SUS316-WPA
SUS302-WPB
SUS304-WPB
SUS304N1-WPB
SUS
631J1-
WPC a)
C 2600 W-H
C 2700 W-H
C 2800 W-H
C 2600
W-EH
C 2700
W-EH
C 7521
W-H
C 7701
W-H
C 5191
W-H
C 1720
W-3/4H b)
0.08
1 650
2150
−
−
−
−
−
−
−
0.09
1 650
2150
−
−
−
−
−
−
−
0.10
1 650
2150
2 200
−
−
−
−
−
−
0.12
1 650
2150
2 200
−
−
−
−
−
−
0.14
1 650
2150
2 200
−
−
−
−
−
−
0.16
1 650
2150
2 200
−
−
−
−
−
−
0.18
1 650
2150
2 200
−
−
−
−
−
−
0.20
1 650
2150
2 200
−
−
−
−
−
−
0.23
1 600
2050
2 180
−
−
−
−
−
−
0.26
1 600
2050
2 180
−
−
−
−
−
−
0.29
1 600
2050
2 180
−
−
−
−
−
−
0.32
1 600
2050
2 180
−
−
−
−
−
−
25
B 2704-1:2018
表7−材料の引張強さ規格値の最小値(続き)
単位 N/mm2
材料の
直径
d
(mm)
材料
SUS302-WPA
SUS304-WPA
SUS304N1-WPA
SUS316-WPA
SUS302-WPB
SUS304-WPB
SUS304N1-WPB
SUS
631J1-
WPC a)
C 2600 W-H
C 2700 W-H
C 2800 W-H
C 2600
W-EH
C 2700
W-EH
C 7521
W-H
C 7701
W-H
C 5191
W-H
C 1720
W-3/4H b)
0.35
1 600
2050
2 180
−
−
−
−
−
−
0.40
1 600
2050
2 180
−
−
665
765
835
1 300
0.45
1 600
1950
2 100
−
−
665
765
835
1 300
0.50
1 600
1950
2 100
685
785
665
765
835
1 300
0.55
1 600
1950
2 100
685
785
665
765
835
1 300
0.60
1 600
1950
2 100
685
785
665
765
835
1 300
0.65
1 530
1850
2 050
685
785
665
765
835
1 300
0.70
1 530
1850
2 050
685
785
665
765
835
1 300
0.80
1 530
1850
2 050
685
785
665
765
835
1 300
0.90
1 530
1850
2 050
685
785
665
765
835
1 300
1.00
1 530
1850
2 050
685
785
665
765
835
1 300
1.20
1 450
1750
1 950
685
785
665
765
835
1 300
1.40
1 450
1750
1 950
685
785
665
765
835
1 300
1.60
1 400
1650
1 850
685
785
665
765
835
1 300
1.80
1 400
1650
1 850
685
785
665
765
835
1 300
2.00
1 400
1650
1 850
685
785
665
765
835
1 300
2.30
1 320
1550
1 750
685
785
665
765
835
1 300
2.50
−
−
−
685
785
665
765
835
1 300
2.60
1 320
1550
1 750
−
−
665
765
835
1 300
2.80
−
−
−
685
785
665
765
835
1 300
2.90
1 230
1450
1 650
−
−
−
−
−
−
3.00
−
−
−
685
785
665
765
835
1 300
3.20
1 230
1450
1 650
685
785
665
765
835
1 300
3.50
1 230
1450
1 650
685
785
665
765
835
1 300
3.80
−
−
−
685
785
−
−
−
−
4.00
1 230
1450
1 650
685
785
665
765
835
1 300
4.20
−
−
−
685
785
−
−
−
−
4.30
−
−
−
685
785
−
−
−
−
4.50
1 100
1350
1 550
685
785
665
765
835
1 300
5.00
1 100
1350
1 550
685
785
665
765
835
1 300
5.50
1 100
1350
1 550
685
785
−
−
−
−
5.80
−
−
−
685
785
−
−
−
−
6.00
1 100
1350
1 550
685
785
−
−
−
−
6.50
1 000
1270
−
685
785
−
−
−
−
6.80
−
−
−
685
785
−
−
−
−
7.00
1 000
1270
−
685
785
−
−
−
−
8.00
1 000
1270
−
685
785
−
−
−
−
9.00
−
1130
−
685
785
−
−
−
−
10.0
−
980
−
685
785
−
−
−
−
12.0
−
880
−
−
−
−
−
−
−
注記 この表は,それぞれの材料(表1参照)の日本工業規格で規定している引張強さの最小値によるものである。
注a) SUS631J1-WPCの値は,析出硬化熱処理を施した後の値である。
b) C 1720 W-3/4Hの値は,時効硬化処理を施した後の値である。



















