B 1759:2019
(1)
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 2
4 記号及び単位 ··················································································································· 2
5 運転試験方法 ··················································································································· 4
5.1 一般 ···························································································································· 4
5.2 運転試験の条件 ············································································································· 5
5.3 標準試験条件 ················································································································ 5
6 試験歯車及び相手歯車 ······································································································· 6
7 試験歯車の歯元曲げ応力 ···································································································· 6
7.1 呼び接線力,トルク,伝達動力,周速及び角速度 ································································· 6
7.2 歯元曲げ応力 ················································································································ 7
7.3 歯形係数 ······················································································································ 7
7.4 応力修正係数 ··············································································································· 10
7.5 ねじれ角係数 ··············································································································· 10
7.6 歯元形状係数 ··············································································································· 10
7.7 リム厚さ係数 ··············································································································· 11
8 歯車の材料の許容歯元曲げ応力 ·························································································· 11
8.1 一般 ··························································································································· 11
8.2 歯車材料の許容曲げ応力及び寿命係数··············································································· 12
8.3 雰囲気温度係数 ············································································································ 12
8.4 温度上昇係数 ··············································································································· 12
8.5 潤滑係数 ····················································································································· 12
8.6 相手歯車係数 ··············································································································· 12
9 歯車の安全性の評価 ········································································································· 13
附属書A(参考)歯元形状係数の算出例 ·················································································· 14
附属書B(参考)許容曲げ応力及び寿命係数の導出例 ································································· 15
附属書C(参考)雰囲気温度係数の導出例 ··············································································· 17
附属書D(参考)潤滑係数の導出例 ························································································ 18
附属書E(参考)相手歯車係数の導出例··················································································· 19
参考文献 ···························································································································· 20
B 1759:2019
(2)
まえがき
この規格は,産業標準化法第16条において準用する同法第12条第1項の規定に基づき,一般社団法人
日本歯車工業会(JGMA)及び一般財団法人日本規格協会(JSA)から,産業標準原案を添えて日本産業規
格を改正すべきとの申出があり,日本産業標準調査会の審議を経て,経済産業大臣が改正した日本産業規
格である。これによって,JIS B 1759:2013は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本産業規格 JIS
B 1759:2019
プラスチック円筒歯車の曲げ強さ評価方法
Estimation of tooth bending strength of cylindrical plastic gears
1
適用範囲
この規格は,平行軸歯車対を構成する円筒歯車(以下,歯車という。)にプラスチック材料を用いたとき,
歯元における曲げ疲労折損に対する当該材料が示す強さの評価方法について規定する。対応国際規格は,
現時点では,制定されていない。評価は,外歯車対の運転試験結果に基づいて歯車材料の許容曲げ応力を
求めることによって行う。
また,この規格の評価法に基づいて既に許容曲げ応力を求めたプラスチック材料製歯車の想定される呼
び接線力に対する安全性評価法も規定する。安全性評価は,呼び接線力から求めた歯元曲げ応力と材料の
許容曲げ応力から求められる許容歯元応力とを比較して行う。安全性評価は,外歯車対だけでなく,内歯
車対にも適用することが可能である。
その他,この規格は,次のa)〜l)の諸元をもつプラスチック歯車及び鋼歯車,又はプラスチック歯車だ
けで構成される外歯車対及び内歯車対に適用することが可能である。
なお,j)〜l)の事項について注意しなければならない。
a) 歯直角モジュール :0.5 mm以上2.0 mm以下
b) 基準円直径
:100 mm以下
c) 圧力角
:14.5°以上25°以下
d) ねじれ角
:25°以下
e) 正面かみ合い率
:1.0を超え2.0未満
f)
歯幅
:25 mm以下
g) 歯車精度
:JIS B 1702-3に規定する精度等級に整合
h) 歯形
:JIS B 1701-1の規定による。ただし,歯直角圧力角については,JIS B 1701-1
に規定する以外[上記c)参照]の歯形にも適用できる。また,基準ラックが創
成する形状以外の歯元すみ肉をもつ歯車についても適用可能である。
i)
その他
:切下げ及び歯先とがりのない歯車で構成され,歯元干渉がなく適切なバックラ
ッシのある中心距離で組み付けられた,歯当たり不良がない歯車対に適用でき
る。また,この規格は,射出成形によって製造したプラスチック歯車に適用す
るが,機械加工したプラスチック歯車にも適用することが可能である。
j)
プラスチック材料一般に対して適用可能であるが,運転試験における損傷モードが歯元疲労折損にな
る場合に限る。
k) 摩耗が極端に進行したときは,歯元付近での折損であっても,損傷モードが異なることがある。この
場合,この規格を適用することはできない。
l)
繊維強化プラスチック製歯車にも適用可能であるが,その強度は,繊維強化の方法及び成形方法に依
2
B 1759:2019
存するので,歯元危険断面(7.3.2参照)位置以外から亀裂が発生することがある[1]。この場合,この
規格を適用することはできない。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0102-1 歯車用語−第1部:幾何形状に関する定義
JIS B 0121 歯車記号−幾何学的データの記号
JIS B 1701-1 円筒歯車−インボリュート歯車歯形−第1部:標準基準ラック歯形
JIS B 1702-1 円筒歯車−精度等級−第1部:歯車の歯面に関する誤差の定義及び許容値
JIS B 1702-3 円筒歯車−精度等級−第3部:射出成形プラスチック歯車の歯面に関する誤差及び両歯
面かみ合い誤差の定義並びに精度許容値
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 0102-1によるほか,次による。
3.1
試験トルク
運転試験中の制御された試験歯車への負荷トルク。動力吸収式の運転試験機を用いる場合は,運転試験
中,負荷トルクを適宜確認し,5.2に規定する範囲を超えないようにする。動力循環式の運転試験機を用い
る場合は,試験歯車歯面の摩耗によって,運転試験中に負荷トルクが減少する可能性があるため,負荷ト
ルクが5.2に規定する範囲を超えたときに自動的に運転試験を中断できるようにすることが望ましい。
3.2
試験歯車の回転速度
運転試験中の試験歯車の制御された回転速度。運転試験中,試験歯車の回転速度を適宜確認し,5.2に規
定する範囲を超えないようにする。
3.3
試験温度
運転試験中の制御された試験歯車周辺の雰囲気温度。油浴又は滴下潤滑においては,潤滑油の制御され
た温度。グリース潤滑の場合は,制御された試験歯車周辺の雰囲気温度。
4
記号及び単位
この規格で用いる記号及び単位は,JIS B 0121によるほか,次による。
BR
:バックアップレシオ
b
:歯幅(mm)
d
:基準円直径(mm)
da
:歯先円直径(mm)
dan
:相当平歯車の歯先円直径(mm)
dbn
:相当平歯車の基礎円直径(mm)
den
:相当平歯車の一歯かみ合い領域の歯先側の点を通る円の直径(mm)
dn
:相当平歯車の基準円直径(mm)
3
B 1759:2019
dNa
:有効歯先円直径(mm)
dw
:かみ合いピッチ円直径(mm)
E
:基準ラック歯元すみ肉半径の中心位置を示す寸法(mm)
Fwt
:呼び接線力(かみ合いピッチ円上)(N)
G
:危険断面歯厚を求めるときの補助係数
H
:危険断面歯厚を求めるときの補助角度(rad)
h
:全歯たけ(mm)
hFe
:曲げモーメントの腕の長さ(mm)
hfp
:基準ラックの歯元のたけ(mm)
L
:危険断面歯厚と曲げモーメントの腕の長さとの比
mn
:歯直角モジュール(mm)
n
:回転速度(min−1)
P
:伝達動力(W)
pbn
:歯直角法線ピッチ(mm)
qs
:危険断面歯厚と歯元すみ肉丸み半径との比
Rc
:基準ラック歯元すみ肉半径(mm)
SF
:曲げ強さに対する安全率
SFmin
:最小安全率
sFn
:歯元危険断面歯厚(mm)
sR
:リム厚さ(mm)
T
:トルク(N·m)
vw
:かみ合いピッチ円上における周速(m/s)
x
:転位係数(外歯車,内歯車を問わず歯厚が大きくなる方を正とする。)[2]
x0
:ピニオンカッタの転位係数
YB
:リム厚さ係数
Yf
:歯元形状係数
YF
:歯形係数
YL
:潤滑係数
YM
:相手歯車係数
YNT
:寿命係数
YS
:応力修正係数
Yβ
:ねじれ角係数
YΔΘ
:温度上昇係数
YΘ
:雰囲気温度係数
z
:歯数(内歯車の歯数は負とする。)[2]
z0
:ピニオンカッタの歯数
zn
:相当平歯車の歯数
αen
:相当平歯車の一歯かみ合い領域の歯先側の点の圧力角(値表示は°,計算はrad)
αFen
:相当平歯車の一歯かみ合い領域の歯先側の点の作用角(値表示は°,計算はrad)(図2及び図
3参照)
4
B 1759:2019
αn
:歯直角圧力角(値表示は°,計算はrad)
αwt
:正面かみ合い圧力角(値表示は°,計算はrad)
β
:ねじれ角(値表示は°,計算はrad)
βb
:基礎円筒ねじれ角(値表示は°,計算はrad)
γe
:相当平歯車の一歯かみ合い領域の歯先側の点の角度(値表示は°,計算はrad)
εα
:正面かみ合い率
εαn
:相当平歯車の正面かみ合い率
εβ
:重なりかみ合い率
εγ
:全かみ合い率
Θ
:試験温度(℃)
θ
:歯元の危険断面位置におけるラック工具又はピニオンカッタの創成角(rad)
ρfp
:基準ラックの歯元すみ肉半径(mm)
ρfpv
:ラック工具又はピニオンカッタの刃先丸み半径(mm)
ρF
:歯元すみ肉丸み半径(mm)
σ
:標準偏差
σF
:歯元曲げ応力(MPa)
σFlim
:歯車材料の許容曲げ応力(MPa)
σFP
:歯車の許容歯元曲げ応力(MPa)
ω
:角速度(rad/s)
5
運転試験方法
5.1
一般
一般事項は,次による。
a) プラスチック歯車の運転試験は,試験歯車の回転速度を一定とし,一定の負荷の下で,試験歯車に損
傷が生じる,又は試験歯車のかみ合い回数が打切り値(106を標準とする。)に達するまで行う。
b) 使用する運転試験機は,動力吸収式歯車運転試験機を基準とするが,負荷トルク変動が5.2の規定を
満足する場合は,動力循環式歯車運転試験機も使用が可能である。
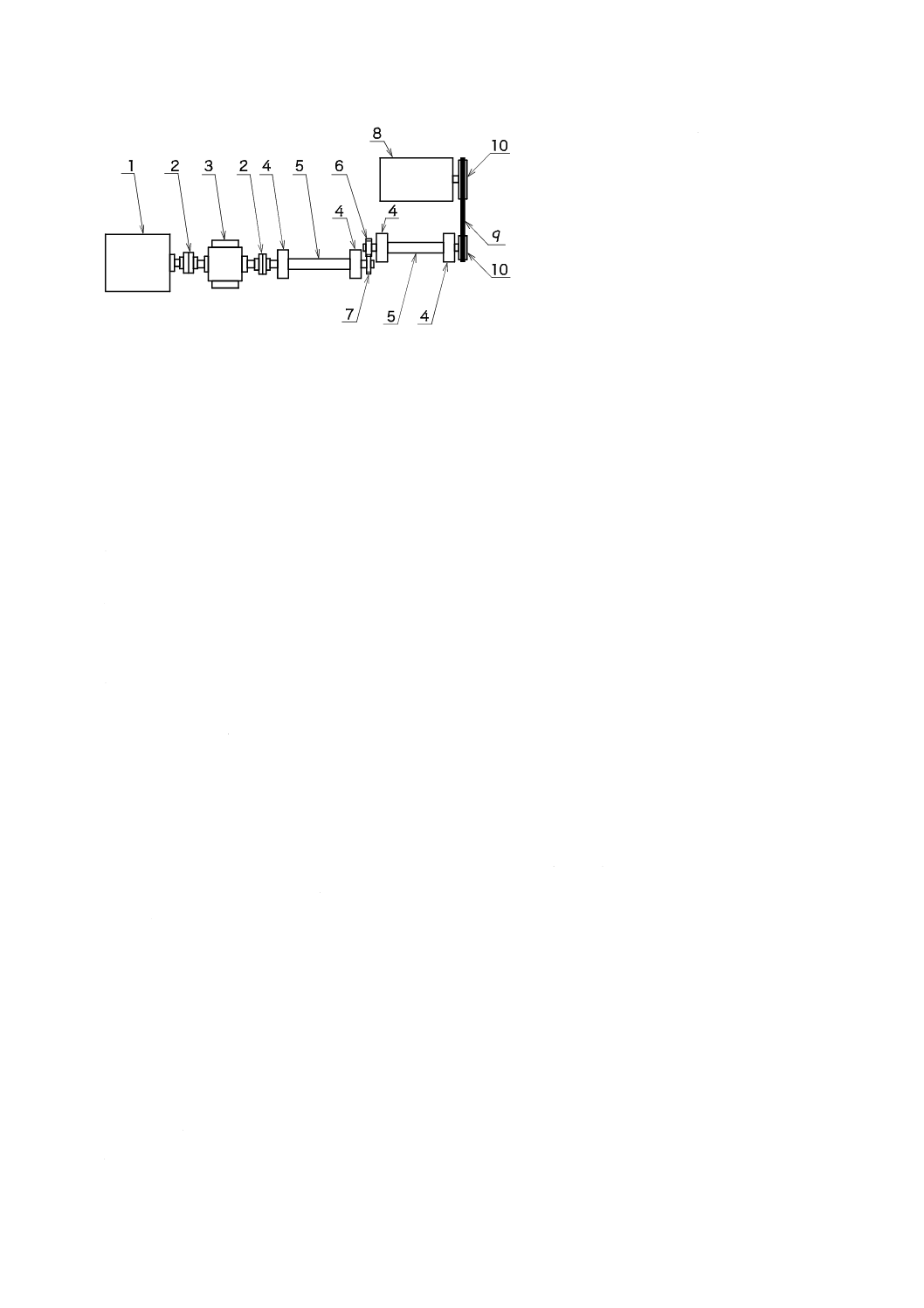
c) 動力吸収式歯車運転試験機の基本構成の例を図1に示す。この図では駆動モータがベルト・プーリを
介して,また,負荷装置が継手を介して歯車軸につながれているが,駆動モータ,負荷装置のつなぎ
方は問わない。
d) 鋼製相手歯車(箇条6参照)を駆動側とし,試験歯車を被動側とする。試験歯車と負荷装置との間に
トルクメータを置き,試験歯車に作用する試験トルクを,回転速度とともに常時監視する。
5
B 1759:2019
1 負荷装置
2 継手
3 トルクメータ
4 軸受
5 歯車軸
6 相手歯車
7 試験歯車
8 駆動モータ
9 ベルト
10 プーリ
図1−動力吸収式歯車運転試験機の基本構成の例
e) 相手歯車と駆動モータとの間にもトルクメータを置き,入出力トルクを比較することによって歯車対
の効率(軸受損失等を含む。)を見積ることが可能である。
5.2
運転試験の条件
運転試験の条件は,次による。
a) 試験歯車材料の強度及びしゅう(摺)動性を考慮し,試験歯車に負荷するトルク及び回転速度を決定
する。
b) 試験歯車の回転速度は,標準試験条件(5.3参照)では,相手歯車が鋼歯車で1 000 min−1とするが,
プラスチック歯車対で試験を行う場合は500 min−1を目安とする。
c) 運転試験機の歯車取付軸の全振れを20 μm以下にして,適切なバックラッシを与え,過度の片当たり
が生じないように試験歯車及び相手歯車,又は試験歯車対を組み付け,運転を開始する。運転試験開
始後,速やかに規定の回転速度を設定値まで加速するとともに,試験トルクを設定値まで増加させる。
d) プラスチック材料は,一般に,線膨張係数が大きいので,運転試験中のバックラッシが小さくなりす
ぎない中心距離を設定しなければならない。また,軸穴をもつ場合は,軸との隙間が大きくなりすぎ
ないような配慮が必要である。
e) 試験歯車の回転速度及び負荷トルクは±5 %に制御しなければならない。これらに加え,試験歯車の
かみ合いに起因すると考えられる振動,騒音,温度上昇などを監視して,できるだけ早く亀裂の発生
を検知することが重要である。
f)
試験歯車の歯の損傷は,亀裂の発生が疑われる時点で運転試験を中断し,目視などで確認する。損傷
の確認は,組付け状態を維持したまま行うことが望ましい。歯元危険断面(7.3.2参照)近傍と認めら
れる位置での歯の折損又は亀裂が確認された時点で寿命と判断し,運転試験を終了する。
g) 損傷が確認できなかった場合は,運転試験を再開する。運転試験の中断は,長くなると試験結果に影
響を及ぼすおそれがあるので,短い方が望ましい。
h) 運転試験の終了が遅れ,全ての歯が失われる場合がある。このようなときには,歯元での折損が確認
できない場合,そのデータを評価に加えることはできない。また,大きな歯の倒れ,歯面の過度の摩
耗,溶融など,歯元疲労折損以外の損傷が認められた場合は,運転条件を見直す必要がある。
5.3
標準試験条件
この規格で定める標準試験条件は,次による。
a) 試験温度:23 ℃±2 ℃
b) 相対湿度:(50±5)%
c) 相手歯車:鋼歯車
6
B 1759:2019
d) 試験歯車回転速度:1 000 min−1
e) 潤滑剤は使用しない。
f)
運転試験前に試験歯車及び相手歯車の歯面を揮発性溶剤などで洗浄する。
6
試験歯車及び相手歯車
試験歯車及び相手歯車の要件は,次による。
a) 試験歯車は,標準基準ラックに対応するモジュール1 mmの標準平歯車で,歯数50及び歯幅10 mm
の歯車と同程度の寸法をもち,十分なリム厚さをもつことが望ましい(以下,標準試験歯車という。)。
b) 相手歯車は,歯幅が試験歯車より大きく,歯数が試験歯車と異なり,歯面研削によって適切な歯先修
整を施した歯車精度等級JIS 5級(JIS B 1702-1)以上の精度をもつ鋼歯車が望ましい。
c) 研削を施さない鋼歯車を用いる場合は,試験歯車の摩耗を少なくするために歯面粗さをRa 0.4/Rz 3.2
以下にする。ホブ切りで歯先修整を施す場合は,専用のホブを用い当該ホブの性能を十分に引き出せ
るホブ盤での加工が望ましい。それが難しい場合は,バレリングを施すなどして歯先に適度な丸みを
付けることが望ましい。
d) 繊維強化プラスチック歯車を試験する場合には,強化繊維が鋼製相手歯車の歯面をきずつける場合が
あるため,歯面性状及び歯面形状の変化に留意するとともに,十分な歯面硬度をもたせる,試験ごと
に交換する,などの対応が必要である。
e) 鋼製相手歯車を用いないで,プラスチック歯車対で試験を行う場合は,同歯数,同歯幅の対での評価
も可能である。ただし,この場合,両歯車の側面をそろえるように取り付けなければならない。
f)
使用するプラスチック歯車は,最終加工後の状態管理に留意し,運転試験開始前には,試験温度23 ℃
±2 ℃,相対湿度(50±5)%の環境下に24時間以上放置する。
g) 他の試験温度で運転試験を行う場合は,状態を調節した後,当該試験温度までゆっくりと加熱,又は
冷却し,30分以上保持した後,運転試験を開始する。
h) 潤滑下の運転試験で用いた鋼製相手歯車を無潤滑の運転試験に使用する場合は,潤滑剤の除去が非常
に困難であるため,注意を要する。
7 試験歯車の歯元曲げ応力
7.1 呼び接線力,トルク,伝達動力,周速及び角速度
歯の曲げ強さを評価するために用いる歯車対が,伝達するかみ合いピッチ円上の接線力(呼び接線力),
トルク,及び動力の間の関係は式(1)〜(3)で定義し,また,かみ合いピッチ円上での周速(以下,単に周速
という。)及び角速度は式(4)及び(5)で求める。添字1及び2は,JIS B 0121による。
呼び接線力
w
2
w
1
w
2,1
2
w
1
w
2,1
wt
2
000
1/
60
/
π
2
2
000
1/
v
P
d
n
P
d
T
F
=
=
=
,
,
········································· (1)
トルク
2,1
2,1
2
w
1
w
wt
2,1
60
/
π
2
2
000
1/
ω
P
n
P
d
F
T
=
=
=
,
········································· (2)
動力
60
/
π
2
2
1
2
1
2
1
2
1
w
wt
,
,
,
,
T
n
ω
T
v
F
P
=
=
=
·············································· (3)
周速
2
000
1/
60
π
2
2
w
w1,
2
1
w
d
n
v
,
=
······························································ (4)
7
B 1759:2019
角速度
60
π
2
2
/
000
1
2,1
2
w
,1
w
w
1,2
n
d
v
=
=
ω
······························································ (5)
7.2
歯元曲げ応力
歯元曲げ応力σFは,歯元表面における最大引張応力であり,式(6)で計算する。σFは,相当平歯車の一歯
かみ合い領域の歯先側の点に力が作用したとき歯元危険断面(7.3.2参照)に発生する曲げ応力から求める。
B
f
β
S
F
n
wt
F
Y
Y
Y
Y
Y
m
b
F
σ =
···························································· (6)
ここに,
mn: 歯直角モジュール(mm)
YF: 歯形係数(7.3参照):一歯かみ合い領域の歯先側の点に力が作用する場合の,
歯元危険断面(7.3.2参照)位置における公称曲げ応力に及ぼす歯の形状の影響
を考慮するための係数
YS: 応力修正係数(7.4参照):一歯かみ合い領域の歯先側の点に力が作用する場合
の,公称曲げ応力から局所歯元曲げ応力を求めるための係数
Yβ: ねじれ角係数(7.5参照):相当平歯車の歯元応力を,はすば歯車の応力に変換
するための係数
Yf: 歯元形状係数(7.6参照):歯元すみ肉形状が標準基準ラック(JIS B 1701-1)に
対応していない場合の歯元曲げ応力の増減を考慮するための係数(標準試験歯
車ではYf=1)
YB: リム厚さ係数(7.7参照):歯元曲げ応力に及ぼすリム厚さの影響を考慮するた
めの係数(標準試験歯車ではYB=1)
7.3
歯形係数[3]
7.3.1
一般
歯形係数YFは,歯車の歯を(歯幅)×(弦歯厚)の長方形断面をもつ単純なはりでモデル化し,一歯か
み合い領域の歯先側の点に力が作用した場合に危険断面位置(7.3.2参照)に生じる最大曲げ応力をU値[Fwt
/(b・mn)]で無次元化したものであり,式(7)で計算する。はすば歯車に対するYFは,相当平歯車(7.3.4参
照)に対して計算する。
wt
2
n
Fn
Fen
n
Fe
F
cos
cos
6
α
α
=
m
s
m
h
Y
····································································· (7)
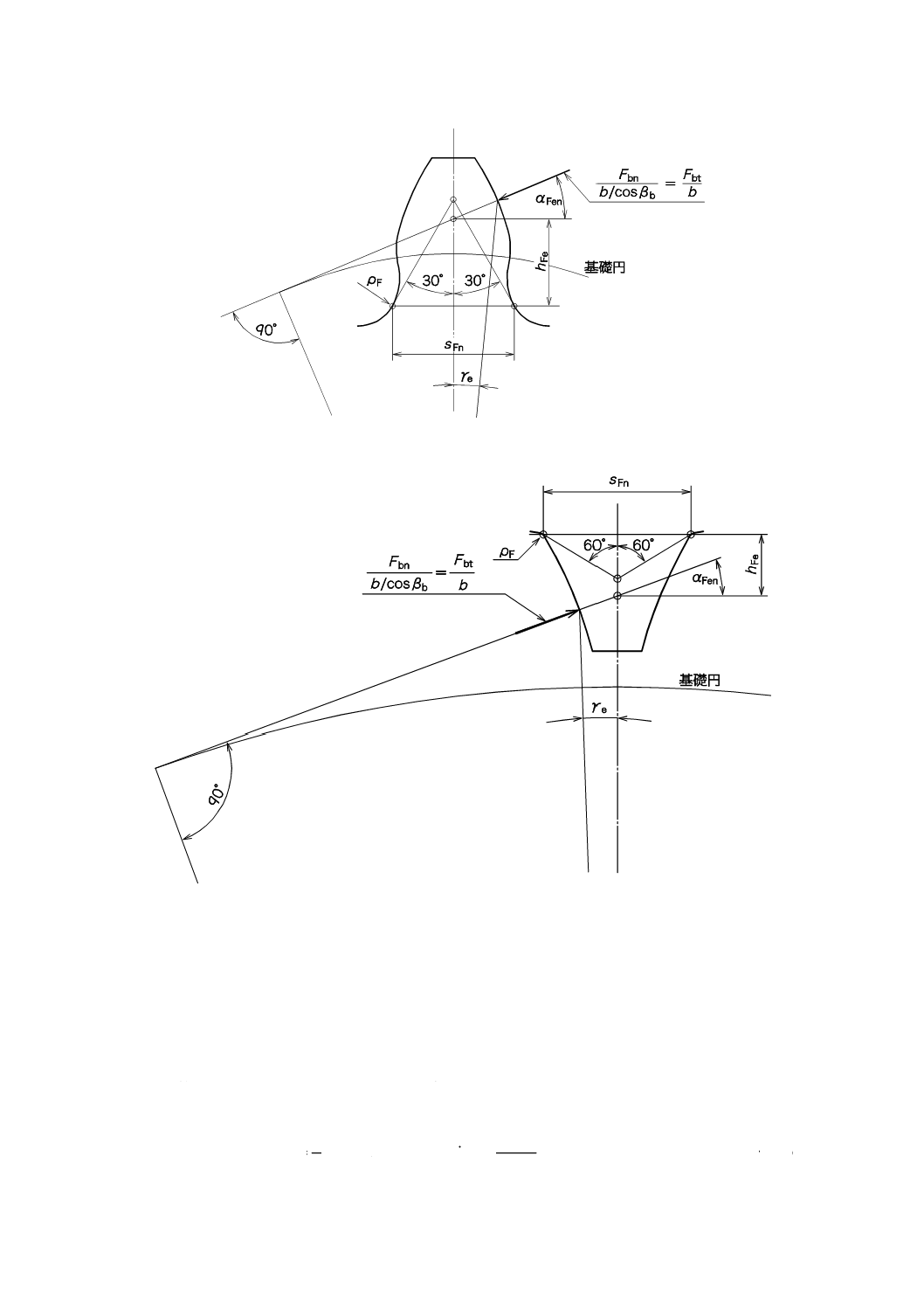
7.3.2
歯元危険断面
歯形係数を求める場合に用いる危険断面位置は,外歯車に対しては30°接線が歯元すみ肉に接する位置,
内歯車に対しては60°接線が歯元すみ肉に接する位置とする(図2及び図3参照)。
8
B 1759:2019
図2−外歯車の危険断面
図3−内歯車の危険断面
7.3.3
歯元危険断面歯厚,曲げモーメントの腕の長さ及び歯元すみ肉丸み半径の決定方法
歯元危険断面歯厚sFn,曲げモーメントの腕の長さhFe,及び歯元すみ肉丸み半径ρFは,式(8)〜(19)によ
って求める。ただし,歯先に丸み又は面取りがある場合は,歯先円直径daを有効歯先円直径dNaに置き換
える必要がある。dNaは,歯先円筒近くの可用歯面の限界を通る円の直径である。
注記 歯元すみ肉丸み半径ρFは,7.4で用いる。
式(7)を計算するに当たり,初めに必要となる補助的な値を決定する。
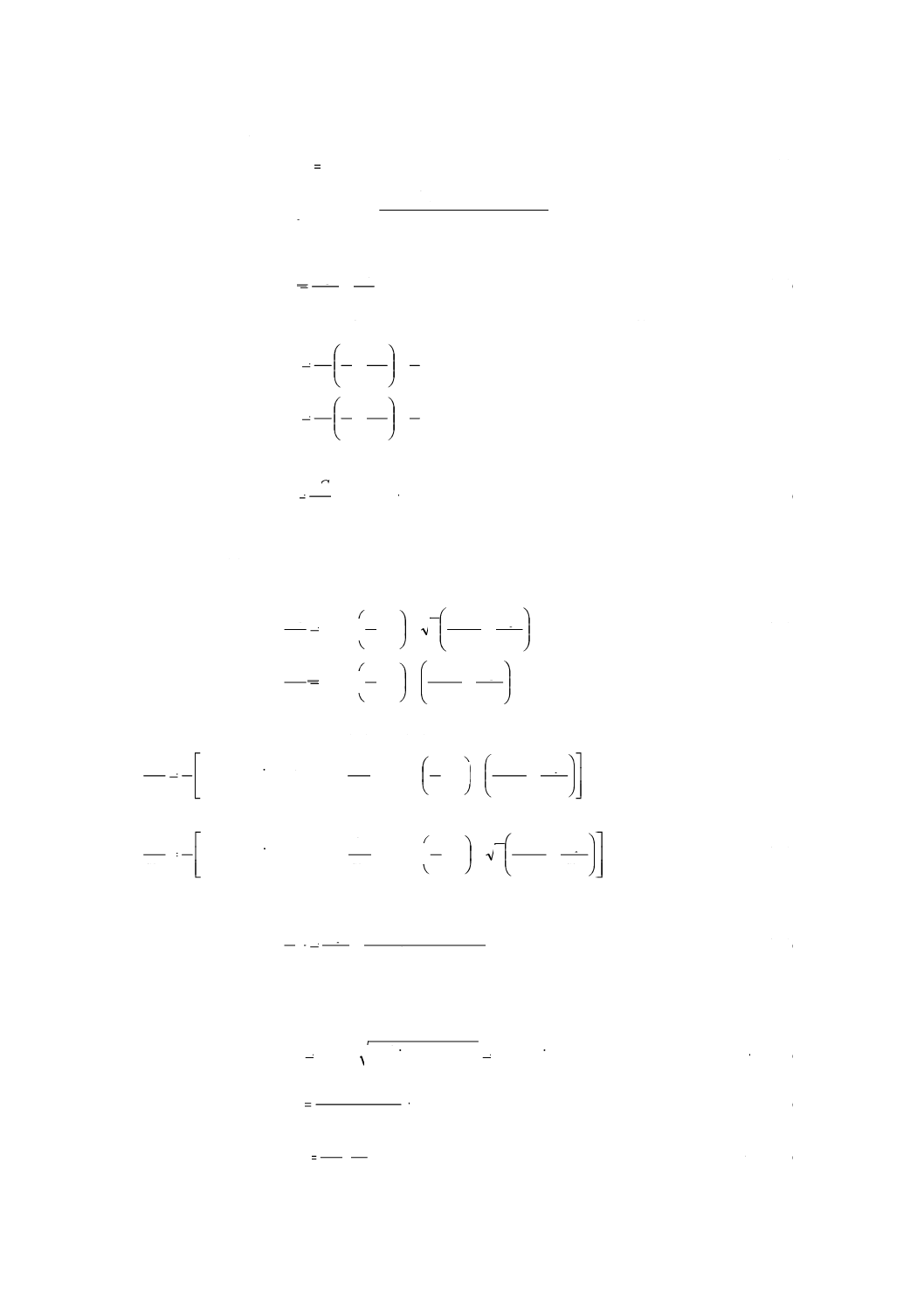
基準ラック歯元すみ肉半径の中心位置を示す寸法Eは,式(8)〜(10)によって計算する。
n
fpv
n
n
fp
n
cos
)
sin
1(
tan
4
π
α
ρ
α
α
h
m
E
−
−
−
=
············································ (8)
9
B 1759:2019
ただし,
fp
fpv
ρ
ρ=
(外歯車の場合) ························································· (9)
(
)
0
036
.1
156
.3
/
/
95
.1
n
fp
n
fp
0
n
fp
fpv
z
m
m
h
x
m
×
−
+
+
≈
ρ
ρ
ρ
(内歯車の場合) ················ (10)
歯元危険断面歯厚を求めるための補助係数Gは,式(11)によって計算する。
x
m
h
m
G
+
−
=
n
fp
n
fpv
ρ
······································································(11)
歯元危険断面歯厚を求めるための補助角度Hは,式(12)又は(13)によって計算する。
3
π
2
π
2
n
n
−
−
=
m
E
z
H
(外歯車の場合) ········································ (12)
6
π
2
π
2
n
n
−
−
=
m
E
z
H
(内歯車の場合) ········································ (13)
これらを用いて,式(14)からθを求める。
H
z
G
−
=
θ
θ
tan
2
n
······································································ (14)
超越方程式(14)をNewton法を用いて解く場合,その初期値として,外歯車に対してはθ=π/6,内歯車に
対してはθ=π/3を用いる。
歯元危険断面歯厚は,式(15)又は(16)によって計算する。
−
+
−
=
n
fpv
n
n
Fn
cos
3
3
π
sin
m
G
z
m
s
ρ
θ
θ
(外歯車の場合) ··················· (15)
−
+
−
=
n
fpv
n
n
Fn
cos
6
π
sin
m
G
z
m
s
ρ
θ
θ
(内歯車の場合) ······················· (16)
曲げモーメントの腕の長さは,式(17)又は(18)によって計算する。
(
)
−
−
−
−
−
=
n
fpv
n
n
en
Fen
e
e
n
Fe
cos
3
π
cos
tan
sin
cos
2
1
m
G
z
m
d
m
h
ρ
θ
θ
α
γ
γ
(外歯車の場合) ········· (17)
(
)
−
−
−
−
−
=
n
fpv
n
n
en
Fen
e
e
n
Fe
cos
3
6
π
cos
tan
sin
cos
2
1
m
G
z
m
d
m
h
ρ
θ
θ
α
γ
γ
(内歯車の場合) ······ (18)
歯元すみ肉丸み半径は,式(19)で求める。
(
)
G
z
G
m
m
2
cos
cos
2
2
n
2
n
fpv
n
F
−
+
=
θ
θ
ρ
ρ
·················································· (19)
7.3.4
相当平歯車に関するパラメータ
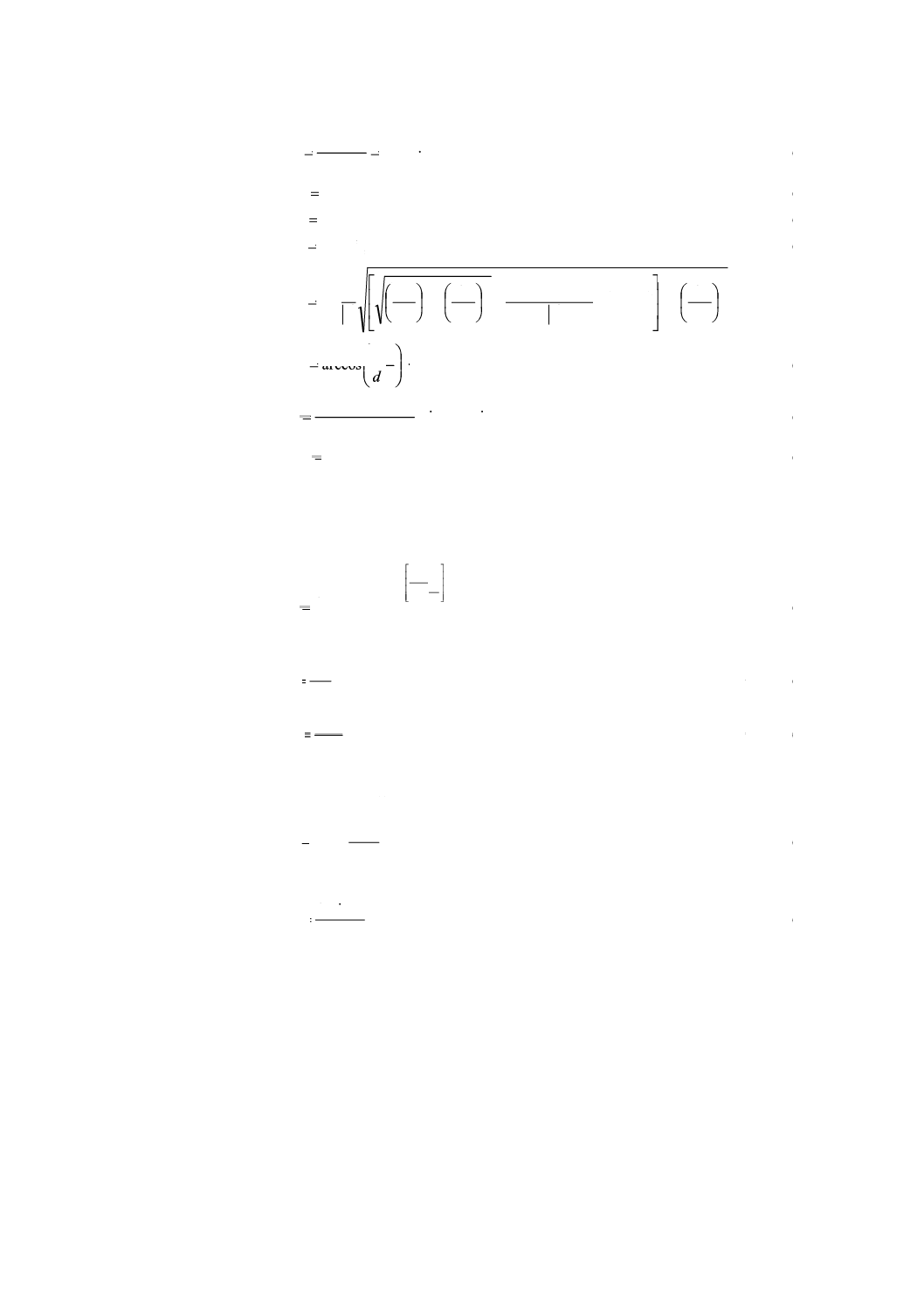
相当平歯車に関するパラメータは,式(20)〜(30)によって計算する。
(
)
(
)
n
2
n
b
cos
sin
arcsin
cos
sin
1
arccos
α
β
α
β
β
=
−
=
··························· (20)
β
βcos
cos
b
2
n
z
z=
···································································· (21)
b
2
α
αn
cosβ
ε
ε=
··········································································· (22)
10
B 1759:2019
n
n
b
2
n
cos
z
m
d
d
=
=
β
·································································· (23)
n
n
bn
cos
π
α
m
p=
······································································ (24)
n
n
bn
cosα
d
d=
········································································ (25)
d
d
d
d
a−
+
=
n
an
······································································ (26)
(
)
2
bn
2
an
n
2
bn
2
an
en
2
1
cos
cos
π
2
2
2
+
−
−
−
×
=
d
z
d
d
d
z
z
d
ε
α
β
····· (27)
=
en
bn
en
arccosdd
α
···································································· (28)
en
n
n
n
e
inv
inv
tan
2
π
5.0
α
α
α
γ
−
+
+
=
z
x
············································· (29)
e
en
Fen
γ
α
α
−
=
········································································· (30)
注記
“inv”は,インボリュート関数と呼ばれ,invα=tanα−α(αはrad)である。
7.4
応力修正係数[3]
応力修正係数YSは,1≦qs<8の場合に対して,式(31)によって計算する。
(
)
+
+
=
L
q
L
Y
3.2
21
.1
1
s
S
13
.0
2.1
··························································· (31)
ここに,
Fe
Fn
h
s
L=
················································································· (32)
F
Fn
s
2ρ
s
q=
··············································································· (33)
7.5
ねじれ角係数[3]
ねじれ角係数Yβは,式(34)によって計算する。
°
−
=
120
1
β
β
β
ε
Y
········································································ (34)
ここで,重なりかみ合い率εβは,式(35)によって計算する。
n
β
π
sin
m
b
=
β
ε
··········································································· (35)
ただし,εβ>1.0のとき,式(34)ではεβ=1とする。
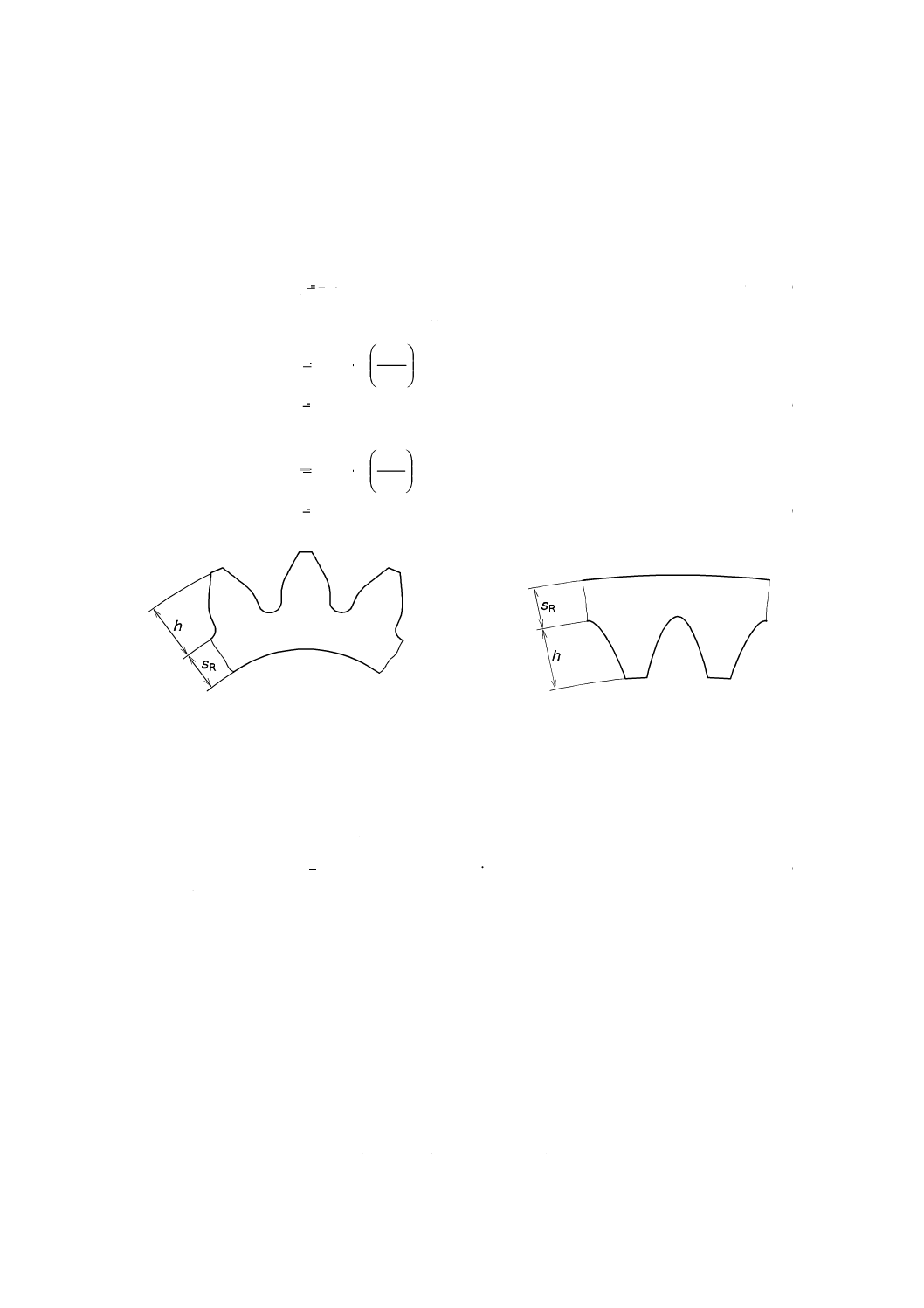
7.6
歯元形状係数
歯元形状係数は,次による。
a) 歯元すみ肉形状が,標準基準ラック(JIS B 1701-1)に対応する場合,Yf=1.0とする。
b) 歯元すみ肉形状が,標準基準ラックに対応しない場合,例えば,円弧のときは,Yf>1.0とする。
c) 詳細な応力解析を行って最適化した歯元形状とした場合は,Yf<1.0とすることができる可能性もある
が,相手歯車の歯先との干渉の危険性も考慮して決定しなければならない。
附属書Aに,ポリアセタール歯車について歯元形状係数を求めた例を示す。
11
B 1759:2019
7.7
リム厚さ係数
射出成形プラスチック歯車は,歯面形状精度を確保するためにリムを薄く製造することが多い。リム厚
さを小さくしすぎると,リム厚さが十分な歯車に比べて負荷容量が減少する[4]。
リム厚さ係数YBは,式(36)で表されるリム厚さの全歯たけに対する比,いわゆるバックアップレシオBR
(図4及び図5参照)を用いて計算する。
h
s
B
R
R=
················································································ (36)
外歯車に対しては,式(37)又は(38)によって計算する。
=
R
B
9.
52
ln
276
.0
B
Y
(0.4<BR<1.4のとき) ·································· (37)
0.1
B=
Y
(BR≧1.4のとき) ························································· (38)
内歯車に対しては,式(39)又は(40)によって計算する。
=
R
B
61
.5
ln
759
.0
B
Y
(0.4<BR<1.5のとき) ·································· (39)
0.1
B=
Y
(BR≧1.5のとき) ························································· (40)
図4−リム厚さ(外歯車)
図5−リム厚さ(内歯車)
8
歯車の材料の許容歯元曲げ応力
8.1
一般
許容歯元曲げ応力σFPは,運転条件を考慮して材料の許容曲げ応力σFlimから求められる歯車の許容され
る歯元曲げ応力で,式(41)によって計算する。
M
L
Δ
NT
Flim
FP
Y
Y
Y
Y
Y
σ
σ =
Θ
Θ
······················································ (41)
ここに,
σFlim
:歯車材料の許容曲げ応力(8.2参照)(MPa)
YNT
:寿命係数(8.2参照):有限寿命に対する許容歯元曲げ応力を与える係数
YΘ
:雰囲気温度係数(8.3参照):雰囲気温度が材料の許容曲げ応力に及ぼす影響を考慮
するための係数(標準試験条件ではYΘ=1.0)
YΔΘ
:温度上昇係数(8.4参照):歯車本体温度の上昇が材料の許容曲げ応力に及ぼす影響
を考慮するための係数(標準試験条件ではYΔΘ=1.0)
YL
:潤滑係数(8.5参照):潤滑が許容歯元曲げ応力に及ぼす影響を考慮するための係数
(標準試験条件ではYL=1.0)
YM
:相手歯車係数(8.6参照):相手歯車の材質が許容歯元曲げ応力に及ぼす影響を考慮
するための係数(標準試験条件ではYM=1.0)
12
B 1759:2019
これらの値は実際のプラスチック歯車に対して運転試験を行い,8.2〜8.6に従って求める。必要に応じ
て解析結果を運転試験結果の補完として用いることもできる。
8.2
歯車材料の許容曲げ応力及び寿命係数
歯車材料の許容曲げ応力σFlim及び寿命係数YNTは,標準試験歯車を用いて標準試験条件の下で行った運
転試験結果から次のように求める。
a) 歯車運転試験における試験トルクは,少なくとも3レベルとし,歯の損傷の確認されるかみ合い回数
が106以下の範囲でなるべく広くなるように選ぶ。かみ合い回数が106を超える寿命に対しても寿命係
数を求める場合は,この3レベルに加え,かみ合い回数が106を超えるまで歯の損傷が認められない
負荷レベルの結果を少なくとも一つ以上含まなければならない。各試験トルクでの運転試験は2回以
上行う。
b) 種々の試験トルクで運転試験を行った結果に基づき,式(6)によって求めた歯元曲げ応力σFと損傷が認
められたときのかみ合い回数Nの関係を両対数グラフにプロットする。これを最小二乗法で直線近似
する。各プロット点のこの近似直線からの偏差に基づき標準偏差σを求め,近似直線を両対数グラフ
上で2.33σだけ下方に平行移動する。この近似直線とN=106の線の交点におけるσFの値を歯車材料の
許容曲げ応力σFlimとする。
c) σFを表すこの近似直線の式をσFlimで無次元化したかみ合い回数Nに関する式を寿命係数YNTとする。
附属書Bにポリアセタール歯車に対して行った運転試験の結果から許容曲げ応力及び寿命係数を求めた
例を示す。
8.3
雰囲気温度係数
標準試験条件以外のある試験温度Θ*における雰囲気温度係数YΘ(at Θ=Θ*)は,当該試験温度による
運転試験結果から求めた歯車材料の許容曲げ応力σFlim(at Θ=Θ*)を用いて式(42)によって計算する。
Flim
*)
at
lim(
F
*)
at
(
Θ
σ
σ
Θ
Θ
Θ
Θ
Y
=
=
=
································································ (42)
附属書Cにポリアセタール歯車に対して行った運転試験の結果から雰囲気温度係数を求めた例を示す。
8.4
温度上昇係数
温度上昇係数YΔΘは,摩擦発熱及びヒステリシス発熱による歯部の温度上昇が歯車材料の許容曲げ応力
に及ぼす影響を考慮するための係数である。温度上昇係数は,次による。
a) 標準試験歯車よりモジュール又は歯幅が小さい場合はYΔΘ>1.0となる。
b) 試験歯車よりモジュール又は歯幅が大きい場合はYΔΘ<1.0となる。
c) 標準試験条件より試験歯車の回転速度が小さい場合はYΔΘ>1.0となる。
d) 標準試験条件より試験歯車の回転速度が大きい場合はYΔΘ<1.0となる。
温度上昇係数を決めるためには詳細な実験及び解析が必要となる。ポリアセタール歯車に対する温度上
昇係数を求めた例が参考文献[5]〜[7]にある。
8.5
潤滑係数
潤滑係数YLは適切な潤滑剤を用いることで負荷容量が大きくなることを考慮するための係数である。適
切な潤滑剤を用いたときはYL>1.0となる。ある種のプラスチック材料では,潤滑剤によってその材料特
性が変化することがある。
附属書Dに,ポリアセタール歯車に対する運転試験の結果から潤滑係数を求めた例を示す。
8.6
相手歯車係数
相手歯車係数YMは,プラスチック歯車と鋼歯車の対に比べ,プラスチック歯車の対の負荷容量が小さ
13
B 1759:2019
くなることを考慮するための係数である。相手歯車係数は,次による。
a) プラスチック歯車を相手歯車としたときはYM<1.0となる。異なるプラスチック材料を対とする場合,
その組合せでYMの大きさは変化する。
b) プラスチック歯車の対で行った運転試験結果から求めた許容曲げ応力σFlim-Pを適用する場合は,鋼製
歯車を相手歯車とするとYM>1.0となる。
附属書Eに,ポリアセタール歯車に対する運転試験の結果から相手歯車係数を求めた例を示す。
9
歯車の安全性の評価
この規格の評価法に基づいて既に許容曲げ応力を求めたプラスチック材料に対して,歯車の許容歯元曲
げ応力を求めるための各係数を適切に定めると,歯車の安全性評価が可能である。歯車の安全性評価は,
次による。
設計諸元によって式(6)を用いて,想定された呼び接線力に対する歯元曲げ応力σFを求め,更に与えられ
た運転条件に対する歯車の許容歯元曲げ応力σFPを式(41)から求める。このときのプラスチック歯車の曲げ
強さに対する安全率SFを式(43)と定義する。
F
FP
F
σ
σ
S=
··············································································· (43)
これが,式(44)を満たすとき,安全であるとみなす。
min
F
F
S
S≥
··············································································· (44)
ここに,SFminは,安全率の最小値で,受渡当事者間の協議による。
内歯車の安全性評価を行う場合には,内歯車対の歯面すべりが外歯車対のそれに比べ小さいこと及び実
のかみ合い率が幾何学的に計算した場合より大きくなることが想定されるため,次の注意が必要である。
a) 標準試験歯車を用いて標準試験条件で行った運転試験結果から求めた潤滑係数及び相手歯車係数は,
若干危険側になる。したがって,SFminを若干大きく設定することが望ましい。
b) 雰囲気温度係数は適用できる。
c) 標準試験歯車を用いて標準試験条件で行った運転試験結果から求めた寿命係数は適用してもよいが,
SFminを小さく設定する場合は,内歯車対での運転試験を行って確認することが望ましい。
d) 温度上昇係数は若干安全側になる。
内歯車の安全性評価の例は,参考文献[8]にある。
14
B 1759:2019
附属書A
(参考)
歯元形状係数の算出例
A.1 一般
この規格は,標準の歯元すみ肉形状をカウンタラックが創成するトロコイド曲線としている。しかし,
成形用金型をワイヤカットで加工する場合には,ワイヤ径に等しい非常に小さな半径をもつ円弧を歯元す
み肉形状とすることも少なくない。このように小さな半径でなくても円弧部で生じる歯元応力は,標準と
している歯元すみ肉形状で生じる応力より大きくなる。この規格では,標準の歯元すみ肉形状に対する歯
元形状係数をYf=1.0としているので,歯元形状が円弧の場合はYf>1.0となる。
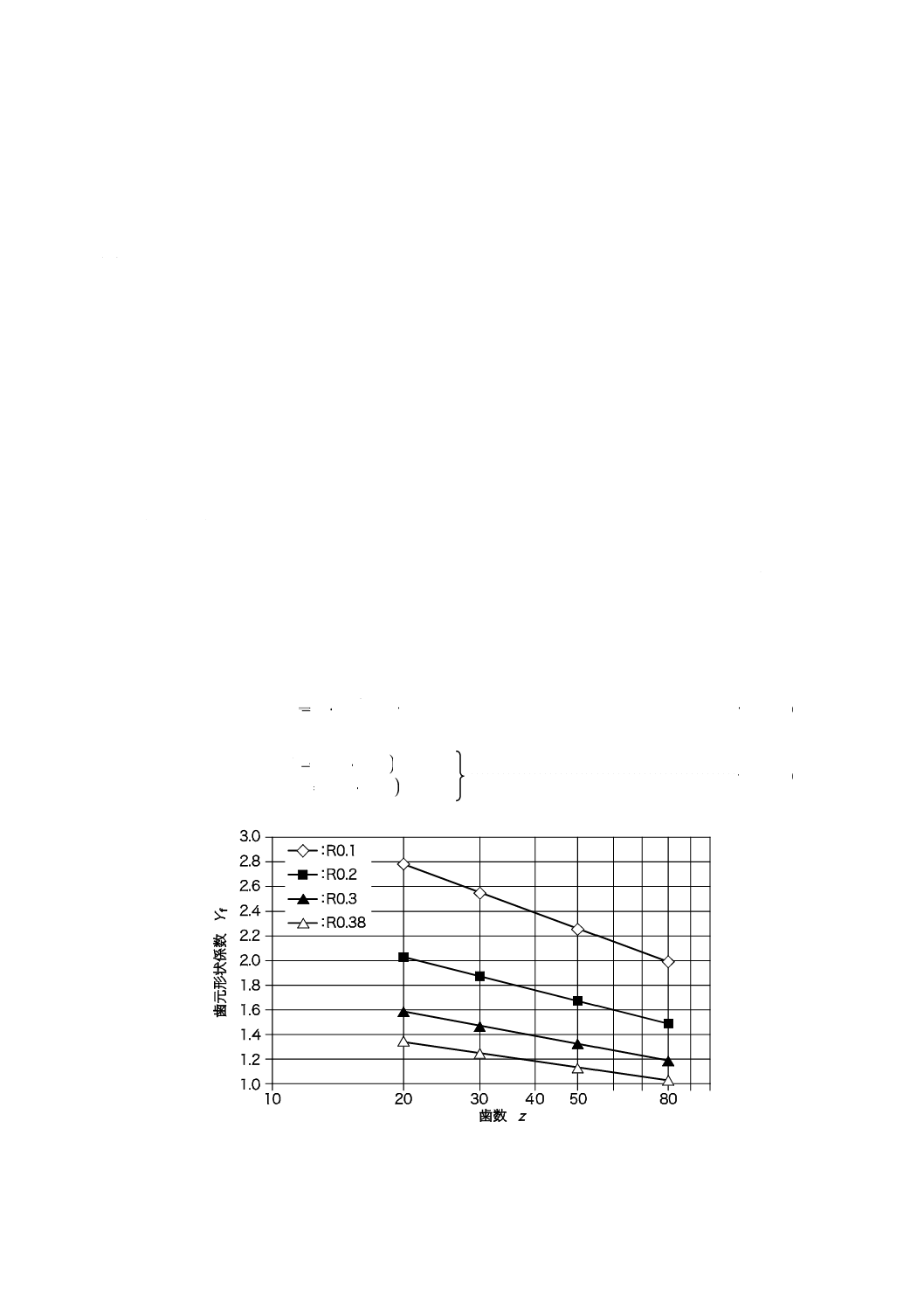
A.2 歯元形状係数
ここでは,歯車の歯元すみ肉形状を円弧とした歯車と,標準の歯元すみ肉形状をもつ歯車とについて有
限要素解析を行い,歯元に生じる最大主応力の最大値を比較することによって,歯元形状係数Yfを見積も
る[9]。有限要素解析は,モジュール1 mm,圧力角20°で歯数20,30,50,及び80のポリアセタール製標
準平歯車のバックラッシが0となる中心距離で同じ諸元をもつ鋼製相手歯車と組み付けたとき,一歯かみ
合いの歯先側の点でかみ合う場合について行った。歯元形状を円弧とした場合とトロコイド曲線とした場
合とについて歯元に生じる最大主応力の最大値σ1R及びσ1Tを求め,それらの比,σ1R/σ1Tを歯元形状係数
Yfとした。図A.1は,歯元円弧半径Rfを0.1,0.2,0.3,及び0.38 mmと変化させて求めたYfを片対数グラ
フで示したものである。
この結果を最小二乗近似してYfを歯数z及び歯元円弧半径Rfの関数として表すと,
()
2
1
f
ln
f
z
f
Y
+
=
····································································· (A.1)
となる。ここに,
()
()
163
.0
ln
89
.1
0380
.0
ln
266
.0
f
2
f
1
+
−
=
+
=
R
f
R
f
······················································· (A.2)
図A.1−歯元形状係数の計算例
15
B 1759:2019
附属書B
(参考)
許容曲げ応力及び寿命係数の導出例
B.1
許容曲げ応力
この規格で用いるプラスチック歯車材料の許容曲げ応力σFlimは,試験歯車を用いて行った運転試験の結
果によって得られた値で,材料試験片を用いて行った曲げ試験の結果によって得られた値ではない。プラ
スチック材料は,一般に明確な疲労限度を示さないため,この規格では,標準試験歯車に対して標準試験
条件で運転試験を行った結果から,かみ合い回数106で損傷確率1 %となる歯元曲げ応力[式(6)から求め
たもの]をプラスチック材料の許容曲げ応力σFlimと定義する。プラスチック歯車対での運転試験結果から
求めた許容曲げ応力は,σFlim-Pと記載する。
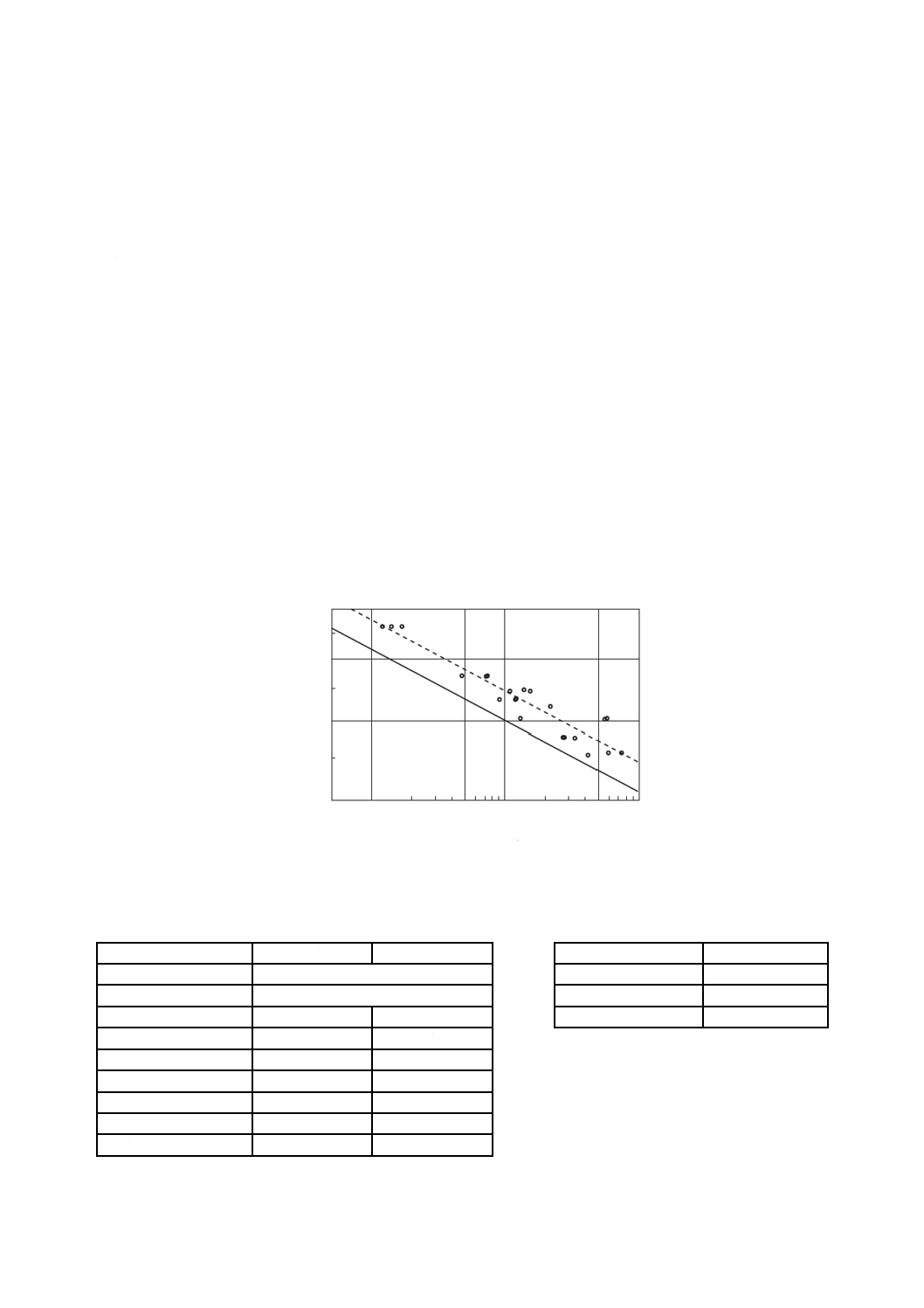
図B.1のプロット点は,表B.1に示す歯車を用いて表B.2に示す条件下で運転試験を行ったときの式(6)
によって求めた歯元曲げ応力σFと損傷が認められたときまでのかみ合い回数Nとの関係を両対数目盛で示
したものである。図B.1中の破線はそれらを最小二乗法で直線近似したものである。その近似直線と各プ
ロット点との偏差から標準偏差σを求め,その破線を2.33σだけ下方に平行移動した直線(図B.1の実線
でかみ合い回数ごとの損傷確率が1 %となる応力レベル)を引くとその直線の式は,式(B.1)となる。
かみ合い回数 N
図B.1−許容曲げ応力及び寿命係数の算出
表B.1−歯車諸元
表B.2−運転条件
相手歯車
試験歯車
試験トルク(N・m)
4.0, 5.0, 7.0
モジュール(mm)
1
回転速度(min−1)
1 000
圧力角(°)
20
試験温度(℃)
25
歯数
67
48
相対湿度(%)
50
ねじれ角(°)
0
0
転位係数
0
0
歯幅(mm)
10.0
8.0
歯先円直径(mm)
69.0
50.0
歯底円直径(mm)
64.5
45.5
材料
SCM415
POM
120
100
80
60
歯
元
曲
げ
応
力
σ
F
(
M
P
a)
105
106
107
16
B 1759:2019
112
.0
F
376
N
σ=
············································································ (B.1)
式(B.1)でN=106としたときのσF=80.0 MPaが,この実験から得られるプラスチック材料の許容曲げ応
力σFlimとなる。
B.2 寿命係数
寿命係数YNTは,かみ合い回数106以下の有限寿命設計を行うときに用いる係数である。必要な場合に
は,106を超える寿命を確保するために用いてもよい。
式(B.1)をB.1で求めたσFlimで無次元化し,寿命係数YNTが式(B.2)のように求められる。
112
.0
NT
70
.4
N
Y
=
·········································································· (B.2)
17
B 1759:2019
附属書C
(参考)
雰囲気温度係数の導出例
C.1 一般
雰囲気温度係数YΘは,雰囲気温度が材料の許容曲げ応力に及ぼす影響を考慮するために用いる係数であ
る。標準試験歯車を用い,標準試験条件の下で,試験温度だけを設定値に変更して運転試験を行い,当該
温度における雰囲気温度係数を求めることが可能である。複数の試験温度レベルに対して運転試験を行う
ことによって,雰囲気温度係数を試験温度の関数として求めることも可能である。
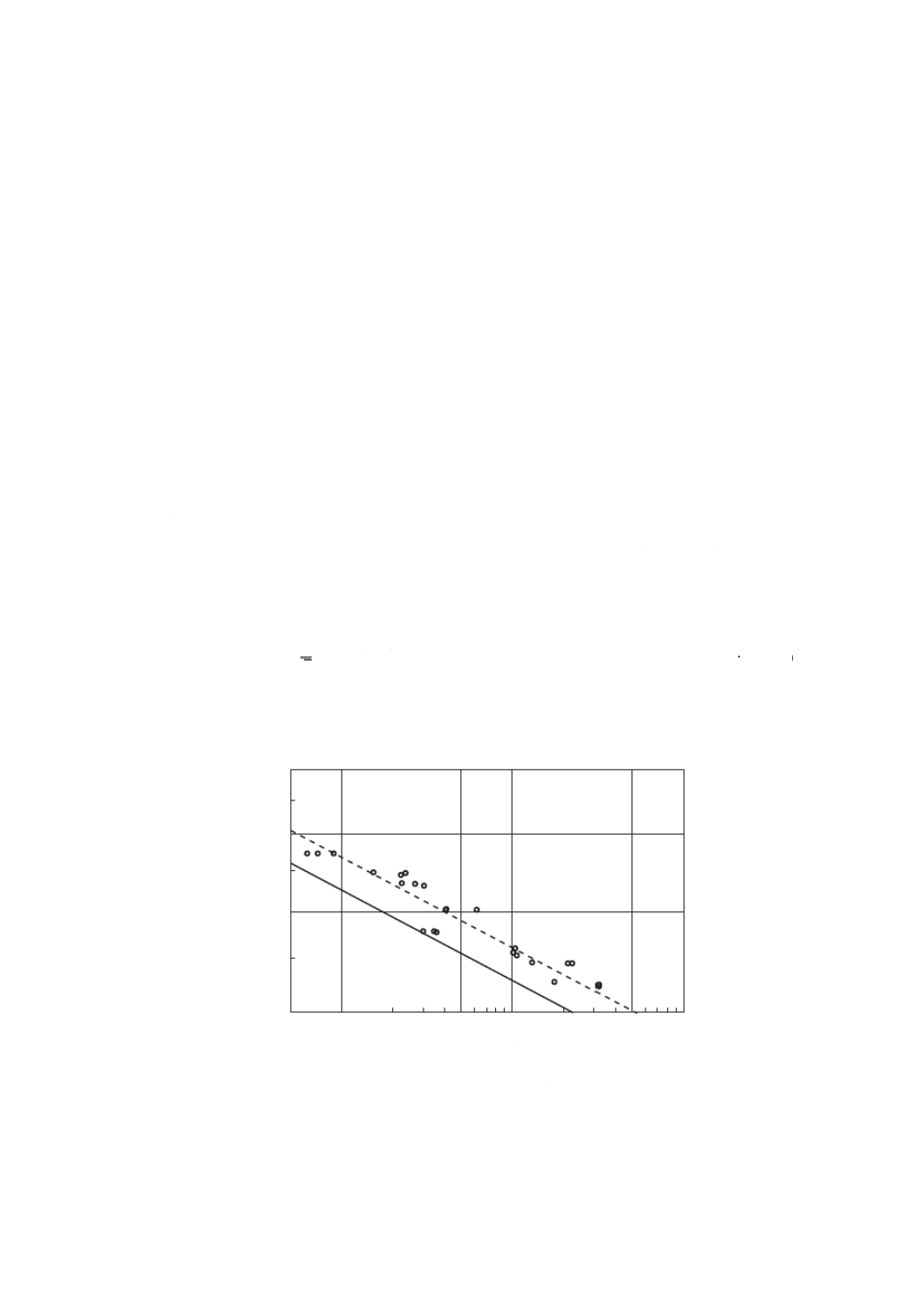
C.2 雰囲気温度係数
図C.1のプロット点は,試験温度だけを80 ℃と高くした場合の運転試験の結果を示している。図の破
線は,これらの結果を図B.1に示した直線と同じ傾きの直線で最小二乗近似したもので,実線は,図B.1
と同じように,1 %の損傷確率となる応力レベルに平行移動した直線である。この直線からかみ合い回数N
=106で損傷確率が1 %となる応力レベルを求めると65.9 MPaとなる。これが80 ℃における材料の許容曲
げ応力σFlim(at 80 ℃)となる。したがって,試験温度80 ℃における雰囲気温度係数YΘ(at 80 ℃)は0.82
(安全側に丸めている)となる。
必要な場合にはσFlimを求めたときの試験温度が25 ℃であったことを考慮し,これらを試験温度Θ (℃)
について線形近似し,雰囲気温度係数YΘを,式(C.1)として見積もることもできる。
07
.1
)
10
12
.3
(
3
+
×
−
=
−
Θ
Θ
Y
························································· (C.1)
しかし,より正確を期すため,試験温度を種々に変えて行った試験結果に基づいてそれぞれの試験温度
に対して雰囲気温度係数YΘを求め,これを試験温度の式で表すことが望ましい。
図C.1−雰囲気温度係数の算出
120
100
80
60
歯
元
曲
げ
応
力
σ
F
(M
P
a)
105
106
107
かみ合い回数 N
18
B 1759:2019
附属書D
(参考)
潤滑係数の導出例
D.1 一般
潤滑係数YLは,潤滑が歯車の許容歯元曲げ応力に及ぼす影響を考慮するための係数である。より正確な
潤滑係数は,雰囲気温度係数と同様に,潤滑剤を用いた運転試験を行い,得られたプラスチック材料の許
容曲げ応力σFlimを標準試験条件での運転試験の結果から得られたそれと比較して決めることが可能である。
しかし,ここでは簡易な方法として安全率の観点から見積もる方法[10]を示す。歯元曲げ応力σFが式(6)か
ら算出でき,歯車の許容歯元曲げ応力σFPを与える式(41)の潤滑係数以外の全ての係数が既知であるとき,
式(43)から求めた安全率が1となるように仮の潤滑係数が求められ,これより潤滑係数を見積もることが
可能である。
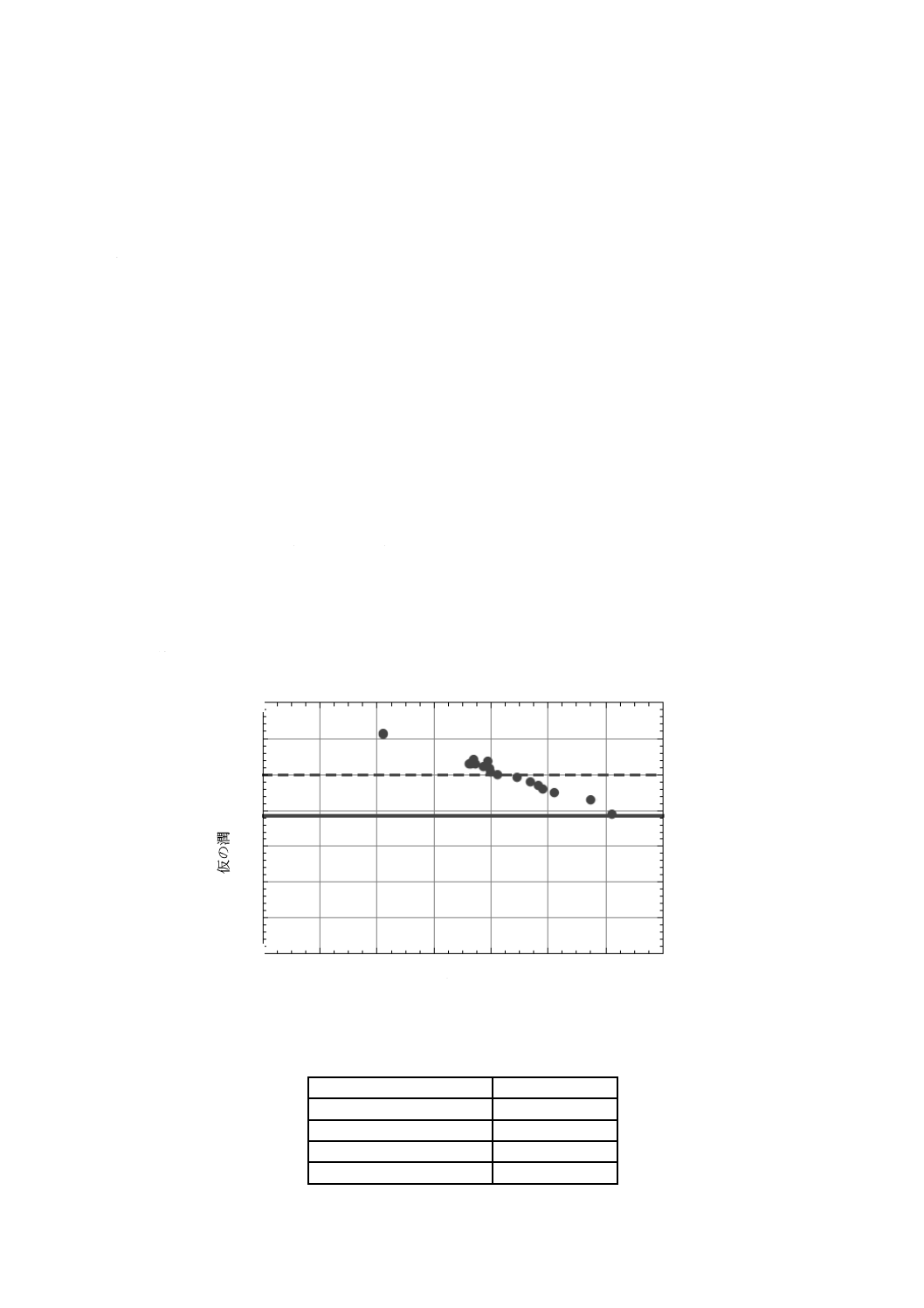
D.2 潤滑係数
図D.1は,表B.1に示した歯車を用いて,表D.1に示す条件下で運転試験を行い,損傷が認められたと
きのかみ合い回数から式(B.2)で計算される寿命係数と仮の潤滑係数との関係を表している。
なお,ここで用いた実験結果は試験温度80 ℃の下で行った運転試験から得られたものなので,雰囲気
温度係数YΘは,C.2に従い0.82とした。
図D.1に示すように,仮の潤滑係数が平均で1.25(図D.1の破線)となっているが,ばらつきを考慮し,
1 %の損傷確率となるように潤滑係数を見積もる。そこで,図D.1の破線を2.33σだけ下方に平行移動(図
D.1の実線)し,この場合には,潤滑係数YLを1.19と見積もることが可能である。
図D.1−潤滑係数の算出
表D.1−運転条件(2)
試験トルク(N・m)
5.0
回転速度(min−1)
1 000
試験温度(℃)
80
相対湿度(%)
50
潤滑油
グリース
1.35
1.30
1.25
1.20
1.15
1.10
1.05
1.00
寿命係数
仮
の
潤
滑
係
数
0.90
0.92
0.94
0.96
0.98
1.00
1.02
1.04
19
B 1759:2019
附属書E
(参考)
相手歯車係数の導出例
E.1
一般
相手歯車係数YMは,相手歯車の材質が許容歯元曲げ応力に及ぼす影響を考慮するための係数である。
相手歯車係数についても潤滑係数と同様に簡易な方法[10]として安全率の観点から見積もることが可能で
ある。
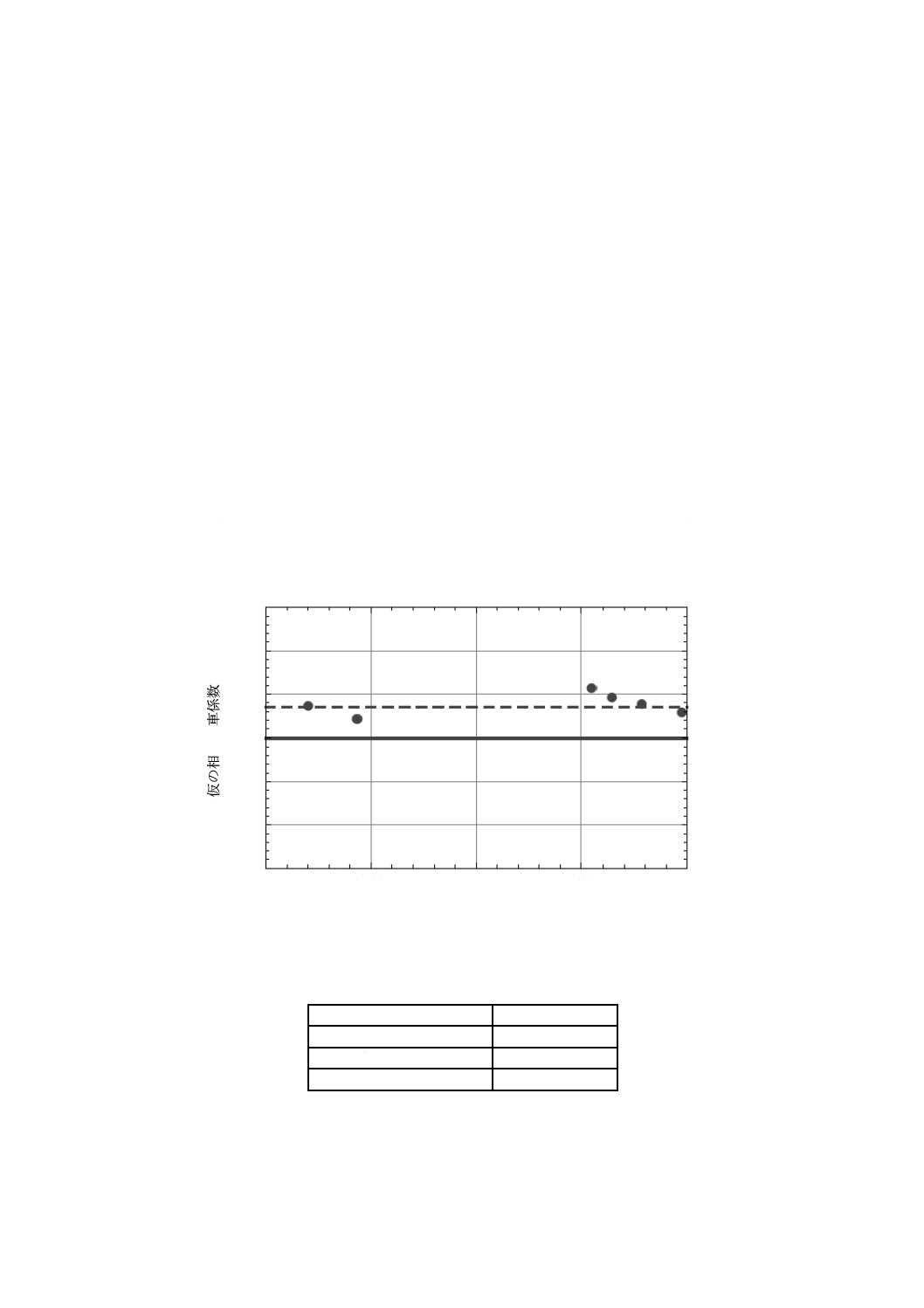
E.2
相手歯車係数
図E.1は,表B.1に示した試験歯車を対として,表E.1に示した条件下で運転試験を行い,損傷が認め
られたときのかみ合い回数から式(B.2)で算出した寿命係数と仮の相手歯車係数の関係を表している。
なお,参考文献[5]〜[7]を参考にして回転速度500 min−1のときの温度上昇係数YΔΘを,伝達トルクが5
N·mでは1.32,4 N·mでは1.23とした。
図E.1に示したように,仮の相手歯車係数が平均で0.685(図E.1の破線)となっているが,ばらつきを
考慮し,1 %の損傷確率となるように相手歯車係数を見積もる。そこで,図E.1の破線を2.33σだけ下方に
平行移動(図E.1の実線)し,この場合,相手歯車係数YMを0.65と見積もることが可能である。
図E.1−相手歯車係数の算出
表E.1−運転条件(3)
試験トルク(N・m)
4.0,5.0
回転速度(min−1)
500
試験温度(℃)
25
相対湿度(%)
50
仮
の
相
手
歯
車
係
数
寿命係数
0.80
0.75
0.70
0.65
0.60
0.55
0.50
0.95
1.00
1.05
1.10
1.15
20
B 1759:2019
参考文献
[1] 森脇一郎,米田紘貴,中村守正,射場大輔,JIS B 1759に基づいたPA66歯車の負荷容量評価,精密
工学会誌,vol.83,No.2,pp.180-185(2017)
[2] ISO 6336-3:2006,Calculation of load capacity of spur and helical gears−Part 3: Calculation of tooth bending
strength
[3] ISO 21771:2007,Gears−Cylindrical involute gears and gear pairs−Concepts and geometry
[4] 森脇一郎,福島隆雄,上田昭夫,中村守正,プラスチック歯車の疲労折損に及ぼすリム厚さの影響,
精密工学会誌,76巻,2号,pp.201-206(2010)
[5] 上田昭夫,吉原正義,高橋秀雄,森脇一郎,プラスチック歯車のかみ合い発熱のコンピュータシミュ
レーション(プラスチック平歯車対の場合),日本機械学会論文集C編,73巻,732号,p.2364(2007)
[6] 上田昭夫,高橋秀雄,中村守正,森脇一郎,プラスチック歯車のかみ合い発熱のコンピュータシミュ
レーション(歯の温度上昇に及ぼす歯幅の影響),日本機械学会論文集C編,74巻748号,pp.3050-3055
(2008)
[7] 上田昭夫,高橋秀雄,中村守正,森脇一郎,プラスチック歯車のかみ合い発熱のコンピュータシミュ
レーション(歯の温度上昇に及ぼすモジュールと回転速度の影響),日本機械学会論文集C編,75巻
752号,pp.1072-1076(2009)
[8] 森脇一郎,村上智哉,立岡晃太,射場大輔,上田昭夫,ポリアセタール(POM)製内歯車の負荷容量
評価に関する研究−内歯車の運転試験から見たJIS B 1759の課題−,精密工学会誌,vol.85,No.6,
pp.591-596(2019)
[9] 上田昭夫,歯元形状係数,成形プラスチック歯車研究専門委員会,プラスチック歯車の設計指針−よ
り良い歯車を設計するために−,pp.30-34(2012)
[10] 森脇一郎,今吉健,中村守正,上田昭夫,プラスチック歯車の負荷容量に及ぼす潤滑剤および相手歯
車材料の影響,精密工学会誌,vol.78,No.11,pp.992-997(2012)









