B 1192-4:2018
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 記号及び添え字 ················································································································ 1
4.1 記号 ···························································································································· 1
4.2 添え字 ························································································································· 2
5 軸方向静剛性R ················································································································ 2
5.1 一般 ···························································································································· 2
5.2 軸方向静剛性R ·············································································································· 4
5.3 ボールねじの軸方向静剛性Rbs ·························································································· 4
5.4 ボールねじ軸の軸方向静剛性Rs ························································································ 5
5.5 ナットの軸方向静剛性Rnu································································································ 5
附属書JA(参考)JISと対応国際規格との対比表 ······································································· 9
B 1192-4:2018
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本工作機器工業会(JMAA)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 1192の規格群には,次に示す部編成がある。
JIS B 1192-1 第1部:用語及び記号
JIS B 1192-2 第2部:呼び径及び呼びリード
JIS B 1192-3 第3部:精度測定方法
JIS B 1192-4 第4部:軸方向静剛性
JIS B 1192-5 第5部:静定格荷重,動定格荷重及び寿命
日本工業規格 JIS
B 1192-4:2018
ボールねじ−第4部:軸方向静剛性
Ball screws-Part 4: Static axial rigidity
序文
この規格は,2006年に第1版として発行されたISO 3408-4を基とし,日本の実情に合わせて一部計算
式の変更など,技術的内容を変更して作成した日本工業規格である。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JAに示す。
1
適用範囲
この規格は,ボールねじの軸方向静剛性について規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 3408-4:2006,Ball screws−Part 4: Static axial rigidity(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この引用
規格は,その最新版(追補を含む。)を適用する。
JIS B 1192-1 ボールねじ−第1部:用語及び記号
注記 対応国際規格:ISO 3408-1,Ball screws−Part 1: Vocabulary and designation
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 1192-1による。
4
記号及び添え字
4.1
記号
この規格で用いる主な記号は,次による。
記号
説明
単位
α
接触角
°
φ
リード角
°
Δl
軸方向弾性変位量
μm
C
材料,寸法,形状によって定まる補助係数
−
d2
ねじ部溝谷径
mm
2
B 1192-4:2018
db0
ねじ軸中空穴径
mm
Dw
ボール径
mm
E
縦弾性係数
MPa
F
軸方向荷重
N
Fpr
予圧荷重
N
i
負荷ボールの巻数
−
k
剛性特性
μm/N2/3
l
取付間距離
mm
ls
荷重作用点間距離
mm
n
回転速度
min−1
q
時間比
%
R
軸方向剛性
N/μm
Sa
バックラッシ
μm
z1
1循環路当たりの負荷ボール数
−
4.2
添え字
この規格で用いる記号の添え字は,次による。
記号
説明
bs
ボールねじを参照
b/t
ねじ溝接触点を参照
e
外部荷重,又はそれによる変位を参照
lim
予圧抜け荷重を参照
m
等価を参照
N
ねじ軸及びナットねじ溝の接触角方向に作用する荷重を参照
nu
ナットを参照
pr
予圧を参照
s
ねじ軸を参照
(1)
ナット1を参照
(2)
ナット2を参照
1
1点接触を参照
2
2点接触を参照
4
4点接触を参照
5
軸方向静剛性R
5.1
一般
ボールねじの軸方向静剛性は,位置決め精度に大きな影響を及ぼす。ボールねじの軸方向静剛性は,ボ
ールねじと支持軸受との組合せに依存するが,次の計算においては,支持軸受及びその組合せについては
考慮しない。
ボールねじの軸方向静剛性は直線的には変化せず,幾つかの線形及び非線形ばね成分の組合せとなる。
そのため,この規格で規定する剛性値は一方向の荷重下に適用する。
変位は,次の要因で発生する。
3
B 1192-4:2018
− ねじ軸及びナットの軸方向変位
− ねじ軸及びナットの半径方向変位
− ボールとねじ溝との接触点での変位
ボール接触による変位の計算はヘルツの理論に基づいており,次の条件に合致しなければならない。
− 接触相手部品の材料は均質・等方性弾性体とする。
− フックの法則が成り立つとする。すなわち,塑性変形はしない。
− 接触部分においては,法線応力だけが作用し,接触面は,平面とする。
さらに,簡易的なヘルツ理論を適用するには,ボールねじ軸,ナット,ボールについて,同一の縦弾性
係数及び横弾性係数の材料とする。
軸方向剛性を計算する場合は,バックラッシがあるナットとバックラッシがないナット(予圧ナット)
とを区別しなければならない。予圧は各種の方法で付加することができる。
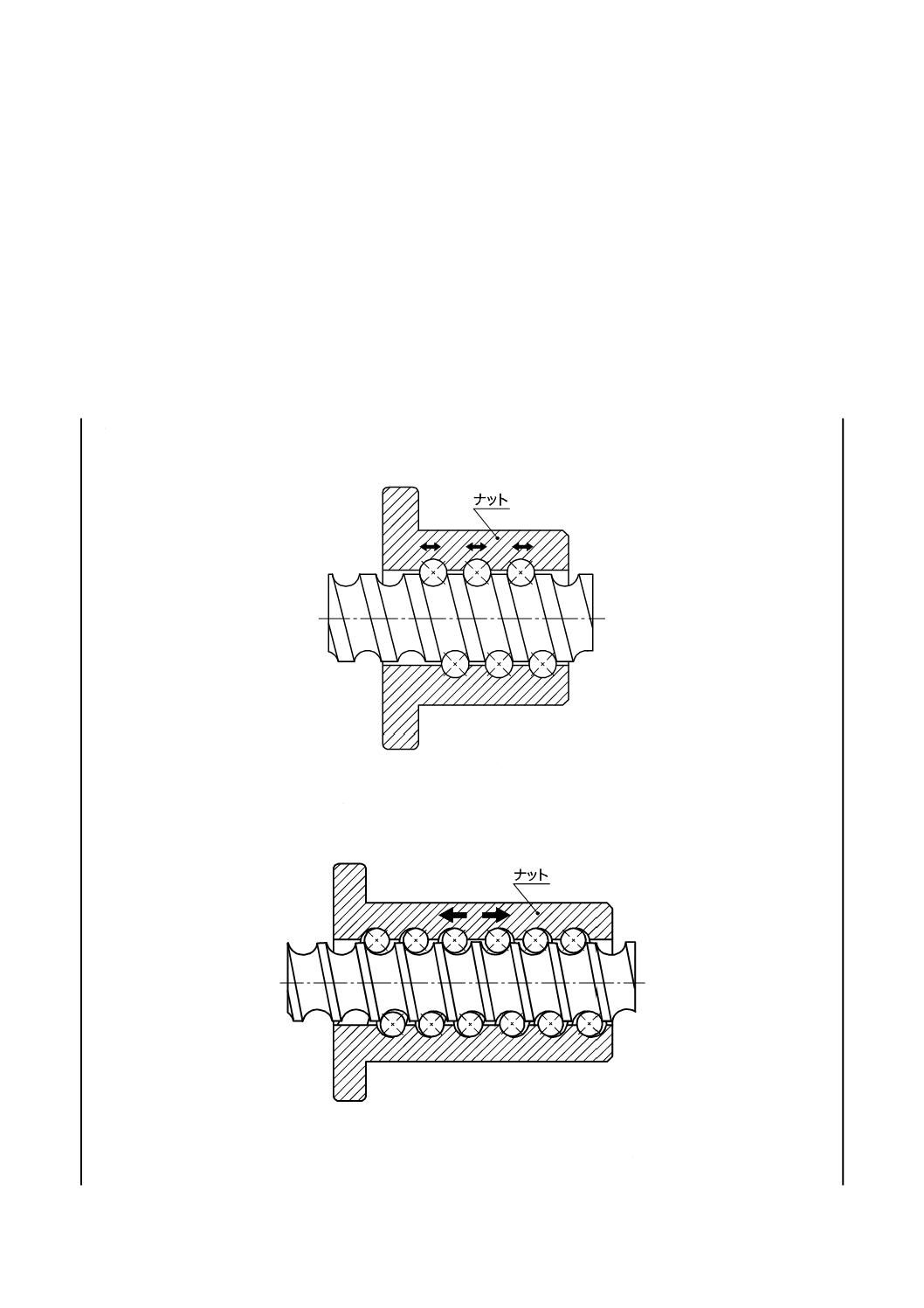
a) オーバーサイズボール予圧 1条ねじのシングルナットにおいて,オーバーサイズボールで予圧を付
加する方法。ボールは4点で接触する(図1参照)。
図1−オーバーサイズボール予圧
b) オフセットリード予圧 シングルナットにおいて,予圧される部分間のリードをシフトすることによ
って予圧を付加する方法。ボールは2点で接触する(図2参照)。
図2−オフセットリード予圧
c) 2条ねじのオフセットリード予圧 2条ねじのシングルナットにおいて,条間のリードをシフトするこ
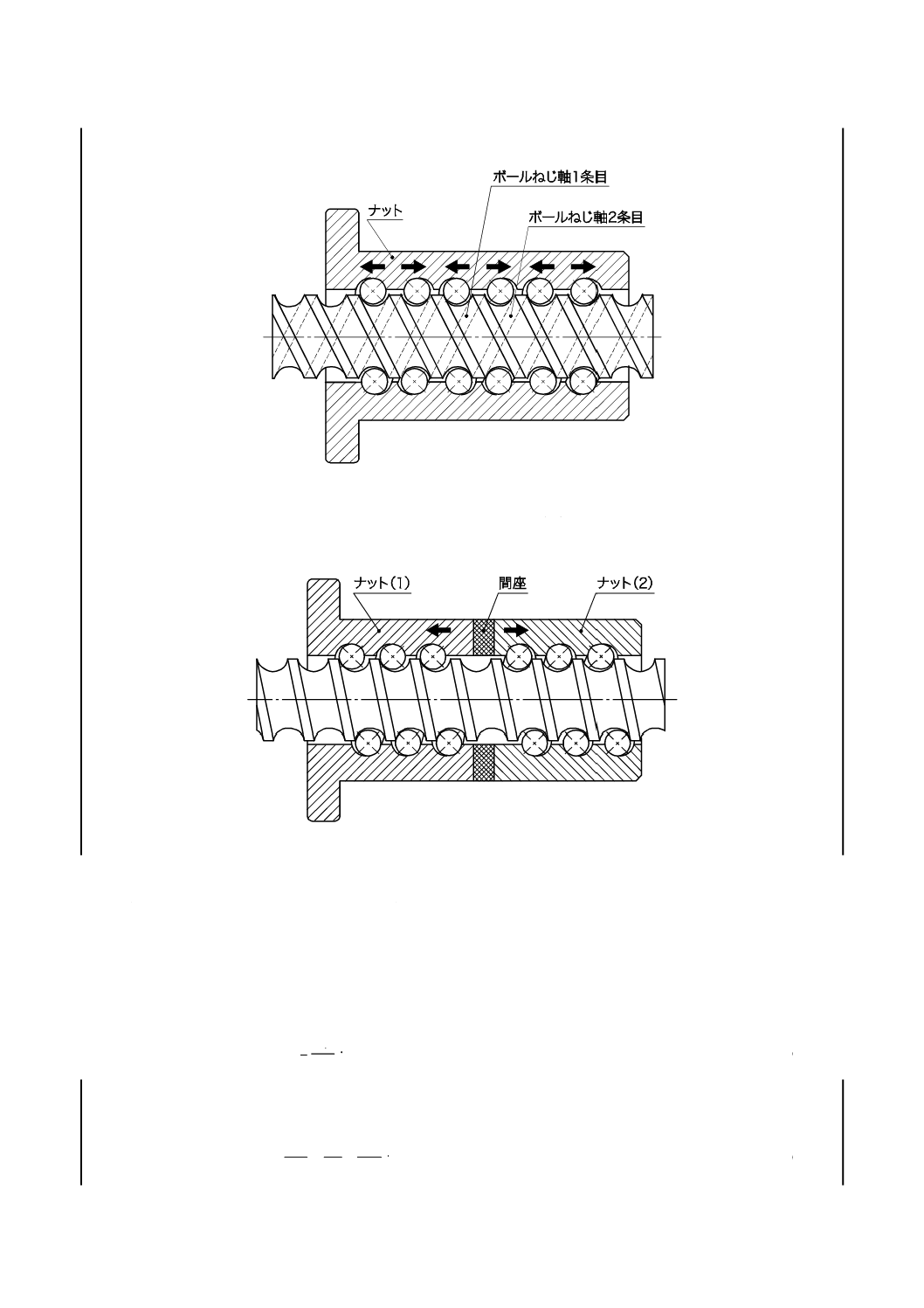
4
B 1192-4:2018
とによって予圧を付加する方法。ボールは2点で接触する(図3参照)。
図3−2条ねじのオフセットリード予圧
d) ダブルナット予圧 二つのシングルナットを組み合わせたダブルナットで,互いのシングルナットが
両方向(軸方向)にシフトして予圧を付加する方法。ボールは2点で接触する(図4参照)。
図4−ダブルナット予圧
この規格における剛性計算式は全ての予圧方式に適用可能である。
計算式に基づき,正確に軸方向変位を計算するには,時間的浪費も大きく,実際の目的にそぐわないた
め,適切に簡略化した計算方法について,5.2〜5.5に規定する。
5.2
軸方向静剛性R
軸方向静剛性Rは,変形に対する抵抗であり,軸方向荷重が作用したとき,1 μmの変位(Δl)を生じる
のに必要な力(ΔF)で表す。
l
F
R
Δ
Δ
=
··················································································· (1)
5.3
ボールねじの軸方向静剛性Rbs
ボールねじ全体の剛性Rbsは各要素の剛性の逆数の和の逆数となる。
nu
s
bs
1
1
1
R
R
R
+
=
·········································································· (2)
5
B 1192-4:2018
5.4
ボールねじ軸の軸方向静剛性Rs
5.4.1
一般
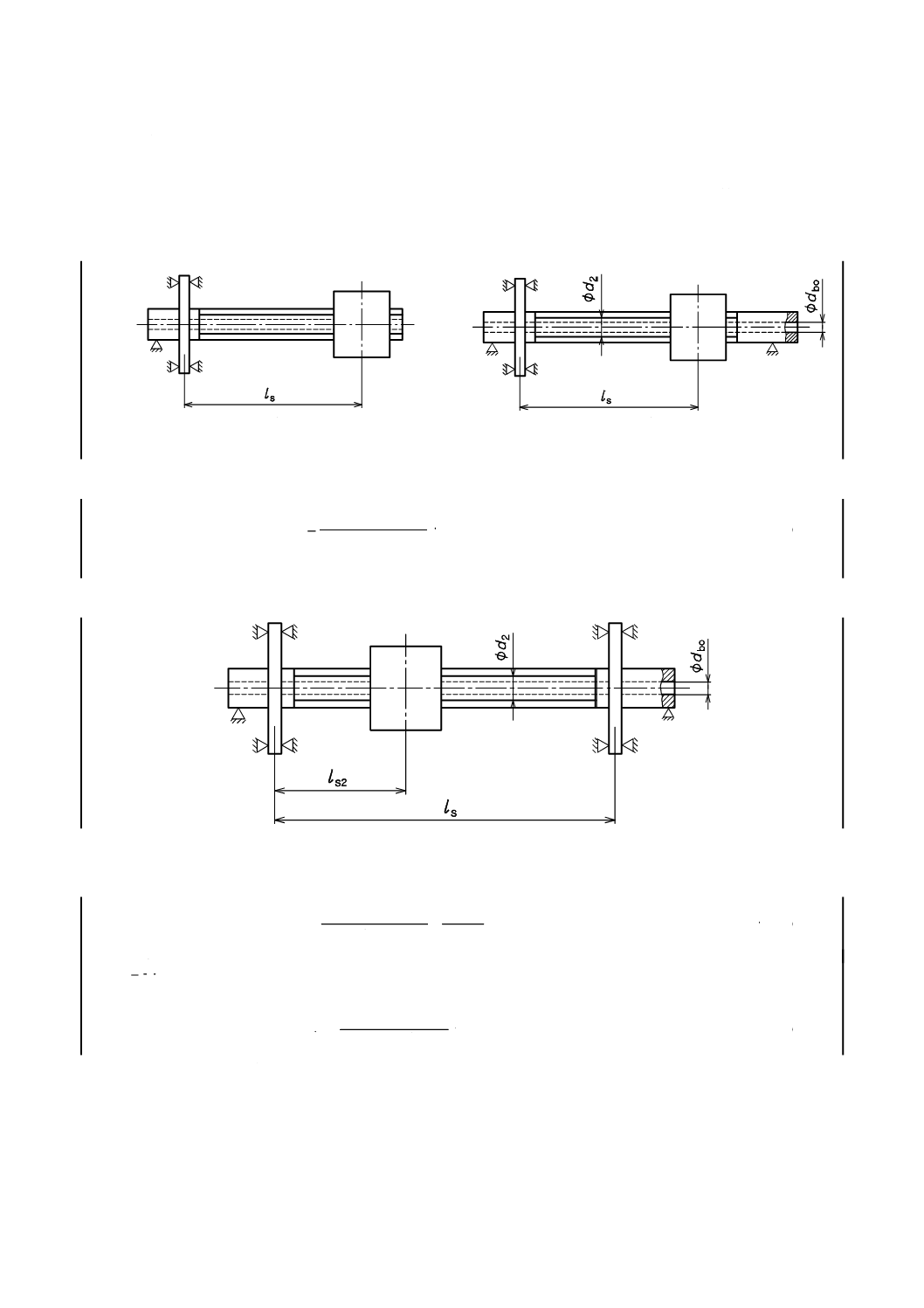
ボールねじ軸の剛性Rsは,軸方向荷重ΔFによって生じるねじ軸の弾性変位Δlsから計算でき,軸端の
軸受支持方法によって異なる。
5.4.2
ねじ軸の一端が固定の場合
a)
b)
図5−ねじ軸の一端が固定の場合の軸方向剛性
図5の取付け方法において,剛性Rs1は次の式で計算する。
3
s
2
bo
2
2
1
s
10
4
)
(π
×
×
×
−
=
l
E
d
d
R
································································· (3)
中実軸の場合 dbo=0
5.4.3
ねじ軸の両端が固定の場合
図6−ねじ軸の両端が固定の場合の軸方向剛性
図6の取付け方法において,剛性Rs2は次の式で計算する。
2
s
s
s
3
2
s
2
bo
2
2
2
s
10
4
)
(π
l
l
l
l
E
d
d
R
−
×
×
×
×
−
=
······················································ (4)
2
s
2
s
l
l =
の箇所で,最小の剛性値となることから,
3
s
2
bo
2
2
min
,2
s
10
)
(π
×
×
−
=
l
E
d
d
R
····························································· (5)
5.5
ナットの軸方向静剛性Rnu
5.5.1
バックラッシのある場合のナットの軸方向静剛性Rnu1
バックラッシのある場合のナットの軸方向剛性Rnu1は,ボールとねじ溝面との剛性Rb/tで代表する。
計算を簡略化するため,ナット及びねじ軸の変形については無視し,次の項目も考慮しない。
6
B 1192-4:2018
− ボール及びねじ溝面に作用する不均一な荷重
− 加工ばらつき
− 接触角の変化
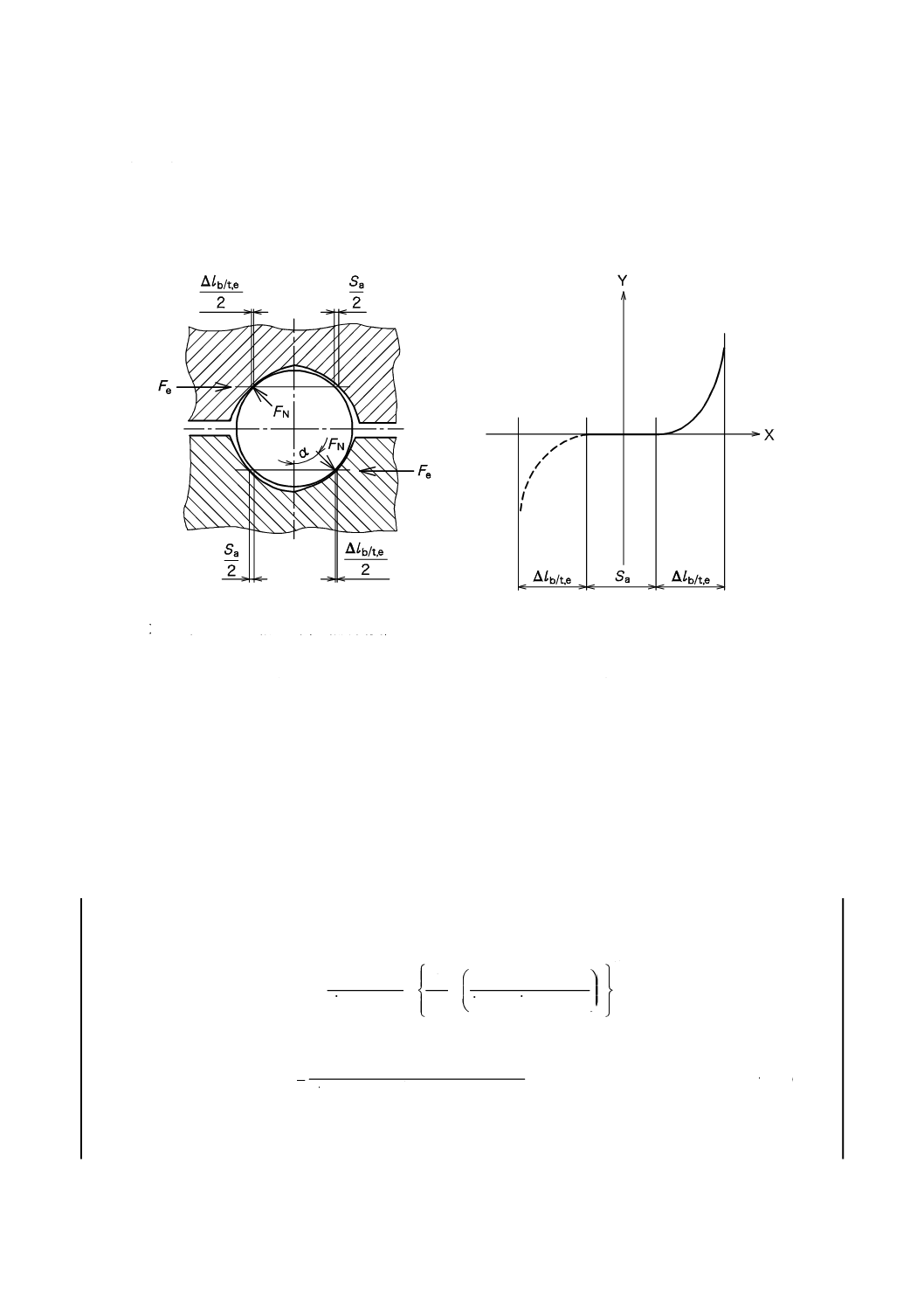
また,軸方向隙間によるナット及びねじ軸の相対的変位は,弾性変形でないため考慮しない[図7のa)
及びb)を参照]。
a)
b)
X:ナットとねじ軸との間の軸方向変位量
Y:外部軸方向荷重,Fe
図7−バックラッシのあるナットのねじ溝接触状態及び弾性変位曲線
ボールとねじ溝面との軸方向変位は,次の要因による。
− 作用荷重
− 呼び径
− ボール径
− 負荷ボール数
− ねじ溝適合度
− 荷重の角度
上記に基づき,バックラッシのあるナットの軸方向変位は,ヘルツ応力の理論からボールとナットねじ
溝面との軸方向弾性変位として,次の式によって近似的に求める。
3
2
3
1
2
1
w
b/t
cos
sin
1
cos
sin
Δ
F
k
α
z
i
F
D
α
C
l
×
=
×
×
×
×
×
×
=
ϕ
ϕ
··············· (6)
ここで,
3
5
3
1
w
3
2
1
)
cos
(sin
)
(
ϕ
×
×
×
×
=
α
D
z
i
C
k
·············································· (7)
C: 材料,形状,寸法によって定まる補助係数(0.52〜0.58)
したがって,ナットの軸方向静剛性Rnu1は,式(6)から軸方向荷重Fに対して次の式で表す。
7
B 1192-4:2018
F
F
k
l
d
3
2
)
Δ
d(
3
/1
b/t
×
×
×
=
−
から,
b/t
e
3/1
e
b/t
b/t
1
nu
Δ
2
3
1
2
3
)
Δ
d(
d
l
F
F
k
l
F
R
R
×
=
×
×
=
=
=
····································· (8)
Fe: 外部軸方向荷重(N)
Δlb/t: 軸方向弾性変位量(μm)
d: 微分演算子
これは荷重に対するばね剛性に依存することを示している。系の剛性は予圧荷重Fprなど,ボールねじ
の軸方向荷重が大きくなるに伴い増加する。
5.5.2
予圧の作用したナットの軸方向静剛性Rnu2,4
予圧の作用したナットの軸方向剛性Rnu2,4は,バックラッシのある場合のナットと同様,ボールとねじ溝
面との剛性Rb/t,prで代表し,ナット及びねじ軸の変形については無視し,次の項目も考慮しない。
− ボール及びねじ溝面に作用する不均一な荷重
− 加工ばらつき
− 接触角の変化
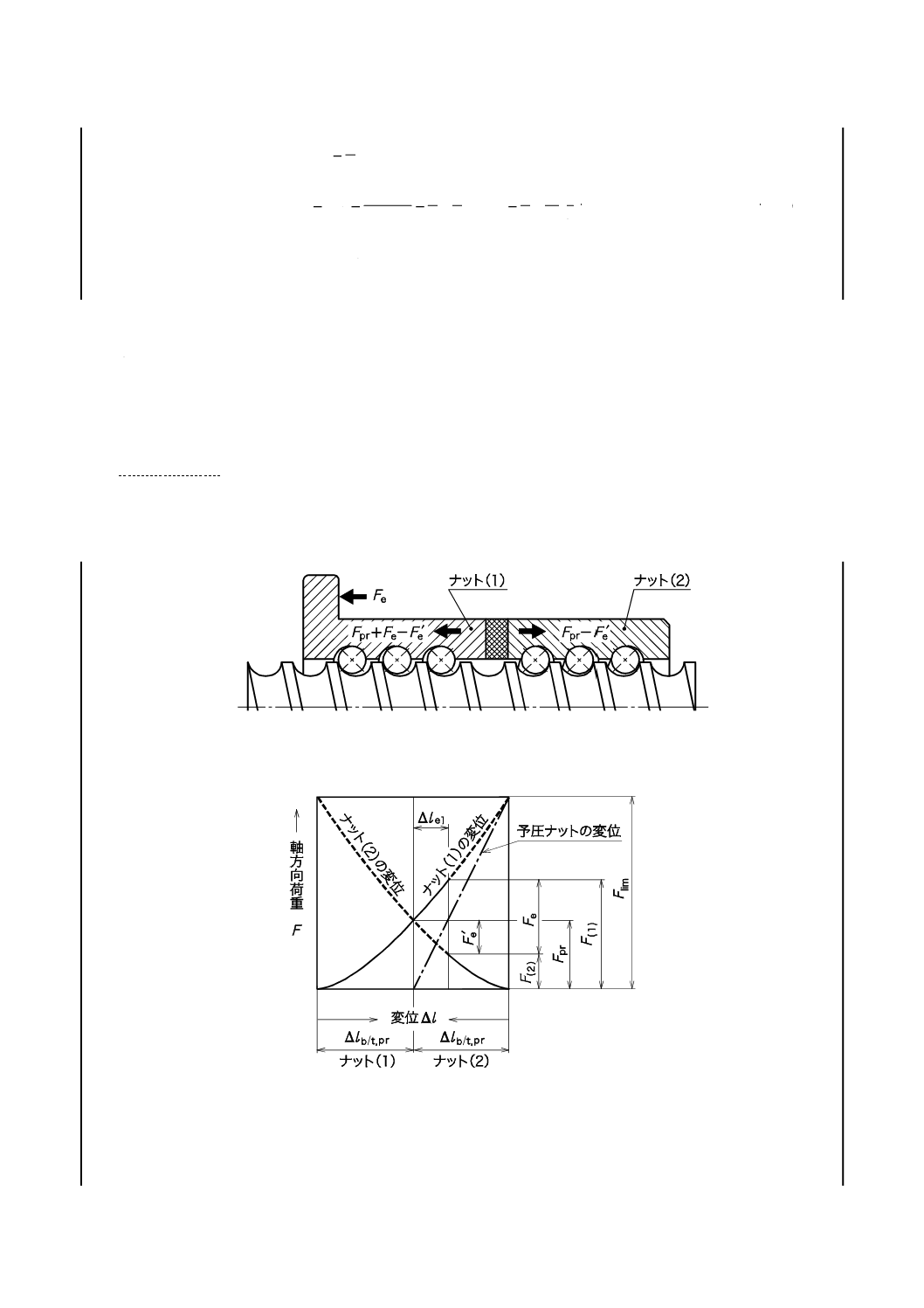
ボールねじ溝面において高い剛性を得るためには,ナットに予圧を付加する(図8参照)。これによって,
個々のナットのバックラッシと低荷重時に生じるボールねじ溝面との変位は除去される。
a)
b)
図8−予圧の作用したナットのねじ溝接触状態及び弾性変位曲線
図8のダブルナット予圧ボールねじにおいて,ナット(1),ナット(2)は予圧荷重Fprによって,あらかじ
8
B 1192-4:2018
めΔlb/t,prだけ弾性変位して組み立てられている。この状態で外部荷重Feがナット(1)に加わると,図8 b)に
示すようにナット(1),ナット(2)のそれぞれの軸方向弾性変位量Δle(1),Δle(2)は,
1
e
pr
b/t,
e(2)
1
e
pr
b/t,
e(1)
Δ
Δ
Δ
Δ
Δ
Δ
l
l
l
l
l
l
−
=
+
=
,
このときナット(1),ナット(2)に作用する荷重はそれぞれ,
e
pr
e(2)
e
e
pr
e(1)
F
F
F
F
F
F
F
′
−
=
′
−
+
=
,
となる。すなわち,予圧を与えることによってナット(1)に作用する荷重はFe−Fe'となり,予圧を与えてい
ない場合に比べてFe'だけ負荷荷重が減少するため,結果として全体の弾性変位は小さくなる。この効果は,
外部荷重による弾性変位がΔlb/t,prとなり,ナット(2)の予圧がなくなるまで働く。予圧が抜けるときの荷重
をFlimとすると,軸方向荷重と弾性変位との関係は図8 b)から次のようになる。
3
2
pr
pr
b/t,
Δ
F
k
l
×
=
········································································ (9)
k: 剛性特性
3
2
lim
pr
b/t,
Δ
2
F
k
l
×
=
···································································· (10)
2
Δ
Δ
2
pr
b/t,
pr
b/t,
3
2
pr
lim
=
=
l
l
F
F
································································(11)
pr
2
3
lim
2
F
F
×
=
········································································· (12)
式(12)及び図8 b)から,予圧荷重の23/2倍の軸方向荷重まで予圧効果がある。
過度の予圧は寿命を短くするため,予圧荷重は慎重に設定する必要がある。予圧荷重の目安は,次の式
となる。
2
3
m
pr
2
F
F=
··············································································· (13)
ここに,Fmは等価荷重を表し,次の式で計算する。
3
i
m
i
1
3
ei
m
q
n
n
F
F
n
i
×
×
=∑
=
······························································· (14)
軸方向荷重が,0<Fe≦Flimの条件下で,予圧ナットのボールねじ溝面における剛性Rnu,b/tは,図8にお
いて,式(9)及び式(12)によって,予圧抜け荷重Flimと予圧による弾性変位量との比で近似する。
3
1
pr
2
3
pr
b/t,
lim
t
b
nu,
2,4
nu
1
2
Δ
F
k
l
F
R
R
×
×
=
=
=
············································ (15)
なお,2点接触(オフセットリード予圧,ダブルナット予圧)の場合,及び4点接触(オーバーサイズ
ボール予圧)の場合も同様にして計算できる。
9
B 1192-4:2018
附属書JA
(参考)
JISと対応国際規格との対比表
JIS B 1192-4:2018 ボールねじ−第4部:軸方向静剛性
ISO 3408-4:2006,Ball screws−Part 4: Static axial rigidity
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの
評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
全体
図題
−
−
追加
JISでは,図番号に図題を追加した。
他の部に合わせ,図題を追加した。
また,使用者にとって分かりやす
いと判断した。
4 記号及び
添え字
4.1 記号
4.1
JISとほぼ同じ
変更
ISO規格では接触点径dcだが,JISで
はねじ部溝谷径d2とした。
5.4によって,国内の実態に合わせ
た。
4.2 添え字
4.2
JISとほぼ同じ
追加
JISでは,接触点数を表す添え字の説明
を追加した。
接触点数の添え字を説明した方が
分かりやすいと判断した。
5 軸方向静
剛性R
5.1 一般
5.1
JISとほぼ同じ
変更
ISO規格は,模式図だが,JISでは,ね
じ溝及びボールを明示した。また,図
題として予圧の名称を追記した。
ねじ溝及びボールを明示した方
が,使用者にとって分かりやすい
と判断した。
5.3 ボールねじの軸
方向静剛性Rbs
5.3
JISとほぼ同じ
変更
JISでは精度係数を考慮したナットの
剛性Rnu,arではなく,ナットの理論剛性
Rnuだけを採用した。
精度等級による剛性の低下は実態
に合わない。今後ISOへ廃止を働
きかけていく。
5.4 ボールねじ軸の
軸方向静剛性Rs
5.4
JISとほぼ同じ
変更
ISO規格では式(3) ,式(5),式(6),図5
及び図6において接触点径を使用して
いるが,JISでは溝谷径を採用した。
接触点径の式(4)を削除したため,以
降の式番号が繰り上げになる。
接触点径が,必ずしもねじ軸の平
均径を表すものでなく,国内での
実態に合わせた。
5.5.1 バックラッシ
のある場合のナット
の軸方向静剛性Rnu1
−
−
追加
JISではラジアル分力による剛性を考
慮しないため,ねじ溝面での剛性に代
表される旨を追加した。
国内の実態に合わせ,この文言を
追加した方が分かりやすいと判断
した。
2
B
1
1
9
2
-4
:
2
0
1
8
10
B 1192-4:2018
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの
評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
5 軸方向静
剛性R
(続き)
−
5.5.1.1 ラジアル分力によるナ
ットとねじ軸との軸方
向静剛性Rn/s
削除
JISでは,ラジアル分力による軸方向剛
性の計算式を削除した。
国内では,この計算式を使用して
いる実態がない。今後ISOへ廃止
を働きかけていく。
5.5.1 バックラッシ
のある場合のナット
の軸方向静剛性Rnu1
5.5.1.2 ボールとねじ溝面との
剛性
変更
ISO規格では弾性変位の結論式(25)の
誘導式(11)〜(24)を記載しているが,JIS
では結論式(6)及び(7)だけを記載した。
また,JISでは,弾性変位の結論式(6)
及び(7)の表記を変更した。
使用者側の分かりやすさを考慮し
て,結論式だけの記載とした。
また,結論式は,従来から使用し
ている表記の方が分かりやすいと
判断した。
−
5.5.1.3 バックラッシのある場
合のナットの軸方向静
剛性Rnu1
削除
JISでは,ラジアル分力による軸方向剛
性の計算式を削除したため,5.5.1に統
合した。
国内では,ラジアル分力を計算し
ている実態がない。
5.5.2 予圧の作用し
たナットの軸方向静
剛性Rnu2,4
−
−
追加
JISではラジアル分力による剛性を考
慮しないため,ねじ溝面での剛性に代
表される旨を追加した。
また,バックラッシのあるナットと同
様に計算における無視する要因を追加
した。
国内の実態に合わせ,この文言を
追加した方が分かりやすいと判断
した。
−
5.5.2.1 予圧下でのナット及び
ねじ軸の軸方向静剛性
Rn/s,pr
削除
JISでは,ラジアル分力による軸方向剛
性の計算式を削除した。
国内では,この計算式を使用して
いる実態がない。今後ISOへ廃止
を働きかけていく。
5.5.2 予圧の作用し
たナットの軸方向静
剛性Rnu2,4
5.5.2.2 予圧下でのボールとね
じ溝面との剛性Rb/t,pr
図8 b)
削除
ISO規格の図8 b)において,剛性線図
における直線近似と実際の曲線との差
異が約6 %である旨の注を削除した。
検証の結果,6 %に近い値である
が,緒元によって誤差は異なる。
JISでは混乱を避けるため記載し
ない。
変更
JISでは,ISO規格の図8 a)をナット全
体の図に変更し,図8 b)に弾性変位の
変化を追加した。
使用者にとって分かりやすいと判
断した。
2
B
1
1
9
2
-4
:
2
0
1
8
11
B 1192-4:2018
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの
評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
5 軸方向静
剛性R
(続き)
5.5.2 予圧の作用し
たナットの軸方向静
剛性Rnu2,4
−
−
追加
JISでは,予圧抜け荷重Flimの計算式(9)
〜(12)を追加した。
剛性の結論式に至るまでの説明が
ISO規格では不足していると判断
した。
今後ISOへは追加を働きかけてい
く。
5.5.2.2 予圧下でのボールとね
じ溝面との剛性Rb/t,pr
変更
JISでは5.5.1において結論式の表現を
簡略化したため,予圧ナットの場合も
それに適合し,式(15)だけとした。
国内生産者が一般的に採用してい
る実態に合わせた。
−
5.5.2.3 2点接触による予圧が
作用したシングルナッ
ト又はダブルナットの
剛性Rnu2
変更
JISでは,ダブルナットの剛性計算式と
同じであるため削除し,5.5.2の計算で
代表できるという文言を追加した。
国内では,2点接触と4点接触と
に分離して計算している実態がな
く,ISO規格では結論式は同一で
あるため,使用者への混乱を招く
と判断した。
−
5.5.2.4 4点接触による予圧が
作用したシングルナッ
トの剛性Rnu4
変更
−
5.5.3
精度等級による剛性値
の補正far
削除
JISでは精度等級による補正係数は採
用しない。
精度等級による剛性の低下は実態
に合わない。今後ISOへ廃止を働
きかけていく。
−
−
附属
書A
(参考)
剛性計算事例
削除
剛性計算の事例はJISでは削除した。
JISで規定する計算式は,ラジア
ル分力などを採用していないため
同一にならず,混乱を招くと判断
した。
−
−
附属
書B
(参考)
荷重方向による剛性値
の補正fal
削除
荷重方向による剛性値の補正係数は,
JISでは採用しない。
国内では使用している実態がな
い。今後ISOへ廃止を働きかけて
いく。
2
B
1
1
9
2
-4
:
2
0
1
8

12
B 1192-4:2018
JISと国際規格との対応の程度の全体評価:ISO 3408-4:2006,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 削除 ················ 国際規格の規定項目又は規定内容を削除している。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
2
B
1
1
9
2
-4
:
2
0
1
8









