B 0681-2:2018
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 領域パラメータの定義 ······································································································· 6
5 プラトー構造表面に対するパラメータの決定 ········································································ 18
附属書A(参考)三次元表面性状規格の背景 ············································································ 21
附属書B(参考)GPSマトリックス ························································································ 23
参考文献 ···························································································································· 25
附属書JA(参考)JISと対応国際規格との対比表 ······································································ 26
B 0681-2:2018
(2)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人日本規格協会(JSA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 0681の規格群には,次に示す部編成がある。
JIS B 0681-2 第2部:用語,定義及び表面性状パラメータ
JIS B 0681-6 第6部:表面性状測定方法の分類
日本工業規格 JIS
B 0681-2:2018
製品の幾何特性仕様(GPS)−表面性状:三次元−
第2部:用語,定義及び表面性状パラメータ
Geometrical product specifications (GPS)-Surface texture: Areal-
Part 2: Terms, definitions and surface texture parameters
序文
この規格は,2012年に第1版として発行されたISO 25178-2を基とし,技術的内容を変更して作成した
日本工業規格である。
この規格は,製品の幾何特性仕様(GPS)の一つで,GPS規格に属し(ISO/TR 14638:1995参照),表面
性状規格チェーンのリンク番号2に関係する。三次元表面性状規格の背景については,附属書Aを参照。
この規格と他のGPS規格との関連についての詳細は,附属書Bを参照。
この規格は,三次元表面性状の用語,概念及びパラメータについて記載する。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。変更の一
覧表にその説明を付けて,附属書JAに示す。
注記 ISO/TR 14638のリンク番号2は,最新版ISO 14638:2015では,リンク番号Bに対応している。
1
適用範囲
この規格は,三次元的な方法によって表面性状を表すための用語,定義及びパラメータについて規定す
る。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 25178-2:2012,Geometrical product specifications (GPS)−Surface texture: Areal−Part 2: Terms,
definitions and surface texture parameters(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,記載の年の版を適用し,その後の改正版(追補を含む。)は適用しない。
ISO 17450-1:2011,Geometrical product specifications (GPS)−General concepts−Part 1: Model for
geometrical specification and verification
ISO/TS 16610-1:2006,Geometrical product specifications (GPS)−Filtration−Part 1: Overview and basic
concepts
注記 ISO/TS 16610-1:2006は2015年に廃止され,代わりにISO 16610-1:2015,Geometrical product
specifications (GPS)−Filtration−Part 1: Overview and basic conceptsが発行されている。
2
B 0681-2:2018
3
用語及び定義
この規格で用いる主な用語及び定義は,ISO 17450-1:2011及びISO/TS 16610-1:2006によるほか,次によ
る。
3.1
一般用語
3.1.1
実表面モデル(non-ideal surface model),スキンモデル(加工物の)(skin model)
加工物が周囲の空間と物理的に接している表面のモデル。
注記1 実表面モデルは,実表面をモデル化した外郭表面であり,図面などで指示された理想的な形
体(図示外殻形体,JIS B 0672-1の2.3参照)を構成する表面モデルではない。また,高さ方
向には厚みをもたない。
注記2 ISO 17450-1:2011の3.2.2参照。
3.1.1.1
機械的な接触で検出する曲面(mechanical surface)
スキンモデルから,半径rの球でエロージョンによって求めた輪郭曲面,又はスキンモデル上を半径r
の理想的な球が転がった場合の,球の中心の軌跡から得られる輪郭曲面。
注記1 エロージョンは,原図形と構造要素との論理積をとるデータ処理の方法である。例えば,触
針式表面粗さ測定機において,スタイラス先端球の中心軌跡として得られたデータから被測
定面を推定する場合の,半径分のオフセット演算がそれに該当する。
注記2 “輪郭曲面”とは,表面性状を表す点群データの総称であり,“機械的な接触で検出する曲面”
のほか,“電磁波によって検出する曲面(3.1.1.2)”,“基礎表面性状曲面(3.1.3)”,“部分基礎
表面性状曲面”,“S-F曲面(3.1.5)”,“S-L曲面(3.1.6)”及び“表面性状曲面(3.1.7)”も,
この“輪郭曲面”に含まれる。
注記3 “輪郭曲面”は,二次元の輪郭曲線方式における“輪郭曲線”に相当する。
注記4 関数及びパラメータにおける“輪郭曲面”は,3.1.7で定義する“表面性状曲面”を指す。
注記5 ISO 14406:2010の3.1.1参照。
3.1.1.2
電磁波によって検出する曲面(electro-magnetic surface)
スキンモデルと電磁波との相互作用によって得られる輪郭曲面。
注記 ISO 14406:2010の3.1.2参照。
3.1.2
座標系(specification coordinate system)
表面性状パラメータを定義する座標系。
注記 基準面が平面又は平面の一部である場合に,座標軸は右手直交座標系を使用する。X軸及びY
軸がその基準面上にあり,Z軸は外側方向(実体から周囲の媒体方向)にある。この座標系を
この規格において適用する。
3.1.3
基礎表面性状曲面(primary surface)
規定したネスティングインデックスの下で,規定の数学モデルによって表現したときに得られる輪郭曲
面の一部分。
注記1 この規格では,基礎表面性状曲面を得るためにSフィルタを使用している。
3
B 0681-2:2018
注記2 信号処理の分野で多用されるウェーブレット変換は,信号を逐次,周波数の低いレベルに分
解する処理手法である。そのレベル番号が“入れ子(ネスト)”の順序に対応するため,順序
付きの番号という意味でネスティングインデックスと表現している。ネスティングインデッ
クスがゼロの場合は,元信号のままである。ガウシアンフィルタの場合のカットオフ値は,
ネスティングインデックスの一例である。モルフォロジカルフィルタに対しては,ネスティ
ングインデックスは構造要素のサイズ(例えば,球の半径)に相当し,表面波長であるカッ
トオフ値の概念とは異なる。この規格におけるネスティングインデックスは,輪郭曲線フィ
ルタのカットオフ値及び前述した構造要素のサイズを包含する。
注記3 ISO/TS 16610-1:2006の3.3参照。
3.1.3.1
測得基礎表面性状曲面(primary extracted surface)
基礎表面性状曲面から抜き取った有限個数の点群データ。
注記 ISO 14406:2010の3.7参照。
3.1.4
輪郭曲面フィルタ(surface filter)
輪郭曲面に適用するフィルタ。
3.1.4.1
Sフィルタ(S-filter)
輪郭曲面から,横方向スケールの小さい成分を除去する輪郭曲面フィルタ。結果として,基礎表面性状
曲面を得る。
注記 Sフィルタは,機械的な接触で検出する曲面(3.1.1.1),又は電磁波によって検出する曲面
(3.1.1.2)に適用する。
3.1.4.2
Lフィルタ(L-filter)
基礎表面性状曲面又はS-F曲面から,横方向スケールの大きい成分を除去する輪郭曲面フィルタ。
3.1.4.3
F演算(F-operation)
基礎表面性状曲面から,形状を除去する演算。
注記1 F演算(当てはめ演算オペレータなど)には,フィルタ処理とは非常に異なる作用をもつも
のがある。この作用は,輪郭曲面の横方向スケールの大きさを制限することができるが,領
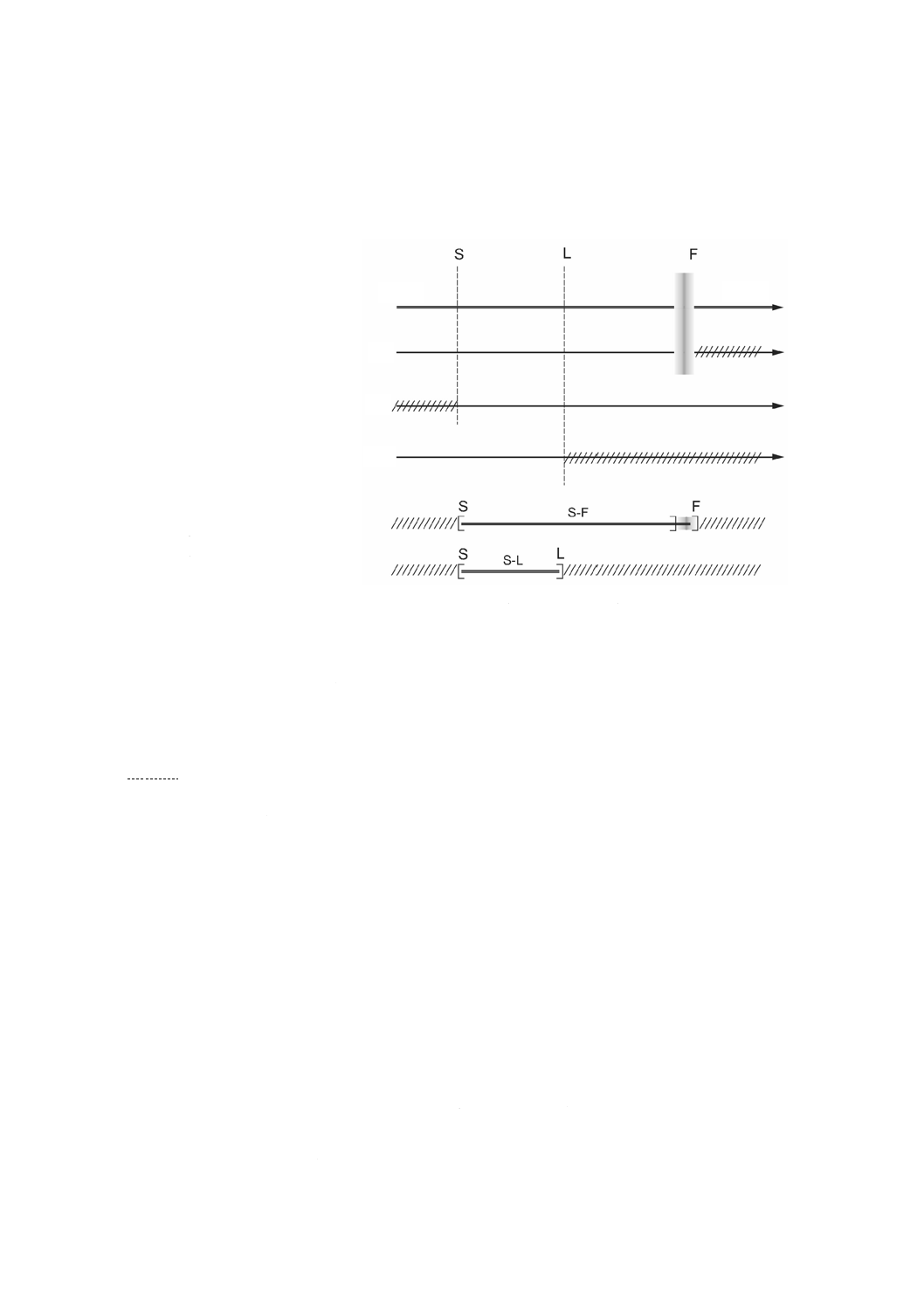
域を分ける境界が非常に不明瞭である。したがって,F演算の作用は,図1のように不明瞭
な線となっている。
注記2 多くのLフィルタは,形状の影響を受けやすい。このようなLフィルタを適用する前に,前
フィルタとしてのF演算が必要となる。
3.1.5
S-F曲面(S-F surface)
F演算によって,基礎表面性状曲面から形状を除いた輪郭曲面。
注記 図1は,S-F曲面,Sフィルタ及びF演算の間の関係を説明している。
3.1.6
S-L曲面(S-L surface)
4
B 0681-2:2018
Lフィルタを用いて,基礎表面性状曲面又はS-F曲面から横方向のスケールの大きい成分を除いた輪郭
曲面。
注記 図1は,S-L曲面並びにSフィルタ及びLフィルタの間の関係を説明している。
a 小さいスケール
b 大きいスケール
c 横方向スケールの軸
d F演算
e Sフィルタ
f Lフィルタ
図1−Sフィルタ,Lフィルタ,F演算,並びにS-F曲面及びS-L曲面の関係
3.1.7
表面性状曲面(scale-limited surface)
S-F曲面又はS-L曲面。
注記1 全ての関数,パラメータなどは,この“表面性状曲面”に関して定義される。
注記2 関数,パラメータなどの定義における“輪郭曲面”は,この“表面性状曲面”を指す。
3.1.8
基準面(reference surface)
ある判定基準に従って,表面性状曲面に当てはめた形状を表す曲面。
注記1 表面性状パラメータに関する基準面として使用する。
注記2 基準面として,平面,円筒及び球面を含む。
3.1.9
評価領域(evaluation area)
特性評価を行うために規定した,表面性状曲面の一部。
注記 補足の情報は,ISO 25178-3:2012を参照。
3.1.10
基準領域(definition area)
表面性状曲面のパラメータを求めるための,評価領域の一部。
3.2
幾何特性パラメータに関する用語(geometrical parameter terms)
3.2.1
領域パラメータ(field parameter)
a
d
e
f
b
c
5
B 0681-2:2018
表面性状曲面上の,全ての点から定義するパラメータ。
注記 領域パラメータは,箇条4で定義する。
3.2.2
Vパラメータ(V-parameter)
実体体積又は空間体積に関する,領域パラメータ。
3.2.3
Sパラメータ(S-parameter)
Vパラメータ以外の,領域パラメータ。
3.2.4
高さ(height)
基準面から表面性状曲面までの符号(正又は負)がある垂直距離。
注記1 距離は,基準面に垂直に定義される。
注記2 点が基準面から実体の内部方向にあるときは,その高さは負となる。
3.2.5
縦座標値(ordinate value)
z(x, y)
表面性状曲面の,任意の位置x, yにおける高さ。
注記 座標系は,基準面が基準となる。
3.2.6
局部勾配ベクトル(local gradient vector)
∂
∂
∂
∂
y
z
x
z,
表面性状曲面の,任意の位置x, yにおける傾斜。
注記 詳細は,ISO 25178-3:2012を参照。
3.2.7
自己相関関数(autocorrelation function)
fACF(tx, ty)
基準領域(A)において,ある表面性状曲面と,その表面性状曲面を(tx, ty)だけ移動した表面性状曲面
との間の相関関係を示す関数。
(
)
(
)(
)
(
)(
)
y
x
y
x
z
y
x
z
y
x
t
y
t
x
z
y
x
z
t
t
f
A
A
y
x
y
x
d
d
,
,
d
d
,
,
,
ACF
∫∫
∫∫
−
−
=
3.2.8
フーリエ変換(Fourier transformation)
F(p, q)
基準領域(A)において,表面性状曲面をフーリエ空間に変換する処理。
(
)
(
)
(
)
y
x
y
x
z
q
p
F
iqy
ipx
A
d
d
e
,
,
+
−
∫∫
=
6
B 0681-2:2018
3.2.8.1
角度スペクトル(angular spectrum)
fAPS(s)
基準領域の平面内において,指定した方向θを基準とした,任意の方向sのパワースペクトル。
()
(
)
(
)
[
]
∫
−
−
=
2
1
2
APS
cos
,
sin
R
R
dr
s
r
s
r
F
r
s
f
θ
θ
ここに,
R1からR2まで: 半径方向の積分範囲
注記1 X軸の正の部分を,角度ゼロと定義する。
注記2 角度は,反時計回りを正とする。
4
領域パラメータの定義
この箇条に収録した用語集において,各用語の次に,そのパラメータ(略語),そして記号が続いている。
略語が複数の文字を含むのに対して,記号は唯一つの文字から成り,必要に応じて添え字を伴う。記号は,
この規格に示す式中で使用する。この違いの理由は,複合文字を式中の数量間の乗法表示と誤解すること
を避けるためである。パラメータ(略語)は,製品文書,図面及びデータシートに使用する。
4.1
高さ方向のパラメータ(height parameters)
全ての高さ方向のパラメータは,基準領域全体で定義する。
4.1.1
輪郭曲面の二乗平均平方根高さ(root mean square height of the scale-limited surface)
Sq
Sq
基準領域(A)における,縦座標値z(x, y) の二乗平均平方根。
(
)
∫∫
=
A
y
x
y
x
z
A
S
d
d
,
1
2
q
4.1.2
輪郭曲面のスキューネス,輪郭曲面のわい(歪)度(skewness of the scale-limited surface)
Ssk
Ssk
Sqの三乗によって無次元化した,基準領域(A)における,縦座標値z(x, y) の三乗平均。
(
)
=
∫∫
A
y
x
y
x
z
A
S
S
d
d
,
1
1
3
3
q
sk
4.1.3
輪郭曲面のクルトシス,輪郭曲面のせん(尖)度(kurtosis of the scale-limited surface)
Sku
Sku
Sqの四乗によって無次元化した,基準領域(A)における,縦座標値z(x, y) の四乗平均。
7
B 0681-2:2018
(
)
=
∫∫
A
y
x
y
x
z
A
S
S
d
d
,
1
1
4
4
q
ku
4.1.4
輪郭曲面の最大山高さ(maximum peak height of the scale limited surface)
Sp
Sp
基準領域における,輪郭曲面山頂の高さの最大値。
4.1.5
輪郭曲面の最大谷深さ(maximum pit depth of the scale limited surface)
Sv
Sv
基準領域における,輪郭曲面谷底の深さの最大値。
4.1.6
輪郭曲面の最大高さ(maximum height of the scale-limited surface)
Sz
Sz
基準領域における,輪郭曲面山頂の最大山高さSpと輪郭曲面谷底の最大谷深さSvとの和。
4.1.7
輪郭曲面の算術平均高さ(arithmetical mean height of the scale limited surface)
Sa
Sa
基準領域(A)における,z(x, y) の絶対値平均。
(
)
∫∫
=
A
y
x
y
x
z
A
S
d
d
,
1
a
4.2
空間パラメータ(spatial parameters)
全ての空間パラメータは,基準領域で定義する。
4.2.1
自己相関長さ(autocorrelation length)
Sal
Sal
0≦s<1の条件下で,自己相関関数fACF(tx, ty) が指定値sまで減衰する,横方向の最短距離。
2
2
al
,
min
y
x
y
x
t
t
R
t
t
S
+
∈
=
ここに,
(
)
(
)
{
}s
t
t
f
t
t
R
y
x
y
x
≦
,
:
,
ACF
=
注記1 指定のない場合,sの標準値は,ISO 25178-3:2012を参照。
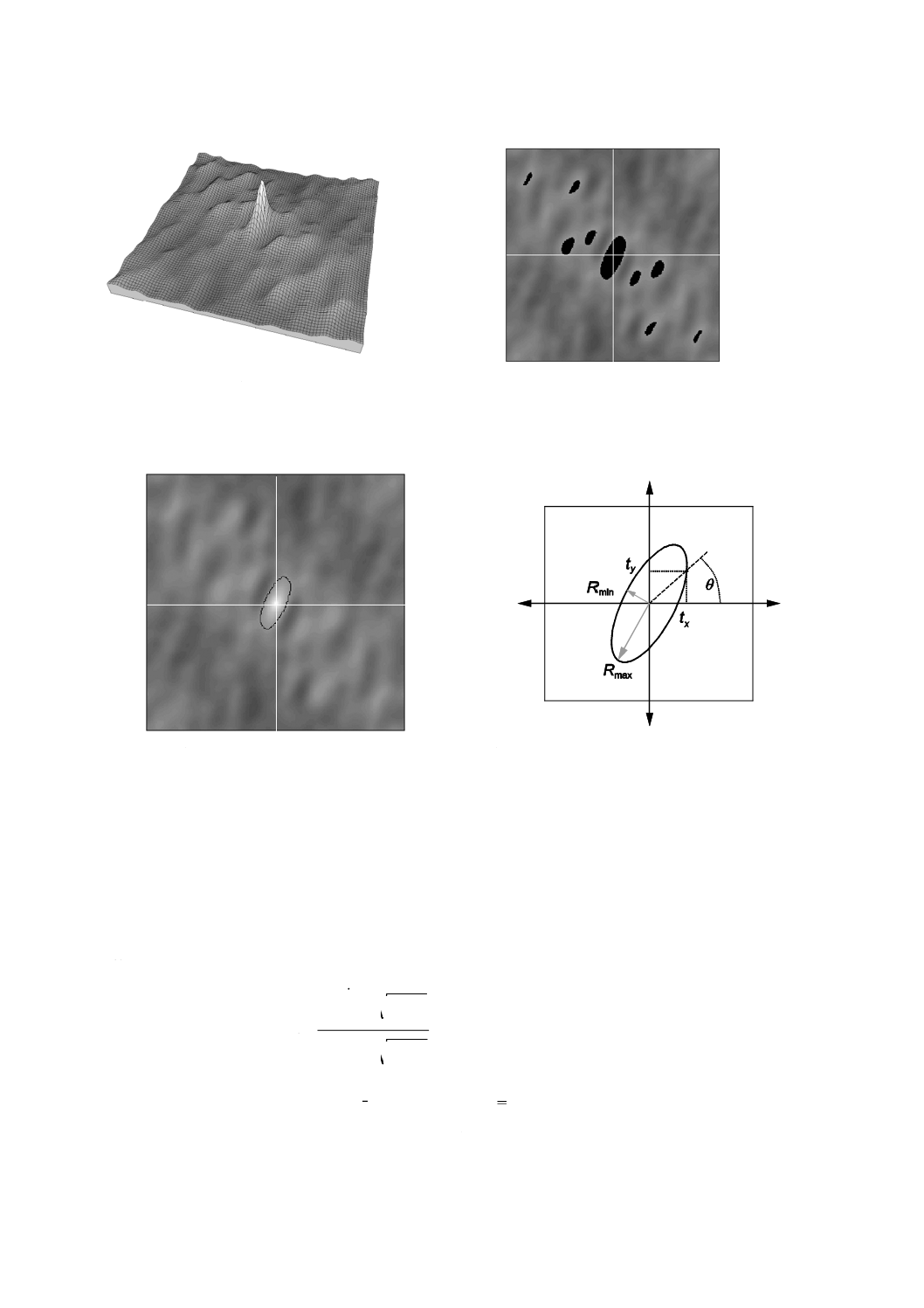
注記2 Salを算出する手順を図2に示す。
8
B 0681-2:2018
a) 表面の自己相関関数
b) sでの自己相関いき(閾)値[黒点がいき(閾)値を超えている。]
Sal=Rmin
Str=Rmin/Rmax
c) 中央部のいき(閾)値境界
d) 任意の方向における自己相関長さを示す極座標
図2−Sal及びStrを算出する手順
4.2.2
テクスチャのアスペクト比(texture aspect ratio)
Str
Str
0≦s<1の条件下で,自己相関関数fACF(tx, ty)が指定値sまで減衰する,横方向の最短距離と最長距離と
の比。
2
2
2
2
tr
,
max
,
min
y
x
y
x
y
x
y
x
t
t
Q
t
t
t
t
R
t
t
S
+
∈
+
∈
=
ここに,
(
)
(
)
{
}s
t
t
f
t
t
R
y
x
y
x
≦
,
:
,
ACF
=
(
)
(
)
{
}*
*
,
:
,
ACF
かつ
≧s
t
t
f
t
t
Q
y
x
y
x
=
**:点(tx, ty) と原点とを結んだ線上でfACF≧sという条件

9
B 0681-2:2018
注記1 指定のない場合,sの標準値は,ISO 25178-3:2012を参照。
注記2 Strを算出する手順を図2に示す。
注記3 Surface textureと表面性状とが対応することから,textureは性状と置き換えるのが自然である
が,テクスチャは単体として十分普及している用語であるため,片仮名表記とした。
4.3
複合パラメータ(hybrid parameters)
4.3.1
輪郭曲面の二乗平均平方根勾配(root mean square gradient of the scale-limited surface)
Sdq
Sdq
基準領域(A)における,局部勾配の二乗平均平方根。
(
)
(
)
y
x
y
y
x
z
x
y
x
z
A
S
A
d
d
,
,
1
2
2
dq
∫∫
∂
∂
+
∂
∂
=
4.3.2
輪郭曲面の展開界面面積率(developed interfacial area ratio of the scale-limited surface)
Sdr
Sdr
基準領域(A)の面積に対する,輪郭曲面の界面の面積と基準領域の面積との差の比。
(
)
(
)
−
∂
∂
+
∂
∂
+
=∫∫
y
x
y
y
x
z
x
y
x
z
A
S
A
d
d
1
,
,
1
1
2
2
dr
注記1 このパラメータの実装方法については,参考文献[13]を参照。
注記2 評価する基準領域内の輪郭曲面において,表面凹凸が全くない場合,輪郭曲面の界面の面積
は基準領域の面積と同じになるため,Sdr=0 %である。
4.4
機能と関連するパラメータ(functions and related parameters)
4.4.1
輪郭曲面の負荷曲線(areal material ratio function of the scale-limited surface)
切断レベルcの関数として表された,輪郭曲面の負荷長さ率の曲線。
注記1 この曲線は,評価領域内の高さz(x, y) の確率と解釈することができる。
注記2 負荷面積率曲線を対象とする場合,対応国際規格には記載はないが,分かりやすくするため
に高さをレベルと表すことがある。
4.4.2
輪郭曲面の負荷面積率(areal material ratio of the scale-limited surface)
Smr(c)
Smr(c)
評価領域に対する切断レベルcにおける,輪郭曲面要素の負荷面積の比。
注記1 通常,Smr(c) は,パーセント(%)で表す。
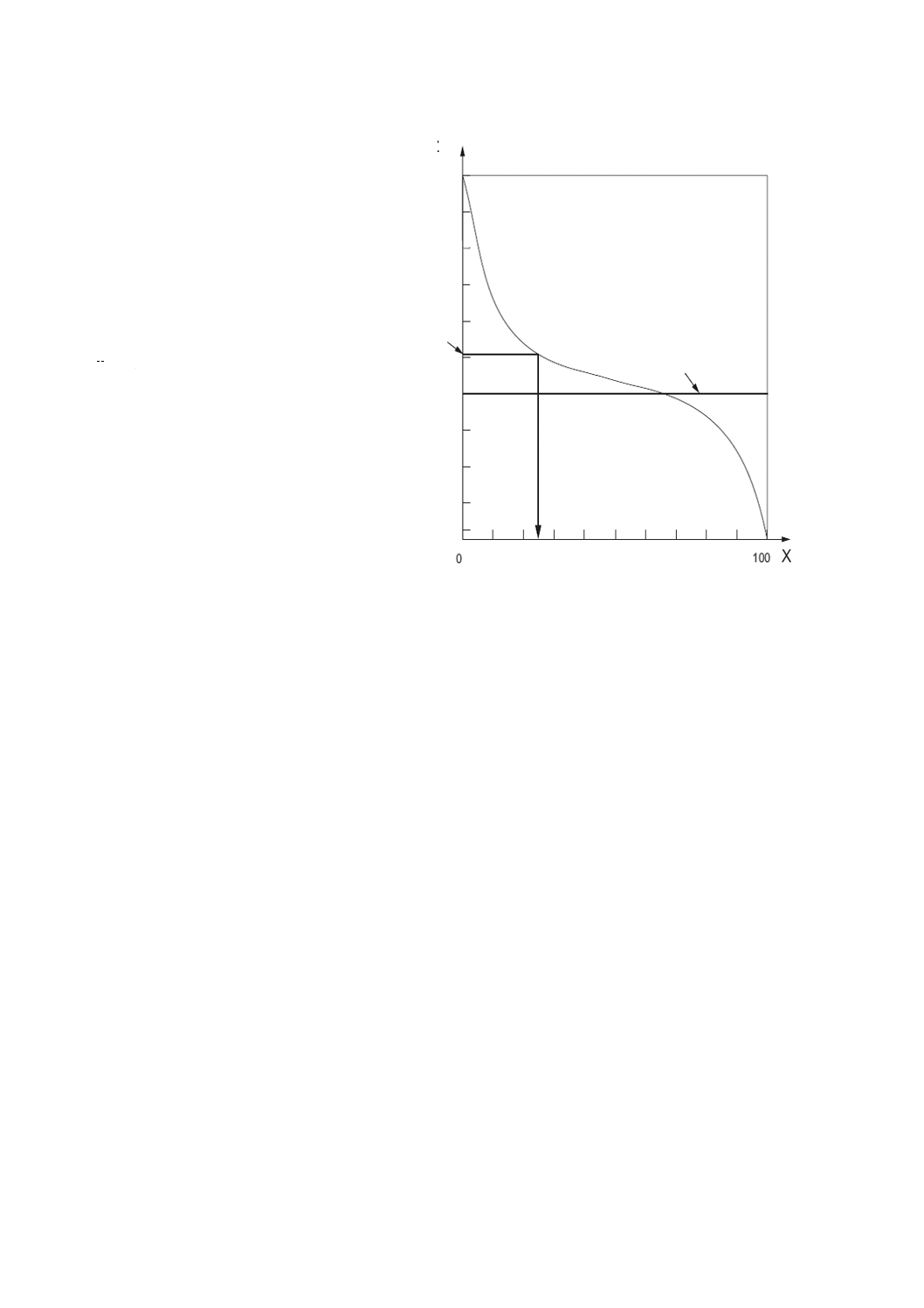
注記2 高さは,基準面からとる。図3参照。
注記3 この関数は,高さ座標値の標本累積確率関数と同類である。
10
B 0681-2:2018
X パーセント表示の負荷面積率Smr(c)
Z 高さ
a 切断レベルc
b 基準面
図3−高さと負荷面積率との関係
Z
a
b
11
B 0681-2:2018
4.4.3
負荷面積率に対応する輪郭曲面の高さ(inverse areal material ratio of the scale-limited surface)
Smc(mr)
Smc(mr)
輪郭曲面の負荷曲線における,負荷面積率に対する切断レベル。
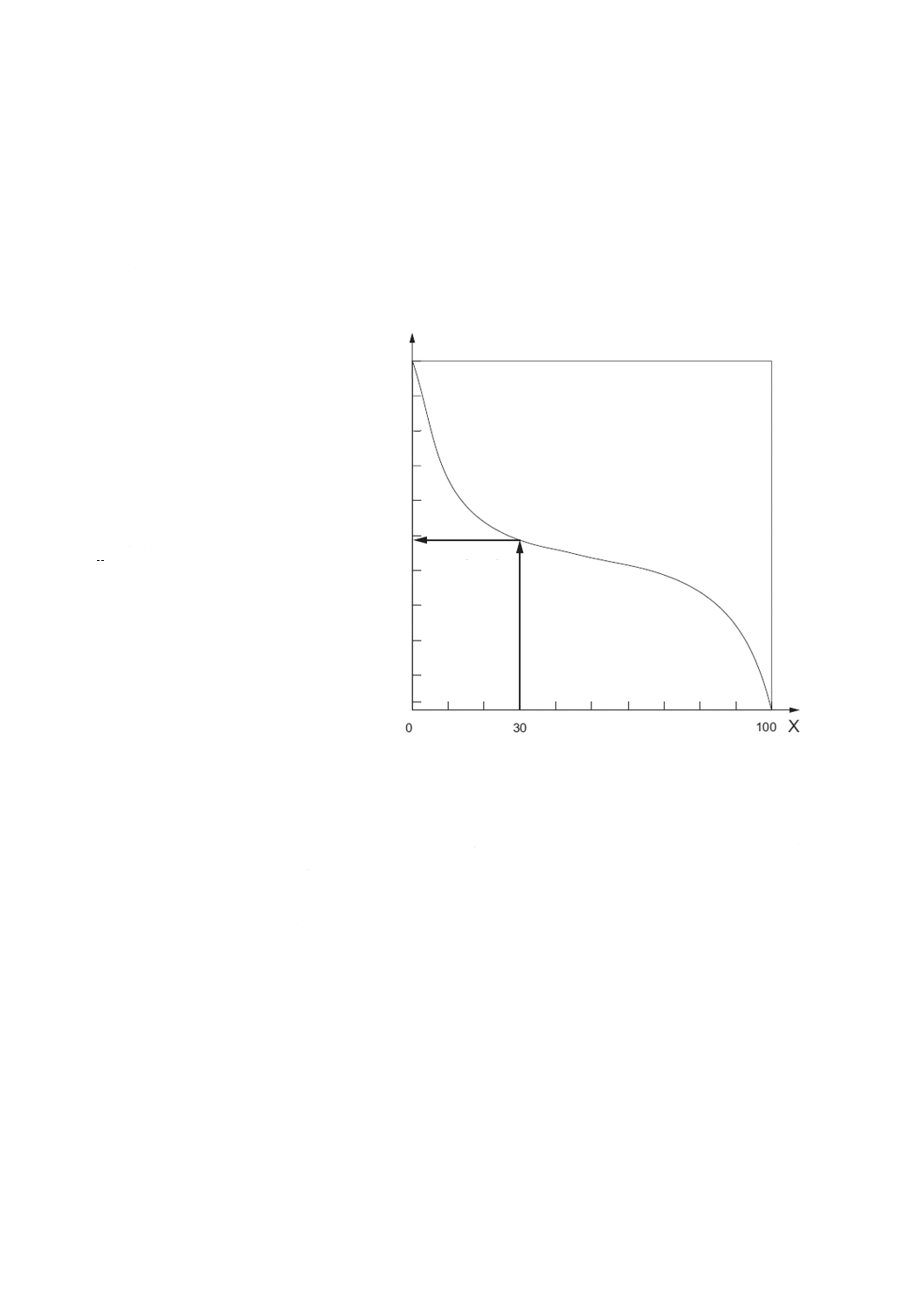
注記 高さは,基準面からとる。図4参照。
X パーセント表示の負荷面積率
Smc(mr)
Z
高さ
図4−負荷面積率と高さとの関係
4.4.4
プラトー構造表面の輪郭曲面パラメータ(areal parameter for the -scale-limited stratified functional surface)
プラトー構造表面の負荷曲線による,高さパラメータ。
4.4.4.1
輪郭曲面コア部(core surface)
高い突出山部及び深い突出谷部を,輪郭曲面から取り除いた曲線。図5参照。
4.4.4.2
コア部のレベル差(core height)
Sk
Sk
輪郭曲面の,コア部の上側レベルと下側レベルとの差。図5参照。
Z
Smc (30 %)
12
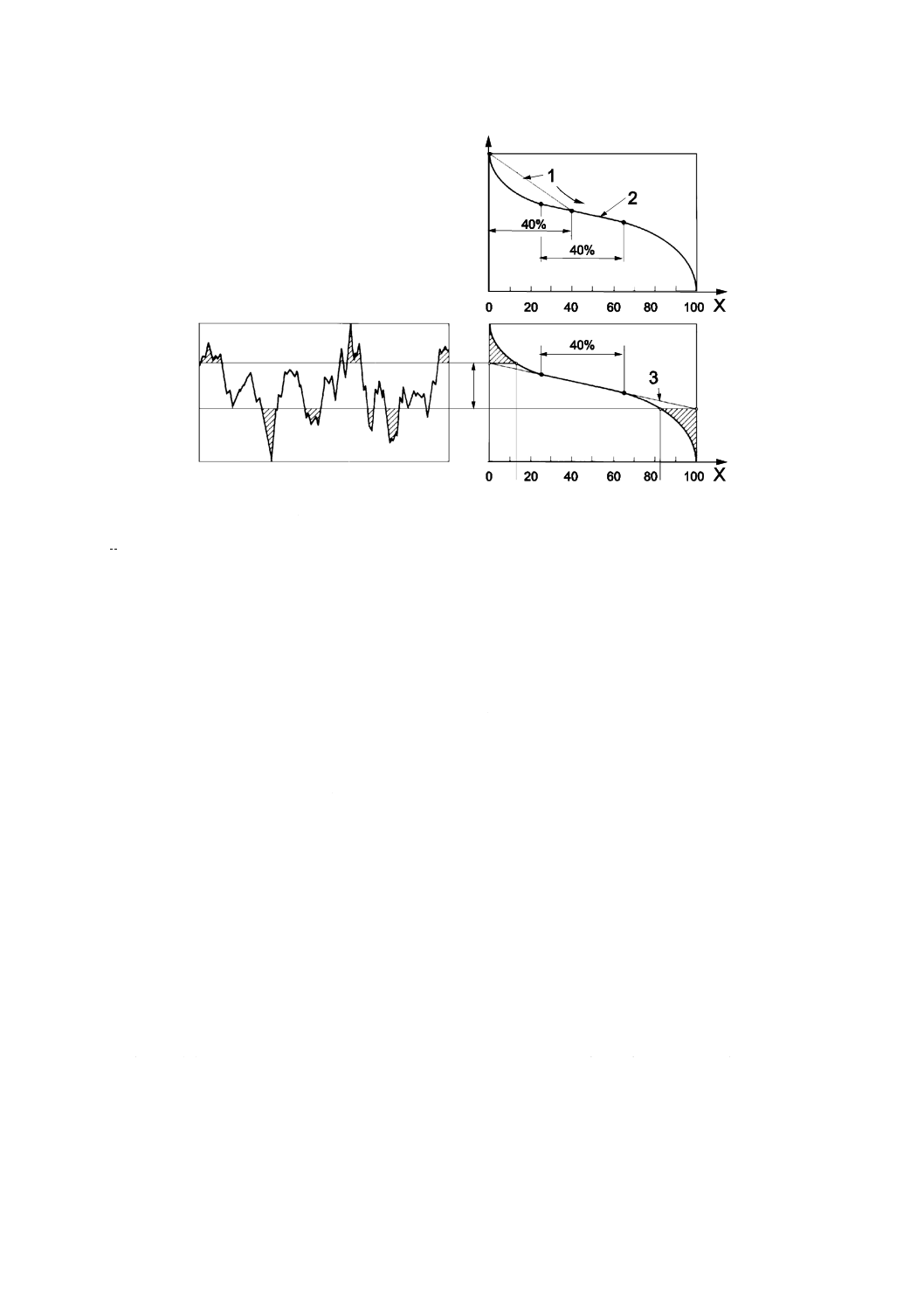
B 0681-2:2018
X
パーセント表示の負荷面積率
Z
高さ
1
割線(かっせん)
2
最も緩い傾斜となる割線
3
等価直線
Sk
コア部のレベル差
Smr1, Smr2
負荷面積率
この図では図説を簡素化するため,輪郭曲面の代わりに輪郭曲線で示す。原理は,輪郭曲面に対するものと同一で
ある。
図5−Sk,Smr1及びSmr2の計算
4.4.4.3
突出山部高さ(reduced peak height)
Spk
Spk
輪郭曲面のコア部の上にある,突出山部の代表高さ。
注記 箇条5の直角三角形を用いた処理は,このパラメータに及ぼす異常値の影響を減らす。
4.4.4.4
突出谷部深さ(reduced dale depth)
Svk
Svk
輪郭曲面のコア部の下にある,突出谷部の代表深さ。
注記 箇条5の直角三角形を用いた処理は,このパラメータに及ぼす異常値の影響を減らす。
4.4.4.5
コア部の負荷面積率(material ratio)
Smr1
Smr1
Smr1
Z
S
k
Smr2
13
B 0681-2:2018
評価領域の突出山部と輪郭曲面のコア部とを分離する直線が負荷曲線と交わる点の,パーセント単位の
負荷面積率。
注記 その比は,パーセント(%)で表す。
4.4.4.6
コア部の負荷面積率(material ratio)
Smr2
Smr2
評価領域の突出谷部と輪郭曲面のコア部とを分離する直線が負荷曲線と交わる点の,パーセント単位の
負荷面積率。
注記 その比は,パーセント(%)で表す。
4.4.4.7
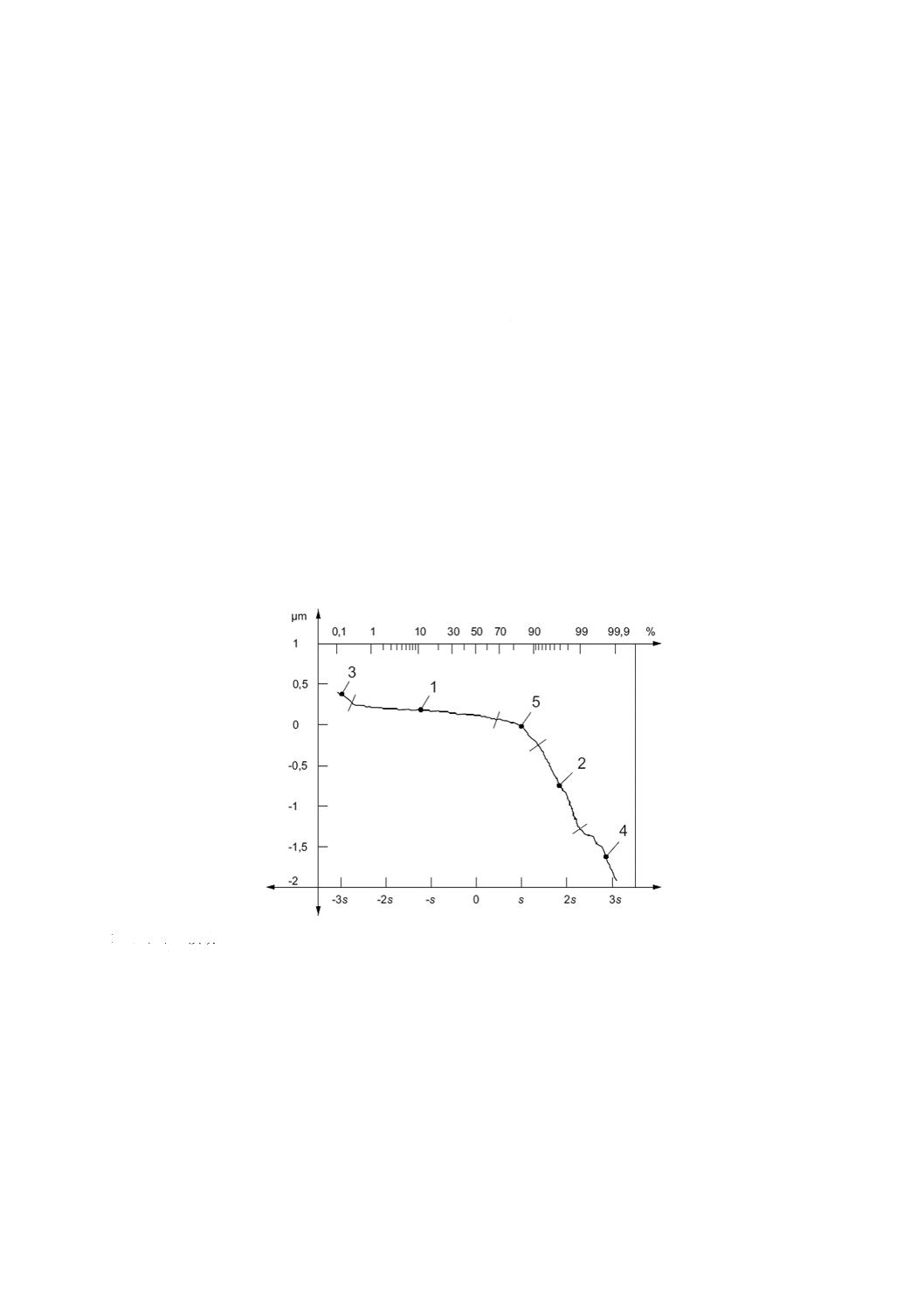
正規確率紙上の輪郭曲面の負荷曲線(areal material probability curve)
標準偏差を単位にして横軸を正規確率スケールとし,それを輪郭曲面の負荷面積率に対して描いた,負
荷曲線の一つの表現。
注記 横軸のスケールは,正規(ガウス)分布に従って標準偏差を単位として等間隔に表示する。こ
のスケールでは,正規分布の負荷曲線は1本の直線となる。二つの正規分布からなるプラトー
構造表面では,二つの線形領域(プラトー領域及び谷領域)が現れる(図6の1及び2を参照)。
1 プラトー領域
2 谷領域
3 データ(輪郭曲面)に含まれる異物又は異常に高い突起領域
4 データ(輪郭曲面)に含まれる深いきず又は異常に深い谷底領域
5 プラトー領域から谷領域への変移点で二つの分布を結ぶ不安定な変移領域(曲線)
図6−正規確率紙上の輪郭曲面の負荷曲線
4.4.4.8
Svqパラメータ(dale root mean square deviation)
Svq
14
B 0681-2:2018
Svq
谷領域に当てはめた回帰直線の傾斜。図7参照。
注記1 Svqは,輪郭曲面の谷領域成分を生成する不規則波形成分のSq値[単位:マイクロメートル
(µm)]と解釈できる。
注記2 谷間域の上限及び下限,並びにプラトー領域の上限及び下限の求め方は,JIS B 0671-3:2002
を参照。
4.4.4.9
Spqパラメータ(plateau root mean square deviation)
Spq
Spq
プラトー領域に当てはめた回帰直線の傾斜。図7参照。
注記 Spqは,輪郭曲面のプラトー領域を生成する不規則波形成分のSq値[単位:マイクロメートル
(µm)]と解釈できる。
4.4.4.10
Smqパラメータ(material ratio)
Smq
Smq
プラトー領域に当てはめた回帰直線と,谷領域に当てはめた回帰直線との交点における負荷面積率。図
7参照。
注記 Smqは,パーセント(%)で表す。
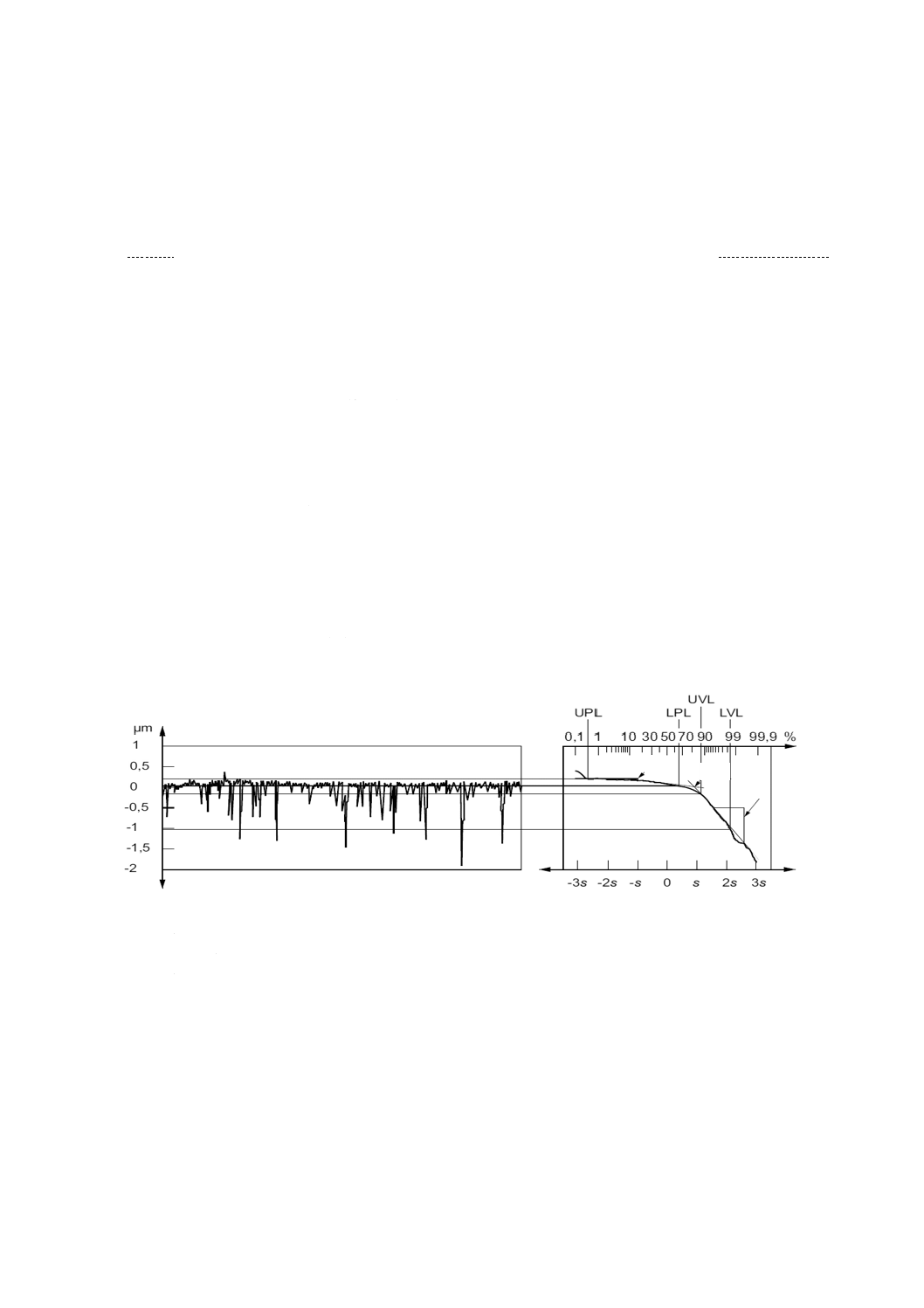
LPL プラトー領域の下限
LVL 谷領域の下限
UPL プラトー領域の上限
UVL 谷領域の上限
Smq プラトー領域に当てはめた回帰直線と谷領域に当てはめた回帰直線との交点における負荷面積率
Spq
プラトー領域に当てはめたられた回帰直線の傾斜
Svq
谷領域に当てはめられた回帰直線の傾斜
この図では図説を簡素化するため,輪郭曲面の代わりに輪郭曲線で示す。原理は輪郭曲面に対するものと同一であ
る。
図7−輪郭曲面及び正規確率紙上の輪郭曲面の負荷曲線並びにパラメータのSpq,Svq及び
Smqの決定に用いる領域
Smq
Svq
Spq
15
B 0681-2:2018
4.4.5
輪郭曲面の空間体積(void volume)
Vv(p)
Vv(p)
輪郭曲面の負荷曲線から計算した,負荷面積率pにおける,単位面積当たりの空間体積。
()
()
()
[
]
∫
−
=
%
100
mc
mc
v
d
%
100
p
q
q
S
p
S
K
p
V
ここに,
K: ミリリットル毎平方メートル(mL/m2)へ換算する定数
4.4.5.1
輪郭曲面の突出谷部空間体積(dale void volume of the scale-limited surface)
Vvv
Vvv
負荷面積率pにおける,谷間の体積。
()p
V
V
v
vv=
注記 pの標準値は,ISO 25178-3:2012を参照。
4.4.5.2
輪郭曲面のコア部空間体積(core void volume of the scale-limited surface)
Vvc
Vvc
負荷面積率pとqとにおける,空間体積の差。
()
()q
V
p
V
V
v
v
vc
−
=
注記 p及びqの標準値は,ISO 25178-3:2012を参照。
4.4.6
輪郭曲面の実体体積(material volume)
Vm(p)
Vm(p)
輪郭曲面の負荷曲線から計算した,ある負荷面積率における単位面積当たりの実体体積。
()
()
()
[
]
∫
−
=
p
q
p
S
q
S
K
p
V
0
dc
mc
m
d
%
100
ここに,
K: ミリリットル毎平方メートル(mL/m2)へ換算する定数
注記 図8参照。
16
B 0681-2:2018
X パーセント表示の輪郭曲面の負荷面積率
Z 高さ
図8−空間体積パラメータ及び実体体積パラメータ
4.4.6.1
輪郭曲面の突出山部実体体積(peak material volume of the scale-limited surface)
Vmp
Vmp
負荷面積率pにおける,実体体積。
注記 pの標準値は,ISO 25178-3:2012を参照。
4.4.6.2
輪郭曲面のコア部実体体積(core material volume of the scale-limited surface)
Vmc
Vmc
負荷面積率pとqとの,実体体積の差。
()
()p
V
q
V
V
m
m
mc
−
=
注記 p及びqの標準値は,ISO 25178-3:2012を参照。
4.4.7
輪郭曲面の切断レベル差(peak extreme height)
Sxp
Sxp
負荷面積率pとqとに一致する,高さ方向の切断レベルの差。
()
()q
S
p
S
S
mc
mc
xp
−
=
注記 p及びqの標準値は,ISO 25178-3:2012を参照。
Z
Vmp
Vmc
Vvc
Vvv
17
B 0681-2:2018
4.4.8
勾配密度関数(gradient density function)
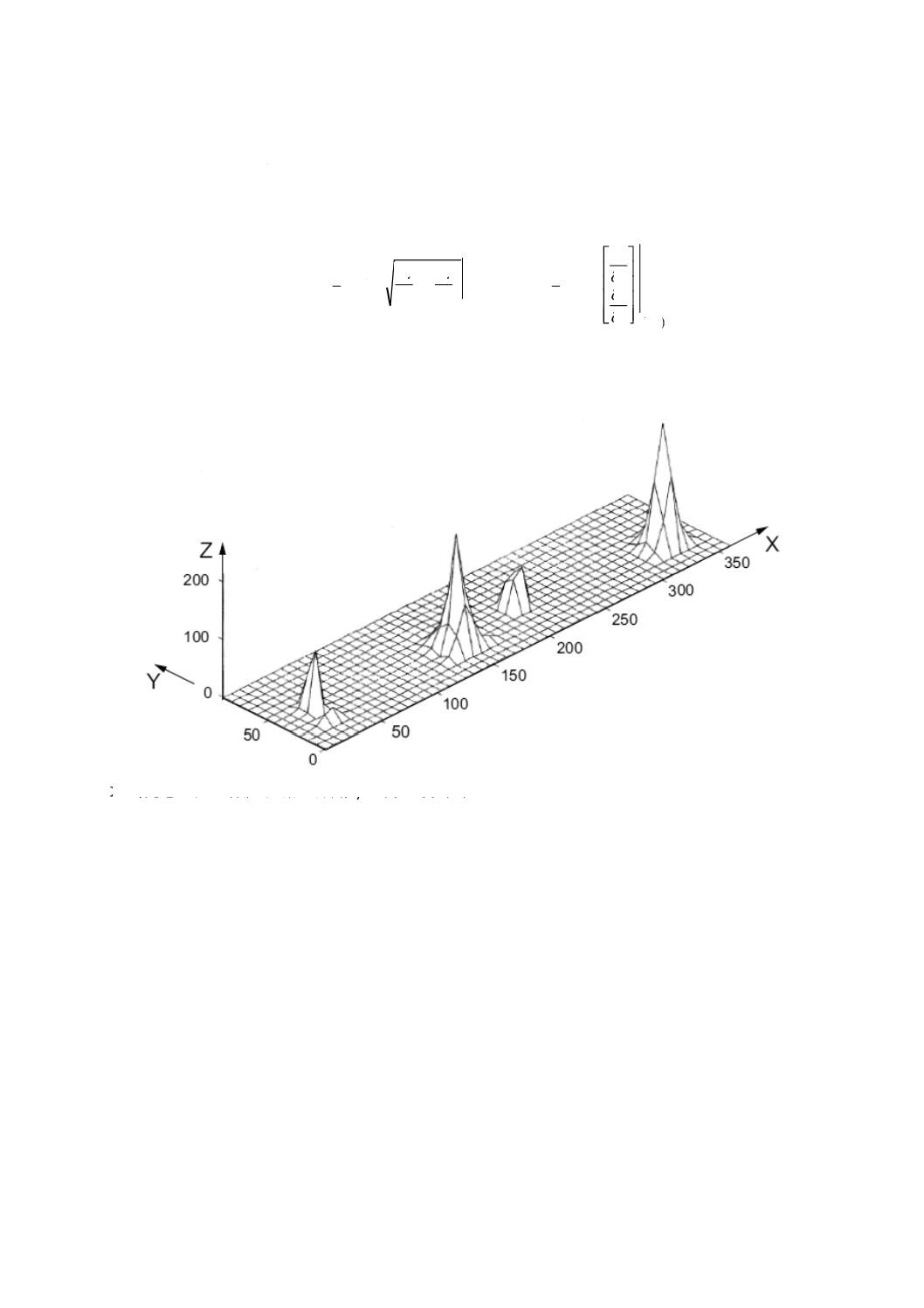
輪郭曲面から算出した勾配密度関数であり,最も急しゅん(峻)な勾配α(x, y) 及び最も急しゅん(峻)
な勾配の方向β(x, y)(角度)に対する相対度数を,x(X)軸から反時計回りで示す(図9参照)。
(
)
(
)
(
)
(
)y
x
y
x
x
z
y
z
y
x
x
z
y
z
y
x
,
,
2
2
arctan
,
arctan
,
∂∂∂∂
=
∧
∂
∂
+
∂
∂
=
β
α
注記1 勾配密度関数の例は,図9を参照。
注記2 最も急しゅん(峻)な勾配α及び最も急しゅん(峻)な勾配の方向βは,図10参照。
X 最も急しゅん(峻)な勾配の方向,β 単位は度(°)
Y 最も急しゅん(峻)な勾配,α 単位は度(°)
Z 出現度数
図9−勾配密度関数の例
18
B 0681-2:2018
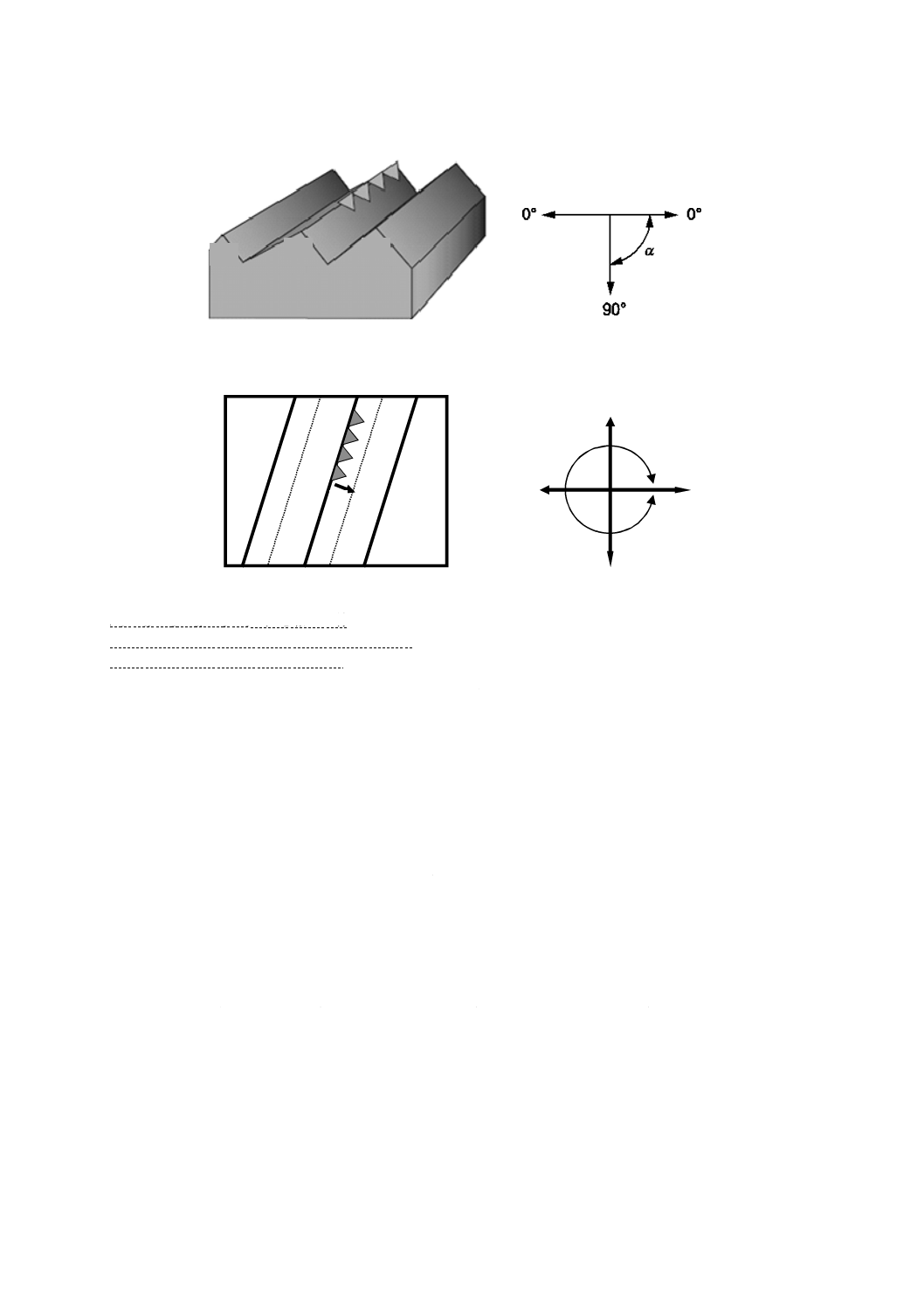
A1-A′1,A2-A′2,A3-A′3:山を結んだ線
B:最も急しゅん(峻)な勾配(図中の三角形)
C:最も急しゅん(峻)な勾配の方向
図10−最も急しゅん(峻)な勾配α及び最も急しゅん(峻)な勾配の方向β
4.5
その他のパラメータ(miscellaneous parameters)
4.5.1
輪郭曲面のテクスチャの方向(texture direction of the scale-limited surface)
Std
Std
指定した方向θに関して,角度スペクトルの絶対値が最大となる角度。
注記 s=Stdは,fAPS(s−θ) の絶対値を最大化する。
5
プラトー構造表面に対するパラメータの決定
5.1
パラメータSk,Smr1及びSmr2の計算
5.2によって計算する等価直線(輪郭曲面の負荷曲線の中央部分に等価な直線をいう。)は,横軸のSmr
=0 %及びSmr=100 %の位置で縦軸と交わる(図5参照)。これらの交わった点から横軸に平行に,突出山
部及び突出谷部を分離して,粗さ曲線のコア部を決めるための2本の直線を引く。
この2本の直線の縦方向間隔が,粗さ曲線のコア部のレベル差Skである。この2本の直線と負荷曲線
との交点の横座標値が,コア部の負荷長さ率Smr1及びSmr2である。
5.2
等価直線の求め方
等価直線は,輪郭曲面の測定点の40 %を含む負荷曲線の中央部分において求める。この“中央部分”は,
180°
0°
90°
270°
B
A1
A2
A3
A′1
A′2
A′3
C
A′1
B
A′2
A′3
A1
A2
A3
19
B 0681-2:2018
負荷面積率の差ΔMrを40 %にして引いた輪郭曲面の負荷曲線の割線(かっせん)が最も緩い傾斜となる
位置にある(図5参照)。これは,図5のように,ΔMr=0 %から負荷曲線に沿ってΔMr=40 %となる割線
を移動させることによって決める。最も緩い傾斜となるΔMr=40 %の割線は,等価直線を計算するための
輪郭曲面の負荷曲線の“中央部分”となる。最も緩い傾斜をもつ部分が複数ある場合には,最初に見つけ
た領域が,使用する“中央部分”となる。“中央部分”に対して,縦軸方向の偏差の二乗和が最小になる直
線(等価直線)を計算する。
輪郭曲面の負荷曲線が有効であるためには,輪郭曲面の縦軸方向量子化のステップ間隔は,“中央部分”
で少なくとも10ステップになるように十分小さくなければならない。測定システムの分解能には限界があ
るので,理想に近いプラトー面をもつ表面では,ステップ間隔を細かくしても意味がない。この場合には,
等価直線の計算に用いた“中央部分”の量子化ステップ数を測定結果に記載しなければならない。
5.3
Spk及びSvkの求め方
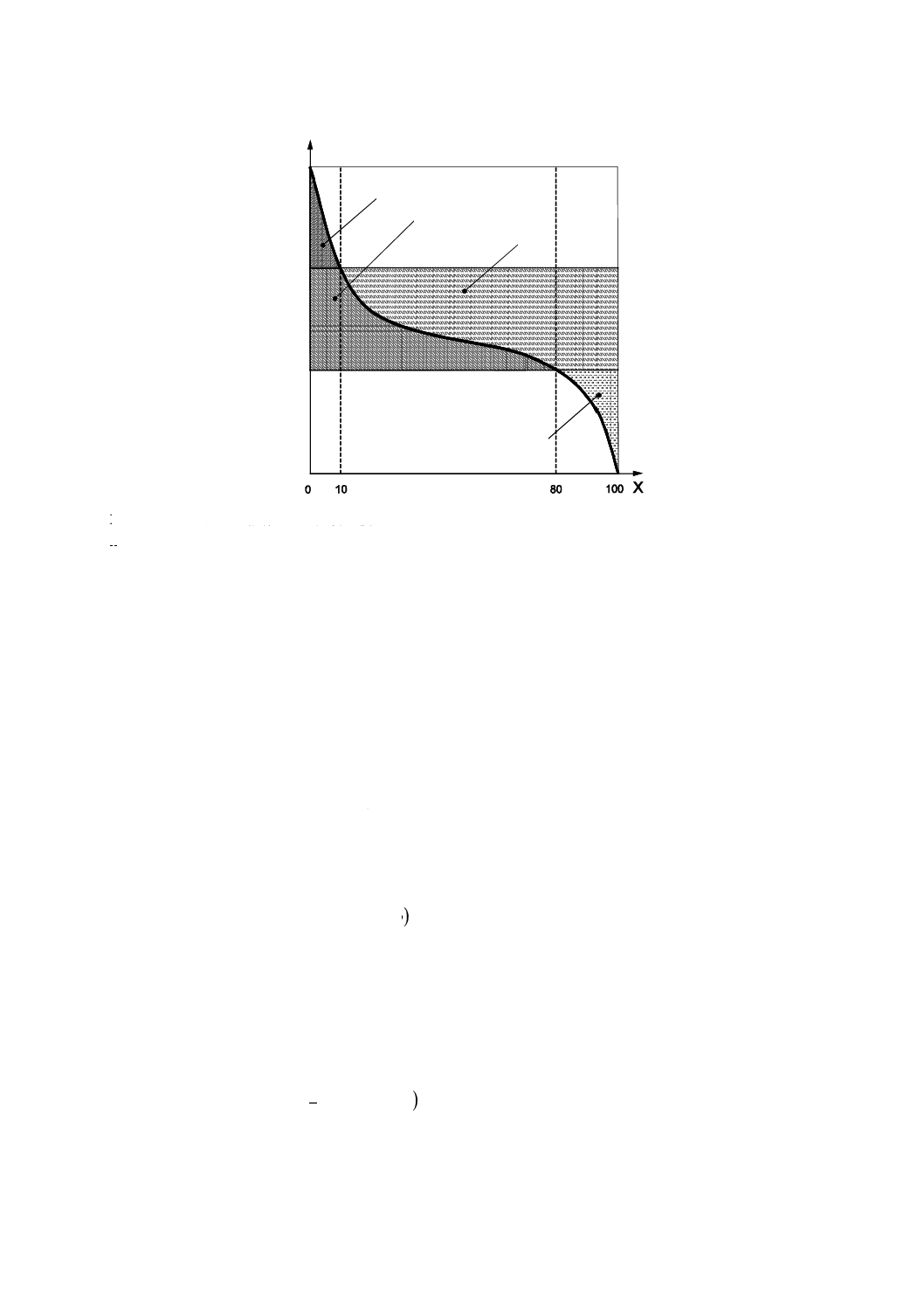
Skで表すコア部の上側の輪郭曲面の負荷曲線及び下側の輪郭曲面の負荷曲線に囲まれた面積を,図11
にハッチングで示す。これらは,輪郭曲面のコア部の外側にある突出山部の体積及び突出谷部の体積に等
しい。
パラメータSpkとSvkとは,それぞれ“突出山部の体積”又は“突出谷部の体積”に等しくなる直角三
角形の高さによって与えられる(図11参照)。“突出山部の体積V1”に相当する直角三角形の底辺はSmr1
であり,“突出谷部の体積V2”に相当する直角三角形の底辺はSmr2と100 %との差である。
パラメータSk,Spk,Svk,Smr1及びSmr2が求められるのは,図5及び図11のように負荷曲線が“S”
字体で,変曲点が1点の場合だけである。経験上,このような性質は,ラップ加工面,研削加工面及びホ
ーニング加工面によく見られる。
5.4
Spq,Svq及びSmqの求め方
二つの加工プロセスの痕跡が残っている表面(二層構造表面という。)の測定データでは,図6に示すよ
うに,正規確率紙上の負荷曲線の3か所に非線形な部分が現れる。正規確率紙上の負荷曲線で正規分布に
十分従う部分だけを用いるために,当てはめ範囲を限定してこれらの非線形な部分を除去しなければなら
ない。
図6の非線形な部分は,次の要因によって生じる。
− データ(輪郭曲面)に含まれる異物又は異常に高い突起(領域3)
− データ(輪郭曲面)に含まれる深いきず又は異常に深い谷底(領域4)
− 二つの分布がつながるプラトー領域から谷領域へ移る点(変移点という。)で生じる不安定領域(領域
5。領域5を変移領域という。)
このような非線形な部分を除去する意図は,対象面の繰り返し測定に対して,パラメータをより安定さ
せることである。図7は,輪郭曲面及びそれに対応した正規確率紙上の負荷曲線,プラトー領域,及び谷
領域を示し,この二つの領域を定めていている輪郭曲面の対応部分を表している。この輪郭曲面は,異常
に高い突起をもっているが,図7はそれがパラメータに影響しないことを示している。図7は対象面の測
定場所によって大きく変化する深い谷底部分は,パラメータ決定に関与しないことも示している。
線形領域の限界決定の手順は,JIS B 0671-3:2002の附属書A(線形領域の限界決定の手順)に規定して
いる。
20
B 0681-2:2018
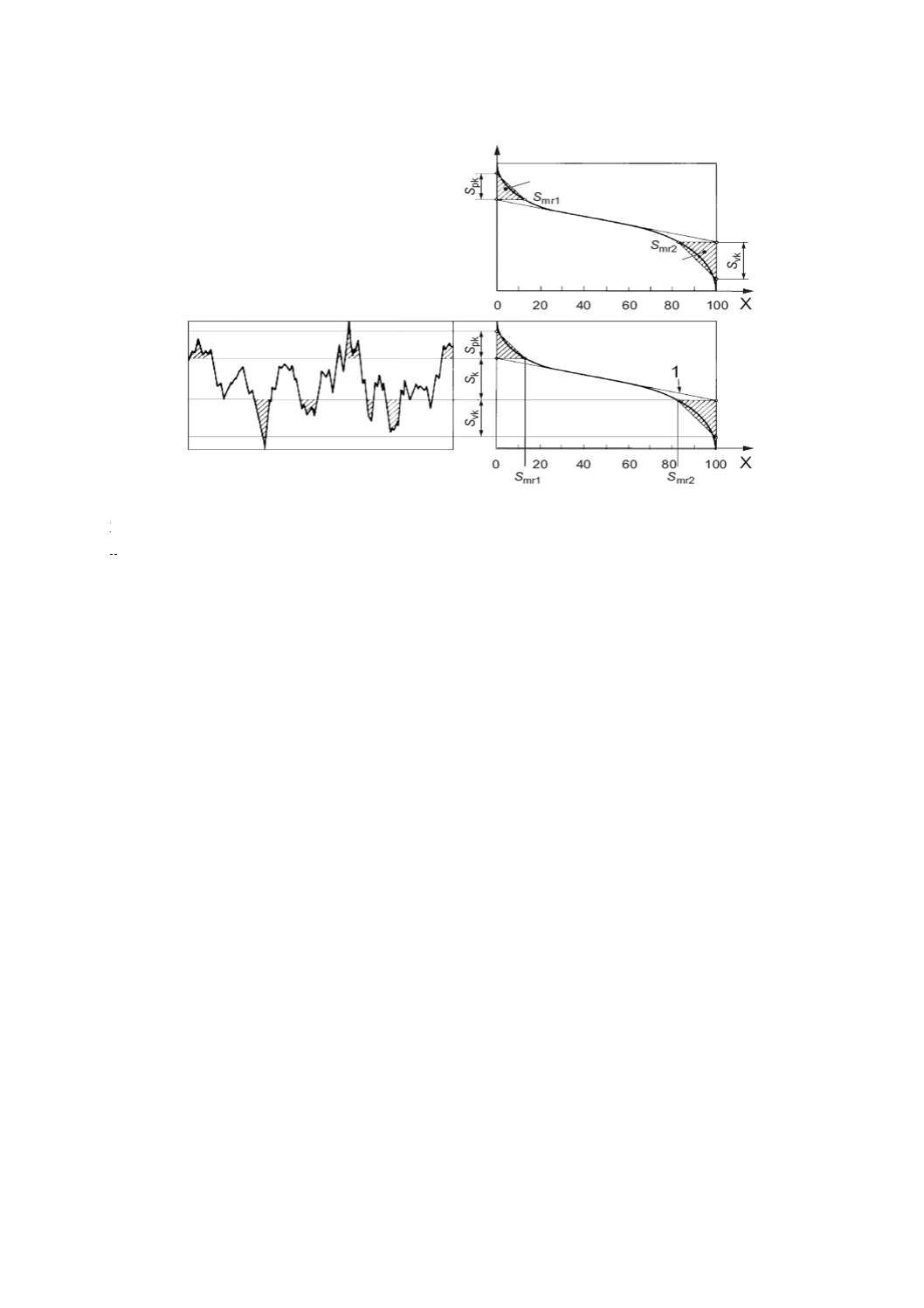
X
パーセント表示の負荷面積率
Z
高さ
1
等価直線
V1
突出山部の体積
V2
突出谷部の体積
Smr1,Smr2
負荷面積率
Sk
コア部のレベル差
Spk
突出山部高さ
Svk
突出谷部深さ
“突出山部の体積”及び“突出谷部の体積”の等面積直角三角形への変換
図11−Rpk及びRvkの計算を基本としたSpk及びSvkの計算
Z
V1
V2
21
B 0681-2:2018
附属書A
(参考)
三次元表面性状規格の背景
A.1 制定の経緯
三次元表面性状に関するこの一連の国際規格が発行された経緯を次に示す。
1990年4月〜1993年4月
バーミンガム大学主導の“三次元粗さの特性評価法の開発”と題するEU基金プロジェクト。こ
のプロジェクトでは,三次元表面性状の特性評価に関する基礎的事項を検討した。当該プロジェク
トの報告書で,“バーミンガム14”三次元表面性状パラメータを紹介し,データファイルのフォー
マットを含む通信プロトコルを整備した。
1993年9月
上記のEU基金プロジェクトに基づいて,詳細な成果を含む“Blue book”[13]を発刊した。
この書籍は,三次元表面性状の特性評価のデファクト標準となった。
1998年4月〜2001年4月
ローバとブルネル大学主導AUTOSURFプロジェクト。このEU基金プロジェクトでは,自動車
用鋼板に対する三次元表面性状の特性評価法を開発した。これは,鋼板の保管中のオイル保持,プ
レス性及び塗装性に対する特性評価を含んでいる。現実の表面性状の問題を解決するために,凹凸
形体のツールボックスを使用した。
1998年5月〜2001年5月
ハダースフィールド大学主導のSURFSTANDプロジェクト。このEU基金プロジェクトで,三次
元表面性状解析の標準化の基礎を確立した。一連の事例研究を通して,“バーミンガム14”パラメ
ータの表面機能に対する有用性を評価した。三次元表面性状の定義を再検討し,結果として,領域
パラメータの定義を厳格化して,凹凸形体のツールボックスを導入した。ロバスト及びウェーブレ
ットフィルタ技術を開発した。最後に,三次元の測定機の校正に関する事項を検討した。
2002年1月
スペインのマドリッドで開催されたISO/TC 213にて,SURFSTAND及びAUTOSURFプロジェク
トの概要を報告した。
2002年6月
三次元表面性状の標準化に対する要求事項を決定するため,ISO/TC 213に表面性状のタスクフォ
ース(特別対策委員会)を設置した。
2003年1月
次世代GPSの一部として新しい表面性状体系を開発するために,ISO/TC 213は新規の作業グル
ープWG 16を設置した。
2003年5月
SURFSTANDプロジェクトの詳細な成果を含む“Green book”[14]を発刊した。
2003年6月
ASME B46.1:2002[15]を発刊した。それは,三次元表面性状のフラクタルによる解析法の基礎及び
表面性状測定機の分類を含んでいる。
22
B 0681-2:2018
A.2 項目ごとの参考資料
三次元表面性状に関する,この一連の規格群で使用した参考資料を,参考文献に示す。JIS及びISO規
格ではない参考資料は,項目分野ごとに分類する。
23
B 0681-2:2018
附属書B
(参考)
GPSマトリックス
B.1
一般
GPSマトリックスの詳細は,ISO/TR 14638:1995を参照。
ISO/TR 14638:1995に示すISO/GPSマスタープランは,この規格もその一部であるISO/TR体系の概要
を示す。ISO 8015に示すISO/GPSの原理原則がこの規格に適用され,JIS B 0641-1に示す決定方式がこの
規格に沿って作成された仕様に適用される。
注記 ISO/TR 14638:1995は廃止され,ISO 14638:2015として発行されている。
B.2
規格及びその利用についての情報
この規格は,表面性状(基礎表面性状曲面,表面性状曲面など)を決定する用語,定義及びパラメータ
を明確にする。
B.3
GPSマトリックスにおける位置付け
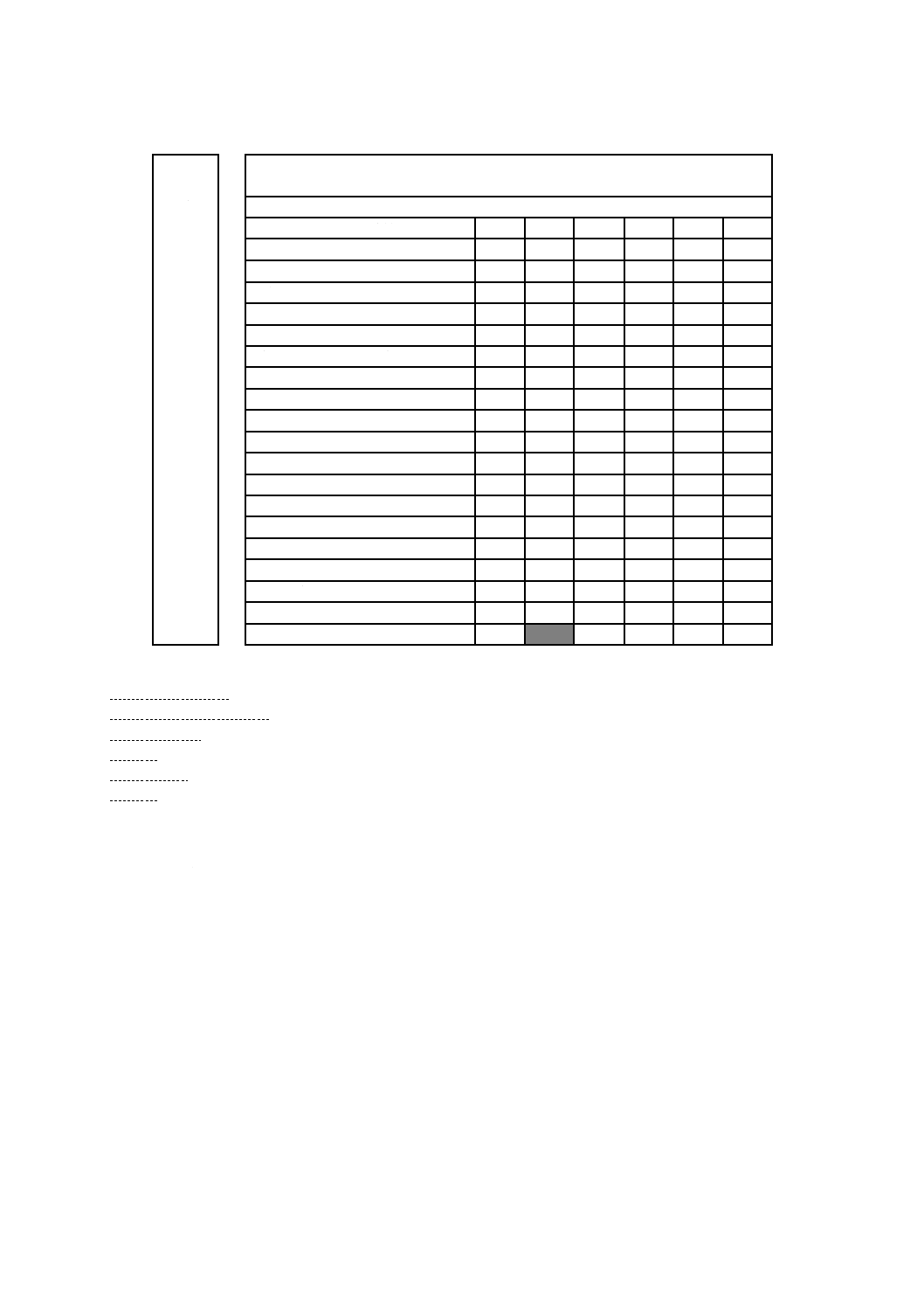
この規格は,図B.1に示すGPSマトリックスの表面性状規格に関するチェーンのリンク番号2に関わる
基本規格である。
24
B 0681-2:2018
GPS
原理
規格
GPS共通規格
GPS基本規格
リンク番号
1
2
3
4
5
6
サイズ
距離
半径
角度
データムに無関係な線の形状
データムに関係する線の形状
データムに無関係な面の形状
データムに関係する面の形状
姿勢
位置
円周振れ
全振れ
データム
粗さ曲線
うねり曲線
断面曲線
表面欠陥
エッジ
三次元表面性状
リンク番号
1:記号及び指示法
2:形体に対する要求事項
3:形体の性質
4:測定
5:測定機器
6:校正
図B.1−GPSマトリックスにおける位置付け
B.4
関連国際規格
関連する国際規格及び日本工業規格は,図B.1に示す規格チェーンに含まれる全ての規格である。
25
B 0681-2:2018
参考文献
[1] JIS B 0641-1:2001 製品の幾何特性仕様(GPS)−製品及び測定装置の測定による検査−第1部:仕
様に対する合否判定基準
注記 対応国際規格:ISO 14253-1:1998,Geometrical Product Specifications (GPS)−Inspection by
measurement of workpieces and measuring equipment−Part 1: Decision rules for proving
conformance or non-conformance with specifications
[2] JIS B 0671-3:2002 製品の幾何特性仕様(GPS)−表面性状:輪郭曲線方式;プラトー構造表面の特
性評価−第3部:正規確率紙上の負荷曲線による高さの特性評価
注記 対応国際規格:ISO 13565-3:1998,Geometrical Product Specifications (GPS)−Surface texture:
Profile method; Surfaces having stratified functional properties−Part 3: Height characterization using
the material probability curve
[3] ISO 8015,Geometrical product specifications (GPS)−Fundamentals−Concepts, principles and rules
[4] ISO 11562:1996,Geometrical Product Specifications (GPS)−Surface texture: Profile method−Metrological
characteristics of phase correct filters
注記 ISO 11562:1996は廃止され,ISO 16610-21:2011,Geometrical product specifications (GPS)−
Filtration−Part 21: Linear profile filters: Gaussian filtersに置き換えられた。
[5] ISO 12085:1996,Geometrical Product Specifications (GPS)−Surface texture: Profile method−Motif
parameters
[6] ISO 13565-2:1996,Geometrical Product Specifications (GPS)−Surface texture: Profile method; Surfaces
having stratified functional properties−Part 2: Height characterization using the linear material ratio curve
[7] ISO 14406:2010,Geometrical product specifications (GPS)−Extraction
[8] ISO/TR 14638:1995,Geometrical product specification (GPS)−Masterplan
[9] ISO 14638:2015,Geometrical product specifications (GPS)−Matrix model
[10] ISO/TS 16610-20:2006,Geometrical product specifications (GPS)−Filtration−Part 20: Linear profile filters:
Basic concepts
[11] ISO 25178-3:2012,Geometrical product specifications (GPS)−Surface texture: Areal−Part 3: Specification
operators
[12] JIS B 0672-1 製品の幾何特性仕様(GPS)−形体−第1部:一般用語及び定義
領域パラメータに関する参考
[13] STOUT, K.J. et al. The development of methods for the characterisation of roughness in three dimensions.
European Report EUR 15178 EN, ISBN 0 7044 1313 2
[14] BLUNT, L. and JIANG, X. Advanced techniques for assessment surface topography−Development of a basis
for the 3D Surface Texture Standards “SURFSTAND”, Kogan Page Science, ISBN 1903996112, 2003
その他
[15] ASME B46.1:2002,Surface Texture, Surface Roughness, Waviness and Lay
事例研究(case study)
参考文献[14]を参照。
26
B 0681-2:2018
附属書JA
(参考)
JISと対応国際規格との対比表
JIS B 0681-2:2018 製品の幾何特性仕様(GPS)−表面性状:三次元−第2部:
用語,定義及び表面性状パラメータ
ISO 25178-2:2012,Geometrical product specifications (GPS)−Surface texture: Areal−
Part 2: Terms, definitions and surface texture parameters
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごと
の評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
3 用語及び
定義
−
3.2.2
feature parameterの定義
削除
対応国際規格のfeature parameterが
JISでは定義されていない。
feature parameterは,新規に導入さ
れたパラメータ群であるが,算出
方法,用語の定義などが確立され
ておらず,多くの不備があり,次
の対応国際規格改訂時に大幅な修
正が予定されている。この変更に
よって用語の定義などが大きく変
わるため,産業界及び学会での混
乱を避けるためにこの規格からは
削除することとした。
3.2.2〜3.2.8.1
3.2.3〜
3.2.9.1
用語及び定義
変更
番号が異なっている。
対応国際規格の3.2.2を削除した
ため。
−
3.3
geometrical featureに関
する用語の定義
削除
対応国際規格のgeometrical feature
に関する用語がJISでは定義され
ていない。
上記feature parameterの削除と同
じ理由による。
4 領域パラ
メータの定
義
−
4.4.9
fractal methodsの定義
削除
対応国際規格のfractal methodsが
JISでは定義されていない。
上記feature parameterの削除と同
じ理由による。
−
−
6
feature characterizationに
関する用語の定義
削除
対応国際規格の
feature
characterizationがJISでは定義され
ていない。
上記feature parameterの削除と同
じ理由による。
8
B
0
6
8
1
-2
:
2
0
1
8

27
B 0681-2:2018
JISと国際規格との対応の程度の全体評価:ISO 25178-2:2012,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 削除 ················ 国際規格の規定項目又は規定内容を削除している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
8
B
0
6
8
1
-2
:
2
0
1
8














