B 0090-12:2012 (ISO 10110-12:2007)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 非球面の数学的な記述 ······································································································· 2
3.1 一般 ···························································································································· 2
3.2 面形状の分類 ················································································································ 3
3.3 特定面の種類 ················································································································ 3
4 図面内の表示 ··················································································································· 6
4.1 理論面の表示 ················································································································ 6
4.2 表面形状公差の表示 ······································································································· 6
4.3 偏心公差の表示 ············································································································· 7
4.4 表面欠陥及び面の肌の表示 ······························································································ 7
5 例·································································································································· 7
5.1 対称的な非球面をもち,機械的な軸と光軸とが一致する部品 ·················································· 7
5.2 対称的な非球面をもち,光軸と機械的な軸とが一致しない部品 ··············································· 9
5.3 回転非対称な非球面部品 ································································································ 11
附属書A(規定)非球面タイプの要約 ····················································································· 14
B 0090-12:2012 (ISO 10110-12:2007)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,日本光学工業協会
(JOIA)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を改正すべき
との申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS B 0090-12:2001は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 0090の規格群には,次に示す部編成がある。
JIS B 0090-1 第1部:通則
JIS B 0090-2 第2部:材料欠陥−応力複屈折
JIS B 0090-3 第3部:材料欠陥−泡及び異物
JIS B 0090-4 第4部:材料欠陥−不均一性及び脈理
JIS B 0090-5 第5部:表面形状公差
JIS B 0090-6 第6部:偏心公差
JIS B 0090-7 第7部:表面欠陥
JIS B 0090-8 第8部:面の肌
JIS B 0090-9 第9部:表面処理及びコーティング
JIS B 0090-10 第10部:光学素子及び接合部品のデータ表示表
JIS B 0090-11 第11部:公差表示のないデータ
JIS B 0090-12 第12部:非球面
JIS B 0090-14 第14部:波面形状公差
JIS B 0090-17 第17部:レーザ放射による損傷しきい値
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 0090-12:2012
(ISO 10110-12:2007)
光学素子及び光学システム用の製図手法−
第12部:非球面
Preparation of drawings for optical elements and systems-
Part 12: Aspheric surfaces
序文
この規格は,2007年に第2版として発行されたISO 10110-12を基に,技術的内容を変更することなく作
成した日本工業規格である。
なお,この規格で点線の下線を施している参考事項は,対応国際規格にはない事項である。
1
適用範囲
JIS B 0090の規格群は,製造及び検査に用いる製図における光学素子及び光学システムに対する設計上
及び機能上の要求事項の表示方法について規定している。
この規格は,非球面の形状,寸法及び公差の表示方法について規定する。
この規格は,フレネル面又は回折格子のような不連続な面には適用しない。
この規格は,仕様に準拠しているかどうかを検査する方法を規定するものではない。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 10110-12:2007,Optics and photonics−Preparation of drawings for optical elements and systems
−Part 12: Aspheric surfaces(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0021 製品の幾何特性仕様(GPS)−幾何公差表示方式−形状,姿勢,位置及び振れの公差表示
方式
注記1 対応国際規格:ISO/DIS 1101:1996,Geometrical Product Specifications (GPS) −Geometrical
tolerancing−Tolerances of form, orientation, location and run-out(IDT)
注記2 対応国際規格:ISO 1101は,2012年版が発行されている。
JIS B 0090-5 光学素子及び光学システム用の製図手法−第5部:表面形状公差
注記 対応国際規格:ISO 10110-5,Optics and photonics−Preparation of drawings for optical elements
and systems−Part 5: Surface form tolerances(IDT)
JIS B 0090-6 光学素子及びシステム用の製図手法−第6部:偏心公差
2
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 対応国際規格:ISO 10110-6,Optics and optical instruments−Preparation of drawings for optical
elements and systems−Part 6: Centring tolerances(IDT)
JIS B 0090-7 光学素子及び光学システム用の製図手法−第7部:表面欠陥
注記 対応国際規格:ISO 10110-7,Optics and photonics−Preparation of drawings for optical elements
and systems−Part 7: Surface imperfection tolerances(MOD)
JIS B 0090-8 光学素子及びシステム用の製図手法−第8部:面の肌
注記 対応国際規格:ISO 10110-8,Optics and optical instruments−Preparation of drawings for optical
elements and systems−Part 8: Surface texture(IDT)
3
非球面の数学的な記述
3.1
一般
3.1.1
座標系
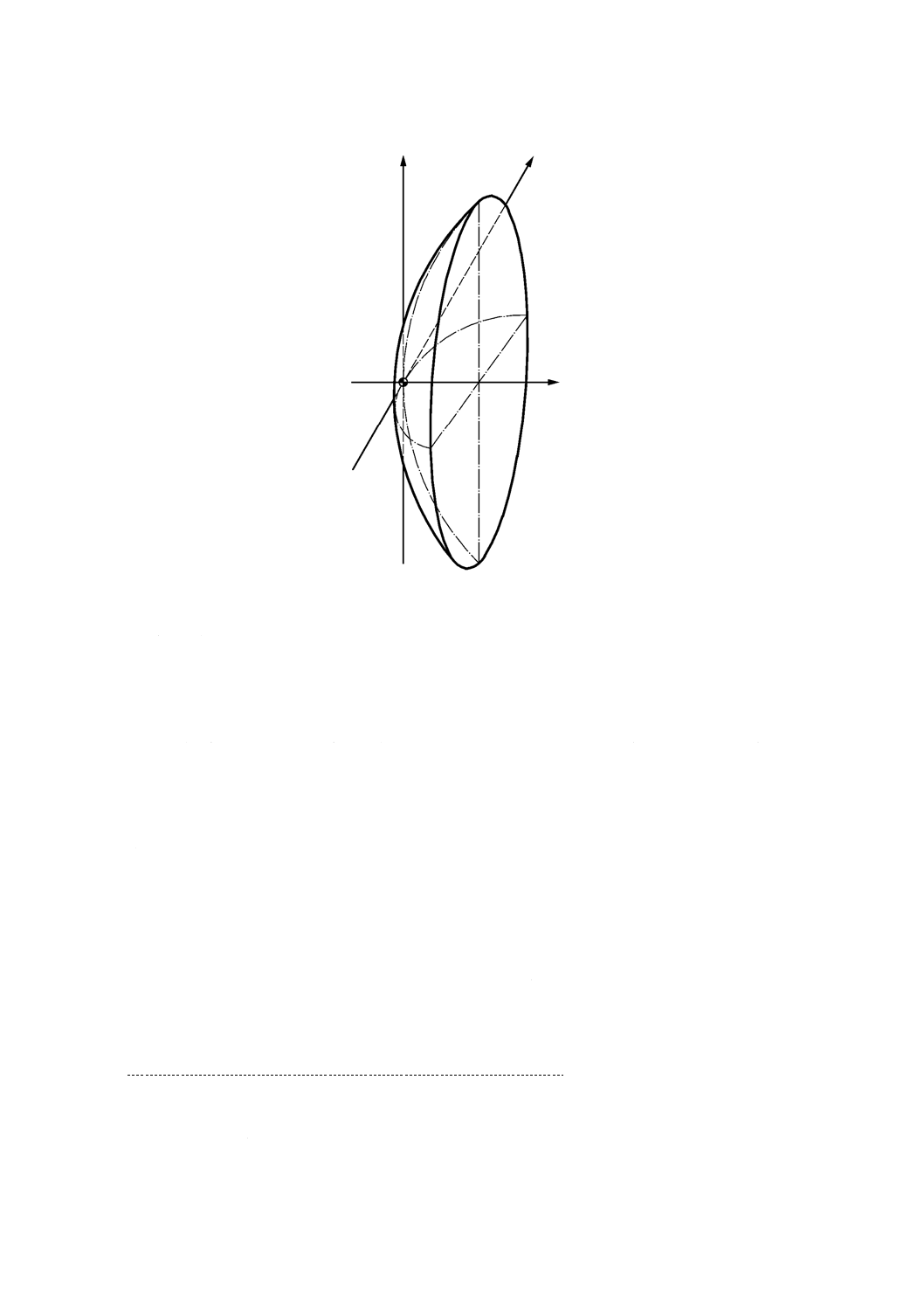
非球面は,Z軸を光軸とする右手直交座標系で記述する。
特記しない限り,Z軸は図面の平面内にあり,正の方向は左から右へ向かう方向とする。
注記 製作(例えば,機械のプログラミング)のため,Z軸の方向を逆にする必要があるとき,半径
の符号及び多項式の非球面係数の符号は共に変化する。しかし,円すい(錐)係数(conic constant)
κの符号は変わらない。
ただ一つの断面を描く場合には,YZ断面を描き,Y軸は図面の平面内にあり,正の方向は下から上へ向
かう方向とする。
二つの断面を描く場合には,XZ断面はYZ断面の下に描く(図5参照)。X軸及びY軸を,明確にするた
めに図面中に示すことができる。
座標系の原点は,非球面の頂点にある(図1参照)。
3
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1−座標系
3.1.2
符号の約束
注記1 3.3に規定するように,様々な非球面は数式によって表す。図面には,選択した数式と対応す
る定数及び係数を指定する。明確な指示を実現するために,定数及び係数の符号の約束を導
入する。
曲率半径(通常,面の頂点で規定する。)の符号は,曲率中心が面の頂点の右側に位置する場合は正であ
り,面の頂点の左側に位置する場合は負である。
非球面上の任意の点の変位量は,その点が面の頂点の右側に位置する場合は正の値であり,面の頂点の
左側に位置する場合は負の値である。
注記2 この変位量をサジッタ量又はサグ量ともいう。
3.2
面形状の分類
光学分野では,次の2種類の非球面を一般的に使用しているため,特に重要である。
− 2次の一般化された面
− 高次関数の面
2次の一般化された面は,円すい面,2次曲面及び放物面を含む。
高次関数の面は,多項式,トーリック面及び面形状の組合せ(例えば,他の面形状に多項式を付加した
ような形状)を含む。
注記 トーリック面には,円環面,トロイダル面などがある。
3.3
特定面の種類
3.3.1
2次関数面
3.3.1.1
2次曲面及び放物面
2次曲面及び放物面の標準形は,式(1)及び式(2)で表す。
Z
Y
X
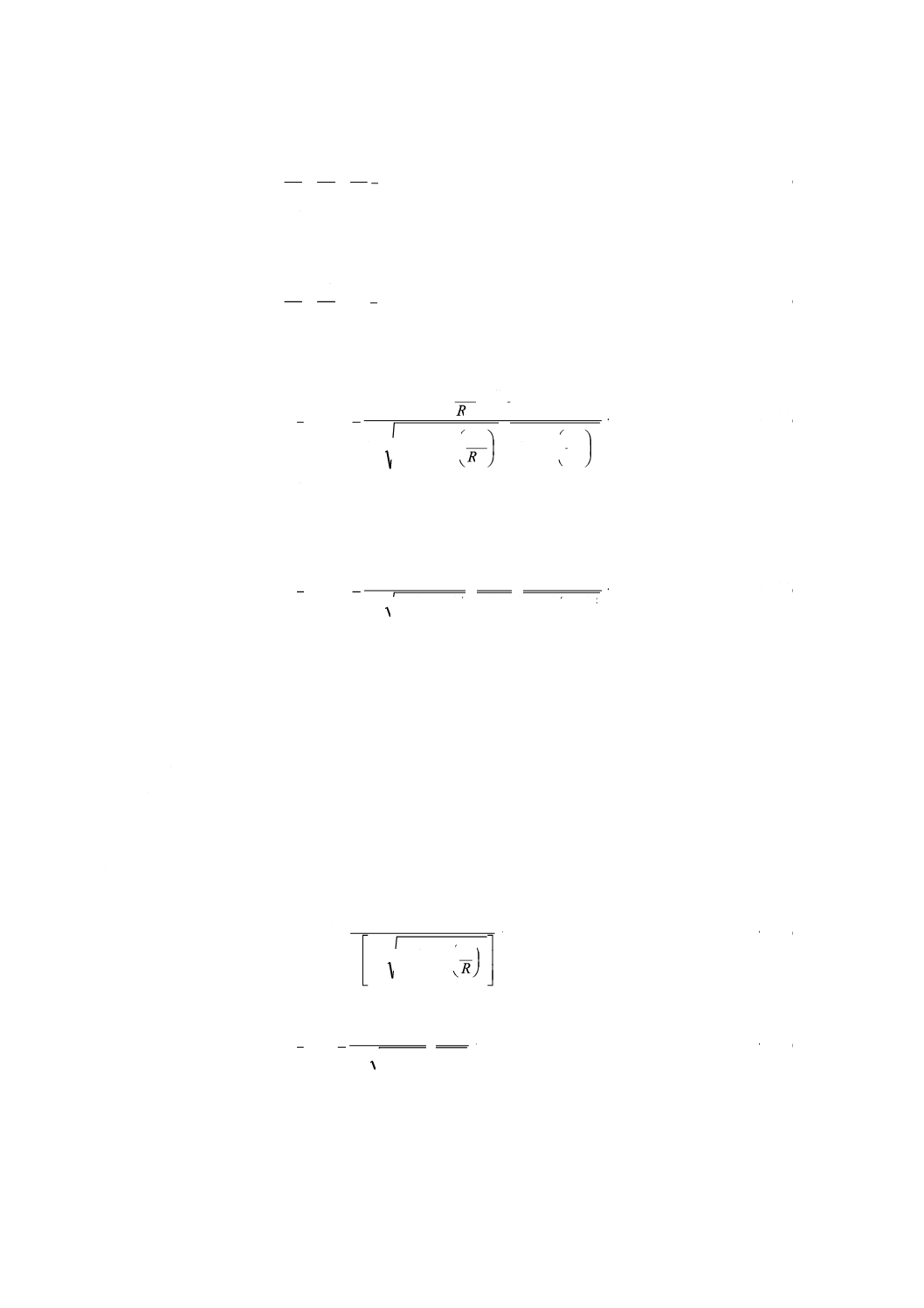
4
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2次曲面
1
2
2
2
2
2
2
=
+
+
c
z
b
y
a
x
········································································ (1)
ここに,
a,b: 実数又は虚数の定数
c: 実数の定数
放物面
0
2
2
2
2
2
=
+
+
z
b
y
a
x
········································································ (2)
ここに,
a,b: 実数又は虚数の定数
式(1)及び式(2)の標準形に基づき,3.1.1で与えた座標系において,2次曲面及び放物面は,式(3)で表す。
(
)
(
)
(
)
2
2
2
2
1
1
1
1
,
+
−
+
−
+
+
=
=
Y
Y
X
X
Y
X
R
y
Rx
R
y
Rx
y
x
f
z
κ
κ
································ (3)
ここに,
RX: XZ平面上における曲率半径
RY: YZ平面上における曲率半径
κX,κY: 円すい定数
曲率半径の代わりに曲率CX=1/RX及びCY=1/RYを用いると,式(4)で表すことができる。
(
)
(
)(
)(
)(
)2
2
2
2
1
1
1
1
,
Y
Y
X
X
Y
X
yC
xC
C
y
C
x
y
x
f
z
κ
κ
+
−
+
−
+
+
=
=
································ (4)
式(3)又は式(4)の面がXZ平面(y=0)又はYZ平面(x=0)と交差すると,κY(又はκX)の値に従って,
次の種類の交線が生じる。
κ>0:
へん平だ円(扁平楕円)
κ=0:
円
−1<κ<0: へん長だ円(扁長楕円)
κ=−1:
放物線
κ<−1:
双曲線
式(3)及び式(4)の特別な場合を,次に示す。
a) 回転対称面
1) 曲率半径による記述 R=RX=RY,κ=κX=κY及びh2=x2+y2のとき,式(3)は,式(5)で表す。
()
(
)
+
−
+
=
=
2
2
1
1
1
Rh
R
h
h
f
z
κ
···················································· (5)
2) 曲率による記述 C=CX=CY,κ=κX=κY及びh2=x2+y2のとき,式(4)は,式(6)で表す。
()
(
)
2
2
2
1
1
1
C
h
C
h
h
f
z
κ
+
−
+
=
=
························································· (6)
式(5)及び式(6)は,Z軸回りに回転対称な面を記述する。
b) 円筒面
1) 曲率半径による記述 RX=∞又はRY=∞のとき,式(3)は,式(7)で表す。
5
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
(
)
+
−
+
=
=
2
U
U
U
2
1
1
1
Ru
R
u
u
f
z
κ
··············································· (7)
2) 曲率による記述 CX=0又はCY=0のとき,式(4)は,式(8)で表す。
()
(
)
2
U
2
U
U
2
1
1
1
C
u
C
u
u
f
z
κ
+
−
+
=
=
······················································· (8)
式(7)及び式(8)は,円筒面を記述する(κUによって,断面は必ずしも円形とは限らない。)。円筒軸は,
u=xのときXZ平面に垂直であり,u=yのときYZ平面に垂直である。
3.3.1.2
円すい面
円すい面の標準形は,式(9)で表す。
0
2
2
2
2
2
2
=
+
+
c
z
b
y
a
x
········································································· (9)
ここに,
a,b: 虚数の定数
c: 実数の定数
式(9)の標準形に基づき,3.1.1で与えた座標系において,円すい面は,式(10)で表すことができる。ただ
しこの場合,a,b及びcは全て実数の定数とする。
2
2
2
2
)
,
(
b
y
a
x
c
y
x
f
z
+
=
=
······························································ (10)
式(10)は,a≠bのとき,Z軸に垂直な断面はだ円であり,a=bのとき,Z軸に垂直な断面は円であり,
その先端が原点にあるすい面を表す。
3.3.2
高次の面
3.3.2.1
多項式
多項式面は,式(11)で表す。
...
...
...
)
,
(
3
3
3
3
6
6
6
6
4
4
4
4
+
+
+
+
+
+
+
+
=
=
y
D
x
C
y
B
x
A
y
B
x
A
y
x
f
z
·············(11)
式(11)に,h2=x2+y2を用いた場合を次に示す。
...
)
(
5
5
4
4
3
3
+
+
+
=
=
h
A
h
A
h
A
h
f
z
··················································· (12)
式(12)は,回転対称多項式面を表しており,シュミット面とも呼ばれている(一般的には,シュミット
補正板として知られている。)。
3.3.2.2
トーリック面
トーリック面は,面内の,任意の定義曲線を,同一面内に存在する軸の回りに回転することによって生
成する。
XZ面内の定義曲線がz=g(x)のとき,回転軸がX軸に平行なトーリック面は,式(13)で表す。
(
)
()
[
]
2
2
,
y
x
g
R
R
y
x
f
z
Y
Y
−
−
=
=
μ
················································· (13)
ここに,RYは,回転軸がZ軸と交差するZ座標である。
この規格の目的に対しては,式(14)は,式(3)においてy=0と設定することによって得られる。

6
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
(
)
+
−
+
=
2
2
1
1
1
X
X
X
Rx
R
x
x
g
κ
·················································· (14)
YZ面内にその定義曲線があり,また,その回転軸がY軸に平行なトーリック面の式は,式(13)及び式(14)
において,xをy,RXをRY,及びκXをκYと交換することによって得られる。
半径RXの円である定義曲線は,式(14)にκx=0を代入し,式(15)で表す。
()
−
−
=
2
1
1
X
X
R
x
R
x
g
··························································· (15)
トーリック面は,式(13)に式(15)を代入し,式(16)で表す。
(
)
2
2
2
1
,
y
R
x
R
R
R
R
y
x
f
z
X
X
X
Y
Y
−
−
+
−
=
=
μ
··························· (16)
3.3.2.3
基礎式とべき級数との和
必要ならば面形状は,基礎式f (x, y)とべき級数f1(x, y)との和に変形できる(附属書A参照)。そのとき面
は,式(17)で表される。
(
)
( )y
x
f
y
x
f
z
,
,
1
+
=
··································································· (17)
ここで,f (x, y)は,式(3)若しくは式(4),又は式(10)に従う基礎式を表している。
トーリック面においても同様に定義曲線g(x)は,べき級数g1(x)との和に変形できる(附属書A参照)。
f1(x, y)及びg1(x)の中の係数の符号は,3.1.1及び3.1.2で定義した約束に従うことに注意を払わなければ
ならない。Z軸の方向が反転する場合は,半径及び曲率並びに係数の符号を変更する。円すい係数の符号
は変更しない。
4
図面内の表示
4.1
理論面の表示
非球面レンズ又は非球面ミラーは,非球面の種類を図面中の半径の表示位置に示す。
式(17)においてf1(x, y)≠0の場合は,“非球面”と表示する。また,f1(x, y)=0の場合は,非球面のタイプ
(例えば,“トーリック面”,“放物面”など)を表示する(JIS B 0090-1参照)。
非球面を記述する式は,円形の断面をもつ円柱面の場合を除いて注記として表示する。
曲率半径は,3.1.2に従って符号を表示する。
非球面が基礎式とべき級数との和で表される場合は,十分な精度をもつ数値で示した変位量を表形式で
図面の中に示さなければならない(図2参照)。
4.2
表面形状公差の表示
表面形状公差は,次のいずれかによって表示する。
a) JIS B 0021による。
b) JIS B 0090-5による。
c) zの許容偏差,すなわち,表示した式によるzの公称値と加工部品の実際の値との差を規定する表形
式で示す(図2参照)。
注記1 干渉計測定によるΔzの値は,面の局部法線に沿って測定する。
7
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
一般的に使用する超精密切削加工による非球面生成において局部的なうねりが発生するため,a)〜c)の
いずれの場合も,表面うねりの許容値に関連する傾斜偏差の公差を付加的に規定することが望ましい。
局部傾斜偏差は,理論面の局部法線と実表面の局部法線とのなす角度の偏差である。
局部傾斜偏差はいかなる場合でも,基準長さにおける平均値として扱う。基準長さは,傾斜量を計算す
る被検面上の横断長さである。
注記2 局部傾斜を求める式は,JIS B 0601の3.2.9を参照。
面全体の傾斜偏差は,局部傾斜偏差の最大値又はRMS値で規定できる。最大傾斜偏差は,全面での傾
斜偏差の最大値である。RMS傾斜偏差は,全面での傾斜偏差の2乗和の平方根である。
傾斜公差を規定する場合は,基準長さ及びデータサンプリング間隔も同様に図面に表示しなければなら
ない。
注記3 局部傾斜偏差は,データサンプリング間隔に大きく依存することに注意が必要である(JIS
B 0601の3.2.9参照)。
形状公差及び傾斜公差の両者共に,異なる断面で異なる数値になってもよい(図4及び図5参照)。
4.3
偏心公差の表示
偏心公差の表示は,JIS B 0021又はJIS B 0090-6のいずれかによる。
4.4
表面欠陥及び面の肌の表示
表面欠陥,並びに粗さと形状の中間空間周波数帯域であるリップル及び面の肌の仕様の表示は,それぞ
れJIS B 0090-7及びJIS B 0090-8による。
5
例
5.1
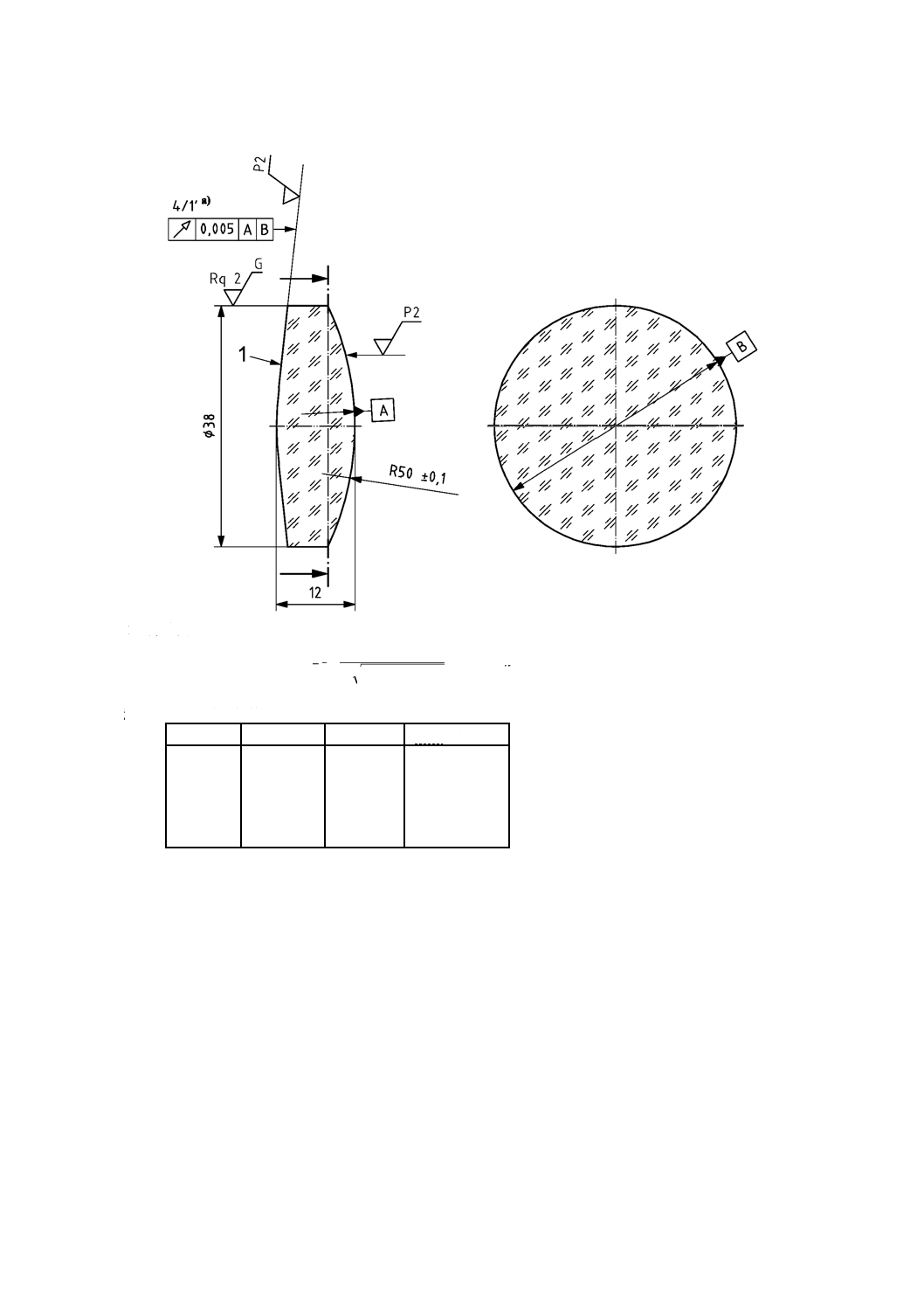
対称的な非球面をもち,機械的な軸と光軸とが一致する部品
図2 a)において,データム軸は,JIS B 0090-6に従って球面の曲率中心及び右の面の中心点を通ってい
る。非球面の形状公差は,表の形で与える。∆zは,与えられたh座標に対するz方向のmmで表した最大
許容偏差である。さらに,局部傾斜公差も表示してある。
JIS B 0021に従って偏心公差は,非球面の円周振れ(軸方向)の最大許容値を示している。また,JIS B
0090-6に従って傾き角の最大許容値を示すこともできる。
図2 b)に図2 a)と幾何学的に同じ形状で反転した(非球面は右側の面)非球面レンズを示す。曲率半径R
とその係数Aiの符号が変化していることに注意する。結果的に変位量(zの値)も同様に符号が変化する。
8
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
1 非球面
(
)
(
)
∑
=
+
+
−
+
=
5
2
2
2
2
2
2
/
)
1(
1
1
i
i
ih
A
R
h
R
h
z
κ
注a) 偏心公差の代替表示
h
z
∆z
局部傾斜公差
R=56.031
0.0
0.000
0.000
0.3′
κ=−3
5.0
0.219 4
0.002
0.5′
A4=−0.432 64E−05
10.0
0.825 3
0.004
0.5′
A6=−0.976 14E−08
15.0
1.600 5
0.006
0.8′
A8=−0.108 52E−11
19.0
1.938 1
0.008
1.0′
A10=−0.122 84E−13
基準長さ=1
データサンプリング間隔0.1
a) 回転対称非球面をもつレンズ
図2−回転対称な非球面レンズ
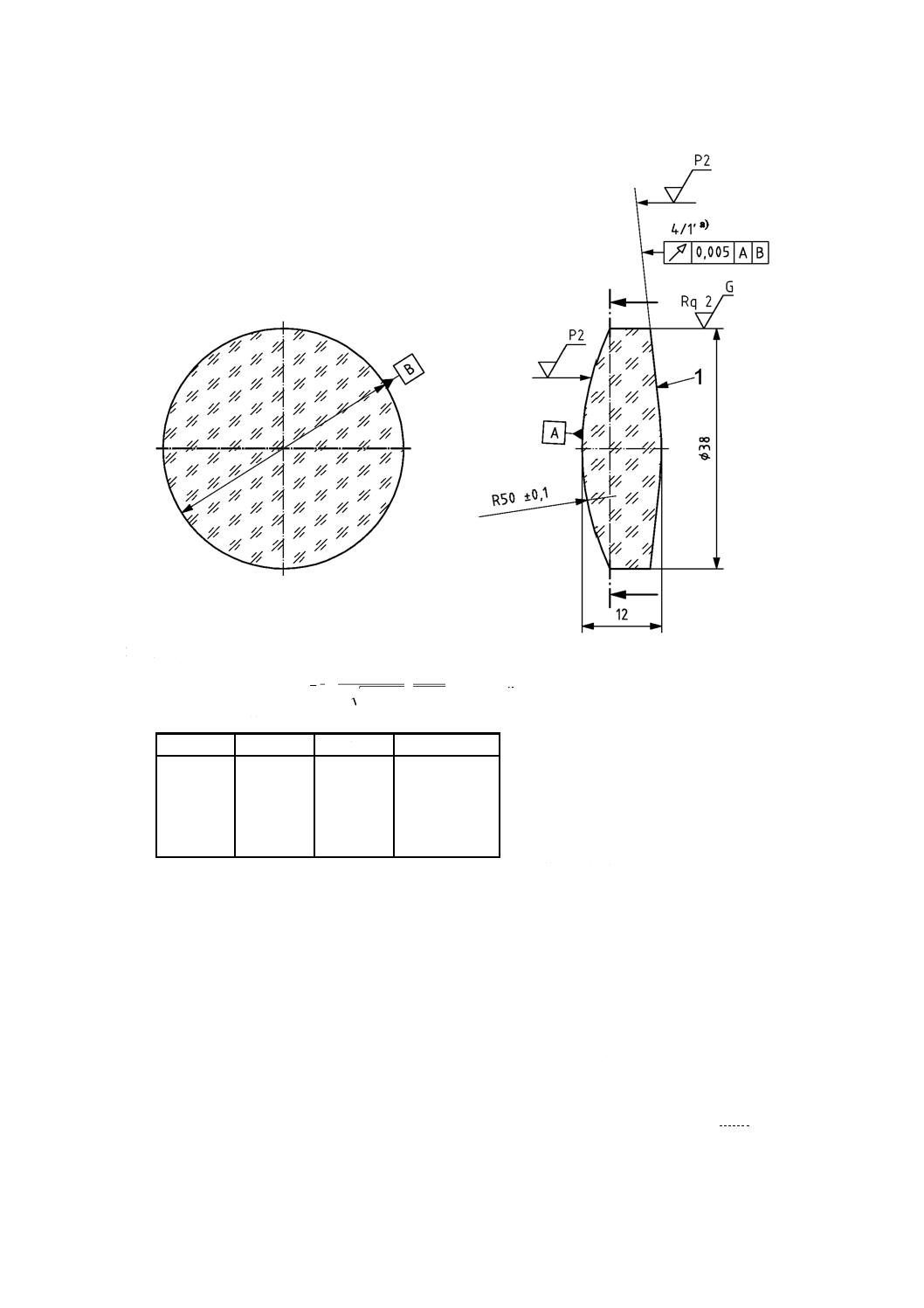
9
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
1 非球面
(
)
(
)
(
)
∑
=
+
+
−
+
=
5
2
2
2
2
2
2
/
1
1
1
i
i
ih
A
R
h
R
h
z
κ
注a) 偏心公差の代替表示
h
z
∆z
局部傾斜公差
R=−56.031
0.0
0.000
0.000
0.3′
κ=−3
5.0
−0.219 4
0.002
0.5′
A4=0.432 64E−05
10.0
−0.825 3
0.004
0.5′
A6=0.976 14E−08
15.0
−1.600 5
0.006
0.8′
A8=0.108 52E−11
19.0
−1.938 1
0.008
1.0′
A10=0.122 84E−13
基準長さ 1
データサンプリング間隔 0.1
b) 反転した図2 a)と同一の非球面レンズ
図2−回転対称な非球面レンズ(続き)
5.2
対称的な非球面をもち,光軸と機械的な軸とが一致しない部品
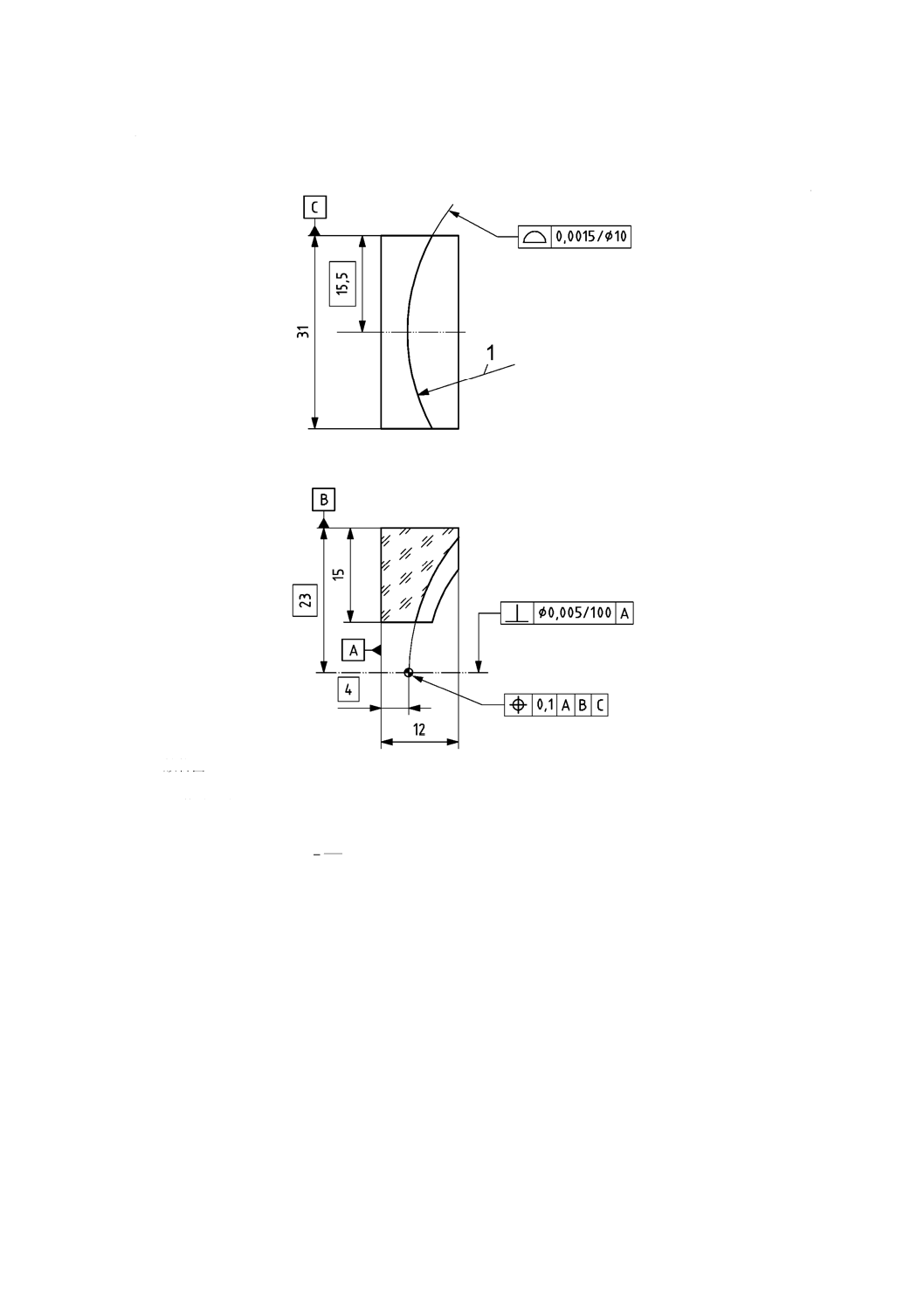
図3 a)は,長方形断面をもつ軸外れ放物面を示す。表面形状公差及び偏心公差は,JIS B 0021に従って
表示してある。
放物面の頂点は,名目上の位置に中心をもつ辺の長さが0.1 mmの立方体である。
放物面の回転軸は,100 mmの長さにわたって0.005 mmの直径をもつデータムAと垂直な円柱内にある。
光学的に有効な面積の表面形状公差は,JIS B 0021によって与える。さらに,面全体の最大傾斜公差も
表示してある。
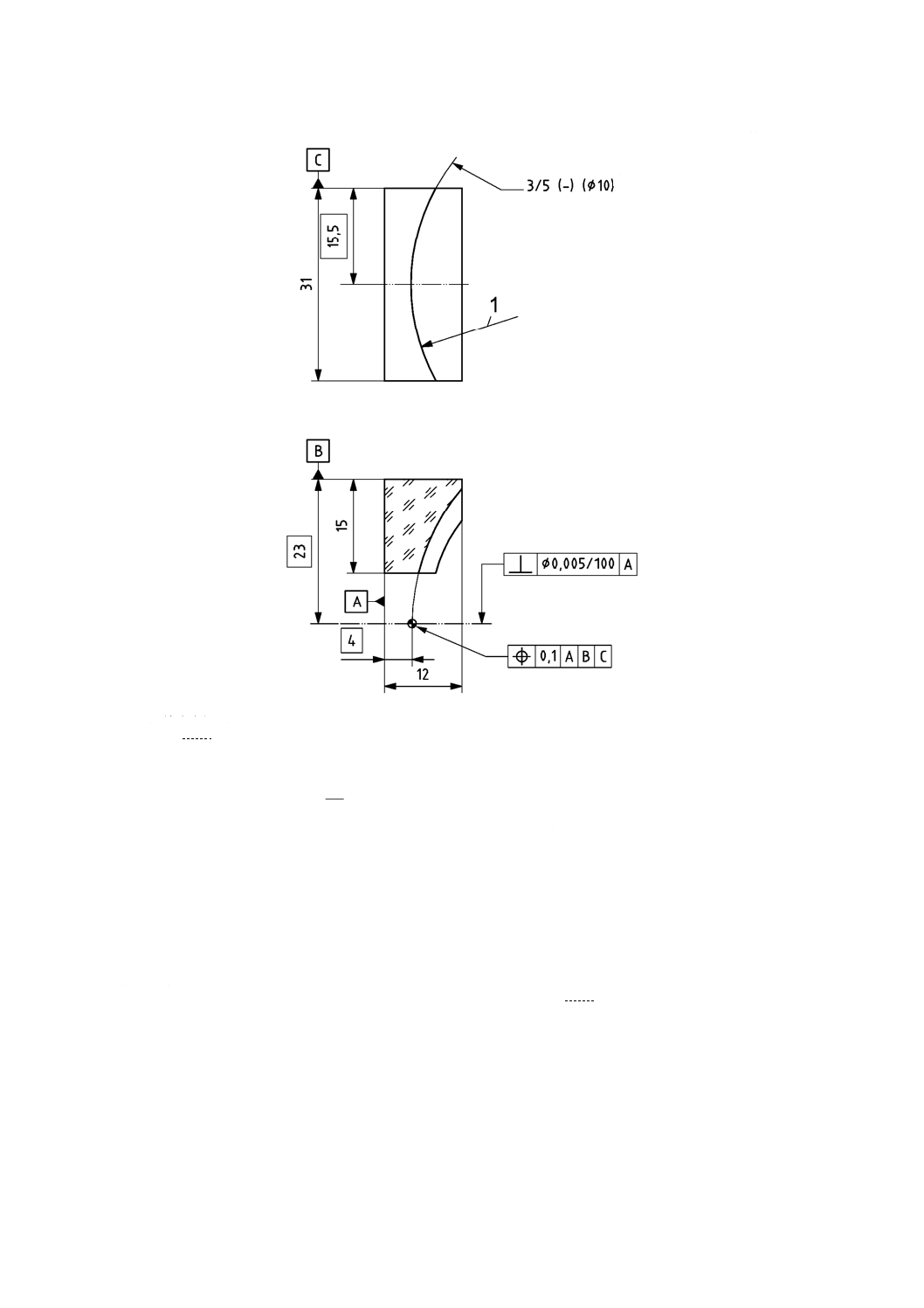
図3 b)は,図3 a)と同じ光学素子を示している。しかし,ここでは,表面形状公差は,JIS B 0090-5に従
10
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
って表示してある。
単位 mm
1 放物面
注a) 最大傾斜公差=0.2ʼ
基準長さ=2
データサンプリング間隔=0.2
R
h
z
2
2
=
R=35.741±0.2
a) JIS B 0021による表面形状公差の表示
図3−軸外れ放物面
a)
11
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
1 放物面
注a) 最大傾斜公差=0.2ʼ
基準長さ=2
データサンプリング間隔=0.2
R
h
z
2
2
=
R=35.741±0.2
b) JIS B 0090-5による表面形状公差の表示
図3−軸外れ放物面(続き)
5.3
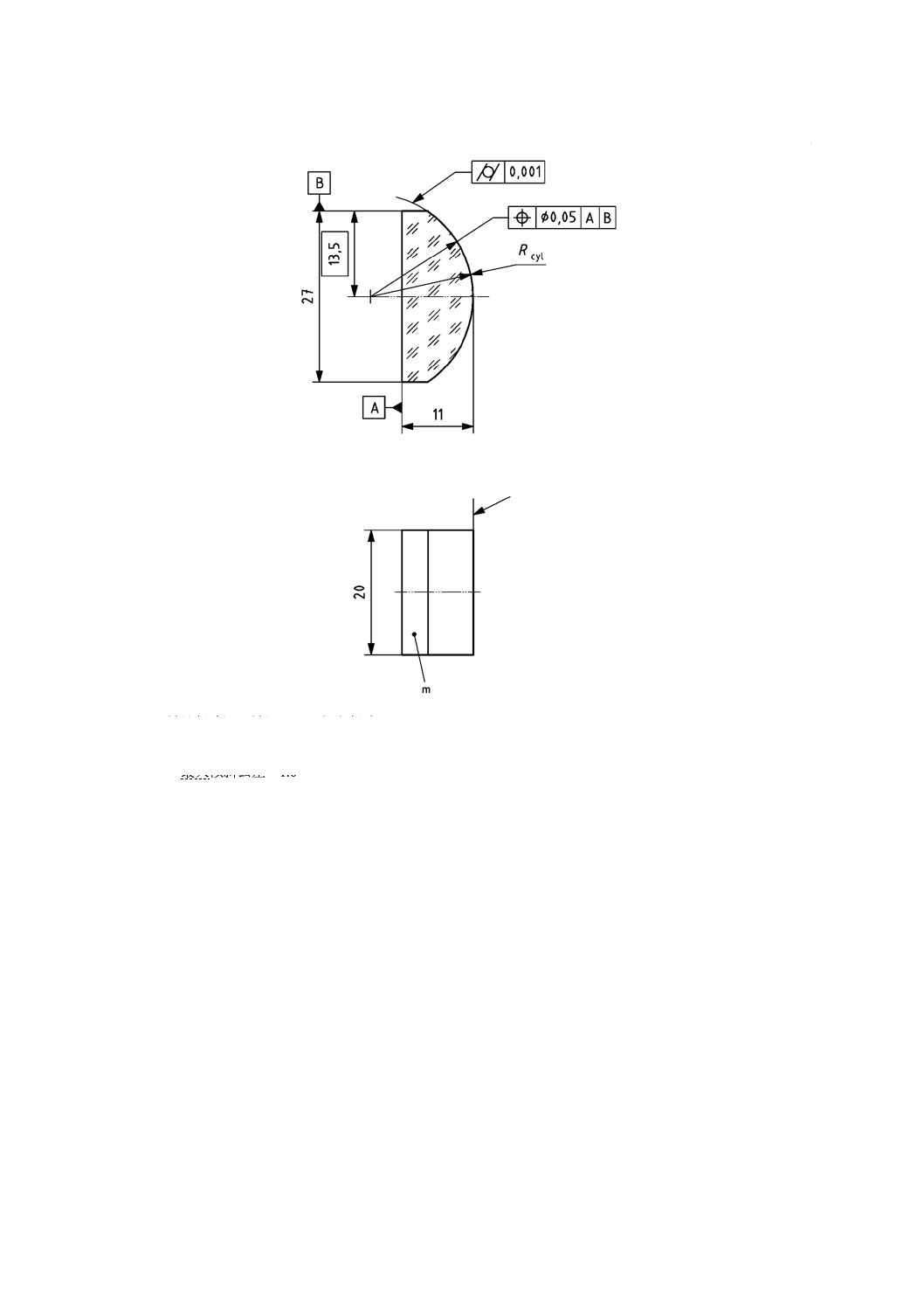
回転非対称な非球面部品
図4は,長方形の断面をもつ平−円柱レンズを示す。データム軸は,面Aと面Bとの交線で与えられる。
円柱面の軸は直径0.05 mmの円柱内にある。
形状公差はJIS B 0021に加えて,二つの断面内の異なる面全体の最大傾斜公差によって規定する。
a)
12
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
m 部品番号又は部品リスト参照番号
RX=∞,RY=17.2±0.2
注a) 最大傾斜公差=0.5ʼ
b) 最大傾斜公差=1.0ʼ
基準長さ=2
データサンプリング間隔=0.2
図4−平−円柱レンズ
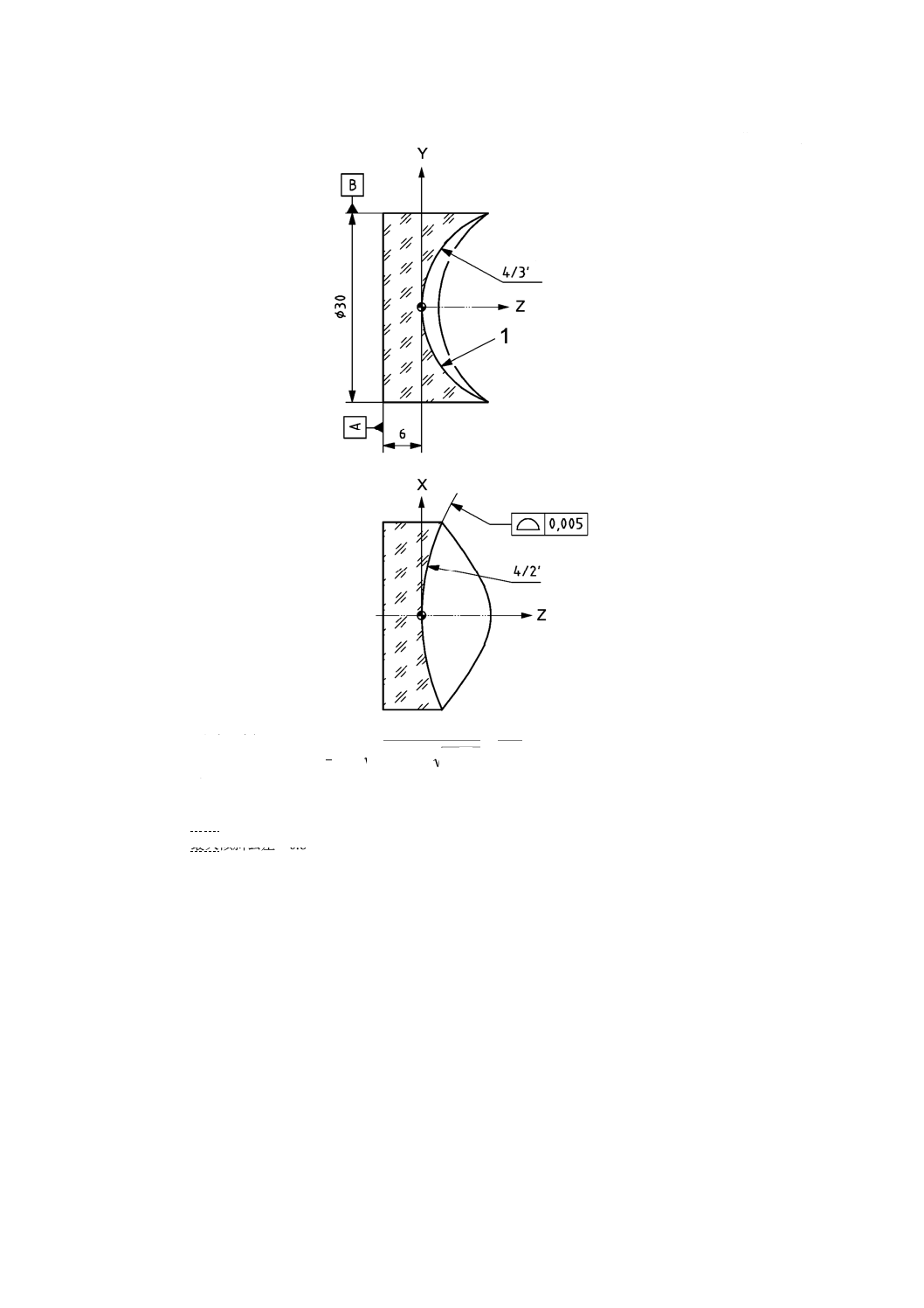
図5は,円形断面をもつ平−トーリックレンズを示す。
データム軸は,外周Bと平面Aとによって与えられる。
図中に示した面の式は,定義弧及び面の回転軸がXZ面内にあることを示している。
二つの断面の面傾斜角度に対してそれぞれ異なる公差が与えられている。また,面全体の最大傾斜公差
も二つの断面で異なる。
b)
a)
13
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
単位 mm
1 トーリック面
[
]
2
2
2
2
y
x
R
R
R
R
Z
X
X
Y
Y
−
−
+
−
−
=
RY=16±0.1
RX=40±0.2
注a) 最大傾斜公差=0.5ʼ
b) 最大傾斜公差=0.8ʼ
基準長さ=3
データサンプリング間隔=0.2
図5−平−トーリックレンズ
b)
a)
14
B 0090-12:2012 (ISO 10110-12:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
非球面タイプの要約
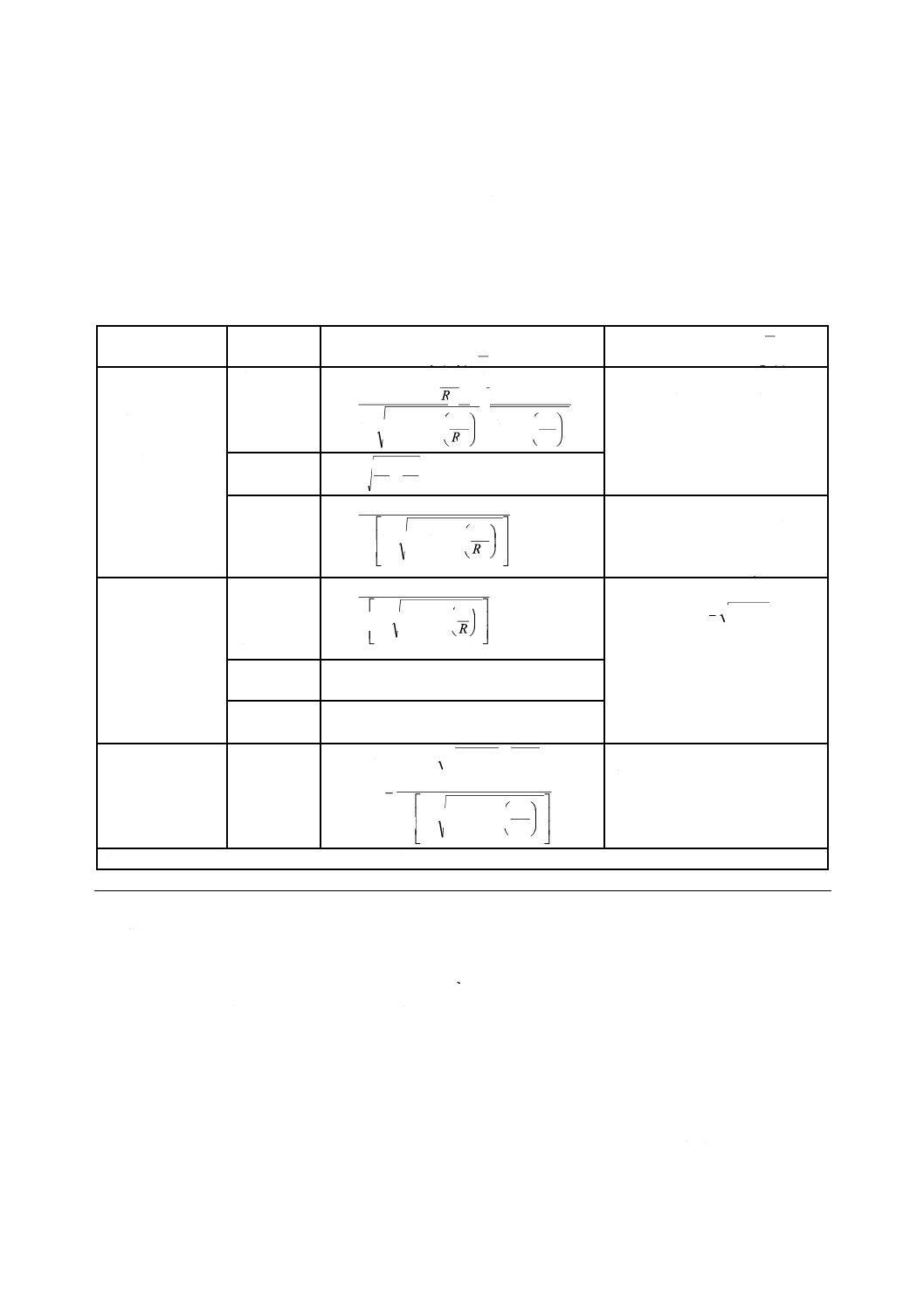
非球面形状を,表A.1に要約する。
表A.1−非球面形状の要約
クラス
基礎面
基礎式
f (x, y) =
べき級数f1 (x, y) =
[トーリック面ではg1(x)]
回転非対称面a)
RX≠RY
κX≠κY
A2i≠B2i
C2i−1≠D2i−1
だ円面
双曲面
放物面
(
)
(
)
2
2
2
2
1
1
1
1
+
−
+
−
+
+
Y
Y
X
X
Y
X
R
y
Rx
R
y
Rx
κ
κ
A4x4+B4y4+A6x6+B6y6+…
+C3 | x |3+…+D3 | y |3+…
すい面
(a≠b)
2
2
2
2
b
y
a
x
c
+
円筒面
(
)
+
−
+
2
U
U
U
2
1
1
1
Ru
R
u
κ
A4x4+A6x6+…+C3 | x |3+…
u=xに対して
B4y4+B6y6+…+D3 | y |3+…
u=yに対して
z軸に関して回転
対称な面
RX=RY=R
κX=κY=κ
h2=y2+x2
だ円面
双曲面
放物面
球面
(
)
+
−
+
2
2
1
1
1
Rh
R
h
κ
A3h3+A4h4+A5h5+…
ここで,
2
2
y
x
h
+
=
すい面
(a=b)
h
a
c
平面(シュミ
ット面)
0
座標軸と一致しな
い回転面
トーリック
面
(
)
[
]
2
2)
(
,
y
x
g
R
R
y
x
f
Y
Y
−
−
=
μ
()
(
)
+
−
+
=
2
2
1
1
1
X
X
X
R
x
R
x
x
g
κ
g1(x)=A4x4+A6x6+…+C3 | x |3
+C5 | x |5+…
注a) 少なくともこれらの不等式の中の一つが有効の場合。
参考文献
JIS B 0633 製品の幾何特性仕様(GPS)−表面性状:輪郭曲線方式−表面性状評価の方式及び手順
注記 対応国際規格:ISO 4288,Geometrical Product Specifications (GPS)−Surface texture: Profile method
−Rules and procedures for the assessment of surface texture(IDT)
JIS B 0090-1 光学素子及びシステム用の製図手法−第1部:通則
注記 対応国際規格:ISO 10110-1,Optics and photonics−Preparation of drawings for optical elements and
systems−Part 1: General(IDT)
JIS B 0601 製品の幾何特性仕様(GPS)−表面性状:輪郭曲線方式−用語,定義及び表面性状パラメー
タ
注記 対応国際規格:ISO 4287,Geometrical Product Specifications (GPS)−Surface texture: Profile method
−Terms, definitions and surface texture parameters(IDT)









