A 3305:2020 (ISO 2394:2015)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 用語及び定義··················································································································· 2
2.1 一般用語 ······················································································································ 2
2.2 設計及びアセスメントに関する用語 ·················································································· 6
2.3 作用,作用効果,環境からの影響に関する用語 ·································································· 10
2.4 構造物の応答,耐力,材料特性,幾何学量に関する用語 ······················································ 12
3 記号······························································································································ 13
3.1 一般 ··························································································································· 13
3.2 ローマ字大文字 ············································································································ 13
3.3 ローマ字小文字 ············································································································ 14
3.4 ギリシャ文字 ··············································································································· 14
3.5 添え字 ························································································································ 15
4 基本事項························································································································ 15
4.1 一般事項 ····················································································································· 15
4.2 構造物に対する要求事項 ································································································ 15
4.3 概念的基礎 ·················································································································· 16
4.4 方法 ··························································································································· 18
4.5 文書化 ························································································································ 21
5 性能のモデル化··············································································································· 21
5.1 一般事項 ····················································································································· 21
5.2 性能モデル ·················································································································· 22
5.3 限界状態 ····················································································································· 23
6 不確定性の表現及びモデル化 ····························································································· 25
6.1 一般事項 ····················································································································· 25
6.2 構造解析のためのモデル ································································································ 27
6.3 結果のモデル ··············································································································· 32
6.4 モデルの不確定性 ········································································································· 32
6.5 実験モデル ·················································································································· 33
6.6 確率モデルの更新 ········································································································· 33
7 リスク情報を活用した意思決定 ·························································································· 34
7.1 一般事項 ····················································································································· 34
7.2 システム同定 ··············································································································· 34
7.3 システムのモデル化 ······································································································ 35
7.4 リスクの定量化 ············································································································ 35
A 3305:2020 (ISO 2394:2015) 目次
(2)
ページ
7.5 意思決定の最適化及びリスク受容 ···················································································· 35
8 信頼性に基づく意思決定 ··································································································· 35
8.1 一般事項 ····················································································································· 35
8.2 更新された確率尺度に基づく決定 ···················································································· 37
8.3 システム信頼性及び部材信頼性 ······················································································· 37
8.4 目標とする破壊確率 ······································································································ 37
8.5 破壊確率の計算 ············································································································ 38
8.6 確率に基づく設計の実現 ································································································ 39
9 準確率論的手法··············································································································· 39
9.1 一般事項 ····················································································································· 39
9.2 基本原則 ····················································································································· 40
9.3 代表値及び特性値 ········································································································· 40
9.4 形式化された安全性検証法 ····························································································· 41
9.5 累積破壊の検証 ············································································································ 43
附属書A(参考)品質マネジメント ························································································ 44
附属書B(参考)構造健全性のライフタイムマネジメント ·························································· 51
附属書C(参考)観測及び実験モデルに基づく設計 ··································································· 58
附属書D(参考)地盤構造物の信頼性 ····················································································· 65
附属書E(参考)コードキャリブレーション ············································································ 73
附属書F(参考)構造のロバスト性························································································· 81
附属書G(参考)人命に対する安全に関する最適化及び基準 ······················································· 92
A 3305:2020 (ISO 2394:2015)
(3)
まえがき
この規格は,産業標準化法第12条第1項の規定に基づき,一般社団法人建築・住宅国際機構(IIBH)
及び一般財団法人日本規格協会(JSA)から,産業標準原案を添えて日本産業規格を制定すべきとの申出
があり,日本産業標準調査会の審議を経て,国土交通大臣が制定した日本産業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。国土交通大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本産業規格 JIS
A 3305:2020
(ISO 2394:2015)
建築・土木構造物の信頼性に関する設計の一般原則
General principles on reliability for structures
序文
この規格は,2015年に第4版として発行されたISO 2394を基に,技術的内容及び構成を変更すること
なく作成した日本産業規格である。
我が国の基規準の要素を取り込みつつ制定され,海外で広く参照されている対応国際規格の技術的内容
について,この規格を通して熟知することは,我が国の建設関係の全ての事業者(ゼネコン,コンサル,
設計事務所など)及び技術者の海外展開に当たり有利になることが期待される。
なお,この規格の附属書A〜附属書Gは,本文の理解を深めるための参考資料である。また,この規格
で点線の下線を施してある参考事項は,対応国際規格にはない事項である。また,この規格は強制的な法
規ではなく,建築物・土木構造物のいずれにおいても,建築基準法などの現行設計基準類への適合が求め
られることに留意されたい。
1
適用範囲
この規格は,建築・土木構造物に関する規準類の作成,並びにその設計及びアセスメントに関する意思
決定のための,リスク情報及び信頼性情報の基礎に関する一般的な原則について規定する。
この規格で提示される原則は,用途の特性又は使用される材料の組合せにかかわらず,大部分の建物,
インフラ構造物及び土木構造物に適用する。また,この規格の適用においては,破壊によって非常に重大
な結果を引き起こす可能性のある特殊な場合では,特定の調整及び詳細化を必要とする。
この規格は,供用期間中の構造物及び構造物を含むシステムの設計及びアセスメントに関する意思決定
に必要な,リスク及び信頼性の原則の活用方法について規定する。互いに関連のある三つのレベルの方法
(リスク情報を活用した方法,信頼性に基づく方法及び準確率論的方法)を利用する。
この規格は,構造物全体[建物,橋りょう(梁),産業施設など],構造物を構成する構造要素及び接合
部の設計に適用する。また,この規格の原則は,建設工程の各段階,構造要素の取扱い,それらの組立て,
現場における全ての作業,維持管理及び補修を含む設計供用期間中における構造物の使用及び撤去を対象
とする。
リスク及び信頼性は,互いに依存する,作用,構造物の応答,耐久性,ライフサイクルにおける性能,
破壊及び損傷による結果,設計規約,施工技量,品質管理手順並びに国の定める要件などの事項に基づき
記載している。
注記1 この規格の適用には,本体及び附属書に記載された内容を超えた知識を必要とする。この知
識が利用可能であり,適用されていることを確認することは,この規格の利用者の責任であ
る。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
2
A 3305:2020 (ISO 2394:2015)
ISO 2394:2015,General principles on reliability for structures(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
用語及び定義
この規格で用いる主な用語及び定義は,次による。
2.1
一般用語
2.1.1
構造物(structure)
様々な作用に対して耐力及び剛性を与えるように設計された,結合された部分を組織的に組み合わせた
もの。地盤構造物を含む。
2.1.2
構造部材(structural member)
物理的に区別できる構造物の部分[例 柱,はり(梁),床・壁及び基礎]。
2.1.3
システム(system)
部分間の相互作用及び部分と環境との相互作用を通じて,環境の中で定義された目的を果たす実体を形
成する,相互に関係,相互に依存又は相互に作用する要素の集まりで境界をもつもの。
2.1.4
構造システム(structural system)
建物又は土木構造物の複数の耐力部材,また,これらの部材がまとまって機能し,環境と相互作用する
働きを包括したもの。
2.1.5
要求(requirement)
人及び環境に対する安全性,機能性,用途,資源投入,費用効率などに関して求められる事項。
2.1.6
適合性(compliance)
定められた要求を満たすこと。
2.1.7
ライフサイクル(life cycle)
要素,システム,建物設備を含む構造物(又はその部分)の計画開始,プロジェクトの定義,設計,建
設,使用開始,運用,維持管理,改修,建替,解体及びその後の処分,リサイクル又は再使用からなる一
連の流れ。
2.1.8
信頼性(reliability)
構造物又は構造部材が,設計時に想定した供用期間中に,所定の要件を満たす能力。
注記1 信頼性は,多くの場合,確率で表している。
注記2 信頼性は,構造物の安全性,使用性及び耐久性を含んでいる。
2.1.9
構造安全性(structural safety)
3
A 3305:2020 (ISO 2394:2015)
所定の期間中,所定の信頼性の水準で,所定の偶発現象効果を含めて,終局限界状態の超過を避ける(構
造物又は構造部材の)能力。
注記 建築基準法令では,終局限界状態に相当するもの以外の状態も想定して,各種の荷重・外力が
作用するときに安全な構造とするための基準が定められている。
2.1.10
耐久性(durability)
環境作用の影響下において,所定の期間にわたり,計画された維持管理を基に設計時に要求された性能
を満足する,構造物又は構造部材の能力。
2.1.11
暴露事象(exposure events)
構造物に対して損傷の原因となる又は性能指標に影響を与える可能性がある事象。
2.1.12
アセスメント(assessment)
既存構造物の信頼性を確かめる目的で行われる一連の活動。
2.1.13
改修(upgrading)
構造性能を向上させる又は用途変更を可能にするために,既存構造物を改変する建設行為。
2.1.14
(構造物の)修復[repair (of a structure)]
損傷を受けたり劣化したりした構造物の状態を元に戻すこと。
2.1.15
補修(rehabilitation)
既存構造物の修復又は改修によって構造物をよみがえらせること。
2.1.16
モニタリング(monitoring)
構造物の状態,作用又は構造物の応答を,頻繁に又は継続的に,通常,長期にわたり,観察したり測定
したりすること。
2.1.17
点検(inspection)
品質管理及び構造物の現況を確かめるための状態評価として実施される現地調査。
2.1.18
(JISでは不採用とした。)
2.1.19
信頼性設計(reliability-based design)
構造物の所定の信頼性水準を確保するための設計手法。
2.1.20
部材信頼性(member reliability)
単一の支配的な破壊モードをもつ単一構造部材の信頼性。
2.1.21
システム信頼性(system reliability)
4
A 3305:2020 (ISO 2394:2015)
複数の部材をもつシステム又は複数の破壊モードをもつ単一構造部材の信頼性。
2.1.22
母集団(population)
同一の確率表現(平均値など)が有効な要素の集合。
2.1.23
標本空間(outcome space)
ランダムな現象の全ての可能な結果の集合。
2.1.24
構成要素(constituent)
性能に寄与する要素又は材料。
2.1.25
性能指標(performance indicator)
構造物の特性を定量的に記載するための尺度となるパラメータ。
2.1.26
構造性能(structural performance)
安全性,使用性,耐久性及びロバスト性に関する構造物の能力(例 耐荷能力,剛性など)の程度。
2.1.27
耐力(resistance)
構造物(又はその一部)が破壊することなく作用に耐える能力。
2.1.28
品質管理(quality control)
構造物の設計,施工,使用及び撤去の品質を管理する活動。
2.1.29
損傷(damage)
構造性能に好ましくない影響を及ぼす可能性のある,構造物の状態の好ましくない変化。
2.1.30
倒壊(collapse)
構造物が崩壊機構に至ること。構造物(又はその一部)の分離及び落下を含む。
2.1.31
劣化(deterioration)
時間とともに,信頼性を含む構造性能が低下すること。
注記 劣化は,自然に発生する化学的,物理的,生物的作用,通常の又は過酷な環境作用,疲労の原
因となるような繰返し作用,使用による摩耗及び構造物の不適切な運用及び維持管理によって
引き起こされる。
2.1.32
使用性(serviceability)
予想されるあらゆる作用下で,通常用途のために適切に機能する,構造物又は構造部材の能力。
2.1.33
シナリオ記述(scenario description)
発生可能性を考慮しながら,性能指標に影響を与えるような様々な一連の事象を,選択して記述するこ
5
A 3305:2020 (ISO 2394:2015)
と。
2.1.34
結果の重大性等級(consequence class)
構造物の破壊の,結果の重大性による分類。
2.1.35
(JISでは不採用とした。)
2.1.36
信頼性水準のレベル分け(reliability differentiation)
予想されるあらゆる破壊の結果及び建設費用を考慮に入れた,建設のための資源の社会経済学的最適化。
2.1.37
ハザードシナリオ(hazard scenario)
システムが経験する可能性があり,システムそのもの,人及び環境に危害を及ぼす可能性がある,過渡
的に変化する状況の集合。
2.1.38
リスク情報を活用した設計(risk-informed design)
人命喪失,負傷,環境の質の被害及び金銭的損失を含むあらゆるリスクを十分考慮して最適化する設計。
注記 リスクに基づく設計は,現時点では一般的に全ての国の国内規格規準においては認められてい
ない。
2.1.39
(JISでは不採用とした。)
2.1.40
リスク(risk)
不確定性が目的に及ぼす影響。
注記 意思決定理論の観点からは,リスクとは望ましくないあらゆる結果の期待値,すなわち,事象
の結果とその確率の積とを全て足し合わせたものである。
2.1.41
追加人命救助費用(marginal lifesaving cost)
追加の安全対策によって更に1人の生命を救うための費用の増分。
2.1.42
リスクスクリーニング(risk screening)
あらゆるハザードの状況に対して同定されるリスクの調査及び分類。
2.1.43
生活の質指標,LQI(Life Quality Index)
GDP,出生時平均余命及び労働時間に対する余暇時間の比の関数として表される,人命安全に関する社
会的選好及び投資能力の指標。
2.1.44
利用計画(utilisation plan)
構造物の(一つ以上の)用途を含み,維持管理要件と対応する要求性能を含む構造物の運用状態を記載
した計画。
6
A 3305:2020 (ISO 2394:2015)
2.1.45
信頼性目標(reliability target)
できる限り近づけるべき,所定の平均的な許容破壊確率で表された目標。
注記 信頼性目標は一般的にはモデル依存であり,それぞれの場合に対して,使用されるモデルに基
づき,設定することが望ましい。
2.1.46
ロバスト性(robustness)
有害かつ予見できない事象(火災,爆発,衝撃など)又は人的過誤の結果に対し,元の原因から不釣合
いな程度に大きい被害を受けることなく耐えることができる構造物の能力。
2.1.46-1
損傷不感性(damage insensitivity)
2.1.46による。
2.1.47
ハザード(hazard)
異常かつ過酷な脅威(例 起こり得る異常な作用又は環境からの影響,不十分な強度及び剛性又は意図
された範囲からの有害な方向への過度な逸脱など。)。
2.2
設計及びアセスメントに関する用語
2.2.1
設計及びアセスメントの局面(design/assessment situations)
関連する限界状態を超過しないことが実証されるべきある特定の期間を示す物理的状態の集合。
注記 設計の局面(design situation)及びアセスメントの局面(assessment situation)とは,設計及びア
セスメントを行うに当たって想定する状況のことを指す。
2.2.2
永続的状況に対する設計の局面(persistent design situation)
構造物にとっての通常の使用状態。
2.2.3
過渡的状況に対する設計の局面(transient design situations)
建設中,修繕中などの,構造物の設計供用期間よりも極めて短い期間における使用又は暴露といった一
時的な状態。
2.2.4
偶発的状況に対する設計の局面(accidental design situations)
浸水,火災,爆発及び局所的破壊を含む,起こり得る例外的な構造物の使用及び暴露の状態を含む設計
の局面。
2.2.5
(JISでは不採用とした。)
2.2.6
破壊(failure)
限界状態を超過して,望ましくない領域に入ること。例えば,構造物若しくは構造部材の耐荷能力の不
足又は不十分な使用性,又は土若しくは岩の強度が抵抗を与える上で重要な役割を担う地盤の破壊若しく
は過度の変形。
7
A 3305:2020 (ISO 2394:2015)
2.2.7
限界状態(limit states)
それを超えると構造物が設計における要求性能を満足できない状態。
2.2.8
終局限界状態(ultimate limit states)
最大耐荷能力に関わる限界状態。
注記 建築基準法令に定める構造計算のうち,限界耐力計算では,最大級の荷重・外力が作用すると
きの状態として“建築物の地上部分が倒壊・崩壊しないこと”を確かめる方法が定められてい
る。これらの方法で想定する状態が,終局限界状態の定義におおむね近いものである。
2.2.9
設計における要求性能(design criteria)
各限界状態に対して満たされるべき状態を定量的に定式化したもの。
2.2.10
使用限界状態(serviceability limit states)
通常の使用に関する機能を決定する基準に関わる限界状態。
注記 建築基準法令が定める構造計算のうち,限界耐力計算では,日常的な荷重・外力が作用すると
きの状態として“建築物の構造耐力上主要な部分に損傷が生じないこと及びそれらの変形又は
振動によって建築物の使用上の支障が生じないこと”,中程度の荷重・外力が作用するときの状
態として“建築物の構造耐力上主要な部分に損傷が生じないこと又は建築物が損傷しないこと”
をそれぞれ確かめる方法が定められている。これらの方法で想定する状態が,使用限界状態の
定義におおむね近いものである。
2.2.11
不可逆的限界状態(irreversible limit states)
超過の原因となった作用が取り除かれても永続的に超過したままであるような限界状態。
2.2.12
可逆限界状態(reversible limit states)
一旦超過しても超過の原因となった作用が取り除かれれば非超過となる限界状態。
2.2.13
形式的限界状態(condition limit state)
明確に定義され,かつ,管理可能な,直接的な負の結果がない限界状態。明確に定義すること又は計算
することが難しい実際の限界状態の近似であることが多い。
注記 耐久性の観点に関連する適用においては,形式的限界状態は耐久限界状態と呼ばれることが多
い。
2.2.14
限界状態関数(limit state function)
基本変数の関数g(X1, X2, …, Xn)。g(X1, X2, …, Xn)=0のとき,限界状態を表す。
注記 限界状態関数の符号が正のときは設計における要求性能を満足している状態で,負のときは満
足していない状態である。
2.2.15
基本変数(basic variables)
8
A 3305:2020 (ISO 2394:2015)
作用,環境からの影響,材料並びに地盤の特性及び幾何量を特徴付ける物理量を表す変数。
2.2.16
設計供用期間(design service life)
構造物又は構造部材が,予期された維持管理の下,実質的な修復を必要とせずに,意図された用途に使
用すると想定される期間。
2.2.17
モデル不確定性(model uncertainty)
物理的又は統計的モデルの正確さに関する不確定性。基本変数として扱う。
2.2.18
偶然的不確定性(aleatory uncertainty)
典型的には荷重環境,構造物の幾何量及び材料特性と関連する固有の不確定性。
2.2.19
認識論的不確定性(epistemic uncertainty)
一般に測定又は理論の進歩によって低減され得る,知識の不足による不確定性。
注記 偶然的不確定性と認識論的不確定性との厳密な境界は必ずしも明確ではない。
2.2.20
不確定性の階層モデル(hierarchical modelling of uncertainty)
他の確率変数の関数として表されるモデル。
2.2.21
確率論的手法(probabilistic methods)
関係する基本変数を,離散的又は連続的な確率変数,確率過程及び確率場として取り扱う検証手法。
2.2.22
信頼性指標,β(reliability index)
破壊確率pfの代わりに用いられるもの。Φ−1を標準正規分布の逆関数として,β=−Φ−1(pf)と表される。
2.2.23
目標信頼性(指標)[target reliability (index)]
許容できる安全性又は許容できる使用性に対応する信頼性(指標)。
2.2.24
準確率論的手法(semi-probabilistic)
代表値及び部分係数,並びに関連があれば付加的な値を用いて基本変数に付随する不確定性及びばらつ
きに対して余裕を付与する検証手法。
注記 部分係数は,個々の確率変数又は包括的な変数と関係する場合がある。
2.2.24-1
部分係数手法(partial factors methods)
2.2.24による。
2.2.25
構造モデル(structural model)
解析,設計及び検証に用いるために,構造物を物理的,数学的又は数量的に理想化したもの。
2.2.26
静的システム(static system)
9
A 3305:2020 (ISO 2394:2015)
静的解析,設計及び検証に用いるために構造物を理想化したもの。
2.2.27
検証レベル(levels of verification)
あらゆる設計及びアセスメントの局面において,目標に適合しているか評価を行うために使用される検
証のレベル。
注記 レベルは,リスクレベル,確率論的な信頼性レベル,準確率論的なレベルが一般に認められて
いる。
2.2.28
一次信頼性手法及び二次信頼性手法,FORM and SORM(First/Second Order Reliability Methods)
信頼性指標βを決定するために用いられる数値的手法。
2.2.29
信頼性要素(reliability elements)
部分係数形式において用いられる数量。それによって所定の目標信頼性の達成を想定する。
注記 一般に信頼性要素は,部分係数及び荷重組合せ係数を含んでいる。
2.2.30
特性値(characteristic value)
所定の超過確率となるよう統計的に定められることが望ましい値。
注記 変動作用に対しては,特性値は次のいずれかに対応する。
− ある特定の基準期間において,あらかじめ定められた非超過確率に対応する上方値又はあ
らかじめ定めた達成確率(超過確率)に対応する下方値。
− 統計的分布が分からない場合に定める公称値。
2.2.31
基準期間(reference period)
信頼性指標又は破壊確率を評価するための期間。変動作用及び/又は偶発作用の設計値を評価するため
の基礎として用いられる。
2.2.32
公称値(nominal value)
例えば,経験,物理的な制約など,非統計的な根拠に基づいて設定される値。
2.2.33
代替荷重経路,ALP(alternative load path)
荷重が作用する点から抵抗する点に伝達される代替経路。
2.2.34
結果の重大さの低減対策(consequence reducing measures)
破壊の直接的又は間接的な結果の重大さを低減することによって,結果として全リスクを低減するため
の対策。
2.2.35
主要素(key element)
構造物の限界状態の性能に関わる構造部材。
2.2.36
コードキャリブレーション(code calibration)
10
A 3305:2020 (ISO 2394:2015)
所定の規準形式において,信頼性目標を達成するための信頼性要素を決定すること。
2.2.37
載荷試験(load testing)
その挙動又は特性を評価したり,耐荷能力を予測したりするために,載荷することによって行う構造物
(又はその一部)の試験。
2.3
作用,作用効果,環境からの影響に関する用語
2.3.1
作用(action)
構造物に作用する集中荷重若しくは分布荷重(直接作用),構造物に強制的に作用したり,拘束したりす
る変位若しくは温度効果又は材料特性若しくは構造物の寸法に経時的な変化をもたらし得る環境からの影
響の総称。
注記 一般に作用は,建築基準法第20条にある“自重,積載荷重,積雪荷重,風圧,土圧及び水圧並
びに地震その他の震動及び衝撃”などの“荷重及び外力”のほか,材料特性又は構造物の寸法
に変化をもたらす可能性のある自然に起こる化学的,物理的又は生物的作用などを含んでいる。
さらに,通常の又は過酷な環境的影響,使用による磨耗,構造物の不適切な使用,維持管理の
不備などによる影響などを含んでいる。また,要素間で相互作用があることがあり,場合によ
っては,作用と構造物の応答との間に相互作用があることもある。
2.3.2
単一作用(individual action single action)
構造物に作用する他のいかなる作用からも時間的,空間的に独立しているとみなすことのできる作用。
2.3.3
永続作用(permanent action)
設計供用期間を通じて継続的に作用すると考えられる,その大きさの時間的なばらつきが平均値に比べ
て小さい作用。
2.3.4
変動作用(variable action)
設計供用期間中に作用すると考えられる,その大きさの時間的なばらつきが無視もできず,単調でもな
い作用。
2.3.5
偶発作用(accidental action)
設計供用期間中に発生する見込みが有意に大きな値でない作用。
2.3.6
固定作用(fixed action)
構造物のある一点を定めれば,構造物全体について,その大きさ及び方向が明確に定められるというよ
うな,固定された分布をもつ作用。
2.3.7
自由作用(free action)
構造物に対して,ある限界内で任意の空間分布をもち得る作用。
2.3.8
(JISでは不採用とした。)
11
A 3305:2020 (ISO 2394:2015)
2.3.9
(JISでは不採用とした。)
2.3.10
(JISでは不採用とした。)
2.3.11
作用の設計値(design value of an action)
準確率論的検証において用いられる,信頼性目標を満足するようにキャリブレーションされた作用値。
注記 部分係数手法では,この値は,作用の代表値に部分係数γFを乗じることで得られる。
2.3.12
(JISでは不採用とした。)
2.3.13
プレストレス(prestress)
強制変形を導入することで構造物に意図的にかけられる力。
2.3.14
地盤作用(geotechnical action)
地盤,盛土又は地下水によって構造物に伝達される作用。
2.3.15
地震作用(seismic action)
地震動によってもたらされる作用。
2.3.16
積載荷重(imposed load)
建物内の人間及び占有物によってもたらされる荷重。
2.3.17
(JISでは不採用とした。)
2.3.18
環境からの影響(environmental influences)
構造物を構成する材料を劣化させる物理的,化学的又は生物的影響。結果的に,使用性及び安全性に悪
影響を及ぼす可能性がある。
2.3.19
荷重配置(load arrangement)
自由作用の作用点,大きさ及び方向を同定すること。
2.3.20
作用の代表値(representative value of an action)
特性値,公称値,組合せ値,頻繁値及び半永続値のうちの一つ。
2.3.21
組合せ値(combination value)
幾つかの値の組合せによって引き起こされる作用効果の超過確率が,単一作用による設計値の超過確率
にほぼ等しいとして定められる値。
注記 “組合せ値”は,係数Ψ0によって低減された特性値として表すことがある。
12
A 3305:2020 (ISO 2394:2015)
2.3.22
作用モデル(action model)
作用の大きさ,位置,方向,継続時間などを表すモデル。
2.3.23
頻繁値[(しばしば)超過する値](frequent value)
選択した期間内で超過する時間の合計が選択期間のうち,所定のほんの一部でしかないとするか,超過
頻度が所定の値に限られているとして定める値。
注記 “頻繁値”は,係数Ψ1によって低減された特性値として表すことがある。
2.3.24
半永続値(quasi-permanent value)
選択した期間内で超過する時間の合計がその期間の半分であるとして定める値。
注記 “半永続値”は,係数Ψ2によって低減された特性値として表すことがある。
2.3.25
荷重状態(load case)
特定の限界状態の詳細な検証で考慮する,矛盾のない荷重配置,一連の変形及び不整。
2.3.26
荷重組合せ(load combination)
所定の限界状態に対する構造物の信頼性を検証する場合に同時に考慮すべき複数の作用及びそれらの設
計値。
2.3.27
(JISでは不採用とした。)
2.3.28
(JISでは不採用とした。)
2.3.29
(JISでは不採用とした。)
2.3.30
(JISでは不採用とした。)
2.3.31
(JISでは不採用とした。)
2.3.32
信頼性解析(reliability analysis)
ある対象物の信頼性を評価するための解析。
2.4
構造物の応答,耐力,材料特性,幾何学量に関する用語
2.4.1
材料モデル(material model)
内力又は応力とひずみを含む変形との関係を表すモデル。
注記 このような関係の変数として,弾性係数,降伏限界,終局強度などがあり,それらは一般に確
率変数と考えられる。それらは時間又は空間に依存している場合もある。変数の間には,しば
しば相関がある。
13
A 3305:2020 (ISO 2394:2015)
2.4.2
剛性(stiffness)
変形とそれを引き起こす作用とを関係付ける特性。
2.4.3
材料特性値(characteristic value of a material property)
供給における材料特性の統計的分布の所定のフラクタイル値。
注記 材料特性値は,JIS A 1108,JIS Z 2241などによって求める値。
フラクタイル値(fractile value)とは,累積確率が設定した確率以下となる確率変数の値:xp
を意味し,例えば,“0.05(すなわち,5 %)フラクタイルはxp”という使い方をする。また,
パーセンタイル値も同じ意味である。
2.4.4
(JISでは不採用とした。)
2.4.5
換算係数,換算関数(conversion factor or function)
試験体から得る特性を計算モデルのそれに変更する係数又は関数。
2.4.6
(JISでは不採用とした。)
2.4.7
幾何学的特性(geometrical properties)
構造物及び構造部材を記載する幾何学的データ(例 寸法,角度など)。
注記 ある構造物は,一般に一次元部材,二次元部材,三次元部材からなるモデルによって記載する
ことが可能である。モデルに含まれる幾何学特性は,通常公称値を参照する。
2.4.8
幾何学量の設計値(design value of a geometrical quantity)
数量を加えたり乗じたりすることで調整される特性値。
3
記号
3.1
一般
この規格で用いる主な記号は,次による(ISO 3898参照)。1か所だけで用いる記号は,その箇所で説明
し,ここでは記載しない。
3.2
ローマ字大文字
A
偶発作用
Ad
偶発作用の設計値
AEd
地震作用の設計値
AEk
地震作用の特性値
C
使用性の制限
F
一般的な作用
Fk
作用の特性値
Frep
作用の代表値
Fd
作用の設計値
14
A 3305:2020 (ISO 2394:2015)
G
永続作用
Gd
永続作用の設計値
Gd,inf
永続作用の下方設計値
Gd,sup
永続作用の上方設計値
Gk,j
j番目の永続作用の特性値
Gk,j,inf
j番目の永続作用の下方設計値
Gk,j,sup
j番目の永続作用の上方設計値
Q
変動作用
Qd
変動作用の設計値
Qk
変動作用の特性値
Qk,1
主の変動作用の特性値
Qk,j
j番目の変動作用の特性値
R
耐力,リスク
Rd
耐力の設計値
Rk
耐力の特性値
S
作用効果
Sd
作用効果の設計値
Sd,dst
不安定作用の設計値
Sd,stb
安定作用の設計値
X
基本変数
Y
モデル出力変数
3.3
ローマ字小文字
a
幾何学量
Δa
付加的幾何学量
m
材料特性
pf
破壊確率
ps
生存確率
pft
目標とする破壊確率
pfs
pfの所定値
t
時間
g(X, t)
限界状態関数
3.4
ギリシャ文字
β
信頼性指標
βt
目標信頼性指標
γ
部分係数
γf
作用に対する部分係数
γF
モデル不確定性及び幾何学的不確定性を考慮した作用に対する一般化部分係数
γG
永続作用に対する部分係数
γQ
変動作用に対する部分係数
γm
材料特性に対する部分係数
15
A 3305:2020 (ISO 2394:2015)
γM
材料,モデル,幾何の不確定性を考慮した耐力に対する一般化部分係数
γS
作用効果に対するモデル不確定性の部分係数
γR
耐力に対するモデル不確定性の部分係数
γI
構造物の重要度,破壊の結果を考慮した係数
θ
モデル不確定性の係数
θS
作用効果のモデル不確定性の係数
θR
耐力のモデル不確定性の係数
Ψ0
作用の組合せ値を決める係数
Ψ1
作用の頻繁値を決める係数
Ψ2
作用の半永続値を決める係数
3.5
添え字
i
基本変数(作用)番号
j
基本変数(作用)番号
k
特性値
d
設計値
1
主の作用
4
基本事項
4.1
一般事項
この箇条では,構造物のリスク及び信頼性を適切な水準で確保するための目的,要求事項,概念的な基
礎,方法及び文書化について規定する。箇条5以降では,これらの原則の最も中心的な部分をより詳細に
規定する。附属書では,実用に供する上での基本的な前提条件としての品質管理の役割及び利用を含めた,
この規格の適用上,特に重要な側面に関する追加的な手引及び情報を提供する。
4.2
構造物に対する要求事項
4.2.1
構造物に対する基本的要求事項
構造物は,その供用期間内に社会的機能を支え,持続可能な社会的発展を促進させるように,計画,設
計,施工,運用,維持管理及び撤去されなければならない。
注記1 構造物が社会に供給する機能に着目すると,社会的機能は構造物の位置付けを包含する。例
えば,電柱は単に電線を支持しているのではなく,産業及び医療への電気の供給もしている。
破壊の結果及び構造物の性能に対する要求事項は,この観点から定められている。
特に,構造物は適切な水準のリスク及び信頼性をもちながら,次の要求性能を満たさなければならない。
− 供用期間を通して,考えられる全ての作用下において適切に機能する。すなわち,サービス及び機能
性を確保する。
− 建設中,想定される使用期間中及び撤去中において発生する,極大及び/又は頻繁に繰り返す作用,
永続的な作用及び環境暴露に耐える。すなわち,損傷及び破壊に関する安全性及び信頼性を確保する。
− 自然ハザード,事故,人的過誤のような異常で予期できない出来事によって深刻な損傷又は連鎖的破
壊を被ることがないようなロバスト性がある。すなわち,十分なロバスト性を確保する。
注記2 持続可能性は,次のような性能指標と関連している。
− 人々の安全性
− 目的の達成に関する信頼性
16
A 3305:2020 (ISO 2394:2015)
− 環境の質
− 費用効率
− 二酸化炭素排出量の最少化
− 自然資源の消費の最少化
− エネルギーの使用の最少化
構造物の供用期間は,構造物の位置付け並びに設計及びアセスメントの全体的な観点を考慮し最適化し
なければならない。通常,構造物の供用期間に関わる決定は,構造物を必要とする期間と個々の要素に対
してレベル分けされた戦略とによって,供用期間中に構造物から得られる便益を最適化する可能性に基づ
かなければならない。耐久性に基づく構造物の設計の概念は,ISO 13823 [21]で取り扱われている。
4.2.2
目標とする性能水準
適切な信頼性の程度は,起こり得る破壊の結果の大きさ,これに伴う費用,破壊及び被害のリスクを低
減するために必要な労力と手続の水準とを考慮して判断しなければならない。
構造設計及びアセスメントにおける意思決定において,構造物の受容可能なリスク,安全性及び信頼性
の水準を確保するには,受容規準及びその他の要求事項を定式化し,評価し,そして満足しなければなら
ない。これらの要求事項の幾つかは,社会によって設定された人の安全及び環境に対する要求に関係しな
ければならない。その他のものは,所有者によって規定されるような構造物の機能性の信頼性と関係しな
ければならない。
人命保護に対する規制において,追加人命救助費用の基本的原則(注記1参照)が当てはまり,また,
利用が推奨される。追加人命救助の原則の使用は,構造物を利用する又は近傍にいる人々の安全性が,あ
る一定の水準を保つことを保証する。一定の水準とは,更なる人命保護のための追加の安全対策に関連す
るコストが,対応する追加人命救助費用を超えることである。
注記1 人命救助の労力をその効率が最も高い活動及び状況に確実に向けるという更なる人命救助費
用の原則に基づくことで,リスク及び信頼性の要求水準のレベル分けが容易となる。この原
則は,附属書Gで記載するように,ALARPの原則の一般的定式化と一貫している。追加人
命救助費用を測るための手法として,生活の質指標(LQI)などがある。同原則は,準確率
論的設計規準のための目標の信頼性水準の同定の基礎を形成し,そこでは目標信頼性は破壊
の結果及び安全性向上効率の関数として与えられている(附属書G参照)。
対象とするプロジェクトの特性に依存しながらも,構造物の要求性能を,環境の質への被害並びに天然
資源の利用及び投入,大気への排出に関連し,考慮しなければならない。そのような場合,要求性能を,
想定した重大な事象の最大年間発生頻度又は合計使用量及び/又は排出量の期待値といった点から明示し,
そして満足しなければならない。これらの要求を,4.4.2.1に規定するように,経済的最適化における制約
条件又は代替の目的関数として理解し,説明しなければならない。
注記2 環境の質,天然資源の利用及び投入並びに大気への排出の要求事項は,これまでのところ一
般的には定式化されていない。しかしながら,ぜい(脆)弱な環境での海底油田,ガス田の
開発,巨大なダム計画など,この点において結果が甚大となる可能性のある特定の計画では,
一般的には,そのような要求に関して特別な考慮をすることが意思決定の根拠の一部となる。
4.3
概念的基礎
4.3.1
構造物に関する決定
構造物に関する決定は,構造物の計画,設計,施工,運用,維持管理及び撤去の過程に関する全ての決
定を含むことを理解しなければならない。
17
A 3305:2020 (ISO 2394:2015)
注記 構造物に関する決定は,耐力,変形,移動,耐久特性,安全性,経済性,材料消費,エネルギ
ー消費などの点から構造物に影響を与え,その結果,それらの性能及び持続可能な発展へのイ
ンパクトにも影響を与える。個別のプロジェクトのレベルにおける,典型的な決定は,次の選
択を含み得る。
− 構造システム
− 材料
− 断面特性
− 接合部及び構造物の構造詳細
− 実験室及び現場における検査,試験並びに監視
− 損傷の検知,防止,低減の能動的及び受動的な手段
− アセスメント,維持管理及び修復
− レトロフィット又は補強
− 撤去
− 更新
構造物に関する決定の基礎となる全ての仮定の妥当性(例 利用可能な知識,情報の妥当性及び不確定
性,使用目的,供用期間,並びに環境による荷重及び運用にかかる荷重)は,制御し,保証し,文書化す
ることが望ましい。又は構造物の性能が,仮定からの起こり得る逸脱又はずれがあってもなお適切である
ということが保証されることが望ましい。
構造物の性能確保のための中心的役割を果たすことから,品質マネジメントを構造物の設計及びアセス
メントに関係する意思決定プロセスの中に,完全に一体化しなければならない(附属書A参照)。特に,
個々のプロジェクトにおいて,品質マネジメント及び品質保証においては,次の点に対応しなければなら
ない。
− 品質計画
− 設計の品質管理
− 建設の品質管理
− 材料,建設機械及び組立ての品質管理
− 作業員の資格,施工技量及び手順の品質管理
− 前提条件の品質管理
− 品質管理及び品質マネジメントの文書化
4.3.2
構造性能のモデル化
設計における決定は,4.2.2に規定した要求性能を通して評価しなければならない。そのため,モデルは
これらの要求性能のために構築することが望ましく,モデル化によって,それら要求性能の定量化が可能
となる。要求性能のモデル化は,構造物の全ライフサイクルを通した,構造物の用途,人々の安全性及び
環境負荷並びに経済性に関係する全ての関連事項を扱わなければならない。構造物及びその周辺の間の相
互作用(すなわち,構造物が受けるあらゆる暴露及び構造物が影響を与え得る暴露),構造物に付随する設
備,例えば,考えられる機械及び電気系統の間の依存性並びに人的組織的過誤の影響のモデル化に,特別
な配慮をしなければならない。そのモデルは,性能に影響を与えるような様々な事象の連鎖に関するシナ
リオ記述を基本として,発生可能性及び結果を考慮しながら構築しなければならない。
関連する事象のシナリオの同定及び説明においては,次の事象を区別しなければならない。
− 暴露事象,すなわち,作用,人的過誤及び化学的環境
18
A 3305:2020 (ISO 2394:2015)
− 構成要素の被害及び破壊事象,すなわち,直接的な結果
− 機能喪失及び/又は連鎖的破壊(進行性破壊),すなわち,間接的な結果
注記1 暴露事象は,構造物に対して損傷をもたらし得るか又は構造物の性能指標に影響を与え得る
全ての事象を表す。ここでの例には,運用にかかる荷重,環境による荷重,腐食性化学物質,
人的過誤,低品質な設計,材料及び建設を含む。荷重及び他の環境・化学的作用の同時作用
のような暴露事象のシナリオを表現することも重要である。
注記2 構成要素の被害及び破壊事象とは,個々の断面及び接合部のような構造物の一部の破壊又は
損傷と関連するものである。個々の要素の性能のモデル化,すなわち,ある暴露シナリオに
対してどの程度被害を受け,損傷するかについては,限界状態関数の定式化及び解析によっ
て裏付けられる(箇条5参照)。
注記3 構成要素の被害及び破壊事象に引き続いて発生し間接的な結果につながる,構造物の機能喪
失及び/又は連鎖的破壊は,ロバスト性と関係がある。関連するリスクの定量化は,附属書
Fで説明している[式(F.4)参照]。
4.3.3
知識の不確定性及びその取扱い
構造物に関する決定では,自然本来のばらつき(偶然的不確定性)及び知識の不足(認識論的不確定性)
のような,性能に関する全ての不確定性を考慮しなければならない。
不確定性は,確率変数,確率過程及び/又は確率場のような確率論的モデルを通して,決定の過程にお
いて表現されなければならない。確率論的モデルでは,考慮する不確定性と事象との間にある時間及び空
間依存性を表現しなければならない。その上で,気候変動及び人口増加の影響のような,考えられる非エ
ルゴード的な現象を,モデル化の中で扱わなければならない。
注記1 ベイズ確率理論は,全面的なリスク及び信頼性に基づく設計及びアセスメントを行うための
基礎を形成する(4.4.2及び箇条5参照)。さらに,ベイズ確率モデルは,キャリブレーショ
ンを通して,準確率論的設計の規準(4.4.3参照)の基礎を形成する(附属書E参照)。
不確定性の定量化及びその確率論的表現は,主観的情報及び利用可能な事実の組込みを容易にするもの
でなければならない。
注記2 新しい構造物が設計されるとき,幾つかの方面についての知識は,まだ極めて一般的な水準
である。関連する不確定性はそのために比較的大きく,様々な品質管理手法,他の仕様の下
で時間をかけて蓄積されたデータ及び経験を考慮して,モデル化している(附属書A及び附
属書C参照)。既存構造物において,試験,監視,検査及び維持管理計画に関連して,確率
論的モデルの(ベイズ)更新の確率から恩恵を受けることが重要である(附属書B参照)。
このように,観測という観点からより多くの事実が評価に用いられるにつれて,リスク及び
信頼性が徐々に更新される。
荷重・耐力係数設計法又は部分安全係数設計法に基づく構造物の設計(4.4.3参照)においては,規定さ
れる設計式,荷重状態及び荷重組合せ係数とともに,設計値及び特性値によって,不確定性を表現しなけ
ればならない。特性値は,必要に応じて,例えば,荷重及び材料特性に関連する利用可能な情報から構成
しなければならない。構造物の設計及びアセスメントの準確率論的方法の詳細は,箇条9で規定する。
4.4
方法
4.4.1
一般事項
設計及びアセスメントにおける決定は,想定されるリスクに関係する情報を基本にしなければならない。
破壊の結果及び損傷が十分に理解され,通常の範囲内である場合には,全面的なリスクアセスメントでは
19
A 3305:2020 (ISO 2394:2015)
なく信頼性に基づく評価が適用可能となる。結果に加えて破壊モード及び不確定性の表現が分類され標準
化することができる場合には,より簡便な準確率論的方法を用いることが望ましい。
リスク情報を活用した方法及び信頼性に基づく方法は,準確率論的設計規準によってカバーされない特
別な構造物並びにプロジェクトのための設計及びアセスメントの決定を支援するためだけでなく,準確率
論的手法のキャリブレーションにも適用しなければならない。
4.4.2
リスク情報を活用した方法及び信頼性に基づく方法
4.4.2.1
リスク情報を活用した,設計及びアセスメントにかかる決定
リスク情報を活用した設計及び/又はアセスメントにおいては,人命の喪失及び負傷,環境の質に対す
る被害並びに金銭的損失を考慮した全リスクを正当に考慮し,決定を最適化しなければならない。全リス
クの評価で考慮する対象期間は,構造物が機能を提供する期間に基づいて決定しなければならない。
全リスクのアセスメントは,シナリオの表現を基本とし(附属書F参照),直接的及び間接的な結果,
暴露,構成要素の損傷及び破壊事象の確率モデルによらなければならない。
受容性の観点から人命の安全及び環境の質に関わる構造物の性能を評価することが望ましい(4.2,箇条
7及び附属書G参照)。これらの制約内において,便益の期待値の最大化に基づいて,決定を最適化しな
ければならない。このプロセスにおいて,この箇条に含まれる原則と調和する限り,他の指標も考慮され
得る。受容規準は,4.2.2で規定したように最適化の制約条件として考慮しなければならず,設計及びアセ
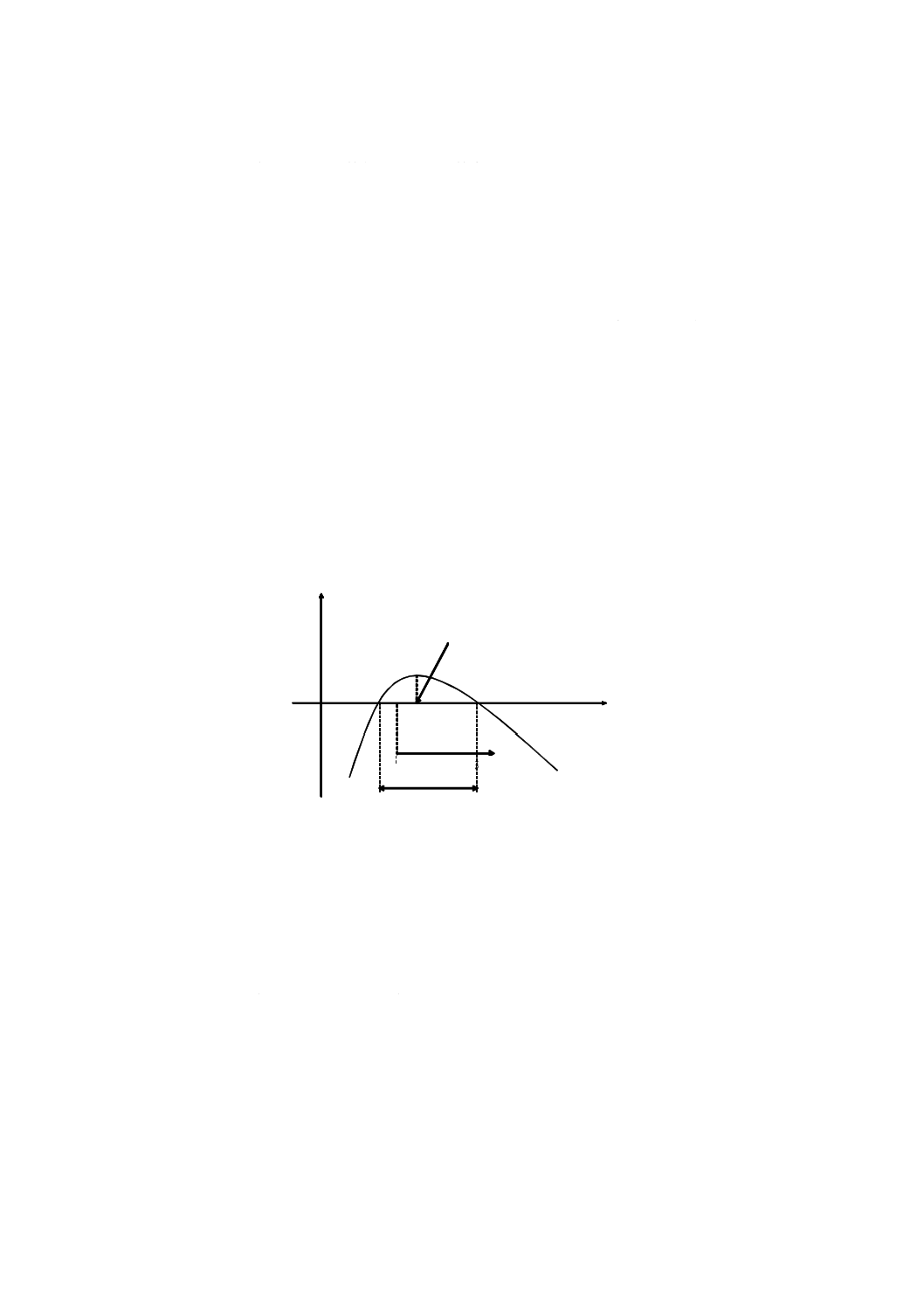
スメントにおける決定の検証に含むことが望ましい。最適化原則は,図1による。
図1−便益最大化による最適化原則の図
注記1 考え得る決定の選択肢は図1の横軸に沿い,右へ行くほど信頼性は高い。縦軸で示される便
益は,考慮する期間における様々な決定に関係する期待純便益を表す。図1で決定は,連続
的に示されているが,離散的な決定又はこれらの組合せについても,同様にまとめられ,表
現され得る。図1から,一部の決定だけが正の純便益を生じており実行可能であることが分
かる。実行可能な決定のうち一つは(便益最大化の観点で)最適であるが,この決定は受容
可能な場合も受容不可能な場合もあり得る。
リスクのアセスメントにおいて,将来に予想される全ての結果を説明しなければならない。これには,
構造物の全ライフサイクルに失われる可能性がある人命に関する補償費用など不確定性と関係のある結果。
例えば,計画された検査,保全などの決定と確定的に関係する結果との両方を含む(附属書B及び附属書
Gを参照。)。
将来コストの純現在価値の評価に用いる利率(割引率)は注意深く選ばれなければならない。未来社会
の変化を考慮するために標準的な年割引率は,長期にわたり平均した年経済成長率であり,国によって異
実行可能な決定
最適な決定
便益
決定の選択肢
受容可能な決定
20
A 3305:2020 (ISO 2394:2015)
なる。人命救助にかかる活動に関連する支出の純現在価値の評価に際しても同様の考え方を適用する。
破壊及び損傷によって極めて深刻な結果が起こり得る構造物においては,リスクに基づくロバスト性評
価を,設計及び/又はアセスメントの検証の一部として実施しなければならない。
注記2 附属書Fは,リスクに基づくロバスト性評価の手法を説明している。実用のためには,破壊
の結果に従った構造物の分類の導入及び構造物の分類に従ってリスクに基づくロバスト性評
価の実施が必要かを決定することが有用となり得る。附属書Fにはそのような分類のための
提案も含まれる。
4.4.2.2
信頼性に基づく設計及びアセスメント
リスク情報を活用した構造物の設計及びアセスメントの代替として,信頼性に基づく方法を選んでもよ
い。この方法では,構造物のある信頼性に対する要求の下で,評価を行い,コストの最小化及び/又は資
源利用の最小化を行わなければならない。信頼性に対する要求は,4.4.2.1に規定したように全面的にリス
ク情報を活用したアセスメントに基づいて評価しなければならず,そのため,破壊の結果及び信頼性向上
のコストの依存関係の中で信頼性水準のレベル分けが容易となる。
注記 信頼性の要求は,一般に人命救助の活動に投資する社会的な能力に依存するので,そのため,
国ごとに固有のものとなる。附属書Gは,幾つかの国に対して,破壊の結果及び信頼性向上の
コストを関数として,信頼性に対する要求を設定し得るかについて記載している。
信頼性に基づく設計及び信頼性に基づく意思決定のための一般的な原則は,箇条8に規定する。
4.4.3
準確率論的方法
破壊及び損傷の結果が十分に理解され,破壊モードが標準的な方法で分類,モデル化され得る構造物で
は,設計及びアセスメントの基礎として準確率論的規準が適切である。規準は,解析,設計,材料,製造,
建設,運用・維持管理及び文書化の品質を確保するのに役立たなければならず,そして,明示的又は暗黙
のうちに構造物の性能に影響を与える不確定性を考慮しなければならない。全ての既知の不確定性を定量
化するように規定を構築することが望ましい。
準確率論的な設計及びアセスメントの規準は,設計及びアセスメントの決定の検証に使用する設計式及
び/又は解析手順を定める形式化された安全性検証法から構成しなければならない。形式化された安全性
検証法は,考慮すべき荷重組合せ及び設計に関する不確定性に関係するような作用,作用効果の設計値,
材料特性及びその他のパラメータを計算するための手順を含まなければならない。
注記1 関連する不確定性に十分配慮し,限界状態,耐力,荷重及び作用をモデル化するための原則
は,箇条5及び箇条6に規定している。
設計及びアセスメントの決定の検証に適用される設計値は,箇条9に規定している信頼性解析の原則を
用いた構造信頼性と,明示的に関係していなければならない。設計及びアセスメントの規準を開発する場
合には,設計値は,規準に従って設計された構造物が達成する信頼性の水準が,その種類及び用途に応じ
た所定の公称信頼性の近傍にあるように,キャリブレーションによって求めなければならない(4.2,8.4
及び附属書G参照)。
注記2 ここで,実構造物の信頼性は,モデル化され定量化された信頼性と異なることを強調するた
めに,公称信頼性と呼んでいる。このような差異は,主にモデル化において人的及び組織的
過誤を除外していることによる。
荷重係数及び耐力係数又は部分安全係数に基づく,構造物の設計及びアセスメントでは,システムの破
壊の結果によって,リスクに基づくロバスト性評価を通して又はロバスト性に対する備えを通して,シス
テムの性能を確保しなければならない。ロバスト性に対する備えは,重要部材の設計,構造的緊結,構造
21
A 3305:2020 (ISO 2394:2015)
的分割を含み,そして,構造システム及びシステムの破壊の結果に依存する(附属書F参照)。
4.5
文書化
構造物の設計に関係する決定事項及び受容規準に関する検証について,全ての関係者にとって追跡可能
で透明性のある形に文書化しなければならない。これは,個別の構造物の設計及びアセスメントに加えて,
規準の開発及びキャリブレーションにも関わる。
文書化は,地点固有のデータ,試験結果,性能指標のモデル,検査結果,損傷,維持管理,修復に関す
る情報,受容規準及びその検証,並びに品質管理手順及び結果を含む構造物の設計及びアセスメントに利
用した全ての関連情報を含まなければならない。
加えて,全ての関連する仮定を特定し,構造物のリスク及び信頼性に関する重要度を議論し,文書化し
なければならない。これは,構造物の所有者によって規定された要求性能だけでなく,構造物の用途及び
予想される維持管理に関わる仮定も含む。
注記 構造物に関する決定の文書化についての更なる詳細は,附属書Aに記載されている。そこでは,
附属書Aでは,しゅん(竣)工時の確認検査済証の発行が推奨される場合があることも記載し
ている。
5
性能のモデル化
5.1
一般事項
5.1.1
構造性能及び限界状態の概念
ある構造物の構造性能を評価するためには,発生し得る構造物の応答を評価し,望ましい状態又は望ま
しくない状態のいずれかに分類しなければならない。これらの二つの状態の境界は限界状態と呼ばれ,望
ましくない領域に入ることを破壊と定義する。限界状態の概念については,5.3にて詳しく規定する。
注記1 一般に,この限界状態の概念は,構造物の性能を評価する際に非常に役に立つ。しかし,機
能不全による損失額の増加を伴いながら,望ましい状態から望ましくない状態へ緩やかに移
行するような場合もある。
注記2 望ましい性能は,出資者,オーナー,住民,運営主体,利用者,近隣住民(建設が住民との
関係に影響を与える場合)及び施工者といった利害関係者によって異なり得る。他の利害関
係者として,政府及び社会が挙げられる。一般に政府及び社会は,安全性及び持続可能性と
いった問題に対して,主な関心がある。
5.1.2
性能及び性能指標
構造性能は,構造物全体又はその部分と関係する。その性能を評価するためには,一連の定量的な性能
指標を選ばなければならず,その指標は要求性能に関して用いる物理状態を表すものである。性能指標は,
次の事項について,様々な抽象化の度合いによって定義する。
− 構造特性(例 剛性,柔性,耐荷能力など)
− 応答パラメータ(例 内力,応力,たわみ,加速度,ひび割れ寸法など)
− 稼働率
− 機能性(例 人の安全性,エネルギー消費量,ロバスト性,使い勝手,可用性,破壊確率など)。様々
な抽象化の度合いの間の関係を構築するように,モデルを作成しなければならない(箇条6参照)。
5.1.3
基本的な要求性能及び設計の局面
次のように分類する全ての関連する設計及びアセスメントの局面において,箇条4に示す要求性能を満
たさなければならない。
22
A 3305:2020 (ISO 2394:2015)
− 永続的局面:構造物が通常の使用下にある状態
− 過渡的局面:構造物の利用又はさらされる状況が一時的である状態
− 偶発的局面:構造物の状態そのもの又はさらされる状況が例外的な状態
様々な設計の局面における要求性能を設定する上では,空間的側面,時間変動及び劣化を,必要に応じ
て考慮しなければならない。
5.1.4
検証レベル
構造物が全ての設計及びアセスメントの局面における目的に適合しているか検証するために,次のレベ
ルのいずれかを用いなければならない。
a) リスク情報を活用する検証レベル 箇条4及び/又は我が国の法・基準にのっとり人の安全面が確保
されるという条件下で,全てのコスト(建設費,維持費など)と(破壊又は機能不全に関する)経済
的リスクとの総和が最小となることを示す。
b) 信頼性に基づく検証レベル 構造物が,最大許容破壊確率又は最小の信頼性レベルとして,定式化す
る一連の信頼性に対する要求を満たす。
c) 準確率論的な検証レベル 構造物が,基本変数の設計値を用いた一連の不等式を満たす。
リスク情報を活用する検証レベルが,最も上位のレベルと考えられる。下位の検証レベルは,箇条9に
示されるコードキャリブレーションの原則を用いることで,より上位の検証レベルと適合するように調整
しなければならない。
注記 通常,このキャリブレーションは,規準作成委員会が実施し,設計者に3番目のレベルc)の検
証手法を用いることを許容することとなる。信頼性に基づく又はリスク情報を活用した検証は,
特別な構造物においてだけ行われる。どのレベルにおいても限界状態の概念及び性能モデルが
用いられなければならない(5.2及び5.3参照)。
5.2
性能モデル
5.2.1
一般事項
構造物がさらされる状況と構造特性との関係を構築し,もう一方で,性能指標を構築するため,一連の
モデルを用いなければならない。
構造物自体,環境(地盤,水及び空気),力学的,物理的,化学的,生物的又は人為的な特性間の相互作
用を表現するように,モデルを構築しなければならない。多くの場合,複数の構造物,環境要素,非構造
要素,設備及び機械,制御システムなどからなるシステムのモデルを考慮することと関連する。
当面の利用に十分であるように,モデルの精度を選択しなければならない。それに見合う程度の不確定
性を同定し,計量可能な量として定義しなければならない。
注記 一般に,リスクスクリーニングの手順から始め,引き続き一連のハザードシナリオを定義して
いる。ハザードシナリオとは,システムが偶然経験し,システム自体又は人々,環境を危険に
さらすような,時間変動する一連の局面である。
5.2.2
時間依存の側面
性能モデルでは,荷重及び構造特性のエルゴード的及び非エルゴード的(ランダム及びシステマティッ
ク)な時間変動を考慮することが望ましい。
その場合は,次を考えなければならない。
− 同時作用による荷重効果を分析する際の時間変動
− 大きな慣性力が働く際の動的影響
− 劣化メカニズム例えば,力学的(疲労及び負荷継続効果),物理的及び化学的性質(腐食及び塩化物浸
23
A 3305:2020 (ISO 2394:2015)
透)又はそれらの組合せ(応力腐食)
劣化を考慮する際には,モデルに,検査,監視及び維持管理を含むことが必要な場合もある。
注記 附属書Bを参照。
5.2.3
システム的側面
要求性能の検証では,次のことを考慮し,含まなければならない。
− 全ての関連する破壊モード
− 破壊モード間の相互作用
− 構造物と環境(風,水,地盤,使用など)との間の相互作用
− 非構造要素(間仕切り,天井,仕上げ,電気・水道・機械設備など)
− 点検・修復活動及び品質マネジメント
− 機能
− 環境的側面(エネルギー消費量,騒音の発生など)
− 持続可能性の側面(人の健康,社会的資産,生物多様性への影響など)
アセスメントの手順において,適切なシステムのレベルを選定しなければならない。物理的及び機能的
境界条件の正しい設定に対して,適切に注意を払わなければならない。
注記 物理的及び機能的境界条件の正しい設定は,関連学会の指針作成委員会などが一連の制約条件
を定義することによって達成されることが一般的である。環境及び持続可能性に関する制約条
件は,いまだ研究段階である。
5.3
限界状態
5.3.1
終局限界状態
終局限界状態とは,次のような望ましくない(網羅的ではない)状態に関連する。
− 構造物又はその一部の剛体としての釣合いの喪失
− 降伏又は破断,過度な変形による断面,部材又は接合部の最大耐力への瞬間的到達
− 破断又は疲労,その他時間依存し累積する効果による部材又は接合部の破壊
− 構造物又はその一部の不安定状態
− 仮定された構造システムから新しいシステムへの急激な移行(例えば,飛び移り座屈現象,大きなひ
び割れの形成など)
− 基礎の破壊
終局限界状態の超過は常に不可逆的で,それが初めて起きた場合に破壊が生じる。終局限界状態は単一
の極大作用事象又は徐々に進む劣化過程の後に生じる(少し小さ目の)極大作用事象による結果として起
こり得る。
終局限界状態は,構造要素及び構造システム全体に対するものであり,構造システム全体に対するもの
にはロバスト性の効果も含む(附属書F参照)。
5.3.2
使用限界状態
使用限界状態は,通常使用に関係する意図した機能の喪失を扱うもので,特に次のような望ましくない
(網羅的ではない)状態に関連する。
− 構造要素又は非構造要素の使い勝手,外観又は設備の機能に影響を与える許容されない変形
− 人に不快感を与えたり,非構造部材又は設備の機能に影響を与えたりする過度な振動
− 構造物の外観,期待される用途の有効性又は機能の信頼性に影響を与える局部損傷
− 構造物の耐久性を減少させる又は構造物の安全な使用を阻害する局部損傷(ひび割れを含む。)。耐久
24
A 3305:2020 (ISO 2394:2015)
限界状態として,しばしば扱われる(例 ISO 13823)。
永続的な局部破壊又は永続的に許容されない変形の場合,使用限界状態の超過は不可逆的であるといわ
れ,最初にこの状態に至ったとき破壊が発生する。
その他の場合,使用限界状態の超過は可逆的であり,次の状況で使用性の喪失が生じる。
− いかなる超過も許容されないと考えられる場合には,使用限界状態を最初に超えるとき
− 超過は許容されるが,構造物が望ましくない状態にある時間が許容される時間より長い場合
− 超過は許容されるが,使用限界状態を超える回数が規定よりも多い場合
− 上記の基準の組合せが生じる場合
これらの場合は,一時的な局部損傷(例 一時的な大きいひび割れ又は漏えい),一時的な大きい変形及
び振動を含むこともある。使用限界状態における限界値は,限界状態を超えた場合の結果に基づいて定義
されることが望ましい。
5.3.3
形式的限界状態
形式的限界状態は,次のような状況に相当し得る。
− 適切に定義できない又は計算が困難な実際の限界状態の近似。終局限界状態として弾性限界を使用し
たり,耐久限界状態として鉄筋の腐食開始を使用(しばしば遷移開始限界状態とされる)したりする
例がある。形式的限界状態での信頼性要求は元の終局限界状態と調和することが望ましい。
注記1 理論上,十分な耐久性に関する要求は,ある期間における安全性又は使用性確保の要求に
既に含まれている。しかし,実用的な理由から特定の耐久性に関する限界状態(ISO 13822
及びISO 13823参照)又はある特定の(危機的ではない)状況に関する限界状態を加える
ことが有効である。
− 構造物の耐久性を低下させたり,構造要素又は非構造要素の機能性及び外観に影響を与えたりする局
部損傷(ひび割れを含む。)
− 連続的に増加する損失関数の場合に追加する限界状態のしきい(閾)値
注記2 5.1.1の注記1に記載したように,限界状態においては,暴露状況が,僅かに変化すると突
然損失が発生すると仮定する。しかし,ある場合には,損失は段階的に生じる。その場合
には,幾つかの損失レベルに対応して望ましくない結果を幾つかの段階に再分割すること
で解決することもある。例えば,地震の解析において,初期の損傷,修復及び倒壊といっ
た限界状態を定義することが有用である。
5.3.4
限界状態関数
構造物の性能を記述する個別の限界状態のモデルのそれぞれにおいて,可能な場合,限界状態関数を規
定し,関連する基本変数を特定しなければならない。
限界状態関数はg(X)で表される。ここで,X=(X1, X2, …)Tは基本(確率)変数である。
式(1)は,限界状態方程式と呼ばれる。
g(X)=0 ···················································································· (1)
式(2)の不等式は,望ましくないXの領域を示す。
g(X)<0 ···················································································· (2)
基本変数Xは,必要な全てのランダムな入力情報をモデルに含むように定義されなければならない。一
般に,基本変数の集合は,次からなる。
a) 作用及び環境からの影響,材料・地盤特性並びに幾何学的寸法を特徴付ける物理量。
b) モデル自体を規定するモデルパラメータ。
25
A 3305:2020 (ISO 2394:2015)
c) 構造システムの性能(使用限界)に関する要求を記述するパラメータ。
限界状態関数は,明確に決定論的なパラメータ及び時間tも含んでいる。
注記1 終局限界状態及び不可逆的使用限界状態については,供用期間中のg(..)の最小値が,通常(構
造物の状態を)決定付ける。一方,可逆限界状態においては,数回の超過又は破壊領域にあ
る程度の(累積)時間であればとどまることは許容され得る。
注記2 使用限界状態は,例えば,構造部材のスパンLのc倍に等しい変位など,使用性の制限を導
入することで定義される。それらの場合,制限値c(例えば,c=1/500)は本来ならば確率変
数であるものに対する設計値と解釈可能である。その場合,cを基本確率変数として導入す
る。
注記3 支配的な破壊モードがある要素の解析においては,限界状態を表す条件は,通常,式(1)によ
る一つの方程式で表される。システムの解析では,支配的な破壊モードが複数あり,複数の
このような方程式が存在する。一般的なシステムにおいては,様々な破壊モードは,直列シ
ステム及び並列システムという論理的システムの混合形式で表現される。
6
不確定性の表現及びモデル化
6.1
一般事項
6.1.1
不確定性の種類
5.3.4で定義した基本変数は,一つ以上の不確定性の要因を表現し得る。例えば,自然現象に固有の変動,
統計的不確定性,計測上の不確定性,新しい情報の精密さに関連した不確定性及びモデルの不確定性であ
る。全ての主要な不確定性の要因を特定しなければならない。
注記1 物理的な不確定性とは,通常,荷重環境,構造物の形態及び材料諸元に関連する不確定性で
あり,しばしば偶然的不確定性と呼んでいる。
注記2 情報量が不十分なことに起因する不確定性,例えば,材料試験の回数の少なさ又は理想化さ
れたモデルに起因する不確定性は,しばしば認識論的不確定性と呼んでいる。
注記3 確率変数は偶然的不確定性と認識論的不確定性との両方を表現可能である。さらに,不確定
性は構造物の供用期間中の異なる局面において,その本質が変わる場合がある。例えば,材
料諸元は構造物の建設前では偶然的不確定性とみなすが,建設後は認識論的不確定性とみな
している。
注記4 地盤構造物の設計において,不確定性の支配的な要因は土質特性及び計算モデルの不確定性
である。これらの主要な要因の不確定性については,附属書Dで記載している。また,附属
書Dは,確率モデルの作成及び不確定性の地盤構造物の信頼性解析及び設計への導入も示し
ている。
6.1.2
不確定性の取扱い
確率論を用いた解析において,構造システムの信頼性評価に重要とみなされる全ての不確定性を考慮し
なければならない。構造信頼性解析では,偶然的不確定性と認識論的不確定性とを区別しないことが望ま
しい。
注記 偶然的不確定性と認識論的不確定性との区別は,追加試験及び詳細調査によってどのように不
確定性が低減できるかという観点に主眼を置く目的だけに導入される。また,その区別はリス
クコミュニケーション及び構造信頼性の更新に関連する項目ともなることがある(附属書B参
照)。
26
A 3305:2020 (ISO 2394:2015)
6.1.3
確率の解釈
構造信頼性解析では,その不確定性の要因とは独立に,確率のベイズの方法による解釈を,不確定性の
一貫した表現をするために最も適切な基本としてみなす。これによって,純主観的に評価された不確定性,
解析的に評価された不確定性及び観察によって得られた事実を同時に考慮することが容易となる。
注記1 ベイズ確率理論では,確率値は,データ,理論的論証及び判断の適切な組合せに基づいて推
定される。そこでは,偶然的不確定性と認識論的不確定性との間に取扱いの区別はない。膨
大なデータがある場合は,ベイズの方法による解釈は頻度論的解釈と一致する。
注記2 基本確率変数(基本確率変数は,基本変数のうち,確定的には定まらず確率変数として取り
扱われるものである。)Xの確率モデルについて考えると,ベイズの方法による確率解析の原
則は,確率モデルの一つ以上のパラメータΘ(平均,標準偏差など)を確率変数としてモデ
ル化することである。Xに関する頻度論的情報又は主観的情報がΘの確率モデルの中で利用
可能である。
6.1.4
確率モデル
信頼性問題の性質によって,基本変数は確率変数,確率過程又は確率場によって,また,離散的又は連
続的に表現され得る。
確率モデルは,個々の基本確率変数の不確定性の特徴を表現するとともに,互いの依存性についても考
慮しなければならない。
注記1 依存性はしばしば,裏に潜んだ現象の因果関係,空間的及び/又は時間的相関性及び/又は
エルゴード性,並びに個々の変数の不確定性に共通に影響を与える統計的及び/又はモデル
の不確定性に起因する。
注記2 確率過程又は確率場を通して不確定現象をモデル化する必要がある場合もあるが,終局限界
状態に関する限り,極値に焦点を当て極値分布によって表現することは,しばしば有用であ
り,かつ,許容される。
確率モデルは,例えば,実験,検査,点検及びモニタリングによって得られた追加情報を組み込むこと
によって更新されることが望ましい。ベイズ更新の公式は,その基本的な方法を与える。
注記3 詳細は,附属書B及び附属書Cを参照。
6.1.5
母集団又は標本空間
確率モデルによる不確定量の表現は,明確に定義された標本空間(又は母集団)に対応しなければなら
ず,信頼性解析の結果は対応する集合に対してだけ有効である。
注記1 偶然的不確定量には母集団という用語がよりふさわしく,認識論的不確定量には標本空間を
用いられている。
標本空間又は母集団の定義のよりどころは多くの場合,変数を規定する又は変数に影響を与える物理現
象から得る。母集団を特徴付ける要因は,次のとおりである。
− 不規則量の特性及び要因
− 空間的条件(例 対象とされる地理的領域)
− 時間的条件(例 設計供用期間)。解析の目的及び利用可能なデータの量及び特性を十分考慮して母集
団を選択しなければならない。
注記2 例えば,母集団を分割して部分母集団に分割(マイクロゾーネーション)することで取扱
いが容易となり得る。この結果を設計の国内規格又は国際規格に用いる場合には,規則が
複雑になりすぎないよう部分母集団同士を結合して再びより大きな母集団とすることが必
27
A 3305:2020 (ISO 2394:2015)
要な場合又はそうすることで取扱いが容易となる場合がある。この場合,変動性は増加す
る。
6.1.6
不確定性の階層モデル
異なる種類の作用及び材料をモデル化する場合には,可能な場合はモデルを階層化することが望ましい。
階層モデルでは,不規則量Xは,それぞれが特定の種類の変動を表すような複数の変数の関数として,次
の式で表される。
Xijk=f(Yi, Yij, Yijk) ········································································· (3)
変数Yi,Yij,Yijkは,様々な要因,変動の時間的スケール,変動の空間的スケールなどを表す。
注記 例えば,Yiは時間変動する現象における定数(時間変動しない変数),Yijはゆっくりとした変動
の時間過程,Yijkは速やかな変動の時間過程を表す。風の場合,Yiは風圧係数Cpにおける(モ
デル)不確定性,Yijは1時間ごとの平均風速vh,Yijkは平均0のガスト過程v(t)として用いるこ
とが可能である。
)
2
(
2
1
2
v
v
v
ρC
X
h
h
p
ijk
+
=
······························································· (4)
ここに,
ρ: 空気密度
コンクリート強度では,Yiは建物ごとの変動,Yijは建物iの階ごとの変動,Yijkはj階の点ご
との変動を表現可能である。
6.2
構造解析のためのモデル
6.2.1
一般事項
構造システムの物理的挙動を表現するための決定要因は,次のように分類可能である。
− 作用及び環境からの影響
− 幾何学的諸元
− 材料諸元及び/又は構造要素の諸元
− アクティブ及びパッシブな制御手段
モデルは,対象とする限界状態までの構造システムの挙動を,記載できなければならない。モデルは,
一般的に,決定的要因を考慮し,重要ではない要因を無視して単純化したものである。モデルにおける不
確定性は,6.4で規定する。
アクティブ及びパッシブな制御手段(例 アクティブダンパー,スプリンクラーの設置など)の信頼性
もモデル化し,全般的なリスク解析に組み入れなければならないが,これについての特定の指針について
は,この規格の範囲外である。
6.2.2
作用及び環境からの影響
6.2.2.1
一般事項
作用の記述は,構造物に対する作用の時間的,空間的及び方向に関する諸元を記述する適切な数学モデ
ルにのっとらなければならない。どの程度詳細なものにするかについては,利用できる情報の質と作用効
果の相応な精度のモデル化との兼ね合いで定めなければならない。当該作用の予測に関する現実性及び精
度の水準の選択は,そのときどきにおいて,設計における暗黙的な意思決定がそれらの水準の選択に与え
る影響及びこれらの意思決定の経済的重みによって導かれる。したがって,同一の作用現象であっても,
検討対象の作用効果及び構造物によって異なる作用モデルとなることがあり得る。
注記 構造システムが置かれた環境は,内力,変形,材料の劣化及びその他の短期的又は長期的効果
を誘発する。これらの効果の原因を作用と呼ぶ。作用を生じさせる環境は,雪,地震及び火災
28
A 3305:2020 (ISO 2394:2015)
のように自然又は人為的なものがある。次の概念は,作用の特性を定める上で有用である。
− 作用は,構造物に作用する集中力又は分布力の集まりである。この種の直接的作用を荷重
とも呼ぶ。
− 作用は,構造物の強制変位及び温度による影響の原因でもある。この種の作用を間接的作
用としばしば呼ぶ。
材料諸元又は構造寸法に関する経時的な変化の原因となるような環境からの影響も,(上記の作用の記載
に対する要求事項と)同様の要求が有効である。
6.2.2.2
分類
作用は,幾つかの特性に応じて分類され得る。作用の種類に関しては,次を考慮しなければならない。
− 構造部材及び非構造部材の自重
− 建物内の積載荷重(例 人及び機器による荷重)
− 産業活動によって発生する荷重(例 サイロ荷重)
− 運搬によって発生する荷重(例 通過交通,パイプラインを流れる液体,クレーン,衝撃など)
− 気象作用(例 雪荷重,風荷重,外部温度など)
− 室内温度及び火災
− 水力学的荷重(例 水圧及び地下水圧)
− 土又は岩からの地盤作用(地震,土圧,地滑り,下層土の振動及び地盤沈下を含む。)
− 製造及び建設時特有の荷重
この分類は全ての作用を含むものではないが,一般的な作用は,ほぼこれらのいずれか又は複数のもの
に該当する。その分類全体が制御不能な作用又は制御可能な作用のいずれかに属するものもあれば,両方
に属するもの(例 水圧)もある。
時間的な変動の観点から,次のように作用を分類しなければならない。
− 永続作用
− 変動作用
− 偶発作用
時間経過に伴う平均からの変動が少なく,かつ,緩やかである場合(例 自重,バラスト,土圧など)
又は変動が最終値まで単調変化する場合(例 プレストレス,施工過程に伴う強制変形,温度の影響,湿
度変動,地盤沈下など)は,永続作用に分類されなければならない。
時間経過に伴う変動がしばしば起こり,かつ,大きい場合(例 構造物の使用,風,雪又は地震のよう
な多くの外的作用が原因で発生する全ての作用など)は,変動作用に分類しなければならない。
非常に程度は大きいが,その構造物の使用が想定される期間に対して発生確率が小さい場合は,偶発作
用に分類しなければならない。ほとんどの場合,偶発作用の継続時間は短い(例 衝撃荷重,爆発,雪崩
など)。衝撃がしばしば発生するような構造物又は場所においては,これらの作用を変動作用として扱うこ
とが望ましい。
注記1 この規格では,偶発作用は必ずしも事故と関連付けるものではない。
注記2 地震活動が低い国及び地域では,地震作用は,偶発作用として扱われることもある。
空間的変動に関しては,固定作用と自由作用とを区別することは有用である。固定作用とは構造物にお
ける作用強さの空間的分布が既知のものである。構造物のある特定の一点における作用強さが特定されれ
ば,構造物全体での作用強さが完全に定義される(例 土水圧)。自由作用とは,作用強さの空間的分布
が変動するものである(例 通常時の積載荷重)。
29
A 3305:2020 (ISO 2394:2015)
6.2.2.3
作用モデル
可能な場合は,その作用の強さ,位置,方向,継続時間などを記載する(一般的には)幾つかの構成要
素からなる完全な作用モデルを考慮しなければならない。場合によっては,個々の要素の相互の影響も考
慮しなければならない。作用及び構造物の応答が相互に影響する場合もあり得る。
多くの場合,2種類の変数が明示的に区別されなければならない。すなわち,作用Fを表現するために
はF0及びωを用いて,次となる。
F=φ(F0, ω) ··············································································· (5)
ここに,
F0: 作用の原因となる事象と直接関連する基準作用変数。可能な
限り構造物とは無関係に定義されるものであることが望ま
しい(例えば,雪荷重においては,F0は地上又は水平平面に
おける積雪荷重である。)。
ω: 基準作用から作用Fへの変換における換算係数又はモデルパ
ラメータ。構造物ごとに異なるものであり,構造物の形及び
大きさなどに左右され得るものである(例えば,雪荷重では,
ωは,地上積雪荷重を屋根雪荷重に変換する係数で,屋根勾
配及び屋根仕上げ材などによって異なる。)。
φ(·,·): 適切な関数。しばしば単純な積になる。
通常,長期間及び短期間における変動はF0に含まれ,ωは時間に左右されないものと考えられる。作用
の空間変動の系統的な部分は,多くの場合,ωに含まれるが,不規則な可能性がある部分はF0又はωに
含まれ得る。式(5)では作用の主要な特徴を考慮することが望ましい。一つの作用に対し,複数のF0及びω
が存在し得る。
いかなる作用モデルも,一連のパラメータ及び変数を含んでおり,これらはモデルを利用する前に評価
しなければならない。確率論的モデル化では,全ての作用変数は通常,確率変数,確率過程又は確率場と
仮定する。一方,パラメータは時間,空間座標及び方向である。例えば,確率モデルを作成する元となる
サンプルの数が小さいことに伴う統計的不確定性を含むとき,パラメータそのものが確率変数となる場合
がある。
式(4)に示すように,作用モデルは,しばしば異なる特徴を示す2個以上の変数を含む。完全な作用モデ
ルを構成するように,個々の変数に対して適切なモデルを選択することが望ましい。
注記 ある特定の期間に対する極値,例えば,年最大風荷重,設計供用期間中の極大交通荷重の分布
などを明示した作用モデルを定義することは,しばしば有用である。
6.2.3
幾何学的特性
構造物の幾何学的特性を適切に表現しなければならない。一般的には,一次元要素[はり(梁),柱,ケ
ーブル,アーチなど],二次元要素(床スラブ,壁,板など),三次元要素(シェル,半無限成層地盤など)
といった標準的な要素が用いられる。モデルに含まれる幾何学量は,一般的に公称値と呼ばれ,すなわち,
図面,解説書などに記載された数値である。通常は,実際の構造物の幾何学量は,公称値とは異なる。す
なわち,構造物は幾何学的不整を伴う。構造物全体の挙動又は要素耐力がこのような不整に対して敏感で
ある場合は,不整はモデルに含まれなければならない。
6.2.4
材料特性
6.2.4.1
一般事項
力又は応力と変形との関係(すなわち,構成則)からなる材料モデルが設定されなければならない。こ
のような関係に含まれる変数は,弾性係数,降伏点,終局強度などであり,一般的には不確定量とみなさ
なければならない。場合によっては,それらの変数は,時間依存性又は空間依存性をもつ。パラメータの
30
A 3305:2020 (ISO 2394:2015)
間には,例えば,コンクリートの弾性係数と終局強度との関係のように,しばしば相関関係がある。
例えば,材料劣化に対する耐性といった,他の材料特性もしばしば同様に扱うことが可能である。しか
しながら,その原則は,対象とする材料の種類及び特性に強く依存する。
6.2.4.2
特性評価
寸法及び状態を定義し,指定された方法に基づいて採取し,合意の得られた方法に従って試験を行い,
その結果が特定の手続に従って評価を受けた材料供試体の特性として,材料特性を定義しなければならな
い。
力学的挙動の主な特性は,一軸応力-ひずみσ-ε線図によって表現される。構造設計の絶対的最低条件と
して,引張及び圧縮の両方に対して次の材料特性を考慮しなければならない。
− 弾性係数
− 材料強度
その他の一軸応力-ひずみσ-ε線図に含まれるパラメータで重要なもの,例えば,次に掲げるものも関連
がある場合がある。
− 降伏応力
− 比例限界
− 破壊時のひずみ及び最大応力時のひずみ
− 摩擦角及び粘着力
破壊時のひずみは局部現象であり,得られる値は供試体の形状及び寸法に大きく依存する。一軸応力-
ひずみσ-ε線図に加えて,次に揚げる事項など,その他の量及び効果に関する情報も重要である。
− 多軸応力-ひずみ関係
− 多相材料(空気及び水を含む土)
− 継続時間及びひずみ速度の効果
− 温度効果
− 湿度効果
− ノッチ及び欠陥の効果
− 化学物質の効果
材料特性の間の依存関係があり得る場合は,これを考慮しなければならない。
6.2.4.3
材料モデル
関連した詳細情報を含む(一般化された)応力-ひずみ関係を記述する関数及びパラメータ(材料特性)
を用いて,構造材料をモデル化しなければならない。対応するモデル不確定性を考慮しなければならない。
材料特性は,時・空間で不規則に変動する。次に掲げるような測定された特性と実際の特性との間に不
整合が生じることがあり,考慮しなければならない。
− 予測における偏りを示唆する,構造特性の実測値と予測値とを関連付ける室内試験から同定される系
統的な偏差
− 一般にモデルで考慮された変数が不十分であることを示唆する,構造特性の実測値と予測値との不規
則な誤差
− 実構造部材に使用された材料と対応する構造材料試験サンプルとの関係における不確定性
− 材料サンプル(実際の構造体から取り出したものではない,架空のもの)の材料特性に影響を与える
ような施工・製作品質の差。すなわち,供給された供試体サンプルに基づいて材料特性をモデル化す
る場合
31
A 3305:2020 (ISO 2394:2015)
− 材料を実構造に用いた場合の,職人の技量の違いによる効果で,対応する材料サンプルには反映され
ていないもの
− 経時変化に伴う不確定性で,室内試験又は現地観測などによって予測可能なもの
− 組立て中又は組立て後の点検手順に関連した不確定性
6.2.5
応答及び耐力
6.2.5.1
分類
必要に応じて,次の力学モデルを用いなければならない。
− 静的応答を表現するモデル
− 時間依存動的応答を表現するモデル
− 時間依存劣化機構を表現するモデル
環境(特に空気,水及び土)と構造物との相互作用を必要に応じて考慮しなければならない。
6.2.5.2
静的応答のためのモデル
解析では,応力,力又はモーメントと対応する変形(又は変形率)との関係を得るために適切なモデル
を選択しなければならない。これらのモデルは,計算の目的及び種類によって異なる。次に,モデルの選
択に当たって考慮しなければならない事項を掲げる。
− 多くの場合,最大応力の箇所において塑性域を形成する弾塑性挙動モデルが十分であるとみなす。
− より高度なモデルには,一般的な材料劣化,明確な又は平均化ひび割れ形成,クリープ,リラクゼー
ション,圧密のような現象などに基づいた軟化挙動を含む。
− 弾性理論は,より一般的な理論の単純化されたものとみなされ,一般に構造物の挙動が弾性状態にと
どまっていると仮定して得られた力及びモーメントの値に限り用いられ得る。安全側の近似となる場
合は,弾性理論をその他の場合に用いてもよい。
− 構造物のある領域[はり(梁)の塑性ヒンジ,床スラブの降伏線など]において,完全塑性領域の形
成を仮定する理論は,終局限界状態に達する前の塑性化挙動を保証し得る変形が起こる場合に限り用
いることが可能である。したがって,ぜい(脆)性破壊,不安定性及び自由変動作用を繰り返し受け
る(シェイクダウンメカニズム)ことによって耐力が限定される場合には,塑性理論を用いた構造物
の耐力の算定に特に注意しなければならない。
− 多くの場合,構造物の変形は幾何学量の公称値から大きく逸脱する原因となる。このような変形が構
造物の挙動に重要な影響を及ぼす場合は,設計において考慮しなければならない。一般に,このよう
な変形の効果は幾何学的非線形又は二次効果と呼ばれる。この種の解析では,初期不整も考慮する必
要がある。
6.2.5.3
動的応答のためのモデル
構造物の動的応答は,作用の大きさ,位置又は方向の比較的速い変化が原因で発生する。しかし,構造
要素の剛性又は耐力の急変が動的挙動の原因となる場合もある。
動的応答のモデルは,一般的に次によって構成する。
− 幾何学的,物理的線形及び非線形挙動を含む剛性モデル
− 材料による減衰,幾何学的減衰,人工的及びアクティブな減衰を含む減衰モデル
− 構造物の質量,内容物の質量,周辺の媒体の質量を含む質量モデル
動的挙動のモデル化では,空気,水,土及び場合によっては隣接する構造物との相互作用を考慮しなけ
ればならない。
動的(ピーク)荷重の継続時間は短いことから,構造物は静的耐荷能力よりも大きな動的荷重に耐え得
32
A 3305:2020 (ISO 2394:2015)
る。この場合,変形の限界があり得ることに対して特に注意しなければならない。地震解析では,これは
いわゆる変形性能に基づく設計法の一部である。
注記 実務では,動的効果が静的荷重にかかる動的増幅係数によって表現できる場合,動的計算はし
ばしば準静的計算で代用する。
6.2.5.4
劣化及び損傷累積のモデル
必要に応じて,構造要素の剛性及び強度に与える損傷の影響を考慮しなければならない。
材料及び構造諸元の劣化は,次の事項に関連するエネルギーが原因となり得る。
− 力学的効果(繰返し作用,長期荷重,沈下,浸食及び摩耗)由来
− 物理的効果(温度,湿度及び紫外線)由来
− 化学的過程(火災,腐食及びアルカリシリカ反応)由来
− 生物的過程(腐食及び木材の腐朽)由来
繰返し作用が原因の疲労破壊の場合,次の2種類のモデルに区別される。
− 実験に基づいたS-Nモデル
− 破壊力学モデル
ひずみの集中が発生しやすい“弱点”に対して,特に注意を払う必要がある。
注記 ISO 13823を参照。
6.3
結果のモデル
リスクに基づく方法では,リスクを評価し,安全対策の最適化及びあり得る制約条件との比較を可能と
するために,構造物の破壊による直接的及び間接的結果のモデルを作成しなければならない。
最低限,次の事項のモデル化によって結果を決定しなければならない。
− 破壊前後の構造物の挙動
− 一次部材及び二次部材の被害の大きさ
− 警報システムなどの可能な減災要因
− 人間の自主的救助活動
− 消防隊のような専門家による救助及び減災活動
− 修復及び再建活動
− 構造的機能の喪失
− 環境的損害
シナリオ解析のような結果解析を実施する場合,フォールトツリー解析及びイベントツリー解析が推奨
される。想定されるシナリオの不確定性を考慮しなければならない。
結果は,人間の死傷者数及び/又は環境被害並びに経済損失を数値的に表現しなければならない。結果
のランク付けで十分な場合もある。
死者数を推定するモデルは,通常,次の2段階で構成される。
a) リスクに暴露される人の総数の算定
b) 暴露される人が実際に死亡又は負傷する確率の算定
6.4
モデルの不確定性
構造解析のためのモデルは,関連する変数の物理的又は経験的な関係であり,これらの変数は一般的に
確率変数である。
Y=f(X1, X2, …, Xn) ······································································ (6)
ここに,
Y: モデルの出力
33
A 3305:2020 (ISO 2394:2015)
X1, X2, …, Xn: 基本変数
ある状況において(例えば,計測によって)Xiの結果が既知の場合には,モデルf(·)は完全で正確となる
場合があり,結果Yは正確に予想され得る。しかし,通常は,モデルは不完全で,不正確である。それは,
知識の不足又は設計者の利便性のためのモデルの意図的な単純化による。これらの側面を採り入れるため
に,式(6)は,次のように改めることが望ましい。
Y=f'(X1, X2, …, Xn, Θ1, Θ2, …, Θm) ··················································· (7)
ここに,
f': モデル不確定性を考慮するために変数Θ=(Θ1, Θ2, …, Θm)T
を用いて拡張した関数f
変数Θ: モデルの不確定性を表現(確率変数として扱う。)
それらの統計的諸元は可能な限り,実験,測定又はより精度の高いモデルによる計算結果から導き出さ
なければならない。これらのパラメータの平均値は,解析モデルが試験結果を正確に予測するよう定める
ことが望ましい。
6.5
実験モデル
適切な計算モデルが存在しないような場合又は既存のモデルが安全側過ぎると思われる場合,設計手順
の一部は,実験モデルに基づいて実施可能である。試験の計画及び評価は,次のとおりであることが望ま
しい。すなわち,実際に設計される構造物は,関連する全ての限界状態及び荷重条件に関して,計算モデ
ルだけに従って設計される構造物と少なくとも同程度の信頼性をもっている。試験において実物と一致さ
せられない条件(例 長期にわたる挙動)は,別途考慮することが望ましい。
実験モデルは,次の仮定を評価又は確認するために用いることが可能である。
− 構造物への荷重(例えば,風洞実験)
− 荷重作用下又は偶発事象時の構造物の応答
− 構造物又は構造部材の強度又は剛性
注記1 材料諸元の標準検査(例 コンクリートの圧縮強度試験,鋼材の引張強度試験など)又はそ
の他の管理試験は,実験モデルに基づいた設計とはみなさない。これらの試験は,既に設計
で立てられた仮定を確認することを目的としている。
試験を行う前には,関連する範囲の変数を包含する計算モデルを可能な限り作成し,試験によって評価
すべき未知の係数及び量を明確に示すことが望ましい。これが不可能な場合は,一連の予備試験を実施す
ることが望ましい。
作用,材料諸元及び幾何学的諸元のように関連する基本変数は,計算モデルに明示されていない場合で
あっても,直接的又は間接的に試験のたびに計測されることが望ましい。これらの基本変数のサンプルは,
代表値である必要はない。例えば,推定された設計値の近傍の値から得るという方法を選択することも可
能である。試験における確率変数の値が計測されない場合,それらは代表サンプルから確実に得ることが
望ましい。
試験結果は,統計的手法に基づいて評価されることが望ましい。通常,選ばれた未知量に関する統計的
不確定性も含んだ確率分布を,試験によって得ることが望ましい。その分布に基づいて,設計値及び部分
係数法に用いる部分係数を導くことが可能である。
注記2 詳細は,附属書Cを参照。
試験の評価結果が経験と整合しない場合は,ずれの詳細な理由を探求し記録することが望ましい。
6.6
確率モデルの更新
作用,構造諸元及び/又はモデルの不確定性が比較的高い場合は,より経済的な設計又はアセスメント
34
A 3305:2020 (ISO 2394:2015)
対応策を達成するために,それらの確率モデルの更新の可能性を検討しなければならない。
更新は,建設中又は建設後の品質保証の手続並びに供用期間中の点検及びモニタリング計画に基づくこ
とが可能である。観測結果を与えることによって確率変数のいわゆる事後分布を得る。破壊の事後確率を
直接計算した方が効率的な場合がある。点検手順における不確定性は,常に考慮しなければならない。
点検は,火災又は地震といった事象の後でも実施可能である。
点検活動の経済的効率性は,いわゆる事前・事後解析に基づく意思決定によって得る。
注記 附属書A及び附属書Bを参照。
7
リスク情報を活用した意思決定
7.1
一般事項
4.2.2に規定しているとおり,便益を確実に最適化し,同時に社会的選好に基づいて生活及び環境の質に
対するリスクが確実に管理されるように,構造物の設計,施工,供用,アセスメント,補修,補強,維持
管理,改修及び撤去における決定をリスクアセスメントに基づいて行わなければならない。
ISO 13824 [21]及び7.2〜7.5の規定に基づいて,リスクアセスメントを実施しなければならない。
注記 リスク情報を活用した意思決定は信頼性情報に基づく意思決定と比較して,決定に関連する全
ての結果を直接的かつ明示的に含む。そこには,構造物の破壊によってもたらされる結果だけ
ではなく,構造物が機能することで達成される利益の観点による結果を含む。したがって,リ
スク情報を活用した意思決定は,利用できる情報によって整合し,構造物のライフサイクルに
わたる決定の最適化のためのより豊かな根拠をもっている。
7.2
システム同定
構造物に関するリスク情報を活用した意思決定における最初の課題として,特に次のシステムを同定し
なければならない。
− システムの空間的及び時間的境界を明確にし,詳細に記述しなければならない。
− 4.3.2に記載されるように,発生の可能性があり,関連する暴露事象,構成要素,直接的結果及び間接
的結果を特定しなければならない。
− リスクを減らし得る様々な対策は,そのコスト,暴露事象に対する効果,直接的及び間接的結果につ
いて特定しなければならない。さらに,構成要素に起こり得る被害の発生前,進展中及び進展後に関
連するリスク低減対策を特定することを考えなければならない。
リスクスクリーニングの観点から,協力体制によってシステムの同定を実施することが推奨される。
協力体制には,構造物の所有者及びその構造物が直面する課題に関する知識をもっている様々な分野
の専門家を含む。
注記1 発生する可能性のあるシナリオ数が膨大になり得るため,関連性が低く詳細なリスクアセス
メントの対象から除外できるシナリオを特定することが重要である。
注記2 リスク低減対策は,受動的方法(例 断面寸法を大きくする,構造的補剛材を設置する,コ
ンクリートの被り厚さを増やすなど)又は能動的方法(例 構造モニタリングの実施,点検
及び維持管理方針の策定,煙及び火災感知器の設置など)がある。さらに,品質管理,現地
地盤調査,材料試験,環境条件の観測などのように,システムを変えるのではなく,むしろ
システムの性能に関する知識を向上するようなリスク低減対策もあり得る。向上した知識は,
システムの物理的変化を含むリスク低減対策の最適化に貢献する。
35
A 3305:2020 (ISO 2394:2015)
7.3
システムのモデル化
システムのモデル化では,4.3.3に示すように,システムに関連する不確定性に着目し,記載しなければ
ならない。これは,暴露事象,システムの構成要素の損傷及び破壊に関連する全ての状態,直接的及び間
接的結果,並びに取り得るリスク低減対策の効果に関するベイズ的確率表現を含む。構成要素の性能は,
箇条5に規定した原則に従ってモデル化しなければならない。
異なる暴露事象間及び構成要素の性能間の依存関係は,リスクに顕著な影響を与えるため,モデル化の
ときに注意深く配慮することが望ましい。
異なるリスク低減対策に関連する便益のモデル化では,全ての結果及び将来発生が予想されるコストに
(現在価値への)割引を適用しなければならない。
7.4
リスクの定量化
可能なものとして特定されたリスク低減対策に関連するリスクは,直接的及び間接的結果の合計の期待
値として評価しなければならない。期待値計算は,システムの性能に影響する全ての不確定性に対して実
施する。必要に応じて,予想最大損失額PML,VaRなど,リスクに関する追加的な指標を評価する。
個々のリスク低減対策aについて,対応するリスクR(a)は,nE個の発生し得る結果に関連する因子から
なる。
∑
=
=
E
n
i
i
iC
P
a
R
1
)
(
·········································································· (8)
ここに, Pi及びCi: それぞれ事象iに関連する確率及び結果の大きさ。発生
し得る結果の数,その確率及びこれに関連する結果の重
大性のいずれも,一般的にリスク低減対策aに依存する。
式(8)中の確率Piは,箇条8で与えられる原則に従って評価しなければならない。結果に関連する事象を
確率論的に表現する場合は,箇条5及び箇条6で規定している不確定性のモデル化の原則及び限界状態の
概念を適用しなければならない。
注記 直接的及び間接的なリスクのアセスメントに基づいて,構造物のロバスト性に関するアセスメ
ントを実施し設計の意思決定に資することが可能である(4.3.2及び附属書F参照)。
7.5
意思決定の最適化及びリスク受容
リスク低減のための意思決定の最適化は,関連する便益のランク付けに基づかなければならない。リス
クに関する情報に基づく意思決定の最適化のための一般原則は,4.4.2.1に規定する。
人命の安全性に関わる意思決定の受容可能性のアセスメントは,4.2.2に規定する原則に従わなければな
らない(詳細は,附属書Gを参照)。
注記 リスク情報を活用した意思決定は,構造物のライフサイクル全体を通した構造物に関する決定
の基本として直接的に適用可能である。また,リスク情報を活用した意思決定は,構造物の最
大許容公称破壊確率にも適用可能である,それによって,信頼性に基づく方法及び準確率論的
な形式化された安全性検証法による定式化及び規定が裏付けられる。
8
信頼性に基づく意思決定
8.1
一般事項
信頼性に基づく意思決定の一般原則は,4.4.2.2に規定している。構造物の設計,補修,補強,維持管理,
供用及び撤去に関する意思決定は,信頼性に対する要求又は等価的に,破壊確率に対する要求を満たさな
ければならない。
36
A 3305:2020 (ISO 2394:2015)
箇条6の不確定性モデルは,確率変数又は確率過程及び確率場で表現し,箇条5の限界状態法は関連す
る事象,例えば,破壊事象をモデル化するために用いることが可能である。さらに,信頼性は,FORM及
びSORM並びにモンテカルロシミュレーション手法のような時変又は時不変の信頼性評価手法によって
評価が可能である。
構造物のライフサイクルにおいて,異なるタイプの意思決定及び変動する情報量に基づく意思決定を行
わなければならない。これらには,次に関する意思決定を含む。
− 終局及び使用限界状態に対する設計
− 構造設計及び工事中における試験及び品質管理の計画。これには,例えば,土質調査,材料試験,供
試体試験片の試験,部材の試験,実物大試験,保証荷重試験,数値試験及び品質管理手続を含む。
− 将来の補修及び維持管理の判断基準のための,供用中の点検及びモニタリングの計画
− 設計供用期間の終了時における構造物の使用期間の延長並びに除去及び建替の意思決定
信頼性に基づく意思決定は,破壊確率pfが指定された目標値pftを超過しないということを意味する(8.4
参照)。
pf≦pft ······················································································ (9)
上記の意思決定に関わる全ての設計の局面に対して,信頼性に対する要求を検証しなければならない。
設計の局面は,構造物の建設中及び使用中において,合理性をもって発生すると予見される条件を全て包
含するように十分に過酷で多様でなければならない。通常,これには,構造物の生涯にわたる種々の段階
における,通常使用時の荷重条件,極限的な環境の荷重条件,例外的かつ偶発的荷重条件が当てはまる。
破壊は,箇条5による限界状態に関連付けられ,時不変の信頼性問題の場合には,好ましくない状態は
限界状態式によって定義する。
g(x)≦0 ·················································································· (10)
ここに,
x: 問題に関連する基本変数Xの実現値を成分とするベクトル
一般的に,変動する作用及び環境からの影響を示す基本変数は,確率過程又は確率場を用いて記述する
ことが望ましい。しかしながら,多くの場合,与えられた基準期間又は領域での最大値の確率分布関数を
もつ確率変数で記述することで十分である。(材料又は幾何学的特性といった)他の基本変数も,時間依存
又は場所依存となり得る。
モデルの不確定パラメータは,通常,基本変数と同様に確率変数として取り扱われる。
多くの終局限界状態及び幾つかの使用限界状態に対しては,破壊確率は,次のように表すことが可能で
ある。
pf=P[g(X)≦0]··········································································(11)
時間依存変数の場合,問題は時間変動し,通常,破壊確率の評価に初通過又はアウトクロッシング法を
適用することが望ましい。しかし,場合によっては,時変問題も時不変問題に容易に変換可能である(ISO
13822参照)。
幾つかの終局限界状態及び多くの使用限界状態では,限界状態の初通過は破壊を意味しない。そのよう
な場合では,更に追加条件を満足する場合だけ破壊が発生するので,個々の場合について破壊のクライテ
リアを定式化しなければならない。
pfは,評価する時間長さに依存するため,あらかじめ指定された期間(基準期間)に関するものでなけ
ればならない。経済的結果が決定的な場合には,建物生涯期間における確率を用いることが可能である。
破壊が人命の脅威となり得る場合は,他の基準期間,典型的には1年が用いられることがある。
破壊確率pfは,次の定義によって信頼性指標βと関連付けられる。
37
A 3305:2020 (ISO 2394:2015)
β=−Φ−1(pf) ··········································································· (12)
ここに, Φ−1: 標準正規確率分布関数の逆関数
信頼性手法は,箇条9に規定される部分係数形式のキャリブレーションに適用可能である。場合によっ
ては,確率に基づく手法は,設計及び意思決定に直接適用可能である。
FORM,SORMなどの近似評価手法ではなく,式(11)で得られた信頼性は,明確に定義された信頼性(例
破壊確率)の確率的尺度となる。この値は,意思決定のための様々な設計の局面間の首尾一貫した比較及
び特定の要求された信頼性の度合いに対するキャリブレーションに用いることが可能である。
注記 一般的に,建設工事の品質マネジメントシステムは,リスクに基づき,かつ,人的過誤,設計
ミス及び施工ミスを含む統合的方法に基づくものでなければならない(附属書A参照)。
信頼性の度合いは,4.2に示すように破壊の結果によってレベル分けすることが可能である。
8.2
更新された確率尺度に基づく決定
試験,品質管理,点検,状態モニタリング,構造ヘルスモニタリングなどによる結果が入手可能な場合
は,ベイズの統計的手法によって,式(11)に用いられる破壊確率を更新することが望ましい(既存構造物
のアセスメントについては,附属書B及び附属書Cを参照。)。
補修及び維持管理,場合によっては改修の意思決定に,更新された破壊確率を用いることが望ましい。
また,式(9)の信頼性に対する要求を構造物の全生涯において確実に満足するための点検計画のよりどころ
として,更新された破壊確率を用いることが望ましい。
8.3
システム信頼性及び部材信頼性
構造システム及び構造物を含むシステムの性能は,4.3.2に規定するように構成要素が破壊のシナリオに
よって表現可能である。シナリオは,例えば,初期破壊から完全崩壊など,構造システムにおける個々の
部材破壊の一連の流れとして表現可能である。
これまでは,設計及びアセスメントにおける信頼性に基づく意思決定は,個々の部材又は個別の限界状
態(使用限界状態及び終局限界状態)に主に適用されてきた。構造の破壊は,通常,システムの破壊の中
で最も深刻な結果をもたらすため,システムの挙動は重要である。そのために,最初に破壊が発生する部
材に引き続いて発生するシステムの破壊の確率の評価を実施することに関心がもたれる。特に,偶発事象
に関する損傷に対する許容性又は構造健全性に関連してシステムの性状を特定することが必要である。部
材に要求される信頼性は,システムの性状によって決めることが望ましい(ロバスト性に対する要求につ
いては,附属書Fを参照。)。
次の項目を考慮に入れて,構造システムの損傷を招く可能性のあるシナリオの確率を明らかにするため
に,信頼性評価を実施することが望ましい。
− システムの破壊モードを招く,個別部材の破壊の一連の流れ
− 所定の破壊状態において,内力を再配分させる構造物の能力
− 内力の再配分が確実に行われるような手段(緊結化)
− 内力の再配分が行われるかが確実でない状況を避けるような手段(分割化)
− 個別要素の破壊モードとシステムの破壊モード間の従属関係
しかしながら,システムの信頼性解析は,現在利用可能な手法がもつ不確定性(精度)を認識し,注意
を払って実施する。
8.4
目標とする破壊確率
目標とする破壊確率,すなわち,pftは,結果及び破壊の性質,経済的損失,社会的不便性,環境への影
響,持続可能な天然資源の利用,破壊確率を低減するために必要な労力及び費用の総計を考慮に入れて選
38
A 3305:2020 (ISO 2394:2015)
択することが望ましい。構造物の破壊に関連する人命の損失のリスクがない場合は,目標破壊確率は経済
的最適性だけによって選択可能である。構造物の破壊が人命の損失のリスクに関連する場合は,更なる人
命の救助費用の原理の適用が推奨される。この原理の適用には,附属書Gに示されるLQI(生活の質指標)
を用いることが可能である。全ての場合において,許容可能な破壊確率は,過去の経験から適切な信頼性
をもつケースとの整合を取ることが望ましい。
注記 終局限界状態に対する試案的な信頼性目標(基準期間1年)は,附属書Gを参照。
時間依存性のある構造特性を取り扱うときは,破壊確率に対する品質管理及び点検・補修手順の影響を
考慮することが望ましい。このことによって,点検結果を反映した目標設定値に補正できる可能性がある。
指定する破壊確率は,常に,採用する計算法と確率モデル及び信頼性評価の手法との関連で考慮すること
が望ましい。
使用限界状態については,目標とする破壊確率は,機能の喪失及び/又は被害の発生を経済的許容範囲
内にとどめるという目的に整合しなければならない。
可逆的使用限界状態については,限界状態を超過する頻度に対する要求がある場合もある(箇条5参照)。
8.5
破壊確率の計算
8.5.1
一般事項
基本的に,破壊確率の計算は,利用可能な知識に基づかなければならず,不確定性の表現は,関連する
因果的及び確率的依存性並びに時間的空間的変動を含まなければならない。破壊確率の計算手法の適切な
選択は,対処する問題,特にその問題が時間に依存しないかどうか,個別の破壊モードなのかシステムな
のかという特性に左右される。
8.5.2
時不変信頼性問題
時間(又は空間)に依存しない問題の場合,又は,例えば,極値を用いて考慮するなど,依存しないよ
うに変換できる場合,一般的には破壊確率pfを算定するのに次の3種類の手法がある。
a) 一次及び二次信頼性手法(FORM及びSORM)
b) シミュレーション手法(例 単純なモンテカルロシミュレーション,重点サンプリング,漸近サンプ
リング,サブセットシミュレーション及びアダプティブサンプリング)
c) 数値積分法
8.5.3
時変問題の時不変問題への変換
次に関連する二つの時間依存問題を考慮する。
− 極値が原因の破壊
− 経時的な効果の累積及び進展が原因の破壊
極値が原因の破壊の場合は,一つの作用過程が定常的であれば,ある選択された基準期間(一般に1年)
における確率過程の極値の特性(最小又は最大)を表す確率変数で代替可能である。二つ以上の確率過程
が含まれる場合は,それらは過程相互の従属性を考慮した上で組み合わせることが望ましい。
累積的劣化(疲労,腐食など)が原因の破壊の場合は,破壊に至るまでの全ての荷重履歴が重要である
可能性がある。このような場合は,対象とする基準期間を幾つかの区間に分割し,破壊確率を個々の時間
区間からなる論理的な直列システムの破壊確率として算定することによって,時間依存性を考慮すること
が可能となる。
注記 ISO 13822に例がある。
8.5.4
アウトクロッシング法
時間区間(0, t)の時間変動過程における破壊確率の厳密で一般的な表現は,式(13)によって,条件付き
39
A 3305:2020 (ISO 2394:2015)
破壊率h(τ)の積分によって導かれる。
−
−
=
∫t
dτ
τ
h
t
p
0
f
)
(
exp
1
)
,0(
······················································· (13)
時刻τ以前に破壊がないものとして,時間区間(τ, τ+dτ)に破壊が発生する確率として,条件付き破壊
率を定義する。破壊のしきい(閾)値が十分高いときに,条件付き破壊率h(τ)は,平均アウトクロッシン
グ率v(τ)に置き換えることが可能である。
{
}
Δ
Δ
τ
X
g
τ
X
g
P
τ
v
Δ
]0
)
(
[
0
)]
(
[
lim
)
(
0
≦
>
+
=
→
Ι
···································· (14)
最初(t=0)の損傷が明示的に考慮される場合は,次の式による。
−
−
+
=
∫t
dτ
τ
v
p
t
p
0
f
f
)
(
exp
1
)0(
)
,0(
··········································· (15)
ここに, pf(0): t=0のときの構造的な破壊の確率
アウトクロッシング率v(τ)の数学的定式化は,荷重過程,構造応答及び限界状態の種類に依存する。実
務的応用として,式(15)は異なる変動スケール及び/又は時不変確率変数を含む幾つかの過程を含むよう
に拡張が必要な場合がある。
注記 破壊は,累積破壊過程及び比較的大きい値をもつ他の荷重との組合せの結果である可能性があ
る。
8.6
確率に基づく設計の実現
設計における意思決定は,8.1〜8.5に従い信頼性に対する特定の要求を満たすことを容易にする確率論
的解析に直接基づいて行うことが可能である。このような方法は,適切な不確定性モデルと信頼性解析手
法が存在し,確率論的解析の専門知識があるという条件の下で適用可能である。
− 不確定性モデル
− 信頼性手法
− 確率論的解析の専門知識
しかし,多くの場合,準確率論的設計手法によって,設計過程の単純化が可能である。
9
準確率論的手法
9.1
一般事項
準確率論的手法は,リスク情報を活用した意思決定及び信頼性に基づく意思決定に代わるものとして,
構造物の設計,施工,補修,補強,維持管理,運用及び撤去に関連する幅広い決定に適用可能である。し
かし,新築及び既存の構造物に関する,受容可能かつ実現可能な決定の同定を容易にするように,形式化
された準確率論的な安全性検証法を策定しなければならない。
構造物のリスク及び信頼性が適切で,かつ,4.4及び8.4で規定する原則と整合することを保証するよう
に,荷重,材料,運用条件,技能者の技量,検査・維持管理,監視(モニタリング)及び品質管理に関連
する一般情報を基本にしなければならない。
形式化された準確率論的な安全性検証法では,予想される限界,その有効性及び適用に関わる仮定に関
連する全ての情報を特定することが望ましい。これには,次の情報を特定することを含む。
− 法的,時間的,地理的限界(例 プロジェクト,有効期限,改定日,高度など)
− 構造物の種類(例 建築構造物,海洋構造物,基礎構造物など)
− 材料種別(例 コンクリート,鋼材,木,複合材料,土など)
40
A 3305:2020 (ISO 2394:2015)
− 荷重の種類(例 永続荷重,風,雪,交通,地震,波浪など)及び永続荷重と変動荷重との組合せ(永
続荷重による安定又は不安定の考慮を含む。)
− 用途種別(例 病院,事務所,倉庫,エネルギー生産,配送など)
注記 準確率論的手法は,通常,確率変数を,特定の利用のための一連の設計値(極端に好ましい又
は好ましくない数値,荷重組合せ値,使用性水準の値など)に落とし込む。より高いレベルの
解析(準確率論的手法に対する高いレベル)へのキャリブレーションは,個別の値に基づいて
一連の設計規則を完備するために行ってもよい。
9.2
基本原則
形式化された準確率論的な安全性検証法には,次の事項を含まなければならない。
− 結果の重大性等級(8.4及び附属書F参照)
− 設計の局面(8.1参照)
− 設計式
− 設計値
設計式は,構造性能をモデル化することを基本に,箇条5及び箇条6で与えられる限界状態関数及び不
確定性の確率的モデル化原則にのっとって策定されなければならない。設計式の基本的な形式は,式(16)
で与えられる。設計式では,全ての関連する構造の破壊モードに対して,断面特性zのような構造物に関
するパラメータの値を,一意に,かつ,リスク及び信頼性の要求に合致するように決定することが可能で
なければならない(8.4参照)。
G(z)=Rd(z)−Sd(z)>0 ································································ (16)
ここに,
z: 設計パラメータのベクトル(例 断面寸法)
Rd(z): 耐力の設計値
Sd(z): 作用効果の設計値
耐力は,次の一般的なモデルで得られるものと仮定する(附属書C参照)。
R=bΘRRn(X, a) ········································································ (17)
ここに, Rn(X, a): 関連する材料規格で定義された耐力モデル
a: 幾何学的パラメータ(設計パラメータzは,一般にaの部
分集合である。)
ΘR: 耐力モデルに関するモデル不確定性(附属書Cに示す手法
で定めることが可能である。)
b: 耐力モデルの偏り(附属書Cに示す手法で定めることが可
能である。)
一般に破壊モードに対して,設計式を定式化しなければならない。通常,破壊モードには構造物の個々
の断面の破壊及び,構造物の複数の断面の破壊の両方が含まれる。
与えられた設計の局面に応じた作用及び耐力に関する不確定性の特性に基づいて,設計式に入力する
様々な作用及び材料特性の設計値を定めることが望ましい。
9.3
代表値及び特性値
9.3.1
作用
永続作用は,一意な特性値をもつことが多い。構造物の自重による作用の場合,幾何学量の指定値及び
材料の平均単位荷重からその値Gkを求めることが望ましい。しかし,永続作用について,上側及び下側の
二つの特性値を定義することが必要となる場合もある。
変動作用は,しばしば,次の代表値Qrepをもつ。
− 特性値Qk
41
A 3305:2020 (ISO 2394:2015)
− 組合せ値Ψ0Qk
− 頻繁値Ψ1Qk
− 半永続値Ψ2Qk
変動作用の特性値は,選択された基準期間において,これを超過する確率が指定された値となるように
選ぶ。
組合せ値は,組合せによる作用効果の値を超過する確率が,単一の作用を考慮した場合とほぼ同じ値と
なるように選ぶ(附属書E参照)。
次のように頻繁値を定める。
− 選択された期間内において,その値を超過する時間の合計が与えられた短い期間に限られている。
− 超過の頻度が与えられた小さな値に限定されている。
注記 設計の局面が異なれば,同じ荷重でも,異なる頻繁値を設定する場合がある。
半永続値は,選択された期間内において,その値を超過する時間の合計が選択された期間の半分となる
ように定める。
偶発作用は,一意な特性値Akをもち,設計値としても用いられる。
9.3.2
耐力
適切な体積の材料に対して材料の特性を定義し,特性値Xkで表す。製造材料に対しては,特性値は,通
常,関連する材料規準の適用範囲内で製造し供給する材料特性の統計的分布における,事前に規定した分
位点として提示することが望ましい。土及び既存構造物についても同様な原則に従って特性値が評価する
ことが望ましく,設計で対象となる実際の地盤又は実際の既存構造物の一部を代表する値となるようにす
る。
非線形解析に用いる材料特性は,安全性に関して一貫性のある考え方を用い,要求する目標信頼性をも
つ設計になるのであれば,設計値,特性値又は平均値のいずれに基づくことも可能である。
9.4
形式化された安全性検証法
9.4.1
一般事項
形式化した準確率論的な安全性検証法は,幾つかの異なる方法を取り得る。異なる方法間で共通すべき
ことは,設計の局面,設計式及び代表値の適切な選択を通して,リスクが許容範囲内であることを保証し
なければならないという点である。
その他の形式化した安全性検証法は,リスク及び信頼性手法を直接的に利用し,適切なリスクの水準及
び/又は信頼性の水準を提供する限り採用可能である。
設計式に入力する設計値は,対象構造物の全ての関連する破壊モードについて,適切かつ十分な水準の
信頼性を達成することを保証するように選ばれなければならない。
部分係数形式は,一般的規則として,形式化した準確率論的な安全性検証法の基本として活用しなけれ
ばならない。
9.4.2
部分係数法
9.4.2.1
作用
特定の荷重ケースiについて,作用効果の設計値Edは,一般に次のように表すことが可能である。
Ed,i=γsS(Gd,i; Qd,i; ad) ································································· (18)
ここに,
ad: 幾何学的設計値をからなるベクトル
γs: 次の不確定性を考慮する部分係数
− 作用効果のモデル化における不確定性。
42
A 3305:2020 (ISO 2394:2015)
− 場合によっては作用のモデル化における不確定性。
注記 より一般的には,作用効果は材料特性に依存する。
永続及び変動作用の設計値は,次の式による。
Gd=γGGk ················································································ (19)
Qd=γQQrep ·············································································· (20)
ここに, γG及びγQ: それぞれ永続及び変動作用に対する部分係数
9.4.2.2
耐力
耐力の設計値Rdは,次のa)〜c)の異なるモデルによって定めることが可能である。
a) モデル1 耐力の設計値が,材料の耐力パラメータの設計値を用いて定められる場合
R
γ
R
R
)
a,
X
(
d
d
n
d=
······································································ (21)
ここに,
ad: 幾何学量の設計値
Xd: 耐力パラメータの設計値
γR: 耐力モデルのモデル不確定性に関する部分係数。実験室から
実構造物への変換に関する不確定性及び耐力モデルの偏りに
関する不確定性を含む。
材料の耐力パラメータの設計値は,次のように定められる。
m
k
d
γ
X
η
X=
············································································· (22)
ここに,
η: 荷重継続効果,湿度,温度,寸法効果などを考慮するための
換算係数
Xk: 一般に5パーセンタイル値で定義される耐力パラメータの特
性値
γm: 材料特性の部分係数
η幾何学量については,設計値adは,通常,設計者によって定められた寸法に対応する。
二つ以上の耐力パラメータが耐力モデルで使用される場合,設計値は,式(21)のそれぞれの耐力パ
ラメータに適用される。
部分係数γmは耐力パラメータの不確定性に依存し,γRは偏りを含む耐力モデルの不確定性に依存す
る。
b
γ
γ
θ
R=
················································································· (23)
ここに,
γθ: モデルの不確定性に関する部分係数
b) モデル2 耐力の設計値が,材料の耐力パラメータの特性値によって得られる場合
M
k
k
n
d
)
a,
X
(
γ
η
R
R=
···································································· (24)
ここに,
γM: 耐力パラメータXの耐力関数Rn(X, a)を介した不確定性に関す
る部分係数
耐力の全不確定性は,モデルの不確定性ΘRと耐力パラメータXに関する耐力関数Rn(X, a)とを介し
た不確定性に依存する。(材料ではなく)耐力の部分安全係数は,それに対応して,次の式によって求
めることが可能である。
b
γ
γ
γ
R
θ
=
M
·············································································· (25)
ここに,
γR: Rn(X, a)を介した耐力パラメータXに関する不確定性に依存す
43
A 3305:2020 (ISO 2394:2015)
る部分係数
γθ: モデル不確定性に依存する部分係数
c) モデル3 耐力の設計値が,試験に基づいて推定された耐力の特性値を用いて定められる場合
M
k
d
γ
R
R=
················································································ (26)
ここに,
Rk: 試験に基づいて推定された耐力の特性値(附属書C参照)
(Rkは一般に5パーセンタイル値として定義される。)
γMは,試験に基づき得られる耐力の統計的不確定性を含む不確定性に関する部分係数である。
関連する破壊モードの生起確率が8.4の目標信頼性水準に近くなるように,荷重の部分係数及び材料の
部分係数γm,γR及びγθをキャリブレーションすることが望ましい。
慣例によって,選択された分位点によって設計式の代表値を定めるのに対して,部分係数及び荷重組合
せ値は,キャリブレーションによって定めることが可能である。
部分係数及び代表値は,対象とする設計の局面及び破壊モードについて関連する偶然的及び認識論的不
確定性を考慮して定めなければならない。通常,作用効果において重要な変数の代表値は,上側の分位点
として選択し,耐力において重要な変数の代表値は,下側の分位点として選択する。
キャリブレーションでは,形式化された準確率論的な安全性検証法が,構造物群に適用されるときに達
成する破壊確率と最大許容破壊確率との差を構造物群全体で最小化するように,部分係数及び荷重組合せ
値を選択しなければならない。部分係数法のコードキャリブレーションの手順は,附属書Eに記載してい
る。
注記 荷重・耐力係数設計(LRFD)法は,基本的に部分係数法と同じ原則に従う。
9.4.3
設計値法
設計値法は,関連する設計の局面と対応する設計式の直接の確認に基づく。設計式には,信頼性評価に
基づき定める基本変数の設計値を用いる。設計値は,附属書Eに示すように,一次信頼性手法(FORM)
を直接利用する簡略法を用いて決定することが可能である。
9.5
累積破壊の検証
累積的で非減少の破壊評価尺度を含む限界状態の場合には,設計供用期間の最終年に対して信頼性の検
証を実施しなければならない。
Rd(X, a, n)>Sd ········································································· (27)
ここに,
n: 設計供用期間の年数
Sd: 年当たりの目標信頼性に基づく最終年における極限作
用効果の設計値
Rd(X, a, n): 元の状態及び供用期間中の全ての作用効果,累積破壊に
基づく,供用期間終了時における耐力の設計値。X及び
aの設計値は,供用期間に関連した目標信頼性に基づく
ことが可能である。
点検プログラムを利用することで,要求を緩和することが可能である(附属書B参照)。
注記 累積破壊の評価尺度は,例えば,構造物の(腐食,疲労などによる)劣化のモデル化に用いる
ことが可能である。
44
A 3305:2020 (ISO 2394:2015)
附属書A
(参考)
品質マネジメント
A.1 目的
この附属書の目的は,リスク及び信頼性に基づく意思決定の過程で用いられる仮定の妥当性について,
品質マネジメント,品質保証及び品質管理を用いることで確認することにある。一般に,品質マネジメン
ト,品質保証及び品質管理は,ISO 9000シリーズに従わなければならない。
一般に,建設工事は,次による。
a) 定められた要求,用途又は目的に合致すること。
b) 顧客の期待を満足するもの。
c) 適用すべき規準及び仕様に適合するもの。
d) 社会の法令(及びその他の)要求に従うもの。
建設工事では,少なくとも最低限の基本的な水準の品質マネジメント,品質保証及び品質管理が要求さ
れる。
A.2 定義
A.2.1 品質マネジメント,品質保証及び品質管理に関する一般的定義
品質,品質マネジメント,品質保証及び品質管理に関する一般的な定義は,ISO 9000:2005に従わなけれ
ばならない。
A.2.2 附属書Aに関連する用語及び定義
A.2.2.1 サンプリング計画(Sampling plan)
サンプリング計画は,品質管理に関してどのように標本を採取すべきかを示す詳細な手順である。これ
には,品質管理で必要となる情報,測定の種類,標本を抽出する時間間隔及び誰がどのようにして情報を
取得しなけばならないかが記載され得る。結果として得られるデータが構成要素又は関心のある特性を代
表する標本からなるように,サンプリング計画を設計することが望ましい。
A.2.2.2 品質水準(Quality level)
目標とする又は達成される定性的又は定量的な品質の程度。
A.2.2.3 合格品質水準,AQL(Acceptable quality level)
コンプライアンス管理の目的の観点から,平均的に許容であるとみなされる品質の最低水準。
A.2.2.4 限界品質,LQ(Limiting quality)
コンプライアンス管理において合格と許容できる,構成要素の特性に関する品質の最低水準。
A.2.2.5 不良率(Fraction defectives)
構成要素の特性の分布において規定値を満足しない割合。
A.2.2.6 平均出検品質,AOQ(Average outgoing quality)
適用されるコンプライアンス管理を行う場合に,構成要素の特性の分布が未知の場合に規定値を満足し
ない割合,すなわち,不良率に,その分布に伴う合格確率を掛け合わせたもの。
A.2.2.7 平均出検品質限界,AOQL(Average outgoing quality limit)
平均出検品質の許容される最大値(適用されるコンプライアンス管理を行った結果としての,構成要素
45
A 3305:2020 (ISO 2394:2015)
の不良率の平均値の最大値に相当)。
A.3 品質マネジメント
品質マネジメントは,品質保証及び品質管理における統合的なリスクに基づく手法を包含しなければな
らない。人的過誤並びに設計及び施工における誤りも,統合的な品質マネジメントシステムの対象の一部
であると考えなければならない。
設計品質のマネジメントをするということは,次のような措置が取られることが望ましいことを意味す
る。
a) 品質についての種々の信頼性の側面を特定する(例 構造安全性,用途の適合性,快適性,耐久性,
美観,費用など)。
b) これらの側面を,品質に対する要求事項一式に変換する(例 機能的特性,温熱特性,構造安全性,
使用性,ロバスト性基準,設計供用期間,費用など)。
c) その品質を確保するのに寄与する主な活動を特定する(例 予備調査,全体計画に関する選択肢,設
計の局面,作用の特性,材料特性,職人の技量水準,用途制限,維持管理の原則など)。構造物のライ
フサイクルの中で品質に影響する様々な活動を特定する。これらの活動は,構造物における品質改善
のループと解釈することが可能である(表A.1参照)。
d) a)〜c)のように考慮した活動は,関連する組織におけるマネジメントによって管理する。
表A.1は,品質計画を準備するための基礎と考えることが可能である。
A.4 品質保証
設計が規定した品質に対する要求を満足していることについての十分な確認に至るための品質保証は,
次の措置を取ることが望ましいことを意味する。
− 規定した品質に対する要求事項の満足を妨げる主要因を,品質計画において考慮することが望ましい
(表A.1参照)。
− 品質に寄与する要因の管理に関する文書を,構造物のライフサイクルを通して編集・保管することが
望ましい。

46
A 3305:2020 (ISO 2394:2015)
表A.1−建設工事の品質改善ループにおける品質マネジメント活動
ライフサイクルの段階
活動
全体計画
− 構造物及び部材の適切な要求性能の確立
− 設計及び/又は供用期間の規定
− 供給元の規定
− 施工及び維持管理の仮規定
− 個人及び組織について適切な資格をもつ関係主体の選択
設計
− 材料,部材及び組立ての性能基準の規定
− 供用期間及び/又はライフサイクルにおける性能の規定
− 性能の受容性及び達成可能性の確認
− 試験の選択肢の規定(実物大模型,現場など)
− 材料の規定
入札
− 性能指定を含めた設計図書の再検討a)
− 要求事項の受諾(請負業者)
− 入札の受諾(顧客)
施工及び検査
− 手順及び工程の管理a)
− サンプリング及び試験a)
− 欠陥の是正a)
− 設計における仮定の評価,是正及び/又は更新a)
− 設計図書に規定されたコンプライアンス試験に従った工事証明a)
工事の完了及び顧客へ
の引渡し
− 稼働検査
− 完成建物の性能検証(例えば,作業荷重下での試験などによる。)a)
使用及び保全
− 性能のモニタリングa)
− 劣化又は破壊の検査a)
− 問題の調査a)
− 構造性能の評価a)
− 作業の証明a)
補修又は除却
− 既存構造物に対する補修における適切な性能水準の確立
− 補修又は除却の必要性の評価a)
− 補修の場合の(上記と同様の)設計,入札,施工,使用及び維持管理にかかる活動a)
注記 除却は,この規格の範囲外である。
注a) 品質マネジメント活動の側面のうち,品質管理に基づいて構成要素の特性をベイズ更新することができるも
の(A.5.5参照)。
構造計算に関する品質保証の場合,一般的に,次の項目を規定することが望ましい。
− 設計の根拠に関する議論,記述を含めた設計規範及びなされた仮定
− 自重,積載荷重及び/又は環境荷重の一覧
− 使用材料の規定
− 地盤工学的情報(関連がある場合)
− 構造要素のしゅん(竣)工時図面
簡易的な感度分析によって関連性がある場合には,それを考慮し,次の項目を含んだ荷重と構造物との
相互作用に関する高度な構造信頼性計算を行う。
− 屋根構造物,床構造,骨組,トラス,柱,壁及び基礎に対する鉛直荷重の解析並びに設計
− 地震作用及び風作用に対する水平荷重の解析並びに設計
− 動的解析
ソフトウェアツールを用いる場合,意味のある計算結果を生むためには,利用者はそのソフトウェアの
基礎となっている原則を知っておくことが望ましい。どのような特徴を正確にモデル化することが望まし
47
A 3305:2020 (ISO 2394:2015)
いか又は単純化することが望ましいかを決めるためには,理にかなった工学的判断が必要である。ソフト
ウェアによる計算は,構造物ごとの安全に関する基本的方針に組み込まれることが望ましい。単純化され
た構造モデルを用いた構造信頼性計算は,参考として用いられることが望ましい。
ある品質マネジメント活動の質の不足が,構造的なロバスト性に不釣合いな影響をもたらす場合には,
これらの活動又は構造物の詳細に対する品質保証及び管理を強化しなければならない。質の不足によって
構造的なロバスト性に不釣合いな影響を与える可能性のある活動を示すために,リスクに基づく手法を用
いることが可能である。
破壊及び損傷の結果が大きい構造物,すなわち,附属書Fで定義される結果の重大性等級3〜5に相当
する構造物に対しては,構造物に対する認証書(我が国の土木構造物においては,各管理者が行う定期点
検報告書がこれに相当する)が発行されなければならない。この認証書が設置され,安全性が確保され,
定期的に更新されることは,所有者の責任である。
構造物に対する認証書は,構造物が所有者に手渡されたときに発行し,次の情報を含まなければならな
い。
− 構造物の幾何学的形状,材料,用途及び性能に対して所有者が規定した要求
− リスク,信頼性又は準確率論的方法のいずれに基づいたのかどうか,構造物の設計及び建設のための
文書化への言及
− 状態管理,検査,維持管理,修復の方策及び手順の仮定に関する事項の文書化
− 材料の生産,設計及び建設に関して行われる品質管理に関する事項の文書化
− 考えられる不適合に関する評価及びそれらの取扱いを含めた“完成時”“使用時”の構造物に関する事
項の文書化
− 実施した状態管理,検査,維持管理,修復及びその他の変更に関する事項の文書化
− 事故及び事象の種類に応じた避難計画並びにその他の損失低減活動計画に関する事項の文書化
− 計画し及び実行した状態管理活動を受けて更新する運用中の“目的適合性”の評価に関する事項の文
書化
A.5 品質管理
A.5.1 一般事項
品質管理の適用とは,次のような措置を取ることが望ましいことを意味する。
− 情報収集
− 収集した情報に基づく判断
− 収集した情報に基づく決定
A.5.2 管理手順
製造及び建設における管理手順に関しては,次の項目間の区別が必要である。
− 生産管理(生産工程の管理)の目的は,生産工程のかじ(舵)を取り,受容可能な結果を保証するこ
とにある。
− 適合性管理(建設工程中若しくは建設工程後に行う管理又は生産工程の結果の管理)の目的は,生産
工程の結果が与えられた仕様に従っていることを保証することである。
注記 建設工事の場合には,例えば,鉄筋の配筋の管理など,適合性管理を建設工程前又は建設工程
中に行うのが最もよいことが多い。
いずれの管理手順も異なる目的をもっているため,生産管理又は適合性管理を行う手法も,一般には区
48
A 3305:2020 (ISO 2394:2015)
別することが望ましい。
管理手順は,考えられる不適合行動とともに,あらかじめ規定しておくことが望ましい。
A.5.3 管理基準及び合否判定ルール
管理は,全数又は統計的に行う。全数管理の場合は,全ての生産単位を検査する。合否判定ルールとは,
一つのロットが良い(合格)か悪い(不合格)かを判定することを示す。管理基準は,定量的な場合,所
定の許容誤差で与えるのが一般的である。
適合性管理に関して,次の区別が可能である。
− あるロットが“良い”状態又は“悪い”状態にあり,決定では“合格”か“不合格”かを決めるとき
の属性による制御
− あるロットが測定の尺度によって評価されるときの変数による制御
統計的管理手順は,一般に次の項目からなる。
− 生産のバッチ処理
− それぞれのバッチの中でのサンプリング
− サンプルの試験
− 結果の統計的判断
− 合否に関する決定
バッチは,管理の対象とする特性に関して(時間的にも空間的にも)同質とみなされるものであること
が望ましい。製品のバッチ化及びサンプリングは,規定されるサンプリング計画に従って実行することが
望ましい。結果の判断は,一般には,次のいずれかの方法で判定することが望ましい。
− 所定の信頼度及び/又は信頼区間
− 合格品質水準(AQL)及び限界品質(LQ)での受容確率又は平均出検品質限界(AOQL)に関する所
定の値のいずれかの,適合性管理に関する検査特性の所定の性能
− ベイズ手法の適用
属性による管理の場合には,合否判定ルールは,ランダム試験を行うサンプルサイズnに占める許容で
きる欠陥数cで規定する。変数による管理の場合には,n個のランダム試験のサンプルに基づく一つ以上
の試験統計からなる適合性関数が,合格領域にあるかどうかで評価する。合格領域は一つ以上の境界から
なる。
A.5.4 管理工程
管理の監督者又は監督組織によって,次のような異なる管理段階の区別をすることが可能である。
− 個人による自己検査
− 内部管理
− プロジェクトマネジメントによって扱う合否管理
− 設計及び/又は施工の独立した外部団体による管理
− 建築主の組織による管理及び監督
品質水準のレベル分け(A.6参照)に依存した必要とされる品質検査水準によって,上記の必要な管理
段階を選択しなければならない。
建築法規及び/又は規格に基づき,公的機関が着手及び実施する追加的な管理もしばしばある。
内部管理は,管理対象となる作業を実施しているのと同じ事務所,工場又は作業場で行う。しかしなが
ら,工事及び管理は,別の組織が行う。
管理工程を,幾つかの段階で構成する場合,これらの段階での活動が,統計的な意味でできる限り互い
49
A 3305:2020 (ISO 2394:2015)
に独立であることが,最終結果にとって重要である。そうでなければ,管理の効率が落ちてしまう。多く
の場合,A.4に従った品質計画の一部として,管理計画を定める必要がある。
A.5.5 品質管理のフィルタリング効果
一般に,品質に対する要求(例 品質マネジメント,生産管理,適合性管理など)があるということは,
質の高い製品の提供が求められるため,構成要素の品質管理を行うことは,その特性値に良好な影響を与
える。この良好なフィルタリング効果は,不確定性の表現(箇条6),確率に基づく意思決定(箇条7)及
び構造ロバスト性の評価(附属書F参照)に影響する。そのため,品質管理の有益な効果は,リスクに基
づく方法にも含まれる。
品質管理の一つ以上の側面,すなわち,品質マネジメント,品質保証又は品質管理(生産管理又は適合
性管理のいずれか)において,ベイズ手法を用いることによる不確定性の表現を考慮に入れることが可能
である。適合性管理の場合,運用特性をベイズ更新におけるゆう(尤)度関数としてみなすことが可能で
ある。後者の場合,確率的なモデルのパラメータの更新は,次のとおり計算することが可能である。
∫∫
=
β
d
β
'f
β
P
β
'f
β
P
β
''
f
β
a
β
a
β
)
(
)
(
)
(
)
(
)
(
······················································· (A.1)
ここに,
β: 更新する統計的母集団の確率モデルのパラメータからなる
ベクトル
)
(β
'fβ
: ベクトルβの事前分布関数
)
(β
''
fβ
: ベクトルβの事後分布関数
Pa(β): 適合性管理の運用特性(パラメータβを用いた確率モデル
によって特徴付けられる母集団の合格確率)
構成要素の特性値のベイズ更新を考慮するような品質管理活動について,暫定的に表A.1に示している。
しかしながら,不確定性の表現及び/又は確率に基づく意思決定において品質管理を考慮する場合には,
品質管理を適切に実施していることを常に保証することが望ましい。
新しい材料又は建設手法を適用する場合には,強化した品質管理を用いて,それがリスク又は信頼性に
基づく手法に与える影響を定量化することによって,材料及びモデルの不確定性を含める場合のリスク又
は信頼性に基づく設計を正当化することが可能となる。事前情報が不足している場合,無情報事前分布又
は少ない情報での専門家判断に基づく事前分布を上記のベイズの方法で用いることが可能である。
A.6 品質水準のレベル分け
考えられる三つの品質水準(QL)を表A.2に示す。品質水準はそれぞれA.3,A.4及びA.5で記載した
品質マネジメント,品質保証及び品質管理と関連付けることが可能である。品質水準を与える際には,三
つの要素(品質マネジメント,品質保証及び品質管理)全てを同時に考慮することが望ましい。
品質水準の区分は,F.1で記載する結果の重大性等級と直接的な関わりがある。そのため,品質水準は
構造物の利用の区分と直接的な関係がある。
注記 この品質水準の区分は,許容した又は仮定する作用効果及び耐力の統計的ばらつき並びにモデ
ル不確定性を考慮して評価した信頼性指標βの区分とも関連し得る。
重大な人命喪失又は経済的・社会的・環境的な結果を伴う建物及び土木構造物,工学システム,すなわ
ち,破壊の結果が重大な公共建築(例 コンサートホール,スタジアム,高層建物など)には,品質水準
QL3を適用しなければならない。必要とされる品質水準の選択は,信頼性に基づく手法に基づくことが可

50
A 3305:2020 (ISO 2394:2015)
能である。
表A.2−品質水準(QL)
品質水準
(QL)
結果の重大性等級
(附属書F参照)
内容
要求事項の明示及び品質検査のための管理体系
QL1
1〜2
基本的な品質水準
自己管理:品質マネジメント,品質保証,品質管理に関す
る要求事項及びライフサイクルにおけるその段階を立案
した人物によって実施される品質検査に関する規定。
QL2
3
高い品質水準
品質マネジメント,品質保証,品質管理に関する要求事項
及び組織的手順に従いライフサイクルにおけるその段階
を立案した個人以外の人物によって実施又は自己検査に
よって実施される体系付けられた品質検査に関する規定。
構造的な主要素に対する建設中の監督及び検査に関する
高い努力。
QL3
4〜5
品質マネジメント,
品質検査,品質管理
に対する拡張方策
を伴う特に高い品
質水準
自己検査及び体系的な品質管理に加え,独立した団体によ
る管理も実施されなければならない:品質マネジメント,
品質保証,品質管理に関する要求事項及び組織的手順に従
いライフサイクルにおけるその段階を立案した組織以外
の組織によって実施される品質検査に関する規定。
(例えば,構造物の設計及び/又は施工に関する)専門知
識をもつ有資格者による主要構造く(躯)体に対する建設
中における徹底的な監督及び品質検査。
51
A 3305:2020 (ISO 2394:2015)
附属書B
(参考)
構造健全性のライフタイムマネジメント
B.1
一般事項
構造健全性マネジメント(SIM)は構造物が4.2.1に規定する目標及び目的を,建設時から解体時までの
全供用期間中に適切な信頼度で満たすことを保証する,継続的なライフタイムにおけるプロセスのことで
ある。たとえ構造物を,上記の目標及び目的に従って設計並びに建設したとしても,それがそれらの目標
及び目的を将来にわたって満たし続ける保証はないため,この過程は必要不可欠である。
構造健全性は,様々な作用及び環境からの影響による劣化並びに損傷によって時間とともに損なわれる
可能性があり,用途及び/又は荷重が変わる可能性があり,設計供用期間を超えた使用期間の延長が必要
となる場合もある。加えて,設計及び施工に誤りがある可能性がある。そのような状況の下では,予想外
の欠陥,損傷及び劣化を検出するために,検査及び維持管理が必要不可欠である。それらの後に,適切な
評価及び構造物の健全性維持に役立つ可能な修復又は改修を行わなければならない。このような活動を構
造物の使用期間にわたって行うことの必要性を,設計及び建設時にも考慮することが望ましい。
注記 検査という用語には,供用期間にわたって構造物の性能に関する情報を収集する活動が含まれ,
一般にモニタリングと呼ぶものも含むと理解することが望ましい。
次にリスク及び信頼性に基づく方法の枠組みにおける一般的なSIMのプロセスを記載する。データ収集,
評価,検査戦略及び計画の構築といったこのプロセスの主な段階を検討する。新しい検査データを用いた
構造信頼性評価の更新に,特に着目する。
B.2
構造健全性マネジメントプロセスの主な段階
SIMのプロセスには,次の段階が含まれる(ISO 19902)。
− (特に検査による)データ収集
− データ評価,必要であればそれに続く構造健全性アセスメント及び是正措置
− 検査戦略の構築
− 詳細な検査計画の構築
このプロセスの各段階を図B.1に示し,この附属書において更に詳細に記載する。
図B.1−構造健全性マネジメントプロセスの段階
図B.1においてSIMのプロセスから設計及び施工に戻る破線矢印は,構造物の設計時にこのプロセスを
計画することの重要性を強調している。これは,供用期間中に損傷及び/又は劣化するおそれのある健全
設計及び
施工
データ
評価
検査戦略
検査計画
52
A 3305:2020 (ISO 2394:2015)
性にとって重要な構造要素を特定することを含む。設計では,検査及び維持管理のためにそれらの要素に
無理なく容易に近づくことを保証することが望ましい。また,それらの要素は構造物の供用期間中に修復
又は交換されることも考慮することが望ましい。このように,実行可能な限り,設計は,このような活動
を比較的容易に行うようにすることが望ましい。SIMのプロセスの最初の計画において,上記の条件が満
たされないことが明らかになる場合には,設計変更が必要となる可能性がある。
B.3
データ収集
SIMのプロセスには構造物に関する最新のデータが不可欠である。データは,構造物の原設計,施工,
検査,構造健全性アセスメント,改修,用途変更,補強,修復及び事故に関する情報を含むことが望まし
い。場合によっては,ひずみ,応力,たわみ,振動,温度,圧力などの構造物のパラメータに関する情報
が,モニタリングによって継続的に収集され得る。モニタリングを行う場合又は行わない場合の構造物に
対する費用便益解析に基づいて,モニタリングの実施は,経済的に正当化することが可能である。収集し
たデータは全て,所有者又は使用者によって,構造物の供用期間全体にわたって保管され,所有者が変わ
る場合には,新しい所有者に渡すことが望ましい。
B.4
評価及び構造健全性アセスメント
B.4.1 データ評価
構造物に関する新しい情報が入手可能になると,構造健全性アセスメント又は検査戦略の更新が必要か
否かを判断するため,まず工学的判断を行い,必要な場合には,より詳細な分析を用いて,関連するあら
ゆるデータを評価する必要がある。検査戦略の更新に関する決断が,詳細な構造健全性アセスメントなし
に行われたり,構造健全性アセスメントをしても必ずしも検査戦略の更新につながるとは限らないことに
注意が必要である。
構造健全性アセスメントは,通常,次のいずれかの場合に必要となる。
a) 構造物の目的及び用途が原設計又は前回の評価から変更された。
b) 構造物の特性が原設計又は前回の評価で採用したものから逸脱した。
構造物の目的及び用途が変化する状況には,次のようなものが含まれる。
− 荷重及び作用の増大
− 用途の変更
− 設計供用期間を超える構造物の使用延長
− 構造物の社会的重要性増大による目標信頼性レベルの上昇
構造物の特性が逸脱する状況には,次のようなものを含む。
− 設計の誤り
− 施工中に発生した構造物の欠陥又は損傷
− (腐食,疲労などによる)構造物の劣化
− 偶発的な事象又は過荷重による構造物の損傷
− 構造物の変更
− 設計規格の改訂による設計要件の変化
構造健全性アセスメントの実施には,更なる検査によるより多くのデータ収集が必要となる場合がある。
劣化が進行しているが関連する損傷はまだ見られない,環境条件が変化した,類似の構造物が満足のい
く性能を発揮しなかったなどの証拠がある場合,評価を行わずに検査戦略の更新が必要であることを決定
53
A 3305:2020 (ISO 2394:2015)
する場合もある。
B.4.2 構造健全性アセスメント
この規格の4.1に規定している性能指標を通じて構造物が意図した目的にかなっているか,改修処置が
必要かを評価によって決定する必要がある。評価においては,構造物の暴露事象,ぜい(脆)弱性及びロ
バスト性を4.2.2に従って,構造物の設計時と同様に考慮する。しかしながら,評価及び設計の状況には,
不確定性に関して根本的な違いがある。
設計においては,不確定性は,その時点で存在していない構造物の荷重及び耐力といったパラメータを
あらかじめ予測することによって生じる。これらの不確定性は,主に材料及び施工の質が異なることによ
る多数の構造物のばらつき,並びに敷地特有の荷重のばらつきを表している。それらを,荷重及び環境の
パラメータの統計的特性に関する一般的なデータとともに構造物の使用材料の製造及び施工の所定の仕様
書に基づいて評価する。
評価においては,荷重,耐力及び環境のパラメータを現場で測定するように,既存の構造物に対して検
査及び試験を行うことが可能である。しかし,これは,供用期間中における検査及び試験に関係する不確
定性があるため,不確定性が完全に解決されるということではない。検査手法は,分解能に限りがある。
したがって,検査結果は,構造物の実際の状況の指標としてだけ考慮可能である。問題は,ある状況の指
標がどの程度実際の状況に関係しているかということである。この目的のため,検出確率(PoD)の概念
が極めて有用である。PoDによって,所定の規模又は範囲の欠陥を検出する確率を用いて検査手法の質が
定量化される[1]。
供用期間中の検査及び試験に関係する不確定性には,次のものが含まれる。
− 計測誤差
− 計測されたパラメータの本来的なばらつき
− 着目しているパラメータを直接計測することが不可能であり,それと対応するものとして計測するパ
ラメータとの間の関係を明らかにするために必要なモデルの不確定性
− 計測数が限られていることによる統計的不確定性
構造健全性アセスメントにおいては,検査に伴う不確定性を考慮することが望ましい。これは,信頼性
解析において,明示的に又は基本変数の特性値及び設計値を更新するために確率的手法を用いることによ
って行うことが可能である。設計及び評価の状況に関係する不確定性が異なる特質をもつため,基本変数
の特性値及び設計規準の部分安全係数の適用性を慎重に調べなければならない。
保守的な設計は,通常は構造物のコストを大きく増加させないが,保守的な評価は不必要かつ高額な修
復又は交換につながり得る。したがって,モデル不確定性を低減するため,設計規準にあるものに比べて
より精緻化された構造モデル(有限要素モデルなど)を既存構造物の評価に用いる場合がある。
情報を収集し,解析によって構造性能を評価し,修復及び補強活動を考案するプロセスは,最も効率の
良い調査及び構造物の使用上の新しい要求を満たすのに必要な改修を特定すること及び/又は構造物の現
況及び将来の性能に関するいかなる疑いも取り除くことを意図した決断のプロセスである。このプロセス
は,構造物の全供用期間の費用を考慮して最適化することが重要である。
一般的な評価手順は,図B.2(ISO 13822の附属書B)に示されるフローチャートに従ってまとめること
が可能である。構造健全性アセスメントに関する更なる情報は,ISO 13822を参照するとよい。
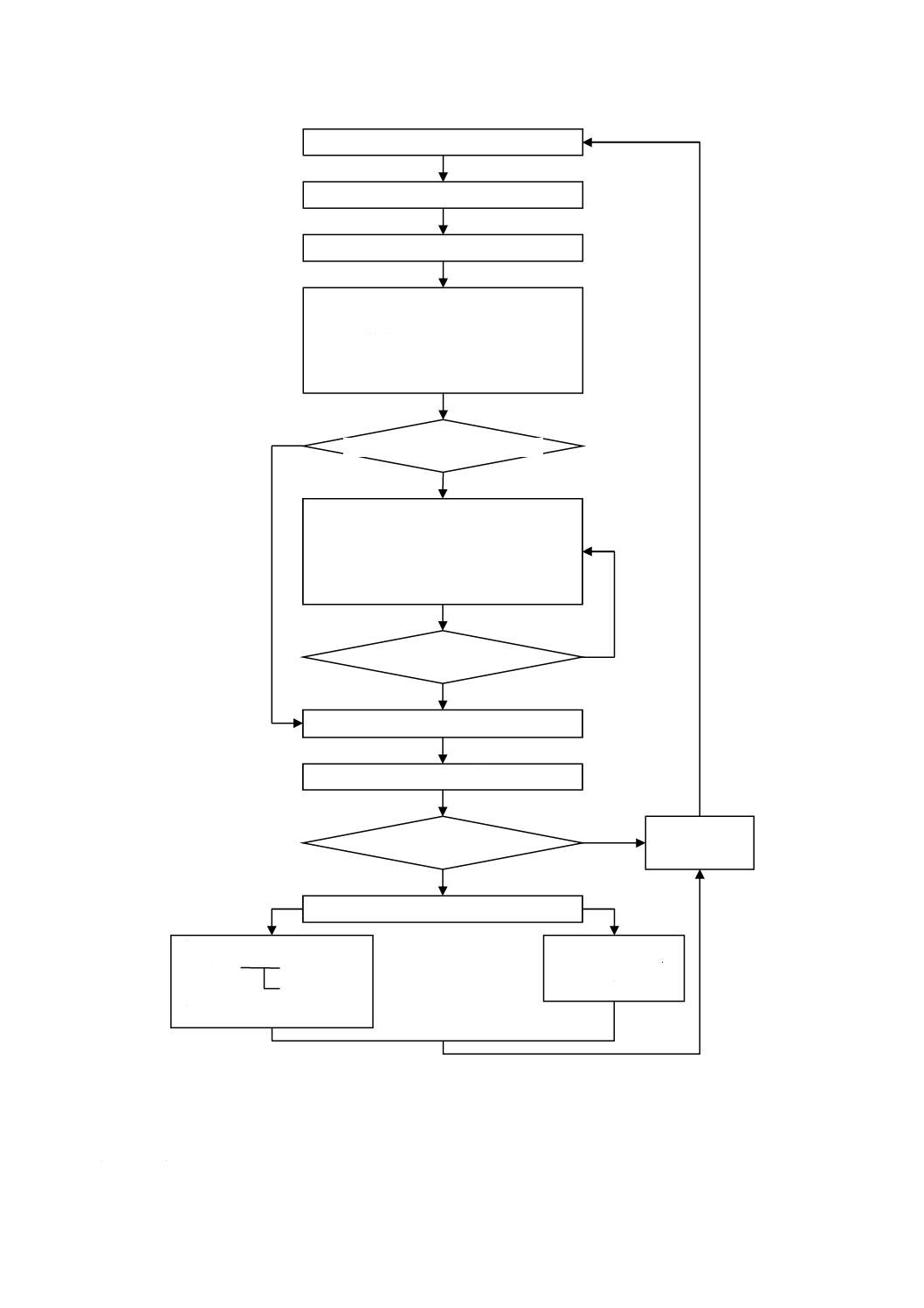
54
A 3305:2020 (ISO 2394:2015)
図B.2−一般的な評価プロセスのフローチャート
B.4.3 情報の更新
構造物の性質に関する情報を更新することは,評価の必要不可欠な部分である。次の二つの相補的な更
新方法が考えられる。
要求
アセスメントの目的の指定
シナリオ
予備的アセスメント
・ 文書及びその他のエビデンスの調査
・ 予備検査
・ 予備確認
・ 即時的な行動の決定
詳細なアセスメントが必要か?
・ 詳細な文書の調査及び再検討
・ 詳細な検査及び材料試験
・ 行動の決定
・ 構造物の特性の決定
・ 構造解析
Yes
Yes
更なる検査が必要か?
No
No
Yes
アセスメントの結果の報告
判断及び決定
十分な信頼性があるか?
No
介入
建設
・ 修繕
・ 取り壊し
・ 修復
・ 改修
運用
・ モニタリング
・ 用途変更
・ 定期検査
・ 維持管理
55
A 3305:2020 (ISO 2394:2015)
a) 保証荷重試験又は過去の性能に関する情報を用いることで構造物全体(又は構造要素)の性能を調べ
る。
b) 供用期間中における検査を行うことで個々の基本変数に関するデータを収集する。過去の入手可能な
不確実情報を新しい検査データを用いて更新することは,通常,ベイズの手法によって行う。更新は,
単一の観測若しくは事象の更新又は複数の観測若しくは分布の更新のいずれかを用いて行うことが可
能である。単一の観測及び事象の更新では,“破壊”を支配するパラメータを計測する。対応する安全
余裕H[=g(X)]の観測が0より大きければ,更新した破壊確率は,次の式で表す。
[
]
[
]
)0
(
0
0
)
(
0
|0
)
(
f
>
>
≦
>
≦
H
p
H
X
g
p
H
X
g
p
pU
Ι
=
=
······························· (B.1)
このような更新の効率は,計測されるパラメータがどの程度破壊に密接に関連しているかに依存する。
複数の観測及び分布の更新を説明するために,確率密度関数が1組のパラメータΘ(平均及び標準偏差
など)に依存する基本変数Xを考える。Θの事前分布をf'θ(θ)と表す。この分布は,供用期間中における検
査の前に,Θについて得られる情報に基づいている。たとえ事前情報が不十分であっても,それがΘ及び
それに次いでXの不確定性を大幅に低減する可能性があるとして,それを考慮することが極めて重要であ
ることに注意しなければならない。xʼ={x1, …, xn}Tを供用期間中における検査の間になされたn個の計測
の結果を含むベクトルであるとする。ベイズの定理によれば,Θの事後分布f''Θ(θ)は,次の式で表す。
∫
=
θ
Θ
dθ
θ
'f
x'
θ
L
θ
'f
x'
θ
L
θ
''
f
)
(
)
|
(
)
(
)
|
(
)
(
Θ
Θ
····················································· (B.2)
ここに, L(θ|x'): 次の式のように測定の条件付き確率fX|θ(xi|θ) (i=1, 2, … n)に
比例するゆう(尤)度関数
∏
=
∝
n
i
i
θ
X
θ
x
f
x'
θ
L
1
|
)
|
(
)
|
(
·························································· (B.3)
次のXの予測分布が更新された破壊確率の推定に用いられる。
∫
=θ
Θ
θ
X
X
dθ
θ
'f
θ
x
f
x
f
)
(
)
|
(
)
(
|
···················································· (B.4)
保証荷重試験は,既存構造物(又はその要素)の耐力を検証するために用いることが可能である。ある
構造物が保証荷重試験に耐えたことが分かったとしても,それは,その構造物の最小耐力が適用された荷
重効果よりも大きいということを示しているだけである。それによって構造物の実際の耐力が明らかにな
ることはなく,構造安全性についての意味のある測定値も提供しない。しかしながら,保証荷重試験の結
果を,確率的(又は信頼性)方法を用いて分析することがある。ある構造物が既知の保証荷重に耐えたな
らば,構造物の耐力の元の累積分布関数F'R(r)は単純にこの既知の荷重効果QPLで切り取られる。その結果,
耐力の更新された分布関数F''R(r)は,次のように与えられる。
)
(
1
)
(
)
(
)
(
PL
PL
Q
F'
Q
F'
r
F'
r
F'
R
R
R
R
−
−
=
························································ (B.5)
供用期間中のT年の間,構造性能が満足な状態にあるということは,構造物の耐力がこの期間中の最大
荷重効果よりも大きいことを意味している。時間Tでの更新された構造耐力の分布関数は,次のように与
えられる。
56
A 3305:2020 (ISO 2394:2015)
∫
∫∞
=
0
0
)
(
)
(
)
(
)
(
)
(
dr
r
'f
r
F
dr
r
'f
r
F
r
F''
R
T
Q
r
R
T
Q
R
······················································· (B.6)
ここに,
T
Q
F: T年最大荷重効果の累積分布
f'R(r): 載荷前の耐力の確率密度関数
B.5
検査戦略
供用期間中の構造物の検査戦略は,類似の荷重及び環境状況にある類似の構造物の一般的なデータに基
づいて,設計段階の構造物に対して最初に練っておくことが極めて望ましい。構造物の設計供用期間中に
おいて,可能性のある機能低下過程の効果をモデル化することによって得る情報も用いることが可能であ
る。構造物のライフサイクルコストについて検査計画を最適化しておくことが重要である。
被害及び欠陥を見つける様々な検査手法(目視検査及び非破壊検査)の能力は検査戦略に依存している。
被害又は潜在的欠陥の考えられる原因を特定することが可能なときには,いつでも適切な検査戦略,すな
わち,どこをどのような手法で,どの程度の頻度で検査するかを考案することが必要である。一方で,構
造健全性を損なう可能性のある,予見できない又は単純に未知の現象を見つけるために定期的な検査の計
画を立てることも必要不可欠である。これは構造物の供用期間の初期において,設計及び施工での誤りを
明らかにし得るという点で特に重要である。この枠組みにおいては,しゅん(竣)工後の構造物の初期状
態を決定する基準となる検査が必要となる。供用期間の後期の段階においては,そのような誤りが事故に
よる被害と関係する可能性がある。事故の後においては,事故の報告書に基づいて当初計画にない検査が
必要になることもある。そのような場合には,一般的に,構造物全体に対する目視検査が有用である。
検査戦略は,構造物の供用期間を通じて,新しいデータの入手,構造健全性アセスメントの結果,SIM
手法に関連する他のデータ及び情報に従う改訂によって,定期的に更新されることが望ましい。検査の頻
度及び範囲は,費用便益分析によって正当性を示すことが望ましい。
検査戦略を最適化するために,リスクに基づく検査(RBI)の計画を活用することが可能である。その
方法は,構造物の要素の破壊に関係するリスクを考慮に入れ,通常,構造物の機能低下及び検査の確率論
的モデルの使用を伴い,機能低下の確率モデルと検査の結果を使用し,ベイズ更新によって結び付けられ
る。最適化は,構造物の破壊,検査及び修復の費用を含み,受容可能な破壊確率を拘束条件とした構造物
の供用期間にわたる期待総費用の最小化に基づく[17]。
検査そのものによって構造物の健全性が向上するわけではないのは明らかである。そのため,検査戦略
とともに,その結果分かる構造物の維持管理,修復及び/又は交換の計画を立てることが不可欠である。
検査,維持管理及び修復活動を含む包括的な戦略は,構造物の全供用期間の費用を最小化することによっ
て作成する[3]。図B.3は様々なシナリオにおける構造物の供用期間にわたるSIMの実施を示す。
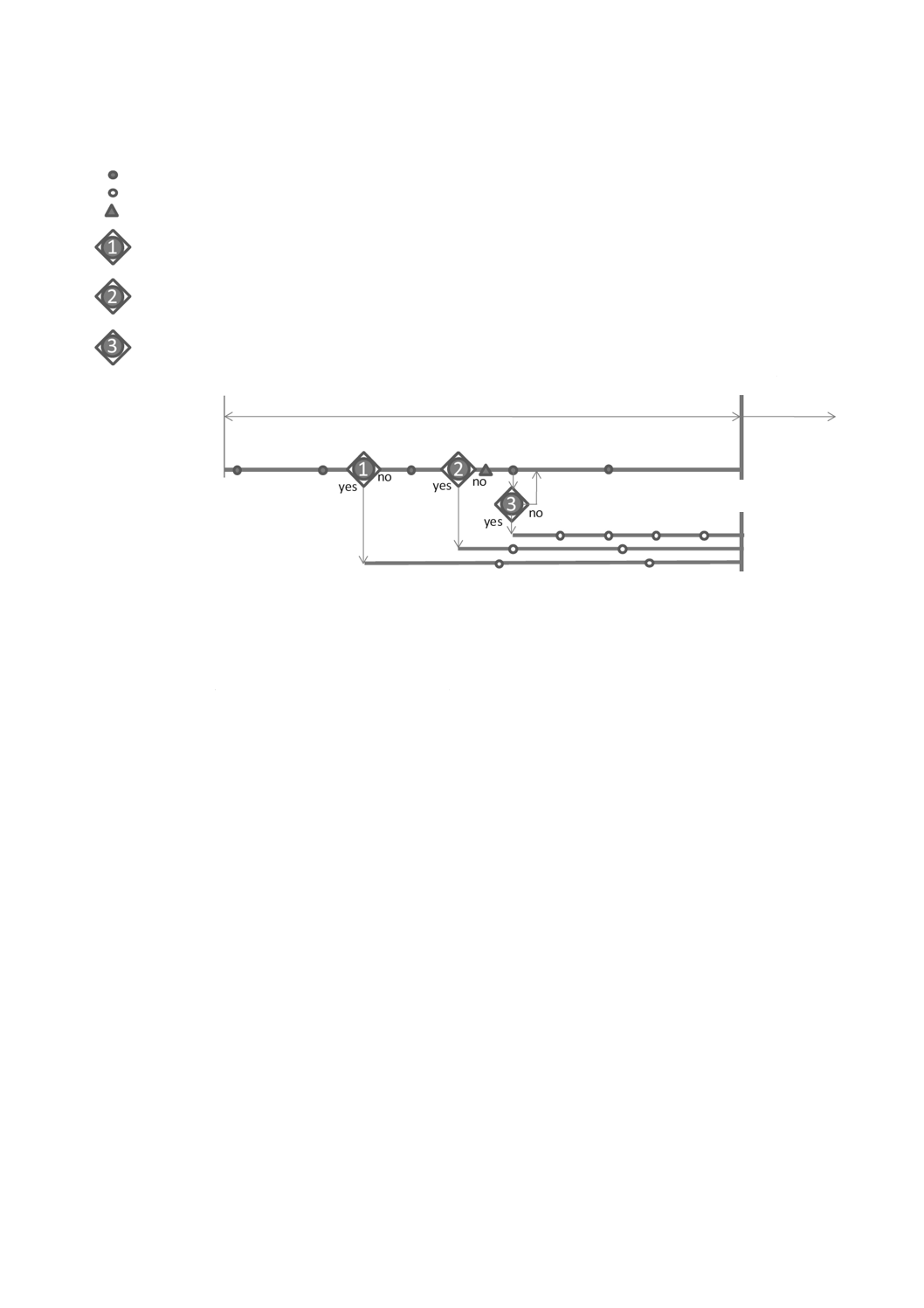
57
A 3305:2020 (ISO 2394:2015)
図B.3−構造の供用期間にわたるSIMに関連する事象及び作用
B.6
検査計画
検査計画は,検査戦略から作成される詳細な活動の範囲である。計画は,工程,予算,人員特性並びに
他の手順,特に適切な検査の手法及び手順を実行前に選択することを必要とする。
設計供用期間
設計及び施工
廃棄
供用期間延長
の可能性
検査によって発見された劣化の兆候
想定外の過大な外力による被害
用途変更
定期検査(元戦略)
定期検査(更新戦略)
計画されていなかった検査
供用期間における事象及び作用
58
A 3305:2020 (ISO 2394:2015)
附属書C
(参考)
観測及び実験モデルに基づく設計
C.1 一般事項
実験モデルに基づく設計(又は,単に“試験による設計”とも呼ぶ。)とは,荷重のパラメータ及び/又
は確定した構造要素及び材料の耐力特性の設計値を設定する手法である。この附属書で記載している手法
は,おおむね,確率論的設計及び部分係数設計の概念に整合した試験結果の統計的評価に基づいている。
適用範囲は,次のとおりである。
− 適切な理論モデル又はデータがないために,設計規準の中で与えられている情報では対処できない場
合
− 非常に特殊なため,一般に計算に使うデータが実態を反映していない場合(例えば,特殊な生産手法
の場合)
− 現行の設計式では極めて安全側の結果となり,限界状態を直接検証することで,より経済的な結果を
もたらすと考える場合
− 新しい設計式を導出する場合
この附属書は,ある特定の材料(例 土質)の非破壊試験及び品質管理試験には適用外であり,これら
については,より詳細な検討及び/又は制限が必要な場合がある。品質管理については,附属書Aを参照。
C.2 一般的な考え方
適切な試験計画を策定するためには,対象とする要素の挙動が危険な状態となるような範囲又は環境を
見つけるための定性的な事前解析を実施することが望ましい。さらに,検討中の限界状態を明確に定義す
ることが望ましい。
供試体は,実際に製作され組み込まれる個体と同一の寸法かつ同一の方法で,また,試験のために無作
為に選ばれた状況で製作したものが望ましい。
最終結果だけを記録するように制限された試験手順であってはならない。境界条件だけではなく,考慮
する限界状態を超過するときに生じる現象,それによって付随する状況,限界状態の機構にも注意しなけ
ればならない(例 境界条件,荷重条件などが,実際の構造物に期待されているものとどの程度異なるの
か。)。
考慮する限界状態を超過する状況,特に破壊を決定付ける破壊モードは,いつも明確であるとは限らな
い。試験プログラムを開発したり,試験結果を評価したりするには,適切な理論的裏付け,試験の経験及
び工学的判断が必要である。
試験から設計値を導出する場合には,試験が(一般に)限られた数しか実施されないということを考慮
することが望ましい。評価は,既存の解析モデル(C.6参照)に基づいて行うことが可能である。そのよ
うなモデルがない場合は,直接評価(C.5参照)することが可能である。
なお,このような統計的な考え方に加えて,構造物の挙動に関する一般理論及び一般に受け入れられて
いる一連の設計規則は,試験による設計を行う場合でも,依然として有効である。
特別な調査から導かれた結論は,その調査の範囲と関連する特性及び/又は生産技術と切り離せない。
その結論を拡大解釈するためには,理論解析に基づき試験結果を別の要素へ拡大して適用することが可能
59
A 3305:2020 (ISO 2394:2015)
でなければ,新たな試験が必要である。
C.3 実際と試験条件との差異の考慮
試験のときの条件は,対象構造物の実際の環境における条件とは異なる可能性がある。そのような違い
を,適切に設定された換算係数又は修正係数によって考慮することが望ましい。
換算係数ηは,一般的な構造理論に基づく実験的又は理論的解析及び/又は経験によって決めることが
望ましい。多くの場合,ある程度の任意性はやむを得ない。
ηによって考慮される影響としては,次のものを含み得る。
− 寸法効果
− 時間効果(試験は一般に短時間の載荷で実施するが,多くの材料の耐荷力及びたわみは長時間の効果
に依存する。)
− 供試体の境界条件(自由か固定かなど)
− 材料特性に影響を与える湿度条件
製作条件,例えば,実際の条件ではなく実験室の条件下での製作は,構造物の特性にかなりの影響を与
えることもあり得る(例 組立構造物の接合部の特性)。これらによる影響が大きいと考えられる場合は,
修正をする又は実際の製作品質をもつ供試体を用いることが望ましい。
C.4 計画
試験実施に先立ち,設計者及び試験機関は試験計画を策定することが望ましい。試験計画には,試験の
目的及び供試体の選択又は製作,試験の実施方法,試験の評価方法に必要な全ての仕様を記載することが
望ましい。特に,試験計画は,次の項目を含まなければならない。
a) 試験に必要な情報の範囲(例 必要なパラメータ及び有効な範囲)。
b) 検討中の限界状態における挙動に影響を与え得る全ての特性及び条件の記載(例 幾何学的パラメー
タ,その許容誤差,材料特性,製作及び組立て手順から影響を受けるパラメータ,寸法効果並びに環
境条件)。
c) 適切な変数を使った破壊モード及び/又は解析モデル。
d) 試験の実施に先立って行った,個々の供試体に関連する特性の計測の結果。関連した基本変数の例と
しては,環境からの影響,材料特性及び幾何学的諸量がある。
e) 供試体の特性の仕様(例 寸法,試作品の材料及び製造法,試料採取方法,並びに制限事項)。
f)
供試体の数及び試料採取方法。
解析モデルが利用可能で,全ての確率変数が計測される場合,試料採取方法は関係しない。その他
の全ての場合には,供試体が当該集団を代表するサンプル集団から選ばれていることを保証すること
が望ましい。異なる生産者による母集団の違いを,例えば,重み係数などで考慮する必要がある可能
性がある。
供試体の数が少ない場合及び/又は破壊モードが基本変数の関数として変化する場合は,設計点近
くの供試体(最も起こりやすい破壊モードに近い供試体)を推奨する。一般にこれは,寸法不整の場
合には,強く推奨する。強度パラメータについては,この考え方には注意深い評価を要する。例えば,
JIS A 5308における呼び強度30のコンクリートの悪いサンプルと呼び強度24のコンクリートの平均
的なサンプルとでは,圧縮強度は同じでも意味に違いがある。
g) 試験における載荷条件及び環境条件についての仕様(例 載荷点,時間的・空間的載荷経路,温度,
60
A 3305:2020 (ISO 2394:2015)
変位又は荷重制御による載荷)。載荷経路は,構造部材に予期される適用範囲を代表するように,起こ
り得る望ましくない経路となるように及び/又は比較のための解析で考慮される経路となるように,
選択しなければならない。
ある構造特性が,系統的には変動しない一つ又は幾つかの作用効果に対して条件付きである場合,
これらの効果は,設計値によって規定することが望ましい。それらが載荷経路の他のパラメータと独
立ならば,推定される荷重組合せの値に関わる設計値を使うことが可能である。
h) 試験準備(載荷装置及び支持装置に十分な強度並びに剛性があること,変形に対して十分なクリアラ
ンスがあることなどを確認する方策も含まれる。)。
i)
観測点,観測及び記録手法(例 変位,速度,加速度,ひずみ,力,圧力の時刻歴,必要な計測頻度・
計測精度,計測装置など)。
C.5 試験結果の直接評価
C.5.1 一般事項
この箇条では,構造要素の耐力又は材料強度を,試験によって直接評価すると仮定する。さらに,供試
体強度を,単一の量で代表し,考慮する破壊メカニズムは全ての試験に対して最も厳しいものであると仮
定する。
試験結果を確率論的設計法と結び付けて使用する場合,試験データは,耐力の統計パラメータがあらか
じめ設定された事前分布を更新するために使用することが可能である。その方法を,C.5.3に示す。部分係
数法を使う場合,C.5.2の手法が適用可能である。
C.5.2 部分係数設計
部分係数法に用いる設計値は,次の式によって評価されることが望ましい。
+
−
=
n
s
t
m
η
R
R
v
R
1
1
d
d
d
························································ (C.1)
ここに,
mR: 標本平均
sR: 標本標準偏差
tνd: t分布の係数(表C.1)
n: 試験数(標本数)
ηd: 換算係数の設計値
tνdの値は表C.1に従う。表C.1では,ν=n−1,βR=αdβである。βは目標信頼性指標,αdはFORMの影
響係数の設計値である。特に指示がない限りは,Rの不確定性が支配的な場合はαd=0.8,その他の場合は
αd=0.3を使うのが望ましい(E.5.2及びE.5.3参照)。
部分係数法で使うには,二つの方法がある。
a) 表C.1中のβR=1.64として式(C.1)を使って特性値Rkを定義し,部分係数をγm=Rk/Rdで求める。
b) その材料及び破壊モードに通常使われるγmの値を使う。この方法では,特性値RkはRk=γmRdで定義
される。この場合,Rkは0.95とは異なる超過確率をもち得ることに注意しなければならない。
いずれの手法を選ぶかは,表現だけの問題である。両方法とも,検証の段階では同じ設計値が使われる。
式(C.1)は,Rは正規分布に従い,標準偏差及び平均値は無情報事前分布に従うとした仮定に基づいてい
る。標準偏差が既知の場合は,標本標準偏差を分布の標準偏差に置き換えて,ν=∞とすればよい。他の
種類の事前情報の取扱いについては,C.5.3に示される式を使用することが可能である。
正規分布は,やや安全側の分布とみなしてもよい。多くの試験に基づく根拠がある場合だけ,対数正規,

61
A 3305:2020 (ISO 2394:2015)
ワイブルなどの他のより好ましい分布を使うことが望ましい。
注記 多くの通常の建築材料については,上記の分布は妥当であるとみなせる。
この箇条で紹介するベイズの手法は,標準偏差が未知の場合は,観測された標準偏差sRに非常に敏感で
ある。危険側の又は非経済的な結果を避けるためには,小さすぎる又は大きすぎる事後の標準偏差は除外
する方がよい。その一つの方法として,たとえ明確な情報がなくても,標準偏差の適切な事前分布を選ぶ
こともあり得る。技術者がある技術的解決法を試験で十分実行可能とみなすといった単なる事実も根拠と
して使用することが可能である。C.5.3で詳細な手順を記載する。
表C.1−tνdの値
βR
Φ(−βR)
自由度,ν
1
2
3
5
7
10
20
30
∞
1.28
0.10
3.08
1.89
1.64
1.48
1.42
1.37
1.33
1.31
1.28
1.64
0.05
6.31
2.92
2.35
2.02
1.89
1.81
1.72
1.70
1.64
2.33
0.01
31.8
6.97
4.54
3.37
3.00
2.76
2.53
2.46
2.33
2.58
0.005
63.7
9.93
5.84
4.03
3.50
3.17
2.84
2.75
2.58
3.08
0.001
318
22.33
10.21
5.89
4.78
4.14
3.55
3.38
3.09
注記 sRが既知の場合は,ν=∞を使う。
例 n=3の供試体のサンプルを考える。標本平均mRは100 kN,標本標準偏差sRは15 kNとする。5 %
の特性値は次の式で計算する(ν=2)。
kN
5.
49
15
37
.3
100
37
.3
3
1
1
92
.2
k
=
×
−
=
−
=
+
−
=
R
R
R
R
s
m
s
m
R
C.5.3 確率論的手法を使った評価
完全に確率論的な取扱いにおいては,まず,耐力Rの未知の分布パラメータのいわゆる事前分布関数を
決める。その分布は,パラメータの全ての利用可能な事前情報を反映したものであることが望ましい。こ
の事前分布及び試験データの統計量を与えると,事後分布は,次の式で与えられる。
f''(θ)=C×L(θ|x)f'(θ) ································································· (C.2)
ここに, f''(θ): θの事後分布
f'(θ): θの事前分布
L(θ|x): 観測結果がxという条件の下でのパラメータθのゆう(尤)
度関数
θ: 分布パラメータのベクトル(例えば,平均値,標準偏差など)
C: 規準化係数
事前情報及び試験データを与えると,更新したRの分布は,次の式で与えられる。
∫
=
dθ
θ
''
f
θ
r
f
r
''
f
R
R
)
(
)
|
(
)
(
······················································· (C.3)
ここに, ∫
)
|
( θ
r
fR
: θの値が与えられた条件下でのRの分布
f''R(r): 更新したRの分布
この更新されたRの分布は,確率論的設計手順において直接使用することが可能である(箇条7及び箇
条8参照)。また,式(C.3)に基づいて設計値を導出することも可能である(箇条9参照)。
次に,Rが正規分布に従う場合を考える。このとき,分布パラメータのベクトルには,平均値μ及び標
準偏差σが含まれる。事前分布は,次の式で表す。
62
A 3305:2020 (ISO 2394:2015)
[
]
−
+
−
=
+
+
−
2
2
2
]1
)
(
[
)
(
)
(
2
1
exp
)
,
(
m'
μ
n'
s'
v'
σ
kσ
σ
μ
'f
n'
δ
v'
···················· (C.4)
ここに, δ(n')=0(n'=0のとき)
δ(n')=1(n'>0のとき)
このような特別な選択によって,積分を解析的に取り扱えるようになる。式(C.4)の事前分布には,m',
n',s'及びν'の四つのパラメータがある。パラメータs',ν'は,標準偏差に関する事前情報を表現する。標
準偏差σの期待値及び変動係数は,近似的に(大きなν'に対して)次のように表現可能である。
E(σ)=s' ················································································ (C.5)
v'
σ
V
2
1
)
(
=
·········································································· (C.6)
平均値に関する事前情報は,m',n'及びs'で表す。平均値μの期待値及び変動係数は,近似的に(大きな
ν'に対して)次のように表現可能である。
E(μ)=m' ··············································································· (C.7)
n'
m'
s'
μ
V
=
)
(
········································································ (C.8)
これらの事前情報は,仮想上の一連の事前試験の結果と解釈することが可能である。一つは,平均値で
あり,もう一つは,標準偏差である。この場合,標準偏差については,次のようになる。
− s' 仮想上の標本標準偏差
− ν' s'の仮想上の自由度数
平均値に関する情報には,二つの追加パラメータが必要である。
− m' 仮想上の標本平均
− n' m'の仮想上の標本数
すなわち,m'及びs'は,平均値及び標準偏差の最良推定値を表す。n'及びν'の選択を行って,推定値に関
する不確定性を表現することが可能である。
試験においては,ν=n−1という関係をよく用いるが,事前パラメータn'とν'とは,互いに独立に選ん
でもよい。
注記1 例えば,情報がほとんどない場合は,n'とν'とは0を選ぶ。この場合は,最終結果は,C.5.2
と同じとなる。過去の経験から平均値及び標準偏差が明確な場合は,n'とν'は比較的大きな
値となる。50だとすると,V(σ)=0.10又はV(μ)=0.14 s'/m'となる。
注記2 多くの場合,平均値に関する事前情報はほとんどないが(したがって,n'=0),σ'については,
かなり良い推定値を得ると仮定するのが妥当である。一例として,σの変動係数が30 %のオ
ーダーだとすると,式(C.6)からν'=5となる。このようなモデルは,平均値のばらつきは大
きいが標準偏差のばらつきは非常に小さいという既存の多くの試験結果に基づき得る。これ
は,コンクリートの強度試験供試体の実際と非常に似ている。この考え方によれば,標本数
が少ない場合でも,非常に不経済になる又は非常に危険側になることは避けられる。
式(C.2)を使うことによって,式(C.4)で表現される事前情報と標本平均m,標本標準偏差sをもつn個の
観測結果とを結び付けることが可能である。その結果,平均値及び標準偏差が未知であるRの事後分布を
式(C.4)が与える。ただし,その場合のパラメータは,次の更新規則によって与えられる。
n''=n'+n ·············································································· (C.9)
ν''=ν'+ν+δ(n') ····································································· (C.10)
63
A 3305:2020 (ISO 2394:2015)
m''n''=n'm'+nm ····································································· (C.11)
[ν''(s'')2+n''(m'')2]=[ν'(s')2+n'(m')2]+(νs2+nm2) ····························· (C.12)
ここに, ν=n−1
n'=0の場合: δ(n')=0
その他の場合: δ(n')=1
式(C.2)を使うと,Rの予測値は,次の式で得られる。
+
−
=
n''
s''
t
m''
R
v''
1
1
·························································· (C.13)
ここに,tν''は,t分布に従い,与えられた超過確率に対するtν''の値は,表C.1で与える。Rが対数正規
分布に従う場合への修正は簡単である。
例 再び,C.5.2の例を考える。ただし,事前の試験で次のことが分かっているとする。
a) 標本平均は,110 kNで,ばらつきは非常に大きい。
b) 標本標準偏差は,平均は20 kNで,変動係数Vは30 %。
式(C.5)〜式(C.8)によって,この事前情報から次の事前分布パラメータが導かれる。
m'=110 kN, n'=0, s'=20 kN, ν'=1/(2V2)=1/(2×0.32)=5
次に,この事前情報をC.5.2の例と同じ試験結果(標本平均m=100 kN,標本標準偏差s=15 kNをもつ
三つの供試体)と結び付ける。その場合,式(C.6)〜式(C.9)から事後分布のパラメータは,次のように導か
れる。
n''=0+3=3
ν''=5+2=7
m''=100 kN
7(s")2+3×1002=5×202+0×1102+2×152+3×1002
から
s''=18.7 kN
式(C.13)及び表C.1を使うと,5 %特性値は次の結果となる。
kN
2.
59
7.
18
18
.2
100
3
1
1
7.
18
89
.1
100
k
=
×
−
=
+
×
−
=
R
···················· (C.14)
特性値が49.5 kNから59.2 kNに変わったのは,事前情報の効果である。設計値の場合は,その差はもっ
と大きくなる可能性がある。
C.6 解析モデルに基づく評価
対象とする構造特性に対して,ある解析モデルが使えると仮定する。そのモデルは,試験から決める一
つの未知係数θを除いては完全であるとする。そのようなモデルは,次のように表すことが可能である。
Y=θg(X, W)·········································································· (C.15)
ここに,
X: 確率変数ベクトル
W: 測定可能な確定値の集合
g(X, W): モデル
Y: モデルの測定可能な出力パラメータ
θ: 実験によって決められる未知係数
パラメータθは,モデル不確定性ともいわれる。他の情報がない場合は,θは対数正規分布と仮定する。
それは,θ'=ln θが正規分布に従うということである。
64
A 3305:2020 (ISO 2394:2015)
次の内容で,一連の実験(i=1, 2, …, n)が実施されたと仮定する。
− Wの値はwi(i=1, 2, …, n)と設定
− Xの値はxi(i=1, 2,…, n)と測定
− Yの値はyi(i=1, 2, …, n)と測定
これらの結果から,未知係数θの観測値の集合を次のように導く。
)
,
(
i
i
i
i
w
x
g
y
θ=
········································································ (C.16)
θ'=ln θの平均値及び標準偏差は,次のとおりである。
∑
=
=
n
i
i
θ'
n
θ'
m
1
1
)
(
····································································· (C.17)
[
]
∑
=
−
−
=
n
i
i
θ'
m
θ'
n
θ'
s
1
2
2
)
(
1
1
)
(
····················································· (C.18)
ここに,θ'iは,次の式で与えられる。
θ'i=ln[yi/g(xi, wi)]···································································· (C.19)
設計値θdは,次の式で与えられる。
[
]
+
±
=
n
θ'
s
t
θ'
m
θ
v
1
1
)
(
exp
)
(
exp
d
d
············································ (C.20)
係数exp[m(θ')]は,偏り係数ということがある。m(θ')=0ならば,exp[m(θ')]=1.0となり,そのモデルは
不偏という。
tνdの値は表C.1に従う。表C.1においては,ν=n−1,βR=αdβ,ここに,βは目標信頼性指標,αdはFORM
の影響係数の設計値である。特に指示がない限りは,Rの不確定性が支配的な場合はαd=0.8,その他の場
合はαd=0.3を使う(附属書E参照)。
試験によって設計される構造要素の設計耐力Rdは,次のように計算することが可能である。
)
w
,
x(
1
d
d
d
d
g
η
γ
R=
································································· (C.21)
ここに, γd=1/θd
ηd: モデル不確定性の設計値
65
A 3305:2020 (ISO 2394:2015)
附属書D
(参考)
地盤構造物の信頼性
D.1 一般事項
この附属書の目的は,この規格の要求事項の地盤設計への適用を補足することである。信頼性に基づく
設計の原則は,一般に地盤工学に適用可能であるが,地盤設計パラメータ及びその他の現場条件にみられ
るような,より大きなばらつきに対応することが不可欠である。6.1.1の注記4に記載されているように,
不確定性の表現がこの規格及び地盤設計を議論する上で重要な部分であり,この附属書で取り扱う。
確率論的モデルコード(JCSS 2001 [8])によると,地盤構造物の特徴は土質特性の不確定性が支配的役割
であるということである。これは,地盤設計の実務において様々な方法論が採用されていることと直接的
に関係している。
この附属書では,地盤の信頼性に基づく設計プロセスの重要な要素の特定及び特徴付けに重点を置く。
これらの要素は,既存の決定論的地盤工学の実務では考慮されていない。重要な特徴的要素は,次のとお
りである。
a) 地盤材料は,自然起因であり原位置でのばらつきを低減できないため,地盤設計パラメータの変動係
数(COVs)は,本質的に大きくなり得る(これに対し,ほとんどの構造物の材料は,品質管理の下生
産される。)。
b) 地盤設計パラメータは,それらを測定する手順に応じて,一意に決まらず広範に変動し得る。
c) 地盤設計パラメータの特徴は場所によって異なるため,現場ごとに調査を行うのが一般的である。こ
のため,統計的な不確定性は十分注意して扱うことが望ましい。
d) 現地調査又は現位置調査では,室内試験及び野外試験の両方を行うのが一般的である。地盤設計パラ
メータは,通常,複数の実験室及び/又は現場試験での指標と関連する。一貫性のある情報が増加す
ると,設計パラメータの変動係数が減少するため,可能な場合には,この多変量相関構造を考慮する
ことが重要である。
e) 構造物との相互作用を考慮する地盤の空間的スケールは構造物の代表長さの数倍であり,この特性長
さ(例 傾斜の高さ,トンネルの直径,掘削孔の深さなど)は,一般的に設計パラメータの変動長さ
スケールよりも,特に鉛直方向において大きい。このため,地盤設計パラメータの空間的変動は,(空
間的平均化の効果により)容易に解消することが可能である。
f)
同じ設計上の問題に対して,通常,多くの異なる地盤工学的計算モデルが存在する。したがって,現
地試験及び現地での経験に基づくモデルのキャリブレーションが重要である。モデルの数及びキャリ
ブレーションデータベースの数が多いために,サイト固有の条件を指定するための条件の増加が予想
される。
g) 群くい(杭),斜面などの地盤の破壊を扱う問題は,互いに相関をもつ複数の破壊モードを含むシステ
ム信頼性問題である。これらの問題の幾つかは,破壊面が地盤媒体の空間変動と結び付いていること
が更に問題を複雑にしている。
66
A 3305:2020 (ISO 2394:2015)
D.2 地盤設計パラメータの不確定性表現
D.2.1 地盤設計パラメータの推定
地盤設計パラメータの変動係数は,地盤固有の統計的特性ではない。それは,サイト条件,測定手法及
び変換(相関)モデルに依存する。したがって,変動係数は一意の値ではなく幅をもつ。地盤タイプ,測
定手法及び変換モデルの関数としての一般的な設計パラメータの標準的な変動係数に関する幾つかのガイ
ドラインを次に示す。
D.2.2 不確定性の発生源
地盤設計パラメータの根底にある不確定性全体は,図D.1に示すように,多くの異なる不確定性に由来
する。地盤の不確定性には,(1)固有の変動性,(2)測定誤差及び(3)変換の不確定性の三つの主な発生源があ
る。第1の発生源は,原位置で土塊が生成され,形状が連続的に変化する自然の地質学的プロセスから主
として生じたものである。第2の発生源は,機器,手順及び作業者,並びに試験の無作為性の影響による
ものである。不確定性の第3の発生源は,現場又は実験室の測定値を経験的モデル又は他の相関モデルに
よって設計パラメータに変換する際に混入するものである。
図D.1−地盤設計パラメータの不確定性全体に寄与する不確定性の発生源[13]
不確定性の様々な発生源は,全不確定性を導出するための入力として,それぞれ個別に特徴付けること
が望ましい。全ばらつきの分析に関する文献に一般的に報告されている変動係数を使用することは,不確
定性の過大評価につながる可能性がある。これは,次の理由による。
a) 異なる地質からの土質データが混在している。
b) 機材及び手順の管理一般が不十分である。
c) 土質データの確定論的なトレンドが除去されていない。
d) 地盤データの収集が長期間にわたっている。
D.2.3 固有のばらつき
空間的なばらつきは,なだらかな変化傾向がある関数と変動成分とに分解することが可能である。変動
する成分を均質なランダム関数としてモデル化することによって定量化することが可能である。D.2.7に記
載するように,変動スケールもまた重要である。
D.2.4 測定誤差
測定誤差のうち,機器の影響は,計測機器の不正確性並びに所定の試験に使用される機器の形状及びシ
ステムのばらつきに起因する。手順の実施に伴う作業者の影響は,既存の標準的試験方法及びその遵守の
仕方に限界があることに起因する。ランダムな試験誤差とは,試験結果の残りのばらつきを指す。測定誤
差は,単純な加法確率モデルを用いて原位置での測定値から抽出する又は実験室試験結果との比較によっ
土
現地計測
変換モデル
推定された
土質特性
地盤固有の
ばらつき
データの
ばらつき
統計的
不確定性
モデルの
不確定性
地盤固有の
ばらつき
計測誤差
67
A 3305:2020 (ISO 2394:2015)
て直接決定する。
D.2.5 不確定性の変換
試験測定結果を,設計に用いられている適切な材料特性に関連付けるためには,変換モデルが必要であ
る。地盤工学におけるほとんどの変換モデルは,経験的又は半経験的なデータフィッティングによって得
られるため,不確定性を導入している。変換モデルは,通常,回帰分析を用いて評価し,回帰曲線に関す
るデータの広がりを,平均ゼロの確率変数εとしてモデル化する。εの標準偏差は,変換の不確定性の大
きさの指標である。
ほとんどの変換モデルは,特定の地盤材料タイプ及び/又は特定の場所のものとして構築する。サイト
固有のモデルは,一般に,多くのサイトをカバーするデータによって調整した“グローバル”モデルより
も正確である。ただし,別のサイトに適用すると,大幅な偏りが生じる可能性がある。この“サイト固有”
の制限は,地盤工学実務に特有かつ一般的な特徴である。地盤の信頼性設計では,“地盤における真実”を
過度に単純化することを避けるために,この制限を考慮に入れることが望ましい。
D.2.6 全不確定性
全不確定性は,地盤固有の変動性,測定誤差及び変換の不確定性の組合せからなる。これらの構成要素
は,単純な確率論的方法である2次モーメント法を使用する又はより高度な不確定性解析手法を使用して
一貫した形で組み合わせることが可能である。全体の変動係数を決定する場合には,個々の限界状態を支
配する特性設計パラメータを同定する必要がある。
終局限界状態の問題では,設計で用いる特性パラメータは,一般に最も重大な破壊経路にわたって空間
的に平均した強度である。空間的変動の存在下では,この空間的に平均化した強度の変動係数は,局所的
な強度の変動係数よりも小さい。変動係数減小の程度は,D.2.7に記載する変動スケールの関数である。変
動の空間スケールが破壊経路の特性長さ(例 斜面の高さ,トンネルの直径,掘削孔の深さなど)に比べ
て短いため,特徴的な変動係数の減小が大きい問題に局所的な変動係数を適用することは不適切である。
代案として,確率有限要素法を,終局限界状態の解析に用いる。そこでは,モンテカルロ法の枠組みにお
いて,確率場と決定論的有限要素とを結び付けている。
地盤設計のパラメータとして単一の代表値を割り当てることは,現実的ではないことに留意すべきであ
る。例えば,良質の実験室での測定,コーン貫入試験などの現場測定からの直接的な相関関係に対してで
あれば,非排水せん断強度に対して30 %の変動係数とすることが適切である可能性がある。しかし,標準
貫入試験に基づく間接的な相関モデルに対しては適していない可能性がある。このことが実際の実務に与
える影響は,簡略化された信頼性設計の枠組みにおいて,キャリブレーションを行い,単一の耐力又は部
分係数を求めることが現実的ではないということである。
D.2.7 変動スケール
D.2.3に示した空間的変動の,なだらかな変化の傾向t(z)及び変動成分w(z)への分解について図D.2に示
す。物理的に均質な地盤の層は必ずしも統計的に均質ではないことは,注目に値する。固有の変動性を記
述するために必要な重要な統計的パラメータは,相関距離又は変動スケールである。変動スケールは,特
性値が比較的強い相関を示す距離の指標を提供する。
注記 変動スケールを決定する簡単な近似法を,図D.2の右図に示している。
変動係数の推定において,合理的な変動スケール,すなわち,合理的で現実的な空間変動を考慮する実
務上の重要性を,D.2.6に明示している。地盤のパラメータを独立と仮定すると,空間平均に対する変動係
数の危険側の評価に低下をもたらす。地盤のパラメータを完全相関と仮定すると,空間平均に対する変動
係数の減少をもたらさず,これは過度に安全側の評価である。変動係数の減少に加えて,破壊のメカニズ
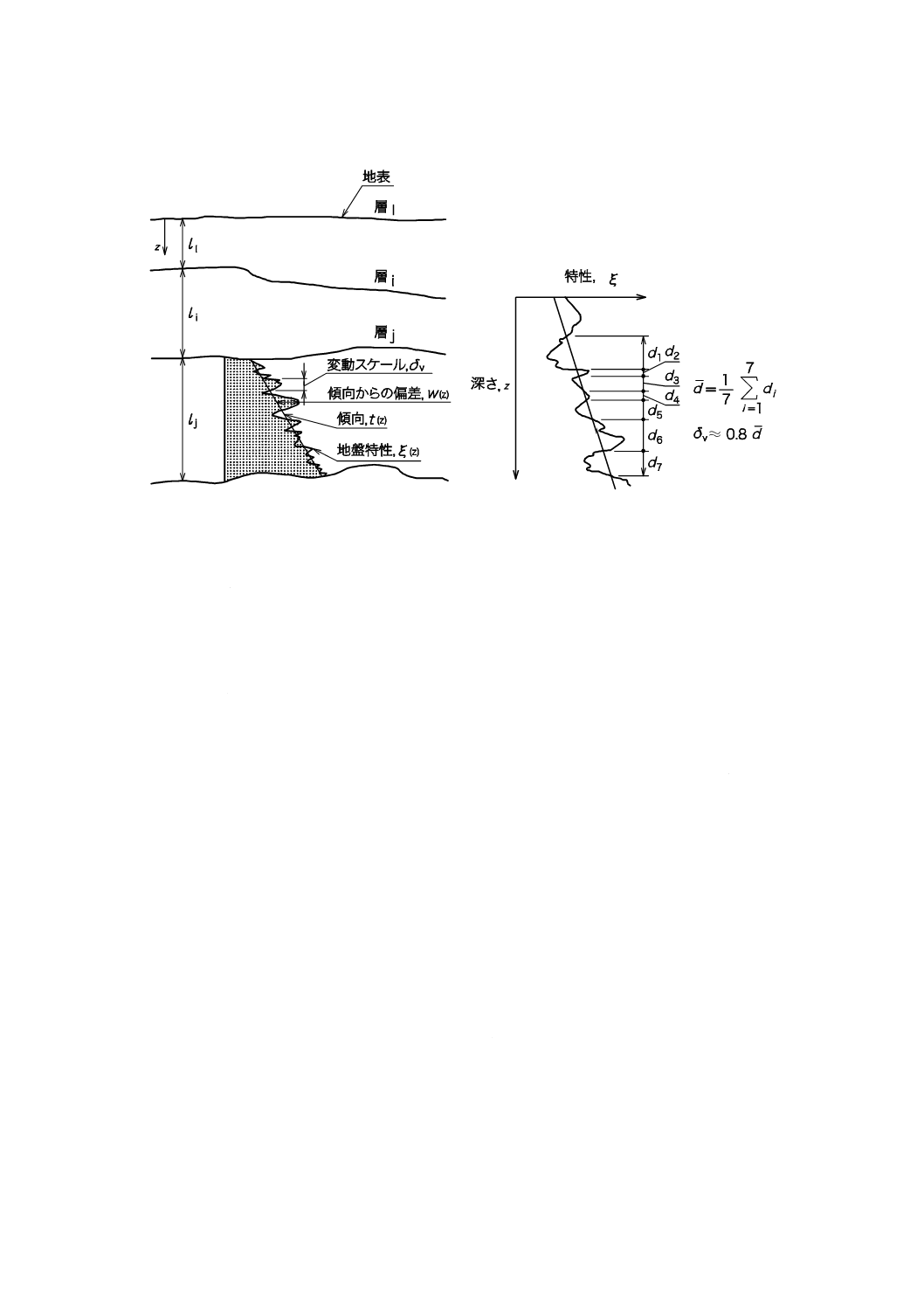
68
A 3305:2020 (ISO 2394:2015)
ムは,空間変動に関連していることを指摘することが重要である。
注記 Phoon and Kulhawy 1999aに加筆 [13]。
図D.2−固有の地盤変動の確率場モデル
D.3 多変量地盤データの統計的特徴付け
D.3.1 一般事項
多変量情報は,通常,標準的な敷地調査によって入手可能である。例えば,su-N及びsu-OCR(過圧密
比)の二つの土質パラメータ間の相関については,一般的に利用可能であるため,多変量正規分布は,変
換の不確定性が存在する場合の地盤のパラメータ間の多変量依存性を捉えるための理にかなった実用的な
選択肢である。多変量データを考慮することの実用的な意義は,複数のパラメータとの依存関係を考慮す
ることによって,設計パラメータの変動係数が一般に減少することである。したがって,多変量試験によ
る不確定性の減少は,信頼性設計を用いることによって設計における省力化,すなわち,節約に直接つな
がる可能性がある。そのため,現地調査は費用がかかる項目ではなく投資項目である。決定論的な設計法
では,現地調査の質及び量と設計における省力化との間の重要なつながりを,体系的に対処することは不
可能である。
D.4 モデル係数の統計的特徴付け
D.4.1 一般事項
モデル不確定性は,工学的挙動を予測する解析モデルの不完全性から生じる。任意の物理的プロセスの
数学的モデル化では,一般に,実用的なモデルを作成するために単純化が必要となる。必然的に,結果と
して生じるモデルは,複雑な現実世界の現象の単純化となる。したがって,モデルへの入力が確実に分か
っていたとしても,モデルによる予測には不確定性が存在する。地盤工学を含む様々な分野におけるモデ
ル不確定性の統計学の現状は,予測した性能と測定した性能とを比較することを含む。
モデル不確定性は,一般にモデル係数の観点で表す。モデル係数は,浅い基礎,くい(杭)基礎,擁壁
構造物,斜面などの様々な地盤構造について特性化する必要がある。モデル係数は,特定の組の条件(例
破壊モード,計算モデル,局所的条件,経験基盤など)に適用する。したがって,モデル係数の条件を指
69
A 3305:2020 (ISO 2394:2015)
定するための数の急増が予想される。
モデル係数は,一般に,計算した耐力に対する測定した耐力の比として定義する。
p
m
Q
Q
M=
··············································································· (D.1)
ここに,
Qm: 載荷試験から測定された“耐力”
Qp: 極限平衡モデルを用いて一般に予測される“耐力”
M: モデル係数
ロバストなモデル係数の統計値は,次のa)〜c)を使用するときだけ評価をすることが可能である。多く
の地盤計算モデルにおけるモデル誤差について,ロバストな統計的評価を行うために利用できる試験デー
タは,基礎を除き,十分ではない。
a) 実物大に近い模型試験
b) 十分に大きく代表的なデータベース
c) 本質的でない不確定性が十分に管理されている適度に高品質な試験
D.5 地盤の信頼性設計実施における問題
D.5.1 一般事項
この規格の一般原則は,地盤の信頼性設計にも同様に適用可能である。地盤構造物については,箇条5
に規定されている限界状態の手続によって適切なレベルの性能が,達成可能である。これは,箇条7で与
えるリスクに基づくレベル,箇条8に規定した信頼性に基づくレベル又は箇条9に規定した準確率論に基
づく設計のいずれかによって達成可能である。地盤工学的不確定性の表現は,箇条6に規定した原則に基
づくことが可能である。
D.5.2 目標及び課題
地盤の信頼性設計の重要な目標は,既存の許容応力度設計で示唆しているものと比較してより均一レベ
ルの信頼性を達成することである。準確率論的方法に関していえば,信頼性に関するキャリブレーション
が,地盤工学分野においてより困難となることを強調することが重要である。重要な理由の一つは,異な
る地盤特性推定の方法論に起因する変動係数の範囲など,キャリブレーションのときに考慮すべき設計シ
ナリオの多様性である。多様性のもう一つの原因は,都市規模においても様々な地層構造が見られること
にある。
現実的(広範な設計シナリオを扱う)かつロバストな(妥当な精度で目標信頼性指標を達成する)地盤
の信頼性設計を実現するための課題を,この箇条で記載する。確率に基づく意思決定(すなわち,箇条8
の直接確率に基づく設計,システム信頼性及び信頼性目標)及び準確率論的手法(すなわち,箇条9の部
分係数法及び特性値)に関連する(地盤の信頼性設計)実施についての幾つかの詳細について,次に記載
する。
D.5.3 信頼性に基づく設計法
信頼性に基づく設計(箇条8)は,地盤設計に見られる多数の状態,破壊モード,不確定性などを表現
するのに特に適している。信頼性に基づく設計は,地盤工学の実務にそのまま適用可能である。信頼性解
析に必要な入力は,地盤のパラメータ及び荷重の確率分布である。限られたデータからの適切な確率分布
の同定及び,これらの分布(例 平均,変動係数など)に関する適切なモデルパラメータの選択は,統計
的不確定性の影響を受ける。

70
A 3305:2020 (ISO 2394:2015)
D.5.4 準確率論的手法
実践的な検討のために,地盤の信頼性設計では,一般に,単純化された準確率論的手法,より具体的に
は部分係数法(9.4.2参照)が適用される。地盤設計の特徴は,多くの地盤計算モデルは比較的“単純”で
あり,地盤工学分野のこれまでの伝統が経験的な性質をもつために,通常は同じ設計問題に対して多くの
異なる計算モデルが存在することである。キャリブレーションの手順では,“最良の”(決定論的)地盤計
算モデルを直接使用することが望ましい。
信頼性のキャリブレーションのために,“最良の”計算モデル(現場測定又はそれがない場合の実験室試
験及び数値シミュレーションと比較したときの最小偏り及び最小変動性)を選択することが望ましい。し
かし,地盤材料の挙動,施工及び設計の経験は,主に地点特有のものであるため,地盤工学においては,
地域特有の慣行が尊重されることが望ましい。
したがって,“最良の”モデルとは,地域における最良の慣行であると定義する方がより現実的である。
結論としては,単一の物理モデル(例 CPT法)又は単一の確率モデル(例 全耐力を単一の対数正規変
数へ一括化すること)を強要することは不可能であり,地盤の信頼性設計のキャリブレーションプロセス
は,既存の多様な現地の慣行に適合できる程度に十分に一般的であることが望ましい。信頼性設計のキャ
リブレーションにおける唯一の必須要件は,モデルの偏差を適切な方法で定量化することである。
地盤設計パラメータ(D.2参照)の変動係数は極めて大きいことから,影響が大きい設計パラメータの
範囲及びそのばらつきを幾つかの部分又は領域に分けることは賢明である(図D.3参照)。次に,キャリブ
レーション手順において変数の均一な範囲を確保し,入力パラメータ及びそれらの変動性の範囲にわたっ
て一貫した設計リスクを実現するように,各部分又は各領域内のキャリブレーション点が選択可能である。
図D.3−耐力係数のキャリブレーションのためのパラメータ空間の分割[10],[12]
D.5.5 特性値
“特性値”の概念は,本質的に準確率論的形式,特に部分係数法と関連する。終局限界状態を例とする
と,この方法では,地盤のパラメータ(例 非排水せん断強度)の“特性値”を強度部分係数で除して“設
計”値を生成し,この設計値に基づく地盤の耐力は設計荷重(特性荷重に荷重係数を掛けた値)よりも大
71
A 3305:2020 (ISO 2394:2015)
きくすることが望ましい。
地盤のパラメータは,限界状態関数に関連する形で定義することが望ましい。例えば,単一の非排水せ
ん断強度のパラメータが斜面安定方程式に現れる場合,限界状態関数と関連した物理的定義は,最も重大
な破壊経路に沿った空間平均となる。それは,土塊中の一点における非排水せん断強度でも,土塊におけ
る所定の線に沿った空間平均でもない。地盤工学の文献では,特性値のこの物理的側面を明確にすること
に重点を置いている。
不確定性の側面を合理的に検討する前に,地盤のパラメータの特性値の物理的意味を明確にする必要が
ある。例えば,くい(杭)の周面摩擦力に関する非排水せん断強度の特性は,くい(杭)の長さに沿った
空間平均である。一方,くい(杭)先端の支持力に対する非排水せん断強度の特性値は,くい(杭)先端
の下の圧力球根内の空間平均である。信頼性解析が行われる場合,限界状態関数は,これらの空間平均に
対して二つの異なる確率分布に従う二つの確率変数を含むことになる。
準確率論的設計を行う場合,各確率分布に対して一つの特性値を選択する必要がある。この値として,
平均値又は下位5 %分位点を参照可能である。これらの特性値の統計的推定は,信頼性解析に現れる確率
分布に対する統計的不確定性の影響を受ける。明らかに,特性値のこの統計的側面は,特性値の物理的特
性と区別する。
原理的には,特性値の任意の統計的定義に対して,所定の目標信頼性指標を達成するために,部分係数
をキャリブレーションすることが可能である。実際には,平均値に対してキャリブレーションされた部分
係数の場合,入力の確率変数の変動係数が変化すると,大きく変化し得ることが知られている。この欠点
は,下位5 %分位点を用いてキャリブレーションされた部分係数に対しては,それほど重大なことにはな
らない。したがって,入力の確率変数の変動係数が,設計コードがカバーする設計シナリオの範囲内の広
い範囲にわたって変化し,部分係数の表現について変動係数の関数ではなく単一の数として表現を簡略化
する実用的な必要性がある場合,下位5 %分位点での定義が好ましい(ただし,特別な考慮をしなければ
ならない非線形応答を考慮する場合を除く。)。繰り返しになるが,信頼性設計コードの重要な機能は,特
定の設計シナリオに対してではなく,一般的に発生する設計シナリオの範囲にわたって,規定された目標
信頼性指標(通常は限界状態及び構造物の重要度の関数)を達成することである。特性値の統計的定義は,
これまでの実務又は信頼性キャリブレーションと切り離した要素に固執するのではなく,信頼性設計コー
ドが何を実現したのかというよりも広い枠組みの中で考えることが望ましい。すなわち,設計は,特性値
単体を用いるのではなく,特性値と部分係数/耐力係数との積である設計値によって生み出される。(1)限
られたデータから高い信頼性で分位点を推定すること及び(2)下限のない確率分布関数を不適切に選択す
ることによって分位点が既知の下限(例 残留摩擦角)を下回ることに関する実用上の懸念がある。しか
し,二つの懸念事項は特性値に影響を与えることはほとんどなく,基本的には,コードキャリブレーショ
ンの基礎となる信頼性解析の方に影響する。
D.5.6 分位点に基づく設計
コードキャリブレーション法は,地盤設計パラメータ及びモデル係数の変動係数が一定ではなく,広い
範囲(D.2及びD.4参照)にわたって変化する可能性があり,D.5.4で強調されているようにキャリブレー
ション領域を分割する必要があるため,扱いにくいことが認識されている。均一でない変動係数を用いた
地盤設計上の問題では,一定の部分係数で均一な目標信頼性指標を維持することはできない一方で,固定
された分位点を用いることでそのような均一性を保持できる可能性がある。
D.5.7 システム信頼性
地盤構造の大部分は複数の破壊モードをもつため,ほとんどの地盤の信頼性設計は,実際にはシステム
72
A 3305:2020 (ISO 2394:2015)
信頼性問題(8.3参照)となる。例えば,簡易重力式擁壁は,擁壁基部に沿った水平滑動,擁壁先端周り
の転倒又は回転及び擁壁下部の地盤の支持力不足の少なくとも三つの破壊モードをもつ。異なる破壊モー
ドの荷重及び耐力が相関し得るため,これらの破壊モードは,互いに相互作用する傾向がある。例えば,
滑動及び転倒による破壊モードに対する主要な耐力の発生源である重力式擁壁の自重は,同時に支持力の
破壊モードの荷重の主要な発生源でもある。
くい(杭)基礎は,幾つかの群くい(杭)からなるくい(杭)システムであり,各群くい(杭)は幾つ
かの個々のくい(杭)から構成されている。くい(杭)システムの信頼性の評価には,個々のくい(杭)
の信頼性,群くい(杭)効果及びくい(杭),並びに上部構造物との相互作用に起因する効果を考慮する必
要がある。
多くの地盤構造物(例 斜面,トンネル,深い掘削孔など)は,周囲の地盤に生じる破壊メカニズムを
形成することで終局限界状態に至る。土塊中の各潜在滑り面は破壊モードである。FORMによって特定す
る“最も可能性の高い”破壊モードに関連する破壊確率は,システムの破壊確率の下限を提供するだけで
ある。滑動面が地盤とくい(杭)との間の境界面にほとんど制限されているくい(杭)基礎とは対照的に,
土塊中の滑り面の軌道は,確率場の特定の実現に結び付いており,有限要素解析又は同等の数値解析法だ
けによって特定し得る。力学及び空間変動性が絡むため,この類のシステム信頼性問題は複雑である。し
かし,地盤工学では珍しいことではない。
73
A 3305:2020 (ISO 2394:2015)
附属書E
(参考)
コードキャリブレーション
E.1
一般事項
新しい設計規準(コード)を制定する場合又は既存の設計規準を改定する場合には,一般にキャリブレ
ーションが要求される。ここでキャリブレーションとは,所定の設計規準形式中の全てのパラメータの値
を決定することを指す。コードキャリブレーションは,判断と当てはめ,最適化又はこれらの組合せによ
って行われる。この附属書では,コードキャリブレーションの方法を記載する。ここで記載する方法は,
この規格に記載する構造信頼性理論の原則に明確に基づいている。
E.2
キャリブレーションに用いる確率モデル
基本確率変数の確率モデルは,極めて慎重に選定することが望ましい。選定の指針はJoint Committee of
Structural Safety (JCSS)による確率論に基づくモデルコード(JCSS 2001)で参照することが可能である。一
般に,次のa)〜d)を推奨している。
a) 強度又は耐力変数は,しばしば対数正規分布によってモデル化する。これによって,負の値が生じる
可能性を排除可能である。状況によっては,材料特性にワイブル分布を用いることも検討に値する。
特に,強度が材料のぜい(脆)性,寸法効果及び材料の欠陥に支配される場合が,これに該当する。
変動係数は,材料の種類によって様々であり,鋼材及び鉄筋は5 %,コンクリートの圧縮強度は15 %,
構造部材として用いられる木材の曲げ強度については15〜20 %というのが一般的な値である。特性値
には,一般に(下側)5パーセンタイル値を用いる。
b) 変動作用(積載及び環境)は様々な方法でモデル化する。最も簡単なモデルは,基準期間(多くは1
年)中の最大値の確率分布モデルである。この変数は,一般にグンベル分布などの極値分布でモデル
化する。変動係数は,一般に20〜40 %程度であるが,特に地震荷重の場合のように,かなり大きな値
となることもある。特性値には,年最大値の確率分布の98パーセンタイル値(再現期間50年の値)
を用いてもよい。
注記 日本では一般社団法人日本建築学会の荷重指針では,年最大値の99 %(再現期間100年の値)
が基本値として規定されている。
c) 永続作用は,多くの異なった要因によることから,一般に正規分布によってモデル化する。変動係数
は,一般に5〜10 %程度で,特性値には50パーセンタイル値(中央値)を用いる。
d) モデル化の不確定性は多くの場合,それらが確率変数の積の形でもたらされる場合には対数正規分布
で,確率変数の和の形でもたらされる場合には正規分布でモデル化する。一般的な変動係数の大きさ
は3〜15 %程度であるが,慎重に設定することが望ましい。特性値としては,一般に中央値を用いる。
E.3
最適化問題としてのコードキャリブレーション
究極的に構造設計規準は,通常の荷重状態,使用条件及び環境条件の下に建つ一般的な構造物を設計す
るための,簡単かつ安全で,経済的に効率的な原理を提供することを目的として作られる。その結果,設
計規準は,構造工学に関する日々の仕事を大いに容易にするだけでなく,構造工学における手順の標準化
を推し進める役割も担っている。この標準化は,最終的には個々人にとっての利益のために,社会の資源
74
A 3305:2020 (ISO 2394:2015)
の最適な使用を推し進める。
したがって,コードキャリブレーションは,設計規準中のパラメータを最適化することによって社会の
期待純益を最大化する意思決定最適化問題と捉えることが可能である。定式化においては,全ての関連す
る利益と構造物に関連する結果,すなわち,社会にとっての利益一般,建設費用,設計供用期間中の維持
管理費用及び破壊による損失を考慮することが望ましい。原理的には目標信頼性も,定式化の中で最適化
することが可能である。しかしながら,構造物の供用期間中に起こる全ての利益及び結果を,適切に考慮
しながら目的関数を定式化することは,一般に困難である。特に,人命のように金銭に換算できない利益
並びに費用及び損失を,どのように目的関数に取り込むかという点については,議論の余地がある(附属
書G参照)。
このような理由から,より現実的に実現可能な方法を推奨する。このような方法のうちの一つを次に記
載する。この方法は,信頼性に基づく最適化に基礎を置いており,準確率論的設計規準形式のコードキャ
リブレーションの枠組みの中で記載する。
E.4
信頼性に基づく設計規準の最適化
E.4.1 設計式及び限界状態関数
信頼性に基づくコードキャリブレーションの手順を記載する前に,準確率論的設計規準における設計式
と限界状態関数との対応を示す。個々の破壊モードに関する限界状態関数は,次の式で示す。
gj(x, pj, z)=0 ·········································································· (E.1)
ここに,
x: 基本確率変数Xの実現値
pj: 確定値であるパラメータで構成されるベクトル
z: 設計変数の集合
設計規準の適用範囲は,L個の異なるベクトルpj,j=1, …, Lの集合Iによって記述される。集合Iは,例
えば,構造物の異なる幾何学的構成,確率変数の異なるパラメータ及び異なる統計モデルを含む。式(E.1)
の限界状態関数に対応した確定的な設計式は,次の式で表す。
Gj(xc, pj, z, γ)≧0 ······································································ (E.2)
ここに,
xc: 基本確率変数の特性値で構成されるベクトル
γ: 部分係数ベクトル
部分係数γの集合は,性質上の不確定な変動に関する偶然的不確定性だけではなく,例えば,荷重及び
耐力の分布に関する統計的不確定性並びに採用したモデルの単純化などに起因する認識論的不確定性も考
慮することが望ましい。
E.4.2 手順
E.4.2.1 段階的手順
コードの最適化は,一般に次の手順で進める。
− 手順1:設計規準の適用範囲の定義
− 手順2:設計規準の目標の定義
− 手順3:設計規準形式の定義
− 手順4:代表的な破壊モード及び確率モデルの特定
− 手順5:近接度の尺度の設定
− 手順6:選択した設計規準形式に用いる最適な部分係数の決定
− 手順7:部分係数の検証及び決定
75
A 3305:2020 (ISO 2394:2015)
E.4.2.2 手順1:設計規準の適用範囲の定義
対象とする構造物のクラスと関連する破壊モードの種類を定義する。
E.4.2.3 手順2:設計規準の目標の定義
設計規準の目標は,対象とする構造物の用途及びクラスごとの目標とする信頼性指標又は目標とする破
壊確率によって定義することが可能である。これらは,既存の設計規準において暗示的又は明示的に示さ
れる信頼性指標を参照することによって又は例えばLQIの概念(附属書G参照)といった他の規準を元に
決定することが可能である。したがって,設計規準の最適化は部分係数1)だけの最適化に置き換えられる。
注1) ここで,部分係数は,確率変数の不確定性を考慮するために設計式に導入した係数一般を意味
している。
E.4.2.4 手順3:設計規準形式の定義
設計規準形式は,次のa)〜d)を含む。
a) 幾つの部分係数及び荷重組合せ係数を使うのか。
b) 荷重に乗ずる部分係数は,材料に依存するかしないか。
c) 材料に乗ずる部分係数は,荷重の種類に依存するかしないか。
d) 設計式の規定において,どのように荷重組合せの部分係数を使うか。
一般に実用性の観点からは,部分係数はできる限り少ない数で,かつ,一般的であることが望ましい。
一方,広い範囲の種類の異なる構造物を対象に,経済的かつ安全な構造物を設計するためには,多数の部
分係数が必要となる。
E.4.2.5 手順4:代表的な破壊モード及び確率モデルの同定
設計規準で対象とする構造物のクラスの範囲において,一般的な破壊モードを同定する。限界状態式及
び設計式を定式化し,限界状態式内のパラメータの確率モデルを選定する。また,各種の安全点検を実行
する頻度を決定する。
E.4.2.6 手順5:近接度の尺度の定義
部分係数ベクトルγは,L個の異なるベクトルpjに対応する信頼性指標が目標信頼性指標βtargetにできる
限り近づくようにキャリブレーションを行う。したがって,近接度の尺度は,次の式で定式化する。
[
]
∑
=
−
L
j
j
j
β
γ
β
w
1
2
target
)
(
······························································· (E.3)
ここに,
βj(γ): 部分係数ベクトルγを用いたことによって得る信
頼性指標
wj(j=1, 2 …, L): 各設計の局面の相対的な出現頻度又は重要さを表
す係数(
1
1
=
∑
=
L
i
i
w
)
式(E.3)において,信頼性指標の代わりに破壊確率を用いる。また,目標よりも小さな信頼性指標に,よ
り大きな重みを与える非線形の目的関数を用いてもよい。上記の定式化は,各破壊モードの信頼性の下限
を含める場合にも簡単に拡張可能である。
E.4.2.7 手順6:選択した設計規準形式に用いる最適な部分係数の決定
次に,最適化問題を定式化する。式(E.3)によって定義される近接度の尺度を部分係数ベクトルγについ
て最小化する。手順5の最適化問題の数値解析の解によって最適な部分係数ベクトルを得る。
最適化の過程において,部分係数ベクトルγが与える設計シナリオjにおける信頼性指標βi(γ)は,次の2
段階の手順によって得る。
76
A 3305:2020 (ISO 2394:2015)
まず,与えられた部分係数ベクトルγから設計値z*を決定する。設計変数の数が一つの場合は,最適な
設計値z*を設計式(E.2)の解として得る。設計変数の数が二つ以上の場合は,設計変数最適化問題を定式化
する。
)z(
min
zC
··············································································· (E.4)
N
i
z
z
z
m
m
i
c
m
i
c
t
s
ui
i
li
j
i
j
i
,
,2
,1
,
,
,1
,0
)z,
p,
x(
,
,2
,1
,0
)z,
p,
x(
..
e
c
e
c
Κ
Κ
Κ
=
+
=
=
=
≦
≦
≧
C(z)は目的関数,ci (i=1, 2 …, m)は制約条件である。目的関数C(z)には,しばしば構造物の重量を用いる。
式(E.4)中にあるme個の等式の制約条件は,設計条件(例 幾何学的寸法に関わる制約条件)をモデル化す
るために,また,構造物に作用する荷重と応答とを関係付ける(例 有限要素方程式)ために用いてもよ
い。構造解析は,不等式の制約条件に直接組み込まれるので,等式の制約条件はしばしば避けることが可
能である。式(E.4)中の不等式の制約条件は,変位及び応力といった応答が設計式(E.2)で表す規準値を超え
ないことを保証する。不等式の制約条件はまた,設計変数に関する一般的な設計要求条件を含むことが可
能である。式(E.4)にあるziの下限zil及び上限ziuは,単純な上下限である。Nは,設計変数の数である。一
般に設計式(E.2)は非線形であり,また,非凸である。
次に,式(E.4)のように定式化された設計変数の最適化問題の解として得られたz*を用い,式(E.1)で表さ
れる限界状態関数に基づき信頼性指標βi(γ)を,FORM及びSORM又はシミュレーションによって評価する。
これらの2段階の手順は,式(E.3)のように定式化された近接度の尺度を最小化する部分係数ベクトルが
見つかるまで繰り返す。
E.4.2.8 手順7:部分係数の検証及び決定
部分係数ベクトルの初期値を,手順6の最適化問題を解くことによって求める。これを元に,最終的な
部分係数ベクトルを工学的判断及び慣例を考慮に入れながら決定する。
E.5
部分係数のキャリブレーションの例2)
注2) ここに記載された手順に沿ってコードキャリブレーションをすることが可能である,JCSSによ
って開発されたCodeCalというソフトウェアが入手可能である(www.jcss.byg.dtu参照)。
E.5.1 問題の設定
次に,単純ではあるが,代表的な限界状態関数を示す。
g=zRXR−{φG+(1−φ)[φQQ1+(1−φQ)Q2]} ···································· (E.5)
ここに,
R: 耐荷力
XR: モデルの不確定性
z: 設計変数
G: 永続作用
Q1: タイプ1の変動作用(例 風荷重)
Q2: タイプ2の変動作用(例 雪荷重)
φ: 永続作用及び変動作用の割合をモデル化する係数で,0から1
の間の値
φQ: タイプ1及びタイプ2の変動作用の割合をモデル化する係数
で,0から1の間の値
表E.1に,これらの基本確率変数の確率モデルの例を示す。全ての基本確率変数は,互いに統計的に独
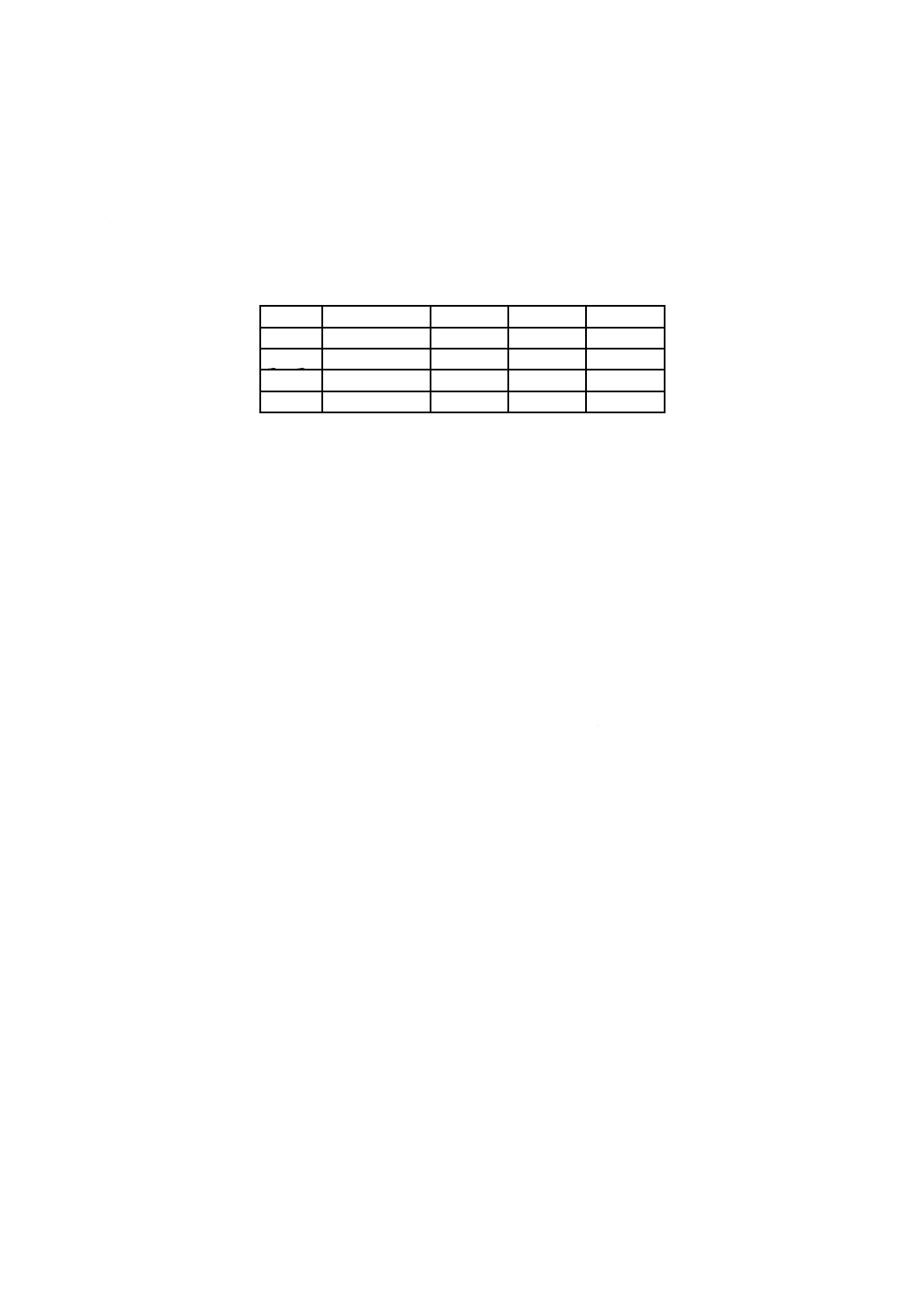
77
A 3305:2020 (ISO 2394:2015)
立であると仮定する。荷重組合せは,Ferry-Borges-Castanheta荷重モデル[6]でモデル化され,変動作用の大
きさが変化をする回数は,次のように仮定する。
a) 風荷重 年当たり360回
b) 雪荷重 雪荷重が生じると想定する地域において,5か月間で10回
c) 積載荷重 10年に1回
表E.1−基本確率変数の確率モデル
変数
分布の種類
平均値
変動係数
特性値
G
正規分布
1.00
0.10
50 %
Q1,Q2
グンベル分布
1.00
0.40
98 %
R
対数正規分布
1.00
0.05
5 %
XR
対数正規分布
1.00
0.03
50 %
対応する設計式は,次の式で表す。
g=zRc/γm−{φγGGc+(1−φ)γQ[φQQ1c+(1−φQ)ψQ2c]} ························· (E.6)
添え字のcは特性値であることを示す。また,γmは耐力に乗ずる部分安全係数,γGは永続作用に乗ずる
部分安全係数,φQは変動作用に乗ずる部分安全係数,ψは荷重組合せ係数である。この定式化は,荷重の
組合せを考慮するとともに,部分安全係数が耐力項及び作用項の両方に用いられる場合に相当する。単一
の作用が支配的な場合には,二つ目の変動作用は無視してもよい。したがって,φQ=1と設定する。
年当たりの目標信頼性指標βtarget=4.2,φの値は,典型的な値として0.2〜0.9の間を0.1間隔で,重み係
数wjは均等に1/8 (j=1, 2, …, 8)と設定して,二つのキャリブレーション例を次に示す。最初の例では単一
の作用が支配的,二つ目の例では二つの変動作用を考慮する。
E.5.2 例1:一つの変動作用に対して荷重及び耐力の両方の項に部分係数
この例は,設計式(E.6)においてφQ=1とした場合に対応する。式(E.6)中の三つの部分係数の値は任意で
あり,ここでは,γG=1とする。したがって,設計式は,次の式に置き換わる。
g=zRc/γm−[φGc+(1−φ)γQQ1c]···················································· (E.7)
E.4.2に示した手順に従うと,部分係数はγm=1.15,γQ=1.65となる。異なるφを用いることによって達
成される信頼性指標を図E.1に示す。
78
A 3305:2020 (ISO 2394:2015)
凡例
---- 目標信頼性指標
○ 達成される信頼性指標
図E.1−φの関数としての信頼性指標
E.5.3 例2:二つの変動作用に対して荷重及び耐力の両方の項に部分係数
次のケースについて,目標信頼性指標がβtarget=4.2となるように荷重組合せ係数ψを定める。
a) 環境からの作用及び支配的でない積載荷重 ψI,E
b) 積載荷重及び支配的でない環境からの作用 ψE,I
c) 雪荷重及び支配的でない風荷重 ψW,S
d) 風荷重及び支配的でない雪荷重 ψS,W
表E.2にφQ=0.1,0.3,0.5,0.7及び0.9としたときの結果を示す。
表E.2−荷重組合せ係数
φQ=0.1
φQ=0.3
φQ=0.5
φQ=0.7
φQ=0.9
ψI,E
0.75
0.6
0.3
0.25
0.0
ψE,I
0.6
0.45
0.3
0.05
0.0
ψW,S
0.9
0.6
0.1
0.0
0.0
ψS,W
0.7
0.45
0.1
0.0
0.0
参考文献[4]を参照。より複雑なケースへ適用する際には,CodeCalの説明書を参照することが望ましい。
古典的な方法でキャリブレーションを行う場合は,ISO 2394:1998の附属書F及び附属書Gを参照するこ
とが望ましい。
E.6
設計値法における設計値のキャリブレーション
E.6.1 FORMによる設計値
変数Xiの設計値xidは,次の事項に依存する。
− 変数Xiの確率分布のパラメータ
− 仮定された確率分布の種類
係数
信
頼
性
指
標

79
A 3305:2020 (ISO 2394:2015)
− 限界状態に対する目標信頼性指標β及び対象とする設計の局面
− 限界状態に到達する際のXiの変動の敏感さを表す係数αi。αiはFORMの計算において定義する。
任意の分布関数F(xi)に従うXiの設計値は,次の式で与える。
F(xi)=Φ(−αiβ) ······································································· (E.8)
Xiが正規分布に従うならば,
xid=μi(1−αiβVi) ······································································ (E.9)
ここに,μi及びViは,それぞれ確率変数Xiの平均値及び変動係数である。
Xiが対数正規分布に従う場合は,設計値を次の式で与える。
xid=ξiexp(−αiβvi) ··································································· (E.10)
ここに,
2
1
i
i
i
V
μ
ξ
+
=
)
1
ln(
2i
i
V
v
+
=
Viの値が小さい場合(例 Vi<0.25)には,ξi=μiかつvi=Viとしてもよい。
E.6.2 FORMによる感度係数(分離係数)
確率変数が互いに統計的に独立な場合は,FORMの解析で用る係数αiは,次の特性をもつ。
−1≦αi≦1············································································ (E.11)
1
2=
∑iα
············································································ (E.12)
一般的に,αiの値は,FORMによる代表的な計算例で求めることが望ましい。これは多くの収束計算を
必要とし,常に不便である。しかしながら,表E.3に示すような標準化されたαiの値一式が,経験に基づ
き提案されている。安全側の評価のため,二乗和は1より大きくなり得ることに注意すべきである。表E.3
を使う場合の誤差を小さくするために,一般に0.16<σS/σR<6.6という条件が付けられている。ここで,σ
は標準偏差,Sは支配的な作用,Rは支配的な耐力のパラメータである。
表E.3−感度係数
Xi
αi
支配的な耐力のパラメータ
0.8
その他の耐力のパラメータ
0.4×0.8=0.32
支配的な作用のパラメータ
−0.7
その他の作用のパラメータ
−0.4×0.7=−0.28
注記 標準化されたαの値の計算原理は,ISO 2394:1998の附属書B
で既に示しており,そこでは表E.3と同じ値を提案している。
表E.3を適用する場合,事前にはどの変数を“支配的”とした方がよいかは分からない。これを見つけ
出す唯一の方法は,全ての変数を順次“支配的”として取り扱い,どれが設計を決定するかを調べること
である。これは,設計規準作成者の段階で行われることもあれば,設計者の役割(例 様々な荷重状態に
対する検証をする場合)となることもある。
例 初歩的な例として,一つの耐力R及び一つの作用Sを考える。ともに正規分布に従うとする。目
標信頼性指標β=3.8とすると,式(E.9)から,
Rd=μR−3.04σR 及び Sd=μS+2.66σS
ここに,Rd>Sdとなっていることの確認を行う。作用Sが対数正規分布に従う場合は,式(E.9)ではなく
式(E.10)を用いる(VS<0.25ならば)。
80
A 3305:2020 (ISO 2394:2015)
Sd=μSexp(2.66VS)
そして,Rd>Sdとなっていることの確認を行う。
E.7
S-N曲線に基づく疲労に対する部分係数設計
E.7.1 S-N曲線
S-N曲線を用いる方法は,疲労を対象とした設計にしばしば用いられ,疲労のメカニズムにおける三つ
の全ての相を取り扱っており,また,完全に実験に基づくものである。多くの試験体に,破壊に至るまで
一定の大きさの繰返し荷重を与える。応力の振幅Sと破壊に至るまでの繰返し回数Nとの関係をプロット
することで,S-N曲線を得る。S-N曲線は,平均応力の大きさに依存する場合もあれば,依存しない場合
もある。構造物に実際に加わる荷重の大きさは変動することから,これに対応するためには累積損傷則を
適用しなければならない。最も広く使われるものは,Palmgren-Minerによる線形累積損傷則である。この
法則に従えば,次の条件を満たせば破壊に至る。
c
i
i
D
N
n=
∑
·········································································· (E.13)
ここに,
ni: 応力の振幅Siで繰り返し載荷をした回数
Ni: 応力の振幅Siで載荷したときに破壊に至るまでの繰返し回数
Dc: 破壊度の限界値
応力の振幅Siは,局所応力集中(例 溶接の先端)の影響も含むと仮定する。
各応力振幅Siでの繰返し回数niを知るためには,特殊な計数手順(例 レインフロー法)が必要となる。
Palmgren-Miner則は載荷順序の効果を考慮に入れていない。限界値Dcは,理想的な場合には1.0となるが,
一般には荷重の履歴,環境及び材料の種類に依存する。
E.7.2 部分係数設計法における検証の手順
形式化した安全性検証法は,解析方法に依存する。S-N曲線を用いた累積損傷法の場合には,検証法を
次の式で示す。
dγ
D
N
n
c
i
i<
∑
·········································································· (E.14)
=
Mf
fc
Ff
,γ
γ
R
S
N
N
i
i
i
······························································· (E.15)
ここに, ni, Si: 荷重履歴の最良推定量
Rfc: 疲労耐力の特性値
γFf: 荷重の大きさと荷重のモデルにおける不確定性とを考慮した
部分係数
γMf: 材料モデルにおける不確定性を考慮した部分係数
γd: 累積損傷則,設計供用期間及び破壊による結果の重大さにお
ける不確定性を考慮した部分係数
部分係数の大きさは,次の事項に依存することが望ましい。
− 確率変数の不確定性及び敏感さ
− 損傷に対する構造物の耐性,すなわち,亀裂が生じた構造物に,代替荷重経路があるか否か
− 点検の間隔及び亀裂を検出できる確率
− 効果的な補修能力
疲労設計に部分係数を用いたキャリブレーションの例は,参考文献[11]を参照。
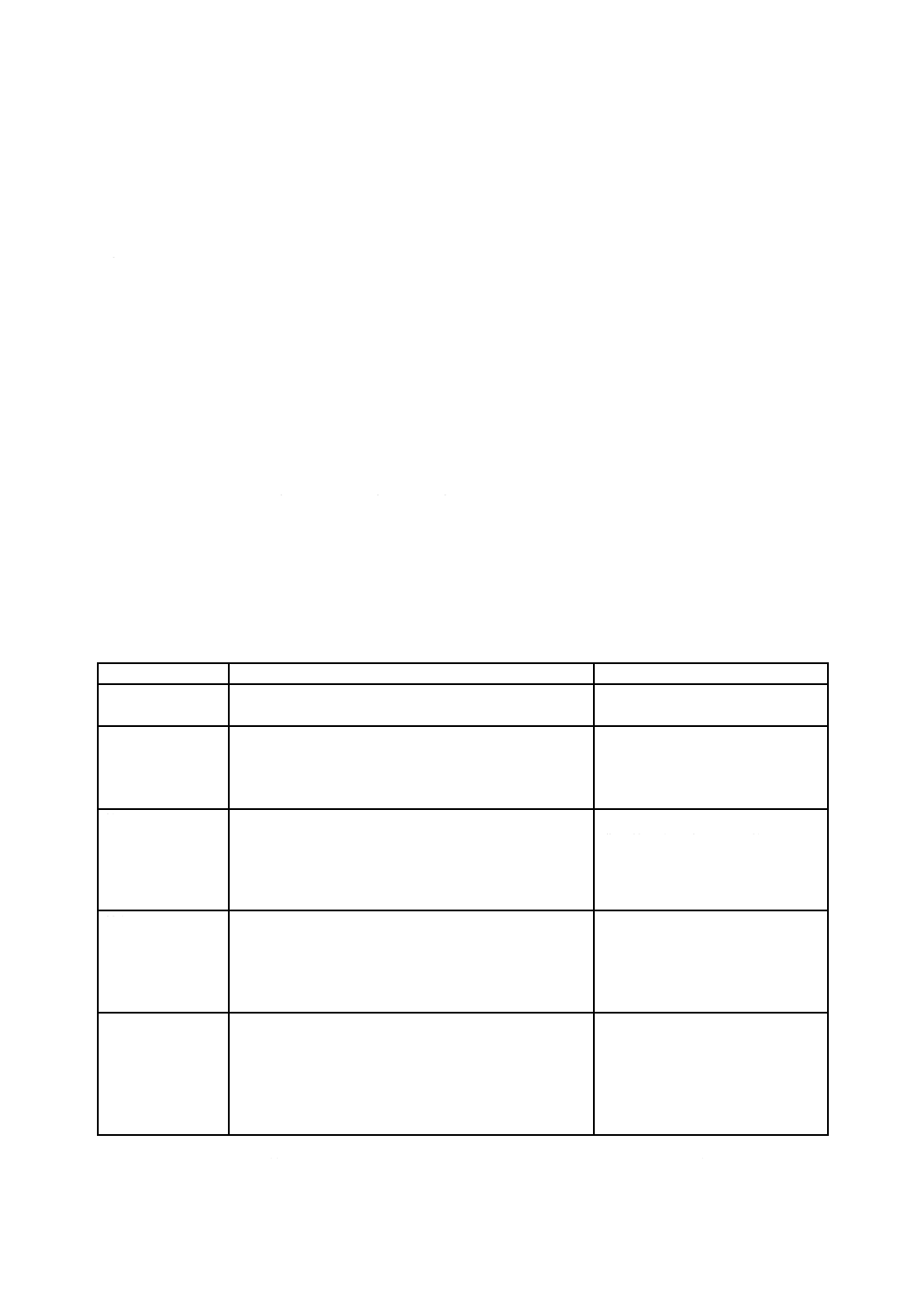
81
A 3305:2020 (ISO 2394:2015)
附属書F
(参考)
構造のロバスト性
F.1
一般事項
箇条4では,構造物の設計は,構造システム及びシステムの破壊の結果だけではなく,構造に作用する
暴露(荷重,外力及び環境)に基づいて,リスクに基づくロバスト性の評価及び/又はロバスト性に対す
る考慮の裏付けがなければならないことを示している。この附属書では,そのような(ロバスト性の)評
価及び適切な備えの見極めに役立つ系統的な枠組みを概説する。
まず,所与の状況において,リスクベースの評価及び設計をする必要があるかどうか,並びに必要な労
力はどの程度かを経験則で評価することができる構造の分類を示す。その後,リスクベースの評価が必要
でない場合において,適切なロバスト性の設計戦略及び備えを選択するための指針を示す。最後に,全体
的なリスク又は信頼性に基づくロバスト性の評価のため,理論的な枠組みを示す。
この附属書は,COST Action TU0601 Robustness of Structures(参考文献[2]を参照)の結果に基づいており,
本文,表及び図の大部分は,そこから引用したものか翻案したものである。
F.2
結果の重大さに従った構造物の分類
表F.1に示した結果の重大さの分類によって,構造物の分類が容易になる。
表F.1−結果の重大さの分類(Eurocode EN 1991-1-7:2006から一部引用)
結果の重大性等級
予想される結果の説明
構造物の例
等級1
主として重大でない部材の損傷。
ほとんど人がいないような低層建
物,小型の風車,畜舎など。
等級2
所有者及び管理者にとって重大な部材の損傷並びに機能
の喪失であるが,社会的な影響は僅か又は皆無。
数週間足らずで完全に回復できる程度の環境の質への被
害。死者数の期待値は5人未満。
比較的小規模の建物,産業施設,小
型の橋,大型の風車,小規模又は無
人の海洋施設など。
等級3
数週間にわたり,地域の混乱を招いたり,重要な社会サ
ービスに遅れをきたしたりするような,社会的に影響の
大きい部材の損傷及び機能喪失。数週間足らずで回復で
きる,破壊事象の周囲の環境の質に限定した被害。
死者数の期待値は50人未満。
大抵の住宅,典型的な橋,トンネル,
典型的な海洋施設,比較的大規模の
及び/又は有害物質を扱う産業施
設
等級4
何箇月にもわたり国家レベルで社会サービスの深刻な損
失,混乱及び遅延を引き起こすような災害事象。数箇月
程度では部分的にしか回復できず,破壊事象の周囲だけ
ではなく著しく広がり国家規模で影響を受けるような環
境の質への被害。死者数の期待値は500人未満。
高層建物,競技場観覧席,大型の橋,
トンネル,堤防,ダム,比較的小規
模の海洋施設,パイプライン,精製
所及び化学プラント。
等級5
何年にもわたり国家規模を超えて社会サービスの深刻な
損失,混乱及び遅延を引き起こすような大災害の事象。
数年から数十年程度では部分的にしか回復できない,著
しく広がって国家規模を超えて影響を受けるような環境
の質への被害。
死者数の期待値は500人以上。
国家的な重要性をもった建物,大規
模の有害物質の格納庫,貯蔵庫,大
規模の海洋施設,大規模ダム及び堤
防。
適切なロバスト性の対策及び適切な状況分析手法は,結果の重大さのカテゴリーに依存し得る。例えば,
82
A 3305:2020 (ISO 2394:2015)
次に示すような方法がある。
− 結果の重大性等級1 ロバスト性については特に考慮しない。
− 結果の重大性等級2 該当の構造物の周囲の状況に依存する。理想化した荷重,構造性能モデルの下
で簡単な分析及び/又は規定どおりの設計及び詳細設計を行う。
− 結果の重大性等級3 構造物の崩壊につながるようなシナリオを系統的に明らかにし,それらに対す
る戦略を立てる。構造性能の分析は,正当な理由があれば簡単で理想化したモデルに基づくことが可
能である。規定どおりの設計及び詳細設計を用いることも可能だが,明らかにしたシナリオを具体的
に扱うことが望ましい。簡素化及び理想化の根拠として,直接的及び間接的な結果を扱う信頼性分析
とリスク分析を用いることが望ましい。
− 結果の重大性等級4 全ての関連分野の専門家を招き,リスクスクリーニング会議を行い,構造物の
崩壊につながるシナリオの更なる検討及び分析を行う。動的及び非線形構造解析並びに厳密に直接的
及び間接的な結果を扱ったリスク分析による詳細な評価を行う。
− 結果の重大性等級5 等級4を踏襲するが,これに加えて,品質管理のために外部の専門家又は審査
委員会の参加が必要である。
表F.1に示される結果の重大さは,結果の期待値として考えるべきであり,暗黙的に主要なハザードへ
の暴露,構造性能及びリスク低減策に依存している。表には明確に記載していないが,原子力施設は結果
の重大性等級5に従って扱うことが可能である。
F.3
適切な設計戦略及びロバスト性の備えの選択のための指針
F.3.1
一般事項
リスク及び信頼性に基づく方法が不必要な場合は,適切なロバスト性の備えを見極めるために設計手法
を,次のように分類する(表F.2参照)。
a) 事象の制御(EC,Event control) この手法は,ハザードHの発生確率に影響を及ぼす。この手法は,
明らかとなったハザードに対して設計するときだけ適用可能。
b) 特定荷重に対する耐力(SLR,Specific load resistance) この手法は,ハザードHが発生したときに局
所的損傷Lが発生する確率に影響を及ぼす。すなわち,構造物及び部材のぜい(脆)弱性を減らす。
局所的損傷は,より一般的には直接的な損傷として知られている。
c) 代替荷重経路(ALP,Alternative load paths) この手法は,局所的損傷が起こった後での建物の崩壊の
ように,更なる(続けて起こる)損傷の確率に影響を及ぼす。緊結のような構造的な備えは,ALPを
与えるのに役立つ。
d) 破壊の結果,特に間接的な結果の重大さを低減させる方法。
方法a)及びd)は間接的な手法であるのに対し,方法b)及びc)は,不釣合いによる崩壊を防ぐ直接的な手
法である。直接的な手法に対する設計は,特定のハザードのシナリオが起こり,構造物に影響を与えると
きにその構造が特定の目標性能を満足することを証明することで,設計過程において崩壊に対する耐力を
明示的に保証することを目的としている。したがって,直接的な手法に対する設計は構造解析に強く依拠
している。一方,間接的な手法に対する設計は,目標性能を達成するのに役立つ合意された設計上の特徴
を取り入れることでハザードの効果を暗黙的に減らすことを目的としている。

83
A 3305:2020 (ISO 2394:2015)
表F.2−設計手法の分類
方法
低減する対象
取り組む課題
a) 事象の制御(EC)
事故事象の発生確率及び/
又は強度
− モニタリング,品質管理,補正及び予防
b) 特定荷重に対する耐力
(SLR)
事故事象による局所的な損
傷の確率
− 強度及び剛性
− ひずみ硬化の便益
− じん(靭)性破壊対ぜい(脆)性破壊
− 座屈後の耐力
− 機械的装置
c) 代替荷重経路法(ALP),
結合材の用意を含む
局所的損傷が起きた場合の
更なる損傷の確率
− 複数の荷重伝達経路及び冗長性
− 進行性破壊対ジッパーストッパー
(ファスナーの留め具)
− 第二の防衛線
− 保有耐力設計及びヒューズ要素
− 壊れてもよい保護装置
− 試験
− 強度及び剛性
− 連続性及びじん(靭)性
d) 結果の重大さの低減
進行性破壊のように続けて
起こる破壊の結果
− 構造の分割
− 警告・能動的干渉・救出作業
− 施設のサービスの冗長性
F.3.2
事象の制御
事象の制御は,不釣合いな破壊につながる可能性がある出来事から回避する又は保護することを意味す
る。この方法は,不釣合いな破壊に対する構造物本来の耐力を増加させるものではない。一旦,建物の使
用が開始されると,この手法の有効性は,建物の運用及び使用が設計者による仕様及び推奨に従ってどの
ようになされるかにかかっている。しかしながら,高い強度のハザードが現れる確率を低減し得る予防策
には,例えば,次のような方法がある。
− 構造物の場所の計画
− 外周の退避距離の備え
− 警報・警備システムのような監視システムの備え
− 爆発物の貯蔵の禁止
− 衝撃力を防ぐための構造物の周囲の保護対策
− ガス検知器及びガスの自動供給停止装置
− 発火物の管理又は制限
− 火災荷重の制限
− 火災鎮圧システム
− 煙検知器及び煙警報器の導入
− 構造ヘルスモニタリングシステムの使用
− 建設,維持保全及び修復活動の品質管理
これらの防止策を講じることで,高い強度のハザードが発生する確率P(H)を小さくし,対応する再現期
間を長くすることが可能である。
F.3.3
特定荷重に対する耐力(SLR)
この手法では,事故又は誤用による破壊に耐えるための十分な強度を,建物の特定の部分の構造部材に
84
A 3305:2020 (ISO 2394:2015)
与えることによって,偶発荷重に耐えられるようにする。この目的のため,構造物が残存するための重要
度に応じて部材を分類し,いわゆる主要素(キーエレメント)を同定する必要がある。主要素を喪失する
と,建物全体として十分強い荷重代替経路を発現させることができなくなるため,主要素の破壊は,目標
性能の達成を妨げる更なる損傷を引き起こすことが予想される。主要素になるものの例としては,建物で
は柱及び耐力壁,連続橋では橋脚又はケーブル支持構造物ではケーブルが挙げられる。
最初の損傷に対してより高い安全性を保証するためには,より高い設計荷重を用いたり,保護対策を講
じたりするだけでは十分ではないことを念頭に置く必要がある。最初の損傷は,腐食又は火災といった事
象によっても引き起こされる可能性がある。こうした事象を,設計荷重を大きくすることよりも,腐食防
止策,定期点検,防火対策及び消火システムといった“事象の制御”の対策によって,より効果的に抑制
する。
SLR法は,同定可能な主要素の数が限られた構造に適しており,費用対効果が高い。しかしながら,多
数の主要素をもつ構造であっても,他の手法が困難な又は実用的でない場合にはSLRを用いる。例えば,
構造システムが代替荷重経路をもっておらず,事象の制御及び結果の制御を実施することが不可能でない
にしても困難な場合である。
F.3.4
代替荷重経路(ALP)
代替荷重経路(ALP)は,構造のロバスト性が向上する直接的な手法である。この方法では,典型的に
は構造部材を一つ一つ取り除いていくことで,荷重が作用点から支持点まで伝達される代替経路を評価し
ていく。これによって,もともと破壊した部材が受けもっていた力を再分配し,破壊が広がることを防ぐ
ことが可能である(新しい経路は十分に耐力があることが前提。)。ALPは,次の例のような荷重伝達機構
によって形成することが可能である。
− 曲げ荷重伝達の反転(破壊した柱の上部におけるかまぼこ型の柱頭の曲げから垂れ下がりの曲げへ)。
− 曲げから引張り荷重伝達への移行(ケーブル的な働き)。
− 平面的な荷重伝達から空間的な荷重伝達への移行(一方向スラブから二方向スラブへ)。
この直接的な手法では,設計者は,構造物に一つ以上の構造要素の破壊(又は仮想的な除去)があった
としても,更に発生する可能性のある損傷レベルを特定の限界以下にとどめ,目標性能を満たすことがで
きることを示さなければならない。この手法は,ハザードが特定できる場合にも,特定できない場合にも
用いることが可能である。なぜならば,代替荷重経路法を用いる場合に考える仮想的な損傷は,特定のハ
ザードを考えているわけではないからである。ハザードを特定して代替荷重経路法を用いるときには,ま
ず初めに予備解析によって偶発事象によって生じる可能性のある最初の損傷を決定する。多くの建築設計
規準では,建築構造に懸垂線状の働き(カテナリーアクション)が生まれたり,じん(靭)性を保証した
りすることができるよう設計規定でつなぎ材を推奨している。ほとんどの規定化された対策の目的は,何
らかの方法で代替荷重経路を用意することである。
基本的にALP法では,どのような事象によっても一つ以上の構造部材[はり(梁),柱及び壁]が損傷
を受け,通常の荷重負担能力を完全に失っている状況を想定している。
何かの原因である要素が取り除かれてしまう確率は,構造の種類に依存する。ハザードを特定しないで
設計する場合,ALP法は,最初の損傷の合理的なシナリオを想定することから始まる。その後,この局所
的な最初の損傷の拡大が限られた範囲にとどまるように構造を設計する。
構造に最小レベルの強度,連続性及びじん(靭)性を確保することは,詳細な位置又は構造を明示的に
考慮しなかったとしても,代替荷重経路の生成に役立つ。例えば,次に挙げるものは,建物のロバスト性
を向上できる良好な方法である。
85
A 3305:2020 (ISO 2394:2015)
− 良好な平面配置計画
− 一体化したつなぎ材システム
− 壁の返し(自立した壁の端部に取り付ける垂直に交わる短い壁)
− 冗長性
− じん(靭)性を高める構造詳細
− 構造部材の耐火性
しかしながら,構造が大規模な場合,部分を全てつなぎ合わせず,構造を分割することがよい場合もあ
る。これによって,破壊が区分を越えて広がらないよう止めることが可能である。
F.3.5
結果の重大さの低減対策
結果の重大さの低減対策の実施は,破壊による直接的及び間接的な結果,すなわち,総リスクの低減を
目的とする。こうした対策には,例えば,次のようなものがある。
− 構造的,建築的対策
− 電気・機械的(装置)対策
− 非常事態の計画を含む組織的対策
− 自己救助及び他者による救助
− バックアップ施設
構造的及び建築的に重要な対策は,例えば,構造の可能な分割又は区画化,そして有効な脱出及び避難
経路の用意が挙げられる。
電気・機械的装置による対策は,例えば,自動スプリンクラーシステム,避難用警報システム,ビデオ
モニタリングシステムをもつ管理センターなどが挙げられる。組織的な対策は,例えば,明快な危機管理
システム並びに構造物の職員及び使用者全員の安全意識が挙げられる。自己救助及び他の方法による救助
は,洪水及び火災時の訓練といった定期的な模擬訓練をすることによってより効果的なものにすることが
可能である。
重要な構造の損失の結果は,短期の間,同じ目的で使用できる代替施設をもつことによって緩和するこ
とが可能である。銀行の場合,記録をコピーし,どこか別のところに保管することで,機能不全に陥った
支店の機能を別の支店が引き継ぐことが可能である。
F.4
ロバスト性評価のリスクに基づく方法
F.4.1
一般事項
構造システムのリスク評価において,システムの性能を向上させる意思決定の選択肢を明確にし,その
リスク低減効果に従ってランク付けすることを容易にするようなシステムの表現を用いることは有益であ
る。以下では,そのような枠組みを紹介し,構造システムのロバスト性評価の概説する。
F.4.2
構造システムのリスク評価
意思決定を目的とする本格的なリスク評価においては,次の三つのステップで構成するシナリオ法を用
いることが可能である。
− ステップ1 ハザード(暴露)Hiのモデル化。
− ステップ2 直接的な損失Djの評価。
− ステップ3 引き続き生じる構造物の挙動Skの評価と対応する結果の総和C(Sk)の評価。
関連する(条件付き)確率が与えられると,構造システムに関わるリスクは,次のように表すことが可
能である。
86
A 3305:2020 (ISO 2394:2015)
dir,
ind,
(
|
)(
)
(
|
)(
|
)(
)
ij
j
i
i
ijk
k
j
i
j
i
i
i
j
k
i
j
R
C
PDHPH
C
PSD
HPDHPH
=
+
∑∑
∑∑∑
∩
······ (F.1)
ここに,
Cdir,ij: 暴露Hiによる損傷(局所的な破壊)Djの結果(費用)
の期待値
Cind,ijk: 暴露Hiによって局所的損傷Djが生じたときに(引き続
き生じる)損傷Skの結果(費用)の期待値
P(Hi): 暴露Hiの発生確率
P(Dj|Hi): 暴露Hiが発生したときに損傷Djが生じる確率
P(Sk|Dj∩Hi): 暴露Hiが発生し局所的損傷Djが生じたときに広い範囲
にわたる損傷Skが生じる確率
結果Cの評価尺度は二つある。一つは通貨単位(しばしば単位時間当たり)である。もう一つは死者数
であり,これは生命の安全性だけを考慮する場合に用いる。死者数は,一般的に,社会的リスクと個人リ
スクを評価する場合に用いる。箇条7に規定したように,関連する結果は,リスク分析で考えるシステム
の範囲に依存することになる。
所定のシステムのリスク評価は,図F.1に示すような一般的な表現を考えることによって容易に行うこ
とが可能である。ハザードへの暴露は,システムの構成要素に作用する可能性のある異なった暴露事象に
よって表す。
図F.1−リスク評価における一般的なシステム表現
(引き続き起こる結果は,“間接的な”結果としても知られる。)
システムの構成要素は,ハザードに対する最初の防護とみなすことが可能である。構成要素の破壊が引
き起こすシステムの損傷は,“直接の結果”と関連しているとみなせる。直接的な結果は,金銭的な損失,
人命の損失,環境への被害又はシステムの構成要素の特性の変化といった,様々な特質から構成する(表
F.3参照)。各構成要素の破壊事象及びそれによって生じる結果の組合せによって,引き続き起こる(又は
“間接的”)結果が発生する可能性がある。構造物がロバスト性を備えていれば,この引き続き起こる結果
の重大性は小さくなる。反対に構造物がロバスト性を備えていないならば,引き続き起こる結果の重大性
は大きくなる。
……….
暴露事象
構成要素の破壊事象
及び直接的な結果
引き続き起こる結果
87
A 3305:2020 (ISO 2394:2015)
F.4.3
ハザードの表現
考慮すべきハザードは,建物の状況に強く依存する。ハザードは,三つのカテゴリーに分類可能である。
− カテゴリー1は,多かれ少なかれ自然又は一般的な人間の活動によって生じるハザードである。自然
災害としては,強風及び地震などを,意図的でない人為的なハザードとしては爆発事故を含む。しか
し,構造設計をする際には,これらの違いはほとんど関係がない。
− カテゴリー2は,(人間による)意図的な作用であり,破壊行為及び悪意のある攻撃といったものを含
む。荷重を与える側はより大きな作用(反作用)を与えられるので,ある程度構造強度を高めても,
これらのハザードに耐えるのに役立たない可能性がある。2001年9月11日の米国同時多発テロ事件
以降,このカテゴリーのハザードがより重要になっている。
− カテゴリー3は,誤り及び見落としによるハザードである。この種のハザードと品質管理及び監視と
の間には直接的な関連がある。こうしたハザードは,構造物のライフサイクルの全ての段階にわたり
監視及び品質管理をよく行うこと,並びにロバスト性を高める一般的な対策の実施によって,同定不
可能な作用に対して適切に対処することでうまく制御される。
潜在的に発生の可能性があるハザードとしては,表F.3に示したものを考慮することが望ましい。
表F.3−リスク評価及び構造の安全性のための関連するハザードの概観
ハザード
カテゴリー
屋内ガス爆発
1
屋内粉じん(塵)爆発
1
屋内爆弾爆発
2
屋外爆弾爆発
2
屋内の火事
1
屋外の火事
1
自動車の衝突
1
飛行機・船舶の衝突
1
地震
1
地滑り
1
採掘に伴う地盤沈下
1
竜巻並びに台風,ハリケーン及びサイクロン
1
雪崩
1
落石
1
地下水位の上昇
1
洪水
1
高潮
1
火山噴火
1
過酷な環境(高温,塩分など)
1
津波
1
破壊行為
2
治安悪化の影響
2
設計・評価の誤り
3
材料の誤り
3
施工の誤り
3
使用者の誤り
3
維持管理の不足(劣化)
3
コミュニケーション不足
3
88
A 3305:2020 (ISO 2394:2015)
注記 あるハザードが別のハザードを引き起こし,より一層深刻な影響を構造システムに与えること
も考えられる。そのような例を,次に示す。
− 地震の後のガス爆発及び/又は火事
− 地震の後の津波
− ガス爆発又は爆弾の爆発の後の火事
− 竜巻又は他の強風の後の火事
− 偶発作用による損傷の後の要素の劣化
F.4.4
直接的な結果及び間接的な結果
結果の重大さは,例えば,各要素の破壊と関連する金銭的損失の合計及び各要素の破壊の複合的な効果
によって生じる,全体としてのシステムの物理的な変化によって表現することが可能である。
システムのリスク評価においては,その後に起こる結果が大きな影響を及ぼしており,これらをモデル
化することを重視することが望ましい。システムの中のどのような要素であっても,それ自身がシステム
としてモデル化できることに留意することが望ましい。例えば,道路ネットワークシステムを考えると,
橋りょう(梁)を要素としている。今度は橋りょう(梁)について考えると,橋りょう(梁)自体が構造
部材から構成するシステムとなっている。リスク評価の詳細度に応じて,システムの定義,暴露量及び構
成要素と結果は異なる。
状況に応じて,表F.4に示した結果が考慮され得る。
表F.4−望ましくない事象の結果の種類
結果の種類
結果
健康
死亡
けが
重要施設(例 病院)の被害による感染症のまん(蔓)延
健康に対する影響の長期化
心理的影響
経済・資産
建物・構造の損傷
建物の周囲の資産の損傷
建物内の物品の損傷
事業継続
収入の減少
顧客の喪失
重要なサービス及び/又は活動を提供できないこと
う(迂)回及び遅延によるコスト
地域経済に与えるコスト
環境
回復可能な環境への被害
回復不可能な環境への被害
社会及び政治
評判の悪化
住民の不安の増加
政治的支援の喪失,新たな厳しい対策法令の施行
都市環境の荒廃・避難の長期化
建物の倒壊につながるシナリオに関連した結果の進展の例として,図F.2で示したような建物の上層階
で爆発が起きることを考えた場合,ここで直接の結果は,(建物の)挙動の変化及び/又は爆発に(直接)
さらされる部材による損失と定義することが可能である(図F.2のステップ2参照)。この応答の度合いに
よっては,建物の他の部分の挙動がその後に続き,その結果又は間接的な結果をもたらし得る(図F.2の
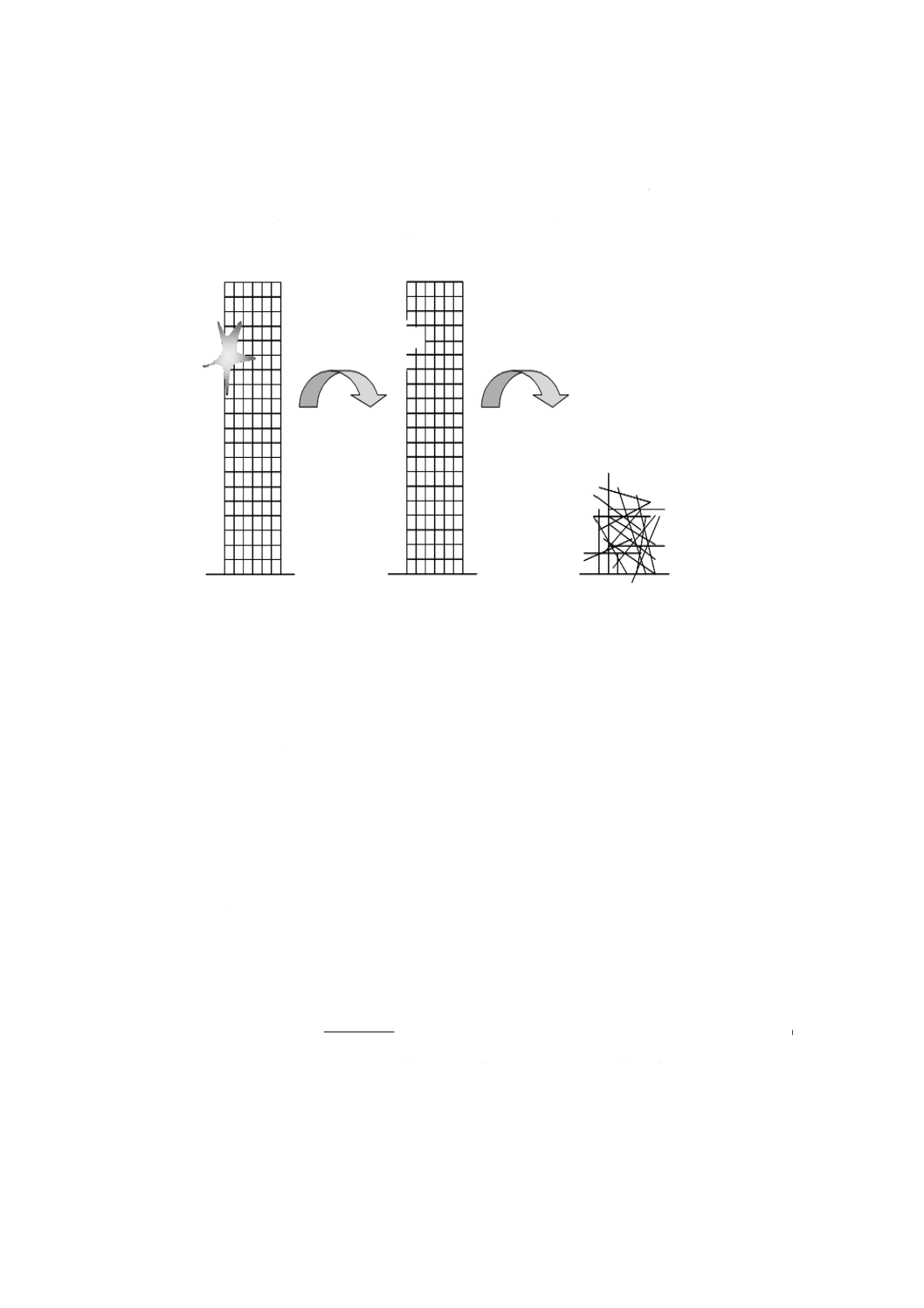
89
A 3305:2020 (ISO 2394:2015)
ステップ3参照)。
図F.2−結果の分析のステップ
考慮するシステムの境界の定義によって,結果及びリスクの総和が変わることに注意が必要である。シ
ステムの境界は,構造物自身と関連する結果だけを考慮するように定義することが可能である。この場合,
直接の結果は構造物の構成要素及び内容物の損傷に関連したものを併せた結果である。間接的な結果は,
構成要素の連鎖的な破壊及び最終的に構造の崩壊によって構造物全体を失うことと関連している。しかし,
多くの場合,特に結果の重大性等級が3以上の場合,対象構造物以外に影響する結果についても考慮する
ことが重要である。このことは,営業損失及び評判の悪化だけでなく,環境の質への被害という観点で結
果を考えるときに特に重要になる。
F.4.5
リスク及び構造物のロバスト性の更なる特性
破壊のリスクは式(F.1)で与えられるが,無次元量のロバスト性の指標があると,ロバスト性を向上する
ために異なる意思決定の選択肢を比較するのに役立つ。
リスクに基づくロバスト性指標(Irob)は,次のように定義することが可能である。
Ind
Dir
Dir
rob
R
R
R
I
+
=
····································································· (F.2)
ここに, RDir: 第1項及び第2項に関わる直接的な結果のリスク
RInd: 第1項及び第2項に関わる間接な結果のリスク
この指標は0〜1までの値をとり,値が大きいほどロバスト性が大きいことを意味する。
最適な意思決定は,リスクの総和を最小にするものであり,それは式(F.1)の第1項又は第2項の値を減
少させることによって得られるものである。全体的なリスク分析では,直接的な結果及び間接的な結果の
ステップ1設計
ステップ2
ステップ3
関連する偶発的ハザードの
同定及びモデル化
種々のハザードによる構造物
の損傷状態の評価
損傷を受けた構造物の性能
の評価
様々な大きさ及び様々な種
類のハザードについて
発生確率の評価
所定のハザードに対する種々
の損傷状態の確率と対応する
結果の評価
損傷を受けた構造物の性能が不十分となる確
率を対応する結果とともに評価
90
A 3305:2020 (ISO 2394:2015)
両方に影響するような意思決定を自由に行うことが可能である。このことを考慮すると,このロバスト性
指標は,全体的なリスク分析と必ずしも結果が整合するとは限らない。しかし,実務的には,規準によっ
て直接的な結果の大部分を解決するため,結果的にロバスト性の向上は,主に間接的な結果について対処
している。したがって,ロバスト性指標は,リスク分析の原則に基づいたロバスト性を表す有効な指標と
みなすことが可能である。一般に,直接的なリスクは,規準に基づく限界状態に関係するため,通常,間
接的なリスクよりも正確に推定できる。
この指標は,構造性能の特性だけではなく,損傷後のシステムの性能と関連する全ての結果を説明する。
さらに,ロバスト性に関わる構造性能を向上する又はぜい(脆)弱性を減らす(要素の信頼性を向上する)
ために採用し得る全ての方法(意思決定の選択肢)を明確に説明可能である。注意しなければならないの
は,ロバスト性の指標は,構造信頼性と同様に条件によって変わることである。ロバスト性指標は,直接
的な結果と間接的な結果の割合だけでなく,個々の構成要素の信頼性レベル及びシステムの破壊モード(直
接的な結果のレベル)によっても変わるものと考えた方がよい。構造要素及び破壊モードの信頼性は,確
率的モデル,適切に設計する技術及び設計の手腕に依存する。
ハザード事象が十分に把握されず確率的に定量化できない場合には,ハザード事象が発生したという条
件付きのリスク及びそれに対応する条件付きのロバスト性指標が意思決定に役立つ。そうした場合,ハザ
ードが発生し,損傷状態ベクトルD=(D1, D2, …, Dm)Tによって定義したあるレベルの損傷が発生すると想
定して構造のロバスト性を決定する。nは,構造システムの要素に対する損傷状態の定義の数である。対
応する条件付きリスクは,次のように評価される。
∑∑
∑
+
=
k
j
j
j
k
k
j
j
j
D
D
P
D
S
P
C
D
P
C
R
)
(
)
|
(
)
(
|
,
ind
,
dir
··························· (F.3)
式(F.3)においては,考慮している損傷状態の発生確率を1に設定することによって,損傷の状態を強制
的にシステムに与えている。
F.4.6
ロバスト性に関わる代替策
リスクに基づくロバスト性指標の他に,信頼性に基づく冗長性指標(RI)を,次のように定義すること
が可能である[Frangopol & Curley (1987)]。
)
intact
(f
)
intact
(f
)
damaged
(f
P
P
P
RI
−
=
···························································· (F.4)
ここに, Pf(damaged): 一部損傷した構造システムの破壊確率
Pf(intact): 損傷していない構造システムの破壊確率
この冗長性指標によって,構造システムの冗長性を測ることが可能である。この指標は,0から∞まで
の値をとり,値が小さい方がロバスト性が大きい。
最後に示すのは,海洋産業分野で用いられる構造物の冗長性の簡単で実用的な尺度で,いわゆる残留影
響率(Residual Influence Factor, RIF)値(ISO 19902 [22]参照)に基づいている。
保有耐力比(Reserve Strength Ratio, RSR)は,次のように定義する。
c
c
RSR
S
R
=
·············································································· (F.5)
ここに,
Rc: 海洋プラットフォーム(典型的には,鋼構造ジャケットプラ
ットフォーム)のベースシア耐力特性値
Sc: 終局状態に対する設計荷重
構造部材iの完全な損傷(又は機能の喪失)の構造耐力への影響を測るため,次の式のいわゆるRIF値
[しばしば損傷時耐力比(Damaged Strength Ratio)]を用いる。
91
A 3305:2020 (ISO 2394:2015)
intact
fail,
RSR
RSR
RIF
i
i=
······································································ (F.6)
ここに, RSRintact: 損傷を受けていない構造物のRSR値
RSRfail,i: 部材iが破壊したとき又は除去されたときの構造物のRSR
値
RIFは0から1までの間の値をとり,大きな値ほど冗長性が高いことを表している。
92
A 3305:2020 (ISO 2394:2015)
附属書G
(参考)
人命に対する安全に関する最適化及び基準
G.1
一般事項
経済的に最適化された実現可能な決定が,健康及び人命の安全に関する社会的選好とも合致することを
保証するため,4.4.2.1では,どのような前提下で,そのような決定が受容可能となると考えられるかを規
定している。この目的に関する原則が追加人命救助費用(MLSC)であり,そこでは,更に1人の人命を
救い得る手段にかかる費用が,ある個人を1人救うために社会が自発的に支払う費用と釣り合うときに,
その手段は人命の安全向上に効果のあると受容できると考える。追加人命救助費用(MLSC,marginal
lifesaving cost)の原則は,生活の質指標(LQI)を用いて適切に実装することが可能である。
この附属書では,4.2.2及び4.4.2.1の実務での使用に関して重要な側面を選択して,概要を次に記載する。
− 原則は,現状の最良な実践とどのように関係するか。
− 最適化の根拠となる便益の期待値をどのように計算するか。
− LQIに基づき人命救助費用の限界値をどのように計算するか。
− 原則を実務にどのように適用するか。
G.2
追加人命救助費用の原則と現状の最良な実践との関係
人命に関するリスクの受容に関わる規制の基準は,通常,合理的に実現可能な限り低くするという
(ALARP,As Low As Reasonably Possible/Practicable)形式で規定する。ALARPは図G.1にその形式を示す
ように,リスクはその大きさによって無視可能,受忍可能又は受容不可のいずれかに評価できるという考
え方である。
図G.1−人命に関するリスク規制における典型的なALARP原則の図
表G.1には,欧州諸国においてALARPの枠組みの中で適用されたリスク基準を事例として示す。国に
よって,リスク基準の選定に多少のばらつきがあることが分かる。
Riskisintolerable
Riskistolerable isALARP
Riskisbroadlyacceptable
The activitycannotbeaccepted
exceptin extraordinarycases
The activityistolerable only if
further reduction of risk is impracticable
or its cost is grossly disproportionate
to the improvement gained
The activityisacceptableanditis
not requiredtodemonstrateALARP
リスクが受忍できない
ALARPリスクが受忍できる
(ALARPである)
リスクが広く許容できる
特別な場合を除きその活動は受容され
ない
更なるリスク低減の実現可能性がないか
そのコストが得られる改善効果と比べ活
動が極めて不釣合いなときに限り,その活
動が受忍される
その活動は許容され,ALARPであること
を実証することは要求されない
93
A 3305:2020 (ISO 2394:2015)
ALARPに加えて,いわゆる予防原則にも触れるべきである。欧州におけるリスク規制の枠組みで形成
されたこの原則を,今日では世界中の多くの国が適用している。この原則は,いろいろと議論はあるもの
の,社会にとって不釣合いに大きい結果をもつ(技術的)開発に対して社会を守るための手段と解釈する
ことが可能である。予防原則は,経験がなく,そのうえ,受容できない負の結果をもつ可能性について疑
いがある活動の評価に関して適用する。そのような状況においては,既存の最良な実践の技術を用いて十
分な形で管理し,マネジメントがなされることができることを保証するように,より多くの知見を集める
ことが求められる。
一般的なALARPの枠組みは,追加人命救助費用の原則と非常に近いことが理解できる。しかし,これ
を確かなものにするためには,ALARPの枠組みについて具体的な解釈が必要である。
表G.1−EUにおける年当たり死亡率に関するリスク基準の概要
年当たり死亡率
英国
オランダ
ハンガリー
チェコ共和国
10−4
公衆の受忍不可能な限界
10−5
ALARP領域
既存の場合の限界(ALARP)
上限
既存の場合の限界
リスクの低減がなされ
なければらない
3×10−6
土地利用計画規準
下限
新規導入の場合の限界
10−6
広く受容可能
新規導入の場合の限界,2010
年以降の一般限界(ALARP)
ALARP形式における追加人命救助費用の原則の実装は,次のように定式化が可能である。
a) リスクが他の仕様規定的な規準等によって規制されていると文書化できるか,リスクが無視できるこ
とが文書化できる場合を除き,後述する原則に関して人命リスクに関わる決定及び活動を評価するこ
とが望ましい。
b) リスク分析は,Risk Assessment in Engineering−Principles, System Representation & Risk Criteria(JCSS,
2008参照)及び関連するISO規格などに示される最良な実践に従って行われなければならない。
c) 諸活動は,追加人命救助費用の原則に従って社会的な受容に関して評価されなければならない。人命
リスクは,最良の技術的,組織的及び手続的な方策で,更なる人命リスクの低減が追加人命救助費用
(G.4に記載)を超える水準まで低減されていることを実証することが望ましい。一般的に,リスク
低減の方策は,与えられた状況において不適切である又は不十分であると証明される場合を除き,規
格規準にて記載するような最良の実践の中から探されなければならない。
d) 該当する人命リスクの絶対値の水準を考慮して,受容可能と判断される活動を評価することが望まし
い。人命リスクの絶対値の水準がしきい(閾)値を超える場合には,アセスメントの全段階で最良の
実践に従っているかどうかについて特に評価することが望ましい。その上で,考慮されている事例が
最良な実践手法で適切に取り扱われているか又は予防原則に従う更なるアセスメントを実施するべき
かについて評価することが望ましい。これらが当てはまらなければ,その活動が受容可能であると考
えられる。
追加人命救助費用の原則は,受容可能な人命リスクについて,絶対値を規定することを強制するもので
も認めるものでもないが,実用において実装する場合には,受容可能なリスクの境界を要求することが可
能である。受容可能な境界を守るために,第一に,リスクが十分小さく,人命リスクを,特定の(しばし
ば仕様規定的な)規制及び規格規準によって十分に管理していると理解する状況においては,全体的な定
量的リスクアセスメントを要求しない。第二に,リスクの絶対値が一般的なリスクと比較して高い場合に
94
A 3305:2020 (ISO 2394:2015)
は,最新知見に準拠してそれ自身のアセスメントを実施し,その活動が予防原則の下でアセスメントを行
うことが望ましい活動には分類しない。最後に,人命の安全に対する必要投資額に対応するリスク水準は,
G.5で記載するように構造物の設計規格のキャリブレーションの根拠として活用することが可能である。
G.3
最適化の根拠となる便益の期待値の計算方法
G.3.1 一般事項
便益の期待値の計算に関して,二つの状態,すなわち,1) 民間企業又は個人所有者が構造物の設計に関
する決定を最適化する場合と,2) 公共機関又は規格策定委員会が構造物の設計を最適化したり最適な設計
規格をキャリブレーションしたりする場合とを(附属書Eに記載されるように)区別する必要がある。
G.3.2 民間所有の場合
民間所有の場合,便益の計算に何を含めどのように計算するかという問題は,自由市場の原理及び時と
して行われる行政による奨励に完全に委ねられている。構造物から得られる収益としては,プロジェクト
の資金繰り及び適用される契約の枠組みのスキームなど,目下の特定の状況に強く依存する。費用面では,
次の費用項目を含めるとよい。
− 設計及び品質保証の費用
− 建設費用
− 検査及び維持管理費用
− 稼働停止の費用
− 修復費用
− 再建設費用
− 補償費用(人命及び負傷,環境への被害並びに第三者に対するその他の不便及び被害)又は代替とし
ての保険料
− 評判喪失に関わる費用
− 撤去費用
ライフサイクルに基づくリスクアセスメントにおいて,上記の費用項目を含めることを推奨する。そこ
では,想定するライフサイクルの期間中に費用が発生する確率を考慮に入れた費用の期待値を計算し,適
切な形で現在価値に割り引く。
G.3.3 公共所有の場合
公共の所有の場合(例 規準化の作業も同様の状況である。),考慮の対象となる構造物(関心の対象と
なる特定のプロジェクトである又は設計規格及び関連する規制によって規定されるプロジェクトである。)
から生じる社会的便益に関して,入手可能な最良の知識に基づいて,その便益を計算することを推奨する。
この場合,それらの発生に関する確率を適切に考慮に入れた上で,上記の全ての費用項目をライフサイ
クルにおける便益の計算に含めることが望ましい。この目的のために,リスクアセスメント及び信頼性評
価を用いることが望ましい。対象となる構造設計の特徴をよく考慮に入れてライフサイクルを評価するこ
とが望ましい。特定の1品生産のプロジェクトの場合には,ライフサイクルを対象となる特定の構造物の
プロジェクトの供用期間と一致させて考えることが合理的である。しかし,一般の場合及び特に設計規格
の場合,ライフサイクルとして個々の構造物の供用期間に着目するのではなく,構造物が全うすることを
目指すよう要求する期間に着目することを推奨する。これは,実際には,100年を超える供用期間に相当
する可能性もある。
社会経済学的持続性を保証するために,ライフサイクルコストの現在価値の計算において,割引は慎重
95
A 3305:2020 (ISO 2394:2015)
に評価した長期にわたる経済成長率に基づくことが望ましい。今日では,最も成長した経済圏においては
年1〜3 %程度,多くの発展途上の経済圏においては5〜8 %程度である。
G.4
LQIに基づく人命救助費用の限界値の計算方法
G.4.1 一般事項
生活の質指標(LQI)は,1997年に提案された[11]。LQIの背景となる根本原理は,健康及び人命の安全
の向上への投資に対する社会的な選好が,出生時平均寿命,1人当たりの国民総生産(GDP)及び労働時
間と余暇時間との比で記述することができるということにある。LQIは,もともと社会経済学的な理論的
考察に基づき提案されたものではあるが,その妥当性については,それ以降経験的に証明されている。LQI
は,人命の安全への投資に関する社会的な選好との整合性に関する決定についての評価を容易にするもの
である。LQIに基づけば,人命救助費用に関する限界値,すなわち,1人の命を追加で救助するために必
要かつ支払い可能な支出を導出することが可能である。仮想人命価値評価などの経済学の分野におけるそ
れ以外の方法論においても,LQIの結果と同等の結果を得ることが明らかとなっている。
LQIを通して評価する追加人命救助費用は,対象とする社会における人命の安全への投資に対する経済
的能力及び選好並びに人命救助のための方策の人口全体に対する効果に依存する。これによって,次の疑
問が提起される。
− 社会的な経済的能力及び選好がどのように追加人命救助費用に影響するか。
− 人口全体に対する人命救助の方策の効果をどのように説明するか。
これらの疑問に答えるため,LQIの背景にある基本的な方法論を,次に要約して記載する[11]。
G.4.2 LQIに基づく追加人命救助費用の評価
LQIは,次の基本的形式で表すことができる。
qe
g
e
g
L
=
)
,
(
·········································································· (G.1)
ここに,
g: 1人当たりのGDP
e: 平均寿命
q: 消費に使用できる資金と健康寿命とのトレードオフに関する
尺度
qは,経済活動に割り振られる時間の比w(自由時間に対する勤務時間の比,一般的には0.18から0.2)
に依存し,さらに,GDPの一部が労働によって実現し,その他の部分を投資の利益として得るという事実
による。e及びwは,国の規模で評価する。定数qは,次のように評価する。
β
w
w
q
)
1(−
=
·········································································· (G.2)
ここに,
β: コブ・ダグラス型の弾力性の定数(ここでは0.7と設定)
社会的支払意思額(SWTP,Societal Willingness To Pay)及び社会における統計的生命価値(SVSL,Societal
Value of a Statistical Life)は,次のように評価する。
dm
G
dm
C
q
g
e
de
q
g
x
x
=
≈
=
d
d
SWTP
················································ (G.3)
d
SVSL
e
q
g
=
·········································································· (G.4)
ここに,
ed: 平均寿命を割り引いた年齢
Cx: 特定の死亡率の集団xに対する人口動態定数
96
A 3305:2020 (ISO 2394:2015)
Gx: WTPの死亡率mに関する単位変化
edの評価に当たっては,異なる人命の安全性改善の戦略が,様々な年齢集団に対して異なる影響を与え
る可能性があるということを考慮するために,年齢の平均化を導入する。人命を救うのは将来であるとい
うことを考慮するために現在価値への割引を導入する。
SWTPは,人命リスク低減活動によって1人の人命を救うために投資することが望ましい金額に相当す
るものである。SVSLは,1人の死亡に対して補償されることが望ましい金額に相当するものである。ここ
で規定されるSVSLは,指針値とみなすことが可能である。国ごとに異なる実際の法体系では,補償に対
する慣例も異なる。
人命リスク低減策を個別構造物の枠組み及び設計規格のキャリブレーションの枠組みにおいて設計戦略
の一部として実装する場合には,リスク低減策の影響は,上記のように,社会における年齢集団ごとに異
なる可能性がある。これは一方で,社会的観点から見た人命リスク低減の効率性に影響する。これを評価
に含めるためには,様々な設計戦略の人命リスク低減策について,人口全体に対する評価として,現在価
値に割り引いた平均余命の年齢平均を計算することが可能である。これを死亡率低減計画と呼ぶ。
ここでは,SWTP及びSVSLの計算のために,二つの異なる死亡率低減の枠組みを考えるが,他の適切
な形式がある場合にはそれを用いてもよい。第一は枠組みΠ(パイ)で,人命リスク低減に関する設計戦
略が全年齢の死亡率に比例的変化を与える。枠組みΔ(デルタ)は,設計戦略におけるリスク低減が全年
齢に対して一様であるような場合である。リスク低減策が年齢に関係なく全個々人へ同様に影響をするの
で,構造物の安全性に関しては大抵の場合,枠組みΔが適切である。コホート生存率表から得られる情報
に基づきSWTP GΠとSWTP GΔを計算する方法の詳細は,文献[5]が示している。
表G.2に年割引率を2 %,3 %及び4 %とした場合の様々な国における結果を示す[5]。対応するSVSLの
値も併せて示す。計算においては,全GDPが人命リスク低減のために利用可能であると仮定している。
97
A 3305:2020 (ISO 2394:2015)
表G.2−国ごとの,異なる人命リスク低減計画,異なる割引率に対する追加人命救助費用
(全数字の単位:千ppp米国ドル)[5](pppとは,主要購買力平価を指す。)
国
2008年1人
当たりGDP
SWTP−GΠ
SWTP−GΔ
SVSL
2 %
3 %
4 %
2 %
3 %
4 %
2 %
3 %
4 %
オーストラリア
35624
3061
2614
2279
4840
4298
3843
6551
5261
4356
ブラジル
9517
548
470
399
804
712
634
1074
864
724
カナダ
36102
2821
2369
2038
4062
3636
3236
5494
4412
3679
中国
5515
252
213
184
353
314
279
482
397
335
コロンビア
8125
390
330
285
475
424
380
443
362
304
コンゴ共和国
290
11
9
8
16
14
12
20
17
14
デンマーク
34005
2334
2007
1704
3842
3431
3064
3127
2549
2113
フランス
30595
1969
1677
1459
2935
2601
2307
2233
1820
1523
ドイツ
33668
2090
1785
1544
3219
2849
2527
2625
2158
1824
香港
40599
1864
1592
1384
2875
2561
2300
2243
1805
1511
インド
2721
128
110
96
175
156
139
172
140
118
日本
31464
1435
1227
1045
2286
2036
1812
1702
1404
1178
マリ
1043
40
34
29
54
48
43
70
56
47
モザンビーク
774
33
28
25
40
36
32
51
42
35
オランダ
38048
2329
1,989
1700
3812
3385
3016
2967
2406
2016
ノルウェー
49416
2794
2380
2038
3937
3500
3129
3531
2839
2348
ポーランド
16418
1006
846
729
1369
1218
1080
1221
989
819
シンガポール
45553
2114
1799
1554
2735
2448
2191
2771
2267
1893
スウェーデン
33769
2249
1891
1630
2710
2406
2137
2561
2113
1743
スイス
37788
2943
2517
2134
4206
3727
3332
3464
2792
2332
イギリス
34204
2600
2178
1873
4105
3665
3270
3127
2505
2117
アメリカ合衆国
42809
2488
2100
1822
3187
2833
2542
4293
3508
2953
表G.2に示す数値に基づき,人命の安全に対する一般的な社会的選好の観点から構造物に関する決定の
整合性を評価する。このため,Risk Assessment in Engineering−Principles, System Representation & Risk
Criteria(JCSS 2008参照)に記載されるような,全リスクのアセスメントが一般に必要となる。決定の代
替案が離散的特徴及び連続的特徴をもつ場合,双方においてどのようにリスクをアセスメントするかにつ
いては,JCSS [8]に例を示しているが,追加人命救助費用が大部分の構造物に対して十分に簡潔な形で直ち
に適用できる方法の概要を,次に記載する。
G.5
実務において本原則を利用する方法
G.5.1 一般事項
要約すると,構造設計のプロセスは制約条件下における便益(の期待値)の最適化又は費用(の期待値)
の最小化であると考えることが可能である。制約条件によって人命の安全に対する十分かつ支払い可能な
投資が確実なものとなる(図G.2参照)。
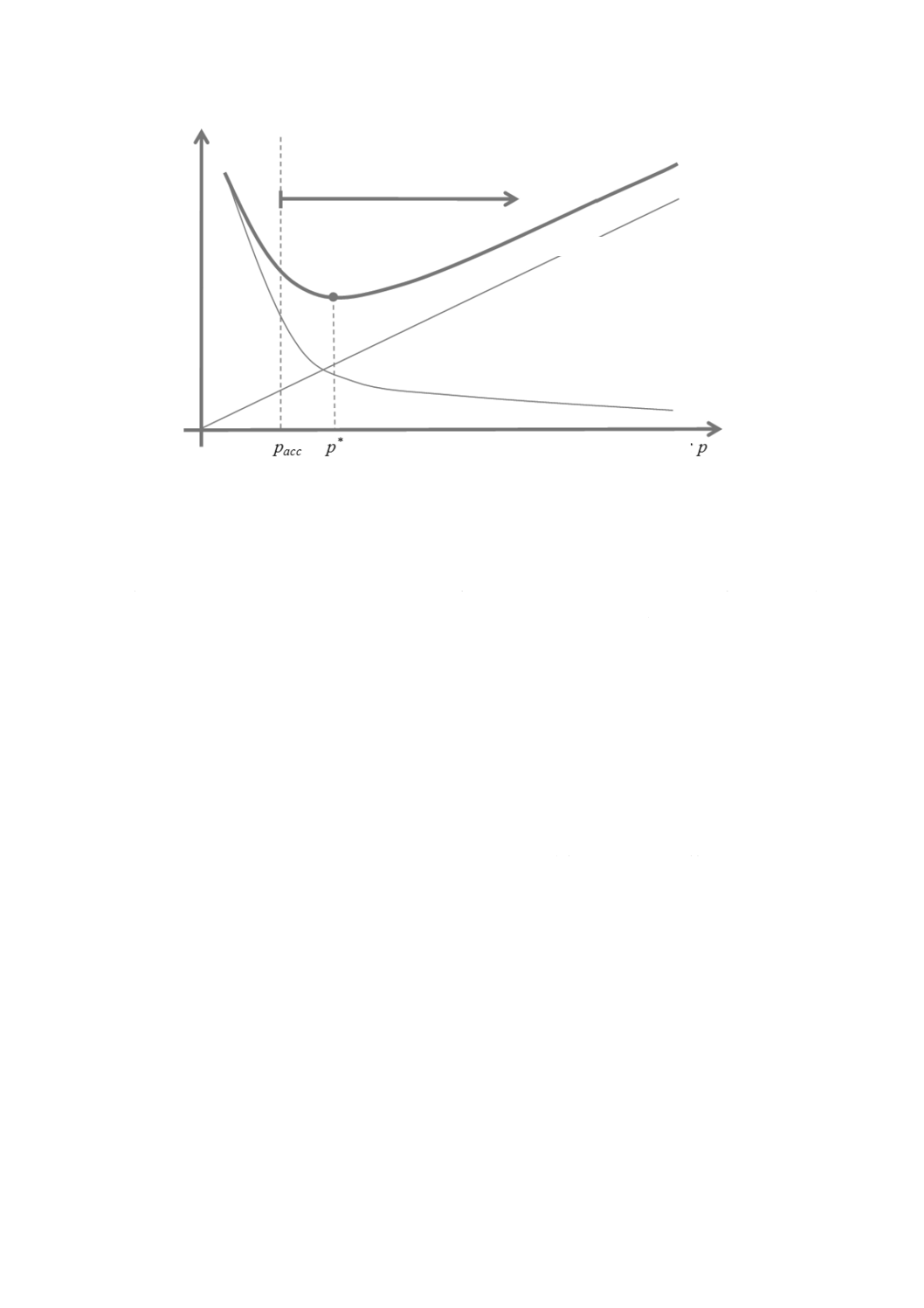
98
A 3305:2020 (ISO 2394:2015)
図G.2−金銭的最適化の境界条件としてのLQI許容基準
G.1〜G.5では,人命リスクに関する制約条件に着目してきたが,箇条4で規定しているように,環境へ
のリスク,天然資源の利用,排出,予想する最大損失など,その他の制約条件についてもこの最適化の過
程で考慮することが可能である。
人命リスクをもたらさない構造物については,通常,設計及びアセスメントにおける決定は,純粋に経
済的な最適化の観点からしてもよい。しかし,実際には,そのような状況は存在するとしても極めてまれ
(稀)である。全ての構造物は,その供用期間の一部において,人命リスクをもたらす。
経済的観点から,ライフサイクルにおける最適化をする場合に考えられる人命喪失は,補償費用,すな
わち,SVSLとして考慮するべきである。人命の安全に関して必要な投資の制約条件を考える場合には,
SWTPを言及することが望ましく,すなわち,実装する設計戦略がSWTPと同程度の追加人命救助費用と
なっていることを示すべきである。SWTPを超える追加人命救助費用は,通常支払いが困難であるが,金
銭的最適化によって要求されるのであれば目標とすることも可能である(図G.2の安全性改善費用)。
G.2で記載したように,追加人命救助費用の原則は,ALARPの枠組みにおいて直接適用することが可能
である。特定の構造物及びプロジェクトを考えた個別の設計における決定において,この手順は明快であ
る。しかし,極めて重要なのは,ALARPの検証を,詮索及び不整合を避けるために管理した計画として
実施することである。
民間組織の側からの詮索を避けるためには,評価する人命救助に関する活動に関わる費用を最低限度に,
かつ,関係する民間組織において考えられる負の便益を取り除いて評価することを保証することが重要で
ある。負の便益が人命救助方策に関わる費用に含まれている場合,社会的費用に限定することが望ましい。
さらに,人命救助費用の評価においては,正味現在費用を計算するときに適用する参照時間は(コホート
生存率表が示す最長老の人を含み)100年程度とすることが望ましい。現状の規制要求は,一つの特定の
プロジェクト又は構造物に限ったものではなく,プロジェクト及び構造物の集合に対してのものであると
考えることを求めている。
表G.2に示される追加人命救助費用に基づき,追加人命救助費用の原則に従うような設計における決定
に対応する人命リスクを評価するパラメータスタディを行うことが可能である。そのようなパラメータス
タディを実施することで,追加人命救助費用の原則を,設計規格における人命の安全に関する信頼性受容
費用
限界安全性改善費用
(LQI基準)
許容範囲
意思決定パラメータ
限界破壊・破壊費用
99
A 3305:2020 (ISO 2394:2015)
規準の特定のために用いることが容易となる。パラメータスタディは,人命リスクを低減する費用を,設
計・建設費用という固定費用に対して変動させることで適切に実施することが可能である。さらに,結果
の重大性,不確定性,ばらつき,検討対象となる構造物に対する荷重及び耐力に関するその他の特徴に関
して異なる状況を想定して実施することが可能である。
G.5.2 受容可能な目標破壊確率の最大値
破壊事象が,次の限界状態関数[7]によって表される理想的な場合について,制約条件付き最適化問題を
表すことが可能である。
g=R−S ················································································ (G.5)
ここに, R及びS: それぞれ耐力及び荷重を表す確率変数
意思決定パラメータpを,耐力の期待値と荷重の期待値との比(大域安全係数)と定義する。
]
[
]
[
R
E
S
E
p=
·············································································· (G.6)
以上によって,いわゆるLQI許容基準は,次のように表すことが可能である。
1
F
1
F
1
f
)
(
/
)
(
)
(
K
N
G
ω
γ
C
N
qC
g
ω
γ
C
dp
p
dP
x
S
x
S
=
+
=
+
−
≦
······································· (G.7)
ここに,
C1: 考慮される安全対策に関連する限界費用
γS: 社会を代表して意思決定する際の利率(すなわち,適切に選
ばれた経済成長率)
ω: 1年当たりの陳腐化率
NF: 構造物が破壊した場合の死者数の期待値
それ以外の用語は,G.4.2で定義されたとおりである。
不等式の右辺の分子C1(γS+ω)は,大域安全係数pが単位量増加するときの年当たりの安全コストの増加
量を表す(γSは資金調達費用,ωは陳腐化した場合の構造物の再建費用に解釈することが可能である。)。
分母は,構造物の破壊による人的結果NFに,追加で1人を救うためのSWTPを乗じることで貨幣単位に
変換されたものである。LQIに対して目標とする信頼性指標は,与えられたR及びSの確率モデルに対し
て定数K1の関数として導出される。
耐力及び荷重が両方とも対数正規分布に従い,R及びSの変動係数Vが0.1から0.3までの範囲であると
仮定すると,1年当たりの目標とする破壊確率が,式(G.7)中の定数K1の関数として求められる[3]。
表G.3−LQI許容基準に基づく基準期間を1年としたときの終局限界状態に対する
目標最小信頼性指標の暫定値
相対的な
人命救助費用
定数K1の範囲
LQIに基づく
目標信頼性
大
10−3〜10−2
β=3.1 (Pf≈10−3)
中
10−4〜10−3
β=3.7 (Pf≈10−4)
小
10−5〜10−4
β=4.2 (Pf≈10−5)
目標とする破壊確率は,基本確率変数の変動係数が大きい場合には,5倍程度増加する可能性がある。
一方,小さい変動係数に対しては1/2倍程度減少する。
G.5.3 経済的最適化に基づく目標信頼性
JCSS [8]が出版した確率論的モデルコードは,経済的最適化に基づく様々な構造物等級に対する目標信頼
性指標の暫定値を提示している(表G.4参照)。目標信頼性指標を,リスク低減対策の費用及び破壊の場合
の結果の大きさの関数として与え,いずれも対象とする構造物の初期建設費用と関連して定義する。目標
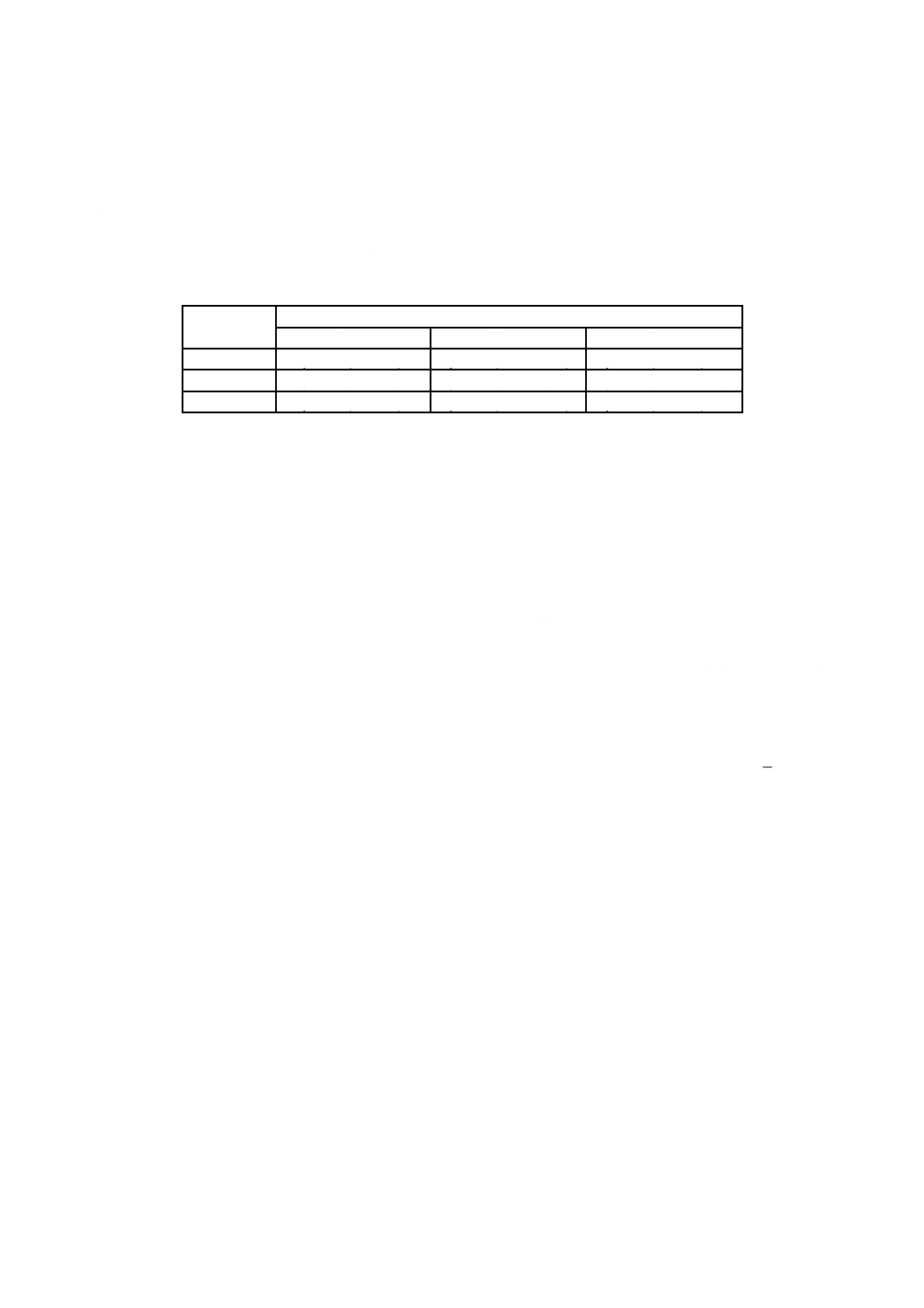
100
A 3305:2020 (ISO 2394:2015)
信頼性指標は構造物の破壊事象と関係し,そのため,部材の破壊から構造物の部分崩壊,完全崩壊に至る
破壊事象に対して,破壊の結果の大きさを調節し,用いることが可能である。一般に,構造システムの目
標信頼性指標[15]は,表G.4に示すように,安全のための費用及び破壊の結果の大きさに関係する可能性が
ある。
表G.4−LQI許容基準に基づく基準期間を1年としたときの終局限界状態に対する
目標信頼性指標の最小値の暫定値[8]
安全対策の
相対的費用
破壊の結果の重大性(表F.1に示す等級)
等級2
等級3
等級4
大
β=3.1 (Pf≈10−3)
β=3.3 (Pf≈5×10−4)
β=3.7 (Pf≈10−4)
中
β=3.7 (Pf≈10−4)
β=4.2 (Pf≈10−5)
β=4.4 (Pf≈5×10−6)
小
β=4.2 (Pf≈10−5)
β=4.4 (Pf≈5×10−6)
β=4.7 (Pf≈10−6)
表G.4に示す目標信頼性指標は,経済的最適化を補足するものと理解することが望ましく,人命安全の
リスクに関する問題において受容できない可能性もある。これについては,G.5.1及びG.5.2のように,常
に個別に確認することが望ましい。
表G.3及び表G.4に示す目標信頼性指標の背景にあるリスク低減の相対費用は同義ではないので,以下
においては,それぞれの結果の重大性等級に対して式(G.7)中の定数K1がリスク低減費用と建設費用との比
の関数として表G.4が与える信頼性指標と同じように計算することを示す。
表G.5には,異なるリスク低減策の相対費用(C1/C0)及び破壊時の結果の大きさ(NF)に対して,建設
費用C0の異なる2種類の構造物を例として,式(G.7)に基づき計算された定数K1の値を示す。表G.5の(a)
は,建設費用がC0=2 000 CHF(スイスフラン)/m2である典型的なスイスの事務所建物であり,死者数の
期待値NFは建物の床面積1 m2当たりで評価している。表G.5の(b)は,[例 橋りょう(梁)のような]総
建設費用がC0=10×106CHFである構造物に対するK1の値を示す。この場合,構造物全体に対して死者数
の期待値NFを評価しなければならない。さらに,両方の構造物の計算においては,年当たりの陳腐化率ω
として2 %,社会的利率γSとして3 %を仮定している。1人を救助する人命に対するSWTP,
x
x
C
q
g
G=
は,
5.1×106 CHFと設定する。
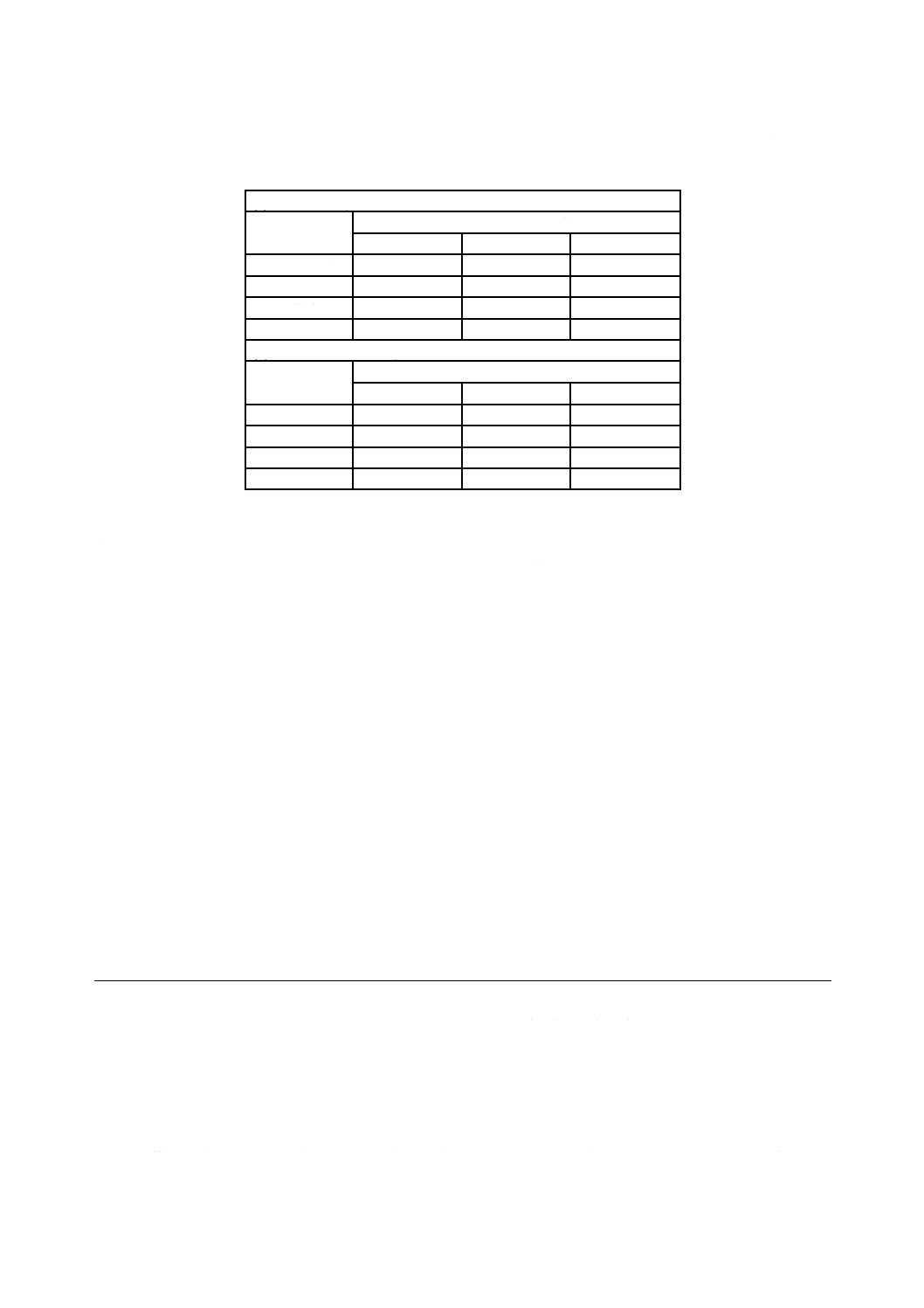
101
A 3305:2020 (ISO 2394:2015)
表G.5−建設費用C0の異なる2種類のスイスの構造物に対する,安全対策の相対費用及び
破壊時の人的結果の関数としてのK1の値
(a) 事務所,C0=2 000 CHF/m2
NF/m2
C1/C0−安全の相対費用
0.001(小)
0.01(通常)
0.1(大)
0.000 1
2E-04
2E-03
2E-02
0.001
2E-05
2E-04
2E-03
0.01
2E-06
2E-05
2E-04
0.1
2E-07
2E-06
2E-05
(b) 橋りょう(梁),C0=10×106 CHF
NF
C1/C0−安全の相対費用
0.001(小)
0.01(通常)
0.1(大)
0.1
1E-03
1E-02
1E-01
1
1E-04
1E-03
1E-02
10
1E-05
1E-04
1E-03
100
1E-06
1E-05
1E-04
K1の値は,安全コスト,破壊時の結果の大きさ及び人命の安全に対するSWTPに関する情報を含む。現
在,表G.5のK1の値に基づき,対応する目標信頼性指標の最小値を表G.4に求めることが可能である。死
者数の期待値が100人となる橋りょう(梁)において,安全対策の相対費用が0.01である場合には,係数
K1は10-5となる。表G.3から,対応する年当たりの目標信頼性指標の最小値βは4.2となる。
参考文献
[1] Berens A.P., & Hovey P.M.. In: Probabilistic Fracture Mechanics and Fatigue Methods: Applications for
Structural Design and Maintenance, ASTM STP 798, (Bloom J.M., & Ekevall J.C. eds.). American Society
for Testing and Materials, 1983, pp. 79-94.
[2] Canisius G. Robust Structural Design for Practicing Engineers, (Ed.), Final Report COST Action TU0601,
Robustness of Structures, 2011. http://www.cost.eu/domains̲actions/tud/Actions/TU0601
[3] Ellis H., Jiang M., Corotis R.B. Inspection, maintenance, and repair with partial observability. J. Infrastruct.
102
A 3305:2020 (ISO 2394:2015)
Syst. 1995, 1 (2) pp. 92-99
[4] Faber M.H., & Sorensen J.D. Reliability based code calibration−The JCSS approach, Applications of
Statistics and Probability in Civil Engineering, 2003, ISBN 90 5966 004 8
[5] Faber M.H., & Virguez-Rodriguez E. Supporting decisions on global health and life safety investments, 11th
International Conference on Applications of Statistics and Probability in Civil Engineering, ICASP11. 01-04
August
2011,
Zurich,
Switzerland.
http://www.staff.dtu.dk/mihf/Publications/
〜
/media/056B85B198694534B85CA0C71A3DE650.ashx
[6] Ferry Borges J., & Castanheta M. Structural Safety, course 101. Laboratorio National de, Engenharia Civil,
Lisbon, Second Edition, 1971
[7] Fischer
K.,
Bernardo
C.,
Faber
M.H.
Deriving
target
reliabilities
from
the
LQI,
http://www.jcss.byg.dtu.dk/upload/subsites/jcss/events/lqi%20symposium/fischerbarnardofaber̲lqisymp2012
.pdf, LQI-Symposium, DTU Denmark, August 2013
[8] Joint Committee on Structural Safety (JCSS). Probabilistic Model Code, ISBN 978-3-909386-79-6,
www.jcss.byg.dtu.dk/Publications/Probabilistic̲Model̲Code.aspx, 2001
[9] Joint Committee on Structural Safety (JCSS). Risk Assessment in Engineering−Principles, System
Representation & Risk Criteria,
Edited
by
M.
H.
Faber,
ISBN
978-3-909386-78-9,
http://www.jcss.byg.dtu.dk/Publications/Risk̲Assessment̲in̲Engineering.aspx, June 2008
[10] Kulhawy F.H., Phoon K.K., Wang Y. Reliability-Based Design of Foundations−A Modern View,
GeoCongress 2012. ASCE, 2012
[11] Nathwani J.S., Lind N., Pandey M. Affordable Safety by Choice: The Life Quality Method. University of
Waterloo, Waterloo, 1997
[12] Phoon K.K., Kulhawy F.H., Grigoriu M.D. Reliability-based Design of Foundations for Transmission Line
Structures, Report TR-105000, Electric Power Research Institute, Palo Alto [available online at EPRI.COM],
1995
[13] Phoon K.K., & Kulhawy F.H. Characterization of Geotechnical Variability. Can. Geotech. J. 1999a, 36 (4) pp.
612-624
[14] Phoon K.K., Kulhawy F.H., Grigoriu M.D. Multiple Resistance Factor Design (MRFD) for Spread
Foundations. J. Geotech. Geoenviron. Eng. 2003b, 129 (9) pp. 807-818
[15] Rackwitz R. Optimization−The basis of code-making and reliability verification. Struct. Saf. 2000, 22 (1) pp.
27-60
[16] Sorensen J.D. Reliability-based calibration of fatigue safety factors for offshore wind turbines. International
Journal of Offshore and Polar Engineering. 2012, 22 (3) pp. 234-241
[17] Straub D., & Faber M.H. Risk-based inspection planning for structural systems. Struct. Saf. 2005, 27 (4) pp.
335-355
[18] EN 1990:2007,Basis of structural design
[19] ISO 13822:2010,Bases for design of structures−Assessment of existing structures
[20] ISO 13823:2008,General principles on the design of structures for durability
[21] ISO 13824:2009,Bases for design of structures−General principles on risk assessment of systems involving
structures
[22] ISO 19902,Petroleum and natural gas industries−Fixed steel offshore structures